电子科技大学研究生试题图论及其应用参考答案

11年研究生试卷(答案)

解：T=1+2+1+2+1+3+4=13
五．(10分)今有赵、钱、孙、李、周五位教师，要承担语文、数学、物理、化学、英语五门课程。已知赵熟悉数学、物理、化学三门课程，钱熟悉语文、数学、物理、英语四门课程，孙、李、周都只熟悉数学、物理两门课程。问能否安排他们都只上他们熟悉的一门课程，使得每门课程都有人教（用图论方法求解）。
3．设是图的推广邻接矩阵，则的行列元等于由中顶点到顶点的长度为_n_途径数目。
4．完全图的邻接矩阵的最大特征值为_n_。
5.不同构的3阶单图共有___4___个。
6.设阶图是具有个分支的森林，则其边数。
7. 阶树( )的点连通度为___1___；边连通度为____1___；点色数为__2___；若其最大度为，则边色数为___ __。
8.图是连通的，则中任意点对间至少有_k__条内点不交路。
9.5阶度极大非哈密尔顿图族为___ ___和__ _____。
10.完全图能够分解为个边不相交的一因子之并。
11. 设连通平面图具有5个顶点，9条边，则其面数为__6_； ( )阶极大平面图的面数等于__ ___； ( )阶极大外平面图的顶点都在外部面边界上时，其内部面共有个。
A1: LA, S ; A2: MA, LA, G ; A3: MA, G, LA;
A4: G, LA, AC ; A5: AC, LA, S ; A6: G, AC;
A7: GT, MA, LA ; A8: LA,GT, S ; A9: AC, S, LA;
A10: GT, S。人只上一门自己所熟悉的课程。
六．(6分)设是赋权完全偶图G=(V,E)的可行顶点标号，若标号对应的相等子图含完美匹配 ,则是G的最优匹配。

电子科技大学研究生试题《图论及其应用》(参考答案)

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间：120分钟一．填空题(每题3分，共18分)1．4个顶点的不同构的简单图共有__11___个；2．设无向图G 中有12条边，已知G 中3度顶点有6个，其余顶点的度数均小于3。

则G 中顶点数至少有__9___个；3．设n 阶无向图是由k(k ?2)棵树构成的森林，则图G 的边数m= _n-k____;4．下图G 是否是平面图？答__是___; 是否可1-因子分解？答__是_.5．下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。

图G二．单项选择(每题3分，共21分)1．下面给出的序列中，是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2．已知图G 如图所示，则它的同构图是（ D ）3．下列图中，是欧拉图的是（ D ）4．下列图中，不是哈密尔顿图的是（B ）5．下列图中，是可平面图的图的是（B ）AC DA B CD6．下列图中，不是偶图的是（ B ）7．下列图中，存在完美匹配的图是（B ）三．作图(6分)1．画出一个有欧拉闭迹和哈密尔顿圈的图；2．画出一个有欧拉闭迹但没有哈密尔顿圈的图；3．画出一个没有欧拉闭迹但有哈密尔顿圈的图；解：四．(10分)求下图的最小生成树，并求其最小生成树的权值之和。

解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20.五．(8分)求下图G 的色多项式P k (G).解：用公式(G P k -G 的色多项式：)3)(3)()(45-++=k k k G P k 。

六．(10分) 22，n 3个顶点的度数为3，…，n k 个顶点的度数为k ，而其余顶点的度数为1，求1度顶点的个数。

解：设该树有n 1个1度顶点，树的边数为m.一方面：2m=n 1+2n 2+…+kn k另一方面：m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得：n 1=n 2+2n 3+…+(k -1)n k七．证明：(8分) 设G 是具有二分类(X,Y)的偶图，证明(1)G 不含奇圈；（2）若|X |≠|Y |，则G 是非哈密尔顿图。

电子科技大学-图论第二次作业

复杂性分析：在第 k 次循环里，找到点 u0 与 v0，要做如下运算: (a) 找出所有不邻接点对----需要 n(n-1)/2 次比较运算；(b) 计算不邻接点对度和----需要做 n(n-1)/2-m(G)次加法运算;(c ),选出度和最大的不邻接点对----需要 n(n-1)/2-m(G)次
2) 若 ek 不在 Ck 中，令 Gk-1=Gk-ek, Ck-1=Ck; 否则转 3); 3) 设 ek=u0v0 ∈Ck, 令 Gk-1=Gk-ek; 求 Ck 中两个相邻点 u 与 v 使得 u0,v0,u,v 依序排列在 Ck 上，且有：uu0,vv0 ∈E(Gk-1),令：
Ck1 Ck u0v0,uvuu0,vv0
如果在
中有 H 圈
如下： Ck1 (u0 , v0 , v1,..., vn2 , u0 )
我们有如下断言：在Ck1上，vi , vi1, 使得u0vi , v0vi1 E(Gk )
若不然，设
那么在 Gk 中，至少有 r 个顶点与 v0 不邻接，则
≦(n-1)-r < n-r，这样与 u0，v0 在 Gk 中度和大于等于 n 矛盾！
图的闭包算法：
1) 令 =G ,k=0;
2) 在中求顶点与 ,使得：
dGk (u0 ) dGk (v0 ) max dGk (u) dGk (v) uv E(Gk )
3) 如果此时得到 G 的闭包；
dGk (u0 ) dGk (v0 ) n
则转 4);否则，停止，
4) 令
,
,转 2).
则是非 Hamilton 图
(2)因为是具有二分类的偶图，又因为
，在这里假设
,则有
,也就是说：对于

电子科技大学《图论及其应用》复习总结--第四章欧拉图与哈密尔顿图

电⼦科技⼤学《图论及其应⽤》复习总结--第四章欧拉图与哈密尔顿图第四章欧拉图与哈密尔顿图(⼀)、欧拉图及其性质(1)、问题背景---欧拉与哥尼斯堡七桥问题问题：对于图G，它在什么条件下满⾜从某点出发，经过每条边⼀次且仅⼀次，可以回到出发点？注：⼀笔画----中国古⽼的民间游戏（存在欧拉迹）要求：对于⼀个图G, 笔不离纸, ⼀笔画成.拓展：三笔画：在原图上添加三笔，可使其变为欧拉图。

定义1 对于连通图G，如果G中存在经过每条边的闭迹，则称G为欧拉图，简称G为E图。

欧拉闭迹⼜称为欧拉环游，或欧拉回路。

定理1 下列陈述对于⾮平凡连通图G是等价的：(1) G是欧拉图；(2) G的顶点度数为偶数；(3) G的边集合能划分为圈。

推论1 连通图G是欧拉图当且仅当G的顶点度数为偶。

推论2 连通⾮欧拉图G存在欧拉迹当且仅当G中只有两个顶点度数为奇数。

证明：若G和H是欧拉图，则G×H是欧拉图。

若G是⾮平凡的欧拉图，则G的每个块也是欧拉图。

(⼆)、Fleury算法(欧拉图中求出⼀条具体欧拉环游的⽅法)⽅法是尽可能避割边⾏⾛(三)、中国邮路问题（最优欧拉环游，管梅⾕）定理2 若W是包含图G的每条边⾄少⼀次的闭途径，则W具有最⼩权值当且仅当下列两个条件被满⾜：(1) G的每条边在W中最多重复⼀次；(2) 对于G的每个圈上的边来说，在W中重复的边的总权值不超过该圈⾮重复边总权值。

(四)、哈密尔顿图的概念定义1 ：如果经过图G的每个顶点恰好⼀次后能够回到出发点，称这样的图为哈密尔顿图，简称H图。

所经过的闭途径是G的⼀个⽣成圈，称为G的哈密尔顿圈。

定义2: 如果存在经过G的每个顶点恰好⼀次的路，称该路为G的哈密尔顿路，简称H路。

(五)、哈密尔顿图性质与判定1、性质定理【必要条件】；定理1 (必要条件) 若G为H图，则对V(G)的任⼀⾮空顶点⼦集S，有：w(G−S)≤|S|注：不等式为G是H图的必要条件，即不等式不满⾜时，可断定对应图是⾮H、图。

电子科大研究生图论考试附答案

1电子科技大学研究生试卷（考试时间：至，共__2_小时）课程名称图论及其应用教师学时 60 学分教学方式讲授考核日期_2013__年_6__月__20__日成绩考核方式：（学生填写）一．填空题(每空2分，共20分)1． n 阶k 正则图G 的边数m =_____。

2．4个顶点的不同构单图的个数为________。

3．完全偶图,r s K (,2r s ≥且为偶数)，则在其欧拉环游中共含____条边。

4．高为h 的完全2元树至少有_______片树叶。

5. G 由3个连通分支124,,K K K 组成的平面图，则其共有_______个面。

6. 设图G 与5K 同胚，则至少从G 中删掉_______条边，才可能使其成为可平面图。

7. 设G 为偶图，其最小点覆盖数为α，则其最大匹配包含的边数为________。

8. 完全图6K 能分解为________个边不重合的一因子之并。

9. 奇圈的边色数为______。

10. 彼得森图的点色数为_______。

二．单项选择(每题3分，共15分) 1．下面说法错误的是( )学号姓名学院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集，在其补图中的点导出子图必为一个完全子图；(B) 若图G 连通，则其补图必连通； (C) 存在5阶的自补图； (D) 4阶图的补图全是可平面图. 2．下列说法错误的是（） (A) 非平凡树是偶图；(B) 超立方体图(n 方体,1n ≥)是偶图； (C) 存在完美匹配的圈是偶图； (D) 偶图至少包含一条边。

3.下面说法正确的是( )(A) 2连通图一定没有割点（假定可以有自环）； (B) 没有割点的图一定没有割边；(C) 如果3阶及其以上的图G 是块，则G 中无环，且任意两点均位于同一圈上；(D) 有环的图一定不是块。

电子科大12年研究生图论试卷

电子科技大学研究生试卷学号姓名学院…………………… 密……………封……………线……………以……………内……………答……………题……………无……………效……………………（考试时间：至，共__2_小时）课程名称图论及其应用教师学时 60 学分教学方式讲授考核日期_2012__年___月____日成绩考核方式：（学生填写）一、填空题（填表题每空1分，其余每题2分，共30分)1．阶正则图G的边数=；2．3个顶点的不同构的简单图共有个；3．边数为的简单图的不同生成子图的个数有个；4. 图与图的积图的边数为；5. 在下图中，点到点的最短路长度为；6. 设简单图的邻接矩阵为，且，则图的边数为；7. 设是n阶简单图，且不含完全子图，则其边数一定不会超过；8．的生成树的棵数为;9. 任意图的点连通度、边连通度、最小度之间的关系为；10. 对下列图，试填下表（是类图的打〝√ 〞，否则打〝〞）。

①②③能一笔画的图Hamilton图偶图可平面图①√√②√√③√√√二、单项选择(每题2分，共10分)1．下面命题正确的是 ( B )对于序列，下列说法正确的是：(A) 是简单图的度序列；(B) 是非简单图的度序列;(C) 不是任意图的度序列;(D) 是图的唯一度序列.2．对于有向图，下列说法不正确的是 ( D )(A) 有向图中任意一顶点只能处于的某一个强连通分支中；(B) 有向图中顶点可能处于的不同的单向分支中;(C) 强连通图中的所有顶点必然处于强连通图的某一有向回路中;(D) 有向连通图中顶点间的单向连通关系是等价关系。

3.下列无向图可能不是偶图的是 ( D )(A) 非平凡的树；(B) 无奇圈的非平凡图；(C) 方体；注意：n方体是n正则二部图。

(D) 平面图。

4.下列说法中正确的是 ( C )(A) 连通3正则图必存在完美匹配；(B) 有割边的连通3正则图一定不存在完美匹配；(C) 存在哈密尔顿圈的3正则图必能1因子分解；(D) 所有完全图都能作2因子分解。

07年研究生试卷(答案)备课讲稿

07年研究生试卷(答案)仅供学习与交流，如有侵权请联系网站删除谢谢2 电子科技大学研究生试卷（考试时间：至，共_____小时）课程名称图论及其应用教师学时 60 学分教学方式讲授考核日期_2007__年___月____日成绩考核方式：（学生填写）一．填空题(每题2分，共12分) 1．简单图G=(n,m)中所有不同的生成子图(包括G 和空图)的个数是____个； 2．设无向图G=(n,m)中各顶点度数均为3，且2n=m+3,则n=_ 6__; m=_9__； 3．一棵树有i n 个度数为i 的结点，i=2,3,…,k,则它有个度数为1的结点； 4．下边赋权图中，最小生成树的权值之和为__20___; 5、某年级学生共选修9门课。

期末考试时，必须提前将这9门课先考完，每天每人只在下午考一门课，则至少需要___9__天才能考完这9门课。

二．单项选择(每题2分，共10分)1．下面给出的序列中，不是某简单图的度序列的是( D )学姓名学院 …………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效…………………… v 5v 4v v v 11624568107496(A) (11123); (B) (22222); (C) (3333); (D) (1333). 2．下列图中，是欧拉图的是（D）A B3．下列图中，不是哈密尔顿图的是（B）A D 4．下列图中，是可平面图的图的是（B）A B C D5．下列图中，不是偶图的是（B）A B DC三、 (8分)画出具有7个顶点的所有非同构的树解：仅供学习与交流，如有侵权请联系网站删除谢谢3仅供学习与交流，如有侵权请联系网站删除谢谢4……四，用图论的方法证明：任何一个人群中至少有两个人认识的朋友数相同(10分) 证明：此题转换为证明任何一个没有孤立点的简单图至少有两个点的度数相同。

电子科技大学图论及其应用5班第4-5章作业

习题43： 1）、画一个有Euler闭迹和Hamilton圈的图。

2）、画一个有Euler闭迹但没有Hamilton圈的图。

3）、画一个有Hamilton圈但没有Euler闭迹的图4）、画一个既没有Hamilton圈也没有Euler闭迹的图7、证明：将G中的孤立点去掉后的图为G1，则G1也是没有奇度点的，且G1的最小度大于等于2.则G1存在一个圈S1，在G1 –S1中去除孤立的点，得到一个新的图G2，显然G2也没有奇度的点，且G2的最小度大于等于2.这样G2中也存在一个圈S2，这样一直下去，指导Gm中有圈Sm，且Gm-Sm都是孤立的点。

这样E(G) = E(G1)并E(G2)…..并E(Gm).命题得证。

10、证明：1）、如果G不是而连通的图，那么G存在割点v或则G是不连通的，G-v的连通分支数大于等于2.由定理：若G是H图，则对于V的每个飞空真子集S，均有G-S的连通分支数小于等于S的顶点数，知，G是非H图。

2）、G 是2部图，且|X|<|Y|,则有G-X的连通分支数等于|Y|>|X|由上边的定理知，G是非H图。

12、证明：假设G中新加入的一点，为V,它和G中的每一个顶点均相连，这样得到新的图G^,这样G^的度序列为(d1+1,d2+1……,dv+1,V)。

因为不存在正整数m<(v+1)/2,使其满足dm<m和dv-m+1<v-m,即不存在m<(v+1)/2,满足dm+1<=m和dv-m+1<v-m+1 = (v+1) –m。

由定理知，G^中含有Hamilton圈C，这样G^-C就是G的H路，命题得证。

习题51、1）、证明：每个k方体都有完美匹配(k>=2)。

假设K方体的顶点坐标为：(x1,x2…,xk)，取(x1,x2,….,xk-1,0)和(x1,x2,…,xk-1,1)两个顶点之间的边的全体集合为M，这样M,中的边均不相邻，所以M是一个匹配，且|M| = 2^(k-1)。

2019电子科技大学研究生试卷答案

2019电⼦科技⼤学研究⽣试卷答案电⼦科技⼤学研究⽣试卷（考试时间：⾄，共 2 ⼩时）课程名称图论及应⽤教师学时 60 学分 3 教学⽅式堂上授课考核⽇期 2019 年 5 ⽉⽇成绩考核⽅式：（学⽣填写）⼀．填空题(每空3分，共15分) 1. 图G 的邻接矩阵为0111101111001100?? ? ? ? ? ???, 则G 的⽣成树的棵数为 8 . 2. 设1G 是11(,)n m 简单图,2G 是22(,)n m 简单图,则1G 和2G 的(Cartesian)积图12G G ?的边数()m G =1221n m n m +. 3. 图1中最⼩⽣成树T 的权值()W T = 23 .4. 图2中S 到T 的最短路的长度为 8 .5. 设G 是n 阶简单图,且不包含三⾓形,则其边数⼀定不超过24n . ⼆．单项选择题(每题3分，共15分) 学号姓名学院……………………密……………封……………线……………以……………内……………答……………题……………⽆……………效……………………座位号图1 图21. 关于彼得森(Petersen)图, 下⾯说法正确的是 ( B )A. 彼得森图是哈密尔顿图;B. 彼得森图是超哈密尔顿图;C. 彼得森图可1-因⼦分解;D. 彼得森图是可平⾯图.2. 下⾯说法正确的是 ( C )A. 有割点的三正则图⼀定没有完美匹配;B. 有割边的三正则图⼀定没有完美匹配;C. 存在哈密尔顿圈的三正则图必能1因⼦分解;D. 正则的哈密尔顿图必能2因⼦分解.3. 关于图的度序列, 下⾯说法正确的是 ( B )A. 任意两个有相同度序列的图都同构;B. 若图G 度弱于图H ，则图G 的边数⼩于等于图H 的边数;C. 若⾮负整数序列12(,,,)n d d d π=满⾜1ni i d =∑为偶数，则它⼀定是图序列;D. 如果图G 所有顶点的度和⼤于或等于图H 所有顶点的度和，则图G 度优于图H.4. 关于图的补图, 下⾯说法错误的是 ( A )A. 若图G 连通，则其补图必连通;B. 若图G 不连通，则其补图必连通;C. 图G 中的⼀个点独⽴集，在其补图中的点导出⼦图必为⼀个团;D. 存在5阶的⾃补图.5. 关于欧拉图, 下⾯说法正确的是 ( D )A. 每个欧拉图有唯⼀的欧拉环游;B. 每个顶点的度均为偶数的图是欧拉图;C. 欧拉图中⼀定没有割点;D. 欧拉图中⼀定没有割边.(三).(10分)若阶为25且边数为62的图G 的每个顶点的度只可能为3，4，5或6，且有两个度为4的顶点，11个度为6的顶点，求G 中5度顶点的个数。

图论作业电子科大杨春

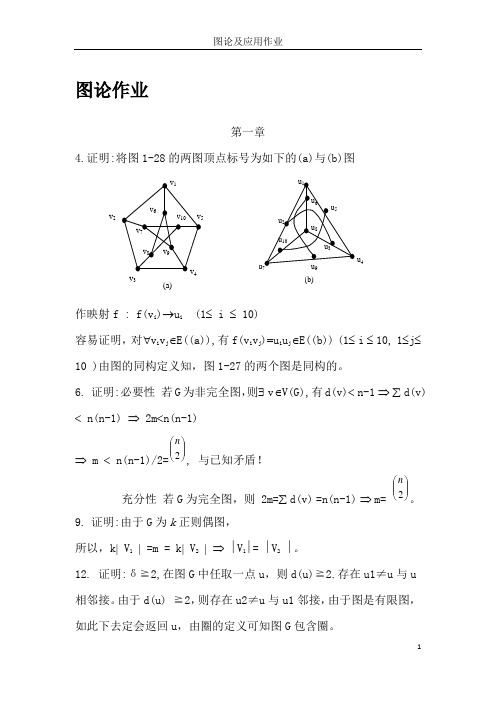
图论作业第一章4.证明:将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 )由图的同构定义知，图1-27的两个图是同构的。

6. 证明:必要性若G 为非完全图，则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾！充分性若G 为完全图，则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。

9. 证明:由于G 为k 正则偶图，所以，k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。

12. 证明:δ≧2,在图G 中任取一点u ，则d(u)≧2.存在u1≠u 与u 相邻接。

由于d(u) ≧2，则存在u2≠u 与u1邻接，由于图是有限图，如此下去定会返回u ，由圈的定义可知图G 包含圈。

(a)v 2 3u 4u (b)17.证明：设u、v是G的任意两个顶点。

若u和v在G中不邻接，则在中他们邻接。

若u和v在G中邻接，他们属于G的同一分支。

在另一个分支中有一点w，在中u和v均与w邻接，即uwv是一条通路，故是连通图。

第二章2.证明：由题意可知如果一棵树恰有两个1度的顶点，则其他顶点的度必为2（如果树其他顶点至少有一个大于2，则该树度为1的顶点树必然大于2），连通的无圈图称为树，一棵树恰有两个1度的顶点而且其他顶点的度数为2，显然这样的树均是路。

16.对于（1）和（2）都可以用Kruskal算法。

具体用法是：对（1）有两种方法：<1>把Kruskal算法中的“小”字换为“大”字。

<2>重新规定图的权为：W’(e)=1/w(e) 当w(e)≠0M（充分大）当w(e)＝0这样就可直接用Kruskal算法。

电子科大图论第二次作业(4、5章) 答案

习题四3.（1）画一个有Euler 闭迹和Hamilton圈的图；（2）画一个有Euler 闭迹但没有Hamilton圈的图；（3）画一个有Hamilton圈但没有Euler闭迹的图；（4）画一个即没有Hamilton圈也没有Euler闭迹的图；解：找到的图如下：(1)一个有Euler 闭迹和Hamilton圈的图；(2)一个有Euler闭迹但没有Hamilton圈的图；(3) 一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.7. 将G中的孤立点去掉后的图为G1，则G1也是没有奇度点的，且G1的最小度大于等于2.则G1存在一个圈S1，在G1 –S1中去除孤立的点，得到一个新的图G2，显然G2也没有奇度的点，且G2的最小度大于等于2.这样G2中也存在一个圈S2，这样一直下去，指导Gm中有圈Sm，且Gm-Sm都是孤立的点。

这样E(G) = E(G1)并E(G2)…并E(Gm).命题得证。

10．证明：若：（1）不是二连通图，或者（2）是具有二分类的偶图，这里,则是非Hamilton图。

证明：（1）不是二连通图，则不连通或者存在割点,有,由于课本上的相关定理：若是Hamilton图，则对于的任意非空顶点集，有：,则该定理的逆否命题也成立，所以可以得出：若不是二连通图，则是非Hamilton图(2)因为是具有二分类的偶图，又因为，在这里假设,则有,也就是说：对于的非空顶点集，有：成立，则可以得出则是非Hamilton图。

习题五1.(1)证明：每个k方体都有完美匹配(k大于等于2)(2) 求K2n和K n,n中不同的完美匹配的个数。

证明一：证明每个k方体都是k正则偶图。

事实上，由k方体的构造：k方体有2k个顶点，每个顶点可以用长度为k的二进制码来表示，两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同。

如果我们划分k方体的2k个顶点，把坐标之和为偶数的顶点归入X，否则归入Y。

图论及应用参考答案

图论及应用参考答案图论及应用参考答案图论是数学中的一个重要分支，研究的是图的性质和图之间的关系。

图由节点（顶点）和边组成，节点代表对象，边代表对象之间的关系。

图论不仅在数学中有广泛的应用，也在计算机科学、物理学、生物学等领域中发挥着重要的作用。

本文将介绍图论的基本概念和一些应用。

一、图论的基本概念1. 图的类型图分为有向图和无向图。

有向图中的边有方向，表示节点之间的单向关系；无向图中的边没有方向，表示节点之间的双向关系。

2. 图的表示方法图可以用邻接矩阵或邻接表来表示。

邻接矩阵是一个二维数组，其中的元素表示节点之间是否有边相连；邻接表是一个链表数组，数组中的每个元素对应一个节点，链表中存储了该节点相邻的节点。

3. 图的性质图的性质包括节点的度、连通性和路径等。

节点的度是指与该节点相连的边的数量；连通性指的是图中任意两个节点之间是否存在路径；路径是指由边连接的节点序列。

二、图论在计算机科学中的应用1. 最短路径算法最短路径算法是图论中的经典问题之一，它用于计算图中两个节点之间的最短路径。

著名的最短路径算法有迪杰斯特拉算法和弗洛伊德算法。

这些算法在网络路由、地图导航等领域中有广泛的应用。

2. 最小生成树算法最小生成树算法用于找到一个连通图的最小生成树，即包含所有节点且边的权重之和最小的子图。

普里姆算法和克鲁斯卡尔算法是常用的最小生成树算法。

这些算法在电力网络规划、通信网络设计等领域中有重要的应用。

3. 图的着色问题图的着色问题是指给定一个图，将每个节点着上不同的颜色，使得相邻节点之间的颜色不同。

这个问题在地图着色、任务调度等方面有实际应用。

三、图论在物理学中的应用1. 粒子物理学在粒子物理学中，图论被用来描述和分析粒子之间的相互作用。

图论模型可以帮助研究粒子的衰变、散射等过程，为理解物质的基本结构提供了重要的工具。

2. 统计物理学图论在统计物理学中也有应用。

例如，渗透模型中的图可以用来研究流体在多孔介质中的渗透性质，为石油勘探、水资源管理等提供了理论基础。

电子科大图论-第二次作业

图论及其应用第二次作业要求：1、交电子档给助教【助教给每个班设置邮箱，助教设置提交回复】；2、第7章授课结束前均可以提交；3、希望能够独立完成。

1．判断图4-43所示的四个图是否可以一笔画。

上面四个图都是连通图，看是否能一笔画成问题本质上看图是否存在欧拉迹；连通图有欧垃迹当且仅当G 最多有两个奇点。

（a ）不可以有4个奇点（b ）可以一个奇点（c ）可以两个奇点（d ）可以没有奇点2.（1）画一个有欧拉闭迹和哈密尔顿圈的图；（2）画一个有欧拉闭迹但没有哈密尔顿圈的图；(3) 画一个有哈密尔顿圈但没有欧拉闭迹的图；（4）画一个既没有欧拉闭迹也没有哈密尔顿圈的图。

3. 设n 阶无向简单图G 有m 条边。

证明：若m ≥⎪⎪⎭⎫ ⎝⎛-21n +2，则G 是哈密尔顿图。

(b) (c) (d ) 图4-43证明：G 是H 图。

若不然，因为G 是无向简单图，则n ≥3，由定理1：若G 是n ≥3的非单图，则G 度弱于C m,n 。

于是有：2,1()()(2)(1)(1)21111(1)(2)(1)(21) 1.222m n E G E C m n m n m m n n n m m m n m ⎡⎤≤=+---+-⎣⎦--⎛⎫⎛⎫=+-------≤+ ⎪ ⎪⎝⎭⎝⎭ 这与条件矛盾！所以G 是H 图。

4. 在图4-45中，哪些图是哈密尔顿图？哪些图中有哈密尔顿路？(a)非哈密尔顿图，没有哈密尔顿路(b)哈密尔顿图（abcdejhfiga)(c)哈密尔顿图（kjdhbagciefk)(d)非哈密尔顿图有哈密尔顿路（hjaidebcgf)(e)不是哈密尔顿图，因为有割点a ，有哈密尔顿路（jaibcedkgfh ）5. 证明：若G 没有奇点，则存在边不重的圈C 1, C 2,…, C m ，使得，E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。

证明：将G 中孤立点除去后的图记为G 1，则G 1也没有奇点，且δ（G 1)，则G 1含圈C 1，在去掉()11G E C -的孤立点后，得图G 2，显然G 2仍无奇度点，且δ（G 2）≥ 2，从而G 2含圈C 1，如此重复下去，直到圈C m ，且G m －E (C m )全为孤立点为止，于是得到E (G ) = E (C 1)∪E (C 2)∪…∪E (C m )。

电子科大图论-第二次作业(4、5章)-答案

(2) 我们用归纳法求 K2n 和 Kn,n 中不同的完美匹配的个数。 K2n 的任意一个顶点有 2n-1 种不同的方法被匹配。所以 K2n 的不同完美匹配个数等于(2n-1)K2n-2,如此推下去，可以归纳出 K2n 的不同完美匹配个数为：(2n-1)!! 同样的推导方法可归纳出 K n, n 的不同完美匹配个数为：n!
习题四
3.（1）画一个有 Euler 闭迹和 Hamilton 圈的图；
（2）画一个有 Euler 闭迹但没有 Hamilton 圈的图；（3）画一个有 Hamilton 圈但没有 Euler 闭迹的图；（4）画一个即没有 Hamilton 圈也没有 Euler 闭迹的图；解：找到的图如下： (1) 一个有 Euler 闭迹和 Hamilton 圈的图；
(2) 一个有 Euler 闭迹但没有 Hamilton 圈的图；
(3) 一个有 Hamilton 圈但没有 Euler 闭迹的图;
(4)一个即没有 Hamilton 圈也没有 Euler 闭迹的图.
7. 将 G 中的孤立点去掉后的图为 G1，则 G1 也是没有奇度点的，且 G1 的最小
度大于等于 2.则 G1 存在一个圈 S1，在 G1 –S1 中去除孤立的点，得到一个新的图 G2，显然 G2 也没有奇度的点，且 G2 的最小度大于等于 2.这样 G2 中也存在的点。这样 E(G) = E(G1)并 E(G2)…并 E(Gm).命题得证。
则是非 Hamilton 图
(2)因为是具有二分类的偶图，又因为
，在这里假设
,则有
,也就是说：对于
的非空顶点集，有：
成
立，则可以得出则是非 Hamilton 图。
习题五
1. (1)证明：每个 k 方体都有完美匹配(k 大于等于 2)

电子科大研究生图论05-14年图论期末试题

亚特兰大：波士顿，芝加哥，迈阿密，纳什维尔
波士顿：亚特兰大，芝加哥，纳什维尔
芝加哥：亚特兰大，波士顿，丹佛，路易维尔
丹佛：芝加哥，路易维尔，迈阿密，纳什维尔
路易维尔：芝加哥，丹佛，迈阿密
迈阿密：亚特兰大，丹佛，路易维尔，纳什维尔
纳什维尔：亚特兰大，波士顿，丹佛，迈阿密
(要求用图论方法求解)
九．(8分)求下图G的色多项式Pk(G).
由T8导出的树中a到b路就是最短路。
2006研究生图论期末试题(120分钟)
一、填空题(15分，每空1分)
1、若两个图的顶点与顶点之间，边与边之间都存在对应，而且它们的关联关系也保持其关系，则这两个图同构。
2、完全图的生成树的数目为；阶为6的不同构的树有棵。
3、设无向图有12条边，已知中度为3的结点有6个，其余结点的度数均小于3，则
六．(10分)设是赋权完全偶图G=(V,E)的可行顶点标号，若标号对应的相等子图含完美匹配 ,则是G的最优匹配。
七.(10分)求证：在n阶简单平面图G中有，这里是G的面数。
八、(10分)来自亚特兰大，波士顿，芝加哥，丹佛，路易维尔，迈阿密，以及纳什维尔的7支垒球队受邀请参加比赛，其中每支队都被安排与一些其它队比赛(安排如下所示)。每支队同一天最多进行一场比赛。建立一个具有最少天数的比赛时间表。
2．设V(G)= ，则图的补图是（）
3.下列图中，既是欧拉图又是哈密尔顿图的是( )
4.下列说法中不正确的是( )
(A)每个连通图至少包含一棵生成树；
(B)k正则偶图(k>0)一定存在完美匹配；
(C)平面图 ,其中表示G的对偶图；
(D)完全图可一因子分解。
三、(10分)设图G的阶为14，边数为27，G中每个顶点的度只可能为3，4或5，且G有6个度为4的顶点。问G中有多少度为3的顶点？多少度为5的顶点？

电子科大图论第二次作业45章答案

习题四3.（1）画一个有Euler 闭迹和Hamilton圈的图；（2）画一个有Euler 闭迹但没有Hamilton圈的图；（3）画一个有Hamilton圈但没有Euler闭迹的图；（4）画一个即没有Hamilton圈也没有Euler闭迹的图；解：找到的图如下：(1)一个有Euler 闭迹和Hamilton圈的图；(2)一个有Euler闭迹但没有Hamilton圈的图；(3) 一个有Hamilton圈但没有Euler闭迹的图;(4)一个即没有Hamilton圈也没有Euler闭迹的图.7. 将G中的孤立点去掉后的图为G1，则G1也是没有奇度点的，且G1的最小度大于等于2.则G1存在一个圈S1，在G1 –S1中去除孤立的点，得到一个新的图G2，显然G2也没有奇度的点，且G2的最小度大于等于2.这样G2中也存在一个圈S2，这样一直下去，指导Gm中有圈Sm，且Gm-Sm都是孤立的点。

这样E(G) = E(G1)并E(G2)…并E(Gm).命题得证。

10．证明：若：（1）不是二连通图，或者（2）是具有二分类的偶图，这里,则是非Hamilton图。

证明：（1）不是二连通图，则不连通或者存在割点,有,由于课本上的相关定理：若是Hamilton图，则对于的任意非空顶点集，有：,则该定理的逆否命题也成立，所以可以得出：若不是二连通图，则是非Hamilton图(2)因为是具有二分类的偶图，又因为，在这里假设,则有,也就是说：对于的非空顶点集，有：成立，则可以得出则是非Hamilton图。

习题五1.(1)证明：每个k方体都有完美匹配(k大于等于2)(2) 求K2n和K n,n中不同的完美匹配的个数。

证明一：证明每个k方体都是k正则偶图。

事实上，由k方体的构造：k方体有2k个顶点，每个顶点可以用长度为k的二进制码来表示，两个顶点连线当且仅当代表两个顶点的二进制码只有一位坐标不同。

如果我们划分k方体的2k个顶点，把坐标之和为偶数的顶点归入X，否则归入Y。

图论第一章课后习题解答

bi 个 (i = 1,2,…,s)，则有列。定理 7
bi = n。故非整数组(b ,b ,…, b )是 n 的一个划分，称为 G 的频序
1 2 s
s
i 1
一个 n 阶图 G 和它的补图 G 有相同的频序列。
§1.2 子图与图的运算
且 H 中边的重数不超过 G 中对应边的定义 1 如果 V H V G ，E H E G ，重数，则称 H 是 G 的子图，记为 H G 。有时又称 G 是 H 的母图。当 H G ，但 H G 时，则记为 H G ，且称 H 为 G 的真子图。G 的生成子图是指满足 V(H) = V(G)的子图 H。假设 V 是 V 的一个非空子集。以 V 为顶点集，以两端点均在 V 中的边的全体为边集所组成的子图，称为 G 的由 V 导出的子图，记为 G[ V ]；简称为 G 的导出子图，导出子图 G[V\ V ]记为 G V ；它是 G 中删除 V 中的顶点以及与这些顶点相关联的边所得到的子图。若 V = {v}, 则把 G-{v}简记为 G–v。假设 E 是 E 的非空子集。以 E 为边集，以 E 中边的端点全体为顶点集所组成的子图称为 G 的由 E 导出的子图，记为 G E ；简称为 G 的边导出子图，边集为 E \ E 的 G 的导出子图简记为 G E 。若 E e ，则用 G–e 来代替 G-{e}。定理 8 简单图 G 中所有不同的生成子图（包括 G 和空图）的个数是 2m 个。定义 2 设 G1，G2 是 G 的子图。若 G1 和 G2 无公共顶点，则称它们是不相交的；若 G1 和 G2 无公共边，则称它们是边不重的。G1 和 G2 的并图 G1∪G2 是指 G 的一个子图，其顶点集为 V(G1)∪V(G2)，其边集为 E(G1)∪E(G2)；如果 G1 和 G2 是不相交的，有时就记其并图为 G1+G2。类似地可定义 G1 和 G2 的交图 G1∩G2，但此时 G1 和 G2 至少要有一个公共顶点。

电子科技大学研究生试题图论及其应用参考答案

11年研究生试卷(答案)