杭州学军中学NOIP2011模拟赛DAY2-2011-10-5题解
noip2011模拟试题二

N oip2011模拟试题二题目一:精度计算(a.pas)[问题描述]输入两个10000以内的正整数X、Y,求X除以Y的值。
要求精确到小数点后100位,如果在100位内出现循环节,请用括号标出。
如:51/7=7.(285714)。
[输入输出]注意:文件名写错该题得0分输入文件:a.in输出文件:a.out[输入输出样例][样例一]输入:(两个整数中间有一个空格,前面的数字表示X,后面的数字表示Y)517输出:7.(285714)[样例二]输入:(两个整数中间有一个空格,前面的数字表示X,后面的数字表示Y)217输出:3题目二:分解因式(Factor.pas)问题描述:一个自然数N的正因子个数记为F(N),例如18的所有正因子为1、2、3、6、9、18,所以F(18)=6。
现在给出K,求所有满足F(N)=K的N中最小的数。
输入格式:从文件读入数据,第一行为K,其中0<K<=80。
输出格式:输出到文件第一行,如果存在不大于20000的解,则输出这个N,否则输出“NO SOLUTION”。
样例1:Factor.in Factor.out936样例2:Factor.in Factor.out17NO SOLUTION题目三:最少步数(c.pas)[问题描述]在各种棋中,一种棋子的走法总是一定的,如中国象棋中马走“日”。
有一位小学生就想如果马能有两种走法将更加增加趣味性,因此,他规定马既能按“日”飞,也能各象一样走“田”字。
他的同桌平时喜欢下围棋,知道这件事后觉得很有趣,就和他玩一种新游戏,在围棋盘上(19*19)任选两点A、B,A点放上黑子,B点放上白子,代表两匹马。
棋子可以按“日”字走,也可以按“田”字走,俩人一个走黑马,一个走白马。
谁用最少的步数走到左上角坐标为(1,1)的点时,谁获胜。
现在他请你帮忙,给你A,B两点的坐标,想知道两个位置到(1,1)点的可能最少步数。
[输入输出]注意:文件名写错该题得0分输入文件:c.in输出文件:c.out[输入输出样例][样例]输入:(每行的两个整数中间有一个空格)1216注:A点坐标1810注:B点坐标输出:8注:A到(1,1)的可能最少步数9注:B到(1,1)的可能最少步数题目四:变音量(song.pas)[问题描述]你将要在元旦演奏一场吉他专场。
NOIP2011DAY2解题报告

NOIP2011DAY2解题报告——by北京一零一中学张子威(c++)今天的题还蛮有意思的,虽然做的没有昨天好吧,随便写两笔,可能是我OI生涯最后一份解题报告了。
一.数学题就是一个数学题,模型化简为(a^n)*(b^m)*c(n,k)(组合数),其中前两项可以很简单算出(因为n,m<=1000,都不需要用快速幂),而c(n,k)=c(n-1,k)+c(n-1,k-1),利用这个公式,用一个简单的DP或者记忆化都可以写完,时间复杂度O(n*K)二.qc首先可以证明,算出来的那个求和值(同样忘了叫啥了,就叫F吧)F(W)随你选定的W增大而减小,所以可以二分,如果F(middle)>s,则left=middle(就是说你选的超重了,提高点标准),不然就right=middle(还得多选点,降低标准),但要注意,一开始的区间是[0,w[max]+1](我就忘了加这个1!!!)最后只需要计算W=left和W=right中,跟S相差的绝对值最小的一个。
对于选定的一个W值,就可以模拟去算每个区间内的Σ值,此处可以用区间和优化,预处理中记Num[X]为前X个中满足题意的石头个数,Sum[X]为前X个中满足题意石头的总重量,则[P,Q]之间的Σ=(Num[Q]-Num[P-1])*(Sum[Q]-Sum[P-1]),所以每次模拟的复杂度为O(N+M),总复杂度为O(logw*(n+m)),可以做完。
三.bus这题挺好玩的,应该是贪心+DP什么的,但考场上我想了40分钟没想明白,就果断骗分了。
1.对于K=0和K=1的情况,可以直接模拟(K=1时把每个非0的d值都减1,取其中ans最小的),可以得到30分。
2.对于K<=20的情况,个人感觉可以DFS,但没有去测,反正也就多得10分3.对于K>20的情况,我就不知道怎么做了,直接写了两个贪心取其中最小的,但很可能一个都过不了。
对了,有一种特殊情况,如果k值大于Σd,那就把所有d改成0,不知道有没有这种数据= =~无论如何,我的NOIP历程算是就此结束了,考好也罢,考砸也罢,就这样了,坐等一周后出分。
noip2011模拟day2
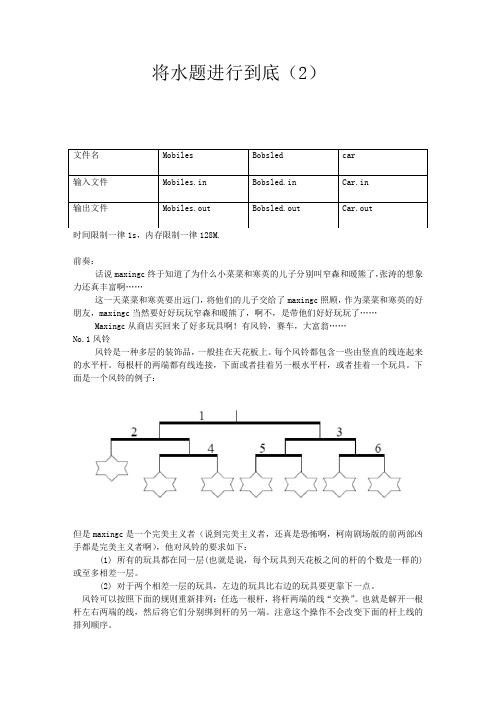
将水题进行到底(2)时间限制一律1s,内存限制一律128M.前奏:话说maxingc终于知道了为什么小菜菜和寒英的儿子分别叫窄森和暖熊了,张涛的想象力还真丰富啊……这一天菜菜和寒英要出远门,将他们的儿子交给了maxingc照顾,作为菜菜和寒英的好朋友,maxingc当然要好好玩玩窄森和暖熊了,啊不,是带他们好好玩玩了……Maxingc从商店买回来了好多玩具啊!有风铃,赛车,大富翁……No.1风铃风铃是一种多层的装饰品,一般挂在天花板上。
每个风铃都包含一些由竖直的线连起来的水平杆。
每根杆的两端都有线连接,下面或者挂着另一根水平杆,或者挂着一个玩具。
下面是一个风铃的例子:但是maxingc是一个完美主义者(说到完美主义者,还真是恐怖啊,柯南剧场版的前两部凶手都是完美主义者啊),他对风铃的要求如下:(1) 所有的玩具都在同一层(也就是说,每个玩具到天花板之间的杆的个数是一样的)或至多相差一层。
(2) 对于两个相差一层的玩具,左边的玩具比右边的玩具要更靠下一点。
风铃可以按照下面的规则重新排列:任选一根杆,将杆两端的线“交换”。
也就是解开一根杆左右两端的线,然后将它们分别绑到杆的另一端。
注意这个操作不会改变下面的杆上线的排列顺序。
Maxingc给窄森一个风铃,让他在1s中之内将它调整到所要求的样子,否则就不让他吃午饭,可怜的窄森怎么会在1s内完成,所以要求助于学oi的你。
你只需在一秒钟内说出最少需要几次交换就行了。
考虑上面的例子,上图中得风铃满足条件1,却不满足条件2。
但是,我们可以通过下面的步骤把这个风铃变成一个符合要求的。
Input输入的第一行包含一个整数n (1 ≤ n ≤ 100000),表示风铃中有多少根杆。
接下来的n行描述杆的连接信息。
这部分的第i行包含两个由空格分隔的整数li和ri,描述杆i的左右两端悬挂的东西。
如果挂的是一个玩具,则对应的值为-1,否则为挂在下面的杆的编号。
如果杆i下面挂有其它杆,则这些杆的编号将严格大于i。
NOIP2011模拟试题及解析

NOIP2011模拟试题及解析128MClass(class.pas/c/cpp)【问题描述】信息班这期的课将要结束了,老师要从现在班上的同学中选出比较优秀的同学进入下一期的学习。
而录取标准则是将平时作业和考试一起考虑,综合成绩排在前面的则录取。
经过一番思考,老师作了以下的筛选计划:1、设计两个参数x,y,学生总成绩为平时成绩的x%和考试成绩的y%。
2、将同学按总成绩排名,招收总成绩在前15的学生,不够15则全部录取。
注:总成绩在第15的如果有多人,则可以被同时录取。
例如:18个人总成绩从大到小依次为95,93,93,88,87,84,80,75,70,68,66,65,60,58,57,57,56,55。
那么93,93同为第2名,而88为第4名,57,57同为第15名,都被录取。
而56,55则不被录取。
老师因为招生培训的事情很忙,所以现在她把信息班学生的成绩表给了你,希望你能告诉她哪些同学被录取了。
【输入】输入文件class.in第一行有三个数N,x,y。
表示信息班有N个同学以及参数x,y。
第二行N个数,分别为A1,A2,A3 … AN。
Ai表示编号为i的同学的平时成绩。
第三行N个数,分别为B1,B2,B3 … BN。
Bi表示编号为i的同学的考试成绩。
【输出】输出文件class.out共一行,为被录取同学的编号,按照升序输出。
【输入输出样例】【数据说明】1<=N<=1000<=x,y<=1000<=平时成绩,考试成绩<=100以上数据皆为整数模拟。
首先求出所有人的总分,然后进行快排(注意第15名的并列情况),人数小于15时,输出1到n;否则将入围人员的编号进行排序升序输出。
程序如下:program zk;varp,k,h,zong:array [0..200] of longint;i,j,a,b,c,n,x,y,xian,f:longint;procedure qsort(x,y:longint);varxo,yo,zz,mid,z:longint;beginxo:=x; yo:=y;mid:=zong[(xo+yo) div 2];repeatwhile zong[xo]>mid do inc(xo);while zong[yo]<mid do dec(yo);if xo<=yo thenbeginz:=zong[xo];zong[xo]:=zong[yo];zong[yo]:=z;zz:=h[xo];h[xo]:=h[yo];h[yo]:=zz;inc(xo); dec(yo);end;until xo>yo;if x<yo then qsort(x,yo);if xo<y then qsort(xo,y);end;procedure qsorth(x,y:longint); varxo,yo,zz,mid,z:longint;beginxo:=x; yo:=y;mid:=h[(xo+yo) div 2]; repeatwhile h[xo]<mid do inc(xo);while h[yo]>mid do dec(yo);if xo<=yo thenbeginzz:=h[xo];h[xo]:=h[yo];h[yo]:=zz;inc(xo); dec(yo);end;until xo>yo;if x<yo then qsorth(x,yo);if xo<y then qsorth(xo,y); end;beginassign(input,'class.in'); assign(output,'class.out'); reset(input);rewrite(output);readln(n,x,y);for i:=1 to n doread(p[i]);readln;for i:=1 to n dobeginh[i]:=i;read(k[i]);end;for i:=1 to n dozong[i]:=p[i]*x+k[i]*y;qsort(1,n);xian:=15;if n>=15 thenbeginf:=zong[xian];while zong[xian+1]=f doxian:=xian+1;endelse xian:=n;qsorth(1,xian);for i:=1 to xian dowrite(h[i],' ');close(input);close(output);end.Clean(clean.pas/c/cpp)【问题描述】最近甲型H1N1流感病毒肆虐。
2011noip解题报告

输入输出样例1
carpet.in 3 1023 0233 2133 22 carpet.out 3
样例分析
carpet.in 3 1023 0233 2133 22 carpet.out 3 如图,1 号地毯用实线表 示,2 号地毯用虚线表示, 3 号用双实线表示,覆盖 点(2,2)的最上面一张 地毯是 3 号地毯。
数据范围
对于 30%的数据,有 n≤2; 对于 50%的数据,0≤a, b, g, k≤100; 对于 100%的数据,有 0≤n≤10,000,0≤a, b, g, k≤100,000。
输入输出
【输入】 carpet.in 输入共 n+2行。 第一行,一个整数 n,表示总共有 n张地毯。 接下来的 n行中,第 i+1行表示编号 i的地毯的信息,包含四个 正整数 a,b,g,k,每两个整数之间用一个空格隔开,分别表 示铺设地毯的左下角的坐标(a,b)以及地毯在 x 轴和 y轴方向 的长度。 第 n+2 行包含两个正整数 x 和 y,表示所求的地面的点的坐标 (x,y) 。 【输出】 carpet.out 输出共 1 行,一个整数,表示所求的地毯的编号;若此处没有被 地毯覆盖则输出-1。
铺地毯
为了准备一个独特的颁奖典礼,组织者在会场的一片矩 形区域(可看做是平面直角坐标系的第一象限)铺上一些矩 形地毯。一共有 n张地毯,编号从 1 到n。现在将这些地毯 按照编号从小到大的顺序平行于坐标轴先后铺设,后铺的地 毯覆盖在前面已经铺好的地毯之上。 地毯铺设完成后,组织者想知道覆盖地面某个点的最上面的 那张地毯的编号。注意:在矩形地毯边界和四个顶点上的点 也算被地毯覆盖。
算法分析
枚举 按编号枚举每一块地毯,保留覆盖统计点 的最后一张地毯。
NOIP2011初赛提高组答案详细解析

NOIP2011初赛提高组答案详细解析一、单项选择二、多项选择5. C是显然要选的,本题因为有300+400=700的情况,所以B也是可以的。
7.首先要知道逆序对的定义:序列A[1..n]里,对于i<j的A[i]>A[j],则称A[i]与A[j]为一对逆序对。
将给定的序列中所有逆序对列出来,统计其中数字只出现过3次的。
8.阶码肯定是要选的,D较长的尾数也是浮点数的一个特点,它只是保正了浮点数一定的精度,并不是它可以表示很大或者很小的数的原因。
9.本题描述有点含糊,它的本意可能是在计算S到B点的距离时出现有值。
三、问题求解1.9平面图中点数n与边数m之间的关系是:m<=3n-6,当n=5时,m的最大值为9。
2. 4求出给定的长度为n的字符串的最长上升序列的长度m,最小的操作次数为n-m。
四、阅读程序题1. 3先是统计出各个数字出现的次数存放在a数组里,然后I从1开始累加a[i],直到总数超过n的一半,最后输出i。
2.1 2 5 13 34斐波那契数列间隔输出3.150求遍历图中各个点所有边长的和的最大值。
本题4个点,求3条不同边的边长和的最大值。
4.57344 (213*7)本题稍有些难度,观察m*n的0-1矩阵,可以看出m=2n,此矩阵其实就是所有7位的二进制数。
每一列中有2n-1个1和个0,在一列里每个1都有2^(n-1)个0与它不同,同样每个0也有2^(n-1)个1与它不同,即每列的结果为22n-2*2=22n-1,n列的结果为n*22n-1,所以本题的结果为213*7.此题也可以从递推的角度来求解:f(n)=4n/(n-1)*f(n-1) (因为列增加1时行变为原来两倍,01的个数也对应为原来2倍)f(1)=2由此递推式子也可以得到通项公式:f(n)=n*22n-1。
再分析此题,发现就是从0开始由小到大每次增加1构造出所有n位二进制数,如果将低位写在右边更符合平常习惯,更易看出结果。
[独家]2011年浙江省杭州学军中学高考模拟考试(文综)
![[独家]2011年浙江省杭州学军中学高考模拟考试(文综)](https://img.taocdn.com/s3/m/991ec82a6edb6f1aff001f60.png)
2011年杭州学军中学高考模拟考试文科综合试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分。
考试时间150分钟。
满分150分。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
第I 卷 选择题部分(共140分)本卷共35小题。
在每小题给出的四个选项中,只有一项是符合题目要求的。
图1为“世界上某种气候类型的局部地区分布示意图”,读图回答1—3题。
1.与甲地区相比,造成乙地区该种气候类型分布范围较狭窄的最主要因素是A .纬度位置B .洋流C .海陆轮廓D .地形2.该气候类型在乙、丙两区域分布的最高纬度有较大差异,其主要的影响因素是A.海陆分布B.海拔高低C.山脉阻挡D.大气环流3.该气候区的农作物一般具有A .耐高温干旱的特点B .耐低温干旱的特点C .喜高温多雨的特点D .喜阴喜湿的特点读图2、图3,回答4-5题。
4.Q 地为该城市规划预留地,最适宜建A .客货物流区B .高新技术区C .旅游度假区D .行政办公区5.依据该城市大气中SO 2地面浓度,判断此时季节最有可能是A .春、夏季节B .冬、春季节C .夏、秋季节D .秋、冬季节 2008年韩国对29个OECD (经合组织)成员国的粮食自给率进行了比较。
结果,法国以329%高居榜首,韩国(26位,25.3%)、日本(第27位,22.4%)冰岛(第29位,甲乙 丙 图 1 图2图30%)。
完成6~8小题:6.韩国和日本粮食自给率倒数的原因,主要是A .本国工业发达,不生产粮食B .粮食产量低C .山地面积大、没有耕地D .人均耕地少7.冰岛粮食自给率居末位的原因是A .多岩浆、火山活动,不能生产粮食B .从事粮食生产的人口少,C .纬度高,气候寒冷,不能生产粮食D .海拔高、气温低人们在选择工作及居住地时多受就业机会、文化及自然环境等因素影响。
下图是针对美国大学生的居住及工作地选择情况,抽样调查所绘制的“偏好指数”空间分布图。
读图回答8—9题。
8.甲地区成为“偏好指数”偏低的区域,主要是因为A.河湖密布,地形起伏大B.平原地形,人口密度高C.大陆性气候,以农牧业为主D.以矿产资源开采为主,经济落后9.东北部地区成为“偏好指数”较高的区域,与20世纪70年代后出现的人口回流有关。
杭州学军中学NOIP2011模拟赛DAY2-2011-10-5题解

NOIP2011模拟赛题解最大公约数首先可以排除所有GCD(a,b)不等于1的数对因为他们同除以公约数后可以得到一样优的解其次可以排除在辗转过程中出现a<=b div2的情况如果b mod a=c可以将b变成a+c可以得到一样优的解并且原来的b变小则可以将所有没被排除掉的数表示成如下形式a,b->b-a,a->….->1,x(经过L次)对于所有的1,x明显x=2得到的序列更优所以只考虑这个序列1,2->2,3->3,5->5,8->8,13….即由Fibonacci数列前后两项所构成的序列做法:用高精度计算fib数列知道列尾数字大于n输出倒数第二和倒数第三项即可序列游戏如果我们枚举Gy,Nsk翻转的位置,然后再进行计算,显然是O(N^3)的。
这个做法通过记录区间和能够非常容易的做到O(N^2),但如果要通过所有的测试数据还有一定困难。
因此我们接下来对这题作一些研究。
显然的,假如Gy的决策已经确定了,Nsk的决策是确定的。
我们猜想这之中有一定的单调性,但是显然Nsk的决策和Gy的决策构不成单调关系。
事实上,要处理原问题,我们只需要解决下面的两个子问题即可。
1.Gy和Nsk的选择集合严格不相交。
2.Gy和Nsk的选择集合存在相交部分。
这两个子问题都是可以做的。
我们先来考虑第一个子问题。
如果Gy和Nsk的选择集合严格不相交的话怎么处理。
显然这个问题可以通过记录后缀最小值单调处理,时间复杂度O(N)。
如果Gy和Nsk的选择集合存在相交部分,假设Gy当前决策是i,Nsk相对的最优决策是j(j<=i),我们记这样的决策为(i,j)。
显然Nsk的最优决策不会在[0,j-1],因为这与(i,j)为Nsk在i处的最优决策相矛盾。
同理最优决策不会在[j+1,i]。
因此,当Gy的决策由i变成i+1时,实际上Nsk下一步只有两种决策的可能1.Nsk的决策仍为j;2.Nsk的决策变为i+1。
Noip2011解题报告

Noip2011解题报告1.题意:将一个数数字位颠倒,符号不变。
注意:由题意,不会出现-0情况。
算法:模拟。
时间复杂度:o(n log10)空间复杂度:o(1)代码:Program reverse;varn:longint;procedure init;beginassign(input,'reverse.in');assign(output,'reverse.out');reset(input);rewrite(output);end;procedure clo;beginclose(input);close(output);end;begininit;readln(n);if n<0 thenbeginwrite('-');n:=abs(n);end;while (n mod 10=0)and(n>0) don:=n div 10;while n>0 dobeginwrite(n mod 10);n:=n div 10;end;writeln;clo;End.测试情况:题号时间(s) 题号时间(s)1 0.05 6 0.042 0.03 7 0.033 0.03 8 0.044 0.05 9 0.035 0.04 10 0.052.题意:在一个字符串中寻找单词注意:单词过长,用ansistring操作更简单,空间更小。
算法:(1)从前向后搜,时间:o(n^2)空间:o(1)代码:Program stat;vars1:ansistring;s,s2:string;i,num,first,i1:longint;procedure init;beginassign(input,'stat.in');assign(output,'stat.out');reset(input);rewrite(output);end;procedure clo;beginclose(input);close(output);end;begininit;readln(s);for i:=1 to length(s) doif (s[i]>='A')and(s[i]<='Z') thens[i]:=chr(ord(s[i])-ord('A')+ord('a'));readln(s1);for i:=1 to length(s1) doif (s1[i]>='A')and(s1[i]<='Z') thens1[i]:=chr(ord(s1[i])-ord('A')+ord('a'));{大小写}s1:=s1+' ';{方便以后操作}i:=0;first:=0;num:=0;while i<length(s1) dobegininc(i);while (s1[i]=' ')and(i<length(s1)) do inc(i);s2:='';i1:=i;while s1[i]<>' ' dobegins2:=s2+s1[i];inc(i);end;if s2=s thenbegininc(num);if first=0 then first:=i1;end;end;{从前向后搜}if num=0 then writeln('-1')elsewriteln(num,' ',first-1);clo;end.优化:本题数据量较小,优化与不优化差别不大。
NOIP2011复赛题解

NOIP2011复赛题解noip2011普及组解题报告NOIP2011普及组解题报告——ahbbzeq 2011.11.25 转载请注明来源一、数字反转没得满分只能说明一个问题,你的程序写的太少了。
program reverse;vars:string;i,sta:longint;beginassign(input,'reverse.in');reset(input);assign(output,'reverse.out');rewrite(output);readln(i);str(i,s);sta:=1;if s[1]='-' thenbeginwrite('-');sta:=2;end;i:=length(s);while (s[i]='0') and (i>sta) dodec(i);while (i>=sta) dobeginwrite(s[i]);dec(i);end;close(input);close(output);end.二、统计单词个数考你的基本功,和对程序的理解,尤其是细节上的优化。
直接在文章中选出单词,与给定单词长度一致时才比较,函数传参数时也不要传字符串(会很慢的,具体慢多少没试)。
program stat;vars,p:ansistring;i,j,first,num,len,c,k:longint;function cmp(x:longint):boolean;vari:longint;beginfor i:= 1 to c doif s[i]<> p[x+i-1] then exit(false);exit(true);end;beginassign(input,'stat.in');reset(input);assign(output,'stat.out');rewrite(output);readln(s);readln(p);s:=upcase(s);p:=upcase(p);c:=length(s); len:=length(p);i:=1; num:=0; first:=-1;while (s[i]=' ')and (i<=len) do inc(i);while (i<=len) dobeginj:=i+1;while (p[j]<>' ') and (j<=len) doinc(j);if (j-i = c) and cmp(i) thenbeginif first=-1 then first:=i;inc(num);end;i:=j; while (p[i]=' ') and (i<=len) do inc(i); end;if first=-1 thenwriteln(-1)else writeln(num,' ',first-1);close(input);close(output);end.三、瑞士轮实践证明,如果单纯的排序r次,必然结果是超时。
浙江省杭州学军中学10-11学年高一下学期期中考试(数学实验班)

3
5
11
25
∴恰有 4 个正整数 n 使不等式 2an p an
bn 1
p8
成立的正整数 p 值为 3.
bn
20.解:( 1)令 x1 x2 0, 得
f (0) f (xo ) 2 f (0)
f ( xo ) f (0) ①
令 x1 1, x2 0,得 f (xo ) f ( xo ) f (1) f ( 0) 由①②得 f ( xo ) f (1), 又因为 f ( x)是单调函数
2
2
(A) 奇函数
(B) 偶函数
(C) 非奇非偶函数
(D) 既奇又偶函数
二、填空题:本大题共 6 小题,每小题 4 分,共 24 分.
11、已知 cos x
2,x
,3 .则 sin x =______ __ .
4 10
24
12. 若 x 表示不超过 x 的最大整数(如 1.3
1,
1 2
4
3 等等)则
( 1)求通项 a n , bn ;
( 2)求数列 { an bn } 的前 n 项和 Sn ;
( 3)若恰有 4 个正整数 n 使不等式 2an p an
bn 1
p8 成立,求正整数 p 的值.
bn
20.已知定义域在 R 上的单调函数 y f ( x) ,存在实数 x0 ,使得对于任意的实数 x1, x2 ,
(写出正确的序号)
(0, ) 4
三、解答题:本大题共 4 小题,共 46 分.解答应写出文字说明、证明过程或演算步骤
17. 如图,四边形 ABCD 中, E,F 分别为 AC 、 BD 的中点,设向量
r
r
r
a (4cos ,sin ), b (sin , 4cos ), c (cos , 4sin ) ,且
杭州学军中学NOIP2011模拟赛DAY2-2011-10-5

NOIP2011模拟赛By 杭州学军中学中文题目名称最大公约数序列游戏纪念品题目名gcd.pas/c/cpp game.pas/c/cpp senzo.pas/c/cpp 时间限制1s 1s 1s空间限制256M 256M 256M编译命令:(以题目名A为例)对于pascal语言:fpc A.pas对于C语言:gcc -o A A.c -lm对于C++语言:g++ -o A A.cpp -lm代码长度限制:50KB请根据实际评测的机器配置适当放大或缩小时间和空间限制为了评测及整理方便起见,文件夹名请使用"学校名-选手名"的格式,里面不需要使用子文件夹,谢谢合作。
出题人:Gy , Chnlich , Nsk最大公约数题目描述刚刚上完小学四年级的Gy和Nsk在讨论有关用辗转相除法求最大公约数的问题。
他们想知道,对于求GCD(a,b) (a<=b<=N),辗转最多的一对是哪一对。
辗转次数的定义:对于数对A,B(A<=B),令A'=B mod A,B'=A,每次将(A,B)变为(A',B'),直到最终A'=gcd(A,B)时总共进行的变换次数。
辗转次数的具体解释:比如在N=10时4,6 -> 2,4 ==> 2GCD(4,6)是2辗转了1次3,8 -> 2,3 -> 1,2 ==> 1GCD(3,8)是1辗转了2次2,9 -> 1,2 ==> 1GCD(2,9)是1辗转了1次所以(3,8)比(2,9)和(4,6)辗转的多。
输入格式一行,包含一个整数N,含义如题所述。
输出格式两行各一个整数,分别表示辗转次数最多的数对的a和b。
如果辗转次数一样,取b最小的(如果b也一样,取a最小的)。
样例输入4样例输出23数据范围对于20% 的数据N<=10^4对于50% 的数据N<=10^18对于100% 的数据3<=N<=10^12000序列游戏题目描述给定一个整数数列Q,小学刚毕业的Gy和Nsk将分别对这个数列进行一次操作。
2011noip提高组复赛题解

Noip 2011 提高组(Day 1)解题报告及程序一、铺地毯正着扫一遍判断每个矩形是否覆盖询问的点,覆盖则更新结果或者倒着扫一遍,找到第一个覆盖询问点的矩形,输出即可,时间复杂度O(n)Procedure:#include <cstdio>#define MaxLength 10000inline int Getint(){char c = getchar();while (c<'0' || c>'9') c = getchar();int ret = 0;while (c>='0' && c<='9'){ret = ret*10 + (c-'0');c = getchar();}return ret;}int sx[MaxLength+5], sy[MaxLength+5], ex[MaxLength+5], ey[MaxLength+5], n; void Init(){n = Getint();for (int i=1; i<=n; i++){sx[i] = Getint(), sy[i] = Getint(), ex[i] = Getint(), ey[i] = Getint();ex[i] += sx[i], ey[i] += sy[i];}return ;}int x0, y0, ans = -1;void Solve(){x0 = Getint(), y0 = Getint();for (int i=n; i;i--)if(x0>=sx[i] && x0<=ex[i] && y0>=sy[i] && y0<=ey[i]){ans = i;break;}printf("%d", ans);return ;}int main(){Init();Solve();getchar(); getchar();return 0;}二、选择客栈f [i][j]表示前i个客栈以第j种颜色的方案数,先以客栈划分第一阶段,以颜色划分第二阶段,如果颜色相同的客栈,则以前一客栈相同颜色的方案数+1,否则同其一样;计算答案时记一下前一个比最高消费限制低的客栈编号pos[i],路径压缩,时间复杂度O(nm)Procedure:#include <cstdio>#define MaxNode 200000#define MaxType 50inline int Getint(){char c = getchar();while (c<'0' || c>'9') c = getchar();int ret = 0;while (c>='0' && c<='9'){ret = ret*10 + (c-'0');c = getchar();}return ret;}int color[MaxNode+5], price[MaxNode+5], n, m, low;void Init(){n = Getint(), m = Getint(), low = Getint();for (int i=1; i<=n; i++) color[i] = Getint(), price[i] = Getint();return ;}int f[MaxNode+5][MaxType+5], pos[MaxNode+5], ans = 0;void Dp(){for (int i=1; i<=n; i++)for (int j=0; j<m; j++)if (color[i]==j) f[i][j] = f[i-1][j]+1;else f[i][j] = f[i-1][j];for (int i=1; i<=n; i++)if (price[i]<=low){pos[i] = i;ans += f[i-1][color[i]];}else{pos[i] = pos[i-1];ans += f[pos[i]][color[i]];}printf("%d", ans);return ;}int main(){Init();Dp();getchar(); getchar();return 0;}三、Mayan纯暴力DFS,加可行性剪枝,如同一种颜色小于3块无法消除,同一颜色交换无意义,下落无法完成左右移动,再加模拟其过程时间复杂度O( n^(?) )Procedure:#include <cstdio>#include <memory>inline int Getint(){char c = getchar();while (c<'0' || c>'9') c = getchar();int ret = 0;while (c>='0' && c<='9'){ret = ret*10 + (c-'0');c = getchar();}return ret;}inline void Swap(int &a, int &b){int temp = a; a = b; b = temp;return ;}int map[10][10], point[10], color[15], n, type = 0;void Init(){n = Getint();for (int i=0; i<5; i++){map[i][0] = Getint();if (type<map[i][point[i]]) type = map[i][point[i]];color[ map[i][point[i]] ]++;while (map[i][point[i]]){map[i][++point[i]] = Getint();if (type<map[i][point[i]]) type = map[i][point[i]];color[ map[i][point[i]] ]++;}point[i]--;}return ;}bool Fall(int k){int top = -1;for (int i=0; i<=point[k]; i++)if (map[k][i]) map[k][++top] = map[k][i];if (top!=point[k]){for (int i=top+1; i<=point[k]; i++) map[k][i] = 0;point[k] = top;return true;}return false;}bool Check_Fall(){bool flag = false;for (int i=0; i<5; i++)if (Fall(i)) flag = true;return flag;}bool sign[10][10];void Clear(){int pmax = 0;for (int i=0; i<5; i++)if (point[i]>pmax) pmax = point[i];for (int i=0; i<5; i++)if (point[i]>=2){int k = point[i], j = k-1;for (; j>=0; j--)if (map[i][j]!=map[i][k]){if (k-j>=3)for (; k>j; k--) sign[i][k] = true;else k = j;}if (k-j>=3)for (; k>j; k--) sign[i][k] = true;}for (int i=0; i<=pmax; i++){int k = 0, j = 1;for (; j<5; j++)if (map[j][i]!=map[k][i]){if (j-k>=3)for (; k<j; k++) sign[k][i] = true;else k = j;}if (j-k>=3)for (; k<j; k++) sign[k][i] = true;}for (int i=0; i<5; i++)for (int j=pmax; j>=0; j--)if (sign[i][j]){sign[i][j] = false;color[map[i][j]]--;map[i][j] = 0;}return ;}void Solve(int x, int y){Fall(x), Fall(y);Clear();while (Check_Fall()) Clear();return ;}bool Check_Point(){for (int i=0; i<5; i++)if (point[i]>=0)return false;return true;}bool Check_Color(){for (int i=1; i<=type; i++)if (color[i]==1 || color[i]==2) return false;return true;}struct Ac{int m[10][10], p[10], c[15];}a[10];inline void Copy(int k){memcpy(a[k].m, map, sizeof(map));memcpy(a[k].p, point, sizeof(point));memcpy(a[k].c, color, sizeof(color));return ;}inline void Turn_Copy(int k){memcpy(map, a[k].m, sizeof(a[k].m));memcpy(point, a[k].p, sizeof(a[k].p));memcpy(color, a[k].c, sizeof(a[k].c));return ;}int ans[10][10];bool Dfs(int deep){if (!Check_Color()) return false;Copy(deep);for (int i=0; i<5; i++)for (int j=0; j<=point[i]; j++){ans[deep][0] = i, ans[deep][1] = j;if (i<4){ans[deep][2] = 1;Swap(map[i][j], map[i+1][j]);if (point[i+1]<j) point[i+1] = j;Solve(i, i+1);if (deep==n && Check_Point()) return true;if (deep<n && Dfs(deep+1)) return true;Turn_Copy(deep);}if (i && point[i-1]<j){ans[deep][2] = -1;Swap(map[i][j], map[i-1][j]);point[i-1] = j;Solve(i, i-1);if (deep==n && Check_Point()) return true;if (deep<n && Dfs(deep+1)) return true;Turn_Copy(deep);}}return false;}int main(){Init();if (!Dfs(1)) printf("-1");elsefor (int i=1; i<=n; i++)printf("%d %d %d\n", ans[i][0], ans[i][1], ans[i][2]);getchar(); getchar();return 0;}Noip 2011 提高组(Day 2)解题报告及程序一、计算系数二项式定理,杨辉三角,注意Mod就可以了,时间复杂度O(k^2)Procedure:#include <cstdio>#define MaxNode 1000#define Mod 10007int f[MaxNode+5][MaxNode+5], a, b, k, n, m;void Init(){scanf("%d %d %d %d %d", &a, &b, &k, &n, &m);a %= Mod,b %= Mod, k++;for (int i=1; i<=k; i++) f[i][1] = f[i][i] = 1;for (int i=2; i<=k; i++)for (int j=2; j<i; j++)f[i][j] = (f[i-1][j-1] + f[i-1][j])%Mod;return ;}void Solve(){int x = k, y = k-n;for (int i=1; i<=n; i++) f[x][y] = (f[x][y] * a)%Mod;for (int j=1; j<=m; j++) f[x][y] = (f[x][y] * b)%Mod;printf("%d", f[x][y]%Mod);return ;}int main(){Init();Solve();getchar(); getchar();return 0;}二、聪明的质检员由观察得随着参数W的上升检验值temp会减小,据函数Abs(标准值-temp)有最小值,故可二分查找得出答案其中每次调整参数W时扫描一次矿石中大于W的,num[]表示其数量前缀和,val[]表示其价值前缀和,故可在一个区间的检验值计算中以O(1)的时间得出答案时间复杂度O(log(w)*(n+m))Procedure:#include <cstdio>#define MaxNode 200000#define INF ((0x7fffffffffffffffll)>>1)inline int Getint(){char c = getchar();while (c<'0' || c>'9') c = getchar();int ret = 0;while (c>='0' && c<='9'){ret = ret*10 + (c-'0');c = getchar();}return ret;}long long Abs(long long a){if (a>0) return a;return -a;}int w[MaxNode+5], val[MaxNode+5], l[MaxNode+5], r[MaxNode+5], n, m, lw, rw; long long standard;void Init(){n = Getint(), m = Getint(), scanf("%I64d", &standard);for (int i=1; i<=n; i++){w[i] = Getint(), val[i] = Getint();if (rw<w[i]) rw = w[i]+1;}for (int i=1; i<=m; i++) l[i] = Getint(), r[i] = Getint();return ;}int num[MaxNode+5];long long sum[MaxNode+5];long long Calc(int left, int right){return (sum[right]-sum[left]) * (num[right]-num[left]);}long long Sieve(int Limit){long long ret = 0;sum[0] = num[0] = 0;for (int i=1; i<=n; i++){num[i] = num[i-1];sum[i] = sum[i-1];if (w[i]>=Limit){num[i]++;sum[i] += val[i];}}for (int i=1; i<=m; i++) ret += Calc(l[i]-1, r[i]);return ret;}long long ans = INF;void Binary_Search()while (lw<rw){int mid = (lw+rw)>>1;long long temp = Sieve(mid);long long value = Abs(standard - temp);if (temp<standard) rw = mid;else lw = mid+1;if (ans>value) ans = value;}printf("%I64d", ans);return ;}int main(){Init();Binary_Search();getchar(); getchar();return 0;}三、观光公交贪心令t[i]表示当前到达第i个站的时间,sumoff[i]表示目的地为i的乘客数,arrtime[i]表示第i个乘客到站等车的时刻题目给定加速器的作用就是可以把某个t[i]减去1并把与其相关联的t[i]全部减小1。
NOIP2011提高组一试参考题解

3.Mayan游戏
思路1:直接输出-1
复杂度O(1) 期望得分0-10分
对于对一行进行搜索,依次枚举每一个格子向左移动或向右移动,层数限制为N,若在N层恰好全部消除完,则输出方案。对于判重问题可以写hash表,将一行的状态转换成10进制映射到一个数上。 复杂度O(10^5)期望得分30
思路3:爆搜+各种剪枝 复杂度O(?) 期望得分 ?
思路3:可以用ST算法O(1)时间求出两个区间的最小值 复杂度O(NlogN+N^2) 期望得分 50-60
思路4:对于每一个客栈,我们考虑和当前点前面的客栈进行配对。预处理出Pre表示i点(包含i点)前面第一个<=p的客栈。对于每一个颜色,求出sum表示前i个点有多少个点的颜色等于当前枚举的颜色。依次枚举每一个客栈,若当前客栈最低消费<=p,当前客栈可以和前面任意一个客栈进行匹配,并且pre一定等于i,所以答案可以累加sum[pre]-1;对于当前客栈最低消费>p,则当前客栈只能和pre以及之前的客栈进行匹配,故答案可以累加sum[pre]。 复杂度O(NK) 期望得分100
NOIP2011题解
铺地毯:
顺序处理每一个长方形,并判断当前的点是否在长方形内,并记录尽可能靠后的长方形编号,输出即可。 复杂度O(N) 期望得分100
选择客栈:
按照题目要求的进行模拟,每次选择两个进行判断,若满足以下条件:
1.
两个客栈颜色相同
2.
两个客栈中间(包含两个客栈)中存在一家咖啡店最低消费小于等于p的
即算作一个满足条件的解。
思路1:枚举两个客栈,判断颜色是否相同,并顺序枚举求两个客栈的最小值,看是否小于等于p
复杂度O(N^3) 期望得分30-40
NOIP2011 提高组 Day2
全国信息学奥林匹克联赛(NOIP2011)复赛提高组day2 全国信息学奥林匹克联赛(NOIP2011)复赛提高组 day2(请选手务必仔细阅读本页内容)一.题目概况注意事项:1、文件名(程序名和输入输出文件名)必须使用英文小写。
2、C/C++中函数main()的返回值类型必须是int,程序正常结束时的返回值必须是0。
3、全国统一评测时采用的机器配置为:CPU P4 3.0GHz,内存1G,上述时限以此配置为准。
4、特别提醒:评测在NOI Linux 下进行。
全国信息学奥林匹克联赛(NOIP2011)复赛提高组day2【问题描述】1.计算系数(factor.cpp/c/pas)给定一个多项式(ax + by)k ,请求出多项式展开后x n y m 项的系数。
【输入】输入文件名为factor.in。
共一行,包含5 个整数,分别为a,b,k,n,m,每两个整数之间用一个空格隔开。
【输出】输出文件名为factor.out。
输出共1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对10007 取模后的结果。
【输入输出样例】对于30%的数据,有0≤k≤10;对于50%的数据,有a = 1,b = 1;对于100%的数据,有0≤k≤1,000,0≤n, m≤k,且n + m = k,0≤a,b≤1,000,000。
【问题描述】2.聪明的质监员(qc.cpp/c/pas)小T 是一名质量监督员,最近负责检验一批矿产的质量。
这批矿产共有n 个矿石,从1 到n 逐一编号,每个矿石都有自己的重量w i 以及价值v i。
检验矿产的流程是:1、给定m 个区间[L i,R i];2、选出一个参数W;3、对于一个区间[L i,R i],计算矿石在这个区间上的检验值Y i :Yi=∑1* ∑v j ,j ∈[L i , R i ] 且w j ≥W ,j 是矿石编号j jm这批矿产的检验结果Y 为各个区间的检验值之和。
noip2011提高组day2题解转载

若time[i+1]减少了1 我们可以用同样的方法判断time[i+2]直到最后是否变化
若time[i+1]不变 则time[i+2]及之后的time值都不会变化
**所以 当我们令某个d[i]减少1时 从time[i]开始会有一段区间的time值均减少1
所以二分找到两个距离给定的值k最近的两个s即可
每次求解s时 用部分和的方法
即先用O(n)的时间算出从最开始到中间某一处总的可以取的零件数和其v值之和
之后对于每一个区间 可以用O(1)的时间算出该范围内可以取的零件数和其v值之和
不需要高精度 因为当w取最大时s为0 此时abs(k-s)=s 优于所有s爆度的情况
时间复杂度O(kn)
d[i]为从i走到i+1所用的时间
很明显的 我们可以利用这个递推关系式用O(n)的时间求解time[i]
当我们令d[i]减少1时
time[1..i-1]不会变化
time[i]会减少1
考虑time[i+1]
由前面的式子得出time[i+1] = max{time[i], last[i+1]} + d[i+1]
由于人到达起始站的时间题目给出不会变化
所以求解一个最优的车到达目的站的时间即可
假设到达第i+1站的时间是time[i]
从前往后逐个求解到站时间
可以得出time[i] = max{time[i-1], last[i]} + d[i]
noip2011初赛试题及答案(完美Word版)-推荐下载

第十七届全国青少年信息学奥林匹克联赛初赛试题(提高组Pascal语言两小时完成)●●全部试题答案均要求写在答卷纸上,写在试卷纸上一律无效●●一、单项选择题(共20题,每题1.5分。
共计30分。
每题有且仅有一个正确选项。
)B 1.在二进制下,1100011 +()= 1110000。
A.1011B.1101C.1010 D.1111B 2.字符“A”的ASCII码为十六进制41,则字符“Z”的ASCII码为十六进制的()。
A.66 B.5A C.50 D.视具体的计算机而定A 3.右图是一棵二叉树,它的先序遍历是()。
A.ABDEFC B.DBEFAC C.DFEBCA D.ABCDEFD 4.寄存器是()的重要组成部分。
A.硬盘B.高速缓存C.内存D.中央处理器(CPU)B 5.广度优先搜索时,需要用到的数据结构是()。
A.链表B.队列C.栈D.散列表A 6.在使用高级语言编写程序时,一般提到的“空间复杂度”中的“空间”是指()。
A.程序运行时理论上所占的内存空间B.程序运行时理论上所占的数组空间C.程序运行时理论上所占的硬盘空间D.程序源文件理论上所占的硬盘空间C 7.应用快速排序的分治思想,可以实现一个求第K大数的程序。
假定不考虑极端的最坏情况,理论上可以实现的最低的算法时间复杂度为()。
A.O(n2)B.O(n log n)C.O(n)D.O(1)D 8.为解决Web应用中的不兼容问题,保障信息的顺利流通,()制定了一系列标准,涉及HTML、XML、CSS等,并建议开发者遵循。
A.微软B.美国计算机协会(ACM)C.联台国教科文组织D.万维网联盟(W3C)B 9.体育课的铃声响了,同学们都陆续地奔向操场,按老师的要求从高到矮站成一排。
每个同学按顺序来到操场时,都从排尾走向排头,找到第一个比自己高的同学,并站在他的后面。
这种站队的方法类似于()算法。
A.快速排序B.插入排序C.冒泡排序D.归并排序A 10.1956年()授予肖克利(William Shockley)、巴丁(John Bardeen)和布拉顿(Walter Brattain),以表彰他们对半导体的研究和晶体管效应的发现。
浙江省学军中学2011届高三高考模拟考试(数学理)

2011年学军中学高考模拟考试数学(理科)试卷注意事项:1.本科考试分试题卷和答题卷,考生须在答题卷上作答。
答题前,请在答题卷的密封线内填写学校、班级、学号、姓名;2.本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分。
全卷满分150分,考试时间120分钟。
参考公式:球的表面积公式 柱体体积公式24R S π= V sh = 球的体积公式 其中S 表示柱体的底面积,h 表示柱体的高343V Rπ=台体的体积公式其中R 表示球的半径121()3V h S S =+锥体体积公式 其中12,S S 分别表示台体的上、下底面积,h 表示台体的高Sh V 31=如果事件A 、B 互斥,其中S 表示锥体的底面积,h 表示锥体的高 那么P (A+B )=P (A )+P (B )第Ⅰ卷(共50分)一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.集合{}k y y x P ==),(, {}1,0,1),(≠>+==a a a y y x Q x,已知∅=Q P ,那么实数k 的取值范围是( )A. (-∞,1)B. (-∞,1]C. (1,+∞)D. (-∞,+∞) 2.若R a ∈,则1=a 是复数i a a z )1(12++-=是纯虚数的 ( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既不充分也不必要条件 3.一个几何体的三视图如图所示,则该几何体的体积为( )A .2B .1C .23D .134.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球, 这些小球除标注的数字外完全相同.现从中随机取出2个小球, 则取出的小球标注的数字之和为3或6的概率是( )5. 为了得到函数sin(2)6y x π=+的图像,只需把函数sin(2)3y x π=-的图像( )A .向左平移4π个长度单位 B .向右平移4π个长度单位C.向左平移2π个长度单位 D.向右平移2π个长度单位6.已知m 、n 是两条不重合的直线,γβα,,是三个两两不重合的平面,给出下列四个命题:①若βαβα//,,则⊥⊥m m ; ②若βαβα//,//,,则n m n m ⊂⊂;③若βαγβγα//,,则⊥⊥; ④若m 、n 是异面直线,βααββα//,//,,//,则n n m m ⊂⊂ 其中真命题是 ( )A .①和②B .①和③C .③和④D .①和④7.如下图所示的程序框图输出的结果是 ( ) A .6 B .-6 C .5 D .-5 8.对于定义在R 上的函数)(x f ,有下述命题:①若)(x f 是奇函数,则)1(-x f 的图象关于点A (1,0)对称 ②若函数)1(-x f 的图象关于直线1=x 对称,则)(x f 为偶函数 ③若对R x ∈,有)(),()1(x f x f x f 则-=-的周期为2④函数)1()1(x f y x f y -=-=与的图象关于直线1=x 对称. 其中正确命题的个数是( )A . 1B . 2C . 3D . 49.已知平面内一点},16)sin 2()cos 2(|),{(22R y x y x P ∈=-+-∈ααα,则满足条件的点P 在 平面内所组成的图形的面积是 ( ) A .36π B .32π C .16π D .4π 10.从双曲线)20(12222a b by ax <<=-的左焦点F 引圆222a yx =+的切线,切点为T,延长FT 交双曲线右支于点P,O 为坐标原点,M 为PF 的中点 则 ||||MT MO -与a b -的大小关系为( ) a b MT MO A ->-||||. a b MT MO B -=-||||. a b MT MO C -<-||||. D.不能确定二、填空题(本大题共7小题,每小题4分,共28分) 11.()()6211x x x ++-展开式中3x 项的系数是_______。
NOIP2011提高组解题报告day2

计算系数【问题描述】给定一个多项式(ax + by)^k,请求出多项式展开后(x^n)*(y^m)项的系数。
【输入】输入文件名为 factor.in。
共一行,包含 5 个整数,分别为a,b,k,n,m,每两个整数之间用一个空格隔开。
【输出】输出文件名为 factor.out。
输出共 1 行,包含一个整数,表示所求的系数,这个系数可能很大,输出对10007 取模后的结果。
【输入输出样例】【数据范围】对于 30%的数据,有0≤k≤10;对于 50%的数据,有a = 1,b = 1;对于 100%的数据,有0≤k≤1,000,0≤n, m≤k,且n + m = k,0≤a,b≤1,000,000。
【考察知识点】数论/二项式系数/组合【思路】学OI的应该知道二项式系数/组合数/杨辉三角,再不行手推几个也就能知道ans=C(k,n)*(a^n)*(b^m)这里由于是取模,同余只能用于加和乘。
但又要算组合数,而组合数公式里有除法,我因此纠结了很久很久,甚至最后都有写高精加减乘除模的想法。
瞬间灵光一闪,C(k,n)=C(k-1,n)+C(k-1,n-1),行了!注意要边加边mod,否则跟没想到一样。
【时间复杂度】O(k^2)program factor;//uses sysutils;constproname='factor';yu=10007;varfin,fout:text;i,j,k,m,n,l,r,s,t,x,y:longint;a,b:int64;ans:int64;c:array[0..1100,0..1100]of longint;procedure pin;i,j:longint;beginreadln(fin,a,b,k,n,m);end;function getc(n,r:int64):int64;vari,j:longint;beginfillchar(c,sizeof(c),0);c[0,0]:=1;c[1,0]:=1;c[1,1]:=1;for i:=2 to n dobeginc[i,0]:=1;for j:=1 to i doc[i,j]:=(c[i-1,j]+c[i-1,j-1]) mod yu;end;exit(c[n,r] mod yu);end;procedure main;vari,j:longint;beginans:=1;a:=a mod yu;b:=b mod yu;for i:=1 to n doans:=ans*a mod yu;for i:=1 to m doans:=ans*b mod yu;if n>m thent:=melset:=n;ans:=ans*getc(k,t) mod yu;end;procedure pout;vari,j:longint;beginwriteln(fout,ans);end;beginassign(fin,proname+'.in');assign(fout,proname+'.out');reset(fin);rewrite(fout);//time:=now;pin;main;pout;//writeln(fout,(now-time)*24*3600*1000:0:0);close(fin);close(fout);end.聪明的质监员【问题描述】小 T 是一名质量监督员,最近负责检验一批矿产的质量。
学军中学Crazy Land 模拟赛2011-10-4

学军中学Crazy Land 模拟赛(NOIP2011提高组赛前联合训练)By crazygirl3小时这套题数学味有点重,自认为数学不好的童鞋自求多福这一天,crazygirl醒来了……一片虚空中,只有Crazy Land两个硕大的单词悬浮在空中……突然一个声音响起……人类,你来到了一个你不该来到的地方……然后,crazygirl的背后出现了一个巨大的漩涡……(难道说……传说中的虫洞?)猫和老鼠Tom and Jerry题目描述crazygirl先被漩涡吸了进去,旋即又被吐了出来。
只是这一进一出着实让晕车的crazygirl成功的“晕漩涡”了。
当crazygirl清醒的时候,眼前竟然出现了……猫和老鼠???是的,一只名为Tom的猫和一只名为Jerry的老鼠正在赛跑。
Tom和Jerry每天都要赛跑。
注意是猫和老鼠赛跑,不是龟兔赛跑。
他们的场地是一个边长为整数且最长边为a的长方体,起点和终点互为对角。
Tom可以在任意表面跑,Jerry则可以在长方体里打洞。
两个人,哦不应该是两只动物,都会走最短路。
但是,Tom表示它很讨厌小数,所以如果这个场地的最短路不是整数那么它会拒绝比赛。
现在,Tom和Jerry想知道在所有最长边为a的不同可比赛长方体上两只动物的最短路平方的平均数输入格式有多组数据第一行一个数T,表示数据组数每组数据进一行,一个整数a输出格式对于每一组数据,输出一行先输出Tom的最短路平方平均数,再输出Jerry的,用一个空格隔开两个数均用最简分数输出如果分母为零,则输出“NULL/NULL”cat.in223cat.outNULL/NULL NULL/NULL25/1 18/1数据范围对于20%的数据 T = 2,1 <= a <= 100对于100%的数据 1 <= T <= 20,1 <= a <= 2000Hints旋转或翻转后相同的长方体视为同一个场地,即将三条边长排序后对应边长相等即视为同一个长方体样例解释,对于a = 2,没有可以比赛的长方体对于a = 3,只有两个可比赛长方体,分别为3 * 3 * 1 和3 * 2 * 2EndTomJerryStartTom和Jerry表示,如果crazygirl可以正确的回答它们的问题,它们就会带着crazygirl去参观它们居住的城市——双城双城记 A Tale of Two Cities题目描述帮助Tom和Jerry解决了问题后,它们愉快的带着crazygirl来到了双城。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NOIP2011模拟赛题解
最大公约数
首先可以排除所有GCD(a,b)不等于1的数对
因为他们同除以公约数后可以得到一样优的解
其次可以排除在辗转过程中出现a<=b div2的情况如果b mod a=c可以将b变成a+c可以得到一样优的解并且原来的b变小
则可以将所有没被排除掉的数表示成如下形式
a,b->b-a,a->….->1,x(经过L次)
对于所有的1,x明显x=2得到的序列更优
所以只考虑这个序列
1,2->2,3->3,5->5,8->8,13….
即由Fibonacci数列前后两项所构成的序列
做法:
用高精度计算fib数列知道列尾数字大于n
输出倒数第二和倒数第三项即可
序列游戏
如果我们枚举Gy,Nsk翻转的位置,然后再进行计算,显然是O(N^3)的。
这个做法通过记录区间和能够非常容易的做到O(N^2),但如果要通过所有的测试数据还有一定困难。
因此我们接下来对这题作一些研究。
显然的,假如Gy的决策已经确定了,Nsk的决策是确定的。
我们猜想这之中有一定的单调性,但是显然Nsk的决策和Gy的决策构不成单调关系。
事实上,要处理原问题,我们只需要解决下面的两个子问题即可。
1.Gy和Nsk的选择集合严格不相交。
2.Gy和Nsk的选择集合存在相交部分。
这两个子问题都是可以做的。
我们先来考虑第一个子问题。
如果Gy和Nsk的选择集合严格不相交的话怎么处理。
显然这个问题可以通过记录后缀最小值单调处理,时间复杂度O(N)。
如果Gy和Nsk的选择集合存在相交部分,假设Gy当前决策是i,Nsk相对的最优决策是j(j<=i),我们记这样的决策为(i,j)。
显然Nsk的最优决策不会在[0,j-1],因为这与(i,j)为Nsk在i处的最优决策相矛盾。
同理最优决策不会在[j+1,i]。
因此,当Gy的决策由i变成i+1时,实际上Nsk下一步只有两种决策的可能
1.Nsk的决策仍为j;
2.Nsk的决策变为i+1。
我们只要求出这两种决策的最优值并记录下来即可,可以在O(N)
的时间内解决。
这样一来,在O(N)的时间内,我们可以求出两种情况下Nsk的最优决策取min即可,然后再在全局取max即为答案,完美解决了这个问题。
最终时间复杂度为O(N),空间复杂度为O(N),C/C++选手可能需要读入优化才能通过此题。
纪念品
根据题目给的条件,我们首先可以算出一些块的总和。
一个显而易见的结论是,对于一个块,如果它没有任意一个节点被覆盖到,花费为0;如果全部被覆盖到,花费为它的代价;否则花费最大值为它的代价,最小值为0。
对于每个询问的两个点x和y,不妨设它们的LCA为z。
假如我们能够预处理出每个点到根这条链上的权值,设第i个点的预处理权值为Si,第i个点所属块的价值为Vi。
由于最大值和最小值是独立的,我们可以分开来考虑。
先考虑最大值。
(注意最大值和最小值对应的Si是不同的)最大值的特点是:只要一个块有一个元素被路径覆盖了,这个块的权值就要加入答案中。
可以发现,z上方的点被重复算了2次,z被多算了1次,因此答案就是Sx+Sy-2*Sz+Vz。
再考虑最小值。
最小值的特点是:只有一个块中所有元素都被路径覆盖,这个块的权值才能加入答案中。
我们进行分情况讨论:
1.z所属的块不是一条链。
显然答案即为Sx+Sy-2*Sz。
2.z所属块是一个点。
此时答案为Sx+Sy-2*Sz+Vz。
3.z是链的端点。
分三种情况讨论得到的答案均为Sx+Sy-2*Sz。
4.z是链的中间点。
我们继续分情况讨论:
(1)z所在链两端点分别在x子树和y子树上并被x到y的路径
包含。
此时答案为Sx+Sy-2*Sz+Vz。
(2)z所在链两端点分别在x子树和y子树上但不被x到y的路
径包含。
此时答案为Sx+Sy-2*Sz。
(3)z所在链两端点一个在x(或y)子树上,另一个在z的其它子
树上。
此时答案为Sx+Sy-2*Sz。
(4)z所在链两端点一个在x(或y)子树上,另一个在z到根的路
径上。
此时答案为Sx+Sy-2*Sz-Vz。
(5)z所在链两端点均不在x,y子树上。
答案为Sx+Sy-2*Sz。
最后是刚才没有解决的预处理部分。
我们先处理出每个点在哪个块内,记录块的大小信息,然后从根节点开始进行一遍dfs,动态维护每个块的大小信息来计算两个S数组即可。
总时间复杂度为O(N)。
为了方便起见,标程的LCA使用了O(NlogN)的写法。
事实上上述分类讨论仍然可以再简化。
