二年级上册数学一课一练-2.7立方体拼图 浙教版(含答案)
二年级上册数学一课一练-2.7立方体拼图 浙教版(含答案)

二年级上册数学一课一练-2.7立方体拼图一、单选题1.下面()个正方体正好可以拼成一个较大的大正方体.A. 8B. 64C. 27D. 1252.一个长6分米,宽4分米,高5分米的长方体盒子,最多能放()个棱长是2分米的正方体木块.A. 5个B. 14个C. 12个3.至少用()个相同的小正方体才能拼成一个大正方体.A. 4B. 6C. 8D. 24.两个同样大小的长方体,长为6cm,宽为3cm,高为6cm,能否拼成一个正方体,表面积是多少?正确的选项是( )。
A. 能,108cm2B. 不能C. 能,216cm2D. 能,54cm25.用12个小正方体可以拼成()种不同的长方体.A. 3B. 4C. 5D. 6二、判断题6.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
7.两个正方体一定能拼成一个长方体。
8.一块豆腐切三刀,最多能切7块.9.把一个长方体木料截成两段,它们的表面积和体积都不变。
()三、填空题10. 一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.11.如图,形体是由________个小正方体拼搭成的.至少还需要________块同样大小的小正方体,才能拼搭成一个大正方体.12.把一个圆柱体平均分成若干份切开,拼成一个近似的长方体。
这个长方体的长等于圆柱________,它的宽等于圆柱的________。
13.下面的图形是由体积为1立方厘米的小正方体堆积成的,露在外面的面积是________平方厘米,体积是________立方厘米。
14.1cm3的小正方体木块,堆成一个1m3的大正方体,需要________个小正方体木块,如果把这些小正方体密铺成一排,长________千米.四、解答题15.有一个长方体,如右图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有________种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?五、综合题16.将整箱装有28块正方体木块的积木:(1)如果拼成一个大的长方体图案,有几种拼法?(2)可以拼成一个大的正方体图案吗?设计一下这样做至少需要几箱子这样的积木?六、应用题17.把一个棱长是10厘米的正方体,分割成2个同样大小的长方体,这个长方体的长、宽、高分别是多少?每个长方体的棱长之和是多少?18.把长8厘米,宽12厘米,高5厘米的木块锯成棱长2厘米的正方体木块.可锯多少块?答案解析部分一、单选题1.【答案】B【解析】【解答】解:因为8是2的立方;27是3的立方;64是4的立方;125是5的立方,都能拼成一个大正方体;所以在上述数字中,只有64是立方数,所以能拼成大正方体.故选:B.【分析】拼成大正方体的小正方体的个数,应该是一个数的立方数,1的立方除外,如2的立方8个,3的立方27个,4的立方64个,5的立方125个等.2.【答案】C【解析】【解答】解:以长为边最多放:6÷2=3(块),以宽为边最多放:4÷2=2(块),以高为边最多放:5÷2=2(块)…1(分米),所以:3×2×2=12(块);答:最多能放12块.故选:C.【分析】先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算即可解答.解答此题时不要用大体积除以小体积来计算块数,因为高还有剩余.3.【答案】C【解析】【解答】解:由正方体的特征即可知道至少用8个相同的正方体才能拼成一个较大的正方体.如:棱长为2米的正方体是由8个棱长为1米的小正方体拼成.故选:C.【分析】根据正方体的特征即可知道至少用8个相同的正方体才能拼成一个较大的正方体.本题考查了正方体的认识,8个相同的较小的正方体才能拼成一个较大的正方体.4.【答案】C【解析】【解答】解:把这样的两个长方体正方形的面拼在一起就能拼出一个正方体,表面积:6×6×6=216(cm²)故答案为:C【分析】这个长方体有两个正方形的面,且高是长的一半,所以能拼出一个棱长6厘米的正方体;用棱长×棱长×6计算表面积即可.5.【答案】B【解析】【解答】解:根据题干分析去掉重复的数据可得:拼组后的长方体的棱长可以分别为:①1、1、12;②1、2、6;③1、3、4;④2、2、3;共可以拼组成4种不同的长方体.故选:B.【分析】设小正方体的棱长为1,要用12个棱长为1的正方体木块拼成一个长方体,拼成一个长方体有下列特点:当高为1时的每组长和宽一组因数,可以为1和12,2和6,3和4;当高为2时的每组长和宽一组因数,可以为1和6,2和3;当高为3时的每组长和宽一组因数,可以为1和4,2和2;当高为4时的每组长和宽一组因数,可以为1和3;由此删去长宽高重复出现的图形,即可得出答案进行选择.此题也可以利用分解质因数的方法解答:12可以写成三个数的乘积的形式为:1×1×12;1×2×6;1×3×4;2×2×3;由此也可以确定拼组后的长方体的长宽高的值.二、判断题6.【答案】正确【解析】【解答】虽然形状发生了变化,但是体积没有变化。
二年级上册数学一课一练-2.7立方体拼图 浙教版(含解析)

二年级上册数学一课一练-2.7立方体拼图一、判断题1.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
2.判断对错.三个小正方体不管怎样叠放在一起,体积总是不变的.3.判断题.四个小正方体可以拼成一个大正方体.二、填空题4. 一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.5.下面的物体都是由棱长1厘米的正方体摆成的.它们的体积各是多少立方厘米.________立方厘米________立方厘米6.用12个棱长1厘米的正方体木块摆成不同形状的长方体,它的体积是________立方厘米.三、单选题7.选择截面的形状连起来是(1)()A. B. C.(2)()A. B. C.(3)()A. B. C.8.将一根半径为5厘米的圆木锯成3段,表面积增加()平方厘米.A. 3.14×52×3B. 3.14×52×6C. 3.14×52×4D. 3.14×5×2×69.用两个棱长为20厘米的小正方体拼成一个长方体,发生了什么变化?()A. 体积变大,表面积变小B. 体积变小,表面积变大C. 体积不变,表面积变大D. 体积不变,表面积变小四、解答题10.有一个长方体,如右图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有________种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?五、综合题11.将整箱装有28块正方体木块的积木:(1)如果拼成一个大的长方体图案,有几种拼法?(2)可以拼成一个大的正方体图案吗?设计一下这样做至少需要几箱子这样的积木?六、应用题12.一根12米长的长方体木料,侧面是正方形,把木料锯成各6米长的两段后,表面积增加了32平方分米,求原来木料的表面积.参考答案一、判断题1.【答案】正确【解析】【解答】虽然形状发生了变化,但是体积没有变化。
精选2019-2020年浙教版小学数学二年级上册7、立方体拼图习题精选四十九

精选2019-2020年浙教版小学数学二年级上册7、立方体拼图习题精选四十九第1题【单选题】最少要( )个同样的小方块才能拼成一个较大的正方体。
A、4B、6C、8【答案】:【解析】:第2题【单选题】两个同样大小的长方体,长为6cm,宽为3cm,高为6cm,能否拼成一个正方体,表面积是多少?正确的选项是( )。
A、能,108cm^2B、不能C、能,216cm^2D、能,54cm^2【答案】:【解析】:第3题【单选题】至少要用( )个同样的正方体才能拼成一个新的正方体.A、8B、16C、4【答案】:【解析】:第4题【单选题】把一个圆柱体截成三个小圆柱体,则表面积增加( )A、2个底面B、3个底面C、4个底面D、6个底面【答案】:【解析】:第5题【判断题】用4块棱长是1厘米的小正方体就可以拼成一个较大的正方体.A、正确B、错误【答案】:【解析】:第6题【判断题】一块豆腐切三刀,最多能切7块.A、正确B、错误【答案】:【解析】:第7题【判断题】把两个一样的正方体拼成一个长方体后,体积和表面积都不变.(判断对错)A、正确B、错误【答案】:【解析】:第8题【填空题】把一根长5分米、宽2分米、高1分米的长方体木料,锯成棱长1分米的正方体木块,最多能锯______块。
A、10【答案】:【解析】:第9题【填空题】至少要用______个相同的小正方体才能拼成一个大正方体。
【答案】:【解析】:第10题【填空题】数一数.有______个。
【答案】:【解析】:第11题【填空题】下图是由棱长为2厘米的小正方体搭成的,它的体积是______立方厘米,表面积是______平方厘米。
【答案】:【解析】:第12题【填空题】A、18【答案】:【解析】:第13题【填空题】数学小组的同学将一个圆柱按下面的左图切割开,然后拼成下面右图所示的物体。
观察填空:拼出的物体是一个近似的______体,它的高与圆柱的高______,它的底面积与圆柱的底面积______,圆柱的体积与它的体积______,所以圆柱的体积计算公式是______。
小学数学浙教版二年级上册立方体拼图(二年级)同步测试.doc
小学数学浙教版二年级上册立方体拼图(二年级)同步测试
姓名:_____________ 年级:____________ 学号:______________
题型选择题填空题简答题xx
题xx题xx题总分得分
一、xx题
(每空xx 分,共xx分)
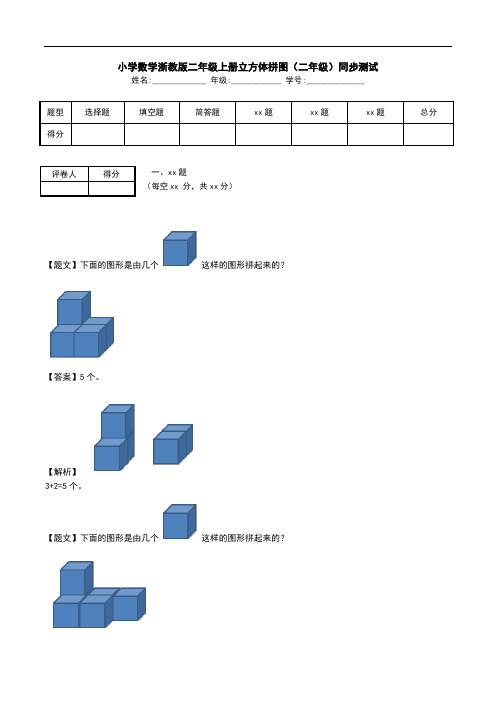
【题文】下面的图形是由几个这样的图形拼起来的?
【答案】5个。
【解析】
3+2=5个。
【题文】下面的图形是由几个这样的图形拼起来的?
评卷人得分
【答案】6个。
【解析】
3+2+1=6(个)
【题文】右边的图形是由几个拼起来的?数一数列式计算。
【答案】5+3+2=10;
【解析】考查学生对立体图形的认识和连加的计算能力。
【题文】右边的图形是由几个
{l
【解析】考查立体图形的认识能力。
【题文】右边的图形是由几个拼起来的?数一数列式计算。
【答案】7+4+1=12;
【解析】考查学生对立体图形的认识和连加的计算能力。
【题文】右边的图形是由几个拼起来的?数一数列式计算。
【答案】6+3+2=11;
【解析】考查学生对立体图形的认识和连加的计算能力。
【题文】右边的图形是由几个拼起来的?数一数列式计算。
【答案】5+3+1=9;
【解析】考查学生对立体图形的认识和连加的计算能力。
二年级上册数学一课一练-2.图形小世界 浙教版(含答案)

二年级上册数学一课一练-2.图形小世界一、单选题1. 用长12厘米,宽9厘米的长方形拼正方形,最少要用该长方形纸()张.A. 8B. 6C. 24D. 122.下图中,有________个小正方体。
( )A. 10B. 13C. 14D. 153.用两个三角板的角可以拼出的角是()A. 75度B. 100度C. 160度4.两个完全一样的等腰梯形可以拼成一个()A. 长方形B. 正方形C. 平行四边形D. 梯形5.一张12 cm 9 cm的长方形纸,最多能剪出直径是2 cm的圆( )个。
A. 27B. 26C. 34D. 24二、判断题6.两个面积相等的三角形一定能拼成一个平行四边形.7.把两个一样的正方体拼成一个长方体后,体积和表面积都不变。
8.4个同样大小正方形,可以拼成一个大的正方形,也可以拼成一个长方形.9.判断对错两个相同的直角三角形可以拼成一个正方形.三、填空题10.数一数.看得见的小正方体有________块,看不见的小正方体有________块,一共有________块小正方体.11.观察这些图形,将图片对应的序号填入横线中。
________ ________ ________ ________ ________________ ________12.请你先数一数,再填一填吧。
有________个13.摆下面的图形,需要几个小正方体.________个14.看图数正方体________个正方体四、解答题15.将一张长方形的纸剪出四个大小一样的长方形,用这些小长方形能拼出哪些图形?16.用三角形拼四边形,你能拼出几种四边形?五、综合题17.如图有三个完全相同的长方形,请按下面三个不同的要求在长方形内各画出一条直线.(1)图(1)分成两部分,使这两部分能拼成平行四边形.(2)图(2)分成两部分,使这两部分既能拼成平行四边形,又能拼成三角形.(3)图(3)分成两部分,使这两部分既能拼成平行四边形,又能拼成三角形和梯形.六、应用题18.工厂里生产了一批长方体的包装箱,长0.6米,宽0.4米,高0.5米,要用一辆卡车把他们拉走,这辆卡车厢的底面积是7.2平方分米,且只能码两层,问最多可以装多少个包装箱?参考答案一、单选题1.【答案】D2.【答案】C3.【答案】A4.【答案】C5.【答案】D二、判断题6.【答案】错误7.【答案】错误8.【答案】正确9.【答案】错误三、填空题10.【答案】4;1;511.【答案】④;⑥;①;⑦;⑤;②;③12.【答案】713.【答案】514.【答案】7四、解答题15.【答案】可以16.【答案】解:1.任取两个三角形,拼组四边形.这两个三角形无法拼成一个四边形.发现这两个三角形没有一条相等的边,不能拼成四边形.2.取有一条边相等的两个三角形,拼组四边形.当两个三角形有一条边长度相等时,就可以拼成四边形.3.用相同的三角形拼四边形.①两个相同的普通三角形拼四边形.②两个相同的直角三角形拼四边形.③两个相同的等腰直角三角形拼四边形.④用三个相同的三角形拼四边形.答:可以拼出长方形、正方形、梯形、平行四边形、普通四边形.五、综合题17.【答案】(1)解:分割方法如下:(2)解:分割方法如下:(3)解:分割方法如下:六、应用题18.【答案】解:7.2÷(0.5×0.4)×2 =7.2÷0.2×2=72(个)答:最多可以装72个包装箱.。
二年级上册数学一课一练-2.6图形的分与合 浙教版(含答案)

二年级上册数学一课一练-2.6图形的分与合一、单选题1.下图中,有________个小正方体。
( )A. 6B. 8C. 10D. 122.一个立体图形从正面看是,从左面看是,搭这个立体图形最少需要( )个小正方体。
A. 4B. 5C. 63.用12个同样大小的正方形,可以拼成( )种不同的长方形。
A. 4B. 3C. 24.两个完全一样的梯形不能拼成一个( )。
A. 长方形B. 三角形C. 正方形D. 平行四边形二、判断题5.两个相同的三角形可以拼成一个平行四边形。
6.两个面积相等的三角形一定能拼成一个平行四边形。
()7.两个面积相等的三角形一定可以拼成一个平行四边形.(判断对错)8.把两个一样的正方体拼成一个长方体后,体积和表面积都不变。
三、填空题9.下面的图中各有多少个小正方体?把它填在________里.(1)________个(2)________个(3)________个10.比一比,看谁数得快又对.________个11.补瓷砖。
这面墙缺了________块瓷砖12.数一数,下面的图形是由几个长方体或正方体组成的.________个四、解答题13.按要求画一画。
(1)分成2个梯形和1个长方形。
(2)分成4个三角形和1个四边形。
14.每种图形里有哪些数(1)□里有()和()。
(2)△里有( )和( )。
(3)○里有( )和( )。
(4)里有( )和( )和( )和( )。
五、综合题15.有两个大小一样的长方形,长24厘米、宽12厘米。
(1)拼成一个长方形,它的面积是多少平方厘米?周长是多少厘米?(2)拼成一个正方形,它的面积是多少平方厘米?周长是多少厘米?六、应用题16.用棱长是2厘米的正方体,拼成一个正方体,最少需要几个小正方体?拼成的正方体的棱长之和是多少厘米?参考答案一、单选题1.【答案】D【解析】2.【答案】B【解析】【解答】解:拼出这个图形下层需要4个,上层需要1个,共至少需要5个小正方形.故答案为:B【分析】这个图形有两层,下层前排3个小正方形,后排1个小正方形,上层前排1个正方形.3.【答案】B【解析】【解答】因为12=3×4=2×6=1×12,所以一共可以拼成3种不同的长方形.故选:B.【分析】本题考点:图形的拼组.本题考查了学生利用因数的分解解决实际问题的灵活应用.根据12的因数,可知12=3×4,12=2×6,12=1×12,用12个相同的小正方形拼成不同的长方形,它的长和宽就应是(3,4),(2,6),(1,12),一共有3种不同的长方形.4.【答案】B【解析】【解答】解:两个完全一样的梯形无论怎样拼都不能拼出一个三角形。
2021年小学数学浙教版二年级上册立方体拼图
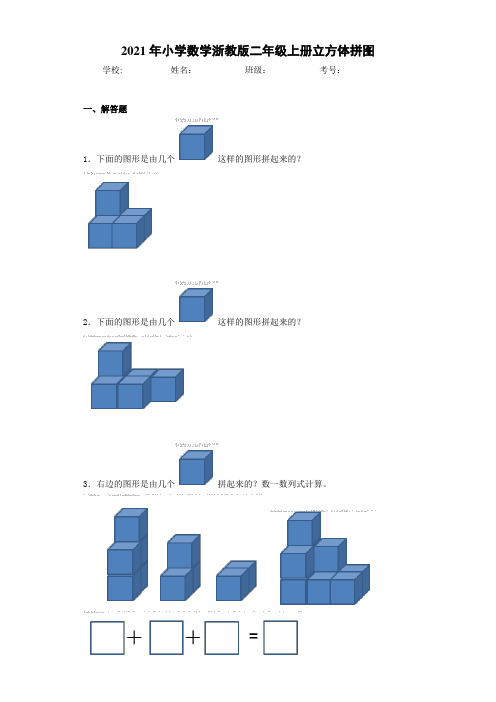
2021年小学数学浙教版二年级上册立方体拼图学校:___________姓名:___________班级:___________考号:___________
一、解答题
1.下面的图形是由几个这样的图形拼起来的?
2.下面的图形是由几个这样的图形拼起来的?
3.右边的图形是由几个拼起来的?数一数列式计算。
4.右边的图形是由几个拼起来的?数一数列式计算。
5.左边的图形拼起来后是右面的那个图形,对应的连起来。
6.
二、填空题
7.右边的图形是由几个拼起来的?数一数列式计算。
8.右边的图形是由几个拼起来的?数一数列式计算。
9.右边的图形是由几个拼起来的?数一数列式计算。
10.右边的图形是由几个拼起来的?数一数列式计算。
参考答案
1.5个。
【解析】
3+2=5个。
2.6个。
【解析】
3+2+1=6(个)
3.5+3+2=10;
【解析】考查学生对立体图形的认识和连加的计算能力。
4.5+3+1=9;
【解析】考查学生对立体图形的认识和连加的计算能力。
5.
【解析】考查立体图形的认识能力。
6.
【解析】考查立体图形的认识能力。
7.6+3+1=10;
【解析】考查学生对立体图形的认识和连加的计算能力。
8.7+4+1=12;
【解析】考查学生对立体图形的认识和连加的计算能力。
9.6+3+2=11;
【解析】考查学生对立体图形的认识和连加的计算能力。
10.5+3+1=9;
【解析】考查学生对立体图形的认识和连加的计算能力。
二年级上册数学一课一练-2.7立方体拼图 浙教版(含答案)

二年级上册数学一课一练-2.7立方体拼图一、判断题1.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
2.一块豆腐切三刀,最多能切7块.3.一个立体图形是由10个小正方体拼搭成的.至少还需要17个同样大小的小正方体,才能拼搭成一个大正方体.4.由6个小正方体可以拼成一个大正方体。
二、填空题5.一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.6.至少用________个棱长1厘米的小正方体可以拼成一个较大的正方体.拼成的这个正方体的表面积是________平方厘米,体积是________立方厘米.7.一根长方体木料,它的横截面的面积是10dm2,把它截成4段,表面积增加了________dm2。
8.把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了________平方厘米.三、单选题9.选择截面的形状连起来是(1)()A.B.C.(2)()A.B.C.(3)()A.B.C.10.将一根半径为5厘米的圆木锯成3段,表面积增加()平方厘米.A. 3.14×52×3B. 3.14×52×6C. 3.14×52×4D. 3.14×5×2×611.一个长6分米,宽4分米,高5分米的长方体盒子,最多能放()个棱长是2分米的正方体木块.A. 5个B. 14个C. 12个12.如图是用棱长1cm的小正方体摆成的,在这个基础上,至少还要用()个这样的小正方体才能摆成一个较大的正方体.A. 10B. 18C. 19D. 2四、解答题13.有一个长方体,如右图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有________种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?14.照下面的样子,用三块正方体木块还能摆出哪些模型?请你试一试.五、应用题15.把一个棱长是10厘米的正方体,分割成2个同样大小的长方体,这个长方体的长、宽、高分别是多少?每个长方体的棱长之和是多少?参考答案一、判断题1.【答案】正确【解析】【解答】虽然形状发生了变化,但是体积没有变化。
浙教版二年级数学上册二图形小世界7《立方体拼图》

复习巩固
立体图形能拼搭和拆分吗?
下面的图形是由几个立方体拼起来的?
(1)从上往下看。
1 + 3 + 3 = 7 (个)
3 × 2+ 1 = 7(个)
(2)从左往右看。
5 + 2 = 7 (个)
(3)从前往后看。
2 + 2 + 3 = 7 (个) 2 × 2+ 3 = 7(个)
下面的图形是由几个立方体拼起来的?
(1)从上往下看。
1 + 3 + 6 = 10 (个)
4 + 6 = 10 (个)
(2)从左往右看。
5 + 3 + 2 = 10 (个)
把下面的图形拼一拼。
•
9、 人的价值,在招收诱惑的一瞬间被决定 。2021/ 4/22021 /4/2Fri day, April 02, 2021
•
13、生气是拿别人做错的事来惩罚自 己。202 1/4/22 021/4/2 2021/4 /22021 /4/24/2 /2021
•
14、抱最大的希望,作最大的努力。2 021年4 月2日 星期五2 021/4/ 22021/ 4/22021 /4/2
•
15、一个人炫耀什么,说明他内心缺 少什么 。。202 1年4月 2021/4 /22021 /4/2202 1/4/24 /2/2021
•
16、业余生活要有意义,不要越轨。2 021/4/ 22021/ 4/2April 2, 2021
•
17、一个人即使已登上顶峰,也仍要 自强不 息。202 1/4/22 021/4/2 2021/4 /22021 /4/2
谢谢大家
பைடு நூலகம்
•
10、低头要有勇气,抬头要有低气。2 021/4/ 22021/ 4/22021 /4/24/ 2/2021 4:49:22 PM
2019-2020学年度小学二年级上册数学7、立方体拼图浙教版练习题第一篇

2019-2020学年度小学二年级上册数学7、立方体拼图浙教版练习题第一篇第1题【单选题】下面( )个正方体正好可以拼成一个较大的大正方体.A、8B、64C、27D、125【答案】:【解析】:第2题【单选题】至少要用( )个同样的正方体才能拼成一个新的正方体.A、8B、16C、4【答案】:【解析】:第3题【单选题】将一根半径为5厘米的圆木锯成3段,表面积增加( )平方厘米.A、3.14×5^2×3B、3.14×5^2×6C、3.14×5^2×4D、3.14×5×2×6【答案】:【解析】:第4题【单选题】用长为4厘米,宽为3厘米,高为2厘米的长方体来拼一个实心的正方体,至少需要( )个这样的长方体.A、4B、24C、48D、72【答案】:【解析】:第5题【单选题】把一个棱长是6cm的正方体切成棱长是3cm的小正方体,可以得到( )个小正方体。
A、3B、8C、27【答案】:【解析】:第6题【单选题】把一个长方体分割成5个小正方体,( )与原来相比保持不变。
A、体积之和B、棱长之和C、表面积之和【答案】:【解析】:第7题【单选题】用12个小正方体可以拼成( )种不同的长方体.A、3B、4C、5D、6【答案】:【解析】:第8题【判断题】判断对错.三个小正方体不管怎样叠放在一起,体积总是不变的.A、正确B、错误【答案】:【解析】:第9题【判断题】把一个长方体木料截成两段,它们的表面积和体积都不变。
( )A、正确B、错误【答案】:【解析】:第10题【填空题】把两个棱长为4厘米的正方体拼成一个长方体,表面积减少了______平方厘米.A、32【答案】:【解析】:第11题【填空题】1cm^3的小正方体木块,堆成一个1m^3的大正方体,需要______个小正方体木块,如果把这些小正方体密铺成一排,长______千米.A、1000000B、10【答案】:【解析】:第12题【填空题】一根圆柱形木料横截成4段小圆柱,增加了______个底面。
二年级上册数学一课一练-2.7立方体拼图 浙教版(含解析)

二年级上册数学一课一练-2.7立方体拼图一、单选题1.下面()个正方体正好可以拼成一个较大的大正方体.A. 8B. 64C. 27D. 1252.一个长9厘米、宽6厘米、高3厘米的长方体,切割成3个体积相等的长方体,表面积最大可增加()A. 36平方厘米B. 72平方厘米C. 108平方厘米D. 216平方厘米3.把一个棱长是6cm的正方体切成棱长是3cm的小正方体,可以得到()个小正方体。
A. 3B. 8C. 274.最少要()个同样的小方块才能拼成一个较大的正方体。
A. 4B. 6C. 8二、判断题5.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
6.两个正方体一定能拼成一个长方体。
7.判断对错.三个小正方体不管怎样叠放在一起,体积总是不变的.三、填空题8. 一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.9.1cm3的小正方体木块,堆成一个1m3的大正方体,需要________个小正方体木块,如果把这些小正方体密铺成一排,长________千米.10.用12个棱长1厘米的正方体木块摆成不同形状的长方体,它的体积是________立方厘米.11.如图,形体是由________个小正方体拼搭成的.至少还需要________块同样大小的小正方体,才能拼搭成一个大正方体.四、解答题12.下图是棱长为5厘米的正方体,如果在这个正方体中切去一个棱长为3厘米的小正方体,剩下几何体的表面积是多少平方厘米?请作具体分析。
五、综合题13.将整箱装有28块正方体木块的积木:(1)如果拼成一个大的长方体图案,有几种拼法?(2)可以拼成一个大的正方体图案吗?设计一下这样做至少需要几箱子这样的积木?六、应用题14.民生包装公司要为某品牌饮料设计一个能放12瓶的包装箱(饮料瓶的尺寸如图).请你帮他们想想办法,设计一种用料最少的包装箱.请写出计算过程.参考答案一、单选题1.【答案】B【解析】【解答】解:因为8是2的立方;27是3的立方;64是4的立方;125是5的立方,都能拼成一个大正方体;所以在上述数字中,只有64是立方数,所以能拼成大正方体.故选:B.【分析】拼成大正方体的小正方体的个数,应该是一个数的立方数,1的立方除外,如2的立方8个,3的立方27个,4的立方64个,5的立方125个等.2.【答案】D【解析】【解答】解:9×6×4=216(平方厘米),答:表面积最大可增加216平方厘米.故选:D.【分析】根据长方体切割小长方体的特点可得:要使切割后表面积增加的最大,可以平行于原长方体的最大面,即9×6面,进行切割,这样表面积就会增加4个原长方体的最大面;据此解答.3.【答案】B【解析】【解答】解:6÷3=2,2×2×2=8(个)故答案为:B【分析】用大正方体的棱长除以小正方体的棱长,求出每条棱长可以切出正方体的个数,这个个数的三次方就是可以得到小正方体的个数。
二年级上册数学一课一练-2.7立方体拼图 浙教版含答案

二年级上册数学一课一练-2.7立方体拼图一、单选题1.下面()个正方体正好可以拼成一个较大的大正方体.A. 8B. 64C. 27D. 1252.一个长6分米,宽4分米,高5分米的长方体盒子,最多能放()个棱长是2分米的正方体木块.A. 5个B. 14个C. 12个3.至少用()个相同的小正方体才能拼成一个大正方体.A. 4B. 6C. 8D. 24.两个同样大小的长方体,长为6cm,宽为3cm,高为6cm,能否拼成一个正方体,表面积是多少?正确的选项是( )。
A. 能,108cm2B. 不能C. 能,216cm2D. 能,54cm25.用12个小正方体可以拼成()种不同的长方体.A. 3B. 4C. 5D. 6二、判断题6.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
7.两个正方体一定能拼成一个长方体。
8.一块豆腐切三刀,最多能切7块.9.把一个长方体木料截成两段,它们的表面积和体积都不变。
()三、填空题10. 一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.11.如图,形体是由________个小正方体拼搭成的.至少还需要________块同样大小的小正方体,才能拼搭成一个大正方体.12.把一个圆柱体平均分成若干份切开,拼成一个近似的长方体。
这个长方体的长等于圆柱________,它的宽等于圆柱的________。
13.下面的图形是由体积为1立方厘米的小正方体堆积成的,露在外面的面积是________平方厘米,体积是________立方厘米。
14.1cm3的小正方体木块,堆成一个1m3的大正方体,需要________个小正方体木块,如果把这些小正方体密铺成一排,长________千米.四、解答题15.有一个长方体,如右图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有________种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?五、综合题16.将整箱装有28块正方体木块的积木:(1)如果拼成一个大的长方体图案,有几种拼法?(2)可以拼成一个大的正方体图案吗?设计一下这样做至少需要几箱子这样的积木?六、应用题17.把一个棱长是10厘米的正方体,分割成2个同样大小的长方体,这个长方体的长、宽、高分别是多少?每个长方体的棱长之和是多少?18.把长8厘米,宽12厘米,高5厘米的木块锯成棱长2厘米的正方体木块.可锯多少块?答案解析部分一、单选题1.【答案】B【解析】【解答】解:因为8是2的立方;27是3的立方;64是4的立方;125是5的立方,都能拼成一个大正方体;所以在上述数字中,只有64是立方数,所以能拼成大正方体.故选:B.【分析】拼成大正方体的小正方体的个数,应该是一个数的立方数,1的立方除外,如2的立方8个,3的立方27个,4的立方64个,5的立方125个等.2.【答案】C【解析】【解答】解:以长为边最多放:6÷2=3(块),以宽为边最多放:4÷2=2(块),以高为边最多放:5÷2=2(块)…1(分米),所以:3×2×2=12(块);答:最多能放12块.故选:C.【分析】先求出每条棱长上最多能放的块数,再借助长方体的体积公式进行计算即可解答.解答此题时不要用大体积除以小体积来计算块数,因为高还有剩余.3.【答案】C【解析】【解答】解:由正方体的特征即可知道至少用8个相同的正方体才能拼成一个较大的正方体.如:棱长为2米的正方体是由8个棱长为1米的小正方体拼成.故选:C.【分析】根据正方体的特征即可知道至少用8个相同的正方体才能拼成一个较大的正方体.本题考查了正方体的认识,8个相同的较小的正方体才能拼成一个较大的正方体.4.【答案】C【解析】【解答】解:把这样的两个长方体正方形的面拼在一起就能拼出一个正方体,表面积:6×6×6=216(cm²)故答案为:C【分析】这个长方体有两个正方形的面,且高是长的一半,所以能拼出一个棱长6厘米的正方体;用棱长×棱长×6计算表面积即可.5.【答案】B【解析】【解答】解:根据题干分析去掉重复的数据可得:拼组后的长方体的棱长可以分别为:①1、1、12;②1、2、6;③1、3、4;④2、2、3;共可以拼组成4种不同的长方体.故选:B.【分析】设小正方体的棱长为1,要用12个棱长为1的正方体木块拼成一个长方体,拼成一个长方体有下列特点:当高为1时的每组长和宽一组因数,可以为1和12,2和6,3和4;当高为2时的每组长和宽一组因数,可以为1和6,2和3;当高为3时的每组长和宽一组因数,可以为1和4,2和2;当高为4时的每组长和宽一组因数,可以为1和3;由此删去长宽高重复出现的图形,即可得出答案进行选择.此题也可以利用分解质因数的方法解答:12可以写成三个数的乘积的形式为:1×1×12;1×2×6;1×3×4;2×2×3;由此也可以确定拼组后的长方体的长宽高的值.二、判断题6.【答案】正确【解析】【解答】虽然形状发生了变化,但是体积没有变化。
2019年精选浙教版小学数学二年级上册二 图形小世界7、立方体拼图练习题【含答案解析】第七十六篇

2019年精选浙教版小学数学二年级上册二图形小世界7、立方体拼图练习题【含答案解析】第七十六篇第1题【单选题】将1立方米的大正方体锯成体积是1立方厘米的小正方体,然后将它们一个个叠成一竖列,估计它的高度约有( )A、30层楼高B、300层楼高C、3000层楼高【答案】:【解析】:第2题【单选题】两个同样大小的长方体,长为6cm,宽为3cm,高为6cm,能否拼成一个正方体,表面积是多少?正确的选项是( )。
A、能,108cm^2B、不能C、能,216cm^2D、能,54cm^2【答案】:【解析】:第3题【单选题】用1立方厘米的小正方体堆成一个大正方体,至少需要( )A、4个B、6个C、8个D、16个5^3等于( )A、5×5×5B、5×3C、5+5+5D、5×5【答案】:【解析】:第4题【单选题】把一个棱长是6cm的正方体切成棱长是3cm的小正方体,可以得到( )个小正方体。
A、3B、8C、27【答案】:【解析】:第5题【填空题】一个底面直径是5厘米、高是2厘米的圆柱,沿它的底面直径,把圆柱切成形状、大小完全一样的两块,截面是______形,它的宽是圆柱的______,它的长是圆柱的______.【答案】:【解析】:第6题【填空题】下面的物体都是由棱长1厘米的正方体摆成的.它们的体积各是多少立方厘米.______立方厘米______立方厘米【答案】:【解析】:第7题【填空题】下图是由棱长为2厘米的小正方体搭成的,它的体积是______立方厘米,表面积是______平方厘米。
【答案】:【解析】:第8题【填空题】一个棱长为5的正方体是由125个木制的棱长是1的小正方体堆叠而成的.那么,你从一个角度最多能看到棱长是1的小正方体______个.A、61【答案】:【解析】:第9题【填空题】某砖长24厘米,宽12厘米,高5厘米,用这样的砖堆成一个正方体,用砖的块数可以为______ . 【答案】:【解析】:第10题【解答题】一个长32厘米,宽4厘米,厚4厘米的长方体木块,最多可以切成多少个棱长是4厘米的正方体?【答案】:【解析】:第11题【解答题】下图是棱长为5厘米的正方体,如果在这个正方体中切去一个棱长为3厘米的小正方体,剩下几何体的表面积是多少平方厘米?请作具体分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二年级上册数学一课一练-2.7立方体拼图一、单选题1.下面()个正方体正好可以拼成一个较大的大正方体.A. 8B. 64C. 27D. 1252.如图是用棱长1cm的小正方体摆成的,在这个基础上,至少还要用()个这样的小正方体才能摆成一个较大的正方体.A. 10B. 18C. 19D. 23.把一个棱长是6cm的正方体切成棱长是3cm的小正方体,可以得到()个小正方体。
A. 3B. 8C. 274.两个同样大小的长方体,长为6cm,宽为3cm,高为6cm,能否拼成一个正方体,表面积是多少?正确的选项是( )。
A. 能,108cm2B. 不能C. 能,216cm2D. 能,54cm2二、判断题5.如果将一块长方体的橡皮泥捏成一个正方体,我们看到它的形状变化,但是它所占的空间的大小没变。
6.把两个一样的正方体拼成一个长方体后,体积和表面积都没变。
7.用4块棱长是1厘米的小正方体就可以拼成一个较大的正方体.8.一个立体图形是由10个小正方体拼搭成的.至少还需要17个同样大小的小正方体,才能拼搭成一个大正方体.三、填空题9.一个长方体,如果沿水平方向切开,得到两个完全相同的正方体,已知每个正方体的表面积是60平方厘米,则这个长方体的表面积是________平方厘米.10.至少用________个棱长1厘米的小正方体可以拼成一个较大的正方体.拼成的这个正方体的表面积是________平方厘米,体积是________立方厘米.11.两个棱长都是2厘米的正方体拼成了一个长方体: ,这个长方体的表面积是________平方厘米,体积是________立方厘米。
12.一个棱长为5的正方体是由125个木制的棱长是1的小正方体堆叠而成的.那么,你从一个角度最多能看到棱长是1的小正方体________个.四、解答题13.一个长32厘米,宽4厘米,厚4厘米的长方体木块,最多可以切成多少个棱长是4厘米的正方体?五、应用题14.一根12米长的长方体木料,侧面是正方形,把木料锯成各6米长的两段后,表面积增加了32平方分米,求原来木料的表面积.15.把一个高3分米的圆柱体底面平均分成若干扇形,然后把圆柱体切开,拼成一个与它等底等高的近似长方体,长方体的表面积比圆柱体的表面积增加120平方厘米,原来圆柱体的体积是多少?参考答案一、单选题1.【答案】B【解析】【解答】解:因为8是2的立方;27是3的立方;64是4的立方;125是5的立方,都能拼成一个大正方体;所以在上述数字中,只有64是立方数,所以能拼成大正方体.故选:B.【分析】拼成大正方体的小正方体的个数,应该是一个数的立方数,1的立方除外,如2的立方8个,3的立方27个,4的立方64个,5的立方125个等.2.【答案】C【解析】【解答】解:观察图形可知,图中一共有5+3=8个小正方体,拼组后的大正方体的棱长至少需要3个小正方体,所以拼组这个大正方体至少需要:3×3×3=27(个),27﹣8=19(个),答:至少还需要19个这样的小正方体才能摆成较大的正方体.故选:C.【分析】观察图形可知,图中一共有5+3=8个小正方体,最长的棱长是3个小正方体组成的,所以拼组后的大正方体的棱长最小由3个小正方体组成,由此利用正方体的体积公式求出所需要的小正方体的总个数,再减去图中已有的8个小正方体即可进行选择.此题主要考查学生观察图形解决问题的能力,关键是确定出拼组后的大正方体的棱长进行解答.3.【答案】B【解析】【解答】解:6÷3=2,2×2×2=8(个)故答案为:B【分析】用大正方体的棱长除以小正方体的棱长,求出每条棱长可以切出正方体的个数,这个个数的三次方就是可以得到小正方体的个数。
4.【答案】C【解析】【解答】解:把这样的两个长方体正方形的面拼在一起就能拼出一个正方体,表面积:6×6×6=216(cm²) 故答案为:C【分析】这个长方体有两个正方形的面,且高是长的一半,所以能拼出一个棱长6厘米的正方体;用棱长×棱长×6计算表面积即可.二、判断题5.【答案】正确【解析】【解答】虽然形状发生了变化,但是体积没有变化。
所以正确。
【分析】注意形状发生变化后,所占空间的大小没有发生变化。
6.【答案】错误【解析】【解答】解:把两个一样的正方体拼成一个长方体后,体积不变,表面积减少,原题说法错误。
故答案为:错误【分析】拼成的长方体的体积就是两个正方体的体积之和,拼成的长方体的表面积比原来少了2个正方形面的面积。
7.【答案】错误【解析】【解答】解:2×2×2=8(个),所以利用小正方体拼组大正方体至少需要8个,原题说法错误.故答案为:错误.【分析】小正方体拼成一个较大的正方体,每条棱长上至少需要2个小正方体,由此利用正方体的体积公式计算即可求出至少需要的小正方体个数.此题考查了小正方体拼组大正方体的方法的灵活应用.8.【答案】正确【解析】【解答】解:因为2×2×2=8(个),10>8个,所以至少还需:3×3×3﹣10,=27﹣10,=17(个);故答案为:正确.【分析】因为2×2×2=8(个),3×3×3=27(个),现在有10个,如果搭成一个大正方体,至少搭长3个,宽3个,高3个的小正方体,共需要27个小正方体,因为现在有10个,则至少还需要:27﹣10=17个;据此判断即可.解答此题的关键是:看要拼搭成的大正方体棱长是由几个小正方体棱长组成,进而根据正方体的体积计算公式求出所需个数.三、填空题9.【答案】100【解析】【解答】解:60×2﹣(60÷6)×2=120﹣20=100(平方厘米).答:这个长方体的表面积是100平方厘米.故答案为:100.【分析】两个正方体拼在一起组成原来的长方体,减少了2个面,所以只要用两个正方体的表面积之和减去2个面的面积即可.10.【答案】8;24;8【解析】【解答】解:每层4个小正方体,两层共8个小正方体能拼成一个大正方体,表面积:1×1×24=24(平方厘米),体积:1×1×1×8=8(立方厘米)故答案为:8;24;8【分析】至少每层摆4个小正方体,共摆2层;大正方体的表面积共有24个小正方形的面,用小正方形面的面积乘24就是大正方体的表面积;计算出每个小正方体的体积,再乘8就是大正方体的体积.11.【答案】40;16【解析】【解答】体积:2×2×2×2=8×2=16(立方厘米)表面积:2×2×10=40(平方厘米).答:这个长方体的表面积是40平方厘米,体积是16立方厘米.故答案为:40平方厘米,16立方厘米.【分析】解答此类题的思路是:把两个正方体拼成一个长方体,长方体的表面积就比原来两个正方体的表面积之和减少了两个面,即等于正方体10个面的面积,也可根据长方体的长、宽、高求得长方体的表面积;长方体的体积即两个正方体的体积之和.12.【答案】61【解析】【解答】解:从正面看到的是:5×5=25(个);从侧面看到的是:(5﹣1)×5=20(个);从上面看到的是:(5﹣1)×(5﹣1)=4×4=16(个);一共是:25+20+16=61(个);答:从一点最多能看到棱长是1的小正方体是61个.故答案为:61.【分析】根据正方体的特征,12条棱的长度都相等,6个面的面积都相等;再根据在一点观察一个正方体最多能看到它的3个面,9条棱;棱长为5的正方体每个面是由(5×5)个小正方体拼成的,由于最多看到的3个面(正面、侧面、上面)中有3条棱长是重复计算了,由此计算出3个面上小正方体的个数减去3条棱上的个数;由此列式解答.考查了组合图形的计数和从不同方向观察物体和几何体,此题解答的关键是理解从一点最多能看到一个正方体的3个面,9条棱,根据正方体的特征每个面都是面积相等的正方形,所有的棱的长度都相等,据此解答.四、解答题13.【答案】解:(32÷4)×(4÷4)×(4÷4)=8×1×1=8(个)答:最多可以切成8个棱长是4厘米的正方体.【解析】【分析】可以用长、宽、高分别除以4,然后再把三个商相乘即可求出切成正方体的个数.五、应用题14.【答案】解:32÷2=16(平方分米)16=4×44分米=0.4米(12×0.4+12×0.4+0.4×0.4)×2=(4.8+4.8+0.16)×2=9.76×2=19.52(平方米)答:原来木料的表面积是19.52平方米【解析】【分析】每截一次就增加2个长方体的侧面,由此可求得长方体的侧面积,进一步得到侧面的边长,然后利用长方体的表面积公式即可解决问题.抓住表面积增加部分求出长方体侧面的边长是解本题的关键.15.【答案】解:3分米=30厘米圆柱的底面半径是:120÷2÷30=2(厘米)圆柱的体积是:3.14×22×30=3.14×4×30=376.8(立方厘米)答:这个圆柱的体积是376.8立方厘米.【解析】【分析】首先明确增加的表面积是2个以底面半径和高为边长的长方形的面的面积,再由圆柱的高是3分米,由此可以求出圆柱的底面半径,再根据圆柱的体积=底面积×高,代入数据计算即可解答.。
