数据结构、算法与应用 第10章
数据结构算法和应用--C++ 语言描述

• 小写o符号
f(n)=o(g(n) ):当且仅当f(n)=O(g(n))且f(n)≠ Ω(g(n))。
2021/4/15
例一 递归问题
递归函数是一个自己调用自己的函数。 递归函数包括两种
2021/4/15
什么是数据结构?
在计算机科学中,数据结构(data structure)是计算 机中存储、组织数据的方式。
什么是 算法?
算法是指完成一个任务所需要的具体步骤和方法。也 就是说给定初始状态或输入数据,能够得出所要求或 期望的终止状态或输出数据。
--维基百科
2021/4/15
数据结构算法与应用 --C++ 语言描述
f(n)=O(g(n)):当且仅当存在正的常数c和n0,使得对于所有的n≥n0 , 有f(n)≤cg(n)。
Ω符号与大O 符号类似,它用来估算函数f 的下限值。
f(n)= Ω (g(n)):当且仅当存在正的常数c 和n0,使得对于所有的n≥n0, 有f(n) ≥cg(n)。
Θ符号适用于同一个函数g 既可以作为f 的上限也可以作为f 的下限 的情形。
P36 练习7 计算n!的非递归程序 int factorial (int n) { //非递归计算n! if (n <= 1) return 1; int fact = 2; for (int i = 3; i <= n; i++)
fact *= i; return fact; }
2021/4/15
程序 性能
运行一个程序所需要的内存大小和时间 分析的方法 实验的方法
数据结构及应用算法教程修订版

20
假如中序遍历二叉排序树,所得序列将是有 序旳,即实现了对原始数据旳排序,二叉排序 树即由此得名。
原始序列数据 (49,38,65,76,49,13,27,52)
构造旳二叉排序树 49
38
65
13
49
7627Leabharlann 52中序遍历二叉排序树
for ( i=H.length; i>1; --i ) { // 调整堆来实现排序 H.r[1]←→H.r[i]; // 将堆顶统计和目前未经排序子序列 // H.r[1..i]中最终一种统计相互互换 HeapAdjust(H.r, 1, i-1); // 对 H.r[1] 进行筛选
} 13
} // HeapSort
13
s->data = T ->data;
s->next = head->next;
38
head->next = s; degression(T ->rchild ); } }
s 插入结点
旳指针操作
40
降序排列旳动态模型演示
49
38
76
13
40
134738069
1343890
143308
3138
13
32
字母集: s, t, a, e, i
出现频度: 5, 6, 2, 9, 7
编码: 101, 00, 100, 11, 01
29
0
1
电文: eat
13 01
16 01
6 00
7 01
7 0
1
9 11
数据结构、算法及其应用PPT(共70页)

Leftist Trees(左高树)
▪ 堆结构是一种隐式数据结构,用完全二叉树表 示的堆在数组中是隐式存贮的。由于没有存贮 结构信息,这种描述方法空间利用率很高。
▪ 尽管堆结构的时间和空间效率都很高,但它不 适合于所有优先队列的应用,尤其是当需要合 并两个优先队列或多个长度不同的队列时。因 此需要借助于其他数据结构来实现这类应用, 左高树就能满足这种要求。
if(!root) throw OutOfBounds(); x=root->data;//最大元素 HBLTNode<T> *L=root->LeftChild; HBLTNode<T> *R=root->RightChild; delete root; root=L; Meld(root,R); return *this; }
▪ 例-CPU调度
优先队列
▪ 优先队列是0个或多个元素的集合,每个元素 都有一个优先权或值。
▪ 对优先队列执行的操作有:
• 查找 • 插入一个新元素 • 删除
优先队列的线性表描述
▪ 描述最大优先队列最简单的方法是采用无序线 性表。
▪ 假设有一个具有n个元素的优先队列,插入操作 可以十分容易地在表的右端末尾执行,插入所 需时间为Θ(1)。删除操作时必须查找优先权最 大的元素,即在未排序的n个元素中查找具有最 大优先权的元素,所以删除操作所需时间为 Θ(n)。
优先队列的线性表描述
▪ 如果利用链表,插入操作在链头执行,时间为 Θ(1),而每个删除操作所需时间为Θ(n)。
优先队列的线性表描述
▪ 另一种描述方法是采用有序线性表,当使用公 式化描述时元素按递增次序排列,使用链表时 则按递减次序排列,这两种描述方法的删除时 间均为Θ(1),插入操作所需时间为Θ(n)。
《数据结构与算法分析》课件第10章

n
(10-3)
递归产生无穷序列x1,x2,…,xk,…。
对于i=2k,k=0, 1, 2, …,以及2k≤j≤2k+1,Pollard算法计
算xj-xi与n的最大公因子为
d=gcd(xj-xi, n)
(10-4)
如果d是n的非平凡因子,则在实现对n的一次因子分割时,
该算法输出n的因子d。
10.1.4 蒙特卡罗算法 在实际应用中常会遇到一些特殊的问题,即无论是采用
E),其中每一条边(v, u)E有一个非负整数费用c(v, u),要求找 出G的最小费用哈密顿回路。
从实际应用中抽象出的旅行售货员问题常常具有一些特 殊性质,如费用函数c往往具有三角不等式性质。当图G中的 顶点是平面上的点时,任意两个顶点间的费用就是这两个顶 点间的欧氏距离,故费用函数c具有三角不等式性质。下面 介绍具有三角不等式性质的旅行售货员问题的近似算法。
n=
p1m1
p
m 2
2
p
mk k
其中,p1<p2<…<pk是k个素数;m1,m2,…,mk是k个整 数。如果n是合数,则n必有一个非平凡因子x,1<x<n,使 得x可以整除n。给定一个合数n,求n的一个非平凡因子的问 题称为因子分割问题。
下面算法可实现整数的因子分割:
int Split(int n) { int m = floor(sqrt( <= m; i++) if(n%i == 0)return i; return 1;
SF
X S,则称C覆盖了X。
SC
集合覆盖问题是要找出F中覆盖X的最小子集C*,使得
| C*| min{| C |, C F且C覆盖X}
(10-9)
图10-5所示是一个集合覆盖的例子,其中,用12个黑点 表示集合X;F={S1, S2, S3, S4, S5, S6}。可以看出,对于这个 例子,最小集合覆盖为C={S3, S4, S5}。
数据结构第10章习题

三、填空题
1. 设用希尔排序对数组{98,36,-9,0,47,23, 1,8,10,7}进行排序,给出的步长(也称增量 序列)依次是4,2,1则排序需__________趟, 写出第一趟结束后,数组中数据的排列次序 __________。 【南京理工大学 1997 三、5 (2分)】 2.若不考虑基数排序,则在排序过程中,主要进行 的两种基本操作是关键字的______和记录的 _____。 【北京邮电大学 2001 二、7 (4分)】 3.分别采用堆排序,快速排序,冒泡排序和归并排 序,对初态为有序的表,则最省时间的是_____ 算法,最费时间的是______算法。【福州大学 1998 二、10 (2分)】
பைடு நூலகம்
12.就排序算法所用的辅助空间而言,堆排序,快 速排序,归并排序的关系是( a ) A.堆排序〈 快速排序〈归并排序 B.堆排序 〈 归并排序〈 快速排序 C.堆排序〉 归并排序 〉快速排序 D.堆排 序 > 快速排序 > 归并排序 E.以上答案都不 对 【西安交通大学 1996 三、1 (3分)】 13.将两个各有N个元素的有序表归并成一个有序表, 其最少的比较次数是( a ) A.N B.2N-1 C.2N D.N-1
2.比较次数与排序的初始状态无关的排序方法是 ( d )。【北方交通大学 2000 二、2(2分)】
A.直接插入排序 D.简单选择排序 B.起泡排序 C.快速排序
3.数据序列(8,9,10,4,5,6,20,1,2)只能是 下列排序算法中的( c )的两趟排序后的结果。 【合肥工业大学 1999 一、3 (2分)】 A.选择排序 B.冒泡排序 C.插入排序 D.堆排序 4.数据序列(2,1,4,9,8,10,6,20)只能是下 列排序算法中的( a )的两趟排序后的结果。 A. 快速排序 B. 冒泡排序 C. 选择排序 D. 插入排序 5.对序列{15,9,7,8,20,-1,4}进行排序,进行 一趟后数据的排列变为{4,9,-1,8,20,7,15}; 则采用的是( c )排序。【南京理工大学 1998 一、8(2分)】 A. 选择 B. 快速 C. 希尔 D. 冒泡
数据结构及应用算法教程参考答案

第1章绪论1.1 简述下列术语:数据,数据元素、数据对象、数据结构、存储结构、数据类型和抽象数据类型。
解:数据是对客观事物的符号表示。
在计算机科学中是指所有能输入到计算机中并被计算机程序处理的符号的总称。
数据元素是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
数据对象是性质相同的数据元素的集合,是数据的一个子集。
数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
存储结构是数据结构在计算机中的表示。
数据类型是一个值的集合和定义在这个值集上的一组操作的总称。
抽象数据类型是指一个数学模型以及定义在该模型上的一组操作。
是对一般数据类型的扩展。
1.2 试描述数据结构和抽象数据类型的概念与程序设计语言中数据类型概念的区别。
解:抽象数据类型包含一般数据类型的概念,但含义比一般数据类型更广、更抽象。
一般数据类型由具体语言系统内部定义,直接提供给编程者定义用户数据,因此称它们为预定义数据类型。
抽象数据类型通常由编程者定义,包括定义它所使用的数据和在这些数据上所进行的操作。
在定义抽象数据类型中的数据部分和操作部分时,要求只定义到数据的逻辑结构和操作说明,不考虑数据的存储结构和操作的具体实现,这样抽象层次更高,更能为其他用户提供良好的使用接口。
1.3 设有数据结构(D,R),其中,,试按图论中图的画法惯例画出其逻辑结构图。
解:1.4 试仿照三元组的抽象数据类型分别写出抽象数据类型复数和有理数的定义(有理数是其分子、分母均为自然数且分母不为零的分数)。
解:ADT Complex{数据对象:D={r,i|r,i为实数}数据关系:R={<r,i>}基本操作:InitComplex(&C,re,im)操作结果:构造一个复数C,其实部和虚部分别为re和imDestroyCmoplex(&C)操作结果:销毁复数CGet(C,k,&e)操作结果:用e返回复数C的第k元的值Put(&C,k,e)操作结果:改变复数C的第k元的值为eIsAscending(C)操作结果:如果复数C的两个元素按升序排列,则返回1,否则返回0IsDescending(C)操作结果:如果复数C的两个元素按降序排列,则返回1,否则返回0Max(C,&e)操作结果:用e返回复数C的两个元素中值较大的一个Min(C,&e)操作结果:用e返回复数C的两个元素中值较小的一个}ADT ComplexADT RationalNumber{数据对象:D={s,m|s,m为自然数,且m不为0}数据关系:R={<s,m>}基本操作:InitRationalNumber(&R,s,m)操作结果:构造一个有理数R,其分子和分母分别为s和mDestroyRationalNumber(&R)操作结果:销毁有理数RGet(R,k,&e)操作结果:用e返回有理数R的第k元的值Put(&R,k,e)操作结果:改变有理数R的第k元的值为eIsAscending(R)操作结果:若有理数R的两个元素按升序排列,则返回1,否则返回0IsDescending(R)操作结果:若有理数R的两个元素按降序排列,则返回1,否则返回0Max(R,&e)操作结果:用e返回有理数R的两个元素中值较大的一个Min(R,&e)操作结果:用e返回有理数R的两个元素中值较小的一个}ADT RationalNumber1.5 试画出与下列程序段等价的框图。
数据结构1800试题-第10章 排序 - 答案
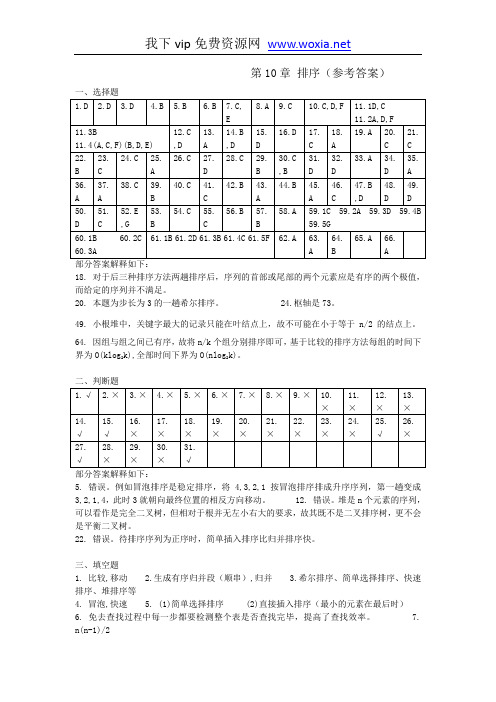
第10章排序(参考答案)部分答案解释如下:18. 对于后三种排序方法两趟排序后,序列的首部或尾部的两个元素应是有序的两个极值,而给定的序列并不满足。
20. 本题为步长为3的一趟希尔排序。
24.枢轴是73。
49. 小根堆中,关键字最大的记录只能在叶结点上,故不可能在小于等于n/2的结点上。
64. 因组与组之间已有序,故将n/k个组分别排序即可,基于比较的排序方法每组的时间下界为O(klog2k),全部时间下界为O(nlog2k)。
二、判断题5. 错误。
例如冒泡排序是稳定排序,将4,3,2,1按冒泡排序排成升序序列,第一趟变成3,2,1,4,此时3就朝向最终位置的相反方向移动。
12. 错误。
堆是n个元素的序列,可以看作是完全二叉树,但相对于根并无左小右大的要求,故其既不是二叉排序树,更不会是平衡二叉树。
22. 错误。
待排序序列为正序时,简单插入排序比归并排序快。
三、填空题1. 比较,移动2.生成有序归并段(顺串),归并3.希尔排序、简单选择排序、快速排序、堆排序等4. 冒泡,快速5. (1)简单选择排序 (2)直接插入排序(最小的元素在最后时)6. 免去查找过程中每一步都要检测整个表是否查找完毕,提高了查找效率。
7. n(n-1)/28.题中p指向无序区第一个记录,q指向最小值结点,一趟排序结束,p和q所指结点值交换,同时向后移p指针。
(1)!=null (2)p->next (3)r!=null (4)r->data<q->data(5)r->next (6)p->next9. 题中为操作方便,先增加头结点(最后删除),p指向无序区的前一记录,r指向最小值结点的前驱,一趟排序结束,无序区第一个记录与r所指结点的后继交换指针。
(1)q->link!=NULL (2)r!=p (3)p->link (4)p->link=s (5)p=p->link10.(1)i<n-i+1 (2)j<=n-i+1 (3)r[j].key<r[min].key (4)min!=i (5)max==i(6)r[max]<-->r[n-i+1]11.(1)N (2)0 (3)N-1 (4)1 (5)R[P].KEY<R[I].KEY (6)R[P].LINK(7)(N+2)(N-1)/2(8)N-1 (9)0 (10)O(1)(每个记录增加一个字段) (11)稳定(请注意I的步长为-1)12. 3,(10,7,-9,0,47,23,1,8,98,36) 13.快速14.(4,1,3,2,6,5,7)15.最好每次划分能得到两个长度相等的子文件。
第10章-数据结构与算法ppt课件(全)

考点3 数据结构的定义
数据对象:是性质相同的数据元素的集合,是数据的一 个子集。
1. 数据的逻辑结构
数据的逻辑结构:是对数据元素之间的逻辑关系的描述, 它可以用一个数据元素的集合和定义在此集合中的若干关系 来表示。
数据的逻辑结构与它们在计算机中的存储位置无关。 数据的逻辑结构有两个要素: 一是数据元素的集合,通常记为D; 二是D上的关系,它反映了数据元素之间的前后件关系, 通常记为R。
进行软件开发的能力。 6. 掌握数据库的基本知识,了解关系数据库的设计。
公共基础知识考试大纲
数据结构与算法考试内容: 1. 算法的基本概念;算法复杂度的概念和意义。 2. 数据结构的定义;数据的逻辑结构与存储结构;
数据结构的图形表示;线性结构与非线性结构的 概念。 3. 线性表的定义;线性表的顺序存储结构及其插入 与删除运算。 4. 栈和队列的定义;栈和队列的个数据结构可以表示成 B=(D,R)
其中 B 表示数据结构。为了反映 D 中各数据元素之间的前后 件关系,一般用二元组来表示。
例 一年四季的数据结构可以表示成 B =(D,R) D = {春,夏,秋,冬} R = {(春,夏),(夏,秋),(秋,冬)}
例 家庭成员数据结构可以表示成 B =(D, R) D = {父亲,儿子,女儿} R = {(父亲,儿子),(父亲,女儿)}
则称为非线性结构。 如 家庭成员之间辈分关系的数据结构是非线性
结构。
考点5 线性表的基本概念
10.3 线性表及其顺序存储结构
线性表(Linear List),由一组数据元素构成, 数据元素的位置只取决于自己的序号,元素之间的 相对位置是线性的。
线性表是由 n(n≥0) 个数据元素组成的一个有限 序列,表中的每一个数据元素,除了第一个外,有 且只有一个前件,除了最后一个外,有且只有一个 后件。
《数据结构、算法与应用(C++语言描述)》习题参考答案doc.

第1章概论1.数据、数据元素、数据结构、数据类型的含义分别是什么?数据:对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并由计算机程序处理的符号的总称。
数据元素:数据的基本单位,在计算机程序中通常作为一个整体考虑。
数据结构:数据元素之间的关系+运算,是以数据为成员的结构,是带结构的数据元素的集合,数据元素之间存在着一种或多种特定的关系。
数据类型:数据类型是用来区分不同的数据;由于数据在存储时所需要的容量各不相同,不同的数据就必须要分配不同大小的内存空间来存储,所有就要将数据划分成不同的数据类型。
数据类型包含取值范围和基本运算等概念。
2.什么是数据的逻辑结构?什么是数据的物理结构?数据的逻辑结构与物理结构的区别和联系是什么?逻辑结构:数据的逻辑结构定义了数据结构中数据元素之间的相互逻辑关系。
数据的逻辑结构包含下面两个方面的信息:①数据元素的信息;②各数据元素之间的关系。
物理结构:也叫储存结构,是指逻辑结构的存储表示,即数据的逻辑结构在计算机存储空间中的存放形式,包括结点的数据和结点间关系的存储表示。
数据的逻辑结构和存储结构是密不可分的,一个操作算法的设计取决于所选定的逻辑结构,而算法的实现依赖于所采与的存储结构。
采用不同的存储结构,其数据处理的效率是不同的。
因此,在进行数据处理时,针对不同问题,选择合理的逻辑结构和存储结构非常重要。
3.数据结构的主要操作包括哪些?对于各种数据结构而言,他们在基本操作上是相似的,最常用的操作有:●创建:建立一个数据结构;●清除:清除一个数据结构;●插入:在数据结构中增加新的结点;●删除:把指定的结点从数据结构中删除;●访问:对数据结构中的结点进行访问;●更新:改变指定结点的值或改变指定的某些结点之间的关系;●查找:在数据结构中查找满足一定条件的结点;●排序:对数据结构中各个结点按指定数据项的值,以升序或降序重新排列。
4.什么是抽象数据类型?如何定义抽象数据类型?抽象数据类型(Abstract Data Type 简称ADT)是指一个数学模型以及定义在此数学模型上的一组操作。
数据结构与算法应用指南

数据结构与算法应用指南第1章数据结构基础 (4)1.1 简单数据类型 (4)1.1.1 整型 (4)1.1.2 浮点型 (4)1.1.3 字符型 (4)1.1.4 布尔型 (4)1.2 复杂数据类型 (5)1.2.1 数组 (5)1.2.2 字符串 (5)1.2.3 结构体 (5)1.2.4 联合 (5)1.2.5 枚举 (5)1.3 数据结构功能分析 (5)1.3.1 时间复杂度 (5)1.3.2 空间复杂度 (6)第2章线性表 (6)2.1 顺序存储结构 (6)2.1.1 定义及特点 (6)2.1.2 顺序存储结构的实现 (6)2.1.3 顺序存储结构的优缺点 (6)2.2 链式存储结构 (6)2.2.1 定义及特点 (6)2.2.2 链式存储结构的实现 (6)2.2.3 链式存储结构的优缺点 (6)2.3 线性表的应用 (7)2.3.1 线性表的合并 (7)2.3.2 线性表的排序 (7)2.3.3 线性表的查找 (7)2.3.4 线性表的其他应用 (7)第3章栈与队列 (7)3.1 栈 (7)3.1.1 栈的定义 (7)3.1.2 栈的抽象数据类型 (7)3.1.3 栈的实现 (7)3.1.4 栈的应用示例 (7)3.2 队列 (8)3.2.1 队列的定义 (8)3.2.2 队列的抽象数据类型 (8)3.2.3 队列的实现 (8)3.2.4 循环队列 (8)3.2.5 队列的应用示例 (8)3.3.1 算术表达式求值 (8)3.3.2 括号匹配 (8)3.3.3 函数调用栈 (8)3.3.4 逆波兰表达式求值 (8)3.3.5 队列在图算法中的应用 (8)3.3.6 队列在操作系统中的应用 (8)第4章串 (8)4.1 串的定义与存储 (8)4.1.1 串的定义 (8)4.1.2 串的存储 (9)4.2 串的基本操作 (9)4.2.1 串的创建 (9)4.2.2 串的插入与删除 (9)4.2.3 串的连接 (9)4.2.4 串的截取 (9)4.2.5 串的查找 (9)4.2.6 串的替换 (9)4.3 串的模式匹配算法 (9)4.3.1 BF算法 (9)4.3.2 KMP算法 (9)4.3.3 BM算法 (10)4.3.4 Sunday算法 (10)第5章树与二叉树 (10)5.1 树的基本概念 (10)5.1.1 树的定义与性质 (10)5.1.2 树的表示方法 (10)5.1.3 树的遍历 (10)5.2 二叉树 (11)5.2.1 二叉树的定义与性质 (11)5.2.2 二叉树的存储结构 (11)5.2.3 二叉树的遍历算法 (11)5.2.4 二叉树的应用 (11)5.3 算法设计与分析 (11)5.3.1 二叉树查找算法 (11)5.3.2 二叉树插入与删除算法 (11)5.3.3 算法分析 (11)5.4 树的应用 (11)5.4.1 文件系统 (11)5.4.2 决策树 (11)5.4.3 数据库索引 (12)第6章图 (12)6.1 图的基本概念 (12)6.1.1 图的定义与术语 (12)6.1.3 图的抽象数据类型 (12)6.2 图的存储结构 (12)6.2.1 邻接矩阵 (13)6.2.2 邻接表 (13)6.2.3 边列表 (13)6.2.4 邻接多重表 (13)6.3 图的遍历算法 (13)6.3.1 深度优先搜索(DFS) (13)6.3.2 广度优先搜索(BFS) (13)6.4 图的应用 (14)6.4.1 最短路径算法 (14)6.4.2 最小树算法 (14)6.4.3 拓扑排序 (14)6.4.4 关键路径 (14)第7章排序算法 (14)7.1 内部排序算法 (14)7.1.1 冒泡排序 (14)7.1.2 选择排序 (14)7.1.3 插入排序 (14)7.1.4 快速排序 (15)7.1.5 归并排序 (15)7.1.6 希尔排序 (15)7.2 外部排序算法 (15)7.2.1 多路归并排序 (15)7.2.2 波浪排序 (15)7.2.3 聚集排序 (15)7.3 排序算法功能分析 (15)7.3.1 时间复杂度 (15)7.3.2 空间复杂度 (15)7.3.3 稳定性 (16)7.3.4 适用场景 (16)第8章查找算法 (16)8.1 顺序查找 (16)8.2 二分查找 (16)8.3 散列表查找 (16)8.4 查找算法应用 (17)第9章算法设计与分析 (17)9.1 算法设计策略 (17)9.1.1 算法设计的一般策略 (17)9.1.2 算法设计策略的选择 (18)9.2 分治算法 (18)9.2.1 分治算法的基本步骤 (18)9.2.2 分治算法的应用 (18)9.3.1 动态规划算法的基本步骤 (19)9.3.2 动态规划算法的应用 (19)9.4 贪心算法 (19)9.4.1 贪心算法的基本步骤 (19)9.4.2 贪心算法的应用 (19)第10章算法应用实例 (20)10.1 算法在数值计算中的应用 (20)10.2 算法在组合问题中的应用 (20)10.3 算法在实际问题中的应用与优化 (20)10.4 算法在人工智能领域的应用前景展望 (20)第1章数据结构基础数据结构是计算机存储、组织数据的方式,良好的数据结构可以有效地提高程序的执行效率和数据的处理速度。
数据结构与算法分析第10章答案LarryNyhoff清华大学出版社

Chapter 10: ADT Implementations: Recursion, Algorithm Analysis, and Standard AlgorithmsProgramming ProblemsSection 10.11./*------------------------------------------------------------------- Driver program to test recursive digit-counting function ofExercise 21.Input: Nonnegative integersOutput: Number of digits in each integer-------------------------------------------------------------------*/ #include <iostream>using namespace std;int numDigits(unsigned n);/*------------------------------------------------------------------- Recursively count the digits in a nonnegative integer -- Exer. 21.Precondition: n >= 0Postcondition: Number of digits in n is returned.-------------------------------------------------------------------*/ int main(){int n;for (;;){cout << "Enter a nonnegative integer (-1 to stop): ";cin >> n;if (n < 0) break;cout << "# digits = " << numDigits(n) << endl;}}//-- Definition of numDigits()int numDigits(unsigned n){if (n < 10)return 1;elsereturn 1 + numDigits(n / 10);}2. Just replace the function definition in 1 with that in Exercise 22./*------------------------------------------------------------------- Driver program to test reverse-print function of Exercise 23.Input: Nonnegative integersOutput: The reversal of each integer.-------------------------------------------------------------------*/ #include <iostream>using namespace std;void printReverse(unsigned n);/*------------------------------------------------------------------- Recursively display the digits of a nonnegative integer in reverse order -- Exer. 23.Precondition: n >= 0Postcondition: Reversal of n has been output to cout.-------------------------------------------------------------------*/ int main(){int n;for (;;){cout << "\nEnter a nonnegative integer (-1 to stop): ";cin >> n;if (n < 0) break;cout << "Reversal is: ";printReverse(n);}}//-- Definition of printReverse()void printReverse(unsigned n){if (n < 10)cout << n << endl;else{cout << n % 10;printReverse(n / 10);}}4. Just replace the function definition in 3 with that in Exercise 24./*------------------------------------------------------------------- Driver program to test power function of Exercise 25.Input: Integer exponents and real basesOutput: Each real to that integer power-------------------------------------------------------------------*/ #include <iostream>using namespace std;double power(double x, int n);/*------------------------------------------------------------------- Recursively compute integer powers of real numbers -- Exer. 25.Precondition: NonePostcondition: n-th power of x is returned.-------------------------------------------------------------------*/ int main(){double base;int exp;for (;;){cout << "\nEnter a real base and an integer exponent (0 0 to stop): ";cin >> base >> exp;if (base == 0 && exp == 0) break;cout << base << '^' << exp << " = " << power(base, exp) << endl;}}//-- Definition of power()double power(double x, int n){if (n == 0)return 1;else if (n < 0)return power(x, n + 1) / x;elsereturn power(x, n - 1) * x;}6. Just replace the function definition in 5 with that in Exercise 26.7-9./*------------------------------------------------------------------- Driver program to test the recursive array reversal, array sum, and array location functions of Exercise 27-29.Input: Integer exponents and real basesOutput: Each real to that integer power-------------------------------------------------------------------*/ #include <iostream>using namespace std;typedef int ElementType;const int CAPACITY = 100;typedef ElementType ArrayType[CAPACITY];void reverseArray(ArrayType arr, int first, int last);/*------------------------------------------------------------------- Recursively reverse an array -- Exer. 27.Precondition: Array arr has elements in positions first through last.Postcondition: Elements in positions first through last of arrare reversed.-------------------------------------------------------------------*/ ElementType sumArray(ArrayType arr, int n);/*------------------------------------------------------------------- Recursively sum the elements of an array -- Exer. 28.Precondition: Array arr has n elements.Postcondition: Sum of the elements is returned-------------------------------------------------------------------*/ int location(ArrayType arr, int first, int last, ElementType item);/*------------------------------------------------------------------- Recursively search the elements of an array -- Exer. 28.Precondition: Array arr has elements in positions first through last.Postcondition: Location of item in arr is returned; -1 if itemisn't found.-------------------------------------------------------------------*/ void display(ArrayType arr, int n);/*------------------------------------------------------------------- Display the elements of an array.Precondition: Array arr has n elements.Postcondition: Elements of arr have been output to cout.-------------------------------------------------------------------*/int main(){ArrayType x;cout << "Enter at most " << CAPACITY << " integers (-1 to stop):\n"; int item, count;for (count = 0; count < CAPACITY; count++){cin >> item;if (item < 0) break;x[count] = item;}cout << "Original array: ";display(x, count);reverseArray(x, 0, count - 1);cout << "Reversed array: ";display(x, count);cout << "\nSum of array elements = " << sumArray(x, count) << endl; ElementType toFind;for(;;){cout << "Enter an item to search for (-1 to stop): ";cin >> toFind;if (toFind < 0) break;cout << "Location of item = " << location(x, 0, count - 1, toFind) << endl << "where -1 denotes item note found)\n";}}//-- Definition of reverseArray()void reverseArray(ArrayType arr, int first, int last){if (first < last){ElementType temp = arr[first];arr[first] = arr[last];arr[last] = temp;reverseArray(arr, first + 1, last - 1);}}//-- Definition of sumArray()ElementType sumArray(ArrayType A, int n){if (n == 0)return 0;if (n == 1)return A[0];elsereturn A[n - 1] + sumArray(A, n - 1);}//-- Definition of location()int location(ArrayType arr, int first, int last, ElementType item) {if (first == last && item != arr[first])return -1;else if (item == arr[last])return last;elsereturn location(arr, first, last-1, item);}//-- Definition of display()void display(ArrayType arr, int n){for (int i = 0; i < n; i++)cout << arr[i] << " ";cout << endl;}10./*------------------------------------------------------------------- Driver program to test the recursive string reversal function of Exercise 30.Input: A stringOutput: The reversal of the string-------------------------------------------------------------------*/ #include <iostream>#include <string>using namespace std;string reverse(string word);/*------------------------------------------------------------------- Recursively reverse a string -- Exer. 30.Precondition: NonePostcondition: String word has been reversed.-------------------------------------------------------------------*/ int main(){string s;cout << "Enter a string: ";getline(cin, s);cout << "Original string: " << s << endl;cout << "Reversed string: " << reverse(s) << endl;}//-- Definition of reverse()string reverse(string word){if (word.length() == 1)return word;elsereturn reverse(word.substr(1, word.length() - 1)) + word[0];}11. Simply replace the definition of reverse() in Problem 10 with the nonrecursive versionfrom Exercise 31.12./*------------------------------------------------------------------- Driver program to test the recursive palindrome checking function of Exercise 32.Input: An integerOutput: An indication of whether the integer is a palindrome-------------------------------------------------------------------*/ #include <iostream>#include <cmath>using namespace std;bool palindrome (unsigned number, int numDigits);/*------------------------------------------------------------------- Recursively check if an integer is a palindrome -- Exer. 32.Precondition: number has numDigits digits.Postcondition: True is returned if number is a palindrome, andfalse otherwise.-------------------------------------------------------------------*/ int main(){int x, n;cout << "Enter integer & number of digits: ";cin >> x >> n;cout << "Palindrome? " << (palindrome(x, n) ? "Yes" : "No") << endl;}//-- Definition of palindrome()bool palindrome (unsigned number, int numDigits){if (numDigits <= 1)return true;else{unsigned powerOf10;powerOf10 = (unsigned)pow(10.0, numDigits - 1);unsigned firstDigit = number / powerOf10 ;unsigned lastDigit = number % 10;if (firstDigit != lastDigit)return false;elsereturn palindrome((number % powerOf10) / 10, numDigits - 2);}}13./*------------------------------------------------------------------- Driver program to test the recursive palindrome checking function of Exercise 32.Input: An integerOutput: An indication of whether the integer is a palindrome-------------------------------------------------------------------*/ #include <iostream>using namespace std;int gcd(int a, int b);/*------------------------------------------------------------------- Recursively compute gcd of two integers -- Exer. 33.Precondition: Not both of a and b are zero.Postcondition: GCD of a and b is returned.-------------------------------------------------------------------*/ int main(){int a, b;for (;;){cout << "\nEnter two integers (0 0 to stop): ";cin >> a >> b;if (a == 0 && b == 0) break;cout << "GCD = " << gcd(a, b) << endl;}}//-- Definition of gcd()int gcd(int a, int b){if (a < 0)a = -a;if (b < 0)b = -b;if (b == 0)return a;elsereturn gcd(b, a % b);}14. Simply replace the recursive function gcd() in Problem 13 with the nonrecursive versionfrom Exercise 34.15./*------------------------------------------------------------------- Driver program to test the recursive binomial coefficient function of Exercise 35.Input: Pairs of integerOutput: The binomial coefficient corresponding to that pair.-------------------------------------------------------------------*/ #include <iostream>using namespace std;int recBinomCoef(int n, int k);/*------------------------------------------------------------------- Recursively compute a binomial coefficient -- Exer. 35.Precondition: 0 <= k <= n && n != 0.Postcondition: The binomial coefficient "n above k" is returned.-------------------------------------------------------------------*/ int main(){int a, b;for (;;){cout << "\nEnter two integers with first >= second (0 0 to stop): ";cin >> a >> b;if (a == 0 && b == 0) break;if (a >= b)cout << "C(" << a << ", " << b << ") = " << recBinomCoef(a, b) << endl;}}//-- Definition of binomCoeff()int recBinomCoef(int n, int k){if (n == k || k == 0)return 1;elsereturn recBinomCoef(n - 1, k - 1) + recBinomCoef(n - 1, k);}16./*------------------------------------------------------------------- Driver program to time the recursive binomial coefficient function of Exercise 35 and the nonrecursive version of Exercise 36.Input: Pairs of integerOutput: The binomial coefficient corresponding to that pair andthe times to compute it both recursively andnonrecursively.NOTE: Binomial coefficients are being computed as doubles because large ones need to be computed to achieve nonzero times,and integer values will overflow.-------------------------------------------------------------------*/ #include <iostream>using namespace std;#include "Timer.h"double recBinomCoef(int n, int k);/*------------------------------------------------------------------- Recursively compute a binomial coefficient -- Exer. 35.Precondition: 0 <= k <= n && n != 0.Postcondition: The binomial coefficient "n above k" is returned.-------------------------------------------------------------------*/ double nonrecBinomCoef(int n, int k);/*------------------------------------------------------------------- Iteratively compute a binomial coefficient -- Exer. 36.Precondition: 0 <= k <= n && n != 0.Postcondition: The binomial coefficient "n above k" is returned.-------------------------------------------------------------------*/ int main(){int a, b;for (;;){cout << "\nEnter two integers with first >= second (0 0 to stop): ";cin >> a >> b;if (a == 0 && b == 0) break;if (a >= b){double recCoeff, // recursive binom coeff.nonRecCoeff; // use double due to integer overflor Timer tRec, tNonrec;tRec.start();recCoeff = recBinomCoef(a, b);tRec.stop();tNonrec.start();nonRecCoeff = nonrecBinomCoef(a, b);tNonrec.stop();// Display the timescout << "C(" << a << ", " << b << ") = " << recCoeff << endl;cout << "*** Recursive binom. coeff. took: ";tRec.print(cout);cout << endl;cout << "C(" << a << ", " << b << ") = " << nonRecCoeff << endl; cout << "*** Nonrecursive binom. coeff. took: ";tNonrec.print(cout);cout << endl;}}}//-- Definition of recBinomCoeff()double recBinomCoef(int n, int k){if (n == k || k == 0)return 1;elsereturn recBinomCoef(n - 1, k - 1) + recBinomCoef(n - 1, k);}//-- Definition of nonRecBinomCoeff()double nonrecBinomCoef(int n, int k){double num = n, denom = 1;if (k > n/2)k = n - k;for (int i = n-1; i >= k + 1; i--)num *= i;for (int i = 2; i <= n-k; i++)denom *= i;return num/denom;}17./*------------------------------------------------------------------- Program to trace recursive calls of a function. Here the function f() of Exercise 13 is used.Input: An integerOutput: Trace of recursive calls and returns and the value off at that integer-------------------------------------------------------------------*/ #include <iostream> // cin, cout, >>, <<using namespace std;void indent(int numSpaces);/*------------------------------------------------------------------- Indent the output numSpaces spaces from current position.Precondition: NonePostcondition: Output has advanced spaces.-------------------------------------------------------------------*/ unsigned f(unsigned n);/*------------------------------------------------------------------- Modification of function f of Exercise 13 -- statements are added to output a trace of the recursive calls to and returns from f().Precondition: NonePostcondition: Trace of recursive calls and returns was output to cout and the value of f returned.-------------------------------------------------------------------*/ int main(){int number;cout << "Enter a positive integer: ";cin >> number;f(number);}//-- Definition of indent()void indent(int numSpaces){while (numSpaces--)cout << " ";}//-- Definition of f()unsigned f(unsigned n){static int level = 0; // static variable to control indentation if (n < 2){indent(level);cout << "f(" << n << ") returns 0\n";return 0;}else{indent(level);cout << "f(" << n << ") = 1 + f(" << (n / 2) << ")\n";level++;unsigned value = 1 + f(n / 2);level--;indent(level);cout << "f(" << n << ") returns " << value << '\n';return value;}}18./*------------------------------------------------------------------- Program to trace recursive calls of the function printReverse()of Exercise 23.Input: An integerOutput: Trace of recursive calls and returns and the reversal of that integer.-------------------------------------------------------------------*/ #include <iostream> // cin, cout, >>, <<using namespace std;int level = 0; // global variable to control indentation void indent(int numSpaces);/*------------------------------------------------------------------- Indent the output numSpaces spaces from current position.Precondition: NonePostcondition: Output has advanced spaces.-------------------------------------------------------------------*/ void printReverse(unsigned n);/*------------------------------------------------------------------- Recursively display the digits of a nonnegative integer in reverse order -- Exer. 23.Precondition: n >= 0Postcondition: Reversal of n has been output to cout.-------------------------------------------------------------------*/ int main(){int number;cout << "Enter a positive integer: ";cin >> number;printReverse(number);}//-- Definition of indent()void indent(int numSpaces){while (numSpaces--)cout << " ";}//-- Definition of printReverse()void printReverse(unsigned number){static int level = 0; // static variable to control indentation indent(level);cout << "printReverse(" << number << "): Output ";cout << number % 10; // output the rightmost digitint leftDigits = number / 10; // leftmost part of Numberif (leftDigits) // inductive step:{cout << ", then call printReverse(" << leftDigits << ").\n";level++;printReverse(leftDigits); // ... output the rest recursively level--;}else // anchor case:{cout << " and \\n.";cout << endl; // ... generate a new line}indent(level);cout << "printReverse(" << number << ") returns.\n";}19./*------------------------------------------------------------------- Program to display the lyrics of the song "Bingo."Output: lyrics of "Bingo"-------------------------------------------------------------------*/ #include <iostream> // cin, cout, <<, >>using namespace std;void printSong(int verseNum);/*------------------------------------------------------------------- Display the lyrics of the song "BINGO" beginning with a givenverse.Precondition: NonePostcondition: The song beginning with verse verseNum.-------------------------------------------------------------------*/int main(){printSong(1);}//-- Definition of printSong()void printSong(int verseNum){const char BINGO[] = "BINGO";cout << "There was a farmer had a dog;\n""And Bingo was his name-o.\n";if (verseNum > 1){cout << "(Clap";for (int i = 2; i < verseNum; i++)cout << ", clap";cout << (verseNum < 6 ? ")-" : ")\n");}for (int i = verseNum; i <= 5; i++)cout << BINGO[i-1] << (i < 5 ? "-" : "!\n");cout << "And Bingo was his name-o!\n\n";if (verseNum < 6)printSong(verseNum + 1);}20./*------------------------------------------------------------------- Driver program to test a recursive function to display a number with commas.Input: An integerOutput: That integer with commas in correct locations-------------------------------------------------------------------*/ #include <iostream> // cin, cout, >>, <<using namespace std;void printNumberWithCommas(long int number);/*------------------------------------------------------------------- Display a number with commas in the appropriate locations.Precondition: NonePostcondition: number, with commas, has been output to cout.-------------------------------------------------------------------*/ int main(){long int n;for (;;){cout << "\nEnter an integer n (negative to stop): ";cin >> n;if (n < 0) break;printNumberWithCommas(n);}}//-- Definition of printNumberWithCommas()void printNumberWithCommas(long int number){if (number < 1000)cout << number;else{printNumberWithCommas(number / 1000);cout << ','<< (number % 1000) / 100<< (number % 100) / 10<< (number % 10);}}21.//-- BlobGrid.h --/*------------------------------------------------------------------- Interface for class BlobGrid-------------------------------------------------------------------*/ #include <iostream> // istream, ostream#include <vector> // vector<T>using namespace std;typedef vector<char> CharRow;typedef vector<CharRow> CharTable;class BlobGrid{public:BlobGrid(unsigned rows, unsigned columns);/*------------------------------------------------------------------- Constructs an empty BlobGrid with specified rows and columns.Precondition: NonePostcondition: The constructed BobGrid has myRows == rows,myColumns == columns, and myGrid is a rows x columns array.-------------------------------------------------------------------*/ void readGrid(istream & in);/*------------------------------------------------------------------- Input a BlobGrid.Precondition: istream in is open.Postcondition: BlobGrid object has been input and removed from in.-------------------------------------------------------------------*/ void displayGrid(ostream & out) const;/*------------------------------------------------------------------- Output a BlobGrid.Precondition: ostream out is open.Postcondition: BlobGrid object has been output to out.-------------------------------------------------------------------*/ unsigned eatAllBlobs();/*------------------------------------------------------------------- Remove all blobs from a BlobGrid.Precondition: NonePostcondition: All blobs have been removed from myGrid and thenumber of blobs removed is returned.-------------------------------------------------------------------*/ void eatOneBlob(unsigned row, unsigned col);/*------------------------------------------------------------------- A recursive function used internally by eatBlobs().Precondition: NonePostcondition: The blob in the specified row and column col hasbeen removed from myGrid.-------------------------------------------------------------------*/ private:unsigned myRows,myColumns;CharTable myGrid;};//-- Definition of constructorinline BlobGrid::BlobGrid(unsigned rows, unsigned columns): myRows(rows), myColumns(columns){CharTable temp(rows, CharRow(columns, '.'));myGrid = temp;}inline istream & operator>>(istream & in, BlobGrid & b)/*-------------------------------------------------------------------Input operator.Precondition: istream in is open.Postcondition: BlobGrid object has been input and removed from inand in is returned.-------------------------------------------------------------------*/ {b.readGrid(in);return in;}inline ostream & operator<<(ostream & out, const BlobGrid & b)/*------------------------------------------------------------------- Output operator.Precondition: ostream out is open.Postcondition: BlobGrid object has been output to out and out isreturned.-------------------------------------------------------------------*/ {b.displayGrid(out);return out;}//-- BlobGrid.cpp --/*------------------------------------------------------------------- Implements the operations for class BlobGrid.-------------------------------------------------------------------*/ #include <iostream>using namespace std;#include "BlobGrid.h"//-- Definition of readGrid()void BlobGrid::readGrid(istream & in){char ch;for (int row = 0; row < myRows; row++)for (int col = 0; col < myColumns; col++)in >> myGrid[row][col];}//-- Definition of displayGrid()void BlobGrid::displayGrid(ostream& out) const{for (int row = 0; row < myRows; row++){for (int col = 0; col < myColumns; col++)out << myGrid[row][col] << ' ';out << endl;}}//-- Definition of eatAllBlobs()unsigned BlobGrid::eatAllBlobs(){unsigned number = 0;for (int row = 0; row < myRows; row++){for (int col = 0; col < myColumns; col++){if (myGrid[row][col] == '*'){eatOneBlob(row, col);number++;}}}return number;}//-- Definition of eatOneBlob()void BlobGrid::eatOneBlob(unsigned row, unsigned col){if ( (row >= myRows) || (col >= myColumns) )return;if (myGrid[row][col] != '*')return;myGrid[row][col] = '.';eatOneBlob(row-1, col);eatOneBlob(row+1, col);eatOneBlob(row, col-1);eatOneBlob(row, col+1);}/*------------------------------------------------------------------- Driver program to test class BlobGrid.Input: size of grid and locations of *'sOutput: The grid and the number of blobs in it.-------------------------------------------------------------------*/ #include <iostream> // cin, cout, >>, <<using namespace std;#include "BlobGrid.h"int main(){unsigned numRows, numColumns;cout << "Enter number of rows and number of columsn in grid: ";cin >> numRows >> numColumns;BlobGrid blobs(numRows, numColumns);cout << "\nEnter " << numRows << " x " << numColumns。
数据结构与算法(10):查找

× (high − low)
也就是将上述的比比例例参数1/2改进为自自适应的,根据关键字在整个有序表中所处的位置,让mid值 的变化更更靠近关键字key,这样也就间接地减少了了比比较次数。
基本思想:基于二二分查找算法,将查找点的选择改进为自自适应选择,可以提高高查找效率。当然, 插值查找也属于有序查找。
if __name__ == '__main__': LIST = [1, 5, 7, 8, 22, 54, 99, 123, 200, 222, 444] result = binary_search(LIST, 444) print(result)
3.3 斐波那契查找
在介绍斐波那契查找算法之前,我们先介绍一一下和它很紧密相连并且大大家都熟知的一一个概念—— ⻩黄金金金分割。 ⻩黄金金金比比例例又又称为⻩黄金金金分割,是指事物各部分间一一定的数学比比例例关系,即将整体一一分为二二,较大大部 分与较小小部分之比比等于整体与较大大部分之比比,其比比值约为1:0.618。 0.618倍公认为是最具有审美意义的比比例例数字,这个数值的作用用不不仅仅体现在诸如绘画、雕塑、 音音乐、建筑等艺术领域,而而且在管理理、工工程设计等方方面面有着不不可忽视的作用用。因此被称为⻩黄金金金分 割。 大大家记不不记得斐波那契数列列:1,1,2,3,5,8,13,21,34,55,89......(从第三个数开 始,后面面每一一个数都是前两个数的和)。然后我们会发现,随着斐波那契数列列的递增,前后两个 数的比比值会越来越接近0.618,利利用用这个特性,我们就可以将⻩黄金金金比比例例运用用到查找技术中。
算法与数据结构考研试题精析(第二版)第10章 排序

第10章排序一、选择题1.某内排序方法的稳定性是指( )。
【南京理工大学 1997 一、10(2分)】A.该排序算法不允许有相同的关键字记录 B.该排序算法允许有相同的关键字记录C.平均时间为0(n log n)的排序方法 D.以上都不对2.下面给出的四种排序法中( )排序法是不稳定性排序法。
【北京航空航天大学 1999 一、10 (2分)】A. 插入B. 冒泡C. 二路归并D. 堆积3.下列排序算法中,其中()是稳定的。
【福州大学 1998 一、3 (2分)】A. 堆排序,冒泡排序B. 快速排序,堆排序C. 直接选择排序,归并排序D. 归并排序,冒泡排序4.稳定的排序方法是()【北方交通大学 2000 二、3(2分)】A.直接插入排序和快速排序 B.折半插入排序和起泡排序C.简单选择排序和四路归并排序 D.树形选择排序和shell排序5.下列排序方法中,哪一个是稳定的排序方法?()【北方交通大学 2001 一、8(2分)】A.直接选择排序 B.二分法插入排序 C.希尔排序 D.快速排序6.若要求尽可能快地对序列进行稳定的排序,则应选(A.快速排序 B.归并排序 C.冒泡排序)。
【北京邮电大学 2001 一、5(2分)】7.如果待排序序列中两个数据元素具有相同的值,在排序前后它们的相互位置发生颠倒,则称该排序算法是不稳定的。
()就是不稳定的排序方法。
【清华大学 1998 一、3 (2分)】A.起泡排序 B.归并排序 C.Shell排序 D.直接插入排序 E.简单选择排序8.若要求排序是稳定的,且关键字为实数,则在下列排序方法中应选()排序为宜。
A.直接插入 B.直接选择 C.堆 D.快速 E.基数【中科院计算所 2000 一、5(2分)】9.若需在O(nlog2n)的时间内完成对数组的排序,且要求排序是稳定的,则可选择的排序方法是()。
A. 快速排序B. 堆排序C. 归并排序D. 直接插入排序【中国科技大学 1998 二、4(2分)】【中科院计算所 1998 二、4(2分)】10.下面的排序算法中,不稳定的是()【北京工业大学 1999 一、2 (2分)】A.起泡排序B.折半插入排序C.简单选择排序D.希尔排序E.基数排序F.堆排序。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
46
More Tournament Tree Applications
• k-way merging of runs during an external merge sort • Truck loading
47
Truck Loading
n packages to be loaded into trucks each package has a weight each truck has a capacity of c tons minimize number of trucks
1 3
6
3
2
4 4 3 6
8 8 1
5 5 7
7 3 2
6 6 9
9 4 5 2 5 8
38
Min Loser Tree For 16 Players
1 3
2
6
3
4
2
4 4 3 6
8 8 1
5 5 7
7 3 2
6 6 9
9 4 5
5 2 5
8 8
39
Min Loser Tree For 16 Players
2 3
2
3
3
2
2
3 4 1 3 2 6
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
2 2 5
5 8
Sorted array.
17
Sort 16 Numbers
2 3
2
3
3
4
2
3 4 1 3 2 6
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
2 2 5
5 8
Sorted array.
18
44
1 2 2 3
Winner
3
2
6
3 5
4
5
4 4 3 6
8 8 9 1
5 9 5 7
7 3 2
6 6 9
9 4 5
5 2 5
8 8
Replace winner with 9 and replay matches. 45
Complexity Of Replay
• One match at each level that has a match node. • O(log n) • More precisely Theta(log n).
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
5 2 5
5 8
Sorted array.
24
Sort 16 Numbers
3 3
4
3
3
4
5
3 4 1 3 2 2 6
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
5 2 5
5 8
Sorted array.
25
Sort 16 Numbers
3 3
• Get winner
O(1) time
• Remove/replace winner and replay
O(log n) time more precisely Theta(log n)
数据结构算法与应用
28
10.3 The CLASS WinnerTree
The left-most internal node at the lowest level is numbered 2s where s = ⎣log 2 ( n − 1) ⎦ . Therefore the number of internal nodes at the lowest level is n-2s, and the number LowExt of external nodes at the lowest level is twice this number.
Sorted array.
20
Sort 16 Numbers
2 3
2
3
3
4
2
3 4 1 3 2 2 6
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
2 2 5
5 8
Sorted array.
21
Sort 16 Numbers
2 3
2
3
3
4
2
3 4 1 3 2 2 6
6 8 1
5 5 7
3 3 2
Chapter 10 Tournament Trees
信息科学与技术学院 黄方军
huangfj@
东校区实验中心B502
数据结构算法与应用
1
10.1 Introduction
• • Winner trees. Loser Trees.
数据结构算法与应用
2
Winner Trees
7
Applications
Sorting. Put elements to be sorted into a winner tree. Repeatedly extract the winner and replace by a large value.
8
Sort 16 Numbers
1 1
2
3
3 3 2
2 6 9
4 4 5
2 2 5
5 8
Sorted array.
11
Sort 16 Numbers
1 1
2
3
1
2
2
3 4 1 3 6
6 8 1
5 5 7
3 3 2
2 6 9
4 4 5
2 2 5
5 8
Sorted array.
12
Sort 16 Numbers
1 1
2
3
3
2
2
3 4 1 3 6
4
3
3
4
5
3 4 1 3 2 2 6
6 8 3 1
5 5 7
3 3 2
6 6 9
4 4 5
5 2 5
5 8
Sorted array.
26
Time To Sort
• Initialize winner tree.
O(n) time
• Remove winner and replay.
O(log n) time
35
Min Loser Tree For 16 Players
3
4 4 3 6
8 8 1 5 7 3 2 6 9 4 5 2 5 8
36
Min Loser Tree For 16 Players
3
6
1
4 4 3 6
8 8 1
5 5 7
7 3 2 6 9 4 5 2 5 8
37
Min Loser Tree For 16 Players
Sort 16 Numbers
2 3
2
3
3
4
2
3 4 1 3 2 6
6 8 1
5 5 7
3 3 2
6 6 9
4 4 5
2 2 5
5 8
Sorted array.
19
Sort 16 Numbers
2 3
2
3
3
42ຫໍສະໝຸດ 3 4 1 3 2 66 8 1
5 5 7
3 3 2
6 6 9
4 4 5
2 2 5
5 8
2 3
2
6
3
4
5
4 4 3 6
8 8 1
5 5 7
7 3 2
6 6 9
9 4 5
5 2 5
8 8
42
1 2
Winner
3
2
6
3
4
5
4 4 3 6
8 8 1
5 5 7
7 3 2
6 6 9
9 4 5
5 2 5
8 8
43
Complexity Of Loser Tree Initialize
• • • • One match at each match node. One store of a left child winner. Total time is O(n). More precisely Theta(n).
1 1
2
3
1
2
2
3 4 3 6
6 8 1
1 5 7
3 3 2
2 6 9
4 4 5
2 2 5
5 8
Replace winner with 6.
31
Replace Winner And Replay
1 1
2
3
1
2
2
3 4 3 6
6 8 6
1 5 7
3 3 2
2 6 9
4 4 5
2 2 5
5 8
Replay matches on path to root.
• Complete binary tree with n external nodes and n - 1 internal nodes. • External nodes represent tournament players. • Each internal node represents a match played between its two children; the winner of the match is stored at the internal node. • Root has overall winner.
