应力与应变间的关系

合集下载

应力和应变之间的关系

s2 0
即为平面应力状态，有
1
1 E
s 1 s 3
3
1 E
s 3 s 1
联立两式可解得：
s1
E 1
2
1 3
210 10 1 0 .3
2
9
240
0 . 3 160 10
6
s3
44 . 3 M Pa 9 E 210 10 3 1 160 0 . 3 240 10 2 2 1 1 0 .3
利用空间应力状态下最大切应力的计算式可得：
t max s1 s3
2 7.25MPa
§7-5 平面应力状态下的电测法
对各向同性材料图示平面应力状态，在线弹性、小变形条件下，sx、sy与切应变无关，即有：
sy sx
x y
1 E 1 E
s s
E
x
s s s
y

y F a
sy sx sz
x
a
(a)
z
(b)
解：铜块应力状态如图b所示，横截面上的压应力为：
s
y

F A
30 MPa
受钢槽的限制，铜块在另两个方向的应变为零，并产生压应力，即有：
x z
1 E 1 E
s s

x
s s
y
s s
z
0 0
所以，应变能密度为： v
d V dxdydz

1tx 2 G
而对纯剪应力状态，其主应力为：
s 1 tx
s2tx
s1 t
x
s
2

材料力学中的应力与应变关系

材料力学中的应力与应变关系材料力学是研究材料在受力作用下的力学行为和性能的学科，应力与应变关系是其中的核心内容之一。

本文将讨论材料力学中的应力与应变的概念及其数学表示，以及应力与应变之间的线性关系与非线性关系。

一、应力的概念及表示应力是指材料单位面积上的内部力，常用符号σ表示。

根据受力情况的不同，可以分为正应力、切应力和体积应力。

正应力是指与作用力方向垂直的内部力，常用符号σ表示；切应力是指与作用力方向平行的内部力，常用符号τ表示；体积应力是指作用在体积内的内部力，常用符号p表示。

正应力的数学表示为σ = F/A，其中F为作用力的大小，A为受力面积。

切应力的数学表示为τ = F/A，其中F为切力的大小，A为受力面积。

体积应力的数学表示为p = F/V，其中F为体积力的大小，V为受力体积。

二、应变的概念及表示应变是指材料在受力作用下产生的形变程度，常用符号ε表示。

根据变形方式的不同，可以分为线性应变和体积应变。

线性应变是指在受力作用下，材料产生的长度或角度发生变化，常用符号ε表示；体积应变是指在受力作用下，材料产生的体积发生变化，常用符号η表示。

线性应变的数学表示为ε = ΔL/L0，其中ΔL为长度变化量，L0为原始长度。

体积应变的数学表示为η = ΔV/V0，其中ΔV为体积变化量，V0为原始体积。

三、应力与应变的线性关系在一定范围内，应力与应变之间可以表现为线性关系。

根据胡克定律（Hooke's Law），线性弹性材料的应力与应变之间满足σ = Eε，其中E为弹性模量。

弹性模量是材料刚度的度量，表示材料单位应力产生的单位应变。

常见的弹性模量有杨氏模量、剪切模量和泊松比。

杨氏模量的数学表示为E = σ/ε，其中σ为应力，ε为线性应变。

剪切模量的数学表示为G = τ/γ，其中τ为切应力，γ为切应变。

泊松比的数学表示为ν = -εv/εh，其中εv为垂直方向的线性应变，εh为水平方向的线性应变。

应力与应变间的关系

22
例题7-7 边长 a = 0.1m 的铜立方块, 无间隙地放入体积较
大, 变形可略去不计的钢凹槽中, 如图所示。已知铜的弹性模量 E=100GPa, 泊松比 =0.34, 当受到P=300kN 的均布压力作用时, 求该铜块的主应力. 体积应变以及最大剪应力。
P a
y
z
x
23
y
解：铜块上截面上的压应力为
9
3、特例
（1）平面应力状态下(假设 Z = 0 )
x
1 E
(
x
y)
y
1 E
(
y
x)
z E ( x y)
xy
xy
G
10
（2）广义胡克定律用主应力和主应变表示时三向应力状态下：
1
1
E [ 1
(
2
3)]
2
1 E
[
2
(
3
1)]
3
1 E
[
3
( 1
2)]
(7-7-6)
11
平面应力状态下设 3 = 0, 则
x y z x y y z z x
y
σy
上面
x y z x y y z z x
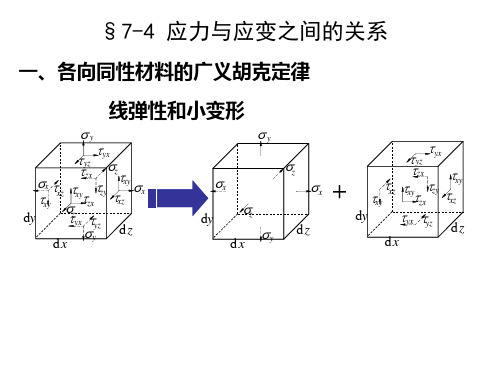
1、各向同性材料的广义胡克定律（1）符号规定
τ yx
τ τ yz
xy
τ τ zy xz
τ zx
右侧面
σx
(a)三个正应力分量：拉应力为正
σz
x
o
压应力为负。 z
前面
3
(b)三个剪应力分量: 若正面(外法线与坐标轴
dxdydz
dxdydz(1 1 2 3) dxdydz
dxdydz

流体力学中应力应变关系

流体力学中应力应变关系
流体力学是研究流体运动和变形的学科，应力和应变是流体力学中关键的概念。

应力是流体内部各点受到的力，应变是流体形变程度的度量。

在流体力学中，应力和应变之间存在一定的关系，通常用应力张量和应变张量来描述。

应力张量包含了流体各点在各个方向上受到的应力大小和方向信息，应变张量则包含了流体在各个方向上的形变程度。

在牛顿流体中，应力张量和应变张量之间的关系是线性的，即应力与应变成比例关系，比例系数被称为粘度。

而在非牛顿流体中，应力与应变的关系则更加复杂。

流体力学中的应力应变关系是研究流体运动和变形的基础，对于工程应用和科学研究都具有重要意义。

在许多工程领域，如航空、水利、化工等，流体力学的应用广泛，深入研究应力应变关系可以为工程设计和实际应用提供更加准确和可靠的理论基础。

- 1 -。

应变和应力关系

生物医学工程：利用应变和应力原理，开发出更符合人体生理需求的医疗器械和生物材料，提高医疗效果和人体健康水平。
新能源技术：利用应变和应力原理，优化风力发电机叶片设计，提高风能利用率和发电效率。
机器人技术：通过研究应变和应力与机器人关节运动的关系，提高机器人的灵活性和稳定性，拓展机器人的应用领域。
应变和应力对未来科技发展的影响
增强材料性能：通过深入研究应变和应力，可以开发出性能更强的新型材料，为未来的科技发展提供物质基础。
智能制造：利用应变和应力的知识，可以优化制造过程中的材料性能，提高生产效率和产品质量，推动智能制造的发展。
生物医学应用：在生物医学领域，应变和应力的研究有助于更好地理解和控制人体生理机制，为未来的生物医学应用提供支持。
压痕法：利用压痕仪在物体表面压出一定形状的压痕，通过测量压痕的尺寸来计算应力
应变和应力的相互影响
应变和应力之间的关系：应变是应力作用下的物体形状变化，应力是抵抗变形的力。
应变和应力的测量方法：通过应变计和应力计进行测量，应变计测量物体变形，应力计测量物体受到的力。
应变和应力的相互影响：应变和应力之间存在相互影响，例如在材料屈服点附近，应变和应力之间会发生突变。
应力的概念
分类：正应力、剪应力、弯曲应力等
定义：物体受到外力作用时，内部产生的反作用力
单位：帕斯卡（Pa）作用效果：使物体产生形变
应变和应力的关系
应变是物体形状的改变，应力是物体内部抵抗变
形的力
应变和应力之间存在线性关系，即应变正比于应
力
应变和应力之间的关系可以用胡克定律表示，即应力=弹性模量
应变和应力关系
汇报人：XX
应变和应力的定义应变和应力的测量方法应变和应力的应用领域应变和应力的研究进展应变和应力的未来展望

应变和应力的概念

应变和应力的概念一、引言应变和应力是材料力学中重要的概念，在工程和科学研究中有着广泛的应用。

应变是描述物体形变程度的物理量，而应力则是描述物体内部受力状态的物理量。

本文将详细介绍应变和应力的概念，并深入探讨两者之间的关系。

二、应变的概念2.1 应变的定义应变是描述物体形变程度的物理量，通常用符号ε表示。

应变可分为线性应变和非线性应变两种情况。

线性应变发生在物体受到小的力引起的形变情况下，其应变与受力成正比。

非线性应变则发生在物体受到大的力引起的形变情况下，其应变与受力不成正比。

2.2 应变的分类1.纵向应变2.横向应变3.剪切应变4.体积应变三、应力的概念3.1 应力的定义应力是描述物体内部受力状态的物理量，通常用符号σ表示。

应力分为正应力和剪应力两种情况。

正应力是指垂直于物体截面的力在单位面积上的分布情况，剪应力是指平行于物体截面的力在单位面积上的分布情况。

3.2 应力的分类1.纵向应力2.横向应力3.剪切应力4.欧拉应力四、应变与应力的关系应变与应力之间存在着密切的关系，可以由材料的应力-应变曲线来描述。

应力-应变曲线显示了材料在受力下的变形和应力的关系，以此来研究材料的力学性质。

4.1 弹性阶段在弹性阶段，材料受力后会发生一定程度的形变，但当去除外力时，材料可以恢复到原先的形状。

此时应力与应变呈线性关系，称为胡克定律。

4.2 屈服阶段当外力超过了材料的弹性极限时，材料会进入屈服阶段。

此时材料会产生更大的形变，但仍能回复到非常接近原来形状的状态。

4.3 塑性阶段当外力超过了材料的屈服极限时，材料将进入塑性阶段，并发生不可逆的形变。

在这个阶段，应力与应变之间的关系不再是线性的，材料会呈现出时间依赖性和屈服后的流变行为。

4.4 断裂阶段当外力继续增加，超过了材料的断裂强度，材料将发生断裂并失去原有的结构完整性。

五、总结应变和应力是描述材料力学性质的重要概念。

应变是描述物体形变程度的物理量，而应力是描述物体内部受力状态的物理量。

应力与应变之间的关系

因主应力和主应变相对应，则由题意可得：解：因主应力和主应变相对应，则由题意可得：
σ2 = 0
即为平面应力状态，即为平面应力状态，有
1 ε 1 = (σ 1 −νσ 3 ) E
1 ε 3 = (σ 3 −νσ 1 ) E
8
E 210 ×10 (ε1 +νε 3 ) = (240 − 0.3 ×160)×10 −6 σ1 = 1 −ν 2 1 − 0.32 = 44.3MPa E 210 ×109 (ε 3 +νε 1 ) = (− 160 + 0.3 × 240)×10−6 σ3 = 1 −ν 2 1 − 0. 3 2 = −20.3MPa 主应变ε2为： ν 0.3 (44.3 − 20.3)×106 ε 2 = − (σ 1 + σ 3 ) = − E 210 ×109 = −34.3 ×10 −6
§10-5 应力与应变之间的关系 101、各向同性材料的广义胡克定律单向应力状态： 1）单向应力状态：
s
σ ≤ σ P 时， ε x =
横向线应变：横向线应变：
σ
E
ε y = −ν
纯剪应力状态： 2）纯剪应力状态：
tx
σ
E
ε z = −ν
σ
E
τ ≤ τ P 时，
γ xy =
τx
G
1
gxy
空间应力状态： 3）空间应力状态：
1 ε x = (σ x −νσ y ) E 1 ε y = (σ y −νσ x ) E
εz = − γ xy
ν
E 1 = τ xy G
(σ
x
+σ y )
5
若用主应力和主应变来表示广义胡克定律，若用主应力和主应变来表示广义胡克定律，有：

应力与应变间的关系

τ xy
右侧面
σx τ xz
x
γ xy
γ yz
γ zx
O
∠ xOy ∠ yOz
∠zox 。
z
σz
前面
2、各向同性材料的广义胡克定、律
(1)线应变的推导线应变的推导分别单独存在时, 在σx σy σz 分别单独存在时 x 方依次为: 向的线应变 εx 依次为
x σ
z
x
x σ
εx ' =
σx
τ = Gγ
或
γ=
τ
G
τ γ γ τ
为剪切弹性模量，单位为N/m G 为剪切弹性模量，单位为N/m2.
三、复杂应力状态下应力与应变的关系 σx σy σz τ x y τ y z τ z x εx ε y ε z γ x y γ y z γ z x
1、各向同性材料的广义胡克定律（1）符号规定） (a)三个正应力分量拉应力为正 (a)三个正应力分量三个正应力分量：拉应力为正
因此, 该圆筒变形后的厚度并无变化, 因此该圆筒变形后的厚度并无变化仍然为 t =10mm .
G G G
在线弹性范围内, 小变形条件下, 在线弹性范围内小变形条件下各向同性材料。各向同性材料。
1 εx = σx ν (σ y +σz ) E 1 E
[
]
公式的适用范围 : 在线弹性范围内,小在线弹性范围内小变形条件下, 变形条件下各向同性材料。
ε y = [σ y ν (σz +σx )]
ν ν ε z = (σ x + σ y ) = (τmax + τmax ) = 0 E E
同理可得,圆筒中任一点该点到圆筒横截面中心的距离为该点到圆筒横截面中心的距离为ρ 同理可得圆筒中任一点 (该点到圆筒横截面中心的距离为ρ) 处的径向应变为

应变与应力的关系

应变与应力的关系
应变与应力的关系可以用胡克定律来描述。

胡克定律指出，在物体恒定温度下，其弹性变形所产生的应变与其所受的应力成正比。

换句话说，应变与应力之间的关系是线性的。

具体来说，该定律的数学表达式为：
应力 = 弹性模量 ×应变
其中，应力是物体所受的力除以其受力面积；弹性模量是物体材料对应力的敏感程度，也称为弹性系数；应变是物体长度、面积或体积的相对变化量。

因此，应变与应力之间的关系是密切相关的。

当施加的应力增加时，物体的应变也会随之增加；反之，当应力减小时，应变也会相应减小。

应力应变之间关系

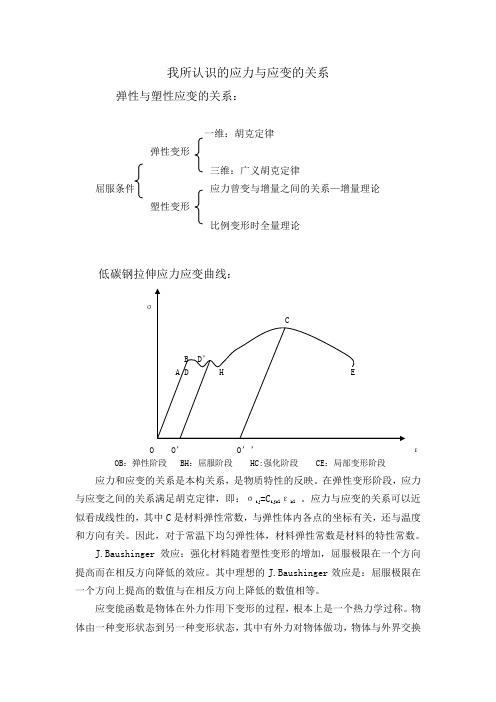
我所认识的应力与应变的关系弹性与塑性应变的关系：一维：胡克定律弹性变形三维：广义胡克定律屈服条件应力曾变与增量之间的关系—增量理论塑性变形比例变形时全量理论低碳钢拉伸应力应变曲线：σO O’ O’’εOB：弹性阶段 BH：屈服阶段 HC:强化阶段 CE：局部变形阶段应力和应变的关系是本构关系，是物质特性的反映。

在弹性变形阶段，应力与应变之间的关系满足胡克定律，即：σij =Cijklεkl。

应力与应变的关系可以近似看成线性的，其中C是材料弹性常数，与弹性体内各点的坐标有关，还与温度和方向有关。

因此，对于常温下均匀弹性体，材料弹性常数是材料的特性常数。

J.Baushinger效应：强化材料随着塑性变形的增加，屈服极限在一个方向提高而在相反方向降低的效应。

其中理想的J.Baushinger效应是：屈服极限在一个方向上提高的数值与在相反方向上降低的数值相等。

应变能函数是物体在外力作用下变形的过程，根本上是一个热力学过称。

物体由一种变形状态到另一种变形状态，其中有外力对物体做功，物体与外界交换能量，物体的总能量发生变化。

热力学定律证明,理想弹性体存在应变能，即udu U ⎰=。

应变能函数是应变状态的单值函数，仅取决于应变的起始状态和最终状态，与变形过程无关，对于线弹性体，ij ij u εσ21=。

格林公式是弹性体的应力分量等于应变能对相应应变分量的偏导数，即ij ij ij u εεσ∂∂=)(，该公式适用于所有弹性体。

应力分析、应变分析的结果适合于连续介质力学的所有问题，与材料物质特性无关。

本构关系的影响因素有：材料、环境、加载类型、加载速度，用函数表达式表示为：),,(T t f εσ=单一曲线假设认为不管何种应力状态，加载时，应力强度和应变强度的关系是一种单一曲线关系，可由简单加载的应力应变获得。

等向强化模型是认为加载时，在各个方向强化的程度相同。

随动强化模型是认为一个方向强化的程度等于相反方向弱化的程度。

应力与应变间的关系共31页

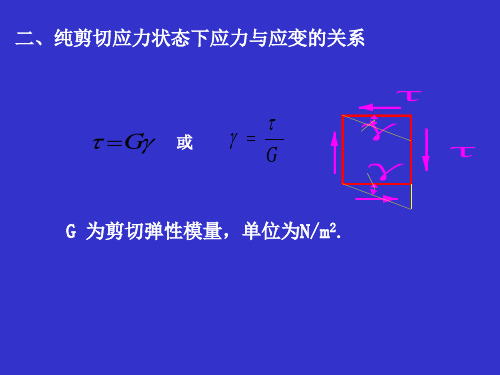
P a
y
z
x
y 解：铜块上截面上的压应力为
yP A30 0 .1 1 20 3 0
y x
3M 0 Pa
x
(b) Z z
1[ ( )]0
x Ex
y
z
由
1[ ( )]0
z Ez
x
y
解得
x
z
(1 1 2
)
y
0.314-(01.3042.34)(30)
-15.5MPa
铜块的主应力为
σ 1 σ 2 1 .5 M 5 σ P 3 3 a M 0 ,P
体积应变和最大剪应力分别为
1 E 2(123 ) 1 .9 5 1 4 0
max 1 2(13)7.25MPa
例题9-8 壁厚 t =10mm , 外径 D=60mm 的薄壁圆筒, 在表面上 k 点处与其轴线成 45°和135° 角即 x, y 两方向分别贴上应变片,然后在圆筒两端作用矩为 m 的扭转力偶,如图所示已知圆筒材料的弹性模量为 E = 200GPa 和 = 0.3 ,若该圆筒的变形在弹性范围内,且 max = 80MPa , 试求k点处的线应变 x ,y 以及变形后的筒壁厚度。
在x y z同时存在时, y,z方向的线应变为
y E 1[y (z x)] z E 1[z (x y)]
(2)剪应变的推导剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为
xy
xy G
yz
yz G
zx
zx G
公式的适用范围 : 在线弹性范围内, 小变形条件下, 各向同性材料。
右侧面
σx
τ xz x
前面
2、各向同性材料的广义胡克定

应力与应变间的关系

210 × 10 9 = ( − 160 + 0 .3 × 240 ) × 10 − 6 = − 20 .3MPa 1 − 0 .3 2 6
∴σ 1 =44 .3 MPa ;σ 2 =0;σ 3 = − 20 .3MPa ;
0.3 ε 3 = − (σ 3 + σ 1 ) = − ( − 22.3 + 44.3) × 10 6 = − 34.3 × 10 − 6 E 210 × 10 9 实际上从排序的角度来看是求得 ε 2
µ
注意:主应力和主应变的方向是相同的注意主应力和主应变的方向是相同的. 主应力和主应变的方向是相同的
2011-11-30
7
§7-4 应力与应变间的关系
一、单拉下的应力--应变关系单拉下的应力--应变关系 -y
σx
εx=
σx
E
ε y =− σ x
E
γ ij ≈ 0 (i,j = x,y,z )
µ
ε z =− σ x
E
µ
z
x
y
二、纯剪的应力--应变关系纯剪的应力--应变关系 --
γ xy =
2011-11-30
τ xy
1 − 2µ θ = (σ 1 + σ 2 + σ 3 ) E 1 − 2µ = (σ x + σ y + σ z ) E
2011-11-30
3(1 − 2 µ ) (σ 1 + σ 2 + σ 3 ) σ m θ = = E 3 k 体积胡克定律， k 为体积弹性模量，
σ m 是三个主应力的平均值
所以，所以，该点处为平面应力状态
′ σ2
E [ε 1 + µε 2 ] ∴σ 1 = 2 1− µ 210 × 10 9 = ( 240 − 0 .3 × 160 ) × 10 − 6 = 44 .3MPa 1 − 0 .3 2

固体力学中的材料应变和应力关系

固体力学中的材料应变和应力关系固体力学是研究物体在受力作用下的形变和力学性能的学科。

在固体力学中，材料的应变和应力关系是一个重要的研究内容。

应变是物体在受力作用下发生的形变程度，而应力则是物体在受力作用下所产生的内部分子间的力。

材料的应变和应力关系可以用应力-应变曲线来表示。

应力-应变曲线是通过对材料进行拉伸或压缩试验得到的。

在拉伸试验中，材料在受到外力拉伸后会发生形变，形变的程度可以通过应变来表示。

应变可以分为线弹性应变、非线弹性应变和塑性应变等不同类型。

线弹性应变是指材料在受力作用下，应变与应力之间呈线性关系的情况。

在这种情况下，材料的应力-应变曲线呈直线，斜率代表了材料的弹性模量。

弹性模量是材料抵抗形变的能力的量度，可以用来描述材料的刚度。

不同材料的弹性模量不同，可以通过对材料进行拉伸试验来测定。

非线弹性应变是指材料在受力作用下，应变与应力之间呈非线性关系的情况。

在这种情况下，材料的应力-应变曲线呈曲线形状，不再是直线。

非线弹性应变通常是由于材料的微观结构发生变化导致的，比如晶体的滑移和位错运动。

非线弹性应变的研究对于了解材料的变形行为以及材料的强度和韧性具有重要意义。

塑性应变是指材料在受力作用下，形变不可逆的情况。

当材料的应力超过一定的临界值时，材料会发生塑性变形，形变不会随着外力的消失而恢复原状。

塑性应变是材料的塑性变形特性，可以通过对材料进行压缩试验来研究。

塑性应变的研究对于了解材料的可塑性、延展性和可加工性具有重要意义。

除了应力-应变曲线，材料的应变和应力关系还可以通过材料的本构关系来描述。

本构关系是指材料的应力与应变之间的函数关系。

常见的本构关系有线弹性本构关系、非线弹性本构关系和塑性本构关系等。

不同的材料具有不同的本构关系，可以通过对材料进行试验来确定。

总之，固体力学中的材料应变和应力关系是一个复杂而重要的研究内容。

通过对材料进行拉伸、压缩等试验，可以得到材料的应力-应变曲线，进而了解材料的弹性、塑性等性能。

应力和应变关系

第四章应力和应变关系一. 内容介绍前两章分别从静力学和运动学的角度推导了静力平衡方程，几何方程和变形协调方程。

由于弹性体的静力平衡和几何变形是通过具体物体的材料性质相联系的，因此，必须建立了材料的应力和应变的内在联系。

应力和应变是相辅相成的，有应力就有应变；反之，有应变则必有应力。

对于每一种材料，在一定的温度下，应力和应变之间有着完全确定的关系。

这是材料的固有特性，因此称为物理方程或者本构关系。

对于复杂应力状态，应力应变关系的实验测试是有困难的，因此本章首先通过能量法讨论本构关系的一般形式。

分别讨论广义胡克定理；具有一个和两个弹性对称面的本构关系一般表达式；各向同性材料的本构关系等。

本章的任务就是建立弹性变形阶段的应力应变关系。

二. 重点1. 应变能函数和格林公式；2. 广义胡克定律的一般表达式；3. 具有一个和两个弹性对称面的本构关系；4. 各向同性材料的本构关系；3. 材料的弹性常数。

知识点应变能原理应力应变关系的一般表达式完全各向异性弹性体正交各向异性弹性体本构关系弹性常数各向同性弹性体应变能格林公式广义胡克定理一个弹性对称面的弹性体本构关系各向同性弹性体的应力和应变关系应变表示的各向同性本构关系§4.1 弹性体的应变能原理学习思路:弹性体在外力作用下产生变形，因此外力在变形过程中作功。

同时，弹性体内部的能量也要相应的发生变化。

借助于能量关系，可以使得弹性力学问题的求解方法和思路简化，因此能量原理是一个有效的分析工具。

本节根据热力学概念推导弹性体的应变能函数表达式，并且建立应变能函数表达的材料本构方程。

根据能量关系，容易得到由于变形而存储于物体内的单位体积的弹性势能，即应变能函数。

探讨应变能的全微分，可以得到格林公式，格林公式是以能量形式表达的本构关系。

如果材料的应力应变关系是线性弹性的，则单位体积的应变能必为应变分量的齐二次函数。

因此由齐次函数的欧拉定理，可以得到用应变或者应力表示的应变能函数。

应力和应变之间的关系

应力和应变的关系曲线
描述
应力和应变的关系曲线是描述应力与应变之间关系的图形表示。
形状
在弹性范围内，曲线呈直线上升；超过弹性极限后，曲线出现弯曲。
应用
通过应力和应变的关系曲线，可以确定材料的弹性模量、屈服点和极限强度等机械性能参数。
04
应力和应变的应用
弹性力学
弹性力学是研究弹性物体在外力作用下变形和内力的规律的科学。在弹性力学中，应力和应变是描述物体变形和受力状态的基本物理量。
公式
σ=Eεsigma = E varepsilonσ=Eε
解释
σ为应力，E为弹性模量，ε为应变。当应力增加时，应变也相应增加，且两者成正比关系。
非线性关系
描述
当材料受到超过其弹性极限的应力时，应力与应变之间的关系不再是线性的，而是呈现非线性关系。
特征
在非线性阶段，应变随应力的增加而急剧增加，可能导致材料发生屈服或断裂。
设计优化
优化结构设计
通过对应力和应变的分析，优化结构设计，提高结构的承载能力和稳定性。
考虑材料特性
在设计过程中，充分考虑材料的力学特性和性能，合理选择和使用材料，以降低应力和应变对结构的影响。
引入减震和隔震措施
通过引入减震和隔震措施，降低地震等外部载荷对结构产生的应力和应变，提高结构的抗震性能。
时间
蠕变
在长期恒定应力作用下，材料会发生缓慢的塑性变形，即蠕变。蠕变会影响材料的应力和应变关系，特别是在高温和长期载荷作用下。
时间依赖性
某些材料的力学性能会随时间发生变化，对应力和应变的关系产生影响。例如，疲劳和时效等现象会导致材料性能随时间发生变化。
07
应力和应变在工程实践中的注意事项

应力与应变间的关系

压应力为负。 z
前面
(b)三个剪应力分量: 若正面(外法线与坐标轴
正向一致的平面)上剪应力矢的指向与坐标轴正向一致, 或负面(外法线与坐标轴负向一致的平面)上剪应力矢的指向与坐标轴负向一致，则该剪应力为正, 反之为负。
y
o
z σz
σy
τ yx τ yz τ zy τ zx
上面
τ xy
右侧面
)

y

0.34(1 0.34) 1- 0.342
(30)
-15.5MPa
铜块的主应力为
σ1 σ2 15.5MPa , σ3 30MPa
体积应变和最大剪应力分别为

1 2
E
(1
2
3)

1.95 104
max

1 2
(1

3
)
7.25MPa
（1）概念:构件每单位体积的体积变化, 称为体积应变用θ表示。
（2）各向同性材料在空间应力状态下的体积应变
公式推导
2
设单元体的三对平面为主平面, 其三个边长为d x, d y, d z 变形后的边长分别为 d x(1+ , d y(1+2 , d z(1+3 , 因此变形后单元体的体积为:
y

1 E
[ y
( z
x )]
z

1 E
[ z
( x
y )]
(2)剪应变的推导
剪应变 xy , yz ,zx与剪应力xy ,yz ,zx之间的关系为

xy

xy
G

yz

试说明弹性力学中应力,应变,位移三者之间的关系

试说明弹性力学中应力,应变,位移三者之间的关系.
应力和应变之间的关系是可以用弹性力学的材料模型来表示的，它们之间的关系可表示为受力的物体会产生一个应变，这个应变是受力强度和材料的模量来决定的，当应力变化时，物体产生的应变也会变化，关系可以用弹性力学方程来表示：应力= 应变× 模量。

另外，应力和位移之间也有关系，当施加力时，物体会产生一个位移，而位移又是一个受力强度和材料模量共同决定的参数，可用弹性力学方程来表示：应力 = 位移× 模量。

另外，弹性模量有时也称为弹性常数，它可用来衡量材料的弹性程度，以及材料在受力时所受到的影响，它是决定应力和应变、应力和位移关系的一个基本参数，物理现象中可以用来描述物体变形的程度，将应力与物体变形程度结合起来可以确定应力对物体变形的影响。

同时，这种参数也可以用来描述弹性体在受力作用下所产生的变形量。

由于弹性模量的作用，物体对于受力时大小的变形量可以用模量值来确定：弹性模量越大，物体几乎不变形，弹性模量越小，则物体的变形量越大；另外，弹性模量也能够描述物体在受力作用下所产生的力和位移关系，弹性模量越大，物体受到相同力量作用时，其所受到的变形量和位移量也会更小，反之，弹性模量越小，受到相同力量作用时，其所受到的变形量和位移量也会更大。

因此，弹性模量可以决定物体受力后的变形情况，以及材料的弹性程度。