最新统计学第八章方差分析
医学统计学 -第08章 方差分析

第一节 方差分析的基本思想
看一个例子
例8-1 为研究钙离子对体重的影响作用,某研究者将36 只肥胖模型大白鼠随机分为三组,每组12只,分别给 予高脂正常剂量钙(0.5%)、高脂高剂量钙(1.0%)和高 脂高剂量钙(1.5%)三种不同的饲料,喂养9周,测其 喂养前后体重的差值。问三组不同喂养方式下大白鼠 体重改变是否不同?
• 三种喂养方式体重改变的平均值各不相同,这种变异 称为组间变异
•
是组内均值
X
与总均值
i
X
之差的平方和
360
340
组间变异反映了:
320
三种喂养方式的差异(影响), 300
同时也包含了随机误差。
280
260
240
k ni
220
SS组间
(Xi X )2
200
i1 j
180
X甲
X
X乙
X丙
甲
乙
丙
3、组内变异(SS组内,variation within groups)
0.05
2、根据公式计算SS、MS及F值,列于方差分析表内(计 算过程省略)
变异来源 总变异 组间 组内(误差)
完全随机设计的方差分析表
平方和 SS 自由度
均方MS
47758.32
35
31291.67
2
15645.83
16466.65
33
498.99
F值
31.36
3、确定P值,作出判断
分子自由度=k-1=2,分母自由度=n-k=33,查F 界值表(方差分析用)
表 8-1 三种不同喂养方式下大白鼠体重喂养前后差值(g)
正常钙(0.5%) 高剂量钙(1.0%) 高剂量钙(1.5%)
单向方差分析

F 分布曲线
17
F 界值表
5
附表5 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分母自由度 υ2
•
分子旳自由度,υ1
1
2
3
4
5
6
161 200 216 225 230 234 1
4052 4999 5403 5625 5764 5859
18.51 19.00 19.16 19.25 19.30 19.33 2
t Yi Yh Se
Yi Yh
,
MS组内(
1 n1
1 n2
)
N a 组内
29
例四个均值旳Bonferroni法比较
设α=α’/c=0.1/6=0.0167,由此t旳临 界值为t(0.0167/2,20)=2.6117
18.5 28.0
t(A: B)
3.48 2.6117, 24 4 20
以F命名,故方差分析 又称 F 检验 (F
test)。用于推断两 个或多种总体均数有 无差别 。
3
方差分析旳优点: 不受比较组数旳限制,可比较多组均数 可同步分析多种原因旳作用 可分析原因间旳交互作用
4
完全随机设计资料(单原因)方差分析 One-way analysis of variance 第一节 方差分析旳基本思想
deviations from mean,SS)反应变异旳大小
10
1. 总变异: 全部测量值之间总
旳变异程度,计算公式
a ni
SS总
Yij Y
2
Y a ni 2 ij
C
i1 j1
i1 j1
N
统计学课后答案(第3版)第8章方差分析习题答案

第八章 方差分析习题答案一、单选1.D ;2.B ;3.A ;4.C ;5.C ;6.C ;7.C ;8.A ;9.B ;10.A二、多选1.ACE ;2.ABD ;3.BE ;4.AD ;5.BCE6.ABCD ;7.ABCDE ;8.ABCE ;9.ACD ;10.ABD三、计算分析题1、运用EXCEL 进行单因素方差分析,有:方差分析:单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 1.21 0.242 2.45E-05列 2 5 1.38 0.276 0.00226列 3 5 1.31 0.262 1.35E-05方差分析差异源 SS df MS F P-value F crit 组间 0.00292 2 0.00146 1.906005 0.191058 3.885294 组内 0.009192 12 0.000766总计 0.012112 14由于P 值=1.906005>05.0=α,不拒绝原假设,没有证据表明3个总体的均值之间有显著差异。
(或用F 值判断,有同样结论)2、运用EXCEL 进行单因素方差分析,有:方差分析:单因素方差分析SUMMARY组 观测数 求和 平均 方差列 1 5 222 44.4 28.3列 2 5 150 30 10列 3 5 213 42.6 15.8方差分析差异源 SS df MS F P-value F crit 组间 615.6 2 307.8 17.06839 0.00031 3.885294 组内 216.4 12 18.03333总计 832 14由于由于P 值=0.00031<05.0=α,拒绝原假设,表明3个总体的均值之间有显著差异。
(或用F 值判断,有同样结论)进一步用LSD 方法见教材P2063、(1)按行依次为:420、2、1.478(第一行);27、142.07(第二行);4256(第三行)。
(2)由于P 值=0.245946>05.0=α,不拒绝原假设,没有证据表明3种方法组装产品数量有显著差异。
第八章:方差分析

SSE xij xi
k ni i 1 j 1
2
计算结果为: SSE = 2708
三个离差平方和的关系
总离差平方和(SST)、组内离差平方和(SSE) 、组间离差平方和 (SSA) 之间的关系:
x
k i 1 j 1
ni
ij
x ni xi x xij x
外包装底色对产品销量是否有显著影响?
市场 北京 上海 深圳 西安 成都 红色 36 35 27 29 38 橙色 28 26 31 30 24 紫色 30 32 28 26 35 蓝色 22 27 20 21 29
什么是方差分析?
【 例 】为了对几个行业的服务质量进行评价,消费者协会 在4个行业分别抽取了不同的企业作为样本。最近一年中消 费者对总共23家企业投诉的次数如下表:
2.
方差分析的基本假定
1. 每个总体都服从正态分布 (每个行业被投诉的次数必须服从正态分布) 2. 各个总体的方差相同 ( 4个行业被投诉次数的方差都相等) 3. 观测值是独立的 (每个行业被投诉的次数与其他行业被投诉的次数独立)
方差分析的基本假设
H 0 : m1 m2 mk H1 : m1 , m2 , , mk 不全相等
2.计算误差
计算全部观测值的均值以及各水平下的组均值 计算总误差 计算组内误差 计算组间误差
计算总误差( SST)
1. 全部观察值 xij 与总平均值 x 的离差平方和 2. 反映全部观察值的离散状况 3. 其计算公式为
SST xij x
k ni i 1 j 1 2
方差分析
差异源
组间 组内
SS
1456.609 2708
卫生统计学第八章正交试验方差分析

WENKU DESIGN
正交试验设计定义与原理
正交试验设计定义
正交试验设计是研究多因素多水平的一种设计方法,它是根 据正交性从全面试验中挑选出部分有代表性的点进行试验, 这些有代表性的点具备了“均匀分散,齐整可比”的特点。
正交试验设计原理
正交试验设计是利用正交表来安排与分析多因素试验的一种 设计方法。它是由试验因素的全部水平组合中,挑选部分有 代表性的水平组合进行试验的,通过对这部分试验结果的分 析,了解全面试验的情况。
THANKS
感谢观看
REPORTINGΒιβλιοθήκη https://VS
正交表特点
每列中不同数字出现的次数相等;任意两 列中数字的排列方式齐全而且均衡。
正交试验设计步骤
挑因素,选水平
根据试验的目的和专业知识,挑选出与考察指标有关的因素。对选出的因素要分清主次,合理安排。 选取的水平数应根据实际情况而定,过少会导致结果不准确,过多则可能数据分布的规律性较差,代 表性差;
通过建立线性模型来描述各因素 与结果之间的关系,从而进行方 差分析和参数估计。
PART 03
正交试验方差分析步骤
REPORTING
WENKU DESIGN
数据整理与描述性统计
整理试验数据
按照试验因素和水平整理数据,列出试验指标的观察值。
计算总均值和总变异
计算所有观察值的总和、均值、离差平方和等描述性统计量。
选正交表,进行表头设计
根据确定的列数(C)与水平数(t)选择相应的正交表。选择的原则是首先满足列数,其次是水平数。若 有2个或2个以上正交表满足条件时则应选取行数最少的一个;
正交试验设计步骤
明确试验方案,进行试验;
医学统计学-8-方差分析

第二节 单因素方差分析
单因素方差分析
单因素方差分析:研究的是一个处理因素的 不同水平间效应的差别。
处 理 因 素
水平1 水平2 水平1 水平2 水平c
单因素方差分析
例1、某地用A、B和C三种方案治疗血红蛋 白含量不满10g的婴幼儿贫血患者,A方案 为每公斤体重每天口服2.5%硫酸亚铁1ml, B方案为每公斤体重每天口服2.5%硫酸亚 铁0.5ml,C方案为每公斤体重每天口服3g 鸡肝粉,治疗一月后,记录下每名受试者血 红蛋白的上升克数,资料见下表,问三种治 疗方案对婴幼儿贫血的疗效是否相同?
A、B、C三种方案治疗婴幼儿贫血的疗效观察表
治疗方案 A n=20
血红蛋白增加量(g) 1.8 1.4 0.5 1.2 2.3 2.3 3.7 0.7 2.4 0.5 2.0 1.4 1.5 1.7 2.7 3.0 1.1 3.2 0.9 2.5
B
n=19
0.2
0.0 2.1 -0.7
0.5
1.6 1.9 1.3
q XA XB
MSe 1 1 2 nA nB
ν=νe
一、q检验
例、在前面对某地用A、B和C三种方案治疗 血红蛋白含量不满10g的婴幼儿贫血患者的 例题(完全随机设计方差分析例1)进行了 方差分析,我们得出三组总体不等的结论。 究竟哪些总体均数之间存在着差别,我们需 要在前方差分析基础之上,再对该资料作两 两比较的q检验。
随机因素是无法避免的,而实质性差异是我们 需要得到的。 如何排除随机因素的干扰,利用样本信息对总 体均数间是否存在差异作出推断?
方差分析的基本思想
按照设计类型将总变异分解为处理因素引 起的变异和随机因素造成的变异; 以处理因素变异与随机因素变异之比来构 造检验统计量F。
统计学课件第八章 方差分析

.1 00 0t j
学
习
网
统计学
统
(两类方差)
计 学 习 网
1. 组内方差
中 华
tj .c
统
中华统计学习网
华
8 - 14 8 - 14
计 学
习 网
计
因素的不同水平(不同总体)下各样本之间的方差 比如,A1、A2、A3、A4四种颜色饮料销售量之间的 方差 组间方差既包括随机误差,也包括系统误差
解释方差分析的概念 解释方差分析的基本思想和原理 掌握单因素方差分析的方法及应用 掌握双因素方差分析的方法及应用
华 统 中 om 中 华 统 计
ww w. 10 00 tj .c
经济、管理类 经济、管理类 基础课程 基础课程
om
中华统计学习网
圣才学习网
华
8-8 8-8
计 学
习 网
计
1. 检验饮料的颜色对销售量是否有影响,也就 是检验四种颜色饮料的平均销售量是否相同 2. 设μ1为无色饮料的平均销售量,μ2粉色饮料的 平均销售量,μ3为橘黄色饮料的平均销售量, μ4为绿色饮料的平均销售量,也就是检验下面 的假设 H0: μ1 = μ2 = μ3 = μ4 H1: μ1 , μ2 , μ3 , μ4 不全相等 3. 检验上述假设所采用的方法就是方差分析
方差分析的基本思想和原理
ww w
om
中华统计学习网
圣才学习网
.1 00 0t j
学
习
网
统计学
计 统 华
(方差的比较)
计 学 习 网
1. 如果不同颜色(水平)对销售量(结果)没有影响,那
么在组间方差中只包含有随机误差,而没有系统 误差。这时,组间方差与组内方差就应该很接近 ,两个方差的比值就会接近1 如果不同的水平对结果有影响,在组间方差中除 了包含随机误差外,还会包含有系统误差,这时 组间方差就会大于组内方差,组间方差与组内方 差的比值就会大于1 当这个比值大到某种程度时,就可以说不同水平 之间存在着显著差异
方差分析法PPT课件

计算各样本平均数 y 如i 下:
表 6-2
型号
ABCDE F
yi
9.4 5.5 7.9 5.4 7.5 8.8
•5
引言 方差分析的基本概念和原理
两个总体平均值比较的检验法 把样本平均数两两组成对:
y 1与 y ,2 与y 1 ,…y 3 与 y ,1 与y 6 ,…y ,2 与y 3 ,共有y (5
6.3 显著性检验
利用(6-17)式来检验原假设H0是否成立.对于给定的显著水
平,可以从F分布表查出临界值
A的值.
F(k1,k(再m根1)据),样本观测值算出F
当 FAF(k1,时k(m ,拒1绝))H0,
当 FAF(k1,,时k(m ,接1 受))H0。
即:如果H0成立,F应等于1;相反应大于1,而且因素的影响越大, F值也越大
m
km
T Tj Yij
•38
j1
作统计假设:6种型号的生产线平均维修时数无显 著差异,即
H0: i=0(i=1,2,…,6),H1:i不全为零
•37
6.3 显著性检验
计算SA及SE
k
SA
k
m
i1
(Yi
Y)2
Ti2
i1
m
T2 km
k
km
km
Ti2
SE i1
(Yij Yi)2
j1
i1
j1Yij2i1m
m
Ti Yij
j 1
相当于检验假设
H0 : i 0 (i=1,2,…,k) , H1 : αi不全为零
•29
6.3 显著性检验
可以证明当H0为真时,
ST
2
~2(k
统计学原理——假设检验与方差分析

二、假设检验中的两类错误**
第Ⅰ类错误/弃真错误 (type Ⅰ error)
当原假设为真时拒绝原假设。犯第Ⅰ类错误的概率
通常记为 。
第Ⅱ类错误/取伪错误(type Ⅱ error)
n1 P 40010.2 320 f 5
所以为大样本分布,检验统计量 Z 近似服从 正态分布。样本数据显示:
p 100 0.25 400
Z p P0 0.25 0.20 0.05 2.5
P 1 P 0.21 0.2 0.02
n
400
在显著性水平 0.05 情况下,查表可知,
比RMB 245.95小或者比RMB 274.05大。所以,在双侧 检验(见下图8-1)中有两个拒绝域。
拒绝域
接受域
拒绝域
245.95
260.00
274.05
图8-1 双边检验的拒绝域与接受域
[例8-2] 在例8-1的假设检验中,如果样本的均值
为 X 240.00 ,当显著性水平为0.05时,原假设是否被 拒绝。
重点是三种不同情况下的假设检验方法,总体方差已 知时正态总体均值和总体比例的假设检验。
难点是总体方差未知时正态总体均值的假设检验和方 差分析。
第一节 假设检验
一、假设检验的概念
一、假设检验的概念
假设(hypothesis),又称统计假设,是对总体参数 的具体数值所作的陈述。
假设检验(hypothesis test) 是先对总体参数提出 某种假设,然后利用样本信息判断假设是否成立的过程。
(3) H0:μ = μ0 H1:μ<μ
应用统计学8-方差分析(1)

Yi = µi + ε i
( 8-1)
其中, μi 纯属Ai作用的结果,称为在Ai条件下Yi的真值(也称为在 Ai条件下Yi的理论平均). εi 是试验误差(也称为随机误差)。
2 ε ~ N ( 0 , σ ) 且相互独立,则 Yi ~ N ( µ i , σ 2 ) 假定 i
且也是相互独立的
第八章
第八章
方差分析
8. 2 单因素试验的方差分析
数学模型和数据结构 参数点估计 分解定理 自由度 显著性检验 多重分布与区间估计
第八章
方差分析
8. 2. 1 数学模型和数据结构
在单因素试验中,为了考察因素A的k个水平A1, A2, …, Ak对Y的影响(如k 种型号对维修时间的影响),设想在固定的 条件Ai下作试验。所有可能的试验结果组成一个总体Yi (i=1, 2, …, k),它是一个随机变量,可以把它分解为两部分
第八章
方差分析
8. 2. 2 参数点估计
2 , , , , µ α α α σ 估计参数 1 2 k 和
估计方法:最小二乘法
最小偏差平方和原则:使观测值与真值的偏差平方和 达到最小
第八章
偏差平方和
方差分析
8. 2. 2 参数点估计
2 S ε = ∑∑ ε ij = ∑∑ (Yij − µ i ) 2 = ∑∑ (Yij − µ − α i ) 2 i =1 j =1 k m
eij = Yij − Y i
第八章
最小二乘估计量
方差分析
8. 2. 2 参数点估计
ˆ =Y µ ˆ i = Yi − Y α µ ˆ i = Yi
可以证明,这三个估计量均为参数μ、 αi和μi的无偏估计量
最新11-第8章 单因素方差分析汇总

11-第8章单因素方差分析仅供学习与交流,如有侵权请联系网站删除 谢谢140+第八章 单因素方差分析第一节 方差分析的基本问题一、方差分析要解决的问题t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验;而多个平均数间的差异显著性检验,必须用方差分析法。
1、检验过程繁琐一试验包含5个处理,采用t 检验法要进行25C 10=次两两平均数的差异显著性检验;若有k 个处理,则要作k (k-1)/2次类似的检验。
2、无统一的试验误差,误差估计的精确性和检验的灵敏性低 12X -X s如表8-1,试验有5个处理,每个处理重复6次,共有30个观测值。
进行t 检验时,每次只能利用两个处理共12个观测值估计试验误差,误差自由度为2(6-1)=10;若利用整个试验的30个观测值估计试验误差,显然估计的精确性高,且误差自由度为5(6-1)=25。
可见在用t检法进行检验时,由于估计误差的精确性低,误差自由度小,使检验的灵敏性降低,容易掩盖差异的显著性。
3、推断的可靠性低,检验的I型错误率大用t检验法进行多个处理平均数间的差异显著性检验,由于没有考虑相互比较的两个平均数的秩次问题,因而会增大犯I型错误的概率,降低推断的可靠性。
假设每一对检验接受零假设的概率都是1-α=0.95,而且这些检验都是相互独立的,那么10对检验都接受概率是(0.95)10=0.60,犯错误的概率α׳=1-0.60=0.40犯I型错误的概率明显增加。
由于上述原因,多个平均数的差异显著性检验不宜用t检验,须采用方差分析法。
二、方差分析的几个概念方差分析(analysis of variance)是由英国统计学家R.A.Fisher于1923年提出的。
这种方法是将a个处理的观测值作为一个整体看待,把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度,进而获得不同变异来源总体方差估计值;通过计算这些总体方差的估计值的适当比值,就能检验各样本所属总体平均数是否相等。
《医学统计学》医统-第八章方差分析

编辑课件
公共卫生系 流行病与统计学教研室
祝晓明
例 8-1 在评价某药物耐受性及安全性的I 期临床试验中,对符合纳入标准的30名健 康自愿者随机分为3组每组10名,各组注 射剂量分别为0.5U、1U、2U,观察48小 时部分凝血活酶时间(s)试问不同剂量的 部分凝血活酶时间有无不同?
编辑课件
编辑课件
• 方差分析
F=3.55, F>F0.05(2,18),P<0.05,三组大鼠 MT 含量的总体均值不全相同。
编辑课件
第三节 多个样本均数的两两比较
证实性研究
探索性研究
证实性研究 与探索性研究
编辑课件
Dunnett-t 检验 LSD-t 检验
SNK-q检验 Tukey检验 Schéffe检验
两个均数的比较时,同一资料所得结果与t检验等
价,即有如下关系 t 2 。F
2.方差分析的基本思想:将全部观测值的总变异按 影响因素分解为相应的若干部分变异,在此基础 上,计算假设检验的统计量 F 值,实现对总体均 数是否有差别的推断。
编辑课件
3. 方差分析有多种设计类型,但基本思想和计算步骤 相同,只是分组变量的个数不同,使用统计软件很容 易实现。 4.多重比较有多种方法,如 Dunnett-t 检验、LSD-t检 验、SNK-q (Student-Newman-Keuls)法 、Tukey法、 Schéffe法、Bonferroni t 检验和 Sidak t 检验。学习 中注意各种方法的适用性。
k1
的
2 分布, 2
2 ,
,认为方差不齐。
编辑课件
例8-1 资料方差齐性检验 提出检验假设,确定检验水准 H0:σ12=σ22=σ32 H1:三组方差不全相等 α=0.05
医学统计学:04 方差分析

1.4 f( F)
1.2
1.0
0.8
0.6
0.4
0.2
0.0
0
1
F 分布曲线
1 1, 2 5
1 5, 2 5
1 10,2 10
2F
3
4
F 界值表
附表4 F界值表(方差分析用,单侧界值) 上行:P=0.05 下行:P=0.01
分母自由度
υ2
1
161 1
4052
18.51 2
98.49
4.21 27
• 随机区组设计又称随机单位组设计、配伍组设计,也叫双因 素方差分析(two--way ANOVA)。是配对设计的扩展。
具体做法:
① 将受试对象按性质(如性别、年龄、病情等) (这些性质是
非处理因素,可能影响试验结果)相同或相近者组成m个单位 组(配伍组),每个单位组中有k个受试对象,分别随机地分 配到k个处理组。
2
7
33.4
18
2
8
38.3
19
2
9
38.4
20
2
10
39.8
21
3
1
32.9
22
3
2
37.9
23
3
3
30.5
24
3
4
31.1
25
3
5
34.7
26
3
6
37.6
27
3
7
40.2
28
3
8
38.1
29
3
9
32.4
30
3
10
35.6
35.51667
(Xij X )2
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案
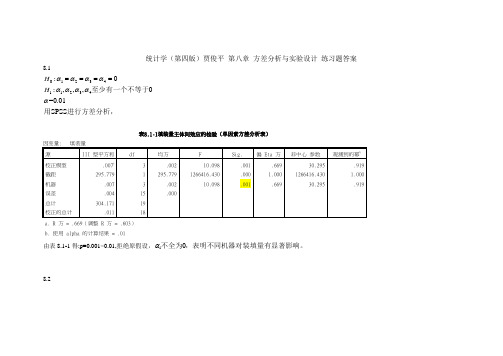
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
方差分析PPT课件

方差分析的用途
1. 用于多个样本平均数的比较 2. 分析多个因素间的交互作用 3. 回归方程的假设检验 4. 方差的同质性检验
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
第一节 方差分析的基本问题
▪ 一、方差分析问题的提出 问题:为了探索简便易行的发展大学生心 血管系统机能水平的方法,在某年级各项 身体发育水平基本相同,同年龄女生中抽 取36人随机分为三组,用三种不同的方法 进行训练,三个月后,测得哈佛台阶指数 如表 1 ,试分析三种不同的训练方法对女 大学生心血管系统的影响有无显著性差异。
结果的好坏和处理效应的高低,实际中具体测 定的性状或观测的项目称为试验指标。常用的 试验指标例如有:身高、体重、日增重、酶活 性、DNA含量等等。
影响因素( experimental factor): 观测中所
研究的影响观测指标的定性变量称之为因素。 当考察的因素只有一个时,称为单因素试验; 若同时研究两个或两个以上因素的影响时,则 称为两因素或多因素试验。
N (3, 2)
A3
61.31 60.00
┆ 67.26 69.05
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
分析
根据研究目的,这里有三个正态总体 N (1, 2),N (2, 2 ), N (3 , a2 ) 。三组数据分别为来自三个总体的样本,问题是 推断 1 ,2 和 3 之间有无显著差异。 由 x1, x2, x3不相等,不能直接得出1, 2, 3不尽相等的结论, 原因是:造成 x1, x2, x3不相等可能有两个方面因素:一是 1, 2, 3 不等,二是1 2 3,但由于抽样误差,造成 x1, x2, x3 之间有差异。现在的任务是通过样本推断1, 2, 3之间有无 显著性差异。
统计学第八章 单因素方差分析(1)

称为处理平方 处理平方 和,记为 SSA
总平方和SST=处理平方和SSA+误差平方和SSe
即, ( y ij − y •• ) = n∑ ( y i • − y •• ) + ∑∑ ( y ij − y i• ) 2 ∑∑
2 i =1 j =1 i =1 i =1 j =1 a n 2 a a n
i =1 j =1
a
n
= n∑ ( y i• − y •• ) + 2∑ [( y i• − y •• )∑ ( y ij − y i• )] + ∑∑ ( y ij − y i • )
2 i =1 i =1 j =1 i =1 j =1
a
a
n
a
n
j =1
∑ ( y ij − y i • ) = 0
换句话说,采用两两t检验法,要进行45次t检验,程序太繁琐。
原因(2):检验的I 型错误增大,从而检验的 可靠性低
a = 2 时, H 0 只有一个,即
µ 1= µ 2
a = 3 时, H 0 有 3 个,即 µ 1= µ 2, µ 2= µ 3, µ 1= µ 3
a = 5时,H 0 有10个,即µ1=µ 2,µ 2=µ3, , µ 4=µ5 L
二、方差分析的几个概念
1、方差分析(analysis of variance):将试验数据的总变异分 解成不同来源的变异,从而评定不同来源的变异相对重要性 的一种统计方法。 2、试验指标(experiment index):为衡量试验结果的好坏或 处理效应的高低,在试验中具体测定的性状或观测的项目。 3、试验因素(experiment factor):试验中所研究的影响试验 指标的因素:单因素、双因素或多因素试验。 4、因素水平(level of factor):因素的具体表现或数量等级。
统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案

统计学(第四版)贾俊平 第八章 方差分析与实验设计 练习题答案8.10123411234:0:,,,0=0.01SPSS H H ααααααααα====至少有一个不等于用进行方差分析,表8.1-1填装量主体间效应的检验(单因素方差分析表)因变量: 填装量 源 III 型平方和df均方F Sig.偏 Eta 方非中心 参数观测到的幂b校正模型 .007a3 .002 10.098 .001 .669 30.295 .919 截距 295.7791 295.7791266416.430.000 1.000 1266416.4301.000 机器 .007 3 .002 10.098.001.66930.295.919误差 .004 15 .000总计 304.17119 校正的总计.01118a. R 方 = .669(调整 R 方 = .603)b. 使用 alpha 的计算结果 = .01由表8.1-1得:p=0.001<0.01,拒绝原假设,i 0α不全为,表明不同机器对装填量有显著影响。
8.201231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.2-1满意度评分主体间效应的检验(单因素方差分析表)因变量: 评分 源III 型平方和df 均方 F Sig.校正模型 29.610a2 14.805 11.756 .001 截距 975.156 1 975.156 774.324 .000 管理者 29.610 2 14.805 11.756.001误差 18.890 15 1.259总计 1061.000 18 校正的总计48.50017a. R 方 = .611(调整 R 方 = .559)由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明管理者水平不同会导致评分的显著差异。
8.301231123:0:,,0=0.05SPSS H H ααααααα===至少有一个不等于用进行方差分析,表8.3-1电池寿命主体间效应的检验(单因素方差分析表)因变量: 电池寿命 源III 型平方和df 均方 F Sig. 偏 Eta 方 非中心 参数 观测到的幂b校正模型 615.600a2 307.800 17.068 .000 .740 34.137 .997 截距 22815.000 1 22815.000 1265.157 .000 .991 1265.157 1.000 企业 615.600 2 307.800 17.068.000.74034.137.997误差 216.400 12 18.033总计 23647.000 15 校正的总计832.00014a. R 方 = .740(调整 R 方 = .697)b. 使用 alpha 的计算结果 = .05由表8.2-1得:p=0.001<0.05,拒绝原假设,i 0α不全为,表明3个企业生产的电池平均寿命之间存在显著差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H1: 1 , 2 , 3 , …, s 不全相等
• 至少有两个不相等 (其它可能相同!)
• 不意味着有: 1 2 ... s
One-Factor ANOVA:
H0: 1 = 2 = 3 = ... = c
请注意其含义
H1: not all the k are equal
之间的平均效果 (均值) 差异足够大, 方案之内的差异相对
小. 反之, 就接受 H0 , 即不同方案的效果没有显著性差异.
注: 用 SPSS 做方差分析中, 输出的结果是: 统计值 f 右侧 的概率, 其与给定显著性水平 进行比较.
如: 查F表得: f , 当 f f ,
在SPPS 的结果中是输出 f 值右侧概率 p .
The Null Hypothesis is True
One Factor ANOVA:
H0: 1 = 2 = 3 = ... = c H1: not all the k are equal
The Null Hypothesis is
NOT True
Total Variation 总变异
s
n i
SST
( X ij X )2
i1 j1
Xij = the ith observation in group i ni = the number of observations in group i
n = the total number of observations in all groups
s
n i
SStotal [
( xij X total )2 ]
i1 j 1
s i 1
ni
(
X
i
X total
)2
s i 1
( x n i
j 1 ij
Xi )2
SS Among SSWithin
MSA SS Among /(s 1), MSW SSWithin /(n s)
F MSA / MSB ~ F (s 1, n s)
MSW =
SSW/(n - S)
Total
n - 1 SST = SSA+SSW
根据观测值, 计算出f 值, 若 f > f (s-1, n-s) (显著性水平为), 则表明 SSb 较大, Xi – Xtotal 的平方和较大, 对应的总体参数
是 i - 的绝对值较大,所以拒绝 H0 , 即至少有两个方案
One-Factor Analysis of Variance 单因子方差分析
单因素方差分析是对多套实验方案的效果的对比 分析,可以用来检验多组相关样本之间均值有无显著 性差异。
如:s 组人员的工资水平、s 种同功能药品的效果、s 种 训练方法的训练效果、 等问题,有无显著性差异。
假设条件: 样本是随机并独立地抽取 (这个条件一定要满足) 所有总体都服从正态分布 所有总体的方差都相等
Among-Group Variation 组间变异
s
SSA ni ( X i X )2 i 1
MSA SSA s 1
ni = the number of observations in group i
s = the number of groups
_
Xi the sample mean of group i
•
••
(ns
1)S
2 s
(n1 1) (n2 1) • • • (ns 1)
• If more than 2 groups, use F Test.
• For 2 groups, use t-Test. F Test more limited.
i
One-Way ANOVA Summary Table 单因子方差分析表
p
f f
One-Factor ANOVA F Test Example
As production manager, you Machine1 Machine2
Source of Degrees
Variation
of
Freedom
Among (Factor)
s-1
Sum of Squares
SSA
Mean
F Test
Square Statistic
(Variance) MSA =
= MSA MSW
SSA/(s - 1)
Within (Error)
n -s
SSW
__
X the overall or grand mean
i j Variation Due to Differences Among Groups.
Within-Group Variation 组内变异
s
n i
SSW
( X ij X i )2
i1 j1
MSW SSW ns
X ij the jth observation in group i
X i the sample mean of group i
Summing the variation within each group and then adding over all groups.
i
Within-Group Variation
MSW SSW ns
(n1
1)S12
(n2
1)S22
s = the number of groups
s
n j
X ij
X j 1 i1 n
2、总变异的分解……方差分析的关键!!!
s
n i
X total [
xij ] / n, n n1 n2 ... ns ij
]/
ni ,
j
1,2,...,s;
第八章 方差分析(ANOVA) Analysis of Variance
在参数假设检验中,我们经常检验两个总 体分布的均值是否相同,其中运用的统计量主 要是 t 统计量。
如果有多个总体,则必须进行两两比较检 验,显然很繁琐。而方差分析,可以一次完成 对多个总体的均值是否相同的检验:
H0: 1 = 2 = 3 = ... = s
多个独立样本均值的比较--单因素方差分析
1、资料类型
方案 1 x11
x12
方案 2 x21
x22
方案 3 x31
x32
…
…
…
方案 s xs1
xs2
…… …… …… …… ……
x1n 1
x2n 2
x3n 3
…
xsn s
注意,s 个样本中含量不必相等!!!
单因素方差分析的假设检验
H0: 1 = 2 = 3 = ... = s =
