讲稿 matlab最优控制仿真
控制系统matlab仿真讲义

应用MATLAB控制系统仿真

01
根据系统性能要求,设计比例、积分、微分控制器参数,优化
系统性能。
状态反馈控制器设计
02
通过状态反馈控制器设计,实现系统的最优控制。
鲁棒控制器设计
03
针对不确定性系统,设计鲁棒控制器,提高系统对参数变化的
适应性。
04
控制系统仿真的动态行为,通过建立和求解微 分方程来模拟系统的动态响应。
性能等。
05
Matlab控制系统仿真实 例
一阶系统仿真
总结词:简单模拟
详细描述:一阶系统是最简 单的控制系统,其动态行为 可以用一个一阶微分方程描 述。在Matlab中,可以使用 `tf`函数创建一个一阶传递函 数模型,然后使用`step`函 数进行仿真。
总结词:性能分析
详细描述:通过仿真,可以 观察一阶系统的响应曲线, 包括超调和调节时间等性能 指标。使用Matlab的绘图功 能,可以直观地展示系统的 动态行为。
THANKS FOR WATCHING
感谢您的观看
适用于模拟数字控制系统、采样控制系统等。
实时仿真
01
在实际硬件上实时模拟控制系统的动态行为,通过将
控制算法嵌入到实际控制系统中进行实时仿真。
02
使用Matlab中的`real-time workshop`等工具箱进
行建模和仿真,可以方便地实现实时仿真。
03
适用于模拟实际控制系统、验证控制算法的正确性和
实时仿真
Matlab支持实时仿真,可以在实 际硬件上运行控制算法,进行系 统测试。
02
控制系统数学模型
线性时不变系统
线性时不变系统(LTI)是指系统的输出与输入之间的关系 可以用线性常数来描述的系统。在控制系统中,LTI系统是 最常见的系统类型之一。
自动化专业课程设计——MATLAB控制系统仿真 ppt课件

锅炉过热蒸汽温度控制的基本任务 就是维持过热器出口温度在允许范围内,
高参数电厂540150o C 保护设备安全,
并使生产过程经济、高效的持续运行。
影响蒸汽温度的因素:
➢ 减温水量 QW (控制量) ➢ 蒸汽流量 D ➢ 烟气热量 QH
PPT课件
29
(二)蒸汽温度系统开环模型建立
减温水量对蒸汽温度的影响
对于倒立摆系统,由于其本身是自不稳定的系统,实验建模 存在一定的困难。但是经过假设忽略掉一些次要的因素后,倒立摆 系统就是一个典型的运动的刚体系统,可以在惯性坐标系内应用 经典力学理论建立系统的动力学方程关系。
PPT课件
11
(一)一级倒立摆系统的数学模型
系统的组成系统由小 车、小球和轻质杆组成。 倒摆通过转动关节安装在 驱动小车上,杆子的一端 固定在小车上,另一端可 以自由地左右倒下。通过 对小车施加一定的外部驱 动力,使倒摆保持一定的 姿势。
27设计过程设计过程11建立倒立摆的数学模型建立倒立摆的数学模型劢力学数学模型劢力学数学模型非线性微分方程形式非线性微分方程形式状态空间表达式非线性状态空间表达式非线性状态空间表达式线性状态空间表达式线性状态空间表达式线性状态空间表达式线性22倒立摆的状态空间分析法设计倒立摆的状态空间分析法设计采用状态反馈进行极点配置采用状态反馈进行极点配置基亍全维观测器用状态反馈进行极点配置基亍全维观测器用状态反馈进行极点配置33基亍基亍matlabmatlab的倒立摆系统仿真设计的倒立摆系统仿真设计matlabmatlab语言程序设计和语言程序设计和simulinksimulink模型建立模型建立建立倒立摆的开环仿真模型观察输出曲线建立倒立摆的开环仿真模型观察输出曲线设计状态反馈进行极点配置分析曲线设计状态反馈进行极点配置分析曲线设计观测器和状态反馈进行极点配置分析曲线设计观测器和状态反馈进行极点配置分析曲线根据根据非线性数学模型非线性数学模型建立开环仿真模型观察输出曲线建立开环仿真模型观察输出曲线采用以上设计的观测器和状态反馈进行控制分析曲线采用以上设计的观测器和状态反馈进行控制分析曲线28及控制系统仿真课程设计二锅炉过热汽温控制系统设计及仿真分数占比2029锅炉出口过热蒸汽温度是蒸汽的重要质量指标是整个锅炉汽水通道中温度最高的直接关系到设备的安全和系统的生产效率
matlab控制系统仿真设计

matlab控制系统仿真设计Matlab控制系统仿真设计控制系统是现代工业领域中的关键技术之一,用于实现对系统行为的预测和调节。
在控制系统设计中,仿真是一个重要的工具,可以帮助工程师和研究人员理解和评估系统的性能。
在本文中,我们将以Matlab的控制系统仿真设计为主题,介绍控制系统仿真的基本概念、方法和工具。
一、控制系统仿真基础1.1 什么是控制系统仿真?控制系统仿真是指通过计算机模拟系统的动态行为来评估和验证控制策略的一种方法。
仿真可以帮助工程师在构建实际系统之前,通过计算机模型对系统的运行过程进行预测和分析。
1.2 为什么要进行控制系统仿真?控制系统仿真可以帮助工程师在实际系统建造之前对系统进行评估和优化。
它可以提供系统的动态响应、稳定性、鲁棒性等信息,帮助工程师优化控制策略和设计参数。
此外,仿真还可以帮助工程师调试和验证控制算法,减少实际系统建造和测试的成本和风险。
1.3 Matlab在控制系统仿真中的作用Matlab是一款功能强大的科学计算软件,也是控制系统仿真的重要工具之一。
Matlab提供了丰富的控制系统设计和分析工具箱,使得控制系统仿真变得更加简单和高效。
二、Matlab控制系统仿真设计的步骤2.1 确定系统模型在进行控制系统仿真设计之前,首先需要确定系统的数学模型。
系统模型可以通过物理原理、实验数据或系统辨识方法得到。
在Matlab中,可以使用符号计算工具箱或数值计算工具箱来建立系统的数学模型。
2.2 设计控制器根据系统模型和性能要求,设计合适的控制器。
常用的控制器设计方法包括PID控制、根轨迹设计、频率响应设计等。
在Matlab中,可以使用Control System Toolbox来设计控制器,并进行性能分析和优化。
2.3 仿真系统响应利用Matlab的仿真工具,对系统进行动态仿真,观察系统的响应。
仿真可以根据预先设定的输入信号和初始条件,计算系统的状态和输出变量随时间的变化。
MATLAB控制系统的仿真
C R
x1 x2
0 1
L
u
L
y [1
0]
x1 x2
[0]u
•
x Ax bu
y CT x du
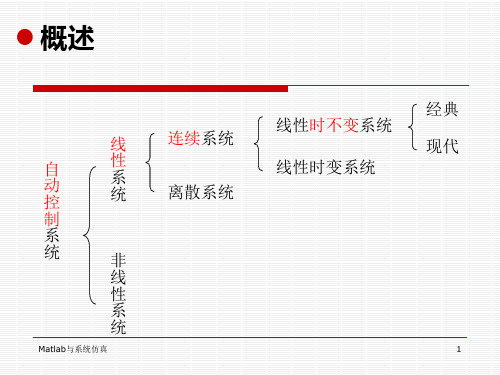
• 没有良好的计算工具前:系统建立、变换、分析、设 计、绘图等相当复杂。
• MATLAB控制系统软件包以面向对象的数据结构为基 础,提供了大量的控制工程计算、设计库函数,可以 方便地用于控制系统设计、分析和建模。
Transfer function:
s+1 ------------s^2 + 5 s + 6
Matlab与系统仿真
22
应用——系统稳定性判断
系统稳定性判据: 对于连续时间系统,如果闭环极点全部在S平面左半平面,
则系统是稳定的;
若连续时间系统的全部零/极点都位于S左半平面, 则系统是——最小相位系统。
Matlab与系统仿真
38
4.2 动态特性和时域分析函数
(一)动态特性和时域分析函数表 (二)常用函数说明 (三)例子
Matlab与系统仿真
39
(一)动态特性和时域分析函数表 ——与系统的零极点有关的函数
表8.6前部分p263
Matlab与系统仿真
40
——与系统的时域分析有关的函数
Matlab与系统仿真
Matlab与系统仿真
8
4.1 控制工具箱中的LTI对象
Linear Time Invariable
(一)控制系统模型的建立 (二)模型的简单组合 (三)连续系统和采样系统变换(*略)
Matlab与系统仿真
9
(一)控制系统模型的建立
➢ MATLAB规定3种LTI子对象:
• Tf 对象—— 传递函数模型 • zpk 对象—— 零极增益模型 • ss 对象—— 状态空间模型
如何使用Matlab进行控制系统仿真

如何使用Matlab进行控制系统仿真概述控制系统在工程领域中扮演着重要角色,它用于控制和管理各种工程过程和设备。
而控制系统仿真则是设计、开发和测试控制系统的关键环节之一。
Matlab作为一种功能强大的工程计算软件,提供了丰富的工具和功能,可以帮助工程师进行控制系统仿真。
本文将简要介绍如何使用Matlab进行控制系统仿真,以及一些实用的技巧和建议。
1. Matlab的基础知识在开始控制系统仿真之前,有一些Matlab的基础知识是必要的。
首先,了解Matlab的基本语法和命令,熟悉Matlab的工作环境和编辑器。
其次,学会使用Matlab的集成开发环境(IDE)进行编程和数学建模。
熟悉Matlab的常用函数和工具箱,并了解如何在Matlab中导入和导出数据。
2. 定义系统模型在进行控制系统仿真之前,需要定义系统的数学模型。
根据具体情况选择合适的建模方法,如传递函数、状态空间或差分方程等。
在Matlab中,可以使用tf、ss 或zpk等函数来创建系统模型,并指定系统的参数和输入信号。
此外,Matlab还提供了Simulink这一强大的图形化建模环境,方便用户以图形化界面设计系统模型。
3. 设计控制器控制系统仿真的关键是设计合适的控制器,以实现所需的控制目标。
Matlab提供了各种控制器设计方法和工具,如PID控制器、根轨迹法、频域方法等。
用户可以使用Matlab的Control System Toolbox来设计和分析控制器,并在仿真中进行验证。
此外,Matlab还支持自适应控制和模糊控制等高级控制方法,可根据具体需求选择合适的方法。
4. 进行仿真实验在完成系统模型和控制器设计后,可以开始进行控制系统仿真实验。
首先,确定仿真实验的输入信号,如阶跃信号、正弦信号或随机信号等。
然后,使用Matlab中的sim函数将输入信号应用到系统模型中,并观察系统的输出响应。
通过调整控制器参数或设计不同的控制器,分析系统的性能和稳定性,并优化控制器的设计。
自动控制原理实验讲义--MATLAB仿真

控制系统的模拟试验和MATLAB 仿真1 MATLAB 简介MATLAB 是Mathworks 公司开发的一种集数值计算、符号计算和图形可视化三大基本功能于一体的功能强大、操作简单的优秀工程计算使用软件。
MATLAB 不仅可以处理代数问题和数值分析问题,而且还具有强大的图形处理及仿真模拟等功能。
从而能够很好的帮助工程师及科学家解决实际的技术问题。
MATLAB 的含义是矩阵实验室(Matrix Laboratory ),最初主要用于方便矩阵的存取,其基本元素是无需定义维数的矩阵。
经过十几年的扩充和完善,现已发展成为包含大量实用工具箱(Toolbox )的综合使用软件,不仅成为线性代数课程的标准工具,而且适合具有不同专业研究方向及工程使用需求的用户使用。
MATLAB 最重要的特点是易于扩展。
它允许用户自行建立完成指定功能的扩展MATLAB 函数(称为M 文件),从而构成适合于其它领域的工具箱,大大扩展了MATLAB 的使用范围。
目前,MATLAB 已成为国际控制界最流行的软件,控制界很多学者将自己擅长的CAD 方法用MATLAB 加以实现,出现了大量的MATLAB 配套工具箱,如控制系统工具箱(control systems toolbox ),系统识别工具箱(system identification toolbox ),鲁棒控制工具箱(robust control toolbox ),信号处理工具箱(signal processing toolbox )以及仿真环境SIMULINK 等。
(1) MATLAB 的安装本节将讨论操作系统为Microsoft Windows 环境下安装MATLAB7的过程。
将MATLAB7的安装盘放入光驱,系统将自动运行auto-run.bat 文件,进行安装;也可以执行安装盘内的setup.exe 文件启动MATLAB 的安装程序。
启动安装程序后,屏幕将显示安装MATLAB 的初始界面,根据Windows 安装程序的常识,不断单击[Next],输入正确的安装信息,具体操作过程如下:输入正确的用户注册信息码;选择接收软件公司的协议;输入用户名和公司名;选择MATLAB 组件(Toolbox );选择软件安装路径和目录;单击[Next]按钮进入正式的安装界面。
matlab仿真讲稿4

– 不画图,通过函数返回值得到响应的相关数据。
[y,x,t]=step(sys,t) [y,x]=step(sys,t) y=step(num,den,t) 其中y为各个仿真时刻的输出向量,x为自动选择的状态 向量的时间响应数据,t为时间向量。
Copyright © by ARTCOM PT All rights reserved.
Copyright © by ARTCOM PT All rights reserved.
19 www.art-com.co.kr
例题 已知系统的开环传递函数:
Company
Logo
G ( s) H ( s)
k ( s 2)( s 3) s( s 1)
绘制出闭环系统的根轨迹,并求出当闭环极点p=[-0.707,-2.6]时,系统所对 应的增益k值。
z=[-2 -3];p=[0 -1]; k=1; g=zpk(z,p,k); pzmap(g) [p,z]=pzmap(g) rlocus(g) [k,poles]=rlocfind(g) [k,poles]=rlocfind(g,[-0.707,-2.6]) r=rlocus(g,0.4854) [r,k]=rlocus(g)
Company
Logo
2], 系统的输入为单位阶跃函数, 求有初始条件的零输入响应曲线和总的 输出响应曲线。
A=[-2 -2.5 -0.5;1 0 0;0 1 0]; B=[1;0;0]; C=[0 1.5 1]; D=0; G=ss(A,B,C,D); t=0:.2:100; step(G,t) hold on y1=step(G,t); y=initial(G,[1 0 2],t); plot(t,y) xlabel('t'); ylabel('y')
第5讲 控制系统Matlab仿真讲解

带有纯滞后环节的传递函数表示
G(s)
s2 s3
3s 4s
4
e5s
num=[1 3 0]; den=[1 0 4 4]; sys=tf(num,den,'iodelay',5)
4.1.2 状态空间描述
经典控制理论用传递函数描述输入-输出关系 现代控制理论则用状态空间描述法(状态方程
3s
8)
试在Matlab中将上述传递函数模型表示出来。
s=tf('s'); G=7*(2*s+3)/(s^2*(3*s+1)*(s+2)^2*(5*s^3+3*s+8))
4.1.1 传递函数模型
*离散系统的脉冲传递函数模型
G(z)
Y (z) U (z)
cm zm an zn
cm1zm1 ... c1z c0 an1zn1 ... a1z a0
2s 9
s4 3s3 2s2 4s 6
试在Matlab中将上述传递函数模型表示出来。
num=[2, 9]; den=[1 3 2 4 6]; G=tf(num,den)
4.1.1 传递函数模型
一、连续系统的传递函数模型举例:
已知系统传递函数为:
G(s)
s2 (3s
7(2s 3) 1)(s 2)2 (5s3
举例:
G(s)
(s 5)(s 6)
(s 1)(s 2)(s 3 4i)(s 3 4i)
Z=[-5,-6]; P=[-1 -2 -3-4i, -3+4i]; K=1; sys=zpk(Z,P,K)
控制系统的MATLAB仿真课件(99页)

x1 1 x2 0 x3 0 x4 0 c=
x1 x2 x3 x4 y1 6 12 6 10 d=
u1 y1 0 Continuous-time model.
19
第7章
控制系统的MATLAB仿真
由以上数据可写出系统的状态空间模型为:
?
?? 2 ? 3 ? 1 ? 1?
?1?
? ??X?(t)?
series()函数命令还可以将多个环节按两两串联的形式多 次递归调用加以连接,进行等效化简。
sys= series(sysl,sys2命) 令可以用命令 sys=sys1*sys2* …*sysn取代,不仅省掉“series(”)字符,且 可以实现多个环节的串联等效传递函数的求取。
23
第7章
控制系统的MATLAB仿真
形式之一。控制系统的环节串联及其化简就是模块方框图模 型的串联及其化简。可以用MATLAB 的函数命令series(将) 串 联模块进行等效变换。
使用series(函) 数命令不必做多项式的乘除运算即可实现 两个环节传递函数的串联连接。如果令sys1= tf(num1,den1) , sys2= tf(num2,den2) ,其命令格式为: sys= series(sysl,sys2)
zp2tf
将系统零极点增益模型转换为传递函数模型
15
第7章
控制系统的MATLAB仿真
【例7.2】 已知某系统的传递函数为: G (s)? 12s3 ? 24s2 ? 12s ? 20 2s4 ? 4s3 ? 6s2 ? 2s ? 2
试用MATLAB 语言求出该系统的传递函数模型、状态空 间模型和零极点增益模型。
22
第7章
控制系统的MATLAB仿真
Matlab控制模型及仿真技术

系统优化与改进
参数优化
通过Matlab的优化工具箱,对控制系统的参数进行优化,提高 系统性能。
结构优化
对控制系统的结构进行改进,如采用串级控制、解耦控制等。
算法改进
对控制算法进行改进,以提高系统的响应速度和稳定性。
05
Matlab控制模型及仿真技术案 例分析
02
控制模型的建立
传递函数模型
总结词
传递函数模型是控制系统中最常用的数学模型之一,它描述递函数模型基于系统的输入和输出信号,通过拉普拉斯变换或Z变换等方法, 将时域中的系统响应转换为频域中的传递函数。传递函数模型具有明确的物理 意义,能够直观地反映系统的动态特性。
案例三:离散时间系统仿真与分析
01
3. 使用Matlab的控制系统工具 箱进行系统分析和设计。
02
4. 进行仿真实验,验证系统的 性能。
03
案例应用:例如设计一个数字 通信系统,通过分析系统的误 码率和信噪比等参数,优化系 统的性能。
THANKS
感谢观看
案例二:非线性控制系统仿真
2. 建立非线性系统的数学 模型。
1. 确定系统的非线性特性。
设计步骤
01
03 02
案例二:非线性控制系统仿真
01
3. 使用Matlab的控制系统工具箱进行系统分析和设
计。
02 4. 进行仿真实验,验证系统的性能。
03
案例应用:例如设计一个飞行器控制系统,通过控制
飞行器的姿态和高度等参数,实现稳定的飞行。
案例三:离散时间系统仿真与分析
• 离散时间系统:离散时间系统是指系统的状态只在离散时刻发生变化,而在其 他时刻系统的状态保持不变的系统。在Matlab中,可以使用Simulink等工具 进行建模和仿真。
matlab控制系统仿真课件

3.模块的删除、剪切和拷贝
选定一个模块, 可以作如下操作。 删除:按Delete键,可以将选定的模块删除。 剪切:选择Edit菜单中的Cut命令, 可以将被选 定模块移到Windows的剪切板上。可供Paste命令重 新粘贴。 拷贝:选择Edit菜单中的Copy命令, 然后将光 标移到要粘贴的地方, 再运行Edit菜单中的Paste命 令,就会在选定的位置上复制出相应的模块。
9. 属性设定 (Block Properties)
包括Description属性、 Priority优先级属性、 Tag属性、Open function属性、 Attributes format string 属性。 其中Open function 属性是一个很有用的属 性,通过它指定一个函 数名,则当该模块被双 击之后,Simulink就会 调用该函数执行,这种 函数在MATLAB中称为 回调函数。
一、解题器(Solver)参数的设定 (1) 在仿真时间(simulation time)中选择: ●start time —— 开始时间; ●stop time —— 停止时间;
(2) 在解题选项(solver options)中选择:
●变步长(variable-step)或固定步长(fixed-step);
8. 参数设定(Block Parameters)
设置每一个模块的特定参数。例如:
双击一个模块,可 直接打开该模块的Block Parameters对话框。
在菜单Edit中选择 Block Parameters , 可打开该模块的Block Parameters对话框。
参数设定窗口包含 了该模块的基本功能帮 助,为获得更详尽的帮 助,可以点击其上的 help按钮。通过对模块 的参数设定,就可以获 得需要的功能模块。
先进PID控制MATLAB仿真

1.3.2 连续系统的数字PID控制仿真
本方法可实现D/A及A/D的功能,符合数字 实时控制的真实情况,计算机及DSP的实时 PID控制都属于这种情况。 采用MATLAB语句形式进行仿真。被控对象 为一个电机模型传递函数: 1 G(s) Js 2 Bs
式中,J=0.0067,B=0.10
k
式中,Ki=Kp/Ti,Kd=KpTd,T为采样周期,K 为采样序号,k=1,2,……,e (k-1)和e (k) 分别为第(k-1)和第k时刻所得的偏差信号。
1.3.1 位置式PID控制算法
位置式PID控制系统
1.3.1 位置式PID控制算法
根据位置式PID控制算法得 到其程序框图。 在仿真过程中,可根据实 际情况,对控制器的输出 进行限幅:[-10,10]。
1.1 PID控制原理
PID控制器各校正环节的作用如下:
比例环节:成比例地反映控制系统的偏差信号e(t),偏差 一旦产生,控制器立即产生控制作用,以减小偏差。 积分环节:主要用于消除静差,提高系统的无差度。积 分作用的强弱取决于积分时间常数T,T越大,积分作用 越弱,反之则越强。 微分环节:反映偏差信号的变化趋势,并能在偏差信号 变得太大之前,在系统中引入一个有效的早期修正信号, 从而加快系统的动作速度,减少调节时间。
控制工程与控制理论课程设计讲座
先进PID控制及其 MATLAB仿真
主讲人 付冬梅 自动化系
第1章 数字PID控制
1.1 PID控制原理 1.2 连续系统的模拟PID仿真
1.3 数字PID控制
1.1 PID控制原理
模拟PID控制系统原理框图
1.1 PID控制原理
PID是一种线性控制器,它根据给定值rin(t)与实 际输出值yout(t)构成控制方案:
Matlab控制系统仿真(1)

一. 控制系统的模型与转换目前大多数控制系统的分析设计方法都要求系统的模型已知。
所以,控制系统的数学模型是控制系统分析和设计的基础。
获得数学模型的方法有两种:一种是从已知的物理规律出发,用数学推导的方法建立系统的数学模型,另外一种就是利用试验数据拟合。
前一种方法称为系统的物理建模方法,而后者称为系统辨识,两者各有优势和适用场合。
一般的分析研究中将控制系统分为连续系统和离散系统,描述连线性连续系统常用的方式是传递函数(传递函数矩阵)和状态空间模型,相应的离散系统可以用离散传递函数和离散状态方程表示。
各种模型之间还可以进行相互转换。
1.1连续线性系统的数学模型连续线性系统一般可以用传递函数描述,也可以用状态方程描述。
前者是经典控制的常用模型,而后者是现代控制理论的基础。
它们是描述同一个系统的不同描述方式。
除此之外,还可以用零极点的形式表示连续线性系统模型。
本章着重介绍这些数学模型,并侧重介绍这些模型在控制系统的Matlab 环境下的表示方法。
高阶线性常微分方程通常是描述线性连续系统的最传统的方法,其基本表达式为: )()()()()()()()(11111111t u b dtt du b dtt u db dtt u d b t y a dtt dy a dtt y da dtt y d m m m m mmn n n n n n++++=++++------ 其中)(t u ,)(t y 分别是控制系统的输入和输出信号,他们均是时间t 的函数,n 是系统的阶次。
利用Laplace 引入的积分变换(拉氏变换),可以在另初始条件下对该微分方程进行变换,得到控制系统的传递函数: nn n n mm m ma s a sa sb s b s b s b s G ++++++++=----1111110)( (n m ≤)传递函数的引入使得控制系统的研究变得简单,它是控制理论中线性系统模型的一种主要描述方式。
讲稿 matlab最优控制仿真

最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
分析小车水平方向所受的合力,可以得到以下方程:
(1)
由摆杆水平方向的受力进行分析可以得到下面等式:
即 把这个等式代入式(1)中,就得到系统的第一个运动方程:
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
最优控制仿真-matlab函数
3、dare ——解离散系统的代数Riccati方程 4、dlqr——离散系统线性二次型状态调节器 5、lqry——连续系统线性二次型输出调节器 6、lqrd——连续时间系统的离散状态调节器
最优控制仿真-一级倒立摆
M 小车质量 m 摆杆质量 b 小车摩擦系数 l 摆杆转动轴心到杆质 心的长度 I 转动惯量 F 加在小车上的力 x 小车位置 φ 摆杆与垂直向上方向 的夹角 θ 摆杆与垂直向下方向 的夹角
一、建立对象模型-牛顿力学方法
⎡x⎤ ⎢ &⎥ ⎡1 0 0 0⎤ ⎢ x ⎥ ⎡0⎤ y=⎢ ⎥ ⎢ Φ ⎥ + ⎢0 ⎥ u ⎣ ⎦ ⎣0 0 1 0 ⎦ ⎢&⎥ ⎣Φ ⎦
最优控制仿真-一级倒立摆
一、建立对象模型-物理量
小车质量
M = 0.5kg
小车的摩擦系数 b = 0.1 倒立摆的转动惯量为
I = 0.006kg ⋅ m 2
端点到小车质心的距离为
l = 0.3m
最优控制仿真-一级倒立摆
二、控制要求
1. 2. 3. 输出的过渡过程时间小于2s; 输出的上升时间<0.5s 输出的超调量<20
最优控制仿真-一级倒立摆
三、仿真实现
1、 对象的阶跃响应
最优控制的MATLAB实现讲解学习

最优控制的M A T L A B实现最优控制的MATLAB实现摘要线性二次型最优控制是一种普遍采用的最优控制系统设计方法。
使用MATLAB软件设计的GUI控制界面实现最优控制,有较好的人机交互界面,便于使用。
线性二次型最优控制又叫做LQ最优控制或者称为无限长时间定常系统的状态调节控制器。
本文分别从连续系统线性二次型最优控制的MATLAB实现,离散系统相形二次型最优控制的MATLAB实现,最优观测器的MATLAB实现,线性二次性Guass最优控制的MATLAB实现四个研究方案。
本论文就是从这四个方面分别以不同的性能指标设计不同的GUI界面以及不同的程序实现其功能并说明其各自的应用范围。
关键词:线性二次型,最优控制, GUI控制界面,最优观测器, Guass最优控制The Linear Quadratic Optimal Control of MATLABAbstractLinear quadratic optimal control is a widely used to optimal control system design method. Use of MATLAB software design GUI interface control to realize the optimal control, Have good man-machine interface, easy to use. The linear quadratic optimal control and called LQ optimal control or an infinite long time of the system state regulation and constant controller.This paper respectively from the continuous system linear quadratic optimal control MATLAB, Discrete system in quadratic optimal control MATLAB, The optimal observer MATLAB, sexual Guass linear quadratic optimal control MATLAB four research plan. This paper is from the four aspects of the performance index respectively in different design different GUI interface and Different programs that realize its function and their application scope.Keywords:Linear quadratic, The optimal control, GUI control interface, The best Guass observer, the optimal control目录1 引言 (1)1.1 概述 (1)1.2课题研究的背景、意义及研究概况 (1)1.3本文研究的主要内容 (2)2 最优控制的基本概念 (3)2.1最优控制基本思想 (3)2.2最优控制的性能指标 (4)2.2.1 积分型性能指标 (4)2.2.2 末值型性能指标 (6)2.3最优控制问题的求解方法 (6)3 最连续系统最优控制的MATLAB实现 (7)3.1连续系统线性二次型最优控制 (7)3.2连续系统线性二次型最优控制的MATLAB实现 (9)3.3连续系统线性二次型最优控制的MATLAB实现示例 (9)4 离散系统线性二次型最优控制的MATLAB实现 (20)4.1离散系统稳态线性二次型最优控制 (20)4.2离散系统线性二次型最优控制的MATLAB实现与示例 (22)5 最优观测器的MATLAB实现 (27)5.1 连续时不变系统的KALMAN滤波 (27)5.2K ALMAN滤波的MATLAB实现 (28)5.3K ALMAN滤波的MATLAB实现示例 (29)6 线性二次型GUASS最优控制的MATLAB实现 (36)6.1LQG最优控制的求解 (36)6.2LQG最优控制的MATLAB实现与示例 (38)7 结论 (43)参考文献: (44)致谢 (46)1 引言1.1 概述随着计算机技术的飞速发展,控制系统的计算机辅助设计与分析得到了广泛的应用,目前已达到了相当高的水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最优控制仿真-matlab函数
3、dare ——解离散系统的代数Riccati方程 4、dlqr——离散系统线性二次型状态调节器 5、lqry——连续系统线性二次型输出调节器 6、lqrd——连续时间系统的离散状态调节器
最优控制仿真-一级倒立摆
M 小车质量 m 摆杆质量 b 小车摩擦系数 l 摆杆转动轴心到杆质 心的长度 I 转动惯量 F 加在小车上的力 x 小车位置 φ 摆杆与垂直向上方向 的夹角 θ 摆杆与垂直向下方向 的夹角
满足性能指标要求
最优控制仿真-一级倒立摆
三、仿真实现
4、LQR控制, 非零初始条件 x=5000;y=100; U=zeros(size(T)); x0=[2,0,0,0]';
满足性能指标要求
此时也暗示着x1(小车位 移)的权重大,x3(倒立 摆的角度)的权重小更 好
对摆杆垂直方向上的合力进行分析,可以得到下面方程:
力矩平衡方程如下: 合并这两个方程,约去P 和N,得到第二个运动方程:
假设φ 与1(单位是弧度)相比很小,即φ <<1,则近似 处理:
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
用u 来代表被控对象的输入力F,线性化后两个运动方程如下:
& ⎧ ( I + ml 2 )φ& − mglφ = ml&& x ⎨ && x & ⎩( M + m) && + bx − mlφ = u
2
0⎤ 0 ⎡ ⎤ 2 ⎡x⎤ ⎢ ⎥ ⎥ I + ml 0⎥ ⎢ & ⎥ ⎢ 2⎥ ⎢ x ⎥ + ⎢ I ( M + m) + Mml ⎥u ⎥ 0 ⎥ ⎢Φ ⎥ ⎢ 0 ⎥ ml ⎢&⎥ ⎢ ⎥ 0 ⎥ ⎣Φ ⎦ 2 ⎥ ⎢ I ( M + m) + Mml ⎥ ⎦ ⎣ ⎦最优控制仿真 Nhomakorabea一级倒立摆
最优控制仿真-matlab函数
1、[X,L,G,rr]=care(A,B,Q,R,S,E)——解连续系统的代 数Riccati方程 X:Riccati方程的解
L:闭环状态方程的特征值 G: 最优反馈增益阵 rr:残留矩阵的Frobenius范数
2、[K,S,e]=lqr(A,B,Q,R,N)——连续系统线性二次型状 态调节器 K:最优反馈增益阵 S:Riccati方程的解 e:闭环系统特征值
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
分析小车水平方向所受的合力,可以得到以下方程:
(1)
由摆杆水平方向的受力进行分析可以得到下面等式:
即 把这个等式代入式(1)中,就得到系统的第一个运动方程:
最优控制仿真-一级倒立摆
一、建立对象模型-牛顿力学方法
相应的状态方程:
⎡0 &⎤ ⎢ ⎡x ⎢ && ⎥ ⎢0 ⎢x⎥ = ⎢ & ⎢Φ ⎥ ⎢0 ⎢ && ⎥ ⎢ ⎣Φ ⎦ ⎢0 ⎣ 1 − ( I + ml 2 )b I ( M + m) + Mml 2 0 − mlb I ( M + m) + Mml 2 0 m gl 2 I ( M + m) + Mml 2 0 mgl ( M + m) I ( M + m) + Mml 2
I = 0.006kg ⋅ m 2
端点到小车质心的距离为
l = 0.3m
最优控制仿真-一级倒立摆
二、控制要求
1. 2. 3. 输出的过渡过程时间小于2s; 输出的上升时间<0.5s 输出的超调量<20
最优控制仿真-一级倒立摆
三、仿真实现
1、 对象的阶跃响应
最优控制仿真-一级倒立摆
三、仿真实现
2、LQR控制,参数1 x=1;y=1; Q = [ x,0,0,0; 0,0,0,0; 0,0,y,0; 0,0,0,0]; R =1;
最优控制仿真-一级倒立摆
三、仿真实现
3、LQR控制,引入 参考输入 x=1;y=1; Q = [ x,0,0,0; 0,0,0,0; 0,0,y,0; 0,0,0,0]; R =1; 不满足性能指标要求
最优控制仿真-一级倒立摆
三、仿真实现
3、LQR控制, 参数2+参考输入 x=5000;y=100; Q = [ x,0,0,0; 0,0,0,0; 0,0,y,0; 0,0,0,0]; R =1;
一、建立对象模型-牛顿力学方法
⎡x⎤ ⎢ &⎥ ⎡1 0 0 0⎤ ⎢ x ⎥ ⎡0⎤ y=⎢ ⎥ ⎢ Φ ⎥ + ⎢0 ⎥ u ⎣ ⎦ ⎣0 0 1 0 ⎦ ⎢&⎥ ⎣Φ ⎦
最优控制仿真-一级倒立摆
一、建立对象模型-物理量
小车质量
M = 0.5kg
小车的摩擦系数 b = 0.1 倒立摆的转动惯量为
