第六章习题答案

合集下载

第六章、七章、八章课后习题答案

第六章课后练习题1、三通公司拟发行5年期、利率6%、面额1000元债券一批；预计发行总价格为550元，发行费用率2%；公司所得税率33%。

要求：试测算三通公司该债券的资本成本率。

参考答案：可按下列公式测算：=1000*6%*（1-33%）/550*（1-2%）=7.46%2、四方公司拟发行优先股50万股，发行总价150万元，预计年股利率8%，发行费用6万元。

要求：试测算四方公司该优先股的资本成本率。

参考答案：可按下列公式测算：其中：=8%*150/50=0.24=（150-6）/50=2.88=0.24/2.88=8.33%3、五虎公司普通股现行市价为每股20元，现准备增发8万份新股，预计发行费用率为5%，第一年每股股利1元，以后每年股利增长率为5%。

要求：试测算五虎公司本次增发普通股的资本成本率。

参考答案：可按下列公式测算：=1/19+5%=10.26%4、六郎公司年度销售净额为28000万元，息税前利润为8000万元，固定成本为3200万元，变动成本为60%；资本总额为20000万元，其中债务资本比例占40%，平均年利率8%。

要求：试分别计算该公司的营业杠杆系数、财务杠杆系数和联合杠杆系数。

参考答案：可按下列公式测算：DOL=1+F/EBIT=1+3200/8000=1.4DFL=8000/（8000-20000*40%*8%）=1.09DCL=1.4*1.09=1.535、七奇公司在初创时准备筹集长期资本5000万元，现有甲、乙两个备选筹资方案，有关资料如下表：筹资方式筹资方案甲筹资方案乙筹资额（万元）个别资本成本率（%）筹资额（万元）个别资本成本率（%）长期借款公司债券普通股800120030007.08.514.0110040035007.58.014.0合计5000 —5000 —要求：试分别测算该公司甲、乙两个筹资方案的综合资本成本率，并据以比较选择筹资方案。

参考答案：（1）计算筹资方案甲的综合资本成本率：第一步，计算各种长期资本的比例：长期借款资本比例=800/5000=0.16或16% 公司债券资本比例=1200/5000=0.24或24%普通股资本比例 =3000/5000=0.6或60%第二步，测算综合资本成本率：Kw=7%*0.16+8.5%*0.24+14%*0.6=11.56%（2）计算筹资方案乙的综合资本成本率：第一步，计算各种长期资本的比例：长期借款资本比例=1100/5000=0.22或22% 公司债券资本比例=400/5000=0.08或8%普通股资本比例 =3500/5000=0.7或70%第二步，测算综合资本成本率：Kw=7.5%*0.22+8%*0.08+14%*0.7=12.09%由以上计算可知，甲、乙两个筹资方案的综合资本成本率分别为11.56%、12.09%，可知，甲的综合资本成本率低于乙，因此选择甲筹资方案。

第六章习题及答案

六、补充练习题（一）单项选择题1．在使用收款凭证、付款凭证、转账凭证的单位，与货币资金无关的业务，填制的凭证是（）A．收款凭证B．付款凭证C．转账凭证D．通用凭证2．下列凭证属于外来原始凭证的是（）A．领料单B．发料汇总表C．上缴税金的收据D．产品交库单3．下列凭证中属于自制原始凭证的是（）A．银行收款通知B．付款凭证C．从购买方获得的销售发票D．销售商品所开具的销售发票4．按填制程序和功能不同，会计凭证分为（）A．收款凭证、付款凭证和转账凭证B．一次凭证和累计凭证C．原始凭证和记账凭证D．外来凭证和自制凭证5．（）是用来编制会计分录的依据，（）是用来作为登记账户的依据。

A．原始凭证B．一次凭证C．记账凭证D．累计凭证6．下列有关记账凭证的说法不正确的有（）A．记账凭证的填制与审核的作用主要在于：一方面防止不该登入账簿的业务进入会计账簿，另一方面确保该登入的都正确地进入会计账簿B．在课堂上讲的会计分录在我国会计实际工作中是没有的，其对应的是记账凭证C．在会计电算化的情况下，记账凭证分为收款凭证、付款凭证和转账凭证的意义已经不大了D．记账凭证登记的依据全部是原始凭证7．付款凭证表头列示的会计科目是（）A．借方科目B．贷方科目C．有时为借方科目，有时为贷方科目D．不能肯定8．下列费用中，直接抵减当期损益的有（）A．生产工人工资B．广告费C．生产车间机器设备的折旧费D．生产产品所耗的材料费9．下列费用中，不应计入产品成本的有（）A．直接材料费B．直接人工费C．期间费用D．制造费用10．月末，如果某种产品一部分完工一部分未完工，归集在产品成本明细账中的费用总额，还要采用适当的分配方法，在（）之间进行分配，然后才能计算完工产品成本。

A．产品品种B．产品批别C．产品生产步骤D．完工产品和在产品11．“累计折旧”账户属于（）类账户。

A．资产B．负债C．费用D．成本12．下列项目属于管理费用的有（）A．银行借款利息B．厂部管理人员工资C．车间管理人员工资D．车间水电费13．“利润分配”账户年末贷方余额表示（）A．已分配的利润额B．未分配的利润额C．未弥补的亏损额D．已实现的净利润14．下列账户中不可能与“制造费用”账户发生对应关系的账户是（）A．原材料B．累计折旧C．应付职工薪酬D．库存商品15．下列不计入当期损益的是（）A．管理费用B．财务费用C．所得税费用D．制造费用16．产品生产间接耗用的费用，先归入（）然后计入有关产品成本中去。

第六章++课后习题+参考答案

第6章完全垄断市场下的价格与产量课后习题参考答案一、单选题1.对完全垄断厂商来说（C）。

A.提高价格一定能够增加收益B.降低价格一定会减少收益C.提高价格未必能增加收益，降低价格未必减少收益D.以上都不对解析：完全垄断市场上，厂商的总收益TR曲线是先增加后减少。

因此，对完全垄断厂商来说，提高价格未必能增加收益，降低价格未必减少收益。

选C。

2.垄断厂商利润极大时，（C）。

A.P=MR=MCB.P>MR=ACC.P>MR=MCD.P>MC=AC解析：垄断厂商定价时遵循利润最大化原则，此时有边际收益等于边际成本MR=MC，而当垄断厂商利润极大时，价格P显然高于边际成本MC。

3.垄断利润或者说超额利润（A）。

A.不是一种成本，因为它不代表生产中使用的资源所体现的替换成本B.不能为垄断者在长期中所获取，因为价格在最优产出水平上必须等于长期平均成本C.为保证资本继续进入该行业所必需D.能为完全竞争者和垄断者一样在长期中获取解析：BCD选项均有明显错误。

垄断利润或者说超额利润不是一种成本，选A。

4.在短期，完全垄断厂商（D）。

A.无盈余B.取得最大利润C.发生亏损D.以上任何一种情况都有可能出现解析：完全垄断厂商在短期均衡点上可能获得超额利润，可能只获得正常利润，还可能发生亏损。

因此选D。

5.在完全垄断厂商的最好或最优产量处（D）。

A.P=MCB.P=SAC的最低点的值C.P最高D.MR=MC解析：根据利润最大化原则，边际收益等于边际成本MR=MC时的价格和产量是最优的。

因此选D。

二、简答题1.成为垄断者的厂商可以任意定价，这种说法对吗？这种说法不正确。

从理论上讲，垄断者是价格的制定者，其产品没有替代品，其他厂商无法进入垄断行业，厂商是产品唯一的卖者。

然而在实际上，如果垄断厂商定价过高，购买量就会下降，从而使总收益和利润下降；其他厂商如看到有丰厚的利润，尽管没有替代品，但相似的替代品总是会生产的，因而垄断厂商如果定价过高，会使自己产品失去销路，市场被相似替代品夺去；国家也会对垄断厂商的定价加以控制，有些国家会通过制定反垄断法，规定最高限价，还可用征税等办法加以控制。

大学物理课后习题答案第六章

第6章真空中的静电场习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。

一试验电荷置于x 轴上何处，它受到的合力等于零？解：根据两个点电荷对试验电荷的库仑力的大小及方向可以断定，只有试验电荷0q 位于点电荷q +的右侧，它受到的合力才可能为0，所以200200)1(π4)1(π42-=+x qq x qq εε故 223+=x2. 电量都是q 的三个点电荷，分别放在正三角形的三个顶点。

试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解：(1) 以A 处点电荷为研究对象，由力平衡知，q '为负电荷，所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。

3. 如图所示，半径为R 、电荷线密度为1λ的一个均匀带电圆环，在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段，该线段的一端处于圆环中心处。

求该直线段受到的电场力。

解：先求均匀带电圆环在其轴线上产生的场强。

在带电圆环上取dl dq 1λ=，dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε根据电荷分布的对称性知，0==z y E E23220)(41cos R x xdqdE dE x +==πεθR Oλ1λ2lxy z式中：θ为dq 到场点的连线与x 轴负向的夹角。

⎰+=23220)(4dq R x xE x πε232210)(24R x Rx+⋅=πλπε232201)(2R x xR +=ελ下面求直线段受到的电场力。

在直线段上取dx dq 2λ=，dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ 方向沿x 轴正方向。

(完整版)第六章线性空间练习题参考答案

第六章线性空间练习题参考答案一、填空题1.已知0000,,00V a bc a b c R c b ⎧⎫⎛⎫⎪⎪ ⎪=+∈⎨⎬ ⎪⎪⎪ ⎪+⎝⎭⎩⎭是33R ⨯的一个子空间，则维（V ）＝ 3 ， V 的一组基是000000000100,100,010*********⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.2．在P 4中，若1234(1,2,0,1),(1,1,1,1),(1,,1,1),(0,1,,1)k k αααα===-=线性无关，则k 的取值范围是3k ≠（以1234,,,αααα为行或者列构成的行列式不为零）. 3．已知a 是数域P 中的一个固定的数，而1{(,,,),1,2,,}n i W a x x x P i n =∈=是P n+1的一个子空间，则a ＝ 0 ，而维(W)＝n 4．维数公式为12dim dim V V +=1212dim()dim()V V V V ++.5．设123,,εεε是线性空间V 的一组基，112233x x x αεεε=++，则由基123,,εεε到基231,,εεε的过渡矩阵T ＝001100010⎛⎫⎪⎪ ⎪⎝⎭，而α在基321,,εεε下的坐标是321(,,)x x x 由基123,,εεε到基233112,,εεεεεε+++的过渡矩阵为T ＝011101110⎛⎫⎪⎪ ⎪⎝⎭.6．数域P 上n 级对称矩阵全体构成数域P 上(1)2n n +维线性空间，数域P 上n 级反对称矩阵全体构成数域P 上(1)2n n -维线性空间，数域P 上n 级上三角矩阵全体构成数域P 上(1)2n n +维线性空间，数域P 上n 级对交矩阵全体构成数域P 上n 维线性空间，数域P 上n 级数量矩阵全体构成数域P 上 1 维线性空间.二、判断题1.设n n V P ⨯=，则{,0}n n W A A P A ⨯=∈=是V 的子空间.错.行列式为零的两个方阵的和的行列式未必为零，因此W 中矩阵关于矩阵的加法运算不封闭，不能成为子空间.）2.已知{(,),,,}V a bi c di a b c d R =++∈为R 上的线性空间，且维(V ）＝2. 错.是子空间，但是是4维的，其基为(1,0),(,0),(0,1),(0,)i i .3.设,n n A B P ⨯∈，V 是0A X B ⎛⎫= ⎪⎝⎭的解空间，V 1是AX ＝0的解空间，V 2是(A ＋B)X ＝0的解空间，则12V V V =.正确. 12V V 中的向量既满足AX ＝0，又满足(A ＋B)X ＝0，因此也满足BX ＝0，即满足0A X B ⎛⎫= ⎪⎝⎭，即为V 中的向量.反之，V 中的向量既在1V 中，又在2V 中，即为12V V 中的向量.因此12V V V =.4.设线性空间V 的子空间W 中每个向量可由W 中的线性无关的向量组12,,,s ααα线性表出，则维(W)＝s.正确.根据定理1.5.设W 是线性空间V 的子空间，如果,,V αβ∈但,W W αβ∉∉且则必有.W αβ+∉错误.可能.W αβ+∈如取,αβ为一对互为负向量，则0.W αβ=+∈ 6. }0|),,{(33321=∈=x R x x x W 是3R 的子空间.正确. 基为（1,0,0），（0,1,0），维数为2. 7.}1|),,{(23321=∈=x R x x x W 是3R 的子空间. 错误.不包含零向量.8.}|),,{(3213321x x x R x x x W ==∈= 是3R 的子空间. 正确.基为（1,1,1），维数为1.9.}|),,{(3213321x x x R x x x W -=∈= 是3R 的子空间. 正确. 基为（1,1,0），（1,0，-1），维数为2. 三、计算题1.求所有与A 可交换的矩阵组成的nn P ⨯的子空间()C A 的维数与一组基，其中100020003A ⎛⎫⎪= ⎪ ⎪⎝⎭.解：设矩阵33()ij B b ⨯=与A 可交换，即有AB BA =.即111213111213212223212223313233313233100100020020003003b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.111213111213212223212223313233313233232222333323b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以有,()0,,1,2,3.ij ij ij ib b j i j b i j =-==当i j ≠时，0ij b =，因此11223300()0000b C A b b ⎧⎫⎛⎫⎪⎪⎪=⎨⎬ ⎪⎪⎪ ⎪⎝⎭⎩⎭ 维数为3，基为112233,,E E E .2.在线性空间P 4中，求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵，并求(1,4,2,3)α=在基1234,,,αααα下的坐标，其中1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=- 1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====--- 解：令过渡矩阵为T ，则有10111432131401238761001232210001T --⎛⎫⎛⎫⎪⎪- ⎪ ⎪=⎪ ⎪- ⎪⎪-⎝⎭⎝⎭因此1143210112379801231314633100128761232100132213221T ------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪==⎪ ⎪ ⎪- ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭. 令1234114324012320012301x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭112341432114113611010123401274210012200122400013000133x x x x -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪===⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (1,4,2,3)α=在基1234,,,αααα下的坐标为（-101,21，-4,3）四、证明题1.V 为定义在实数域上的函数构成的线性空间，令12{()(),()()},{()(),()()}W f x f x V f x f x W f x f x V f x f x =∈=-=∈=--证明：W 1、W 2皆为V 的子空间，且12.V W W =⊕证明：W 1、W 2 分别为偶函数全体及奇函数全体构成的集合，显然W 1、W 2均为非空的.由奇偶函数的性质可得W 1、W 2皆为V 的子空间.()()()()(),()22f x f x f x f x f x V f x +---∀∈=+. 而12()()()(),22f x f x f x f x W W +---∈∈，因此12.V W W =+又12{0}.W W =所以12.V W W =⊕2.设W 是P n 的一个非零子空间，若对于W 的每一个向量12(,,,)n a a a 来说，或者120n a a a ====，或者每一个i α都不等于零，证明：维(W)＝1.证明：由W 是P n 的一个非零子空间，可得W 中含有非零向量设1212(,,,),(,,,)n n a a a b b b αβ==是W 中的任二个非零向量，由题意可得每一个,i i a b 都不等于零.考虑向量11112112121211(,,,)(,,,)(0,,,)n n n n b a b a a a a b b b b a a b b a a b W αβ-=-=--∈.由题设条件有1212110n n b a a b b a a b -==-=，即有1212n na a ab b b ===.即W 中的任二个非零向量均成比例，因此维(W)＝1.。

第六章习题答案 1. (1)临界分切应力n及取向因子数据如附表23 …

第六章习题答案1．(1)临界分切应力n及取向因子数据如附表2.3所示。

以上数据表明，实验结果符合临界分切应力定律τk ＝σm。

(2)屈服应力σs与取向因子，m之间的关系如附图2.17所示。

6．单滑移是指只有一个滑移系进行滑移。

滑移线呈一系列彼此平行的直线。

这是因为单滑移仅有一组多滑移是指有两组或两组以上的不同滑移系同时或交替地进行滑移。

它们的滑移线或者平行，或者相交成一定角度。

这是因为一定的晶体结构中具有一定的滑移系，而这些滑移系的滑移面之间及滑移方向之间都交滑移是指两个或两个以上的滑移面沿共同的滑移方向同时或交替地滑移。

它们的滑移线通常为折线或波纹状。

只是螺位错在不同的滑移面上反复“扩展”的结果。

10．滑移带一般不穿越晶界。

如果没有多滑移时，以平行直线和波纹线出现，如附图2.19(a)，它可以通过抛光而去除。

机械孪晶也在晶粒内，因为它在滑移难以进行时发生，而当孪生使晶体转动后，又可使晶体滑移。

所以一般孪晶区域不大，如附图2．19(b)所示。

孪晶与基体位向不同，不能通过抛光去除。

退火孪晶以大条块形态分布于晶内，孪晶界面平直，一般在金相磨面上分布比较均匀，如附图2。

19(c)所示，且不能通过抛光去除。

11．低碳钢的屈服现象可用位错理论说明。

由于低碳钢是以铁素体为基的合金，铁素体中的碳(氮)原子与位错交互作用，总是趋于聚集在位错线受拉应力的部位以降低体系的畸变能，形成柯氏气团对位错起“钉扎”作用，致使σs 升高。

而位错一旦挣脱气团的钉扎，便可在较小的应力下继续运动，这时拉伸曲线上又会出现下屈服点。

已经屈服的试样，卸载后立即重新加载拉伸时，由于位错已脱出气团的钉扎，故不出现屈服点。

但若卸载后，放置较长时间或稍经加热后，再进行拉伸时，由于熔质原子已通过热扩散又重新聚集到位错线周围形成气团，故屈服现象又会重新出现。

吕德斯带会使低碳薄钢板在冲压成型时使工件表面粗糙不平。

其解决办法，可根据应变时效原理，将钢板在冲压之前先进行一道微量冷轧(如1％～2％的压下量)工序，使屈服点消除，随后进行冲压成型，也可向钢中加入少量Ti，A1及C，N等形成化合物，以消除屈服点。

有机化学-第六章-卤代烃-习题答案

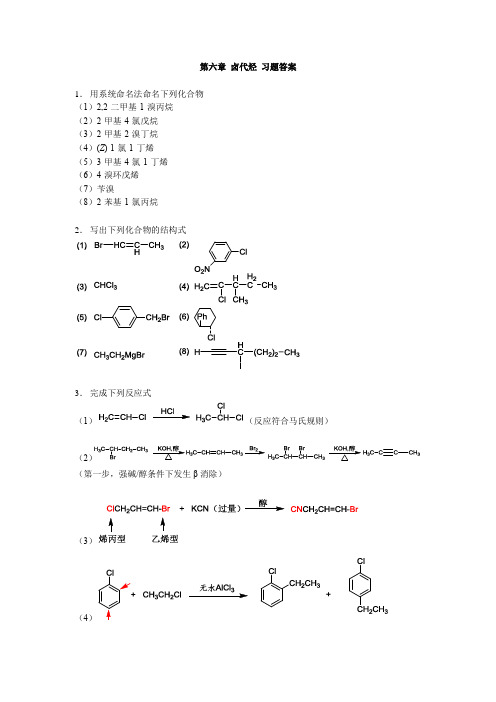
第六章卤代烃习题答案1．用系统命名法命名下列化合物（1）2,2-二甲基-1-溴丙烷（2）2-甲基-4-氯戊烷（3）2-甲基-2-溴丁烷（4）(Z)-1-氯-1-丁烯（5）3-甲基-4-氯-1-丁烯（6）4-溴环戊烯（7）苄溴（8）2-苯基-1-氯丙烷2．写出下列化合物的结构式3．完成下列反应式（1）（反应符合马氏规则）（2（第一步，强碱/醇条件下发生β消除）（3）（4（5（Cl离去生成稳定的苄基碳正离子）（6（优先生成π-π共轭产物）（7）（由于乙醇钠写在反应式左侧，应该为反应原料，因此发生威廉姆森反应生成醚；如果写在箭头上方表示为碱，加热条件下发生消除反应）（8（注意硝酰氧基的正确写法，不能写成-NO3）4．用化学方法鉴别下列化合物（1）（2）（3）5．按要求将下列各组化合物排序（1）C6H5CHBrC6H5>CH3CHBrCH3>CH3CH2CH2Br （依据碳正离子稳定性）（2）1-溴丁烷>2-溴丁烷>2-甲基-2-溴丙烷（根据位阻大小来判断）（3）（前面两个都是烯丙型，后面两个都是乙烯型，活性肯定是烯丙型最高因为烯丙型碳正离子更稳定，乙烯型活性最差。

作为离去基团，溴的离去活性相对于氯更高，因此可以得出以上活性排序）6．试判断在下列各种情况下卤代烷水解是属于S N1机理还是S N2机理（1）S N2 （2）S N1 （3）S N2 （4）S N17．完成下列转化。

（1）（2）（利用格氏试剂与二氧化碳的反应来增加一个碳原子）8．推断题9．推断题。

习题答案(第六章)

1、R n 中分量满足下列条件的全体向量1(,,)n x x 的集合，是否构成R n的子空间？①10n x x ++=；②120n x x x ⋅⋅⋅=；③2211n x x ++=。

解：①是，设(){}111,,|0n n V x x x x =++=，显然V 1≠∅，1,,,a b F V ξη∀∈∀∈，设1212(,,),(,,)x x y y ξη==，则()()()1111,,,,,,n n n n a b a x x b y y ax by ax by ξη+=+=++，而1111()()()()000n n n n ax by ax by a x x b y y a b ++++=+++++=+=所以1a b V ξη+∈，所以V 1是R n 的子空间； ②不是，取(1,0,,0),(0,1,,1)αβ==，则(){}11,,,|0n n V x x x x αβ∈=⋅⋅=，但(1,1,,1)V αβ+=∉，所以V 不是R n 的子空间；③不是，取(1,0,,0),(0,1,0,,0)αβ==，则(){}2211,,,|1n n V x x x x αβ∈=++=，但(1,1,0,,0)V αβ+=∉，所以V 不是R n 的子空间。

2、子集{}1|,,V X AX XB A B n ==为已知的阶矩阵是否是()n M F 的子集？解：是()n M F 的子集；证：显然1V ≠∅，1,,,X Y V a b F ∀∈∈，有()()A aX bY aAX bAY aXB bYB aX bY B +=+=+=+，所以1aX bY V +∈，所以1V 是()n M F 的子集。

3、设12(1,0,1,0),(1,1,2,0)αα==-，求含12,αα的R 4的一组基。

解：因为101010101010112001100010⎛⎫⎛⎫⎛⎫→→⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭，取34(0,0,1,0),(0,0,0,1)αα==，所以{}1234,,,αααα为R 4的一组基。

第六章习题及答案

第六章方差分析一、单项选择题1、方差分析是对多个正态总体（）这一假设进行检验。

A 、方差相等B 、方差相异C 、均值相等D 、均值不等2、方差分析使用的统计量F （）A 、是正态分布B 、是正偏态的C 、是负偏态的D 、取值小于零 3、设单因素方差分析中误差项离差平方和为125.00，水平项离差平方和为375，那么总离差平方和为（）A 、250B 、125.00C 、375.00D 、500 4、因素A 共4个水平，每个水平下重复5次实验，数据的平方和为1250，数据总和为150，A 、125 B 、-125 C 、无法计算 D 、14005、在单因素方差分析中，已知总离差平方和的自由度为24，水平项离差平方和的自由度为7，那么误差项离差平方和的自由度为（）A 、17B 、24C 、7D 、31 6、在一个双因素方差分析中，F A =2.300,F B =4.55相应的P － value 依次为0.11和0.0018，那么结论是（）A 、A 的作用显著，B 的作用不显著 B 、A 的作用不显著，B 的作用显著C 、A 的作用不显著，B 的作用不显著D 、A 的作用显著，B 的作用显著7、已知,8,6,30,560,700,1440======B A T f f f SSB SSA SST 那么F A =( )A 、1440B 、700C 、116.67D 、10.37 8、如果,16,25.2,5,00.8,4,25.12======E B A f MSE f MSB f MSA 那么SST ( )A 、无法计算B 、22.5C 、25D 、125二、多项选择题1、方差分析假定的内容有（）A 、数据来自正态总体B 、数据来自二项总体C 、各总体相互独立D 、各总体不相关E 、各总体方差相等2、一个单因素方差分析中，因素的水平为5，每个水平下的样本容量是6，SST =120,SSA=75那么以下正确的是（） A 、n=30 B 、df A = 4 C 、MSE=1.8 D 、df T =29 E 、F=10.423、在一个单因素方差分析问题中，因素的水平为4，每个水平下的样本容量是5,那么下列说法正确的是（）A 、检验的原假设为43210:μμμμ===HB 、检验的临界值为)5,4(αFC 、检验的原假设为543210:μμμμμ====HD 、检验的临界值为)16,3(αFE 、检验的统计量为163SSE SSA F =4、一个因素A 有6水平，因素B 有4水平的双因素方差分析中，以下正确的有（）A 、数据共24个B 、误差平方和的自由度为15C 、SSA 的自由度为6D 、SST 的自由度为3E 、SST=SSA+SSB+SSE5、一个因素A 有7水平，因素B 有8水平的双因素方差分析中，SST=225,SSA=78,SSB=140以下正确的有（）A 、SSE=2B 、SSE=7C 、78=A FD 、MSE=0.1667E 、因素A 的作用显著三、填空题1、方差分析的英文缩写为：_____________________________________________________。

第六章完全竞争市场习题+答案

第六章完全竞争市场一、单项选择题1、在完全竞争市场上，厂商实现短期均衡的条件是（）A、P＝ARB、P＝MRC、P＝SMCD、P＝SAC2、在微观经济学中，对（）行业的长期均衡状态的分析通常被用来作为对消费者统治说法的一种证明。

A、完全垄断B、完全竞争C、垄断竞争D、寡头竞争3、短期内，一个完全竞争厂商所得到的价格若低于以下哪种成本就会停止营业（）。

A、平均总成本B、平均可变成本C、短期边际成本D、平均固定成本4、根据完全竞争市场的条件，下列（）行业最接近完全竞争行业。

A、自行车行业B、服装行业C、玉米行业D、烟草行业5、在一个完全竞争的市场上，厂商所面临的需求曲线与其长期平均成本曲线相切是（）。

A、厂商在长期内要得到超额利润的条件B、该行业内厂商的数目不再变化的条件C、厂商在长期内要得到最大利润的条件D、以上说法中B和C都是正确的6、在短期内，（）是完全竞争厂商的关闭点。

A、SAC曲线与SMC曲线的交点B、MR曲线与SMC曲线的交点C、AVC曲线与SMC曲线的交点D、AFC曲线与SMC曲线的交点7、假定一个完全竞争行业内某厂商在目前产量水平上的边际成本、平均总成本和平均收均等于1美元，则这家厂商（）。

A、肯定只得到正常利润B、肯定没得到最大利润C、是否得到了最大利润还不能确定D、肯定得到了最少利润8、在短期内，（）是完全竞争厂商的收支相抵点。

A、SAC曲线与SMC曲线的交点B、MR曲线与SMC曲线的交点C、AVC曲线与SMC曲线的交点D、MR曲线与SAC曲线的切点9、在完全竞争的条件下，如果厂商把产量调整到平均总成本曲线最低点所对应的水平（）。

A、他将获得最大利润B、他不能获得最大利润C、他是否获得最大利润仍无法确定D、他一定亏损10、如果某厂商的边际收益大于边际成本，那么为了取得最大利润（）。

A、他在完全竞争的条件下应该增加产量，在不完全竞争条件下则不一定B、他在不完全竞争条件下应该增加产量，在完全竞争条件则不一定C、任何条件下都应该增加产量D、任何条件下都应该减少产量11、在MR=MC的均衡产量上，企业（）。

生物化学第六章维生素辅酶和激素习题含答案

第六章维生素、辅酶和激素一、是非题1.胡萝卜中含有的β-胡萝卜素是维生素A的前体。

2.维生素A预防夜盲症是因为它可转变为视黄醛。

3.泛酸中含有β-丙氨酸。

4.维生素E又称α-生育酚，所以它与人的生育能力有关。

5.维生素K的存在是维持人和动物凝血因子正常功能的必要条件。

6.TPP是许多种脱氢酶如琥珀酸脱氢酶、谷氨酸脱氢酶等的辅酶。

7.作为氢的载体NAD+可以接受两个氢质子和两个电子。

8.在传递氢的过程中，NAD+和NADP+有严格的立体专一性。

9.NAD+和NADP+脱下的氢都是通过呼吸链交给分子氧生成水。

10.尼克酸（烟酸）合成的主要原料是含组氨酸丰富的蛋白质。

11.维生素和激素对人和动物的作用都是一样的，因为它们在体内的含量都非常少。

12.严格地说硫辛酸不属于维生素，因为它可以在动物体内合成。

13.维生素C（即抗坏血酸）可以在动物体内合成，所以不能算做维生素。

14.缺乏维生素C会引起坏血病，维生素C可提高机体的抗病能力和解毒作用。

15.GPT在血液中的含量是检查肝功能的指标之一，GPT实际上是一种转氨酶。

16.甾醇类激素作用于靶细胞后必定会有某种蛋白质的量在细胞内升高。

17.高等动物体内的激素只能由内分泌腺体细胞生成和分泌。

18.催产素和加压素的空间结构是其行使功能的必要条件。

19.下丘脑有调节垂体前叶激素分泌的功能，它本身分泌的激素主要是促进或抑制其它激素的分泌。

20.肾上腺分泌的所有激素以及性激素都是甾醇类物质。

21.胰岛素是由β-胰岛的细胞分泌的胰岛素原转化来的。

22.对于富含葡萄糖的细胞来说，胰岛素的分泌可以看成是合成代谢的信号。

23.甲状腺肿大是由于缺少碘，生物体补偿发育的结果。

24.胰岛素受体含有酪氨酸激酶活性，与胰岛素结合后自动使受体磷酸化。

25.cAMP可以作为所有激素的第二信使。

二、填空题1.胡萝卜素有α，β和γ三种，其中转变为维生素A的效率最高。

2.维生素A的化学名称是，它的化学组成是聚合物。

No3.第6章习题及答案

1) 将 F 中依赖右部属性单一化： F1＝{ E→G,G→E,F→E,F→G,H→E,H→G,FH→E }
2) 对于 FH→E，由于有 F→E,则为多余的：
-4-
第六章习题答案
5
F2＝{ E→G,G→E,F→E,F→G,H→E,H→G }
3) 在 F2 中的 F→E 和 F→G 以及 H→E 和 H→G 之一是多余的，则为：
R 属于______ NF。
答案：AB，2
-1-
第六章习题答案
2
二、选择题：
1.在二元关系模式 R（U，F）中，X、Y 都是单一属性，如果 X→Y，则 R 一定可以达到（）
A．2NF B. 3NF C. BCNF D. 4NF
答案：D
2．在关系模式）
F3＝{ E→G,G→E,F→G, H→G }
F3＝{ E→G,G→E,F→G, H→E }
F3＝{ E→G,G→E,F→E, H→E }
F3＝{ E→G,G→E,F→E, H→G }
3）.设有关系模式 R（A,B,C,D），其上的函数依赖集：F＝{A→C,C→A,B→AC,D→AC}，试计算： A）(AD)+； B）F的最小等价依赖集F‘； C）R 的关键字；答案： 1) 令X={AD}，X(0)={AD}，X(1)={ACD}，X(2)={ACD}，故(AD)＋={ACD}。 2)
第六章习题答案
1
《数据库系统概论》第 6 章习题答案
题型：
1、填空题： 10 题 2、选择题： 10 题 2、综合题： 3 题
一、填空
1. 与 1NF 相比，2NF 消除了非主属性对候选关键字的_________。
答案：部分函数依赖
2.与 2NF 相比，3NF 消除了非主属性对候选关键字的_________。

第六章习题及答案

第六章社会主义社会及其发展一、单项选择题1.迄今为止资本主义社会的发展，大体可分为A.自由竞争资本主义和垄断资本主义两个阶段B.垄断资本主义和非垄断资本主义两个阶段C.商品经济和市场经济两个阶段D.国内垄断和国际垄断两个阶段2，一般垄断资本主义阶段大体形成于A.16世纪资产阶级革命以后B.18世纪工业革命以后C.19世纪末20世纪初D.第二次世界大战以后3.垄断产生的物质条件和基础是A.社会分工的发展B.自然分工的发展C.社会化生产力的发展D．商品经济的发展4.垄断资本主义的产生并占统治地位是A.资本原始积累的结果B:争夺短缺资源的产物C.生产和资本集中发展到一定程度的必然结果D.资本主义国际竞争的结果5.垄断资本主义时期处于垄断地位的大银行A.只是一般的借贷中介人B.已成为社会经济生活中的万能垄断者C.已控制了整个国民经济D.已掌握了国民经济的命脉6.马列主义政治经济学中的金融资本概念是指A.垄断的工业资本B.垄断的银行资本C.垄断的工业资本和银行资本融合生长构成的资本形式D.私人垄断资本和国家垄断资本结合的资本形式7.金融寡头在经济上的统治主要是A二通过实行“参与制”实现的 B.通过“个人联合”实现的C.通过与国家政权相结合实现的D.通过自由竞争实现的8.金融寡头在政治上的统治主要是A.通过实行“参与制”实现的B.通过“个人联合”实现的C.通过与国家政权相结合实现的D.通过自由竞争实现的9.垄断资本主义可进一步分为A.私人垄断和一般垄断两个阶段B.私人垄断和国家垄断两个阶段C.国内垄断和国际垄断两个阶段D.国家垄断和国际垄断两个阶段10.国家垄断资本主义的产生和发展是A.资产阶级自觉适应生产力发展的产物B.资本主义国家力量逐渐增强的表现C.对资本主义生产无政府状态的反映D.资本主义基本矛盾加剧的必然结果11.为了获得高额垄断利润、垄断组织在采购原材料时多采取A.垄断高价B.垄断低价C.自由价格D.市场价格12.垄断价格的出现A.违背了价值规律B.否定了价值规律C.使价值规律的作用范围受到了严重限制D.使价值规律的作用形式发生了变化13.垄断利润的产生说明A.垄断可以创造新价值B.垄断能转移更多旧价值C.价值规律不再起决定价值的作用D.价值规律作用的形式发生了变化14.国家垄断资本主义管理和调控经济的主要机制是A.自由市场经济制度B.经济政策引导C.国民经济计划化D.国家调节市场、市场引导企业15.资本主义国有经济一般不涉足的领域是A.基础设施建设B.大型科研项目C.普通消费品生产D.公共产品生产16.资本主义国家对国民经济的调控最主要是采取A.经济手段B.法律手段C.行政手段D.计划手段17.国家垄断资本主义对国民经济的调节和管理A.完全符合社会化大生产的客观内在要求B.代表了全社会的利益C.维护了垄断资产阶级的整体利益D.对社会经济发展起负作用18.垄断资本主义国家中的计划管理的作用是A.可以根除资本主义基本矛盾B.在资本主义制度内部缓解其矛盾C.导致资本主义向社会主义和平过渡D.可以消除资本主义经济危机19.垄断资本主义阶段、大量资本输出的原因是A.垄断资本主义国内不需要继续投资发展了B.发展中国家急需大量建设资金C.垄断资本的利润率太低D.对垄断资本追求高额垄断利润的需求来说资本过剩了20.垄断资本主义时期资本输出的财力基础是A.资本的原始积累B.剩余价值的资本化C.“过剩资本”的出现D.银行垄断的形成21.发达资本主义国家对发展中国家的“经济援助”A.一般都是无偿的B.是新殖民主义的一种方式C.对发展中国家是完全不利的D.是发展中国家的内在要求22.打着“援助”的旗号对发展中国家进行经济剥削和政治控制属于A.老殖民主义B.新殖民主义C.新老帝国主义的一贯做法D.发展中国家的内在要求23.当代资本主义国家在经济关系方面的一系列新变化表明A.其社会性质已经根本改变B.其基本矛盾已经彻底解决C.其社会状况并无变化D.其社会发生了阶段性的部分质变24.以下不属于当代资本主义国家经济关系方面新变化的是A.出现资本社会化趋势B.工会的产生和发展C.社会福利事业的发展D.出现工人持股现象25.资产阶级造就的置自身于死地的社会力量是A.工人阶级B.社会化的生产力C.科学技术D.巨大的社会财富26.垄断资本主义为向社会主义过渡准备了日益完备的社会经济基础主要是指A.无产阶级的产生和壮大B.社会化大生产的发展C.社会矛盾的加剧D.国家管理经济的经验二、多项选择题1.垄断价格A.是垄断组织规定的旨在保证最大限度利润的市场价格B.并未否定价值规律．C.由垄断组织随主观愿望制定D.不能由垄断组织随心所欲制定2.垄断高价和垄断低价并未否定价值规律，因为A.垄断高价和垄断低价不能完全离开商品的价值B.按垄断价格进行买卖仍然是等价交换C.全社会商品价格总额仍然等于商品的价值总额D.垄断价格改变的只是价值规律的表现形式3.垄断和竞争的关系是A.垄断是在竞争的基础上产生的B.垄断没有也不可能消除竞争C.垄断使竞争更加剧烈和复杂D.垄断与竞争并存4.资本主义国家宏观经济管理与调节的主要目标包括A.促进充分就业B.保持一定程度的经济增长C.保持币值和物价稳定D.促进国内国际收支平衡5.国家垄断资本主义宏观调控的目标一般包括A.经济增长B.币值稳定C.充分就业D.收支平衡6.资本主义国家对经济的调控手段主要包括A.经济手段B.法律手段C.必要的行政手段D.计划手段7.发达市场经济中国家调节的主要对象是A.商品市场B.资本市场C.劳动力市场D.外汇市场8.发达市场经济国家调控货币量的主要手段有A.公开市场业务B.最低准备金率政策C.再贴现利率政策D．利率政策9.垄断资本主义时期资本输出的必要性在于A.垄断资本主义国家出现大量过剩资本B．国内生产已充分满足需要、无需继续投资C.利用资本输出可使垄断资本获得高额利润D.利用资本输出可带动商品输出、扩大市场10.战后资本输出的重要特点是A.多采取“援助”的方式输出资本B.在输出流向上发展为多方向输出C.资本输出的附加条件比战前进一步减少D.国家资本输出增长更快、地位日益提高11.经济全球化的内容大体可以分为A.生产的全球化B.贸易的全球化C.销售的全球化D.资本的全球化12.资本主义生产在其自身范围内的调整包括A.股份公司的出现B.从自由竞争到垄断C.从私人垄断到国家垄断D.国际垄断资本和国际垄断同盟的发展【答案详解】一、单项选择题1.A2.C3.C4.C5.B6.C7.A8.B9.D10.B11.B12.D13.D14.D15.C16.A17.C18.B19.D20.C21.B22.B23.D24.B25.A26.B二、多项选择题1.ABD2.ACD3.ABCD4.ABCD5.ABCD6.ABCD7.ABCD8.ABC9.ACD10.ABC11.ABD12.ABCD。

微积分课后习题参考答案第六章

第六章微分方程与差分方程§1微分方程的基本概念习题 6 — 11.验证下列各题中函数是所给微分方程的解，并指出解的类型： ⑴03=+'y y x ，3-=Cx y ；解：3-=Cx y 是03=+'y y x 的通解；⑵ax xyy +='，bx ax y +=2，其中a ，b 为常数；解：bx ax y +=2是ax xy y +='的特解（因为b 不是任意常数）；⑶()()022='-'+'+''-y y y y x y x xy ，()xy y ln =；解：()xy y ln =是()()022='-'+'+''-y y y y x y x xy 的特解；⑷0127=+'-''y y y ，x xe C e C y 4231+=；解：x xe C eC y 4231+=是0127=+'-''y y y 的通解；⑸x y y y 2103=-'+''，50355221--+=-x e C e C y x x. 解：50355221--+=-x e C eC y x x是x y y y 2103=-'+''的通解. 知识点：，定义6.2（若一个函数代入微分方程后，能使方程两端恒等，则称这个函数为微分方程的解）和若微分方程的解中含有独立的任意常数且个数与微分方程的阶数相同，这样的解叫做微分方程的通解，不含任意常数的解称为特解。

2.在曲线族()xex C C y 221+=中找出满足条件10==x y ，10='=x y 的曲线.解：由题意得：()xe x C C C y 222122++='，∵10==x y ，10='=x y ， ∴解得11=C ,12-=C ，故所求曲线为()xex y 21-=（xxe y 2=）。

第六章有机化学课后习题答案

第六章卤代烃1.回答下列问题(1).在CH3CH2Cl(I),CH2═CHCl(II),CH≡CCl(III),C6H5Cl(IV)四种一氯代烃中，按C-X键键长次序排列，并讨论其理由。

解: IV< II < III <I(2).将四种化合物(A) CH3CH2CH2F，(B) CH3CH2CH2I ，(C) CH3CH2CH2Br ，(D) CH3CH2CH2Cl的沸点从最高到低排列，并讨论其理由。

解: B> C> D> A(3).四种化合物(A) CH3CHClCH2OH，(B) CH3CHNH2CH2Br ，(C) HC≡CCH2Cl，(D) CH3CONHCH2CH2Cl 中，哪些能生成稳定的格氏试剂？为什么？解: D(4).比较(A) CH3CH2CH2CH2Cl，(B) (CH3)2CHCH2Cl，(C) CH3CH2CH(Cl)CH3，(D) (CH3)3CCl四个氯代烃，它们发生S N2反应情况如何。

解: A> B> C> D(5).将①苄溴，②溴苯，③1–苯基–1–溴乙烷，④1–溴–2–苯基乙烷四个化合物按 S N1 反应的反应活性顺序排列，并讨论其理由。

解: ③>①>④>②(6).不活泼的乙烯型卤代烃能否生成格氏试剂？为什么？解:由于卤原子与双键间的 p-π共轭效应,使C-X键之间的键能增加,难以断裂。

(7).化合物：(A)正溴戊烷，(B)叔溴戊烷，(C)新戊基溴，(D)异戊基溴分别与水反应生成相应的醇，讨论它们的反应速率的差异？解: A> D> C> B(8).用极性溶剂代替质子溶剂对(A) S N1，(B) S N2，(C) 烯的亲电加成， (D) 醇的失水反应有何影响?解: 极性溶剂有利于S N1反应和烯的亲电加成反应的进行,不利于S N2反应和醇的失水反应的发生。

(9). 2–氯环己醇的反式异构体可以跟碱反应转化成环氧化物, 但顺式异构体却不能, 为什么?解: 2–氯环己醇的反式异构体跟碱反应时,进行反式消除,热力学能量低,反应速率快, 顺式异构体则不能。

第六章习题参考答案

第六章习题参考答案1、举例说明下列各词的意义。

（1）旋光体（2）比旋光度（3）对映异构体（4）非对映异构体（5）外消旋体（6）内消旋体解：略2、下列化合物分子中有无手性碳原子（用*表示手性碳原子）。

(1)(2)(3)(4)BrCH 2 CHDCH 2ClCOOHCHCl COOH OHClCH 3CHOH CH 2CH 3解：(1)(2)(3)(4)BrCH 2 CHDCH 2ClCOOH CHCl COOH OH ClCH 3CHOH CH 2CH 3无****3、写出分子式为C 3H 6DCl 所有构造异构体的结构式。

在这些化合物中哪些有手性？用投影式表示它们的对映异构体。

解：分子式为C 3H 6DCl 的化合物共有5个构造异构体，其中3个有对映异构体。

无*ClDCHCH 2CH 3CH 3CDClCH 3DCH 2CH 2CH 2Cl(5)(1)(2)(3)无*ClCH 2CHCH 3D*DCH 2CHCH 3Cl(4)(1)(3)Cl HD CH 2CH 3Cl DH CH 2CH 3CH 2Cl H D CH 3CH 2Cl DH CH 3CH 2D H Cl CH 3CH 2D Cl H CH 3(4)4、（1）丙烷氯化已分离出二氯化合物C 3H 6Cl 2的四种构造异构体，写出它们的构造式。

（2）从各个二氯化物进一步氯化后，可得到三氯化物（C 3H 5Cl 3）的数目已由气相色谱法确定。

从A 得出一个三氯化物，B 给出二个，C 和D 各给出三个，试推出A 、B 的结构。

（3）通过另一合成方法得到有旋光性的化合物C ，那么C 的构造式是什么？D 的构造式是怎样的？（4）有旋光性的C 氯化时，所得到的三氯丙烷化合物中有一个E 是有旋光性的，另二个是无旋光性的，它们的构造式是怎样的？解：（1）Cl 2CHCH 2CH 3 CH 3CCl 2CH 3 ClCH 2CHClCH 3 ClCH 2CH 2CH 2Cl （2）A 的构造式为：CH 3CCl 2CH 3（3）C 的构造式为：ClCH 2C*HClCH 3 ，D 的构造式为：Cl 2CHCH 2CH 3 （4）E 的构造式为：Cl 2CHC*HClCH 3另外两个的构造式为：ClCH 2CCl 2CH 3 ClCH 2CHClCH 2Cl 5、写出下列构型式是R 或S 。

第六章课后练习答案

第六章具体经济业务的核算课后习题答案习题一（一）计算题1、目的：练习所有者权益各项目的构成及相互关系的确定。

资料：利和股份公司所属A公司200×年年初所有者权益总额为2 318 000元，年内接受某投资人的实物投资800 000元，接受现金投资260 000元，用资本公积金转增资本120 000元。

要求：计算年末公司的所有者权益总额是多少？解答：期末的所有者权益= 期初的所有者权益+ 本期增加的所有者权益- 期末所有者权益。

利和股份公司所属A公司年末的所有者权益= 2 318 000 +（800 000 + 260 000）= 3 378 000（元）2、目的：练习权责发生制与收付实现制假设下企业损益额的确定。

资料：利和股份公司200×年6月发生下列业务：（1）销售商品520 000元，其中400 000元当即收款，存入银行；另120 000元尚未收到。

（2）收到上个月提供劳务的款项100 000元存入银行。

（3）用银行存款支付本月的水电费7 200元。

（4）用现金30 000元预付下半年的房租。

（5）用银行存款6 000元支付本季度银行借款利息（其中本月2 000元）。

（6）本月提供劳务获得收入48 000元，款项未收到。

（7）按照合同规定预收客户的订货款200 000元，存入银行。

（8）本月负担年初已付预收款的产品本月销售，价款280 000元。

（9）本月负担的修理费5 000元（款项在下个月支付）。

要求：分别按收付实现制和权责发生制计算公司本月的收入、费用和利润各是多少，并对两种原则下确定的经营成果进行简要说明。

根据题意做如下的解答：（1）收付实现制：收入= 400 000 + 100 000 + 200 000 = 700 000（元）费用= 7 200 + 30 000 + 6 000 = 43 200（元）利润= 700 000 – 43 200 = 656 800（元）（2）权责发生制：收入= 520 000 +48 000 + 280 000 = 848 000（元）费用= 7 200 + 2 000 + 5 000 = 14 200（元）利润= 848 000 – 14 200 = 833 800（元）（二）业务题1.目的：练习有关资金筹集业务的核算。

大学物理第六章课后习题答案

第六章静电场中的导体与电介质 6 －1 将一个带正电的带电体A 从远处移到一个不带电的导体B 附近，则导体B 的电势将（）（A ）升高（B ）降低（C ）不会发生变化（D ）无法确定分析与解不带电的导体B 相对无穷远处为零电势。

由于带正电的带电体A 移到不带电的导体B 附近时，在导体B 的近端感应负电荷；在远端感应正电荷，不带电导体的电势将高于无穷远处，因而正确答案为（A ）。

6 －2 将一带负电的物体M 靠近一不带电的导体N ，在N 的左端感应出正电荷，右端感应出负电荷。

若将导体N 的左端接地（如图所示），则（）（A ） N 上的负电荷入地（B ）N 上的正电荷入地（C ） N 上的所有电荷入地（D ）N 上所有的感应电荷入地分析与解导体N 接地表明导体N 为零电势，即与无穷远处等电势，这与导体N 在哪一端接地无关。

因而正确答案为（A ）。

6 －3 如图所示将一个电量为q 的点电荷放在一个半径为R 的不带电的导体球附近，点电荷距导体球球心为d ，参见附图。

设无穷远处为零电势，则在导体球球心O 点有（）（A ）d εq V E 0π4,0== （B ）dεq V d εq E 020π4,π4== （C ）0,0==V E（D ）R εq V d εq E 020π4,π4==分析与解达到静电平衡时导体内处处各点电场强度为零。

点电荷q 在导体球表面感应等量异号的感应电荷±q′，导体球表面的感应电荷±q′在球心O 点激发的电势为零，O 点的电势等于点电荷q 在该处激发的电势。

因而正确答案为（A ）。

6 －4 根据电介质中的高斯定理，在电介质中电位移矢量沿任意一个闭合曲面的积分等于这个曲面所包围自由电荷的代数和。

下列推论正确的是( )（A ）若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内一定没有自由电荷（B ）若电位移矢量沿任意一个闭合曲面的积分等于零，曲面内电荷的代数和一定等于零（C ）若电位移矢量沿任意一个闭合曲面的积分不等于零，曲面内一定有极化电荷（D ）介质中的高斯定律表明电位移矢量仅仅与自由电荷的分布有关（E ）介质中的电位移矢量与自由电荷和极化电荷的分布有关分析与解电位移矢量沿任意一个闭合曲面的通量积分等于零，表明曲面内自由电荷的代数和等于零；由于电介质会改变自由电荷的空间分布，介质中的电位移矢量与自由电荷与位移电荷的分布有关。

近代史第六章习题(含答案)

第六章中华民族的抗日战争重要知识点1.日本发动灭亡中国的侵略战争2.中国人民奋起抗击日本侵略者3.抗日战争的正面战场4.抗日战争的中流砥柱5.抗日战争的胜利及其意义练习题一、选择题（一）单选题1.毛泽东明确地提出“马克思主义的中国化”这个命题是在中国共产党的( )A.二大B.七大C.六届六中全会D.八七会议2.近代以来中国第一次取得反侵略完全胜利的战争是（）A.中法战争B.甲午战争C.抗日战争D.抗美援朝战争3.全国抗战爆发后，国民党正面战场取得的第一个大的胜利是（）A.平型关战役B.枣宜战役C.豫湘桂战役D.台儿庄战役4.全国抗战爆发后，共产党领导的敌后战场取得的第一个大的胜利是（）A.平型关伏击战B.台儿庄战役C.百团大战D.淞沪会战5.1927年日本召开“东方会议”，制定了（）A.《对华政策纲要》B.《昭和十二年度对华作战计划》C.《反共产国际协定》D.《大陆政策》6.抗日战争进入相持阶段的时间是（）A.1937年7月B.1938年5月C.1938年10月D.1941年12月7.1936年，东北各抗日武装统一为（）A.东北抗日联军B.东北义勇军C.东北人民革命军D.抗日游击队8.抗日战争进入相持阶段后，日本帝国主义对国民党采取的政策是（）A.军事打击为主，政治诱降为辅B.政治诱降为主，军事打击为辅C.军事打击和政治诱降齐头并进D.政治诱降取代军事进攻9.1939年1月，国民党确定“防共、限共、溶共、反共”方针的会议是（）A.国民党五届三中全会B.国民党五届五中全会C.国民党五届六中全会D.国民党临时全国代表大会10.日本开始实施变中国为其独占殖民地的事件是（）A.“九一八”事变B.华北事变C.皇姑屯事变D.卢沟桥事变11.确立毛泽东思想为全党的指导思想的会议是（）A.遵义会议B.瓦窑堡会议C.洛川会议D.中共七大12.面对日军的大举侵略，蒋介石在1931年7月的方针是（）A.“绝对不抵抗”B.“以华制华”C.“自强之术，必先练兵”D.“攘外必先安内”13.延安整风运动的最主要任务是（）A.反对主观主义以整顿学风B.反对宗派主义以整顿党风C.反对党八股以整顿文风D.反对官僚主义以整顿作风14.1941年中共中央批准颁布的、全面体现党关于根据地建设基本方针的是（）A.《论持久战》B.《关于若干历史问题的决议》C.《陕甘宁边区施政纲领》D.《停战议和一致抗日通电》15.中国人民抗日战争取得完全胜利的标志是（）A.1945年8月14日，日本政府表示接受波茨坦公告B.1945年8月15日，日本天皇发表终战诏书C.1945年9月2日，日本向同盟国投降签字D.1945年10月25日，中国收回被日本占领的台湾及澎湖列岛16.标志以国共合作为基础的抗日民族统一战线正式形成的是（）A.西安事变的和平解决B.国民党五届三中全会确定实行联共政策C.国民党公布了合作宣言和蒋介石发表承认中共合法地位的谈话D.7月17日，周恩来，秦邦宪等在庐山同蒋介石、张冲等进行谈判17.毛泽东在《论持久战》中分析交战的中日双方存在着相互矛盾的特点是（）A.敌强我弱；敌退步我进步；敌小国我大国；敌寡助我多助B.抗日战争是持久战，最后胜利是中国的C.战争要经过战略防御、战略相持、战略反攻D.中国是正义战争，日本是侵略战争18.在新民主主义革命时期，曾以“团结的大会，胜利的大会”载入中国共产党史册的一次具有最重要意义的会议是（）A.瓦窑堡会议B.六届六中全会C.党的“七大”D.洛川会议19.抗日战争时期，中国共产党解决农民问题的基本政策是（）A.土地国有B.没收地主土地C.减租减息D.按人口平均分配土地20.抗日战争时期，国民党第二次反共高潮达到顶点的标志是（）A.晋西事变B.陇东事变C.平江惨案D.皖南事变21.毛泽东比较完整阐明新民主主义基本理论、纲领和政策的著作是（）A.《论反对日本帝国主义的策略》B.《新民主主义论》C.《中国共产党在民族战争中的地位》D.《抗日游击战争的战略问题》22.下列关于抗战历史意义的表述，不恰当的是（）A.是中国人民近百年来第一次取得的反对帝国主义侵略斗争的完全胜利B.增强了全国人民的自尊心和自信心C.是世界反法西斯战争的重要组成部分D.结束了中国半殖民地半封建社会的历史23.中国共产党领导的民主政权实行“三三制”原则是（）A.解放战争时期B.抗日战争时期C.土地革命时期D.大革命时期24.最早为中国抗日战争提供援助的国家是（）A美国B英国C法国D苏联25.1938年5月，毛泽东发表的论述抗日战争发展规律的著作是（）A.《论反对日本帝国主义的策略》B.《论持久战》C.《中国共产党在民族战争中的地位》D.《抗日游击战争的战略问题》26.标志着中国人民抗日救亡运动新高潮的到来的是（）A.第十九路军抗战B.卢沟桥抗战C.华北事变D.一二九运动27.中国共产党内反复出现“左”、右倾错误的思想认识根源是（）A.经验主义B.宗派主义C.官僚主义D.主观主义28.抗战后期，国民党军队遭到大溃败的战役是（）A.长沙会战B.豫湘桂战役C.淞沪会战D.武汉会战29.1937年8月，中国共产党制定《抗日救国十大纲领》的会议是（）A.瓦窑堡会议B.中共七大C.洛川会议D.中共扩大的六届六中全会30.中国共产党在抗日民族统一战线中必须坚持独立自主原则的实质是（）A.力争中国共产党对抗日战争的领导权B.扩充自己的军事实力C.防止国民党顽固派的反共政策D.独自抗击日本侵略者参考答案1.C2.C3.D4.A5.A6.C7.A8.B9.B 10.A 11.D 12.D 13.A 14.C 15.D 16.C 17.A 18.C 19.C 20.D 21.B 22.D 23.B 24.D 25.B 26.D27.D 28.B 29.C 30.A（二）多选题1.1938年9月至11月，中国共产党在延安举行的扩大的六届六中全会，会议纠正了王明的右倾错误是（）A.一切经过统一战线B.轻视共产党领导的游击战争C.关门主义D.一切服从统一战线2.延安整风运动是一场伟大的思想解放运动。

第六章习题答案

第六章、七章、八章课后习题答案

第六章习题及答案

第六章++课后习题+参考答案

大学物理课后习题答案第六章

(完整版)第六章线性空间练习题参考答案

第六章 习题答案 1. (1)临界分切应力n及取向因子数据如附表23 …

有机化学-第六章-卤代烃-习题答案

习题答案(第六章)

第六章 习题及答案

第六章完全竞争市场习题+答案

生物化学第六章维生素辅酶和激素习题含答案

No3.第6章习题及答案

第六章习题及答案

微积分课后习题参考答案第六章

第六章有机化学课后习题答案

第六章习题参考答案

第六章 课后练习答案

大学物理第六章课后习题答案

近代史第六章 习题(含答案)

第六章习题答案 1. (1)临界分切应力n及取向因子数据如附表23 …

第六章习题及答案

第六章课后练习答案

近代史第六章习题(含答案)