2019年安徽省皖智“1号卷”A10联盟高三下学期开学联考理科数学试题(含答案)
安徽省皖中名校联盟2019届高三10月联考数学(理)试题(原卷版)

皖中名校联盟2019届高三10月联考数学试题卷(理科)第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.每一小题给出的四个选项中只有一项是符合题目要求的.1.命题“4,0x R x x ∀∈+≥”的否定是( ) A. 4,0x R x x ∀∈+< B. 4,0x R x x ∀∈+≤ C. 4000,0x R x x ∃∈+≥D. 4000,0x R x x ∃∈+<2.已知2{|430},{|P x x x Q y y =-+<==,则P Q =( )A. [0,1)B. [0,2)C. (1,2]D. (1,2)3.由曲线3,y x y == )A.512B.13 C. 14 D. 12 4.已知向量AB 与AC的夹角为3π,()2,3,,AB AC AM AB AC R λμλμ===+∈,且A M B C ⊥,则λμ=( ) A.16B. 6C.14D. 45.设函数21()1xxf x e e x -=+-+,则使得(2)(1)f x f x >+成立的x 的取值范围是( ) A. (,1)-∞B. (1,)+∞C. 1(,1)3- D. 1(,)(1,)3-∞-+∞U6.“0a ≥”是“函数()(1)f x ax x =+在区间(0,)+∞上单调递增”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7.已知数列{}n a 为等差数列,其前n 项和为n S ,且13623a a S +=,给出以下结论: ①100a =;②10S 最小;③712S S =;④190S =. 其中一定正确的结论是( )A. ①②B. ①③④C. ①③D. ①②④8.函数4lg x x y x=的图象大致是( )A.B.C.D.9.已知函数()()sin 0,0,2f x A x A πωφωφ⎛⎫=+>><⎪⎝⎭,其图象相邻两条对称轴之间的距离为2π,且()f x 的图象关于点,012π⎛⎫- ⎪⎝⎭对称,则下列判断正确的是( ) A. 要得到函数()f x的图象只将2y x =的图象向右平移6π个单位B. 函数()f x 的图象关于直线512x π=对称 C. 当,66x ππ⎡∈-⎤⎢⎥⎣⎦时,函数()f x 的最小值为D. 函数()f x 在,63ππ⎡⎤⎢⎥⎣⎦上单调递增10.已知定义在R 上的奇函数()f x 满足(2)()f x f x +=-,当01x <<时,()21x f x =-,则2(log 9)f =( )A. 79-B. 8C. 10-D. 259-11.设函数121,1(),4,1x x f x x x +⎧-≤⎪=⎨->⎪⎩若互不相等的实数,,p q r 满足()()(),f p f q f r ==则222p q r ++的取值范围是( ) A. (8,16)B. (9,17)C. (9,16)D. 1735(,)2212.已知2()f x x ax b =++,集合{|()0}A x f x =≤,集合{|[()]3}B x f f x =≤,若A B =≠∅,则实数a 的取值范围是( )A .[6,2]-B.C. [2,-D. [6,--第П卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.请将答案填写在答题卷相应位置上.13.已知平面向量,a b 满足2,1,223a b a b ==+=,则a b r r与的夹角为___________.14.函数()y f x =的图象和函数log (0a y x a =>且1)a ≠的图象关于直线y x =-对称,且函数()(1)3g x f x=--,则函数()y g x =图象必过定点___________。
安徽省A10联盟2019届高三第三次模拟考试数学(理)试题

安徽省A10联盟2019届高三第三次模拟考试数学(理)试题本试题卷共6页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{|A x y ==,{|21}x B x =≥,则A B =( )A .{|03}x x ≤≤B .{|13}x x -≤≤C .{|01}x x ≤≤D .{|11}x x -≤≤2.若a R ∈,则“cos α=”是“sin 21α=”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要3.若等差数列{}n a 的前n 项和n S ,且330S =-,840S =-,则11S =( ) A .-16 B . -18 C . -20 D . -224.如图,在平行四边形ABCD 中,AC 与BD 交于点O ,,E F 分别为,AD CD 的中点,则BF =( )A.1433BE OF+B.3122BE OF+ C.1322BE OF+D.4133 BE OF+5.函数3sin()1cos2xf xx=+的图像大致为()A.B.C.D .6.定义在R 上的函数()f x 的图像连续且关于原点对称,当(,0]x ∈-∞时,'()0f x >,若(1)3f -=-,则不等式|(34)|3f x -≥的解集为( )A .5[1,]3 B .5(,0][1,]3-∞ C. 5(0,1][,)3+∞ D .5(,1][,)3-∞+∞7.已知2(tan )sin sin 2f x x x =-,记1s i n ()2fα=,其中α是第四象限角,则tan()4πα+=( ) A .17 B .17- C. 7 D .-7 8.已知函数)sin()(ϕω+=x A x f )||,0,0(πϕω<>>A 的部分图像如图所示,将函数()f x 的图像上所有点的横坐标缩短为原来的13,得到新函数()g x 图像的一条对称轴为( )A .6x π=B .12x π=C. 6x π=-D .3x π=-9.已知131log 2a =,5log 6b =,6log 7c =,则,,a b c 的大小关系是( ) A .c b a << B .a b c << C. b a c << D .a c b <<10.已知函数5,3()log ,3ax x f x x x -+≤⎧=⎨>⎩(0a >且1a ≠),若函数()f x 无最小值,则实数a 的值不可能为( ) A .12 B .32C. 2 D .4 11.在ABC ∆中,内角,,A B C 的对边分别为,,a b c ,若ABC ∆的面积为218c ,则a bb a+的最大值为( )A . 2B .4 C..12.已知曲线321()2(0)32a f x x x x a =-+->与直线13y kx =-相切,且满足条件的k 值有且只有3个,则实数a 的取值范围是( )A .[2,)+∞B .(2,)+∞ C. [1,)+∞ D .(1,)+∞第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知向量(1,3)a =-,(8,)b m =,且向量b 在向量a 方向上的投影是,则||b = .14.已知实数,x y 满足103(4)x x y y m x -≥⎧⎪≤-⎨⎪≥-⎩,其中0m >,若2z x y =+的最小值为1,则实数m 的值为 .15.已知实数,(0,)m n ∈+∞且1m n +=,则4133m n m n+++的最小值为 .16.在数列{}n a 中,12a =-,23a =,34a =,31(1)2n n n a a +++-=,记n S 是数列{}n a 的前n 项和,则41S 的值为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 已知命题:[1,0]p x ∀∈-,2log (2)2x m +<;命题q :关于x 的方程2220x x m -+=有两个不同的实数根.(1)若()p q ⌝∧为真命题,求实数m 的取值范围;(2)若p q ∨为真命题,p q ∧为假命题,求实数m 的取值范围. 18. 已知数列{}n a 的前n 项和n S ,且423n n a S -=. (1)求数列{}n a 的通项公式; (2)设41log n nb a =,求数列12{}n n b b ++的前n 项和n T .19. 在ABC ∆中,角,,A B C 的对边分别为,,a b c ,8a =,1cos 3c b a B -=. (1)若ABC ∆有两解,求b 的取值范围;(2)若ABC ∆的面积为B C >,求b c -的值. 20. 已知函数()2sin(2)(0)6f x x πωω=+>.(1)若点5(,0)8π是函数()f x 图像的一个对称中心,且(0,1)ω∈,求函数()f x 在3[0,]4π上的值域;(2)若函数()f x 在2(,)33ππ上单调递增,求实数ω的取值范围.21. 已知函数1()f x x x=+.(1)若关于x 的不等式(3)32x xf m ≤+在[2,2]-上恒成立,求实数m 的取值范围; (2)若函数2()(|21|)32|21|xx tg x f t =-+---有四个不同的零点,求实数t 的取值范围.22. 已知函数2()ln f x mx x x =++,0m ≤. (1)讨论函数()f x 的单调性;(2)若(0,)x ∃∈+∞,使得关于x 的不等式3()()xf x n mx n Z ≤+∈成立,求n 的最小值.试卷答案一、选择题1.A 由题意得:{|13}A x x =-≤≤,{|0}B x x =≥,∴{|03}AB x x =≤≤,故选A.2.B 若sin 21α=,则c o s 20α=,此时22cos 10α-=,解得:cos α=;若c o s 2α=±,则c os20α=,∴sin 21α=±;故“cos 2α=±”是“sin 21α=”的必要不充分条件,故选B3.D 法一:设等差数列{}n a 的公差为d ,根据题意得:11333082840a d a d +=-⎧⎨+=-⎩,解得112a =-,2d =,∴11111011(12)2222S ⨯=⨯-+⨯=-,故选D法二:836510S S a -==-,∴62a =-,∴1161122S a ==-,故选D 4.C 1113()2222BF BO OF BD OF BE ED OF BE OF =+=+=++=+,故选C 5.A 因为()()f x f x -=-,故函数()f x 为奇函数,排除C ;因为1cos 20x +≠,故()2x k k Z ππ≠+∈,排除B ;33sin34()0341cos 2f πππ=>+,排除D ;故选A. 6.D 由题意得:函数()f x 为奇函数,故(1)(1)3f f -=-=-,即(1)3f =,∴ |(34)|(1)|(1)|f x f f -≥=,易知函数|()|f x 为偶函数,故|34|1x -≥,解得53x ≥或1x ≤,故选D7.A ∵22222sin 2sin cos tan 2tan (tan )sin cos tan 1x x x x xf x x x x --==++,∴13()25f =-,即3sin 5α=-,又α是第四象限角,∴4cos 5α=,∴3tan 4α=-,∴1tan 1tan()41tan 7πααα++==-,故选A8.C 由题意得:2A =,2()434T ππππω=-⨯==,解得23ω=,则2232k ππϕπ+=+,k Z ∈,∵6πϕ=-,∴2()2sin()36f x x π=-,∴()2sin(2)6g x x π=-,令262x k πππ-=+,k Z ∈,解得:32k x ππ=+,k Z ∈,故选C 9.D ∵3log 21a =<,1b >,1c >,∴选项A ,C 排除;又256lg6lg7(lg6)lg5lg7log 6log 7lg5lg6lg5lg6b c --=-=-=,∵222lg 5lg 7lg 5lg 7()(lg 6)2+<=<,∴b c >,∴a c b <<,故选D 10.B 由题意得:当01a <<时,函数()f x 无最小值,符合题意;当1a >时,若函数()f x 无最小值,结合图像可知,log 32a <,解得a >a 的取值范围为(0,1)(3,)+∞,故选B11.C 由题意得,211sin 28S ab C c ==,∴24sin c ab C =,又2222cos c a b ab C =+-,∴2222cos a b c ab C +=+,∴2222cos a b a b c ab Cb a ab ab +++==4sin 2cos 4sin 2cos ab C ab CC C ab+==+)C ϕ=+,则a bb a+的最大值为 C 12.B 由题意得:2'()2f x x ax =-+-,设切点321(,2)32a P t t t t -+-, 则其切线的斜率为2'()2k f t t at ==-+-,所以切线方程为32212(2)()32a y t t t t at x t +-+=-+--,又点1(0,)3-在切线上, ∴322112(2)(0)332a t t t t at t -+-+=-+--,即322110323t at -+=,由题意得,方程322110323t at -+=有三个不同的实数解,记32211()323h t t at =-+,则2'()2h t t at =-,当0a >时,令'()0h t >,解得0t <或2a t >,令'()0h t <,解得02a t <<,则函数()h t 在(,0)-∞上单调递增,在(0,)2a 上单调递减,在(,)2a+∞上单调递增,∵1(0)3h =,311()2243a h a =-+,∴要使方程322110323t at -+=有三个不同的实数解,则()02ah <,解得2a >,故选B二、填空题 13. 10由题意知,||10a b a ==6m =,∴||10b = 14.13作出不等式组所表示的平面区域如图中阴影部分所示,其中(1,3)A m -,34(,)11m mB m m +-++,(1,2)C ,观察可知,当直线2z x y =+过点A 时,z 有最小值,即231m -=,解得13m =.15.94令3m n x +=,3m n y +=,∴4x y +=,∴4141141()()334x y m n m n x y x y +=+=++++149(5)44y x x y =++≥,当且仅当2,4x y x y =+=,即84,33x y ==,即51,66m n ==时等号成立. 16.458由题意知,当n 是奇数时,312n n a a ++-=,又23a =,∴数列{}n a 中的偶数是以3为首项,2为公差的等差数列,∴24640201920324402a a a a ⨯++++=⨯+⨯=;当n 是偶数时,312n n a a +++=,∴数列{}n a 中的相邻的两个奇数项之和均等于2, ∴13573941135793941()()()a a a a a a a a a a a a a ++++++=+++++++22018-+=∴4144018458S =+=. 三、解答题17.(1)令2()log (2)f x x =+,则函数()f x 在[1,0]-上是增函数, 故当[1,0]x ∈-时,()f x 最大值为(0)1f =. 当命题p 为真时,则21m >,解得12m >. 当命题q 为真时,则2440m ∆=->,解得11m -<<. 若()p q ⌝∧为真,则p 假q 真,∴1211m m ⎧≤⎪⎨⎪-<<⎩,解得112m -<≤, 即实数m 的取值范围为1(1,]2-.(2)若p q ∨为真命题,p q ∧为假命题,则,p q 一真一假,若p 真q 假,则1211m m m ⎧>⎪⎨⎪≤-≥⎩或,解得1m ≥; 若p 假q 真,则1211m m ⎧≤⎪⎨⎪-<<⎩,解得112m -<≤. 综上所述,实数m 的取值范围为1(1,][1,)2-+∞.18.(1)∵423n n a S -=, ∴当2n ≥时,11423n n a S ---=,两式相减得,134()n n n a a a -=-, ∴14n n a a -=,即14nn a a -=, 由11342S a =-,得12a =,∴数列{}n a 是以2为首项,4为公比的等比数列. ∴121*242()n n n a n N --=⨯=∈. (2)由(1)知,214421log log 22n n n a --==, ∴221n b n =-, ∴124112()(21)(23)2123n n b b n n n n ++==-++++,∴1111112()35572123n T n n =-+-++-++2423(23)3(23)n nn n =⨯=++. 19.(1)∵1cos 3c b a B -=,∴1sin sin sin cos 3C B A B -=, ∴1sin cos sin cos sin sin cos 3A B B A B A B +-=.∵sin 0B ≠,∴1cos 3A =,∴sin A =若ABC ∆有两解,∴sin 8b A b <<,解得8b <<b 的取值范围为.(2)由(1)知,1122sin 822ABC S bc A bc ∆===24bc =, ∵2222cos a b c bc A =+-24()3b c bc =-+, ∴224()824323b c -=-⨯=,∵B C >,∴b c -=20.(1)由题意得:5,46k k Z ππωπ+=∈, ∴41()56k ω=-,k Z ∈, ∵(0,1)ω∈,∴23ω=, ∴4()2sin(2)2sin()636f x x x ππω=+=+, ∵3[0,]4x π∈,∴47[,]3666x πππ+∈, ∴41sin()[,1]362x π+∈-, 故函数()f x 在3[0,]4π上的值域为[1,2]-. (2)令222,262k x k k Z ππππωπ-+≤+≤+∈, 解得36k k x ππππωωωω-≤≤+, ∵函数()f x 在2(,)33ππ上单调递增, ∴002(,)(,)3336k k ππππππωωωω⊆-+,0k Z ∈,∴0033263k k πππωωπππωω⎧-≤⎪⎪⎨⎪+≥⎪⎩,即0031614k k ωω≤+⎧⎨+≥⎩, 又2123322πππω-≤,∴302ω<≤, ∴01566k -<≤,∴00k =, ∴104ω<≤,即ω的取值范围为1(0,]4. 21.(1)由题意得:13323x x x m +≤+在[2,2]x ∈-上恒成立, 故211()2()133x x m ≥-+在[2,2]x ∈-上恒成立, 令13x s =,∵[2,2]x ∈-,∴1[,9]9s ∈, 则2221(1)m s s s ≥-+=-在1[,9]9s ∈上恒成立, 又当9s =时,2max (1)64s -=,∴64m ≥.即实数m 的取值范围为[64,)+∞.(2)方程2(|21|)320|21|x x t f t -+--=-, 即12|21|320|21||21|x x x t t -++--=--, ∴2|21|(32)|21|(21)0x x t t --+-++=(|21|0x ->).令|21|x r =-,则2(32)(21)0r t r t -+++=,(0,)r ∈+∞,故问题转化为关于r 的方程2(32)(21)0r t r t -+++=有两个不相等的实数根1r 和2r , 且101r <<,201r <<,记2()(32)(21)h r r t r t =-+++,则2(32)4(21)0(0)210(1)032012t t h t h t t ⎧∆=+-+>⎪=+>⎪⎪⎨=->⎪+⎪<<⎪⎩,∴409102203t t t t ⎧><-⎪⎪⎪-<<⎨⎪⎪-<<⎪⎩或,解得1429t -<<-, 即实数t 的取值范围为14(,)29--. 22.(1)由题意得,函数()f x 的定义域为(0,)+∞,2121'()21mx x f x mx x x++=++=, 若0m =,1'()10f x x=+>恒成立,则函数()f x 在(0,)+∞上单调递增; 若0m <,设2()21h x mx x =++,令()0h x =,180m ∆=->, 则12102x x m +=->,12102x x m =<,故104x m-=>,∴当x ∈时,'()0f x >;当)x ∈+∞时,'()0f x <, 则函数()f x在上单调递增,在)+∞上单调递减, 综上所述,当0m =时,函数()f x 在(0,)+∞上单调递增;当0m <时,函数()f x在上单调递增,在)+∞上单调递减. (2)由题意得:323ln ()mx x x x n mx n Z ++≤+∈,即2ln ()x x x n n Z +≤∈.令2()ln g x x x x =+,则'()2ln 1g x x x =++,函数'()g x 在(0,)+∞上单调递增, 1'()2ln 202g =->,15'()ln 8084g =-<, 则存在唯一011(,)82x ∈,使得0'()0g x =,即000'()2ln 10g x x x =++=. 当0(0,)x x ∈时,'()0g x <,当0(,)x x ∈+∞时,'()0g x >,∴22min 0000000()()ln (21)g x g x x x x x x x ==+=+--2200011()24x x x =--=-++ ∵011(,)82x ∈,∴039()464g x -<<-, 由题意得,0()n g x ≥,且n Z ∈,故n 的最小值为0.。
2019届安徽省示范联盟高三下学期5月大联考数学(理)试题(解析版)

2019届安徽省示范联盟高三下学期5月大联考数学(理)试题一、单选题1.已知集合{}|21,A x x x Z =-<≤∈,则集合A 中元素的个数为( ) A .0 B .1C .2D .3【答案】D【解析】直接根据集合的定义即可得结果. 【详解】{}{}|21,1,0,1A x x x Z =-<≤∈=-,所以集合A 中元素的个数为3.故选:D. 【点睛】本题主要考查了集合的表示方法——描述法,属于基础题.2.设复数12z i =+(i 是虚数单位),则复数()z z i +在复平面内对应点在( ) A .第一象限 B .第二象限C .第三象限D .第四象限【答案】A【解析】根据共轭复数的概念结合复数的运算求出()z z i +,最后根据复数的几何意义即可得结果. 【详解】()()()()()12121213z z i i i i i i i +=+-+=+-=+,对应的点为()3,1,即复数()z z i +在复平面内对应点在第一象限, 故选:A. 【点睛】本题主要考查了共轭复数的概念,复数的运算,复数的几何意义,属于基础题. 3.我国古代的“割圆术”相当于给出已知圆的半径r ,计算其面积S 的近似值,进一步计算圆周率的近似值.根据 3.14159π=⋅⋅⋅判断,下列近似公式中最接近π的是( )A .r ≈B .r ≈C .r ≈D .r ≈【答案】C【解析】先阅读理解题意,再通过运算进行简单的合情推理即可得解. 【详解】 由2S r π=得Sr π=,由A 得,1573.1450π≈≈;由B 得,3π≈; 由C 得,22 3.142897π≈≈;由D 得,27 3.3758π≈≈. 即最接近π的值为3.143, 故选:C . 【点睛】本题主要考查了阅读能力及简单的合情推理,属中档题.4.下面程序框图是为了求出m ,n 的最大公约数,那么在①②③三个空白框中,可以依次填入( )A .n r = m n = 输出nB .m n = n r = 输出nC .m n = n r = 输出mD .n r = m n = 输出m【答案】B【解析】根据求m ,n 的最大公约数的步骤,进行判断即可. 【详解】设m nk r =+,若0r =,则m ,n 的最大公约数为n ;若0r ≠,则需要令m n =,n r =,如法炮制,直到m 被n 整除, 故选:B. 【点睛】本题主要考查程序框图的识别和判断,根据求m ,n 的最大公约数步骤是解决本题的关键,属于中档题.5.如图所示为三棱锥的三视图以及尺寸,则三棱锥的体积为( )A .83B .2C .3D .4【答案】A【解析】直接利用三视图的转换,进一步利用几何体的体积公式的应用求出结果. 【详解】三视图对应的三棱锥为如图的三棱锥ABCD ,且4BD =,2CD =,A 到平面BCD 的距离为2,所以三棱锥的体积为11182423323BCD S h ⎛⎫⋅=⨯⨯⨯⨯= ⎪⎝⎭△. 故选:A.【点睛】本题考查的知识要点:三视图和几何体之间的转换,几何体的体积公式的应用,主要考查学生的运算能力和转换能力,属于基础题型.6.如图,在正方形ABCD 中,以AB ,AD 边为直径向正方形内作两个半圆交于O 点,若某机械手向正方形ABCD 内随机投入一个质点,则该质点落入这两个半圆的并集所在区域内的概率为( )A .3216π+ B .4π C .28π+ D .68π-【答案】C【解析】这是一个几何概型,设正方形边长为2,再求得两个半圆的并集所在区域的面积,代入公式求解. 【详解】设正方形边长为2,则这两个半圆的并集所在区域的面积为21121422πππ⎛⎫⋅-⨯-=+⎪⎝⎭, 所以该质点落入这两个半圆的并集所在区域内的概率为12248ππ++=.故选:C 【点睛】本题主要考查几何概型的概率,还考查了运算求解的能力,属于基础题.7.在四边形ABCD 中,若AD u u u r ,BC uuu r不共线,E ,F 分别为AB ,CD 上的点,且13AE AB =u u u r u u u r ,13DF DC =u u u r u u u r ,则EF =u u u r( )A .1133AD BC +u u u r u u u rB .2133AD BC +u u ur u u u rC .1133AD BC -u u u r u u u r D .1233AD BC +u u ur u u u r【答案】B【解析】连接AC ,在AC 取一点O ,使得13AO AC =u u u r u u u r,连接OE ,OF ,结合题意易知EO uuu r 和BC uuu r ,OF uuu r 和AD u u u r的关系,进而可得结果.【详解】连接AC ,在AC 取一点O ,使得13AO AC =u u u r u u u r,连接OE ,OF .因为13AE AB =u u u r u u u r ,13DF DC =u u u r u u u r,所以13EO BC =u u u r u u u r ,23OF AD =u u u r u u u r ,所以1233EF EO OF BC AD =+=+u u u r u u u r u u u r u u u r u u u r .故选:B. 【点睛】本题主要考查了平面向量基本定理的应用,但是本题不好建立坐标系,作辅助线结合向量共线定理是解题的关键,属于中档题. 8.已知4log 5a =,3log 2b =,1161log 36c =,则a ,b ,c 从小到大排序为( )A .a b c <<B .b c a <<C .c b a <<D .b a c <<【答案】D【解析】直接利用对数函数的单调性即可得出结果. 【详解】由已知得,342116log 21log 5136log log b a c =<<==<=162log 36log ==故选:D . 【点睛】本题主要考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.9.一个圆经过以下三个点12A ⎫⎪⎭,(3,0)B -,(0,2)C -,且圆心在y 轴上,则圆的标准方程为( )A .22211344x y ⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭ B .22251344x y ⎛⎫⎛⎫+±= ⎪ ⎪⎝⎭⎝⎭C .2251344x y ⎛⎫+-= ⎪⎝⎭ D .22251344x y ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭ 【答案】D【解析】根据题意设出圆心,利用圆心到三点的距离相等建立等式,从而求得标准方程. 【详解】解:设圆心坐标为()0,b ,半径为r ,则圆的方程为()222x y b r +-=,则()222222110292b rb r b r ⎧⎛⎫+-=⎪ ⎪⎝⎭⎪⎪+=⎨⎪+=⎪⎪⎩,解得54b =,216916r =.∴圆的标准方程为22251344x y ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭.故选:D . 【点睛】本题主要考查圆的标准方程,重点找出圆心及半径是关键,难度不大.10.设函数()322x ax x f b x =+++,且()()112f x f x ++-=,则曲线()y f x =在1x =处的切线方程为( )A .0y =B .1y =C .y x =D .23y x =-+【答案】D【解析】根据()()112f x f x ++-=,得到函数()322x ax x f b x =+++的图象关于点()1,1对称,令()()()3111f x x k x =-+-+,利用待定系数法求得()f x ,然后利用导数的几何意义求切线方程. 【详解】因为()()112f x f x ++-=,所以函数()322x ax x f b x =+++的图象关于点()1,1对称,所以函数()()()()33211133f x x k x x x k x k =-+-+=-++-, 所以3a =-,3b k =+,2k -=, 解得,3a =-,1b =, 所以()3232f x x x x =-++,所以()2'361f x x x =-+,()()'12,11f f =-=所以曲线()y f x =在1x =处的切线方程为()()()1'11y f f x -=-, 即23y x =-+. 故选:D 【点睛】本题主要考查由函数的对称性求解析式以及导数的几何意义,还考查了运算求解的能力,属于中档题.11.设抛物线C :24y x =的焦点为F ,点A 的坐标为()2,0-,直线()20x ky k +=>与C 交于M ,N 两点,2AN AM =u u u r u u u u r ,则FM FN ⋅=uuu r uuu r( ) A .8 B .7 C .6D .5【答案】A【解析】抛物线方程与直线方程联立,得到2480y ky -+=,根据2AN AM =u u u r u u u u r,得到212y y =,再利用韦达定理求得1y ,2y ,k ,再根据()1,0F ,利用数量积公式求解FM FN ⋅u u u u r u u u r .【详解】由24y x =与()20x ky k +=>,联立得,2480y ky -+=,设M ,N 的坐标分别为()11,x y ,()22,x y ,所以121248y y ky y +=⎧⎨=⎩,因为2AN AM =u u u r u u u u r ,所以212y y =,所以12y =,24y =,32k =,因为()1,0F ,所以()111,FM x y =-u u u u r ,()221,FN x y =-u u u r,所以()()121211FM FN x x y y ⋅=--+u u u u r u u u r 12123333822y y y y ⎛⎫⎛⎫=--+= ⎪⎪⎝⎭⎝⎭.故选:A 【点睛】本题主要考查直线与抛物线的位置关系以及平面向量的基本运算,还考查了运算求解的能力,属于中档题.12.在四棱锥E ABCD -中,已知1AB =,BC,2CD =,DA =形BDE 是边长为2的正三角形,当四棱锥E ABCD -的外接球的体积取得最小值时,则以下判断正确的是( )A .四棱锥E ABCD -的体积取得最小值为612,外接球的球心必在四棱锥E ABCD -内B .四棱锥E ABCD -的体积取得最小值为64+,外接球的球心可在四棱锥E ABCD -内或外C .四棱锥E ABCD -的体积为612,外接球的球心必在四棱锥E ABCD -内 D .四棱锥E ABCD -E ABCD -内或外 【答案】C【解析】根据22222AB AD BC CD BD +=+=,得到AB AD ⊥,BC CD ⊥,说明四边形ABCD 有一个外接圆,且圆心为BD 的中点设为1O ,设外接球的球心为O ,利用截面圆的性质,则1OO ⊥平面ABCD ,设1OO x =,同理过O 作平面BDE 的垂线,垂足为F ,F 为正三角形BDE 的外心,设OF y =,外接球的半径为r ,则有222221r x y =+=+,然后根据当四棱锥E ABCD -外接球的体积取得最小时,外接球的半径最小求解. 【详解】当四棱锥E ABCD -外接球的体积取得最小时,外接球的半径最小.由已知得,22222AB AD BC CD BD +=+=,所以AB AD ⊥,BC CD ⊥, 所以四边形ABCD 有一个外接圆,且圆心为BD 的中点设为1O , 设外接球的球心为O ,则1OO ⊥平面ABCD ,设1OO x =, 过O 作平面BDE 的垂线,垂足为F ,则F 为三角形BDE 的外心,设OF y =,外接球的半径为r ,则222221r x y =+=+,所以221133x y =+≥,所以3x ≥,当且仅当0y =时,外接球的体积取得最小值,此时平面BDE ⊥平面ABCD ,243r =可得四棱锥E ABCD -的体积为1161322212⎛⎫+⨯⨯= ⎪ ⎪⎝⎭,且外接球的球心必在四棱锥E ABCD -内. 故选:C 【点睛】本题主要考查球的截面性质,还考查了空间想象和运算求解的能力,属于中档题.二、填空题13.sin 330°–cos 240°+tan 150°的值为__________.【答案】3-【解析】利用诱导公式结合特殊角三角函数值求解即可 【详解】sin330°–cos240°+tan150°=sin (360°–30°)–cos (180°+60°)+tan (180°–30°)=–sin30°+cos60°–tan30°113 223=-+-33=-.故答案为3-.【点睛】本题考查诱导公式,特殊角三角函数值求解,熟记公式准确计算是关键,是基础题14.设x,y满足约束条件1124x yx yx y-≥⎧⎪+≥⎨⎪-≤⎩,已知当1x=,0y=时,mx y-+取得最大值,则m的取值范围是______.【答案】[)1,+∞【解析】作出不等式组对于的平面区域,利用数形结合即可得到结论.【详解】作出x,y满足约束条件1124x yx yx y-≥⎧⎪+≥⎨⎪-≤⎩,对应的平面区域如图:由z mx y=-+,得y mx z=+,则当y mx z=+截距最大时,z也取得最大值,要使若z mx y=-+在点()10,处取得最大值,则不等式组对应的平面区域在直线y mx z=+的下方,则1mm>⎧⎨≥⎩,解得m1≥,故答案为:[)1,+∞.【点睛】本题主要考查线性规划的应用,利用z 的几何意义,利用数形结合是解决本题的关键,属于中档题.15.记n S 为数列{}n a 的前n 项和.若221n n S a n n =+-+,则6a =______.【答案】11【解析】根据数列通项与前n 项和间的关系,由221n n S a n n =+-+,得到211(1)2(1)1n n S a n n ++=++-++,两式相减求解.【详解】因为221n n S a n n =+-+,所以211(1)2(1)1n n S a n n ++=++-++,两式相减得:2211(1)2(1)2n n n a a a n n n n ++=-++--++,即21n a n =-, 所以611a =. 故答案为:11 【点睛】本题主要考查数列通项与前n 项和间的关系,还考查了运算求解的能力,属于中档题. 16.已知圆锥的母线l 长为3,侧面积为S ,体积为V ,则VS取得最大值时圆锥的底面半径为______.【答案】2【解析】设圆锥的底面半径为r ,高为h ,根据圆锥的几何特征,则有222r h l +=,再由2139r h V rhS rl ππ==,利用重要不等式求解. 【详解】设圆锥的底面半径为r ,高为h ,则222239r h l +===,所以222111913992922r h V rh r h S rl ππ+==≤⨯=⨯=,当且仅当2r h ==时取等号.故答案为:2【点睛】本题主要考查圆锥的几何特征,体积,侧面积的求法以及重要不等式的应用,还考查了运算求解的能力,属于中档题.三、解答题17.在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ;()2cos sin 1cos c A B a C b ⋅-=-.(1)求角B 的大小;(2)在锐角三角形'''A B C 中,角'A ,'B ,'C 的对边分别为'a ,'b ,'c ,若'b ='a =+'2B B ∠=∠,求三角形'''A B C 的内角平分线''B D 的长.【答案】(1)6π(2)【解析】(1)利用正弦定理将2cos (sin 1)cos c A B a C b ⋅-=-中的边转化为角,然后利用两角和的公式化简,根据锐角三角形确定角B .(2)根据'2B B =,得到'3B π=.,在三角形'''A B C 中,由余弦定理解得边'c ,利用正弦定理解得 'C ,'A ,然后根据''B D 为内角平分线求解. 【详解】(1)因为2cos (sin 1)cos c A B a C b ⋅-=-, 所以2sin cos (sin 1)sin cos sin C A B A C B ⋅-=-, 所以2sin cos (sin 1)sin cos sin()C A B A C A C ⋅-=-+, 所以2sin cos (sin 1)sin cos C A B C A ⋅-=-, 在锐角三角形ABC 中,0,2A π⎛⎫∈ ⎪⎝⎭,即cos 0A ≠,sin 0C >, 所以2(sin 1)1B -=-,所以1sin 2B =, 因为B 为锐角,所以6B π=;(2)因为'2B B =,所以'3B π=.在三角形'''A B C 中,由余弦定理得,'2'2'2'''2cos b a c a c B =+-,()()()22'2'2362262cos3c c π=++-+,即()'2'624340cc -++-=, 解得,'22c =或'62c =-.当'62c =-时,()()()222'2'2'2236262b c a +-=+--+12830=-<,所以此时角'A 为钝角,不符合三角形ABC 为锐角三角形,所以'22c =.由正弦定理得,''''sin sin c b C B=, 所以''''22sin 232sin s 3i 2n c BC bπ===, 所以'4C π=,'512A π=, 因为''B D 为内角平分线,所以'''''''512A DBC BD C π∠=∠+=, 所以''''A D B A ∠=,所以''''22B D B A ==. 【点睛】本题主要考查正弦定理,余弦定理和两角和正弦公式的应用,还考查了运算求解的能力,属于中档题.18.在直四棱柱1111ABCD A B C D -中,四边形ABCD 为平行四边形,E 为1DD 的中点,BC BD a ==,12AB AA a==.(1)求证:平面1A BE ⊥平面1BDC ; (2)求直线1BD 与直线1C D 所成角θ的余弦值.【答案】(1)证明见解析 (2)36【解析】(1)取1CC 的中点F ,连接FE ,1FB ,在矩形11BCC B 中,得到11B F BC ⊥,易得BD ⊥平面11BCC B ,从而得到1BD B F ⊥,利用线面垂直的判定定理得到1B F ⊥平面1C BD ,由直四棱柱的几何特征,知11//A E B F ,有1A E ⊥平面1C BD ,再利用面面垂直的判定定理得到平面1A BE ⊥平面1BDC .(2)建立空间直角坐标系D xyz -,分别求得1C D u u u u r ,1BD u u u u r的坐标,代入公式1111cos C D BD C D BD θ⋅=u u u u r u u u u ru u u u r u u u u r 求解.【详解】 (1)如图所示:取1CC 的中点F ,连接FE ,1FB .在直四棱柱1111ABCD A B C D -中,四边形11A B FE 为平行四边形,所以11//A E B F , 在矩形11BCC B 中,因为BC a =,112BB AA a ==, 所以11111tan 2BB B C B B C ∠==,11111tan 2B CB FC C F∠== 所以1111B C B B FC ∠=∠,所以11B F BC ⊥,因为BC BD a ==,12AB AA a =,所以222BC BD AB +=,所以BD BC ⊥, 因为1BB ⊥平面ABCD ,所以1BB BD ⊥,因为1BC BB B =I ,所以BD ⊥平面11BCC B ,所以1BD B F ⊥, 因为1BD BC B =I ,所以1B F ⊥平面1C BD ,所以1A E ⊥平面1C BD , 因为1A E ⊂平面1A BE ,所以平面1A BE ⊥平面1BDC ; (2)建立如图的坐标系D xyz -,则()0,0,0D,()1,C a a -,()0,,0B a,()1D ,所以()1,,C D a a =-u u u u r,()10,BD a =-u u u u r,所以1111co 6s C D BD C D BD θ==⋅=u u u u r u u u u r u u u ur u u u u r 【点睛】本题主要考查直棱柱的几何特征,线面垂直,面面垂直的判定定理以及空间向量法求角,还考查逻辑推理和运算求解的能力,属于中档题.19.某市教育局为了监控某校高一年级的素质教育过程,从该校高一年级16个班随机抽取了16个样本成绩,制表如下:令i x 为抽取的第i 个学生的素质教育测评成绩,1,2,,16i =⋅⋅⋅,经计算得,161196.3116i i x ==∑ 2.08≈.以下计算精确到0.01.(1)设ξ为抽取的16个样本的成绩,用频率估计概率,求ξ的分布列、数学期望()E ξ和标准方差σ;(2)在抽取的样本成绩中,如果出现了在()()()3,3E E ξσξσ-+之外的成绩,就认为本学期的素质教育过程可能出现了异常情况,需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议.从该校抽样的结果来看,是否需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议?(3)列出不小于()E ξ的所有样本成绩,设列出的这些成绩的中位数为a ,每次从列出的这些成绩中随机抽取1个成绩,有放回地连续抽取3次,求恰好有2次抽得的成绩为a 的概率.【答案】(1)分布列见解析, ()96.31E ξ=,方差 2.08σ≈(2)需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议 (3)108343【解析】(1)根据表中数据,利用频率代替概率,列出ξ的分布列,然后求期望和方差.(2)根据(1)中期望和方差,则有()()()()3,390.07,102.55E E ξσξσ-+=,然后看有无数据在此之外即可.(3))根据(1)中期望,按顺序列出不小于()E ξ的所有样本成绩,找出中位数,然后利用二项分布求解. 【详解】(1)ξ的分布列为()96.31E ξ=,方差 2.08σ≈;(2)由已知得,()()()()3,390.07,102.55E E ξσξσ-+=,由样本数据可以看出抽取的第4个测评成绩90在()90.07,102.55以外,因此需对本学期的素质教学过程进行反思,同时对下学期的素质教育过程提出指导性的建议. (3)不小于()E ξ的所有样本成绩为97,97,98,98,98,99,,99,中位数98a =. 每次从列出的这些成绩中随机抽取1个成绩,又放回地连续抽取3次,每次抽得成绩为a 的概率为37, 则恰好有2次抽得的成绩为a 的概率22333108177343p C ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭. 【点睛】本题主要考查离散型随机变量的分布列,期望,方差,正态分布和二项分布,还考查理解辨析和运算求解的能力,属于中档题.20.已知椭圆C :()222210x y a b a b+=>>,1A ,2A 为椭圆C 的左、右顶点,椭圆的右焦点为F ,椭圆C 的离心率为e .(1)设直线y =与椭圆交于D ,E 两点,且DF EF ^,求e 的值;(2)设过点F 且斜率为1的直线与椭圆交于P ,Q (其中P ,Q 分别在x 轴的上、下方)两点,当2e =时,记2PA Q △、1PAQ △的面积分别为2PA Q S △、1PA Q S △,求211PA Q PA QS S +△△的最小值,并求此时椭圆的标准方程.【答案】(1)1e =(2)最小值为)21,此时椭圆的标准方程为221332x y += 【解析】(1)设D 在x 轴上方,根据DF EF ^,利用直角三角形中线定理得到OF OD c ==,,再由直线的倾斜角为60o,得到12D c ⎛⎫ ⎪ ⎪⎝⎭,然后代入22221x y a b +=求解。
安徽省1号卷A10联盟2019届高三下学期4月联考数学(文科)试题+答案+详解

A10联盟2019届高三下学期4月联考数学(文科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.请在答题卷上作答.第Ⅰ卷 选择题(共60分)一、选择题:(本大题共12小题,每小题5分,共60分,每小题分别给出四个选项,只有一个选项符合题意)1.设集合1124xA x N⎧⎫⎪⎪⎛⎫=∈⎨⎬ ⎪⎝⎭⎪≤⎪⎩⎭,{1,2,3,4}B =,则A B ⋂=( ). A .{1} B .∅ C .{3,4} D .{2,3,4} 2.已知复数z 满足(12)26i z i -=+(i 是虚数单位),则复数z 的虚部为( ). A .2 B .2- C .2i D .4-3.某小学六年级一班学生期末测试数学成绩统计如下图所示,则该班学生测试成绩的中位数为( ).A .77.5B .76.5C .77D .764.过双曲线2222:1(0,0)x y C a b a b-=>>的右焦点F 作其实轴的垂线l ,若l 与双曲线C 及其渐近线在第一象限分别交于点A ,B ,且2FB FA =u u u r u u u r,则该双曲线的离心率为( ).ABCD5.如图1是我国古代著名的“赵爽弦图”的示意图,它由四个全等的直角三角形围成,其中3sin 5BAC ∠=,现将每个直角三角形的较长的直角边分别向外延长一倍,得到如图2的数学风车,岩在该数学风车内随机取一点,则该点恰好取自“赵爽弦图”外面(图中阴影部分)的概率为( ).A .2543 B .1843C .2549D .24496.已知函数()2||101()x x f x x e+=⋅,则函数()f x 的图象大致为( ).A .B .C .D .7.运行如图所示的程序框图,若输入S 的值为2019,则输出S 的值为( ).A .1441-B .441-C .431-D .440-8.已知某几何体的三视图如图所示,则图中点A 、B 在该几何体中对应的两点间的距离等于( ).A. B. C. D.9.已知函数224,1()log (1),1x x m x f x x x ⎧++≤-=⎨+>-⎩,若函数()()1g x f x =+有三个零点,则实数m 的取值范围是( ).A .(2,)+∞B .(2,3]C .[2,3)D .(1,3) 10.记函数()2cos 26f x x π⎛⎫=+ ⎪⎝⎭,将函数()f x 的图象向右移动512π个单位后,得到函数()g x 的图象.现有如下命题:1p :函数()g x 的图象关于直线12x π=对称;2p :函数()g x 在区间35,44ππ⎛⎫⎪⎝⎭上单调递增;3p :函数()g x 在区间0,2π⎡⎤⎢⎥⎣⎦上的值域为[1,2]-.则下列命题是真命题的为( ).A .12p p ∨B .()13p p ∨⌝C .()33p p ⌝∧D .12p p ∧11.已知三棱锥D ABC -的体积为6,在ABC V 中,2AB =,4AC =,60BAC ︒∠=,且三棱锥D ABC -的外接球的球心O 恰好是AD 的中点,则球O 的表面积等于( ). A .323π B .643πC .43πD .42π 12.定义在R 上的函数()f x 的导函数为()f x ',若()()f x f x '<,则不等式4(2)(34)x e f x e f x ⋅<⋅-的解集是( ).A .(,2)-∞B .(2,)+∞C .(4,)+∞D .(,4)-∞第Ⅱ卷 非选择题(共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分.)13.若实数x ,y 满足约束条件0129x y x x y ≥⎧⎪≥+⎨⎪+≤⎩,则3z x y =+的最大值是________.14.在四边形ABCD 中,AD BC =u u u r u u u r ,(2,4)AB =u u u r ,(3,5)BD =--u u u r ,则AC u u u r 在AB u u u r上的投影为________.15.已知抛物线2:2(0)C x py p =>上一点(,2)(0)P a a >到焦点F 的距离为3,过焦点F 的直线l 与抛物线C 相交于M 、N 两点,点P 到直线l 的距离为d ,当d 取得最大值时,PMN V 的面积等于________.16.已知在ABC V 中,线段AC 的垂直平分线与线段AB 的垂直平分线交于点P ,若230AP CB BA ++=u u u r u u u r u u u r ,则sin A 的值为________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分) 已知数列{}n a 满足26a =,()*1nn na n n N a a +=∈-.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设n S 为数列{}n a 的前n 项和,求数列1n S ⎧⎫⎨⎬⎩⎭的前n 项和n T . 18.(本小题满分12分)如图,已知111ABC A B C -是直三棱柱,AC BC ⊥,11AC BC CC ===,点D 为1AA 的中点,点E 在AC 上,且DE ∥平面1A BC .(Ⅰ)求证:平面11A BC ⊥平面11A B C ; (Ⅱ)求三棱锥11E A B C -的体积. 19.(本小题满分12分)某教师将寒假期间该校所有学生阅读小说的时间统计如下图所示,并统计了部分学生阅读小说的类型,得到的数据如下表所示:(Ⅰ)是否有99.9%把握认为“性别”与“阅读小说的类型”有关?(Ⅱ)求学生阅读小说时间的众数和平均数(同一组数据用该组区间的中点值作代表);(Ⅲ)若按照分层抽样的方法从阅读时间在[16,18)、[18,20]的学生中随机抽取6人,再从这6人中随机挑选2人介绍选取小说类型的缘由,求所挑选的2人阅读时间都在[16,18)的概率.附:22()()()()()n ad bc K a b c d a c b d -=++++,n a b c d =+++.20.(本小题满分12分)已知椭圆22:13x C y +=,斜率为l 的直线l 与椭圆C 交于()11,A x y ,()22,B x y 两点,且12x x >. (Ⅰ)若A ,B 两点不关于原点对称,点D 为线段AB 的中点,求直线OD 的斜率; (Ⅱ)若存在点()03,E y ,使得45EBA AEB ︒∠=∠=,求直线AB 的方程. 21.(本小题满分12分)已知函数2()ln f x x x x λ=+,R λ∈.(Ⅰ)若1λ=-,求曲线()f x 在点(1,(1)) f 处的切线方程;(Ⅱ)若关于x 的不等式()f x λ≤在[1,)+∞上恒成立,求实数λ的取值范围.请考生在第22、23题中任选一题作答.注意:只能做选定的题目,如果多做,则按所做的第一题记分,解答时请写清题号.22.(本小题满分10分)选修4-4:坐标系与参数分程 已知在极坐标系中,曲线1Ccos 04m πθ⎛⎫++= ⎪⎝⎭.以极点为原点,极轴所在直线为x 轴建立平面直角坐标系,曲线2C的参数方程为1x y αα⎧=+⎪⎨=⎪⎩(α为参数).(Ⅰ)求曲线1C 的直角坐标方程以及曲线2C 的极坐标方程;(Ⅱ)若曲线1C ,2C 交于M ,N 两点,且(0,)A m ,||||2AM AN ⋅=,求m 的值. 23.(本小题满分10分)选修4-5:不等式选讲 已知函数()|1||2|f x x x a =+++,a R ∈. (Ⅰ)当0a =时,求不等式()5f x ≤的解集;(Ⅱ)若()2f x ≥对于x R ∀∈恒成立,求a 的取值范围.1号卷·A10联盟2019届高三下学期4月联考数学(文科)参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.D 由题意得,{|2}A x N x =∈≥,故{2,3,4}A B ⋂=,故选D . 2.A 由题意得,(26)(12)2461222(12)(12)5i i i i z i i i ++++-===-+-+,则复数z 的虚部为2,故选A .3.B 由茎叶图知,共有30个数据,将数据按照从小到大排列之后,第15个数为76,第16个数为77,则所求中位数为76.5,故选B .4.A 设(,0)(0)F c c >,则2,b A c a ⎛⎫ ⎪⎝⎭,,bc B c a ⎛⎫ ⎪⎝⎭.又2FB FA =u u u r u u u r ,则22bc b a a =,2c b ==,化简得2a =,则离心率3c e a ==.故选A . 5.D 在Rt ABC V 中,3sin 5BAC ∠=,不妨设3BC =,则5AB =,4AC =,则阴影部分的面积为1443242⨯⨯⨯=,数学风车的面积为224549+=,∴所求概率2449P =.故选D . 6.A 由题意得,函数()f x 的定义域为(,0)(0,)-∞⋃+∞,关于原点对称,且()22||10110()1()()x xx x f x f x x e x e -⎡⎤+-+⎣⎦-==-=--⋅⋅r,故函数()f x 为奇函数,则函数()f x 的图象关于原点对称,排除B ;因为20(1)0f e =>,排除C ;又552(5)2f e=<,排除D ;故选A . 7.B 第一次循环,201932016S =-=,3n =;第二次循环,3201631989S =-=,5n =;第三次循环,5198931746S =-=,7n =;第四次循环,717463441S =-=-,9n =;此时0S n +<0,则输出的S 的值为441-,故选B .8.C 作出该几何体的直观图如图所示,点A 和点B 在几何体中对应的位置如图所示,则||AB ==C .9.C 令()0g x =,故()1f x =-,故当1x ≤-时,函数2()4f x x x m =++的图象与直线1y =-有两个交点,结合图象可知(2)41(1)31f m f m -=-<-⎧⎨-=-≥-⎩,解得23m ≤<,故选C .10.C 由题意得,552()2cos 22cos 22sin 2126636g x f x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-+=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭;将12x π=代入()g x ,得012g π⎛⎫=⎪⎝⎭,故命题1p 为假命题;函数()g x 在35,44ππ⎛⎫⎪⎝⎭上先减后增,故命题2p 为假命题;当0,2x π⎡⎤∈⎢⎥⎣⎦时,52,666x πππ⎡⎤-∈-⎢⎥⎣⎦,∴()[1,2]g x ∈-,故命题3p 为真命题.综上,12p p ∨、()13p p ∨⌝、12p p ∧为假命题,()23p p ⌝∧为真命题,故选C .11.C 在ABC V中,由余弦定理得BC =222AB BC AC +=,∴ABC V 是直角三角形.设三棱锥D ABC -的高为h ,则112632V h =⨯⨯⨯=6,解得h =.取AC 边的中点为1O ,连接1OO ,则1OO ⊥平面ABC,且122h OO ==,则R OA ====,∴球O 的表面积2443S R ππ==,故选C .12.D 由题意得,()()0f x f x '-<,即2()()0x x x e f x e f x e '-<,∴()0x f x e '⎡⎤<⎢⎥⎣⎦,故函数()()x f x g x e =在R 上单调递减.∵4(2)(34)x e f x e f x ⋅<⋅-,∴234(2)(34)x x f x f x e e--<,即(2)(34)g x g x <-,∴234x x >-,解得4x <,故选D .二、填空题:本大题共4小题,每小题5分. 13.353作出不等式组所表示的平面区域如图阴影部分所示,其中(0,9)A ,(0,1)B ,811,33C ⎛⎫⎪⎝⎭.作直线:30l x y +=,平移直线l ,当其经过点811,33C ⎛⎫⎪⎝⎭时,z 取得最大值,∴max353z =.14.5由AD BC =u u u r u u u r得四边形ABCD 是平行四边形, 且(2,4)(3,5)(1,1)AD AB BD =+=+--=--u u u r u u u r u u u r, 则(2,4)(1,1)(1,3)AC AB AD =+=+--=u u u r u u u r u u u r,∴AC u u u r 在AB u u u r上的投影为||cos 5||AB AC AC AB θ⋅===u u u r u u u ru u u r u u u r . 15.54 由题意得,232p+=,解得2p =,则抛物线C 的方程为24x y =.则点P的坐标为,当d 取得最大值时,PF l ⊥,∵4PF k =,∴直线l的斜率k =-,则直线l的方程为1y =-+,联立241x y y ⎧=⎪⎨=-+⎪⎩,得240x +-=,∴12x x +=-,124x x =-,∴12||36MN x =-=,∴11||||3635422PMN S MN PF =⋅=⨯⨯=V . 16由题意得,点P 为ABC V 的外心.不妨设ABC V 外接圆的半径2R =,因为230AP CB BA ++=u u u r u u u r u u u r,故2AC AP AB BP =-=u u u r u u u r u u u r u u u r ①,故112AC BP ==.取AC 的中点M ,则PM AC ⊥,如图所示,且B 与A 位于直线PM 同侧,∵AC PB ∥, ∴1cos cos 4MC BPC PCM PC ∠=-∠=-=-;在BPC V 中,由余弦定理得,BC ==在ABC V 中,由正弦定理得sin 2BC BAC R ∠==. 三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分12分) (Ⅰ)∵26a =,()*1nn na n n N a a +=∈-,∴13a =且1(1)n n a n a +=+,即11n n a n a n++=; 2分 由累乘法得12111121123121n n n n n a a a n n a a a na n a a a n n ----=⋅⋅⋅⋅=⨯⨯⨯⨯==--……, 则数列{}n a 是等差数列,其通项公式为3n a n =. 5分(Ⅱ)由(Ⅰ)知,2(33)3322n n n n nS +⋅+==, 则122113(1)31n S n n n n ⎛⎫==- ⎪++⎝⎭, 8分∴21111121211322313133n n T n n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪+++⎝⎭⎝⎭…. 12分 18.(本小题满分12分)(Ⅰ)由题意得,四边形11BCC B 是正方形,∴11B C BC ⊥,又AC BC ⊥,∴1111AC B C ⊥. 1分在直三棱柱111ABC A B C -中,1CC ⊥平面111A B C ,11A C ⊂平面111A B C ,∴111AC CC ⊥, 2分又1111CC C B C ⋂=,111,CC C B ⊂平面11BCC B ,∴11A C ⊥平面11BCC B .又1B C ⊂平面11BCC B ,∴111AC B C ⊥. 4分∵1111AC BC C ⋂=,111,AC BC ⊂平面11A BC ,∴1B C ⊥平面11A BC , 6分又1B C ⊂平面11A B C ,∴平面11A BC ⊥平面11A B C . 7分(Ⅱ)∵D 是1AA 的中点,点E 在AC 上,∴DE ⊂平面11ACC A ,∵DE ∥平面1A BC ,平面11ACC A ⋂平面11A BC AC =,∴1DE AC ∥, ∴E 为AC 的中点. 10分 ∴11111111111111332212E A B C B EA C A CE V V S B C --==⋅=⨯⨯⨯⨯=V . 12分 19.(本小题满分12分)(Ⅰ)由题意得,完善列联表如下表所示:∴22200(80703020)50.50510.82811090100100K ⨯⨯-⨯=≈>⨯⨯⨯, 3分 ∴有99.9%的把握认为“性别”与“阅读小说的类型”有关. 4分(Ⅱ)由题意得,所求众数为15; 5分所求平均数为110.16130.24150.3170.2 1.76 3.12 4.5 3.4 1.914.6190.81⨯+⨯+⨯+⨯+⨯++++==. 8分(Ⅲ)由题意得,抽取的6人阅读时间在[16,18)的有4人,记为A ,B ,C ,D ,阅读时间在[18,20)的有2人,记为a ,b ,则从6人中挑选2人,所有的情况共15种,它们是:(,)A B ,(,)A C ,(,)A D ,(,)A a ,(,)A b ,(,)B C ,(,)B D ,(,)B a ,(,)B b ,(,)C D ,(,)C a ,(,)C b ,(,)D a ,(,)D b ,(,)a b . 其中满足条件的有6种,故所求概率62155P ==. 12分 20.(本小题满分12分) (Ⅰ)由题意得,221122221313x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩, 两式相减得,()()()()1212121203x x x x y y y y -++-+=, 2分 故21122112113AB y y x x k x x y y -+==-⋅=-+, 3分 则12121212012302OD y y y y k x x x x +-+===-++-. 5分 (Ⅱ)设直线AB 的方程为y x m =+, 联立2213x y y x m ⎧+=⎪⎨⎪=+⎩,得2246330x mx m ++-=,令223648480m m ∆=-+>,解得22m -<<. ∴1232x x m +=-,()212314x x m =-. 7分 在ABE V 中,45EBA AEB ︒∠=∠=,且直线l 的倾斜角也为45︒,∴BE x ∥轴. 8分过点A 作BE 的垂线,则垂足F 为线段BE 的中点.设点F 的坐标为(),F F x y ,则2132F x x x +==. 9分 由方程组()12212213231432x x m x x m x x ⎧+=-⎪⎪⎪=-⎨⎪+⎪=⎪⎩,化简得2210m m ++=,解得1m =-. 11分 而1(2,2)m =-∈-,则直线AB 的方程为1y x =-. 12分21.(本小题满分12分)(Ⅰ)当1 λ=-时,2()ln f x x x x =-,则()ln 12f x x x '=+-,故(1)1f '=-,又(1)1f =-,故所求切线方程为(1)1(1)y x --=-⋅-,即0x y +=. 4分(Ⅱ)由题意得,2ln x x x λλ+≤在[1,)+∞上恒成立.设函数()2()ln 1g x x x x λ=+-,则()ln 12g x x x λ'=++,故对任意[1,)x ∈+∞,不等式()0(1)g x g ≤=恒成立. ①当()0g x '≤,即ln 12x xλ+≤-恒成立时,函数()g x 在[1,)+∞上单调递减. 设ln 1()x r x x +=,则2ln ()0x r x x -'=≤, ∴max ()(1)1r x r ==,即12λ≤-,解得12λ≤-,符合题意; 8分 ②当0λ≥时,()0g x '≥恒成立,此时函数()g x 在[1,)+∞上单调递增.则不等式()(1)0g x g ≥=对任意[1,)x ∈+∞恒成立,不符合题意; 9分 ③当102λ-<<时,设()()ln 12q x g x x x λ'==++,则1()2q x xλ'=+, 令()0q x '=,解得112x λ=->. 当11,2x λ⎛⎫∈- ⎪⎝⎭时,()0q x '>,此时()q x 单调递增,∴()(1)120q x q λ>=+>, 故当11,2x λ⎛⎫∈- ⎪⎝⎭时,函数()g x 单调递增,∴当11,2x λ⎛⎫∈- ⎪⎝⎭时,()0g x >成立,不符合题意. 11分 综上所述,实数λ的取值范围为1,2⎛⎤-∞- ⎥⎝⎦. 12分 请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.作答时请写清题号.22.(本小题满分10分)选修4-4:坐标系与参数方程cos 04m πθ⎛⎫++= ⎪⎝⎭,∴(cos sin )0m ρθρθ-+=,1分 则曲线1C 的直角坐标方程为0x y m -+=.∵22(1)2x y -+=,∴22210x y x +--=,则曲线2C 的极坐标方程为22cos 10ρρθ--=. 5分(Ⅱ)设曲线1C的参数方程为22x y m ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数),代入22210x y x +--=中,整理得2210t t m +-+-=,7分 22460m m ∆=--+>,解得31m -<<.设M ,N 对应的参数分别为1t ,2t ,则2121t t m ⋅=-,8分 由t 的几何意义得,212||||12AM AN t t m ⋅=⋅=-=,9分解得m =又31m -<<,∴m = 10分23.(本小题满分10分)选修4-5:不等式选讲(Ⅰ)当0a =时,()|1||2|5f x x x =++≤,则1315x x <-⎧⎨--≤⎩或1015x x -≤≤⎧⎨-+≤⎩或0315x x >⎧⎨+≤⎩,2分分别解得21x -≤<-或10x -≤≤或403x <≤,∴不等式()5f x ≤的解集为42,3⎡⎤-⎢⎥⎣⎦. 5分 (Ⅱ)方法一:()|1||2||1|122a a f x x x a x x =+++≥+++-…, 当且仅当2a x =-时取等号, 8分 ∴min ()122a f x =-≥,解得2a ≤-或6a ≥, 即a 的取值范围是(,2][6,)-∞-⋃+∞. 10分方法二:当2a <时,31,1()|1||2|1,1231,2x a x a f x x x a x a x a x a x ⎧⎪---<-⎪⎪=+++=-+--≤≤-⎨⎪⎪++>-⎪⎩, 则函数在,2a ⎛⎤-∞- ⎥⎝⎦上单调递减,在,2a ⎡⎫-+∞⎪⎢⎣⎭上单调递增, ∴min ()1222a a f x f ⎛⎫=-=-≥ ⎪⎝⎭,解得2a ≤-; 7分 当2a =时,()3|1|f x x =+,最小值是0,不符合题意; 8分当2a >时,31,2()|1||2|1,1231,1a x a x a f x x x a x a x x a x ⎧---<-⎪⎪⎪=+++=+--≤≤-⎨⎪++>-⎪⎪⎩. 则函数在,2a ⎛⎤-∞- ⎥⎝⎦上单调递减,在,2a ⎡⎫-+∞⎪⎢⎣⎭上单调递增, 此时min ()1222a a f x f ⎛⎫=-=-≥ ⎪⎝⎭,解得6a ≥. 9分 综上所述,a 的取值范围是(,2][6,)-∞-⋃+∞. 10分。
安徽省1号卷A10联盟2019届高三开年考理科综合试题
A10联盟2019届高三开年考理科综合试题可能用到的相对原了质量:H-1 L-7 C-12 N-14 O-16 Mg-24 Al-27 S-32 Fe-56Ni-58.5 Cu-64 I-127第Ⅰ卷选择题一、选择题;本题共有13小题,每小题6分。
每小题编出的四个选项中,只有一个选项是最符合题目要求的。
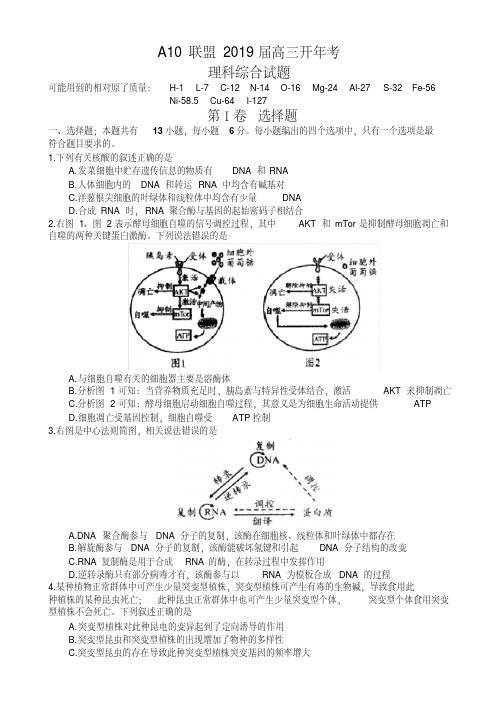
1.下列有关核酸的叙述正确的是A.发菜细胞中贮存遗传信息的物质有DNA和RNAB.人体细胞内的DNA和转运RNA中均含有碱基对C.洋葱根尖细胞的叶绿体和线粒体中均含有少量DNAD.合成RNA时,RNA聚合酶与基因的起始密码子相结合2.右图1、图2表示酵母细胞自噬的信号调控过程,其中AKT和mTor是抑制酵母细胞凋亡和自噬的两种关键蛋白激酶。
下列说法错误的是A.与细胞自噬有关的细胞器主要是溶酶体B.分析图1可知:当营养物质充足时,胰岛素与特异性受体结合,激活AKT来抑制凋亡C.分析图2可知:酵母细胞启动细胞自噬过程,其意义是为细胞生命活动提供ATPD.细胞凋亡受基因控制,细胞自噬受ATP控制3.右图是中心法则简图,相关说法错误的是A.DNA聚合酶参与DNA分子的复制,该酶在细胞核、线粒体和叶绿体中都存在B.解旋酶参与DNA分子的复制,该酶能破坏氢键和引起DNA分子结构的改变C.RNA复制酶是用于合成RNA的酶,在转录过程中发挥作用D.逆转录酶只有部分病毒才有,该酶参与以RNA为模板合成DNA的过程4.某种植物正常群体中可产生少量突变型植株,突变型植株可产生有毒的生物碱,导致食用此种植株的某种昆虫死亡;此种昆虫正常群体中也可产生少量突变型个体,突变型个体食用突变型植株不会死亡。
下列叙述正确的是A.突变型植株对此种昆电的变异起到了定向诱导的作用B.突变型昆虫和突变型植株的出现增加了物种的多样性C.突变型昆虫的存在导致此种突变型植株突变基因的频率增大D.此种昆虫和此种植物之间的相互选择能够实规二者的共同进化5.下列有关植物生命活动调节的说法正确的是A.赤霉素可能参与α-淀粉酶基因表达过程的调控来促进种子的萌发B.色氨酸通过脱水缩合反应直接形成生长素C.植物激素几乎控制着植物所有的生命活动D.在生长素类似物促进扦插枝条生根的实验中,处理浓度不同,枝条生根数一定不同6.我国西北沙化地区为恢复生态系统釆用乔、灌、草相结合的方法,通过栽种多种植被来防风沙,取得了良好的效果。
安徽省A10联盟2018-2019学年高三下学期开学考试理科数学试题(带答案解析)

(2)已知直线 与曲线 交于 两点,直线 与曲线 交于 两点,求 的最大值.
23.已知函数 , .
(1)当 时,求不等式 的解集;
(2)若 的解集包含 ,求实数 的取值范围.
参考答案
1.D
【解析】
【分析】
根据不等式解法得到集合A,再由集合补集得到结果.
【详解】
由题意得, , , ,
3.B
【解析】
【分析】
由题意分析在何区间内等待时间可以控制在5分钟之内,再由概率计算公式即可求出结果.
【详解】
此人在25分到30分或55分到60分之间的5分钟内到达,等待时间不多于5分钟,所以他等待时间不多于 分钟的概率为 .故选B
【点睛】
本题主要考查几何概型,熟记公式即可求解,属于基础题型.
4.C
附: , , ,
21.已知函数 的最大值为 (其中 为自然对数的底数), 是 的导函数.
(1)求 的值;
(2)任取两个不等的正数 ,且 ,若存在正数 ,使得 成立.求证: .
22.在平面直角坐标系 中,直线 的普通方程是 ,曲线 的参数方程是 ( 为参数).在以 为极点, 轴的正半轴为极轴建立的极坐标系中,曲线 的极坐标方程是 .
A. B. C. D.
4.已知偶函数 在 上单调递减, ,若 ,则 的取值范围是()
A. B. C. D.
5.执行如图所示的程序框图,则输出的结果为()
A.7B.8C.9D.11
6. 展开式中 的系数为()
A.-7B.28C.35D.42
7.设 , 满足约束条件 ,且 的最小值为2,则 ()
A.1B.-1C. D.
【详解】
∵二项式 的通项为 ,分别令 ,则 的系数为 .故选B.
安徽省1号卷A10联盟2019届高三下学期4月联考数学(理科)试题+答案+详解

1号卷·A10联盟2019届高三下学期4月联考数学(理科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.请在答题卷上作答.第Ⅰ卷 选择题(共60分)一、选择题:(本大题共12小题,每小题5分,共60分,每小题分别给出四个选项,只有一个选项符合题意)1.已知集合03x A xx ⎧⎫=≥⎨⎬-⎩⎭,{|4}B x k x =≤<,则A B=⋂( ). A .{|34}x x ≤< B .{|01}x x ≤≤ C .{|14}x x ≤< D .{|13}x x ≤<2.若复数12miz i-=+(i 是虚数单位)为纯虚数,则实数m 的值为( ). A .2 B .12- C .3 D .31-3.下图给出的是2017年11月-2018年11月某工业原油产量的月度走势图,则以下说法正确的是( ).A .2018年11月份原油产量约为51.8万吨B .2018年11月份原油产量相对2017年11月增加1.0%C .2018年11月份原油产量比上月减少54.9万吨D .2018年1-11月份原油的总产量不足15000万吨4.记等差数列{}n a 的前n 项和为n S ,若311139a a a ++=,则17S =( ). A .57 B .51 C .42 D .395.图1是我国古代著名的“赵爽弦图”的示意,它由四个全等的直角三角形围成,其中3sin 5BAC ∠=,现将每个直角三角形的较长的直角边分别向外延长一倍,得到如图2的数学风车,若在该数学风车内随机取一点,则该点恰好取自“赵爽弦图”外面(图中阴影部分)的概率为( ).A .2543 B .1843C .2549D .24496.过双曲线2222:1(0,0)x y C a b a b-=>>的右焦点F 作其实轴的垂线l ,若l 与双曲线C 及其渐近线在第一象限分别交于点A ,B ,且2FB FA =u u u r u u u r,则该双曲线的离心率为( ).A B C D 7.下图中小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( ).A .2432π+B .2424π+C .2032π+D .2024π+8.设函数()()x x f x x e ae -=+的导函数为()f x ',若()f x '是奇函数,则曲线()y f x =在点(1,(1))f --处切线的斜率为( ). A .12e-B .1-C .eD .2e - 9.已知在正方形ABCD 中,点E 为CD 的中点,点F 为CB 上靠近点C 的三等分点,O 为AC 与BD 的交点,则DB =u u u r( ).A .81855AE OF -+u u u r u u u rB .141255AE OF -+u u u r u u u rC .18855AE QF -+u u u r u u u rD .121455AE OF -+u u ur u u u r10.已知函数243,1()1(1),12x x x f x x x ⎧++≤-⎪=⎨+>-⎪⎩,若关于x 的不等式()(2)f x m x <+恰有2个整数解,则实数m的取值范围为( ).A .81,00,34⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦ B .81,00,33⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦C .31,00,24⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦ D .31,00,23⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦11.将函数()sin()f x x ϕ=+图象上所有点的横坐标变为原来的1(1)ωω>(纵坐标不变),得函数()g x 的图象.若16g π⎛⎫=⎪⎝⎭,203g π⎛⎫= ⎪⎝⎭,且函数()g x 在,62ππ⎛⎫⎪⎝⎭上具有单调性,则ω的值为( ). A .2 B .3 C .5 D .7 12.已知以正八面体各面的中心为顶点能构造一个正方体,若正八面体的体积为3,则正方体外接球的表面积为( ). A .43π B .83π C .89π D .49π 第Ⅱ卷 非选择题(共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.二、填空题(本大题共4小题,每小题5分,共20分)13.已知实数x ,y 满足0129x y x x y ≥⎧⎪≥+⎨⎪+≤⎩,则3z x y =-的最大值为________.14.若二项式2nx ⎛- ⎝的展开式中,只有第5项的二项式系数最大,则展开式中1x -的系数为________.(用数字作答)15.已知抛物线2:2(0)C y px p =>的焦点为F ,准线为l ,过F 作斜率大于0的直线与抛物线C 交于M ,N 两点(M 在x 轴上方),且与直线l 交于点Q .若||3||4FN NQ =,||16MF =,则p 的值为________.16.首项为1的数列{}n a 满足:当2n ≥时,211n n n a a a ---=,记数列11n a ⎧⎫⎨⎬+⎩⎭的前n 项和为n P ,前n 项积为n Q ,则n n P Q +=________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,且1cos 3A =,a =. (Ⅰ)若6B π=,求cos b C 的值;(Ⅱ)若ABC V 的面积是b c +的值. 18.(本小题满分12分)如图,在正三棱柱111ABC A B C -中,ABC V ,12AA AB =.点E 为线段BC 的中点.(Ⅰ)在线段11B C 上找出一点F ,使得平面1AB E ∥平面1A CF ,并证明; (Ⅱ)求二面角1E AB B --的余弦值. 19.(本小题满分12分)某超市开展年终大回馈,设计了两种答题游戏方案:方案一:顾客先回答一道多选题,从第二道开始都回答单选题; 方案二:顾客全部选择单选题进行回答.其中每道单选题答对得2分,每道多选题答对得3分,无论单选题还是多选题答错都得0分,每名参与的顾客至多答题3道.在答题过程中得到3分或3分以上立刻停止答题,并获得超市回馈的赠品. 为了调查顾客对方案的选择情况,研究人员调查了参与游戏的500名顾客,所得结果如下表所示:(Ⅰ)是否有95%的把握认为方案的选择与性别有关?(Ⅱ)小明回答每道单选题的正确率为0.8,多选题的正确率为0.75.(ⅰ)若小明选择方案一,记小明的得分为X ,求X 的分布列及期望;(ⅱ)如果你是小明,你觉得选择哪种方案更有可能获得赠品,请通过计算说明理由.附:22()()()()()n ad bc K a b c d a c b d -=++++,n a b c d =+++.20.(本小题满分12分)已知椭圆2222:1(0)x y C a b a b+=>>上的一点到两个焦点的距离之和为4,离心率为2,点A 为椭圆C 的左顶点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)设圆222:(2)(02)M x y r r +-=<<,过点A 作圆M 的两条切线分别交椭圆C 于点B 和D ,求证:直线BD 过定点. 21.(本小题满分12分)已知函数()ln()fx x m x m=-+,m R ∈. (Ⅰ)讨论函数()f x 的单调性;(Ⅱ)若(0,)m ∈+∞,()xme x f x m -+>恒成立,求实数m 的取值范围.请考生在第22、23题中任选一题作答.注意:只能做选定的题目,如果多做,则按所做的第一题记分,解答时请写清题号.22.(本小题满分10分)选修4-4:坐标系与参数分程 已知在极坐标系中,曲线1C cos 04m πθ⎛⎫++= ⎪⎝⎭.以极点为原点,极轴所在直线为x 轴建立平面直角坐标系,曲线2C 的参数方程为1x y αα⎧=+⎪⎨=⎪⎩(α为参数).(Ⅰ)求曲线1C 的直角坐标方程以及曲线2C 的极坐标方程;(Ⅱ)若曲线1C ,2C 交于M ,N 两点,且(0,)A m ,||||2AM AN ⋅=,求m 的值. 23.(本小题满分10分)选修4-5:不等式选讲已知函数()|1||2|f x x x a =+++,a R ∈. (Ⅰ)当0a =时,求不等式()5f x ≤的解集;(Ⅱ)若()2f x ≥对于x R ∀∈恒成立,求a 的取值范围.1号卷·A10联盟2019届高三4月联考数学(理科)参考答案一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.D 由题意得,{|03}A x x =≤<,∴{|13}A B x x ⋂=≤<.故选D .2.A 由题意得,2(1)(2)22221(2)(2)555mi i mi i mi m m z i i ----+-+===-+-, 故20210m m -=⎧⎨+≠⎩,解得2m =.故选A .3.C 由题意得,2018年11月份原油的日均产量为51.8万吨,则11月份原油产量为51.8301554⨯=万吨,10月份原油产量为51.9311608.9⨯=万吨,故A 错误;2018年11月份原油产量的同比增速为 1.0%-,原油产量相对2017年11月减少1.0%,则B 错误;又11月份原油产量比上月减少1608.9155454.9-=万吨,则C 正确;1-11月份共334天,而1-11月份日均原油产量都超过50万吨,故1-11月份原油的总产量会超过15000万吨,故D 错误.故选C .4.B 设等差数列{}n a 的公差为d ,则311131932439a a a a d a ++=+==,即93a =.由等差数列性质可得,1791751S a ==.故选B . 5.D 在Rt ABC V 中,3sin 5BAC ∠=,不妨设3BC =,则5AB =,4AC =,则阴影部分的面积为1434242⨯⨯⨯=,数学风车的面积为224549+=,∴所求概率2449P =.故选D .6.A 设(,0)(0)F c c >,则2,b A c a ⎛⎫ ⎪⎝⎭,,bc B c a ⎛⎫ ⎪⎝⎭,又2FB FA =u u u r u u u r ,则22bc b a a =,2c b ==,化简得2a =,则离心率3c e a ==.故选A . 7.C 由题意得,所求几何体的体积1462444220322V πππ=⨯+⨯⨯-⨯⨯=+.故选C . 8.D 由题意得,()(1)(1)xxf x x e a x e-'=++-.∵()f x '是奇函数,∴(0)0f '=,即10a +=,解得1a =-,∴()(1)(1)x x f x x e x e -'=+--,则(1)2f e '-=-,即曲线()y f x =在点(1,(1))f --处切线的斜率为2e -.故选D .9.A 以D 为原点,DC ,DA 所在直线分别为x ,y 轴建立如图所示的平面直角坐标系.设6AB =,则(0,6)A ,(6,6)B ,(3,3)O ,(3,0)E ,(6,2)F ,∴(6,6)DB =u u u r ,(3,6)AE =-u u u r ,(3,1)OF =-u u u r.设DB mAE nOF =+u u u r u u u r u u u r ,即63366m n m n =+⎧⎨=--⎩,解得85185m n ⎧=-⎪⎪⎨⎪=⎪⎩,故81855DB AE OF =-+u u u r u u u r u u u r .故选A .10.C 若0m =,显然不等式()(2)f x m x <+仅有1个整数解2-;若0m <,如图(1)所示,不等式()(2)f x m x <+的整数解为3-和2-,即9123(32)16163(42)m m -+<-+⎧⎨-+≥-+⎩,解得302m -≤<;若0m >,如图(2)所示,不等式()(2)f x m x <+的整数解为2-和1-,即143(12)122m m -+<-+⎧⎪⎨≥⎪⎩,解得104m <≤.综上所述,实数m 的取值范围为31,00,24⎡⎫⎛⎤-⋃⎪ ⎢⎥⎣⎭⎝⎦,故选C .11.B 由题意得,()sin()g x x ωϕ=+,最小正周期2T πω=.若16g π⎛⎫=⎪⎝⎭,203g π⎛⎫= ⎪⎝⎭,∴()*221364n T n N ππ--=∈,∴()*21n n N ω=-∈.∵函数()g x 在,62ππ⎛⎫ ⎪⎝⎭上具有单调性,∴26223642T T πππωπππω⎧-≤=⎪⎪⎨⎪-≥=⎪⎩,解得13ω≤≤,又1ω>,()*21n n N ω=-∈,∴3ω=.故选B . 12.B 设正八面体的棱长为a,则3133V a =⨯=,解得2a =.作出图形如图所示,设G ,H 分别为平面ABE 与平面ADE 的中心,分别延长AG ,AH 交BE ,DE 于G ',H '.则21333G H H D G B ==='',故所求外接球半径r ==,则所求表面积2843S ππ=⨯=.故选B .二、填空题:本大题共4小题,每小题5分. 13.133作出不等式组所表示的平面区域(如图中阴影部分所示),其中(0,9)A ,(0,1)B ,811,33C ⎛⎫⎪⎝⎭.当直线3z x y =-经过点C 时,z 取得最大值,max 811133333z =⨯-=.14.1792由题意得,展开式共有9项,则8n =,故82x ⎛- ⎝展开式的通项857882218822(1)rrr r r r r r T C x C x x ---+⎛⎫⎛⎫=⋅⋅-=⋅⋅-⋅ ⎪ ⎪⎝⎭⎝⎭.令7812r -=-,解得2r =,故所求系数为26282(1)28641792C ⨯⨯-=⨯=.15.4过M ,N 分别作l 的垂线,垂足分别为1M ,1N ,过F 作1MM 的垂线,垂足为P . ∵||3||4FN NQ =,∴13||4NN NQ =,∴||3||4MP MF =,∴3||||4MP MF =, ∴13||||||4MF MM MP p MF p ==+=+,∴4p =. 16.1由题意得,()211n n n n n a a a a a +=+=+,故()1111n n n a a a +=+,即 111111n n n n n a a a a a ++==-+,由111n n n aa a +=+,可以求得 121223*********n n n n n a a a Q a a a a a a a ++=⋅⋅⋅=⋅⋅⋅=+++……;由11111n n n a a a +=-+,可以求得 1212231111111111111111n n n n n P a a a a a a a a a a ++=+++=-+-++-=-+++……, 故1n n P Q +=.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.) 17.(本小题满分12分) (Ⅰ)∵1cos 3A =,∴sin 3A =. 1分∴cos cos()sin sin cos cos C A B A B A B =-+=-1132326=-⨯=. 3分由正弦定理得,sin sin b a B A=,即123b =,解得3b =. 5分∴cos b C =. 6分 (Ⅱ)∵1sin 2ABC S bc A =V,∴123⨯=6bc =. 8分 由余弦定理得,2222cos a b c bc A =+-, ∴222228()33a b c bc b c bc =+-=+-, 10分 ∴232()16b c =+-,∴b c += 12分 18.(本小题满分12分)(Ⅰ)取11B C 的中点F ,连接1A F ,EF ,CF .∵1CE B F =,1CE B F ∥,∴四边形1CEB F 为平行四边形,∴1CF B E ∥,∵CF ⊄平面1AB E ,1B E ⊂平面1AB E ,∴CF ∥平面1AB E ; 3分 同理可得,四边形1AEFA 为平行四边形,∴1A F ∥平面1AB E ; 4分 ∵1A F CF F ⋂=,1A F ⊂平面1A CF ,CF ⊂平面1A CF , ∴平面1AB E ∥平面1A CF . 5分(Ⅱ)取AB 中点D ,11A B 的中点G ,分别以DA ,DG ,DC 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.∵ABC S =V 12AA AB =,∴2AB =,14AA =. 6分由题意得,(1,0,0)A ,(1,0,0)B -,C ,1(1,4,0)B -,122E ⎛⎫- ⎪ ⎪⎝⎭,则3,0,22AE ⎛=- ⎝⎭u u u r ,1(2,4,0)AB =-u u u r.设平面1AB E 的法向量为(,,)n x y z =r,则100n AE n AB ⎧⋅=⎪⎨⋅=⎪⎩u u u r r u u u u r r,即3022240x z x y ⎧-+=⎪⎨⎪-+=⎩,即12z y x ⎧=⎪⎨=⎪⎩. 令2x =,则1y =,z =n =r. 9分 又平面1ABB 的一个法向量为(0,0,1)m =r, 10分∴cos ,||||17m n m n m n ⋅<>===⋅r rr r r r , 由图可知,二面角1E B AB --为锐角, 故二面角1E B AB --的余弦值为17. 12分19.(本小题满分12分)(Ⅰ)由题意,完善列联表如下表所示:∴22500(150********) 4.831 3.841230270300200K ⨯⨯-⨯=≈>⨯⨯⨯, 3分 故有95%的把握认为方案的选择与性别有关. 4分 (Ⅱ)(ⅰ)X 的所有可能取值为0,2,3,4, 则1111(0)455100P X ==⨯⨯=,1142(2)245525P X ==⨯⨯⨯=, 3(3)4P X ==,1444(4)45525P X ==⨯⨯=. 7分 故X 的分布列为:∴4()0234 3.0510025425E X =⨯+⨯+⨯+⨯=. 9分(ⅱ)小明选择方案一得分不低于3分的概率为134(3)0.91425P P X =≥=+=, 小明选择方案二得分不低于3分的概率为21444411220.89655555125P =⨯⨯⨯+⨯==,∵21P P <,∴小明选择方案一时更有可能获得赠品.12分 20.(本小题满分12分)(Ⅰ)由题意得,242a c a =⎧⎪⎨=⎪⎩,解得2c a ⎧=⎪⎨=⎪⎩2221b a c =-=. ∴椭圆C的标准方程为2214x y +=. 3分 (Ⅱ)设切线AB ,AD 的方程为(2)y k x =+,r =,即()2224840r k k r --+-=,设两切线AB ,AD 的斜率为1k ,2k ,则121k k =. 5分联立22(2)14y k x x y =+⎧⎪⎨+=⎪⎩,得()222214161640k x k x k +++-=,设()11,B x y ,()22,D x y ,则211212814k x k -=+,1121414k y k =+, 同理2221222212828144k k x k k --==++,212222144144k k y k k ==++, 8分 则()11221112221112211443414282841414BDk k k k k k k k k k k -++==--+-++,∴直线BD 的方程为()21112221114328141441k k k y x k k k ⎛⎫--=- ⎪+++⎝⎭, 10分 整理得()121310341k y x k ⎛⎫=+ ⎪+⎝⎭, 故直线BD 过定点10,03⎛⎫-⎪⎝⎭. 12分 21.(本小题满分12分)(Ⅰ)由题意得,函数()f x 的定义域为(,)m -+∞,()1m xf x x m x m'=-=++. 1分 若0m =,则()10f x '=>,故函数()f x 在(0,)+∞上单调递增; 2分 若0m >,则0m -<,故当(,0)x m ∈-时,()0f x '<,当(0,)x ∈+∞时,()0f x '>, 则()f x 在(,0)m -上单调递减,在(0,)+∞上单调递增; 3分 若0m <,则0m ->,故()0f x '>,故函数()f x 在(,)m -+∞上单调递增;综上所述,当0m ≤时,()f x 在(,)m -+∞上单调递增;当0m >时,()f x 在(,0)m -上单调递减,在(0,)+∞上单调递增. 5分(Ⅱ)∵()xme x f x m -+>,∴1ln()xe x m ->+.又1x e x -≥,∴若ln()x x m >+,则1ln()xe x m ->+. 6分 令()ln()()x x x m x m ϕ=-+>-,则1()1x x mϕ'=-+, 令()0x ϕ'=,解得1x m =-.当(,1)x m m ∈--时,()0x ϕ'<,则函数()x ϕ在(,1)m m --上单调递减, 当(1,)x m ∈-+∞时,()0x ϕ'>,则函数()x ϕ在(1,)m -+∞上单调递增, ∴min ()(1)10x m m ϕϕ=-=->,解得1m <. 9分 当1m ≥时,存在0x =,使得1ln()xe x m -≤+成立, 这与1ln()xe x m ->+矛盾,∴1m <,又0m >,故实数m 的取值范围为(0,1). 12分请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.作答时请写清题号. 22.(本小题满分10分)选修4-4:坐标系与参数方程cos 04m πθ⎛⎫++= ⎪⎝⎭,∴(cos sin )0m ρθρθ-+=, 1分 则曲线1C 的直角坐标方程为0x y m -+=. ∵22(1)2x y -+=,∴22210x y x +--=,则曲线2C 的极坐标方程为22cos 10ρρθ--=. 5分(Ⅱ)设曲线1C的参数方程为22x y m ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数), 代入22210x y x +--=中,整理得2210t t m +-+-=, 7分22460m m ∆=--+>,解得31m -<<.设M ,N 对应的参数分别为1t ,2t ,则2121t t m ⋅=-, 8分由t 的几何意义得,212||||12AM AN t t m ⋅=⋅=-=, 9分解得m =31m -<<,∴m = 10分 23.(本小题满分10分)选修4-5:不等式选讲(Ⅰ)当0a =时,()|1||2|5f x x x =++≤, 1分则1315x x <-⎧⎨--≤⎩或1015x x -≤≤⎧⎨-+≤⎩或0315x x >⎧⎨+≤⎩, 3分分别解得21x -≤<-或10x -≤≤或403x <≤, ∴不等式()5f x ≤的解集为42,3⎡⎤-⎢⎥⎣⎦. 5分(Ⅱ)方法一:()|1||2||1|122a a f x x x a x x =+++≥+++-…,当且仅当2ax =-时取等号, 8分 ∴min ()122af x =-≥,解得2a ≤-或6a ≥, 即a 的取值范围是(,2][6,)-∞-⋃+∞. 10分方法二:当2a <时,31,1()|1||2|1,1231,2x a x a f x x x a x a x a x a x ⎧⎪---<-⎪⎪=+++=-+--≤≤-⎨⎪⎪++>-⎪⎩,则函数在,2a ⎛⎤-∞- ⎥⎝⎦上单调递减,在,2a ⎡⎫-+∞⎪⎢⎣⎭上单调递增,∴min ()1222a a f x f ⎛⎫=-=-≥ ⎪⎝⎭,解得2a ≤-; 7分 当2a =时,()3|1|f x x =+,最小值是0,不符合题意; 8分当2a >时,31,2()|1||2|1,1231,1a x a x a f x x x a x a x x a x ⎧---<-⎪⎪⎪=+++=+--≤≤-⎨⎪++>-⎪⎪⎩.则函数在,2a ⎛⎤-∞- ⎥⎝⎦上单调递减,在,2a ⎡⎫-+∞⎪⎢⎣⎭上单调递增,此时min ()1222a af x f ⎛⎫=-=-≥ ⎪⎝⎭,解得6a ≥. 9分 综上所述,a 的取值范围是(,2][6,)-∞-⋃+∞. 10分。
1号卷A10联盟2019届高三下学期4月联考理科数学试卷含答案解析

微信公众号:“免费下载站”第费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
微信公众号:“免费下载站”第一时间更新初高中所有大型考试的试题和答案,免费提供下载
安徽省A10联盟2019届高三摸底考数学(理科)试题含答案

A10联盟2019届高三摸底考数学(理科)试题巢湖一中 合肥八中 淮南二中 六安一中 南陵中学 舒城中学 太湖中学天长中学 屯溪一中 宣城中学 滁州中学 池州中学 阜阳一中第Ⅰ卷 选择题(共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要示的.1.已知集合}032|{2<--=x x x A ,)}1lg(|{-==x y x B ,则B A =( )A .(-1,3)B .(-3,1)C .(1,3)D .(-1,1)2.若复数z 满足i i z -=+1)2((i 为虚数单位),则z 的虚部分为( )A .53B .53-C .i 53D .i 53- 3.若α,β,γ是三个不同的平面,m ,n 是两条不同的直线,则下列命题正确的是( )A .若m =βα ,α⊂n ,n m ⊥,则βα⊥B .若βα⊥,m =βα ,n =γα ,则n m ⊥C .若m 不垂直于平面α,则m 不可能垂直于平面α内的无数条直线D .若α⊥m ,β⊥n ,m ∥n ,则α∥β4.七巧板是一种古老的中国传统智力游戏,被誉为“东方魔板”.如图,这是一个用七巧板拼成的正方形,其中1号板和2号板为两个全等的等腰直角三角形,3号板和5号板为两个全等的等腰直角三角形,7号板为一个等腰直角三角形,4号板为一个正方形,6号板为一个平行四边形.现从这个正方形内任取一点,由此点取自阴影部分的概率为( )A .81 B .41 C .163 D .83 5.函数x x f x x cos 2121)(⋅+-=,⎥⎦⎤⎢⎣⎡-∈22ππ, x 的图象大致为( )6.设等比数列}{n a 的前n 项和为n S ,若0221=+S S ,且15)(842=-a a ,则51a a =( )A .94B .49C .8116D .16817.若函数)sin()(θ+=x x f (0<θ<π)的图象关于直线3π=x 对称,则)(x f 在[0,π]上的单调递减区间为( ) A .⎥⎦⎤⎢⎣⎡ππ,3 B .⎥⎦⎤⎢⎣⎡323ππ, C .⎥⎦⎤⎢⎣⎡320π, D .⎥⎦⎤⎢⎣⎡ππ,32 8.设F 1,F 2分别是双曲线12222=-by a x (a >0,b >0)的左、右焦点,以线段F 1F 2为为边作等边 △MF 1F 2,若线段MF 1的中点P 在双曲线上,则该双曲线的离心率为( )A .324+B .13+C .213+ D .3 9.在△ABC 中,=,且32||=CP ,8||=CA ,∠ACB =32π,则CA CP ⋅=( ) A .24 B .12 C .324 D .31210.已知某几何体的三视图如图所示,俯视力中的3个小三角形全等,则该几何体的外接球衣的表面积为( )A .314πB .27136πC .64165πD .449π 11.已知直线l 过点(33,0)且不与x 轴垂直,圆C :0222=-+y y x ,若直线l 上存在一点M ,OM交圆C 于点N ,且23=,其中O 为坐标原点,则直线l 的斜率的最小值为( ) A .-1 B .3- C .6- D .33- 12.设)('x f 是函数)(x f 的导函数,12)1(')0(21)(-+-=x e f x f x x f ,若x x x f x g +-=221)()(,且 方程02=-⎪⎪⎭⎫ ⎝⎛-x x a x g 有且只有一个实数根,则实数a 的取值范围是( ) A .}0{)0( ,-∞ B .]10()0(,, -∞ C .]10(, D .[)∞+,1 第Ⅱ卷 非选择题(共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知角θ的终边经过点(54-,53),则2sin 2θ的值为 . 14.已知实数x ,y 满足⎪⎩⎪⎨⎧≥+≥+≥y x y x x y 2422,则y x z 3-=的最大值为 .15.6)2(z y x --的展开式中含z y x 32项的系数为 .16.设抛物线x y 42=的焦点为F ,过点(2,0)的直线交抛物线于A ,B 两点,交抛物线的准线于点C . 若52=∆∆BCF ACF S S ,则=||AF . 三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且B c a C b cos )2(cos -=.(Ⅰ)求角B 的大小;(Ⅱ)若△ABC 外接圆的半径为334,求△ABC 面积的最大值.18.(本小题满分12分)已知数列}{n a 是单调递增数列,首项11=a ,其前n 项和为S n ,且满足12212+-=-n n n S a S (n ≥2且*N n ∈).(Ⅰ)求数列}{n a 的通项公式;(Ⅱ)设11+⋅=n n n a a b ,数列}{n b 的前n 项和为n T ,求证:n T <21.如图,在多面体ABCDEF中,四边形ABCD是梯形,四边形ADEF是正方形,ED⊥平面ABCD.AB ∥DC,AB=AD=1,CD=2,AC=5.(Ⅰ)求证:平面EBC⊥平面EBD;(Ⅱ)设M为线段EC上一点,满足EC=3EM.求二面角M-BD-E的余弦值.20.(本小题满分12分)某市政府为了节约用电,计划在本市试行居民生活用电定额管理,即确定一户居民用电标准a,用电量不超过a的部分按平价收费,超过a的部分按议价收费.为此,政府随机调查了100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.(Ⅰ)根据频率分布直方图中的数据,求x的值,并估计该市每户居民月平均用电量μ的值(同一组数据用该组区间的中点值作代表);(Ⅱ)用频率估计概率,利用(Ⅰ)的结果,假设该市每户居民月平均用电量X服从正态分布σ),求“μ<X<240”的概率;N(μ,2(Ⅲ)利用(Ⅱ)的结果,从该市所有居民中随机抽取3户,记月平均用电量介于(μ,240)度之间的户数为Y,求Y的分布列及数学期望E(Y).已知椭圆C :12222=+by a x (a >b >0)过点A (2,1),离心率为23.直线l :t x y +=21(0≠t ) 与椭圆C 交于E (1x ,1y ),F (2x ,2y )两点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)若直线AE 、AF 分别与x 轴正半轴交于P 、Q 两点,求证:||||OQ OP +为定值.22.(本小题满分12分)已知函数b x x e x f x ++-+=1232)(2的图象在0=x 处的切线方程为2+=ax y ,其中a ,b 为常数. (Ⅰ)求函数)(x f 的单调区间与极值;(Ⅱ)若存在实数x ,使得k x x x f 2232)(2----≤0成立,求整数k 的最小值.。
安徽省皖中名校联盟2019届高三10月联考数学(理)试卷(含答案)

又 ABC 中, sin A 0
故 cosC 1 2
得 C .………6 分 3
(2)由 CD 1 (CA CB) 得 2
3 1 (22 a2 2 2 a cos 60) 4
从而 a 2 或 a= 4(舍)
故 S ABC
1 ab sin C 2
2
皖中名校联盟 2019 届高三 10 月联考
数学试题卷(理科)参考答案
一、选择题
题号 1
2
3
4
5
6
7
8
9 10 11 12
答案 D D A B D C B D A A B B
二、填空题
13. 3
14. (1,4)
三、解答题
15. 2
16.0 或 1
17.解:命题 p : 令 u(x) 2 mx u(x) 在 x [0,1] 上单减
2
12
()
A.要得到函数 f (x) 的图象,只需将 y
2 cos 2x 的图象向右平移 个单位
6
B.函数 f (x) 的图象关于直线 x 5 对称 12
C.当 x [ , ] 时,函数 f (x) 的最小值为 2 66
D.函数 f (x) 在[ , ] 上单调递增
m 1
又 u(x) 0 u(x)min u(1) 2 m 0 1 m 2 ………3 分
命题 q :
x
|
x
m
|
2x m,
x
m, x m
m
x | x m | 1的解集为 R 分
只需 (x | x m |)min m 1 ………6
安徽省1号卷 A10联盟2019届高三开年考理科综合试题
A10联盟2019届高三开年考理科综合试题可能用到的相对原了质量:H-1 L-7 C-12 N-14 O-16 Mg-24 Al-27 S-32 Fe-56Ni-58.5 Cu-64 I-127第Ⅰ卷选择题一、选择题;本题共有13小题,每小题6分。
每小题编出的四个选项中,只有一个选项是最符合题目要求的。
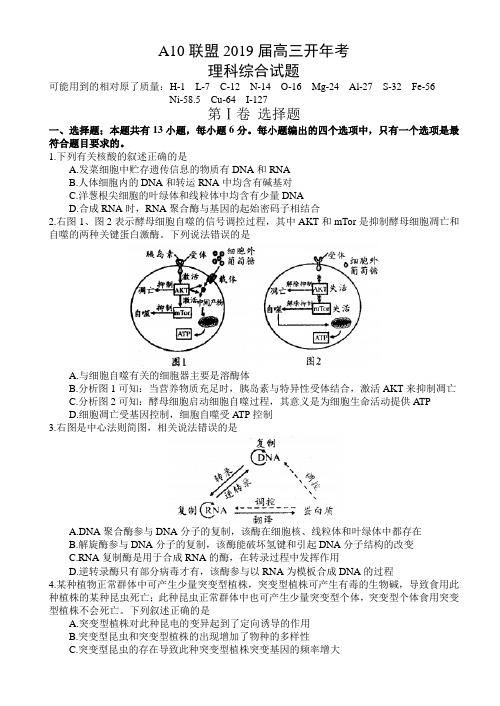
1.下列有关核酸的叙述正确的是A.发菜细胞中贮存遗传信息的物质有DNA和RNAB.人体细胞内的DNA和转运RNA中均含有碱基对C.洋葱根尖细胞的叶绿体和线粒体中均含有少量DNAD.合成RNA时,RNA聚合酶与基因的起始密码子相结合2.右图1、图2表示酵母细胞自噬的信号调控过程,其中AKT和mTor是抑制酵母细胞凋亡和自噬的两种关键蛋白激酶。
下列说法错误的是A.与细胞自噬有关的细胞器主要是溶酶体B.分析图1可知:当营养物质充足时,胰岛素与特异性受体结合,激活AKT来抑制凋亡C.分析图2可知:酵母细胞启动细胞自噬过程,其意义是为细胞生命活动提供A TPD.细胞凋亡受基因控制,细胞自噬受A TP控制3.右图是中心法则简图,相关说法错误的是A.DNA聚合酶参与DNA分子的复制,该酶在细胞核、线粒体和叶绿体中都存在B.解旋酶参与DNA分子的复制,该酶能破坏氢键和引起DNA分子结构的改变C.RNA复制酶是用于合成RNA的酶,在转录过程中发挥作用D.逆转录酶只有部分病毒才有,该酶参与以RNA为模板合成DNA的过程4.某种植物正常群体中可产生少量突变型植株,突变型植株可产生有毒的生物碱,导致食用此种植株的某种昆虫死亡;此种昆虫正常群体中也可产生少量突变型个体,突变型个体食用突变型植株不会死亡。
下列叙述正确的是A.突变型植株对此种昆电的变异起到了定向诱导的作用B.突变型昆虫和突变型植株的出现增加了物种的多样性C.突变型昆虫的存在导致此种突变型植株突变基因的频率增大D.此种昆虫和此种植物之间的相互选择能够实规二者的共同进化5.下列有关植物生命活动调节的说法正确的是A.赤霉素可能参与α-淀粉酶基因表达过程的调控来促进种子的萌发B.色氨酸通过脱水缩合反应直接形成生长素C.植物激素几乎控制着植物所有的生命活动D.在生长素类似物促进扦插枝条生根的实验中,处理浓度不同,枝条生根数一定不同6.我国西北沙化地区为恢复生态系统釆用乔、灌、草相结合的方法,通过栽种多种植被来防风沙,取得了良好的效果。
安徽省a10联盟2019届高三下学期开学数学试卷(理科)Word版含解析

安徽省a10联盟2019届高三下学期开学数学试卷(理科)Word版含解析2018-2019学年安徽省A10联盟高三(下)开学数学试卷(理科)一、选择题:(本大题共12小题,每小题5分,共60分,每小题分别给出四个选项,只有温馨提示:多少汗水曾洒下,多少期待曾播种,终是在高考交卷的一刹尘埃落地,多少记忆梦中惦记,多少青春付与流水,人生,总有一次这样的成败,才算长大。
高考保持心平气和,不要紧张,像对待平时考试一样去做题,做完检查一下题目,不要直接交卷,检查下有没有错的地方,然后耐心等待考试结束。
一个选项符合题意)1.已知复数,其中i是虚数单位,则|z|=()A.2B.2C.3D.32.若p是q的充分不必要条件,则下列判断正确的是()A.¬p是q的必要不充分条件B.¬q是p的必要不充分条件C.¬p是¬q的必要不充分条件D.¬q是¬p的必要不充分条件3.抛物线x2=4y上一点P到焦点的距离为3,则点P到y轴的距离为()A.2B.1 C.2 D.34.已知a为锐角,且7sinα=2cos2α,则sin(α+)=()A.B.C. D.5.已知函数为偶函数,则m+n=()A.1 B.﹣1 C.2 D.﹣26.某小区有1000户,各户每月的周电量近似服从正态分布N,则用电量在320度以上的户数约为()(参考数据:若随机变量ξ服从正态分布N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=68.26%,P (μ﹣2σ<ξ<μ+2σ)=95.44%,P(μ﹣3σ<ξ<μ+3σ)=99.74%.)A.17 B.23 C.34 D.467.执行如图所示的程序框图,则输出的b值为()A.8 B.30 C.92 D.968.一个半球与一个正四棱锥组成的几何体的正视图与俯视图如图所示,其中正视图中的等腰三角形的腰长为3.若正四棱锥的顶点均在该半球所在球的球面上,则此球的半径为()A.2 B.C.D.9.双曲线中,F2为其右焦点,A1为其左顶点,点B(0,b)在以A1F2为直径的圆上,则此双曲线的离心率为()A.B.C.D.10.已知函数f(x)=2cos(x+φ)图象的一个对称中心为(2,0),且f(1)>f(3),要得到函数,f(x)的图象可将函数y=2cos x的图象()A.向左平移个单位长度B.向左平移个单位长度C.向右平移个单位长度D.向右平移个单位长度11.已知A、B、C三点不共线,且=﹣+2,则=()A.B.C.6 D.12.已知函数f(x)=﹣k(+lnx),若x=2是函数f(x)的唯一一个极值点,则实数k的取值范围为()A.(﹣∞,e]B.[0,e]C.(﹣∞,e)D.[0,e)二、填空题:(本大题共4小题,每小题5分,共20分.把答案填在题中横线上.)13.(x﹣2y)6展开式中二项式系数最大的项的系数为(用数字作答).14.已知圆C:(x+2)2+y2=4,直线l:kx﹣y﹣2k=0(k∈R),若直线l与圆C恒有公共点,则实数k的最小值是.15.已知实数x,y满足不等式组,则z=|x|+y的取值范围为.16.在△ABC中,内角A,B,C的对边分别为a,b,c,角B为锐角,且8sinAsinC=sin2B,则的取值范围为.三、解答题:(解答应写出必要的文字说明,证明过程或演算步骤.)17.已知数列{a n}为等差数列,数列{b n}为等比数列,a1=b1=1,且数列{a n?b n}的前n项和S n=k﹣(k是常数,n∈N*).(1)求k值,并求数列{a n}与数列{b n}的通项公式;(2)求数列{S n}的前n项和T n.18.某地交通管理部门从当地驾校学员中随机抽取9名学员参加交通法规知识抽测,活动设有A、B、C三个等级,分别对应5分,4分,3分,恰好各有3名学员进入三个级别,现从中随机抽取n名学员(假设各人被抽取的可能性是均等的,1≤n≤9),再将抽取的学员的成绩求和.(I)当n=3时,记事件A={抽取的3人中恰有2人级别相同},求P(A);(Ⅱ)当n=2时,若用ξ表示n个人的成绩和,求ξ的分布列和期望.19.已知在底面为矩形的四棱锥D﹣ABCE中,AB=1,BC=2,AD=3,DE=,二面角D ﹣AE﹣C的平面角的正切值为﹣2.(1)求证:平面ADE⊥平面CDE;(2)求二面角A﹣BD﹣C的大小.20.已知椭圆C:的离心率为,且焦距为4(I)求椭圆C的方程;(Ⅱ)设直线l:y=kx+m与椭圆C交于A、B两点,且△AOB的面积为4,其中O为坐标原点,求实数m的取值范围.21.若函数y=f(x)对任意x1,x2∈(0,1],都有,则称函数y=f(x)是“以π为界的类斜率函数”.(I)试判断函数y=是否为“以π为界的类斜率函数”;(Ⅱ)若实数a>0,且函数f(x)=x2+x+alnx是“以π为界的类斜率函数”,求实数a的取值范围.请考生在第22、23、24题中任选一题作答.,注意:只能做选定的题目,如果多做,则按所做的第一题记分,解答时请写清题号.(共1小题,满分10分)[选修4-1:几何证明选讲] 22.如图,⊙O内接四边形ABCD的两条对角线AC、BD交于点M,AP为⊙O的切线,∠BAP=∠BAC(I)证明:△ABM≌△DBA;(II )若BM=2,MD=3,求BC的长.[选修4-4:坐标系与参数方程]23.已知在直角坐标系xOy中,直线l的参数方程是(t是参数,m是常数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C极坐标方程为ρ=asin(θ+),点M的极坐标为(4,),且点M在曲线C上.(I)求a的值及曲线C直角坐标方程;(II )若点M关于直线l的对称点N在曲线C上,求|MN|的长.[选修4-5:不等式选讲]24.设函数f(x)=|x﹣2|﹣|2x+l|.(I)求不等式f(x)≤x的解集;(II )若不等式f(x)≥t2﹣t在x∈[﹣2,﹣1]时恒成立,求实数t的取值范围.2015-2016学年安徽省A10联盟高三(下)开学数学试卷(理科)参考答案与试题解析一、选择题:(本大题共12小题,每小题5分,共60分,每小题分别给出四个选项,只有一个选项符合题意)1.已知复数,其中i是虚数单位,则|z|=()A.2B.2C.3D.3【考点】复数求模.【分析】根据复数的运算性质求出z,从而求出z的模.【解答】解:∵=3﹣3i,∴|z|==3,故选:C.2.若p是q的充分不必要条件,则下列判断正确的是()A.¬p是q的必要不充分条件B.¬q是p的必要不充分条件C.¬p是¬q的必要不充分条件D.¬q是¬p的必要不充分条件【考点】必要条件、充分条件与充要条件的判断.【分析】本题考查的知识点是四种命题及充要条件的定义,根据p是q的充分不必要条件,我们易得到p?q与q?p的真假,然后根据逆否命题真假性相同,即可得到结论.【解答】解:∵p是q的充分不必要条件,∴p?q为真命题,q?p为假命题,故¬p?¬q为假命题,¬q?¬p为真命题,故¬p是¬q的必要不充分条件故选:C.3.抛物线x2=4y上一点P到焦点的距离为3,则点P到y轴的距离为()A.2B.1 C.2 D.3【考点】抛物线的简单性质.【分析】先根据抛物线方程求得焦点坐标及准线方程,进而根据抛物线的定义可知点p到焦点的距离与到准线的距离相等,进而推断出y p+1=2,求得y p,代入抛物线方程即可求得点p的横坐标即可.【解答】解:根据抛物线方程可求得焦点坐标为(0,1),准线方程为y=﹣1,根据抛物线定义,∴y p+1=3,解得y p=2,代入抛物线方程求得x=±2,∴点P到y轴的距离为:2.故选:A.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学精品复习资料
2019.5
安徽1号卷.A10联盟高三开年考
数学(理科)试题
巢湖一中合肥八中淮南二中六安一中南陵中学
舒城中学太湖中学天长中学屯溪一中宣城中学
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
第I 卷选择题(共60分)
一、选择题:(本大题共12小题,每小题
5分,共60分,每小题分别给出四个选项,只有一个选项符合题意)
1.已知复数
10233z i ,其中i 是虚数单位,则|x|=( ) A .22B .23c .32D .33
2.若p 是q 的充分不必要条件,则下列判断一摩军确的是
( ) A .p 是q 的必要不充分条件
B .-q 是p 的必要不充分条件
C .p 是q 的必要不充分条件
D .q 是p 的必要不充分条件
3.抛物线x 2 =4y 上一点P 到焦点的距离为
3,则点P 到y 轴的距离为( ) A .22B .1 C .2 D .3
4.已知a 为锐角,且7 sina=2cos 2a ,则sin(a+3
)=( ) A .135
8B .153
8C .135
8D .153
8
5.已知函数
22log 2sin ,0()log ()sin ,0m x x x f x x n x x 为偶函数,则m+n= ( ) A .1 B .-1
C .2
D .-2 6.某小区有1000户,各户每月的周电量近似服从正态分布N(300,l02),则用电量在320度以上的户数约为( )
(参考数据:若随机变量
服从正态分布N (μ,σ2),则=68.26%,= 95.44%,。
