第3-4章等值线等值面的生成
等值面提取

等值面提取等值面提取是地理信息系统中常用的一种数据处理方法,用于将连续的数据转换为离散的等值线或等值面。
等值面是在地图上表示相同数值的点的连线形成的区域,通过等值面可以直观地展示地理现象的变化规律。
等值面提取的过程一般包括数据预处理、插值方法选择、等值线生成和等值面生成四个步骤。
首先,需要对原始数据进行预处理,包括数据清洗、空值填充等操作,以确保数据的准确性和完整性。
然后,根据具体的需求和数据特点选择合适的插值方法,常用的插值方法有反距离加权法、克里金插值法、样条插值法等。
选择合适的插值方法可以在一定程度上减小插值误差,提高等值面的精度。
在等值线生成阶段,通过将插值后的数据按照一定的数值间隔绘制等值线,即将相同数值的点连接起来,形成等值线。
等值线的绘制需要根据数据的分布情况和数值间隔进行调整,以保证等值线的连续性和平滑性。
在等值线生成的基础上,可以进一步生成等值面。
等值面是由相邻等值线之间的区域填充而成的,可以通过填充颜色或阴影来区分不同数值区域,达到直观展示数据分布的目的。
等值面提取在地理信息系统中具有广泛的应用。
例如,在地形分析中,可以使用等值面提取方法生成数字高程模型,通过等值面展示地形高度的变化;在气象学中,可以利用等值面提取方法绘制气温、降雨量等气象要素的分布图,以便分析和预测气候变化;在地质勘探中,可以通过等值面提取方法绘制地下水位、地下水质等地质要素的分布图,为地下水资源的开发和利用提供参考。
等值面提取是一种重要的数据处理方法,可以将连续的数据转换为离散的等值线或等值面,在地理信息系统中具有广泛的应用。
通过等值面可以直观地展示地理现象的变化规律,为地理分析和决策提供有力的支持。
在使用等值面提取方法时,需要注意合理选择插值方法、调整等值线的间隔和样式,以及合理解释等值面的含义,以确保提取结果的准确性和可靠性。
等值线的数学规律研究

1500 1600
1450
1500 1450 1550
1700 1650
1700 15156050
1350 等高线
凸低比两侧高 公 路
1550 155城0 区
1600
1600
11.对图中城区威胁最大的自然灾害是 ( )
A. 暴雨
B.泥石流
C. 滑坡
D.洪涝
县城建在狭窄的山脊上,两侧极其容易发生滑坡事故
难点:通过经纬网进行区域认知
分界规律
4 月 15 日 4 月 15 日
3 月 15 日
n
①
5 月 15 日
5 月 15 日 5月1日
4 月 15 日
E
②
2 月下旬
4-1 F
③
33-月11 日
④4 月 1 日
33月-118 8日
m
9.造成③、④两地入春时间差异的原因是 ( ) A.③地太阳高度较④大,获得太阳辐射多 B.③地大陆性较④强,春季气温回升较快 C.④地受海洋调节作用较③强,春季来得早 D.④地受冬季风影响较③大,春季来得晚
用地理学原理来解释, 不是用数学规律
读等高线示意图,已知a>b,读图完成1~3题。
求:B、M、N的取值范围。(必备铺垫知识)
B:b<B<a M:a<M<2a-b N:2b-a<N<a
M比a大0到(a-b)范围 N比b小0到(a-b)范围
a
M
N
B
b
1.有关M、N两处地形的正确叙述( ) A.M为山坡上的小丘,N为山坡上的洼地 B.N 为山坡上的小丘,M为山坡上的洼地 C.M、N均为山坡上的小丘 D.M、N均为山坡上的洼地
高考地理知识总结等值线地图综合分析和判读

2019高考地理学问总结-等值线地图综合分析和判读高考地理备考系列(四)等值线地图综合分析和判读等值线图是将某种地理事物或某种地理现象取其数值相等的点所做的连线图。
中学地理的等值线有许多类型,如等高线、等温线、等压线、等降水量线、等盐度线、等酸雨pH值线、等太阳辐射线、等太阳高度线、等时线、等深线、等潜水线、等物质线、降水变率等值线、等水温压线、等震线、等地价线等等。
其中等高线、等温线、等压线最重要。
地理事象的空间分布、空间演化以及地理各要素之间的相互联系都可以通过等值线图来展示。
它可以充分考查学生的空间概念、空间想像,以及分析计算实力,历年来高考都特别重视对等值线图的考查。
所以,了解等值线的基本特点,把握等值线图的判读方法和综合分析特别重要。
一、等值线的基本特点1.同一条等值线上的数值相等。
2.等值线为闭合曲线。
3.两条等值线一般不能相交。
等高线图上悬崖可以显示为重合状态。
4.相邻的两条等值线数值相等或差一个等值距。
二、判读的一般方法1.读数值一等值差(每相邻的两条线数值差相等或为0);改变规律(这是做题的基础)2.看疏密状况一了解影响因素3.看走向和形态一了解影响因素4.留意等值线的弯曲处—可添加协助线,变抽象为直观三.综合应用(一)、等高线地形图1.坡度问题:一看等高线疏密,密集的地方坡度陡,稀疏的地方坡度缓;二计算,坡度的正切=垂直相对高度/水平实地距离2.通视问题:通过作地形剖面图来解决,假如过已知两点作的地形剖面图无山地或山脊阻挡,则两地可相互通视;留意凸坡(等高线上疏下密)不行见,凹坡(等高线上密下疏)可见;留意题中要求,分析图中景观图是仰视或俯视可见。
3.引水线路:留意让其从高处向低处引水,以实现自流,且线路要尽可能短,这样经济投入才会较少。
4.交通线路选择:利用有利的地形地势,既要考虑距离长短,又要考虑路途平稳(间距、坡度等),一般是在两条等高线间绕行,沿等高线走向(延长方向)分布,以削减坡度,只有必要时才可穿过一、两条等高线;尽可能少地通过河流,少建桥梁等,以削减施工难度和投资;避开通过断崖、沼泽地、沙漠等地段。
surfer与ArcGIS生成等值线和等值面

surfer
与 Arcgis 生成等值线和等直面的步骤如下: 准备 surfer 用的 book1.dat 文件,格式如下: Y 40.8 40.72 Z 1 116.24 … …
2、在 surfer 中,选择 Grid->data 菜单,打开 book1.dat 文件,单击 OK,生成 book1.grd 文件 3、在 surfer 中,选择 file->open 菜单,打开 book1.grd 文件,然后选 择 File->Save as ,保存为 book1.dem 4、在 Arcgis 中打开 book1.dem 文件,用 spatial analyst->surface analysis->contour 工具,在弹出的对话框中,等高线间隔根据需要设 置,确定,生成 contour.shp 5、用准备好的区域的边界去剪切等高线,生成 contour_clip.shp 6、用 feature to point 工具,生成 contour_clip_FeatureToPoint.shp 7、用 feature to polygon 工具,选择区域图层和 contour_clip.shp,lable layer 选 contour_clip_FeatureToPoint.shp 生成等值面, 注意如果区域图 层和 contour_clip.shp 没有相交,要用 buffer 工具向内(-0.005)生成 新的区域,然后再用 feature to ploygon 工具处理
web前端利用turf.js生成等值线、等值面

} console.log(pointGrid.features.length); //等值线的级数 var breaks = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
}
var map = L.map("map", { center: [31.59, 120.29], zoom: 12, layers: [normal], zoomControl: false
}); // 创建等值线区域 var extent = [0, 30, 20, 50]; var cellWidth = 100; var pointGrid = turf.pointGrid(extent, cellWidth, { units: 'miles' });
#map {
height: 2000px; width: 1500px; } </style> <script src="Script/leaflet/leaflet.js"></script> <script src="Script/leaflet/leaflet.ChineseTmsProviders.js"></script> <script src='https:///@turf/turf/turf.min.js'></script> </head> <body> <div id="map"></div>
等值线图的制作流程课件

84
点属性标注
点属性标注 标注属性选择 可选标注域名 (字段名) 添加到文件 (保存注释的文件)
等值线图的制作流程
85
点属性标注
点属性标注 设置属性标注注释
等值线图的制作流程
86
点属性标注
点属性标注 效果
如何取消 1.关闭文件 2.不保存修改 3.重新打开
等值线图的制作流程
87
等值线图的制作流程
47
纸张大小设置
等值线图的制作流程
48
编辑图片
等值线图的制作流程
49
缓冲区分析
缓冲区分析:
包括点缓冲区分析 线缓冲区分析 区缓冲区分析
要点:
半径 缓冲区类型 图元
等值线图的制作流程
50
操作流程 1输入半径
等值线图的制作流程
51
操作流程 2选择类型
等值线图的制作流程
3375006
等值线图的制作流程
2
处理导出到 txt文档
导出:选择数据复制,粘贴到文本文件 保存为SourceData.txt,如图
等值线图的制作流程
3
2. 投影变换
准备投影变换参数: 投影前WGS84坐标 获取参考GPS参数设置 地图的投影坐标 请查看地图参数:地图的说明,
如湖南省小土壤图附投影参数说明
等值线图的制作流程
99
区属性标注
区属性标注 示例
等值线图的制作流程
100
生成裁剪边界弧段区文件、区文件
在工程中添加弧段的区文件 在区编辑中选择区编辑生成区,然后保存。
等值线图的制作流程
68
保存区文件、打开区文件
等值线图的制作流程
69
生成区,保存后从工程删除区文件
高中数学等值线

_______________________。 高度角大,太阳辐射强
(2)在相同纬度太阳总辐射量分布 特点是______________,其形 西多东少 成的主要原因是_____________ 西部处于山脉
背风坡,云雨少,对太阳辐射削弱作用小 ____________________________。
2、如果锋面系统都能引起降水,那么图中A、B、C、D出 现降水区域的是: B、C
四、等降水量线图
1、判断降水的地区分布差异大小: 等降水量线密集——降水的地区分布差 异大,稀疏——降水的地区分布差别小 2、判断等降水量线延伸方向。 (1)受海陆影响:等降水量线与海岸线大 致平行——降水自沿海向内陆减少。 (2)受地形影响,等降水量线与等高线大 致平行。如新疆天山南北的降水分布。 3、判断迎风坡和背风坡 多雨——迎风坡 少雨——背风坡
5.判断地形
等温线闭合:
内线数值大→中心气温高→中心地势低→盆地(洼地)
内线数值小→中心气温低→中心地势高→山地(高原) 等温线不闭合: 等温线向高值方向凸→中间比两侧气温低→中间地势高→山脊 等温线向低值方向凸→中间比两侧气温高→中间地势低→山谷
山地
8℃
10℃
12℃
平原
6.判读等温线的走向,分析等温线与纬线、海岸线与地 形的关系,进而判断影响因素 ①等温线与纬线平行:这是全球等温线分布的基本趋 势,它是太阳辐射从赤道向两极递减的结果。 ②等温线与海岸线大致平行:在北半球中纬度的大陆 东西两岸比较明显,这是因为海洋对气温起了调节作用, 沿海地区受海洋的影响较大。
·
·
⑷ 气压系统的判读
①凡等压线闭合,中心气压高于四周气压的区域,叫做高气压; 凡等压线闭合,中心气压低于四周气压的区域,叫做低气压
等值线等值面生成算法在矿山储量计算剖面图中的应用

第5卷 第4 9 期
有 色 金 属 ( 部分) 矿山
20 年7 07 月
等值线等值面生成算法在矿山储量计算剖面图中的应用
鞠 霞 徐 兵 田 宜平
( 中国地 质大 学资 源 学院 国土资 源信 息 系统研 究所 )
摘 要: 在利用克里格方法对紫金矿 山进行储量分析 的过程 中, 储量计算剖 面图是重 要的图件之 一。 因此,
I f r ain Sy tm n ttt ft e Chia Un v r i fGe s inc s,c n r aiet e f cin h q v e tlneta ig no m t se I siu eo h n ie st o o ce e o y a e z h un to o te e uia n i r cn l f l a d t quv e ts fa e g ne ain o hes ai e r t a l aa o n o p ci g ln n hee ia n ur c e r to ft p ta s paa e s mp e d t n a y prs e tn ie ̄ s cin,whih prv d l l et o c o ie
Al o ih i h l c l t n o i e s r e r f e g rt m n t e Ca u a i fM n Re e v s P o o s i
J a Xu B n T a pn u Xi ig in Yiig ( ada dR sucsI om t nS s m Istt,aut o at R suc , hn nvri f esi cs Ln n eore n r ai yt tueF cl f r eore C iaU ie t o G oc n e) f o e ni y E h sy e A s atI epoeso s gK i gf n l i o inMi  ̄r evs h acl i f eevs r l i bt c: t rcs f i r raa s f j n e re,t c ua o o sre o e s r nh un  ̄n o y s Zi e s el tn r p f i
等值线等值面的生成

• 如图所示,(x0, y0) 为“-”,(x0, y1) 为“+”,则交点为
xt x0 Ft F00 yt y0 F F ( y1 y0 ) 01 00 y0 ( F01 Ft ) y1 ( Ft F00 ) F01 F00
网格序列法
• 如何从中选择一种正确的连接方式呢?这可从单元内的双线性插 值函数分析入手。由于在单元边上采用了线性插值,由此单元面 上函数值的变化是双线性的,
F ( x , y ) a a x a y a xy 0 1 2 3
• 即等值线在单元内不是直线段而是双曲线。二义性连接可通过求 该双曲线两条渐近线交点处的函数值来判定,这是因为渐近线的 交点总是与其中一对顶点落入同一区域内 ,如渐近线交点为 “+”,则取图5a的连接方式;如为“-”,则取图5b的连接方 式。即在图5a中,表示单元中部为“+”,在图5b中,表示单元 中部为“-”。在实际计算中,为简化计算,往往采用单元对角 线交点代替渐近线交点的计算。
一 Cuberille方法(立方体方法)
网格序列法
• (1) 将网格点分为“IN”和“OUT”两种状态,表示该点在等值线 内,或在等值线外。如果 Fij≤Ft ,则顶点 (xi, yj) 为“ IN” ,记为 “-”;如果Fij﹥Ft,则顶点(xi, yj)为“OUT”,记为“+”。 • (2) 如果单元四个顶点全为“+”,或全为“-”,则网格单元 与值为Ft的等值线无交点,否则 • (3) 对于两个顶点分别为“+”、“-”的单元边,可用线性插 值计算等值线在这条边上的交点。
第 3章
二维标量场等值线的生成
二维标量场可看成是定义于某一个面上的二维标量函 数F=F(x, y),所谓等值线是由所有点(xi, yi)构成,其中F(xi, yi) =Ft(为一给定值),将这些点按一定顺序连接起来就 组成了函数值为Ft的等值线。对于二维标量场,其数据往 往是分布在规则网格点上的,常用的等值线抽取方法有网 格序列法和单元剖分法。
如何用Section作平面等值线图

如何用Section作平面等值线图
在我们平时的工作中,常常会遇到需作等高线或等值线图的情况,如根据煤层底板作煤层底板等高线图,根据GPS点高层数据作地形等高线图等情况。
以前我也为这事烦恼,有了Section这件事就变得简单了,下面我就根据自己的实际操作步骤写出来,和大家一起分享。
1、平时我们可以将各地质点的X、Y、Z作好一个Excel表,等
要作图时将其另存为文本文件。
2、打开Section—1辅助工具—绘制等值线---高程数据网格化----
找到要作等值线的那个文本文件,打开。
此时弹出如下界面:
3、在数据列中,选择好X、Y、Z所对应的列和网格化方法,确
定。
4、Section—1辅助工具—绘制等值线---高程数据网格化—平面
等值线图,找到刚才网格化得到的文件,打开。
5、设置等值线参数:
⑴设置是否等值线套区,保留边界;
⑵等值线是否光滑处理;
⑶图幅范围一般选择原始数据范围;
⑷等值层值可以根据需要设置,只要双击就可以设置;设置线参数;
⑸点击注记参数,可以设置标注字体、格式、起始层、频度等;
⑹单击区中和颜色可以修改不同等值范围的颜色;
⑺全部设置完成后,点击确定。
6、然后点击1:1,即可看到等值线了。
7、将这个文件的点、线、文件保存,然后添加到相应的图中,就形成了底板等高线或等值线图了。
16种等值线图的解读与应用

16种等值线图的解读与应用一、等值线的原理1、等值性或同距性原理在等值线图中,相邻的两条等值线要么等值,要么同距。
2、低高低和高低高原理低值凸向高值,凸处的值变低高值凸向低值,凸处的值变高3、疏差小和密差大原理等值线越稀疏,单位距离的差值越小等值线越密集,单位距离的差值越大二、等值线的类型中学地理主要有:等高线、等深线、等温线(等气温线、等水温线)、等压线(水平面等压线、垂直面等压线)、等降水量线、等太阳辐射量线、等盐度线、等PH值线、等太阳高度线、等潜水位线、等承压水位线等等。
三、主要等值线的应用1、通过判读等高线来判断地形的种类(山地、盆谷、轮廓、山脊线、山谷线、陡崖)坡度的陡与缓,确定山脉的走向,选择水库大坝的位置、修筑公路线的走向选择、地形剖面图的绘制及工程土方的估计等。
2、通过判读等深线来判断海洋地形的种类如大陆架、海沟、海盆、海岭、海底火山等;甚至判断地形图所在的具体海域;确定港口的区位条件。
3、通过判读大气等压线来判断气压中心的名称:如气旋、反气旋、高压脊、低压糟、轮廓;判断不同部位的天气特点,风向与风力大小。
也可以从全球范围的等压线图来判定典型的气压中心名称。
4、通过判读大气等温线来判断所在地的南北半球、季节与天气、以及该季节大陆与海洋上的气压中心、季风盛行方向(亚洲东部和南部)。
5、通过判读海洋等水温线判定洋流的性质,洋流的南北半球位置及大陆东西岸位置,以及洋流对环境的影响。
6、通过判读等降水量线结合具体的地形轮廓判定山地的迎风坡与背风坡,具体离海远近、山脉走向等。
7、判读太阳辐射等值线,判断回答太阳辐射极大值、极小值出现的地区及原因,分布的总体规律及对人类的影响。
8、通过判读等震线判定地表某点地震的烈度、震源位置及震中距等。
9、通过判读海底岩石年龄等值线判定海岭、海沟的位置,及海底张裂地带与碰撞地带的位置与走向。
10、通过判读人口密度等值线分析某地区人口分布的规律及其影响的自然、历史、社会、经济诸因素。
第三章优化设计的数学基础

第三章优化设计的数学基础一等值(线)面目标函数是n维变量的函数,它的函数图像只能在n+1维空间中描述出来。
为了在n维设计空间中反映目标函数的变化情况,常采用目标函数等值面的方法。
对于可计算的函数f(x),给定一个设计点X(k),f(x)总有一个定值c 与之对应;而当f(x)取定值 c 时,则有无限多个设计点X(i)(i=1,2, …)与之对应,这些点集构成一个曲面,称为等值面。
即具有相等目标函数值的设计点构成的平面曲线或曲面称为等值线或等值面。
目标函数F(x)的等值面(线)数学表达式为:F(x)=C当 c 取c1,c2, …等值时,就获得一族曲面族,称为等值面族。
等值线的“心”(以二维为例)一个“心”:是单峰函数的极(小)值点,是全局极(小)值点。
没有“心”:例,线性函数的等值线是平行的,无“心”,认为极值点在无穷远处。
多个“心”:不是单峰函数,每个极(小)值点只是局部极(小)值点,必须通过比较各个极值点和“鞍点”(须正确判别)的值,才能确定极(小)值点。
等值线的形状:同心圆族、椭圆族,近似椭圆族;严重非线性函数——病态函数的等值线族是严重偏心和扭曲、分布疏密严重不一的曲线族。
等值线的疏密:沿等值线密的方向,函数值变化快;沿等值线疏的方向,函数值变化慢。
等值线的疏密定性反应函数值变化率。
二 方向导数与梯度1 方向导数二元函数在点x 0处沿某一方向s 的方向导数方向导数是偏导数概念的推广。
方向导数与偏导数之间的数量关系是n 元函数在点x 0处沿s 方向的方向导数2 梯度二元函数的梯度▽F (x 0)为函数F (x 1,x 2)在x 0点处的梯度。
设010*********(,)(,)lim S F F x x x x F x x s s ∆→∂+∆+∆-=∂∆x 0001212cos cos F F F s x x θθ∂∂∂=+∂∂∂x x x 0000012121cos cos cos cos n n n ii i F F F F s x x x F x θθθθ=∂∂∂∂=+++∂∂∂∂∂=∂∑x x x xx O x 110x 0001212cos cos F F F s x x θθ∂∂∂=+∂∂∂x x x 01212cos cos F F x x θθ⎡⎤⎡⎤∂∂=⎢⎥⎢⎥∂∂⎣⎦⎣⎦x 0010122()T F x F F F F x x x ∂⎡⎤⎢⎥∂⎡⎤∂∂⎢⎥∇==⎢⎥∂∂∂⎢⎥⎣⎦⎢⎥∂⎣⎦x x x 12cos cos s θθ⎡⎤=⎢⎥⎣⎦s 方向和梯度方向重合时,方向导数值最大。
绘制等值线(等高线)方法

如何根据离散点自动绘制等值线(等高线)之三角形法自动绘制等值线的方法从技术方向上看可以分为两大类,插值和曲线拟合.其中曲线拟合总的来说效果不如插值算法经典和应用广泛,效果也较逊色.这里着重介绍插值算法.其中插值算法中,按照方式不同分为离散点客观化和三角网方式.两者区别在于三角网计算主要在生成三角网过程,省去了插值到格点的过程.而客观分析过程则是将离散点分析到格点后再内插到细网格,然后大多利用追踪法生成等值线,也有在这里再使用曲线拟合.1、三角形算法a、首先生成delaunay三角形,这一点在我的帖子"delaunay triangulation之丰衣足食“内有源程序,大家可以参考。
b、随后需要在三角形的边上插补等值点。
要确定某个三角形的边上是否有等值点,需要进行判断和处理。
注意:如果某原始数据点和等值线值相同,将该点改变一个微量。
如果一个三角形三顶点的值相同则各边无等值点。
如果一个三角形的任意边两端点(A、B〕的Z值(Za、Zb)满足满足(Zd-Za)*(Zd-Zb)<0,其中Zd代表等值线的值,则该边必有等值点,其平面位置是Xd=Xa+(Xb-Xa)*(Zd-Za)/(Zd-Za) , Yd=Ya+(Yb-Ya)*(Zd-Za)/(Zb-Za)。
每个三角形上不可能三边都有同值的等值点,另一边上必定有同值的等值点。
c、等值点的追踪。
为了能将内插的等值点顺序追踪排列,绘出等值线,还必须找出相互重叠的环形网内所计算的等值点间的平面位置关系。
因每个环形网都是由多个三角形组成的,我们先简单分析一下单个三角形中存在等值点的情况。
由于不必考虑等值线穿过端点,如果一个三角形的边上存在等值点的话,只可能在某两条边上存在等值点,而不可能三条边上同时都有。
也就是说,只要三角形一边上存在等值点,则其余的两条边中必有一边存在等值点。
根据上面的约定,我们再研究等值线穿过任一环形网中两条及两条以上相邻的径边时,可能出现的几种情形:① 等值线不通过环形网的界边。
面绘制方法

嵌套树Nesting tree
• 嵌套树:描述每一断 层上轮廓线的嵌套关 系。树中每一结点对 应于一条轮廓线,其 根结点对应于一虚拟 的包围所有轮廓线的 外轮廓线,树中每一 结点的后续结点对应 于被该结点的轮廓线 所直接包围的所有轮 廓线。
合,将该集合称为一个“水平集”。 • 分析“水平集”中双曲线拓扑性质的变化,可以简单直观
地确定体素内部曲面的拓扑和几何形状。
临界点与临界线
• 4种存在二义性的体素 中的等值面都存在临 界点(右图中两条点划 线的交点),“水平集” 中过临界点的等值线 (图中点划线),称 之为临界曲线。
确定临界点与临界线
• 连通分叉:在一个层面上有嵌套的两条等 值线,在另一个层面上是一条等值线。
马鞍面三角片的处理
马鞍面三角片的处理: • 在层面间引入附加点来重构等值面。 • 当层面间距离较小时,也可直接将附加点加在某一层面上,
不会产生太大的视觉误差。如上页图所示,两条轮廓线被 归类到单条轮廓线。 另外一种三角面片——极值点三角片:建立平面三角片网。
• 计算法向量:采用中心差 分计算出体素顶点处的梯 度,再用线性插值计算等 值点处的梯度值作为该点 的法向量。
二义性
• 在14种模式中,某 3A
3B
些模式存在二义性,
如右图示。
• 下节将着重讨论4
7B
7C
种存在二义性的体
素中等值面的重构
方法。
12A
12B
6A
6B
7D
10A
13A
13B
13E
(a)
(b)
高考地理专题一 第二讲:等值线图的判读与应用

知识点一
等值线(面)的类型和判读
1.等值线(面)类型与影响分布的因素 等值线(面)类型 等高线 等深线 等温线
Copyright 2004-2009 版权所有 盗版必究
影响分布的因素 地质作用(内力、外力) 地质作用(内力、外力) 纬度、海陆、地形、洋流、 大气环流等
等降水量线
线之间的高度差。
(3)等高线是封闭的曲线:无论怎样迂回曲折, 终必环绕成圈,但在一幅图上不一定全部闭合。 (4)两条等高线决不能相交,因为一般情况下, 同一地点不会有两个高度。但在垂直壁立的峭壁悬 崖,等高线可以重叠。
Copyright 2004-2009 版权所有 盗版必究
(5)等高线疏密反映坡度缓陡:等高线稀疏的地方表示缓坡, 密集的地方表示陡坡,间隔相等的地方表示均匀坡。 (6)等高线与山脊线或山谷线垂直相交:等高线穿过山脊线时, 山脊线两侧的等高线略呈平行状。等高线穿过河谷(山谷线或集 水线)时,向上游弯曲,成反“V”字形。 (7)两对等高线凸侧互相对称时,为山地的鞍部。 (8)示坡线表示降坡方向:示坡线是与等高线垂直相交的短线, 总是指向海拔较低的方向,有时也叫做降坡线。 (9)坡面上物体自然运动的方向为最大坡度方向,即与等高线垂 直的方向。 (10)几条特殊的等高线:0米线表示海平面,也是海岸线; 200米线区分平原和低丘;500米、1 000米线显示低山丘陵或高 原,2 000米、3 000米反映中山和高原;4 000米反映青藏高原和 高山的特征。
差异体现了
A.纬度地带分异规律 C.垂直地带分异规律
(
D.地方性分异规律
)
B.干湿度地带分异规律
Copyright 2004-2009 版权所有 盗版必究
第一课双狐软件常用操作

输入csv或地震 导出文件
越大,允许变化的范围越大
越大精度越 高,速度慢
第二部分:数据成图
(1)常规等值线生成—利用井点数据直接生成或利用软件导出的等值线生成 另选盘文件
最后,二维显示 查看平面图
第二部分:数据成图
(2)断层分盘
Background-单击 选中-右键-另存为
曲线处理
输入上步导出的构 造等值线曲面文
图层必须是可编辑的情况下:
矩形范围外的删除 首先画个任意形状,然后拾取式 给出精确的坐标范围
第三部分:常用操作与小技巧
(11)等值线清绘,与生成背景
首先点击 左下角的 定位点, 输入坐标, 再按顺时 针方向点 击剩余三 个点。
第三部分:常用操作与小技巧
(11)等值线清绘,与生成背景
精品课件!
精品课件!
(3)深度校正
Derth.txt
井号、 X、 Y、 钻井分层、构造曲面值、误差值
拖至快捷方式 dfdraw中打开
删除---条件删 除---十字空心 箭头—框选
文件---保存
第二部分:数据成图
(3)深度校正
修改各项参数
可暂时不加边界,视情况而定
二维显示后
第二部分:数据成图
(3)深度校正
输入校正量曲面
(2)井轨迹
第一部分:数据的导入
数据格式
文件-导入
第一部分:数据的导入
(2)等值线和断层
等值线格式
断层格式
等值线导入
断层导入
第二部分:数据成图
(1)常规等值线生成—利用井点数据直接生成或利用软件导出的等值线生成
x,y,z值
常规等值线勾绘
地震导出数据(DAT格式要转换为双狐格式)
总第讲等值线图①同线等高;②同图等高距一致;③等高线是封闭曲线(图内..
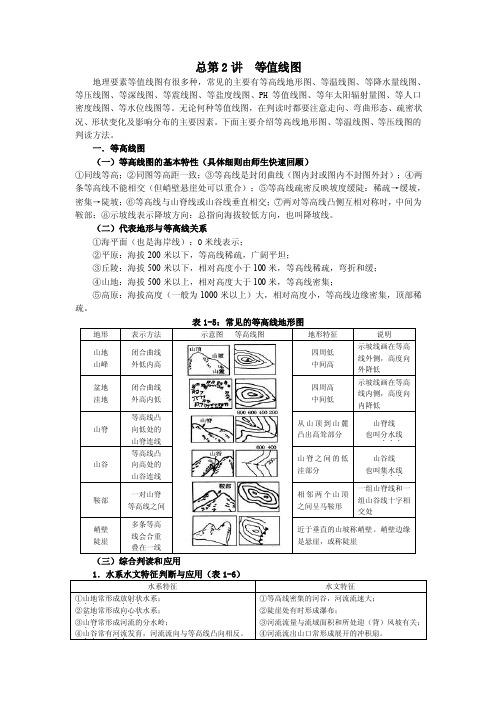
总第2讲等值线图地理要素等值线图有很多种,常见的主要有等高线地形图、等温线图、等降水量线图、等压线图、等深线图、等震线图、等盐度线图、PH等值线图、等年太阳辐射量图、等人口密度线图、等水位线图等。
无论何种等值线图,在判读时都要注意走向、弯曲形态、疏密状况、形状变化及影响分布的主要因素。
下面主要介绍等高线地形图、等温线图、等压线图的判读方法。
一.等高线图(一)等高线图的基本特性(具体细则由师生快速回顾)①同线等高;②同图等高距一致;③等高线是封闭曲线(图内封或图内不封图外封);④两条等高线不能相交(但峭壁悬崖处可以重合);⑤等高线疏密反映坡度缓陡:稀疏→缓坡,密集→陡坡;⑥等高线与山脊线或山谷线垂直相交;⑦两对等高线凸侧互相对称时,中间为鞍部;⑧示坡线表示降坡方向:总指向海拔较低方向,也叫降坡线。
(二)代表地形与等高线关系①海平面(也是海岸线):0米线表示;②平原:海拔200米以下,等高线稀疏,广阔平坦;③丘陵:海拔500米以下,相对高度小于100米,等高线稀疏,弯折和缓;④山地:海拔500米以上,相对高度大于100米,等高线密集;⑤高原:海拔高度(一般为1000米以上)大,相对高度小,等高线边缘密集,顶部稀疏。
(三)综合判读和应用2.气候特征判断与应用分析等高线与气候特征关系应结合地势高低(水热状况变化)、坡向(降水和气温差别)等因素。
①相对高度较大处应考虑气温的垂直变化,对流层下部的垂直变化率为0.60C/100m 。
②山区应考虑迎风坡和背风坡,迎风坡降水多、背风坡降水少。
③盆地不易散热,又容易引起污染空气的滞留,易成雾,造成污染。
4.地形剖面图的绘制及其应用(1)地形剖面图是以等高线地形图为基础转绘而成的,它也是一种平面直角坐标图。
地形剖面图的主要制作步骤是:①根据要求选取剖面线,如图1-12甲图中的AB 线。
②选择适当的水平比例尺将等高线图上的剖面线转绘到剖面图中作横轴,一般地说剖面图的水平比例尺与等高线图的比例尺相同,如图2-11中乙图的A ′B ′线;用等高线图的高度确定合理的垂直比例尺作纵轴,一般地说垂直比例尺比水平比例尺大若干倍,以体现地势起伏。
Arcgis 生成等值线和等值面的步骤

surfer9 与Arcgis生成等值线和等值面的步骤如下:1.准备surfer 用的Book1.dat 文件,格式如下:"x" "y" "z" 116.471992 40.809975 232 116.335556 40.700542 1235 116.541626 40.713333 214 116.73349 40.798607 566 2.在surfer 中,选择Grid->data 菜单,打开book1.dat 文件,单击ok 生成book1.grd 文件 3.在surfer 中,选择file->open 菜单,打开book1.grd 文件,然后选择File->save as ,保存为book1.dem 4.在Arcgis中打开book1.dem文件,用spatial anylyst->surface anylisys->contour 工具在弹出的对话框中,等高线间隔填50(根据你的数据定)基高-50,确定生成contour.shp 5.用你准备好的区域的边界去剪切此等高线层,生成contour_clip.shp,见下图1。
6.用feature to point 工具生成contour_Clip_FeatureToPoint.shp(为生成等值面做准备)7. 用feature to polygon 工具,选择区域图层和contour_clip.shp ,lable layer 选contour_Clip_FeatureToPoint.shp 生成等值面,注意如果区域图层和contour_clip.shp 没有相交,要用buffer 工具向内(-0.005)生成新的区域,然后在用feature to polygon 工具,结果如图2 所示以上步骤生成的等值线和等值面带属性,光滑,可谓完美。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
网格序列法
• (1) 将网格点分为“IN”和“OUT”两种状态,表示该点在等值线 内,或在等值线外。如果Fij≤Ft ,则顶点(xi, yj)为“IN”,记为 “-”;如果Fij﹥Ft,则顶点(xi, yj)为“OUT”,记为“+”。 • (2) 如果单元四个顶点全为“+”,或全为“-”,则网格单元 与值为Ft的等值线无交点,否则 • (3) 对于两个顶点分别为“+”、“-”的单元边,可用线性插 值计算等值线在这条边上的交点。
Cuberille方法(立方体方法)
• Cuberrille算法的主要优点是简单易行,其主要缺点是 出现严重的走样,显示的图象给人一种“块状的感觉”, 尤其在物体边界处锯齿形走样特别明显,而且画面较粗 糙,不能很好地显示对象的细节。
• 立方体法的另一个缺点是面的重叠冗余问题。两个相邻 边界体元的公共面重复出现,实际上它们都不会出现在 显示画面上,因为无论从哪个角度进行观察,它们都会 被这两个体元的其它面遮挡。改进的立方体法删除了边 界体元之间的公共面,减少了显示过程需要处理的多边 形的数量。
• 如图所示,(x0, y0) 为“-”,(x0, y1) 为“+”,则交点为
xt x 0 Ft F00 ( y1 y 0 ) yt y0 F01 F00 y 0 ( F01 Ft ) y1 ( Ft F00 ) F01 F00
• 当三维离散数据的密度较高,即每个体元很小时,可以假定函数 值沿体元边界呈线性变化。因此,等值面与体元边界的交点可以 通过该边两端点函数值的线性插值求出,公式为:
• 可以利用两种不同的对称性将256种不同的情况简化为15种。
• ① 互补对称性:如果将一个体元的顶点状态颠倒,即“0”变成 “1”,“1”变成“0”,则等值面与体元中8个顶点之间的拓扑关 系将不会改变,该体元与等值面的相交情况与原来一致,即新生 成的等值面与原等值面是相同的。也就是说,大于等值面的点与 小于等值面的点是可以相互替换的,因此,只要考虑4个以下 (含4个)的顶点值大于Ft就够了。根据这种互补对称性,可将 体元的模式由256种减少为128种。
二 Marching Cubes(MC)方法
• Marching Cubes ( 移 动 立 方 体 ) 方 法 是 由 W.E.Lorenson 和 H.E.Cline在1987年提出来的。由于这一方法原理简单,易于实 பைடு நூலகம்,目前已经得到了较为广泛的应用,成为三维数据等值面生成 的经典算法,Marching Cubes算法又简称为MC算法。
网格序列法
• 如何从中选择一种正确的连接方式呢?这可从单元内的双线性插 值函数分析入手。由于在单元边上采用了线性插值,由此单元面 上函数值的变化是双线性的,
F ( x, y) a0 a1 x a2 y a3 xy
• 即等值线在单元内不是直线段而是双曲线。二义性连接可通过求 该双曲线两条渐近线交点处的函数值来判定,这是因为渐近线的 交点总是与其中一对顶点落入同一区域内,如渐近线交点为 “+”,则取图5a的连接方式;如为“-”,则取图5b的连接方 式。即在图5a中,表示单元中部为“+”,在图5b中,表示单元 中部为“-”。在实际计算中,为简化计算,往往采用单元对角 线交点代替渐近线交点的计算。
Marching Cubes(MC)方法
• (1) 确定包含等值面的体元及对应的等值面片模式
• 一个体元由8个数据点构成,这8个数据点分别位于该体元的8个 顶点上。 • 首先对体元的8个顶点进行分类,判定是位于等值面之外,还是 位于等值面之内。再根据8个顶点的状态,确定等值面的模式。 • 设等值面的值为Ft,顶点分类规则为: • 若某顶点的值≥Ft,则定义该顶点位于等值面之外,记为“0”。 • 若某顶点的值<Ft,则定义该顶点位于等值面之内,记为“1”。
Cuberille方法(立方体方法)
• 每个单元均为一正六面体,包括6个多边形面。对组成所有边界 体元的多边形面进行绘制,即可产生最终的图象结果。在绘制多 边形过程中应采用合适的光照模型和消隐技术。 • 如果在具有硬件深度缓存(Z-buffer)功能的计算机上运行立方体 方法,可以将这组多边形不分次序地提交给硬件,由硬件完成消 除隐藏面的任务。如果以软件方式执行立方体方法,在算法中必 须考虑多边形的遮挡问题。一个有效的方法是把遍历体元集合与 显示两个步骤合二为一,遍历体元集合时采用从后至前的次序。 发现一个边界体元,就立刻显示它的6个面。后显示到屏幕上去 的多边形将覆盖先显示的多边形,这样就达到了消除隐藏面的目 的,这就是画家算法的思想。
网格序列法
• 在每一单元内计算出等值线与该网格单元边的交点后,利用这些 交点,就能构成在该单元内的等值线段。为了正确地连接交点生 成等值线段,必须规定等值线的方向。等值线的方向定义如下: • 沿等值线走,大于等值线值的点在等值线的左边,小于等值线值 的点在等值线的右边。也就是“-”点在等值线的右边,“+” 点在等值线的左边。在规定了等值线的走向后,等值线的连接对 于矩形单元可分如下四种情况进行:
• 如果某体元一条边的一个顶点在等值面之内,而另一个顶点在等 值面之外,那么,该边必然与等值面相交。根据这一原理就可以 判断所求等值面将与哪些体元相交,或者说将穿过哪些体元。
Marching Cubes(MC)方法
• 由于每个体元有8个顶点,每个顶点又有0、1两种状态,因此每 个体元按其8个顶点的0、1分布而言,共有28=256种不同的状态。 尽管判断等值面将与哪些体元相交在原理上很容易理解,但是要 根据这256种不同的情况求出每个体元中的等值面却是很繁琐的, 而且也容易出错。
• 1.MC方法的基本原理
• 在Marching Cubes方法中,假定原始数据是离散的三维空间规则 数据,一个体元定义为由相邻层上的8个顶点组成的一个长方体。 为了在三维数据中构造等值面,应先给定所求等值面的值,该方 法的基本原理是逐个处理所有的体元,将体元各顶点处的值与给 定的阈值进行比较,首先找出与等值面相交的体元,然后通过插 值求等值面与体元棱边的交点,并将各交点连成三角形来构成等 值面片,所有体元中的三角形集合就构成了等值面。由于这一方 法是逐个处理所有的体元,因此被称为Marching Cubes方法。 MC方法的主要步骤如下:
第4章
等值面的生成
所谓等值面是指空间中的一个曲面,在该曲面上函数 F(x, y, z)的值等于某一给定值Ft ,即等值面是由所有点 SFt = {(x, y, z):F(x, y, z) = Ft}组成的一个曲面。
等值面技术在可视化中应用很广,许多标量场的可视 化问题都可归纳为等值面的抽取和绘制,如各种等势面、 等位面、等压面、等温面等。等值面技术除生成等值面的 几何表示外,还包括显示技术,如要考虑合适的光照模型、 解决等值面的相互遮挡等。等值面的生成和显示也是可视 化研究中的一个重要领域。
网格序列法
• 网格序列法(grid sequence)的基本思想是按网格单元的排列次序, 逐个处理每一单元,寻找每一单元内相应的等值线段,在处理完 所有单元后,就自然生成了该网格中的等值线分布。 • 规则网格数据等值线的生成 • 设一规则网格数据如图所示,网格线是相互正交的,每一网格单 元是一矩形,其中四个顶点分别为(x0, y0)、(x0, y1)、(x1, y0)、(x1, y1),对应的值分别为F00 、F01、F10 、F11。要在该单元内生成值 为Ft的等值线,其主要计算步骤为: • 逐个计算每一网格单元与等值线的交点; • 连接该单元内等值线的交点,生成在该单元中的等值线线段; • 由一系列单元内的等值线线段构成该网格中的等值线。 • 网格单元与等值线的交点计算主要是求各单元的边线与等值线的 交点。假设函数在单元内呈线性变化,可以采用顶点判定,边上 插值的方法计算交点,具体步骤为:
• 在实现时,对一个体元可按照它的8个顶点的状态构造一个一字 节(8位)的状态表,如图3所示,其中的每一位表示该体元中一 个顶点的0或1状态,根据这个状态表就可判断出当前体元属于哪 一种模式、等值面将与哪一条边相交以及体元内三角面片的连接 方式。
Marching Cubes(MC)方法
• (2) 计算等值面与体元边界的交点,并连接成三角形
第3章
二维标量场等值线的生成
二维标量场可看成是定义于某一个面上的二维标量函 数F=F(x, y),所谓等值线是由所有点(xi, yi)构成,其中 F(xi, yi) =Ft(为一给定值),将这些点按一定顺序连接起 来就组成了函数值为Ft的等值线。对于二维标量场,其数 据往往是分布在规则网格点上的,常用的等值线抽取方法 有网格序列法和单元剖分法。
Marching Cubes(MC)方法
• ② 旋转对称性:如果某一模式的体元经过旋转后与另一模式的 体元一致,即顶点位臵及其状态值相同,那么这两种模式的体元 可以合并为一种。根据这种旋转对称性,体元模式可以最终归纳 为15种,见图2。其中第0种情况表示所有8个顶点的值均大于 (或小于)Ft,因而该体元与等值面不相交。第一种情况表示有 一个顶点的函数值大于(或小于)Ft,其余7个顶点均与此相反, 因而该体元内的等值面将是一个三角面片。在考虑了上面两种对 称性后,这一种情况实际上代表了16种情况。如此类推,图2中 的15种模式反映了一个体元中8个顶点可能存在的全部256种状态。
一 Cuberille方法(立方体方法)
• Cuberrille等值面方法又称Opaque Cube算法,最初由Herman等 人提出,后来又多次改进。算法主要分为两个步骤。 • (1) 确定边界单元 • 对于规则网格数据,其网格单元可看成是正六面体单元,整个三 维数据就是由这种正六面体组成的,这种组成三维图象的基本正 六面体单元称为体元。对于给定的阈值Ft,遍历体数据中的各个 单元,将组成体元8个顶点上的值与Ft进行比较,找出顶点值跨 越Ft的所有体元,即体元中有的顶点值大于阈值,有的顶点值小 于阈值,因此体元内包含等值面片,这就是边界单元。 • (2) 绘制各边界单元的6个多边形面,即将等值面看成是由各单元 的六个外表面拼合而成。
