用凯特摆测量重力加速度
用凯特摆测量重力加速度 (7)

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mgh I T π2=(1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2 (2)代入式(1)得:mgh mh I T G 22+=π (3)对比单摆周期的公式gl T π2= 可得 mhmh I l G 2+=(4),称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
左图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π (5) 22222mgh mh I T G +=π (6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l即为等效摆长。
由式(5)和(6)消去I G ,可得:()22222121214222T T T T a b g l h l π+-=+=+- (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l ,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l 的值,粗略估算T 值。
初中物理凯特摆测量重力加速度

凯特摆测量重力加速度1818年凯特提出的倒摆,经雷普索里德作了改进后,成为当时测量重力加速度g 最精确的方法。
波斯坦大地测量研究所曾用五个凯特摆用了8年时间(1896-1904),测得当地的重力加速度g=(981.274±0.003)cm/s 2,许多地区的g 值都曾以此为根据。
凯特摆测量重力加速度的方法不仅在科学史上有着重要的价值,而且在实验设计上亦有值得学习的技巧。
教学目的:1. 学习凯特摆的实验设计思想和技巧。
2. 掌握一种比较精确的测量重力加速度的方法。
教学重点及难点:1. 复摆的原理2. 凯特摆的结构及原理3. 利用凯特摆测量重力加速度的方法教学内容:一.实验原理图一是复摆的示意图,设一质量为m 的刚体,其重心G 到转轴O的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为mghI T π2= (1) 式中g 为当地的重力加速度。
设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有2mh I I G += (2)代入式(1)得 mgh mh I T G 22+=π (3) 对比单摆周期的公式gl T π2=,可得mh mh I l G 2+= (4)l 称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
复摆的周期我们能测得非常精确,但利用mhmh I l G 2+=来确定l 是很困难的。
因为重心G 的位置不易测定,因而重心G 到悬点O 的距离h 也是难以精确测定的。
同时由于复摆不可能做成理想的、规则的形状,其密度也难绝对均匀,想精确计算I G 也是不可能的。
我们利用复摆上两点的共轭性可以精确求得l 。
在复摆重心G 的两旁,总可找到两点O 和O ’,使得该摆以O 悬点的摆动周期T 1与以O ’为悬点的摆动周期T 2相同,那么可以证明'OO 就是我们要求的等效摆长l 。
图一 复摆示意图 图二 凯特摆摆杆示意图 图二是凯特摆摆杆的示意图,对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
用凯特摆测量重力加速度

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验仪器:凯特摆、光电探头、米尺和VAFN多用数字测试仪。
实验原理:1,复摆。
质量为m的刚体,其重心G到转轴O的距离为h,绕O轴的转动惯量为I。
当摆幅很小时,刚体绕O转动的周期为(1)设复摆绕通过重心G的转动惯量为,当G轴与O轴平行时有:(2)代入(1)得:(3)对比单摆周期公式,可得:(4)l称为复摆的等效摆长,因此只要测出周期和等效摆长便可球的重力加速度。
2,凯特摆。
如左图对凯特摆而言,两刀口间距就是该摆的等效摆长l。
在实验种当两刀口位置确定后,通过调节A、B、C、D四摆锤的位置可以使正、倒悬挂时的摆动周期和基本相等,即。
由公式(3):(5)(6)当时,即为等效摆长。
由公式(5)和(6)可得:(7)此式中,l、T1、T2都是可以精确测定的量,而h1则不易测准。
由此可知,a项可以精确求得,而b项则不易精确求得。
但当T1=T2以及|2h1-l| 的值较大时,b项的值相对a项是非常小的,这样b项的不精确对测量结果产生的影响就微乎其微了。
实验步骤:1,仪器调节调节摆锤A、B、C、D到合适位置,是正,倒悬的摆动周期相等。
2,测量摆动周期测量凯特摆正,倒悬摆动10个周期的时间,等效摆长和转轴O到G的距离,记录如下:的A类不确定度:的B类不确定度:所以的展伸不确定度:同理,的展伸不确定度:同上,同上,将具体的数值代入一步写清楚3,计算重力加速度及其不确定度根据公式(7):所以:g=以下求的合成不确定度。
已知:(8)对(8)式等号两边取对数:等号两边求导并合并同类项:所以的合成不确定度公式为:(9)将上述数据代入(9):所以:注意单位由于,很小可以忽略,所以只合成g和的不确定度。
类似(8)到(9)的过程:所以:最后可得:不确定度取一到两位有效数字思考题:1,凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度设计特点是:减少一些量的测量,提高实验精度。
用凯特摆测量重力加速度实验报告 (7)

用凯特摆测量重力加速度化学物理系04级龚晓李PB042060022005-12-5实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复摆绕通过重心G的转轴的转动惯量为I G 。
当G轴与O轴平行时,有I=I G+mh2∴∴复摆的等效摆长l=( I G+mh2 )/mh2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg 。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg 。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,u A =σ/=0.01764cm,∴ΔA =t P·u A =1.32*0.01764=0.02328cmu B=ΔB /C=0.1/3=0.03333cm∴u L ==0.04066cmT e ==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,u A =σ/=1.129*10¯⁴s∴ΔA =t P·u A =1.14*0.0001129=1.287*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T1 ==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,u A =σ/=0.6570*10¯⁴s∴ΔA =t P·u A =1.14*0.00006570=0.7489*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T2 ==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]}=9.813m/s²∴u g0.68 =g·{l¯²* u L²+[2 T₁/(T₁²+T₂²)]²·u T1²+[2 T₂/(T₁²+T₂²)]²·u T2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴u g0.95 =2* u g0.68 =0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
用凯特摆测量重力加速度 (4)
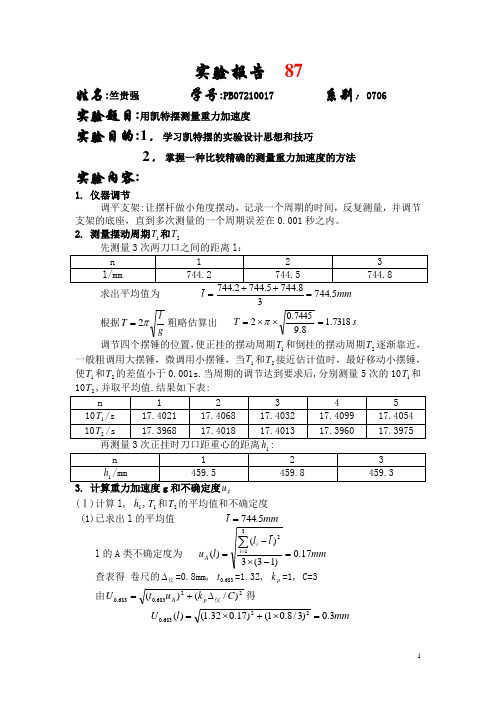
实验报告 87姓名:竺贵强 学号:PB07210017 系别:0706 实验题目:用凯特摆测量重力加速度实验目的:1.学习凯特摆的实验设计思想和技巧2.掌握一种比较精确的测量重力加速度的方法实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动,记录一个周期的时间,反复测量,并调节支架的底座,直到多次测量的一个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=⨯⨯=π 调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,一般粗调用大摆锤,微调用小摆锤,当1T 和2T 接近估计值时,最好移动小摆锤,使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=⨯+⨯=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=⨯+⨯=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5)()(512111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=⨯=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(512222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=⨯=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=⨯+=下面求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-⨯-= (3)比较a 和b 的大小,%15.0%100=⨯ab ,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =⨯= 所以 20.004)m /s 9.708(±=g P=0.683误差分析:1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同5. 在实验过程中,可能会形成不易察觉的锥面摆6. 从数据果看出,测得的十个周期数据并不理想,在调节时,两个周期分别为1.74005和1.74003,但在测量十个周期时周期的偏差比较大,可能是由于等待稳定的时间选的不好,导致周期有偏差改进方法:先测量一个周期,当稳定后,再迅速调到十个周期的档测量(这样能保证摆动已经稳定)。
凯特摆测量重力加速度带数据

凯特摆测量重力加速度带数据1. 简介凯特摆是一种单摆实验装置,可以用来测量重力加速度。
在该实验中,摆球被固定在一个可以自由摆动的杆上,当杆被释放后,摆球将开始摆动。
通过测量摆球摆动的周期,可以计算出重力加速度的数值。
2. 实验装置和方法2.1 实验装置凯特摆实验所需的装置包括:•一个摆球:用于摆动的重物,可以选择一个小球或者其他形状的物体。
•一个杆:用于支撑摆球并使其能够自由摆动,可以选择一个细长的棍子或者其他合适的杆状物体。
•一个计时器:用于精确测量摆动的时间。
•一个测量尺:用于测量摆球摆动的振幅。
2.2 实验方法1.将摆球固定在杆的一端,确保摆球能够自由摆动。
2.将杆支撑在一个适当的支架上,使摆球摆动的幅度合适。
3.使用计时器测量摆球摆动的时间,记录下每次摆动的周期。
4.重复多次实验,取平均值以提高测量结果的准确性。
5.根据测得的摆动周期和摆长,利用凯特摆公式计算出重力加速度的数值。
3. 实验数据和结果在进行凯特摆实验时,我们进行了5次摆动周期的测量,并记录下了每次测量的数据。
具体测量数据如下表所示:实验次数摆动周期(s)1 1.252 1.303 1.274 1.295 1.26根据上述测量数据,我们可以计算平均摆动周期,并利用凯特摆公式计算出重力加速度的数值。
首先,计算平均摆动周期:平均摆动周期 = (1.25 + 1.30 + 1.27 + 1.29 + 1.26) / 5 = 1.274 s然后,根据凯特摆公式计算重力加速度:摆长为L(单位:米),摆动周期为T(单位:秒),重力加速度为g(单位:m/s^2),凯特摆公式为:T = 2 * π * √(L / g)根据上述公式,可以解得:g = (4 * π^2 * L) / T^2设摆长L为1.0 m,代入上述数值,可以计算得到:g = (4 * (3.1416)^2 * 1.0) / (1.274^2) = 9.819 m/s^2因此,通过凯特摆实验测得的数据,我们计算得到重力加速度的数值为9.819m/s^2。
用凯特摆测量重力加速度

实验仪器:凯特摆,米尺,光电探头,数字测试仪.实验内容:1.估算T 值,调节仪器,使 T 1 T 2 0 001s ;2.测量摆动周期T 1和T 2 ;3.计算重力加速度g 及不确定度u g .数据处理:1. T 1所有的 都在 区间内,数据有效.所用数字测试仪 估 , 仪 , 仪 取C= ,,,,2.T2同上, ,,3.l钢尺,取∆估=0.1mm,∆仪=1.2mm,可忽略∆估,则仪. 米尺,误差正态分布,取C=3,,4.h1同上,为0.00040m,5.计算g及U g其中确实有b,在计算不确定度中可以忽略.,,,误差分析:系统误差的来源有,空气阻力对摆的阻碍作用,部分光电探头测出的周期不为一个周期,实验时需要注意;接触线粗糙程度不同产生摩擦阻碍作用,以及钢尺部分已有弯曲.操作误差有,测量l与h1时不能精确地测得,使用钢尺时不能很好地接触测量,读数时有误差;对重心的判断可有mm数量级的差别;摆动时要避免形成圆锥摆.要注意让光电探头对准小孔.思考题:1.利用共轭性质精确地求得了等效摆长l,避免了对转动惯量的测量或计算,降低了h1的测量精度.实验上通过调节摆锤使T1与T2逐渐接近,近似达到共轭条件,较精确地测量周期来实现.2.影响因素主要有T的测量精确度,l的精确度.实验地纬度为北纬31.52°,查得北纬31.20°处g为9.7940,与实验值相比,误差仅略大于0.01%,说明凯特摆法测g值是较准确的.3.周期和摆角的关系:V形刀承至底端尖端距离s=84.28cm 摆角对实验数据进行简单处理,有:在测量范围内,周期是随摆角增加而增加的,当摆角更大时,凯特摆易形成圆锥摆,测量时发现周期反而减小了.如果不考虑圆锥摆现象,周期会随着摆角增加而增加.。
凯特摆测量重力加速度实验报告

凯特摆测量重力加速度实验报告一、实验目的本实验旨在利用凯特摆测量当地的重力加速度,加深对摆动规律和物理原理的理解,并通过实验操作提高实验技能和数据处理能力。
二、实验原理凯特摆是一种特殊的物理摆,由两个质量不同但长度相等的摆杆组成。
通过调节摆杆上的两个质量块,可以使凯特摆的摆动周期与摆长之间呈现特定的关系。
根据物理摆的周期公式:$T = 2\pi\sqrt{\frac{I}{mgd}}$,其中$T$为摆动周期,$I$为转动惯量,$m$为摆的质量,$g$为重力加速度,$d$为摆的质心到转动轴的距离。
对于凯特摆,通过合理设计其结构,可以得到一个较为简单的周期与摆长的关系式:$T = A\sqrt{L + B}$,其中$A$和$B$为常数,$L$为凯特摆的等效摆长。
通过测量不同摆长下凯特摆的摆动周期,然后进行数据拟合,即可求得重力加速度$g$的值。
三、实验仪器凯特摆装置、光电门、计数器、米尺、游标卡尺、天平。
四、实验步骤1、调节凯特摆的两个质量块,使其重心位于摆杆的中心线上。
2、用米尺测量凯特摆的摆杆长度$l$,用游标卡尺测量摆杆的直径$d$,多次测量取平均值。
3、用天平测量凯特摆的质量$m$。
4、将光电门安装在合适的位置,使其能够准确测量凯特摆的摆动周期。
5、选择不同的摆长$L$,从较小的值开始逐渐增加,每次增加一定的长度。
6、让凯特摆摆动,通过光电门和计数器测量每个摆长下的摆动周期$T$,每个摆长测量多次,取平均值以减小误差。
五、实验数据记录与处理|摆长$L$ (m) |摆动周期$T$ (s) |周期平方$T^2$ (s²) |||||| 050 | 141 | 19881 || 060 | 158 | 24964 || 070 | 172 | 29584 || 080 | 185 | 34225 || 090 | 198 | 39204 || 100 | 210 | 441 |以摆长$L$为横坐标,周期平方$T^2$为纵坐标,绘制散点图。
用凯特摆测量重力加速度实验报告

用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法。
实验原理:1、当摆幅很小时,刚体绕O轴摆动的周期:刚体质量m,重心G到转轴O的距离h,绕O轴的转动惯量I,复。
摆绕通过重心G的转轴的转动惯量为IG当G轴与O轴平行时,有I=I+mh2G∴+mh2 )/mh∴复摆的等效摆长l=( IG2、利用复摆的共轭性:在复摆重心G旁,存在两点O和O´,可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同,可证得|OO´|=l,可精确求得l。
3、对于凯特摆,两刀口间距就是l,可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。
∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器:凯特摆、光电探头、米尺、数字测试仪。
实验内容:1、仪器调节选定两刀口间得距离即该摆得等效摆长l,使两刀口相对摆杆基本对称,并相互平行,用米尺测出l的值,粗略估算T值。
将摆杆悬挂到支架上水平的V形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒挂也如此。
将光电探头放在摆杆下方,让摆针在摆动时经过光电探测器。
让摆杆作小角度摆动,待稳定后,按下reset钮,则测试仪开始自动记录一个周期的时间。
2、测量摆动周期T₁和T₂调整四个摆锤的位置,使T₁和T₂逐渐靠近,差值小于0.001s,测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。
3、计算重力加速度g及其标准误差σg。
将摆杆从刀承上取下,平放在刀口上,使其平衡,平衡点即重心G。
测出|GO|即h₁,代入公式计算g。
推导误差传递公式计算σg。
实验数据处理:1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ=0.03055cm,uA=σ/=0.01764cm,∴ΔA =tP·uA=1.32*0.01764=0.02328cmu B=ΔB/C=0.1/3=0.03333cm∴uL==0.04066cmTe==1.729s2、T₁和T₂的值T₁=1.72746sσ=2.525*10¯⁴s,uA=σ/=1.129*10¯⁴s∴ΔA =tP·uA=1.14*0.0001129=1.287*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT1==1.329*10¯⁴sT₂=1.72751sσ=1.469*10¯⁴s,uA=σ/=0.6570*10¯⁴s∴ΔA =tP·uA=1.14*0.00006570=0.7489*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT2==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]} =9.813m/s²∴ug0.68 =g·{l¯²* uL²+[2 T₁/(T₁²+T₂²)]²·uT1²+[2 T₂/(T₁²+T₂²)]²·uT2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴ug0.95 =2* ug0.68=0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题:1、凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量,利用复摆上两点的共轭性,对难以精确测定的量,有些避免了对其的测量,不能避免的则降低了其测量精度。
用凯特摆测量重力加速度(4)

⽤凯特摆测量重⼒加速度(4)实验报告 87姓名:竺贵强学号:PB07210017 系别:0706 实验题⽬:⽤凯特摆测量重⼒加速度实验⽬的:1.学习凯特摆的实验设计思想和技巧2.掌握⼀种⽐较精确的测量重⼒加速度的⽅法实验内容:1. 仪器调节调平⽀架:让摆杆做⼩⾓度摆动,记录⼀个周期的时间,反复测量,并调节⽀架的底座,直到多次测量的⼀个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=??=π调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,⼀般粗调⽤⼤摆锤,微调⽤⼩摆锤,当1T 和2T 接近估计值时,最好移动⼩摆锤,使1T 和2T 的差值⼩于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-?-=∑= 查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=?+?=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-?-=∑=查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=?+?=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5) ()(512111=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=?=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(51 2222=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=?=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=?+=下⾯求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带⼊数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(?+?+?+?+??=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-?-= (3)⽐较a 和b 的⼤⼩,%15.0%100=?ab ,可见b 与a 相⽐,b 项可以忽略不计,从⽽可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带⼊数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =?= 所以 20.004)m /s 9.708(±=g P=0.683误差分析:1. 使⽤⽶尺测量长度,误差太⼤;2. 在实验过程中⽀架底座很难调平,从⽽造成每个周期之间会有偏差;3. 实验中的偶然因素(⽐如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有⼀定关系,从⽽每次的振幅不同也会造成周期的不同5. 在实验过程中,可能会形成不易察觉的锥⾯摆6. 从数据果看出,测得的⼗个周期数据并不理想,在调节时,两个周期分别为1.74005和1.74003,但在测量⼗个周期时周期的偏差⽐较⼤,可能是由于等待稳定的时间选的不好,导致周期有偏差改进⽅法:先测量⼀个周期,当稳定后,再迅速调到⼗个周期的档测量(这样能保证摆动已经稳定)。
用凯特摆测量重力加速度 (14)
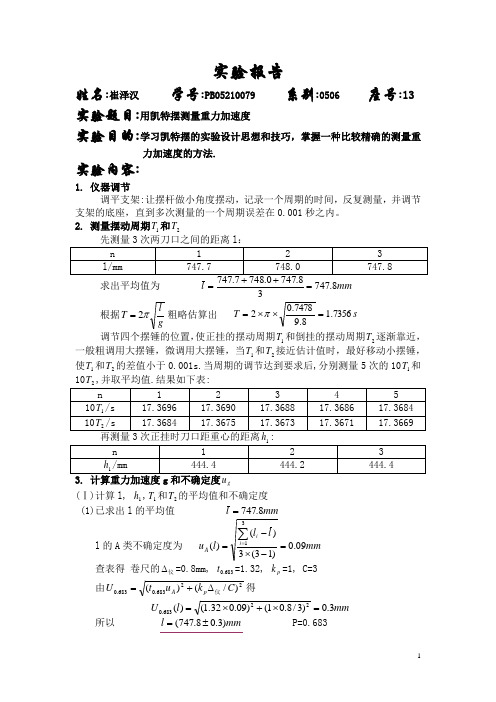
实验报告姓名:崔泽汉 学号:PB05210079 系别:0506 座号:13 实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方法.实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动,记录一个周期的时间,反复测量,并调节支架的底座,直到多次测量的一个周期误差在0.001秒之内。
2. 测量摆动周期1T 和2T求出平均值为 mm l 8.7473== 根据gl T π2=粗略估算出 s T 7356.18.97478.02=⨯⨯=π 调节四个摆锤的位置,使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近,一般粗调用大摆锤,微调用大摆锤,当1T 和2T 接近估计值时,最好移动小摆锤,使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度(1)已求出l 的平均值 mm l 8.747=l 的A 类不确定度为 mm l l l u i i A 09.0)13(3)()(31=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()09.032.1()(22683.0=⨯+⨯= 所以 mm l )3.08.747(±= P=0.683(2)求出1h 的平均值 mm h 3.44434.4442.4444.4441=++=1h 的A 类不确定度为 mm h h h u i i A 07.0)13(3)()(31111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()07.032.1()(221683.0=⨯+⨯=所以 mm h )3.03.444(1±= P=0.683(3)求出1T 的平均值 s T T i 73689.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00002.0)15(5)()(51111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00002.000002.014.1)(1683.0=⨯=所以 s T )00002.073689.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73674.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00003.0)15(5)()(51222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00003.000003.014.1)(2683.0=⨯=所以 s T )00003.073674.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220339.47478.0273674.173689.1s m a -=⨯+=下面求a 的不确定度传递公式:两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl ldT T T T dT T T Tda a 1221222212122211-+++=系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07478.01()00003.073674.173689.173674.12()00002.073674.173689.173689.12(0339.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0016m s =所以 2-10.0016)m 0339.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220018.0)7478.04443.02(273674.173689.1s m b -=-⨯-= (3)比较a 和b 的大小,%04.0%100=⨯ab,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.787m /s 0339.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号,最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00016.00339.4787.9)(s m g U =⨯= 所以 20.004)m /s 9.787(±=g P=0.683误差分析:1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同.思考题:1.凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?该实验在设计中避免了一些不易直接或精确测量的量的测量,并在计算过程中利用数学技巧把这些量消去.避免了重心到悬点距离h和复摆转动惯量I的测量.G降低了周期T的测量精度.I;利用复摆的两点共轭性可以精确求得等效摆长l,而不必去测量h和G利用数字测试仪精确测10T,可精确求得周期T.2.结合误差计算,你认为影响凯特摆测g精度的主要因素是什么?将所得到的实验结果与当地的重力加速度的公认值相比较,你能得到什么结论?若有偏差是分析之。
利用凯特摆测定重力加速度g值(精)

複擺
5.移動滑體,改變重心位置,重覆步驟1.、 2.、3.、4.,求g值。 B.曲線法 1.量取O1O2距離L。 2.以O1為懸點,利用測量法之步驟2.並將滑體位置定在10公分, 測出週期T1, 重複三次,逐次移動滑體10公分再測量週期T1 , 至 位置80公分為止。 3.再以O2為懸點,仿步驟2.來量測週期T2。 4.以滑體位置為橫軸,週期T為縱軸,畫出T1 、 T2的曲線並找出 交點所對應的時間T0,帶入式(6) ,求g值。
複擺
一、目的 利用凱特擺測定重力加速度g值。 二.原理 (A)測量法:固定滑體和黑色圓形重物的位置, 找出質心並利用複擺求得重力加速度g值。 凱特(Kater)擺是兩端不對稱的複擺,做小角 度擺動時,運動方程式為τ = Iα (1)
(τ是力矩,I 是轉動慣量,α是角加速度,θ為擺角)
複擺
圖一 複擺結構裝置與示意圖
定值,即使不同交點,T1=T2=T0=T'1= T'2仍存在】
複擺
三、儀器與裝置 儀器:複擺支座、複擺刀口、複擺、水平儀、 平衡支架、光時閘、光電計時器 四、步驟
A.測量法 1.用平衡支架找出複擺重心位置G,量得O1G、O2G距離h1、h2。 2.先以O1為懸點,使其自由擺動,但擺幅不得超過5度,記錄擺 動10次的平均時間,即得擺動週期T1,重覆四次,取平均值。 3.以O2為懸點,重覆步驟2.,求得T2之平均值。 4.將T1、T2、h1、h2帶入式(5),即可求得g值。
複擺
以O1為懸點,轉動θ角時,複擺所受力矩大小為τ =-M g h1sinθ~-M g h1θ (2)其解 為 (A、δ為常數,由初始條件決定, I為複擺
對懸點O1的轉動慣量,且I=Icm+Mh12=M(R2+h12)【Icm為複擺 以質心G點為轉軸的轉動慣量,假設Icm=MR2,R未知且與質量 分佈有關】 )
用凯特摆测量重力加速度 (15)

一实验报告906系07级 姓名:刘贝 实验日期:2008-10-14 No.PB07210063 一.实验题目:用凯特摆测量重力加速度.二.实验目的:学习凯特摆的实验设计思想与技巧.掌握一种比较精确地测量重力加速度的 方法.三.实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h,绕O 轴的转动惯量为I,当摆幅很小时,刚体绕O 轴摆的周期T 为mghI T π2= (1)式中g 为当地的重力加速度.设复摆通过重心G 的转动惯量为I G ,当G 轴与O 轴平行时有2mhI I G +=.mghmh I G T 22+=π(2)对比单摆周期的公式gl T π2= (3).可得:mhmh I G l 2+= (4) 复摆示意图l 称为复摆的等效摆长.对于凯特摆而言,两刀口间的距离就是该摆的等效摆长l.在实验中当两刀口位置确定后,通过调节A,B,C,D 四摆锤的位置可使正,倒悬挂时的摆动周期T 1和T 2基本相等,即T 1≈T 2.由公式可得:12121mgh mh I G T +=π(5).22222mgh mh I G T +=π(6).ba l h T T lT T g+=+=--+)2(2241222122212π (7).凯特摆摆杆结构示意图 此式中,l,T 1,T 2都是可以精确测定的量,而h 1则不易测准,由此可知,a 项可以精确求得,而b 项则不易精确测得.但当T 1=T 2以及|2h 1-l|的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确度对测量结果产生的影响就微乎其微了.四.实验数据处理:(1)实验中用米尺测得等效摆长l 的值分别如下:3次测量等效摆长所得到的数据表等效摆长l次数 1 2 3 l(cm)75.4575.4375.42取参考g 值(g ≈9.80m/s 2),利用公式(3)粗略估算T 值.而等效摆长的平均值二l=(l 1+l 2+l 3)/3=(75.42+75.43+75.45)/3=226.3/3=75.433cm. 所以参考值T=2π√(75.433)/9.80=1.7432 s.cmx i i l x 2210)*69.109.089.2(31210*528.1)13/()(4-++=-==--=-∑σ∴μl =σl /√2=1.0807*10-2cm.(2)在满足实验条件的情况下(即T 1与T 2的差值小于0.001s)分别测量5次10T 1和5次10T 2得到的数据如下:由以上数据可得到10T 1的平均值为10T 1=(17.4296+17.4287+17.4326+17.4315+17.4290)/5=17.43032 s.sx i i T x 3410)*7424.13924.11984.56244.25184.0(5121010*6938.1)15/()(61-++++=-==--=-∑σ所以取T 1=17.43032/10=1.74303 s.σT1=σ10T1/10=1.6938*10-4 s. ∴μT1=σT1/√5=0.7575*10-4 s.在同样情况下测量5次10T 2得到的数据如下:由以上数据可得到10T 1的平均值为10T 2=(17.4300+17.4267+17.4317+17.4318+17.4305)/5=17.43014 s.sx i i T x 3410)*96.1256.27536.24336.118396.1(5121010*7196.2)15/()(82-++++=-==--=-∑σ所以取T 2=17.43014/10=1.74301 s.σT2=σ10T2/10=2.7196*10-4s.∴μT2=σT2/√5=1.2163*10-4 s.(3)实验中所测得的相应的h 1得到的数据如下:由以上数据可得到h 1的平均值为cmh i i h477.293/)50.2948.2945.29(3/311=++==∑=-.三cmx i i h x 2210)*29.509.029.7(31210*5169.22/)(41-++=-==-=-∑σ.∴μh1=σh1/√3=1.4532*10-2cm.将以上相关数据代入公式(7),则有:.02727.432958.010*97208.650866.1076098.6)75433.029477.0*2*(274301.174303.175433.0*27430.17430.1)2(224522221222122212=-=+=+=+=---+--+ba l h T T lT T gπ所以有:./80277.9202727.44422s m g ba ===+ππ由于在测量周期中n 的值为5,所以若取P=0.68,t=1.14,T 1的不确定度为μT1=1.14*0.7575*10-4=0.86355*10-4. P=0.95,t=2.78,T 1的不确定度为μT1=2.78*0.7575*10-4=2.10585*10-4. P=0.99,t=4.60,T 1的不确定度为μT1=4.60*0.7575*10-4=3.4845*10-4. 由于在测量周期中n 的值为5,所以若取P=0.68,t=1.14,T 2的不确定度为μT2=1.14*1.2163*10-4=1.3866*10-4. P=0.95,t=2.78,T 2的不确定度为μT2=2.78*1.2163*10-4=3.3813*10-4. P=0.99,t=4.60,T 2的不确定度为μT2=4.60*1.2163*10-4=5.5949*10-4. 在测量h 1中n 的值为3,所以若取P=0.68,t=1.32,h 1的不确定度为μh1=1.32*1.4532*10-2=1.9182*10-2. P=0.95,t=4.30,h 1的不确定度为μh1=4.30*1.4532*10-2=6.2488*10-2. P=0.99,t=9.93,h 1的不确定度为μh1=9.93*1.4532*10-2=14.4303*10-2. 在测量l 中n 的值为3,所以若取P=0.68,t=1.32,l 的不确定度为μl =1.32*1.0807*10-2=1.4265*10-2. P=0.95,t=4.30,l 的不确定度为μl =4.30*1.0807*10-2=4.6470*10-2. P=0.99,t=9.93,l 的不确定度为μl =9.93*1.0807*10-2=10.7313*10-2.由不确定度的传递公式有(P=0.68):T 12的不确定度为2*μT1*T 1=2*0.86355*10-4*1.74303=3.0104*10-4. T 22的不确定度为2*μT2*T 2=2*3.3813*10-4*1.74301=11.7872*10-4.T 12+T 22的不确定度为3.0104*10-4+11.7872*10-4=14.7978*10-4.T 12-T 22的不确定度为3.0104*10-4-11.7872*10-4=8.7769*10-4.(2h1-l)的不确定度为2*μh1-μl=2*1.9182*10-2-1.4265*10-2=2.4099*10-4.a的不确定度为(yΔx+xΔy)/2y2=(14.7978*10-4*0.75433+1.4265*10-4*6.0761)/(2*0.5690)=1.7425*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*8.7769*10-4+1.8257*10-4*6.97208*10-5)/(2*0.02716)=2.6626*10-3.所以a+b的不确定度为(1.7425+2.6626)*10-3=4.4051*10-3.由公式(7)有g=4π2/(a+b).所以g的不确定度σg=4π2*(4.4051*10-3)/16.2206=1.0721*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.01072)m/s2.而σg/g=0.01072*10-2/9.80277=1.0938*10-3<0.2%.所以认为这个数据是理想的.由不确定度的传递公式有(P=0.95):T12的不确定度为2*μT1*T1=2*2.10585*10-4*1.74303=7.3411*10-4.T22的不确定度为2*μT2*T2=2*3.3813*10-4*1.74301=11.7872*10-4.T12+T22的不确定度为7.3411*10-4+11.7872*10-4=19.1284*10-4.T12-T22的不确定度为7.3411*10-4-11.7872*10-4=4.4461*10-4.(2h1-l)的不确定度为2*μh1-μl=2*6.2488*10-4-4.6470*10-4=7.8506*10-4.a的不确定度为(yΔx+xΔy)/2y2=(19.1284*10-4*0.75433+4.6470*10-4*6.0761)/(2*0.5690)=3.7491*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*4.4461*10-4+1.8257*10-4*6.97208*10-5)/(2*0.02716)=2.4782*10-3.所以a+b的不确定度为(3.7491+2.4782)*10-3=6.2273*10-3.由公式(7)有g=4π2/(a+b).所以g的不确定度σg=4π2*(6.2273*10-3)/16.2206=1.5156*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.01516)m/s2.而σg/g=0.01516*10-2/9.80277=1.5461*10-3<0.2%.所以认为这个数据是理想的.由不确定度的传递公式有(P=0.99):T12的不确定度为2*μT1*T1=2*3.4845*10-4*1.74303=12.1472*10-4.T22的不确定度为2*μT2*T2=2*5.5949*10-4*1.74301=19.5039*10-4.T12+T22的不确定度为12.1472*10-4+19.5039*10-4=31.6511*10-4.T12-T22的不确定度为12.1472*10-4-19.5039*10-4=7.3567*10-4.(2h1-l)的不确定度为2*μh1-μl=2*14.4303*10-4-10.7313*10-4=18.1293*10-4.a的不确定度为(yΔx+xΔy)/2y2=(31.6511*10-4*0.75433+10.7313*10-4*6.0761)/(2*0.5690)=7.8278*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*7.3567*10-4+18.1293*10-4*6.97208*10-5)/(2*0.02716)=1.2123*10-3.所以a+b的不确定度为(7.8278+1.2123)*10-3=9.0401*10-3.由公式(7)有g=4π2/(a+b).四所以g的不确定度σg=4π2*(9.0401*10-3)/16.2206=2.2002*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.02200)m/s2.而σg/g=0.02200*10-2/9.80277=2.244*10-3<0.3%.所以认为这个数据是理想的.综上数据分析可得,当地的重力加速度的实验值为:(1)P=0.68时, g=(9.80277±0.01072)m/s2.(2)P=0.95时, g=(9.80277±0.01516)m/s2.(3)P=0.99时, g=(9.80277±0.02200)m/s2.五.实验分析及总结:本实验学到了一种可以比较精确测量当地重力加速度的方法--用凯特摆测量重力加速度.由以上实验数据得到了当地的重力加速度的实验值.由实验数据分析所得到的结果分析来看,认为这次实验是成功的,得到的实验数据值也是较为理想的.另外,实验中仍存在着一些细节需要注意和一些可以再进一步改进的地方.T1和T2的值应当尽量接近.当然,让它们相等是很难的.这其中有仪器自身的原因,也有实验者人为的原因影响.另外,在测量等效摆长l和h1时由于使用的是米尺,所以精确度还不是太高.加之人为的读取数据和数据的取舍影响了实验数据的精确度.所以,若用较为精确的测量仪器并保证在读取数据时能尽可能的精确和在实验数据计算处理过程中也尽可能的精确,则得到的实验数据将会更加精确,更加接近其真实值.六.思考题:1.用凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上成功避免和减少了一些不易测量量对实验结果的影响,减少了单摆测重力加速度中一些非理想情况对实验结果的影响(如摆线的质量和摆的体积等),避免了测重力加速度中对摆长的测量,同时降低了悬挂点与重心距离的测量精度.避免测量摆长,采用测量等效摆长的方法来实现,降低悬挂点与重心距离的测量精度.在实验上使用正悬和倒悬分别测量周期的方法来实现.2.结合误差计算,你认为影响凯特摆测重力加速度精度的主要因素是什么?将所得的实验结果与当地的重力加速度的公认值相比较,你能得到什么结论?若有偏差,试分析之.答:影响重力加速度的主要因素有T1和T2的测量精度和等效摆长以及悬挂点与重心距离的测量精度.与当地的重力加速度公认值比较,有偏差.这偏差主要来自实验中T1和T2的测量偏差以及等效摆长和悬挂点与重心距离的测量偏差以及实验数据处理中对实验数据的取舍偏差有关.五。
凯特摆测量重力加速度实验报告

实验报告214系 09级 卢焘 2010-12-01 PB09214047 得分:实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确地测量重力加速度的方法。
实验仪器:凯特摆、光电探头、米尺、VAFN 多用数字测试仪。
实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mghI T π2= (1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2(2)代入式(1)得:mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2= 可得mhmh I l G 2+=(4)称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π(5)22222mgh mh I T G +=π(6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得:()l h T T l T T g --++=12221222122224π =a+b(7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
实验内容:1,仪器调节:固定刀口(使两刀口对称且平行),测量亮刀口间距即等效摆长l (用米尺测三次),由此粗略估计出T 作为调节T 1=T 2的依据。
凯特摆测重力加速度

凯特摆测重力加速度简介凯特摆是一种通过摆动的周期和长度来测量地球重力加速度的装置。
通过测量凯特摆的周期和长度之间的关系,可以计算出重力加速度的数值。
本文将介绍凯特摆的原理、实验步骤以及数据处理方法。
原理凯特摆是由一个线形摆线和一个重力体组成。
当重力体被拉向一侧释放后,由于重力的作用,重力体将开始摆动。
摆动的周期和长度的关系可以通过重力加速度公式来求得:T = 2π * √(L / g)其中,T为周期,L为摆长,g为重力加速度。
实验步骤以下是测量重力加速度的凯特摆的实验步骤:1.准备工作:确定实验场地,将凯特摆悬挂在一个固定的支撑物上。
2.在凯特摆上设置一个固定的摆长,例如 1 米。
3.将重力体拉至一侧,并释放。
4.记录重力体摆动的周期,可以使用计时器或计时器应用程序来记录摆动时间。
5.根据测得的周期和已知的摆长,使用重力加速度公式计算重力加速度的数值。
6.重复步骤 2-5,至少进行三次实验以获得可靠的结果。
7.取多次实验的平均值,计算重力加速度的最终数值。
数据处理在进行实验的过程中,我们得到了多次实验的周期和摆长数据。
为了计算重力加速度的数值,我们需要处理这些数据。
以下是数据处理的步骤:1.将周期数据转换为秒,并计算平均周期。
2.将摆长数据转换为米,并计算平均摆长。
3.使用平均摆长和平均周期,使用重力加速度公式计算重力加速度的数值。
4.使用所有实验的重力加速度数值,计算平均值并计算标准偏差,以评估实验结果的可靠性。
5.根据标准偏差的大小,判断实验结果的可靠性。
如果标准偏差较小,则实验结果较为可靠。
结论通过使用凯特摆来测量重力加速度,我们可以获得重力加速度的数值。
通过多次实验取平均值,并计算标准偏差,可以评估实验结果的可靠性。
凯特摆测重力加速度是一种简单而有效的方法,可以在物理实验中广泛应用。
【精品】凯特摆测重力加速度

【精品】凯特摆测重力加速度
凯特摆是定义在一个摆臂中有一个重物和另一个轻物,它们交叉把摆臂组成一个锤子
状物体,该系统由两个主要物理参量控制:重力加速度和动能。
它可用于测量重力加速度,或者可以测量和记录摆臂的周期,因此它经常用于物理实验室实验,以及其他研究重力的
任务。
由于重力加速度是凯特摆在运动中最重要的参量,因此可以用重力加速度这个参量来
分析凯特摆的运动模式。
首先,使用一个精确的测量仪器对凯特摆进行测量,以求得在水
平方向和垂直方向的重力加速度分量,其相对准确的结果是取决于测量仪器的精确度。
第二,从测量结果中,可以计算出重力加速度的总值,称为凯特摆的自由加速度,它
提供了一种评估的标准,用于指示凯特摆运动的状态。
自由加速度是指一种独立的参量,
它不会受到重力和空气阻力的影响;也就是说,它是一个纯粹的物理参量,它可以反映出
物体运动的完整性,而不会受到外界因素的影响。
此外,测量凯特摆的运动还可以帮助我们了解物体运动的模式,并使用这些资料进行
控制。
通过观察凯特摆的运动模式和重力加速度以及动能的相互作用,可以为我们提供实
用的参考,用于了解物体运动的性质和内在规律。
用凯特摆测量重力加速度

用凯特摆测量重力加速度1818年Kater 设计出一种物理摆,他巧妙地利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响,提高了测量重力加速度的精度。
19世纪60年代雷普索里德对此作了改进,成为当时测重力加速度的最精确方法。
波斯坦大地测量所曾同时以五个Kater 摆花了八年时间(1896-1904)测得当地重力加速度的值g= ( 981.274 ± 0.003 ) cm / s 2 。
凯特摆测量重力加速度的方法不仅在科学史上有重要价值,而且在实验设计思想上亦有值得学习的地方。
实验原理设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mghIT π2= (1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2(2)代入式(1)得:mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2=可得mhmh I l G 2+=(4)称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
上图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π(5)22222mgh mh I T G +=π(6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得:()l h T T l T T g --++=12221222122224π (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
凯特摆测重力加速度实验

凯特摆测重力加速度实验
一、故障及排除方法:
1.现象:测单个周期时,周期读数的重复性不好,相差较大。
原因:
(1)空气阻力对测量周期有很大影响。
(2)刀口太粗糙了。
(3)振动周期测量毫秒仪本身工作不正常。
(4)凯特摆两端的挡光金属部分在实验过程中没有调节好。
(5)凯特摆在摆动时不在平面内摆动。
(6)凯特摆没有在刀口上放好,导致摩擦增大,影响周期读数。
排除方法:
(1)关上实验室电风扇,如果天气风速较大,要关闭好窗户,减少空气阻力的影响。
(2)可适当加些润滑油改善。
(3)更换振动周期测量毫秒仪。
(4)调节好激光光电门使之满足挡光的要求。
(5)尽量不要形成圆锥摆。
(6)要把凯特摆在刀口上放好位置,减少摩擦力。
2.现象:实验过程中,毫秒仪显示的周期只有实际周期的一半。
原因:激光光电门的入射光偏离了接收小孔。
排除方法:调整即可。
二、注意的问题:
1.测量一个周期时,将周数预置档设置成01。
2.测量10个周期时,只需把周数预置档设置成10即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告:用凯特摆测量重力加速度张贺 PB07210001一、实验题目:用凯特摆测量重力加速度二、实验目的:学习凯特摆的实验设计思想和技巧,掌握一种比较精确地测量重力加速度的方法。
三、实验仪器:凯特摆、光电探头、米尺、VAFN 多用数字测试仪四、实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h ,绕O 轴的转动惯量为I ,当摆幅很小时,刚体绕O 轴摆动的周期T 为:mghI T π2= (1)式中g 为当地的重力加速度。
设复摆绕通过重心G 的轴的转动惯量为I G ,当G 轴与O 轴平行时,有I=I G +mh 2(2)代入式(1)得:mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2=可得mhmh I l G 2+=(4)称为复摆的等效摆长。
因此只要测出周期和等效摆长便可求得重力加速度。
下图是凯特摆摆杆的示意图。
对凯特摆而言,两刀口间的距离就是该摆的等效摆长l 。
在实验中当两刀口位置确定后,通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。
由公式(3)可得12112mgh mh I T G +=π(5)22222mgh mh I T G +=π(6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。
当T 1≈T 2时,h 1+h 2=l 即为等效摆长。
由式(5)和(6)消去I G ,可得:()l h T T l T T g --++=12221222122224π (7)此式中,l 、T 1、T 2都是可以精确测定的量,而h 1则不易测准。
由此可知,a 项可以精确求得,而b 项则不易精确求得。
但当T 1=T 2以及 |2h 1-l | 的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确对测量结果产生的影响就微乎其微了。
五、实验内容:1 仪器调节:固定刀口,用米尺测出l 的值,取参考g 值,利用单摆周期公式粗略估算T 值,作为调节21T T =的参考值。
将摆杆悬挂到支架上水平的V 形刀承上,调节底座上的螺丝,借助于铅垂线,使摆杆能在铅垂面内自由摆动,倒过来悬挂也是如此。
将光电探头放在摆杆下方,调整它的位置和高度,让摆针在摆动时经过光电探测器,接通电源。
2 测量摆动周期1T 和2T :调节四个摆锤的位置,使1T 与1T 逐渐靠近,一般粗调用大摆锤,微调用小摆锤。
当1T 和2T 的差值小于0.001s 。
当周期的调节达到要求后,测量凯特摆正、倒摆动10个周期的时间,110T 和210T 各测量5次取平均值。
3 计算重力加速度g 及标准误差g σ:测出1h ,代入公式(7)中计算g 值,自己推到误差传递公式,计算g σ。
六、数据处理:1 实验原始数据:2 数据处理: (1)两刀口距离l :cm cmcm cm l l l l 40.75340.7541.7539.753321=++=++=()()()()()cm l l l l l l 01.0cm 240.7541.7540.7539.751322232221=-+-=--+-+-=σcm cm nu A 0057.0301.0===σcm cmCu B 0333.031.0==∆=仪 ()()()()cm cm u t u t u B k A p l 0697.00333.096.10057.030.42222=⨯+⨯=+=95.0=p(2)1h :44.8267cm cm 381.4485.4482.4431312111=++=++=h h h h ()()()()()()cmh h h h h h28267.4481.448267.4485.448267.4482.4413222211321122111--+-=--+-+-=σ cm 0208.0=cm cm u A 0120.030208.03===σcm cm Cu B 0333.031.0==∆=仪 ()()()()cm cm u t u t u B k A ph 0832.00333.096.10120.030.422221=⨯+⨯=+=95.0=p(3)凯特摆正挂时的十个周期110T :s s T T i4454.1754458.174455.174453.174450.174455.175101011=++++==∑()+-+-+-=--=∑22211)4454.174453.17()4454.174450.17()4454.174455.17[(151010T Tiσ s s 0003.0)15/(])4454.174455.17()4454.174455.17(22=--+-s s u A 0001.050003.05===σs s C u B 000033.030001.0==∆=仪()()()()s s u t u tu B k A pT 0003.0000033.096.10001.078.22222101=⨯+⨯=+=95.0=ps s T T 7445.1104454.17101011===s s u u T T 00003.0100003.0101110===95.0=p(4)凯特摆倒挂时的十个周期210T :s s TT i4400.1754401.174401.174399.174401.174400.175101022=++++==∑()+-+-+-=--=∑222221)4400.174399.17()4400.174401.17()4400.174400.17[(151010T Tiσ s s 0001.0)15/(])4400.174401.17()4400.174401.17(22=--+-s s u A 00004.050001.05===σs s C u B 000033.030001.0==∆=仪()()()()s s u t u tu B k A pT 0001.0000033.096.100004.078.22222102=⨯+⨯=+=95.0=ps s T T 7440.1104400.17101022===s s u u T T 00001.0100001.0102210===95.0=p(5)对重力加速度g 的分析:()()l h T T l T T g l h T T l T T g --++=⇒--++=1222122212122212221222242224ππ ()()2222221222122212/7540.04483.0227440.17445.17540.027440.17445.142224s m l h T T l T T g -⨯⨯-+⨯+=--++=ππ 7691.9=2/s m 推导误差传递公式:222128T T l g +≈π取对数()2221222212ln ln 8ln 8ln ln T T l T T lg +++=+=ππ 求微分()2222121222112221222122dT T T T dT T T T l dlT T T T d l dl g dg ++++=+++=系数取绝对值并改成不确定度符号212221222211221T T l gu T T T u T T T u l g u ++++=22227440.17445.100001.07440.127440.17445.100003.07445.1240.750697.0+⨯⨯++⨯⨯+==0.0009476 95.0=p 得到22/0093.00009476.0/7691.9s m s m u g =⨯= 95.0=p得到的重力加速度的最终表达式为:()2/0093.07691.9s m g ±= 95.0=p七、误差分析:1 测量仪器在正常使用过程中测量环境和仪器性能随机涨落的影响。
2 当摆倒置时,各个摆锤都有微小的移动,从而导致实验的误差。
3 无法完全保证支架的竖直,从而摆杆无法完全在铅锤面内自由摆动,引起的误差。
4 摆杆与支架的摩擦导致的误差。
八、注意事项:1开始做实验时,将凯特摆两大圆柱与两小圆柱放置对称使之有最大调解范围,且可抵消实验室空气浮力的影响以及可以减小阻力的影响。
2 固定刀口时要注意使两刀口相对摆杆基本对称两刀口相互平行。
且刀口与刀承应是线接触。
3 调节凯特摆时,可根据算出的T 理论值进行调整。
4 调节摆锤位置时,一般粗调用大摆锤,微调用小摆锤。
当T 1和T 2比较接近估算值T 时,最好移动小摆锤。
九、思考题:1 凯特摆侧重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现? 答:(1)特点:巧妙地利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响,提高了测量重力加速度的精度。
(2)避免了复摆绕通过重心G 的轴的转动惯量I G 的测量。
(3)降低了重心G 到悬点O 的距离h 的测量精度。
(4)首先通过固定刀口确定了其距离l ,然后再在l 一定的基础上,通过调节摆锤来改变摆的重心,最后得到以l 为等效摆长的凯特摆。
2 结合误差计算,你认为影响凯特摆测g 精度的主要因素是什么?将所得的实验结果与当地的重力加速度的公认值相比较,你能得到什么结论?若有偏差,试分析之。
答:(1)通过误差计算,发现h 1对重力加速度的精度几乎没有影响;主要影响g 的因素是等效摆长l 、凯特摆正摆与倒摆的周期T 1和T 2。
(2)已知合肥地区的重力加速度g=9.795m/s 2。
测量值略小于理论值。
测量值与理论值的相对误差为:%26.0%100795.97691.9795.9%10000=⨯-=⨯-=g g g E r 误差在可接受范围内,原因详见上页误差分析。
