理论力学答案(谢传峰版)资料
《理论力学》试题答案以及复习要点汇总(完整版)最新最全面(完整版)

《理论力学》试题答案以及复习要点汇总(试题附后面)第一部分静力学第1 章.静力学基本概念和物体的受力分析1.静力学基本概念力是物体间相互的机械作用,这种作用使物体运动状态发生变化或使物体产生变形。
前者称为力的运动效应,后者称为力的变形效应。
力对物体的作用决定力的三要素:大小、方向、作用点。
力是一定位矢量。
刚体是在力作用下不变形的物体,它是实际物体抽象化的力学模型。
等效若两力系对物体的作用效应相同,称两力系等效。
用一简单力系等效地替代一复杂力系称为力系的简化或合成。
2.静力学基本公理力的平行四边形法则解成两个力的分解法则。
给出了力系简化的一个基本方法,是力的合成法则,也是一个力分二力平衡公理是最简单的力系平衡条件。
加减平衡力系公理是研究力系等效变换的主要依据。
作用与反作用定律概括了物体间相互作用的关系。
刚化公理给出了变形体可看作刚体的条件。
3. 约束类型及其约束力限制非自由体位移的周围物体称为约束。
工程中常见的几种约束类型及其约束力光滑接触面约约束力作用在接触点处,方向沿接触面公法线并指向受力物体。
束柔索约束约束力沿柔索而背离物体。
约束力在垂直销钉轴线的平面内,并通过销钉中心。
约束力的方向不能预铰链约束先确定,常以两个正交分量 F x 和F y 表示。
滚动支座约束约束力垂直滚动平面,通过销钉中心。
约束力通过球心,但方向不表示。
能预先确定,常用三个正交分量F x,F y,F z球铰约束止推轴承约束约束力有三个分量Fx,F y ,F z 。
4. 受力分析对研究对象进行受力分析、画受力图时,应先解除约束、取分离体,并画出分离体所受的全部已知载荷及约束力。
画受力图的要点(1)熟知各种常见约束的性质及其约束力的特点。
判断二力构件及三力构件,向。
并根据二力平衡条件及三力平衡条件确定约束力的方(2)(3)熟练、正确表出作用力与反作用力。
受力分析三步曲:分离物体、画主动力、画约束力(约束个数、约束类型、用约束力代替约束)第2、3 章.平面力系1. 力矩力矩是度量力对物体转动效果的物理量。
理论力学答案(谢传峰版)精编版
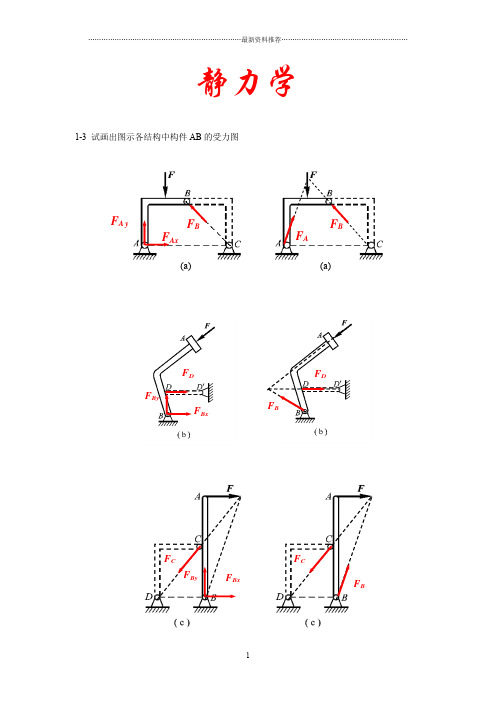
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学课后答案-谢传峰、王琪-动力学第九章、第十章

1 2
2l m dx(
x sin )2 0 2l
2 ml 2
2 sin2 3
O C
系统的动能 T T1 T2 。 取 900 为势能零点,则系统的势能为:
V mgl cos
则拉格朗日函数:
L T V 2 ml2 (2
2 sin2 ) mgl cos 3
x
楔块 B 的速度 vB ,以及 B 相对于 A 的相对速度
满足如下的矢量关系(方向如图所示):
vB vA vBr
系统的动能为:
vBr vA
T
1 2
m
Av
A
2
1 2
mBvB 2
P1 2g
x 2
P2 2g
[(x
s cos)2
(ssin)2 ]
1 2g
(P1
P2 )x 2
度
转动。物体的质心 G 在垂直于 O1O2 的直线上,O3G l 。设 O1O2 和 O3G 是物体过 O3
点的惯量主轴,转动惯量为 J1 和 J 2 ,物体对另一过 O3 点的惯量主轴的转动惯量为 J 3 ,试
求物体的动能表达式并建立物体的运动微分方程。 解:
以该物体为研究对象,有一个自由度,取 O3G 和 OC 的夹角 为广义坐标。若以框架 O1O2OC 为动系,则物体的相对运动是以角速度 绕轴 O1O2 的定轴转动,牵连运动是以角 速度
垂直于 O1O2 的平面
z’
O3
θ G
y’
坐标系 O3 x y z 的三个坐标轴为过 O3 点的三个惯量主轴,则系统的动能为:
T
理论力学答案(谢传峰版)61453
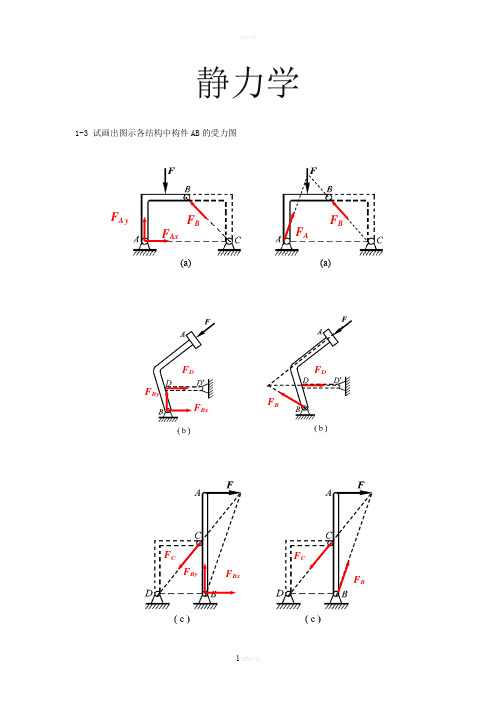
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yFB(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A yF D F ByF A F BxF B F AF Ax F A yF Dy T E F CxF C yN’F BF DF ANF AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
45030对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学(附答案)-谢传峰、王琪-动力学部分

m 2R4 x2
(x2
R
2
)
5 2
,
FN
mg
m 2R5x
(x2
R
2
)
5 2
1-13 解:动点:套筒 A;
动系:OA 杆; 定系:机座; 运动分析: 绝对运动:直线运动; 相对运动:直线运动; 牵连运动:定轴转动。 根据速度合成定理
va ve vr
va
ve
vr
有: va cos ve ,因为 AB 杆平动,所以 va v ,
2014-北航考研-永爱渣渣
《动力学 I》第一章 运动学部分习题参考解答
1-3 解:
运动方程: y l tan ,其中 kt 。
将运动方程对时间求导并将 300 代入得 v y l lk 4lk
cos2 cos2 3
a y 2lk 2 sin 8 3lk 2
ve
va
R
, va
vr
R
,1
ve O1 A
R 2R
0.5
根据加速度合成定理有
aa aet aen ar aC
(b)
将(b)式在垂直于 O1A 杆的轴上投影得
v02l 2 x3
(负号说明滑块 A 的加速度向上)
取套筒 A 为研究对象,受力如图所示,根据质点矢量形式的运动微分方程有:
ma F FN mg
将该式在 x, y 轴上投影可得直角坐标形式的运动微分方程: mx mg F cos my F sin FN
x
(
x2
理论力学问题详解(谢传峰版)32531
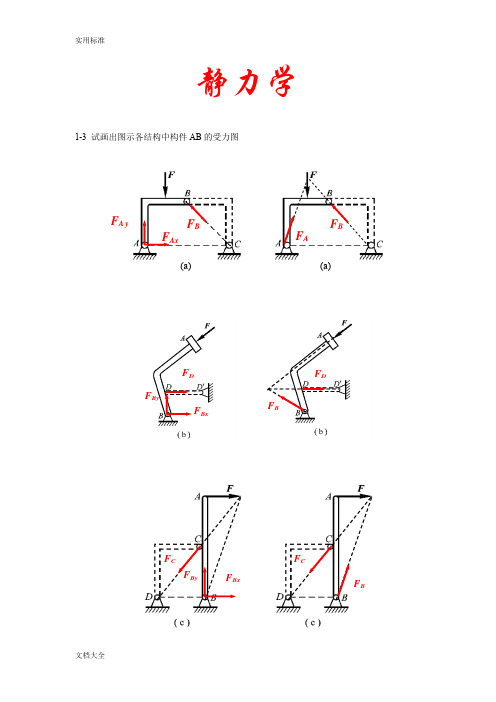
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F D F ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF B y F Cx F Dy F Bx T EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =FF450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
理论力学第三版课后习题答案

理论力学第三版课后习题答案【篇一:理论力学教程思考题答案第三版.doc】2r?.。
这表示质点的径向与横向运动在相互影响,它们一起才?2,a??rar??r??r?能完整地描述质点的运动变化情况1.3答:内禀方程中,an是由于速度方向的改变产生的,在空间曲线中,由于a恒位于密切面内,速度v总是沿轨迹的切线方向,而an垂直于v指向曲线凹陷一方,故an总是沿助法线方向。
质点沿空间曲线运动时,ab?0,fb?0z何与牛顿运动定律不矛盾。
因质点除受作用力f,还受到被动的约反作用力r,二者在副法线方向的分量成平衡力fb?rb?0,故ab?0符合牛顿运动率。
有人会问:约束反作用力靠谁施加,当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。
有人也许还会问:某时刻若fb与rb大小不等,ab就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同,质点的位置也在改变,副法线在空间中方位也不再是原来ab所在的方位,又有了新的副法线,在新的副法线上仍满足fb?rb?0即ab?0。
这反映了牛顿定律得瞬时性和矢量性,也反映了自然坐标系的方向虽质点的运动而变。
1.4答:质点在直线运动中只有a?而无an,质点的匀速曲线运动中只有an而无a?;质点作变速运动时即有at又有an。
1.5而dr即反应位矢r大小的改变又反映其方向的改变,是质点运动某时刻的速度矢量,dtdrdr?j而dr?r?i?r??。
在直线运动中,?r只表示r大小的改变。
如在极坐标系中,dtdtdt规定了直线的正方向后,drdrdrdr。
且的正负可表示的指向,二者都可表示质点dtdtdtdt的运动速度;在曲线运动中drdrdrdr?,且也表示不了的指向,二者完全不同。
dtdtdtdtdvdv表示质点运动速度的大小,方向的改变是加速度矢量,而只是质点运动速度大小dtdtdvdvaan,而?a?。
dtdt的改变。
在直线运动中规定了直线的正方向后,二者都可表示质点运动的加速度;在曲线运动中,二者不同,1.6答:不论人是静止投篮还是运动投篮,球对地的方向总应指向篮筐,其速度合成如题1.6v球对人v人对地题1-6图图所示,故人以速度v向球网前进时应向高于篮筐的方向投出。
工程力学课后习题答案【整理版】

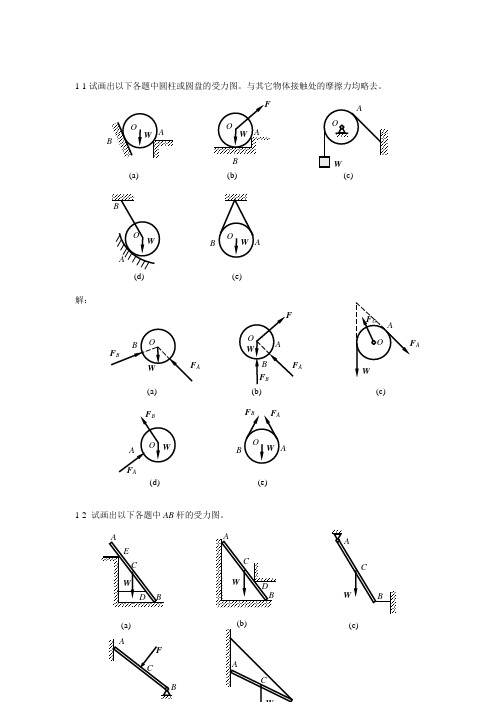
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解� 1-2 试画出以下各题中A B 杆的受力图。
BA OW(a ) B A O WF(b ) OW (c ) AAO W(d ) BA O W (e ) BFB FABO W (a ) BA OW F(b ) F A F BAO W(c )FA FO AO W (d ) F B F A A O W (e ) BF B FA A WC B (c ) D(a ) AW CEB (b ) AW C DB《工程力学》习题选解 。
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案解�1-3试画出以下各题中A B 梁的受力图。
ABF (d ) CABW (e ) CAB W (e ) C FB FA AB F(d ) CFB F A (a ) FD FB FE DAW CEB (b ) AW CD B F D FB FA (c ) A WC B FB FA AWCB(a ) W ABCD(c ) AB Fq D (b ) C CABFW DA’ D ’ B’ (d ) AB Fq (e )解�1-4 试画出以下各题中指定物体的受力图。
(a ) 拱A B C D �(b ) 半拱A B 部分�(c ) 踏板A B �(d ) 杠杆A B �(e ) 方板A B C D �(f ) 节点B 。
解� A WCB(a ) FB FAA BFqD(b ) FC FD W ABC(c ) FC FB CAB F WD(d ) FB FA FD ABFq(e ) FB x FB y FA AB F (a ) D C WAF(b ) DB (c ) F ABD D ’ A B F(d ) C DW A B CD(e ) W A BC(f ) A BF(a ) D CWFA x FA y FD AF (b ) B FB FA (c ) FA B DF B FD1-5 试画出以下各题中指定物体的受力图。
(完整word版)理论力学课后习题及答案解析.docx

理论力学教科书课后习题及解析第一章偶,大小是260Nm,转向是逆时针。
习题 4- 1.求图示平面力系的合成结果,长度单位为m。
习题 4- 3.求下列各图中平行分布力的合力和对于 A 点之矩。
解: (1) 平行力系对 A 点的矩是:解: (1) 取 O 点为简化中心,求平面力系的主矢:取 B 点为简化中心,平行力系的主矢是:求平面力系对O 点的主矩:平行力系对 B 点的主矩是:(2)合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;向 A 点简化的结果是一个力R A和一个力偶M A,且:如图所示;将 R B向下平移一段距离d,使满足:最后简化为一个力R ,大小等于R B。
其几何意义是: R 的大小等于载荷分布的将 R A向右平移一段距离d,使满足:矩形面积,作用点通过矩形的形心。
(2)取 A 点为简化中心,平行力系的主矢是:最后简化为一个力R,大小等于R A。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
平行力系对 A 点的主矩是:列平衡方程:习题 4-4 .求下列各梁和刚架的支座反力,长度单位为m。
解方程组:反力的实际方向如图示。
校核:解: (1) 研究 AB 杆,受力分析,画受力图:结果正确。
(2) 研究 AB 杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:(3) 研究 ABC ,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:列平衡方程:反力的实际方向如图示。
校核:解方程组:结果正确。
反力的实际方向如图示。
校核:结果正确。
习题 4-5 .重物悬挂如图,已知G=1.8kN ,其他重量不计;求铰链 A 的约束反力和杆 BC 所受的力。
列平衡方程:解方程组:解: (1) 研究整体,受力分析(BC 是二力杆),画受力图:反力的实际方向如图示。
列平衡方程:习题 4-8 .图示钻井架,G=177kN ,铅垂荷载P=1350kN ,风荷载 q=1.5kN/m ,水平力 F=50kN ;求支座 A 的约束反力和撑杆CD 所受的力。
工程力学(静力学与材料力学) 单祖辉 谢传峰合编 课后习题答案
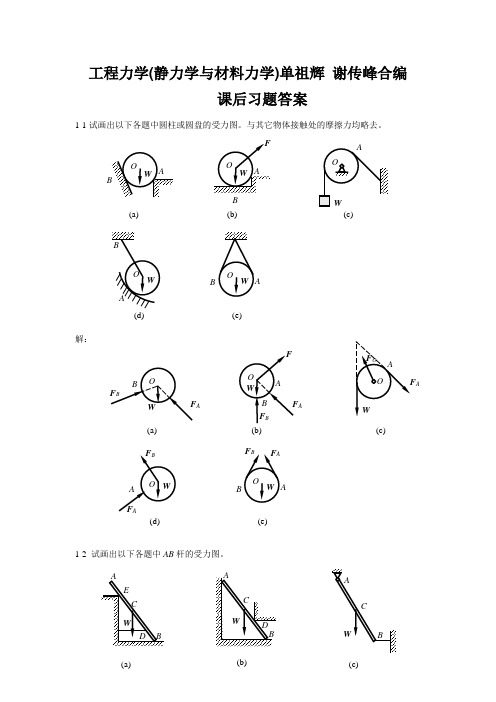
工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a)(b)c)(d)A(e) A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(d)FC(e)WB(f)F FBC(c)(d)(b)e)解:(a)(b)(c)(d)(e)ATF BAFCAA C’CDDC’B2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos 6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
2016新编理论力学谢传锋第九章习题解答
第九章部分习题解答9-2解:取整个系统为研究对象,不考虑摩擦,该系统具有理想约束。
作用在系统上的主动力为重力g M g M 21,。
如图(a )所示,假设重物2M 的加速度2a 的方向竖直向下,则重物1M 的加速度1a 竖直向上,两个重物惯性力I2I1,F F 为11I1a M F = 22I2a M F =(a )该系统有一个自由度,假设重物2M 有一向下的虚位移2x δ,则重物1M 的虚位移1x δ竖直向上。
由动力学普遍方程有 (a )02I21I12211=--+-=x F x F x g M x g M W δδδδδ (b )根据运动学关系可知2121x x δδ=2121a a =(c )将(a)式、(c)式代入(b)式可得,对于任意02≠x δ有212122m/s 8.2424=+-=g M M M M a (b )方向竖直向下。
取重物2M 为研究对象,受力如图(b )所示,由牛顿第二定律有222a M T g M =-解得绳子的拉力N 1.56=T 。
本题也可以用动能定理,动静法,拉格朗日方程求解。
9-4解:如图所示该系统为保守系统,有一个自由度,取θ为广义坐标。
系统的动能为2])[(21θθ R l m T +=取圆柱轴线O 所在的水平面为零势面,图示瞬时系统的势能为]cos )(sin [θθθR l R mg V +-=M 1gM 2g F I2F I1δx 2δx 1M 2gT a 2拉格朗日函数V T L -=,代入拉格朗日方程0)(=∂∂-∂∂θθL L dt d 整理得摆的运动微分方程为0sin )(2=+++θθθθg R R l 。
9-6解:如图所示,该系统为保守系统,有一个自由度,取弧坐标s 为广义坐标。
系统的动能为221S m T = 取轨线最低点O 所在的水平面为零势面,图示瞬时系统的势能为m g h V =由题可知b s ds dh 4sin ==ϕ,因此有b s d b s h So8s 42==⎰。
工程力学(静力学与材料力学) 单祖辉 谢传峰合编 课后习题答案.doc
工程力学(静力学与材料力学)单祖辉 谢传峰合编课后习题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 解:1-3 试画出以下各题中AB 梁的受力图。
(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)DBF D1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(d)FC(e)WB(f)F FBC(c)(d)(b)(e)解:(a)(b)(c)(d)(e)ATF BAFCAA C’CDDB2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点,如图所示。
如不计刚架重量,试求支座A 和D 处的约束力。
《理论力学》——期末考试答案

《理论力学》——期末考试答案一、单选题1.力对点之矩决定于( )。
A.力的大小B.力臂的长短C.力的大小和力臂的长短D.无法确定正确答案:C2.动点相对于动坐标系的运动称为( )的运动。
A.牵连运动B.相对运动C.绝对运动D.圆周运动正确答案:B3.动点的牵连速度是指该瞬时牵连点的速度,它相对的坐标系是( )。
A.动坐标系B.不必确定的C.静坐标系D.静系或动系都可以正确答案:C4.在质点系动能定理中,应注意外力或内力做的功之和不等于合外力或( )做的功。
A.重力B.浮力C.合内力D.牵引力正确答案:C5.将平面力系向平面内任意两点进行简化,所得主矢量和主矩都相等,且主矩不为零,则该力系简化的最后结果为( )。
A.合力偶B.合力C.平衡力系D.无法进一步合成正确答案:A6.超静定结构的超静定次数等于结构中( )。
A.约束的数目B.多余约束的数目C.结点数D.杆件数正确答案:B7.静不定系统中,多余约束力达到3个,则该系统静不定次数为( )A.3次B.6次C.1次D.不能确定正确答案:A8.关于平面力偶系、平面汇交力系、平面一般力系,最多能够得到的相互独立的平衡方程的个数依次是( )。
A.2、1、3B.2、2、3C.1、2、2D.1、2、3正确答案:D9.平面任意力系向一点简化,应用的是( )。
A.力的平移定理B.力的平衡方程C.杠杆原理D.投影原理正确答案:A10.对于平面力系,一个平衡方程可解( )未知量。
A.1个B.2个C.3个D.不一定正确答案:A11.一平面力系由两组平面平行力系组成(这两组平面平行力系之间互不平行),若力系向某A点简化结果为一合力,下述说法正确的是( )。
A.这两组平面平行力系必然都各自向A点简化为一合力B.这两组平面平行力系可能都各自简化为一力偶C.可能一组平面平行力系向A点简化得到一个力和一个力偶,而另一组平面平行力系向A点简化得到一合力D.可能这两组平面平行力系都各自向A点简化得到一个力和一个力偶正确答案:D12.在任何情况下,在几何可变体系上增加一个二元体后构成的体系是几何( )体系。
工程力学_静力学与材料力学_(单辉祖_谢传锋_着)_高等教育出版社_课后答案
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解:1-2 试画出以下各题中AB 杆的受力图。
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案解:1-3 试画出以下各题中AB 梁的受力图。
(d)(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(e)BB(c)(a)(b)(a) B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ;(b) 半拱AB 部分;(c) 踏板AB ;(d) 杠杆AB ;(e) 方板ABCD ;(f) 节点B 。
解:1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ,结点B ;(b) 圆柱A 和B 及整体;(c) 半拱AB ,半拱BC 及整体;(d) 杠杆AB ,切刀CEF 及整体;(e) 秤杆AB ,秤盘架BCD 及整体。
(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D(d)F C(e)WB (f)F F BC(c)(d) (b)(e)解:(a)(b)(c)(d)(e)2-2 杆AC、BC在C处铰接,另一端均与墙面铰接,如图所示,F1和F2作用在销钉C上,F1=445 N,F2=535 N,不计杆重,试求两杆所受的力。
解:(1) 取节点C为研究对象,画受力图,注意AC、BC都为二力杆,(2) 列平衡方程:12140 sin600530 cos6005207 164oy ACox BC ACAC BCF F F FF F F FF N F N=⨯+-==⨯--=∴==∑∑AC与BC两杆均受拉。
2-3 水平力F作用在刚架的B点,如图所示。
如不计刚架重量,试求支座A和D处的约束力。
理论力学第三版课后习题答案

理论力学第三版课后习题答案【篇一:理论力学教程思考题答案第三版.doc】2r?.。
这表示质点的径向与横向运动在相互影响,它们一起才?2,a??rar??r??r?能完整地描述质点的运动变化情况1.3答:内禀方程中,an是由于速度方向的改变产生的,在空间曲线中,由于a恒位于密切面内,速度v总是沿轨迹的切线方向,而an垂直于v指向曲线凹陷一方,故an总是沿助法线方向。
质点沿空间曲线运动时,ab?0,fb?0z何与牛顿运动定律不矛盾。
因质点除受作用力f,还受到被动的约反作用力r,二者在副法线方向的分量成平衡力fb?rb?0,故ab?0符合牛顿运动率。
有人会问:约束反作用力靠谁施加,当然是与质点接触的周围其他物体由于受到质点的作用而对质点产生的反作用力。
有人也许还会问:某时刻若fb与rb大小不等,ab就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同,质点的位置也在改变,副法线在空间中方位也不再是原来ab所在的方位,又有了新的副法线,在新的副法线上仍满足fb?rb?0即ab?0。
这反映了牛顿定律得瞬时性和矢量性,也反映了自然坐标系的方向虽质点的运动而变。
1.4答:质点在直线运动中只有a?而无an,质点的匀速曲线运动中只有an而无a?;质点作变速运动时即有at又有an。
1.5而dr即反应位矢r大小的改变又反映其方向的改变,是质点运动某时刻的速度矢量,dtdrdr?j而dr?r?i?r??。
在直线运动中,?r只表示r大小的改变。
如在极坐标系中,dtdtdt规定了直线的正方向后,drdrdrdr。
且的正负可表示的指向,二者都可表示质点dtdtdtdt的运动速度;在曲线运动中drdrdrdr?,且也表示不了的指向,二者完全不同。
dtdtdtdtdvdv表示质点运动速度的大小,方向的改变是加速度矢量,而只是质点运动速度大小dtdtdvdvaan,而?a?。
dtdt的改变。
在直线运动中规定了直线的正方向后,二者都可表示质点运动的加速度;在曲线运动中,二者不同,1.6答:不论人是静止投篮还是运动投篮,球对地的方向总应指向篮筐,其速度合成如题1.6v球对人v人对地题1-6图图所示,故人以速度v向球网前进时应向高于篮筐的方向投出。
(完整版)理论力学答案(谢传峰版)
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
(完整版)工程力学_静力学与材料力学课后习题答案_(单辉祖_谢传锋_着)_高等教育出版社_
(2)列平衡方程:
AC与BC两杆均受拉。
2-3水平力F作用在刚架的B点,如图所示。如不计刚架重量,试求支座A和D处的约束力。
解:(1)取整体ABCD为研究对象,受力分析如图,画封闭的力三角形:
(2)由力三角形得
2-4在简支梁AB的中点C作用一个倾斜45o的力F,力的大小等于20KN,如图所示。若梁的自重不计,试求两支座的约束力。
(2)列平衡方程:
AB的约束力:
3-8在图示结构中,各构件的自重都不计,在构件BC上作用一力偶矩为M的力偶,各尺寸如图。求支座A的约束力。
解:(1)取BC为研究对象,受力分析,画受力图;
(2)取DAC为研究对象,受力分析,画受力图;
画封闭的力三角形;
解得
4-1试求题4-1图所示各梁支座的约束力。设力的单位为kN,力偶矩的单位为kNm,长度单位为m,分布载荷集度为kN/m。(提示:计算非均布载荷的投影和与力矩和时需应用积分)。
(2)选F点为矩心,列出平衡方程;
(3)不翻倒的条件;
4-13活动梯子置于光滑水平面上,并在铅垂面内,梯子两部分AC和AB各重为Q,重心在A点,彼此用铰链A和绳子DE连接。一人重为P立于F处,试求绳子DE的拉力和B、C两点的约束力。
解:
1-5试画出以下各题中指定物体的受力图。
(a)结点A,结点B;(b)圆柱A和B及整体;(c)半拱AB,半拱BC及整体;(d)杠杆AB,切刀CEF及整体;(e)秤杆AB,秤盘架BCD及整体。
解:(a)
(b)
(c)
(d)
(e)
2-2杆AC、BC在C处铰接,另一端均与墙面铰接,如图所示,F1和F2作用在销钉C上,F1=445N,F2=535N,不计杆重,试求两杆所受的力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):=∑M 0)45sin(100=-+⋅⋅M a F A θaM F A 354.0= 其中:31tan =θ。
对BC 杆有: aMF F F A B C 354.0=== 。
A ,C 两点约束力的方向如图所示。
2-4四连杆机构在图示位置平衡,已知OA=60cm,BC=40cm,作用在BC 上力偶的力偶矩M 2=1N ·m 。
试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力AB F 。
各杆重量不计。
解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有:0=∑M 030sin 20=-⋅⋅M C B F B 对AB 杆有:A B F F =对OA 杆有:0=∑M01=⋅-A O F M A求解以上三式可得:m N M ⋅=31, N F F F C O AB5===,方向如图所示。
F B F Aθ θ F BF C F AF OO F AF B F BF C C2-6等边三角形板ABC,边长为a ,今沿其边作用大小均为F 的力321,,F F F ,方向如图a,b 所示。
试分别求其最简简化结果。
解:2-6a坐标如图所示,各力可表示为:j F i F F ρρρ23211+=,i F F ρρ=2,j F i F F ρρρ23213+-=先将力系向A 点简化得(红色的): j F i F F R ρρρ3+=, k Fa M A ρρ23=方向如左图所示。
由于A R M F ρρ⊥,可进一步简化为一个不过A 点的力(绿色的),主矢不变,其作用线距A 点的距离a d 43=,位置如左图所示。
2-6b同理如右图所示,可将该力系简化为一个不过A 点的力(绿色的),主矢为:i F F R ρρ2-=其作用线距A 点的距离a d 43=,位置如右图所示。
简化中心的选取不同,是否影响最后的简化结果?2-13图示梁AB 一端砌入墙内,在自由端装有滑轮,用以匀速吊起重物D 。
设重物重为P, AB 长为l ,斜绳与铅垂方向成α角。
试求固定端的约束力。
法1 解:整个结构处于平衡状态。
选择滑轮为研究对象,受力如图,列平衡方程(坐标一般以水平向右为x 轴正向,竖直向上为y 轴正向,力偶以逆时针为正):∑=0x F 0sin =+Bx F P α∑=0y Fcos =--αP P F By选梁AB 为研究对象,受力如图,列平衡方程:xy F RM AF R dxF RM AF R d yPB F Bx FByP∑=0x F 0=-Bx Ax F F ∑=0y F 0=-By Ay F F 0=∑A M 0=⋅-l F M By A求解以上五个方程,可得五个未知量ABy Bx Ay Ax M F F F F ,,,,分别为:αsin P F F Bx Ax -==(与图示方向相反))cos 1(α+==P F F By Ay (与图示方向相同) l P M A )cos 1(α+= (逆时针方向)法2 解:设滑轮半径为R 。
选择梁和滑轮为研究对象,受力如图,列平衡方程:∑=0x F0sin =+αP F Ax∑=0y F 0cos =--αP P F Ay0=∑AM02tansin )(cos )(=-----αααR P R l P R l P M A求解以上三个方程,可得AAy Ax M F F ,,分别为:αsin P F Ax -= (与图示方向相反))cos 1(α+=P F Ay (与图示方向相同)l P M A )cos 1(α+= (逆时针方向)2-18均质杆AB 重G ,长l ,放在宽度为a 的光滑槽内,杆的B 端作用着铅垂向下的力F ,如图所示。
试求杆平衡时对水平面的倾角α。
解:选AB 杆为研究对象,受力如图所示,列平衡方程:0=∑A M 0cos cos 2cos =⋅-⋅-⋅αααl F lG a N D ∑=0y F 0cos =--F G N D α求解以上两个方程即可求得两个未知量α,D N ,其中:31])2()(2arccos[l G F a G F ++=α未知量不一定是力。
M A F Bx F ByF AxF A yM APF Ax F A y PAN AN DD2-27如图所示,已知杆AB 长为l ,重为P ,A 端用一球铰固定于地面上,B 端用绳索CB 拉住正好靠在光滑的墙上。
图中平面AOB 与Oyz 夹角为α,绳与轴Ox 的平行线夹角为θ,已知N P m c m a o 200,45,43tan ,4.0,7.0=====θα。
试求绳子的拉力及墙的约束力。
解:选杆AB 为研究对象,受力如下图所示。
列平衡方程:=∑yM0tan sin cos tan 21=⋅-⋅-⋅αθθαc F c F c P BC BCN F BC 6.60= 0'=∑x M0sin 21=⋅-⋅-⋅a F c F a P BC B θ N F B 100=由∑=0y F和∑=0z F可求出Az Ay FF ,。
平衡方程=∑xM可用来校核。
思考题:对该刚体独立的平衡方程数目是几个?2-29图示正方形平板由六根不计重量的杆支撑,连接处皆为铰链。
已知力F 作用在平面BDEH 内,并与对角线BD 成o 45角,OA=AD 。
试求各支撑杆所受的力。
解:杆1,2,3,4,5,6均为二力杆,受力方向沿两端点连线方向,假设各杆均受压。
选板ABCD 为研究对象,受力如图所示,该力系为空间任意力系。
采用六矩式平衡方程:0=∑DE M045cos 02=⋅F 02=F0=∑AO M 045cos 45cos 45cos 0006=⋅-⋅-a F a FF F 226-= (受拉) 0=∑BH M 045cos 45cos 0604=⋅-⋅-a F a FF F 224=(受压) 0=∑AD M 045sin 45cos 061=⋅-⋅+⋅a F a F a FF F 2211+=(受压) 0=∑CD M045sin 031=⋅-⋅+⋅a F a F a FFF 213-= (受拉) 0=∑BC M045cos 0453=⋅-⋅+⋅a F a F a F05=F本题也可以采用空间任意力系标准式平衡方程,但求解代数方程组非常麻烦。
类似本题的情况采用六矩式方程比较方便,适当的选择六根轴保证一个方程求解一个未知量,避免求解联立方程。
2-31如图所示,欲转动一置于V 形槽中的棒料,需作用一力偶,力偶矩cm N M ⋅=1500。
已知棒料重N P 400=,直径cm D 25=。
试求棒料与V 形槽之间的静摩擦因数s f 。
解:取棒料为研究对象,受力如图所示。
列平衡方程:⎪⎩⎪⎨⎧===∑∑∑000Oy x M F F⎪⎪⎩⎪⎪⎨⎧=-⋅+=+-=-+02)(045sin 045cos 21102201M D F F N p F N p F补充方程:⎩⎨⎧==2211N f F N f F s s五个方程,五个未知量s f N F N F ,2211,,,,可得方程:02222=+⋅⋅-⋅M f D p f M S S解得491.4,223.021==S S f f 。
当491.42=S f 时有:0)1(2)1(2221<+-=S S f f p N即棒料左侧脱离V 型槽,与题意不符,故摩擦系数223.0=S f 。
2-33均质杆AB 长40cm ,其中A 端靠在粗糙的铅直墙上,并用绳子CD 保持平衡,如图所示。
设cm AD cm BC 25,15==,平衡时α角的最小值为o45。
试求均质杆与墙之间的静摩擦因数s f 。
解:当045=α时,取杆AB 为研究对象,受力如图所示。
列平衡方程:⎪⎩⎪⎨⎧===∑∑∑000Ay x M F F⎪⎪⎩⎪⎪⎨⎧=⋅-⋅-⋅=-+=-0sin 2cos sin sin cos 0cos 0sin ααθαθθθABp AC T C AC T p T F T F S N 附加方程:N S S F f F =四个方程,四个未知量s S N f T F F ,,,,可求得646.0=s f 。
2-35在粗糙的斜面上放着一个均质棱柱体,A ,B 为支点,如图所示。
若AC BC AB ==,A 和B 于斜面间的静摩擦因数分别为1s f 和2s f,试求物体平衡时斜面与水平面所形成的最大倾角α。
