初中数学奥林匹克初中训练题五套
初中数学奥林匹克竞赛题包括答案.docx

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题 1 分,共 10 分)1.如果 a,b 都代表有理数,并且a+b=0 ,那么 ( ) A.a,b 都是 0B.a,b 之一是 0C.a,b 互为相反数D. a,b 互为倒数答案: C解析:令 a=2 , b= - 2,满足 2+( - 2)=0 ,由此 a、b 互为相反数。
2.下面的说法中正确的是( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案: D3都是单项式.两个单项式33A。
两个单项式解析: x2, x x , x2之和为 x +x 2是多项式,排除x2, 2x2之和为3x2是单项式,排除 B。
两个多项式x3+x2 与 x3-x2之和为2x3 是个单项式,排除 C,因此选 D。
3.下面说法中不正确的是( )A.有最小的自然数B.没有最小的正有理数Word资料C.没有最大的负整数D.没有最大的非负数答案: C解析:最大的负整数是-1 ,故 C 错误。
4.如果 a,b 代表有理数,并且a+b 的值大于 a- b 的值,那么( ) A.a,b 同号B.a,b 异号C.a>0D. b> 0答案: D5.大于-π并且不是自然数的整数有( )A.2 个B.3 个C.4 个D.无数个答案: C解析:在数轴上容易看出:在-π右边0的左边(包括0 在)的整数只有-3,- 2,-1 ,0 共 4 个.选 C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
Word资料这四种说法中,不正确的说法的个数是( )A.0 个B.1 个C.2 个D. 3 个答案: B解析:负数的平方是正数,所以一定大于它本身,故 C 错误。
7.a 代表有理数,那么, a 和- a 的大小关系是( )A.a 大于- aB.a 小于- aC.a 大于- a 或 a 小于- aD. a 不一定大于- a答案: D解析:令 a=0 ,马上可以排除A、 B、 C,应选 D。
数学奥林匹克初中训练题_121_

°第 9期课外训练 37数学奥林匹克初中训练题 ( 121)第 一 试一、选择题 (每小题 7分 , 共 42分 )且 AD B C 于点 D. 小明从点 D 出发 , 经过边 AB 上一点及边 AC 上一点 , 最后回到 D 处. 则小明走的最短路程是 ( ) .1. 将 16+ 1 24 + 1 60 + 1 120 + 1 210 + 1 加 上336(A ) 5 6 (B ) 10 3 (C ) 10 6 (D ) 20 6 二、填空题 (每小题 7分 ,共 28分 ) 一个数后 , 使七个数之和等于 1. 那么 , 加上4的这个数是 () . 1. 已知x x 2+ 3x + 18 - x x 2- 6x + 18 = 1.1 1 1 1 则 2x x2 - 6x + 18 - 9x 3的 值为.(A ) 56 (B ) 84 (C ) 112 (D ) 2242. 二次函数 y = ax 2+ bx + c 的图像如图 1 所示. 下列结论正确的是( ) .(A ) 3 | a | + | c | > 2 | b | (图 1( C ) 3 | a | + | c | < 2 | b | (D ) 3 | a | + | c | ≤2 | b |3. 如图 2, O的直径 AB 与弦 CD 2. 如图 3, 在 △AB C中 , BD 平 分 AB C ,CD BD 于 点 D ,BAC = ACD , B C =5, BA = 11. 则 △AB C 的面积是 .图 3 3. 对于任意实数 x 、y,不等式| x - 1 | + | x - 3 | + | x - 5 | ≥k (2 - | y - 9 | ) 恒成立. 则实数 k 的最大值是 .4. 已知四边形 AB CD 是梯形 , AD ∥B C, 点 E 、F 分别在 AD 、B C 上 , AD = B F = 3, ED =(非直径 ) 所在的直 线交于圆外一点 P, 图 2PA = AB = 4. 则 PD的取值范围是 () .EF =12.FC = 2. 则 D - B 的度数是第 二 试(A ) 4 < PD < 8(B ) 4 2 < PD < 8 ( C ) 4 < PD < 4 2(D ) 4 2 ≤PD ≤8一、( 20分 )已知二次函数 y = x 2- 2kx + 4. 方程 x 3+ x 2+ x - 2 = 0 的根的情况是() .(A )有一个正实根 (B )有两个正实根( C )有一个负实根 (D )有两个负实根5. 若质数 p 、q 满足 p 2- 5q - 36 = 0, 则样本 p 、q 、9、16的中位数是 () . (A ) 16 (B ) 13( C ) 11(D ) 13156. 有一块三角形的活动场地 , 边 AB = 20,B = 60 ,C = 75°, AD 是一条石灰线 , 3k + 1, 自变量 x 和实数 a 、b 满足 4a 2x + 6ab = 2, y 最小值 = 1. 求常数 k 的值.二、( 25 分 ) 如图 4, AB 是 O 的直径 , C 是 O 外一点 , CD AB 于点D, O 于点 E. EF是非直径的弦, 且 图 4CF = CE. FG AB+ 9b 2 =+ 5 -- -- 38于点 G, EF 于点 H, 点 D 、G 在点 O 的两侧 , DHG = 45°. 求 EF 2 ∶AB 2的值.三、( 25分 )已知关于 x 的方程 x 2+a - 2 009x a - 2 061= 02有两个整数根. 求所有满足条件的实数 a 的值.参 考 答 案第 一 试过 点 P 作 PE 切 O 于点 E, 联结EC 、ED.由切割线定理 得PE 2= PA ·PB= 4 ×8 = 32.于是 , PE = 4 2. 中 等 数 学图 5一、1. C .加上的这个数易知 PED >PEC =EDC.从而 , PD > PE, 即 PD > 4 2. 1 1 = 4 6 1 + 24 1 + 60 1 + 120 1 + 210 1+ 336 综上 , 4 2 < PD < 8.4. A.1 1 = 4 1 ×2 ×3 1 + 2 ×3 ×4 1+ 3 ×4 ×5 + 显然 , x ≠0. x 3 + x 2+ x - 21 1 1于是 ,x= 0, 即4 ×5 ×6 + 5 ×6 ×7 + 6 ×7 ×8221 1 = 1 - 1 1 1 + + x + x + 1 = x.4 2 1 ×2 2 ×3 2 ×3 3 ×4 令 y 1 = x 2+ x + 1,1 - 1+1 ×5 - 1+ 1 - y 2 =2 . 如图 6, 作出x1 6 ×72. C.1+6 7- 17 ×8两个函数图像. 由图像可知 , 两个函数图像只有一个交点且在第一象限内. 故原方 由图像可知 a < 0, b > 0, c < 0. 当 x = 1时 , y > 0, 即a +b +c > 0. ①程有一个正实根.图 65. D.由 p 2- 5q - 36 = 0 得因 为 - b> 1, 所以 ,( p + 6) ( p - 6) = 5q = q 5 = 1 ×5q = 5q ×1.2a2a + b > 0. ②因此 ,p + 6 = 5, p - 6 = q; p + 6 = q, p - 6 = 5;由式 ①、②得 3a + 2b + c > 0.则 3 | a | + | c | - 2 | b | = - 3a - c - 2bp + 6 = 1,p - 6 = 5q; p + 6 = 5q,p - 6 = 1.= - ( 3a + 2b + c ) < 0.( p, q ) = ( - 1, ) ( ) , (11, 17) ,故 3 | a | + | c | < 2 | b |.3. B.- 5, - 115(舍去 ) , 7, 13 (舍去 ) .如图 5,联结 OD. 在 △POD 中 , 有PO - OD < PD < PO + OD.则 4 < PD < 8.故样本为 11, 17, 9, 16, 其中位数是11 + 16 = 1315.21 1 1 11 = 4 -2 2 - 56 = 11 . 2x 2+ 3x + 18 = 1 22009年第 9期6. C. 如图 7, 作点D 关于 AB 的对称点 D 1 , 关于 AC 的对称 点 D 2 , 联 结D 1 D 2 分别交 AB 、AC 于点 E 、F. 则D E + EF + FD 就图 7是小明走的最短路程.理由如下 : 在 AB 上任取一点 E ′, 在 AC 上任取一点 F ′, 联结 D E ′、E ′F ′、F ′D 、E ′D 1 、F ′D 2 、AD 1 、AD 2. 易知E ′D = E ′D 1 , ED = ED 1 ,F ′D = F ′D 2 , FD = FD 2.故 D E + EF + FD = D 1 E + EF + FD 2= D 1 D 2 ,D E ′+ E ′F ′+ F ′D = D 1 E ′+ E ′F ′+ F ′D 2.39上式与已知等式相减得2x x 2- 6x + 18 = 9x 3- 1.故 2x x 2 - 6x + 18 - 9x 3= - 1.2. 1325如图 8, 延长 CD 交AB 于点 E. 易知△B ED △B CD.所以 , B E = B C = 5,ED = CD.图 8故 A E = AB - B E= 11 - 5 = 6.又 BAC =ACD , 则 CE = A E = 6.因 此 , CD 1CE = 3.2由勾股定理得BD = B C 2- CD 2= 52- 32= 4.根据“两点之间线段最短 ”可知 , D 1 D 2 ≤D 1 E ′+ E ′F ′+ F ′D 2(当 E ′与 E 重合且 F ′与 F 重合时取等号 ) ,即 1 1故 S △B CD = 2 BD ·CD = 2因而 , S △B EC = 2S △B CD = 12.×4 ×3 = 6.D E + EF + FD ≤D E ′+ E ′F ′+ F ′D.AB 则 S = S 11 132 = ×12 = 因此 , D E + EF + FD 就是小明走的最短路程.3. 2.△AB C B E △B EC 5 5 .因 为 AD = AB sin B = 20 sin 60°= 10 3, 所以 , AD 1 = AD 2 = AD = 10 3.由绝对值的几何意义可知 , | x - 1 | +| x - 3 | + | x - 5 |的最小值为 4 (此时 x = 3 ) , 而 2 - | y - 9 |的最大值为 2 (此时 y = 9 ) . 根 又 D 1 AB = DAB , D 2 AC =DAC,则D 1 AD 2 = 2BAC = 2 ( 180°-B -C ) = 90°. 根据勾股定理得 据条件得 4≥k ·2, 所以 , k ≤2. 故 k 的最大值是 2.4. 90°.D D = =(10 3) 2×2 =10 6.如图 9, 过点 E 作 EG ∥AB 交 B C 于 因此 , D E + EF + FD = 10 6. 二 、 1. - 1.注意到x + x x 2 ( x 2 + 3x + 18) - x 2 ( x 2- 6x + 18)=x x 2 + 3x + 18 - x x 2- 6x + 18 点 G, 作 EH ∥CD 交B C 于点 H. 易知四图 9边形 AB GE 和 CD EH 都是平行四边形. 所以 ,B G = A E = AD - D E = 1, CH = ED = 2.于是 , GF = B F - B G = 2,HF = FC - CH = 2.x 2·9x 31=1= 9x . 则 GF = HF = 2, EF = 2GH = 2.AD +AD 22 12x 2- 6x + 18.a - 2 009 = 240故 △GEH 为直角三角形,且 GEH = 90°.故 y 最小值 中 等 数 学= 32 - 2k ·3 + 3k + 1 = 1.因此 , EGH + EHG = 90°. 又 B EGH, C EHG, 则B + C = 90°. 由 A + B + C + D = 360°,得 A + D = 270°.因为 A + B = 180°, 所以 ,D - B = 90°.第 二 试一、由已知得4a 2- 6ab + 9b 2= x.①又 4a 2 + 9b 2= 2,② ② - ①得 2a ·3b = 2 - x .③由式 ②、③可得( 2a + 3b ) 2= 4a 2+ 9b 2+ 12ab= 2 + 2 ( 2 - x ) = 6 - 2x.所 以 , 2a + 3b = ± 6 - 2x.因而 , 2a 、3b 是关于 t 的一元二次方程t 2u6 - 2x t + 2 - x = 0的两个实数根.故Δ = (u 6 - 2x ) 2- 4 (2 - x ) =2x - 2≥0. 于是 , x ≥1.又 6 - 2x ≥0, 则 x ≤3.因此 , y = x 2- 2kx + 3k + 1中的 x 的取值范围是 1≤x ≤3.解得 k = 3 (舍去 ) .综上所述 , 常数 k 的值为 - 1和 3. 二、如图 10, 联结 OH 、O E 、O F.图 10由 CE = CF, CH EF, 有 EH = FH. 由垂径定理得 OH EF. 又 FG AB ] FHO + FGO = 180° ] O 、G 、F 、H 四点共圆] GFO = GHO. 同理 , D EO = DHO.故 GFO + D EO = GHO + DHO = DHG = 45°. 由 ED ∥FG ] GFE D EF = 180°] EO F = 180°- ( O FE + O EF ) = 45°. 设 O 的半径为 R. 则 AB = 2R. 过 F 作 F O E 于点 I . 则O I = F I = FO sin EO F = R sin 45° 2R.2于是 , E I = O E - O I = 1 - 2 R.2二次函数 y = x 2- 2kx + 3k + 1 的顶点坐标是 ( k, - k 2+ 3k + 1) .( 1)若 k < 1, x = 1 时的二次函数值就是 y 的最小值.由勾股定理得EF 2 = F I 2 + E I 2= ( 2 - 2) R 2.22+1 -2 R 2故 y 最小值 = 1 - 2k ·1 + 3k + 1 = 1. 解 得 k = - 1.( 2)若 1 ≤k ≤3, 二次函数图像顶点的纵坐标值就是 y 的最小值.故 EF 2∶AB 2= ( 2 - 2) R 2∶( 2R ) 2= ( 2 - 2) ∶4.三、设方程的两个整数根为 x 1 、x 2. 故 y 最小值 = - k 2 + 3k + 1 = 1. 由韦达定理得 x 1 + x 2 = - 是解得 k = 3或 k = 0.整数 , x x a - 2 061 = .1 22是整数 因为 1≤k ≤3, 所以 , k = 3.( 3)若 k > 3, x = 3 时的二次函数值就是 y 的最小值.故原方程为整系数一元二次方程 , 且a - 2 009 为完全平方数 , a 为奇数.不妨设 a - 2 009 = k 2( k 为自然数且 k 为2R 21 2 3 4 5 6 =2009年第 9期 41数学奥林匹克高中训练题 ( 121)第 一 试一、填空题 (每小题 7分 , 共 56分 )1. 从 { 1, 2, , 100 }中任取 5 个数 (可以相同) . 则取到合数的个数的数学期望是.2. 椭圆面积公式 S ab 可由圆的面积公式 S = r 2得出 : 只需将圆沿着一个方向 “拉长 ”即可. 仿此 , 若一个椭圆半长轴、半短6. 称一个函数是“好函数 ”当且仅当其满足 :( 1)定义在 R 上;( 2) 存在 a < b, 使其在 ( - ∞, a ) 、( b,+ ∞)上单调递增 , 在 ( a, b )上单调递减.则以下函数是好函数的有 .①y = x | x - 2 | ,②y = x 3- x + 1③y = 2x 3 - 3x 2 - 6x - 1, ④y = 2x 7+ 7x 4+ 28x + 3.轴分别为 a 、b, 将其以长轴为轴旋转 , 得到 7. p 2+ p 2+ p 2+ p 2+ p 2= p 2的正质数解 的“椭球 ”的体积为 .3. 半径为 R 的圆的内接三角形的面积的最大值是.n 3- 2n - 2( p 1 , p 2 , p 3 , p 4 , p 5 , p 6 )有组.8. 某班教室桌椅 6 排 7 列 , 有 40 名同学. 空出最后一排的某两个位置 , 其余人按身高和视力排座位. 班中有 24 人身高高 , 有 18 4. 已 知 a 1 = 1, a n + 1 = 2a n +则 { a n }的通项公式为.n 2+ n .人视力好 , 其中 , 有 6名同学同时具备此两个条件. 已知若一名同学个子矮视力又不好 , 则 5. f (θ)1 - 2sin θ7 - 6 sin θ+4 +2 cos θ+ 4的取值范围是.他必须坐在前三排; 若一名同学个子高视力又好 , 则他必须坐在最后三排. 设排座位的方法是 A , 则 A 的质因数分解中的 2 的次数是.偶数 ) .于是 , a = k 2 + 2 009.Δa - 2 061 条件;( 2)当 k = 2时 ,Δ = 100, a = k 2+ 2 009 =2 013. 这时方程为 x 2+ 2x - 24 = 0, 其根为 x又 = a - 2 009 - 4 × 2= - ( k 2+ 2 009) - 2 009 + 2 ×2 061 = - k 2+ 104≥0.解得 - 104≤k ≤ 104.由 k ≥0, 知 0≤k ≤ 104 ( k 为偶数 ) . 则 k = 0, 2, 4, 6, 8, 10.( 1)当 k = 0, 4, 6, 8 时 ,Δ都不是完全平方数 , 原方程都没有整数根 , 不符合题设1 = 4, x2 = - 6, 符合题设条件;( 3)当k = 10 时,Δ= 4, a = k2 + 2 009 = 2 109, 这时方程为x2 + 10x + 24 = 0, 其根为x1 = - 4, x2 = - 6, 也符合题设条件.综上所述, 所有满足条件的实数 a 的值为2013 和 2 109.(周东庭汪伟林湖北省黄冈市浠水县实验中学, 438200)。
初中数学奥林匹克竞赛全真试题(全国联赛卷)(详解版)

初中数学奥林匹克竞赛全真试题(全国联赛卷)(详解版)初中数学奥林匹克竞赛全真试题(全国联赛卷)(详解版)一、填空题1. 如果函数 f(x)=x^2-2x+1的根为 a,b,那么a + b 等于_____.答案:-12. 已知正整数 m、n 满足 mx+ny=1(m、n 都不为 0),若 m + n 等于 8,则 m - n 等于_____.答案:73. 若等差数列{an}的前 n 项和为 Sn,且 a1=3,Sn=15,则 n 的值是_____.答案:64. 在△ABC 中,已知 a=4,b=4,c=8,若 AB+AC=9,则∠B =_____.答案:45°二、选择题5. 已知 A、B 两点的坐标分别为(3,1)、(5,-1),则 AB 是_______.A. 水平的直线B. 斜率为 1 的直线C. 斜率为 -1/3 的直线D. 竖直的直线答案:B6. 若正方形的边长为 x,周长为 5x,则 x 的值等于_______.A. 4B. 5C. 8D. 10答案:A7. 已知tanα=2,cotβ=-3,则 tan(α-β)等于_______.A. 5B. -5C. -1/5D. 1/5答案:B8. 把一个正整数分成 K 份,第一份的数量是剩下的 K-1 份的总和的()A. 1/2B. 3/2C. 2/3D. 3/4答案:B三、解答题9. 已知函数 f(x)=2x+1,若直线 4x+3y=37 与曲线 f(x) 相切,求该曲线上点 P 的坐标答:设点 P 的坐标为 (x,y),因为直线 4x+3y=37 与曲线 f(x) 相切,所以曲线上点 P 的 y 值可由 4x+3y=37 中求得,即 y=12-4/3x,由函数 f(x)可得 12-4/3x=2x+1,故 x=7,代入 y=12-4/3x 可得 y=12-4/3(7)=8。
点 P的坐标即为 (7, 8)。
10. 已知△ABC 中,a=3,b=3,∠A=120°,求 B 的坐标答:由△ABC 中 A 的坐标为(0,0),a=3,b=3 可知 C 的坐标为(3,0),∠A=120°,∠C=60°,因为∠B=60,则以 C 为外接圆圆心,半径为3 的圆○上可得点B,即B(√3,1),综上所述,点B 的坐标为(√3,1)。
初中数学奥林匹克训练题及答案五

又 AD ∥BC ,故 ∠ABC + ∠BAD = 180°,
即 ∠ADC + ∠BAD = 180°.
所以 ,AB ∥CD ,四边形 ABCD 是平行四边形.
5. (A) . 因为 aabb = 1 000 a + 100 a + 10 b + b
= 11 (100 a + b) , 由题意可设 100 a + b = 11 c2 ( c 是正整数) , 所以 ,101 < 100 a + b = 11 c2 < 999 , 即 9 < c2 < 90. 于是 ,4 ≤c ≤9. 经检验 , c = 8 时满足条件 ,此时 a = 7 , b = 4. 故 a + b = 11.
数学奥林匹克初中训练题
第一试
一 、选择题 (每小题 7 分 ,共 42 分) 1. 若 a 、b 都是质数 ,且 a2 + b = 2 003 , 则 a + b 的值等于 ( ) . (A) 1 999 (B) 2 000 (C) 2 001 (D) 2 002
2.设 a > 0 > b > c , a + b + c = 1 , M =
所以 , x - 8 = 30 ,知 x = 38.
即汽车在途中排除故障花了 38 min.
ab - ac = 360 ,则 abc 的最大值是 .
3. 若
abc
=
1
,
1
+
x a+
ab
+ 1+
x b+
bc
+
1
+
x c+
初中数学奥林匹克竞赛模拟试卷(八年级)

初中数学奥林匹克竞赛模拟试卷(八年级)全国初中数学奥林匹克竞赛试卷(八年级)一、选择题1、已知三点A(2,3),B(5,4),C(-4,1)依次连接这三点,则三点在同一直线上。
解析:AB的解析式为y= 3x+3,当x= -4时,y=1,即点C在直线AB上,∴选D。
2、边长为整数,周长为20的三角形个数是8个。
解析:设三角形的三边为a、b、c且a≥b≥c,a+b+c=20,a≥7,又b+c>a,2a<20a<10,又7≤a≤9,可列出(a、b、c)有:(9,9,2)(9,8,3)(9,7,4)(9,6,5)(8,8,4)(8,7,5)(8,6,6)(7,7,6)共八组,选C。
3、N=++,则N的个位数字是9.解析:的个位数字为3,的个位数字为9,的个位数字为7,∴N的各位数字为9,选C。
4、P为正方形ABCD内一点,若解析:过P作BP’⊥BP,且使BP’=BP,连P’A。
易得△P’AB≌△PBC,则P’A=PC,设PA=k,则PB=2k,PC=P’A=3k,连PP’,则Rt△PBP’中,∠P’PB=45°且PP’=22k,在△P’AP中有:P’A2=P’P2+PA2,∴∠P’PA=90°,∴∠APB=135°选B。
5、在函数y= -x(a为常数)的图象上有三点:(-1,y1)(-4,y2)(2,y3),则函数值y1,y2,y3的大小关系是y3<y1<y2.解析:-(a2+1)<0,∴在每个象限,y随x的增大而增大,因此y1<y2.又∵(-1,y1)在第二象限,而(2,y3)在第四象限,∴y3<y1,选C。
6、已知a+b+c≠0,且c=a=b。
解析:由c=a=b,可得a=b=c,代入a+b+c≠0中,得3a≠0,∴a≠0,选D。
初中数学奥林匹克考试试题

初中数学奥林匹克考试试题本文将提供一些经典的初中数学奥林匹克考试试题,旨在帮助学生提升数学解题能力和思维能力。
以下是一些题目供大家练习:1. 在平面直角坐标系中,点A(-2, 4)和B(3, 1)在坐标轴上的垂直平分线所交的点为C,求AC的长度。
2. 若x能被3整除,且由x的各位数字组成的3位数能被27整除,求满足条件的最小正整数x。
3. 甲、乙两车,相向而行,甲车的速度是乙车速度的4倍,甲车行驶8小时后,与乙车相距960公里,求甲车和乙车的速度分别是多少。
4. 求4/7与21/50的和的最简分数形式。
5. 若a、b、c均为正整数,且满足方程式:1/a + 1/b + 1/c = 1/2求满足条件的最小正整数解。
6. 在等腰三角形ABC中,AC=BC,角ACB的角度为120°,D是AB的中点,连接AD和BD,求角ACD的度数。
7. 若x和y是正整数,满足x^3 + x^2y + xy^2 + y^3 = (x + y)^3,求x与y的和。
8. 若正整数m、n均满足m/n = 12.3456789...,求m与n的最大公约数。
9. 设a、b、c为正整数,满足a+b+c=99,且a^2 + b^2 + c^2 =3(abc),求a、b、c的值。
10. 在等腰梯形ABCD中,AB//CD,AB+CD=15,AC=10,BD=12,求AB的长度。
以上是一些初中数学奥林匹克考试的典型题目,希望能对大家的数学学习有所帮助。
通过练习,可以提高解题能力和思维能力,培养逻辑思维和分析问题的能力。
希望大家能够积极参与数学竞赛,挑战自我,不断进步!。
初一数学奥林匹克竞赛题(含标准答案)

初一数学奥林匹克竞赛题(含答案)初一奥数题一甲多开支100元,三年后负债600元.求每人每年收入多少?S的末四位数字的和是多少?4.一个人以3千米/小时的速度上坡,以6千米/小时的速度下坡,行程12千米共用了3小时20分钟,试求上坡与下坡的路程.5.求和:6.证明:质数p除以30所得的余数一定不是合数.8.若两个整数x,y使x2+xy+y2能被9整除,证明:x和y能被3整除.9.如图1-95所示.在四边形ABCD中,对角线AC,BD的中点为M,N,MN的延长线与AB边交于P点.求证:△PCD的面积等于四边形ABCD的面积的一半.解答:所以x=5000(元).所以S的末四位数字的和为1+9+9+5=24.3.因为a-b≥0,即a≥b.即当b≥a>0或b≤a<0时,等式成立.4.设上坡路程为x千米,下坡路程为y千米.依题意则有由②有2x+y=20,③由①有y=12-x.将之代入③得 2x+12-x=20.所以x=8(千米),于是y=4(千米).5.第n项为所以6.设p=30q+r,0≤r<30.因为p为质数,故r≠0,即0<r<30.假设r 为合数,由于r<30,所以r的最小质约数只可能为2,3,5.再由p=30q+r 知,当r的最小质约数为2,3,5时,p不是质数,矛盾.所以,r一定不是合数.7.设由①式得(2p-1)(2q-1)=mpq,即(4-m)pq+1=2(p+q).可知m<4.由①,m>0,且为整数,所以m=1,2,3.下面分别研究p,q.(1)若m=1时,有解得p=1,q=1,与已知不符,舍去.(2)若m=2时,有因为2p-1=2q或2q-1=2p都是不可能的,故m=2时无解.(3)若m=3时,有解之得故 p+q=8.8.因为x2+xy+y2=(x-y)2+3xy.由题设,9|(x2+xy+y2),所以3|(x2+xy +y2),从而3|(x-y)2.因为3是质数,故3|(x-y).进而9|(x-y)2.由上式又可知,9|3xy,故3|xy.所以3|x或3|y.若3|x,结合3(x-y),便得3|y;若3|y,同理可得,3|x.9.连结AN,CN,如图1-103所示.因为N是BD的中点,所以上述两式相加另一方面,S△PCD=S△CND+S△CNP+S△DNP.因此只需证明S△AND=S△CNP+S△DNP.由于M,N分别为AC,BD的中点,所以S△CNP=S△CPM-S△CMN=S△APM-S△AMN=S△ANP.又S△DNP=S△BNP,所以S△CNP+S△DNP=S△ANP+S△BNP=S△ANB=S△AND.初一奥数题二1.已知3x2-x=1,求6x3+7x2-5x+2000的值.2.某商店出售的一种商品,每天卖出100件,每件可获利4元,现在他们采用提高售价、减少进货量的办法增加利润,根据经验,这种商品每涨价1元,每天就少卖出10件.试问将每件商品提价多少元,才能获得最大利润?最大利润是多少元?3.如图1-96所示.已知CB⊥AB,CE平分∠BCD,DE平分∠CDA,∠1+∠2=90°.求证:DA⊥AB.4.已知方程组的解应为一个学生解题时把c抄错了,因此得到的解为求a2+b2+c2的值.5.求方程|xy|-|2x|+|y|=4的整数解.6.王平买了年利率7.11%的三年期和年利率为7.86%的五年期国库券共35000元,若三年期国库券到期后,把本息再连续存两个一年期的定期储蓄,五年后与五年期国库券的本息总和为47761元,问王平买三年期与五年期国库券各多少?(一年期定期储蓄年利率为5.22%)7.对k,m的哪些值,方程组至少有一组解?8.求不定方程3x+4y+13z=57的整数解.9.小王用5元钱买40个水果招待五位朋友.水果有苹果、梨子和杏子三种,每个的价格分别为20分、8分、3分.小王希望他和五位朋友都能分到苹果,并且各人得到的苹果数目互不相同,试问他能否实现自己的愿望?解答:1.原式=2x(3x2-x)+3(3x2-x)-2x+2000 =2x×1+3×1-2x+2000=2003.2.原来每天可获利4×100元,若每件提价x元,则每件商品获利(4+x)元,但每天卖出为(100-10x)件.如果设每天获利为y元,则y =(4+x)(100-10x)=400+100x-40x-10x2=-10(x2-6x+9)+90+400=-10(x-3)2+490.所以当x=3时,y最大=490元,即每件提价3元,每天获利最大,为490元.3.因为CE平分∠BCD,DE平分∠ADC及∠1+∠2=90°(图1-104),所以∠ADC+∠BCD=180°,所以AD∥BC.①又因为 AB⊥BC,②由①,②AB⊥AD.4.依题意有所以a2+b2+c2=34.5.|x||y|-2|x|+|y|=4,即|x|(|y|-2)+(|y|-2)=2,所以(|x|+1)(|y|-2)=2.因为|x|+1>0,且x,y都是整数,所以所以有6.设王平买三年期和五年期国库券分别为x元和y元,则因为y=35000-x,所以 x(1+0.0711×3)(1+0.0522)2+(35000-x)(1+0.0786×5)=47761,所以 1.3433x+48755-1.393x=47761,所以 0.0497x=994,所以 x=20000(元),y=35000-20000=15000(元).7.因为 (k-1)x=m-4,①m为一切实数时,方程组有唯一解.当k=1,m=4时,①的解为一切实数,所以方程组有无穷多组解.当k=1,m≠4时,①无解.所以,k≠1,m为任何实数,或k=1,m=4时,方程组至少有一组解.8.由题设方程得z=3m-y.x=19-y-4(3m-y)-m=19+3y-13m.原方程的通解为其中n,m取任意整数值.9.设苹果、梨子、杏子分别买了x,y,z个,则消去y,得12x-5z=180.它的解是x=90-5t,z=180-12t.代入原方程,得y=-230+17t.故x=90-5t,y=-230+17t,z=180-12t.x=20,y=8,z=12.因此,小王的愿望不能实现,因为按他的要求,苹果至少要有1+2+3+4+5+6=21>20个.初一奥数题三1.解关于x的方程2.解方程其中a+b+c≠0.3.求(8x3-6x2+4x-7)3(2x5-3)2的展开式中各项系数之和.4.液态农药一桶,倒出8升后用水灌满,再倒出混合溶液4升,再用水灌满,这时农药的浓度为72%,求桶的容量.5.满足[-1.77x]=-2x的自然数x共有几个?这里[x]表示不超过x的最大整数,例如[-5.6]=-6,[3]=3.6.设P是△ABC一点.求:P到△ABC三顶点的距离和与三角形周长之比的取值围.7.甲乙两人同时从东西两站相向步行,相会时,甲比乙多行24千米,甲经过9小时到东站,乙经过16小时到西站,求两站距离.8.黑板上写着三个数,任意擦去其中一个,将它改写成其他两数的和减1,这样继续下去,最后得到19,1997,1999,问原来的三个数能否是2,2,2?9.设有n个实数x1,x2,…,x n,其中每一个不是+1就是-1,且求证:n是4的倍数.解答:1.化简得6(a-1)x=3-6b+4ab,当a≠1时,2.将原方程变形为由此可解得x=a+b+c.3.当x=1时,(8-6+4-7)3(2-1)2=1.即所求展开式中各项系数之和为1.依题意得去分母、化简得7x2-300x+800=0,即7x-20)(x-40)=0,5.若n为整数,有[n+x]=n+[x],所以[-1.77x]=[-2x+0.23x]=-2x+[0.23x].由已知[-1.77x]=-2x,所以-2x=-2x+[0.23x],所以 [0.23x]=0.又因为x为自然数,所以0≤0.23x<1,经试验,可知x可取1,2,3,4,共4个.6.如图1-105所示.在△PBC中有BC<PB+PC,①延长BP交AC于D.易证PB+PC<AB+AC.②由①,②BC<PB+PC<AB+AC,③同理 AC<PA+PC<AC+BC,④AB<PA+PB<AC+AB.⑤③+④+⑤得AB+BC+CA<2(PA+PB+PC)<2(AB+BC+CA).所以7.设甲步行速度为x千米/小时,乙步行速度为y千米/小时,则所求距离为(9x+16y)千米.依题意得由①得16y2=9x2,③由②得16y=24+9x,将之代入③得即 (24+9x)2=(12x)2.解之得于是所以两站距离为9×8+16×6=168(千米).8.答案是否定的.对于2,2,2,首先变为2,2,3,其中两个偶数,一个奇数.以后无论改变多少次,总是两个偶数,一个奇数(数值可以改变,但奇偶性不变),所以,不可能变为19,1997,1999这三个奇数.。
数学奥林匹克初中训练题15套

数学奥林匹克初中训练题(一)第 一 试一. 选择题 1、已知33333a b c abca b c++-=++,则22()()()()a b b c a b b c -+-+--的值为:A .1B .2C .3D .42、规定”Δ”为有序实数对的运算,如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为: A .(0,1) B .(1,0) C .(-1,0) D .(0,-1)3、在ΔABC 中,211a b c=+,则∠A:A .一定是锐角B .一定是直角C .一定是钝角D .非上述答案4、下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2();a a =③若点(,)P a b 在第三象限,则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是:A .2个B .3个C .4个D .5个5、设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点,22S AP BP =+,那么: A . 22CP S < B .22CP S = C .22CP S > D .不确定6、满足方程222()x y x y xy +=++的所有正整数解有:A .一组B .二组C .三组D .四组 二. 填空题1、一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问再过 分钟,货车追上了客车.2、若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .3、如图1, ∠AOB=30O , ∠AOB 内有一定点P ,且OP=10.在OA 上有一点Q ,OB 上有一点R.若ΔPQR 周长最 小,则最小周长是 .4、已知二次函数2(1)y ax a =≥的图象上两点A ,B 的横坐标分别为1,2-,O 是坐标原点,如果ΔAOB 是直角三角形,则ΔAOB 的周长为 .第 二 试一、已知实数,,a b c 满足不等式,a b c b c a ≥+≥+,c a b ≥+,求a b c ++的值.二、如图2,点D 在ΔABC 的边BC 上,且与B ,C 不重合,过点D 作AC 的平行线DE 交AB 于E ,作AB 的平行线DF 交AC 于点F.又知BC=5.(1)设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长.(2)若2,AC AB =且DF 经过ΔABC 的重心G ,求E ,F 两点的距离.三、已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=,则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论.数学奥林匹克初中训练题(二)第 一 试一、选择题1、有铅笔,练习本,圆珠笔三种学习用品.若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本10本,圆珠笔1支共需4.2元.现购铅笔,练习本,圆珠笔各1件,共需:A .1.2元B .1.05元C .0.95元D .0.9元2、三角形的三边,,a b c 都是整数,且满足7abc bc ca ab a b c ++++++=,则此三角形的面积等于: A .32B .24C .34D .223、如图1,ΔABC 为正三角形,PM ⊥AB ,PN ⊥AC.设四边形AMPN , ΔABC 的周长分别是,m n ,则有: A .5321<<n m B .4332<<nm C .%79%78<<nm D .%83%80<<nm4、满足22(3)(3)6x y -+-=的所有实数对(,)x y ,使y x取最大值,此最大值为:A .322+B .42+C .533+D .53+5、设333717171p a b c =+++++371d ++.其中,,,a b c d 是正实数,且满足1a b c d +++=.则p 满足:A .p >5B .p <5C .p <2D .p <36、如图2,点O 是正六边形ABCDEF 的中心,OM ⊥CD ,N 为OM 的中点.则:ABN BC N S S 等于:A .9:5B .7:4C .5:3D .3:2二、填空题1、若实数,x y 满足22(1)(1)1x x y y ++++=,则 x y += .2、如图3,CD 为直角ΔABC 斜边AB 上的高,DE ⊥AC.设ΔADE ,ΔCDB ,ΔABC 的周长分别是12,,p p p .当12p p p +取最大值时,∠A= .3、若函数2543kx y kx kx +=++中自变量的取值范围是一切实数,则实数k 的取值范围是 .4、如图4所示,线段AB 与CD 都是⊙O 中的弦,其 108,,36,O O AB AB a CDCD b ====,则⊙O 的半径R= .第 二 试一.(共20分)n 是一个三位数,b 是一个一位数,且22,1a a bb ab ++都是整数,求a b +的最大值与最小值.二.(共25分)如图5,在ΔABC 中,∠A=60O ,O ,I ,H 分别是它的外心,内心,垂心.试比较ΔABC 的外接圆与ΔIOH 的外接圆的大小,证明你的论断.三.(共25分)求方程组33333x y z x y z ++=⎧⎨++=⎩的所有整数解.数学奥林匹克初中训练题(三)第 一 试一、选择题1、在112,,0.2002,(3222),7223n n π----(n 是大于3的整数)这5个数中,分数的个数为:A .2B .3C .4D .52、如图1,正方形ABCD 的面积为256,点F 在AD 上,点E 在AB 的延长线上,Rt ΔCEF 的面积为200,则BE 的长为: A .10 B .11 C .12 D .153、已知,,a b c 均为整数,且满足2223a b c +++<32ab b c ++.则以,a b c b +-为根的一元二次方程是:A .2320x x -+=B .2280x x +-=C .2450x x --=D .2230x x --=4、如图2,在Rt ΔABC 中,AF 是高,∠BAC=90O,且 BD=DC=FC=1,则AC 为:A .32 B .3 C .2 D .335、若222a b c a b c k cba+++===,则k 的值为:A .1B .2C .3D .非上述答案6、设0,0,26x y x y ≥≥+=,则224363u x xy y x y =++--的最大值是: A .272B .18C .20D .不存在二、填空题1、方程222111013x x x x++=+的实数根是 .2、如图3,矩形ABCD 中,E ,F 分别是BC ,CD 上的点,且4,3,2===∆∆∆ADF CEF ABE S S S ,则AEF S ∆= .3、已知二次函数2(1)y x a x b =+++(,a b 为常数).当3x =时,3;y =当x 为任意实数时,都有y x ≥.则抛物线的顶点到原点的距离为 .4、如图4,半径为2cm ,圆心角为90O 的扇形OAB 的 AB 上有一运动的点P .从点P 向半径OA 引垂线PH 交OA 于点H.设ΔOPH 的内心为I ,当点P 在 AB 上从点A 运动到点B 时,内心I 所经过的路径长为 .第 二 试一、(20分)在一个面积为1的正方形中构造一个如下的小正方形;将单位正方形的各边n 等分,然后将每个顶点和它相对应顶点最接近的分点连结起来,如图5所示.若小正方形的面积恰为13281,求n 的值.二、(25分)一条笔直的公路l 穿过草原,公路边有一卫生站A ,距公路30km 的地方有一居民点B ,A ,B 之间的距离为90km .一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60/km h ,在草地上行驶的最快速度是30/km h .问司机应以怎样的路线行驶,所用的行车时间最短?最短时间是多少?三、(25分)从1,2,3,……,3919中任取2001个数。
初中数学奥林匹克训练题4(试卷)

初中数学奥林匹克训练题(4)第一试一、填空题1、一个直角三角形的两条直角边长为b a ,满足不等式31634192622≤+-++-b b a a ,则这个直角三角形的斜边长为2、数812934756是一个包含1至9每个数字恰好一次的九位数,它具有如下性质:数字1至6在其中是从小到大排列的,但是数字1至7不是从小到大排列的.这样的九位数共有 ______________个.3、对每一个正整数k ,设ka k 1211 ++=,则 49493212500)99753(a a a a a -++++等于______________4、集合{}7,6,5,4,3,2,1=S 的五元子集共有21个,每个子集的数从小到大排好后,取出中间的数,则所有这些数之和是( )4、函数32)(2+-=x x x f ,若a x f -)(<2恒成立的充分条件是21≤≤x ,则实数a 的取值范围是 .5、在直角坐标平面上,正方形ABCD 的顶点A 、C 的坐标分别为(12,19)、(3,22),则顶点B 、D 的坐标分别为 .(A 、B 、C 、D 依逆时针顺序排列)6、方程10033100=+y x 的正整数解),(y x 有 组.7、正整数集合k A 的最小元素为1,最大元素为2007,并且各元素可以从小到大排成一个公差为k 的等差数列,则并集1759A A 中的元素个数为8、若实数,x y 满足:1031031031031,125263536xy x y+=+=++++,则x y += .9、把一个长方体切割成k 个四面体,则k 的最小值是 .10、将各位数码不大于3的全体正整数m 按自小到大的顺序排成一个数列{}n a ,则2007a = .二、解答题1、已知二次函数c bx ax x f ++=2)(和一次函数bx x g -=)(,其中c b a ,,满足c b a >>,0=++c b a ,),,(R c b a ∈.(1)求证:两函数的图像交于不同的两点A 、B ; (2)求线段AB 在x 轴上的射影11B A 的范围。
初中数学奥林匹克竞赛题及答案

初中数学奥林匹克竞赛题及答案初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么 ( )A.a,b都是0B.a,b之一是0C.a,b互为相反数D.a,b互为倒数答案:C解析:互为相反数。
b,由此a、-2,满足2+(-2)=0令a=2,b=2.下面的说法中正确的是 ( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案:D33222解析:3是多项式,排除A+x之和为xx,x。
两个单项都是单项式.两个单项式x,x22223之和为2x3x是个单-之和为3xx是单项式,排除B。
两个多项式x3+x2式x2x,与。
,因此选D项式,排除C3.下面说法中不正确的是 ( )A. 有最小的自然数B.没有最小的正有理数C.没有最大的负整数D.没有最大的非负数答案:C解析:错误。
C最大的负整数是-1,故4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号B.a,b异号C.a>0D.b>0答案:D5.大于-π并且不是自然数的整数有 ( )A.2个B.3个C.4个D.无数个答案:C解析:在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,13/ 1初中数学奥林匹克竞赛题及答案。
个.选C0共4-1,6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
这四种说法中,不正确的说法的个数是 ( )A.0个B.1个C.2个D.3个答案:B解析:负数的平方是正数,所以一定大于它本身,故C错误。
7.a代表有理数,那么,a和-a的大小关系是 ( )A.a大于-aB.a小于-aC.a大于-a或a小于-aD.a不一定大于-a答案:D解析:。
,应选D、B、C,马上可以排除令a=0A8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( )A.乘以同一个数B.乘以同一个整式C.加上同一个代数式D.都加上1答案:D解析:对方程同解变形,要求方程两边同乘不等于0的数,所以排除A。
数学奥林匹克初中训练题
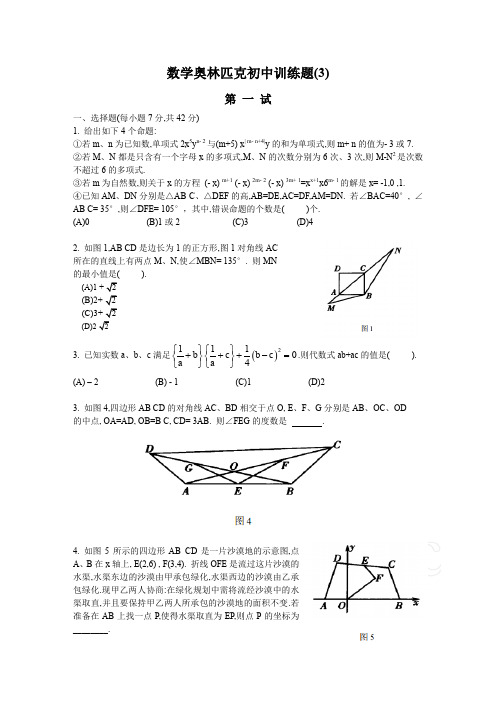
数学奥林匹克初中训练题(3)第 一 试一、选择题(每小题7分,共42分)1. 给出如下4个命题:①若m 、n 为已知数,单项式2x 5y n- 2与(m+5) x | m- n+4|y 的和为单项式,则m+ n 的值为- 3或7. ②若M 、N 都是只含有一个字母x 的多项式,M 、N 的次数分别为6次、3次,则M-N 2是次数不超过6的多项式.③若m 为自然数,则关于x 的方程 (- x) m+1 (- x) 2m- 2 (- x) 3m+ 1=x x+1x6m- 1的解是x= -1,0 ,1. ④已知AM 、DN 分别是△AB C 、△DEF 的高,AB=DE,AC=DF,AM=DN. 若∠BAC=40°, ∠AB C= 35°,则∠DFE= 105°,其中,错误命题的个数是( )个.(A)0 (B)1或2 (C)3 (D)42. 如图1,AB CD 是边长为1的正方形,图1对角线AC所在的直线上有两点M 、N,使∠MBN= 135°. 则MN的最小值是( ).3. 已知实数a 、b 、c 满足()211104b c b c a a ⎧⎫⎧⎫+++-=⎨⎬⎨⎬⎩⎭⎩⎭.则代数式ab+ac 的值是( ). (A) – 2 (B) - 1 (C)1 (D)23. 如图4,四边形AB CD 的对角线AC 、BD 相交于点O, E 、F 、G 分别是AB 、OC 、OD 的中点, OA=AD, OB=B C, CD= 3AB. 则∠FEG 的度数是.4. 如图5所示的四边形AB CD 是一片沙漠地的示意图,点A 、B 在x 轴上, E(2,6) , F(3,4). 折线OFE 是流过这片沙漠的水渠,水渠东边的沙漠由甲承包绿化,水渠西边的沙漠由乙承包绿化.现甲乙两人协商:在绿化规划中需将流经沙漠中的水渠取直,并且要保持甲乙两人所承包的沙漠地的面积不变.若准备在AB 上找一点P,使得水渠取直为EP,则点P 的坐标为________.。
2023年全国中学生数学奥林匹克竞赛题目

2023年全国中学生数学奥林匹克竞赛题目1. 题目一设函数$f(x)$在区间$[a,b]$上连续,且满足$f(a)=-1$,$f(b)=3$。
证明:对于任意实数$k$,在区间$[a,b]$上至少存在一点$c$,使得$f(c)-f(a)=k(c-a)$。
2. 题目二已知正整数$n>1$,且$n$与$n+1$互质。
定义数列$\{a_k\}$满足$a_1=n$,$a_2=n+1$,且对于$k\geq 1$有\[a_{k+2}=\frac{a_{k+1}+a_k}{\text{gcd}(a_{k+1},a_k)}.\]证明:数列$\{a_k\}$中不存在连续的三个不等于1的整数。
3. 题目三平面上有$2023$个点,任意三点不共线。
现将这些点两两连接,得到若干条线段。
试证明:存在至少$10$条线段,它们共点于同一点上。
4. 题目四设$a,b$为正整数,且满足$(a+1)^{b+1}-(a-1)^{b+1}=2023$。
求$(a,b)$的所有可能的整数解。
5. 题目五将正整数$n$表示为两个不同素数的乘积,即$n=pq$,其中$p$和$q$均为素数,且$p < q$。
设$S=(p+1)^2+q^2$。
求满足条件的$n$的所有可能取值,并给出满足条件的所有$n$对应的$S$的最大值。
6. 题目六已知三角形$ABC$的三个内角$A,B,C$满足$\cos A+\cos B+\cos C = 2$。
证明:三角形$ABC$为等边三角形。
7. 题目七设函数$f(x)$在区间$[0,1]$上连续,且满足$f(0)=0$,$f(1)=1$。
证明:对于任意$\epsilon > 0$,存在有理数$m/n$,其中$m$为自然数,$n$为正整数,且$\left| \frac{m}{n} - f\left(\frac{m}{n}\right) \right| < \epsilon$。
8. 题目八已知正整数$a,b,c$满足$ab+bc+ca=2023$。
初中数学奥林匹克训练题(五)及答案

数学奥林匹克初中训练题(五)第 一 试一. 选择题.(每小题7分,共42分)( )1.若,a b 均为质数,且22003a b +=,则a b +的值为:(A)1999 (B)2000 (C)2001 (D)2002( )2.设0,1,a b c a b c ++=f f f ,,,b c a c a b M N P a b c +++===,则,,M N P 之间的关系是:(A)M N P f f (B)N P M f f(C)P M N f f (D)M P N f f( )3.设ΔABC 的三边长为,,a b c 满足28,1252b c bc a a +==-+,则ΔABC 的周长是: (A)10 (B)14 (C)16 (D)不能确定( )4.下面四个命题:①直角三角形的两边长为3,4,则第三边长为5;②1x x x-=-,③对角线相等且互相垂直的四边形是正方形;④若四边形ABCD 中,AD ∥BC,且 AB+BC=AD+DC,则四边形ABCD 是平行四边形.其中正确的命题的个数为:(A)0 (B)1 (C)2 (D)3( )5.一个四位数aabb u u u u u r 为平方数,则a b +的值为:(A)11 (B)10 (C)9 (D)8( )6.如果满足60,12,O ABC AC BC k ∠===的ΔABC 恰有一个,那么k 的取值范围是:(A)83k = (B)012k ≤p (C)12k ≥ (D)012k ≤p 或83k =二. 填空题.(每小题7分,共28分)1.已知,,a b c 为实数,且多项式32x ax bx c +++能被234x x +-整除,则22a b c --的值是 .2.设正整数,,a b c 满足518,360ab bc ab ac +=-=,则abc 的最大值是 . 3,若abc =1,2003111x x x a ab b bc c ac++=++++++,则x = . 4.如图1,AB 是半圆O 的直径,四边形CDMN 和DEFG 都是正方形,其中C,D,E 在AB 上,F,N 在半圆上.若AB=10,则正方形CDMN 的面积与正方形DEFG 的面积之和是 .第 二 试一.(20分)若AD 是ΔABC 角平分线,I 是线段AD 上的点,且1902O BIC BAC ∠=+∠. 求证:I 是ΔABC 的内心.二.(25分)用汽船拖载重量相等满载货物的小船若干只,在两港之间来回送货物.已知每次拖4只小船,一日能来回16次;每次拖7只小船,一日能来回10次.每日来回次数是拖小船只数的一次函数(一天中每次拖小船只数不变).问每日来回多少次,每次拖多少只小船,才能使运货问题达到最大?三.(25分)设,,a b c 是从1到9的互不相同的整数,求a b c abc++的最大的可能值.。
初中数学奥林匹克模拟试卷1-10套

数学奥林匹克模拟试卷(一)一、选择题:1、已知311=-=-b b a a ,且3>+b a ,则33ab b a -的值是( )。
(A )521(B )1321(C )533(D )13332、如果二次函数()522++++=k x k x y 的图象与x 轴的两个不同交点的横坐标是正的,那么k 值应为( )(A )4>k 或5.-<k (B )45-<<-k (C )4.-≥k 或5-≤k (D )45-≤≤-k3、如图,∆ABC 为锐角三角形,BE ⊥AC 于F ,则ABCAEF S S ∆∆:的值为( )(A )A sin (B )A cos (C )A 2sin (D )A 2cos4、方程1997111=+y x 的正整数解的组数为( ) (A )1(B )2(C )3(D )大于等于45、P 为∆ABC 内一点,PA 、PB 、PC 把∆ABC 的面积分成三等分,则P 点是∆ABC 的( )(A )内心(B )外心(C )垂心(D )重心6、抛物线122++=bx x y 与直线ab ax y 22+=的图象至多有一个交点,则的最大值是( )(A )1(B )23(C )22(D )0 二、填空题:1、已知四个实数的乘积为1,其中任意一个数与其余三个数的积的和都等于1000,则此四数的和是_________。
2、如果c yz b xz a xy ===,,,而且它们都不等于0,则222z y x ++=_________。
AB CE F A B CED G3、若抛物线()242+++=a x ax y 全在x 轴的上方,a 的范围是_________。
4、如图,在图形ABCD 中,AB ∥CD ,∠A=900,E 为BC 重点,GE ⊥BC 于,交DA 延长线于G ,DC=17cm ,AB=25cm ,BC=10cm ,则CE=_________。
数学奥林匹克初中训练题_58_

故 x > y , x < z . 所以 , y < x < z . 5. (D) . 12 y =3x + . 当 x = 1 ,2 ,3 ,4 ,6 ,12 时 , y = 15 ,12 ,
x
∵
3 ≤AM ≤ 1,∴ 3 ≤PA + PC ≤ 2 3. 2
第二试
一、 由题意知 4 + 2 p + q = - 1 ,即 2 p + q = - 5.
从而 , a + b < 即
a + b 6 6 > a + b
4 4
6
6
a + b ,a + b <
4 4
4
4
4
4
a + b ,
4
4
a + b
4
4
a + b
,
a + b 6 6 < a + b
4
4
a + b 6 . a + b
6
4
= AO ( AN + CM) (1 + ON + 1 + OM) = 1 + 1 + 1 = 3. = 1・ 3 故 PA + PC = .
三、 取 4 个无理数
2, 3,- 2,- 3
, 显然不
满足条件 ,故 n ≥ 5. 设 5 个无理数 a 、 b、 c、 d、 e ,视为 5 个点 . 若两数和为有 理数 ,则相应两点连成红线 ,否 则连成蓝线 . (1) 无 红 色 三 角 形 . 若 不 然 ,不妨设 a + b 、 b + c、 c+ a 图 11 都是有理数 . 由于 ( a + b) + ( c + a) - ( b + c) = 2 a ,与 a 为无理数矛盾 . (2) 必有同色三角形 . 否则 ,图中必有一个红圈 , 顶点上 5 个数中 ,两两之和均为有理数 . 设 a + b 、 b+ c、 c + d、 d + e、 e + a 为有理数 ,由 ( a + b) - ( b + c) + ( c + d) - ( d + e) + ( e + a) = 2 a 推出矛盾 . 这样 ,同色 三角形必为蓝色三角形 . 因此 , n 的最小值是 5.
数学奥林匹克竞赛试卷初中

一、选择题(每题5分,共50分)1. 下列各数中,能被3整除的是()A. 2B. 7C. 12D. 252. 一个等腰三角形的底边长为6cm,腰长为8cm,那么这个三角形的周长是()A. 20cmB. 22cmC. 24cmD. 26cm3. 已知函数y=2x+1,若x=3,则y的值为()A. 5B. 6C. 7D. 84. 在下列各组数中,有最大公约数4的是()A. 16,24B. 12,18C. 20,28D. 15,215. 一个长方体的长、宽、高分别为5cm、4cm、3cm,那么它的体积是()A. 60cm³B. 72cm³C. 80cm³D. 90cm³6. 已知x²-5x+6=0,则x的值为()A. 2B. 3C. 4D. 57. 在直角坐标系中,点A(-2,3)关于原点的对称点是()A. (-2,-3)B. (2,-3)C. (-2,3)D. (2,3)8. 下列各图中,是轴对称图形的是()A.B.C.D.9. 下列各数中,有最小公倍数120的是()A. 24,40B. 30,48C. 36,50D. 42,6010. 已知a²+b²=c²,则下列结论正确的是()A. a、b、c都是正数B. a、b、c都是负数C. a、b、c都是整数D. a、b、c都是正整数二、填空题(每题5分,共50分)11. 若a+b=5,ab=6,则a²+b²的值为______。
12. 0.5+0.2+0.1+…+0.05+0.01+0.005+…+0.0005+0.0001的和为______。
13. 一个数的平方根是±2,那么这个数是______。
14. 下列各数中,是质数的是______。
15. 一个圆的半径增加了50%,那么这个圆的面积增加了______。
16. 若一个等边三角形的边长为a,那么它的周长是______。
最新整理初中奥数试题大全及解析汇总

数学奥林匹克初中训练题(2)及答案解析
参考答案: 一.1.(B)
数学奥林匹克初中训练题(2)及答案解析
数学奥林匹克初中训练题(3)及答案解析
数学奥林匹克初中训练题(3)及答案解析
数学奥林匹克初中训练题(3)及答案解析
数学奥林匹克初中训练题(4)及答案解析
数学奥林匹克初中训练题(4)及答案解析
数学奥林匹克初中训练题(5)及答案解析
数学奥训练题(5)及答案解析
1 2 下一页 上一页 1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学奥林匹克初中训练题(1)第 一 试一. 选择题.(每小题7分,共42分)( )1.已知33333a b c abc a b c++-=++,则22()()()()a b b c a b b c -+-+--的值为: (A)1 (B)2 (C)3 (D)4( )2.规定”Δ”为有序实数对的运算,如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为:(A)(0,1) (B)(1,0) (C)(1,0)- (D)(0,1)-( )3.在ΔABC 中,211a b c=+,则∠A: (A)一定是锐角 (B)一定是直角 (C)一定是钝角 (D)非上述答案( )4.下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2();a a =③若点(,)P a b 在第三象限,则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是:(A)2个 (B)3个 (C)4个 (D)5个( )5.设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点,22S AP BP =+,那么:(A)22S CP p (B)22S CP = (C)22S CP f (D)不确定( )6.满足方程222()x y x y xy +=++的所有正整数解有:(A)一组 (B)二组 (C)三组 (D)四组二. 填空题.(每小题7分,共28分)1.一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问再过分钟,货车追上了客车.2.若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .3.如图1, ∠AOB=30O , ∠AOB 内有一定点P,且OP=10.在OA 上有一点Q,OB 上有一点R.若ΔPQR 周长最小,则最小周长是 . 4.已知二次函数2(1)y ax a =≥的图象上两点A,B 的横坐标分别为1,2-,O 是坐标原点,如果ΔAOB 是直角三角形,则ΔAOB 的周长为 .第 二 试一.(20分)已知实数,,a b c 满足不等式,a b c b c a ≥+≥+,c a b ≥+,求a b c ++的值.二.(25分)如图2,点D 在ΔABC 的边BC 上,且与B,C 不重合,过点D 作AC 的平行线DE 交AB 于E,作AB 的平行线DF 交AC 于点F.又知BC=5.(1) 设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长.(2) 若2,AC AB =且DF 经过ΔABC 的重心G,求E,F 两点的距离.三.(25分)已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=,则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论.数学奥林匹克初中训练题(2)第 一 试一. 选择题.(每小题7分,共42分)( )1.有铅笔,练习本,圆珠笔三种学习用品.若购铅笔3支,练习本7本,圆珠笔1支共需3.15元;若购铅笔4支,练习本10本,圆珠笔1支共需4.2元.现购铅笔,练习本,圆珠笔各1件,共需:(A)1.2元 (B)1.05元 (C)0.95元 (D)0.9元( )2.三角形的三边,,a b c 都是整数,且满足7abc bc ca ab a b c ++++++=,则此三角形的面积等于:(A)32 (B)24 (C)34 (D)22 ( )3.如图1,ΔABC 为正三角形,PM ⊥AB,PN ⊥AC.设四边形AMPN, ΔABC 的周长分别是,m n ,则有:(A)1325m n p p (B)2334m n p p (C)80%83%m n p p (D)78%79%m np p ( )4.满足22(3)(3)6x y -+-=的所有实数对(,)x y ,使y x 取最大值,此最大值为:(A)322+ (B)42+ (C)533+ (D)53+( )5.设333717171p a b c =+++++371d ++.其中,,,a b c d 是正实数,且满足1a b c d +++=.则p 满足: (A)p >5(B)p <5 (C)p <2 (D)p <3( )6.如图2,点O 是正六边形ABCDEF 的中心,OM ⊥CD,N为OM 的中点.则:ABN BCN S S V V 等于:(A)9:5 (B)7:4 (C)5:3 (D)3:2二. 填空题.(每小题7分,共28分)1.若实数,x y 满足22(1)(1)1x x y y ++++=,则x y += .2.如图3,CD 为直角ΔABC 斜边AB 上的高,DE ⊥AC.设ΔADE,ΔCDB,ΔABC 的周长分别是12,,p p p .当12p p p+ 取最大值时,∠A= .3.若函数2543kx y kx kx +=++中自变量的取值范围是一切实数,则实数k 的取值范围是 .4.如图4所示,线段AB 与CD 都是⊙O 中的弦,其中»»108,,36,O O AB AB a CDCD b ====,则⊙O 的半径R= .第 二 试一.(共20分)n 是一个三位数,b 是一个一位数,且22,1a a b b ab ++都是整数,求a b +的最大值与最小值.二.(共25分)如图5,在ΔABC 中,∠A=60O ,O,I,H 分别是它的外心,内心,垂心.试比较ΔABC 的外接圆与ΔIOH 的外接圆的大小,证明你的论断.三.(共25分)求方程组33333x y z x y z ++=⎧⎨++=⎩的所有整数解.参考答案一.1.(B)数学奥林匹克初中训练题(三)第 一 试三. 选择题.(每小题7分,共42分)( )1.在112,,0.2002,(3222),722n n π----(n 是大于3的整数)这5个数中,分数的个数为: (A)2 (B)3 (C)4 (D)5( )2.如图1,正方形ABCD 的面积为256,点F 在AD上,点E 在AB 的延长线上,Rt ΔCEF 的面积为200,则BE 的长为:(A)10 (B)11 (C)12 (D)15( )3.已知,,a b c 均为整数,且满足2223a b c +++<32ab b c ++.则以,a b c b +-为根的一元二次方程是:(A)2320x x -+= (B)2280x x +-=(C)2450x x --= (D)2230x x --=( )4.如图2,在Rt ΔABC 中,AF 是高,∠BAC=90O ,且BD=DC=FC=1,则AC 为:(A)32 (B)3 (C)2 (D)33( )5.若222a b c a b c k c b a+++===,则k 的值为: (A)1 (B)2 (C)3 (D)非上述答案 ( )6.设0,0,26x y x y ≥≥+=,则224363u x xy y x y =++--的最大值是:(A)272(B)18 (C)20 (D)不存在 四. 填空题.(每小题7分,共28分)1.方程222111013x x x x++=+的实数根是 . 2.如图3,矩形ABCD 中,E,F 分别是BC,CD 上的点,且2,3,4ABE CEF ADF S S S ===V V V ,则AEF S V = .3.已知二次函数2(1)y x a x b =+++(,a b 为常数).当3x =时,3;y =当x 为任意实数时,都有y x.则抛物线的顶点到原点的距离为.4.如图4,半径为2cm,圆心角为90O的扇形OAB的»AB上有一运动的点P.从点P向半径OA引垂线PH交OA于点H.设ΔOPH的内心为I,当点P在»AB上从点A运动到点B时,内心I所经过的路径长为.第二试一.(20分)在一个面积为1的正方形中构造一个如下的小正方形;将单位正方形的各边n等分,然后将每个顶点和它相对应顶点最接近的分点连结起来,如图5所示.若小正方形的面积恰为13281,求n的值.二.(25分)一条笔直的公路l穿过草原,公路边有一卫生站A,距公路30km的地方有一居民点B,A,B之间的距离为90km.一天某司机驾车从卫生站送一批急救药品到居民点.已知汽车在公路上行驶的最快速度是60/km h,在草地上行驶的最快速度是30/km h.问司机应以怎样的路线行驶,所用的行车时间最短?最短时间是多少?三.(25分)从1,2,3,……,3919中任取2001个数。
证明:一定存在两个数之差恰好为98。
数学奥林匹克初中训练题(四)第 一 试五. 选择题.(每小题7分,共42分)( )1.若,a b 均为质数,且22003a b +=,则a b +的值为:(A)1999 (B)2000 (C)2001 (D)2002( )2.设0,1,a b c a b c ++=f f f ,,,b c a c a b M N P a b c +++===,则,,M N P 之间的关系是:(A)M N P f f (B)N P M f f(C)P M N f f (D)M P N f f( )3.设ΔABC 的三边长为,,a b c 满足28,1252b c bc a a +==-+,则ΔABC 的周长是: (A)10 (B)14 (C)16 (D)不能确定( )4.下面四个命题:①直角三角形的两边长为3,4,则第三边长为5;②1x x x-=-,③对角线相等且互相垂直的四边形是正方形;④若四边形ABCD 中,AD ∥BC,且 AB+BC=AD+DC,则四边形ABCD 是平行四边形.其中正确的命题的个数为:(A)0 (B)1 (C)2 (D)3( )5.一个四位数aabb u u u u u r 为平方数,则a b +的值为:(A)11 (B)10 (C)9 (D)8( )6.如果满足60,12,O ABC AC BC k ∠===的ΔABC 恰有一个,那么k 的取值范围是:(A)83k = (B)012k ≤p (C)12k ≥ (D)012k ≤p 或83k =六. 填空题.(每小题7分,共28分)1.已知,,a b c 为实数,且多项式32x ax bx c +++能被234x x +-整除,则22a b c --的值是 .2.设正整数,,a b c 满足518,360ab bc ab ac +=-=,则abc 的最大值是 . 3,若abc =1,2003111x x x a ab b bc c ac++=++++++,则x = . 4.如图1,AB 是半圆O 的直径,四边形CDMN 和DEFG 都是正方形,其中C,D,E 在AB 上,F,N 在半圆上.若AB=10,则正方形CDMN 的面积与正方形DEFG 的面积之和是 .第 二 试一.(20分)若AD 是ΔABC 角平分线,I 是线段AD 上的点,且1902O BIC BAC ∠=+∠. 求证:I 是ΔABC 的内心.二.(25分)用汽船拖载重量相等满载货物的小船若干只,在两港之间来回送货物.已知每次拖4只小船,一日能来回16次;每次拖7只小船,一日能来回10次.每日来回次数是拖小船只数的一次函数(一天中每次拖小船只数不变).问每日来回多少次,每次拖多少只小船,才能使运货问题达到最大?三.(25分)设,,a b c 是从1到9的互不相同的整数,求a b c abc++的最大的可能值.数学奥林匹克初中训练题(五)第 一 试七. 选择题.(每小题7分,共42分)( )1.正实数,x y 满足1xy =,那么44114x y +的最小值为: (A)12 (B)58 (C)1 (D)2 ( )2.33333333(21)(31)(41)(1001)(21)(31)(41)(1001)----++++g g g g g g g g 的值最接近于: (A)12 (B)23(C)35 (D)58 ( )3.如图1, ΔABC 中,AB=AC,∠A=40O ,延长AC 到D,使CD=BC,点P 是ΔABD 的内心,则∠BPC=:(A)145O (B)135O (C)120O (D)105O( )4.,,,a b c d 为两两不同的正整数,且,a b cd ab c d +==+,则满足上述要求的四元数组 ,,,a b c d 共有: (A)4组 (B)6组 (C)8组 (D)10组( )5. ΔABC 的三边长皆为整数,且24a bc b ca +++=,当ΔABC 为等腰三角形时,它的面积的答案有:(A)1种 (B)2种 (C)3种 (D)4种( )6. ΔABC 的∠A,∠B 皆为锐角,CD 是高,已知2()AD AC DB BC=,则ΔABC 是: (A) 直角三角形 (B)等腰三角形 (C)等腰直角三角形 (D)等腰三角形或直角三角形八. 填空题.(每小题7分,共28分)1.使方程1223x x x c ---+-=恰好有两个解的所有实数c 为 .2.如图2,正方形ABCD 中,延长边BC 到E,AE 分别交BD,CD 于点P,Q.当AP=QE 时,PQ:AE= .3.如图3, ΔABC 内接于⊙O,,,BC a CA b ==∠A -∠B=90O ,则⊙O 的面积为 .4.某中学生暑期社会调查团共17人到几个地方去考察,事先预算住宿费平均每人每天不超过x 元.一日到达某地,该地有两处招待所A,B.A 有甲级床位8个,乙级床位11个;B 有甲级床位10个,乙级床位4个,丙级床位6个.已知甲,乙,丙床位每天分别为14元,8元,5元.若全团集中住在一个招待所里,按预算只能住B 处,则整数x = .第 二 试一.(20分)一批货物准备运往某地,有甲,乙,丙三辆卡车可雇用.已知甲,乙,丙三辆车每次运货量不变,且甲乙两车单独运这批货物分别用2,a a 次;若甲,丙两车合运相同次数,运完这批货物,甲车共运了180t ;若乙,丙两车合运相同次数,运完这批货物,乙车共运了270t .现甲,乙,丙合运相同次数把这批货物运完,货主应付车方运费各多少元?(按每吨运费20元计算)?二.(25分)如图4,在圆外切凸六边形ABCDEF 中,AB ∥DE,BC∥EF,CD ∥FA.求证: 凸六边形ABCDEF 是中心对称图形.三.(25分)试求出所有这样的正整数a 使得关于x 的二次方程22(21)4(3)0ax a x a +-+-=至少有一个整数根.。
