立方半导体光学声子形变势的LMTO计算方法
高二物理竞赛课件半导体的声子和等离子体的光学性质

对激发能量,集体激发不能被个别e-h对
激发产生,也不能衰变为个别e-h对激发.
在 k kc 区域, 等离子振荡衰变,只存在 对激发. 3. 等离子激元-纵光学声子耦合模 ●半导体中 pl TO Eg . ●半金属以及某些窄带半导体中,如
x 0.10 0.20,Cdx Hg1xTe pl TO Eg .
0 bme ,h
0,
total b 1 02
f
2
0 PL
2
2
.
0
晶格离子 等离子共振 两者之和
说明: A.三维材料中 P0L 的空间色散可以忽略, 但是低维系统中不可以忽略。 B.如果所有晶格离子频率都比PL 高(或 低)得多, 它们对等离子共振的影响都可
以用 s 或b 描述.
晶格
ne 2
总
晶格
0me ,h i 2
.
晶格离子
自由电子气
在
0 PL
区域,介电函数实部小于0,
相应折射
率为纯虚数,反射率接近1.
●k=0附近,光学声子和等离子激元空间色
散都很弱.
total
b
1
02
f
2 i
0 PL
2
2 i,Βιβλιοθήκη 其中f Ne2 ,
0 bm
0 PL
2
ne2 .
等离子激元 纵极化电场 纵光学声子模
产生等离子激元-纵光学声子耦合模上支 和下支 (可根据非交叉原理分析). ●对于下支 的理解: 在载流子密度较小时, LO TO当载流子密 度很大时,由于自由载 流子气屏蔽了离子间
的库仑作用,导致 LO TO , 因此 趋近于 TO .
运动方程为 me ,h x me ,h x eE0eit , 解方程可得电导率为
能带论自洽lmto方法计算金属铜的零温物态方程

能带论自洽lmto方法计算金属铜的零温物态方程能带论自洽LMTO方法是一种非常重要的计算金属材料物态方程的方法之一。
在这篇文章中,我们将分步骤阐述如何使用这种方法计算铜的零温物态方程。
第一步:准备工作在开始计算前,需要准备以下几个方面的工作:1. 选择一个适合的软件包,比如WIEN2k或者VASP等。
2. 确认金属铜的晶体结构,因为不同的晶体结构需要不同的计算方法。
3. 确定计算模型,例如是使用密度泛函理论(DFT)进行计算,还是采用紧束缚模型等。
4. 初始化计算模型参数,例如电荷密度、初始轨道等。
5. 确定计算所需的格点(网格)等计算参数。
第二步:计算电子结构在完成上述准备工作后,接下来需要计算电子结构。
这一步需要使用LMTO方法,该方法采用紧束缚近似,得到的能带结构通常比较准确。
为使计算更准确,需要进行自洽迭代计算,即先假定电荷密度分布,然后求解薛定谔方程,得到能带结构和电荷密度。
然后将这个电荷密度代回原方程中,重新求解薛定谔方程,最终得到真正的电荷密度分布和能带结构。
在计算时,需要将k空间划分为一系列点阵,对于每个点阵,需要求解薛定谔方程,计算出各个轨道的真实能量,然后以此构建能带结构图。
第三步:计算零温物态方程在得到了能带结构后,接下来可以计算物态方程,即压力-体积曲线。
这是因为给定温度下的压力和体积呈线性关系,可以获得材料在不同温度下的状态。
计算物态方程可以通过计算固体各自的自由能来完成。
自由能与能带结构有关,具体来说,它是所有能态加上化学势的和。
这个化学势就是金属电子的费米能级,因此需要知道金属的费米能级。
一旦这些参数都已经确定,就可以计算自由能了。
最终,通过根据体积对自由能的最小化,可以得到零温物态方程。
总结:能带论自洽LMTO方法是一个相对准确的计算材料物态方程的方法之一。
按照上述的步骤,可以使用LMTO方法计算铜的零温物态方程。
这个过程需要大量的计算,包括自洽迭代计算、能带结构计算、自由能的最小化等,因此需要在相应的软件平台上进行计算。
半导体物理与器件公式以及全参数

半导体物理与器件公式以及参数KT=0.0259ev N c=2.8∗1019N v=1.04∗1019 SI材料的禁带宽度为:1.12ev. 硅材料的n i=1.5∗1010Ge材料的n i=2.4∗1013 GaAs材料的n i=1.8∗106介电弛豫时间函数:瞬间给半导体某一表面增加某种载流子,最终达到电中性的时间,ρ(t)=ρ(0)e−(t/τd),其中τd =ϵσ,最终通过证明这个时间与普通载流子的寿命时间相比十分的短暂,由此就可以证明准电中性的条件。
E F热平衡状态下半导体的费米能级,E Fi本征半导体的费米能级,重新定义的E Fn是存在过剩载流子时的准费米能级。
准费米能级:半导体中存在过剩载流子,则半导体就不会处于热平衡状态,费米能级就会发生变化,定义准费米能级。
n0+∆n=n i exp(E Fn−E FikT) p0+∆p=n i exp[−(E Fp−E Fi)kT]用这两组公式求解问题。
通过计算可知,电子的准费米能级高于E Fi,空穴的准费米能级低于E Fi,对于多子来讲,由于载流子浓度变化不大,所以准费米能级基本靠近热平衡态下的费米能级,但是对于少子来讲,少子浓度发生了很大的变化,所以费米能级有相对比较大的变化,由于注入过剩载流子,所以导致各自的准费米能级都靠近各自的价带。
过剩载流子的寿命:半导体材料:半导体材料多是单晶材料,单晶材料的电学特性不仅和化学组成相关而且还与原子排列有关系。
半导体基本分为两类,元素半导体材料和化合物半导体材料。
GaAs主要用于光学器件或者是高速器件。
固体的类型:无定型(个别原子或分子尺度内有序)、单晶(许多原子或分子的尺度上有序)、多晶(整个范围内都有很好的周期性),单晶的区域成为晶粒,晶界将各个晶粒分开,并且晶界会导致半导体材料的电学特性衰退。
空间晶格:晶格是指晶体中这种原子的周期性排列,晶胞就是可以复制出整个晶体的一小部分晶体,晶胞的结构可能会有很多种。
晶体材料的声子计算

晶体材料的声子计算晶体材料声子计算是材料科学和固体物理领域的重要研究内容之一、声子即晶体中的声波振动,是材料性质研究的基础。
声子计算可以用于预测材料的热力学性质、电子输运性质以及光学性质等,对材料设计和材料性能优化具有重要意义。
声子计算的理论基础可以追溯到量子力学。
根据量子力学的原理,声子的存在是由晶体的周期性结构决定的。
声子的振动模式以及频率可以通过求解晶体中的原子间相互作用和原子质量关于位移的势能函数获得。
声子的频率可以由动力学矩阵和力常数矩阵确定,这些矩阵可以通过密度泛函理论(DFT)计算获得。
声子计算主要包括两个方面的内容,即声子能谱计算和声子密度计算。
声子能谱计算是指计算晶体中的声子频率和振动模式,是声子计算的核心内容。
声子能谱可以通过解析解或数值解的方式得到。
在解析解的方法中,可以采用周期性格点振动的假设,并且通过Bloch定理将声子问题转化为一个广义特征值问题。
在数值解的方法中,可以采用有限元法或有限差分法求解声子的本征频率和本征振动模式。
声子密度计算是指计算晶体中声子的态密度,以及声子与其他物理量之间的关系。
声子态密度是声子能谱的统计特性,可以反映晶体中声子的分布情况。
声子态密度与材料的热力学性质、声学性质和电子性质等密切相关,可以通过声子密度计算来预测材料性质。
此外,声子计算还可以计算声子的热容、热导率、热膨胀系数等热力学性质,以及声子的声子-声子散射、声子-电子散射等输运性质。
声子计算在材料科学和固体物理领域具有广泛的应用。
例如,在材料设计方面,声子计算可以用于预测材料的热学性能,从而优化材料的热导率和热膨胀系数。
在催化剂设计方面,声子计算可以用于研究声子-表面模式的相互作用,从而提高催化剂的效率。
在光伏材料方面,声子计算可以用于预测材料的光学性质,从而提高材料的光电转换效率。
总之,声子计算是材料科学和固体物理研究中的重要内容。
通过声子计算,可以预测材料的热力学性质、电子输运性质以及光学性质等,对材料设计和材料性能优化具有重要意义。
声子群速度计算

声子群速度计算
声子群速度是材料中声波的传播速度。
在固体和液体中,声波是通
过固体或液体分子之间的相互作用传播的,它们的速度与材料的密度
和模量有关。
根据声子群速度公式:v = √(C/ρ),其中v是声子群速度,C是弹性常数,ρ是密度。
下面是声子群速度计算的步骤:
1. 计算材料的密度。
材料密度可以通过称重法测量,也可以通过材料
的化学式计算。
2. 确定材料的弹性常数。
弹性常数包括杨氏模量、剪切模量和体积弹
性模量。
弹性常数可以通过实验和模拟计算等方式获得。
3. 根据声子群速度公式计算声子群速度。
将所得弹性常数和密度代入
公式计算。
下面是一个具体的例子:
某固体材料的密度为7.8g/cm³,杨氏模量为180GPa。
根据声子群速度
公式,可计算出该材料中的声子群速度。
步骤1:材料密度为7.8g/cm³。
步骤2:杨氏模量为180GPa。
步骤3:将所得弹性常数和密度代入声子群速度公式,得到声子群速度v = √(C/ρ) = √(180GPa × 10³ kg/m³ / 7.8×10³ kg/m³) ≈ 4730 m/s。
声子群速度计算的结果可用于研究材料的声学性质和机械性质,对于材料设计和工程性能的优化具有重要意义。
总之,声子群速度计算是材料物理学和声学领域中的重要内容,需要结合材料的物理性质、实验数据和计算方法来进行分析。
comsol计算声子晶体算例
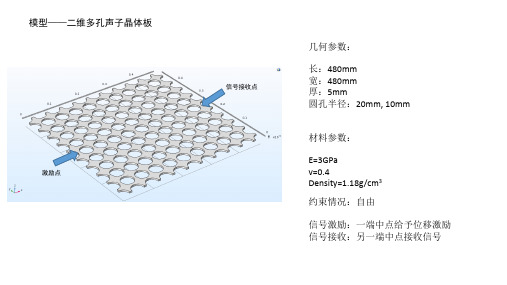
信号接收点
长:480mm 宽:480mm 厚:5mm 圆孔半径:20mm, 10mm
材料参数: E=3GPa v=0.4 Density=1.18g/cm3 约束情况:自由 信号激励:一端中点给予位移激励 信号接收:另一端中点接收信号
激励点
定义相关参数
新建一个工作平面创建二维图形(利用阵列、布尔操作等变换), 转换为实体后进行拉伸创建三维模型
另一端中点接收信号激励点信号接收点定义相关参数新建一个工作平面创建二维图形利用阵列布尔操作等变换转换为实体后进行拉伸创建三维模型定义材料参数设置激励点并给一个单位位移激励在对边中点设置一个域点探针接收响应在参数化扫描中设置输入频率的起始值及步长在频域设置中设置频率单位设置网格参数并划分网格计算后将结果表格输出按照以下公式计算20lg????????????????????????????????????????????????????绘制该值与频率k之间的图像即为频谱图
定义材料参数
设置激励点并给一个单位位移激励
在对边中点设置一个域点探针接收响应
在参数化扫描中设置输入频率的起始值及步长
在频域设置中设置频率单位
设置网格参数并式计算
绘制该值与频率k之间的图像即为频谱图
半导体材料光学带隙的计算

半导体材料光学带隙的计算
1.势能法:势能法是一种比较简单的计算光学带隙的方法。
它基于半导体能带结构的理论,假设电子在晶体中的势能与电子自由状态的势能有所不同。
通过求解晶格势能与电子能级之间的薛定谔方程,可以计算得到光学带隙。
2.密度泛函理论:密度泛函理论(DFT)是一种使用波函数的基态电子密度分布来计算材料性质的方法。
在计算光学带隙时,可以使用DFT方法计算材料的密度泛函,然后通过求解光学跳跃的频率依赖响应函数来计算光学带隙。
3.自洽场方法:自洽场方法是一种通过迭代求解薛定谔方程得到平衡态的方法。
在计算光学带隙时,可以使用自洽场方法来计算材料的电子结构,并从中得到波函数的电子势能。
然后可以通过求解晶格势能与电子能级之间的薛定谔方程来计算光学带隙。
4.傅里叶变换方法:傅里叶变换方法是一种通过对周期晶格进行傅里叶变换来计算材料性质的方法。
在计算光学带隙时,可以使用傅里叶变换方法来计算材料的能带结构,并从中获得光学带隙。
应用以上方法计算光学带隙时需要考虑的因素包括材料的晶体结构、成分、温度等。
此外,还需要考虑电子-空穴相互作用的影响,例如考虑材料的多体效应和激子形成。
总而言之,计算材料的光学带隙是一个复杂的过程,需要考虑多个因素和使用不同的方法。
在光学带隙的计算中,可以选择合适的方法来获得准确的结果。
通过计算光学带隙,可以更好地理解材料的电子结构和光学特性,为材料的设计和应用提供理论指导。
载流子迁移率计算方法(VASP,ORIGIN)

计算公式:之老阳三干创作
时间:二O二一年七月二十九日
半导体物理书上也有载流子迁移率的公式,但是上面的是带有平均自由时间的公式,经过变换推倒,就成了上面的那个公式,因此要用vasp计算的参数有,Sl,me,md,El这四个参数,其他的都是常数,可以查询出来带入公式.
参数:Sl
,就是需要我们先用vasp计算出声子谱,我们要对声子谱求导,取导带底处的值,对应的就是电子迁移率的Sl 所以需要学会怎么使用phonopy
me
:就是电子的有效质量,要用origin对能带图求二次导,取导带底对应的值.
md:
mx就是布里渊区X标的目的的有效质量,my就是y 标的目的的有效质量,先用笔算出G 到K,M向量,然后辨别作这两个向量的垂直向量,在这两个向量标的目的上取20个权重为0的点,放到KPOINTS中,依照以前的办法,算出来的能带就是x标的目的上的和y标的目的上的,然后就可以算出x,y标的目的上的有效质量.
El
把公式变形一下,El,放在一边,其他的放在另一边,δV就是原来晶胞的体积改动量,δE就是对应能量的该变量,V0就是晶胞原来的体积,也就是说,我要把原来的晶胞
任意改动一下大小,算出导带底能量的变更量,进而就算出了El这个量.
以上这四个量算出来之后,带入公式计算就可以得出电子的迁移率公式.
电子迁移率主要受到:声学支波散射,光学支波散射,电离杂质杂质散射的影响,因为后两者没有第一个影响大,所以我们计算的迁移率包含的就是在声学支波散射作用下的迁移率.(半导体物理书上都很仔细的介绍.)。
声子谱计算范文

声子谱计算范文声子是晶体中的晶格振动模式的量子化激发,可以通过离散频率来描述。
声子能谱是描述晶体中声子能量与动量关系的函数,可以提供关于材料的晶格振动模式和能级分布的信息。
要计算声子谱,首先需要得到晶体的势能函数,即晶格势能和杂质势能。
在理论计算中,可以使用第一性原理方法,如密度泛函理论(DFT)或者分子动力学模拟,从头计算得到晶体的波函数和能量。
然后,通过引入微扰来计算声子的振动模式和能量。
在计算声子振动模式时,可以采用周期性边界条件,将晶体看作无限重复的单元。
然后,使用线性响应理论,通过矩阵元素的计算,可以得到晶格动力学矩阵,描述晶体中原子的振动行为。
计算声子谱的方法有多种,其中最常见的包括密度泛函微扰论(DFT-Perturbation Theory)和模型哈密顿量的对角化方法。
在DFT微扰论中,声子谱可以通过计算系统在外施加微扰下的响应来得到。
而模型哈密顿量的对角化方法,通过构造一个包含原子振动的模型哈密顿量,然后对其进行对角化,可以得到声子振动的能量和波函数。
声子谱计算可以提供丰富的信息,用于解释材料的热导率、声学、光学和电子输运等性质。
例如,在光学性质的研究中,可以利用声子谱计算得到材料的光学吸收谱,帮助解释材料的吸收和发射机制。
在热导率的研究中,可以通过声子谱计算得到声子输运的散射机制,解释热导率的波长和温度依赖关系。
声子谱计算在材料科学、凝聚态物理和固体化学等领域有着广泛的应用。
例如,在材料的设计和优化中,可以通过计算不同材料的声子谱,来预测材料的热导率、光学性质和电子输运等性能。
此外,声子谱计算还可以帮助解析实验中的谱线,对材料的特性进行表征和分析。
总结起来,声子谱计算是一种研究晶体中声子能谱的理论和计算方法,通过计算晶体的波函数和能量,以及引入微扰和线性响应理论,可以得到材料的振动模式和能谱。
声子谱计算在材料科学和物理学中有着广泛的应用,对于研究材料的结构和性能具有重要的意义。
基于COMSOL的声子晶体带结构计算新方法

基于COMSOL的声子晶体带结构计算新方法付子义;王晨旭;王立国;长谷川弘治【摘要】结合声波与电磁波的物理特性,建立光子晶体与声子晶体物理量之间的联系,通过类比光子晶体能带结构的求解过程,对声子晶体能带结构进行仿真计算.以二维声子晶体为研究对象,通过重新建立数学模型,利用Born-von-karman周期性边界条件和布洛赫态,推导出声子晶体偏微分形式的本征方程,基于有限元仿真软件COMSOL Multiphysics系数偏微分模块(coefficient form PDE),求解出相应的本征频率从而求解出能带.与已有计算方法相比,该方法在适用性,难易程度等方面具有明显的优越性.【期刊名称】《软件》【年(卷),期】2018(039)012【总页数】4页(P6-9)【关键词】声子晶体;能带结构;有限元;PDE;本征方程【作者】付子义;王晨旭;王立国;长谷川弘治【作者单位】河南理工大学电气工程与自动化学院,河南焦作 454150;河南理工大学电气工程与自动化学院,河南焦作 454150;河南理工大学电气工程与自动化学院,河南焦作 454150;室兰工业大学情报电子工学系,日本室兰 0500071【正文语种】中文声子晶体是由嵌入均匀主体材料中的声波散射体组成的有限尺寸周期阵列的人造晶体。
声波与周期性排列的散射体之间的相互作用导致形成声波不能通过该结构的频带。
这种频带被称为带隙。
基于这一特性使得声子晶体具有广阔的应用前景。
声子晶体的概念是由光子晶体的概念演绎而来的,因此与光子晶体相类似的是,能带结构也是声子晶体最重要的研究内容之一。
文献[1]基于TMM方法,对声子晶体能带结构进行求解计算,但是TMM方法主要用于一维声子晶体的能带计算。
虽然结合PWE方法可用于二维情况,但计算量较大。
文献[2]基于PWE方法,但是PWE方法对于组分材料声学参数相差较大的声子晶体需要更多的计算时间和内存,而且不易给出正确结果。
【半导体物理与器件】【尼曼】【课后小结与重要术语解释】汇总

第一章、固体晶体结构1.小结1.硅是最普遍的半导体材料2.半导体和其他材料的属性很大程度上由其单晶的晶格结构决定。
晶胞是晶体中的一小块体积,用它可以重构出整个晶体。
三种基本的晶胞是简立方、体心立方和面心立方。
3.硅具有金刚石晶体结构。
原子都被由4个紧邻原子构成的四面体包在中间。
二元半导体具有闪锌矿结构,它与金刚石晶格基本相同。
4.引用米勒系数来描述晶面。
这些晶面可以用于描述半导体材料的表面。
密勒系数也可以用来描述晶向。
5.半导体材料中存在缺陷,如空位、替位杂质和填隙杂质。
少量可控的替位杂质有益于改变半导体的特性。
6.给出了一些半导体生长技术的简单描述。
体生长生成了基础半导体材料,即衬底。
外延生长可以用来控制半导体的表面特性。
大多数半导体器件是在外延层上制作的。
2.重要术语解释1.二元半导体:两元素化合物半导体,如GaAs。
2.共价键:共享价电子的原子间键合。
3.金刚石晶格:硅的原子晶体结构,亦即每个原子有四个紧邻原子,形成一个四面体组态。
4.掺杂:为了有效地改变电学特性,往半导体中加入特定类型的原子的工艺。
5.元素半导体:单一元素构成的半导体,比如硅、锗。
6.外延层:在衬底表面形成的一薄层单晶材料。
7.离子注入:一种半导体掺杂工艺。
8.晶格:晶体中原子的周期性排列9.密勒系数:用以描述晶面的一组整数。
10.原胞:可复制以得到整个晶格的最小单元。
11.衬底:用于更多半导体工艺比如外延或扩散的基础材料,半导体硅片或其他原材料。
12.三元半导体:三元素化合物半导体,如AlGaAs。
13.晶胞:可以重构出整个晶体的一小部分晶体。
14.铅锌矿晶格:与金刚石晶格相同的一种晶格,但它有两种类型的原子而非一种。
第二章、量子力学初步3.小结1.我们讨论了一些量子力学的概念,这些概念可以用于描述不同势场中的电子状态。
了解电子的运动状态对于研究半导体物理是非常重要的。
2.波粒二象性原理是量子力学的重要部分。
粒子可以有波动态,波也可以具有粒子态。
半导体有效质量的计算公式

半导体有效质量的计算公式半导体有效质量这个概念,对于很多人来说可能有点陌生,甚至觉得高深莫测。
但其实啊,只要咱们一步一步来,它也没那么可怕。
咱先来说说啥是半导体。
半导体这玩意儿,就像是一个有点“纠结”的家伙。
它的导电性既不像导体那么爽快,电流可以畅通无阻;也不像绝缘体那样坚决拒绝,电流完全过不去。
半导体处于这两者之间,有时候让电流通过,有时候又有点“扭捏”。
那半导体有效质量又是啥呢?简单来说,它反映了半导体中电子或者空穴在外力作用下的“运动难易程度”。
就好比一个人在不同的道路上跑步,有的路平坦好跑,有的路崎岖难行。
在半导体里,电子或者空穴就像是在不同“路况”下运动,有效质量就是描述这种“路况”的一个重要指标。
说到这半导体有效质量的计算公式,那可有点复杂。
不过别担心,我来慢慢给您解释。
一般常用的公式是:有效质量m* = ħ² / (d²E / dk²) 。
这里的ħ是约化普朗克常数,E 是能量,k 是波矢。
这公式看起来是不是有点头疼?我给您举个例子吧。
就像我们在操场上跑步,速度快的时候感觉轻松,速度慢的时候就觉得累。
在半导体里,电子或者空穴的运动也类似。
当它们的能量变化和波矢变化的关系不同时,有效质量也就不同。
还记得我之前有一次去实验室做实验,就是研究半导体的特性。
那时候,我们反复测量各种数据,计算、分析,就为了能更准确地得到半导体有效质量的值。
当时为了保证实验的准确性,每一个步骤都小心翼翼,每一个数据都反复核对。
有时候,因为一点点的误差,就得重新再来。
那过程真是既紧张又充满期待。
其实,在实际应用中,半导体有效质量的计算对于设计和制造半导体器件非常重要。
比如说,在制造芯片的时候,如果能准确掌握半导体有效质量,就能更好地控制电流的流动,提高芯片的性能。
总之,半导体有效质量的计算公式虽然复杂,但只要我们耐心去理解、去研究,就能逐渐掌握其中的奥秘,为半导体相关的技术发展贡献一份力量。
半导体材料光学带隙的计算

半导体材料光学带隙的计算禁带宽度是半导体的一个重要特征参量,其大小主要决定于半导体的能带结构,即与晶体结构和原子的结合性质等有关。
禁带宽度的大小实际上是反映了价电子被束缚强弱程度的一个物理量,也就是产生本征激发所需要的最小能量。
禁带宽度可以通过电导率法和光谱测试法测得,为了区别用电导率法测得禁带宽度值,用光谱测试法测得的禁带宽度值又叫作光学带隙。
下面以光谱测试法为例介绍半导体材料光学带隙的计算方法:对于半导体材料,其光学带隙和吸收系数之间的关系式为[1]:αhν=B(hν-Eg)m ( 1)其中α为摩尔吸收系数,h为普朗克常数,ν为入射光子频率, B 为比例常数, Eg为半导体材料的光学带隙,m的值与半导体材料以及跃迁类型相关:(1)当 m=1/2 时,对应直接带隙半导体允许的偶极跃迁;( 2)当 m=3/2 时,对应直接带隙半导体禁戒的偶极跃迁;( 3)当m=2 时,对应间接带隙半导体允许的跃迁;( 4)当m=3 时,对应间接带隙半导体禁戒的跃迁。
下面介绍两种禁带宽度计算公式的推导方法:推导 1:根据朗伯比尔定律可知:A=αb c(2)其中 A 为样品吸光度,b 为样品厚度,c 为浓度,其中 bc 为一常数,若B1=(B/bc)1/m,则公式(1)可为:(Ahν)1/m=B1(hν-Eg) (3)根据公式(3),若以hν 值为 x 轴,以(Ahν)1/m 值为 y 轴作图,当 y=0 时,反向延伸曲线切线与 x 轴相交,即可得半导体材料的光学带隙值 Eg。
推导 2:根据 K-M 公式可知:F(R∞)=(1- R∞)2/2 R∞=K/S (4)其中R∞为绝对反射率(在日常测试中可以用以硫酸钡做参比测得的样品相对反射率代替[2]), K 为吸收系数, S 为散射系数。
若假设半导体材料分散完全或者将样品置于 600入射光持续光照下可认为K=2α[3]。
因在一定温度下样品散射系数为一常数,假设比例常数为 B2, ,我们可通过公式(4)和公式(1)可得:(F(R∞) hν)1/m=B2(hν-Eg) (5)根据公式(5),若以hν 值为 x 轴,以(F(R∞) hν)1/m值为 y 轴作图,当 y=0 时,反向延伸曲线切线与 x 轴相交,即可得半导体材料的光学带隙值Eg。
MZM及EAM的原理即特性公式推导

RoF 系统主要由以下元件组成:光源,光调制器,光放大器和光电探测器。
在射频频率范围超出10GHz 的情况下,通常会采用外调制器。
外调制技术是将射频信号通过一个外部光学调制器调制到光载波上。
光调制器是通过电压或电场的变化最终调控输出光的折射率、吸收率、振幅或相位的器件。
它依据的基本理论是各种不同形式的电光效应、声光效应、磁光效应、Fang-Keldgsh 效应、量子阱Stark 效应、载流子色散效应等。
光调制器主要包括相位调制器(PM )和强度调制器,由于光电探测器的输出电信号直接与入射光强相关,而相位调制和频率调制必须采用外差接收机来解调,在技术上实现比较困难,所以目前光通信中普遍采用的是光强度调制,尤其是在RoF 系统中,需要实现信号的模拟调制,强度调制主要有铌酸锂MZM (LN-MZM )和电吸收调制器EAM 。
MZM因为铌酸锂材料本身非常稳定,有低损耗、使用寿命长、受温度及系统波长影响小等特点,且马赫增德尔调制器可以处理的信号带宽和光功率都较高,具有波长无关调制特性,能够较好地控制调制性能以及调制光强度和相位,可以实现40 Gbit/ s 以上高数据速率的调制,成为许多先进光调制格式产生的基础。
下图为LN-MZM 结构图其中111()DC V V v t =+222()DC V V v t =+1DC V 为上臂的直流偏置电压,2DC V 为下臂直流偏置电压,1()v t 为上臂的驱动电压,2()v t 为下臂的驱动电压。
MZM 调制器是由一个铌酸锂的衬底和共面型相位调制器组成。
在这种调制器中,两个分支的相位调制和由基材的电光特性有关,每一个分支的相位变化转换为输出光功率的变化。
MZ 调制器可以看作由两个相位调制器组成。
首先介绍相位调制器。
设输入光场为00()0()j t in E t E e ωϕ+= ,其中E 0为输入光场的振幅,00,ωφ 为光的频率与初相位。
相位调制器的驱动电压为()cos()DC RF RF V t V V t ωϕ=++,其中DC V 为直流偏置电压,RF V 为驱动电压的振幅,0,RF ωϕ分别为驱动电压频率与初相位。
半导体光学8局域声子模
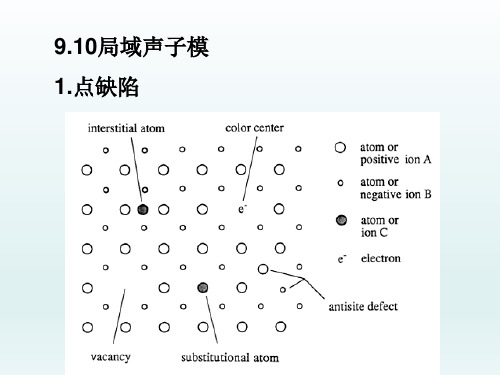
3.能带的产生 离子键:阴离子满壳层形成价带;
阳离子 空壳层形成导带. CdS:S原子3s 23p 4 ,Cd原子 4d 105s 2. S 2 : 3s 23p 6 ,3p满壳层形成价带, Cd 2 : 4d 10, 5s空壳层形成导带. 共价键:成键态形成价带;
反成键态形成导带.
E
E原 子p
E杂化
E原子s
E反成键 E成键
导带 带隙 价带
4.半导体材料概述
• IV a族
最重要的半导体是硅Si:基于 sp3 杂化轨道, 反成键态产生导带,反成键态产生价带, 完全的共价键, 室温下 Eg 1.1eV , 金刚石 结构晶体 Oh (锗Ge也是) ,间接半导体 . 灰锡Sn:半金属,金刚石结构. SiC: 间接半导体,带隙约为3eV.
●J为相邻两电子波函数的重叠积分
J d ra1 rb2 ,0 J 1.
当两个原子核相距很远时, 两原子的电子
云不重叠, J 0; 反之, 当两个原子核 相距很近时, 两原子的电子云重叠, J 1; 一般情况 0 J 1. ● Z为配位数,每一格点最邻近的原子数. 如立方格子中,Z=6. 紧束缚近似:相邻原子的电子波函数相 互交叠相当小J. 0. ④图示
简约 扩展 周期能带结构.
⑤价带VB:低能带,T=0,完全填满. 导带CB:高能带,部分填满或空带. 能隙 E g : 导带与价带之间距.
半导体中电子系统的光学性质是由较高的 价带和较低导带间电子跃迁决定的. 10.2 金属 半导体 绝缘体 1.电子能带结构 金属: 存在一个或多个部分填充的导带,或一个 完全填满的导带与另一个空导带重叠(碱 土金属).费米能级位于导带中.
即 k G 与 k 实际上是等效的.
金刚石结构晶体Λ,△轴光学声子形变势的LMTO-ASA计算

金刚石结构晶体Λ,△轴光学声子形变势的LMTO-ASA计算柯三黄;王仁智;黄美纯
【期刊名称】《半导体学报:英文版》
【年(卷),期】1992(13)7
【摘要】本文在LMTO-ASA 自治能带计算的基础上,采用冻结声子模型,对C、Si、Ge、Sn在A轴和△轴的光学声子形变势(ODPs)进行了第一原理计算,并考察了自
治电荷密度计算中所取用的特殊k点的数目对ODPs计算结果的影响以及在Γ点
附近各形变势之间的相互关系.讨论了同一材料各形变势随k的变化规律以及不同
材料之间各形变势的变化趋势.
【总页数】7页(P393-399)
【关键词】金刚石;晶体;ODPS;能带;计算
【作者】柯三黄;王仁智;黄美纯
【作者单位】厦门大学物理系
【正文语种】中文
【中图分类】TN304.18
【相关文献】
1.Ⅲ-Ⅴ族化合物半导体∧轴光学声子形变势的研究 [J], 王仁智;郑永梅;吴孙桃;黄
美钝
2.GaAs和AlAs光学声子形变势的第一性原理研究 [J], 王仁智;黄美纯
3.Ga1-xAlxAs光学声子形变势研究 [J], 王仁智;黄美纯
4.三元混晶双势垒结构中光学声子辅助共振隧穿及压力效应 [J], 朱金广;班士良
5.基于声子晶体异质位错结结构的大尺寸楔形变幅杆的优化设计 [J], 林基艳;林书玉
因版权原因,仅展示原文概要,查看原文内容请购买。
