最新解直角三角形的应用测试题带答案
人教版数学九年级下《解直角三角形的应用》测试题(含答案及解析)

人教版数学九年级下《解直角三角形的应用》测试题(含答案及解析)时间:100分钟总分:100题号一二三四总分得分1.小明应用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1米,那么旗杆PA的高度为()A. 11−sinαB. 11+sinαC. 11−cosαD. 11+cosα2.如图,长4m的楼梯AB的倾斜角∠ABD为60∘,为了改善楼梯的平安功用,预备重新建造楼梯,使其倾斜角∠ACD为45∘,那么调整后的楼梯AC的长为()A. 2√3mB. 2√6mC. (2√3−2)mD. (2√6−2)m3.一座楼梯的表示图如下图,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,CA=4米,楼梯宽度1米,那么地毯的面积至少需求()A. (4+4sinθ)米 2B. 4米 2cosθ)米 2 D. (4+4tanθ)米 2C. (4+4tanθ4.上午9时,一条船从A处动身,以每小时40海里的速度向正西方向飞行,9时30分抵达B处(如图).从A、B两处区分测得小岛M在北偏东45∘和北偏西方15∘向,那么在B处船与小岛M的距离为()A. 20海里B. 20√2海里C. 15√3海里D. 20√3海里5.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为()A. ℎsinαB. ℎtanαC. ℎcosαD. ℎ−sinα6.如下图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30∘,再向电视塔方向行进120米到达F处,又测得电视塔顶端A的仰角为60∘,那么这个电视塔的高度AB(单位:米)为()A. 60√3B. 61C. 60√3+1D. 1217.某校八年级生物兴味小组租两艘快艇去微山湖生物调查,他们从同一码头动身,第一艘快艇沿北偏西方70∘向飞行50千米,第二艘快艇沿南偏西方20∘向飞行50千米,假设此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇飞行的方向和距离区分是()A. 南偏东25∘,50√2千米B. 北偏西25∘,50√2千米C. 南偏东70∘,100千米D. 北偏西20∘,100千米8.如图,一艘海轮位于灯塔P的南偏西方45∘向,距离灯塔60nmile的A处,它沿正南方向飞行一段时间后,抵达位于灯塔P的北偏西方30∘向上的B处,这时,B处与灯塔P的距离为()A. 60√3nmileB. 60√2nmileC. 30√3nmileD. 30√2nmile9.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度i=1:1.5,那么坝底AD的长度为()A. 26米B. 28米C. 30米D. 46米10.如图是某水库大坝的横截面表示图,AD//BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提矮小坝的防洪才干,需对大坝停止加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,那么大坝底端添加的长度CF是()米.A. 7B. 11C. 13D. 20二、填空题〔本大题共10小题,共30.0分〕11.为增强防汛任务,某市对一拦水坝停止加固,如图,加固前拦水坝的横断面是梯形ABCD.迎水坡面AB=12米,背水坡面CD=12√3米,∠B=60∘,加固后拦水坝的√3,那么CE的长为______ 米.横断面为梯形ABED,tanE=31312.如图,航拍无人机从A处测得一幢修建物顶部B的仰角为30∘,测得底部C的俯角为60∘,此时航拍无人机与该修建物的水平距离AD为90米,那么该修建物的高度BC约为______ 米.(准确到1米,参考数据:√3≈1.73)13.小明沿着坡度i为1:√3的直路向上走了50m,那么小明沿垂直方向降低了______m.14.如图,长4m的楼梯AB的倾斜角∠ABD为60∘,为了改善楼梯的平安功用,预备重新建造楼梯,使其倾斜角∠ACD为45∘,那么调整后楼梯AC长为______ 米.15.如图,一名滑雪运发动沿着倾斜角为34∘的斜坡,从A滑行至B,AB=500米,那么这名滑雪运发动的高度下降了______米.(参考数据:sin34∘≈0.56,cos34∘≈0.83,tan34∘≈0.67)16.如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为30∘,朝楼房AB方向行进10米抵达点D,再次测得A点的仰角为60∘,那么此楼房的高度为______ 米(结果保管根号).17.如图,从热气球C处测无暇中A、B两点的俯角区分为30∘、45∘,假设此时热气球C处的高度为200米,点A、B、C在同不时线上,那么AB两点间的距离是______米(结果保管根号).18.如图,水库堤坝的横断面是梯形,测得BC长为30m,CD长为20√5m,斜坡AB的坡比为1:3,斜坡CD的坡比为1:2,那么坝底的宽AD为______m.19.如图,某堤坝的斜坡AB的斜角是α,坡度是1:√3,那么α=______.20.某兴味小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在空中C处同一方向上区分测得A处的仰角为75∘,B处的仰角为30∘.无人飞机的飞行速度为3米/秒,那么这架无人飞机的飞行高度为(结果保管根号)______ 米.三、计算题〔本大题共4小题,共24.0分〕21.如图,某数学兴味小组要测量一栋五层居民楼CD的高度.该楼底层为车库,高2.5米;下面五层寓居,每层高度相等.测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60∘,在B处测得四楼顶部点E的仰角为30∘,AB=14米.求居民楼的高度(准确到0.1米,参考数据:√3≈1.73)22.某兴味小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在空中C处同一方向上区分测得A处的仰角为75∘,B处的仰角为30∘.无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保管根号)23.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18∘,教学楼底部B的俯角为20∘,量得实验楼与教学楼之间的距离AB= 30m.(1)求∠BCD的度数.(2)讨教学楼的高BD.(结果准确到0.1m,参考数据:tan20∘≈0.36,tan18∘≈0.32) 24.如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30∘,小红在斜坡下的点C处测得楼顶B的仰角为60∘,在斜坡上的点D处测得楼顶B的仰角为45∘,其中点A、C、E在同不时线上.(1)求斜坡CD的高度DE;(2)求大楼AB的高度(结果保管根号)四、解答题〔本大题共2小题,共16.0分〕25.如图,大楼AB右侧有一阻碍物,在阻碍物的旁边有一幢小楼DE,在小楼的顶端D处测得阻碍物边缘点C的俯角为30∘,测得大楼顶端A的仰角为45∘(点B,C,E在同一水平直线上),AB=80m,DE=10m,求阻碍物B,C两点间的距离(结果准确到0.1m)(参考数据:√2≈1.414,√3≈1.732)26.如图,某湖中有一孤立的小岛,湖边有一条蜿蜒的观光小道AB,现决议从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同窗在观光道AB上测得如下数据:AB=100米,∠PAB=45∘,∠PBA=30∘.央求出小桥PQ的长.(√2≈1.414,√3≈1.732,结果准确到0.1米)答案和解析【答案】1. A2. B3. D4. B5. A6. C7. B8. B9. D10. C11. 812. 20813. 2514. 2√615. 28016. 5√317. 200(√3+1)18. 13019. 30∘20. 9√3+921. 解:设每层楼高为x米,由题意得:MC′=MC−CC′=2.5−1.5=1米,∴DC′=5x+1,EC′=4x+1,在Rt△DC′A′中,∠DA′C′=60∘,∴C′A′=DC′tan60∘=√33(5x+1),在Rt△EC′B′中,∠EB′C′=30∘,∴C′B′=EC′tan30∘=√3(4x+1),∵A′B′=C′B′−C′A′=AB,∴√3(4x+1)−√33(5x+1)=14,解得:x≈3.17,那么居民楼高为5×3.17+2.5≈18.4米.22. 解:如图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75∘,∠BCH=30∘,AB//CH,∴∠ABC=30∘,∠ACB=45∘,∵AB=32m,∴AD=CD=16m,BD=AB⋅cos30∘=16√3m,∴BC=CD+BD=(16√3+16)m,那么BH=BC⋅sin30∘=(8√3+8)m.23. 解:(1)过点C作CE⊥BD,那么有∠DCE=18∘,∠BCE=20∘,∴∠BCD=∠DCE+∠BCE=18∘+20∘=38∘;(2)由题意得:CE=AB=30m,在Rt△CBE中,BE=CE⋅tan20∘≈10.80m,在Rt△CDE中,DE=CD⋅tan18∘≈9.60m,∴教学楼的高BD=BE+DE=10.80+9.60≈20.4m,那么教学楼的高约为20.4m.24. 解:(1)在Rt△DCE中,DC=4米,∠DCE=30∘,∠DEC=90∘,∴DE=12DC=2米;(2)过D作DF⊥AB,交AB于点F,∵∠BFD=90∘,∠BDF=45∘,∴∠BFD=45∘,即△BFD为等腰直角三角形,设BF=DF=x米,∵四边形DEAF为矩形,∴AF=DE=2米,即AB=(x+2)米,在Rt△ABC中,∠ABC=30∘,∴BC=ABcos30∘=x+2√32=2x+4√3=√3(2x+4)3米,BD=√2BF=√2x米,DC=4米,∵∠DCE=30∘,∠ACB=60∘,∴∠DCB=90∘,在Rt△BCD中,依据勾股定理得:2x2=(2x+4)23+16,解得:x=4+4√3,那么AB=(6+4√3)米.25. 解:如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.那么DE=BF=CH=10m,在直角△ADF中,∵AF=80m−10m=70m,∠ADF=45∘,∴DF=AF=70m.在直角△CDE中,∵DE=10m,∠DCE=30∘,∴CE=DEtan30∘=10√33=10√3(m),∴BC=BE−CE=70−10√3≈70−17.32≈52.7(m).答:阻碍物B,C两点间的距离约为52.7m.26. 解:设PQ=x米,在直角△PAQ中,tan∠PAQ=x AQ,∴AQ=xtan45∘=x,在直角△PBQ中,tan∠PBQ=x BQ,∴BQ=xtan30∘=√3x,∵AB=100米,∴x+√3x=100,解得:x=50√3−50≈36.6(米).答:小桥PQ的长度约是36.6米.【解析】1. 解:设PA=PB=PB′=x,在RT△PCB′中,,∴x−1x=sinα,∴x−1=xsinα,∴(1−sinα)x=1,∴x=11−sinα.应选:A.设PA=PB=PB′=x,在RT△PCB′中,依据,列出方程即可处置效果.此题考察解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.2. 解:在Rt△ABD中,∵sin∠ABD=ADAB,∴AD=4sin60∘=2√3(m),在Rt△ACD中,∵sin∠ACD=ADAC,∴AC=2√3sin45∘=2√6(m).应选B.先在Rt△ABD中应用正弦的定义计算出AD,然后在Rt△ACD中应用正弦的定义计算AC即可.此题考察了解直角三角形的运用−坡度坡角:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的峻峭水平,普通用i表示,常写成i=1:m的方式.把坡面与水平面的夹角α叫做坡角,坡度i与坡角α之间的关系为:i=tanα.3. 解:在Rt△ABC中,BC=AC⋅tanθ=4tanθ(米),∴AC+BC=4+4tanθ(米),∴地毯的面积至少需求1×(4+4tanθ)=4+4tanθ(米 2);应选:D.由三角函数表示出BC,得出AC+BC的长度,由矩形的面积即可得出结果.此题考察了解直角三角形的运用、矩形面积的计算;由三角函数表示出BC是处置效果的关键.4. 解:如图,过点B作BN⊥AM于点N.=20海里,∠ABM=105∘.由题意得,AB=40×12作BN⊥AM于点N.在直角三角形ABN中,BN=AB⋅sin45∘=10√2.在直角△BNM中,∠MBN=60∘,那么∠M=30∘,所以BM=2BN=20√2(海里).应选B.过点B作BN⊥AM于点N.依据三角函数求BN的长,从而求BM的长.解普通三角形,求三角形的边或高的效果普通可以转化为解直角三角形的效果,处置的方法就是作高线.5. 解:∵sina=ℎ,m∴m=ℎ.sina应选A.依据三角函数的定义即可求解.此题考察了三角函数的定义,了解定义是关键.6. 【剖析】依据题意求出CE的长,依据三角形的外角的性质和等腰三角形的性质求出AE的长,依据正弦的定义计算即可.此题考察的是解直角三角形的运用−仰角俯角效果,了解仰角的概念、熟记锐角三角函数的定义是解题的关键.【解答】解:由题意得,CE=DF=120m,∠EAC=∠AEG−∠ACE=30∘,∴∠EAC=∠ECA,∴AE=DF=120m,∴AG=AE×sin∠AEG=60√3m,∴AB=AG+GB=(60√3+1)m.应选:C.7. 解:∵第一艘快艇沿北偏西方70∘向,第二艘快艇沿南偏西方20∘向,∴∠BOA=90∘,∵BO=AO=50km,∴AB=50√2km,∠B=∠OAB=45∘,∵第二艘快艇沿南偏西方20∘向,∴∠1=∠CAO=20∘,∴∠2=45∘−20∘=25∘,∴第二艘快艇飞行的方向和距离区分是:北偏西25∘,50√2千米.应选:B.依据题意得出AO=BO以及∠BOA=90∘,进而得出第二艘快艇飞行的方向和距离.此题主要考察了方向角以及勾股定理,正确掌握方向角的定义是解题关键.8. 解:如图作PE⊥AB于E.在Rt△PAE中,∵∠PAE=45∘,PA=60nmile,∴PE=AE=√22×60=30√2nmile,在Rt△PBE中,∵∠B=30∘,∴PB=2PE=60√2nmile,应选:B.如图作PE⊥AB于E.在Rt△PAE中,求出PE,在Rt△PBE中,依据PB=2PE即可处置效果.此题考察方向角、直角三角形、锐角三角函数的有关知识.解普通三角形的效果普通可以转化为解直角三角形的效果,处置的方法就是作高线.9. 解:∵坝高12米,斜坡AB的坡度i=1:1.5,∴AE=1.5BE=18米,∵BC=10米,∴AD=2AE+BC=2×18+10=46米,应选:D.先依据坡比求得AE的长,CB=10m,即可求得AD.此题考察了解直角三角形的运用中的坡度坡角的效果及等腰梯形的性质的掌握状况,将相关的知识点相结合更利于解题.10. 解:过D作DG⊥BC于G,EH⊥BC于H,∴GH=DE=2,∵DG=EH=15,背水坡CD的坡度i=1:0.6,背水坡EF的坡度i=3:4,∴CG=9,HF=20,∴CF=GH+HF−CG=13米,应选C.过D作DG⊥BC于G,EH⊥BC于H,解直角三角形即可失掉结论.此题考察了解直角三角形的运用,解答此题的关键是了解坡度、坡比的含义,结构直角三角形,应用三角函数表示相关线段的长度,难度普通.11. 解:区分过A、D作AF⊥BC,DG⊥BC,垂点区分为F、G,如下图.∵在Rt△ABF中,AB=12米,∠B=60∘,∴sin∠B=AFAB,∴AF=12×√32=6√3,∴DG=6√3.∵在Rt△DGC中,CD=12√3,DG=6√3米,∴GC=√CD2−DG2=18.∵在Rt△DEG中,tanE=313√3,∴6√3GE =313√3,∴GE=26,∴CE=GE−CG=26−18=8.即CE的长为8米.故答案为8.区分过A、D作下底的垂线,设垂足为F、G.在Rt△ABF中,坡面长和坡角的度数,可求得铅直高度AF的值,也就失掉了DG的长;在Rt△CDG中,由勾股定理求CG的长,在Rt△DEG中,依据正切函数定义失掉GE的长;依据CE=GE−CG即可求解.此题考察的是解直角三角形的运用−坡度坡角效果,锐角三角函数的定义,勾股定理.作辅佐线结构直角三角形是解答此类题的普通思绪.12. 解:由题意可得:tan30∘=BDAD =BD90=√33,解得:BD=30√3,tan60∘=DCAD =DC90=√3,解得:DC=90√3,故该修建物的高度为:BC=BD+DC=120√3≈208(m),故答案为:208.区分应用锐角三角函数关系得出BD,DC的长,进而求出该修建物的高度.此题主要考察了解直角三角形的运用,熟练运用锐角三角函数关系是解题关键.13. 解:如图,过点B作BE⊥AC于点E,∵坡度:i=1:√3,∴tan∠A=1:√3=√33,∴∠A=30∘,∵AB=50m,∴BE=12AB=25(m).∴他降低了25m.故答案为:25.首先依据题意画出图形,由坡度为1:√3,可求得坡角∠A=30∘,又由小明沿着坡度为1:√3的山坡向上走了50m,依据直角三角形中,30∘所对的直角边是斜边的一半,即可求得答案.此题考察了坡度坡角效果.此题比拟复杂,留意能结构直角三角形并用解直角三角形的知识求解是解此题的关键,留意数形结合思想的运用.14. 解:在Rt△ABD中,∵sin∠ABD=ADAB,∴AD=4sin60∘=2√3(m),在Rt△ACD中,∵sin∠ACD=ADAC,∴AC=2√3sin45∘=2√6(m).故答案是:2√6.先在Rt△ABD中应用正弦的定义计算出AD,然后在Rt△ACD中应用正弦的定义计算AC即可.此题考察了解直角三角形的实践运用中的坡度坡角效果,难度不大,留意细心运算即可.15. 解:如图在Rt△ABC中,AC=AB⋅sin34∘=500×0.56≈280m,∴这名滑雪运发动的高度下降了280m.故答案为280如图在Rt△ABC中,AC=AB⋅sin34∘=500×0.56≈280m,可知这名滑雪运发动的高度下降了280m.此题考察解直角三角形、坡度坡角效果、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.16. 解:∵在直角三角形ADB中,∠D=30∘,∴ABBD=tan30∘,∴BD=ABtan30∘=√3AB,∵在直角三角形ABC中,∠ACB=60∘,∴BC=ABtan60∘=√33AB,∵CD=10,∴CD=BD−BC=√3AB−√33AB=10,解得:AB=5√3.故答案为:5√3.首先依据题意剖析图形;此题触及到两个直角三角形,应应用其公共边AB及CD=BD−BC=10结构方程关系式,进而可解,即可求出答案.此题考察解直角三角形的运用−仰角俯角效果,要求先生能借助仰角结构直角三角形,并结合图形应用三角函数解直角三角形.17. 解:∵从热气球C处测无暇中A、B两点的俯角区分为30∘、45∘,∴∠BCD=90∘−45∘=45∘,∠ACD=90∘−30∘=60∘,∵CD⊥AB,CD=200m,∴△BCD是等腰直角三角形,∴BD=CD=200m,在Rt△ACD中,CD=200m,∠ACD=60∘,∴AD=CD⋅tan60∘=200×√3=200√3m,∴AB=AD+BD=200√3+200=200(√3+1)m.故答案为:200(√3+1).先依据从热气球C处测无暇中A、B两点的俯角区分为30∘、45∘可求出∠BCD与∠ACD的度数,再由直角三角形的性质求出AD与BD的长,依据AB=AD+BD即可得出结论.此题考察的是解直角三角形的运用−仰角俯角效果,熟知锐角三角函数的定义是解答此题的关键.18. 解:作BE⊥AD于E,CF⊥AD于F,∵斜坡CD的坡比为1:2,即CFDF =12,∴DF=2CF,又CD=20√5m,∴CF=20m,DF=40m,由题意得,四边形BEFC是矩形,∴BE=CF=20m,EF=BC=30m,∵斜坡AB的坡比为1:3,∴BEAE =13,即AE=3BE=60m,∴AD=AE+EF+DF=130m,故答案为:130m.作BE⊥AD于E,CF⊥AD于F,依据坡度的概念区分求出AE、DF,结合图形计算即可.此题考察的是解直角三角形的运用−坡度坡角效果,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键,掌握矩形的判定和性质的运用.19. 解:tanα=1:√3,那么α=30∘.故答案是:30∘.依据坡度就是坡角的正切值即可求解.此题主要考察了坡度的定义,了解坡度和坡角的关系是解题的关键.20. 解:如图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75∘,∠BCH=30∘,AB//CH,∴∠ABC=30∘,∠ACB=45∘,∵AB=3×12=36m,∴AD=CD=18m,BD=AB⋅cos30∘=18√3m,∴BC=CD+BD=(18√3+18)m,∴BH=BC⋅sin30∘=(9√3+9)m.故答案为:9√3+9.作AD⊥BC,BH⊥水平线,依据题意确定出∠ABC与∠ACB的度数,应用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.此题考察了解直角三角形的运用−仰角俯角效果,熟练掌握锐角三角函数定义是解此题的关键.21. 设每层楼高为x米,由MC−CC′求出MC′的长,进而表示出DC′与EC′的长,在直角三角形DC′A′中,应用锐角三角函数定义表示出C′A′,同理表示出C′B′,由C′B′−C′A′求出AB的长即可.此题属于解直角三角形的运用−仰角俯角效果,熟练掌握锐角三角函数定义是解此题的关键.22. 如图,作AD⊥BC,BH⊥水平线,依据题意确定出∠ABC与∠ACB的度数,应用锐角三角函数定义求出AD与BD的长,由CD+BD求出BC的长,即可求出BH的长.此题考察了解直角三角形的运用−仰角俯角效果,熟练掌握锐角三角函数定义是解此题的关键.23. (1)过点C作CE与BD垂直,依据题意确定出所求角度数即可;(2)在直角三角形CBE中,应用锐角三角函数定义求出BE的长,在直角三角形CDE中,应用锐角三角函数定义求出DE的长,由BE+DE求出BD的长,即为教学楼的高.此题考察了解直角三角形的运用−仰角俯角效果,熟练掌握锐角三角函数定义是解此题的关键.24. (1)在直角三角形DCE中,应用锐角三角函数定义求出DE的长即可;(2)过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设BF= DF=x,表示出BC,BD,DC,由题意失掉三角形BCD为直角三角形,应用勾股定理列出关于x的方程,求出方程的解失掉x的值,即可确定出AB的长.此题考察了解直角三角形−仰角俯角效果,坡度坡角效果,熟练掌握勾股定理是解此题的关键.25. 如图,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H.经过解直角△AFD失掉DF的长度;经过解直角△DCE失掉CE的长度,那么BC=BE−CE.此题考察了解直角三角形−仰角俯角效果.要求先生能借助仰角结构直角三角形并解直角三角形.26. 设PQ=x米,在直角△PAQ和直角△PBQ中区分应用x表示出AQ和BQ的长,依据AB=AQ+BQ,即可列方程求得x的值.此题考察了解直角三角形的运用,解答此题的关键是结构直角三角形,应用三角函数表示出相关线段的长度,难度普通.。
九年级数学下册《第二十八章 解直角三角形及其应用》练习题附答案解析-人教版

九年级数学下册《第二十八章解直角三角形及其应用》练习题附答案解析-人教版班级:___________姓名:___________考号:____________一、单选题1.图,在Rt△ABC中△ACB=90°,CE是斜边AB上的中线,过点E作EF⊥AB交AC于点F,若BC=4,sin△CEF= 3,则△AEF的面积为()5A.3B.4C.5D.62.小丽在小华北偏东40°的方向,则小华在小丽的()A.南偏西50°B.北偏西50°C.南偏西40°D.北偏西40°3.如图,小明在距离地面30米的P处测得A处的俯角为15︒,B处的心角为60︒,若斜面坡度为,则斜面AB的长是()米.A.B.C.D.4.如图,某渔船正在海上P处捕鱼,先向北偏东30°的方向航行10km到A处.然后右转40°再航行到B处,在点A的正南方向,点P的正东方向的C处有一条船,也计划驶往B处,那么它的航向是()A .北偏东20°B .北偏东30°C .北偏东35°D .北偏东40°5.如图,某建筑物的顶部有一块宣传牌CD .小明在山坡的坡脚A 处测得宣传牌底部D 的仰角为60°,沿山坡向上走到B 处测得宣传牌顶部C 的仰角为45°,已知斜坡AB 的坡角为30°,10AB =米,15AE =米,则宣传牌CD 的高度是( )米A .20-B .20+C .15+D .56.如图,已知正六边形ABCDEF 内接于半径为r 的O ,随机地往O 内投一粒米,落在正六边形内的概率为( )A B C D .以上答案都不对7.如图,小明利用标杆BE 测量建筑物DC 的高度,已知标杆BE 的长为1.2米,测得AB =85米,BC =425米,则楼高CD 是( )A .6.3米B .7.5米C .8米D .68.如图,点E 是⊥ABCD 的边AB 上一点,过点E 作EF ∥BC ,交CD 于F ,点P 为EF 上一点,连接PB 、PD .下列说法不正确的是( )A .若⊥ABP =⊥CDP ,则点P 在⊥ABCD 的对角线BD 上B .若AE :EB =2:3,EP :PF =1:2,则S △BEP :S △DFP =3:4C .若S △BEP =S △DFP ,则点P 在AC 上D .若点P 在BD 上,则S △BEP =S △DFP9.如图,一棵大树被台风拦腰刮断,树根A 到刮断点P 的距离是4米,折断部分PB 与地面成40︒的夹角,那么原来这棵树的高度是( )A .44cos 40+︒⎛⎫ ⎪⎝⎭米B .44sin 40+︒⎛⎫ ⎪⎝⎭米C .()44sin 40+︒米D .()44tan 40+︒米10.如图,等腰Rt △ABC 中⊥A =90°,AB =AC ,BD 为△ABC 的角平分线,若2CD =,则AB 的长为( )A.3 B .2 C .4 D 2+二、填空题11.在Rt ABC 中90C ∠=︒,有一个锐角为60︒,6AB =若点P 在直线..AB 上(不与点A ,B 重合),且30PCB ∠=︒,则AP 的长为_______.12.如图,将扇形AOB 沿OB 方向平移,使点O 移到OB 的中点O '处,得到扇形A O B '''.若⊥O =90°,OA =2,则阴影部分的面积为______.13.如图,在一次数学实践活动中小明同学要测量一座与地面垂直的古塔AB 的高度,他从古塔底部点处前行30m 到达斜坡CE 的底部点C 处,然后沿斜坡CE 前行20m 到达最佳测量点D 处,在点D 处测得塔顶A的仰角为30︒,已知斜坡的斜面坡度i =A ,B ,C ,D ,在同一平面内,小明同学测得古塔AB 的高度是___________.14.如图,在直角坐标系中点A 的坐标为(0,点B 为x 轴的正半轴上一动点,作直线AB ,⊥ABO 与⊥ABC 关于直线AB 对称,点D ,E 分别为AO ,AB 的中点,连接DE 并延长交BC 所在直线于点F ,连接CE ,当⊥CEF 为直角时,则直线AB 的函数表达式为__.15.如图,平行四边形OABC 的顶点O 是坐标原点,A 在x 轴的正半轴上,B ,C 在第一象限,反比例函数1y x =的图象经过点C ,()0k y k x=≠的图象经过点B .若OC AC =,则k =________.16.在⊥ABC 中AB =6AC =且45B ∠=,则BC =______________.17.如图,大坝横截面的迎水坡AB 的坡比为1:2,(即BC :AC=1:2),若坡面AB 的水平宽度AC 为12米,则斜坡AB 的长为________米.18.如图,等边ABC 中115,125AOB BOC ∠=︒∠=︒,则以线段,,OA OB OC 为边构成的三角形的各角的度数分别为______________________________.三、解答题19.实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线MN 的距离皆为100cm .王诗嬑观测到高度90cm 矮圆柱的影子落在地面上,其长为72cm ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线MN 互相垂直,并视太阳光为平行光,测得斜坡坡度1:0.75i =,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:(1)若王诗嬑的身高为150cm ,且此刻她的影子完全落在地面上,则影子长为多少cm ?(2)猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否正确?(3)若同一时间量得高圆柱落在坡面上的影子长为100cm ,则高圆柱的高度为多少cm ?20.八年级二班学生到某劳动教育实践基地开展实践活动,当天,他们先从基地门口A 处向正北方向走了450米,到达菜园B 处锄草,再从B 处沿正西方向到达果园C 处采摘水果,再向南偏东37°方向走了300米,到达手工坊D 处进行手工制作,最后从D 处回到门口A 处,手工坊在基地门口北偏西65°方向上.求菜园与果园之间的距离.(结果保留整数)参考数据:sin65°≈ 0.91,cos65°≈0.42,tan65°≈2.14,sin37°≈ 0.60,cos37°≈ 0.80,tan37°≈0.7521.如图是某水库大坝的横截面,坝高20m CD =,背水坡BC 的坡度为11:1i =.为了对水库大坝进行升级加固,降低背水坡的倾斜程度,设计人员准备把背水坡的坡度改为2i =求背水坡新起点A 与原起点B之间的距离. 1.41 1.73≈结果精确到0.1m )参考答案与解析1.C【分析】连接BF ,由已知CE AE BE ==得到A FBA ACE ==∠∠∠,再得出CEF ∠与CBF ∠的关系,由三角函数关系求得CF 、BF 的值,通过BF AF =,用三角形面积公式计算即可.【详解】解:连接BF⊥CE 是斜边AB 上的中线 ⊥12CE AE BE AB ===(直角三角形斜边上的中线等于斜边的一半)⊥A FBA ACE ==∠∠∠又⊥90BCA BEF ==︒∠∠在⊥ABC 中180902CBF ACB A ABF A =︒-∠-∠-∠=︒-∠∠在⊥AEC 中180902CEF AEF A ACE A =︒-∠-∠-∠=︒-∠∠⊥CEF CBF ∠=∠3sin sin 5CBF CEF ∴∠=∠=4BC =,设3,5CF x BF x ==则222BC CF BF +=,即()()222435x x +=解得1x =(负值舍掉)3,5CF BF ∴== ⊥EF 是AB 的垂直平分线, ⊥5BF AF ==11·541022AFB S AF BC ∴==⨯⨯=△ 152AEF ABF S S ∴==△△故选:C .【点睛】本题综合考查了垂直平分线的性质、直角三角形和等腰三角形的性质、勾股定理及三角函数等相关知识,熟练利用相关定理和性质进行计算是解决本题的关键.2.C【分析】画出示意图,确定好小丽和小华的的方向和位置即可.【详解】解:如图所示,当小丽在小华北偏东40°的方向时,则小华在小丽的南偏西40°的方向.故选:C【点睛】本题考查了方位角的知识点,确定好物体的方向和位置是解题的关键.3.B【分析】过点A 作AF BC ⊥于点F ,根据三角函数的定义得到30ABF ∠=︒,根据已知条件得到3045HPB APB ∠∠=︒=︒,求得60HBP ∠=︒,解直角三角形即可得到结论.【详解】如图所示:过点A 作AF BC ⊥于点F斜面坡度为AF tan ABF BF ∠∴=== 30ABF ∠∴=︒在P 处进行观测,测得山坡上A 处的俯角为15︒,山脚B 处的俯角为60︒3045HPB APB ∠∠∴=︒=︒,60HBP ∠∴=︒9045PBA BAP ∠∠∴=︒=︒,PB AB ∴=303060PH PH m sin PB PB =︒===,解得:)PB m =故AB =故选:B .【点睛】此题主要考查了解直角三角形的应用-仰角俯角问题,解直角三角形的应用-坡度坡角问题,正确得出PB AB =是解题关键.4.C【分析】连接BC ,由锐角三角函数定义得AC A = km ,则AC =AB ,再由等腰三角形的性质得⊥ACB =⊥ABC =35°,即可得出结论.【详解】解:如图,连接BC由题意得:⊥ACP =⊥ACD =90°,⊥P AC =30°,P A =10km ,⊥BAE =40°,AB =⊥⊥BAC =180°—⊥P AC —⊥BAE =180°—30°—40°=110°⊥cos⊥P AC =ACPA =cos30°=⊥AC =P A =×10= km⊥AC =AB⊥⊥ACB =⊥ABC =12×(180°—⊥BAC )=12×(180°—110°)=35°即B 处在C 处的北偏东35°方向故选:C .【点睛】本题考查了解直角三角形的应用—方向角问题,等腰三角形的性质,锐角三角函数定义等知识,由锐角三角函数定义求出AC 的长是解题的关键.5.A【分析】过点B 分别作AE 、DE 的垂线,垂足分别为G 、F ,在Rt ⊥ABG 中由已知可求得BG 、AG 的长,从而可易得EF 及EG 、BF 的长度,由等腰直角三角形的性质可得CF 的长度,在Rt ⊥DAE 中由正切函数关系可求得DE 的长度,从而可求得CD 的长度.【详解】过点B 分别作AE 、DE 的垂线,垂足分别为G 、F ,如图在Rt ⊥ABG 中⊥BAG =30゜⊥152BG AB ==米,cos3010AG AB =︒==⊥15)EG AG AE =+=米⊥BG ⊥AE ,BF ⊥ED ,AE ⊥ED⊥四边形BGEF 是矩形⊥EF =BG =5米,15)BF EG ==米⊥⊥CBF =45゜,BF ⊥ED⊥⊥BCF =⊥CBF =45゜⊥15)CF BF ==米在Rt ⊥DAE 中⊥DAE =60゜,AE =15米⊥tan DE AE DAE =∠=米)⊥155(20CD CF EF DE =+-=+-=-米故选:A【点睛】本题考查了解直角三角形的实际应用,理解坡角、仰角的含义,构造辅助线得到直角三角形是解题的关键.6.A【分析】连接OB ,过点O 作OH ⊥AB 于点H ,由正六边形的特点可证得⊥OAB 是等边三角形,由特殊角的三角函数值可求出OH 的长,利用三角形的面积公式即可求出⊥OAB 的面积,进而可得出正六边形ABCDEF 的面积,即可得出结果.【详解】解:如图:连接OB ,过点O 作OH ⊥AB 于点H⊥六边形ABCDEF 是正六边形⊥⊥AOB =60°⊥OA =OB =r⊥⊥OAB 是等边三角形⊥AB =OA =OB =r ,⊥OAB =60°在Rt OAH △中sin OH OA OAB r =⋅∠==⊥21122OAB S AB OH r =⋅==△⊥正六边形的面积226== ⊥⊥O 的面积=πr 2⊥米粒落在正六边形内的概率为:222rπ 故选:A .【点睛】本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、解直角三角形;熟练掌握正六边形的性质,通过作辅助线求出⊥OAB 的面积是解决问题的关键.7.B【分析】先判断出⊥ABE ⊥⊥ACD ,再根据相似三角形对应边成比例解答.【详解】⊥AB =85,BC =425 ⊥AC =AB +BC =10⊥BE ⊥AC ,CD ⊥AC⊥BE ⊥CD⊥AB :AC =BE :CD ⊥85:10=1.2:CD⊥CD =7.5米.故选:B .【点睛】本题只要是把实际问题抽象到相似三角形中利用相似三角形的相似比,列出方程,通过解方程求出建筑物的高度,体现了方程的思想.8.D【分析】根据平行四边形的性质和判定进行判断即可.【详解】解:A 、若⊥ABP =⊥CDP ,则点P 在⊥ABCD 的对角线BD 上,说法正确;B 、若AE :EB =2:3,EP :PF =1:2则S △BEP :S △DFP =3:4,说法正确;C 、过点P 作GH AB ∥,分别交AD ,BC 于G ,H⊥GH AB ∥ GA HB ∥⊥四边形ABHG 是平行四边形同理:四边形CDGH 、四边形BHPE ,四边形DGPE 都是平行四边形 ⊥12BEP BHPE S S =△ 12DFP DGPF S S =△又BEP DFP S S =△△⊥BEPH DGPF SS = ⊥ABHG ADFE S S =同理:BCFE CDGH S S =⊥点P 在AC 上,C 说法正确;D 、若点P 在BD 上,不能得出EP =PF ,所以S △BEP 不一定等于S △DFP ,说法错误;故选:D .【点睛】此题考查平行四边形的判定和性质,掌握平行四边形的性质是解题的关键.9.B【分析】通过解直角三角形即可求得.【详解】解:在Rt ABP △中4==sin sin 40AP BP ABP ∠︒ 故原来这棵树的高度为:4=4sin 40AP BP ⎛⎫++ ⎪︒⎝⎭(米) 故选:B .【点睛】本题考查了解直角三角形的应用,熟练掌握和运用解直角三角形的方法是解决本题的关键.10.D【分析】过点D 作DE ⊥BC 于点E ,设AB =AC =x ,则AD =x -2,根据等腰Rt △ABC 中90,A AB AC ∠=︒= 得到⊥C =45°,根据BD 为△ABC 的角平分线,⊥A =90°,DE ⊥BC ,推出DE =AD =x -2,运用⊥C 的正弦即可求得.【详解】解:过点D 作DE ⊥BC 于点E ,则⊥DEB =⊥DEC =90°设AB =AC =x ,则AD =x -2⊥等腰Rt △ABC 中,⊥A =90°,AB =AC ,⊥⊥C =(180°-⊥A )=45°⊥BD 为△ABC 的角平分线⊥DE =AD =x -2⊥sin sin 452DE C CD ︒===⊥22x -⊥2x ,即2AB =.故选D .【点睛】本题主要考查了等腰直角三角形,角平分线,解直角三角形,熟练掌握等腰直角三角形的性质,角平分线的性质,正弦的定义和45°的正弦值,是解决问题的关键.11.92或9或3 【分析】分⊥ABC =60、⊥ABC =30°两种情况,利用数形结合的方法,分别求解即可.【详解】解:当⊥ABC =60°时,则⊥BAC =30°⊥132BC AB ==⊥AC ==当点P 在线段AB 上时,如图⊥30PCB ∠=︒⊥⊥BPC =90°,即PC ⊥AB⊥9cos 2AP AC BAC =⋅∠==;当点P 在AB 的延长线上时⊥30PCB ∠=︒,⊥PBC =⊥PCB +⊥CPB⊥⊥CPB =30°⊥⊥CPB =⊥PCB⊥PB =BC =3⊥AP =AB +PB =9;当⊥ABC =30°时,则⊥BAC =60°,如图⊥132AC AB ==⊥30PCB ∠=︒⊥⊥APC =60°⊥⊥ACP =60°⊥⊥APC =⊥P AC =⊥ACP⊥⊥APC 为等边三角形⊥P A =AC =3.综上所述,AP 的长为92或9或3. 故答案为:92或9或3 【点睛】本题是解直角三角形综合题,主要考查了含30度角的直角三角形、解直角三角形,等边三角形的判定和性质等,分类求解是本题解题的关键.12.3π【分析】设A O '与扇形AOB 交于点C ,连接OC ,解Rt OCO ',求得60O C COB '=∠=︒,根据阴影部分的面积为()OCO A O B OCB S S S ''''--扇形扇形,即可求解.【详解】如图,设A O '与扇形AOB 交于点C ,连接OC ,如图O '是OB 的中点11122OO OB OA '∴===, OA =2 AOB ∠=90°,将扇形AOB 沿OB 方向平移90A O O ''∴∠=︒1cos 2OO COB OC '∴∠== 60COB ∴∠=︒sin 60O C OC '∴=︒=∴阴影部分的面积为()OCO A O B OCB S S S''''--扇形扇形 OCO AOB OCB S S S ''=-+扇形扇形22906012213603602ππ=⨯-⨯+⨯3π=故答案为:3π+【点睛】本题考查了解直角三角形,求扇形面积,平移的性质,求得60COB ∠=︒是解题的关键.13.(20m +【分析】过D 作DF ⊥BC 于F ,DH ⊥AB 于H ,设DF =x m ,CF m ,求出x =10,则BH =DF =,CF =,DH =BF ,再求出AH DH ,即可求解. 【详解】解:过D 作DF ⊥BC 于F ,DH ⊥AB 于H⊥DH =BF ,BH =DF⊥斜坡的斜面坡度i =1⊥:DF CF =设DF =x m ,CFm⊥CD 220x ==⊥x =10⊥BH =DF =10m ,CF =⊥DH =BF =(m )⊥⊥ADH =30°⊥AH 10=+m ) ⊥AB =AH +BH =20103(m )故答案为:(20m +【点睛】本题考查了解直角三角形的应用-仰角俯角问题、坡角坡度问题,正确的作出辅助线构造直角三角形是解题的关键.14.y【分析】证明⊥ABO ⊥⊥ABC ,于是可知⊥CBA =⊥ABO =30°,得出OB =3即可求出直线AB 的函数表达式.【详解】解:⊥⊥ABO 与⊥ABC 关于直线AB 对称⊥⊥ACB =⊥AOB =90°⊥点E 是AB 的中点⊥CE =BE =EA⊥⊥EAC =⊥ECA⊥⊥ECA +⊥ECF =90°,⊥ECF +⊥CFE =90°⊥⊥CFE =⊥BAC而点D ,E 分别为AO ,AB 的中点⊥DF ∥OB⊥⊥CFE =⊥CBO =2⊥CBA =2⊥ABO⊥⊥ABO 与⊥ABC 关于直线AB 对称⊥⊥ABO ⊥⊥ABC⊥⊥OAB =⊥CAB =2⊥ABO⊥⊥ABO =30°而点A 的坐标为(0,即OAAB ∴=⊥OB =3即点B 的坐标为(3,0)于是可设直线AB 的函数表达式为y =kx +b ,代入A 、B 两点坐标得30b k b ⎧=⎪⎨+=⎪⎩解得kb故答案为y【点睛】本题考查的是三角形的全等,并考查了用待定系数法求函数解析式,找到两个已知点的坐标是解决本题的关键.15.3【分析】过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E ,先证四边形CDEB 为矩形,得出CD =BE ,再证Rt △COD ⊥Rt △BAE (HL ),根据S 平行四边形OCBA =4S △OCD =2,再求S △OBA =112OCBA S =平行四边形即可. 【详解】解:过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E⊥CD ⊥BE⊥四边形ABCO 为平行四边形⊥CB OA ∥ ,即CB DE ∥,OC =AB⊥四边形CDEB 为平行四边形⊥CD ⊥OA⊥四边形CDEB 为矩形⊥CD =BE⊥在Rt △COD 和Rt △BAE 中OC AB CD EB =⎧⎨=⎩⊥Rt △COD ⊥Rt △BAE (HL )⊥S △OCD =S △ABE⊥OC =AC ,CD ⊥OA⊥OD =AD⊥反比例函数1yx=的图象经过点C⊥S△OCD=S△CAD=12⊥S平行四边形OCBA=4S△OCD=2⊥S△OBA=11 2OCBAS=平行四边形⊥S△OBE=S△OBA+S△ABE=13 122 +=⊥3232k=⨯=.故答案为3.【点睛】本题考查反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质,掌握反比例函数k的几何意义,平行四边形的性质与判定,矩形的判定与性质,三角形全等判定与性质.16.3或3【分析】画出图形,分⊥ABC为锐角三角形和钝角三角形两种情况讨论即可.【详解】解:情况一:当⊥ABC为锐角三角形时,如图1所示:过A点作AH⊥BC于H⊥⊥B=45°⊥⊥ABH为等腰直角三角形⊥363322ABAH BH在Rt⊥ACH中由勾股定理可知:2236273CH AC AH⊥333BC BH CH.情况二:当⊥ABC为钝角三角形时,如图2所示:由情况一知:363322ABAH BH2236273CH AC AH⊥333BC BH CH .故答案为:3或3.【点睛】本题考察了等腰直角三角形的性质及勾股定理的应用,本题的关键是能将⊥ABC 分成锐角三角形或钝角三角形分类讨论.17.【分析】根据坡面AB 的坡比以及AC 的值,求出BC ,再利用勾股定理即可求出斜面AB 的长.【详解】解:⊥大坝横截面的迎水坡AB 的坡比为1:2,AC=12米⊥1212BC BC AC == ⊥BC=6⊥AB =故答案为:【点睛】本题主要考查学生对坡度坡角的掌握及三角函数的运用能力,能根据坡度求出BC 是解题关键. 18.55°,60°,65°.【分析】通过旋转AOB 至CDB △,可得BOD 是等边三角形,将,,OA OB OC 放在一个三角形中进而求出各角大小。
解直角三角形 试题及答案

向东航行 30 分钟后到达 C处,发现灯塔 B在它的南偏东 15°方向,则此时货轮与灯塔 B的距离为
km.
图 K23-8
10、 如图 K23-9,在一笔直的沿湖道路上有 A,B两个游船码头,观光岛屿 C在码头 A北偏东 60°的方向,在码头 B北偏 西
45°的方向,AC=4 km.游客小张准备从观光岛屿 C乘船沿 CA回到码头 A或沿 CB回到码头 B,设开往码头 A,B的游船
∵∠CNP=46°,∴∠PNA=44°,
∴PA=PN·sin∠PNA=60×0.6947≈41.68(海里).
6【答案】25
如图,过点 B作 BE⊥AE于点 E,
∵坡度 i=1∶ 3,
∴tanA=1∶ 3= 3,∴3∠A=30°,
∵AB=50 m,∴BE=1AB=25(m)
.
2
∴他升高了 25 m.
∴BD=CD·tan37°≈27.2×0.75=20.4(海里).
�� 3
答:还需航行的距离 BD的长为 20.4 海里.
12【答案】解:如图,过点 C作 CD⊥AB于点 D,
设 BD为 x海里,
在 Rt△ACD中,∠DAC=45°,
∴AD=DC=(x+5)海里,
4
在 Rt△BCD中,由 tan53°=����
126
米.
5【答案】B
如图,过点 P作 PA⊥MN于点 A,
MN=30×2=60(海里),
∵∠MNC=90°,∠CNP=46°,
∴∠MNP=∠MNC+∠CNP=136°,
∵∠BMP=68°,
∴∠PMN=90°-∠BMP=22°,
∴∠MPN=180°-∠PMN-∠PNM=22°,
解直角三角形的应用测试题带答案

解直角三角形的应用测试题一、选择题(本大题共10小题,共分)1.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度如图,旗杆PA的高度与拉绳PB的长度相等小明将PB拉到的位置,测得为水平线,测角仪的高度为1米,则旗杆PA的高度为A. B. C. D.2.如图,长4m的楼梯AB的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后的楼梯AC的长为A. B. C. D.2 3 43.楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为现要在楼梯上铺一条地毯,已知米,楼梯宽度1米,则地毯的面积至少需要A. 米B. 米C. 米D. 米4.上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处如图从A、B两处分别测得小岛M在北偏东和北偏东方向,那么在B处船与小岛M的距离为5. A. 20海里 B. 海里 C. 海里 D. 海里6.如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为A. B. C. D.7.如图所示,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为,再向电视塔方向前进120米达到F处,又测得电视塔顶端A 的仰角为,则这个电视塔的高度单位:米为A. B. 61 C. D. 1216 7 88.某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西方向航行50千米,第二艘快艇沿南偏西方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是A. 南偏东,千米B. 北偏西,千米C. 南偏东,100千米D. 北偏西,100千米9.如图,一艘海轮位于灯塔P的南偏东方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东方向上的B处,这时,B处与灯塔P的距离为10. A. nmile B. nmile C. nmile D. nmile11.如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度:,则坝底AD的长度为A. 26米B. 28米C. 30米D. 46米9 10 1112.如图是某水库大坝的横截面示意图,已知,且AD、BC之间的距离为15米,背水坡CD的坡度:,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度:4,则大坝底端增加的长度CF是米.A. 7B. 11C. 13D. 20二、填空题(本大题共10小题,共分)13.为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形已知迎水坡面米,背水坡面米,,加固后拦水坝的横断面为梯形ABED,,则CE的长为______ 米14.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为______ 米精确到1米,参考数据:15.16.17.小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了______18.如图,长4m的楼梯AB的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后楼梯AC长为______ 米19.如图,一名滑雪运动员沿着倾斜角为的斜坡,从A滑行至B,已知米,则这名滑雪运动员的高度下降了______米参考数据:,,20.如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为,则此楼房的高度为______ 米结果保留根号.16 17 18 21.如图,从热气球C处测得地面A、B两点的俯角分别为、,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是______米结果保留根号.22.如图,水库堤坝的横断面是梯形,测得BC长为30m,CD长为,斜坡AB的坡比为1:3,斜坡CD的坡比为1:2,则坝底的宽AD为______23.如图,某堤坝的斜坡AB的斜角是,坡度是,则______.24.25.26.某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为3米秒,则这架无人飞机的飞行高度为结果保留根号______ 米三、计算题(本大题共4小题,共分)27.如图,某数学兴趣小组要测量一栋五层居民楼CD的高度该楼底层为车库,高米;上面五层居住,每层高度相等测角仪支架离地米,在A处测得五楼顶部点D的仰角为,在B处测得四楼顶部点E的仰角为,米求居民楼的高度精确到米,参考数据:28.某兴趣小组借助无人飞机航拍校园如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为4米秒,求这架无人飞机的飞行高度结果保留根号29.如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为,教学楼底部B的俯角为,量得实验楼与教学楼之间的距离.30.求的度数.31.求教学楼的高结果精确到,参考数据:,32.如图,在大楼AB的正前方有一斜坡CD,米,坡角,小红在斜坡下的点C处测得楼顶B的仰角为,在斜坡上的点D处测得楼顶B的仰角为,其中点A、C、E在同一直线上.33.求斜坡CD的高度DE;34.求大楼AB的高度结果保留根号四、解答题(本大题共2小题,共分)35.如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点B,C,E在同一水平直线上,已知,,求障碍物B,C两点间的距离结果精确到参考数据:,36.37.38.39.如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:米,,请求出小桥PQ的长,结果精确到米答案和解析【答案】1. A2. B3. D4. B5. A6. C7. B8. B9. D10. C11. 812. 20813. 2514.15. 28016.17.18. 13019.20.21. 解:设每层楼高为x米,由题意得:米,,,在中,,,在中,,,,,解得:,则居民楼高为米.22. 解:如图,作,水平线,由题意得:,,,,,,,,,则.23. 解:过点C作,则有,;由题意得:,在中,,在中,,教学楼的高,则教学楼的高约为.24. 解:在中,米,,,米;过D作,交AB于点F,,,,即为等腰直角三角形,设米,四边形DEAF为矩形,米,即米,在中,,米,米,米,,,,在中,根据勾股定理得:,解得:,则米.25. 解:如图,过点D作于点F,过点C作于点H.则,在直角中,,,.,.答:障碍物B,C两点间的距离约为.26. 解:设米,在直角中,,,在直角中,,,米,,解得:米.答:小桥PQ的长度约是米.【解析】1. 解:设,在中,,,,,.故选:A.设,在中,根据,列出方程即可解决问题.本题考查解直角三角形、三角函数等知识,解题的关键是设未知数列方程,属于中考常考题型.2. 解:在中,,,在中,,.故选B.先在中利用正弦的定义计算出AD,然后在中利用正弦的定义计算AC即可.本题考查了解直角三角形的应用坡度坡角:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,它是一个比值,反映了斜坡的陡峭程度,一般用i表示,常写成:m的形式把坡面与水平面的夹角叫做坡角,坡度i与坡角之间的关系为:.3. 解:在中,米,米,地毯的面积至少需要米;故选:D.由三角函数表示出BC,得出的长度,由矩形的面积即可得出结果.本题考查了解直角三角形的应用、矩形面积的计算;由三角函数表示出BC是解决问题的关键.4. 解:如图,过点B作于点N.由题意得,海里,.作于点N.在直角三角形ABN中,.在直角中,,则,所以海里.故选B.过点B作于点根据三角函数求BN的长,从而求BM的长.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.5. 解:,.故选A.根据三角函数的定义即可求解.本题考查了三角函数的定义,理解定义是关键.6. 【分析】根据题意求出CE的长,根据三角形的外角的性质和等腰三角形的性质求出AE的长,根据正弦的定义计算即可.本题考查的是解直角三角形的应用仰角俯角问题,理解仰角的概念、熟记锐角三角函数的定义是解题的关键.【解答】解:由题意得,,,,,,.7. 解:第一艘快艇沿北偏西方向,第二艘快艇沿南偏西方向,,,,,第二艘快艇沿南偏西方向,,,第二艘快艇航行的方向和距离分别是:北偏西,千米.故选:B.根据题意得出以及,进而得出第二艘快艇航行的方向和距离.此题主要考查了方向角以及勾股定理,正确把握方向角的定义是解题关键.8. 解:如图作于E.在中,,,,在中,,,故选:B.如图作于在中,求出PE,在中,根据即可解决问题.本题考查方向角、直角三角形、锐角三角函数的有关知识解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.9. 解:坝高12米,斜坡AB的坡度:,米,米,米,故选:D.先根据坡比求得AE的长,已知,即可求得AD.此题考查了解直角三角形的应用中的坡度坡角的问题及等腰梯形的性质的掌握情况,将相关的知识点相结合更利于解题.10. 解:过D作于G,于H,,,背水坡CD的坡度:米,故选C.过D作于G,于H,解直角三角形即可得到结论.本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.11. 解:分别过A、D作,,垂点分别为F、G,如图所示.在中,米,,,,.在中,,米,.在中,,,,.即CE的长为8米.故答案为8.分别过A、D作下底的垂线,设垂足为F、在中,已知坡面长和坡角的度数,可求得铅直高度AF的值,也就得到了DG的长;在中,由勾股定理求CG的长,在中,根据正切函数定义得到GE的长;根据即可求解.本题考查的是解直角三角形的应用坡度坡角问题,锐角三角函数的定义,勾股定理作辅助线构造直角三角形是解答此类题的一般思路.12. 解:由题意可得:,解得:,,解得:,故该建筑物的高度为:,故答案为:208.分别利用锐角三角函数关系得出BD,DC的长,进而求出该建筑物的高度.此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.13. 解:如图,过点B作于点E,坡度::,:,,,.他升高了25m.故答案为:25.首先根据题意画出图形,由坡度为1:,可求得坡角,又由小明沿着坡度为1:的山坡向上走了50m,根据直角三角形中,所对的直角边是斜边的一半,即可求得答案.此题考查了坡度坡角问题此题比较简单,注意能构造直角三角形并用解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.14. 解:在中,,,在中,,.故答案是:.先在中利用正弦的定义计算出AD,然后在中利用正弦的定义计算AC即可.本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可.15. 解:如图在中,,这名滑雪运动员的高度下降了280m.故答案为280如图在中,,可知这名滑雪运动员的高度下降了280m.本题考查解直角三角形、坡度坡角问题、锐角三角函数等知识,解题的关键是熟练掌握锐角三角函数的定义,属于中考常考题型.16. 解:在直角三角形ADB中,,,,在直角三角形ABC中,,,,,解得:.故答案为:.首先根据题意分析图形;本题涉及到两个直角三角形,应利用其公共边AB及构造方程关系式,进而可解,即可求出答案.本题考查解直角三角形的应用仰角俯角问题,要求学生能借助仰角构造直角三角形,并结合图形利用三角函数解直角三角形.17. 解:从热气球C处测得地面A、B两点的俯角分别为、,,,,,是等腰直角三角形,,在中,,,,.故答案为:.先根据从热气球C处测得地面A、B两点的俯角分别为、可求出与的度数,再由直角三角形的性质求出AD与BD的长,根据即可得出结论.本题考查的是解直角三角形的应用仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.18. 解:作于E,于F,斜坡CD的坡比为1:2,即,,又,,,由题意得,四边形BEFC是矩形,,,斜坡AB的坡比为1:3,,即,,故答案为:130m.作于E,于F,根据坡度的概念分别求出AE、DF,结合图形计算即可.本题考查的是解直角三角形的应用坡度坡角问题,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键,掌握矩形的判定和性质的应用.19. 解::,则.故答案是:.根据坡度就是坡角的正切值即可求解.本题主要考查了坡度的定义,理解坡度和坡角的关系是解题的关键.20. 解:如图,作,水平线,由题意得:,,,,,,,,,.故答案为:.作,水平线,根据题意确定出与的度数,利用锐角三角函数定义求出AD与BD的长,由求出BC的长,即可求出BH的长.此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.21. 设每层楼高为x米,由求出的长,进而表示出与的长,在直角三角形中,利用锐角三角函数定义表示出,同理表示出,由求出AB的长即可.此题属于解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.22. 如图,作,水平线,根据题意确定出与的度数,利用锐角三角函数定义求出AD与BD的长,由求出BC的长,即可求出BH的长.此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.23. 过点C作CE与BD垂直,根据题意确定出所求角度数即可;在直角三角形CBE中,利用锐角三角函数定义求出BE的长,在直角三角形CDE中,利用锐角三角函数定义求出DE的长,由求出BD的长,即为教学楼的高.此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数定义是解本题的关键.24. 在直角三角形DCE中,利用锐角三角函数定义求出DE的长即可;过D作DF垂直于AB,交AB于点F,可得出三角形BDF为等腰直角三角形,设,表示出BC,BD,DC,由题意得到三角形BCD为直角三角形,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出AB的长.此题考查了解直角三角形仰角俯角问题,坡度坡角问题,熟练掌握勾股定理是解本题的关键.25. 如图,过点D作于点F,过点C作于点通过解直角得到DF的长度;通过解直角得到CE的长度,则.本题考查了解直角三角形仰角俯角问题要求学生能借助仰角构造直角三角形并解直角三角形.26. 设米,在直角和直角中分别利用x表示出AQ和BQ的长,根据,即可列方程求得x的值.本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数表示出相关线段的长度,难度一般.。
中考数学复习《解直角三角形的实际应用 》专项检测卷(附带答案)
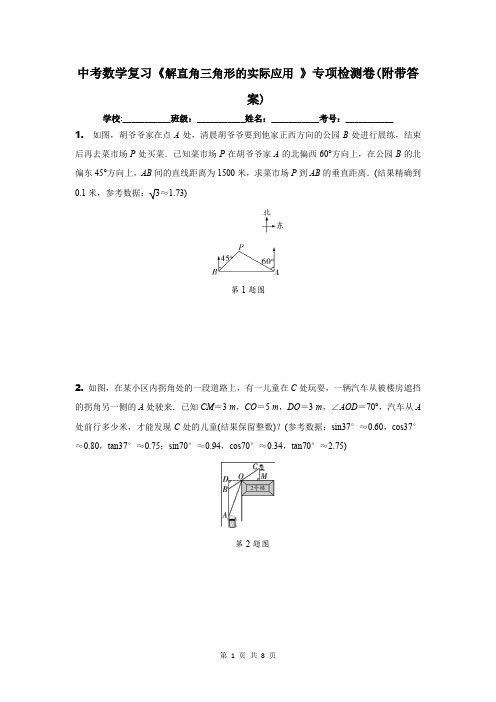
中考数学复习《解直角三角形的实际应用》专项检测卷(附带答案)学校:___________班级:___________姓名:___________考号:___________1.如图,胡爷爷家在点A处,清晨胡爷爷要到他家正西方向的公园B处进行晨练,结束后再去菜市场P处买菜.已知菜市场P在胡爷爷家A的北偏西60°方向上,在公园B的北偏东45°方向上,AB间的直线距离为1500米,求菜市场P到AB的垂直距离.(结果精确到0.1米,参考数据:3≈1.73)第1题图2.如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来.已知CM=3 m,CO=5 m,DO=3 m,∠AOD=70°,汽车从A 处前行多少米,才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)第2题图3.如图,在数学综合实践活动课上,九年级(1)班数学兴趣小组的同学们利用所学的数学知识测量建筑物CD的遮光板DE的长度,先测得建筑物CD的高为10 m,然后在A处测得建筑物CD的遮光板外沿E的仰角为30°,向正前方走9 m到达B处后测得遮光板内沿D的仰角为45°,求遮光板DE的长.(点A、B、C在一条直线上,DE∥AC,结果保留根号)第3题图4.小明周末与父母一起到遂宁湿地公园进行数学实践活动,在A处看到B、C处各有一棵被湖水隔开的银杏树,他在A处测得B在北偏西45°方向,C在北偏东30°方向,他从A 处走了20米到达B处,又在B处测得C在北偏东60°方向.(1)求∠C的度数;(2)求两棵银杏树B、C之间的距离(结果保留根号).第4题图5.王刚同学在学习了解直角三角形及其应用的知识后,尝试利用所学知识测量河对岸大树AB的高度,他在点C处测得大树顶端A的仰角为45°,再从C点出发沿斜坡走210米到达斜坡上D点,在点D处测得树顶端A的仰角为30°,若斜坡CF的坡比为i=1∶3(点E、C、B在同一水平线上).(1)求王刚同学从点C到点D的过程中上升的高度;(2)求大树AB的高度(结果保留根号).第5题图6.拓展小组研制的智能操作机器人,如图①,水平操作台为l,底座AB固定,高AB为50 cm,连杆BC长度为70 cm,手臂CD长度为60 cm,点B,C是转动点,且AB,BC与CD始终在同一平面内.(1)转动连杆BC,手臂CD,使∠ABC=143°,CD∥l,如图②,求手臂端点D离操作台l的高度DE的长(精确到1 cm,参考数据:sin53°≈0.8,cos53°≈0.6);(2)物品在操作台l上,距离底座A端110 cm的点M处,转动连杆BC,手臂CD,手臂端点D能否碰到点M?请说明理由.第6题图创新题7.白塔市位于呼和浩特市东临17公里的白塔村,原为辽代丰州古城内一座佛教寺院中的藏经塔.某数学活动小组在学习完“锐角三角函数”之后,决定测量白塔的高度.为了减小误差,该数学活动小组在测量仰角的度数及两个测量点之间的距离时,都分别测量了两次并取他们的平均值作为测量结果,测量数据如下表(不完整):活动课题测量白塔的高度活动工具测角仪和皮尺测量示意图第7题图说明:如图,他们先在点C处测得古塔顶端A的仰角为∠ACB,再在点D处测得古塔顶端A的仰角为∠ADB,且B、C、D在同一条直线上测量数据测量项目第一次第二次平均值∠ACB40.5°39.5°40°∠ADB30.2°29.8°30°C、D之间的距离29.6 m29.4 m……(1)两次测量C、D之间的距离的平均值是_____________________________________m;(2)根据以上测量结果,请你帮助该数学活动小组计算白塔AB的高度.(结果精确到1 m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,3≈1.73)参考答案1.解:如解图,过点P作PD⊥AB于点D第1题解图则∠PDB =∠PDA =90°由题意,得∠BPD =45°,∠APD =60°,AB =1500 设菜市场P 到AB 的垂直距离PD 为x ∴AD =PD ·tan60°=3x ,BD =PD =x ∴AB =AD +BD =3x +x =1500 解得x ≈547.5.答:菜市场P 到AB 的垂直距离约为547.5米. 2. 解:∵CM =3,CO =5,∠CMO =90° ∴在Rt △CMO 中,MO =52-32=4. ∵∠BOD =∠COM ,∠BDO =∠CMO =90° ∴△BDO ∽△CMO ∴BD CM =DO MO即BD 3=34,∴BD =2.25. 在Rt △ADO 中,tan ∠AOD =ADOD∴tan70°=AD3∴AD ≈3×2.75=8.25∴AB =AD -BD =8.25-2.25=6(m ).答:汽车从A 处前行约6 m ,才能发现C 处的儿童.3. 解:如解图,过点E 作EF ⊥AC 于点F ,可得四边形EFCD 是矩形第3题解图由题意得∠EAC =30°,∠DBC =45°,AB =9,CD =10∴EF =CD =10,DE =CF .在Rt △AEF 中,AF =EFtan30°=103在Rt △BCD 中,BC =CDtan45°=10∴CF =AC -AF =AB +BC -AF =19-103 ∴DE =CF =19-103答:遮光板DE 的长为(19-103)m . 4. 解:(1)由题意知,BE ∥AD ,∠EBD =60° ∴∠BDA =∠EBD =60°.∵∠BDA =∠C +∠CAD ,∠CAD =30° ∴∠C =∠BDA -∠CAD =30°; (2)如解图,过点B 作BG ⊥AD 于点G . ∴∠AGB =∠BGD =90°.在Rt △AGB 中,AB =20,∠BAG =45° ∴AG =BG =20×sin45°=10 2. 在Rt △BGD 中,∠BDA =60° ∴BD =BG sin60°=2063,DG =BG tan60°=1063.∵∠C =∠CAD =30°∴CD =AD =AG +DG =102+1063∴BC =BD +CD =102+106=10(2+6)米. 答:两棵银杏树B 、C 之间的距离为10(2+6)米.第4题解图5. 解:(1)如解图,过点D 作DH ⊥CE 于点H 在Rt △CDH 中,i =DH CH =13∴CH =3DH .∵CH2+DH2=CD2∴(3DH)2+DH2=(210)2解得DH=2或-2(舍去)∴王刚同学从点C到点D的过程中上升的高度为2米;(2)如解图,延长AD交CE于点G由题意,得∠AGC=30°∴GH=DHtan∠AGC=233=2 3.∵CH=3DH=6∴GC=GH+CH=23+6.在Rt△BAC中,∠ACB=45°∴AB=BC∴tan∠AGB=ABBG=ABBC+CG=ABAB+23+6=33解得AB=6+43答:大树AB的高度为(6+43)米.第5题解图6.解:(1)如解图①,过点C作CP⊥AE于点P,过点B作BQ⊥CP于点Q第6题解图①由题意,得∠ABC=143°,∠ABQ=90°∴∠CBQ=53°∴在Rt△BCQ中,CQ=BC·sin53°≈70×0.8=56.∵CD∥l,PQ=AB=50∴DE=CP=CQ+PQ=56+50=106答:手臂端点D离操作台l的高度DE长为106 cm;(2)能.理由如下:如解图②,当点B,C,D共线时第6题解图②BD=60+70=130,AB=50在Rt△ABD中,AD=BD2-AB2=1302-502=120.∵120>110∴手臂端点D能碰到点M.7.解:(1)29.5;(2)由题意,设白塔AB的高度为x m在Rt△ABC中,∠ACB=40°,tan∠ACB=xBC∴BC=xtan40°.在Rt△ABD中,∠ADB=30°,tan∠ADB=x BD∴BD=x tan30°.∵BD-BC=29.5∴xtan30°-xtan40°=29.5解得x≈55.答:白塔AB的高度约为55 m.。
中考数学复习《解直角三角形的应用》专项检测卷-附带答案

中考数学复习《解直角三角形的应用》专项检测卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.小王同学学习了锐角三角函数后,通过观察广场的台阶与信号塔之间的相对位置,他认为利用台阶的可测数据与在点A,B处测出点D的仰角度数,可以求出信号塔DE的高.如图,AB的长为5m,高BC为3m.他在点A处测得点D的仰角为45°,在点B处测得点D的仰角为38.7°.A,B,C,D,E在同一平面内.你认为小王同学能求出信号塔DE的高吗?若能,请求出信号塔DE的高;若不能,请说明理由.(参考数据:sin38.7°≈0.625,cos38.7°≈0.780,tan38.7°≈0.80,结果保留整数)2.如图,太阳能电池板宽为AB,点O是AB的中点,OC是灯杆,地面上三点D,E与C在一条直线上,DE=10.5m,EC=5m.在D处测得电池板边缘点B的仰角为37°,在E处测得电池板边缘点B的仰角为45°.此时点A、B与E在一条直线上,求太阳能电池板宽AB的长度.(结果精确到0.1m.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,√2≈1.41,√3≈1.73)3.为积极响应绿色出行的号召,骑车出行已经成为人们的新风尚.图①是某品牌自行车放在水平地面上的实物图,图②是其示意图,其中AB∥CD∥l,车轮半径为32cm,∠ABC=64°,BC=60cm,坐垫E与点B的距离BE为10cm.(1)求坐垫E到地面的距离;(2)根据经验,当坐垫E到CD的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为84cm,现将坐垫E调整至坐骑舒适高度位置E′,求EE′的长.(结果精确到0.lcm.参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)4.在学校的数学学科周上,李老师指导学生测量学校旗杆AB的高度.在旗杆附近有一个斜坡,坡长CD=10米,坡度i=3:4,小华在C处测得旗杆顶端A的仰角为60°,在D处测得旗杆顶端A的仰角为45°.求旗杆AB的高度.(点A,B,C,D在同一平面内,B,C在同一水平线上,结果保留根号)5.如图1是某商场的入口,它是由立柱、斜杆、支撑杆组成的支架撑起的,如图2是它的示意图,点P、A、C在同一水平线上,经过测量,支架的立柱BC与地面PC垂直(∠ACB=90°),BC=3米,支撑杆DE⊥AB于点E,∠BDE=α且sinα=25,从点B观测点D的仰角为45°,又测得BE =4米.(1)求该支架的边BD的长;(2)求支架的边BD的顶端点D到地面PC的距离DF.(结果保留根号)6.桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子•备城门》,是一种利用杠杆原理的取水机械.如图2所示的是桔槔示意图,OM是垂直于水平地面的支撑杆,OM=3米,AB是杠杆,且AB=6米,OA:OB=2:1.当点A位于最高点时,∠AOM=127°.(1)求点A位于最高点时到地面的距离;(2)当点A从最高点逆时针旋转54.5°到达最低点A1时,求此时水桶B上升的高度.(参考数据:sin37°≈0.6,sin17.5°≈0.3,tan37°≈0.8)7.某班同学在一次综合实践课上,测量校园内一棵树的高度.如图,测量仪在A处测得树顶D的仰角为45°,在C处测得树顶D的仰角为37°(点A、B、C在同一条水平直线上).已知测量仪高度AE=CF=1.65米,AC=28米,求树BD的高度.(结果精确到0.1米)【参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75】8.如图,某工厂坐落在东西方向公路MN的北侧,H,E分别是矩形生产车间ABCD的入口和出口(AD∥MN,HE⊥BC),车间宽度EH=80m,生产出来的产品沿北偏西53°的厂内道路EF运送到库房F存放,EF=500m,工厂大门G在库房F南偏西26.6°的方向,求大门与车间入口之间的距离GH的长.(点G,B,H,C在直线MN上.参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.5,sin53°≈45,cos53°≈35,tan53°≈43)9.数学兴趣小组测量某楼房的高度.如图所示,楼房剖面和台阶的剖面在同一平面,在台阶底部点A处测得楼顶端点E的仰角∠GAE=50.2°,台阶AB长39米,台阶坡面AB的坡度i=5:12,然后在点B处测得楼顶端点E的仰角∠EBF=63.4°,则楼顶到地面的高度EF约为多少米.(参考数据:tan50.2°≈1.20,tan63.4°≈2.00,sin50.2°≈0.77,sin63.4°≈0.89)10.“工欲善其事,必先利其器”,如图为钓鱼爱好者购买的神器“晴雨伞”,其截面示意图是轴对称图形,对称轴是垂直于地面的支杆AD,用绳子拉直AC后系在树干PQ上的点E处,使得A,C,E在一条直线上,AB=AC=2m,DQ=3m.(1)垂钓时打开“晴雨伞”,若∠α=60°,求遮蔽宽度BC(结果精确到0.01m);(2)若由(1)中的位置收合“晴雨伞”,使得∠BAC=106°,求点E下降的高度(结果精确到0.1m).(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33,√3≈1.73)参考答案1.解:能,过B作BF⊥DE于F则EF=BC=3m,BF=CE在Rt△ABC中,∵AB=5m,BC=3m∴AC=√AB2−BC2=4(m)在Rt△ADE中,∵∠DAE=45°∴AE=DE设AE=DE=x m∴BF=(4+x)m,DF=(x﹣3)m在Rt△BDF中,tan38.7°=DFBF =x−34+x≈0.80解得x=31∴DE=31m答:信号塔DE的高为31m.2.解:过B作BM⊥ED于M,BN⊥CO于N ∴∠DMB=90°,∠ONB=90°∵∠BEM=45,∠BDE=37°,∠OCE=90°∴△OEC,OBN是等腰直角三角形设BN=MC=x m∴ME=(5﹣x)m,MD=(5.5﹣x)m在Rt△BMD中,∠DMB=90°∴tan∠BDM=BMDM =5−x5.5−x=0.75∴x=0.5∵∠BEM=45°,∠ECO=90°∴OB=√22∴AB=2OB=√2≈1.4(m)答:太阳能电池板宽AB的长度约为1.4m.3.解:过点E作EG⊥CD于点G∴∠EGC=90°.∵BC=60cm,坐垫E与点B的距离BE为10cm ∴CE=70(cm).∵∠ABC=64°,AB∥CD∴∠ECD=64°.∴EG=EC•sin64°≈70×0.90=63(cm).∵CD∥l,CF⊥l,l与⊙D相切,车轮半径为32cm ∴CF=32(cm).∴坐垫E到地面的距离为:63+32=95(cm).答:坐垫E到地面的距离为95cm;(2)过点E′作E′G′⊥CD于点G′∴∠E′G′C=90°.∵小明的腿长约为84cm∴E′G′=84×0.8=67.2(cm).∵∠ECD=64°∴CE′=67.2sin64°=67.20.90≈74.67(cm).∴EE′=CE′﹣CE=74.67﹣70=4.67≈4.7(cm).答:EE′长4.7cm.4.解:过点D作DE⊥BC,垂足为E,过点D作DF⊥AB,垂足为F由题意得:DF=BE,BF=DE∵坡长CD=10米,坡度i=3:4∴DECE=34∴设DE=3x米,则CE=4x米在Rt△CDE中,CD=√CE2+DE2=√(4x)2+(3x)2=5x(米)∴5x=10解得:x=2∴CE=8米,DE=BF=6米设BC=y米∴DF=BE=BC+CE=(y+8)米在Rt△ABC中,∠ACB=60°∴AB=BC•tan60°=√3y(米)在Rt△ADF中,∠ADF=45°∴AF=DF•tan45°=(y+8)米∵AB=AF+BF∴√3y=y+8+6解得:y=7√3+7∴AB=√3y=(21+7√3)米∴旗杆AB的高度为(21+7√3)米.5.解:(1)∵DE⊥AB∴△DBE是直角三角形在Rt△DBE中,sinα=BEDB=25∵BE=4∴BD=10即该支架的边BD的长为10米;(2)根据已知可得,在Rt△DBG中∠DBG=45°,且BD=10∴sin∠DBG=sin45°=DGDB即DG10=√22解得:DG=5√2在矩形GFCB中,GF=BC=3∴DF=DG+GF=(5√2+3)米.6.解:(1)过O作EF⊥OM于O,过A作AG⊥EF于G ∵AB=6米,OA:OB=2:1∴OA=4米,OB=2米∵∠AOM=127°,∠EOM=90°∴∠AOE=127°﹣90°=37°在Rt△AOG中,AG=AO×sin37°≈4×0.6=2.4(米)点A位于最高点时到地面的距离为2.4+3=5.4(米)答:点A位于最高点时到地面的距离为5.4米;(2)过O作EF⊥OM,过B作BC⊥EF于C,过B1作B1D⊥EF于D ∵∠AOE=37°∴∠BOC=∠AOE=37°,∠B1OD=∠A1OE=17.5°∵OB1=OB=2(米)在Rt△OBC中,BC=sin∠OCB×OB=sin37°×OB≈0.6×2=1.2(米)在Rt△OB1D中,B1D=sin17.5°×OB1≈0.3×2=0.6(米)∴BC+B1D=1.2+0.6=1.8(米)∴此时水桶B上升的高度为1.8米.7.解:连接EF交树BD于点G.由题意知;AE⊥AC,CF⊥AC,BD⊥AC又∵AE=CF=1.65米∴四边形EAGB、CFGB是矩形.∴BG=AE=1.65米.∠DGE=∠DGF=90°AB=EG,BC=GF.在Rt△EGD中∵∠DEG=45°∴AB=DG=EG=(DB﹣1.65)米.在Rt△FGD中∵tan∠DFG=DGGF∴BC=GF=DGtan∠DFG ≈DB−1.650.75米.∵AB+BC=AC=28∴DB﹣1.65+DB−1.65=280.75∴DB=13.65≈13.7(米).答:树BD的高度为13.7米.8.解:过F作FP⊥BG于P,延长EA交FP于Q则四边形PHEQ是矩形∴PQ=EH=80m,EQ=PH在Rt△EFQ中,∠FQE=90°,∠EFQ=53°,EF=500m∴FQ=EF•cos53°≈500×3=300(m),EQ=EF•sin53°≈500×45=400(m)5∴PH=EQ=400m,PF=FQ+PQ=300+80=380(m)在Rt△PFG中,∠FPG=90°,∠PFG=26.6°∴PG=PF•tan26.6°≈380×0.5=190(m)∴GH=PG+PH=190+400=590(m)答:大门与车间入口之间的距离GH的长约为590m.9.解:如图,延长EF交AG于点H,则EH⊥AG,作BP⊥AG于点P,则四边形BFHP是矩形∴FB=PH,FH=PB由i=5:12,可以假设BP=5x,AP=12x∵PB2+P A2=AB2∴(5x)2+(12x)2=392∴x=3或﹣3(舍去)∴PB=FH=15,AP=36设EF=a米,BF=b米∵tan∠EBF=EFBF∴ab≈2∴a≈2b①∵tan∠EAH=EHAH =EF+HFAP+PH=EF+BPAP+BF∴a+1536+b≈1.2②由①②得a≈70.5,b≈35.25答:塔顶到地面的高度EF约为70.5米.10.解:(1)∵AB=AC=2m,AO⊥BC ∴BC=2OC在Rt△AOC中,∠α=60°∴OC=AC•sin60°=2×√32=√3(m)∴BC=2OC=2√3≈3.46(m)∴遮蔽宽度BC约为3.46m;(2)过点E作EF⊥AD,垂足为F由题意得:EF=DQ=3m当∠α=60°时在Rt△AFE中,AF=EFtan60°=√3=√3(m)当∠BAC=106°时∵AB=AC,AO⊥BC∴∠EAF=12∠BAC=53°在Rt△AFE中,AF=EFtan53°≈31.33≈2.26(m)∴点E下降的高度=2.26﹣1.73≈0.5(m)∴点E下降的高度约为0.5m.第11页共11页。
解直角三角形测试题与答案

解直角三角形测试题与答案一、选择题(每小题 5 分,共 25 分)1、在直角三角形中,若一个锐角为 30°,斜边与较小直角边的和为 12,则斜边的长为()A 4B 6C 8D 10答案:C解析:设较小直角边为 x,则斜边为 2x,由题意得 2x + x = 12,解得 x = 4,所以斜边为 8。
2、在 Rt△ABC 中,∠C = 90°,sinA =,则 tanB 的值为()A B C D答案:D解析:因为 sinA =,设 BC = 4x,AB = 5x,则 AC = 3x,所以tanB =。
3、如图,在△ABC 中,∠C = 90°,AC = 8,∠A 的平分线 AD =,则 BC 的长为()A 12B 10C 8D 6答案:B解析:因为 AD 是∠A 的平分线,所以∠CAD =∠BAC。
在Rt△ACD 中,cos∠CAD =,即,解得 CD = 6。
在 Rt△ABC 中,BC =。
4、已知在 Rt△ABC 中,∠C = 90°,tanA =,则 sinA 的值为()A B C D答案:B解析:设 BC = 3x,AC = 4x,则 AB = 5x,所以 sinA =。
5、如图,在菱形 ABCD 中,DE⊥AB,cosA =,BE = 2,则tan∠DBE 的值是()A B 2C D答案:C解析:因为 cosA =,设 AD = 5x,AE = 3x,则 DE = 4x。
因为BE = 2,所以 5x 3x = 2,解得 x = 1,所以 DE = 4。
在 Rt△BDE 中,tan∠DBE =。
二、填空题(每小题 5 分,共 25 分)1、在 Rt△ABC 中,∠C = 90°,若 sinA =,AB = 10,则 BC=________。
答案:6解析:因为 sinA =,所以,设 BC = 3x,AB = 5x,因为 AB =10,所以 5x = 10,解得 x = 2,所以 BC = 6。
解直角三角形测试题与答案

解直角三角形测试题与答案一、选择题(每小题 3 分,共 30 分)1、在直角三角形中,若一个锐角为 30°,斜边与较小直角边的和为 12,则斜边的长为()A 4B 6C 8D 10答案:C解析:在直角三角形中,30°角所对的直角边等于斜边的一半。
设较小直角边为 x,则斜边为 2x,由题意得 2x + x = 12,解得 x = 4,所以斜边为 8。
2、已知在 Rt△ABC 中,∠C = 90°,sinA =,则 tanB 的值为()A B C D答案:A解析:因为 sinA =,所以设 BC = 3x,AB = 5x,则 AC = 4x。
所以 tanB =。
3、在△ABC 中,∠C = 90°,AB = 15,sinA =,则 BC 等于()A 9B 12C 10D 6答案:B解析:因为 sinA =,所以 BC = AB×sinA = 15×= 9。
4、如图,在 Rt△ABC 中,∠C = 90°,AC = 4,AB = 5,则cosB 的值是()A B C D答案:A解析:因为在 Rt△ABC 中,∠C = 90°,AC = 4,AB = 5,所以BC = 3。
所以 cosB =。
5、一个直角三角形的两条直角边分别为 6 和 8,则其斜边上的高为()A 48B 5C 3D 10答案:A解析:根据勾股定理可得斜边为 10,设斜边上的高为 h,根据面积相等可得 ×6×8 = ×10×h,解得 h = 48。
6、在 Rt△ABC 中,∠C = 90°,若 sinA =,则 cosA 的值为()A B C D答案:B解析:因为 sin²A + cos²A = 1,sinA =,所以 cosA =。
7、如图,在 Rt△ABC 中,∠ACB = 90°,CD⊥AB 于点 D,若AC =,BC = 2,则 sin∠ACD 的值为()A B C D答案:A解析:因为∠ACB = 90°,AC =,BC = 2,所以 AB = 3。
人教新版九年级下册《28.2_解直角三角形及其应用》2024年同步练习卷(13)+答案解析

人教新版九年级下册《28.2解直角三角形及其应用》2024年同步练习卷(13)一、选择题:本题共9小题,每小题3分,共27分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,,则拉线BC的长度为、D、B在同一条直线上()A.B.C.D.2.身高相同的甲、乙、丙三人放风筝,各人放出线长分别为300米、250米、200米,线与地面的夹角分别为、、假设风筝线是拉直的,三人所放风筝()A.甲的最高B.乙的最高C.丙的最高D.一样高3.如图,一艘海轮位于灯塔P的南偏东方向的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔P的北偏东的N处,则N处与灯塔P的距离为()A.40海里B.60海里C.70海里D.80海里4.如图,在地面上的点A处测得树顶B的仰角为度,,则树高BC为用含的代数式表示()A.B.C.D.5.如图,这是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为()A. B. C. D.24m6.如图,斜面AC的坡度与AD的比为1:2,米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若米,则旗杆BC的高度为()A.5米B.6米C.8米D.米7.如图,小明利用一个锐角是的三角板测操场旗杆的高度,已知他与旗杆之间的水平距离BC为15m,AB为即小明的眼睛与地面的距离,那么旗杆的高度是()A.B.C.D.8.如图,在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡,斜坡CD的坡度为:,坡顶D到BC的垂直距离米,点A、B、C、D、E在同一面内,在点D处测得建筑物顶点A的仰角为,则建筑物AB的高度约参考数据:,,A.米B.米C.米D.米9.如图,为了测量某建筑物BC高度,小明采用了如下的方法:先从与某建筑物底端B在同一水平线上的A 点出发,先沿斜坡AD行走260米至坡顶D处,再从D处沿水平方向继续前行若干米后至点E处,在E点测得该建筑物顶端C的仰角为,建筑物底端B的俯角为,其中点A、B、C、D、E在同一平面内,斜坡AD的坡度:,根据小明的测量数据,计算得出建筑物BC的高度约为计算结果精确到米,参考数据:,,,()A.米B.米C.米D.米二、填空题:本题共2小题,每小题3分,共6分。
中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)

中考数学总复习《解直角三角形的应用题》专题测试卷(附答案)1.如图,小明为了测量学校旗杆CD的高度,在地面离旗杆底部C处22米的A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,求旗杆的高度CD.(结果精确到0.1米)【参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62】2.如图,在一次数学实践活动中,小明同学为了测量学校旗杆EF的高度,在观测点A处观测旗杆顶点E的仰角为45°,接着小明朝旗杆方向前进了7m到达C点,此时,在观测点D处观测旗杆顶点E的仰角为60°.假设小明的身高为1.68m,求旗杆EF的高度.(结果保留一位小数.参考数据:√2≈1.414,√3≈ 1.732)3.如图,在徐州云龙湖旅游景区,点A为“彭城风华”观演场地,点B为“水族展览馆”,点C为“徐州汉画像石艺术馆”.已知∠BAC=60°,∠BCA=45°,AC=1640m.求“彭城风华”观演场地与“水族展览馆”之间的距离AB(精确到1m).(参考数据:√2≈1.41,√3≈1.73)4.大连作为沿海城市,我们常常可以在海边看到有人海钓.小华陪爷爷周末去东港海钓,爷爷将鱼竿AB摆成如图所示.已知AB=2.4m,在有鱼上钩时,鱼竿与地面的夹角∠BAD=45°.此时鱼线被拉直,鱼线BO= 3m.点O恰好位于海面,鱼线BO与海面OH的夹角∠BOH=60°.求海面OH与地面AD之间的距离DH的长.(结果保留一位小数,参考数据:√2=1.414,√3=1.73)5.让运动挥洒汗水,让青春闪耀光芒.重庆某中学倡议全校师生“每天运动一小时,快乐学习每一天”,响应学校号召,小明决定早睡早起,每天步行上学.如图,小明家在A处,学校在C处,从家到学校有两条线路,他可以从点A经过点B到点C,也可以从点A经过点D到点C.经测量,点B在点A的正北方向,AB=300米.点C在点B的北偏东45°;点D在点A的正东方向,点C在点D的北偏东30°方向CD=2900米.(1)求BC的长度(精确到个位);(2)小明每天步行上学都要从点A到点C,路线一;从点A经过点B到点C,路线二;从点A经过点D到点C,请计算说明他走哪一条路线较近?(参考数据:√2≈1.414,√3≈1.732,√6≈2.449)6.拉杆箱是外出旅行常用工具.某种拉杆箱示意图如图所示(滚轮忽略不计),箱体截面是矩形BCDE,BC 的长度为60cm,两节可调节的拉杆长度相等,且与BC在同一条直线上.如图1,当拉杆伸出一节(AB)时,AC与地面夹角∠ACG=53°;如图2,当拉杆伸出两节(AM、MB)时,AC与地面夹角∠ACG=37°,两种情况下拉杆把手A点距离地面高度相同.求每节拉杆的长度.(参考数据:sin53°≈45,sin37°≈35,tan53°≈4 3,tan37°≈34)7.某中学凤栖堂前一尊孔子雕像矗立于萋萋芳草间,小刚站在雕像前,自C处测得雕像顶A的仰角为53°,小强站凤栖堂门前的台阶上,自D处测得雕像顶A的仰角为45°,此时,两人的水平距离EC为0.45m,已知凤栖堂门前台阶斜坡CD的坡比为i=1:3.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)(1)计算台阶DE的高度;(2)求孔子雕像AB的高度.8.如图为某景区平面示意图,C为景区大门,A,B,D分别为三个风景点.经测量,A,B,C在同一直线上,且A,B在C的正北方向,AB=240米,点D在点B的南偏东75∘方向,在点A的东南方向.(参考数据:√2≈1.414,√3≈1.732)(1)求B,D两地的距离;(结果精确到0.1米)(2)大门C在风景点D的南偏西60∘方向,景区管理部门决定重新翻修CD之间的步道,求CD间的距离.9.小明和小玲游览一处景点,如图,两人同时从景区大门A出发,小明沿正东方向步行60米到一处小山B处,再沿着BC前往寺庙C处,在B处测得亭台D在北偏东15°方向上,而寺庙C在B的北偏东30°方向上,小玲沿着A的东北方向上步行一段时间到达亭台D处,再步行至正东方向的寺庙C处.(1)求小山B与亭台D之间的距离;(结果保留根号)(2)若两人步行速度一样,则谁先到达寺庙C处.(结果精确到个位,参考数据:√2≈1.41,√3≈1.73,√6≈2.45)10.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动,同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.数据采集:如图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角∠ACD=18.4°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD=37°,当到达点A正上方的点E处时,测得AE=9米数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算纪念碑顶部点A到地面的距离AB的长.(结果精确到1米.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin18.4°≈0.32,cos18.4°≈0.95,tan18.4°≈0.33)11.【综合与实践】如图1,光线从空气射入水中会发生折射现象,其中α代表入射角,β代表折射角.学习小组查阅资料了解到,若n=sinαsinβ,则把n称为折射率.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43)【实践操作】如图2,为了进一步研究光的折射现象,学习小组设计了如下实验:将激光笔固定在MN处,光线可沿PD照射到空容器底部B处,将水加至D处,且BF=12cm时,光点移动到C处,此时测得DF=16cm,BC=7cm四边形ABFE是矩形,GH是法线.【问题解决】(1)求入射角∠PDG的度数;(2)请求出光线从空气射入水中的折射率n.12.数学兴趣小组设计了一款含杯盖的奶茶纸杯(如图1),图2为该纸杯的透视效果图,在图3的设计草图中,由AF、线段EF和ED构成的图形为杯盖部分,其中AF、与ED均在以AD为直径的⊙O上,且AF= ED,G为EF的中点,点G是吸管插孔处(忽略插孔直径和吸管直径),由点A,B,C,D构成的图形(杯身部分)为等腰梯形,已知杯壁AB=13.6cm,杯底直径BC=5.8cm,杯壁与直线l的夹角为84°.(1)求杯口半径OD的长;(2)若杯盖顶FE=3.2cm,吸管BH=22cm,当吸管斜插,即吸管的一端与杯底点B重合时,求吸管漏出杯盖部分GH的长.(参考数据:sin84∘≈0.995,cos84∘≈0.105,tan84∘≈9.514,√15.93≈3.99,17.5222≈307.02,√315.43≈17.76,结果精确到0.1cm).13.为了保护小吉的视力,妈妈为他购买了可升降夹书阅读架(如图1),将其放置在水平桌面上的侧面示意图(如图2),测得底座高AB为2cm,∠ABC=150°,支架BC为18cm,面板长DE为24cm,CD为6cm.(厚度忽略不计)(1)求支点C离桌面l的高度:(计算结果保留根号)(2)小吉通过查阅资料,当面板DE绕点C转动时,面板与桌面的夹角α满足30°≤α≤70°时,能保护视力.当α从30°变化到70°的过程中,问面板上端E离桌面l的高度是增加了还是减少了?增加或减少了多少?(精确到0.1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)14.如图,四边形ABCD是某公园的游览步道(步道可以骑行),把四个景点连接起来,为了方便,在景点C的正东方设置了休息区K,其中休息区K在景点A的南偏西30°方向800√2米处,景点A在景点B的北偏东75°方向,景点B和休息区K两地相距400√5米(∠ABK<90°),景点D分别在休息区K、景点A的正东方向和正南方向.(参考数据:√2≈1.41,√5≈2.24,√6≈2.45)(1)求步道AB的长度;(2)周末小明和小宏相约一起去公园游玩,他们在景点C一起向正东出发,不久到达休息区K,他们发现有两条路线到达景点A,于是小宏想比赛看谁先到达景点A.他们分别租了一辆共享单车,两人同时在K点出发,小明选择①K−B−A路线,速度为每分钟320米;小宏选择②K−D−A路线,速度为每分钟240米,其中两人在各个景点停留的时间不计.请你通过计算说明,小明和小宏谁先到达景点A呢?15.某公园里有一座凉亭,亭盖呈圆锥状,如图所示,凉亭的顶点为O,点O在圆锥底面、地面上的正投影分别为点O1,O2,点P为圆锥底面的圆上一点,数据显示,该圆锥的底面半径为2米(即O1P=2米),圆锥底面离地面的高度为3米(即O1O2=3米).(1)若OO1=2米,求圆锥的侧面积;(2)现计划对亭盖的外部进行喷漆作业,需测算亭盖的外部面积(即圆锥的侧面积).因凉亭内堆积建筑材料,导致无法直接测量OO2的高度,工人先在水平地面上选取观测点A,B(A,B,O2在同一直线上),利用测角仪分别测得点O的仰角为α,β,其中tanα=12,tanβ=25,再测得A,B两点间的距离为m米(即AB=MN=m米),已知测角仪的高为1米(即MA=NB=QO2=1米),求亭盖的外部面积(用含m的代数式表示).16.赤水河畔的“美酒河”三个大字,是世界上最大的摩崖石刻汉字.小茜想测量绝壁上“美”字AG的高度,根据平面镜反射原理可推出入射光线与镜面的夹角等于反射光线与镜面的夹角(如图中∠DEC=∠AEB,∠DFC=∠GFB),具体操作如下:将平面镜水平放置于E处,小茜站在C处观测,俯角∠MDE=45°时,恰好通过平面镜看到“美”字顶端A处(CD为小茜眼睛到地面的高度),再将平面镜水平放置于F处观测,俯角∠MDF=36.9°时,恰好通过平面镜看到“美”字底端G处.测得BE=163.3m,CE=1.5m,点C,E,F,B在同一水平线上,点A,G,B在同一铅垂线上.(参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75)(1)CD的高度为__________m,CF的长为__________m;(2)求“美”字AG的高度.17.风能是一种清洁无公害的可再生能源,利用风力发电非常环保.如图1所示,是一种风力发电装置;如图2为简化图,塔座OD建在山坡DF上(坡比i=3:4,DE垂直于水平地面EF,O,D,E三点共线),坡面DF长10m,三个相同长度的风轮叶片OA,OB,OC可绕点O转动,每两个叶片之间的夹角为120°;当叶片静止,OA与OD重合时,在坡底F处向前走25米至点M处,测得点O处的仰角为53°,又向前走23.5米至点N处,测得点A处的仰角为30°(点E,F,M,N在同一水平线上).(1)求叶片OA的长;(2)在图2状态下,当叶片绕点O顺时针转动90°时(如图3),求叶片OC顶端C离水平地面EF的距离.(参考数据:sin53°≈45,cos53°≈35,tan53°≈43,√3≈1.7,结果保留整数)18.贵州旅游资源丰富.某景区为给游客提供更好的游览体验,拟在如图①景区内修建观光索道.设计示意图如图②所示,以山脚A为起点,沿途修建AB,CD两段长度相等的观光索道,最终到达山顶D处,中途设计了一段与AF平行的观光平台BC为50m.索道AB与AF的夹角为15°,CD与水平线的夹角为45°,A,B 两处的水平距离AE为576m,DF⊥AF,垂足为点F.(图中所有点都在同一平面内,点A,E,F在同一水平线上)(1)求索道AB的长(结果精确到1m);(2)求水平距离AF的长(结果精确到1m).(参考数据:sin15°≈0.26cos15°≈0.97tan15°≈0.27√2≈1.41)19.春天是踏青的好季节小明和小华决定去公园出游踏青.如图已知A为公园入口景点B位于A点东北方向400√2米处景点E位于A点南偏东30°方向景点B在景点E的正北方向景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.景点F既位于景点E的正东方向又位于景点D的正南方向.DF=400米.(参考数据:√2≈1.41,√3≈1.73,sin37.5°≈35,cos37.5°≈45,tan37.5°≈34)(1)求BE的长;(精确到个位)(2)小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/分小明在景点B、C处各停留了10分钟、5分钟.小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/分.小华在景点E、F处各停留了9分钟、8分钟.请通过计算说明:小明和小华谁先到达景点D处.20.如图是一种家用健身卷腹机由圆弧形滑轨⌒AB可伸缩支撑杆AC和手柄AD构成.图①是其侧面简化示意图.滑轨⌒AB支撑杆AC与手柄AD在点A处连接其中D A B三点在一条直线上.(1)如图① 固定∠DAC=120°,若BC=30√6cm,AC=60cm,求∠ABC的度数;(2)如图② 固定∠DAC=100°若AC=50cm,∠ABC=30°时圆弧形滑轨AB所在的圆恰好与直线BC 相切于点B求滑轨⌒AB的长度.(结果精确到0.1 参考数据:π取3.14 sin70°≈0.940)参考答案:1.解:由题意得BE⊥CD于EBE=AC=22米∠DBE=32°在Rt△DBE中DE=BE⋅tan∠DBE=22×0.62≈13.64(米)CD=CE+DE=1.5+13.64≈15.14(米)答:旗杆的高CD约为15.14米.2.解:延长AD交EF于点G设EG=x∵AD∥BF,EF⊥BF∵AG⊥EF∵∠B=∠F=∠AGF=90°∵四边形ABFG是矩形∠AGE=90°∵∠EAG=45°∵∠AEG=90°−∠EAG=45°∵AG=EG=x∵AD=7∵DG=x−7∵∠EDG=60°=√3∵tan∠EDG=EGDG=√3∵xx−7∵x=7(3+√3)2∵EG=7(3+√3)2∵GF=AB=1.68∵EF=EG+GF=7(3+√3)2+1.68≈7(3+1.732)2+1.68 =16.562+1.68=18.242≈18.2.故旗杆EF的高度约18.2m.3.解:过B作BH⊥AC于H设AH=xm∵∠BAC=60°∵∠ABH=90°−60°=30°∵AB=2AH=2xm∵tanA=tan60°=BHAH=√3∵BH=√3xm∵∠BCA=45°∠BHC=90°∵△BHC是等腰直角三角形∵CH=BH=√3xm∵AH+CH=√3x+x=AC=1640≈600.7∵x=√3+1∵AB=2x≈1201(m).答:“彭城风华”观演场地与“水族展览馆”之间的距离AB约是1201m.4.解:过点B作BC⊥OH交OH于点C延长AD交BC于点E∵四边形DECH是矩形∵DH=CE.根据题意可知∠BAD=45°,∠BOH=60°在Rt△ABE中AB=2.4m∵sin∠BAE=BEAB即sin45°=BE2.4=1.2×1.41=1.692.解得BE=2.4×√22在Rt△BOC中BO=3m∵sin∠BOC=BCBO即sin60°=BC3=1.5×1.73=2.595解得BC=3×√32∵DH=CE=BC−BE=0.903≈0.9(m).所以海面OH与地面AD之间得距离DH的长0.9m.5.(1)解:过点C作CM⊥AD交AD的延长线于点M过点B作BN⊥AM交AM于点N过点D作DH⊥BN 交BN于点H.由题可知:∠CBN=45°∠A=90°∠CDM=60°.∵四边形ABNM、四边形ABHD、四边形DMNH都是矩形△BCN是等腰直角三角形.在Rt△CMD中∵∠CDM=60°CD=2900米∵DM=12DC=1450米CM=√3DM=1450√3米∵AB=MN=300米∵CN=CM−MN=(1450√3−300)米在Rt△CBN中∠CBN=45°∵CB=√2CN=(1450√6−300√2)米≈3127米答:BC的长度为3127米.(2)解:路线一:AB+BC=(300+1450√6−300√2)米≈3427米∵AM=BN=CN=(1450√3−300)米∵AD=AM−DM=(1450√3−1750)米∵路线二:AD+CD=(1450√3+1150)米≈3361米∵3427<3361∵路线二较近.6.解:如图1 作AF⊥CG垂足为F设AB=xcm则AC=60+x∵sin53°=AFAC =AF60+x∴AF=(60+x)⋅sin53°如图2 作AH⊥CG垂足为H则AC=60+2x∴AH=(60+2x)⋅sin37°∵AF=AH∴(60+x)⋅sin53°=(60+2x)⋅sin37°∴4(60+x)5=3(60+2x)5解得:x=30.答:每节拉杆的长度为30cm.7.(1)解:∵凤栖堂门前台阶斜坡CD的坡比为i=1:3EC为0.45m∵DE EC =13∴DE=EC3=0.15m即台阶DE的高度为0.15m;(2)解:如图所示设AB的对边为MN作DF⊥MN于F∵由题意得四边形NFDE是矩形∵FN=DE=0.15m DF=NE设MN=xm则MF=(x−0.15)m在Rt△MFD中∠MDF=45°∵FD=MF=(x−0.15)m∵NC=NE−EC=(x−0.15)−0.45=(x−0.6)m∵tan53°=MNNC ≈43即xx−0.6=43解得x=2.4经检验x=2.4是原方程的解答:孔子雕像AB的高度约2.4m.8.(1)解:过点B作BP⊥AD于点P由题意知∠BAD=45∘∠CBD=75∘∴∠ADB=30∘∠ABP=45∘=∠A∴BD=2BP AP=BP在Rt△ABP中AB=240米∴AP=BP=AB=120√2(米)sin45∘∴BD=2BP=240√2≈339.4(米).答:B、D两地的距离约为339.4米;(2)解:过点B作BM⊥CD于点M由(1)得BD=2BP=240√2(米)∵∠CDB=180∘−60∘−75∘=45∘∠CBD=75∘∠DCB=60∘∴∠DBM=45∘=∠CDB∴BM=DM在Rt△BDM中BD=240√2sin45∘=BMBD∴BM=DM=BD⋅sin45∘=240√2×√2=240(米)2在Rt△BCM中∠CBM=75∘−45∘=30∘∴CM=BM⋅tan30∘=80√3(米)∴DC=DM+CM=240+80√3(米).9.解:(1)作BE⊥AD于点E由题意知AB=60∠A=45°∠ABD=90°+15°=105°∠CBA=90°+30°=120°在Rt△ABE中在Rt△BDE中ED=√3BE=30√6BD=2BE=60√2∴小山B与亭台D之间的距离60√2米(2)延长AB作DF⊥BA于点F作CG⊥BA于点G则∠CBG=180°−∠CBA=60°由题意知CD∥AB∵四边形CDFG是矩形∵CG=DF,CD=FG.∵AE=30√2ED=30√6∴AD=30√2+30√6在Rt△AFD中DF=AF=√2=30+30√3CG=DF=30+30√3米在Rt△BCG中BG=√3=10√3+30∴CD=FG=AB+BG−AF=60−20√3∴S玲=AD+CD=30√2+30√6+60−20√3≈141.2米S明=AB+BC=60+60+20√3≈154.6米∵141.2<154.6且两人速度一致∴小玲先到.答:小玲先到达寺庙C处.10.解:如图:延长CD交AB于点H则四边形CMBH为矩形∴CM=HB=20在Rt△ACH中∠AHC=90°∠ACH=18.4°∴tan∠ACH=AH CH∴CH=AHtan∠ACH=AHtan18.4°≈AH0.33在Rt△ECH中∠EHC=90°∠ECH=37°∴tan∠ECH=EH CH∴CH=EHtan∠ECH=EHtan37°≈EH0.75设AH=x.∵AE=9∴EH=x+9∴x0.33=x+90.75解得x≈7.1∴AB=AH+HB≈7.1+20=27.1≈27(米).答:点A到地面的距离AB的长约为27米.11.(1)解:如图1 ∵GH∥FB∴∠DBF=∠PDG,∵BF=12cm,DF=16cm,∴tan∠DBF=DFBF=1612=43,∵tan53°≈4 3∴入射角∠PDG约为53°.(2)解:如图2 作DM⊥AB于点T在Rt△BDF中BF=12cm,DF=16cm∴BD=√DF2+BF2=20cm,在Rt△DTC中TC=DF−BC=16−7=9cm,DT=BF=12cm∴CD=√DT2+TC2=√122+92=15cm,∴光线从空气射入水中的折射率∴光线从空气射入水中的折射率n=43.12.(1)解:过点B作BP⊥AD于点D过点C作CQ⊥AD于点Q延长BC到点R ∵四边形BCQP是矩形∵BC=QP BP=CQ∵AB=13.6cm杯底直径BC=5.8cm杯壁与直线l的夹角为84°点A B C D构成的图形(杯身部分)为等腰梯形∵AD∥BC CD=AB=13.6cm QP=BC=5.8cm∵∠A=∠D=∠DCR=84°∵BP=CQ CD=AB∵Rt△ABP≌Rt△DCQ(HL)∵AP=DQ∵AP=DQ=CDcosD=13.6×0.105=1.428(cm)CQ=CDsinD=13.6×0.995=13.532(cm)∵AD=2AP+PQ=DQ=2×1.428+5.8=8.656(cm)AD=4.328≈4.3(cm)∵OD=12故杯口半径OD的长为4.3cm.(2)解:连接GO并延长交BC于点N∵G为EF的中点EF=1.6(cm)∵GO⊥EF,EG=FG=12连接FD∵ AF=ED,∵∠EFD=∠ADF,∵AD∥EF∵GO⊥AD∵ AD∥BC∵GO⊥BC∵NO=13.532(cm)∵GO=√(4.3)2−(1.6)2≈4.0(cm)∵GN≈17.532(cm)∵GB=√(17.532)2+(2.9)2≈17.77(cm)∵GH=BH−GB=22−17.77≈4.2(cm)13.(1)解:过点C作CF⊥l于点F过点B作BM⊥CF于点M∴∠CFA=∠BMC=∠BMF=90°.由题意得:∠BAF=90°∴四边形ABMF为矩形∴MF=AB=2cm∠ABM=90°.∵∠ABC=150°∴∠MBC=60°.∵BC=18cm∴CM=BC⋅sin60°=18×√32=9√3(cm).∴CF=CM+MF=(9√3+2)cm.答:支点C离桌面l的高度为(9√3+2)cm;(2)解:过点C作CN∥l过点E作EH⊥CN于点H∴∠EHC=90°.∵DE=24cm CD=6cm∴CE=18cm.当∠ECH=30°时EH=CE⋅sin30°=18×12=9(cm);当∠ECH=70°时EH=CE⋅sin70°≈18×0.94=16.92(cm);∴16.92−9=7.92≈7.9(cm)∴当α从30°变化到70°的过程中面板上端E离桌面l的高度是增加了增加了约7.9cm.14.(1)解:由题意得∠DAK=30°∠BAD=75°∠D=90°AK=800√2米BK=400√5米∵∠BAK=∠BAD−∠DAK=75°−30°=45°过点K作KH⊥AB于H则∠AHK=∠BHK=90°∵△AHK为等腰直角三角形∵AH=KH=√22AK=√22×800√2=800米∵BH=√BK2−KH2=√(400√5)2−8002=400米∵AB=AH+BH=800+400=1200米;(2)解:∵AK=800√2∠DAK=30°∠D=90°∵DK=12AK=400√2米AD=AK·cos30°=800√2×√32=400√6米∵路线②K−D−A的路程为KD+AD=400√2+400√6≈1544米∵小宏到达景点A的时间为1544÷240≈6.43分钟∵路线①K−B−A的路程为KB+BA=400√5+1200≈2096米∵小明到达景点A的时间为2096÷320≈6.55分钟∵6.43<6.55∵小宏先到达景点A.15.(1)解:由题意得:∠OO1P=90°.∵OO1=2米O1P=2米∴OP=2√2(米).∴圆锥的侧面积=π×2√2×2=4√2π(米2).答:圆锥的侧面积为4√2π平方米;(2)解:由题意得:∠OQM=90°.设OQ长x米.∵tanα=1 2∴MQ=2x米.∵MN=m米∴NQ=(m+2x)米.∵tanβ=2 5∴xm+2x =25.解得:x=2m.∵O1O2=3米QO2=1米∴OO1=2m+1−3=(2m−2)米.∵O1P=2米∠OO1P=90°.∴OP=√22+(2m−2)2=√4m2−8m+8=2√m2−2m+2(米).∴圆锥的侧面积=π×2√m2−2m+2×2=4π√m2−2m+2(米2).答:亭盖的外部面积为4π√m2−2m+2平方米.16.(1)解:∵∠MDE=45°∴∠DEC=45°∵DC⊥BC∴△DCE是等腰直角三角形∴DC=CE=1.5m 在Rt△DCF中∠DFC=36.9°DC=1.5m∴DF=DCsin36.9°=1.50.60=2.5(m)∴CF=√DF2−DC2=√2⋅52−1⋅52=2(m);故答案为:1.52;(2)∵∠DEC=45°∴∠AEB=45°∴∠BAE=45°∴AB=BE=163.3m由题意可知∠MDF=36.9°∴∠GFB=∠DFC=∠MDF=36.9°∵EF=CF−CE=2−1.5=0.5(m)∴BF=163.3−0.5=162.8(m)在Rt△BFG中BG=tan∠GFB⋅BF≈0.75×162.8=122.1(m)∴AG=163.3−122.1=41.2(m)即“美”字的高度AG约为41.2m.17.(1)解:∵DE垂直于水平地面EF∵∠E=90°∵坡比i=3:4∵DE EF =34设DE=3xm则EF=4xm ∵坡面DF长10m∵(3x)2+(4x)2=102解得:x=2(负值舍去)∵DE=6m EF=8m∵MF=25m∵ME=MF+EF=33m由题意得:∠OME=53°=44m∵OE=ME⋅tan53°≈33×43∵MN=23.5m∵NE=ME+MN=56.5m.由题意得:∠N=30°≈32m∵AE=NE⋅tan30°=56.5×√33∵OA=OE−AE=44−32=12m.(2)如图过点C作CH⊥OE于点M CG⊥NE于G∵∠CHE=∠HEG=∠CGE=∠CHO=90°∵四边形HEGC是矩形∵EH=CG∵叶片绕点O顺时针转动90°∵∠AOE=90°∵∠AOC=120°∵∠COH=30°由题意得:OC=OA=12m=6√3m∵OH=OCcos∠COH=12×√32∵CG=HE=OE−OH=44−6√3≈34m.∵叶片OC顶端C离水平地面EF的距离为34m.18.(1)解:在Rt△ABE中∠AEB=90°∠A=15°AE=576m∴AB=AEcosA =576cos15°≈594(m).答:索道AB的长约为594m.(2)延长BC交DF于点G∵BC∥AF DF⊥AF∴DG⊥CG.∵四边形BEFG为矩形.∴EF=BG.∵CD=AB≈594m∠DCG=45°∴CG=CD·cos∠DCG≈594×cos45°=297√2(m).∴AF=AE+EF=AE+BG=AE+BC+CG≈576+50+297√2≈1045(m).答:水平距离AF的长约为1045m19.(1)解:如图所示过点A作AH⊥BE于点H∵∠BAH=45°,AB=400√2米∴AH=BH=√22AB=400米∵∠AEB=30°∴HE=√3AH=400√3米AE=2AH=800米∴BE=400+400√3≈1092(米).∴BE长约1092米.(2)解:小华先到达景点D处理由如下:如图过点C作CN⊥EF于点N过点D作DM⊥BE于点M交CN于点G则四边形BCNE和四边形DFNG都是矩形∴BC=EN BE=CN=(400+400√3)米GN=DF=400米DG=NF∴CG=CN−GN=400√3米∵景点C既位于景点B正东方向310米处又位于景点D的北偏西37.5°方向.∴BC=310(米)∠DCN=37.5°在Rt△CGD中cos∠DCN=CGCD tan∠DCN=DGCG∴CD=CGcos37.5°=400√345≈865(米)DG=CG⋅tan37.5°=400√3×34≈519(米)∴EF=EN+NF=BC+DG≈829(米)∵小明选择了游览路线①:A−B−C−D小明行驶的平均速度是72米/秒.小明在景点B、C处各停留了10分钟、5分钟∴小明的游览时间为400√2+310+86572+10+5≈39(分钟)在Rt△AEH中AH=400米∠EAH=60°∴AE=AHcos60°=40012=800(米)∵小华选择了游览路线②:A−E−F−D小华行驶的平均速度为96米/秒.小华在景点E、F处各停留了9分钟、8分钟∴小华的游览时间为800+829+40096+9+8≈38(分钟)∴小华的游览时间更短先到达景点D处.20.(1)解:如图过点C作CE⊥AB垂足为E∵∠DAC=120°∴∠EAC=180°−∠DAC=60°在Rt△AEC中AC=60cm∴CE=AC⋅sin60°=60×√32=30√3(cm)在Rt△BEC中BC=30√6cm∴sin∠EBC=ECBC=√330√6=√22∴∠ABC=45°∴∠ABC的度数约为45°;(2)解:如图过点A作AF⊥BC垂足为F∵圆弧形滑轨⌒AB所在的圆恰好与直线BC相切于点B ∴过点B作HB⊥BC作AB的垂直平分线MG交HB于点O连接OA∴OB=OA∴圆弧形滑轨⌒AB所在的圆的圆心为O∵∠DAC=100°∠ABC=30°∴∠ACF=∠DAC−∠ABC=100°−30=70°在Rt△AFC中AC=50cm∴AF=AC⋅sin70°≈50×0.940=47(cm)在Rt△AFB中∠ABC=30°∴AB=2AF=2×47=94(cm)∵OB⊥BC∴∠OBC=90°∴∠OBA=∠OBC−∠ABC=60°∴△OBA为等边三角形∴OB=AB=94cm∠BOA=60°∴滑轨⌒AB的长度=60π×94180≈98.4(cm)∴滑轨AB⌒AB的长度约为98.4cm.。
解直角三角形测试题

解直角三角形测试题一、选择题(每小题 3 分,共 30 分)1、在 Rt△ABC 中,∠C = 90°,若 sinA = 1/2,则∠A 的度数是()A 30°B 45°C 60°D 90°2、已知在 Rt△ABC 中,∠C = 90°,AC = 4,BC = 3,则 tanA的值是()A 3/4B 4/3C 3/5D 4/53、在 Rt△ABC 中,∠C = 90°,AB = 5,AC = 3,则 cosB 的值是()A 3/5B 4/5C 3/4D 4/34、若一个直角三角形的两条直角边的长分别为 5 和 12,则斜边上的高为()A 60/13B 13/60C 13D 605、在 Rt△ABC 中,∠C = 90°,sinA = 4/5,则 cosA 的值是()A 3/5B 4/5C 3/4D 4/36、如图,在 Rt△ABC 中,∠C = 90°,CD⊥AB 于点 D,若 AC= 5,BC = 12,则 CD 的长为()A 60/13B 120/13C 13/60D 5/127、已知α为锐角,且cosα = 06,则()A 0°<α < 30°B 30°<α < 45°C 45°<α < 60°D 60°<α < 90°8、在 Rt△ABC 中,∠C = 90°,若∠A = 30°,AB = 6,则 BC 的长为()A 3B 3√3C 2√3D 4√39、如图,在△ABC 中,∠C = 90°,∠B = 30°,AD 是∠BAC 的平分线,若 CD = 2,则 BD 的长为()A 2B 4C 6D 810、已知在 Rt△ABC 中,∠C = 90°,tanA = 3/4,则 sinA 的值是()A 3/5B 4/5C 3/4D 4/3二、填空题(每小题 3 分,共 18 分)11、在 Rt△ABC 中,∠C = 90°,AB = 13,BC = 5,则 sinA =________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形测验
解直角三角形的应用测试题
一、选择题(本大题共10小题,共30.0分)
1. 小明利用测角仪和旗杆的拉绳测量学校旗杆的高度如图,旗杆PA的高度与拉绳PB的长度相等小明将PB拉到的位置,测得为水平线,测角仪的高度为1米,则旗杆PA的高度为
A. B. C. D.
2. 如图,长4m的楼梯AB的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后的楼梯AC的长为
A. B. C. D.
2 3 4
3. 楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为现要在楼梯上铺一条地毯,已知米,楼梯宽度1米,则地毯的面积至少需要
A. 米
B. 米
C. 米
D. 米
4. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,9时30分到达B处如图从A、B两处分别测得小岛M在北偏东和北偏东方向,那么在B处船与小岛M的距离为 A. 20海里 B. 海里 C. 海里 D. 海里
5. 如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长m为
A. B. C. D.
6. 如图所示,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为,再向电视塔方向前进120米达到F处,又测得电视塔顶端A的仰角为,则这个电视塔的高度单位:米为
A. B. 61 C. D. 121
6 7 8
7. 某校八年级生物兴趣小组租两艘快艇去微山湖生物考察,他们从同一码头出发,第一艘快艇沿北偏西方向航行50千米,第二艘快艇沿南偏西方向航行50千米,如果此时第一艘快艇不动,第二艘快艇向第一艘快艇靠拢,那么第二艘快艇航行的方向和距离分别是
A. 南偏东,千米
B. 北偏西,千米
C. 南偏东,100千米
D. 北偏西,100千米
8. 如图,一艘海轮位于灯塔P的南偏东方向,距离灯塔60nmile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东方向上的B处,这时,B处与灯塔P的距离为 A. nmile B. nmile C. nmile D. nmile
9. 如图,一河坝的横断面为等腰梯形ABCD,坝顶宽10米,坝高12米,斜坡AB的坡度:,则坝底AD的长度为
A. 26米
B. 28米
C. 30米
D. 46米
9 10 11
10. 如图是某水库大坝的横截面示意图,已知,且AD、BC之间的距离为15米,背水坡CD 的坡度:,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD 加宽了2米,背水坡EF的坡度:4,则大坝底端增加的长度CF是米.
A. 7
B. 11
C. 13
D. 20
二、填空题(本大题共10小题,共30.0分)
11. 为加强防汛工作,某市对一拦水坝进行加固,如图,加固前拦水坝的横断面是梯形已知迎水坡面米,背水坡面米,,加固后拦水坝的横断面为梯形ABED,,则CE的长为______ 米
12. 如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离AD为90米,那么该建筑物的高度BC约为______ 米精确到1米,参考数据:
12 14 15
13. 小明沿着坡度i为1:的直路向上走了50m,则小明沿垂直方向升高了______
14. 如图,长4m的楼梯AB的倾斜角为,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角为,则调整后楼梯AC长为______ 米
15. 如图,一名滑雪运动员沿着倾斜角为的斜坡,从A滑行至B,已知米,则这名滑雪运动员的高度下降了______米参考数据:,,
16. 如图,为测量某栋楼房AB的高度,在C点测得A点的仰角为,朝楼房AB方向前进10米到达点D,再次测得A点的仰角为,则此楼房的高度为______ 米结果保留根号.
16 17 18
17. 如图,从热气球C处测得地面A、B两点的俯角分别为、,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是______米结果保留根号.
18. 如图,水库堤坝的横断面是梯形,测得BC长为30m,CD长为,斜坡AB的坡比为1:3,斜坡CD的坡比为1:2,则坝底的宽AD为______
19. 如图,某堤坝的斜坡AB的斜角是,坡度是,则______.
20. 某兴趣小组借助无人飞机航拍,如图,无人飞机从A处飞行至B处需12秒,在地面C 处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为3米秒,则这架无人飞机的飞行高度为结果保留根号 ______ 米
三、计算题(本大题共4小题,共24.0分)
21. 如图,某数学兴趣小组要测量一栋五层居民楼CD的高度该楼底层为车库,高米;上面五层居住,每层高度相等测角仪支架离地米,在A处测得五楼顶部点D的仰角为,在B处测得四楼顶部点E的仰角为,米求居民楼的高度精确到米,参考数据:
22. 某兴趣小组借助无人飞机航拍校园如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为,B处的仰角为已知无人飞机的飞行速度为4米秒,求这架无人飞机的飞行高度结果保留根号
23. 如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为,教学楼底部B的俯角为,量得实验楼与教学楼之间的距离.求的度数.求教学楼的高结果精确到,参考数据:,
24. 如图,在大楼AB的正前方有一斜坡CD,米,坡角,小红在斜坡下的点C处测得楼顶B 的仰角为,在斜坡上的点D处测得楼顶B的仰角为,其中点A、C、E在同一直线上.求斜坡CD的高度DE;求大楼AB的高度结果保留根号
四、解答题(本大题共2小题,共16.0分)
25. 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为,测得大楼顶端A的仰角为点B,C,E在同一水平直线上,已知,,求障碍物B,C两点间的距离结果精确到参考数据:,
26. 如图,某湖中有一孤立的小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PQ通往小岛,某同学在观光道AB上测得如下数据:米,,请求出小桥PQ的长,结果精确到米
答案和解析
【答案】
1. A
2. B
3. D
4. B
5. A
6. C
7. B
8. B
9. D 10. C
11. 8
12. 208
13. 25
14.
15. 280
16.
17.
18. 130
19.
20.
21. 解:设每层楼高为x米,由题意得:米,,,在中,,,在中,,,,,解得:,则居民楼高为米.
22. 解:如图,作,水平线,由题意得:,,,,,,,,,则.
23. 解:过点C作,则有,,;由题意得:,在中,,在中,,教学楼的高,则教学楼的高约为.
(六)DIY手工艺品的“创作交流性”24. 解:在中,米,,,米;过D作,交AB于点F,,,,即为等腰直角三角形,设米,四边形DEAF为矩形,米,即米,在中,,米,米,米,,,,在中,根据勾股定理得:,解得:,则米.。
