考点综合提升练(三)

合集下载

【步步高】高三语文总复习(浙江专用)【配套课件】文言文阅读第二章考点综合提升练(三)

)
一
1
2
3
4
5
二
6
7
8
9
10
2．下列各组句子中，加点词的意义和用法相同的一组是( 始足为忠义者戒． A. 巡船所物色经北舰十余里，为．
义所当死，死贤于生． B. 朝既而以吴民之乱请于．盖有舍生以取义者焉． C. 赂者丧不赂者以． Nhomakorabea)
连词，来/介词，何期拥兵则岁月犹存． D. 因为。长桥卧波，未云何龙．
一
1
2
3
4
5
二
6
7
8
9
10
犹记去岁华函见及某之报书有宁为文山之语至今日敢有食言夫自古废兴亦屡矣废兴之际何代无忠臣义士何代无逋臣处
士？义所当死，死贤于生；义所当生，生贤于死。盖有舍生以．．取义者焉，未闻求生以害仁者也。某之忧患已过乎文山，隐遁殆几于叠山矣。而被执以来，视死如归，非好死而恶生也。亦谓得从文山、叠山，异代同游，于事毕矣！
视：对比，赊：遥远，远离
比较。冀：希冀，希望 D．伏冀台下立赐处决．
一
1
2
3
4
5
二
6
7
8
9
10
2．下列各组句子中，加点词的意义和用法相同的一组是( 始足为忠义者戒． A. 巡船所物色经北舰十余里，为．
义所当死，死贤于生． B. 朝既而以吴民之乱请于．盖有舍生以取义者焉． C. 赂者丧不赂者以．何期拥兵则岁月犹存． D. 龙长桥卧波，未云何．
③
在，可考而知也。卒触天祐之怒，执之北去，叠山遂不食而死。盖未尝不叹古人守义之坚，殉节之笃也！

2023年钎焊高频考点训练3卷合壹(带答案)试题号42

2023年钎焊高频考点训练3卷合壹（带答案）（图片大小可自由调整）全文为Word可编辑，若为PDF皆为盗版，请谨慎购买！卷I一.全能考点(共100题)1.【判断题】钎焊复杂件用的感应圈和内热式感应器可借助氧磁体来控制高频磁场和增加感应圈的效率。

参考答案：√2.【单选题】钎料的选择应满足的基本要求,下列说法错误的是()。

A、适当(低于母材)的熔点B、较高的温度C、具有良好的润湿性能及填缝性能参考答案：B3.【判断题】真空环境下,金属不易挥发。

参考答案：×4.【判断题】炉中钎焊时,对可能经炉衬短路的电热设备,在测量绝缘电阻之后,应把炉衬充分烘干并冷却到环境温度。

参考答案：×5.【单选题】转盘式自动感应钎焊机的导承材质为()。

A、加碳橡胶B、石棉水泥C、高锰钢参考答案：B6.【单选题】气关式调节阀是随着输入信号压力的()而开大的调节阀。

A、减小B、增大C、不变参考答案：A7.【判断题】爆炸过程极短,仅1s左右,瞬间造成人员伤亡、财产损失环境破坏,其突发性大,破坏严重。

参考答案：√8.【单选题】下列哪项不是现场急救原则？A、先排险后施救B、先救命后治伤C、先疏导后救伤参考答案：C9.【判断题】乙炔与氧混合燃烧形成的火焰,称为氧-乙炔焰。

参考答案：√10.【单选题】冷壁真空炉炉体结构不包括()。

A、辐射屏B、热交换器C、电炉参考答案：C11.【单选题】沸腾钢中的杂质较多,一般有()。

A、硫B、镍C、硅参考答案：A12.【判断题】气瓶不要进行定期检验。

参考答案：×13.【单选题】下列不属于职业病管理管理依据的是()。

A、《中华人民共和国职业病防治法》B、《职业安全卫生管理体系试行标准》C、《职业病诊断与鉴定管理办法》参考答案：B14.【单选题】我国目前试行的高频电磁场卫生学参考标准电场为()V/m。

A、10B、20C、30参考答案：B15.【判断题】电热元件常用的材料有金属和非金属两大类。

中考数学提升作业考点系统复习第三章函数第五节反比例函数的综合题

3．★如图，在平面直角坐标系中，菱形OABC的边OA在x轴的正半轴上，反 k
比例函数y＝ x (x＞0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为12，则k的值为 4 .
4．(2022·深圳)如图，已知在Rt△ABO中，AO＝1，将△ABO绕O点旋转 k
至△A′B′O的位置，且点A′为OB中点，点B′在反比例函数y＝ x 上，则k的值为 3 .
k ∵反比例函数y1＝x(k≠0)的图象经过点D， ∴k＝6×4＝24，
24 ∴反比例函数的解析式为y＝ x .
(2)若AB所在直线解析式为y2＝ax＋b(a≠0)，当y1＞y2时，求x的取值范围．Βιβλιοθήκη ∵A(0，2)，B(6，8)，
∴把点A，B的坐标代入y2＝ax＋b得
b＝2，
a＝1，
6a＋b＝8，解得b＝2，
第五节反比例函数的综合题
1．如图，在平面直角坐标系中，点O为坐标原点，▱OBAD的顶点B在反比
例函数y＝
6 x
的图象上，顶点A在反比例函数y＝
k x
的图象上，顶点D在x轴
的负半轴上．若▱OBAD的面积是10，则k的值是
( D)
A．4
B．2
C．－2
D．－4
2．(2022·株洲)如图，矩形ABCD的顶点A，D在y轴上，顶点C在第一象限， x轴为该矩形的一条对称轴，且矩形ABCD的面积为6.若反比例函数y＝kx的图象经过点C，则k的值为 3 .
长的最小值是 2 2 .
(2)求反比例函数与一次函数的解析式；
将A(－2，4)代入y＝mx，得－8＝m， 8
∴反比例函数的解析式为y＝－x. 将A(－2，4)，B(－4，2)代入y＝ax＋b，得 4＝－2a＋b， a＝1， 2＝－4a＋b，解得b＝6， ∴一次函数的解析式为y＝x＋6.

事业单位招聘综合类考点强化练习经济考点(2023年版)_3

事业单位招聘综合类考点强化练习经济考点(2023 年最新版) 事业单位考试题库考点强化练习：1、单选题财政政策与货币政策一样都是通过调节_____来实现政府宏观经济目标的。

A : 总供给B : 总需求C : 总供给和总需求D : 总供给或总需求参考答案: B本题解释:【答案】B。

2、单选题下列有关需求的表述，不正确的是_____A : 对消费者需求量影响最大的是消费者的偏好B : 奢侈品的需求较富有弹性，而低档商品的需求较缺乏弹性C : 替代商品的价格越高，数量越少，消费者对本商品的需求量就越大D : 互补商品的价格越高，数量越少，消费者购买本商品的数量就越少参考答案: A本题解释:【答案】A。

解析：对消费者需求量影响最大的是价格因素。

3、多选题凯恩斯总需求决定理论所基于的三大心理规律是_____A : 流动性偏好B : 货币供给C : 资本边际效率递减D : 边际消费倾向递减参考答案: ACD本题解释:ACD[解析]凯恩斯经济学的核心理论是有效需求不足理论，造成有效需求不足的三大心理规律包括边际消费倾向递减规律、资本边际效率递减规律和流动偏好规律。

4、单选题为抑制商品房价格过快上涨，促进房地产市场健康发展，我国政府采取了一系列增加保障性住房供给的措施，如增加价格明显低于商品房的经济适用房、供低收人者租用的廉价房等。

政府出台这些措施是因为_____。

①增加经济适用房可以减少商品房购买需求②增加廉租房就能抑制商品房有效需求③经济适用房与廉租房互为替代品④增加保障性住房能缓解房地产市场的过度炒作A : ①②B : ②③C : ①④D : ③④参考答案: C本题解释:C[解析]②说法过于绝对，排除；廉租房与商品房是互为替代品，经济适用房与廉租房为互补品，③说法错误，排除；政府采取增加价格明显低于商品房的经济适用房、供低收入者租用的廉价房等措施是为了抑制商品房过热，①、④正确。

5、单选题以下哪种贷款的特点是用于环保、教育、扶贫和农业开发项目_____A : 国际金融组织贷款B : 国际产业贷款C : 外国政府贷款D : 出口信贷参考答案: C本题解释:【答案】C。

九年级中考数学考点提升训练——专题：《一次函数：动点综合》(四)(Word版,带答案)

九年级中考数学考点提升训练——专题：《一次函数：动点综合》（四）1．如图，平面直角坐标系xOy中，直线y＝﹣x+3交x轴于点A，交y轴于点B，点P是线段OA上一动点（不与点A重合），过点P作PC⊥AB于点C．（1）当点P是OA中点时，求△APC的面积；（2）连接BP，若BP平分∠ABO，求此时点P的坐标；（3）设点D是x轴上方的坐标平面内一点，若以点O，B，C，D为顶点的四边形是菱形，求点D的坐标及此时OP的长．2．如图①，在△ABC中，∠C＝90°，AB＝10，BC＝8．点D，E分别是边AC，BC上的动点，连接DE．设CD＝x（x＞0），BE＝y，y与x之间的函数关系如图②所示．（1）求出图②中线段PQ所在直线的函数表达式；（2）将△DCE沿DE翻折，得△DME．①点M是否可以落在△ABC的某条角平分线上？如果可以，求出相应x的值；如果不可以，说明理由；②直接写出△DME与△ABC重叠部分面积的最大值及相应x的值．3．数学课上，李老师提出问题：如图1，在正方形ABCD中，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F．求证：AE＝EF．经过思考，小聪展示了一种正确的解题思路．取AB的中点H，连接HE，则△BHE为等腰直角三角形，这时只需证△AHE与△ECF全等即可．在此基础上，同学们进行了进一步的探究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（不含点B，C）的任意一点”，其他条件不变，那么结论“AE＝EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程，如果不正确，请说明理由；（2）小华提出：如图3，如果点E是边BC延长线上的任意一点，其他条件不变，那么结论“AE＝EF”是否成立？（填“是”或“否”）；（3）小丽提出：如图4，在平面直角坐标系xOy中，点O与点B重合，正方形的边长为1，当E为BC边上（不含点B，C）的某一点时，点F恰好落在直线y＝﹣2x+3上，请直接写出此时点E的坐标．4．如图1，在平面直角坐标系中，OB＝10，F是y轴正半轴上一点．（1）若OF＝2，求直线BF的解析式；（2）设OF＝t，△OBF的面积为s，求s与t的函数关系（直接写出自变量t的取值范围）；（3）如图3，在（2）的条件下，过点B作BA⊥x轴，点C在x轴上，OF＝OC，连接AC，CD⊥直线BF于点D，∠ACB＝2∠CBD，AC＝13，OF＝OC，AC．BD交于点E，求此时t的值．5．如图，在平面直角坐标系中，直线l1：y＝x+6与y轴交于点A，直线l2：y＝kx+b与y轴交于点B，与l1相交于C（﹣3，3），AO＝2BO．（1）求直线l2：y＝kx+b的解析式；（2）求△ABC的面积．6．（1）已如：如图，正方形ABCD中，∠EDF＝45°，DE、DF分别交边AB、BC平点E、F，求证：EF＝AE+CF．（2）在平面直角坐标系中、正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点，将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y＝x上停止，旋转过程中，AB边交直线y＝x于点M，BC边交x轴于点N．设△MBN的周长为P，在旋转正方形OABC的过程中，P值是否有变化？请证明你的结论．7．如图，一次函数y＝2x+b的图象与x轴交于点A（2，0），与y轴交于点B．（1）求b的值．＝4，求点C坐标．（2）若直线AB上的点C在第一象限，且S△AOC8．如图，已知直线y＝x+2交x轴于A，交y轴于B，过B作BC⊥AB，且AB＝BC，点C 在第四象限，点R（3，0）．点P、Q分别在直线AB和BC上，△PQR是以RQ为斜边的等腰直角三角形，求出点P的坐标．9．小东同学根据函数的学习经验，对函数y＝|x﹣1|+|x+3|进行了探究，下面是他的探究过程：（1）已知x＝﹣3时|x+3|＝0；x＝1时|x﹣1|＝0，化简：①当x＜﹣3时，y＝；②当﹣3≤x≤1时，y＝；③当x＞1时，y＝；（2）在平面直角坐标系中画出y＝|x﹣1|+|x+3|的图象，根据图象，写出该函数的一条性质：；（3）根据上面的探究，解决下面问题：已知A（a，0）是x轴上一动点，B（1，0），C（﹣3，0），则AB+AC的最小值是．10．如图，在平面直角坐标系中，直线l：y＝x+4分别与x轴、y轴交于点B、C，且1：y＝x交于点A．与直线l2（1）分别求出点A、B、C的坐标；（2）若D是线段OA上的点，且△COD的面积为6，求直线CD的函数表达式；（3）在（2）的条件下，设P是射线CD上的点，在平面内是否存在点Q，使以O、C、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．参考答案1．解：（1）如图，连接BP，∵直线y＝﹣x+3交x轴于点A，交y轴于点B，∴点A（4，0），点B（0，3），∴AO＝4，OB＝3，∴AB＝＝＝5，∵点P是OA中点，∴AP＝OP＝2，∵S＝×AP×OB＝×AB×CP，△ABP∴CP＝，∴AC＝＝＝，∴S＝×AC×PC＝；△APC（2）∵BP平分∠ABO，∴∠OBP＝∠CBP，又∵BP＝BP，∠BOP＝∠BCP＝90°，∴△BOP≌△BCP（AAS），∴BO＝BC＝3，OP＝CP，∴AC＝AB﹣BC＝5﹣3＝2，∵AP2＝PC2+AC2，∴（4﹣OP）2＝OP2+4，∴OP＝，∴点P（，0）；（3）若OB为边，如图2，设点C（a，﹣a+3），连接OD，∵四边形OCDB是菱形，∴OC＝CD＝BD＝OB＝3，BO∥CD，OD⊥BC，∴（a﹣0）2+（﹣a+3﹣0）2＝9，∴a1＝0（不合题意舍去），a2＝，∴点C（，），∵BO∥CD，OB＝CD＝3，∴点D（，），∴直线OD解析式为：y＝x，∵PC∥OD，∴设直线PC解析式为y＝x+b，∴＝×+b，∴b＝﹣3，∴直线PC解析式为y＝x﹣3，∴当y＝0时，x＝，∴点P（，0），∴OP＝；若OB为对角线，如图3，设点C（a，﹣a+3），连接CD，∵四边形OCBD是菱形，∴OB与CD互相垂直平分，∴点C在OB的垂直平分线上，∴＝﹣a+3，∴a＝2，∴点C（2，），∵BO垂直CD，∴点D（﹣2，），设直线PC解析式为y＝x+b，∴＝×2+b，∴b＝﹣，∴设直线PC解析式为y＝x﹣，当y＝0时，x＝，∴点P（，0），∴OP＝；综上所述：当OP＝时，点D（﹣2，）或当OP＝时，点D（，）．2．解：（1）设线段PQ所在直线的函数表达式为y＝kx+b，将P（3，4）和Q（6，0）代入得，，解得，∴线段PQ所在直线的函数表达式为y＝﹣x+8；（2）①如图1，连接CM并延长CM交AB于点F，∵∠C＝90°，AB＝10，BC＝8，∴AC＝＝6，由（1）得BE＝﹣x+8，∴CE＝x，∴，∵∠DCE＝∠ACB，∴△DCE∽△ACB，∴∠DEC＝∠ABC，∴DE∥AB，∵点C和点M关于直线DE对称，∴CM⊥DE，∴CF⊥AB，＝AB•CF，∵S△ABC∴6×8＝10×CF，∴CF＝，∵∠C＝90°，CD＝x，CE＝x，∴DE＝＝x，∴CM＝x，MF＝x，过点M作MG⊥AC于点M，过点M作MH⊥BC于点H，则四边形GCHM为矩形，∵∠GCM+∠BCF＝∠BCF+∠ABC＝90°，∴∠GCM＝∠ABC，∵∠MGC＝∠ACB＝90°，∴△CGM∽△BCA，∴，即，∴MG＝x，CG＝x，∴MH＝x，（Ⅰ）若点M落在∠ACB的平分线上，则有MG＝MH，即x，解得x＝0（不合题意舍去），（Ⅱ）若点M落在∠BAC的平分线上，则有MG＝MF，即x，解得x＝，（Ⅲ）若点M落在∠ABC的平分线上，则有MH＝MF，即x＝x，解得x＝．综合以上可得，当x＝或x＝时，点M落在△ABC的某条角平分线上．②当0＜x≤3时，点M不在形外，△DME与△ABC重叠部分面积为△DME的面积，∴S＝，当x＝3时，S的最大值为＝6．当3＜x≤6时，点M在形外，如图2，由①知CM ＝2CQ ＝x ， ∴MT ＝CM ﹣CF ＝，∵PK ∥DE ，∴△MPK ∽△MDE ， ∴＝＝，∴S △MPK ＝S △MDE •，∵S 四边形DEKP ＝S △MDE ﹣S △MPK ，∴S 四边形DEKP ＝＝，化简得S 四边形DEKP ＝﹣2x 2+16x ﹣24＝﹣2（x ﹣4）2+8，∴当x ＝4时，△DME 与△ABC 重叠部分面积的最大值为8．综合可得，当x ＝4时，△DME 与△ABC 重叠部分面积的最大值为8．3．解：（1）仍然成立，如图2，在AB 上截取BH ＝BE ，连接HE ，∵四边形ABCD 是正方形，∴AB＝BC，∠ABC＝90°＝∠BCD，∵CF平分∠DCG，∴∠DCF＝45°，∴∠ECF＝135°，∵BH＝BE，AB＝BC，∴∠BHE＝∠BEH＝45°，AH＝CE，∴∠AHE＝∠ECF＝135°，∵AE⊥EF，∴∠AEB+∠FEC＝90°，∵∠AEB+∠BAE＝90°，∴∠FEC＝∠BAE，∴△AHE≌△ECF（ASA），∴AE＝EF；（2）如图3，在BA的延长线上取一点N，使AN＝CE，连接NE．∵AB＝BC，AN＝CE，∴BN＝BE，∴∠N＝∠FCE＝45°，∵四边形ABCD是正方形，∴AD∥BE，∴∠DAE＝∠BEA，∴∠NAE＝∠CEF，在△ANE和△ECF中，，∴△ANE≌△ECF（ASA）∴AE＝EF，故答案是：是；（3）如图4，在BA上截取BH＝BE，连接HE，过点F作FM⊥x轴于M，设点E（a，0），∴BE＝a＝BH，∴HE＝a，由（1）可得△AHE≌△ECF，∴CF＝HE＝a，∵CF平分∠DCM，∴∠DCF＝∠FCM＝45°，∵FM⊥CM，∴∠CFM＝∠FCM＝45°，∴CM＝FM＝＝a，∴BM＝1+a，∴点F（1+a，a），∵点F恰好落在直线y＝﹣2x+3上，∴a＝﹣2（1+a）+3，∴a＝，∴点E（，0）．4．解：（1）∵OB＝10，OF＝2，∴B（﹣10，0），F（0，2），设直线BF的解析式为y＝kx+b，∵直线y＝kx+b经过点B（﹣10，0），F（0，2），∴，解得：，∴直线BF的解析式为y＝x+2；（2）△OBF的面积为S＝＝5t（t＞0）；（3）如图，延长AB至点R，使BR＝AB，连接CR，延长CD交y轴于点T，过点T，作TM ∥x轴交BA的延长线于点M，过点T作TK⊥CR交RC的延长线于点K，连接RT，∵AB⊥BC，AB＝BR，∴BC垂直平分AR，∴AC＝CR＝13，∴∠ACB＝∠RCB，设∠CBD＝α，则∠ACB＝2α，∵BD⊥CD，∴∠BDC＝90°，∴∠BCD＝90°﹣α，∵∠ACB＝∠RCB＝2α，∴∠ACK＝180°﹣4α，∴∠KCT＝∠BCK﹣∠BCD＝∠BCA+∠ACK﹣∠BCD＝90°﹣α，∴∠KCT＝∠BCD，∵TK⊥KR，OT⊥OC，∴OT＝TK，∵TC＝TC，∴Rt△OTC≌Rt△KTC（HL），∴OC＝CK＝t，∵OF＝OC，∠BOF＝∠TOC，∠FBO＝∠OTC，∴△BOF≌△TOC（AAS），∴OB＝OT＝10，∴TK＝10，∵∠ABO+∠BOT＝90°+90°＝180°．∴MB∥OT，∵MT∥OB，∴四边形OBMT为平行四边形，∵OB＝OT，∠BOT＝90°．∴四边形OBMT为正方形，∴MB＝MT＝OT＝10，∴MT＝TK，∵RT＝RT，∴Rt△RMT≌Rt△RTK（HL），∴RK＝RM＝CR+CK＝13+t，∴BR＝RM﹣MB＝3+t，∵BC＝OB+OC＝10+t，在Rt△BRC中，BR2+BC2＝RC2，∴（3+t）2+（10+t）2＝132，解得：t＝2（t＝﹣15舍去）．∴t的值为2．：y＝x+6与y轴交于点A，5．解：（1）∵直线l1∴当x＝0时，y＝0+6＝6，∴A（0，6），∵AO＝2BO，∴B（0，﹣3），∵C（﹣3，3），代入直线l：y＝kx+b中得，2解得．的解析式为y＝﹣2x﹣3；故直线l2＝AB•|x C|＝×（6+3）×3＝．（2）S△ABC6．（1）证明：∵四边形ABCD为正方形，∴DA＝DC，∠A＝∠ADC＝∠ACB＝90°，把△DAE绕点D逆时针旋转90°得到△DCG，如图1，∴∠EDG＝90°，DE＝DG，AE＝CG，∠DCG＝∠A＝90°，∵∠DCB+∠DCG＝180°，∴B、C、G三点共线，∵∠EDF＝45°，∴∠GDF＝∠EDG﹣45°＝45°，∴∠EDF＝∠GDF，在△DFE和△DFG中，∴△DFE≌△DFG（SAS），∴EF＝FG，∴EF＝FC+CG＝FC+AE；（2）解：在旋转正方形OABC的过程中，P值不变．理由如下：∵直线y＝x为第一、三象限的角平分线，∴∠MON＝45°，由（1）的结论得MN＝AM+CN，∴P＝BM+BN+MN＝BM+AM+BN+CN＝BA+BC＝2AB，而AB为正方形的边长，∴P的值为定值．7．解：（1）将A（2，0）代入直线y＝2x+b中，得2×2+b＝0解得b＝﹣4；＝4，点A（2，0），（2）∵S△AOC∴OA＝2，∴•OA•y C＝4，解得y C＝4，把y＝4代入y＝2x﹣4得2x﹣4＝4，解得x＝4，∴C（4，4）．8．解：∵直线AB为：y＝x+2，BC⊥AB，∴直线BC为：y＝﹣x+2，①当点P在第二象限时，如下图，过点P作y轴的平行线交过点Q与x轴的平行线于点G，交x轴于点H，延长GQ交y轴于点M，∵∠GAQ+∠HPR＝90°，∠HPR+∠PRH＝90°，∴∠PRH＝∠GAQ，又∠QGA＝∠PHR＝90°，PR＝PQ，∴△PHR≌△QGP（AAS），∴GQ＝PH，HR＝PG，设：点P、Q的坐标分别为（m，m+2）、（n，﹣n+2），GQ＝PH，即：n﹣m＝m+2…①，HR＝PG，即：﹣n+2﹣m﹣2＝3﹣m…②，联立①②并解得：m＝﹣，故点P的坐标（﹣，），②当点P在第一象限时，同理可得：点P的坐标为（，），故：点P的坐标为（﹣，）或（，）．9．解：（1）∵x＝﹣3时|x+3|＝0；x＝1时|x﹣1|＝0∴当x＜﹣3时，y＝1﹣x﹣x﹣3＝﹣2﹣2x；②当﹣3≤x≤1时，y＝1﹣x+x+3＝4；③当x＞1时，y＝x﹣1+x+3＝2x+2；故答案为：﹣2﹣2x；4；2x+2．（2）在平面直角坐标系中画出y＝|x﹣1|+|x+3|的图象，如图所示：根据图象，该函数图象不过原点．故答案为：函数图象不过原点；（3）根据上面的探究可知当A（a，0）位于点B（1，0）和点C（﹣3，0）之间时，AB+AC 有最小值4．故答案为：4．10．解：（1）∵y＝x+4分别与x轴、y轴交于点B、C，∴点C坐标为（0，4），点B坐标为（8，0），∵直线l1：y＝x+4与直线l2：y＝x交于点A．∴﹣x+4＝x，∴x＝，∴点A坐标为（，）；（2）设点D坐标为（x，x），∵△COD的面积为6，∴×4×|x|＝6，∴x＝±3，∵D是线段OA上的点，∴x＝3，∴点D（3，1），设直线CD解析式为：y＝kx+4，∴1＝3k+4，∴k＝﹣1，∴直线CD解析式为：y＝﹣x+4；（3）若以OC为边，设点P（a，﹣a+4）（a≥0），如图，当四边形OCPQ是菱形，∴OC＝CP＝4，PQ∥OC，PQ＝OC＝4，∴4＝，∴a1＝2，a2＝﹣2（舍去），∴点P（2，4﹣2），∴点Q（2，﹣2）；当四边形OCQ'P'是菱形，∴OC＝OP'＝4，PQ'＝OC＝4，PQ'∥OC，∴4＝，∴a1＝0（舍去），a2＝4，∴点P'（4，0），∴点Q'（4，4）；若OC为对角线，∵以O、C、P、Q为顶点的四边形是菱形，∴CO与PQ互相垂直平分，∴点P的纵坐标为2，∴点P（2，2），∴点Q坐标为（﹣2，2）；综上所述：点Q的坐标为（﹣2，2）或（4，4）或（2，﹣2）．。

2023年中考九年级数学高频考点提升练习--圆的综合题(含答案)

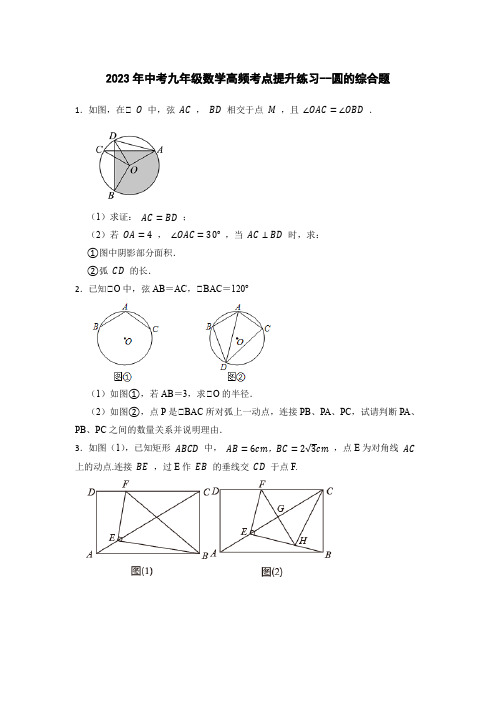
2023年中考九年级数学高频考点提升练习--圆的综合题1．如图，在⊙ O中，弦AC，BD相交于点M，且∠OAC=∠OBD．（1）求证：AC=BD；（2）若OA=4，∠OAC=30°，当AC⊥BD时，求：①图中阴影部分面积．②弧CD的长．2．已知⊙O中，弦AB＝AC，⊙BAC＝120°（1）如图①，若AB＝3，求⊙O的半径．（2）如图②，点P是⊙BAC所对弧上一动点，连接PB、PA、PC，试请判断PA、PB、PC之间的数量关系并说明理由．3．如图（1），已知矩形ABCD中，AB=6cm，BC=2√3cm，点E为对角线AC 上的动点.连接BE，过E作EB的垂线交CD于点F.（1）探索BE与EF的数量关系，并说明理由.（2）如图（2），过F作AC垂线交AC于点G，交EB于点H，连接CH.若点E从A出发沿AC方向以2√3cm/s的速度向终点C运动，设E的运动时间为ts.①是否存在t，使得H与B重合？若存在，求出t的值；若不存在，说明理由；②t为何值时，△CFH是等腰三角形；③当CG=GH时，求△CGH的面积.4．如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD交BA的延长线于点E.（1）求证：CD是⊙O的切线；（2）求证：⊙C＝2⊙DBE.（3）若EA＝AO＝2，求图中阴影部分的面积.（结果保留π）5．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”.如图1，⊙ABC中，点D 是BC边上一点，连结AD，若AD2=BD⋅CD，则称点D是⊙ABC中BC边上的“好点”.（1）如图2，⊙ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”.（2）⊙ABC中，BC=9，tanB=43，tanC=23，点D是BC边上的“好点”，求线段BD的长.（3）如图3，⊙ABC是⊙O的内接三角形，OH⊙AB于点H，连结CH并延长交⊙O于点D.①求证：点H是⊙BCD中CD边上的“好点”.②若⊙O的半径为9，⊙ABD=90°，OH=6，请直接写出CHDH的值.6．如图，⊙O为等边⊙ABC的外接圆，半径为2，点D在劣弧上运动（不与点A，B 重合），连接DA，DB，DC.（1）求证：DC是⊙ADB的平分线；（2）设四边形ADBC的面积为S，线段DC的长为x，试用含x的代数式表示S；（3）若点M，N分别在线段CA，CB上运动（不含端点），经过探究发现，点D 运动到每一个确定的位置，⊙DMN的周长有最小值t，随着点D的运动，t的值会发生变化，求所有t值中的最大值.7．在⊙ABC中，D，E分别是⊙ABC两边的中点，如果弧DE（可以是劣弧、优弧或半圆）上的所有点都在⊙ABC的内部或边上，则称弧DE为⊙ABC的中内弧．例如，图1中弧DE是⊙ABC其中的某一条中内弧．（1）如图2，在边长为4 √3的等边⊙ABC中，D，E分别是AB，AC的中点．画出⊙ABC的最长的中内弧DE，并直接写出此时弧DE的长；（2）在平面直角坐标系中，已知点A（2 √3，6），B（0，0），C（t，0），在⊙ABC中，D，E分别是AB，AC的中点．①若t＝2 √3，求⊙ABC的中内弧DE所在圆的圆心P的纵坐标的取值范围；②请写出一个t的值，使得⊙ABC的中内弧DE所在圆的圆心P的纵坐标可以取全体实数值．8．如图，⊙O是⊙ABC的外接圆，AC是直径，过点O作OD⊙AB于点D，延长DO 交⊙O于点P，过点P作PE⊙AC于点E，作射线DE交BC的延长线于F点，连接PF．（1）若⊙POC=60°，AC=12，求劣弧PC的长；（结果保留π）（2）求证：OD=OE；（3）求证：PF是⊙O的切线．9．如图，点A和动点P在直线l上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ：AB=3：4，作△ABQ的外接圆O.点C在点P右侧，PC=4，过点C作直线m⊥l，过点O作OD⊥m于点D，交AB右侧的圆弧于点E.在射线CD上取点F，使DF=32CD，以DE，DF为邻边作矩形DEGF.设AQ=3x.（1）用关于x的代数式表示BQ=，DF=.（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长.（3）当点P在点A右侧时，作直线BG交⊙O于点N，若BN的弦心距为1，求AP的长.10．如图，⊙ABC中，⊙ACB=90°，D是边AB上一点，且⊙A=2⊙DCB．E是BC边上的一点，以EC为直径的⊙O经过点D．（1）求证：AB是⊙O的切线；（2）若CD的弦心距为1，BE=EO，求BD的长．11．已知：A、B两点在直线l的同一侧，线段AO，BM均是直线l的垂线段，且BM 在AO的右边，AO=2BM，将BM沿直线l向右平移，在平移过程中，始终保持⊙ABP=90°不变，BP边与直线l相交于点P．（1）当P与O重合时（如图2所示），设点C是AO的中点，连接BC．求证：四边形OCBM是正方形；（2）请利用如图1所示的情形，求证：ABPB=OMBM；（3）若AO=2 √6，且当MO=2PO时，请直接写出AB和PB的长．12．（问题情境）如图①，小区A、B位于一条笔直的道路l的同侧，为了方便A，B两个小区居民投放垃圾，现在l上建一个垃圾分类站C，使得C与A，B的距离之比为2：1.（1）（初步研究）在线段AB上作出点C，使CACB=2.如图，做法如下：第一步：过点A作射线AM，以A为圆心，任意长为半径画弧，交AM于点P1；以P1为圆心，AP1长为半径画弧，交AM于点P2；以P2为圆心，AP1长为半径画弧，交AM于点P3.第二步：连接BP3，作∠AP2C=∠AP3B，交AB于点C.则点C即为所求.请证明所作的点C满足CACB=2.（2）（深入思考）如图，点C在线段AB上，点D在直线AB外，且DADB=CACB=2.求证：DC是∠ADB的平分线.（3）（问题解决）如图，已知点A，B和直线l，点C在线段AB上，且CACB=2.用直尺和圆规完成下列作图.（保留作图痕迹，不写作法）（⊙）在直线AB上作出点E（异于点C），使EAEB=2；（⊙）在直线l上作出点F，使FAFB=2.13．在矩形ABCD中，BC=2AB，点E是对角线AC上任意一点，过点E作AD的垂线分别交AD，BC于点F，G，作FH平行AC交CD于点H．（1）证明：EF=CH．（2）连结GH交AC于点K，若AE：CK=3，求AE：EK的值．（3）作⊙FGH的外接圆⊙O，且AB=1．①若⊙O与矩形的边相切时，求CH的长．②作点E关于GH的对称点E'，当E'落在⊙O上时，直接写出⊙FGH的面积。

2023高考化学综合提升训练题及答案

2023高考化学综合提升训练题及答案高考化学综合提升训练题及答案一、选择题(16小题，每小题3分，共48分，每小题只有一个正确答案)1.化学在生产和生活中有重要的应用，下列说法正确的是()A.新型材料聚酯纤维、光导纤维都属于有机高分子化合物B.14C可用于文物年代的鉴定，14C与12C互为同素异形体C.福美林可作食品的保鲜剂D.“开发利用新能源”、“汽车尾气催化净化”都能提高空气质量【答案】D考点：考查化学与生活的判断2.NA为阿伏加德罗常数的值，下列说法正确的是A.标准状况下，2.24LO2中含有的共键数为0.4NAB.0.1molH2S和0.1molSO2混合后，体系中的硫原子数0.2NAC.100g质量分数为16.2%HBr溶液中的氢原子数为NAD.3.9gNa2O2晶体中所含的离子总数为0.5NA【答案】B考点：考查阿伏加德罗常数的正误判断3.将铜和氧化铁的混和物溶于足量稀盐酸中，向所得溶液中滴入2滴KSCN溶液后出现红色。

下列有关说法错误的是A.容器中可能有固体残渣B.所得溶液中一定存在Fe2+C.反应过程中水的电离程度增大D.再加入铜后，溶液红色逐渐退去【答案】A【解析】试题分析：将铜和氧化铁的混和物溶于足量稀盐酸中，发生反应Fe2O3+6HCl=2FeCl3+3H2O，2FeCl3+Cu=2FeCl2+CuCl2，向所得溶液中滴入2滴KSCN溶液后出现红色，说明铁离子过量，铜在溶液中一定全部溶解，生成氯化铜，部分铁元素变化为亚铁盐。

A、氧化铁溶于过量的稀盐酸，生成的氯化铁过量铜全部溶解，容器中不可能有固体残渣，故A错误;B、向所得溶液中滴入2滴KSCN溶液后出现红色，说明铁离子过量，铜在溶液中一定全部溶解，生成氯化铜，部分铁元素变化为亚铁盐，故B 正确;C、氧化铁溶解于盐酸，氢离子浓度减小，生成的氯化铜、氯化亚铁和氯化铁溶液中水解溶液显酸性，对水的电离起到促进作用，反应过程中水的电离程度增大，故C正确;D、分析可知铁离子过量，向所得溶液中滴入2滴KSCN溶液后出现红色，Fe3++3SCN-Fe(SCN)3，加入铜发生反应2FeCl3+Cu=2FeCl2+CuCl2，Fe3++3SCN-Fe(SCN)3，平衡逆向进行，铁离子消失后溶液红色褪去，故D正确;故选A。

2023高考地理高频考点技能提升练习：生态建设(附答案解析)

2023高考地理高频考点技能提升练习：生态建设（附答案解析）一、选择题2018年2月,国务院批复同意《呼包鄂榆城市群发展规划》(以下简称《规划》),《规划》指出,呼包鄂榆城市群的战略定位为全国高端能源化工基地、向北向西开放战略支点、西北地区生态文明合作共建区、民族地区城乡融合发展先行区。

《规划》要求打造四大优势产业集群--高端能源化工产业集群、金属加工和装备制造产业集群、战略性新兴产业集群、绿色农畜产品生产加工产业集群。

努力提升人口和经济集聚水平,将呼包鄂榆城市群培育发展成为中西部地区具有重要影响力的城市群。

下图为呼包鄂榆城市群规划范围示意图。

据此完成下面小题。

1．国家规划发展呼包鄂榆城市群的重要意义是（）A．推动产业分工协作和转型升级B．带动西北地区矿产资源开发C．推进中国与朝鲜经济走廊建设D．推动东部地区人口向西部地区迁移2．呼包鄂榆城市群建设高端能源化工基地的区位优势是（）A．人口稠密,劳动力丰富且廉价B．有众多高校科研院所,科技力量雄厚C．交通便利,对外联系方便D．能源矿产资源富集,原料、燃料充足【答案】1．A2．D【解析】1．国家规划发展呼包鄂榆城市群的重要性在于立足其资源条件和产业基础，推动产业分工协作和转型升级，加快淘汰落后产能，大力发展优势产业、战略性新兴产业和现代服务业，故 A 正确；对西北地区而言，呼包鄂榆城市群定位为西北地区生态文明合作共建区，不能带动西北地区矿产资源开发，并且由于西北地区环境相对恶劣，在矿产资源开发过程中可能会对生态环境造成破坏，故 B 错误；呼包鄂榆城市群的战略定位为向北向西开放战略支点，该城市群与朝鲜距离较远，故该城市群的规划发展不能推进中国与朝鲜经济走廊建设，故 C 错误；现代社会人口迁移主要受经济因素影响，东部地区比西部地区经济发达，故该城市群的规划发展不能推动东部地区人口向西部地区迁移，故D错误。

故本题选A。

2．呼包鄂榆城市群人口相对稀疏，并且高端产业发展要求劳动力素质较高，故 A 错误；呼包鄂榆城市群高校科研院所相对较少，故 B 错误；交通相对落后，立体交通运输网络正在构建，交通基础设施不完善，对外联系不方便，故 C 错误；高端能源化工业的能源、原料投入较大。

2015高考语文一轮文档：现代文阅读第2章专题2 考点综合提升练1

考点综合提升练(一)一、阅读下面的文字，完成文后题目。

文学与人生(节选)朱光潜从前中国人有“文以载道”的说法，后来有人嫌这看法的道学气太重，把“诗言志”一句老话抬出来，以为文学的功用只在言志；释志为“心之所之”，因此言志包含表现一切心灵活动在内。

文学理论家于是分文学为“载道”“言志”两派，仿佛以为这两派是极端，绝不相容——“载道”是“为道德教训而文艺”，“言志”是“为文艺而文艺”。

其实这问题的关键全在“道”字如何解释。

如果释“道”为狭义的道德教训，载道就显然小看了文学。

文学没有义务要变成劝世文或是修身科的高头讲章。

如果释“道”为人生世相的道理，文学就决不能离开“道”，“道”就是文学的真实性。

志为心之所之，也就要合乎“道”，情感思想的真实本身就是“道”，所以“言志”即“载道”，根本不是两回事。

哲学科学所谈的是“道”，文艺所谈的仍然是“道”，所不同者哲学科学的道是抽象的，是从人生世相中抽绎出来的，好比从盐水中所提出来的盐；文艺的道是具体的，是含蕴在人生世相中的，好比盐溶于水，饮者知咸，却不辨何者为盐，何者为水。

用另一个比喻来说，哲学科学的道是客观的、冷的、有精气而无血肉的；文艺的道是主观的、热的，通过作者的情感与人格的渗沥，精气与血肉凝成完整生命的。

换句话说，文艺的“道”与作者的“志”融为一体。

我常感觉到，与其说“文以载道”，不如说“因文证道”。

《楞严经》记载佛有一次问他的门徒从何种方便之门，发菩提心，证圆通道。

几十个菩萨罗汉轮次回答，有人说从声音，有人说从颜色，有人说从香味，大家总共说出二十五个法门。

读到这段文章，我心里起了一个幻想，假如我当时在座，轮到我起立作答时，我一定说我的方便之门是文艺。

我不敢说我证了道，可是从文艺的玩索，我窥见了道的一斑。

文艺到了最高的境界，从理智方面说，对于人生世相必有深广的观照与彻底的了解，如阿波罗凭高远眺，华严世界尽成明镜里的光影，大有佛家所谓万法皆空，空而不空的景象；从情感方面说，对于人世悲欢好丑必有平等的真挚的同情，冲突化除后的谐和，不沾小我利害的超脱，高等的幽默与高度的严肃，成为相反者之同一。

【省级联考】四川省2024届高三综合能力提升卷(三)物理高频考点试题

【省级联考】四川省2024届高三综合能力提升卷(三)物理高频考点试题一、单项选择题：本题共8小题，每小题3分，共24分，在每小题给出的答案中，只有一个符合题目要求。

(共8题)第(1)题均匀介质中，波源位于O点的简谐横波在水平面内传播，波面为圆。

某时刻第一象限内第一次出现如图（a）所示的波面分布，其中实线表示波峰，虚线表示相邻的波谷，从此时刻开始计时，坐标（，）处质点的振动图像如图（b）所示，轴正方向竖直向上。

下列说法正确的是（）A．该水波的波长为6mB ．，P点偏离平衡位置的位移为0.5cmC．，P点正在平衡位置的上方且向下运动D．若波源从平衡位置起振，则波源的起振方向一定向上第(2)题在一些电子显示设备中，让阴极发射的电子束通过适当的非匀强电场，可以使发散的电子束聚集。

下列4幅图中带箭头的实线表示电场线，如果用虚线表示电子可能的运动轨迹，其中正确的是（）A．B．C．D．第(3)题某探险者在野外攀岩时，踩落一小石块，约5s后听到石头直接落到崖底的声音，探险者离崖底的高度最接近的是（）A．25m B．50m C．110m D．150m第(4)题呼吸机是治疗新冠肺炎的重要设备，其核心元件为呼吸机马达（即电动机）。

图为某品牌呼吸机马达的技术参数，用图示交流电源通过理想变压器给马达供电，使其正常工作。

则（）A．马达内线圈的电阻为120ΩB．马达正常工作时理想变压器原、副线圈的匝数比为55∶6C．该交流电源的电压有效值为311VD．该交流电源每秒内电流方向变化50次第(5)题银河系中存在大量的铝同位素，核衰变的衰变方程为，测得核的半衰期为72万年，下列说法正确的是（）A．核的质量等于核的质量B．核的中子数大于核的中子数C．将铝同位素放置在低温低压的环境中，其半衰期不变D．银河系中现有的铝同位素将在144万年后全部衰变为第(6)题磁感应强度B的单位T等价于（）A．B．C．D．第(7)题为了节能减排绿色环保，新能源汽车成为未来汽车发展的方向。

考点三关联速度问题

考点三关联速度问题星I知识梳戛1. 模型特点沿绳（或杆）方向的速度分量大小相等.2. 思路与方法合速度T绳拉物体的实际运动速度v其一：沿绳（或杆的速度V i分速度T'R其二：与绳（或杆垂直的分速度V2方法：V i与V2的合成遵循平行四边形定则.3. 解题的原则把物体的实际速度分解为垂直于绳（杆）和平行于绳（杆）的两个分量，根据沿绳（杆）方向的分速度大小相等求解.常见的模型如下图所示.命题点1绳牵连物体运动问题6•如图所示，A、B两球分别套在两光滑的水平直杆上，两球通过一轻绳绕过一定滑轮相连，现在将A球以速度v向左匀速移动，某时刻连接两球的轻绳与水平方向的夹角分别为a、伏下列说法正确的是（）TCOS a A .此时B球的速度为COS] vB •此时B球的速度为sn a vC.在B增大到90。

的过程中，B球做匀速运动D .在B增大到90。

的过程中，B球做加速运动【解析】由速度的合成与分解知，A、B两球沿绳方向的分速度相等，则VCOS a V B COS cca zB可得V B = cos常，A正确，B错误；在A球向左匀速运动的过程中，a减小、B增大，余弦函数为减函数，故在B增大到90°的过程中，B球做加速运动，C错误，D正确.【答案】AD命题点2杆牵连物体运动问题7•在光滑的水平面内建立如图所示的直角坐标系，长为L的光滑细杆AB的两个端点A、B被分别约束在x轴和y轴上运动，现让A沿x轴正方向以v o匀速运动，已知P点为杆的中点，杆AB与x 轴的夹角为0,下列关于P点的运动轨迹和P点的运动速度大小v的表达式正确的是（）A . P点的运动轨迹是一条直线B. P点的运动轨迹是圆的一部分C. P点的运动速度大小v = v o tan 0v oD . P点的运动速度大小v=2Sin~0【解析】设P点坐标为（x, y）,则A、B点的坐标分别为（2x,0）、（0,2y）, AB长度一定, 设为L,根据勾股定理，有（2x）2+ （2y）2= L2，解得x2+ y2= £2,故P点的运动轨迹是圆的一部分，故A错误，B正确.画出运动轨迹，如图所示，速度v与杆的夹角a= 90 °—2 0由于杆不可伸长，故P点的速度沿杆方向的分速度与A点速度沿杆方向的分速度相等,VCOS a= V 0COS 0, vcos (90 — 2 0 = v o cos 0 解得v= 2sn 0，故C错误，D 正确.【答案】 BD绳（杆）端速度分解思路物理建模系列（五）小船渡河模型分析1.模型构建在运动的合成与分解问题中，两个匀速直线运动的合运动仍是匀速直线运动，其中一个速度大小和方向都不变，另一个速度大小不变，方向在180°范围内（在速度不变的分运动所在直线的一侧）变化，我们对合运动或分运动的速度、时间、位移等问题进行研究•这样的运动系统可看作"小船渡河模型”.2•模型展示合运気分近动一：黑密水泠流的込动 , 木施的 Sfi 度船和时丁-弭运曲二:iUfi 时于挣成的创杆运总”专仟泄水屮的3.三种速度：V 1（水的流速卜V 2（船在静水中的速度）、v （船的实际速度）.4. 三种情景过河要求过河方法图象沿着绳（杆）方I 旬分解垂直绳（杆）方向分解f 沿绳或杆方向的分速度大小相等例一小船渡河，河宽d= 180 m,船在静水中的速度为v t = 5 m/s,水流速度v2= 2.5 m/s. 求：(1) 欲使船在最短的时间内渡河，船头应朝什么方向？用多长时间？位移是多少？(2) 欲使船渡河的航程最短，船头应朝什么方向？用多长时间？位移是多少？【解析】(1)欲使船在最短时间内渡河，船头应朝垂直河岸方向当船头垂直河岸时，如图甲所示，合速度为倾斜方向，垂直分速度为v i= 5 m/s.d 180t=書=” 36 sv= .v2+ v2= 2 . 5 m/sx= vt= 90 . 5 m.乙(2)欲使船渡河航程最短，合速度应垂直于河岸，船头应朝上游与垂直河岸方向成某一夹角a如图乙所示, 有v i sin a= V2,得a= 30°所以当船头向上游垂直河岸方向偏30°时航程最短.x' = d= 180 m.d = 180 v i cos 30 °5 - 2^3=24 3 s.【答案】(1)垂直河岸方向36 s 90 5 m(2)向上游垂直河岸方向偏30° 24.3 s 180 m1. 解这类问题的关键是：正确区分分运动和合运动.2. 运动分解的基本方法：按实际运动效果分解.(1) 确定合速度的方向(就是物体的实际运动方向);(2) 根据合速度产生的的实际运动效果确定分速度的方向；(3) 运用平行四边形定则进行分解.3. 小船渡河问题的处理(1)小船渡河问题，无论v船〉V水，还是V船V V水，渡河的最短时间均为t min = _L(L为河V船宽).⑵当v船〉v水时，船能垂直于河岸渡河，河宽即是最小位移；当v船V v水时，船不能垂直于河岸渡河，但此时仍有最小位移渡河，可利用矢量三角形定则求极值的方法处理.A考能提升莎点演练k［高考真题］1. (2016课标卷I, 18)一质点做匀速直线运动，现对其施加一恒力，且原来作用在质点上的力不发生改变，则()A •质点速度的方向总是与该恒力的方向相同B .质点速度的方向不可能总是与该恒力的方向垂直C.质点加速度的方向总是与该恒力的方向相同D .质点单位时间内速率的变化量总是不变【解析】因为质点原来做匀速直线运动，合外力为0,现在施加一恒力，质点的合力就是这个恒力，所以质点可能做匀变速直线运动，也有可能做匀变速曲线运动，这个过程中加速度不变且一定与该恒力的方向相同，但若做匀变速曲线运动，单位时间内速率的变化量船渡河，去程时船头指向始终与河岸垂直，回程时行驶路线与河岸垂直.间的比值为k,船在静水中的速度大小相冋，则小船在静水中的速度大小为去程与回程所用时（）是变化的，故C正确，D错误.若做匀变速曲线运动，则质点速度的方向不会总是与该恒力的方向相同，故A错误；不管做匀变速直线运动，还是做匀变速曲线运动，质点速度的方向不可能总是与该恒力的方向垂直，故B正确.【答案】BC2. （2015广东卷，14）如图所示，帆板在海面上以速度v朝正西方向运动，帆船以速度v朝正北方向航行，以帆板为参照物（）A •帆船朝正东方向航行，速度大小为vB .帆船朝正西方向航行，速度大小为vC.帆船朝南偏东45。

2021年中考物理考点提升训练——热学、电学综合计算

2021年中考物理考点提升训练——热学、电学综合计算1．（2021鞍山模拟）如图表是从某电热饮水机说明书上收集到的信息。

当开关S闭合时，饮水机处于加热状态，S断开时，饮水机处于保温状态。

为了测量它加热时的实际功率，小明断开其它所有用电器，只将该饮水机接入家庭电路中，闭合开关S，测得热水箱中的水（装满）从25℃升高到100℃，所用时间为7.5min，同时观察到家中标有“1200r/kW•h”字样的电能表转盘转过120转（r）．不考虑温度对阻值的影响；根据以上信息，求：（1）饮水机热水箱中的水从25℃升高到100℃时所吸收的热量[c水＝4.2×103J/（kg•℃）]。

（2）饮水机此加热过程中的热效率（η＝×100%）。

（3）饮水机加热时的实际电压。

2．（2021抚顺模拟）有一只电热水壶，其铭牌上标有“220V 1210W”的字样，不考虑温度对电阻的影响，水的比热容c＝4.2×103J/（kg•℃），g＝10N/kg。

求：（1）它正常工作时通过电阻丝的电流有多大。

（2）它正常工作时电阻丝的电阻有多大。

（3）当实际电压为220V时，该电热水壶的效率为80%，在一标准大气压下将壶内1kg的水由20℃加热至沸腾，加热多少分钟。

3．（2021娄底模拟）学校购置了一批温热型饮水机，配置每个班级。

其电路图和铭牌如图所示。

小东查阅说明书了解到，通电后开关S和S0闭合饮水机进入加热状态；当瓶胆内水的温度被加热到90℃时，加热状态就停止，S0断开而进入保温状态；当胆内水的温度下降到60℃时，加热状态就又会自动启动。

请解答以下问题：（1）饮水机在加热状态下正常工作的电流是多大？电热丝R2的规格？（2）小东同学通过观察发现：瓶胆内装满初温20℃的水，通电后正常工作，加热状态10min 后停止，间隔15min后加热状态又启动。

求饮水机在这25min工作过程中消耗的电能和对外损失的能量是多少？[c水＝4.2×103J/（kg•℃）]（3）根据以上信息从物理学的角度对这种温热型饮水机进行合理评价。

散文阅读考点综合提升练(三)

考点综合提升练(三)一、阅读下面的文字，完成1～4题。

故乡的沉沦曾看到过一幅照片：一个农民在故乡新建成的楼房前呆坐，他的肤色是久在风雨暴晒下才有的酱色。

我心中涌动起莫名的风雨飘絮的黍离之情，只觉得无边的乡村在沉沦，或者说在一点点坍塌。

乡土的中国，故乡的中国，真的转换这么快？一夜之间，土地里不再种出庄稼，而是种出了成片的高楼。

“农民上楼”，就如镰刀割下了谷子，这不是一次收割的事件，而是一个精神的事件。

有人说这世界消失的方式不是一声巨响，而是一声呜咽。

谷穗碰到镰刀是呜咽，大树遭遇斧头是呜咽，而故乡田园风光的消逝更是呜咽。

有一个成语叫背井离乡，“背”是背离，这是孩子都能理解的。

但我宁愿理解“背”为背负，一个背负着故乡井水的人是有底气的，无论走到哪里都有故乡井水的滋润，有故乡做依靠。

记得，在一次文人雅集的酒桌上，友人问我，你的眼睛为何这样亮？我说那是故乡的水井！又问，你的头上隐隐像有什么东西，那是什么呢？也许，是我醉酒的缘故，我回答：那是故乡的屋檐。

友人愣住了，不知如何应答，他有点黯然，然后醉了。

他说，我没有故乡的屋檐。

然后就伏在桌子上呜呜大哭起来。

故乡是一个人的血地。

台湾把故乡叫作原乡，作家钟离和说“原乡人的血，只有回到原乡，他的血才能停止沸腾”，真是透到了骨髓，彻骨彻肤。

故乡是一种容器，故乡是收藏我们童年哭声的地方，一石一础，一草一叶，井栏树冠，那都是我们的见证，那里勾留了我们的年轮，涂抹了黄昏时我们读书的影子，还有那塞满草的窗子。

当我们夜晚背诵课文的时候，常仰着脖颈望着星空，像是背诵着夜。

现在那里的夜还是那样纯净么？没有一丝阴翳，没有污染，没有毁容？一个人不能没有灵魂。

曾记得一个台湾老兵的故事。

他把装着故乡泥土的玻璃瓶子弄丢了，他的魂魄也随之丢失了。

老兵住院，什么样的医术也疗救不了他这种思乡之痛。

他的事传播开来，人们同情他，一个研究生翻找资料，在实验室里为老兵配制了他家乡的土。

土里特别多放了一点盐分，用以配出老兵家人在这土地上流过的汗水。

【步步高】(新课标)高考语文大一轮总复习语言基础知识考点综合提升练(三)(含解析)

考点综合提升练(三)题组一1.依次填入下列各句横线处的成语，最恰当的一组是()①历史其实无处不在。

在你我生活的城市里，每一幢由逝去时代留下的老建筑都是一页________的活的史书。

②以“侃”“凑”“加”为核心的剧本写作模式肯定会破坏故事的思想性和整体性，剧中人物的情感和生命轨迹的展现也很难做到________。

③试想一下，如果不是马云拜访王林的一张照片，使王林重回公众视野，那么，会不会有《新京报》的记者去采访，以及引发接下来令人________的问题呢？A.触手可及水到渠成眼花缭乱B.唾手可得水到渠成眼花缭乱C.触手可及一以贯之目不暇接D.唾手可得一以贯之目不暇接答案 C解析触手可及：近在手边，一伸手就可以接触到。

唾手可得：动手就可以取得。

形容非常容易得到。

一以贯之：用一种思想理论贯穿于始终。

水到渠成：意指水流到之处便有渠道，比喻有条件之后，事情自然成功，即功到自然成。

目不暇接：形容东西太多，眼睛看不过来。

眼花缭乱：形容眼睛看见纷繁复杂的东西而感到迷乱。

2.下列各句中，没有语病的一句是()A.省环境监测中心的分析报告认为，造成此次较严重的区域性灰霾污染的主要原因是区域性焚烧秸秆，加上静风、低压等不利于污染物扩散的气象条件等导致的。

B.最新出台的医疗保险政策最大限度地关注了工薪阶层的就医问题，完善和增强了医疗保险制度和医保专用资金的使用效率。

C.《中国汉字听写大会》使传承华夏文明的信念得以增强，使中华汉字书写的魅力得以展示，对汉字文化传统的回归将产生积极影响。

D.目前，合肥幸福邮局正从实体店向网络发展，致力于打造一个集交友、纪念、联络情感等多种服务于一体，融合函件、集邮、报刊、电子商务、分销等各项业务。

答案 C解析A项“造成……的主要原因是……导致的”句式杂糅，可删去“导致的”。

B项“增强”与“效率”搭配不当，可改为“提高”。

D项成分残缺，“打造”后无宾语中心语，可在句末加“的现代化邮政平台”。

【2021中考数学】四边形综合：动点与相似(三)含答案

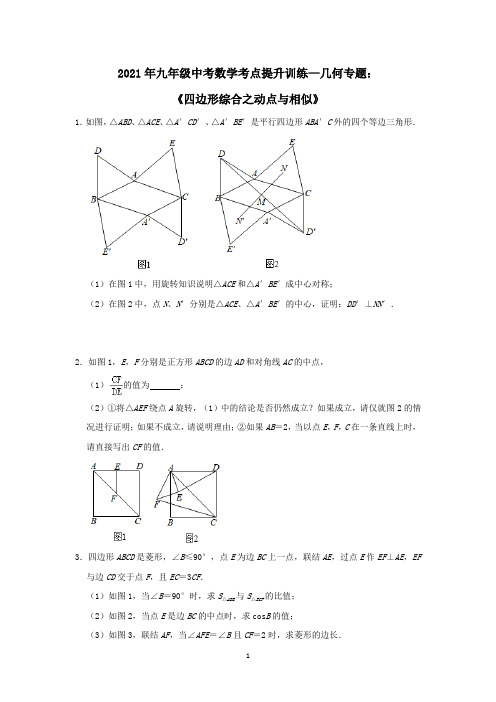
2021年九年级中考数学考点提升训练—几何专题：《四边形综合之动点与相似》1．如图，△ABD、△ACE、△A′CD′、△A′BE′是平行四边形ABA′C外的四个等边三角形．（1）在图1中，用旋转知识说明△ACE和△A′BE′成中心对称；（2）在图2中，点N、N′分别是△ACE、△A′BE′的中心，证明：DD′⊥NN′．2．如图1，E，F分别是正方形ABCD的边AD和对角线AC的中点，（1）的值为；（2）①将△AEF绕点A旋转，（1）中的结论是否仍然成立？如果成立，请仅就图2的情况进行证明；如果不成立，请说明理由；②如果AB＝2，当以点E，F，C在一条直线上时，请直接写出CF的值．3．四边形ABCD是菱形，∠B≤90°，点E为边BC上一点，联结AE，过点E作EF⊥AE，EF 与边CD交于点F，且EC＝3CF．（1）如图1，当∠B＝90°时，求S△ABE 与S△ECF的比值；（2）如图2，当点E是边BC的中点时，求cos B的值；（3）如图3，联结AF，当∠AFE＝∠B且CF＝2时，求菱形的边长．4．在矩形ABCD中，AB＝6，AD＝8，点E在CD边上，tan∠EAD＝．点F是线段AE上一点，联结BF，CF．（1）如图1，如果tan∠CBF＝，求线段AF的长；（2）如图2，如果CF＝BC，①求证：∠CFE＝∠DAE；②求线段EF的长．5．如图，在长方形ABCD中，AB＝4，BC＝6．延长BC到点E，使CE＝3，连结DE．动点P 从点B出发，沿着BE以每秒1个单位的速度向终点E运动，点P运动的时间为t秒．（1）DE的长为．（2）连结AP，求当t为何值时，△ABP≌△DCE．（3）连结DP．①求当t为何值时，△PDE是直角三角形．②直接写出当t为何值时，△PDE是等腰三角形．6．将一个矩形纸片OABC放置在平面直角坐标系中，点O（0，0），点A（8，0），点C（0，6）．P是边OC上的﹣一点（点P不与点O，C重合），沿着AP折叠该纸片，得点O的对应点O'．（Ⅰ）如图①，当点O'落在边BC上时，求点O'的坐标；（Ⅱ）若点O'落在边BC的上方，O'P，O'A与分别与边BC交于点D，E．①如图②，当∠OAP＝30°时，求点D的坐标；②当CD＝O'D时，求点D的坐标（直接写出结果即可）．7．如图，在平行四边形ABCD中，∠B＝90°，且AD＝9cm，AB＝4cm，延长BC至点E，使CE＝3cm，连接DE．若动点P从A点出发，以每秒2cm的速度沿线段AD向点D运动；动点Q从E点出发以每秒3cm的速度沿EB向B点运动，当点P、Q有一个到达指定位置时，动点P、Q同时停止运动，设点P、Q同时出发，并运动了t秒，回答下列问题：（1）求DE的长；（2）当t为多少时，四边形PQED成为平行四边形；（3）请直接写出使得△DQE是等腰三角形时t的值．8．如图1，在正方形ABCD（正方形四边相等，四个角均为直角）中，AB＝8，P为线段BC 上一点，连接AP，过点B作BQ⊥AP，交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交AD于点N．（1）求证：BP＝CQ；（2）若BP＝PC，求AN的长；（3）如图2，延长QN交BA的延长线于点M，若BP＝x（0＜x＜8），△BMC'的面积为S，求S与x之间的函数关系式．9．已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA 的中点，动点P在线段BC上以每秒2个单位长的速度由点C向B运动．设动点P的运动时间为t秒（1）当t为何值时，四边形PODB是平行四边形？（2）在直线CB上是否存在一点Q，使得O、D、Q、P四点为顶点的四边形是菱形？若存在，求t的值，并求出Q点的坐标；若不存在，请说明理由．（3）在线段PB上有一点M，且PM＝5，当P运动秒时，四边形OAMP的周长最小，并画图标出点M的位置．10．四边形ABCD是正方形，将线段CD绕点C逆时针旋转2α（0°＜α＜45°），得到线段CE，连接DE，过点B作BF⊥DE交DE的延长线于F，连接BE．（1）依题意补全图1；（2）直接写出∠FBE的度数；（3）连接AF，用等式表示线段AF与DE的数量关系，并证明．参考答案1．解：（1）如图1，连接AA'，BC相交于O，连接OE'，OE，∵四边形ABA'C是平行四边形，∴AC∥BA'，OA＝OA'，AC＝A'B，将△ACE绕点O顺时针旋转180°得到△A'BF，∵△ACE和△A'BE'是等边三角形，∴AE＝A'E'，∠CAE＝∠BA'E'＝60°，∵AC∥BA'，∴∠OAC＝∠OA'B，∴∠CAE+∠OAC＝BA'E'+∠OA'B，∴∠OAE＝∠OA'E，∴△OAE≌△OA'E'（SAS），∴OE＝OE'，∠AOE＝∠A'OE'，∵∠AOE+∠A'OE＝180°，∴∠A'OE'+∠A'OE＝180°，∴点E，O，E'在同一条线上，∴点F与点E'重合，即△ACE和△A′BE′成中心对称；（2）如图2，连接AN，BN'，DN，DN'，D'N'，D'N，A'N'，由（1）知，△ACE和△A′BE′成中心对称，∵点N，N'分别是等边△ACE和等边△A'BE'的中心，∴AN＝BN'，∠CAN＝∠A'BN'＝30°，设∠ABA'＝α，∵四边形ABA'C是平行四边形，∴AC∥BA'，∴∠ABA'+∠BAC＝180°，∴∠BAC＝180°﹣α，∵△ABD是等边三角形，∴BD＝AD，∠BAD＝∠ABD＝60°，∴∠DBN'＝∠ABD+∠ABA'+∠A'BN'＝90°+α，∠DAN＝360°﹣（∠BAD+∠BAC+∠CAN）＝360°﹣（60°+180°﹣α+30°）＝90°+α，∴∠DBN'＝∠DAN，∴△DBN'≌△DAN（SAS），∴DN＝DN'，同理：D'N＝D'N'，同理：∠D'A'N'＝90°+α，∴∠DBN'＝∠D'A'N'，∵四边形ABA'C是平行四边形，∴AB＝A'C，∵△ABD和△A'CD'是等边三角形，∴AB＝DB，AC＝A'D'，∴DB＝D'A'，∵点N'是△A'BE'的中心，∴BN'＝A'N'，∴△DBN'≌△D'A'N'（SAS），∴DN'＝D'N'，∴DN'＝D'N'＝D'E＝DN，∴四边形DN'D'N是菱形，∴DD′⊥NN′．2．解：（1）∵四边形ABCD是正方形，∴AD＝CD，∠D＝90°，∴AC＝AD，∵E，F分别是正方形ABCD的边AD和对角线AC的中点，∴EF是△ACD的中位线，AE＝AD，AF＝AC，∴EF∥CD，∴＝＝＝，故答案为：；（2）①（1）中的结论仍然成立，理由如下：由（1）得：＝＝，△AFE和△ACD都是等腰直角三角形，∴∠FAE＝∠CAD＝45°，∴∠FAE+∠CAE＝∠CAD+∠CAE，即∠FAC＝∠EAD，∴△ACF∽△ADE，∴＝＝；②如图3所示：∵四边形ABCD是正方形，∴AD＝CD＝AB＝2，∠ADC＝90°，∴AC＝AD＝2，同②得：EF＝AE＝AD＝1，∠AEF＝90°，∵点E，F，C在一条直线上，∴∠AEC＝90°，∴CE＝＝＝，∴CF＝CE+EF＝+1．3．解：（1）∵四边形ABCD是菱形，∠B＝90°，∴四边形ABCD是正方形，∴∠B＝∠C＝90°，∵EF⊥AE，∴∠AEB+∠CEF＝∠AEB+∠BAE＝90°，∴∠BAE＝∠CEF，∴△ABE≌△CEF，∴，∵EC＝3CF，设CF＝x，AB＝a，则EC＝3x，BE＝a﹣3x，∴，解得，a＝4.5x，∴；（2）过点A作AM⊥BC于点M，过点F用FN⊥BC于点H，如图2，则∠AME＝∠CNF＝90°，∵四边形ABCD是菱形，∴AB＝BC，AB∥CD，∴∠B＝∠FCN，设CF＝x，则CE＝3x，∵E是BC的中点，∴BE＝CE＝3x，AB＝BC＝2CE＝6x，∴BM＝AB•cos B＝6x cos B，AM＝AB•sin B＝6x sin B，CN＝CF•cos∠FCN＝x cos B，FN＝CF•sin ∠FCN＝x sin B，∴ME＝BE﹣BM＝3x﹣6x cos B，EN＝EC+CN＝3x+x cos B，∵∠AEF＝90°，∴∠AEM+∠NEF＝∠AEM+∠MAE＝90°，∴∠MAE＝∠NEF，∴△AME∽△ENF，∴，即，即，整理得，2sin2B＝3﹣5cos B﹣2cos2B，∴2＝3﹣5cos B，∴cos B＝；（3）过点A作AM⊥BC于点M，过点F用FN⊥BC于点H，如图3，则∠AME＝∠CNF＝90°，∵四边形ABCD是菱形，∴AB＝BC，AB∥CD，∴∠B＝∠FCN，∵∠AEF＝90°，∴∠AEM+∠NEF＝∠AEM+∠MAE＝90°，∴∠MAE＝∠NEF，∴△AME∽△ENF，∴＝，∵∠AFE＝∠B，tan B＝，tan∠AFE＝，∴，∴，∴BM＝EN，设菱形ABCD的边长为a，则AB＝BC＝a，∴BM＝a cos B，CN＝CF•cos∠FCN＝CF•cos B，∴a cos B＝EC+CF•cos B，∵CF＝2，EC＝3CF，∴EC＝6，∴a cos B＝6+2cos B，∴cos B＝，∵，AM＝AB•sin B＝a sin B，EN＝6+2cos B，ME＝a﹣a cos B﹣6，NF＝CF•sin∠FCN＝2sin B，∴，化简得，2a（sin2B+cos2B）＝6a﹣4a cos B﹣12cos B﹣36，2a＝6a﹣4a cos B﹣12cos B﹣36，a﹣a cos B﹣3cos B﹣9＝0，∵cos B＝，∴a﹣﹣﹣9＝0，解得，a＝17，或a＝0（舍），∴菱形的边长为17．4．解：（1）如图1，∵四边形ABCD是矩形，∴∠BAC＝∠ABC＝90°，过点F作FG⊥AB于G，∴AD∥GF∥BC，∴∠DAE＝∠AFG，∵tan∠EAD＝，∴tan∠AFG＝，在RtAGF中，tan∠AFG＝＝，设AG＝m，则FG＝2m，∵FG∥BC，∴∠BFG＝∠CBF，∵tan∠CBF＝，∴tan∠BFG＝，在RtBGF中，tan∠BFG＝＝，∴，∴BG＝m，∵AB＝AG+BG＝6，∴m+m＝6，∴m＝，∴AG＝，FG＝2m＝，根据勾股定理得，AF＝＝＝；（2）①如图2，∵四边形ABCD是矩形，∴AD∥BC，BC＝AD＝8，CD＝AB＝6，∠D＝90°，在Rt△ADE中，tan∠DAE＝＝，∴DE＝AD＝×8＝4，∴CE＝CD﹣DE＝2，延长AE，BC相交于点H，∵AD∥BC，∴△ADE∽△HCE，∴，∴，∴CH＝4，∵CF＝BC＝4，∴CF＝CH，∴∠H＝∠CFE，∵AD∥BC，∴∠H＝∠DAE，∴∠CFE＝∠DAE；②如图3，过点F作FP⊥CD于P，∴AD∥FP，∴∠PFE＝∠DAE，∵tan∠DAE＝，∴tan∠PFE＝，在Rt△EPF中，tan∠PFE＝＝，设PE＝n，则PF＝2n，由①知，CE＝2，∴CP＝n+2，在Rt△CPF中，CF＝4，根据勾股定理得，CF2＝PF2+CP2，∴42＝（2n）2+（n+2）2，∴n＝﹣2（舍）或n＝，∴PE＝，PE＝2n＝，根据勾股定理得，EF＝＝＝．5．解：（1）∵四边形ABCD是矩形，∴AB＝CD＝4，CD⊥BC，在Rt△DCE中，DE＝＝＝5，故答案为 5．（2）如图1，在长方形ABCD中，AB＝DC，∠B＝∠DCB＝90°，∴∠DCE＝∠B＝90°，∵△ABP≌△DCE，∴BP＝CE，∴1×t＝3，∴t＝3；（3）①当∠PDE＝90°时，如图2，在Rt△PDE中，PD2＝PE2﹣DE2，在Rt△PCD中，PD2＝PC2+CD2，∴PE2﹣DE2＝PC2+CD2，∴（9﹣t）2﹣52＝（6﹣t）2+42，∴t＝．当∠DPE＝90°时，此时点P与点C重合，∴BP＝BC，∴t＝6．综上所述，当t＝或t＝6时，△PDE是直角三角形；②若△PDE为等腰三角形，则PD＝DE或PE＝DE或PD＝PE，当PD＝DE时，如图3，∵PD＝DE，DC⊥BE，∴PC＝CE＝3，∵BP＝BC﹣CP＝3，∴t＝＝3，当PE＝DE＝5时，如图4，∵BP＝BE﹣PE，∴BP＝9﹣5＝4，∴t＝＝4，当PD＝PE时，如图5，∴PE＝PC+CE＝3+PC，∴PD＝3+PC，在Rt△PDC中，DP2＝CD2+PC2，∴（3+PC）2＝16+PC2，∴PC＝，∵BP＝BC﹣PC，∴BP＝，∴t＝＝，综上所述：当t＝3秒或4秒或秒时，△PDE为等腰三角形．6．解：（Ⅰ）∵点A（8，0），点C（0，6），OABC为矩形，∴AB＝OC＝6，OA＝CB＝8，∠B＝90°．根据题意，由折叠可知△AOP≌△AO'P，∴O'A＝OA＝8．在Rt△AO'B中，BO'＝＝2．∴CO'＝BC﹣BO'＝8﹣2．∴点O'的坐标为（8﹣2，6）．（Ⅱ）①∵∠OAP＝30°，∴∠OPA＝60°，∵∠OPA＝∠O'PA，∴∠CPD＝180°﹣∠OPA﹣∠O'PA＝60°．∵OA＝8，∴OP＝OA•tan30°＝．∴CP＝6﹣OP＝6﹣．∴CD＝CP•tan60°＝6﹣8．∴点D的坐标为（6﹣8，6）．②连接AD，如图：设CD＝x，则BD＝BC﹣CD＝8﹣x，O'D＝CD＝x，根据折叠可知AO'＝AO＝8，∠PO'A＝∠POA＝90°，∴在Rt△ADO'中，AD2＝AO'2+DO'2＝82+x2＝x2+64；在Rt△ABD中，AD2＝BD2+AB2＝（8﹣x）2+62＝x2﹣16x+100；∴x2+64＝x2﹣16x+100，解得：x＝，∴D（，6）．7．解：（1）∵四边形ABCD是平行四边形，∴AB＝CD＝4，AB∥CD，∴∠DCE＝∠B＝90°，在Rt△DCE中，CE＝3，根据勾股定理得，DE＝＝5cm；（2）根据题意得，AP＝2t，PD＝9﹣2t，EQ＝3t，∵四边形PQED是平行四边形，∴PD＝EQ，∴9﹣2t＝3t，∴t＝，即：当t为秒时，四边形PQED成为平行四边形；（3）根据题意得，EQ＝3t，由（1）知，DE＝5，∵△DQE是等腰三角形，∴①当DQ＝DE时，∵∠DCE＝90°，∴CQ＝CE，∴EQ＝2CE＝6，∴3t＝6，∴t＝2；②当DQ＝EQ时，如图，则DQ＝3t，CQ＝EQ﹣CE＝3t﹣3，在Rt△DCE中，根据勾股定理得，CD2+CQ2＝DQ2，∴42+（3t﹣3）2＝（3t）2，③当DE＝EQ时，∴3t＝5，∴t＝；即：△DQE是等腰三角形时，t的值为2秒或秒或秒．8．解：（1）证明：∵∠ABC＝90°∴∠BAP+∠APB＝90°∵BQ⊥AP∴∠APB+∠QBC＝90°，∴∠QBC＝∠BAP，在△ABP于△BCQ中，，∴△ABP≌△BCQ（ASA），∴BP＝CQ，（2）由翻折可知，AB＝BC'，连接BN，在Rt△ABN和Rt△C'BN中，AB＝BC'，BN＝BN，∴Rt△ABN≌△Rt△C'BN（HL），∴AN＝NC'，∵BP＝PC，AB＝8，∴BP＝2＝CQ，CP＝DQ＝6，设AN＝NC'＝a，则DN＝8﹣a，∴在Rt△NDQ中，（8﹣a）2+62＝（a+2）2解得：a＝4.8，即AN＝4.8．（3）解：过Q点作QG⊥BM于G，由（1）知BP＝CQ＝BG＝x，BM＝MQ．设MQ＝BM＝y，则MG＝y﹣x，∴在Rt△MQG中，y2＝82+（y﹣x）2，∴．∴S△BMC′＝S△BMQ﹣S△BC'Q＝＝，＝．9．解：（1）∵四边形OABC为矩形，A（10，0），C（0，4），∴BC＝OA＝10，AB＝OC＝4，∵点D是OA的中点，∴OD＝OA＝5，由运动知，PC＝2t，∴BP＝BC﹣PC＝10﹣2t，∵四边形PODB是平行四边形，∴PB＝OD＝5，∴10﹣2t＝5，∴t＝2.5；（2）①当Q点在P的右边时，如图1，∵四边形ODQP为菱形，∴OD＝OP＝PQ＝5，∴在Rt△OPC中，由勾股定理得：PC＝3∴2t＝3；∴t＝1.5，∴Q（8，4）②当Q点在P的左边且在BC线段上时，如图2，同①的方法得出t＝4，∴Q（3，4），③当Q点在P的左边且在BC的延长线上时，如图3，同①的方法得出，t＝1，∴Q（﹣3，4），（3）如图4，由（1）知，OD＝5，∵PM＝5，∴OD＝PM，∵BC∥OA，∴四边形OPMD时平行四边形，∴OP＝DM，∵四边形OAMP的周长为OA+AM+PM+OP＝10+AM+5+DM＝15+AM+DM，∴AM+DM最小时，四边形OAMP的周长最小，∴作点A关于BC的对称点E，连接DE交PB于M，∴AB＝EB，∵BC∥OA，∴BM＝AD＝，∴PC＝BC﹣BM﹣PM＝10﹣5﹣＝，∴t＝÷2＝，10．解：（1）补全图形，如图所示：（2）∠FBE＝45°．设DF与AB交于点G，如图所示：由题意得，CD＝CE＝CB，∠ECD＝2α，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，∴∠EDC＝90°﹣α，∠BCE＝90°﹣2α，∴∠CBE＝45°+α，∠ADF＝α，∴∠ABE＝45°﹣α．∵BF⊥DE，∴∠BFD＝90°．∵∠AGD＝∠FGB，∴∠FBG＝α∴∠FBE＝∠FEB＝45°．（3）DE＝AF．证明：如图，作AH⊥AF，交BF的延长线于点H，由（2）得∠FBE＝∠FEB＝45°．∴FB＝FE．∵AH⊥AF，∠BAD＝90°，∴∠HAB＝∠FAD，∵∠BFG＝∠DAG＝90°，∠BGF＝∠DGA，∴∠FBG＝∠ADG，即∠ABH＝∠ADF，∴△HAB≌△FAD（ASA），∴HB＝FD，AH＝AF，∴HF＝DE，∠H＝45°．∴HF＝AF．∴DE＝AF．。

2023年中考数数学高频考点提升练习三角形动点问题综合(含解析)

2023年中考九年级数数学高频考点提升练习--三角形动点问题综合1．如图，在△ABC中，∠C=90°，CA=3厘米，CB=2厘米．动点P从点C出发，沿CB方向以1厘米/秒的速度向B运动，动点Q从点B同时出发，沿BC方向以1厘米/秒的速度向C运动．当点P到达点B时，P、Q两点同时停止运动，以CP为一边向上作正方形CPDE，过点Q作QF∥AB，交AC于点F．设点P的运动时间为t秒，正方形CPDE和梯形AFQB重合部分的面积为S平方厘米．（1）当t=秒时，点P于点Q重合；（2）当t=秒时，点D在QF上；（3）当点P在Q、B两点之间（不包括Q、B两点）时，求S与t之间的函数关系式．2．如图，在△ABC中，已知AB=AC=10cm，BC=16cm，AD△BC于D，点E、F分别从B、C两点同时出发，其中点E沿BC向终点C运动，速度为4cm/s；点F沿CA、AB向终点B运动，速度为5cm/s，设它们运动的时间为x（s）．（1）求x为何值时，△EFC和△ACD相似；（2）是否存在某一时刻，使得△EFD被AD分得的两部分面积之比为3：5，若存在，求出x的值，若不存在，请说明理由；（3）若以EF为直径的圆与线段AC只有一个公共点，求出相应x的取值范围．3．如图，直线y=kx+b(k≠0)与坐标轴分别交于A、B两点，OA=8，OB=6.动点P从O点出发，沿路线O→A→B以每秒2个单位长度的速度运动，到达B点时运动停止.（1）则A点的坐标为，B两点的坐标为；（2）当点P在OA上，且BP平分△OBA时，则此时点P的坐标为；（3）设点P的运动时间为t秒（0≤t≤4），△BPA的面积为S，求S与t之间的函数关系式：并直接写出当S=8时点P的坐标.4．如图，在Rt△ABC中，∠B=90°，AC=40cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤10）．过点D作DF⊥BC于点F，连接DE，EF．（1）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；（2）当t为何值时，ΔDEF为直角三角形？请说明理由．5．如图1，OA=2，OB=4，以A点为顶点、AB为腰在第三象限作等腰Rt△ABC，（1）求C点的坐标；（2）如图2，P为y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，以P为顶点，PA为腰作等腰Rt△APD，过D作DE△x轴于E点，求OP−DE的值；（3）如图3,已知点F坐标为(−2,−2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持△GFH=90△,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0)，当G点在y轴的负半轴上沿负方向运动时，以下两个结论：①m−n为定值；②m+n为定值，其中只有一个结论是正确的，请找出正确的结论，并求出其值. 6．如图（1）如图1，点E在四边形ABCD的边BC上，EA＝ED，且△AED＝△B＝△C．判断AB、BC、CD三边的数量关系，并说明理由；（2）如图2，在Rt△ABC中，△C＝90°，AC＝6，BC＝8，点D在线段BC上，CD ＝3，点E是AC边上一动点，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，当AE的值为多少时，线段BF有最小值？并求出线段BF的最小值．7．如图，在Rt△ABC中，△ACB＝90°，AC＝6cm，BC＝8cm，点P从点A出发沿线段AB以每秒1cm的速度运动，同时点Q从点B出发沿折线B﹣C﹣A以每秒2cm的速度运动．其中一点停止则另一点也随之停止，设运动时间为t秒．（1）①直接写出t的取值范围：；②当点P运动到AB中点时，连结PQ，PC，BQ，求证：△CPQ△△ABQ；（2）当△BPQ是直角三角形时，求t的值．8．已知△ABC中，∠BAC=90∘，AB=AC，点D为直线BC上的一动点(点D不与点B、C重合)，以AD为边作△ADE，使∠DAE=90∘，AD=AE，连接CE．发现问题：如图1，当点D在边BC上时，（1）请写出BD和CE之间的位置关系为，并猜想BC和CE、CD之间的数量关系：．（2）如图2，当点D在边BC的延长线上且其他条件不变时，(1)中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；（3）如图3，当点D在边CB的延长线上且其他条件不变时，若BC=6，CE= 2，求线段ED的长．9．如图，P、Q分别是边长4cm为的等边ΔABC的边AB，BC上的动点，点P从顶点A，点Q从顶点B同时出发，分别沿AB，BC边运动，点P到点B停止，点Q到点C停止.社运动时间为t秒，他们的速度都为1cm/s.（1）连接AQ，CP相交于M，在点P，Q的运动过程中∠CMQ的大小是否变化？若变化，说明理由；若不变，求出它的度数；（2）当t取何值时，ΔPBQ是直角三角形.10．如图所示，点B坐标为(6，0)，点A坐标为(6，12)，动点P从点O开始沿OB以每秒1个单位长度的速度向点B移动，动点Q从点B开始沿BA以每秒2个单位长度的速度向点A移动，如果P，Q分别从O，B同时出发，用t（秒）表示移动的时间(0<t≤6)．（1）用含t的式子来表示BP=．AQ=．（2）当t为何值时，以点P、B、Q为顶点的三角形与△AOB相似？（3）若四边形OPQA的面积为y，试写出y与t的函数关系式，并求出t取何值时，四边形OPQA的面积最小？（4）在y轴上是否存在点E，使点P、Q在移动过程中，以B、E、Q、P为顶点的四边形的面积是一个常数？若存在请求出点E的坐标；若不存在，请说明理由．11．如图，在平面直角坐标系中，等边△ABC的顶点A，B的坐标分别为（0，0），（6，0），点D是x轴上的一个动点，连接CD，将△ACD绕点C逆时针旋转60°得到△BCE，连接DE．（1）点C的坐标为，△CDE为三角形；（2）当点D在线段AB上运动时，四边形CDBE的周长是否存在最小值？若存在，求出四边形CDBE的周长最小值及此时点D的坐标；若不存在，请说明理由；（3）当△BDE是直角三角形时，请直接写出点D的坐标．12．如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．（1）如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA 上由点C向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，则经过秒后，点P与点Q第一次在△ABC的AC边上相遇？（在横线上直接写出答案，不必书写解题过程）13．如图，点A坐标是(0，0)，点C坐标是(2，2)，现有E、F两点分别从点D(0，2)和点B(2，0)向下和向右以每秒一个单位速度移动，Q为EF中点．设运动时间为t．（1）在运动过程中始终与线段EC相等的线段是；四边形CEAF面积＝．（2）当t＝1秒时，求线段CQ的长．（3）过点B作BP平行于CF交EC于点P．当t＝▲ 时，线段AP最短，此时作直线EP与x轴交于点K，试证明，点K是线段AB的黄金分割点．14．如图1，已知△ABC是边长为3cm的等边三角形，动点P，Q同时从A，B两点出发，分别沿AB，BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P，Q两点都停止运动，设点P的运动时间为t(s)．（1）当运动时间为t秒时，则BQ的长为cm，BP的长为cm．（用含t的式子表示）（2）当t为何值时，△PBQ是直角三角形；（3）如图2，连接AQ，CP相交于点M，则点P，Q在运动的过程中，∠CMQ的大小会变化吗？若变化，请说明理由．若不变，请直接写出它的度数．15．旋转是一种重要的图形变换，当图形中有一组邻边相等时往往可以通过旋转解决问题．（1）尝试解决：如图①，在等腰Rt△ABC中，∠BAC=90°，AB=AC，点M 是BC上的一点，BM=1cm，CM=2cm，将△ABM绕点A旋转后得到△ACN，连接MN，则AM=cm．（2）类比探究：如图②，在“筝形”四边形ABCD中，AB=AD=a，CB= CD，AB⊥BC于点B，AD⊥CD于点D，点P、Q分别是AB、AD上的点，且∠PCB+∠QCD=∠PCQ，求△APQ的周长．（结果用a表示）（3）拓展应用：如图③，已知四边形ABCD，AD=CD，∠ADC=60°，∠ABC=75°，AB=2√2，BC=2，求四边形ABCD的面积．16．如图，在矩形ABCD中，AB=6cm，BC=8cm，动点P以2cm/s的速度从点A出发，沿AC向点C移动，同时动点Q以1cm/s的速度从点C出发，沿CB向点B移动，设P、Q两点移动ts（0<t<5）后，ΔCQP的面积为Scm2．（1）在P、Q两点移动的过程中，ΔCQP的面积能否等于3.6cm2？若能，求出此时t的值；若不能，请说明理由；（2）当运动时间为多少秒时，ΔCPQ与ΔCAB相似．答案解析部分1．【答案】（1）1（2）34（3）解：点P 与点Q 重合时，由（1）知t =1；当点D 在AB 上时，如下图所示：此时DP =CP =BQ =t ，∵∠DPB =∠ACB =90°，∠DBP =∠ABC ，∴△DBP ∽△ABC ，∴DP PB =CA CB =32，∴PB =23DP =23t ，∵CP +PB =CB ，∴t +23t =2，解得t =65， ∴CE =65．∵QF ∥AB ，∴∠FQC =∠ABC ，又∠FCQ =∠ACB =90°，∴△FQC ∽△ABC ，∴CQ CB =CF CA ，即2−652=CF 3， ∴CF =65，∴t =65时，点E 与点F 重合；当点P 到达B 点时，此时t =2．当点P 在Q 、B 两点之间（不包括Q 、B 两点）时，其运动过程可分析如下：①当1<t≤65时，如下图所示，此时重合部分为梯形GDPQ．则PQ=CP+BQ−CB=2t−2，PD=t，由△FQC∽△ABC得：CF=32CQ=32×(2−t)=3−32t，∴EF=CF−CE=3−32t−t=3−52t，∵QF∥AB，∴∠A=∠EFG，又∠ACB=∠FEG=90°，∴△ABC∽△FGE，∴FE CA=EG CB，∴EG=23EF=23×(3−52t)=2−53t，∴DG=ED−EG=t−(2−53t)=83t−2，∴S梯形GDPQ=12(PQ+DG)⋅DP=12(2t−2+83t−2)⋅t=73t2−2t，∴S=73t2−2t；②当65<t<2时，如下图所示，此时重合部分为一个多边形．则CP=BQ=t，CQ=BP=2−t，易知△ABC∽△FQC∽△MBP∽△MND，可得CF=32CQ=32(2−t)=3−32t，MP=32BP=32(2−t)=3−32t，∴DM=DP−MP=t−(3−32t)=52t−3，∴DN=23DM=23×(52t−3)=53t−2，∴S=S正方形EDPC−S△CFQ−S△MDN=CP2−12CF⋅CQ−12DM⋅DN=t2−12(3−32t)⋅(2−t)−12(52t−3)⋅(53t−2)=−116t2+8t−6；综上，当点P在Q、B两点之间（不包括Q、B两点）时，S与t之间的函数关系式为：S={73t2−2t(1<t≤65)−116t2+8t−6(65<t<2)．2．【答案】（1）解：如图1中，点F在AC上，点E在BD上时，①当CFCE=CDAC时，△CFE△△CDA，∴5t16−4t=810，∴t= 64 41，②当CFCE=ACCD时，即5t16−4t= 108，∴t=2，当点F在AB上，点E在CD上时，不存在△EFC和△ACD相似，综上所述，t= 6441s或2s时，△EFC和△ACD相似．（2）解：不存在．理由：如图2中，当点F在AC上，点E在BD上时，作FH△BC 于H，EF交AD于N．∵CF=5t．BE=4t，∴CH=CF•cosC=4t，∴BE=CH，∵AB=AC，AD△BC，∴BD=DC，∴DE=DH，∵DN△FH，∴EDDH=ENNF=1，∴EN=FN，∴S△END=S△FND，∴△EFD被AD分得的两部分面积相等，同法可证当点F在AB上，点E在CD上时，△EFD被AD分得的两部分面积相等，∴不存在某一时刻，使得△EFD被AD分得的两部分面积之比为3：5．（3）解：①如图3中，当以EF为直径的△O经过点A时，△O与线段AC有两个交点，连接AE，则△EAF=90°．由ACEC=cosC= 45，可得1016−4t=45，∴t=78，∴0≤t＜78时，△O与线段AC只有一个交点．②如图4中，当△O与AC相切时，满足条件，此时t= 6441．③如图5中，当△O与AB相切时，cosB= BFBE，即45=20−5t4t，解得t= 10041．④如图6中，△O 经过点A 时，连接AE ，则△EAF=90°．由cosB= AB AE = 45 ，即 104t = 45 ，t= 258， ∴258＜t≤4时，△O 与线段AC 只有一个交点．综上所述，当△O 与线段AC 只有一个交点时，0≤t ＜ 78 或 6441 或 10041 或 258＜t≤4 3．【答案】（1）（8，0）；（0，6）（2）（3，0）（3）解：∵OA=8，v=2，∴t=8÷2=4，∴P 从O 运动到A 的时间为4秒，∴当0≤t≤4时，P 在线段OA 上运动.OP=2t ，PA=8－OP=8－2t ，S=S △BAP = 12 •PA•OB= 12•（8-2t ）•6=24－6t. 当S=8时，8=24－6t ，解得：t= 83 ，∴OP=2t =2× 83 = 163 ，∴P （ 163，0）.答：S= 24－6t （0≤t≤4），当S=8时，P （ 163，0）.4．【答案】（1）解：能．理由如下：在ΔDFC中，∠DFC=90°，∠C=30°，DC=4t，∴DF=2t，又∵AE=2t，∴AE=DF，∵AB⊥BC，DF⊥BC，∴AE//DF，又∵AE=DF，∴四边形AEFD为平行四边形，当AE=AD时，四边形AEFD为菱形，即40−4t=2t，解得t=20 3．∴当t=203秒时，四边形AEFD为菱形．（2）解：①当∠DEF=90°时，由（1）知四边形AEFD为平行四边形，∴EF//AD，∴∠ADE=∠DEF=90°，∵∠A=60°，∴∠AED=30°，∴AD=12AE=t，又AD=40−4t，即40−4t=t，解得t=8；②当∠EDF=90°时，四边形EBFD为矩形，在RtΔAED中∠A=60°，∴∠ADE=90°−∠A=30°，∴AD=2AE，即40−4t=4t，解得t=5．③若∠DFE =90°，则E 与B 重合，D 与A 重合，此种情况不存在．综上所述，当t =8或5秒时，ΔDEF 为直角三角形．5．【答案】（1）解：过C 作CM△x 轴于M 点，如图1，∵CM△OA ，AC△AB ，∴△MAC+△OAB= 90° ,△OAB+△OBA= 90°则△MAC=△OBA在△MAC 和△OBA 中 {∠CMA =∠AOB =90∠MAC =∠OBA AC =BA∘则△MAC△△OBA(AAS)则CM=OA=2,MA=OB=4,则点C 的坐标为(−6,−2)；（2）解：过D 作DQ△OP 于Q 点,如图2,则OP−DE=PQ,△APO+△QPD= 90° ，△APO+△OAP= 90° ，则△QPD=△OAP ，在△AOP 和△PDQ 中 {∠AOP =∠PQD =90∘∠QPD =∠OAP AP =PD则△AOP△△PDQ(AAS)∴OP−DE=PQ=OA=2；（3）解：结论②是正确的，m+n=−4，如图3,过点F 分别作FS△x 轴于S 点,FT△y 轴于T 点,则FS=FT=2，△FHS=△HFT=△FGT ，在△FSH 和△FTG 中 {∠FSH =∠FTG =90∘∠FHS =∠FGT FS =FT则△FSH△△FTG(AAS)则GT=HS ，又∵G(0,m),H(n,0),点F 坐标为(−2,−2)，∴OT═OS=2，OG=|m|=−m ，OH=n ，∴GT=OG−OT=−m−2，HS=OH+OS=n+2，则−2−m=n+2，则m+n=−4.6．【答案】（1）解：AB ，BC ，CD 三边的数量关系是：AB+CD ＝BC ，理由如下：∵△AEB+△AED ＝△BED ，△EDC+△C ＝△BED ，且△AED ＝△C ，∴△AEB ＝△EDC ，在△ABE 和△ECD 中，{∠B =∠C ∠AEB =∠EDC AE =ED，∴△ABE△△ECD （AAS ），∴AB ＝EC ，BE ＝DC ，∴AB+CD ＝BE+EC ＝BC ；（2）解：如图，过D 作BD 垂线B'D 且使得B'D ＝BD ，连接B'E ，∵△EDF ＝△B'DB ＝90°，∴△BDF+△B'DF ＝△B'DF+△B'DE ，∴△BDF ＝△B'DE ，在△B'DE 与△BDF 中，{B ′D =BD ∠BDF =∠B ′DE DE =DF，∴△B'DE△△BDF （SAS ），∴BF ＝B'E ，∵点到直线垂线段最短，∴B'E△AC 时，B'E 取最小值，过点B'作B'G△AC 交AC 于G ，∵△C ＝△CDB'＝△CGB'＝90°，∴四边形CDB'G 为矩形，∴B'G ＝CD ＝3，CG ＝B'D ＝BD ＝8﹣3＝5，∴BF 取最小值时AE ＝AG ＝AC ﹣CG ＝1，BF 最小值为B'G ＝3．7．【答案】（1）0≤t≤7；解：②证明：如图1中，由题意点P 运动到AB 的中点时，t ＝5， ∴CQ ＝5×2﹣8＝2， ∵△ACB ＝90°，PA ＝PB ，∴PC ＝PA ＝PB ＝5， ∴△PCQ ＝△A ， ∵QC AQ =24=12 ， CP AB =12， ∴QC AQ =CP AB ， ∴△QCP△△CAB ，（2）解：①如图2中，当PQ△AC 时，△PQB ＝△C ＝90°，∵PQ△AC ，∴BQ BC =BP AB，∴2t 8=10−t 10，解得： t =207； ②如图3中，当△QPB ＝90°时，∵△QPB ＝△ACB ＝90°，△B ＝△B ，∴△BPQ△△BCA ，∴PB BC =BP BA， ∴10−t 8=2t 10，解得： t =5013；综上所述，满足条件的t 的值为： 207 或 5013. 8．【答案】（1）BD△CE ；BC=CD+CW 尝试探究：（2）解： BD ⊥CE 成立，数量关系不成立，关系为 BC =CE −CD ．理由：如图2中，由 (1) 同理可得，∵∠BAC =∠DAE =90∘ ，∴∠BAC +∠CAD =∠DAE +∠CAD即 ∠BAD =∠CA E ，∴ 在 △ABD 和 △ACE 中，{AB =AC ∠BAD =∠CAE AD =AE，∵△ABD △ △ACE(SAS) ，∴BD =CE ， ∠ACE =∠ABC ，∵AB =AC ，∴∠ABC =∠ACB =45∘ ，∴BD =BC +CD ，即 CE =BC +CD ， ∠ACE +∠ACB =90∘ ， ∴BC =CE −CD ； BD ⊥CE ；拓展延伸：（3）解：如图3中，由 (1) 同理可得，∵∠BAC=∠DAE=90∘，∴∠BAC−∠BAE=∠DAE−∠BAE，即∠BAD=∠EAC，易证△ABD△ △ACE(SAS)，∴BD=CE=2，∠ACE=∠ABD=135∘，∴CD=BC+BD=BC+CE=8，∵∠ACB=45∘∴∠DCE=90∘，在Rt△DCE中，由勾股定理得DE2=DC2+CE2=82+22=68，∴DE=2√17．9．【答案】（1）∵△ABC为等边三角形，∴AB=AC，△B=△PAC=60°，∵点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，∴AP=BQ，在△APC和△BQA中{AP＝BQ∠PAC＝∠B AC＝AB，∴△APC△△BQA（SAS），∴△BAQ=△ACP，∴△CMQ=△CAQ+△ACP=△BAQ+△CAQ=△BAC=60°，∴在P、Q运动的过程中，△CMQ不变，△CMQ=60°；（2）∵运动时间为ts，则AP=BQ=t，∴PB=4-t，①当△PQB=90°时，∵△B=60°，∴PB=2BQ，∴4-t=2t，解得t=4 3，②当△BPQ=90°时，∵△B=60°，∴BQ=2PB ，∴t=2（4-t ），解得 t =83， ∴当t 为 43 s 或 83s 时，△PBQ 为直角三角形 10．【答案】（1）6-t ；12-2t（2）解：当 ∠BPQ =∠BOA 时，即 PQ//OA ，则 △BPQ ∼△BOA ， ∴BP BO =BQ BA ，即 6−t 6=2t 12，解得： t =3 ；当 ∠BPQ =∠A 时，则 △BPQ ∼△BAO ，∴BP BA =BQ BO ，即 6−t 12=2t 6，解得： t =65； ∴当 t =65秒或3秒时，以点P 、B 、Q 为顶点的三角形与 △AOB 相似（3）解： y =S △OAB −S △BPQ =12×6×12−12×2t ×(6−t)=t 2−6t +36=(t −3)2+27 ，∵a =1 ，∴t =3 时，y 有最小值是27；（4）解：存在，理由如下：当E 在y 轴负半轴上时，以B 、Q 、E 、P 为顶点不能形成四边形；当E 在y 轴正半轴上时，设 E(0，m) ，∴以B 、Q 、E 、P 为顶点的四边形的面积=梯形 BQEO 的面积- △OPE 的面积，即 12×6×(m +2t)−12×m ×t =(6−12m)t +3m ，当以B 、Q 、E 、P 为顶点的四边形的面积是一个常数，则 6−12m =0 ，解得： m =12 ，∴点E 的坐标为 (0，12) ；11．【答案】（1）（3，3 √3 ）；等边（2）解：存在，理由如下：∵△ABC 为等边三角形，∴△ACD+△DCB=60°，∵△DCE为等边三角形，∴△BCE+△DCB=60°，∴△ACD=△BCE，在△ACD和△BCE中，{CA＝CB∠ACD＝∠BCECD＝CE，∴△ACD△△BCE（SAS）∴AD=BE，∴四边形CDBE的周长=CD+DB+BE+CE=CD+DB+AD+CE=6+2CD，当CD最小时，四边形CDBE的周长存在最小值，由垂线段最短可知，CD△AB时，CD最小，CD的最小值为3 √3，∴四边形CDBE的周长最小值为6+6 √3，此时点D的坐标为（3，0）（3）解：由（2）可知，△ACD△△BCE，∴BE=AD，∴△DBE=120°或60°，不能为90°，如图②，△DEB=90°时，△DBE=60°，∴△BDE=30°，∴DB=2BE，∵BE=AD，∴AD=AB=6，此时，点D的坐标为（-6，0），如图③，当△BDE=90°时，△ADC=90°-60°=30°，∵△CAD=60°，∴△ACD=90°，又△ADC=30°，∴AD=2AC=12，此时，点D的坐标为（12，0），综上所述，当△BDE是直角三角形时，点D的坐标为（-6，0）或（12，0）．12．【答案】（1）解：①全等，理由如下：∵t=1秒，∴BP=CQ=1×1=1厘米，∵AB=6cm，点D为AB的中点，∴BD=3cm.又∵PC=BC−BP，BC=4cm，∴PC=4−1=3cm，∴PC=BD.∴△BPD≅△CQP；②假设△BPD≅△CQP，∵v P≠v Q，∴BP≠CQ，又∵△BPD≅△CQP，∠B=∠C，则BP=CP=2，BD=CQ=3，∴点P，点Q运动的时间t=BP1=2秒，∴v Q=CQ t=32=1.5cm/s；（2）2413．【答案】（1）FC；4（2）解：∵△CDE△△CBF，∴EC＝FC，△DCE＝△BCF，∵△DCE+△ECB＝90°，∴△BCF+△ECB＝90°，即△ECF＝90°，∴△ECF是等腰直角三角形，当t＝1时，DE＝1，在Rt△CDE中，由勾股定理得：CE＝√DE2+CD2＝√12+22＝√5，∴EF＝√2CE＝√2× √5＝√10，∵Q为EF中点，∴CQ＝12EF＝12×√10＝√102；（3）解：t＝（√5+1）s∵BP△CF，△ECF＝90°，∴△BPC＝90°，∴点P的轨迹在以BC为直径的圆弧上，设BC的中点为G，连接AG，如图2所示：当点P在AG上时，AP最短，此时，PG＝BG＝1，在Rt△ABG中，由勾股定理得AG＝√AB2+BG2＝√22+12＝√5，∴AP＝AG﹣PG＝√5﹣1，∵BC△DE，∴△AEP＝△GCP，∵GC＝GP，∴△GCP＝△GPC，∵△GPC＝△APE，∴△AEP＝△APE，∴AP＝AE＝√5﹣1，∴E （0，1﹣ √5 ），∴DE ＝2﹣（1﹣ √5 ）＝ √5 +1，∴t ＝（ √5 +1）s ，故答案为：（ √5 +1）s ；设CE 的解析式为：y ＝kx+b （k≠0），将C （2，2）、E （0，1﹣ √5 ）代入解析式得： {2k +b =2b =1−√5，解得： {k =√5+12b =1−√5，∴CE 的解析式为：y ＝ √5+12x+1﹣ √5 ，令y ＝0，x ＝3﹣ √5 ，∴K （3﹣ √5 ，0），∴BK ＝2﹣（3﹣ √5 ）＝ √5 ﹣1，∴BK AB ＝ √5−12， ∴点K 是线段AB 的黄金分割点．14．【答案】（1）t ；（3-t ）（2）解：由（1）得：AP =BQ =tcm ，BP =(3−t)cm ，①如图1，当∠PQB =90°时，∵△ABC 是等边三角形，∴∠B =60°，∴∠BPQ =30°，∴PB =2BQ ，即3−t =2t ，解得：t =1，②如图2，当∠BPQ =90°时，∵∠B=60°，∴∠BQP=30°，∴BQ=2BP，即t=2(3−t)，解得：t=2，∴当t=1或t=2时，△PBQ为直角三角形；（3）解：不变，∠CMQ=60°．15．【答案】（1）√102（2）解：∵AD⊥CD，CB=CD，AB⊥BC，∴将△BCP绕点C旋转后得到△DCM，此时BC与DC重合，∴△BCP△△DCM，∴△DCM=△PCB，BP=DM，PC=CM，∵∠PCB+∠QCD=∠PCQ，∴∠DCM+∠QCD=∠PCQ，∴∠QCM=∠PCQ，∵PC=CM，QC=QC，∴△QCP△△QCM，∴PQ=QM，∴△APQ的周长=AQ+AP+PQ= AQ+AP+QM= AQ+AP+DQ+DM= AQ+AP+DQ+BP=AD+AB，∵AB=AD=a，∴△APQ的周长=2a；（3）解：如图3，连接BD，由于AD=CD，所以可将△BCD绕点D顺时针方向旋转60°，得到△DAB′，连接BB′，延长BA，作B′E△BE；{AD=CD∠CDB=∠ADB′BD=B′D∴△BCD△△B′AD∴S四边形ABCD=S四边形BDB′A，∵△ABC=75°，△ADC=60°，∴△BAB′=135°∴△B′AE=45°，∵B′A=BC=2∴B′E=AE= √2，∴BE=AB+AE=2 √2+ √2= 3√2，∴BB′=√(√2)2+(3√2)2=2√5∵等边△DBB′，∴BB′上的高= =2√5×√32=√15，∴.SΔABB′=12⋅AB⋅B′E=12×2√2×√2=2∴SΔBDB′=12×2√5×√15=5√3，∴S四边形ABCD=S四边形BDB′A=S△BDB′-S△ABB′= =5√3−2；16．【答案】（1）解：在矩形ABCD中，∵AB=6cm，BC=8cm，∴AC=10cm，AP=2tcm，PC=(10−2t)cm，CQ=tcm，过点P作PH⊥BC于点H，则PH=35(10−2t)cm根据题意，得12t•35(10−2t)=3.6，解得：t1=2，t2=3，∴ΔCQP的面积等于3.6cm2时，t的值为2或3．（2）解：如图1，当∠PQC=90∘时，PQ⊥BC，∵AB⊥BC，AB=6，BC=8，QC=t，PC=10−2t，∴ΔPQC△ ΔABC，∴PCAC=CQBC，即10−2t10=t8，解得t=4013（秒）如图2，当∠CPQ=90∘时，PQ⊥AC，∵∠ACB=∠QCP，∠B=∠QPC，∴ΔCPQ△ ΔCBA，∴CPBC=CQAC，即10−2t8=t10，解得t=257（秒）综上所述，t为4013秒与257时，ΔCPQ与ΔCBA相似．。

2023年中考九年级数学高频考点提升练习--圆的综合(含答案)

2023年中考九年级数学高频考点提升练习--圆的综合1．如图，AB是⊙O的直径，点C为⊙O上一点，OE⊥BC于点H，交⊙O于点E，点D为OE的延长线上一点，DC的延长线与BA的延长线交于点F﹐且∠BOD=∠BCD，连结BD、AC、CE.（1）求证：DF为⊙O的切线；（2）过E作EG⊥FD于点G，求证：△CHE≌△CGE；（3）如果AF=1，sin∠FCA=√33，求EG的长.2．如图，在平面直角坐标系中，直线y=−12x+2与x轴交于点A，与y轴交于点B，抛物线y=−23x 2+bx+c过点B且与直线相交于另一点C(52,34).（1）求抛物线的解析式；（2）点P是抛物线上的一动点，当∠PAO=∠BAO时，求点P的坐标；（3）点N(n,0) (0<n<52)在x轴的正半轴上，点M(0,m)是y轴正半轴上的一动点，且满足∠MNC=90°.①求m与n之间的函数关系式；②当m在什么范围时，符合条件的N点的个数有2个？3．综合与探究如图，抛物线y=−x2+bx+c经过A(−1,0)，D(3,4)两点，直线AD与y 轴交于点Q．点P(m,n)是直线AD上方抛物线上的一个动点，过点P作PF⊥x轴，垂足为F，并且交直线AD于点E．（1）请直接写出抛物线与直线AD的函数关系表达式；（2）当CP//AD时，求出点P的坐标；（3）是否存在点P，∠CPE=∠QFE？若存在，求出m的值；若不存在，请说明理由．4．如图，在梯形ABCD中，AD⊙BC，⊙B=90°，BC=6，AD=3，⊙DCB=30°．点E、F同时从B点出发，沿射线BC向右匀速移动，已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边⊙EFG，设E点移动距离为x（x＞0）．（1）⊙EFG的边长是（用含有x的代数式表示），当x=2时，点G的位置在；（2）若⊙EFG与梯形ABCD重叠部分面积是y，求y与x之间的函数关系式；（3）探究（2）中得到的函数y在x取何值时，存在最大值？并求出最大值．5．如图，抛物线y=−34x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N．（1）求抛物线的解析式，并写出此抛物线的对称轴；（2）如果以点P、N、B、O为顶点的四边形为平行四边形，求m的值；（3）若△BPN与△OPM面积相等，直接写出点M的坐标．6．在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”.（1）当⊙O的半径为2时，﹣12)⊙O的“完①点M( 32，0)⊙O的“完美点”，点(﹣√32美点”；(填“是”或者“不是”)②若⊙O的“完美点”P在直线y＝34x上，求PO的长及点P的坐标；（2）设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围.7．平面直角坐标系xOy中有点P和某一函数图象M，过点P作x轴的垂线，交图象M 于点Q ，设点P ，Q 的纵坐标分别为 y P ， y Q ．如果 y P >y Q ，那么称点P 为图象M 的上位点；如果 y P =y Q ，那么称点P 为图象M 的图上点；如果 y P <y Q ，那么称点P 为图象M 的下位点．（1）已知抛物线 y =x 2−2 .① 在点A (-1，0)，B (0，-2)，C (2，3)中，是抛物线的上位点的是；② 如果点D 是直线 y =x 的图上点，且为抛物线的上位点，求点D 的横坐标 x D 的取值范围；（2）将直线 y =x +3 在直线 y =3 下方的部分沿直线 y =3 翻折，直线 y =x +3 的其余部分保持不变，得到一个新的图象，记作图象G ．⊙H 的圆心H 在x 轴上，半径为 1 ．如果在图象G 和⊙H 上分别存在点E 和点F ，使得线段EF 上同时存在图象G 的上位点，图上点和下位点，求圆心H 的横坐标 x H 的取值范围．8．在平面直角坐标系xOy 中，⊙O 的半径为1，点A 在⊙O 上，点P 在⊙O 内，给出如下定义：连接AP 并延长交⊙O 于点B ，若AP =kAB ，则称点P 是点A 关于⊙O 的k 倍特征点．（1）如图，点A 的坐标为(1，0)．①若点P 的坐标为(−12，0)，则点P 是点A 关于⊙O 的 ▲倍特征点；②在C 1(0，12)，C 2(12，0)，C 3(12，−12)这三个点中，点 ▲是点A 关于⊙O 的12倍特征点； ③直线l 经过点A ，与y 轴交于点D ，∠DAO =60°.点E 在直线l 上，且点E 是点A 关于⊙O 的12倍特征点，求点E 的坐标；（2）若当k取某个值时，对于函数y=−x+1(0<x<1)的图象上任意一点M，在⊙O上都存在点N，使得点M是点N关于⊙O的k倍特征点，直接写出k的最大值和最小值．9．如图，已知抛物线y=x2+bx-3c经过点A(1,0)和点B(0,-3)，与x 轴交于另一点C ．（1）求抛物线的解析式；（2）若点P 是抛物线上的动点，点Q 是抛物线对称轴上的动点，是否存在这样的点P ，使以点A、C、P、Q 为顶点的四边形是平行四边形？若存在，求出点P 的坐标；若不存在，请说明理由．10．如图，在⊙ABC中，⊙ACB =90°，AB=10，AC=8，CD是边AB的中线．动点P 从点C出发，以每秒5个单位长度的速度沿折线CD-DB向终点B运动．过点P作PQ⊙AC于点Q，以PQ为边作矩形PQMN，使点C、N始终在PQ的异侧，且PN= 2．设矩形PQMN与⊙ACD重叠部分图形的面积是S，点P的运动时间为t(s)3PQ（t>0）．（1）当点P在边CD上时，用含t的代数式表示PQ的长．（2）当点N落在边AD上时，求t的值．（3）当点P在CD上时，求S与t之间的函数关系式．（4）连结DQ，当直线DQ将矩形PQMN分成面积比为1：2的两部分时，直接写出t的值．11．如图1，在平面直角坐标系中，抛物线y= √36x2﹣114x+3 √3与x轴交于点A、B两点（点A在点B的左侧），与y轴交于点C，过点C作CD⊙x轴，且交抛物线于点D，连接AD，交y轴于点E，连接AC．（1）求S⊙ABD的值；（2）如图2，若点P是直线AD下方抛物线上一动点，过点P作PF⊙y轴交直线AD于点F，作PG⊙AC交直线AD于点G，当⊙PGF的周长最大时，在线段DE上取一点Q，当PQ+ 35QE的值最小时，求此时PQ+35QE的值；（3）如图3，M是BC的中点，以CM为斜边作直角⊙CMN，使CN⊙x轴，MN⊙y 轴，将⊙CMN沿射线CB平移，记平移后的三角形为⊙C′M′N′，当点N′落在x轴上即停止运动，将此时的⊙C′M′N′绕点C′逆时针旋转（旋转度数不超过180°），旋转过程中直线M′N′与直线CA交于点S，与y轴交于点T，与x轴交于点W，请问⊙CST是否能为等腰三角形？若能，请求出所有符合条件的WN′的长度；若不能，请说明理由．12．在平面直角坐标系xOy中，把与x轴交点相同的二次函数图象称为“共根抛物线”．如图，抛物线L1：y=12x2−32x−2的顶点为D，交x轴于点A、B（点A在点B左侧），交y轴于点C．抛物线L2与L1是“共根抛物线”，其顶点为P．（1）若抛物线L2经过点（2，﹣12），求L2对应的函数表达式；（2）当BP﹣CP的值最大时，求点P的坐标；（3）设点Q是抛物线L1上的一个动点，且位于其对称轴的右侧．若⊙DPQ与⊙ABC相似，求其“共根抛物线”L2的顶点P的坐标．13．如图，已知抛物线与x轴交于A(−1，0)、B(3，0)两点，与y轴交于点C(0，3)．（1）求抛物线的解析式；（2）点D是第一象限内抛物线上的一个动点（与点C、B不重合），过点D作DF⊥x 轴于点F，交BC于点E，过点D作DM⊥BC，垂足为M．求线段DM的最大值；（3）已知P为抛物线对称轴上一动点，若△PBC是直角三角形，求出点P的坐标．14．如图，D是⊙ABC的BC边上一点，连接AD，作⊙ABD的外接圆，将⊙ADC沿直线AD折叠，点C的对应点E落在⊙O上.（1）求证：AE＝AB.（2）填空：①当⊙CAB＝90°，cos⊙ADB＝13，BE＝2时，边BC的长为.②当⊙BAE＝时，四边形AOED是菱形.15．如图，在平面直角坐标系xOy中，已知点A（0，4），点B是x轴正半轴上一点，连结AB，过点A作AC⊙AB，交x轴于点C，点D是点C关于点A的对称点，连结BD，以AD为直径作⊙Q交BD于点E，连结AE并延长交x轴于点F，连结DF.（1）求线段AE的长；（2）若AB﹣BO＝2，求tan⊙AFC的值；（3）若⊙DEF与⊙AEB相似，求BEDE的值.16．如图，已知AB为⊙O的直径，C为⊙O上一点，BG与⊙O相切于点B，交AC的延长线于点D（点D在线段BG上），AC = 8，tan⊙BDC = 4 3（1）求⊙O的直径；（2）当DG= 52时，过G作GE//AD，交BA的延长线于点E，说明EG与⊙O相切.答案解析部分1．【答案】（1）证明：如图，连结OC ，∵OE⊙BC ， ∴⊙OHB=90°， ∴⊙OBH+⊙BOD=90°， ∵OB=OC ， ∴⊙OBH=⊙OCB ， ∵⊙BOD=⊙BCD ， ∴⊙BCD+⊙OCB=90°， ∴OC⊙CD ，∵点C 为⊙O 上一点， ∴DF 为⊙O 的切线（2）证明：∵⊙OCD=90°， ∴⊙ECG+⊙OCE=90°， ∵OC=OE ， ∴⊙OCE=⊙OEC ， ∴⊙ECG+⊙OEC=90°， ∵⊙OEC+⊙HCE=90°， ∴⊙ECG=⊙HCE ，在⊙CHE 和⊙CGE 中， {∠CHE ＝∠CGE ＝90°∠ECG ＝∠HCE CE ＝CE，∴⊙CHE⊙⊙CGE （AAS ）（3）解：∵AB 是⊙O 的直径，∴⊙ACB=90°， ∴⊙ABC+⊙BAC=90°， ∵DF 为⊙O 的切线， ∴⊙OCA+⊙FCA=90°， ∵OA=OC ， ∴⊙OAC=⊙OCA ， ∴⊙FCA=⊙ABC ，∴sin∠ABC =sin∠FCA =√33，设AC= √3a ，则AB=3a ，∴BC =√AB 2−AC 2=√(3a)2−(√3a)2=√6a ， ∵⊙FCA=⊙ABC ，⊙AFC=⊙CFB ， ∴⊙ACF⊙⊙CFB ，∴AF CF =CF BF =AC BC =1√2，∵AF=1， ∴CF= √2 ， ∴BF =(√2)21=2 ，∴BF-AF=AB=1，∴OC =12,BC =√63，∵OE⊙BC ，∴CH =12BC =√66，∴OH =√OC 2−CH 2=(12)2−(√66)2=√36，∴HE=OE-OH= 12−√36，∵⊙CHE⊙⊙CGE ，∴EG=HE= 12−√36.2．【答案】（1）解：∵直线 y =−12x +2 与x 轴交于点A ，与y 轴交于点B ，令x=0，则y=2，令y=0，则x=4， ∴A （4，0），B （0，2），∵抛物线 y =−23x 2+bx +c 经过B （0，2）， C(52,34) ，∴{2=c 34=−23×254+52b +c ，解得： {b =76c =2 ， ∴抛物线的表达式为： y =−23x 2+76x +2 ；（2）解：当点P 在x 轴上方时，点P 与点C 重合，满足 ∠PAO =∠BAO ， ∵C(52,34) ，∴P(52,34) ，当点P 在x 轴下方时，如图，AP 与y 轴交于点Q ，∵∠PAO =∠BAO ，∴B ，Q 关于x 轴对称，∴Q （0，-2），又A （4，0），设直线AQ 的表达式为y=px+q ，代入，{−2=q0=4p +q ，解得： {p =12q =−2 ，∴直线AQ 的表达式为： y =12x −2 ，联立得：{y =12x −2y =−23x 2+76x +2，解得：x=3或-2，∴点P 的坐标为（3， −12 ）或（-2，-3），综上，当 ∠PAO =∠BAO 时，点P 的坐标为： (52,34) 或（3，−12 ）或（-2，-3）；（3）解：①如图，⊙MNC=90°，过点C 作CD⊙x 轴于点D ，∴⊙MNO+⊙CND=90°，∵⊙OMN+⊙MNO=90°，∴⊙CND=⊙OMN,又⊙MON=⊙CDN=90°，∴⊙MNO⊙⊙NCD ，∴MO ND =NO CD ，即 m 52−n =n 34 ，整理得： m =−43n 2+103n ； ②如图，∵⊙MNC=90°，以MC 为直径画圆E ，∵N(n,0) (0<n <52) ， ∴点N 在线段OD 上（不含O 和D ），即圆E 与线段OD 有两个交点（不含O 和D ）， ∵点M 在y 轴正半轴，当圆E 与线段OD 相切时，有NE= 12 MC ，即NE 2= 14MC 2， ∵M （0，m ）， C(52,34) ， ∴E （ 54， 38+m 2 ）， ∴(38+m 2)2 = 14[(52)2+(m −34)2] ，解得：m= 2512，当点M 与点O 重合时，如图，此时圆E 与线段OD （不含O 和D ）有一个交点，∴当0＜m ＜ 2512时，圆E 与线段OD 有两个交点，故m 的取值范围是：0＜m ＜ 2512. 3．【答案】（1）解：∵抛物线 y =−x 2+bx +c 经过 A(−1,0) ， D(3,4) 两点，∴{−(−1)2+b ×(−1)+c =0−32+b ×3+c =4，解之得： {b =3c =4 ∴抛物线的函数关系表达式为 y =−x 2+3x +4 ，设直线 AD 的函数关系表达式为 y =kx +b ，∵直线 AD 经过 A(−1,0) ， D(3,4) 两点，∴{k ×(−1)+b =0k ×3+b =4，解之得： {k =1b =1 ∴直线 AD 的函数关系表达式为 y =x +1 ．（2）解：把 x =0 代入 y =−x 2+3x +4 ，得 y =4 ．∴点 C 坐标是（0，4），∵CP//AD∴k CP =k AD =1 ，设直线 CP 的函数关系表达式为 y =x +b ，∵将点 C （0，4），代入 y =x +b 得： b =4 ，∴直线 CP 的函数关系表达式为 y =x +4 ，∵直线 CP 与抛物线 y =−x 2+3x +4 相交于 P ，则有： x +4=−x 2+3x +4 ，解之得： x 1=0 ， x 2=2 ，把 x =2 代入 y =x +4 ，得 y =6 ，∴点P 的坐标是（2，6）．（3）解：存在点 P ，使得 ∠CPE =∠QFE ．过点 C 作 CG ⊥PF ，垂足为 G ．过点 Q 作 QH ⊥PF ，垂足为 H ．则四边形CGHQ为矩形．∴CG=QH，∠CGP=∠QHF=90°．∴当PG=HF时，△CGP≌△QHF，这时∠CPG=∠QFH，即∠CPE=∠QFE．设P(m,−m2+3m+4)，则PG=−m2+3m+4−4=−m2+3m．∵HF=QO=1．∴−m2+3m=1，解得m=3+√52或m=3−√52．4．【答案】（1）x；D（2）解：①当0＜x≤2时，⊙EFG在梯形ABCD内部，所以y= √34x2；②分两种情况：⊙．当2＜x＜3时，如图1，点E、点F在线段BC上，⊙EFG与梯形ABCD重叠部分为四边形EFNM，∵⊙FNC=⊙FCN=30°，∴FN=FC=6﹣2x．∴GN=3x﹣6．∵在Rt⊙NMG中，⊙G=60°，GN=3x﹣6，∴GM= 12（3x﹣6），由勾股定理得：MN= √32（3x﹣6），∴S⊙GMN= 12×GM×MN= 12× 12（3x﹣6）× √32（3x﹣6）= √38（3x﹣6）2，所以，此时y= √34x2﹣√38（3x﹣6）2=﹣7√38x2+9√32x−9√32；⊙．当3≤x≤6时，如图2，点E在线段BC上，点F在射线CH上，⊙EFG与梯形ABCD重叠部分为⊙ECP，∵EC=6﹣x，∴y= √38（6﹣x）2= √38x2﹣3√32x+ 9√32，⊙．当x＞6时，点E，F都在线段BC的延长线上，没公共部分，∴y=0（3）解：当0＜x≤2时，∵y= √34x2，在x＞0时，y随x增大而增大，∴x=2时，y最大= √3；当2＜x＜3时，∵y=﹣9√37x 2+9√32x−9√32在x= 187时，y最大= 9√37；当3≤x≤6时，∵y= √38x−3√32x+9√32，在x＜6时，y随x增大而减小，∴x=3时，y最大= 9√38．综上所述：当x= 187时，y最大=9√37．5．【答案】（1）解：∵抛物线y=−34x2+bx+c与x轴交于点A(4，0)，与y轴交于点B(0，3)，∴{−34×16+4 b+c=0c=3，解得{b=94c=3，∴抛物线y=−34x 2+94x+3=−34(x−32)2+7516；∴抛物线的对称轴为直线x=32（2）解：设直线A(4，0)，B(0，3)的解析式为y=ax+d，∴{4a+d=0d=3，解得{a=−34 d=3，∴直线AB的表达式为：y=−34x+3；∵点M(m，0)为线段OA上一动点，过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P，N，∴PN//y轴，即PN//OB，且点N在点P上方，若以点P、N、B、O为顶点的四边形为平行四边形，则只需要PN=OB，∴−34m2+94m+3−(−34m+3)=3，解得m=2；即当m=2时，以点P、N、B、O为顶点的四边形为平行四边形．（3）解：M（1，0）6．【答案】（1）不是；是；解：如图1，根据题意，|PA−PB|＝2，∴|OP+2−(2−OP)|＝2，∴OP＝1. 若点P在第一象限内，作PQ⊙x轴于点Q，∵点P在直线y＝34x上，OP＝1，∴OQ=45,PQ=3 5 .∴P( 45,35). 若点P在第三象限内，根据对称性可知其坐标为(﹣45，﹣35). 综上所述，PO的长为1，点P的坐标为( 45,35)或（−45,−35）).（2）解：对于⊙C的任意一个“完美点”P都有|PA﹣PB|＝2，∴|CP+r﹣(r﹣CP)|＝2.∴CP＝1.∴对于任意的点P，满足CP＝1，都有|CP+r﹣(r﹣CP)|＝2，∴|PA﹣PB|＝2，故此时点P为⊙C的“完美点”.因此，⊙C的“完美点”是以点C为圆心，1为半径的圆.设直线y＝﹣2x+1与y轴交于点D，如图2，当⊙C 移动到与y 轴相切且切点在点D 的上方时，t 的值最大.设切点为E ，连接CE ，∵⊙C 的圆心在直线y ＝﹣2x+1上，∴此直线和y 轴，x 轴的交点D(0，1)，F( 12，0)， ∴OF ＝ 12，OD ＝1， ∵CE⊙OF ，∴⊙DOF⊙⊙DEC ，∴OD DE =OF CE， ∴1DE =12， ∴DE ＝2，∴OE ＝3，t 的最大值为3，当⊙C 移动到与y 轴相切且切点在点D 的下方时，t 的值最小.同理可得t 的最小值为﹣1.综上所述，t 的取值范围为﹣1≤t≤3.7．【答案】（1）解：① A ，C ②∵点D 是直线 y =x 的图上点，∴点D 在 y =x 上. 又∵点D 是 y =x 2−2 的上位点， ∴点D 在 y =x 与y =x 2−2 的交点R ，S 之间运动. ∵{y =x 2−2,y =x.∴{x 1=−1,y 1=−1. {x 2=2,y 2=2.∴点R( −1 ， −1 )，S( 2 ， 2 ). ∴−1<x D <2 .（2）解：如图，当圆与两条直线的反向延长线相切时，为临界点，临界点的两边都满足要求.将y=x+3沿直线y=3翻折后的直线的解析式为y=−x+3当y=x+3=0时，x=−3，∴A(-3,0),OA=3当x=0时，y=x+3=3∴C(0,3),OC=3∴OA=OC∵∠AOC=90°∴∠CAO=45°∴AH1=rsin45°=1√22=√2∵A(-3,0)∴x H1=−3+√2同理可得x H2=3−√2∴线段EF上同时存在图象G的上位点，图上点和下位点，圆心H的横坐标x H的取值范围为x H>3−√2或x H<−3+√2.8．【答案】（1）解：①34②C3③如图所示，设直线AD交圆O于B，连接OE，过点E作EF⊙x轴于F，∵点E 是点A 关于⊙O 的12倍的特征点， ∴AE AB =12， ∴E 是AB 的中点，∴OE⊙AB ，∵⊙EAO=60°，∴⊙EOA=30°，∴AE =12OA =12，EF =12OE ， ∴OE =√OA 2−AE 2=√32， ∴EF =√34， ∴OF =√OE 2−EF 2=34， ∴点E 的坐标为（34，√34）；（2）k 的最小值为2−√24，k 有最大值为2+√249．【答案】（1）解：把A （1，0），B （0，-3）代入 y=x 2+bx-3c ，得 {1+b −3c =0−3c =−3解得 {b =2c =1∴抛物线的解析式为y=x 2+2x-3；（2）解：对于y=x 2+2x-3，∵x =−b 2a=−1 ，A(1，0)∴C 点坐标为（-3,0），AC=4，Q点的横坐标为-1.如图所示：若以点A、C、P、Q 为顶点的平行四边形以AC为边，则PQ=AC=4.①当P点的横坐标为x1=-1-4=-5时，y1=x2+2x−3=25−10−3=12，即P1(-5,12）②当P点的横坐标为x2=-1+4=3时，y2=x2+2x−3=9+6−3=12，即P2(3,12）；若以点A、C、P、Q为顶点的平行四边形以AC为对角线，则设P3的横坐标为x3，则有x3−12=−3+12，解得x3=-1，y3=x2+2x−3=1−2−3=−4，即P3(-1，-4)。

2江苏省2024高考考前综合模拟(三)卷物理核心考点试题

2江苏省2024高考考前综合模拟（三）卷物理核心考点试题一、单选题 (共7题)第(1)题具有相同质子数和不同中子数的原子称为同位素．让氢的三种同位素原子核（、和）以相同的速度从带电平行板间的P点沿垂直于电场的方向射入电场，其中氘核恰好能离开电场，轨迹如图所示．不计粒子的重力，则（）A．不能离开电场B．在电场中受到的电场力最大C．在电场中运动的时间最短D．在电场中运动的过程中电场力对做功最少第(2)题以下四幅图是生活和科技中常见的现象，关于这些现象的描述，下列说法正确的是（）A．图甲，起重机将物体匀减速向上提升时，物体的机械能一定增加B．图乙，嫦娥三号探测器在月球表面软着陆减速落向月球表面时，探测器处于失重状态C．图丙，皮带传动中（皮带与滑轮间不打滑），主动轮和从动轮转动的角速度等大D．图丁，在医院做颈椎牵引治疗时，头部给牵引带的压力是因为牵引带发生形变引起的第(3)题有a、b、c、d四种单色光，在水中的折射率分别为n a、n b、n c、n d。

a光和b光从水中斜射向空气的折射光路如题图甲所示：b光和c光从空气斜射向水中的折射光路如题图乙所示；c光和d光从水中斜射向空气，d光的折射光路如题图丙所示（c光发生全反射）。

则可判断（）A．n d<n c<n b<n a B．n c<n d<n b<n aC．n d<n b<n c<n a D．n d<n c<n a<n b第(4)题磷是构成DNA的重要元素，2023年科学家在土卫二的海洋中检测到磷。

此发现意味着土卫二有可能存在生命。

目前探测器已经测出了土卫二的密度为，现发射一颗贴近土卫二表面的人造卫星对土卫二进一步观测，已知万有引力常量为G，则根据题中所给数据可以计算出（）A．人造卫星的周期B．土卫二的质量C．人造卫星的向心加速度大小D．人造卫星与土卫二之间的万有引力大小第(5)题一个光滑圆环固定在竖直平面内，质量为m的小球（可视为质点）套在圆环上，如图所示，已知重力加速度为g，将小球从圆环最高点A静止释放，小球沿圆环下滑至最低点C的过程中，下列说法正确的是（）A．从A运动到B的过程中，圆环对小球的弹力始终沿半径向外B．从A运动到C的过程中，小球在B点的机械能最大C．当圆环对小球的作用力为零时，小球的向心力大小为D．当小球运动到C点时，对圆环的弹力大小为第(6)题某部队进行一场实战演习。

九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》(四)(Word版,带答案)

九年级中考数学考点提升训练——专题：《三角形综合：全等与相似》（四）1．如图1，在平面直角坐标系中，直线AB分别交y轴、x轴于点A（0，a），点B（b，0），且a、b满足a2﹣4a+4+＝0．（1）求a，b的值；（2）以AB为边作Rt△ABC，点C在直线AB的右侧且∠ACB＝45°，求点C的坐标；（3）若（2）的点C在第四象限（如图2），AC与x交于点D，BC与y轴交于点E，连接DE，过点C作CF⊥BC交x轴于点F．①求证CF＝BC；②直接写出点C到DE的距离．2．已知：如图，点P是等边△ABC内一点，连接PC，以PC为边作等边三角形△PDC，连接PA，PB，BD．（1）求证：∠APC＝∠BDC；（2）当∠APC＝150°时，试猜想△DPB的形状，并说明理由；（3）当∠APB＝100°且DB＝PB，求∠APC的度数．3．如图，在△ABC中，AB＝AC，AD⊥BC于点D．点E为AD上一点，点F为BE延长线上一点，且AF＝AC．（1）如图1，若∠FBC＝∠BAC＝30°．①判断△BAF的形状，并证明；②若AE＝（+1）BE，则＝．（直接写出结果）（2）如图2，若∠FBC＝45°，作AG⊥BF于G，求证：EF＝BE+2AG．4．如图1，Rt△ABC中，点D，E分别为直角边AC，BC上的点，若满足AD2+BE2＝DE2，则称DE为Rt△ABC的“完美分割线”．显然，当DE为△ABC的中位线时，DE是△ABC的一条完美分割线．（1）如图1，AB＝10，cos A＝，AD＝3，若DE为完美分割线，则BE的长是．（2）如图2，对AC边上的点D，在Rt△ABC中的斜边AB上取点P，使得DP＝DA，过点P画PE⊥PD交BC于点E，连结DE，求证：DE是直角△ABC的完美分割线．（3）如图3，在Rt△ABC中，AC＝10，BC＝5，DE是其完美分割线，点P是斜边AB的中点，连结PD、PE，求cos∠PDE的值．5．如图1，张老师在黑板上画出了一个△ABC，其中AB＝AC．让同学们进行探究．（1）探究一：如图2，小明以BC为边在△ABC内部作等边△BDC，连接AD．请直接写出∠ADB的度数；（2）探究二：如图3，小彬在（1）的条件下，又以AB为边作等边△ABE，连接CE．判断CE与AD的数量关系，并说明理由；（3）探究三：如图3，小聪在（2）的条件下，连接DE．若∠DEC＝60°，DE＝2，求AE的长．6．如图1，在Rt△ABC中，∠ACB＝90°，AB＝20，AC＝16，CD是斜边AB上的中线，P是边AC上一点，连接DP，以DP为直角边作等腰直角三角形DPE（点E始终在直线AB右侧）．（1）求点D到边AC的距离；（2）当△PEC是以PE为腰的等腰三角形时，求所有满足要求的AP长．（3）如图2，当斜边DE与AC有交点时，记交点为Q，若AP＝CQ，则S△DPE ＝．（直接写出答案）7．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC，E为BC上一点，连接AE，作AF ⊥AE且AF＝AE，BF交AC于D．（1）如图1，求证：D为BF中点；（2）如图1，求证：BE＝2CD；（3）如图2，若＝，直接写出的值．8．在△ABC中，AC＝BC＝4，∠ACB＝90°，E为BC上一个动点，CF⊥AE于G，交AB于F．（1）如图1，当AE平分∠CAB时，求BE的长．（2）如图2，当E为BC中点时．①求CG的长．②连接EF，求GF+EF的值．（3）如图3，在E运动过程中，连接BG，则BG的最小值为．9．已知在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝BC．（1）连接BD，如图1，若∠BAD＝90°，AD＝3，求DC的长；（2）点E，F分别在射线DC，DA上．①如图2，若点E，F分别在线段CD，AD上，且满足∠EBF＝90°﹣∠ADC，求证：EF＝AF+CE；②如图3，若点E，F分别在线段DC延长线与DA延长线上，且满足EF＝AF+CE，请直接写出∠EBF与∠ADC之间的数量关系．10．（1）已知△ABC中，AB＝AC，∠BAC＝120°．①如图1，点M、N在底边BC上，且∠ANB＝45°，∠MAN＝60°．请在图中作出∠NAD＝60°，且AD＝AM，连接ND、CD；并直接写出BM与CN的数量关系．②如图2，点M在BC上，点N在BC的上方，且∠MBN＝∠MAN＝60°，求证：MC＝BN+MN；（2）如图3，在四边形ABCD中，∠CAB＝50°，BD平分∠ABC，若∠ADC与∠ABD互余，则∠DAC的大小为（直接写出结果）．参考答案1．解：（1）∵，∴，∵（a﹣2）2≥0，，∴a﹣2＝0，2b+2＝0，∴a＝2，b＝﹣1；（2）由（1）知a＝2，b＝﹣1，∴A（0，2），B（﹣1，0），∴OA＝2，OB＝1，∵△ABC是直角三角形，且∠ACB＝45°，∴只有∠BAC＝90°或∠ABC＝90°，Ⅰ、当∠BAC＝90°时，如图1，∵∠ACB＝∠ABC＝45°，∴AB＝CB，过点C作CG⊥OA于G，∴∠CAG+∠ACG＝90°，∵∠BAO+∠CAG＝90°，∴∠BAO＝∠ACG，在△AOB和△BCP中，，∴△AOB≌△CGA（AAS），∴CG＝OA＝2，AG＝OB＝1，∴OG＝OA﹣AG＝1，∴C（2，1），Ⅱ、当∠ABC＝90°时，如图2，同Ⅰ的方法得，C（1，﹣1）；即：满足条件的点C（2，1）或（1，﹣1）（3）①如图3，由（2）知点C（1，﹣1），过点C作CL⊥y轴于点L，则CL＝1＝BO，在△BOE和△CLE中，，∴△BOE≌△CLE（AAS），∴BE＝CE，∵∠ABC＝90°，∴∠BAO+∠BEA＝90°，∵∠BOE＝90°，∴∠CBF+∠BEA＝90°，∴∠BAE＝∠CBF，在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴BE＝CF，∴；②点C到DE的距离为1．如图4，过点C作CK⊥ED于点K，过点C作CH⊥DF于点H，由①知BE＝CF，∵BE＝BC，∴CE＝CF，∵∠ACB＝45°，∠BCF＝90°，∴∠ECD＝∠DCF，∵DC＝DC，∴△CDE≌△CDF（SAS），∴∠BAE＝∠CBF，∴CK＝CH＝1．2．解：（1）如图，∵△ABC，△PDC是等边三角形，∴AC＝BC，PC＝PD＝CD，∠ACB＝∠PCD＝60°，∴∠ACP＝∠BCD，且AC＝BC，PC＝CD，∴△ACP≌△BCD（SAS）∴∠APC＝∠BDC；（2）△DPB是直角三角形．理由：∵∠BDC＝∠APC＝150°，∠PDC＝60°∴∠BDP＝∠BDC﹣∠PDC＝90°，∴△DPB是直角三角形；（3）设∠APC＝x，则∠BPD＝200°﹣x，∠BDP＝x﹣60°∵PB＝DB，∴∠BPD＝∠BDP，∴200°﹣x＝x﹣60°，∴x＝130°，∴∠APC＝130°3．解：（1）①△BAF为等腰直角三角形．证明：∵AB＝AC，AD⊥BC，∠FBC＝∠BAC＝30°，∴∠ABC＝∠C＝75°，∠BAD＝∠CAD＝15°，∵AF＝AC，∴AB＝AF，∴∠ABF＝45°，∴△BAF为等腰直角三角形；②如图1，过点A作AM⊥BF于点M，设BE＝x，则AE＝（+1）x，∵∠FBC＝30°，∴DE＝BE＝x，∠BED＝∠AEF＝60°，∴∠EAM＝30°，∴EM＝AE（+1）x，∵△ABF为等腰直角三角形，AM⊥BF，∴AM＝MF＝BM，∴BM＝EB+EM＝x+x＝x，∴EF＝EM+MF＝x＝（2+）x，∴＝4+2．故答案为：4+2．（2）证明：如图2，过点A作AH⊥AE，交BC于点H，∵∠FBC＝45°，AD⊥BC，∴∠BED＝∠AEH＝45°，∴∠AHE＝∠AEH＝45°，AE＝AH，∴∠AEB＝∠AHF＝135°，∵AF＝AC，∴AB＝AF，∠ABF＝∠F，在△ABE和△AFH中，，∴△ABE≌△AFH（AAS），∴BE＝FH，∴AG＝EG＝GH，∴EH＝2AG，∴EF＝FH+EH＝BE+2AG．4．解：（1）∵AB＝10，cos A＝，∴cos A＝，∴AC＝8，CD＝5，∴＝＝6，设BE＝x，则CE＝6﹣x，在Rt△CDE中，DE2＝CD2+CE2＝52+（6﹣x）2，∵DE为完美分割线，∴AD2+BE2＝DE2，∴32+x2＝52+（6﹣x）2，解得：x＝．∴BE＝．故答案为：．（2）证明：如图2，∵DA＝DP，∴∠DAP＝∠DPA，∵PE⊥PD，∴∠DPA+∠EPB＝90°，又∠A＝∠B，∴∠EPB＝∠B，∴EP＝EB，∴AD2+BE2＝DP2+EP2＝DE2，∴DE是直角△ABC的完美分割线．（3）解：延长DP至F，使PF＝PD，连接BF，EF，∵AP＝BP，∠APD＝∠BPF，∴△APD≌△BPF（SAS），∴AD＝BF，∠A＝∠FBP，∴∠EBF＝∠CBA+∠FBP＝∠CBA+∠A＝90°，∵DE是完美分割线，∴DE2＝AD2+BE2＝BF2+BE2＝EF2，即ED＝EF．又PD＝PF，∴∠EPD＝90°，过点P作PM⊥AC，PN⊥BC，则∠MPD＝∠NPE＝90°﹣∠MPE，∴△MPD∽△NPE，∴，设PD＝a，则PE＝2a，则DE＝＝a，∴cos∠PDE＝＝．5．解：（1）探究一：∵△BDC是等边三角形，∴BD＝DC，∠BDC＝60°，在△ADB和△ADC中，，∴△ADB≌△ADC（SSS），∴∠ADB＝∠ADC，∵∠ADB+∠ADC＝360°﹣60°，∴∠ADB＝150°，故答案为：150°．（2）探究二：结论：CE＝AD．理由：∵△BDC、△ABE都是等边三角形∴∠ABE＝∠DBC＝60°，AB＝BE，BD＝DC．∴∠ABE﹣∠DBE＝∠DBC﹣∠DBE∴∠ABD＝∠EBC，在△ABD和△EBC中，∴△ABD≌△EBC（SAS）．∴AD＝CE．（3）探究三：∵△ABD≌△EBC，∴∠BDA＝∠ECB＝150°，∵∠BCD＝60°，∴∠DCE＝90°，∵∠DEC＝60°，∴∠CDE＝30°，∵DE＝2，∴CE＝1，由勾股定理得，DC＝BC＝，∵∠BDE＝60°+30°＝90°，DE＝2，BD＝．由勾股定理得，BE＝＝．∵△ABE是等边三角形∴AE＝BE＝．6．解：（1）过D用DF⊥AC于点H，如图1，则DF∥BC，∵D是AB的中点，∴AF＝CF，∴DF＝，∵BC＝，∴DF＝6，故点D到边AC的距离为6；（2）当PE＝CE时，如图1，过点E作EG⊥PC于点G，∴PG＝CG，∵∠DPE＝90°，∴∠DPF+∠EPG＝∠DPF+∠PDF＝90°，∴∠PDF＝∠EPG，∵PD＝EP，∠DFP＝∠PGE＝90°，∴△DPF≌△PEG（AAS），∴DF＝PG＝CG＝6，∴AP＝AC﹣PC＝16﹣6﹣6＝4；当PE＝PC时，如备用图1，过D作DF⊥AC于点F，过点E作EG⊥AC于点G，则DF∥BC，AF＝CF＝8，DF＝BC＝6，∵∠DPE＝90°，∴∠DPF+∠EPG＝∠DPF+∠PDF＝90°，∴∠PDF＝∠EPG，∵∠DFP＝∠PGE＝90°，DP＝EP，∴△PDF≌△EPG（AAS），∴DPG＝6，PF＝EG，设PE＝PC＝x，则EG＝FP＝8﹣x，由勾股定理得，PE2﹣EG2＝PG2，∴x2﹣（8﹣x）2＝62，解得，x＝，即PC＝，∴AP＝AC﹣PC＝16﹣，综上，AP＝4或；（3）过点D作DF⊥AC于点F，过点E作EG⊥AC于G，则DF∥EG∥BC，∵D是AB的中点，∴AF＝CF＝8，DF＝，∵AP＝CQ，∴PF＝QF，设AP＝CQ＝x，则PF＝QF＝，∵∠DPE＝90°，∠DFP＝90°，∴∠DPF+∠EPG＝∠DPF+∠PDF＝90°，∴∠PDF＝∠EPF，∵∠DFP＝∠PGE＝90°，DP＝PE，∴△DPF≌△PEG（AAS），∴DF＝PG＝6，PF＝EG＝8﹣x，∴QG＝PG﹣PQ＝6﹣2（8﹣x）＝2x﹣10，∵DF∥EG，∴△DFQ∽△EGQ，∴，即，解得，x＝14+6＞16（舍），或x＝14﹣6，∴PF＝QF＝EG＝8﹣x＝6﹣6，∴＝．另一解法：过D作DF⊥AC于点F，延长DF至M，使得DF＝FM，过M作MN⊥DE，与DE的延长线交于点N，如图2，则DF∥BC，∴QD＝QM，∴∠QDM＝∠QMD，∵D是AB的中点，DF∥BC，∴AF＝CF＝8，DF＝，∴DM＝12，∵AP＝CQ，∴PF＝QF，∴DP＝DQ，∴∠PDF＝∠QDF，∴∠PDF＝∠QMF，∴DP∥QM，∴∠MQN＝∠PDE＝45°，∴∠NMQ＝45°＝∠MQN，∴MN＝QN，不妨设MN＝QN＝x，则DP＝QD＝QM＝，∵DN2+MN2＝DM2，∴，解得，，∴，∴，∴．故答案为：72﹣36．7．证明：（1）如图1，过F点作FG⊥AC于点G，∵∠FAG+∠CAE＝90°，∠FAG+∠AFG＝90°，∴∠CAE＝∠AFG，在△AGF和△ECA中，，∴△AGF≌△ECA（AAS），∴AG＝EC，FG＝AC，∵AC＝BC，∴BC＝FG，又∵∠FGD＝∠DCB＝90°，∠FDG＝∠CDB，∴△FGD≌△BCD（AAS），∴DF＝BD，即D为BF的中点；（2）证明：∵△FGD≌△BCD，∴DC＝GD，∴CG＝2CD，∵AG＝CE，AC＝BC，∴CG＝BE，∴BE＝2CD；（3）解：如图2，过F点作FG⊥AC于点G，∵，∴，∵AC＝CB，∴，由（1），（2）可知△AGF≌△ECA，△FGD≌△BCD，∴CE＝AG，CD＝DG，∴，∴，∴，∴．∴．8．解：（1）∵AE平分∠CAB，∴点E到AC，AB的距离相等，∴，∵AC＝BC＝4，∠ACB＝90°，∴AB＝AC＝4，∴，∴，∴BE＝×4＝4（2﹣）＝8，即BE＝8﹣4；（2）①∵点E是BC的中点，∴CE＝BE＝BC＝2，∴AE＝＝2，∵CF⊥AE，∴S△ACE＝AE•CG＝AC•CE，∴CG＝．②过点B作BM⊥BC交CF延长线于点M，∵BM⊥BC，∴∠CBM＝90°，∴∠CBM＝∠ACE＝90°，∵∠ACG+∠BCM＝90°，∠ACG+∠CAE＝90°，∴∠BCM＝∠CAE，在△CBM和△ACE中，，∴△CBM≌△ACE（ASA），∴AE＝CM＝2，CE＝BM，∵CE＝BE，∴BM＝BE，∵∠CAB＝∠CBA＝45°，∴∠EBF＝∠MBF＝45°，在△EBF和△MBF中，，∴△EBF≌△MBF（SAS），∴EF＝MF，∴GF+EF＝GF+MF＝GM＝CM﹣CG＝2﹣．∴GF+EF＝．（3）取AC的中点N，连接NG，BN，∵点N是AC的中点，∴AN＝CN＝AC＝2，∴BN＝＝2，∵CF⊥AE，∴∠AGC＝90°，∴NE＝AC＝2，∴BG≥BN﹣NG，当且仅当B，G，N三点共线时，BG取得最小值，∴BG的最小值为2﹣2．故答案为：2﹣2．9．（1）解：∵∠ABC+∠ADC＝180°，∴∠A+∠C＝180°，又∵∠A＝90°，∴∠C＝90°＝∠A，在Rt△ABD和Rt△CBD中，，∴Rt△ABD≌Rt△CBD（HL），∴DC＝DA＝3；（2）证明：如图2，延长DC到G，使得CG＝AF，连接BG，∵∠ABC+∠BCD+∠ADC+∠A＝360°，∠ABC+∠ADC＝180°，∴∠A+∠BCD＝180°，且∠BCD+∠BCG＝180°，∴∠A＝∠BCG，∵AB＝BC，CG＝AF，∴△ABF≌△CBG（SAS），∴BF＝BG，∠ABF＝∠CBG，又∵∠ABC+∠ADC＝180°，∴∠EBF＝90°﹣∠ADC＝∠ABC＝∠ABF+∠EBC＝∠CBG+∠EBC＝∠EBG，∵BE＝BE，∴△EBF≌△EBG（SAS），∴EF＝EG＝EC+CG＝CE+AF；（3）解：∠EBF与∠ADC之间的数量关系为：∠EBF＝90°+∠ADC．在CD的延长线上截取CH＝AE，连接BH，∵∠ABC+∠BCD+∠ADC+∠DAB＝360°，∠ABC+∠ADC＝180°，∴∠DAB+∠BCD＝180°，且∠DAB+∠EAB＝180°，∴∠BCD＝∠EAB，且AB＝BC，AE＝CH，∴△AEB≌△CHB（SAS），∴BE＝BH，∠EBA＝∠HBC，∵EF＝AE+CF，∴EF＝CH+CF＝HF，且BF＝BF，BE＝BH，∴△EBF≌△HBF（SSS），∴∠EBF＝∠HBF，∵∠EBF+∠HBF+∠EBA+∠ABH＝360°，∴2∠EBF+∠HBC+∠ABH＝360°，∴2∠EBF+∠ABC＝360°，∴2∠EBF+180﹣∠ADC＝360°，∴∠EBF＝90°+∠ADC．10．解：（1）①BM＝2CN．如图1，作出∠NAD＝60°，且AD＝AM，连接ND、CD；∵∠MAN＝60°，∠BAC＝120°，∴∠BAM+∠CAN＝60°，∵∠CAD+∠CAN＝60°，又∵AD＝AM，AB＝AC，∴△ABM≌△ACD（SAS），∴BM＝CD，∠B＝∠ACD＝30°，∵AM＝AD，∠MAN＝∠DAN，AN＝AN，∴△AMN≌△ADN（SAS），∴∠ANM＝∠AND＝45°，∴∠MND＝90°，又∵∠DCN＝∠ACB+∠ACD＝60°，∴∠CDN＝30°，∴CD＝2CN，∴BM＝2CN．故答案为：BM＝2CN．②如图2，在CB上截取CG＝BN，连接AG，∵AB＝AC，∠BAC＝120°，∴∠C＝∠ABC＝30°，∵∠NBM＝60°，∴∠ABN＝30°，在△ABN和△ACG中，，∴△ABN≌△ACG（SAS），∴∠BAN＝∠CAG，AN＝AG，∴∠BAN+∠BAM＝∠BAM+∠CAG＝∠MAN＝60°，∴∠MAG＝∠BAC﹣∠BAM﹣∠CAG＝60°，在△AMN和△AMG中，，∴△AMN≌△AMG（SAS），∴MN＝MG，∴MC＝MG+GC＝MN+BN．（2）如图3，过点D作DM⊥BA于点M，DN⊥BC于点N，在AM上截取MK＝CN，连接DK，∵BD平分∠ABC，∴∠ABC＝2∠ABD，DM＝DN，∵∠ADC＝90°﹣∠ABD，∠MDN＝180°﹣2∠ABD，∴∠MDN＝2∠ADC，在△DMK和△DNC中，，∴△DMK≌△DNC（SAS），∴DC＝DK，∠MDK＝∠CDN，∴∠NDC+∠ADM＝∠MDK+∠ADM＝∠ADC，∴∠ADC＝∠ADK，∵AD＝AD∴△ADC≌△ADK（SAS），∴∠DAC＝∠DAM＝．故答案为：65°．。