改进欧拉法的Matlab程序
MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名:樊元君学号:02 日期:一、实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
:二、实验内容1、分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
求,步长h=。
*2、实验注意事项的精确解为,通过调整步长,观察结果的精度的变化^)三、程序流程图:●改进欧拉格式流程图:~|●四阶龙格库塔流程图:]四、源程序:●改进后欧拉格式程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');…x0=input('x0=');y0=input('y0=');disp('输入的范围是:');X=input('X=');Y=input('Y=');n=round((Y-X)/h);\i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);%·yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);%y1=(yp+yc)/2;x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y);:endend●四阶龙格库塔程序源代码:function [] = LGKT(h,x0,y0,X,Y)。
format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是:');"X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:n~x1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);% k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);% k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);%…y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4);%x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.7f,%.7f\n',x1,y1,y);end·end*五、运行结果:改进欧拉格式结果:;}四阶龙格库塔结果:步长分别为:和时,不同结果显示验证了步长减少,对于精度的提高起到很大作用,有效数字位数明显增加。
欧拉方法matlab

欧拉方法matlab欧拉方法matlab是数值计算中常用的一种方法,通过一系列的计算来逼近函数的解,并与真实解进行比较。
下面分步骤阐述欧拉方法在matlab中的实现过程。
第一步,定义微分方程。
首先需要明确待求解的微分方程,以y'=f(x,y)为例。
f为函数,表示自变量x和因变量y的关系。
在matlab中可以写成一个函数或者匿名函数的形式,如f=@(x,y)-2*x*y。
第二步,确定初始条件。
欧拉方法需要确定初始条件y0和初始值x0,以便进行迭代计算。
在matlab中,可以直接赋值给y0和x0,如y0=1和x0=0。
第三步,定义步长和迭代次数。
步长h表示每个小步长的大小,步数N表示需要到达的最终的x值,通常可以根据需要自行设定。
在matlab中,可以通过输入变量N和h来实现,如N=10,h=0.1。
第四步,进行欧拉方法的迭代计算。
具体的计算公式为y(i+1)=y(i)+h*f(x(i),y(i)),其中i表示当前的小步长编号。
在matlab中,可以通过for循环来实现,如下所示:for i=1:Ny(i+1)=y(i)+h*f(x(i),y(i));x(i+1)=x(i)+h;end第五步,绘制函数的图像。
通过上述计算可以获得欧拉方法逼近的函数值,可以使用plot函数将其描绘成一条曲线。
在matlab中,可以通过以下语句来实现:plot(x,y,'-ro')其中,'-ro'表示使用红色圆点曲线来描绘函数的图像。
综上所述,欧拉方法在matlab中的实现过程需要分别确定微分方程、初始条件、步长和迭代次数,进行迭代计算,并绘制函数的图像。
通过这些步骤的实现,可以更全面地理解欧拉方法的计算原理,更好地应用于实际问题的求解。
matlab软件欧拉算法教程

y( xn1 ) y( xn ) hK
*
寻求计算平均斜率的算法
考察欧拉法,以xn的斜率值
K1 f ( xn , yn )
作为平均斜率
考察改进的欧拉法,可以将其改写为:
1 1 yi 1 yn h K1 K 2 2 2 K1 f ( x n , yn ) K 2 f ( xn h, yn hK1 )
xn
h f ( x , y( x ))dx f ( xn , y( xn )) f ( xn1 , y( xn1 )) O( h3 ) 2
h yn1 yn [ f ( xn , yn ) f ( xn1 , yn1 )] 梯形格式 2
梯形格式是显式Euler格式与隐式Euler格式的 算术平均 Euler格式是显式算法,计算量小,但精度低 梯形格式,精度较高,但是隐式算法,需要通过 迭代过程求解,计算量大
四、四阶Runge-Kutta方法
继续上述过程,可以进一步导出四阶Runge-Kutta 格式
yn1 yn h K1 2 K 2 2 K 3 K 4 , 6 K f x , y , n n 1 h K 2 f x n 1 , yn K1 , 2 2 K f x , y h K , n 1 n 2 3 2 2 K 4 f xn1 , yn hK 3 . Biblioteka 利用数值积分求积分项的方法离散
(1)左矩形法
xn1
f ( x , y( x ))dx hf ( xn , y( xn )) O( h2 )
xn
y( xn1 ) y( xn ) hf ( xn , y( xn ))
欧拉法(euler)求解常微分方程的matlab程序及案例

欧拉法(euler)求解常微分方程的matlab程序及案例欧拉方法是最初用于求解常微分方程的数值方法之一,它是一种显式的一步法,具有易于实施的优点,特别适合初学者使用。
本文将介绍欧拉法的原理和使用MATLAB求解常微分方程的具体方法,同时给出一个简单的实例进行说明。
一、欧拉法原理考虑一个一阶常微分方程y'=f(t,y),欧拉法的基本思想是将时间步长Δt均分成n个小步长,从y(t0)开始依次计算每个时刻的值,得到一列估计值y1, y2, …, yn。
欧拉法的计算公式为:(1)y1=y(t0+Δt)=y(t0)+Δtf(t0, y0)(2)y2=y(t0+2Δt)=y(t0+Δt)+Δtf(t0+Δt, y1)(3)yn=y(t0+nΔt)=y(t0+(n-1)Δt)+Δtf(t0+(n-1)Δt, yn-1)可以看出,欧拉法的核心在于利用已知的t和y计算f(t,y),从而获得y的逼近值。
但是需要注意的是,步长Δt越小,计算所需的时间和内存就越多,而精度却并不一定提高。
因此在实际应用中需要结合具体问题选择合适的步长。
二、MATLAB求解常微分方程的具体方法(1)定义常微分方程我们以一个简单的例子开始,考虑求解y'=1-y,y(0)=0.5在[0,1]区间内的积分。
首先定义匿名函数dydt,将其传到ode45中求解:dydt=@(t,y)1-y;[t,y]=ode45(dydt,[0 1],0.5);plot(t,y,'-o')运行以上代码可以得到结果,其中plot函数用于绘制图像。
但是,由于求解过程中计算机执行到ode45函数时可能需要很长时间,因此需要更快捷的方法。
(2)利用欧拉法求解方程欧拉法求解方程首先需要定义步长Δt,这里设Δt为0.1。
定义起始值y=[0.5]、时间向量t=0:Δt:1,然后计算列向量y的估计值:t=0:0.1:1;y=zeros(size(t));y(1)=0.5;for n=1:length(t)-1y(n+1)=y(n)+0.1*(1-y(n));endplot(t,y,'-o')以上代码的执行结果与前面的ode45方法相同,但是速度更快。
解微分方程欧拉法,R-K法及其MATLAB实例

解微分方程的欧拉法,龙格-库塔法及其MATLAB简单实例欧拉方法(Euler method)用以对给定初值的常微分方程(即初值问题)求解分为前进EULER法、后退EULER法、改进的EULER法。
缺点:欧拉法简单地取切线的端点作为下一步的起点进行计算,当步数增多时,误差会因积累而越来越大。
因此欧拉格式一般不用于实际计算。
改进欧拉格式:为提高精度,需要在欧拉格式的基础上进行改进。
采用区间两端的斜率的平均值作为直线方程的斜率。
改进欧拉法的精度为二阶。
算法为:微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值。
对于常微分方程:x∈[a,b]y(a) = y0可以将区间[a,b]分成n段,那么方程在第xi点有y'(xi) = f(xi,y(xi)),再用向前差商近似代替导数则为:在这里,h是步长,即相邻两个结点间的距离。
因此可以根据xi点和yi点的数值计算出yi+1来:i=0,1,2,L这就是向前欧拉格式。
改进的欧拉公式:将向前欧拉公式中的导数f(xi,yi)改为微元两端导数的平均,即上式便是梯形的欧拉公式。
可见,上式是隐式格式,需要迭代求解。
为了便于求解,使用改进的欧拉公式:数值分析中,龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。
实际上,龙格-库塔法是欧拉方法的一种推广,向前欧拉公式将导数项简单取为f(xn,yn),而改进的欧拉公式将导数项取为两端导数的平均。
龙格-库塔方法的基本思想:在区间[xn,xn+1]内多取几个点,将他们的斜率加权平均,作为导数的近似。
龙格库塔法的家族中的一个成员如此常用,以至于经常被称为“RK4”或者就是“龙格库塔法”。
令初值问题表述如下。
则,对于该问题的RK4由如下方程给出:其中这样,下一个值(y n+1)由现在的值(y n)加上时间间隔(h)和一个估算的斜率的乘积决定。
该斜率是以下斜率的加权平均:k1是时间段开始时的斜率;k2是时间段中点的斜率,通过欧拉法采用斜率k1来决定y在点tn + h/2的值;k3也是中点的斜率,但是这次采用斜率k2决定y值;k4是时间段终点的斜率,其y值用k3决定。
微分方程数值解之欧拉法在MATLAB下的应用

科教论坛 !"#!$%&$'(') *+&,-./&$01$21(3$&)%)$$%%(3
微分方程数值解之欧拉法在 J7<97F下的应用
梁春叶4王桥明4孙远通4叶晓艳4曾宝莹
玉林师范学院数学与统计学院!广西玉林!(#+$$$
摘4要微分方程在实际应用中十分广泛涉及领域众多但对于微分方程的数值解的计算仍然有很大挑战 本文着重 对微分方程数值解求解的常用的一类基础方法欧拉法进行在 EH#[HC的应用下的一个简单介绍
求出$ 以下为在 50;"0)中实现!
F8/F68& 6'
+'
Copyright©博看网 . All Rights Reserved.
科教论坛
%I&Fh(J>>& 8'hh63t3i8326% KG&( h+ 8&$'hh( 27, % 8h(FG*H%& %I&F#KG&(' 由此得该方程的精确解为!
科技风 "#"$ 年 % 月
8hFJ/E*J>8& 8' 由此得解析解为!8h67 i63 N6N$' $
)% $) $) )% 使用欧拉法求解#如下! A h%3$% >hu& 6#8' 63t(i63t)% 6h+$!A!$%, % -hFJ9%& 6#)' i$% 8$ h+) 27#9%$GF&$#-' , % >G$& h$!8$& &N$'h8$& &' NA!>& 6& &' #8$& &' ' % %&( 8h63t732)%i63t332$)N632$)N$' 2)%% E*G7& 6#8#pGBp#6#8$#pN@p' *%L%&(& p,6?K7p#p,+*%$p' 运行程序可输出结果为!
欧拉方法matlab

欧拉方法matlab
欧拉方法是一种数值解微分方程的方法,适用于一阶常微分方程和某些高阶微分方程。
本文将介绍如何使用MATLAB实现欧拉方法。
首先,我们需要定义微分方程和初始条件。
例如,对于一阶常微分方程dy/dx = f(x,y),初始条件为y(x0) = y0,我们可以定义函数f和初始值x0和y0:
function dydx = f(x,y)
dydx = ... % 定义f(x,y)的具体表达式
end
x0 = ... % 初始值x0
y0 = ... % 初始值y0
接下来,我们需要设置步长和计算区间。
步长越小,计算结果越精确,但计算量也会增加。
计算区间可以根据需要设置。
h = ... % 步长
xspan = ... % 计算区间
然后,我们可以使用欧拉方法计算微分方程的数值解。
欧拉方法的基本思想是在每个步长上使用当前值和导数的近似值(如斜率)来估计下一个值。
首先,我们可以定义一个数组来存储计算结果,设初始值为y0: y = [y0];
然后,我们可以使用for循环来计算每个步长上的结果。
在每个步长上,我们需要计算当前值的导数,以及使用欧拉方法计算下一个
值。
改进的欧拉公式的应用

0.5000
处的数值解为
1.4164
微分方程y’=y-(2*x)/y在点
0.6000
处的数值解为
1.4860
微分方程y’=y-(2*x)/y在点
0.7000
处的数值解为
1.5525
微分方程y’=y-(2*x)/y在点
0.8000
处的数值解为
1.6165
微分方程y’=y-(2*x)/y在点
0
处的数值解为
1
微分方程y’=y-(2*x)/y在点
0.1000
处的数值解为
1.0959
微分方程y’=y-(2*x)/y在点
0.2000
处的数值解为
1.1841
微分方1.2662
微分方程y’=y-(2*x)/y在点
0.4000
处的数值解为
1.3434
改进欧拉公式欧拉公式的应用欧拉公式欧拉公式证明欧拉公式推导欧拉公式是什么材料力学欧拉公式matlab欧拉公式
改进的欧拉公式的应用
例如求解微分方程y'=y-(2*x)/y在区间[0 1]上的数值解,初始条件y(1)=1
在matlab中运行结果如下
h =
0.1000
x =
0
y =
1
微分方程y’=y-(2*x)/y在点
0.9000
处的数值解为
1.6782
微分方程y’=y-(2*x)/y在点
1.0000
处的数值解为
1.7379
欧拉及改进的欧拉法求解常微分方程

生物信息技术0801徐聪U200812594
#include<stdio.h>
#include<math.h>
void f1(double *y,double *x,double *yy)
{
y[0]=2.0;
x[0]=0.0;
yy[0]=2.0;
f1(y,x,yy);
}
{
y[0]=2.0;
x[0]=0.0;
yy[0]=2.0;
for(int =1;i<=9;i++)
{
x[i]=x[i-1]+0.2;
y0[i]=y[i-1]+0.2*(y[i-1]-x[i-1]);
y[i]=y[i-1]+0.1*(y[i-1]-x[i-1]+y0[i-1]-x[i-1]);
yy[i]=x[i]+1+exp(x[i]);
printf("若x=%f,计算值是%f,真实值是%f,截断误差是%f\n ",x[i],y[i],yy[i],y[i]-yy[i]);
}
};
void f4(double *y,double *x,double *yy,double *y0)
{
y[0]=1.0;
x[0]=0.0;
yy[0]=1.0;
}
};
void f2(double *y,double *x,double *yy)
{
y[0]=1.0;
x[0]=0.0;
yy[0]=1.0;
for(int i=1;i<=9;i++)
微分方程数值解第一次报告——matlab改进欧拉法与四阶龙格-库塔求解

微分方程数值解第一次报告徐松松41345053计1304一:实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
二:实验内容分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
{y′=−xy2y(0)=2(0<=x<=5) , 步长h=0.25。
三:源程序改进后欧拉格法程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是');X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);% yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);% y1=(yp+yc)/2; x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('½á¹û=%.3f,%.8f,%.8f\n',x1,y1,y); endend四阶龙格库塔法源程序:function [] = LGKT(h,x0,y0,X,Y)format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是');X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:nx1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);%k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);%k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);% y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4); %x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('½á¹û=%.3f,%.7f,%.7f\n',x1,y1,y);endend四:运行结果改进欧拉法:四阶龙格库塔法:。
用欧拉法、改进欧拉法、四阶龙格-库塔法解初值问题

常微分方程的数值解一、实验名称:用欧拉法、改进欧拉法、四阶龙格-库塔法解初值问题[])( b a, x ),(00⎪⎩⎪⎨⎧=∈=y x y y x f dx dy 要求输出:x ,真值,欧拉法,改进欧拉法,龙格库塔法二、算法:(1)欧拉法公式:),(1n n n n y x f h y y +=+(2)改进欧拉法公式:[]),(),(2111+++++=n n n n n n y x f y x f h y y (3)龙格—库塔法公式: ()⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++=⎪⎭⎫ ⎝⎛++=⎪⎭⎫ ⎝⎛++==++++=+342312143211,2,212,21),()22(6hk y h x f k k h y h x f k k h y h x f k y x f k k k k k h y y n n n n n n n n n n 三、源程序(见附件)1. 常微分方程见f.m2. 欧拉法、改进欧拉法、龙格库塔法及真值对比见cwffc.m四、数值例子以讲义例9.2为例:⎪⎩⎪⎨⎧=-=1)0(2y y x y dxdy 在区间[0,1.5]上,取h=0.11.在命令窗口输入: cwffc(@f,1,0.1,0,1.5)、回车输出:欧拉法、改进欧拉法、龙格库塔法的计算结果及真值五、分析总结由以上的实例可以看出这三种方法的计算精度:龙格库塔>改进欧拉法>欧拉法,由于欧拉法采取的实际是左矩形公式,随着计算次数的增多,其误差越来越大,改进欧拉法较欧拉法的精度要高,而龙格库塔法具有收敛、稳定、计算过程中可以改变步长等优点。
六、操作手册1.双击启动matlab;2.在命令窗口依次输入cwffc(@fx,y0,h,a,b),回车(输入时给y0赋初始值,h赋步长,a赋左端点值,b赋右端点值,常微分方程的修改在f.m 中进行),即可输出真值和欧拉法、改进欧拉法、龙格库塔法的计算结果。
改进的欧拉法
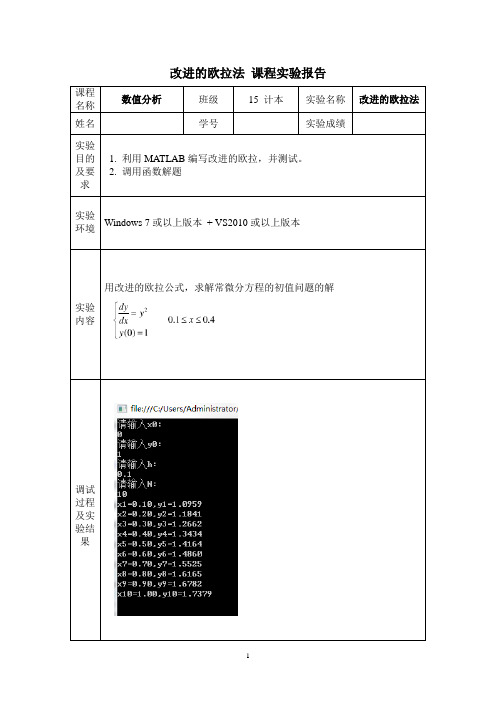
}
Console.ReadKey();
}
}
}
通过这次实验我掌握了将得到的解进一步精确,而且要学会比较这几种方法的精确性,显然,四阶龙格库达比改进欧拉发精确,改进欧拉发比欧拉法精确。
实验难度不大,要比较n的取值不同,产生的影响不同。
代码
using System;
using System.Collections.Generic;
using System.Linq;
double x1 = 0, y1 = 0, yp, yc;
for (int n = 1; n <= N; n++)
{
x1 = x0 + h;
yp = y0 + h * f(x0, y0);
yc = y0 + h * f(x1, yp);
y1 = (yp + yc) / 2;
Console.WriteLine("x{0}={1:f2},y{2}={3:f4}", n, x1, n, y1);
Console.WriteLine("请输入h:");
double h = Convert.ToDouble(Console.ReadLine());
Console.WriteLine("请输入N:");
double N = Convert.ToDouble(Console.ReadLine());
{
Console.WriteLine("请输入x0:");
double x0 = Convert.ToDouble(Console.ReadLine());
