欧拉法matlab程序
MATLAB改进欧拉法与四阶龙格-库塔求解一阶常微分方程

姓名:樊元君学号:02 日期:一、实验目的掌握MATLAB语言、C/C++语言编写计算程序的方法、掌握改进欧拉法与四阶龙格-库塔求解一阶常微分方程的初值问题。
掌握使用MATLAB程序求解常微分方程问题的方法。
:二、实验内容1、分别写出改进欧拉法与四阶龙格-库塔求解的算法,编写程序上机调试出结果,要求所编程序适用于任何一阶常微分方程的数值解问题,即能解决这一类问题,而不是某一个问题。
实验中以下列数据验证程序的正确性。
求,步长h=。
*2、实验注意事项的精确解为,通过调整步长,观察结果的精度的变化^)三、程序流程图:●改进欧拉格式流程图:~|●四阶龙格库塔流程图:]四、源程序:●改进后欧拉格式程序源代码:function [] = GJOL(h,x0,y0,X,Y)format longh=input('h=');…x0=input('x0=');y0=input('y0=');disp('输入的范围是:');X=input('X=');Y=input('Y=');n=round((Y-X)/h);\i=1;x1=0;yp=0;yc=0;for i=1:1:nx1=x0+h;yp=y0+h*(-x0*(y0)^2);%yp=y0+h*(y0-2*x0/y0);%·yc=y0+h*(-x1*(yp)^2);%yc=y0+h*(yp-2*x1/yp);%y1=(yp+yc)/2;x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.8f,%.8f\n',x1,y1,y);:endend●四阶龙格库塔程序源代码:function [] = LGKT(h,x0,y0,X,Y)。
format longh=input('h=');x0=input('x0=');y0=input('y0=');disp('输入的范围是:');"X=input('X=');Y=input('Y=');n=round((Y-X)/h);i=1;x1=0;k1=0;k2=0;k3=0;k4=0;for i=1:1:n~x1=x0+h;k1=-x0*y0^2;%k1=y0-2*x0/y0;%k2=(-(x0+h/2)*(y0+h/2*k1)^2);%k2=(y0+h/2*k1)-2*(x0+h/2)/(y0+h/2*k1);% k3=(-(x0+h/2)*(y0+h/2*k2)^2);%k3=(y0+h/2*k2)-2*(x0+h/2)/(y0+h/2*k2);% k4=(-(x1)*(y0+h*k3)^2);%k4=(y0+h*k3)-2*(x1)/(y0+h*k3);%…y1=y0+h/6*(k1+2*k2+2*k3+k4);%y1=y0+h/6*(k1+2*k2+2*k3+k4);%x0=x1;y0=y1;y=2/(1+x0^2);%y=sqrt(1+2*x0);%fprintf('结果=%.3f,%.7f,%.7f\n',x1,y1,y);end·end*五、运行结果:改进欧拉格式结果:;}四阶龙格库塔结果:步长分别为:和时,不同结果显示验证了步长减少,对于精度的提高起到很大作用,有效数字位数明显增加。
有限差分的欧拉法

西北农林科技大学实习报告学院:理学院 专业年级:信计061 姓名:袁金龙 学号:15206012 课程:微分方程数值解 报告日期:2008-11-26实习一、一维问题的有限差分方法-----Euler 法一)实习问题:用欧拉法,龙格库塔法,米尔恩法求解下面的初值问题:'2(0)1tu u e u ⎧+=⎨=⎩二)算法描述:⑴欧拉法:1(,),0,1,2,...,1m m m m u u hf t u m n +=+=-⑵龙格库塔法的中点法:111(,(,)),0,1,2,...,122m m m m m m u u hf t h u hf t u m n +=+++=-⑶米尔恩法:2211(4),0,1,2,...,23m m m m m u u h f f f m n +++=+++=-⑷初始值的确定: 泰勒级数法1'1000()()()...()(1)q q j jh u u t u t jh ut q --=+++- ⑸雅可比迭代法1[1][]0[0]11(,)()()k n n m k k m k m k j m j j m j j m km k m k u h f t u u h f u uhf Euler βαβ-++++++=++-+-⎧=--⎪⎨⎪=⎩∑三)matlab 程序: ⑴问题函数:function [f1]=f(t,u) f1=-2*u+exp(t);*************************************************** ⑵欧拉法:function []=oula(a,b,u0,n) %[a,b]表示t 的取值区间%u0表示初值%n表示将[0,1]区间分成的分数h=(b-a)/n;t0=a;u(1)=u0+h*(f(t0,u0));for i=1:nt(i)=a+i*h;endtfor i=2:nu(i)=u(i-1)+h*f(t(i-1),u(i-1));endu%精确解的求法for i=1:nu1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1plot(t,u,t,u1)title('欧拉法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');*********************************************************** ⑶龙格库塔法的中点法:function []=zhongdian(a,b,u0,n)%[a,b]表示t的取值区间%u0表示初值%n表示将[0,1]区间分成的分数h=(b-a)/n;t0=a;u(1)=u0+h*(f((t0+(1/2)*h),(u0+(1/2)*h*f(t0,u0))));for i=1:nt(i)=a+i*h;endtfor i=2:nu(i)=u(i-1)+h*(f((t(i-1)+(1/2)*h),(u(i-1)+(1/2)*h*f(t(i-1),u(i-1))))); endu%精确解的求法for i=1:nu1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1plot(t,u,t,u1)title('中点法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');**************************************************************⑷米尔恩法:function []=Milne(n,e)%n表示区间[0,1]要分的份数%对于初值精度我们选择q=3阶的%初值的求解%经过计算运用泰勒级数法求解初值%q(i)表示第i次迭代满足精度的最终值t0=0;for i=1:nt(i)=(1/n)*i;endu0=1;h=1/n;u2(1,1)=1-h+2.5*h*h%Jacobi迭代求解隐式法u2(2,1)=u2(1,1)+h*f(t(1),u2(1,1))for i=2:1000000u2(2,i)=h*(1/3)*f(t(2),u2(2,i-1))+u0+h*(1/3)*f(t0,u0)+h*(4/3)*f(t(1),u2(1,1));if abs(u2(2,i)-u2(2,(i-1)))<eu2(3,1)=u2(2,i)+h*f(t(2),u2(2,i));break;endendfor i=3:nfor j=2:1000000u2(i,j)=h*(1/3)*f(t(i),u2(i,j-1))+u2(i-2,1)+h*(1/3)*f(t(i-2),u2(i-2,1))+h*(4/3)*f(t(i-1),u2(i-1,1));if abs(u2(2,j)-u2(2,(j-1)))<eu2(i+1,1)=u2(i,j)+h*f(t(i),u2(i,j));break;endendendq(1)=u2(1,1);for i=2:n-1q(i)=u2(i+1,1);end%精确解的求法for i=1:n-1t1(i)=(1/n)*i;endfor i=1:n-1u1(i)=(2/3)*exp(-2*t(i))+(1/3)*exp(t(i));endu1;plot(t1,q,t1,u1)title('Milne法中的预测值与真实值的比较');xlabel('采样点');ylabel('幅度');grid;legend('预测值','真实值');*********************************************************四)图形显示的计算结果:⑴欧拉法:表1:欧拉法中的预测值与真实值的比较(n=20时)真实值预测值误差(%)0.9500 0.9536 0.38260.9076 0.9142 0.72710.8721 0.8812 1.03170.8430 0.8540 1.29550.8197 0.8324 1.51810.8020 0.8158 1.70050.7893 0.8041 1.84400.7813 0.7968 1.95110.7777 0.7938 2.02490.7784 0.7948 2.06860.7830 0.7997 2.08620.7913 0.8082 2.08150.8033 0.8202 2.05850.8188 0.8356 2.02070.8376 0.8544 1.97160.8597 0.8764 1.91430.8850 0.9017 1.85140.9135 0.9301 1.78530.9451 0.9616 1.71790.9799 0.9963 1.6506表2:欧拉法中的预测值与真实值的比较(n=10时)真实值 预测值 误差(%)0.9000 0.9142 1.5544 0.8305 0.8540 2.7514 0.7866 0.8158 3.5882 0.7642 0.7968 4.0910 0.7606 0.7948 4.3105 0.7733 0.8082 4.31150.8009 0.8356 1.638 0.8421 0.8764 1.6736 0.8962 0.9301 1.6943 0.96290.99631.70540.10.20.30.40.50.60.70.80.910.750.80.850.90.951欧拉法中的预测值与真实值的比较采样点幅度图1:欧拉法中的预测值与真实值的比较(分成20份时)说明:从图1及表1和表2中可以看出:采用欧拉法对初值问题的近似比较准确,且从算法中可以推断,随着n (将[a,b]区间分成的分数)值的增大,误差将会越来越小。
用MATLAB程序生动地演示欧拉公式

⽤MATLAB程序⽣动地演⽰欧拉公式下⾯的MA TLAB 程序⽣动地演⽰欧拉公式Exp(t) = cos(t) + j sin(t)% Henry-104% 本程序演⽰欧拉公式% Jan.25th,2012%h_fig1 = figure;set(h_fig1, 'unit', 'normalized', 'position', [0.1, 0.1, 0.9, 0.9]);set(h_fig1, 'defaultuicontrolunits', 'normalized');h_text1 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.73, 0.25, 0.05],... % 创建⽂本框'String', '▲是cos 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_text2 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.78, 0.25, 0.05],... % 创建⽂本框'String', 'Δ是sin 和exp 曲线的起点', 'ForegroundColor', 'r', 'FontName', '⿊体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_pushbutton1 = uicontrol(h_fig1, 'Style', 'PushButton', 'Position', [0.82, 0.12, 0.07, 0.06],...'string', '退出', 'BackgroundColor', [0.8 0.9 0.8], 'ForegroundColor', 'r', 'FontSize', 14, 'FontWeight', 'Bold',...'callback', 'delete(h_fig1),')h_axes0 = axes('Box', 'on', 'Position', [0.15, 0.18, 0.56, 0.68], 'FontSize', 8)set(gcf,'color','w');w = 0.1*pit = 0:40; % 在前进⽅向绕了2 圈%a = -ones(1,length(t));plot3(cos(w*t),t,sin(w*t),'b', 'LineWidth', 2);grid on; hold on;hc = plot3(cos(w*t),t,a,'k--'); hold on;set(hc, 'Color', 'r', 'LineWidth', 2);a=-a;hs = plot3(a,t,sin(w*t),'r-.'); hold on;set(hs, 'Color', 'k', 'LineWidth', 2);text(0.7,0.3,0.6, ' <-- CCW', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,-1, ' ▲Cos', 'Color', 'r', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,0, ' Δ Sin', 'FontSize', 14, 'FontWeight', 'Bold');%xlabel('x', 'FontSize', 14, 'FontWeight', 'Bold');ylabel('t', 'FontSize', 14, 'FontWeight', 'Bold');zlabel('y', 'FontSize', 14, 'FontWeight', 'Bold');title('演⽰欧拉公式y = exp(jwt) = cos(wt) + jsin(wt)', 'Color', 'b', …'FontSize', 18, 'FontWeight', 'Bold');%line([-1,-1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,40],[-1,-1],'LineWidth',3, 'Color', 'k');line([-1,1],[0,0],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,0],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[40,40],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');line([-1,1],[40,40],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');text(0,0,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'r') text(0,40,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'b')程序运⾏结果如下所⽰。
欧拉法求解一阶微分方程matlab

为了更好地理解欧拉法求解一阶微分方程在Matlab中的应用,我们首先来了解一些背景知识。
一阶微分方程是指只含有一阶导数的方程,通常表示为dy/dx=f(x,y),其中f(x,y)是关于x和y的函数。
欧拉法是一种常见的数值解法,用于求解微分方程的近似数值解。
它是一种基本的显式数值积分方法,通过将微分方程转化为差分方程来进行逼近。
在Matlab中,我们可以利用欧拉法求解一阶微分方程。
我们需要定义微分方程的函数表达式,然后选择合适的步长和初始条件,最后使用循环计算逼近解。
下面我们来具体讨论如何在Matlab中使用欧拉法来求解一阶微分方程。
我们假设要求解的微分方程为dy/dx=-2x+y,初始条件为y(0)=1。
我们可以通过以下步骤来实现:1. 我们需要在Matlab中定义微分方程的函数表达式。
在Matlab中,我们可以使用function关键字来定义函数。
在这个例子中,我们可以定义一个名为diff_eqn的函数,表示微分方程的右侧表达式。
在Matlab中,这个函数可以定义为:```matlabfunction dydx = diff_eqn(x, y)dydx = -2*x + y;end```2. 我们需要选择合适的步长和初始条件。
在欧拉法中,步长的选择对于数值解的精度非常重要。
通常情况下,可以先尝试较小的步长,然后根据需要进行调整。
在这个例子中,我们可以选择步长h=0.1,并设置初始条件x0=0,y0=1。
3. 接下来,我们可以使用循环来逼近微分方程的数值解。
在每一步,根据欧拉法的迭代公式y(i+1) = y(i) + h * f(x(i), y(i)),我们可以按照下面的Matlab代码计算逼近解:```matlabh = 0.1; % 步长x = 0:h:2; % 定义计算区间y = zeros(1, length(x)); % 初始化y的值y(1) = 1; % 设置初始条件for i = 1:(length(x)-1) % 欧拉法迭代y(i+1) = y(i) + h * diff_eqn(x(i), y(i));end```通过上述步骤,在Matlab中就可以用欧拉法求解一阶微分方程。
微分方程数值解之欧拉法在MATLAB下的应用

科教论坛 !"#!$%&$'(') *+&,-./&$01$21(3$&)%)$$%%(3
微分方程数值解之欧拉法在 J7<97F下的应用
梁春叶4王桥明4孙远通4叶晓艳4曾宝莹
玉林师范学院数学与统计学院!广西玉林!(#+$$$
摘4要微分方程在实际应用中十分广泛涉及领域众多但对于微分方程的数值解的计算仍然有很大挑战 本文着重 对微分方程数值解求解的常用的一类基础方法欧拉法进行在 EH#[HC的应用下的一个简单介绍
求出$ 以下为在 50;"0)中实现!
F8/F68& 6'
+'
Copyright©博看网 . All Rights Reserved.
科教论坛
%I&Fh(J>>& 8'hh63t3i8326% KG&( h+ 8&$'hh( 27, % 8h(FG*H%& %I&F#KG&(' 由此得该方程的精确解为!
科技风 "#"$ 年 % 月
8hFJ/E*J>8& 8' 由此得解析解为!8h67 i63 N6N$' $
)% $) $) )% 使用欧拉法求解#如下! A h%3$% >hu& 6#8' 63t(i63t)% 6h+$!A!$%, % -hFJ9%& 6#)' i$% 8$ h+) 27#9%$GF&$#-' , % >G$& h$!8$& &N$'h8$& &' NA!>& 6& &' #8$& &' ' % %&( 8h63t732)%i63t332$)N632$)N$' 2)%% E*G7& 6#8#pGBp#6#8$#pN@p' *%L%&(& p,6?K7p#p,+*%$p' 运行程序可输出结果为!
欧拉法

欧拉法的MATLAB实现班级:123082--04 姓名:应业敏学号:20081001088摘要:在数学和计算机科学中,欧拉方法(Euler method)命名自它的发明者莱昂哈德·欧拉,是一种一阶数值方法,用以对给定初值的常微分方程(即初值问题)求解。
它是一种解决常微分方程数值积分的最基本的一类显型方法(Explicit method)。
欧拉法(euler method)是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法。
它不直接追究质点的运动过程,而是以充满运动液体质点的空间——流场为对象。
研究各时刻质点在流场中的变化规律。
将个别流体质点运动过程置之不理,而固守于流场各空间点。
通过观察在流动空间中的每一个空间点上运动要素随时间的变化,把足够多的空间点综合起来而得出的整个流体的运动情况。
基本思想:基本思想是迭代。
其中分为前进的EULER法、后退的EULER法、改进的EULER法。
所谓迭代,就是逐次替代,最后求出所要求的解,并达到一定的精度。
误差可以很容易的计算出来。
特点:单步,显式,一阶求导精度,截断误差贰阶缺点:欧拉法简单地取切线的端点作为下一步的起点进行计算,当步数增多时,误差会因积累而越来越大。
因此欧拉格式一般不用于实际计算。
改进欧拉格式:为提高精度,需要在欧拉格式的基础上进行改进。
采用区间两端的函数值的平均值作为直线方程的斜率。
改进欧拉法的精度为二阶。
算法为:微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值,这个过程称为离散化。
实现离散化的基本途径是用向前差商来近似代替导数,这就是欧拉算法实现的依据。
欧拉(Euler)算法是数值求解中最基本、最简单的方法,但其求解精度较低,一般不在工程中单独进行运算。
所谓数值求解,就是求问题的解y(x)在一系列点上的值y(xi)的近似值yi。
对于常微分方程:,x∈[a,b]y(a) = y0可以将区间[a,b]分成n段,那么方程在第x i点有y'(x i) = f(x i,y(x i)),再用向前差商近似代替导数则为:,在这里,h是步长,即相邻两个结点间的距离。
用 MATLAB 程序生动地演示欧拉公式

下面的MA TLAB 程序生动地演示欧拉公式Exp(t) = cos(t) + j sin(t)% Henry-104% 本程序演示欧拉公式% Jan.25th,2012%h_fig1 = figure;set(h_fig1, 'unit', 'normalized', 'position', [0.1, 0.1, 0.9, 0.9]);set(h_fig1, 'defaultuicontrolunits', 'normalized');h_text1 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.73, 0.25, 0.05],... % 创建文本框'String', '▲是cos 曲线的起点', 'ForegroundColor', 'r', 'FontName', '黑体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_text2 = uicontrol(h_fig1, 'Style', 'text', 'Position', [0.71, 0.78, 0.25, 0.05],... % 创建文本框'String', 'Δ是sin 和exp 曲线的起点', 'ForegroundColor', 'r', 'FontName', '黑体',...'FontSize', 12, 'FontWeight', 'Bold', 'BackgroundColor', [1, 1, 1]);h_pushbutton1 = uicontrol(h_fig1, 'Style', 'PushButton', 'Position', [0.82, 0.12, 0.07, 0.06],...'string', '退出', 'BackgroundColor', [0.8 0.9 0.8], 'ForegroundColor', 'r', 'FontSize', 14, 'FontWeight', 'Bold',...'callback', 'delete(h_fig1),')h_axes0 = axes('Box', 'on', 'Position', [0.15, 0.18, 0.56, 0.68], 'FontSize', 8)set(gcf,'color','w');w = 0.1*pit = 0:40; % 在前进方向绕了2 圈%a = -ones(1,length(t));plot3(cos(w*t),t,sin(w*t),'b', 'LineWidth', 2);grid on; hold on;hc = plot3(cos(w*t),t,a,'k--'); hold on;set(hc, 'Color', 'r', 'LineWidth', 2);a=-a;hs = plot3(a,t,sin(w*t),'r-.'); hold on;set(hs, 'Color', 'k', 'LineWidth', 2);text(0.7,0.3,0.6, ' <-- CCW', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,-1, ' ▲Cos', 'Color', 'r', 'FontSize', 14, 'FontWeight', 'Bold'); text(1,0,0, ' Δ Sin', 'FontSize', 14, 'FontWeight', 'Bold');%xlabel('x', 'FontSize', 14, 'FontWeight', 'Bold');ylabel('t', 'FontSize', 14, 'FontWeight', 'Bold');zlabel('y', 'FontSize', 14, 'FontWeight', 'Bold');title('演示欧拉公式y = exp(jwt) = cos(wt) + jsin(wt)', 'Color', 'b', …'FontSize', 18, 'FontWeight', 'Bold');%line([-1,-1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[39.9,39.9],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([1,1],[0,0],[-1,1],'LineWidth',3, 'Color', 'r');line([-1,-1],[0,40],[-1,-1],'LineWidth',3, 'Color', 'k');line([-1,1],[0,0],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[40,40],[-1,-1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[1,1],'LineWidth',3, 'Color', 'b')line([-1,1],[0,0],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,0],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[40,40],[-1,1],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');line([-1,1],[40,40],[0,0],'LineWidth',2, 'Color', 'k');line([0,0],[0,40],[0,0],'LineWidth',2, 'Color', 'k');text(0,0,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'r')text(0,40,0.12,'O', 'FontSize', 14, 'FontWeight', 'Bold', 'Color', 'b')程序运行结果如下所示。
数值分析Matlab作业龙格库塔欧拉方法解二阶微分方程
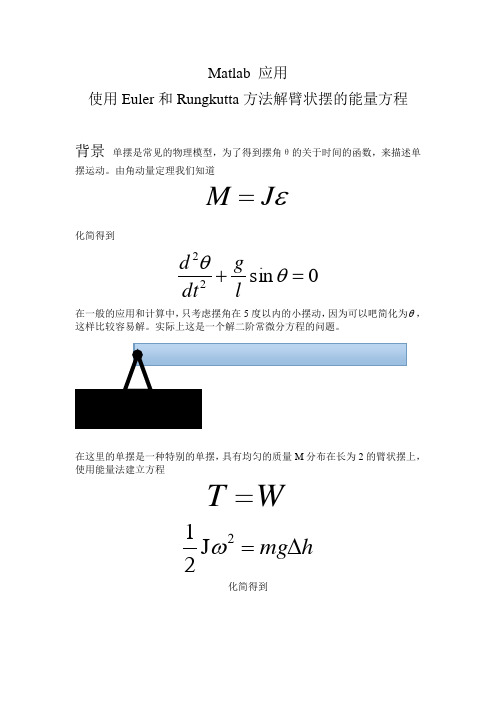
% K3 and L3
K4=RK_z(i)+h*L3; L4=rightf_sys1(x(i)+h,RK_y(i)+h*K3,RK_z(i)+h*L3);% K4and L4
RK_y(i+1)=RK_y(i)+1/6*h*(K1+2*K2+2*K3+K4);
RK_z(i+1)=RK_z(i)+1/6*h*(L1+2*L2+2*L3+L4);
end
plot(x,Euler_y,'r-',x,RK_y,'b-');
[y,T]=max(RK_y);
fprintf('角度峰值等于%d',y)%角度的峰值也就是π
运行第三个程序:在一幅图中显示欧拉法和RK4法,随着截断误差的积累,欧拉法产生了较大的误差
h=0.01
h=0.0001,仍然是开始较为稳定,逐渐误差变大
总结:RK4是很好的方法,很稳定,而且四阶是很常用的方法,因为到五阶的时候精度并没有相应提升。通过这两种方法计算出角度峰值y=3.141593,周期是1.777510。
y(0)=0
z(0)=0
精度随着h的减小而更高,因为向前欧拉方法的整体截断误差与h同阶,(因为是用了泰勒公式)所以欧拉方法的稳定区域并不大。
2.RK4-四阶龙格库塔方法
使用四级四阶经典显式Rungkutta公式
稳定性很好,RK4法是四阶方法,每步的误差是h5阶,而总积累误差为h4阶。所以比欧拉稳定。
matlab实例讲解欧拉法求解微分方程

欧拉法是数值分析中常用的一种方法,用于求解常微分方程的数值解。
在MATLAB中,可以通过编写相应的代码来实现欧拉法求解微分方程。
下面我们将通过具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
我们要了解欧拉法的基本原理。
欧拉法是一种通过迭代逼近微分方程解的方法,它基于微分方程的定义,通过离散化的方法逼近微分方程的解。
其基本思想是利用微分方程的导数定义,将微分方程以差分形式进行逼近。
具体而言,欧拉法通过将微分方程转化为差分方程的形式,然后通过迭代逼近得到微分方程的数值解。
接下来,我们通过一个具体的实例来讲解MATLAB中如何使用欧拉法求解微分方程。
假设我们要求解以下的一阶常微分方程:(1) dy/dx = x + y(2) y(0) = 1现在我们来编写MATLAB代码来实现欧拉法求解这个微分方程。
我们需要确定微分方程的迭代步长和迭代范围。
假设我们将x的范围取为0到10,步长为0.1。
接下来,我们可以编写MATLAB代码如下:```matlab欧拉法求解微分方程 dy/dx = x + y定义迭代步长和范围h = 0.1;x = 0:h:10;初始化y值y = zeros(1,length(x));y(1) = 1;使用欧拉法迭代求解for i = 1:(length(x)-1)y(i+1) = y(i) + h * (x(i) + y(i));end绘制图像plot(x,y,'-o');xlabel('x');ylabel('y');title('欧拉法求解微分方程 dy/dx = x + y');```在这段MATLAB代码中,我们首先定义了迭代的步长和范围,并初始化了微分方程的初始值y(0) = 1。
然后通过for循环使用欧拉法进行迭代求解微分方程,最后绘制出了微分方程的数值解的图像。
通过以上的实例讲解,我们可以看到,在MATLAB中使用欧拉法求解微分方程是非常简单而直观的。
matlab用欧拉法求常微分方程初值

Matlab中欧拉法求解常微分方程初值问题一、概念介绍在数学和工程领域,常微分方程初值问题是一个广泛应用的数学概念。
它描述了一个未知函数在给定初始条件下的行为。
而欧拉法则是一种常用的数值方法,用来解决常微分方程初值问题。
在Matlab中,我们可以利用欧拉法来求解常微分方程问题,从而得到函数在给定初始条件下的近似解。
二、欧拉法的基本原理欧拉法的基本思想是通过离散化微分方程,将其转化为递推的差分方程。
考虑一个一阶常微分方程初值问题:\[ \frac{dy}{dx} = f(x, y), \quad y(x_0) = y_0 \]在欧拉法中,我们采用递推的方式,根据已知的初始条件和微分方程的性质,通过迭代来得到逼近解的数值结果。
具体地,我们首先将自变量$x$的范围进行等间距分割,得到$x_0, x_1, x_2, ..., x_n$,并将步长记为$h$。
根据微分方程的性质,我们可以根据已知的初始条件$y(x_0) = y_0$,通过迭代计算得到近似解$y(x_1), y(x_2), ..., y(x_n)$。
三、Matlab中的欧拉法求解在Matlab中,我们可以利用欧拉法来求解常微分方程初值问题。
以求解一阶常微分方程为例,假设我们需要求解以下的常微分方程初值问题:\[ \frac{dy}{dx} = -2xy, \quad y(0) = 1 \]我们可以利用欧拉法的思想,将自变量$x$的范围进行离散化,然后根据欧拉法的递推公式,利用迭代的方式得到近似解的数值结果。
具体地,在Matlab中,我们可以编写如下代码来实现欧拉法的求解过程:```matlabfunction y = euler_method(f, x0, y0, h, n)% 初始化存储结果的数组x = zeros(1, n+1);y = zeros(1, n+1);% 将初始条件存入数组x(1) = x0;y(1) = y0;% 利用欧拉法进行迭代for i = 1:nx(i+1) = x(i) + h;y(i+1) = y(i) + h * f(x(i), y(i));end% 返回近似解的数值结果plot(x, y); % 绘制解的图像end```在上述代码中,我们定义了一个名为`euler_method`的函数,其中包含了欧拉法的计算过程。
matlab软件欧拉算法教程

y( xn1 ) y( xn ) hK
*
寻求计算平均斜率的算法
考察欧拉法,以xn的斜率值
K1 f ( xn , yn )
作为平均斜率
考察改进的欧拉法,可以将其改写为:
1 1 yi 1 yn h K1 K 2 2 2 K1 f ( x n , yn ) K 2 f ( xn h, yn hK1 )
Step 1: 将 K2 在 ( xn , yn ) 点作 Taylor 展开
K 2 f ( xn ph , yn phK1 ) f ( xn , yn ) phf x ( xn , yn ) phK1 f y ( xn , yn ) O( h2 )
y( xn ) phy( xn ) O(h2 )
Euler法
xn Yn
0.1 1.1 0.2 1.1918
改进Euler法
0.0046 1.0959 0.0086 1.1841 0.0005 0.0009
准确解
1.0954 1.1832
|yn-y(xn)| Yn
|yn-y(xn)| y(xn)
0.3 1.2774
0.4 1.3582 0.5 1.4351 0.6 1.5090 0.7 1.5803 0.8 1.6498 0.9 1.7178 1.0 1.7848
Y
x1 b
N 结束
例题3
例2
求解初值问题 步长h 0.1) ( 2x y y y y ( 0) 1 (0 x 1)
解
f ( x, y) y 2 x / y
y p yn hf ( xn , yn ) 改进Euler格式 yc yn hf ( xn1 , y p ) yn1 1 ( y p yc ) 2
有效独立法 matlab

有效独立法 matlab
MATLAB是一种非常强大的数学软件,广泛应用于工程、科学和
数学领域。
在MATLAB中,独立法通常指的是一种用于解决微分方程
的数值方法。
独立法也被称为Euler法或者前进欧拉法,它是一种
基本的数值积分方法,用于求解常微分方程的初值问题。
独立法的基本思想是通过离散化微分方程,将微分方程转化为
差分方程,然后通过迭代的方式逐步逼近微分方程的解。
具体来说,对于给定的微分方程dy/dx=f(x,y),初始条件y(x0)=y0,独立法通
过以下迭代公式进行计算,y(x0+h) = y(x0) + hf(x0, y0),其中
h是步长。
这个公式直观地表示了在点(x0, y0)处的斜率f(x0, y0)
与步长h的乘积,即为下一个点的增量,通过不断迭代可以逼近微
分方程的解。
在MATLAB中,可以使用独立法来求解常微分方程的数值解。
通
过编写MATLAB脚本或者函数,可以实现独立法的迭代计算过程。
MATLAB提供了丰富的数值计算和绘图函数,可以方便地进行独立法
的实现和结果可视化。
此外,MATLAB还提供了一些内置的数值积分
函数,如ode45等,可以更方便地求解微分方程的数值解。
总之,独立法是一种常用的数值方法,用于求解微分方程的数值解,在MATLAB中可以方便地实现并得到结果。
当然,在使用独立法时需要注意选择合适的步长以及对数值误差进行控制,以获得准确的数值解。
解微分方程欧拉法RK法及其MATLAB实例

解微分方程的欧拉法,龙格-库塔法及其MATLAB简单实例欧拉方法(Euler method)用以对给定初值的常微分方程(即初值问题)求解分为前进EULER法、后退EULER法、改进的EULER法。
缺点:欧拉法简单地取切线的端点作为下一步的起点进行计算,当步数增多时,误差会因积累而越来越大。
因此欧拉格式一般不用于实际计算。
改进欧拉格式:为提高精度,需要在欧拉格式的基础上进行改进。
采用区间两端的斜率的平均值作为直线方程的斜率。
改进欧拉法的精度为二阶。
算法为:微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值。
对于常微分方程:?x∈[a,b]y(a) = y0可以将区间[a,b]分成n段,那么方程在第xi点有y'(xi) = f(xi,y(xi)),再用向前差商近似代替导数则为:在这里,h是步长,即相邻两个结点间的距离。
因此可以根据xi点和yi点的数值计算出yi+1来:i=0,1,2,L这就是向前欧拉格式。
改进的欧拉公式:将向前欧拉公式中的导数f(xi,yi)改为微元两端导数的平均,即上式便是梯形的欧拉公式。
可见,上式是隐式格式,需要迭代求解。
为了便于求解,使用改进的欧拉公式:数值分析中,龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。
实际上,龙格-库塔法是欧拉方法的一种推广,向前欧拉公式将导数项简单取为f(xn,yn),而改进的欧拉公式将导数项取为两端导数的平均。
龙格-库塔方法的基本思想:在区间[xn,xn+1]内多取几个点,将他们的斜率加权平均,作为导数的近似。
龙格库塔法的家族中的一个成员如此常用,以至于经常被称为“RK4”或者就是“龙格库塔法”。
令初值问题表述如下。
则,对于该问题的RK4由如下方程给出:其中这样,下一个值(y n+1)由现在的值(y n)加上时间间隔(h)和一个估算的斜率的乘积决定。
该斜率是以下斜率的加权平均:k1是时间段开始时的斜率;k2是时间段中点的斜率,通过欧拉法采用斜率k1来决定y在点tn + h/2的值;k3也是中点的斜率,但是这次采用斜率k2决定y值;k4是时间段终点的斜率,其y值用k3决定。
matlab编程例题自由落体运动

自由落体运动是物理学中的一个基础概念,它描述了在没有空气阻力作用下物体在重力场中运动的规律。
在实际工程和科学研究中,我们常常需要使用matlab编程来模拟自由落体运动,并分析物体的轨迹、速度、加速度等参数。
本文将通过实际例题,介绍如何利用matlab编程来模拟自由落体运动,并分析其运动规律。
1. 问题描述假设有一个质量为m的物体从高度h自由落体,重力加速度为g,求在不考虑空气阻力的情况下,物体落地时的速度、运动时间以及运动过程中的轨迹。
2. 解决思路为了解决上述问题,我们可以采用matlab编程,利用欧拉法对自由落体运动进行模拟。
欧拉法是一种常用的数值求解算法,其基本思想是根据微分方程的定义,通过离散化时间和空间,逐步迭代计算物体运动过程中的位置、速度等参数。
3. matlab代码实现下面是利用matlab编写的自由落体运动模拟程序代码:```matlabclearclch = input('请输入初始高度h:'); 初始高度g = 9.8; 重力加速度t = sqrt(2*h/g); 运动时间v = g*t; 落地时的速度disp(['物体落地时的速度为:', num2str(v)]);disp(['物体运动时间为:', num2str(t)]);模拟自由落体运动轨迹t = 0:0.01:t; 时间间隔y = h - 0.5*g*t.^2; 物体高度plot(t, y);xlabel('时间');ylabel('高度');title('自由落体运动轨迹');```4. 代码说明上述matlab代码首先输入初始高度h,并利用公式计算出运动时间t 和落地时的速度v,然后利用plot函数绘制自由落体运动的轨迹图。
在模拟运行程序后,我们可以得到落地时的速度、运动时间以及运动轨迹,并通过图形直观地观察物体的运动规律。
