[教育]阵列信号处理课件第八章阵列信号稳健处理方法
阵列信号处理 ARRAY ppt课件

阵列信号处理
January 19, 2005
School of Communication and Information Engineering
总述
概述 阵列的基本知识(阵列流形) 波束形成 文献分析
精品资料
• 你怎么称呼老师?
• 如果老师最后没有总结一节课的重点的难点,你 是否会认为老师的教学方法需要改进?
盲波束形成
早期的盲波束形成技术依赖方向估计 方向估计分为参数化方法和非参数化方
法两大类 非参数化方法是基于谱的方法
——以空间角为自变量分析到达波的空 间分布(空间谱)
多天线系统的信道容量(1)
全向单天线系统:在收、发两个全向天线之 间只存在一条信道,这时的容量由香农公式 得到:
CBlo2(g 1SN Om R )ni
波束形成的目的
目的是从信号、干扰和噪声混在一起的 输人信号中提取期望信号。在接收模式 下,使得来自窄波束之外的信号被抑制, 而在发射模式下,能使期望用户接收的 信号功率最大,同时使窄波束范围以外 的非期望用户受到的干扰最小。
波束形成的优点
在智能天线中,波束形成是关键技 术之一,是提高信噪比、增加用户 容量的保证,能够成倍地提高通信 系统的容量,有效地抑制各种干扰, 并改善通信质量。
S
N足 R够M 大{Blo2(gSNOR m}ni
多天线系统的信道容量比较
CBe a m sBlo2g(1M2SNORm)n i SN足 R 够B大 {2lo2g(M.SNORm}ni
MIMO天线系统示意图
独立信道
天线阵
天线阵2
多天线系统的信道容量(3)
如果发射功率分散到M个独立的信道中, 并且各个信道具有相同的路径损耗,则信 道容量为:
阵列信号处理某高校课程ppt

第一章
绪论
信号处理研究的内容
信号处理主要 研究方向
从复杂环境中 提取有用信号
由检测到的信号中 提取信息
信号处理的发展
起源于17世纪 50年代前期 分离元件 速度低 体积大 可靠性差
速度高 体积小 可靠性高
60年代后期 集成电路
信号处理的发展
信号处理前期
信号处理后期
时域信号处理 (一维)
图像处理
特点: 与时间频率相对应,反映相位在空间的变化; 其值为:
v k = 2π / λ
是矢量函数,与方向有关; 与波长成反比; 是传播媒质的函数; 也称为相位常数;
慢矢量: 慢矢量: v v 定义 α = k / ω 示为:
,则波动方程的解可以表
v v v s( x, t ) = A exp[ jω(t − α ⋅ x )]
2 y
+ k
2 2
2 z
c
2.8
则波动方程有解,且其解为:
s ( x, y, z , t ) = A exp[ j (ωt − k x x − k y y − k z z )]
平面波定义: 在任意时刻 t ,在一个平面内 0 即, C为常数。 理论上真正的平面波不存在。 单频的平面波可以表示为:
v s( x , t 0 )
波束形成;
窗函数; 阵列的形成; 数字波束形成等;
阵列处理方法;
抗干扰; 超分辨;
空间目标参数的获取和估计; 两大类: 空间滤波; 空间谱估计;
阵列信号处理的主要目的: 1)增加信噪比 空间采样; 空间滤波; 2)利用阵列信号处理,对波源的个数、传播 方向、位置等参数进行估计。 3)对运动目标进行跟踪。
v s( x , t ) =
阵列信号处理
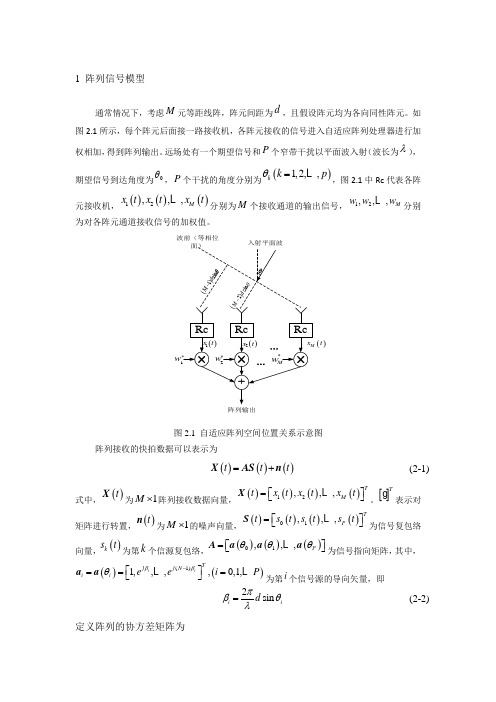
1 阵列信号模型通常情况下,考虑M 元等距线阵,阵元间距为d ,且假设阵元均为各向同性阵元。
如图2.1所示,每个阵元后面接一路接收机,各阵元接收的信号进入自适应阵列处理器进行加权相加,得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射(波长为λ),期望信号到达角度为0θ,P 个干扰的角度分别为()1,2,,k k p θ= ,图2.1中Rc 代表各阵元接收机,()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号,12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前(等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中,()t X 为1M ⨯阵列接收数据向量,()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置,()t n 为1M ⨯的噪声向量,()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量,()k s t 为第k 个信源复包络,()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵,其中,()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量,即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中,()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵,I 为M 维单位矩阵,2n σ为阵元的噪声功率,本文中约定,[]T表示转置,[]*表示共轭,[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替,即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型,阵列的M 个通道接收信号经加权处理后,最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ,可以改变阵列的方向图,即改变各个方向上入射信号增益。
阵列信号处理

宽带信号中的三种二维平面阵DOA估计宽带信号中的三种二维平面阵DOA 估计一. 背景目前关于阵列窄带信号的高分辨算法已比较成熟,但是随着信号处理技术的发展,信号环境日趋复杂,信号形式多样,信号密度日渐增大,窄带阵列探测系统的确定逐渐显示出来。
由于宽带信号具有目标回波携带的信息量大,有利于目标探测、参量估计和目标特征提取等特点,在有源探测系统中越来越多地得到应用。
而在无源探测系统中,利用目标辐射的宽带连续谱进行目标检测是有效发现目标的一种重要手段。
ISM 方法把宽带信号在频域分解为J 个窄带分量,然后在每一个子带上直接进行窄带处理。
因为信号为调频信号,所以信号在时域的分段实际上就是频域的分段。
将信号分解为窄带信号后,我们就可以利用窄带算法进行处理,最后将各个结果进行加权综合,即可得到最终的结果。
二维DOA 估计是阵列信号处理中的重要内容,通过二维DOA 估计可以得到信号源在平面中的角度信息。
一般采用L 型、面阵和平行阵或矢量传感器实现二维参数的估计,多数有效的二维DOA 估计算法是在一维DOA 估计的基础上,直接针对空间二维谱提出的,如二维MUSIC 算法以及二维CAPON 算法等。
这两种算法可以产生渐进无偏估计,但要在二维参数空间搜索谱峰,计算量相当大。
而采用二维ROOT MUSIC 算法可以减小计算量,但是需要付出精度下降的代价。
本次报告将结合宽带信号和二维DOA 估计算法,进行相关的算法介绍和仿真。
二. 算法介绍1. 接收信号模型:图 1 平面阵列示意图如图1所示,设平面阵元数为M ×N ,信源数为K 。
信源的波达方向为11(,),,(,)k k θφθφ ,第i 个阵元与参考阵元之间的波程差为:2(cos sin sin sin cos )/i i i x y z βπφθφθθλ=++设子阵1沿x 轴的方向矩阵为x A ,而子阵2的每个阵元相对于参考阵元的波程差就等于子阵1的阵元的波程差加上2sin sin /d πφθλ,所以接收信号为121()()()y x y x y M x A D A A D A X S N A D A -⎡⎤⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎣⎦协方差矩阵为H H H s s s n n n R XX E D E E D E ==+其中,s D 代表由最大的K 个特征值构成的一个K ×K 对角阵,n D 代表由MN-k 个较小的特征值构成的对角矩阵, s E 和n E 分别代表由s D 和n D 对应的特征值构成的特征矢量。
阵列信号处理技术(pdf 66页)

① 随机信号
例如:舰船发动机的噪声、推进器的噪声、未知的通信 信号、传感器热噪声、环境噪声、干扰信号,本质上都是随 机的。这些噪声都典型地来自大量独立微弱源的合成效应, 故应用统计学中心极限定理,可取合成噪声信号的数学模型 为高斯(Gauss)随机过程(通常是平稳高斯随机过程)。 高斯信号的统计学性质特别有利于分析计算,因为高斯随机 过程的一阶矩和二阶矩给出了这种随机信号的全部信息特征。
(2.1.4) (2.1.5) (2.1.6)
二、信号环境 1、传感器中的信号: ① 有用信号(desired signal) 也叫所需信号,这种信号的部分信息已知的,例如 方向、 频谱特性、调制特性、波形以及极化特性等。 ② 噪声及干扰 噪声: 系统本身固有的热噪声,往往可以假设为高斯热噪声。 干扰:敌方的干扰(压制式、回答式) 多径信号:有用信号经过多次反(散)射进入接收机的信号。
x1 (t )
X
(t )
=
x
2
(
t
)
M
xN (t)
0≤t ≤T(2.2.Βιβλιοθήκη )t 的范围为观察时间间隔
接收信号矢量中所需信号成份记为S(t),噪声成份记为n(t), 那么,接收信号矢量为:
X (t) = S(t) + n(t)
0≤t ≤T
(2.2.5)
其中n(t)中包含热噪声和干扰。 所需信号和噪声的矢量可以表达为:
求解约束性问题:
min W T RW (输出功率) s.t CTW = H (设置某一方向的增益为固定值)
图2.2 方向图
两个信号: 一个干扰, 一个有用信
号(方向θ1 )
确保有用信号的输入
CT (θ1)W = H
现代数字信号处理课件:阵列信号处理

阵列信号处理
2. 阵列信号协方差矩阵分解 阵列信号协方差矩阵R=E[XXH]可以写作
R
E[ x1 x1 ] E[x2 x1]
E[ x1 x2 ] E[x2 x2]
E[ x1 xM E[x2 xM
] ]
E[
xM
x1
]
E[xM x2]
E[
xM
xM
]
(7.1.11)
这是一个Hermitian方阵,则其特征分解为
di l c
1 c
( xi
sin
cosj
yi
cos
cosj
zi
sinj )
(7.1.4)
通常情况下,考虑空间有N个独立远场窄带信号入射到
M个阵元的阵列上,且有零均值高斯白噪声n(t),可以得到
阵列的输出为
x1(t) exp( j2πf011)
x2 (t
)
exp(
j2πf0
21 )
UHRU=Σ
(7.1.13)
将R=ARSAH+σ2I代入上式,可得
UH(ARSAH+σ2I)U=Σ 而酉矩阵U满足UHU=I,因此
(7.1.14)
UHARSAHU=Σ-σ2I
(7.1.15)
由上面的分析可知,Σ可分为两部分: 一是与信号对应
的大特征值,由ARSAH和RN提供;二是与噪声对应的小特征 值σ2,由RN提供。即
则各阵元第k次快拍的采样值的矩阵形式为
X(k)=AS(k)+N(k)
(7.1.7)
由于S(k)随k变化,且其初相通常为均匀分布,一阶统
计量(均值)为零,所以不能直接采用一阶统计量来提取方向
信息。而二阶统计量可以消除信号S(k)的随机初相,可以用
阵列信号处理全.ppt

▪平面阵
图1.5
▪立体阵
图1.6
b. 参数化数据模型
假设N元阵分布于二维平面上,阵 元位置为:
rl xl , yl ,l 1,2, , N
一平面波与阵面共面,传播方向矢
量为: 1 cos ,sin T
c
y
r
x 图1.7:二维阵列
几何结构
阵元
l 接收信号为:xl
t s rl,t
滤波:增强信噪比 获取信号特征:信号源数目 传输方向(定位)及波形 分辨多个信号源
定义:
➢传感器——能感应空间传播信号并且能以某 种形式传输的功能装置
➢传感器阵列(sensors array)——由一组传感 器分布于空间不同的位置构成
由于空间传播波携带信号是空间位置和时
间的四维函数,所以:
连续:面天线
波动方程的任意解可以分解为无穷多个“单频”
解的迭加(传播方向和频率分量均任意)。
波动方程的单频解可以写成单变量的函数:
sr,t Aexp[ j(t kT r) Aexp[ j t T r ]
式中 k ,其大小等于传播速度的倒数,其方向与 传播方向相同,常称为慢速矢量(slowness vector)。
2. G.Strang,"Linear Algerbra and Its Applications", Academic Press,New York ,1976.(有中译本, 侯自新译,南开大学出版社,1990)
§2.1线性空间和希尔伯特空间
一、符号及定义
1. 符号
以后我们常用字母加低杆表示矢量和矩阵,
实际阵列
空间采样方式 虚拟阵列(合成阵列如SAR)
空时采样示意图如下:
第8章 阵列信号处理与空域滤波

sK
n
vM
1
n
以后讨论没特殊说明均设各阵元的噪声为零均值, 方差为 2的高斯白噪声,不同阵元的接收噪声相互独立 且信号与噪声也相互独立 ,即
Ev n 0
Ev nvH l 2I n l EsnvH l 0
e j
s
t
xM 1 t
e
j
(
M
1)
定义列向量 xt x0 t x1 t
xM 1 t T
和 a 1 e j
e jM 1 T ,
2 d sin
(8.1.8)可表示为 x t a s t a s t e j0t
12
阵元 pmn 对参考点(坐标原点)时延
mn
pmn , r c
mdx sin cos ndy sin sin
c
(8.1.26)
信号相移为
mn
,
2
mdx sin cos ndy sin sin
mx ny
m 0,1, , M 1, n 0,1, , N 1
(8.1.7)
定义空间相位 2 f0d sin c 2 d sin
( f0 是入射信号载波频率,l 是波长,c f0 )
4
取 m = 0,1,L ,M - 1 , (8.1.7)写为向量形式
x0 t 1
x1 t
(8.1.8)
(8.1.9) (8.1.10)
向量 a 称为方向向量或导向向量(steering vector)
阵列信号处理

阵列信号处理是信号处理的一个年青的分支,属于现代信号处理的重要研究内容之一,其应用范围很广,可用于雷达、声呐、通信、地震勘察、射电天文和医用成像等众多领域。
阵列信号处理是将一组传感器在空间的不同位置按一定规则布置形成的传感器阵列(尽管采用的传感器的类型可以不同,如天线、水听器、听地器、超声探头、X射线检测器,但是传感器的功能是相同的,它是连接信号处理器和感兴趣的空间纽带),用传感器阵列发射能量和(或)接收空间信号,获得信号源的观测数据并加以处理。
阵列信号处理的目的是从这些观测数据中提取信号的有用特征,获取信号源的属性等信息。
目前,阵列信号处理在雷达及移动通信等领域有着广泛而重要的应用。
在相控阵雷达体制中,自适应波束形成技术在抑制杂波干扰方面起着关键的作用。
在移动通信中,基于阵列信号处理的波达方向估计技术,使移动通信进入一个崭新的阶段。
本论文首先介绍阵列信号处理的基础知识。
在此基础上,着重讨论阵列波束形成技术,非理想线性阵列的雷达信号波达方向和多普勒频率估计,均匀圆形阵列的信号波达方向估计和复杂信号的波达方向及参数估计等四方面内容。
这些内容都是阵列信号处理领域的研究热点。
它们无论对阵列信号处理的理论发展还是实际应用,都有重要的意义。
目前,人们普遍关注在阵列响应矢量未知情况下,自适应波束形成问题,即盲自适应波束形成技术。
本文第一方面介绍了最基本的阵列波束形成方法,即最小均方误差波束形成器,线性约束最小方差波束形成器和基于特征空间的波束形成器(ESB)。
在此基础上,提出一个基于特征空间的盲自适应波束形成算法。
此算法首先根据高分辨波达方向估计方法,估计信号源的波达方向,然后以此方向形成约束导向矢量,进而计算出ESB波束形成算法的最优权矢量,最后,对期望目标形成笔状波束。
此算法能够有效地抑制信号的对消现象,并且能够应用于在波束中有多个期望信号的场合。
当阵列存在各种误差时,一般高分辨波达方向估计方法(如MUSIC)的估计性能严重下降。
阵列信号处理的基本知识PPT课件

6
将整个阵列的输出信号写成矩阵形式为:
x (t) A (t) sn (t)
A [a (1) ,,a (P)]为阵列流行矩阵、空间信
号方向矢量、阵列响应矩阵。
a ( ) [ 1 e , ,e ] j2 d si /n
j2( M 1 ) d si /n T
s [s(t) ,,s(t)T]为信号源矢量。
阵列信号处理中的若干问 题与研究
.
1
主要内容
阵列信号处理的基本知识 阵列信号处理的主要内容 当前的一些研究热点和新技术 应用领域的一些实例
• 仿真结果 • 实测数据处理
.
2
一、阵列信号处理的基本知识
阵列信号处理系统构成 阵列系统模型假设
阵列信号数学模型 对阵列及其通道的假设 对信号和噪声的假设
.
11
各通道同步采集假设
阵列接收信号需要进行采样和A/D变换 为数字信号后进入DSP处理器进行算法处 理。
Nyquist采样率
宽频段信号:采用欠采样率(空时欠采 样),需要解模糊算法。
.
12
对信号和噪声的假设
窄带假设
信号带宽远小于信号波前跨越阵列最大口径 所需要的时间的倒数,即有如下假设:
2. 快速算法(子空间跟踪与更新,权系数更新)。
3. 相干信号和宽带信号环境。
4. 低信噪必(弱信号)、短数据环境下的检测与估 计。
5. 新方法(MCMC,SMC(particle filter),SVB, Stochastic Resonance)。
.
18
波束形成:
1. Robust Beamforming(steering vector error, array error, coherent signals, Robust Capon beamforming) . 2. Array Pattern Synthesis. The problem of designing complex weights for individual array elements to achieve properties such as high directive gain or to spatially filter signals by their angle of arrival.
阵列信号处理 ARRAY

智能天线技术
波束成形
– 天线单元之间的间距小于半个波长 – 发射机和接收机必须预知方向 – 在蜂窝系统中通过形成的,窄波束减少干扰
从而增加复用系数,增加系统容量 – 通过天线增益,降低发射功率 – 通过空间滤波抑制可分离的空间干扰,抑制
时延扩展、减少瑞利衰落,对于衰落没有分 集增益。
阵列流形(1)
空间复用
利用空间散射信道,在各个收发天线对之间 形成多路独立的传输信道。
传输相同数据可以提高传输可靠性
传输不同的数据可以提高传输容量
Transmit
Receive
M elements
N elements
文章结构与框架
引言 MIMO—OFDM系统模型 自适应半盲波束形成算法
分布多天线阵
阵列信号处理的系统分类
有源系统 –具有发射传感器阵的系统
无源系统 –不具有发射传感器阵的系统
阵列信号处理主要研究什么
超分辨
在传感器阵列的物理孔径一定的条件下,通 过信号处理,获得比常规的波束形成器处理方
法高得多的空间分辨率。 自适应
如何能在复杂的干扰背景下最优地检测信号。
5、结论(2)
此外,这种算法充分利用了OFDM的导 频特性,波束形成器能自适应调整权矢 量,其更新方式与TDMA和CDMA相似, 所以本算法可直接用于有天线阵列基于 OFDM的第三代和以后的无线通信系统, 在多天线通信系统的矩阵信道估计和提 高天线增益方面有广泛的应用前景.
盲波束形成
早期的盲波束形成技术依赖方向估计 方向估计分为参数化方法和非参数化方
法两大类 非参数化方法是基于谱的方法
——以空间角为自变量分析到达波的空 间分布(空间谱)
阵列信号处理某高校课程

医学成像中的阵列信号处理
总结词
医学成像中的阵列信号处理主要用于提高成像质量和诊断准确率。
详细描述
医学成像技术如超声成像、核磁共振成像等,利用不同频率的声波或电磁波获取人体内部结构的信息 。阵列信号处理技术可以对接收到的信号进行处理,实现图像增强、去噪和分辨率提升。阵列信号处 理在医学成像中能够提高成像质量和诊断准确率,对于医疗诊断和治疗具有重要意义。
阵列信号处理将进一步与其他 领域的技术融合,如机器学习 、人工智能等。通过跨域协同 ,可以实现更高效、更精准的 信号处理和分析。
随着传感器技术的发展,阵列 的构成和排列方式也将不断创 新。未来的阵列信号处理系统 将更加灵活、多样化和智能化 。
阵列信号处理技术的应用领域 将继续拓展,如智能感知、无 人系统、物联网等新兴领域。 通过与这些领域的交叉融合, 阵列信号处理将发挥更大的作 用和价值。
信号的波束形成
通过调整阵列天线接收信号的相位和幅度,实现信号的 波束形成,增强特定方向的信号强度。
阵列信号的传播特性
信号的空间传播
阵列信号在空间中传播时,会受到环境因素的影 响,如多径效应、阴影衰落等。
信号的方向特性
阵列信号的方向特性包括方向图、波束宽度、副 瓣电平等,这些特性决定了阵列对信号的接收和 定向发射能力。
05
课程总结与展望
课程总结
阵列信号处理的基本原理
阵列信号处理是一门研究如何通过多个传感器接收信号,并通过对这些信号的处理和分析,实现对信号源的定位、跟 踪和识别的学科。其基本原理包括信号的传播、阵列的几何排列、信号的波束形成等。
课程内容与学习目标
本课程介绍了阵列信号处理的基本概念、原理和方法,包括信号模型、阵列模型、信号参数估计、波束形成等。通过 学习,学生应能掌握阵列信号处理的基本理论和方法,并能够运用所学知识解决实际问题。
阵列信号处理基础教程

波动方程的单频解可以写成单变量的函数:
sr,t Aexp[ j(t kT r) Aexp[ j t T r ]
式中 k ,其大小等于传播速度的倒数,其方向与 传播方向相同,常称为慢速矢量(slowness vector)。
Q 1 所以 T r表示从原点 o 传播到位置 r所需时间。
仰角和方位角 • 信源分离--确定各个信源发射的信号
波形,根据各个信源不同的波达 方向加以区分 • 信道估计--确定信源与阵列之间的传 输信道的参数(多径参数)
西安电子科技大学雷达信号处理实验室
6.阵列信号处理的主要问题(技术):
• 波束形成技术(DBF)--使阵列方向图的主 瓣指向所需的方向
• 零点形成技术--使天线的零点对准干扰方向 • 空间谱估计--对空间信号波达方向的分布进
西安电子科技大学雷达信号处理实验室
空间谱估计的系统结构
通道1
处
通道2
理
信
器
源
通道M
目标空间
观察空间
估计空间
注意:在观察空间中,通道与阵元并非一一对应,
通道可由空间的一个、几个或所有阵元合成的。
西安电子科技大学雷达信号处理实验室
二、阵列信号的应用
• 雷达:相控阵天线系统、波束灵活控制、高 分辨测向、干扰置零、成像(SAR/ISAR)
它与一般的信号处理方式不同,因为其阵列是 按一定方式布置在空间不同位置上的传感器组,主 要利用信号空域特征来增强信号及有效提取信号空 域信息,因此阵列信号处理也称为空域信号处理。
西安电子科技大学雷达信号处理实验室
1.阵列信号处理的目的:
提取阵列所接收的信号及其特征信息(参数),同 时抑制干扰和噪声或不感兴趣的信息。
阵列信号处理课件西电共8页文档

信号子空间:设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑在无噪声条件下,()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ为信号子空间,是N 维线性空间中的P 维子空间,记为P N S 。
PN S 的正交补空间称为噪声子空间,记为N P N N -。
正交投影设子空间m S R ∈,如果线性变换P 满足, 则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑,其中矢量()i ia θ称为导向矢量,当改变空间角θ,使其在空间扫描,所形成的矩阵称为阵列流形,用符号A 表示,即(){|(0,2)}a A θθπ=∈波束形成波束形成(空域滤波)技术与时间滤波相类似,是对采样数据作加权求和,以增强特定方向信号的功率,即()()()()HHy t W X t s t W a θ==,通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ,其中θ为参数集合,使条件概率()12,,,N f X X X θ最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源,N 元阵列,则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元,其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆,则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵,阵元间隔为半个波长,当信源与阵列共面时: 首先建立阵列几何模型:对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为故:()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时: 首先将信源投影到阵列平面 然后建立阵列模型对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为故:()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则(LCMV )的自适应波束形成算法 对于信号模型:()()()0X t s t a J N θ=++, 波束形成输出:()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下,求取使得()HWJ N +方差最小的W 作为最有权值,即:()0min .H X WHW R Ws t W a Fθ⎧⎪⎨⎪=⎩,其中F 为常数利用拉格朗日乘子法可解得:()10X opt W R a μθ-=当取1F =时,则()()11H X a R a μθθ-=,μ的取值不影响SNR 和方向图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5•
•§ 8.3.3利用多普勒信息提高阵列处理的稳健性
•信号模型: ••其中
•快拍
矢量 ,相应的
•若利用上述信号波形结构,只有2个未知变量。
•由
,估计未知参数
中的未知变量。由于待估计变量减少,则估计方差
CRB下界变小。
•西安电子科技大学雷达信号处理实验室
6•
➢传统ML方法与利用多普勒信息的ML方法比较:
•2)
•西安电子科技大学雷达信号处理实验室
8•
3) 矩阵累量对自变量对称,即与顺序无关。
4) 若随机变量
可以划分成任意两个或
多个统计独立的组,则它们的n阶
累量等
于0,但一般矩不成立。
5) 若随机变量
与
统计独立,
则:
•但矩不成立。
6) 若随机变量
是联合高斯的,则阶
数 的高阶累量等于0。
•西安电子科技大学雷达信号处理实验室
•旁瓣:电平升高 •误差使超低旁瓣电平天线实现困难。
•自适应波束形成:“自适应”对系统本身的误差具 备调节能力。有指向误差:引起目标信号相消。
2) 对高分辨处理的影响
•Music
信号子空间/噪声子空间
•谱峰搜索:由于阵列误差未知,只能用理论阵列 流形计算谱函数。DOA估计与分辨性能下降甚至 恶化。
•西安电子科技大学雷达信号处理实验室
5•
•§ 8.2对阵列误差具有容差能力的稳健方法
1. 利用阵列相关矩阵结构先验知识提高阵列处理 的稳健性
•在独立源(加白噪声)情况下 为Toeplitz矩阵 。•在系统误差下:不再是Toeplitz,强制对 进行 Toeplitz化。 2. 利用信源方向的大致范围的先验知识提高稳健性 •角度:Sector •对Sector角度构造理想阵列流形及其相关矩阵 :
•[电子学报 1998 2001 廖桂生、张林让]
•安电子科技大学雷达信号处理实验室
。
•在
未知的情况下,如何实现波束形成?
•多信号源分离成单信号源法(在不 •方法分类 同 域分开)
•利用
的波形结构信息和MSE准
•例如:多普则勒信号结构
•记最优波束形成的权矢量为
•西安电子科技大学雷达信号处理实验室
0•
•目标函数:
• 其中
•此方法仅利用了多普勒信号的结构,可实现多普 勒频率 -DOA联合估计
•方法1:4阶累量Music方法 : •关键定义(构造)4阶累量矩阵。
•在 个独立源情况下 :
•西安电子科技大学雷达信号处理实验室
1•
•这里假定了噪声信号是高斯过程
•其中 累量:
, 为第 个信号源的4阶
•由
,运用Music方法,实现DOA估
计。
➢在有限采样数据条件下,高阶累量的估计方差
较大(相对低阶)
•西安电子科技大学雷达信号处理实验室
4•
•§ 8.3.2基于循环平稳性阵列处理
➢时变(非平稳):统计特性随时间变化的信号。 ➢特例:相关函数随时间按周期或多周期规律变 化——循环平稳信号。 ➢基于循环平稳性的阵列处理特点:利用各信号 源的不同循环频率,在循环频率域信号自动分离 (包括噪声)。
•西安电子科技大学雷达信号处理实验室
9•
➢高阶统计量用于阵列处理的动机: a) 抑制未知相关矩阵的高斯色噪声,利用高斯过
程阶数 以上的高阶累量等于0。 b) 虚拟孔径扩展。
•西安电子科技大学雷达信号处理实验室
0•
2. 基于高斯统计量的几种高分辨DOA估计方法
•在 元阵列信号中,至少有
种高阶统计量
,由这些高阶统计量构成矩阵的方法也有很多。
•方法2:基于高阶累量的ESPRIT方法(一)
2•
•此方法适用于等距线阵,其中:
•西安电子科技大学雷达信号处理实验室
3•
•累量域的ESPRIT方法(二) •对任意的阵列结构, 元阵列信号为 。 •定义新的矢量
•计算 与
的4阶累量矩阵:
•由 和 运用ESPRIT方法可以计算出 及 ,只需已知阵元1和阵元2的距离。 ➢用于校正和盲波束形成。
1. 传统ML方法(仅利用空间阵列流形)
•似然函数 •波形参数
, 估计为:
2. 利用多普勒信号结构信息: •将 次快拍数据(相干脉冲串)排成矢量:
•西安电子科技大学雷达信号处理实验室
7•
•信号矢量改写:
8•
•其中
时域导向矢量。
•西安电子科技大学雷达信号处理实验室
9•
•§ 8.4盲阵列信号处
•盲波束理形成:
•西安电子科技大学雷达信号处理实验室
6•
•§ 8.3 利用信号的时域信息提高
•
阵列处理的性能
•§ 8.3.1基于高阶统计量的阵列处理
1. 高阶矩、高阶累量的定义与性质
•已知随机矢量 矩定义为
,其联合的
阶
•式中
为随机矢量PDF的特征函数。
•西安电子科技大学雷达信号处理实验室
7•
•累量定义:
•其中 •性质: • 1) 零均值情况:
4•
•二、系统误差的校正技术
•校正技 术
•基于测试技术:测出离散角度的实际 •阵列流形
•联合处理法: •基于数据 •DOA、误差参数联合寻 •(自校正)•优子空间处理法:
•单信源相关矩阵 仅有 一个大特征值,其特征矢 量就是真实的阵列流形
•具体实现方法又分为有源自校正和无源校正。
•西安电子科技大学雷达信号处理实验室
[教育]阵列信号处理课件第 八章阵列信号稳健处理方法
2•
•空域误差使得阵列流形 有变化:
•其中
, 为复数。
•在有误差的情况下的阵列信号模型:
•互耦情况下:用互耦矩阵 表示, 一般不是对 角阵。
•阵列信号模型:
•西安电子科技大学雷达信号处理实验室
3•
➢幅相误差对阵列信号的影响: 1) 波束形成 •主瓣:指向有偏差
