小学比例应用题25道含答案

合集下载

小学数学六年级比的应用题针对性训练题后面带答案

比的应用训练针对性训练题1．甲数是乙数的4/5，乙数是丙数的5/8，甲、乙、丙三数的比是（）：（）：（）。

2．甲数是乙数的4/5，甲数是丙数的4/9，甲、乙、丙三数的比是（）：（）：（）。

3．甲数是丙数的3/7，乙数是丙数的2又1/2，甲、乙、丙三数的比是（）：（）：（）。

4、光明小学将五年级的140名学生，分成三个小组进行植树活动，已知第一小组和第二小组人数的比是2：3，第二小组和第三小组人数的比是4：5。

这三个小组各有多少人？5．某农场把61600公亩耕地划归为粮田与棉田，它们之间的比是7：2，棉田与其他作物面积的比6：1。

每种作物各是多少公亩？6．黄山小学六年级的同学分三组参加植树。

第一组与第二组的人数的比是5：4，第二组与第三组人数的比是3：2。

已知第一组的人数比二、三组人数的总和少15人。

六年级参加植树的共有多少人？7．科技组与作文组人数的比是9：10，作文组与数学组人数的比是5：7。

已知数学组与科技组共有69人。

数学组比作文组多多少人？8、甲、乙两校原有图书本数的比是7：5，如果甲校给乙校650本，甲、乙两校图书本数的比就是3：4。

原来甲校有图书多少本？9．小明读一本书，已读的和未读的页数比是1：5。

如果再读30页，则已读和未读的页数之比为3：5。

这本书共有多少页？10.甲、乙两包糖的重量比是4：1。

从甲包取出130克放入乙包后，甲、乙两包糖的重量比为7：5。

原来甲包有多少克糖？11.五年级三个班举行数学竞赛。

一班参加比赛的占全年级参赛总人数的1/3，二班与三班参加比赛人数的比是11：13，二班比三班少8人。

一班有多少人参加了数学竞赛？12.从前有个农民，临死前留下遗言，要把17头牛分给三个儿子，其中大儿子分得1/2，二儿子分得1/3，小儿子分得1/9，但不能把牛卖掉或杀掉。

三个儿子按照老人的要求怎么也不好分。

后来一位邻居顺利地把17头牛分完了，你知道这到底是怎么回事吗？13．图书室取出一批书，按照一年级得1/2，二年级得1/3，三年级得1/7，正好是41本，各年级各得多少本？14．古罗马富豪约翰逊再临终前，对怀孕的妻子写下这样一份遗嘱：如果生下来是个男孩，就把遗产的三分之二给儿子，母亲拿三分之一；如果生下来的是女孩就把遗产的三分之一给女儿，三分之二给母亲。

比例练习题带答案十道

比例练习题带答案十道1、张大妈家上个月用了8吨水，水费是12.8元。

李奶奶家用了10吨水，李奶奶家的水费是多少钱？2、有一批书，这批书如果每包20本，要捆18包。

如果每包30本，要捆多少包？3、一根木料，锯3段需要9分钟，如果锯6段，需要多少分钟？4、一辆汽车2小时行了140km，照这样的速度，甲地到乙地的距离是400km，需要行驶多少小时？5、“万达”修路队修筑一条公路，原计划每天修400m，15天可以修完。

结果12天就完成了任务，实际每天修多少米？6、学校用同样的方砖铺地，铺5㎡需要方砖120块，照这样计算，再铺32㎡，一共需要这种方砖多少块？7、发电厂运来一批煤，计划每天用30吨，12天用完，实际每天节约5吨煤，实际比计划多用了多少天？8、装修一间客厅，用边长5dm的方砖铺地，需要80块，用边长4dm的方砖铺地，需要多少块？需要X块5*5：4*4=X：8016X=2000X=2000/16X=125需要125块9、制作一批零件，甲单独完成要8小时，已知甲、乙的工作效率比是4:3，那么乙单独完成要多长时间？已知甲单独完成需要8小时，可以设甲的效率为每小时完成1/8批零件。

甲乙效率比4:3,。

设乙的效率为x。

则:x=4:3可求得x=*3/4=3/32则乙单独工作需要时间为2/3小时也就是10小时40分钟10、王明在100m赛跑冲到终点时领先李明10m，领先王亮15m。

如果李明和王亮按原来的速度继续冲向终点，那么当李明到达终点时，王亮还差多少米到达终点？X5=1200-150x=304x=1201200/120=10比和比例练习题一、填空： 1.甲乙两数的比是11:9,甲数占甲、乙两数和的，乙数占甲、乙两数和的。

甲、乙两数的比。

是3:2，甲数是乙数的倍，乙数是甲数的2. 某班男生人数与女生人数的比是34，女生人数与男生人数的比是，男生人数和女生人数的比是。

女生人数是总人数的比是。

.一本书，小明计划每天看27，这本书计划看完。

小学数学比例练习题及答案

小学数学比例练习题及答案【小学数学练习题及答案】题一：某商品原价为800元，现已降价20%，请问现在的售价为多少？A. 600元B. 640元C. 720元D. 760元答案：D. 760元题二：一个矩形的长和宽成比例，长边为12cm，短边为4cm，求这个矩形的长边和短边的比值是多少？A. 1:2B. 2:1C. 3:1D. 1:3答案：A. 1:2题三：小明购买了一箱苹果，每箱有20个苹果，他打算将苹果平均分给4个朋友，每人分多少个？A. 3个B. 4个C. 5个D. 6个答案：D. 6个题四：小明的爸爸购买了一辆新车，他发现每行驶100公里需要消耗10升汽油，那么行驶80公里需要消耗多少升汽油？A. 8升B. 12升C. 16升D. 20升答案：A. 8升题五：某商店一个月的营业额为40000元，其中销售商品的总利润为6000元，那么这个月该商店的利润率是多少？A. 12%B. 15%C. 18%D. 20%答案：B. 15%题六：玛丽每天早上骑自行车上学，上学路程是她家到学校路程的3/4，她到学校用了20分钟，那么她家到学校的路程需要多少分钟？A. 15分钟B. 16分钟C. 25分钟D. 30分钟答案：C. 25分钟题七：一个正方形的边长是x，另一个正方形的边长是x+5，求较大正方形的面积与较小正方形的面积的比值是多少？A. x:x+5B. x+5:xC. x^2:(x+5)^2D. (x+5)^2:x^2答案：D. (x+5)^2:x^2题八：某班级一共有50个学生，其中男生占总人数的1/4，女生人数是男生人数的3倍，求女生的人数。

A. 10人B. 15人C. 20人D. 25人答案：C. 20人题九：小明的体重是45千克，小红的体重是小明体重的3/5，两人体重的差是多少千克？A. 9千克B. 18千克C. 27千克D. 36千克答案：B. 18千克题十：某商品原价为120元，打折后降价20%，再经过一次满减活动，实际支付80元，满减的金额是多少？A. 10元B. 20元C. 30元D. 40元答案：A. 10元。

苏教版数学六年级下册专项～比例解决问题【含答案】

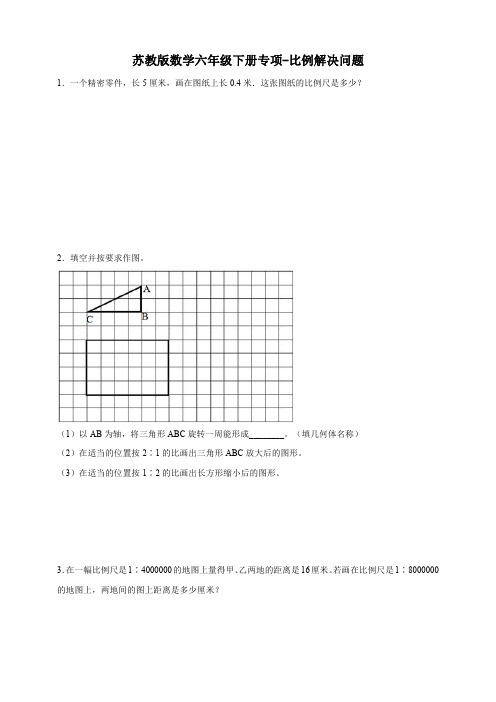
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。

（1）以AB为轴，将三角形ABC旋转一周能形成________。

（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。

（3）在适当的位置按1∶2的比画出长方形缩小后的图形。

3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。

若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。

（1）按3∶1的比画出图形A放大后得到的图形B。

（2）按1∶2的比画出图形B缩小后得到的图形C。

我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。

5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。

（单位：分米）12．根据图中提供的信息，完成下列问题。

（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。

（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。

广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。

乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。

解比例典型例题及答案

解比例答案典题探究例1．按下面的条件列出比例并解比例．（1）5和8的比等于20和X的比．（2）4和12的比等于8和X的比．（3）等号左端的比是4.5：X，等号右端的比是0.3：4．（4）比的两个外项分别是X和1.5，两个内项分别是2.8和3．考点：解比例．专题：比和比例．分析：（1）根据题意先列出比例式5：8=20：x，再根据两内项之积等于两外项之积把比例式转化为乘积式，然后再根据等式的性质方程两边同除5，即可得解；（2）根据题意先列出比例式4：12=8：x，再根据两内项之积等于两外项之积把比例式转化为乘积式，然后再根据等式的性质方程两边同除4，即可得解；（3）根据题意先列出比例式4.5：x=0.3：4，再根据两内项之积等于两外项之积把比例式转化为乘积式，然后再根据等式的性质方程两边同除0.3，即可得解；（4）根据题意先列出比例式x：2.8=3：1.5，再根据两内项之积等于两外项之积把比例式转化为乘积式，然后再根据等式的性质方程两边同除1.5，即可得解；解答：解：（1）5：8=20：x；5x=20×85x÷5=160÷5x=32；（2）4：12=8：x4x=12×84x÷4=96÷4x=24；（3）4.5：x=0.3：40.3x=4×4.50.3x÷0.3=18÷0.3x=60；（4）x：2.8=3：1.51.5x=3×2.81.5x÷1.5=8.4÷1.5x=5.6．点评：此题考查解比例的方法：根据两内项之积等于两外项之积，把比例式转化为乘积式是解题的关键．例2．求未知数x的值．（1）7：x=0.8：2.4；（2）=；（3）x：=18：．考点：解比例．专题：比和比例．分析：（1）根据比例的基本性质可得：0.8x=7×2.4，再利用等式的性质，两边同时除以0.8求解；（2）根据比例的基本性质可得：15x=20×0.8，再利用等式的性质，两边同时除以15求解；（3）根据比例的基本性质可得：x=×18，再利用等式的性质，两边同时除以求解．解答：解：（1）7：x=0.8：2.40.8x=7×2.40.8x÷0.8=16.8÷0.8x=21；（2）=15x=20×0.815x÷15=16÷15x=；（3）x：=18：x=×18x=x=．点评：此题考查了比例的基本性质和等式的性质的计算应用．例3．若自然数A、B满足﹣=，且A：B=4：5．那么A=8，B=10．考点：解比例．专题：简易方程．分析：把﹣=的左边通分成，由A：B=4：5，根据比例的性质，可得5A=4B，推出A=B，把A=B代人=中，即可求得B的数值，进而求得A的数值．解答：解：因为A：B=4：5，所以5A=4B，A=B；﹣=，=，把A=B代人=中，得：=，=，×=，=，B=10；把B=10代入A=B中，A=B=×10=8；故答案为：8，10．点评：用含B的式子表示出A是解答此题的关键，进而代入方程即可得解．例4．只列算式（或方程），不计算．（1）比例的两个内项分别是5和2，两个外项分别是x和3.5．（2考点：解比例；分数除法应用题．专题：压轴题．分析：（1）根据比例的基本性质“两外项之积等于两内项之积”，据此列出方程即可；（2）根据图意，可知把这根绳子的总长看做单位“1”，用去了，还剩下300米；要求单位“1”的量，要先求出还剩下的300米对应的分率是多少列式为：1﹣，进而用具体的数量除以具体的数量对应的分率即可解答．解答：解：（1）x：2=5：3.5；（2）300÷（1﹣）．点评：此题考查根据题意或图意，列比例式或算式，解决关键是要分析好题意或图意，灵活的解答即可．演练方阵A档（巩固专练）一．选择题（共7小题）1．在2、3、这三个数中插入第四个数X，使得这四个数能组成比例，那么X最小是（）A．B．C．D．考点：解比例；比例的意义和基本性质．专题：比和比例．分析：根据比例的性质：两内项之积等于两外项之积．要使插入的第四个数X最小，即要使两内项之积或两外项之积最小，积最小为：2×，据此解答即可．解答：解：由分析可得：2×=3X，所以X=．故选：C．点评：解答本题的关键是，分析出要使插入的第四个数X最小，即要使两内项之积或两外项之积最小．2．（•静宁县）在比例中，两个外项互为倒数，两个内项（）A．成正比例B．成反比例C．不成比例考点：解比例；正比例和反比例的意义．分析：根据倒数的定义结合比例的基本性质，即可得出两个内项的关系．解答：解：因为在比例中，两个外项互为倒数，所以两个内项的积=1，所以两个内项成反比例．故选：B．点评：本题考查了正比例和反比例的意义，得到两个内项的积=1是解题的关键．3．（•厦门）如果a÷=b×（a、b都不等于零），那么（）A．a＞b B．a=b C．a＜b考点：解比例；比与分数、除法的关系．专题：压轴题．分析：可令a÷=b×的值为1，求得a，b，再比较a，b的关系．解答：解：令a÷=b×=1，则a=，b=，则a＜b．故选C．点评：考查了比例中的大小比较问题，常用举特例的方法解决这类问题．4．2：x=：，x=（）A．40B．4C．0.4D．1考点：解比例．分析：根据两内项之积等于两外项之积把比例式转化为乘积式，然后再解关于x的一元一次方程即可．解答：解：x=2×，x=，解得x=1．故选D．点评：本题主要考查了解比例，根据两内项之积等于两外项之积把比例式转化为乘积式是解题的关键，是基础题，难度不大．5．在=中，a的值是（）A．2B．4C．6D．8考点：解比例．分析：利用比例的基本性质“两内项之积等于两外项之积”由此可求得a，进而选择正确答案．解答：解：根据比例的基本性质可解得：a=4，故选：B．点评：紧扣比例的基本性质即可解决此类问题．6．当：4=x：5时，x的值是（）A．B．C．D．考点：解比例．分析：根据比例的性质，把比例先改写成两个内项的积等于两个外项的积的形式，再进一步求出比例中的未知项，再进行选择．解答：解：：4=x：5，4x=×5，4x=3，x=．故选：B．点评：此题考查比例性质的运用即解比例．7．已知，则x=（）A．40B．4C．0.4D．1考点：解比例．分析：解比例的方法：根据比例的性质先把比例式转化成两外项积等于两内项积的形式，就是已学过的简易方程，再解简易方程即可．解答：解：，x=2×，x=，x=，x=1．故选：D．点评：此题考查根据比例的性质解比例：把比例式先转化成两外项积等于两内项积的形式，再解方程即可．二．填空题（共10小题）8．（1）如果：5=16%：7，那么=；（2）若（0.5+÷）=，则=．考点：解比例；整数、分数、小数、百分数四则混合运算．专题：运算顺序及法则；简易方程．分析：（1）把五角星未知数看作x，根据比例基本性质：两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以7求解，（2）把正方形看作未知数x，依据等式的性质，方程两边同时除以，再同时减0.5，然后同时乘x，最后同时除以求解．解答：解：（1）把原题中五角星未知数看作x，原题化为：x：5=16%：7，7x=5×16%，7x=0.8，7x÷7=0.8÷7，x=，即=，故应填：；（2）把原题中的正方形看作未知数x，原题化为：（0.5+÷x）=，（0.5+÷x）=，0.5+÷x﹣0.5=﹣0.5，x×x=x，x，x=，即=，故应填：．点评：本题主要考查学生依据等式的性质，以及比例基本性质解方程的能力，解方程时注意对齐等号．9．在X：1=3：4中，X=．考点：解比例．分析：本题按照比例的基本性质两内项之积等于两外项之积来求解．解答：解：X：1=3：4解：4X=×34X=X=；故答案为：．点评：解比例使用比例的基本性质来求解．10．0.8：4=8：x中，x=0.4，×．（判断对错）考点：解比例．专题：比和比例．分析：0.8：4=8：x，根据比例的基本性质得：0.8x=4×8，两边同时除以0.8解出x即可．解答：解：0.8：4=8：x0.8x=4×80.8x=32x=32÷0.8x=40x=40而不是0.4，故这句话是错误的．故答案为：×．点评：本题主要考查学生依据等式的性质，以及比例基本性质解方程的能力，解答时注意对齐等号．11．9：6=15：10．考点：解比例．专题：比和比例．分析：根据比的基本性质“两内项之积等于两外项之积”，先求出两內项之积，进而用积除以已知的外项，即可得出未知的外项．解答：解：6×15÷9=90÷9=10；故答案为：10．点评：解决此题也可以根据比的意义，先求出前一个比的比值，进而用后一个比的内项除以比值求解．12．6：1.5=8：2．填上合适的数．4：3=36：2724：80=1.8：6考点：解比例．专题：比和比例．分析：每一道题都设要求的数为x，进而写出比例：（1）根据比例的基本性质，先把比例式转化成等式4x=3×36，再根据等式的性质，在方程两边同时除以4得解；（2）根据比例的基本性质，先把比例式转化成等式1.8x=24×6，再根据等式的性质，在方程两边同时除以1.8得解；（3）根据比例的基本性质，先把比例式转化成等式1.5x=6×2，再根据等式的性质，在方程两边同时除以1.5得解．解答：解：每一道题都设要求的数为x：（1）4：3=36：x，4x=3×36，4x÷4=108÷4，x=27；（2）24：x=1.8：6，1.8x=24×6，1.8x÷1.8=144÷1.8，x=80；（3）6：1.5=x：2，1.5x=6×2，1.5x÷1.5=12÷1.5，x=8．故答案为：27，80，8．点评：本题主要考查了解比例，根据比例的性质先把比例式转化为乘积式是解题的关键；注意等号要对齐．13．解比例：：=X：24X：=：0.6．考点：解比例．分析：根据两内项之积等于两外项之积把比例式转化为乘积式，然后再解关于x的一元一次方程即可．解答：解：（1）x=24×，x=9，解得x=10；（2）0.6x=×，0.6x=，解得x=；（3）4x=5.2×6.5，4x=33.8，解得x=8.45；（4）0.6x=1.2×4，0.6x=4.8，解得x=8．点评：本题主要考查解比例，根据两内项之积等于两外项之积把比例式转化为乘积式是解题的关键，是基础题，难度不大．14．（•金寨县模拟）甲数比乙数少，甲数和乙数的比是2：9．考点：解比例．分析：甲数=（1﹣）×乙数，依此可求甲数与乙数的比．解答：解：甲数和乙数的比=（1﹣）：1=2：9．故答案为：2：9．点评：考查了求比的问题，解题的关键是将乙数看作单位1，依此得到甲数．15．如果x：=0.15：2.5，那么x=0.048．考点：解比例．专题：比和比例．分析：根据比例的基本性质变为：2.5x=×0.15，然后化简，再在方程的两边同时除以2.5求解．解答：解：x：=0.15：2.52.5x=×0.152.5x=0.122.5x÷2.5=0.12÷2.5x=0.048故答案为：0.048．点评：本题考查了利用比例的基本性质解比例．16．能与：组成比例的比是B、CA.2：3B.9：6C.：D.：．考点：解比例．分析：先化简：，再分别计算各选项，与：进行比较，比值相等的即为所求．解答：解：：=3：2．A、因为2：3≠3：2，所以不能组成比例，故选项错误；B、因为9：6=3：2，所以能组成比例，故选项正确；C、因为：=3：2，所以能组成比例，故选项正确；D、因为：=2：3≠3：2，所以不能组成比例，故选项错误．故选：B和C．点评：本题考查了比例线段的定义：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如a：b=c：d（即ad=bc），我们就说这四条线段是成比例线段，简称比例线段．17．在横线里填上适当的数．5：4=30：241.5：0.18=150：188：15=24：4536：12=9：30.9：0.5=9：5．考点：解比例．专题：比和比例．分析：设未知数为x，列出比例，根据比例的基本性质，两外项之积等于两内项之积，求出未知数即可．解答：解：（1）5：4=x：244x=5×244x÷4=5×24÷4x=30；（2）1.5：0.18=x：180.18x=1.5×180.18x÷0.18=1.5×18÷0.18x=150；（3）8：15=24：x8x=15×248x÷8=15×24÷8x=45；（4）36：12=9：x36x=12×936x÷36=12×9÷36x=3；（5）x：0.5=9：55x=0.5×95x÷5=0.5×9÷5x=0.9．故答案为：30，150，45，3，0.9．点评：此题主要是考查解比例，解比例与解方程类似，要注意书写格式．解比例的依据是比例的基本性质及等式的性质．三．解答题（共11小题）18．计算：4：5=（χ+5）：10．考点：解比例．专题：简易方程．分析：根据两内项之积等于两外项之积，把比例式转化成方程，再根据等式的性质求解即可．解答：解：4：5=（x+5）：104×10=5×（x+5）40=5x+255x=40﹣25x=15÷5x=3．点评：掌握比例的基本性质是解题的关键．19．解比例．（1）6：15=x：20（2）：x=3：8（3）：=：x（4）=（5）x：15=1：2.4（6）8：x=3：1．考点：解比例．专题：比和比例．分析：根据两内项之积等于两外项之积，把比例式转化成方程，再根据等式的性质求解即可．解答：解：（1）6：15=x：2015x=6×2015x÷15=120÷15x=8（2）：x=3：83x=3x÷3=6÷3x=2（3）x=（4）0.75x=0.5×60.75x÷0.75=3÷0.75x=4（5）x：15=1：2.42.4x=1×152.4x÷2.4=15÷2.4x=6.25（6）8：x=3=8×x=3点评：掌握比例的基本性质是解题的关键．20．求未知数x的值．：0.05=1：x x﹣1=x+x+x+x+x．考点：解比例；方程的解和解方程．专题：用字母表示数．分析：（1）根据比例的基本性质转化为x=×，再根据等式的基本性质，方程的两边同除以即可；（2）先计算x+x+x+x+x=x，再根据等式的基本性质，方程的两边同x，再加上1即可．解答：解：：0.05=1：x，x=×，x÷=×÷，x=；（2）x﹣1=x+x+x+x+x，x﹣1=x，x﹣1﹣x=x﹣x，x﹣1=0，x﹣1+1=0+1，x=1，x=32．点评：本题主要考查学生依据等式的性质，以及比例基本性质解方程的能力，解答时注意对齐等号．21．解方程．X：1.2=3：4=30%X﹣X=．考点：解比例；方程的解和解方程．专题：简易方程．分析：（1）根据比例的基本性质：两内项之积等于两外项之积可得4x=1.2×3，再利用等式的性质两边同时除以4即可解答；（2）可以写成x：4=3：10，根据比例的基本性质：两内项之积等于两外项之积可，10x=4×3，再利用等式的性质两边同时除以10即可解答；（3）先把左边计算出来得：x=，再利用等式的性质，两边同时乘，即可解答．解答：解：（1）x：1.2=3：4，4x=1.2×3，4x÷4=3.6÷4，x=0.9，（2）=30%，x：4=3：10，10x=4×3，10x÷10=12÷10，x=1.2，（3）x﹣x=，x=，x×=×，x=2．点评：此题考查了利用比例的基本性质解比例和利用等式的性质解方程的方法．22．一个数和的比等于8和1.6的比，求这个数．考点：解比例．分析：根据题意可以设这个数为x，组成比例，解比例即可．解答：解：设这个数为x．x：=8：1.61.6x=×8x=×8÷1.6x=4答：这个数是4．点评：此题主要考查解比例的方法．23．（•河池）求未知数x的值．（1）：x=：8（2）1.7x﹣0.4x=3.9．考点：解比例；方程的解和解方程．专题：简易方程．分析：（1）根据比例基本性质，两内项之积等于两外项之积化简方程，再依据等式的性质，方程两边同时除以求解，（2先化简方程，再依据等式的性质，方程两边同时除以1.3求解．解答：解：（1）：x=：8，x=×8，x=，x=4；（2）1.7x﹣0.4x=3.9，1.3x=3.9，1.3x÷1.3=3.9÷1.3，x=3．点评：本题主要考查学生依据等式的性质以及比例的基本性质解方程的能力，解答时注意对齐等号．24．（•东莞市模拟）求x的值．6x﹣0.5×5=9.5：x=：0.75考点：解比例；方程的解和解方程．专题：简易方程．分析：①根据比例的性质变成x=×，再根据等式的性质，方程的两边同时除以即可；②6x﹣0.5×5=9.5，先计算0.5×5=2.5，再根据等式的性质，方程的两边同时加上2.5，再除以6即可；解答：解：①：x=：0.75，x=×，x=，x÷=÷，x=；②6x﹣0.5×5=9.5，6x﹣2.5=9.5，6x﹣2.5+2.5=9.5+2.5，6x=12，6x÷6=12÷6，x=2．点评：此题考查根据等式的性质和比例的性质解比例和解方程的能力，注意等号对齐．25．解比例：8：20=7.6：x．考点：解比例．专题：比和比例．分析：根据比例的基本性质，先把比例式转化成等式8x=20×7.6，再根据等式的性质，在方程两边同时除以2.5得解．解答：解：8：20=7.6：x8x=20×7.68x=1528x÷8=152÷8x=19．点评：本题主要考查了解比例，根据比例的性质先把比例式转化为乘积式是解题的关键；注意等号要对齐．26．解方程．（1）4.2：x=25（2）3.6x：=3.5（3）x：=（4）x：0.25=4．考点：解比例．专题：比和比例．分析：（1）根据比例的基本性质，两内项之积等于两外项之积，方程可化为25x=4.2，再依据等式的性质，两边同除以25即可求解；（2）根据比例的基本性质，两内项之积等于两外项之积，方程可化为3.6x= 3.5，再依据等式的性质，两边同除以3.6即可求解；（3）根据比例的基本性质，两内项之积等于两外项之积，方程可化为x=×，化简计算即可；（4）根据比例的基本性质，两内项之积等于两外项之积，方程可化为x=0.25×4，化简计算即可；解答：解：（1）4.2：x=2525x=4.225x÷25=4.2÷25x=0.168（2）3.6x：=3.53.6x= 3.53.6x÷3.6=1.75÷3.6x=0.486（3）x：=x=×x=（4）x：0.25=4x=0.25×4x=1点评：本题主要考查运用等式的性质以及比例的基本性质解方程的能力，注意等号对齐．27．解方程或解比例：8x÷（1.8÷3）=1.5．：=：（4﹣x）考点：解比例；方程的解和解方程．专题：简易方程．分析：（1）先化简方程的左边，变成8x÷0.6=1.5，然后方程的两边同时乘上0.6，再同时除以8即可；（2）根据比例的基本性质，把方程变成×（4﹣x）=×，然后方程的两边同时除以，再同加上x，最后同时减去即可．解答：解：（1）8x÷（1.8÷3）=1.58x÷0.6=1.58x÷0.6×0.6=1.5×0.68x=0.98x÷8=0.9÷8x=0.1125；（2）：=：（4﹣x）×（4﹣x）=××（4﹣x）÷=÷4﹣x=4﹣x+x=+xx+﹣=4﹣x=3．点评：本题考查了根据比例的基本性质以及等式的性质解方程的方法，计算时要细心，注意把等号对齐．28．求未知数x（1）6.5：x=314：4（2）8（x﹣2）=2（x+7）考点：解比例；方程的解和解方程．专题：简易方程；比和比例．分析：（1）先根据比例基本性质：两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以314即可；（2）先化简方程，再根据等式的性质，在方程两边同时减2x，加16，再同时除以6求解．解答：解：（1）6.5：x=314：4314x=6.5×4314x÷314=26÷314x=；（2）8（x﹣2）=2（x+7）8x﹣16=2x+148x﹣16+16﹣2x=2x+14﹣2x+166x=306x÷6=30÷6x=5．点评：此题考查了根据等式的性质解方程，即等式两边同时加、减、乘同一个数或除以同一个不为0的数，等式的左右两边仍相等；注意等号上下要对齐．B档（提升精练）一．选择题（共14小题）1．当x=（）时，的比值恰好是最小的质数．A．B．C．考点：解比例．专题：比和比例．分析：最小的质数是2，所以可得的一个等式：=2，根据比与除法的关系即比的前项相当于除法的被除数，比的后项相当于除法的除数，比值相当于除法的商，然后再进行计算得到答案．解答：解；=2x=÷2，x=，答：当x=时，的比值恰好是最小的质数．故选：C．点评：解答此题的关键是确定比与除法之间的关系，然后再进行计算即可．2．解比例是根据（）A．比的基本性质B．比例的基本性质C．比例的意义．考点：解比例．专题：比和比例．分析：解比例是求比例的解的过程，即先把比例改写成两个内项的积等于两个外项的积的形式，再进一步求出比例中的未知项，所以根据的是比例的基本性质．据此即可判断．解答：解：解比例是先把比例改写成两个内项的积等于两个外项的积的形式，再进一步求出比例中的未知项，所以解比例是根据比例的基本性质．故选：B．点评：本题考查了解比例的依据，明确解比例的定义是关键．3．如果3：5=x：2，那么x应该是（）A．B．C．D．考点：解比例．专题：比和比例．分析：根据比例的性质，可得5x=3×2，再利用等式的性质两边同时除以5，即可得出x=，据此即可选择．解答：解：3：5=x：2，5x=3×2，5x÷5=6÷5，x=．故选：A．点评：熟练运用比例的基本性质，掌握比例式和等式的转化．4．解比例：=2：1，x=（）A．6B．1.5C．0.7D．9考点：解比例．专题：比和比例．分析：根据比例的基本性质：两内项之积等于两外项之积，得出关于x的方程，再利用等式的性质解方程即可解答问题．解答：解：=2：1x：3=2：1x=6．故选：A．点评：此题考查了比例的基本性质和等式的性质的应用．5．解比例的根据是（）A．比的基本性质B．比例的基本性质C．分数的基本性质考点：解比例．分析：首先要知道什么是解比例，然后分析每个选项，看哪一个最适合用来作为解比例的根据．解答：解：因为求比例的解的过程，叫做解比例．所以选项A：比的基本性质“比的前项和后项同时乘或除以相同的数（0除外），比值不变．”不能作为解比例的根据．选项B：比例的基本性质“两外项之积等于两内项之积”可以作为解比例的根据．选项C：分数的基本性质“分子和分母同时扩大或缩小相同的倍数，分数值不变．”也不能作为解比例的根据．故选B．点评：做这道题的关键是分清比、分数和比例的基本性质．6．（X﹣0.1）：0.4=0.6：1.2 则X=（）A．X=0.3B．X=0.9C．X=0.8考点：解比例．专题：比和比例．分析：根据比例基本性质，两内项之积等于两外项之积，化简方程，再依据等式的性质求解．解答：解：（X﹣0.1）：0.4=0.6：1.2，（X﹣0.1）×1.2=0.6×0.4，（X﹣0.1）×1.2÷1.2=0.24÷1.2，X﹣0.1=0.2，X﹣0.1+0.1=0.2+0.1，X=0.3．故选：A．点评：本题主要考查学生依据等式的性质以及比例的基本性质解方程的能力，解方程时注意对齐等号．7．x=是比例（）的解．A．2.6：x=1：8B．3：6=x：8C．：x=考点：解比例．专题：比和比例．分析：根据比例的基本性质，把x=代入各选项即可判断．解答：解：A、把x=代入2.6：x=2.6：=52：25，52：25≠1：8，所以把x=不是2.6：x=1：8的解；B、把x=代入x：8=：8=5：32，3：6≠5：32，所以把x=不是3：6=x：8的解；C、把x=代入：x=：=2：1，：=2：1，所以把x=是：x=：的解．故选：C．点评：本题主要考查学生依据等式的性质以及比例基本性质解方程的能力．8．（•荔波县模拟）如果比例的两个外项互为倒数，那么比例的两个内项（）A．成反比例B．成正比例C．不成比例考点：解比例．专题：压轴题．分析：根据互为倒数的定义和比例的两内项之积等于两外项之积，可得比例的两个内项之积等于1，再根据成反比例的定义即可求解．解答：解：因为比例的两个外项互为倒数，那么比例的两个内项之积=1（为恒指），则比例的两个内项成反比例．故选：A．点评：本题考查了倒数的定义和成反比例的条件，两种相关联的量，一种量变化，另一种量也随着变化，这两种量中相对应的两个数的积一定．这两种量叫做成反比例的量．它们的关系叫做反比例关系．9．已知：x=0.2：0.3，则x的值为（）A．B．C．3考点：解比例．专题：比和比例．分析：先根据比例基本性质，两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以0.2求解．解答：解：：x=0.2：0.3，0.2x=0.3×，0.2x=0.15，0.2x÷0.2=0.15÷0.2，x=，故选：A．点评：解答本题的关键是依据比例基本性质求解．解答时注意对齐等号．10．用4，0.8，5和x组成比例，并解比例，x有（）种不同的解．A．1B．2C．3D．4考点：解比例．专题：比和比例．分析：根据比例的基本性质，4，0.8，5和x，组成比例的情况有12种，两内项之积等于两外项之积，这四个数可写成三个等式．据此解答．解答：解：根据分析知，4，0.8，5和x组成比例的情况有12种：（1）5：0.8=x：4，0.8：5=4：x，0.8：5=4：x，4：0.8=x：5，它们变形后都能写成0.8x=5×4，解相同．同理也有四个比例式变形后写成5x=4×0.8，和4x=5×0.8．故选：C．点评：本题考查了学生根据比例的基本性质解答问题的能力．11．解比例30：x=2：0.1，x=（）A．6B．1.5C．0.7D．9考点：解比例．专题：比和比例．分析：先根据比例基本性质：两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以2求解．解答：解：30：x=2：0.1，2x=30×0.1，2x÷2=3÷2，x=1.5，故应选：B．点评：本题主要考查学生依据等式的性质以及比例基本性质解方程的能力，解方程时注意对齐等号．12．x=1.25是哪个比例的解？（）A．2.6：x=6：3B．3：6=x：8C．：x=：考点：解比例．专题：简易方程．分析：把三个选项中的比例式，依据等式的性质，以及比例的基本性质，求出方程的解，再与x=1.25比较即可解答．解答：解：在选项A中：2.6：x=6：36x=2.6×36x÷6=7.8÷6x=1.3；在选项B中：3：6=x：86x=3×86x÷6=24÷6x=4；在选项C中：：x=：x=x=x=1.25故选：C．点评：依据等式的性质，以及比例的基本性质，求出选项中各方程的解，是解答本题的关键．13．若已知2：3=（5﹣x）：x，那么x等于（）A．2B．3C．4D．6考点：解比例．专题：比和比例．分析：先根据比例基本性质：两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时加3x，最后同时除以5求解．解答：解：2：3=（5﹣x）：x，15﹣3x=2x，15﹣3x+3x=2x+3x，15÷5=5x÷5，x=3．故选：B．点评：本题考查知识点：依据等式的性质，以及比例基本性质解方程．14．如果和相等，则m等于（）A．B．C．D．考点：解比例．专题：比和比例．分析：依据题意可列比例式：=，先根据比例基本性质：两内项之积等于两外项之积，化简方程，再依据等式的性质，方程两边同时除以18即可求解．解答：解：=，18m=11×12，18m÷18=132÷18，m=，m=7．故答案为：A．点评：等式的性质，以及比例基本性质是解方程的依据，解方程时注意对齐等号．二．填空题（共14小题）15．（•新干县）若a与b互为倒数，且=，那么x=．√．（判断对错）考点：解比例．专题：比和比例．分析：若a与b互为倒数，且=，根据比例的基本性质可得：5x=ab=1，那么x=．解答：解：=，根据比例的基本性质可得：5x=ab=1，那么x=；故答案为：√．点评：此题考查了比例的基本性质的运用．16．（•东莞模拟）如果ҳ：=：，那么ҳ=．考点：解比例．分析：根据比例的性质，把比例先改写成两个内项的积等于两个外项的积的形式，再进一步求出比例中的未知项．解答：解：ҳ：=：，X=×，X=，X=．故答案为：．点评：此题考查比例性质的运用即解比例．17．（•铁山港区模拟）下面表格中，如果x与y成正比例，“？”是32：如果x和y成反比例，“？”是8X16？y4896考点：解比例．专题：比和比例．分析：（1）如果x与y成正比例，由正比例的意义可得16：48=？：96，把？看作未知数，根据比例的基本性质进行解比例即可；（2）如果x和y成反比例，由反比例的意义可得96？=16×48，把？看作未知数，根据等式的性质进行解方程即可．解答：解：根据题意可得：（1）16：48=？：96，48？=16×96，48？=1536，48？÷48=1536÷48，？=32；所以，如果x与y成正比例，“？”是32；（2）96？=16×48，96？=768，96？÷96=768÷96，？=8；所以，如果x和y成反比例，“？”是8．故答案为：32，8．点评：本题主要考查正反比例的意义，然后根据题意列出比例或方程再进一步解答即可．18．（•沿河县模拟）根据比例关系填表：x43918152y601024考点：解比例．专题：比和比例．分析：判断两个相关联的量之间成什么比例，就看这两个量是对应的比值一定，还是对应的乘积一定；如果是比值一定，就成正比例；如果是乘积一定，则成反比例．解答：解：因为24×15=360（一定）所以xy成反比例关系．360÷4=90，360÷3=120，360÷60=6，360÷9=40，360÷10=36，360÷18=20，360÷2=180．x43693618152y901206040102024180点评：此题属于辨识成正、反比例的量，就看这两个量是对应的比值一定，还是对应的乘积一定，再做判断．19．（•靖江市）如果x与y成正比例，那么表中的△是 4.5；如果x与y成反比例，那么△是2．x3△y120180考点：解比例．专题：比和比例．分析：（1）如果表中x和y成正比例，说明x和y对应的比值一定，根据两个比的比值相等列比例，并解比例即可；（2）如果表中x和y成反比例，说明x和y对应的乘积一定，根据两个比的乘积相等列方程，并解方程即可．解答：解：（1）3：120=x：180，120x=3×180，120x÷120=540÷120，x=4.5；（2）180x=3×120，180x=360，180x÷180=360÷180，x=2；故答案为：4.5，2．点评：此题考查根据正、反比例的意义，解答时要根据已知两种相关联的量，看比值一定还是积一定．20．（•广州模拟）0.4：x=1：10．考点：解比例．分析：根据比例的基本性质，把原式转化为x=0.4×10，再根据等式的性质，在方程两边同时乘上求解，解答：解：0.4：x=1：10，x=0.4×10，x×=4×，x=．点评：本题主要考查了学生根据比例的基本性质和等式的性质解方程的能力．21．（•广州模拟）6：2.8=2.4：x．考点：解比例．分析：根据比例的基本性质，把原式转化为6x=2.8×2.4，再根据等式的性质，在方程两边同时除以6求解．解答：解：6：2.8=2.4：x，6x=2.8×2.4，6x÷6=6.72÷6，x=1.12．点评：本题考查了学生根据比例的基本性质和等式的性质解方程的能力，注意等号对齐．22．（•江宁区模拟）如果A与B成正比例，那么“？”是 3.2；如果A与B成反比例，那么“？”是5．A4？B200160考点：解比例．分析：这一题可由正比例的意义和反比例的意义解答即可．解答：解：（1）A与B成正比例，△，x=3.2；（2）A与B成反比例，160x=4×200，x=5；故答案为：3.2，5．点评：此题考查了对正比例与反比例意义的理解以及应用的能力，要灵活掌握正反比例的公式．23．（•广州模拟）：=4：x．考点：解比例．分析：根据比例的基本性质，把原式转化为，再根据等式的性质，在方程两边同时乘上求解．解答：解：：=4：x，，，x=．点评：本题考查了学生根据比例的基本性质和等式的性质解方程的能力，注意等号对齐．。

六年级百分比应用题10道

六年级百分比应用题10道1. 问题：一个班级有40名学生，其中男生占60%，那么女生有多少人？解答：首先计算男生的人数：40 x 60% = 24人。

然后计算女生的人数：40 - 24 = 16人。

所以女生有16人。

2. 问题：一个工厂生产了100个产品，其中有80个是合格的，那么合格率是多少？解答：合格率= (合格的产品数/ 总产品数) x 100% = (80 / 100) x 100% = 80%。

3. 问题：一个公司的员工中，有75%的人有大学学历，那么没有大学学历的员工有多少人？解答：首先计算有大学学历的员工人数：总员工数x 75% = 总员工数x 0.75。

然后计算没有大学学历的员工人数：总员工数- 有大学学历的员工人数。

4. 问题：一个商店卖出了120件衣服，其中男装占50%，女装占50%，那么男装和女装各卖出了多少件？解答：首先计算男装的数量：120 x 50% = 60件。

然后计算女装的数量：120 - 60 = 60件。

所以男装卖出了60件，女装卖出了60件。

5. 问题：一个学校的男生占学生总数的65%，女生占学生总数的35%，那么这个学校一共有多少学生？解答：设学生总数为x，那么男生数量为0.65x，女生数量为0.35x。

由于男生和女生的总数等于学生总数，所以有0.65x + 0.35x = x。

解这个方程得到x = 100。

所以这个学校一共有100名学生。

6. 问题：一个城市的居民中，有25%的人是年轻人，那么老年人占多少比例？解答：老年人的比例= 1 - 年轻人的比例= 1 - 25% = 75%。

7. 问题：一个公司的销售额中，产品A占40%，产品B占30%，产品C占30%，那么产品A、B、C的销售额分别是多少？解答：设总销售额为x，那么产品A的销售额为0.4x，产品B 的销售额为0.3x，产品C的销售额为0.3x。

8. 问题：一个班级的学生中，有70%的人喜欢数学，那么喜欢英语的学生占多少比例？解答：喜欢英语的学生的比例= 1 - 喜欢数学的学生的比例= 1 - 70% = 30%。

小学数学6年级应用题100道附答案(完整版)

小学数学6年级应用题100道附答案(完整版)题目1某工厂有男工25 人，女工20 人，男工人数是女工人数的百分之几？答案：25÷20×100% = 125%题目2一个数的30%是15，这个数是多少？答案：15÷30% = 50题目3果园里有苹果树120 棵，梨树比苹果树少20%，梨树有多少棵？答案：120×(1 - 20%) = 96（棵）题目4一套衣服原价200 元，现在打八折出售，现价是多少元？答案：200×80% = 160（元）题目5一本书300 页，第一天看了全书的20%，第二天看了全书的25%，两天一共看了多少页？答案：300×(20% + 25%) = 135（页）题目6六年级有学生180 人，其中男生占60%，女生有多少人？答案：180×(1 - 60%) = 72（人）题目7一项工程，甲单独做10 天完成，乙单独做15 天完成，两人合作几天完成？答案：1÷(1/10 + 1/15) = 6（天）题目8一个圆形花坛的周长是62.8 米，它的半径是多少米？答案：62.8÷3.14÷2 = 10（米）题目9一堆煤，用去了40%，还剩12 吨，这堆煤原来有多少吨？答案：12÷(1 - 40%) = 20（吨）题目10商店运来一批水果，其中苹果有180 千克，梨比苹果多20%，梨有多少千克？答案：180×(1 + 20%) = 216（千克）题目11一辆汽车从甲地开往乙地，已经行驶了全程的40%，离乙地还有120 千米，甲乙两地相距多少千米？答案：120÷(1 - 40%) = 200（千米）题目12在一个直径为8 米的圆形花坛周围铺一条宽1 米的小路，小路的面积是多少平方米？答案：内圆半径= 8÷2 = 4（米），外圆半径= 4 + 1 = 5（米），小路面积= 3.14×(5²- 4²) = 28.26（平方米）13一本书，第一天读了全书的25%，第二天读了全书的30%，第一天比第二天少读10 页，这本书共有多少页？答案：10÷(30% - 25%) = 200（页）题目14一个圆锥形沙堆，底面半径是2 米，高是1.5 米，这个沙堆的体积是多少立方米？答案：1/3×3.14×2²×1.5 = 6.28（立方米）题目15某商品按20%的利润定价，然后按八八折出售，共得利润84 元，这件商品的成本是多少元？答案：设成本为x 元，(1 + 20%)x×88% - x = 84，解得x = 1500题目16小明把5000 元存入银行，定期2 年，年利率是 2.52%，到期时他可得利息多少元？答案：5000×2.52%×2 = 252（元）题目17一个长方体的棱长总和是48 厘米，长、宽、高的比是3:2:1，这个长方体的体积是多少立方厘米？答案：48÷4 = 12（厘米），长= 12×3/(3 + 2 + 1) = 6（厘米），宽= 12×2/(3 + 2 + 1) = 4（厘米），高= 12×1/(3 + 2 + 1) = 2（厘米），体积= 6×4×2 = 48（立方厘米）题目18一件工作，甲单独做8 小时完成，乙单独做10 小时完成，甲、乙合作几小时完成？答案：1÷(1/8 + 1/10) = 40/9（小时）题目19六年级学生参加植树活动，成活了95 棵，5 棵没成活，成活率是多少？答案：95÷(95 + 5)×100% = 95%题目20一辆汽车从甲地到乙地，去时每小时行60 千米，返回时每小时行50 千米，往返的平均速度是多少？答案：设甲乙两地距离为“1”，去时时间= 1÷60 = 1/60，返回时间= 1÷50 = 1/50，往返总路程= 2，平均速度= 2÷(1/60 + 1/50) = 600/11（千米/时）题目21学校买来120 本图书，按3:2 的比例分给六年级和五年级，六年级分得多少本？答案：120×3/(3 + 2) = 72（本）题目22在比例尺是1:5000000 的地图上，量得两地的距离是 6 厘米，两地的实际距离是多少千米？答案：6÷1/5000000 = 30000000（厘米）= 300（千米）题目23一个圆柱的底面半径是3 厘米，高是5 厘米，它的侧面积是多少平方厘米？答案：2×3.14×3×5 = 94.2（平方厘米）题目24一个圆柱和一个圆锥等底等高，圆柱的体积是27 立方分米，圆锥的体积是多少立方分米？答案：27÷3 = 9（立方分米）25有含盐率为10%的盐水80 克，加入多少克水就能得到含盐率为8%的盐水？答案：80×10%÷8% - 80 = 20（克）题目26某班男生人数是女生人数的4/5，女生人数比男生人数多百分之几？答案：(5 - 4)÷4×100% = 25%题目27一个数增加20%后是120，这个数是多少？答案：120÷(1 + 20%) = 100题目28光明小学有男生360 人，女生比男生少20%，女生有多少人？答案：360×(1 - 20%) = 288（人）题目29一件商品原价150 元，现降价20%出售，现价是多少元？答案：150×(1 - 20%) = 120（元）题目30一本书，已经看了全书的35%，还剩130 页没看，这本书一共有多少页？答案：130÷(1 - 35%) = 200（页）题目31六年级一班有48 人，其中1/3 参加了数学兴趣小组，参加数学兴趣小组的有多少人？答案：48×1/3 = 16（人）题目32一个圆的直径是10 厘米，它的面积是多少平方厘米？答案：3.14×(10÷2)²= 78.5（平方厘米）题目33一个长方体的长、宽、高分别是6 厘米、5 厘米、4 厘米，它的表面积是多少平方厘米？答案：(6×5 + 6×4 + 5×4)×2 = 148（平方厘米）题目34一项工作，甲、乙合作8 天完成，甲单独做12 天完成，乙单独做几天完成？答案：1÷(1/8 - 1/12) = 24（天）题目35某工厂五月份生产零件2000 个，六月份比五月份增产15%，六月份生产零件多少个？答案：2000×(1 + 15%) = 2300（个）题目36在一个边长为10 厘米的正方形内画一个最大的圆，这个圆的面积是多少平方厘米？答案：3.14×(10÷2)²= 78.5（平方厘米）题目37修一条公路，已经修了全长的45%，距离中点还有200 米，这条公路全长多少米？答案：200÷(50% - 45%) = 4000（米）题目38一个等腰三角形，顶角与底角的度数比是2:1，这个三角形的顶角是多少度？答案：180×2/(2 + 1 + 1) = 90（度）题目39把一个棱长为 6 分米的正方体木块削成一个最大的圆锥，这个圆锥的体积是多少立方分答案：1/3×3.14×(6÷2)²×6 = 56.52（立方分米）题目40六年级同学参加体育达标测试，达标的有196 人，未达标的有4 人，达标率是多少？答案：196÷(196 + 4)×100% = 98%题目41一种商品，现在的售价是80 元，比原价降低了20 元，降低了百分之几？答案：20÷(80 + 20)×100% = 20%题目42一个圆柱形水桶，底面直径是4 分米，高是5 分米，这个水桶能装多少升水？答案：3.14×(4÷2)²×5 = 62.8（立方分米）= 62.8（升）题目43学校举行绘画比赛，参赛作品共有125 幅，其中一等奖6 幅，二等奖占参赛作品的16%，三等奖的数量比二等奖的数量多40%，三等奖有多少幅？答案：二等奖数量：125×16% = 20（幅），三等奖数量：20×(1 + 40%) = 28（幅）题目44从甲地到乙地，客车要行驶8 小时，货车要行驶10 小时，客车速度比货车速度快百分之几？答案：(1/8 - 1/10)÷1/10×100% = 25%题目45某服装店同时卖出两件衣服，每件各卖180 元，其中一件赚了20%，另一件亏了20%，这个服装店卖出这两件衣服是赚了还是亏了？答案：第一件成本：180÷(1 + 20%) = 150（元），第二件成本：180÷(1 - 20%) = 225（元），总成本：150 + 225 = 375（元），总售价：180×2 = 360（元），亏了：375 - 360 = 15（元）题目46一个环形铁片，外圆半径是8 厘米，内圆半径是5 厘米，这个环形铁片的面积是多少平方厘米？答案：3.14×(8²- 5²) = 122.46（平方厘米）题目47有一堆煤，第一天运走了总数的25%，第二天运走了总数的35%，还剩下120 吨，这堆煤一共有多少吨？答案：120÷(1 - 25% - 35%) = 300（吨）题目48把20 克糖溶解在80 克水中，糖水的含糖率是多少？答案：20÷(20 + 80)×100% = 20%题目49一个长方形的长和宽的比是5:3，长比宽多12 厘米，这个长方形的面积是多少平方厘米？答案：长：12÷(5 - 3)×5 = 30（厘米），宽：12÷(5 - 3)×3 = 18（厘米），面积：30×18 = 540（平方厘米）题目50小明家十月份用电80 度，比九月份节约了20%，九月份用电多少度？答案：80÷(1 - 20%) = 100（度）题目51一个直角三角形，两条直角边分别是6 厘米和8 厘米，斜边是10 厘米，斜边上的高是多答案：6×8÷10 = 4.8（厘米）题目52一批零件，甲单独做20 小时完成，乙单独做30 小时完成，两人合作完成时，甲比乙多做60 个，这批零件一共有多少个？答案：两人合作时间：1÷(1/20 + 1/30) = 12（小时），甲比乙每小时多做：(1/20 - 1/30)，零件总数：60÷[(1/20 - 1/30)×12] = 300（个）题目53一个圆柱的侧面积是188.4 平方厘米，高是10 厘米，它的体积是多少立方厘米？答案：底面周长：188.4÷10 = 18.84（厘米），底面半径：18.84÷3.14÷2 = 3（厘米），体积：3.14×3²×10 = 282.6（立方厘米）题目54学校有足球20 个，篮球比足球多25%，篮球有多少个？答案：20×(1 + 25%) = 25（个）题目55一个数的40%比它的30%多12，这个数是多少？答案：12÷(40% - 30%) = 120题目56在比例尺是1:2000000 的地图上，量得A、B 两地的距离是20 厘米，A、B 两地的实际距离是多少千米？答案：20×2000000 = 40000000（厘米）= 400（千米）题目57一个圆锥的体积是75.36 立方厘米，底面半径是3 厘米，高是多少厘米？答案：75.36×3÷(3.14×3²) = 8（厘米）题目58一辆汽车3 小时行驶了180 千米，照这样的速度，5 小时能行驶多少千米？答案：180÷3×5 = 300（千米）题目59王师傅加工一批零件，第一天加工了总数的20%，第二天加工了总数的25%，两天共加工了90 个，这批零件一共有多少个？答案：90÷(20% + 25%) = 200（个）题目60一种盐水，盐和水的质量比是1:9，现有盐5 克，能配制这种盐水多少克？答案：5×(1 + 9) = 50（克）题目61一个长方体的水箱，长8 分米，宽 6 分米，高5 分米，把120 升水倒入这个水箱中，水深多少分米？答案：120 升= 120 立方分米，120÷(8×6) = 2.5（分米）题目62果园里桃树和梨树的棵数比是5:3，桃树有200 棵，梨树有多少棵？答案：200÷5×3 = 120（棵）题目63学校买了12 个篮球和8 个足球，一共用去1120 元，篮球每个60 元，足球每个多少元？- 12某工厂4 月份用水120 吨，5 月份比4 月份节约用水20%，5 月份用水多少吨？答案：120×(1 - 20%) = 96（吨）题目65一个圆柱的底面周长是12.56 分米，高是6 分米，求它的表面积。

小学数学比和比例问题知识汇总及解析例题

小学数学知识总结之比和比例应用题【求比的问题】例1 两个同样容器中各装满盐水。

第一个容器中盐与水的比是2∶3，第二个容器中盐与水的比是3∶4，把这两个容器中的盐水混合起来，则混合溶液中盐与水的比是____。

（无锡市小学数学竞赛试题）则混合溶液中，盐与水的比是：某电子产品去年按定价的80％出售，能获利20％，由于今年买入价降（1994年全国小学数学奥林匹克决赛试题）即：【比例问题】例1 甲、乙两包糖的重量比是4∶1，如果从甲包取出10克放入乙包后，甲、乙两包糖的重量比变为7∶5 那么两包糖重量的总和是____克。

（1989年全国小学数学奥林匹克初赛试题）例2 甲容器中有纯酒精11升，乙容器中有水15升，第一次将甲容器中的一部分纯酒精倒入乙容器，使酒精与水混合。

第二次将乙容器中的一部分混合液倒入甲容器。

这样甲容器中纯酒精含量为62.5％，乙容器中纯酒精含量为25％，那么，第二次从乙容器倒入甲容器的混合液是____升。

（1991年全国小学数学奥林匹克决赛试题）讲析：因为现在乙容器中纯酒精含量为25％，所以，乙容器中酒精与水的比为25％∶（1-25％）=1∶3第一次从甲容器中倒5升纯酒精到乙容器，才使得乙容器中纯酒精与水的比恰好是5∶15=1∶3又甲容器中纯酒精含量为62.5％，则甲容器中酒精与水的比为62.5％∶（1-62.5％）=5∶3第二次倒后，要使甲容器中纯酒精与水的比为5∶3，不妨把从甲容器中倒入乙容器的混合液中纯酒精作1份，水作3份。

那么甲容器中剩下的纯酒精便是11-5=6（升）6升算作4份，这样可恰好配成5∶3。

而第二次从乙容器倒入甲容器的混合液共为1＋3=4（份），所以也应是6升。

一.比的意义和性质（1）比的意义两个数相除又叫做两个数的比。

“：”是比号，读作“比”。

比号前面的数叫做比的前项，比号后面的数叫做比的后项。

比的前项除以后项所得的商，叫做比值。

同除法比较，比的前项相当于被除数，后项相当于除数，比值相当于商。

比例尺应用题60题(有答案过程)

比例尺应用题60题(有答案过程)比例尺应用题专项练习60题（有答案）1．一幅地图的比例尺是1：800000，在一幅地图上量得甲乙两地的距离是2.5厘米，，则甲乙两地的实际距离是多少千米？2．在比例尺是的地图上，测得甲乙两地的距离是8厘米，在另一幅1：4000000的地图上，甲乙两地相距多少厘米？3．在一幅地图上量得北京到沈阳的铁路长5厘米，地图的比例尺是1：7000000，北京到沈阳的铁路实际有多少千米？4．在比例尺是1：100的图纸上，量得一个正方形花坛的边长是10厘米这个花坛的实际面积是多少平方米？5．在比例尺是1：5000的图纸上，量得一个长方形花园的长是10cm，宽是8cm，这个花园的实际面积是多少平方米？6．在比例尺的地图上，量得A、B两地的距离长12厘米，甲乙两车同时从AB两地相对开出，经过4小时两车相遇，已知甲乙两车的速度比是3：2，甲乙两车的速度各是多少千米？7．某县人民政府门前的广场是一个长方形，长180米，宽100米．请你选择一个合适的比例尺，在下边的图纸内画出广场的平面图，并在图上注明长和宽．我设计的比例尺是_________．8．在比例尺是的地图上，有一段长是40厘米的道路．一辆时速是50千米的汽车走完这段路需要多少分钟？9．北京到上海大约相距1050千米，在比例尺为1：30000000的一幅地图上，量得两地相距多少厘米？10．在一张比例尺是1：5000000的地图上，小明量得北京到上海的距离是28.8cm，已知火车每小时行120千米，姥姥四月三十日晚7：00上车，小明应最晚在什么时候去接站？11．在如图中量出所需的数据（取整厘米数），再计算．A、B两地相距80千米，A、C两地相距多少千米呢？12．在标有比例尺的地图上，量得两地间相距12厘米，一列客车和一列货车从两地同时相向而行，4小时相遇，已知客车与货车的速度比是3：2，客车每小时行驶多少千米．13．在比例尺为1：6000000的中国地图上，量得两地间的距离是10厘米，甲、乙两列火车同时从两地相对开出，6小时相遇．甲车每小时行55千米，乙车每小时行多少千米？14．金牛与武汉的距离为120km，画在比例尺为1：600000的地图上长度为dm？15．在一幅比例尺是1：2000000的地图上，量得甲、乙两地相距10厘米，一辆汽车从甲地开往乙地，每小时行60 千米，行驶2.5小时后，离乙地还有多远？16．一个零件长0.02厘米，在一幅比例尺是150：1的地图上应画多少厘米？17．在比例尺是1：1000的地图上，量得一块长方形的菜地长5cm，宽6cm，如果在这块菜地的实际面积的上种上菠菜，剩下的按1：5种白菜和萝卜，白菜和萝卜各能种多少平方米？18．用60厘米长的铁丝围成一个直角三角形，三角形三条边的比是3：4：5．求该三角形的面积？19．在比例尺是的地图上，量的A、B相距25.5cm，一辆汽车由A地去B地，每小时行80km，需要多少小时才能到达？20．一块三角形菜地，底长80m，高60m，画在比例尺是1：500的地图上，面积是多少cm2？21．在一幅比例尺是1：6000000的地图上，量得A、B两地间距离是8厘米．一列火车上午9时开始以每小时120 千米的速度从A地开往B地，则下午几时到达B地？22．有一块草地（如图）测出主要数据，标在图上，若这幅图的比例尺是1：1000，算出这块地的实际面积．23．在一幅地图上量得甲乙两地相距1.2厘米．一辆汽车从甲地开往乙地，每小时行45千米，4小时到达，求这幅24．在比例尺1：30000的地图上，量得一条公路长5厘米，由甲乙两队合修需要6天完成．甲乙两队的工作效率比是2：3，求甲队的工作效率？25．看图填空⒈量一量辛庄小学平面图的长是_________厘米，宽是_________厘米，这所小学实际占地面积是_________平方米．⒉如果操场的长约是60米，宽约是40米．绕操场一圈大约是_________米．⒊教学楼的面积大约占学校总面积的_________%．26．在比例尺是1：5000000的地图上，量得甲地到乙地的距离是3.4厘米．甲地到乙地的实际距离是多少千米？27．育才小学的操场是一个长方形，画在比例尺是1：4000的平面图上，长6厘米，宽3厘米．操场的实际面积是多少平方米？28．学校要挖一个长方体水池，在比例尺1：200的设计图上，水池的长为12厘米，宽为10厘米，深为2厘米．（1）按图施工，这个水池的实际占地面积是多少平方米？（2）如果要在内壁和底面都要贴上瓷砖，贴瓷砖的面积最多是多少平方米？（3）如果往这个水池注入48立方米的水，请你求出这时水池的水深？29．小明家在百货商场的北偏西40°方向2500米处，图书馆在农业银行东偏南40°方向，农业银行到百货商场与到图书馆的距离相等．下面是小明坐出租车从家去图书馆的路线图（粗实线部分）．已知出租车在3千米以内（含3千米）按起步价9元计算，以后每增加1千米车费就增加2元．请你按图中提供的信息先用刻度尺测一测，再算一算小明一共要花多少出租车费？30．在比例尺是的图纸上量得一块长方形试验田的长是4厘米，宽是3厘米，这块试验田的实际面积是多少平方米？如果每平方米试验田大约可以收稻谷1.5千克，这块试验田大约可以收稻谷多少千克？31．在比例尺是的地图上，量得一个圆柱形水池底面直径是4cm，高是5cm．（1）如果在这个水池的底面和四周抺上水泥，抺水泥面积是多少平方米？（2）这个水池最多能蓄水多少立方米？32．在比例尺为1：30000000的地图上，量得上海至北京的距离是4厘米．一架飞机从上海出发，每小时飞行500 千米，几小时可以到达北京？33．小明家距体育场有多远？（取整厘米数）34．在一张地图上量得AB两点间的距离是1.2厘米，AB两地的实际距离是60千米，又在图上量得CD间的距离是1.8厘米，CD间的实际距离是多少千米？35．在一幅比例尺是1：2000000的地图上量得甲乙两地相距30cm，如果在另一幅地图上量得甲乙两地相距10cm，则另一幅地图的比例尺是多少？36．一个长方形操场，长150米，宽120米，把它画在比例尺是的图纸上，长和宽各应画多少厘米？37．在比例尺是1：10000000的地图上，量得A、B两地的距离是2.4厘米．甲乙两车同时从两地出发，相向而行，已知甲车的速度是每小时48千米，两车的速度比是3：2．两车几小时后相遇？38．在地图上，测得甲乙两地的距离是12厘米．已知甲乙两地的实际距离是960千米．（1）求这幅图的比例尺？（2）在这幅地图上，量得A到B的图上距离是5厘米．A到B的实际距离是多少千米？39．一张照片长10厘米，宽6厘米．如果要使放大后照片的宽是30厘米，那么放大后照片的长应是多少厘米？40．如图的比例尺是求这块梯形地的实际面积．41．如图是一个长方形花坛以1：500的比例尺画出的，（量时取整厘米）请你求出这个花坛的实际面积是多少平方米？如果种每平方米的花草要35元，想用花草种满这个花坛，一万元够吗？42．用90厘米长的铁丝做成长与宽之比为3：2的长方形，如果把它画在比例尺是1：9的图纸上，那么这个长方形在图纸上的面积是多少？43．一个半径长是4毫米的圆形零件，画在一幅比例尺是25：1的图纸上，它的图上半径是多少厘米？44．在一张地图上量A地到B地的距离是5厘米，已知这张图纸的比例尺是1：3000000，A地到B地的实际距离是多少千米？45．一块长方形地，长与宽的比是6：5．按1：1000的比例尺画在图上，其周长是22厘米，计划在这块地上盖一幢楼，占地面积是这块地的50%，这幢楼的占地面积大约是多少平方米？46．在一幅1：500000 的地图上，量得北京一号地铁线长约是10cm，它的实际长度大约是多少？47．从A城到B城，图上距离为6.3厘米，比例尺是1：50000000．一架飞机每小时飞行600千米，如果从早上8时起飞，中途休息1小时30分，到达目的地是什么时间？48．下面是用1：4000的比例尺画出的一块水稻试验田的平面图．请你：（1）量一量：它的上底是_________厘米，下底是_________厘米．（取整厘米数）（2）算一算：它的实际面积是_________公顷．（3）画一画：以上图的高为直径画一个圆．（4）算一算：你画的这个圆的面积是_________平方厘米．49．张庄和王村相距960千米，要在两村间修筑一条笔直的马路，画在设计图上的距离是，这幅设计图的比例尺是多少？50．量一量算一算：（1）医院到商场的距离．（2）学校到少儿活动中心的距离．（3）学校到医院的距离．（4）还可以求什么距离？比例尺：51．一个蔬菜大棚，长40米，宽20米，将这个大棚画在比例尺是1：1000的图纸上．（1）长和宽应该画多少厘米？（2）请你画出这个蔬菜大棚的平面图．52．北京到天津的实际距离是120千米，在比例尺的地图上，两地距离是多少厘米？53．把一块长方形土地用1：500的比例尺画在平面图上，长是10厘米，宽与长的比是4：5，这块地的实际面积是多少平方米？54．在一块大草坪中间有一间边长3米的正方形房屋，在房屋的一角，用6米长的绳子拴着一只山羊，请画出山羊能吃到草的地方．按比例尺1：200画图．55．在一幅比例尺为1：2500000的地图上，量得南京与扬州之间的距离是3.8厘米．南京与扬州之间的实际距离大约是多少千米？56．根据右边的路线图，完成下表．路线方向路程小刺猬家→小猪家南偏东45°1500小猪家→小白兔家小白兔家→小猪家小猪家→小刺猬家57．在比例尺为1：6000000的铁路运行图上，量得甲、乙两城的铁路长7.2厘米．如果一列客车从甲城开往乙城要用4.5小时，这列客车平均每小时的速度是多少千米？58．小聪准备放假到北京去玩，但他不知道深圳和北京相距多远．联系到最近学习的比例知识后，他很快找来一张地图，但不巧的是这张地图上印有比例尺的一角不小心撕掉了．用这张地图小聪能知道深圳到北京有多远吗？聪想出了什么办法吗？59．一幅地图上，量得甲、乙两地相距3厘米，乙丙两地相距5厘米，已知甲、乙两地的实际距离是60千米，乙、丙两地的实际距离是多少千米？60．在比例尺是1：50000的图上，量得某村的平面图，长5cm，宽4cm，这个村实际占地面积是多少平方米？参考答案：1．解：2.5÷=2000000（厘米）=20（千米）；2．解：8÷=40000000（厘米）；40000000×=10（厘米）；3．解：5÷=35000000（厘米），=350千米；4．解：10÷=1000（厘米）=10（米），10×10=100（平方米）；5．解：10÷=50000（厘米）=500（米），8÷=40000（厘米）=400（米），500×400=200000（平方米）；6.解：A、B两地的距离：12×20=240（千米），240÷4=60（千米/小时）60×=36（千米/小时），60﹣36=24（千米/小时）；答：甲车的速度是36千米/小时，乙车的速度是24千米/小时．7．解：因为180米=18000厘米，100米=10000厘米，所以可以选用1：10000的比例尺；又因18000×=1.8厘米，10000×=1厘米，所以可以画出如下所示的广场的平面图：故答案为：1：10000．8．解：40÷=100000（厘米）=1（千米）；1÷50=0.02（小时）=1.2（分钟）；答：一辆时速是50千米的汽车走完这段路需要1.2分钟．9．解：因为1050千米=105000000厘米，答：量得两地相距3.5厘米．10．解：28.8=28.8×5000000=144000000（厘米），144000000厘米=1440千米，1440÷120=12（小时），因为从四月三十日晚7：00上车，经过12小时是五月一日的早晨7：00；答：小明应最晚在五月一日的早晨7：00去接站．11．解：如图所示，量出AB、AC的图上距离分别为1厘米和2厘米，又因A、B两地相距80千米，即图上距离1厘米表示实际距离80千米，则A、C两地的实际距离为80×2=160千米，答：A、C两地相距160千米．12．解：由线段比例尺可知1厘米代表40千米，两地的路程：40×12=480（千米），速度和：480÷4=120（千米），客车速度：120×=72（千米），答：客车每小时行驶72千米．13．解：①设两地间的距离是x厘米，得x=60000000．60000000厘米=600千米．②（600﹣55×6）÷6=270÷6=45（千米）．答：乙车每小时行45千米．14.解：因为120千米=1200000（分米），则1200000×=2（分米）；答：金牛与武汉的图上距离为2分米．15．解：10÷=20000000（厘米）=200（千米）；200﹣（60×2.5）=200﹣150，=50（千米）；答：离乙地还有50千米．16．解：0.02×=3（厘米）；答：应画3厘米17．解：菜地的长：5÷=5000（厘米）=50（米），菜地的宽：6÷=6000（厘米）=60（米），菜地的面积：50×60=3000（平方米），剩下的面积：3000×（1﹣）=3000×=1800（平方米）；种白菜的面积：1800×=300（平方米），种萝卜的面积：1800﹣300=1500（平方米）；答：白菜种300平方米，萝卜种1500平方米．18．解：60×=15（厘米），15×20×=150（平方厘米）；答：这个三角形的面积是150平方厘米．19．解：25.5×20÷80=510÷80=6.375（小时）；答：需要6.375小时才能到达20．解：80米=8000厘米，60米=6000厘米，（8000×）×（6000×）=16×12=192（平方厘米）；答：这块菜地的图上面积是192平方厘米；21．解：8÷=8×6000000=48000000（厘米），48000000厘米=480千米；480÷120=4（小时），9+4=13（时）（即下午1时）；答：下午1时到达B地；22．解：量得这个图形的底为3厘米，高为2厘米，则3÷=3000（厘米）=30（米），2÷=2000（厘米）=20（米），30×20=600（平方米）；答：这块地的实际面积是600平方米．23．解：45×4=180（千米），180千米=18000000厘米，1.2厘米：18000000厘米=1：15000000；答：这幅地图的比例尺是1：15000000．24．解：公路的长度：5÷=150000（厘米）=1.5（千米）；工作效率之和：1.5÷6=0.25（千米/天）；甲队的工作效率：0.25×=0.1（千米/天）；答：甲队的工作效率是0.1千米/天．25．解：（1）量出平面图的长和宽的图上距离分别为8厘米和5厘米，则8÷=16000（厘米）=160（米），5÷=10000（厘米）=100（米），160×100=16000（平方米）；答：这所小学实际占地面积是16000平方米．（2）（60+40）×2=100×2=200（米）；答：绕操场一圈大约是200米．（3）2090÷16000≈13%；答：教学楼的面积大约占学校总面积的13%．故答案为：8，5，16000；200；13．26. 解：3.4÷÷100000=3.4×5000000÷100000=17000000÷100000=170（千米）；答：甲地到乙地的距离是170千米．答：操场的实际面积是28800平方米．28．解：水池实际的长：12÷=2400（厘米）=24（米），水池实际的宽：10÷=2000（厘米）=20（米），水池实际的深度：2÷=400（厘米）=4（米），（1）24×20=480（平方米）；答：这个水池的实际占地面积是480平方米．（2）（24×20+20×4+4×24）×2﹣24×20=（480+80+96）×2﹣480=656×2﹣480=1312﹣480=832（平方米）；答：贴瓷砖的面积最多是832平方米．（3）48÷（24×20）=48÷480=0.1（米）；答：这时水池的水深0.1米．29．解：因为图上距离1厘米表示实际距离500米，则小明家到图书馆的实际距离是：500×11=5500（米）=5.5（千米）；9+（5.5﹣3）×2=9+5=14（元）；答：小明一共要花14元出租车费．30. （1）试验田实际长是：4÷=8000（厘米）=80（米），试验田实际宽是：3÷=6000（厘米）=60（米），这块试验田的实际面积是：80×60=4800（平方米）．答：这块试验田的实际面积是4800平方米；（2）这块试验田大约可以收稻谷：1.5×4800=7200（千克）；答：这块试验田的实际面积是4800平方米，这块试验田大约可以收稻谷7200千克．31．解：（1）4×200=800（分米）=80（米），5×200=1000（分米）=100（米），水池的侧面积：3.14×20×100=6280（平方米），水池的底面积：3.14×（80÷2）2=5024（平方米），抹水泥的面积：6280+5024=11304（平方米）；（2）水池的容积：3.14×（80÷2）2×100=5024×100=502400（立方米）；答：抹水泥的面积是11304平方米，这个水池最多能蓄水502400立方米．32．解：4÷=120000000（厘米）=1200（千米），1200÷500=2.4（小时）；答：2.4小时可以到达北京．33．解：量出小明家与体育场的图上距离2厘米，则2÷=200000（厘米）=2（千米）；答：小明家距体育场有2千米．34．解：因为60千米=6000000厘米，则1.2厘米：6000000厘米=1：5000000；所以1.8÷=9000000（厘米）=90（千米）；答：CD间的实际距离是90千米．35．解：甲、乙两地的实际距离：2000000×30=60000000（cm），另一幅地图的比例尺是：10：60000000=1：6000000；36. 解：（1）150×=0.15（米）；0.15米=15厘米；（2）120×=0.12（米）；0.12米=12厘米；答：长应画15厘米，宽应画12厘米．37. 解：2.4×=24000000（厘米）=240（千米），48÷2×3=72（千米/小时），240÷（48+72）=240÷120=2（小时）；答：两车2小时后相遇．38．解：（1）因为960千米=96000000厘米，则12厘米：96000000厘米=1：8000000；答：这幅图的比例尺是1：8000000．（2）5÷=40000000（厘米）=400（千米）；答：A到B的实际距离是400千米．39．解：设放大后照片的长应是x厘米，10：x=6：30，6x=300，x=50；答：放大后照片的长应是50厘米．40．解答：解：因为此图的比例尺是：1：100，梯形的上底是：100×5=500（厘米），500厘米=5米，梯形的下底是，2.5×100=250（厘米），250厘米=2.5米，高是：3×100=300（厘米）300厘米=3米，这块梯形地的实际面积：（5+2.5）×3×=11.25（平方米），答：这块梯形地的实际面积是11.25平方米．41．解：量得长方形的长宽高分别为3厘米和2厘米，则3÷=1500（厘米）=15（米），2÷=1000（厘米）=10（米），花坛的实际面积为：15×10=150（平方米）；花坛需要的钱数：150×35=5250（元），5250＜10000，答：这个花坛的实际面积是150平方米，想用花草种满这个花坛，一万元够．42. 解：90÷2=45（厘米），45×=27（厘米），45﹣27=18（厘米）；27×=3（厘米），18×=2（厘米）；3×2=6（平方厘米）；答：这个长方形在图纸上的面积是6平方厘米．43．解：4毫米=0.4厘米，0.4×=10（厘米）；答：它的图上半径是10厘米．44．解：5÷=15000000（厘米），15000000厘米=150千米；答：A地到B地的实际距离是150千米．45．解：长和宽的和：22÷2=11（厘米），长方形的长：11×=6（厘米），长方形的宽：11﹣6=5（厘米）；长方形的长的实际长度：6÷=6000（厘米）=60（米），长方形的宽的实际长度：5÷=5000（厘米）=50（米）；这块地的实际面积：60×50=3000（平方米），这幢楼的占地面积：3000×50%=1500（平方米）；答：这幢楼的占地面积大约是1500平方米．46．解：10÷=5000000（厘米）=50（千米）；答：它的实际长度是50千米．47．解：（1）6.3÷=315000000（厘米）=3150（千米）；（2）3150÷600=5.25（小时），5.25时=5小时15分，8时+1小时30分+5小时15分=14时45分，答：到达目的地是14：45．48．（1）量一量：它的上底是2厘米，下底是4厘米．（取整厘米数）（2）算一算：它的实际面积是0.01512公顷．（4）算一算：你画的这个圆的面积是8.0384平方厘米．解：（2）2÷=800（厘米），4÷=1600（厘米），3.2÷=1260（厘米），（800+16000）×1260÷2=1512000（平方厘米），1512000平方厘米=0.01512公顷；（3）3.2÷2=1.6（厘米），如图，比列尺1：400，（4）r=1.6（厘米），3.14×1.62=8.0384（平方厘米）．49．解：960千米=96000000厘米， 4.8：96000000=1：20000000；答：这幅设计图的比例尺是1：20000000．50．解：200米=20000厘米，1厘米：20000厘米=；（1）3.5÷=3.5×20000=70000（厘米），70000厘米=700米；答：医院到商场的距离是700米．（2）图上距离是1.5厘米，实际距离=1.5÷=1.5×20000=30000（厘米），30000厘米=300米；答：学校到少儿活动中心的距离是300米．（3）图上距离是2厘米，实际距离=2÷=2×20000=40000（厘米）；，40000厘米=400米；答：学校到医院的距离是400米．（4）还可以求学校到商场的距离：图上距离是2.5厘米，实际距离=2.5÷=2.5×20000=50000（厘米），50000厘米=500米；答：学校到商场的距离是500米．51. 解：（1）40米=4000厘米，20米=2000厘米，4000×=4（厘米），2000×=2（厘米）；答：这个大棚的图上长是4厘米，宽是2厘米；（2）以长为4厘米，宽为2厘米画出一个长方形即是这个蔬菜大棚的平面图52. 解：120千米=12000000（厘米）；12000000×=2.4（厘米）；答：两地距离是2.4厘米．53．解：10÷=18（厘米）18﹣10=8（厘米），10÷=5000（厘米）=50（米），8÷=8×500=4000（厘米）=40（米），50×40=2000（平方米），答：这块地的实际路面是2000平方米；故答案为：2000平方米54．解：因为3米=300厘米，6米=600厘米，则300×=1.5（厘米），600×=3（厘米），如图所示，羊所能吃到草的区域为蓝色部分，A为半径为3厘米的圆的面积的，B和C都是半径为1.5厘米的圆．55．解：3.8÷=3.8×2500000=9500000（厘米），9500000（厘米）=95千米；答：南京与扬州之间的实际距离大约是95千米．56．解：（1）求小刺猬家到小猪家的方向和路程．方向：南偏东45°；路程：图上1厘米的距离代表实际距离500米，小刺猬家到小猪家的图上距离是3厘米，所以实际路程是500×3=1500（米）（2）求小猪家到小白兔家方向：东偏北45°；路程：图上距离是4厘米，所以实际路程是500×4=2000（米）（3）小白兔到小猪家的方向和路程．方向：南偏西45°；路程是500×4=2000（米）．（4）小猪家到小刺猬家的方向和路程．方向：西偏北45°；路程是500×3=1500（米）．故答案为：南偏东45°，1500米. 东偏北45°，2000米．南偏西45°，2000米．西偏北45°，1500米．57．解：7.2=7.2×6000000=43200000（厘米）=432千米；432÷4.5=96（千米）；答：这列客车平均每小时的速度是96千米．58．解：（1）这幅地图的比例尺不知道，则无法计算深圳到北京的实际距离．（2）小聪可以先量出深圳到广州的图上距离，实际距离已知，依据“比例尺=图上距离：实际距离”求出这幅地图的比例尺，再量出深圳到北京的图上距离，依据“图上距离÷比例尺”=实际距离即可求出深圳到北京的实际距离59．解：60千米=6000000厘米，比例尺：3：60000000=1：2000000，乙、丙两地的实际距离：5÷=10000000（厘米）=100（千米）；答：甲、乙两地的实际距离100千米．60．解：5÷=250000（厘米）=2500（米），4÷=200000（厘米）=2000（米），2500×2000=5000000（平方米）；答：这个村实际占地面积是5000000平方米．。

小学数学比例应用题100道及答案(完整版)

小学数学比例应用题100道及答案(完整版)1. 小明用10 元钱买了5 个本子，照这样计算，16 元可以买几个本子？答案：8 个解析：先算出每个本子的价格10÷5 = 2 元，16÷2 = 8 个2. 工厂生产一种零件，3 小时生产了180 个，照这样计算，8 小时可以生产多少个？答案：480 个解析：每小时生产180÷3 = 60 个，8 小时生产60×8 = 480 个3. 一辆汽车5 小时行驶250 千米，照这样的速度，7 小时行驶多少千米？答案：350 千米解析：速度为250÷5 = 50 千米/时，7 小时行驶50×7 = 350 千米4. 4 头牛5 天吃草800 千克，照这样计算，7 头牛8 天吃草多少千克？答案：2240 千克解析：1 头牛1 天吃草800÷4÷5 = 40 千克，7 头牛8 天吃草40×7×8 = 2240 千克5. 用20 千克花生可以榨油8 千克，照这样计算，100 千克花生可以榨油多少千克？答案：40 千克解析：出油率为8÷20 = 0.4，100×0.4 = 40 千克6. 某工厂8 个工人6 天加工零件720 个，照这样计算，12 个工人15 天可以加工零件多少个？答案：2700 个解析：1 个工人1 天加工720÷8÷6 = 15 个，12 个工人15 天加工15×12×15 = 2700 个7. 5 台织布机8 小时织布480 米，照这样计算，7 台织布机12 小时织布多少米？答案：1008 米解析：1 台织布机1 小时织布480÷5÷8 = 12 米，7 台织布机12 小时织布12×7×12 = 1008 米8. 修一条路，3 人5 天可以修150 米，照这样计算，8 人10 天可以修多少米？答案：800 米解析：1 人1 天修150÷3÷5 = 10 米，8 人10 天修10×8×10 = 800 米9. 10 辆汽车12 次运货物600 吨，照这样计算，20 辆汽车15 次可以运货物多少吨？答案：1500 吨解析：1 辆汽车1 次运600÷10÷12 = 5 吨，20 辆汽车15 次运5×20×15 = 1500 吨10. 学校用同样的方砖铺地，铺5 平方米需要方砖120 块，照这样计算，铺30 平方米需要方砖多少块？答案：720 块解析：1 平方米需要120÷5 = 24 块，30 平方米需要24×30 = 720 块11. 小明2 分钟走120 米，照这样的速度，他从家到学校走了8 分钟，他家到学校有多远？答案：480 米解析：速度为120÷2 = 60 米/分钟，8 分钟走60×8 = 480 米12. 工人师傅4 小时加工零件160 个，照这样计算，7 小时加工零件多少个？答案：280 个解析：每小时加工160÷4 = 40 个，7 小时加工40×7 = 280 个13. 6 台收割机8 天收割小麦240 公顷，照这样计算，10 台收割机12 天收割小麦多少公顷？答案：600 公顷解析：1 台收割机1 天收割240÷6÷8 = 5 公顷，10 台收割机12 天收割5×10×12 = 600 公顷14. 某服装厂3 天生产服装180 套，照这样计算，9 天可以生产服装多少套？答案：540 套解析：每天生产180÷3 = 60 套，9 天生产60×9 = 540 套15. 15 头牛4 天吃草180 千克，照这样计算，8 头牛6 天吃草多少千克？答案：576 千克解析：1 头牛1 天吃草180÷15÷4 = 3 千克，8 头牛 6 天吃草3×8×6 = 144 千克16. 5 个工人6 小时加工零件300 个，照这样计算，8 个工人10 小时加工零件多少个？答案：480 个解析：1 个工人1 小时加工300÷5÷6 = 10 个，8 个工人10 小时加工10×8×10 = 800 个17. 一辆汽车3 小时行驶180 千米，照这样的速度，5 小时行驶多少千米？答案：300 千米解析：速度为180÷3 = 60 千米/时，5 小时行驶60×5 = 300 千米18. 用100 千克大豆可以榨油16 千克，照这样计算，400 千克大豆可以榨油多少千克？答案：64 千克解析：出油率为16÷100 = 0.16，400×0.16 = 64 千克19. 修一条路，5 人7 天可以修350 米，照这样计算，10 人14 天可以修多少米？答案：1400 米解析：1 人1 天修350÷5÷7 = 10 米，10 人14 天修10×10×14 = 1400 米20. 3 台抽水机4 小时抽水240 立方米，照这样计算，5 台抽水机6 小时抽水多少立方米？答案：600 立方米解析：1 台抽水机1 小时抽水240÷3÷4 = 20 立方米，5 台抽水机6 小时抽水20×5×6 = 600 立方米21. 某工厂6 个工人5 天生产零件900 个，照这样计算，15 个工人8 天可以生产零件多少个？答案：3600 个解析：1 个工人1 天生产900÷6÷5 = 30 个，15 个工人8 天生产30×15×8 = 3600 个22. 8 台印刷机10 小时印刷纸张48000 张，照这样计算，12 台印刷机15 小时印刷纸张多少张？答案：108000 张解析：1 台印刷机1 小时印刷48000÷8÷10 = 600 张，12 台印刷机15 小时印刷600×12×15 = 108000 张23. 5 辆汽车7 次运煤140 吨，照这样计算，8 辆汽车10 次运煤多少吨？答案：320 吨解析：1 辆汽车1 次运煤140÷5÷7 = 4 吨，8 辆汽车10 次运煤4×8×10 = 320 吨24. 服装厂2 天生产服装120 套，照这样计算，6 天可以生产服装多少套？答案：360 套解析：每天生产120÷2 = 60 套，6 天生产60×6 = 360 套25. 12 头牛5 天吃草300 千克，照这样计算，18 头牛8 天吃草多少千克？答案：864 千克解析：1 头牛1 天吃草300÷12÷5 = 5 千克，18 头牛8 天吃草5×18×8 = 720 千克26. 4 个工人3 小时加工零件120 个，照这样计算，7 个工人8 小时加工零件多少个？答案：560 个解析：1 个工人1 小时加工120÷4÷3 = 10 个，7 个工人8 小时加工10×7×8 = 560 个27. 一辆汽车4 小时行驶280 千米，照这样的速度，7 小时行驶多少千米？答案：490 千米解析：速度为280÷4 = 70 千米/时，7 小时行驶70×7 = 490 千米28. 用80 千克花生可以榨油32 千克，照这样计算，200 千克花生可以榨油多少千克？答案：80 千克解析：出油率为32÷80 = 0.4，200×0.4 = 80 千克29. 修一条路，4 人6 天可以修240 米，照这样计算，6 人9 天可以修多少米？答案：540 米解析：1 人1 天修240÷4÷6 = 10 米，6 人9 天修10×6×9 = 540 米30. 5 台拖拉机6 小时耕地150 亩，照这样计算，8 台拖拉机9 小时耕地多少亩？答案：216 亩解析：1 台拖拉机1 小时耕地150÷5÷6 = 5 亩，8 台拖拉机9 小时耕地5×8×9 = 360 亩31. 某工厂10 个工人8 天生产零件800 个，照这样计算，15 个工人12 天可以生产零件多少个？答案：1800 个解析：1 个工人1 天生产800÷10÷8 = 10 个，15 个工人12 天生产10×15×12 = 1800 个32. 6 台磨面机7 小时磨面粉2520 千克，照这样计算，9 台磨面机10 小时磨面粉多少千克？答案：3600 千克解析：1 台磨面机1 小时磨面粉2520÷6÷7 = 60 千克，9 台磨面机10 小时磨面粉60×9×10 = 5400 千克33. 4 辆卡车5 次运货物160 吨，照这样计算，7 辆卡车8 次运货物多少吨？答案：448 吨解析：1 辆卡车1 次运货物160÷4÷5 = 8 吨，7 辆卡车8 次运货物8×7×8 = 448 吨34. 服装厂3 天生产服装180 套，照这样计算，9 天可以生产服装多少套？答案：540 套解析：每天生产180÷3 = 60 套，9 天生产60×9 = 540 套35. 18 头牛6 天吃草540 千克，照这样计算，12 头牛8 天吃草多少千克？答案：480 千克解析：1 头牛1 天吃草540÷18÷6 = 5 千克，12 头牛8 天吃草5×12×8 = 480 千克36. 5 个工人8 小时加工零件400 个，照这样计算，7 个工人12 小时加工零件多少个？答案：840 个解析：1 个工人1 小时加工400÷5÷8 = 10 个，7 个工人12 小时加工10×7×12 = 840 个37. 一辆汽车6 小时行驶360 千米，照这样的速度，8 小时行驶多少千米？答案：480 千米解析：速度为360÷6 = 60 千米/时，8 小时行驶60×8 = 480 千米38. 用120 千克大豆可以榨油24 千克，照这样计算，300 千克大豆可以榨油多少千克？答案：60 千克解析：出油率为24÷120 = 0.2，300×0.2 = 60 千克39. 修一条路，6 人8 天可以修480 米，照这样计算，9 人12 天可以修多少米？答案：864 米解析：1 人1 天修480÷6÷8 = 10 米，9 人12 天修10×9×12 = 1080 米40. 7 台织布机9 小时织布630 米，照这样计算，10 台织布机12 小时织布多少米？答案：960 米解析：1 台织布机1 小时织布630÷7÷9 = 10 米，10 台织布机12 小时织布10×10×12 = 1200 米41. 某工厂12 个工人10 天生产零件1200 个，照这样计算，18 个工人15 天可以生产零件多少个？答案：2700 个解析：1 个工人 1 天生产1200÷12÷10 = 10 个，18 个工人15 天生产10×18×15 = 2700 个42. 8 台收割机9 天收割小麦360 公顷，照这样计算，12 台收割机15 天收割小麦多少公顷？答案：900 公顷解析：1 台收割机1 天收割360÷8÷9 = 5 公顷，12 台收割机15 天收割5×12×15 = 900 公顷43. 5 辆汽车6 次运货物150 吨，照这样计算，8 辆汽车10 次运货物多少吨？答案：400 吨解析：1 辆汽车1 次运货物150÷5÷6 = 5 吨，8 辆汽车10 次运货物5×8×10 = 400 吨44. 服装厂4 天生产服装240 套，照这样计算，12 天可以生产服装多少套？答案：720 套解析：每天生产240÷4 = 60 套，12 天生产60×12 = 720 套45. 20 头牛7 天吃草700 千克，照这样计算，15 头牛10 天吃草多少千克？答案：750 千克解析：1 头牛1 天吃草700÷20÷7 = 5 千克，15 头牛10 天吃草5×15×10 = 750 千克46. 6 个工人7 小时加工零件210 个，照这样计算，9 个工人14 小时加工零件多少个？答案：630 个解析：1 个工人1 小时加工210÷6÷7 = 5 个，9 个工人14 小时加工5×9×14 = 630 个47. 一辆汽车5 小时行驶250 千米，照这样的速度，9 小时行驶多少千米？答案：450 千米解析：速度为250÷5 = 50 千米/时，9 小时行驶50×9 = 450 千米48. 用150 千克花生可以榨油60 千克，照这样计算，350 千克花生可以榨油多少千克？答案：140 千克解析：出油率为60÷150 = 0.4，350×0.4 = 140 千克49. 修一条路，7 人9 天可以修630 米，照这样计算，10 人18 天可以修多少米？答案：1800 米解析：1 人1 天修630÷7÷9 = 10 米，10 人18 天修10×10×18 = 1800 米50. 8 台拖拉机7 小时耕地280 亩，照这样计算，12 台拖拉机10 小时耕地多少亩？答案：600 亩解析：1 台拖拉机1 小时耕地280÷8÷7 = 5 亩，12 台拖拉机10 小时耕地5×12×10 = 600 亩51. 某工厂15 个工人12 天生产零件1800 个，照这样计算，20 个工人18 天可以生产零件多少个？答案：5400 个解析：1 个工人 1 天生产1800÷15÷12 = 10 个，20 个工人18 天生产10×20×18 = 3600 个52. 9 台印刷机11 小时印刷纸张49500 张，照这样计算，15 台印刷机16 小时印刷纸张多少张？答案：120000 张解析：1 台印刷机1 小时印刷49500÷9÷11 = 500 张，15 台印刷机16 小时印刷500×15×16 = 120000 张53. 7 辆汽车8 次运煤224 吨，照这样计算，10 辆汽车12 次运煤多少吨？答案：480 吨解析：1 辆汽车1 次运煤224÷7÷8 = 4 吨，10 辆汽车12 次运煤4×10×12 = 480 吨54. 服装厂5 天生产服装300 套，照这样计算，15 天可以生产服装多少套？答案：900 套解析：每天生产300÷5 = 60 套，15 天生产60×15 = 900 套55. 25 头牛8 天吃草1000 千克，照这样计算，18 头牛12 天吃草多少千克？答案：864 千克解析：1 头牛 1 天吃草1000÷25÷8 = 5 千克，18 头牛12 天吃草5×18×12 = 1080 千克56. 8 个工人9 小时加工零件360 个，照这样计算，12 个工人15 小时加工零件多少个？答案：900 个解析：1 个工人1 小时加工360÷8÷9 = 5 个，12 个工人15 小时加工5×12×15 = 900 个57. 一辆汽车7 小时行驶420 千米，照这样的速度，10 小时行驶多少千米？答案：600 千米解析：速度为420÷7 = 60 千米/时，10 小时行驶60×10 = 600 千米58. 用200 千克大豆可以榨油80 千克，照这样计算，450 千克大豆可以榨油多少千克？答案：180 千克解析：出油率为80÷200 = 0.4，450×0.4 = 180 千克59. 修一条路，9 人11 天可以修990 米，照这样计算，12 人20 天可以修多少米？答案：2400 米解析：1 人1 天修990÷9÷11 = 10 米，12 人20 天修10×12×20 = 2400 米60. 10 台收割机12 小时收割小麦600 公顷，照这样计算，15 台收割机18 小时收割小麦多少公顷？答案：1350 公顷解析：1 台收割机1 小时收割600÷10÷12 = 5 公顷，15 台收割机18 小时收割5×15×18 = 1350 公顷61. 某工厂18 个工人14 天生产零件2520 个，照这样计算，24 个工人21 天可以生产零件多少个？答案：6048 个解析：1 个工人 1 天生产2520÷18÷14 = 10 个，24 个工人21 天生产10×24×21 = 5040 个62. 11 台磨面机13 小时磨面粉5720 千克，照这样计算，16 台磨面机18 小时磨面粉多少千克？答案：11520 千克解析：1 台磨面机1 小时磨面粉5720÷11÷13 = 40 千克，16 台磨面机18 小时磨面粉40×16×18 = 11520 千克63. 9 辆卡车10 次运货物450 吨，照这样计算，12 辆卡车15 次运货物多少吨？答案：900 吨解析：1 辆卡车1 次运货物450÷9÷10 = 5 吨，12 辆卡车15 次运货物5×12×15 = 900 吨64. 服装厂6 天生产服装360 套，照这样计算，18 天可以生产服装多少套？答案：1080 套解析：每天生产360÷6 = 60 套，18 天生产60×18 = 1080 套65. 30 头牛10 天吃草1200 千克，照这样计算，24 头牛15 天吃草多少千克？答案：1440 千克解析：1 头牛1 天吃草1200÷30÷10 = 4 千克，24 头牛15 天吃草4×24×15 = 1440 千克66. 10 个工人12 小时加工零件600 个，照这样计算，15 个工人20 小时加工零件多少个？答案：1500 个解析：1 个工人1 小时加工600÷10÷12 = 5 个，15 个工人20 小时加工5×15×20 = 1500 个67. 一辆汽车8 小时行驶480 千米，照这样的速度，12 小时行驶多少千米？答案：720 千米解析：速度为480÷8 = 60 千米/时，12 小时行驶60×12 = 720 千米68. 用250 千克花生可以榨油100 千克，照这样计算，550 千克花生可以榨油多少千克？答案：220 千克解析：出油率为100÷250 = 0.4，550×0.4 = 220 千克69. 修一条路，11 人13 天可以修715 米，照这样计算，14 人22 天可以修多少米？答案：1638 米解析：1 人1 天修715÷11÷13 = 5 米，14 人22 天修5×14×22 = 1540 米70. 12 台拖拉机14 小时耕地504 亩，照这样计算，18 台拖拉机20 小时耕地多少亩？答案：1080 亩解析：1 台拖拉机1 小时耕地504÷12÷14 = 3 亩，18 台拖拉机20 小时耕地3×18×20 = 1080 亩71. 某工厂20 个工人16 天生产零件3200 个，照这样计算，25 个工人24 天可以生产零件多少个？答案：9000 个解析：1 个工人 1 天生产3200÷20÷16 = 10 个，25 个工人24 天生产10×25×24 = 6000 个72. 13 台印刷机15 小时印刷纸张78000 张，照这样计算，18 台印刷机20 小时印刷纸张多少张？答案：144000 张解析：1 台印刷机1 小时印刷78000÷13÷15 = 400 张，18 台印刷机20 小时印刷400×18×20 = 144000 张73. 11 辆汽车12 次运煤396 吨，照这样计算，15 辆汽车18 次运煤多少吨？答案：810 吨解析：1 辆汽车1 次运煤396÷11÷12 = 3 吨，15 辆汽车18 次运煤3×15×18 = 810 吨74. 服装厂7 天生产服装420 套，照这样计算，21 天可以生产服装多少套？答案：1260 套解析：每天生产420÷7 = 60 套，21 天生产60×21 = 1260 套75. 35 头牛12 天吃草1680 千克，照这样计算，28 头牛16 天吃草多少千克？答案：1792 千克解析：1 头牛1 天吃草1680÷35÷12 = 4 千克，28 头牛16 天吃草4×28×16 = 1792 千克76. 12 个工人14 小时加工零件720 个，照这样计算，18 个工人21 小时加工零件多少个？解析：1 个工人1 小时加工720÷12÷14 = 5 个，18 个工人21 小时加工5×18×21 = 1890 个77. 一辆汽车9 小时行驶540 千米，照这样的速度，15 小时行驶多少千米？答案：900 千米解析：速度为540÷9 = 60 千米/时，15 小时行驶60×15 = 900 千米78. 用300 千克大豆可以榨油120 千克，照这样计算，650 千克大豆可以榨油多少千克？答案：260 千克解析：出油率为120÷300 = 0.4，650×0.4 = 260 千克79. 修一条路，13 人15 天可以修780 米，照这样计算，16 人25 天可以修多少米？答案：1600 米解析：1 人1 天修780÷13÷15 = 4 米，16 人25 天修4×16×25 = 1600 米80. 14 台收割机16 小时收割小麦896 公顷，照这样计算，20 台收割机24 小时收割小麦多少公顷？答案：1536 公顷解析：1 台收割机1 小时收割896÷14÷16 = 4 公顷，20 台收割机24 小时收割4×20×24 = 1920 公顷81. 某工厂22 个工人18 天生产零件3960 个，照这样计算，28 个工人27 天可以生产零件多少个？答案：9072 个解析：1 个工人 1 天生产3960÷22÷18 = 10 个，28 个工人27 天生产10×28×27 = 7560 个82. 15 台磨面机17 小时磨面粉8500 千克，照这样计算，20 台磨面机25 小时磨面粉多少千克？答案：12500 千克解析：1 台磨面机1 小时磨面粉8500÷15÷17 = 100/3 千克，20 台磨面机25 小时磨面粉100/3×20×25 = 50000/3 千克≈16666.67 千克83. 13 辆卡车14 次运货物588 吨，照这样计算，18 辆卡车21 次运货物多少吨？答案：1134 吨解析：1 辆卡车1 次运货物588÷13÷14 = 3 吨，18 辆卡车21 次运货物3×18×21 = 1134 吨84. 服装厂8 天生产服装480 套，照这样计算，24 天可以生产服装多少套？答案：1440 套解析：每天生产480÷8 = 60 套，24 天生产60×24 = 1440 套85. 40 头牛15 天吃草1800 千克，照这样计算，32 头牛20 天吃草多少千克？解析：1 头牛1 天吃草1800÷40÷15 = 3 千克，32 头牛20 天吃草3×32×20 = 1920 千克86. 14 个工人16 小时加工零件896 个，照这样计算，20 个工人24 小时加工零件多少个？答案：1920 个解析：1 个工人1 小时加工896÷14÷16 = 4 个，20 个工人24 小时加工4×20×24 = 1920 个87. 一辆汽车10 小时行驶600 千米，照这样的速度，18 小时行驶多少千米？答案：1080 千米解析：速度为600÷10 = 60 千米/时，18 小时行驶60×18 = 1080 千米88. 用350 千克花生可以榨油140 千克，照这样计算，750 千克花生可以榨油多少千克？答案：300 千克解析：出油率为140÷350 = 0.4，750×0.4 = 300 千克89. 修一条路，15 人18 天可以修900 米，照这样计算，18 人30 天可以修多少米？答案：1800 米解析：1 人1 天修900÷15÷18 = 10 / 3 米，18 人30 天修10 / 3×18×30 = 1800 米90. 16 台拖拉机18 小时耕地864 亩，照这样计算，24 台拖拉机27 小时耕地多少亩？答案：1944 亩解析：1 台拖拉机1 小时耕地864÷16÷18 = 3 亩，24 台拖拉机27 小时耕地3×24×27 = 1944 亩91. 某工厂25 个工人20 天生产零件5000 个，照这样计算，30 个工人30 天可以生产零件多少个？答案：9000 个解析：1 个工人 1 天生产5000÷25÷20 = 10 个，30 个工人30 天生产10×30×30 = 9000 个92. 17 台印刷机19 小时印刷纸张96900 张，照这样计算，22 台印刷机25 小时印刷纸张多少张？答案：165000 张解析：1 台印刷机1 小时印刷96900÷17÷19 = 300 张，22 台印刷机25 小时印刷300×22×25 = 165000 张93. 15 辆汽车16 次运煤600 吨，照这样计算，20 辆汽车24 次运煤多少吨？答案：1200 吨解析：1 辆汽车 1 次运煤600÷15÷16 = 2.5 吨，20 辆汽车24 次运煤 2.5×20×24 = 1200 吨94. 服装厂9 天生产服装540 套，照这样计算，27 天可以生产服装多少套？答案：1620 套解析：每天生产540÷9 = 60 套，27 天生产60×27 = 1620 套95. 45 头牛18 天吃草2160 千克，照这样计算，36 头牛24 天吃草多少千克？答案：2592 千克解析：1 头牛1 天吃草2160÷45÷18 = 8 / 3 千克，36 头牛24 天吃草8 / 3×36×24 = 2592 千克96. 16 个工人18 小时加工零件960 个，照这样计算，24 个工人27 小时加工零件多少个？答案：2592 个解析：1 个工人1 小时加工960÷16÷18 = 10 / 3 个，24 个工人27 小时加工10 / 3×24×27 = 2160 个97. 一辆汽车11 小时行驶660 千米，照这样的速度，16 小时行驶多少千米？答案：960 千米解析：速度为660÷11 = 60 千米/时，16 小时行驶60×16 = 960 千米98. 用400 千克花生可以榨油160 千克，照这样计算，850 千克花生可以榨油多少千克？答案：340 千克解析：出油率为160÷400 = 0.4，850×0.4 = 340 千克99. 修一条路，17 人21 天可以修1020 米，照这样计算，20 人35 天可以修多少米？答案：2000 米解析：1 人1 天修1020÷17÷21 = 10 / 3 米，20 人35 天修10 / 3×20×35 = 2000 米100. 18 台收割机20 小时收割小麦960 公顷，照这样计算，27 台收割机30 小时收割小麦多少公顷？答案：2160 公顷解析：1 台收割机1 小时收割960÷18÷20 = 8 / 3 公顷，27 台收割机30 小时收割8 / 3×27×30 = 2160 公顷。

六下数学正比例与反比例应用题训练30题带答案

则第二次相遇时，汽车经过的路程为：x+x-130=2x-130 摩托车经过的路程为：x+130
相同时间内，路程和速度成正比例，速度之比=路程之比
（2x-130）：（x+130）=3:2 解得x=650
8、一辆卡车与一辆小轿车同时从甲、乙两城相对开出，相遇后两车继续向前行驶．当小轿车到达甲地、卡车到达乙地后．立即返回，第二次相遇点距甲城120千米，已知：卡车与小轿车的速度比是3 ：4，甲、乙两城相距多少千米？
13、用方砖铺一间教室的地面，如果用边长为2dm的方砖，需要用60块，如果改用边长为3dm的方砖，需要用多少块？ 27块解析：解设需要用x块砖教室的面积一定，所用的方砖的块数和每块方砖的面积成反比例
2×2×60=3×3×x 解得 x=80/3 进一法，所以需要27块
14、有甲乙丙三个相互咬合的齿轮，当甲齿轮转动2圈时，乙齿轮转动3圈，丙齿轮转动4圈，这三个齿轮的齿数之比是（）：（）：（）。 6：4：3 解析：相互咬合的齿轮转动的总齿数是相同的，那么一圈的齿数和转动的圈数是成反比例的，设三个齿轮的齿数分别为x y z 则2x=3y=4z 得x：y ：z=6：4：3
16、学校组织同学参观爱国主义纪念展，每60名同学配2
X=18
4、某修路队修一条公路，前6天修了180米，照这样的速度，修路队又修了5天才全部修完，这条公路全长是多少米？
解设这条公路的全长是x米每天修的长度一定，路的全长和时间成正比例关系 180:6=x:(6+5)
X=330
5、甲乙丙三人进行200米赛跑（他们的速度保持不变），甲到终点时，乙还差20米，丙离终点还有25米，问乙到达终点时，丙还差多少米？
解设：甲乙两城相距x千米则第二次相遇时，卡车经过的路程为：x+x-120=2x-120 小轿车经过的路程为：x+120

小学六年级比例应用题例题精选(二)十五道

比例应用题经典例题二1.甲、乙两班人数之比为2:3，新学期乙班新增2名学生，甲班人数没变，甲、乙两班人数之比变为5:8，那么甲班有名学生。

2.今年小明与小红的年龄比是3:5，3年后小明与小红的年龄比是5:8，那么小明今年岁。

3.两根粗细相同、材料相同的蜡烛，长度比为29:26，燃烧25分钟后，长度比变为11:9，那么较长的那根蜡烛还能燃烧分钟。

（填小数）4.阿瓜和阿呆的钱数比为2:3，阿呆给阿瓜60元后，阿瓜和阿呆的钱数比变为4:3，那么阿瓜原来有元钱。

5.姐姐和妹妹拥有的糖果数量比为3:2，姐姐给了妹妹22颗糖后，姐姐与妹妹的糖数比变为2:5，那么姐姐原来有颗糖。

6.一根冰糕售价3元，如果阿童木买这根冰糕，那么阿童木和机器猫剩余的钱数之比为2:5，如果机器猫买了这根冰糕，那么两人的剩余钱数之比为8:13，原来阿童木有元钱。

7.一瓶盐水，盐和水的重量比是1:24，如果再放入75克水，这时盐与水的重量比是1:27，原来瓶内盐水重克。

8.甲、乙两包糖果的重量比是3:1，如果从甲中取出25克放入乙，甲、乙的重量比变为7:5，那么两包糖果的重量和为克。

9.某小学男、女生人数比为16:13，有几名女生转学来到这所学校后，男、女生人数比变为6:5，这时全校共有学生880名，那么转学的女生共有名。

10.亮亮读一本书，已读和未读的页数比是1:5，如果再读30页，已读和未读的页数比为3:5，那么这本书共有页。

11.隔壁班的男、女生人数比为6:5，后来转走了5名男生，班上的男、女生人数比变成了1:1，那么班里一共有女生名。

12.姐姐和妹妹微信钱包里的钱数比为4:3，后来妹妹给姐姐发了两元红包后，姐姐和妹妹的钱数比变为了25:17，那么原来姐姐有元钱。

13.5年前，高高和思思的年龄比是3：4，3年后，高高和思思的年龄比变成了5:6，那么今年高高和思思的年龄和是岁。

14.一杯糖水，糖和水的重量比为1:5，加了100克水后，糖和水的重量比变成了1:10，现在这杯糖水的总重量为克。

人教版六年级下册数学第四单元比例应用题训练(含简单答案)

人教版六年级下册数学第四单元比例应用题训练1．曲港高速公路（曲阳至黄骅港）是河北省“东出西联”出海通道，其定州段连通京昆和京港澳高速，填补安国、博野两地无高速公路的空白，项目建设里程约为92千米，在一幅1∶4000000的地图上，这条高速公路的长度是多少？2．一个骑兵俑模型身高是18厘米，模型高度与实际高度的比是1∶10。

这个骑兵俑的实际身高是多少？（用比例解）3．在的地图上量得甲乙两地的距离是4厘米，甲乙两地的实际距离是多少？把它画在1∶4000000的地图上应画多长？4．在一幅比例尺为1∶2000000的地图上，量得甲乙两地之间的公路长10厘米。

一辆汽车和一辆货车从两地同时出发相向而行，汽车以每小时55千米的速度行驶，2小时后在超过中点10千米的地方相遇。

货车每小时行多少千米？5．在比例尺1∶4000000的地图上，量得天津到北京的距离是3厘米。

一辆汽车以每小时60千米的速度从天津开往北京，几小时能到达？6．一种药水，药液与水的比是1∶180，如果配制905千克的药水，需要药液多少千克？（用比例解）7．学校把制作爱心贺卡的任务按5∶4分配给六年级和五年级。

六年级实际制作了108张贺卡，超过原分配任务的20%，原计划五年级制作多少张爱心贺卡？8．小红去银行换港币，当天人民币与港币的兑换比是1∶1.25，小红要兑换1000元港币，她需要给银行多少元人民币？（用比例解）9．某市修一条道路，计划每天修120米，8天可以修完。

但因为天气原因，12天才完成任务，实际每天修多少米？（用比例方法解）10．一列动车从A城开往B城前3小时行了540千米，照这样的速度，动车还要行驶4小时才能到达B城，A城和B城相距多远？（用比例的方法解答）11．小明和小英住在同一个小区、小明家上个月用电102度，电费是61.2元。

小英家上个月用电85度，小英家上个月的电费是多少元？（用比例知识解答）12．小东家的客厅是正方形的，用边长0.6m的方砖铺地，正好需要100块。

正比例方程应用题专项练习90题

正比例应用题专项练习90题(有答案）1．某测量小组把一根长3米的竹竿直立在地上，测得影长为1.2米，同时测得一水塔的影长为7.2米，这座水塔的高是多少米？2．水果店3天售出苹果吨．照这样计算，剩下的吨苹果还要几天售完？3．修一条公路，开工3天修了1.5千米，照这样的速度，再修21天就可以完成任务，这条公路长多少千米？（用比例解）4．王华5天看完一本115页的书，照这样的速度，要看207页的一本书，需要多少天？（用比例方法解答）5．蜗牛5分钟爬行了31厘米，照这样的速度，蜗牛爬行了55.8厘米要几分钟？6．一辆汽车5小时行400km，照这样的速度7小时行多少千米？（用比例解答）7．兰兰家里搞装修．用同样大小的瓷砖铺一间18平方米的房间和一间27平方米的客厅．已知铺房间正好用了200块瓷砖，铺客厅要用多少块瓷砖？（用比例）8．农民伯伯按1：50的比例配制一种杀虫剂，有一瓶200ml的农药，可以配制多少升杀虫剂？9．240千克油菜籽可以榨油86.4千克，要榨得270吨油需要油菜籽多少吨？10．小明为了测量一棵大树的高度，他测量的结果是：标尺高度12分米，它的影长是2.5分米；测得大树的影长是3米．请你帮小明算一算大树的高度．11．挖一条长1800米的水渠，7天挖了840米，照这样的速度，完成这样的工程还需多少天？12．一种金属合金中银和铝的重量比是5：6．现有480千克铝，需要加多少千克的银，才可以制成这种合金？（用比例思路解）13．某车间计划加工540个零件，前2天做了180个，照这样计算，做完零件需要多少天？（用比例知识解答）14．一辆汽车前4小时共行驶240千米，以同样的速度又行驶5小时，后5小时行驶了多少千米？15．万丰集团生产一批汽车零件，前8天生产了1200箱，照这样计算，剩下的刚好4天完成．这批零件共有多少箱？（用比例解）16．某化肥厂7小时生产化肥630吨，照这样计算，要生产1350吨化肥需要多少小时？17．五一节假期中，小华原计划每天花40分钟，共读儿童小说60页．照这样算，如果他把每天的读书时间调整为50分钟，共可读多少页？（用比例解）18．修一条公路总长12千米，开工前3天修了3600米，照这样计算，修完这条路还需多少天？19．甲乙2人比赛爬楼梯，已知每层楼梯相同，当甲到3层时，乙到2层，照这样计算，当甲到9层时，乙到几层．20．“五一”假期，欣宇连续3天看了84页书，照这样计算，这个月一共可看书多少页？21．修一段高速公路，计划每天修500米，24天可以完成．实际5天修3000米，实际多少天完成？（用正、反比例两种方法解）22．一瓶“84”消毒液写明：清洗浴缸时，需要将原液和清水按1：300配制，李阿姨倒出原液10克清洗浴缸，要加清水多少千克？（用比例知识解答）23．小东身高1.4米，站在操场上他的影长是1米．同时测得教学楼的影长是7米，教学楼有多高？（用比例解）24．一根木料锯3段需要9分钟，照这样计算，如果锯6段，需要多少分钟．（用比例知识解答）25．某修路队修一条长1200米的路，前3天修72米，照这样计算，修完这条路还需多少天？26．工程队修筑公路，5天修了600米，照这样计算，再修3天，一共可以修筑公路多少米？27．一台织布机4小时可以织布24米，照这样计算，要织布54米，需要几小时？（用比例解）28．王师傅3天加工了120个零件，照这样计算，加工360个零件需要多少天？（用比例的思路解）29．食堂买3桶油用780元，照这样计算，买8桶同样的油要用多少钱？（用比例解）30．甲、乙两地相距504千米，一辆汽车从甲地开往乙地，6小时行了全程的，以这样的速度，还需几小时到达乙地？（用比例解）31．在一幅地图上，用3厘米的线段表示实际距离的900千米，一条长480千米的高速公路，在这幅地图上是多少厘米？（用比例解）32．修一条公路，总长12千米，开工3天修了1.5千米．照这样计算，修完这条公路还需要多少天？（用比例解）33．汽车从学校出发到太湖玩，小时行驶了全程的，这时距太湖边还有4千米．照这样的速度，行完全程共用多少小时？34．100克蜂蜜里含30葡萄糖，多少克蜂蜜里含有240克葡萄糖？35．用5辆同样汽车运粮食一次能运22.5吨，照这样计算，要把36吨粮食一次运完，需要增加多少辆这样的汽车？36．一本书，如果每天读30页，6天可以读完，若每天读20页，要多少天才能读完？37．要测量一棵树的高度，量得树的影子长度是8.4米，同时用一根2米长的标杆直立在地面上，量得影子长度是1.2米，这棵树高是多少米？38．一种农药，由药粉和水按照1：400混合而成的．（1）2.5千克药粉，应加水多少千克？（2）用水600千克，需要药粉多少千克？39．学校买来塑料绳342米做短跳绳，先剪下同样长的5根，一共用去9米，照这样计算，买来的塑料绳可以做短跳绳多少根？40．一台收割机4小时收割小麦4.8公顷，照这样计算，收割72公顷小麦需要多少小时？（用比例知识解）41．服装厂生产制服，前3个月生产0.48万套，照这样计算，今年可以生产制服多少万套？42．飞机每小时飞行480千米，汽车每小时行60千米．飞机行4小时的路程，汽车要行多少小时？（用比例方法解）43．一列火车从甲地开往乙地，5小时行了350千米，照这样计算，共要行9小时．甲乙两地相距多少千米？44．雨上小学开展节约用水活动，7天节约用水112吨．照这样计算，今年2月该校共节约用水多少吨？45．测量小组把一米长的竹竿直立在地面上，测得它的影子长度是1.6米，同时测得电线杆的影子长度是4米，求电线杆高多少米？46．一台织布机7小时织布105米，照这样的速度，再织8小时，一共可以织布多少米？47．桃每千克售价1.8元，梨每千克售价2.4元．买40千克桃的钱，可以买多少千克梨？48．A地到B地480千米，一辆汽车前3.5小时行了全程的，按这样的速度，行完全程需要多少小时？（比例解）49．100克蜂蜜里含有34.5克葡萄糖．照这样计算，多少克蜂蜜里含有207克葡萄糖？（用比例的方法解）50．40千克小麦能磨面粉32千克，照这样计算，7吨小麦能磨面粉多少千克？51．钟面上，分针从上午11时到下午2时针尖走了188.4厘米，照这样计算，针尖一天能走多少厘米？（用比例解）52．某工厂2002年二月份前4天用电2.8万度，照这样计算，全月共用电多少万度？53．修一段长400米的路，3天修了120米，照这样计算，修完这段路还需几天？54．一辆汽车从甲地开往乙地，甲乙两地相距405千米，头4小时行驶了180千米，剩下的路程还要行多少小时？55．一本《趣味数学》共96页，小敏前3天看了24页．照这样的速度，看完全书还需多少天？56．某印刷厂计划三月份印刷课本20000本，结果上旬就印刷7000本，照这样速度，三月份可以多印刷多少本？57．某工程队修一条路，12天共修780米，还剩下325米没有修．照这样速度，修完这条公路，共需要多少天？（比例解）58．一种药水中药液和水重量的比是1：2000，5克药液要加水多少千克？如果用6千克水，需要用多少克药液？59．50千克花生仁可以榨油19千克．要榨200千克花生油需多少千克花生仁？（比例解）60．100吨甘蔗可以榨糖12吨，照这样计算，6000吨甘蔗可以榨糖多少吨？如果要榨糖360吨，需要用甘蔗多少吨？61．小杰家离学校的距离为1200米，学校到体育场的距离为2千米．小杰早晨从家步行到学校需要9分钟，如果下午放学后他用同样的速度步行去体育场，需要多少分钟？62．景区有一条面积为4200平方米的步行街，正在铺方砖，小林得知工人们已经干了2天，铺完了1000平方米．照这样的速度，铺完整条步行街还需要多少天？（用比例知识解答）63．用比例方法求解：一支粗细均匀的足够长的蜡烛点燃6分钟，蜡烛缩短3厘米，照这样的速度，蜡烛点燃16分钟缩短多少厘米？64．红红用25毫升蜂蜜和200毫升水调剂了一杯蜂蜜水．如果仍按这样的比例，800毫升水中应加入多少毫升蜂蜜？65．修路队3天修路120米．照这样计算，修完600米长的一段路需要多少天？66．公园里有13条游船，平均每天收入975元．照这样计算，32条游船一天可以收入多少元钱？67．某施工队要安装900米的下水道，6天安装了300米，照这样的速度剩下的任务，还要多少天可以完成？（用比例解）68．法国巴黎的埃菲尔铁塔高320m．北京的“世界公园”里有一座埃菲尔铁塔的模型，它的高度与原塔高度的比是1：10．这座模型高多少米？（用比例解）69．有两个用同一种钢铁制成的零件，一个零件重9吨，体积是1.2立方米．另一个重7.9吨，它的体积是多少立方分米？70．4辆卡车共运480箱苹果，照这样计算，再增加3辆卡车一共可以运多少箱？71．一种药水是按药粉和水的比1：5000配制成的．现在用药粉30克配制成这样的药水，需要加水多少千克？（用比例解）72．修路队修一条长750米的路，前2天修了150米，照这样计算，修完这条路一共需要几天完成？（用比例解）73．一个晒盐场用100克海水可以晒出3克盐．照这样计算，25000吨这样的海水可以晒出多少吨盐？74．自然小组把4米长的竹竿直立在地上，量得它的影子长3.8米，同时量得水塔影子长17.1米．水塔的实际高度是多少米？75．吴师傅带领车工小组加工一批零件，前6天完成330个零件．照这样的速度，又用了14天完成了其余的任务，这批零件共有多少个？（用比例解）76．把2米长的竹竿直立在地上，量得它的影长是l.6米，同时量得一棵大树的影长是5.6米．你知道这棵大树有多高吗？（用比例解．）77．修路队修一段公路，前7天修了357米，照这样，又用了13天把路修完，这段路全长多少米？（比例解）78．学校领来一批树苗，按2：3：4分给四、五、六年级种植．已知四年级分到树苗24棵．五、六年级各分到多少棵？79．某车间要加工540个零件，前2天加工了180个，照这样计算，剩下的还要几天才能完成任务？（用比例解）80．张老师4分钟走了360米．照这样的速度，他从家到学校要走18分钟，张老师家到学校的路程是多少？（用比例知识解答）81．食堂买来5吨煤，6天烧了1.5吨，照这样计算，这批煤可以捎多少天？（用比例解）82．一本故事书共120页，李丽4天看了32页，照这样的速度，看完这本书还需多少天？（用比例解）83．一辆汽车从A城出发，4小时行了364千米，照这样计算，再行2小时就到达B城．AB两城相距多少千米？（用比例知识解答）84．甲、乙两个码头相距308.7千米，一艘轮船从甲码头开往乙码头，3小时行了73.5千米．照这样的速度，几小时可以到达乙码头？85．李洋看一本职工作264页的小说，前3天已经看了72页，照这样计算，这本小说他还要看多少天才能看完？86．某小区维修线路，需停电半小时，妈妈找来一根长20厘米的蜡烛，点燃8分钟后，还剩15厘米，请问，这根蜡烛够燃烧到送电吗？（用比例知识解答并简要说明理由）87．小红在同一时间、同一地点，测得自己的身高与影子的长度比是2：3，这时教学楼的影子长24米，则教学楼的高度是多少米？（用比例解）88．甲工厂有120人，乙工厂有80人．从乙工厂调几人到甲工厂才能使甲工厂与乙工厂人数的比是5：3？89．白寨距郑州有20km，一辆公交车从白寨开往郑州，2小时可以行60km，照这样计算．这辆公交车几小时可到达目的地？（用比例解答）90．李庄要修一条长1200千米长的水渠，前3天修了全长的60%．照这样计算，修完这条水渠一共要用多少天？参考答案1．设这座水塔的高是x米．3：1.2=x：7.2；1.2x=3×7.2；x=；x=18；答：这座水塔的高是18米．2．设剩下的吨苹果还要x天售完，由题意得3：=x ：，x=3×，x=8．答：还要8天售完．3．设21天修路的长度为x千米，则有1.5：3=x：21，3x=21×1.5，3x=31.5，x=10.5；10.5+1.5=12（千米）；答：这条公路长12千米4．设需要x天，115：5=207：x，115x=207×5，115x=1035，x=9；答：需要9天5．蜗牛5分钟爬行了31厘米，照这样的速度，蜗牛爬行了55.8厘米要几分钟？31：5=55.8：x．设蜗牛爬行了55.8厘米要x分钟，31：5=55.8：x；x=9．6．设7小时行x千米；400：5=x：7，5x=400×7，x=，x=560，答：7小时行560千米．7．设铺客厅要用x块瓷砖，18：200=27：x，18x=27×200，18x=5400，x=300；答：铺客厅要用300块瓷砖．8．设可以配制xml杀虫剂，1：（50+1）=200：x，x=200×52，x=10400；10400毫升=10.4升，答：可以配制10.4升杀虫剂9．设要榨得270吨油需要油菜籽x吨，86.4：240=270：x，86.4x=240×270，x=，x=750；答：要榨得270吨油需要油菜籽750吨10．设大树的高度为x米，2.5：12=3：x，2.5x=12×3，x=，x=14.4，答：大树的高度为14.4米．11．设完成这样的工程还需x天．840：7=（1800﹣840）：x840x=7×960x=8；答：完成这样的工程还需8天12．需要加x千克的银，x：480=5：6，6x=480×5，6x=2400，x=400；答：需要加400千克的银，才可以制成这种合金．13．设做完零件需要x天，180：2=540：x，180x=2×540，180x=1080，x=6；答：做完零件需要6天．14．设后5小时行驶了x千米；240：4=x：5，4x=240×5，x=，x=300；答：后5小时行驶了300千米15．设这批零件共有x箱，1200：8=x：（8+4），8x=1200×12，x=，x=1800，答：这批零件共有1800箱16．设要生产1350吨化肥需要x小时，则有：630：7=1350：x，630x=1350×7，630x=9450，x=15；答：要生产1350吨化肥需要15小时17．设如果他把每天的读书时间调整为50分钟，共可读x页，则有60：40=x：50，40x=50×60，40x=3000，x=75；答：如果他把每天的读书时间调整为50分钟，共可读75页18．设修完这条路还需X天，12千米=12000米，3600：3=（12000﹣3600）：x3600x=8400×3，3600x=25200，x=7；答：修完这条路还需7天．19．甲乙的速度之比：（3﹣1）：（2﹣1）=2：1，乙跑的层数：（9﹣1）×=4（层），乙所在的楼层：4+1=5（层）；答：当甲到9层时，乙到5层20．设这个月一共可看书x页，84：3=x：31，3x=84×31，x=，x=868；答：这个月一共可看书868页21．设实际x天完成，（1）（3000÷5）x=500×24，600x=12000，x=20；（2）（500×24）：x=3000：5，12000：x=3000：5，3000x=12000×5，3000x=60000，x=20；答：实际20天完成．22．设要加水x千克．1：300=10：xx=300×10x=3000；3000克=3千克；答：要加水3千克．23．设教学楼的高度是x米，则1.4：1=x：7，x=1.4×7，x=9.8；答：教学楼的高度是9.8米．24．设需要x分钟，9：（3﹣1）=x：（6﹣1），9：2=x：5，2x=9×5，x=，x=22.5；答：需要22.5分钟．25．设修完这条路还需x天，72：3=（1200﹣72）：x，72x=1128×3，x=3384÷72，x=47；答：修完这条路还需47天26．一共可以修筑公路x米；x：（5+3）=600：5，5x=600×（5+3），5x=600×8，x=，x=960；答：一共可以修筑公路960米27．需要x小时，24：4=54：x，24x=54×4，x=，x=9，答：需要9小时28．设加工360个零件需要x天，则有120：3=360：x，120x=360×3，120x=1080，x=9；答：加工360个零件需要9天29．设买8桶同样的油要用x元，x：8=780：3，3x=780×8，x=，x=2080；答：买8桶同样的油要用2080元30．设还需X小时到达乙地．：6=（1﹣）：XX=6×，X=2；答：还需2小时到达乙地．31．设在这幅地图上是x厘米，3：900=x：480，900x=480×3，x=，x=1.6答：在这幅地图上是1.6厘米32．设修完这条公路还需要x天，1.5：3=（12﹣1.5）：x，1.5x=3×（12﹣1.5），1.5x=31.5，x=31.5÷1.5，x=21；答：修完这条公路还需要21天33．1÷（），=1÷（×），=1÷，=（小时），答：行完全程共用小时34．设x克蜂蜜里含有240克葡萄糖，30：100=240：x，30x=100×240，x=24000÷30，x=800；答：800克蜂蜜里含有240克葡萄糖．35．设需要增加x辆这样的汽车．36：（x+5）=22.5：5，22.5×（x+5）=36×5，22.5x+22.5×5=180，22.5x=180﹣112.5，x=3；或：设要把36吨粮食一次运完，需要x辆这样的汽车．36：x=22.5：5，22.5x=36×5，x=180÷22.5，x=8；8﹣5=3（辆）；答：需要增加3辆这样的汽车36．设要x天才能读完．20x=30×6x=180÷20x=9；答：要9天才能读完．37．这棵树高是x米，2：1.2=x：8.4，1.2x=8.4×2，x=14；答：这棵树高是14米．38．（1）设应加水x千克，1：400=2.5：xx=400×2.5x=100；答：应加水100千克．（2）设需要药粉y千克，1：400=y：600400y=600y=1.5；答：需要药粉1.5千克．39．设买来的塑料绳可以做短跳绳x根，9：5=342：x，9x=342×5，x=，x=190，答：买来的塑料绳可以做短跳绳190根40．设收割72公顷小麦需要x小时4.8：4=72：x4.8x=72×44.8x=288x=60答：收割72公顷小麦需要60小时．41．设今年可以生产制服x万套．0.48：3=x：123x=0.48×12x=1.92；答：今年可以生产制服1.92万套．42．设汽车要行x小时，则480×4=60x60x=2160x=36答：汽车要行36小时．43．甲乙两地相距x千米=5x=350×9x=630；答：甲乙两地相距630千米．44．因为今年的二月份有28天，设今年2月该校共节约用水x吨，则112：7=x：287x=112×287x=3136x=448答：今年2月该校共节约用水448吨．45．设电线杆的高是x米．1：1.6=x：41.6x=4x=2.5；答：电线杆的高是2.5米．46．设一共可以织布x米，105：7=x：（8+7），7x=105×（8+7），7x=105×15，x=，x=225，答：一共可以织布225米47．1.8×40÷2.4=72÷2.4=30（千克）答：可以买30千克梨．48．把全程看作单位“1”，设行完全程需要x小时，：3.5=1：x，x=3.5，x=3.5÷，x=3.5×，x=10；答：行完全程需要10小时49．设x克蜂蜜里含有207克葡萄糖；100：34.5=x：207，34.5x=100×207，x=，x=600；答：600克蜂蜜里含有207克葡萄糖50．设7吨小麦能磨面粉x千克．7吨=7000千克40：32=7000：x40x=32×7000x=5600答：7吨小麦能磨面粉5600千克．51．因为，从上午11时到下午2时针尖一共走了3小时：又因为一天是24小时，所以，设针尖一天能走x厘米，188.4：3=x：24，3x=188.4×24，x=，x=1507.2，答：针尖一天能走1507.2厘米52．设全月用电x万度．2.8：4=x：284x=2.8×28x=x=19.6；答：全月共用电19.6万度．53．修完这段路还需要x天．120：3=（400﹣120）：x，120x=3×280，x=7；答：修完这段路还需要7天54．设剩下的路程还要行x千米．180：4=（405﹣180）：x180x=4×225x=5；答：剩下的路程还要行5小时55．设看完全书还需x天，则：（96﹣24）：x=24：3，24x=72×3，x=9；答：看完全书还需9天56．7000÷10×31﹣20000，=21700﹣20000，=1700（本）；答：三月份可以多印1700本57．设共需要x天，（780+325）：x=780：12，780x=1105×12，780x=13260，x=17；答：修完这条公路，共需要17天．58．①设需要加水x克．1：2000=5：x，x=2000×5，x=10000，10000克=10千克；②6千克=6000克设需要用y克药液．1：2000=y：6000，2000y=6000，y=3．答：5克药液要加水10千克．如果用6千克水，需要用3克药液59．设榨200千克花生油需x千克花生仁，由此可得比例：50：19=x：200，19x=10000，x≈526.32；答：大约需要526.32千克花生仁．60．（1）6000吨甘蔗可以榨糖x吨，100：12=6000：x，100x=12×6000，x=720；（2）如果要榨糖360吨，需要用甘蔗y吨，100：12=y：360，12y=100×360，y=，y=3000；答：6000吨甘蔗可以榨糖720吨；如果要榨糖360吨，需要用甘蔗3000吨61．设需要x分钟，则1200：9=2000：x，1200x=2000×9，1200x=18000，x=15；答：需要15分钟．62．设铺完整条步行街还需要x天，则1000：2=（4200﹣1000）：x，1000x=3200×2，1000x=6400，x=6.4；答：铺完整条步行街还需要6.4天63．设蜡烛点燃16分钟缩短x厘米，6：3=16：x，6x=3×16，6x=48，x=8；答：蜡烛点燃16分钟缩短8厘米．64．设800毫升水中应加入x毫升蜂蜜，25：200=x：800，200x=800×25，x=，x=100；答：800毫升水中应加入100毫升蜂蜜．65．设需要x天，120：3=600：x，120x=600×3，x=，x=15；答：需要15天66．设32条游船一天可以收入x元钱，则有975：13=x：32，13x=975×32，13x=31200，x=2400；答：32条游船一天可以收入2400元钱．67．还要x天可以完成，300：6=（900﹣300）：x300x=6×600x=12答：还要12天可以完成．68．设这座模型高x米，则x：320=1：10，10x=320，x=32；答：这座模型高32米．69．设它的体积是x立方米，9：1.2=7.9：x，9x=1.2×7.9，x=，x≈1.053，1.053立方米=1053立方分米，答：它的体积是1053立方分米70．设再增加3辆卡车一共可以运x箱；x：（4+3）=480：4，4x=480×（4+3），x=，x=840；答：再增加3辆卡车一共可以运840箱71．设需要加水x克，1：5000=30：x，x=30×5000，x=150000，150000克=150千克，答：需要加水150千克72．设修完这条路一共需要x天完成，750：x=150：2，150x=750×2，x=，x=10；答：修完这条路一共需要10天完成73．设25000吨这样的海水可以晒出x吨盐，3：100=x：25000，100x=3×25000，x=750，答：25000吨这样的海水可以晒出750吨盐74．设水塔的实际高度是x米，3.8：4=17.1：x，3.8x=4×17.1，3.8x=68.4，x=18．答：水塔的实际高度是18米75．设这批零件共有x个，330：6=x：（6+14），6x=330×（6+14），6x=330×20，x=，x=1100，答：这批零件共有1100个76．设这棵大树有x米高，1.6：2=5.6：x，1.6x=5.6×2，1.6x=11.2，x=11.2÷1.6，x=7；答：这棵大树有7米高．77．设这段路全长x米；357：7=x：（7+13），7x=357×（7+13），7x=357×20，x=，x=1020；答：这段路全长1020米．78．总份数：2+3+4=9（份）；树苗总数：24÷=108（棵）；五年级分到的棵树：108×=36（棵）；六年级分到的棵树：108×=48（棵）．答：五、六年级各分到36、48棵79．设剩下的还要x天才能完成任务，180：2=（540﹣180）：x，180x=（540﹣180）×2，180x=360×2，x=，x=4，答：剩下的还要4天才能完成任务80．设张老师家到学校的路程是x米，360：4=x：18，4x=360×18，x=，x=1620；答：张老师家到学校的路程是1620米．81．这批煤可以烧x天，1.5：6=5：x，1.5x=6×5，x=，x=20；答：这批煤可以烧20天82．设看完这本书还需x天，则32：4=（120﹣32）：x，32x=4×88，32x=352，x=11；答：看完这本书还需11天．83．设AB两城相距x千米，则有364：4=x：（2+4），4x=364×（2+4），4x=2184，x=546；答：AB两城相距546千米84．设x小时到达乙码头，则73.5：3=（308.7﹣73.5）：x，73.5x=（308.7﹣73.5）×3，73.5x=235.2×3，73.5x=705.6，x=9.6；答：照这样的速度，9.6小时可以到达乙码头85．设还要看x天才能看完，72：3=（264﹣72）：x，72：3=192：x，72x=192×3，x=，x=8，答：还要看8天才能看完．86．20厘米的蜡烛燃烧所用的时间为x分钟，（20﹣15）：8=20：x，5：8=20：x，5x=8×20，x=，x=32，因为半小时=30分钟，32＞30，所以这根蜡烛够燃烧到送电；答：这根蜡烛够燃烧到送电87．教学楼的高度是x米；2：3=x：24，3x=24×2，x=，x=16；答：教学楼的高度是16米．88．80﹣（120+80）×，=80﹣200×，=80﹣75，=5（人）；答：从乙工厂调5人到甲工厂才能使甲工厂与乙工厂人数的比是5：3．89．设这辆公交车x小时可到达目的地；60：2=20：x，60x=20×2，x=，x=；答：这辆公交车小时可到达目的地90．设修完这条水渠一共要用x天，则有（1200×60%）：3=1200：x，720：3=1200：x，720x=1200×3，720x=3600，x=5；答：修完这条水渠一共要用5天。

高斯小学奥数五年级上册含答案_比例应用题

第十七讲比例应用题在研究两个量之间的关系时，经常用到和的关系、差的关系以及倍数关系. 之前我们学过的和差倍问题就是关于这些关系的. 而倍数关系还有一种比较常见的表现形式，就是比的关系.比如，甲有3个苹果，乙有2个苹果，我们可以说甲的苹果是乙的 1.5倍，也可以说甲和乙的苹果数之比是 3:2,读作3比2.如果甲有6个苹果，乙有4个苹果，甲的苹果仍然是乙的1.5倍，甲和乙的苹果数之比是 6:4.我们发现，比的关系和倍数关系可以如下转化：倍数关系由此可见，比的概念与除法的概念密切相关，我们定义：两个数相除又叫做这两个数的比.在两个数的比中，比号前面的数叫做比的除以比的后项所得的商叫做比值.例如：比的关系3 2 1.53:2 1.5倍 6:46 4 1.51.5倍前项，比号后面的数叫做比的后项，比的前项比的前项比的后项3: 7 3 7比值比值通常用分数表示，也可以用小数或整数表示.比号请你想一想：比的前项、后项和比值分别相当于除法算式和分数中的什么? 以是0吗？与除法和分数一样，比的前项和后项同时乘或除以相同的数（变.利用这个性质，我们可以像约分一样，将比化简.比如6:4=3:2 .比的后项可 0除外），比值不像这种表示两个比相等的式子叫做比例（式）•要判断两个比是否成比例，就要看它们的比值是否相等•两个比的比值相等，这两个比能组成比例，否则不能组成比例•比例有四个项，分别是两个内项和两个外项.在3:4=9:12中，其中3与12叫做比例的外项， 4与9叫做比例的内项.比例的四个数均不能为 0.在任意一个比例中，两个外项的积等于两个内项的积.即:1. 求比值：2:5 = _________ ; 7:3 = _______ ; 10:4= ________2. 把比化成最简整数比：6:15 = ________ ；8:12= ______ ；0.2:0.5 = _______ .3. 如果3a 4b，那么a:b=():();4. 我国《国旗法》规定，国旗长宽之比为3:2,若国旗宽是128厘米，则长是 ____________厘米.在表示两个量之间的关系时，可以用到和的关系、差的关系、倍数关系和分数倍关系.除了这些之外，比例也可以用来表示两个量之间的倍数关系. 知道了两个量之间的比，我们可以方便的按照比例将两个对象的数量分配好，这也是本讲要重点学习的：按比例分配.例题1. (1)水果店运来了西瓜和哈密瓜共234个.如果西瓜和哈密瓜的个数比为5:4,那么水果店运来西瓜和哈密瓜各多少个？(2)阿呆和阿瓜一起去买包子，两人买的包子数之比是13:6 •又知道阿呆比阿瓜多买了21个包子，那么两人一共买了多少个包子？「分析」根据比例设份数，比如西瓜和哈密瓜的个数比是5:4，那么可设西瓜有5份，哈密瓜有4份.(1 )卡莉娅和萱萱一共买了50块巧克力，卡莉娅的巧克力块数和萱萱的比是7:3，那么卡莉娅比萱萱多多少块巧克力？(2)小山羊和老山羊去吃草，小山羊和老山羊吃的草量比为5:9,并且老山羊比小山羊多吃了200克的草，那么小山羊吃了多少克的草？例题2•红旗小学共有师生 1081人•其中老师与学生的人数之比为数之比为5:4 .请问：红旗小学的老师、男生和女生各有多少人？「分析」如何通过师生的人数比求出学生的总人数？又如何利用男、各有多少？把这两个问题搞清楚了，本题也就解决了.512名士兵分成龙、虎两个营，将龙营分成甲、乙两个连，再将乙连分成 A 、B 两个排.如果每次都按5:3的人数比来分，那么 A 排有多少名士兵？比例除了可以表示两个量之间的倍数关系，还可以表示多个量之间的倍数关系. 我们把两个数之间的比称为简单比，多个数的比称为连比•简单比与连比之间可以互相转化.如果甲:乙 =2:3，乙:丙 =5:4，那么甲:乙 :丙是多少?甲乙丙2 :35 :4甲:乙 :丙=10:15:1210 : 15 : 12例题3•机器人制造厂一月份与二月份生产机器人的个数比为 4:5 •后来改进生产技术，三月份生产的机器人的个数与二月份的产量之比为 5:3.(1 )请写出三个月的产量的连比；(2)如果三月份比一月份多生产了 78个机器人.请问，这家工厂第一季度共生产多少个机器人？「分析」题目中给出了两个比，这两个比之间存在什么样的关系呢？你能通过这两个比求出一月份、二月份和三月份这三个月产量的连比吗？育才小学五年级学生分成三批去参观博物馆.第一批与第二批的人数比是与第三批的人数比是 3:2.已知第一批的人数比第二、三批的总和少 55人.请问：育才小学2:45，男生与女生的人女比例，求出男、女生5:4,第二批五年级一共有多少人?对于数量发生变化的题，题目中比的每一份的含义往往也是不一样的，不能直接来计算•那么对于这类问题，我们通常要从题中找到不变量，根据它来统一份数•我们来看看下面这道题，题中的量是如何变化的？你能找到其中的不变量吗？例题4•慢羊羊村长开了一间学校，招了好多小羊和小狼，上学期小羊和小狼的数量比为 1:3 , 新学期时又转来了 20只小羊，导致开学的时候小羊和小狼的数量比变为 3:5，那么开学时一共有多少只小羊？「分析」题目中也给出了两个比，这两个比之间存在什么样的关系？我们能像例 1那样，把上学期的小羊和小狼设成 1份和3份，这学期的设成 3份和5份吗？史蒂文森高中去年男生和女生的人数比为 5:3,今年转来了 200名男生，使得女生和男生的人数比变为1:2，那么今年史蒂文森高中一共有多少名学生？例题5.如下图，甲、乙、丙三根木棒插在水池中，它们的长度之和是水面上、下的长度之比为 3:1，乙木棒在水面上、下的长度之比为下的长度之比为2:3.请问：水深是多少厘米?「分析」题目中的三个比涉及到了甲、乙、丙三根木棒的水上部分和水下部分，它们之间有公共的量吗？例题 6．甲、乙两包糖的重量比是 5:3,如果从甲包取出 10 克放入乙包后,甲、乙两包糖的重量比变360厘米.甲木棒在 4:3，丙木棒在水面上、为7:5．请问：这两包糖重量的总和是多少克？「分析」甲包少了10克,乙包多了10 克．什么没有变呢？黄金分割把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比。

(完整版)比例尺应用题及答案

比例尺应用题及答案比例尺是表示图上一条线段的长度与地面相应线段的实际长度之比。

比例尺应用题及答案1 应用题1. 在一幅比例尺是1 ：3000000的地图上，甲乙两地的距离是7.5厘米，甲乙两地的实际距离是多少千米2. 英华小学有一块长120米、宽80米的长方形操场，画在比例尺为1 ：4000的平面图上，长和宽各应画多少厘米？3. 一个机器零件长5毫米，画在图纸上是4厘米，求这幅图纸的比例尺。

4. 一幅地图的线段比例尺是：0 40 80 120 160千米，甲乙两城在这幅地图上相距18厘米，两城间的实际距离是多少千米？丙丁两城相距660千米，在这幅地图上两城之间的距离是多少厘米5. 某建筑工地挖一个长方形的地基，把它画在比例尺是1 ：2000的平面图上，长是6厘米，宽是4厘米，这块地基的面积是多少？6. 在比例尺是1 ：2500000的地图上，量得甲乙两城之间的距离是7.2厘米。

一辆汽车从甲城到乙城，每小时行80千米，需要多少小时？7. 一种精密零件，画在图上是12厘米，而实际的长度是3毫米。

求这幅图的比例尺。

8. 在比例尺是1 ：2000000的地图上，量得甲乙两地的距离是3.6厘米。

如果汽车以每小时30千米的速度于上午8时整从甲地开出，走完这段路程，到达乙地时是什么时间？9. 在比例尺是1：12000000的地图上，量得济南到青岛的距离是4厘米。

在比例尺是1：8000000的地图上，济南到青岛的距离是多少厘米？10.在一幅比例尺为1:500的平面图上量得一间长方形教室的长是3厘米，宽是2厘米。

（1）求这间教室的图上面积与实际面积。

（2）写出图上面积和实际面积的比。

并与比例尺进行比较，你发现了什么？答案1.实际距离=图上距离/比例尺=7.5*3000000=22500000cm=225Km2.图上距离=实际距离*比例尺图上长=120*100*（1/4000）=3cm图上宽=8*100*（1/4000）=2cm3.比例尺=图上距离/实际距离=4cm/5mm=4/0.5=8:14.先求出比例尺，比例尺=图上距离/实际距离=1/(40*1000*100)=1:4000000地图上相距18厘米的两城间的实际距离=图上距离/比例尺=18/(1:4000000)=72000000cm=720Km丙丁图上距离=实际距离*比例尺=660*1000*100*（1:4000000）=16.5cm以下几题的公式省略，只写计算过程和结果5.实际长=6*2000=12000cm=120m实际宽=4*2000=8000=80m实际面积=实际长*实际宽=120*80=9600m26.甲乙两城的实际距离=7.2*2500000=18000000cm=180Km 时间=180/80=2.25h7.比例尺=图上距离/实际距离=12cm/3mm=12/（0.3）=40:18.甲乙两地实际距离=3.6*2000000=7200000cm=72km时间=72/30=2.4h=2小时24分钟，到达乙地时间是10时24分，即上午10:249.济南到青岛的实际距离=4*12000000=48000000=480km，在1：8000000的图上的图上距离是48000000/8000000=6cm10.实际长=3*500=1500cm=15m实际宽=2*500=1000cm=10m(1)图上面积=3*2=6cm2实际面积=15*10=150m2(2)图上面积/实际面积=6cm2/150m2=6cm2/(150*10000cm2)=1/250000=(1/500)2 发现图上面积/实际面积=比例尺的平方比例尺应用题及答案2 应用题1. 在一幅地图上，用3厘米的线段来表示实际距离600千米。

第四单元《比例》应用题(试题)人教版六年级下册数学

人教版六年级下册数学第四单元《比例》应用题1．铺一间客厅的地面，用边长为60cm的方砖需要100块，若改用边长为50cm的方砖，需要多少块？（用比例的知识解答）2．在比例尺是1∶5000000的地图上，量得北京到南京的铁路线长24厘米，李老师乘坐时速为100千米的列车从北京出发，到达南京时要用多长时间？3．李师傅计划加工一批零件，前五天加工了120个，照这样计算，再用18天就可以做完，这批零件一共有多少个？（用比例解）4．小亮看一本故事书，如果每天看12页，需要15天看完，如果要提前3天看完，每天要看多少页？（用比例解）5．爸爸打算给李明的小书房铺上方砖，用边长3分米的方砖需要40块，如果改用边长2分米的方砖，则需要多少块？（用比例解）6．在比例尺是12000000的地图上，量得甲、乙两地的距离是25厘米，两辆汽车同时从甲、乙两地相对开出，甲车每小时行驶54千米，乙车每小时行驶46千米，几小时后两车相遇？7．一种消毒液，用酒精和蒸馏水按2:5配制而成，要配制这种消毒液840升，需要酒精多少毫升？（用方程解答）8．学校组织同学们参观科技博物馆，如果每辆车坐35人，需要12辆车；如果每辆车坐28人，需要多少辆车？（用比例解）9．一间长4.8米，宽3.6米的房间，用边长0.15米的正方形砖铺地面、需要768块，在长6米、宽4.8米的房间里，如果用同样的砖来铺，要几块？（用比例解）10．一个圆柱形零件的高是5毫米，在图纸上的高是2厘米，这幅图纸的比例尺是多少？11．某建筑工地挖一块长方形的地基，把它画在比例尺是1∶4000的平面图上，长是6厘米，宽是4厘米。

这块地基的实际面积是多少平方米？12．在比例尺是12000000的地图上，量得甲、乙两地的距离是25cm，甲车每小时行驶54km，乙车每小时行驶46km，几小时后相遇？13．给一间房子铺地砖，用边长为3分米的正方形地砖要1000块，若选用边长为5分米的正方形地砖，需要多少块？14．一块长方形地长和宽的比是7∶4，将其画在比例尺为1∶1000的图纸上，所得图形的周长是44厘米。

比例练习题100道答案

比例练习题参考答案化简下列各比（1）()()35:105=3535:105351:3÷÷= （2）91:13=(9113):(1313)=7:1÷÷ （3）77:3=(9):(39)7:2799⨯⨯=（4）446:(67):(7)42:421:277=⨯⨯== （5）1111:(10):(10)5:22525=⨯⨯=（6）11811:(49):(49)56:1749749=⨯⨯= （7）1790.7:2(20):(20)14:454104=⨯⨯= （8）333:0.75(20):(20)2:510104=⨯⨯= （9）1.6:2.5(1.610):(2.510)16:25=⨯⨯= （10）3.5:8.4(3.510):(8.410)5:12=⨯⨯= （11）3132131.05:1:(40):(40)42:15(423):(153)14:58208208==⨯⨯==÷÷= （12）5511561:2.44:2200:200125:4888825825⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭（13）36:0.2836:28(364):(284)9:79:7=÷÷厘米米=厘米厘米厘米厘米=厘米厘米=36:0.28=036:0.2809:0.7(0910):(0.710)9:79:7=⨯⨯=或厘米米.米米=.米米.米米=米米（14）48:1.648:164816):(1616)=÷÷分米米=分米分米=(分米分米=3分米:1分米3:1（15）4:1254=601248:12(4812):(1212)5⎛⎫⨯==÷÷ ⎪⎝⎭时分分:分分分分分=4:1（16）120:4120:(60)20:15(205):(155)4:34:34⨯==÷÷==分时=分分分分分分分分（17）220:5220:(1000)20:400(2020):(40020)5⨯=÷÷克千克=克克=克克克克=1:20（18）33:50053333(1000):6:(65):(5)==500555=⨯==⨯⨯千克克克克克克克克30克:3克10:1（19）71:101022121700(7002)=22==⨯⨯升毫升毫升:毫升毫升:(2)毫升=1400毫升:21毫升200:3（20）44:24=(100)2455=8024=103=10:3⨯平方米平方分米平方分米：平方分米平方分米：平方分米平方分米:平方分米解比例方程（21）2:4:189x x ==（22）:518:452x x ==（23）20:74:75x x ==（24）51:817:83xx ==（25）125::64600x x ==（26）12:7:33311x x ==（27）542::6531x x ==（28）62248::933554855x x ==（29）1.8:9:10.2x x ==（30）0.14:4.8:123.5x x ==（31）1.6:4.80.2:0.6xx ==（32）:2.1 1.6:8.40.4x x ==（33）40.16::1553x x ==（34）614.4::151.2x x ==（35）7:6.3:4.990.1xx==（36）35:0.8:86169xx==（37）1.225750.4xx==（38）24:335210xx==（39）5235::857336125xx==（40）2639:1:1.53737xx==（41）2781632xx+==（42）3741157xx=+=（43）5312157xxx=+=（44）13758xxx+=+=（45）(1):512:303xx-==（46）4:(3)2:915xx+==（47）13:91(21):493xx=+=（48）5:855:(412)25xx=-=（49）(32):(23)4:72x xx-+==（50）(4):5(32):9233x xx+=-=比例应用题（51）小白的身高1.4米，他的影长是2.8米。

小学数学正反比例的应用题(含答案)

正反比例的应用题1、用同样的方砖铺地，铺20 平方米要320 块，如果铺42 平方米，要用多少块方砖？2、一间教室，用面积是0.16 平方米的方砖铺地，需要275 块，如果用面积是0.25 平方米的方砖铺地，需要方砖多少块？3、建筑工地原来用4 辆汽车，每天运土60 立方米，如果用 6 辆同样的汽车来运，每天可以运土多少立方米？4 我国发射的人造地球卫星绕地球运行3 周约3.6 小时，运行20 周约需多少小时？5、一种铁丝，7.5 米长重3 千克，现在有19.5 米长的这种铁丝，重多少千克？6、汽车在高速公路上3 小时行240千米，照这样计算，5 小时行多少千米？7、修一条公路，4 天修了200米，照这样计算，又修了 6 天，又修了多少米8、小明读一本书，每天读12 页，8 天可以读完。

如果每天多读 4 页，几天可以读完？9、今春分配给学校一些植树任务，每天栽200 棵6 天可以完成任务，现在需要 4 天完成任务，实际每天比原计划多栽多少棵？10、农场用3 辆拖拉机耕地，每天共耕225 公顷，照这样速度，用 5 辆同样拖拉机，每天共耕地多少公顷？11、一艘轮船，从甲地从开往乙地，每小时航行20千米，12 小时到达，从乙地返回甲地时，每小时多航行4 千米，几小时可以到达？12、100 千克黄豆可以榨油13 千克，照这样计算，要榨豆油 6.5 吨，需黄豆多少吨？13、学校计划买54张桌子，每张30 元，如果这笔钱买椅子，可以买90 张，每张椅子多少钱？14、一对互相咬合的齿轮，主动轮有20 个齿，每分钟转60 转，如果要使从动轮每分钟转40 转，从动轮的齿数应是多少？15、把3米长的竹竿直立在地面上，测得影长1.2 米，同时测得一根旗杆的影长为 4.8 米，求旗杆的高是多少米？16、一个机器零件长5毫米，画在图纸上是4 厘米，求这幅图纸的比例尺。

（5 分）17、地图上的26厘米，在比例尺为1 : 1300000的地图上约是多少千米？（ 5 分）18、李师傅计划生产450 个零件，工作8 小时后还差330 个零件没有完成，照这样速度，共要几小时完成任务？19、用一批纸装订同样的练习本，如果每本30 页，可以装订80 本。