08011331计控实验-纯滞后系统大林控制
一种用于具有纯滞后系统的新控制方法

一种用于具有纯滞后系统的新控制方法
马竹梧;宗书强
【期刊名称】《信息与控制》
【年(卷),期】1989(18)3
【摘要】具有纯滞后的系统是一类比较难于控制的系统,对于这类系统较为有效的解决方法是 Smith (?)估器。
这种方法对于参考输入能够给出良好响应,但在其它性能上却有不少缺陷。
首先,它不能很好的消除外加干扰的影响,甚至带来稳态偏差,其次,它的鲁棒性不强、对模型偏差很敏感。
为了改善这些性能,近年来提出了一些改进方案,但这些工作均有一定局限性。
本文提出一个新的改进方案,这个方案在综合前人工作的基础上,兼顾了系统的各个主要方面,因而具有较好的总体性能,并以电渣炉数据为例,证明它具有较优越的性能。
【总页数】6页(P1-6)
【关键词】纯滞后系统;Smith预估器;鲁棒性
【作者】马竹梧;宗书强
【作者单位】冶金部自动化研究院
【正文语种】中文
【中图分类】TP13
【相关文献】
1.一种具有大纯滞后系统的自适应Smith控制方法 [J], 文方
2.大纯滞后系统一种新预估模糊控制 [J], 于标
3.一种新的纯滞后预估控制系统 [J], 李传辉
4.大纯滞后系统的一种PID预估控制方法 [J], 吕群;于标
5.一种具有大纯滞后系统的Smith控制 [J], 袁铸钢;曲守宁
因版权原因,仅展示原文概要,查看原文内容请购买。
第五章(一) 纯滞后控制技术--达林(DAHLIN)算法(全)

2014-2-26
3
前言 对这类具有纯滞后环节系统的控制要求,快速性往往 是第二位的,通常要求系统稳定,要求系统的超调量要小, 而调整时间允许在较多的采样周期内结束。 这样的一种大时间滞后系统采用PID控制或采用最少拍 控制,控制效果往往不好。本节介绍能满足上述要求的一种 直接数字控制器设计方法 ——达林(Dahlin)算法 1968年,美国IBM公司DAHLIN提出。
2014-2-26
32
大林算法小结 过程纯延迟对控制质量的影响 达林算法 设计思想 一阶被控对象的达林算法 二阶被控对象的达林算法 达林算法的递推表达式 达林算法的参数整定 振铃(Ringing)现象 产生原因;振铃幅度RA;振铃现象的抑制
2014-2-26
33
式中: Tτ为闭环系统的时间常数,实际使用时需要整定;τ为 纯滞后时间,与被控对象的相同,并且与采样周期T有整数 倍的关系τ=NT(N=1,2,…)。
2014-2-26
8
达林算法
2014-2-26
9
达林算法
2014-2-26
10
达林算法
2014-2-26
11
达林算法
2014-2-26
12
达林算法
31
大林算法的设计步骤 根据系统性能要求,确定期望闭环系统的参数Tτ,给出 振铃幅度RA的指标; 根据振铃幅度RA的要求,确定采样周期T。如果T有多 解,则选择较大的T; 确定整数N=τ/T; 求广义对象的脉冲传递函数及期望闭环系统的脉冲传递 函数; 求数字控制器的脉冲传递函数D(z); 将D(z)转变为差分方程,以便于编制相应算法程序。
2014-2-26
4
过程纯延迟对控制质量的影响 纯延迟是某些物理系统常有的一种性质。由于它的存 在,系统对输入信号的响应被推迟了。所谓纯延迟,是指 在输入信号作用后,看不到系统对输入信号响应的这段时 间。它与输入信号无关,量纲为时间。 当物质和能量沿着特定的路径传输时,就会出现纯延 迟。路径的长度和运动速度是构成纯延迟的因素。 纯延迟都是由于传输才引起的,故称为传输滞后。
08011331计控实验-纯滞后系统大林控制

东南大学自动化学院实验报告课程名称:计算机控制技术基础第四次实验实验名称:具有纯滞后系统的大林控制院(系):自动化学院专业:自动化姓名:郭劲廷学号:08011331实验室:常州楼419 实验组别:同组人员:实验时间:2014 年 4 月28 日评定成绩:审阅教师:实验五 具有纯滞后系统的大林控制一、实验目的1.了解大林控制算法的基本原理;2.掌握用于具有纯滞后对象的大林控制算法及其在控制系统中的应用。
二、实验设备1.THBDC-1型 控制理论·计算机控制技术实验平台 2.PCI-1711数据采集卡一块3.PC 机1台(安装软件“VC++”及“THJK_Server ”)三、实验原理在生产过程中,大多数工业对象具有较大的纯滞后时间,对象的纯滞后时间τ对控制系统的控制性能极为不利,它使系统的稳定性降低,过渡过程特性变坏。
当对象的纯滞后时间τ与对象的惯性时间常数T1之比,即τ/T1≥0.5时,采用常规的比例积分微分(PID )控制,很难获得良好的控制性能。
长期以来,人们对纯滞后对象的控制作了大量的研究,比较有代表性的方法有大林算法和纯滞后补偿(Smith 预估)控制。
本实验以大林算法为依据进行研究,大林算法的被控对象是带纯滞后的一阶或二阶惯性环节。
即1)(1+=-s T Ke s G sτ 或 )1)(1()(21++=-s T s T Ke s G sτ本实验被控对象为带纯滞后的一阶惯性环节。
式中:τ为纯滞后时间,为方便起见假设为采样周期T 的整数倍NT =τ大林算法的主要设计目标是系统在单位阶跃输入作用下,整个闭环系统的传递函数相当于一个延迟环节和一个惯性环节相串联。
即1)(0+=-s T e s H sτ (5-1) 要求整个闭环系统的纯滞后时间等于被控对象的纯滞后时间。
与H(s)相对应的闭环系统脉冲传递函数为01()[]1sT NTse e H z Z s T s ---=⋅+101(1)[](1)Nzz Z s T s--=-+ 01111(1)(1)(1)(1)TT NT T ez zz z e z --------=---00(1)1(1)1T T N T T ez ez --+---=- (5-2)将上式代入式1()()()1()H z D z G z H z =⋅-中,得 0(1)1(1)(1)()()[1(1)]T T N T T T T N ez D z G z ez e z --+----+-=--- (5-3)当对象为一阶惯性环节加纯滞后时11()[]1sT NTse Ke G z Z s T s ---=⋅+111(1)[](1)N Kz z Z s T s --=-+111111(1)(1)(1)(1)T T NT T ez Kzz z e z --------=---11(1)1(1)1T T N T T e Kz ez --+---=- (5-4)将式(5-4)代入式(5-3)得一阶惯性环节的控制器的D(z)为01111(1)(1)(1)()(1)[1(1)]T T T T T T T T T T N eez D z K eez ez --------+--=----由上式,控制算法为)1()1()1()()1(1)1()1()1()(11100------+---+-=-------k e eK eek e e K eN k u e k u ek u T T T T T T T T T T T T T T四、实验步骤1、仔细阅读“PCI-1711数据采集卡驱动函数说明.doc ”和“THJK-Server 软件使用说明.doc ”文档,掌握PCI-1711数据采集卡的数据输入输出方法和THJK-Server 软件(及相关函数)的使用方法。
实验三 纯滞后控制实验
实验三 纯滞后控制实验班级:自控081班 学号:200808602 姓名:樊军艳一. 实验目的与要求(1) 掌握应用达林算法进行纯滞后系统)(z D 的设计;(2) 掌握纯滞后系统消除振铃的方法。
二. 实验原理在一些工业过程(如热工、化工)控制中,由于物料或能量的传输延迟,许多被控制对象具有纯滞后性质。
例如,一个用蒸汽控制水温的系统,蒸汽量的边比划要经过长度为L的路程才能反映出来。
这样,就造成水温的变化要滞后一段时间τ(v L /=τ,v 是蒸汽的速度)。
对象的这种纯滞后性质常会英气系统产生超调和振荡。
因此,对于这一类系统,采用一般的随动系统设计方法是不行的,而用PID 控制往往效果也欠佳。
本实验采用达林算法进行被控制对象具有纯滞后系统设计。
设被控对象为有纯滞后的一阶惯性环节或二阶惯性环节,达林算法的设计目标是使整个闭环系统所期望的传递函数)(s Φ,相当于一个延时环节和一个惯性环节串联,即 1)(+=Φ-s e s sτθ ,NT =θ 该算法控制将调整时间的要求放在次要,而超调量小甚至没有放在首位。
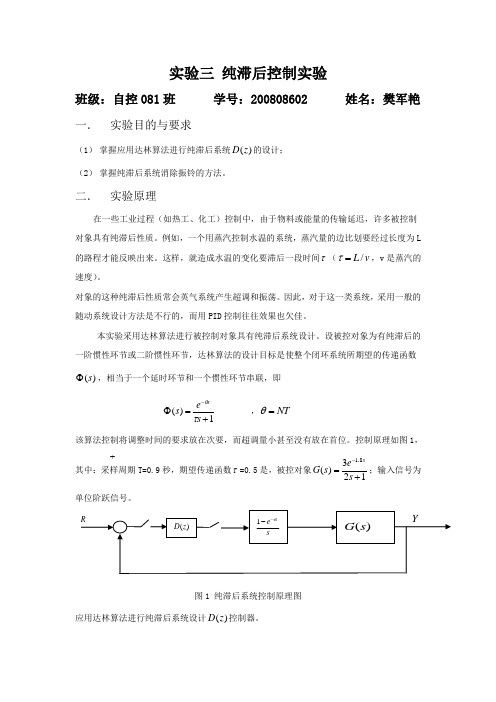
控制原理如图1,其中:采样周期T=0.9秒,期望传递函数τ=0.5是,被控对象123)(8.1+=-s e s G s;输入信号为单位阶跃信号。
图1 纯滞后系统控制原理图应用达林算法进行纯滞后系统设计)(z D 控制器。
三. 实验内容与步骤(1)按照纯滞后控制系统的要求设计)(z D ;按照系统原理图,在simulink 下构造系统结构图模型。
,观察输入输出的波形,标明参(2)数,打印结果;(3)尝试用M 文件实现dalin 算法控制四. 实验设计图1 纯滞后控制Simulink 仿真图图2 纯滞后控制器输出曲线图3 纯滞后系统输出曲线五.思考与分析(1)纯滞后控制系统对阶跃信号有无超调?为什么?答: 阶跃肯定会有超调,而且会很大。
对于单位阶跃信号,含有极点z=1,如果Φu(z)的极点在z平面的负实轴上,且与z=-1点相近,那么数字控制器的输出序列u(kT)中将含有这两种幅值相近的瞬态项,而且瞬态项的符号在不同的时刻是不相同的。
CMAC与大林的复合控制在纯滞后系统中的应用

dsd atgso n dut gt eo al l rh . h eut o M t t l cnrl rnMA L B f i lt ni i vnae fo gajsn i f hi a oi m T ersl f x e ot l T A rs a o a l i m D n g t s e f i oe i o mu i s
p e e t d a d t e rt g t e ag r h i t n t n u e n S MUL NK smu ai n I g e t mp o e e p a t a i t f r s n e , n h n w i l o t m o f c i s d i I i n h i n u o I i lt . t r al i r v st r c i b l y o o y h c i t ec n r l lo t m. h o t g r h oa i Ke r s t — ea y tm ;Da l lo t m ;C y wo d : i d ly s s me e hi agr h n i MAC;c mp st o to ;S MUL NK s l t n o oi c nrl I e I i ai mu o
大 多 数 工 业 过 程 中 , 如 锅 炉 温 度 控 制 过 程 , 纸 、 工 例 造 化
过 程 控 制 等 , 控 制 系 统 一 般 为 纯 滞 后 系 统 , 滞 后 性 质 会 其 纯
使 系 统 的 过 渡 过 程 时 间 加 长 、 生 大 幅 度 的 超 调 . 而 使 控 产 从
关 键 词 :纯 滞后 系统 ;大林 算 法 ; MA 复 合 控 制 ; I U I K 仿 真 C C; SM LN 中图 分 类 号 : P 7 T 23 文献标识码 : A 文 章 编 号 :1 7 — 2 6 2 1 ) 0 0 9 — 3 6 4 6 3 (0 2 2 — 0 3 0
实验8实验指导书具有纯滞后系统的大林控制

实验8实验指导书具有纯滞后系统的大林控制实验8具有纯滞后系统的大林控制系统一、实验目的1.了解算法的基本原理;2.掌握纯滞后对象的控制算法及其在控制系统中的应用。
2、实验设备1.thbcc-1型信号与系统?控制理论及计算机控制技术实验平台2.thbxd数据采集卡一块(含37芯通信线、16和usb电缆线各1根))三、实验内容1.纯滞后一阶惯性环节达林算法的实现。
2.采用纯滞后二阶惯性环节实现达林算法。
4、实验原理在生产过程中,大多数工业对象具有较大的纯滞后时间,对象的纯滞后时间?对控制系统的控制性能极为不利,它使系统的稳定性降低,过渡过程特性变坏。
当对象的纯滞后时间? 与对象的惯性时间常数相比,传统的比例积分微分(PID)控制难以获得良好的控制性能制性能。
长期以来,人们对纯滞后对象的控制作了大量的研究,比较有代表性的方法有大林算法和纯滞后补偿预估)控制。
本实验基于达林算法。
Dalin算法的综合目标不是最小拍频响应,而是具有纯滞后时间的一阶滞后响应。
其等效闭环传递函数为要求的等效环节的时间常数,t为采样周期。
通过对零阶holder方法进行离散,可以得到系统的闭环传递函数:v.实验步骤1、实验接线1.1根据图8-1,连接惯性链接的模拟电路;1.2用导线将该电路输出端与数据采集卡的输入端“ad1”相连,电路的输入端与数据采集卡的输入端“da1”相连;2.脚本程序运行2.1启动计算机,在桌面双击图标“thbcc-1”,运行实验软件;2.2顺序点击虚拟示波器界面上的开始钮和工具栏上的脚本编程器2.3点击脚本编辑器窗口文件菜单下的“打开”按钮,选择“计算机控制算法VBS\\basic algorithm of computer control technology”文件夹下的“Dalin algorithm”脚本程序并打开。
阅读并理解节目,2.4点击脚本编辑器窗口的调试菜单下“启动”;用虚拟示察图输出端的响应曲线;2.5点击脚本编辑器的调试菜单下“停止”,修改程序中n(可模拟对象的滞后时间,滞后时间为n*运行步长,单位为ms;当运行步长,n的取值范围为1~5)值以修改对象的滞后时间,再点击“启动”按钮。
计控实验3 大林算法

T
2、用MATLAB和Simulink仿真并检查输出结果是否符 合控制系统设计要求。
二、实验内容 2 S e 1、已知被控对象的传递函数 G ( s) s( s 1) ,若采样期 T=1s,用大林算法设计数字控制器D(Z),并用MATLAB 检验系统的性能。
HG(Z)
r(t) T R(Z) E(Z) × ○ D(Z) T H0(S) G(S)
实验三:大林算法
一、实验目的:
1、对应纯滞后的被控对象,应采用大林算法。 (1)大林算法的设计准则:对于一阶或二阶滞后系 统,设计数字控制器D(z),使整个闭环系统的滞后与 被控对象的滞后相同,消除滞后环节对系统稳定性的 s Ke 影响。 G( s ) 1 T 1s 一阶滞后系统可表示为: e s Gc (s) 1 THS 闭环系统的传递函数:
(二)Simulink的模块库
通用模块
连续模块 非连续模块 离散模块 接收模块
输入信号源
数学运算 端口与子系统
1.输入信号源模 块库(Sources)
主要有: Constant(常数) Step(阶跃信号) Ramp(线性信号) Sine Wave(正弦信号) Signal Generator(信 号发生器) From File(文件获取) From Workspace(矩阵 读数据) Clock(仿真时钟) In(输入模块)
1、启动MATLAB
下载软件或用光盘进行MATLAB的安装。
点击 图标 ,启动MATLAB,出现操作窗口:
操作界面分为以下几部分: (1)菜单 (2)工具栏 (3)工作空间窗口
(4)命令窗口 (5)历史命令窗口口
命令 窗口
历史 命令 窗口 开始按钮
纯滞后控制实验报告

一、实验目的1. 理解纯滞后控制系统的概念及其在工业控制系统中的应用。
2. 掌握大林算法在纯滞后控制系统中的应用原理。
3. 通过实验验证大林算法在纯滞后控制系统中的控制效果。
二、实验原理1. 纯滞后控制系统:纯滞后控制系统是指被控对象具有纯滞后特性,即输入信号到输出信号的传递过程中存在一定的时间延迟。
这种时间延迟会使得控制作用不及时,从而影响系统的稳定性和动态性能。
2. 大林算法:大林算法是一种针对纯滞后控制系统的控制策略,其基本思想是在设计闭环控制系统时,采用一阶惯性环节代替最少拍多项式,并在闭环控制系统中引入与被控对象相同的纯滞后环节,以补偿系统的滞后特性。
三、实验设备1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 设计实验模型:根据实验要求,设计一个具有纯滞后特性的被控对象模型,并确定其参数。
2. 构建大林算法控制器:根据大林算法的原理,设计一个大林算法控制器,并确定其参数。
3. 进行仿真实验:在MATLAB软件中搭建实验平台,将设计的被控对象模型和大林算法控制器进行联接,进行仿真实验。
4. 分析实验结果:观察实验过程中系统的动态性能,分析大林算法在纯滞后控制系统中的应用效果。
五、实验结果与分析1. 实验结果(1)无控制策略:在无控制策略的情况下,被控对象的输出信号存在较大的超调和振荡,系统稳定性较差。
(2)大林算法控制:在采用大林算法控制的情况下,被控对象的输出信号超调量明显减小,振荡幅度减小,系统稳定性得到提高。
2. 分析(1)无控制策略:由于被控对象具有纯滞后特性,系统动态性能较差,导致输出信号存在较大超调和振荡。
(2)大林算法控制:大林算法通过引入与被控对象相同的纯滞后环节,有效补偿了系统的滞后特性,使得控制作用更加及时,从而提高了系统的动态性能和稳定性。
六、实验结论1. 纯滞后控制系统在实际工业生产中普遍存在,对系统的稳定性、动态性能和抗干扰能力具有较大影响。
计算机控制技术课程设计--具有纯滞后一阶惯性系统的计算机控制系统设计

《计算机控制技术》课程设计具有纯滞后一阶惯性系统的计算机控制系统设计班级:姓名:学号:指导老师:日期:目录一、设计任务 (1)1.1 题目 (1)1.2内容与要求 (1)二、设计思想与方案 (2)2.1控制策略的选择 (2)2.2 硬件设计思路与方案 (2)2.3 软件设计思路与方案 (3)三、硬件电路设计 (3)3.1温度传感器输出端与ADC的连接 (3)3.2 ADC与单片机8051的连接 (4)3.3 单片机8051与DAC的连接 (4)3.4 整机电路 (5)四、系统框图 (7)五、程序流程图 (8)5.1 主程序流程图 (8)5.2 子程序流程图 (9)六、数字调节器的求解 (11)6.1 基本参数的计算 (11)七、系统的仿真与分析 (13)7.1 θ=0时系统的仿真与分析 (13)7.2 θ=0时系统的可靠性与抗干扰性分析 (14)7.2 θ=0.4461时系统的仿真与分析 (16)7.3 θ=0.4461时系统的可靠性与抗干扰性分析 (17)八、设计总结与心得体会 (20)参考资料 (21)一、 设计任务一、题目设计1. 针对一个具有纯滞后的一阶惯性环节()1sKe G s Ts τ-=+的温度控制系统和给定的系统性能指标:✧ 工程要求相角裕度为30°~60°,幅值裕度>6dB✧ 要求测量范围-50℃~200℃,测量精度0.5%,分辨率0.2℃2. 书面设计一个计算机控制系统的硬件布线连接图,并转化为系统结构图 具体要求:✧ 温度传感器、执行机构的选型✧ 微型计算机的选型(MCS51、A VR 等等)✧ 温度传感器和单片机的接口电路✧ 其它扩展接口电路(主要是输入输出通道)✧ 利用Protel 绘制原理图,制作PCB 电路板(给出PCB 图)3. 软件部分:✧ 选择一种控制算法(最少拍无波纹或Dalin 算法)设计出控制器(被控对象由第4步中的参数确定),给出控制量的迭代算法,并借助软件工程知识编写程序流程图✧ 写出主要的单片机程序4. 用MATLAB 和SIMULINK 进行仿真分析和验证对象确定:K=10*log(C*C-sqrt(C)),rand(‘state ’,C), T=rand(1)考虑θ=0或T/2两种情况,即有延时和延时半个采样周期的情况。
纯滞后控制系统讲解

过程控制实验报告实验名称:纯滞后控制系统班级:姓名:学号:实验五 纯滞后系统一、实验目的1) 通过本实验,掌握纯滞后系统的基本概念和对系统性能的影响。
2) 了解纯滞后系统的常规控制方法和史密斯补偿控制方法。
二、 实验原理在工业生产中,被控对象除了容积延迟外,通常具有不同程度的纯延迟。
这类控制过程的特点是:当控制作用产生后,在滞后时间范围内,被控参数完全没有响应,使得系统不能及时随被控制量进行调整以克服系统所受的扰动。
因此,这样的过程必然会产生较明显的超调量和需要较长的调节时间。
所以,含有纯延迟的过程被公认为是较难控制的过程,其难控制程度随着纯滞后时间与整个过程动态时间参数的比例增加而增加。
一般认为,纯滞后时间与过程的时间常数之比大于0.3时,该过程是大滞后过程。
随此比值增加时,过程的相位滞后增加而使超调增大,在实际的生产过程中甚至会因为严重超调而出现聚爆、结焦等事故。
此外,大滞后会降低整个控制系统的稳定性。
因此大滞后过程的控制一直备受关注。
前馈控制系统主要特点如下:1) 在纯滞后系统控制中,为了充分发挥PID 的作用,改善滞后问题,主要采用常规PID 的变形形式:微分先行控制和中间微分控制。
微分先行控制和中间微分控制都是为了充分发挥微分作用提出的。
微分的作用是导前,根据变化规律提前求出其变化率,相当于提取信息的变化趋势,所以对滞后系统,充分利用微分作用,可以提前预知变化情况,进行有效的“提前控制”。
微分先行和中间微分反馈方法都能有效地克服超调现象,缩短调节时间,而且不需特殊设备。
因此,这两种控制形式都具有一定的实际应用价值。
但是这两种控制方式都仍有较大超调且响应速度很慢,不适于应用在控制精度要求很高的场合。
2) 史密斯补偿控制的基本思路是:在控制系统中某处采取措施(如增加环节,或增加控制支路等),使改变后系统的控制通道以及系统传递函数的分母不含有纯滞后环节,从而改善控制系统的控制性能及稳定性等。
天津大学计算机控制系统——第8.8课 (掌握)纯滞后控制系统设计—达林算法

8.4 纯滞后系统的设计—达林算法
5. 举例——基本达林算法设计
b)把G(z)带入标准控制器形式中 <1>选择T τ ,τ,写闭环z传递函数的形式, T 2s e 2 s p s 取 则 2s 2s 1
D z (1 e T T )(1 e T T1 z 1 )(1 e T T2 z 1 ) K (C1 C2 z 1 )[1 e T T z 1 1 e T T z N 1 ]
8.4 纯滞后系统的设计—达林算法
5. 举例——基本达林算法设计
输出 控制量
1 0.393z 3 Y z Rz z 1 z 1 1 0.607z 1 0.393z 3 0.632z 0.775z 5 0.865z 6 0.918z 7 0.950z 8
5. 举例——基本达林算法设计
已知
e 2 s Gp s , T 1s 1 s s
,试用达林算法设计
【解】 a)广义对象的离散化
1 e Ts 1 G z Z G p s z 2 1 z 1 Z 2 s s 1 s 1 3 0 . 368 1 0 . 718 z z 1 z 1 1 0 .368 z 1
1 e s T s 1
T 期望的闭环系统惯性时间常数
为对象纯滞后时间, NT ,N=1,2...
按照期望闭环特性,可保证系统具有一阶惯性环节和纯 滞后时间特性,以此代替最小拍多项式
8.4 纯滞后系统的设计—达林算法
3 达林算法的控制器特性
大林算法实验报告【范本模板】

大林算法实验报告 一、实验目的1、掌握大林控制算法的基本概念和实现方法;2、进一步熟悉MATLAB 的使用方法;3、掌握在MA TLAB 下大林算法控制器的调试方法;4、观察振铃现象,并且尝试消除振铃现象二、实验原理1.大林算法的原理及推导大林算法是IBM 公司的大林(Dahlin)在1968年提出了一种针对工业生产过程中含有纯滞后对象的控制算法。
其目标就是使整个闭环系统的传递函数 相当于一个带有纯滞后的一阶惯性环节。
该算法具有良好的控制效果。
大林控制算法的设计目标是使整个闭环系统所期望的传递函数φ(s ) 相当于一个延迟环节和一个惯性环节相串联,即:整个闭环系统的纯滞后时间和被控对象G 0(s )的纯滞后时间τ相同。
闭环系统的时间常数为T τ ,纯滞后时间τ与采样周期T 有整数倍关系, τ=NT 。
其控制器形式的推导的思路是用近似方法得到系统的闭环脉冲传递函数,然后再由被控系统的脉冲传递函数,反推系统控制器的脉冲传递函数。
由大林控制算法的设计目标,可知整个闭环系统的脉冲传递函数应 当是零阶保持器与理想的φ(s )串联之后的Z 变换,即φ(z )如下:对于被控对象为带有纯滞后的一阶惯性环节即:其与零阶保持器相串联的的脉冲传递函数为:1()1ss eT s ττφ-=+1/1()1(1)()=()11T s ττT/T s NT T -Y z e ee z z Z z R z s T s ezττφ------⎡⎤--==⋅=⋅⎢⎥+-⎣⎦011()11s NTs Ke KeG s T s T sτ--==++11/1/1111()11T T Ts sN T T eKe eG z Z Kz s T s ezτ-------⎡⎤--=⋅=⎢⎥+-⎣⎦于是相应的控制器形式为:11111(1)(1)()(1)1(1)T T T T T T T T N e e z D z K e e z e z τττ-----------=⎡⎤----⎣⎦2.振铃现象及其消除按大林算法设计的控制器可能会出现一种振铃现象,即数字控制器的输出以二分之一的采样频率大幅度衰减振荡,会造成执行机构的磨损. 在有交互作用的多参数控制系统中,振铃现象还有可能影响到系统的稳 定性。
大林控制算法实验报告

一、实验目的1. 理解大林控制算法的基本原理及其设计过程。
2. 掌握大林控制算法在计算机控制系统中的应用。
3. 通过实验验证大林控制算法在解决纯滞后系统控制问题上的有效性。
二、实验原理大林控制算法(Dahlin Control Algorithm)是一种针对具有纯滞后特性的控制对象而设计的新型控制算法。
该算法的核心思想是将期望的闭环响应设计成一阶惯性加纯延迟形式,然后通过反向设计得到满足这种闭环响应的控制器。
对于具有纯滞后特性的被控对象,其传递函数可以表示为:\[ G(s) = \frac{K}{T_s s + 1} \cdot e^{-\frac{s}{T}} \]其中,\( K \) 为系统增益,\( T_s \) 为采样周期,\( T \) 为纯滞后时间。
大林控制算法要求选择闭环传递函数 \( W(s) \) 时,采用相当于连续一阶惯性环节的 \( W(s) \) 来代替最少拍多项式。
如果对象有纯滞后,则 \( W(s) \) 应包含有同样的纯滞后环节。
带有纯滞后的控制系统闭环传递函数为:\[ W(s) = \frac{K}{T_s s + 1} \cdot e^{-\frac{s}{T}} \]根据大林控制算法,可以设计出满足期望闭环响应的数字控制器 \( D(z) \):\[ D(z) = \frac{K_1 e^{-\frac{1}{T}}}{(1 - e^{-\frac{1}{T_1}}) (1 - e^{-\frac{1}{T_2}})} \cdot \frac{1}{[1 - e^{-\frac{1}{T_1}} (1 - e^{-\frac{1}{T_2}})] (1 - e^{-\frac{1}{T} z^{-1}})} \]其中,\( K_1 \)、\( T_1 \) 和 \( T_2 \) 为大林算法的参数。
三、实验仪器1. MATLAB 6.5软件一套2. 个人PC机一台四、实验步骤1. 启动MATLAB软件,创建一个新的脚本文件。
计算机控制09.大林控制算法

常用控制算法>>大林控制算法
大林控制算法控制器D(z)的基本形式 的基本形式 大林控制算法控制器
Simulink仿真结构图为 仿真结构图为
Scope2 1-0.779z-1 1-0.607z-1 +-0.393z-3 controller
Scope1 1 4s+1 Zero-Order Hold Transfer Fcn Transport Delay Scope
其与零阶保持器相串联的的脉冲传递函数为: 其与零阶保持器相串联的的脉冲传递函数为:
1 − e −Ts K (C1 + C2 z −1 ) z − N −1 Ke − NTs G( z) = Z ⋅ = s (1 + T1s )(1 + T2 s ) (1 − e −T T1 z −1 )(1 − e −T T2 z −1 ) 1 C1 = 1 + (T1e−T / T1 − T2e−T / T2 ) T2 − T1 1 1 −T + C = e T1 T2 + 1 (T e −T / T2 − T e −T / T1 ) 1 2 2 T2 − T1
0.1493z−2(1+0.733z−1) G(z) = 1−0.7413z−1
选取φ(z),时间常数为 τ=2s,纯滞后时间为 时间常数为T 纯滞后时间为τ=1s。则N=1,于是 选取 时间常数为 纯滞后时间为 。 于是
−1/ 2 (1−e−T/Tτ )z−1 )z−1 0.3935z−2 −1 (1−e ⋅ =z ⋅ = −T /T -1 −1/2 -1 τ 1−e z 1−e z 1−0.6065z−1
CMAC与大林的复合控制在纯滞后系统中的应用

CMAC与大林的复合控制在纯滞后系统中的应用高小凤;李虹【摘要】一般工业控制中都会存在纯滞后现象,针对于纯滞后性质对控制系统稳定性的影响,采用在大林算法的基础上加入CMAC(小脑神经网络)的方法,CMAC 用于前馈控制,对大林控制器的输出进行学习,从而提高系统的响应速度,克服大林算法调节时间长的缺点。
文中给出了在MATLAB中编写的M文本文件控制器的仿真结果,进而将控制算法编写成函数文件,运用到SIMULINK仿真中,大大的提高了控制算法的实用性。
%General industrial control exists time delay,it influences the stability of the control system,adopting Dahlin andCMAC(Cerebella Model Articulation Controller)composite control can solve this problem,CMAC used for feed forward control to learn output of the Dahlin controller,thereby it improves the response speed of the system,and overcomes the disadvantages of long adjusting time of Dahlin algorithm.The results of M text file controller in MATLAB for simulation is presented,and then writing the algorithm into function used in SIMULINK simulation.It greatly improves the practicability of the control algorithm.【期刊名称】《电子设计工程》【年(卷),期】2012(020)020【总页数】3页(P93-95)【关键词】纯滞后系统;大林算法;CMAC;复合控制;SIMULINK仿真【作者】高小凤;李虹【作者单位】太原科技大学电子信息工程学院,山西太原030024;太原科技大学电子信息工程学院,山西太原030024【正文语种】中文【中图分类】TP273大多数工业过程中,例如锅炉温度控制过程,造纸、化工过程控制等,其控制系统一般为纯滞后系统,纯滞后性质会使系统的过渡过程时间加长、产生大幅度的超调,从而使控制品质变差,甚至会影响稳定性。
3.具有纯滞后系统的大林控制

实验三 具有纯滞后系统的大林控制一.实验目的通过混合仿真实验,学习并掌握用于具有纯滞后系统的大林控制算法的设计及其实现。
二.实验内容针对一个具有纯滞后的被控对象,设计并实现大林控制,并通过混合仿真实验观察振铃现象。
三.实验步骤1.设计并连接模拟具有一个惯性环节的被控对象的电路,利用C8051F060构成的数据处理系统完成计算机控制系统的模拟量输入、输出通道的设计和连接,利用上位机模拟被控对象的纯滞后。
利用上位机的虚拟仪器功能对此模拟被控对象的电路进行测试,根据测试结果调整电路参数,使它满足实验要求。
2.编制程序并运行,完成所设计的大林算法的控制计算,观察系统输出中的振铃现象。
3.对实验结果进行分析,并写出实验报告。
四.实验内容1.被控对象模拟与计算机闭环控制系统的构成 实验系统被控对象的传递函数为01()1s s Ke KG s T s θθ--=+上式中,滞后时间,这里取θT 为采样周期。
0T 按控制要求选择。
作为闭环控制的综合目标,与()s φ相对应的00/1/11(1)()[()]1T T Ts n T T e e z z Z s s e z φφ--------=⋅=- (8-3)而包含零阶保持器被控对象的S 传递函数为0111()()1Ts Ts se e Ke G s G s s s T s θ-----=⋅=⋅+ 离散化后得到11/1/1(1)()[()]1T T n T T K e z G z Z G s e z------==- (8-4)于是可以得到大林算法控制器的Z 传递函数01001//1///11(1)(1)()(1)[1(1)]T T T T T T T T T T n e e z D z K e e z e z -----------=---- (8-5)由此得到大林算法0000111///////()(1)(1)(1)(1)(1)()(1)(1)(1)T T T T T T T T T T T T T T u k e u k e u k n e e e e k e k K e K e -------=-+-----+⋅---- (8-6)五.实验过程1.模拟电路如图8.1所示。
纯滞后控制技术大林算法PPT学习教案

第15页/共19页
例:设
2.524(1 0.6065z 1) D(z)
(1 z 1)(1 z 1)(2 z 1)
如何消除振铃现象?
解:极点为:z1=1,z2=-1,z3=-0.5,z2和z3会产 生振铃现象,为了消除振铃现象,令z=1代入极点z2=- 1和z3=-0.5,得:
2.524(1 0.6065z 1) 2.524(1 0.6065z 1)
纯滞后控制技术大林算法
会计学
1
4.3.2 达林(Dahlin)算法
由于超调是主要的设计目标,一般的离散化设计方法 是不行的,PID效果也欠佳。
IBM公司的Dahlin在1968年提出了针对工业生产过程 中含有纯滞后控制对象的控制算法,取得了良好的效果。
1、数字控制器D(z)的形式
控制对象:Gc (s)由一或二阶惯性环节和纯滞后组成:
象 G(s) 1 ,经e1.4过6s T=1s的采样保持后,其广义对象的
3.34s 1
脉冲传递函数为
G(z)Biblioteka 0.1493z2 (1 0.733z1) 1 0.7413z1
选取Φ(z),时间常数为Tτ=2s,纯滞后时间为1s。则:
(
z
)
1
0.3935 z 2 0.6065z1
D(z)
1 G(z)
1
2
3
4
5
6
3
2.5
2
1.5
1
0.5
0
1
2
3
4
5
从图中,系统输出的采样值可按期望指数形式变化,但控 制量有大幅度的振荡,而且是衰减的振荡。
第9页/共19页
(A)带纯滞后的一阶惯性环节的系统
基于大林算法模型失配时滞控制系统的研究

基于大林算法模型失配时滞控制系统的研究郑仲桥;张燕红【摘要】研究工业控制对象的大时延特性所引起的不利影响,使系统能够得到有效控制,对于保证安全生产,实现工业过程的连续化、提高产品质量与经济效益都有着举足轻重的作用.本文针对典型的时滞系统退火炉为研究对象,炉中温度带有很大的滞后特性,使得系统控制变得困难,其严重影响系统的稳定性,会导致系统的超调量变大,调节时间也大大加长,甚至出现振荡和发散现象,系统的动态品质很差,研究应用大林算法实现稳定的控制并给出系统模型发生参数失配时的仿真结果.【期刊名称】《应用能源技术》【年(卷),期】2014(000)008【总页数】5页(P1-5)【关键词】时滞系统;退火炉;稳定性;大林算法;模型失配【作者】郑仲桥;张燕红【作者单位】常州工学院电子信息与电气工程学院,江苏常州213000;常州工学院电子信息与电气工程学院,江苏常州213000【正文语种】中文【中图分类】TF061.20 引言工业生产的大规模化使工业过程变得更为复杂,大时滞对工业过程控制系统的设计提出了更高的要求,因此需要更高级、更快速、更可靠和更有效的控制方法[1]。
在基于参数模型的控制方法中,Smith预估控制和Dahlin控制是最经典和最成熟的方法,它不仅使设定值和外部扰动输入的稳态误差为零,还可以结合很多智能控制方法形成各种改进的智能控制系统,提高控制的品质。
对于时滞系统模型的不确定性,非参数模型显得更为有效,因此智能控制开始进入时滞系统,其中模糊控制和神经网络控制可以发挥很大的作用。
神经网络有学习与适应严重不确定性动态特性的能力,并且具有很强的鲁棒性和容错性,模糊控制理论具有处理不精确信息的能力,从而使模糊控制能模仿人的经验对复杂被控对象进行专家式的控制,但是对于时滞过程,如何获得有效的控制规则仍然是一个难题。
自适应控制方法的出现又丰富了时滞系统的控制方法,它的其他方法结合形成了各种有效实用的新方法,有很大的优越性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
东南大学自动化学院
实验报告
课程名称:计算机控制技术基础
第四次实验
实验名称:具有纯滞后系统的大林控制
院(系):自动化学院专业:自动化
姓名:郭劲廷学号:08011331
实验室:常州楼419 实验组别:
同组人员:实验时间:2014 年 4 月28 日评定成绩:审阅教师:
实验五 具有纯滞后系统的大林控制
一、实验目的
1.了解大林控制算法的基本原理;
2.掌握用于具有纯滞后对象的大林控制算法及其在控制系统中的应用。
二、实验设备
1.THBDC-1型 控制理论·计算机控制技术实验平台 2.PCI-1711数据采集卡一块
3.PC 机1台(安装软件“VC++”及“THJK_Server ”)
三、实验原理
在生产过程中,大多数工业对象具有较大的纯滞后时间,对象的纯滞后时间τ对控制系统的控制性能极为不利,它使系统的稳定性降低,过渡过程特性变坏。
当对象的纯滞后时间
τ与对象的惯性时间常数T1之比,即τ/T1≥0.5时,采用常规的比例积分微分(PID )控制,
很难获得良好的控制性能。
长期以来,人们对纯滞后对象的控制作了大量的研究,比较有代表性的方法有大林算法和纯滞后补偿(Smith 预估)控制。
本实验以大林算法为依据进行研究,大林算法的被控对象是带纯滞后的一阶或二阶惯性环节。
即
1
)(1+=
-s T Ke s G s
τ 或 )
1)(1()(21++=-s T s T Ke s G s
τ
本实验被控对象为带纯滞后的一阶惯性环节。
式中:τ为纯滞后时间,为方便起见假设为采样周期T 的整数倍
NT =τ
大林算法的主要设计目标是系统在单位阶跃输入作用下,整个闭环系统的传递函数相当于一个延迟环节和一个惯性环节相串联。
即
1
)(0+=
-s T e s H s
τ (5-1) 要求整个闭环系统的纯滞后时间等于被控对象的纯滞后时间。
与H(s)相对应的闭环系统脉冲传递函数为
01()[]1
sT NTs
e e H z Z s T s ---=⋅+
101(1)[]
(1)N
z
z Z s T s
--=-+ 0
1
1
11(1)(1)
(1)(1)
T
T N
T T e
z z
z z e z -
-------=---00
(1)
1
(1)1T T N T T e
z e
z -
-+-
--=
- (5-2)
将上式代入式1()()()1()
H z D z G z H z =
⋅-中,得 0
(1)
1(1)(1)()()[1(1)]
T T N T T T T N e
z D z G z e
z e z -
-+----+-=
--- (5-3)
当对象为一阶惯性环节加纯滞后时
11()[]1
sT NTs
e Ke G z Z s T s ---=⋅+
111
(1)[
](1)
N Kz z Z s T s --=-+
1
1
1
1
11(1)(1)
(1)(1)
T T N
T T e
z Kz
z z e z -
-------=---
1
1
(1)
1
(1)
1T T N T T e Kz e
z -
-+-
--=- (5-4)
将式(5-4)代入式(5-3)得一阶惯性环节的控制器的D(z)为
01
1
11(1)(1)(1)
()(1)[1(1)]
T T T T T T T T T T N e
e
z D z K e
e
z e
z -
-
--
----+--=
----
由上式,控制算法为
)1()
1()1()()
1(1)1()1()1()(1
1
1
00
------+
---+-=-
-
-
--
--k e e
K e
e
k e e K e
N k u e k u e
k u T T T T T T T T T T T T T T。
