最新四川德阳市数学七年级试卷(含答案)

合集下载

四川省德阳市德阳中学校2023-2024学年七年级下学期期中数学试题

四川省德阳市德阳中学校2023-2024学年七年级下学期期中数学试题一、单选题1．16 的平方根是( )A ．8B ．256C ．±4D ．42．在平面直角坐标中，点(2,3)M -在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 3．下列各式中，正确的是（）A 2=-B 123C 34=±D 0.6= 4．如图，若AB ，CD 相交于点O ，过点O 作OE ⊥AB ，则下列结论不正确的是（）A ．∠1与∠2互为余角B ．∠3与∠2互为余角C ．∠2与∠AOE 互为补角D ．∠AOC 与∠BOD 是对顶角5．如图，直角坐标系中四边形的面积是（）A ．4B ．5.5C ．4.5D ．56．把一根10m 长的钢管裁成2m 长和1m 长两种规格的钢管（每种规格至少有一根），在不浪费的情况下，它的裁法有（）A ．3种B ．4种C ．5种D ．6种7．在平面直角坐标系中，点A 坐标为（﹣3，2），AB ∥x 轴，且AB ＝5，则点B 的坐标为（）A．（﹣8，2）B．（﹣8，2）或（2，2）C．（﹣3，7）D．（﹣3，7）或（﹣3，﹣3）8．如图，已知P是三角形ABC的边AB上一个动点，AB＝6，三角形ABC的面积为12，则CP的最小长度为（）A．1 B．2 C．3 D．49．如图，把两个边长分别为1，2的小长方形沿对角线剪开，将所得的4个直角三角形拼在一起，就得到一个正方形ABCD（中间空心部分记为正方形A′B′C′D′．下列说法错误的是（）A．小正方形A'B'C′D′的边长为1 B．每个直角三角形的面积为1C．大正方形ABCD面积是小正方形A′B′C′D′面积的4倍D．大正方形ABCD的边长为10．若关于x，y的方程组48ax byax by-=-⎧⎨+=⎩的解是23xy=⎧⎨=⎩，则方程组(3)(1)4(3)(1)8a xb ya xb y+--=-⎧⎨++-=⎩的解是（）A．14xy=-⎧⎨=⎩B．23xy=⎧⎨=⎩C．14xy=⎧⎨=-⎩D．52xy=⎧⎨=⎩11．《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，根据题意得（）A ．11910813x y y x x y =⎧⎨+-+=⎩（）（） B ．10891311y x x y x y +=+⎧⎨+=⎩C ．91181013x y x y y x （）（）=⎧⎨+-+=⎩ D ．91110813x y y x x y =⎧⎨+-+=⎩（）（） 12．如图，在一个单位为1的方格纸上，△A 1A 2A 3，△A 3A 4A 5，△A 5A 6A 7，…，是斜边在x 轴上，斜边长分别为2，4，6，…的等腰直角三角形．若△A 1A 2A 3的顶点坐标分别为A 1（2，0），A 2（1，﹣1），A 3（0，0），则依图中所示从律，A 2022的纵坐标为（）A ．﹣1010B ．1010C ．﹣1011D ．1011二、填空题13．164的立方根是． 14．已知P （1﹣m ，m ＋2）在x 轴上，则点P 的坐标是．15．若关于x ，y 的方程351225a b x y -+-=是二元一次方程，则a b +=．16．如图，把长方形ABCD 沿着直线EF 对折，折痕为EF ，若∠AFE ＝62°，则∠CEB ′＝．17．如果方程组23759x y x y +=⎧⎨-=⎩，的解是方程716x my +=的一个解，则m 的值为． 18．如图，直线MN ∥PQ ，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连接AB ．∠ABM 的平分线BC 交PQ 于点C ，连接AC ，过点A 作AD ⊥PQ 交PQ 于点D ，作AF ⊥AB 交PQ于点F ，AE 平分∠DAF 交PQ 于点E ，若∠CAE=45°，∠ACB =52∠DAE ，则∠ACD 的度数是．三、解答题19．（1）计算：5| （2）解方程：30()271125x --+=；（3）解方程组：20346x y x y +=⎧⎨+=⎩①②． 20．如图，正方形ABCD 的顶点A ，C 的坐标分别为()5,6-和()1,2-．(1)画出平面直角坐标系，并写出点B ，D 的坐标；(2)将正方形ABCD平移，使4个顶点到原点的距离相等，画出平移后的正方形EFGH，并写出平移方式．21．如表中每一对x，y的值满足方程ax＋by＝2．（1）求a，b的值；（2）若关于x，y的方程组423ax by mx y m-=+⎧⎨+=⎩的解满足方程3x﹣2y＝﹣10，求m的值．22．完成下面的证明与解题．如图，AD∥BC，点E是BA延长线上一点，∠E＝∠DCE．（1）求证：∠B＝∠D．证明：∵AD∥BC，∴∠B＝∠______________（______________）∵∠E＝∠DCE，∴AB∥CD（______________）．∴∠D＝∠______________（______________）．∴∠B＝∠D．（2）若CE平分∠BCD，∠E＝50°，求∠B的度数．23．小丽购买学习用品的收据如表，因污损导致部分数据无法识别，根据下表，解决下列问题：(1)小丽买了自动铅笔、记号笔各几支？(2)若小丽再次购买软皮笔记本和自动铅笔两种文具，共花费15元，则有哪几种不同的购买方案？24．已知AB CD ∥，AM 平分BAP ∠．(1)如图1，当点P ，M 在CD 上时，写出APC ∠与AMC ∠的数量关系，并说明理由．(2)如图2，当点P 在AB ，CD 之间，且在AC 连线右侧，点M 仍在CD 上时，写出P ∠，C ∠，AMC ∠间的数量关系，并说明理由．25．如图，在平面直角坐标系中，点A （a ，0）在x 轴负半轴上，点C （2,0）在x 正半轴上，点B （0，b ）在y 轴正半轴上，并且a 、b 是方程组2356a b a b +=-⎧⎨+=⎩的解，连接AB 、BC ．（1）a =________，b =________；（2）经过计算AB=10，动点M 从点A 出发，沿射线AB 以每秒2个单位长度的速度匀速运动，连接MC ，设点M 的运动时间为t （t>0）秒，用含t 的式子表示△BCM 的面积S ，并直接写出t 的取值范围；（3）在（2）的条件下，点N 在线段BC 上，且BN=2CN ，连接MN.当三角形BMN 的面积为8时，求t 值，并直接写出点M 的坐标.。

德阳市七年级上册数学期末试卷(含答案)

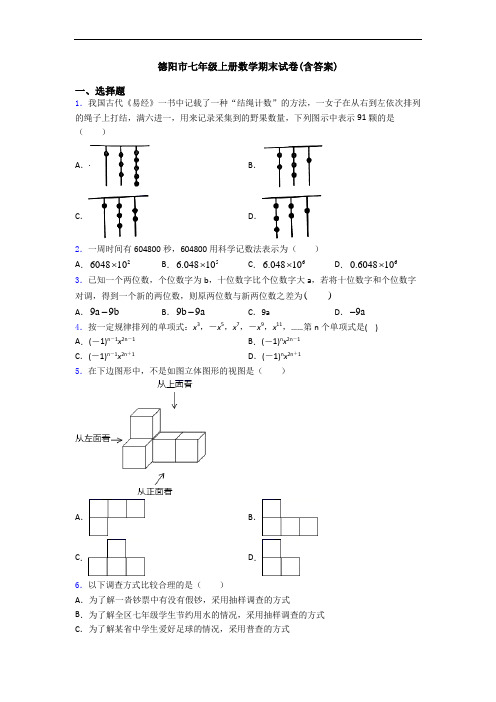
德阳市七年级上册数学期末试卷(含答案)一、选择题1．我国古代《易经》一书中记载了一种“结绳计数”的方法，一女子在从右到左依次排列的绳子上打结，满六进一，用来记录采集到的野果数量，下列图示中表示91颗的是（）A ．B ．C ．D ．2．一周时间有604800秒，604800用科学记数法表示为（） A ．2604810⨯B ．56.04810⨯C ．66.04810⨯D ．60.604810⨯3．已知一个两位数，个位数字为b ，十位数字比个位数字大a ，若将十位数字和个位数字对调，得到一个新的两位数，则原两位数与新两位数之差为( ) A ．9a 9b - B ．9b 9a -C ．9aD ．9a -4．按一定规律排列的单项式：x 3，－x 5，x 7，－x 9，x 11，……第n 个单项式是( )A ．(－1)n －1x 2n －1B ．(－1)n x 2n －1C ．(－1)n －1x 2n ＋1D ．(－1)n x 2n ＋15．在下边图形中，不是如图立体图形的视图是（）A ．B ．C ．D ．6．以下调查方式比较合理的是（）A ．为了解一沓钞票中有没有假钞，采用抽样调查的方式B ．为了解全区七年级学生节约用水的情况，采用抽样调查的方式C ．为了解某省中学生爱好足球的情况，采用普查的方式D ．为了解某市市民每天丢弃塑料袋数量的情况，采用普查的方式 7．点()5,3M 在第( )象限． A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 8．下列各数中,有理数是( )A ．2B ．πC ．3.14D ．379．若a<b,则下列式子一定成立的是( ) A ．a+c>b+cB ．a-c<b-cC ．ac<bcD ．a b c c< 10．估算15在下列哪两个整数之间( ) A ．1，2 B ．2，3C ．3，4D ．4，511．“植树时只要定出两棵树的位置，就能确定这一行树所在的直线”，用数学知识解释其道理应是（） A ．两点确定一条直线 B ．两点之间，线段最短C ．直线可以向两边延长D ．两点之间线段的长度，叫做这两点之间的距离12．某商店有两个进价不同的计算器都卖了135元，其中一个盈利25%，另一个亏本25%，在这次买卖中，这家商店( ) A ．不赔不赚 B ．赚了9元 C ．赚了18元 D ．赔了18元 13．若2m ab -与162n a b -是同类项，则m n +=（）A ．3B ．4C ．5D ．714．如图，两块直角三角板的直角顶点O 重叠在一起，且OB 恰好平分COD ∠，则AOD∠的度数为（）A ．100B ．120C ．135D ．15015．如图为一无盖长方体盒子的展开图（重叠部分不计），可知该无盖长方体的容积为（）A ．8B ．12C ．18D ．20二、填空题16．一个角的余角等于这个角的13，这个角的度数为________. 17．2019年11月11日是第11个“双十一”购物狂欢节，天猫“双十一”总成交额为2684亿，再创历史新高；其中，“2684亿”用科学记数法表示为__________． 18．若x ＝2是关于x 的方程5x +a ＝3（x +3）的解，则a 的值是_____．19．甲、乙两地海拔高度分别为20米和﹣9米，那么甲地比乙地高_____米．20．若523m x y +与2n x y 的和仍为单项式，则n m =__________.21．﹣213的倒数为_____，﹣213的相反数是_____． 22．若12x y =⎧⎨=⎩是方程组72ax by bx ay +=⎧⎨+=⎩的解，则+a b =_________.23．15030'的补角是______．24．学校某兴趣活动小组现有男生30人，女生8人，还要录取女生多少人，才能使女生人数占该活动小组总人数的三分之一？设还要录取女生x 人，依题意列方程得_____． 25．已知线段AB=8cm ，在直线AB 上画线段BC ，使它等于3cm ，则线段AC=______cm ． 26．规定：用{m }表示大于 m 的最小整数，例如{52}= 3，{4} = 5，{-1.5}= -1等；用[m ] 表示不大于 m 的最大整数，例如[72]= 3， [2]= 2，[-3.2]= -4，如果整数 x 满足关系式：3{x }+2[x ]=23，则 x =________________.27．一个水库的水位变化情况记录：如果把水位上升5cm 记作+5cm ，那么水位下降3cm 时水位变化记作_____．28．单项式()26a bc -的系数为______，次数为______.29．已知7635a ∠=︒'，则a ∠的补角为______°______′.30．如图都是由同样大小的黑棋子按一定规律摆出的图案，第①个图案有4个黑棋子，第②个图案有9个黑棋子，第③个图案有14个黑棋子，…，依此规律，第n 个图案有2019个黑棋子，则n=______．三、压轴题31．如图1，O 为直线AB 上一点，过点O 作射线OC ，∠AOC ＝30°，将一直角三角板（其中∠P ＝30°）的直角顶点放在点O 处，一边OQ 在射线OA 上，另一边OP 与OC 都在直线AB 的上方．将图1中的三角板绕点O 以每秒3°的速度沿顺时针方向旋转一周．（1）如图2，经过t 秒后，OP 恰好平分∠BOC ． ①求t 的值；②此时OQ 是否平分∠AOC ？请说明理由；（2）若在三角板转动的同时，射线OC 也绕O 点以每秒6°的速度沿顺时针方向旋转一周，如图3，那么经过多长时间OC 平分∠POQ ？请说明理由；（3）在（2）问的基础上，经过多少秒OC 平分∠POB ？（直接写出结果）．32．如图，以长方形OBCD 的顶点O 为坐标原点建立平面直角坐标系，B 点坐标为（0，a ），C 点坐标为（c ，b ），且a 、b 、C 满足6a ++|2b+12|+（c ﹣4）2＝0．（1）求B 、C 两点的坐标；（2）动点P 从点O 出发，沿O→B→C 的路线以每秒2个单位长度的速度匀速运动，设点P 的运动时间为t 秒，DC 上有一点M （4，﹣3），用含t 的式子表示三角形OPM 的面积；（3）当t 为何值时，三角形OPM 的面积是长方形OBCD 面积的13？直接写出此时点P 的坐标．33．如图，数轴上有A ， B 两点，分别表示的数为a ，b ，且()225350a b ++-=．点P 从A 点出发以每秒13个单位长度的速度沿数轴向右匀速运动，当它到达B 点后立即以相同的速度返回往A 点运动，并持续在A ，B 两点间往返运动．在点P 出发的同时，点Q 从B 点出发以每秒2个单位长度向左匀速运动，当点Q 达到A 点时，点P ，Q 停止运动．（1）填空：a = ，b = ；（2）求运动了多长时间后，点P ，Q 第一次相遇，以及相遇点所表示的数；（3）求当点P ，Q 停止运动时，点P 所在的位置表示的数；（4）在整个运动过程中，点P 和点Q 一共相遇了几次．（直接写出答案）34．如图，直线l上有A、B两点，点O是线段AB上的一点，且OA=10cm，OB=5cm．（1）若点C是线段AB的中点，求线段CO的长．（2）若动点P、Q分别从 A、B同时出发，向右运动，点P的速度为4c m/s，点Q的速度为3c m/s，设运动时间为x秒，①当x=__________秒时，PQ=1cm；②若点M从点O以7c m/s的速度与P、Q两点同时向右运动，是否存在常数m，使得4PM+3OQ﹣mOM为定值，若存在请求出m值以及这个定值；若不存在，请说明理由．（3）若有两条射线OC、OD均从射线OA同时绕点O顺时针方向旋转，OC旋转的速度为6度/秒，OD旋转的速度为2度/秒.当OC与OD第一次重合时，OC、OD同时停止旋转，设旋转时间为t秒，当t为何值时，射线OC⊥OD？35．如图：在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a、c满足|a+2|+（c-7）2=0．（1）a=______，b=______，c=______；（2）若将数轴折叠，使得A点与C点重合，则点B与数______表示的点重合；（3）点A、B、C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，假设t秒钟过后，若点A与点B之间的距离表示为AB，点A与点C之间的距离表示为AC，点B与点C 之间的距离表示为BC．则AB=______，AC=______，BC=______．（用含t的代数式表示）.（4）直接写出点B为AC中点时的t的值.36．如图，A、B、P是数轴上的三个点，P是AB的中点，A、B所对应的数值分别为-20和40．（1）试求P点对应的数值；若点A、B对应的数值分别是a和b，试用a、b的代数式表示P点在数轴上所对应的数值；（2）若A、B、P三点同时一起在数轴上做匀速直线运动，A、B两点相向而行，P点在动点A和B之间做触点折返运动（即P点在运动过程中触碰到A、B任意一点就改变运动方向，向相反方向运动，速度不变，触点时间忽略不计），直至A、B两点相遇，停止运动．如果A、B、P运动的速度分别是1个单位长度/s，2个单位长度/s，3个单位长度/s，设运动时间为t．①求整个运动过程中，P点所运动的路程．②若P点用最短的时间首次碰到A点，且与B点未碰到，试写出该过程中，P点经过t秒钟后，在数轴上对应的数值（用含t的式子表示）；③在②的条件下，是否存在时间t，使P点刚好在A、B两点间距离的中点上，如果存在，请求出t值，如果不存在，请说明理由．37．问题一：如图1，已知A，C两点之间的距离为16 cm，甲，乙两点分别从相距3cm的A，B两点同时出发到C点，若甲的速度为8 cm/s，乙的速度为6 cm/s，设乙运动时间为x（s），甲乙两点之间距离为y（cm）．(1)当甲追上乙时，x = ．(2)请用含x的代数式表示y．当甲追上乙前，y= ；当甲追上乙后，甲到达C之前，y= ；当甲到达C之后，乙到达C之前，y= ．问题二：如图2，若将上述线段AC弯曲后视作钟表外围的一部分，线段AB正好对应钟表上的弧AB（1小时的间隔），易知∠AOB=30°．(1)分针OD指向圆周上的点的速度为每分钟转动 cm；时针OE指向圆周上的点的速度为每分钟转动 cm．(2)若从4：00起计时，求几分钟后分针与时针第一次重合．38．如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.(1)若点P到点A，B的距离相等，求点P对应的数x的值．(2)数轴上是否存在点P，使点P到点A，B的距离之和为8？若存在，请求出x的值；若不存在，说明理由．(3)点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以5个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间．当点A与点B重合时，点P经过的总路程是多少？【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【解析】【分析】由于从右到左依次排列的绳子上打结，满六进一，所以从右到左的数分别进行计算，然后把它们相加即可得出正确答案．【详解】解：A 、5+3×6+1×6×6＝59（颗），故本选项错误； B 、1+3×6+2×6×6＝91（颗），故本选项正确； C 、2+3×6+1×6×6＝56（颗），故本选项错误； D 、1+2×6+3×6×6＝121（颗），故本选项错误；故选：B ．【点睛】本题是以古代“结绳计数”为背景，按满六进一计数，运用了类比的方法，根据图中的数学列式计算；本题题型新颖，一方面让学生了解了古代的数学知识，另一方面也考查了学生的思维能力．2．B解析：B 【解析】【分析】科学记数法的表示形式为10n a ⨯的形式，其中110,a n ≤<为整数．确定n 的值时，要看把原数变成a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同．当原数绝对值1>时，n 是正数；当原数的绝对值1<时，n 是负数．【详解】604800的小数点向左移动5位得到6.048，所以数字604800用科学记数法表示为56.04810⨯，故选B ．【点睛】本题考查科学记数法的表示方法．科学记数法的表示形式为10n a ⨯的形式，其中110,a n ≤<为整数，表示时关键要正确确定a 的值以及n 的值． 3．C解析：C 【解析】【分析】分别表示出愿两位数和新两位数，进而得出答案．【详解】解：由题意可得，原数为：()10a b b ++；新数为：10b a b ++，故原两位数与新两位数之差为：()()10a b b 10b a b 9a ++-++=．故选C ．【点睛】本题考查列代数式，正确理解题意得出代数式是解题关键．4．C解析：C 【解析】【分析】观察可知奇数项为正，偶数项为负，除符号外，底数均为x ，指数比所在项序数的2倍多1，由此即可得. 【详解】观察可知，奇数项系数为正，偶数项系数为负，∴可以用1(1)n --或1(1)n +-，(n 为大于等于1的整数)来控制正负，指数为从第3开始的奇数，所以指数部分规律为21n ， ∴第n 个单项式是 (－1)n －1x 2n ＋1 ，故选C. 【点睛】本题考查了规律题——数字的变化类，正确分析出哪些不变，哪些变，是按什么规律发生变化的是解题的关键.5．C解析：C 【解析】【分析】直接利用简单组合体的三视图进而判断得出答案．【详解】解：A 选项为该立体图形的俯视图，不合题意；B 选项为该立体图形的主视图，不合题意；C 选项不是如图立体图形的视图，符合题意；D 选项为该立体图形的左视图，不合题意．故选：C ．【点睛】此题主要考查了简单组合体的三视图，正确掌握观察角度是解题关键．6．B解析：B【分析】抽取样本注意事项就是要考虑样本具有广泛性与代表性，所谓代表性，就是抽取的样本必须是随机的，即各个方面，各个层次的对象都要有所体现．【详解】解：A ．为了解一沓钞票中有没有假钞，采用全面调查的方式，故不符合题意； B ．为了解全区七年级学生节约用水的情况，采用抽样调查的方式，故符合题意； C ．为了解某省中学生爱好足球的情况，采用抽样调查的方式，故不符合题意； D ．为了解某市市民每天丢弃塑料袋数量的情况，采用抽样调查的方式，故不符合题意；故选：B ．【点睛】本题考查的是抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．7．A解析：A 【解析】【分析】根据平面直角坐标系中点的坐标特征判断即可. 【详解】 ∵5>0,3>0,∴点()5,3M 在第一象限．故选A. 【点睛】本题考查了平面直角坐标系中点的坐标特征.第一象限内点的坐标特征为（+，+），第二象限内点的坐标特征为（-，+），第三象限内点的坐标特征为（-，-），第四象限内点的坐标特征为（+，-），x 轴上的点纵坐标为0，y 轴上的点横坐标为0.8．C解析：C 【解析】【分析】根据有理数及无理数的概念逐一进行分析即可得. 【详解】B. π是无理数，故不符合题意；C. 3.14是有理数，故符合题意；D. 故选C.本题考查了有理数与无理数，熟练掌握有理数与无理数的概念是解题的关键.9．B解析：B【解析】【分析】根据不等式的基本性质逐一进行分析判断即可.【详解】A.由a<b，两边同时加上c，可得 a+c<b+c，故A选项错误，不符合题意；B. 由a<b，两边同时减去c，得a-c<b-c，故B选项正确，符合题意；C. 由a<b，当c>0时，ac<bc，当c<0时，ac<bc，当c=0时，ac=bc，故C选项错误，不符合题意；D.由 a<b，当a>0，c≠0时，a bc c<，当a<0时，a bc c>，故D选项错误，故选B.【点睛】本题考查了不等式的基本性质，熟练掌握不等式的基本性质是解题的关键.10．C解析：C【解析】【分析】.【详解】∵9<15<16，∴，故选C.【点睛】本题考查了无理数的估算，现实生活中经常需要估算，估算应是我们具备的数学能力，“夹逼法”是估算的一般方法，也是常用方法．11．A解析：A【解析】【分析】根据题目可知：两棵树的连线确定了一条直线，可将两棵树看做两个点，再运用直线的公理可得出答案.【详解】解：“植树时只要定出两棵树的位置，就能确定这一行树所在的直线”，这种做法运用到的数学知识是“两点确定一条直线”.故答案为：A.【点睛】本题考查的知识点是直线公理的实际运用，易于理解掌握.12．D解析：D【解析】试题分析：设盈利的这件成本为x 元，则135－x=25%x ，解得：x=108元；亏本的这件成本为y 元，则y －135=25%y ，解得：y=180元，则135×2－(108+180)=－18元，即赔了18元．考点：一元一次方程的应用.13．C解析：C【解析】【分析】根据同类项的概念求得m 、n 的值，代入m n +即可．【详解】解：∵2m ab -与162n a b -是同类项，∴2m=6，n-1=1，∴m=3，n=2，则325m n +=+=．故选：C ．【点睛】本题考查了同类项的知识，解答本题的关键是掌握同类项定义中的两个“相同”：相同字母的指数相同．14．C解析：C【解析】【分析】首先根据角平分线性质得出∠COB=∠BOD=45°，再根据角的和差得出∠AOC=45°，从而得出答案．【详解】解：∵OB 平分∠COD ，∴∠COB=∠BOD=45°，∵∠AOB=90°，∴∠AOC=45°，∴∠AOD=135°．故选：C ．【点睛】本题考查了角的平分线角的性质和角的和差，角平分线的性质是将两个角分成相等的两个角．15．A解析：A【解析】【分析】根据观察、计算可得长方体的长、宽、高，根据长方体的体积公式，可得答案．【详解】解：由图可知长方体的高是1，宽是3-1=2，长是6-2=4，长方体的容积是4×2×1=8，故选：A．【点睛】本题考查了几何体的展开图.能判断出该几何体为长方体的展开图，并能根据展开图求得长方体的长、宽、高是解题关键.二、填空题16．【解析】【分析】设这个角度的度数为x度，根据题意列出方程即可求解.【详解】设这个角度的度数为x度，依题意得90-x=解得x=67.5故填【点睛】此题主要考查角度的求解，解题的关键是解析：67.5【解析】【分析】设这个角度的度数为x度，根据题意列出方程即可求解.【详解】设这个角度的度数为x度，依题意得90-x=1 3 x解得x=67.5故填67.5【点睛】此题主要考查角度的求解，解题的关键是熟知补角的性质. 17．684×1011【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．解析：684×1011【解析】【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【详解】解：将 2684 亿用科学记数法表示为：2.684×1011．故答案为：2.684×1011【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．18．5【解析】【分析】把x＝2代入方程求出a的值即可．【详解】解：∵关于x的方程5x+a＝3（x+3）的解是x＝2，∴10+a＝15，∴a＝5，故答案为5．【点睛】本题考查了方程的解解析：5【解析】【分析】把x＝2代入方程求出a的值即可．【详解】解：∵关于x的方程5x+a＝3（x+3）的解是x＝2，∴10+a＝15，∴a＝5，故答案为5．【点睛】本题考查了方程的解，掌握方程的解的意义解答本题的关键.19．【解析】【分析】根据题意可得20﹣（﹣9），再根据有理数的减法法则进行计算即可．【详解】解：20﹣（﹣9）＝20+9＝29，故答案为：29．【点睛】此题主要考查了有理数的减法，关键是解析：【解析】【分析】根据题意可得20﹣（﹣9），再根据有理数的减法法则进行计算即可．【详解】解：20﹣（﹣9）＝20+9＝29，故答案为：29．【点睛】此题主要考查了有理数的减法，关键是掌握减去一个数，等于加上这个数的相反数． 20．9【解析】根据与的和仍为单项式,可知与是同类项,所以,解得,所以,故答案为:9. 解析：9【解析】根据523m x y +与2n x y 的和仍为单项式,可知523m x y +与2n x y 是同类项,所以52m +=,解得m 3,n 2=-=,所以()239n m =-=,故答案为:9.21．﹣ 2【解析】【分析】根据乘积是1的两数互为倒数；只有符号不同的两个数叫做互为相反数可得答案．【详解】﹣2的倒数为﹣，﹣2的相反数是2．【点睛】本题考查的是相反数和倒数，解析：﹣37 213【解析】【分析】根据乘积是1的两数互为倒数；只有符号不同的两个数叫做互为相反数可得答案．【详解】﹣213的倒数为﹣37，﹣213的相反数是213．【点睛】本题考查的是相反数和倒数，熟练掌握两者的性质是解题的关键.22．3【解析】【分析】把x与y的值代入方程组得到关于a和b的方程组，然后整体求出a＋b的值即可．【详解】解：把代入方程组得：，①＋②得：3（a＋b）＝9，则a＋b＝3，故答案为：3.【解析：3【解析】【分析】把x与y的值代入方程组得到关于a和b的方程组，然后整体求出a＋b的值即可．【详解】解：把12xy=⎧⎨=⎩代入方程组得：2722a bb a+=⎧⎨+=⎩，①＋②得：3（a＋b）＝9，则a＋b＝3，故答案为：3.【点睛】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．23．【解析】【分析】利用补角的意义：两角之和等于180°，那么这两个角互为补角其中一个角叫做另一个角的补角直接列式计算即可．【详解】解：．故答案为．【点睛】此题考查补角的意义，以及度分秒解析：2930'【解析】【分析】利用补角的意义：两角之和等于180°，那么这两个角互为补角其中一个角叫做另一个角的补角直接列式计算即可．【详解】解：18015030'2930'-=．故答案为2930'．【点睛】此题考查补角的意义，以及度分秒之间的计算，注意借1当60．24．8+x ＝（30+8+x ）．【解析】【分析】设还要录取女生人，则女生总人数为人，数学活动小组总人数为人，根据女生人数占数学活动小组总人数的列方程．【详解】解：设还要录取女生人，根据题意得：解析：8+x ＝13（30+8+x ）．【解析】【分析】设还要录取女生x 人，则女生总人数为8x +人，数学活动小组总人数为308x ++人，根据女生人数占数学活动小组总人数的13列方程．【详解】解：设还要录取女生x 人，根据题意得：18(308)3x x +=++．故答案为：18(308)3x x +=++．【点睛】此题考查了由实际问题抽象出一元一次方程，关键是准确表示还要录取后女生的人数及总人数．25．5或11【解析】【分析】由于C 点的位置不能确定，故要分两种情况考虑AC 的长，注意不要漏解．【详解】由于C 点的位置不确定，故要分两种情况讨论：当C 点在B 点右侧时，如图所示：AC=AB+解析：5或11【解析】【分析】由于C 点的位置不能确定，故要分两种情况考虑AC 的长，注意不要漏解．【详解】由于C 点的位置不确定，故要分两种情况讨论：当C 点在B 点右侧时，如图所示：AC=AB+BC=8+3=11cm ；当C 点在B 点左侧时，如图所示：AC=AB ﹣BC=8﹣3=5cm ；所以线段AC 等于11cm 或5cm.26．4【解析】【分析】由题意可得，求解即可.【详解】解：解得故答案为：4【点睛】本题属于新定义题型，正确理解{m}和[m]的含义是解题的关键.解析：4【解析】【分析】由题意可得{}[]1,x x x x =+=，求解即可.【详解】解：{}[]323(1)25323x x x x x +=++=+=解得4x =故答案为：4【点睛】本题属于新定义题型，正确理解{m }和[m ]的含义是解题的关键. 27．﹣3cm【解析】【分析】首先审清题意，明确“正”和“负”所表示的意义，再根据题意作答．【详解】解：因为上升记为+，所以下降记为﹣，所以水位下降3cm 时水位变化记作﹣3c m ．故答案为：﹣3解析：﹣3cm【解析】【分析】首先审清题意，明确“正”和“负”所表示的意义，再根据题意作答．【详解】解：因为上升记为+，所以下降记为﹣，所以水位下降3cm 时水位变化记作﹣3cm ．故答案为：﹣3cm ．【点睛】此题主要考查有理数的应用，解题的关键是熟知有理数的意义.28．【解析】【分析】根据定义：单项式的次数是指单项式中所有字母的指数和；单项式的系数是单项式中的数字因数，即可得解.【详解】单项式的系数为；次数为2+1+1=4；故答案为；4.【点睛】此解析：16- 【解析】【分析】根据定义：单项式的次数是指单项式中所有字母的指数和；单项式的系数是单项式中的数字因数，即可得解.单项式()26a bc -的系数为16-；次数为2+1+1=4；故答案为16-；4. 【点睛】此题主要考查对单项式系数和次数的理解，熟练掌握，即可解题.29．25【解析】【分析】根据补角的概念，两个角加起来等于180°，就是互为补角，即可求解.【详解】的补角为故答案为103；25.【点睛】此题主要考查补角的求解，熟练掌握，即可解题解析：25【解析】【分析】根据补角的概念，两个角加起来等于180°，就是互为补角，即可求解.【详解】a ∠的补角为180762313550'='︒-︒︒故答案为103；25.【点睛】此题主要考查补角的求解，熟练掌握，即可解题.30．404【解析】【分析】仔细观察每一个图形中黑棋子的个数与图形序列号的关系，找到规律，利用规律求解即可．【详解】解：观察图1有5×1-1=4个黑棋子；图2有5×2-1=9个黑棋子；图3有解析：404【解析】仔细观察每一个图形中黑棋子的个数与图形序列号的关系，找到规律，利用规律求解即可．【详解】解：观察图1有5×1-1=4个黑棋子；图2有5×2-1=9个黑棋子；图3有5×3-1=14个黑棋子；图4有5×4-1=19个黑棋子；…图n有5n-1个黑棋子，当5n-1=2019，解得：n=404，故答案：404.【点睛】本题考查探索与表达规律——图形类规律探究.能根据题中已给图形找出黑棋子的数量与序数之间的规律是解决此题的关键.三、压轴题31．（1）①5；②OQ平分∠AOC，理由详见解析；（2）5秒或65秒时OC平分∠POQ；（3）t＝703秒．【解析】【分析】（1）①由∠AOC＝30°得到∠BOC＝150°，借助角平分线定义求出∠POC度数，根据角的和差关系求出∠COQ度数，再算出旋转角∠AOQ度数，最后除以旋转速度3即可求出t 值；②根据∠AOQ和∠COQ度数比较判断即可；（2）根据旋转的速度和起始位置，可知∠AOQ＝3t，∠AOC＝30°+6t，根据角平分线定义可知∠COQ＝45°，利用∠AOQ、∠AOC、∠COQ角之间的关系构造方程求出时间t；（3）先证明∠AOQ与∠POB互余，从而用t表示出∠POB＝90°﹣3t，根据角平分线定义再用t表示∠BOC度数；同时旋转后∠AOC＝30°+6t，则根据互补关系表示出∠BOC度数，同理再把∠BOC度数用新的式子表达出来．先后两个关于∠BOC的式子相等，构造方程求解．【详解】（1）①∵∠AOC＝30°，∴∠BOC＝180°﹣30°＝150°,∵OP平分∠BOC，∴∠COP＝12∠BOC＝75°,∴∠COQ＝90°﹣75°＝15°,∴∠AOQ＝∠AOC﹣∠COQ＝30°﹣15°＝15°, t＝15÷3＝5；②是，理由如下：∵∠COQ＝15°，∠AOQ＝15°，∴OQ平分∠AOC；（2）∵OC平分∠POQ，∴∠COQ＝12∠POQ＝45°．设∠AOQ＝3t，∠AOC＝30°+6t，由∠AOC﹣∠AOQ＝45°，可得30+6t﹣3t＝45，解得：t＝5，当30+6t﹣3t＝225，也符合条件，解得：t＝65，∴5秒或65秒时，OC平分∠POQ；（3）设经过t秒后OC平分∠POB，∵OC平分∠POB，∴∠BOC＝12∠BOP，∵∠AOQ+∠BOP＝90°，∴∠BOP＝90°﹣3t，又∠BOC＝180°﹣∠AOC＝180°﹣30°﹣6t，∴180﹣30﹣6t＝12（90﹣3t），解得t＝70 3．【点睛】本题主要考查一元一次方程的应用，根据角度的和差倍分关系，列出方程，是解题的关键. 32．（1）B点坐标为（0，﹣6），C点坐标为（4，﹣6）（2）S△OPM＝4t或S△OPM＝﹣3t+21（3）当t为2秒或133秒时，△OPM的面积是长方形OBCD面积的13．此时点P的坐标是（0，﹣4）或（83，﹣6）【解析】【分析】（1）根据绝对值、平方和算术平方根的非负性，求得a，b，c的值，即可得到B、C两点的坐标；（2）分两种情况：①P在OB上时，直接根据三角形面积公式可得结论；②P在BC上时，根据面积差可得结论；（3）根据已知条件先计算三角形OPM的面积为8，根据（2）中的结论分别代入可得对应t 的值，并计算此时点P 的坐标．【详解】（1）∵6a ++|2b +12|+（c ﹣4）2=0，∴a +6=0，2b +12=0，c ﹣4=0，∴a =﹣6，b =﹣6，c =4，∴B 点坐标为（0，﹣6），C 点坐标为（4，﹣6）．（2）①当点P 在OB 上时，如图1，OP =2t ，S △OPM 12=⨯2t ×4=4t ； ②当点P 在BC 上时，如图2，由题意得：BP =2t ﹣6，CP =BC ﹣BP =4﹣（2t ﹣6）=10﹣2t ，DM =CM =3，S △OPM =S 长方形OBCD ﹣S △0BP ﹣S △PCM ﹣S △ODM =6×412-⨯6×（2t ﹣6）12-⨯3×（10﹣2t ）12-⨯4×3=﹣3t +21．（3）由题意得：S △OPM 13=S 长方形OBCD 13=⨯（4×6）=8，分两种情况讨论： ①当4t =8时，t =2，此时P （0，﹣4）； ②当﹣3t +21=8时，t 133=，PB =2t ﹣626188333=-=，此时P （83，﹣6）．综上所述：当t 为2秒或133秒时，△OPM 的面积是长方形OBCD 面积的13．此时点P 的坐标是（0，﹣4）或（83，﹣6）．【点睛】本题考查了一元一次方程的应用，主要考查了平面直角坐标系中求点的坐标，动点问题，求三角形的面积，还考查了绝对值、平方和算术平方根的非负性、解一元一次方程，分类讨论是解答本题的关键．33．（1）25- ，35 （2）运动时间为4秒，相遇点表示的数字为27 ；（3）5;(4) 一共相遇了7次.【解析】【分析】（1）根据0+0式的定义即可解题；（2）设运动时间为x 秒,表示出P ,Q 的运动路程,利用路程和等于AB 长即可解题；（3）根据点Q 达到A 点时，点P ，Q 停止运动求出运动时间即可解题；（4）根据第三问点P 运动了6个来回后，又运动了30个单位长度即可解题.【详解】。

德阳市七年级上册数学期末试卷(含答案)

德阳市七年级上册数学期末试卷(含答案)一、选择题1．在数3，﹣3，13，13-中，最小的数为（） A ．﹣3B ．13C ．13-D ．32．如图，已知线段AB 的长度为a ，CD 的长度为b ，则图中所有线段的长度和为( )A ．3a+bB ．3a-bC ．a+3bD ．2a+2b3．下列数或式：3(2)-，61()3-，25- ，0，21m +在数轴上所对应的点一定在原点右边的个数是（） A ．1B ．2C ．3D ．44．把一根木条固定在墙面上，至少需要两枚钉子，这样做的数学依据是（） A ．两点之间线段最短 B ．两点确定一条直线 C ．垂线段最短 D ．两点之间直线最短5．直线3l 与12,l l 相交得如图所示的5个角，其中互为对顶角的是（）A ．3∠和5∠B ．3∠和4∠C ．1∠和5∠D ．1∠和4∠6．已知线段AB a ，,,C D E 分别是,,AB BC AD 的中点，分别以点,,C D E 为圆心，,,CB DB EA 为半径作圆得如图所示的图案，则图中三个阴影部分图形的周长之和为（）A ．9a πB ．8a πC ．98a πD ．94a π7．解方程121123x x +--=时，去分母得（） A ．2（x +1）＝3（2x ﹣1）＝6B ．3（x +1）﹣2（2x ﹣1）＝1C ．3（x +1）﹣2（2x ﹣1）＝6D ．3（x +1）﹣2×2x ﹣1＝6 8．下列四个数中最小的数是（） A ．﹣1B ．0C ．2D ．﹣（﹣1）9．下列变形不正确的是（） A ．若x ＝y ，则x+3＝y+3 B ．若x ＝y ，则x ﹣3＝y ﹣3 C ．若x ＝y ，则﹣3x ＝﹣3y D ．若x 2＝y 2，则x ＝y 10．已知a ＝b ，则下列等式不成立的是（）A ．a+1＝b+1B ．1﹣a ＝1﹣bC ．3a ＝3bD ．2﹣3a ＝3b ﹣211．如图，在数轴上有A ，B ，C ，D 四个整数点(即各点均表示整数)，且2AB ＝BC ＝3CD ，若A ，D 两点表示的数分别为-5和6，点E 为BD 的中点，在数轴上的整数点中，离点E 最近的点表示的数是（）A ．2B ．1C ．0D ．-112．如图，已知点C 在线段AB 上，点M 、N 分别是AC 、BC 的中点，且AB ＝8cm ，则MN的长度为（）cm ．A ．2B ．3C ．4D ．6二、填空题13．若代数式mx 2+5y 2﹣2x 2+3的值与字母x 的取值无关，则m 的值是__． 14．如图，数轴上点A 与点B 表示的数互为相反数，且AB =4则点A 表示的数为______.15．定义-种新运算:22a b b ab ⊕=-,如21222120⊕=-⨯⨯=，则(1)2-⊕=__________．16．16的算术平方根是．17．中国古代数学著作《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这道题的意思是：今有若干人乘车，每三人乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车？如果我们设有x 辆车，则可列方程_____．18．如图，将1～6这6个整数分别填入如图的圆圈中，使得每边上的三个数之和相等，则符合条件的x 为_____．19．计算7a 2b ﹣5ba 2＝_____．20．某校全体同学的综合素质评价的等级统计如图所示,其中评价为C 等级所在扇形的圆心角是____度.21．已知二元一次方程2x-3y=5的一组解为x ay b=⎧⎨=⎩，则2a-3b+3=______. 22．如图，已知线段16AB cm =，点M 在AB 上:1:3AM BM =，P Q 、分别为AM AB 、的中点，则PQ 的长为____________．23．线段AB=2cm ，延长AB 至点C ，使BC=2AB ，则AC=_____________cm.24．设一列数中相邻的三个数依次为m ，n ，p ，且满足p=m 2﹣n ，若这列数为﹣1，3，﹣2，a ，b ，128…，则b=________.三、压轴题25．如图，在数轴上的A 1，A 2，A 3，A 4，……A 20，这20个点所表示的数分别是a 1，a 2，a 3，a 4，……a 20．若A 1A 2＝A 2A 3＝……＝A 19A 20，且a 3＝20，|a 1﹣a 4|＝12．（1）线段A 3A 4的长度＝；a 2＝；（2）若|a 1﹣x |＝a 2+a 4，求x 的值；（3）线段MN 从O 点出发向右运动，当线段MN 与线段A 1A 20开始有重叠部分到完全没有重叠部分经历了9秒．若线段MN ＝5，求线段MN 的运动速度．26．如图，数轴上点A 表示的数为4-，点B 表示的数为16，点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动.设运动时间为t 秒(t 0)>．()1A ，B 两点间的距离等于______，线段AB 的中点表示的数为______；()2用含t 的代数式表示：t 秒后，点P 表示的数为______，点Q 表示的数为______； ()3求当t 为何值时，1PQ AB 2=？()4若点M 为PA 的中点，点N 为PB 的中点，点P 在运动过程中，线段MN 的长度是否发生变化？若变化，请说明理由；若不变请直接写出线段MN 的长．27．对于数轴上的点P ，Q ，给出如下定义：若点P 到点Q 的距离为d(d≥0)，则称d 为点P 到点Q 的d 追随值，记作d[PQ]．例如，在数轴上点P 表示的数是2，点Q 表示的数是5，则点P到点Q的d追随值为d[PQ]=3．问题解决：(1)点M，N都在数轴上，点M表示的数是1，且点N到点M的d追随值d[MN]=a(a≥0)，则点N表示的数是_____(用含a的代数式表示)；(2)如图，点C表示的数是1，在数轴上有两个动点A，B都沿着正方向同时移动，其中A 点的速度为每秒3个单位，B点的速度为每秒1个单位，点A从点C出发，点B表示的数是b，设运动时间为t(t>0)．①当b=4时，问t为何值时，点A到点B的d追随值d[AB]=2；②若0<t≤3时，点A到点B的d追随值d[AB]≤6，求b的取值范围．28．如图，已知数轴上点A表示的数为10，B是数轴上位于点A左侧一点，且AB=30，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为秒.(1)数轴上点B表示的数是________，点P表示的数是________(用含的代数式表示)；(2)若M为线段AP的中点，N为线段BP的中点，在点P运动的过程中，线段MN的长度会发生变化吗?如果不变，请求出这个长度；如果会变化,请用含的代数式表示这个长度；(3)动点Q从点B处出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、Q同时出发，问点P运动多少秒时与点Q相距4个单位长度?29．如图，以长方形OBCD的顶点O为坐标原点建立平面直角坐标系，B点坐标为（0，a），C点坐标为（c，b），且a、b、C满足6a +|2b+12|+（c﹣4）2＝0．（1）求B、C两点的坐标；（2）动点P从点O出发，沿O→B→C的路线以每秒2个单位长度的速度匀速运动，设点P 的运动时间为t秒，DC上有一点M（4，﹣3），用含t的式子表示三角形OPM的面积；（3）当t为何值时，三角形OPM的面积是长方形OBCD面积的13？直接写出此时点P的坐标．30．数轴上线段的长度可以用线段端点表示的数进行减法运算得到，例如：如图①，若点A，B在数轴上分别对应的数为a，b(a<b)，则AB的长度可以表示为AB=b－a．请你用以上知识解决问题：如图②，一个点从数轴上的原点开始，先向左移动2个单位长度到达A点，再向右移动3个单位长度到达B点，然后向右移动5个单位长度到达C点．（1）请你在图②的数轴上表示出A，B，C三点的位置．（2）若点A以每秒1个单位长度的速度向左移动，同时，点B和点C分别以每秒2个单位长度和3个单位长度的速度向右移动，设移动时间为t秒．①当t=2时，求AB和AC的长度；②试探究：在移动过程中，3AC－4AB的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值．31．如图所示，已知数轴上A，B两点对应的数分别为－2，4，点P为数轴上一动点，其对应的数为x.(1)若点P到点A，B的距离相等，求点P对应的数x的值．(2)数轴上是否存在点P，使点P到点A，B的距离之和为8？若存在，请求出x的值；若不存在，说明理由．(3)点A，B分别以2个单位长度/分、1个单位长度/分的速度向右运动，同时点P以5个单位长度/分的速度从O点向左运动．当遇到A时，点P立即以同样的速度向右运动，并不停地往返于点A与点B之间．当点A与点B重合时，点P经过的总路程是多少？32．如图①，点O为直线AB上一点，过点O作射线OC，使∠AOC=120°，将一直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（1）将图①中的三角板OMN摆放成如图②所示的位置，使一边OM在∠BOC的内部，当OM平分∠BOC时，∠BO N= ；（直接写出结果）（2）在（1）的条件下，作线段NO的延长线OP（如图③所示），试说明射线OP是∠AOC的平分线；（3）将图①中的三角板OMN摆放成如图④所示的位置，请探究∠NOC与∠AOM之间的数量关系．（直接写出结果，不须说明理由）【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【解析】【分析】有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．【详解】解：∵3＞13＞13-＞﹣3，∴在数3，﹣3，13，13-中，最小的数为﹣3．故选：A．【点睛】此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．2．A解析：A【解析】【分析】依据线段AB长度为a，可得AB=AC+CD+DB=a，依据CD长度为b，可得AD+CB=a+b，进而得出所有线段的长度和．【详解】∵线段AB长度为a，∴AB=AC+CD+DB=a，又∵CD长度为b，∴AD+CB=a+b，∴图中所有线段的长度和为：AB+AC+CD+DB+AD+CB=a+a+a+b=3a+b，故选A．【点睛】本题考查了比较线段的长度和有关计算，主要考查学生能否求出线段的长度和知道如何数图形中的线段．3．B解析：B【解析】【分析】点在原点的右边，则这个数一定是正数，根据演要求判断几个数即可得到答案.【详解】()32-=-8，613⎛⎫- ⎪⎝⎭=1719，25-=-25 ，0，21m +≥1 在原点右边的数有613⎛⎫- ⎪⎝⎭和 21m +≥1 故选B 【点睛】此题重点考察学生对数轴上的点的认识，抓住点在数轴的右边是解题的关键.4．B解析：B【解析】因为两点确定一条直线,所以把一根木条固定在墙面上,至少需要两枚钉子故选B.5．A解析：A 【解析】【分析】两条直线相交后所得的有公共顶点，且两边互为反向延长线的两个角互为对顶角，据此逐一判断即可．【详解】A.3∠和5∠只有一个公共顶点，且两边互为反向延长线，是对顶角，符合题意，B.3∠和4∠两边不是互为反向延长线，不是对顶角，不符合题意，C.1∠和5∠没有公共顶点，不是对顶角，不符合题意，D.1∠和4∠没有公共顶点，不是对顶角，不符合题意，故选：A. 【点睛】本题考查对顶角，两条直线相交后所得的有公共顶点且两边互为反向延长线的两个角叫做对顶角；熟练掌握对顶角的定义是解题关键.6．D解析：D 【解析】【分析】根据中点的定义及线段的和差关系可用a 表示出AC 、BD 、AD 的长，根据三个阴影部分图形的周长之和等于三个圆的周长之和即可得答案. 【详解】∵AB a ，C 、D 分别是AB 、BC 的中点， ∴AC=BC=12AB=12a ，BD=CD=12BC=14a ， ∴AD=AC+BD=34a ，∴三个阴影部分图形的周长之和=aπ+12aπ+34aπ=94a π，故选：D. 【点睛】本题考查线段中点的定义，线段上一点,到线段两端点距离相等的点是线段的中点；正确得出三个阴影部分图形的周长之和等于三个圆的周长之和是解题关键.7．C解析：C 【解析】【分析】方程两边都乘以分母的最小公倍数即可．【详解】解：方程两边同时乘以6，得：3(1)2(21)6x x +--=，故选：C ．【点睛】本题主要考查了解一元一次方程的去分母，需要注意，不能漏乘，没有分母的也要乘以分母的最小公倍数．8．A解析：A 【解析】【分析】首先根据有理数大小比较的方法，把所给的四个数从大到小排列即可．【详解】解：﹣（﹣1）＝1， ∴﹣1＜0＜﹣（﹣1）＜2，故选：A ．【点睛】此题主要考查了有理数大小比较的方法，要熟练掌握正数都大于0，负数都小于0，正数大于一切负数．两个负数比较大小，绝对值大的反而小．9．D解析：D 【解析】【分析】根据等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．【详解】解：A 、两边都加上3，等式仍成立，故本选项不符合题意． B 、两边都减去3，等式仍成立，故本选项不符合题意． C 、两边都乘以﹣3，等式仍成立，故本选项不符合题意．D、两边开方，则x＝y或x＝﹣y，故本选项符合题意．故选：D．【点睛】本题主要考查了等式的基本性质．解题的关键是掌握等式的基本性质，等式的两边同时加上（或减去）同一个数（或字母），等式仍成立；等式的两边同时乘以（或除以）同一个不为0数（或字母），等式仍成立．10．D解析：D【解析】【分析】根据等式的基本性质对各选项进行逐一分析即可．【详解】A、∵a＝b，∴a+1＝b+1，故本选项正确；B、∵a＝b，∴﹣a＝﹣b，∴1﹣a＝1﹣b，故本选项正确；C、∵a＝b，∴3a＝3b，故本选项正确；D、∵a＝b，∴﹣a＝﹣b，∴﹣3a＝﹣3b，∴2﹣3a＝2﹣3b，故本选项错误．故选：D．【点睛】本题考查了等式的性质，掌握等式的基本性质是解答此题的关键．11．A解析：A【解析】【分析】根据A、D两点在数轴上所表示的数，求得AD的长度，然后根据2AB=BC=3CD，求得AB、BD的长度，从而找到BD的中点E所表示的数．【详解】解：如图：∵|AD|=|6-（-5）|=11，2AB=BC=3CD，∴AB=1.5CD，∴1.5CD+3CD+CD=11，∴CD=2，∴AB=3，∴BD=8，∴ED=12BD=4，∴|6-E|=4，∴点E所表示的数是：6-4=2．∴离线段BD的中点最近的整数是2．故选：A．【点睛】本题考查了数轴、比较线段的长短．灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．12．C解析：C【解析】【分析】根据MN＝CM+CN＝12AC+12CB＝12（AC+BC）＝12AB即可求解．【详解】解：∵M、N分别是AC、BC的中点，∴CM＝12AC，CN＝12BC，∴MN＝CM+CN＝12AC+12BC＝12（AC+BC）＝12AB＝4．故选：C．【点睛】本题考查了线段中点的性质，找到MC与AC，CN与CB关系，是本题的关键二、填空题13．2【解析】解：mx2+5y2﹣2x2+3=（m﹣2）x2+5y2+3，∵代数式mx2+5y2﹣2x2+3的值与字母x的取值无关，则m﹣2=0，解得m=2．故答案为2．点睛：本题主要考查合并同类解析：2【解析】解：mx2+5y2﹣2x2+3=（m﹣2）x2+5y2+3，∵代数式mx2+5y2﹣2x2+3的值与字母x的取值无关，则m﹣2=0，解得m=2．故答案为2．点睛：本题主要考查合并同类项的法则．即系数相加作为系数，字母和字母的指数不变．与字母x的取值无关，即含字母x的系数为0．14．-2【解析】【分析】根据图和题意可得出答案.【详解】解：表示的数互为相反数，且，则A 表示的数为：.故答案为：.【点睛】本题考查的是数轴上距离的含义，解题关键是对数轴距离的理解.解析：-2【解析】【分析】根据图和题意可得出答案.【详解】解：,A B 表示的数互为相反数，且4AB =，则A 表示的数为：2-.故答案为：2-.【点睛】本题考查的是数轴上距离的含义，解题关键是对数轴距离的理解.15．8【解析】【分析】根据题意原式利用题中的新定义计算将-1和2代入计算即可得到结果．【详解】解：因为；所以故填8.【点睛】本题结合新定义运算考查有理数的混合运算，熟练掌握运算法则是解解析：8【解析】【分析】根据题意原式利用题中的新定义计算将-1和2代入计算即可得到结果．【详解】解：因为22a b b ab ⊕=-；所以2(1)222(1)28.-⊕=-⨯-⨯=故填8.【点睛】本题结合新定义运算考查有理数的混合运算，熟练掌握运算法则是解本题的关键．16．【解析】【分析】【详解】正数的正的平方根叫算术平方根，0的算术平方根还是0；负数没有平方根也没有算术平方根∵∴16的平方根为4和-4∴16的算术平方根为4解析：【解析】【分析】【详解】正数的正的平方根叫算术平方根，0的算术平方根还是0；负数没有平方根也没有算术平方根∵2(4)16±=∴16的平方根为4和-4∴16的算术平方根为4 17．3（x ﹣2）＝2x+9【解析】【分析】根据每三人乘一车，最终剩余2辆车，每2人共乘一车，最终剩余9个人无车可乘，进而表示出总人数得出等式即可．【详解】设有x 辆车，则可列方程：3（x ﹣2）解析：3（x ﹣2）＝2x+9【解析】【分析】根据每三人乘一车，最终剩余2辆车，每2人共乘一车，最终剩余9个人无车可乘，进而表示出总人数得出等式即可．【详解】设有x 辆车，则可列方程：3（x ﹣2）＝2x+9．故答案是：3（x ﹣2）＝2x+9．【点睛】本题考查一元一次方程，解题的关键是读懂题意，掌握列一元一次方程.18．2【解析】直接利用有理数的加法运算法则得出符合题意的答案．【详解】解：如图所示：x的值为2．故答案为：2．【点睛】此题主要考查了有理数的加法，正确掌握相关运算法则是解题关键解析：2【解析】【分析】直接利用有理数的加法运算法则得出符合题意的答案．【详解】解：如图所示：x的值为2．故答案为：2．【点睛】此题主要考查了有理数的加法，正确掌握相关运算法则是解题关键．19．2a2b【解析】【分析】根据合并同类项法则化简即可．【详解】故答案为：【点睛】本题考查了合并同类项，解题的关键是熟练运用合并同类项的法则，本题属于基础题型．解析：2a2b【解析】【分析】根据合并同类项法则化简即可．()2222﹣﹣．7a b5ba=75a b=2a b2a b故答案为：2【点睛】本题考查了合并同类项，解题的关键是熟练运用合并同类项的法则，本题属于基础题型．20．72【解析】【分析】用360度乘以C等级的百分比即可得.【详解】观察可知C等级所占的百分比为20%，所以C等级所在扇形的圆心角为：360°×20%=72°，故答案为：72.【点睛】解析：72【解析】【分析】用360度乘以C等级的百分比即可得.【详解】观察可知C等级所占的百分比为20%，所以C等级所在扇形的圆心角为：360°×20%=72°，故答案为：72.【点睛】本题考查了扇形统计图，熟知扇形统计图中扇形圆心角度数的求解方法是解题的关键. 21．8【解析】【分析】根据二元一次方程解的定义可得2a-3b=5，继而整体代入即可求得答案.【详解】把代入方程2x-3y=5得2a-3b=5，所以2a-3b+3=5+3=8，故答案为：8解析：8【解析】【分析】根据二元一次方程解的定义可得2a-3b=5，继而整体代入即可求得答案.把x ay b=⎧⎨=⎩代入方程2x-3y=5得2a-3b=5，所以2a-3b+3=5+3=8，故答案为：8.【点睛】本题考查了二元一次方程的解，代数式求值，熟练掌握二元一次方程解的定义以及整体代入思想是解题的关键.22．6cm【解析】【分析】根据已知条件得到AM=4cm．BM=12cm，根据线段中点的定义得到AP=AM=2cm ，AQ=AB=8cm，从而得到答案．【详解】解：∵AB=16cm，AM：BM=1解析：6cm【解析】【分析】根据已知条件得到AM=4cm．BM=12cm，根据线段中点的定义得到AP=12AM=2cm，AQ=12AB=8cm，从而得到答案．【详解】解：∵AB=16cm，AM：BM=1：3，∴AM=4cm．BM=12cm，∵P，Q分别为AM，AB的中点，∴AP=12AM=2cm，AQ=12AB=8cm，∴PQ=AQ-AP=6cm；故答案为：6cm．【点睛】本题考查了线段的长度计算问题，把握中点的定义，灵活运用线段的和、差、倍、分进行计算是解决本题的关键．23．6【解析】如图，∵AB=2cm，BC=2AB，∴BC=4cm，∴AC=AB+BC=6cm.故答案为：6.解析：6【解析】如图，∵AB=2cm，BC=2AB，∴BC=4cm，∴AC=AB+BC=6cm.故答案为：6.24．-7【解析】【分析】先根据题意求出a的值，再依此求出b的值.【详解】解：根据题意得：a=32-（-2）=11，则b=(-2)2-11=-7．故答案为：-7.【点睛】本题考查探索与表解析：-7【解析】【分析】先根据题意求出a的值，再依此求出b的值.【详解】解：根据题意得：a=32-（-2）=11，则b=(-2)2-11=-7．故答案为：-7.【点睛】本题考查探索与表达规律——数字类规律探究. 熟练掌握变化规律，根据题意求出a和b是解决问题的关键．三、压轴题25．（1）4，16；（2）x＝﹣28或x＝52；（3）线段MN的运动速度为9单位长度/秒．【解析】【分析】（1）由A1A2＝A2A3＝……＝A19A20结合|a1﹣a4|＝12可求出A3A4的值，再由a3＝20可求出a 2＝16；（2）由（1）可得出a 1＝12，a 2＝16，a 4＝24，结合|a 1﹣x|＝a 2+a 4可得出关于x 的含绝对值符号的一元一次方程，解之即可得出结论；（3）由（1）可得出A 1A 20＝19A 3A 4＝76，设线段MN 的运动速度为v 单位/秒，根据路程＝速度×时间（类似火车过桥问题），即可得出关于v 的一元一次方程，解之即可得出结论．【详解】解：（1）∵A 1A 2＝A 2A 3＝……＝A 19A 20，|a 1﹣a 4|＝12，∴3A 3A 4＝12，∴A 3A 4＝4．又∵a 3＝20，∴a 2＝a 3﹣4＝16．故答案为：4；16．（2）由（1）可得：a 1＝12，a 2＝16，a 4＝24，∴a 2+a 4＝40．又∵|a 1﹣x|＝a 2+a 4，∴|12﹣x|＝40，∴12﹣x ＝40或12﹣x ＝﹣40，解得：x ＝﹣28或x ＝52．（3）根据题意可得：A 1A 20＝19A 3A 4＝76．设线段MN 的运动速度为v 单位/秒，依题意，得：9v ＝76+5，解得：v ＝9．答：线段MN 的运动速度为9单位长度/秒．【点睛】本题考查了一元一次方程的应用、数轴、两点间的距离以及规律性：图形的变化类，解题的关键是：（1）由相邻线段长度相等求出线段A 3A 4的长度及a 2的值；（2）由（1）的结论，找出关于x 的含绝对值符号的一元一次方程；（3）找准等量关系，正确列出一元一次方程．26．（1）20,6；（2）43t -+，162t -；（3）t 2=或6时；（4）不变，10，理由见解析.【解析】【分析】（1）由数轴上两点距离先求得A ，B 两点间的距离，由中点公式可求线段AB 的中点表示的数；（2）点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动同时点Q 从点B 出发，向右为正，所以-4+3t ；Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动，向左为负，16-2t.（3）由题意,1PQ AB 2=表示出线段长度，可列方程求t 的值；（4）由线段中点的性质可求MN 的值不变．【详解】解：()1点A 表示的数为4-，点B 表示的数为16，A ∴，B 两点间的距离等于41620--=，线段AB 的中点表示的数为41662-+= 故答案为20，6 ()2点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右匀速运动，∴点P 表示的数为：43t -+，点Q 从点B 出发，以每秒2个单位长度的速度向左匀速运动，∴点Q 表示的数为：162t -，故答案为43t -+，162t -()13PQ AB 2= ()43t 162t 10∴-+--=t 2∴=或6答：t 2=或6时，1PQ AB 2= ()4线段MN 的长度不会变化，点M 为PA 的中点，点N 为PB 的中点，1PM PA 2∴=，1PN PB 2= ()1MN PM PN PA PB 2∴=-=- 1MN AB 102∴== 【点睛】本题考查了一元一次方程的应用，数轴上两点之间的距离，找到正确的等量关系列出方程是本题的关键．27．(1)1＋a 或1－a ；(2)12或52；(3)1≤b≤7. 【解析】【分析】(1)根据d 追随值的定义，分点N 在点M 左侧和点N 在点M 右侧两种情况，直接写出答案即可；(2)①分点A 在点B 左侧和点A 在点B 右侧两种情况，类比行程问题中的追及问题，根据“追及时间=追及路程÷速度差”计算即可；②【详解】解：(1)点N在点M右侧时，点N表示的数是1+a；点N在点M左侧时，点N表示的数是1-a；(2)①b=4时，AB相距3个单位，当点A在点B左侧时，t=(3-2)÷(3-1)=12，当点A在点B右侧时，t=(3+2)÷(3-1)=52；②当点B在点A左侧或重合时，即d≤1时，随着时间的增大，d追随值会越来越大，∵0<t≤3，点A到点B的d追随值d[AB]≤6，∴1-d+3×(3-1)≤6，解得d≥1，∴d=1，当点B在点A右侧时，即d>1时，在AB重合之前，随着时间的增大，d追随值会越来越小，∵点A到点B的d追随值d[AB]≤6，∴d≤7∴1<d≤7，综合两种情况，d的取值范围是1≤d≤7.故答案为(1)1＋a或1－a；(2)①12或52；②1≤b≤7.【点睛】本题考查了数轴上两点之间的距离和动点问题.28．（1）-20，10-5t；（2）线段MN的长度不发生变化，都等于15．（3）13秒或17秒【解析】【分析】(1)根据已知可得B点表示的数为10-30；点P表示的数为10-5t；(2)分类讨论：①当点P在点A、B两点之间运动时，②当点P运动到点B的左侧时，利用中点的定义和线段的和差易求出MN．(3) 分①点P、Q相遇之前，②点P、Q相遇之后，根据P、Q之间的距离恰好等于2列出方程求解即可；【详解】解：（1））∵点A表示的数为10，B在A点左边，AB=30，∴数轴上点B表示的数为10-30=-20；∵动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒，∴点P表示的数为10-5t；故答案为-20，10-5t；（2）线段MN的长度不发生变化，都等于15．理由如下：①当点P在点A、B两点之间运动时，∵M为线段AP的中点，N为线段BP的中点，∴MN=MP+NP=AP+BP=（AP+BP）=AB=15；②当点P运动到点B的左侧时：∵M为线段AP的中点，N为线段BP的中点，∴MN=MP-NP=AP-BP=（AP-BP）=AB=15，∴综上所述，线段MN的长度不发生变化，其值为15．（3）若点P、Q同时出发，设点P运动t秒时与点Q距离为4个单位长度．①点P、Q相遇之前，由题意得4+5t=30+3t，解得t=13；②点P、Q相遇之后，由题意得5t-4=30+3t，解得t=17．答：若点P、Q同时出发，13或17秒时P、Q之间的距离恰好等于4；【点睛】本题考查了数轴一元一次方程的应用，用到的知识点是数轴上两点之间的距离，关键是根据题意画出图形，注意分两种情况进行讨论．29．（1）B点坐标为（0，﹣6），C点坐标为（4，﹣6）（2）S△OPM＝4t或S△OPM＝﹣3t+21（3）当t为2秒或133秒时，△OPM的面积是长方形OBCD面积的13．此时点P的坐标是（0，﹣4）或（83，﹣6）【解析】【分析】（1）根据绝对值、平方和算术平方根的非负性，求得a，b，c的值，即可得到B、C两点的坐标；（2）分两种情况：①P在OB上时，直接根据三角形面积公式可得结论；②P在BC上时，根据面积差可得结论；（3）根据已知条件先计算三角形OPM的面积为8，根据（2）中的结论分别代入可得对应t的值，并计算此时点P的坐标．【详解】（1）∵6a+|2b+12|+（c﹣4）2=0，∴a+6=0，2b+12=0，c﹣4=0，∴a=﹣6，b=﹣6，c =4，∴B点坐标为（0，﹣6），C点坐标为（4，﹣6）．（2）①当点P在OB上时，如图1，OP=2t，S△OPM12=⨯2t×4=4t；②当点P在BC上时，如图2，由题意得：BP =2t ﹣6，CP =BC ﹣BP =4﹣（2t ﹣6）=10﹣2t ，DM =CM =3，S △OPM =S 长方形OBCD ﹣S △0BP ﹣S △PCM ﹣S △ODM =6×412-⨯6×（2t ﹣6）12-⨯3×（10﹣2t ）12-⨯4×3=﹣3t +21．（3）由题意得：S △OPM 13=S 长方形OBCD 13=⨯（4×6）=8，分两种情况讨论： ①当4t =8时，t =2，此时P （0，﹣4）； ②当﹣3t +21=8时，t 133=，PB =2t ﹣626188333=-=，此时P （83，﹣6）．综上所述：当t 为2秒或133秒时，△OPM 的面积是长方形OBCD 面积的13．此时点P 的坐标是（0，﹣4）或（83，﹣6）．【点睛】本题考查了一元一次方程的应用，主要考查了平面直角坐标系中求点的坐标，动点问题，求三角形的面积，还考查了绝对值、平方和算术平方根的非负性、解一元一次方程，分类讨论是解答本题的关键．30．（1）详见解析；（2）①16；②在移动过程中，3AC ﹣4AB 的值不变【解析】【分析】（1）根据点的移动规律在数轴上作出对应的点即可；（2）①当t =2时，先求出A 、B 、C 点表示的数，然后利用定义求出AB 、AC 的长即可； ②先求出A 、B 、C 点表示的数，然后利用定义求出AB 、AC 的长，代入3AC －4AB 即可得到结论．【详解】（1）A ，B ，C 三点的位置如图所示：．（2）①当t =2时，A 点表示的数为－4，B 点表示的数为5，C 点表示的数为12，∴AB =5－(－4)=9，AC =12－(－4)=16．②3AC －4AB 的值不变．当移动时间为t 秒时，A 点表示的数为－t －2，B 点表示的数为2t ＋1，C 点表示的数为3t＋6，则：AC=(3t＋6)－(－t－2)=4t＋8，AB=(2t＋1)－(－t－2)=3t＋3，∴3AC－4AB=3(4t＋8)－4(3t＋3)=12t＋24－12t－12=12．即3AC﹣4AB的值为定值12，∴在移动过程中，3AC﹣4AB的值不变．【点睛】本题考查了数轴上的动点问题．表示出对应点所表示的数是解答本题的关键．31．(1)x=1;(2) x＝－3或x＝5;(3) 30.【解析】【分析】（1）根据题意可得4－x＝x－（－2），解出x的值；（2）此题分为两种情况，当点P在B的右边时，当点P在B的左边时，分别列出方程求解即可；（3）设经过x分钟点A与点B重合，根据题意得：2x＝6＋x进而求出即可.【详解】（1）4－x＝x－（－2），解得：x＝1，（2）①当点P在B的右边时得：x－（－2）＋x－4＝8，解得：x＝5，②当点P在B的左边时得：－2－x＋4－x＝8，解得：x＝－3，则x＝－3或x＝5.（3）设经过x分钟点A与点B重合，根据题意得：2x＝6＋x，解得：x＝6，则5x＝30，故答案为30个单位长度.【点睛】本题主要考查了一元二次方程的应用，解此题的要点在于根据数轴得出点的位置. 32．（1）60°；（2）射线OP是∠AOC的平分线；（3）30°．【解析】整体分析：(1)根据角平分线的定义与角的和差关系计算；(2)计算出∠AOP的度数，再根据角平分线的定义判断；(3)根据∠AOC，∠AON，∠NOC，∠MON，∠AOM的和差关系即可得到∠NOC 与∠AOM之间的数量关系．解：(1)如图②，∠AOC=120°，∴∠BOC=180°﹣120°=60°，又∵OM平分∠BOC，∴∠BOM=30°，又∵∠NOM=90°，∴∠BOM=90°﹣30°=60°，故答案为60°；(2)如图③，∵∠AOP=∠BOM=60°，∠AOC=120°，∴∠AOP=12∠AOC，∴射线OP是∠AOC的平分线；(3)如图④，∵∠AOC=120°，∴∠AON=120°﹣∠NOC，∵∠MON=90°，∴∠AON=90°﹣∠AOM，∴120°﹣∠NOC=90°﹣∠AOM，即∠NOC﹣∠AOM=30°．。

2023-2024学年四川省德阳市七年级(下)期末数学试卷(含详解)

2023-2024学年四川省德阳市七年级（下）期末数学试卷一、选择题：本题共12小题，每小题4分，共48分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列图中，不是同位角的是( )A. B.C. D.2.二元一次方程的自然数解有( )A. 个B. 个C. 个D. 无数个3.点先向右平移个单位，再向下平移个单位得对应点，则点坐标是( )A. B. C. D.4.下列调查中，适宜采用全面调查方式的是( )A. 对市场上一次性筷子的卫生情况的调查B. 为保证“神舟十八号”载人航天飞船的成功发射，对其零部件进行检查C. 对年春节联欢晚会满意度的调查D. 检测一批灯的使用寿命5.如图，将直角三角形沿着的方向平移得到三角形，已知，，，平移距离为，则阴影部分的面积为( )A.B.C.D.6.为了了解七年级名学生期中数学考试的情况，从中抽取了名学生的数学成绩进行统计，下列说法：这种调查方式是抽样调查；名学生是总体；每名学生的数学成绩是个体；名学生是总体的一个样本；名是样本容量，其中，正确的有( )A. 个B. 个C. 个D. 个7.如图所示，要求添加一个条件，使得，则不能得到的是( )A. B.C. D.8.已知甲、乙两种商品的进价和为元，为了促销而打折销售，若甲商品打八折，乙商品打六折，则可赚元，若甲商品打六折，乙商品打八折，则可赚元，甲、乙两种商品的定价分别为( )A. 元、元B. 元、元C. 元、元D. 元、元9.将正整数的算术平方根按如图所示的规律排列下去若用有序实数对表示第排，从左到右第个数，如表示实数，则表示的实数是( )第一排第二排第三排第四排A. B. C. D.10.在平面直角坐标系中，第四象限内的点到轴的距离是，到轴的距离是，已知平行于轴且，则点的坐标是( )A. B.C. 或D. 或11.已知是直线外一点，以为一个端点作线段，使端点在直线上，并且使线段的长为，这样的线段的条数不可能的是( )A. B. C. D.12.若数使关于的方程有非负数解，且关于的不等式组恰好有两个偶数解，则符合条件的所有整数的和是( )A. B. C. D.二、填空题：本题共6小题，每小题4分，共24分。

2023-2024学年四川省德阳市广汉市七年级(上)期末数学试卷+答案解析

2023-2024学年四川省德阳市广汉市七年级（上）期末数学试卷一、选择题：本题共12小题，每小题4分，共48分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.在2，，0，四个数中，最大的数是()A.2B.C.0D.2.2023年5月17日10时49分，我国在西昌卫星发射中心成功发射第五十六颗北斗导航卫星，北斗系统作为国家重要基础设施，深刻改变着人们的生产生活方式.目前，某地图软件调用的北斗卫星日定位量超300000000000次.将数据300000000000用科学记数法表示为()A. B. C. D.3.如图，被墨迹污染的数可能是()A. B. C. D.4.下列各式中，正确的是()A. B.C. D.5.下列变形中，不正确的是()A.如果，那么B.如果，那么C.如果，那么D.如果，那么6.下列说法中正确的是()A.单项式的系数是，次数是3B.单项式m的系数是1，次数是0C.单项式的系数是2，次数是4D.单项式的系数是，次数是27.把用度、分、秒表示，正确的是()A. B. C. D.8.如果的值为2，则代数式的值是()A. B. C.2 D.59.如图，由下面正方体的平面展开图可知，原正方体“我”字所在的面的对面的汉字是()A.巴B.蜀C.梦D.的10.如图所示，C、D为线段AB的三等分点，点E是线段CD的中点.若，则DE的长为()A.2B.3C.4D.511.《孙子算经》是中国古代重要的数学著作，是《算经十书》之一，书中记载了这样一个题目：今有木，不知长短，引绳度之，余绳五尺：屈绳量之，不足一尺，木长几何？其大意是：用一根绳子去量一根长木，绳子还剩余5尺：将绳子对折再量长木，长木还剩余1尺，问木长多少尺？设木长x尺，则可列方程为()A. B. C. D.12.数轴上某一个点表示的数为a，比a小2的数用b表示，那么的最小值为()A.0B.1C.2D.3二、填空题：本题共6小题，每小题4分，共24分。

德阳市七年级上册数学期末试卷(含答案)

德阳市七年级上册数学期末试卷(含答案)一、选择题1．如果一个角的补角是130°，那么这个角的余角的度数是（） A ．30° B ．40° C ．50° D ．90°2．已知max{}2,,x x x 表示取三个数中最大的那个数，例如：当x ＝9时，max {}{}22,,max 9,9,9x x x =＝81．当max {}21,,2x x x =时，则x 的值为（） A ．14-B ．116C ．14D ．123．如图，直线AB ⊥直线CD ，垂足为O ，直线EF 经过点O ,若35BOE ∠=，则FOD ∠=( )A ．35°B ．45°C ．55°D ．125°4．下列方程是一元一次方程的是（）A ．213+x ＝5xB ．x 2+1＝3xC ．32y＝y+2D ．2x ﹣3y ＝15．已知2a ﹣b ＝3，则代数式3b ﹣6a+5的值为( )A ．﹣4B ．﹣5C ．﹣6D ．﹣76．如图，∠ABC=∠ACB ，AD 、BD 、CD 分别平分△ABC 的外角∠EAC 、内角∠ABC 、外角∠ACF ，以下结论：①AD ∥BC ；②∠ACB=2∠ADB ；③∠ADC+∠ABD=90°；④∠BDC=∠BAC ；其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个7．如果方程组223x y x y +=⎧⎨-=⎩的解为5x y =⎧⎨=⎩，那么“口”和“△”所表示的数分别是( )A ．14，4B ．11，1C ．9，-1D ．6，-4 8．一个几何体的表面展开图如图所示，则这个几何体是( )A ．四棱锥B ．四棱柱C ．三棱锥D ．三棱柱 9．若代数式3x ﹣9的值与﹣3互为相反数，则x 的值为（）A ．2B ．4C ．﹣2D ．﹣410．赣州是中国脐橙之乡，据估计2013年全市脐橙总产量将达到150万吨，用科学计数法表示为 ( )吨. A ．415010⨯B ．51510⨯C ．70.1510⨯D ．61.510⨯11．某商店有两个进价不同的计算器都卖了80元，其中一个赢利60%，另一个亏本20%，在这次买卖中，这家商店（） A ．赚了10元B ．赔了10元C ．赚了50元D ．不赔不赚12．某中学为检查七年级学生的视力情况，对七年级全体300名学生进行了体检，并制作了如图所示的扇形统计图，由该图可以看出七年级学生视力不良的学生有（）A ．45人B ．120人C ．135人D ．165人二、填空题13．若x ＝2是关于x 的方程5x +a ＝3（x +3）的解，则a 的值是_____． 14．将0.09493用四舍五入法取近似值精确到百分位，其结果是_____．15．单项式22ab -的系数是________.16．将一个含有30°角的直角三角板如图所示放置.其中，含30°角的顶点落在直线a 上，含90°角的顶点落在直线b 上.若//221a b ∠=∠，;,则1∠=__________°.17．如图，在长方形ABCD 中，10,13.,,,AB BC E F G H ==分别是线段,,,AB BC CD AD 上的定点，现分别以,BE BF 为边作长方形BEQF ,以DG 为边作正方形DGIH .若长方形BEQF 与正方形DGIH 的重合部分恰好是一个正方形，且,BE DG=,Q I均在长方形ABCD内部.记图中的阴影部分面积分别为123,,s s s.若2137SS=,则3S=___18．如图所示，ABC90∠=，CBD30∠=，BP平分ABD.∠则ABP∠=______度.19．如图，已知OC是∠AOB内部的一条射线，∠AOC＝30°，OE是∠COB的平分线．当∠BOE＝40°时，则∠AOB的度数是_____．20．中国古代数学著作《孙子算经》中有个问题：今有三人共车，二车空；二人共车，九人步，问人与车各几何？这道题的意思是：今有若干人乘车，每三人乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车？如果我们设有x辆车，则可列方程_____．21．如图，已知O为直线AB上一点，OC平分∠AOD，∠BOD＝4∠DOE，∠COE＝α，则∠BOE的度数为___________.(用含α的式子表示)22．已知二元一次方程2x-3y=5的一组解为x ay b=⎧⎨=⎩，则2a-3b+3=______.23．我国高速公路发展迅速，据报道，到目前为止，全国高速公路总里程约为118000千米，用科学记数法表示为_____千米．24．通常山的高度每升高100米，气温下降0.6C︒，如地面气温是4C-︒，那么高度是2400米高的山上的气温是____________________. 三、压轴题25．已知120AOB ∠︒＝ (本题中的角均大于0︒且小于180︒)(1)如图1，在AOB ∠内部作COD ∠，若160AOD BOC ∠∠︒＋＝，求COD 的度数；(2)如图2，在AOB ∠内部作COD ∠，OE 在AOD ∠内，OF 在BOC ∠内，且3DOE AOE ∠∠＝，3COF BOF ∠=∠，72EOF COD ∠=∠，求EOF ∠的度数；(3)射线OI 从OA 的位置出发绕点O 顺时针以每秒6︒的速度旋转，时间为t 秒(050t <<且30t ≠)．射线OM 平分AOI ∠，射线ON 平分BOI ∠，射线OP 平分MON ∠．若3MOI POI ∠=∠，则t = 秒．26．如图1，已知面积为12的长方形ABCD ，一边AB 在数轴上。

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)一、幂的运算易错压轴解答题1．若 (a > 0，且a≠1，m、n 是整数），则 m = n.你能利用上面的结论解决下面的问题吗？（1）如果2×8x ×16x =229 ，求x的值；（2）如果，求x的值.2．化简下列多项式：（1）（2）（3）若，求的值.（4）先化简，再求值：(2x﹣1)2﹣(3x+1)(3x﹣1)+5x(x﹣1)，其中x=﹣2．3．阅读理解：乘方的定义可知：（个相乘）．观察下列算式回答问题：（7个3相乘）（7个4相乘）（7个5相乘）（1） ________；（2） ________；（3）计算：．二、平面图形的认识（二）压轴解答题4．如图，已知AB∥CD，CE、BE的交点为E，现作如下操作：第一次操作，分别作∠ABE 和∠DCE的平分线，交点为E1，第二次操作，分别作∠ABE1和∠DCE1的平分线，交点为E2，第三次操作，分别作∠ABE2和∠DCE2的平分线，交点为E3，…，第n次操作，分别作∠ABE n﹣1和∠DCE n﹣1的平分线，交点为E n.（1）如图①，已知∠ABE=50°，∠DCE=25°，则∠BEC = ________°；（2）如图②，若∠BEC=140°，求∠BE1C的度数；（3）猜想：若∠BEC＝α度，则∠BE n C = ________ °.5．如图，，，，点D，C，E在同一条直线上.（1）完成下面的说理过程∵，（已知）∴，（垂直的定义）.∴ .∴，（________）.∴ .（________）又∠B=∠D，∴∠B=∠BCE，∴AB//CD. （________）（2）若∠BAD=150°，求∠E的度数.6．如图1，AD∥BC，∠BAD的平分线交BC于点G，∠BCD＝90°．（1）求证：∠BAG＝∠BGA；（2）如图2，若∠ABG＝50°，∠BCD的平分线交AD于点E、交射线GA于点F．求∠AFC 的度数；（3）如图3，线段AG上有一点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，请直接写出的值．三、整式乘法与因式分解易错压轴解答题7．某同学利用若干张正方形纸片进行以下操作：（1）从边长为a的正方形纸片中减去一个边长为b的小正方形，如图1，再沿线段AB把纸片剪开，最后把剪成的两张纸片拼成如图2的等腰梯形，这一过程所揭示的公式是________.（2）先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出两张边长分别为a和b的长方形纸片，如图3，最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式？（3）先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出三张边长分别为a和占的长方形纸片，如图5，你能否把图5中所有纸片拼成一个长方形？如果可以，请画出草图，并写出相应的等式.如果不能，请说明理由.8．【阅读与思考】整式乘法与因式分解是方向相反的变形.如何把二次_一项式ax2+bx+c进行因式分解呢?我们已经知道，(a1x+c1)(a2x+c2)=a1a2x2+a1c2x+a2c1x+c1c2=a1a2x2+(a1c2+a2c1)x+c1c2.反过来，就得到：a1a2x2+(a1c2+a2c1)x+c1c2=(a1x+c1)(a2x+c2).我们发现，二次项的系数a分解成a1a2，常数项c分解成c1c2，并且把a1， a2， c1，c2，如图①所示摆放，按对角线交叉相乘再相加，就得到a1c2+a2c1，如果a1c2+a2c1的值正好等于ax2+bx+c的一次项系数b，那么ax2+bx+c就可以分解为(a1x+c1)(a2x+c2)，其中a1， c1位于图的上一行，a2， c2位于下一行.像这种借助画十字交叉图分解系数，从而帮助我们把二次三项式分解因式的方法，通常叫做“十字相乘法”.例如，将式子x2-x-6分解因式的具体步骤为：首先把二次项的系数1分解为两个因数的积，即1=1×1，把常数项-6也分解为两个因数的积，即-6=2×（-3)；然后把1，1，2，-3按图②所示的摆放，按对角线交叉相乘再相加的方法，得到1×(-3)+1×2=-1，恰好等于一次项的系数-1，于是x2-x-6就可以分解为(x+2)(x-3).（1）请同学们认真观察和思考，尝试在图③的虚线方框内填入适当的数，并用“十字相乘法”分解因式：x2+x-6=________.（2）【理解与应用】请你仔细体会上述方法，并尝试对下面两个二次三项式进行分解因式：Ⅰ.2x2+5x-7=________；Ⅱ.6x2-7xy+2y2=________ .（3）【探究与拓展】对于形如ax2+bxy+cy2+dx+ey+f的关于x，y的二元二次多项式也可以用“十字相乘法”来分解.如图④，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np=b，pk+qj=e，mk+nj=d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式=(mx+py+j)(nx+qy+k)，请你认真阅读上述材料并尝试挑战下列问题：Ⅰ.分解因式3x2+5xy-2y2+x+9y-4=________ .Ⅱ.若关于x，y的二元二次式x2+7xy-18y2-5x+my-24 可以分解成两个一次因式的积，求m的值.________Ⅲ.己知x，y为整数，且满足x2+3xy+2y2+2x+3y=-1，请写出一组符合题意的x，y的值.________9．如果一个正整数能表示为两个连续奇数的平方差，那么我们称这个正整数为“和谐数”，如8=32-12， 16=52-32， 24=72-52，因此，8，16，24这三个数都是“和谐数”．（1）在32，75，80这三个数中，是和谐数的是________；（2）若200为和谐数，即200可以写成两个连续奇数的平方差，则这两个连续奇数的和为________；（3）小鑫通过观察发现以上求出的“和谐数”均为8的倍数，设两个连续奇数为2n-1和2n+1（其中n取正整数），请你通过运算验证“和谐数是8的倍数”这个结论是否符合题意．四、二元一次方程组易错压轴解答题10．某学校准备购买若干台A型电脑和B型打印机.如果购买1台A型电脑，2台B型打印机，一共需要花费6200元；如果购买2台A型电脑，1台B型打印机，一共需要花费7900元。

四川省德阳市旌阳区2022-2023学年七年级数学上学期期末试卷(含答案)

2022年秋期期末七年级地方学业质量监测数学试卷考生注意:1.考生须将自己的姓名、准考证号填写到试卷和答题卡规定的位置.2.非选择题用黑色墨水笔或签字笔在答题卡上作答，在试题卷上作答无效.3.全卷共25个小题，满分150分，考试时间120分钟.第I 卷(选择题，共48分)一、选择题(本大题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求的).1. - 2023的绝对值是( ※)A . 2023B .- 12023C .- 2023D . 120232.2022年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车' 被火星“捕获”。

在制动捕获过程中，探测器距离地球的距离为1920000000 公里，数据1920000000用科学记数法表示为(※)A .19.2x 107B . 19.2x 108C .1.92x 108D .1.92x 1093.一个正方体相对的表面上所标的数都是互为相反数的两个数，如图是这个正方体的表面展开图，那么图中x 的值是(※)A . -3B . -8C .3D . -24.、下列说法: ①-a 一定是一个负数;②相反数、绝对值都等于它本身的数只有0; ③一个有理数不是整数就是分数;④一个数的绝对值越大，则表示它的点在数轴上离原点的距离越远;⑤当a ≠0时，|a |总是大于0,正确的有(※)A .4个B .3个C .2个D .1个5.下列等式变形错误的是(※)A .若a =b ，则a +2=b +2B .若a =b ，则a -3=b -3C .若a =b ，则22a b x xD .若a =b ，则-4a =-4b6.下列叙述正确的是( ※)A .画直线AB =10厘米B .两点之间的线段叫做这两点之间的距离C .把弯曲的公路改直，就能缩短路程，数学原理是“两点确定一条直线”D .已知A ，B , C 三点在同-条直线上，线段AB =8，BC =5,则AC 的长是13或37.下列说法错误的是(※)A .0是单项式B .2πr 2的次数是3C . xy +1是二次二项式D .多项式-4a 2b +3ab -5的常数项为-58.《九章算术》中有一道阐述“盈不足术”的问题，原文如下:今有人共买物，人出八，盈三;人出七，不足四，问人数，物价各几何?译文为:现有一些人共同买一个物品，每人出8元，还盈余3元;每人出7元，则还差4元，问共有多少人?这个物品的价格是多少?设共有x 人，则可列方程为( )A .8x - 3= 7x +4B .8x +3=7x - 4c .4738x x =-+ D . 4738x x =+- 9. 如图，把四张形状大小完全相同的小长方形卡片(如图1)，不重叠地放在一个长为 acm 、宽为bcm 长方形内(如图2)，未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长和是(※)A .4a cmB .4b cmC .2(a + b )cmD .4(a - b )cm10.某超市出售某种商品，标价为a 元，由于市场行情的变化，超市进行了第- -次调价，在此基础上后来又进行了第二次调价，下列四种方案中，两次调价后售价最低的是(※)A .第一次打九折，第二次打九折B .第一次提价60%，第二次打五折C .第一次提价40%，第二次降价40%D .第一次提价20%，第二次降价30%11.阅读:关于x 的方程ax =b 在不同的条件下解的情况如下: (1) 当a ≠0时，有唯一解b x a=; (2)当a =0, b =0时有无数解; (3) 当a =0，b ≠0时无解。

德阳市七年级上册数学期末试卷(含答案)

德阳市七年级上册数学期末试卷(含答案)一、选择题1．如图，已知线段AB 的长度为a ，CD 的长度为b ，则图中所有线段的长度和为( )A ．3a+bB ．3a-bC ．a+3bD ．2a+2b 2．以下选项中比-2小的是（）A ．0B ．1C ．-1.5D ．-2.53．下列方程中，以32x =-为解的是（） A ．33x x =+B ．33x x =+C ．23x =D ．3-3x x =4．根据等式的性质，下列变形正确的是（） A ．若2a ＝3b ，则a ＝23b B ．若a ＝b ，则a +1＝b ﹣1 C ．若a ＝b ，则2﹣3a ＝2﹣3bD ．若23a b=，则2a ＝3b 5．晚上七点刚过，小强开始做数学作业，一看钟，发现此时时针和分针在同一直线上；做完数学作业八点不到，此时时针和分针又在同一直线上，则小强做数学作业花了多少时间（） A ．30分钟B ．35分钟C ．42011分钟 D ．36011分钟 6．-2的倒数是（） A ．-2B ．12- C ．12D ．27．下列选项中，运算正确的是（） A ．532x x -= B ．2ab ab ab -= C ．23a a a -+=-D ．235a b ab +=8．下列分式中，与2x yx y ---的值相等的是()A ．2x y y x+-B ．2x y x y+-C ．2x y x y--D ．2x y y x-+9．如图，直线AB ∥CD ，∠C ＝44°，∠E 为直角，则∠1等于（）A ．132°B ．134°C ．136°D ．138°10．下列方程变形正确的是（） A ．方程110.20.5x x --=化成1010101025x x--= B ．方程 3﹣x=2﹣5（x ﹣1），去括号，得 3﹣x=2﹣5x ﹣1 C ．方程 3x ﹣2=2x+1 移项得 3x ﹣2x=1+2D ．方程23t=32，未知数系数化为 1，得t=1 11．方程3x +2＝8的解是（）A ．3B ．103C ．2D ．1212．方程312x -=的解是（） A ．1x =B ．1x =-C ．13x =-D ．13x =13．如果+5米表示一个物体向东运动5米，那么-3米表示( )． A ．向西走3米 B ．向北走3米 C ．向东走3米 D ．向南走3米 14．若2m ab -与162n a b -是同类项，则m n +=（）A ．3B ．4C ．5D ．715．某同学晚上6点多钟开始做作业，他家墙上时钟的时针和分针的夹角是120°，他做完作业后还是6点多钟，且时针和分针的夹角还是120°，此同学做作业大约用了（） A ．40分钟B ．42分钟C ．44分钟D ．46分钟二、填空题16．甲乙两个足够大的油桶各装有一定量的油，先把甲桶中的油的一半给乙桶，然后把乙桶中的油倒出18给甲桶，若最终两个油桶装有的油体积相等，则原来甲桶中的油是乙桶中油的______倍。

四川省德阳市中江县2023-2024学年七年级下学期期中数学试题(解析版)

2024年春教学质量监测（二）七年级数学试卷说明：1．本试卷分为第Ⅰ卷和第Ⅱ卷．第Ⅰ卷为选择题，第Ⅱ卷为非选择题，全卷共4页．考生作答时，须将答案答在答题卡上，在本试卷、草稿纸上答题无效，考试结束后，将答题卡交回．2．本试卷满分150分，监测时间为120分钟．第Ⅰ卷选择题（48分）一、选择题（本大题共12个小题，每小题4分，满分48分）在每小题给出的四个选项中，有且仅有一项是符合题目要求的．1. 下列各数中，是无理数的是（）A. 2024B.C.D. 【答案】C【解析】【分析】本题考查无理数的概念．无理数指无限不循环小数，逐项判断即可．【详解】解：A.2024是整数，属于有理数，此项不符合题意；B.是整数，属于有理数，此项不符合题意；开方开不尽，是无限不循环小数，属于无理数，此项符合题意；D.是分数，属于有理数，此项不符合题意．故选：C ．2. 如图，将沿向右平移得到，若，，则的长是（）A. 2B.C. 3D. 5【答案】A【解析】【分析】利用平移的性质得到，即可得到的长．【详解】解：∵沿方向平移至处．∴，故选：A ．2024-120242024-12024ABC BC DEF 5BC =2BE =CF 2.5BE CF =CF ABC BC DEF 2BE CF ==【点睛】本题考查了平移的性质：把一个图形整体沿某一直线方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同；新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点．连接各组对应点的线段平行（或共线）且相等．3. 如图是小周同学在校运会上投掷实心球场景，当投掷完毕时，测量员选取的长度作为小周的成绩，其依据是（）A. 垂线段最短B. 两点之间线段最短C. 两点确定一条直线D. 过一点有且只有一条直线与已知直线垂直【答案】A【解析】【分析】此题考查了垂线段最短的性质的运用．由点到直线的距离的定义及投掷实心球比赛的规则作出判断．【详解】解：投掷完毕时，测量员选取的长度作为小周的成绩，其依据是垂线段最短，故选：A ．4. 下列命题正确的是（）A. 两条直线被第三条直线所截，同位角相等B. 对顶角相等，相等的角也是对顶角C.若，则或D. 过一点有且只有一条直线与已知直线垂直【答案】C【解析】【分析】本题考查命题的真假．真命题指正确的命题，假命题指错误的命题，逐项判断即可．【详解】解：A ．两条平行的直线被第三条直线所截，同位角相等，此项不符合题意；B ．对顶角相等，相等的角不一定是对顶角，此项不符合题意；C ．若，则或，此项符合题意；D ．在同一平面内，过一点有且只有一条直线与已知直线垂直，此项不符合题意．的AB AB a b =a b =a b=-a b =a b =a b =-故选：C ．5. 如图，，平分，则（）A. B. C. D. 【答案】B【解析】【分析】根据平行线的性质得出，再由角平分线确定，利用三角形内角和定理求解即可．【详解】解：∵，∴，∵平分，∴，∵，∴，故选：B ．【点睛】题目主要考查平行线的性质及角平分线的计算，三角形内角和定理，理解题意，综合运用这些知识点是解题关键．6. 把点A 先向左平移2个单位长度，再向上平移3个单位长度得到点B ，点B 正好落在轴上，则点B 的坐标为（）A. B. C. D. 【答案】B【解析】【分析】由平移方式可得平移后的坐标为，再根据x 轴上的点的纵坐标为0求出m 的值，即可得出点B 的坐标．【详解】解：点A 先向左平移2个单位长度，对应点的坐标为，AE CD ∥AC BCD ∠235,60D ︒︒∠=∠=B ∠=52︒50︒45︒25︒1235∠=∠=︒70BCD ∠=︒AE CD ∥1235∠=∠=︒AC BCD ∠2170BCD ∠=∠=︒60D ∠=︒18050B BCD D ∠=︒-∠-∠=︒(),2m m +x ()50-，()70-，()40，()30，()2,5m m -+(),2m m +()2,2m m -+再向上平移3个单位长度得到点B 的坐标为，即，点B 正好落在轴上，，，点B 的坐标为，即．故选：B ．【点睛】本题考查由平移方式确定点的坐标，解题的关键是根据平移方式用含m 的代数式表示出平移后的坐标．7. 一个正方体的体积扩大为原来的8倍，它的棱长变为原来的（）A. 2倍B. 3倍C. 4倍D. 5倍【答案】A【解析】【分析】根据正方体的体积计算公式和立方根的定义即可求解．【详解】解：设原来棱长为x ，那么现在的体积为，，∴它的棱长变为原来的2倍，故选：A ．【点睛】此题主要考查了立方根与立方体的体积公式，解题关键是利用立方根的定义准确的求出新立方体的棱长，从而求出棱长之间的关系．8. 如图，将△ABC 沿着某一方向平移一定的距离得到△DEF ，则下列结论：①AD =CF ；②AC ∥DF ；③∠ABC =∠DFE ；④∠DAE =∠AEB ．其中正确的是（）A. 仅①②B. 仅①②④C. 仅①②③D. ①②③④【答案】B【解析】的()2,23m m -++()2,5m m -+ x ∴50m +=∴5m =-∴()52,0--()70-，38x 2x =【分析】根据平移的性质，对应点的连线互相平行且相等，平移变换只改变图形的位置不改变图形的形状与大小对各小题分析判断即可得解．【详解】解：∵△ABC 沿着某一方向平移一定的距离得到△DEF ，①AD =CF ，正确；②AC ∥DF ，正确；③∠ABC =∠DEF ，故原命题错误；④∠DAE =∠AEB ，正确．所以，正确的有①②④．故选：B ．【点睛】本题主要考查了平移的性质，是基础题，熟记性质是解题的关键．9. 已知关于的二元一次方程组的解满足，则m 的值为（）A. 0B. 1C. 2D. 3【答案】B【解析】【分析】将方程组的两个方程相减，可得到，代入，即可解答．【详解】解：，得，，代入，可得，解得，故选：B ．【点睛】本题考查了根据解的情况求参数，熟练利用加减法整理代入是解题的关键．10. 某学校课后兴趣小组在开展手工制作活动中，美术老师要求用14张卡纸制作圆柱体包装盒，准备把这些卡纸分成两部分，一部分做侧面，另一部分做底面．已知每张卡纸可以裁出2个侧面，或者裁出3个底面，如果1个侧面和2个底面可以做成一个包装盒，这些卡纸最多可以做成包装盒的个数为（）A. 6B. 8C. 12D. 16【答案】C ,x y 34125x y m x y m -=+⎧⎨+=-⎩4x y -=3x y m -=+4x y -=34125x y m x y m -=+⎧⎨+=-⎩①②-①②2226x y m -=+3x y m ∴-=+4x y -=34m +=1m =【解析】【分析】设用x 张卡纸做侧面，用y 张卡纸做底面，则做出侧面的数量为2x ，底面的数量为3y ，然后根据等量关系：底面数量=侧面数量的2倍，列出方程组即可．【详解】解：设用x 张白卡纸做侧面，用y 张白卡纸做底面，由题意得，．解得．，答：这些卡纸最多可以做成包装盒的个数为12个．故选：C ．【点睛】本题考查了由实际问题抽象出二元一次方程组，解答本题的关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组．还需注意本题的等量关系是：底面数量=侧面数量的2倍．11. 如图，已知平分平分，且．则下列结论：①平分，②，③，④点是线段上任意一点，则．正确有（）个．A. 1个B. 2个C. 3个D. 4个【答案】C【解析】【分析】本题考查平行线的判定与性质，角平分线的判定与性质．由，平分，平分，得，，，再由，可得，①正确；进而得，②正确；由得，③正确；点是线段上任意一点，由与不平行，与不平行，得的14223x y x y +=⎧⎨⨯=⎩68x y =⎧⎨=⎩212x =,AC BD BC ∥,ABD CE ∠DCM ∠BC CE ⊥CB ACD ∠AB CD A BDC ∠=∠P BE APM BAP PCD ∠=∠+∠AC BD ∥BC ABD ∠CE DCM ∠DBC ACB ∠=∠ABC DBC ∠=∠DCE MCE ∠=∠90MCE BCD ∠+∠=︒90MCE ACB ∠+∠=︒ACB BCD ∠=∠ABC BCD ∠=∠AB CD 180,180A ABD BDC ABD ∠+∠=︒∠+∠=︒A BDC ∠=∠P BE AB PC CD PM，故，④不正确，所以有3个正确．【详解】解：平分平分平分,故①正确；,故②正确；，故③正确；如图，点是线段上任意一点与不平行，与不平行，故④不正确，所以，正确的个数有3个．,BAP APC PCD CPM ∠≠∠∠≠∠APM BAP PCD ∠≠∠+∠AC BDDBC ACB∴∠=∠BC ABD∠ABC DBC∴∠=∠ABC ACB∴∠=∠CE DCM∠DCE MCE∴∠=∠BC CE⊥ 90BCD DCE ∴∠+∠=︒90MCE BCD ∴∠+∠=︒90MCE ACB ∠+∠=︒ACB BCD∴∠=∠CB ∴ACD ∠ABC BCD∴∠=∠AB CD ∴∥∥,∥AC BD AB CD180,180A ABD BDC ABD ∴∠+∠=︒∠+∠=︒A BDC ∴∠=∠P BE AB PC CD PM ,BAP APC PCD CPM∴∠≠∠∠≠∠APM BAP PCD ∴∠≠∠+∠故选：C ．12. 如图，点，点，点，点，点…，按照这样的规律下去，点的坐标为( )A. B. C. D. 【答案】D【解析】【分析】本题考查了图形坐标规律探索，并用代数式表示规律，分类思想，通过发现特殊点的坐标与序号的关系，得出横坐标，纵坐标与点的序号之间关系，从而确定规律求解即可．【详解】解：观察图形可得：点，，…，，，…．∵2024是偶数，且，∴，∴，故选：D ．第Ⅱ卷（非选择题，共102分）二、填空题（每小题4分，满分28分，将答案填在答题卡对应的题号后的横线上）13. 把命题“对顶角相等”改写成“如果…那么…”的形式为__________．【答案】如果两个角是对顶角，那么这两个角相等【解析】【分析】本题考查了命题的概念，命题是由题设和结论两部分组成，根据命题的概念作答即可．【详解】把命题“对顶角相等”改写成“如果…那么…”的形式为：如果两个角是对顶角，那么这两个角相等．(0,1)A 1(2,0)A ()23,2A 3(5,1)A 4(6,3)A 2024A ()3035,1011()3036,1011()3035,1013()3036,10131(2,0)A 3(5,1)A ()58,2A ()2131,1n A n n ---()23,2A 4(6,3)A ()69,4A ()23,1n A n n +20242n =1012n =()20243036,1013A =故答案为：如果两个角对顶角，那么这两个角相等．14.____．【答案】±3【解析】【分析】根据算术平方根、平方根解决此题．【详解】解：，的平方根是．故答案为：．【点睛】本题主要考查算术平方根、平方根，熟练掌握算术平方根、平方根是解题的关键．15. 已知是二元一次方程的一个解，则代数式的值是_________．【答案】【解析】【分析】根据是二元一次方程的一个解，得到，利用整体思想代入代数式求值即可．【详解】解：∵是二元一次方程的一个解，∴，∴；故答案为：．【点睛】本题考查二元一次方程的解，代数式求值．熟练掌握二元一次方程的解是使等式成立的未知数的值，利用整体思想代入求值，是解题的关键．16. 已知 ∠1 的两边分别平行于 ∠2 的两边，若 ∠1 = 40°，则 ∠2 的度数为__．【答案】40°或140°【解析】【分析】如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补. 根据题意, ∠1=∠2或∠1是 9=∴3=±3±x a y b=⎧⎨=⎩278x y -=17414a b -+1x a y b=⎧⎨=⎩278x y -=278a b -=x a y b =⎧⎨=⎩278x y -=278a b -=()1741417227a b a b -+=--1728=-⨯1716=-1=1和∠2互补.【详解】解:根据题意,得 ∠1=∠2=40°或∠2=180°-∠1=180°-40°=140°故答案为40°或140°.【点睛】本题考查了平行线的性质，如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.17. 如图，若，，，将三角形沿方向平移，得到三角形，连接，则阴影部分的周长为______．【答案】11【解析】【分析】本题考查的是平移的性质，掌握平移不改变图形的形状和大小、经过平移，对应点所连的线段平行且相等，对应线段平行且相等是解答本题的关键．根据平移的性质得到，根据周长公式计算，得到答案．【详解】由平移的性质，可知：∴，∴阴影部分的周长为故答案为：11．18.的最小值为______．【答案】6【解析】知，整数的最小值为6即可．【详解】解：整数的最小值为6．故答案为：6．19. 在初中数学文化节游园活动中，被称为“数学小王子”的王小明参加了“智取九宫格”游戏比赛，活动规则是：在九宫格中，除了已经填写的三个数之外的每一个方格中，填入一个数，使每一横行、每一竖4cm AB =5cm =BC 2cm =AC ABC BC ()cm 05a a <<DEF AD cm 4cm,cm DE AB AD BE a ====4cm,cm DE AB AD BE a ====(5)cm EC a =-11cmAD EC AC DE +++=n =n =∴n列以及两条对角线上的3个数之和分别相等，且均为m ．王小明抽取到的题目如图所示，他运用初中所学的数学知识，很快就完成了这个游戏，则_________．1674【答案】39【解析】【分析】设第一列中间的数为，则三个数之和为，再一次把表格的每一个数据填好，从而可得答案．【详解】解：如图，设第一列中间的数为，则三个数之和为，可得：1674∴，故答案为：39【点睛】本题考查的是列代数式，整式的加减运算的应用，理解题意，设出合适的未知数是解本题的关键．三、解答题（本大题7个小题，满分74分）20. （1）计算：，（2）解方程：，（3）解方程组：．【答案】（1；（2）；（3）【解析】【分析】本题考查实数的运算，一元二次方程的解法，二元一次方程组的解法．（1）先算绝对值，算术平方根，去括号，立方根，再算加减即可；m =x 16420x x ++=+x 16420x x ++=+13x+x136x +1016131039m =++=31ππ-+-225(1)360x +-=3249513x y x y -=⎧⎨-=⎩12111,55x x ==-21x y =⎧⎨=⎩（2）先移项，然后用直接开方法解即可；（3）用加减消元解即可．【详解】解：（1）原式（2）或；（3），得把代入①，得原方程组的解为．21. 如图，将三角形放在单位长度为1的正方形网格中，顶点均在格点上．（1）直接写出点A ，B ，C 的坐标；（2）将三角形的顶点A 平移到，B ，C 分别平移到，求点的坐标；352ππ=-++-22== 225(1)360x +-=236(1)25x ∴+=∴615x +=615x +=-12111,55x x ∴==-3249513x y x y -=⎧⎨-=⎩①②3⨯-①②1y -=-1y =∴1y =2x =∴21x y =⎧⎨=⎩ABC ABC ()112，A 11,BC 11,B C（3）求三角形的面积．【答案】（1），，；（2），；（3）8【解析】【分析】（1）根据点的位置写出坐标即可；（2）利用平移变换的性质作出图形可得结论；（3）把三角形的面积看成矩形的面积减去周围的三个三角形面积即可．【小问1详解】解：，，；【小问2详解】解：如图，即为所求，，；【小问3详解】解：三角形的面积．【点睛】本题考查坐标与图形变化平移，三角形的面积等知识，解题的关键是掌握平移变换的性质，属于中考常考题型．22. 已知：如图，点D ，E ，F 分别是三角形ABC 的边BC ，CA ，AB 上的点，DF ∥CA ，∠FDE ＝∠A ；（1）求证：DE ∥BA．111A B C ()1,3A -()3,1B --()2,1C ()11,2B --()14,0C ()1,3A -()3,1B --()2,1C 111A B C △()11,2B --()14,0C 111A B C 111452423258222=⨯-⨯⨯-⨯⨯-⨯⨯=-（2）若∠BFD ＝∠BDF ＝2∠EDC ，求∠B 的度数．【答案】（1）见解析（2）36°【解析】【分析】(1)根据平行线的性质与判定方法证明即可；(2)设∠EDC =x °，由∠BFD =∠BDF = 2∠EDC 可得∠BFD =∠BDF = 2x °，根据平行线的性质可得∠DFB = ∠FDE = 2x °，再根据平角的定义列方程可得x 的值，进而得出∠B 的度数．小问1详解】证明：∵DF ∥CA ，∴∠DFB =∠A ，又 ∵∠FDE =∠A ，∴∠DFB =∠FDE ，∴DE ∥AB ；【小问2详解】解：设∠EDC =x º，∵∠BFD =∠BDF =2∠EDC ，∴∠BFD =∠BDF =2x º，由（1）可知∠DFB =∠FDE =2x º，∴∠BDF +∠EDF +∠EDC =2x º+2x º+x º=180º，∴x =36，又∵DE ∥AB ，∴∠B =∠EDC =36 º．【点睛】本题主要考查了平行线的性质与判定的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．23. 先阅读然后解答提出的问题：设a 、b 是有理数，且满足，求b a 的值．解：由题意得，因为a 、b 都是有理数，所以a ﹣3，b+2也是有理数，是无理数，所以a-3=0，b+2=0，所以a=3，b=﹣2，所以．【3=-a (3)(0-++=a b 3(2)8=-=-a b问题：设x 、y 都是有理数，且满足x+y 的值．【答案】7或-1.【解析】【分析】根据题目中给出的方法，对所求式子进行变形，求出x 、y 的值，进而可求x+y 的值.【详解】解：∵∴，∴=0=0∴x=±4，y=3当x=4时，x+y=4+3=7当x=-4时，x+y=-4+3=-1∴x+y 的值是7或-1.【点睛】本题考查实数的运算，解题的关键是弄清题中给出的解答方法，然后运用类比的思想进行解答.24. 探究题：已知为直线上的一点，以为顶点作，射线平分．（1）如图1，若，则______，______；（2）若将绕点旋转至图2的位置，射线仍然平分，请写出与之间的数量关系，并说明理由；（3）若将绕点旋转至图3的位置，射线仍然平分，求的度数．【答案】（1），（2），理由见解析（3）【解析】【分析】（1）利用角的加减，角平分线定义计算；（2）由图②，可以得到各个角之间的关系，从而可以得到和之间的数量系；（3）由图③和已知条件可以建立各个角之间的关系，从而可以得到的度数．2210x y -+=+2210x y -=+()22100x y --+-=2210x y ---O AD O 90COE ∠︒＝OF AOE ∠54DOE ∠︒＝AOC ∠＝COF ∠＝COE ∠O OF AOE ∠COF ∠DOE ∠COE ∠O OF AOE ∠2COF DOE ∠+∠36︒27︒COF ∠=12DOE ∠360︒COF ∠DOE ∠2COF DOE ∠+∠【小问1详解】解：故答案为：,【小问2详解】解：，理由如下：【小问3详解】解：54DOE ∠=︒18054126AOE ∴∠=︒-︒=︒90COE ∠=︒1269036AOC AOE COE ∴∠=∠-∠=︒-︒=︒OF AOE∠ 平分1632AOF FOE AOE ∴∠=∠=∠=︒906327FOC COE FOE ∴∠=∠-∠=︒-︒=︒36︒27︒12COF DOE ∠=∠()1290901190902218011901802212OF AOE AOF AOE COE AOC AOE COF AOC AOF AOE AOE AOE AOE DOECOF DOE DOE COF DOE ∠∴∠=∠∠=︒∴∠=︒-∠∴∠=∠-∠=︒-∠∠=︒-∠∠=︒-∠∴∠=︒-︒-∠=∠∴∠=∠ 平分＋90COE ∠=︒()1809090222232339090360AOE COD OF AOEAOE EOFCOF DOECOE EOF COE CODCOE EOF COE CODCOE EOF CODCOE AOE COD∴∠∠=︒-︒=︒∠∴∠=∠∴∠∠=∠∠∠∠=∠∠∠∠=∠∠∠=∠∠∠=⨯︒︒=︒＋平分＋＋＋＋＋＋＋＋＋＋＋＋故答案为：【点睛】本题考查了角平分线的定义以及角的计算，解题的关键是找出各个角之间的关系，利用数形结合的思想找出所求问题需要的条件．25. 塘栖枇杷是余杭的特色产品，肉质细嫩、汁多味鲜，塘栖枇杷有着非常悠久的历史，据相关文献记载，塘栖枇杷的种植距今已经有 1400多年的历史．某销售商将塘栖枇杷分成型、型两种礼盒进行销售，①型每盒，每盒售价元；②型每盒，每盒售价比型价格的2倍少50元．某位顾客买了一盒型，两盒型，一共花费340 元．（1）请问型、型售价分别是多少元？（2）假设用这两种包装方式恰好包装完所有的枇杷．销售总收入为9820元．①若这批塘栖枇杷全部售完，请问型、型分别有多少盒？②若该销售商留下盒型礼盒送人，剩余礼盒全部售出，求出的值．【答案】（1）型售价88元、型售价126元；（2）①型礼盒装40盒，型礼盒50盒；②【解析】【分析】本题主要考查了一元一次方程的应用以及二元一次方程的应用，（1）根据题意列出一元一次方程，解方程求解；（2）①设型礼盒装共包装了盒，型礼盒装共包装了盒,根据题意列出二元一次方程，解方程求解即可； ②由题意得出，，结合，，，得出m 的值即可；【小问1详解】解：由题意得型礼盒售价为元，得，解得：，则元，答：型售价88元、型售价126元；【小问2详解】①设型礼盒装共包装了盒，型礼盒装共包装了盒，由题意得：，360︒255kg A B A 2kg a B 3.5kg A A B A B A B (0)m m >A m A B A B 14m =A x B y 22507m y =-11402m x =+0x ≥0y ≥0m >B ()250a -()2250340a a +-=88a =250126a -=A B A x B y 2 3.5255881269820x y x y +=⎧⎨+=⎩解得，答：型礼盒装40盒，型礼盒50盒；②由①知，可得．由题意得，，解得：，，，，都是整数，且，，，．26. 如图1，，将线段平移至线段，点（不与点重合）在线段上．（1）若，求的度数；（2）求证：；（3）如图2，已知点在上，分别交的延长线于点，垂足为点．设，且满足，求的值．【答案】（1）（2）见详解（3）8【解析】【分析】本题考查平行线的性质，平移的性质，三角形内角和定理，非负数的性质．（1）先用三角形内角和求，再用平行线的性质即可；4050x y =⎧⎨=⎩A B 2 3.5255x y +=51074y x -=51078812698204y m y -⎛⎫⨯-+=⎪⎝⎭22507m y =-11402m x ∴=+x y m 0x ≥0y ≥0m >14m ∴=AB CD ∥AB EF E C BC 15,120ACB BAC ∠=︒∠=︒BEF ∠ACB CEF BAC ∠=∠-∠G CD ,,EG AB AM AB AM =⊥,,EF CD FG ,,,K H M MN EG ⊥N ,AK a KH b ==,ab 1120a b --+=MA MN -45︒B ∠（2）先用平行线的性质得，，再用等量代换得，最后化简即可；（3）先根据非负数的性质求出，连接，过点作于，得,利用即得到，最后由即可．【小问1详解】解：线段平移至线段；【小问2详解】即；【小问3详解】解得180ACB BCD BAC ∠+∠+∠=︒180BCD CEF ∠+∠=︒ACB BCD BAC BCD CEF ∠+∠+∠=∠+∠,a b EM G GQ EF ⊥Q GQ KH =EFG EFM EGM S S S =- 111222EF KM EG MN EF KH ⋅-⋅=⋅KM MN KH -=AM MN AK KM MN AK KH -=+-=+ 15,120ACB BAC ∠=︒∠=︒1801512045B ∴∠=︒-︒-︒=︒AB EF AB EF∴45BEF B ∴∠=∠=︒ AB CD∥180ACD BAC ∴∠+∠=︒180ACB BCD BAC ∠+∠+∠=︒AB EF∥EF CD∴ 180BCD CEF ∴∠+∠=︒ACB BCD BAC BCD CEF∴∠+∠+∠=∠+∠∴ACB CEF BAC ∠=∠-∠ 1120a b --+=11202130a b a b --=⎧∴⎨+-=⎩53a b =⎧⎨=⎩5,3AK KH ∴==,EG AB EF AB==连接，过点作于，，．即的值为8．EG EF∴=EM G GQ EF ⊥Q EF CD GQ KH∴=EFG EFM EGMS S S =- 111222EF KM EG MN EF KH ∴⋅-⋅=⋅3KM MN KH ∴-==538AM MN AK KM MN AK KH ∴-=+-=+=+=MA MN -。

七年级上册德阳数学期末试卷测试卷(word版,含解析)

七年级上册德阳数学期末试卷测试卷（word版，含解析）—、选择题1.自南京地铁四号线开通以来，最髙单日线路客运量是2017年12月7日的191000人次，数字191000用科学计数法表示为（）A. 19.1x104B. 1.91X105C. 19.1XJ05D. 0.191xl062.如图1是AD//BC的一张纸条，按图I T图2 —图3,把这一纸条先沿EF折叠并压平，再沿折叠并压平，若图3中ZCFE = 24°,则图2中ZAEF的度数为（）B 下列四个图形中，能用Zl, ZAOB.ZO三种方法表示同一个角的是（）3.4.D.两点之间线段最短A.C. 一个角的补角一定大于这个角5.如图的平面展开图折叠成正方体后，相对而上的数都互为相反数，那么d的值是（）对顶角相等-2 C.6.某种商品的进价为100元，由于该商品积压, 16元，则标价为（）A. X6 元B. 245 元3 D. -b商店准备按标价的8折销售，可保证利润C. 150元D. 160 元①经过两点有且只有一条直线；②连接两点的线段叫两点的距离：③两点之间的所有连线中，垂线段最短；④过直线外一点有且只有一条直线与已知直线平行.A.0个B. 1个C. 2个D. 3个二、填空题16.如图，已知ZAOB=75\ ZCOD=35\ ZCOD在ZAOB的内部绕着点0旋转(0C与OA 不重合，0D 与0B不重合)，若0E为ZAOC的角平分线.贝I] 2ZBOE-ZBOD的值为17.计算：x(x・2y)二__________18.太阳与地球的平均距离大约是150 000 000千米，数据150 000 000用科学记数法表示为_______ .19.若a-b = 3,则代数式2b-2a +1的值等于____________ •20.如图是一把剪刀，若ZAOB+ZCOD = 60\则ZBOD= °・21._______________________________________________________ 如图，一副三角尺有公共的顶点A ,则ZDAB_ZEAC= _____________________________________22.如图，田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分.发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是_______ ・23・已知月球与地球之间的平均距离约为384 000km,把384 000km用科学记数法可以表 zj\ km ・24.在-2、-3、4、5中选取2个数相除，则商的最小值是___________ :325.若代数式4十+3_4的值为则代数式l-x1 2 3 4--x的值为________________ ・4三、解答题26.如图，数轴上线段AB二2 （单位长度），CD二4 （单位长度），点A在数轴上表示的数是-&点C在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动，同时线段CD以2个单位长度/秒的速度也向右匀速运动.A B0 CD（1） _________________________________ 运动t秒后，点B表示的数是:点C表示的数是.（用含有t的代数式表示）（2）求运动多少秒后，BC二4 （单位长度）；（3）P是线段AB上一点，当B点运动到线段CD上时，是否存在关系式加-AP = 4PQ, 若存在，求线段PD的长：若不存在，请说明理由.1 1 3 127.先化简，再求值：-x-2（x--r）+（--x+-r）, K中如y满足乙丿厶丿2（x + 2）2+y~- =028.如图所示的几何体是由若干个相同的小正方体组成的.（2）画出它的三个视图.（作图必须用黑色水笔描黑）29.如图，已知点A, B, C,直线/及上一点M,请你按着下列要求画出图形.1 画射线3M;2 画线段BC、AM，且相交于点D：3 画出点A到直线/的垂线段AE：4 请在直线/上确疋一点6使点O到点A和点B的距离之和（OA + OB）最小.，cA •30・(探索新知)如图1,点C将线段人B分成AC和BC两部分，若BC=nAC,则称点C 是线段的圆周率点，线段AC、BC称作互为圆周率伴侣线段.(1)若AC=39则_________ :(2)若点D也是图1中线段处的圆周率点(不同于C点)，贝WC_DB；丨 1 !A C B图1(深入研究)如图2,现有一个直径为1个单位长度的圆片，将圆片上的某点与数轴上表示1的点重合，并把圆片沿数轴向右无滑动地滚动1周，该点到达点C的位置.(\ i \o y c ./—,——-—,—.—------------------------------- >■0 I 2 3 4图2(3)若点M、A/均为线段0C的圆周率点，求线段M/V的长度.(4〉图2中，若点D在射线0C上，且线段CD与以0、C、D中某两个点为端点的线段互为圆周率伴侣线段，请直接写出点D所表示的数.31.计算题(1)-(-3) + 7-|-8|<2) -32-|-6|-3X(-|)+(-2)2^1.232.如图，C为线段A3上一点，D在线段AC上，且AD = -AC, E为BC的中点,3若AC = 6, BE=\，求线段DE的长.A D CEB33.解方程或不等式(1)—-1 = ^^; (2) 2(x + 3)>4x-(x-3)2 3四、压轴题34.点A、B在数轴上分別表示数u,b, A、B两点之间的距离记为\AB\.我们可以得到\AB\ = \a-b\t(1)数轴上表示2和5的两点之间的距离是_:数轴上表示-2和-5两点之间的距离是_;数轴上表示1和Q的两点之间的距离是(2)若点A、B在数轴上分别表示数-1和5,有一只电子蚂蚁在数轴上从左向右运动，设电子蚂蚁在数轴上的点C对应的数为c .①求电子蚂蚁在点A的左侧运动时\AC\ + \BC\的值，请用含C的代数式表示：②求电子蚂蚁在运动的过程中恰好使W|c+l| + |c-5| = ll, c表示的数是多少？③在电子蚂蚁在运动的过程中，探索|c+l| + |c-5|的最小值是一.35.如图①，点0为直线A3上一点，过点0作射线0C,将一直角三角板如图摆放（ZMON=90）•（1）若ZBOC = 35 ,求ZMOC的大小.（2）将图①中的三角板绕点0旋转一立的角度得图②，使边OM恰好平分ZBOC, I nJ: ON 是否平分ZAOC?请说明理由.（3）将图①中的三角板绕点0旋转一泄的角度得图③，使边ON任乙BOC的内部，如果ZBOC = 50，则ABOM与ZNOC之间存在怎样的数屋关系？请说明理由.图①_图②图③36.泄义：若a — 0 = 9O ,且90 <a<180 ,则我们称0是Q的差余角.例如：若 a = 110 ,则&的差余角0 = 20 .（1）如图1,点0在直线上，射线0E是ZBOC的角平分线，若ZCOE是ZAOC 的差余角，求ZBOE的度数.（2）如图2,点0在直线A3上，若ZBOC是ZAOE的差余角，那么ZBOC与ZBOE 有什么数量关系.（3）如图3,点0在直线AB上，若ZCOE是乙40C的差余角，且0E与OC在直线A3的同侧，请你探究厶""一W是否为定值？若是,请求出立值；若不是，请说ZCOE明理由.图1 图2 图337.数轴上有两点A, B,点C, D分别从原点0与点B出发，沿BA方向同时向左运动. （1）如图，若点N为线段0B上一点，AB=16, 0N=2,当点C, D分别运动到AO, BN的中点时，求CD的长；（2）若点C在线段0A上运动，点D在线段0B上运动，速度分别为每秒lcm, 4cm,在点MC, D运动的过程中，满足0D二4AC,若点M为直线AB上一点，且AM-BM=OM,求二石OM的值.6 6 AV 6 小 6 Bi38.对于数轴上的A、B,C三点，给出如下泄义：若荘中一个点与其他两个点的距离恰好满足2倍的数量关系，则称该点是其他两点的"倍联点".例如数轴上点A,B,C所表示的数分别为2, 3, 4,满足AB = 2BC，此时点3是点A,C的“倍联点A B C0 1 2 3 4 5若数轴上点M表示-3,点N表示6,回答下列问题：(1)数轴上点分別对应0, 3.5和口，贝IJ点_________________ 是点M,N的“倍联点”，点N是________ 这两点的“倍联点”：(2)已知动点P在点N的右侧，若点N是点PM的倍联点，求此时点尸表示的数.39.已知 ZAOB是锐角，ZAOC = 2ZBOD.(1)如图，射线OC,射线0D在ZAOB的内部(ZAOD>ZAOC), ZAOB与ZCOD互余；①若ZAOB =60°,求ZBOD的度数；②若OD平分ZBOC，求ZBOD的度数.(2)若射线O D/±.ZAOB的内部，射线OC在乙4OB的外部，ZAOB与ZCOD互补.方方同学说ZBOD的度数是确定的：圆圆同学说：这个问题要分类讨论，一种情况下 ZBOD的度数是确左的，另一种情况下ABOD的度数不确左•你认为谁的说法正确?为什么？40.综合与探究问题背景数学活动课上，老师将一副三角尺按图(1)所示位置摆放，分别作出ZAOC, ZBOD的平分线OM、ON,然后提出如下问题：求出ZM0N的度数.特例探究“兴趣小组”的同学决定从特例入手探究老师提出的问题，他们将三角尺分别按图2、图3所示的方式摆放，0M和ON仍然是ZAOC和ZBOD的角平分线.其中，按图2 方式摆放时，可以看成是ON、OD、0B在同一直线上.按图3方式摆放时，ZAOC和 ZBOD相等.（1） _________________________________________________________ 请你帮助“兴趣小组”进行计算：图2中ZMON的度数为_______________________________ ° .图3中ZMON的度数为________ ° .发现感悟解决完图2,图3所示问题后，“兴趣小组”又对图1所示问题进行了讨论：小明：由于图1中ZAOC和ZBOD的和为90° ,所以我们容易得到ZMOC和ZNOD的和，这样就能求出ZMON的度数.小华：设ZBOD为X。

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)一、幂的运算易错压轴解答题1．解答下列问题（1）已知2x＝3，2y＝5，求2x+y的值；（2）已知3m＝4，3n＝2，求的值；（3）若，求的值．2．综合题（1）填空：21﹣20=2（________）， 22﹣21=2（________）， 23﹣22=2（________）…（2）探索（1）中式子的规律，试写出第n个等式，并说明第n个等式成立；（3）运用上述规律计算：20﹣21﹣22﹣…﹣22017+22018。

3．计算（1）|﹣1|+（﹣2）3+（7﹣π）0﹣（）﹣1（2）（﹣a2）3﹣6a2•a4（3）3x﹣2（x﹣1）﹣3（x+1）（4）（m4）2+m5•m3+（﹣m）4•m4．二、平面图形的认识（二）压轴解答题4．小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决一下.（1）如图1，已知，则成立吗？请说明理由.（2）如图2，已知，平分，平分 . 、所在直线交于点，若，，求的度数.（3）将图2中的线段沿所在的直线平移，使得点B在点A的右侧，若，，其他条件不变，得到图3，请你求出的度数（用含m，n的式子表示）.5．在中，为直线AC上一点，E为直线AB上一点，（1）如图1，当D在AC上，E在AB上时，求证；（2）如图2，当D在CA的延长线上，E在BA的延长线上时，点G在EF上，连接AG，且，求证：（3）如图3，在（2）的条件下，连接BG,当BG平分时，将沿着AG折至探究与的数量关系．6．将一副三角板中的两块直角三角尺的直角顶点按如图所示的方式叠放在一起（其中，，），固定三角板，另一三角板的边从边开始绕点顺时针旋转，设旋转的角度为．（1）当时；若，则的度数为________；（2）若，求的度数；（3）由（1）（2）猜想与的数量关系，并说明理由；（4）当时，这两块三角尺是否存在一组边互相垂直？若存在，请直接写出所有可能的值，并指出哪两边互相垂直（不必说明理由）；若不存在，请说明理由．三、整式乘法与因式分解易错压轴解答题7．[数学实验探索活动]实验材料现有若干块如图①所示的正方形和长方形硬纸片.实验目的：用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积，写出相应的等式有a2+3ab+2b2=（a+2b）（a+b）或（a+2b）（a+b）=a2+3ab+2b2.问题探索：（1）小明想用拼图的方法解释多项式乘法（2a+b）（a+b）=2a2+3ab+b2，那么需要两种正方形纸片________张，长方形纸片________张；（2）选取正方形、长方形硬纸片共8块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；（3）试借助拼图的方法，把二次三项式2a2+5ab+2b2分解因式，并把所拼的图形画在虚线方框3内.8．提出问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”探究发现：如图所示，小敏用4个完全相同的、邻边长度分别为a、b的长方形拼成一个边长为（a+b）的正方形（其中a、b的和不变，但a、b的数值及两者的大小关系都可以变化）.仔细观察拼图，我们发现，如果右图中间有空白图形F，那么它一定是正方形（1）空白图形F的边长为________；（2）通过计算左右两个图形的面积，我们发现（a+b）2、（a﹣b）2和ab之间存在一个等量关系式.①这个关系式是________；②已知数x、y满足：x+y＝6，xy＝，则x﹣y＝________；问题解决：问题：“周长一定的长方形，当邻边长度满足什么条件时面积最大？”①对于周长一定的长方形，设周长是20，则长a和宽b的和是________面积S＝ab的最大值为________，此时a、b的关系是________；②对于周长为L的长方形，面积的最大值为________.活动经验：周长一定的长方形，当邻边长度a、b满足________时面积最大.9．阅读下面材料:通过整式运算一章的学习，我们发现要验证一个结论的正确性可以有两种方法：例如：要验证结论方法1：几何图形验证：如下图，我们可以将一个边长为（a+b）的正方形上裁去一个边长为(a-b)的小正方形则剩余图形的面积为4ab,验证该结论正确。

德阳初一数学考试题及答案

德阳初一数学考试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是正整数？A. -2B. 0C. 1D. 0.5答案：C2. 一个数的相反数是它自己，这个数是？A. 0B. 1C. -1D. 2答案：A3. 计算2x + 3y = 7，当x = 1时，y的值是？A. 1B. 2C. 3D. 4答案：B4. 以下哪个图形是轴对称图形？A. 平行四边形B. 矩形C. 等边三角形D. 任意梯形答案：C5. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 0答案：C6. 计算(a+b)^2的结果是？A. a^2 + b^2B. a^2 - 2ab + b^2C. a^2 + 2ab + b^2D. a^2 + b^2 + 2ab答案：C7. 一个数的平方根是2，这个数是？A. 4B. -4C. 2D. -2答案：A8. 计算3x - 5 = 10，x的值是？A. 5B. 3C. 7D. 1答案：C9. 一个数的立方是-8，这个数是？A. 2B. -2C. 8D. -8答案：B10. 计算以下哪个表达式的结果是偶数？A. 2x + 3B. 2x - 1C. 2x + 1D. 2x答案：D二、填空题（每题4分，共20分）11. 一个数的平方是25，这个数是______。

答案：±512. 计算2^3 + 3^2的结果是______。

答案：1713. 一个数的倒数是1/4，这个数是______。

答案：414. 计算(2x - 3)/(x + 1) = 1，x的值是______。

答案：215. 一个数的绝对值是3，这个数可能是______或______。

答案：3或-3三、解答题（每题10分，共50分）16. 解方程：4x - 7 = 9。

答案：x = 417. 计算表达式：(3a + 2b)(a - b)。

答案：3a^2 - ab - 2b^218. 证明：(a + b)^2 = a^2 + 2ab + b^2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

最新四川德阳市数学七试卷（含答案）
第Ⅰ卷选择题（共30分）
一、选择题（本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）
1．在1，0，-1，1/2这四个数中，最小的数是（）
A. 1
B. 0
C. -1
D. 1/2
2．某市一天的最高气温为2℃，最低气温为﹣8℃，那么这天的最高气温比最低气温高
（）
A．﹣10℃B．﹣6℃C．10℃D．6℃
3．（﹣1）2015的相反数是（）
A．1B．﹣1C．2015D．﹣2015
4．如果m和n互为相反数，则化简（3m﹣2n）﹣（2m﹣3n）的结果是（）
A．﹣2B．0C．2D．3
5.钟表上2时25分时，时针与分针所成的角是 ( )
A. 77.5 °
B. 77 °5′
C. 75°
D. 76°
6．下列说法正确的是( ) A．过一点有且仅有一条直线与已知直线平行
B．两点之间的所有连线中，线段最短
C．相等的角是对顶角
D．若AC＝BC，则点C是线段AB的中点
7．“十一”黄金周，商场为促销开始打折，某商品原价a元，打m折后的售价为……………（）
A．am B．a/m C．am%D．0.1am
8. 若 x 表示一个两位数， y 也表示一个两位数，小明想用 x、 y来组成一个四位数，且把
x 放在 y 的右边
．．，你认为下列表达式中哪一个是正确的 ( )
A、 yx
B、 x + y
C、 100x + y
D、 100y + x
9.计算
等于（）
A.－1
B.1
C.－4
D.4 10．若x 的相反数是3，|y|＝5，则x ＋y 的值为（）
A ．－8
B ．2
C ．8或－2
D ．－8或2
第Ⅱ卷非选择题（共90分）
二、填空题（本大题共5个小题，每小题3分，共15分）
11. 化简-9/3的结果是 .
12、如果a 与1互为相反数，则︱a+2︱= .
13.甲乙丙三地的海拔高度分别为20米, －15米, －10
米,那么最高的地方比最低的地方高（）
A ．5米
B ．10米
C ．25米
D ．35米
14．如图是每个面上都有一个汉字的正方体的一种展开图，那么在正方体的表面，与“明”相对
的面上的汉字是（）
15．请阅读一小段约翰·斯特劳斯的作品，根据乐谱中的信息，确定最后一个音符的时间长应为______ ( )
三、解答题（本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤） 16．（1）计算：（﹣2）3﹣8÷（﹣2）×（﹣）+（﹣1）2016 （2）解方程：=1﹣．
17．解方程
(1) 3(x －4)＝12； (2) x －x －12 ＝2－x ＋23．
18．先化简，再求值：
已知5x y 2－[x2 y－2( 3xy 2－x2 y )]－4 x2y，其中x、y满足(x－2)2 +∣y+1∣=0．
19．下表为国外几个城市与北京的时差（正数表示同一时刻比北京时间早的时数，负数表示同一时刻比北京时间晚的时数）：
城市东京巴黎伦敦纽约莫斯科悉尼
时差（时）+1﹣7﹣8 ﹣13﹣5+2
（1）北京6月11日20时是巴黎的什么时间？
（2）北京6月11日20时是悉尼的什么时间？
（3）小莹的爸爸于6月11日20时从北京乘飞机，经过16小时的航行到达纽约，到达纽
约时北京时间是多少？
20、如图1，CE平分∠ACD，AE平分∠BAC，∠EAC+∠ACE=90°
（1）请判断AB与CD的位置关系并说明理由；
（2）如图2，当∠E=90°保持不变，移动直角顶点E，使∠MCE=∠ECD，当直角顶点E点移动时，问∠BAE与∠MCD否存在确定的数量关系？并说明理由；；
（3）如图3，P为线段AC上一定点，点Q为直线CD上一动点，①当点Q在射线CD上运动时（点C除外）∠CPQ+∠CQP与∠BAC有何数量关系？猜想结论并说明理由．②当点Q在射线CD的反向延长线上运动时（点C除外）∠
CPQ+∠CQP与∠BAC有何数量关系？直接写出猜想结论，不需说明理由．
21、已知数轴上有A、B、C三点，分别表示有理数-26，-10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒．
（1）用含t的代数式表示P到点A和点C的距离：PA=________，PC=_____________
（2）当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回点A，当点Q开始运动后，请用t的代数式表示P、Q两点间的距离。

（友情提醒：注意考虑P、Q的位置）
22、如图1是一个三角形，分别连接这个三角形三边的中点得到图2，在分别连接图b中间的小三角形三边中点，得到图3，按此方法继续下去，请你根据每个图中三角形个数的规律，完成下列问题：
图1 图2 图3
图形编号 1 2 3 4 5 ……
三角形个数 1 5
23.如图，在Rt△ABC中，∠C=90°，AC=12，BC=16，动点P从点A出发沿AC边向点C以每
秒3个单位长的速度运动，动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动。

P、Q分别从点A，C同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程
中，△PCQ关于直线PQ对称的图形是△PDQ．设运动时间为t
（秒）。

（1）设四边形PCQD的面积为y，求y与t的函数关系式；
（2）t为何值时，四边形PQBA是梯形？
（3）是否存在时刻t，使得PD∥AB？若存在，求出t的值；若
不存在，请说明理由。

（第28题图）
A
B
C
P
D
Q。

最新四川德阳市数学七年级试卷(含答案)

最新德阳市数学七年级统考试题(含答案)下载

四川省德阳市德阳中学校2023-2024学年七年级下学期期中数学试题

最新德阳市数学七年级试卷

德阳市七年级上册数学期末试卷(含答案)

德阳市七年级上册数学期末试卷(含答案)

2023-2024学年四川省德阳市七年级(下)期末数学试卷(含详解)

2023-2024学年四川省德阳市广汉市七年级(上)期末数学试卷+答案解析

德阳市七年级上册数学期末试卷(含答案)

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)

四川省德阳市旌阳区2022-2023学年七年级数学上学期期末试卷(含答案)

德阳市七年级上册数学期末试卷(含答案)

四川省德阳市中江县2023-2024学年七年级下学期期中数学试题(解析版)

七年级上册德阳数学期末试卷测试卷(word版,含解析)

德阳市七年级数学试卷七年级苏科下册期末专题练习(及答案)

德阳初一数学考试题及答案