七年级数学下册《实数》课件 新人教版
合集下载
人教版数学七年级下册 6.3 .1实数 课件(共21张PPT)

9,
•
0.6,
64, 0, 3
0.13
(5)正实数数集合:
9 , 3 5,
64,
,
0.
•
6,
3,
0.13
(6)负实数集合: 3 ,
4
(7) 实数集合: 9 , 3 5, 64,
,
•
0.6,
3, 4
0,
3, 0.13
解:
课堂小结
1. 无理数及实数的概念 无限不循环小数叫做无理数;有理数与无理数统称实数. 2. 实数的分类
5 , 3 , 27 ,11, 9 2 5 4 9 11
它们都可以化 成有限小数或 无限循环小数 的形式
思考1:(1)整数能写成小数的形式吗?3可以看成是3.0吗?
可以 (2)由此你可以得到什么结论?
任何一个有理数都可以写成有限小数或无限循环小数; 反过来,任何有限小数或无限循环小数也都是有理数. 思考2:除了有限小数和无限循环小数,还有什么其他类 型的小数吗?
无限不循环小数 叫做无理数
它们都是无限 不循环小数, 是无理数
π
练一练
把下列各数分别填入相应的集合内:
17 , 4
π
3,
4,
0.101,
, 3
2, 5
64, 2.121, 0.3737737773(相邻两个3之间7的个数逐渐加1)
...
有理数集合
...
无理数集合
有理数和无理数统称实数,实数的分类如下:
(1)按定义分
整数
有理数:
有限小数或无限循环小数
实
分数
数
无理数: 无限不循环小数
含开方开不尽的数
π 含有 的数
人教版数学七年级下册《实数》ppt
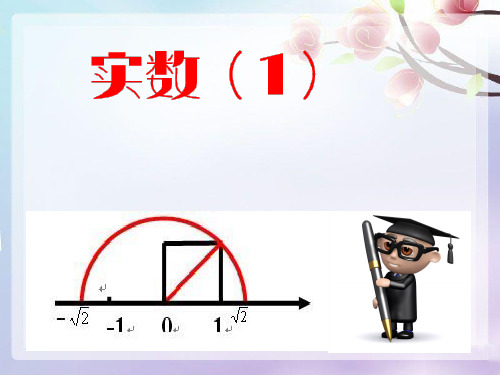
(1)如何用数轴上的点表示 2 ? 2 呢?
2.你能在数轴上找到 7 对应的点吗?试试看吧! 3. 2, 2 , 7这三个点分别介哪两个整数之间?
1、如果将所有有理数都标到数轴上,那么数轴 被填满了吗?
数轴未被填满,数轴上的点还可以表示无理数。
2、实数和数轴上的点的关系是怎样的?
实数和数轴上的点是一一对应的。
1 5
4……2
4 38 0
9
有理数集合
3 2 7
20
2 3 5
0.373 7737773…(相邻两个3
之间7的个数…逐…次增加1)
无理数集合
实数
实数:有理数和无理数统称实数。
实数的分类:
有理数
实 数
无理数
整数 分数
(1) 你能把下列各数分别填入相应的集合内吗?
, 1
3 2,
, 4
7,
5, 2
2,
20 , 3
5, 3 8,
4, 9
0,
0.3737737773 (个相数邻逐两次个加31之)间的7的
正数集合
0
负数集合
实数的分类:
按是否是有理数分: 按符号的正负分:
整数
有理数
实
分数
数
无理数
正有理数 正实数
正无理数
实 数
0
负有理数
负实数
负无理数
在给实数分类的时候,一定要按照同一 标准不重不漏。
把下列个数填入相应的集பைடு நூலகம்内:
有理数集合{ 无理数集合{ 正实数集合{ 负实数集合{
…} …} …} …}
1.阅读课本104页“议一议”,解决下列问题:
2.你能在数轴上找到 7 对应的点吗?试试看吧! 3. 2, 2 , 7这三个点分别介哪两个整数之间?
1、如果将所有有理数都标到数轴上,那么数轴 被填满了吗?
数轴未被填满,数轴上的点还可以表示无理数。
2、实数和数轴上的点的关系是怎样的?
实数和数轴上的点是一一对应的。
1 5
4……2
4 38 0
9
有理数集合
3 2 7
20
2 3 5
0.373 7737773…(相邻两个3
之间7的个数…逐…次增加1)
无理数集合
实数
实数:有理数和无理数统称实数。
实数的分类:
有理数
实 数
无理数
整数 分数
(1) 你能把下列各数分别填入相应的集合内吗?
, 1
3 2,
, 4
7,
5, 2
2,
20 , 3
5, 3 8,
4, 9
0,
0.3737737773 (个相数邻逐两次个加31之)间的7的
正数集合
0
负数集合
实数的分类:
按是否是有理数分: 按符号的正负分:
整数
有理数
实
分数
数
无理数
正有理数 正实数
正无理数
实 数
0
负有理数
负实数
负无理数
在给实数分类的时候,一定要按照同一 标准不重不漏。
把下列个数填入相应的集பைடு நூலகம்内:
有理数集合{ 无理数集合{ 正实数集合{ 负实数集合{
…} …} …} …}
1.阅读课本104页“议一议”,解决下列问题:
人教版《实数》优秀课件初中数学ppt

品比赛,小红很高兴,他 想裁出一块面积为25dm2 的正方形画布,画上自己 的得意之作参加比赛,这 块正方形画布的边长应取 多少?你能帮小明算一算 吗?
二、推进新课
填表1
正方形的边长 1 正方形的面积 1
3 0.1 9 0.01
思考:你能从表格中发现什么共同点吗?
已知一个正数,求这个正数的平方, 这就是平方运算。
一、创设情境,导入新课 一、创设情境,导入新课 算数平方根的数学符号表示 会用根号表示一个数的算术平方根(重点); 一个正数有两个算术平方根,且互为相反数。 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 第1课时 算术平方根 了解算术平方根的概念; 思考:你从表2中能发现什么? 算术平方根具有双重非负性 算数平方根的数学符号表示 已知一个数的平方,求这个数的运算叫做开平方。 会用根号表示一个数的算术平方根(重点); 了解算术平方根的概念; 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 一个正数有两个算术平方根,且互为相反数。 用大小完全相同的250块正方形地板砖,铺一间面积为160 m2的地面,每块地板砖的边长是多少? 第1课时 算术平方根 会用根号表示一个数的算术平方根(重点); 已知一个正数,求这个正数的平方,这就是平方运算。
已知一个数的平方,求这个数的运算叫做开平方。
算数平方根的数学符号表示
所以m+n=2
了解算术平方根的概念;
算术平方根具有双重非负性
问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方
二、推进新课
填表1
正方形的边长 1 正方形的面积 1
3 0.1 9 0.01
思考:你能从表格中发现什么共同点吗?
已知一个正数,求这个正数的平方, 这就是平方运算。
一、创设情境,导入新课 一、创设情境,导入新课 算数平方根的数学符号表示 会用根号表示一个数的算术平方根(重点); 一个正数有两个算术平方根,且互为相反数。 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 第1课时 算术平方根 了解算术平方根的概念; 思考:你从表2中能发现什么? 算术平方根具有双重非负性 算数平方根的数学符号表示 已知一个数的平方,求这个数的运算叫做开平方。 会用根号表示一个数的算术平方根(重点); 了解算术平方根的概念; 问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方 形画布的边长应取多少?你能帮小明算一算吗? 一个正数有两个算术平方根,且互为相反数。 用大小完全相同的250块正方形地板砖,铺一间面积为160 m2的地面,每块地板砖的边长是多少? 第1课时 算术平方根 会用根号表示一个数的算术平方根(重点); 已知一个正数,求这个正数的平方,这就是平方运算。
已知一个数的平方,求这个数的运算叫做开平方。
算数平方根的数学符号表示
所以m+n=2
了解算术平方根的概念;
算术平方根具有双重非负性
问题:学校要举行美术作品比赛,小红很高兴,他想裁出一块面积为25dm2的正方形画布,画上自己的得意之作参加比赛,这块正方
七年级数学下册:第六章实数6.3实数第2课时实数的运算教学课件(新版新人教版)

18、只要愿意学习,就一定能够学会。——列宁 19、如果学生在学校里学习的结果是使自己什么也不会创造,那他的一生永远是模仿和抄袭。——列夫·托尔斯泰
20、对所学知识内容的兴趣可能成为学习动机。——赞科夫 21、游手好闲地学习,并不比学习游手好闲好。——约翰·贝勒斯 22、读史使人明智,读诗使人灵秀,数学使人周密,自然哲学使人精邃,伦理学使人庄重,逻辑学使人善辩。——培根 23、我们在我们的劳动过程中学习思考,劳动的结果,我们认识了世界的奥妙,于是我们就真正来改变生活了。——高尔基 24、我们要振作精神,下苦功学习。下苦功,三个字,一个叫下,一个叫苦,一个叫功,一定要振作精神,下苦功。——毛泽东 25、我学习了一生,现在我还在学习,而将来,只要我还有精力,我还要学习下去。——别林斯基、学习外语并不难,学习外语就像交朋友一样,朋友是越交越熟的,天天见面,朋友之间就亲密无间了。——高士其 2、对世界上的一切学问与知识的掌握也并非难事,只要持之以恒地学习,努力掌握规律,达到熟悉的境地,就能融会贯通,运用自如了。——高士其 3、学和行本来是有联系着的,学了必须要想,想通了就要行,要在行的当中才能看出自己是否真正学到了手。否则读书虽多,只是成为一座死书库。——谢觉哉、你的假装努力,欺骗的只有你自己,永远不要用战术上的勤奋,来掩饰战略上的懒惰。 11、时间只是过客,自己才是主人,人生的路无需苛求,只要你迈步,路就在你的脚下延伸,只要你扬帆,便会有八面来风,启程了,人的生命才真正开始。 12、不管做什么都不要急于回报,因为播种和收获不在同一个季节,中间隔着的一段时间,我们叫它为坚持。 13、你想过普通的生活,就会遇到普通的挫折。你想过最好的生活,就一定会遇上最强的伤害。这个世界很公平,想要最好,就一定会给你最痛。
D. 8
11.计算: (1)3 3-5 3; (2)1- 2+ 3- 2; (3)2 3+3 2-5 3-3 2; (4)| 3-2|+| 3-1|.
20、对所学知识内容的兴趣可能成为学习动机。——赞科夫 21、游手好闲地学习,并不比学习游手好闲好。——约翰·贝勒斯 22、读史使人明智,读诗使人灵秀,数学使人周密,自然哲学使人精邃,伦理学使人庄重,逻辑学使人善辩。——培根 23、我们在我们的劳动过程中学习思考,劳动的结果,我们认识了世界的奥妙,于是我们就真正来改变生活了。——高尔基 24、我们要振作精神,下苦功学习。下苦功,三个字,一个叫下,一个叫苦,一个叫功,一定要振作精神,下苦功。——毛泽东 25、我学习了一生,现在我还在学习,而将来,只要我还有精力,我还要学习下去。——别林斯基、学习外语并不难,学习外语就像交朋友一样,朋友是越交越熟的,天天见面,朋友之间就亲密无间了。——高士其 2、对世界上的一切学问与知识的掌握也并非难事,只要持之以恒地学习,努力掌握规律,达到熟悉的境地,就能融会贯通,运用自如了。——高士其 3、学和行本来是有联系着的,学了必须要想,想通了就要行,要在行的当中才能看出自己是否真正学到了手。否则读书虽多,只是成为一座死书库。——谢觉哉、你的假装努力,欺骗的只有你自己,永远不要用战术上的勤奋,来掩饰战略上的懒惰。 11、时间只是过客,自己才是主人,人生的路无需苛求,只要你迈步,路就在你的脚下延伸,只要你扬帆,便会有八面来风,启程了,人的生命才真正开始。 12、不管做什么都不要急于回报,因为播种和收获不在同一个季节,中间隔着的一段时间,我们叫它为坚持。 13、你想过普通的生活,就会遇到普通的挫折。你想过最好的生活,就一定会遇上最强的伤害。这个世界很公平,想要最好,就一定会给你最痛。
D. 8
11.计算: (1)3 3-5 3; (2)1- 2+ 3- 2; (3)2 3+3 2-5 3-3 2; (4)| 3-2|+| 3-1|.
人教版七年级下册数学第六章实数课件:6.3 实数

正有理数
正实数
实数
正无理数
0 负实数
负有理数
负无理数
4.实数与数轴上的点是一一对应的.
教学课件 七年级数学下册(RJ)
第六章 实数
6.3 实根(2)
课前预习
带着问题自学课本P54“思考”
1.无理数也有相反数吗?怎么表示? 2.有绝对值吗?怎么表示? 3.有倒数吗?怎么表示?
探究新知
(1) 2的相反数是 ____2___ -π的相反数是____π_____ 0的相反数是____0_____
无理数的概念
所有的数都可以写成有限小数和无限循 环小数的形式吗?
2 =1.41421356237309504880168… 3 5 =1.70997594667669698935310…
π=3.1415926535897932384626…
1.01001000100001…(两个1之间依次多一个0)
解:- 的相反数是 π -3.14的相反数是3.14-π
(2)指出 - 5 ,1- 3 3 分别是什么数的相反数;
(2)- 是 的相反数; 1- 是 -1 的相反数;
例题讲解
(3)求 3 64 的绝对值;
|
|=|-4|=4.
(4)已知一个数的绝对值是 3 ,求这个数。
绝对值为 的数是 或-
实数的运算
35
9
3 4
0.6
(6)实数集合: 9 3 5
0.6
3 4
3 9 3 0.13
64
0.6
3
3
4
0.13
3 9
64 3
3 9
实数课件人教版数学七年级下册[2]
![实数课件人教版数学七年级下册[2]](https://img.taocdn.com/s3/m/ef4457ee6bd97f192379e947.png)
12.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动), 圆上的一点由原点到达点O′,点O′所对应的数值是__π__.
13.有一个数值转换器,原理如下:当输入的 x 为 64 时,输出的 y 是 ___8______.
14.请将图中数轴上标有字母的各点与下列实数对应起来. 2 ,-0.5,- 3 , 5 ,π,3.
有限小数或无限循环小数
正无理数
无理数
无限不循环小数
负无理数
(2)按大小分:
正实数 实数 0
负实数
正有理数 正无理数
负有理数 负无理数
实数的分类有不同 的方法,但不论用 哪一种分类方法, 都要做到不重不漏.
(1)对实数进行分类时,某些数应先进行计算或化简, 然后根据最后结果进行分类,不能看到带根号的数, 就认为是无理数,不能看到有分数线的数,就认为 是有理数. (2)在实数范围内,一个数不是有理数, 那么它一定是无理数,反之亦成立.
④无理数一定都是实数.其中正确的有________.
有理数和无理数统称为实数.
整数、小数、分数、百分数. 12.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′所对应的数值是____.
无理数都是无限小数,但无限小数不一定是无理数,只有无限不循环小数才是无理数. 事实上,如果把整数看成小数点后是 0 的小数,那么任何一个有理数都可以写成有限小数或无限循环小数的形式.
巩固新知
把下列各数填在相应的大括号内.
非负整数:{ 整数:{ 负分数:{
…}; …}; …};
把下列各数填在相应的大括号内.
|a|>4
B.
(1)对实数进行分类时,某些数应先进行计算或化简,然后根据最后结果进行分类,不能看到带根号的数,就认为是无理数,不能看到有分数线的数,就认为是有理数.
实数课件人教版数学七年级下册3

填空:设a,b,c是任意实数,则
(1)a+b = b+a (2)(a+b)+c = a+(b+c) (3)a+0 = 0+a = a
(加法交换律); (加法结合律);
;
(4)a+(-a) = (-a)+a = 0
;
(5)ab = ba
(乘法交换律);
(6)(ab)c =a(bc) (乘法结合律);
(1)( 3 2) 2;
(2)3 3 2 3.
解:(1)( 3 2) 2 3 2 2 3
(2)3 3 2 3 (3 2) 3 5 3
在实数运算中,当遇到无理数并且需要求出结果的近似值时, 可以按照所要求的精确度用相应的近似有限小数去代替无理 数,再进行计算.
例3 计算(结果保留小数点后两位):
(1)规定用符号[m]表示实数 m 的整数部分,例如:[23 ]=0,[ 6 ]=2, 按此规定[ 10 +1]的值为__4__;
(2)若 7 的整数部分为 a,小数部分为 b,且|c|= 7 ,求 c(a-b)- 4(c-2)的值.
解:(2)∵ 4 < 7 < 9 ,即 2< 7 <3,∴a=2,b= 7 -2, ∴a-b=2-( 7 -2)=4- 7 ,∵|c|= 7 ,∴c=± 7 .当 c= 7 时,原式= 7 (4- 7 )-4( 7 -2)=4 7 -7-4 7 +8=1;当 c =- 7 时,原式=- 7 (4- 7 )-4(- 7 -2)=-4 7 +7+ 4 7 +8=15,即 c(a-b)-4(c-2)的值为 15 或 1
(乘法对于加法的分配律),
在进行实数的运算时,有理数的运算法则及运算性质等同样适用.
七年级数学人教版下册第六章6.3.1实数及其分类课件

101 001 000 1…(相邻两个1之间0的个数逐次加1), A.无理数包括正无理数、0和负无理数
正有理数
有
理
数
0
负 有 理 数
8, ,-4.
限小数或无限循环小数的形式.
正数:{ ,…};
∵
,∴
是有理数.∵
,
8, ,…};
合作探究
知识点 1 无理数
探究 我们知道有理数包括整数和分数,请把下列分数写成 小数的形式,你有什么发现?
3
2
(相邻两个1之间0的个数逐次加1), 3 9
,-
.
有理数:{ -7,0.32, 1 ,3.14·,0,…}; 2
3
无理数:{ 8 , 1 ,0.101 001 000 1…(相邻两个1 2
之间0的个数逐次加1), 3 9 ,- ,…}; 2
正实数:{ 0.32,1 3
,3.14·,
8
,
1 2
这样的无限不循环小数.
例1 下列各数:3.141 59, 3 8 ,0.131 131 113…(每相
邻两个3之间依次多1个1),-π,
2 5 ,
1 7
中,无
理数有( B )
A.1个
B.2个
C.3个
D.4个
导引:∵3.141 59是有限小数,∴3.141 59是有理数.
∵ 3 8 2 ,∴ 3 8 是有理数.∵ 25 5 ,
人教版数学七年级下册
第六章
6.3.1 实数及其分类
学习目标
1.了解无理数和实数的概念以及实数的分 类。
2.知道实数与数轴上的点具有一一对应的 关系。
复习导入
…};
(1)如图,OA=OB,数轴上点A对应的数是什么?它介
正有理数
有
理
数
0
负 有 理 数
8, ,-4.
限小数或无限循环小数的形式.
正数:{ ,…};
∵
,∴
是有理数.∵
,
8, ,…};
合作探究
知识点 1 无理数
探究 我们知道有理数包括整数和分数,请把下列分数写成 小数的形式,你有什么发现?
3
2
(相邻两个1之间0的个数逐次加1), 3 9
,-
.
有理数:{ -7,0.32, 1 ,3.14·,0,…}; 2
3
无理数:{ 8 , 1 ,0.101 001 000 1…(相邻两个1 2
之间0的个数逐次加1), 3 9 ,- ,…}; 2
正实数:{ 0.32,1 3
,3.14·,
8
,
1 2
这样的无限不循环小数.
例1 下列各数:3.141 59, 3 8 ,0.131 131 113…(每相
邻两个3之间依次多1个1),-π,
2 5 ,
1 7
中,无
理数有( B )
A.1个
B.2个
C.3个
D.4个
导引:∵3.141 59是有限小数,∴3.141 59是有理数.
∵ 3 8 2 ,∴ 3 8 是有理数.∵ 25 5 ,
人教版数学七年级下册
第六章
6.3.1 实数及其分类
学习目标
1.了解无理数和实数的概念以及实数的分 类。
2.知道实数与数轴上的点具有一一对应的 关系。
复习导入
…};
(1)如图,OA=OB,数轴上点A对应的数是什么?它介
人教版七年级数学下册全册第六章《实数》PPT课件

… 0.25 0.790 6 2.5 7.906 25 79.06 250 …
规律:被开方数的小数点向右每移动 2 位,它的 算术平方根的小数点就向右移动 1 位;被开方数 的小数点向左每移动 2 位,它的算术平方根的小 数点就向左移动 1 位.
(2)用计算器计算 3(精确到0.001),并利用你在(1) 中发现的规律说出 0.03, 300, 30 000 的近似值,你 能根据 3 的值说出 30 是多少吗?
2.会求非负数的算术平方根,掌握算术平方根的非负 性.(重点、难点)
导入新课
历史感悟
毕达哥拉斯(公元前570年~公元前500年) 公元前500多年古希腊的哲学家、数学家、天文学家。
导入新课
万物皆数
导入新课
情境引入 学校要举行美术作品比赛,小明很高兴,他想
裁出一块面积为25dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应取多少? 你能帮小明算一算吗?
所以这个数是3或-3. 会不会是巧合呢?
解:设每块地板砖的边长为x m.由题意得
240x2 60, x2 1 . 4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
拓展提升
已知:|x+2y|+ 3x 7 (5y z)2 0
求x-3y+4z的值. 解:由题意得:
3x 7 0, x 2y 0,5y z 0,
所以正数 t 4 2 (秒). 即铁球到达地面需要2秒.
当堂练习
1.填空:(看谁算得又对又快) (1) 一个数的算术平方根是3,则这个数是 9 . (2) 一个自然数的算术平方根为a,则这个自然数 是_a_2_;和这个自然数相邻的下一个自然数是 a2+1 .
规律:被开方数的小数点向右每移动 2 位,它的 算术平方根的小数点就向右移动 1 位;被开方数 的小数点向左每移动 2 位,它的算术平方根的小 数点就向左移动 1 位.
(2)用计算器计算 3(精确到0.001),并利用你在(1) 中发现的规律说出 0.03, 300, 30 000 的近似值,你 能根据 3 的值说出 30 是多少吗?
2.会求非负数的算术平方根,掌握算术平方根的非负 性.(重点、难点)
导入新课
历史感悟
毕达哥拉斯(公元前570年~公元前500年) 公元前500多年古希腊的哲学家、数学家、天文学家。
导入新课
万物皆数
导入新课
情境引入 学校要举行美术作品比赛,小明很高兴,他想
裁出一块面积为25dm2的正方形画布,画上自己的得 意之作参加比赛,这块正方形画布的边长应取多少? 你能帮小明算一算吗?
所以这个数是3或-3. 会不会是巧合呢?
解:设每块地板砖的边长为x m.由题意得
240x2 60, x2 1 . 4
x 1 1 0.5 42
故每块地板砖的边长是0.5 m.
拓展提升
已知:|x+2y|+ 3x 7 (5y z)2 0
求x-3y+4z的值. 解:由题意得:
3x 7 0, x 2y 0,5y z 0,
所以正数 t 4 2 (秒). 即铁球到达地面需要2秒.
当堂练习
1.填空:(看谁算得又对又快) (1) 一个数的算术平方根是3,则这个数是 9 . (2) 一个自然数的算术平方根为a,则这个自然数 是_a_2_;和这个自然数相邻的下一个自然数是 a2+1 .
6.3 实数 课件3(数学人教版七年级下册)

2.运用新知 把下列各数填入相应的集合内:
2 3 15 , 4 , 16 , , 27 , 0.15 , 7.5 , π, 0, 2.3 . 3
①有理数集合:{
…};
②无理数集合:{
③正实数集合:{
…};
…};
④负实数集合:{
…}.
把下列各数填入相应的集合内:
9 3 4
3
5
3
64
随堂练习
二、填空 1、正实数的绝对值是 它本身 ,0的绝对值是
0 ,
负实数的绝对值是 它的相反数 .
2、 3 的相反数是 3、绝对值等于 5 的数是
3
,绝对值是
3
.
5,
4 3
7 的平方 是
7
.
4、比较大小:-7
5、一个数的绝对值是
p 2
,则这个数是
p 2
.
图形坐标 已知如图,等边三角形 ABC 的边长为 2 ,求 各顶点的坐标。
3.运用新知 例1 (1)分别写出 6 ,π 3.14 的相反数;
6
5
3
3.14 π
3 (2)指出 5 , 1 3 是什么数的相反数;
(3)求
3
3 1 64 的绝对值;4
(4)已知一个数的绝对值是 3 ,求这个数.
3或
3
3.运用新知 例2 计算下列各式的值: (1) ( 3 2 ) 2
2 =
0=
,-π = .
,
2.探究新知 结合有理数相反数和绝对值的意义, 你能说说实数关于相反数和绝对值的意义吗? 数 a 的相反数是 a ,
一个正实数的绝对值是它本身; 一个负实数的绝对值是它的相反数; 0的绝对值是0. a , 当a 0时; a 0,当a 0时; - a , 当a 0时.
人教版七年级数学下册第六章实数全章优质教学课件

三 、研学教材
认真阅读课本第40页内容,完成下 面练习并体验知识点的形成过程.
三、研学教材
知识点一 算术平方根的概念
问题:学校要举行美术作品比赛,小欧 想裁出一块面积为25dm2的正方形画布 ,画上自己的得意之作参加比赛,这 块正方形画布的边长应取多少?
分析: ∵( 5 )2=25 ∴这个正方形画布的边长应取
(3)∵( 3)2= 32 ∴32的算术平方根 是__3___ 即 32 =___3___;
2、求下列各式的值:
(1)
1
;(2)
9 25
;(3)
22
解:(1)∵12=1
∴ 1 =1
9
(2) 25 3 2 9
解:(2)∵ 5 = 25
∴ 9= 3
(3) 22
25 5
解:(3)∵(2)2=22
∴ 2 2 =2
温馨提示:正数和0统称非负数.
练一练
1、你能根据等式:122=144,说出144的 算术平方根是多少吗?用等式表示出来
解:∵122=___1_4_4__ ∴__1_4_4__的算术平方根是12,
即 144 =___1_2_____
2、225的算术平方根是__1_5,0的 算术平方根是__0___.
思考: 2 它到底是个多大的数? 因为 12 =_1__, 2 2 =__4_,所以1< 2 <2 因为 1.42= _1_._96_,1.52=_2_.2_5_, 所以__1_.4_< 2 <__1_._5_;......
事实上, 2 =1.414 213 562 373..., 它是一个无限不循环小数.
引导学生读懂数学书
四、归纳小课件结制作:李周林
人教版七年级数学课件《实数的相关概念及分类》

3.14-π.
3
3
3
3
(2)因为-(- 5)= 5,-( 3-1)=1- 3,所以,- 5,1- 3分别是 5, 3-1的相反数.
3
3
3
(3)因为 −64=- 64 =-4,所以| −64|=|-4|=4.
(4)因为| 3|= 3,|- 3|= 3,所以绝对值是 3的数是 3或- 3.
针对练习
人教版数学七年级下册
± 11
右
12.数轴上表示-3.14的点在表示-π的点的______侧.
13.若将三个数- 3, 7, 11表示在数轴上,其中能被如图所示
7
的墨迹覆盖的数是______.
达标检测
人教版数学七年级下册
14.请将图中数轴上标有字母的各点与下列实数对应起来:
3
解:A:-3,B:-2.5,C: 3,D:2 2,E: 15.
正实数
实数
正无理数
0
负有理数
负实数
负无理数
小结梳理
人教版数学七年级下册
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数以后,实数与数轴上的点是一一对应的,
即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个
点都表示一个实数.
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的
圆上的一点由原点到达点O',点O'对应的数是多少?
OO'的长是这个圆的周长π,所以点O'的坐标为π.
无理数π可以用数轴上的点来表示出.
知识精讲
人教版数学七年级下册
如图,以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示 2,与负半轴
3
3
3
3
(2)因为-(- 5)= 5,-( 3-1)=1- 3,所以,- 5,1- 3分别是 5, 3-1的相反数.
3
3
3
(3)因为 −64=- 64 =-4,所以| −64|=|-4|=4.
(4)因为| 3|= 3,|- 3|= 3,所以绝对值是 3的数是 3或- 3.
针对练习
人教版数学七年级下册
± 11
右
12.数轴上表示-3.14的点在表示-π的点的______侧.
13.若将三个数- 3, 7, 11表示在数轴上,其中能被如图所示
7
的墨迹覆盖的数是______.
达标检测
人教版数学七年级下册
14.请将图中数轴上标有字母的各点与下列实数对应起来:
3
解:A:-3,B:-2.5,C: 3,D:2 2,E: 15.
正实数
实数
正无理数
0
负有理数
负实数
负无理数
小结梳理
人教版数学七年级下册
事实上,每一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数以后,实数与数轴上的点是一一对应的,
即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个
点都表示一个实数.
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点所表示的
圆上的一点由原点到达点O',点O'对应的数是多少?
OO'的长是这个圆的周长π,所以点O'的坐标为π.
无理数π可以用数轴上的点来表示出.
知识精讲
人教版数学七年级下册
如图,以单位长度为边长画一个正方形,以原点为圆心,
正方形对角线为半径画弧,与正半轴的交点就表示 2,与负半轴
2020人教版七年级数学下册第六章6.3实数(1)实数的概念课件(共32张PPT)

6,
••
, 1. 2 3,
22 , 36
2
7
1.232232223 (两个3之间依次多一个 2)
有理数是:1.
•
2
•
3
22
,7
36
无理数是: 6
,,
2
1.232232223 ,(两个3之间依次多一个 2)
思考:无理数一般有哪些形式?
(1)像 7, 3, 12 的开不尽方的数是无理数。
020
002
000
02…是无
理数吗?
1.57079632679...
2
它们都是无限 不循环小数,
2.02002000200002…
是无理数
常见的一些无理数:
(1)含 π 的一些数;
(2)含开不尽方的数; (3)有规律但不循环的小数,如1.01001000100001…
例:判断下列数哪些是有理数?哪些是无理数?
人教版七年级数学 下册
6.3 实 数 第1课时 实数的概念
1.了解实数的意义,并能将实数按要求进 行准确的分类;
2.熟练掌握实数大小的比较方法;(重点) 3.了解实数和数轴上的点一一对应,能用 数轴上的点 表示无理数.(难点)
认真阅读课本中6.3 实数的 内容,完成下面练习并体验知 识点的形成过程。
• 这个矛盾说明, 2 不能写成分数的形式, 即 2 不是有理数。
• 实际上, 2 是无限不循环小数。
实数的概念:
在前面的学习中,我们知道,许多数的平方根和 立方根都是无限不循环小数,它们不能化成分数.我 们给无限不循环小数起个名字,叫“无理数”.有理 数和无理数统称为实数.
思考:
七年级数学下册教学课件《实数的概念》
2. 求下列各数的相反数与绝对值:
【教材P56 练习 第2题】
相反数: 绝对值:
2.5 , 7 , π , 3 2 , 0 2
π
-2.5
7
2
2 3 0
π
2.5
7
2
2 3 0
3. 求下列各式中的实数x:
(1)x 2; 3
x2 3
(3)x 10;
x 10
【教材P56 练习 第3题】
(2)x 0;
∴ 5,1 3 3分别是 5,3 3 1的相反数
例1 (3)求 3 64 的绝对值;
∵3 64 3 64 4 ∴ 3 64 4 4
【教材P55 例1】
(4)已知一个数的绝对值是 3 ,求这个数.
∵ 3 3
3 3
∴绝对值是 3的数是 3或 3
随堂训练
1. 下列说法正确的是( B ) A.带根号的数和分数统称实数 B.正实数包括正有理数和正无理数 C.实数包括正实数和负实数 D.无理数包括正无理数、负无理数和0
9 3,是有理数
2.将下列各数分别填入下列相应的括号内:
3 9 ,1 ,7 ,π,- 16 , 5 , 8 , 4 ,0 ,
4
9
25 ,0.525225……
无理数:
3 9 ,7 ,π, 5 ,0.525225……
有理数: 正实数: 负实数:
1 ,- 16 , 8 ,4 ,0 ,25
4
9
3 9 ,1 ,7 ,π,4 ,0 ,25 ,0.525225……
不能写成分数的形式 以看成分母是1的分数)
有
理 数
实数
和
无
分数
理
有理数
数
无理数
6.3.1实数-人教版七年级数学下册课件

你能求出下列各数的相反数、倒数和绝对值吗?
限 47 限 设点C表示的实数为x,则点A到点C的距离为-1-x,
5 . 8 7 5 2.会在实数范围内求一个数的相反数、倒数、绝对值.
小 8 循 思考: 是无理数吗?2.
反过来,数轴上的每一点都表示一个实数,即实数和数轴上的点是一一对应的。
数 环 ⑤无理数一定都带根号.
(√) (√) (√) (× ) (× ) (√) (× ) (√)
2、把下列各数分别填在相应的集合里
22 , 3.1415926, 7, 8, 3 2 , 0.6, 0,
7 36 ,
,
3
..
1.652,
0.3131131113
有理数集合
无理数集合
4. 下列说法不正确的是 A.|3-π|= 3-π C.2的相反数是-2
|-π|=___π_____,|3-π|=__π_-__3___.
2.我们在有理数范围内学过的运算法则和运算律是 否在实数范围内还能继续用呢?
在实数范围内,相反数、倒数、绝对值的意义和有理 数范围内的相反数、倒数、绝对值的意义完全一样。
学以致用 知行并进
你能求出下列各数的相反数、 倒数和绝对值吗?
7.如图所示,数轴上A,B两点表示的数分别为-1 和 3 ,点B关于点A的对称点为C,求点C所表示的 实数.
解:∵数轴上A,B两点表示的数分别为-1和 3 , ∴点B到点A的距离为1+ 3 ,则点C到点A的距离为 1+ 3 , 设点C表示的实数为x,则点A到点C的距离为-1-x, ∴-1-x=1+ 3 , ∴x=-2- 3
02002000200002… 有理数和无理数统称为实数
它们都是无限不循环小数,是无理数
人教版数学七年级下册课件:6.3实数(第一课时)

正有理数{
3 8、22 、 1.414 7
…}
负有理数{ 3.141、 7 、 0.020202 … }
8
正无理数{ 3、 、0.1010010001 … }
3
负无理数{ 3 2、- 7 …}
3、将图中字母与下列实数对应起来:
2 ,-1.5, 5 , ,3
-2
0
4
A
B CDE
解:点A、B、C、D、E分别对应
第六章 6.3实数(1)
自学课本P 53-54练习前,思考: 1、什么叫无理数?什么叫实数?你会给实数分 类吗?
2、完成P54页探究,你能在数轴上表示2 吗?
-3 2 呢? 3、实数与数轴上的点是什么关系? 4、完成P56页练习1
1、任何一个有理数都可以写成__有__限__小数或者 无限循环小数的形式.反过来,任何有限小数或
即每一个实数都可以用__数_轴___上的点来表示;
反过来,数轴上的每一个点都是表示一个 实数 .
练一练
1.下列各数中,哪些是有理数?哪些是无理 数?
0.4583
•
,3.7
,
π
,
1
,18,
2.
7
2把下列各数分别填入相应的集合里:
3 8, 3, 3.141, , 22 , 7 , 3 2,
37 8 0.1010010001 ,1.414, 0.020202 , 7
__正___实数
__0___
__负___实数
有限小数或无限循环小数
_______________________Hale Waihona Puke ___________________
无限不循环小数
_______________________________________
人教版初中数学《实数》_上课课件

【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
七年级数学下册(RJ)
【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载 【获奖课件ppt】人教版初中数学《实 数》_ 上课课 件1-课 件分析 下载
【新】人教版七年级数学下册第六章《 实 数》公开课课件.ppt

famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about. 。2020年12月15日星期二2020/12/152020/12/152020/12/15
【预习导学】
②用一张硬纸片前一个半径为1cm的小圆,计算圆的周长,周长是有理 数还是无理数?如何在数轴上表示圆的周长呢?
归纳总结:实数与数轴上的点是 一一对应的 ,即任何一个都可以用数轴上的一 个点来表示;反过来,数轴上的每一个点都表示一个实数。数轴上的任意两个 点,右边的点表示的数总比左边的点表示的数 大 。
1、有理数的运算法则及运算律同样适用于实数的运算;当 遇到无理数并需要求出结果的近似值时,应按照要求的精 确度用相应的近似有限小数去代替无理数,再进行计算。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/152020/12/15Tuesday, December 15, 2020
【预习导学】
一、自学指导 1、自学1:自学课本P53-54页,完成54页“探究”,掌握实数的相关概念,理解实数与
数轴上的点的对应关系,完成下列填空。5分钟 归纳总结: 有理数 和 无理数 统称实数。 实数按正负分可分为 正实数 、 0 、 负实数 。
点拨精讲:带根号的不一定都是无理数;所有的无限循环小数都可以化成分数。
解:没有最大的实数,没有最小的实数,绝对值最小的实数是0. 2、设a是最小的自然数,b是最大的负整数,c是绝对值最小的实数,求
【预习导学】
②用一张硬纸片前一个半径为1cm的小圆,计算圆的周长,周长是有理 数还是无理数?如何在数轴上表示圆的周长呢?
归纳总结:实数与数轴上的点是 一一对应的 ,即任何一个都可以用数轴上的一 个点来表示;反过来,数轴上的每一个点都表示一个实数。数轴上的任意两个 点,右边的点表示的数总比左边的点表示的数 大 。
1、有理数的运算法则及运算律同样适用于实数的运算;当 遇到无理数并需要求出结果的近似值时,应按照要求的精 确度用相应的近似有限小数去代替无理数,再进行计算。
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/12/152020/12/15Tuesday, December 15, 2020
【预习导学】
一、自学指导 1、自学1:自学课本P53-54页,完成54页“探究”,掌握实数的相关概念,理解实数与
数轴上的点的对应关系,完成下列填空。5分钟 归纳总结: 有理数 和 无理数 统称实数。 实数按正负分可分为 正实数 、 0 、 负实数 。
点拨精讲:带根号的不一定都是无理数;所有的无限循环小数都可以化成分数。
解:没有最大的实数,没有最小的实数,绝对值最小的实数是0. 2、设a是最小的自然数,b是最大的负整数,c是绝对值最小的实数,求
