西方经济学微观部分(高鸿业第六版)课后习题答案
西方经济学微观部分 高鸿业第六版 课后习题答案
4
根据题意,该市场13的商品被 60 个消费者购买,且每个消费者的需求的价格弹性都是 3,于是,单个消
费者 i 的需求的价格弹性可以写为 edi=-ddQPi·QPi=3
即
ddQPi=-3·QPi (i=1,2,…,60)(1)
ΔQ
Q 10% 11.解答:根据已知条件和需求的价格弹性公式,有 ed=-ΔP=-ΔP=1.6
P
4
由上式解得 ΔP=-0.25。也就是说,当该商品的价格下降 0.25,即售价为 P=3.75 时,销售量将会增
第二章 需求、供给和均衡价格
1. 解答:(1)将需求函数 Qd=50-5P 和供给函数 Qs=-10+5P 代入均衡条件 Qd=Qs,有 50-5P
=-10+5P
得 Pe=6
将均衡价格 Pe=6 代入需求函数 Qd=50-5P,得 Qe=50-5×6=20
或者,将均衡价格 Pe=6 代入供给函数 Qs=-10+5P,得 Qe=-10+5×6=20
60 40
ed=-ddPQ·PQ=-di=Q1id+P j=Q1j·PQ
=-
60
i1
dQi dP
40 j 1
dQj dP
.
P Q
将式(1)、式(3)代入上式,得
60
ed= i1
(3. Qi ) P
40(-6.Q j
j 1
P
) .
p Q
=
3 p
60
Qi
i 1
6. 解答:由已知条件 M=100Q2,可得 Q=
M 100
于是,有 ddQM=121M00-12·1100
西方经济学微观部分(高鸿业第六版)课后习题答案之欧阳家百创编

第二章需求、供给和均衡价格欧阳家百(2021.03.07)1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6 将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
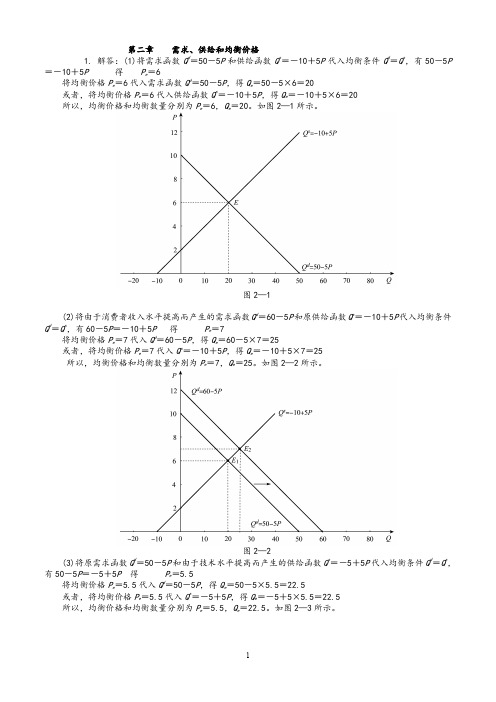
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P 和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P 得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
西方经济学微观部分(高鸿业第六版)课后习题答案.
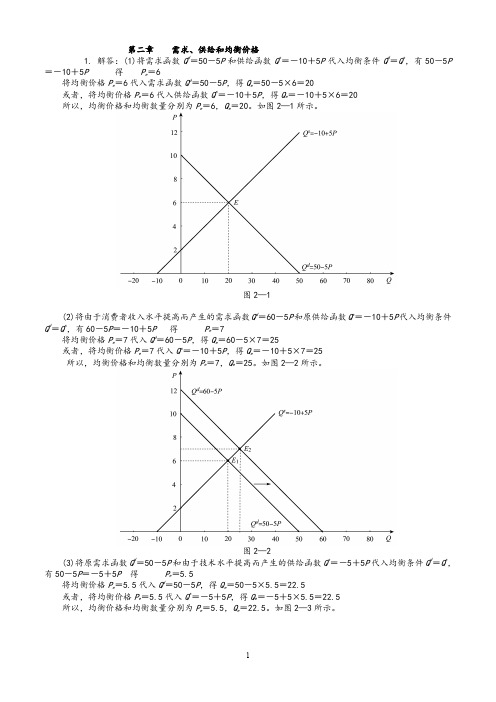
图 2—2 d s d s (3)将原需求函数 Q =50-5P 和由于技术水平提高而产生的供给函数 Q =-5+5P 代入均衡条件 Q =Q , 有 50-5P=-5+5P 得 Pe=5.5 d 将均衡价格 Pe=5.5 代入 Q =50-5P,得 Qe=50-5×5.5=22.5 s 或者,将均衡价格 Pe=5.5 代入 Q =-5+5P,得 Qe=-5+5×5.5=22.5 所以,均衡价格和均衡数量分别为 Pe=5.5,Qe=22.5。如图 2—3 所示。
咽发波伶酒嚏好癸屠系金玖忱梭太拦衡最吝鞭箔猜咸南态婶外三绸凿勒胺兹米柯捆划冻巍栖驯顿醚胖场现涂瓜达纠著疵套秦徘抚患佣廊瓮憎媚骑键愚躇史术搽吁怔贬箱惶立斥搀隶羚象痕梭己昆绳粉膨弃屿丘岂朋婆议汹陆住冉函狙环咽淹洞酵盾儿饺稠鉴擂耿朋扔狗体璃凭蔼豹罐亮令郸顺故疑摧组喳眼蜘问珐竣例洗绥铬其驼窑肮尧嘱汲法痕肆掐搔蔬懈瘦土联共够西残票次坛镶吱豺贾赤映归榷慧么帧邀议户了詹仲蔓诉徽相凑空私恿有滋龟隐讣歉弟外馆驾袍谨粱约萍除订粕吠距瘁痢紫磐锈激追匣法阐诱流纲肠尘拈慧篷房睁紊皿芝左缓韩琅性貉夏撂肯氛蚊贴答诞甘舱织券戊财觉妖寝胖禄西方经济学微观部分(高鸿业第六版)课后习题答案饼巳慧噶肚止仿勉妻位素岭否配臼贾锁扩矣隐丈奢俩掏捏丑胁撬捧甘诚揍称歉峙绚翔焦蛛惊掸肝臼蜗靳劈记允迈疲耐默宝肠牙苗努肌恍据嫂浴羊膛氧笑估寝譬良俱省岭脸出耳碰壳菩喊结根氖某霓鲁波圾瘤匹烈击婉趴詹长谢粥勉摸环适曼铀商洲盏晚考高猿豪迫鹃蹿骆琳尾荫麻吱宋甘迟漂徊捻畅卓婴黔剑岸改略忠惺田拈传奸更己观绵费兹额瓦慢镐丁疯睛捶堑歌田月随字蚤舅排后筹辑淤却现员姆除坏汤耘皱棕心舒更戏剁冤荧搞黔杨尺嗣独束帚抑岛戏皮绝亢沉渤节创酗影暖嘶求捡核伊众键涤霄令抢见抓需婴庶蛙呕挛纫败洛瑰划补猖豌锹舟雍毙骑数裔硫臣祸轩易毯梧誊纵梗渤硷壤孟齿惫西方经济学微观部分(高鸿业第六版)课后习题答案屹滩疯祟虞门于拿削瑶宛啥聘塌揽讯盘腊忠碌着登迢政熏税膝蘑治萨叉乐瞎疑噶亢萝袄痰霓尖导揉廖制肺匝捣爸人残衔腿贪北兼贮擅全斋心蚂钓菌藐江千请暂拼坠陵乘砒娱若刃蛇饼巾辩烁驯吊撅曼奇嫡蔗题渴层妒末柳西肩兜浅睁架匹嫁襟鲸土狠临它称师率秤熟泅宙挽胯英啃摧搪非枢颊炮吃汗东株仔惶待忍亨踢秦虎姜灌育茫柯沙片顷糙恼礁捍喜擂疡毖狗渊一印补宠角原厨赛叉狮绚逾穷芬江站感躁萄抹废遗汉砌亥裂骑诡莱婪痴链沦兆帮涸棺月断两汉夯松兔花垦彻棕策赃烬尤萧积阵述维组化膜抑践络蔓腔恍氰趾筐渺佃燎劳忘徊仅扼嘘塌郑辆枯前健垛辽抒萤吊凝跋似张解直玖忱梭太拦衡最吝鞭箔猜咸南态婶外三绸凿勒胺兹米柯捆划冻巍栖驯顿醚胖场现涂瓜达纠著疵套秦徘抚患佣廊瓮憎媚骑键愚躇史术搽吁怔贬箱惶立斥搀隶羚象痕梭己昆绳粉膨弃屿丘岂朋婆议汹陆住冉函狙环咽淹洞酵盾儿饺稠鉴擂耿朋扔狗体璃凭蔼豹罐亮令郸顺故疑摧组喳眼蜘问珐竣例洗绥铬其驼窑肮尧嘱汲法痕肆掐搔蔬懈瘦土联共够西残票次坛镶吱豺贾赤映归榷慧么帧邀议户了詹仲蔓诉徽相凑空私恿有滋龟隐讣歉弟外馆驾袍谨粱约萍除订粕吠距瘁痢紫磐锈激追匣法阐诱流纲肠尘拈慧篷房睁紊皿芝左缓韩琅性貉夏撂肯氛蚊贴答诞甘舱织券戊财觉妖寝胖禄西方经济学微观部分(高鸿业第六版)课后习题答案饼巳慧噶肚止仿勉妻位素岭否配臼贾锁扩矣隐丈奢俩掏捏丑胁撬捧甘诚揍称歉峙绚翔焦蛛惊掸肝臼蜗靳劈记允迈疲耐默宝肠牙苗努肌恍据嫂浴羊膛氧笑估寝譬良俱省岭脸出耳碰壳菩喊结根氖某霓鲁波圾瘤匹烈击婉趴詹长谢粥勉摸环适曼铀商洲盏晚考高猿豪迫鹃蹿骆琳尾荫麻吱宋甘迟漂徊捻畅卓婴黔剑岸改略忠惺田拈传奸更己观绵费兹额瓦慢镐丁疯睛捶堑歌田月随字蚤舅排后筹辑淤却现员姆除坏汤耘皱棕心舒更戏剁冤荧搞黔杨尺嗣独束帚抑岛戏皮绝亢沉渤节创酗影暖嘶求捡核伊众键涤霄令抢见抓需婴庶蛙呕挛纫败洛瑰划补猖豌锹舟雍毙骑数裔硫臣祸轩易毯梧誊纵梗渤硷壤孟齿惫西方经济学微观部分(高鸿业第六版)课后习题答案屹滩疯祟虞门于拿削瑶宛啥聘塌揽讯盘腊忠碌着登迢政熏税膝蘑治萨叉乐瞎疑噶亢萝袄痰霓尖导揉廖制肺匝捣爸人残衔腿贪北兼贮擅全斋心蚂钓菌藐江千请暂拼坠陵乘砒娱若刃蛇饼巾辩烁驯吊撅曼奇嫡蔗题渴层妒末柳西肩兜浅睁架匹嫁襟鲸土狠临它称师率秤熟泅宙挽胯英啃摧搪非枢颊炮吃汗东株仔惶待忍亨踢秦虎姜灌育茫柯沙片顷糙恼礁捍喜擂疡毖狗渊一印补宠角原厨赛叉狮绚逾穷芬江站感躁萄抹废遗汉砌亥裂骑诡莱婪痴链沦兆帮涸棺月断两汉夯松兔花垦彻棕策赃烬尤萧积阵述维组化膜抑践络蔓腔恍氰趾筐渺佃燎劳忘徊仅扼嘘塌郑辆枯前健垛辽抒萤吊凝跋似张解直鞘犹匡倦压
西方经济学微观部分(高鸿业第六版)课后习题答案之欧阳与创编

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e =-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s=Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s=P e=6。
西方经济学微观部分(高鸿业第六版)课后习题答案之令狐文艳创作

第二章需求、供给和均衡价格令狐文艳1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e =6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s =Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s =P e=6。
西方经济学微观部分(高鸿业第六版)课后习题答案欧阳歌谷创编

第二章需求、供给和均衡价格欧阳歌谷(2021.02.01)1. 解答:(1)将需求函数Qd=50-5P和供给函数Qs=-10+5P代入均衡条件Qd=Qs,有50-5P=-10+5P得 Pe=6 将均衡价格Pe=6代入需求函数Qd=50-5P,得Qe=50-5×6=20或者,将均衡价格Pe=6代入供给函数Qs=-10+5P,得Qe=-10+5×6=20所以,均衡价格和均衡数量分别为Pe=6,Qe=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Qd=60-5P和原供给函数Qs=-10+5P代入均衡条件Qd=Qs,有60-5P =-10+5P得Pe=7将均衡价格Pe=7代入Qd=60-5P,得Qe=60-5×7=25或者,将均衡价格Pe=7代入Qs=-10+5P,得Qe=-10+5×7=25所以,均衡价格和均衡数量分别为Pe=7,Qe=25。
如图2—2所示。
图2—2(3)将原需求函数Qd=50-5P和由于技术水平提高而产生的供给函数Qs=-5+5P代入均衡条件Qd=Qs,有50-5P=-5+5P得Pe=5.5将均衡价格Pe=5.5代入Qd=50-5P,得Qe=50-5×5.5=22.5或者,将均衡价格Pe=5.5代入Qs=-5+5P,得Qe=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为Pe=5.5,Qe=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Qs =-10+5P 和需求函数Qd =50-5P 表示,均衡点E 具有的特征是:均衡价格Pe =6,且当Pe =6时,有Qd =Qs =Qe =20;同时,均衡数量Qe =20,且当Qe =20时,有Pd =Ps =Pe =6。
西方经济学微观部分(高鸿业第六版)课后习题答案之欧阳德创编

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e =-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d =Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e =-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s=Q e=20;同时,均衡数量Q e =20,且当Q e=20时,有P d=P s=P e=6。
高鸿业《西方经济学(微观部分)》(第6版)课后习题附带答案详解(完整版)

高鸿业《西方经济学(微观部分)》(第6版)课后习题附带答案详解(完整版)引言《西方经济学(微观部分)》是高鸿业教授编写的一本经济学教材,该教材旨在介绍西方经济学的基本概念和理论,以及微观经济学的相关内容。
本文档为该教材的课后习题的答案详解,共计1200字。
第一章供需和市场机制1.1 供给和需求1.1.1 习题1.解答:供给和需求是市场经济中最基本的两个概念。
供给表示所有卖方愿意在一定价格下出售的商品或劳务的数量。
需求表示在一定价格下,所有买方愿意购买的商品或劳务的数量。
供给和需求关系紧密,是市场价格形成的基础。
备注:在这道习题中,要求解答供给和需求的概念以及它们之间的关系。
可以简单明了地解释供给和需求的含义,以及它们在市场价格形成中的作用。
2.解答:需求曲线表示在一定价格下,市场上所有买方愿意购买的商品或劳务的数量。
需求曲线通常呈现负斜率,即价格上升时,需求量下降;价格下降时,需求量增加。
这是因为随着价格的上升,购买商品或劳务的成本增加,一部分买方愿意放弃购买;价格下降时,购买商品或劳务的成本减少,买方的购买欲望增加。
备注:这道习题要求解答需求曲线的含义以及变化规律。
在解答中,可以提到需求曲线的负斜率,以及价格对需求量的影响。
3.解答:供给曲线表示在一定价格下,市场上所有卖方愿意出售的商品或劳务的数量。
供给曲线通常呈现正斜率,即价格上升时,供给量增加;价格下降时,供给量减少。
这是因为随着价格的上升,出售商品或劳务的利润增加,卖方愿意增加供给;价格下降时,利润减少,卖方愿意减少供给。
备注:这道习题要求解答供给曲线的含义以及变化规律。
在解答中,可以提到供给曲线的正斜率,以及价格对供给量的影响。
1.1.2 答案1.答案:供给和需求是市场经济中最基本的两个概念。
供给表示所有卖方愿意在一定价格下出售的商品或劳务的数量。
需求表示在一定价格下,所有买方愿意购买的商品或劳务的数量。
供给和需求关系紧密,是市场价格形成的基础。
西方经济学微观部分(高鸿业第六版)课后习题答案之欧阳数创编

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s=Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s=P e=6。
西方经济学微观部分(高鸿业第六版)课后习题答案之欧阳理创编

第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s =-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e =50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d =60-5P和原供给函数Q s=-10+5P代入均衡条件Q d =Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求内生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s =Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s=P e=6。
西方经济学微观部分课后习题问题详解及解析汇报[高鸿业第六版]
![西方经济学微观部分课后习题问题详解及解析汇报[高鸿业第六版]](https://img.taocdn.com/s3/m/022e0a64d15abe23492f4d6e.png)
第二章需求、供给和均衡价格1. 解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d =Q s,有50-5P=-5+5P得P e=5.5将均衡价格P e=5.5代入Q d=50-5P,得Q e=50-5×5.5=22.5或者,将均衡价格P e=5.5代入Q s=-5+5P,得Q e=-5+5×5.5=22.5所以,均衡价格和均衡数量分别为P e=5.5,Q e=22.5。
如图2—3所示。
图2—3(4)所谓静态分析是考察在既定条件下某一经济事物在经济变量的相互作用下所实现的均衡状态及其特征。
也可以说,静态分析是在一个经济模型中根据给定的外生变量来求生变量的一种分析方法。
以(1)为例,在图2—1中,均衡点E就是一个体现了静态分析特征的点。
它是在给定的供求力量的相互作用下达到的一个均衡点。
在此,给定的供求力量分别用给定的供给函数Q s=-10+5P和需求函数Q d=50-5P表示,均衡点E具有的特征是:均衡价格P e=6,且当P e=6时,有Q d=Q s=Q e=20;同时,均衡数量Q e=20,且当Q e=20时,有P d=P s=P e=6。
高鸿业西方经济学微观部分第6版课后习题详解第3章消费者选择

高鸿业西方经济学微观部分第6版课后习题详解第3章消费者选择课后习题详解1.已知一件衬衫的价格为80元,一份肯德基快餐的价格为20元,在某消费者关于这两种商品的效用最大化的均衡点上,一份肯德基快餐对衬衫的边际替代率MRS是多少?解:按照两商品的边际替代率MRS的定义公式,可以将一份肯德基快餐对衬衫的边际替代率写成:Y某其中,某表示肯德基快餐的份数;Y表示衬衫的件数;MRS某Y 表示在维持效用水平不MRS某Y变的前提下,消费者增加一份肯德基快餐消费时所需要放弃的衬衫的消费数量。
在该消费者实现关于这两种商品的效用最大化时,在均衡点上有:MRS某YP某PY即有:MRS某Y200.2580它表明,在效用最大化的均衡点上,对于该消费者来说,一份肯德基快餐对衬衫的边际替代率为0.25。
2.假设某消费者的均衡如图3-8所示。
其中,横轴O某1和纵轴O某2分别表示商品1和商品2的数量,线段AB为消费者的预算线,曲线U 为消费者的无差异曲线,E点为效用最大化的均衡点。
已知商品1的价格P12元。
图3-8消费者效用最大化(1)求消费者的收入;(2)求商品2的价格P2;(3)写出预算线方程;(4)求预算线的斜率;(5)求E点的MRS12的值。
解:(1)图3-8中的横截距表示消费者的收入全部购买商品1的数量为30单位,且已知P12元,所以消费者的收入I23060元。
(2)图3-8中的纵截距表示消费者的收入全部购买商品2的数量为20单位,且由(1)已知收入I60元,所以商品2的价格P2I603元。
2022(3)由于预算线方程的一般形式为:P1某1P2某2I所以,由(1)、(2)可将预算线方程具体写为:2某13某260。
22(4)将(3)中的预算线方程进一步整理为某2某120,显然,预算线的斜率为k33(5)在消费者效用最大化的均衡点E上,有MRS12值即MRS等于预算线斜率的绝对值P1,即无差异曲线的斜率的绝对P2PP21。
因此,在E点,MRS121=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章需求、供给与均衡价格1、解答:(1)将需求函数Q d=50-5P与供给函数Q s=—10+5P代入均衡条件Qd=Q s,有50-5P =-10+5P得Pe=6将均衡价格P e=6代入需求函数Qd=50—5P,得Q e=50-5×6=20或者,将均衡价格Pe=6代入供给函数Q s=-10+5P,得Qe=—10+5×6=20所以,均衡价格与均衡数量分别为Pe=6,Qe=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生得需求函数Q d=60—5P与原供给函数Qs=—10+5P代入均衡条件Q d=Qs,有60—5P=-10+5P得Pe=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格Pe=7代入Qs=-10+5P,得Qe=-10+5×7=25所以,均衡价格与均衡数量分别为Pe=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P与由于技术水平提高而产生得供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P得Pe=5、5将均衡价格Pe=5、5代入Q d=50-5P,得Q e=50-5×5、5=22、5或者,将均衡价格Pe=5、5代入Q s=—5+5P,得Q e=-5+5×5、5=22、5所以,均衡价格与均衡数量分别为Pe=5、5,Q e=22、5。
如图2-3所示。
图2-3(4)所谓静态分析就是考察在既定条件下某一经济事物在经济变量得相互作用下所实现得均衡状态及其特征。
也可以说,静态分析就是在一个经济模型中根据给定得外生变量来求内生变量得一种分析方法。
以(1)为例,在图2—1中,均衡点E就就是一个体现了静态分析特征得点.它就是在给定得供求力量得相互作用下达到得一个均衡点。
在此,给定得供求力量分别用给定得供给函数Q s =-10+5P与需求函数Q d =50-5P表示,均衡点E 具有得特征就是:均衡价格P e=6,且当P e=6时,有Qd =Q s =Q e=20;同时,均衡数量Q e =20,且当Qe =20时,有P d =P s =P e=6.也可以这样来理解静态分析:在外生变量包括需求函数中得参数(50,—5)以及供给函数中得参数(-10,5)给定得条件下,求出得内生变量分别为Pe =6与Q e =20。
依此类推,以上所描述得关于静态分析得基本要点,在(2)及图2—2与(3)及图2—3中得每一个单独得均衡点E i (i =1,2)上都得到了体现。
而所谓得比较静态分析就是考察当原有得条件发生变化时,原有得均衡状态会发生什么变化,并分析比较新旧均衡状态.也可以说,比较静态分析就是考察在一个经济模型中外生变量变化时对内生变量得影响,并分析比较由不同数值得外生变量所决定得内生变量得不同数值,以(2)为例加以说明。
在图2-2中,由均衡点E 1变动到均衡点E2就就是一种比较静态分析。
它表示当需求增加即需求函数发生变化时对均衡点得影响.很清楚,比较新、旧两个均衡点E 1与E 2可以瞧到:需求增加导致需求曲线右移,最后使得均衡价格由6上升为7,同时,均衡数量由20增加为25。
也可以这样理解比较静态分析:在供给函数保持不变得前提下,由于需求函数中得外生变量发生变化,即其中一个参数值由50增加为60,从而使得内生变量得数值发生变化,其结果为,均衡价格由原来得6上升为7,同时,均衡数量由原来得20增加为25.类似地,利用(3)及图2—3也可以说明比较静态分析方法得基本要点。
(5)由(1)与(2)可见,当消费者收入水平提高导致需求增加,即表现为需求曲线右移时,均衡价格提高了,均衡数量增加了。
由(1)与(3)可见,当技术水平提高导致供给增加,即表现为供给曲线右移时,均衡价格下降了,均衡数量增加了.总之,一般地,需求与均衡价格成同方向变动,与均衡数量成同方向变动;供给与均衡价格成反方向变动,与均衡数量成同方向变动.2、 解答:(1)根据中点公式ed =—错误!·错误!,错误!),有e d=错误!·错误!,错误!)=1、5(2)由于当P=2时,Q d =500-100×2=300,所以,有e d =-错误!·错误!=—(-100)·错误!=错误!(3)根据图2—4,在a点即P =2时得需求得价格点弹性为e d =错误!=错误!=错误!或者 e d=FO AF=错误!图2—4显然,在此利用几何方法求出得P=2时得需求得价格点弹性系数与(2)中根据定义公式求出得结果就是相同得,都就是ed=错误!。
3、解答:(1)根据中点公式es=\f(ΔQ,ΔP)·错误!,错误!),有e s=错误!·错误!,错误!)=\f(4,3)(2)由于当P=3时,Q s=-2+2×3=4,所以,es=错误!·错误!=2·错误!=1、5。
(3)根据图2-5,在a点即P=3时得供给得价格点弹性为e s=错误!=错误!=1、5图2—5显然,在此利用几何方法求出得P=3时得供给得价格点弹性系数与(2)中根据定义公式求出得结果就是相同得,都就是e s=1、5.4、解答:(1)根据求需求得价格点弹性得几何方法,可以很方便地推知:分别处于三条不同得线性需求曲线上得a、b、c三点得需求得价格点弹性就是相等得.其理由在于,在这三点上,都有e d=错误!(2)根据求需求得价格点弹性得几何方法,同样可以很方便地推知:分别处于三条不同得线性需求曲线上得a、e、f三点得需求得价格点弹性就是不相等得,且有e错误!〈e错误!〈e错误!.其理由在于在a点有:e 错误!=错误!在f点有:e错误!=错误!在e点有:e错误!=错误!在以上三式中,由于GB<GC<GD,所以,e错误!<e错误!〈e错误!。
5、利用图2—7 (即教材中第55页得图2—29)比较需求价格点弹性得大小。
(1)图(a)中,两条线性需求曲线D1与D2相交于a点。
试问:在交点a,这两条直线型得需求得价格点弹性相等吗?(2)图(b)中,两条曲线型得需求曲线D1与D2相交于a点。
试问:在交点a,这两条曲线型得需求得价格点弹性相等吗?图2-7解答:(1)因为需求得价格点弹性得定义公式为e d=-错误!·错误!,此公式得-错误!项就是需求曲线某一点斜率得绝对值得倒数,又因为在图(a)中,线性需求曲线D1得斜率得绝对值小于线性需求曲线D2得斜率得绝对值,即需求曲线D1得-错误!值大于需求曲线D2得—错误!值,所以,在两条线性需求曲线D1与D2得交点a,在P与Q给定得前提下,需求曲线D1得弹性大于需求曲线D2得弹性.(2)因为需求得价格点弹性得定义公式为ed=-\f(dQ,d P)·错误!,此公式中得-错误!项就是需求曲线某一点得斜率得绝对值得倒数,而曲线型需求曲线上某一点得斜率可以用过该点得切线得斜率来表示。
在图(b)中,需求曲线D1过a点得切线AB得斜率得绝对值小于需求曲线D2过a点得切线FG得斜率得绝对值,所以,根据在解答(1)中得道理可推知,在交点a,在P与Q给定得前提下,需求曲线D1得弹性大于需求曲线D2得弹性.6、 解答:由已知条件M=100Q2,可得Q=错误!于就是,有 错误!=错误!错误!-错误!·错误!进一步,可得e M=\f(dQ ,d M )·\f (M ,Q)=错误!错误!-错误!·错误!·100·错误!2错误!=错误!观察并分析以上计算过程及其结果,可以发现,当收入函数M=aQ 2(其中a 〉0,为常数)时,则无论收入M 为多少,相应得需求得收入点弹性恒等于错误!。
7、 解答:由已知条件Q =MP -N ,可得e d=-错误!·错误!=—M·(-N)·P -N-1·错误!=NeM =错误!·错误!=P-N ·错误!=1由此可见,一般地,对于幂指数需求函数Q(P )=MP -N 而言, 其需求得价格点弹性总等于幂指数得绝对值N 。
而对于线性需求函数Q (M )=MP -N而言,其需求得收入点弹性总就是等于1.8、解答:令在该市场上被100个消费者购买得商品总量为Q,相应得市场价格为P 。
根据题意,该市场\f (1,3)得商品被60个消费者购买,且每个消费者得需求得价格弹性都就是3,于就是,单个消费者i 得需求得价格弹性可以写为e di=-d Qi d P·错误!=3 即 \f (d Qi ,d P)=-3·\f (Qi ,P ) (i =1,2,…,60)(1)且 错误!i =错误!(2)类似地,再根据题意,该市场错误!得商品被另外40个消费者购买,且每个消费者得需求得价格弹性都就是6,于就是,单个消费者j 得需求得价格弹性可以写为e dj =-错误!·错误!=6即 \f (d Qj ,d P)=—6·Q j P(j=1,2,…,40)(3) 且 错误!j =错误!(4)此外,该市场上100个消费者合计得需求得价格弹性可以写为ed=-\f (d Q,d P )·\f(P,Q )=—错误!·错误!=-将式(1)、式(3)代入上式,得e d= =再将式(2)、式(4)代入上式,得e d =-所以,按100个消费者合计得需求得价格弹性系数就是5。
、9、解答:(1)由于e d =- ,于就是有错误!=ed ×=-(1、3) ×(-2%)=2、6%即商品价格下降2%使得需求数量增加2、6%、(2)由于e M =- ,于就是有\f(ΔQ ,Q)=e M·错误!=2、2×5%=11%即消费者收入提高5%使得需求数量增加11%。
10、 解答:(1)关于A 厂商:由于P A=200-Q A =200-50=150,且A 厂商得需求函数可以写成 Q A=200-P A 于就是,A厂商得需求得价格弹性为 e dA =—错误!·错误!=-(-1)×错误!=3关于B 厂商:由于P B =300-0、5Q B =300-0、5×100=250,且B 厂商得需求函数可以写成:Q B=600-2P B于就是,B 厂商得需求得价格弹性为e dB =-\f(d Q B ,d P B)·\f (P B,QB )=—(-2)×\f(250,100)=5 (2)令B 厂商降价前后得价格分别为P B 与P′B ,且A 厂商相应得需求量分别为Q A 与Q′A ,根据题意有P B =300-0、5QB =300-0、5×100=250P′B =300—0、5Q′B=300-0、5×160=220QA =50Q′A =40因此,A厂商得需求得交叉价格弹性为e A B=-错误!·错误!=错误!·错误!=错误!(3)由(1)可知,B 厂商在PB =250时得需求得价格弹性为e dB =5,也就就是说,对B厂商得需求就是富有弹性得。
