全国物理竞赛复赛试题解答

合集下载

2023年全国中学生物理竞赛复赛试题及答案

全国中学生物理竞赛复赛试卷姓名（）总分（）本卷共九题，满分160 分．计算题的解答应写出必要的文字说明、方程式和重要的演算环节．只写出最后结果的不能得分．有数字计算的题．答案中必须明确写出数值和单位．填空题把答案填在题中的横线上，只要给出结果，不需写出求解的过程．一、（15 分）蛇形摆是一个用于演示单摆周期与摆长关系的实验仪器（见图）．若干个摆球位于同一高度并等间距地排成一条直线，它们的悬挂点在不同的高度上，摆长依次减小．设重力加速度g = 9 . 80 m/ s2 ,1 ．试设计一个包含十个单摆的蛇形摆（即求出每个摆的摆长），规定满足：( a ）每个摆的摆长不小于0 . 450m ，不大于1.00m ; ( b ）初始时将所有摆球由平衡点沿x 轴正方向移动相同的一个小位移xo ( xo <<0.45m ) ，然后同时释放，通过40s 后，所有的摆可以同时回到初始状态．2 ．在上述情形中，从所有的摆球开始摆动起，到它们的速率初次所有为零所通过的时间为________________________________________.二、（20 分）距离我们为L 处有一恒星，其质量为M ，观测发现其位置呈周期性摆动，周期为T ，摆动范围的最大张角为△θ．假设该星体的周期性摆动是由于有一颗围绕它作圆周运动的行星引起的，试给出这颗行星的质量m所满足的方程．若L=10 光年，T =10 年，△θ= 3 毫角秒，M = Ms （Ms为太阳质量），则此行星的质量和它运动的轨道半径r各为多少？分别用太阳质量Ms 和国际单位AU （平均日地距离）作为单位，只保存一位有效数字．已知1 毫角秒=11000角秒，1角秒=13600度，1AU=1.5×108km,光速 c = 3.0×105km/s.三、（22 分）如图，一质量均匀分布的刚性螺旋环质量为m，半径为R ，螺距H =πR ，可绕竖直的对称轴OO′，无摩擦地转动，连接螺旋环与转轴的两支撑杆的质量可忽略不计．一质量也为m 的小球穿在螺旋环上并可沿螺旋环无摩擦地滑动,一方面扶住小球使其静止于螺旋环上的某一点A ，这时螺旋环也处在静止状态．然后放开小球，让小球沿螺旋环下滑，螺旋环便绕转轴O O′，转动．求当小球下滑到离其初始位置沿竖直方向的距离为h 时，螺旋环转动的角速度和小球对螺旋环作用力的大小．四、（ 12 分）如图所示，一质量为m、电荷量为 q ( q > 0 ）的粒子作角速度为ω、半径为 R 的匀速圆周运动.一长直细导线位于圆周所在的平面内，离圆心的距离为d ( d > R ) ，在导线上通有随时间变化的电流I, t= 0 时刻，粒子速度的方向与导线平行，离导线的距离为d+ R .若粒子做圆周运动的向心力等于电流 i ,的磁场对粒子的作用力，试求出电流 i 随时间的变化规律．不考虑变化的磁场产生的感生电场及重力的影响．长直导线电流产生的磁感应强度表达式中的比例系数 k 已知．五、（20分）如图所示，两个固定的均匀带电球面，所带电荷量分别为+Q和-Q (Q >0) ，半径分别为R和R/2，小球面与大球面内切于C点，两球面球心O和O’的连线MN沿竖直方在MN与两球面的交点B、0和C 处各开有足够小的孔因小孔损失的电荷量忽略不计，有一质量为m，带电荷为q(q>0的质点自MN线上离B点距离为R的A点竖直上抛。

第25届全国高中生物理竞赛答案(复赛)

第25届全国中学生物理竞赛复赛理论试题参考解答一、答案1. 14103.1⨯ 2. 31122kg m s -⋅⋅ 51.0610-⨯(答51.0510-⨯也给分)3.34T T 二、参考解答：1. 椭圆半长轴a 等于近地点和远地点之间距离的一半，亦即近地点与远地点矢径长度（皆指卫星到地心的距离）n r 与f r 的算术平均值，即有 ()()()()n f n f n f111222a r r H R H R H H R =+=+++=++⎡⎤⎣⎦ (1) 代入数据得43.194610a =⨯km (2) 椭圆半短轴b 等于近地点与远地点矢径长度的几何平均值，即有b = (3)代入数据得41.94210km b =⨯ (4) 椭圆的偏心率ab a e 22-=(5) 代入数据即得0.7941e = (6)2. 当卫星在16小时轨道上运行时，以n v 和f v 分别表示它在近地点和远地点的速度，根据能量守恒，卫星在近地点和远地点能量相等，有22n f n f1122GMm GMmm m r r -=-v v (7) 式中M 是地球质量，G 是万有引力常量. 因卫星在近地点和远地点的速度都与卫星到地心的连线垂直，根据角动量守恒，有n n f f m r m r =v v (8) 注意到g RGM=2(9)由(7)、(8)、(9)式可得n =v (10)n f n f r r ==v v (11) 当卫星沿16小时轨道运行时，根据题给的数据有n n r R H =+ f f r R H =+ 由(11)式并代入有关数据得f 1.198=v km/s (12)依题意，在远地点星载发动机点火，对卫星作短时间加速，加速度的方向与卫星速度方向相同，加速后长轴方向没有改变，故加速结束时，卫星的速度与新轨道的长轴垂直，卫星所在处将是新轨道的远地点.所以新轨道远地点高度4f f 5.093010H H '==⨯km ，但新轨道近地点高度2n6.0010H '=⨯km .由(11)式，可求得卫星在新轨道远地点处的速度为 f 1.230'=v km/s (13) 卫星动量的增加量等于卫星所受推力F 的冲量，设发动机点火时间为∆t ，有()f f m F t '-=∆v v (14) 由(12)、(13)、(14)式并代入有关数据得∆t=21.510s ⨯ (约2.5分) (15) 这比运行周期小得多.3. 当卫星沿椭圆轨道运行时，以r 表示它所在处矢径的大小，v 表示其速度的大小，θ表示矢径与速度的夹角，则卫星的角动量的大小sin 2L rm m θσ==v (16 ) 其中1sin 2r σθ=v （17）是卫星矢径在单位时间内扫过的面积，即卫星的面积速度.由于角动量是守恒的，故σ是恒量.利用远地点处的角动量，得f f 12r σ=v (18)又因为卫星运行一周扫过的椭圆的面积为πS ab = (19) 所以卫星沿轨道运动的周期σST =(20)由(18)、(19)、(20) 式得f f2πabT r =v (21) 代入有关数据得45.67810T =⨯s (约15小时46分) (22)注：本小题有多种解法.例如，由开普勒第三定律，绕地球运行的两亇卫星的周期T 与T 0之比的平方等于它们的轨道半长轴a 与a 0之比的立方，即2300T a T a ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭若0a 是卫星绕地球沿圆轨道运动的轨道半径，则有202002πGMmma a T ⎛⎫= ⎪⎝⎭得22203204π4πT a GM gR ==从而得T =代入有关数据便可求得(22)式.4. 在绕月圆形轨道上，根据万有引力定律和牛顿定律有2m m 2m m2π()GM m mr r T = (23) 这里m m r r H =+是卫星绕月轨道半径，m M 是月球质量. 由(23)式和(9)式，可得23mm 22m4πr M M gR T = (24) 代入有关数据得m0.0124M M= (25)三、参考解答：足球射到球门横梁上的情况如图所示（图所在的平面垂直于横梁轴线）.图中B 表示横梁的横截面，O 1为横梁的轴线；11O O '为过横梁轴线并垂直于轴线的水平线；A 表示足球，O 2为其球心；O 点为足球与横梁的碰撞点，碰撞点O 的位置由直线O 1OO 2与水平线11O O '的夹角θ 表示.设足球射到横梁上时球心速度的大小为v 0，方向垂直于横梁沿水平方向，与横梁碰撞后球心速度的大小为v ，方向用它与水平方向的夹角ϕ表示(如图).以碰撞点O 为原点作直角坐标系Oxy ，y 轴与O 2OO 1重合.以α0表示碰前速度的方向与y 轴的夹角，以α表示碰后速度的方向与y 轴(负方向)的夹角，足球被横梁反弹后落在何处取决于反弹后的速度方向，即角α的大小.以F x 表示横梁作用于足球的力在x 方向的分量的大小，F y 表示横梁作用于足球的力在y 方向的分量的大小，∆t 表示横梁与足球相互作用的时间，m 表示足球的质量，有x 0x x F t m m ∆=-v v (1) y y 0y F t m m ∆=+v v (2) 式中0x v 、0y v 、x v 和y v 分别是碰前和碰后球心速度在坐标系Oxy 中的分量的大小.根据摩擦定律有x y F F μ= (3) 由（1）、（2）、（3）式得 0x xy 0yμ-=+v v v v (4)根据恢复系数的定义有y 0y e =v v （5）因0x00ytan α=v v （6） xytan α=v v （7）由（4）、（5）、（6）、（7）各式得⎪⎭⎫⎝⎛+-=e e 11tan 1tan 0μαα （8）由图可知αθϕ+= （9）若足球被球门横梁反弹后落在球门线内，则应有90ϕ≥ (10) 在临界情况下，若足球被反弹后刚好落在球门线上，这时90ϕ= .由（9）式得()tan 90tan θα-=(11)因足球是沿水平方向射到横梁上的，故θα=0，有⎪⎭⎫⎝⎛+-=e e 11tan 1tan 1μθθ (12) 这就是足球反弹后落在球门线上时入射点位置θ所满足的方程.解（12）式得tan θ=13)代入有关数据得tan 1.6θ= (14) 即58θ=(15)现要求球落在球门线内，故要求58θ≥ (16)四、参考解答：1. 当阀门F 关闭时，设封闭在M 和B 中的氢气的摩尔数为n 1，当B 处的温度为T 时，压力表显示的压强为 p ，由理想气体状态方程，可知B 和M 中氢气的摩尔数分别为 RTpV n BB 1=(1) 0MM 1RT pV n = (2) 式中R 为普适气体恒量.因1M 1B 1n n n =+ (3) 解（1）、（2）、（3）式得 1MB B 011n R V T V p V T =- (4) 或1MB B 0p T n R V p V V T =- (5) (4)式表明，T 1与p1成线性关系，式中的系数与仪器结构有关.在理论上至少要测得两个已知温度下的压强，作T 1对p1的图线，就可求出系数. 由于题中己给出室温T 0时的压强p 0，故至少还要测定另一己知温度下的压强，才能定量确定T 与p 之间的关系式.2. 若蒸气压温度计测量上限温度v T 时有氢气液化，则当B 处的温度v T T ≤时，B 、M 和E 中气态氢的总摩尔数应小于充入氢气的摩尔数.由理想气体状态方程可知充入氢气的总摩尔数 ()0B M E 20p V V V n RT ++=（6）假定液态氢上方的气态氢仍可视为理想气体，则B 中气态氢的摩尔数为 v B2B vp V n RT =（7）在（7）式中，已忽略了B 中液态氢所占的微小体积.由于蒸气压温度计的其它都分仍处在室温中，其中氢气的摩尔数为()νM E 2M 2Ep V V n n RT ++= （8）根据要求有2B 2M 2E 2n n n n ++≤ （9）解（6）、（7）、（8）、（9）各式得 ()B vv 0v00v E M V T p p T p T p V V --≥+ (10)代入有关数据得M E B 18V V V +≥ (11)五、答案与评分标准：1．59.022122=-=+(3分) 2 (2分)2．如图(15分.代表电流的每一线段3分，其中线段端点的横坐标占1分，线段的长度占1分，线段的纵坐标占1分)六、参考解答：如果电流有衰减，意味着线圈有电阻，设其电阻为R ，则在一年时间t 内电流通过线圈因发热而损失的能量为Rt I E 2=∆ （1）以ρ 表示铅的电阻率，S 表示铅丝的横截面积，l 表示铅丝的长度，则有 SlR ρ= （2）电流是铅丝中导电电子定向运动形成的，设导电电子的平均速率为v ，根据电流的定义有 I S ne =v （3）所谓在持续一年的时间内没有观测到电流的变化，并不等于电流一定没有变化，但这变化不会超过电流检测仪器的精度∆I ，即电流变化的上限为mA 0.1=∆I .由于导电电子的数密度n 是不变的，电流的变小是电子平均速率变小的结果，一年内平均速率由v 变为 v -∆v ，对应的电流变化I neS ∆=∆v （4）导电电子平均速率的变小，使导电电子的平均动能减少，铅丝中所有导电电子减少的平均动能为()221122k E lSn m m ⎡⎤∆=--∆⎢⎥⎣⎦v v v l S n m ≈∆v v （5）由于∆I<<I ，所以∆v <<v ，式中∆v 的平方项已被略去.由（3）式解出 v ，（4）式解出 ∆v ，代入（5）式得2k lmI IE ne S∆∆=(6) 铅丝中所有导电电子减少的平均动能就是一年内因发热而损失的能量，即E E k ∆=∆ （7）由(1)、(2)、(6)、(7)式解得2Δm I ne Itρ= （8）式中7365243600s =3.1510s t =⨯⨯⨯ （9）在（8）式中代入有关数据得261.410Ωm ρ-=⨯⋅ (10)所以电阻率为0的结论在这一实验中只能认定到m Ω104.126⋅⨯≤-ρ (11)七、参考解答：按照斯特藩-玻尔兹曼定律，在单位时间内太阳表面单位面积向外发射的能量为 4s s W T σ=(1)其中σ为斯特藩-玻尔兹曼常量，T s 为太阳表面的绝对温度.若太阳的半径为R s ，则单位时间内整个太阳表面向外辐射的能量为2s s s 4πP R W= (2) 单位时间内通过以太阳为中心的任意一个球面的能量都是s P .设太阳到地球的距离为r se ，考虑到地球周围大气的吸收，地面附近半径为R 的透镜接收到的太阳辐射的能量为 ()2s 2seπ14πP P R r α=- (3)薄凸透镜将把这些能量会聚到置于其后焦面上的薄圆盘上，并被薄圆盘全部吸收.另一方面，因为薄圆盘也向外辐射能量.设圆盘的半径为D R ，温度为D T ，注意到簿圆盘有两亇表面，故圆盘在单位时间内辐射的能量为24D D D 2πP R T σ=⋅⋅ (4)显然，当D P P = (5) 即圆盘单位时间内接收到的能量与单位时间内辐射的能量相等时，圆盘达到稳定状态，其温度达到最高.由(1)、(2)、(3)、(4)、(5)各式得 ()1224s D s 22se D12R R T T r R α⎡⎤=-⎢⎥⎣⎦(6) 依题意，薄圆盘半径为太阳的像的半径s R '的2倍，即D 2s R R '=.由透镜成像公式知s sseR R f r '= (7) 于是有sD se2R R f r = (8) 把(8)式代入(6)式得()124D s 218R T T f α⎡⎤=-⎢⎥⎣⎦(9) 代入已知数据，注意到s s (273.15)T t =+K ， T D =1.4×103K (10)即有3o D D 273.15 1.110C t T =-=⨯ (11) 八、参考解答：1．根据爱因斯坦质能关系，3H 和3He 的结合能差为()332n p H He B m m m m c ∆=--+ (1)代入数据，可得763.0=∆B MeV (2) 2．3He 的两个质子之间有库仑排斥能，而3H 没有.所以3H 与3He 的结合能差主要来自它们的库仑能差.依题意，质子的半径为N r ，则3He 核中两个质子间的库仑排斥能为2C N2e E k r = (3)若这个库仑能等于上述结合能差，C E B =∆，则有2N 2Δke r B= (4)代入数据，可得N 0.944r =fm (5)3．粗略地说，原子核中每个核子占据的空间体积是 3N (2)r .根据这个简单的模型，核子数为A 的原子核的体积近似为33N N (2)8V A r Ar == (6)另一方面，当A 较大时，有 343V R π=（7）由（6）式和（7）式可得R 和A 的关系为1/31/31/3N 06πR r A r A ⎛⎫== ⎪⎝⎭(8)其中系数1/30N 6πr r ⎛⎫= ⎪⎝⎭(9)把(5)式代入(9)式得17.10=r fm (10) 由(8)式和(10)式可以算出Pb 208的半径Pb 6.93fm R =。

第28届全国中学生物理竞赛复赛试卷(含答案)

第28届全国中学生物理竞赛复赛试题一、（20分）如图所示，哈雷彗星绕太阳S 沿椭圆轨道逆时针方向运动，其周期T 为76.1年，1986年它过近日点P 0时与太阳S 的距离r 0=0.590AU ，AU 是天文单位，它等于地球与太阳的平均距离，经过一段时间，彗星到达轨道上的P 点，SP 与SP 0的夹角θP =72.0°。

已知：1AU=1.50×1011m ，引力常量G=6.67×10－11Nm 2/kg 2，太阳质量m S =1.99×1030kg ，试求P 到太阳S 的距离r P 及彗星过P 点时速度的大小及方向（用速度方向与SP 0的夹角表示）。

二、（20分）质量均匀分布的刚性杆AB 、CD 如图放置，A 点与水平地面接触，与地面间的静摩擦系数为μA ，B 、D 两点与光滑竖直墙面接触，杆AB 和CD 接触处的静摩擦系数为μC ，两杆的质量均为m ，长度均为l 。

1、已知系统平衡时AB 杆与墙面夹角为θ，求CD 杆与墙面夹角α应该满足的条件（用α及已知量满足的方程式表示）。

2、若μA =1.00，μC =0.866，θ=60.0°。

求系统平衡时α的取值范围（用数值计算求出）。

三、（25分）在人造卫星绕星球运行的过程中，为了保持其对称转轴稳定在规定指向，一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴转，但有时为了改变卫星的指向，又要求减慢或者消除卫星的旋转，减慢或者消除卫星旋转的一种方法就是所谓消旋法，其原理如图所示。

一半径为R ，质量为M 的薄壁圆筒，，其横截面如图所示，图中O 是圆筒的对称轴，两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q 、Q ′（位于圆筒直径两端）处，另一端各拴有一个质量为2m的小球，正常情况下，绳绕在圆筒外表面上，两小球用插销分别锁定在圆筒表面上的P 0、P 0′处，与卫星形成一体，绕卫星的对称轴旋转，卫星自转的角速度为ω0。

第 23届全国中学生物理竞赛复赛参考解答

第23届全国中学生物理竞赛复赛题参考解答及评分标准一、参考解答：解法一小球沿竖直线上下运动时，其离开玻璃管底部的距离h 随时间t 变化的关系如图所示．设照片拍摄到的小球位置用A 表示，A 离玻璃管底部的距离为h A ，小球开始下落处到玻璃管底部的距离为H .小球可以在下落的过程中经过A 点，也可在上升的过程中经过A 点.现以τ表示小球从最高点（即开始下落处）落到玻璃管底部所需的时间（也就是从玻璃管底部反跳后上升到最高点所需的时间），1τ表示小球从最高点下落至A 点所需的时间（也就是从A 点上升至最高点所需的时间），2τ表示小球从A 点下落至玻璃管底部所需的时间（也就是从玻璃管底部反跳后上升至A 点所需的时间）.显然，12τττ+=.根据题意，在时间间隔T 的起始时刻和终了时刻小球都在A 点．用n 表示时间间隔 T 内（包括起始时刻和终了时刻）小球位于A 点的次数（n ≥2）.下面分两种情况进行讨论：1．A 点不正好在最高点或最低点．当n 为奇数时有()()()12111T n n n τττ=-+-=- 3,5,7,n = （1）在（1）式中，根据题意1τ可取10ττ<<中的任意值，而21τττ=-（2）当n 为偶数时有()()211222T n n n n ττττ=+-=+- 2,4,6,n = （3）由（3）式得12ττ=（4）由（1）、（3）、（4）式知，不论n 是奇数还是偶数，都有()1T n τ=- 2,3,4,n =（5）因此可求得，开始下落处到玻璃管底部的距离的可能值为th2211221n T H g g n τ⎛⎫== ⎪-⎝⎭2,3,4,n = （6）若用n H 表示与n 对应的H 值，则与n H 相应的A 点到玻璃管底部的距离 2112A n h H g τ=-2,3,4,n = （7）当n 为奇数时，1τ可取10ττ<<中的任意值，故有0A n h H << 2121n T H g n ⎡⎤⎛⎫=⎢⎥ ⎪-⎝⎭⎢⎥⎣⎦n=3,5,7,·· · （8）可见与n H 相应的A h 的可能值为0与n H 之间的任意值．当n 为偶数时，112ττ=，由（6）式、（7）式求得n H 的可能值34A n h H =2121n T H g n ⎡⎤⎛⎫=⎢⎥ ⎪-⎝⎭⎢⎥⎣⎦n=2,4,6,·· · （9） 2．若A 点正好在最高点或最低点．无论n 是奇数还是偶数都有()21T n τ=- n=2,3,4,· · ·（10）()22112221n T H g g n τ⎡⎤==⎢⎥-⎢⎥⎣⎦n=2,3,4,·· · （11）A n h H = ()21221n T H g n ⎧⎫⎡⎤⎪⎪=⎨⎢⎥⎬-⎢⎥⎪⎪⎣⎦⎩⎭n=2,3,4,·· · （12）或0A h =（13）解法二因为照相机每经一时间间隔T 拍摄一次时，小球都位于相片上同一位置，所以小球经过该位置的时刻具有周期性，而且T 和这个周期的比值应该是一整数．下面我们就研究小球通过某个位置的周期性．设小球从最高点（开始下落处）落下至管底所需时间为τ ，从最高点下落至相片上小球所在点（A 点）所需时间为1τ，从A 点下落至管底所需时间为2τ，则12τττ=+（1）（小球上升时通过相应路程段所需时间与下落时同一路程所需时间相同，也是τ、1τ和2τ）从小球在下落过程中经过A 点时刻开始，小球经过的时间22τ后上升至A 点，再经过时间12τ后又落到A 点，此过程所需总时间为12222τττ+=．以后小球将重复这样的运动．小球周期性重复出现在A 点的周期是多少？分两种情况讨论：（1）． 12ττ≠，1τ和2τ都不是小球在A 点重复出现的周期，周期是2τ．（2）． 12ττ=，小球经过时间22ττ=回到A 点，再经过时间12ττ=又回到A 点，所以小球重复出现在A 点的周期为τ．下面就分别讨论各种情况中H 的可能值和A 点离管底的距离A h 的可能值．（如果从小球在上升过程中经过A 点的时刻开始计时，结果一样，只是1τ和2τ对调一下）1．H 的可能值（1）．较普遍的情况，12ττ≠．T 与2τ的比值应为一整数，τ的可能值应符合下式2Tk τ=， 1,2,3,k = （2）由自由落体公式可知，与此相应的k H 的数值为2211222k T H g g k τ⎛⎫== ⎪⎝⎭1,2,3,k = （3）（2）．12ττ=．τ的可能值应符合下式Tk τ'= 1,2,3,k '= （4）故k H '的可能值为221122k T H g g k τ'⎛⎫== ⎪'⎝⎭1,2,3,k '= （5）当k '为偶数时，即2,4,6,k '=时，（5）式与（3）式完全相同．可见由（3）式求得的H 的可能值包含了12ττ≠的全部情况和12ττ=的一部分情况．当k '为奇数时，即1,3,5,k '=时，由（5）式得出的H 的可能值为212k T H g k '⎛⎫= ⎪'⎝⎭1,3,5,k '= （6）它们不在（3）式之内，故（3）式和（6）式得出的H 合在一起是H 的全部的可能值． 2．与各H 值相应的A h 的可能值 a.与k H 相应的A h 的可能值由于在求得（3）式时未限定A 点的位置，故A h 的数值可取0和k H 之间的任意值，即0A k h H ≤≤ 2122k T H g k ⎡⎤⎛⎫=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ 1,2,3,k = （7）b. 与k H '（k '为奇数）相应的A h 的可能值这些数值与A 位于特定的位置，122τττ==，相对应，所以对于每一个k H '对应的A h 是一个特定值，它们是21122A k T h H g k '⎛⎫=- ⎪'⎝⎭212k T H g k '⎡⎤⎛⎫=⎢⎥ ⎪'⎝⎭⎢⎥⎣⎦1,3,5,k '= （8）评分标准：本题23分二、参考解答：1．求刚碰撞后小球A 、B 、C 、D 的速度设刚碰撞后，小球A 、B 、C 、D 的速度分别为A v 、B v 、C v 、D v ，并设它们的方向都与0v 的方向相同．由于小球C 位于由B 、C 、D 三球组成的系统的质心处，所以小球C 的速度也就是这系统的质心的速度．因碰撞前后四小球组成的质点组的动量守恒，故有0A C 3M M m =+v v v（1）碰撞前后质点组的角动量守恒，有C D 02ml ml =+v v（2）这里角动量的参考点设在与B 球重合的空间固定点，且规定顺时针方向的角动量为正．因为是弹性碰撞，碰撞前后质点组的动能相等，有222220A B C D 11111+22222M M m m =++v v mv v v （3）因为杆是刚性杆，小球B 和D 相对于小球C 的速度大小必相等，方向应相反，所以有B C C D --v v =v v（4）解（1）、（2）、（3）、（4）式，可得两个解C v =0（5）和C 0456MM m=+v v（6）因为C v 也是刚碰撞后由B 、C 、D 三小球组成的系统的质心的速度，根据质心运动定律，碰撞后这系统的质心不可能静止不动，故（5）式不合理，应舍去．取（6）式时可解得刚碰撞后A 、B 、D 三球的速度 A 05656M mM m -=+v v（7）B 01056M M m=+v v（8）D 0256MM m=-+v v（9）2．讨论碰撞后各小球的运动碰撞后，由于B 、C 、D 三小球组成的系统不受外力作用，其质心的速度不变，故小球C 将以（6）式的速度即C 0456MM m=+v v 沿0v 方向作匀速运动．由（4）、（8）、（9）式可知，碰撞后，B 、D 两小球将绕小球C 作匀角速度转动，角速度的大小为656B M l M m ω-==+C v v v l（10）方向为逆时针方向．由（7）式可知，碰后小球A 的速度的大小和方向与M 、m 的大小有关，下面就M 、m 取值不同而导致运动情形的不同进行讨论：（i ）A 0v =，即碰撞后小球A 停住，由（7）式可知发生这种运动的条件是即65M m = （11）（ii ）A 0v <，即碰撞后小球A 反方向运动，根据（7）式，发生这种运动的条件是65M m < （12）（iii ）A 0v >但A C <v v ，即碰撞后小球A 沿0v 方向作匀速直线运动，但其速度小于小球C 的速度．由（7）式和（6）式，可知发生这种运动的条件是 560M m ->和m M M 654->即665m M m << （13）（iv ）A C >v v ，即碰撞后小球A 仍沿0v 方向运动，且其速度大于小球C 的速度，发生这种运动的条件是6M m > （14）（v ）A C =v v ，即碰撞后小球A 和小球C 以相同的速度一起沿0v 方向运动，发生这种运动的条件是6M m =（15）在这种情形下，由于小球B 、D 绕小球C 作圆周运动，当细杆转过180时，小球D 将从小球A 的后面与小球A 相遇，而发生第二次碰撞，碰后小球A 继续沿0v 方向运动．根据质心运动定理，C 球的速度要减小，碰后再也不可能发生第三次碰撞．这两次碰撞的时间间隔是()056πππ6M m l lt Mω+===v v （16）从第一次碰撞到第二次碰撞，小球C 走过的路程C 2π3ld t ==v （17）3．求第二次碰撞后，小球A 、B 、C 、D 的速度刚要发生第二次碰撞时，细杆已转过180，这时，小球B 的速度为D v ，小球D 的速度为B v ．在第二次碰撞过程中，质点组的动量守恒，角动量守恒和能量守恒．设第二次刚碰撞后小球A 、B 、C 、D 的速度分别为A 'v 、B 'v 、C 'v 和D 'v ，并假定它们的方向都与0v 的方向相同．注意到（1）、（2）、（3）式可得0AC 3M M m ''=+v v v （18） C B 02ml ml ''=+v v（19）222220A B C D 11111+22222M M m m ''''=++v v mv v v（20）由杆的刚性条件有D C C B ''''-=-v v v v（21）（19）式的角动量参考点设在刚要发生第二次碰撞时与D 球重合的空间点．把（18）、（19）、（20）、（21）式与（1）、（2）、（3）、（4）式对比，可以看到它们除了小球B 和D 互换之外是完全相同的．因此它们也有两个解C0'=v （22）和C0456MM m'=+v v（23）对于由B 、C 、D 三小球组成的系统，在受到A 球的作用后，其质心的速度不可能保持不变，而（23）式是第二次碰撞未发生时质心的速度，不合理，应该舍去．取（22）式时，可解得 A 0'=v v （24）B 0'=v（25）D 0'=v（26）（22）、（24）、（25）、（26）式表明第二次碰撞后，小球A 以速度0v 作匀速直线运动，即恢复到第一次碰撞前的运动，但已位于杆的前方，细杆和小球B 、C 、D 则处于静止状态，即恢复到第一次碰撞前的运动状态，但都向前移动了一段距离2π3ld =，而且小球D 和B 换了位置．评分标准：本题25分．三、参考解答：由k pV =α， 1>α （1）可知，当V 增大时，p 将随之减小（当V 减小时，p 将随之增大），在p V -图上所对应的曲线（过状态A ）大致如图所示．在曲线上取体积与状态B 的体积相同的状态C ．现在设想气体从状态A 出发，保持叶片不动，而令活V塞缓慢地向右移动，使气体膨胀，由状态A 到达状态C ，在此过程中，外界对气体做功11111C A k W V V ααα--⎡⎤=-⎢⎥-⎣⎦（2）用U A 、U C 分别表示气体处于状态A 、C 时的内能，因为是绝热过程，所以内能的增量等于外界对气体做的功，即11111C A C A k U U V V ααα--⎡⎤-=-⎢⎥-⎣⎦（3）再设想气体处于状态C 时，保持其体积不变，即保持活塞不动，令叶片以角速度ω 做匀速转动，这样叶片就要克服气体阻力而做功，因为缸壁及活塞都是绝热的，题设缸内其它物体热容量不计，活塞又不动（即活塞不做功），所以此功完全用来增加气体的内能．因为气体体积不变，所以它的温度和压强都会升高，最后令它到达状态B ．在这过程中叶片转动的时间用∆t 表示，则在气体的状态从C 到B 的过程中，叶片克服气体阻力做功W L t ω'=∆ （4）令U B 表示气体处于状态B 时的内能，由热力学第一定律得B C U U L t ω-=∆（5）由题知1p L t Vαω∆-=⋅∆ （6）由（4）、（5）、（6）式得()1BB C BC V U U p p α-=-- （7）（7）式加（3）式，得()111111B B A B C C A V k U U p p V V αααα--⎡⎤-=-+-⎢⎥--⎣⎦（8）利用pV k α=和C B V V =得()11B A B B A A U U p V p V α-=-- （9）评分标准：本题23分．四、参考解答：答案：D u 如图1所示，B u 如图2 所示． u D．附参考解法：二极管可以处在导通和截止两种不同的状态.不管D 1和D 2处在什么状态，若在时刻t ，A 点的电压为u A ，D 点的电压为u D ，B 点的电压为u B ，电容器C 1两极板间的电压为u C 1，电容器C 2两极板间的电压为u C 2，则有1D A C u u u =- （1）2B C u u =（2） 11C A D q u u u C =-=（3）22C B G qu u u C=-=（4）式中q 1为C 1与A 点连接的极板上的电荷量，q 2为C 2与B 点连接的极板上的电荷量.若二极管D 1截止，D 2导通，则称电路处在状态I . 当电路处在状态I 时有D B u u = 0D u >（5）若二极管D 1和D 2都截止，则称电路处在状态II . 当电路处在状态II 时有D B u u < 0D u >（6）若二极管D 1导通，D 2截止，则称电路处在状态III .当电路处在状态III 时有D B u u < 0=D u（7）电路处在不同状态时的等效电路如图3所示.在0t =到2t T =时间间隔内，u D 、u B 随时间t 的变化情况分析如下：1. 从0t =起，u A 从0开始增大，电路处在状态 I ，C 1、C 2与电源组成闭合回路. 因C 1、C 2的电容相等，初始时两电容器都不带电，故有在u A 达到最大值即u A = U 时，对应的时刻为14t T =，这时12D B u U ==，也达到最大值. u A 达到最大值后将要减小，由于D 2的单向导电性，电容器C 1、C 2都不会放电，1C u 和2C u 保持不变，u D 将要小于12U ，即将要小于u B ，D 2将由导通变成截止，电路不再处于状态I . 所以从t = 0到14t T =时间间隔内，u D 、u B随时间t 变化的图线如图4、图5中区域I 内的的直线所示．2. 从14t T =起，因u D 小于u B ，D 2处在截止状态，电路从状态 I 变为状态 II . 因为二极管的反向电0 2TT 图2C 1D 1 C 2 D u A G A BD 2 C 1 D 1 2 Du A GA BD 2C 1D 1 C 2 D u A GA B D 2 状态I 状态II 状态III图3阻为无限大，电容器C 1、C 2都不会放电，两极板间的电压都保持不变.当电路处在状态II 时，D 点的电压 B 点的电压随着u A 从最大值U 逐渐变小，u D 亦变小；当12A u U =时，对应的时刻为38t T =，0D u =.如果u A 小于12U ，则u D 将小于0，D 1要从截止变成导通，电路不再处在状态II .所以在14t T =到38t T =时间间隔内，u D 、u B 随t 变化的图线如图4和图5中区域 II 1 内的直线所示.3.从38t T =起，u A 从12U 开始减小，D 1导通，但D B u u <，D 2仍是截止的，电路从状态II 变为状态III .当电路处在状态 III 时有在u A 减小的过程中，C 1两极板间的电压u C 1（= u A ）也随之改变，从而维持u D 为0. 当u A 达到反向最大值即A u U =-时，对应的时刻为34t T =，1C u U =-.若u A 从U -开始增大（U -减小），因D 1的单向导电性，电容器C 1不会放电，1C u U =-保持不变，10D A C u u u =->，D 1要从导通变成截止，电路不再处于状态III .所以在38t T =到34t T =时间间隔内，u D 、u B 随t 变化的图线如图4和图5中区域 III 1 内的直线所示.4. 从34t T =起，u A 从U -开始增大， D 1变为截止状态，D A u u U =+从零开始增大，只要u D 仍小于u B ，D 2仍是截止的，电路从状态III 变为状态II . 当电路处在状态 II 时，C 1和C 2不会放电，电容器两极板间的电压保持不变. 故有当u A 增大至12U -时，对应的时刻为78t T =，12D B u u U ==. 若u A 再增大，u D 将要大于u B ，D 2将要从截止变为导通，D B u u =，电路不再处于状态II . 所以在34t T =到78t T =时间间隔内，u D 、u B 随t 变化的图线如图4和图5中区域 II 2 中的直线所示.5. 从78t T =起，u A 要从12U -增大， D 2变为导通状态，这时D 1仍是截止的，电路又进入状态I . 当电路处在状态I 时，电源与C 1、C 2构成闭合回路，而当u A 变化时，12q q +将随之变化，但由导通的二极管D 2连接的C 1、C 2的两块极板所带的总电荷量12q q -+是恒定不变的.由于在78t T =时刻，1C u U =-，212C u U =，此时1q CU =-，212q CU =，故有由以上有关各式得u D 、u B 随着u A 的增大而增大. 当u A 达到最大值即A u U =时，对应的时刻为54t T =，54D B u u U ==．由于D 2单向导电，2B C u u =只增不减，u A 从最大值减小时，1C u 不变，u D 将要小于54U ，而2B C u u =保持为54U ，因而D B u u <，D 2从导通变成截止，电路不再是状态I . 所以在78t T =到T t 45=时间间隔内，u D 、u B 随t 变化的图线如图4和图5中 I 2中的直线所示.6. 从54t T =起，u A 从U 开始减小， D 2变为截止状态，这时D 1仍是截止的，电路又进入状态II . 当电路处在状态 II 时，C 1和C 2不会放电，电容器两极板间的电压保持不变. 由54t T =时刻的u D 和u A 的值可知此时114C u U =-. 故有当u A 减少至14U -时，对应的时刻为=t 2516T ，0D u =，以后D 1将由截止变为导通，电路不再处在状态II . 所以在54t T =到2516t T =时间内，u D 、u B 随t 变化的图线如图4和图5中 II 3中的直线所示.7. 从2516t T =起，u A 从14U -开始减小，D 1变为导通状态，但D 2仍是截止的，电路又进入状态III ，故有在u A 减小的过程中，C 1两端的电压u C 1也随之改变，开始阶段D 1保持导通，u D = 0. 但当u A 减小至-U 时，对应的时刻为74t T =，u C 1 = U . 因D 1单向导电，且D B u u <，C 1右极板的正电荷只增不减，u A 到达-U 后要增大，u D 要大于0，D 1要从导通变为截止，电路不再处于状态III . 所以在2516t T =到74t T =时间间隔内，u D 、u B 随t 变化的图线如图4和图5中III 2内的直线所示.8. 从74t T =起，u A 从-U 开始增大，D 1变为截止状态，D 2仍是截止的，电路又进入状态II . 当电路处于状态II 时，C 1和C 2不会放电，电容器两极板间的电压保持不变.由74t T =时刻的u D 和u A 的值可知，此时1C u U =-.故有u D 将随着u A 的增大而增大.当u A =14U 时，对应的时刻33216t T T =>，u D =54U ，与u B 相等.以后u D 要大于54U ，D 2要从截止变为导通，电路不再是状态II . 所以在74t T =到2t T =时间间隔内，u D 、u B 随t 变化的图线如图4和图5中II 4内的直线所示.总结以上讨论，各时段起讫时刻及D u 和B u 变化值如下表所示：时段 1 2 3 4 5 6 7 8 I 1II 1III 1II 2I 2II 3III 2II 4u D评分标准：本题25分五、参考解答：1．题给的磁场(),B x t 随时间和空间的变化具有周期性，在某时刻t ，磁场的空间分布为在t t +∆时刻，磁场的空间分布为比较上面两式，不难看出，t 和t t +∆这两个时刻的磁场的空间分布规律是相同的，只是t 时刻原位于x t k ω⎛⎫-∆ ⎪⎝⎭处的磁场，经历t ∆时间，在t t +∆时刻，出现在x 处．即整个磁场的分布经时间间隔t ∆沿x轴的正方向平移了一段距离平移速度0x t kω∆==∆v （1）平移速度0v 为恒量．由此可见，题给出的磁场()()0,cos B x t B t kx ω=-可视为一在空间按余弦规律分布的非均匀磁场区域以速度0v 沿x 轴的正方向平移．如果金属框移动的速度小于磁场区域平移的速度，那么通过金属框的磁通将随时间发生变化，从而在金属框中产生感应电流，感应电流将受到磁场的安培力作用．由题已知，在时刻t ，金属框移动的速度为v ，金属框MN 边位于坐标x 处，PQ 边位于坐标x d +处．设此时金属框的磁通为Φ（规定由纸内到纸外Φ为正）；经过一很短的时间间隔t ∆，整个磁场分布区域向x 方向移动了一段距离0t ∆v ，金属框向x 方向移动了一段距离t ∆v ，其结果是：MN 边左侧穿过面积为()0l t -∆v v 的磁通()()0,B x t l t -∆v v 移进了金属框，PQ 边左侧穿过面积为()0l t -∆v v 的磁通()()0,B x d t l t +-∆v v 移出了金属框，故在t t +∆时刻，通过金属框的磁通为在t ∆时间间隔内，通过金属框的磁通增量为()()()0,,B x t B x d t l t ΦΦΦ'∆=-=⎡-+⎤-∆⎣⎦v v（2）规定框内的感应电动势()t E 沿顺时针方向（沿回路MNPQM 方向)为正，由电磁感应定律，可得t 时刻的感应电动势()t tΦ∆=∆E （3）规定金属框内的感应电流()i t 沿顺时针方向（沿回路MNPQM 方向)为正，可得t 时刻的感应电流为()i t R=E (4)磁场对于上下两边NP 和MQ 的安培力的大小相等，方向相反，二者的合力为零．规定向右的力为正，则磁场作用于金属框MN 边的安培力为()(),i t B x t l ；由于PQ 边和MN 边的电流方向相反，磁场作用于金属框PQ 边的安培力为 ()(),i t B x d t l -+，故金属框的安培力的合力()()()()(),,f t i t B x t l i t B x d t l =-+（5）由（1）、（2）、（3）、（4）、（5）式及题给定的磁场分布规律，得()()(){}2202cos cos B l k f t t kx t kx kd ωωω⎛⎫- ⎪⎝⎭=--⎡--⎤⎣⎦v R（6）利用三角学公式，得()()()220222042sin sin sin 222B l t kx kd kd kd k f t F t kx ωωω⎛⎫- ⎪⎡--⎤⎛⎫⎡⎤⎝⎭==--⎢⎥ ⎪⎢⎥⎝⎭⎣⎦⎣⎦v R （7）0F 称为安培力()f t 的幅度．从（7）式可以看出，安培力()f t 在0F 的幅度内随时间变化，但其值不会小于零，表示磁场作用于金属框的安培力始终向右．2．讨论安培力的大小与线框几何尺寸的关系就是讨论0F 与线框几何尺寸的关系．0F 与金属框长度l 的平方成正比，与金属框的宽度d 有关：当2πkd n =，即2π0,1,2,n d n k== （8）得00F =（9）当()21πkd n =+，即()21π 0,1,2,n d n k+== （10）0F 达最大值()2200max 4B l k F ω⎛⎫- ⎪⎝⎭=v R（11）当d 取其它值时，0F 介于0与最大值()0max F 之间．评分标准：本题25分．六、参考解答：1．圆筒内光学元件的相对位置如图1所示．各元件的作用如下：22 观察屏P ：位于L 2焦平面上，光源的谱线即在此屏上．透镜L 3：与P 的距离≤f 3，是人眼观察光谱线所用的放大镜（目镜）．2．已知钠黄光的谱线位于P 的中央，S 的像位于L 2 的焦点上，由此可知，对分光棱镜系统来说，钠黄光的入射光束和出射光束都与轴平行，由于棱镜系统是左右对称，因此钠黄光在棱镜内的光路应该是左右对称的，在中间棱镜中的光路应该与轴平行，分光元件中的光路图如图2所示，左半部的光路如图3．用i 1、r 1、i 2、r 2分别表示两次折射时的入射角和折射角，用n 1、n 2分别表示两块棱镜对D 线的折射率，由图3可以看出，在两棱镜界面上发生折射时，22i r >，表明21n n >，即中间的棱镜应用折射率较大的火石玻璃制成，两侧棱镜用冕牌玻璃制成，故有D n n =1D n n '=2由几何关系可得122i r α==（1）12r i α+=（2）由折射定律可得111sin sin i n r =（3）1222sin sin n i n r =（4）从以上各式中消去1i 、2i 、1r 和2r 得22212sin 2n n α⎛⎫-= ⎪⎝⎭（5）解（5）式得图2图3图1()()221222124142sin n n n n -+-=⎪⎭⎫⎝⎛α （6）以5170.11=n ，7200.12=n 代入，得123.6α= （7）评分标准：本题23分．七、参考解答：带电粒子在静电场内从S 到T 的运动过程中，经历了从S 到N 和从N 到T 的两次加速，粒子带的电荷量q 的大小均为191.6010C -⨯，若以U 表示N 与地之间的电压，则粒子从电场获得的能量2E qU ∆=(1)质子到达T 处时的质量m =(2)式中v 为质子到达T 时的速度．质子在S 处的能量为20m c ，到达T 处时具有的能量为2mc ，电子的质量与质子的质量相比可忽略不计，根据能量守恒有220mc E m c =∆+（3）由（1）、（2）、（3）式得代入数据解得74.3410m/s =⨯v（4）评分标准：本题16分．。

第28届全国中学生物理竞赛复赛试题(清晰扫描版)及参考解答

第28届全国中学生物理竞赛复赛试题参考解答及评分标准一、参考解答：解法一取直角坐标系Oxy ，原点O 位于椭圆的中心，则哈雷彗星的椭圆轨道方程为22221x y a b += （1） a 、b 分别为椭圆的半长轴和半短轴，太阳S 位于椭圆的一个焦点处，如图1所示．以e T 表示地球绕太阳运动的周期，则e 1.00T =年；以e a 表示地球到太阳的距离（认为地球绕太阳作圆周运动），则e 1.00AU a =，根据开普勒第三定律，有3232a T a T =e e（2）设c 为椭圆中心到焦点的距离，由几何关系得c a r =-0 （3）22c a b -= （4）由图1可知，P 点的坐标cos P P x c r θ=+ （5） sin P P y r θ= （6）把（5）、（6）式代入（1）式化简得()2222222222sin cos 2cos 0P P P P P ab r b cr bc a b θθθ+++-= （7）根据求根公式可得()22222cos sin cos P P P Pb ac r a b θθθ-=+ （8）由(2)、(3)、(4)、(8)各式并代入有关数据得0.896AU P r = (9) 可以证明，彗星绕太阳作椭圆运动的机械能为 s2Gmm E =a-(10) 式中m 为彗星的质量．以P v 表示彗星在P 点时速度的大小，根据机械能守恒定律有2s s 122P P Gmm Gmm m r a ⎛⎫+-=- ⎪⎝⎭v （11）得图1P=v（12）代入有关数据得414.3910m sP-⨯⋅v=(13)设P点速度方向与SP的夹角为ϕ(见图2)，根据开普勒第二定律[]sin2P P Prϕθσ-=v（14）其中σ为面积速度，并有πabTσ=（15）由（9）、（13）、（14）、（15）式并代入有关数据可得127ϕ= （16）解法二取极坐标，极点位于太阳S所在的焦点处，由S引向近日点的射线为极轴，极角为θ，取逆时针为正向，用r、θ表示彗星的椭圆轨道方程为1cospreθ=+（1）其中，e为椭圆偏心率，p是过焦点的半正焦弦，若椭圆的半长轴为a，根据解析几何可知()21p a e=-（2）将（2）式代入（1）式可得()θcos112eear+-=（3）以eT表示地球绕太阳运动的周期，则e1.00T=年；以ea表示地球到太阳的距离（认为地球绕太阳作圆周运动），则e1.00AUa=，根据开普勒第三定律，有3232a Ta T=e e（4）在近日点0=θ，由（3）式可得1rea=-0（5）将Pθ、a、e的数据代入（3）式即得0.895AUPr=（6）可以证明，彗星绕太阳作椭圆运动的机械能s2GmmE=a-(7)式中m为彗星的质量．以Pv表示彗星在P点时速度的大小，根据机械能守恒定律有2s s122PPGmm Gmmmr a⎛⎫+-=-⎪⎝⎭v（8）可得P=v（9）代入有关数据得414.3910m sP-⨯⋅v=(10)设P点速度方向与极轴的夹角为ϕ，彗星在近日点的速度为0v，再根据角动量守恒定律，有()sinP P Pr rϕθ-=v v00（11）根据（8）式，同理可得=v（12）由（6）、（10）、(11)、(12)式并代入其它有关数据127ϕ= (13)评分标准：本题20分解法一（2）式3分，（8）式4分，（9）式2分，（11）式3分，(13) 式2分,（14）式3分,（15）式1分，（16）式2分．解法二（3）式2分，（4）式3分，（5）式2分，（6）式2分，（8）式3分，(10) 式2分,（11）式3分,（12）式1分，（13）式2分．二、参考解答：1．建立如图所示坐标系Oxy.两杆的受力情况如图：1f为地面作用于杆AB的摩擦力，1N为地面对杆AB的支持力，2f、2N为杆AB作用于杆CD的摩擦力和支持力，3N、4N分别为墙对杆AB和CD的作用力，mg为重力.取杆AB和CD构成的系统为研究对象，系统平衡时, 由平衡条件有431N N f+-=（1）120N mg-=（2）以及对A点的力矩()3411sin sin sin cos cos cos022mgl mg l l N l N l l CFθθαθθα⎛⎫+---+-=⎪⎝⎭即()3431sin sin cos cos cos022mgl mgl N l N l l CFθαθθα---+-=（3）式中CF待求.F是过C的竖直线与过B的水平线的交点，E为BF与CD的交点．由几何关系有sin cot CF l αθ= （4）取杆CD 为研究对象，由平衡条件有422cos sin 0N N f θθ+-= （5） 22sin cos 0N f mg θθ+-= （6）以及对C 点的力矩41cos sin 02N l mgl αα-= （7）解以上各式可得41tan 2N mg α=（8） 331sin 1tan sin tan tan 22cos 2sin N mg αααθαθθ⎛⎫=--+ ⎪⎝⎭ （9）13tan sin 1tan sin 2cos 2sin f mg θαααθθ⎛⎫=-+ ⎪⎝⎭ （10）12N mg = （11）21sin tan cos 2N mg θαθ⎛⎫=-⎪⎝⎭ （12） 21cos tan sin 2f mg θαθ⎛⎫=+ ⎪⎝⎭（13） CD 杆平衡的必要条件为22c f N μ≤ （14）由（12）、（13）、（14）式得()2sin cos tan cos sin C C μθθαμθθ-≤+ （15）AB 杆平衡的必要条件为11A f N μ≤ (16)由（10）、（11）、（16）式得tan sin 2sin 43tan sin cos A αααμθθθ-≤- （17）因此，使系统平衡，α应满足的条件为（15）式和（17）式．2．将题给的数据代入（15）式可得 arctan 0.38521.1α︒≤= (18) 将题给的数据代入（17）式，经数值计算可得19.5α≥︒ (19) 因此，α的取值范围为 19.521.1α≤≤(20)评分标准：本题20分第1问15分（1）、（2）、（3）式共3分，（4）式1分，（5）、（6）、（7）式共3分，(9) 、(10) 式各1分,(12)到（17）式各1分．第2问5分（18）式1分，（19）式3分，（20）式1分．三、参考解答：'解法一1．设在时刻t ，小球和圆筒的运动状态如图1所示，小球位于P 点，绳与圆筒的切点为T ，P 到T 的距离即绳的拉直部分的长度为l圆筒的角速度为ω，小球的速度为v .小球的速度可以分解成沿着绳子方向的速度1v 和垂直于绳子方向的速度2v 两个分量.根据机械能守恒定律和角动量守恒定律有()()()()22222001211112222M R m R M R m ωωω+=++v v (1) 2220012+=++MR mR MR mR ml ωωωv v (2)因为绳子不可伸长，1v 与切点T 的速度相等，即ωR =1v (3) 解(1)、(2)、(3)式得()()02222ωωml R m M ml R m M ++-+= (4) ()()022222ωmlR m M l R m M +++=v (5) 由(4)式可得l = (6)这便是在卫星角速度减至ω时绳的拉直部分的长度l ．2．由（6）式，当0=ω得=L （7）这便是绳的总长度L .3．如图2所示，从时刻t 到t t +∆，切点T 跟随圆筒转过一角度1t ωθ∆=∆，由于绳子的拉直部分的长度增加了l ∆，切点相对圆筒又转过一角度2lRθ∆=∆，到达T '处，所以在t ∆时间内，切点转过的角度12lt Rθθωθ∆∆=∆=+∆+∆ （8）切点从T 变到T '也使切线方向改变了一个同样的角度θ∆，而切线方向的改变是小球具有垂直于绳子方向的速度2v 引起的，故有2tlθ∆∆=v （9）由(1)、(2)、(3)式可得 ()20l ωω=+v （10）2()2t由(8)、（9）、（10）三式得0l R t ω∆=∆ （11）（11）式表示l 随t 均匀增加，故l 由0增加到L所需的时间为0s L t R ω== （12）解法二1．撤去插销后两个小球的运动情况相同，故可取一个小球作为对象进行研究，先研究任何时刻小球的速度.在t 时刻，相对卫星系统质心参考系小球运动状态如图1所示，绳子的拉直部分与圆筒面的切点为T ，小球到切点T 的距离即绳的拉直部分的长度为l ，小球到转轴O 的距离为r ，圆筒的角速度为ω.由于圆筒的转动和小球相对圆筒的运动，绳将展开，切点位置和绳的拉直部分的长度都要改变.首先考察小球相对于圆筒的运动.在t 时刻，OT 与固定在圆筒上的半径0OP 的夹角为φ，如图2所示.由于小球相对圆筒的运动，经过时间t ∆，切点从圆筒上的T 点移到T '点，OT '与0OP 的夹角变为φφ+∆，绳的拉直部分的长度由l 变为l '，小球由P 运动到P '，PP '便是小球相对圆筒的位移.当t ∆很小时l l '≈，故PP l l φφ''=∆≈∆于是小球相对圆筒的速度大小为ll tφφφω∆==∆v (1) 方向垂直于TP ．φω是切点相对圆筒转动的角速度．再考察圆筒相对质心参考系的转动，即与圆筒固连在一起的转动参考系相对质心参考系的运动.当圆筒的角速度为ω时，位于转动参考系中的P 点(小球所在处)相对质心系的速度r ωω=v (2)方向垂直于OP ．可以把ωv 分解成沿着TP 方向的分量1ωv 和垂直TP 方向的分量2ωv ，如图3所示，即1R ωω=v(3)2l ωω=v (4)小球相对质心系的速度 v 是小球相对圆筒的速度和圆筒参考系中的P 点相对质心系速度的合成，由图3可得v 的2m12φω+ v大小=v (5)因 l R φ= (6) 故有=v （7）因为系统不受外力作用，故系统的动能和角动量守恒，故有()()222220011112222M R mR M R m ωωω+=+v （8） ()2220012MR mR MR mR ml ωωφωωω+=+++v v v （9）由(7)、(8)两式有()22220mM mφωωωωφ=+++ （10）由(1)、(3)、(4)、(6)、(9)各式得()20mM mφωωφωω=+++ （11）由(10)、(11)两式得φωωωω+=+0 故有0ωωφ= （12）上式说明绳子与圆筒的切点相对圆筒转动的角速度等于卫星的初始角速度，是一个恒量，将(12）式代入（11）式得φ=（13）由(6)、(13)两式得l = （14）这便是在卫星角速度减至ω时绳的拉直部分的长度l ．2．由（14）式，当0=ω得绳总长度, 即L = （15） 3．因φω是一个恒量，φ随时间的t 的变化规律为t 0ωφ= （16）当0=ω时，由（13）式可得卫星停旋时的φs φ=（17）设卫星停转所用的时间为s t ，由（16）、（17）式得0s s t φω==（18）评分标准：本题25分．解法一第1问12分．（1）、（2）式各3分，（3）式2分，（6）式4分．第2问3分．（7）式3分．第3问10分．（8）、（9）式各3分，（10）式2分，（11）、（12）式各1分．解法二第1问18分．（1）式3分，（2）式2分，（7）式2分，（8）式3分，（9）式3分，（12）式2分，（14）式3分，第2问3分．（15）式3分．第3问4分．（16）式2分，（17）式1分，（18）式1分．四、参考解答：1．根据题意，粒子的初速度只有y 方向和z 方向的分量，设它们为0y v 和0z v .因为粒子在z 方向不受电场力和磁场力作用，故粒子在z 方向以初速度0z v 作匀速运动.粒子在Oxy 面内的运动可以看作由以下两部分运动的合成：可把粒子在y 方向的初速度表示为 001001y y y y =-++v v v v (1) 其中0010y E B =-v (2) 沿y 负方向．与01y v 相关的磁场力 010Bx y f q B =-v (3) 沿x 负方向.粒子受到的电场力0E Ex f f qE == (4)沿x 正方向．由(2)、(3)、(4)式可知，粒子在x 方向受到的电场力和磁场力正好抵消，故粒子以大小为E B 的速度沿y 负方向运动．除此之外，由（1）式可知，粒子还具有初速度00200y y E B =+v v (5) 沿y 正方向，与02y v 相关的磁场力使粒子以速率02y v 在Oxy 面内作匀速圆周运动，以r 表示圆周运动的半径，有202020y y q B mr=v v (6) 可得020y m r qB =v (7)由周期的定义和(7)式可得圆周运动的周期02mT =qB π (8) (8)式表明，粒子运动的周期与粒子在y 方向的初速度无关．经过时间T 或T 的整数倍所考察的粒子就能同时回到Oyz 平面.2．增加的电场2E对粒子在Oxy 平面内的运动无影响，但粒子在z 方向要受到此电场力作用．以z a 表示在此电场力作用下的加速度，有 0c o s z m a q E t ω= (9) 或0cos z qE a =t mω (10) 这是简谐运动的加速度，因而有 2z a =z ω- （11）由(10)、（11）可得t mqE z ωωcos 102-= (12) 因未增加电场时，粒子在z 方向作初速度为0z v 的匀速运动，增加电场后，粒子在z 方向的运动是匀速运动与简谐运动的叠加，即有0021cos z qE z t t mωω=-v （13）粒子在Oxy 平面内的运动不受电场2E的影响．设0ω为粒子在Oxy 平面内作圆周运动的角速度，则有202πqB T mω== (14) 由图示可得与圆周运动相联系的粒子坐标随时间t 的变化关系()01cos x r t ω'=- (15) 0sin y r t ω'= (16)考虑到粒子在y 方向还具有速度为01y v 的匀速运动，并利用(2)、(5)、(7)、(14)以及己知条件，可得带电粒子的运动规律：000001cos y E qB m x t qB B m ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭v (17) 0000000siny E E qB m y t t B qB B m⎛⎫=-++ ⎪⎝⎭v (18) 00020cos z mE qB z t t qB m=-v (19)评分标准：本题20分．第1问12分．（2）、（3）、（4）式共5分，（5）、（6）、（7）式共4分，（8）式及相关说明共3分．第2问8分．（12）式2分，（14）式到（19）式各1分. 五、答案与评分标准本题15分．1．01TV V L I I e ⎛⎫-- ⎪ ⎪⎝⎭ (2分），L I （2分），0ln 1L T I V I ⎛⎫+ ⎪⎝⎭ （2分），01TVV L VI VI e ⎛⎫-- ⎪ ⎪⎝⎭（1分）．2．0.62V （2分）；0.54V （2分）；49mW （2分）；6.0Ω （2分）．六、参考解答：在电加热器对A 室中气体加热的过程中，由于隔板N 是导热的，B 室中气体的温度要升高，活塞M 将向右移动.当加热停止时，活塞M 有可能刚移到气缸最右端，亦可能尚未移到气缸最右端. 当然亦可能活塞已移到气缸最右端但加热过程尚未停止.1. 设加热恰好能使活塞M 移到气缸的最右端，则B 室气体末态的体积02B V V = （1）根据题意，活塞M 向右移动过程中，B 中气体压强不变，用B T 表示B 室中气体末态的温度，有00BBV V T T =（2）由(1)、(2)式得02B T T = （3）由于隔板N 是导热的，故A 室中气体末态的温度02A T T = （4）下面计算此过程中的热量m Q .在加热过程中，A 室中气体经历的是等容过程，根据热力学第一定律，气体吸收的热量等于其内能的增加量，即 05()2A A Q R T T =- （5）由(4)、(5)两式得052A Q RT = （6）B 室中气体经历的是等压过程，在过程中B 室气体对外做功为00()B B W p V V =- （7）由(1)、(7)式及理想气体状态方程得 0B W R T = （8）内能改变为05()2B B U R T T ∆=- （9）由(4)、(9)两式得052∆=B U RT （10）根据热力学第一定律和(8)、(10)两式，B 室气体吸收的热量为 072=∆+=B B B Q U W RT (11) 由(6)、(11) 两式可知电加热器提供的热量为06m A B Q Q Q RT =+= （12）若0m Q Q =，B 室中气体末态体积为02V ，A 室中气体的末态温度02T .2．若0m Q Q >，则当加热器供应的热量达到m Q 时，活塞刚好到达气缸最右端，但这时加热尚未停止，只是在以后的加热过程中气体的体积保持不变，故热量0m Q Q -是A 、B 中气体在等容升温过程中吸收的热量.由于等容过程中气体不做功，根据热力学第一定律，若A 室中气体末态的温度为AT '，有 00055(2)(2)22m AA Q Q R T T R T T ''-=-+- （13）由(12)、(13)两式可求得00455AQ T T R '=+ （14） B 中气体的末态的体积02BV =V ' （15） 3. 若0m Q Q <，则隔板尚未移到气缸最右端，加热停止，故B 室中气体末态的体积BV ''小于02V ，即02BV V ''<．设A 、B 两室中气体末态的温度为A T ''，根据热力学第一定律，注意到A 室中气体经历的是等容过程，其吸收的热量05()2A AQ R T T ''=- （16） B 室中气体经历的是等压过程，吸收热量0005()()2B AB Q R T T p V V ''''=-+- （17）利用理想气体状态方程，上式变为()072B AQ R T T ''=- （18）由上可知006()A B AQ Q Q R T T ''=+=- （19）所以A 室中气体的末态温度 006AQ T T R''=+ （20） B 室中气体的末态体积 00000(1)6BA V QV T V T RT ''''==+ （21）评分标准：本题20分．得到0m Q Q =的条件下（1）、（4）式各1分；（12）式6分，得到0m Q Q >的条件下的（14）式4分，（15）式2分；得到0m Q Q <的条件下的（20）式4分，（21）式2分．七、答案与评分标准：本题20分．1． 3R (3分) 2． 6R (3分)第1第3空格各2分；其余3个空格全对3分，有一个错则不给这3分．八、参考解答：1. 反应能()()332p n H He Q m m m m c ⎡⎤=+-+⎣⎦（1）式中c 为光速．代入数据得0.764MeV Q =- （2）上式表明这是一吸能核反应．2．为了求入射质子阈能，反应前后各粒子都应沿同一直线运动．设质子的入射速度大小为p v ，反应后32He 的速度大小为3He v ，中子的速度大小为n v ，根据动量守恒和能量守恒有33p p n n He He m m m =+v v v (3)33222p p n n He He 111222m m m Q =++v v v （4）由（3）、（4）式可得3333322n n p p p n22He He n p n p He He He220m m m m m m m m Q m m m ⎛⎫⎛⎫+--++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭v v v v (5) 令333332n nHe He p n pHe 2p p 2Hep He22m m m a m m m b m m m m c Qm ⎫+⎪=⎪⎪⎪=-⎬⎪⎪-⎪=+⎪⎭v v (6) 把(6)式代入(5)式得2n n 0a b c ++=v v (7)(7)式有解的条件是240b ac -≥ (8)由(6)式可知，c 可能大于零，亦可能小于零.若0c <，则(8)总成立，中子速度一定有解，反应一定能发生；若0c >，则由 (6)、(8)两式得33n 2He p p n pHe 12m m m Q m m m +≥+-v (9) 即只有当入射质子的动能满足(9)式时，中子速度才有解，反应才能发生，所以入射质子的阈能为3pn p He 1th m T Q m m m ⎛⎫=+⎪ ⎪+-⎝⎭ (10) 利用(1)式，在忽略2Q 项的情况下，(10)式可简化为 3p H1th m T Q m ⎛⎫=+⎪ ⎪⎝⎭(11) 代入有关数据得 1.02MeV th T = (12)3．由动量守恒和能量守恒有33p p n n He He =+m m m v v v (12)33222p p n n He He 111222m m m Q =++v v v (13) 以θ表示反应中产生的中子速度方向与入射质子速度方向的夹角，如图所示，根据余弦定律有 ()()()33222n n p p n p n p He He 2cos m m m m m θ=+-v v v v v (14)令2p p p 12T m =v (15) 2n n n 12T m =v (16) 3332He He He 12=T m v (17) 把(15)、(16)、(17)式代入(13)、(14)两式得3He Q T T T =--p n （18）p p m v33n n p p He He 222m T m T m T θ=+- （19）由（18）、（19）式，消去3He T 后，得()3333p p HeHe n nnHe He 0m m T Q m T m m θ---=+ （20）令3nHe S θ=，()333p p HeHe nHe m m T Q m R m m --=+ （21）得n 20T R -= （22）根据题给的入射质子的动能和第1问求得的反应能Q 的值，由(21)式可知0R >，故（22）式的符合物理意义的S = （23）将具体数据代入（21）、（23）式中，有n 0.132MeV T = (24) (如果得到 131.0=n T MeV ,也是对的.)第2问的其他解法解法一为了研究阈能，只考虑碰撞前后各粒子都沿同一直线运动的情况．若碰撞后32He 和中子的速度相同，即粘在一起运动(完全非弹性碰撞)，则在碰撞过程中损失的机械能最多，若所损失的机械能正好等于反应能，则入射质子的动能最小，这最小动能便是阈能. 设质子的入射速度大小为p v ，反应后32He 和中子的速度大小为v ，根据动量守恒和能量守恒有3p p n He ()m m m =+v v (1)322p p n He 11()22m m m Q =++v v (2) 由（1）、（2）式可得 33n 2He p p n pHe 12m m m Q m m m +=+-v (3) 所以阈能为3p n p He 1th m T Q m m m ⎛⎫=+⎪ ⎪+-⎝⎭(4) 利用第1问中的(1)式，并注意到32H 1<<Q m c有333332n pHe H H 2H H 11111⎛⎫==- ⎪ ⎪+-⎛⎫⎝⎭+⎪ ⎪⎝⎭Q m m m m m c Q m m c 在忽略2Q 项的情况下，(4)式可简化为 3p H 1th m T Q m ⎛⎫=+⎪ ⎪⎝⎭(5) 代入有关数据得 1.02M e Vth T = (6)第2问8分(1)、(2)式各3分，(4)式或(5)式1分，(6)式1分．解法二在牛顿力学中可以证明，质点系的总动能可以表示为质点系的总质量以质心速度运动的动能即所谓质心动能与各质点相对质心运动的动能之和.若质点系不受外力作用，则质点系的动量守恒，质心速度不变，故质心动能亦恒定不变；如果质点系内部的相互作用导致质点系机械能的变化，则可变化的机械能只能是各质点相对质心运动的动能. 在本题中，如果质子p 与氚31H 发生反应后，生成的中子n 和氦32He 相对质心都静止，则质子p 与氚31H相对质心运动的动能之和全部转化成反应能，反应后系统的动能只有质心的动能，在这请况下，转化成其他形式能量的机械能最多，入射质子的动能最小，这最小动能便是阈能.所以入射质子的阈能等于系统质心的动能与反应能之和.以p 'v 和3H 'v 分别表示质子p 和氚31H 相对质心的速度，有3322p p H H 1122Q =m m ''+v v (1) 因系统质心的速度 3p p c p H=+m m m v v (2)而33p H p p c p Hm m '=-=+v v v v m (3) 33p p c Hp H0m m '=-=-+v v v m (4)由(1)、(3)、(4)式得 332H p pp H12m Q m m m =+v (5) 在牛顿力学中，系统的总质量是恒定不变的，这就导致系统质心的动能在反应前后恒定不变的结论，但在本题中，损失掉的机械能导致系统总质量的变化，使反应前系统的总质量与反应后系统的总质量不相等，即33p n H He +≠+m m m m ．如果仍沿用牛顿力学的结论，对一个孤立系统，其质心速度是不会改变的，故反应后质心的动能应为 ()()33222c n c p c c 2He H 111222=+=++Q E m m m m cv v v 而 ()33322p p p 2c 2222p H Hp HQ 1122m m Q QQ c c c m m m m m =⋅=⋅⋅++v v 由此可见，在忽略2Q 的条件下 ()()3322n p He H 1122c c m m m m +=+v v 而入射质子的阀能 ()32p H 12th c T m m Q =++v (6) 由(2)、(5)、(6)式得 3p H 1th m T Q m ⎛⎫=+⎪ ⎪⎝⎭(7) 代入有关数据得 1.02MeV th T = (8)第2问8分(1)、(5) 、(6)式各2分， (7)式1分，、(8)式1分. 解法三考虑反应前后各粒子都沿同一直线运动的情况，若入射质子与与静止的31H 发生完全非弹性碰撞，即反应后产生的中子和32He 以相同的速度运动，则入射质子的动能就是阈能.以10m 表示质子的静止质量，20m 表示31H 的静止质量，30m 表示中子的静止质量，40m 表示31He 的静止质量，设质子的入射速度大小为p v ，反应后32He 和中子的速度大小都为v ，根据动量守恒和能量守恒有1pm m m +=v(1)222120m m c m c m c++=(2)式中1m 是质子的动质量.由(1)、(2)两式得 1p 120+m m m v v =(3)把(3)式代入(1)式，经整理得 ()()2222221201p 3040+-=+m m c m m m c v (4)由 1m =(5)可得221p221102-=m m m cv (6)若入射质子的阈能为th E ，有22110th m c m c E =+ (7) 由(4)、(6)、(7)式可得 ()()2230401020202thm m m m E m +-+= (8)利用题给条件并引入反应能，得 333p n H HeH2th m m m m E Q m +++=(9)或有 ()3333p 2H p H H H22th Q+m m m m c E Q Q m m ++=≈ (10)代入有关数据得 1.02M e Vth T = (11) 第2问8分(1)、(2) 、(8)式各2分， (9)或(10)式1分， (11)式1分。

第39届全国中学生物理竞赛复赛试题及答案

第39届全国中学生物理竞赛复赛试题（2022年9月17日上午9:00-12:00）考生必读1、考生考试前请务必认真阅读本须知。

2、本试题共7道题，4页，总分为320分。

3、如遇试题印刷不清楚情况，请务必向监考老师提出。

4、需要阅卷老师评阅的内容一定要写在答题纸上；写在试题纸和草稿纸上的解答一律不能得分。

一、（40分）迈克尔逊干涉仪是光学干涉仪中最常见的一种，发明者是美国物理学家阿尔伯特·亚伯拉罕·迈克尔逊。

最初设计迈克尔逊干涉仪的目的是为测量“以太”（假想的传播光的媒质）的漂移速度，目前它广泛应用于精密测量。

迈克尔逊干涉仪的光路图如图1a所示：图1a图1b照明光为单色激光，入射光经过半反半透的镜子分为沿干涉仪的两个臂（反射臂和透射臂）传播的两束光。

半反半透镜与入射光轴方向之间的夹角为45°，反射臂和透射臂相互垂直。

在两个臂端上各放置与相应的臂垂直的反射镜，反射镜可以沿臂的方向移动。

反射和透射光线经反射镜反射，再次经过半反半透镜透射和反射，两束光在空间重叠，发生干涉。

如果照明光为发散光源，我们观察到的干涉条纹为同心圆环。

半反半透镜是在一个平整的石英基板上蒸镀一层薄金属膜制成，迈克尔逊干涉仪中参与叠加的两束光都经过半反半透镜的反射，一束光是在石英和金属界面上的反射，另一束光是在空气和金属界面上的反射。

因为反射界面不同，所以两束光反射时相位突变不同，两者的差异为ϕ∆。

开始时，观察到干涉场中心是亮斑，干涉场最外侧是亮圆环，一共20个∆，下面我们通过实验测量ϕ亮条纹（计及中心亮斑）。

现在缓慢调节一个臂的反射镜，让反射镜沿臂的方向平移，观察到干涉条纹发生明暗变化，并发现同心圆环条纹越来越稀疏。

干涉场中心明暗变化了23个周期，干涉场最外侧的明暗变化了20个周期。

（本题中，条纹数目均视为精确计数值，干涉仪两臂的长度在cm量级。

）（1）求相位突变差异ϕ∆。

（2）反射镜移动后，可以观察到多少个干涉亮条纹（计及中心亮斑）？（3）使用此干涉仪测量某一透明液体的折射率，将扁平的石英空槽插入迈克尔逊干涉仪的一个臂，使得石英槽的θ=︒；在角度改变过程中，干涉场中心明暗表面与臂的方向垂直。

第24届全国中学生物理竞赛复赛试卷及参考答案

第24届全国中学生物理竞赛复赛试卷（本题共七大题，满分160分）一、（20分）如图所示，一块长为的光滑平板PQ固定在轻质弹簧上端，弹簧的下端与地面固定连接。

平板被限制在两条竖直光滑的平行导轨之间（图中未画出竖直导轨），从而只能地竖直方向运动。

平板与弹簧构成的振动系统的振动周期。

一小球B放在光滑的水平台面上，台面的右侧边缘正好在平板P端的正上方，到P端的距离为。

平板静止在其平衡位置。

水球B与平板PQ的质量相等。

现给小球一水平向右的速度，使它从水平台面抛出。

已知小球B与平板发生弹性碰撞，碰撞时间极短，且碰撞过程中重力可以忽略不计。

要使小球与平板PQ发生一次碰撞而且只发生一次碰撞，的值应在什么范围内？取二、（25分）图中所示为用三角形刚性细杆AB、BC、CD连成的平面连杆结构图。

AB和CD杆可分别绕过A、D的垂直于纸面的固定轴转动，A、D两点位于同一水平线上。

BC杆的两端分别与AB杆和CD杆相连，可绕连接处转动（类似铰链）。

当AB杆绕A轴以恒定的角速度转到图中所示的位置时，AB杆处于竖直位置。

BC杆与CD杆都与水平方向成45°角，已知AB杆的长度为，BC杆和CD杆的长度由图给定。

求此时C点加速度的大小和方向（用与CD杆之间的夹角表示）三、（20分）如图所示，一容器左侧装有活门，右侧装有活塞B，一厚度可以忽略的隔板M将容器隔成a、b两室，M上装有活门。

容器、隔板、活塞及活门都是绝热的。

隔板和活塞可用销钉固定，拔掉销钉即可在容器内左右平移，移动时不受摩擦作用且不漏气。

整个容器置于压强为P0、温度为T0的大气中。

初始时将活塞B用销钉固定在图示的位置，隔板M固定在容器PQ处，使a、b两室体积都等于V0；、关闭。

此时，b室真空，a室装有一定量的空气（容器内外气体种类相同，且均可视为理想气体），其压强为4P0/5，温度为T0。

已知1mol空气温度升高1K时内能的增量为C V，普适气体常量为R。

1.现在打开，待容器内外压强相等时迅速关闭（假定此过程中处在容器内的气体与处在容器外的气体之间无热量交换），求达到平衡时，a室中气体的温度。

2023年全国中学生物理竞赛复赛试题参考解答

全国中学生物理竞赛复赛试题参考解答、评分标准一、参考解答令表达质子的质量, 和分别表达质子的初速度和到达a 球球面处的速度, 表达元电荷, 由能量守恒可知2201122mv mv eU =+ （1）由于a 不动, 可取其球心为原点, 由于质子所受的a 球对它的静电库仑力总是通过a 球的球心, 所以此力对原点的力矩始终为零, 质子对点的角动量守恒。

所求的最大值相应于质子到达a 球表面处时其速度方向刚好与该处球面相切（见复解20-1-1）。

以表达的最大值, 由角动量守恒有 max 0mv l mvR = （2）由式（1）、（2）可得20max 1/2eU l R mv =- （3）代入数据, 可得max 22l R = （4）若把质子换成电子, 则如图复解20-1-2所示, 此时式（1）中改为。

同理可求得 max 62l R =（5）评分标准: 本题15分。

式（1）、（2）各4分, 式（4）2分, 式（5）5分。

二、参考解答在温度为时, 气柱中的空气的压强和体积分别为, （1）1C V lS = （2）当气柱中空气的温度升高时, 气柱两侧的水银将被缓慢压入A 管和B 管。

设温度升高届时 , 气柱右侧水银刚好所有压到B 管中, 使管中水银高度增大C BbS h S ∆= （3）由此导致气柱中空气体积的增大量为C V bS '∆= （4）与此同时, 气柱左侧的水银也有一部分进入A 管, 进入A 管的水银使A 管中的水银高度也应增大 , 使两支管的压强平衡, 由此导致气柱空气体积增大量为A V hS ''∆=∆ （5）所以, 当温度为时空气的体积和压强分别为21V V V V '''=+∆+∆ （6）21p p h =+∆ （7）由状态方程知112212p V p V T T = （8）由以上各式, 代入数据可得2347.7T =K （9）此值小于题给的最终温度 K, 所以温度将继续升高。

第13届全国中学生物理竞赛(含参考答案)

第十三届全国物理竞赛复赛试题解答一、在各段电路上，感应电流的大小和方向如图复解13 - 1所示电流的分布，已考虑到电路的对称性，根据法拉第电磁感应定律和欧姆定律，对半径为α的圆电路，可得 π2a k = 21r 1I + 1r 1I ' 对等边三角形三个边组成的电路，可得332a k / 4 = 22r 2I + 22r 2I '对由弦AB 和弧AB 构成的回路，可得（π2a -332a / 4）k / 3 = 1r 1I - 2r 2I考虑到，流进B 点的电流之和等于流出B 点电流之和，有1I + 2I =1I ' + 2I ' 由含源电路欧姆定律可得A U -B U = π2a k /3 - 1I 1r由以上各式及题给出的 2r = 21r / 3可解得A U -B U = - 32a k / 32二、解法一：1、分析和等效处理根据棱镜玻璃的折射率，棱镜斜面上的全反射临界角为c α= arcsin ( 1 / n ) ≈ 42 注意到物长为4mm ，由光路可估算，进入棱镜的近轴光线在斜面上的入射角大多在 45左右，大于临界角，发生全反射。

所以对这些光线而言，棱镜斜面可看成是反射镜。

本题光路可按反射镜成像的考虑方法，把光路“拉直”如图复解13 – 2 - 1所示。

现在，问题转化为正立物体经过一块垂直于光轴、厚度为6cm 的平玻璃板及其后的会聚透镜、发散透镜成像的问题。

2、求像的位置；厚平玻璃板将使物的近轴光线产生一个向右侧移动一定距离的像，它成为光学系统后面部分光路的物，故可称为侧移的物。

利用沿光轴的光线和与光轴成α角的光线来讨论就可求出这个移动的距离。

设轴上的物点为B 。

由于厚平玻璃板的作用（即侧移的物点）为B ′（如图复解13 – 2 - 2所示）。

画出厚平玻图复解13 - 111I图复解13 - 2 - 2图复解13 - 2 - 1璃板对光线的折射，由图可知 Δl = d （ctg α）而 d = D （tg α- tg β）所以 Δl = D （1 – tg α/ tg β）当α为小角度时 tg β/ tg α≈sin β/ sin α= 1/n 故得 Δl = D （1 – 1 / n ）= 2 cm这也就是物AB 与它通过厚玻璃板所成的像之间的距离。

第31届全国中学生物理竞赛复赛试题及答案

第31届全国中学生物理竞赛复赛试题及答案31届全国中学生物理竞赛复赛理论考试试题解答一、(12分)题目一：球形液滴的振动频率假设球形液滴振动频率与其半径r、密度ρ和表面张力系数σ之间的关系式为f=kρσr，其中k是常数。

根据单位分析法，可以得到单位等式[f]=[ρ][σ][r]。

力学的基本物理量包括质量m、长度l和时间t，分别对应的单位是千克(kg)、米(m)和秒(s)。

根据单位等式，[f]=[t]^-1，[r]=[l]，[ρ]=[m][l]^-3，[σ]=[m][t]^-2.将这些单位代入单位等式，得到[t]^-1=[l]^-3[m]^[ρ][t]^-2[σ]，即[t]^-1=[l]^[ρ][m]^[σ][t]^-2.由此可以得到三个未知量的关系式：α-3β=0，β+γ=0，2γ=1.解得α=-1，β=-1，γ=1/2.解法二：假设球形液滴振动频率与其半径r、密度ρ和表面张力系数σ之间的关系式为f=kρσr，其中k是常数。

根据单位分析法，可以得到单位等式[f]=[ρ][σ][r]。

在国际单位制中，振动频率的单位是赫兹(Hz)，半径r的单位是米(m)，密度ρ的单位是千克每立方米(kg/m^3)，表面张力系数σ的单位是牛每米(N/m)=千克每秒平方(m/s^2)。

根据单位等式，[f]=s^-1，[r]=m，[ρ]=kg/m^3，[σ]=kg/s^-2.将这些单位代入单位等式，得到[s]^-1=[m][ρ][σ]，即[s]^-1=[m][kg/m^3][kg/s^-2]。

将这个式子代入f=kρσr，得到k=f/ρσr。

1.(V。

T)。

(p。

V。

T)和(pf。

V。

T)分别表示气体在初态、中间态和末态的压强、体积和温度。

留在瓶内的气体先后满足绝热方程和等容过程方程：p1 * V1^γ = p2 * V2^γ (绝热方程)V1 = V2 * (p1/p2) (等容过程方程)联立以上两式可得：p1/T1 = p2/T2 = pf/Tf由此得到以下式子：p1/pf = (p1/pf)^(1/γ)ln(p1/pf) = ln(p1) - ln(pf) = (1/γ) * ln(p1/pf)pf = p1 / (e^(γ * ln(p1/pf)))2.根据力学平衡条件，有：pi = p + ρghipf = p + ρghf其中，p是瓶外大气压强，ρ是U型管中液体的密度，g 是重力加速度大小。

2024年9月第41届全国中学生物理竞赛复赛试题参考解答

第41届全国中学生物理竞赛复赛试题参考解答（2024年9月21日9:00-12:00）一、（45分）（1）（1.1）记质量为M 的振子偏离平衡位置的位移为x （向左为正），单摆的偏转角为θ（向左为正），摆臂上的张力为T ，按牛顿第二定律，摆锤在水平方向上的运动方程为m ẍ+lθcos θ−lθ sin θ =−T sin θ ①在竖直方向上的运动方程为m −l sin θθ−lθ cos θ =m g −T cos θ ② 利用小幅度振动条件，保留到小量θ的领头阶，有sin cos 1 ， ③将③式代入①②式，并保留到小量θ的领头阶，得T mg ④ ẍ+lθ+g θ=0⑤【注: 利用悬点不动的非惯性系也可更方便地得到上述结果。

在悬点不动的非惯性系中，摆锤额外受到横向的惯性力−mẍ，有角向运动方程mlθ=−m g sin θ−mẍcosθ ①′ 同时也有径向运动方程2θcosθsin ml mx g T m ②′进一步利用小摆幅条件，保留到小量θ的领头阶，即得⑤④式。

】质量为M 的振子在水平方向上做一维运动，由牛顿第二定律得Mẍ=−kx +T sin θ+H cos ωt ⑥由③④⑥式得Mẍ+kx −m g θ=H cos ωt ⑦只考虑系统在强迫力下的稳定振动，稳定振动的圆频率为ω，设cos(x x A t ) ⑧ cos()l B t ⑨其中φ 、φ 是稳定振动与所受强迫力之间的位相差。

将⑧⑨式代入方程⑤⑦后，所得出的两个方程对任意时间 t 均成立，故有00x ，⑩进而有22M m k A m B H⑪ 22200A B⑫由⑪⑫式得2202222200()()()HA k M m⑬222222222000()()H B A k M m⑭其中（1.2）由⑬式可知，当没有阻尼器时（这时0m ），有2HA k M ⑮即当风的频率为⑯时，大楼受迫振动幅度最大。

当风的频率取⑮式所示的值、但有阻尼器时，由⑬式得k g H H kl Mg M l A g k gkm m l M⑰为了调节阻尼器的参数m 、l 使得A 最小，可取Mgl k， ⑱或m 尽可能大。

第41届全国中学生物理竞赛复赛试题及答案

第41届全国中学生物理竞赛复赛试题（2024年9月21日上午9:00-12:00）考生须知1、考生考试前请务必认真阅读本须知。

2、本试题共7道题，5页，总分为320分。

3、如遇试题印刷不清楚的情况，请务必及时向监考老师提出。

4、需要阅卷老师评阅的内容一定要写在答题纸上；写在试题纸和草稿纸上的解答一律不给分。

一、（45分）高层建筑（大楼）在风的作用下会发生晃动。

在特定条件下，大楼的晃动幅度会变得较大，影响到安全。

（1）为了减小晃动幅度，通常会在高层建筑上加装阻尼器，例如悬点固定在大楼上、摆锤质量为m 、摆臂长度为l 的摆，摆臂是刚性的，质量可以忽略；大楼在风作用下的运动可简化为谐振子的强迫振动，谐振子的质量为M ，恢复力等效为劲度系数为k 的弹簧，大楼在运动过程中可视为刚体。

整个摆和谐振子系统如图1a 所示，系统的总质量为m 与M 之和。

风可视为水平方向上的强迫力F （向左为正），它随时间t 的变化为cosωF t H t其中振幅H 和频率ω均为常量。

重力加速度大小为g 。

为简单起见，只考虑摆和谐振子的小幅度振动（因而摆便成为单摆）。

（1.1）求谐振子因强迫力F 的作用产生的稳定振动的振幅；（1.2）指出在没有阻尼器的情况下，风的频率为多大时，大楼受迫振动的振幅最大？对此频率的风，阻尼器应满足何种条件会最大限度地减小大楼的受迫振动？（2）若风的频率为第（1.2）问中求出的风的频率的√0.99倍，在没有阻尼器的情况下，求此时大楼受迫振动的振幅有多大? 若安装的阻尼器参数l 符合第（1.2）问中得到的条件，为了使得大楼在此风的作用下的受迫振动的振幅减到无阻尼器时的1%，阻尼器的质量m 应该为M 的多少倍？（3）实际的阻尼器还装有其他装置以提供阻尼力，通常做法是将摆锤浸泡在固定于建筑物上的油池中（相对于建筑物的质量，油的质量可以忽略；油池质量可视为已包含在大楼的质量之内）。

已知当摆锤与油的相对速度为 v 时，摆锤受到的阻尼力为f v其中γ为常量。

第25届全国中学生物理竞赛复赛试题(含答案)

第25届全国中学生物理竞赛复赛试卷本卷共八题，满分160分一、（15分） 1．（5分）蟹状星云脉冲星的辐射脉冲周期是0．033s 。

假设它是由均匀分布的物质构成的球体，脉冲周期是它的旋转周期，万有引力是唯一能阻止它离心分解的力，已知万有引力常量113126.6710G m kg s ---=⨯⋅⋅，由于脉冲星表面的物质未分离，故可估算出此脉冲星密度的下限是 3kg m -⋅。

2．（5分）在国际单位制中，库仑定律写成122q q F kr =，式中静电力常量9228.9810k N m C -=⨯⋅⋅，电荷量q 1和q 2的单位都是库仑，距离r 的单位是米，作用力F 的单位是牛顿。

若把库仑定律写成更简洁的形式122q q F r=，式中距离r 的单位是米，作用力F 的单位是牛顿。

若把库仑定律写成更简洁的形式122q qF r=，式中距离r 的单位是米，作用力F 的单位是牛顿，由此式可这义一种电荷量q 的新单位。

当用米、千克、秒表示此新单位时，电荷新单位= ；新单位与库仑的关系为1新单位= C 。

3．（5分）电子感应加速器（betatron ）的基本原理如下：一个圆环真空室处于分布在圆柱形体积内的磁场中，磁场方向沿圆柱的轴线，圆柱的轴线过圆环的圆心并与环面垂直。

圆中两个同心的实线圆代表圆环的边界，与实线圆同心的虚线圆为电子在加速过程中运行的轨道。

已知磁场的磁感应强度B 随时间t 的变化规律为0cos(2/)B B t T π=，其中T 为磁场变化的周期。

B 0为大于0的常量。

当B 为正时，磁场的方向垂直于纸面指向纸外。

若持续地将初速度为v 0的电子沿虚线圆的切线方向注入到环内（如图），则电子在该磁场变化的一个周期内可能被加速的时间是从t= 到t= 。

二、（21分）嫦娥1号奔月卫星与长征3号火箭分离后，进入绕地运行的椭圆轨道，近地点离地面高22.0510n H km =⨯，远地点离地面高45.093010f H km =⨯，周期约为16小时，称为16小时轨道（如图中曲线1所示）。

第19届全国中学生物理竞赛复赛试题及解答

第十九届全国中学生物理竞赛复赛试卷全卷共七题，总分为140分。

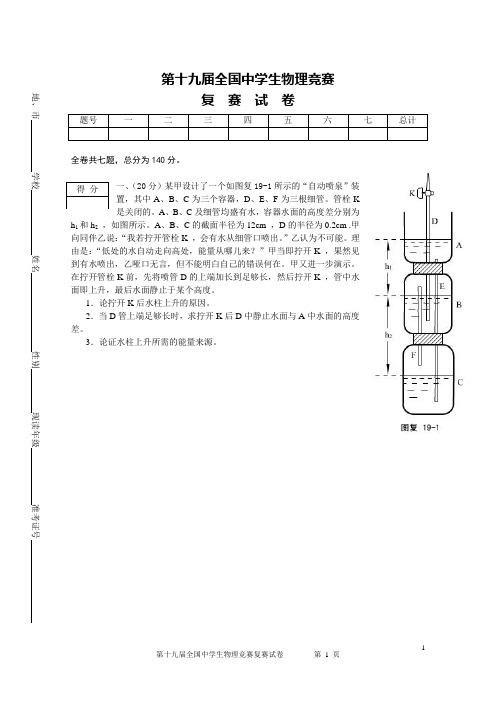
一、（20分）某甲设计了一个如图复19-1所示的“自动喷泉”装置，其中A 、B 、C 为三个容器，D 、E 、F 为三根细管。

管栓K 是关闭的。

A 、B 、C 及细管均盛有水，容器水面的高度差分别为h 1和h 2 ，如图所示。

A 、B 、C 的截面半径为12cm ，D 的半径为0.2cm .甲向同伴乙说：“我若拧开管栓K ，会有水从细管口喷出。

”乙认为不可能。

理由是：“低处的水自动走向高处，能量从哪儿来？”甲当即拧开K ，果然见到有水喷出，乙哑口无言，但不能明白自己的错误何在。

甲又进一步演示。

在拧开管栓K 前，先将喷管D 的上端加长到足够长，然后拧开K ，管中水面即上升，最后水面静止于某个高度。

1．论拧开K 后水柱上升的原因。

2．当D 管上端足够长时，求拧开K 后D 中静止水面与A 中水面的高度差。

3．论证水柱上升所需的能量来源。

二、（18分）在图复19-2中，半径为R的圆柱形区域内有匀强磁场，磁场方向垂直图面指向纸外，磁感强随时间均匀变化，变化率ΔB/Δt = K（K为一正值常数）。

圆柱形区域外空间中没有磁场。

沿图中AC弦的方向画一直线，并向外延长，弦AC与半径OA的夹角α= π/4 。

直线上有一任意点，设该点与A点的距离为x ，求从A沿直线到该点的电动势大小。

三、（18分）如图复19-3所示，在水平光滑的绝缘桌面上，有三个带正电的质点Array1、2、3 ，位于边长为L的等边三角形的三个顶点处，C为三角形的中心。

三个质点的质量皆为m ，带电量皆为q 。

质点1、3之间和2、3之间用绝缘的轻而细的刚性杆相连，在3的连接处为无摩擦的铰链。

已知开始时三个质点的速度为零，在此后运动过程中，当质点3运动到C处时，其速度为多少？四、（18分）有人设计了下述装置用以测量线圈的自感系数。

在图复19-4-1中，E为可调的直流电源，K为电键，L为待测线圈的自感系数，r L为线圈的直流电阻，D为理想二极管，r为用电阻丝做成的电阻器，A为电流表。

全国中学生物理竞赛复赛试题及参考答案

全国中学生物理竞赛复赛考试试题解答与评分标准一、（15分）一半径为R 、内侧光滑的半球面固定在地面上，开口水平且朝上. 一小滑块在半球面内侧最高点处获得沿球面的水平速度，其大小为0v (00≠v ). 求滑块在整个运动过程中可能达到的最大速率. 重力加速度大小为g .参考解答：以滑块和地球为系统，它在整个运动过程中机械能守恒. 滑块沿半球面内侧运动时，可将其速度v 分解成纬线切向 (水平方向)分量ϕv 及经线切向分量θv . 设滑块质量为m ，在某中间状态时，滑块位于半球面内侧P 处，P 和球心O 的连线与水平方向的夹角为θ. 由机械能守恒得2220111sin 222m mgR m m ϕθθ=-++v v v (1) 这里已取球心O 处为重力势能零点. 以过O 的竖直线为轴. 球面对滑块的支持力通过该轴，力矩为零；重力相对于该轴的力矩也为零. 所以在整个运动过程中，滑块相对于轴的角动量守恒，故0cos m R m R ϕθ=v v . (2)由 (1) 式，最大速率应与θ的最大值相对应max max ()θ=v v . (3)而由 (2) 式，q 不可能达到π2. 由(1)和(2)式，q 的最大值应与0θ=v 相对应，即max ()0θθ=v . (4)[(4)式也可用下述方法得到：由 (1)、(2) 式得22202sin tan 0gR θθθ-=≥v v .若sin 0θ≠，由上式得220sin 2cos gRθθ≤v .实际上，sin =0θ也满足上式。

由上式可知max 22max 0sin 2cos gRθθ=v .由(3)式有222max max 0max ()2sin tan 0gR θθθθ=-=v v . (4’)将max ()0θθ=v 代入式(1)，并与式(2)联立，得()2220max max max sin 2sin 1sin 0gR θθθ--=v . (5)以max sin θ为未知量，方程(5)的一个根是sin q =0，即q =0，这表示初态，其速率为最小值，不是所求的解. 于是max sin 0θ≠. 约去max sin θ，方程(5)变为22max 0max 2sin sin 20gR gR θθ+-=v . (6)其解为20maxsin 14gR θ⎫=-⎪⎪⎭v . (7)注意到本题中sin 0θ≥，方程(6)的另一解不合题意，舍去. 将(7)式代入(1)式得，当max θθ=时，(22012ϕ=v v ,(8) 考虑到(4)式有max ==v评分标准：本题15分. (1)式3分， (2) 式3分，(3) 式1分，(4) 式3分， (5) 式1分，(6) 式1分，(7) 式1分， (9) 式2分.二、（20分）一长为2l 的轻质刚性细杆位于水平的光滑桌面上，杆的两端分别固定一质量为m 的小物块D 和一质量为m α（α为常数）的小物块B ，杆可绕通过小物块B 所在端的竖直固定转轴无摩擦地转动. 一质量为m 的小环C 套在细杆上（C 与杆密接），可沿杆滑动，环C 与杆之间的摩擦可忽略. 一轻质弹簧原长为l ，劲度系数为k ，两端分别与小环C 和物块B 相连. 一质量为m 的小滑块A 在桌面上以垂直于杆的速度飞向物块D ，并与之发生完全弹性正碰，碰撞时间极短. 碰撞时滑块C 恰好静止在距轴为r （r >l ）处.1. 若碰前滑块A 的速度为0v ，求碰撞过程中轴受到的作用力的冲量；2. 若碰后物块D 、C 和杆刚好做匀速转动，求碰前滑块A 的速度0v 应满足的条件.参考解答：1. 由于碰撞时间t ∆很小，弹簧来不及伸缩碰撞已结束. 设碰后A 、C 、D 的速度分别为A v 、C v 、D v ，显然有D C2l r =v v . (1)以A 、B 、C 、D 为系统，在碰撞过程中，系统相对于轴不受外力矩作用，其相对于轴的角动量守恒D C A 0222m l m r m l m l ++=v v v v . (2)由于轴对系统的作用力不做功，系统内仅有弹力起作用，所以系统机械能守恒. 又由于碰撞时间t ∆很小，弹簧来不及伸缩碰撞已结束，所以不必考虑弹性势能的变化. 故2222D C A 011112222m m m m ++=v v v v . (3) 由 (1)、(2)、(3) 式解得2200022222248,,888C D A lr l r l r l r l r===-+++v v v v v v (4)[代替 (3) 式，可利用弹性碰撞特点0D A =-v v v . (3’) 同样可解出(4). ]设碰撞过程中D 对A 的作用力为1F '，对A 用动量定理有221A 0022428l r F t m m m l r+'∆=-=-+v v v ,(5)方向与0v 方向相反. 于是，A 对D 的作用力为1F 的冲量为221022428l r F t m l r+∆=+v (6)方向与0v 方向相同.以B 、C 、D 为系统，设其质心离转轴的距离为x ，则22(2)2mr m l l r x m αα++==++. (7)质心在碰后瞬间的速度为C 0224(2)(2)(8)l l r x r l r α+==++v v v . (8) 轴与杆的作用时间也为t ∆，设轴对杆的作用力为2F ，由质心运动定理有()210224(2)28l l r F t F t m m l rα+∆+∆=+=+v v . (9) 由此得2022(2)28r l r F t m l r-∆=+v . (10) 方向与0v 方向相同. 因而，轴受到杆的作用力的冲量为2022(2)28r l r F t m l r -'∆=-+v ,(11) 方向与0v 方向相反. 注意：因弹簧处在拉伸状态，碰前轴已受到沿杆方向的作用力；在碰撞过程中还有与向心力有关的力作用于轴. 但有限大小的力在无限小的碰撞时间内的冲量趋于零，已忽略.[代替 (7)-(9) 式，可利用对于系统的动量定理21C D F t F t m m ∆+∆=+v v . ][也可由对质心的角动量定理代替 (7)-(9) 式. ]2. 值得注意的是，(1)、(2)、(3) 式是当碰撞时间极短、以至于弹簧来不及伸缩的条件下才成立的. 如果弹簧的弹力恰好提供滑块C 以速度02248C lrl r =+v v 绕过B 的轴做匀速圆周运动的向心力，即()222C 022216(8)l r k r m m r l r -==+v v(12) 则弹簧总保持其长度不变，(1)、(2)、(3) 式是成立的. 由(12)式得碰前滑块A 的速度0v 应满足的条件0=v (13)可见，为了使碰撞后系统能保持匀速转动，碰前滑块A 的速度大小0v 应满足(13)式.评分标准：本题20分.第1问16分，(1)式1分， (2) 式2分，(3) 式2分，(4) 式2分， (5) 式2分，(6) 式1分，(7) 式1分，(8) 式1分，(9) 式2分，(10) 式1分，(11) 式1分；第2问4分，(12) 式2分，(13) 式2分.三、（25分）一质量为m 、长为L 的匀质细杆，可绕过其一端的光滑水平轴O 在竖直平面内自由转动. 杆在水平状态由静止开始下摆， 1. 令mLλ=表示细杆质量线密度. 当杆以角速度ω绕过其一端的光滑水平轴O 在竖直平面内转动时，其转动动能可表示为 k E k L αβγλω=式中，k 为待定的没有单位的纯常数. 已知在同一单位制下，两物理量当且仅当其数值和单位都相等时才相等. 由此求出α、β和γ的值.2. 已知系统的动能等于系统的质量全部集中在质心时随质心一起运动的动能和系统在质心系（随质心平动的参考系）中的动能之和，求常数k 的值.3. 试求当杆摆至与水平方向成θ角时在杆上距O 点为r 处的横截面两侧部分的相互作用力. 重力加速度大小为g .提示：如果)(t X 是t 的函数，而))((t X Y 是)(t X 的函数，则))((t X Y 对t 的导数为d (())d d d d d Y X t Y Xt X t=例如，函数cos ()t θ对自变量t 的导数为dcos ()dcos d d d d t t tθθθθ=参考解答：1. 当杆以角速度ω绕过其一端的光滑水平轴O 在竖直平面内转动时，其动能是独立变量λ、ω和L 的函数，按题意可表示为k E k L αβγλω= (1)式中，k 为待定常数（单位为1）. 令长度、质量和时间的单位分别为[]L 、[]M 和[]T （它们可视为相互独立的基本单位），则λ、ω、L 和k E 的单位分别为 1122[][][],[][],[][],[][][][]k M L T L L E M L T λω---==== (2)在一般情形下，若[]q 表示物理量q 的单位，则物理量q 可写为 ()[]q q q = (3)式中，()q 表示物理量q 在取单位[]q 时的数值. 这样，(1) 式可写为 ()[]()()()[][][]k k E E k L L αβγαβγλωλω= (4)在由(2)表示的同一单位制下，上式即()()()()k E k L αβγλω= (5) [][][][]k E L αβγλω= (6)将 (2)中第四式代入 (6) 式得22[][][][][][]M L T M L T αγαβ---= (7)(2)式并未规定基本单位[]L 、[]M 和[]T 的绝对大小，因而(7)式对于任意大小的[]L 、[]M 和[]T 均成立，于是1,2,3αβγ=== (8)所以23k E k L λω= (9)2. 由题意，杆的动能为,c ,r k k k E E E =+ (10)其中， 22,cc 11()222k L E m L λω⎛⎫== ⎪⎝⎭v (11) 注意到，杆在质心系中的运动可视为两根长度为2L的杆过其公共端（即质心）的光滑水平轴在铅直平面内转动，因而，杆在质心系中的动能,r k E 为 32,r2(,,)222k k L L E E k λωλω⎛⎫== ⎪⎝⎭(12)将(9)、 (11)、 (12)式代入(10)式得2323212222L L k L L k λωλωλω⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭(13)由此解得16k = (14)于是E k =16lw 2L 3. (15)3. 以细杆与地球为系统，下摆过程中机械能守恒sin 2k L E mg θ⎛⎫= ⎪⎝⎭(16) 由(15)、(16)式得w =以在杆上距O 点为r 处的横截面外侧长为()L r -的那一段为研究对象，该段质量为()L r λ-，其质心速度为22c L r L rr ωω-+⎛⎫'=+= ⎪⎝⎭v . (18) 设另一段对该段的切向力为T (以θ增大的方向为正方向)，法向(即与截面相垂直的方向)力为N (以指向O 点方向为正向)，由质心运动定理得()()cos t T L r g L r a λθλ+-=- (19) ()()sin n N L r g L r a λθλ--=- (20)式中，t a 为质心的切向加速度的大小()3cos d d d d d 2d 2d dt 4ct L r g L r L r a t t Lθωωθθ+'++====v (21) 而n a 为质心的法向加速度的大小()23sin 22n L r g L r a Lθω++==. (22) 由(19)、(20)、(21)、(22)式解得 ()()23cos 4L r r L T mg L θ--= (23)()()253sin 2L r L r N mg L θ-+=(24)评分标准：本题25分.第1问5分， (2) 式1分， (6) 式2分，(7) 式1分，(8) 式1分；第2问7分， (10) 式1分，(11) 式2分，(12) 式2分， (14) 式2分；不依赖第1问的结果，用其他方法正确得出此问结果的，同样给分；第3问13分，(16) 式1分，(17) 式1分，(18) 式1分，(19) 式2分，(20) 式2分，(21) 式2分，(22) 式2分，(23) 式1分，(24) 式1分；不依赖第1、2问的结果，用其他方法正确得出此问结果的，同样给分.四、（20分）图中所示的静电机由一个半径为R 、与环境绝缘的开口（朝上）金属球壳形的容器和一个带电液滴产生器G 组成. 质量为m 、带电量为q 的球形液滴从G 缓慢地自由掉下（所谓缓慢，意指在G 和容器口之间总是只有一滴液滴）. 液滴开始下落时相对于地面的高度为h . 设液滴很小，容器足够大，容器在达到最高电势之前进入容器的液体尚未充满容器. 忽略G 的电荷对正在下落的液滴的影响.重力加速度大小为g . 若容器初始电势为零，求容器可达到的最高电势max V .参考解答：设在某一时刻球壳形容器的电量为Q . 以液滴和容器为体系，考虑从一滴液滴从带电液滴产生器 G 出口自由下落到容器口的过程. 根据能量守恒有2122Qq Qqmgh km mgR kh R R+=++-v . (1) 式中，v 为液滴在容器口的速率，k 是静电力常量. 由此得液滴的动能为 21(2)(2)2()Qq h R m mg h R kh R R-=---v . (2) 从上式可以看出，随着容器电量Q 的增加，落下的液滴在容器口的速率v 不断变小；当液滴在容器口的速率为零时，不能进入容器，容器的电量停止增加，容器达到最高电势. 设容器的最大电量为max Q ，则有 max (2)(2)0()Q q h R mg h R kh R R---=-. (3)由此得 max ()mg h R RQ kq-=. (4)容器的最高电势为maxmax Q V kR= (5) 由(4) 和 (5)式得 max ()mg h R V q-=(6) 评分标准：本题20分. (1)式6分， (2) 式2分，(3) 式4分，(4) 式2分， (5) 式3分，(6) 式3分.五、（25分）平行板电容器两极板分别位于2dz =±的平面内，电容器起初未被充电. 整个装置处于均匀磁场中，磁感应强度大小为B ，方向沿x 轴负方向，如图所示.1. 在电容器参考系S 中只存在磁场；而在以沿y 轴正方向的恒定速度(0,,0)v （这里(0,,0)v 表示为沿x 、y 、z 轴正方向的速度分量分别为0、v 、0，以下类似）相对于电容器运动的参考系S '中，可能既有电场(,,)xy z E E E '''又有磁场(,,)x y z B B B '''. 试在非相对论情形下，从伽利略速度变换，求出在参考系S '中电场(,,)xy z E E E '''和磁场(,,)x y z B B B '''的表达式. 已知电荷量和作用在物体上的合力在伽利略变换下不变.2. 现在让介电常数为ε的电中性液体（绝缘体）在平行板电容器两极板之间匀速流动，流速大小为v ，方向沿y 轴正方向. 在相对液体静止的参考系（即相对于电容器运动的参考系）S '中，由于液体处在第1问所述的电场(,,)xy z E E E '''中，其正负电荷会因电场力作用而发生相对移动（即所谓极化效应），使得液体中出现附加的静电感应电场，因而液体中总电场强度不再是(,,)xy z E E E '''，而是0(,,)xy z E E E εε'''，这里0ε是真空的介电常数. 这将导致在电容器参考系S 中电场不再为零. 试求电容器参考系S 中电场的强度以及电容器上、下极板之间的电势差. （结果用0ε、ε、v 、B 或（和）d 表出. ）参考解答：1. 一个带电量为q 的点电荷在电容器参考系S 中的速度为(,,)x y z u u u ，在运动的参考系S '中的速度为(,,)x y z u u u '''. 在参考系S 中只存在磁场(,,)(,0,0)x y z B B B B =-，因此这个点电荷在参考系S 中所受磁场的作用力为0,,x y z z y F F qu B F qu B==-= (1) 在参考系S '中可能既有电场(,,)xy z E E E '''又有磁场(,,)x y z B B B '''，因此点电荷q 在S '参考系中所受电场和磁场的作用力的合力为(),(),()x x y z z y y yx z z x z z x y y x F q E u B u B F q E u B u B F q E u B u B '''''''=+-'''''''=-+'''''''=+-(2) 两参考系中电荷、合力和速度的变换关系为 ,(,,)(,,),(,,)(,,)(0,,0)x y z x y z x y z x y z q q F F F F F F u u u u u u '='''='''=-v (3)由(1)、 (2)、 (3)式可知电磁场在两参考系中的电场强度和磁感应强度满足 ()0,,()xy z z y yx z z x z z x yy x y E u B u B E u B u B u B E u B u B u B '''+--='''-+=-'''+--=v v (4)它们对于任意的(,,)x y z u u u 都成立，故(,,)(0,0,),(,,)(,0,0)xy z xy z E E E B B B B B '''='''=-v (5)可见两参考系中的磁场相同，但在运动的参考系S '中却出现了沿z 方向的匀强电场.2. 现在，电中性液体在平行板电容器两极板之间以速度(0,,0)v 匀速运动. 电容器参考系S 中的磁场会在液体参考系S '中产生由(5)式中第一个方程给出的电场. 这个电场会把液体极化，使得液体中的电场为(,,)(0,0,)xy z E E E B εε'''=v . (6) 为了求出电容器参考系S 中的电场，我们再次考虑电磁场的电场强度和磁感应强度在两个参考系之间的变换，从液体参考系S '中的电场和磁场来确定电容器参考系S 中的电场和磁场. 考虑一带电量为q 的点电荷在两参考系中所受的电场和磁场的作用力. 在液体参考系S '中，这力(,,)x y z F F F '''如(2)式所示. 它在电容器参考系S 中的形式为(),(),()x x y z z y y y x z z x z z x y y x F q E u B u B F q E u B u B F q E u B u B =+-=-+=+-(7) 利用两参考系中电荷、合力和速度的变换关系(3)以及(6)式，可得 00,,()x y z z y y x z z x z z x y y x y E u B u B E u B u B u B BE u B u B u B εε+-=-+=-+-=+-v v (8)对于任意的(,,)x y z u u u 都成立，故 0(,,)(0,0,(1)),(,,)(,0,0)x y z x y z E E E B B B B B εε=-=-v (9) 可见，在电容器参考系S 中的磁场仍为原来的磁场，现由于运动液体的极化，也存在电场，电场强度如(9)中第一式所示.注意到(9)式所示的电场为均匀电场，由它产生的电容器上、下极板之间的电势差为z V E d =-. (10)由(9)式中第一式和(10)式得01V Bd εε⎛⎫=- ⎪⎝⎭v . (11)评分标准：本题25分.第1问12分， (1) 式1分， (2) 式3分， (3) 式3分，(4) 式3分，(5) 式2分；第2问13分， (6) 式1分，(7) 式3分，(8) 式3分， (9) 式2分， (10) 式2分，(11) 式2分.六、（15分）温度开关用厚度均为0.20 mm 的钢片和青铜片作感温元件；在温度为20C ︒时，将它们紧贴，两端焊接在一起，成为等长的平直双金属片. 若钢和青铜的线膨胀系数分别为51.010-⨯/度和52.010-⨯/度. 当温度升高到120C ︒时，双金属片将自动弯成圆弧形，如图所示. 试求双金属片弯曲的曲率半径. (忽略加热时金属片厚度的变化. )参考解答：设弯成的圆弧半径为r ，金属片原长为l ，圆弧所对的圆心角为φ，钢和青铜的线膨胀系数分别为1α和2α，钢片和青铜片温度由120C T =︒升高到2120C T =︒时的伸长量分别为1l ∆和2l ∆. 对于钢片1()2dr l l φ-=+∆ (1)1121()l l T T α∆=- (2) 式中，0.20 mm d =. 对于青铜片2()2dr l l φ+=+∆ (3)2221()l l T T α∆=- (4) 联立以上各式得2122121212()()2.010 mm 2()()T T r d T T αααα++-==⨯-- (5)评分标准：本题15分. (1)式3分， (2) 式3分，(3) 式3分，(4) 式3分， (5) 式3分.七、（20分）一斜劈形透明介质劈尖，尖角为θ，高为h . 今以尖角顶点为坐标原点，建立坐标系如图(a)所示；劈尖斜面实际上是由一系列微小台阶组成的，在图(a)中看来，每一个小台阶的前侧面与xz 平面平行，上表面与yz 平面平行. 劈尖介质的折射率n 随x 而变化，()1n x bx =+，其中常数0b >. 一束波长为λ的单色平行光沿x 轴正方向照射劈尖；劈尖后放置一薄凸透镜，在劈尖与薄凸透镜之间放一档板，在档板上刻有一系列与z 方向平行、沿y 方向排列的透光狭缝，如图(b)所示. 入射光的波面（即与平行入射光线垂直的平面）、劈尖底面、档板平面都与x 轴垂直，透镜主光轴为x 轴. 要求通过各狭缝的透射光彼此在透镜焦点处得到加强而形成亮纹. 已知第一条狭缝位于y =0处；物和像之间各光线的光程相等.1. 求其余各狭缝的y 坐标；2. 试说明各狭缝彼此等距排列能否仍然满足上述要求.图(a) 图(b) 参考解答：1. 考虑射到劈尖上某y 值处的光线，计算该光线由0x =到x h =之间的光程()y δ. 将该光线在介质中的光程记为1δ，在空气中的光程记为2δ. 介质的折射率是不均匀的，光入射到介质表面时，在0x = 处，该处介质的折射率()01n =；射到x 处时，该处介质的折射率()1n x bx =+. 因折射率随x线性增加，光线从0x =处射到1x h =（1h 是劈尖上y 值处光线在劈尖中传播的距离）处的光程1δ与光通过折射率等于平均折射率()()()1111110111222n n n h bh bh =+=++=+⎡⎤⎣⎦ (1) 的均匀介质的光程相同，即2111112nh h bh δ==+ (2)x忽略透过劈尖斜面相邻小台阶连接处的光线（事实上，可通过选择台阶的尺度和档板上狭缝的位置来避开这些光线的影响），光线透过劈尖后其传播方向保持不变，因而有21h h δ=- (3)于是()212112y h bh δδδ=+=+. (4)由几何关系有1tan h y θ=. (5)故()22tan 2b y h y δθ=+. (6)从介质出来的光经过狭缝后仍平行于x 轴，狭缝的y 值应与对应介质的y 值相同，这些平行光线会聚在透镜焦点处. 对于0y =处，由上式得d 0()=h . (7)y 处与0y =处的光线的光程差为()()220tan 2b y y δδθ-=. (8)由于物像之间各光线的光程相等，故平行光线之间的光程差在通过透镜前和会聚在透镜焦点处时保持不变；因而(8)式在透镜焦点处也成立. 为使光线经透镜会聚后在焦点处彼此加强，要求两束光的光程差为波长的整数倍，即22tan ,1,2,3,2b y k k θλ==. (9)由此得y A θθ===. (10) 除了位于y =0处的狭缝外，其余各狭缝对应的y 坐标依次为,,,,A . (11)2. 各束光在焦点处彼此加强，并不要求(11)中各项都存在. 将各狭缝彼此等距排列仍可能满足上述要求. 事实上，若依次取,4,9,k m m m =，其中m 为任意正整数，则49,,,m m m y y y ===. (12)，光线在焦点处依然相互加强而形成亮纹. 评分标准：本题20分.第1问16分， (1) 式2分， (2) 式2分， (3) 式1分，(4) 式1分，(5) 式2分，(6) 式1分，(7) 式1分，(8) 式1分， (9) 式2分， (10) 式1分，(11) 式2分；第2问4分，(12) 式4分（只要给出任意一种正确的答案，就给这4分）.八、（20分）光子被电子散射时，如果初态电子具有足够的动能，以至于在散射过程中有能量从电子转移到光子，则该散射被称为逆康普顿散射. 当低能光子与高能电子发生对头碰撞时，就会出现逆康普顿散射. 已知电子静止质量为e m ，真空中的光速为 c . 若能量为e E 的电子与能量为E γ的光子相向对碰，1. 求散射后光子的能量；2. 求逆康普顿散射能够发生的条件；3. 如果入射光子能量为2.00 eV ，电子能量为 1.00´109 eV ，求散射后光子的能量. 已知 m e =0.511´106 eV /c 2. 计算中有必要时可利用近似：如果1x <<»1-12x .参考解答：1. 设碰撞前电子、光子的动量分别为e p （0e p >）、p γ（0p γ<），碰撞后电子、光子的能量、动量分别为,,,ee E p E p γγ''''. 由能量守恒有 E e +E g =¢E e +¢E g . (1)由动量守恒有cos cos ,sin sin .e eep p p p p p γγγαθαθ''+=+''=. (2)式中，α和θ分别是散射后的电子和光子相对于碰撞前电子的夹角. 光子的能量和动量满足E g =p g c ,¢E g =¢p g c . (3)电子的能量和动量满足22224e e e E p c m c -=，22224e e e E p c m c ''-= (4)由(1)、(2)、(3)、(4)式解得e E E E γγ'=[由(2)式得22222()2()cos ee e p c p c p c p c p c p c p c γγγγθ'''=++-+此即动量p '、ep '和e p p γ+满足三角形法则. 将(3)、(4)式代入上式，并利用(1)式，得 22(2)()22cos 2e e e E E E E E E E E E E E γγγγγγγγθθ''+-+=+--此即(5)式. ]当0θ→时有e E E E γγ'=(6)2. 为使能量从电子转移到光子，要求¢E g >E g . 由(5)式可见，需有E E γγ'-=>此即E γ 或 e p p γ>(7)注意已设p e >0、p g <0.3. 由于2e e E m c >>和e E E γ>>，因而e p p p γγ+>>，由(5)式可知p p γγ'>>，因此有0θ≈. 又242e e em cE E -. (8)将(8)式代入(6)式得¢E g »2E e E g2E g +m e 2c 42E e. (9) 代入数据，得¢E g »29.7´106eV . (10)评分标准：本题20分.第1问10分， (1) 式2分， (2) 式2分， (3) 式2分，(4) 式2分，(5) 或(6)式2分；第2问5分，(7) 式5分；第3问5分，(8) 式2分， (9) 式1分， (10) 式2分.。