2017年中考数学专题复习八：几何证明题

合集下载

2017河北中考复习之几何证明

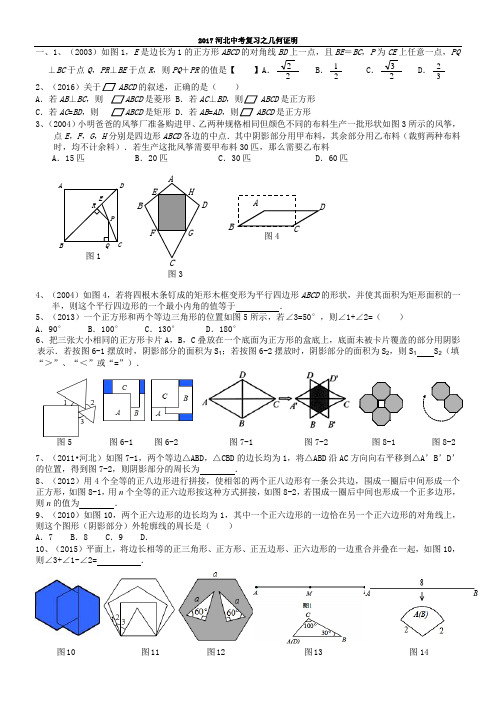
一、1、（2003）如图1，E是边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是【】A．2B．1C．3 D．2A．若⊥，则B．若⊥，则C．若AC=BD，则D．若AB=AD，则3、（2004）小明爸爸的风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图3所示的风筝，点E，F，G，H分别是四边形ABCD各边的中点．其中阴影部分用甲布料，其余部分用乙布料（裁剪两种布料时，均不计余料）．若生产这批风筝需要甲布料30匹，那么需要乙布料A．15匹B．20匹C．30匹D．60匹4、（2004）如图4，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于．5、（2013）一个正方形和两个等边三角形的位置如图5所示，若∠3=50°，则∠1+∠2=（）A．90°B．100°C．130°D．180°6、把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图6-1摆放时，阴影部分的面积为S1；若按图6-2摆放时，阴影部分的面积为S2，则S1S2（填“＞”、“＜”或“=”）．7、（2011•河北）如图7-1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A’B’D’的位置，得到图7-2，则阴影部分的周长为．8、（2012）用4个全等的正八边形进行拼接，使相邻的两个正八边形有一条公共边，围成一圈后中间形成一个正方形，如图8-1，用n个全等的正六边形按这种方式拼接，如图8-2，若围成一圈后中间也形成一个正多边形，则n的值为．9、（2010）如图10，两个正六边形的边长均为1，其中一个正六边形的一边恰在另一个正六边形的对角线上，则这个图形（阴影部分）外轮廓线的周长是（）A．7 B．8 C．9 D．10、（2015）平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图10，则∠3+∠1-∠2=．图5 图6-1 图7-1 图8-2图6-2 图7-2 图8-1图14 图10 图11 图12 图13D图3图4ABDCERPQ图1图15C ．点M 在BC 上，且距点B 较近，距点C 较远D ．点M 在BC 上，且距点C 较近，距点B较远14、如图14，将长为8cm 的铁丝首尾相接围成半径为2cm 的扇形．则扇形s =15、（2006）小宇同学在一次手工制作活动中，先把一张矩形纸片按图9—1的方式进行折叠，使折痕的左侧部分比右侧部分短1cm ；展开后按图9—2的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长1cm ，再展开后，在纸上形成的两条折痕之间的距离是A ．0.5cm B ．1cm C ．1.5cmD ．2cm16、（2009）如图15，等边△ABC 的边长为1cm ，D 、E 分别是AB 、AC 上的点，将△ADE 沿直线DE 折叠，点A 落在点A ′处，且点A ′在△ABC 外部，则阴影部分图形的周长为cm ．17、（2014）如图16，△ABC 中，D ，E 分别是边AB ，AC 的中点．若DE=2，则BC=（）A ．2 B ．3 C ．4 D ．5 18、（2014）如图17，将长为2、宽为1的矩形纸片分割成n 个三角形后，拼成面积为2的正方形，则n ≠（） A ．2 B ．3 C ．4 D ．5迹是（）A ．B ．C ．D ．20、（2015）如图15，∠BOC=9°，点A 在OB 上，且OA=1，按下列要求画图：以A 为圆心，1为半径向右画弧交OC 于点A 1，得第1条线段AA 1；再以A 1为圆心，1为半径向右画弧交OB 于点A 2，得第2条线段A 1A 2；再以A 2为圆心，1为半径向右画弧交OC 于点A 3，得第3条线段A 2A 3；…这样画下去，直到得第n 条线段，之后就不能再画出符合要求的线段了，则n= 21、（2016）如图16，步骤1：以C 为圆心，CA 为半径画弧○1；步骤2：以B 为圆心，BA 为半径画弧○2，将弧○1于点D ；步骤3：连接AD ，交BC 延长线于点H.下列叙述正确的是（） A ．BH 垂直分分线段AD B ．AC 平分∠BAD C ．S △ABC=BC ·AH D ．AB=AD22、如图17，∠AOB=120°，OP 平分∠AOB ，且OP=2.若点M ，N 分别在左右左右第二次折叠第一次折叠图9－1 图9－2 图15 图16 图14 图17图16OA ，OB 上，且△PMN 为等边三角形，则满足上述条件的△PMN 有（） A ．1个 B ．2个 C ．3个 D ．3个以上23、如图，点B ，F ，C ，E 在直线l 上（F ，C 之间不能直接测量），点A ，D 在l 异侧，测得AB=DE ，AC=DF ，BF=EC. （1）求证：△ABC ≌△DEF ；（2）指出图中所有平行的线段，并说明理由.24、（2015）嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD ，并写出了如下不完整的已知和求证．已知：如图1，在四边形ABCD 中，BC=AD ，AB=CD 求证：四边形ABCD 是平行四边形．（1）在方框中填空，以补全已知和求证；（2）按嘉淇的想法写出证明；（3）用文字叙述所证命题的逆命题为平行四边形两组对边分别相等（2015考试说明）求证：角平分线上的点到这个角的两边距离相等. 已知：求证：证明 25、（2014•河北）如图，△ABC 中，AB=AC ，∠BAC=40°，将△ABC 绕点A 按逆时针方向旋转100°．得到△ADE ，连接BD ，CE 交于点F ．（1）求证：△ABD ≌△ACE ；（2）求∠ACE 的度数；（3）求证：四边形ABFE 是菱形．25、如图，在四边形ABCD 中，AB=AD ，CB=CD ，E 是CD 上一点，BE 交AC于F ，连接DF ．（1）证明：∠BAC=∠DAC ，∠AFD=∠CFE ．（2）若AB ∥CD ，试证明四边形ABCD 是菱形；（3）在（2）的条件下，又知∠EFD=∠BCD ，请问你能推出什么结论？（直接写出一个结论，要求结论中含有字母E ）图1426、如图，在▱ABCD中，点E，F分别在AB，DC上，且ED⊥DB，FB⊥BD．（1）求证：△AED≌△CFB；（2）若∠A=30°，∠DEB=45°，求证：DA=DF．27．在▱ABCD中，过点D作DE⊥AB于点E，点F 在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB．28、（2009）在图14-1至图14-3中，点B是线段AC的中点，点D是线段CE的中点．四边形BCGF和CDHN都是正方形．AE的中点是M．（1）如图14-1，点E在AC的延长线上，点N与点G重合时，点M与点C重合，求证：FM = MH，FM⊥MH；（2）将图14-1中的CE绕点C顺时针旋转一个锐角，得到图14-2，求证：△FMH是等腰直角三角形；（3）将图14-2中的CE缩短到图14-3的情况，△FMH还是等腰直角三角形吗？（不必说明理由）29、（17预测）我们经常能够看到如下练习：如图1，⊿ABC 中，AB =AC ，∠BAC =40°，AB 的垂直平分线交边AB 于E ，交边AC 点D ，则∠DBC =°变式1：⊿ABC 中，AB =AC ，∠BAC =α，AB 的垂直平分线交直线．．AC 点于D ，交边 AB于E ，那么1）如果α=40°时，∠DBC =°2）如果α=70°时，∠DBC =° 3）如果α=110°时，∠DBC =° 变式2：⊿ABC 中，AB =AC ，∠BAC =α，AB 的垂直平分线交直线．．AC 于D ，交边AC 点D ，请通过画图分析问题，并用α表示∠DBC ，同时写出α范围30、(2008)在一平直河岸l 同侧有A ，B 两个村庄，A ，B 到l 的距离分别是3 km 和2 km ， AB = a km （a ＞1）．现计划在河岸l 上建一抽水站P ，用输水管向两个村庄供水．方案设计某班数学兴趣小组设计了两种铺设管道方案：图13-1是方案一的示意图，设该方案中管道长度为d 1，且d 1=PB+BA （km ）（其中BP ⊥ l 于点P ）；图13-2是方案二的示意图，设该方案中管道长度为d 2，且d 2=PA +PB （km ）（其中点A '与点A 关于l 对称，A 'B 与l 交于点P ）．观察计算（1）在方案一中，d 1=km （用含a 的式子表示）；（2）在方案二中，组长小宇为了计算d 2的长，作了如图13-3所示的辅助线，请你按小宇同学的思路计算，d 2=km（用含a 的式子表示）．探索归纳（1）①当a = 4时，比较大小： d 1d 2（填“＞”、“=”或“＜”）； ②当a = 6时，比较大小： d 1d 2（填“＞”、“=”或“＜”）；（2）请你参考右边方框中的方法指导，就a （当a ＞1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？24、在正方形ABCD 中，点E 是AD 上一动点，MN ⊥AB 分别交AB ，CD 于M ，N ，连接BE 交MN 于点O ，过O 作OP ⊥BE 分别交AB ，CD 于P ，Q ．l 图13 -1 l图13 -2 图13 -3 l探究：（1）如图①，当点E 在边AD 上时，请你动手测量三条线段AE ，MP ，NQ 的长度，猜测AE 与MP+NQ 之间的数量关系，并证明你所猜测的结论；探究：（2）如图②，若点E 在DA 的延长线上时，AE ，MP ，NQ 之间的数量关系又是怎样请直接写出结论；再探究：（3）如图③，连接并延长BN 交AD 的延长线DG 于H ，若点E 分别在线段DH 和射线HG 上时，请在图③中完成符合题意的图形，并判断AE ，MP ，NQ 之间的数量关系又分别怎样？请直接写出结论．25、2005）操作示例对于边长均为a 的两个正方形ABCD 和EFGH ，按图11—1所示的方式摆放，再沿虚线BD ，EG 剪开后，可以按图中所示的移动方式拼接为图11—1中的四边形BNED ．从拼接的过程容易得到结论： ①四边形BNED 是正方形；②S 正方形ABCD +S 正方形EFGH =S 正方形BNED ．实践与探究（1）对于边长分别为a ，b （a ＞b ）的两个正方形ABCD 和EFGH ，按图11—2所示的方式摆放，连结DE ，过点D 作DM ⊥DE ，交AB 于点M ，过点M 作MN ⊥DM ，过点E 作EN ⊥DE ，MN 与EN 相交于点N ．①证明四边形MNED 是正方形，并用含a ，b 的代数式表示正方形MNED 的面积；②在图11—2中，将正方形ABCD 和正方形EFGH 沿虚线剪开后，能够拼接为正方形MNED ．请简略说明你的拼接方法（类比图11—1，用数字表示对应的图形）．（2）对于n （n 是大于2的自然数）个任意的正方形，能否通过若干次拼接，将其拼接为一个正方形？请简要说明你的理由．A B FM 图11—2图11—126、（2005课改）如图14—1，14—2，四边形ABCD 是正方形，M 是AB 延长线上一点．直角三角尺的一条直角边经过点D ，且直角顶点E 在AB 边上滑动（点E 不与点A ，B 重合），另一条直角边与∠CBM 的平分线BF 相交于点F ．（1）如图14—1，当点E 在AB 边的中点位置时： ①通过测量DE ，EF 的长度，猜想DE 与EF 满足的数量关系是；②连接点E 与AD 边的中点N ，猜想NE 与BF 满足的数量关系是；③请证明你的上述两个猜想．（2）如图14—2，当点E 在AB 边上的任意位置时，请你在AD 边上找到一点N ，使得NE =BF ，进而猜想此时DE 与EF 有怎样的数量关系．27、如图13－1，一等腰直角三角尺GEF 的两条直角边与正方形ABCD 的两条边分别重合在一起．现正方形ABCD 保持不动，将三角尺GEF 绕斜边EF 的中点O （点O 也是BD 中点）按顺时针方向旋转．（1）如图13－2，当EF 与AB 相交于点M ，GF 与BD 相交于点N 时，通过观察或测量BM ，FN 的长度，猜想BM ，FN 满足的数量关系，并证明你的猜想；（2）若三角尺GEF 旋转到如图13－3所示的位置时，线段FE 的延长线与AB 的延长线相交于点M ，线段BD 的延长线与GF 的延长线相交于点N ，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．30、(2007)在图14-1—14-5中，正方形ABCD 的边长为a ，等腰直角三角形FAE 的斜边AE ＝2b ，且边AD 和AE 在同一直线上．操作示例当2b ＜a 时，如图14-1，在BA 上选取点G ，使BG ＝b ，连结FG 和CG ，裁掉△FAG 和△CGB 并分别拼接到△FEH 和△CHD 的位置构成四边形FGCH ．思考发现小明在操作后发现：该剪拼方法就是先将△FAG 绕点F 逆时针旋转90°到△FEH 的位置，易知EH 与AD 在同一直线上．连结CH ，由剪拼方法可得DH =BG ，故△CHD ≌△CGB ，从而又可将△CGB 绕点C 顺时针旋转90°到△CHD 的位置．这样，对于剪拼得到的四边形FGCH （如图14-1），过点F 作FM ⊥AE 于点M （图略），利用SAS 公理可判断△HFM ≌△CHD ，易得FH =HC =GC =FG ，∠FHC =90°．进而根据正方形的判定方法，可以判断出四边形FGCH 是正方形．实践探究（1）正方形FGCH 的面积是；（用含a ，b 的式子表示）（2）类比图14-1的剪拼方法，请你就图14-2—图14-4的三种情形分别画出剪拼成一个新正方形的示意图．图14—1 A B CD E MF 图14—2E图14-1 （2b ＜a ）图13－2 G 图13－3图13－1 A () B (E )D (F )联想拓展小明通过探究后发现：当b ≤a 时，此类图形都能剪拼成正方形，且所选取的点G 的位置在BA 方向上随着b 的增大不断上移．当b ＞a 时，如图14-5的图形能否剪拼成一个正方形？若能，请你在图中画出剪拼的示意图；若不能，简要说明理由．(2008)如图14-1，△ABC 的边BC 在直线l 上，AC ⊥BC ，且AC =BC ；△EFP 的边FP 也在直线l 上，边EF 与边AC 重合，且EF =FP ．（1）在图14-1中，请你通过观察、测量，猜想并写出AB 与AP 所满足的数量关系和位置关系；（2）将△EFP 沿直线l 向左平移到图14-2的位置时，EP 交AC 于点Q ，连结AP ，BQ ．猜想并写出BQ 与AP 所满足的数量关系和位置关系，请证明你的猜想；（3）将△EFP 沿直线l 向左平移到图14-3的位置时，EP 的延长线交AC 的延长线于点Q ，连结AP ，BQ ．你认为（2）中所猜想的BQ 与AP 的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由．在△ABC 中，AB =AC ，CG ⊥BA 交BA 的延长线于点G ．一等腰直角三角尺按如图15-1所示的位置摆放，该三角尺的直角顶点为F ，一条直角边与AC 边在一条直线上，另一条直角边恰好经过点B ．（1）在图15-1中请你通过观察、测量BF 与CG 的长度，猜想并写出BF 与CG满足的数量关系，然后证明你的猜想；图（b ＞a）图14-1 B C (F ) P A (E ) lC 图14-2 l l 图14-3图15-3图15-1（2）当三角尺沿AC方向平移到图15-2所示的位置时，一条直角边仍与AC边在同一直线上，另一条直角边交BC 边于点D，过点D作DE⊥BA于点E．此时请你通过观察、测量DE、DF与CG的长度，猜想并写出DE＋DF与CG之间满足的数量关系，然后证明你的猜想；（3）当三角尺在（2）的基础上沿AC方向继续平移到图15-3所示的位置（点F在线段AC上，且点F与点C 不重合）时，（2）中的猜想是否仍然成立？（不用说明理由）。

2017年长沙中考数学之几何经典专题(含解析)

2017年长沙中考数学之几何经典专题1.女口图，ABCD 为正方形，0 为 AC 、BD 的交点，△ DCE 为 Rt △，/ CED=90 ° Z DCE=30 °若 0E= 「〜,2则正方形的面积为( ) A . 5 B . 4 C . 3 D . 2 3. 如图，正方形 ABCD 中，点E 是AD 边中点，BD 、CE 交于点H , BE 、AH 交于点G ,则下列结论: ① AG 丄BE ;② BG=4GE ;③ JBHE =S A CHD ；④ Z AHB= Z EHD . 其中正确的个数是()A . 1 B . 2 C . 3 D . 4 4.已知点D 与点A (0, 6), B( 0, - 4), C( x, y )是平行四边形的四个顶点，其中x, y 满足3x - 4y+12=0 , 则CD 长的最小值为() A . 10 B . 2 " C . — D .42.如图，正方形 ABCD 的边长为6，点E 、F 分别在AB ,AD 上，若 CE=3 ，，且Z ECF=45 ，贝U CF的长为（）A . 2 —i B .3 -55. _____________________________________________________________________ 如图，已知平行四边形ABCD中，AB=BC , BC=10 ,Z BCD=60 °两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动，连接OA，则OA的长的最小值是 ____________________________________________________ .7. 如图，在 △ ABC 中，/ BAC=90 ° AB=6 , AC=8，点P 是BC 边上任意一点(B 、C 除外)PE 丄AB 于点E , PF 丄AC 于点F ,连接EF ，则EF 的最小值为 ___________________________ .& 如图，正方形 ABCD 的对角线交于点 0,以AD 为边向外作 Rt △ ADE , / AED=90 °连接0E , DE=6 , 0E=8二，则另一直角边 AE 的长为 _____________________ .9.若顺次连接四边形 ABCD 各边的中点所得四边形是矩形，则四边形 ABCD 一定是10. 如图，正方形 0ABC 的边0A , 0C 在坐标轴上，点 B 的坐标为(-3, 3).点P 从点A 出发，以每秒1个单位长度的速度沿 x 轴向点0运动；点Q 从点0同时出发，以相同的速度沿 x 轴的正方向运动，规定点P 到达点0时，点Q 也停止运动.连接 BP ，过P 点作BP 的垂线，与过点 Q 平行于y 轴的直线I 相交于点D . BD 与y 轴交于点E ,连接PE .设点P 运动的时间为t ( s ).(1) 求/ EBP 的度数；(2) 求点D 运动路径的长；(3) 探索△ P0E 周长是否随时间t 的变化而变化？若变化，说明理由；若不变，试求这个定值.AC=12 , P 为边BC 上一动点，PE 丄AB 于E , PF 丄AC11. 如图，把△ EFP按图示方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4，EF=4 近，/ BAD=60 ° 且AB > 4 晶.(1)求/ EPF的大小；(2)若AP=6，求AE+AF 的值；(3)若厶EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值.12. 知，四边形ABCD是正方形，/ MAN=45 °它的两边AM、AN分别交CB、DC与点M、N，连接MN，作AH丄MN，垂足为点H(1)如图1，猜想AH与AB有什么数量关系？并证明；(2)如图2，已知/ BAC=45 ° AD丄BC于点D，且BD=2 , CD=3，求AD的长；小萍同学通过观察图① 发现，△ ABM和厶AHM关于AM对称，△ AHN和厶ADN关于AN对称，于是她巧妙运用这个发现，将图形如图③ 进行翻折变换，解答了此题.你能根据小萍同学的思路解决这个问题吗？图②13. 如图1 , BC是O O的直径，点A在O O上，点D在CA的延长线上，DE丄BC ,垂足为点E, DE与O O相交于点H，与AB相交于点I，过点A作O O的切线AF，与DE相交于点F.(1)求证：/ DAF= / ABO ;(2)当AB=AD 时，求证：BC=2AF ;(3)如图2，在(2)的条件下，延长FA, BC相交于点G,若tan/ DAF= ' , EH=2 ~，求线段CG的长.14. 如图，一次函数y= - x+4的图象与x轴、y轴分别相交于点A、B，过点A作x轴的垂线I，点P为直线I上的动点，点Q为直线AB与厶OAP外接圆的交点，点P、Q与点A都不重合.(1) 写出点A的坐标；(2) 当点P在直线I上运动时，是否存在点P使得△ OQB与厶APQ全等？如果存在，求出点P的坐标；如果不存在，请说明理由.(3) 若点M在直线l上，且/ POM=90 °记厶OAP外接圆和△ OAM外接圆的面积分别是参考答案与试题解析一 •选择题（共4小题）1. 女口图，ABCD 为正方形，0 为 AC 、BD 的交点，△ DCE 为 Rt △，/ CED=90 ° Z DCE=30 °若 0E== 一 A . 5 B . 4 C . 3 D . 2【解答】解：如图，过点 0作0M 丄CE 于M ,作ON 丄DE 交ED 的延长线于 N ,•••Z CED=90 °•••四边形OMEN 是矩形，•••Z MON=90 °• Z COM+ Z DOM= Z DON+ Z DOM ,• Z COM= Z DON ,• •四边形ABCD 是正方形，• OC=OD ,在厶COM 和厶DON 中，Nc 陆 ZDON-ZN=ZCIO-90QL OC =OD•••△ COM ◎△ DON （AAS ）,• OM=ON ,•四边形OMEN 是正方形，设正方形ABCD 的边长为2a ,• Z DCE=30 ° Z CED=90 °• DE=a , CE= ■ . a ,设 DN=x , x+DE=CE - x ，解得: （V5+1）a• NE=x+a=——: -----------2 •/ OE = G 「NE ,• —_ -= p 一后:71• a=1,• S 正方形ABCD =4 故选B .2. 如图，正方形 ABCD 的边长为6，点E 、F 分别在AB , AD 上，若CE=3伍，且/ ECF=45 °则CF 的长为（）x= （V3 - 1）a则正方形的面积为（A. 2 厂B. 3 =C.-」D.上:，【解答】解：如图，延长FD到G,使DG=BE ; 连接CG、EF;•••四边形ABCD为正方形，在△ BCE与△ DCG中，r CB=CD-ZCBE=ZCDG ,,BE=DG•••△ BCE◎△ DCG (SAS),••• CG=CE，/ DCG= / BCE,•••/ GCF=45 °在厶GCF与厶ECF中，r GC=EC£ZGCF=ZECF ,L CF=CF•••△ GCF ◎△ ECF ( SAS),•GF=EF,•/ CE=3 二，CB=6 ,•BE= J 「J=：：」,"3，•AE=3 ,设AF=x，贝U DF=6 - x, GF=3+ (6 - x) =9 - x,•EF=• J=，2 2••( 9 - x) =9+x ,•x=4 ,即AF=4 ,•GF=5,•DF=2,•CF=-二「厂1宀二=2 ''，故选：A.3. 如图，正方形ABCD中，点E是AD边中点，BD、CE交于点H , BE、AH交于点G,则下列结论:① AG 丄BE;② BG=4GE ;③ S^BHE=S^CHD；④/ AHB= / EHD .其中正确的个数是（）【解答】证明：•••四边形ABCD是正方形，E是AD边上的中点, ••• AE=DE , AB=CD，/ BAD= / CDA=90 °在△ BAE和△ CDE中r AB=DEiAB二CD•△ BAE ◎△ CDE (SAS),•••/ ABE= / DCE ,•••四边形ABCD是正方形，•AD=DC，/ ADB= / CDB=45 °,•••在△ ADH和厶CDH中，r AD=CD円ZADH=ZCDH,L DH=DH•△ ADH ◎△ CDH ( SAS),•••/ HAD= / HCD ,•••/ ABE= / DCE•••/ ABE= / HAD ,•••/ BAD= / BAH+ / DAH=90 °•••/ ABE+ / BAH=90 °•••/ AGB=180。

中考数学专题复习八几何证明题

专题八：几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位．根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低．但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型．热点探究类型一：关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2．1求证：BD=CE；2求证：∠M=∠N．分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可．解答1证明：在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE；2证明：∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得：△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N．点评本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．类型二：关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG．1请判断四边形EBGD的形状;并说明理由；2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值．考点平行四边形的判定与性质；角平分线的性质．分析1结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题．解答解：1四边形EBGD是菱形．理由：∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=．MC=3;∴EC===10．∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10．点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型．同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．类型三：关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证：1四边形EBFD是矩形；2DG=BE．考点正方形的性质；矩形的判定；圆周角定理．分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案；2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG．解答证明：1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形；2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．类型四：关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F．1求证：△ACD∽△BFD；2当tan∠ABD=1;AC=3时;求BF的长．考点相似三角形的判定与性质．分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明．2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题．解答1证明：∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD．2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3．同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=．1试判断△ABC 的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD 的值．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线．1求证：△ADE ≌△CBF ；2若∠ADB 是直角;则四边形BEDF 是什么四边形证明你的结论．5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上．设∠PCB=α;∠POC=β．求证：tanα tan=．DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．参考答案类型一：关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．考点等腰三角形的性质．分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数；2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论．解答1①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE．∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC．在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE．②解：∵△ACD≌△BCE;∴∠ADC=∠BEC．∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°．∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．2证明：∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°．∵CM⊥DE;∴∠CMD=90°;DM=EM．在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°．在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN．∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM．点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是：1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；2找出线段AD、DE的长．本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键．类型二：关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．考点正方形的性质．分析1根据正方形的性质以及勾股定理即可求得；2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM．解答解：1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1；2CN=CM．证明：∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM．类型三：关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．思路分析：本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点．故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线；对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得；对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得．解题过程：1证明：连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线；2证明：∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD．∴BC2=2CD OE；3解：∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15．又∵AC=2OE;∴OE=12AC=152．规律总结：熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键．要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可．类型四：关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可；2①BP＝5；②71解析1证明：∵∠ACP＝∠B;∠BAC＝∠CAP;∴△ACP∽△ABC;∴AC：AB＝AP：AC;∴AC2＝AP·AB；2①如图;作CQ∥BM交AB延长线于Q;设BP＝x;则P Q＝2x∵∠PBM＝∠ACP;∠PAC＝∠CAQ;∴△APC∽△ACQ;由AC2＝AP·AQ得：22＝3－x35即BP②如图：作CQ⊥AB 于点Q;作CP 0＝CP 交AB 于点P 0;∵AC ＝2;∴AQ＝1;CQ ＝BQ; 设P0Q ＝PQ ＝1－x;BP －1＋x;∵∠BPM＝∠CP 0A ;∠BMP＝∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C ＝2012P C ==AP 0 BP ＝1＋x;解得x ∴BP ＝－11-．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．考点正方形的性质；全等三角形的判定与性质．分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论；2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析．解答解：1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．考点三角形例行;特殊四边形的性质与判定..1证明：∵点E 是AD 的中点;∴AE ＝DE ．∵AF ∥BC;∴∠AFE ＝∠DCE;∠FAE ＝∠CDE ．∴△EAF ≌△EDC ．∴AF ＝DC ．∵AF ＝BD;∴BD ＝DC;即D 是BC 的中点．2四边形AFBD 是矩形．证明如下：∵AF ∥BD;AF ＝BD;∴四边形AFBD 是平行四边形．∵AB ＝AC;又由1可知D 是BC 的中点;∴AD ⊥BC ．DC EF B A图6∴□AFBD是矩形．3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=．1试判断△ABC的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD的值．思路分析：1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形；2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解．解题过程：解：1△ABC为等腰三角形．理由如下：连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形；2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===．规律总结：本题考查了圆周角定理：在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半．推论：半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质和勾股定理．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线．1求证：△ADE≌△CBF；2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．分析：1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF；2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形．解答：1证明：∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS；2若∠ADB是直角;则四边形BEDF是菱形;理由如下：解：由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形．点评：本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键．5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上．设∠PCB=α;∠POC=β．求证：tanα tan=．解析：连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=．解答：证明：连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===．点评：本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=．6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．所有分析： 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE;故可得出结论；2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论．解答： 1证明：∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP；2解：由勾股定理得;BP===4．∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=．由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．考点：切线的判定．分析： 1如图;连接OE．欲证明PE是⊙O的切线;只需推知OE⊥PE即可；2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论；3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长．解答： 1证明：如图;连接OE．∵CD是圆O的直径;∴∠CED=90°．∵OC=OE;∴∠1=∠2．又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线；2证明：∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等．又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP；3解：设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=．点评：本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键．。

中考数学几何专题复习

专题几何专题题型一考察概念基础知识点型例1如图1,等腰△ABC 的周长为21,底边BC ＝ 5,AB 的垂直平分线是DE ,则△BEC 的周长为 ; 例2 如图2,菱形ABCD 中,60A ∠=°,E 、F 是AB 、AD 的中点,若2EF=,菱形边长是______．图1 图2 图3 例3 已知AB 是⊙O 的直径,PB 是⊙O 的切线,AB ＝3cm,PB ＝4cm,则BC ＝．题型二折叠题型：折叠题要从中找到对就相等的关系,然后利用勾股定理即可求解; 沿DE 折叠,若48CDE ∠=°,则APD ∠等例4 D E ，分别为AC ,BC 边的中点,于 ;例5如图4.矩形纸片ABCD 的边长AB =4,AD =2．将矩形纸片沿 EF 折叠, 使点A 与点C 重合,折叠后在其一面着色图,则着色部分的面积为A ． 8B ．112C ． 4D ．52EDBC A P图4图5 图6题型三涉及计算题型：常见的有应用勾股定理求线段长度,求弧长,扇形面积及圆锥体积,侧面积,三角函数计算等;例6如图3,P 为⊙O 外一点,PA 切⊙O 于A,AB 是⊙O 的直径,PB 交⊙O 于C,PA ＝2cm,PC ＝1cm,则图中阴影部分的面积S 是A.2235cm π- B 2435cm π- C 24235cm π- D 2232cm π- 图3 题型四证明题型：第二轮复习之几何一——三角形全等判定方法1：SAS例1如图,AC 是菱形ABCD 的对角线,点E 、F 分别在边AB 、AD 上,且 AE=AF; 求证：△ACE ≌△ACF例2 在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED ． 1求证：△BEC ≌△DEC ；2延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数．BD GFF ADFEBCDCBA EFG判定方法2：AASASA例3 如图,ABCD 是正方形,点G 是BC 上的任意一点,DE AG ⊥于 E ,BF DE ∥,交 AG 于F ,求证：AFBF EF =+．例4如图,在□ABCD 中,分别延长BA,DC 到点E,使得AE=AB, CH=CD 连接EH,分别交AD,BC 于点F,G;求证：△AEF ≌△CHG.判定方法3：HL 专用于直角三角形例5在△ABC 中,AB=CB,∠ABC=90o,F 为AB 延长线上一点,点E在BC上, 且AE=CF. 1求证:Rt △AB E ≌Rt △CBF; 2若∠CAE=30o,求∠ACF 度数.对应练习1.如图,在平行四边形ABCD 中,E 为BC 中点,AE 的延长线与DC 的延长线相交于点F.1证明：∠DFA = ∠FAB； 2证明: △ABE≌△FCE.2.如图,点E 是正方形ABCD 内一点,CDE ∆是等边三角形,连接EB 、EA ,延长BE 交边AD 于点F . 1求证:BCE ADE ∆≅∆；5分2求AFB ∠的度数.5分3．如图,已知∠ACB ＝90°,AC ＝BC ,BE ⊥CE 于E ,AD ⊥CE 于D ,CE 与AB 相交于F ．1求证：△CEB ≌△ADC ；2若AD ＝9cm,DE ＝6cm,求BE 及EF 的长．第二轮复习之几何二——三角形相似Ⅰ.三角形相似的判定例1如图,在平行四边形ABCD 中,过点A 作AE ⊥BC,垂足为E,连接DE,F 为线段DE 上一点,且∠AFE ＝∠B. 1求证：△ADF ∽△DEC2若AB ＝4,AD ＝33,AE ＝3,求AF 的长. 例2如图9,点P 是正方形ABCD 边AB 上一点不与点A ．B重合,连接PD 并将线段PD 绕点P 顺时针方向旋转90°得到线段PE, PE 交边BC 于点F ．连接BE 、DF;E B D A CF AF DEB CABCEFABCDF EF ED CBA 1求证：∠ADP=∠EPB ； 2求∠CBE 的度数； 3当APAB的值等于多少时．△PFD ∽△BFP 并说明理由．2.相似与圆结合,注意求证线段乘积,一般是转化证它所在的三角形相似;将乘积式转化为比例式→比例式边长定位到哪个三角形→找条件证明所在的三角形相似例3 如图,在△ABC 中,AB=AC,以AB 为直径的⊙O 交AC 与E,交BC 与D ．求证：1D 是BC 的中点；2△BEC∽△ADC； 3BC 2=2AB CE ．3.相似与三角函数结合,①若题目给出三角函数值一般会将给出的三角函数值用等角进行转化,然后求线段的长度②求某个角的三角函数值,一般会先将这个角用等角转化,间接求三角函数值例4如图,点E 是矩形ABCD 中CD 边上一点,⊿BCE 沿BE 折叠为⊿BFE,点F 落在AD 上.1求证：⊿ABE∽⊿DFE ;2若sin∠DFE=31,求tan∠EBC 的值. 练习一、选择题1、如图1,将非等腰ABC △的纸片沿DE 折叠后,使点A 落在BC 边上的点F 处．若点D 为AB 边的中点,则下列结论：①BDF △是等腰三角形；②DFE CFE ∠=∠；③DE 是ABC △的中位线,成立的有 A ．①②B ．①③C ．②③D ．①②③图1 图22.如图,等边△ABC 中,BD=CE,AD 与BE 相交于点P,则∠APE 的度数是A ．45° B．55° C．60° D．75° 3.如图3,在ABC △中,13AB AC ==,10BC =,点D 为BC 的中点,DE DE AB ⊥,垂足为点E ,则DE等于A ．1013 B ．1513 C ．6013 D ．7513MEDCBA图3 图4 图5GFE CBADAO BCXY4.如图4,⊿ABC 和⊿CDE 均为等腰直角三角形,点B,C,D 在一条直线上,点M 是AE 的中点,下列结论：①tan∠AEC=CDBC;②S ⊿ABC +S ⊿CDE ≧S ⊿ACE ;③BM⊥DM;④BM=DM.正确结论的个数是 A1个 B2个 C3个 D4个5.如图5,等边三角形ABC 中,D 、E 分别为AB 、BC 边上的两个动点,且总使AD=BE ,AE 与CD 交于点F ,AG ⊥CD 于点G,则FGAF= ． 6.如图6,已知点A 、B 、C 、D 均在已知圆上,AD ∥BC ,AC 平分∠BCD ,∠ADC = 120°,四边形ABCD 的周长为10cm ．图中阴影部分的面积为 A. 32B.3C. 23D. 43图6 图7对折,使点A 落在点1A 处;已知7.如图7,在直角坐标系中,将矩形OABC 沿OB3=OA ,1=AB ,则点1A 的坐标是 ; A 、23,23 B 、23,3 C 、23,23 D 、21,23 三、解答题1如图,矩形ABCD 中,点E 是BC 上一点,AE ＝AD,DF⊥AE 于F,连结DE.求证：DF ＝DC ．2.如图,四边形ABCD 是矩形,△PBC 和△QCD 都是等边三角形,且点P 在矩形上方,点Q 在矩形内．求证：1∠PBA =∠PCQ =30°；2PA =PQ ．3.如图9,已知点D 为等腰直角△ABC 内一点,∠CAD ＝∠CBD ＝15°,E 为AD 延长线上的一点,且CE ＝CA ．1求证：DE 平分∠BDC ；2若点M 在DE 上,且DC=DM ,求证： ME=BD ． 4.如图5AB 是⊙O 的直径,AC 是弦,CD 是⊙O 的切线,C 为切点,AD ⊥CD 于点D ．求证：1∠AOC =2∠ACD ； 2AC 2＝AB ·AD ．、5．把一张矩形ABCD 纸片按如图方式折叠,使点A 与点E 重合,点C 与点F 重合E 、F 两点均在BD 上,折痕分别为BH 、DG;1求证：△BHE ≌△DGF ；2若AB ＝6cm,BC ＝8cm,求线段FG 的长;6．如图8,在Rt △ABC 中,∠BAC=90°,AC=2AB,点D 是AC 的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A 、D 重合, 连结BE 、EC ．试猜想线段BE 和EC 的数量及位置关系,并证明你的猜想．ABCDEAC B DPQABCDEF 第二轮复习之几何三——四边形例1 如图,分别以Rt△ABC 的直角边AC 及斜边AB 向外作等边△ACD、等边△ABE;已知∠BAC=30o,EF⊥AB,垂足为F,连结DF;1试说明AC=EF ；2求证：四边形ADFE 是平行四边形;例2如图,AD ∥FE,点B 、C 在AD 上,∠1＝∠2,BF ＝BC⑴求证：四边形BCEF 是菱形⑵若AB ＝BC ＝CD,求证：△ACF ≌△BDE例3如图,四边形ABCD 是边长为2的正方形,点G 是BC 延长线上一点,连结AG,点E 、F 分别在AG 上,连接BE 、DF,∠1=∠2 ,∠3=∠4.1证明：△ABE≌△DAF； 2若∠AGB=30°,求EF 的长.例4如图,在等腰梯形ABCD 中,已知AD BC ∥,AB DC =,2AD =, 4BC =延长BC 到E ,使CE AD =．1证明：BAD DCE △≌△；2如果AC BD ⊥,求等腰梯形ABCD 的高DF 的值．对应练习1.如图,在菱形ABCD 中,∠A=60°,点P 、Q 分别在边AB 、BC 上,且AP=BQ ． 1求证：△BDQ ≌△ADP ；2已知AD=3,AP=2,求cos ∠BPQ 的值结果保留根号．2、如图,E F ，是四边形ABCD 的对角线AC 上两点,AF CE DF BE DFBE ==，，∥．求证：1AFD CEB △≌△．2四边形ABCD 是平行四边形．3．如罔7,在一方形ABCD 中．E 为对角线AC 上一点,连接EB 、ED,1求证：△BEC ≌△DEC ：2延长BE 交AD 于点F,若∠DEB=140°．求∠AFE 的度数．4.如图,在梯形ABCD 中,AD ∥BC ,延长CB 到点E ,使BE =AD ,连接DE 交AB 于点M .1求证：△AMD ≌△BM E ；2若N 是CD 的中点,且M N=5,BE =2,求BC 的长.第二轮复习之几何四——圆Ⅰ、证线段相等例1：如图,AB 是⊙O 的直径,C 是的中点,CE ⊥AB 于 E ,BD 交CE 于点F ．1求证：CF=BF ；2若CD =6, AC =8,则⊙O 的半径为 ___ ,CE 的长是 ___ ．ABDEFCDAB EC F ACBDEFO2、证角度相等例2如图,AB 是⊙O 的直径,C 为圆周上一点,30ABC ∠=︒,过点B 的切线与CO 的延长线交于点D ．:求证：1CAB BOD ∠=∠；2ABC ∆≌ODB ∆． 3、证切线点拨：证明切线的方法——连半径,证垂直;根据：过半径的外端且垂直于半径的直线是圆的切线例3如图,四边形ABCD 内接于⊙O,BD 是⊙O 的直径, AE⊥CD 于点E,DA 平分∠BDE;1求证：AE 是⊙O 的切线;2若∠DBC=30°,DE=1cm,求BD 的长;例4如图,点A 、B 、C 、D 都在⊙O 上,OC⊥AB,∠ADC=30°． 1求∠BOC 的度数；2求证：四边形AOBC 是菱形．对应练习1．如图,已知⊙O 的直径AB 与弦CD 互相垂直,垂足为点E . ⊙O 的切线BF 与弦AD的延长线相交于点F ,且AD =3,cos ∠BCD= . 1求证：CD ∥BF ； 2求⊙O 的半径； 3求弦CD 的长.2.如图,点D 是⊙O 的直径CA 延长线上一点,点B 在⊙O 上,且AB ＝AD ＝AO ．1求证：BD 是⊙O 的切线．2若点E 是劣弧BC 上一点,AE 与BC 相交于点F,且△BEF 的面积为8,cos∠BFA＝32,求△ACF 的面积．1.一副三角板,如图所示叠放在一起,则图中∠α的度数是A ．75B ．60C ．65D ．55图1 图22．如图2,在边长为4的等边三角形ABC 中,AD 是BC 边上的高,点E 、F 是AD 上的两点,则图中阴影部分的面积是A ．43B ．33C ．23D ．33.如图3,△ABC 中,∠C =90°,AC =3,∠B =30°,点P 是BC 边上的动点,则AP 长不可能是DCBOADOBCA E 例7图43DOEC O图 8OFE BCADCB A O P D图3 图4 A B C D74. 如图4,直角三角形纸片的两直角边长分别为6,8,现将ABC △如图那样折叠,使点A 与点B 重合,折痕为DE ,则tan CBE ∠的值是 A ．247B ．73C ．724D ．135.如图5,ABC △是等腰直角三角形,BC 是斜边,将ABP △绕点A 逆时针旋转后,能与ACP '△重合,如果3AP =,那么PP '的长等于 A ．32B ．23C ．42 D ．336. 图6,已知等边△ABC 中,点D,E 分别在边AB,BC 上,把△BDE 沿直线DE 翻折,使点B 落在点B ˊ处,DB ˊ,EB ˊ分别交边AC 于点F,G,若∠ADF=80o ,则∠EGC 的度数为图5 图67．如图,已知：在平行四边形ABCD 中,AB=4cm,AD=7cm,∠ABC 的平分线交AD•于点E,交CD 的延长线于点F,则DF=______cm ．8．如图,矩形ABCD 中,AB ＝2,BC ＝3,对角线AC 的垂直平分线分别交AD,BC 于点E 、F,连接CE,则CE 的长________.9.如图,BD 是⊙O 的直径,OA ⊥OB,M 是劣弧错误!上一点,过点M 作⊙O 的切线MP 交OA 的延长线于P 点,MD 与OA 交于点N; 1求证：PM=PN ； 2若BD=4,PA=32AO,过B 点作BC ∥MP 交⊙O 于C 点,求BC 的长． 10．如图,在△ABC 中,以AB 为直径的⊙O 交BC 于点P,PD ⊥AC 于点D,且PD 与⊙O 相切．1求证：AB ＝AC ；2若BC ＝6,AB ＝4,求CD 的值．11．一副直角三角板如图放置,点C 在FD 的延长线上,AB ∥CF,∠F=∠ACB=90°, ∠ E=45°,∠A=60°,AC=10,试求CD 的长．12．如图,四边形ABCD 是边长为a 的正方形,点G ,E 分别是边AB ,BC 的中点,∠AEF =90o,且EF 交正方形外角的平分线CF 于点F ． 1证明：∠BAE =∠FEC ； 2证明：△AGE ≌△ECF ； 3求△AEF 的面积．13．如图,矩形ABCD 中,53AB AD ==，．点E 是CD 上的动点,以AE 为直径的O ⊙与AB 交于点F ,过点F 作FG BE ⊥于点G ．1当E 是CD 的中点时：①tan EAB ∠的值为______________； ② 证明：FG 是O ⊙的68CEABD切线；2试探究：BE 能否与O ⊙相切若能,求出此时DE 的长；若不能,请说明理由．几何之——解直角三角形1在△ABC 中,∠C＝90°,sinA＝45,则tanB ＝A ．43B ．34C ．35D ．452、在 ABC 中,若｜sinA-22 |+23-cosB 2=0, ∠A.∠B 都是锐角,则∠C 的度数是A. 750B. 9003、如下左图,在△ABC 中,∠C=90°,AB=13,BC=5,则sinA 的值是A 、513B 、1213 C 、512D 、1354如上右图,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点,若EF=2, BC=5,CD=3,则tanC 等于A 、34B 、43C 、35D 、455、如,在矩形ABCD 中,DE⊥AC 于E,设∠ADE=α,且53cos =α, AB = 4, 则AD 的长为． A3 B316 C 320 D 516 6在锐角△ABC 中,∠BAC=60°,BD、CE 为高,F 为BC 的中点,连接DE 、DF 、EF,则结论：①DF=EF；②AD：AB=AE ：AC ；③△DEF 是等边三角形；④BE+CD=BC；⑤当∠ABC=45°时,BE=√2DE 中,一定正确的有A 、2个B 、3个C 、4个D 、5个7.084sin 45(3)4-︒+-π+-=为528.某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离米,则这个破面的坡度为 . 9.如图,已知直线1l∥2l ∥3l ∥4l ,相邻两条平行直线间的距离都是1,如果正方形ABCD 的四个顶点分别在四条直线上,则sin α= ．直角三角形常见模型1 张华同学在学校某建筑物的C 点处测得旗杆顶部A 点的仰角为30°,旗杆底部B 点的俯角为45°．若旗杆底部B 点到建筑物的水平距离BE=9米,旗杆台阶高1米,试求旗杆AB 的高度;2．海船以5海里/小时的速度向正东方向行驶,在A 处看见灯塔B 在海船的北偏东DE OCBG FAABC DαAABCDEADBE图6i =1:3C60°方向,2小时后船行驶到C 处,发现此时灯塔B 在海船的北偏西45方向,求此时灯塔B 到C 处的距离; 3某年入夏以来,松花江哈尔滨段水位不断下降,一条船在松花江某段自西向东沿直线航行,在A 处测得航标C 在北偏东60°方向上;前进100m 到达B 处,又测得航标C 在北偏东45°方向上如图,在以航标C 为圆心,120m 为半径的圆形区域内有浅滩,如果这条船继续前进,是否有被浅滩阻碍的危险4如图6,梯形ABCD 是拦水坝的横断面图,图中3:1=i 是指坡面的铅直高度DE 与水平宽度CE 的比,∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD 的面积．结果保留三位有效数字.参考数据：3≈,2≈3 1.73≈。

中考复习初中数学几何证明经典试题(含答案)

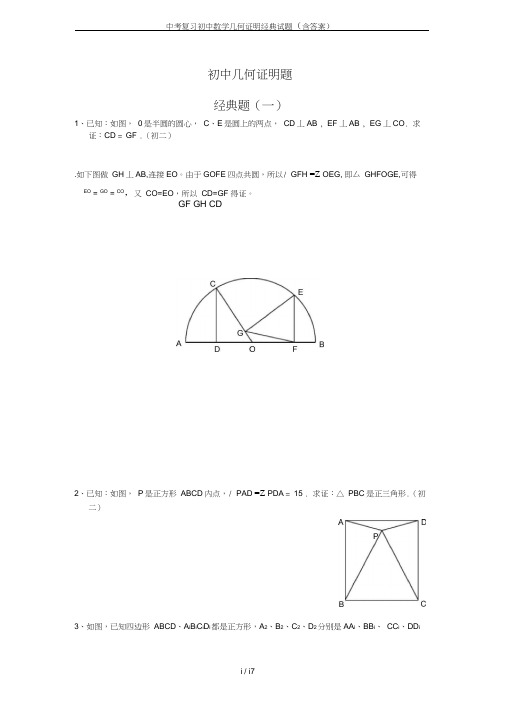
初中几何证明题经典题（一）1、已知：如图，0是半圆的圆心，C、E是圆上的两点，CD丄AB , EF丄AB , EG丄CO. 求证：CD = GF .（初二）.如下图做GH丄AB,连接EO。

由于GOFE四点共圆，所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO，又CO=EO，所以CD=GF 得证。

GF GH CD2、已知：如图，P是正方形ABCD内点，/ PAD =Z PDA = 15°. 求证：△ PBC是正三角形.（初二）3、如图，已知四边形ABCD、A i B i C i D i都是正方形，A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证：AP = AQ .（初二）3、如果上题把直线 MN 由圆外平移至圆内，则由此可得以下命题:设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN P 、Q .4、 1、求证：四边形 A 2B 2C 2D 2是正方形.（初二）已知: 求证: 如图，在四边形的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中，AD = BC , M 、N 分别是 AB 、CD 的中点，AD 、BC 于E 、F .经典题（二）已知： (1) 求证：AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心（各边高线的交点），0为外心，且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线，过O 作OA 丄MN 于A ，自A 引圆的两条直线，交圆于DCGN求证：AP = AQ .（初二）ECAM NP4、如图，分别以厶 ABC 的AC 和BC 为一边，在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ，点P 是EF 的中点.求证：点P 到边AB 的距离等于 AB 的一半.（初二）经典题（二）1、如图，四边形 ABCD 为正方形, 求证：CE = CF .（初二）2、如图，四边形 ABCD 为正方形，DE // AC ,且CE = CA ，直线EC 交DA 延长线于F . 求证：AE = AF .（初二）DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图，PC 切圆0于C , AC 为圆的直径，PEF 为圆的割线，AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形，求证： AB • CD + AD • BC = AC • BD .（初三）B 、D .求证: AB = DC , BC = AD .（初三）1、已知：△ ABC 是正三角形，P 是三角形内一点求：/ APB 的度数.（初二）2、设P 是平行四边形 ABCD 内部的一点，且/求证：/ PAB = Z PCB .（初二）4、平行四边形 ABCD 中，设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证：/ DPA =Z DPC .（初二）AO DB EFC求证:4、如图，△ ABC 中，/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点，/ DCA = 30°, / EBA = 20°，求/ BED 的度数. LiB C经典题（一）1•如下图做GH丄AB,连接E0。

初中数学几何证明题经典例题(超全)

求证：BE=AF
完整版ppt
9
• 已知：如图正方形ABCD，P、Q分别是BC、 DC上的点，若∠1=∠2 求证：PB+QD=PA
完整版ppt
10
• 已知：如图正方形ABCD，AC、BD交于点 O，E、F分别是BC、OD的中点求证： AF⊥EF
完整版ppt
11
• 已知：如图，，AB=BC，D、E分别是AB、 BC上一点，DM⊥AE交AC于M， BN⊥AE 交AC于N，若BD=BE求证：MN=NC。
完整版ppt
20
• 如图，在四边形ABCD中，AB=DC，E、F 分别是AD、BC的中点，G、H分别是BD、 AC的中点，猜一猜EF与GH的位置关系，并证明你的结论．
完整版ppt
21
• 如图，分别以△ABC的三边为边长，在BC 的同侧作等边三角形ABD，等边三角形 BCE，等边三角形ACF，连接DE，EF。求证：四边形ADE 2，AB=3AC，BE⊥AD，
求证：AD=DE
完整版ppt
15
• 已知：如图，AB//CD， D=90 o， BE=EC=DC，求证： AEC=3 BAE
完整版ppt
16
• 已知如图，AB=DC，AE=DE，BF=FC，
FE交BA、CD的延长线于G、H，求证：1= 2。
完整版ppt
17
• 已知:如图，正方形ABCD中，E是DC上一点，DF⊥AE交BC于F 求证：OE⊥OF
完整版ppt
18
• 已知：如图，AB//CD， ADC=90o ， BE=EC，求证： AED=2 EDC
完整版ppt
19
• 已知:如图，正方形ABCD中，E是DC上一点，DF⊥AE交BC于F 求证：OE⊥OF

初二数学几何证明题（5篇可选）

初二数学几何证明题（5篇可选）第一篇：初二数学几何证明题1.在△ABC中，AB=AC，D在AB上，E在AC的延长线上，且BD=CE，线段DE交BC于点F，说明：DF=EF。

2.已知：在正方形ABCD中，M是AB的中点，E是AB延长线上的一点，MN垂直DM于点M，且交∠CBE的平分线于点N.（1）求证：MD＝MN.（2）若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变，则（1）的结论还成立吗？如果成立，请证明，如果不成立，请说明理由。

3.。

如图，点E,F分别是菱形ABCD的边CD和CB延长线上的点，且DE=BF，求证∠E=∠F。

4，如图，在△ABC中，D,E,F,分别为边AB,BC,CA,的中点，求证四边形DECF为平行四边形。

5.如图，在菱形ABCD中，∠DAB=60度，过点C作CE垂直AC 且与AB的延长线交与点E，求证四边形AECD是等腰梯形？6.如图，已知平行四边形ABCD中，对角线AC,BD，相交与点0，E是BD延长线上的点，且三角形ACE是等边三角形。

1.求证四边形ABCD是菱形。

2.若∠AED=2∠EAD，求证四边形ABCD是正方形。

7.已知正方形ABCD中，角EAF=45度，F点在CD边上，E点在BC边上。

求证：EF=BE+DF第二篇：初二几何证明题1如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE的延长线于F，且AF=DCCF．（1）求证：D是BC的中点；（2）如果AB=ACADCF的形状，并证明你的结论AEB第三篇：初二几何证明题初二几何证明题1.已知：如图，在△ABC中，AD⊥BC，垂足为D，BE⊥AC，垂足为E。

M为AB中点，联结ME,MD、ED求证：角EMD=2角DAC证明：∵M为AB边的中点，AD⊥BC，BE⊥AC，∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图，已知四边形ABCD中，AD=BC,E、F分别是AB、CD中点，AD、BC的延长线与EF的延长线交于点H、D求证：∠AHE=∠BGE证明：连接AC，作EM‖AD交AC于M，连接MF.如下图：∵E是CD的中点，且EM‖AD，∴EM=1/2AD，M是AC的中点，又因为F是AB的中点∴MF‖BC，且MF=1/2BC.∵AD=BC，∴EM=MF，三角形MEF为等腰三角形，即∠MEF=∠MFE.∵EM‖AH，∴∠MEF=∠AHF ∵FM‖BG，∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。

中考数学总复习——几何证明分类试题汇编

C ABD中考数学总复习——几何证明分类试题汇编三角形总复习题1、求证等腰三角形两腰上的高线相等（先画出图，再写出已知、求证和证明）。

2．求证：有两条高相等的三角形是等腰三角形（先画出图，再写出已知、求证和证明）1.如图，已知在△ABC 中，CD ⊥AB 于D ，AC ＝20，BC ＝15，DB ＝9。

(1)求DC 的长。

(2)求AB 的长。

2.如图所示的一块地，∠ADC=90°，AD=12m ，CD=9m ，AB=39m ，BC=36m ，求这块地的面积。

ADEBC3．如图，铁路上A ，B 两点相距25km ，C ，D 为两村庄，DA ⊥AB 于A ，CB ⊥AB 于B ，已知DA=15km ，CB=10km ，现在要在铁路AB 上建一个土特产品收购站E ，使得C ，D 两村到E 站的距离相等，则E 站应建在离A 站多少km 处？18．如图６，A 、D 、F 、B 在同一直线上，AD=BF ,AE =BC , 且 AE ∥BC ．E求证：（1）△AEF≌△BCD；(2)EF∥CD．4.如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：(1)AD=CB；(2)AE=CF；(3)∠B=∠D；(4)AD∥BC。

请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程.18．如图10，在△AFD 和△CEB 中，点A 、E 、F 、C 在同一条直线上，有下面四个结断：①AD =CB ；②AE =CF ；③∠B =∠D ；④AD ∥BC ．请用其中三个作为条件，余下的一个作为结论编一道数学题，并证明结论成立．5.如图，AD ⊥CD ，AB=10，BC=20，∠A=∠C=30°，求AD 、CD 的长.CABEF D图6. 已知，如图，⊿ABC 中，∠A = 900，AB =AC ，D 是BC 边上的中点，E 、F 分别是AB 、AC 上的点，且BE = AF ，求证：ED ⊥FD7.已知：如图，AB ＝AC ，CE ⊥AB 于E ，BD ⊥AC 于D ，求证：BD ＝CE .DBCEF8.已知：如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使CE＝CD．求证：BD＝DE．9．如图：已知在ABC，D为BC边的中点，过点D作△中，AB AC，.⊥，⊥，垂足分别为E FDE AB DF AC（1）求证：BED CFD △≌△；（2）若90A ∠=°，求证：四边形DFAE 是正方形.10.如图，△ABC 中，AB =AC ，AD 、AE 分别是∠BAC 和∠BAC 和外角的平分线，BE ⊥AE ．（1）求证：DA ⊥AE ；（2）试判断AB 与DE 是否相等？并证明你的结论．DCBE AFA BCD EF11. 已知，如图，O 是△ABC 的∠ABC 、∠ACB 的角平分线的交点，OD∥AB 交BC 于D ，OE ∥AC 交BC 于E ，若12. 已知，如图⊿ABC 中，∠ACB 的平分线交AB 于E ，∠ACB 的补角∠ACD 的平分线为CG ，EG ∥BC 交AC 于F ，EF 会与FG 相等吗？为什么？C13.（2012临沂）如图，点A．F、C．D在同一直线上，点B和点E 分别在直线AD的两侧，且AB=DE，∠A=∠D，AF=DC．（1）求证：四边形BCEF是平行四边形，（2）若∠ABC=90°，AB=4，BC=3，当AF为何值时，四边形BCEF是菱形．ADEF 14.（2012•恩施州）如图，在△ABC 中，AD ⊥BC 于D ，点D ，E ，F 分别是BC ，AB ，AC 的中点．求证：四边形AEDF 是菱形．15．（2012•南通）（本小题满分10分）如图，菱形ABCD 中，∠B ＝60º，点E 在边BC 上，点F 在边CD 上．(1)如图1，若E 是BC 的中点，∠AEF ＝60º，求证：BE ＝DF ； (2)如图2，若∠EAF ＝60º，求证：△AEF 是等边三角形．16.（2011广东）如图，分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE 。

中考数学几何证明复习题

中考数学几何证明复习题第一篇：中考数学几何证明复习题几何证明练习1.如图13－1，一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起．现正方形ABCD保持不动，将三角尺GEF绕斜边EF的中点O（点O也是BD中点）按顺时针方向旋转．（1）如图13－2，当EF与AB相交于点M，GF与BD相交于点N时，通过观察或测量BM，FN的长度，猜想BM，FN满足的数量关系，并证明你的猜想；（2）若三角尺GEF旋转到如图13－3所示的位置时，线段FE的延长线与AB的延长线相交于点M，线段BD的延长线与GF的延长线相交于点N，此时，（1）中的猜想还成立吗？若成立，请证明；若不成立，请说明理由．A(E)图13－1 图13－2图13－32.将两块全等的含30°角的三角尺如图(1)摆放在一起，它们的较短直角边长为3．(1)将△ECD沿直线l向左平移到图(2)的位置，使E点落在AB上，则CC′=______；(2)将△ECD绕点C逆时针旋转到图(3)的位置，使点E落在AB上，则△ECD绕点C旋转的度数=______；(3)将△ECD沿直线AC翻折到图(4)的位置，ED′与AB相交于点F，求证AF=FD′A A A AE E’ E’D’ F’l B(2)(3)D’(4)3.填空或解答：点B、C、E在同一直线上，点A、D在直线CE的同侧，AB＝AC，EC＝ED，∠BAC＝∠CED，直线AE、BD交于点F。

(1)如图①，若∠BAC＝60°，则∠AFB＝_________；如图②，若∠BAC＝90°，则∠AFB＝_________；(2)如图③，若∠BAC＝α，则∠AFB＝_________(用含α的式子表示)；(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合)，得图④或图⑤。

在图④中，∠AFB与∠α的数量关系是________________；在图⑤中，∠AFB与∠α的数量关系是________________。

（完整版）八年级几何证明题集锦及解答值得收藏

（完整版）八年级几何证明题集锦及解答值得收藏八年级几何全等证明题归纳1.如图，梯形ABCD中，AD∥BC，∠DCB=45°，BD⊥CD．过点C作CE⊥AB 于E，交对角线BD于F，点G为BC中点，连接EG、AF．求证：CF=AB+AF．证明：在线段CF上截取CH=BA，连接DH，∵BD⊥CD，BE⊥CE，∴∠EBF+∠EFB=90°，∠DFC+∠DCF=90°，∵∠EFB=∠DFC，∴∠EBF=∠DCF，∵DB=CD，BA=CH，∴△ABD≌△HCD，∴AD=DH，∠ADB=∠HDC，∵AD∥BC，∴∠ADB=∠DBC=45°，∴∠HDC=45°，∴∠HDB=∠BDC—∠HDC=45°，∴∠ADB=∠HDB，∵AD=HD，DF=DF，∴△ADF≌△HDF，∴AF=HF，∴CF=CH+HF=AB+AF，∴CF=AB+AF．2.如图，ABCD为正方形，E为BC边上一点，且AE=DE，AE与对角线BD交于点F，连接CF，交ED于点G．判断CF与ED的位置关系，并说明理由．解：垂直．理由：∵四边形ABCD为正方形，∴∠ABD=∠CBD，AB=BC，∵BF=BF，∴△ABF≌△CBF，∴∠BAF=∠BCF，∵在RT△ABE和△DCE中，AE=DE，AB=DC，∴RT△ABE≌△DCE，∴∠BAE=∠CDE，∴∠BCF=∠CDE，∵∠CDE+∠DEC=90°，∴∠BCF+∠DEC=90°，∴DE⊥CF．3.如图，在直角梯形ABCD中，AD∥BC，∠A＝90o，AB＝AD，DE⊥CD交AB于E，DF平分∠CDE交BC于F，连接EF．证DA明：CF＝EF解：EB F C过D作DG⊥BC于G．由已知可得四边形ABGD为正方形，∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG，∴∠ADE=∠GDC．又∵∠A=∠DGC且AD=GD，∴△ADE≌△GDC，∴DE=DC且AE=GC．在△EDF和△CDF中∠EDF=∠CDF，DE=DC，DF为公共边，∴△EDF ≌△CDF，∴EF=CF4.已知：在⊿ABC中，∠A=900，AB=AC，D是AC的中点，AE⊥BD，AE延长线交BC于F，求证：∠ADB=∠FDC。

20102017年成都中考数学真题之几何证明题汇编含答案解析

2010-2017年成都市中考数学真题几何证明题部分汇编安博教育杨老师编制1、（2010成都17．）已知：如图，AB 与O 相切于点C ，OA OB =，O 的直径为4,8AB =．（1）求OB 的长；（2）求sin A 的值．2、（2010成都18．）如图，已知反比例函数ky x=与一次函数y x b =+的图象在第一象限相交于点(1,4)A k -+．（1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B 的坐标，并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．3、（2010成都20．）已知：在菱形ABCD 中，O 是对角线BD 上的一动点．（1）如图甲，P 为线段BC 上一点，连接PO 并延长交AD 于点Q ，当O 是BD 的中点时，求证：OP OQ =；（2）如图乙，连结AO 并延长，与DC 交于点R ，与BC 的延长线交于点S ．若460,10AD DCB BS ===，∠，求AS 和OR 的长．4、（2010成都27．）已知：如图，ABC ∆内接于O ，AB 为直径，弦CE AB ⊥于F ，C是AD 的中点，连结BD 并延长交EC 的延长线于点G ，连结AD ，分别交CE 、BC 于点P 、Q ．（1）求证：P 是ACQ ∆的外心；（2）若3tan ,84ABC CF ∠==,求CQ 的长；（3）求证：2()FP PQ FP FG +=．5、（2010成都28．）在平面直角坐标系xOy 中，抛物线2y ax bx c =++与x 轴交于A B 、两点（点A 在点B 的左侧），与y 轴交于点C ，点A 的坐标为(30)-，，若将经过A C 、两点的直线1y kx b =+沿y 轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线2x =-．（1）求直线AC 及抛物线的函数表达式；（2）如果P 是线段AC 上一点，设ABP ∆、BPC ∆的面积分别为ABP S ∆、BPC S ∆，且:2:3ABP BPC S S ∆∆=，求点P 的坐标；（3）设Q 的半径为l ，圆心Q 在抛物线上运动，则在运动过程中是否存在Q 与坐标轴相切的情况？若存在，求出圆心Q 的坐标；若不存在，请说明理由．并探究：若设⊙Q 的半径为r ，圆心Q 在抛物线上运动，则当r 取何值时，⊙Q 与两坐轴同时相切？6、（2011成都19.）如图，已知反比例函数(0)k y k x =≠的图象经过点(12，8)，直线y x b =-+经过该反比例函数图象上的点Q(4，m)．(1)求上述反比例函数和直线的函数表达式；(2)设该直线与x 轴、y 轴分别相交于A 、B 两点，与反比例函数图象的另一个交点为P ，连结0P 、OQ ，求△OPQ 的面积．7、（2011成都20）如图，已知线段AB∥CD，AD 与B C 相交于点K ，E 是线段AD 上一动点。

中考数学专题复习8几何初步及三角形相关计算(原卷版)

几何初步及三角形相关计算复习考点攻略考点一直线、射线、线段相关概念和性质1．直线的性质（1）两条直线相交.只有一个交点；（2）经过两点有且只有一条直线.即两点确定一条直线；（3）直线的基本事实：经过两点有且只有一条直线．2．线段的性质：两点确定一条直线.两点之间.线段最短.两点间线段的长度叫两点间的距离．3．线段的中点性质：若C是线段AB中点.则AC=BC=12AB；AB=2AC=2BC．4．两条直线的位置关系在同一平面内.两条直线只有两种位置关系：平行和相交．5．垂线的性质（1）两条直线相交所构成的四个角中有一个角是直角.则这两条直线互相垂直.其中一条直线叫做另一条直线的垂线；（2）①经过一点有且只有一条直线与已知直线垂直；②直线外一点与直线上各点连接的所有线段中.垂线段最短．6．点到直线的距离：从直线外一点向已知直线作垂线.这一点和垂足之间线段的长度叫做点到直线的距离．7. 角：有公共端点的两条射线组成的图形．8．角平分线（1）定义：在角的内部.以角的顶点为端点把这个角分成两个相等的角的射线（2）角平分线的性质：①若OC是∠AOB的平分线.则∠AOC=∠BOC=12∠AOB.∠AOB=2∠AOC =2∠BOC．②角平分线上的点到角两边的距离相等。

9．度、分、秒的运算方法1°=60′.1′=60″.1°=3600″．1周角=2平角=4直角=360°．10．余角和补角（1）余角：∠1＋∠2＝90°⇔∠1与∠2互为余角；（2）补角：∠1＋∠2＝180°⇔∠1与∠2互为补角．（3）性质：同角（或等角）的余角相等；同角（或等角）的补角相等．11．方向角和方位角在描述方位角时.一般应先说北或南.再说偏西或偏东多少度.而不说成东偏北（南）多少度或西偏北（南）多少度．当方向角在45°方向上时.又常常说成东南、东北、西南、西北方向．【例1】如图.在数轴上有A、B、C、D四个整数点（即各点均表示整数）.且2AB=BC=3CD.若A、D两点表示的数分别为-5和6.且AC的中点为E.BD的中点为M.BC之间距点B的距离为13BC的点N.则该数轴的原点为A．点E B．点FC．点M D．点N【例2】如图.∠AOB=180°.∠BOC=80°.OD平分∠AOC.∠DOE=3∠COE.求∠BOE．【例3】如图.要修建一条公路.从A村沿北偏东75°方向到B村.从B村沿北偏西25°方向到C 村．若要保持公路CE与AB的方向一致.则∠ECB的度数为A．80°B．90°C．100°D．105°【例4】计算：18°30′=__________°考点二立体图形1．常见的立体图形有：球、柱体和锥体．圆柱和棱柱的区别：圆柱的底面是圆.棱柱的底面是多边形；圆柱的侧面是曲面.棱柱的侧面是四边形；圆锥和棱锥的区别：圆锥的底面是圆.侧面是曲面；棱锥的底面是多边形.侧面是三角形．2．点动成线.线动成面.面动成体.线没有粗细.点没有大小．3．设立体图形的面数为F.顶点数为V.棱数为E.则F+V-E=2．4．正方体的平面展开图有如下11种类型：【例5】如图是一个正方体包装盒的表面积展开图.若在其中的三个正方形A、B、C内分别填上适当的数.使得将这个表面展开图沿虚线折成正方体后.相对面上的两数互为相反数.则填在A、B、C内的三个数依次为A．0.-2.1 B．0.1.2C．1.0.-2 D．-2.0.1考点三三角形的基本概念(1)三角形的概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

中考数学第一轮复习专题八三角形(2)(无答案) 浙教版(2021年整理)

2017届中考数学第一轮复习专题八三角形（2）（无答案）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2017届中考数学第一轮复习专题八三角形（2）（无答案）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2017届中考数学第一轮复习专题八三角形（2）（无答案）浙教版的全部内容。

三角形（2）班级姓名学号一、选择题1.如图,△ABC中，AB=AC，AD是∠BAC的平分线．已知AB=5，AD=3，则BC的长为（）A．5 B．6 C．8 D．102.如图，在△ABC中，∠ABC=90°，AB=8,BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为（）A．7 B．8 C．9 D．103.已知3是关于x的方程x2﹣（m+1）x+2m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为（）A．7 B．10 C．11 D．10或114.如图，在矩形ABCD中（AD＞AB)，点E是BC上一点,且DE=DA，AF⊥DE,垂足为点F，在下列结论中，不一定正确的是（)A．△AFD≌△DCE B．AF=AD C．AB=AF D．BE=AD﹣DF5。

如图，在正方形ABCD中,连接BD，点O是BD的中点，若M、N是边AD上的两点,连接MO、NO，并分别延长交边BC于两点M′、N′，则图中的全等三角形共有（)A．2对 B．3对 C．4对 D．5对6。

如图，点O在△ABC内，且到三边的距离相等．若∠BOC=120°，则tanA的值为（）A． B． C． D．7。

【名师点睛】2017-2018学年八年级数学上册全等三角形证明题专题复习46题（含答案）

【名师点睛】2017-2018学年⼋年级数学上册全等三⾓形证明题专题复习46题（含答案）2017-2018学年⼋年级数学上册全等三⾓形证明题专题复习45题1.如图,在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证：AF平分∠BAC.2.如图，∠DCE=90°，CD=CE，AD⊥AC，BE⊥AC，垂⾜分别为A．B．试说明AD+AB=BE．3.如图,点D是AB上⼀点,DF交AC于点E,DE=FE,FC∥AB.求证：AE=CE．4.如图，AB=AE，∠1=∠2，∠C=∠D．求证：△ABC≌△AED．5.如图，已知△EFG≌△NMH，∠F与∠M是对应⾓．（1）写出相等的线段与⾓．（2）若EF=2.1cm，FH=1.1cm，HM=3.3cm，求MN和HG的长度．6.如图，AB=DC，AC=DB，求证：AB∥CD．7.如图，E、A．C三点共线，AB∥CD，∠B=∠E,，AC=CD。

求证：BC=ED。

8.如图，在Rt△ABC中，∠ABC=90°，点D在边AB上，使DB=BC，过点D作EF⊥AC，分别交AC于点E，CB的延长线于点F．求证：AB=BF．9.如图，点A，B，C，D在⼀条直线上，△ABF≌△DCE．你能得出哪些结论？（请写出三个以上的结论）10.如图，在△AEC中，点D是EC上的⼀点，且AE=AD，AB=AC，∠1=∠2．求证：BD=EC．11.如图，已知DE⊥AC，BF⊥AC，垂⾜分别是E、F，AE=CF，DC∥AB，（1）试证明：DE=BF；（2）连接DF、BE，猜想DF与BE的关系？并证明你的猜想的正确性．12.如图，△ABC和△ADE都是等腰三⾓形，且∠BAC=90°，∠DAE=90°，B，C，D在同⼀条直线上．求证：BD=CE．13.已知：如图AC，BD相交于点O，∠A=∠D，AB=CD，求证：△AOB≌△DOC．14.如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，BD的延长线垂直于过C点的直线于E，直线CE交BA的延长线于F．求证：BD=2CE．15.如图，OM平分∠POQ，MA⊥OP,MB⊥OQ，A．B为垂⾜，AB交OM于点N．求证：∠OAB=∠OBA16.如图：AD 是△ABC 的⾼，E 为AC 上⼀点，BE 交AD 于F ，且有BF=AC ，FD=CD 。

中考数学几何证明题--(专题练习答案详解)

几何证明题专题1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H在边BF上，且∠HDF=∠E，连接CH，求证：∠BCH=45°﹣∠EBC．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．7、已知：如图，ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD 为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．30、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．参考答案1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．证明：（1）已知等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，∴AB=DC，∠BAE=∠CDE，AE=DE，∴△BAE≌△CDE，∴BE=CE；（2）延长CD和BE的延长线交于H，∵BF⊥CD，∠HEC=90°，∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH，又∠BEC=∠CEH=90°，BE=CE（已证），∴△BEG≌△CEH，∴EG=EH，BG=CH=DH+CD，∵△BAE≌△CDE（已证），∴∠AEB=∠GED，∠HED=∠AEB，∴∠GED=∠HED，又EG=EH（已证），ED=ED，∴△GED≌△HED，∴DG=DH，∴BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：∵ED平分∠AEF，∠A=∠DFE=90°，∴AD=DF，∵DF=DC﹣FC，∵△EBH≌△GFC，∴FC=BH=1，∴AD=4﹣1=3．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．（2）过E点作EM⊥DB于点M，四边形FDME是矩形，FE=DM，∠BME=∠BCE=90°，∠BEC=∠MBE=60°，△BME≌△ECB，BM=CE，继而可证明BD=DM+BM=EF+CE．（1）解：∵AD=CD，∴∠DAC=∠DCA，∵DC∥AB，∴∠DCA=∠CAB，∴，∵DC∥AB，AD=BC，∴∠DAB=∠CBA=60°，∴∠ACB=180°﹣（∠CAB+∠CBA）=90°，∴∠BCE=180°﹣∠ACB=90°，∵BE⊥AB，∴∠ABE=90°，∴∠CBE=∠ABE﹣∠ABC=30°，在Rt△BCE中，BE=2CE=2，，∴…（5分）（2）证明：过E点作EM⊥DB于点M，∴四边形FDME是矩形，∴FE=DM，∵∠BME=∠BCE=90°，∠BEC=∠MBE=60°，∴△BME≌△ECB，∴BM=CE，∴BD=DM+BM=EF+CE…（10分）4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E作EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．解答：（1）证明：延长EF交AD于G（如图），在平行四边形ABCD中，AD∥BC，AD=BC，∵EF∥CA，EG∥CA，∴四边形ACEG是平行四边形，∴AG=CE，又∵，AD=BC，∴，∵AD∥BC，∴∠ADC=∠ECF，在△CEF和△DGF中，∵∠CFE=∠DFG，∠ADC=∠ECF，CE=DG，∴△CEF≌△DGF（AAS），∴CF=DF，∵四边形ABCD是平行四边形，∴OB=OD，∴OF∥BE．（2）解：如果梯形OBEF是等腰梯形，那么四边形ABCD是矩形．证明：∵OF∥CE，EF∥CO，∴四边形OCEF是平行四边形，∴EF=OC，又∵梯形OBEF是等腰梯形，∴BO=EF，∴OB=OC，∵四边形ABCD是平行四边形，∴AC=2OC，BD=2BO．∴AC=BD，∴平行四边形ABCD是矩形．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H 在边BF 上，且∠HDF=∠E ，连接CH ，求证：∠BCH=45°﹣∠EBC ．（1）解：连接BD ，由∠ABC=90°，AD ∥BC 得∠GAD=90°，又∵BF ⊥CD ，∴∠DFE=90°又∵DG=DE ，∠GDA=∠EDF ，∴△GAD ≌△EFD ，∴DA=DF ，又∵BD=BD ，∴Rt △BAD ≌Rt △BFD （HL ），∴BF=BA=，∠ADB=∠BDF 又∵CF=6，∴BC=，又∵AD ∥BC ，∴∠ADB=∠CBD ，∴∠BDF=∠CBD ，∴CD=CB=8．（2）证明：∵AD ∥BC ，∴∠E=∠CBF ，∵∠HDF=∠E ，∴∠HDF=∠CBF ，由（1）得，∠ADB=∠CBD ，∴∠HDB=∠HBD ，∴HD=HB ，由（1）得CD=CB ，CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ，∴∠DCH=∠BCH ，∴∠BCH=∠BCD==．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．解：（1）连AC，过C作CM⊥AD于M，如图，在Rt△ABC中，AB=6，sin∠ACB==，∴AC=10，∴BC=8，在Rt△CDM中，∠D=45°，∴DM=CM=AB=6，∴AD=6+8=14，∴梯形ABCD的面积=•（8+14）•6=66（cm2）；（2）证明：过G作GN⊥AD，如图，∵∠D=45°，∴△DNG为等腰直角三角形，∴DN=GN，又∵AD∥BC，∴∠BFH=∠FHN，而∠EFH=∠FHG，∴∠BFE=∠GHN，∵EF=GH，∴Rt△BEF≌Rt△NGH，∴BE=GN，BF=HN，∴DA=AN+DN=AN+DG=BF+BE．7、已知：如图，▱ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．（1）证明：如图．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵DF=CD，∴AB∥DF．∵DF=CD，∴AB=DF．∴四边形ABDF是平行四边形，∴AE=DE．（2）解：∵四边形ABCD是平行四边形，且AB=BC，∴四边形ABCD是菱形．∴AC⊥BD．∴∠COD=90°．∵四边形ABDF是平行四边形，∴AF∥BD．∴∠CAF=∠COD=90°．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．（1）证明：在△DAE和△DCE中，∠ADE=∠CDE（正方形的对角线平分对角），ED=DE（公共边），AE=CE（正方形的四条边长相等），∴△DAE≌△DCE（SAS），∴∠DAE=∠DCE（全等三角形的对应角相等）；（2）解：如图，由（1）知，△DAE≌△DCE，∴AE=EC，∴∠EAC=∠ECA（等边对等角）；又∵CG=CE（已知），∴∠G=∠CEG（等边对等角）；而∠CEG=2∠EAC（外角定理），∠ECB=2∠CEG（外角定理），∴4∠EAC﹣∠ECA=∠ACB=45°，∴∠G=∠CEG=30°；过点C作CH⊥AG于点H，∴∠FCH=30°，∴在直角△ECH中，EH=CH，EG=2CH，在直角△FCH中，CH=CF，∴EG=2×CF=3CF．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．（1）证明：连接PC．∵ABCD是正方形，∴∠ABE=∠ADF=90°，AB=AD．∵BE=DF，∴△ABE≌△ADF．（SAS）∴∠BAE=∠DAF，AE=AF．∴∠EAF=∠BAD=90°．∵P是EF的中点，∴PA=EF，PC=EF，∴PA=PC．又AD=CD，PD公共，∴△PAD≌△PCD，（SSS）∴∠ADP=∠CDP，即DP平分∠ADC；（2）作PH⊥CF于H点．∵P是EF的中点，∴PH=EC．设EC=x．由（1）知△EAF是等腰直角三角形，∴∠AEF=45°，∴∠FEC=180°﹣45°﹣75°=60°，∴EF=2x，FC=x，BE=2﹣x．在Rt△ABE中，22+（2﹣x）2=（x）2解得x1=﹣2﹣2（舍去），x2=﹣2+2．∴PH=﹣1+，FD=（﹣2+2）﹣2=﹣2+4．=（﹣2+4）×=3﹣5．∴S△DPF10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．（1）证明：∵AD∥BC，∴∠DAE=∠F，∠ADE=∠FCE．∵E为CD的中点，∴ED=EC．∴△ADE≌△FCE．∴EF=EA．（5分）（2）解：连接GA，∵AD∥BC，∠ABC=90°，∴∠DAB=90°．∵DG⊥BC，∴四边形ABGD是矩形．∴BG=AD，GA=BD．∵BD=BC，∴GA=BC．由（1）得△ADE≌△FCE，∴AD=FC．∴GF=GC+FC=GC+AD=GC+BG=BC=GA．∵由（1）得EF=EA，∴EG⊥AF．（5分）11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，∴AF=AD，∠FAD=60°（1分）∵∠DAB=90°，∠EAD=15°，AD=AB（2分）∴∠FAE=∠BAE=75°，AB=AF，（3分）∵AE为公共边∴△FAE≌△BAE（4分）∴EF=EB（5分）（2）解：如图，连接EC．（6分）∵在等边三角形△ADF中，∴FD=FA，∵∠EAD=∠EDA=15°，∴ED=EA，∴EF是AD的垂直平分线，则∠EFA=∠EFD=30°．（7分）由（1）△FAE≌△BAE知∠EBA=∠EFA=30°．∵∠FAE=∠BAE=75°，∴∠BEA=∠BAE=∠FEA=75°，∴BE=BA=6．∵∠FEA+∠BEA+∠GEB=180°，∴∠GEB=30°，∵∠ABC=60°，∴∠GBE=30°∴GE=GB．（8分）∵点G是BC的中点，∴EG=CG∵∠CGE=∠GEB+∠GBE=60°，∴△CEG为等边三角形，∴∠CEG=60°，∴∠CEB=∠CEG+∠GEB=90°（9分）∴在Rt△CEB中，BC=2CE，BC2=CE2+BE2∴CE=，∴BC=（10分）；解法二：过C作CQ⊥AB于Q，∵CQ=AB=AD=6，∵∠ABC=60°，∴BC=6÷=4．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．（1）证明：∵AB=DC，∴梯形ABCD为等腰梯形．∵∠C=60°，∴∠BAD=∠ADC=120°，又∵AB=AD，∴∠ABD=∠ADB=30°．∴∠DBC=∠ADB=30°．∴∠BDC=90°．（1分）由已知AE⊥BD，∴AE∥DC．（2分）又∵AE为等腰三角形ABD的高，∴E是BD的中点，∵F是DC的中点，∴EF∥BC．∴EF∥AD．∴四边形AEFD是平行四边形．（3分）∴AE=DF（4分）∵F是DC的中点，DG是梯形ABCD的高，∴GF=DF，（5分）∴AE=GF．（6分）（2）解：在Rt△AED中，∠ADB=30°，∵AE=1，∴AD=2．在Rt△DGC中∠C=60°，并且DC=AD=2，∴DG=．（8分）由（1）知：在平行四边形AEFD中EF=AD=2，又∵DG⊥BC，∴DG⊥EF，∴四边形DEGF的面积=EF•DG=．（10分）13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．解答：（1）证明：∵∠ABC=90°，DE⊥AC于点F，∴∠ABC=∠AFE．∵AC=AE，∠EAF=∠CAB，∴△ABC≌△AFE，∴AB=AF．∴AE﹣AB=AC﹣AF，即FC=BE；（2）解：∵AD=DC=2，DF⊥AC，∴AF=AC=AE．∴AG=CG，∴∠E=30°．∵∠EAD=90°，∴∠ADE=60°，∴∠FAD=∠E=30°，∴FC=，∵AD∥BC，∴∠ACG=∠FAD=30°，∴CG=2，∴AG=2．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，（1）证明：∵AD∥BC，∴∠BAD+∠ABC=180°，∵∠ABC=90°，∴∠BAD=∠ABC=90°，∵DE⊥EC，∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°，∴∠BEC=∠ADE，∵∠DAE=∠EBC，AE=BC，∴△EAD≌△EBC，∴AD=BE．（2）答：△ABF是等腰直角三角形．理由是：延长AF交BC的延长线于M，∵AD∥BM，∴∠DAF=∠M，∵∠AFD=∠CFM，DF=FC，∴△ADF≌△MFC，∴AD=CM，∵AD=BE，∴BE=CM，∵AE=BC，∴AB=BM，∴△ABM是等腰直角三角形，∵△ADF≌△MFC，∴AF=FM，∴∠ABC=90°，∴BF⊥AM，BF=AM=AF，∴△AFB是等腰直角三角形．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．解答：（1）证明：连接AC，∵AB∥CD，∴∠ACD=∠BAC，∵AB=BC，∴∠ACB=∠BAC，∴∠ACD=∠ACB，∵AD⊥DC，AE⊥BC，∴∠D=∠AEC=90°，∵AC=AC，∴，∴△ADC≌△AEC，（AAS）∴AD=AE；（2）解：由（1）知：AD=AE，DC=EC，设AB=x，则BE=x﹣4，AE=8，在Rt△ABE中∠AEB=90°，由勾股定理得：82+（x﹣4）2=x2，解得：x=10，∴AB=10．说明：依据此评分标准，其它方法如：过点C作CF⊥AB用来证明和计算均可得分．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．（1）证明：∵AD∥CB，∴∠ADB=∠CBD，又BD平分∠ABC，∴∠ABD=∠CBD，∴∠ADB=∠ABD，∴AB=AD，∴△ABD是等腰三角形，已知E是BD的中点，∴AE⊥BD．（2）解：延长AE交BC于G，∵BD平分∠ABC，∴∠ABE=∠GBE，又∵AE⊥BD（已证），∴∠AEB=∠GEB，BE=BE，∴△ABE≌△GBE，∴AE=GE，BG=AB=AD，又F是AC的中点（已知），所以由三角形中位线定理得：EF=CG=（BC﹣BG）=（BC﹣AD）=×（14﹣4）=5．答：EF的长为5．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．（1）证明：∵AD∥BC，∴∠DAC=∠BCE，而BE⊥AC，∴∠D=∠BEC=90°，AC=BC，∴△BCE≌△CAD．∴CD=BE．（2）解：在Rt△ADC中，根据勾股定理得AC==5，∵△BCE≌△CAD，∴CE=AD=3．∴AE=AC﹣CE=2．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．解：如图，过点D作DF∥AB，分别交AC，BC于点E，F．（1分）∵AB⊥AC，∴∠AED=∠BAC=90度．∵AD∥BC，∴∠DAE=180°﹣∠B﹣∠BAC=45度．在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×=2（2分）在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=．∴CE=AC﹣AE=．（4分）在Rt△DEC中，∠CED=90°，∴DC==．（5分）19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．证明：∵FC=F′C，EC=EC，∠ECF'=∠BCF+∠DCE=∠ECF，∴△FCE≌△F′CE，∴EF′=EF=DF′+ED，∴BF=EF﹣ED；（2）解：∵AB=BC，∠B=80°，∴∠ACB=50°，由（1）得∠FEC=∠DEC=70°，∴∠ECB=70°，而∠B=∠BCD=80°，∴∠DCE=10°，∴∠BCF=30°，∴∠ACF=∠BCA﹣∠BCF=20°．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．解：（1）作EM⊥AB，交AB于点M．∵AE=BE，EM⊥AB，∴AM=BM=×6=3；∵∠AME=∠MAF=∠AFE=90°，∴四边形AMEF是矩形，∴EF=AM=3；在Rt△AFE中，AE==5；（2）延长AF、BC交于点N．∵AD∥EN，∴∠DAF=∠N；∵∠AFD=∠NFC，DF=FC，∴△ADF≌△NCF（AAS），∴AD=CN；∵∠B+∠N=90°，∠BAE+∠EAN=90°，又AE=BE，∠B=∠BAE，∴∠N=∠EAN，AE=EN，∴BE=EN=EC+CN=EC+AD，∴CE=BE﹣AD．．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．解：（1）证明：过D作DE∥AC交BC延长线于E，（1分）∵AD∥BC，∴四边形ACED为平行四边形．（2分）∴CE=AD，DE=AC．∵四边形ABCD为等腰梯形，∴BD=AC=DE．∵AC⊥BD，∴DE⊥BD．∴△DBE为等腰直角三角形．（4分）∵DH⊥BC，∴DH=BE=（CE+BC）=（AD+BC）．（5分）（2）∵AD=CE，∴．（7分）∵△DBE为等腰直角三角形BD=DE=6，∴．∴梯形ABCD的面积为18．（8分）注：此题解题方法并不唯一．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．（1）证明：∵△ABC是等边三角形，DG∥BC，∴∠AGD=∠ABC=60°，∠ADG=∠ACB=60°，且∠BAC=60°，∴△AGD是等边三角形，AG=GD=AD，∠AGD=60°．∵DE=DC，∴GE=GD+DE=AD+DC=AC=AB，∵∠AGD=∠BAD，AG=AD，∴△AGE≌△DAB；（2）解：由（1）知AE=BD，∠ABD=∠AEG．∵EF∥DB，DG∥BC，∴四边形BFED是平行四边形．∴EF=BD，∴EF=AE．∵∠DBC=∠DEF，∴∠ABD+∠DBC=∠AEG+∠DEF，即∠AEF=∠ABC=60°．∴△AFE是等边三角形，∠AFE=60°．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．解：（1）证明：∵EF=EC，∴∠EFC=∠ECF，∵EF∥AB，∴∠B=∠EFC，∴∠B=∠ECF，∴梯形ABCD是等腰梯形；（2）△DCF是等腰直角三角形，证明：∵DE=EC，EF=EC，∴EF=CD，∴△CDF是直角三角形（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形），∵梯形ABCD是等腰梯形，∴CF=（BC﹣AD）=1，∵DC=，∴由勾股定理得：DF=1，∴△DCF是等腰直角三角形；（3）共四种情况：∵DF⊥BC，∴当PF=CF时，△PCD是等腰三角形，即PF=1，∴PB=1；当P与F重合时，△PCD是等腰三角形，∴PB=2；当PC=CD=（P在点C的左侧）时，△PCD是等腰三角形，∴PB=3﹣；当PC=CD=（P在点C的右侧）时，△PCD是等腰三角形，∴PB=3+．故共四种情况：PB=1，PB=2，PB=3﹣，PB=3+．（每个1分）24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．解答：（1）证明：∵在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，∴AB=CD，∵AD=DC，∴BA=AD，∠BAE=∠ADF=120°，∵DE=CF，∴AE=DF，在△BAE和△ADF中，，∴△ABE≌△DAF（SAS）．（2）解：∵由（1）△BAE≌△ADF，∴∠ABE=∠DAF．∴∠BPF=∠ABE+∠BAP=∠BAE．而AD∥BC，∠C=∠ABC=60°，∴∠BPF=120°．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？解答：解：（1）∵AD∥BC，∴∠ADB=∠DBC，∵AB=AD，∴∠ADB=∠ABD，∴∠DBC=∠ABD，∵在梯形ABCD中AB=DC，∴∠ABC=∠DCB=2∠DBC，∵BD⊥DC，∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°（2）过点D作DH⊥BC，垂足为H，∵∠DBC=30°，BC=8，∴DC=4，∵CF=CD∴CF=4，∴BF=12，∵∠F+∠FDC=∠DCB=60°，∠F=∠FDC∴∠F=30°，∵∠DBC=30°，∴∠F=∠DBC，∴DB=DF，∴，在直角三角形DBH中，∴，∴，∴，即△DBF的面积为．26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．（1）证明：连接BE，∵梯形ABCD中，AB=DC，∴AC=BD，可证△ABC≌△DCB，∴∠GCB=∠GBC，又∵∠BGC=∠AGD=60°∴△AGD为等边三角形，（2）解：∵BE为△BCG的中线，∴BE⊥AC，在Rt△ABE中，EF为斜边AB上的中线，∴EF=AB=5cm．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．解：（1）∵∠BEC=75°，∠ABC=90°，∴∠ECB=15°，∵∠ECD=45°，∴∠DCF=60°，在Rt△DFC中：∠DCF=60°，FC=3，∴DF=3，DC=6，由题得，四边形ABFD是矩形，∴AB=DF=3，∵AB=BC，∴BC=3，∴BF=BC﹣FC=3﹣3，∴AD=DF=3﹣3，∴C=3×2+6+3﹣3=9+3，梯形ABCD答：梯形ABCD的周长是9+3．（2）过点C作CM垂直AD的延长线于M，再延长DM到N，使MN=BE，∴CN=CE，可证∠NCD=∠DCE，∵CD=CD，∴△DEC≌△DNC，∴ED=EN，∴ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．（1）证明：∵AD∥BC，E是AB的中点，∴AE=BE，∠B=∠EAF，∠BCE=∠F．∴△BCE≌△AFE（AAS）．（2）解：∵AD∥BC，∴∠DAB=∠ABC=90°．∵AE=BE，∠AEF=∠BEC，∴△BCE≌△AFE．∴AF=BC=4．∵EF2=AF2+AE2=9+16=25，∴EF=5．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．（1）∵DC=BC，∠1=∠2，CF=CF，∴△DCF≌△BCF．（2）延长DF交BC于G，∵AD∥BG，AB∥DG，∴四边形ABGD为平行四边形．∴AD=BG．∵△DFC≌△BFC，∴∠EDF=∠GBF，DF=BF．又∵∠3=∠4，∴△DFE≌△BFG．∴DE=BG，EF=GF．∴AD=DE．（3）∵EF=GF，DF=BF，∴EF+BF=GF+DF，即：BE=DG．∵DG=AB，∴BE=AB．∵C=DF+FE+DE=6，△DFE∴BF+FE+DE=6，即：EB+DE=6．∴AB+AD=6．又∵AD=2，∴AB=4．∴DG=AB=4．∵BG=AD=2，∴GC=BC﹣BG=5﹣2=3．又∵DC=BC=5，在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°．=（AD+BC）•DG∴S梯形ABCD=（2+5）×430、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．解答：解：（1）证明：∵AD∥BC，DE2=CD2+CE2=42+32=25，∴∠OAD=∠OEB，∴DE=5又∵AB=AD，AO⊥BD，∴AD=BE=5，=．∴OB=OD，∴S梯形ABCD又∵∠AOD=∠EOB，∴△ADO≌△EBO（AAS），∴AD=EB，又∵AD∥BE，∴四边形ABCD是平行四边形，又∵AB=AD∴四边形ABCD是菱形．（2）∵四边形ABCD是菱形，∴AD=DE=BE，。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题八：几何证明题【问题解析】几何证明题重在训练学生应用数学语言合情推理能力，几何证明题和计算题在中考中占有重要地位•根据新的课程标准，对几何证明题证明的方法技巧上要降低，繁琐性、难度方面要降低•但是注重考查学生的基础把握推理能力，所以几何证明题是目前常考的题型.【热点探究】类型一：关于三角形的综合证明题【例题11(2016 •四川南充)已知△ ABN和厶ACM位置如图所示，AB=ACAD=AE /仁/ 2.(1) 求证：BD=CE(2) 求证：/ M=/ N.【分析】(1)由SAS证明△ ABD^A ACE得出对应边相等即可(2)证出/BAN/ CAM由全等三角形的性质得出/ B=/ C,由AAS证明△ ACI WA ABN 得出对应角相等即可.【解答】(1)证明：在厶ABD和厶ACE中，’IL*•••△ABD^A ACE( SAS,••• BD=CE(2)证明：T/ 1=/ 2,• / 1+/ DAE/ 2+/ DAE 即/ BAN/ CAM由(1)得：△ ABD^A ACE• / B=/ C,r zc=z&«AC=AB在厶ACM^n^ ABN 中，| Z CM=Z BAN,•••△ ACMmABN( ASA,•••/ M= N.【点评】本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键.【同步练】(2016 •山东省荷泽市・3 分)如图，△ ACB和厶DCE均为等腰三角形，点A，D, E在同一直线上，连接BE(1)如图1，若/ CAB M CBA M CDE M CED=50①求证：AD=BE②求/ AEB的度数.(2)如图2,若/ ACB M DCE=120 , CM^^ DCE中DE边上的高，BN%A ABE 中AE边类型二：关于四边形的综合证明题【例题2] (2016 •山东省滨州市•10分)如图，BD是△ ABC的角平分线，它的垂直平分线分别交AB, BD BC于点E，F，G,连接ED DG(1)请判断四边形EBGD勺形状，并说明理由；(2)若/ ABC=30，/ C=45, , 点H是BD上的一个动点，求HG+HC勺最小值.【考点】平行四边形的判定与性质；角平分线的性质.【分析】（1）结论四边形EBGD是菱形.只要证明BE=ED=DG=G即可.（2）作EM L BC于M, DN^ BC于N,连接EC交BD于点H 此时HG+H（最小，在RT^ EMC 中，求出EM MC即可解决问题.【解答】解：（1）四边形EBGD是菱形.理由：••• EG垂直平分BD••• EB=ED GB=GD•••/ EBD=/ EDB•••/ EBD=/ DBC•••/ EDF玄GBF在厶EFD和△ GFB中，r ZEPF=ZGBF“ ZEFD^ZGFB,DF=BF•△EFD^A GFB• ED=BG• BE=ED=DG=GB•四边形EBGD是菱形.（2）作EM L BC于M, DNL BC于N ,连接EC交BD于点H ,此时HG+HC t小,在RT^ EBM 中，I/ EMB=90 , / EBM=30 , EB=ED=^Q ,• EM=7BE= I ',•••DE// BC, EMIBC, DN!BC,• EM// DIN EM=DN= , MN=DE=2可!',在RT^ DNC中 , DNC=90 , / DCN=45 ,NDC/ NCD=45 ,• DN=NC= ,••• MC=3 | ,在RT^ EMC中，•••/ EMC=90 , EM= - . MC=3 ,•EC粕珊5腿也』（帧）S （3负）'=10履.•/ HG+HC=EH+HC=,EC• HG+HC勺最小值为10 | -.B M 仔N C【点评】本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识，解题的关键是利用对称找到点H的位置，属于中考常考题型.【同步练】(2016 •山东省济宁市• 3分)如图，正方形ABCD勺对角线AC BD相交于点0,延长CB至点F,使CF=CA连接AF,/ ACF的平分线分别交AF, AB, BD于点E, N, M,连接E0.(1)已知BD=",求正方形ABCD勺边长；(2)猜想线段EM与CN的数量关系并加以证明.类型三：关于圆的综合证明题【例题3】(2016 •山东潍坊)正方形ABCD内接于O 0,如图所示，在劣弧—上取一点E,连接DE BE,过点D作DF// BE交OO于点F,连接BF、AF,且AF与DE相交于点G 求证：(1)四边形EBFD是矩形；（2）DG=BE【分析】(1)直接利用正方形的性质、圆周角定理结合平行线的性质得出/ BED=/ BAD=90，/ BFD2 BCD=90，/ EDF=90，进而得出答案；(2)直接利用正方形的性质疋的度数是90°,进而得出BE=DF则BE=DG【解答】证明：(1厂••正方形ABCD内接于O 0,•••/ BED d BAD=90，/ BFD2 BCD=90 ,又• DF// BE•••/ EDF+d BED=180 ,•••/ EDF=90 ,•四边形EBFD是矩形;(2)) •正方形ABCD内接于O 0,•「的度数是90°,•••/ AFD=45 ,又GDF=90 ,•••/ DGF d DFC=45 ,• DG=DF又••在矩形EBFD中, BE=D【同步练】(枣庄市2015 中考-24 )如图，在△ ABC中，/ ABC=90，以AB的中点0为圆心、0A为半径的圆交AC于点D, E是BC的中点，连接DE, 0E(1)判断DE与OO的位置关系，并说明理由；(2)求证：BC=CD?20；(3)若cos / BAD=3, BE=6,求0E 的长.5类型四：关于相似三角形的证明问题【例题4】（2016 •黑龙江齐齐哈尔・8 分）如图，在△ ABC中，ADL BQ BEL AC垂足分别为D, E, AD与BE相交于点F.(1) 求证：△ AC SA BFD(2) 当tan / ABD=1 AC=3时，求BF 的长.【考点】相似三角形的判定与性质.【分析】（1）由/ C+Z DBF=90 , / C+Z DAC=90 ,推出/ DBF2 DAC 由此即可证明.（2）先证明AD=B»由厶ACDo^ BFD得丛=奧=1，即可解决问题.EF BD【解答】（1）证明：T AD L BC, BE L AC,•••Z BDF Z ADC Z BEC=90 , •••Z C+Z DBF=90 , Z C+Z DAC=90 ,• Z DBF Z DAC(2)v tan Z ABD=1 Z ADB=90「A• AD=BDAC EF ⑴ ⑵ V C3 S 图1 图？ BE•••BF=AC=3BP 的长. 【同步练】（2016 •湖北武汉• 10分）在厶ABC 中，P 为边AB 上一点.① 如图2,若/ PBM^Z ACP AB= 3，求BP 的长;②如图3,若/ ABC= 45°,/ A =Z BM = 60°,直接写出如图 1，若/ ACP=/ B,求证： AC = AP- AB若M 为CP 的中点，AC = 2,【达标检测】1. （2016 •黑龙江哈尔滨・8 分）已知：如图，在正方形ABCD中，点E在边CD上, AQL BE 于点Q DPI AQ 于点P.（1）求证：AP=BQ（2）在不添加任何辅助线的情况下，请直接写出图中四对线段，使每对中较长线段与2. （2016 •四川内江）（9分）如图6所示，△ ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F,且AF= BD连接BF.⑴求证：D是BC的中点；（2）若AB= AC,试判断四边形AFBD的形状，并证明你的结论.图63. （烟台市2015中考-23 ）如图，以△ ABC的一边AB为直径的半圆与其它两边AC, BC的交点分别为D、E,且「上f -.（1）试判断△ ABC的形状，并说明理由.（2）已知半圆的半径为5, BC=12求sin /ABD的值.4. (2015?内蒙古呼伦贝尔兴安盟，第22题7分)如图，在平行四边形ABCD中, E、F 分别为边AB CD的中点，BD是对角线.(1)求证：△ ADE^A CBF；(2)若/ ADB是直角，则四边形BEDF是什么四边形？证明你的结论.5. (烟台市2014中考-24 )如图，AB是OO的直径，延长AB至P,使BP=OB BD垂直于弦BC垂足为点B,点D在PC上.设/ PCB=a，/ POC=3 .求证：tan a ?tan 卫-=2.2 36. (2015?梧州，第25题12分)如图，在正方形ABCD中，点P在AD上，且不与A、D 重合，BP的垂直平分线分别交CD AB于E、F两点，垂足为Q过E作EF U AB于H.(1)求证：HF=AR(2)若正方形ABCD的边长为12, AP=4,求线段EQ的长.2__亡D7. (2015?北海,第25题12分)如图，AB CD为O O的直径，弦AE// CD连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使/ PED=/ C.(1)求证：PE是O O的切线；(2)求证：ED平分/ BEP(3)若O O的半径为5, CF=2EF,求PD的长.【参考答案】类型一：关于三角形的综合证明题【同步练】（2016 •山东省荷泽市・3 分）如图，△ ACB 和厶DCE 均为等腰三角形，点 A , D, E 在同一直线上，连接 BE（1）如图 1，若/ CAB=/ CBA=/ CDE M CED=50① 求证：AD=BE② 求/ AEB 的度数.(2)如图 2,若/ ACB M DCE=120 , CM ^^ DCE 中 DE 边上的高，ABE 中 AE 边【考点】等腰三角形的性质.【分析】（1 ［①通过角的计算找出/ ACD M BCE 再结合△ ACB 和厶DCE 均为等腰三角形可得出“ AC=BC DC=EC ，利用全等三角形的判定（SAS 即可证出厶ACD^^ BCE 由此即可得出结论AD=BE②结合①中的△ ACD^^ BCE 可得出/ ADC M BEC 再通过角的计算即可算出/ AEB 的度数；（2）根据等腰三角形的性质结合顶角的度数，即可得出底角的度数，利用（1）的结论，通过解直角三角形即可求出线段 AD DE 的长度，二者相加即可证出结论. 【解答】（1）①证明：•••/ CAB M CBA M CDE M CED=50 ,•••/ ACB d DCE=180 - 2X 50° =80°•••/ ACB d ACD # DCB / DCE M DCB # BCE•••/ ACD M BCE•/△ ACB 和厶DCE 均为等腰三角形，• AC=BC DC=EC上的高，试证明: AE=2 CMAC^BC ZACD^Z BCE , DC=EC •••△ ACD^A BCE( SAS ,••• AD=BE②解：•••△ ACD^^ BCE•••/ ADC M BEC •••点A, D, E 在同一直线上，且/ CDE=50 ,•••/ ADC=180 -Z CDE=130 ,•••/ BEC=130 .vZ BEC Z CED Z AEB 且 Z CED=50 ,• Z AEB Z BEC-Z CED=130 - 50° =80°.(2)证明：•••△ ACB 和厶DCE 均为等腰三角形，且Z ACB Z DCE=120 ,• Z CDM Z CEM=- X( 180°- 120°) =30°. 1•/ CM L DE• Z CMD=9°0 , DM=EM在 Rt △ CMD 中, Z CMD=9° , Z CDM=3° ,vZ BEC Z ADC=180 - 30° =150°, Z BEC Z CEM Z AEB• Z AEB Z BEC-Z CEM=15° - 30° =120° ,• Z BEN=180 - 120° =60°在 Rt △ BNE 中，Z BNE=90 , Z BEN=60 ,v AD=BE AE=AD+DE【点评】本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算，解题的关键是：(1)通过角的计算结合等腰三角形的性质证出△ ACD^^ BCE(2)找出线段AD DE 的长.本题属于中档题，难度不大，但稍显繁琐，解决该题型题目时， I• BE= ginZBEN• DE=2DM=2• AE=BE+DE BN+2. 「CM利用角的计算找出相等的角，再利用等腰三角形的性质找出相等的边或角，最后根据全等三角形的判定定理证出三角形全是关键.类型二：关于四边形的综合证明题【同步练】(2016 •山东省济宁市• 3分)如图，正方形ABCD勺对角线AC BD相交于点0,延长CB至点F,使CF=CA连接AF,/ ACF的平分线分别交AF, AB, BD于点E, N, M,连接E0.(1)已知BD= •・.，求正方形ABCD勺边长；(2)猜想线段EM与CN的数量关系并加以证明.尸月C【考点】正方形的性质.【分析】(1)根据正方形的性质以及勾股定理即可求得；(2)根据等腰三角形三线合一的性质证得CE! AF,进一步得出/ BAF=/ BCN然后通过证得△ ABF^A CBN得出AF=CN进而证得厶ABF^A COM根据相似三角形的性质和正方形的性质即可证得CN=「■ CM【解答】解：(1)v四边形ABCD是正方形，•••△ABD是等腰直角三角形，•••2AB^B D,•- BD= ■-,• AB=1,•正方形ABCD的边长为1;(2) CN=. ：CM证明：••• CF=CA AF是/ACF的平分线，• CE! AF,•/ AEN/ CBN=90 ,•••/ ANE/ CNB•/ BAF=/ BCN在厶ABF和厶CBN中 ,ZBAF=ZBCNI ZABF=ZCBN=90°，AB=BC•••△ ABF ^A CBN( AAS ,••• AF=CN•••/ BAF=/ BCN / ACN=/ BCN•••/ BAF=/ OCM•••四边形ABCD 是正方形，• AC 丄 BD,• / ABF=/ COM=90 ,• △ ABF^A COM即 CN= [ CM类型三：关于圆的综合证明题【同步练】(枣庄市2015 中考-24 )如图，在△ ABC 中，/ ABC=90，以 AB 的中点O 为圆心、OA 为半径的圆交AC 于点D, E 是BC 的中点，连接DE OE(1) 判断DE 与OO 的位置关系，并说明理由；(2) 求证：BC=CD?2O ；3(3) 若 cos / BAD= , BE=6,求 OE 的长.5思路分析：本题考查了切线的判定，垂径定理以及相似三角形的判定与性质等知识点. 故对于题(1) ,也2 c- C---E O-AJo- c X-疔M N c-Alc c可以连接OD BD,由AB为圆O的直径，得到/ ADB为直角，从而得出三角形BCD为直角三角形，E为斜边BC的中点，利用斜边上的中线等于斜边的一半，得到CE=DE利用等边对等角得到一对角相等，再由OA=OD利用等边对等角得到一对角相等，由直角三角形ABC中两锐角互余，利用等角的余角相等得到/ ADO与/CDE互余，可得出/ ODE为直角，即DE垂直于半径OD可得出DE为圆0的切线；对于题(2)首先可证明OE：＞A ABC的中位线，贝U AC=2OE然后证明厶ABS A BDC根据相似三角形的对应边的比相等，即可证得；对于题(3)在直角△ ABC中，利用勾股定理求得AC的长，之后根据三角形中位线定理OE的长即可求得.解题过程：(1)证明：连接OD BD•/ AB为圆O的直径，•••/ ADB=90 ,在Rt△ BDC中，E为斜边BC的中点，1• CE=DE=BE= BC2•••/ C=Z CDE•/ OA=OD•••/ A=Z ADO•••/ ABC=90，即/ C+Z A=90 ,•••/ ADO Z CDE=90，即Z ODE=90 ,• DELOD又OD为圆的半径，• DE为OO的切线；(2)证明：TE是BC的中点，O点是AB的中点，•••。