中考数学专题复习八几何证明题
初三几何证明练习题和答案

初三几何证明练习题和答案几何证明是初中数学中的重要内容,通过练习不同类型的几何证明题,可以帮助学生理解并掌握几何证明的基本方法与技巧。
本文将为大家提供一些初三几何证明的练习题和答案,希望对同学们的学习有所帮助。
1. 题目:已知ABCD是平行四边形,证明∠ABC + ∠ADC = 180°。
证明:解:连接AC,根据平行四边形的性质可知∠ADC = ∠ACB,所以要证明∠ABC + ∠ADC = 180°,只需证明∠ABC + ∠ACB = 180°。
由角的内外(对顶、同旁)定理可知∠ACB + ∠ABC = 180°,即∠ABC + ∠ACB = 180°。
所以,∠ABC + ∠ADC = 180°得证。
2. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = 5cm,BC= 12cm,证明AB = 13cm。
证明:解:根据勾股定理可得AB² = AC² + BC²。
代入已知条件,即可得AB² = 5² + 12² = 25 + 144 = 169。
开方可得AB = 13cm。
所以,AB = 13cm得证。
3. 题目:已知直角三角形ABC中,∠ACB = 90°,AC = BC,证明∠ABC = 45°。
证明:解:连接AB,根据等腰直角三角形的性质可知∠ACB = ∠CAB。
所以,∠ABC = 180° - ∠ACB - ∠CAB = 180° - ∠ACB - ∠ACB = 180° - 2∠ACB。
由于∠ACB = 90°,代入得∠ABC = 180° - 2 × 90° = 0°。
所以,∠ABC = 0°,即∠ABC = 45°得证。
4. 题目:已知ABCD是一个平行四边形,E为AD的中点,证明BE平分∠CBD。
人教版八年级数学上册专题复习证明三角形全等的常见题型

证明三角形全等的常见题型全等三角形是初中几何的重要内容之一,全等三角形的学习是几何入门最关键的一步,这部分内容学习的好坏直接影响着今后的学习。
而一些初学的同学,虽然学习了几种判定三角形全等的公理和推论,但往往仍不知如何根据已知条件证明两个三角形全等。
在辅导时可以抓住以下几种证明三角形全等的常见题型,进行分析。
一、已知一边与其一邻角对应相等1.证已知角的另一边对应相等,再用SAS证全等。
例1已知:如图1,点E、F在BC上,BE=CF,AB=DC,∠B=∠C .求证:AF=DE。
证明∵BE=CF(已知),∴BE+ EF=CF+EF,即 BF=CE。
在△ABF和△DCE中,∴△ABF≌△DCE(SAS)。
∴ AF=DE(全等三角形对应边相等)。
2.证已知边的另一邻角对应相等,再用ASA证全等。
例2已知:如图2,D是△ABC的边AB上一点,DF交AC于点E,DE=FE,FC∥AB。
求证:AE=CE。
证明∵ FC∥AB(已知),∴∠ADE=∠CFE(两直线平行,内错角相等)。
在△ADE和△CFE中,∴△ADE≌△CFE(ASA).∴ AE=CE(全等三角形对应边相等)3.证已知边的对角对应相等,再用AAS证全等。
例3(同例2).证明∵ FC∥AB(已知),∴∠A=∠ECF(两直线平行,内错角相等).在△ADE和△CFE中,∴△ADE≌△CFE(AAS).∴ AE=CE(全等三角形对应边相等)。
二、已知两边对应相等1.证两已知边的夹角对应相等,再用SAS证等。
例4已知:如图3,AD=AE,点D、E在BCBD=CE,∠1=∠2。
求证:△ABD≌△ACE.证明∵∠1=∠2(已知),∠ADB=180°-∠1,∠AEC=180°-∠2(邻补角定义),∴∠ADB = ∠AEC,在△ABD和△ACE中,∴△ABD≌△ACE(SAS).2.证第三边对应相等,再用SSS证全等。
例5已知:如图4,点A、C、B、D在同一直线AC=BD,AM=CN,BM=DN。
中考复习初中数学几何证明 试题(含答案)
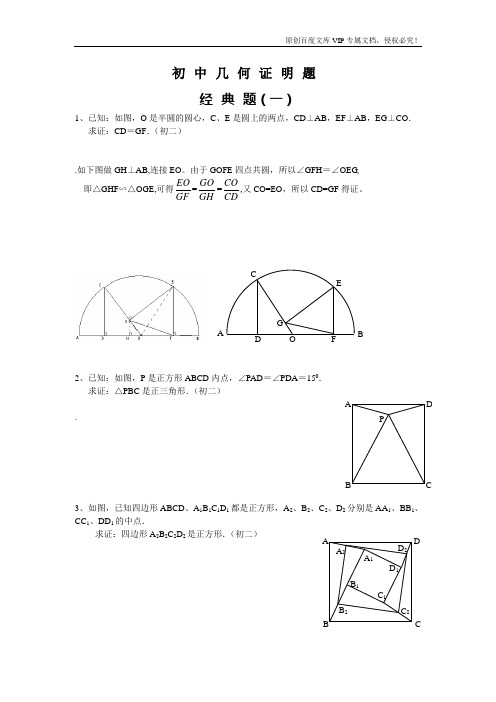
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二).3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)APCDB D 2C 2 B 2 A 2D 1C 1B 1C B DA A 1 AFGCEBOD4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.BF求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值. A P CB P A D CB C B D A F PD E CB A APCB3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
经典初二数学几何证明题

A DB C E最新中考数学几何证明(平行四边形,菱形矩形正方形)经典 1.(本题10分)如图,已知: ABCD 中,BCD ∠的平分线CE 交边AD 于E ,ABC∠的平分线BG 交CE 于F ,交AD 于G .求证:AE DG =.2.在正方形ABCD 中,AC 为对角线,E 为AC 上一点,连接EB 、ED . (1)求证:△BEC ≌△DEC ;(2)延长BE 交AD 于F ,当∠BED =120°时,求∠EFD 的度数.3.(本小题满分5分)如图,在△ABC 中,点D 、E 分别在边AC 、AB 上,BD=CE ,∠DBC=∠求证:AB=AC 。
4.(本小题满分7分)如图,在△ABC 中,AB=AC ,D 为BC 中点,四边形ABDE 是平行四边形。
是矩形。
5.(10分)在□ABCD 中,AC 是一条对角线,∠B =∠CAD ,延长BC 至点接DE .(1)求证:四边形ABED 是等腰梯形.(2)若AB =AD =4,求梯形ABED 的面积. 6、(本小题7分)如图,点A 、E 、B 、D 在同一条直线上,AE=DB ,AC=DF ,AC ∥DF. 请探索BC 与EF 有怎样的位置关系?并说明理由。
7.如图,已知BE ⊥AD ,CF ⊥AD ,且BE =CF .(1) 请你判断AD 是△ABC 的中线还是角平分线?请证明你的结论.(2)连接BF 、CE ,若四边形BFCE 是菱形,则△ABC 添加一个条件 ▲8.(广东广州,18,9分)如图5,在等腰梯形ABCD 中,AD ∥BC .求证:∠A +∠C =180°10.如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分∠BCD ,CD=CE .(1)求证:△ACD≌△BCE;(2)若∠D=50°,求∠B 的度数. 11.(本题6分)如图,在△ABC 中,D 是BC 边上的点(不与B ,C 重合),F ,E 分别是AD 及其延长线上的点,CF ∥BE. 请你添加一个条件,使△BDE ≌△CDF (不再添加其它线段,不再标注或使用其他字母),并给出证明.(1)你添加的条件是: ▲ ;(2)证明:.12.(8分)如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD 是平行四边形,并予以证明.(写出一种即可)B A CBD FE(第11题)B CDE F A 关系:①AD ∥BC ,②CD AB =,③C A ∠=∠,④︒=∠+∠180C B . 已知:在四边形ABCD 中, , ; 求证:四边形ABCD 是平行四边形. 13.(本题满分9分)将三角形纸片ABC (AB >AC )沿过点A 的直线折叠,使得AC 落在AB 边上,折痕为AD ,展平纸片,如图(1);再次折叠该三角形纸片,使得点A 与点D 重合,折痕为EF ,再次展平后连接DE 、DF ,如图2,证明:四边形AEDF 是菱形.14.如图10,已知ABC ADE Rt △≌Rt △,90ABC ADE ∠=∠=°,BC 与DE 相交于点F ,连接CD ,EB .(1)图中还有几对全等三角形,请你一一列举. (2)求证:.CF EF = 15.(本小题满分8分)如图,已知:点B 、F 、C 、E 在一条直线上,FB =CE ,AC=DF .能否由上面的已知条件证明AB ∥ED ?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件.......,添加到已知条件中,使AB ∥ED 成立,并给出证明. 供选择的三个条件(请从其中选择一个): ①AB =ED ; ②BC =EF ; ③∠ACB =∠DFE . 16.(6分)已知:正方形ABCD 中,E 、F 分别是边CD 、DA 上的点,且CE =DF ,AE 与BF 交于点M . (1)求证:△ABF ≌△DAE ;(2)找出图中与△ABM 相似的所有三角形(不添加任何辅助线).17.(6分)如图,在△ABC 中,BC >AC ,点D 在BC 上,且DC =AC ,∠ACB 的平分线CF 交AD 于点F .点E 是AB 的中点,连接EF .(1)求证:EF ∥BC ;(2)若△ABD 的面积是6,求四边形BDFE 的面积.18.(本小题满分8分)如图,四边形ABCD 的对角线AC 、DB 相交于点O ,现给出如下三个条件:AB CD(1)(2) ABDCCDBF AE图10 DE(第15题)A EB DA G EB CF D AB DC AC DB OBC OCB ==∠=∠①②③.(1)请你再增加一个..条件:________,使得四边形ABCD 为矩形(不添加其它字母和辅助线,只填一个即可,不必证明);(2)请你从①②③中选择两个条件________(用序号表示,只填一种情况),使得AOB DOC △≌△,并加以证明.19.如图,在直角梯形ABCD 中,AD ∥BC ,∠A =90o ,AB =AD =6,DE ⊥CD交AB 于E ,DF 平分∠CDE 交BC 于F ,连接EF . (1)证明:CF =EF ; (2)当tan ∠ADE = 13时,求EF 的长.20.(10分)如图,在□ABCD 中,E 、F 分别是边AB 、CD的中点,AG ∥BD 交CB 的延长线于点G .(1)求证:△ADE ∽≌△CBF ;(2)若四边形BEDF 是菱形,则四边形AGBD 是什么特 殊四边形?请说明你的理由. 21.(本题满分8分)如图,在ABCD 中,点E 、F 是对角线AC 上两点,且CF AE =.求证:FDE EBF =∠.22.(8分)如图,四边形ABCD 是矩形,∠EDC=∠CAB , ∠DEC=90°。
初中经典几何证明练习题(含问题详解)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
中考数学题型八 几何图形探究题

例2 (2020·东营)如图①,在等腰三角形ABC中,∠A=120°,AB=AC,
点D,E分别在边AB,AC上,AD=AE,连接BE,点M,N,P分别为DE,
BE,BC的中点.
(1)观察猜想 图①中,线段NM,NP的数量关系是___N__M_=__N__P____,∠MNP的大小为 ____6_0_°___;
2. (2020·泰安)小明将两个直角三角形纸片如图①那样拼放在同一平面上, 抽象出如图②的平面图形,∠ACB与∠ECD恰好为对顶角,∠ABC= ∠CDE=90°,连接BD,AB=BD,点F是线段CE上一点.
探究发现: (1)当点F为线段CE的中点时,连接DF(如图②),小明经过探究,得到结 论:BD⊥DF.你认为此结论是否成立?_是___.(填“是”或“否” )
又∵AB=BC,∴∠ACB=∠CAB=∠FAE, ∵EF∥BC,∴∠F=∠FCB, ∴EF=AE,∴AE=FE=FM+ME=CF+BC;
(3)解:CF=18或CF=6, 当DE=2AE=6时,题图①中,由(1)得:AE=3,BC=AB=BD+DE +AE=15, ∴CF=AE+BC=3+15=18; 题图②中,由(2)得:AE=AD=3,BC=AB=BD+AD=9,∴CF= BC-AE=9-3=6; 题图③中,DE小于AE,故不存在.故答案为18或6.
拓展创新:解:AD 的长为 5 .[解法提示]如解图②,过点 A 作 AB 的垂线, 过点 D 作 AD 的垂线,两垂线交于点 M,连接 BM,∵∠BAD=30°,∴∠DAM =60°,∴∠AMD=30°,
∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴MBDD
=DDCA ,又∠BDC=∠ADM,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM
初中数学几何证明题经典例题(超全)
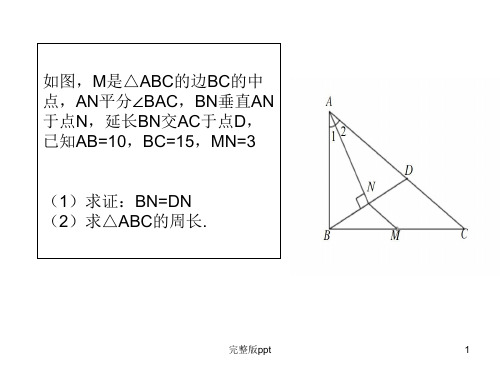
完整版ppt
9
• 已知:如图正方形ABCD,P、Q分别是BC、 DC上的点,若∠1=∠2 求证:PB+QD=PA
完整版ppt
10
• 已知:如图正方形ABCD,AC、BD交于点 O,E、F分别是BC、OD的中点 求证: AF⊥EF
完整版ppt
11
• 已知:如图,,AB=BC,D、E分别是AB、 BC上一点,DM⊥AE交AC于M, BN⊥AE 交AC于N,若BD=BE求证:MN=NC。
完整版ppt
20
• 如图,在四边形ABCD中,AB=DC,E、F 分别是AD、BC的中点,G、H分别是BD、 AC的中点,猜一猜EF与GH的位置关系, 并证明你的结论.
完整版ppt
21
• 如图,分别以△ABC的三边为边长,在BC 的同侧作等边三角形ABD,等边三角形 BCE,等边三角形ACF,连接DE,EF。求 证:四边形ADE 2,AB=3AC,BE⊥AD,
求证:AD=DE
完整版ppt
15
• 已知:如图,AB//CD, D=90 o, BE=EC=DC,求证: AEC=3 BAE
完整版ppt
16
• 已知如图,AB=DC,AE=DE,BF=FC,
FE交BA、CD的延长线于G、H,求证:1= 2。
完整版ppt
17
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
完整版ppt
18
• 已知:如图,AB//CD, ADC=90o , BE=EC,求证: AED=2 EDC
完整版ppt
19
• 已知:如图,正方形ABCD中,E是DC上一 点,DF⊥AE交BC于F 求证:OE⊥OF
初二数学几何证明题(5篇可选)

初二数学几何证明题(5篇可选)第一篇:初二数学几何证明题1.在△ABC中,AB=AC,D在AB上,E在AC的延长线上,且BD=CE,线段DE交BC于点F,说明:DF=EF。
2.已知:在正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直DM于点M,且交∠CBE的平分线于点N.(1)求证:MD=MN.(2)若将上述条件中的“M是AB的中点”改为“M 是AB上任意一点”其余条件不变,则(1)的结论还成立吗?如果成立,请证明,如果不成立,请说明理由。
3.。
如图,点E,F分别是菱形ABCD的边CD和CB延长线上的点,且DE=BF,求证∠E=∠F。
4,如图,在△ABC中,D,E,F,分别为边AB,BC,CA,的中点,求证四边形DECF为平行四边形。
5.如图,在菱形ABCD中,∠DAB=60度,过点C作CE垂直AC 且与AB的延长线交与点E,求证四边形AECD是等腰梯形?6.如图,已知平行四边形ABCD中,对角线AC,BD,相交与点0,E是BD延长线上的点,且三角形ACE是等边三角形。
1.求证四边形ABCD是菱形。
2.若∠AED=2∠EAD,求证四边形ABCD是正方形。
7.已知正方形ABCD中,角EAF=45度,F点在CD边上,E点在BC边上。
求证:EF=BE+DF第二篇:初二几何证明题1如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DCCF.(1)求证:D是BC的中点;(2)如果AB=ACADCF的形状,并证明你的结论AEB第三篇:初二几何证明题初二几何证明题1.已知:如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E。
M为AB中点,联结ME,MD、ED求证:角EMD=2角DAC证明:∵M为AB边的中点,AD⊥BC,BE⊥AC,∴MD=ME=MA=MB(斜边上的中线=斜边的一半)∴△MED为等腰三角形∵ME=MA∴∠MAE=∠MEA∴∠BME=2∠MAE∵MD=MA∴∠MAD=∠MDA,∴∠BMD=2∠MAD,∵∠EMD=∠BME-∠BMD=2∠MAE-2∠MAD=2∠DAC2.如图,已知四边形ABCD中,AD=BC,E、F分别是AB、CD中点,AD、BC的延长线与EF的延长线交于点H、D求证:∠AHE=∠BGE证明:连接AC,作EM‖AD交AC于M,连接MF.如下图:∵E是CD的中点,且EM‖AD,∴EM=1/2AD,M是AC的中点,又因为F是AB的中点∴MF‖BC,且MF=1/2BC.∵AD=BC,∴EM=MF,三角形MEF为等腰三角形,即∠MEF=∠MFE.∵EM‖AH,∴∠MEF=∠AHF ∵FM‖BG,∴∠MFE=∠BGF∴∠AHF=∠BGF.3.写出“等腰三角形两底角的平分线相等”的逆命题,并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知BD平分∠ABC,CE平分∠ACB,BD=CE,求证:AB=AC证明:BD平分∠ABC==>BE/AE=BC/AC==>BE/AB=BC/(BC+AC)==>BE=AB*BC/(BC+AC)同理:CD=AC*BC/(BC+AB)假设AB≠AC,不妨设AB>AC.....(*)AB>AC==>BC+ACAC*BC==>AB*AB/(BC+AC)>AC*BC/(BC+AB)==>BE>CDAB>AC==>∠ACB>∠ABC∠BEC=∠A+∠ACB/2,∠BDC=∠A+∠ABC/2==>∠BEC>∠BDC过B作CE平行线,过C作AB平行线,交于F,连DF则BECF为平行四边形==>∠BFC=∠BEC>∠BDC (1)BF=CE=BD==>∠BDF=∠BFDCF=BE>CD==>∠CDF>∠CFD==>∠BDF+∠CDF>∠BFD+∠CFD==>∠BDC>∠BFC (2)(1)(2)矛盾,从而假设(*)不成立所以AB=AC。
2024年数学八年级几何证明专项练习题1(含答案)

2024年数学八年级几何证明专项练习题1(含答案)试题部分一、选择题:1. 在三角形ABC中,若∠A = 90°,AB = 6cm,BC = 8cm,则AC 的长度为()。
A. 2cmB. 10cmC. 4cmD. 5cm2. 下列哪个条件不能判定两个三角形全等?()A. SASB. ASAC. AASD. AAA3. 在直角坐标系中,点A(2,3)关于原点对称的点是()。
A. (2,3)B. (2,3)C. (2,3)D. (3,2)4. 下列哪个比例式是正确的?()A. 若a∥b,则∠1 = ∠2B. 若a∥b,则∠1 + ∠2 = 180°C. 若a⊥b,则∠1 = 90°D. 若a⊥b,则∠1 + ∠2 = 180°5. 在等腰三角形ABC中,若AB = AC,∠B = 70°,则∠C的度数为()。
A. 70°B. 40°C. 55°D. 110°6. 下列哪个条件可以判定两个角相等?()A. 对顶角B. 邻补角C. 内错角D. 同位角7. 在平行四边形ABCD中,若AD = 8cm,AB = 6cm,则对角线AC 的长度()。
A. 10cmB. 14cmC. 12cmD. 15cm8. 下列哪个图形是轴对称图形?()A. 等腰三角形B. 等边三角形C. 矩形D. 梯形9. 在三角形ABC中,若a = 8cm,b = 10cm,c = 12cm,则三角形ABC是()。
A. 锐角三角形B. 钝角三角形C. 直角三角形D. 不能确定10. 下列哪个条件不能判定两个直线平行?()A. 内错角相等B. 同位角相等C. 同旁内角互补D. 两直线垂直二、判断题:1. 若两个三角形的两边和夹角分别相等,则这两个三角形全等。
()2. 在等腰三角形中,底角相等。
()3. 平行线的同位角相等,内错角相等。
()4. 若两个角的和为180°,则这两个角互为补角。
(完整版)八年级几何证明题集锦及解答值得收藏

(完整版)八年级几何证明题集锦及解答值得收藏八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE,∴∠BCF=∠CDE,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE⊥CF.3.如图,在直角梯形ABCD中,AD∥BC,∠A=90o,AB=AD,DE⊥CD交AB于E,DF平分∠CDE交BC于F,连接EF.证DA明:CF=EF解:EB F C过D作DG⊥BC于G.由已知可得四边形ABGD为正方形,∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG,∴∠ADE=∠GDC.又∵∠A=∠DGC且AD=GD,∴△ADE≌△GDC,∴DE=DC且AE=GC.在△EDF和△CDF中∠EDF=∠CDF,DE=DC,DF为公共边,∴△EDF ≌△CDF,∴EF=CF4.已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
中考数学-几何证明

2020年-春季-初三下-【入学考试】1.(初2020级BZ初三下入学测试)如图,正方形ABCD中,对角线AC, BD交于点。
,点E.点OB ,线段AB上,且AF OE ,连接AE交OF于G , 连接DG交AO于H.F分别在线段⑴如图1,若点E为线段BO中点,AE J5,求BF的长:(2)如图2,若AE平分BAC,求证:FG HG;(3)如图3,点E在线段BO (含端点)上运动,连接HE,当线段HE长度取得最大值时,直接写出cos HDO的值.2.(初2020级BS初三下入学测试)如图,平行四边形ABCD中,AB=2BC, B 60 . 曲 DC中点,连接AE . F为AD上一点,连接CF交AE与点G , CM平分FCB交AB于点M .(1)如图1,若BC 3,AF 1 求sin DCF 的值.(2)求证:EG BM CG(3)如图2, CN AB于点N ,若AG=4, MN : BN=3: 5.求CG 的长度.3.(初2020级YZ初三下入学测试)在0ABCD中BAC=90 , AB=AE,延长BE交CD 于点F . AG BE交BE于点H点,M是BC边上的点.(1)如图1,若点M与点G重合,AH 5, AD 显26 ,求CF的长:2(2)如图2.若AM是BAD的角平分线,连接MH , HMG MAH ,求证:AM 2 .2HM(3)如图3,若点M为BC的中点,作点B关于AM的对称点N,连接AN、MN、EN,请直接写出AMH、NAE、MNE之间的角度关系.4.(初2020级YZ 初三下入学测试)在正方形 ABCD 中,E 为边CD 上一点(不与点 C 、D 第4页共34重合),垂直于BE 的一条直线 MN 分别交BC 、BE 、AD 于点M 、P 、N,正方形ABCD 的边长为6.(1)如图1,当点M 和点C 重合时,若AN =4,求线段PM 的长度;(2)如图2,当点M 在边BC 上时,判断线段AN 、MB 、EC 之间的数量关系,并说明理由;(3)如图3,当垂足P 在正方形 ABCD 的对角线 AC 上运动时,连接 NB,将^ BPN 沿着BN 翻折,点P 落在点P 处,AB 的中点为Q,直接写出PQ 的最小值.5.(万二中初2020级初三下入学测试)在4ABC与4ADF中,/BAC=/DAF=90° ,AB=AC,AD=AF, DF的延长线交BC于点E,连接DB、CF.(1)如图1,当点C、A、D三点在同一直线上,且AC=g AF, AF=超时,求CE的长;(2)如图2,当/ AFC = 90°时,求证:E是BC的中点;(3)如图3,若CF平分/ ACB,且CF的延长线与DB交于点G,请直接写出BG、DG、FG之间的数量关系.[ D6.(万中初2020级初三下入学测试) 如图,在?ABCD中,/ACB = 45° , AEXBC于点E, 过点C 作CFLAB于点F,交AE于点M.点N在边BC上,且AM = CN ,连结DN .(1)若AB= 10Q , AC = 4,求BC 的长;(2)求证:AD+AM= 22DN .(3)如图,连接EF、探究AF、EF、CF之间存在的数量关系,直接写出数量关系不需要证明.2020年-春季-初三下-【第一次诊断】1.(初2020级YW初三下第一次诊断)如图,在平行四边形ABCD中,AC为对角线,过点D作DELDC交直线AB于点E,过点E作EHXAD于点H,过点B作BFXAD于点F.(1)如图,若/ BAD=60° , AF=3, AH=2,求AC 的长.(2)如图,若BF=DH,在AC上取一点G,连接DG、GE, 若/ DGE=75° ,/CDG=45° -/CAB,求证:DG 立CG22.如图,已知ABCD中,/ B=45° , CE^AD于G,交BA延长线E, CF平分/ DCE ,连接EF, ED.(1)如果AB=5, AD = 372,求线段DE的长.(2)如果/ CFE=90° ,求证:CD 2DF 版AG .(3)如图,在(2)的条件下,若FG J5,点M、N是线段CF、CD上的动点,DM+MN 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由 ^3.(初2020级BZ初三下第一次诊断)已知△ ABC是等边三角形,CD,AB交AB于M, DBXBC, E是AC上一点,EHXBC,垂足为H, EH与CD交于点F,连接BE.(1)如图,若EC=-AC , EH=6,求BE 的长. 5(2)如图,连接AF,将AF绕点A顺时针旋转,使F点落在BD边上的G点处,AG交CD 于Q,求证:BG=CF.(3)如图,在(2)的条件下,连接FG,交BE于N,连接MN,若竺勺,4AGF的面QG 3积为49户,求MN的长.3.(万州国本中学初三下期中考试)已知,在0ABCD中,AB BD, AB BD, E为射线BC上一点,连接AE交BD于点F .(1)如图1,若点E与点C重合,且AF 2胫,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG AE于G ,延长DG交BC于H ,连接FH ,求证:AF DH FH ;(3)如图3,当点E在射线BC上运动时,过点D作DG AE于G , M为AG的中点,点N在BC边上且BN 1 ,已知AB 4 J2 ,请直接写出MN的最小值.4 .(万州国本中学初三下第一次诊断) 【问题背景】如图1所示,在gABC 中,AB= BC, ABC=90,点D 为直线BC 上的一个动点(不与 B 、C 重合),连结AD,将线段AD 绕点D 按顺时针方向旋转90。
中考数学专题复习8几何初步及三角形相关计算(原卷版)

几何初步及三角形相关计算复习考点攻略考点一直线、射线、线段相关概念和性质1.直线的性质(1)两条直线相交.只有一个交点;(2)经过两点有且只有一条直线.即两点确定一条直线;(3)直线的基本事实:经过两点有且只有一条直线.2.线段的性质:两点确定一条直线.两点之间.线段最短.两点间线段的长度叫两点间的距离.3.线段的中点性质:若C是线段AB中点.则AC=BC=12AB;AB=2AC=2BC.4.两条直线的位置关系在同一平面内.两条直线只有两种位置关系:平行和相交.5.垂线的性质(1)两条直线相交所构成的四个角中有一个角是直角.则这两条直线互相垂直.其中一条直线叫做另一条直线的垂线;(2)①经过一点有且只有一条直线与已知直线垂直;②直线外一点与直线上各点连接的所有线段中.垂线段最短.6.点到直线的距离:从直线外一点向已知直线作垂线.这一点和垂足之间线段的长度叫做点到直线的距离.7. 角:有公共端点的两条射线组成的图形.8.角平分线(1)定义:在角的内部.以角的顶点为端点把这个角分成两个相等的角的射线(2)角平分线的性质:①若OC是∠AOB的平分线.则∠AOC=∠BOC=12∠AOB.∠AOB=2∠AOC =2∠BOC.②角平分线上的点到角两边的距离相等。
9.度、分、秒的运算方法1°=60′.1′=60″.1°=3600″.1周角=2平角=4直角=360°.10.余角和补角(1)余角:∠1+∠2=90°⇔∠1与∠2互为余角;(2)补角:∠1+∠2=180°⇔∠1与∠2互为补角.(3)性质:同角(或等角)的余角相等;同角(或等角)的补角相等.11.方向角和方位角在描述方位角时.一般应先说北或南.再说偏西或偏东多少度.而不说成东偏北(南)多少度或西偏北(南)多少度.当方向角在45°方向上时.又常常说成东南、东北、西南、西北方向.【例1】如图.在数轴上有A、B、C、D四个整数点(即各点均表示整数).且2AB=BC=3CD.若A、D两点表示的数分别为-5和6.且AC的中点为E.BD的中点为M.BC之间距点B的距离为13BC的点N.则该数轴的原点为A.点E B.点FC.点M D.点N【例2】如图.∠AOB=180°.∠BOC=80°.OD平分∠AOC.∠DOE=3∠COE.求∠BOE.【例3】如图.要修建一条公路.从A村沿北偏东75°方向到B村.从B村沿北偏西25°方向到C 村.若要保持公路CE与AB的方向一致.则∠ECB的度数为A.80°B.90°C.100°D.105°【例4】计算:18°30′=__________°考点二立体图形1.常见的立体图形有:球、柱体和锥体.圆柱和棱柱的区别:圆柱的底面是圆.棱柱的底面是多边形;圆柱的侧面是曲面.棱柱的侧面是四边形;圆锥和棱锥的区别:圆锥的底面是圆.侧面是曲面;棱锥的底面是多边形.侧面是三角形.2.点动成线.线动成面.面动成体.线没有粗细.点没有大小.3.设立体图形的面数为F.顶点数为V.棱数为E.则F+V-E=2.4.正方体的平面展开图有如下11种类型:【例5】如图是一个正方体包装盒的表面积展开图.若在其中的三个正方形A、B、C内分别填上适当的数.使得将这个表面展开图沿虚线折成正方体后.相对面上的两数互为相反数.则填在A、B、C内的三个数依次为A.0.-2.1 B.0.1.2C.1.0.-2 D.-2.0.1考点三三角形的基本概念(1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
中考数学几何证明题--(专题练习 答案详解)

几何证明题专题1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H在边BF上,且∠HDF=∠E,连接CH,求证:∠BCH=45°﹣∠EBC.6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°.(1)若AB=6cm,,求梯形ABCD的面积;(2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.7、已知:如图, ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD 为边在直角梯形ABCD外作等边三角形ADF,点E是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.求证:(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.30、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.参考答案1、如图,等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,连接BE,CE(1)求证:BE=CE;(2)若∠BEC=90°,过点B作BF⊥CD,垂足为点F,交CE于点G,连接DG,求证:BG=DG+CD.证明:(1)已知等腰梯形ABCD中,AD∥BC,AB=DC,E为AD中点,∴AB=DC,∠BAE=∠CDE,AE=DE,∴△BAE≌△CDE,∴BE=CE;(2)延长CD和BE的延长线交于H,∵BF⊥CD,∠HEC=90°,∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH,又∠BEC=∠CEH=90°,BE=CE(已证),∴△BEG≌△CEH,∴EG=EH,BG=CH=DH+CD,∵△BAE≌△CDE(已证),∴∠AEB=∠GED,∠HED=∠AEB,∴∠GED=∠HED,又EG=EH(已证),ED=ED,∴△GED≌△HED,∴DG=DH,∴BG=DG+CD.2、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,E为AB延长线上一点,连接ED,与BC交于点H.过E作CD的垂线,垂足为CD上的一点F,并与BC交于点G.已知G 为CH的中点.(1)若HE=HG,求证:△EBH≌△GFC;(2)若CD=4,BH=1,求AD的长.(1)证明:∵HE=HG,∴∠HEG=∠HGE,∵∠HGE=∠FGC,∠BEH=∠HEG,∴∠BEH=∠FGC,∵G是HC的中点,∴HG=GC,∴HE=GC,∵∠HBE=∠CFG=90°.∴△EBH≌△GFC;(2)解:∵ED平分∠AEF,∠A=∠DFE=90°,∴AD=DF,∵DF=DC﹣FC,∵△EBH≌△GFC,∴FC=BH=1,∴AD=4﹣1=3.3、如图,梯形ABCD中,AB∥CD,AD=DC=BC,∠DAB=60°,E是对角线AC延长线上一点,F是AD延长线上的一点,且EB⊥AB,EF⊥AF.(1)当CE=1时,求△BCE的面积;(2)求证:BD=EF+CE.(2)过E点作EM⊥DB于点M,四边形FDME是矩形,FE=DM,∠BME=∠BCE=90°,∠BEC=∠MBE=60°,△BME≌△ECB,BM=CE,继而可证明BD=DM+BM=EF+CE.(1)解:∵AD=CD,∴∠DAC=∠DCA,∵DC∥AB,∴∠DCA=∠CAB,∴,∵DC∥AB,AD=BC,∴∠DAB=∠CBA=60°,∴∠ACB=180°﹣(∠CAB+∠CBA)=90°,∴∠BCE=180°﹣∠ACB=90°,∵BE⊥AB,∴∠ABE=90°,∴∠CBE=∠ABE﹣∠ABC=30°,在Rt△BCE中,BE=2CE=2,,∴…(5分)(2)证明:过E点作EM⊥DB于点M,∴四边形FDME是矩形,∴FE=DM,∵∠BME=∠BCE=90°,∠BEC=∠MBE=60°,∴△BME≌△ECB,∴BM=CE,∴BD=DM+BM=EF+CE…(10分)4、如图.在平行四边形ABCD中,O为对角线的交点,点E为线段BC延长线上的一点,且.过点E作EF∥CA,交CD于点F,连接OF.(1)求证:OF∥BC;(2)如果梯形OBEF是等腰梯形,判断四边形ABCD的形状,并给出证明.解答:(1)证明:延长EF交AD于G(如图),在平行四边形ABCD中,AD∥BC,AD=BC,∵EF∥CA,EG∥CA,∴四边形ACEG是平行四边形,∴AG=CE,又∵,AD=BC,∴,∵AD∥BC,∴∠ADC=∠ECF,在△CEF和△DGF中,∵∠CFE=∠DFG,∠ADC=∠ECF,CE=DG,∴△CEF≌△DGF(AAS),∴CF=DF,∵四边形ABCD是平行四边形,∴OB=OD,∴OF∥BE.(2)解:如果梯形OBEF是等腰梯形,那么四边形ABCD是矩形.证明:∵OF∥CE,EF∥CO,∴四边形OCEF是平行四边形,∴EF=OC,又∵梯形OBEF是等腰梯形,∴BO=EF,∴OB=OC,∵四边形ABCD是平行四边形,∴AC=2OC,BD=2BO.∴AC=BD,∴平行四边形ABCD是矩形.5、如图,梯形ABCD中,AD∥BC,∠ABC=90°,BF⊥CD于F,延长BF交AD的延长线于E,延长CD交BA的延长线于G,且DG=DE,AB=,CF=6.(1)求线段CD的长;(2)H 在边BF 上,且∠HDF=∠E ,连接CH ,求证:∠BCH=45°﹣∠EBC .(1)解:连接BD ,由∠ABC=90°,AD ∥BC 得∠GAD=90°,又∵BF ⊥CD ,∴∠DFE=90°又∵DG=DE ,∠GDA=∠EDF ,∴△GAD ≌△EFD ,∴DA=DF ,又∵BD=BD ,∴Rt △BAD ≌Rt △BFD (HL ),∴BF=BA=,∠ADB=∠BDF 又∵CF=6,∴BC=,又∵AD ∥BC ,∴∠ADB=∠CBD ,∴∠BDF=∠CBD ,∴CD=CB=8.(2)证明:∵AD ∥BC ,∴∠E=∠CBF ,∵∠HDF=∠E ,∴∠HDF=∠CBF ,由(1)得,∠ADB=∠CBD ,∴∠HDB=∠HBD ,∴HD=HB ,由(1)得CD=CB ,CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ,∴∠DCH=∠BCH ,∴∠BCH=∠BCD==.6、如图,直角梯形ABCD中,AD∥BC,∠B=90°,∠D=45°.(1)若AB=6cm,,求梯形ABCD的面积;(2)若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点,且满足EF=GH,∠EFH=∠FHG,求证:HD=BE+BF.解:(1)连AC,过C作CM⊥AD于M,如图,在Rt△ABC中,AB=6,sin∠ACB==,∴AC=10,∴BC=8,在Rt△CDM中,∠D=45°,∴DM=CM=AB=6,∴AD=6+8=14,∴梯形ABCD的面积=•(8+14)•6=66(cm2);(2)证明:过G作GN⊥AD,如图,∵∠D=45°,∴△DNG为等腰直角三角形,∴DN=GN,又∵AD∥BC,∴∠BFH=∠FHN,而∠EFH=∠FHG,∴∠BFE=∠GHN,∵EF=GH,∴Rt△BEF≌Rt△NGH,∴BE=GN,BF=HN,∴DA=AN+DN=AN+DG=BF+BE.7、已知:如图,▱ABCD中,对角线AC,BD相交于点O,延长CD至F,使DF=CD,连接BF交AD于点E.(1)求证:AE=ED;(2)若AB=BC,求∠CAF的度数.(1)证明:如图.∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵DF=CD,∴AB∥DF.∵DF=CD,∴AB=DF.∴四边形ABDF是平行四边形,∴AE=DE.(2)解:∵四边形ABCD是平行四边形,且AB=BC,∴四边形ABCD是菱形.∴AC⊥BD.∴∠COD=90°.∵四边形ABDF是平行四边形,∴AF∥BD.∴∠CAF=∠COD=90°.8、已知:如图,在正方形ABCD中,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F.(1)求证:∠DAE=∠DCE;(2)当CG=CE时,试判断CF与EG之间有怎样的数量关系?并证明你的结论.(1)证明:在△DAE和△DCE中,∠ADE=∠CDE(正方形的对角线平分对角),ED=DE(公共边),AE=CE(正方形的四条边长相等),∴△DAE≌△DCE(SAS),∴∠DAE=∠DCE(全等三角形的对应角相等);(2)解:如图,由(1)知,△DAE≌△DCE,∴AE=EC,∴∠EAC=∠ECA(等边对等角);又∵CG=CE(已知),∴∠G=∠CEG(等边对等角);而∠CEG=2∠EAC(外角定理),∠ECB=2∠CEG(外角定理),∴4∠EAC﹣∠ECA=∠ACB=45°,∴∠G=∠CEG=30°;过点C作CH⊥AG于点H,∴∠FCH=30°,∴在直角△ECH中,EH=CH,EG=2CH,在直角△FCH中,CH=CF,∴EG=2×CF=3CF.9、如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.(1)求证:DP平分∠ADC;(2)若∠AEB=75°,AB=2,求△DFP的面积.(1)证明:连接PC.∵ABCD是正方形,∴∠ABE=∠ADF=90°,AB=AD.∵BE=DF,∴△ABE≌△ADF.(SAS)∴∠BAE=∠DAF,AE=AF.∴∠EAF=∠BAD=90°.∵P是EF的中点,∴PA=EF,PC=EF,∴PA=PC.又AD=CD,PD公共,∴△PAD≌△PCD,(SSS)∴∠ADP=∠CDP,即DP平分∠ADC;(2)作PH⊥CF于H点.∵P是EF的中点,∴PH=EC.设EC=x.由(1)知△EAF是等腰直角三角形,∴∠AEF=45°,∴∠FEC=180°﹣45°﹣75°=60°,∴EF=2x,FC=x,BE=2﹣x.在Rt△ABE中,22+(2﹣x)2=(x)2解得x1=﹣2﹣2(舍去),x2=﹣2+2.∴PH=﹣1+,FD=(﹣2+2)﹣2=﹣2+4.=(﹣2+4)×=3﹣5.∴S△DPF10、如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,BD=BC,E为CD的中点,交BC的延长线于F;(1)证明:EF=EA;(2)过D作DG⊥BC于G,连接EG,试证明:EG⊥AF.(1)证明:∵AD∥BC,∴∠DAE=∠F,∠ADE=∠FCE.∵E为CD的中点,∴ED=EC.∴△ADE≌△FCE.∴EF=EA.(5分)(2)解:连接GA,∵AD∥BC,∠ABC=90°,∴∠DAB=90°.∵DG⊥BC,∴四边形ABGD是矩形.∴BG=AD,GA=BD.∵BD=BC,∴GA=BC.由(1)得△ADE≌△FCE,∴AD=FC.∴GF=GC+FC=GC+AD=GC+BG=BC=GA.∵由(1)得EF=EA,∴EG⊥AF.(5分)11、如图,直角梯形ABCD中,∠DAB=90°,AB∥CD,AB=AD,∠ABC=60度.以AD为边在直角梯形ABCD外作等边三角形ADF,点E 是直角梯形ABCD内一点,且∠EAD=∠EDA=15°,连接EB、EF.(1)求证:EB=EF;(2)延长FE交BC于点G,点G恰好是BC的中点,若AB=6,求BC的长.(1)证明:∵△ADF为等边三角形,∴AF=AD,∠FAD=60°(1分)∵∠DAB=90°,∠EAD=15°,AD=AB(2分)∴∠FAE=∠BAE=75°,AB=AF,(3分)∵AE为公共边∴△FAE≌△BAE(4分)∴EF=EB(5分)(2)解:如图,连接EC.(6分)∵在等边三角形△ADF中,∴FD=FA,∵∠EAD=∠EDA=15°,∴ED=EA,∴EF是AD的垂直平分线,则∠EFA=∠EFD=30°.(7分)由(1)△FAE≌△BAE知∠EBA=∠EFA=30°.∵∠FAE=∠BAE=75°,∴∠BEA=∠BAE=∠FEA=75°,∴BE=BA=6.∵∠FEA+∠BEA+∠GEB=180°,∴∠GEB=30°,∵∠ABC=60°,∴∠GBE=30°∴GE=GB.(8分)∵点G是BC的中点,∴EG=CG∵∠CGE=∠GEB+∠GBE=60°,∴△CEG为等边三角形,∴∠CEG=60°,∴∠CEB=∠CEG+∠GEB=90°(9分)∴在Rt△CEB中,BC=2CE,BC2=CE2+BE2∴CE=,∴BC=(10分);解法二:过C作CQ⊥AB于Q,∵CQ=AB=AD=6,∵∠ABC=60°,∴BC=6÷=4.12、如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于点E,F是CD的中点,DG是梯形ABCD的高.(1)求证:AE=GF;(2)设AE=1,求四边形DEGF的面积.(1)证明:∵AB=DC,∴梯形ABCD为等腰梯形.∵∠C=60°,∴∠BAD=∠ADC=120°,又∵AB=AD,∴∠ABD=∠ADB=30°.∴∠DBC=∠ADB=30°.∴∠BDC=90°.(1分)由已知AE⊥BD,∴AE∥DC.(2分)又∵AE为等腰三角形ABD的高,∴E是BD的中点,∵F是DC的中点,∴EF∥BC.∴EF∥AD.∴四边形AEFD是平行四边形.(3分)∴AE=DF(4分)∵F是DC的中点,DG是梯形ABCD的高,∴GF=DF,(5分)∴AE=GF.(6分)(2)解:在Rt△AED中,∠ADB=30°,∵AE=1,∴AD=2.在Rt△DGC中∠C=60°,并且DC=AD=2,∴DG=.(8分)由(1)知:在平行四边形AEFD中EF=AD=2,又∵DG⊥BC,∴DG⊥EF,∴四边形DEGF的面积=EF•DG=.(10分)13、已知,如图在直角梯形ABCD中,AD∥BC,∠ABC=90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点E,且AE=AC,连AG.(1)求证:FC=BE;(2)若AD=DC=2,求AG的长.解答:(1)证明:∵∠ABC=90°,DE⊥AC于点F,∴∠ABC=∠AFE.∵AC=AE,∠EAF=∠CAB,∴△ABC≌△AFE,∴AB=AF.∴AE﹣AB=AC﹣AF,即FC=BE;(2)解:∵AD=DC=2,DF⊥AC,∴AF=AC=AE.∴AG=CG,∴∠E=30°.∵∠EAD=90°,∴∠ADE=60°,∴∠FAD=∠E=30°,∴FC=,∵AD∥BC,∴∠ACG=∠FAD=30°,∴CG=2,∴AG=2.14、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,点E是AB边上一点,AE=BC,DE⊥EC,取DC的中点F,连接AF、BF.(1)求证:AD=BE;(2)试判断△ABF的形状,并说明理由.(1)证明:∵AD∥BC,∴∠BAD+∠ABC=180°,∵∠ABC=90°,∴∠BAD=∠ABC=90°,∵DE⊥EC,∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°,∴∠BEC=∠ADE,∵∠DAE=∠EBC,AE=BC,∴△EAD≌△EBC,∴AD=BE.(2)答:△ABF是等腰直角三角形.理由是:延长AF交BC的延长线于M,∵AD∥BM,∴∠DAF=∠M,∵∠AFD=∠CFM,DF=FC,∴△ADF≌△MFC,∴AD=CM,∵AD=BE,∴BE=CM,∵AE=BC,∴AB=BM,∴△ABM是等腰直角三角形,∵△ADF≌△MFC,∴AF=FM,∴∠ABC=90°,∴BF⊥AM,BF=AM=AF,∴△AFB是等腰直角三角形.15、(2011•潼南县)如图,在直角梯形ABCD中,AB∥CD,AD⊥DC,AB=BC,且AE⊥BC.(1)求证:AD=AE;(2)若AD=8,DC=4,求AB的长.解答:(1)证明:连接AC,∵AB∥CD,∴∠ACD=∠BAC,∵AB=BC,∴∠ACB=∠BAC,∴∠ACD=∠ACB,∵AD⊥DC,AE⊥BC,∴∠D=∠AEC=90°,∵AC=AC,∴,∴△ADC≌△AEC,(AAS)∴AD=AE;(2)解:由(1)知:AD=AE,DC=EC,设AB=x,则BE=x﹣4,AE=8,在Rt△ABE中∠AEB=90°,由勾股定理得:82+(x﹣4)2=x2,解得:x=10,∴AB=10.说明:依据此评分标准,其它方法如:过点C作CF⊥AB用来证明和计算均可得分.16、如图,已知梯形ABCD中,AD∥CB,E,F分别是BD,AC的中点,BD平分∠ABC.(1)求证:AE⊥BD;(2)若AD=4,BC=14,求EF的长.(1)证明:∵AD∥CB,∴∠ADB=∠CBD,又BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AB=AD,∴△ABD是等腰三角形,已知E是BD的中点,∴AE⊥BD.(2)解:延长AE交BC于G,∵BD平分∠ABC,∴∠ABE=∠GBE,又∵AE⊥BD(已证),∴∠AEB=∠GEB,BE=BE,∴△ABE≌△GBE,∴AE=GE,BG=AB=AD,又F是AC的中点(已知),所以由三角形中位线定理得:EF=CG=(BC﹣BG)=(BC﹣AD)=×(14﹣4)=5.答:EF的长为5.17、如图,在梯形ABCD中,AD∥BC,∠D=90°,BE⊥AC,E为垂足,AC=BC.(1)求证:CD=BE;(2)若AD=3,DC=4,求AE.(1)证明:∵AD∥BC,∴∠DAC=∠BCE,而BE⊥AC,∴∠D=∠BEC=90°,AC=BC,∴△BCE≌△CAD.∴CD=BE.(2)解:在Rt△ADC中,根据勾股定理得AC==5,∵△BCE≌△CAD,∴CE=AD=3.∴AE=AC﹣CE=2.18、如图,在梯形ABCD中,AD∥BC,AB⊥AC,∠B=45°,AD=1,BC=4,求DC的长.解:如图,过点D作DF∥AB,分别交AC,BC于点E,F.(1分)∵AB⊥AC,∴∠AED=∠BAC=90度.∵AD∥BC,∴∠DAE=180°﹣∠B﹣∠BAC=45度.在Rt△ABC中,∠BAC=90°,∠B=45°,BC=4,∴AC=BC•sin45°=4×=2(2分)在Rt△ADE中,∠AED=90°,∠DAE=45°,AD=1,∴DE=AE=.∴CE=AC﹣AE=.(4分)在Rt△DEC中,∠CED=90°,∴DC==.(5分)19、已知梯形ABCD中,AD∥BC,AB=BC=DC,点E、F分别在AD、AB上,且.(1)求证:BF=EF﹣ED;(2)连接AC,若∠B=80°,∠DEC=70°,求∠ACF的度数.证明:∵FC=F′C,EC=EC,∠ECF'=∠BCF+∠DCE=∠ECF,∴△FCE≌△F′CE,∴EF′=EF=DF′+ED,∴BF=EF﹣ED;(2)解:∵AB=BC,∠B=80°,∴∠ACB=50°,由(1)得∠FEC=∠DEC=70°,∴∠ECB=70°,而∠B=∠BCD=80°,∴∠DCE=10°,∴∠BCF=30°,∴∠ACF=∠BCA﹣∠BCF=20°.20、如图,梯形ABCD中,AD∥BC,点E在BC上,AE=BE,且AF⊥AB,连接EF.(1)若EF⊥AF,AF=4,AB=6,求AE的长.(2)若点F是CD的中点,求证:CE=BE﹣AD.解:(1)作EM⊥AB,交AB于点M.∵AE=BE,EM⊥AB,∴AM=BM=×6=3;∵∠AME=∠MAF=∠AFE=90°,∴四边形AMEF是矩形,∴EF=AM=3;在Rt△AFE中,AE==5;(2)延长AF、BC交于点N.∵AD∥EN,∴∠DAF=∠N;∵∠AFD=∠NFC,DF=FC,∴△ADF≌△NCF(AAS),∴AD=CN;∵∠B+∠N=90°,∠BAE+∠EAN=90°,又AE=BE,∠B=∠BAE,∴∠N=∠EAN,AE=EN,∴BE=EN=EC+CN=EC+AD,∴CE=BE﹣AD..21、如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.(1)求证:DH=(AD+BC);(2)若AC=6,求梯形ABCD的面积.解:(1)证明:过D作DE∥AC交BC延长线于E,(1分)∵AD∥BC,∴四边形ACED为平行四边形.(2分)∴CE=AD,DE=AC.∵四边形ABCD为等腰梯形,∴BD=AC=DE.∵AC⊥BD,∴DE⊥BD.∴△DBE为等腰直角三角形.(4分)∵DH⊥BC,∴DH=BE=(CE+BC)=(AD+BC).(5分)(2)∵AD=CE,∴.(7分)∵△DBE为等腰直角三角形BD=DE=6,∴.∴梯形ABCD的面积为18.(8分)注:此题解题方法并不唯一.22、已知,如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE,BD.(1)求证:△AGE≌△DAB;(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.(1)证明:∵△ABC是等边三角形,DG∥BC,∴∠AGD=∠ABC=60°,∠ADG=∠ACB=60°,且∠BAC=60°,∴△AGD是等边三角形,AG=GD=AD,∠AGD=60°.∵DE=DC,∴GE=GD+DE=AD+DC=AC=AB,∵∠AGD=∠BAD,AG=AD,∴△AGE≌△DAB;(2)解:由(1)知AE=BD,∠ABD=∠AEG.∵EF∥DB,DG∥BC,∴四边形BFED是平行四边形.∴EF=BD,∴EF=AE.∵∠DBC=∠DEF,∴∠ABD+∠DBC=∠AEG+∠DEF,即∠AEF=∠ABC=60°.∴△AFE是等边三角形,∠AFE=60°.23、如图,梯形ABCD中,AD∥BC,DE=EC,EF∥AB交BC于点F,EF=EC,连接DF.(1)试说明梯形ABCD是等腰梯形;(2)若AD=1,BC=3,DC=,试判断△DCF的形状;(3)在条件(2)下,射线BC上是否存在一点P,使△PCD是等腰三角形,若存在,请直接写出PB的长;若不存在,请说明理由.解:(1)证明:∵EF=EC,∴∠EFC=∠ECF,∵EF∥AB,∴∠B=∠EFC,∴∠B=∠ECF,∴梯形ABCD是等腰梯形;(2)△DCF是等腰直角三角形,证明:∵DE=EC,EF=EC,∴EF=CD,∴△CDF是直角三角形(如果一个三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形),∵梯形ABCD是等腰梯形,∴CF=(BC﹣AD)=1,∵DC=,∴由勾股定理得:DF=1,∴△DCF是等腰直角三角形;(3)共四种情况:∵DF⊥BC,∴当PF=CF时,△PCD是等腰三角形,即PF=1,∴PB=1;当P与F重合时,△PCD是等腰三角形,∴PB=2;当PC=CD=(P在点C的左侧)时,△PCD是等腰三角形,∴PB=3﹣;当PC=CD=(P在点C的右侧)时,△PCD是等腰三角形,∴PB=3+.故共四种情况:PB=1,PB=2,PB=3﹣,PB=3+.(每个1分)24、如图,在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,AD=DC,E、F分别在AD、DC的延长线上,且DE=CF.AF交BE于P.(1)证明:△ABE≌△DAF;(2)求∠BPF的度数.解答:(1)证明:∵在梯形ABCD中,AD∥BC,∠ABC=∠BCD=60°,∴AB=CD,∵AD=DC,∴BA=AD,∠BAE=∠ADF=120°,∵DE=CF,∴AE=DF,在△BAE和△ADF中,,∴△ABE≌△DAF(SAS).(2)解:∵由(1)△BAE≌△ADF,∴∠ABE=∠DAF.∴∠BPF=∠ABE+∠BAP=∠BAE.而AD∥BC,∠C=∠ABC=60°,∴∠BPF=120°.25、如图,在梯形ABCD中,AD∥BC,AB=AD=DC,BD⊥DC,将BC延长至点F,使CF=CD.(1)求∠ABC的度数;(2)如果BC=8,求△DBF的面积?解答:解:(1)∵AD∥BC,∴∠ADB=∠DBC,∵AB=AD,∴∠ADB=∠ABD,∴∠DBC=∠ABD,∵在梯形ABCD中AB=DC,∴∠ABC=∠DCB=2∠DBC,∵BD⊥DC,∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°(2)过点D作DH⊥BC,垂足为H,∵∠DBC=30°,BC=8,∴DC=4,∵CF=CD∴CF=4,∴BF=12,∵∠F+∠FDC=∠DCB=60°,∠F=∠FDC∴∠F=30°,∵∠DBC=30°,∴∠F=∠DBC,∴DB=DF,∴,在直角三角形DBH中,∴,∴,∴,即△DBF的面积为.26、如图,梯形ABCD中,AD∥BC,AB=DC=10cm,AC交BD于G,且∠AGD=60°,E、F分别为CG、AB的中点.(1)求证:△AGD为正三角形;(2)求EF的长度.(1)证明:连接BE,∵梯形ABCD中,AB=DC,∴AC=BD,可证△ABC≌△DCB,∴∠GCB=∠GBC,又∵∠BGC=∠AGD=60°∴△AGD为等边三角形,(2)解:∵BE为△BCG的中线,∴BE⊥AC,在Rt△ABE中,EF为斜边AB上的中线,∴EF=AB=5cm.27、已知,如图,AD∥BC,∠ABC=90°,AB=BC,点E是AB上的点,∠ECD=45°,连接ED,过D作DF⊥BC于F.(1)若∠BEC=75°,FC=3,求梯形ABCD的周长.(2)求证:ED=BE+FC.解:(1)∵∠BEC=75°,∠ABC=90°,∴∠ECB=15°,∵∠ECD=45°,∴∠DCF=60°,在Rt△DFC中:∠DCF=60°,FC=3,∴DF=3,DC=6,由题得,四边形ABFD是矩形,∴AB=DF=3,∵AB=BC,∴BC=3,∴BF=BC﹣FC=3﹣3,∴AD=DF=3﹣3,∴C=3×2+6+3﹣3=9+3,梯形ABCD答:梯形ABCD的周长是9+3.(2)过点C作CM垂直AD的延长线于M,再延长DM到N,使MN=BE,∴CN=CE,可证∠NCD=∠DCE,∵CD=CD,∴△DEC≌△DNC,∴ED=EN,∴ED=BE+FC.28、(2005•镇江)已知:如图,梯形ABCD中,AD∥BC,E是AB的中点,直线CE交DA的延长线于点F.(1)求证:△BCE≌△AFE;(2)若AB⊥BC且BC=4,AB=6,求EF的长.(1)证明:∵AD∥BC,E是AB的中点,∴AE=BE,∠B=∠EAF,∠BCE=∠F.∴△BCE≌△AFE(AAS).(2)解:∵AD∥BC,∴∠DAB=∠ABC=90°.∵AE=BE,∠AEF=∠BEC,∴△BCE≌△AFE.∴AF=BC=4.∵EF2=AF2+AE2=9+16=25,∴EF=5.29、已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF 的延长线交DC于点E.(1)△BFC≌△DFC;(2)AD=DE;(3)若△DEF的周长为6,AD=2,BC=5,求梯形ABCD的面积.(1)∵DC=BC,∠1=∠2,CF=CF,∴△DCF≌△BCF.(2)延长DF交BC于G,∵AD∥BG,AB∥DG,∴四边形ABGD为平行四边形.∴AD=BG.∵△DFC≌△BFC,∴∠EDF=∠GBF,DF=BF.又∵∠3=∠4,∴△DFE≌△BFG.∴DE=BG,EF=GF.∴AD=DE.(3)∵EF=GF,DF=BF,∴EF+BF=GF+DF,即:BE=DG.∵DG=AB,∴BE=AB.∵C=DF+FE+DE=6,△DFE∴BF+FE+DE=6,即:EB+DE=6.∴AB+AD=6.又∵AD=2,∴AB=4.∴DG=AB=4.∵BG=AD=2,∴GC=BC﹣BG=5﹣2=3.又∵DC=BC=5,在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°.=(AD+BC)•DG∴S梯形ABCD=(2+5)×430、如图,梯形ABCD中,AD∥BC.∠C=90°,且AB=AD.连接BD,过A点作BD的垂线,交BC于E.(1)求证:四边形ABED是菱形;(2)如果EC=3cm,CD=4cm,求梯形ABCD的面积.解答:解:(1)证明:∵AD∥BC,DE2=CD2+CE2=42+32=25,∴∠OAD=∠OEB,∴DE=5又∵AB=AD,AO⊥BD,∴AD=BE=5,=.∴OB=OD,∴S梯形ABCD又∵∠AOD=∠EOB,∴△ADO≌△EBO(AAS),∴AD=EB,又∵AD∥BE,∴四边形ABCD是平行四边形,又∵AB=AD∴四边形ABCD是菱形.(2)∵四边形ABCD是菱形,∴AD=DE=BE,。
中考复习初中数学几何证明经典试题(含答案)
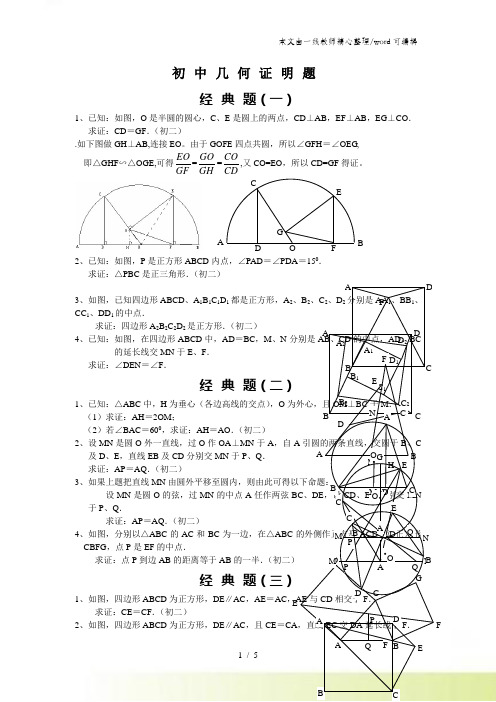
P CG FAD E初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二).如下图做GH ⊥AB,连接EO 。
由于GOFE 四点共圆,所以∠GFH =∠OEG , 即△GHF ∽△OGE,可得EO GF =GO GH =COCD,又CO=EO ,所以CD=GF 得证。
2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 的延长线交MN 于E 、F .求证:∠DEN =∠F . 经典1、已知:△ABC 中,H 为垂心(各边高线的交点),O (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典题(三) 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .AQ P NM · O B D AF D AFGCEBO D求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二) 4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,=AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5. 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA DPC .(初二) 经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数. 经典题(一)1.如下图做GH ⊥AB,连接EO 。
(完整版)八年级几何证明题集锦及解答值得收藏
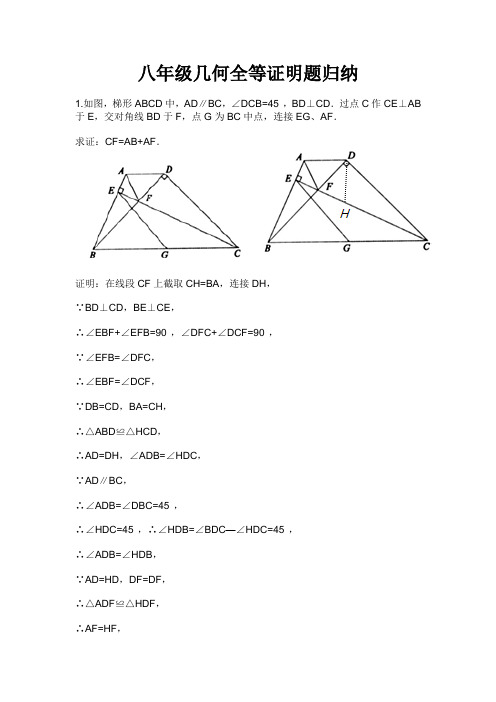
八年级几何全等证明题归纳1.如图,梯形ABCD中,AD∥BC,∠DCB=45°,BD⊥CD.过点C作CE⊥AB 于E,交对角线BD于F,点G为BC中点,连接EG、AF.求证:CF=AB+AF.证明:在线段CF上截取CH=BA,连接DH,∵BD⊥CD,BE⊥CE,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°,∵∠EFB=∠DFC,∴∠EBF=∠DCF,∵DB=CD,BA=CH,∴△ABD≌△HCD,∴AD=DH,∠ADB=∠HDC,∵AD∥BC,∴∠ADB=∠DBC=45°,∴∠HDC=45°,∴∠HDB=∠BDC—∠HDC=45°,∴∠ADB=∠HDB,∵AD=HD,DF=DF,∴△ADF≌△HDF,∴AF=HF,∴CF=CH+HF=AB+AF,∴CF=AB+AF.2.如图,ABCD为正方形,E为BC边上一点,且AE=DE,AE与对角线BD交于点F,连接CF,交ED于点G.判断CF与ED的位置关系,并说明理由.解:垂直.理由:∵四边形ABCD为正方形,∴∠ABD=∠CBD,AB=BC,∵BF=BF,∴△ABF≌△CBF,∴∠BAF=∠BCF,∵在RT△ABE和△DCE中,AE=DE,AB=DC,∴RT△ABE≌△DCE,∴∠BAE=∠CDE,∴∠BCF=∠CDE,∵∠CDE+∠DEC=90°,∴∠BCF+∠DEC=90°,∴DE⊥CF.3.如图,在直角梯形ABCD中,AD∥BC,∠A=90º,AB=AD,DE⊥CD交AB于E,DF平分∠CDE交BC于F,连接EF.证DA明:CF=EF解:EB F C过D作DG⊥BC于G.由已知可得四边形ABGD为正方形,∵DE⊥DC∴∠ADE+∠EDG=90°=∠GDC+∠EDG,∴∠ADE=∠GDC.又∵∠A=∠DGC且AD=GD,∴△ADE≌△GDC,∴DE=DC且AE=GC.在△EDF和△CDF中∠EDF=∠CDF,DE=DC,DF为公共边,∴△EDF ≌△CDF,∴EF=CF4.已知:在⊿ABC中,∠A=900,AB=AC,D是AC的中点,AE⊥BD,AE延长线交BC于F,求证:∠ADB=∠FDC。
专题08 全等模型巩固练习(基础)-冲刺2021年中考几何专项复习(解析版)

全等模型巩固练习1. 王强同学用10块高度都是2cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC =BC ,∠ACB =90°),点C 在DE 上,点A 和B 分别与木墙的顶端重合.(1)求证:△ADC ≌△CEB ;(2)求两堵木墙之间的距离.【解答】(1)见解析;(2)20cm【解析】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠DAC =90°,∴∠BCE =∠DAC在△ADC 和△CEB 中{∠ADC =∠CEB∠DAC =∠BCE AC =BC,∴△ADC ≌△CEB (AAS );(2)由题意得:AD =2×3=6cm ,BE =7×2=14cm ,∵△ADC ≌△CEB ,∴EC =AD =6cm ,DC =BE =14cm ,∴DE =DC +CE =20(cm ),答:两堵木墙之间的距离为20cm .2. 如图,小明站在堤岸的A 点处,正对他的S 点停有一艘游艇,他想知道这艘游艇距离他多远,于是他沿堤岸走到电线杆B 旁,接着再往前走相同的距离,到达C 点,然后他向左直行,当看到电线杆与游艇在一条直线上时停下来.此时他位于D 点.那么C 、D 两点间的距离就是在A 点处小明与游艇的距离,你知道这是为什么吗?【解答】见解析【解析】在△ABS 与△CBD 中,{∠A =∠C =90°AB =CB ∠ABS =∠CBD,∴△ABS ≌△CBD (ASA ),∴AS =CD .3. 如图,工人师傅要在墙壁的O 处用钻打孔,要使孔口从墙壁对面的B 点处打开,墙壁厚是35cm ,B 点与O 点的铅直距离AB 长是20cm ,工人师傅在旁边墙上与AO 水平的线上截取OC =35cm ,画CD ⊥OC ,使CD =20cm ,连接OD ,然后沿着DO 的方向打孔,结果钻头正好从B 点处打出,这是什么道理呢?请你说出理由.【解答】见解析【解析】∵OC =35cm ,墙壁厚OA =35cm ,∴OC =OA ,∵墙体是垂直的,∴∠OAB =90°且CD ⊥OC ,∴∠OAB =∠OCD =90°,在Rt △OAB 和Rt △OCD 中,{∠OAB =∠OCD =90°OC =OA ∠AOB =∠COD,∴Rt △OAB ≌Rt △OCD (ASA ),∴DC =AB ,∵DC =20cm ,∴AB =20cm ,∴钻头正好从B 点处打出.4. 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图AD ⊥DE ,BE ⊥DE .(1)求证:△ADC ≌△CEB ;(2)若三角板的一条直角边AC =25cm ,请你帮小明求出砌墙砖块的厚度a 的大小(每块砖的厚度相等).【解答】(1)见解析;(2)5cm .【解析】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠DAC =90°,∴∠BCE =∠DAC ,在△ADC 和△CEB 中,{∠ADC =∠CEB∠DAC =∠BCE AC =BC,∴△ADC ≌△CEB (AAS );(2)∵一块墙砖的厚度为a ,∴AD =4a ,BE =3a ,由(1)得:△ADC ≌△CEB ,∴DC =BE =3a ,AD =CE =4a ,∴AC =√AD 2+CD 2=5a =25,∴a =5,答:砌墙砖块的厚度a 为5cm .5. 某大学计划为新生配备如图1所示的折叠凳图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB 和CD 的长相等,O 是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD 设计为30cm ,由以上信息能求出CB 的长度吗?如果能,请求出BC 的长度,如果不能,请你说明理由.【解答】30cm【解析】∵O 是AB 、CD 的中点,∴OA =OB ,OC =OD ,在△AOD 和△BOC 中,{OA =OB∠AOD =∠BOC OC =OD,∴△AOD ≌△BOC (SAS ),∴CB =AD ,∵AD =30cm ,∴CB =30cm .6. 在测量一个小口圆形容器的壁厚时,小明用“X 型转动钳”按如图方法进行测量,其中OA =OD ,OB =OC ,只需测得AB =a ,EF =b ,就可以知道圆形容器的壁厚了.(1)请你利用所学习的数学知识说明AB =CD ;(2)求出圆形容器的壁厚.(用含有a ,b 的代数式表示)【解答】(1)见解析;(2)12(b ﹣a ) 【解析】(1)连接AB .在△AOB 和△DOC 中,{OA =OD ∠AOB =∠DOC BO =OC,∴△AOB≌△DOC(SAS),∴AB=CD;(2)∵EF=b,AB=CD=a,(b﹣a).∴圆形容器的壁厚是127.如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作ED⊥BD交AC的延长线于点E,垂足为点D.(DE≠CD)(1)线段的长度就是A、B两点间的距离(2)请说明(1)成立的理由.【解答】(1)DE;(2)见解析【解析】(1)线段DE的长度就是A、B两点间的距离;故答案为:DE;(2)∵AB⊥BC,DE⊥BD∴∠ABC=∠EDC=90°又∵∠ACB=∠DCE,BC=CD∴△ABC≌△CDE(ASA)∴AB=DE.8.某风景区改建中,需测量湖两岸游船码头A、B间的距离,于是工作人员在岸边A、B的垂线AF上取两点E、D,使ED=AE.再过D点作出AF的垂线OD,并在OD上找一点C,使B、E、C在同一直线上,这时测得CD 长就是AB 的距离.请说明理由.【解答】见解析【解析】证明:∵AB ⊥AD ,CD ⊥AD∴∠A =∠CDE =90°又∵ED =AE ,∠AEB =∠CED∴△ABE ≌△CED (AAS )所以AB =CD .9. 课间,王二丁拿着老师的等腰直角三角板的三角板玩,不小心掉到两墙之间,如图所示AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE(1)求证:△ADC ≌△CEB ;(2)已知DE =42cm ,请你帮王二丁求出砌墙的厚度a 的大小(每块砖的厚度相等).【解答】(1)见解析;(2)6【解析】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,∴∠ADC =∠CEB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠DAC =90°,∴∠BCE =∠DAC ,在△ADC 和△CEB 中,{∠ADC =∠CEB∠DAC =∠BCE AC =BC,∴△ADC ≌△CEB (AAS );(2)由题意得:∵一块墙砖的厚度为a ,∴AD =4a ,BE =3a ,由(1)得:△ADC ≌△CEB ,∴DC=BE=3a,AD=CE=4a,∴DC+CE=BE+AD=7a=42,∴a=6,答:砌墙的厚度a为6cm.10.如图,小明站在乙楼BE前方的点C处,恰好看到甲、乙两楼楼顶上的点A和E重合为一点,若B、C 相距30米,C、D相距60米,乙楼高BE为20米,小明身高忽略不计,则甲楼的高AD是多少米?【解答】40米【解析】∵AD⊥DC,EB⊥BC,∴AD∥BE,∴∠AEF=∠C,∵B、C相距30米,C、D相距60米,∴EF=DB=BC=30米,∵∠AFE=∠EBC=90°,∴△AEF≌△ECB(ASA),∴AF=BE,∵DF=BE,∴AD=2BE=2×20=40(米).答:甲楼的高AD是40米.11.雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=13AB,AF=13AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.【解答】∠BAD =∠CAD【解析】雨伞开闭过程中二者关系始终是:∠BAD =∠CAD ,理由如下:∵AB =AC ,AE =13AB ,AF =13AC , ∴AE =AF ,在△AOE 与△AOF 中,{AE =AF AO =AO OE =OF,∴△AOE ≌△AOF (SSS ),∴∠BAD =∠CAD .12.如图,O 为海港码头,A ,B 是到海港码头O 距离相等的两座灯塔,OA ,OB 为海岸线,一艘渔船离开码头,计划沿∠AOB 的平分线方向航行,在航行途中,测得渔船到灯塔A ,B 的距离始终相等.(1)渔船是否偏离预定的航线?为什么?(C 表示渔船航行途中的某一位置)(2)已知灯塔A ,B 距离码头17海里,灯塔A ,B 相距16海里,若渔船航行到距离灯塔17海里的E 处,渔船离开海港码头多远?【解答】(1)渔船没偏离预定的航线;(2)30海里【解析】(1)没有偏离预定航行,理由如下:连接AC ,BC ,在△AOC 与△BOC 中,{OA =OBOC =OC AC =BC,∴△AOC ≌△BOC (SSS ).∴∠AOC =∠BOC ,即点C 在∠AOB 的平分线上,∴渔船没偏离预定的航线;(2)连接AE ,AB 交OC 于∵OA =OB ,∠AOC =∠BOC ,∴OC ⊥AB ,AC =BC =12AB =8, 由题意得,OA =OB =AE =17,AB =16,∴OC =√OA 2−AC 2=√172−82=15,∵AO =AE ,AC ⊥OE ,∴OE =2OC =30,故渔船离开海港码头30海里.13.如图,A 、B 两建筑物位于河的两岸,要测得它们之间的距离,可以从B 点出发沿河岸画一条射线BF ,在BF 上截取BC =CD ,过D 作DE ∥AB ,使E 、C 、A 在同一直线上,则DE 的长就是A 、B 之间的距离,请你说明道理.【解答】见解析【解析】∵DE ∥AB ,∴∠CED =∠CAB ,{∠CAB =∠CED∠ACB =∠ECD BC =CD∴△ABC ≌△EDC (AAS ),∴AB =ED ,答:DE 的长就是A 、B 之间的距离.14.如图所示,有两个长度相等的滑梯,左边滑梯BC 的高AC 与右边滑梯EF 水平方向的长度DF 相等,两滑梯倾斜角∠ABC 和∠DFE 有什么关系?【解答】∠ABC 与∠DFE 互余【解析】证明:在Rt △ABC 和Rt △DEF 中,{BC =EF AC =DF∴Rt △ABC ≌Rt △DEF (HL )∴∠ABC =∠DEF又∵∠DEF +∠DFE =90°∴∠ABC +∠DFE =90°即两滑梯的倾斜角∠ABC 与∠DFE 互余.。
中考数学几何证明题汇编

AMNEFP几何证明题分类汇编一、证明两线段相等1.如图3,在梯形ABCD 中,AD BC ∥,EA AD ⊥,M 是AE 上一点,BAE MCE =∠∠,45MBE =∠.〔1〕求证:BE ME =.〔2〕假设7AB =,求MC 的长.2、〔8分〕如图11,一张矩形纸片ABCD ,其中AD=8cm ,AB=6cm ,先沿对角线BD 折叠,点C 落在点C ′的位置,BC ′交AD 于点G. 〔1〕求证:AG=C ′G ;〔2〕如图12,再折叠一次,使点D 与点A 重合,的折痕EN ,EN 角AD 于M ,求EM 的长.2、类题演练3如图,分别以Rt △ABC 的直角边AC 及斜边AB 向外作等边△ACD 、等边△ABE .∠BAC =30º,EF ⊥AB ,垂足为F ,连结DF . 〔1〕试说明AC =EF ;〔2〕求证:四边形ADFE 是平行四边形.4如图,在△ABC 中,点P 是边AC 上的一个动点,过点P 作直线MN ∥BC ,设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F . (1)求证:PE =PF ;(2)*当点P 在边AC 上运动时,四边形BCFE 可能是菱形吗?说明理由;(3)*假设在AC 边上存在点P ,使四边形AECF 是正方形,且 AP BC =32.求此时∠A 的大小.图3A BCDMEA B CD E F第20题图二、证明两角相等、三角形相似及全等1、〔9分〕AB 是⊙O 的直径,点E 是半圆上一动点〔点E 与点A 、B 都不重合〕,点C 是BE 延长线上的一点,且CD ⊥AB ,垂足为D ,CD 与AE 交于点H ,点H 与点A 不重合。
〔1〕〔5分〕求证:△AHD ∽△CBD〔2〕〔4分〕连HB ,假设CD=AB=2,求HD+HO 的值。
2、〔此题8分〕如图9,四边形ABCD 是正方形,BE ⊥BF ,BE=BF ,EF 与BC 交于点G 。
专题八 几何证明之四边形中的三角形全等问题 2020年中考数学冲刺难点突破 几何证明问题(解析版)

2020年中考数学冲刺难点突破几何证明问题专题八几何证明之四边形中的三角形全等问题1、如图1,已知正方形ABCD,E是线段BC上一点,N是线段BC延长线上一点,以AE为边在直线BC的上方作正方形AEFG.(1)连接GD,求证DG=BE;(2)连接FC,求tan∠FCN的值;(3)如图2,将图1中正方形ABCD改为矩形ABCD,AB=3,BC=8,E是线段BC上一动点(不含端点B,C),以AE为边在直线BC的上方作矩形AEFG,使顶点G恰好落在射线CD上.当点E由B向C运动时,判断tan∠FCN的值是否为定值?若是,求出该定值;若不是,请说明理由.解:(1)如图1,∵正方形ABCD和正方形AEFG中,∴∠BAD=∠EAG=90°,AB=AD,AE=AG,∴△BAE≌△GAD(SAS),∴DG=BE;(2)如图2,过点F作FM⊥BN于M,则∠B=∠AEF=∠FME=90°,∴∠BAE+∠AEB=∠FEM+∠AEB=90°,即∠BAE=∠FEM,又AE=EF,∴△BAE≌△MEF(ASA),∴FM=BE,EM=AB,又BE+EC=AB,EM=EC+CM,∴CM=FM,在Rt△FCM中,tan∠FCN==1;(3)如图2,过点F作FM⊥BN于M,则∠B=∠AEF=∠FME=90°,∴∠BAE+∠AEB=∠FEM+∠AEB=90°,同理可证∠GAD=∠FEM,又AG=EF,∴△DAG≌△MEF,△BAE∽△MEF,∴EM=AD=BC=8,=,设BE=a,则EM=EC+CM=BC=BE+EC,∴CM=BE=a,∴=,∴FM=,∴tan∠FCN===,即tan∠FCN的值为定值.2、【操作发现】如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.【拓展】(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.【实践探究】(1)解:∵四边形ABCD是正方形,∴AB=CD=AD,∠BAD=∠C=∠D=90°,由旋转得:△ABE≌△ADM,∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,即∠EAM=90°,∵∠MAN=45°,∴∠EAN=90°﹣45°=45°,∴∠MAN=∠EAN,在△AMN和△EAN中,,∴△AMN≌△EAN(SAS),∴MN=EN.∵EN=BE+BN=DM+BN,∴MN=BN+DM.在Rt△CMN中,MN===5,则BN+DM=5,设正方形ABCD的边长为x,则BN=BC﹣CN=x﹣3,DM=CD﹣CM=x﹣4,∴x﹣3+x﹣4=5,解得:x=6,即正方形ABCD的边长是6;故答案为:6;(2)EF2=BE2+DF2,理由如下:如图②,将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABH,连结EH,∴∠ADF=∠ABH,DF=BH,∠DAF=∠BAH,AH=AF,∵∠EAF=45°,∴∠DAF+∠BAE=45°=∠BAH+∠BAE,∴∠HAE=45°=∠EAF,又∵AH=AF,AE=AE,∴△EAH≌△EAF(SAS),∴HE=EF,∵BN=DM,BN∥DM,∴四边形BMDN是平行四边形,∴DN∥BM,∴∠AND=∠ABM,∵∠ADN+∠AND=90°,∴∠ABH+∠ABM=90°=∠HBM,∴BE2+BH2=HE2,∴EF2=BE2+DF2;(3)如图③,延长AB至P,使BP=BN=1,过P作BC的平行线交DC的延长线于Q,延长AN交PQ 于E,连接EM,则四边形APQD是正方形,∴PQ=DQ=AP=AB+BP=4,设DM=x,则MQ=4﹣x,∵PQ∥BC,∴△ABN∽△APE,∴,∴PE=BN=,∴EQ=PQ﹣PE=4﹣=,由(1)得:EM=PE+DM=+x,在Rt△QEM中,由勾股定理得:()2+(4﹣x)2=(+x)2,解得:x=2,即DM的长是2.3、如图,将▱ABCD的边AB延长到点E,使BE=AB,连接DE,交BC边于点F.(1)求证:△BEF≌△CDF;(2)连接BD、CE,请探究:当∠BFD与∠A之间满足怎样的数量关系时,能使四边形BECD成为矩形?为什么?(1)证明:∵四边形ABCD是平行四边形,∵AB=CD,AB∥CD.∵BE=AB,∴BE=CD.∵AB∥CD,∴∠BEF=∠CDF,∠EBF=∠DCF,在△BEF与△CDF中,,∴△BEF≌△CDF(ASA);(2)解:∠BFD=2∠A时,四边形BECD成为矩形.证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠A=∠DCB,∵AB=BE,∴CD=EB,∴四边形BECD是平行四边形,∴BF=CF,EF=DF,∵∠BFD=2∠A,∴∠BFD=2∠DCF,∴∠DCF=∠FDC,∴DF=CF,∴DE=BC,∴四边形BECD是矩形.4、已知在△ABC中,AB=AC,点D在BC上,以AD、AE为腰做等腰三角形ADE,且∠ADE=∠ABC,连接CE,过E作EM∥BC交CA延长线于M,连接BM.(1)求证:△BAD≌△CAE;(2)若∠ABC=30°,求∠MEC的度数;(3)求证:四边形MBDE是平行四边形.(1)证明:∵AB=AC,∴∠ABC=∠ACB,∴∠BAC=180°﹣2∠ABC,∵以AD、AE为腰做等腰三角形ADE,∴AD=AE,∴∠ADE=∠AED,∴∠DAE=180°﹣2∠ADE,∵∠ADE=∠ABC,∴∠BAC=∠DAE,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,,∴△BAD≌△CAE(SAS);(2)解:∵AB=AC,∴∠ACB=∠ABC=30°,∵△BAD≌△CAE,∴∠ABD=∠ACE=30°,∴∠ACB=∠ACE=30°,∴∠ECB=∠ACB+∠ACE=60°,∵EM∥BC,∴∠MEC+∠ECD=180°,∴∠MEC=180°﹣60°=120°;(3)证明:∵△BAD≌△CAE,∴DB=CE,∠ABD=∠ACE,∵AB=AC,∴∠ABD=∠ACB,∴∠ACB=∠ACE,∵EM∥BC,∴∠EMC=∠ACB,∴∠ACE=∠EMC,∴ME=EC,∴DB=ME,又∵EM∥BD,∴四边形MBDE是平行四边形.5、如图,在四边形ABCD中,∠A=90°,AD∥BC,BC=BD,CE⊥BD,垂足为E.(1)求证:△ABD≌△ECB;(2)若AD=4,CE=3,求CD的长.证明:(1)∵AD∥BC,∴∠ADB=∠EBC,∵CE⊥BD,∠A=90°,∴∠A=∠BEC=90°,在△ABD和△ECB中,,∴△ABD≌△ECB(AAS);(2)∵△ABD≌△ECB,∴AB=CE=3,∵AD=4,∴在Rt△ABD中,由勾股定理可得:BD=5,∵△BD≌△ECB,∴D=BE=4,∴DE=BD﹣BE=1,∴在Rt△CDE中,由勾股定理得:CD=.6、已知:矩形ABCD中,点E、F为对角线AC上两点,AF=CE.(1)如图1,求证:BE∥DF;(2)如图2,当AB=BE=AD时,连接DE、BF,在不添加任何辅助线的情况下,请直接写出四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.(1)证明:∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴∠DAF=∠BCE,在△AFD和△CEB中,,∴△AFD≌△CEB(SAS),∴∠AFD=∠CEB,∴BE∥DF;(2)解:△ABF,△CDE,△ADF,△BCE;理由如下:由(1)得:△AFD≌△CEB,同理:△ABF≌△CDE(SAS),∴△AFD的面积=△CEB的面积,△ABF的面积=△CDE的面积,作BG⊥AC于G,如图2所示:∵四边形ABCD是矩形,∴∠ABC=90°,BC=AD,∵AB=BE=AD,∴AB=BE=BC,∴BC=2AB,AC==AB,AG=EG,∵△ABC的面积=AC×BG=AB×BC,∴BG===AB,∴AG===AB,∴AE=2AG=AB,∵AF=CE,∴△ABF的面积=△BCE的面积,CF=AE=AB,∴AF=AC﹣CF=AB﹣AB=AB,∴△ABF的面积=AF×BG=×AB×AB=AB2,∵矩形ABCD的面积=AB×BC=AB×2AB=2AB2,∴△ABF的面积=矩形ABCD面积的,∴△ABF的面积=△CDE的面积=△ADF的面积=△BCE的面积=矩形ABCD面积的.7、如图,在平行四边形ABCD中,点G在CD上,点H在AB上,且DG=BH,点E.F在AC上,且AE=CF.连接GF,FH,HE,EG.(1)求证:△CFG≌△AEH;(2)若AG=GC,则四边形EHFG是什么特殊四边形?请说明理由.证明:(1)∵在平行四边形ABCD中,AB∥CD,AB=CD,∴∠GCF=∠HAE,∵DG=BH,∴GC=AH,在△CFG与△AEH中,,∴△CFG≌△AEH(SAS);(2)∵△CFG≌△AEH,∴GF=EH,∠AEH=∠GFC,∴∠FEH=∠EFG,∴四边形EGFH是平行四边形,∵AG=GC,∴∠GAE=∠GCF,在△GAE与△GCF中,∴△GAE≌△GCF(SAS),∴EG=GF,∴平行四边形EGFH是菱形.8、如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD边上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.(1)求证:△BDF≌△CDE.(2)若DE=BC,求证:四边形BECF是正方形.(1)证明:∵AD是BC边上的中线,AB=AC,∴BD=CD,∴∠DBF=∠DCE,∵∠BDF=∠CDE,∴△BDF≌△CDE(ASA);(2)证明:∵△BDF≌△CDE,∴BF=CE,DE=DF,∵BF∥CE,∴四边形BECF是平行四边形,∵AB=AC,AD是中线,∴四边形BECF是菱形,∵DE=BC,DE=DF=EF,∴EF=BC,∴四边形BECF是正方形.9、阅读材料:教育部基础教育司负责人解读“2020新中考”时强调要注重学生分析与解决问题的能力,要增强学生的创新精神和综合素质.王老师想尝试改变教学方法,将以往教会学生做题改为引导学生会学习.于是她在菱形的学习中,引导同学们解决菱形中的一个问题时,采用了以下过程(请解决王老师提出的问题):先出示问题(1):如图1,在等边三角形ABC中,D为BC上一点,E为AC上一点,如果BD=CE,连接AD、BE,AD、BE相交于点P,求∠APE的度数.学习,王老师请同学们说说自己的收获.小明说发现一个结论:在这个等边三角形ABC中,只要满足BD=CE,则∠APE的度数就是一个定值,不会发生改变.紧接着王老师出示了问题(2):如图2,在菱形ABCD中,∠A=60°,E为BC上一点,F为CD上一点,BE=CF,连接DE、BF,DE、BF相交于点P,如果DP=4,BP=3,求出菱形的边长.问题(3):通过以上的学习请写出你得到的启示(一条即可).解:问题(1)∵△ABC是等边三角形,∴∠ABD=∠C=60°,AB=BC,在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),∴∠BAD=∠EBC,∵∠APE=∠ABP+∠BAP,∴∠APE=∠ABP+∠EBC=∠ABC=60°;问题(2)过点D作DG⊥BF交BF于点G,如图2所示:∵四边形ABCD是菱形,∴∠C=∠A=60°,BC=CD,∴△BCD是等边三角形,∴BC=CD=BD,由(1)可知∠DPG=60°,在Rt△DPG中,sin60°=,即=,解得:DG=2,cos60°=,即=,解得:PG=2,∴BG=BP+PG=3+2=5,在Rt△BDG中,由勾股定理得:BD2=BG2+DG2=52+(2)2=37,∴BD=,∴BC=BD=,∴菱形的边长为;问题(3)平时应该注意基本图形的积累,在学习过程中做个有心人.10、如图1,在正方形ABCD(正方形四边相等,四个角均为直角)中,AB=8,P为线段BC上一点,连接AP,过点B作BQ⊥AP,交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交AD于点N.(1)求证:BP=CQ;(2)若BP=PC,求AN的长;(3)如图2,延长QN交BA的延长线于点M,若BP=x(0<x<8),△BMC'的面积为S,求S与x之间的函数关系式.解:(1)证明:∵∠ABC=90°∴∠BAP+∠APB=90°∵BQ⊥AP∴∠APB+∠QBC=90°,∴∠QBC=∠BAP,在△ABP于△BCQ中,,∴△ABP≌△BCQ(ASA),∴BP=CQ,(2)由翻折可知,AB=BC',连接BN,在Rt△ABN和Rt△C'BN中,AB=BC',BN=BN,∴Rt△ABN≌△Rt△C'BN(HL),∴AN=NC',∵BP=PC,AB=8,∴BP=2=CQ,CP=DQ=6,设AN=NC'=a,则DN=8﹣a,∴在Rt△NDQ中,(8﹣a)2+62=(a+2)2解得:a=4.8,即AN=4.8.(3)解:过Q点作QG⊥BM于G,由(1)知BP=CQ=BG=x,BM=MQ.设MQ=BM=y,则MG=y﹣x,∴在Rt△MQG中,y2=82+(y﹣x)2,∴.∴S△BMC′=S△BMQ﹣S△BC'Q==,=.11、已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B、C重合),以AD为边做正方形ADEF,连接CF.(1)如图①,当点D在线段BC上时,直接写出线段CF、BC、CD之间的数量关系.(2)如图②,当点D在线段BC的延长线上时,其他件不变,则(1)中的三条线段之间的数量关系还成立吗?如成立,请予以证明,如不成立,请说明理由;(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC两侧,其他条件不变;若正方形ADEF的边长为4,对角线AE、DF相交于点O,连接OC,请直接写出OC的长度.解:(1)∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴BD=CF,∵BD+CD=BC,∴CF+CD=BC;故答案为:CF+CD=BC;(2)CF+CD=BC不成立,存在CF﹣CD=BC;理由:∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS)∴BD=CF∴BC+CD=CF,∴CF﹣CD=BC;(3)∵∠BAC=90°,∠ABC=45°,∴∠ACB=∠ABC=45°,∴AB=AC,∵四边形ADEF是正方形,∴AD=AF,∠DAF=90°,∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,∴∠BAD=∠CAF,∵在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴∠ACF=∠ABD,∵∠ABC=45°,∴∠ABD=135°,∴∠ACF=∠ABD=135°,∴∠FCD=135°﹣45°=90°,∴△FCD是直角三角形.∵正方形ADEF的边长4且对角线AE、DF相交于点O.∴DF=AD=4,O为DF中点.∴Rt△CDF中,OC=DF=×=.13、已知四边形ABCD和四边形CEFG都是正方形,且AB>CE.(1)如图1,连接BG、DE.求证:BG=DE;(2)如图2,如果正方形CEFG绕点C旋转到某一位置恰好使得CG∥BD,BG=BD.①求∠BDE的度数;②若正方形ABCD的边长是,请求出△BCG的面积.(1)证明:∵四边形ABCD和四边形CEFG为正方形,∴BC=DC,CG=CE,∠BCD=∠GCE=90°.∴∠BCD+∠DCG=∠GCE+∠DCG,∴∠BCG=∠DCE.在△BCG和△DCE中,,∴△BCG≌△DCE(SAS).∴BG=DE;(2)解:①连接BE,如图2所示:由(1)可知:BG=DE,∵CG∥BD,∴∠DCG=∠BDC=45°,∴∠BCG=∠BCD+∠DCG=90°+45°=135°,∵∠GCE=90°,∴∠BCE=360°﹣∠BCG﹣∠GCE=360°﹣135°﹣90°=135°,∴∠BCG=∠BCE,在△BCG和△BCE中,,∴△BCG≌△BCE(SAS),∴BG=BE,∵BG=BD=DE,∴BD=BE=DE,∴△BDE为等边三角形,∴∠BDE=60°;②延长EC交BD于点H,过点G作GN⊥BC于N,如图3所示:在△BCE和△DCE中,,∴△BCE≌△BCG(SSS),∴∠BEC=∠DEC,∴EH⊥BD,BH=BD,∵BC=CD=,∴BD=BC=2,∴BE=2,BH=1,∴CH=1,在Rt△BHE中,由勾股定理得:EH===,∴CE=﹣1,∵∠BCG=135°,∴∠GCN=45°,∴△GCN是等腰直角三角形,∴GN=CG=(﹣1),∴S△BCG=BC•GN=××(﹣1)=.15、利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.(1)如图①,B,C,D三点共线,AB⊥BD于点B,DE⊥BD于点D,AC⊥CE,且AC=CE.若AB+DE=6,求BD的长.(2)如图②,在平面直角坐标系中,△ABC为等腰直角三角形,直角顶点C的坐标为(1,0),点A 的坐标为(﹣2,1).求直线AB与y轴的交点坐标.(3)如图③,∠ACB=90°,OC平分∠AOB,若点B坐标为(b,0),点A坐标为(0,a).则S四边形AOBC=.(只需写出结果,用含a,b的式子表示)解:(1)∵AB⊥BD,DE⊥BD,AC⊥CE,∴∠ABC=∠CDE=∠ACE=90°,∴∠A+∠ACB=90°,∠ECD+∠ACB=180°﹣∠ACE=90°,∴∠A=∠ECD,在△ABC和△CDE中,,∴△ABC≌△CDE(AAS),∴AB=CD,BC=DE,∴BD=CD+BC=AB+DE=6;(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,如图②所示:∵△ABC为等腰直角三角形∴∠ADC=∠CEB=∠ACB=90°,AC=CB,∴∠DAC+∠ACD=90°,∠ECB+∠ACD=180°﹣∠ACB=90°,∴∠DAC=∠ECB,在△ADC和△CEB中,,∴△ADC≌△CEB(AAS),∴AD=CE,CD=BE,∵点C的坐标为(1,0),点A的坐标为(﹣2,1),∴CO=1,AD=1,DO=2,∴OE=OC+CE=OC+AD=2,BE=CD=CO+DO=3,∴点B的坐标为(2,3),设直线AB的解析式为y=kx+b,将A、B两点的坐标代入,得,解得:,∴直线AB的解析式为:y=x+2,当x=0时,解得y=2,∴直线AB与y轴的交点坐标为(0,2);(3)过点C作CD⊥y轴于D,CE⊥x轴于E,如图③所示:∵OC平分∠AOB,∴CD=CE∴四边形OECD是正方形∴∠DCE=90°,OD=OE,∵∠ACB=90°,∴∠DCA+∠ACE=∠ECB+∠ACE=90°,∴∠DCA=∠ECB,在△DCA和△ECB中,,∴△DCA≌△ECB(ASA),∴DA=EB,S△DCA=S△ECB,∵点B坐标为(b,0),点A坐标为(0,a),∴OB=b,OA=a,∵OD=OE,∴OA+DA=OB﹣BE,即a+DA=b﹣DA,∴DA=,∴OD=OA+DA=a+=,∴S=S四边形AOEC+S△ECB=S四边形AOEC+S△DCA=S正方形DOEC=OD2=()2=,四边形AOBC故答案为:.16、如图1,将边长为2的正方形OABC如图放置在直角坐标系中.(1)如图2,若将正方形OABC绕点O顺时针旋转30°时,求点A的坐标;(2)如图3,若将正方形OABC绕点O顺时针旋转75°时,求点B的坐标.解:(1)过点A作AD⊥x轴于点D,如图2所示:则∠AOD=30°,∵正方形OABC的边长为2,∴AO=2,∴AD=AO=1,∴OD===,∴点A的坐标为:(,﹣1);(2)连接OB,过点B作BE⊥x轴于点E,如图3所示:则∠AOE=75°,∵四边形OABC是正方形,∴∠AOB=45°,OB=AO=2,在Rt△BOE中,∠BOE=∠AOE﹣∠AOB=30°,∴BE=OB=,OE=BE=,∴点B的坐标为(,﹣).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题八:几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位.根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低.但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型.热点探究类型一:关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2.1求证:BD=CE;2求证:∠M=∠N.分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可.解答1证明:在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE;2证明:∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得:△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N.点评本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键.同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE.1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证:AD=BE;②求∠AEB的度数.2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明:AE=2CM+BN.类型二:关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG.1请判断四边形EBGD的形状;并说明理由;2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值.考点平行四边形的判定与性质;角平分线的性质.分析1结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题.解答解:1四边形EBGD是菱形.理由:∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形.2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=.MC=3;∴EC===10.∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10.点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型.同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO.1已知BD=;求正方形ABCD的边长;2猜想线段EM与CN的数量关系并加以证明.类型三:关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证:1四边形EBFD是矩形;2DG=BE.考点正方形的性质;矩形的判定;圆周角定理.分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案;2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG.解答证明:1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形;2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE.1判断DE与⊙O的位置关系;并说明理由;2求证:BC2=CD 2OE;3若cos∠BAD=35;BE=6;求OE的长.类型四:关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F.1求证:△ACD∽△BFD;2当tan∠ABD=1;AC=3时;求BF的长.考点相似三角形的判定与性质.分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明.2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题.解答1证明:∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD.2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3.同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点.1 如图1;若∠ACP=∠B;求证:AC2=AP·AB;2 若M为CP的中点;AC=2;① 如图2;若∠PBM=∠ACP;AB=3;求BP的长;② 如图3;若∠ABC=45°;∠A=∠BMP=60°;直接写出BP的长.达标检测1. 2016·黑龙江哈尔滨·8分已知:如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P .1求证:AP=BQ ;2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长.2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF =BD;连接BF .1求证:D 是BC 的中点;2若AB =AC;试判断四边形AFBD 的形状;并证明你的结论.3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=.1试判断△ABC 的形状;并说明理由.2已知半圆的半径为5;BC=12;求sin∠ABD 的值.4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线.1求证:△ADE ≌△CBF ;2若∠ADB 是直角;则四边形BEDF 是什么四边形 证明你的结论.5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上.设∠PCB=α;∠POC=β.求证:tanα tan=.DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H.1求证:HF=AP;2若正方形ABCD的边长为12;AP=4;求线段EQ的长.7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C.1求证:PE是⊙O的切线;2求证:ED平分∠BEP;3若⊙O的半径为5;CF=2EF;求PD的长.参考答案类型一:关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE.1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证:AD=BE;②求∠AEB的度数.2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明:AE=2CM+BN.考点等腰三角形的性质.分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE;②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数;2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论.解答1①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°.∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE.∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC.在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE.②解:∵△ACD≌△BCE;∴∠ADC=∠BEC.∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°.∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.2证明:∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°.∵CM⊥DE;∴∠CMD=90°;DM=EM.在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM.∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°.在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN.∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM.点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是:1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE;2找出线段AD、DE的长.本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键.类型二:关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO.1已知BD=;求正方形ABCD的边长;2猜想线段EM与CN的数量关系并加以证明.考点正方形的性质.分析1根据正方形的性质以及勾股定理即可求得;2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM.解答解:1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1;2CN=CM.证明:∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM.类型三:关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE.1判断DE与⊙O的位置关系;并说明理由;2求证:BC2=CD 2OE;3若cos∠BAD=35;BE=6;求OE的长.思路分析:本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点.故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线;对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得;对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得.解题过程:1证明:连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线;2证明:∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD.∴BC2=2CD OE;3解:∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15.又∵AC=2OE;∴OE=12AC=152.规律总结:熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键.要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可.类型四:关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点.1 如图1;若∠ACP=∠B;求证:AC2=AP·AB;2 若M为CP的中点;AC=2;① 如图2;若∠PBM=∠ACP;AB=3;求BP的长;② 如图3;若∠ABC=45°;∠A=∠BMP=60°;直接写出BP的长.考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可;2①BP=5;②71解析1证明:∵∠ACP=∠B;∠BAC=∠CAP;∴△ACP∽△ABC;∴AC:AB=AP:AC;∴AC2=AP·AB;2①如图;作CQ∥BM交AB延长线于Q;设BP=x;则P Q=2x∵∠PBM=∠ACP;∠PAC=∠CAQ;∴△APC∽△ACQ;由AC2=AP·AQ得:22=3-x35即BP②如图:作CQ⊥AB 于点Q;作CP 0=CP 交AB 于点P 0;∵AC =2;∴AQ=1;CQ =BQ; 设P0Q =PQ =1-x;BP -1+x;∵∠BPM=∠CP 0A ;∠BMP=∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C =2012P C ==AP 0 BP =1+x;解得x ∴BP =-11-.达标检测1. 2016·黑龙江哈尔滨·8分已知:如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P .1求证:AP=BQ ;2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长.考点正方形的性质;全等三角形的判定与性质.分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论;2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析.解答解:1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF =BD;连接BF .1求证:D 是BC 的中点;2若AB =AC;试判断四边形AFBD 的形状;并证明你的结论.考点三角形例行;特殊四边形的性质与判定..1证明:∵点E 是AD 的中点;∴AE =DE .∵AF ∥BC;∴∠AFE =∠DCE;∠FAE =∠CDE .∴△EAF ≌△EDC .∴AF =DC .∵AF =BD;∴BD =DC;即D 是BC 的中点.2四边形AFBD 是矩形.证明如下:∵AF ∥BD;AF =BD;∴四边形AFBD 是平行四边形.∵AB =AC;又由1可知D 是BC 的中点;∴AD ⊥BC .DC EF B A图6∴□AFBD是矩形.3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=.1试判断△ABC的形状;并说明理由.2已知半圆的半径为5;BC=12;求sin∠ABD的值.思路分析:1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形;2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解.解题过程:解:1△ABC为等腰三角形.理由如下:连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形;2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===.规律总结:本题考查了圆周角定理:在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半.推论:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.也考查了等腰三角形的判定与性质和勾股定理.4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线.1求证:△ADE≌△CBF;2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.分析:1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF;2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形.解答:1证明:∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS;2若∠ADB是直角;则四边形BEDF是菱形;理由如下:解:由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形.点评:本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键.5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上.设∠PCB=α;∠POC=β.求证:tanα tan=.解析:连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=.解答:证明:连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===.点评:本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=.6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H.1求证:HF=AP;2若正方形ABCD的边长为12;AP=4;求线段EQ的长.考点:正方形的性质;全等三角形的判定与性质;勾股定理.所有分析: 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE;故可得出结论;2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论.解答: 1证明:∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°.∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM.在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP;2解:由勾股定理得;BP===4.∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=.由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=.点评:本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C.1求证:PE是⊙O的切线;2求证:ED平分∠BEP;3若⊙O的半径为5;CF=2EF;求PD的长.考点:切线的判定.分析: 1如图;连接OE.欲证明PE是⊙O的切线;只需推知OE⊥PE即可;2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论;3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长.解答: 1证明:如图;连接OE.∵CD是圆O的直径;∴∠CED=90°.∵OC=OE;∴∠1=∠2.又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线;2证明:∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等.又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP;3解:设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=.点评:本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键.。
