信号与线性系统分析复习题及答案.doc
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
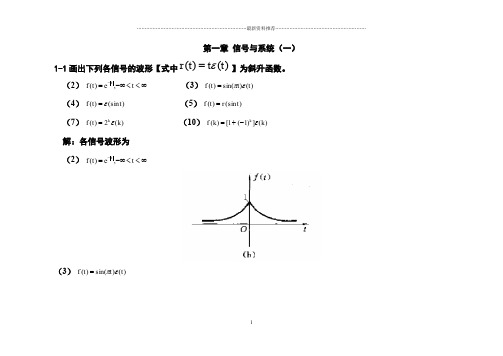
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析 (吴大正 第四版)第四章习题答案

第四章习题4、6 求下列周期信号得基波角频率Ω与周期T。
(1) (2)(3) (4)(5) (6)4、7 用直接计算傅里叶系数得方法,求图4-15所示周期函数得傅里叶系数(三角形式或指数形式)。
图4-154、10 利用奇偶性判断图4-18示各周期信号得傅里叶系数中所含有得频率分量。
图4-184-11 某1Ω电阻两端得电压如图4-19所示,(1)求得三角形式傅里叶系数。
(2)利用(1)得结果与,求下列无穷级数之与(3)求1Ω电阻上得平均功率与电压有效值。
(4)利用(3)得结果求下列无穷级数之与图4-194、17 根据傅里叶变换对称性求下列函数得傅里叶变换(1)(2)(3)4、18 求下列信号得傅里叶变换(1) (2)(3) (4)(5)4、19 试用时域微积分性质,求图4-23示信号得频谱。
图4-234、20 若已知,试求下列函数得频谱: (1) (3) (5)(8) (9)4、21 求下列函数得傅里叶变换(1)(3)(5)4、23 试用下列方式求图4-25示信号得频谱函数(1)利用延时与线性性质(门函数得频谱可利用已知结果)。
(2)利用时域得积分定理。
(3)将瞧作门函数与冲激函数、得卷积之与。
图4-254、25 试求图4-27示周期信号得频谱函数。
图(b)中冲激函数得强度均为1。
图4-274、27 如图4-29所示信号得频谱为,求下列各值[不必求出] (1) (2)(3)图4-294、28 利用能量等式计算下列积分得值。
(1) (2)4、29 一周期为T 得周期信号,已知其指数形式得傅里叶系数为,求下列周期信号得傅里叶系数(1) (2)(3) (4)4、31 求图4-30示电路中,输出电压电路中,输出电压对输入电流得频率响应,为了能无失真得传输,试确定R1、R2得值。
图4-304、33 某LTI系统,其输入为,输出为式中a为常数,且已知,求该系统得频率响应。
4、34 某LTI系统得频率响应,若系统输入,求该系统得输出。
信号与线性系统分析 (吴大正 第四版)第七章习题答案

7.3 如图7-5的RC 带通滤波电路,求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ,其系统函数)(s H 的零点、极点分布如图7-12所示,且已知当∞→s 时,1)(=∞H 。
(1)求出系统函数)(s H 的表达式。
(2)写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2,极点在31j ±-,且21)0(=Z ,求R 、L 、C 的值。
7.14 如图7-27所示的离散系统,已知其系统函数的零点在2,极点在-0.6,求各系数a,b。
7.18 图7-29所示连续系统的系数如下,判断该系统是否稳定。
(1)3,210==a a ; (2)3,210-=-=a a ; (3)3,210-==a a 。
7.19 图7-30所示离散系统的系数如下,判断该系统是否稳定。
(1)1,2110-==a a ; (2)1,2110==a a ;(3)1,2110=-=a a 。
7.20 图7-31所示为反馈系统,已知44)(2++=s s ss G ,K 为常数。
为使系统稳定,试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y(1) 若该系统为因果系统,求系统的单位序列响应h(k)。
(2) 若该系统为稳定系统,求系统的单位序列响应h(k),并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图,求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
信号与系统复习题及答案

1.系统的激励是,响应为,若满足,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?)2.求积分的值为 5 。
3.当信号是脉冲信号时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4.若信号的最高频率是2kHz ,则的乃奎斯特抽样频率为 8kHz 。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6.系统阶跃响应的上升时间和系统的 截止频率 成反比。
7.若信号的,求该信号的。
8.为使LTI 连续系统是稳定的,其系统函数的极点必须在S 平面的 左半平面 。
9.已知信号的频谱函数是,则其时间信号为。
10.若信号的,则其初始值 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足 ( √ )2.满足绝对可积条件的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × )得分)t (e )t (r dt)t (de )t (r =dt )t ()t (212-+⎰∞∞-δf(t)f(t)t)f(23s F(s)=(s+4)(s+2)=)j (F ωj 3(j +4)(j +2)ωωω)s (H ))00(()j (F ωωδωωδω--+=f(t)01sin()t j ωπf(t)211)s (s )s (F +-==+)(f 0)()(t t -=δδ∞<⎰∞∞-dt t f )(3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分,6题15分,共60分)1.信号,信号,试求。
信号与线性系统分析试卷
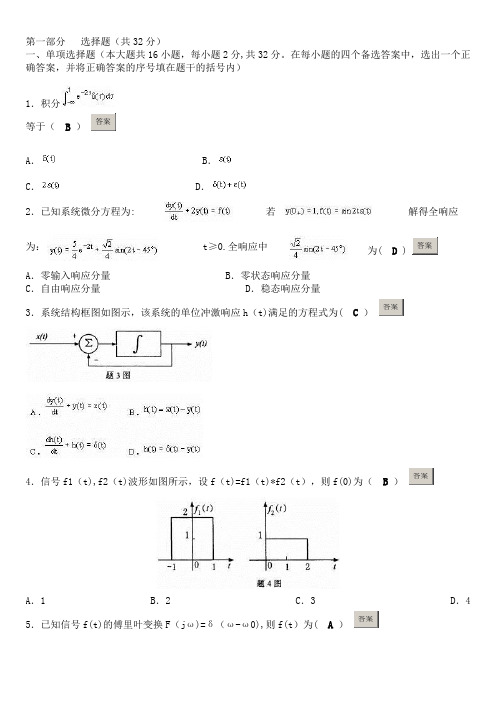
第一部分选择题(共32分)一、单项选择题(本大题共16小题,每小题2分,共32分。
在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内)1.积分等于(B)答案A. B.C. D.2.已知系统微分方程为: 若解得全响应为:t≥0.全响应中为( D ) 答案A.零输入响应分量 B.零状态响应分量C.自由响应分量 D.稳态响应分量3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( C)答案4.信号f1(t),f2(t)波形如图所示,设f(t)=f1(t)*f2(t),则f(0)为(B)答案A.1 B.2 C.3 D.4 5.已知信号f(t)的傅里叶变换F(jω)=δ(ω-ω0),则f(t)为( A)答案6.已知信号f(t)如图所示,则其傅里叶变换为(C)答案7.f(t)=ε(t)-ε(t—1)的拉氏变换为(A)答案8. 的拉氏反变换为(D)答案9.图(a)中ab段电路是某复杂电路的一部分,其中电感L和电容C都含有初始状态,请在图(b)中选出该电路的复频域模型。
(B ) 答案10.离散信号f(n)是指(B)答案A.n的取值是连续的,而f(n)的取值是任意的信号B.n的取值是离散的,而f(n)的取值是任意的信号C.n的取值是连续的,而f(n)的取值是连续的信号D.n的取值是连续的,而f(n)的取值是离散的信号11.若序列f(n)的图形如图(a)所示,那么f(—n+1)的图形为图(b)中的( D)答案12.差分方程的齐次解为,特解为,那么系统的稳态响应为( B ) 答案13.已知离散系统的单位序列响应和系统输入如图所示,f(n)作用于系统引起的零状态响应为,那么序列不为零的点数为(C)答案A.3个 B.4个C.5个 D.6个第二部分非选题(共68分)二、填空题(本大题共9小题,每小题2分,共18分)14.=()。
答案15.GLC并联电路发生谐振时,电容上电流的幅值是电流源幅值的(Q)倍。
信号和线性系统分析(吴大正第四版)第四章习题答案解析

第四章习题4.6求下列周期信号的基波角频率Ω和周期T解 ⑴角频率为Ω = IOO rad∕s,周期丁=盲=p÷ξ ⑵角频率为I fi=号■rad∕s,周期= 4 s(3) 角频率为Ω = 2 rad 倉,周期T = ~ = Tr S (4) 角频率为Q =兀rad∕ s,周期T=^ = 2 sΩ(5) 角频率为 Ω — rad∕s*周期 T=-^ = 8 s4 12⑹角频率为C =話rad∕s,周期T = -jy = 60 s4.7用直接计算傅里叶系数的方法, 求图4-15所示周期函数 的傅里叶系数(三角形式或指数形式)(1) e j100t(2) cos[,t - 3)](3) cos(2t) sin(4t) ⑷ cos(2 兀 t) +cos(3πt) +cos(5 兀 t)(5)π π cos( t) sin( t)2 4(6)JEJITEcos( t) cos( t) cos( t)2 35-2 -1 O 12 3 r(IJ)图4-15f>~ 十解 ⑴周期T = 4,1Ω = Y =亍r 则有H ,4⅛ - 1 ≤ r ≤ 4⅛+ 1/⑺=II∣07 4⅛ + 1 < r < 4⅛ + 3由此可得-Tu rt = ~∖ ' τ fit) cost nΩt)dt= -∣^∣ /(f)cos(^ψ^)df J- J —⅛ 乙-.:—2 I(2}周期丁=2・0 =年=兀,则有由此可得1 + e -jrhr2π( I - √ )所含有的频率分量)dr =2 J -[2『亍=Wl f(t)sm(ττΩt)dt =1 J -T2——SInnπ (才),= om 小山(竽)出ISin(Jrt) 9fm=! 0,2⅛ ≤ r ≤ 2⅛ + 12⅛ + 1 < r < 2⅛ + 2F ri ]ft1 Γl=TJV Cf)^dr =⅛J r ∣/(r)e-7iβ,dr — -7- Sin(^f)e -dr -I ZJV4.10利用奇偶性判断图4-18示各周期信号的傅里叶系数中扣 =O* ± 1 * + 2・・图 4-18解 (1)由旳⑺的波形可矩Λ<r) =√√-n =-∕l (f ⊂f)亠 IU Jr = f(t)cos( riΩt )df 则有丿 丁人 ,jj = 0.1,2,-[仇=0"[J =盘?=应丄=*" =QE=仇=仏=*八=0 则∕√r)的傅里叶级数中含有的频率分量为奇次余弦波亠 (2)由f 2(t)的波形可知则有— ■ ??f(t)s}n(tιΩt )d r ⅛ =A rz fl , J Tni JJO则f 2(t)的傅里叶级数中含有的频率分量为正弦波*(3)由 f 3(t)的波形可⅛l∕3<f) = f 3(~r)则有Γ⅛ = 0, n/(z)cos( fiΩt >d;(4)% 4召=亍即ΛG)的傅里叶级数中含有的频率分量为偶次余弦波* 由/<(0的波形可知,人⑺为奇谐函数■即fdι) =一 fZ 土 £)b 2 = h A = b 6 =・*・=0则有 U即人")的傅里叶级数中只含有奇次谐波•包括正弦波和余弦披"4-11 求u(t)的三角形式傅里叶系数。
信号与线性系统分析 (吴大正 第四版)第四章习题答案

创作编号:BG7531400019813488897SX 创作者: 别如克*第四章习题4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 (7)151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ (2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dtt df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)tdt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=000,1,)(j ωωωωωF (3))(3cos 2)(j ωω=F(5)ωωωω1)(2n -20sin 2)(j +=∑=j n e F4.23 试用下列方式求图4-25示信号的频谱函数创作编号:BG7531400019813488897SX创作者:别如克*(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
信号与线性系统分析_(吴大正_第四版)第四章习题答案

第四章习题4.6求下列周期信号的基波角频率Q和周期T。
(1 ) e j100t( 2) cos^td)](3) cos(2t) sin( 4t) ( 4) cos(2p cos(3二t) cos(5「:t)(5) cos^-t) sinqt) ( 6) cos^t) cos^t) cos铸t)解(l)角频率为0=100 rad/s,周期丁=三=亍2 s0 100o⑵角频率为Q =今rad/s T周期T = -^ = 4 s(3) 角频率为Q = 2rad豊,周期T =—=沢s(4) 角频率为Q = Jr rad/s,周期T = ^ = 2 s12(5) 角频率为Q =耳rad/s*周期T = = 8 s4 £2⑹角频率为C =盒rad/s,周期T = yy = 60 S4.7用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-159 ft1啓料十b n = -= /(r)sin(nOr)dt =万 /(f)sin(-^-)dj=£ I stn 年Q == 1,2"・2 J-L 2(2)周期丁 = 2』=年=兀,则有:sin(rtz),心0,由此可得1 ft^i ri^ i ri . 帀 T )e _ r ^' dr = — /(r )e _:rlfirdr —可 sin( n-f )e _ dfJ J —-Jr —『=|2 J 01上厂檢2iz( 1 — ?i 2)所含有的频率分量mkvv_T _f i 7 f 2 2 1NT ;VN~T/^i J.it/子/"Tk/I'r(h >(1)周期 T = 4/=2囂=h—亍—戈円则有 由此可得a n = -^= f T T /(t )cos (riflt )dz = /(Z)cos( J J —苗 乙J —2] ■j] T /= —sin2?j;r2 >drJ??r2J-j 4.10利用奇偶性判断图4-18示各周期信号的傅里叶系数中» = 0, ± 1, + 2 …(t)(1)rtr 化⑺的波形可知=厲(一小=一八匕二寻)“G =盘?=盘』=*"=佻=仇=% = *八=0 则fAn 的傅里叶级数中含有的频率分量为奇次余弦波亠(2)由/2(r )的波形可知b 2 = b A = Z?6 == 0即人")的傅里叶级数中只含有奇次谐波•包括正弦波和余弦波"利用(1)的结果和u (2)「,求下列无穷级数之和求1 Q 电阻上的平均功率和电压有效值 。
(完整版)信号与线性系统分析_(吴大正_第四版)习题答案

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t (7))t(k=f kε)(2(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析 (吴大正 第四版)第三章习题答案精编版

第三章习题3.1、试求序列k01(k)=2f ⎧⎪⎛⎫⎨ ⎪⎪⎝⎭⎩, 的差分(k)f ∆、(k)f ∇和i=-(i)kf ∞∑。
3.6、求下列差分方程所描述的LTI 离散系统的零输入相应、零状态响应和全响应。
1)()-2(-1)(),()2(),(-1)-1y k y k f k f k k y ε===3)()2(-1)(),()(34)(),(-1)-1y k y k f k f k k k y ε+==+= 5)1()2(-1)(-2)(),()3()(),(-1)3,(-2)-52k y k y k y k f k f k k y y ε++====3.8、求下列差分方程所描述的离散系统的单位序列响应。
2)()-(-2)()=y k y k f k5)()-4(-1)8(-2)()+=y k y k y k f k3.9、求图所示各系统的单位序列响应。
(a)(c)3.10、求图所示系统的单位序列响应。
3.11、各序列的图形如图所示,求下列卷积和。
(1)12()()f k f k *(2)23()()f k f k *(3)34()()f k f k *(4)[]213()-()()f k f k f k *3.13、求题3.9图所示各系统的阶跃响应。
3.14、求图所示系统的单位序列响应和阶跃响应。
3.15、若LTI 离散系统的阶跃响应()()()0.5k g k k ε=,求其单位序列响应。
3.16、如图所示系统,试求当激励分别为(1)()()f k k ε= (2)()()0.5()kf k k ε=时的零状态响应。
3.18、如图所示的离散系统由两个子系统级联组成,已知()1=2cos4k h k π,()()2=k h k k a ε,激励()()()=--1f k k a k δδ,求该系统的零状态响应()zs k y 。
(提示:利用卷积和的结合律和交换律,可以简化运算。
)3.22、如图所示的复合系统有三个子系统组成,它们的单位序列响应分别为()()1=h k k ε,()()2=-5h k k ε,求复合系统的单位序列响应。
信号与线性系统分析吴大正习题答案

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第2讲第一章信号与系统(二)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t (5))f=t(sin)(tr(7))(2)(k t f k ε=(10))(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
信号与线性系统分析试题及答案(10套)

标准答案(一)一、填空题(每空1分,共30分)1、无线电通信中,信号是以电磁波形式发射出去的。
它的调制方式有调幅、调频、调相。
2、针对不同的调制方式有三种解调方式,分别是检波、鉴频、和鉴相。
3、在单调谐放大器中,矩形系数越接近于1、其选择性越好;在单调谐的多级放大器中,级数越多,通频带越窄、(宽或窄),其矩形系数越(大或小)小。
4、调幅波的表达式为:uAM(t)= 20(1 +0.2COS100πt)COS107πt(V);调幅波的振幅最大值为24V,调幅度Ma为20℅,带宽fBW为100Hz,载波fc为5*106Hz。
5、在无线电技术中,一个信号的表示方法有三种,分别是数学表达式、波形、频谱。
6、调频电路有直接调频、间接调频两种方式。
7、检波有同步、和非同步检波两种形式。
8、反馈式正弦波振荡器按照选频网络的不同,可分为LC、RC、石英晶振等三种。
9、变频器可由混频器、和带通滤波器两部分组成。
10、列出三个常见的频谱搬移电路调幅、检波、变频。
11、用模拟乘法器非线性器件实现调幅最为理想。
二、选择题(每小题2分、共20分)将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息(C )A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含(B )A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于( A )分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中,石英谐振器相当于(C )元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为( B )A、|AF|=1,φA+φF= 2nπB、|AF| >1,φA+φF = 2nπC、|AF|>1,φA+φF ≠2nπD、|AF| =1,φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在(B )状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为( B )A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为( B )A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是(D )A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中,由于检波电容放电时间过长而引起的失真是(B)A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题,对的打“√”,错的打“×”(每空1分,共10分)1、谐振放大器是采用谐振回路作负载的放大器。
信号与线性系统分析复习题及答案

信号与线性系统复习题单项选择题;1. 已知序列3()cos()5f k k π=为周期序列,其周期为 C A . 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 B图题2A .()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+-3.已知sin()()()t f t t dt t πδ∞-∞=⎰,其值是 AA .π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 AA . 1 B. 2 C. 3 D. 45.为了使信号无失真传输,系统的频率响应函数应为 D A . ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 B A .13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 AA .0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ,则(3)f t +的傅里叶变换为 C A .()jwF jw e B. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f kεα=,)2()(-=k k h δ,则()()f k h k *的值为 BA .)1(1--k k εαB. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα10.连续时间系统的零输入响应的“零”是指 A A. 激励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列kjek f 3)(π=为周期序列,其周期为A . 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为A .)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ,则 12()()f t f t *的值是 A .)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(,则其对应的原函数为A .)(t δ B. )('t δ C. )(''t δ D. )('''t δ15.连续因果系统的充分必要条件是 A . 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为A .1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=,则其单位冲激响应()h t 为A .)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ,则)5(t f 的拉普拉斯变换为tA .)5(s F B. )5(31s F C. )5(51s F D. )5(71s F 19.已知)2()(2-=-k k f k εα,)2()(-=k k h δ,则()()f k h k *的值为A .)1(1--k k εα B. )2(2--k k εαC. )3(3--k k εαD. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ,则)(jt F 的傅里叶变换为 A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 下列微分或差分方程所描述的系统是时变系统的是 A . )(2)()(2)(''t f t f t y t y -=+B. )()(sin )('t f t ty t y =+C. )()]([)(2't f t y t y =+D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==,则)()(21t f t f *的值是 A .)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 A .ωj 1 B. ωj 2 C. ωj 3 D. ωj 424.连续系统是稳定系统的充分必要条件是 A . M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ,则原函数)(t f 的初值为A . 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ,则该系统的单位冲激响应为 A .)(t e tε- B.)(2t e tε- C.)(3t e tε- D. )(4t e tε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα,则)()(k h k f *的值为A .)(k kεα B.)1(1--k k εα C.)2(2--k k εα D. )3(3--k k εα28. 系统的零输入响应是指 A.系统无激励信号 B. 系统的初始状态为零C. 系统的激励为零,仅由系统的初始状态引起的响应D. 系统的初始状态为零,仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中A .只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形,则)2(t f 的波形为 A .将()f t 以原点为基准,沿横轴压缩到原来的12B. 将()f t 以原点为基准,沿横轴展宽到原来的2倍C. 将()f t 以原点为基准,沿横轴压缩到原来的14D. 将()f t 以原点为基准,沿横轴展宽到原来的4倍 填空题1. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________;2.()(2)t e t t dt δ∞--∞++=⎰____________________________;3.当LTI 离散系统的激励为单位阶跃序列()k ε时,系统的零状态响应称为_________________;4.已知函数4()23F s s =+,其拉普拉斯逆变换为____________________; 5.函数()f t 的傅里叶变换存在的充分条件是________________________;6. 已知11()10.5X z z -=+(0.5)z >,则其逆变换()x n 的值是______________;7.系统函数(1)(1)()1()2z z H z z -+=-的极点是___________________________;8.已知()f t 的拉普拉斯变换为()F s ,则00()()f t t t t ε--的拉普拉斯变换为_________________; 9.如果系统的幅频响应()H jw 对所有的ω均为常数,则称该系统为__________________________; 10. 已知信号)(t f ,则其傅里叶变换的公式为______________; 11. 已知象函数223()(1)s F s s +=+,其原函数的初值(0)f +为___________________; 12.()(2)t e t t dt δ∞--∞++=⎰____________________________;13.当LTI 离散系统的激励为单位阶跃序列()k ε时,系统的零状态响应称为_________________;14.已知函数4()23F s s =+,其拉普拉斯逆变换为____________________; 15.函数()f t 的傅里叶变换存在的充分条件是________________________;16. 已知11()10.5X z z-=+(0.5)z >,则其逆变换()x n 的值是______________; 17.系统函数(1)(1)()1()2z z H z z -+=-的极点是___________________________;18.已知()f t 的拉普拉斯变换为()F s ,则00()()f t t t t ε--的拉普拉斯变换为_________________; 19.如果系统的幅频响应()H jw 对所有的ω均为常数,则称该系统为__________________________; 20. 已知信号)(t f ,则其傅里叶变换的公式为______________; 21.)(63t e tε-的单边拉普拉斯变换为_________________________;22.=-⎰∞∞-dt t t t f )()(0δ ____________________________;23.)(5t δ的频谱函数为______________________;24.一个LTI 连续时间系统,当其初始状态为零,输入为单位阶跃函数所引起的响应称为__________响应; 25.序列)()21()(k k f kε=的z 变换为___________________________;26.时间和幅值均为______________的信号称为数字信号; 27.系统函数)6.0)(4.0()1()(+-+=z z z z z H 的极点是___________________________;28.LTI 系统的全响应可分为自由响应和__________________;29. 函数)(1t f 和)(2t f 的卷积积分运算=*)()(21t f t f _______________________; 30. 已知函数23)(+=s s F ,其拉普拉斯逆变换为____________________; 简答题.;1.简述根据数学模型的不同,系统常用的几种分类;2.简述稳定系统的概念及连续时间系统时域稳定的充分必要条件; 3.简述单边拉普拉斯变换及其收敛域的定义; 4.简述时域取样定理的内容; 5.简述系统的时不变性和时变性; 6.简述频域取样定理;7.简述-0时刻系统状态的含义;8. 简述信号拉普拉斯变换的终值定理;9.简述LTI 连续系统微分方程经典解的求解过程; 10.简述傅里叶变换的卷积定理;11.简述LTI 离散系统差分方程的经典解的求解过程;12.简述信号z 变换的终值定理;13.简述全通系统及全通函数的定义; 14.简述LTI 系统的特点; 15.简述信号的基本运算 计算题1.描述离散系统的差分方程为1)1(,0)1(9.0)(=-=--y k y k y ,利用z 变换的方法求解)(k y ; 2.描述某LTI 系统的微分方程为)(3)()(3)(4)(''''t f t f t y t y t y -=++ ,求其冲激响应)(t h ;3.给定微分方程 )(3)()(2)(3)(''''t f t f t y t y t y +=++,1)0(),()(==-y t t f ε,2)0('=-y ,求其零输入响应;4.已知某LTI 离散系统的差分方程为),()1(2)(k f k y k y =--)(2)(k k f ε=, y-1=-1,求其零状态响应;5.当输入)()(k k f ε=时,某LTI 离散系统的零状态响应为)(])5.1()5.0(2[)(k k y k k zs ε-+-=,求其系统函数;6.描述某LTI 系统的方程为),(3)()(3)(4)(''''t f t f t y t y t y -=++求其冲激响应)(t h ;7.描述离散系统的差分方程为 )1()(2)2(43)1()(--=---+k f k f k y k y k y ,,求系统函数和零、极点; 8. 已知系统的微分方程为)()(3)(4)('''t f t y t y t y =++,1)0()0('==--y y )()(t t f ε=,求其零状态响应;9.用z 变换法求解方程2)1(),(1.0)1(9.0)(=-=--y k k y k y ε的全解10.已知描述某系统的微分方程)(4)()(6)(5)(''''t f t f t y t y t y +=++,求该系统的频率响应).(jw H11.已知某LTI 系统的阶跃响应)()1()(2t e t g tε--=,欲使系统的零状态响应)()1()(22t te e t y t t zs ε--+-=,求系统的输入信号)(t f ;12.利用傅里叶变换的延时和线性性质门函数的频谱可利用已知结果,求解下列信号的频谱函数;13.若描述某系统的微分方程和初始状态为 )(4)(2)(4)(5)(''''t f t f t y t y t y -=++5)0(,1)0('==--y y ,求系统的零输入响应;14.描述离散系统的差分方程为 )2()()2(21)1()(--=-+--k f k f k y k y k y , 求系统函数和零、极点;15.若描述某系统的差分方程为)()2(2)1(3)(k k y k y k y ε=-+-+,已知初始条件5.0)2(,0)1(=-=-y y ,利用z 变换法,求方程的全解;信号与线性系统分析复习题答案单项选择题1. C2.B3.A4.A5.D6.B 7 .A 8.C 9.B 10.A 11. C 12.A 13. D 14.B 15.B 16. D17. A 18.C 19. D 20.C 21.B 22.C 23. B 24.A 25.B 26.C 27. D 28.C 29. B 30. B填空题1. 22. 22e - 3. 单位阶跃响应/阶跃响应 4. )(223t et ε- 5.()f t dt ∞-∞<∞⎰6.)()5.0(k k ε- 7.128. 0()st F s e - 9. 全通系统 10. dt e t f jw F jwt⎰∞∞--=)()( 11.卷积和 12. 1 13.)()(d t t kf t y -= 14. )()()()(3121t f t f t f t f *+* 15.齐次解和特解16. 系统函数分子 17. 2 18.63-z z 19.)(2w πδ 20.齐次 21.36+s 22.)(0t f - 23. 5 24. 单位阶跃响应 25. 122-z z26. 离散 27. 0.4,-0.6 28. 强迫响应 29.τττd t f f )()(21-⎰∞∞- 30. )(32t e t ε-简答题1.答:1加法运算,信号1()f ⋅与 2()f ⋅之和是指同一瞬时两信号之值对应相加所构成的“和信号”,即12()()()f f f ⋅=⋅+⋅2乘法运算,信号1()f ⋅与 2()f ⋅之积是指同一瞬时两信号之值对应相乘所构成的“积信号”,即12()()()f f f ⋅=⋅⋅3反转运算:将信号()f t 或()f k 中的自变量t 或k 换为t -或k -,其几何含义是将信号()f ⋅以纵坐标为轴反转;4平移运算:对于连续信号()f t ,若有常数00t >,延时信号0()f t t -是将原信号沿t 轴正方向平移0t 时间,而0()f t t +是将原信号沿t 轴负方向平移0t 时间;对于离散信号()f k ,若有整常数00k >,延时信号0()f k k -是将原序列沿k 轴正方向平移0k 单位,而0()f k k +是将原序列沿k 轴负方向平移0k 单位; 5尺度变换:将信号横坐标的尺寸展宽或压缩,如信号()f t 变换为()f at ,若1a >,则信号()f at 将原信号()f t 以原点为基准,将横轴压缩到原来的1a倍,若01a <<,则()f at 表示将()f t 沿横轴展宽至1a 倍2.答:根据数学模型的不同,系统可分为4种类型. 即时系统与动态系统; 连续系统与离散系统; 线性系统与非线性系统 时变系统与时不变系统3.答:1一个系统连续的或离散的如果对任意的有界输入,其零状态响应也是有界的则称该系统是有界输入有界输出稳定系统;2连续时间系统时域稳定的充分必要条件是()h t dt M ∞-∞≤⎰4.信号的单边拉普拉斯正变换为:dt e t f s F st ⎰∞-=)()(逆变换为:ds e s F j t f jwjwst ⎰+-=δδπ)(21)(收敛域为:在s 平面上,能使0)(lim =-∞→tt et f δ满足和成立的δ的取值范围或区域,称为)(t f 或)(s F 的收敛域;5.答:一个频谱受限的信号)(t f ,如果频谱只占据m m w w ~-的范围,则信号)(t f 可以用等间隔的抽样值唯一表示;而抽样间隔必须不大于mf 21m m f w π2=,或者说,最低抽样频率为m f 2; 6.答:如果系统的参数都是常数,它们不随时间变化,则称该系统为时不变或非时变系统或常参量系统,否则称为时变系统; 描述线性时不变系统的数学模型是常系数线性微分方程或差分方程,而描述线性时变系统的数学模型是变系数线性微分或差分方程;7.答:一个在时域区间),(m m t t -以外为零的有限时间信号)(t f 的频谱函数)(jw F ,可唯一地由其在均匀间隔)21(m s s t f f <上的样点值)(s jnw F 确定;)()()(ππn wt Sa t n j F jw F m n m -=∑∞-∞=,sm f t 21=8.答:在系统分析中,一般认为输入)(t f 是在0=t 接入系统的;在-=0t 时,激励尚未接入,因而响应及其导数在该时刻的值)0()(-j y与激励无关,它们为求得0>t 时的响应)(t y 提供了以往的历史的全部信息,故-=0t 时刻的值为初始状态;9.答:若)(t f 及其导数dt t df )(可以进行拉氏变换,)(t f 的变换式为)(s F ,而且)(lim t f t ∞→存在,则信号)(t f 的终值为)(lim )(0lim s sF t f s t →∞→=;终值定理的条件是:仅当)(s sF 在s 平面的虚轴上及其右边都为解析时原点除外,终值定理才可用;10.答:1列写特征方程,根据特征方程得到特征根,根据特征根得到齐次解的表达式 2 根据激励函数的形式,设特解函数的形式,将特解代入原微分方程,求出待定系数得到特解的具体值. 3 得到微分方程全解的表达式, 代入初值,求出待定系数 4 得到微分方程的全解11.答:1时域卷积定理:若)()(),()(2211ωωj F t f j F t f ↔↔,则)()()()(2121ωωj F j F t f t f ↔* 2 频域卷积定理:若)()(),()(2211ωωj F t f j F t f ↔↔,则)()(21)()(2121ωωπj F j F t f t f *↔12..答:1列写特征方程,得到特征根,根据特征根得到齐次解的表达式 2 根据激励函数的形式,设特解的形式,将特解代入原差分方程,求出待定系数, 得到特解的具体值. 3 得到差分方程全解的表达式, 代入初始条件,求出待定系数, 4 得到差分方程的全解 13.答:终值定理适用于右边序列,可以由象函数直接求得序列的终值,而不必求得原序列;如果序列在M k < 时,0)(=k f ,设∞<<↔z z F k f α),()(且10<≤α,则序列的终值为)(1lim)(lim )(1z F zz k f f z k -==∞→∞→或写为)()1(lim )(1z F z f z -=∞→上式中是取1→z 的极限,因此终值定理要求1=z 在收敛域内10<≤α,这时)(lim k f k ∞→存在;14.答 全通系统是指如果系统的幅频响应)(jw H 对所有的w 均为常数,则该系统为全通系统,其相应的系统函数称为全通函数;凡极点位于左半开平面,零点位于右半开平面,且所有的零点与极点为一一镜像对称于jw 轴的系统函数即为全通函数;15.答:当系统的输入激励增大α 倍时,由其产生的响应也增大α倍,则称该系统是齐次的或均匀的;若两个激励之和的响应等于各个激励所引起的响应之和,则称该系统是可加的;如果系统既满足齐次性又满足可加性,则称系统是线性的;如果系统的参数都是常数,它们不随时间变化,则称该系统为时不变系统或常参量系统;同时满足线性和时不变的系统就称为线性时不变系统LTI 系统;描述线性时不变系统的数学模型是常系数线性微分差分方程;线性时不变系统还具有微分特性;计算题1解:令)()(z Y k y ↔,对差分方程取z 变换,得 0)]1()([9.0)(1=-+--y z Y z z Y将1)1(=-y 代入上式并整理,可得 9.09.09.019.0)(1-=-=-z zz z Y 取逆变换得 )()9.0()(1k k y k ε+=2.解:令零状态响应的象函数为)(s Y zs ,对方程取拉普拉斯变换得:)(3)()(3)(4)(2s F s sF s Y s sY s Y s zs zs zs -=++于是系统函数为343)()()(2++-==s s s s F s Y s H zs )()23()(3t e e t h t t ε---=3.系统的特征方程为0232=++λλ特征根为:1,221-=-=λλ 所以,零输入响应为t zi tzi zi e C e C t y --+=221)(所以:22)0(1)0(21'21=--==+=++zi zi zi zi zi zi C C y C C y故:4321=-=zi zi C C所以:t t zi e e t y --+-=43)(24.解:零状态响应满足:2)1(2)(=--k y k y zs zs ,且0)1(=-zs y 该方程的齐次解为:kzs C 2设特解为p,将特解代入原方程有:22=-p p从而解得2)(-=k y p所以22)(-=k zs zs C k y 将2)0(=zs y 代入上式,可解得4=zs C故,)()224()(k k y k zs ε-⋅=5.解:1)(-=z z z F )5.1)(5.0)(1()5.02()(2+--+=z z z z z z Y zs 75.05.02)()()(22-++==z z z z F z Y z H zs 6.解:令零状态响应的象函数为)(s Y zs ,对方程取拉普拉斯变换得:)(3)()(3)(4)(2s F s sF s Y s sY s Y s zs zs zs -=++ 系统函数为:3312)()()(+++-==s s s F s Y s H zs 故冲激响应为)()23()(3t e e t h t t ε---=7. 解:对差分方程取z 变换,设初始状态为零;则:)()2()()431(121z F z z Y z z ----=-+于是系统函数)21)(23()12()()()(-+-==z z z z z F z Y z H 其零点为21,021==ζζ, 极点为21.2321=-=p p 8. 解: 方程的齐次解为:t zs t zs e C e C 321--+方程的特解为:31 于是:31)(321++=--t zs t zs zs e C e C t y 031)0(21=++=+zs zs zs C C y 03)0(21'=--=+zs zs zs C C y得61,2121=-=zs zs C C 于是:)()312161()(3t e et y t t zs ε+-=--9. 解:令)()(z Y k y ↔,对差分方程取z 变换,得11.0)]1()([9.0)(1-=-+--z z y z Y z z Y 将2)1(=-y 代入上式,并整理得 )9.0)(1()8.19.1()(---=z z z z z Y )(])9.0(1[)(1k k y k ε++=10.解:令)()(),()(jw Y t y jw F t f ↔↔,对方程取傅里叶变换,得 )(4)()()(6)()(5)()(2jw F jw F jw jw Y jw Y jw jw Y jw +=++ 654)()()(2++-+==jw w jw jw F jw Y jw H 11. 解:)(2)()(2t e dtt dg t h t ε-==22)(+=s s H 2)2(43)(++=s s s s Y zs 2211)()()(++==s s s H s Y s F zs )()211()(2t e t f t ε-+= 12 解:)(t f 可看作两个时移后的门函数的叠合;)2()2()(22-++=t g t g t f因为)(2)(2w Sa t g ↔所以由延时性和线性性有: )2cos()(4)(2)(2)(22w w Sa e w Sa e w Sa jw F w j w j =+=- 13.解:特征方程为:0452=++λλ 4,121-=-=λλt zi t zi zi e C e C t y 421)(--+=t zi t zi zi e C e C t y 421'4)(----=令,0=t 将初始条件代入上式中,得1)0(21=+=+zi zi zi C C y 54)0(21'=--=+zi zi zi C C y 可得: 2,321-==zi zi C C0,23)(4≥-+=--t e e t y t t zi14.解:对差分方程取z 变换,设初始状态为零,则 )()1()()211(221z F z z Y z z ----=+- 211)()()(22+--==z z z z F z Y z H 其零点1,121-==ζζ;极点21212,1j p ±= 15. 解:令)()(z Y k y ↔,对差分方程取z 变换,得112111)]2()1()((2)]1()([3)(----+=-+-++-++zy y z z Y z y z Y z z Y)1)(23()(22-++=z z z z z Y )(])2(32)1(2161[)(k k y k k ε---+=。
信号与系统复习资料及答案

信号与系统复习资料及答案2.设系统零状态响应与激励的关系是:"s (r )=∣∕α)∣,则以下表述不对的是(.A )。
B.系统是时不变的C.系统是因果的D.系统是稳定的4 .设一个矩形脉冲的面积为S,则矩形脉冲的FT (傅氏变换)在原点处的函数值等)o5 .信号(£(t )-£(t-2))的拉氏变换的收敛域为(C )。
6 .已知连续系统二阶微分方程的零输入响应κ,⑺的形式为A/+8",则其2个7 .函数£⑺是(8 .周期矩形脉冲序列的频谱的谱线包络线为()09 .能量信号其(B )010 .在工程上,从抽样信号恢复原始信号时需要通过的滤波器是(B )0A.高通滤波器C.带通滤波器D.带阻滤波器 二、填空题L 系统的激励是e(“,响应为若满足也乜,则该系统为线性、时不dt 变、因果。
一、选择题L 线性系统具有 D)o A.分解特性 B.零状态线性C.零输入线性D.ABC A.系统是线性的 3.零输入响应是( )0A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差A.S/2B.S/3C.S/4D.SA.Re[s]>OB.Re[s]>2C.全S 平面D.不存在特征根为(AA. -1,-2)o B. -1,2 C. 1,-2 D. 1,2 A.奇函数B.偶函数C.非奇非偶函数D.奇谐函数 A. δ函数B. Sa 函数C. £函数D.无法给出 A.能量E=OB.功率P=OC.能量E=8D.功率P=OOB.低通滤波器2.求积分Jjr2+∖)δ(t-2)dt的值为o3.当信号是脉冲信号/⑺时,其低频分量主要影响脉冲的顶部,其高频分量主要影响脉冲的跳变沿。
4.若信号/⑺的最高频率是2kHz,则"2。
的乃奎斯特抽样频率为8kHz。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为相频特性为o6.系统阶跃响应的上升时间和系统的截止频率成反比。
《信号与系统复习题(有答案)》

信号与系统复习题说明: 以下给出了绝大多数题目的答案, 答案是我个人做的,不保证正确性,仅供参考.请务必把复习题弄明白并结合复习题看书.请务必转发给每个同学!!!补充要点(务必搞明白):1 教材p.185例6-12 已知离散时间LTI 系统的单位冲激响应为h(n)=…,又已知输入信号x(n)=…,则系统此时的零状态响应为h(n)和x(n)的卷积.3 已知连续时间LTI 系统在输入信号为f(t)时的零状态响应为y(t),则输入信号为f(t)的导函数时对应的零状态响应为y(t)的导函数(即输入求导,对应的零状态响应也求导)4 教材p.138倒数第3行到139页上半页,请理解并记忆,必考.一、单项选择题1.信号5sin 410cos3t t ππ+为 ( A )A.周期、功率信号B.周期、能量信号C.非周期、功率信号D.非周期、能量信号2.某连续系统的输入-输出关系为2()()y t f t =,此系统为 ( C )A.线性、时不变系统B.线性、时变系统C.非线性、时不变系统D.非线性、时变系统3.某离散系统的输入-输出关系为()()2(1)y n f n f n =+-,此系统为 ( A )A.线性、时不变、因果系统B.线性、时变、因果系统C.非线性、时不变、因果系统D.非线性、时变、非因果系统4.积分(t t dt t--⎰20)()δ等于( B )A.-2δ()tB.2()u t -C.(2)u t -D.22δ()t - 5. 积分(3)t e t dt δ∞--∞-⎰等于( C )(此类题目务必做对)A.t e -B.(3)t e t δ--C. 3e -D.06.下列各式中正确的是 ( B )A.12()(2)2t t δδ=B.1(2)()2t t δδ= C. (2)()t t δδ= D. (2)2()t t δδ= 7.信号)(),(21t f t f 波形如图所示,设12()()*()f t f t f t =,则(1)f 为( D )A .1B .2C .3D .48.已知f(t)的波形如图所示,则f(5-2t)的波形为( C )9. 描述某线性时不变连续系统的微分方程为()3()()y t y t x t '+=。
信号与线性系统分析 (吴大正 第四版)第四章习题答案(完整资料).doc

【最新整理,下载后即可编辑】 第四章习题 4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++ 4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 ......7151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ(2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dt t df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)tdt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=0,1,)(jωωωωωF(3))(3cos2)(jωω=F(5)ωωωω1)(2n-2sin2)(j+=∑=jneF4.23 试用下列方式求图4-25示信号的频谱函数(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t
(t ), f2(t )
(t)
A.0.1t2(t )
B.
0.3t2(t )
,则f1(t )f2(t)的值是()
C.0.5t2(t )D.0.7t2(t)
23.符号函数sgn(t )的频谱函数为()
A.1
B.
2
C.
3
D.
4
j
j
j
j
24.连续系统是稳定系统的充分必要条件是
(
)
A.
h(t )dt
A.2
B. 4
C. 6
D. 8
12.
题2图所示f (t )的数学表达式为
(
)
f(t
1
-
0
1
t
A.f (t)
(t
1)
(t
1)
B.
f (t )
(t
1)
(t
1)
C.
f (t )
(t )
(t
1)
D.
f (t)
(t)
(t
1)
13.
已知
f1(t)
(t
1),
f2(t)
(t
2),则
f1(t )
f2(t)的值是
(
)
A.(t )
(D
)
A.H ( jw )
C.H ( jw )
6.已知序列
z
A.
ejwtd
B.
H ( jw)
ejwtd
Kejwtd
D.
H ( jw )
Kejwtd
f (k ) (1)k
(k ),其z变换为
(B
)
3
B.
z
C.
z
D.
z
z
1
3
z1
z
1
z
1
3
4
4
7.离散因果系统的充分必要条件是
(
A
)
A.h(k)
0,k
0
B.
(k
2),则f ( k)
h(k )的值为(B
)
A.k 1( k 1)
B.
k 2
(k
2)
C.
k 3(k
3)
D.
k 4(k 4)
10.
连续系统的零输入响应的“零”是指(
A)
A.激励为零
B.
系统的初始状态为零
C.系统的冲激响应为零
D.
系统的阶跃响应为零
11.
已知序列f (k)
j
k
(
)
e3
为周期序列,其周期为
(k)时,系统的零状态响应称为
_________________。
4.
已知函数F (s)
4
,其拉普拉斯逆变换为____________________。
2s
3
5.
函数f (t)的傅里叶变换存在的充分条件是________________________。
6.
已知X ( z)
1
( z
0.5),则其逆变换x(n)的值是______________。
h( k)
0, k
0
C.
h(k)
0,k
0
D.
h( k)
0, k
0
8.已知f (t)的傅里叶变换为F ( jw ),则f (t 3)
的傅里叶变换为
(C
)
A.F ( jw )ejw
B.
F ( jw )ej 2w
C.
F ( jw )ej 3 w
D.
F ( jw )ej 4 w
9.已知f (k)
k(k),h(k)
M
B.
h(t) dt
M
C.
h(t)dt
M
D.
h(t)dt
M
25.已知函数f (t)的象函数F ( s)
( s 6)
,则原函数f (t)
的初值为
(
)
( s
2)(s
5)
A.0
B. 1
C. 2
D. 3
26.已知系统函数H ( s)
3
,则该系统的单位冲激响应为
(
)
s
1
A.et(t )
B.
2et
(t )
C.
3et(t)
D.
4et
(t )
27.已知f ( k)
k 1(k
1), h(k )
( k
2),则f (k )
h( k)的值为
(
)
A.k
(k)
B.
k 1(k
1)
C.
k 2
(k 2)
D.
k
3(k 3)
28.系统的零输入响应是指()
A.系统无激励信号
B.系统的初始状态为零
C.系统的激励为零,仅由系统的初始状态引起的响应
信号与线性系统复习题
单项选择题。
1.
已知序列f ( k)
cos(3k )为周期序列,其周期为
(C)
5
A.2B. 5
C. 10D. 12
2.
题2图所示f (t)的数学表达式为
(B
)
f(t正弦函数
10
01
t
图题2
A.f (t )
10sin(
t )[
(t)
(t
1)]
B.
f (t )
10sin(
t)[ (t )
B.
1F (s)
C.
1F (s)D.
1F (s)
5
3
5
5
5
7
5
19.
已知f ( k)
k 2( k
2),h( k)
(k
2),则f (k)
h(k )的值为(
)
A.k 1( k
1)
B.
k 2(k 2)
C.
k 3( k
3)
D.
k 4
( k 4)
20.
已知f (t)的傅里叶变换为F ( j
),则F ( jt )的傅里叶变换为(
2倍
C.将f (t )以原点为基准,沿横轴压缩到原来的
1
4
D.将f (t )以原点为基准,沿横轴展宽到原来的
4倍
填空题
1.
已知象函数F (s)
2s
3ห้องสมุดไป่ตู้
f (0 )
为___________________。
(s 1)2,其原函数的初值
(et
t ) (t 2)dt
。
3.
当LTI离散系统的激励为单位阶跃序列
(
)
A.z, z
1
B.
z
z, z
1C.
z, z
1
D.
z, z
1
z 1
1
z
1
z 1
17.
已知系统函数H ( s)
1,则其单位冲激响应
h(t )为
(
)
s
A.(t )
B.
t (t )
C.
2t
(t )
D.
3t
(t)
18.
已知f (t)的拉普拉斯变换为F ( s),则f (5t )的拉普拉斯变换为
(
)
A.F (s)
B.
(t
1)
C.
(t
2)
D.
(t
3)
14.
已知F ( j )
j
,则其对应的原函数为
(
)
A.(t )
B.
'(t )
C.
' '(t )
D.
'' '(t)
15.
连续因果系统的充分必要条件是
(
)
A.h(t )
0,t
0
B.
h(t )
0,t
0
C.
h(t )
0, t
0
D.
h(t )
0,t
0
16.
单位阶跃序列
(k)的z变换为
0.5z
1
1
7.
系统函数H (z)
(z
1)(z
1)的极点是___________________________。
D.系统的初始状态为零,仅由系统的激励引起的响应
29.偶函数的傅里叶级数展开式中
(
)
A.只有正弦项B.只有余弦项
C.
只有偶次谐波
D.只有奇次谐波
10.已知信号f (t )的波形,则f (t)的波形为
(
)
2
A.将f (t )以原点为基准,沿横轴压缩到原来的
1
2
B.将f (t )以原点为基准,沿横轴展宽到原来的
(t
1)]
C.
f (t )
10sin(
t )[
(t)
(t
2)]
D.
f (t)
10sin(
t )[ (t)
(t
2)]
3.
已知f (t)
sin(
t)
(t )dt,其值是
(A)
t
A.
B.
2
C.
3
D.
4
4.
冲激函数(t)的拉普拉斯变换为
(A
)
A.1
B. 2
C. 3
D. 4
5.
为了使信号无失真传输,系统的频率响应函数应为
)
A.
f (
)
B.
f ( )
C.
2 f (
