拉格朗日插值法使用MATLAB做的例题
拉格朗日插值法matlab程序

拉格朗日插值法matlab程序拉格朗日插值法是一种用于构造插值多项式的方法,它可以通过已知数据点来估计函数在其他位置的值。
在数值分析和工程应用中,拉格朗日插值法被广泛使用,尤其在数据处理和曲线拟合方面。
在本文中,我将为您介绍拉格朗日插值法的原理和应用,并共享一个用于实现该方法的简单matlab程序。
让我们来了解一下拉格朗日插值法的原理。
拉格朗日插值法是通过在已知数据点上构造一个插值多项式来实现的。
假设我们有n+1个不同的数据点(x0, y0), (x1, y1), ..., (xn, yn),我们希望通过这些数据点来估计函数在其他位置的值。
拉格朗日插值多项式的一般形式为:P(x) = Σ(yi * li(x))i=0 to n其中,li(x)是拉格朗日基础多项式,它的表达式为:li(x) = Π(x - xj) / (xi - xj)j=0 to n, j ≠ i通过以上公式,我们可以得到拉格朗日插值多项式P(x),从而实现对函数在其他位置的估计。
在matlab中,我们可以通过编写一个简单的程序来实现拉格朗日插值法。
下面是一个用于计算拉格朗日插值多项式的matlab程序:```matlabfunction [L, P] = lagrange_interp(x, y, xx)n = length(x);m = length(xx);L = zeros(n, m);for i = 1:nt = ones(1, m);for j = [1:i-1, i+1:n]t = t .* (xx - x(j)) / (x(i) - x(j));endL(i,:) = t;endP = y * L;end```在上面的程序中,x和y分别表示已知数据点的横纵坐标,xx表示我们希望估计函数值的位置。
程序返回的L矩阵存储了插值多项式的系数,P向量存储了估计函数值的结果。
通过这个简单的程序,我们就可以快速实现拉格朗日插值法的计算。
MATLAB作业拉格朗日三阶样条插值函数牛顿插值

Lagrange插值M函数syms xx0=[0,1,2];y0=[1,2,3];n=length(x0);for i=1:na=1;for j=1:nif j~=ia=expand(a*(x-x0(j)));endendb=1;for k=1:nif k~=ib=b*(x0(i)-x0(k));endendA(i)=expand(a/b);endL=0;for p=1:nL=L+y0(p)*A(p);endL>> LanguageL =x + 1三阶样条插值M函数function m=naspline(x,y,dy0,dyn,xx)n=length(x)-1;h=diff(x);lemda=h(2/n)./(h(1:n-1)+h(2:n));mu=1-lemda;g=3*(lemda.*diff(y(1:n))./h(1:n-1)+mu.*diff(y(2:n+1))./h(2:n)); g(1)=g(1)-lemda(1)*dy0;g(n-1)=g(n-1)-mu(n-1)*dyn;dy=nachase(lemda,2*ones(1:n-1),mu,g);m=[dy0;dy;dyn];if nargin>=5s=zeros(size(xx));for i=1:nif i==1,kk=find(xx<=x(2));elseif i==nkk=find(xx>x(n));elsekk=find(xx>x(i)&xx<=x(i+1));endxbar=(xx(kk)-x(i))/h(i);s(kk)=alpha0(xbar)*y(i)+alpha1(xbar)*y(i+1)+...h(i)*beta0(xbar)*m(i)+h(i)*beta1(xbar)*m(i+1);endm=s;endfunction x=nachase(a,b,c,d)n=length(a);for k=2:nb(k)=b(k)-a(k)/b(k-1)*c(k-1);d(k)=d(k)-a(k)/b(k-1)*d(k-1);endx(n)=d(n)/b(n);for k=n-1:-1:1x(k)=(d(k)-c(k)*x(k+1))/b(k);endx=x(:);function y=alpha0(x)y=2*x.^3-3*x.^2+1;function y=alpha1(x)y=-2*x.^3+3*x.^2;function y=beta0(x)y=x.^3-2*x.^2+x;function y=beta1(x)y=x.^3-x.^2;naspline([-1 0 1],[-1 0 1],0,-1)ans =1.7500-1.0000>> naspline([-1 0 1],[-1 0 1],0,-1,-1:0.25:1)ans =-1.0000 -0.9258 -0.7188 -0.4023 0 0.4492 0.8438 1.06641.0000ans =Columns 1 through 5-1.0000 -0.9258 -0.7188 -0.4023 0 Columns 6 through 90.4492 0.8438 1.0664 1.0000牛顿插值多项式function yi=Newton(x,y,xi)n=length(x);m=length(y);if n~=merror;return;end%计算均差表YY=zeros(n);Y(:,1)=y';for k=1:n-1for i=1:n-kif abs(x(i+k)-x(i))<epserror;return;endY(i,k+1)=(Y(i+1,k)-Y(i,k))/(x(i+k)-x(i));endend%计算牛顿插值公式yi=0;for i=1:nz=1;for k=1:i-1z=z*(xi-x(k));endyi=yi+Y(1,i)*z;endEnd>>format compact>> x=pi*[1/6 1/4 1/3];y=[0.5 0.7071 0.866];xi=2*pi/9;0.550.60.650.70.750.450.50.550.60.650.70.75>> yi=Newton(x,y,xi)yi =0.6434>>fplot(‘sin ’,[pi/6 pi/4 pi/3]);hold on;>>plot(x,y,’o ’xi,0.6434,’rv ’);hold off;牛顿迭代M 函数function x=nanewton(fname,dfname,x0,e,N) if nargin<5,N=500;endif nargin<4,e=1e-4;endx=x0;x0=x+2*e;k=0;while abs(x0-x)>e&k<N,k=k+1;x0=x;x=x0-feval(fname,x0)/feval(dfname,x0); disp(x)endif k==N,warning('已达迭代次数上限');end >> fun=inline('x^3-x-1');dfun=inline('3*x^2-1'); >> nanewton(fun,dfun,1.5,0.5e-3)1.34781.32521.3247ans =1.32470.550.60.650.70.750.450.50.550.60.650.70.75。
matlab实现lagrange插值和分段线性插值
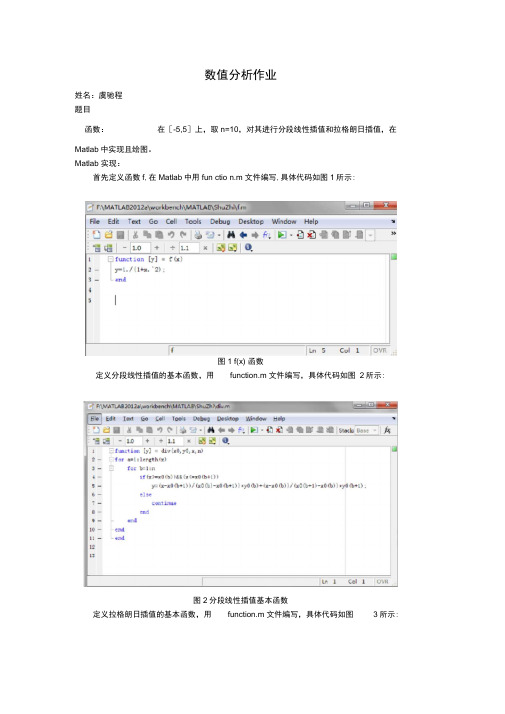
数值分析作业姓名:虞驰程题目函数:在[-5,5]上,取n=10,对其进行分段线性插值和拉格朗日插值,在Matlab中实现且绘图。
Matlab 实现:首先定义函数f,在Matlab中用fun ctio n.m 文件编写,具体代码如图1所示:图1 f(x) 函数定义分段线性插值的基本函数,用function.m 文件编写,具体代码如图2所示:图2分段线性插值基本函数定义拉格朗日插值的基本函数,用function.m 文件编写,具体代码如图3所示:图3拉格朗日插值的基本函数进行分段线性插值并绘图和原函数进行对比的Matlab实现代码如图4所示:图4分段线性插值函数绘制其结果如图5所示,其中红色代表分段线性插值结果,蓝色代表原函数:图5分段线性插值和原函数对比同理可以进行拉格朗日插值并绘图,其Matlab实现代码如图6所示,其结果如图Ffe Edit Tesrt Go C«ll TooU D«bug Oesktop Wind Help *1 D 已■ | $ ■•勺◊Qi 勺-it • * F;iL ・昌电T・• ■ ■ ■ | MadgJBmr ■血*S肓匸1必」•* _U■「鬲迢[0 _L 1- IWEU I1『inpirt ftji')2 - ■Elinus:""卜氐£11*1〕3 - \-\t^£ 15* —yslftErflnfeiwQpiftrtl,!!) ■5 —told An:ft - plfft <45- r* * E X).7 - jlflrt(i p fCx)/lb J kE — d.isp(-x):9 - -end2 u"含m al=n' taufwi图6拉格朗日插值函数绘制图7拉格朗日插值和原函数对比7所示:最后我们可以将分段线性插值、拉格朗日插值和原函数进行对比,其实现代码如图8所示,最终结果如图9所示(黑色代表原函数,蓝色是分段线性插值,红色是拉格朗日插值)图8两种插值方法和原函数对比实现图9两种插值方法和原函数对比。
2、拉格朗日插值的matlab实现

syms t;
if(length(x)==length(y))
n=length(x);
else
disp('x和y的维数不相等!');
return;
end%检错
f=0.0;
for(i=1:n)
l=y(i);
for(j=1:i-1)
l=l*(t-x(j))/(x(i)-x(j));
end;
[f,f0]=Language(x,y,1.6)%计算输出的拉格朗日插值多项式
%计算x=1.6时的插值输出值f0
运行结果
f =
-799/3125*t*(t-1)*(t-3/2)*(t-2)*(t-5/2)*(t-3)+561/500*t*(t-1/2)*(t-3/2)*(t-2)*(t-5/2)*(t-3)-133/75*t*(t-1/2)*(t-1)*(t-2)*(t-5/2)*(t-3)+3031/2500*t*(t-1/2)*(t-1)*(t-3/2)*(t-5/2)*(t-3)-399/1250*t*(t-1/2)*(t-1)*(t-3/2)*(t-2)*(t-3)+1411/112500*t*(t-1/2)*(t-1)*(t-3/2)*(t-2)*(t-5/2)
for(j=i+1:n)
l=l*(t-x(j))/(x(i)-x(j));%计算拉格朗日基函数
end;
f=f+l;%计算拉格朗日插值函数
simplify(f);%化简
end
f0=subs(f,'t',x0);%计算插值点的函数值
运行程序;
x=0:0.5:3;
y=[0 0.4794 0.8415 0.9975 0.9093 0.5985 0.1411];
matlab实现拉格朗日函数,拉格朗日插值多项式

matlab实 现 拉 格 朗 日 函 数 , 拉 格 朗 日 插 值 多 项 式
%拉格朗日插值多项式 利用矩阵求解 x=1:0.2:3;%已知数据点x坐标向量:x y=sin(x);%已知数据点x坐标向量:y x1=1.1:0.2:3.1;%插值点的x坐标:x1 L=zeros(11,11);%另L矩阵为0
for i=1:11 A=ones(10,1);%另A矩阵为10行1列的矩阵 x2=x; x2(i)=[]; x2';%10行一列 B=ones(1,11);%另B矩阵为1行11列的矩阵 A*x1;%10行11列 (x2')*B;%10行11列 A*x1-(x2')*B;%11行11列 ones(10,11); x(i);%提取x的第i个元素 ones(10,11)*x(i);%10行11列的矩阵 prod(A*x1-(x2')*B);%基函数的分子 ones(10,11)*(x(i))-(x2')*B;%基函数的分母 C=prod(A*x1-(x2')*B)./prod(ones(10,11)*(x(i))-(x2')*B);%对x2进行转置%C矩阵是一个1行11列的矩阵 L(i,:)=C; %将A的第一行元素全部变为10 %将得到的矩阵赋值基函数的1,2,3。。。。11行
end L;%11行11列 y;%1行11列 y1=y*L
结.9636 0.9975 0.9917 0.9463 0.8632 0.7457
8 至 11 列
0.5985 0.4274 0.2392 0.0416
用拉格朗日插值法求解函数值 matlab

**使用拉格朗日插值法求解函数值的MATLAB实现**拉格朗日插值法是一种常用的插值方法,通过已知的若干点构造一个多项式来近似一个未知的函数。
下面我们将详细介绍如何在MATLAB中使用拉格朗日插值法来求解函数值。
**1. 拉格朗日插值法的基本原理**给定n+1个点(x0, y0), (x1, y1), ..., (xn, yn),拉格朗日插值多项式L(x)可以表示为:L(x) = Σ[yi * li(x)] (i从0到n)其中,li(x) 是拉格朗日基函数,定义为:li(x) = Π[(x - xj) / (xi - xj)] (j从0到n,且j≠i)**2. MATLAB实现**以下是一个简单的MATLAB脚本,用于计算给定点的拉格朗日插值多项式及其值。
```matlab% 假设我们有一些点的数据:xi, yi(其中i = 0,1,2,...,n)xi = [1, 2, 3, 4]; % 自变量数据点yi = [1, 4, 9, 16]; % 因变量数据点% 要计算插值的点x = 2.5;n = length(xi); % 点的数量L = 0; % 初始化插值多项式% 计算拉格朗日插值多项式在点x处的值for i = 1:nli = 1; % 初始化基函数for j = 1:nif i ~= jli = li * (x - xi(j)) / (xi(i) - xi(j)); % 计算基函数endendL = L + yi(i) * li; % 更新插值多项式enddisp(['拉格朗日插值结果:', num2str(L)]); % 显示结果```在此脚本中,我们首先定义了已知的数据点`xi`和`yi`,并选择一个特定的`x`来计算对应的函数近似值。
然后,我们使用两个嵌套的循环来计算拉格朗日插值多项式在所选点`x`处的值。
外部循环遍历每个数据点,而内部循环计算相应的基函数。
最后,我们显示计算得到的插值结果。
拉格朗日插值matlab程序例题

拉格朗日插值是一种常用的数据拟合方法,它可以通过已知数据点来估计出未知数据点的值。
在数学和工程领域中,拉格朗日插值经常被用来进行数据的近似和预测。
在本文中,我们将深入探讨拉格朗日插值的原理和应用,并以Matlab程序例题来展示其实际运用。
1. 拉格朗日插值的原理拉格朗日插值是利用已知数据点来构造一个多项式,通过这个多项式来拟合数据并进行预测。
它的原理基于拉格朗日多项式的概念,即通过已知的n个点来构造一个n-1次的拉格朗日多项式,利用这个多项式来估计其他点的数值。
2. 拉格朗日插值的公式假设有n个已知的数据点(x1, y1), (x2, y2), …, (xn, yn),则拉格朗日插值多项式可以表示为:L(x) = Σ(yi * li(x)), i=1 to n其中li(x)是拉格朗日基函数,定义为:li(x) = Π((x - xj) / (xi - xj)), j=1 to n, j≠i利用这个公式,我们可以得到拉格朗日插值多项式,进而进行数据的拟合和预测。
3. 拉格朗日插值的Matlab程序实现下面我们将以一个具体的例题来展示如何使用Matlab来实现拉格朗日插值。
假设有如下数据点:y = [10, 5, 8, 3, 6];我们希望利用这些数据点来构造拉格朗日插值多项式,并使用这个多项式来估计x=3.5处的数值。
我们可以编写Matlab程序来实现拉格朗日插值。
代码如下:```matlabfunction result = lagrange_interpolation(x, y, xx)n = length(x);result = 0;for i = 1:ntemp = y(i);for j = 1:nif i ~= jtemp = temp * (xx - x(j)) / (x(i) - x(j));endendresult = result + temp;endend```我们可以调用这个函数来进行插值计算:```matlaby = [10, 5, 8, 3, 6];xx = 3.5;result = lagrange_interpolation(x, y, xx)disp(result);```通过这段程序,我们可以得到x=3.5处的插值结果为6.75。
实验四用MATLAB实现拉格朗日插值分段线性插值

实验四用MATLAB实现拉格朗日插值分段线性插值实验四用M A T L A B实现拉格朗日插值分段线性插值The final edition was revised on December 14th, 2020.实验四用MATLAB实现拉格朗日插值、分段线性插值一、实验目的:1)学会使用MATLAB软件;2)会使用MATLAB软件进行拉格朗日插值算法和分段线性差值算法;二、实验内容:1用MATLAB实现y = 1./(x.^2+1);(-1<=x<=1)的拉格朗日插值、分段线性2.选择以下函数,在n个节点上分别用分段线性和三次样条插值的方法,计算m个插值点的函数值,通过数值和图形的输出,将插值结果与精确值进行比较,适当增加n,再作比较,由此作初步分析:(1).y=sinx;( 0≤x≤2π)(2).y=(1-x^2)(-1≤x≤1)三、实验方法与步骤:问题一用拉格朗日插值法1)定义函数:y = 1./(x.^2+1);将其保存在文件中,程序如下:function y = f1(x)y = 1./(x.^2+1);2)定义拉格朗日插值函数:将其保存在文件中,具体实现程序编程如下:function y = lagrange(x0,y0,x)m = length(x); /区间长度/n = length(x0);for i = 1:nl(i) = 1;endfor i = 1:mfor j = 1:nfor k = 1:nif j == kcontinue;endl(j) = ( x(i) -x0(k))/( x0(j) - x0(k) )*l(j); endendendy = 0;for i = 1:ny = y0(i) * l(i) + y;end3)建立测试程序,保存在文件中,实现画图:x=-1::1; y = 1./(x.^2+1);p=polyfit(x,y,n);py=vpa(poly2sym(p),10)plot_x=-5::5;f1=polyval(p,plot_x);figureplot(x,y,‘r',plot_x,f1)二分段线性插值:建立文件。
建模实验 拉格朗日插值

建模实验插值方法【实验目的】1.掌握用MATLAB计算拉格朗日、分段线性、三次样条三种插值的方法,改变节点的数目,对三种插值结果进行初步分析;2.掌握用MATLAB及梯形公式、辛普森公式计算数值积分;3.通过实例学习用插值和数值积分解决实际问题。
【实验内容】题1(3)选择一些函数,在n个节点上(n不要太大,如5~11)用拉格朗日、分段线性、三次样条三种插值的方法,计算m个插值点的函数值(m要适中,如50~100)。
通过数值和图形输出,将三种插值结果与精确值进行比较,适当增加n,再作比较,由此作初步分析。
下列函数供选择参考:(3)y=cos10x,-2≤x≤2解:当n=8,m=50时,在matlab中编程如下:x=-2:0.5:2;y=(cos(x)).^10;a=-2:4/50:2;yy=(cos(a)).^10;y1=lagr(x,y,a);y2=interp1(x,y,a);y3=interp1(x,y,a,'spline');[a;yy;y1;y2;y3]'数值输出如下:-2 0.00015576 0.00015576 0.00015576 0.00015576-1.92 2.1987e-005 -0.99289 0.00013084 0.0019267-1.84 1.771e-006 -1.2394 0.00010592 0.0027391-1.76 5.538e-008 -1.078 8.0997e-005 0.0027867-1.68 2.3645e-010 -0.74009 5.6075e-005 0.0022632-1.6 4.5057e-016 -0.37345 3.1153e-005 0.0013621-1.52 1.1388e-013 -0.063296 6.2305e-006 0.00027724-1.44 1.4242e-009 0.1509 0.00025442 -0.00079778-1.36 1.6085e-007 0.26129 0.00059364 -0.0016693-1.28 3.7541e-006 0.28038 0.00093287 -0.0021436-1.2 3.9028e-005 0.23209 0.0012721 -0.0020271-1.12 0.00024643 0.14495 0.0016113 -0.001126-1.04 0.0011051 0.047167 0.0019505 0.0007532-0.96 0.0038502 -0.03686 0.023626 0.0039155-0.88 0.011026 -0.088593 0.066638 0.011223-0.8 0.026946 -0.096401 0.10965 0.028094-0.72 0.057684 -0.055717 0.15266 0.06006-0.64 0.11022 0.031477 0.19567 0.11265 -0.56 0.19061 0.15766 0.23869 0.19139 -0.48 0.30145 0.3111 0.30011 0.30176 -0.4 0.43942 0.4774 0.41676 0.44195 -0.32 0.59394 0.64102 0.5334 0.59603 -0.24 0.74766 0.78685 0.65005 0.74643 -0.16 0.87937 0.90159 0.7667 0.8756 -0.08 0.96847 0.97483 0.88335 0.96597 0 1 1 1 1 0.08 0.96847 0.97483 0.88335 0.96597 0.16 0.87937 0.90159 0.7667 0.8756 0.24 0.74766 0.78685 0.65005 0.74643 0.32 0.59394 0.64102 0.5334 0.59603 0.4 0.43942 0.4774 0.41676 0.44195 0.48 0.30145 0.3111 0.30011 0.30176 0.56 0.19061 0.15766 0.23869 0.19139 0.64 0.11022 0.031477 0.19567 0.11265 0.72 0.057684 -0.055717 0.15266 0.06006 0.8 0.026946 -0.096401 0.10965 0.028094 0.88 0.011026 -0.088593 0.066638 0.0112230.96 0.0038502 -0.03686 0.023626 0.00391551.04 0.0011051 0.047167 0.0019505 0.0007532 1.12 0.00024643 0.14495 0.0016113 -0.001126 1.2 3.9028e-005 0.23209 0.0012721 -0.0020271 1.28 3.7541e-006 0.28038 0.00093287 -0.0021436 1.36 1.6085e-007 0.26129 0.00059364 -0.0016693 1.44 1.4242e-009 0.1509 0.00025442 -0.00079778 1.52 1.1388e-013 -0.063296 6.2305e-006 0.00027724 1.6 4.5057e-016 -0.37345 3.1153e-005 0.0013621 1.682.3645e-010 -0.74009 5.6075e-005 0.0022632 1.76 5.538e-008 -1.078 8.0997e-005 0.0027867 1.84 1.771e-006 -1.2394 0.00010592 0.00273911.922.1987e-005 -0.99289 0.00013084 0.00192672 0.00015576 0.00015576 0.00015576 0.00015576再观察图形:plot(a,yy,'k*',a,y1,'r',a,y2,'b',a,y3,'c')从图中可以看出,三次样条插值函数(青色)与原函数(黑色*)符合地最好,分段线性插值得到的函数(蓝色)符合的较差,而拉格朗日插值函数(红色)在小范围内符合的较好,但大范围内波动较大。
MATLAB程序设计插值实验题目

1、当2,1,1-=x 时,4,3,0)(-=x f ,求x =0时的值。
2、给出x x f ln )(=的数值表用线性插值及二次插值计算54.0ln 的近似值。
3、4()31f x x x =++,已知x =0,1,2处的值,计算x =0.11的近似值。
4.求i =3和5时的值。
5. 给定数据表,采用牛顿插值方法求i =3和5时的值。
6. 已知函数y =在4, 6.25,9x x x ===的近似值。
7. 已知函数y =在4,9,16x x x ===的近似值。
8. 已知函数y =在0,1,4,9x x x x ==== 9. 给定数据表:构造出函数()f x 的差商表,并计算x =0.5时的值.10. 已知函数y =在8,27,64x x x ===的近似值。
11. 已知函数sin()y x =在0,/4,/2x x x ππ===处的函数值,试通过一个二次插值函数求sin(/5)π的近似值。
12. 已知函数cos()y x =在0,/4,/2x x x ππ===处的函数值,试通过一个二次插值函数求cos(/5)π的近似值。
13. 已知函数tan()y x =在0,/4,/3x x x ππ===处的函数值,试通过一个二次插值函数求tan(/5)π的近似值。
14. 已知函数4y x =在1,2,3x x x ===处的函数值,试通过一个二次插值函数求 1.111x =的近似值。
15. 已知函数sin()y x =在0,/4,/2x x x ππ===处函数值,通过一个二次插值函数求1sin(2/5)π-的近似值。
16. 已知函数cos()y x =在0,/4,/2x x x ππ===处函数值,通过一个二次插值函数求1+cos(/5)π的近似值。
17. 已知函数5y x =在1,2,3x x x ===处的函数值,试通过一个二次插值函数求 1.121x =的近似值。
18. 已知函数41/y x =在1,2,3x x x ===处的函数值,试通过一个二次插值函数求 1.211x =的近似值。
拉格朗日插值龙格现象的matlab实现

拉格朗日插值龙格现象的MATLAB 实现姓名:袁宽 学号:2 专业:电气工程题目:对于函数211)(x x f +=,55≤≤-x 进行拉格朗日插值。
10=n ,按等距节点求分段线性插值,把)(x f 和插值多项式的曲线画在同一张图上进行比较。
观察Lagrange 插值及数值积分中的分段性插值。
f.m :function f= f( x )f=1./(1+x.^2);endLagrange.mfunction y=Lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;End拉格朗日插值的曲线:x=[-5:1:5];y=1./(1+x.^2);x0=[-5:0.001:5];y0=Lagrange(x,y,x0);y1=1./(1+x0.^2);plot(x0,y0,'b')hold onplot(x0,y1,'r')使用龙格现象观察分段性插值的曲线:syms y x lx;y=1/(1+x^2);x0=-5:1:5;y0=zeros(1,length(x0));for i=1:11x=x0(i);y0(i)=eval(y);endM = -5:0.01:5;y1 = zeros(1,length(M));n = 1;for i=2:11for x=-5:0.01:5if x<x0(i) && x>=x0(i-1)lx(1)=y0(i-1)*(x-x0(i))/(x0(i-1)-x0(i));lx(2)=y0(i)*(x-x0(i-1))/(x0(i)-x0(i-1));y1(n) = lx(1)+lx(2);n = n+1;endendendezplot(y,[-5,5])hold onA =-5:0.01:5;plot(A,y1,'r');分别运行两个文件后的得到两个图形曲线:拉格朗日插值曲线分段插值曲线。
拉格朗日插值函数matlab例题

拉格朗日插值函数是一种常用的数学工具,它可以用于拟合数据、逼近函数和插值等多种数学问题。
在本文中,我将通过介绍拉格朗日插值函数的原理和应用,以及使用Matlab进行实例演示,帮助你更好地理解这一主题。
1. 拉格朗日插值函数的原理拉格朗日插值函数是通过拉格朗日插值多项式来实现插值的过程。
拉格朗日插值多项式是由一组互不相同的节点和函数值得到的,并且满足通过这些节点的所有函数值。
它的数学表达式如下所示:\[P(x) = \sum_{i=0}^{n} y_i l_i(x)\]其中 \(P(x)\) 是拉格朗日插值多项式,\(n\) 是节点数,\(y_i\) 是函数在节点 \(x_i\) 处的函数值,\(l_i(x)\) 是拉格朗日基函数。
2. 拉格朗日插值函数的应用拉格朗日插值函数广泛应用于各种领域,包括数值分析、数值计算和工程应用等。
它可以用于曲线拟合、图像处理、信号处理等多种领域,并且在实际问题中具有重要的作用。
3. 使用Matlab进行拉格朗日插值函数的实例演示接下来,我将使用Matlab进行一个简单的拉格朗日插值函数的实例演示,以便更直观地理解这一主题。
```matlab% 拉格朗日插值函数的实例演示x = [1, 2, 3, 4]; % 设定节点y = [1, 4, 9, 16]; % 对应的函数值xx = 1:0.1:4; % 生成插值点yy = zeros(size(xx)); % 初始化插值结果for i = 1:length(x)L = ones(size(xx));for j = 1:length(x)if j ~= iL = L.*(xx-x(j))/(x(i)-x(j));endendyy = yy + y(i)*L; % 计算插值结果endplot(x,y,'o',xx,yy,'-'); % 绘制插值结果xlabel('x'); ylabel('y');legend('节点','插值结果');```在这个实例中,我们首先定义了一组节点\(x\) 和对应的函数值\(y\),然后生成了插值点 \(xx\),利用拉格朗日插值多项式计算了插值结果\(yy\),最后使用Matlab进行了绘图展示。
