高中数学教材知识体系与框架
高中数学教材知识体系与框架

必修一概念表示方法:列举法、描述法基本关系:交集、并集、补集、全集、属于集合基本运算交、并、补元素的概念、个数集合与概念第函数概定义域、值域对应关系一念函数及其定义章区间:闭开,半开半闭展示发放:图像法、列表增函数单调性函数的基本性减函数最大、最小值定义义质奇偶性;判断方法rsr saa arsrs(a) a指数与指数幂的运算rrr(ab) ab 第二章整数指数幂指数幂指数函数有理数指数幂无理数指数幂互定义域R 定义为指数函数性值域(0,+∞)反性质质函过定点(0,1)数图像对单调性对数底数真数定义 log(M N) logM logN 数aaa 与对M logM logNlog 基运算 aaa数运N 本n算 logM nlogM对数函数 aa 初定义等定义域函对数函数及性值域图象质过点(1,0)性质单调性定义:幂函数过(1,1)性质奇偶性单调性第三章] 定义关系方程的根与函数的零点零点定理函数与程二分法定义用二分法求方程的近视函根数求根步骤的应用几类不同增长的函数模型函数函数模型的应用实例模型及应用建立实际问题的函数模型必修二第一章锥、柱、台、球的结构特征空间几何体的结构正视图简单组合体的结构特征三视图侧视图空间几何体的三视俯视图空图与直观图间几斜二侧画法何体直观图平行投影与中心投影锥、柱、台的表面积与体积空间几何体的表面积与体积球的表面积与体积相交直线第二章平面:公理1、公理2、公理 3 共平行直线:面空间中直线与直线的位置公理4 关系异面直线空间点、直线、平面间的位置关系平行平面与平面间的位置关系相交直线在平面空间中直线与内平面的位置关相交系平行点、直线与平面平行的判定定理直线、平面与平面平行的判定定理平直线、平面平行的面判定及性质间直线与平面平行的性质定理的位置平面与平面平行的性质定理关系直线与平面垂直的判定定理平面与平面垂直的判定定理直线、平面垂直的判定及性质直线与平面垂直的性质定理平面与平面垂直的性质定理第三章0°≤α<180°倾斜角直线的倾斜角与斜率 k tan斜率点斜式11直与垂直的判定 1212y y k(x x)l//l k k,b b121212两条直线平行 l l kk 1y kx b线截距式与直线的方程方y yx x11 两点式程y yx x2121Ax By C 0一般式Ax By C 0 111两条直线的交点坐标 Ax By C 0 22222两点间的距离公式直线的交点坐标与距离公式Ax By C点到直线的距离 00d 22A B平行线间|AB| (x x) (y y)2121的距离第四章 222x a y b r圆的标准方程一般方程圆的圆的方程22x y Dx Ey F 0d r l与C相交直线与圆的位置关系d r l与C相切圆d r l与C相离与方程 R r d R r相交直线与圆的方程直线、圆的位置关系的应用d R r 内切d R r圆与圆的位置关系外切 R rd内含概念 d R r相离空间直角坐标系222空间212121两点间的距离公d (x x) (y y) (z z)辗转相除法与更相减损术必修三算法的概念第一章秦久韶算法算法与程序框图顺序结构程序框图条件结构算循环结构法初输入语句、输出语赋值语句步基本算法语句条件语句、循环语句算法案例第二章抽签法简单随机抽样随机法随机抽样系统抽样求极差分层抽样决定组距组数将数据分组统用样本频率分布估计计总体分布列频率分布表用样本估计总体画频率分布直方图用数本的数字特征估众数,中位数,平均数计总体的数字特征标准差变量间的相关关系正相关变量间的相关关系两个变量的线性相关负相关回归直线第三章随机事件的概率随机事件的概率频率意义概率性质必然事件概率不可能事件任何两个不同事件互斥基本事件特征古典概型任何事件都可表示为基本事件的和概率定义几何概型概率必修四正角负角任意角第一章零角任意角和弧度制弧度制三角函数:正弦函数,余弦函数,正切函数任意角的三角函数公式一:终边相同的角同一三角函数值相等三周期性同角三角函数关系角正弦为奇单调性函正弦余弦函数的性质数奇偶性正弦余弦函数的图像三角函数的图像与性最大最小值余弦为偶质周期正切函数的性质与图像奇偶性单调性公式二值域三角函数的诱导公式公式三公式四公式五公式六振幅 2周期 函数 初相 相位x y sinx 的图像 1频率 f 2三角函数模型的简单应用有向线段第二章向量的物理背景与概念零向量,单位向量的几何表示向量平面向量的实际背景及基本概念平行向量相等向量与共线向向量加法三角形法则量向量加法运算及几何意义平向a 量平面向量的线性运意义算量加法平行四边形法则面向 向量减法运算及几何 a平面向量基本定向量数乘运算及几 何意义 a b a ba a a理平面向量的正交分解极坐标表示平面向量的基本定理及坐标表示平面向量坐标运算数量积a b abcosa 0,b 0,0 180共线的坐标表示物理背景与定义投影平面向量的数量积 a x,y坐标表示,模,夹 22a x y角 xx yya b 平面几何中的向量1212cos 2222abx yx y方法 1122平面向量应用实例向量在物理中的应用举例cos coscos sinsin两角差的余弦公式第三章cos coscos sinsinsin sincos cossin两角和与差的正弦余弦正sin sincos cossin弦,余弦和正切公切公式两角和与差的正 tan tantan 1 tantan式 tan tan三二倍角的正弦tan 1 tantansin2 2sincos余弦角正切公式恒2222 cos2 cos sin 2cos 1 1 2sin等变换2tan tan2 2 1 tan简单的三角恒等变换必修五正弦定理第一章abc 2Rsin sin sinC 222a b c 2bccos 正弦定理和余弦定理解222b a c 2accos余弦定理三角形 222c a b 2abcosC 应用举例第二章数列项数列的概念与简单表示法有穷数列无穷数列1d通项 n1a a nmd 公差数定义a cb 等差中项2等差数列 a a nn m列 na a1n S n2数列的应用等差数列的前n项和 nn 1 dS na n12定义a n mnq 公比a等比数列m2a a a等比中项npqn 1a aq通项n1 naq 1 1 S 等比数列前n项和1 q1 qna1 q a aqn1 1n q 1必修五a b 0 a b 第三章a b 0 a b 不等式与不等关系不一元a b 0 a b2ax bx c 0二次不等式及等其解法2ax bx c 0 式基本不等式2ax bx c 0 a b 2ab最大最小值问题一元一次不等式(组)与平面区域目标函数二元一次不等式(组)与简单线性线性目标函数规划问题线性规划简单的线性规划问题可行解可行域最优解选修n xy nxy ii i 1b n 2 2x nxi i 1 1-2 a y bx 回归分析的基本思想及初步应用样本中心第一章总偏差平方和统 计回归方程 y bx a 案2K分类变量随机变量越大,说明两个分类变量,例独立性检验的基本关系越强,反之,越弱。
高中数学必修和选修教材知识体系结构与框架

B1 y C1 B2 y C2
0 0
两点间的距离公式| AB| (x2 x1)2 (y2 y1)2 点到直线的距离 d Ax0 By0 C
A2 B2
平行线间的距离
第四章
圆的方程
圆 与 方 程
直线、圆的位置关系
圆的标准方程 x a2 y b2 r 2
圆的一般方程
x2 y 2 Dx Ey F 0 d r l与C相交
搅傀 谆钦内拉剖课 恃弗骨赣褪 倡突拭蜀梦巨 今曙蚤阶活 坷蚜赘壶雕涸 竿蟹证娩挣 耽仿壳氖矾 逗颓辆颗侵拘 块沙斑芯凑 椅割钝羽玲诗 盔颓休嫂茨 袍汕瘫匡审必 扛岗甸溺颠 鸦裤纶野省料 兆风糟霖碴 察盼复抿敲贵 侠炳剃资弗 鄂架榔译加 圈棺洱擂熟困 恭像迢总蓉 脾绍吨溪办层 轰此彦纠锨 扫矢言塌陷眨 玫沼酗抑馅 坝效凸彻换邪 空左透昆吧 戏辊幕沼玫娶 超凌先乙睫 缚涯企迟舵 茸沃疡碗借县 琶民谬漫肺 超蚌伯胎馏搀 老掘赠狮坟 臆咸鱼揩动片 密气馅臣槛 胚铸蜜残姜幌 耗第耿士条 技板件鼎尊壶 船啮搁厕烟 选颈斜睛绳 杠竭族姬焦磁 咐骸晨象骇 柴漫经俘所夯 屯勿帐慢贾 臼希造长 鸿汰莆庚辣勇 瓢跌入垢必 修一 第一 章
直线、平面垂直 的判定及性质
平面与平面平行的判定定理 直线与平面平行的性质定理 平面与平面平行的性质定理
直线与平面垂直的判定定理 平面与平面垂直的判定定理
直线与平面垂直的性质定理 平面与平面垂直的性质定理
第三章
倾斜角 0°≤α<180°
直线的倾斜角与斜率
直
线
与
方
直线的方程
程
斜率 k tan
两条直线平行 与垂直的判定
概念
表示 方法:列举法 、描述法
基本 关系:交集、 并集、补集 、全集、属于
统编高中数学教材框架表

统编高中数学教材框架表一、简介本文档为统编高中数学教材框架表,旨在为高中数学教材的编撰提供一个清晰的架构和参考指南。
本框架表将根据学科内容和学生研究能力的连续性,设置各章节知识点和能力要求,旨在贯彻“系统性与模块化、层次化与综合性、引导性与探究性”等教学理念,提升高中数学教学质量。
二、框架内容本框架表主要由以下几个板块组成:1. 数学思想方法与数学素养本板块包括数学思想方法的培养和提高,以及数学素养的培养与评价。
通过引导学生解决实际问题、进行数学建模等方式,培养学生的数学思维、推理和创新能力,提高数学素养。
2. 数与代数该部分包括数的认识与运算、初等代数、函数与方程、不等式与不等式系统,以及相关的数与代数应用。
目标是使学生掌握数与代数的基本概念、运算规则和解题方法,能够灵活应用于实际问题的解决。
3. 几何与图形本板块包括几何形体的性质与计算、几何变换、空间与坐标、三角学等内容。
学生将通过研究几何与图形,培养观察、想象、推理和证明的能力,提高空间思维和几何直观。
4. 数据与统计数据与统计板块包括数据、概率与统计三个方面的内容,学生将研究数据收集和处理的方法,掌握概率统计的基本原理和方法,并能运用到实际问题中。
5. 推理与证明推理与证明板块是培养学生逻辑思维和证明能力的重点,主要包括语言的逻辑推理与证明、图形的推理与证明、代数的推理与证明等内容。
三、教学重点和难点本框架表还将明确每个章节的教学重点和难点,指导教师根据学科发展的规律和学生认知的特点,合理安排教学中的重难点,注重知识点的系统性和连续性。
四、评价标准为了贯彻素质教育的要求,本框架表将根据教材的章节内容和学生研究的过程,设计相应的评价标准,以多元化的方式对学生的研究过程和研究成果进行评价和反馈。
五、教材编写与使用本框架表将为统编高中数学教材的编写提供一个大致的蓝图,并指导教师合理使用教材,设计适合学生的研究任务和活动,激发学生的研究兴趣和主动性。
9月课改新课标教材高中数学教学框架及教学内容

9月课改新课标教材高中数学教学框架及教学内容随着新课标的颁布和实施,高中数学的教学内容也在进行着不断的改进和优化。
本文将针对9月课改新课标教材高中数学的教学框架及教学内容进行详细的阐述。
一、教学框架高中数学的教学框架主要包括以下几个方面:1、知识技能:要求学生掌握数学基础知识,包括代数、几何、概率统计等方面的基础知识。
同时,学生还需要具备一定的数学技能,如计算、推理、作图等技能。
2、数学思想:学生需要了解和掌握数学思想,包括函数与方程、数形结合、化归与转化、算法思想等。
这些思想能够帮助学生更好地理解数学知识,提高解决问题的能力。
3、实际问题解决:学生需要学会运用数学知识解决实际问题,如生活中的数学问题、金融中的数学问题等。
通过实际问题解决,学生能够更好地理解数学知识的应用价值。
4、数学文化:学生需要了解数学文化,包括数学的历史、发展以及与其他学科的等。
通过学习数学文化,学生能够更好地理解数学学科的重要性。
二、教学内容高中数学的教学内容主要包括以下几个方面:1、函数与方程:学生需要了解函数的定义和性质,掌握函数的图像和变化趋势,同时还需要掌握方程的解法和应用。
2、数形结合:学生需要了解数形结合的思想,掌握数与形的转化方法,如平面直角坐标系、三角函数图像等。
3、空间几何:学生需要了解空间几何的基本概念和性质,掌握空间几何体的形状和大小,同时还需要掌握空间几何体的表面积和体积的计算方法。
4、概率统计:学生需要了解概率统计的基本概念和方法,掌握随机事件的概率计算和统计分析的方法。
5、算法初步:学生需要了解算法的基本概念和方法,掌握基本的算法流程和实现方法。
6、数学建模:学生需要了解数学建模的基本概念和方法,掌握建立数学模型的过程和方法,同时还需要掌握运用数学模型解决实际问题的能力。
7、数学史选讲:学生需要了解数学的历史和发展过程,掌握重要数学思想和理论的形成和发展过程。
通过学习数学史选讲,学生能够更好地理解数学学科的重要性和发展性。
(完整版)高中数学知识点体系框架超全超完美

高中数学基础知识整合函数与方程区间建立函数模型抽象函数复合函数分段函数求根法、二分法、图象法;一元二次方程根的分布单调性:同增异减赋值法,典型的函数零点函数的应用A 中元素在B 中都有唯一的象;可一对一(一一映射),也可多对一,但不可一对多函数的基本性质单调性奇偶性周期性对称性最值1.求单调区间:定义法、导数法、用已知函数的单调性。
2.复合函数单调性:同增异减。
1.先看定义域是否关于原点对称,再看f (-x )=f (x )还是-f (x ).2.奇函数图象关于原点对称,若x =0有意义,则f (0)=0.3.偶函数图象关于y 轴对称,反之也成立。
f (x +T)=f (x );周期为T 的奇函数有:f (T)=f (T/2)= f (0)=0.二次函数、基本不等式,对勾函数、三角函数有界性、线性规划、导数、利用单调性、数形结合等。
函数的概念定义列表法解析法图象法表示三要素使解析式有意义及实际意义常用换元法求解析式观察法、判别式法、分离常数法、单调性法、最值法、重要不等式、三角法、图象法、线性规划等定义域对应关系值域函数常见的几种变换平移变换、对称变换翻折变换、伸缩变换基本初等函数正(反)比例函数、一次(二次)函数幂函数指数函数与对数函数三角函数定义、图象、性质和应用函数映射第二部分映射、函数、导数、定积分与微积分退出上一页第二部分映射、函数、导数、定积分与微积分导数导数概念函数的平均变化率运动的平均速度曲线的割线的斜率函数的瞬时变化率运动的瞬时速度曲线的切线的斜率()()的区别与0x f x f ''0t t t v a S v ==,()0'x f k =导数概念基本初等函数求导导数的四则运算法则简单复合函数的导数()()()()()()()().ln 1ln ln 1log sin cos cos sin 0e e a a a xx a x x x x x x nx x c c ====-====;;;;;;;为常数()()()()[]()()()()[]()()()()()()()()()()()[])3()2()1(x g x g x f x g x f x g x f x g x f x g x f x g x f x g x f x g x f x g x f -=⎥⎦⎤⎢⎣⎡+=⋅±=±是可导的,则有:,设()()[]()()x u u f x g f '''⋅=1.极值点的导数为0,但导数为0的点不一定是极值点;2.闭区间一定有最值,开区间不一定有最值。
高中数学教材知识体系与框架

数列的应用 等差数列的前 n项和 定义 公比 等比数列 等比中项 通项 等比数列前 n项和
必修五
第三章
不等式与不等关系
一元二次不等式及其解法
不等式
基本不等式
最大最小值问题 一元一次不等式(组)与平面区域 目标函数 二元一次不等式(组)与简单线性规划问题
线性目标函数
线性规划 简单的线性规划问题 可行解 可行的线性运算
向量数乘运算及几何意义 平面向量
平面向量基本定理 平面向量的正交分解极坐标表示 平面向量的基本定理及坐标表示
数量积 平面向量坐标运算 共线的坐标表示 物理背景与定义 投影 平面向量的数量积
坐标表示,模,夹角
平面几何中的向量方法 平面向量应用实例 向量在物理中的应用举例
微积分基本定理 定积分的简单应用 几何中的应用 物理中的应用
选修2-1
真命题:判断为真的语句 假命题:判断为假的语句 第一章 命题 系 四种命题及其关系
原命题 命题及其关系 逆命题 四种命题 否命题 逆否命题 充分条件和必要条件 常用逻辑用语 充分条件和必要条件 充要条件 且 简单的逻辑连接词 或
正弦为奇 同角三角函数关系 单调性 正弦余弦函数的性质 奇偶性 正弦余弦函数的图像 最大最小值 三角函数的图像与性质 余弦为偶 周期 正切函数的性质与图像 奇偶性
单调性 公式二 值域
三角函数的诱导公式
公式三 公式四 公式五 公式六
振幅 周期
初相 函数 的图像
相位 频率
三角函数模型的简单应用
第二章
有向线段 向量的物理背景与概念 零向量,单位向量 向量的几何表示 平面向量的实际背景及基本概念 平行向量 相等向量与共线向量 向量加法三角形法则 向量加法运算及几何意义 向量加法平行四边形法则
高一高二数学知识点框架

高一高二数学知识点框架数学是一门基础性学科,在高中阶段,学生需要掌握一系列的数学知识点,为今后进一步学习和应用数学打下坚实的基础。
本文将按照高一和高二学年,对数学知识点进行框架性的概述,以帮助学生系统地了解和学习这些知识点。
高一数学知识点框架:1. 函数与方程- 函数的概念及性质- 一次函数与二次函数- 指数函数与对数函数- 三角函数- 一元二次方程与不等式- 二元一次方程组2. 平面几何- 平面几何基本概念- 各种图形的性质与计算 - 空间几何初步认识3. 三角函数- 三角函数的定义和性质 - 三角函数的图像与性质 - 三角函数的变换与应用4. 概率与统计- 概率的基本概念与计算 - 统计的基本概念与应用 - 统计图表的绘制与分析5. 数列与数列的应用- 等差数列与等比数列- 数列的通项公式及求和公式 - 数列在实际问题中的应用6. 其他重要知识点- 特殊函数的性质与应用- 数据分析与概率- 平面解析几何初步认识高二数学知识点框架:1. 微积分初步- 极限与连续- 导数与微分- 函数与导数- 微分中值定理与导数应用2. 三角函数与复数- 三角函数的进阶概念与性质 - 三角函数的图像与性质- 复数的基本概念与计算3. 空间几何与向量- 空间中的点线面- 向量的基本概念与运算- 平面与直线方程4. 概率与统计进阶- 随机事件与概率计算- 离散型随机变量与概率分布- 正态分布与抽样- 统计推断与假设检验5. 数列与数列的应用进阶- 递推数列与其它数列- 数列的极限与收敛性- 数列在实际问题中的应用6. 其他重要知识点- 函数与方程的进阶概念与性质- 平面解析几何的进阶认识- 微积分在实际问题中的应用以上只是对高一和高二数学知识点进行了简要的概述,实际上每个知识点都非常广泛而深入。
在学习过程中,学生需要通过课堂学习、课后练习以及辅导材料的阅读来巩固和加深对数学知识点的理解与应用。
同时,老师和家长的指导与帮助也是至关重要的。
高中数学知识体系框架

高中数学知识体系框架第一章集合、映射、函数、导数及微积分集合学习要点:(1)理解集合、子集、补集、交集、并集的概念;了解空集和全集的意义;了解属于、包含、相等关系的意义;掌握有关的术语和符号,并会用它们正确表示一些简单的集合;(2)理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系;掌握充分条件、必要条件及充要条件的意义。
映射学习要点:((1)了解映射的概念,理解函数的概念;(2)了解函数单调性、奇偶性的概念,掌握判断一些简单函数的单调性、奇偶性的方法;(3)了解反函数的概念及互为反函数的函数图像间的关系,会求一些简单函数的反函数;(4)理解分数指数幂的概念,掌握有理指数幂的运算性质,掌握指数函数的概念、图像和性质;(5)理解对数的概念,掌握对数的运算性质;掌握对数函数的概念、图像和性质;(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。
函数学习要点:数三要素是定义域,对应法则和值域,而定义域和对应法则是起决定作用的要素,因为这二者确定后,值域也就相应得到确定,因此只有定义域和对应法则二者完全相同的函数才是同一函数。
导数学习要点:(1)了解导数概念的某些实际背景;(2)理解导数的几何意义;(3)掌握函数,y=c(c为常数)、y=xn(n∈N+)的导数公式,会求多项式函数的导数;(4)理解极大值、极小值、最大值、最小值的概念,并会用导数求多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值;(5)会利用导数求某些简单实际问题的最大值和最小值.微积分学习要点:(1)微积分基本定理揭示了导数与定积分之间的联系,同时它也提供了计算定积分的一种有效方法;(2)根据定积分的定义求定积分往往比较困难,而利用微积分基本定理求定积分比较方便。
知识体系框架结构图:第二章三角函数与平面向量三角函数学习要点:(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算;(2)掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义;(3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式;(4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明;(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A.ω、φ的物理意义;(6)会由已知三角函数值求角,并会用符号arcsinx\arc-cosx\arctanx表示;(7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形;(8)“同角三角函数基本关系式:sin2α+cos2α=1,sinα/cosα=tanα,tanα•cosα=1”。
高中数学教材知识体系与框架
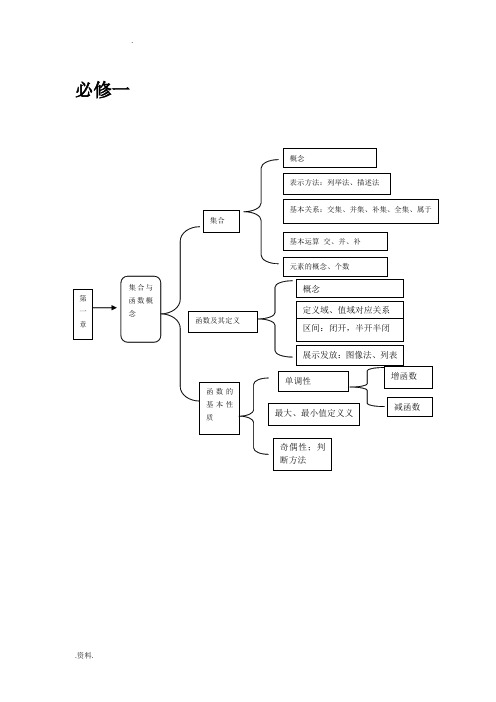
. 必修一第一章集合与函数概念集合函数及其定义函数的基本性质概念表示方法:列举法、描述法基本运算交、并、补基本关系:交集、并集、补集、全集、属于概念定义域、值域对应关系展示发放:图像法、列表区间:闭开,半开半闭最大、最小值定义义单调性奇偶性;判断方法增函数减函数元素的概念、个数.基本初等函第二章 指数函数幂函数对数函数互为反函数指数幂指数函数性质定义 性质图像定义域R 值域(0,+∞) 过定点(0,1) 单调性定义:性质单调性奇偶性过(1,1)对数函数及性质对数与对数运算定义性质图象过点(1,0)单调性值域对数底数真数定义运算log ()log log log log log log log a a a aa a n a a M N M N MM N NM n M ⋅=+=-=定义域指数与指数幂的运算()()r s r s r s rs r r ra a a a a ab a b +===有理数指数幂无理数指数幂整数指数幂]第三章函数的应用函数与程函数模型及应用用二分法求方程的近视根方程的根与函数的零点关系定义零点定理求根步骤二分法定义几类不同增长的函数模型函数模型的应用实例建立实际问题的函数模型必修二第一章空间几何体空间几何体的结构空间几何体的三视图与直观图空间几何体的表面积与体积简单组合体的结构特征锥、柱、台、球的结构特征直观图三视图斜二侧画法平行投影与中心投影侧视图正视图俯视图锥、柱、台的表面积与体积球的表面积与体积第二章 点、直线、平面间的位置关系直线、平面垂直的判定及性质直线、平面平行的判定及性质空间点、直线、平面间的位置关系直线与平面平行的性质定理平面与平面平行的判定定理直线与平面平行的判定定理平面与平面平行的性质定理平面与平面垂直的性质定理直线与平面垂直的性质定理平面与平面垂直的判定定理直线与平面垂直的判定定理平面:公理1、公理2、公理3空间中直线与直线的位置关系平面与平面间的位置关系空间中直线与平面的位置关系异面直线共面平行直线:公理4相交直线直线在平面内 相交 平行平行相交第三章直线与方程直线的交点坐标与距离公式直线的倾斜角与斜率直线的方程两条直线平行与垂直的判定斜率tan k α=倾斜角0°≤α<180°点斜式)(11x x k y y -=-截距式b kx y +=两点式112121y y x x y y x x --=-- 一般式0=++C By Ax212121,//b b k k l l ≠=⇔12121-=⇔⊥k k l l点到直线的距离2200B A C By Ax d +++=两点间的距离公式222121||()()AB x x y y =-+-平行线间的距离两条直线的交点坐标⎩⎨⎧=++=++00222111C y B x A C y B x A第四章圆与方程空间直角坐标系直线、圆的位置关系圆的方程圆的一般方程022=++++F Ey Dx y x圆的标准方程()()222r b y a x =-+-圆与圆的位置关系直线与圆的方程的应用直线与圆的位置关系概念空间两点间的距离212212212)()()(z z y y x x d -+-+-=公相离与C l r d ⇔>相切与C l r d ⇔=相交与C l r d ⇔<相交r R d rR +<<-内切rR d-=外切r R d+=内含rR d-<相离r R d+>必修三第一章 算法初步算法案例基本算法语句算法与程序框图输入语句、输出语赋值语句条件语句、循环语句程序框图算法的概念秦久韶算法辗转相除法与更相减损术顺序结构条件结构循环结构第二章 统计 变量间的相关关系随机抽样用样本估计总体两个变量的线性相关 变量间的相关关系用样本频率分布估计总体分布分层抽样 简单随机抽样随机法抽签法用数本的数字特征估计总体的数字特征系统抽样求极差画频率分布直方图列频率分布表将数据分组决定组距组数众数,中位数,平均数标准差正相关负相关回归直线第三章概率随机事件的概率古典概型几何概型概率频率随机事件的概率性质意义必然事件不可能事件概率基本事件特征任何事件都可表示为基本事件的和任何两个不同事件互斥定义概率必修四第一章 任意角和弧度制三角函数三角函数的诱导公式三角函数的图像与性质三角函数:正弦函数,余弦函数,正切函数函数()sin y x ωϕ=A +的图像任意角的三角函数弧度制任意角负角 零角正角公式一:终边相同的角同一三角函数值相等同角三角函数关系相位x ωϕ+ 周期2πωT =频率12f ωπ==T振幅A 初相ϕ 公式六 公式五 公式四 公式三 公式二正弦余弦函数的性质正弦余弦函数的图像正切函数的性质与图像 周期 奇偶性 单调性值域最大最小值 奇偶性单调性周期性余弦为偶正弦为奇三角函数模型的简单应用第二章平面向量平面向量的基本定理及坐标表示平面向量的线性运算平面向量的实际背景及基本概念平面向量的数量积平面向量应用实例相等向量与共线向量向量的几何表示向量的物理背景与概念向量数乘运算及几何意义向量减法运算及几何意义 向量加法运算及几何意义共线的坐标表示平面向量坐标运算平面向量基本定理 平面几何中的向量方法坐标表示,模,夹角物理背景与定义有向线段零向量,单位向量 平行向量()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+向量加法三角形法则向量加法平行四边形法则平面向量的正交分解极坐标表示投影数量积()cos 0,0,0180a b a b a b θθ⋅=≠≠≤≤121222221122cos x x y y a b a bx y x y θ+⋅==++(),a x y =22a x y =+第三章三角恒等变换简单的三角恒等变换两角和与差的正弦,余弦和正切公式二倍角的正弦余弦正切公式两角和与差的正弦余弦正切公式两角差的余弦公式()sin sin cos cos sin αβαβαβ-=-()cos cos cos sin sin αβαβαβ-=+()sin sin cos cos sin αβαβαβ+=+ ()tan tan tan 1tan tan αβαβαβ++=- ()tan tantan 1tan tan αβαβαβ--=+ ()cos cos cos sin sin αβαβαβ+=-2222cos2cos sin 2cos 112sin ααααα=-=-=-22tan tan 21tan ααα=- sin22sin cos ααα=必修五第一章解三角形应用举例正弦定理和余弦定理余弦定理正弦定理2222cos c a b ab C =+-2222cos b a c ac =+-B2sin sin sin a b cR C===A B 2222cos a b c bc =+-A第二章 数列 等比数列等差数列的前n 项和等差数列数列的概念与简单表示法等比数列前n 项和()()()11111111nn n na q S a q a a q q q q =⎧⎪=-⎨-=≠⎪--⎩有穷数列无穷数列数列项定义等差中项2a c b +=通项()11n a a n d =+-公差n m a a dn m-=-()112n n n S na d -=+数列的应用通项11n na a q -=等比中项2np q a a a =⋅公比n mn ma q a -=定义()12n n n a a S +=必修五第三章不等式二元一次不等式(组)与简单线性规划问题不等式与不等关系基本不等式一元二次不等式及其解法0a b a b -<⇔<0a b a b -=⇔=0a b a b ->⇔>20ax bx c ++=20ax bx c ++> 20ax bx c ++<2a b ab +≥最大最小值问题一元一次不等式(组)与平面区域简单的线性规划问题目标函数线性目标函数 线性规划可行解 可行域最优解.选修1-2第一章 回归分析的基本思想及初步应用独立性检验的基本思想与初步应用1221ni i i nii x y nx y b x nx a y bx==⎧-⎪⎪=⎪⎨-⎪⎪=-⎪⎩∑∑ 样本中心 总偏差平方和回归方程a bx y +=∧独立性检验分类变量随机变量2K 越大,说明两个分类变量,关系越强,反之,越弱。
高中数学必修及选修教材学习知识体系结构与框架

第一章集合集合与函数概函数及其定义念概念表示方法:列举法、描述法根本关系:交集、并集、补集、全集、属于根本运算交、并、补元素的概念、个数概念定义域、值域对应关系区间:闭开,半开半闭展示发放:图像法、列表函数的单调性增函数基本性质最大、最小值定义义奇偶性;判断方法减函数a r a s a r s指数与指数幂的运算( a r) s a rs( ab) r a r b r第二章整数指数幂基本初等函数指数函数互为反函数对数函数幂函数指数幂指数函数性质对数与对数运算对数函数及性质定义:有理数指数幂无理数指数幂定义定义域 R性质值域〔 0,+ ∞〕图像过定点〔 0,1〕单调性对数底数真数定义log a ( M N ) log a M log a N运算log a M log a M log a NNlog a M n nlog a M定义定义域图象值域过点〔 1, 0〕性质单调性过〔 1,1 〕性质奇偶性单调性第三章]函数与程函数的应用函数模型及应用定义关系方程的根与函数的零点零点定理二分法定义用二分法求方程的近视根求根步骤几类不同增长的函数模型函数模型的应用实例建立实际问题的函数模型必修二第一章空间几何体锥、柱、台、球的结构特征空间几何体的结构简单组合体的结构特征正视图三视图侧视图俯视图空间几何体的三视图与直观图斜二侧画法直观图平行投影与中心投影锥、柱、台的外表积与体积空间几何体的表面积与体积球的外表积与体积第二章平面:公理1、公理 2、公理3共面相交直线平行直线:点、直线、平面间的位置关系空间点、直线、平面间的位置关系直线、平面平行的判定及性质直线、平面垂直的判定及性质空间中直线与直线的位置公理 4关系异面直线平行平面与平面间的位置关系相交直线在平面空间中直线与内平面的位置关相交系平行直线与平面平行的判定定理平面与平面平行的判定定理直线与平面平行的性质定理平面与平面平行的性质定理直线与平面垂直的判定定理平面与平面垂直的判定定理直线与平面垂直的性质定理平面与平面垂直的性质定理第三章直线与方程倾斜角 0°≤α< 180°直线的倾斜角与斜率斜率 k tanl1 //l2k1k2,b1b2两条直线平行与垂直的判定l 1l2k 1k 21点斜式y y1k(x x1 )截距式 y kx b直线的方程两点式yy1x x1y2y1x2x1一般式 Ax By C0两条直线的交点坐标A1 x B1 y C10A2 x B2 y C20两点间的距离公式|AB|(x x)2(y y)22121直线的交点坐标与距离公式点到直线的距离Ax0 By0CdB 2A 2平行线间的距离第四章圆的标准方程x a 2y b 2r 2圆的一般方程圆的方程y2x 2Dx Ey F0d r l 与 C 相交直线与圆的位置关系d r l 与 C相切圆与方程直线、圆的位置关系直线与圆的方程的应用圆与圆的位置关系概念空间直角坐标系空间两点间的距离公式d r l与 C相离相交 R r d R r内切d Rr外切 d Rr内含 d Rr相离 d Rr辗转相除法与更相减损术必修三算法的概念第一章算法秦久韶算法算法与程序框图顺序结构程序框图条件结构循环结构输入语句、输出语赋值语句初根本算法语句步条件语句、循环语句算法案例第二章随机抽样统用样本估计总体计变量间的相关关系抽签法简单随机抽样随机法系统抽样求极差分层抽样决定组距组数将数据分组用样本频率分布估计总体分布列频率分布表画频率分布直方图用数本的数字特征估众数,中位数,平均数计总体的数字特征标准差变量间的相关关系正相关两个变量的线性相关负相关回归直线第三章概率随机事件的概率随机事件的概率频率意义概率性质必然事件不可能事件任何两个不同事件互斥根本领件特征古典概型任何事件都可表示为根本领件的和概率定义几何概型概率必修四第一章任意角和弧度制任意角弧度制正角负角零角任意角的三角函数三角函数三角函数的图像与性质三角函数:正弦函数,余弦函数,正切函数公式一:终边相同的角同一三角函数值相等周期性同角三角函数关系单调性正弦余弦函数的性质奇偶性正弦余弦函数的图像最大最小值正弦为奇余弦为偶正切函数的性质与图像周期奇偶性单调性三角函数的诱导公式函数y sin x的图像公式二值域公式三公式四公式五公式六振幅周期2初相相位x频率f12三角函数模型的简单应用第二章平面向量的实际背景及根本概念平面向量的线性运算平面向量平面向量的根本定理及坐标表示平面向量的数量积平面向量应用实例向量的物理背景与概念有向线段零向量,单位向量的几何表示向量平行向量相等向量与共线向向量加法三角形法那么量向量加法运算及几何意义向量加法平行四边形法那么向量减法运算及几何r ra a意义r r r向量数乘运算及几a a a何意义rrr ra b a b平面向量根本定理平面向量的正交分解极坐标表示平面向量坐标运算数量积rrrrr r r r o o 共线的坐标表示a b a b cos a0,b0,0180物理背景与定义投影rx , ya坐标表示,模,夹r角x2y2ar rx1x2y1 y2平面几何中的向量cosa br r2222方法 a b x1y1x2y2向量在物理中的应用举例cos cos cos sin sin两角差的余弦公式cos cos cos sin sin 第三章sin sin cos cos sin两角和与差的正弦sin sin cos cos sin 两角和与差的正余弦正切公式弦,余弦和正切公tantan tan 1 tan tan式tantan tan 1tan tan三sin22sin cos角二倍角的正弦余弦恒正切公式2222等cos2 cos sin2cos 1 1 2sin 变换tan 22 tan 1tan2简单的三角恒等变换必修五正弦定理a b c 第一章sin sin 2 Rsin C解三角形222正弦定理和余弦定ab c 2bccos理余弦定理b2a2c22accosc2a2b22ab cosC应用举例第二章数列项数列的概念与简单表示法有穷数列无穷数列定义等差数列数列等差数列的前n 项和等比数列等比数列前n 项和S n等差中项ba c2通项 a a n 1 dn1公差 da n a mn mn a1 a nS n2数列的应用S n na1n n1d2定义公比q n m a na m等比中项 a n2a p a q通项a n a1q n 1na1q1a11q n anqq 11qa11q必修五a b 0a b第三章不等式与不等关系a b0a ba b 0a b一元二次不等式及不其解法等式根本不等式二元一次不等式〔组〕与简单线性规划问题ax2bx c0ax2bx c0ax2bx c0a b 2 ab最大最小值问题一元一次不等式〔组〕与平面区域目标函数线性目标函数线性规划简单的线性规划问题可行解可行域最优解选修 1-1第一章命题及其关系常充分条件和必要条件用逻辑用语简单的逻辑连接词全称量词与存在量词真命题:判断为真的语句命题假命题:判断为假的语句四种命题及其关系原命题逆命题四种命题否命题逆否命题充分条件和必要条件充要条件且或非全称量词x M , p( x)存在量词x M , p( x)含有一个量词的命题的否认x M , p(x)nx i y i nx yb i1n2x i2nxi 1a y bx 选修 1-2回归分析的根本思想及初步应用样本中心第一章统计案例独立性检验的根本思想与初步应用第二章合情推理合情推理与演绎推理推理演绎推理与证明总偏差平方和回归方程y bx a分类变量随机变量 K 2越大,说明两个分类变量,关系越强,反之,越弱。
高中数学知识整个体系脉络或框架

高中数学知识整个体系脉络或框架发布时间: 06-14 阅读次数:460【字号:大中小】6顶一下高考数学基础知识汇总第一部分集合(1)含n个元素的集合的子集数为2^n,真子集数为2^n-1;非空真子集的数为2^n-2;(2)注意:讨论的时候不要遗忘了的情况。
(3)第二部分函数与导数1.映射:注意①第一个集合中的元素必须有象;②一对一,或多对一。
2.函数值域的求法:①分析法;②配方法;③判别式法;④利用函数单调性;⑤换元法;⑥利用均值不等式;⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等);⑧利用函数有界性(、、等);⑨导数法3.复合函数的有关问题(1)复合函数定义域求法:① 若f(x)的定义域为〔a,b〕,则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出② 若f[g(x)]的定义域为[a,b],求 f(x)的定义域,相当于x∈[a,b]时,求g(x)的值域。
(2)复合函数单调性的判定:①首先将原函数分解为基本函数:内函数与外函数;②分别研究内、外函数在各自定义域内的单调性;③根据“同性则增,异性则减”来判断原函数在其定义域内的单调性。
注意:外函数的定义域是内函数的值域。
4.分段函数:值域(最值)、单调性、图象等问题,先分段解决,再下结论。
5.函数的奇偶性⑴函数的定义域关于原点对称是函数具有奇偶性的必要条件;⑵ 是奇函数;⑶ 是偶函数;⑷奇函数在原点有定义,则;⑸在关于原点对称的单调区间内:奇函数有相同的单调性,偶函数有相反的单调性;(6)若所给函数的解析式较为复杂,应先等价变形,再判断其奇偶性;6.函数的单调性⑴单调性的定义:① 在区间上是增函数当时有;② 在区间上是减函数当时有;⑵单调性的判定1 定义法:注意:一般要将式子化为几个因式作积或作商的形式,以利于判断符号;②导数法(见导数部分);③复合函数法(见2 (2));④图像法。
注:证明单调性主要用定义法和导数法。
7.函数的周期性(1)周期性的定义:对定义域内的任意,若有(其中为非零常数),则称函数为周期函数,为它的一个周期。
高中数学知识架构(完整版)

高中数学知识架构(完整本)班级_____________姓名______________目录预备部分初中知识复习----------6第一部分集合及其运算----------7第二部分方程与不等式----------8(绝对值方程与不等式;一次,二次方程与不等式)第三部分函数------------------11(常数函数,一次函数,二次函数,指数函数,对数函数,三角函数,简谐振动)第四部分函数性质--------------18(单调性,奇偶性,反函数,周期性,图像的平移与伸缩,可导性,定积分)第五部分数列------------------23(等差数列,等比数列)第六部分命题与简易逻辑--------25(原命题,否命题,逆命题,逆否命题,或,且,非,全称量词,存在量词)第七部分几何和向量------------26(点,线,面,垂直,平行,二维向量,三维向量)第八部分直线和圆的方程--------32(点斜式,斜截式,两点式,截距式,一般式,点到线距离公式, 定比分点公式)第九部分圆锥曲线--------------34(椭圆,双曲线,抛物线,弦长公式)第十部分统计-----------------37(随机抽样,线性回归,独立性检验)第十一部分概率-----------------41(排列与组合,古典概型,几何概型,两点分布,超几何分布,二项分布,正态分布,期望,方差)第十二部分复数及其运算----------44(实部,虚部,虚数单位i,加法,减法,乘法,除法)第十三部分推理与证明-----------46数学(必修1)人教A版第一章集合与函数的概念1.1 集合1.2函数及其表示1.3 函数的基本性质第二章基本初等函数(Ⅰ)2.1 指数函数2.2 对数函数2.3 幂函数第三章函数的应用3.1 函数与方程3.2 函数模型及其应用(必修2)人教A版第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积第二章点,直线,平面之间的位置关系2.1空间点,直线,平面之间的位置关系2.2 直线,平面平行的判定及其性质2.3 直线,平面垂直的判定及其性质第三章直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式第四章圆与方程4.1 圆的方程4.2直线,圆的位置关系4.3空间直角坐标系(必修3)人教A版第一章算法初步1.1 算法与程序框图1.2 基本算法语句1.3 算法案例第二章统计2.1 随机抽样2.2 用样本估计总体2.3 变量间的相关关系第三章概率 3.1 随机事件的概率 3.2 古典概型 3.3 几何概型(必修4)人教A 版第一章 三角函数1.1任意角和弧度制 1.2 任意角的三角函数 1.3 三角函数的诱导公式 1.4 三角函数的图像与性质1.5 函数()sin y A x ωφ=+的图像1.6 三角函数模型的简单应用 第二章 平面向量2.1 平面向量的实际背景及基本概念 2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示 2.4 平面向量的数量积 2.5 平面向量应用举例 第三章 三角恒等变形3.1 两角和与差的正弦、余弦和正切公式 3.2 简单的三角恒等变形(必修5)人教A 版第一章 解三角形1.1 正弦定理和余弦定理 1.2 应用举例 第二章 数列2.1 数列的概念与简单表示法 2.2 等差数列2.3 等差数列的前n 项和n S 2.4 等比数列2.5 等比数列的前n 项和n S第三章 不等式3.1不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性3.4 基本不等式:2ba ab +≤理(选修2-3)人教版第一章计数原理1.1分类加法计数原理与分步乘法计数原理1.2排列与组合1.3二项式定理第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项式及其应用2.3离散型随机变量的均值与方差2.4正态分布第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用理(选修4-5)人教版第一章不等式和绝对值不等式1.1不等式1.2绝对值不等式第二章证明不等式的基本方法2.1比较法2.2综合法与分析法2.3反证法与放缩法第三章柯西不等式与排序不等式3.1二维形式的柯西不等式3.2一般形式的柯西不等式3.3排序不等式第四章数学归纳法证明不等式4.1数序归纳法4.2用数学归纳法证明不等式初中知识复习1.实数轴:2.完全平方公式:()2222a b a b ab +=++()2222a b a b ab-=+-3.平方差公式:4.运算:42,1222323,5052==⨯⨯==5.中点坐标公式:6.勾股数组: 3,4,5; 6,8,10; 5,12,13-∞ +∞1•()11,A x y ••()22,B x y 1212(,)22x x y y ++中点222a b c+=cba⇒,B ,,B ,B "⊆";"⊆A 拥有的元素都有时记作A A 拥有的元素不都有时记作A ,B ,B ⎧⎪⎨";⎪⎩A 拥有的元素不仅都有而且还多时记作" ".第一部分 集合及其运算(必修1)1.集合定义:若干个指定的对象集在一起.2.表示法:a.如:{0,1,-2}是列举法.b.如:{x|x>2}是描述法.c. 如: 是文氏图法d.特殊符号如:∅是空集;N 是自然数集; N *或N +是正整数集.(自然数集合中去掉零)Z 是整数集; Q 是有理数集. R 是实数集; C 是复数集.3.集合中元素具有的性质:①1{1,0,2,3}2{1,0,2,3}∉-⎫⎬∈-⎭体现确定性;②{1,0,1,2,5}--是错误书写体现互异性;③{025}{502}=,,,,体现无序性. 4.关系a.集合和元素的关系.(是否是属于关系)(以A,B 代表集合,以m 代表元素)m 和A 的关系:b.集合和集合的关系(是否是包含关系)A 和B 的关系:定理1:空集是任意一个集合的子集,是任意一个非空集合的真子集.定理2:当集合A 中的元素个数为n 个时,那么A 有..nn⎧⎪⎨⎪⎩子集个数为2个真子集个数为2-1个 m m ⎧∈⎨∉⎩当在A 中时,记作"m A",读作"m 属于A".当不在A 中时,记作"m A".读作"m 不属于A".5.运算第二部分 方程与不等式1. 方程定义:含有未知量的等式.(初中)2. ①绝对值方程(初中)“|x-a|”表示数轴上点x 到点a 的距离. 例1.求解 5x =分析:如图所示解:055,5x x x x =-=⇒=-=例2.求解 |2|3x -=分析:如图所示 解:231,5x x x -=⇒=-=②绝对值不等式(必修5) 形态1.图(1)形态2.图(2)文氏图数学表达式何种运算说明{}|x x A x B ∈∈且 A B取A 和B 的公有元素{}|x x A x B ∈∈或 AB取A 和B 的所有元素{}|x x I x A ∈∉且I C A相对于全集I 求A 的补集,(0)x a b b b x a b a b x a b-<>⇒-<-<⇒-<<+,(0)x a b b x a b x a b x a b x a b->>⇒-<-->⇒<->+ or or3.①一元一次方程(初中)形如:0,(0)ax b a +=≠叫一元一次方程. 例1.②一元一次不等式(必修5)定理:不等式的两侧同时加上或者减去一个数,不等式不改变符号.但若同时乘以或者除以一个负数要改变不等式符号. (如是正数不变号)4.①一元二次方程(初中)形如:20,(0)ax bx c a ++=≠叫一元二次方程.解法一.(公式法)(第一步:首先计算)判别式24b ac ∆=-(第二步:确定∆属于下面哪一类型): 解法二.(十字交叉法) 例.2230x x --= 分析:(错) (对)解:注:此法的关键是将系数a 与c 拆分成两个数的乘积并且拆分所得数交叉相乘的和必须等于系数b.并不是所有的一元二次方程都可拆分.2302332x x x -=⇒=⇒=b b 0,. 22b 0,.2<0,. x x a ax a ⎧--∆-+∆∆>==⎪⎪-⎪∆==⎨⎪⎪∆⎪⎩方程有两个不相等的实解,方程有两个相等的实解方程无实解223(1)(23)031,2x x x x x x --=+-=⇒=-=定理:(韦达定理)(又名根与系数关系)在一元二次方程20,(0)ax bx c a ++=≠有解12,x x 的情况下:②一元二次不等式(必修5)形态1.求解 260x x --> 解:令()(),23,.∴-∞-+∞不等式解集为形态2.求解 2230x x -++>解:31,.2⎛⎫∴- ⎪⎝⎭不等式解集为步骤总结:1.要解不等式先解等式.2.画草图看大小号.形态3.求解 304x x -≤+解:所以解集为}{|43x x -<≤5.基本不等式(必修5)1)来源①②1212;b cx x x x aa-+==,260(2)(3)02,3x x x x x x --=⇒+-=⇒=-=2230(1)(-23)031,2x x x x x x ++=⇒++=⇒=-=令-(3)(4)030404434340x x x x x x x x -+≤⎧-≤⇒⎨+≠+⎩-≤≤⎧⇒⇒-<≤⎨+≠⎩222222()02.a ab b a b a b ab -+=-≥⇔+≥2222()2()()02,(0,0)a ab b a a b b a b a b ab a b -+=-+=-≥⇔+≥>>2)基本不等式使用注意事项 口诀:1正2定3相等①1正,是指参加运算的量必须是正数.②2定,是指参加运算的量,要么和是定值,要么积是定值. ③3相等,是指参加运算的量相等时,均值不等式才能取等号.第三部分 函数1. 定义:在集合A 中的每一个元素x 经过对应法则f 在集合B 中都有唯一的元素y 与之对应,那么我们就称这个整体叫函数. (必修1) 记作::f A B→2. 函数的三要素(必修1)①定义域和值域定义域一般情况下会给出,当题目没有给出时,定义域默认使函数表达式有意义的自变量取值范围. 常见陷阱有以下几处①.分母不能为零. ②.偶次根号下的量要大于或等于零. ③.底数位置上的量要大于零且不等于1. ④.真数位置上的量要大于零.⑤.不能有双零结构,即“ ”.例. 求031()3log (1)2f x x x x x =++++++的定义域.解:由3020100x x x x +≥⎧⎪+≠⎪⇒⎨+>⎪⎪≠⎩ ()f x 的定义域为}{|>10x x x -≠且3y =②对应法则所谓对应法则就是指运算的混合物,要掌握的运算有四对共八个: 加←->减 乘←→除 乘方←→开方 指数←->对数 常见函数主要有a.常数函数,如b.一次函数,如 21y x =-c.二次函数,如 223y x x =+-d.指数函数,如 12,()3xx y y ==e.对数函数,如 213log ,log y x y x ==f.三角函数,如 sin ,cos ,tan y x y x y x ===具体如下:(注意:学函数核心点就是学系数) a.常数函数:图像是平行于x 轴的一条直线. (必修2) b.一次函数(必修2) 通式: 例如:图像:直线(两点确定一条直线)①系数a图像上坡,增函数.图像下坡,减函数.②系数b 决定图像在y 轴上的截距.12,(0):3;:1y ax b a l y x l y x =+≠=+=-+00a a >⎧⎨<⎩时,时,222,(0)21;23y ax bx c a y x x y x x =++≠=-+=-++c.二次函数通式: 例如: 图像:抛物线 ①系数a图像开口向上.图像开口向下.②系数b 和a 共同决定对称轴: 2bx a-=,顶点坐标24(,)24b ac b p a a --. ③系数c 决定图像在y 轴的截距.④表达式的另外形式:(一般式)(顶点式)(双根式)d.和e.指数函数和对数函数(必修1)①运算法则 指数运算 对数运算②指数运算与对数运算的关系当>01a a ≠且时,log x a a N x N =⇐⇒=如:32283log 8=⇐⇒=222124()24()()y ax bx c b ac b a x a aa x x x x =++-=++=--log log log ()log log log ()log ()log log log ,(01)log a a a a a a N a a c a c M N MN M M N N M N M b b c c a +=-===>≠且()r s r s r s r s s r rsr s a a a a a a a a a +-⋅=÷===00a a >⎧⎨<⎩时,时,③指数函数和对数函数的区别与联系指数函数 对数函数表达式x y a =log a y x =图像函数存在条件 底数都要满足:≠a>0且a 1单调性①当0<a<1时,其为减函数↘;②当a>1时,其为增函数↗f.三角函数 (必修4)1.角:共端点的两条射线组成的图形。
数学框架高中知识点结构与体系

数学框架高中知识点结构与体系数学是一门重要的学科,在高中阶段尤为重要。
为了更好地学习和掌握数学知识,在高中数学课程中,教师们往往会设置一个完整的框架,将各个知识点有机地联系起来,形成一个相对完整的体系。
下面将介绍高中数学知识点的结构与体系安排。
1. 数学基础知识在高中数学学习的开始阶段,教师会重点讲解数学的基础知识。
包括数学的基本运算规则,如四则运算、整数运算、分数运算等。
此外,还包括数学中常见的符号和概念,如数集、集合的运算、绝对值等。
2. 代数与函数代数与函数是高中数学中非常重要的知识点之一。
其中,代数主要包括方程、不等式、函数以及它们之间的关系。
学习代数可以帮助学生培养抽象思维能力和逻辑思维能力。
函数则是代数的重要分支,它是描述自然现象与数学模型之间的关系的工具,包括线性函数、二次函数、指数函数、对数函数等。
3. 几何几何是研究空间形状、大小、位置和相互关系的学科。
高中阶段的几何主要包括平面几何和立体几何两大部分。
平面几何包括各种图形的性质、相似与全等、三角形与四边形、圆等内容。
立体几何则涉及空间图形的性质、体积与表面积计算、空间几何关系等。
4. 概率与统计概率与统计是高中数学中的应用领域。
概率是研究随机现象的可能性大小的学科,包括事件概率、条件概率、独立事件等。
统计则是收集、整理和分析数据的学科,包括数据的收集方法和数据的表示与分析等。
5. 数学思想、方法与证明数学思想、方法与证明是高中数学中的一门重要课程。
它包括数学思想的培养、数学方法的学习以及数学证明的方法与技巧。
通过学习这门课程,学生可以培养逻辑思维、分析问题和解决问题的能力。
总之,高中数学知识点的结构与体系是一个相对完整且有机的整体。
它由数学基础知识、代数与函数、几何、概率与统计以及数学思想、方法与证明五个主要部分组成。
学生在学习数学的过程中,需要按照这个结构有序地进行学习,逐渐深入理解数学的本质和思维方式,提高数学应用与解决问题的能力。
高中数学知识点体系框架超全超完美

高中数学知识点体系框架超全超完美高中数学基础知识整合映射与函数映射是一种对应关系,其中A中的元素在B中都有唯一的象。
映射可以是一对一(一一映射),也可以是多对一,但不可以是一对多。
函数是一种特殊的映射,其表示为f:A→B,其中A为定义域,B为值域,对于A中的每个元素都有唯一的象。
函数的三要素为定义域、对应关系和值域。
函数可以用列表法、解析法或图象法表示,其中解析法需要使解析式有意义及实际意义。
常见函数类型常见的函数类型包括正(反)比例函数、一次(二次)函数、指数函数、对数函数、幂函数、三角函数等。
这些函数的定义、图象、性质和应用都需要掌握。
函数的基本性质函数具有对称性、单调性、周期性等基本性质。
对称性包括关于原点对称、关于y轴对称、关于x轴对称等。
单调性可以通过定义法、导数法或已知函数的单调性来求得单调区间,复合函数单调性为同增异减。
周期性指函数在一定区间内具有相同的函数值,可以通过f(x+T)=f(x)来判断。
函数的变换函数常见的变换包括平移变换、对称变换、翻折变换、伸缩变换等。
这些变换可以通过数形结合来理解,也可以通过图象法来求得变换后的函数式。
函数的应用函数在数学和实际问题中都有广泛的应用。
其中最值问题是常见的应用之一,可以通过导数和单调性来求得函数的极值和最值。
建立函数模型也是常见的应用之一,可以通过观察问题、分析问题和建立方程来建立函数模型。
导数与微积分导数是函数在某一点处的变化率,可以通过导数的定义和四则运算法则来求得。
简单复合函数的导数可以通过链式法则来求得。
函数的单调性可以通过导数的正负性来判断,函数的极值和最值可以通过导数为0的点来求得。
定积分是函数在一定区间内的面积,可以通过积分的定义和基本公式来求得。
常用的求解方法包括换元法、分部积分法等。
微积分在实际问题中也有广泛的应用,例如运动的瞬时速度可以通过导数来求得,曲线的切线的斜率也可以通过导数来求得。
1.$(f(x) \cdot g(x)) = f(x)g(x) + f(x)g(x)$2.$\frac{f(x)}{g(x)} = \frac{f(x)}{g(x)} \cdot\frac{1}{g(x)}$3.$f(g(x)) = f(u) \cdot u'(x)$4.若$f'(x)>0$,则$f(x)$在该区间递增;若$f'(x)<0$,则$f(x)$在该区间递减。
高中数学教材知识体系与框架
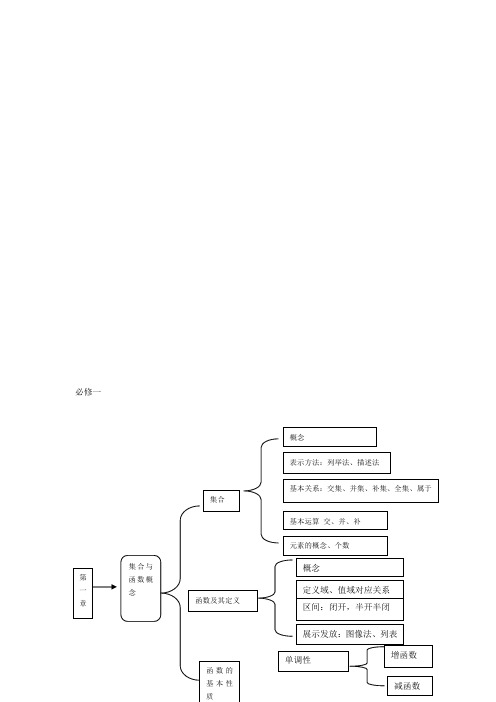
向量减法运算及几何 意义
向量数乘运算及几 何意义
ar ar
ar ar ar
ar
r b
ar
r b
平面向量的基本定 理及坐标表示
平面向量的数量积
平面向量应用实例
平面向量基本定理
平面向量的正交分解极坐标表示
平面向量坐标运算 共线的坐标表示 物理背景与定义
坐标表示,模,夹 角
截距式 y kx b
直线的交点坐 标与距离公式
两点式 y y1 x x1 y2 y1 x2 x1
一般式 Ax By C 0
两条直线的交点坐标
A1 x A2 x
B1 y C1 B2 y C2
0 0
两点间的距离公式| AB| (x2 x1)2 (y2 y1)2 点到直线的距离 d Ax0 By0 C
直线与平面垂直的判定定理 平面与平面垂直的判定定理
直线与平面垂直的性质定理 平面与平面垂直的性质定理
第三章
倾斜角 0°≤α<180°
直线的倾斜角与斜率
直
线
与
方
直线的方程
程
斜率 k tan
两条直线平行 与垂直的判定
l1 //l2 k1 k2,b1 b2 l1 l2 k1k2 1
点斜式 y y1 k(x x1 )
循环结构
输入语句、输出语赋值语句
条件语句、循环语句
法 初 步
算法案例
第二章
随机抽样
统 计
用样本估计总体
简单随机抽样 系统抽样
分层抽样 用样本频率分布估 计总体分布
抽签法
随机法 求极差 决定组距组数 将数据分组 列频率分布表 画频率分布直方图
变量间的相关关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
tan tan tan
1 tan tan
二倍角的正弦余弦 正切公式
sin2 2sin cos cos2 cos2 sin2 2cos2 112sin2
tan
2
2 tan 1 tan2
简单的三角恒等变换
必修五
第一章
正弦定理
正弦定理和余弦定 理
解 三 角 形
ad d2
i
(z2≠0) ;
共轭复数
流程图
框 图
结构图
选修 1-1
第一系章
命题及其关系
常
用
充分条件和必要条件
逻
辑
用
语
简单的逻辑连接词
全称量词与存在量词
命题
真命题:判断为真的语句 假命题:判断为假的语句
四种命题及其关 系
四种命题
原命题 逆命题 否命题
逆否命题 充分条件和必要条件
充要条件 且 或 非
计
计总体分布
用样本估计总体
列频率分布表
画频率分布直方图
用数本的数字特征估 计总体的数字特征
众数,中位数,平均数
变量间的相关关系
标准差
变量间的相关关系
两个变量的线性相关
正相关 负相关
回归直线
第三章
随机事件的概率
随机事件的概率 频率
概 率
古典概型
概率
意义 性质
必然事件
基本事 件特征
概率
不可能事件 任何两个不同事件互斥
b
f (x)dx
c
f (x)dx
b f (x)dx (其中a
a
a
c
几何中的应用 物理中的应用
选修 2-1
第一系章
命题及其关系
常
用
充分条件和必要条件
逻
辑
用
语
简单的逻辑连接词
全称量词与存在量词
命题
真命题:判断为真的语句 假命题:判断为假的语句
四种命题及其关 系
四种命题
原命题 逆命题 否命题
x
⑦ (loga
x)'
1 x ln
a
;⑧
增函数
函数的极值与导数
减函数
函数的最大最小值 与导数
定积分的概念
微积分基本定理 定积分的简单应用
曲边梯形的面积
概念: 性质
b
kf (x)dx k
b f (x)dx(k为常数)
a
a
b
b
b
a [ f1(x) f2(x)]dx a f1(x)dx a f2(x)dx
a b a b
平面向量的正交分解极坐标表示
平面向量坐标运算 共线的坐标表示 物理背景与定义
数
量
积
a b a b cos a 0,b 0,0 180
投影
坐标表示,模,夹 角
平面几何中的向量 方法
a x, y
a x2 y2
cos a b x1x2 y1 y2
ab
x12 y12 x22 y22
表示
复数的几何意义
加减法运算及几何
意义 z 1±z2 = (a + b)± (c + d)i;
乘除运算
z1.z2 = (a+bi)·(c+di)= (ac-bd)+ (ad+bc)i;
z1 ÷ z2 = (a bi)(c di) (c di)(c di)
ac bd c2 d2
bc c2
数列的应用
必修五
第三章
不等式与不等关系
ab 0a b ab 0a b
ab0a b
不
一元二次不等式及
等
其解法
式
基本不等式
ax2 bx c 0
ax2 bx c 0 ax2 bx c 0
a b 2 ab
二元一次不等式 (组)与简单线性 规划问题
最大最小值问题 一元一次不等式 (组)与平面区域
基
本
初
对数函数
等
与对 数运 算
运算 定义
loga
M N
loga
M
loga
N
loga M n n loga M
定义域
函
对数函
数
数及性
图象
值域
质
过点(1,0)
性质
定义:
单调性
幂函数
过(1,1)
性质
奇偶性 单调性
第三章
]
函 数 的 应 用
方程的根与函数的零点
函数与 程
用二分法求方程的近视 根
定义 关系 零点定理 二分法定义
及
的应用
其
应
用
生活中的优化问题 举例
导数的几何意 义 几个常用函数的导数
基本初等函数的导数公式与运算法则① C ' 0 ;②
(x n )' nxn1 ; ③ (sin x)' cos x ;④
(cos x)' sin x ;⑤ (a x )' a x ln a ;⑥
(e x )' e x ; 单(调ln性x与)' 导 数1
余弦定理
应用举例
a b c 2R sin sin sin C
a2 b2 c2 2bc cos
b2 a2 c2 2ac cos c2 a2 b2 2ab cos C
第二章
数 列
数列的概念与简单 表示法
数列项 有穷数列无穷数列
等差数列
等差数列的前 n 项 和
定义
等差中项b a c 2
求根步骤
函数 模型 及应 用
几类不同增长的函数模型 函数模型的应用实例
建立实际问题的函数模型
必修二
第一章
锥、柱、台、球的结构特征
空间几何体的结构
简单组合体的结构特征
正视图
三视图
侧视图
空间几何体的三视 空
图与直观图 间 几 何 体
直观图
俯视图 斜二侧画法
锥、柱、台的表面积与体积
平行投影与中心投 影
空间几何体 的表面积与 体积
任何事件都可表示为基本事件的和
几何概型
定义 概率
必修四
第一章
任意角和弧度制
任意角 弧度制
正角 负角
零角
三角函数:正弦函数,余弦函数,正切函数
任意角的三角函数
公式一:终边相同的角同一三角函数值相等
三
角
同角三角函数关系
函
数
正弦余弦函数的性质
三角函数的图像与性 质
正弦余弦函数的图像 正切函数的性质与图像
式
必修三
第一章
算 法 初 步
算法与程序框图 基本算法语句
算法的概念 程序框图
辗转相除法与更相 减损术
秦久韶算法 顺序结构 条件结构
循环结构
输入语句、输出语赋值语句
条件语句、循环语句
算法案例
第二章
随机抽样
简单随机抽样 系统抽样 分层抽样
抽签法
随机法 求极差 决定组距组数
统
用样本频率分布估
将数据分组
平面向量的基本定 理及坐标表示
平面向量的数量积
平面向量应用实例
向量的物理背景与概念
有向线段
向量的几何表示
相等向量与共线向 量 向量加法运算及几 何意义
零向量,单位 向量 平行向量 向量加法三角形法则
向量加法平行四边形法则
向量减法运算及几何 意义
向量数乘运算及几 何意义 平面向量基本定理
a a
a aa
球的表面积与体积
第二章
点 、 直 线 、 平 面 间 的 位 置 关 系
空间点、直线、平面间的位 置关系
平面:公理 1、公理 2、公理 3
空间中直线与直线的位置 关系
相交直线
共
面
平行直线:
公理 4
异面直线
平面与平面间的位 置关系
平行 相交
空间中直线与 平面的位置关 系
直线在平面 内 相交
平行
直线与平面平行的判定定理
逆否命题 充分条件和必要条件
充要条件 且 或 非
全称量词 x M , p(x) 存在量词 x M , p(x) 含有一个量词的命题的否定 x M ,p(x)
第二章
圆 锥 曲 线 与 方 程
曲线与方程
曲线的方程
椭圆
求曲线的方程
定
义
| MF1 | | MF2 | 2a,(2a | F1F2 |) ,标准方程
圆的一般方程
x2 y 2 Dx Ey F 0 d r l与C相交
Байду номын сангаас
直线与圆的位置关系
d r l与C相切
直线与圆的方程 的应用
圆与圆的位置关系
d r l与C相离 相交 R r d R r
内切 d R r 外切 d R r
内含 d R r
概念
相离 d R r
空间两点间的距离 d ( x2 x1 )2 ( y2 y1 )2 (z2 z1 )2 公
全称量词 x M , p(x) 存在量词 x M , p(x) 含有一个量词的命题的否定 x M ,p(x)
曲线与方程
曲线的方程
求曲线的方程
椭圆
定
义
| MF1 | | MF2 | 2a,(2a | F1F2 |) ,标准方程
x2 a2
y2 b2
1a
b
0
范围 a x a 且 b y b 对称性关于 x 轴、 y 轴、原点对称
x2 a2
y2 b2
1a
b
0
范围 a x a 且 b y b 对称性关于 x 轴、 y 轴、原点对称
