1 一、矩阵秩的概念
矩阵的秩及其求法-求秩的技巧

第五节:矩阵的秩及其求法之五兆芳芳创作一、矩阵秩的概念 1. k 阶子式 定义1 设 在A 中任取k 行k 列穿插处元素按原相对位置组成的阶行列式,称为A 的一个k 阶子式.例如共有个二阶子式,有 个三阶子式矩阵 A 的第一、三行,第二、四列相交处的元素所组成的二阶子式为 而为 A 的一个三阶子式.显然, 矩阵 A 共有 个k 阶子式.2. 矩阵的秩 定义2 设 有r 阶子式不为0,任何r +1阶子式(如果存在的话)全为0 ,称r 为矩阵A 的秩,记作R (A )或秩(A ).规则: 零矩阵的秩为 0 .注意:(1) 如 R ( A ) = r ,则 A 中至少有一个 r 阶子式所有 r + 1 阶子式为 0,且更高阶子式均为 0,r 是 A 中不为零的子式的最高阶数,是唯一的 .(2) 有行列式的性质,(3) R(A ) ≤m , R (A ) ≤n , 0 ≤R (A ) ≤min { m , n } .(4) 如果An ×n , 且 则 R ( A ) = n .反之,如 R()nm ij a A ⨯={}),min 1(n m k k ≤≤43334=C C 1015643213-=D nm ⨯()nm ij a A ⨯=0,r D ≠()().T R A R A =0,A ≠0.A ≠( A ) = n ,则因此,方阵 A 可逆的充分需要条件是 R ( A ) = n . 二、矩阵秩的求法 1、子式判别法(定义).例1 设 为阶梯形矩阵,求R (B ). 解 由于 存在一个二阶子式不为0,而任何三阶子式全为0,则R (B ) = 2.结论:阶梯形矩阵的秩=台阶数.例如 一般地,行阶梯形矩阵的秩等于其“台阶数”——非零行的行数. 例2 设 如果 求a .解 或例3则 2、用初等变换法求矩阵的秩定理2矩阵初等变换不改动矩阵的秩. 即则注: 只改动子行列式的符号. 是 A 中对应子式的k 倍.2021≠⎪⎪⎪⎭⎫ ⎝⎛=010*********A ⎪⎪⎪⎭⎫ ⎝⎛=001021B ⎪⎪⎪⎭⎫ ⎝⎛=100010011C 125034000D ⎛⎫ ⎪= ⎪ ⎪⎝⎭21235081530007200000E ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭⎪⎪⎪⎭⎫ ⎝⎛=a a a A 111111(),3<A R ()3<A R 1=∴a 2-=a ()3=A R =K 3-BA →)()(B R A R =ji r r ↔.1irk .2是行列式运算的性质.求矩阵A 的秩办法:1)利用初等行变换化矩阵A 为阶梯形矩阵B 2)数阶梯形矩阵B 非零行的行数即为矩阵A 的秩. 例4求 解R(A ) = 2例5三、满秩矩阵定义3A 为n 阶方阵时,称 A 是满秩阵,(非奇异矩阵) 称 A 是降秩阵,(奇异矩阵) 可见:对于满秩方阵A 施行初等行变换可以化为单位阵E ,又按照初等阵的作用:每对A 施行一次初等行变换,相当于用一个对应的初等阵左乘A,由此得到下面的定理. 定理3设A 是满秩方阵,则存在初等方阵 使得对于满秩矩阵A ,它的行最简形是n 阶单位阵 E . 例如A 为满秩方阵.关于矩阵的秩的一些重要结论:ji krr +.3().A R μλμλ,2,6352132111,求)(且设=⎪⎪⎪⎭⎫⎝⎛--=A R A (),n A R =(),n A R <()0≠⇔=A nA R EA P P P P s s =-121,定理5R (AB )R (A ),R (AB )R (B ),即R (AB )min{R (A ),R (B )}设A 是 矩阵,B 是 矩阵, 性质1性质2 如果 A B = 0 则性质3 如果 R (A )= n, 如果A B = 0 则 B = 0. 性质4 设A,B 均为矩阵,则例8 设A 为n 阶矩阵,证明R (A+E )+R (A-E )≥n 证: ∵ (A+E )+(E-A )=2E∴R (A+E )+ R ( E-A )≥ R (2E )=n而 R ( E-A )=R ( A-E ) ∴ R (A+E )+R (A-E )≥n≤nm ⨯tn ⨯).()()(AB R n B R A R ≤-+.)()(n B R A R ≤+nm ⨯).()()(B R A R B A R +≤±。
矩阵秩的证明方法及技巧

矩阵秩的证明方法及技巧矩阵的秩是描述矩阵行(列)向量空间维数的重要指标,广泛应用在线性代数和矩阵理论中。
下面将介绍矩阵秩的定义、性质以及一些证明方法和技巧。
一、矩阵秩的定义和性质:1. 矩阵秩的定义:对于任意一个m×n矩阵A,它的秩(rank)定义为其所有非零行(列)向量的极大无关组的向量个数,即r(A) = r(A^T),其中A^T为A的转置矩阵。
2.矩阵秩的基本性质:a) r(A) ≤ min(m, n),即矩阵秩r(A)不会超过矩阵的行数m和列数n的较小值。
b)如果r(A)=m,即矩阵的秩与行数相等,则称矩阵为满秩矩阵。
c)两个矩阵的行等价(列等价),它们的秩相等。
d)对于一个n阶方阵A,如果A可逆,则r(A)=n,即满秩方阵。
e)若A和B为同型矩阵,则r(A+B)≤r(A)+r(B)。
二、矩阵秩的证明方法和技巧:1.行变换法证明矩阵秩:行变换可以通过初等行变换来实现,包括交换两行、行乘以一个非零常数、行加上另一行的k倍。
行变换不改变矩阵的秩,因此可以通过行变换来找到矩阵的极大无关组,从而确定矩阵的秩。
2.列空间法证明矩阵秩:列空间是由矩阵的所有列向量张成的向量空间,可以通过检查矩阵的列向量组是否线性无关来确定矩阵的秩。
如果列向量组线性无关,则矩阵的秩等于列向量组的向量个数;否则,删除线性相关的列向量,再次检查新的列向量组是否线性无关,直至找到一个线性无关的列向量组为止。
3.奇异值分解法证明矩阵秩:对于任意一个m×n矩阵A,可以进行奇异值分解为A=UΣV^T,其中U和V为正交矩阵,Σ为对角矩阵,其对角元素为矩阵A的奇异值。
矩阵A的秩等于非零奇异值的个数。
4.行列式法证明矩阵秩:矩阵A的秩等于其最高阶非零子式的阶数。
通过计算矩阵A的各个阶数的子式的行列式是否为零,可以确定矩阵的秩。
5.矩阵的分解法证明矩阵秩:常用的矩阵分解方法包括LU分解、QR分解和SVD分解等。
通过对矩阵进行适当的分解,可以得到新的矩阵形式,从而更容易确定矩阵的秩。
矩阵的秩

k 2 个元素按照原来的顺序所组成的k阶行列式,称为矩阵A 的一个k阶子式。
定理3.4.3 矩阵A的秩为r的充要条件是:矩阵A中有一个 r阶子式不为零,而所有的r+1阶子式全为零。
注意:要说明矩阵A的秩为r,必须找到一个r阶子式不为 零;而所有的r+1阶子式全为零。
第三章 线性方程组
定理3.4.3 矩阵A的秩为r的充要条件是:矩阵A中有一个 r阶子式不为零,而所有的r+1阶子式全为零。 证明:充分性。设在矩阵A中有一个r阶子式不为零,而所 有的r+1阶子式全为零。不妨设这r阶子式在A的左上角,即 a11 a12 a1r a21 a22 a2 r ≠ 0 。由定理3.4.2知这r个行组成的向量组线
a11 a21 A= a n1 0 a12 a22 − a21 a11 a an 2 − 12 an1 a11 0 a1n a2 n − a21 a11 a ann − 1n an1 a11
=
a11 a21 a n1
0 ′ a22 ′ an 2
0 ′ a2 n ′ ann
其中
′ (0, a2 i ,
rank ( A), r ( A), R( A) 注1、 若 A = 0, 则 R( A) = 0 。 , 则 R( A) ≤ min( m , n) 。 2、 设 A = ( aij ) m× n
3、若 R( A) = m , 则称A为行満秩的矩阵; 4、若
R( A) = n , 则称A为列満秩的矩阵。
第三章 线性方程组
必要性。设矩阵A的秩为r,即矩阵A中行向量组的秩为r。 而任意r+1个行向量必线性相关,线性相关向量组的“缩短”向 下证A中 量组也线性相关,故矩阵A的任意r+1阶子式全为零。 至少有一个r阶子式不为零。 设这r个线性无关的向量正是A的前 a1n ⎞ ⎛ a11 a12 ⎜ ⎟ a2 n ⎟ ⎜ a21 a22 r个行向量,把这r个向量取出得矩阵:A1 = ⎜ ⎟ ⎜ ⎟ arn ⎠ ⎝ ar 1 ar 2 矩阵 A1 的行秩为r,其列秩也为r, 不妨设前r列线性无关,于
第四节 矩 阵 的 秩

例如,在矩阵
1 1 3 1
A
0 0
2 0
1 0
4
5
0
0
0
0
中,选第 1, 3 行和第 3, 4 列,它们交点上的元素
所成的 2就是一个 2 级子式. 又如选第 1, 2, 3 行和第1, 2, 4
列,相应的 3 级子式就是
求向量组的极大线性无关组的方法是:把向量 组中的每一个向量作为矩 阵的一列构成一个矩阵, 然后用矩阵的初等行变换把矩阵化成阶梯形矩阵, 在阶梯形矩阵中,每个阶梯中的第一个非零元所在 的列所对应的向量即为极大线性无关组中的向量.
若要用极大线性无关组来表示其余向量,则需进一 步把阶梯形矩阵化成行最简形,这时,不在极大线 性无关组中的列中的元素即为用极大线性无关组表 示该列所对应的向量的表示系数.
2 3
,
3
3 5
,
4
7
;
1
1
1
4
1
本若请本若请本若请本若请本本若若请请本若节想请单节想本单若节想请单节想本单若节节想想请单单节想内结本单若击内请结节击想内结本单若击内请结节击想内 内结 结本单若击击内请结容束节击想返本容单若束内请返结容束节击想返本容单若束内请返结容 容束 束节击想返返本容单若束已本内请返结回节已击想本本容单若回束已本内请返结回节已击想本本容单若回束已 已本 本内请返结回回节已击想本结本堂容单若回束按内结请返结本堂若节已击想按本结请本 本堂容单若 若回束按内结请 请返结本堂若节已击想按本结 结请本堂 堂容单若回束按按内结请返结堂束节课已击想按本钮容束单回束节课想内结返结钮堂束单节 节课已击想 想按本钮容束单单回束节课想内结返结钮堂束 束单节课 课已击想按本钮钮容束单回束课内,结返结钮堂.已击按本内,!结容束回束课.击内 内,结!返结 结钮堂.已击击按本内,!结容束回束课.击内,,结!返结钮堂..已击按本,!!容束回束课.结!返钮堂容束已按本,返容 容束回束 束课.结!返返钮堂容束已按本,返容束回束课.结!返钮堂已按本,束回课.已本结!钮堂回已 已按本 本,束回回课.已本结!钮堂回已按本,束回课.结!钮堂按,结堂束课.按结 结!钮堂堂按按,结堂束课.按结!钮堂按,束课.!钮束课,钮束束课课.!钮钮束课,钮束课.!钮,.,!.,,!..,!!.,!.!
矩阵的秩

若r ( A) m, 则称A为行满秩;
若r ( A) n, 则称A为列满秩.
若r ( A) m n, 则称A为满秩.
(2) r( AT ) r( A) ; r(kA) r( A) ( k 0 ); (3) 若 A 有一个 r 阶子式不为零,则 r( A) r ;
若 A 的所有 r 1 阶子式全为零,则r( A) r ; (4) 对于 n 阶方阵 A 而言,有 r( A) n | A | 0 ;
10
2 1 0 3 2
例3
求矩阵
B
0 0
0
3 0
1 0
2 4
5 3
的秩.
0 0 0 0
解 B是一个阶梯形矩阵,其非零行有3行,
r(B) 3 .
11
3 2 0 5 0
例4
设
A
3 2 1
2 0 6
3 1 4
6 5 1
413, 求 矩 阵 A 的 秩 .
解
A
r1 r4
1 3 2
类似有矩阵的初等列变换 .
矩阵的初等行变换和初等列变换合称为矩阵的 初等变换.
定理 矩阵的初等变换不改变矩阵的秩. 证略. 7
阶梯形矩阵
若矩阵的每行第一个非零元的下方及左下方全为零,
则称之为阶梯形矩阵.
例如, 2 3 2 0 4
0 1 2 5 0
0 0
0 0
7 0
1 0
3 0
1 2 0 0 2
§2.6
1
一、矩阵的秩的概念
定义 在一个 m n 矩阵 A 中任意选定 k 行 k 列(k , min{ m , n}) 位于这些选定的行和列的交点上的k 2 个元
素按原来的顺序所组成的 k 阶行列式,称为 A 的一个 k 阶 子式.
第三节矩阵的秩

1 0 3 6
1 2 3 4 1 0 5 1
r2 2 r1 r3 2 r1
r4 3 r1
1 0 0 0
2 0 0 0
2 4 2 61 2 1 3r2 2 r3 r 2
r4 3 r2
1 0 0 0 1 0 0 0
1 2 r2 r3 3 0 ~ r1 2 r 2 0 0
0 1 0 0
1 3 2 3 0 0
0 0 1 0
16 9 1 9 , 1 3 0
最后一个行阶梯形矩阵具有下述特性: 每一个非零行的第一个非零元素均为1,且含这些元素的 列的其它元素都为0. 这个矩阵称为矩阵A的行最简形
4 3 1 0
1 1 5 5
4 1 3 0
r1 r4 r2 r4 r3 2 r1 r4 3 r1
1 0 0 0
6 4 12 16
4 3 9 12
1 1 7 8
1 11 12 4
矩阵I称为A的标准形,其特点是:I的左上角是一个r 阶单位阵 ( r R ( A )), 其它元素都是0. 可见若 A ~ B , 则A与B有相同的标准形.
特别地,当A为n阶方阵且 A 0 时, 可知 R ( A ) n , 故A的标准形为单位阵E,即 A ~ E . 因此称行列式值 不为零的方阵为满秩方阵; 称行列式值为零的方阵为 降秩方阵
从这个行阶梯形矩阵不仅可看出矩阵的秩. 继续施行 初等行变换,还可化为最简单的形式:
1 0 0 0 2 3 0 0 1 2 0 0 0 2 3 0 2 1 1 0
1 1 r2 0 3 ~ 1 r3 3 0 0
矩阵秩的概念

矩阵秩的概念矩阵秩的概念矩阵是线性代数中的重要概念,它是由若干行和列组成的矩形数组。
在矩阵中,每个元素都可以用一个行列坐标来表示。
而矩阵秩则是描述了一个矩阵所包含的信息量大小的指标。
一、定义在数学中,一个m×n(m行n列)的矩阵A的秩,也称为矩阵A的维数或者等级,通常记作rank(A)。
它表示该矩阵所包含信息量大小的指标。
简单来说,就是该矩阵所包含非零行或非零列的最大个数。
二、求解方法1. 高斯消元法高斯消元法就是将一个增广矩阵通过初等变换化为行最简形式,然后统计出非零行(列)个数即可得到该矩阵的秩。
2. 初等变换法初等变换法就是将一个矩阵通过初等变换化为行最简形式,然后统计出非零行(列)个数即可得到该矩阵的秩。
3. 行列式法对于一个n*n方阵A,在进行初等变换时如果其主对角线上有0,则可以通过行列式法将其转化为一个上三角矩阵。
此时,该矩阵的秩就等于其主对角线上非零元素的个数。
三、性质1. 对于任意矩阵A,rank(A) <= min(m,n),其中m和n分别表示A 的行数和列数。
2. 对于任意矩阵A,rank(A) = rank(A^T),其中A^T表示A的转置矩阵。
3. 对于任意矩阵A和B,有rank(AB) <= min(rank(A), rank(B))。
4. 对于任意矩阵A和B,有rank(A+B) <= rank(A) + rank(B)。
四、应用1. 线性方程组求解对于一个线性方程组Ax=b,如果rank(A)=rank([A|b]),则该方程组有唯一解;如果rank(A)<rank([A|b]),则该方程组无解;如果rank(A)<n且rank([A|b])=n,则该方程组有无限多解。
2. 线性变换求解对于一个线性变换T:V→W(其中V和W分别表示两个向量空间),其维数为dim(V)*dim(W),而T的秩则是指T所映射出来的向量空间的维数。
线性代数课件第三章矩阵的秩课件

VS
矩阵的秩可以用于判断两个矩阵是否相似。如果两个矩阵相似,则它们的秩相同。
特征值和特征向量
矩阵的秩还可以用于确定矩阵的特征值和特征向量的个数。对于给定的矩阵,其秩等于其非零特征值的个数。
矩阵相似
矩阵的秩可以用于矩阵分解,如奇异值分解(SVD)和QR分解等。这些分解方法将一个复杂的矩阵分解为几个简单的、易于处理的矩阵,有助于简化计算和解决问题。
1 2 3 | 0 0 -3
7 8 9 | 0 0 0`
```
由于非零行的行数为2,所以矩阵B的秩为2。
题目3
求矩阵C=[1 -2 3; -4 5 -6; 7 -8 9]的秩。
解答
首先,将矩阵C进行初等行变换,得到行阶梯矩阵
```
继续进行初等行变换,得到
1 -2 3 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0 -6 -9 | 0
矩阵秩的应用
03
线性方程组的解
矩阵的秩可以用来判断线性方程组是否有解,以及解的个数。如果系数矩阵的秩等于增广矩阵的秩,则方程组有唯一解;否则,方程组无解或有无数多个解。
最小二乘法
矩阵的秩还可以用于最小二乘法,通过最小化误差平方和来求解线性方程组。最小二乘法的解就是使残差矩阵的秩等于其行数或列数的最小二乘解。
矩 阵 的 秩

即
R(A E) R(A 4E) n
(1.2)
又 ( A E)( A 4E) A2 3A 4E O ,由性质9,得
R(A E) R(A 4E) n
(1.3)
所以
R(A E) R(A 4E) n
性质10 设A 为n(n≥2)阶矩阵,则
n,若R( A) n R( A) 1,若R( A) n 1
个k
阶子式。
定义2 若矩阵A 中存在一个r 阶子式Dr 不等于 零,而所有的r+1阶子式(如果存在的话)全等 于零,则不等于零的r 阶子式Dr 称为矩阵A 的最高阶非零子式。
定义3 矩阵A 的最高阶非零子式的阶数 称为矩阵A 的秩,记为R(A)。
例1 求矩阵
1 1 3 0
(A
B)
2 121 1 1 5 2
性质5 设A 为m ×n 矩阵,P 为m 阶可逆矩阵,Q
为n 阶可逆矩阵.则R(PAQ) R(PA) R( AQ) R( A)
1 1 1
例4
设4×3矩阵A
的秩R(A)=2,A
0 0
2 0
2 3
,试求R(AB)。
解 显然B 为可逆矩阵,则R(AB)=R(A)=2。
性质6 设A 为m ×s矩阵,B 为m ×t矩阵,
0 0 7
1
1
4
3
0
0
7
4
1 1 3 1
r3 r2
r4 r2
0 0 7 4
0 0 0
则R(A)=2
0
0
0
0
(2)因为R(A)=2<3,所以R(A* )=0,则A* =O.
线性代数
1 1 3 1
例6
设四阶矩阵
线性代数1同济大学第五版课件3-2

机动
目录
上页
下页
返回
设 A 经初等列变换变为
B,
则 A
T
经初等行变换变为
T T
B ,
T
R ( A ) R ( B ),
T T
且 R ( A ) R ( A ), R ( B ) R ( B ),
R ( A ) R ( B ).
R ( B ) 3,
机动
目录
上页
下页
返回
故 B 中必有
3 阶非零子式
. 且共有
4 个.
计算 B 的前三行构成的子式
3 2 3
2 0 2
5
3
2 0 0
5 5 11
5 2 6 6
2
2 6
5 11
16 0 .
则这个子式便是A 的一个最高阶非零子式.
机动
目录
上页
下页
返回
例4
1 2 设A 2 3
则 D r D r 0 , 也有 R ( B ) r .
若A经一次初等行变换变为 ,则 R( A ) R( B ). B
由于 B 也可经过一次初等行变 换变为 A ,
故也有 R( B ) R( A). 因此 R( A) R( B ).
经一次初等行变换矩阵的秩不变,即可知经 有限次初等行变换矩阵的秩仍不变.
对于 A , 显有 R ( A ) R ( A ).
T T
对 A m n,有 0 R ( A ) min m , n
0,则 R ( A ) s ;
矩阵的秩的运算

矩阵的秩的运算一、矩阵秩的定义1. 基本概念- 对于一个m× n矩阵A,它的秩r(A)是矩阵A中线性无关的行向量(或列向量)的最大个数。
- 例如,对于矩阵A=begin{pmatrix}1&2&32&4&6end{pmatrix},通过观察可以发现第二行是第一行的2倍,所以矩阵A的行向量中最多只有一个线性无关的向量,r(A) = 1。
2. 等价定义- 矩阵A的秩等于矩阵A的行最简形矩阵中非零行的行数。
例如,将矩阵A=begin{pmatrix}1&1&11&2&31&3&5end{pmatrix}化为行最简形begin{pmatrix}1&0& - 10&1&20&0&0end{pmatrix},非零行有2行,所以r(A)=2。
二、矩阵秩的基本运算性质1. r(A)=r(A^T)- 矩阵A与其转置矩阵A^T具有相同的秩。
这是因为矩阵A中行向量的线性相关性与A^T中列向量的线性相关性是对应的。
例如,若A=begin{pmatrix}1&2&34&5&6end{pmatrix},A^T=begin{pmatrix}1&42&53&6end{pmatrix},通过计算可知r(A)=2,r(A^T) = 2。
2. r(kA)- 若k≠0为常数,r(kA)=r(A)。
这是因为数乘矩阵只是对矩阵的每个元素进行数乘,不会改变向量之间的线性相关性。
例如,设A=begin{pmatrix}1&23&4end{pmatrix},2A=begin{pmatrix}2&46&8end{pmatrix},r(A)=2,r(2A)=2。
- 当k = 0时,r(0A)=0(零矩阵的秩为0)。
3. r(A + B)≤ r(A)+r(B)- 设A=begin{pmatrix}1&00&0end{pmatrix},B=begin{pmatrix}0&00&1end{pmatrix},r(A)=1,r(B)=1,A +B=begin{pmatrix}1&00&1end{pmatrix},r(A + B)=2,此时r(A + B)=r(A)+r(B);再设A=begin{pmatrix}1&00&0end{pmatrix},B=begin{pmatrix}-1&00&0end{pmatrix},r(A)=1,r(B)=1,A +B=begin{pmatrix}0&00&0end{pmatrix},r(A + B)=0,r(A + B)<r(A)+r(B)。
线性代数 矩阵的秩

1 2 2 1 0 2 4 8 B 2 4 2 3 3 6 0 6 1 2 0 0 0 0 0 0
求矩阵 A的列向量组的一个最大 无关组。
解 对A施行初等行变换变为 行阶梯形矩阵
1 0 0 0 1 2 1 4 1 1 1 0 , 0 0 1 3 0 0 0 0
A
初等行变换
知R( A) 3,
故列向量组的最大无关 组含3个向量.
而三个非零行的非零首元在1、、三列, 24 故 a1 , a2 , a4 , 为列向量组的一个最大无关组.
1 2 3 4
初等行变换
2 1 1 2 1 0 0 0 1 0 0 0
R( A) 2, R( B ) 3.
例5 已知两个2×4矩阵
2 0 1 3 1 A T 3 2 1 1 2
由阶梯形矩阵有三个非零行可知 R( A) 3.
1 2 2 1 1 0 2 4 8 2 例4 设A 2 4 2 3 , b 3 3 6 0 6 4
求矩阵A及矩阵B ( A b )的秩.
说明
(1)ቤተ መጻሕፍቲ ባይዱ等变换不改变矩阵的秩
(2)用初等行(列)变换把矩阵化成行(列) 阶梯时,非零行(列)的个数就是矩阵的秩 (3)把矩阵A化成行(列)阶梯矩阵B,则B的 列(行)向量组中任意最大无关组所对应的A的 列(行)向量组构成A的一个最大无关组。
第三章-矩阵的秩

的一个最高阶非零子式. 则这个子式便是 A 的一个最高阶非零子式
线性代数——第 3章
1 0 例7 求矩阵A = 2 3
1 1 1 −1 3 a 5 1
1 b 的秩, 其中a, b为参数. 4 7
线性代数——第 3章
三、矩阵秩的性质
( 1)
(2 )
R ( AT ) = R ( A )
线性代数——第 3章
定义2 定义2
设在矩阵中有一个不等于 的 阶子式 阶子式D, 设在矩阵中有一个不等于0的r阶子式 ,且 有一个不等于
所有r 所有 + 1阶子式(如果存在的话)全等于 ,那么 阶子式(如果存在的话)全等于0 那么D 称为矩阵A的最高阶非零子式, 称为矩阵 的秩, 称为矩阵A的秩 称为矩阵 的最高阶非零子式,数r称为矩阵 的秩, 记作R (A), 并规定零矩阵的秩等于零 记作 , 并规定零矩阵的秩等于零.
线性代数——第 3章
§3 矩阵的秩
一、矩阵秩的概念 二、矩阵秩的求法 三、矩阵秩的性质 小结、 四、小结、思考题
线性代数——第 3章
一、矩阵秩的概念
任何矩阵 Am × n , 总可经过有限次初等行 变换 把它变为行阶 梯形,行阶 梯形矩阵中非零行的行 梯形, 数是唯一确定的 .
矩阵的秩
线性代数——第 3章
解
r1 ↔ r4 r2 − r4
r3 − 2r1 r4 − 3r1
6 4 −4 −1 1 3 1 −1 0 − 4 0 − 12 9 7 − 11 0 − 16 12 8 − 12
线性代数——第 3章
r3 − 3r2
r4 − 4r2
1 6 − 4 −1 4 1 − 1 0 − 4 3 0 0 0 4 − 8 0 0 0 4 − 8
第二章 第一讲 矩阵的秩

互换变换:A的i行与j行交换变为B,则B 的子式或为A的子式,或与A的子式差一个符号, 秩不变。 倍乘变换:A的i 行元素乘以 k (k≠0) 得到B, 则B 的子式成为A的子式,或与A的子式差一个 因子 k≠0。则秩不变。
首页 上页 返回 下页 结束 铃
倍加变换:A由i行的k倍加到 j行,得到
矩阵B。 :B的一个子式若不包含第j行元素,则 也为A的一个子式;
1 2 1 1 0 3 4 4 , 0 5 1 0
5 0 , 由r(A)=2, 得 1 0
5. 即 1
首页
上页
返回
下页
结束
铃
四、小结
1. 矩阵秩的概念 2. 求矩阵秩的方法 (1) 利用定义 寻找矩阵中非零子式的最高阶数; (2) 初等变换法
解: 对A作初等行变换,变成行阶梯形矩阵。
1 1 2 1 A 1 2 4 1
首页
2 2 0 4
1 4 3 2
上页
r2 2 r1 r3 r1 r4 4 r1
返回
1 1 2 1 0 3 2 2 0 3 2 2 0 3 4 2
对A作初等行变换,变成行 阶梯形矩阵:
1 r r 1 3 2 5 1 1 8 1 1 3 4 7 3 5 0 1 2 4 11
解
A
7 11
首页
上页
返回
下页
结束
铃
5 1 2 1 7 1 11 8 r2 2r1
无解。
返回 下页
因此,r(A) = 2 , r(B) = 3.
上页
结束
一矩阵秩的概念

当A ? r?i ??rj ? B或 A ? r?i???k B 时, 在 B 中总能找到与 Dr 相对应的子式 Dr ,.
由于 Dr ? Dr 或 Dr ? ? Dr 或 Dr ? kDr ,
因此 Dr ? 0,从而 R(B ) ? r. 当A ? r?i ??krj ? B时,分三种情况讨论: (1)Dr中不含第 i行; (2)Dr中同时含第 i行和第 j行; (3)Dr中含第 i行但不含第 j行;
若D?r ? 0, 则 Dr ? Dr ? 0,也有 R(B ) ? r. 若A经一次初等行变换变为 B,则 R( A) ? R(B ).
又由于 B 也可经一次初等变换变 为 A, 故也有 R(B ) ? R( A).
因此 R( A) ? R(B ).
经一次初等行变换矩阵的秩不变,即可知经 有限次初等行变换矩阵的秩仍不变.
子式的最高阶数 .
对于 AT, 显有 R( AT ) ? R( A).
?1 2 3 ?
例1
求矩阵
A
?
? ?2
3
?
5
? ?
的秩.
??4 7 1 ??
解
在 A 中,1
2 ? 0.
23
又? A的 3 阶子式只有一个 A,且 A ? 0,
? R( A) ? 2.
?2 ? 1 0 3 ? 2?
?
?
例2
求矩阵
另解
对矩阵
A
?
?? ?
1 0
3 2
?2 ?1
2 3
?? ?
做初等变换,
??? 2 0 1 5??
?? 1 3 ? 2 2?? ??1 3 ? 2 2?? ? ? 0 2 ? 1 3? ~ ?0 2 ? 1 3?,
2.6 矩阵的秩
A 中阶数大于 r 的子式必等于零 .
A 中不等于零的子式的阶 数 r 秩 R( A) . 1 2 3 例如,矩阵 A 2 4 6 4 8 12 0, 在 A 中显然有不等于 0 的1 阶子式 2,所有2阶子式都为 此时, R( A) 1. 2 即为矩阵 A的最高阶非零子式 ,
因 R( A) 2 , 故A的行阶梯形矩阵只能有两个非零行. 而B的2,3行都不为零,因此必有一行会被消成零. 0 8 5 4 k 0 3 4 4 0 0 0 0 或 0 3 4 4 l 0 8 5 4 0 0 0 0 5 0 5 即 1 0 1
行最简形矩阵: 行阶梯形矩阵; 非零行的第一个非零元为1, 且这些非零元所在的列的其他元素都为0
行阶梯形矩阵的秩
行阶梯形矩阵中非零行的行 数就是该矩阵的秩
例
3 2 2 1 0 3 1 2 5 0 求矩阵 B 的秩. 0 0 0 4 3 0 0 0 0 0
而
R( A E ) R( E A) ,故 R( A E ) R( A E ) n
三、小结
1. 矩阵秩的概念
2. 求矩阵秩的方法 (1)利用定义 (即寻找矩阵中最高非零子式的阶数); (2)初等变换法 定理2.5:初等变换不改变矩阵的秩。
初等变换求矩阵秩的方法
(把矩阵用初等行变换变成为行阶梯形矩阵,行 阶梯形矩阵中非零行的行数就是矩阵的秩).
解
在 A 中,
1 2
2 3
0.
且 A 0, 又 A的 3 阶子式只有一个 A,
R( A) 2.
行阶梯形矩阵的秩
行阶梯形矩阵: 任意一行的第一个非零元素所在的列中, 在这个非零元素的下方全为0。 特点: 可画出一条阶梯线,线的下方全为0; 每个台阶只有一行,台阶数即为非零行的行数,阶梯线 的竖线(每段竖线的长度为一行)后面的第一个元素为 非零元,也就是非零行的第一个非零元。
矩阵的秩学习课件

定理2.11 设 均为 矩阵,则 (2.16) 例22 设 为 阶幂等矩阵,即 ,证明 . 证 由 ,有 .由(2.15)式,有 另一方面,由(2.16)式,有 ,故 .
例20 求下列矩阵的秩(1) ,(2) 解 (1)A 是一个行阶梯形矩阵,容易看出 A的所有4阶子式均为零,有一个三阶子式 故 . (2) 的最大子式为三阶,共有4个:
将 分块: ,其中 为 矩阵, 为 矩阵。于是 再由定理2.8,有 。同理可证, 。 定理2.10(Sylvester) 设 分别为 和 n×k 矩阵,则 (2.14)特别地,若 ,则 (2.15)
矩阵的秩既不超过其行数,也不超过其列数。对于矩阵的乘积与和的秩,有下列结果 定理2.9 两个矩阵乘积的秩不超过每个因子的秩。即 (2.13) 证 设 A为 矩阵, B为 矩阵,由定理2.5,存在 阶可逆矩阵 和 阶可逆矩阵 ,使于是 , 。
的所有3阶子式皆为零,且有一个二阶子式 ,故 . 当矩阵的阶数较高时,按定义求该矩阵的秩是比较麻烦的。2.6.2 用初等变换求矩阵的秩 从例20第(1)小题可以看出,行阶梯形矩阵容易求秩,其秩就是其非零行的行数。标准形就更容易求秩了。而任意矩阵可经过初等变换化为标准形,问题是初等变换是否改变矩阵的秩呢?我们不加证明的给出下面的定理。
定理2.7 初等变换不改变矩阵的秩. 例21 用初等变换求下列矩阵的A的秩。 解 故r(A)=3.
实际计算时,并不一定要将A用初等变换化为标准形,只需将A 化为一眼就能看出它的秩的矩阵即可。 既然初等变换不改变矩阵的秩,又注意到可逆矩阵可表为若干个初等矩阵的乘积,我们有 定理2.8 设A是一个 矩阵, P,Q分别是m阶和n阶可逆矩阵,则 ; ; 。即 A 左乘或右乘一个可逆矩阵,其秩不改变。2.6.3 矩阵秩的不等式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
15
关于矩阵的秩的一些重要结论: R(AB) R(A), R(AB) R(B),即 定理5 R(AB) min{R(A),R(B)}。 设A是 m n 矩阵, B是 n t 矩阵, R( A) R( B) n R( AB). 性质1 性质2 如果 A B = 0 则 R( A) R( B) n. 性质3 如果 R(A)= n, 如果 A B = 0 则 B = 0。 性质4 设A,B均为m n 矩阵,则 R( A B) R( A) R( B).
R(A) = 2
11
1 例5 设A 3 5 1 1 A 3 5 3 1 1 0 3 0 5
2 1 2 , 且R(A) 2,求 , 3 6 1 2 1 2 1 1 1 2 0 3 4 4 0 8 5 4 6 1 2 R( A) 2, 4 4 5 0, 1 0 1 0 5, 1 1
(3) R(A) ≤m, R(A) ≤n, 0 ≤R(A) ≤min { m , n } .
(4) 如果 An×n , 且 A 0 , 则 R ( A ) = n . 反之,如 R ( A ) = n ,则 A 0 .
因此,方阵 A 可逆的充分必要条件是 R ( A ) = n .
5
二、矩阵秩的求法
1
12
三、满秩矩阵
定义3 A 为 n 阶方阵时, R A n, 称 A 是满秩阵,(非奇异矩阵) R A n, 称 A 是降秩阵,(奇异矩阵) 可见:R A n A 0
对于满秩方阵A施行初等行变换可以化为单位阵E, 每对A施行一次初等行变换, 又根据初等阵的作用: 相当于用一个对应的初等阵左乘A, 由此得到下面的 定理.
13
定理3
设A是满秩方阵,则存在初等方阵
使得 P 1, P 2 , , P s.
Ps Ps 1 , P2 P 1A E
14
对于满秩矩阵A, 它的行最简形是 n 阶单位阵 E .
R A n A ~ E
2 1
例如
1 A 2 3 1 0 0
1 0
子式(如果存在的话)全为0 , 称r为矩阵A的秩, 记作R(A)或秩(A)。
4
规定: 零矩阵的秩为 0 . 注意:(1) 如 R ( A ) = r,则 A 中至少有一个 r 阶子 式 Dr 0 , 所有 r + 1 阶子式为 0,且更高阶
子式均为 0,r 是 A 中不为零的子式的最高阶
数,是唯一的 . R( A) R( AT ) . (2) 有行列式的性质,
16
例8
设A为n阶矩阵,证明R(A+E)+R(A-E)≥n 证: ∵ (A+E)+(E-A)=2E R(A+E)+ R( E-A )≥ R(2E)=n 而 R( E-A )=R( A-E ) R(A+E)+R(A-E)≥n
∴ ∴
17
作业
P109 1 2 3
18
1 K 1 1
1 1 K 1
9
2、用初等变换法求矩阵的秩
矩阵初等变换不改变矩阵的秩。 即 A B 则 R( A) R( B) 注: 1. ri r j 只改变子行列式的符号。 2. k ri 是 A 中对应子式的 k 倍。 3. ri kr j 是行列式运算的性质。 求矩阵A的秩方法: 1)利用初等行变换化矩阵A为阶梯形矩阵B 2)数阶梯形矩阵B非零行的行数即为矩阵A的秩。 定理2
1、子式判别法(定义)。
1 2 3 4 例1 设 B 0 2 7 0 为阶梯形矩阵, 求R(B)。 0 0 0 0 1 2 0 ,存在一个二阶子式不为0,而 解 由于 0 2
则 R(B) = 2. 任何三阶子式全为0,
结论:阶梯形矩阵的秩=台阶数。
6
例如 1 2 3 0 A 0 1 0 1 0 0 1 0
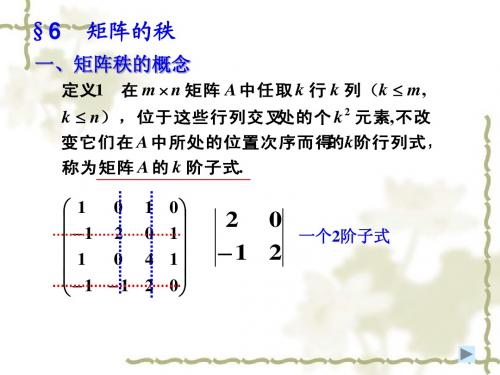
矩阵A 的第一、三行,第二、四列相交处的元素 所构成的二阶子式为
D2
3
2 1 0 1
1 2
而
D3 4 6
5 为 A 的一个三阶子式。
1 0 1
k k 个 k 阶子式。 m n 矩阵 A 共有 cm cn 显然,
3
2. 矩阵的秩
定义2 设 A a ij
mn
,有r 阶子式不为0,任何rБайду номын сангаас1阶
10
例4
1 0 2 4 A 2 1 3 6 1 1 1 2
求 R A.
1 0 2 4 1 0 2 4 r2 2 r1 0 1 1 2 , 解 A r 0 1 1 2 3 r 1 0 0 0 0 0 1 1 2
1 0
R A n A ~ En 3 3 1 2 1 0 0 2 0 3 4 0 1 1 0 2 3 0 2 3 2 0 A为满秩方阵。 R A 3 0 E 1
1 2 B 0 1 0 0
2 1 0 0 3 5 7 0 5 3 2 0
1 1 0 C 0 1 0 0 0 1
R A 3 RB 2 RC 3
2 1 1 2 5 0 8 D 0 3 4 E 0 0 0 0 0 0 0
R D 2 R E 3
一般地, 行阶梯形矩阵的秩等于其“台阶数”—— 非零行的行数。
7
a 1 1 例2 设 A 1 a 1 1 1 a a 解 R A 3 A 1 1 a 1 或 a 2
如果 R A 3 , 求 a .
1 1 a 1 (a 2)(a 1) 2 0 1 a
8
例3
R A 3
1 1 A K 3 1 1
K 1 A 1 1
1 K 1 1 则
1 1 K 1
K 3
1 1 3 ( K 1) ( K 3) 1 K
1 1 1 K
第五节 矩阵的秩及其求法
一、矩阵秩的概念
第二章
二、矩阵秩的求法 三、满秩矩阵
1
一、矩阵的秩的概念
1. k 阶子式 定义1 设 A aij
mn
在A中任取k 行k 列交叉
处元素按原相对位置组成的 k
(1 k min m, n)
阶行列式, 称为A的一个k 阶子式。
2
1 2 3 1 2 2 例如 A 4 6 5 4 共有 设 , C 3 C 4 18 1 0 1 1 3 3 个二阶子式,有 C 4 C 3 4 个三阶子式。
