第二章一元线性回归模型(Stata)
02一元线性回归模型ppt课件

xi (xi X) xi2
xi2 xi2
X
xi xi2
1
故: ˆ1 1 kii
E(ˆ1) E(1 kii ) 1 ki E(i ) 1
ˆ0 wiYi wi(0 1Xi i)0 wi 1 wiXi wii
由于:wi (1/nXki)1Xki 1
wiXi
二、普通最小二乘法〔OLS)
普通最小二乘法是一种参数估计方法,确定估计参数的 准则是使全部观察值的残差平方和最小,即 ei2 min, 由 此得出选择回归参数 b0 , b1 的最小二乘估计式。
(谁提出的呢?) Y
e3 e1 e2
e5 e6
e4
X1 X2 X3
X4
X5 X6
X
(C F Gauss, 1777-1855)
▪ 回归模型存在两个特点。 ▪ (1〕回归函数不能百分之百地再现所研究的经济
过程。 ▪ (2〕也正是由于这些假定与抽象,才使我们能够
透过复杂的经济现象,深刻认识到该经济过程的 本质。
总体回归方程随机形式 总体回归方程
Y i E Y iX i i 0 1 X i i
系统变 化部分
非系统 变化部分
C F Gauss 1809年提出OLS估计方法。
残差平方和
n ei2 n (YiYˆ)2 n Yi(o1Xi)2
i1
i1
i1
使偏导数为零
( e oi2)2 (Yi o1Xi)0 ( e 1i2)2 (Yio1X i)X i0
得正规方程
Yi = nβo + β 1 Xi XiYi = β o Xi + β 1 Xi2
其中,ci ki di ,di 为不全为零的常数。 E(ˆ1* ) E( ciYi ) ci E(Yi ) ci ( 0 1 X i ) 0 ci 1 ci X i
一元线性回归模型

几个常用结果以及注释 1. Σei =0
2. Σei
Xi=0
3.样本回归方程过( X , Y )点 样本回归方程过( 4.截距为0的一元线性回归模型参数估 计式 一元线性回归模型参数估计举例( P23页)
四、估计量的统计学性质
1. 线性性:b , b 都是Yi的线性函数。
0 1
∑ x y = ∑ x (Y Y ) = ∑ x Y b = ∑ x ∑ x ∑ x ∑ xY = ∑ x x 令: K = 则: b = ∑ K Y 是 Y ∑ x
4.线性回归模型 的普遍性
在实际经济分析中,由于经济变量之间的关系 在实际经济分析中 由于经济变量之间的关系 往往是非常复杂的,所以直接的精确线性模型是较 往往是非常复杂的 所以直接的精确线性模型是较 所以直接的精确线性模型 少的。 少的。 但是,由于第一,线性模型比较容易研究;第 但是,由于第一,线性模型比较容易研究; 二,现实经济分析中许多非线性问题可以经过简 单的数学处理转化为线性模型;第三, 单的数学处理转化为线性模型;第三,非线性模 型的分析基础是线性模型。 型的分析基础是线性模型。 所以,我们研究的思路是先学习线性回归模型, 所以,我们研究的思路是先学习线性回归模型, 然后学习非线性问题。 然后学习非线性问题。
表示 Xi ,Yi…… 离差形式用小写字母表示 xi ,yi……
三、举例说明
计量经济学模型为什么引入随机扰动项ui ? 例题:需求模型 如前所述需求量Q受到商品价格P、当期 收入Yt 、其它商品价格P1 、前期收入Y t-1 、 经济政策G 、……等因素影响。所以, Q=f(P、 Y t 、P1、Y t-1、G……)
i i i i i 1 2 2 2 i i i i i 2 i i i 2 1 i i i
计量经济学第二章--一元线性回归模型

2 、同方差假定:每一个随机误差项的方差为常数,即:
经 济
Var(Yi ) Var(i ) 2 (常数)
学
该假定表明:给定X对应的每个条件
分布都是同方差的,每个Y值以相同
的分布方式在它的期望值E(Y)附近波
动
10
3、无自相关假定:任意两个随机误差项之间不相关,用数学
形式表示为:
Cov(i, j ) E (i E(i ))( j E( j )) 0
)
xiYi Y xi2
xi
xi 0
bˆ1
xiYi xi2
(bˆi
x12
x1Y1 x22
xn2
x12
x2Y2 x22
xn2
...
x12
xnYn x22
xn2
)
19
令
ki
xi xi2
则
bˆi
kiYi
(1) k i
(
xi xi2
)
xi xi2
0
计 量 经 ki的性质 济 学
2 n
2k1k21 2
2kn1kn n1 n
)
量
经
k12
E
(12
)
k22
E
(
2 2
)
kn2
E
(
2 n
)
2k1k2
E
(1
2
)
2kn
1kn
E
(
n1
n
)
济
学 由古典线性回归模型的假定可知,对每一个随机变量,有
E(i2) 2, E(i j ) 0(当i j时)
Var(bˆ1)
k12 E (12
第二章二计量经济学-一元线性回归分析.ppt课件

2
1 n
2 n
X
ki X 2
xi
x
2 i
2
2
1 n
X2
x
2 i
2
x
2 i
nX
2
2
X
2 i
2
n
x
2 i
n
x
2 i
(2.2.11)
精选
34
(2)证明最小方差性
假设ˆ1* 是其他方法得到的关于1 的线性无偏估计量: ˆ1* ciYi
其中,ci ki di ,di 为不全为零的常数。 E(ˆ1* ) E( ciYi ) ci E(Yi ) ci (0 1 X i ) 0 ci 1 ci X i
由ˆ1* 的无偏性,即E(ˆ1* ) 1 可知: 0 ci 1 ci X i 1
从而有: ci 0 ,ci Xi 1
精选
35
的 ˆ
* 1
方
差
var(
ˆ
* 1
)
var(
ciYi )
c
2 i
var(
Yi)
c
2 i
var(
i)
c
2 i
2
= ( k i d i ) 2 2
变量置换得到
Z 0 1 X 1 2 X 2 3 X 3
精选
9
结论:
• 实际经济活动中的许多问题,都可以最终化为线 性问题,所以,线性回归模型有其普遍意义。
• 即使对于无法采取任何变换方法使之变成线性 的非线性模型,目前使用得较多的参数估计方 法——非线性最小二乘法,其原理仍然是以线 性估计方法为基础。
(Gauss-Markov theorem) 在给定经典线性回归的假定下,最小二乘
第二讲 一元线性回归模型

E(i Xi ) 0, i 1,2,, n
• (2)同方差假设。 Var( X ) 2 , i 1, 2,, n i i • (3)序列不相关假设。
Cov(i , j ) 0, i, j 1, 2,, n, i j
(4)正态性假设。 一般假设随机项服从正态分布。
3、可决系数R2统计量
ESS RSS R 1 TSS TSS
2
• 是一个非负的统计量。取值范围:[0,1] • 越接近1,说明实际观测点离回归线越近, 拟合优度越高。
• 拟合优度越高,说明回归结果越好。
二、变量的显著性检验
T检验(检验单个回归系数是否显著不为零)
二、变量的显著性检验:T检验(检验 单个变量的回归系数是否显著不为零)
ˆ ˆ yt 0 1xt et MinQ (Y Y ) 2 e2 ˆ i i i
n n
ˆ ˆ ˆ yt 0 1xt
1
1
ˆ X )) 2 (Yi ( 0 ˆ1 i
1
n
2、正规方程组
Q 0 0 Q 1 0
第二章 经典单方程计量经济学模型: 一元线性回归模型 The Classical Single Equation Econometric Model: Simple Regression Model
本章内容
• §2.1一元线性回归模型的设定与古典假
设
• §2.2一元线性回归模型的参数估计 • §2.3一元线性回归模型的检验 • §2.4一元线性回归模型的预测
二、经典线性回归模型的基本假设 The Basic Assumptions of Classical Linear Regression Model(CLRM)
第二章一元线性回归模型(Stata)

第⼆章⼀元线性回归模型(Stata)1. 中国居民⼈均消费模型从总体上考察中国居民收⼊与消费⽀出的关系。
表2.1给出了1990年不变价格测算的中国⼈均国内⽣产总值(GDPP )与以居民消费价格指数(1990年为100)所见的⼈均居民消费⽀出(CONSP )两组数据。
表2.1 中国居民⼈均消费⽀出与⼈均GDP (单位:元/⼈)年份 CONSP GDPP 年份 CONSP GDPP 1978 395.8000 675.1000 1990 797.1000 1602.300 1979 437.0000 716.9000 1991 861.4000 1727.200 1980 464.1000 763.7000 1992 966.6000 1949.800 1981 501.9000 792.4000 1993 1048.600 2187.900 1982 533.5000 851.1000 1994 1108.700 2436.100 1983 572.8000 931.4000 1995 1213.100 2663.700 1984 635.6000 1059.200 1996 1322.800 2889.100 1985 716.0000 1185.200 1997 1380.900 3111.900 1986 746.5000 1269.600 1998 1460.600 3323.100 1987 788.3000 1393.600 1999 1564.400 3529.300 1988 836.4000 1527.000 20001690.8003789.7001989779.70001565.9001) 建⽴模型,并分析结果。
2)输出结果为:对应的模型表达式为:201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出,拟合度较好,截距项和斜率项系数均通过了t 检验。
计量经济学 第二章 一元线性回归模型
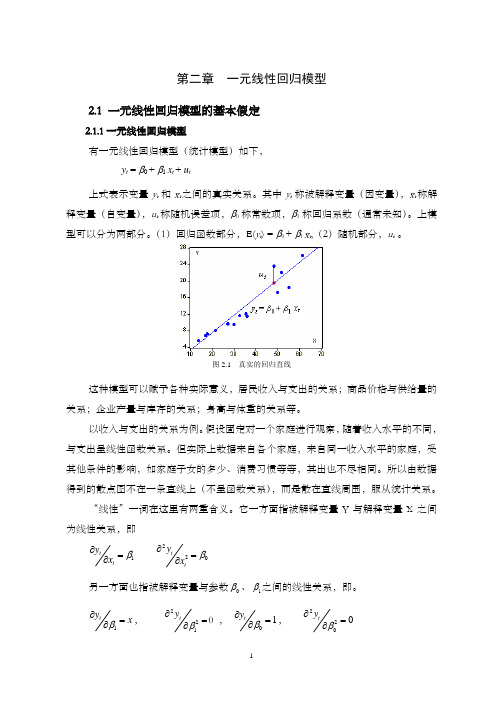
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
21一元线性回归模型.ppt

同理,p(Y= ? /X=260)=1/7
条件均值(条件期望 ) :
对Y的每一条件概率分布,我们能算出它 的均值 :
记做E(Y/X=Xi)
[简写为E(Y/Xi) ]
并读为“在X取特定Xi值时的Y的期望值”。
计算方法:
将表2.1中的有关列乘以表2.2中的相应列 的条件概率,然后对这些乘积求和便是。
第二章 一元线性回归模型
§2.1 一元线性回归模型概念基础 回归是计量经济学的主要工具 一、“回归”一词的历史渊源
Francis Galton F.加尔顿
回归一词最先由F.加尔顿 (FrancisC,alton)引入
加尔顿的普遍回归定律还被他的朋友 K.皮尔逊(KartPearson)证实
Karl Pearson K.皮尔逊
综合来看,回归分析一般可以用来:
(1) 通过已知变量的值来估计因变量的均值。
(2)对独立性进行假设检验―――根据经济理 论建立适当的假设。
例如,对于需求函数,你可以检验假设:需求的 价格弹性为-1.0;即需求曲线具有单一的价格 弹性。也就是说,在其他影响需求的因素保持 不变的情况下,如果商品的价格上涨1%,平 均而言,商品的需求量将减少1%。
P (
1/7 1/5 1/5 1/6 1/5 1/7 1/5 1/7 1/5
Y/ 1/7 1/5 1/5 1/6 1/5 1/7 1/5 1/7 1/5
Xi ) 1/7
1/6
1/7
1/7
1/7
1/7
1/7
Y的条 48 46 44 42 40 38 36 34 32 30
件均值
E(Y/X=Xi) Y的条件均值
·
·
·
· ·
第二章 一元线性回归模型 知识点
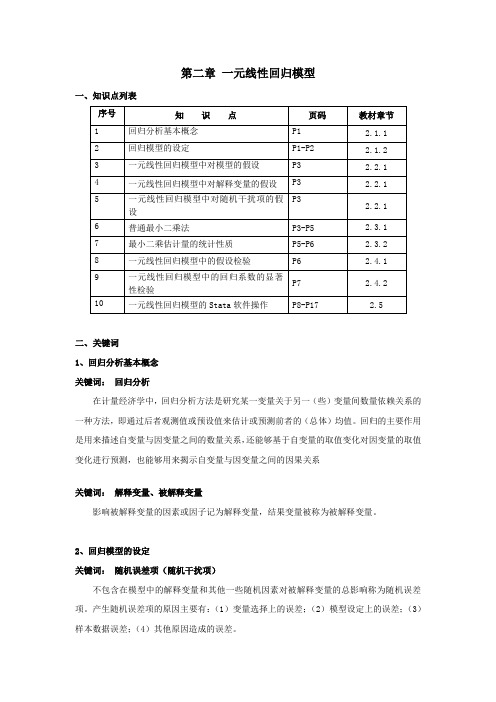
第二章一元线性回归模型一、知识点列表二、关键词1、回归分析基本概念关键词:回归分析在计量经济学中,回归分析方法是研究某一变量关于另一(些)变量间数量依赖关系的一种方法,即通过后者观测值或预设值来估计或预测前者的(总体)均值。
回归的主要作用是用来描述自变量与因变量之间的数量关系,还能够基于自变量的取值变化对因变量的取值变化进行预测,也能够用来揭示自变量与因变量之间的因果关系关键词:解释变量、被解释变量影响被解释变量的因素或因子记为解释变量,结果变量被称为被解释变量。
2、回归模型的设定关键词:随机误差项(随机干扰项)不包含在模型中的解释变量和其他一些随机因素对被解释变量的总影响称为随机误差项。
产生随机误差项的原因主要有:(1)变量选择上的误差;(2)模型设定上的误差;(3)样本数据误差;(4)其他原因造成的误差。
关键词:残差项(residual )通过样本数据对回归模型中参数估计后,得到样本回归模型。
通过样本回归模型计算得到的样本估计值与样本实际值之差,称为残差项。
也可以认为残差项是随机误差项的估计值。
3、一元线性回归模型中对随机干扰项的假设 关键词:线性回归模型经典假设线性回归模型经典假设有5个,分别为:(1)回归模型的正确设立;(2)解释变量是确定性变量,并能够从样本中重复抽样取得;(3)解释变量的抽取随着样本容量的无限增加,其样本方差趋于非零有限常数;(4)给定被解释变量,随机误差项具有零均值,同方差和无序列相关性。
(5)随机误差项服从零均值、同方差的正态分布。
前四个假设也称为高斯马尔科夫假设。
4、最小二乘估计量的统计性质关键词:普通最小二乘法(Ordinary Least Squares ,OLS )普通最小二乘法是通过构造合适的样本回归函数,从而使得样本回归线上的点与真实的样本观测值点的“总体误差”最小,即:被解释变量的估计值与实际观测值之差的平方和最小。
ββ==---∑∑∑nn n222i i 01ii=111ˆˆmin =min ()=min ()i i i i u y y y x关键词:无偏性由于未知参数的估计量是一个随机变量,对于不同的样本有不同的估计量。
一元线性回归模型ppt课件

差e的原因.
例1.(多选)在如图所示的四个散点图,适合用一元线性回
归模型拟合其中两个变量的是( AC ).
例2.在一元线性回归模型中,下列关于Y=bx+a+e的说法正确的是( C )
A.Y=bx+a+e是一次函数
B.响应变量Y是由解释变量x唯一确定的
C.响应变量Y除了受解释变量x的影响外,可能还受到其他因素的影响,这
Y bx a e
(1)
2
E (e ) 0,D(e ) .
追问3.对于父亲身高为xi的某一名男大学生,他的身高yi一定是bxi+a吗?
对于父亲身高为的某一名男大学生,他的身高 并不一定为
bxi+a ,它仅是该子总体的一个观测值,这个观测值与均值有一个误
差项ei=yi -(+a).
相关程度较高.
编号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
父亲身高/cm 174
170
173
169182172180172168
166
182
173
164
180
儿子身高/cm 176
176
170
170
185
176
178
174
170
168
178
172
165
182
问题2.根据表中的数据,儿子身高和父亲身高这两个变量之间的关系可以
参数;e是Y与bx+a之间的随机误差. 模型中的Y也是随机变量,其值虽不能由变
量x的值确定,但却能表示为bx+a与e的和,前一部分由x所确定,后一部分是随
《一元线性回归》ppt课件

做该样本的散点图 样本散点图近似于一条直线,这与 总体中表达的X和Y的关系是一致的。 画一条直线以尽能够地拟合该散点 图,由于样本取自总体,可用该线近 似地代表总体回归线。 该线称为样本回归线〔sample regression lines〕。
记样本回归线的函数方式为:
Y ˆif(X i)ˆ0ˆ1X i
计量经济学
Econometrics
第二章 一元线性回归模型
§ 2.1 回归分析概述 § 2.2 一元线性回归模型的参数估计 § 2.3 一元线性回归模型的统计检验 § 2.4 一元线性回归模型的运用:预测 § 2.5 实例:时间序列问题
§2.1 回归分析概述
一、回归分析的根本概念 二、总体回归函数 三、随机干扰项 四、样本回归函数
1969 1991 2046 2068 2101
968 1045 1243 1474 1672 1881 1078 1254 1496 1683 1925
2189 2233
1122 1298 1496 1716 1969 1155 1331 1562 1749 2013
2244 2299
1188 1364 1573 1771 2035 1210 1408 1606 1804 2101
3500 1/6
2585
〔4〕描出散点图发现:随着收入X的添加,消费“平均地说〞也在添加, 且Y的条件均值均落在一条正斜率的直线上。这条线,我们称为总体回归 线〔population regression line,PRL〕
每 月 消 费 支 出 Y 〔元〕
3500 3000 2500 2000 1500 1000
A2:回归分析与因果关系
虽然回归分析通常用于研讨具有因果关系的变量之间的详细依赖关系, 但是回归关系式本身并不一定意味着因果关系
[经济学]第二章 一元线性回归模型计量经济学ppt课件
![[经济学]第二章 一元线性回归模型计量经济学ppt课件](https://img.taocdn.com/s3/m/6239f6d031126edb6e1a1016.png)
比较三个模型拟合程度的优劣,用最好的模型估计2009年的预 测值(2009:59942.7,5383,86396.8),给出样本值和预 测值的时间序列图,并求2009年的农业总产值95%的预测区间
4、如果增加一个地区,该地区年可支配收入是12000元,求 该地区的消费支出的点预测值,和该地区人均消费支出95%置 信水平的区间预测。
2021/5/19
台州学院《计量经济学》讲义
34
2021/5/19
台州学院《计量经济学》讲义
35
yˆi 725.346 0.665xi
t (1.589) (22.496)
2021/5/19
台州学院《计量经济学》讲义
33
例3:利用给出的2008年我国城镇居民人均消费支出与人均 可支配收入数据(数据来源:中国统计年鉴2009),回答问题:
1、建立一元线性回归模型,写出回归方程,如何解释斜率?
2、给出显著性水平5%,对参数进行显著性检验
3、弹性定义为自变量变动百分之一所引起的因变量变动的百 分比,用数学形式表示为弹性=斜率*(x/y)。假设仅根据2得 到的回归结果,能求出支出对收入的弹性吗?如果不能,计算 此弹性还需要其它什么信息?
一、重视数据的收集和甄别
一些变量无法直接观测,一些现实数据不能公开 数据缺失或出现异常数据 数据量不够,样本太小 数据不准确、不一致、有矛盾
2021/5/19
台州学院《计量经济学》讲义
29
二、合理确定数据的单位
适当的选取变量的单位,使模型中各变量的数量级大体 一致
2021/5/19
台州学院《计量经济学》讲义
计量经济学第2章-一元线性回归模型PPT课件

E(Y
/
X1i,X
,
2i
,X ki)
(f X1i,X
,
2i
,X
)
ki
(2-5)
表示对于解释变量 X1、X 2、
、X k的每一组取值
X1i、X
、
2i
、X ki
,都有被解释变量Y的条件期望
E(Y
/
X
1i,X
,
2i
,X
)
ki
与之对应,E(Y
/
X
1i,X
,
2i
,X ki)是
X1、X 2 、
、X k 的函数。
经济变量之间的关系
确定的函数关系 不确定的相关关系
第4页/共111页
函数关系
指某一经济变量可直接表示为其他经济变量的确定的函数, 函数表达式中没有未知参数,不存在参数估计的问题。
例如:
1) 某一商品的销售收入Y与单价P、销售数量Q之间的关系Y = PQ 2) 某一农作物的产量Q与单位面积产量q 、种植面积S之间的关系Q = q S
第8页/共111页
相关关系的分类
c)按照相关的性质
正相关
指不同经济变量的变化趋势一致,即一个经济变量的 取值由小变大时,另一经济变量的取值也由小变大;
负相关
指不同经济变量的变化趋势相反,即一个经济变量的 取值由小变大时,另一经济变量的取值由大变小。
第9页/共111页
相关关系的分类
c)按照相关的性质
Va(r X)、Va(r Y)分别是变量X、Y的方差。
第13页/共111页
如果给定变量X、Y 的一组样本 Xi,Yi ,i 1,2,n,,
则总体相关系数的估计——样本相关系数为
第2章一元线性回归模型

布图上的点接近于一条曲线时,称为非线性相关。简单相关按
符号又可分为 正相关 (见图2.3.4 )、负相关 (见图2.3.8 )和零 相关 (见图2.3.6 )。两个变量趋于在同一个方向变化时,即同
增或同减,称为变量之间存在正相关;当两个变量趋于在相反
方向变化时,即当一个变量增加,另一个变量减少时,称为变 量之间存在负相关;当两个变量的变化相互没有关系时,称为
4、普通最小二乘法
为什么要使用OLS? (1)OLS的应用相对简便; (2)以最小化残差平方和为目标在理论很合理; (3)OLS估计量有很多有用的性质。 1)估计的回归线通过Y和X的均值。下列等式总是
ˆ ˆX 严格成立的:设下,可以证明,OLS是 “最优”的估计方法。
2.2.2 最小二乘估计量的性质
一个用于考察总体的估计量,可从如下几个方面考察其
优劣性: (1)线性。即它是否是另一个随机变量的线性函数;
(2)无偏性。即它的均值或期望是否等于总体的真实值;
(3)有效性。即它是否在所有的线性无偏估计量中具有 最小方差; (4)渐近无偏性。 即样本容量趋于无穷大时,它的均值 序列趋于总体的真值; (5)一致性。即样本容量趋于无穷大时,它是否依概率 收敛于总体的真值;
1.总变差的分解
ˆ b ˆX ˆ b Yt的估计值位于估计的回归线 Y t 0 1 t 上,Y围绕其均值的变异 (Y Y )可被分解为两部分:
ˆ Y ) (1) (Y t
ˆ) (2) (Yt Y t
样本回归函数:
3.相关系数检验
(1)变量相关的定义和分类
相关:指两个或两个以上变量间相互关系的程度或强度。
2 2 ˆ e ( Y Y ) i i OLS 最小化 i i 1 i 1
一元线性模型回归Stata上机

2
其中:n-kБайду номын сангаас1为残差平方和的自由度,n-1为总体平 方和的自由度。 调整的可决系数多大才是合适的?
15
ˆ 已经估计出后: 在实际计算可决系数时,在 β 1
2 x ∑ i 2 2 ˆ R = β1 ∑ y2 i
2
使偏导数为零
∂(∑ ei2 ) = − 2∑ (Yi − β o − β 1 Xi) = 0 ∂β o ∧ ∧ ∂(∑ ei2 ) = − 2∑ (Yi − β o − β 1 Xi) Xi = 0 ∂β 1
4
∧
∧
2、正规方程组
∂ Q $ =0 ∂β 0 ∂ Q =0 $ ∂β 1
Y的i个观测值与样本均 值的离差
ˆ ) + (Y ˆ −Y ) = e + y ˆi y i = Yi − Y = (Yi − Y i i i
离差分解为两 部分之和 回归直线不能 解释的部分 由回归 直线解 释的部 分
10
如果Yi=Ŷi 即实际观测值落在样本回归“线”上,则拟合最好。 可认为,“离差”全部来自回归线,而与“残差”无关。
) = ∑( (
2 n i =1
ˆ +β ˆX Yi − β 0 1 i
))
2
e5 e6 e3 e1 e2 e4
X1
X2
X3
X4
X5
X6
3
X
残差平方和
ˆ) ∑ e = ∑ (Y − Y
n i =1 2 i n i i =1
2
∧ n = ∑ Yi − (β i =1
o
一元线性回归模型及参数估计

步骤:收集数据、建立模型、 计算参数、评估模型
优点:简单易行,适用于线 性回归模型
最大似然估计法
定义:最大似然 估计法是一种基 于概率的参数估 计方法,通过最 大化样本数据的 似然函数来估计
参数。
原理:利用已知 样本数据和概率 分布函数,计算 出样本数据出现 的概率,然后选 择使得概率最大 的参数值作为估
参数估计的性质
无偏性
定义:参数估计量是 无偏估计时,其期望 值等于参数的真实值。
性质:无偏性是线性 回归模型参数估计的 最基本性质之一,是 评价估计量优劣的重 要标准。
证明:可以通过数学 推导证明无偏性,具 体过程可以参考相关 教材或论文。
应用:在回归分析中, 无偏性可以保证估计 的参数具有最小误差, 从而提高预测的准确 性和可靠性。
计值。
优点:简单易行, 适用于多种分布 类型的数据,具
有一致性。
局限:对样本数 据的要求较高, 当样本数据量较 小或分布不均时, 估计结果可能不
准确。
最小绝对误差准则
定义:最小化预测值与实际值之间的绝对误差
优点:对异常值不敏感,能够更好地处理数据中的噪声和异常值
缺点:可能导致模型过于复杂,过拟合数据 应用场景:适用于预测连续变量,尤其是当因变量和自变量之间的关系是 非线性的情况
行处理。
处理方法:包括 删除不必要的自 变量、合并相关 性较高的自变量、 使用其他模型等
方法。
模型预测与决策应用
预测未来趋势
利用一元线性回 归模型预测未来 趋势
模型参数估计的 方法和步骤
预测结果的解读 与决策应用
模型预测的局限 性及改进方法
制定决策依据
利用回归方程进行 预测
ห้องสมุดไป่ตู้
【统计学】一元线性回归模型课件

• 因此,给定收入X的值Xi,可得消费支出Y的 条件均值(conditional mean)或条件期望 (conditional expectation):E(Y|X=Xi)。
• 注意:
–不存在线性相关并不意味着不相关。 –存在相关关系并不一定存在因果关系。 – 相关分析对称地对待任何(两个)变量,两个变量
都被看作是随机的。 – 回归分析对变量的处理方法存在不对称性,即区分
因变量(被解释变量)和自变量(解释变量),前 者是随机变量,后者不一定是。
Our greatest weakness lies in giving up. The most certain way to succeed is alway s to try just one more time
圆 面 f,半 积 径 半 2 径
• 统计依赖或相关关系:研究的是非确定性现象 随机变量间的关系。
农作 f气 ,物 降 温 ,阳 产 雨 ,施 光 量 量 肥
Our greatest weakness lies in giving up. The most certain way to succeed is alway s to try just one more time
1、条件均值(conditional mean)
• 例2.1.1:一个假想的社区有99户家庭组成,欲 研究该社区每月家庭消费支出Y与每月家庭可 支配收入X的关系。 即如果知道了家庭的月收 入,能否预测该社区家庭的平均月消费支出水 平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 中国居民人均消费模型从总体上考察中国居民收入与消费支出的关系。
表2.1给出了1990年不变价格测算的中国人均国内生产总值(GDPP )与以居民消费价格指数(1990年为100)所见的人均居民消费支出(CONSP )两组数据。
表2.1 中国居民人均消费支出与人均GDP (单位:元/人)年份 CONSP GDPP 年份 CONSP GDPP 1978 395.8000 675.1000 1990 797.1000 1602.300 1979 437.0000 716.9000 1991 861.4000 1727.200 1980 464.1000 763.7000 1992 966.6000 1949.800 1981 501.9000 792.4000 1993 1048.600 2187.900 1982 533.5000 851.1000 1994 1108.700 2436.100 1983 572.8000 931.4000 1995 1213.100 2663.700 1984 635.6000 1059.200 1996 1322.800 2889.100 1985 716.0000 1185.200 1997 1380.900 3111.900 1986 746.5000 1269.600 1998 1460.600 3323.100 1987 788.3000 1393.600 1999 1564.400 3529.300 1988 836.4000 1527.000 20001690.8003789.7001989779.70001565.9001) 建立模型,并分析结果。
2)输出结果为:对应的模型表达式为:201.1070.3862CONSP GDPP =+(13.51) (53.47) 20.9927,2859.23,0.55R F DW ===从回归估计的结果可以看出,拟合度较好,截距项和斜率项系数均通过了t 检验。
中国人均消费增加10000元,GDP增加3862元。
2.线性回归模型估计表2.2给出黑龙江省伊春林区1999年16个林业局的年木材采伐量和相应伐木剩余物数据。
利用该数据(1)画散点图;(2)进行OLS回归;(3)预测。
表2.2 年剩余物y t和年木材采伐量x t数据林业局名年木材剩余物y t(万m3)年木材采伐量x t(万m3)乌伊岭26.13 61.4东风23.49 48.3新青21.97 51.8红星11.53 35.9五营7.18 17.8上甘岭 6.80 17.0友好18.43 55.0翠峦11.69 32.7乌马河 6.80 17.0美溪9.69 27.3大丰7.99 21.5南岔12.15 35.5带岭 6.80 17.0朗乡17.20 50.0桃山9.50 30.0双丰 5.52 13.8合计202.87 532.00(1)画散点图得散点图(2)OLS估计得到输出结果如图由输出结果可以看出,对应的回归表达式为:ˆ0.76290.4043t t yx =-+ (-0.625) (12.11)20.9129,146.7166, 1.48R F DW ===(3)x=20条件下模型的样本外预测方法首先修改工作文件范围(不会)3. 表2.3列出了中国1978—2000年的参政收入Y 和国内生产总值GDP 的统计资料。
做出散点图,建立财政收入随国内生产总值变化的一元线性回归方程。
表2.3年份财政收入Y GDP 年份财政收入Y GDP 1978 1132.260 3624.100 1990 2937.100 18547.90 1979 1146.380 4038.200 1991 3149.480 21617.80 1980 1159.930 4517.800 1992 3483.370 26638.10 1981 1175.790 4862.400 1993 4348.950 34634.40 1982 1212.330 5294.700 1994 5218.100 46759.40 1983 1366.950 5934.500 1995 6242.200 58478.10 1984 1642.860 7171.000 1996 7407.990 67884.60 1985 2004.820 8964.400 1997 8651.140 74462.60 1986 2122.010 10202.20 1998 9875.950 78345.20 1987 2199.350 11962.50 1999 11444.08 82067.50 1988 2357.240 14928.30 2000 13395.23 89403.60 1989 2664.900 16909.201) 做散点图:得到散点图如下:2) 进行回归分析:输出结果如下:对应的表达式是:556.60.12Y GDP =+(2.52) (22.72) 20.96,516.3R F ==从上面的结果可以看出,模型的你拟合度较高,各个系数均通过了t 检验。
财政收入增加10000元,GDP 增加1200元。
4. 表2.4给出了某国1990—1996年间的CPI 指数与S&P500指数。
(1)以CPI 指数为横轴,S&P500指数为纵轴作图;(2)做回归模型,并解释结果。
表2.4年份 CPI 指数 S&P500指数 年份 CPI 指数 S&P500指数 1990 130.7000 334.5900 1994 148.2000 460.3300 1991 136.2000 376.1800 1995 152.4000 541.6400 1992 140.3000 415.7400 1996 159.6000 670.83001993 144.5000 451.41001) 作散点图:得散点图如下:2)做回归估计:得到如下结果:对应的回归表达式为:&1137.8311.08S P CPI =-+(-6.39) (9.02)回归结果显示,CPI 指数与S&P 指数正相关,斜率表示当CPI 指数变化1个点,会使S&P 指数变化11.08个点;截距表示当CPI 指数为0是,S&P 指数为-1137.83,此数据没有明显的经济意义。
5.表2.5给出了美国30所知名学校的MBA学生1994年基本年薪(ASP),GPA分数(从1—4共四个等级),GMAT分数,以及每年学费(X)的数据。
(1)用双变量回归模型分析GPA分数是否对ASP有影响?(2)用合适的回归模型分析GMAT分数是否与ASP有关?(3)每年的学费与ASP有关吗?如果两变量之间正相关,是否意味着进到最高费用的商业学校是有利的?(4)高学费的商业学校意味着高质量的MBA成绩吗?为什么?表2.5学校ASP/美元GPA分数GMAT分数X/美元Harvard 102630.0 3.400000 650.0000 23894.00Stanford 100800.0 3.300000 665.0000 21189.00Columbian 100480.0 3.300000 640.0000 21400.00Dartmouth 95410.00 3.400000 660.0000 21225.00Wharton 89930.00 3.400000 650.0000 21050.00 Northwestern 84640.00 3.300000 640.0000 20634.00 Chicago 83210.00 3.300000 650.0000 21656.00MIT 80500.00 3.500000 650.0000 21690.00Virginia 74280.00 3.200000 643.0000 17839.00UCLA 74010.00 3.500000 640.0000 14496.00Berkeley 71970.00 3.200000 647.0000 14361.00Cornell 71970.00 3.200000 630.0000 20400.00NUY 70660.00 3.200000 630.0000 20276.00Duke 70490.00 3.300000 623.0000 21910.00CarnegieMellon 59890.00 3.200000 635.0000 20600.00 North Carolina 69880.00 3.200000 621.0000 10132.00 Michigan 67820.00 3.200000 630.0000 20960.00Texas 61890.00 3.300000 625.0000 8580.000Indiana 58520.00 3.200000 615.0000 14036.00Purdue 54720.00 3.200000 581.0000 9556.000 Case Western 57200.00 3.100000 591.0000 17600.00Georgetown 69830.00 3.200000 619.0000 19584.00Michigan State 41820.00 3.200000 590.0000 16057.00Penn State 49120.00 3.200000 580.0000 11400.00SouthernMethodist 60910.00 3.100000 600.0000 18034.00Tulane 44080.00 3.100000 600.0000 19550.00Illinois 47130.00 3.200000 616.0000 12628.00Lowa 41620.00 3.200000 590.0000 9361.000 Minnesota 48250.00 3.200000 600.0000 12618.00Washington 44140.00 3.300000 617.0000 11436.00(1)以ASP为因变量,GPA为自变量进行回归分析。
结果如下:从回归结果可以看出,GPA分数的系数是显著的,对ASP有正的影响。
(与Eviews系数结果不一致,仔细核实一下)(2)以ASP为因变量,GMAT为自变量做回归分析。
结果如下:从回归结果可以看出,GMAT分数与ASP是显著正相关的。
(与Eviews系数结果不一致,仔细核实一下)(3)以ASP为因变量,X为自变量进行回归分析。
