Verilog 实现一个16位超前进位加法器
组成原理课程设计(16位全加器电路的设计与实现)

16位全加器电路的设计与实现学生姓名:杨传福指导老师:王新摘要本课程设计主要利用门电路完成一个16位的全加器电路的设计与实现。
本设计采用逐步求解的方法,即先设计一位全加器,再利用一位全加器设计出四位全加器,最后在四位全加器的基础上设计出16位全加器,并使用VHDL语言编写程序,在MAX-PLUSⅡ仿真平台上进行仿真。
仿真结果表明,本课程设计中设计出的16位全加器能正确完成16位二进制数的加法运算。
关键词全加器;门电路;先行进位Abstract:This curriculum design primarily use the gate circuit to complete a 16-bit full-adder circuit.The design solve this problem with step-by-step approach, namely start designing one full-adder, and then use one full-adder design a four full-adder , the last design the 16-bit full-adder based on the four full-adder,and use VHDL language programming, at MAX-PLUS Ⅱsimulation on simulation platform. The simulation results show that the design of the curriculum design of the 16-bit full-adder to add a 16-bit binary number addition operations.Keywords:Full-adder; Gate circuit; First binary1引言1.1课程设计的背景随着计算机科学技术的发展,人们获得信息的途径更加多样,获取信息的速度更加快捷。
×16位移位相加乘法器设计

16×16位移位相加乘法器设计(总40页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除本科学生毕业论文 2012年 6 月 13日论文题目: 16×16位移位相加乘法器设计 学院: 电子工程学院 年 级:2009级 专 业:集成电路设计与集成系统 姓 名:于昊 学 号:指导教师: 曹贝摘要随着集成电路设计技术的不断进步,乘法器的芯片设计实现的研究与应用越来越广泛,对乘法器进行ASIC芯片设计,具有设计实现过程简单、所用到的EDA工具完善而且成熟、硬件开销小、易于在VLSI电路或系统级芯片中集成。
通常,数字电路设计的流程对于芯片的实现而言,需要RTL级的HDL描述,并要对各层次的设计进行功能仿真验证,在验证电路能按预期设计功能工作后,即可对RTL级的HDL描述进行综合、优化,形成门级网表。
整个设计流程可称为数字电路的前端设计。
本课题基于移位相加算法的研究,设计16位移位相加乘法器,并在功能仿真通过后,将所设计的Verilog RTL级代码进行综合,采用Synopsys公司Design Compiler EDA工具进行电路综合,获得16位移位相加乘法器的门级网表与电路实现。
关键词数字电路设计;移位相加乘法器;综合;AbstractAbstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract abstract.(英文摘要内容必须与中文摘要完全对应。
16位超前进位加法器实验报告
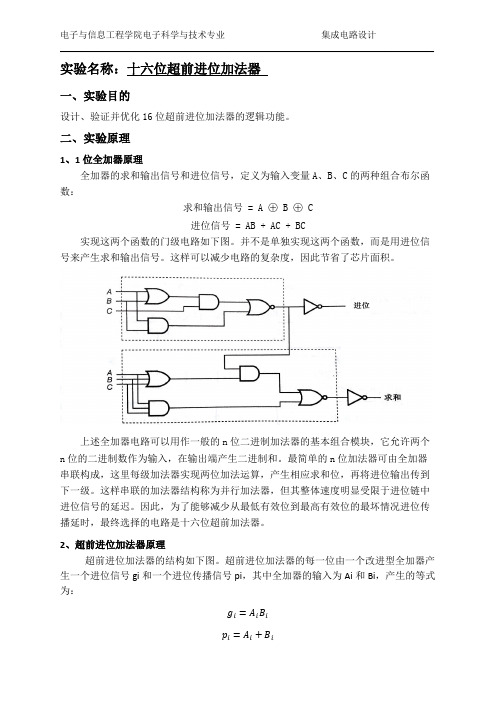
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号 = A ⊕ B ⊕ C进位信号 = AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
verilog实现加法器

verilog实现加法器半加器如果不考虑来⾃低位的进位将两个1⼆进制数相加,称为半加。
实现半加运算的逻辑电路称为半加器。
真值表>> 逻辑表达式和s=ab′+a′b>> 逻辑表达式进位输出co=abverilog codemodule halfadder(output s, //sumoutput co, //carryinput a,input b);assign s = a ^ b;assign co = a & b;//assign {co,s} = a + b;endmoduletestbenchmodule halfadder_tb;wire s;wire co;reg a;reg b;initialbegina = 0;b = 0;#10 a = 0 ;b = 0;#10 a = 0 ;b = 1;#10 a = 1 ;b = 0;#10 a = 1 ;b = 1;#10 $finish;endinitial begin$fsdbDumpfile("test.fsdb");$fsdbDumpvars();endhalfadder u_halfadder(.s(s),.co(co),.a(a),.b(b));endmodule全加器在将两位多位⼆进制数相加时,除了最低位以外,每位都应该考虑来⾃低位的进位,即将两个对应位的加数和来⾃低位的进位3个数相加。
这种运算称为全加,所⽤的电路称为全加器。
真值表逻辑表达式和s=(a′b′ci′+ab′ci+a′bci+abci′)′>> 逻辑表达式进位输出co=(a′b′+b′ci′+a′ci′)′verilog codemodule fulladder(output s, //sumoutput co, //carry to high bitinput a,input b,input ci //carry from low bit);//RTL levelassign s = ~((~a&~b&~ci)||(a&~b&ci)||(~a&b&ci)||(a&b&~ci));assign co = ~((~a&~b)||(~b&~ci)||(~a&~ci));//assign {co,s} = a + b + ci;endmoduletestbenchmodule fulladder_tb;wire s;wire co;reg a;reg b;reg ci;initialbeginci = 0; a = 0 ;b = 0;#10 ci = 0; a = 0 ;b = 1;#10 ci = 0; a = 1 ;b = 0;#10 ci = 0; a = 1 ;b = 1;#10 ci = 1; a = 0 ;b = 0;#10 ci = 1; a = 0 ;b = 1;#10 ci = 1; a = 1 ;b = 0;#10 ci = 1; a = 1 ;b = 1;#10 $finish;endinitial begin$fsdbDumpfile("test.fsdb");$fsdbDumpvars();endfulladder u_fulladder(.s(s),.co(co),.a(a),.b(b),.ci(ci));endmodule多位加法器串⾏进位加法器依次将低位全加器的进位输出co接到全加器的进位输⼊端ci,就可以构成多位加法器。
verilog乘法运算和加法运算

verilog乘法运算和加法运算【实用版】目录1.引言2.Verilog 乘法运算2.1 乘法运算原理2.2 乘法运算实例3.Verilog 加法运算3.1 加法运算原理3.2 加法运算实例4.总结正文1.引言Verilog 是一种硬件描述语言,常用于数字系统硬件的描述和仿真。
在数字电路中,乘法运算和加法运算是基本的运算。
本文将介绍如何在Verilog 中实现乘法运算和加法运算。
2.Verilog 乘法运算2.1 乘法运算原理在 Verilog 中,乘法运算通常使用循环来实现。
基本原理是将一个数不断乘以 2,直到达到目标数值。
例如,实现一个 4 位乘以 4 位的乘法器,需要将一个 4 位数不断乘以 2,直到结果达到 16 位。
2.2 乘法运算实例以下是一个简单的 4 位乘以 4 位的 Verilog 乘法运算实例:```verilogmodule multiplier_4bit(input [3:0] a, input [3:0] b, output reg [7:0] result);integer i, j;reg [7:0] temp;always @(*)for (i = 0; i < 4; i = i + 1) begintemp = temp + a * b[i];endresult = temp;endmodule```3.Verilog 加法运算3.1 加法运算原理在 Verilog 中,加法运算非常简单,只需要将两个数相加即可。
需要注意的是,如果结果超过某个范围,需要进行溢出处理。
3.2 加法运算实例以下是一个简单的 4 位加法器的 Verilog 实例:```verilogmodule adder_4bit(input [3:0] a, input [3:0] b, output reg [3:0] result);always @(*)result = a + b;endmodule```4.总结通过以上实例,我们可以看到在 Verilog 中实现乘法运算和加法运算的基本方法。
16位超前加法器实验报告

16位超前加法器设计实验一、实验分析:四位超前进位加法器HDL程序:module add4_head ( a, b, ci, s, pp, gg);input[3:0] a;input[3:0] b;input ci;output[3:0] s;output pp;output gg;wire[3:0] p;wire[3:0] g;wire[2:0] c;assign p[0] = a[0] ^ b[0];assign p[1] = a[1] ^ b[1];assign p[2] = a[2] ^ b[2];assign p[3] = a[3] ^ b[3];assign g[0] = a[0] & b[0];assign g[1] = a[1] & b[1];assign g[2] = a[2] & b[2];assign g[3] = a[3] & b[3];assign c[0] = (p[0] & ci) | g[0];assign c[1] = (p[1] & c[0]) | g[1];assign c[2] = (p[2] & c[1]) | g[2];assign pp = p[3] & p[2] & p[1] & p[0];assign gg = g[3] | (p[3] & (g[2] | p[2] & (g[1] | p[1] & g[0])));assign s[0] = p[0] ^ ci;assign s[1] = p[1] ^ c[0];assign s[2] = p[2] ^ c[1];assign s[3] = p[3] ^ c[2];endmodulep表示进位否决信号(pass),如果p为0就否决调前一级的进位输入。
否决的意思就是即使前一级有进位,本级也不会向后一级产生进位输出。
Verilog实现加减乘除计算器

Verilog实现加减乘除计算器主要内容: 1. 按键按下后,进⾏加减乘除操作 2. Verilog往TXT⽂本⽂件中写⼊数据 3. 完成计算模块 4. 最终实现加减乘除计算器1. 实现按键按下后,选择option,进⾏加减乘除操作,除法计算结果为商&余数module jsq(clk,rst_n,key,option,x,y,result,quotient,remainder);parameter N = 16; // 输⼊数的位数input clk; // 输⼊时钟input rst_n; // 低电平有效的复位(清零)input key;input [1:0]option;input [N-1:0] x;input [N-1:0] y;output [2*N-1:0] result;output [N-1:0] quotient; //输出计算的商output [N-1:0] remainder; //输出计算的余数reg [2*N-1:0] result_r;reg [N-1:0] quotient_r,remainder_r;always @ (posedge clk or negedge rst_n)beginif (!rst_n)beginresult_r <= 1'b0;quotient_r <= 1'b0;remainder_r <= 1'b0;endelsebeginif (key == 1'b0)begin//按键按下case(option)2'b00: result_r = x + y;2'b01: result_r <= x + (~y + 1'b1);2'b10: result_r = x * y;2'b11: //result_r = x / y;beginquotient_r = x / y;remainder_r = x % y;endendcaseendelsebegin// 按键释放result_r <= 1'b0;quotient_r <= 1'b0;remainder_r <= 1'b0;endendendassign result = result_r ;assign quotient= quotient_r;assign remainder = remainder_r;endmoduleView Code`timescale 1ns/1ps`define clock_period 20module jsq_tb;reg clk;reg rst_n;reg key;reg [1:0]option;reg [15:0] x,y;wire [31:0] result;wire [15:0] quotient;wire [15:0] remainder;initial beginclk = 1'b1;rst_n = 1'b0;key = 1'b1; // 复位时,按键释放# 20//复位20nsrst_n = 1'b1;# 20key = 1'b0;option = 2'b10;# 100key = 1'b1;# 20key = 1'b0;option = 2'b11;# 100// key = 1'b1;// # 20$stop;endalways #(`clock_period/2) clk = ~clk; //50Mjsq #(.N(16)) jsq_0(.clk(clk),.rst_n(rst_n),.key(key),.option(option),.x(x),.y(y),.result(result),.quotient(quotient),.remainder(remainder));initial beginx = 0;repeat(20)#(`clock_period) x = {$random}%100; //通过位拼接操作{}产⽣0—59范围的随机数endinitial beginy = 0;repeat(20)#(`clock_period) y = {$random}%50;end/*integer i;initial beginx = 0;y = 0;for(i = 0; i < 20; i = i + 1)begin//利⽤$random系统函数产⽣随机数。
用verilog编写16位加法器乘法器自动售货机

Verilog课程实验报告实验1十六位超前进位加法器系统设计要求用超前进位加法器实现一个有符号位的16位加法器,并且考虑溢出的情况详细设计根据超前进位加法器的原理Co = G | ( P & Ci ) S = P ^ Ci 设计出4位加法器的子模块,然后通过4个4位加法器的相连来得到十六位的加法器。
原理如下图所示。
溢出用flag=0表示。
F A F A F A F AP 0G 1P 0G1P 2G2P 3G 3C o ,3C o ,2Co ,1Co ,0C i ,0F A F A F A F AP 0G1P 0G1P 2G2P 3G 3Co ,2C o ,1Co ,0C i,0C o ,3M u l t i p l e x e rB P =P o P 1P 2P 3Id e a : If (P 0 a n d P 1 a n d P 2 a n d P 3 = 1)th e n C o 3 = C 0, e ls e “k ill” o r “g e n e r a te ”.程序"module sixteenaddertest;wire [15:0] s;reg [15:0]a,b;wire flag;parameter times=5;a=-10743,,b==11372没有溢出,sto=0.通过这个实验验证了s=a+b,实现了带符号位的加法器。
实验二十六位加减法器系统设计要求将加法器和减法器结合到一起,实现带符号位的16位加减法运算,并考虑溢出。
详细设计在16位加法器的基础上,加上一条判断语句,如果出现减的操作,被减数取反加一,这样就实现了减的运算,用add_sub来表示加减运算符,当add_sub=0时候实现的是减运算,add_sub=1的时候实现的是加运算。
程序"module adder_sub_test;wire [15:0] s;reg [15:0]a,b;reg add_sub;wire flag;initial当a=-4659 b=12817 add_sub=0,减操作,输出s=-17476,无溢出,flag=0.当a=562 b=-24223 add_sub=1,加操作,输出s=-23661,无溢出,flag=0.通过以上的结果分析,此程序实现了带符号位的加减法的功能。
74181 ALU的设计及16位加法功能验证

74181 ALU的设计及16位加法功能验证This is a controlled document.Printed copies must have the revision number verified prior to each use.修改记录分工情况目录修改记录................................................................................................... 错误!未定义书签。
分工情况................................................................................................... 错误!未定义书签。
目录................................................................................................... 错误!未定义书签。
1.0B关于本文 ......................................................................................... 错误!未定义书签。
1.1 4B目的............................................................................................ 错误!未定义书签。
1.2 5B术语列表........................................................................................ 错误!未定义书签。
1.3 6B相关文档........................................................................................ 错误!未定义书签。
基于FPGA的模可变16进制加法器的设计

课程设计任务书学生姓名:兰翔专业班级:电子科学与技术2班指导教师:葛华工作单位:信息工程学院题目:模可变16位加法计数器设计初始条件:QuartusII6.0,微机要求完成的主要任务:深入学习Verilog HDL语言与FPGA理论知识。
利用QuartusII强大的硬件语言处理功能,数字电路仿真功能以及波形处理功能,实现模可变16位加法计数器设计。
1.利用Verilog HDL语言描述计数器功能;2.用QuartusII对Verilog HDL语言进行仿真;3. 撰写《EDA技术应用实践》课程设计说明书。
时间安排:学习Verilog HDL语言的概况第1天学习Verilog HDL语言的基本知识第2、3天学习QuartusII的应用环境,仿真功能。
第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)A BSTRACT.......................................................... I I1.设计任务 (1)1.1初始条件 (1)1.2课题要求 (1)1.3设计要求 (1)2.Q UARTUS II简介 (2)3.课题内容 (3)3.1 总体框图 (3)3.2 各部分功能 (3)3.2.1按键触发 (3)3.2.2 LED显示部分 (5)3.2.3计数部分 (6)4.心得体会 (8)参考文献 (9)附录一V ERILOG HDL原程序 (10)附录二总原理图 (15)摘要FPGA(Field Programmable Gate Array)即“现场可编程门阵列”是应着当代微电子技术迅猛发展而产生的一种技术,到现在为止,已经存在了27年。
由于其电路执行速度快、上市时间短、成本低廉、可靠性高、易于维护升级而被人们所青睐,目前已经广泛用于通信、信号处理、嵌入式处理器、图形处理和工业控制的领域。
本次课设就是在Altera公司的FPGA设计平台QuartusII上进行的计数器设计。
verilog 16bit加法

在Verilog中,你可以使用内置的"+"运算符来实现16位整数的加法。
以下是一个简单的16位加法器的示例:
```verilog
module adder16(
input [15:0] a,
input [15:0] b,
output reg [15:0] sum
);
always @* begin
sum = a + b;
end
endmodule
```
在这个模块中,`a`和`b`是两个16位宽的输入,而`sum`是输出。
在always块中,我们执行加法操作并将结果存储在`sum`中。
注意,如果`a`和`b`的和超过16位,结果将被截断为16位。
你可以通过以下方式使用此模块:
```verilog
module top;
reg [15:0] a, b;
wire [15:0] sum;
adder16 adder(.a(a), .b(b), .sum(sum));
initial begin
a = 16'hA5; // 十进制数173
b = 16'h5A; // 十进制数138
#10;
$display("Sum = %h", sum); // 显示结果
end
endmodule
```
在这个顶层模块中,我们实例化了一个`adder16`模块,并连接了它的输入和输出。
然后我们设定了`a`和`b`的值,并在仿真开始时显示了它们的和。
数字集成电路课程设计16位加法器

数字集成电路课程设计——16位加法器设计参数:*输入两个16位的补码*输出一个17位的补码*允许采用流水线、单元复用等技术实现设计要求:*使用RTL级Verilog描述加法器架构*使用门级验证加法器功能(ModelSim等仿真)*优化方向:加法器等效总门数最少*等效门数计算示例:INV=1, NOR2=NAND2=2, DFF=4最终优化结果:图1.1单个全加器单元的最终优化方案图1.2 第17位结果的运算电路最终总共等效门数= 16 X 17 + 7 = 279仿真结果:1 2 3 4 5图2. ModelSim仿真结果如图2所示,箭头1所指区域为两个16位全0的加数,无进位,输出和为0;箭头2所指区域为0与1000000000000000(-32768)相加,无进位,输出和为11000000000000000(-32768);箭头3所指区域为0与1111111111111111(-1)相加,无进位,输出和为11111111111111111(-1);箭头4所指区域为-1与1000000000000000(-32768)相加,无进位,输出和为10111111111111111(-32769);箭头4所指区域为-1与1000000000000000(-32768)相加,进位为1,输出和为11000000000000000(-32768)。
可见已正确实现了16位补码加法器的功能。
设计思路:首先,我们需要明确加法器的设计。
按照题目的要求,我们的加法器必须满足以下几个原则:1、16位加法器,且可以计算出第17位的进位;2、可以计算补码;3、设计出的结构门数最少.由上面的要求,我们可以有对应的设计:1.我们假定16位数据本身就是以补码形式储存的,那么最高位就是符号位,0代表正数,1代表负数;由此,我们可以根据二进制加法的规则得知,计算补码不需要对储存的补码进行任何形式的修改,利用正常的全加器结构就可以计算出正确的结论,包括位数扩展的要求也能满足;2.要完成17位的补码计算,需要进行符号位扩展,也就是将加数和被加数的最高位重复一次变成17位的数据,如1000000000000000变为11000000000000000;在编码的时候,需要17个加法器,但是最后一个加法器的加数和被加数重复使用16位的数据,而进位则采用16位得到的进位;3.加法器必须是一般意义上的加法器,除非采用流水线结构,否则不应使用时序逻辑,如下图所示的设计就不合理。
16位超前进位加法器的verilog实现

H a r b i n I n s t i t u t e o f T e c h n o l o g yv e r i l o g实验报告(1)设计题目: 16位超前进位加法器班级:姓名:学号:工业大学2015年6月一、功能描述加法运算是最基本的运算,所有其他基本算术运算都是以加法运算为基础。
但因为加法运算存在进位问题,使得某一位计算结果的得出和所有低于它的位相关,因此,为了减少进位传输所耗的时间,提高计算速度,我们可以采用超前进位加法器,它是利用输入信号来预先产生高位进位信号,从而减少进位从低位到高位的传递时间。
超前进位加法器,不同于串行进位加法器,对于每一位的结果是否有进位,不需要等前一位的进位结果计算出来,而是只要输入A,B 到来就可以经过一些列的逻辑运算同时计算出各位是否有进位。
理论上讲无论多少位的加法器都可以设计成为超前进位加法器,但是当位数很大的时候,超前进位加法器的逻辑会变得异常复杂,而失去了使用的意义,所以大多数超前进位加法器做到4位,而多于4位的要求,就用多个超前进位加法器级联实现,所以本设计要进行16位的加法运算,我们可以将其分成四组,组采用超前进位,组间采用串行进位,既提高了运算速度,又不至于采用过多的门数。
二、设计方案1.设计原理首先做两个传递函数;进位产生函数Gi和进位传送函数Gi=Ai BiPi=Ai^Bi当Gi=1时会产生进位,而当Pi=1时会使进位输入传到输出。
根据全加器原理,第i位的进位及和的输出可表示为Ci =Gi+PiCi-1Si =Pi^Ci-1由此可得各位的进位输出表达式C1=G1+P1C0C2=G2+P2G1+P2P1C0C3=G3+P3G2+P3P2G1+P3P2P1C0C4=G4+P4G3+P4P3G2+P4P3P2G1+P4P3P2P1C0…这样经过函数Pi和函数Qi产生一级时间延迟,经过计算C产生一级时延迟,则A,B输入一旦产生即可算出结果。
性能改进的16位超前进位加法器_李嘉

性能改进的16位超前进位加法器李 嘉,蒋 林(西安邮电学院 陕西西安 710061)摘 要:加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
在不同的场合使用的加法器对其要求也不同,有的要求速度更快,有的要求面积更小。
基于速度更快的要求,对3种常用加法器从结构与性能上进行比较,给出了综合面积与速度的比较。
进而对超前进位加法器进行了进一步改进,加入了流水线结构设计,大大提高了其速度性能。
关键词:串行进位加法器;超前进位加法器;流水线;逻辑综合中图分类号:T P342+.21 文献标识码:B 文章编号:1004-373X(2007)22-172-03A 16-bit C LA with Improved PerformanceL I Jia,JIA N G L in(Xi an Institute o f P ost and T elecom municat i o ns,Xi an,710061,Chi na)Abstract :T he addition o perat ion is the mo st impo rtant fundamental o per ation,all other o perat ions including subtr action multiplication division and modular mult iplication can be implemented by addition operatio n.A dders using at var ious cases are different since the requirement are different.Some ask for faster,others ask for smaller.T hree co mmon used adder s are com -pared in the st ruct ur al and perfo rmance,based o n the requirement o f faster.T hen so me amelio ratio ns on the CL A are made by adding pipline str ucture to impro ve its perfo rmance fo r w or king faster.Keywords :ripple adder ;car ry loo k -ahead adder;pipeline;log ic sy nthesis收稿日期:2007-04-23加法运算是最重要最基本的运算,所有的其他基本算术运算,减、乘、除、模乘运算最终都能归结为加法运算。
16位超前进位加法器实验报告
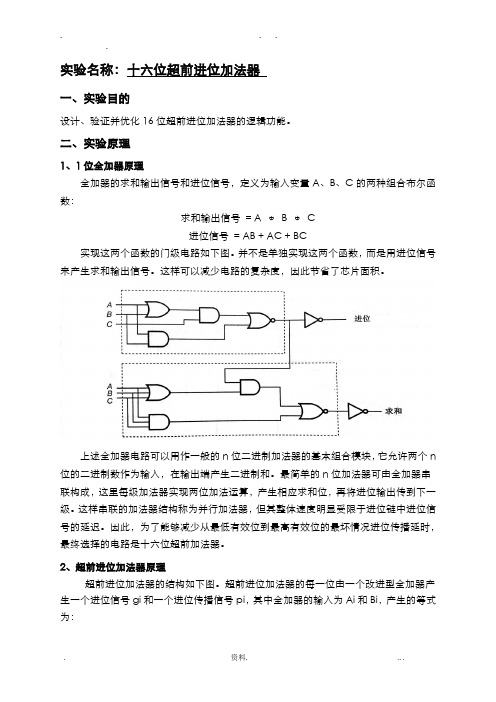
实验名称:十六位超前进位加法器一、实验目的设计、验证并优化16位超前进位加法器的逻辑功能。
二、实验原理1、1位全加器原理全加器的求和输出信号和进位信号,定义为输入变量A、B、C的两种组合布尔函数:求和输出信号= A ⊕B ⊕C进位信号= AB + AC + BC实现这两个函数的门级电路如下图。
并不是单独实现这两个函数,而是用进位信号来产生求和输出信号。
这样可以减少电路的复杂度,因此节省了芯片面积。
上述全加器电路可以用作一般的n位二进制加法器的基本组合模块,它允许两个n 位的二进制数作为输入,在输出端产生二进制和。
最简单的n位加法器可由全加器串联构成,这里每级加法器实现两位加法运算,产生相应求和位,再将进位输出传到下一级。
这样串联的加法器结构称为并行加法器,但其整体速度明显受限于进位链中进位信号的延迟。
因此,为了能够减少从最低有效位到最高有效位的最坏情况进位传播延时,最终选择的电路是十六位超前加法器。
2、超前进位加法器原理超前进位加法器的结构如下图。
超前进位加法器的每一位由一个改进型全加器产生一个进位信号gi和一个进位传播信号pi,其中全加器的输入为Ai和Bi,产生的等式为:改进的全加器的进位输出可由一个进位信号和一个进位传输信号计算得出,因此进位信号可改写为:式中可以看出,当gi = 1(Ai = Bi = 1)时,产生进位;当pi = 1(Ai =1或Bi = 1)时,传输进位输入,这两种情况都使得进位输出是1。
近似可以得到i+2和i+3级的进位输出如下:下图为一个四位超前进位加法器的结构图。
信号经过pi和gi产生一级时延,经过计算C产生一级时延,则A,B输入一旦产生,首先经过两级时延算出第1轮进位值C’不过这个值是不正确的。
C’再次送入加法器,进行第2轮2级时延的计算,算出第2轮进位值C,这一次是正确的进位值。
这里的4个4位超前进位加法器仍是串行的,所以一次计算经过4级加法器,一级加法器有2级时延,因此1次计算一共经过8级时延,相比串行加法器里的16级时延,速度提高很多。
verilog乘法运算和加法运算

verilog乘法运算和加法运算【原创实用版】目录1.Verilog 简介2.乘法运算的实现2.1 4 位乘 2 位2.2 扩展到任意位数3.加法运算的实现3.1 4 位加 4 位3.2 扩展到任意位数4.总结正文一、Verilog 简介Verilog 是一种硬件描述语言,主要用于数字系统的设计和验证。
它的语法简单易学,可以描述各种数字电路,包括组合逻辑、时序逻辑和混合信号电路。
Verilog 中包含各种基本的逻辑门、寄存器、计数器等组件,用户可以根据需要进行组合和连接。
二、乘法运算的实现1.4 位乘 2 位的乘法运算在 Verilog 中,我们可以使用循环来实现乘法运算。
例如,实现 4 位乘 2 位的乘法运算,可以使用以下代码:```verilogmodule multiplier_4bit_2bit (input [3:0] a,input [1:0] b,output [7:0] result);reg [7:0] temp;integer i;always @(*) beginfor (i = 0; i < 4; i = i + 1) begintemp[i] = a[i] * b;endresult = temp;endendmodule```2.扩展到任意位数如果要实现任意位数的乘法运算,可以采用类似的方法,只需要将循环次数和寄存器位数相应地调整即可。
例如,实现 16 位乘 16 位的乘法运算,可以使用以下代码:```verilogmodule multiplier_16bit_16bit (input [15:0] a,input [15:0] b,output [31:0] result);reg [31:0] temp;integer i;always @(*) beginfor (i = 0; i < 16; i = i + 1) begintemp[i] = a[i] * b[i];endresult = temp;endendmodule```三、加法运算的实现1.4 位加 4 位的加法运算在 Verilog 中,实现加法运算同样可以使用循环。
16位超前进位加法器的设计_谢莹

第27卷第4期合肥工业大学学报(自然科学版)Vol.27No.4 2004年4月JO URN AL O F HEFEI UN IV ERSITY O F TECHNO LOGY Apr.2004 16位超前进位加法器的设计谢 莹, 陈 琳(安庆师范学院教育技术系,安徽安庆 246011)摘 要:电子计算机是由具有各种逻辑功能的逻辑部件组成的,加法器就属于其中的组合逻辑电路。
如果对传统的加法器电路进行改进,在超前进位链的基础上,用一种新的超前进位链树的设计方法不仅可以克服串行进位加法器速度低的缺点,也可以解决单纯的超前进位加法器带负载能力不足等问题,从而在实际电路中使加法器的运算速度达到最优。
根据这种理论,可以推导得到最优的任意位加法器。
关键词:半加器;全加器;超前进位加法器;4位超前进位加法器;16位超前进位加法器中图分类号:T P342.21 文献标识码:A 文章编号:1003-5060(2004)04-0450-05Design of16-bit carry look-ahead adderXIE Ying, CHEN Lin(Dept.of Ed ucational Technology,Anqing Teachers College,Anqing246011,China)Abstract:A com puter is com prised of so me logic parts w hich hav e serial lo gic functions,and the adder is one o f the combine logic circuits.In o rder to im prov e the traditio nal adder circuit,based on the carry lo ok-ahead techno logy,a new desig n o f ca rry look-ahead chain is presented so tha t the low speed of serial adders and the less car ry capacity of the pure carry look-ahead adder ca n be ov erco me.Thus the o ptimum com pute speed can be achiev ed in the real circuit.Based on the presented idea,the ex cellent ra ndo m bit adder can be deduced.Key words:half adder;full adder;carry look-ahead adder;4-bit carry look-ahead adder;16-bit carry lo ok-ahead adder0 引 言电子计算机是由具有各种逻辑功能的逻辑部件组成的,这些逻辑部件按其功能结构又可分为组合逻辑电路和时序逻辑电路。
用verilog编写的32位超前进位加法器代码

//超前进位加法器`define word_size 32`define word [`word_size-1:0]`define n 4`define slice [`n-1:0]`define s0 (1*`n)-1:0*`n`define s1 (2*`n)-1:1*`n`define s2 (3*`n)-1:2*`n`define s3 (4*`n)-1:3*`n`define s4 (5*`n)-1:4*`n`define s5 (6*`n)-1:5*`n`define s6 (7*`n)-1:6*`n`define s7 (8*`n)-1:7*`nmodule c_adder (a,b,cin,s,cout); //顶层模块input`word a,b;input cin;output`word s;output cout;wire[7:0] gg,gp,gc; //wire[3:0] ggg,ggp,ggc; //wire gggg,gggp; ////first levelbitslice i0(a[`s0],b[`s0],gc[0],s[`s0],gp[0],gg[0]); bitslice i1(a[`s1],b[`s1],gc[1],s[`s1],gp[1],gg[1]); bitslice i2(a[`s2],b[`s2],gc[2],s[`s2],gp[2],gg[2]); bitslice i3(a[`s3],b[`s3],gc[3],s[`s3],gp[3],gg[3]); bitslice i4(a[`s4],b[`s4],gc[4],s[`s4],gp[4],gg[4]); bitslice i5(a[`s5],b[`s5],gc[5],s[`s5],gp[5],gg[5]); bitslice i6(a[`s6],b[`s6],gc[6],s[`s6],gp[6],gg[6]); bitslice i7(a[`s7],b[`s7],gc[7],s[`s7],gp[7],gg[7]); //second levelcla c0(gp[3:0],gg[3:0],ggc[0],gc[3:0],ggp[0],ggg[0]); cla c1(gp[7:4],gg[7:4],ggc[1],gc[7:4],ggp[1],ggg[1]); assign ggp[3:2]=2'b11;assign ggg[3:2]=2'b00;//third levelcla c2(ggp,ggg,cin,ggc,gggp,gggg);assign cout=gggg|(gggp&cin);endmodule//求和并按输出a,b,cin分组module bitslice(a,b,cin,s,gp,gg);input`slice a,b;input cin;output`slice s;output gp,gg;wire`slice p,g,c;pg i1(a,b,p,g);cla i2(p,g,cin,c,gp,gg);sum i3(a,b,c,s);endmodule//计算传播值和产生值的PG模块module pg(a,b,p,g);input`slice a,b;output `slice p,g;assign p=a|b;assign g=a&b;endmodule//计算sum值的sum模块module sum(a,b,c,s);input`slice a,b,c;output`slice s;wire`slice t=a^b;assign s=t^c;endmodule//n-bit 超前进位模块module cla (p,g,cin,c,gp,gg);input`slice p,g; //输出的propagate bit (传送值)和generate bit(生成值)input cin; //进位输入output`slice c; //为每一位产生进位output gp,gg; //传播值和进位制function [99:0] do_cla; //该函数内将为每个位计算其进位值input `slice p,g;input cin;begin: labelinteger i;reg gp,gg;reg`slice c;gp=p[0];gg=g[0];c[0]=cin;for (i=1;i<`n;i=i+1)begin//C0=G0+P0C_1//C1=G1+P1C0=(G1+P1G0)+P1P0C_1 gp=gp&p[i];gg=(gg&p[i])|g[i];c[i]=(c[i-1]&p[i-1])|g[i-1]; enddo_cla={c,gp,gg};endendfunctionassign {c,gp,gg}=do_cla(p,g,cin); endmodule。
