1-2第二节 公路测设中的测量坐标系
测量中的常用坐标系及坐标转换概述

测量中的常用坐标系及坐标转换概述在测量领域中,常用的坐标系包括直角坐标系、极坐标系和球坐标系。
不同的坐标系适用于不同的测量任务和数据处理需求,而坐标转换则是将不同坐标系下的测量数据相互转换的方法。
本文将对常用坐标系及坐标转换进行概述。
1.直角坐标系直角坐标系是最常见的坐标系之一,通常用于描述二维或三维空间中的点的位置。
在二维直角坐标系中,一个点的位置可以由两个坐标值(x,y)表示。
而在三维直角坐标系中,一个点的位置可以由三个坐标值(x,y,z)表示。
直角坐标系中的坐标轴是相互垂直的,可以方便地描述点的位置和进行测量。
2.极坐标系极坐标系是另一种常用的坐标系,通常用于描述平面上的点的位置。
极坐标系由一个极径和一个极角组成。
极径表示点到原点的距离,极角表示点与正x轴的夹角。
在极坐标系中,一个点的位置可以由(r,θ)表示。
极坐标系在一些特定情况下对测量任务更加方便,例如描述圆形或对称物体的位置。
3.球坐标系球坐标系用于描述三维空间中的点的位置。
球坐标系由一个极径、一个极角和一个方位角组成。
极径表示点到原点的距离,极角表示点与正z轴的夹角,方位角表示点在xy平面上的投影与正x轴的夹角。
在球坐标系中,一个点的位置可以由(r, θ, φ)表示。
球坐标系在描述球体或对称物体的位置时非常有用。
在测量中,常常需要在不同的坐标系之间进行转换以满足不同的需求。
以下是常见的坐标转换方法:1.直角坐标系到极坐标系的转换从直角坐标系到极坐标系的转换可以通过以下公式实现:极径 r = sqrt(x^2 + y^2)极角θ = atan2(y, x)其中,sqrt表示平方根,atan2表示求反正切值。
2.极坐标系到直角坐标系的转换从极坐标系到直角坐标系的转换可以通过以下公式实现:x = r * cos(θ)y = r * sin(θ)3.直角坐标系到球坐标系的转换从直角坐标系到球坐标系的转换可以通过以下公式实现:极径 r = sqrt(x^2 + y^2 + z^2)极角θ = acos(z / r)方位角φ = atan2(y, x)4.球坐标系到直角坐标系的转换从球坐标系到直角坐标系的转换可以通过以下公式实现:x = r * sin(θ) * cos(φ)y = r * sin(θ) * sin(φ)z = r * cos(θ)需要注意的是,在进行坐标转换时,要确保所使用的公式和单位系统是一致的,否则会导致转换结果错误。
工程测量的平面直角坐标系和数学坐标系

工程测量的平面直角坐标系和数学坐标系1. 引言工程测量中使用的平面直角坐标系和数学坐标系是确定地理空间位置和方向的基本工具。
它们是工程测量中不可或缺的一部分,用于准确测量、标定和规划工程项目。
本文将介绍平面直角坐标系和数学坐标系的定义、特点和应用。
2. 平面直角坐标系平面直角坐标系是一种常用的表示平面位置的坐标系。
它由两条相互垂直的直线组成,分别称为X轴和Y轴。
这两条直线的交点被称为原点,用坐标(0, 0)表示。
X轴和Y轴上的单位长度可以是任意选择的,常用的单位有米、公里等。
在平面直角坐标系中,任意一点的位置可以用有序数对(x, y)表示,其中x表示点在X轴上的坐标值,y表示点在Y轴上的坐标值。
坐标值的正负表示点在原点的左侧、右侧、上方或下方。
平面直角坐标系的特点是简单直观、易于计算,适用于平面上大部分工程测量问题。
它广泛应用于工程建设、地理测量、土木工程等领域。
3. 数学坐标系数学坐标系是一种更广义的坐标系,用于表示多维空间中的位置。
它与平面直角坐标系类似,但可以扩展到三维甚至更高维空间。
数学坐标系常用的表示方式是通过多个坐标轴来描述空间的各个方向。
在二维数学坐标系中,除了X轴和Y轴之外,还可以引入Z轴。
三维数学坐标系中的任意一点的位置可以用有序数对(x, y, z)表示,其中x表示点在X轴上的坐标值,y表示点在Y轴上的坐标值,z表示点在Z轴上的坐标值。
类似于平面直角坐标系,坐标值的正负表示点在原点的位置关系。
数学坐标系有许多重要的应用,如计算机图形学、物理学、工程测量等。
通过数学坐标系,我们可以更准确地描述和计算三维空间中的各种问题。
4. 应用4.1 工程建设平面直角坐标系在工程建设中有广泛的应用。
在建筑和土木工程中,平面直角坐标系用于确定建筑物、道路、桥梁等的准确位置和方向。
通过对不同建筑元素的平面定位,可以实现各个部分的精确拼接和施工。
4.2 地理测量在地理测量和地理信息系统中,平面直角坐标系被用于将地球曲面上的地理位置转换为平面上的坐标值。
测量中的坐标系有哪些

测量中的坐标系有哪些在测量领域中,坐标系是用来描述和定位物体、点或空间位置的重要工具。
不同的测量任务和应用需要使用不同类型的坐标系。
本文将介绍测量中常见的几种坐标系。
1. 直角坐标系直角坐标系是最常见和最基本的坐标系之一。
它使用直角坐标来描述一个点在平面或空间中的位置。
在二维情况下,直角坐标系由水平的 x 轴和垂直的 y 轴组成;在三维情况下,直角坐标系由 x、y 和 z 轴组成。
每个轴上的刻度表示该方向上的距离。
直角坐标系以原点为起始点,通过坐标轴上的正负方向来确定一个点的位置。
例如,在二维直角坐标系中,一个点的位置可以由两个坐标值(x, y)表示,其中 x表示点与 y 轴的距离,y 表示点与 y 轴的距离。
2. 柱坐标系柱坐标系是一种用极坐标来描述点位置的坐标系。
它通常用于描述平面上的点。
柱坐标系由一个极径和一个极角组成。
极径表示点到原点的距离,极角表示点到极轴(一条从原点引出的射线)的角度,一般使用弧度作为单位。
在柱坐标系中,点的坐标表示为(r, θ)。
其中,r 表示极径,θ 表示极角。
例如,一个点的坐标为(2, π/4),表示该点到原点的距离为 2,与极轴的夹角为π/4。
3. 球坐标系球坐标系是一种在三维空间中描述点位置的坐标系。
与柱坐标系类似,球坐标系也使用极径和极角来表示点的坐标。
但是,球坐标系添加了一个与垂直轴的角度。
球坐标系中,点的坐标表示为(r, θ, φ)。
其中,r 表示点到原点的距离,θ 表示与正 x 轴的夹角,φ 表示与垂直轴的夹角。
例如,一个点的坐标为(3, π/4, π/2),表示该点到原点的距离为 3,与正 x 轴的夹角为π/4,与垂直轴的夹角为π/2。
4. 区域坐标系区域坐标系是一种二维坐标系,通常用于描述一个区域或区域中的点的位置。
在区域坐标系中,通常会选择一个特定的参考点作为坐标原点,并定义一个规则来测量点与原点的位置。
区域坐标系常用于地理测量和地图制作。
在地理测量中,经纬度就是一种区域坐标系。
测量中常用的坐标系统

测量中常用的坐标系一、坐标系类型1、大地坐标系定义:大地测量中以参考椭球面(不准确)为基准面建立起来的坐标系。
一定的参考椭球和一定的大地原点上的大地起算数据,确定了一定的坐标系。
通常用参考椭球参数和大地原点上的起算数据作为一个参心大地坐标系建成的标志。
大地坐标(地理坐标):将某点投影到椭球面上的位置用大地经度L和大地纬度B表示,( B , L)统称为大地坐标。
大地高H:某点沿投影方向到基准面(参考椭球面)的距离。
在大地坐标系中,某点的位置用(B , L,H)来表示。
2、空间直角坐标系定义:以椭球体中心为原点,起始子午面与赤道面交线为X 轴,在赤道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴。
在空间直角坐标系中,某点的位置用(X,Y,Z)来表示。
3、平面直角坐标系在小区域进行测量工作若采用大地坐标来表示地面点位置是不方便的,通常采用平面直角坐标系。
测量工作以x轴为纵轴,以y轴为横轴投影坐标:为了建立各种比例尺地形图的控制及工程测量控制,一般应将椭球面上各点的大地坐标按照一定的规律投影到平面上,并以相应的平面直角坐标表示。
4、地方独立坐标系基于限制变形、方便、实用和科学的目的,在许多城市和工程测量中,常常会建立适合本地区的地方独立坐标系,建立地方独立坐标系,实际上就是通过一些参数来确定地方参考椭球与投影面。
二、国家大地坐标系1.1954年北京坐标系(BJ54旧)坐标原点:前苏联的普尔科沃。
参考椭球:克拉索夫斯基椭球。
平差方法:分区分期局部平差。
存在问题:(1)椭球参数有较大误差。
(2)参考椭球面与我国大地水准面存在着自西向东明显的系统性倾斜。
(3)几何大地测量和物理大地测量应用的参考面不统一。
(4)定向不明确。
2.1980年国家大地坐标系(GDZ80)坐标原点:陕西省泾阳县永乐镇。
参考椭球:1975年国际椭球。
平差方法:天文大地网整体平差。
特点:(1)采用1975年国际椭球。
(2)参心大地坐标系是在1954年北京坐标系基础上建立起来的。
(整理)公路测量坐标系的建立

摘要】本文以公路测量为例,较详细地论述了在线路测量中应考虑的变形因素,以及解决变形的办法,详细地叙述了建立独立坐标系的作用及建立这种坐标系的六种方法,并介绍了因提高归化高程面而产生新椭球后的一些椭球常数的计算方法和步骤。
此外,本文还对当路线跨越相邻投影带时,需要进行相邻带的坐标换算这一问题进行了阐述。
【关键字】独立坐标系高斯投影带抵偿高程面新椭球常数坐标转换归化高程面线路控制测量中坐标系统的建立与统一方法第一章概述铁路、公路、架空送电线路以及输油管道等均属于线型工程,它们的中线统称线路。
一条线路的勘测和设计工作,主要是根据国家的计划与自然地理条件,确定线路经济合理的位置。
为达此目的,必须进行反复地实践和比较,才能凑效。
线路在勘测设计阶段进行的控制测量工作,称线路控制测量,在线路控制测量过程中,由于每条线路不可能距离较短,有的可能跨越一个带,二个带甚至更多,所以,在线路控制测量中,长度变形是一个不可避免的问题,但我们可以采取一些措施来使长度变形减弱,将长度变形根据施测的精度要求和测区所处的精度范围控制在允许的范围之内。
最有效的措施就是建立与测区相适应的坐标系统.坐标系统是所有测量工作的基础.所有测量成果都是建立在其之上的,一个工程建设应尽可能地采用一个统一的坐标系统.这样既便于成果通用又不易出错.对于一条线路,如果长度变形超出允许的精度范围,我们将建立新的坐标系统加以控制.这就涉及到一个非常关键的问题,既,坐标系统的建立与统一.对于不同的情况,我们可以采用适应的方法尽可能建立统一的坐标系统,且使其长度变形在允许范围之内.本文以公路控制测量为例,详细论述了线路控制测量中坐标系统的建立与统一方法.第二章坐标系统的建立当对一条线路进行控制测量时,首先应根据已有资料判断该测区是否属同一投影带和长度变形是否在允许范围之内.这样我们就可以判断是否需要建立新的坐标系统和怎样建立,下面对此进行详细讨论.§2.1 相对误差对变形的影响与国家点联测的情况:我们的每项测量工作都是在地球表面上进行的,而要将实地测量的真实长度归化到高斯平面上,应加入二项改正.这样就改变了其真实长度,这种高斯投影平面上的长度与地面长度之差,称之为长度综合变形,其计算公式为,£=+Ym²*S/2R²-Hm*s/Ra取:R=Ra=6371Km.S=s将其写成相对变形的形式并代入数子:£/s=(0.00123y²-15.7H)*10y:测区中心横坐标(Km)H:测区平均高程(Km)依据我国的工程测量规范规定,建立平面控制网的坐标系统应该保证长度综合变形不超过2.5cm/km.(相对变形不超过1/40000)。
测量坐标系定义

测量坐标系定义1. 引言在测量学中,坐标系是非常重要的概念。
测量坐标系是用来描述和表示对象位置和方向的方法。
通过定义一个适当的坐标系,可以实现对对象的准确测量和定位。
本文将介绍测量坐标系的定义及其主要特征。
2. 坐标系的概念坐标系是由坐标轴和原点组成的空间结构。
在二维坐标系中,通常有两个坐标轴,分别是水平的x轴和垂直的y轴。
在三维坐标系中,除了水平的x轴和垂直的y轴外,还有一个竖直的z轴。
坐标轴上的每个点都有一个唯一的坐标值,用于表示该点在各轴上的位置。
3. 测量坐标系的定义测量坐标系是一种特殊的坐标系,用于测量和描述物体的位置和方向。
其定义如下:1.原点:测量坐标系的原点是一个固定的参考点,用作坐标轴的交汇点。
通常选取物体的某个特定点作为原点。
2.坐标轴:测量坐标系至少有两个坐标轴,分别是水平的x轴和垂直的y轴。
在三维空间中,还会有一个竖直的z轴。
坐标轴的方向和单位需要根据实际情况进行定义。
3.坐标系方向:坐标系方向通常遵循右手法则。
在二维坐标系中,x轴正方向指向右侧,y轴正方向指向上方。
在三维坐标系中,x轴正方向指向前方,y轴正方向指向右方,z轴正方向指向上方。
4.坐标值:坐标值用于表示物体在各轴上的位置。
在二维坐标系中,坐标值为一个二元组(x, y)。
在三维坐标系中,坐标值为一个三元组(x, y, z)。
4. 测量坐标系的特征测量坐标系具有以下几个特征:1.唯一性:每个对象在测量坐标系中都有唯一的坐标值,能够准确描述其位置和方向。
2.相对性:测量坐标系是相对于测量对象而言的。
不同的对象可以采用不同的测量坐标系,以便更好地描述各自的位置和方向。
3.转换性:测量坐标系之间可以进行转换。
通过合适的坐标转换公式,可以将一个坐标系的坐标值转换为另一个坐标系中的坐标值。
4.精度和误差:测量坐标系的精度取决于测量设备和方法。
测量误差会对坐标的准确性产生影响,因此需要采取适当的措施来减小误差。
5. 总结测量坐标系是用来描述和表示物体位置和方向的方法。
详细论述公路测量中坐标系统确定方法及若干问题

详细论述公路测量中坐标系统确定方法及若干问题摘要:本文笔者结合公路测量工作的特殊性,详细论述了不同地形条件下坐标系统的确定方法,从而有效解决了控制网中长度综合变形对于测量精度所造成的影响,对于实际测量工作具有一定的指导和借鉴意义。
关键词:公路测量;坐标系统;确定方式0前言随着国家经济建设的快速发展,我国公路建设范围的扩大,在高原、山地、丘陵等地区的公路工程也日益增多,而不同地表形态所引起的长度综合变形的主要原因也不尽相同,所以,工程控制网如果采用国家统一的坐标系统,就容易使控制网各边的实际长度发生变化,导致长度的变形,这对于公路测量工作来说有着较大危害。
除此之外,公路测量工作本身也具有着自身的特殊性,如果测量的跨越区域较长且地域狭窄,就会使测量必须经过不同的地形区域,很难满足对于测量精度的要求。
想要对投影长度变形进行有效控制,就必须对国家统一坐标系统的适用范围、长度变形的来源和允许数值等内容进行分析,形成相应的抵偿方法,以便满足不同地形条件下的测量精度要求。
1长度变形的产生及允许值在测量工作中,将真实长度归化到国家统一椭圆球面上时,测量人员应注意加入下面的改正数,即:△s=—(Hm/RA)s(1)在公式(1)中,Hm表示的是长度所在高程相对于椭圆球面的高差;RA 表示的是长度所在方向的椭圆球面的曲率半径;s表示的是实际测量的水平距离。
随后,将椭圆球面的长度投影到高斯平面上,并加入下面的改正数,即:△S=+(y2m/2R2)S(2)在公式(2)中,ym表示的是测量区域中心位置的横坐标;R表示的是测量区域中点位置的曲率半径的平均值。
经过两次改正计算之后,地面上距离的真实长度被改变,像这种在高斯投影面上与地面长度之间的差异,就是长度综合变形,我们可以通过下面的公式对其进行计算,即:δ=+(y2m/2R2)S—(Hm/RA)s(3)想要在不损失精度的同时使计算变得更加简便,我们认为R≈RA≈6371m,S≈s,在将公式(3)转化为相对变形的形式后,我们得出公式(4),即:δ/s=(y2m/2R2)—Hm/R(4)由公式(4)我们可以发现,由国家统一坐标系统所导致的综合变形,与测量区域的平均高程以及所处的投影带位置有关。
公路测量坐标系的选择

摘要:高等级公路勘测主要包括平面控制测量、高程控制测量、地形测量、路线定线与放线、中桩测量、横断面测量,以及路基路面防护排水勘查、沿线设施勘测与调查、环境保护勘测与调查、临时工程勘测与调查、征地动迁勘测与调查等内容。
本文将介绍和研究上述前六项内容。
关键词:高等级公路;勘测;内容一、平面控制测量1、测量坐标系为了确定地面点的空间位置,需要建立测量坐标系。
常见的测量坐标系有大地坐标系,高斯平面直角坐标系和WGS—84坐标系。
⑴大地坐标系。
地面上一点的位置(如P),可用大地坐标(L,B)表示。
大地坐标系是以参考椭球面作为基准面,以起始子午面(即通过格林尼治天文台的子午面)和赤道面作为在椭球面上确定某一点投影位置的两个参考面。
如图1所示,过地面某点的子午面与起始子午面之间的夹角,称为该点的大地经度,用L表示。
规定从起始子午面起算,向东为正,由0°至180°称为东经;向西为负,由0°至180°称为西经。
过地面某点的椭球面法线(PP)与赤道面的交角,称为该点的大地纬度,用B表示。
规定从赤道面起算,由赤道面向北为正,从0°到90°称为北纬;由赤道面向南为负,从0°到90°称为南纬。
⑵高斯平面直角坐标系。
投影面上,中央子午线和赤道的投影都是直线。
以中央子午线和赤道的交点O作为坐标原点,以中央子午线的投影为纵坐标轴X,规定X轴向北为正;以赤道的投影为横坐标轴Y,Y轴向东为正,这样便形成了高斯平面直角坐标系,如图2所示。
图1大地坐标系图2高斯平面直角坐标系高斯投影中,除中央子午线外,各点均存在长度变形,且距中央子午线愈远,长度变形愈大。
为了控制长度变形,将地球椭球面按一定的经度差分成若干范围不大的带,称为投影带。
带宽一般分为经差6°、3°,分别称为6°带、3°带。
⑶WGS—84坐标系。
如图3所示,图3 空间直角坐标系以O为原点,起始子午面与赤道面交线为X轴,赤道面上与X轴正交的方向为Y轴,椭球体的旋转轴为Z轴,指向符合右手规则。
公路勘察GPSRTK测量中坐标系定义方法

《交通标准化》2006年第8期COMMUNICATIONS STANDARDIZATION.No.8,20064.2.4控制沥青用量:混合料中沥青的用量不宜过多。
自由沥青相当于润滑油,它不但会大幅度地降低矿料的内摩擦力,而且会显著降低其粘结力,从而导致沥青混凝土强度的降低。
4.3控制集料的级配和密实度适当增大集料的粒径,可以提高抗车辙能力。
沥青混合料的密实度决定着其空隙率(VTM的大小,密实度越大,空隙率越小,混合料的抗辙槽能力就越强,但VTM也不能太小, Superpave认为,当VTM<4%时,路面的抗车辙能力明显下降。
4.4控制沥青面层的厚度半刚性基层的沥青面层厚度不宜太大,厚的沥青面层容易产生车辙,但也不宜过薄,否则沥青面层容易损坏基层,出现沥青面层底部开裂现象。
国外柔性路面沥青混合料层通常在30cm以上,半刚性路面沥青面层的厚度通常为10cm ̄20cm,半刚性组合路面沥青层的厚度为4cm ̄8cm。
参考文献[1]Brown E R,Handdock J E,Mallicks R B andLynn T A.Development of Mixture Design Procedure for stone Matrix Asphalt[J]. AAPT,1997,26(3:8-12.[2]Brown E R and Mallicks R B.Evaluation of Stone-on-stone Contact in Stone-Matrix Asphalt[J].TRR,1998,35(6:43-46.[3]Corry R W,Dolan C W.Strengthening and Repair of a Column Bracket Using a Carbon Fiber Reinforced Polymer(CFRP Fabric[J].PIC Journal,2001,(4:28-32.[4]Banfill P F G,Saunders D C.The Relationship Between the Retardation of Hydration[J].Cementand Concrete Research.1986,(3:12-16.[5]Insights intoPavement Preservation[R].Washington:U.S.Federal Highway Administration,April2003.[6]Prevention of Rut in Pavement[R].A.Vanelstraete,L.Francken.RILEM Report 18,1997.收稿日期:2005-12-28李峰伟(河南省交通规划勘察设计院,河南郑州450052摘要:公路勘察GPS RTK测量是公路工程的基础,其中正确定义坐标系求解不同坐标系间的转化参数是RTK 测量的关键,因此就公路勘察GPS RTK测量中点在不同坐标系下的坐标转换方法及坐标转换中的注意事项进行探讨,具有一定的实用价值。
公路测量坐标系选择及坐标转换方法

公路测量坐标系选择及坐标转换方法一、公路测量坐标系选择在公路测量中,选择合适的坐标系是非常重要的,它直接影响到测量结果的准确性和后续数据处理的方便性。
常见的公路测量坐标系有以下几种:1. 平面直角坐标系:平面直角坐标系是最常用的坐标系之一。
它以测量起点为原点,建立一个平面,将测量线路分为东西方向和南北方向两个坐标轴。
这种坐标系适用于较小范围的测量,精度较高。
2. 地理坐标系:地理坐标系使用经度和纬度来表示位置,是一种全球通用的坐标系。
在公路测量中,如果需要与其他地理信息系统进行数据交换,就需要使用地理坐标系。
但由于地理坐标系的测量精度较低,一般不适用于高精度的公路测量。
3. 工程测量坐标系:工程测量坐标系是根据具体工程测量任务而建立的坐标系。
它可以根据需要选择不同的坐标原点和坐标轴方向,以适应具体的测量需求。
工程测量坐标系一般用于较大范围的测量,如公路工程中的大地坐标系。
二、坐标转换方法在公路测量中,常常需要进行不同坐标系之间的转换。
以下介绍几种常见的坐标转换方法:1. 平面直角坐标系和地理坐标系的转换:平面直角坐标系和地理坐标系之间的转换需要考虑地球的曲率和投影等因素。
常用的转换方法有高斯投影法和椭球面坐标转换法。
高斯投影法是将地理坐标系投影到平面直角坐标系上,常用于大范围的测量。
椭球面坐标转换法是将地理坐标系的经纬度转换为平面直角坐标系的x、y坐标,常用于小范围的测量。
2. 平面直角坐标系和工程测量坐标系的转换:平面直角坐标系和工程测量坐标系之间的转换可以通过坐标原点和坐标轴的平移和旋转来实现。
一般先将平面直角坐标系的原点平移到工程测量坐标系的原点,然后根据需要进行坐标轴的旋转,最后得到工程测量坐标系的坐标。
3. 地理坐标系和工程测量坐标系的转换:地理坐标系和工程测量坐标系之间的转换需要考虑地理坐标系的经纬度和高程与工程测量坐标系的坐标之间的关系。
常用的转换方法有大地坐标系转换法和高程转换法。
常用坐标计算及公路路线坐标计算
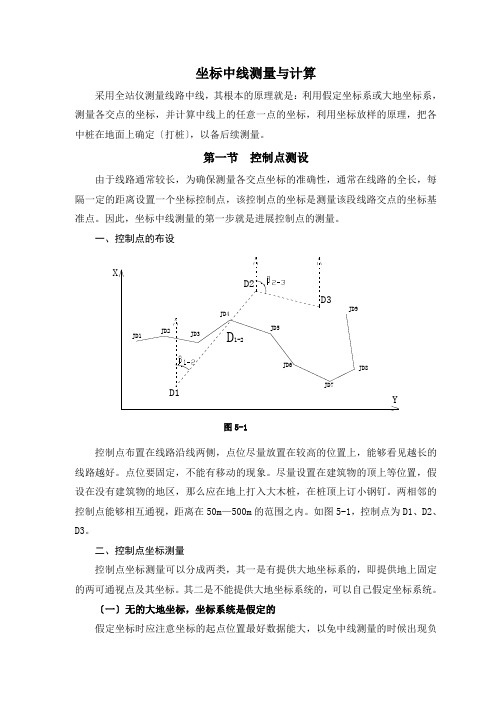
坐标中线测量与计算采用全站仪测量线路中线,其根本的原理就是:利用假定坐标系或大地坐标系,测量各交点的坐标,并计算中线上的任意一点的坐标,利用坐标放样的原理,把各中桩在地面上确定〔打桩〕,以备后续测量。
第一节控制点测设由于线路通常较长,为确保测量各交点坐标的准确性,通常在线路的全长,每隔一定的距离设置一个坐标控制点,该控制点的坐标是测量该段线路交点的坐标基准点。
因此,坐标中线测量的第一步就是进展控制点的测量。
一、控制点的布设图5-1控制点布置在线路沿线两侧,点位尽量放置在较高的位置上,能够看见越长的线路越好。
点位要固定,不能有移动的现象。
尽量设置在建筑物的顶上等位置,假设在没有建筑物的地区,那么应在地上打入大木桩,在桩顶上订小钢钉。
两相邻的控制点能够相互通视,距离在50m—500m的范围之内。
如图5-1,控制点为D1、D2、D3。
二、控制点坐标测量控制点坐标测量可以分成两类,其一是有提供大地坐标系的,即提供地上固定的两可通视点及其坐标。
其二是不能提供大地坐标系统的,可以自己假定坐标系统。
〔一〕无的大地坐标,坐标系统是假定的假定坐标时应注意坐标的起点位置最好数据能大,以免中线测量的时候出现负坐标。
如第一点的坐标假定为〔10000,10000〕。
图5-2 控制点测量程序1〔二〕有的大地坐标,坐标系统是的大地坐标系统是的,必须提供的两点坐标和实地的点位。
其测量出来的坐标均是大地坐标。
如提供两点点位与坐标,S1、S2。
图5-3 控制点测量程序2第二节坐标计算一、某点的坐标,求另一点的坐标 置罗盘仪于D1,后视D2,瞄准JD 1,得方位角β0,测JD 1—D1的距离L 1得 X JD1 = X D1 +L 1cos β0Y JD1 = Y D1 +L 1sinβ0 同理测JD 2、JD 3……的坐标。
二、二点坐标,求方位角与距离。
JD A 〔X A 、Y A 〕 JD B 〔X B 、Y B 〕 用L AB =22)()(A B A B Y Y X X -+-βAB =arctgAB AB X X Y Y --+n*1800注意:计算βAB 的时候必须是B 点坐标减A 点坐标。
测量坐标系的定义

测量坐标系的定义1. 引言在测量学中,坐标系是用来描述和定位物体在空间中位置的工具。
坐标系的定义和使用对于各种测量工作都至关重要,不管是进行地理测绘、机械零件加工还是进行建筑设计。
本文将介绍测量坐标系的定义、常见的坐标系类型以及其在测量中的应用。
2. 坐标系的定义坐标系是一种用来描述和定位空间中点、线、平面或者其他物体的参考系统。
通常,一个坐标系由固定的原点、坐标轴、单位长度等要素组成。
原点位于坐标系的中心,坐标轴则用来表示空间中不同的方向。
在二维空间中,常见的坐标系有直角坐标系和极坐标系。
直角坐标系由两条互相垂直的线段组成,其中一条表示水平方向,称为x轴,另一条表示垂直方向,称为y轴。
点在直角坐标系中的位置可以由其在x轴和y轴上的坐标值确定。
而极坐标系则由原点、极径和极角组成,点在极坐标系中的位置可以由其相对于原点的极径和极角确定。
在三维空间中,常见的坐标系有笛卡尔坐标系和球坐标系。
笛卡尔坐标系以三个相互垂直的坐标轴为基础,分别标记为x轴、y轴和z轴。
点在笛卡尔坐标系中的位置可以由其在x轴、y轴和z轴上的坐标值确定。
而球坐标系则由一个原点、一个极径、一个极角和一个方位角组成,点在球坐标系中的位置可以由其相对于原点的极径、极角和方位角确定。
3. 坐标系的应用坐标系在测量学中具有广泛的应用。
以下是一些常见的应用场景:地理测绘在地理测绘中,使用地理坐标系来描述地球表面上的点的位置。
地理坐标系采用经度和纬度来表示点在地球上的位置。
经度表示点相对于本初子午线的偏移角度,纬度表示点相对于赤道的偏移角度。
地理坐标系的标准是WGS84,其坐标单位为度。
机械零件加工在机械零件加工中,使用机械坐标系来描述零件上不同特征点的位置。
机械坐标系通常是一个三维直角坐标系,其原点位于零件的某个基准面上。
通过测量零件上特定点相对于机械坐标系原点的偏移量,可以确定不同特征的位置,从而实现加工的精度控制。
建筑设计在建筑设计中,使用本地坐标系来描述建筑物在三维空间中的位置。
测量中坐标系

测量中坐标系引言在测量学中,测量中坐标系是一种用于描述空间位置和方向的系统。
它是测量工作的基础,能够帮助我们准确地记录和表示测量结果。
本文将介绍测量中坐标系的概念、组成以及在测量过程中的作用。
什么是测量中坐标系测量中坐标系是一个三维空间参考系统。
它是由三个坐标轴和一个原点组成的,用来确定点和物体在空间中的位置和方向。
一般来说,我们用笛卡尔坐标系作为测量中坐标系,其中有一个主轴作为基准轴,并与其他两个轴相互垂直。
组成测量中坐标系主要由以下几个组成部分:1.坐标轴:测量中坐标系中的三个坐标轴分别是X轴、Y轴和Z轴。
它们是相互垂直的,构成了一个空间直角坐标系。
2.原点:测量中坐标系的原点是空间中的一个点,通常被定义为坐标轴的交点。
所有的测量都是相对于原点进行的。
3.坐标系方向:在测量中坐标系中,坐标轴有正负方向。
一般来说,我们可以通过定义正负方向来确定坐标系的朝向。
作用测量中坐标系在测量工作中起到了至关重要的作用。
它具有以下几个主要作用:1.确定位置:通过测量中坐标系,我们可以准确地确定点和物体在空间中的位置。
测量结果可以用坐标值来表示,使得位置信息得以记录和传递。
2.定位方向:测量中坐标系可以帮助我们准确地描述空间方向。
通过指定坐标轴和正负方向,我们可以确定物体的朝向和方向。
3.比较和分析:测量中坐标系提供了一个统一的标准,使得不同地点和时间的测量结果可以进行比较和分析。
通过将测量结果转化到相同的坐标系中,我们可以消除坐标系的差异,得到更加准确的比较和分析结果。
4.网格与坐标:测量中坐标系还可以用来构建网格和坐标系线。
这些网格和线可以作为辅助工具,帮助我们更好地观察和分析测量结果。
总结测量中坐标系是测量学中一种用于描述空间位置和方向的系统。
它由三个相互垂直的坐标轴和一个原点组成,并具有确定位置、定位方向、比较和分析以及构建辅助工具的功能。
测量中坐标系在测量过程中扮演着重要的角色,并有助于提高测量的准确性和可重复性。
测量坐标系及坐标转换

(
)[
]
2.高斯坐标反算 ( x, y ) → (L, B ) 1 B = B f − V f2 t f 2 ⎡⎛ y ⎢⎜ N ⎢⎜ ⎣⎝ f ⎞ 2 2 2 ⎟ − 1 5 + 3t 2 f + η f − 9η f t f ⎟ 12 ⎠
2
(
)
⎛ y ⎜ ⎜N ⎝ f
⎞ 4 ⎟ + 1 61 + 90t 2 f + 45t f ⎟ 360 ⎠
三.高斯平面直角坐标系
1.高斯坐标正算 (L, B ) → ( x, y ) l = L − L0 x=X + N N N t cos 2 Bl 2 + t 5 − t 2 + 9η 2 + 4η 4 cos 4 Bl 4 + t 61 − 58t 2 + t 4 cos 6 Bl 6 2 24 720 N N y = N cos Bl + 1 − t 2 + η 2 cos 3 Bl 3 + 5 − 18t 2 + t 4 + 14η 2 − 58η 2 t 2 cos 5 Bl 5 6 120
⎤ ⎥ ⎥ ⎡ΔX O ⎤ cos B ρ ′′⎥ ⋅ ⎢ ΔYO ⎥ ⎢ ⎥ + M +H ⎥ sin B ⎥ ⎢ ⎣ ΔZ O ⎥ ⎦B ⎥ ⎦
0
测绘信息网http;//www.othermap.com网友提供
⎡ tan B cos L ⎢ ⎢ − sin L ⎢ 2 Ne B cos B sin L sin ⎢− ⎢ ρ ′′ ⎣
⎡ΔX o ⎤ ⎢ΔY ⎥ ⎢ o⎥ ⎢ΔZ o ⎥ ⎡X 2 ⎤ ⎢ ⎥ ⎢ ⎥ ⎢a1 ⎥ + ⎢Y2 ⎥ ⎢a ⎥ ⎢ ⎣Z 2 ⎥ ⎦ ⎢ 2 ⎥ a ⎢ 3 ⎥ ⎢a ⎥ ⎣ 4 ⎦
测量中的常用坐标系及坐标转换概述

测量中的常用坐标系及坐标转换概述1.引言在测量与空间信息处理中,坐标系是非常重要的概念。
通过坐标系,可以将现实世界中的点、线、面等空间要素进行数学建模和描述。
常用的坐标系包括笛卡尔坐标系、极坐标系、球坐标系等。
坐标系之间的转换是测量与空间信息处理中常用的操作。
2.笛卡尔坐标系笛卡尔坐标系是最常见的坐标系,由三个互相垂直的坐标轴构成。
在二维情况下,有两个坐标轴分别表示横坐标和纵坐标;在三维情况下,有三个坐标轴分别表示横坐标、纵坐标和高度坐标。
笛卡尔坐标系广泛应用于地理信息系统、测绘工程、建筑设计等领域。
3.极坐标系极坐标系由极径和极角两个坐标轴构成。
极径表示点到坐标原点的距离,极角表示点在平面上相对于一个基准线的角度。
极坐标系常用于极坐标测量仪器中,如激光扫描仪,雷达等。
极坐标系优点之一是可以简化角度变化的描述,适用于自然界中的很多环境和场景。
4.球坐标系球坐标系由球半径、极角和方位角三个坐标轴构成。
球半径表示点到坐标原点的距离,极角表示点距离球心的水平角度,方位角表示点在水平面上相对于一个基准线的角度。
球坐标系常用于天文学、地理学等领域,描述地球表面上各个点的位置。
5.坐标转换在实际测量中,经常需要在不同的坐标系之间进行转换,以实现测量数据的互通。
常见的坐标转换包括坐标系之间的旋转、平移和缩放等操作。
下面以笛卡尔坐标系和极坐标系为例,介绍一下坐标转换的基本原理。
-笛卡尔坐标系到极坐标系的转换:假设有一个点在笛卡尔坐标系中的坐标为(x,y),则可以通过以下公式将其转换为极坐标系中的坐标(r,θ):r=√(x²+y²)θ = arctan(y/x)-极坐标系到笛卡尔坐标系的转换:假设有一个点在极坐标系中的坐标为(r,θ),则可以通过以下公式将其转换为笛卡尔坐标系中的坐标(x,y):x = r * cos(θ)y = r * sin(θ)在实际测量中,常常需要进行坐标系之间的转换,比如将地理坐标转换为笛卡尔坐标,或者将局部坐标系转换为全球坐标系等。
测量中常用的坐标系有哪几种

测量中常用的坐标系有哪几种在测量领域中,坐标系是一个非常重要的概念,用于描述和定位物体在空间中的位置和方向。
不同的测量任务和应用需要使用不同的坐标系。
下面将介绍一些测量中常用的坐标系。
直角坐标系(笛卡尔坐标系)直角坐标系,也称为笛卡尔坐标系,是最常见和最基本的坐标系形式。
它由三个相互垂直的轴组成,通常用于描述平面或三维空间中的位置。
在二维平面上,直角坐标系由X轴和Y轴组成,原点为(0, 0)。
在三维空间中,直角坐标系由X轴、Y轴和Z轴组成,原点为(0, 0, 0)。
直角坐标系通过给定一个点的X、Y和Z坐标值来表示一个位置。
例如,一个点的坐标可以表示为(2, 3)或(2, 3, 4),其中2表示X轴上的位置,3表示Y轴上的位置,4表示Z轴上的位置。
极坐标系极坐标系是另一种描述平面上位置的坐标系。
它以原点为中心,使用角度和半径两个参数来定位一个点。
极坐标系中,角度通常用弧度表示,表示一个点与X轴正方向之间的旋转角度。
半径表示一个点到原点的距离。
使用极坐标系可以方便地描述某些特定形状的物体,比如圆形。
在某些测量任务中,例如雷达和声纳测量,极坐标系也常常被使用。
地理坐标系地理坐标系是用于在地球表面定位位置的坐标系。
地理坐标系使用经度和纬度两个参数来描述一个位置。
经度表示一个点在东西方向上的位置,以本初子午线(通常为格林尼治子午线)为参考。
经度的取值范围从-180°到180°,东经为正,西经为负。
纬度表示一个点在南北方向上的位置,以赤道为参考。
纬度的取值范围从-90°到90°,北纬为正,南纬为负。
地理坐标系在全球定位系统(GPS)和地图绘制中广泛应用,用于确定地球上任何一个点的精确位置。
本地坐标系本地坐标系是指相对于特定物体或参考物体而言的坐标系。
相对于一个参考物体建立的本地坐标系可以使测量更加精确和方便。
例如,航空航天和汽车工业中常用的局部坐标系是以飞机或汽车为参考,将其位置和方向与自身的坐标系相关联。
1-2第二节 公路测设中的测量坐标系

3、投影带
L6, 0 6 N 3 带号与中央子午线经度的关系为 L3, 0 3n
4、国家统一坐标
我国位于北半球,在高斯平面直 角坐标系内,X坐标均为正值,而 Y坐标值有正有负。 为避免Y坐标出现负值,规定将 X坐标轴向西平移500km,即所有 点的Y坐标值均加上500km。 为了便于区别某点位于哪一个投 影带内,还应在横坐标值前冠以 投影带带号,这种坐标称为国家 统一坐标。
新北京1954年北京坐标系
新北京1954坐标系是由1980西安坐标系转换得来的,它是在采用 1980西安坐标系的基础上,仍选用克拉索夫斯基椭球为基准椭 球,并将椭球中心平移,使其坐标轴与1980西安坐标系的坐标 轴平行。其特点如下: 1:是采用克拉索夫斯基椭球; 2:采用多点定位,但椭球面同大地水准面在我国境内并不是最 佳拟合; 3:椭球定向明确,其短轴指向与我国地极原点JYD1968.0方向平 行,大地起始子午面平行我国起始天文子午面。 4:大地高程基准面采用1956黄海高程系统; 5:大地原点与1980西安坐标系相同,但起算数据不同;
正常高 正高 大地高
高程系统的由来及特点:
正常高系统和正高系统是有区别的,主要是由于重力场的影响 不同,重力线就会产生一些偏移。 我国高程系统日常测量中采用的是正常高,GPS测量得到的是 大地高。 我国采用青岛验潮站1950-1956年观测成果求得的黄海平均海 水面作为高程的零点,称为“1956年黄海高程系”。后经复查, 发现该高程系验潮资料过短,准确性较差,改用青岛验潮站 1950-1979年的观测资料重新推算,并命名为“1985年国家高 程基准”。 国家水准点设于青岛市观象山,1956年黄海平均海水面的水准 原点高程为72.289m,“1985国家高程基准”的水准原点高程 为72.260m。 在有限范围内两点之间的高差与高程起算面无关 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、投影带
带号与中央子午线经度的关系为
L6, 0
L
3,
0
6N 3n
3
4、国家统一坐标
我国位于北半球,在高斯平面直 角坐标系内,X坐标均为正值,而 Y坐标值有正有负。 为避免Y坐标出现负值,规定将 X坐标轴向西平移500km,即所有 点的Y坐标值均加上500km。 为了便于区别某点位于哪一个投 影带内,还应在横坐标值前冠以 投影带带号,这种坐标称为国家 统一坐标。
我国高程系统日常测量中采用的是正常高,GPS测量得到的是 大地高。
我国采用青岛验潮站1950-1956年观测成果求得的黄海平均海 水面作为高程的零点,称为“1956年黄海高程系”。后经复查, 发现该高程系验潮资料过短,准确性较差,改用青岛验潮站 1950-1979年的观测资料重新推算,并命名为“1985年国家高 程基准”。
我国现行的坐标参考系是我国北京54坐标系及我国80坐标 系,它是一个参心坐标系。
西安80坐标系
参心坐标系,大地原点位于我国陕西省泾阳县永乐镇。
1:采用的国际大地测量和地球物理联合会于1975年推荐的椭球参 数,简称1975旋转椭球。它有四个基本参数:
地球椭球长半径
a=6378140m
地心引力常数
GM3.9860015014m3 / s2
地球重力场二阶带谐系数 J21.08263108
地球自转角速度
7.292111505rad/ s
2:椭球面同大地水准面在我国境内最为拟合;
3:椭球定向明确,其短轴指向我国地极原点JYD1968.0方向,大 地起始子午面平行于格林尼治平均天文台的子午面。
4:大地高程基准面采用1956黄海高程系统。
新北京1954年北京坐标系
新北京1954坐标系是由1980西安坐标系转换得来的,它是在采用 1980西安坐标系的基础上,仍选用克拉索夫斯基椭球为基准椭 球,并将椭球中心平移,使其坐标轴与1980西安坐标系的坐标 轴平行。其特点如下:
1:是采用克拉索夫斯基椭球;
2:采用多点定位,但椭球面同大地水准面在我国境内并不是最 佳拟合;
国家水准点设于青岛市观象山,1956年黄海平均海水面的水准 原点高程为72.289m,“1985国家高程基准”的水准原点高程 为72.260m。
在有限范围内两点之间的高差与高程起算面无关 。
四、空间直角坐标系
以O为原点,起始子午面与赤道面 交线为X轴,赤道面上与 X轴正交的 方向为Y轴,椭球体的旋转轴为 Z轴, 指向符合右手规则。在该坐标系中, P点的点位用OP在这三个坐标轴上 的投影X,Y,Z表示。
标的完整性。
2、地心地固坐标系
地心地固坐标系就是能解决上述问题的地心坐标系。地心地固 坐标系原点在地球质心,Z轴指向国际习用原点CIO,X轴指向 格林尼治子午线与对应CIO的赤道面的交点,是右手系。 WGS-84坐标系是地心地固坐标系。
WGS-84坐标系的几何定义是:原点是地球质心,Z轴指向 BIH1984.0定义的协议地球极(CTP)方向,轴指向BIH1984.0 的零子午面和CTP赤道的交点,Y轴与Z轴、轴构成右手坐标系。
GPS测量中所使用的地球坐标系统为WGS-84坐标系。
2、地心地固坐标系
表示方法: 笛卡尔直角坐标系:X,Y,Z 大地坐标:B,L,H 球坐标:,,r
换算公式(1-4,1-5)
3、局部坐标系
基于限制变形、方便、实用和科学的目的,在许多城市和工程 测量中,常常会建立适合本地区的地方独立坐标系,建立地方
空间直角坐标系又可分为:参心坐 标系、地心地固坐标系、局部坐标 系
1、参心坐标系
参心坐标系通常是选取一参考椭球面作为基本参考面,选 一参考点作为大地测量的起算点(或称为大地原点),并 且利用大地原点的天文观测量,来确定参考椭球体在地球 内部的位置及方位,且该参考椭球体的中心一般不会与地 球的质心重合。这种原点位于地球质心附近的坐标系即为 地球参心坐标系。
❖ 2、 正高系统 以大地水准面为基准面的高程系
统。大地水准面为平均海平面通过大陆 延伸勾画出的一个封闭连续的封闭曲面。
❖ 3、 正常高 以似大地水准面为基准的高程系
统。似大地水准面为从地面点沿正常重 力线量取正常高所得端点构成的封闭曲 面。
正常高
正高
大地高
高程系统的由来及特点:
正常高系统和正高系统是有区别的,主要是由于重力场的影响 不同,重力线就会产生一些偏移。
独立坐标系,实际上就是通过一些参数来确定地方参考椭球与 投影面。
地方参考椭球一般选择与当地平均高程相对应的参考椭球,该
椭球的中心、轴向和扁率与国家参考椭球相同,其椭球半径a
增大为:
11 1Hm10
式中, H m 为当地平均海拔高程, 0 为该地区平均高程异
常
在地方投影面的确定过程中,应当选取过测区中心的经线为独 立中央子午线,并选取当地平均高程面为投影面。
3:椭球定向明确,其短轴指向与我国地极原点JYD1968.0方向平 行,大地起始子午面平行我国起始天文子午面。
4:大地高程基准面采用1956黄海高程系统;
5:大地原点与1980西安坐标系相同,但起算数据不同;
参心坐标系,就整个地球空间而言,有以下缺点: (1)不适合建立全球统一的坐标系统; (2)不便于研究全球重力场; (3)水平控制网和高程控制网分离,破坏了空间三维坐
例:P点的高斯平面直角坐标 Xp=3 275 611.188Biblioteka Yp=-376 543.211m
若该点位于第19带内,则P点的 国家统一坐标表示为:
xp=3 275 611.188m yp=19 123 456.789m
三、高程系统
❖ 1、 大地高系统 参考椭球面为基准面的高程系统。
大地高也称为椭球高,是一个纯几何量, 不具有物理意义,同一个点,在不同的 基准下,具有不同的大地高。
第二节 公路测设中的测量坐标系
二、高斯平面直角坐标系
1、高斯投影
将椭球面上各点的大地坐标按照一定的规律投影到平面 上,并以相应的平面直角坐标表示。
2、高斯平面直角坐标系
在投影面上,中央子午线和赤道的投影都是直线。以中央 子午线和赤道的交点O作为坐标原点,以中央子午线的投影为 纵坐标轴X,规定X轴向北为正;以赤道的投影为横坐标轴Y, Y轴向东为正,这样便形成了高斯平面直角坐标系。
