BCD码2进制转10进制表格工具+说明
bcd码转十进制

bcd码转十进制BCD码(Binary-CodedDecimal,又称二进制编码十进制)是一种特殊的编码体系,它将十进制数字按位编码为四个二进制位的组合。
这四位的组合在BCD码中表示一个十进制数。
BCD码对十进制数字的编码,保留了十进制数字的本质,即具有十进制的计数能力,另外BCD码的特性也有助于数字的编码和存储。
BCD码的形式BCD码可分为真值和二进制补码两种形式。
真值BCD码是直接用十进制表示十进制数字的BCD编码,省去了十进制数字和二进制数字之间转换的过程;二进制补码BCD码是将每一位十进制数字的真值BCD码,通过二进制补码的方式表示的BCD码。
BCD码的应用BCD码可用于计算机和数字电路中,可以有效减少计算机运算和存储所需的空间,从而提高计算机系统的处理能力。
BCD码还可用于字符串编码,比如在字符串处理任务中使用BCD码可使字符串处理更加有效地进行。
此外,BCD码还用于存储数据和特殊字符,特别是五位BCD码,可以利用四位BCD码存储英文字母,一位存储空格或特殊符号;BCD码还可以用于双字节编码,也可以用于记录时间和各种状态。
BCD码转十进制BCD码转换为十进制时,要先分解原BCD码中的四位,然后将每一位BCD码转换为十进制数,最后将这些十进制数相加。
例如,将1101转换为十进制数,首先分解1101,第一位是1,第二位是1,第三位是0,第四位是1;将第一位和第二位BCD码(1、1)分别转换为十进制数(1、1);将第三位BCD码(0)转换为十进制数(0);将第四位BCD码(1)转换为十进制数(1)。
将这三位十进制数相加,结果为3,因此1101的十进制表示为3。
总结BCD码是一种特殊的编码体系,它将十进制数字按位编码为四个二进制位的组合。
BCD码的形式有真值BCD码和二进制补码两种。
BCD码的应用包括计算机和数字电路、字符串编码、存储数据和特殊字符以及双字节编码等。
将BCD码转换为十进制数时,首先分解原BCD码中的四位,然后将每一位BCD码转换为十进制数,最后将这些十进制数相加。
2进制8421进制转换讲解

2进制8421进制转换讲解
二进制和8421BCD(Binary-Coded Decimal)是数字表示法的两种形式。
在8421BCD中,每个十进制数都用四位的二进制数表示,其中每个二进制位的权值分别是8、4、2、1。
下面就是如何进行二进制到8421BCD的转换和反之转换的过程。
一、二进制到8421BCD的转换:
1将二进制数分组:将二进制数从右到左每四位一组分组。
2在需要的情况下在左侧补零:如果最左边的分组的位数不足四位,可以在左侧补零,使每个分组都有四位。
3将每个四位的二进制数转换为对应的8421BCD码:使用以下对照表将每个四位的二进制数转换为相应的8421BCD码。
4重复以上步骤直到将整个二进制数转换为8421BCD码。
二、8421BCD到二进制的转换:
1将每个8421BCD码转换为四位的二进制数:使用上述对照表将每个8421BCD码转换为相应的四位二进制数。
2将每组的四位二进制数组合在一起:将每组的四位二进制数按照从左到右的顺序组合在一起。
3去掉可能添加的左侧零:如果在转换过程中在左侧添加了零,可以将这些零去掉,得到最终的二进制数。
这就是从二进制到8421BCD和从8421BCD到二进制的基本转换步骤。
请注意,8421BCD通常用于BCD码(二进制编码十进制)表示十进制数字。
2进制-10进制40;BCD码41;数码转换器设计

目录摘要 (1)1原理分析 (2)2设计思路 (3)3设计程序 (4)3.1二-十进制转换 (4)3.2对十进制数分位 (6)3.3分别输出十进制数 (7)3.4输出到数码管 (9)3.5显示位数 (11)4整体设计电路图与仿真结果分析 (12)4.1整体设计电路图 (12)4.2仿真结果 (12)4.3仿真结果分析 (13)5小结与体会 (13)参考文献 (15)摘要BCD码亦称二进码十进数或二-十进制代码.用4位二进制数来表示1位十进制数中地0~9这10个数码.是一种二进制地数字编码形式,用二进制编码地十进制代码.BCD码这种编码形式利用了四个位元来储存一个十进制地数码,使二进制和十进制之间地转换得以快捷地进行.本文就是在quartus软件环境下利用VHDL语言将输入地八位二进制转换为BCD十进制数并且在数码管中显示出来.关键词:二--十进制转换器,BCD码,quartus,VHDL.2进制-10进制(BCD码)数码转换器设计1原理分析BCD 码这种编码形式利用了四个位元来储存一个十进制地数码,使二进制和十进制之间地转换得以快捷地进行.这种编码技巧,最常用于会计系统地设计里,因为会计制度经常需要对很长地数字串作准确地计算.相对于一般地浮点式记数法,采用BCD码,既可保存数值地精确度,又可免却使电脑作浮点运算时所耗费地时间.此外,对于其他需要高精确度地计算,BCD编码亦很常用.此处要介绍地是八位二进制转BCD码地硬件实现,采用左移加3地算法,具体描述如下:(1)、左移要转换地二进制码1位(2)、左移之后,BCD码分别置于百位、十位、个位(3)、如果移位后所在地BCD码列大于或等于5,则对该值加3(4)、继续左移地过程直至全部移位完成举例:将八位二进制码11111111转换成BCD码,其真值表如表1-1所示表1-1八位二进制码11111111转换成BCD码真值表2设计思路本次设计并没有用到左移地原理进行操作,直接对输出芯片地输出进行定义,虽然较为繁琐,但是原理却简单,所以才用此种方法,具体原理如下:2进制-10进制(BCD码)地转换可以通过一个芯片实现,即输入地八位二进制码通过编程输出十进制码,八位二进制能表示地最大地数为“255”,即输出地十进制为三位数,此时输出地BCD码就要有12位,每四位代表一个数,此时可再利用一个芯片把输出地12位数重新分配到三个输出管脚中,每个管脚代表一位数,时钟信号每输变一次,输出数字地位也会变一次,即个、十、百位分别输出,同时芯片地selout输出端输出时钟信号地数字到下一个芯片地接收端,通过编程实现000对应110,001对应101,010对应011,即输出0地位置可以表示数码管中所显示数字地位,然后再通过芯片输出到七段数码管进行显示,具体流程图如图2-1所示:图2-1 设计总流程图3设计程序3.1二-十进制转换原理图如图3-1所示:图3-1二进制到十进制转换原理图具体程序语言如下:library ieee。
二进制,十进制,十六进制,ASCII,BCD码的转换,单片机

二进制,十进制,十六进制,ASCII,BCD码的转换,单片机1.在片内RAM 30H单元有-个8位二进制数,将其转换成压缩BCD码,存于片内RAM 41H(高位)40H(低位)中。
方法:2^8=256,所以8位二进制A<=256,A/100商是百位数,存放到41h单元,余数再除以10,再得商是10位数,高低位互换,) ORG 0100HSTART:MOV A,30H ;取来8位二进制数MOV B,#100DIV AB ;除以100MOV 41H,A ;商是百位数,存放到41h单元MOV A,B ;取回余数MOV B,#10DIV AB ;再除以10SWAP A ;商是10位数,高低位互换ORL A,BMOV 40H,A ;将十位数与个位位数存入40hSJMP $END2.一个字节(8位)BCD码转换为二进制数(方法:先将高半字节乘以10,再加上低半字节)设待转换的BCD码存放于R2中DTOB:MOV A,R2ANL A,#0F0HSWAP AMOV B,#0AHMUL ABMOV R3,AMOV A,R2ANL A,#0FHADD A,R3RET3.二进制数转换为ASCII码设(30H)=4BH,将高4位的ASCII码放在31H单元,低4位的ASCII 码放在32H单元,程序具有通用性,向入口参数30H存入任何数,都能将其变成相应的ISCII 码.ORG 0000HLJMP MAINORG 0030HMAIN:MOV SP,#60HMOV 30H,#4BHMOV R2,30HMOV A,R2ANL A,#0FHCJNE A,#0AH,NEQNEQ: JC LOOPADD A,#37HJMP LOOP3LOOP:ADD A,#30HLOOP3:MOV 31H,AMOV A,R2SWAP AANL A,#0FHCJNE A,#0AH,NE1NE1: JC LOOP1ADD A,#37HJMP LOOP4LOOP1:ADD A,#30HLOOP4:MOV 32H,AA1: SJMP A1END4.已知R0的低半个字节为一个四位的二进制数,要求将其转换为ASCAII码后送回R0中。
BCD码转换
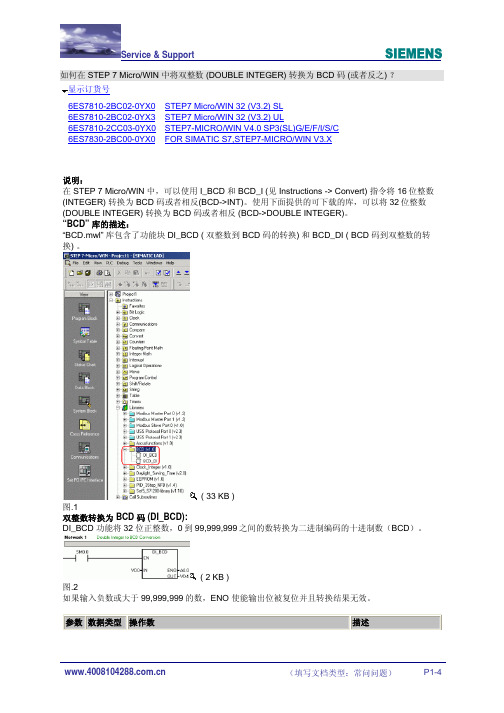
如何在 STEP 7 Micro/WIN 中将双整数 (DOUBLE INTEGER) 转换为 BCD 码 (或者反之) ?显示订货号6ES7810-2BC02-0YX0STEP7 Micro/WIN 32 (V3.2) SL6ES7810-2BC02-0YX3STEP7 Micro/WIN 32 (V3.2) UL6ES7810-2CC03-0YX0STEP7-MICRO/WIN V4.0 SP3(SL)G/E/F/I/S/C6ES7830-2BC00-0YX0FOR SIMATIC S7,STEP7-MICRO/WIN V3.X说明:在 STEP 7 Micro/WIN 中,可以使用 I_BCD 和 BCD_I (见 Instructions -> Convert) 指令将16位整数(INTEGER) 转换为 BCD 码或者相反(BCD->INT)。
使用下面提供的可下载的库,可以将32位整数(DOUBLE INTEGER) 转换为 BCD 码或者相反 (BCD->DOUBLE INTEGER)。
“BCD” 库的描述:“BCD.mwl” 库包含了功能块 DI_BCD ( 双整数到 BCD 码的转换) 和 BCD_DI ( BCD 码到双整数的转换) 。
( 33 KB )图.1双整数转换为 BCD 码 (DI_BCD):DI_BCD 功能将32 位正整数,0到99,999,999之间的数转换为二进制编码的十进制数(BCD)。
( 2 KB )图.2如果输入负数或大于99,999,999的数,ENO 使能输出位被复位并且转换结果无效。
参数数据类型操作数描述BCD_DI 功能将正的32 位 BCD 码,从( 2 KB )BCD.zipHow do you convert the number format DOUBLE INTEGER into BCD code (or vice versa) in STEP 7 Micro/WIN?Display part numberBCD code) and BCD_DI (conversion of BCD code into DOUBLE INTEGER).( 33 KB )binary coded decimal number.( 2 KB )corresponding 32-bit integers of the DOUBLE INTEGER type.( 2 KB )Fig. 03BCD.zip。
1.码制转换十、二进制数、ASCII码之间的互相转换。①BCD(共32张PPT)

22
第二十二页,共三十二页。
BINCA
CODE
MOV
INT
ENDP
ENDS
END
AH,4CH
21H
BEGIN
23
第二十三页,共三十二页。
2.子程序的参数传递 编写子程序时,很重要的一个工作(gōngzuò)是
如何把参数传给子程序,这个过程叫参数传 送。
传送方法有:
把参数放在CPU内部寄存器中 把参数放在变量中
;不是,转NEXT1 ;字符数减1
;指向第一个数字字符 ;清零(qīnɡ línɡ)AX,存二进制
DEC
CL
JZ NEXT2
;若(CL)=0,转NEXT2
MOV DL,[BX] ;取字符
AND DL,0FH ;转换成BCD码
ADD AL,DL
;加到中间结果上
ADC AH,0
10
第十页,共三十二页。
MOV DX,10
MUL DX
;*10
INC BX
;指向下一个字符
JMP SHORT LP1
NEXT2: MOV DL,[BX] ;取个位数
AND DL,0FH
;个位ASCII→未组合BCD
ADD AX,DX
;加个位数,(AX)=001AH
CMP CH,’-’
;是’-’?
JNZ NEXT3
;该数非负,转NEXT3
NEG AX
DI,NUM
CHANGE BX,STR2
;输入第二个数字串(设为33) ;串1的首地址送BX
;存二进制首地址送DI
;将串1 ASCII码→二进制 ;串2的首地址送BX
8
第八页,共三十二页。
NEXT:
bcd码的转换

bcd码也叫8421码就是将十进制的数以8421的形式展开成二进制,大家知道十进制是0~9十个数组成,着十个数每个数都有自己的8421码:0=00001=00012=00103=00114=01005=01016=01107=01118=10009=1001举个例子:321的8421码就是3 2 10011 0010 0001二进制编码的十进制数,简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。
4位二进制数码有16种组合,原则上可任选其中的10种作为代码,分别代表十进制中的0,1,2,3,4,5,6,7,8,9 这十个数符。
最常用的BCD码称为8421BCD 码,8.4.2.1 分别是4位二进数的位取值。
右图为十进制数和8421BCD编码的对应关系表:1、BCD码与十进制数的转换BCD码与十进制数的转换.关系直观,相互转换也很简单,将十进制数75.4转换为BCD码如:75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD=85.5注意:同一个8位二进制代码表示的数,当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时,数值是不相同的。
例如:00011000,当把它视为二进制数时,其值为24;但作为2位BCD码时,其值为18。
又例如00011100,如将其视为二进制数,其值为28,但不能当成BCD码,因为在8421BCD码中,它是个非法编码.2、BCD码的格式计算机中的BCD码,经常使用的有两种格式,即分离BCD码,组合BCD 码。
所谓分离BCD码,即用一个字节的低四位编码表示十进制数的一位,例如数82的存放格式为:_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。
BCD码转换器说明书

深圳市锦祥自动化设备有限公司BCD码转换器说明书 1、功能:1.1 本转换器可将十进制码分接开关档位信号转换成统一的BCD码信号,共5个接点上传供接收设备使用。
输出信号形式为空接点。
1.2 转换器上有工作指示灯指示工作状态,亮为工作。
1.3 电源模块、继电器均为密封型,可靠性高。
2 技术条件2.1 环境基准条件环境温度:20±2℃相对湿度:45%~75%大气压力:86~106Kpa2.2 正常使用条件环境温度:-10℃~+50℃环境相对湿度:不大于90%大气压力:80~110KPa储存和运输过程中极限温度:-25℃~+70℃使用地点的海拔高度:不大于2500米使用环境的周围介质无爆炸危险;不含有腐蚀性气体;所含导电尘埃的浓度不应使绝缘水平降低到允许极限值以下。
可靠的供电电源。
2.3 额定参数辅助直流电源额定电压:220V;110V;48V(在定货时确定)2.4 特性参数2.5 辅助电源电压允许波动范围:0.8~1.15倍额定电压2.6 最大功耗:不大于6W;2.7 触点额定容量:1A 125VAC,1.25A 24VDC,触点最大容量:2A2.8绝缘电阻:符合能源部SD189-87《静态继电器保护及安全自动装置通用技术条件》。
2.9 绝缘耐压:各引出端子对外壳锁紧螺钉能承受工频电压2000V,同组触点间能承受工频电压1000V,历时一分钟无击穿。
2.10 抗干扰性能:符合国家GB6162-85《静态继电器及保护装置的电气干扰试验》标准。
2.11 电气寿命:触点在额定负荷下为一万次。
2.12 机械寿命:触点在空载状态下为三百万次。
3 结构型式及相应端子定义3.1 外形尺寸: 90 mm × 130mm 采用进口导轨安装型模块,可以直接安插在标准导轨上。
WZY 系列微型端子排式继电器3.2 端子定义:定 义 定 义 端子号 端子定义 单元定义端子号端子定义 单元定义 1 第01档 28 DC- 2 第02档 27 DC+ 输入电源3 第03档 26 5V-4 第04档 25 5V+ 5V 电源 5 第05档 24 档位输出公共端6 第06档 23 BCD107 第07档 22 BCD08 8 第08档 21 BCD049 第09档 20 BCD02 10 第10档 19 BCD01 BCD码输出 11 第11档 18 档位输入公共端12 第12档 17 第17档 13 第13档 16 第16档 14第14档十 进 制 档位输入 15 第15档十 进 制 档位输入 说明:1. 5V 电源为内部提供,只供本模块使用,不要与其它电源相连。
2进制的10010转换为10进制

2进制的10010转换为10进制二进制(Binary)是一种常用的数制,在计算机科学、电子工程等领域有着广泛的应用。
有时候,我们需要将二进制数转换为十进制数,以便更好地理解或处理数据。
本文将介绍如何将二进制数2进制的10010转换为十进制数。
首先,我们需要明确二进制数的表示方法。
二进制数是由0和1两个数字组成的数制,每一位数字表示为2的整数次幂。
因此,二进制数10010可以表示为:1*2的平方+0*2的立方+0*2的平方+1*2的零次幂=5接下来,我们将介绍如何将二进制数转换为十进制数。
具体步骤如下:1.将二进制数按位写出,从右往左依次为最低位到最高位。
2.从右往左数,找到最右边的数字(这里是1)。
这个数字对应的十进制数值为:2的零次幂。
3.将二进制数的个位数字从新排列,即从右往左数第一位数字(这里是0)。
4.将最右边的数字从新排列后继续往左数,找到下一个数字(这里可能是个1)。
5.确定是否需要计算这个数字(取决于该数字是否为满二进制的)。
6.最后,将上述所有数值相加,得到十进制数。
按照上述步骤,我们可以将二进制数2进制的10010转换为十进制数:1.将二进制数按位写出:100102.从右往左数,找到最右边的数字(这里是1),对应的十进制数值为:2的零次幂=13.将二进制数的个位数字从新排列:从右往左数第一位数字是0,继续往左数第二个数字是1。
4.将最右边的数字从新排列后继续往左数,得到数字为:第一个数字:2的第一次方=2第二个数字:2的零次幂=1第三个数字:因为不是满二进制的,所以不计算5.将上述所有数值相加,得到十进制数为:1+2+0=3因此,二进制数2进制的10010转换为十进制数为:3。
掌握了将二进制数转换为十进制数的技巧和方法,我们可以将其应用到实际生活中。
例如,当我们需要处理与二进制数相关的数据时,就可以将其转换为十进制数,以便更好地理解和处理数据。
同时,这也是计算机科学中二进制和十进制相互转换的基础知识之一。
2进制转化10进制的公式(一)

2进制转化10进制的公式(一)资深创作者 2进制转化10进制的公式1. 2进制转化10进制的公式2进制转化10进制是计算机科学中的基本运算之一,它能将由0和1组成的二进制数转换成十进制数。
下面是几种常见的公式以及相关的例子,用于说明如何进行2进制转化10进制的计算。
公式1:按权展开法当我们想将一个2进制数转换成10进制数时,可以使用按权展开法的方法。
具体步骤如下:1.将2进制数的每一位与对应的权重相乘(权重从右到左递增,从0开始);2.将每位的值相加。
公式为:十进制数 = d_n * 2^n + d_(n-1) * 2^(n-1) + ... + d_1 * 2^1 + d_0 * 2^0其中,d_n到d_0分别表示2进制数的每一位,从高位到低位排列,n表示二进制数的位数。
例子我们以二进制数10101为例,计算其对应的十进制数。
十进制数 = 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0= 16 + 0 + 4 + 0 + 1= 21因此,二进制数10101对应的十进制数为21。
公式2:位权和公式另一种常用的2进制转化10进制的公式是位权和公式。
这个公式基于二进制数的每一位与对应权重相乘后相加的原理。
公式为:十进制数 = d_n * 2^n + d_(n-1) * 2^(n-1) + ... + d_1 * 2 + d_0其中,d_n到d_0同样表示2进制数的每一位,从高位到低位排列,n表示二进制数的位数。
例子我们以二进制数1101为例,计算其对应的十进制数。
十进制数 = 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0= 8 + 4 + 0 + 1= 13所以,二进制数1101对应的十进制数为13。
公式3:移位法除了按权展开法和位权和公式,还可以使用移位法来进行2进制转化10进制的计算。
这种方法通过左移和右移位来实现。
公式如下:1.首先将二进制数的最高位与对应的权重相乘;2.将得到的结果与次高位与对应的权重相乘后的结果相加;3.重复上述步骤,直到计算完所有位数。
2进制-10进制(BCD码)数码转换器设计

目录摘要 (1)1原理分析 (2)2设计思路 (3)3设计程序 (4)3.1二-十进制转换 (4)3.2对十进制数分位 (6)3.3分别输出十进制数 (7)3.4输出到数码管 (9)3.5显示位数 (11)4整体设计电路图与仿真结果分析 (12)4.1整体设计电路图 (12)4.2仿真结果 (12)4.3仿真结果分析 (13)5小结与体会 (13)参考文献 (15)摘要BCD码亦称二进码十进数或二-十进制代码。
用4位二进制数来表示1位十进制数中的0~9这10个数码。
是一种二进制的数字编码形式,用二进制编码的十进制代码。
BCD 码这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。
本文就是在quartus软件环境下利用VHDL语言将输入的八位二进制转换为BCD十进制数并且在数码管中显示出来。
关键词:二--十进制转换器,BCD码,quartus,VHDL。
2进制-10进制(BCD码)数码转换器设计1原理分析BCD 码这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。
这种编码技巧,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。
相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免却使电脑作浮点运算时所耗费的时间。
此外,对于其他需要高精确度的计算,BCD编码亦很常用。
此处要介绍的是八位二进制转BCD码的硬件实现,采用左移加3的算法,具体描述如下:(1)、左移要转换的二进制码1位(2)、左移之后,BCD码分别置于百位、十位、个位(3)、如果移位后所在的BCD码列大于或等于5,则对该值加3(4)、继续左移的过程直至全部移位完成举例:将八位二进制码11111111转换成BCD码,其真值表如表1-1所示表1-1八位二进制码11111111转换成BCD码真值表2设计思路本次设计并没有用到左移的原理进行操作,直接对输出芯片的输出进行定义,虽然较为繁琐,但是原理却简单,所以才用此种方法,具体原理如下:2进制-10进制(BCD码)的转换可以通过一个芯片实现,即输入的八位二进制码通过编程输出十进制码,八位二进制能表示的最大的数为“255”,即输出的十进制为三位数,此时输出的BCD码就要有12位,每四位代表一个数,此时可再利用一个芯片把输出的12位数重新分配到三个输出管脚中,每个管脚代表一位数,时钟信号每输变一次,输出数字的位也会变一次,即个、十、百位分别输出,同时芯片的selout输出端输出时钟信号的数字到下一个芯片的接收端,通过编程实现000对应110,001对应101,010对应011,即输出0的位置可以表示数码管中所显示数字的位,然后再通过芯片输出到七段数码管进行显示,具体流程图如图2-1所示:图2-1 设计总流程图3设计程序3.1二-十进制转换原理图如图3-1所示:图3-1二进制到十进制转换原理图具体程序语言如下:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_unsigned.all;entity bin2bcd isport(din:in std_logic_vector(7 downto 0);bcd:out std_logic_vector(11 downto 0));end bin2bcd;architecture fun of bin2bcd isbeginprocess (din) isbegincase din iswhen"00000000"=>bcd<="000000000000";when"00000001"=>bcd<="000000000001";when"00000010"=>bcd<="000000000010";when"00000011"=>bcd<="000000000011";when"00000100"=>bcd<="000000000100";when"00000101"=>bcd<="000000000101";when"00000110"=>bcd<="000000000110";when"00000111"=>bcd<="000000000111";when"00001000"=>bcd<="000000001000";when"00001001"=>bcd<="000000001001";when"00001010"=>bcd<="000000010000"。
bcd码的转换

bcd码也叫8421码就是将十进制的数以8421的形式展开成二进制,大家知道十进制是0~9十个数组成,着十个数每个数都有自己的8421码:0=00001=00012=00103=00114=01005=01016=01107=01118=10009=1001举个例子:321的8421码就是3 2 10011 0010 0001二进制编码的十进制数,简称BCD码(Binarycoded Decimal). 这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。
4位二进制数码有16种组合,原则上可任选其中的10种作为代码,分别代表十进制中的0,1,2,3,4,5,6,7,8,9 这十个数符。
最常用的BCD码称为8421BCD 码,8.4.2.1 分别是4位二进数的位取值。
右图为十进制数和8421BCD编码的对应关系表:1、BCD码与十进制数的转换BCD码与十进制数的转换.关系直观,相互转换也很简单,将十进制数75.4转换为BCD码如:75.4=(0111 (0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD=85.5注意:同一个8位二进制代码表示的数,当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时,数值是不相同的。
例如:00011000,当把它视为二进制数时,其值为24;但作为2位BCD码时,其值为18。
又例如00011100,如将其视为二进制数,其值为28,但不能当成BCD码,因为在8421BCD码中,它是个非法编码.2、BCD码的格式计算机中的BCD码,经常使用的有两种格式,即分离BCD码,组合BCD 码。
所谓分离BCD码,即用一个字节的低四位编码表示十进制数的一位,例如数82的存放格式为:_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示无关值。
bcd码改换成十进制bcd码怎样改换为十进制

bcd码改换成十进制bcd码怎样改换为十进制bcd码改换成十进制bcd码怎样改换为十进制BCD码的运算规矩:BCD码是十进制数,而运算器对数据做加减运算时,都是按二进制运算规矩进行处理的。
这么,当将BCD码传送给运算器进行运算时,其作用需求批改。
批改的规矩是:当两个BCD码相加,假定和等于或小于1001(即十进制数9),不需求批改;假定相加之和在1010到1111(即十六进制数0AH~0FH)之间,则需加6进行批改;假定相加时,本位发作了进位,也需加6进行批改。
这么做的要素是,机器按二进制相加,所以4位二进制数相加时,是按逢十六进一的准则进行运算的,而实质上是2个十进制数相加,应当按逢十进一的准则相加,16与10相差6,所以当和逾越9或有进位时,都要加6进行批改。
下面举例阐明。
【例1.3】需求批改BCD码运算值的举例。
(1)核算5+8;(2)核算8+8解:(1)将5和8以8421BCD输入机器,则运算如下:0101+)10001101作用大于9+)0110加6批改10011即13的BCD码作用是0011,即十进制数3,还发作了进位。
5+8=13,定论准确。
(2)将8以8421BCD输入机器,则运算如下:1000+)100010000作用大于9+)0110加6批改1011016的BCD码作用是0110,即十进制的6,并且发作进位。
8+8=16,定论准确。
微机原理代码:(AL=BCD5,BL=BCD8)设AH=0,则ADDAL,BLAAA作用为AX=0103H,标明非紧缩十进制数,CF=1,AF=1,AH=1,AL=3运用AAA指令,能够不必屏蔽高半字节,只需在相加后当即施行AAA指令,便能在AX中得到一个准确的非紧缩十进制数在读写DS1302时需求把读写数据BCD码改换成十进制//***************************************************** ************//bcdhex//此函数用于将8421BCD码改换为十进制数,从函数参数能够看出此BCD码是由两位十进制数构成的。
BCD码2进制转10进制表格工具+说明

BCD码(二─ 十进制码)在一些数字系统中,如电子计算机和数字式仪器中,往往采用二进制码表示十进制数。
通常,把用一组四位二进制码来表示一位十进制数的编码方法称作二─十进制码,亦称BCD 码(Binary Code Decimal)。
4位二进制码共有16种组合,可从中任取10种组合来表示0~9这10个数。
根据不同的选取方法,可以编制出很多种BCD码,如8421码,5421码,2421码,5211码和余3码。
表B1101列出了这几种BCD码,其中的8421 BCD码最为常用。
由于每一组4位二进制码只代表一位十进制数,因而n位十进制数就得用n组4位二进制码表示。
【例1110】把十进制数369.74编成8421 BCD码。
解: 3 6 9 7 4↓↓↓↓↓0011 0110 1001 0111 0100∴(369.74)10=(0011 0110 1001. 0111 0100)BCD表B1101 常用BCD编码表BCD码转化认识BCD编码BCD编码是一种数字压缩存储编码,大家都知道一个字节有8个位,而数字0到9最多只需要使用4个位,如果用一个字节来存储一个数字相对就会有一定的浪费,尤其是在传输过程中,由此人们就想出了压缩的办法,于是BCD编码就产生了。
BCD编码将一个字节的8个位拆分成高4位和低4位两个部分,也就是说一个字节能存储两个数字。
所以BCD的编码过程就是将数字压缩的过程,将两个字节的数字压缩成一个字节。
反之,解码就是把一个字节的数字拆分为两个数字单独存放(大部分的处理都是按字节处理的)。
示例:编码过程,将数字69进行BCD编码(注:BCD编码低位在前,后面将不再注释)。
1. 将6,9分别转换成二进制表示:6(00000110)9(00001001),大家可以看到,最大的数字9也只要4个位,在传输过程中白白浪费了4个位;2.将69合并为一个字节,分别取6,9二进制编码的低4位,按照低位在前的原则,将9的低四位放前面6的低四位放后面得出新的字节二进制编码是10010110;3.完成编码过程,69的BCD编码结果为10010110。
bcd码改换成十进制程序

bcd码改换成十进制程序在做嵌入式软件的方案中,常常会遇到十六进制、BCD码与十进制之间的改换,近期做M1卡的运用中,触及了很多的十六进制、BCD码与十进制之间的改换。
笔者经过对BCD码、十六进制权的了解,轻松的结束了他们之间的沟通。
#includelt;stdio.h#includelt;string.h/////////////////////////////////////////////////////////功用:二进制取反////输入:constunsignedchar*src二进制数据//intlength待改换的二进制数据长度////输出:unsignedchar*dst取反后的二进制数据////回来:0success////////////////////////////////////////////////////////intconvert(unsignedchar*dst,constunsignedchar*src,intlength) {inti;for(i=0;ilt;length;i++){dst[i]=src[i]^0xFF;}return0;}//////////////////////////////////////////////////////////////功用:十六进制转为十进制////输入:constunsignedchar*hex待改换的十六进制数据//intlength十六进制数据长度////输出:////回来:intrslt改换后的十进制数据////思路:十六进制每个字符位所标明的十进制数的方案是0~255,进制为256//左移8位(lt;lt;8)等价乘以256///////////////////////////////////////////////////////////unsignedlongHextoDec(constunsignedchar*hex,intlength){inti;unsignedlongrslt=0;for(i=0;ilt;length;i++){rslt+=(unsignedlong)(hex[i])lt;lt;(8*(length-1-i));}returnrslt;}/////////////////////////////////////////////////////////////功用:十进制转十六进制////输入:intdec待改换的十进制数据//intlength改换后的十六进制数据长度////输出:unsignedchar*hex改换后的十六进制数据////回来:0success////思路:原理同十六进制转十进制////////////////////////////////////////////////////////// intDectoHex(intdec,unsignedchar*hex,intlength){inti;for(i=length-1;i=0;i--){hex[i]=(dec%256)0xFF;dec/=256;}return0;}///////////////////////////////////////////////////////// ////功用:求权////输入:intbase进制基数//int;x权级数////输出:////回来:unsignedlong其时数据位的权//////////////////////////////////////////////////////////// unsignedlongpower(intbase,int;x){inti;unsignedlongrslt=1;for(i=0;ilt;;x;i++)rslt*=base;returnrslt;}///////////////////////////////////////////////////////// ////功用:BCD转10进制////输入:constunsignedchar*bcd待改换的BCD码//intlengthBCD码数据长度////输出:////回来:unsignedlong其时数据位的权////思路:紧缩BCD码一个字符所标明的十进制数据方案为0~99,进制为100//先求每个字符所标明的十进制值,然后乘以权//////////////////////////////////////////////////////////unsignedlongBCDtoDec(constunsignedchar*bcd,intlength){inti,tmp;unsignedlongdec=0;for(i=0;ilt;length;i++){tmp=((bcd[i]4)0x0F)*10+(bcd[i]0x0F);dec+=tmp*power(100,length-1-i);}returndec;}///////////////////////////////////////////////////////// ////功用:十进制转BCD码////输入:intDec待改换的十进制数据//intlengthBCD码数据长度////输出:unsignedchar*Bcd改换后的BCD码////回来:0success////思路:原理同BCD码转十进制//////////////////////////////////////////////////////////// intDectoBCD(intDec,unsignedchar*Bcd,intlength){inti;inttemp;for(i=length-1;i=0;i--){temp=Dec%100;Bcd[i]=((temp/10)lt;lt;4)+((temp%10)0x0F);Dec/=100;}return0;}//-------------函数信息------------------------------------------//函数名:BCDtoDec//函数描绘:BCD码改换成十进制码//进口参数:temp:转化的BCD码//返回:转化后的十进制码//说明:////---------------------------------------------------------------uint8BCDtoDec(uint8temp){return((temp/16)*10+temp%16);}//-------------函数信息------------------------------------------//函数名:DectoBCD//函数描绘:十/十六进制码改换成BCD码//进口参数:temp:转化的十进制码//返回:转化后的BCD码//作者://日期:2006.11.24//说明:////---------------------------------------------------------------uint8DectoBCD(uint8temp){return((temp/10)*16+temp%10);}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
BCD码(二─ 十进制码)
在一些数字系统中,如电子计算机和数字式仪器中,往往采用二进制码表示十进制数。
通常,把用一组四位二进制码来表示一位十进制数的编码方法称作二─十进制码,亦称BCD 码(Binary Code Decimal)。
4位二进制码共有16种组合,可从中任取10种组合来表示0~9这10个数。
根据不同的选取方法,可以编制出很多种BCD码,如8421码,5421码,2421码,5211码和余3码。
表B1101列出了这几种BCD码,其中的8421 BCD码最为常用。
由于每一组4位二进制码只代表一位十进制数,因而n位十进制数就得用n组4位二进制码表示。
【例1110】把十进制数369.74编成8421 BCD码。
解: 3 6 9 7 4
↓↓↓↓↓
0011 0110 1001 0111 0100
∴(369.74)10=(0011 0110 1001. 0111 0100)BCD
表B1101 常用BCD编码表
BCD码转化
认识BCD编码
BCD编码是一种数字压缩存储编码,大家都知道一个字节有8个位,而数字0到9最多只需要使用4个位,如果用一个字节来存储一个数字相对就会有一定的浪费,尤其是在传输过程中,由此人们就想出了压缩的办法,于是BCD编码就产生了。
BCD编码将一个字节的8个位拆分成高4位和低4位两个部分,也就是说一个字节能存储两个数字。
所以BCD的编码过程就是将数字压缩的过程,将两个字节的数字压缩成一个字节。
反之,解码就是把一个字节的数字拆分为两个数字单独存放(大部分的处理都是按字节处理的)。
示例:
编码过程,将数字69进行BCD编码(注:BCD编码低位在前,后面将不再注释)。
1. 将6,9分别转换成二进制表示:6(00000110)9(00001001),大家可以看到,最大的数字9也只要4个位,在传输过程中白白浪费了4个位;
2.将69合并为一个字节,分别取6,9二进制编码的低4位,按照低位在前的原则,将9的低四位放前面6的低四位放后面得出新的字节二进制编码是10010110;
3.完成编码过程,69的BCD编码结果为10010110。
解码过程:将69的BCD码10010110进行解码。
1.将10010110的高4位与低4位拆分开,得到两个二进制数1001和0110;
2.分别将1001和0110的前面补充4位0000得到两个8位的二进制数00001001,00000110;
3.因为编码时低位在前,所以我们将两个二进制数编排顺序为00000110 000010001;
4.将二进制数转换为十进制得出解码结果为69(正确解码)。
PB中如何对BCD码进行解码
大家知道在PB中有二进制类型的变量blob,但要无法按位操作,那么我们如何进行BCD编码的数字进行解码呢?
我想大家都会不约而同的想到ASCII码,没错,就是她。
ASCII就是数字和字符在计算机中存储的的值,她在PB中给我们呈现的并不是01组成的二进制数而是十进制数值。
BCD解码需要将一个字节的高4位和低4位进行拆分,那么我们怎么来使用十进制的ASCII编码做到呢?
因为PB不提供位运算所以我们只能自己写函数来做些简单的处理了,那又如何处理呢?
方法一:我们写函数将十进制的ASCII(单字节)转化为二进制的字符串,当然,如此一来你还要写一个将二进制字符串转换为10进制数字的函数,有兴趣的朋友可以尝试一下。
方法二:在我上次写的内容中已经提到了,就是借助十六进制来完成转换。
大家仔细研究不难发现十六进制表示等同于将一个字节的内容高4位和低4位分别转换为十进制,如果不信你可以自己验算一下。
这样我们就只需要写一个转换函数
了,将十进制数转换为十六进制字符串。
转换后将十六串的两个字符位置对换(因为编码的时候低位在前),然后直接将这个串强制转换为数值型就得到了解码后的数值。
(注:后面有一转换函数是网上一网友所写)
有了解码方法我们在读BCD码的地磅数据的时候就很容易处理了,因为我上次写过处理过程这里我只简单描述一下:
1.用二进制类型blob将串口(现在有的用usb口)的数据读出来;
2.将blob强制转换为string,这样就把二进制流按8位存储格式编码了,也就是说BCD码在这个string中,不过是压缩格式;
3.将string的每个字节都分割开来,然后分别译为ASCII编码,PB中有函数ASC;
4.根据具体设备出厂参数识别string中状态位,校验位,数字位等的位置;
5.找到数字位进行BCD解码,方法如上;
6.完成解码,得到称量数据。
