锐角三角函数的基础测试题及解析
初三数学锐角三角函数试题答案及解析

初三数学锐角三角函数试题答案及解析1.(2013四川乐山)如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为()A.B.C.D.【答案】A【解析】如图,过点P作PA⊥x轴于点A,则OA=3.在Rt△POA中,∵,∴.∴.∴.故选A.2.(2013广东汕头)在Rt△ABC中,∠ABC=90°,AB=3,BC=4,则sinA=________.【答案】【解析】∵∠ABC=90°,AB=3,BC=4,∴.∴.3.(2014江苏无锡)如图,□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于________.【答案】【解析】设AC、BD交于点O.在Rt△AEO中,,即,解得.∵四边形ABCD是平行四边形,∴.4.如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC的值为________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)【答案】24【解析】在Rt△ABC中,∠C=90°,所以,即,所以AC=32·tan37°≈32×0.75=24.5. (2014江苏无锡)如图,在□ABCD中,AE⊥BD于E,∠EAC=30°,AE=3,则AC的长等于________.【答案】【解析】如图,在直角△AOE中,,∴.又∵四边形ABCD是平行四边形,∴.6. (2014四川宜宾)规定:sin(-x)=-sinx,cos(-x)=cosx,sin(x+y)=sinx·cosy+cosx·siny.据此判断下列等式中成立的是________(写出所有正确的序号).①;②;③sin2x=2sinx·cosx;④sin(x-y)=sinx·cosy-cosx·siny.【答案】②③④【解析】①,故①错误;②sin75°=sin(30°+45°)=sin30°·cos45°+cos30°·sin45°,故②正确;③sin2x=sinx·cosx+cosx·sinx=2sinx·cosx,故③正确;④sin(x-y)=sinx·cos(-y)+cosx·sin(-y)=sinx·cosy-cosx·siny,故④正确.7. (2014福建三明)如图,在山坡上植树,已知山坡的倾斜角α是20°,小明种植的两棵树之间的坡面距离AB是6米,要求相邻两棵树之间的水平距离AC为5.3~5.7米.问:小明种植的这两棵树是否符合这个要求?(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)【答案】符合要求【解析】在Rt△ACB中,AB=6米,∠A=20°,∴AC=AB·cosA≈6×0.94=5.64(米).又5.3<5.64<5.7,∴小明种植这两棵树符合要求.8. (2014浙江绍兴)某校九(1)班的同学在上学期的社会实践活动中,对学校旁边的山坡护墙和旗杆进行了测量.(1)如图①,第一小组用一根木条CD斜靠在护墙上,使得DB与CB的长度相等,如果测量得到∠CDB=38°,求α的度数.(2)如图②,第二小组用皮尺量得EF的长为16米(E为护墙上的端点),EF的中点距离地面FB的高度为1.9米,请你求出E点距离地面FB的高度.(3)如图③,第三小组利用第一、第二小组的结果,来测量护墙上旗杆的高度,在点P处测得旗杆顶端A的仰角为45°,向前走4米到达点Q处,测得A的仰角为60°,求旗杆的高度AE(精确到0.1米.参考数据:tan60°≈1.732,tan30°≈0.577,,).【解析】(1)∵BD=BC,∴∠CDB=∠DCB,∴α=2∠CDB=2×38°=76°.(2)设EF的中点为M,过M作MN⊥BF,垂足为点N,过点E作EH⊥BF,垂足为点H,如图①.∴MN∥EH,又M为EF的中点,∴MN为△EFH的中位线,又∵MN=1.9米,∴EH=2MN=3.8米,∴E点距离地面FB的高度是3.8米.(3)延长AE,交PB于点C,如图②.设AE=x米,则AC=(x+3.8)米.∵∠APB=45°,∴PC=AC=(x+3.8)米.∵PQ=4米,∴CQ=x+3.8-4=(x-0.2)米.∵,∴,解得x≈5.7,即AE≈5.7米.答:旗杆的高度AE约为5.7米.9.(2014贵州六盘水)为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动.下图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.活动中测得数据如下:①小明的身高DC=1.5m;②小明的影长CE=1.7m;③小明的脚到旗杆底部的距离BC=9m;④旗杆的影长BF=7.6m;⑤从D点看A点的仰角为30°.请选择你需要的数据,求出旗杆的高度.(计算结果精确到0.1,参考数据:,)【答案】6.7m【解析】解法一:选用①、②、④.∵AB⊥FC,CD⊥FC,∴∠ABF=∠DCE=90°.又∵AF∥DE,∴∠AFB=∠DEC.∴△ABF∽△DCE.∴.又∵DC=1.5m,FB=7.6m,EC=1.7m,∴AB≈6.7m.即旗杆高度约为6.7m.解法二:选用①、③、⑤.如图,过D点作DG⊥AB于G点.∵AB⊥FC,CD⊥FC,∴四边形BCDG为矩形.∴CD=GB=1.5m,DG=BC=9m.在Rt△AGD中,∠ADG=30°,∴,∴m.又∵AB=AG+GB,∴(m),即旗杆高度约为6.7m.10.为了响应某市人民政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅.如图所示,在乙建筑物的顶点D处测得条幅顶端点A的仰角为45°,测得条幅底端点E的俯角为30°,求底部不能直接到达的甲、乙两建筑物之间的水平距离BC.(精确到1米)【答案】19米【解析】要求BC的长,即求△ADE中AE边上的高,如图,过点D作DF⊥AB,垂足为F.由题意,得∠ADF=45°,∠EDF=30°,∴AF=DF.在Rt△DFE中,.∵AE=30,∴,解关于DF的方程得.又∵DF=BC,∴.∴甲、乙两建筑物之间的水平距离约为19米.11.如图所示,在△ABC中,∠C=90°,,D为AC上一点,∠BDC=45°,DC=6,求AB的长.【答案】15【解析】先解直角三角形BCD,求得BC=DC=6,再解直角三角形ABC,由正弦的定义可得,从而得.所以在较复杂的图形中求线段的长度时,有时要通过两次或更多次解直角三角形才能达到目的.因为∠C=90°,∠BDC=45°,所以∠DBC=45°,所以BC=DC=6.在Rt△ABC中,,所以,即AB的长为15.12. (2014福建漳州)将一盒足量的牛奶按如图①所示的方式倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图②是它的平面示意图,请根据图中的信息,求出容器中牛奶的高度.(结果精确到0.1cm.参考数据:,)【答案】约5.5cm【解析】过点P作PN⊥AB于点N,由题意可得∠ABP=30°,AB=8cm,则AP=4cm,cm.∵.∴(cm),∴(cm).∴容器中牛奶的高度约为5.5cm.13.如图,某翼装飞行运动员从离水平地面高AC=500m的A处出发,沿着俯角为15°的方向,直线滑行1600米到达D点,然后打开降落伞以75°的俯角降落到地面上的B点.求他飞行的水平距离(结果精确到1m).【答案】1575米【解析】如图,过点D作DE⊥AC,作DF⊥BC,垂足分别为E,F,∵AC⊥BC,∴四边形ECFD是矩形,∴EC=DF.在Rt△ADE中,∠ADE=15°,AD=1600.∴AE=AD·sin∠ADE=1600sin15°,DE=AD·cos∠ADE=1600cos15°,∵EC=AC-AE,∴EC=500-1600sin15°.在Rt△DBF中,BF=DF·tan∠FDB=ECtan15°,∴BC=CF+BF=1600cos15°+(500-1600sin15°)·tan15°≈1575.∴运动员飞行的水平距离约为1575米.14.(2014江苏南通)如图,海中有一灯塔P,它的周围8海里内有暗礁,海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上,航行40分钟到达B处,测得灯塔P在北偏东30°方向上,如果海轮不改变航线继续向东航行,有没有触礁的危险?【答案】没有【解析】如图,过点P作PH⊥AB于点H,则∠PHB=90°.∵海轮的速度是18海里/时,行驶了40分钟,∴(海里),由题意可得∠PAB=90°-60°=30°,∠PBH=90°-30°=60°,∴∠APB=30°,∴∠PAB=∠APB,∴BP=AB=12.在Rt△PBH中,,所以.∵,∴海轮不改变航线继续向东航行,没有触礁的危险.15.已知在△ABC中,∠C=90°,∠B=60°,,求a,b,c的值及∠A的度数.【答案】,b=3,,∠A=30°【解析】先求∠A,再根据∠A的三角函数关系及已知列方程组求a,b,最后利用勾股定理求c.∵∠C=90°,∴∠A+∠B=90°.∵∠B=60°,∴∠A=30°.由直角三角形的边角关系,得,即,所以,又∵,∴解得∴,∴,b=3,,∠A=30°.16.如图,在Rt△ABC中,∠C=90°,BC=8,,点D在BC上,且BD=AD.求AC的长和cos∠ADC的值.【答案】4;【解析】在Rt△ABC中,∵BC=8,,∴AC=4.设AD=x,则BD=x,CD=8-x,由勾股定理,得(8-x)2+42=x2.解得x=5.∴.17.已知:如图,在Rt△ABC中,∠C=90°,.点D为BC边上一点,且BD=2AD,∠ADC=60°,求△ABC的周长.(结果保留根号)【答案】【解析】在Rt△ADC中,∠C=90°,,∠ADC=60°,因为,即,所以AD=2.由勾股定理得:.所以BD=2AD=4,BC=BD+DC=5.在Rt△ABC中,∠C=90°,,BC=5,由勾股定理得:,所以Rt△ABC的周长为.18.已知:如图,在△ABC中,∠B=45°,∠C=60°,AB=6,求BC的长.(结果保留根号)【答案】【解析】如图,过点A作AD⊥BC于点D,在Rt△ABD中,∠B=45°,∴AD=BD,设AD=x,又∵AB=6,∴Rt△ABD中,x2+x2=62,解得,即.在Rt△ACD中,∠ACD=60°,∴∠CAD=30°,∴,即,∴,∴.19. (2014福建厦门)sin30°的值是( )A.B.C.D.1【答案】A【解析】直接根据特殊角的三角函数值进行计算即可..故选A.20. (2014贵州铜仁)cos60°=________.【答案】【解析】.。
黄冈市初中数学锐角三角函数的基础测试题含解析

黄冈市初中数学锐角三角函数的基础测试题含解析一、选择题1.cos60tan45+o o 的值等于( )A .32B .22C .32D .1【答案】A【解析】【分析】根据特殊角的三角函数值计算即可.【详解】解:原式13122=+=. 故选A .【点睛】本题考查了特殊角的三角函数值,解题的关键是熟练掌握特殊角的三角函数值.2.如图,AB 是O e 的弦,直径CD 交AB 于点E ,若3AE EB ==,15C ∠=o ,则OE 的长为( )A .3B .4C .6D .33【答案】D【解析】【分析】 连接OA .证明OAB ∆是等边三角形即可解决问题.【详解】如图,连接OA .∵AE EB =,∴CD AB ⊥,∴»»AD BD=, ∴230BOD AOD ACD ∠=∠=∠=o ,∴60AOB ∠=o ,∵OA OB =,∴AOB ∆是等边三角形,∵3AE =, ∴tan 6033OE AE =⋅=o ,故选D .【点睛】本题考查圆周角定理,勾股定理,垂径定理,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.3.菱形ABCD 的周长为20cm,DE ⊥AB,垂足为E,sinA=35,则下列结论正确的个数有( ) ①DE=3cm; ②BE=1cm; ③菱形的面积为15cm 2; ④BD=210cm .A .1个B .2个C .3个D .4个 【答案】C【解析】【分析】根据菱形的性质及已知对各个选项进行分析,从而得到答案【详解】∵菱形ABCD 的周长为20cm∴AD=5cm∵sinA=35∴DE=3cm (①正确)∴AE=4cm∵AB=5cm∴BE=5﹣4=1cm (②正确)∴菱形的面积=AB×DE=5×3=15cm 2(③正确)∵DE=3cm,BE=1cm∴10(④不正确)所以正确的有三个.故选C .【点睛】本题考查了菱形的性质及锐角三角函数的定义,熟练掌握性质是解题的关键4.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B 之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()A.(543+10) cm B.(542+10) cm C.64 cm D.54cm【答案】C【解析】【分析】过A作AE⊥CP于E,过B作BF⊥DQ于F,则可得AE和BF的长,依据端点A与B之间的距离为10cm,即可得到可以通过闸机的物体的最大宽度.【详解】如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则Rt△ACE中,AE=12AC=12×54=27(cm),同理可得,BF=27cm,又∵点A与B之间的距离为10cm,∴通过闸机的物体的最大宽度为27+10+27=64(cm),故选C.【点睛】本题主要考查了特殊角的三角函数值,特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.5.一个物体的三视图如图所示,其中主视图和左视图是全等的等边三角形,俯视图是圆,根据图中所示数据,可求这个物体的表面积为()A.πB.2πC.3πD.(31)π+【答案】C【解析】【分析】由三视图可知:该几何体是一个圆锥,其轴截面是一个高为3的正三角形.可计算边长为2,据此即可得出表面积.【详解】解:由三视图可知:该几何体是一个圆锥,其轴截面是一个高为3的正三角形.∴正三角形的边长32 sin60==︒.∴圆锥的底面圆半径是1,母线长是2,∴底面周长为2π∴侧面积为12222ππ⨯⨯=,∵底面积为2rππ=,∴全面积是3π.故选:C.【点睛】本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.6.同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.根据以上作图过程及所作图形,下列结论中错误的是()A.∠ABD=90°B.CA=CB=CD C.sinA=32D.cosD=12【答案】D【解析】【分析】由作法得CA=CB=CD=AB,根据圆周角定理得到∠ABD=90°,点C是△ABD的外心,根据三角函数的定义计算出∠D=30°,则∠A=60°,利用特殊角的三角函数值即可得到结论.【详解】由作法得CA=CB=CD=AB,故B正确;∴点B在以AD为直径的圆上,∴∠ABD=90°,故A正确;∴点C是△ABD的外心,在Rt△ABC中,sin∠D=ABAD=12,∴∠D=30°,∠A=60°,∴sinA=3,故C正确;cosD=3,故D错误,故选:D.【点睛】本题考查了解直角三角形,三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和解直角三角形.7.直角三角形纸片的两直角边长分别为6,8,现将ABCV如图那样折叠,使点A与点B 重合,折痕为DE,则tan CBE∠的值是()A.247B7C.724D.13【答案】C【解析】试题分析:根据题意,BE=AE.设BE=x,则CE=8-x.在Rt△BCE中,x2=(8-x)2+62,解得x=254,故CE=8-254=74,∴tan∠CBE=724 CECB=.故选C.考点:锐角三角函数.8.如图,在矩形ABCD 中,BC =2,AE ⊥BD ,垂足为E ,∠BAE =30°,则tan ∠DEC 的值是( )A .1B .12C .32D .33【答案】C【解析】【分析】 先根据题意过点C 作CF ⊥BD 与点F 可求得△AEB ≌△CFD (AAS ),得到AE =CF =1,EF =323-33【详解】过点C 作CF ⊥BD 与点F .∵∠BAE =30°,∴∠DBC =30°,∵BC =2,∴CF =1,BF 3 ,易证△AEB ≌△CFD (AAS )∴AE =CF =1,∵∠BAE =∠DBC =30°,∴BE =33 AE =33, ∴EF =BF ﹣BE 3 3233, 在Rt △CFE 中,tan ∠DEC =323CFEF ==, 故选C .【点睛】此题考查了含30°的直角三角形,三角形全等的性质,解题关键是证明所进行的全等9.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在AC 上找一点B ,取145ABD ∠=o ,500BD m =,55D ∠=o ,要使A ,C ,E 成一直线,那么开挖点E 离点D 的距离是( )A .500sin55m oB .500cos55m oC .500tan55m oD .500cos55m o【答案】B【解析】【分析】根据已知利用∠D 的余弦函数表示即可.【详解】 在Rt △BDE 中,cosD=DE BD, ∴DE=BD •cosD=500cos55°.故选B .【点睛】 本题主要考查了解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键.10.如图,ABC ∆是一张顶角是120︒的三角形纸片,,6AB AC BC ==现将ABC ∆折叠,使点B 与点A 重合,折痕DE ,则DE 的长为( )A .1B .2C 2D 3【答案】A【解析】【分析】 作AH ⊥BC 于H ,根据等腰三角形的性质求出BH ,根据翻折变换的性质求出BD ,根据正切的定义解答即可.【详解】解:作AH ⊥BC 于H ,∵AB=AC ,AH ⊥BC ,BH=12BC=3, ∵∠BAC=120°,AB=AC ,∴∠B=30°,∴AB=30BH cos=23, 由翻折变换的性质可知,DB=DA=3,∴DE=BD •tan30°=1,故选:A .【点睛】此题考查翻折变换的性质、勾股定理的应用,解题关键在于掌握翻折变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.11.如图,平面直角坐标系中,A (8,0),B (0,6),∠BAO ,∠ABO 的平分线相交于点C ,过点C 作CD ∥x 轴交AB 于点D ,则点D 的坐标为( )A .( 163,2) B .( 163,1) C .( 83,2) D .(83,1) 【答案】A【解析】【分析】 延长DC 交y 轴于F ,过C 作CG ⊥OA 于G ,CE ⊥AB 于E ,根据角平分线的性质得到FC =CG =CE ,求得DH =CG =CF ,设DH =3x ,AH =4x ,根据勾股定理得到AD =5x ,根据平行线的性质得到∠DCA =∠CAG ,求得∠DCA =∠DAC ,得到CD =HG =AD =5x ,列方程即可得到结论.【详解】解:延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,∵CD∥x轴,∴DF⊥OB,∵∠BAO,∠ABO的平分线相交于点C,∴FC=CG=CE,∴DH=CG=CF,∵A(8,0),B(0,6),∴OA=8,OB=6,∴tan∠OAB=DHAH=OBOA=34,∴设DH=3x,AH=4x,∴AD=5x,∵CD∥OA,∴∠DCA=∠CAG,∵∠DAC=∠GAC,∴∠DCA=∠DAC,∴CD=HG=AD=5x,∴3x+5x+4x=8,∴x=23,∴DH=2,OH=163,∴D(163,2),故选:A.【点睛】本题考查了等腰三角形的判定和性质,进行的判定和性质,解直角三角形,正确的作出辅助线构造矩形和直角三角形是解题的关键.12.如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若4BC=,1DE AF==,则GF的长为()A .135B .125C .195D .165【答案】A【解析】【分析】根据正方形的性质以及勾股定理求得5BE CF ==,证明BCE CDF ∆≅∆,根据全等三角形的性质可得CBE DCF ∠=∠,继而根据cos cos BC CG CBE ECG BE CE∠=∠==,可求得CG 的长,进而根据GF CF CG =-即可求得答案.【详解】∵四边形ABCD 是正方形,4BC =,∴4BC CD AD ===,90BCE CDF ∠=∠=︒,∵1AF DE ==,∴3DF CE ==, ∴22345BE CF =+=,在BCE ∆和CDF ∆中, BC CD BCE CDF CE DF =⎧⎪∠=∠⎨⎪=⎩,∴()BCE CDF SAS ∆≅∆,∴CBE DCF ∠=∠,∵90CBE CEB ECG CEB CGE ∠+∠=∠+∠=︒=∠,cos cos BC CG CBE ECG BE CE ∠=∠==, ∴453CG =,125CG =, ∴1213555GF CF CG =-=-=, 故选A.【点睛】 本题考查了正方形的性质,勾股定理,全等三角形的判定与性质,三角函数等知识,综合性较强,熟练掌握和灵活运用相关知识是解题的关键.注意数形结合思想的运用.13.如图,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x轴上,将Rt△AOB绕点O顺时针旋转至△RtA'OB',其中点B'落在反比例函数y=﹣2x的图象上,OA'交反比例函数y=kx的图象于点C,且OC=2CA',则k的值为()A.4 B.72C.8 D.7【答案】C【解析】【详解】解:设将Rt△AOB绕点O顺时针旋转至Rt△A'OB'的旋转角为α,OB=a,则OA=3a,由题意可得,点B′的坐标为(acosα,﹣asinα),点C的坐标为(2asinα,2acosα),∵点B'在反比例函数y=﹣2x的图象上,∴﹣asinα=﹣2acosα,得a2sinαcosα=2,又∵点C在反比例函数y=kx的图象上,∴2acosα=k2asinα,得k=4a2sinαcosα=8.故选C.【点睛】本题主要考查反比例函数与几何图形的综合问题,解此题的关键在于先设旋转角为α,利用旋转的性质和三角函数设出点B'与点C的坐标,再通过反比例函数的性质求解即可.14.如图,已知△A1B1C1的顶点C1与平面直角坐标系的原点O重合,顶点A1、B1分别位于x轴与y轴上,且C1A1=1,∠C1A1B1=60°,将△A1B1C1沿着x轴做翻转运动,依次可得到△A2B2C2,△A3B3C3等等,则C2019的坐标为()A .(2018+6723,0)B .(2019+6733,0)C .(40352+6723,3)D .(2020+6743,0) 【答案】B【解析】【分析】根据题意可知三角形在x 轴上的位置每三次为一个循环,又因为20193673÷=,那么2019C 相当于第一个循环体的3673C 个即可算出.【详解】由题意知,111C A =,11160C A B ︒∠=,则11130C B A ︒∠=,11222A B A B ==,1122333C B C B C B ===,结合图形可知,三角形在x 轴上的位置每三次为一个循环,Q 20193673÷=,∴2019673(123)20196733OC =++=+,∴2019C (20196733,0)+,故选B .【点睛】考查解直角三角形,平面直角坐标系中点的特征,结合找规律.理解题目中每三次是一个循环是解题关键.15.如图,在平面直角坐标系中,AOB ∆的顶点B 在第一象限,点A 在y 轴的正半轴上,2AO AB ==,120OAB ∠=o ,将AOB ∠绕点O 逆时针旋转90o ,点B 的对应点'B 的坐标是( )A .3(23)2--B .33(2222---C .3(3,22--D .(3)-【解析】【分析】过点'B 作x 轴的垂线,垂足为M ,通过条件求出'B M ,MO 的长即可得到'B 的坐标.【详解】解:过点'B 作x 轴的垂线,垂足为M ,∵2AO AB ==,120OAB ∠=︒,∴'''2A O A B ==,''120OA B ∠=︒,∴'0'6M B A ∠=︒,在直角△''A B M 中,3==22=B'M B'M 'sin B A M B '''A ∠ , 1==22=A'M A'M 'cos B A M B '''A ∠, ∴'3B M =,'1A M =,∴OM=2+1=3,∴'B 的坐标为(3,3)-.故选:D.【点睛】本题考查坐标与图形变化-旋转,解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.16.如图,△ABC 的顶点是正方形网格的格点,则cos A =( )A .12B .22C 3D 5 【答案】B【解析】【分析】构造全等三角形,证明△ABD 是等腰直角三角形,进行作答.过A作AE⊥BE,连接BD,过D作DF⊥BF于F.∵AE=BF,∠AEB=∠DFB,BE=DF,∴△AEB≌△BFD,∴AB=DB.∠ABD=90°,∴△ABD是等腰直角三角形,∴cos∠DAB=2 .答案选B.【点睛】本题考查了不规则图形求余弦函数的方法,熟练掌握不规则图形求余弦函数的方法是本题解题关键.17.如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE,若AF=1,四边形ABED的面积为6,则∠EBF的余弦值是()A 213B313C.23D13【答案】B【解析】【分析】首先证明△ABF≌△DEA得到BF=AE;设AE=x,则BF=x,DE=AF=1,利用四边形ABED的面积等于△ABE的面积与△ADE的面积之和得到12•x•x+•x×1=6,解方程求出x得到AE=BF=3,则EF=x-1=2,然后利用勾股定理计算出BE,最后利用余弦的定义求解.【详解】∵四边形ABCD为正方形,∴BA=AD,∠BAD=90°,∵DE ⊥AM 于点E ,BF ⊥AM 于点F ,∴∠AFB =90°,∠DEA =90°,∵∠ABF+∠BAF =90°,∠EAD+∠BAF =90°,∴∠ABF =∠EAD ,在△ABF 和△DEA 中BFA DEA ABF EAD AB DA ∠=∠⎧⎪∠=⎨⎪=⎩∴△ABF ≌△DEA (AAS ),∴BF =AE ;设AE =x ,则BF =x ,DE =AF =1,∵四边形ABED 的面积为6, ∴111622xx x ⋅⋅+⋅⨯=,解得x 1=3,x 2=﹣4(舍去), ∴EF =x ﹣1=2, 在Rt △BEF 中,222313BE =+=,∴313cos 1313BF EBF BE ∠===. 故选B .【点睛】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.会运用全等三角形的知识解决线段相等的问题.也考查了解直角三角形.18.如图,等边ABC V 边长为a ,点O 是ABC V 的内心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①ODE V 形状不变;②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一;③四边形ODBE 的面积始终不变;④BDE V 周长的最小值为1.5a .上述结论中正确的个数是( )A .4B .3C .2D .1【答案】A【解析】【分析】连接OB 、OC ,利用SAS 证出△ODB ≌△OEC ,从而得出△ODE 是顶角为120°的等腰三角形,即可判断①;过点O 作OH ⊥DE ,则DH=EH ,利用锐角三角函数可得OH=12OE 和OE ,然后三角形的面积公式可得S △ODE=4OE 2,从而得出OE 最小时,S △ODE 最小,根据垂线段最短即可求出S △ODE 的最小值,然后证出S 四边形ODBE =S △OBC=212即可判断②和③;求出BDE V 的周长=a +DE ,求出DE 的最小值即可判断④.【详解】解:连接OB 、OC∵ABC V 是等边三角形,点O 是ABC V 的内心,∴∠ABC=∠ACB=60°,BO=CO ,BO 、CO 平分∠ABC 和∠ACB∴∠OBA=∠OBC=12∠ABC=30°,∠OCA=∠OCB=12∠ACB=30°∴∠OBA=∠OCB ,∠BOC=180°-∠OBC -∠OCB=120°∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG -∠BOE=∠BOC -∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COEBO COOBD OCE∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形,∴ODE V 形状不变,故①正确;过点O 作OH ⊥DE ,则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12(180°-120°)=30°∴OH=OE·sin ∠OED=12OE ,EH= OE·cos ∠OED=2OE∴∴S △ODE =12DE·2∴OE 最小时,S △ODE 最小,过点O 作OE′⊥BC 于E′,根据垂线段最短,OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a ×33=36a ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB +S △OBE = S △OEC +S △OBE =S △OBC =12BC·OE′=231223=14×2312a ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一,故②正确; ∵S 四边形ODBE 23 ∴四边形ODBE 的面积始终不变,故③正确;∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB +BE +DE= EC +BE +DE=BC +DE=a +DE∴DE 最小时BDE V 的周长最小∵3OE∴OE 最小时,DE 最小而OE 的最小值为3 ∴DE 33=12a ∴BDE V 的周长的最小值为a +12a =1.5a ,故④正确;综上:4个结论都正确,故选A .【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用,掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键.19.如图,一架飞机在点A 处测得水平地面上一个标志物P 的俯角为α,水平飞行m 千米后到达点B 处,又测得标志物P 的俯角为β,那么此时飞机离地面的高度为( )A .cot cot m αβ-千米B .cot cot m βα-千米C .tan tan m αβ-千米 D .tan tan m βα-千米【答案】A【解析】【分析】根据锐角三角函数的概念进行作答.【详解】在P 点做一条直线垂直于直线AB 且交于点O ,由锐角三角函数知,AO=PO cot α,BO=PO cot β,又AB=m=AO-BO= PO cot α- PO cot β=cot cot m αβ-. 所以答案选A. 【点睛】本题考查了锐角三角函数的概念,熟练掌握锐角三角函数是本题解题关键.20.如图,在矩形ABCD 中E 是CD 的中点,EA 平分,BED PE AE ∠⊥交BC 于点P ,连接PA ,以下四个结论:①EB 平分AEC ∠;②PA BE ⊥;③3AD AB =;④2PB PC =.其中结论正确的个数是( )A.4个B.3个C.2个D.1个【答案】A【解析】【分析】根据矩形的性质结合全等三角形的判定与性质得出△ADE≌△BCE(SAS),进而求出△ABE 是等边三角形,再求出△AEP≌△ABP(SSS),进而得出∠EAP=∠PAB=30°,再分别得出AD与AB,PB与PC的数量关系即可.【详解】解:∵在矩形ABCD中,点E是CD的中点,∴DE=CE,又∵AD=BC,∠D=∠C,∴△ADE≌△BCE(SAS),∴AE=BE,∠DEA=∠CEB,∵EA平分∠BED,∴∠AED=∠AEB,∴∠AED=∠AEB=∠CEB=60°,故:①EB平分∠AEC,正确;∴△ABE是等边三角形,∴∠DAE=∠EBC=30°,AE=AB,∵PE⊥AE,∴∠DEA+∠CEP=90°,则∠CEP=30°,故∠PEB=∠EBP=30°,则EP=BP,又∵AE=AB,AP=AP,∴△AEP≌△ABP(SSS),∴∠EAP=∠PAB=30°,∴AP⊥BE,故②正确;∵∠DAE=30°,∴tan∠DAE=DEAD=tan30°=33,∴AD,即2AD=,∵AB=CD,∴③AD AB=正确;∵∠CEP=30°,∴CP=12 EP,∵EP=BP,∴CP=12 BP,∴④PB=2PC正确.综上所述:正确的共有4个.故选:A.【点睛】此题主要考查了四边形综合,全等三角形的判定与性质,等边三角形的判定与性质,含30度角的直角三角形性质以及三角函数等知识,证明△ABE是等边三角形是解题关键.。
锐角三角函数的真题汇编含答案解析

锐角三角函数的真题汇编含答案解析一、选择题1.如图,在平面直角坐标系中,四边形ABCD是菱形,点B的坐标是(0,4),点D的坐标是(83,4),点M和点N是两个动点,其中点M从点B出发,沿BA以每秒2个单位长度的速度做匀速运动,到点A后停止,同时点N从点B出发,沿折线BC→CD以每秒4个单位长度的速度做匀速运动,如果其中一个点停止运动,则另一点也停止运动,设M,N两点的运动时间为x,△BMN的面积为y,下列图象中能表示y与x的函数关系的图象大致是()A.B.C.D.【答案】D【解析】【分析】根据两个点的运动变化,写出点N在BC上运动时△BMN的面积,再写出当点N在CD上运动时△BMN的面积,即可得出本题的答案;【详解】解:当0<x⩽2时,如图1:连接BD,AC,交于点O′,连接NM,过点C作CP⊥AB垂足为点P,∴∠CPB=90°,∵四边形ABCD是菱形,其中点B的坐标是(0,4),点D的坐标是3,4),∴BO′3,CO′=4,∴228',O B O C+'=∵AC=8,∴△ABC是等边三角形,∴∠ABC=60°,∴CP=BC×sin60°=8×32=43,BP=4,BN=4x,BM=2x,242BM x xBP==,2BN xBC=,∴=BM BNBP BC,又∵∠NBM=∠CBP,∴△NBM∽△CBP,∴∠NMB=∠CPB=90°,∴114438322CBPS BP CP=⨯⨯=⨯⨯=V;∴2NBMCBPS BNS BC⎛⎫= ⎪⎝⎭VV,即y=22283=232NBM CBPBN xS S xBC⎛⎫⎛⎫=⨯=⨯⎪ ⎪⎝⎭⎝⎭V V,当2<x⩽4时,作NE⊥AB,垂足为E,∵四边形ABCD是菱形,∴AB∥CD,∴3BM=2x,∴y=11=2434322BM NE x x⨯⨯=g g;故选D.【点睛】本题主要考查了动点问题的函数图象,掌握动点问题的函数图象是解题的关键.2.如图,矩形纸片ABCD,4AB=,3BC=,点P在BC边上,将CDP∆沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP OF=,则cos ADF∠的值为( )A .1113B .1315C .1517D .1719【答案】C【解析】【分析】根据折叠的性质可得出DC=DE 、CP=EP ,由∠EOF=∠BOP 、∠B=∠E 、OP= OF 可得出△OEF ≌AOBP(AAS)根据全等三角形的性质可得出0E=OB 、EF=BP ,设EF=x ,则BP=x 、DF=4-x 、BF=PC=3-x ,进而可得出AF=1+x ,在Rt △DAF 中,利用勾股定理可求出x 的值,再利用余弦的定义即可求出cos ∠ADF 的值.【详解】解:∵矩形纸片ABCD ,点P 在BC 边上,将CDP ∆沿DP 折叠,点C 落在点E 处, 根据折叠性质,可得:△DCP ≌△DEP ,∴.DC=DE=4, CP= EP ,在△OEF 和△OBP 中90 EOF BOP B E OP OF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△OEF ≌△OBP(AAS)∴ОE=OB , EF= ВР.设EF=x,则BP=x ,DF= DE-EF=4-X ,又∵ BF=OB+OF=OE+ OP=PE=PC, РС=ВC-BP=3-x,∴AF=AB-BF=1+x.在Rt △DAF 中,AF 2+AD 2= DF 2,即(1+x) 2+32= (4-x)2解得: x=35∴DF=4-x=175∴cos ∠ADF=1517AD DF = 故选: C.【点睛】本题考查了全等三角形的判定与性质、勾股定理以及解直角三角形,利用勾股定理结合AF=1+x,求出AF的长度是解题的关键.3.如图,在△ABC中,AC⊥BC,∠ABC=30°,点D是CB延长线上的一点,且AB=BD,则tan D的值为()A.3B.33C.23D.23【答案】D【解析】【分析】设AC=m,解直角三角形求出AB,BC,BD即可解决问题.【详解】设AC=m,在Rt△ABC中,∵∠C=90°,∠ABC=30°,∴AB=2AC=2m,BC33,∴BD=AB=2m,DC=3,∴tan∠ADC=ACCD23m m+=23故选:D.【点睛】本题考查解直角三角形,直角三角形30度角的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4.如图,在矩形ABCD中,AB=3,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为()A.3 B.4 C.5 D.7【答案】B【解析】【分析】如图作GM⊥AD于M交BC于N,作HT⊥BC于T.通过解直角三角形求出AM、GM的长,同理可得HT、CT的长,再通过证四边形ABNM为矩形得MN=AB=3BN=AM=3,最后证四边形GHTN为平行四边形可得GH=TN即可解决问题.【详解】解:如图作GM⊥AD于M交BC于N,作HT⊥BC于T.∵△ABE沿着AE翻折后得到△AGE,∴∠GAM=∠BAE,AB=AG=3∵AG分别平分∠EAD,∴∠BAE=∠EAG,∵∠BAD=90°,∴∠GAM=∠BAE=∠EAG=30°,∵GM⊥AD,∴∠AMG=90°,∴在Rt△AGM中,sin∠GAM=GMAG,cos∠GAM=AMAG,∴GM=AG•sin30°3AM=AG•cos30°=3,同理可得HT3CT=3,∵∠AMG=∠B=∠BAD=90°,∴四边形ABNM为矩形,∴MN=AB=3BN=AM=3,∴GN=MN﹣GM3,∴GN=HT,又∵GN∥HT,∴四边形GHTN是平行四边形,∴GH=TN=BC﹣BN﹣CT=10﹣3﹣3=4,故选:B.【点睛】本题考查翻折变换,解直角三角形,矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.5.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于()A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米【答案】C【解析】【分析】根据正切函数可求小河宽PA的长度.【详解】∵PA⊥PB,PC=100米,∠PCA=35°,∴小河宽PA=PCtan∠PCA=100tan35°米.故选:C.【点睛】此题考查解直角三角形的应用,解题关键在于掌握解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.6.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A(1,1),∴OA=,∴BO=,∵直线AC的解析式为y=x,∴直线BD的解析式为y=-x,∵OB=,∴点B的坐标为(−,),∵点B在反比例函数y=的图象上,∴,解得,k=-3,故选C.点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.7.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的切线与AB的延长线交于点P,连接AC,若∠A=30°,PC=3,则⊙O的半径为()A.3B.23C.32D.233【答案】A【解析】连接OC,∵OA=OC,∠A=30°,∴∠OCA=∠A=30°,∴∠COB=∠A+∠ACO=60°,∵PC是⊙O切线,∴∠PCO=90°,∠P=30°,∵PC=3,∴OC=PC•tan30°=3,故选A8.如图,点O为△ABC边 AC的中点,连接BO并延长到点D,连接AD、CD,若BD=12,AC=8,∠AOD=120°,则四边形ABCD的面积为()A.23B.22C.10D.243【答案】D【解析】【分析】分别过点A、C作BD的垂线,垂足分别为M、N,通过题意可求出AM、CN的长度,可计算三角形ABD和三角形CBD的面积,相加即为四边形ABCD的面积.【详解】解:分别过点A、C作BD的垂线,垂足分别为M、N,∵点O为△ABC边 AC的中点,AC=8,∴AO=CO=4,∵∠AOD =120°,∴∠AOB=60°,∠COD=60°, ∴342AM AM sin AOB AO ===∠, 342CN CN sin COD CO ===∠, ∴AM=23,CN=23,∴122312322ABD BD AM S ⨯===g △, 122312322BD CN S ⨯===g △BCD , ∴=123123243ABD BCD ABCD S S S +=+=△△四边形故选:D.【点睛】本题考查了三角函数的内容,熟练掌握特殊角的三角函数值是解题的关键.9.如图,AB 是O e 的弦,直径CD 交AB 于点E ,若3AE EB ==,15C ∠=o ,则OE 的长为( )A .3B .4C .6D .33【答案】D【解析】【分析】 连接OA .证明OAB ∆是等边三角形即可解决问题.【详解】如图,连接OA .∵AE EB =,∴CD AB ⊥,∴»»AD BD=, ∴230BOD AOD ACD ∠=∠=∠=o ,∴60AOB ∠=o ,∵OA OB =,∴AOB ∆是等边三角形,∵3AE =, ∴tan 6033OE AE =⋅=o ,故选D .【点睛】本题考查圆周角定理,勾股定理,垂径定理,解直角三角形等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.10.cos60tan45+o o 的值等于( )A .32B .22C .3D .1【答案】A【解析】【分析】根据特殊角的三角函数值计算即可.【详解】解:原式13122=+=. 故选A .【点睛】本题考查了特殊角的三角函数值,解题的关键是熟练掌握特殊角的三角函数值.11.如图,在Rt △ABC 内有边长分别为a ,b ,c 的三个正方形.则a 、b 、c 满足的关系式是( )A .b=a+cB .b=acC .b 2=a 2+c 2D .b=2a=2c 【答案】A【解析】【分析】利用解直角三角形知识.在边长为a 和b 两正方形上方的两直角三角形中由正切可得a b c b a c-=-,化简得b =a +c ,故选A. 【详解】请在此输入详解!12.如图,ABC V 中,90ACB ∠=︒,O 为AB 中点,且4AB =,CD ,AD 分别平分ACB ∠和CAB ∠,交于D 点,则OD 的最小值为( ).A .1B .22C 21D .222【答案】D【解析】【分析】 根据三角形角平分线的交点是三角形的内心,得到DO 最小时,DO 为三角形ABC 内切圆的半径,结合切线长定理得到三角形为等腰直角三角形,从而得到答案.【详解】解:Q CD ,AD 分别平分ACB ∠和CAB ∠,交于D 点,D ∴为ABC ∆的内心,OD ∴最小时,OD 为ABC ∆的内切圆的半径,,DO AB ∴⊥过D 作,,DE AC DF BC ⊥⊥ 垂足分别为,,E F,DE DF DO ∴==∴ 四边形DFCE 为正方形, O Q 为AB 的中点,4,AB =2,AO BO ∴==由切线长定理得:2,2,,AO AE BO BF CE CF r ======sin 4522,AC BC AB ∴==•︒=222,CE AC AE ∴=-=Q 四边形DFCE 为正方形,,CE DE ∴=222,OD CE ∴==故选D .【点睛】本题考查的动态问题中的线段的最小值,三角形的内心的性质,等腰直角三角形的性质,锐角三角函数的计算,掌握相关知识点是解题关键.13.将一副直角三角板如图放置,点C在FD的延长上,AB∥CF,∠F=∠ACB=90°,∠E =30°,∠A=45°,AC=122,则CD的长为()A.3B.12﹣3C.12﹣3D.3【答案】B【解析】【分析】过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=60°,进而可得出答案.【详解】解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=45°,AC=2,∴BC=AC=2.∵AB∥CF,∴BM=BC×sin45°=2 12212=CM=BM=12,在△EFD中,∠F=90°,∠E=30°,∴∠EDF=60°,∴MD=BM÷tan60°=43∴CD=CM﹣MD=12﹣43故选B.【点睛】本题考查了解直角三角形,难度较大,解答此类题目的关键根据题意建立直角三角形利用所学的三角函数的关系进行解答.14.如图,在Rt△ABC中,∠ABC=90°,AB=23,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )A.5342π-B.5342π+C.23πD.432π【答案】A【解析】【分析】连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,利用∠A的正切值求出∠A=30°,继而可求得OH、AH长,根据圆周角定理可求得∠BOC =60°,然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.【详解】连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,∠ABC=90°,AB=3BC=2,tan∠A=323BCAB==,∴∠A=30°,∴OH=123AH=AO•cos∠3332=,∠BOC=2∠A=60°,∴AD=2AH=3,∴S阴影=S△ABC-S△AOD-S扇形BOD=2603113232322360π⨯⨯-⨯532π-,故选A.【点睛】本题考查了垂径定理,圆周角定理,扇形面积,解直角三角形等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.15.如图,一架飞机在点A 处测得水平地面上一个标志物P 的俯角为α,水平飞行m 千米后到达点B 处,又测得标志物P 的俯角为β,那么此时飞机离地面的高度为( )A .cot cot m αβ-千米B .cot cot m βα-千米C .tan tan m αβ-千米 D .tan tan m βα-千米 【答案】A【解析】【分析】根据锐角三角函数的概念进行作答.【详解】在P 点做一条直线垂直于直线AB 且交于点O ,由锐角三角函数知,AO=PO cot α,BO=PO cot β,又AB=m=AO-BO= PO cot α- PO cot β=cot cot m αβ-. 所以答案选A. 【点睛】本题考查了锐角三角函数的概念,熟练掌握锐角三角函数是本题解题关键.16.如图,在边长为8的菱形ABCD 中,∠DAB =60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E ,交CD 于点G ,则图中阴影部分的面积是 ( )A .183π-B .183πC .32316πD .1839π-【答案】C【解析】由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF,图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF是菱形的高,∴DF⊥AB,∴DF=AD•sin60°=3843⨯=,∴图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积=2120(43)84332316ππ⨯⨯-=-.故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.17.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为()A.2 B3C2D.1 2【答案】B【解析】【分析】连接OA,由圆周角定理可求出∠AOC=60°,再根据∠AOC的正切即可求出PA的值.【详解】连接OA,∵∠ABC=30°,∴∠AOC=60°,∵PA是圆的切线,∴∠PAO=90°,∵tan∠AOC =PA OA,∴PA= tan60°3.【点睛】本题考查了圆周角定理、切线的性质及锐角三角函数的知识,根据圆周角定理可求出∠AOC=60°是解答本题的关键.18.在Rt△ABC中,∠C=90°,如果∠A=α,BC=a,那么AC等于()A.a•tanαB.a•cotαC.a•sinαD.a•cosα【答案】B【解析】【分析】画出图形,根据锐角三角函数的定义求出即可.【详解】如图,∠C=90°,∠A=α,BC=a,∵cotαAC BC ,∴AC=BC•cotα=a•cotα,故选:B.【点睛】本题考查了锐角三角函数的定义的应用,在直角三角形中,锐角的正弦是角的对边与斜边的比;余弦是角的邻边与斜边的比;正切是对边与邻边的比;余切是邻边与对边的比;熟练掌握三角函数的定义是解题关键.19.如图1,在△ABC中,∠B=90°,∠C=30°,动点P从点B开始沿边BA、AC向点C以恒定的速度移动,动点Q从点B开始沿边BC向点C以恒定的速度移动,两点同时到达点C,设△BPQ的面积为y(cm2).运动时间为x(s),y与x之间关系如图2所示,当点P 恰好为AC的中点时,PQ的长为()A.2 B.4 C.23D.43【答案】C【解析】【分析】点P、Q的速度比为3:3,根据x=2,y=63,确定P、Q运动的速度,即可求解.【详解】解:设AB=a,∠C=30°,则AC=2a,BC=3a,设P、Q同时到达的时间为T,则点P的速度为3aT,点Q的速度为3aT,故点P、Q的速度比为3:3,故设点P、Q的速度分别为:3v、3v,由图2知,当x=2时,y=63,此时点P到达点A的位置,即AB=2×3v=6v,BQ=2×3v=23v,y=12⨯AB×BQ=12⨯6v×23v=63,解得:v=1,故点P、Q的速度分别为:3,3,AB=6v=6=a,则AC=12,BC=63,如图当点P在AC的中点时,PC=6,此时点P运动的距离为AB+AP=12,需要的时间为12÷3=4,则BQ=3x=43,CQ=BC﹣BQ=63﹣43=23,过点P作PH⊥BC于点H,PC=6,则PH=PC sin C=6×12=3,同理CH=3,则HQ=CH﹣CQ=333,PQ22PH HQ+39+3,故选:C.【点睛】本题考查的是动点图象问题,此类问题关键是:弄清楚不同时间段,图象和图形的对应关系,进而求解.20.如图,△ABC的外接圆是⊙O,半径AO=5,sinB=25,则线段AC的长为()A.1 B.2 C.4 D.5【答案】C【解析】【分析】首先连接CO并延长交⊙O于点D,连接AD,由CD是⊙O的直径,可得∠CAD=90°,又由⊙O的半径是5,sinB=25,即可求得答案.【详解】解:连接CO并延长交⊙O于点D,连接AD,由CD是⊙O的直径,可得∠CAD=90°,∵∠B和∠D所对的弧都为弧AC,∴∠B=∠D,即sinB=sinD=25,∵半径AO=5,∴CD=10,∴2 sin105AC ACDCD===,∴AC=4,故选:C.【点睛】本题考查了同弧所对的圆周角相等,以及三角函数的内容,注意到直径所对的圆周角是直角是解题的关键.。
锐角三角函数的经典测试题含答案

CE平行于AB,BC的坡度为i 1: 0.75,坡长0.64,cos40BC 140米,则AB的长为( )(精确0.77,tan40 0.84 )A.78.6米【答案】CB.78.7 米C.78.8 米D.78.9 米锐角三角函数的经典测试题含答案一、选择题1.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点 A 测得大桥主架与水面的交汇点C 的俯角为α,大桥主架的顶端D的仰角为β,已知测量点与大桥主架的水平距离AB=a,则此时大桥主架顶端离水面的高解析】【分析】在Rt△ABD和Rt△ABC中,由三角函数得出BC=atan α,BD=atan β,得出CD=BC+BD=atan α +atan即β可.【详解】∴BC=atan α,BD=atan β,∴CD=BC+BD=atan α+atan β,故选C.点睛】本题考查了解直角三角形﹣仰角俯角问题;由三角函数得出BC和BD 是解题的关键.2.在课外实践中,小明为了测量江中信号塔A离河边的距离AB ,采取了如下措施:如图在江边D处,测得信号塔A的俯角为40 ,若DE 55米,DE CE,CE 36米,acos α +acos βC.atan α +atan βaD.tanatan在Rt△ABD 和Rt△ABC中,AB= a ,BC BDtan α=,tan β=AB ABB.答案】CA.533B.C.222D.【分析】如下图,先在Rt△CBF中求得BF、CF的长,再利用Rt△ADG 求AG的长,进而得到AB的长度【详解】如下图,过点C作AB的垂线,交AB延长线于点F,延长DE交AB延长线于点G∵BC 的坡度为1:0.75∴设CF为xm,则BF 为0.75xm ∵BC=140m∴在Rt△BCF中,x20.75x 21402,解得:x=112 ∴CF=112m,BF=84m∵DE⊥CE,CE∥AB,∴DG⊥AB,∴△ ADG 是直角三角形∵ DE=55m,CE=FG=36m∴DG=167m,BG=120m 设AB=ym ∵∠ DAB=40°DG 167 ∴tan40 °= 0.84AG y 120 解得:y=78.8 故选: C【点睛】本题是三角函数的考查,注意题干中的坡度指的是斜边与水平面夹角的正弦值3.如图,在等腰直角△ABC中,∠ C=90°,D为BC的中点,将△ABC折叠,使点A与点D 重合,EF为折痕,则sin∠ BED的值是()35解析】分析】先根据翻折变换的性质得到DEF AEF ,再根据等腰三角形的性质及三角形外角的性质可得到BED CDF ,设CD 1,CF x,则CA CB 2 ,再根据勾股定理即可求解.【详解】解:∵△ DEF是△AEF翻折而成,∴△ DEF≌△ AEF,∠ A=∠ EDF,∵△ ABC是等腰直角三角形,∴∠ EDF=45°,由三角形外角性质得∠ CDF+45°=∠ BED+45°,∴∠ BED=∠ CDF,设CD=1,CF=x,则CA=CB=2,∴DF=FA=2﹣x,∴在Rt△CDF中,由勾股定理得,CF2+CD2=DF2,即x2+1=(2﹣x)2,3解得:x 3,4CFsin BED sin CDFDF故选:B.点睛】本题考查的是图形翻折变换的性质、等腰直角三角形的性质、勾股定理、三角形外角的性质,涉及面较广,但难易适中.4.直角三角形纸片的两直角边长分别为6,8,现将VABC如图那样折叠,使点A与点B 重合,折痕为DE ,则tan CBE 的值是()71 C.D.7 3 24 3 【答案】 C【解析】试题分析:根据题意,BE=AE.设BE=x,则CE=8-x.在Rt△BCE中,x2=(8-x)2+62,25 25 7解得x= 25,故CE=8-25 = ,4 4 4CE 7∴tan ∠CBE= .CB 24故选 C. 考点:锐角三角函数.5.如图,从点A看一山坡上的电线杆PQ ,观测点P的仰角是45 ,向前走6m到达B 点,测得顶端点P和杆底端点Q的仰角分别是60 和30°,则该电线杆PQ 的高度()A.24B.7A.6 2 3 B.6 3 C.10 3 D.8 3【答案】A【解析】【分析】延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x 表示出AE和BE,列出方程求得x 的值,再在直角△BQE中利用三角函数求得QE的长,则问题求解.【详解】解:延长PQ 交直线AB于点E,设PE=x.在直角△APE中,∠ A=45°,AE=PE=x;∵∠ PBE=60°∴∠ BPE=30°在直角△BPE中,BE= 3 PE= 3 x,33∵AB=AE-BE=6米,则x- x=6,3解得:x=9+3 3.则BE=3 3 +3 .在直角△BEQ中,QE= 3 BE= 3(3 3 +3)=3+ 3.33∴PQ=PE-QE=9+3 3-(3+ 3 )=6+2 3.答:电线杆PQ的高度是(6+2 3 )米.故选:A.【点睛】本题考查解直角三角形的实际应用,解答关键是根据题意构造直角三角形解决问题6.如图,在x轴的上方,直角∠ BOA绕原点O按顺时针方向旋转.若∠ BOA的两边分别与12函数y 、y 的图象交于B、A 两点,则∠ OAB大小的变化趋势为()A.逐渐变小B.逐渐变大C.时大时小D.保持不变【答案】D 【解析】【分析】如图,作辅助线;首先证明△BEO∽△OFA,,得到BE OE ;1设 B 为(a,), A 为OF AF a2 1 2(b,),得到OE=-a,EB= ,OF=b,AF= ,进而得到a2b22 ,此为解决问题的关 b a b2键性结论;运用三角函数的定义证明知tan∠ OAB= 2为定值,即可解决问题.2【详解】解:分别过B和A作BE⊥x轴于点E,AF⊥x轴于点F,则△BEO∽△ OFA,∴BE OE∴OF AF ,12设点 B 为(a,),A 为(b,2),a b12则OE=-a,EB= ,OF=b,AF= 2,a b2可代入比例式求得 a 2b 2 2 ,即 a 2 2 , b 2该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问 题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用相似三角形的判 定等知识点来分析、判断、推理或解答.7.如图,要测量小河两岸相对的两点 P ,A 的距离,可以在小河边取 PA 的垂线 PB 上的一解析】 分析】根据正切函数可求小河宽 PA 的长度. 【详解】∵PA ⊥ PB ,PC=100米,∠ PCA=35°,根据勾股定理可得: OB= OE 2EB 2a 212,OA= OF 2 AF 2∴tan ∠OAB=OBOA1 b 22 2 (b 2 b 2) = 2 b b2 b 42 = 22∴∠ OAB 大小是一个定值,因此∠ 故选 DOAB 的大小保持不变 .D . 100tan55 米°a 2a 122 b2b b 42 b 2 b 42点睛】PA 等于( )C . 100tan35米°∴小河宽PA=PCtan∠ PCA=100tan35°米.故选:C.【点睛】此题考查解直角三角形的应用,解题关键在于掌握解直角三角形的一般过程是:① 将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).② 根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.8.某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB 自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12 米,CD=8 米,∠ D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为()米.(精确到0.1 米,参考数据:tan36 °≈0,.7c3os36 °≈0,.8s1in36 °≈)0.59A.5.6 B. 6.9 C.11.4 D.13.9【答案】C【解析】【分析】根据勾股定理,可得CE,BE的长,根据正切函数,可得AE 的长,再根据线段的和差,可得答案.【详解】解:如图,延长DC、AB 交于点E,由斜坡轨道BC的坡度(或坡比)为i=1:2,得BE:CE=1:2.设BE=xm,CE=2xm.在Rt △BCE中,由勾股定理,得BE2+CE2=BC2,即x2+(2x)2=(12 )2,解得x=12,BE=12m,CE=24m ,DE =DC+CE =8+24=32m , 由 tan36 °≈ 0.,73得=0.73,解得 AB =0.73 ×3=2 23.36m . 由线段的和差,得AB =AE ﹣BE =23.36﹣12= 11.36 ≈ 11m.4, 故选: C .【点睛】 本题考查解直角三角形的应用,利用勾股定理得出 切函数,线段的和差.9.如图,对折矩形纸片 ABCD ,使 AD 与 BC 重合,得到折痕 EF ,把纸片展平,再一次折叠 纸片,使点 A 落在 EF 上的点 A ′处,并使折痕经过点 B ,得到折痕 BM ,若矩形纸片的宽 AB=4,则折痕 BM 的长为 ( )1BE= AB ,A ′B=AB=,4∠BA ′M=∠A=90°,∠ ABM=∠MBA ′,可得∠2EA ′B=30°,根据直角三角形两锐角互余可得∠ E BA ′=60 °,进而可得∠ ABM=30°,在Rt △ABM中,利用∠ ABM 的余弦求出 BM 的长即可 .【详解】 ∵对折矩形纸片 ABCD ,使 AD 与 BC 重合, AB=4,1∴BE= AB=2,∠ BEF=90°,2∵把纸片展平,再一次折叠纸片,使点 A 落在 EF 上的点 A '处,并使折痕经过点 B , ∴A ′B=AB=4,∠ BA ′M= ∠ A=90°,∠ ABM=∠ MBA ′, ∴∠ EA ′B=30°, ∴∠ EBA ′=60°, ∴∠ ABM=3°0 ,∴在 Rt △ABM 中, AB=BM cos ∠ ABM ,即 4=BM cos30 °,CE ,BE 的长是解题关键,又利用了正A . 8 33【答案】 A 【解析】 【分析】B . 4 33C .8D . 8 3根据折叠性质可得解得: BM= 8 3 ,3故选 A.【点睛】 本题考查了折叠的性质及三角函数的定义,折叠前后,对应边相等,对应角相等;在直角 三角形中,锐角的正弦是角的对边比斜边;余弦是角的邻边比斜边;正切是角的对边比邻 边;余切是角的邻边比对边;熟练掌握相关知识是解题关键 .故选 B .【点睛】 本题考查了解直角三角形,菱形的性质,等边三角形的判定和性质, 线的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.11.如图 1,在△ABC 中,∠ B =90°,∠ C = 30°,动点 P 从点 B 开始沿边 BA 、AC 向点 C 以 恒定的速度移动,动点 Q 从点 B 开始沿边 BC 向点 C 以恒定的速度移动,两点同时到达点 C ,设△BPQ 的面积为 y (cm 2).运动时间为 x ( s ), y 与 x 之间关系如图 2所示,当点 P 恰好为 AC 的中点时, PQ 的长为( )10. 如图,菱形 ABCD 中, AC 交 BD 于点 O ,DE ⊥BC 于点 E ,连接 OE ,∠ DOE =120°,DE A . 33【答案】 B 【解析】 【分析】证明 △OBE 是等边三角形,然后解直角三角形即可. 【详解】∵四边形 ABCD 是菱形,∴ OD=OB ,CD=BC . ∵DE ⊥BC ,∴∠ DEB=90°,∴OE=OD=OB . ∵∠ DOE=120°,∴∠ BOE=60°,∴△ OBE是等边三角形,∴∠ ∵∠ DEB=90°,∴ BD= DE 2 3 .sin60 3B .23 3D . 3 3DBC=60°直角三角形斜边的中3,解:设 AB =a ,∠ C = 30°,则 AC =2a ,BC = 3 a , 设 P 、 Q 同时到达的时间为 T ,则点 P 的速度为 3a ,点 Q 的速度为 3a ,故点 P 、 Q 的速度比为 3: 3, TT 故设点 P 、 Q 的速度分别为: 3v 、 3 v ,由图 2 知,当 x =2 时,y =6 3,此时点 P 到达点 A 的位置,即 AB =2×3v =6v , BQ = 2×3 v = 2 3 v ,11y =AB ×BQ =6v ×2 3 v = 6 3 ,解得: v =1,22故点 P 、Q 的速度分别为: 3, 3,AB =6v =6=a , 则 AC =12,BC =6 3 ,如图当点 P 在 AC 的中点时, PC =6,此时点 P 运动的距离为 AB+AP =12,需要的时间为 12÷3=4, 则 BQ =3 x =4 3 , CQ = BC﹣ BQ =6 3 ﹣4 3 =2 3 , 过点 P 作 PH ⊥BC 于点 H ,PC = 6,则 PH = PCsinC = 6×1 =3,同理 CH =3 3 ,则 HQ = CH ﹣ CQ = 3 3 ﹣2 3 =2PQ = PH 2 HQ 2 = 3 9 =2 3,D . 4 3【答案】【解析】【分析】 点 P 、 Q 的速度比为【详解】3: 3 ,根据 x =2,y =6 3 ,确定 P 、Q 运动的速度,即可求解.C故选: C .【点睛】本题考查的是动点图象问题,此类问题关键是:弄清楚不同时间段,图象和图形的对应关 系,进而求解.12.一艘轮船从港口 O 出发,以 15海里 /时的速度沿北偏东 60°的方向航行 4小时后到达 A 处,此时观测到其正西方向 50 海里处有一座小岛 B .若以港口 O 为坐标原点,正东方向为 x 轴的正方向,正北方向为 y 轴的正方向, 1 海里为 1 个单位长度建立平面直角坐标系(如解析】分析】 【详解】解: OA=15×4=60海里,∵∠ AOC=60°,∴∠ CAO=30°,∵sin30°= OCAO 2∴CO=30 海里, ∴AC=30 3 海里, ∴BC=(30 3 -50)海里, ∴B ( 30 3 -50, 30) 故选 A点睛】 本题考查掌握锐角三角函数的应用.13.在一次数学活动中,嘉淇利用一根拴有小锤的细线和一个半圆形量角器制作了一个测 角仪,去测量学校内一座假山的高度 CD .如图,嘉淇与假山的水平距离 BD 为 6m ,他的D .(30,30 3 )C .(30 3 ,30)眼睛距地面的高度为1.6m ,嘉淇的视线经过量角器零刻度线OA和假山的最高点C ,此时,铅垂线OE经过量角器的60 刻度线,则假山的高度CD 为()A.2 3 1.6 m B.2 2 1.6 m C.4 3 1.6 m D.2 3m【答案】A【解析】【分析】CK CK根据已知得出AK=BD=6m,再利用tan30 °= ,进而得出CD 的长.AK 6【详解】解:如图,过点 A 作AK CD 于点K∵BD=6 米,李明的眼睛高AB=1.6米,∠ AOE=6°0 ,∴DB=AK,AB=KD=1.6米,∠ CAK=30°,CK CK∴tan30 °= ,AK 6解得:CK=2 3即CD=CK+DK=2 3 +1.6=( 2 3 +1.6)m .故选:A.【点睛】本题考查的是解直角三角形的应用,根据题意构造直角三角形,解答关键是应用锐角三角函数定义.14.如图,△ABC的顶点是正方形网格的格点,则cosA ()答案】 B 【解析】【分析】构造全等三角形,证明 △ABD 是等腰直角三角形,进行作答【详解】过 A 作 AE ⊥ BE ,连接 BD ,过 D 作 DF ⊥BF 于 F. ∵AE=BF ,∠ AEB=∠ DFB ,BE=DF ,∴△ AEB ≌△ BFD ,∴AB=DB.∠ABD=90°,∴△ ABD 是等腰直角三角形,∴cos ∠ DAB= 22 答案选 B.【点睛】 本题考查了不规则图形求余弦函数的方法,熟练掌握不规则图形求余弦函数的方法是本题 解题关键 .15. 如图,矩形 ABCD 的对角线 AC 、 BD 相交于点 O ,AB :BC =2:1,且 BE ∥ AC , CE ∥答案】 B解析】分析】DC 交线段 DC 延长线于点 F ,连接 OE 交BC 于点 G .根据邻边相等的平行四边形是菱形即可判断四边形 OBEC 是菱形,则 OE 与 BC 垂直平分,易得 EF=1 x , 2 1 A . 2B . 2 2C . 3 2D . 55C . 62 3D . 10过点 E 作 EF ⊥直线 B . A .4CF=x.再由锐角三角函数定义作答即可.【详解】解:∵矩形ABCD的对角线AC、BD 相交于点O,AB:BC=2:1,∴BC=AD,设AB=2x,则BC=x.如图,过点 E 作EF⊥直线DC交线段DC延长线于点F,连接OE交BC于点G.∵BE∥AC,CE∥BD,∴四边形BOCE是平行四边形,∵四边形ABCD是矩形,∴OB=OC,∴四边形BOCE是菱形.∴OE与BC垂直平分,∴EF=1 AD=1 x,OE∥ AB,22∴四边形AOEB是平行四边形,∴OE=AB=2x,1∴CF=OE=x.2本题考查矩形的性质、平行四边形的判定与性质、菱形的判定与性质以及解直角三角形,解题的关键是熟练掌握矩形的性质和菱形的判定与性质,属于中考常考题型.16.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m 千米∴tan ∠EDC=EFDF2x xA.m cotcot千米B.cot cot千米C.tan tan千米D.tan tan故选:B.点睛】m m m【答案】A【解析】【分析】根据锐角三角函数的概念进行作答.【详解】在P 点做一条直线垂直于直线AB 且交于点O,由锐角三角函数知,AO=PO cotBO=PO cot m,又AB=m=AO-BO= PO cot - PO cot = . 所以答案选 A. cot cot【点睛】本题考查了锐角三角函数的概念,熟练掌握锐角三角函数是本题解题关键17.如图,在边长为8的菱形ABCD中,∠ DAB=60°,以点D为圆心,菱形的高画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是解析】分析】由菱形的性质得出AD=AB=8,∠ ADC=12°0 ,由三角函数求出菱形的高DF,图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD 是菱形,∠ DAB=60°,∴AD=AB=8,∠ ADC=18°0 -60°=120 °,∵DF是菱形的高,∴DF⊥ AB,∴DF=AD?sin60 °=834 3,2∴图中阴影部分的面积=菱形ABCD 的面积- 扇形DEFG的面积=8 4 3120 (4 3)32 3 16.360故选: C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.DF 为半径C.32 3 16 D.18 3 答案】C18.如图,一艘轮船从位于灯塔 C 的北偏东 60°方向,距离灯塔 60 nmile 的小岛 A 出发, 沿正南方向航行一段时间后,到达位于灯塔小岛 A 的距离是 ( AB 的长.【详解】 CDcos ∠ ACD= ,AC∴CD=AC?cos ∠ACD=6×0 3 30 3 .2在 Rt △DCB 中,∵∠ BCD=∠ B=45°,∴CD=BD=30 3 ,∴AB=AD+BD=30+30 3 .答:此时轮船所在的 B 处与灯塔 P 的距离是( 30+30 3 )nmile .故选 D .【点睛】此题主要考查了解直角三角形的应用 -方向角问题,求三角形的边或高的问题一般可以转化 C 的南偏东 45°方向上的 B 处,这时轮船 B 与A . 30 3 n mile 【答案】 D【解析】【分析】过点 C 作 CD ⊥AB , B . 60 n mile C .120 nmile D . (30 30 3) n mile则在 Rt △ACD 中易得A D 的长,再在直角 △BCD 中求出 BD ,相加可得 在 Rt △ACD中, AC=60.为解直角三角形的问题,解决的方法就是作高线.19.已知 B 港口位于 A 观测点北偏东 45°方向,且其到 A 观测点正北风向的距离 BM 的长 为 10 2 km ,一艘货轮从 B 港口沿如图所示的 BC 方向航行 4 7 km 到达 C 处,测得 C 处 位于 A 观测点北偏东 75°方向,则此时货轮与 A 观测点之间的距离 【答案】 A【解析】【分析】【详解】解:∵∠ MAB=4°5 , BM=10 2 ,∴AB= BM 2 MA 2 = (10 2)2 (10 2)2 =20km , 过点 B 作 BD ⊥AC ,交 AC 的延长线于 D , 在 Rt △ADB 中,∠ BAD=∠MAC ﹣∠ MAB=7°5 ﹣45°=30°, BDtan ∠ BAD=AD∴AD= 3 BD , BD 2 +AD 2 =AB 2,即BD 2+( 3 BD )2=202,∴ BD=10,∴ AD=10 3 ,在 Rt △BCD 中, BD 2+CD 2=BC 2, BC=4 3 ,∴ CD=2 3 , ∴AC=AD ﹣ CD=10 3 ﹣ 2 3 =8 3 km ,答:此时货轮与 A 观测点之间的距离 AC 的长为 8 3 km . 故选 A .【考点】解直角三角形的应用 -方向角问题.AC 的长为( )B . 9 3C . 6 3D . 7 320.如图,一艘轮船位于灯塔 P 的北偏东 60°方向,与灯塔 P 的距离为 30 海里的 A 处,轮 船沿正南方向航行一段时间后,到达位于灯塔 P 的南偏东 30°方向上的 B 处,则此时轮船 所在位置 B 与灯塔 P 之间的距离为 ( )【答案】 D【解析】 【分析】 根据题意得出:∠ B=30°,AP=30 海里,∠ 案.【详解】 解:由题意可得:∠ B=30°, AP=30海里,∠ APB=90°, 故AB=2AP=60(海里),则此时轮船所在位置 B 处与灯塔 P 之间的距离为: BP= AB 2 AP 2 故选:D .【点睛】 此题主要考查了勾股定理的应用以及方向角,正确应用勾股定理是解题关键. B . 45 海里 C .20 3 海里 D .30 3 海里APB=90°,再利用勾股定理得出 BP 的长,求出答 30 3 (海里)。
锐角三角函数的经典测试题及答案

锐角三角函数的经典测试题及答案锐角三角函数的经典测试题及答案一、选择题1.“奔跑吧,兄弟!”节目组预设计一个新的游戏:“奔跑”路线需经过A、B、C、D四地。
如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向。
C地在A地北偏东75°方向。
且BD=BC=30m。
从A地到D地的距离是()A。
303mB。
205mC。
302mD。
156m答案】D解析】过点D作DH垂直于AC,垂足为H,求出∠DAC的度数,判断出△BCD是等边三角形,再利用三角函数求出AB的长,从而得到___的长。
详解】过点D作DH垂直于AC,垂足为H,由题意可知∠DAC=75°-30°=45°。
因为△BCD是等边三角形,所以∠DBC=60°,BD=BC=CD=30m。
因此,DH=3/2×30=45,AD=2DH=90m。
所以,从A地到D地的距离是156m。
故选D。
点睛】本题考查了解直角三角形的应用——方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想。
2.公元三世纪,我国汉代数学家___在注解《周髀算经》时给出的“___图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形。
如果大正方形的面积是125,小正方形面积是25,则(sinθ-cosθ)=()A。
1/5B。
5/5C。
35/5D。
9/5答案】A解析】根据正方形的面积公式可得大正方形的边长为5√5,小正方形的边长为5,再根据直角三角形的边角关系列式即可求解。
详解】解:因为大正方形的面积是125,小正方形面积是25,所以大正方形的边长为5√5,小正方形的边长为5.因此,55cosθ-55sinθ=5,cosθ-sinθ=2/5.因此,(sinθ-cosθ)=1/5.故选:A。
点睛】本题考查了解直角三角形、勾股定理的证明和正方形的面积,难度适中,解题的关键是正确得出cosθ-sinθ=2/5.3.如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点A′处,并使折痕经过点B,得到折痕BM,若矩形纸片的宽AB=4,则折痕BM的长为()A。
锐角三角函数(含答案)

一、基础知识1、1、利用计算器求锐角三角三角函数值。
如求sin63゜52′41″的值.(精确到0.0001)先用如下方法将角度单位状态设定为“度”:再按下列顺序依次按键:显示结果为0.897 859 012.所以sin63゜52′41″≈0.89792、利用计算器根据锐角三角函数值求锐角。
如已知tan x=0.7410,求锐角x.(精确到1′)在角度单位状态为“度”的情况下(屏幕显示出),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4. 所以,x≈36゜32′注意:利用计算器求锐角三角函数值或已知锐角三角函数值求相应的锐角时,不同的计算器操作步骤有所不同。
二、重难点分析重点:用计算器求任意角的三角函数值。
难点:由锐角三角函数值求锐角:例1:如图,工件上有一个V形槽,测得它的上口宽20mm,深19.2mm,求V形角(∠ACB)的大小(结果精确到1°)三、中考感悟(2014•tan56°≈。
(结果精确到0.01)四、专项训练(一)基础练习1、用计算器计算cos44°的结果(精确到0.01)是()A. 0.90B. 0.72C. 0.69D. 0.66【答案】B2、按键,使科学记算器显示回后,求sin90°的值,以下按键顺序正确的是()3、用计算器求下列各式的值:(1)sin47°;(2)sin12°30′;(3)cos25°18′;(4)tan44°59′59″;(5)sin18°+cos55°-tan59°(3)cos25°18′=0.9003;(4)tan44°59′59″=1.0000;(5)sin18°+cos55°-tan59=-0.7817.4、利用计算器求下列各角(精确到1″)(1)sinA=0.75,求A;(2)cosB=0.888 9,求B;(3)tanC=45.43,求C;(4)tanD=0.974 2,求D.6、用计算器验证,下列不等式中成立的是()A.sin37°24′>cos37°24′+cos3°10′B.cos45°32′>sin45°-sin1°12′C.sin63°47′<cos18°21′-cos87°D.2sin30°12′<sin60°24′【解析】使用计算器分别对各选项进行计算,只有B正确.【答案】B(二)提升练习7、先用计算器求:sin20°≈,sin40°≈,sin60°≈,sin80°≈,再按从小到大的顺序用“<”把sin20°,sin40°,sin60°,sin80°连接起来:.归纳:正弦值,角大值。
锐角三角函数基础题1-30

锐角三角函数基础题1-30一、选择题(共12小题)1.(2014•兰州)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cosA的值等于().C D.2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()D米米.C D.4.(2014•广州)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=().C D.5.(2014•湖州)如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是()7.(2014•巴中)在Rt△ABC中,∠C=90°,sinA=,则tanB的值为().C D.2D.9.(2014•义乌市)如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是()10.(2014•凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是()m m.C D.C D.二、填空题(共12小题)(除非特别说明,请填准确值)13.(2014•新疆)如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=_________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)14.(2014•常州)若∠α=30°,则∠α的余角等于_________度,sinα的值为_________.15.(2014•温州)如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是_________.16.(2014•攀枝花)在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C=_________.17.(2014•来宾)如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为_________.18.(2014•天水)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC 的顶点都在方格的格点上,则cosA=_________.19.(2014•本溪)在△ABC中,∠B=45°,cosA=,则∠C的度数是_________.20.(2014•怀化)如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为_________.21.(2014•白银)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C=_________.22.(2014•齐齐哈尔)在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是_________.23.(2014•南昌)在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为_________.24.(2014•铜仁)cos60°=_________.三、解答题(共6小题)(选答题,不自动判卷)25.(2014•河北)如图1,A,B,C是三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=100米.四人分别测得∠C的度数如下表:2,图3:(1)求表中∠C度数的平均数:(2)求A处的垃圾量,并将图2补充完整;(3)用(1)中的作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75)26.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)27.(2014•重庆)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.28.(2014•眉山)如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.29.(2014•乌鲁木齐)如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)30.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)锐角三角函数基础题1-30参考答案与试题解析一、选择题(共12小题)1.(2014•兰州)如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,那么cosA的值等于().C D.AB=cosA=2.(2014•随州)如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为()D米米CM=BC=50BM=CM=50.C D.AB==13=.4.(2014•广州)如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tanA=().C D.tanA==.5.(2014•湖州)如图,已知Rt△ABC中,∠C=90°,AC=4,tanA=,则BC的长是()tanA=,代入求出即可.tanA=,sinA=,cosA=.,7.(2014•巴中)在Rt△ABC中,∠C=90°,sinA=,则tanB的值为().C D.sinA=,=12x=.2D.×9.(2014•义乌市)如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是()=10.(2014•凉山州)拦水坝横断面如图所示,迎水坡AB的坡比是1:,坝高BC=10m,则坡面AB的长度是()m m:tanA=10AB=.C D=.C D..二、填空题(共12小题)(除非特别说明,请填准确值)13.(2014•新疆)如图,在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=24.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75),然后把,即=14.(2014•常州)若∠α=30°,则∠α的余角等于60度,sinα的值为.,.15.(2014•温州)如图,在△ABC中,∠C=90°,AC=2,BC=1,则tanA的值是.tanA=)求出即可.tanA=,故答案为:sinA=,cosA=.16.(2014•攀枝花)在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C=75°.cosB=,求出∠)cosB=17.(2014•来宾)如图,Rt△ABC中,∠C=90°,∠B=30°,BC=6,则AB的长为4.cosB=cosB=,AB==.18.(2014•天水)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点.△ABC的顶点都在方格的格点上,则cosA=.解:如图,,故答案为:19.(2014•本溪)在△ABC中,∠B=45°,cosA=,则∠C的度数是75°.cosA=,20.(2014•怀化)如图,小明爬一土坡,他从A处爬到B处所走的直线距离AB=4米,此时,他离地面高度为h=2米,则这个土坡的坡角为30°.sinA==,21.(2014•白银)△ABC中,∠A、∠B都是锐角,若sinA=,cosB=,则∠C=60°.,cosB=22.(2014•齐齐哈尔)在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是.==故答案为:23.(2014•南昌)在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为6或2或4.==2=42.24.(2014•铜仁)cos60°=..故答案为:三、解答题(共6小题)(选答题,不自动判卷)25.(2014•河北)如图1,A,B,C是三个垃圾存放点,点B,C分别位于点A的正北和正东方向,AC=100米.四2,图3:(1)求表中∠C度数的平均数:(2)求A处的垃圾量,并将图2补充完整;(3)用(1)中的作为∠C的度数,要将A处的垃圾沿道路AB都运到B处,已知运送1千克垃圾每米的费用为0.005元,求运垃圾所需的费用.(注:sin37°=0.6,cos37°=0.8,tan37°=0.75))=37,26.(2014•抚州)如图1所示的晾衣架,支架主视图的基本图形是菱形,其示意图如图2,晾衣架伸缩时,点G在射线DP上滑动,∠CED的大小也随之发生变化,已知每个菱形边长均等于20cm,且AH=DE=EG=20cm.(1)当∠CED=60°时,求C、D两点间的距离;(2)当∠CED由60°变为120°时,点A向左移动了多少cm?(结果精确到0.1cm)(3)设DG=xcm,当∠CED的变化范围为60°~120°(包括端点值)时,求x的取值范围.(结果精确到0.1cm)(参考数据≈1.732,可使用科学计算器)CEH=×=10(CD=20cm20≈DEI=,×=10 DG=2DI=2027.(2014•重庆)如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12,tan∠BAD=,求sinC的值.BAD=BAD==×=9AC==13sinC==28.(2014•眉山)如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.40+x=x+40=60+2060+2029.(2014•乌鲁木齐)如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)CE=≈30.(2014•南昌)图1中的中国结挂件是由四个相同的菱形在顶点处依次串联而成,每相邻两个菱形均成30°的夹角,示意图如图2.在图2中,每个菱形的边长为10cm,锐角为60°.(1)连接CD,EB,猜想它们的位置关系并加以证明;(2)求A,B两点之间的距离(结果取整数,可以使用计算器)(参考数据:≈1.41,≈1.73,≈2.45)cmcmcmcmAB=BD+AD=20。
锐角三角函数检测卷及答案

锐角三角函数单元检测时间:100分钟班级: 姓名: 分数:一、单选题1.已知△ABC 中, ∠C =90°,tan A =12,D 是 AC 上一点, ∠CBD =∠A , 则 cos∠CDB 的值为( )A .12B C D .22.如图,正方形ABCD 中,点E 在边CD 上,且3CD DE =,将ADE 沿AE 对折至AFE △.延长EF 交边BC 于点G ,连接AG 、CF .下列结论:∠ABG AFG △△≌;∠45GAE ∠=︒;∠BG GC =;∠AG CF ∥;∠GCF 是等边三角形,其中正确结论有( )个.A .2B .3C .4D .53.如图,将边长6cm 的正方形纸片沿虚线剪开,剪成两个全等梯形.已知裁剪线与正方形的一边夹角为60°,则梯形纸片中较短的底边长为( )A .(3cm B .(3﹣cm C .(6cm D .(6﹣cm4.三角函数sin40cos16tan50︒︒︒、、之间的大小关系是( ) A .tan50cos16sin40︒>︒>︒ B .cos16sin40tan50︒>︒>︒ C .cos16tan50sin40︒>︒>︒D .tan50sin40cos16︒>︒>︒5.如图,在网格中,小正方形的边长为1,点A 、B 、C 都在格点上,则sin A 的值为( )A B .35C .45D 6.如图,已知窗户高AB m =米,窗户外面上方0.2米的点C 处安装水平遮阳板CD n =米,当太阳光线与水平线成α角时,光线刚好不能直接射入室内,则m n ,的关系式是( )A .n =m tan α-0.2B .n =m tan α+0.2C .m =n tan α-0.2D .m =n tan α+0.27.如图,已知楼高AB 为50m ,铁塔基与楼房房基间的水平距离BD 为50m ,塔高DC ,下列结论中,正确的是( )A .由楼顶望塔顶仰角为60°B .由楼顶望塔基俯角为60°C .由楼顶望塔顶仰角为30°D .由楼顶望塔基俯角为30°8.先化简,再求代数式的值:222111a a a a a +⎛⎫+÷ ⎪+--⎝⎭=( ),其中tan602sin30a =︒-︒.ABCD 9.数学活动小组到某广场测量标志性建筑AB 的高度.如图,他们在地面上C 点测得最高点A 的仰角为22°,再向前70m 至D 点,又测得最高点A 的仰角为58°,点C ,D ,B 在同一直线上,则该建筑物AB 的高度约为( )(精确到1m .参考数据:sin 220.37︒≈,tan220.40︒≈,sin580.85︒≈,tan58 1.60︒≈)A .28mB .34mC .37mD .46m10.如图所示,某办公大楼正前方有一根高度是15米的旗杆ED ,从办公楼顶端A 测得旗杆顶端E 的俯角α是45°,旗杆底端D 到大楼前梯坎底边的距离DC 是20米,梯坎坡长BC 是12米,梯坎坡度i =1AB 的高度为( )(精确到0.1)A .30.4B .36.4C .39.4D .45.411.如图所示一座楼梯的示意图,BC 是铅垂线,CA 是水平线,BA 与CA 的夹角为θ.现要在楼梯上铺一条地毯,已知CA =6米,楼梯宽度4米,则地毯的面积至少需要( )A .24sin θ米2 B .24cos θ米2 C .2424tan θ⎛⎫+⎪⎝⎭米2D .()2424tan θ+米212.如图,在长方形ABCD 中,5AB =,3AD =,点E 在AB 上,点F 在BC 上.若2AE =,1CF =,则()sin 12∠+∠=( )A .12B C D 13.如图,在由小正方形组成的网格中,小正方形的边长均为1,点A ,B ,O 都在小正方形的顶点上,则∠AOB 的正弦值是( )A B C .13D .1214.式子2cos30tan 45︒-︒ )A .0B .C .2D .2-15.如图,网格中的每个小正方形的顶点称为格点,边长均为1,ABC 的顶点均在格点上,则∠ABC 的正弦值为( )A .12B C .35D 16.如图,在正方形方格纸中,每个小方格边长为1,A ,B ,C ,D 都在格点处,AB 与CD 相交于点O ,B ,则cos BOD ∠的值等于( )A .14B .13C D 17.如图,在44⨯网格正方形中,每个小正方形的边长为1,顶点为格点,若ABC 的顶点均是格点,则cos BAC ∠的值是( )A B C D .4518.如图,在Rt ABC 中,90C ∠=︒,BC =D 是AC 上一点,连接BD .若1tan 2A ∠=,1tan 3ABD ∠=,则CD 的长为( )A .B .3CD .219.在直角三角形ABC 中,90,4,C AB BC =∠=︒=3tan 2A的值是( )AB .C .D .320.如图,折叠矩形ABCD 的一边AD ,使点D 落在BC 边的点F 处,若4CF =,3tan 4EFC ∠=,则折痕AE =( )A .B .C .8D .1021.已知:如图,在平面直角坐标系中,有菱形OABC ,点A 的坐标为(10,0),对角线OB 、AC 相交于点D ,双曲线y=kx(x >0)经过点D ,交BC 的延长线于点E ,且OB •AC =160,有下列四个结论:∠双曲线的解析式为y =40x (x >0);∠点E 的坐标是(4,8);∠sin∠COA =45;∠AC +OB 其中正确的结论有( ) A .1个B .2个C .3个D .4个22.如图,在矩形纸片ABCD 中,5AB =,3BC =,将BCD △沿BD 折叠到BED 位置,DE 交AB 于点F ,则cos ADF ∠的值为( )A .817B .715C .1517D .81523.如图,一棵大树被台风拦腰刮断,树根A 到刮断点P 的距离是4米,折断部分PB 与地面成40︒的夹角,那么原来这棵树的高度是( )A .44cos 40+︒⎛⎫ ⎪⎝⎭米B .44sin 40+︒⎛⎫ ⎪⎝⎭米C .()44sin 40+︒米D .()44tan 40+︒米24.中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tan α=( )A .2B .32C .12D 25.如图,在正方形方格纸中,每个小正方形的边长都相等,A 、B 、C 、D 都在格点处,AB 与CD 相交于点P ,则cos∠APC 的值为( )A B C .25D 26.如图,已知菱形ABCD 的边长为4,E 是BC 的中点,AF 平分EAD ∠交CD 于点F , FG AD ∥ 交AE 于点G ,若1cos 4B =,则FG 的长是( )A .3B .83C D .52第II 卷(非选择题)二、解答题27.如图,山坡上有一棵与水平面垂直的大树AB ,且90BHE ∠=︒,一场台风过后,大树被刮倾斜后折断()A C D --倒在山坡上,树的顶部恰好接触到坡面().AB AC CD =+已知山坡的坡角30AEF ∠=︒,量得树干倾斜角45BAC ∠=︒,大树被折断部分CD 和坡面所成的角60ADC ∠=︒,4AD =米.(1)求CAD ∠的度数;(2)求这棵大树折断前AB 的高度.(结果保留根号)28.小明学了《解直角三角形》内容后,对一条东西走向的隧道AB 进行实地测量.如图所示,他在地面上点C 处测得隧道一端点A 在他的北偏东15︒方向上,他沿西北方向前进D ,此时测得点A 在他的东北方向上,端点B 在他的北偏西60︒方向上,(点A 、B 、C 、D 在同一平面内)(1)求点D 与点A 的距离;(2)求隧道AB 的长度.(结果保留根号) 29.(1)已知:对于锐角α满足sin 1cos tan21cos sin ααααα-==+,求tan15°的值;(2)如图,△ABC 中,∠C =90°,∠BAC =30°,延长CA 到D ,使AD =AB ,连接BD ,请利用这个图形求tan15°的值.30.某市政府为了方便市民绿色出行,推出了共享单车服务.图∠是某品牌共享单车放在水平地面上的实物图,图∠是其示意图,其中AB 、CD 都与地面l 平行,车轮半径为32cm ,∠BCD =64°,BC =60cm ,坐垫E 与点B 的距离BE 为15cm .(1)求坐垫E 到地面的距离;(2)根据经验,当坐垫E 到CD 的距离调整为人体腿长的0.8时,坐骑比较舒适.小明的腿长约为80cm ,现将坐垫E 调整至坐骑舒适高度位置E ',求E E '的长.(结果精确到0.1cm ,参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05) 31.计算:1202203(1)|2cos308|(3)π--︒--- 32.在遵义市科技馆楼前,在A 点观测楼顶K 的仰角为30°,然后将观测点沿石梯向楼的水平方向移动了28m ,上升4m ,到达最上一层平台,用高为1.4m 的测角仪,在C 点观测楼顶K 的仰角为45°.(1)求:A ,C 间的距离;(结果保留根号)(2)求:科技馆的楼高KF 的值.1.7)33.计算:212)4cos30|32-⎛⎫--+- ⎪⎝⎭.34.如图,是学生小金家附近的一块三角形绿化区的示意图;为增强体质,他每天早晨都沿着绿化区周边小路AB ,BC ,CA 跑步(小路的宽度不计),观测得点B 在点A 的南偏东30°方向上,点C 在点A 的南偏东60°的方向上,点B 在点C 的北偏西75°方向上,AC 间距离为400米.小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(结果精确到1 1.4≈ 1.7≈)35.图1是笔记本电脑放在散热支架上的实物图,实物图的侧面可抽象成图2,结点B ,C ,D 处可转动,支撑架AB =BC =CD =28cm ,面板DE =28cm ,若DE 始终与AB 平行.(1)直接写出∠ABC ,∠BCD ,∠CDE 之间的数量关系;(2)若ABC BCD CDE ∠=∠=∠,电脑显示屏宽EF =26cm .且105DEF ∠=︒,求笔记本电脑显示屏的端点F 到AB 的距离.(结果精确到0.1cm .参考数据sin750.97︒≈,cos750.26︒≈ 1.73≈)36.有一只拉杆式旅行箱(图1),其侧面示意图如图2所示,已知箱体长AB =50cm ,拉杆BC 的伸长距离最大时可达35cm ,点A 、B 、C 在同一条直线上,在箱体底端装有圆形的滚筒∠A ,∠A 与水平地面切于点D ,在拉杆伸长至最大的情况下,当点B 距离水平地面38cm 时,点C 到水平面的距离CE 为59cm .设AF ∥MN .(1)求∠A 的半径长;(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,某人将手自然下垂在C 端拉旅行箱时,CE 为80cm ,∠CAF =60°.求此时拉杆BC 的伸长距离.37.2022年6月5日,“神舟十四号”载人航天飞船搭载“明星”机械臂成功发射.如图是处于工作状态的某型号手臂机器人示意图,OA 是垂直于工作台的移动基座,AB 、BC 为机械臂,1OA =m ,5AB =m ,2BC =m ,143ABC ∠=︒.机械臂端点C 到工作台的距离6CD =m .(1)求A 、C 两点之间的距离; (2)求OD 长.(结果精确到0.1m ,参考数据:sin370.60︒≈,cos370.80︒≈,tan370.75︒≈ 2.24≈)38.深圳是沿海城市,每年都会受到几次台风侵袭,台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风景,有极强的破坏力.某次,据气象观察,距深圳正南200千米的处有一台风中心,中心最大风力为12级,每远离台风中心30千米,风力就会减弱一级,该台风中心正以20千米/时的速度沿北偏东43°方向向移动,且台风中心风力不变,若城市受到风力达到或超过六级,则称受台风影响. (1)此次台风会不会影响深圳?为什么?(2)若受到影响,那么受到台风影响的最大风力为几级?(3)若受到影响,那么此次台风影响深圳共持续多长时间?(结果可带根号表示)(sin43°≈34,cos42°≈2940,tan42°≈910)39.如图,港口B 位于港口A 的南偏西45︒方向,灯塔C 恰好在AB 的中点处,一艘海轮位于港口A 的正南方向港口B 的南偏东45︒方向的D 处,它沿正北方向航行21km 到达E 处,此时测得灯塔C 在E 的南偏西70︒方向上,E 处距离港口A 有多远?(结果用含非特殊角的三角函数及根式表示即可)40.因东坡文化远近闻名的遗爱湖公园,“国庆黄金周”期间,游人络绎不绝,现有一艘游船载着游客在遗爱湖中游览,当船在A 处时,船上游客发现岸上P 1处的临皋亭和P 2处的遗爱亭都在东北方向;当游船向正东方向行驶600m 到达B 处时,游客发现遗爱亭在北偏西15°方向;当游船继续向正东方向行驶400m 到达C 处时,游客发现临皋亭在北偏西60°方向.则临皋亭P 1处与遗爱亭P 2处之间的距离为 _____.(计算结果保留根号)41.如图,线段EF 与MN 表示某一段河的两岸,EF 平行MN .综合实践课上,同学们需要在河岸MN 上测量这段河的宽度(EF 与MN 之间的距离),已知河对岸EF 上有建筑物C 、D ,且CD =30米,同学们首先在河岸MN 上选取点A 处,用测角仪测得C 建筑物位于A 北偏东45°方向,再沿河岸走10米到达B 处,测得D 建筑物位于B 北偏东55°方向,请你根据所测数据求出该段河的宽度,(用非特殊角的三角函数或根式表示即可)42.图1是某小型汽车的示意图,图2是其后备厢的箱盖打开过程侧面简化示意图,五边形ABCDE 表示该车的后备厢的厢体侧面,在打开后备厢的过程中,箱盖AED 可以绕点A 逆时针方向旋转,当旋转角为60°时,箱盖AED 落在AE D ''的位置.若90EAB ABC BCD ∠=∠=∠=︒,150AED ∠=︒,AE =80厘米,ED =40厘米,DC =25厘米,且后备厢底部BC 离地面的高CN =25厘米.(1)求点D 到地面MN 的距离(结果保留根号);(2)求箱盖打开60°时的宽D ,D 1.73≈ 2.91116.3,结果取整数).43.如图是一种手机三脚架,它通过改变锁扣C 在主轴AB 上的位置调节三脚架的高度,其它支架长度固定不变,已知支脚DE =AB .底座CD ∠AB ,BG ∠AB ,且CD =BG ,F 是DE 上的固定点,且EF :DF =2:3.(1)当点B ,G ,E 三点在同一直线上(如图1所示)时,测得tan∠BED =2.设BC =5a ,则FG =__(用含a 的代数式表示);(2)在(1)的条件下,若将点C 向下移动24cm ,则点B ,G ,F 三点在同一直线上(如图2),此时点A 离地面的高度是__cm .44.图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC =OD =10分米,展开角∠COD =60°,晾衣臂OA =OB =10分米,晾衣臂支架HG =FE =6分米,且HO =FO =4分米.(参考数据:)(1)当90AOC ∠=︒时,求点A 离地面的距离AM 约为多少分米;(结果精确到0.1)(2)当OB 从水平状态旋转到OB '(在CO 延长线上)时,点E 绕点F 随之旋转至OB '上的点E '处,求B E BE ''-为多少分米.45.海绵拖把一般由长杆、U 型挤压器、海绵及连杆(含拉杆)装置组成(如图),拉动拉杆可带动海绵进入挤压器的两压杆间,起到挤水的作用.图1,图2,图3是其挤水原理示意图,A 、B 是拖把上的两个固定点,拉杆AP 一端固定在点A ,点P 与点B 重合(如图1),拉动点P 可使拉杆绕着点A 转动,此时点C 沿着AB 所在直线上下移动(如图2).已知AB =10cm ,连杆PC 为40cm ,FG =4cm ,MN =8cm .当P 点转动到射线BA 上时(如图3),FG 落在MN 上,此时点D 与点E 重合,点I 与点H 重合.(1)求ME 的长;(2)转动AP ,当∠P AC =53°时,∠求点C 的上升高度;∠求点D 与点I 之间的距离(结果精确到0.1).(sin53°≈45,cos53°≈35≈2.45) 参考答案:1.B【分析】由已知条件CBD A ∠=∠,可得1tan tan 2CBD A ∠==,设CD a =,由题意可得1tan 2CD CBD BC ∠==,即可算出2BC a =,在t ΔR CBD 中,根据勾股定理可得BD 答案.【详解】解:CBD A ,1tan tan 2CBD A ∴∠==, 设CD a =,1tan 2CD CBD BC ∴∠==, 2BC a ∴=, 在Rt ΔCBD 中,BD ,cosCD CDB BD ∴∠===. 故选:B 【点睛】本题主要考查了解直角三角形,熟练掌握解直角三角形的方法进行求解是解决本题的关键.2.C【分析】根据翻折变换的性质和正方形的性质可证ABG AFG △△≌;在直角ECG 中,根据勾股定理可证BG GC =;通过证明===∠∠∠∠AGB AGF GFC GCF ,由平行线的判定可得AG CF ∥;由于BG CG =,得到tan 2AGB ∠=,求得60AGB ∠≠︒,根据平行线的性质得到60FCG AGB ∠=∠≠︒,求得GCF 不是等边三角形.【详解】解:由翻折变换可知,AD AF =,DAE FAE ∠=∠,DE FE =,D AFE ∠=∠,∠18090AFG AFE B ∠=︒-∠=︒=∠,在Rt ABG 和Rt AFG 中,AF AB AG AG =⎧⎨=⎩, ∠()≌Rt ABG Rt AFG HL ,因此∠正确;∠BAG FAG ∠=∠,又∠90BAG FAG DAE FAE ∠+∠+∠+∠=︒, ∠190452GAE FAG FAE ∠=∠+=︒∠⨯=︒,因此∠正确; 由翻折变换可知,DE EF =,由全等三角形可知BG GF =,设正方形的边长为a ,BG x =,13DE EF a ==,则CG a x =-,13GE x a =+,1233EC a a a =-=, 在Rt ECG 中,由勾股定理得,222EC GC EG +=, 即()22221=33a a x x a ⎛⎫⎛⎫+-+ ⎪ ⎪⎝⎭⎝⎭,解得12x a =, 即1122BG a BC ==, ∠BG CG =,因此∠正确;∠BG CG FG ==,∠GCF GFC ∠=∠,由三角形全等可得,AGB AGF ∠=∠,又∠180AGB AGF FGC FGC GCF GFC ∠+∠+∠=︒=∠+∠+∠,∠ABG FCG ∠=∠,∠AG FC ∥,因此∠正确,∠BG CG =, ∠12BG AB =, ∠tan 2AGB ∠=,∠60AGB ∠≠︒,∠AG FC ∥,∠60FCG AGB ∠=∠≠︒,∠GCF 不是等边三角形,因此∠不正确;故选:C .【点睛】本题考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,求一个角的正切值,此题综合性较强,难度较大,解题的关键是注意数形结合思想应用.3.A【分析】过M 点作ME ∠AD 于E 点,根据四边形ABCD 是正方形,有AD =CD =6,∠C =∠D =90°,由裁剪的两个梯形全等,可得AN =MC ;再证明四边形MCDE 是矩形,即有MC =ED ,ME =CD =6,进而有AN =ED ,在Rt ∠MNE 中,解直角三角形可得NE =3AN =【详解】如图,过M 点作ME ∠AD 于E 点,∠四边形ABCD 是正方形,边长为6,∠AD =CD =6,∠C =∠D =90°,∠裁剪的两个梯形全等,∠AN =MC ,∠ME ∠AD ,∠四边形MCDE 是矩形,∠MC =ED ,ME =CD =6,∠AN =ED ,根据题意有∠MNE =60°,∠在Rt ∠MNE 中,62tan tan 60ME NE MNE ===∠∠∠6AN ED AD NE +=-=-∠3AN =即梯形中较短的底为3cm ),故选:A .【点睛】本题主要考查了正方形的、矩形的判定与性质、解直角三角形的应用等知识,根据梯形全等得出AN =MC 是解答本题的关键.4.A【分析】首先把sin 40cos16︒︒、转换成相同的锐角三角函数;再根据正弦值是随着角的增大而增大,进行分析,可以知道1sin74sin 40︒︒>>,又根据正切值随着角度增大而增大,因此tan50tan 451︒︒=>,即可得出正确选项.【详解】解:∠()sin cos 90αα=︒-(090α≤≤︒),∠()cos16sin 9016sin74︒=︒-︒=︒,sin901︒=∠1sin74sin 40︒︒>>,∠tan50tan 451︒︒=>,∠tan50sin74sin 40︒>︒>︒,∠tan50cos16sin40︒>︒>︒,故选:A .【点睛】本题考查三角函数值的大小比较,掌握正余弦的转换方法:一个角的正弦值等于它的余角的余弦值;以及正余弦值、正切值的变化规律是本题的关键.5.C【分析】过点B 作BD AC ⊥于点D ,连接BC ,利用面积法求出BD 的长,然后由sin BD A AB=即可获得答案. 【详解】解:过点B 作BD AC ⊥于点D ,连接BC ,如下图,∠小正方形的边长为1,∠AB AC == ∠111333*********ABC S=⨯-⨯⨯-⨯⨯-⨯⨯=,∠11422ABC S AC BD BD =⋅==,∠BD =∠4sin5BD A AB ===. 故选:C .【点睛】本题主要考查了利用三角函数解直角三角形、勾股定理的应用等知识,解题关键是正确作出直角三角形并熟记正弦函数的定义.6.C【分析】根据CB =CA +AB 求出CB 的长,再利用三角函数求出m 的值即可.【详解】解:∠窗子高AB =m 米,窗子外面上方0.2米的点C 处安装水平遮阳板CD =n 米,∠CB =CA +AB =(m +0.2)米,∠光线与水平线成α角,∠∠BDC =α,∠tan∠BDC =CB CD, ∠CB =n •tan α,∠m =n tan α-0.2,故选:C .【点睛】本题主要考查三角函数的应用,熟练利用三角函数解直角三角形是解题的关键.7.C【分析】求CE ,进而求得∠CAE 的正切值即可求得∠CAE 的度数;同理可求得∠EAD 的正切值,得到∠EAD 的度数.【详解】解:过点A 作水平线AE ,则∠EAD 为楼顶望塔基俯角,∠CAE 为由楼顶望塔顶仰角.∠AB =50m∠DE =50m∠CE =CD 50(m)∠tan∠CAE =CE :AE =CE :BD ∠∠CAE =30°.故C 正确,D 错误;∠tan∠EAD =DE :AE =50:BD =1,∠∠EAD =45°.故A 、B 错误;故选:C .【点睛】本题考查解直角三角形的应用,熟练掌握正切的定义,特殊角的三角函数值是解题的关键.8.A【分析】先将题目中的式子化简,再根据锐角三角函数求得a 的值,代入化简后的式子即可解答本题. 【详解】解:222111a a a a a +⎛⎫+÷ ⎪+--⎝⎭ ()()()212111a a a a a a-++-=⨯+-()()3111a a a a a -=⨯+- 31a =+, 当tan602sin30a =︒-︒1212=⨯=时,原式= 故选:A .【点睛】本题考查分式的化简求值、特殊角的三角函数值,解题的关键是明确它们各自的计算方法.9.C【分析】在Rt △ABD 中,解直角三角形求出58DB AB =,在Rt △ABC 中,解直角三角形可求出AB . 【详解】解:在Rt △ABD 中,tan∠ADB =AB DB , ∠5tan 58 1.68AB AB DB AB =≈=︒, 在Rt △ABC 中,tan∠ACB =AB CB , ∠tan 220.45708AB AB ︒=≈+, 解得:112373AB =≈m , 故选:C .【点睛】本题考查了解直角三角形的应用,熟练掌握正切函数的定义是解题的关键.10.C【分析】延长AB 交DC 于H ,作EG ∠AB 于G ,则GH =DE =15米,EG =DH ,设BH =x 米,则CH米,在Rt ∠BCH中,BC =12米,由勾股定理得出方程,解方程求出BH =6米,CHBG 、EG 的长度,证明∠AEG 是等腰直角三角形,得出AG =EG =()(米),即可得出大楼AB 的高度.【详解】解:如图,延长AB 交DC 于H ,作EG ∠AB 于G ,则GH =DE =15米,EG =DH ,∠梯坎坡度i =1∠BH :CH =1设BH =x 米,则CH米,)2=122,由勾股定理得:x2+解得:x=6,∠BH=6米,CH=∠BG=GH﹣BH=15﹣6=9(米),EG=DH=CH+CD=()(米),∠∠α=45°,∠∠EAG=90°﹣45°=45°,∠∠AEG是等腰直角三角形,∠AG=EG=()(米),∠AB=AG+BG=(米);故选:C.【点睛】本题考查了解直角三角形的应用-坡度、俯角问题;通过作辅助线运用勾股定理求出BH,得出EG是解决问题的关键.11.D【分析】在Rt△ABC中,利用锐角三角函数求出BC,然后根据平移的性质可得在楼梯上铺的地毯长,从而求出地毯的面积.【详解】解:在Rt△ABC中,AC=6,∠BAC=θ,∠tanθ=BC,AC∠BC=AC tanθ=6tanθ(米),∠在楼梯上铺的地毯长=BC+AC=(6+6tanθ)米,∠地毯的面积=4(6+6tanθ)=(24+24tanθ)平方米,故选:D.【点睛】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的计算是解题的关键.12.B【分析】连接EF,求证∠DEF是等腰直角三角形,得∠EDF=45°,所以1+245∠∠=,即可求解.【详解】解:连接EF,∠四边形ABCD是长方形,∠∠A=∠B=∠C=∠ADC=90°,BC=AD=3,CD=AB=5,∠22222=+=+=,DE AD AE3213∠AB=5,∠BE=AB-AE=3,∠CF=1,∠BF=BC-CF=2,在在Rt∠EBF中,∠22222=+=+=,EF BE BF3213∠EF=DE在Rt∠CDF中,∠22222=+=+=,DF DC CF5126∠26=13+13,即:222=+,DF DE EF∠∠DEF=90°,∠∠EDF=∠DFE=45°,∠1+2=45∠∠∠-∠=,ADC EDF∠()2∠+∠=sin12sin45=2故选B.【点睛】本题考查长方形的性质、勾股定理及其逆定理、正弦函数,根据勾股定理的逆定理证明出∠DEF是等腰直角三角形是解题的关键.13.B【分析】过点B作BC∠OA于点C.先利用勾股定理求出BO、AO的长,再利用∠AOB的面积求出BC的长,最后在直角∠BCO中求出∠AOB的正弦值.【详解】解:过点B作BC∠OA于点C.BO=,AO==,∠S △AOB 12=×2×2=2, ∠12AO •BC =2,∠BC==sinBC AOB BO ∴∠=== 故选:B .【点睛】本题考查了解直角三角形,构造直角三角形,利用∠的面积求出OA 边上的高是解决本题的关键. 14.A【分析】根据特殊角的三角函数值计算即可.【详解】解:原式21=-11)=-11==0故选:A .【点睛】本题考查特殊角的三角函数值及二次根式的混合运算,解题关键是熟练掌握特殊角的三角函数值. 15.D【分析】根据勾股定理计算得出AB AC BC CE BE =====可得出AE BC ⊥,由勾股定理得AE =从而可得出sin ABC ∠= 【详解】解:如图,连接AE ,由勾股定理得,AB AC ∠AB AC =又BC CE BE ===∠点E 为BC 的中点,∠AE BC ⊥,∠AE ==∠sin AE ABC AB ∠== 故选:D【点睛】本题考查了解直角三角形、勾股定理,利用勾股定理求出AE 的长度是解题的关键.16.D【分析】根据网格的特点找到格点E ,使得AE CD ∥,则BOD A ∠=∠,构造Rt AEF ,即可求解.【详解】如图,5DG CG ==,90G ∠=︒,45CDG ∴∠=︒,1AG GE ==,45AEG ∴∠=︒,∴AE CD ∥,∴BOD A ∠=∠,2,AE AF EF ===22218220,20AE EF AF +=+==, 222AE EF AF ∴+=, ∠∠AEF 是直角三角形,∠AEF =90°,cos cosAE BOD A AF ∴∠=== 故选D 【点睛】本题考查了勾股定理与网格,勾股定理的逆定理,求余弦,构造直角三角形是解题的关键.17.C【分析】过点C 作AB 的垂线,构造直角三角形,利用勾股定理求解即可.【详解】解:过点C 作AB 的垂线交AB 于一点D ,如图所示,∠每个小正方形的边长为1,∠5AC BC AB ===,设AD x =,则5BD x =-,在Rt ACD △中,222DC AC AD =-,在Rt BCD 中,222DC BC BD =-,∠2210(5)5x x --=-,解得2x =,∠cosAD BAC AC ∠== 故选:C .【点睛】本题考查了解直角三角形,勾股定理等知识,解题的关键是能构造出直角三角形.18.C 【分析】先根据锐角三角函数值求出AC =5,AB =过点D 作DE AB ⊥于点E ,依据三角函数值可得11,,23DE AE DE BE ==从而得32BE AE =,再由5AE BE +=得AE =2,DE =1,由勾股定理得AD 可求出CD .【详解】解:在Rt ABC 中,90C ∠=︒,BC = ∠1tan 2BC A AC ∠==∠2AC BC ==由勾股定理得,5AB ==过点D 作DE AB ⊥于点E ,如图,∠1tan 2A ∠=,1tan 3ABD ∠=, ∠11,,23DE DE AE BE ==∠11,,23DE AE DE BE == ∠1123AE BE = ∠32BE AE =∠5,AE BE += ∠352AE AE += ∠2,AE =∠1DE =,在Rt ADE ∆中,222AD AE DE =+ ∠AD∠AD CD AC +==∠CD AC AD =-==故选:C【点睛】本题主要考查了勾股定理,由锐角正切值求边长,正确作辅助线求出DE 的长是解答本题的关键. 19.A【分析】由勾股定理求出AB =2,再由三角函数的意义求出60,A ∠=︒进一步可得出结论.【详解】解:如图,∠90,4,C AB BC =∠=︒=∠2AC ===又tan BC A AC ∠=== ∠60A ∠=︒ ∠302A ∠=︒∠3tan3tan 3032A =︒== 故选:A【点睛】本题主要考查了正切函数的定义,正确求得AC 的长是解题关键.20.B【分析】首先根据折叠及3tan 4EFC ∠=求得EF 的值,进一步知道DC 的长度,后根据BAF EFC ∠=∠,其正切值相同解三角形ABF 得BF 的长度,从而知道AD 的长度,后根据勾股定理求得AE 的长度.【详解】解:由题意4CF =,∠C =90°,3tan 4EC EFC FC ∠== ∠CE =3∠Rt EFC 中,∠C =90°,∠5EF =∠AEF 是ADE 折叠而来∠5ED EF ==,538DC AB ==+=∠矩形ABCD∠90C B AFE ∠=∠=∠=︒∠90BAF AFB ∠+∠=︒,90AFB EFC ∠+∠=︒∠BAF EFC ∠=∠ ∠tan∠BAF =tan∠EFC =34, 即34BF AB =, ∠364BF AB == ∠6410AD BC ==+=∠AE 故选:B【点睛】本题考查了锐角三角函数解直角三角形,勾股定理,矩形的性质,翻折的性质,根据等量变换得到BAF EFC ∠=∠并运用其锐角三角函数相等,求线段长是解决本题的关键.21.C【分析】过点B 作BF x ⊥轴于点F ,先根据菱形的性质可得10AB OA ==,1802OA BF OB AC ⋅=⋅=,OD BD =,从而可得8BF =,再在Rt ABF 中,利用勾股定理可得6AF =,从而可得点B 的坐标,然后根据中点的坐标公式可得点D 的坐标,最后利用待定系数法可得双曲线的解析式,由此可判断∠;根据点E 的纵坐标为8,代入反比例函数即可判断∠;先根据平行线的性质可得COA BAF ∠=∠,再根据正弦的定义即可判断∠;先在Rt OBF △中,利用勾股定理可得OB =160OB AC ⋅=可得AC =AC OB +的值,由此即可判断∠.【详解】解:如图,过点B 作BF x ⊥轴于点F ,点A 的坐标为(10,0),10OA ∴=,四边形OABC 是菱形,且160OB AC ⋅=,10AB OA ∴==,1802OA BF OB AC ⋅=⋅=,OD BD =,AD CD =, 解得8BF =,在Rt ABF 中,6AF ==,16OF OA AF ∴=+=,(16,8)B ∴,又OD BD =,即点D 是OB 的中点,01608(,)22D ++∴,即(8,4)D , 将点(8,4)D 代入反比例函数k y x =得:8432k =⨯=, 则该双曲线解析式为32y x=,结论∠错误; 四边形OABC 是菱形,BC OA ∴,OC AB ∥,∴点E 的纵坐标与点B 的纵坐标相同,即为8,当8y =时,3248x ==, 则点E 的坐标是(4,8),结论∠正确;OC AB ,COA BAF ∴∠=∠,84sin sin 105BF COA BAF AB ∴∠=∠===,结论∠正确;在Rt OBF △中,OB =160OB AC ⋅=,160AC OB∴==,AC OB ∴+==,结论∠正确;综上,正确的结论有3个,故选:C .【点睛】本题考查了菱形的性质、勾股定理、反比例函数、正弦等知识点,熟练掌握菱形的性质是解题关键. 22.C【分析】先根据矩形的性质和折叠的性质,利用“AAS”证明AFD EFB ∆∆≌,得出AF EF =,DF BF =,设AF EF x ==,则5BF x =-,根据勾股定理列出关于x 的方程,解方程得出x 的值,最后根据余弦函数的定义求出结果即可.【详解】解:∠四边形ABCD 为矩形,∠CD =AB =5,AB =BC =3,90A C ∠=∠=︒,根据折叠可知,3BE BC ==,5DE DE ==,90∠=∠=︒E C ,∠在∠AFD 和∠EFB 中903A E AFD EFB AD BE ∠=∠=︒⎧⎪∠=∠⎨⎪==⎩,∠AFD EFB ∆∆≌(AAS ),∠AF EF =,DF BF =,设AF EF x ==,则5BF x =-,在Rt BEF ∆中,222BF EF BE =+,即()22253x x -=+, 解得:85x =,则817555DF BF ==-=, ∠315cos 17175AD ADF DF ∠===,故C 正确.故选:C .【点睛】本题主要考查了矩形的折叠问题,三角形全等的判定和性质,勾股定理,三角函数的定义,根据题意证明AFD EFB ∆∆≌,是解题的关键.23.B【分析】通过解直角三角形即可求得.【详解】解:在Rt ABP △中,4==sin sin 40AP BP ABP ∠︒, 故原来这棵树的高度为:4=4sin 40AP BP ⎛⎫++ ⎪︒⎝⎭(米), 故选:B .【点睛】本题考查了解直角三角形的应用,熟练掌握和运用解直角三角形的方法是解决本题的关键.24.A【分析】首先根据两个正方形的面积分别求出两个正方形的边长,然后结合题意进一步设直角三角形短的直角边为a ,则较长的直角边为a +1,再接着利用勾股定理得到关于a 的方程,据此进一步求出直角三角形各个直角边的边长,最后求出tan α的值即可.【详解】∠小正方形与每个直角三角形面积均为1,∠大正方形的面积为5,∠小正方形的边长为1设直角三角形短的直角边为a ,则较长的直角边为a +1,其中a >0,∠a 2+(a +1)2=5,其中a >0,解得:a 1=1,a 2=-2(不符合题意,舍去),tan α=1a a +=111+=2, 故选:A .【点睛】本题主要考查了勾股定理与一元二次方程及三角函数的综合运用,熟练掌握相关概念是解题关键. 25.B【分析】把AB 向上平移一个单位到DE ,连接CE ,则DE ∠AB ,由勾股定理逆定理可以证明△DCE 为直角三角形,所以cos∠APC =cos∠EDC 即可得答案.【详解】解:把AB 向上平移一个单位到DE ,连接CE ,如图.则DE ∠AB ,∠∠APC =∠EDC .在△DCE 中,有EC DC =5DE =,∠22252025EC DC DE +=+==,∠DCE ∆是直角三角形,且90DCE ∠=︒,∠cos∠APC =cos∠EDC =DC DE = 故选:B .【点睛】本题考查了解直角三角形、平行线的性质,勾股定理,作出合适辅助线是解题关键.26.B【分析】过点A 作AH 垂直BC 于点H ,延长FG 交AB 于点P ,由题干所给条件可知,AG =FG ,EG =GP ,利用∠AGP =∠B 可得到cos∠AGP =14,即可得到FG 的长; 【详解】过点A 作AH 垂直BC 于点H ,延长FG 交AB 于点P ,由题意可知,AB =BC =4,E 是BC 的中点,∠BE =2,又∠1cos 4B =, ∠BH =1,即H 是BE 的中点,∠AB =AE =4,又∠AF 是∠DAE 的角平分线,FG AD ∥,∠∠F AG =∠AFG ,即AG =FG ,又∠PF AD ∥,AP DF ∥,∠PF =AD =4,设FG =x ,则AG =x ,EG =PG =4-x ,∠PF BC ∥,∠∠AGP =∠AEB =∠B ,∠cos∠AGP =12PG AG =22x x-=14, 解得x =83; 故选B .【点睛】本题考查菱形的性质、角平分线的性质、平行线的性质和解直角三角形,熟练掌握角平分线的性质和解直角三角形的方法是解决本题的关键.27.(1)75︒(2)()2米【分析】(1)根据直角三角形的性质求出EAH ∠,根据平角的定义计算,求出CAD ∠;(2)过点A 作AM CD ⊥,垂足为M ,根据正弦的定义求出AM 、根据余弦的定义求出DM ,根据直角三角形的性质求出CM ,根据正弦的定义求出AC ,结合图形计算,得到答案.(1)解:在Rt AHE 中,30AEH ∠=︒, 60EAH ∴∠=︒,45BAC ∠=︒,180604575CAD ∴∠=︒-︒-︒=︒;(2)过点A 作AM CD ⊥,垂足为M ,在Rt ADM △中,60ADC ∠=︒,4AD =米,cos 4cos602DM AD ADC ∠∴=⋅=︒=(米),sin 4sin 60AM AD ADC ∠=⋅=︒=,在Rt ACM △中,180756045C ∠=︒-︒-︒=︒,CM AM ∴==,sin AM AC C==, ()2AB AC CD ∴=+=米,答:这棵大树折断前高为()2米.【点睛】本题考查的是解直角三角形的应用——坡度坡角问题,掌握坡度坡角的概念、熟记锐角三角函数的定义是解答此题的关键.28.(1)点D 与点A 的距离为300米(2)隧道AB 的长为米【分析】(1)根据方位角图,易知60ACD ∠=︒,90ADC ∠=︒,解Rt ADC 即可求解;(2)过点D 作DE AB ⊥于点E .分别解Rt ADE △,Rt BDE 求出AE 和BE ,即可求出隧道AB 的长(1)由题意可知:154560ACD ∠=︒+︒=︒,180454590ADC ∠=︒-︒-︒=︒在Rt ADC 中,∠tan tan 60300AD DC ACD =⨯∠=︒=(米)答:点D 与点A 的距离为300米.(2)过点D 作DE AB ⊥于点E .。
初三数学锐角三角函数测试题及答案
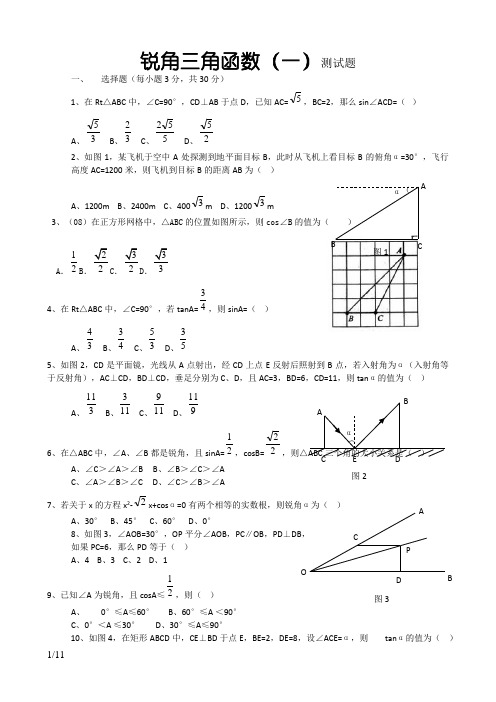
ACOP D B图3锐角三角函数(一)测试题一、 选择题(每小题3分,共30分)1、在Rt △ABC 中,∠C=90°,CD ⊥AB 于点D ,已知AC=5,BC=2,那么sin ∠ACD=( )A 、35B 、32C 、552D 、252、如图1,某飞机于空中A 处探测到地平面目标B ,此时从飞机上看目标B 的俯角α=30°,飞行高度AC=1200米,则飞机到目标B 的距离AB 为( ) A 、1200m B 、2400m C 、4003m D 、12003m3、(08)在正方形网格中,△ABC 的位置如图所示,则cos ∠B 的值为( )A .12B .22C .32D .334、在Rt △ABC 中,∠C=90°,若tanA=43,则sinA=( )A 、34B 、43C 、35D 、535、如图2,CD 是平面镜,光线从A 点射出,经CD 上点E 反射后照射到B 点,若入射角为α(入射角等于反射角),AC ⊥CD ,BD ⊥CD ,垂足分别为C 、D ,且AC=3,BD=6,CD=11,则tan α的值为( )A 、311B 、113C 、119D 、9116、在△ABC 中,∠A 、∠B 都是锐角,且sinA=21,cosB=22ABC 三个角的大小关系是( )A 、∠C >∠A >∠B B 、∠B >∠C >∠A C 、∠A >∠B >∠CD 、∠C >∠B >∠A7、若关于x 的方程x 2-2x+cos α=0有两个相等的实数根,则锐角α为( )A 、30°B 、45°C 、60°D 、0°8、如图3,∠AOB=30°,OP 平分∠AOB ,PC ∥OB ,PD ⊥DB , 如果PC=6,那么PD 等于( ) A 、4 B 、3 C 、2 D 、19、已知∠A 为锐角,且cosA ≤21,则( )A 、 0°≤A ≤60°B 、60°≤A <90°C 、0°<A ≤30°D 、30°≤A ≤90°10、如图4,在矩形ABCD 中,CE ⊥BD 于点E ,BE=2,DE=8,设∠ACE=α,则 tan α的值为( )ABC( α 图1CEDAB图2(αA 、21B 、34C 、43D 、2二、 填空题(每小题3分,共30分)11、直线y=kx-4与y 轴相交所成的锐角的正切值为21,则k 的值为。
第四章《锐角三角函数》(基础卷)(解析版)

第四章锐角三角函数(基础卷)一、选择题(每小题4分,共40分)1、在Rt△ABC中,∠C=90∘,BC=5,AC=12,则sin B的值是()A.512B.125C.513D.1213【答案】D【解析】直接利用勾股定理得出AB的长,再利用锐角三角函数得出答案.【解答】如图所示:∵∠C=90∘,BC=5,AC=12,∴AB=13,∴sin B=ACAB =1213.2、在Rt△ABC中,∠C=90∘,则下列式子定成立的是()A.sin A=sin BB.cos A=cos BC.tan A=tan BD.sin A=cos B【答案】D【解析】根据一个锐角的正弦等于它的余角的余弦解答.【解答】解:∵∠C=90∘,∴∠A+∠B=90∘,∴sin A=cos B.3、已知sinαα是锐角,则α=( )A.75∘B.60∘C.45∘D.30∘【答案】B【解析】根据sin60∘a的值.【解答】解:∵sinαα是锐角,∴α=60∘.4、sin58∘、cos58∘、cos28∘的大小关系是()A.cos28∘<cos58∘<sin58∘B.sin58∘<cos28∘<cos58∘C.cos58∘<sin58∘<cos28∘D.sin58∘<cos58∘<cos28∘【答案】C【解析】先把正弦化成余弦,然后根据锐角三角函数值的变化规律:锐角余弦值随着角度的增大而减小进行排列大小.【解答】sin58∘=cos32∘.∵58∘>32∘>28∘,∴cos58∘<cos32∘<cos28∘,∴cos58∘<sin58∘<cos28∘.5、在Rt△ABC中,∠C=90∘,如果AC=4,BC=3,那么∠A的正弦值是( )A.34B.43C.35D.45【答案】C【解析】根据三角函数的定义即可得到结论.【解答】∵AC=4,BC=3,AB=5,∴sin A=BCAB =35.6、拦水坝横断面如图所示,迎水坡AB的坡比是BC=10m,则坡面AB的长度是()A.15mB.C.D.20m【答案】D【解析】在Rt△ABC中,已知坡面AB的坡比以及铅直高度BC的值,通过解直角三角形即可求出斜面AB的长.【解答】解:Rt△ABC中,BC=10m,tan A=∴AC=BC÷tan A=,∴AB=20m.7、在Rt△ABC中,∠B=90∘.若AC=2BC,则sin C的值是( )A.12B.2【答案】C【解析】利用已知表示出各边长,进而利用锐角三角函数关系得出答案.【解答】解:如图所示:∵AC=2BC,∴设BC=x,则AC=2x,∴AB=,∴sin C=ABAC=8、如图,在平面直角坐标系xOy中,点P(4, 3),OP与x轴正半轴的夹角为α,则tanα的值为()A.35B.45C.34D.43【答案】C【解析】过P作PN⊥x轴于N,PM⊥y轴于M,根据点P的坐标求出PN和ON,解直角三角形求出即可.【解答】过P作PN⊥x轴于N,PM⊥y轴于M,则∠PMO=∠PNO=90∘,∵x轴⊥y轴,∴∠MON=∠PMO=∠PNO=90∘,∴四边形MONP是矩形,∴PM=ON,PN=OM,∵P(4, 3),∴ON=PM=4,PN=3,∴tanα=PNON =34,9、在Rt△ABC中,已知∠C=90∘,∠A=40∘,BC=3,则AC等于()A.3sin40∘B.3sin50∘C.3tan40∘D.3tan50∘【答案】D【解析】根据三角形内角和定理求出∠B的度数,根据正切的概念解答即可.【解答】解:∵∠C=90∘,∠A=40∘,∴∠B=50∘.∵tan B=AC,BC∴AC=BC⋅tan B=3tan50∘.10、我国北斗导航装备的不断更新,极大方便人们的出行.某中学组织学生利用导航到C地进行社会实践活动,到达A地时,发现C地恰好在A地正北方向,导航显示路线应沿北偏东60∘方向走到B地,再沿北偏西37∘方向走才能到达C地.如图所示,已知A,B两地相距6千米,则A,C两地的距离为()(参考数据sin53∘≈0.80,cos53∘≈0.60,tan53∘≈1.32)A.12千米B.(3+千米C.(3+千米D.(12―千米【答案】B【解析】作BD⊥AC于点D,根据题意可得,∠A=60∘,AB=6,∠CBD=53∘,再根据锐角三角函数即可求出AD和CD的值,进而求出A,C两地的距离.【解答】如图,作BD⊥AC于点D,根据题意可知:在Rt△ADB中,∠A=60∘,AB=6,∴AD=3,BD=在Rt△CDB中,∠CBD=53∘,≈∴CD=BD⋅tan53∘≈×1.32≈×43∴AC=AD+CD=3+则A,C两地的距离为(3+千米.二、填空题(本题共计6小题,每题4分,共计24分)11. 已知tan(α+15∘)=α的度数为________∘.【答案】15【解析】根据tan30∘=α+15∘=30∘,再解即可.【解答】∵tan30∘=∴α+15∘=30∘,∴α=15∘,12.已知在Rt△ABC中,∠C=90∘,sin A=5,则tan B的值为________.13【答案】125,设一条直角边BC为5x,斜边AB为13x,根据勾股【解析】根据题意作出直角△ABC,然后根据sin A=513定理求出另一条直角边AC的长度,然后根据三角函数的定义可求出tan∠B.【解答】解:∵sin A=513,∴设BC=5x,AB=13x,则AC=12x,故tan∠B=ACBC =125.13.如图,在△ABC中,∠C=90∘,AC=6,若cos A=35,则BC的长为________.【答案】8【解析】根据锐角三角函数定义和勾股定理求解.【解答】∵在△ABC中,∠C=90∘,AC=6,cos A=35,∴cos A=ACAB =6AB=35,∴AB=10,∴BC8.14. △ABC中,∠C=90∘,AB=8,cos A=34,则BC的长________.【答案】【解析】首先利用余弦函数的定义求得AC的长,然后利用勾股定理即可求得BC的长.【解答】解:如图,∵cos A=ACAB,∴AC=AB⋅cos A=8×34=6,∴BC15. △ABC中,∠A、∠B都是锐角,若sin A cos B=12,则∠C=________.【答案】60∘【解析】先根据特殊角的三角函数值求出∠A、∠B的度数,再根据三角形内角和定理求出∠C即可作出判断.【解答】解:∵△ABC中,∠A、∠B都是锐角sin A cos B=12,∴∠A=∠B=60∘.∴∠C=180∘―∠A―∠B=180∘―60∘―60∘=60∘.16. 如图,BE是△ABC的角平分线,F是AB上一点,∠ACF=∠EBC,BE、CF相交于点G.若sin∠AEB=BG=4,EG=5,则S△ABE=________.【答案】81【解析】如图,过点B作BT⊥AC于T,连接EF.在Rt△BET中,解直角三角形求出BT,ET,BC,由△ECG ∽△EBC,求出EC,CG,再利用相似三角形的性质求出EF,BF,AE,AB,证明点T与点A重合即可解决问题.【解答】如图,过点B作BT⊥AC于T,连接EF.∵BE平分∠ABC,∴∠ABE=∠CBE,∵∠ECG=∠ABE,∴∠ECG=∠CBE,∵∠CEG=∠CEB,∴△ECG∽△EBC,∴ECEB =EGEC=CGCB,∴EC2=EG⋅EB=5×(5+4)=45,∵EC>0,∴EC=在Rt△BET中,∵sin∠AEB=BTBEBE=9,∴BT∴ET==∴CT=ET+CE∴BC=∴CG=EG⋅BCEC=10,∵∠ECG=∠FBG,∴ E ,F ,B ,C 四点共圆,∴ ∠EFG =∠CBG ,∵ ∠FGE =∠BGC ,∴ △EGF ∽△CGB ,∴ EF CB =EGCG ,∴510,∴ EF =5,∵ ∠AFE =∠ACB ,∠EAF =∠BAC ,∴ △EAF ∽△BAC ,∴AE AB=AFAC =EFBC =12,设AE =x ,则AB =2x ,∵ ∠FBG =∠ECG ,∠BGF =∠CGE ,∴ △BGF ∽△CGE ,∴ BF CE =BGCG ,∴410,∴ BF ∵ AE ⋅AC =AF ⋅AB ,∴ x (x =(2x ―⋅2x ,解得x =∴ AE =ET ∴ 点A 与点T 重合,∴ AB =2AE =∴ S △ABE =12×AB ×AE =12××81.三、解答题(本题共计8小题,每题10分,共计86分) 17. 计算(1)tan30∘sin60∘+cos 230∘―sin 245∘tan45∘;(2)2―1+∘+|―5|―(π―2013)0.解:(1)原式=×+―×1=12+34―12=34 .(2)原式=12+―1=12+32+5―1=6 .18. 如图,在△ABC 中,AB =AC =4,BC =6,求cos B 及tan B 的值.解:过点A 作AD ⊥BC 于点D .∵ AB =AC ,∴ BD =CD =3.在Rt △ABD 中,由勾股定理得AD ===∴ cos B =BDAB =34,tan B =ADBD =19. 在△ABC 中,∠A,∠B,∠C 的对边分别为a ,b ,c ,且a :b :c =3:4:5,求证:sin A +sin B =75 证明:设a =3k ,b =4k ,c =5k (k >0).∵ a 2+b 2=(3k )2+(4k )2=25k 2=c 2,∴ △ABC 是直角三角形,且∠C =90∘.∴ sin A =ac =3k5k =35,sin B =bc =4k c=45.∴ sin A +sin B =75.20. 如图,一艘船由西向东航行,在A 处测得北偏东60∘方向上有一座灯塔C ,再向东继续航行60km 到达B 处,这时测得灯塔C 在北偏东30∘方向上,已知在灯塔C 的周围47km 内有暗礁,问这艘船继续向东航行是否安全?解:过点C 作CD ⊥AB ,垂足为D .根据题意可知∠BAC =90∘―30∘=30∘,∠DBC =90∘―30∘=60∘,∵ ∠DBC =∠ACB +∠BAC ,∴ ∠BAC =30∘=∠ACB ,∴ BC =AB =60km ,在Rt △BCD 中,∠CDB =90∘,∠BDC =60∘,sin ∠BCD =ADAC ,∴ sin60∘=CD60,∴ CD =60×sin60∘=60×=km )>47km ,∴ 这艘船继续向东航行安全.21. 如图,王亮为了测量河宽CD,先在A处测得对岸C点在其北偏东45∘方向,然后沿河岸直行100米到B点,在B点测得对岸C点在其北偏西45∘方向,求河宽CD的长度.(结果精确到0.1m,参考数据:≈1.732).解:设GD=x米,由题意得:CD⊥AB,∠ACD=30∘,∠BCD=45∘,∴∠ADC=∠BDC=90∘,∴AD=米,BD=CD=x米,∵AD+BD=AB=100米,∴+x=100,解得:x=6.5,即河宽CD约为63.5米(63.4也对).22. 如图,山坡上有一棵与水平面垂直的大树AB,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部B恰好落在山坡上的点D处,已知山坡的坡角∠AEF=23∘,量得树干倾斜角∠BAC=38∘,大树被折断部分和坡面所成的角∠ADC=60∘,AD=4m.(1)求∠CAE的度数;(2)求这棵大树折断前的高度.(结果保留整数,参考数据≈1.4≈1.7≈2.4).解:(1)如图,延长BA交EF于点G.在Rt△AGE中,∠AEF=23∘,∴∠GAE=90∘―23∘=67∘.又∵∠BAC=38∘,∴∠CAE=180∘―67∘―38∘=75∘.(2)如图,过点A作AH⊥CD,垂足为H.在△ADH中,∠ADC=60∘,AD=4,cos∠ADC=DHAD ,sin∠ADC=AHAD,∴DH=2,AH=在Rt△ACH中,∵∠C=180∘―75∘―60∘=45∘,∴CH=AH=∴AC=∴ CD =CH +DH =+2.∴ AB =AC +CD =+2≈10(米).答:这棵大树折断前高约10米.23. 已知:如图,在平面直角坐标系中,△ABC 是直角三角形.∠ACB =90∘,点A ,C 的坐标分别为A (―4,0),C (2,0),tan ∠BAC =12,AB 与y 轴相交于点D .(1)求过点A ,B 的直线的函数表达式;(2)在y 轴上找一点E ,连接EB ,使得△EDB 与△ABC 相似,求点E 的坐标.解:(1)∵ 点A (―4,0),C (2,0), ∴ AC =6.∵ tan ∠BAC =12=BC AC , ∴ BC =3, ∴B 点坐标为(2,3).设过点A ,B 的直线的函数表达式为:y =kx +b ,则―4k +b =0,2k +b =3, 解得k =12,b =2,∴ 直线AB 的函数表达式为:y =12x +2.(2)①当∠BED =∠ACB =90∘时,即过点B ,作BE //x 轴,与y 轴交于点E ,则∠EBD =∠CAB ,∴ △EDB ∼△CBA ,则DE BC =BE AC ,即DE 3=26,解得DE =1,∴ E (0,3).②当∠DBE =∠ACB =90∘时,即过点B ,作BE ⊥BD ,与y 轴交于点E ,则∠DEB =∠BAC ,∴ △EDB ∼△ABC ,则DE BA =BD BC ,即=DE =5,∴ E (0,7).24、在东西方向的海岸线l 上有一长为1km 的码头MN(如图),在码头西端M 的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A 的北偏西30°,且与A 相距40km 的B 处;经过1小时20分钟,又测得该轮船位于A 的北偏东60°,且与A 相距的C 处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.解:(1)∵∠1=30°,∠2=60°,∴△ABC为直角三角形.∵AB=40km,AC=,∴BC=km).∵1小时20分钟=80分钟,1小时=60分钟,∴80=千米/小时).(2)作线段BR⊥x轴于R,作线段CS⊥x轴于S,延长BC交l于T.∵∠2=60°,∴∠4=90°-60°=30°.∵AC=km),∴CS=30°=km).∴AS=30°=12(km).又∵∠1=30°,∴∠3=90°-30°=60°.∵AB=40km,∴BR=40·sin60°=km).∴AR=40×cos60°=40×12=20(km).易得,△STC∽△RTB,∴STRT=CSBR,STST+20+12=解得:ST=8(km).∴AT=12+8=20(km).又∵AM=19.5km,MN长为1km,∴AN=20.5km.∵19.5<AT<20.5,故轮船能够正好行至码头MN靠岸.。
《锐角三角函数》习题(含答案)

《锐⾓三⾓函数》习题(含答案)《锐⾓三⾓函数》⼀、选择题1. 4sin tan 5ααα=若为锐⾓,且,则为 ( )933425543A B C D ....2.在Rt△ABC 中,∠C = 90°,下列式⼦不⼀定成⽴的是()A .sinA = sinB B .cosA=sinBC .sinA=cosBD .∠A+∠B=90°3.直⾓三⾓形的两边长分别是6,8,则第三边的长为()A .10B .C .10或D .⽆法确定4.在Rt△ABC 中,∠C=90°,当已知∠A 和a 时,求c ,应选择的关系式是()A .c =B .c =C .c = a·tanAD .c = sin a A cos a A tan a A 5、的值等于()o o 45cos 45sin +A. B. C. D. 12213+36.在Rt△ABC 中,∠C=90°,tan A=3,AC 等于10,则S△ABC 等于( )A. 3B. 300C.D. 155037.当锐⾓α>30°时,则cosα的值是()A .⼤于B .⼩于CD 12128.⼩明沿着坡⾓为30°的坡⾯向下⾛了2⽶,那么他下降()A .1⽶B ⽶C .9.如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,则AB=()(A )4 (B )5 (C )(D10.已知Rt△ABC 中,∠C=90°,tanA=,BC=8,则AC 等于()43 A .6 B . C .10 D .12323⼆、填空题11.计算2sin30°+2cos60°+3tan45°=_______.12.若sin28°=cosα,则α=________.13.已知△ABC 中,∠C=90°,AB=13,AC=5,则tanA=______.14.某坡⾯的坡度为1,则坡⾓是_______度.15.在△ABC 中,∠C =90°,AB =10cm ,sinA =,则BC 的长为_______cm .5416.如图,在⾼楼前点测得楼顶的仰⾓为,向⾼楼前进60⽶到点,⼜测得仰⾓为,则该⾼楼的D 30?C 45?⾼度⼤约为A.82⽶B.163⽶C.52⽶D.70⽶17.如图,⼩鸣将测倾器安放在与旗杆AB 底部相距6m 的C 处,量出测倾器的⾼度CD =1m ,测得旗杆顶端B 的仰⾓=60°,则旗杆AB 的⾼度为.(计算结果保留根号)α(16题)三、解答题18.由下列条件解直⾓三⾓形:在Rt△ABC 中,∠C=90°:(1)已知a=4,b=8,(2)已知b=10,∠B=60°.(3)已知c=20,∠A=60°. (4) (2)已知a=5,∠B=35°19.计算下列各题.(1)s in 230°+cos 2sin60°·tan45°;(2)+ sin45°22cos 30cos 60tan 60tan 30?+四、解下列各题20.如图所⽰,平地上⼀棵树⾼为5⽶,两次观察地⾯上的影⼦,第⼀次是当阳光与地⾯成45°时,第⼆次是阳光与地⾯成30°时,第⼆次观察到的影⼦⽐第⼀次长多少⽶?(第21.如图,AB 是江北岸滨江路⼀段,长为3千⽶,C 为南岸⼀渡⼝,为了解决两岸交通困难,拟在渡⼝C 处架桥.经测量得A 在C 北偏西30°⽅向,B 在C 的东北⽅向,从C 处连接两岸的最短的桥长多少?(精确到0.1)22. 如图,点A 是⼀个半径为300⽶的圆形森林公园的中⼼,在森林公园附近有B 、C 两个村庄,现要在B 、C 两村庄之间修⼀条长为1000⽶的笔直公路将两村连通,经测得∠ABC=45o ,∠ACB=30o ,问此公路是否会穿过该森林公园?请通过计算进⾏说明。
银川市初中数学锐角三角函数的基础测试题附解析

银川市初中数学锐角三角函数的基础测试题附解析一、选择题1.如图,在菱形ABCD 中,按以下步骤作图:①分别以点C 和点D 为圆心,大于12CD 为半径作弧,两弧交于点M ,N ;②作直线MN ,且MN 恰好经过点A ,与CD 交于点E ,连接BE ,则下列说法错误的是( )A .60ABC ∠=︒B .2ABE ADE S S ∆=VC .若AB=4,则7BE =D .21sin 14CBE ∠= 【答案】C【解析】【分析】 由作法得AE 垂直平分CD ,则∠AED=90°,CE=DE ,于是可判断∠DAE=30°,∠D=60°,从而得到∠ABC=60°;利用AB=2DE 得到S △ABE =2S △ADE ;作EH ⊥BC 于H ,如图,若AB=4,则可计算出CH=12CE=1,337 ;利用正弦的定义得sin ∠CBE=21EH BE =. 【详解】解:由作法得AE 垂直平分CD ,∴∠AED=90°,CE=DE ,∵四边形ABCD 为菱形,∴AD=2DE ,∴∠DAE=30°,∠D=60°,∴∠ABC=60°,所以A 选项的说法正确;∵AB=2DE ,∴S △ABE =2S △ADE ,所以B 选项的说法正确;作EH ⊥BC 于H ,如图,若AB=4,在Rt △ECH 中,∵∠ECH=60°,CH=12CE=1,EH=3CH=3, 在Rt △BEH 中,BE=22(3)527+=,所以C 选项的说法错误;sin ∠CBE=3211427EH BE ==,所以D 选项的说法正确. 故选C .【点睛】本题考查了基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了菱形的性质和解直角三角形.2.如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在AC 上找一点B ,取145ABD ∠=o ,500BD m =,55D ∠=o ,要使A ,C ,E 成一直线,那么开挖点E 离点D 的距离是( )A .500sin55m oB .500cos55m oC .500tan55m oD .500cos55m o【答案】B【解析】【分析】根据已知利用∠D 的余弦函数表示即可.【详解】 在Rt △BDE 中,cosD=DE BD, ∴DE=BD •cosD=500cos55°.故选B .【点睛】 本题主要考查了解直角三角形的应用,正确记忆三角函数的定义是解决本题的关键.3.如图,某地修建高速公路,要从A 地向B 地修一条隧道(点A ,B 在同一水平面上).为了测量A ,B 两地之间的距离,一架直升飞机从A 地起飞,垂直上升1000米到达C 处,在C 处观察B 地的俯角为α,则AB 两地之间的距离约为( )A .1000sin α米B .1000tan α米C .1000tan α米D .1000sin α米 【答案】C【解析】【分析】 在Rt △ABC 中,∠CAB=90°,∠B=α,AC=1000米,根据tan AC ABα=,即可解决问题. 【详解】 解:在Rt ABC ∆中,∵90CAB ∠=o ,B α∠=,1000AC =米,∴tan AC ABα=, ∴1000tan tan AC AB αα==米. 故选:C .【点睛】 本题考查解直角三角形的应用-仰角俯角问题,解题的关键是熟练掌握基本知识,属于中考常考题型.4.菱形ABCD 的周长为20cm,DE ⊥AB,垂足为E,sinA=35,则下列结论正确的个数有( ) ①DE=3cm; ②BE=1cm; ③菱形的面积为15cm 2; ④BD=210cm .A .1个B .2个C .3个D .4个【答案】C【解析】【分析】根据菱形的性质及已知对各个选项进行分析,从而得到答案【详解】∵菱形ABCD 的周长为20cm∴AD=5cm∵sinA=3 5∴DE=3cm(①正确)∴AE=4cm∵AB=5cm∴BE=5﹣4=1cm(②正确)∴菱形的面积=AB×DE=5×3=15cm2(③正确)∵DE=3cm,BE=1cm∴BD=10cm(④不正确)所以正确的有三个.故选C.【点睛】本题考查了菱形的性质及锐角三角函数的定义,熟练掌握性质是解题的关键5.同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.根据以上作图过程及所作图形,下列结论中错误的是()A.∠ABD=90°B.CA=CB=CD C.sinA 3D.cosD=12【答案】D【解析】【分析】由作法得CA=CB=CD=AB,根据圆周角定理得到∠ABD=90°,点C是△ABD的外心,根据三角函数的定义计算出∠D=30°,则∠A=60°,利用特殊角的三角函数值即可得到结论.【详解】由作法得CA=CB=CD=AB,故B正确;∴点B在以AD为直径的圆上,∴∠ABD=90°,故A正确;∴点C 是△ABD 的外心,在Rt △ABC 中,sin ∠D =AB AD =12, ∴∠D =30°,∠A =60°, ∴sinA =32,故C 正确;cosD =32,故D 错误, 故选:D .【点睛】本题考查了解直角三角形,三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和解直角三角形. 6.如图,在△ABC 中,AC ⊥BC ,∠ABC =30°,点D 是CB 延长线上的一点,且BD =BA ,则tan ∠DAC 的值为( )A .2+3B .23C .3+3D .33【答案】A【解析】【分析】【详解】 设AC=x ,在Rt △ABC 中,∠ABC=30°,即可得AB=2x ,BC=3x ,所以BD=BA=2x ,即可得CD=3x+2x=(3+2)x ,在Rt △ACD 中,tan ∠DAC=(32)32CD x AC x+==+, 故选A.7.如图,从点A 看一山坡上的电线杆PQ ,观测点P 的仰角是45︒,向前走6m 到达B 点, 测得顶端点P 和杆底端点Q 的仰角分别是60︒和30°,则该电线杆PQ 的高度( )A .623+B .63+C .103D .83+【答案】A【解析】【分析】延长PQ交直线AB于点E,设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x 表示出AE和BE,列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则问题求解.【详解】解:延长PQ交直线AB于点E,设PE=x.在直角△APE中,∠A=45°,AE=PE=x;∵∠PBE=60°∴∠BPE=30°在直角△BPE中,BE=3PE=3x,∵AB=AE-BE=6米,则x-33x=6,解得:x=9+33.则BE=33+3.在直角△BEQ中,QE=33BE=33(33+3)=3+3.∴PQ=PE-QE=9+33-(3+3)=6+23.答:电线杆PQ的高度是(6+23)米.故选:A.【点睛】本题考查解直角三角形的实际应用,解答关键是根据题意构造直角三角形解决问题.8.如图,菱形ABCD的两个顶点B、D在反比例函数y=的图象上,对角线AC与BD的交点恰好是坐标原点O,已知点A(1,1),∠ABC=60°,则k的值是()A.﹣5 B.﹣4 C.﹣3 D.﹣2【答案】C【解析】分析:根据题意可以求得点B的坐标,从而可以求得k的值.详解:∵四边形ABCD是菱形,∴BA=BC,AC⊥BD,∵∠ABC=60°,∴△ABC是等边三角形,∵点A(1,1),∴OA=,∴BO=,∵直线AC的解析式为y=x,∴直线BD的解析式为y=-x,∵OB=,∴点B的坐标为(−,),∵点B在反比例函数y=的图象上,∴,解得,k=-3,故选C.点睛:本题考查反比例函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用反比例函数的性质解答.9.如图,4个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点,己知菱形的一∠=()个内角为60°,A、B、C都是格点,则tan ABCA .39B .3C .33D .32 【答案】A【解析】【分析】直接利用菱形的对角线平分每组对角,结合锐角三角函数关系得出EF,的长,进而利用EC tan ABC BE∠=得出答案. 【详解】解:连接DC ,交AB 于点E .由题意可得:∠AFC=30°, DC ⊥AF,设EC=x,则EF=x 3x tan 30︒, ∴BF AF 2EF 23x === EC 3tan ABC BE 23x 3x 33====+∠, 故选:A【点睛】此题主要考查了菱形的性质以及解直角三角形,正确得出EF 的长是解题关键.10.cos60tan45+o o 的值等于( )A .32B .22C .32D .1【答案】A【解析】【分析】根据特殊角的三角函数值计算即可.【详解】解:原式13122=+=. 故选A .【点睛】本题考查了特殊角的三角函数值,解题的关键是熟练掌握特殊角的三角函数值.11.如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为()A.(163,2)B.(163,1)C.(83,2)D.(83,1)【答案】A【解析】【分析】延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,根据角平分线的性质得到FC=CG=CE,求得DH=CG=CF,设DH=3x,AH=4x,根据勾股定理得到AD=5x,根据平行线的性质得到∠DCA=∠CAG,求得∠DCA=∠DAC,得到CD=HG=AD=5x,列方程即可得到结论.【详解】解:延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,∵CD∥x轴,∴DF⊥OB,∵∠BAO,∠ABO的平分线相交于点C,∴FC=CG=CE,∴DH=CG=CF,∵A(8,0),B(0,6),∴OA=8,OB=6,∴tan∠OAB=DHAH=OBOA=34,∴设DH=3x,AH=4x,∴AD=5x,∵CD∥OA,∴∠DCA=∠CAG,∵∠DAC=∠GAC,∴∠DCA=∠DAC,∴CD=HG=AD=5x,∴3x+5x+4x=8,∴x=23,∴DH=2,OH=163,∴D(163,2),故选:A.【点睛】本题考查了等腰三角形的判定和性质,进行的判定和性质,解直角三角形,正确的作出辅助线构造矩形和直角三角形是解题的关键.12.一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A 处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是()A.3,30) B.(30,3-50) C.330) D.(30,3)【答案】A【解析】【分析】【详解】解:OA=15×4=60海里,∵∠AOC=60°,∴∠CAO=30°,∵sin30°=OCAO=12,∴CO=30海里,∴AC3∴BC=(3-50)海里,∴B(3-50,30).故选A【点睛】本题考查掌握锐角三角函数的应用.13.如图,抛物线y=ax2+bx+c(a>0)过原点O,与x轴另一交点为A,顶点为B,若△AOB为等边三角形,则b的值为()A3B.﹣3C.﹣3D.﹣3【答案】B【解析】【分析】根据已知求出B(﹣2,24b ba a-),由△AOB为等边三角形,得到2b4a=tan60°×(﹣2ba),即可求解;【详解】解:抛物线y=ax2+bx+c(a>0)过原点O,∴c=0,B(﹣2,24b ba a-),∵△AOB为等边三角形,∴2b4a=tan60°×(﹣2ba),∴b=﹣3故选B.【点睛】本题考查二次函数图象及性质,等边三角形性质;能够将抛物线上点的关系转化为等边三角形的边关系是解题的关键.14.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x-12x2刻画,斜坡可以用一次函数y=12x刻画,下列结论错误的是( )A.斜坡的坡度为1: 2B.小球距O点水平距离超过4米呈下降趋势C.小球落地点距O点水平距离为7米D.当小球抛出高度达到7.5m时,小球距O点水平距离为3m【答案】D【解析】【分析】求出抛物线与直线的交点,判断A、C;根据二次函数的性质求出对称轴,根据二次函数性质判断B;求出当7.5y=时,x的值,判定D.【详解】解:214212y x xy x⎧=-+⎪⎪⎨⎪=⎪⎩,解得,11xy=⎧⎨=⎩,22772xy=⎧⎪⎨=⎪⎩,72∶7=1∶2,∴A正确;小球落地点距O点水平距离为7米,C正确;2142y x x=-21(4)82x=--+,则抛物线的对称轴为4x=,∴当4x>时,y随x的增大而减小,即小球距O点水平距离超过4米呈下降趋势,B正确,当7.5y=时,217.542x x=-,整理得28150x x-+=,解得,13x=,25x=,∴当小球抛出高度达到7.5m 时,小球水平距O 点水平距离为3m 或5m ,D 错误,符合题意;故选:D【点睛】本题考查的是解直角三角形的-坡度问题、二次函数的性质,掌握坡度的概念、二次函数的性质是解题的关键.15.如图,等边ABC V 边长为a ,点O 是ABC V 的内心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①ODE V 形状不变;②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一;③四边形ODBE 的面积始终不变;④BDE V 周长的最小值为1.5a .上述结论中正确的个数是( )A .4B .3C .2D .1【答案】A【解析】【分析】 连接OB 、OC ,利用SAS 证出△ODB ≌△OEC ,从而得出△ODE 是顶角为120°的等腰三角形,即可判断①;过点O 作OH ⊥DE ,则DH=EH ,利用锐角三角函数可得OH=12OE 和3OE ,然后三角形的面积公式可得S △ODE 32,从而得出OE 最小时,S △ODE 最小,根据垂线段最短即可求出S △ODE 的最小值,然后证出S 四边形ODBE =S △OBC 23即可判断②和③;求出BDE V 的周长=a +DE ,求出DE 的最小值即可判断④.【详解】解:连接OB 、OC∵ABC V 是等边三角形,点O 是ABC V 的内心,∴∠ABC=∠ACB=60°,BO=CO ,BO 、CO 平分∠ABC 和∠ACB ∴∠OBA=∠OBC=12∠ABC=30°,∠OCA=∠OCB=12∠ACB=30° ∴∠OBA=∠OCB ,∠BOC=180°-∠OBC -∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG -∠BOE=∠BOC -∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形,∴ODE V 形状不变,故①正确;过点O 作OH ⊥DE ,则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12(180°-120°)=30° ∴OH=OE·sin ∠OED=12OE ,EH= OE·cos ∠OED=32OE ∴DE=2EH=3OE ∴S △ODE =12DE·OH=3OE 2 ∴OE 最小时,S △ODE 最小,过点O 作OE′⊥BC 于E′,根据垂线段最短,OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a ×33=36a ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB +S △OBE = S △OEC +S △OBE =S △OBC =12BC·OE′=2312∵23a =14×2312a ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一,故②正确; ∵S 四边形ODBE =23a ∴四边形ODBE 的面积始终不变,故③正确;∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB +BE +DE= EC +BE +DE=BC +DE=a +DE∴DE 最小时BDE V 的周长最小∵DE=3OE∴OE 最小时,DE 最小而OE 的最小值为OE′=3a ∴DE 的最小值为3×3a =12a ∴BDE V 的周长的最小值为a +12a =1.5a ,故④正确; 综上:4个结论都正确,故选A .【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用,掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键.16.如图,在ABC V 中,//,,30DE BC AF BC ADE ⊥∠=︒,2,33,DE BC BF ==则DF 的长为()A .4B .23C .33D .3【答案】D【解析】【分析】先利用相似三角形的相似比证明点D 是AB 的中点,再解直角三角形求得AB ,最后利用直角三角形斜边中线性质求出DF .【详解】解:∵//DE BC ,∴ADE ~ABC V V ,∵2DE BC =,∴点D 是AB 的中点,∵,30AF BC ADE ⊥∠=︒,33BF =,∴∠B =30°,∴AB 6cos30BF ==︒, ∴DF=3,故选:D .【点睛】 此题主要考查相似三角形的判定与性质、解直角三角形和直角三角形斜边中线性质,熟练掌握性质的运用是解题关键.17.如图,在边长为8的菱形ABCD 中,∠DAB =60°,以点D 为圆心,菱形的高DF 为半径画弧,交AD 于点E ,交CD 于点G ,则图中阴影部分的面积是 ( )A .183π-B .183πC .32316πD .1839π-【答案】C【解析】【分析】 由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF ,图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD 是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF 是菱形的高,∴DF ⊥AB ,∴DF=AD•sin60°=38432⨯=,∴图中阴影部分的面积=菱形ABCD的面积-扇形DEFG的面积=2120(43)84332316360ππ⨯⨯-=-.故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.18.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )A.303n mile B.60 n mile C.120 n mile D.(30303)+n mile 【答案】D【解析】【分析】过点C作CD⊥AB,则在Rt△ACD中易得AD的长,再在直角△BCD中求出BD,相加可得AB的长.【详解】过C作CD⊥AB于D点,∴∠ACD=30°,∠BCD=45°,AC=60.在Rt△ACD中,cos∠ACD=CD AC,∴CD=AC •cos ∠ACD=60×33032=. 在Rt △DCB 中,∵∠BCD=∠B=45°,∴CD=BD=303,∴AB=AD+BD=30+303.答:此时轮船所在的B 处与灯塔P 的距离是(30+303)nmile .故选D .【点睛】此题主要考查了解直角三角形的应用-方向角问题,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.19.在Rt △ABC 中,∠C=90°,AC=3,BC=4,那么cosA 的值是( )A .45B .35C .43D .34【答案】B【解析】【分析】根据勾股定理,可得AB 的长,根据锐角的余弦等于邻边比斜边,可得答案.【详解】解:在Rt △ABC 中,∠C=90°,AC=3,BC=4,由勾股定理,得AB=22AC BC +=5cosA=AC AB =35故选:B .【点睛】 本题考查锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.20.利用量角器可以制作“锐角余弦值速查卡”.制作方法如下:如图,设1OA =,以O 为圆心,分别以0.05,0.1,0.15,0.2,…,0.9,0.95长为半径作半圆,利用“锐角余弦值速查卡”可以读出相应锐角余弦的近似值.例如:cos300.87︒≈,cos450.71︒=.下列角度中余弦值最接近0.94的是( )A.30°B.50︒C.40︒D.20︒【答案】D【解析】【分析】根据“锐角余弦值速查卡”解答即可.【详解】从“锐角余弦值速查卡”可以读出cos20︒≈0.94,∴余弦值最接近0.94的是20︒,故选:D.【点睛】此题考查“锐角余弦值速查卡”,正确读出“锐角余弦值速查卡”是解题的关键.。
北师大版九年级数学下册《1.1锐角三角函数》同步测试题及答案

北师大版九年级数学下册《1.1锐角三角函数》同步测试题及答案1.如图,在Rt ABC △中,AC=4,BC=3,90C ∠=︒则sin A 的值为( )A.34B.53C.43D.352.在Rt ABC △中90C ∠=︒ 3cos 5A =,AB=10,则BC 的( ) A.3 B.4 C.6 D.83.在Rt ABC △中,各边的长度都扩大4倍,那么锐角A 的余弦值( )A.扩大4倍B.保持不变C.缩小4倍D.扩大2倍4.如图,在Rt ABC △中,CD 是斜边AB 上的高,则下列正确的是( )A.3tan 4DCB ∠=B.5tan 3DCB ∠=C.4cos 5DCB ∠=D.4sin 5DCB ∠= 5.已知A B ∠∠=︒+90,且3cos 5A =,则tanB 的值为( ). A.45 B.35 C.34 D.43 6.ABC △中,A ∠和B ∠,C ∠的对边分别为a ,b ,c .已知6810a b c ===,,,则cos A ∠的值为( )A.35B.34C.45D.43 7.如图,在44⨯网格正方形中,每个小正方形的边长为1,顶点为格点,若ABC △的顶点均是格点,则cos BAC ∠的值是( )A.55B.105C.255D.458.如图,的顶点分别在单位长度为1的正方形网格的格点上,则sin BAC∠的值为( ) A. B.55C. D.2539.已知ABC△中,90C∠=︒和3cos5A=,AC=6,那么AB的长是___________.10.在等腰三角形ABC中10AB AC==,BC=12,则tan B=_____________.11.如图,在44⨯网格正方形中,每个小正方形的边长为1,顶点为格点,若ABC△的顶点均是格点,则sin∠的值为_____.12.如图,在ACD中90C∠=︒,15A∠=︒点B在边AC上,且2AB BD==,则BC= _______________,tan CAD∠=_______________.ABC△51213.如图,在四边形ABCD 中90ABC ∠=︒ 45C ∠=︒ 2CD 3BD =.(1)求sin CBD ∠的值;(2)若3AB =,求AD 的长.14.如图,在平面直角坐标系内,O 为原点,点A 的坐标为(10,0),点B 在第一象限内5BO = 3sin 5BOA ∠=求:(1)点B 的坐标;(2)cos BAO ∠的值.参考答案及解析1.答案:D解析:=4AC =3BC 90C ∠=︒∴2222345AB AC BC =++= ∴3sin 5BC A AB ==; 故选:D.2.答案:D解析:如图在Rt ABC △中 3cos 5AC A AB ==10AB =6AC ∴=在Rt ABC △中 22221068BC AB AC =-=-=. 故选:D.3.答案:B解析:在Rt ABC △中,各边的长度都扩大4倍 ∴各角的大小不变,即A ∠大小不变.一个角的锐角三角函数值只与角的大小有关∴锐角A 的余弦值保持不变.故选:B.4.答案:D解析:Rt ABC △中,CD 是斜边AB 上的高,AC=3,CB=4 5AB ∴= DCB DBC DBC A ∠+∠=∠+∠DCB A ∴∠=∠4tan tan 3DCB CAD ∴∠=∠=,故A 选项不正确; 4tan 3DCB ∴∠=,故B 选项不正确;3cos 5DCB ∴∠,故C 选项不正确; 4sin 5DCB ∴∠=,故D 选项正确 故选:D.5.答案:C解析:如图A B ∠∠=︒+90∴90C ∠=︒3cos5A =∴设3AC x = 5AB x =∴224BC AB AC x =-=∴33tan 44xB x ==故选:C.6.答案:C解析:在ABC △中6a = 8b = 10c =2222683664100a b ∴+=+=+=2100c = 222a b c ∴+=ABC ∴△是直角三角形84cos 105b A c ∴===.故选:C.7.答案:C解析:过点C 作AB 的垂线交AB 于一点D ,如图所示∵每个小正方形的边长为1∵5AC = 10= 5AB =设AD x =,则5BD x =-在Rt ACD △中 222DC AC AD =-在Rt BCD △中 222DC BC BD =-∵2210(5)5x x --=-解得2x =∵25cos 55AD BAC AC ∠=== 故选:C.8.答案:B解析:如图,过B 作BD AC ⊥于点D根据勾股定理得:22345AB =+= 223635AC =+=11111546313463,22222ABC S AC BD ∴=⋅=⨯-⨯⨯-⨯⨯-⨯⨯=△ 5BD ∴=5sin 5BD CAB AB ∴∠== 故选:B.9.答案:10解析:在Rt ABC △中3cos 5AC A AB == 6AC = 10AB ∴=故答案为:10.10.答案:43解析:本题易因忽略求tan B 的前提是将B ∠放在一个直角三角形中而出错. 11.答案:55解析:延长AC 到D ,连接BD ,如图:220AD = 25BD = 225AB = 222AD BD AB ∴+=90ADB ∴∠=︒55sin 525BD BAC AB ∴∠===. 故答案为:55. 12.答案:323/32解析:2AB BD ==∴15A ADB ∠=∠=︒∴30DBC A ADB ∠=∠+∠=︒ 90C ∠=︒∴112CD BD ==在Rt DBC △中,由勾股定理得:2222213BC BD CD =--= ∴23AC AB BC =+= ∴tan 2323CD CAD AC ∠===-+ 故答案为:3 3.13.答案:(1)1sin 3CBD ∠= (2)23AD =解析:(1)如图,过点D 作DE BC ⊥于点E .在Rt CED △中45C ︒∠= 2CD = 1CE DE ∴==.在Rt BDE △中1sin 3DE CBD BD ∠==. (2)如图,过点D 作DF AB ⊥于点F ,则90BFD BED ABC ∠=∠=∠=︒. ∴四边形BEDF 为矩形.1BF DE ∴==.2AF AB BF ∴=-= 2222DF BD BF =-=2223AD AF DF ∴=+.14.答案:(1)(4,3)B (2)2cos 55BAO ∠= 解析:(1)如图,过点B 作BC OA ⊥于点C . 3sin 5BCBOA BO ∠==.22534OC ∴=-=. .(2)易知10OA =.4OC = . 226335AB ∴=+5BO =3BC ∴=(4,3)B ∴6AC ∴=2cos 5535AC BAO AB ∴∠===。
初中—锐角三角函数(锐角三角函数的增减性)基础题与答案

初中—锐角三角函数(锐角三角函数的增减性)基础(1)试题一.选择题(共30小题)1.(2014秋•余姚市期末)在Rt△ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况()A.都扩大2倍B.都缩小2倍C.都不变D.正弦值扩大2倍,余弦值缩小2倍2.(2014秋•福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是()A.tan70°<tan50°<tan20°B.tan50°<tan20°<tan70°C.tan20°<t an50°<tan70°D.tan20°<tan70°<tan50°3.(2013秋•文登市期末)若α为锐角,,则()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°4.(2014秋•昆明校级期末)若0°<α<90°,则下列说法不正确的是()A.sinα随α的增大而增大B.cosα随α的减小而减小C.tanα随α的增大而增大D.sinα=cos(90°﹣α)5.(2014秋•滨江区期末)已知sinα<0.5,那么锐角α的取值范围是()A.60°<α<90° B.30°<α<90° C.0°<α<60°D.0°<α<30°6.(2014秋•莱州市期中)随着锐角α的增大,cosα的值()A.增大B.减小C.不变D.增大还是减小不确定7.(2014秋•锦江区校级期中)如果角α为锐角,且sinα=,那么α在()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°8.(2014秋•怀化校级月考)如果∠A为锐角,sinA=,那么()A.0°<∠A<30°B.30°<∠A<45°C.45°<∠A<60°D.60°<∠A<90°9.(2014秋•慈溪市校级月考)当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是()A.正弦和余弦B.正弦和正切C.余弦和正切D.正弦、余弦和正切10.(2014秋•江阴市校级月考)如图,A(0,8),B(0,2),点E为x轴正半轴上一动点,设tan∠AEB=m,则m的取值范围是()A.0<m≤B.0<m≤C.<m< D.0<m≤11.(2013•清远校级一模)在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值()A.也扩大3倍B.缩小为原来的C.都不变D.有的扩大,有的缩小12.(2013秋•松北区校级期中)在Rt△ABC中,各边都扩大5倍,则角A的三角函数值()A.不变B.扩大5倍 C.缩小5倍 D.不能确定13.(2013•遂宁模拟)已知,则锐角α的取值范围是()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°14.(2013春•聊城期中)下列各式正确的是()A.cos60°<sin45°<tan45°B.sin45°<cos60°<tan45°C.sin45°<tan45°<cos60 D.cos60°<tan45°<sin45°15.(2013秋•龙凤区校级期中)已知α为锐角,下列不等式中正确的是()①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.A.② B.①,②,③C.②,④D.①,②,③,④16.(2013秋•海阳市期中)在Rt△ABC中,∠C=90°,下列结论:(1)sinA<1;(2)若A>60°,则cosA>;(3)若A>45°,则sinA>cosA.其中正确的有()A.0个B.1个C.2个D.3个17.(2013秋•平江区校级期中)若∠A=41°,则cosA的大致范围是()A.0<cosA<1 B.<cosA<C.<cosA<D.<cosA<118.(2012•常德模拟)已知α、β都是锐角,且sinα<sinβ,则下列关系中,正确的是()A.α>βB.tanα>tanβC.cosα>cosβD.α=β19.(2012•天山区校级模拟)当45°<θ<90°时,下列各式中正确的是()A.tanθ>cosθ>sinθB.sinθ>cosθ>tanθC.tanθ>sinθ>cosθD.cosθ>sinθ>tanθ20.(2012秋•安次区校级期末)下列式子正确的是()A.sin66°>sin68°B.tan66°>tan68°C.cos66°>cos68° D.cot66°<cot68°21.(2012秋•大兴区期末)已知∠A为锐角,且sinA<,那么∠A 的取值范围是()A.0°<A<30°B.30°<A<60° C.60°<A<90°D.30°<A<90°22.(2012春•冠县校级期中)若α是锐角,且cosα=0.7,则()A.0°<α<30°B.30°≤α<45°C.45°<α<60° D.60°≤α<90°23.(2012秋•下城区校级月考)若α=40°,则α的正切值h的范围是()A.<h<B.<h<C.1<h<D.<h<24.(2011•茂名)如图,已知:45°<∠A<90°,则下列各式成立的是()A.sinA=cosA B.sinA>cosA C.sinA>tanA D.sinA<cosA25.(2009秋•莆田校级期末)在Rt△ABC中,各边的长度都扩大2倍,那么锐角A的正切值()A.都扩大2倍B.都扩大4倍C.没有变化 D.都缩小一半26.(2011秋•信州区期末)已知90°<∠A<180°,90°<∠B<180°,甲、乙、丙、丁四个同学计算的结果依次为28°、48°、60°、88°,其中只有一个同学计算结果是正确的,那么计算正确的同学是()A.甲 B.乙 C.丙 D.丁27.(2011秋•西湖区校级月考)已知:∠A为锐角,且cosA≥,则()A.0°<∠A≤60° B.60°≤∠A<90°C.O°<∠A≤30°D.30°≤∠A <90°28.(2011秋•巴东县校级月考)下列各式正确的是()A.sin46°<cos46°<tan46°B.sin46°<tan46°<cos46°C.tan46°<cos46°<sin46°D.cos46°<sin46°<tan46°29.(2010•山西)在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值()A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变30.(2010•黔东南州)设x为锐角,若sinx=3K﹣9,则K的取值范围是()A.K<3 B.C.D.考点卡片1.坐标与图形性质1、点到坐标轴的距离与这个点的坐标是有区别的,表现在两个方面:①到x轴的距离与纵坐标有关,到y轴的距离与横坐标有关;②距离都是非负数,而坐标可以是负数,在由距离求坐标时,需要加上恰当的符号.2、有图形中一些点的坐标求面积时,过已知点向坐标轴作垂线,然后求出相关的线段长,是解决这类问题的基本方法和规律.3、若坐标系内的四边形是非规则四边形,通常用平行于坐标轴的辅助线用“割、补”法去解决问题.2.锐角三角函数的增减性(1)锐角三角函数值都是正值.(2)当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).(3)当角度在0°≤∠A≤90°间变化时,0≤sinA≤1,1≥cosA≥0.当角度在0°<∠A<90°间变化时,tanA>0.3.特殊角的三角函数值(1)特指30°、45°、60°角的各种三角函数值.sin30°=;cos30°=;tan30°=;sin45°=;cos45°=;tan45°=1;sin60°=;cos60°=;tan60°=;(2)应用中要熟记特殊角的三角函数值,一是按值的变化规律去记,正弦逐渐增大,余弦逐渐减小,正切逐渐增大;二是按特殊直角三角形中各边特殊值规律去记.(3)特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.28.1.2初中—锐角三角函数(锐角三角函数的增减性)基础(1)参考答案与试题解析一.选择题(共30小题)1.(2014秋•余姚市期末)在Rt△ABC中,若各边的长度同时都扩大2倍,则锐角A的正弦值与余弦值的情况()A.都扩大2倍B.都缩小2倍C.都不变D.正弦值扩大2倍,余弦值缩小2倍【考点】锐角三角函数的增减性.【分析】根据相似三角形的性质及锐角三角函数的定义解答即可.【解答】解:∵Rt△ABC中,若各边的长度同时都扩大2倍,∴扩大后形成的三角形与原三角形相似,锐角A的正弦与余弦的比值不变.故选C.【点评】此题比较简单,解答此题的关键是熟知三角函数值是一个比值,与角的边长无关.2.(2014秋•福田区期末)比较tan20°,tan50°,tan70°的大小,下列不等式正确的是()A.tan70°<tan50°<tan20°B.tan50°<tan20°<tan70°C.tan20°<tan50°<tan70°D.tan20°<tan70°<tan50°【考点】锐角三角函数的增减性.【分析】根据正切函数随锐角的增大而增大,可得答案.【解答】解:由正切函数随角增大而增大,得tan20°<tan50°<tan70°,故C符合题意,故选:C.【点评】本题考查了锐角三角函数的增减性,利用了正切函数随锐角的增大而增大.3.(2013秋•文登市期末)若α为锐角,,则()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°【考点】锐角三角函数的增减性.【分析】先求出sin30°=0.5,sin45°=≈0.707,sin60°=≈0.866,即可得出答案.【解答】解:∵sin30°=0.5,sin45°=≈0.707,sin60°=≈0.866,sinα==0.8,∴45°<α<60°,故选C.【点评】本题考查了特殊角的三角函数值和锐角三角函数的增减性的应用,注意:当0°<α<90°,sinα随角度的增大而增大.4.(2014秋•昆明校级期末)若0°<α<90°,则下列说法不正确的是()A.sinα随α的增大而增大B.cosα随α的减小而减小C.tanα随α的增大而增大D.sinα=cos(90°﹣α)【考点】锐角三角函数的增减性.【分析】根据锐角三角函数的增减性及互余两角的三角函数的关系即可作答.【解答】解:若0°<α<90°,则正弦值随着角度的增大(或减小)而增大(或减小);余弦值随着角度的增大(或减小)而减小(或增大);正切值随着角度的增大(或减小)而增大(或减小);sinα=cos(90°﹣α);所以A、C、D正确,B错误.故选B.【点评】本题考查了锐角三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).也考查了互余两角的三角函数的关系:sinα=cos(90°﹣α),cosα=sin(90°﹣α).5.(2014秋•滨江区期末)已知sinα<0.5,那么锐角α的取值范围是()A.60°<α<90° B.30°<α<90° C.0°<α<60°D.0°<α<30°【考点】锐角三角函数的增减性.【分析】根据锐角函数的正弦值随锐角的增大而增大,可得答案.【解答】解:由sinα=0.5,得α=30°,由锐角函数的正弦值随锐角的增大而增大,得0°<α<30°,故选:D.【点评】本题考查了锐角三角函数的增减性,利用了锐角函数的正弦值随锐角的增大而增大.6.(2014秋•莱州市期中)随着锐角α的增大,cosα的值()A.增大B.减小C.不变D.增大还是减小不确定【考点】锐角三角函数的增减性.【分析】当角度在0°~90°间变化时,余弦值随着角度的增大而减小,依此求解即可.【解答】解:随着锐角α的增大,cosα的值减小.故选B.【点评】本题考查了锐角三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).7.(2014秋•锦江区校级期中)如果角α为锐角,且sinα=,那么α在()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°【考点】锐角三角函数的增减性.【分析】根据特殊角的三角函数值及锐角三角函数的增减性即可求解.【解答】解:∵sin0°=0,sinα=,sin30°=,又0<<,∴0°<α<30°.故选A.【点评】本题考查了锐角三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).同时考查了特殊角的三角函数值.8.(2014秋•怀化校级月考)如果∠A为锐角,sinA=,那么()A.0°<∠A<30°B.30°<∠A<45°C.45°<∠A<60°D.60°<∠A<90°【考点】锐角三角函数的增减性.【分析】首先明确s in30°=,再根据一个锐角的正弦值随着角的增大而增大,进行分析.【解答】解:∵sin30°=,0<<,∴0°<∠A<30°.故选A.【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.9.(2014秋•慈溪市校级月考)当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是()A.正弦和余弦B.正弦和正切C.余弦和正切D.正弦、余弦和正切【考点】锐角三角函数的增减性.【分析】当角度在0°到90°之间变化时,正弦和正切函数值随着角度的增大而增大.【解答】解:当角度在0°到90°之间变化时,函数值随着角度的增大而增大的三角函数是正弦和正切.故选B.【点评】本题考查了锐角三角函数的增减性的应用,主要考查学生的理解能力.10.(2014秋•江阴市校级月考)如图,A(0,8),B(0,2),点E为x轴正半轴上一动点,设tan∠AEB=m,则m的取值范围是()A.0<m≤B.0<m≤C.<m< D.0<m≤【考点】锐角三角函数的增减性;坐标与图形性质.【分析】点E为x轴正半轴上一动点,设tan∠AEB=m,则m>0,再求出m的最大值即可.过A、B、E三点的圆O′与x轴相切时,∠AEB 最大,m的值最大.作O′D⊥AB于D,由垂径定理得出AD=DB=AB=3,OD=OA﹣AD=5,那么⊙O′的半径为5.在直角△O′AD中,由勾股定理得出O′D==4,则AE===4,再作BC⊥AE于C.由S △AOE=OA•OE=S△BOE+S△ABE,求出BC=,CE==,那么m的最大值为==.【解答】解:如图,过A、B、E三点的圆O′与x轴相切时,∠AEB最大.作O′D⊥AB于D,则AD=DB=AB=3,∵OA=8,∴OD=OA﹣AD=5,∴O′E=O′A=OD=5,即⊙O′的半径为5.在直角△O′AD中,由勾股定理得O′D==4,∴OE=O′D=4,∴AE===4,作BC⊥AE于C.∵S△AOE=OA•OE=S△BOE+S△ABE,∴×8×4=×2×4+×4×BC,∴BC=,∵BE2=OB2+OE2=22+42=20,∴CE==,∴m的最大值为==,又∵m>0,∴0<m≤.故选A.【点评】本题主要考查了三角函数的定义,垂径定理,勾股定理,三角形的面积,有一定难度,理解过A、B、E三点的圆与x轴相切时,m的值最大是解题的关键.11.(2013•清远校级一模)在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值()A.也扩大3倍B.缩小为原来的C.都不变D.有的扩大,有的缩小【考点】锐角三角函数的增减性.【分析】理解锐角三角函数的概念:锐角三角函数值即为直角三角形中边的比值.【解答】解:根据锐角三角函数的概念,可知在直角三角形中,各边的长度都扩大3倍,锐角A的三角函数值不变.故选C.【点评】理解锐角三角函数的概念,明白三角函数值与边的长度无关.12.(2013秋•松北区校级期中)在Rt△ABC中,各边都扩大5倍,则角A的三角函数值()A.不变B.扩大5倍 C.缩小5倍 D.不能确定【考点】锐角三角函数的增减性.【分析】易得边长扩大后的三角形与原三角形相似,那么对应角相等,相应的三角函数值不变.【解答】解:∵各边都扩大5倍,∴新三角形与原三角形的对应边的比为5:1,∴两三角形相似,∴∠A的三角函数值不变,故选A.【点评】用到的知识点为:三边对应成比例,两三角形相似;相似三角形的对应角相等.三角函数值只与角的大小有关,与角的边的长短无关.13.(2013•遂宁模拟)已知,则锐角α的取值范围是()A.0°<α<30°B.30°<α<45° C.45°<α<60° D.60°<α<90°【考点】锐角三角函数的增减性.【分析】分别求出tan30°=≈0.644,tan45°=1,tan60°=≈1.732,tanα==1.2,得出tan45°<tanα<tan60°,根据根据正切值随角度的增大而增大即可得出答案.【解答】解:∵tan30°=≈0.644,tan45°=1,tan60°=≈1.732,又∵tanα==1.2,∴tan45°<tanα<tan60°,∵锐角的正切值随角度的增大而增大,∴45°<α<60°,故选C.【点评】本题考查了特殊角的三角函数值和锐角三角形函数的增减性的应用,主要考查学生的理解能力和判断能力,注意:锐角的正切值随角度的增大而增大.14.(2013春•聊城期中)下列各式正确的是()A.cos60°<sin45°<tan45°B.sin45°<cos60°<tan45°C.sin45°<tan45°<cos60 D.cos60°<tan45°<sin45°【考点】锐角三角函数的增减性.【分析】先根据特殊角的三角函数值分别得出cos60°=,sin45°=,tan45°=1,再比较大小即可.【解答】解:∵cos60°=,sin45°=,tan45°=1,又∵<<1,∴cos60°<sin45°<tan45°.故选A.【点评】本题考查了特殊角的三角函数值,实数的大小比较,熟记特殊角的三角函数值是解题的关键.15.(2013秋•龙凤区校级期中)已知α为锐角,下列不等式中正确的是()①tanα>1;②0<sinα<1;③cotα<1;④0<cosα<1.A.② B.①,②,③C.②,④D.①,②,③,④【考点】锐角三角函数的增减性.【分析】根据锐角三角函数的增减性,可得答案.【解答】解:α为锐角,①tanα>0,故①错误;②0<sinα<1,故②正确;③cotα>0,故③错误;④0<cosα<1,故④正确;故选:C.【点评】本题考查了锐角三角函数的增减性,掌握锐角三角函数的增减性是解题的关键.16.(2013秋•海阳市期中)在Rt△ABC中,∠C=90°,下列结论:(1)sinA<1;(2)若A>60°,则cosA>;(3)若A>45°,则sinA>cosA.其中正确的有()A.0个B.1个C.2个D.3个【考点】锐角三角函数的增减性.【分析】由Rt△ABC中,∠C=90°,根据三角形内角和定理可知∠A与∠B都是锐角,再根据特殊角的三角函数值及锐角三角函数的增减性即可求解.【解答】解:∵在Rt△ABC中,∠C=90°,∴∠A与∠B都是锐角,∴sinA<1,(1)正确;∵cos60°=,锐角余弦值随着角度的增大而减小,∴若A>60°,则cosA<,(2)错误;∵cos(90°﹣A)=sinA,锐角正弦值随着角度的增大而增大,∴若A>45°,则sinA>cosA,(3)正确.故选C.【点评】本题主要考查了锐角三角函数的增减性,特殊角的三角函数值,是基础题,比较简单.17.(2013秋•平江区校级期中)若∠A=41°,则cosA的大致范围是()A.0<cosA<1 B.<cosA<C.<cosA<D.<cosA<1【考点】锐角三角函数的增减性.【分析】根据特殊角的三角函数值及余弦函数随角增大而减小解答.【解答】解:∵cos30°=,cos45°=,余弦函数函数值随角度的增大而减小,∴<cosA<.故选C.【点评】本题考查了特殊角的三角函数值,以及三角函数的增减性,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键.18.(2012•常德模拟)已知α、β都是锐角,且sinα<sinβ,则下列关系中,正确的是()A.α>βB.tanα>tanβC.cosα>cosβD.α=β【考点】锐角三角函数的增减性.【专题】计算题.【分析】先根据锐角三角函数的增减性由sinα<sinβ得到α<β,然后再根据锐角三角函数的增减性进行判断即可.【解答】解:∵α、β都是锐角,且sinα<sinβ,∴α<β,∴tanα<tanβ,cosα>cosβ,所以A、B、D选项都是错误的,C选项是正确的.故选C.【点评】本题考查了锐角三角函数的增减性:当0<α<90°,sinα随α的增大而增大;cosα随α的增大而减小;tanα随α的增大而增大.19.(2012•天山区校级模拟)当45°<θ<90°时,下列各式中正确的是()A.tanθ>cosθ>sinθB.sinθ>cosθ>tanθC.tanθ>sinθ>cosθD.cosθ>sinθ>tanθ【考点】锐角三角函数的增减性.【分析】本题可以根据θ的取值范围,从中找到一个特殊值,然后求出其三角函数值比较即可.【解答】解:∵45°<θ<90°,∴可令θ=60°,∴tanθ=,sinθ=,cosθ=,∴tanθ>sinθ>cosθ.故选C.【点评】本题考查了锐角三角函数的增减性,在解决填空或选择时,特殊值也是一种很好的方法.20.(2012秋•安次区校级期末)下列式子正确的是()A.sin66°>sin68°B.tan66°>tan68°C.cos66°>cos68° D.cot66°<cot68°【考点】锐角三角函数的增减性.【分析】根据锐角三角函数值的变化规律:正弦值和正切值都是随着角的增大而增大,余弦值和余切值都是随着角的增大而减小即可判断.【解答】解:根据锐角三角函数的变化规律,知sin66°<sin68°,tan66°<tan68°,cos66°>cos68°,cot66°>cot68°.故A、B、D错误,C正确.故选C.【点评】本题考查了锐角三角函数的增减性,当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小).④余切值随着角度的增大(或减小)而减小(或增大).21.(2012秋•大兴区期末)已知∠A为锐角,且sinA<,那么∠A 的取值范围是()A.0°<A<30°B.30°<A<60° C.60°<A<90°D.30°<A<90°【考点】锐角三角函数的增减性.【分析】根据特殊角的三角函数值求出sin30°=,根据当∠A是锐角时,其正弦随角度的增大而增大,【解答】解:∵∠A为锐角,且sin30°=,又∵当∠A是锐角时,其正弦随角度的增大而增大,∴0°<A<30°,故选A.【点评】本题考查了特殊角的三角函数值和锐角三角函数的增减性的应用,注意:当角是锐角时,其正弦和正切随角度的增大而增大,余弦和余切随角度的增大而减小.22.(2012春•冠县校级期中)若α是锐角,且cosα=0.7,则()A.0°<α<30°B.30°≤α<45°C.45°<α<60° D.60°≤α<90°【考点】锐角三角函数的增减性.【分析】在锐角三角函数中,余切值都是随着角的增大而减小.cos30°=,cos45°=,故知α的范围.【解答】解;:∵在锐角三角函数中,余切值都是随着角的增大而减小,又知cos60°=,cos45°=,故45°<α<60°.故选C.【点评】本题主要考查锐角三角形的增减性,在一个单调区间里,正弦函数和正切函数随角度增大而增大,余弦和余切反之.23.(2012秋•下城区校级月考)若α=40°,则α的正切值h的范围是()A.<h<B.<h<C.1<h<D.<h<【考点】锐角三角函数的增减性;特殊角的三角函数值.【分析】根据特殊角的三角函数值及余弦函数随角增大而减小解答即可.【解答】解:∵tan30°=,tan60°=,一个角的正切值随角的增大而增大,∴tan30°<tan40°<tan60°,即<h<,故选D.【点评】本题考查了锐角三角函数的增减性,熟记特殊角的三角函数值和了解锐角三角函数的增减性是解题的关键.24.(2011•茂名)如图,已知:45°<∠A<90°,则下列各式成立的是()A.sinA=cosA B.sinA>cosA C.sinA>tanA D.sinA<cosA 【考点】锐角三角函数的增减性.【专题】计算题.【分析】根据锐角三角函数的增减性sinA随角度的增大而增大,cosA 随角度的增大而减小,直接得出答案即可.【解答】解:∵45°<A<90°,∴根据sin45°=cos45°,sinA随角度的增大而增大,cosA随角度的增大而减小,当∠A>45°时,sinA>cosA.故选:B.【点评】此题主要考查了锐角三角函数的增减性,正确利用锐角三角函数的增减性是解决问题的关键.25.(2009秋•莆田校级期末)在Rt△ABC中,各边的长度都扩大2倍,那么锐角A的正切值()A.都扩大2倍B.都扩大4倍C.没有变化 D.都缩小一半【考点】锐角三角函数的增减性.【分析】明确概念:在Rt△ABC中,锐角A的正切值等于其对边和邻边的比.【解答】解:根据锐角三角函数的定义,知各边的长度都扩大2倍,那么锐角A的大小不变,所以其正切值不变.故选C.【点评】本题考查三角函数的定义与性质:三角函数的大小只与角的大小有关,与角的两边长度无关.26.(2011秋•信州区期末)已知90°<∠A<180°,90°<∠B<180°,甲、乙、丙、丁四个同学计算的结果依次为28°、48°、60°、88°,其中只有一个同学计算结果是正确的,那么计算正确的同学是()A.甲 B.乙 C.丙 D.丁【考点】锐角三角函数的增减性.【分析】根据90°<∠A<180°,90°<∠B<180°,得出360°>∠A+∠B >180°,进而得出30°<<60°即可得出答案.【解答】解:∵90°<∠A<180°,90°<∠B<180°,∴360°>∠A+∠B>180°,∴30°<<60°,∴甲、乙、丙、丁四个同学计算的结果依次为28°、48°、60°、88°,中只有48°符合要求,故选:B.【点评】此题主要考查了不等式的性质,根据已知得出30°<<60°是解题关键.27.(2011秋•西湖区校级月考)已知:∠A为锐角,且cosA≥,则()A.0°<∠A≤60° B.60°≤∠A<90°C.O°<∠A≤30°D.30°≤∠A <90°【考点】锐角三角函数的增减性.【分析】首先明确cos60°=,再根据余弦函数值随角增大而减小进行分析.【解答】解:∵cos60°=,余弦函数值随角增大而减小,∴当cosA≥时,∠A≤60°.又∠A是锐角,∴0°<A≤60°.故选A.【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.28.(2011秋•巴东县校级月考)下列各式正确的是()A.sin46°<cos46°<tan46°B.sin46°<tan46°<cos46°C.tan46°<cos46°<sin46°D.cos46°<sin46°<tan46°【考点】锐角三角函数的增减性.【分析】根据三角函数的增减性:当角度在0°~90°间变化时,①正弦值随着角度的增大(或减小)而增大(或减小);②余弦值随着角度的增大(或减小)而减小(或增大);③正切值随着角度的增大(或减小)而增大(或减小);以及互余的两个角之间的关系:sinA=cos(90°﹣A);当角度在0°≤∠A≤90°间变化时,0≤sinA≤1,1≥cosA≥0,当角度在0°<∠A<90°间变化时,tanA>0即可作出判断.【解答】解:A、cos46°=sin44°<sin46°故此选项错误;B、sin46°=cos44°>cos46°,故此选项错误;C、cos46°=sin44°<sin46°,∵tan46°>tan45°>1,cos44°<1,∴cos46°<sin46°<tan46°,故此选项错误;D、由C选项的分析可知此选项正确;故选;D.【点评】本题主要考查了三角函数的增减性熟记锐角三角函数的增减性是解题的关键.29.(2010•山西)在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的正弦值()A.扩大2倍 B.缩小2倍 C.扩大4倍 D.不变【考点】锐角三角函数的增减性.【分析】根据三角函数的定义解答即可.【解答】解:∵Rt△ABC中,∠C=90°,将各边长度都扩大为原来的2倍,其比值不变,∴∠A的正弦值不变.故选:D.【点评】此题比较简单,解答此题的关键是熟知三角函数值是一个比值,与角各边长度的变化无关.30.(2010•黔东南州)设x为锐角,若sinx=3K﹣9,则K的取值范围是()A.K<3 B.C.D.【考点】锐角三角函数的增减性.【专题】应用题.【分析】根据锐角x正弦的取值范围0<sinx<1作答即可.【解答】解:根据三角函数的增减性得:0<sinx<1,即0<3K﹣9<1,解得:3<K<,故选:B.【点评】此题考查的知识点是锐角三角函数的增减性,关键是明确锐角x有0<sinx<1.。
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)
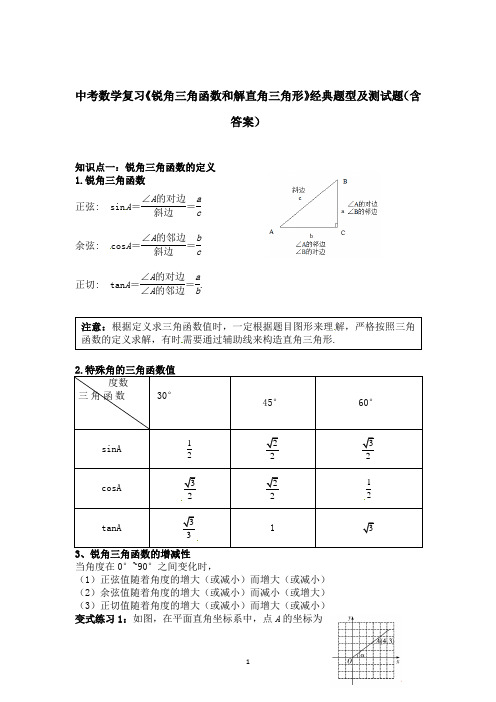
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)知识点一:锐角三角函数的定义 1.锐角三角函数 正弦: sin A =∠A 的对边斜边=ac余弦: cos A =∠A 的邻边斜边=bc正切: tan A =∠A 的对边∠A 的邻边=ab.来源:学&科&网]2.特殊角的三角函数值[来 度数三角函数[来源:Z 。
xx 。
]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时,(1)正弦值随着角度的增大(或减小)而增大(或减小) (2)余弦值随着角度的增大(或减小)而减小(或增大) (3)正切值随着角度的增大(或减小)而增大(或减小) 变式练习1:如图,在平面直角坐标系中,点A 的坐标为注意:根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅助线来构造直角三角形.[(4,3),那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图,过点A 作AB ⊥x 轴于点B ,∵A (4,3),∴OB =4,AB =3,∴OA =32+42=5,∴cos α=OB OA =45.变式练习2:在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,则sinA =________. 【解析】∵在Rt △ABC 中,由勾股定理得AC =22AB BC +=32+42=5,∴sin A =BC AC =45. 变式练习3:在Rt △ABC 中,∠C =90°,sin A =35,BC =6,则AB =( D )A .4B .6C .8D .10变式练习4:如图,若点A 的坐标为(1,3),则sin ∠1=__32__. ,知识点二 :解直角三角形 1.解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形. 2.解直角三角形的常用关系在Rt △ABC 中,∠C=90°,∠A ,∠B ,∠C 所对的边分别为a ,b ,c (1)三边之间的关系:a 2+b 2=c 2;(2)锐角之间的关系:∠A +∠B =90°; (3)边角之间的关系:,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======(sinA==cosB=ac,c osA=sinB=bc,tanA=ab.)变式练习1:在Rt△ABC中,已知a=5,sinA=30°,则c=10,b=5.变式练习2:如图,Rt△ACB中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI =90°.若AC=a,求CI的长.解:在Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB,∴∠A=60°,∵AC=a,∴CD=AC·sin60°=32a,依此类推CH=(32)3a=338a,在Rt△CHI中,∵∠CHI=60°,∴CI=CH·tan60°=338a×3=98a.变式练习3:如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )A.433B.4 C.8 3 D.4 3,灵活选择解直角三角形的方法顺口溜:已知斜边求直边,正弦、余弦很方便;已知直边求直边,理所当然用正切;已知两边求一边,勾股定理最方便;已知两边求一角,函数关系要记牢;已知锐角求锐角,互余关系不能少;已知直边求斜边,用除还需正余弦.变式练习4:如图,一山坡的坡度为i=1∶3,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了__100__米., ,变式练习5:一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为___40+4033___海里/小时.知识点三:解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.(如图①)(2)坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有i=tanα.(如图②)(3)方向角:平面上,通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向),则从点O出发的视线与水平线或铅垂线所夹的角,叫做观测的方向角.(如图③)2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;(3)选择合适的边角关系式,使运算简便、准确;(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.注意:解直角三角形中“双直角三角形”的基本模型:(1)叠合式(2)背靠式解题方法:这两种模型种都有一条公共的直角边,解题时,往往通过这条边为中介在两个三角形中依次求边,或通过公共边相等,列方程求解变式练习1:如图,某数学兴趣小组想测量一棵树CD 的高度,他们先在点A 处测得树顶C 的仰角为30°,然后沿AD 方向前行10 m ,到达B 点,点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上).请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈ 1.732)解:如解图,由题意可知∠CAB =30°,∠CBD =60°,AB =10 m ,∵∠CBD =∠CAB +∠BCA ,∴∠BCA =∠CBD -∠CAB =60°-30°=30°=∠CAB , ∴BC =AB =10 m . 在Rt △BCD 中,∵sin ∠CBD =CDBC,∴CD =BC ·sin ∠CBD =10×sin60°=10×32=53≈5×1.732≈8.7 m . 答:这棵树CD 的高度大约是8.7 m .变式练习2:如图,小山岗的斜坡AC 的坡度是tan α=34,在与山脚C 距离200米的D 处,测得山顶A 的仰角为26.6°,求小山岗的高AB (结果取整数;参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50).解:设AB =x 米,在Rt △ABD 中,∠D =26.6°,∴BD =tan 26.6x≈2x ,在Rt △ABC 中,tan α=AB BC =34,∴BC =43x ,∵BD -BC =CD ,CD =200,∴2x-43x=200,解得x=300.答:小山岗的高AB约为300米.变式练习3:如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B 处测得M的仰角为30°,已知每层楼的窗台离该层的地面高度均为1 m,求旗杆MN的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈1.732)解:如解图,过点M的水平线交直线AB于点H,由题意,得∠AMH=∠MAH=45°,∠BMH=30°,AB=3.5 m,设MH=x m,则AH=x m,BH=x·tan30°=33x≈0.58x m,∴AB=AH-BH=x-0.58x=0.42x=3.5 m,解得x≈8.3,则MN=x+1=9.3 m.答:旗杆MN的高度约为9.3 m.变式练习4:小明去爬山,如图,在山脚看山顶的角度为30°,小明在坡比为5∶12的山坡上走了1300米,此时小明看山顶的角度为60°,则山高为( )A. (600-2505)米B. (6003-250)米C. (350+3503)米D. 500 3 米【解析】B如解图,∵BE∶AE=5∶12,∴设BE=5k,AE=12k,∴AB=2()5K+(12k)2=13k,∴BE∶AE∶AB=5∶12∶13,∵AB=1300米,∴AE=1200米,BE =500米,设EC=FB=x米,∵∠DBF=60°,∴DF=3x米,则DC=(3x+500)米,又∵∠DAC=30°,∴AC=3CD,即1200+x=3(3x+500),解得x=600-2503,∴DF=3x=(6003-750)米,∴CD=DF+CF=(6003-250)米,即山高CD为(6003-250)米.变式练习5:某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)解:如解图,过点A作AD⊥BC交BC于点D,过点B作BH⊥水平线交水平线于点H,由题意∠ACH=75°,∠BCH=30°,AB∥CH,∴∠ABC=30°,∠ACB=45°,∵AB=4×8=32米,∴CD=AD=AB·sin30°=16米,BD=AB·cos30°=32×32=163米,∴BC=CD+BD=(16+163)米,∴BH=BC·sin30°=(16+163)×12=(8+83)米.答:这架无人飞机的飞行高度为(8+83)米.变式练习6:如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中3≈1.732) 解:∵CD∥BE,∴∠EBC+∠DCB=180°.∵∠ABE=60°,∠DCB=30°,∴∠ABC=90°.…………(4分)由题知,BC=80×12=40(海里),∠ACB=60°.在Rt△ABC中,AB=BC·tan60°=403≈40×1.732≈69.3(海里).答:此时渔政船距钓鱼岛A的距离AB的长约为69.3海里.。
必刷基础练【28.1 锐角三角函数】(解析版)

2022-2023学年九年级数学下册考点必刷练精编讲义(人教版)基础第28章《锐角三角函数》28.1 锐角三角函数知识点01:锐角三角函数的定义1.(2022秋•钢城区期中)已知在Rt△ABC中,∠C=90°,tan A=2,BC=8,则AC等于( )A.6B.16C.12D.4解:∵∠C=90°,∴tan A==2,∴AC=BC=×8=4.故选:D.2.(2022秋•晋州市期中)在Rt△ABC中,∠C=90°,AB=10,AC=8,则cos B的值等于( )A.B.C.D.解:∵∠C=90°,AB=10,AC=8,∴BC==6,∴cos B===.故选:A.3.(2022秋•浦东新区期中)在Rt△ABC中,∠C=90°,BC=9,AC=6,下列等式中正确的( )A.tan A=B.sin A=C.cot A=D.cos A=解:∵AB2=BC2+AC2,∴AB2=62+92=117,∴AB=3;A、tan A===,故A不符合题意;B、sin A===,故B不符合题意;C、cot A===,故C符合题意;D、cos A===,故D不符合题意,故选:C.4.(2022秋•杨浦区期中)在Rt△ABC中,∠C=90°,BC=1,AB=3,下列各式中,正确的是( )A.sin A=B.cos A=C.tan A=D.cot A=解:∵∠C=90°,BC=1,AB=3,∴AC===2,∴sin A==,cos A==,tan A===,cot A==2.故选:A.5.(2022秋•黄浦区期中)在Rt△ABC中,∠C=90°,BC=3,AB=4,那么下列各式中正确的是( )A.sin A=B.cos A=C.tan A=D.cot A=解:∵∠C=90°,AB=4,BC=3,∴AC==,∴sin A==,cos A==.tan A===,cot A==.故选:A.6.(2022•睢宁县模拟)如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,则sin B的值是 .解:∵∠C=90°,AC=3,BC=4,∴AB==5,∴sin B==,故答案为:.7.(2021秋•牡丹江期末)在△ABC中,∠A,∠C都是锐角,cos A=,sin C=,则∠B= 60° .解:∵∠A,∠C都是锐角,cos A=,sin C=,∴∠A=60°,∠C=60°,∴∠B=180°﹣∠A﹣∠C=60°,故答案为:60°.8.(2022春•衡阳月考)如图,在△ABC中,∠C=90°,AB=13,AC=12,则tan B= .解:∵∠C=90°,AB=13,AC=12,∴BC==5,∴tan B==.故答案为:.9.(2022秋•惠山区校级期中)在Rt△ABC中,∠ACB=90°,∠A、∠B、∠C的对边分别是a、b、c,(1)a=5,c=2a,求b、∠A.=9,求△ABC的周长.(2)tan A=2,S△ABC解:(1)∵a=5,c=2a=10,∴b===5,∵sin A===,∴∠A=30°;(2)∵tan A==2,∴a=2b,∵S=9,△ABC∴=9,∴=9,解得:b=3(负数舍去),即a=6,由勾股定理得:c===3,∴△ABC的周长为a+b+c=6+3+3=9+3.10.(2022•湖州)如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3.求AC的长和sin A的值.解:∵∠C=90°,AB=5,BC=3,∴AC===4,sin A==.答:AC的长为4,sin A的值为.知识点02:锐角三角函数的增减性11.(2022•五通桥区模拟)若锐角α满足cosα<且tanα<,则α的范围是( )A.30°<α<45°B.45°<α<60°C.60°<α<90°D.30°<α<60°解:∵α是锐角,∴cosα>0,∵cosα<,∴0<cosα<,又∵cos90°=0,cos45°=,∴45°<α<90°;∵α是锐角,∴tanα>0,∵tanα<,∴0<tanα<,又∵tan0°=0,tan60°=,0<α<60°;故45°<α<60°.故选:B.12.(2022•路南区二模)梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )A.sin A的值越大,梯子越陡B.cos A的值越大,梯子越陡C.tan A的值越小,梯子越陡D.陡缓程度与∠A的函数值无关解:根据锐角三角函数值的变化规律,知sin A的值越大,∠A越大,梯子越陡.故选:A.13.(2022秋•晋江市期中)比较大小:tan50° < tan60°.解:∵50°<60°,∴tan50°<tan60°,故答案为:<.14.(2021秋•淮阴区期末)比较大小:sin50° < sin60°(填“>”或“<”).解:由于50°<60°,根据一个锐角的正弦值随着角度的增大而增大可得,sin50°<sin60°,故答案为:<.15.用锐角α的三角函数的定义去说明(1)0<sinα<1(2)0<cosα<1(3)tanα>sinα解:(1)sinα=,0<a<c,0<1,即0<sinα<1;(2)cosα=,0<b<c,0<<1,即0<cosα<1;(3)tanα=,sinα=,由0<b<c,得>,即tanα>sinα.16.(2019春•西湖区校级月考)如图,半径为4的⊙O内一点A,OA=.点P在⊙B上,当∠OPA最大时,求PA的长.解:如图,作OE⊥PA于E,∵sin∠OPA=,∴OE的值取最大值时,sin∠OPA的值最大,此时∠OPA的值最大,∵OE≤OA,∴当OE与OA重合时,即PA⊥OA时,∠OPA的值最大.如图,∵在直角△OPA中,OA=2,OP=4,∴PA==2.知识点03:同角三角函数的关系17.(2022春•巴东县期中)x为锐角,,则cos x的值为( )A.B.C.D.解:∵sin2x+cos2x=1,,∴cos x===.故选:B.18.(2021秋•舟山期末)在直角△ABC中,已知∠C=90°,sin A=,求cos A=( )A.B.C.D.2解:∵sin2A+cos2A=1,∴cos A==.\故选:C.19.(2021•温江区校级开学)计算:(cos230°+sin230°)×tan60°= .解:原式=[()2+()2]×=,故答案为:.20.(2021秋•金牛区校级期中)在△ABC中,∠C=90°,tan A=2,则sin A+cos A= .解:如图,∵tan A=2,∴设AB=x,则BC=2x,AC==x则有:sin A+cos A=+=+=.故答案为:.21.(2020秋•万州区校级期中)计算:sin225°+cos225°﹣tan60°= 1﹣ .解:∵sin225°+cos225°=1,tan60°=,∴sin225°+cos225°﹣tan60°=1﹣,故答案为:1﹣.22.(2021秋•鄞州区校级月考)计算:(1)4sin260°﹣3tan30°;(2)+cos245°+sin245°.解:(1)4sin260°﹣3tan30°=4×=3﹣;(2)+cos245°+sin245°==4+1=5.23.(2021秋•绥宁县月考)计算:(1)sin230°+tan60°﹣sin245°+cos230°;(2)+(1+π)0﹣2cos45°﹣|1﹣|.解:(1)原式=()2+﹣()2+()2=+﹣+=+;(2)原式=2+1﹣2×﹣+1=2+1﹣﹣+1=2.24.(2022秋•蓬莱区期中)计算:(1)﹣4cos30°+20220;(2)已知α为锐角,sin(α+15°)=,计算﹣4cosα+tanα+()﹣1的值.解:(1)原式=|1﹣|﹣4×+1=﹣1﹣2+1=﹣;(2)∵sin60°=,sin(α+15°)=,∴α+15°=60°,∴α=45°,∴﹣4cosα+tanα+()﹣1=2﹣4×+1+3=4.知识点04:互余两角三角函数的关系25.(2022秋•芝罘区期中)在Rt△ABC中,∠C=90°,下列等式成立的是( )A.sin A=sin B B.cos A=cos B C.sin A=cos B D.tan A=tan B 解:∵∠C=90°,∴∠A+∠B=90°,∴sin A=cos B.故选:C.26.(2021秋•怀化期末)已知锐角α,且sinα=cos38°,则α=( )A.38°B.62°C.52°D.72°解:∵锐角α,且sinα=cos38°,sin A=cos(90°﹣∠A),∴sinα=cos(90°﹣α)=cos38°,∴90°﹣α=38°,解得:α=52°.故选:C.27.(2021秋•怀宁县期末)在Rt△ABC中,∠C=90°,cos A=,则sin B= .解:∵在△ABC中,∠C=90°,∴∠A+∠B=90°,∴sin B=cos A=.故答案为:.28.(2020秋•肥东县期末)已知α为锐角,则sinα﹣cos(90°﹣α)= 0 .解:∵α为锐角,∴sinα=cos(90°﹣α),∴sinα﹣cos(90°﹣α)=0.故答案为0.29.(2019秋•双流区期末)已知,在Rt△ABC中,∠C=90°,若sin A=,则tan B= .解:如图.在Rt△ABC中,∵sin A==,∴设BC=x,AB=3x,则AC==2x,故tan B===.故答案为:.30.(2017•吴兴区校级二模)已知cos45°=,求cos21°+cos22°+…+cos289°的值.解:原式=(cos21°+cos289°)+(cos22°+cos288°)+…+(cos244°+cos246°)+cos245=(sin21°+cos21°)+(sin22°+cos22°)+…+(sin244°+cos244°)+cos245=44+()2=44.31.化简下列各式:(1)4cos2(90°﹣θ)+4sin2(90°﹣θ)+4(2).解:(1)原式=4sin2θ+4cos2θ+4=4(sin2θ+cos2θ)+4=4+4=8;(2)原式=﹣1=﹣1=1+tan2θ﹣1=tan2θ.知识点05:特殊角的三角函数值32.(2022秋•巨野县期中)∠β为锐角,且2cosβ﹣1=0,则∠β=( )A.30°B.60°C.45°D.37.5°解:∵∠β为锐角,且2cosβ﹣1=0,∴cosβ=,∴∠β=60°.故选:B.33.(2021秋•梁平区期末)式子2cos30°﹣tan45°﹣的值是( )A.0B.2C.2D.﹣2解:原式=2×﹣1﹣(﹣1)=﹣1﹣+1=0.故选:A.34.(2022秋•乳山市校级月考)在△ABC中,∠A=105°,∠B=45°,sin C的值是( )A.B.C.1D.解:∵∠A=105°,∠B=45°,∴∠C=180°﹣∠A﹣∠C=30°,∴sin C=sin30°=.故选:A.35.(2022秋•虎丘区校级期中)已知∠α为锐角,且sinα=,则∠α= 60° .解:∵∠α为锐角,sinα=,∴∠α=60°.故答案为:60°.36.(2022秋•东平县校级月考)若(3tan A﹣)2+|2sin B﹣|=0,则以∠A、∠B为内角的△ABC的形状是 直角三角形 .解:∵(3tan A﹣)2+|2sin B﹣|=0,∴3tan A﹣=0,2sin B﹣=0,则tan A=,sin B=,∴∠A=30°,∠B=60°,∴以∠A、∠B为内角的△ABC的形状是直角三角形.故答案为:直角三角形.37.(2022秋•铁西区期中)在△ABC中,若sin A=,∠A,∠B都是锐角,则∠C的度数是 75° .解:∵,∠A,∠B都是锐角,∴∠A=45°,∠B=60°,∴∠C=180°﹣45°﹣60°=75°,故答案为:75°.38.(2022秋•垦利区期中)在△ABC中,若|sin A﹣|+(﹣cos B)2=0,则∠C的度数是 105° .解:∵|sin A﹣|+(﹣cos B)2=0,∴sin A﹣=0,﹣cos B=0,即sin A=,cos B=,∴∠A=30°,∠B=45°,∴∠C=180°﹣∠A﹣∠B=105°.故答案为:105°.39.(2022秋•黄浦区期中)计算:.解:原式=﹣=cot30°﹣1﹣=﹣1﹣=﹣1﹣(+1)=﹣1﹣﹣1=﹣2.40.(2022秋•莱西市期中)计算:(1);(2)cos60°﹣2sin245°+tan230°﹣sin30°.解:(1)原式===﹣1﹣=﹣;(2)原式=﹣2×()2+×()2﹣=﹣1+﹣=﹣.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. B. C. D.
【答案】A
【解析】
【分析】
设a= BC,∠B=∠C=α,求出CN、DM、EN的长度,利用y=S△BMD−S△CNE,即可求解.
【详解】
∵AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N,
∴∠ADM=∠MDC=∠NCD=45°,
∴ =CD,
在矩形ABCD中,AB=CD=a,
∴DM+CN=acos45°= a.
故选C.
【点睛】
此题考查矩形的性质,解直角三角形,解题关键在于得到cos45°=
16.如图,基灯塔AB建在陡峭的山坡上,该山坡的坡度i=1:0.75.小明为了测得灯塔的高度,他首先测得BC=20m,然后在C处水平向前走了34m到达一建筑物底部E处,他在该建筑物顶端F处测得灯塔顶端A的仰角为43°.若该建筑物EF=20m,则灯塔AB的高度约为(精确到0.1m,参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)()
又∵点C在反比例函数y= 的图象上,
∴2acosα= ,得k=4a2sinαcosα=8.
故选C.
【点睛】
本题主要考查反比例函数与几何图形的综合问题,解此题的关键在于先设旋转角为α,利用旋转的性质和三角函数设出点B'与点C的坐标,再通过反比例函数的性质求解即可.
2.公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则 ( )
故选A
【点睛】
本题考查掌握锐角三角函数的应用.
15.如图,矩形ABCD中,AB>AD,AB=a,AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N.则DM+CN的值为(用含a的代数式表示)( )
A.aB. aC. D.
【答案】C
【解析】
【分析】
根据“AN平分∠DAB,DM⊥AN于点M,CN⊥AN于点N”得∠MDC=∠NCD=45°,cos45°= ,所以DM+CN=CDcos45°;再根据矩形ABCD,AB=CD=a,DM+CN的值即可求出.
A.100sin35°米B.100sin55°米C.100tan35°米D.100tan55°米
【答案】C
【解析】
【分析】
根据正切函数可求小河宽PA的长度.
【详解】
∵PA⊥PB,PC=100米,∠PCA=35°,
∴小河宽PA=PCtan∠PCA=100tan35°米.
故选:C.
【点睛】
此题考查解直角三角形的应用,解题关键在于掌握解直角三角形的一般过程是:①将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).②根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
为直径,
,
,
,
而 ,
,
,
,
而 ,
,
,
,
在 中, ,
,
, ,
, ,
,
,即 ,
,
.
故选:D.
【点睛】
本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角, 的圆周角所对的弦是直径.也考查了解直角三角形.
8.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )
∴∠EDF=60°,
∴MD=BM÷tan60°= ,
∴CD=CM﹣MD=12﹣ .
故选B.
【点睛】
本题考查了解直角三角形,难度较大,解答此类题目的关键根据题意建立直角三角形利用所学的三角函数的关系进行解答.
13.如图,有一个边长为 的正六边形纸片,若在该纸片上沿虚线剪一个最大圆形纸片,则这个圆形纸片的半径是()
∴∠BOG=∠COG= ∠BOC =30°,
∵OG⊥BC,OB=OC,BC=2cm,
∴BG= BC= ×2=1cm,
∴OB= =2cm,
∴OG= ,
∴圆形纸片的半径为 cm,
故选:A.
【点睛】
本题考查的是正多边形和圆,根据题意画出图形,利用直角三角形的性质及正六边形的性质解答是解答此题的关键.
14.一艘轮船从港口O出发,以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处,此时观测到其正西方向50海里处有一座小岛B.若以港口O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1海里为1个单位长度建立平面直角坐标系(如图),则小岛B所在位置的坐标是( )
A. mB. m
C. mD. m
【答案】A
【解析】
设MN=xm,
在Rt△BMN中,∵∠MBN=45∘,
∴BN=MN=x,
在Rt△AMN中,tan∠MAN= ,
∴tan30∘= =3√3,
解得:x=8( +1),
则建筑物MN的高度等于8( +1)m;
故选A.
点睛:本题是解直角三角形的应用,考查了仰角和俯角的问题,要明确哪个角是仰角,哪个角是俯角,知道仰角是向上看的视线与水平线的夹角,俯角是向下看的视线与水平线的夹角,并与三角函数相结合求边的长.
【详解】
解: , 分别平分 和 ,交于 点,
为 的内心,
最小时, 为 的内切圆的半径,
过 作 垂足分别为
四边形 为正方形,
为 的中点,
由切线长定理得:
四边形 为正方形,
故选D.
【点睛】
本题考查的动态问题中的线段的最小值,三角形的内心的性质,等腰直角三角形的性质,锐角三角函数的计算,掌握相关知识点是解题关键.
∴正三角形的边长 .
∴圆锥的底面圆半径是1,母线长是2,
∴底面周长为
∴侧面积为 ,∵底面积为 ,
∴全面积是 .
故选:C.
【点睛】
本题考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.
6.如图,为了测量某建筑物MN的高度,在平地上A处测得建筑物顶端M的仰角为30°,向N点方向前进16m到达B处,在B处测得建筑物顶端M的仰角为45°,则建筑物MN的高度等于( )
7.如图,四边形 内接于 , 为直径, ,过点 作 于点 ,连接 交 于点 .若 , ,则 的长为()
A.10B.12C.16D.20
【答案】D
【解析】
【分析】
连接 ,如图,先利用圆周角定理证明 得到 ,再根据正弦的定义计算出 ,则 , ,接着证明 ,利用相似比得到 ,所以 .
【详解】
解:连接 ,如图,
此题考查相似三角形的判定和性质、锐角三角函数的定义,掌握相似三角形的对应角相等是解题的关键.
12.将一副直角三角板如图放置,点C在FD的延长上,AB∥CF,∠F=∠ACB=90°,∠E=30°,∠A=45°,AC=12 ,则CD的长为( )
A.4 B.12﹣4 C.12﹣6 D.6
【答案】B
【解析】
A. B. C. D.
【答案】A
【解析】
【分析】
根据题意画出图形,再根据正多边形圆心角的求法求出∠AOB的度数,最后根据等腰三角形及直角三角形的性质解答即可.
【详解】
解:如图所示,正六边形的边长为2cm,OG⊥BC,
∵六边形ABCDEF是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,OG⊥BC,
A. B. C. D.
【答案】A
【解析】
【分析】
根据正方形的面积公式可得大正方形的边长为 ,小正方形的边长为5,再根据直角三角形的边角关系列式即可求解.
【详解】
解:∵大正方形的面积是125,小正方形面积是25,
∴大正方形的边长为 ,小正方形的边长为5,
∴ ,
∴ ,
∴பைடு நூலகம்.
故选:A.
【点睛】
本题考查了解直角三角形、勾股定理的证明和正方形的面积,难度适中,解题的关键是正确得出 .
【点睛】
本题考查了动点问题的函数图象、等腰三角形的性质、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
4.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为()
【分析】
过点B作BM⊥FD于点M,根据题意可求出BC的长度,然后在△EFD中可求出∠EDF=60°,进而可得出答案.
【详解】
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=45°,AC=12 ,
∴BC=AC=12 .
∵AB∥CF,
∴BM=BC×sin45°=
CM=BM=12,
在△EFD中,∠F=90°,∠E=30°,
11.把 三边的长度都扩大为原来的 倍,则锐角 的余弦值()
A.扩大为原来的 倍B.缩小为原来的 C.扩大为原来的 倍D.不变
【答案】D
【解析】
【分析】
根据相似三角形的性质解答.
【详解】
三边的长度都扩大为原来的3倍,
则所得的三角形与原三角形相似,
