MATLAB 非线性 回归 拟合 nlintool
《计量经济学》与MATLAB编程-第六章多项式回归与非线性回归
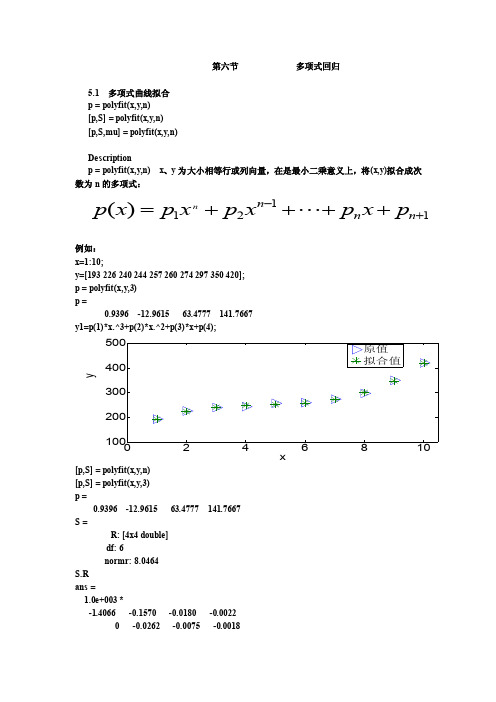
第六节 多项式回归5.1 多项式曲线拟合 p = polyfit(x,y,n) [p,S] = polyfit(x,y,n) [p,S,mu] = polyfit(x,y,n)Descriptionp = polyfit(x,y,n) x 、y 为大小相等行或列向量,在是最小二乘意义上,将(x,y)拟合成次数为n 的多项式:1121)(+-++++=n n n p x p x p x p x p n例如: x=1:10;y=[193 226 240 244 257 260 274 297 350 420]; p = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667y1=p(1)*x.^3+p(2)*x.^2+p(3)*x+p(4);xy[p,S] = polyfit(x,y,n) [p,S] = polyfit(x,y,3) p =0.9396 -12.9615 63.4777 141.7667 S =R: [4x4 double] df: 6normr: 8.0464 S.R ans =1.0e+003 *-1.4066 -0.1570 -0.0180 -0.0022 0 -0.0262 -0.0075 -0.00180 0 -0.0019 -0.00140 0 0 0.0005normr是残差的模,即:norm(y-y1)ans =8.0464[p,S,MU] = polyfit(x,y,n)[p,S,MU] = polyfit(x,y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464MU =5.50003.0277MU是x均值和x的标准差即std(x)S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.0901P它等于:[p,S] = polyfit((x-mean(x))./std(x),y,3)p =26.0768 23.2986 18.6757 255.1312S =R: [4x4 double]df: 6normr: 8.0464>> S.Rans =5.1959 0.0000 2.7682 0.00000 -3.7926 -0.0000 -2.37310 0 1.1562 0.00000 0 0 -2.09015.2 多项式估计y= polyval(p,x)[y,DELT A] = polyval(p,x,S)y= polyval(p,x) 返回给定系数p和变量x值的多项式的预测y = P(1)*x^N + P(2)*x^(N-1) + ... + P(N)*x + P(N+1)x=1:10;y= polyval([3 2],x)y =5 8 11 14 17 20 23 26 29 32[3 2]有两个数,因此为一次多项式,即y=3x+2如:x=1:10;y=[193 226 240 244 257 260 274 297 350 420];p=polyfit(x,3)y1= polyval(p,x)norm(y-y1)ans =8.0464如果是矩阵,则polyval(p,x)为对应x的每一个预测值。
第六章 Matlab插值、拟合与回归

[x,y,z]=meshgrid(-1:0.2:1); [x0,y0,z0]=meshgrid(-1:0.05:1); V=exp(x.^2.*z+y.^2.*x+z.^2.*y).*cos(x.^2.*y.*z+z.^2.*y.*x); V0=exp(x0.^2.*z0+y0.^2.*x0+z0.^2.*y0).*cos(x0.^2.*y0.*z0+z0.^2.*y0.*x0); V1=interp3(x,y,z,V,x0,y0,z0,'spline'); err=V1-V0; max(err(:)) slice(x0,y0,z0,V1,[-0.5,0.3, 0.9],[0.6,-0.1],[-1,-0.5,0.5,1]) title('Slives for Four Dim Figures');
一般多项式拟合的目标是寻找一组多项式系数ai,使得多项式 f(x)=a1xn+a2xn-1 +…+anx+an+1 能够较好的拟合原始数据,使整体拟合误差较 小,在Matlab中使用polyfit()函数实现,调用格式为:p=polyfit(x,y,n),n为选 定的多项式的次数,p是多项式按降幂排列得出的行向量,可以使用 poly2sym转换为多项式,使用polyval()计算多项式的值。
还有三维插值运算函数interp3,n维网格插值interpn,其调用格式同 interp1和interp2,对应的三维网格生成函数为[x,y,z]=meshgrid(x1,y1,z1) 和非网格生成函数griddata3(),griddatan(),他们同g;6*rand(199,1);y=-2+4*rand(199,1); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); plot(x,y,'*');figure;plot3(x,y,z,'*');figure; [x1,y1]=meshgrid(-3:0.2:3,-2:0.2:2); z1=griddata(x,y,z,x1,y1,'cubic'); surf(x1,y1,z1);figure; z2=griddata(x,y,z,x1,y1,'v4');surf(x1,y1,z2); %误差比较 z0=(x1.^2-2*x1).*exp(-x1.^2-y1.^2-x1.*y1); surf(x1,y1,abs(z0-z1));axis([-3,3,-2,2,0,0.15]) figure; surf(x1,y1,abs(z0-z2));axis([-3,3,-2,2,0,0.15])
matlab 多元与非线性回归即拟合问题regress、nlinfit

回归(拟合)自己的总结(20100728)1:学三条命令:polyfit(x,y,n)---拟合成一元幂函数(一元多次) regress(y,x)----可以多元,nlinfit(x,y,’fun ’,beta0) (可用于任何类型的函数,任意多元函数,应用范围最主,最万能的)2:同一个问题,可能这三条命令都可以使用,但结果肯定是不同的,因为拟合的近似结果,没有唯一的标准的答案。
相当于咨询多个专家。
3:回归的操作步骤:(1) 根据图形(实际点),选配一条恰当的函数形式(类型)---需要数学理论与基础和经验。
(并写出该函数表达式的一般形式,含待定系数)(2) 选用某条回归命令求出所有的待定系数所以可以说,回归就是求待定系数的过程(需确定函数的形式)配曲线的一般方法是: (一)先对两个变量x 和y 作n 次试验观察得n i y x ii,...,2,1),,( 画出散点图,散点图(二)根据散点图确定须配曲线的类型. 通常选择的六类曲线如下:(1)双曲线xba y +=1 (2)幂函数曲线y=a bx , 其中x>0,a>0(3)指数曲线y=a bx e 其中参数a>0.(4)倒指数曲线y=a xb e/其中a>0,(5)对数曲线y=a+blogx,x>0(6)S 型曲线x be a y -+=1(三)然后由n 对试验数据确定每一类曲线的未知参数a 和b.一、一元多次拟合polyfit(x,y,n)一元回归polyfit多元回归regress---nlinfit(非线性)二、多元回归分析(其实可以是非线性,它通用性极高)对于多元线性回归模型:e x x y p p ++++=βββ 110设变量12,,,px x x y 的n 组观测值为12(,,,)1,2,,i i ip i x x x y i n= .记 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=np n n p p x x x x x x x x x x 212222111211111,⎪⎪⎪⎪⎪⎭⎫⎝⎛=n y y y y 21,则⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=p ββββ 10 的估计值为排列方式与线性代数中的线性方程组相同()拟合成多元函数---regress 使用格式:左边用b=或[b, bint, r, rint, stats]= 右边用regress(y, x) 或regress(y, x, alpha)---命令中是先y 后x,---须构造好矩阵x(x 中的每列与目标函数的一项对应) ---并且x 要在最前面额外添加全1列/对应于常数项 ---y 必须是列向量---结果是从常数项开始---与polyfit 的不同。
matlab非线性拟合

matlab非线性拟合
Matlab非线性拟合是一种使用Matlab软件调用内置非线性拟合功能的数据处理方法。
由于Matlab具有强大的数学建模和仿真功能,因此,
在许多科学和工程应用中,都通常将其用于数据拟合。
Matlab非线性
拟合可以有效地对各种形式的数据进行拟合,而无需显式的模型表达式。
Matlab非线性拟合可以采用多种算法来实现,包括拟牛顿算法、梯度
下降算法、最小二乘算法和全局最优化算法等。
Matlab非线性拟合可
以帮助我们准确地拟合数据,具有很高的精度和高效率,而且不需要
太多的参数即可实现。
例如,如果我们需要优化一个复杂的多元函数,我们可以使用Matlab非线性拟合来找出最佳的解。
此外,Matlab非线性拟合还可以用来处理不确定性数据和随机噪声。
这些不确定的变量和噪声可以通过拟合技术来解决,这样可以使得拟
合结果更加准确。
此外,Matlab非线性拟合还可以应用于多个变量间
的相关性分析,从而帮助我们更好地了解数据的规律,并提高拟合的
准确性。
因此,Matlab非线性拟合能有效解决我们的实际问题,它具有很高的
精度和高效率,也可以有效处理不确定性和噪声数据,是一种有效的
数据拟合方法。
通过正确使用Matlab非线性拟合,可以有效地提高拟
合的准确性,为解决科研问题和工程实践提供有效的解决方案。
matlab中nlinfit函数用法

matlab中nlinfit函数用法
在MATLAB 中,nlinfit函数用于拟合非线性数据。
它是在MATLAB 的Statistics and Machine Learning Toolbox 中提供的。
以下是一个基本的nlinfit的用法示例:
matlab复制代码
% 导入 Statistics and Machine Learning Toolbox
% 假设我们已经有了输入数据 x 和对应的目标输出 y
x = [1, 2, 3, 4, 5];
y = [2.2, 2.8, 3.6, 4.5, 5.1];
% 定义一个非线性模型函数,这里我们选择一个简单的二次函数
% 这个函数需要接受一个参数,并返回一个预测值
modelfun = @(b, x) b(1)*x.^2 + b(2)*x + b(3);
% 使用 nlinfit 函数进行拟合,这里我们指定初始参数估计值
% nlinfit 将返回最佳拟合参数
beta = nlinfit(x, y, modelfun, [0, 0, 0]);
% 输出最佳拟合参数
disp(beta);
在上述代码中,nlinfit的第一个参数是输入数据x,第二个参数是目标输出y,第三个参数是非线性模型函数modelfun,第四个参数是初始参数估计值[0, 0, 0]。
返回的beta是最佳拟合参数。
注意:在使用nlinfit前,请确保已经正确安装并配置了MATLAB 的Statistics and Machine Learning Toolbox。
matlab非线性参数拟合估计_很好的参考材料

使用nlinfit 、fminsearch 在matlab 中实现基于最小二乘法的非线性参数拟合(整理自网上资源) 最小二乘法在曲线拟合中比较普遍。
拟合的模型主要有1. 直线型2. 多项式型3. 分数函数型4. 指数函数型5. 对数线性型6. 高斯函数型一般对于 LS 问题,通常利用反斜杠运算“”、 fminsearch 或优化工具箱提供的极小化函数求解。
在 Matlab 中,曲线拟合工具箱也提供了曲线拟合的图形界面操作。
在命令提示符后键入: cftool ,即可根据数据,选择适当的拟合模型。
“”命令1. 假设要拟合的多项式是:y=a+b*x+c*xT.首先建立设计矩阵X:X=[o nes(size(x)) x x A2];执行:para=X\ypara 中包含了三个参数: para(1)=a;para(2)=b;para(3)=c;这种方法对于系数是线性的模型也适应。
2. 假设要拟合: y=a+b*exp(x)+cx*exp(xA2)设计矩阵 X 为X=[ones(size(x)) exp(x) x.*exp(x.A2)];para=X\y3. 多重回归(乘积回归)设要拟合: y=a+b*x+c*t ,其中 x 和 t 是预测变量, y 是响应变量。
设计矩阵为X=[ones(size(x)) x t] % 注意 x,t 大小相等!para=X\y polyfit 函数polyfit 函数不需要输入设计矩阵,在参数估计中, polyfit 会根据输入的数据生成设计矩阵。
1. 假设要拟合的多项式是: y=a+b*x+c*xA2 p=polyfit(x,y,2)然后可以使用 polyval 在 t 处预测: y_hat=polyval(p,t)polyfit 函数可以给出置信区间。
[p S]=polyfit(x,y,2) %S 中包含了标准差[y_fit,delta] = polyval(p,t,S) % 按照拟合模型在 t 处预测在每个 t 处的 95%CI为:(y_fit-1.96*delta, y_fit+1.96*delta)2. 指数模型也适应假设要拟合: y = a+b*exp(x)+c*exp(x.?2) p=polyfit(x,log(y),2)fminsearch 函数fminsearch 是优化工具箱的极小化函数。
matlab nlinfit原理

MATLAB中的nlinfit函数用于进行非线性回归分析,其原理是基于最小二乘法的。
非线性回归分析是一种数学工具,用于研究一个变量Y与其他若干变量X之间相互关系。
在非线性回归中,回归函数不是线性函数,而是某种非线性函数。
使用nlinfit进行非线性回归的基本步骤如下:
定义非线性回归模型:首先需要定义一个非线性回归模型,该模型由一个非线性函数原型和一组系数组成。
这些系数是通过非线性回归分析来估计的。
最小二乘法拟合:nlinfit函数使用最小二乘法原理,通过最小化残差平方和来拟合数据。
残差平方和是实际观测值与根据模型预测值之间的差的平方和。
通过迭代计算,nlinfit函数可以找到最佳拟合参数,使得残差平方和最小化。
计算回归系数:在找到最佳拟合参数后,nlinfit函数会返回估计的回归系数。
这些系数可用于预测新的数据点或进行进一步的分析。
需要注意的是,非线性回归分析比线性回归更复杂,因为非线性函数的形式多样,且参数估计可能更加困难。
因此,在使用nlinfit函数时,需要仔细选择合适的非线性模型,并对数据进行适当的预处理和清理。
利用Matlab编程计算非线性回归模型

§5. 利用Matlab编程计算非线性回归模型——以Logistic曲线为例1.原始数据下表给出了某地区1971—2000年的人口数据(表1)。
试分别用Matlab和SPSS软件,对该地区的人口变化进行曲线拟合。
表1 某地区人口变化数据年份时间变量t=年份-1970人口y/人1971133 8151972233 9811973334 0041974434 1651975534 2121976634 3271977734 3441978834 4581979934 49819801034 47619811134 48319821234 48819831334 51319841434 49719851534 51119861634 52019871734 50719881834 50919891934 52119902034 51319912134 51519922234 51719932334 51919942434 51919952534 52119962634 5211997 27 34 523 1998 28 34 525 1999 29 34 525 20003034 527根据上表中的数据,做出散点图,见图1。
337003380033900340003410034200343003440034500346001970197219741976197819801982198419861988199019921994199619982000年份人口图1 某地区人口随时间变化的散点图从图1可以看出,人口随时间的变化呈非线性过程,而且存在一个与横坐标轴平行的渐近线,故可以用Logistic 曲线模型进行拟合。
因为Logistic 曲线模型的基本形式为:tbe a y -+=1所以,只要令:t e x yy -='=',1,就可以将其转化为直线模型: x b a y '+='下面,我们分别用Matlab 和SPSS 软件进行回归分析拟合计算。
数据回归分析和拟合的Matlab实现

数据回归分析和拟合的Matlab 实现目录:一、多元线性回归二、多项式回归一元多项式:polyfit 或者polytool多元二项式:rstool 或者rsmdemo三、非线性回归四、逐步回归一、多元线性回归多元线性回归:1、b=regress(Y, X ) 确定回归系数的点估计值2、[b, bint,r,rint,stats]=regress(Y,X,alpha) 求回归系数的点估计和区间估计、并检验回归模型①bint 表示回归系数的区间估计.②r 表示残差③rint 表示置信区间④stats表示用于检验回归模型的统计量,有三个数值:相关系数r2、F值、与F对应的概率p 说明:相关系数r2越接近1,说明回归方程越显著; F 越大,说明回归方程越显著;与 F 对应的概率p<α时拒绝H0⑤alpha 表示显著性水平(缺省时为0.05)3、rcoplot(r,rint) 画出残差及其置信区间具体参见下面的实例演示4、实例演示,函数使用说明(1)输入数据>>x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]'; >>X=[ones(16,1) x];>>Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';(2)回归分析及检验>> [b,bint,r,rint,stats]=regress(Y ,X)b =-16.07300.7194bint =-33.7071 1.56120.6047 0.83401.2056-3.2331-0.95241.32820.88951.1702-0.98790.29270.57341.85400.1347-1.5847-0.3040-0.0234-0.46210.0992rint =-1.2407 3.6520-5.0622 -1.4040-3.5894 1.6845-1.2895 3.9459-1.8519 3.6309-1.5552 3.8955-3.7713 1.7955-2.5473 3.1328-2.2471 3.3939-0.7540 4.4621-2.6814 2.9508-4.2188 1.0494-3.0710 2.4630-2.7661 2.7193-3.1133 2.1892-2.4640 2.6624stats =0.9282 180.9531 0.0000 1.7437运行结果解读如下参数回归结果为对应的置信区间分别为[-33.7017,1.5612] 和[0.6047,0.834]r2=0.9282(越接近于1,回归效果越显著),F=180.9531,p=0.0000,由p<0.05, 可知回归模型y=-16.073+0.7194x 成立(3)残差分析作残差图rcoplot(r,rint)从残差图可以看出,除第二个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型y=-16.073+0.7194x 能较好的符合原始数据,而第二个数据可视为异常点。
matlab_多元与非线性回归即拟合问题regressnlinfit

回归(拟合)自己的总结(20100728)1:学三条命令:polyfit(x,y,n)---拟合成一元幂函数(一元多次) regress(y,x)----可以多元,nlinfit(x,y,’fun ’,beta0) (可用于任何类型的函数,任意多元函数,应用范围最主,最万能的)2:同一个问题,可能这三条命令都可以使用,但结果肯定是不同的,因为拟合的近似结果,没有唯一的标准的答案。
相当于咨询多个专家。
3:回归的操作步骤:(1) 根据图形(实际点),选配一条恰当的函数形式(类型)---需要数学理论与基础和经验。
(并写出该函数表达式的一般形式,含待定系数)(2) 选用某条回归命令求出所有的待定系数所以可以说,回归就是求待定系数的过程(需确定函数的形式)配曲线的一般方法是: (一)先对两个变量x 和y 作n 次试验观察得n i y x ii,...,2,1),,( 画出散点图,散点图(二)根据散点图确定须配曲线的类型. 通常选择的六类曲线如下:(1)双曲线xb a y +=1 (2)幂函数曲线y=a bx , 其中x>0,a>0(3)指数曲线y=a bx e 其中参数a>0.(4)倒指数曲线y=a xb e/其中a>0,(5)对数曲线y=a+blogx,x>0(6)S 型曲线x be a y -+=1(三)然后由n 对试验数据确定每一类曲线的未知参数a 和b.一、一元多次拟合polyfit(x,y,n)一元回归polyfit多元回归regress---nlinfit(非线性)二、多元回归分析(其实可以是非线性,它通用性极高)对于多元线性回归模型:e x x y p p ++++=βββ 110设变量12,,,p x x x y的n 组观测值为12(,,,)1,2,,i i ip i x x x y i n=.记 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=np n n p p x x x x x x x x x x 212222111211111,⎪⎪⎪⎪⎪⎭⎫⎝⎛=n y y y y 21,则⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=p ββββ 10 的估计值为排列方式与线性代数中的线性方程组相同()拟合成多元函数---regress 使用格式:左边用b=或[b, bint, r, rint, stats]= 右边用regress(y, x) 或regress(y, x, alpha)---命令中是先y 后x,---须构造好矩阵x(x 中的每列与目标函数的一项对应) ---并且x 要在最前面额外添加全1列/对应于常数项 ---y 必须是列向量---结果是从常数项开始---与polyfit 的不同。
matlab回归拟合

matlab回归拟合一、Matlab回归拟合的基本概念Matlab回归拟合是一种利用Matlab软件对数据进行线性或非线性回归分析的方法。
通过回归拟合,我们可以探讨自变量与因变量之间的关系,为后续的数据分析、预测和模型构建提供依据。
二、Matlab回归拟合的常用函数1.线性回归:使用`polyfit`函数进行线性回归分析,可以得到回归系数。
2.非线性回归:使用`nlinfit`函数进行非线性回归分析,可以得到回归系数。
3.曲线拟合:使用`curve_fit`函数进行曲线拟合,可以得到拟合参数。
4.残差分析:使用`residual`函数计算拟合残差,评估拟合效果。
三、Matlab回归拟合的实例分析以下将以一个简单的例子说明Matlab回归拟合的具体操作。
假设我们有一组数据如下:```x = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];```我们希望通过线性回归分析找到y与x之间的关系。
```matlab% 创建数据点X = 1:4;Y = [2 4 6 8 10];% 进行线性回归m = polyfit(X, Y, 1);% 输出回归系数disp(m);```四、Matlab回归拟合的结果分析与优化在进行回归拟合后,我们需要对结果进行分析,评估拟合效果。
常用的方法有:1.评估指标:使用`corrcoef`函数计算自变量与因变量之间的相关系数,判断线性关系。
2.残差分析:使用`residual`函数计算拟合残差,评估拟合效果。
3.优化方法:根据拟合结果,可以尝试调整模型参数或更换其他拟合方法以提高拟合效果。
五、总结与展望Matlab回归拟合是一种强大的数据分析工具,可以帮助我们探索自变量与因变量之间的关系。
通过熟练掌握Matlab回归拟合的常用函数、结果分析与优化方法,我们可以更好地应用于实际问题的解决。
matlab非线性曲线拟合

m atlab非线性曲线拟合最近在用matlab做非线性曲线拟合,发现matlab功能确实很强大,总结其方法有如下几种:一、Matlab非线性拟合工具箱单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。
假设我们要拟合的函数形式是y=a+(b-a)*c^2*(c^2-x^2)/((c^2-x^2)^2+(2*d*x)^2);其中a,b,c,d是待定系数。
在命令行输入数据:x=8:0.01:12.4;y=real(epsilon);2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X data和Y data的下拉菜单读入数据x,y,可修改数据集名“Data set name”,然后点击“Create data set”按钮,退出“Data”窗口,返回工具箱界面,这时会自动画出数据集的曲线图;(3)点击“Fitting”按钮,弹出“Fitting”窗口;(4)点击“New fit”按钮,可修改拟合项目名称“Fit nam e”,通过“Data set”下拉菜单选择数据集,然后通过下拉菜单“Type of fit”选择拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型Exponential:指数逼近,有2种类型, a*exp(b*x) 、a*exp(b*x) + c*exp(d*x)Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w)Gaussian:高斯逼近,有8种类型,基础型是a1*exp(-((x-b1)/c1)^2)Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~ Power:幂逼近,有2种类型,a*x^b 、a*x^b + cRational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型Smoothing Spline:平滑逼近Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1)Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。
MATLAB 非线性 回归 拟合 nlintool

非线性回归非线性回归可用命令nlinfit,nlintool,nlparci,nlpredci来实现。
进行非线性回归时可使用nlinfit指令,其语法如下:beta = nlinfit(X,y,fun,beta0)[beta,r,J] = nlinfit(X,y,fun,beta0)[...] = nlinfit(X, y, fun, beta0, options)回归:回归可用命令[beta,r,J]=nlinfit(x,y,model,beta0) 或者nlintool(x,y,model,beta0,alpha)来实现。
其中:命令 [beta,r,J]=nlinfit(x,y,model,beta0)的作用为确定回归系数;而命令 nlintool(x,y,model,beta0,alpha)产生一个交互式的画面,画面中有拟合曲线和y的置信区间。
通过左下方的Export下拉式菜单,可以输出回归系数等。
这里的输入数据:x、y分别为 m×n 矩阵和n维列向量,对一元非线性回归,x为n维列向量;model是事先用m-文件定义的非线性函数;beta0是回归系数的初值。
Beta是估计出的回归系数,r(残差)、 J(Jacobian矩阵)是估计预测误差需要的数据。
alpha为显著性水平,缺省时为0.05。
预测和预测误差估计:预测和预测误差估计的命令格式为betaci=nlparci(beta,r,J)其用途为记算回归系数的置信区间;[Y,DELTA]=nlpredci(model,x,beta,r,J)其用途为求nlinfit或nlintool所得的回归函数在x处的预测值Y及预测值的显著性为1-alpha的置信区间Y± DELTA;alpha缺省时为0.05。
某些非线性回归也可化为多元线性回归来解。
.................例:在工具箱中,有reaction.mat之资料,这是有关化学反应所到之观察值,其中牵涉到三种化学反应:氢、n-戊烷、同位戊烷等。
MATLAB 常用函数检索表

909附录 MATLAB 常用函数检索表Aabs 函数——数值的绝对值与复数的幅值。
acos 、acosh 函数——反余弦函数与反双曲余弦函数。
acot 、acoth 函数——反余切函数与反双曲余切函数。
acsc 、acsch 函数——反余割函数与反双曲余割函数。
angle 函数——计算复数的相角。
asec 、asech 函数——反正割函数与反双曲正割函数。
asin 、asinh 函数——反正弦函数与反双曲正弦函数。
atan 、atanh 函数——反正切函数与反双曲正切函数。
Bbar 函数——二维垂直条形图。
barh 函数——二维水平条形图。
bdclose 函数——关闭正在打开的仿真系统窗口。
besselap 函数——设计Bessel 低通滤波器。
Bessel 函数——设计Bessel 滤波器。
betafit 函数——计算β分布的参数估计。
Betalike 函数——负分布的对数似然函数。
bicgstab 函数——稳定双共轭梯度方法解方程组。
bicg 函数——双共轭梯度法解方程组。
bilinear 函数——用双线性变换法将模拟滤波器转化为数字滤波器。
binocdf 函数——二项分布的累积概率值。
binofit 函数——二项分布的参数估计。
binopdf 函数——二项分布的密度函数。
binornd 函数——二项分布的随机数据的产生。
binostat 函数——二项分布的均值和方差。
blkdiag 函数——产生以输入元素为对角线元素的矩阵。
boxplot 函数——样本数据的盒图。
break 函数——结束循环。
brighten 函数——色图控制函数。
buttap 函数——设计巴特沃思模拟滤波器。
butter 函数——设计巴特沃思数字滤波器。
Ccapaplot 函数——样本的概率图形。
cat 函数——创建多维数组。
ccode 函数——符号表达式的C 语言代码。
cdf2rdf 函数——复对角矩阵转化为实对角矩阵。
MATLAB 回归分析regress,nlinfit,stepwise函数

MATLAB 回归分析regress,nlinfit,stepwise函数matlab回归分析regress,nlinfit,stepwise函数回归分析1.多元线性重回在matlab统计工具箱中使用命令regress()实现多元线性回归,调用格式为b=regress(y,x)或[b,bint,r,rint,statsl=regess(y,x,alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性重回,挑k=1即可。
alpha为显著性水平(缺省时预设为0.05),输入向量b,bint为回归系数估计值和它们的置信区间,r,rint为残差及其置信区间,stats就是用作检验重回模型的统计数据量,存有三个数值,第一个就是r2,其中r就是相关系数,第二个就是f统计数据量值,第三个就是与统计数据量f对应的概率p,当p拒绝h0,回归模型成立。
图画出来残差及其置信区间,用命令rcoplot(r,rint)实例1:已知某湖八年来湖水中cod浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料,建立污染物y的水质分析模型。
(1)输出数据x1=[1.376,1.375,1.387,1.401,1.412,1.428,1.445,1.477]x2=[0.450,0.475,0.485,0.50 0,0.535,0.545,0.550,0.575]x3=[2.170,2.554,2.676,2.713,2.823,3.088,3.122,3.262]x4=[0.8922,1.1610,0.5346,0.9589,1.0239,1.0499,1.1065,1.1387]y=[5.19,5.30,5.60,5.82,6.00,6.06,6.45,6.95](2)留存数据(以数据文件.mat形式留存,易于以后调用)savedatax1x2x3x4yloaddata(抽出数据)(3)继续执行重回命令x=[ones(8,1),];[b,bint,r,rint,stats]=regress得结果:b=(-16.5283,15.7206,2.0327,-0.2106,-0.1991)’stats=(0.9908,80.9530,0.0022)即为=-16.5283+15.7206xl+2.0327x2-0.2106x3+0.1991x4r2=0.9908,f=80.9530,p=0.00222.非线性重回非线性回归可由命令nlinfit来实现,调用格式为[beta,r,j]=nlinfit(x,y,'model’,beta0)其中,输人数据x,y分别为n×m矩阵和n维列向量,对一元非线性回归,x为n维列向量model是事先用m-文件定义的非线性函数,beta0是回归系数的初值,beta是估计出的回归系数,r是残差,j是jacobian矩阵,它们是估计预测误差需要的数据。
MATLAB 回归分析regress,nlinfit,stepwise函数

回归分析1.多元线性回归在Matlab统计工具箱中使用命令regress()实现多元线性回归,调用格式为b=regress(y,x)或[b,bint,r,rint,statsl = regess(y,x,alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性回归,取k=1即可。
alpha为显著性水平(缺省时设定为0.05),输出向量b,bint为回归系数估计值和它们的置信区间,r,rint为残差及其置信区间,stats是用于检验回归模型的统计量,有三个数值,第一个是R2,其中R是相关系数,第二个是F统计量值,第三个是与统计量F对应的概率P,当P<α时拒绝H0,回归模型成立。
画出残差及其置信区间,用命令rcoplot(r,rint)实例1:已知某湖八年来湖水中COD浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料,建立污染物y的水质分析模型。
(1)输入数据x1=[1.376, 1.375, 1.387, 1.401, 1.412, 1.428, 1.445, 1.477]x2=[0.450, 0.475, 0.485, 0.500, 0.535, 0.545, 0.550, 0.575]x3=[2.170 ,2.554, 2.676, 2.713, 2.823, 3.088, 3.122, 3.262]x4=[0.8922, 1.1610 ,0.5346, 0.9589, 1.0239, 1.0499, 1.1065, 1.1387]y=[5.19, 5.30, 5.60,5.82,6.00, 6.06,6.45,6.95](2)保存数据(以数据文件.mat形式保存,便于以后调用)save data x1 x2 x3 x4 yload data (取出数据)(3)执行回归命令x =[ones(8,1),];[b,bint,r,rint,stats] = regress得结果:b = (-16.5283,15.7206,2.0327,-0.2106,-0.1991)’stats = (0.9908,80.9530,0.0022)即= -16.5283 + 15.7206xl + 2.0327x2 - 0.2106x3 + 0.1991x4R2 = 0.9908,F = 80.9530,P = 0.00222.非线性回归非线性回归可由命令nlinfit来实现,调用格式为[beta,r,j] = nlinfit(x,y,'model’,beta0)其中,输人数据x,y分别为n×m矩阵和n维列向量,对一元非线性回归,x 为n维列向量model是事先用m-文件定义的非线性函数,beta0是回归系数的初值,beta是估计出的回归系数,r是残差,j是Jacobian矩阵,它们是估计预测误差需要的数据。
第七讲_matlab实现非线性拟合

i 1
i 1
其中 是待定的参数,而 ˆ 就是最小二乘法所确定的 最佳参数.
解决此类问题有以下几个步骤:(1)首先作出散点 图,确定函数的类别;(2)根据已知数据确定待定 参数的初始值,利用Matlab软件计算最佳参数;(3) 根据可决系数,比较拟合效果,计算可决系数的公式 为
其中
n
( yi yˆi )2
[x,y]=solve('6.42*(2*a+b)=2','10.76*(16*a+b)=16')
y a(1 becx ) ln b cx ln( y / a 1)
取点:(2,6.42),(8,9.93),(10,10.49)代入上述方程
[a,b,c]=solve('log(b)+c*2=log(6.42/a-1)','log(b)+c*10=log(10.49/a-1)','log(b)+c*8=log(9.93/a-1)')
理查德(Richards)模型: 威布尔(Weibull)模型:
y /[1 exp( x)]1/ y exp( t )
为了实现非线性拟合,首先要定义在线函数
1. inline 定义的函数:用于曲线拟合、数值计算 步骤:(1)建立M文件; (2)fun=inline('f(x) ', '参变量','x')
y1=x./(0.1152+0.0845*x); % 拟合曲线
R2=1-sum((y-y1).^2)/sum((y-mean(y)).^2)
如果是多项式函数,则称为多项式回归,此时
的参数即多项式的系数;如果为指数函数、对数函 数、幂函数或三角函数等,则称为非线性拟合.下面 的图形给出了常见曲线与方程的对应关系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
% Reference:
% [1] Bates, Douglas, and Watts, Donald, "Nonlinear
% Regression Analysis and Its Applications", Wiley
% 1988 p. 271-272.
betaci=nlparci(betahat,f,J);
betaa=[betahat',betaci] %回归系数及其置信区间 betaa=[betahat',betaci] betaa=[betahat,betaci]
[yhat1,delta]=nlpredci(yhat,x,betahat,f,J); % y的预测值及其置信区间半径,置信区间为yhat1 ±delta。
beta0是回归系数的初值。
Beta是估计出的回归系数,
r(残差)、 J(Jacobian矩阵)是估计预测误差需要的数据。
alpha为显著性水平,缺省时为0.05。
预测和预测误差估计:
预测和预测误差估计的命令格式为
betaci=nlparci(beta,r,J)
其用途为记算回归系数的置信区间;
[...] = nlinfit(X, y, fun, beta0, options)
回归:
回归可用命令
[beta,r,J]=nlinfit(x,y,model,beta0) 或者
nlintool(x,y,model,beta0,alpha)
来实现。
其中:
命令 [beta,r,J]=nlinfit(x,y,model,beta0 10
6 14.39 100 190 10
7 2.54 100 80 65
function yhat = hougen(beta,x)
%HOUGEN Hougen-Watson model for reaction kinetics.
% YHAT = HOUGEN(BETA,X) gives the predicted values of the
% reaction rate, YHAT, as a function of the vector of
而命令 nlintool(x,y,model,beta0,alpha)
产生一个交互式的画面,画面中有拟合曲线和y的置信区间。
通过左下方的Export下拉式菜单,可以输出回归系数等。
这里的输入数据:
x、y分别为 m×n 矩阵和n维列向量,对一元非线性回归,x为n维列向量;
model是事先用m-文件定义的非线性函数;
2 3.79 285 80 10
3 4.82 470 300 120
4 0.02 470 80 120
.................
例:
在工具箱中,有reaction.mat之资料,这是有关化学反应所到之观察值,其中牵涉到三种化学反应:氢、n-戊烷、同位戊烷等。
其中之函数hougen已经存在,是使用Hougen-Watson模式建立之反应动能量,其回应值为预设之反应速率。
load reaction
................
% parameters, BETA, and the matrix of data, X.
% BETA must have 5 elements and X must have three
% columns.
%
% The model form is:
% y = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3)
% Copyright 1993-2004 The MathWorks, Inc.
% $Revision: 2.7.2.1 $ $Date: 2004/01/24 09:34:06 $
% B.A. Jones 1-06-95.
b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);
x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);
yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);
....
另有一个nlintool指令函数则可利用图形介面执行,可在指令窗下打入执行之。
11 0.05 100 80 120
12 11.32 285 300 10
13 3.12 285 190 120];
8 4.35 470 190 65
9 13.00 100 300 54
10 8.50 100 300 120
[Y,DELTA]=nlpredci(model,x,beta,r,J)
其用途为求nlinfit或nlintool所得的回归函数在x处的预测值Y及预测值的显著性为1-alpha的置信区间Y± DELTA;
alpha缺省时为0.05。
某些非线性回归也可化为多元线性回归来解。
....
...
close all
clear,clc
yhat = @(beta,x) (beta(4)*x(:,2) - x(:,3)/beta(5))./(1+beta(1)*x(:,1)+beta(2)*x(:,2) + beta(3)*x(:,3));
x0=[1 8.55 470 300 10
x=x0(:,3:5);
y=x0(:,2);
beta=[0.1,0.05,0.02,1,2]; %回归系数的初值 beta = [0.1000 2.0000 1.0000 0.0500 0.0200];
[betahat,f,J]=nlinfit(x,y,yhat,beta); % f,j是下面命令用的信息
yy=[y,yhat1,delta]
用命令nlintool可看到画面。 [beta,r,J,COVB,mse] = nlinfit(X,y,fun,beta0)
nlintool(x,y,yhat1,beta)
[betahat,f,J,COVB,mse] = nlinfit(x,y,yhat,beta)
betafit = nlinfit(reactants,rate,@hougen,beta)
betafit =
1.2526
0.062776
0.040048
0.11242
1.1914
其中之hougen.m可以type hougen,得其內容如下:
非线性回归
非线性回归可用命令nlinfit,nlintool,nlparci,nlpredci来实现。
进行非线性回归时可使用nlinfit指令,其语法如下:
beta = nlinfit(X,y,fun,beta0)
[beta,r,J] = nlinfit(X,y,fun,beta0)
