机械设计--JXSJ2 机械强度
机械设计课程设计--二级减速器圆锥齿轮机械设计

机械设计课程设计说明书专业:机械电子工程2016年12月29日重庆理工大学目录一、任务设计书 (3)二、传动方案的拟订及说明 (3)三、选择电动机 (4)四、计算传动装置的运动和动力参数 (5)五、传动件的设计计算 (6)六、轴的设计计算 (15)七、滚动轴承的选择及计算 (34)八、键联接的选择及校核计算 (37)九、联轴器的选择 (38)十、减速器附件的选择 (39)十一、润滑与密封 (39)十二、箱体数据 (39)十三、设计小结 (40)十四、参考目录 (40)一、任务设计书设计一用于带式运输机上的圆锥圆柱齿轮齿轮减速器。
工作经常满载,空载启动,工作有轻振,不反转,单班制工作。
运输带容许速度误差为5%。
减速器为小批生产,使用期限10年。
(已知带式运输机驱动卷筒的圆周牵引力F=2000N ,带速v=1.2m/s ,卷筒直径D=320m ,设每年工作300天)二、传动方案的拟订和说明计算驱动卷筒的转速如下:min /6.713202.1100060100060r D v n w =⨯⨯⨯=⨯=ππ选用同步转速为1000r/min 或1500r/min 的电动机作为原动机,因此传动装置总传动比约为13,根据总传动比数值, 可拟定以下传动方案:图一三、选择电动机1)电动机类型和结构型式按工作要求和工作条件,选用一般用途的Y (IP44)系列三相异步电动机。
它为卧式封闭结构。
2)电动机容量 (1)卷筒的输出功率P ωkw Fv p w 4.210002.120001000=⨯==(2)电动机输出功率d Pd P P ωη=传动装置的总效率12^3345^26ηηηηηηη∙∙∙∙∙=式中1η、2η…为从电动机至卷筒轴的各传动机构和轴承的效率。
由课程设计教材表2-5查得:V 带传动1η=0.96;滚动轴承2η=0.988;圆柱齿轮传动3η=0.97;圆锥齿轮传动4η=0.96;弹性联轴器5η=0.99;卷筒轴滑动轴承6η=0.96;则0.960.988^30.970.960.990.990.960.81η=⨯⨯⨯⨯⨯⨯=故 kw p 96.281.04.2p d ===ηω(3)电动机额定功率ed P由教材查得选取电动机额定功率 4.0ed P kw =。
机械零件表面接触强度

《机械设计》电子教材 编著 上海铁道大学 李小江
表面接触强度
1. 疲劳点蚀形成过程
2. 表面接触强度的计算
1) 接触应力的概念
两零件构成高副接触,接触处形成较 小的接触面积,产生很大的 应力,该应力称为接触应力。 2) 接触应力的计算
接触应力按弹性力学中赫兹公式计算 a) 线接触
F
Hmax
a
b
F
《机械设计》电子教材 编著 上海铁道大学 李小江
外
内
接
接
触
触
3. 提高表面接触疲劳强度的措施
1) 增大,例外接触改为内接触。 2)提高表面硬度使Hlim 增大。例齿轮。 3) 线接触改为面接触。 4) 提高表面质量减少减轻初始裂纹。 5) 采用适当的润滑油粘度。
JXSJ
JXSJ
H max
1
Fb1源自12E11 1 1 为 1 2
E1、E2 两接触体 1、2 两接触体材
Hmax
《机械设计》电子教材 编著 上海铁道大学 李小江
Hmax
Hmax
b) 点接触 F
H max
3
6
F
1
E1
1 1 1 为 1 2
E1、E2 两接触
1、2 两接触体
JXSJ
机械设计课程设计——二级斜齿齿轮减速器

机械设计课程设计说明书题目:二级展开式斜齿圆柱齿轮减速器目录1.题目及总体分析 (3)2.电动机选择 (3)3.分配传动比 (4)4.传动系统的运动和动力参数计算 (5)5.设计高速级齿轮 (6)6.设计低速级齿轮 (10)7.链传动的设计 (12)8.减速器轴及轴承装置、键的设计 (13)1轴(输入轴)及其轴承装置、键的设计 (13)2轴(中间轴)及其轴承装置、键的设计 (19)3轴(输出轴)及其轴承装置、键的设计 (23)9.润滑与密封 (28)10.箱体结构尺寸 (28)11.设计总结 (29)12.参考文献 (30)一、题目及整体分析题目:设计一个二级展开式斜齿圆柱齿轮减速器给定条件:由电动机驱动,输送带的牵引力F=3200N,运输带速度v=1.0m/s,运输机滚筒直径为D=350mm.带式输送机用于锅炉房运煤。
工作寿命为12年,三班制工作;每班工作8小时,常温下连续、单向运转,载荷平稳。
输送带滚轮效率为0.97。
特点及应用:结构简单,但齿轮相对于轴承的位置不对称,因此要求轴有较大的刚度。
高速级齿轮布置在远离转矩输入端,这样,轴在转矩作用下产生的扭转变形和轴在弯矩作用下产生的弯曲变形可部分地互相抵消,以减缓沿齿宽载荷分布不均匀的现象。
高速级一般做成斜齿,低速级可做成直齿。
整体布置如下:辅助件有:观察孔盖,油标和油尺,放油螺塞,通气孔,吊环螺钉,吊耳和吊钩,定位销,启盖螺钉,轴承套,密封圈等.。
二、电动机的选择目的 过程分析 结论 类型 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W过程分析 结论 类型 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W结论 类型 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P=F×V=3600N×1.0m/s=3600Ww类型 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W类型 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 根据一般带式输送机选用的电动机选择 选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W选用Y系列封闭式三相异步电动机 功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W功率 工作机所需有效功率为P=F×V=3600N×1.0m/s=3600Ww功率 工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W工作机所需有效功率为P w=F×V=3600N×1.0m/s=3600W弹性联轴器传动效率η1=0.99滚动轴承传动效率为η2=0.99圆柱齿轮传动(8级精度)效率为η3=0.97输送机滚筒效率为η4=0.97总效率为η=η1 2η24η3 2η 4 =0.859电动机输出有效功率为P d=P w / η=3.725KW 电动机输出功率为电动机输出功率为P d=3.725KW 型号 查得型号Y132M1-6封闭式三相异步电动机参数如下型号 查得型号Y132M1-6封闭式三相异步电动机参数如下型号 查得型号Y132M1-6封闭式三相异步电动机参数如下查得型号Y132M1-6封闭式三相异步电动机参数如下额定功率p=4 kW满载转速960 r/min同步转速1000 r/min 选用选用型号Y132M1-6封闭式三相异步电动机三、分配传动比其中i 目的 过程分析 结论 分配传动比 传动系统的总传动比EMBED Equation.3是传动系统的总传动比,多级串联传动系统的总传动等于各级传动比的连乘积;n m是电动机的满载转速,r/min;n w 为工作机输入轴的转速,r/min。
国标机械性能等级

机械性能等级钢结构连接用螺栓性能等级分3.6、4.6、4.8、5.6、6.8、8.8、9.8、10.9、12.9等10余个等级,其中8.8级及以上螺栓材质为低碳合金钢或中碳钢并经热处理(淬火、回火),通称为高强度螺栓,其余通称为普通螺栓。
螺栓性能等级标号有两部分数字组成,分别表示螺栓材料的公称抗拉强度值和屈强比值。
例如:性能等级4.6级的螺栓,其含义是:1、螺栓材质公称抗拉强度达400MPa级;2、螺栓材质的屈强比值为0.6;3、螺栓材质的公称屈服强度达400×0.6=240MPa级性能等级10.9级高强度螺栓,其材料经过热处理后,能达到:1、螺栓材质公称抗拉强度达1000MPa级;2、螺栓材质的屈强比值为0.9;3、螺栓材质的公称屈服强度达1000×0.9=900MPa级螺栓性能等级的含义是国际通用的标准,相同性能等级的螺栓,不管其材料和产地的区别,其性能是相同的,设计上只选用性能等级即可。
强度等级所谓8.8级和10.9级是指螺栓的抗剪切应力等级为8.8GPa 和10.9GPa8.8 公称抗拉强度800N/MM2 公称屈服强度640N/MM2一般的螺栓是用"X.Y"表示强度的,X*100=此螺栓的抗拉强度,X*100*(Y/10)=此螺栓的屈服强度(因为按标识规定:屈服强度/抗拉强度=Y/10)如4.8级则此螺栓的抗拉强度为:400MPa;屈服强度为:400*8/10=320MPa。
另:不锈钢螺栓通常标为A4-70,A2-70的样子,意义另有解释度量:当今世界上长度计量单位主要有两种,一种为公制,计量单位为米(m)、厘米(cm)、毫米(mm)等,在欧州、我国及日本等东南亚地区使用较多,另一种为英制,计量单位主要为英寸(inch),相当于我国旧制的市寸,在美国、英国等欧美国家使用较多。
1、公制计量:(10进制)1m =100 cm=1000 mm2、英制计量:(8进制)1英寸=8英分1英寸=25.4 mm 3/8¢¢×25.4 =9.523、1/4¢¢以下的产品用番号来表示其称呼径,如:4#,5#,6#,7#,8#,10#,12#螺纹一、螺纹是一种在固体外表面或内表面的截面上,有均匀螺旋线凸起的形状。
机械零件的强度计算

第三章 机械零件的强度计算第0节 强度计算中的基本定义 一. 载荷1. 按载荷性质分类:1) 静载荷:大小方向不随时间变化或变化缓慢的载荷。
2) 变载荷:大小和(或)方向随时间变化的载荷。
2. 按使用情况分:1)公称载荷(名义载荷): 按原动机或工作机的额定功率计算出的载荷。
2) 计算载荷:设计零件时所用到的载荷。
计算载荷与公称载荷的关系:F ca =kF n M ca =kM n T ca =kT n3) 载荷系数:设计计算时,将额定载荷放大的系数。
由原动机、工作机等条件确定。
二. 应力2.按强度计算使用分1) 工作应力:由计算载荷按力学公式求得的应力。
2) 计算应力:由强度理论求得的应力。
3) 极限应力:根据强度准则、材料性质和应力种类所选择的机械性能极限值σlim 。
4) 许用应力:等效应力允许达到的最大值。
[σ]=σlim /[s σ]稳定变应力 非稳定变应力对称循环变应力脉动应力 规律性非稳定变应力随机性非稳定变应力 静应力 对称循环变应力 脉动应力σ周期变应力第1节 材料的疲劳特性一. 疲劳曲线 1. 疲劳曲线给定循环特征γ=σlim /σmax ,表示应力循 环次数N 与疲劳极限σγ的关系曲线称为疲 劳曲线(或σ-N )。
2. 疲劳曲线方程1) 方程中参数说明a) 低硬度≤350HB ,N 0=107 高硬度>350HB ,N 0=25×107b) 指数m :c) 不同γ,σ-N 不同;γ越大,σ也越大。
…二、 限应力线图1) 定义:同一材料,对于不同的循环特征进行试验,求得疲劳极限,并将其绘在σm -σa坐标系上,所得的曲线称为极限应力线图。
CN N m m N ==0γγσσr N N k mNN σσσγγ==0mNN k N 0=整理:即:其中:N 0--循环基数σγ--N 0时的疲劳极限k N --寿命系数用线性坐标表示的疲劳曲线ND2)简化曲线3)σ-N与σm-σa关系a) σ-N曲线:同一循环特征下、不同循环次数。
华东交通大学机械设计课程设计二级直齿圆柱齿轮减速器设计说明书1
。
1 180 d d 2 d d 1
6、计算带的根数
57.3 57.3 180 224 90 163 120 a 448
(1)计算单根 V 带的额定功率 Pr 由 d d 1 90mm和n 1440 r min 查表可得 P0 1.064kw 根据 n 1440 r min ,i 2.7 和 A 型带,查表可得 P0 0.169kw 、 k 0.956 、
=1364mm 查表可选带的基准长度 Ld 1400mm (3)按计算式计算实际中心距 a
a a0
Ld Ld 0 1400 1364 (430 ) mm 448mm 2 2
中心距的变化范围为 4 2 7 m m 4 9 0 m m 5、验算小带轮上的包角 1
2
二、计算传动装置的运动和动力参数
本装置从电动机到工作机有三轴,依次为Ⅰ,Ⅱ,Ⅲ轴,则 1、各轴转速
n Ⅰ nⅡ nm 1440 576 r min iV 带 2.5
n 576 Ⅰ 135.753r min i1 4.243 nⅢ n Ⅱ 135.753 44.288r min i2 3.031
dd 1n 90 1440 6.782 m s 60 1000 60 1000
因为 5 m s v 30 m s ,故此带速合适。 3、计算大带轮的基准直径 d d 2 按式 (8-15a) 计算大带轮的基准直径 d d 2 iV 带 d d 1 2.5 90 225mm 表 8-8,圆整得
d d 2 224mm
根据教材
。
4、确定 V 带的中心距 a 和基准直径 Ld (1)按计算式初定中心距 a0 500mm (2)按计算式计算所需的基准长度
机械设计课程设计--二级展开式斜齿轮减速器

机械设计课程设计2013-2014第二学期名称:二级展开式斜齿轮减速器学院:机电与汽车工程学院目录绪论第一章概述1.1机械设计的任务及目的 (4)第二章传动方案的分析论证2.1 传动装置的组成与特点 (5)2.2 传动方案的确定及分析 (5)第三章电动机的选择3.1选择电动机的类型 (5)3.2选择电机的功率 (5)3.3电机转速的选择 (6)3.4总传动比计算和分配各级传动比 (6)第四章传动装置运动和动力参数的计算4.1 各轴转速的推算 (7)4.2 各轴功率的计算 (7)4. 3 各轴扭矩的计算 (7)第五章齿轮设计5.1 高速级齿轮设计及校核 (9)5.2低速级齿轮设计及校核 (13)第六章轴、键的设计及校核6.1 高速轴和键的设计及校核 (19)6.2 中间轴和键的设计及校核 (23)6.3低速轴和键的设计及校核 (28)第七章联轴器的选择 (31)第八章轴承的校核8.1高速轴轴承的校核 (32)8.2中间轴轴承的校核 (33)8.3低速轴轴承的校核 (34)第九章箱体的设计 (35)第十章减速器的润滑与密封 (36)第十一章减速器附件的选择及说明 (37)第十二章设计小结 (37)参考文献绪论本论文主要内容是进行二级斜齿硬面齿轮的设计计算,在设计计算中用到了《机械原理》、《机械制图》、《机械设计》等多门课程知识。
并用了《AutoCAD》软件进行绘图,因此是一个非常重要的实践环节,通过对齿轮的设计计算,加深了对已学科目的影响,并通过自主设计,理论与实践结合,是一次对所学知识全面的、系统的、规范的实践训练。
通过训练,使我们在各个方面得到了锻炼和培养。
机械设计课程设计是机械设计课程的重要教学环节。
通过课程设计我们学会了:1、通过课程设计,综合运用机械设计课程和其他课程的理论和实际知识,培养分析和解决问题的能力,掌握了机械设计的一般规律,树立正确的设计思想。
2、学会从机器功能要求出发,合理选择执行机构和传动机构的类型、制定传动方案、合理选择标准部件的类型和型号、正确计算零件的工作能力、确定其尺寸、形状及机构材料、并考虑制造工艺、使用、维护、经济和安全等问题,培养机械设计能力。
机械零件的强度计算.

第三章 机械零件的强度计算第0节 强度计算中的基本定义 一. 载荷1. 按载荷性质分类:1) 静载荷:大小方向不随时间变化或变化缓慢的载荷。
2) 变载荷:大小和(或)方向随时间变化的载荷。
2. 按使用情况分:1)公称载荷(名义载荷): 按原动机或工作机的额定功率计算出的载荷。
2) 计算载荷:设计零件时所用到的载荷。
计算载荷与公称载荷的关系:F ca =kF n M ca =kM n T ca =kT n3) 载荷系数:设计计算时,将额定载荷放大的系数。
由原动机、工作机等条件确定。
二. 应力2.按强度计算使用分1) 工作应力:由计算载荷按力学公式求得的应力。
2) 计算应力:由强度理论求得的应力。
3) 极限应力:根据强度准则、材料性质和应力种类所选择的机械性能极限值σlim 。
4) 许用应力:等效应力允许达到的最大值。
[σ]=σlim /[s σ]稳定变应力 非稳定变应力对称循环变应力脉动应力 规律性非稳定变应力随机性非稳定变应力 静应力 对称循环变应力 脉动应力σ周期变应力第1节 材料的疲劳特性一. 疲劳曲线 1. 疲劳曲线给定循环特征γ=σlim /σmax ,表示应力循 环次数N 与疲劳极限σγ的关系曲线称为疲 劳曲线(或σ-N )。
2. 疲劳曲线方程1) 方程中参数说明a) 低硬度≤350HB ,N 0=107 高硬度>350HB ,N 0=25×107b) 指数m :c) 不同γ,σ-N 不同;γ越大,σ也越大。
…二、 限应力线图1) 定义:同一材料,对于不同的循环特征进行试验,求得疲劳极限,并将其绘在σm -σa坐标系上,所得的曲线称为极限应力线图。
CN N m m N ==0γγσσr N N k mNN σσσγγ==0mNN k N 0=整理:即:其中:N 0--循环基数σγ--N 0时的疲劳极限k N --寿命系数用线性坐标表示的疲劳曲线ND2)简化曲线3)σ-N与σm-σa关系a) σ-N曲线:同一循环特征下、不同循环次数。
机械设计课程设计---二级直齿圆柱齿轮减速器设计说明书

机械设计课程设计计算说明书设计题目:二级展开式圆柱齿轮减速器设计者:指导教师:年月日一、传动方案拟定 (2)二、电动机的选择 (2)三、计算总传动比及分配各级的传动比 (3)四、运动参数及动力参数计算 (3)五、传动零件的设计计算 (4)六、轴的设计计算 (11)七、滚动轴承的选择及校核计算 (13)八、键联接的选择及校核计算 (15)设计参数:1、运输带工作拉力:F=2.7KN2、运输带工作速度:V=1.6m/s3、滚筒直径:D=450mm;4、工作寿命:10年,2班制,大修期3年,所以,;H=2×8×10×3005、工作条件:载荷平稳,空载启动,室内工作,有粉尘;。
传动装置设计:一、传动方案:展开式二级圆柱齿轮减速器。
二、选择电机:1、类型:Y系列一般用途的全封闭自扇冷鼠笼型三相异步电动机;2、型号:工作机所需输入功率:Pw=FV/1000ηKW=2700×1.6/1000×0.95=4.55KW电机所需功率:P0=P/η1=4.55/0.890=5.11KW,其中,Η为电动机轴至卷筒轴的传动装置总效率η1电机转速n选:1500/minr;所以查表选电机型号为:Y132s-4电机参数:额定功率:5.5 Kw满载转速:m n =1440/min r电机轴直径:0.0090.00428mm m d+-=三、 传动比分配:传动装置总传动比i= m n / w n (min /94.67100060r Dvn w =⨯⨯=π)其中:1i 为高速级传动比,2i 为低速级传动比,且12(1.3~1.5)i i =,取214.1i i =,则有:89.3,446.521==i i ;四、传动装置的运动和动力参数1、电机轴: kw p p d m 11.5==;1440/m i n m n r = ;m N n p T m m m .89.33144011.595509550===; 2、高速轴:kW p p m 008.51==联η;11440/m i n m n n r == ;m N n P T .21.331440008.595509550111===;3、中间轴:kW p p 833.412==齿承ηη;m i n /4.264446.51440112r i nn ===;m N n p T .57.1744.264833.495509550222===; 4、低速轴:kW p p 665.423==齿承ηηm i n /97.6789.3/4.264223r i n n ===;m N n p T .45.65597.67665.495509550333===; 5、工作轴:kW p p 55.430==联η;m i n /97.6730r n n ==;m N n p T .29.63997.6755.495509550000===;将以上算得的运动的动力参数列表如下: 轴名参数电动机轴I 轴II 轴III 轴工作轴转速n(r/min) 1440 1440 264.4 67.97 67.97 功率p(kw) 5.11 5.008 4.833 4.665 4.55 转矩T(N ·m ) 33.89 33.21 174.57655.4639.08 传动比i 1.00 5.446 3.89 1.00 效率0.980.9650.9650.975传动零件设计:一、齿轮设计(课本p147)高速级设计参数:ht i r n r n m N T kW p 48000;446.5min;/4.264min;/1440;.21.33;008.512111======寿命 1、选材:大齿轮:45,调质处理表面淬火,硬度40~50HBS ; 小齿轮:45,调质处理表面淬火,硬度40~50 HBS 。
全新—机械设计基础课程设计二级减速器解读

L1 L Z型轴孔
L
L1 L J型轴孔
L1
Y型轴孔
J1型轴孔
Z型轴孔:阶梯形圆锥轴孔。 Y型轴孔:长圆柱轴孔。 J型轴孔: 阶梯形圆柱轴孔。 J1型轴孔:短圆柱轴孔。
14
2.型号选择 按不小于轴的转矩T,转速n和初算最小轴径dmin的值选取 联轴器型号。 低速轴最小轴径应由所选联轴器标准孔径最终确定。 联轴器标记示例说明:
29
S=D2 ③确定凸台高度 按螺栓的扳手空间C1和边缘厚C2得 凸台宽度,由此确定高度h,所得凸台 尺寸应圆整。 c)确定箱盖顶部外表面轮廓 大齿轮一侧:R1=da2/2+△1+ δ1 C2 C1 小齿轮一侧:R2>Rʹ d)确定箱座高度 箱座高度:H >da2/2+30~50+8+3~5 mm e)输油沟的结构确定 轴承采用飞溅润滑时,应在箱座凸缘上开输油沟。输油沟 的结构见P19图4-11。 注意所开输油沟不能与联接螺栓孔通连。
nⅠ= nw· i 1 r/min nⅡ= nw r/min nⅠ, nⅡ:分别为高速轴、低速轴转速。 nW:滚筒转速,r/min。 2.各轴功率 按电动机的所需功率Pd计算: PⅠ=Pd η1 kW PⅡ=PⅠη2 η4 kW PⅠ, PⅡ:分别为高速轴,低速轴功率。 各效率值同前。 3.各轴转矩 TⅠ=9550PⅠ/nⅠ N· m TⅡ=9550PⅡ/nⅡ N· m TⅠ, TⅡ:分别为高速轴,低速轴转矩。
4
二、设计任务
1)在A1图纸上完成减速器装配图一张。 2)在A2图纸上绘制齿轮零件工作图一张。 低速轴大齿轮,参考图样见P55。 3)在A2图纸上绘制轴零件工作图一张。 低速轴,参考图样见P53。 4)完成设计计算说明书一份。 说明书内容、要求及书写格式见P62。
机械设计课程设计说明书型砂搅拌机的传动装置—两级圆柱齿轮减速器

设计题目:型砂搅拌机的传动装置—两级圆柱齿轮减速器姓名:学号:专业班级:目录摘要………………………………………………………………………………第一章绪论引言…………………………………………………………………目的…………………………………………………………………第二章设计项目已知数据……………………………………………………………传动方案的选择……………………………………………………电动机的选择………………………………………………………传动比的计算与分派………………………………………………传动参数的计算……………………………………………………各级传动零件的设计计算…………………………………………轴的尺寸设计——按许用应力计算………………………………联轴器的选择………………………………………………………键的选择——按轴颈选择…………………………………………转动轴承的选择……………………………………………………箱体及减速器附件说明……………………………………………转动轴承的外部密封装置…………………………………………第三章装配图设计…………………………………………………………第四章零件图设计…………………………………………………………第五章个人小结……………………………………………………………第六章参考文献…………………………………………第一章绪论引言机械设计综合课程设计是对咱们一个学年内学习状况的考察,也是锻炼同窗自主创新、设计及试探的一项课题。
本次机械设计课程设计的主题为“二级展开式圆柱齿轮减速器”,在设计进程中涉及到了很多在过去的一年中咱们所学到的知识,例如齿轮、轴和与它们相关的知识。
这次是咱们第一次接触实际进行设计,相信无论对于咱们知识的强化仍是创新能力、试探能力都是一次锻炼和挑战。
1.2目的综合运用机械设计基础、机械制造基础的知识和画图技术,完成传动装置的测绘与分析,通过这一进程全面了解一个机械产品所涉及的结构、强度、制造、装配和表达等方面的知识,培育综合分析、实际解决工程问题的能力。
JCZS-Ⅱ型机械传动性能综合实验台实验指导书

JCZS-Ⅱ型机械传动性能综合实验台实验指导书一、主要结构的组成及调整:该实验台主要由控制(配件)柜、安装平板、驱动源、负载以及减速器、联轴器、传动支承组件、带、链、三角带轮、链轮库等组成。
可根据需要按一定的形式组合成13大类30几种机械传动系统。
其中底座控制(配件)柜、安装平板、驱动源、负载、减速器、传动支承组件为整体结构。
安装平板上加工了T型槽(横向4根纵向6根)可满足不同机械传动系统安装的需要。
减速器有蜗轮减速器、园柱齿轮减速器、摆线针轮减速器等三种。
可拼装组合的类型:1.摆线针轮传动2.圆柱齿轮传动3.蜗轮蜗杆传动4.带传动(1)三角皮带传动(2)平皮带传动(3)同步带传动5.滚子链传动6.带—链组合传动(1)三角皮带—链传动(2)同步带—链传动7. 带—齿轮传动(1)三角皮带—圆柱齿轮传动(2)三角皮带—摆线针轮传动(3)平皮带—圆柱齿轮传动(4)平皮带—摆线针轮传动(5)同步带—圆柱齿轮传动(6)同步带—摆线针轮传动8. 滚子链—齿轮传动(1)滚子链—圆柱齿轮传动(2)滚子链—摆线针轮传动9. 摆线针轮—圆柱齿轮组合传动10. 齿轮—带传动(1)圆柱齿轮—三角皮带传动(2)摆线针轮—三角皮带传动(3)圆柱齿轮—平皮带传动(4)摆线针轮—平皮带传动(5)圆柱齿轮—同步带传动(6)摆线针轮—同步带传动12. 齿轮—滚子链传动(1)圆柱齿轮—滚子链传动(2)摆线针轮—滚子链传动13.弹性柱销联轴器传动1、控制(配件)柜的组成(见图一):图一、控制(配件)柜的组成1.支撑脚2.定向轮3.控制(配件)柜体4.机械传动系统5.安装平板6.磁粉制动控制器7.变频器8.万向轮控制(配件)柜体(3)采用δ3优质钢板经弯曲成型后焊接而成,其框架内内框通过固定有四扇柜门,可自由开启方便零配件的存取。
其下布四角安装有四个支撑脚(1)和定向轮(2)、万向轮(8)各两个。
其上通过螺栓固定有安装平板(5),安装平板(5)作为组装各种不同类型的机械传动系统的安装基准和固定平台。
机械设计课程设计-二级展开式斜齿圆柱齿轮减速器

机械设计课程设计图3-1 轴的弯矩图和扭矩图3.6 按弯扭合成应力校核轴的强度3Ⅵ.按弯扭合成应力校核轴的强度进行校核时,通常只校核轴上承受最大弯矩和扭矩的截面(即危险截面C)的强目录1 电动机的选择及运动参数的计算 (1)1.1电动机的选择 (1)1.2计算传动装置的总传动及其分配 (2)1.3 计算传动装置的运动和动力参数 (3)2 齿轮传动设计 (5)2.1高速轴上的大小齿轮传动设计 (5)2.2低速轴上的大小齿轮传动设计 (8)3 轴的设计计算 (13)3.1 输出轴上的功率转速和转矩 (13)3.2 求作用在齿轮上的力 (13)3.3 初步确定轴的最小直径 (13)3.4 轴的结构设计 (14)3.5 求轴上的载荷 (15)3.6 按弯扭合成应力校核轴的强度 (16)3.7 精确校核轴的疲劳强度 (17)Ⅳ.齿轮轴的结构设计 (21)4 滚动轴承的选择及校核 (25)4.1 轴承的选择(表4-1) (25)4.2 滚动轴承(低速轴)的校核 (25)5 键联接的选择及校核 (27)5.1 与联轴器间键的选择及校核 (27)5.2 与齿轮间键的选择及校核 (27)6 联轴器的选择及校核 (28)7 箱体结构的设计 (29)8 减速器的附件 (30)8.1 视孔盖和窥视孔 (30)8.2 放油孔和螺塞 (30)8.3 油标: (30)8.4 通气孔 (30)8.5 定位销 (30)8.6 吊钩: (30)8.7 起盖螺钉 (31)9 润滑和密封方式的选择 (33)9.1.齿轮的润滑 (33)9.2 滚动轴承的润滑 (33)9.3 润滑油的选择 (33)9.4 密封方式选取: (33)后序设计小结 (34)附录参考文献 (35)。
合成纤维西服套装的机械强度和耐热性测试

合成纤维西服套装的机械强度和耐热性测试合成纤维西服套装已经成为现代时尚界的焦点,其在服装制造业中的重要地位不容忽视。
然而,为了确保这种材料符合消费者对品质和耐用性的要求,合成纤维西服套装的机械强度和耐热性测试变得至关重要。
本文将探讨这些测试的重要性以及常用的测试方法和标准。
首先,机械强度测试是评估合成纤维西服套装耐久性和抗拉性能的关键步骤。
这些测试可以帮助制造商确定该套装能否经受住日常活动和穿着的压力,如行走、坐下和伸展等动作。
通过机械强度测试,人们可以检测出织物的弹性和耐磨性,以确保西服套装在戴用过程中不会过早磨损或损坏。
目前,常用的机械强度测试方法包括抗拉测试、撕裂测试和磨损测试。
抗拉测试是通过将材料拉伸至极限,测量其抗拉强度和断裂伸长率来评估其耐久性。
撕裂测试则是通过切割或撕裂材料,测量其抗撕裂强度和断裂延伸率来评估其耐用性。
磨损测试则是利用磨擦或摩擦装置,模拟日常活动的摩擦过程,以判断材料的耐磨性。
此外,在合成纤维西服套装中,耐热性测试也是至关重要的。
这是因为消费者常常在高温环境中穿着西服套装,如夏季的户外活动或特定职业岗位的工作环境。
因此,耐热性测试可以确认材料在高温环境中的稳定性和安全性,以避免任何潜在的危险情况。
耐热性测试主要涉及高温热湿处理、热变形测试和热传导率测试等方法。
高温热湿处理是将样品置于高温高湿的环境中,模拟真实使用环境下的条件,来评估合成纤维西服套装的变形和稳定性。
热变形测试则是通过将样品加热至高温,测量其热稳定性和形状保持能力。
热传导率测试则是评估材料传导热量的能力,以确认西服套装在高温环境中的舒适度和安全性。
为了确保这些测试的准确性和可靠性,制造商通常参考国际标准化组织(ISO)和其他行业标准。
ISO 13934-1标准规定了织物抗拉强度和伸长率的测量方法。
ISO 13937-1标准则规定了织物断裂强度和断裂伸长率的测量方法。
另外,ASTMD4966标准规定了织物磨损性能的测试方法。
jxsj2

第五章齿轮机构§5—1 齿轮机构的应用和分类一、齿轮机构的应用齿轮机构是在各种机构中应用最为广泛的,且是很重要的一种传动机构。
它可用于传递空间任意两轴间的运动和动力。
与其它传动型式相比,它具有功率范围大、传动效率高、传动比准确稳定、工作可靠且寿命长等优点。
但齿轮传动的缺点是:要求有较高的制造和安装精度,成本较高。
且不适宜于远距离两轴之间的传动。
二、齿轮传动的分类齿轮传动的类型很多,根据一对齿轮在啮合过程中传动比i是否恒定,可将齿轮机构分为定传动比传动的齿轮机构和变传动比传动的齿轮机构两大类。
因定传动比齿轮机构中的齿轮都是圆形(圆柱形和圆锥形),所以前者又称为圆形齿轮机构;而后者一般是非圆形的,故又可称为非圆形齿轮机构。
在各种齿轮机构中应用最广泛的是圆形齿轮机构,它可以保证传动比恒定不变,从而使机械运转平稳。
圆形齿轮机构的类型也很多,按照不同的分类方法有不同的类型,常见的类型如下:1、按照一对齿轮轴线的相对位置及齿向可分类如下(图5—1)。
2、按照齿廓的形状,齿轮传动可分为渐开线齿轮传动、摆线齿轮传动和圆弧齿轮传动三种,其中渐开线齿轮应用最广。
3、按照齿轮传动的工作条件,可分为闭式传动和开式传动两种。
闭式传动的齿轮封闭在刚性很大的箱体内,因而能保证良好的润滑和工件条件。
重要的齿轮传动都采用闭式传动,如变速器等。
开式齿轮传动的齿轮是外露的,不能保证良好的润滑,故齿面容易磨损。
但结构简单,成本低廉,故适用于低速和精度要求不高的场合。
齿轮的种类虽然很多,但最基本的,应用最多的是直齿圆柱齿轮,故我们将重点介绍渐开线直齿圆柱齿轮。
§5—2 齿轮的齿廓曲线对齿轮传动的基本要求是其瞬时角速度之比(或称传动比)必须保持不变,否则,当主动轮以等角速度回转时,从动轮的角速度为变数,就会产生惯性力。
这种惯性力不仅影响齿轮的寿命,而且还引起机器的振动和噪声,从而影响其工作精度。
因此,齿轮的齿廓曲线必须具有一定的形状。
规律性非稳定变应力时的机械零件疲劳强度
F
N1 N,
1
......
N i
N, i
......
N n
N, n
n
Ni ,
N i1 i
失效时:F=1 实际上:F=0.7~2.2
2. 等效稳定变应力及寿命系数
如果在若干应力···i···,循环次数···Ni···等作用下与 在应力v, 循环次数 Nv 作用下的疲劳损伤率相等,则v 则称为等 效应力,
《机械设计》电子教材 编著 上海铁道大学 李小江
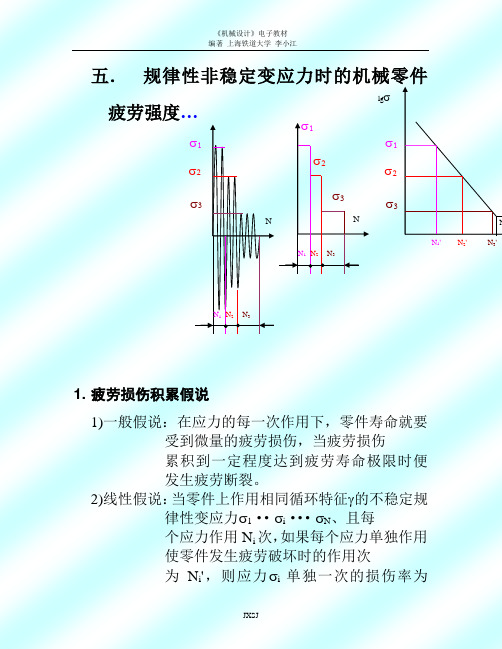
五. 规律性非稳定变应力时的机械零件
疲劳强度…
lg
N
N
N
N1 N2 N3
N1'
N2'
N3'
N1 N2 N3
1. 疲劳损伤积累假说
1)一般假说:在应力的每一次作用下,零件寿命就要 受到微量的疲劳损伤,当疲劳损伤 累积到一定程度达到疲劳寿命极限时便 发生疲劳断裂。
JXSJ
循环 Nv 次零件疲劳破坏时的疲劳极限应力:
由:
m N
Nv
m
N
0
得: v kN
其中: kN
kN---寿命系数 ks---应力情况系数
1 ks
m
N0 Nv
m
N0
i v
m
Ni
3. 强度计算
1) 静强度
=max(1,...i,...,n) s=s/≥s
2) 疲劳强度
a) 取v b) 计算 Nv c) 计算 kN、v d) 按疲劳强度计算 s=kN-1/(Ka) 例:规律性非稳定变应力时强度计算
Nv 称为等效循环次数。 代入疲劳曲线方程:
N1 N,
1
......
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Smin
分析图6得知,凡是工作应力点位于OGC区域内时,在循环特性等于 常数的条件下,极限应力统为屈服极限,都只需进行静强度计算。
第三章 机械零件的强度
2、m=C的情况
当m=C时,需找到一个其平均应力与工作应力的平均应力相同的极限应力。 在图7中,通过M(或N)点作纵轴的平行线MM2(或NN2),则此线上任何一 点代表的应力循环都具有相同的平均应力值。
一、选择题
1、机械设计课程研究的内容只限于 3
。
(1)专用零件和部件;(2)在高速、高压、环境温度过高或过低等特殊条件
下工作的以及尺寸特大或特小的通用零件和部件;(3)在普通工作条件下工作
的一般参数的通用零件和部件;(4)标准化的零件和部件。
2、下列四种叙述中
4 是正确的。
(1)变应力只能由变载荷产生;(2)静载荷不能产生变应力;(3)变应力
是由静载荷产生;(4)变应力是由变载荷产生,也可能由静载荷产生。
第三章 机械零件的强度
3、发动机连杆横截面上的应力变化规律如图所示,则该变应力的应力比r为 2 。
(1)0.24;(2)-0.24;(3)-4.17;(4)4.17。
0
31.2N/mm2 t
-130N/mm2
4、发动机连杆横截面上的应力变化规律如题3图所示,则其应力幅a和平均应力m
其中:max—变应力最大值;min—变应力最小值;m—平均应力; a—应力幅;r—循环特性,-1 r +1。
由此可以看出,一种变应力的状况,一般地可由max、min、m、a及r五个参 数中的任意两个来确定。
第三章 机械零件的强度
三、几种特殊的变应力
特殊点:
0
m t
静应力
max=min=m a=0 r=+1
(1)一个;(2)两个;(3)三个;(4)四个。
第三章 机械零件的强度
6、图示各应力随时间变化的图形分别表示什么类型的应力?它们的应力比
分别是多少?
0
max
t
a)
max
a
m
0
min=
t
0
c)
a
max m
0
mi
t
n
b)
0
max t
a
m=0
d)
解:a)静应力r=1;b)非对称(或稳定)循环变应力 0< r <+1; c)脉动循环r = 0;d)对称循环r=-1。
横轴上任何一点都代表应力幅等于零的应力,即静应力。取C点的坐标值等于材料
的屈服极限s,并自C点作一直线与直线C0成45夹角,交AD延长线于G,则CG上任
何一点均代表 max = m + a = s 的变应力状况。
于是,零件材料(试件)的极限应力曲线即为折线AGC。材料中发生的应力如处于
OAGC区域以内,则表示不发生破坏;
0/2K -1e=-1/K
0/2 -1
a A
D G
45 0 0/2
45 C
m
s
a
A
D
G
0 0/2
45 C
m
s
图3 材料的极限应力线图
图4 零件的极限应力线图
连接A、D得直线AD。由于这条直线与不同循环特性时进行试验所求得的疲劳极 限应力曲线非常接近,所以直线AD上任何一点都代表了一定循环特性时的疲劳极限。
从图上可以看出,应力愈高,则产生疲劳失效的循环次数愈少。
在作材料试验时,常取一规定的应力循环次数N0,称为循环基数,把相应于这一循环次 数的疲劳极限,称为材料的持久疲劳极限,记为rN0(或r)。
第三章 机械零件的强度
疲劳曲线可分成两个区域:有限寿命区和无限寿命区。所谓“无限”寿命,是指零 件承受的变应力水平低于或等于材料的疲劳极限r,工作应力总循环次数可大于N0,零 件将永远不会产生破坏。
max
对称循环变应力
0
t min
max=min=a m=0
r=-1
0
min
max m
t
脉动循环变应力 min=0
a=m=max/2
r=0
不属于上述三类的应力称为非对称循环应力,其r在+1与-1之间,它可 看作是由第一类(静应力)和第二类(对称循环应力)叠加而成。
第三章 机械零件的强度
机械零件的疲劳强度(习题1)
Smin
m
Sa'
=
-1 - min (K + ) a
Smin
图8 min=C时的极限应力
第三章 机械零件的强度 七、不稳定变应力的强度计算
1.应力谱
1
2 3
n1
n2
n3
t
图9不稳定变应力示意图
1
1 2
3
n1
n2 n3
2 3 n
第三章 机械零件的强度
图9为一不稳定变应力的示意图。变应力1(对称循环变应力的最大 应力,或不对称循环变应力的等效对称循环变应力的应力幅)作用了n1次, 2作用了n2次,……等等。
Sca
= max max
= max m +a
=
-1 K a + m
Smin
对应于N点的极限应力点N1位于直线CG上。此时的极限应力 即为屈服极限s。这就是说,工作应力为N点时,首先可能发生的是 屈服失效,故只需进行静强度计算,其强度计算式为:
Sca
= lim
= s max
= s a +m
a
a
A M1 D
M 0 m
G
N N1
C
m
图6 r = C时的极限应力
联解OM及AG两直线的方程式,可以求出M1点的坐标值m及a, 把它们加起来,就可以求出对应于M点的试件的极限应力max:
第三章 机械零件的强度
max
= a
+ m
=
-1 m + a K a + m
于是,安全系数计算值Sca及强度条件为:
45 0 0/2
45 C
m
s
图3材料的极限应力线图
由于对称循环变应力的平均应力m=0,最大应力等于应力幅,所以对称循环疲劳极 限在图中以纵坐标轴上的A点来表示。
由于脉动循环变应力的平均应力及应力幅均为m=a=0/2,所以脉动循环疲劳极限 以由原点0所作45射线上的D点来表示。
第三章 机械零件的强度
min = m - a = C
因此在图8中,通过M(或N)点,作与横坐标轴夹角为45的直 线,则此直线上任何一个点所代表的应力均具有相同的最小应力。
a
A
M3’ D M
G
45
I N N3’
minM 0
minN
C
Sca
=
2 -1 + (K - ) min (K + )( min + 2 a )
a
max
0
m
0
t
min
min a
t m
max
图2稳定循环变应力
第三章 机械零件的强度
max = m + a
min = m - a
m
=
max
+ min
2
a
=
max
- min
2
r
=
min max
a
0 min
max
0
m t
图2稳定循环变应力
min a
t m
max
规定:1、a总为正值; 2、a的符号要与m的符号保持一致。
直线AG的方程,由已知两点坐标A(0,-1)及D(0/2,0/2)求得为(疲劳 区):
第三章 机械零件的强度
-1
= a
+
2
-1
-
0
0
m
令
=
2 -1 - 0 0
—试件的材料特性(等效系数、折算系数);
-1 = a + m
0
-1 t =0
a
t +0
m t
直线GC方程为(静强度区): m + a = s
2、疲劳损伤累积假说—曼耐尔(Miner’s rule法则)
a)金属材料在一定变应力作用下都有一定寿命; b)每增加一次过载的应力(超过材料的持久疲劳极限),就对材料造成一 定的损伤,当这些损伤的逐渐积累其总和达到其寿命相当的寿命时,材料 即造成破坏; c)小于持久疲劳极限,不会对材料造成损伤; d)变应力大小作用的次序对损伤有影响。
tg = a = max - min m max + min
max - min
2 2
=
max max + min
=
11+
r r
=
C
max
因此,在图6中,从坐标原点引射线通过工作应力点M(或N),与极限应力 曲线交于M1(或N1),得到0M1(或0N1),则在此射线上任何一个点所代表 的应力循环都具有相同的循环特性。
在有限寿命区的疲劳曲线上,N<N0所对应的各点的应力值,为有限寿命条件下的 疲劳极限。
对低碳钢而言,循环基数N0=106~25×107; 对合金钢及有色金属,循环基数N0=108或(5×108); 变应力与在此应力作用下断裂时的循环次数N之间有以下关系式:
m rN
N
=
C
此式称为疲劳曲线方程(或—N曲线方程)。其中: rN— 应力比为r时有限寿命疲劳极限应力; N —与rN对应的循环次数; m —与材料有关的指数; C —实验常数;(m、c根据实验数据通过数理统计得到)。
第三章 机械零件的强度
第三章 机械零件的强度
六、疲劳强度计算
弯曲疲劳极限综合影响系数
