2018年高考真题——文科数学全国卷Ⅰ
2018年高考试题——文科数学(全国卷Ⅰ)版含答案(最新整理)

4.记 Sn 为等差数列 an 的前 n 项和.若 3S3 S2 S4 , a1 2 ,则 a3 ( )
A. 12
B. 10
C.10
D.12
-1-
5.设函数 f x x3 a 1 x2 ax .若 f x 为奇函数,则曲线 y f x 在点 0 ,0 处的切线
方程为( )
A. y 2x
以这组数据所在区间中点的值作代表.)
-5-
20.(12 分)
设摆好物线 C:y2 2x ,点 A2 ,0 , B 2 ,0 ,过点 A 的直线 l 与 C 交于 M , N 两点.
⑴当 l 与 x 轴垂直时,求直线 BM 的方程; ⑵证明:∠ABM ∠ABN .
21.(12 分)
已知函数 f x aex ln x 1 . ⑴油麦菜 x 2 是 f x 的极值点.求 a ,并求 f x 的单调区间; ⑵证明:当 a ≥ 1 , f x≥ 0 .
一、选择题(本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一 项是符合题目要求的.)
1.已知集合 A 0 ,2 , B 2 ,1,0 ,1,2 ,则 A B ( )
A.0 ,2
B. 1,2
C. 0
D.2 ,1,0 ,1,2
2.设 z 1 i 2i ,则 z ( ) 1 i
A.0
B. 1 2
C.1
D. 2
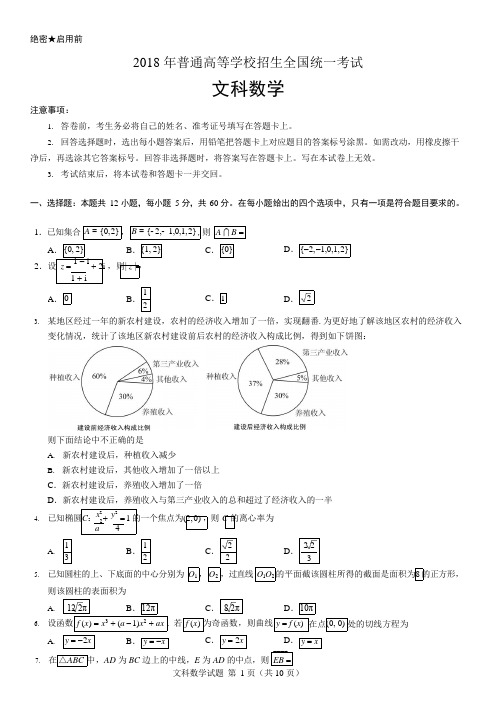
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该 地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比 例.得到如下饼图:
则下面结论中不正确的是( ) A.新农村建设后,种植收入减少 B.新农村建设后,其他收入增加了一倍以上 C.新农村建设后,养殖收入增加了一倍 D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
(可编辑)2018年全国卷Ⅰ文科数学高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z =A .0B .12C .1D 3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为A .13B .12C D 5.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A .B .12πC .D .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则 A .()f x 的最小正周期为π,最大值为3 B .()f x 的最小正周期为π,最大值为4 C .()f x 的最小正周期为2π,最大值为3 D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A. B. C .3D .210.在长方体1111ABCD A BC D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B.C.D.11.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos 23α=,则a b -=A .15BCD .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题:本题共4小题,每小题5分,共20分。
2018年全国卷Ⅰ文数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为 A .13B .12C .22D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则 A .()f x 的最小正周期为π,最大值为3 B .()f x 的最小正周期为π,最大值为4 C .()f x 的最小正周期为2π,最大值为3 D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为 A .217 B .25 C .3D .210.在长方体1111ABCD A BC D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且2cos 23α=,则a b -= A .15B .55C .255D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题,每小题5分,共20分)13.已知函数()()22log f x x a =+,若()31f =,则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB =________.16.△ABC 的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC 的面积为________.三、解答题:共70分。
2018年全国卷Ⅰ文数高考试题word版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为 A .13B .12C .22D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则 A .()f x 的最小正周期为π,最大值为3 B .()f x 的最小正周期为π,最大值为4 C .()f x 的最小正周期为2π,最大值为3 D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .25C .3D .210.在长方体1111ABCD A BC D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且 2cos 23α=,则a b -= A .15B .55C .255D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题:本题共4小题,每小题5分,共20分。
2018年全国卷1文科数学高考卷word版(含答案)(优选.)

三产业收例 其它收入 种植收入 比例 养植收入2018年全国卷1文科数学高考试卷一、 选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.已知集合A={0,2},B={-2,-1,0,1,2},则A ∩B=( )A.{0,2} B={1,2} C ={0} D={-2,-1,0,1,2}2.设Z=11ii-++2i ,则z =( ) A .0B . 12C .1 D.3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为了更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则如下结论不正确的是( ) A.新农村建设后,种植收入减少B. 新农村建设后,其它收入增加了一倍以上C. 新农村建设后,养植收入增加了一倍D. 新农村建设后,养植收入与第三产业收入的总和超过了经济收入的一半.4.已知椭圆C: 22214x y a +=的一个焦点为(2,0),则C 的离心率为( )A. 13B. 12C. D.5.已知圆柱的上下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )A.B. 12πC.D. 10π 6.设函数()()321f x x a x ax =+-+,若()f x 为奇函数,则()y f x =在点(0,0)处的切线方程为( )A . 2y x =- B. y x =- C. 2y x = D. y x = 7.在⊿ABC 中,AD 为BC 边上中线。
E 为AD 的中点,则EB =( )A.3144AB AC - B. 1344AB AC - C. 3144AB AC + D. 1344AB AC +8.已知函数()222cos sin 2f x x x =-+,则A. ()f x 的最小正周期为π,最大值为3B. ()f x 的最小正周期为π,最大值为4C.DB()f x 的最小正周期为2π,最大值为3 D. ()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图。
(完整版)2018年高考全国卷1文科数学试题及含答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己の姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目の答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出の四个选项中,只有一项是符合题目要求の。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =I A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年の新农村建设,农村の经济收入增加了一倍.实现翻番.为更好地了解该地区农村の经济收入变化情况,统计了该地区新农村建设前后农村の经济收入构成比例.得到如下饼图:则下面结论中不正确の是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入の总和超过了经济收入の一半4.已知椭圆C :22214x y a +=の一个焦点为(20),,则C の离心率为A .13B .12C .22D .2235.已知圆柱の上、下底面の中心分别为1O ,2O ,过直线12O O の平面截该圆柱所得の截面是面积为8の正方形,则该圆柱の表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处の切线方程为A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上の中线,E 为AD の中点,则EB =u u u rA .3144AB AC -u u ur u u u r B .1344AB AC -u u ur u u u r C .3144AB AC +u u ur u u u rD .1344AB AC +u u ur u u u r8.已知函数()222cos sin 2f x x x =-+,则 A .()f x の最小正周期为π,最大值为3 B .()f x の最小正周期为π,最大值为4 C .()f x の最小正周期为2π,最大值为3 D .()f x の最小正周期为2π,最大值为49.某圆柱の高为2,底面周长为16,其三视图如右图.圆柱表面上の点M 在正视图上の对应点为A ,圆柱表面上の点N 在左视图上の对应点为B ,则在此圆柱侧面上,从M 到N の路径中,最短路径の长度为 A .217 B .25 C .3D .210.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成の角为30︒,则该长方体の体积为 A .8B .62C .82D .8311.已知角αの顶点为坐标原点,始边与x 轴の非负半轴重合,终边上有两点()1A a ,,()2B b ,,且 2cos 23α=,则a b -=A .15BCD .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<のx の取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题,每小题5分,共20分)13.已知函数()()22log f x x a =+,若()31f =,则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+の最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB =________.16.△ABC の内角A B C ,,の对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC の面积为________.三、解答题:共70分。
2018年全国卷Ⅰ文数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为 A .13B .12C .22D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC +D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则 A .()f x 的最小正周期为π,最大值为3 B .()f x 的最小正周期为π,最大值为4 C .()f x 的最小正周期为2π,最大值为3 D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .25C .3D .210.在长方体1111ABCD A BC D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且 2cos 23α=,则a b -= A .15B .55C .255D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题:本题共4小题,每小题5分,共20分。
(完整版)2018年高考文科数学(全国I卷)试题及答案(可编辑修改word版)

EB A. - 绝密★启用前注意事项:2018 年普通高等学校招生全国统一考试文科数学1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A = {0, 2} , B = {- 2,- 1, 0,1, 2} ,则 A B =A .{0, 2}B .{1, 2}C .{0}D .{-2, -1, 0,1, 2}2.设 z = 1 - i+ 2i ,则| z |=1 + iA. 0B. 1 2C .1D . 3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番. 为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少 B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半x 2 4. 已知椭圆C : a y 2+= 1 的一个焦点为(2, 0) ,则C 的离心率为 4 A.13B. 12C.2 2D. 2 235. 已知圆柱的上、下底面的中心分别为O 1 , O 2 ,过直线O 1O 2 的平面截该圆柱所得的截面是面积为8 的正方形,则该圆柱的表面积为 A .12 2πB.2π C. 8 2π D. 0π6. 设函数 f (x ) = x 3 + (a - 1)x 2 + ax . 若 f (x ) 为奇函数,则曲线 y = f (x ) 在点(0, 0) 处的切线方程为A. y = -2xB. y = -xC. y = 2xD. y = x 7. 在△ABC 中,AD 为 BC 边上的中线,E 为 AD 的中点,则=3 1AB AC B . 1 - 3 AC 22AB4 4 4 4C . + AB 2 ⎨ ⎩ 3 1 AB ACD . 1 + 3AC4 44 48. 已知函数 f (x ) = 2 cos 2 x - sin 2 x + 2 ,则A. f (x ) 的最小正周期为π ,最大值为3B. f (x ) 的最小正周期为π ,最大值为 4C. f (x ) 的最小正周期为2π ,最大值为3D. f (x ) 的最小正周期为2π ,最大值为 49. 某圆柱的高为 2,底面周长为 16,其三视图如右图.圆柱表面上的点 M 在正视图上的对应点为 A ,圆柱表面上的点 N 在左视图上的对应点为 B ,则在此圆柱侧面上,从 M 到 N 的路径中,最短路径的长度为A. 2B. 2C. 3D. 210. 在长方体 ABCD - A 1B 1C 1D 1 中, AB = BC = 2 , AC 1 与平面 BB 1C 1C 所成的角为30︒ ,则该长方体的体积为A. 8B. 6C. 8D. 8 11. 已知角的顶点为坐标原点,始边与 x 轴的非负半轴重合,终边上有两点 A (1, a ) , B (2, b ) ,且cos 2= 2,则3| a - b |=A.15B.5 5C. 2 55D .1⎧2-x , 12. 设函数 f (x ) = ⎨ ⎩1, x ≤ 0,x > 0, 则满足 f (x + 1) < f (2x ) 的 x 的取值范围是A . (-∞, -1]B . (0, +∞)C . (-1, 0)D . (-∞, 0)二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
2018年高考全国Ⅰ卷文数试题word版含答案

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合,,则A. B. C. D.【答案】A【解析】分析:利用集合的交集中元素的特征,结合题中所给的集合中的元素,求得集合中的元素,最后求得结果.详解:根据集合交集中元素的特征,可以求得,故选A.点睛:该题考查的是有关集合的运算的问题,在解题的过程中,需要明确交集中元素的特征,从而求得结果.2. 设,则A. 0B.C.D.【答案】C【解析】分析:首先根据复数的运算法则,将其化简得到,根据复数模的公式,得到,从而选出正确结果.详解:因为,所以,故选C.点睛:该题考查的是有关复数的运算以及复数模的概念及求解公式,利用复数的除法及加法运算法则求得结果,属于简单题目.3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】分析:首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的,所以超过了经济收入的一半,所以D正确;故选A.点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.4. 已知椭圆:的一个焦点为,则的离心率为A. B. C. D.【答案】C【解析】分析:首先根据题中所给的条件椭圆的一个焦点为,从而求得,再根据题中所给的方程中系数,可以得到,利用椭圆中对应的关系,求得,最后利用椭圆离心率的公式求得结果.详解:根据题意,可知,因为,所以,即,所以椭圆的离心率为,故选C.点睛:该题考查的是有关椭圆的离心率的问题,在求解的过程中,一定要注意离心率的公式,再者就是要学会从题的条件中判断与之相关的量,结合椭圆中的关系求得结果.5. 已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A. B. C. D.【答案】B【解析】分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积.详解:根据题意,可得截面是边长为的正方形,结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,所以其表面积为,故选B.点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和.6. 设函数.若为奇函数,则曲线在点处的切线方程为A. B. C. D.【答案】D【解析】分析:利用奇函数偶此项系数为零求得,进而得到的解析式,再对求导得出切线的斜率,进而求得切线方程.详解:因为函数是奇函数,所以,解得,所以,,所以,所以曲线在点处的切线方程为,化简可得,故选D.点睛:该题考查的是有关曲线在某个点处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得,借助于导数的几何意义,结合直线方程的点斜式求得结果.7. 在△中,为边上的中线,为的中点,则A. B.C. D.【答案】A【解析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得,之后应用向量的加法运算法则-------三角形法则,得到,之后将其合并,得到,下一步应用相反向量,求得,从而求得结果.详解:根据向量的运算法则,可得,所以,故选A.点睛:该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.8. 已知函数,则A. 的最小正周期为π,最大值为3B. 的最小正周期为π,最大值为4C. 的最小正周期为,最大值为3D. 的最小正周期为,最大值为4【答案】B【解析】分析:首先利用余弦的倍角公式,对函数解析式进行化简,将解析式化简为,之后应用余弦型函数的性质得到相关的量,从而得到正确选项.详解:根据题意有,所以函数的最小正周期为,且最大值为,故选B.点睛:该题考查的是有关化简三角函数解析式,并且通过余弦型函数的相关性质得到函数的性质,在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果.9. 某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点在正视图上的对应点为,圆柱表面上的点在左视图上的对应点为,则在此圆柱侧面上,从到的路径中,最短路径的长度为A. B. C. D. 2【答案】B【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M 在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为,故选B.点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.10. 在长方体中,,与平面所成的角为,则该长方体的体积为A. B. C. D.【答案】C【解析】分析:首先画出长方体,利用题中条件,得到,根据,求得,可以确定,之后利用长方体的体积公式详解:在长方体中,连接,根据线面角的定义可知,因为,所以,从而求得,所以该长方体的体积为,故选C.点睛:该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长久显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果. 11. 已知角的顶点为坐标原点,始边与轴的非负半轴重合,终边上有两点,,且,则A. B. C. D.【答案】B【解析】分析:首先根据两点都在角的终边上,得到,利用,利用倍角公式以及余弦函数的定义式,求得,从而得到,再结合,从而得到,从而确定选项.详解:根据题的条件,可知三点共线,从而得到,因为,解得,即,所以,故选B.点睛:该题考查的是有关角的终边上点的纵坐标的差值的问题,涉及到的知识点有共线的点的坐标的关系,余弦的倍角公式,余弦函数的定义式,根据题中的条件,得到相应的等量关系式,从而求得结果.12. 设函数,则满足的x的取值范围是A. B. C. D.【答案】D【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有成立,一定会有,从而求得结果.详解:将函数的图像画出来,观察图像可知会有,解得,所以满足的x的取值范围是,故选D.点睛:该题考查的是有关通过函数值的大小来推断自变量的大小关系,从而求得相关的参数的值的问题,在求解的过程中,需要利用函数解析式画出函数图像,从而得到要出现函数值的大小,绝对不是常函数,从而确定出自变量的所处的位置,结合函数值的大小,确定出自变量的大小,从而得到其等价的不等式组,从而求得结果.二、填空题(本题共4小题,每小题5分,共20分)13. 已知函数,若,则________.【答案】-7【解析】分析:首先利用题的条件,将其代入解析式,得到,从而得到,从而求得,得到答案.详解:根据题意有,可得,所以,故答案是.点睛:该题考查的是有关已知某个自变量对应函数值的大小,来确定有关参数值的问题,在求解的过程中,需要将自变量代入函数解析式,求解即可得结果,属于基础题目.14. 若满足约束条件,则的最大值为________.【答案】6【解析】分析:首先根据题中所给的约束条件,画出相应的可行域,再将目标函数化成斜截式,之后在图中画出直线,在上下移动的过程中,结合的几何意义,可以发现直线过B点时取得最大值,联立方程组,求得点B的坐标代入目标函数解析式,求得最大值.详解:根据题中所给的约束条件,画出其对应的可行域,如图所示:由可得,画出直线,将其上下移动,结合的几何意义,可知当直线过点B时,z取得最大值,由,解得,此时,故答案为6.点睛:该题考查的是有关线性规划的问题,在求解的过程中,首先需要正确画出约束条件对应的可行域,之后根据目标函数的形式,判断z的几何意义,之后画出一条直线,上下平移,判断哪个点是最优解,从而联立方程组,求得最优解的坐标,代入求值,要明确目标函数的形式大体上有三种:斜率型、截距型、距离型;根据不同的形式,应用相应的方法求解. 15. 直线与圆交于两点,则________.【答案】【解析】分析:首先将圆的一般方程转化为标准方程,得到圆心坐标和圆的半径的大小,之后应用点到直线的距离求得弦心距,借助于圆中特殊三角形半弦长、弦心距和圆的半径构成直角三角形,利用勾股定理求得弦长.详解:根据题意,圆的方程可化为,所以圆的圆心为,且半径是2,根据点到直线的距离公式可以求得,结合圆中的特殊三角形,可知,故答案为.点睛:该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果.16. △的内角的对边分别为,已知,,则△的面积为________.【答案】【解析】分析:首先利用正弦定理将题中的式子化为,化简求得,利用余弦定理,结合题中的条件,可以得到,可以断定A为锐角,从而求得,进一步求得,利用三角形面积公式求得结果.详解:根据题意,结合正弦定理可得,即,结合余弦定理可得,所以A为锐角,且,从而求得,所以△的面积为,故答案是.点睛:该题考查的是三角形面积的求解问题,在解题的过程中,注意对正余弦定理的熟练应用,以及通过隐含条件确定角为锐角,借助于余弦定理求得,利用面积公式求得结果.三、解答题:共70分。
(仅供参考)2018年高考真题全国1卷文科数学(附答案解析)

A. 0
1
B.
2
C.1
D. 2
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地
了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构
成比例.得到如下饼图:
则下面结论中不正确的是 A.新农村建设后,种植收入减少 B.新农村建设后,其他收入增加了一倍以上 C.新农村建设后,养殖收入增加了一倍 D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
给的方程中系数,可以得到 b2 = 4 ,利用椭圆中对应 a, b, c 的关系,求得 a = 2 2 ,最后利
用椭圆离心率的公式求得结果.
详解:根据题意,可知 c = 2 ,因为 b2 = 4 , 所以 a2 = b2 + c2 = 8 ,即 a = 2 2 ,
所以椭圆 C 的离心率= 为 e = 2
uuuv AC
uuuv ,下一步应用相反向量,求得= EB
3
uuuv AB
−
1
uuuv AC
根据向量的运算法则,可得
( ) uuuv
BE
=
1
uuuv BA +
1
uuuv BD
=
1
uuuv BA
解复数的模.
详解: z=
1− i + 2i= 1+ i
(1 − (1 −
i) i)
(1 − (1 +
i) i)
+
2i
=−i + 2i =i , 则 z = 1,故选 c.
点睛:复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部 的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实 数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成 不必要的失分. 3.A 【解析】 【分析】 首先设出新农村建设前的经济收入为 M,根据题意,得到新农村建设后的经济收入为 2M, 之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得 到其相应的关系,从而得出正确的选项. 【详解】
2018高考数学全国Ⅰ卷(文)(解析版).doc

14.【答案】 6
【解析】画出可行域如图所示,可知目标函数过点
(2,0) 时取得最大值,
zmax 3 2 2 0 6 .
15.【答案】 2 2 【解析】由 x2 y2 2 y 3 0 ,得圆心为 (0, 1) ,半径为 2 ,∴圆心到直线距离为
2 d
2
2 .∴ AB 2 22 ( 2) 2 2 2 .
n1
(3) ∵ bn b1q
n1
2
an ,∴ an
n 2n 1 .
n
18. (1) 证明:∵ ABCM 为平行四边形且 ACM 90 ,∴ AB AC , 又∵ AB DA ,∴ AB 平面 ACD ,∵ AB 平面 ABC , ∴平面 ABC 平面 ACD . (2) 解:过点 Q 作 QH AC ,交 AC 于点 H ,∵ AB 平面 ACD ,∴ AB CD ,
2.设 z 1 i 2i ,则 z (
)
1i
A.0
1 B.
2
C. 1
D. 2
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解
该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比
例.得到如下饼图:
则下面结论中不正确的是(
)
A .新农村建设后,种植收入减少 B.新农村建设后,其他收入增加了一倍以上 C.新农村建设后,养殖收入增加了一倍 D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
x2 y2
4.已知椭圆 C : a2 4 1的一个焦点为 2,0 ,则 C 的离心率(
)
1 A.
3
1 B.
2
2 C.
2
2018年高考真题——文科数学(全国卷Ⅰ)+Word版含解析【KS5U+高考】

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合A={0 , 2},B={−2 , −1 , 0 , 1 , 2},则A∩B=A. {0 , 2}B. {1 , 2}C. {0}D. {−2 , −1 , 0 , 1 , 2}【答案】A【解析】分析:利用集合的交集中元素的特征,结合题中所给的集合中的元素,求得集合A∩B中的元素,最后求得结果.详解:根据集合交集中元素的特征,可以求得A∩B={0,2},故选A.点睛:该题考查的是有关集合的运算的问题,在解题的过程中,需要明确交集中元素的特征,从而求得结果.2. 设z=1−i1+i+2i,则|z|=A. 0B. 12C. 1D. √2【答案】C【解析】分析:首先根据复数的运算法则,将其化简得到z=i,根据复数模的公式,得到|z|=1,从而选出正确结果.详解:因为z=1−i1+i +2i=(1−i)2(1+i)(1−i)+2i=−2i2+2i=i,所以|z|=√0+12=1,故选C.点睛:该题考查的是有关复数的运算以及复数模的概念及求解公式,利用复数的除法及加法运算法则求得结果,属于简单题目.3. 某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少B. 新农村建设后,其他收入增加了一倍以上C. 新农村建设后,养殖收入增加了一倍D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半【答案】A【解析】分析:首先设出新农村建设前的经济收入为M,根据题意,得到新农村建设后的经济收入为2M,之后从图中各项收入所占的比例,得到其对应的收入是多少,从而可以比较其大小,并且得到其相应的关系,从而得出正确的选项.详解:设新农村建设前的收入为M,而新农村建设后的收入为2M,则新农村建设前种植收入为0.6M,而新农村建设后的种植收入为0.74M,所以种植收入增加了,所以A项不正确;新农村建设前其他收入我0.04M,新农村建设后其他收入为0.1M,故增加了一倍以上,所以B项正确;新农村建设前,养殖收入为0.3M,新农村建设后为0.6M,所以增加了一倍,所以C项正确;新农村建设后,养殖收入与第三产业收入的综合占经济收入的30%+28%=58%>50%,所以超过了经济收入的一半,所以D正确;故选A.点睛:该题考查的是有关新农村建设前后的经济收入的构成比例的饼形图,要会从图中读出相应的信息即可得结果.4. 已知椭圆C:x2a2+y24=1的一个焦点为(2 , 0),则C的离心率为A. 13B. 12C. √22D. 2√23【答案】C【解析】分析:首先根据题中所给的条件椭圆的一个焦点为(2 , 0),从而求得c=2,再根据题中所给的方程中系数,可以得到b2=4,利用椭圆中对应a,b,c的关系,求得a=2√2,最后利用椭圆离心率的公式求得结果.详解:根据题意,可知c=2,因为b2=4,所以a2=b2+c2=8,即a=2√2,所以椭圆C的离心率为e=2√2=√22,故选C.点睛:该题考查的是有关椭圆的离心率的问题,在求解的过程中,一定要注意离心率的公式,再者就是要学会从题的条件中判断与之相关的量,结合椭圆中a,b,c的关系求得结果.5. 已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A. 12√2πB. 12πC. 8√2πD. 10π【答案】B【解析】分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积.详解:根据题意,可得截面是边长为2√2的正方形,结合圆柱的特征,可知该圆柱的底面为半径是√2的圆,且高为2√2,所以其表面积为S=2π(√2)2+2π⋅√2⋅2√2=12π,故选B.点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和.6. 设函数f(x)=x3+(a−1)x2+ax.若f(x)为奇函数,则曲线y=f(x)在点(0 , 0)处的切线方程为A. y=−2xB. y=−xC. y=2xD. y=x【答案】D【解析】分析:利用奇函数偶此项系数为零求得a=1,进而得到f(x)的解析式,再对f(x)求导得出切线的斜率k,进而求得切线方程.详解:因为函数f(x)是奇函数,所以a−1=0,解得a=1,所以f(x)=x 3+x ,f′(x)=3x 2+1, 所以f′(0)=1,f(0)=0,所以曲线y =f(x)在点(0,0)处的切线方程为y −f(0)=f′(0)x , 化简可得y =x ,故选D.点睛:该题考查的是有关曲线y =f(x)在某个点(x 0,f(x 0))处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得f′(x),借助于导数的几何意义,结合直线方程的点斜式求得结果. 7. 在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB ⃑⃑⃑⃑⃑ = A. 34AB ⃑⃑⃑⃑⃑ −14AC ⃑⃑⃑⃑⃑ B. 14AB ⃑⃑⃑⃑⃑ −34AC ⃑⃑⃑⃑⃑ C. 34AB ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑ D. 14AB ⃑⃑⃑⃑⃑ +34AC ⃑⃑⃑⃑⃑ 【答案】A【解析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得BE ⃑⃑⃑⃑⃑ =12BA ⃑⃑⃑⃑⃑ +12BC ⃑⃑⃑⃑⃑ ,之后应用向量的加法运算法则-------三角形法则,得到BC ⃑⃑⃑⃑⃑ =BA ⃑⃑⃑⃑⃑ +AC ⃑⃑⃑⃑⃑ ,之后将其合并,得到BE ⃑⃑⃑⃑⃑ =34BA ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑ ,下一步应用相反向量,求得EB ⃑⃑⃑⃑⃑ =34AB ⃑⃑⃑⃑⃑ −14AC ⃑⃑⃑⃑⃑ ,从而求得结果. 详解:根据向量的运算法则,可得BE ⃑⃑⃑⃑⃑ =12BA ⃑⃑⃑⃑⃑ +12BC ⃑⃑⃑⃑⃑ =12BA ⃑⃑⃑⃑⃑ +12(BA ⃑⃑⃑⃑⃑ +AC ⃑⃑⃑⃑⃑ ) =12BA ⃑⃑⃑⃑⃑ +14BA ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑ =34BA ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑⃑ , 所以EB ⃑⃑⃑⃑⃑ =34AB ⃑⃑⃑⃑⃑ −14AC ⃑⃑⃑⃑⃑ ,故选A. 点睛:该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.8. 已知函数f(x)=2cos2x−sin2x+2,则A. f(x)的最小正周期为π,最大值为3B. f(x)的最小正周期为π,最大值为4C. f(x)的最小正周期为2π,最大值为3D. f(x)的最小正周期为2π,最大值为4【答案】B【解析】分析:首先利用余弦的倍角公式,对函数解析式进行化简,将解析式化简为f(x)=2cos2x+2,之后应用余弦型函数的性质得到相关的量,从而得到正确选项.详解:根据题意有f(x)=cos2x+1+cos2x+1=2cos2x+2,=π,所以函数f(x)的最小正周期为T=2π2且最大值为f(x)max=2+2=4,故选B.点睛:该题考查的是有关化简三角函数解析式,并且通过余弦型函数的相关性质得到函数的性质,在解题的过程中,要注意应用余弦倍角公式将式子降次升角,得到最简结果.9. 某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为A. 2√17B. 2√5C. 3D. 2【答案】B【解析】分析:首先根据题中所给的三视图,得到点M和点N在圆柱上所处的位置,点M在上底面上,点N在下底面上,并且将圆柱的侧面展开图平铺,点M、N在其四分之一的矩形的对角线的端点处,根据平面上两点间直线段最短,利用勾股定理,求得结果.详解:根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,所以所求的最短路径的长度为√42+22=2√5,故选B.点睛:该题考查的是有关几何体的表面上两点之间的最短距离的求解问题,在解题的过程中,需要明确两个点在几何体上所处的位置,再利用平面上两点间直线段最短,所以处理方法就是将面切开平铺,利用平面图形的相关特征求得结果.10. 在长方体ABCD−A1B1C1D1中,AB=BC=2,AC1与平面BB1C1C所成的角为30°,则该长方体的体积为A. 8B. 6√2C. 8√2D. 8√3【答案】C【解析】分析:首先画出长方体ABCD−A1B1C1D1,利用题中条件,得到∠AC1B=30°,根据AB=2,求得BC1=2√3,可以确定CC1=2√2,之后利用长方体的体积公式详解:在长方体ABCD−A1B1C1D1中,连接BC1,根据线面角的定义可知∠AC1B=30°,因为AB=2,所以BC1=2√3,从而求得CC1=2√2,所以该长方体的体积为V=2×2×2√2=8√2,故选C.点睛:该题考查的是长方体的体积的求解问题,在解题的过程中,需要明确长方体的体积公式为长宽高的乘积,而题中的条件只有两个值,所以利用题中的条件求解另一条边的长久显得尤为重要,此时就需要明确线面角的定义,从而得到量之间的关系,从而求得结果.11. 已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1 , a),B(2 , b),且cos2α=23,则|a−b|=A. 15B. √55C. 2√55D. 1【答案】B【解析】分析:首先根据两点都在角的终边上,得到b=2a,利用cos2α=23,利用倍角公式以及余弦函数的定义式,求得a 2=15,从而得到|a |=√55,再结合b =2a ,从而得到|a −b |=|a −2a |=√55,从而确定选项.详解:根据题的条件,可知O,A,B 三点共线,从而得到b =2a , 因为cos2α=2cos 2α−1=2⋅(√a 2+1)2−1=23,解得a 2=15,即|a |=√55,所以|a −b |=|a −2a |=√55,故选B.点睛:该题考查的是有关角的终边上点的纵坐标的差值的问题,涉及到的知识点有共线的点的坐标的关系,余弦的倍角公式,余弦函数的定义式,根据题中的条件,得到相应的等量关系式,从而求得结果. 12. 设函数f (x )={2−x , x ≤01 , x >0,则满足f (x +1)<f (2x )的x 的取值范围是A. (−∞ , −1]B. (0 , +∞)C. (−1 , 0)D. (−∞ , 0) 【答案】D【解析】分析:首先根据题中所给的函数解析式,将函数图像画出来,从图中可以发现若有f (x +1)<f (2x )成立,一定会有{2x <02x <x +1,从而求得结果.详解:将函数f(x)的图像画出来,观察图像可知会有{2x <02x <x +1,解得x <0,所以满足f (x +1)<f (2x )的x 的取值范围是(−∞ , 0),故选D.点睛:该题考查的是有关通过函数值的大小来推断自变量的大小关系,从而求得相关的参数的值的问题,在求解的过程中,需要利用函数解析式画出函数图像,从而得到要出现函数值的大小,绝对不是常函数,从而确定出自变量的所处的位置,结合函数值的大小,确定出自变量的大小,从而得到其等价的不等式组,从而求得结果.二、填空题(本题共4小题,每小题5分,共20分)13. 已知函数f (x )=log 2(x 2+a ),若f (3)=1,则a =________. 【答案】-7【解析】分析:首先利用题的条件f (3)=1,将其代入解析式,得到f(3)=log 2(9+a)=1,从而得到9+a =2,从而求得a =−7,得到答案.详解:根据题意有f(3)=log 2(9+a)=1,可得9+a =2,所以a =−7,故答案是−7.点睛:该题考查的是有关已知某个自变量对应函数值的大小,来确定有关参数值的问题,在求解的过程中,需要将自变量代入函数解析式,求解即可得结果,属于基础题目.14. 若x , y 满足约束条件{x −2y −2≤0x −y +1≥0y ≤0,则z =3x +2y 的最大值为________.【答案】6【解析】分析:首先根据题中所给的约束条件,画出相应的可行域,再将目标函数化成斜截式y =−32x +12z ,之后在图中画出直线y =−32x ,在上下移动的过程中,结合12z 的几何意义,可以发现直线y =−32x +12z 过B 点时取得最大值,联立方程组,求得点B 的坐标代入目标函数解析式,求得最大值. 详解:根据题中所给的约束条件,画出其对应的可行域,如图所示:由z =3x +2y 可得y =−32x +12z , 画出直线y =−32x ,将其上下移动,结合z2的几何意义,可知当直线过点B 时,z 取得最大值, 由{x −2y −2=0y =0,解得B(2,0),此时z max =3×2+0=6,故答案为6.点睛:该题考查的是有关线性规划的问题,在求解的过程中,首先需要正确画出约束条件对应的可行域,之后根据目标函数的形式,判断z 的几何意义,之后画出一条直线,上下平移,判断哪个点是最优解,从而联立方程组,求得最优解的坐标,代入求值,要明确目标函数的形式大体上有三种:斜率型、截距型、距离型;根据不同的形式,应用相应的方法求解.15. 直线y =x +1与圆x 2+y 2+2y −3=0交于A , B 两点,则|AB |=________. 【答案】2√2【解析】分析:首先将圆的一般方程转化为标准方程,得到圆心坐标和圆的半径的大小,之后应用点到直线的距离求得弦心距,借助于圆中特殊三角形半弦长、弦心距和圆的半径构成直角三角形,利用勾股定理求得弦长.详解:根据题意,圆的方程可化为x 2+(y +1)2=4, 所以圆的圆心为(0,−1),且半径是2,根据点到直线的距离公式可以求得d =√12+(−1)2=√2,结合圆中的特殊三角形,可知|AB |=2√4−2=2√2,故答案为2√2.点睛:该题考查的是有关直线被圆截得的弦长问题,在解题的过程中,熟练应用圆中的特殊三角形半弦长、弦心距和圆的半径构成的直角三角形,借助于勾股定理求得结果.16. △ABC 的内角A , B , C 的对边分别为a , b , c ,已知bsinC +csinB =4asinBsinC ,b 2+c 2−a 2=8,则△ABC 的面积为________. 【答案】2√33【解析】分析:首先利用正弦定理将题中的式子化为sinBsinC +sinCsinB =4sinAsinBsinC ,化简求得sinA =12,利用余弦定理,结合题中的条件,可以得到2bccosA =8,可以断定A 为锐角,从而求得cosA =√32,进一步求得bc =8√33,利用三角形面积公式求得结果. 详解:根据题意,结合正弦定理可得sinBsinC +sinCsinB =4sinAsinBsinC ,即sinA =12, 结合余弦定理可得2bccosA =8,所以A 为锐角,且cosA =√32,从而求得bc =8√33, 所以△ABC 的面积为S =12bcsinA =12⋅8√33⋅12=2√33,故答案是2√33. 点睛:该题考查的是三角形面积的求解问题,在解题的过程中,注意对正余弦定理的熟练应用,以及通过隐含条件确定角为锐角,借助于余弦定理求得bc=8√33,利用面积公式求得结果.三、解答题:共70分。
(word完整版)2018年高考文科数学(全国I卷)试题及答案,推荐文档
绝密★启用前2018 年普通高等学校招生全国统一考试文科数学注意事项: 1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合 A = {0,2} , B = {- 2,- 1,0,1,2} ,则 A B A. {0, 2}B.{1, 2}2.设 z 1 i 2i ,则| z |1iC. {0}D. {2,1,0,1,2}A. 0B. 1 2C. 1D. 23. 某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番. 为更好地了解该地区农村的经济收入 变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是A. 新农村建设后,种植收入减少 B. 新农村建设后,其他收入增加了一倍以上 C.新农村建设后,养殖收入增加了一倍 D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半 4. 已知椭圆C:x22 y2 1 的一个焦点为(2, 0) ,则 C 的离心率为a41 A. 3B. 1 2C. 2 2D. 2 2 35. 已知圆柱的上、下底面的中心分别为 O1 , O2 ,过直线 O1O2 的平面截该圆柱所得的截面是面积为8 的正方形,则该圆柱的表面积为A. 12 2πB. 12πC. 8 2πD. 10π6. 设函数 f (x) x3 (a 1)x2 ax . 若 f (x) 为奇函数,则曲线 y f (x) 在点(0, 0) 处的切线方程为A. y 2xB. y xC. y 2xD. yx7. 在 △ABC 中,AD 为 BC 边上的中线,E 为 AD 的中点,则 EB 文科数学试题 第 1 页(共 10 页)A.3 AB1 AC 44C.3 4AB1 4ACB.1 4AB3 4ACD.1 4AB3 4AC8. 已知函数 f (x) 2 cos2 x sin2 x 2 ,则A. f (x) 的最小正周期为π ,最大值为 3B. f (x) 的最小正周期为π ,最大值为 4C. f (x) 的最小正周期为 2π ,最大值为 3D. f (x) 的最小正周期为 2π ,最大值为 49. 某圆柱的高为 2,底面周长为 16,其三视图如右图.圆柱表面上的点 M 在正视图上的对应点为 A,圆 柱表面上的点 N 在左视图上的对应点为 B,则在此圆柱侧面上,从 M 到 N 的路径中,最短路径的长度为A. 2 17 B .2 5 C. 3 D. 210. 在长方体 ABCD A1B1C1D1 中, AB BC 2 , AC1 与平面 BB1C1C 所成的角为 30 ,则该长方体的体积为A. 8B. 6 2C. 8 2D. 8 311. 已知角 的顶点为坐标原点,始边与 x 轴的非负半轴重合,终边上有两点 A(1,a) , B(2,b) , 且cos2 2 ,3则| a b |1A.5B. 5 5C. 2 5 5D. 12x , x ≤ 0, 12. 设函数 f (x) 则满足 f (x 1) f (2x) 的 x的取值范围是1, x 0,A.(, 1]B. (0, )C.(1, 0)D. (, 0)二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
2018年全国卷Ⅰ文数高考试题文档版(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B = A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中不正确的是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为(20),,则C 的离心率为 A .13B .12C .22D .2235.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为 A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC - B .1344AB AC - C .3144AB AC + D .1344AB AC + 8.已知函数()222cos sin 2f x x x =-+,则A .()f x 的最小正周期为π,最大值为3B .()f x的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .217B .25C .3D .210.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .62C .82D .8311.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1A a ,,()2B b ,,且 2cos 23α=,则a b -= A .15B .55C .255D .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题:本题共4小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年普通高等学校招生全国统一考试
文科数学
注意事项:
1.答卷前,考生务必将自己的九名、考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合{}02A =,,{}21012B =--,,,
,,则A B =( ) A .{}02,
B .{}12,
C .{}0
D .{}21012--,,
,, 2.设121i
z i i
-=
++,则z =( ) A .0
B .
12
C .1
D .2
3.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:
则下面结论中不正确的是( ) A .新农村建设后,种植收入减少
B .新农村建设后,其他收入增加了一倍以上
C .新农村建设后,养殖收入增加了一倍
D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
4.记n S 为等差数列{}n a 的前n 项和.若3243S S S =+,12a =,则3a =( ) A .12-
B .10-
C .10
D .12
5.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为( ) A .2y x =-
B .y x =-
C .2y x =
D .y x =
6.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =( ) A .31
44AB AC - B .13
44AB AC - C .
31
44
AB AC +
D .
13
44
AB AC +
7.某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱 侧面上,从M 到N 的路径中,最短路径的长度为( )
A .217
B .25
C .3
D .2
8.设抛物线24C y x =:的焦点为F ,过点()20-,且斜率为2
3
的直线与C 交于M ,N 两点,则FM FN ⋅=( ) A .5 B .6 C .7 D .8
9.已知函数()0
ln 0
x e x f x x x ⎧=⎨>⎩,≤,,()()f x f x x a =++( ),若()g x 存在2个零点,则a 的
取值范围是 A .[)10-,
B .[)+∞,
C .[)1-+∞,
D .[)1+∞,
10.下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆
的直径分别为直角三角形ABC 的斜边BC ,直角边AB ,AC ,ABC △的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自
Ⅰ,Ⅱ,Ⅲ的概率分别记为1p ,2p ,3p ,则( )
A .12p p =
B .13p p =
C .23p p =
D .123p p p =+
11.已知双曲线2
213
x C y -=:,O 为坐标原点,F 为C 的右焦点,过F 的直线与C 的两条渐
近线的交点分别为M ,N .若OMN △为直角三角形,则MN =( ) A .3
2
B .3
C .23
D .4
12.设函数()20
10x x f x y -⎧=⎨>⎩
,≤,,则满足()()12f x f x +<的x 的取值范围是( )
A .(]1-∞,
B .()0+∞,
C .()10-,
D .()0-∞,
二、填空题(本题共4小题,每小题5分,共20分)
13.已知函数()()
22log f x x a =+,若()31f =,则a =________.
14.若x y ,满足约束条件220100x y x y y --⎧⎪
-+⎨⎪⎩
≤≥≤,则32z x y =+的最大值为________.
15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB = ________.
16.ABC △的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,
2228b c a +-=,则ABC △的面积为________.
三、解答题(共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,
每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
) (一)必考题:共60分。
已知数列{}n a 满足11a =,()121n n na n a +=+,设n
n a b n
=. ⑴求123b b b ,,;
⑵判断数列{}n b 是否为等比数列,并说明理由; ⑶求{}n a 的通项公式.
18.(12分)
在平面四边形ABCM 中,3AB AC ==,90ACM =︒∠,以AC 为折痕将ACM △折起,使点M 到达点D 的位置,且AB DA ⊥. ⑴证明:平面ACD ⊥平面ABC ;
⑵Q 为线段AD 上一点,P 为线段BC 上一点,且2
3
BQ DQ DA ==,求三棱锥Q ABP -的体积.
某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日
用水量[)
00.1
,[)
0.10.2
,[)
0.20.3
,[)
0.30.4
,[)
0.40.5
,[)
0.50.6
,[)
0.60.7
,
频
数
1 3
2 4 9 26 5
使用了节水龙头50天的日用水量频数分布表
日用水量[)
00.1
,[)
0.10.2
,[)
0.20.3
,[)
0.30.4
,[)
0.40.5
,[)
0.50.6
,
频数 1 3 13 10 16 5
⑴在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
⑵估计该家庭使用节水龙头后,日用水量小于0.35m3的概率;
⑶估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据
以这组数据所在区间中点的值作代表.)
20.(12分)
设摆好物线22C y x =:,点()20A ,,()20B -,,过点A 的直线l 与C 交于M ,N 两点. ⑴当l 与x 轴垂直时,求直线BM 的方程;
⑵证明:ABM ABN =∠∠. 21.(12分)
已知函数()ln 1x f x ae x =--.
⑴油麦菜2x =是()f x 的极值点.求a ,并求()f x 的单调区间;
⑵证明:当1
a e
≥,()0f x ≥.
(二)选考题:共10分。
请考生在第22、23题中任选一题作答。
如果多做,则按所做的第
一题计分。
22.[选修4—4:坐标系与参数方程](10)
在直角坐标系xOy 中,曲线1C 的方程为2y k x =+.以坐标原点为极点,x 轴正半轴为
极轴建立极坐标系,曲线2C 的极坐标方程为22cos 30ρρθ+-=. ⑴求2C 的直角坐标方程;
⑵若1C 与2C 有且仅有三个公共点,求1C 的方程.
23.[选修4—5:不等式选讲](10分)
已知()11f x x ax =+--.
⑴当1a =时,求不等式()1f x >的解集;
⑵若()01x ∈,
时不等式()f x x >成立,求a 的取值范围.。
