七年级规律探索题答案
新初一规律探索题参考答案

前言:七年级上册数学期中考试,主要考察书本前2章,想要考试取得好的成绩,首先应一般能力:①基本知识、基本技能;②计算能力;其次要想获得高分必须具备高分能力:①观察、猜想、推理、验证的能力;②数形结合思想的建立;③分类讨论思想的建立;④方程思想的建立;对于重点中学学生,尤为重要。
高分能力是今后学习领先的有力保障,需要大量练习、总结、体会,七年级涉及的仅仅是一部分。
一、规律探索类题型规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形等条件,要求学生通过:①读题②观察③分析④猜想⑤验证,来探索对象的规律。
它体现了“特殊到一般”、“数形结合”等数学思想方法,考察学生的分析、解决问题能力。
题型可涉及填空、选择或解答。
【题型分类】【1、数字问题】最好具备数列的有关知识(小学奥数有涉及),实际考察的是:经历探索事物间的数量关系,用字母表示数和代数式表示的过程,建立初步的符号感,发展抽象思维,进一步使学生体会到代数式是刻画现实世界的有效数学模型。
如:1、正整数规律1、2、3、4、5、、、、可以表示为n (其中n 为正整数)2、奇数规律1、3、5、7、9、、、、可以表示为21n -(其中n 为正整数)3、偶数规律2、4、6、8、10、、、、可以表示为2n (其中n 为正整数)4、正、负交替规律变化一组数,不看他们的绝对值,只看其性质,为正负交替(1)、-、+、-、+、-、+、-、+可以表示为(1)n -(2)、+、-、+、-、+、-、+、-可以表示为1(1)n +-5、平方数规律1、4、9、16、、、、可以表示为2n (其中n 为正整数),能看得出:上面的规律数+1、+2、-1、-26、等差数列常识按一定次序排列的一列数就叫数列。
例如:(1)1,2,3,4,5,6,…(2)1,2,4,8,16,32;A 、一个数列中从左至右的第n 个数,称为这个数列的第n 项。
专题06 整式中规律探索的三种考法(解析版)-2024年常考压轴题攻略(7年级上册人教版)

专题06整式中规律探索的三种考法类型一、单项式规律性问题例.如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点.若青蛙从数1这点开始跳,第1次跳到数3那个点,如此,则经2015次跳后它停的点所对应的数为()A.5B.3C.2D.1【答案】C【分析】先根据题意,求出前几次跳到的点的位置,发现这是一个循环,按照3、5、2、1成一个循环,再用解循环问题的方法求解.【详解】解:按照题意,第一次在1这个点,下一次就跳到3,再下一次跳到5,再下一次跳到2,2是偶数了,就逆时针跳一个点,又回到了1这个点,发现这是一个循环,3、5、2、1是一个循环,÷ ,20154=5033∴最后到2这个点.故选:C.【点睛】本题考查找规律,解题的关键是通过前几个数发现这是一个循环问题,利用解循环问题的方法求解.【变式训练1】按上面数表的规律.得下面的三角形数表:【点睛】本题考查了数字的变化类,找出数字的变化规律是解题的关键.类型三、图形类规律探索例.根小棒,搭2020个这样的小正方形需要小棒()根.A.8080B.6066C.6061D.6060【答案】C【分析】通过归纳与总结得出规律:每增加1个正方形,火柴棒的数量增加3根,由此求出第n个图形时需要火柴的根数的代数式,然后代入求值即可.【详解】解:搭2个正方形需要4+3×1=7根火柴棒;搭3个正方形需要4+3×2=10根火柴棒;搭n个这样的正方形需要4+3(n﹣1)=3n+1根火柴棒;∴搭2020个这样的正方形需要3×2020+1=6061根火柴棒;故选C.【点睛】本题考查了图形规律型:图形的变化.解题的关键是发现各个图形的联系,找出其中的规律,有一定难度,要细心观察总结.【变式训练1】下列每一个图形都是由一些同样大小的三角形按一定的规律排列组成的,其中第①个图形中有5个小三角形,第②个图形中有10个小三角形,第③个图形中有16个小三角形,按此规律,则第⑨个图中小三角形的个数是()A.69B.73C.77D.83【答案】B【分析】根据已知图形得出第⑨个图形中三角形的个数的特点,据此可得答案.【详解】解:∵第①个图形中三角形的个数5=1+2×(1-1),第②个图形中三角形的个数10=5+2×1+3,第③个图形中三角形的个数16=5+2×2+3+4,第④个图形中三角形的个数23=5+2×3+3+4+5,第⑤个图形中三角形的个数31=5+2×4+3+4+5+6,……【答案】57【分析】根据每个图形增加三角形的个数,找到规律即可.【详解】解:第1个图形中一共有1个三角形,第2个图形中一共有1+4=5个三角形,第3个图形中一共有1+4+4=9个三角形,…,第n个图形中三角形的个数是1+4(n﹣1)=(4n﹣3)个,当n=15时,4n﹣3=4×15﹣3=57.故答案为:57.【点睛】本题考查了图形的变化规律,解题关键是通过图形数量的变化发现规律,并应用规律解决问题.课后训练20192020)a a -。
七年级数学人教课标(上册)38规律探索

规律探索一、选择题1.(5分)(2014•毕节地区,第18题5分)观察下列一组数:,,,,,…,它们是按一定规律排列的,那么这一组数的第n个数是.个数是故答案为:2.(2014•武汉,第9题3分)观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第5个图中共有点的个数是()3. (2014•株洲,第8题,3分)在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是()二.填空题1. (2014•湘潭,16题,3分)如图,按此规律,第6行最后一个数字是16,第672行最后一个数是2014.2. (2014•扬州,第18题,3分)设a1,a2,…,a2014是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,则a1,a2,…,a2014中为0的个数是165.,得到方程组二.填空题1. (2014•珠海,第10题4分)如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…则OA4的长度为8.OA,=;=2OA2.(2014年四川资阳,第16题3分)如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是(,).考点:规律型:点的坐标;等边三角形的性质.菁优网分析:根据O(0,0)A(2,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去,结合图形求出点P6的坐标.解答:解:由题意可得,每一个正三角形的边长都是上个三角形的边长的,第六个正三角形的边长是,故顶点P6的横坐标是,P5纵坐标是=,P6的纵坐标为,故答案为:(,).点评:本题考查了点的坐标,根据规律解题是解题关键.3.(2014年云南省,第14题3分)观察规律并填空(1﹣)=•=;(1﹣)(1﹣)=•••==(1﹣)(1﹣)(1﹣)=•••••=•=;(1﹣)(1﹣)(1﹣)(1﹣)=•••••••=•=;…(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)=.(用含n的代数式表示,n是正整数,且n≥2)考点:规律型:数字的变化类.分析:由前面算式可以看出:算式的左边利用平方差公式因式分解,中间的数字互为倒数,乘积为1,只剩下两端的(1﹣)和(1+)相乘得出结果.解答:解:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣)=••••••…=.故答案为:.点评:此题考查算式的运算规律,找出数字之间的联系,得出运算规律,解决问题.4.(2014•邵阳,第18题3分)如图,A点的初始位置位于数轴上的原点,现对A点做如下移动:第1次从原点向右移动1个单位长度至B点,第2次从B点向左移动3个单位长度至C点,第3次从C点向右移动6个单位长度至D点,第4次从D点向左移动9个单位长度至E点,…,依此类推,这样至少移动28 次后该点到原点的距离不小于41.≥5.(2014•孝感,第18题3分)正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是(63,32).6.(2014•滨州,第18题4分)计算下列各式的值:;;;.观察所得结果,总结存在的规律,应用得到的规律可得= 102014.先计算得到,=100=10=1000=10,=1000=10=100=10=1000=10=1000=107.(2014•德州,第17题4分)如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…A n,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…M n,…都在直线L:y=x上;②抛物线依次经过点A1,A2,A3…A n,….则顶点M2014的坐标为(4027,4027).(((8.(2014•菏泽,第14题3分)下面是一个某种规律排列的数阵:根据数阵的规律,第n(n是整数,且n≥3)行从左到右数第n﹣2个数是(用含n的代数式表示)故答案为:9.(2014年山东泰安,第24题4分)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,4),则点B2014的横坐标为.分析:首先利用勾股定理得出AB的长,进而得出三角形的周长,进而求出B2,B4的横坐标,进而得出变化规律,即可得出答案.解:由题意可得:∵AO=,BO=4,∴AB=,∴OA+AB1+B1C2=++4=6+4=10,∴B2的横坐标为:10,B4的横坐标为:2×10=20,∴点B2014的横坐标为:×10=10070.故答案为:10070.点评:此题主要考查了点的坐标以及图形变化类,根据题意得出B点横坐标变化规律是解题关键.三.解答题1. (2014•安徽省,第16题8分)观察下列关于自然数的等式:32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…根据上述规律解决下列问题:(1)完成第四个等式:92﹣4×42=17;(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.考点:规律型:数字的变化类;完全平方公式.菁优网分析:由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.解答:解:(1)32﹣4×12=5 ①52﹣4×22=9 ②72﹣4×32=13 ③…所以第四个等式:92﹣4×42=17;(2)第n个等式为:(2n+1)2﹣4n2=2(2n+1)﹣1,左边=(2n+1)2﹣4n2=4n2+4n+1﹣4n2=4n+1,右边=2(2n+1)﹣1=4n+2﹣1=4n+1.左边=右边∴(2n+1)2﹣4n2=2(2n+1)﹣1.点评:此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题.。
七年级数学探索规律——图形规律(人教版)(专题)(含答案)

试题难度:三颗星知识点:略
4.有一长条型链子,其外型由边长为1的正六边形排列而成.如图是此链子的任意一段示意图,其中每个黑色六边形与6个白色六边形相邻.若此链子上共有35个黑色六边形,则共有( )个白色六边形.
A.140 B.142
C.210 D.212
答案:B
解题思路:
分析:按照分类的思想来考虑,第1个黑色六边形周围的6个白色六边形可以分成两类,左边的2个白色六边形是一类,剩余的4个白色六边形是一类.黑色六边形每增加1个,白色六边形就增加4个.
第3个图中三角形个数为 ;
将上述规律标序号,如下:
① ;
② ;
③ ;
…
所以第 个图中三角形个数为 ;
当 时, ,
所以第20个图中三角形个数为77.
故选C.
试题难度:三颗星知识点:略
7.下列图形是由同样大小的五角星按一定的规律排列组成,其中第1个图形共有2个五角星,第2个图形共有8个五角星,第3个图形共有18个五角星,…,则第10个图形中五角星的个数为( )
当 时, ,
即此链子上共有35个黑色六边形时,共有142个白色六边形.
故选B.
试题难度:三颗星知识点:略
5.一块瓷砖的图案如图1所示,用这种瓷砖铺设地面,如果铺设成如图2的图案,其中完整的圆一共有5个,如果铺设成如图3的图案,其中完整的圆一共有13个,如果铺设成如图4的图案,其中完整的圆一共有25个,依此规律,第10个图中,完整的圆一共有( )
A.100个B.101个
C.181个D.221个
答案:C
解题思路:
分析:按照分类的思想来考虑,可以分为一块瓷砖自带的圆和多块瓷砖拼成的完整的圆;
第1个图案,自带的圆1个,拼成的圆0个,共 个;
七年级数学上册专题规律探索.doc

专题:规律探索1、观察下列各算式:1+3=4=2的平方,1+3+5二9二3的平方,1+3+5+7=16=4的平方…按此规律(1)试猜想:1+3+5+7+・・・+2005+2007的值?(2)推广: 1+3+5+7+9+・・・+ (2n-l)+ (2n+l)的和是多少?2、下而数列后两位应该填上什么数字呢?2 3 5 8 12 173、请填出下面横线上的数字。
1 123 5 8 _____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?5、有一串数字3 6 10 15 21 第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是()・A. 1B. 2C. 3D. 47、100个数排成一行,其中任意三个相邻数屮,屮间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1, 0,那么这100个数屮“0”的个数为_____________ 个.答案:1、(1) 1004的平方(2) n+1的平方2、23 30o数列中每两个相邻数字间的差分别是1, 2, 3, 4, 5, 6, 7。
3、13o这一数列后面一个数是前面相邻两个数的和。
4、34 o考虑时,可以从第一个数开始,每3个数加一个括号(1, 2, 3), (2, 3, 4), (3, 4, 5),……一共加了33个括号,剩下的一个必是第100个。
每个插号的第一个数分别是1, 2, 3,……因此第100个数必然是34。
5、28o 3+3=6 6+4二10 10+5二15 15+6二21 21+7二2& 所以第6 个是28。
其实一般这类的规律题无非就是在数的基础上加减乘除,有些麻烦点的就是-•个数乘上倍数后在加1或减lo6、 A7、33二、数、式计算规律题1、已知下列等式:%1m%113+23=32;%113+23+33=62;%113+23+33+43= 102;由此规律知,第⑤个等式是________________________ .2、观察下面的几个算式:1+2+1二4,1、13 4-23 +33 +43 +53 = 15210000 (1)343400 或-xlOOxlOlxlO2 (2)-*- /?(/? + \\n +2)(3) — n(n + 卅〃 + 2X" + 3)109.2、 3、 4、1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1 +2+3+・・・+99+100+99+・・・+3+2+1 二 .3、1+2+3+…+100= ?经过研究,这个问题的一般性结论是1+2+3+… + ” = 抑 + 1),其)15是正整数•现在我们来研究一个类似的问题:1 X 2+2X 3+…心 + 1)= ?观察下而三个特殊的等式Ix2 = |(lx2x3-Oxlx2)2x3 = |(2x3x4-lx2x3)3X 4 = |(3X 4X 5-2X 3X 4)将这三个等式的两边相加,可以得到1 X2+2X3+3X4=1x3x4x5 = 20 3读完这段材料,请你思考后回答:(1) 1x2 +2x3 +…+ 100x101 = ____________(2) 1x2x34-2x3x4 + ••• + n{ri + 1)(/? + 2)= ________________⑶ 1X 2X 3 + 2X 3X 4 + ・・・ + n(n + 怆 + 2)= __________.-f z .rl 小2 & 2 小3 「 3 才4 ” 4 °5 “ 5 4^己犬口:2— = 2~ x — ,3 --------------------- — = 3" x — ,4 ---- = 4~ x 一,5= 5~ x—— 3 3 8 8 15 15 24 24…,若10 + - = 102x^符合前面式子的规律,贝h + b = a a ---答案:规律探索专题训练先观察占+圭1 +2 +3 +4 +5 = 15 =(1 +5)x521+3=4=221+3+5=9=321+3+5+7二16二半1+3+5+7+9=25=5?(1)请猜想1+3+5+7+9+ (19)(2)请猜想1+3+5+7+9+・・・+ (2门-1)乘方形式,3分) ______ ;(只填数字,2分)(2n+l) + (2门+3) = ;(只填---- + + ------------- = ( ------- ) + ( ----- ) + ( ------- ) =1 —-=-1x2 2x3 3x4 1 2 2 3 3 4 4 4再计算占+舟+占…祐的值・答案:n/ (n+1)2.若“!”是一种数学运算符号,并且1! =1, 2! =2X1=2, 3! =3X2X1=6,4! =4X3X2X1,…,则巴匕的值为98! ----------------答案:99003.观察下列等式,并回答问题:I+2+3=6=(Z)X321 +2 +3 +4 = 10= (1 + 4)><421 +2 +3 ----- n =并求1 + 2 + 3 +…+ 1000的结果。
七年级数学有理数规律探索性试题解析试题

无棣县埕口中学七年级数学 有理数规律探究性试题解析一、 数阵规律探究问题例1:〔2021年〕把数字按如下图排列起来,从上开场,依次为第一行、第二行、第三行、……,中间用虚线围一列,从上至下依次为1、5、13、…,那么第10个数为__________________。
2827262423222120181716151411108762析解:观察数阵中用虚线围成的数,不难发现:第2个数5比第1个数1多4,第3个数13比第2个数5多8,第4个数25比第3个数13多12,…,第n 个数比它的前一个数多了4的(n-1)倍数,所以被围住的数从上至下分别是1、5、13、25、41、61、85、113、145、181、…,所以第10个数是181。
二、数式规律探究问题例2:〔2021年〕一个正整数数表如下〔表中下一行中数的个数是上一行中数的个数的2倍〕:那么第6行中的最后一个数为【】A.31B.63C.127D.255析解:此题属于表格信息题,解决问题的关键是要通过观察、考虑来发现其中的规律。
因为第1行有1个数,后面每行数的个数都是前面一行数字个数的2倍,所以第4行有8个数,第5行有16个数,第6行有32个数。
观察每行的最后一个数分别是2的行数次幂与1的差,所以第6行的最后一个数为26-1=63。
例3:〔2021年〕观察以下一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2021个数是A.1 B.2 C.3 D.4析解:这是由1、2、3、4这四个数字组成的一组数的排列,可以发现6个数“1,2,3,4,3,2〞恰好一个轮回,而2021=6×334+1,所以第2021个数是这6个数中的第一个数1,应选〔A〕。
三、数形结合探究问题例4:〔2021年〕如下图,按以下方法将数轴的正半轴绕在一个圆〔该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2〕上:先让原点与圆周上数字0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合。
人教版七年级数学上册小专题练习四《有理数-探索规律题》(含答案)

人教版七年级数学上册小专题练习四《有理数-探索规律题》一、选择题1.观察下列各式: - 2x ,4x 2, - 8x 3,16x 4, - 32x 5,…则第n 个式子是( )A.- 2n - 1x nB.( - 2)n - 1x nC.- 2n x nD.( - 2)n x n2.下图是一个运算程序的示意图,若开始输入x 的值为125,则第2 016次输出的结果为( )A.125B.25C.1D.53.如图是由一些点组成的图形,按此规律,第n 个图形中点的个数为( )A.n 2+1B.n 2+2C.2n 2+2D.2n 2 - 14.如图,下列每个图都是由若干个点组成的形如三角形的图案,每条边(包括两个顶点)有n 个点,每个图案的总点数是S ,按此推断S 与n 的关系式为( )A.S=3nB.S=3(n - 1)C.S=3n - 1D.S=3n +15.下面每个表格中的四个数都是按相同规律填写的:根据此规律确定x 的值为( )A.135B.170C.209D.2526.有一列数a 1,a 2,a 3,a 4,…,a n ,从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若a 1=2,则a 2018的值为( )A.2B.- 1C.12D.2018 7.a 是不为1的有理数,我们把称为a 的差倒数,如2的差倒数为=﹣1,﹣1的差倒数=,已知a 1=5,a 2是a 1的差倒数,a 3是a 2的差倒数,a 4是a 3的差倒数…,依此类推,a 2019的值是( )A .5 B.﹣ C . D .8.如下表,从左到右在每个小格子中都填入一个整数..,使得其中任意三个相邻..格子中所填整数之和都相等,则第2014个格子中的数为( )A.3B.2C.0D.-19.已知一列数:1,-2,3,-4,5,-6,7,…将这列数排成下列形式:按照上述规律排下去,那么第100行从左边数第5个数是( )A.-4955B.4955C.-4950D.495010.计算:,,,,,归纳各计算结果中的个位数字规律,猜测22022-1的个位数字是()A.1 B.3 C.7 D.5二、填空题11.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c=________.12.观察下列等式:1=12,1+3=22, 1+3+5=32,1+3+5+7=42,…,则1+3+5+7+…+2 015=_________.13.已知:,,,…,观察上面的计算过程,寻找规律并计算C106=.14.如图,是一个运算程序的示意图,若开始输入x的值为625,则第2020次输出的结果为.15.观察下列数据:﹣2,,﹣,,﹣,…,它们是按一定规律排列的,依照此规律,第11个数据是.16.正整数按如图的规律排列.请写出第20行,第21列的数字.参考答案1.答案为:D2.答案为:D.3.答案为:B4.答案为:B.5.答案为:C6.答案为:C7.答案为:D.8.答案为:B;解析:已知其中任意三个相邻格子中所填整数之和都相等,则3+a+b=a+b+c,a+b+c=b+c-1,所以a=-1,c=3,按要求排列顺序为,3,-1,b,3,-1,b,…,再结合已知表得:b=2,所以每个小格子中都填入一个整数后排列是:3,-1,2,3,-1,2,…,得到:每3个数一个循环,则:2014÷3=670余3,因此第2011个格子中的数为2.故选B9.答案为:B10.答案为:B11.答案为:110.12.答案为:10082.13.答案为:21014.答案为:1解析:依次求出每次输出的结果,根据结果得出规律,即可得出答案.解:当x=625时,x=125,当x=125时,x=25,当x=25时,x=5,当x=5时,x=1,当x=1时,x+4=5,当x=5时,x=1,…依此类推,以5,1循环,(2020﹣2)÷2=1010,即输出的结果是1,故答案为:115.答案为:﹣.解析:∵﹣2=﹣,,﹣,,﹣,…,∴第11个数据是:﹣=﹣.16.答案为:420;。
部编数学七年级上册专题05整式中的两种规律探索问题(解析版)(人教版)含答案

专题05 整式中的两种规律探索问题类型一、数字类规律探索例.观察:(x ﹣1)(x +1)=x 2﹣1,(x ﹣1)(x 2+x +1)=x 3﹣1,(x ﹣1)(x 3+x 2+x +1)=x 4﹣1,据此规律,当(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=0时,代数式x 2019﹣1的值为 _____.【答案】0或﹣2【详解】解:根据题意得∶ (x ﹣1)(x +1)=x 2﹣1,(x ﹣1)(x 2+x +1)=x 3﹣1,(x ﹣1)(x 3+x 2+x +1)=x 4﹣1,……∴(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=x 6﹣1∵(x ﹣1)(x 5+x 4+x 3+x 2+x +1)=0,∴x 6﹣1=0,解得:x =1或x =﹣1,则x 2019﹣1=0或﹣2,故答案为:0或﹣2.【变式训练1】a 是不为1的有理数,我们把11-a 称为a 的差倒数,如2的差倒数为1-11-2=,-1的差倒数为111(1)2=--,已知15a =,2a 是1a 差倒数,3a 是2a 差倒数,4a 是3a 差倒数,以此类推……,2021a 的值是()A .5B .14-C .43D .45【答案】B【解析】∵15a = , 2a 是1a 的差倒数,∴211154a ==--,∵3a 是2a 的差倒数,4a 是3a 的差倒数,∴314151-4a ==æö-ç÷èø,∴415415a ==-,根据规律可得n a 以5,1-4,45为周期进行循环,因为2021=673×3…2,所以202114a =-.故选B .【变式训练2】有2021个数排成一行,对于任意相邻的三个数,都有中间数等于前后两数的和,如果第一个数是0,第二个数是1, 那么前6个数的和是______, 这2021个数的和是______.【答案】0 1【解析】由题意得:第3个数是101-=,第4个数是110-=,第5个数是011-=-,第6个数是101--=-,则前6个数的和是()()0110110++++-+-=,第7个数是1(1)0---=,第8个数是0(1)1--=,归纳类推得:这2021个数是按0,1,1,0,1,1--循环往复的,202163365=´+Q ,且前6个数的和是0,\这2021个数的和与前5个数的和相等,即为()011011++++-=,故答案为:0,1.【变式训练3】有一列数11315,,,,228432---,…,那么第n 个数为______.【答案】()12n nn-【详解】解:()11122-=-´,()221221242==-´,()3333182-=-´,()4414414162==-´,()55551322-=-´,……由此发现:第n 个数为()12n n n -.故答案为:()12n nn-【变式训练4】杨辉三角又称贾宪三角,是二项式系数在三角形中的一种几何排列,如图,观察下面的杨辉三角:按照前面的规律,则()7a b +的展开式中从左起第三项为______.()1a b a b +=+()2222a b a ab b +=++()3322333a b a a b ab b +=+++()4432234464a b a a b a b ab b +=++++LL【答案】5221a b 【详解】解:根据题意,()7a b +=7652433425677213535217a a b a b a b a b a b ab b +++++++,∴()7a b +的展开式中从左起第三项为5221a b ,故答案为:5221a b .类型二、图形类规律探索例.如图,两条直线相交,有1个交点,三条直线相交最多有3个交点,四条直线相交最多有______个交点,n 条直线相交最多有______个交点.【答案】 6 (1)2n n -【详解】解: 如图,两条直线相交最多有1个交点,即()22112´-=;三条直线相交最多有3个交点,即()33132´-=;四条直线相交最多有6个交点,即()44162´-=,五条直线相交最多有10个交点,即()551102´-=,……∴n 条直线两两相交,最多有(1)2n n -个交点(n 为正整数,且n ≥2).故答案为6;(1)2n n -.【变式训练1】如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第_____个图形共有45个小球.【答案】9【详解】解:第1个图中有1个小球,第2个图中有3个小球,3=1+2,第3个图中有6个小球,6=1+2+3,第4个图中有10个小球,10=1+2+3+4,……n(1+n)个小球,照此规律,第n个图形有1+2+3+4+…+n=12n(1+n)=45,∴12解得n=9或-10(舍去),故答案为:9.【变式训练2】为庆祝“六·一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,则n的值为______.【答案】10【详解】解:由题可知:第n个图形有(6n+2)根火柴棒,第(n+1)个图形有(6n+8)根火柴棒,∵摆第n个“金鱼”和第(n+1)个“金鱼”需用火柴棒的根数为130根,∴6n+2+6n+8=130,解得n=10.故答案为:10.【变式训练3】如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数为___个,第n层含有正三角形个数为___个.n-【答案】114 126【解析】根据题意分析可得:从里向外的第1层包括6个正三角形,第2层包括18个正三角形,此后,每层都比前一层多12个,依此递推,第10层中含有正三角形个数是6+12×9=114个,则第n层中含有正三角形个数是6+12×(n-1)=126n-个,故答案为:114,126n-.【变式训练4】观察下列图形:它们是按一定规律排列的,依照此规律,用6064个五角星摆出的图案应该是第_______个图形.【答案】2021【解析】观察发现,第1个图形五角星的个数是:1+3=4,第2个图形五角星的个数是:1+3×2=7,第3个图形五角星的个数是:1+3×3=10,第4个图形五角星的个数是:1+3×4=13,⋯第n个图形五角星的个数是:1+3•n=1+3n,∵6064120213-=,∴用6064个五角星摆出的图案应该是第2021个图形,故答案为:2021.课后训练1.下列图形都是由同样大小的黑色正方形纸片组成,其中第1个图有3张黑色正方形纸片,第2个图有5张黑色正方形纸片,第3个图有7张黑色正方形纸片,…,按此规律排列下去,若第n个图中有201张黑色正方形纸片,则n的值为( )A.99B.100C.101D.102【答案】B【详解】解:观察图形知:第一个图中有3=1+2×1个正方形,第二个图中有5=1+2×2个正方形,第三个图中有7=1+2×2个正方形,…故第n 个图中有1+2×n =2n +1=201(个)正方形,解得n =100故选B .2.如图,将若干颗棋子按箭头方向依次摆放,记第一颗棋子摆放的位置为第1列第1排,第二颗棋子摆放的位置为第2列第1排,第三颗棋子摆放的位置为第2列第2排……,按此规律摆放在第16列第8排的是第( )颗棋子.A .85B .86C .87D .88【答案】B 【详解】偶数列数与排数表:偶数列数排数22436485……n 12n +∴当n =16时,排数为:192n +=,∴前16列共有棋子:()9102123+-3=2-3=872´+++´…9(颗),∴第16列第8排的棋子位次是:87-1=86.故选B .3.将一正方形按如图方式分成n 个完全相同的长方形,上、下各横排三个,中间两行各竖排若干个,则n 的值为( )A .12B .16C .18D .20【答案】C 【详解】解:设长方形的长为a ,宽为b ,根据题意得,2a +2b =3a , 整理得,a =2b ,∴竖排的一行的长方形的个数为3a ÷b =(3×2b )÷b =6,∴n =3×2+6×2=6+12=18.故选:C .4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图(1)就是一个幻方.图(2)是一个未完成的幻方,则x 与y 的和是( )A .9B .10C .11D .12【详解】解:设如图表所示:根据题意可得:x +6+20=22+z +y ,整理得:x -y =-4+z ,x +22+n =20+z +n ,20+y +m =x +z +m ,整理得:x =-2+z ,y =2z -22,∴x -y =-2+z -(2z -22)=-4+z ,解得:z =12,∴x +y =3z -24=12故选:D .5.如图,按此规律,第6行最后一个数字是_____,第_____行最后一个数是2020.【答案】16 674【详解】Q 每一行的最后一个数字分别是1,4,7,10 ,……,\第n 行的最后一个数字为:1+3(1)32n n -=-,\第6行最后一个数字为:36216´-=;322020n -=,解得:674n =,故答案为:16,674.6.如图,每个图形中的三个数之间均具有相同的规律.根据此规律,若图形中11m =,12n =,则M 的值为________.【详解】解:∵1×(2+1)=3,3×(4+1)=15,5×(6+1)=35,∴右下圆圈内的数=上方圆圈内的数×(左下圆圈内的数+1),∴M =m (n +1),∴M =11×(12+1)=143.故答案为:143.7.为了求220211222+++¼+的值,可令220211222S =+++¼+,则220222222S =++¼+,因此2022221S S -=-,所以220212022122221+++¼+=-.按照以上推理计算出1220211333---+++¼+的值是______.【答案】2021332--【详解】解:令1220211333S ---=+++¼+,则1220212022133333S ----=++¼++,因此20221313S S --=-,则20222313S --=-,得:2021332S --=,所以20211220213313332-----+++¼+=.故答案为:2021332--.8.今年“10.1”黄金周,适逢祖国70大庆,广西柳州赛长桌宴,民族风情浓郁,吸引了大量游客如果长桌宴按下图方式就坐(其中□代表桌子,〇代表座位),则拼接n (n 为正整数)张桌子时,最多可就坐_____人.【答案】(6n +2)【详解】解:根据图示知,拼1张桌子,可以坐(2+6)人.拼2张桌子,可以坐[2+(6×2)]人.拼3张桌子,可以坐[2+(6×3)]人.…拼接n (n 为正整数)张桌子,可以坐(6n +2)人.故答案是:(6n +2).9.在日历上,我们可以发现其中某些数满足一定的规律,如图是2012年8月份的日历.我们任意选择其中所示的方框部分,将每个方框部分中4个位置上的数交又相乘,再相减,例如:7136147´-´=,172316247´-´=,不难发现,结果都是7.2012年8月日一二三四五六12345678910111213141516171819202122232425262728293031(1)请你再选择两个类似的部分试一试,看看是否符合这个规律;(2)换一个月的月历试一下,是否有同样的规律?(3)请你利用整式的运算对以上的规律加以证明.【答案】(1)111710187´-´=,符合;(2)392107´-´=;(3)见解析【详解】解:(1)由题意得:111710187´-´=,符合;(2)392107´-´=;答:换一个月的月历试一下还是同样的规律;(3)设上边第一个数为x ,则其后的数为(x +1),第二行的两个数分别为(x +7),(x +8),根据题意,得22(1)(7)(8)8787x x x x x x x x ++-+=++--=.10.(1)你知道下面每一个图形中各有多少个小圆圈吗?第5个图形中应该有多少个小圆圈?为什么?(2)完成下表:边上的小圆圈数12345每个图中小圆圈的总数(3)如果用n 表示六边形边上的小圆圈数,m 表示这个六边形中小圆圈的总数,那么m 和n 的关系是什么?【答案】(1)第1个图形:1个;第2个图形:7个;第3个图形:19个;第4个图形:37个;第5个图形:61个,理由见解析;(2)1,7,19,37,61;(3)2331m n n =-+【详解】(1)观察每个图形的特点,就可以算出第1个图形的小圆圈有1个,第2个图形的小圆圈有2+3+2=7个,第3个图形的小圆圈有3+4+5+4+3=19个,第4个图形的小圆圈有4+5+6+7+6+5+4=37个,由此可推知第5个图形的小圆圈有5+6+7+8+9+8+7+6+5=61个;(2)将(1)算出的结果填入下列表格,如下表所示,边上的小圆圈数12345每个图中小圆圈的总数17193761(3)结合(1)(2)可知,m 与n 之间的函数关系为:()()()()()1...212...1m n n n n n n n n n n=+++++-++-++-++++首尾相加得()()21...(2)1m n n n n n n =+++++-++-éùëû()()21322213312n n n n n --=+-=-+2331m n n =-+.11.对任意一个四位正整数m ,如果m 的百位数字等于个位数字与十位数字之和,m 的千位数字等于十位数字的2倍与个位数字之和,那么称这个数m 为“筋斗数”.例如:m =5321,满足1+2=3,2×2+1=5,所以5321是“筋斗数”.例如:m =8523,满足2+3=5,但2×2+3=7≠8,所以8523不是“筋斗数”.(1)判断9633和2642是不是“筋斗数”,并说明理由;(2)若m 是“筋斗数”,且m 与13的和能被11整除,求满足条件的所有“筋斗数”m .【答案】(1)9633是“筋斗数”;2642不是“筋斗数”; 理由见解析(2)m 的值为9909或2110或6422【解析】(1)解:9633是“筋斗数”,2642不是“筋斗数”,理由如下:∵6=3+3,9=2×3+3,∴9633是“筋斗数”;∵6=4+2,28+2¹,∴2642不是“筋斗数”;(2)设m 的个位数为a ,0≤a ≤9,十位数为0<b ≤9,且a 、b 为整数∵m 是“筋斗数”,∴m 的百位数为a +b ,千位数为2b +a ;∴m =1000(2b +a )+100(a +b )+10b +a =1100a +110b +2000b +a∵m 与13的和能被11整除,∴1100a +110b +2000b +a +13能被11整除,∵2b +a ≤9且a 、b 为整数,∴b ≤4.5∵1100a +110b 能被11整除,∴2000b +a +13能被11整除,∴b =0,a =9或b =1,a =0或b =2,a =2或b =3,a =4,或b =4,a =6,∴a +b =9,2b +a =9或a +b =1,2b +a =2或a +b =4,2b +a =6或a +b =7,2b +a =10(舍去)或a +b =10,2b +a =14(舍去),∴m 的值为9909或2110或642212.看图填空:如图,把一个面积为1的正方形等分成两个面积为12的长方形,接着把面积为12的长方形等分成两个面积为14的长方形,再把面积为14的长方形等分成面积为18的长方形,如此进行下去……(1)试利用图形揭示的规律计算:1111111112481632641282562n ++++++++L =_______.并使用代数方法证明你的结论.(2)请给利用图(2),再设计一个能求:2341111122222n +++++L 的值的几何图形.【答案】(1)112n - ,证明见解析;(2)见解析【解析】(1)解:①由题意可知当最后一个小长方形的面积为12n时 ,1111111112481632641282562n ++++++++L 的值为正方形面积减去最后一个小长方形面积,即:112n - ,1111111111124816326412825622n n \++++++++=-L ;②设1111111112481632641282562n s =++++++++L ,111111111212481632641282n s -=++++++++L ,1212n s s \-=-,即112ns =-,1111111111124816326412825622n n \++++++++=-L ;(2)如图所示,将面积为1的正方形等分成两个面积为12的三角形,接着把面积为12的三角形等分成两个面积为14的三角形,再把面积为14的三角形等分成面积为18的三角形,如此进行下去,则2341111122222n +++++L 的值即为正方形面积减去最后一个小三角形面积:112n -。
2023学年浙江七年级数学上学期专题训练专题02 运算思维之规律探究(解析版)

专题02运算思维之规律探究专练(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知一列数1a ,2a ,3a ,…,具有如下规律:211n n n a a a ++=+,2n n a a =(n 是正整数).若11a =,则37a 的值为( )A .1B .5C .7D .11【答案】D【分析】 根据题干公式寻找规律,从而逐步推出结果.【详解】解:由a 2n +1=a n +a n +1,a 2n =a n (n 是正整数)可得:a 37=a 18+a 19=2a 9+a 10=2(a 4+a 5)+a 5=2a 4+3a 5=2a 2+3(a 2+a 3)=5a 2+3a 3=8a 1+3a 2=11a 1=11. 故选:D .【点睛】本题考查数字变化规律,解题关键是根据题中规律拆项.2.把一根起点为0的数轴弯折成如图所示的样子,虚线最下面第1个数字是0,往上第2个数字是6,第3个数字是21,…,则第5个数字是( )A .78B .80C .82D .89【答案】A【分析】 观察根据排列的规律得到第1个数字为0,第2个数字为0加6个数即为6,第3个数字为从6开始加15个数得到21,第4个数字为从21开始加24个数即45,…,由此得到后面加的数比前一个加的数多9,由此得到第5个数字为0+6+(6+9×1)+(6+9×2)+(6+9×3).【详解】解:∵第一个数字为0,第二个数字为0+6=6,第三个数字为0+6+15=21,第四个数字为0+6+15+24=45,第五个数字为0+6+15+24+33=78,故选:A .【点睛】此题主要考查了数字变化规律,发现数在变化过程中各边上点的数字的排列规律是解题关键.3.有一列数:123,,,,n a a a a …,若112a =-,从第2个数起,每一个数都等于“1与它前面的那个数的差的倒数”,那么2021a 的值为( )A .2-B .12-C .23D .3【答案】C【分析】根据每一个数都等于1与它前面那个数的差的倒数多列举几个数字,找出规律即可.【详解】解:a 1=12-,13122⎛⎫--= ⎪⎝⎭, a 2=23,21133-=, a 3=3,132-=-,a 4=12-, …,从上面的规律可以看出每三个数一循环,2021÷3=673......2,∵a 2021=a 2=23, 故选:C .【点睛】本题主要考查数字的变化规律,总结归纳数字的变化规律是解题的关键.4.定义一种对正整数n 的“F ”运算:∵当n 为奇数时,结果为35n +;∵当n 为偶数时,结果为2k n ;(其中k 是使2k n 为奇数的正整数),并且运算可以重复进行,例如,取26n =.则:26134411F F F −−−→−−−→−−−→①②③第一次第二次第三次若49n =,则第2020次“F 运算”的结果是( )A .152B .19C .62D .31【答案】D【分析】计算出n =49时第1、2、3、4、5、6、7次运算的结果,找出规律再进行解答即可求解.【详解】解:本题提供的“F 运算”,需要对正整数n 分情况(奇数、偶数)循环计算,由于n =49为奇数应先进行F ∵运算,即3×49+5=152(偶数),需再进行F ∵运算,即152÷23=19(奇数),再进行F ∵运算,得到3×19+5=62(偶数),再进行F ∵运算,即62÷21=31(奇数),再进行F ∵运算,得到3×31+5=98(偶数),再进行F ∵运算,即98÷21=49(奇数),再进行F ∵运算,得到3×49+5=152(偶数),…,即第1次运算结果为152,…,第4次运算结果为31,第5次运算结果为98,…,可以发现第6次运算结果为49,第7次运算结果为152,则6次一循环,2020÷6=336…4,则第2020次“F 运算”的结果是31.故选:D .【点睛】本题考查了有理数的混合运算,既渗透了转化思想、分类思想,又蕴涵了次数、结果规律探索问题,检测学生阅读理解、抄写、应用能力.5.观察图形并判断照此规律从左到右第四个图形是() A.B.C.D.【答案】D【详解】观察图形可知:单独涂黑的角顺时针旋转,只有D符合.故选:D.6.如图所示,下列图形都是由相同的玫瑰花按照一定的规律摆成的,按此规律摆下去,第n个图形中有120朵玫瑰花,则n的值为()A.28B.29C.30D.31【答案】C【详解】分析:根据题目中的图形变化规律,可以求得第个图形中玫瑰花的数量,然后令玫瑰花的数量为120,即可求得相应的n的值,从而可以解答本题.详解:由图可得,第n个图形有玫瑰花:4n,令4n=120,得n=30,故选C.点睛:本题考查图形的变化类,解答本题的关键是明确题意,找出题目中图形的变化规律.7.如图,用火柴棍分别搭一排三角形组成的图形和一排正方形组成的图形,三角形、正方形的每一边用一根火柴棒.如果搭这两个图案一共用了2030根火柴棒,且正方形的个数比三角形的个数的少4个,则搭成的三角形的个数是()A.429B.409C.408D.404【答案】C【分析】根据搭建三角形和正方形一共用了2030根火柴,且三角形的个数比正方形的个数多4个,即可得搭建三角形的个数.【详解】解:∵搭建三角形和正方形一共用了2030根火柴,且三角形的个数比正方形的个数多4个,观察图形的变化可知:搭建n个三角形需要(2n+1)根火柴棍,n个正方形需要(3n+1)根火柴棍,所以2n+1+3(n-4)+1=2030,解得n=408.故选:C.【点睛】本题考查了规律型-图形的变化类,解决本题的关键是根据图形的变化寻找规律.8.将图∵所示的正六边形进行分割得到图∵,再将图∵中最小的某一个正六边形按同样的方式进行分割得到图∵,再将图∵中最小的某一个正六边形按同样的方式进行分割,…,则第2014个图形中,共有()个正六边形.A.4027B.6040C.6061D.10066【答案】B【分析】观察第二个图形,有1+3=4个;第三个图形,有1+3+3=7个;依此类推,发现规律即可解答.【详解】解:第二个图形中有1+3=4个;第三个图形中有1+3+3=7个;...∵第n个图形中有1+3(n-1)=3n-2个;∵第2014个图形中有1+3×(2014-1)=6040个;故选B.【点睛】本题考查了图形的变化规律:结合图形观察前几个具体数值,即可发现每一次总是多3个正六边形是关键.二、填空题9.如表是一组密码的一部分,目前已破译出“守初心”的对应口令是“担使命”,根据上述破译方法,破译出“找差距”的对应口令是_______.【答案】抓落实【分析】根据表格中汉字所在行及列的位置以及对应口令所在行和列的位置探索规律,从而求解.【详解】解:由题意“守”位于第3行第4列,其对应口令“担”位于第1行第3列“初”位于第5行第2列,其对应口令“使”位于第3行第1列“心”位于第4行第7列,其对应口令“命”位于第2行第6列∵位于第n行第m列的汉字,其对应口令位于第(n-2)行第(m-1)列,由此,“找”位于第7行第2列,其对应口令位于第5行第1列,即“抓”“差”位于第3行第2列,其对应口令位于第1行第1列,即“落”“距”位于第5行第7列,其对应口令位于第3行第6列,即“实”故答案为:抓落实.【点睛】本题考查规律探索,准确理解题意,分析汉字所在位置的规律是解题关键. 10.如图各网格中四个数之回都有相同的规律,则第9个网格中右下角的数为_________.【答案】119【分析】从图中观察出各个格子中的数据的规律,找出第九个格子的各个数字即可.【详解】解:由图中的数字可知,左上角的数字是一些连续的正整数,从1开始,左下角的数字是对应的左上角的数据加1,右上角的数字是对应的左下角的数字加2, 右下角的数字是左下角的数字与右上角的数字乘积再加左上角数字的和,故第9个正方形中的左上角的数字是9,左下角的数字是10,右上角的数字是11,右下角的数字是:10×11+9=119;故答案为:119.【点睛】本题考查数字变化的规律的相关内容,解题的关键是找出各个数字之间的规律. 11.观察下列各式:∵2204-=;∵22318-=;∵224212-=;∵225316-=;∵226420-=;……;用含自然数n 的等式表示你发现的规律:__________________.【答案】(n +2)2-n 2=4(n +1)【分析】分别列出n =0,1,2,3,4,5…的情况,再进行总结归纳即可.【详解】解:∵n =0,(0+2)2-02=4×1,∵n =1,(1+2)2-12=4×2,∵n =2,(2+2)2-22=4×3,∵n =3,(3+2)2-32=4×4,∵n =4,(4+2)2-42=4×5,…,所以n =n 时,(n +2)2-n 2=4(n +1),故答案为:(n +2)2-n 2=4(n +1).【点睛】本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.12.设123,,a a a ,…是一列正整数,其中1a 表示第一个数,2a 表示第二个数,……,n a 表示第n 个数(n 是正整数).若12a =,()()221411n n n a a a +=---,则(1)2a =_______(2)2021a =______.【答案】4 4042【分析】先将4a n =(a n +1-1)2-(a n -1)2,变形,结合a 1=2,a 1,a 2,a 3……是一列正整数,得出递推公式a n +1=a n +2,进而可得a n =2n ,将n =2021代入即可求得答案.【详解】解:∵a 1=2,4a n =(a n +1-1)2-(a n -1)2,a 1,a 2,a 3……是一列正整数,∵a n -1≥0,(a n +1-1)2=(a n -1)2+4a n =(a n +1)2,∵a n +1-1=a n +1,∵a n +1=a n +2,∵a 1=2,∵a 2=4,a 3=6,a 4=8,a 5=10,…∵a n =2n ,∵a 2021=2×2021=4042.故答案为:4;4042.【点睛】本题考查了数字的变化规律,由已知条件推出递推关系式,进而得出含n 字母的各项的表达式,是解题的关键.13.观察下列等式:22110=-,22321=-,22532=-,…按此规律,则第n 个等式为21n -=__________________. 【答案】()221n n --.【分析】第一个底数是从1开始连续的自然数的平方,减去从0开始连续的自然数的平方,与从1开始连续的奇数相同,由此规律得出答案即可.【详解】解:∵22110=-,22321=-,22532=-,…∵第n 个等式为:()22211n n n -=-- 故答案是:()221n n --.【点睛】本题考查了数字的变化类,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题的关键.14.数202020212022379⋅⋅的个位数字是____.【答案】7【分析】由3n 的个位数字是3,9,7,1四次一循环,7n 的个位数字是7,9,3,1四次一循环,9n 的个位数字是9,1,9,1四次一循环,继而可以求得32009×72010×132011的个位数字.【详解】解:∵3n (n 为从1开始的正整数)的个位数字是3,9,7,1四次一循环, 7n 的个位数字是7,9,3,1四次一循环,9n 的个位数字是9,1,9,1四次一循环,又∵2020÷4=505,2021÷4=505…1,2022÷4=505…2,∵32020的末尾数字为1,72021的末尾数字为7,92022的末尾数字为1,∵1×7×1=7,∵32020×72021×92022的个位数字是7.故答案为:7.【点睛】此题考查了尾数特征.此题难度适中,注意得到3,7,9为底数的整数幂的个位数字的规律是解此题的关键.15.阳阳和明明玩上楼梯游戏,规定一步只能上一级或二级台阶,玩着玩着两人发现:当楼梯的台阶数为一级、二级、三级…逐步增加时,楼梯的上法数依次为1,2,3,5,8,13,21,…(这就是著名的裴波那契数列),请你仔细观察这列数的规律后回答:(1)上10级台阶共有__________种上法.(2)这列数的前2020个数中共有________个偶数.【答案】89 673【分析】(1)认真观察不难发现,这列数中,任意相邻两个数的和都等于相邻的后一个数,也就是第10个数应该是第8个、9个的和;(2)观察发现,每3个数中必有一个偶数,且偶数在3个数中间,依此规律可求出问题答案.【详解】解:(1)∵1+2=3,2+3=5,3+5=8,5+8=13,8+13=21,13+21=34,21+34=55,34+55=89,∵上10级台阶共有89种上法;(2)∵2020÷3=673…1,∵偶数个数为673个.【点睛】本题考查了数字型规律,根据已知条件找寻数列中的规律是解题的关键.16.数列1,1,2,3,5,8,13,21,34,55,…的排列规律:前两个数是1,从第3个数开始,每一个数都是它前两个数的和,这个数列叫做斐波契数列,在斐波契数列前2020个数中共有_______个偶数.【答案】673【分析】由于数列1,1,2,3,5,8,13,21,34,55,…中是两个奇数然后一个偶数,接着又是两个奇数,一个偶数,由此即可确定斐波那契数列的前2020个数中共有多少个偶数.【详解】∵数列1,1,2,3,5,8,13,21,34,55,…,中是两个奇数然后一个偶数,而÷=⋅⋅⋅⋅⋅⋅;余数是1,那么这个数列的第2020个数是奇数,202036731∵斐波那契数列的前2020个数中共有673个偶数.故答案为:673.【点睛】此题主要考查了数字的变化规律,解题时首先正确理解题意,然后根据题意找出隐含的规律即可解决问题.17.如图,每一图中有若干个大小不同的菱形,第一幅图中有1个菱形,第二幅图中有3个菱形,第三幅图中有5个菱形,如果第n幅图中有2021个菱形,则n为____________.【答案】1011【分析】根据题意分析可得:第1幅图中有1个,第2幅图中有2×2-1=3个,第3幅图中有2×3-1=5个,…,可以发现,每个图形都比前一个图形多2个,继而即可得出答案.【详解】解:根据题意分析可得:第1幅图中有1个.第2幅图中有2×2-1=3个.第3幅图中有2×3-1=5个.第4幅图中有2×4-1=7个.….可以发现,每个图形都比前一个图形多2个.故第n幅图中共有(2n-1)个.当图中有2021个菱形时,2n-1=2021,所以:n=1011,故答案为:1011.【点睛】本题考查规律型中的图形变化问题,难度适中,要求学生通过观察,分析、归纳并发现其中的规律.18.如图,边长为12320202021、、、、的正方形套在一起,形成一个庞大的回宫格,则阴影部分的面积是_______.【答案】2043231【分析】若只有1个阴影部分,则面积为20212-20202,有2个阴影部分,面积为(20212-20202)+(20192-20182),…【详解】解:阴影部分的面积为(20212-20202)+(20192-20182)+(20172-20162)+…+(32-22)+1=2021+2020+2019+2018+…+3+2+1=() 1202120212+⨯=1011×2021=2043231,故答案为:2043231.【点睛】本题考查图形的变化规律;得到阴影部分面积的组成是解决本题的难点;找到相应的计算方法是解决本题的突破点.19.如图,各网格中四个数之间都有相同的规律,则第9个网格中右下角的数为______.【答案】119【分析】观察序号与网格中上面最左边的数字的关系,第二个数字与序号的关系,左下角的数字与序号的关系,右下角数字与上面所说三个数字的关系,确定好计算即可【详解】根据题意,得网格中上面最左边的数字等于序号,第二个数字与序号+1,左下角的数字与序号+2,右下角数字等于对角线上的数字积加上序号,∵第n个网格中,右下角的数字=(n+1)(n+2)+n,当n=9时,(n+1)(n+2)+n=10×11+9=119,故答案为:119.【点睛】本题考查了数字中规律,仔细思考各数字与序号的关系是解题的关键.2,3,20.把所有的正整数按如图所示规律排列形成数表.若正整数6对应的位置记为() 12,7对应的正整数是_______.则()【答案】138【分析】2,3,可得表示方法,观察出1行1根据表格中的数据,以及正整数6对应的位置记为()列数的特点为12-0,2行2列数的特点为22-1,3行3列数的特点为32-2,…n行n列数的特点为(n2-n+1),且每一行的第一个数字逆箭头方向顺次减少1,由此进一步解决问题.【详解】2,3,解:∵正整数6对应的位置记为()即表示第2行第3列的数,12,7表示第12行第7列的数,∵()由1行1列的数字是12-0=12-(1-1)=1,2行2列的数字是22-1=22-(2-1)=3,3行3列的数字是32-2=32-(3-1)=7,…n行n列的数字是n2-(n-1)=n2-n+1,∵第12行12列的数字是122-12+1=133,∵第12行第7列的数字是138,故答案为:138.【点睛】此题考查观察分析归纳总结顾虑的能力,解答此题的关键是找出两个规律,即n 行n 列数的特点为(n 2-n +1),且每一行的第一个数字逆箭头方向顺次减少1,此题有难度. 21.数轴上,点A 的初始位置表示的数为1,现点A 做如下移动:第1次点A 向左移动3个单位长度至点1A ,第2次从点1A 向右移动6个单位长度至点2A ,第3次从点2A 向左移动9个单位长度至点3A ,…,按照这种移动方式进行下去,如果点n A 与原点的距离不小于20,那么n 的最小值是_______. 【答案】13 【分析】序号为奇数的点在点A 的左边,各点所表示的数依次减少3,序号为偶数的点在点A 的右侧,各点所表示的数依次增加3,于是可得到A 13表示的数为-17-3=-20,A 12表示的数为16+3=19,则可判断点A n 与原点的距离不小于20时,n 的最小值是13. 【详解】解:第一次点A 向左移动3个单位长度至点A 1,则A 1表示的数,1-3=-2; 第2次从点A 1向右移动6个单位长度至点A 2,则A 2表示的数为-2+6=4; 第3次从点A 2向左移动9个单位长度至点A 3,则A 3表示的数为4-9=-5; 第4次从点A 3向右移动12个单位长度至点A 4,则A 4表示的数为-5+12=7; 第5次从点A 4向左移动15个单位长度至点A 5,则A 5表示的数为7-15=-8; …则A 7表示的数为-8-3=-11,A 9表示的数为-11-3=-14,A 11表示的数为-14-3=-17,A 13表示的数为-17-3=-20,A 6表示的数为7+3=10,A 8表示的数为10+3=13,A 10表示的数为13+3=16,A 12表示的数为16+3=19,所以点A n 与原点的距离不小于20,那么n 的最小值是13. 故答案为13. 【点睛】本题考查了规律型问题,认真观察、仔细思考,找出点表示的数的变化规律是解决问题的关键.22.下列图形是由同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,每一个小正方形表示一块地砖,如果按图1、2、3 的次序铺设地砖,把第n 个图形用图n 表示,那么图100中的白色小正方形地砖的块数是_______.【答案】703 【分析】根据图象中地砖个数发现规律,图n 中有()32n +块黑色地砖,图n 中一共有()105n +块地砖,就可以得到白色地砖数,令100n =即可求出结果. 【详解】解:图1中有5块黑色地砖,图2中比图1中多3块黑色地砖,有8块黑色地砖, 图3中比图2中多3块黑色地砖,有11块黑色地砖, …图n 中有()53132n n +-=+块黑色地砖, 图1中一共有5315⨯=块地砖, 图2中一共有5525⨯=块地砖, 图3中一共有5735⨯=块地砖, …图n 中一共有()521105n n +=+块地砖,∵图100中白色小正方形地砖的块数是:()10100531002703⨯+-⨯+=(块). 故答案是:703. 【点睛】本题考查找规律,解题的关键是找出图形中的规律,并用n 将规律通过代数式表示出来. 23.2020年6日1日,湖州市政府发布了全新湖洲城市形象标识,小周同学对新形象标识很感兴趣,用电脑绘画软件绘制了如下图形,其中第(1)个图形有3个形象标识,第(2)个图形有7个形象标识,第(3)个图形有13个形象标识,按此规律绘制下去.(1)小周绘制的第(5)个图形中有_________个形象标识.(2)小周绘制的第(n)个图形中有_________个形象标识.【答案】31 (n2+n+1)【分析】观察图形可知,每个图形中形象标识的个数为序号数的平方+序号数+1,依此可求第5个和第n个图有多少个形象标识.【详解】解:由图形可知,第1个图形有12+1+1=3个形象标识,第2个图形有22+2+1=7个形象标识,第3个图形有32+3+1=13个形象标识,第4个图形有42+4+1=21个形象标识,(1)小周绘制的第(5)个图形中有52+5+1=31个形象标识.(2)小周绘制的第(n)个图形中有(n2+n+1)个形象标识.故答案为:31;(n2+n+1).【点睛】此题考查图形的变化规律,找出图形之间的联系,找出规律是解决问题的关键.三、解答题24.探究:211112222122-=⨯-⨯=,32222-=⨯-⨯=,222212243333-=⨯-⨯=,2222122……(1)请仔细观察,写出第4个等式;(2)请你找规律,写出第n个等式;(3)计算:12320192020++++-.22222【答案】(1)25-24=2×24-1×24=24;(2)2n+1-2n=2×2n-1×2n=2n;(3)-2【分析】(1)根据给出的内容,直接可以仿写25-24=2×24-1×24=24,(2)2n +1-2n =2×2n -1×2n =2n ,(3)将原式进行变形,即提出负号后,就转化为原题中的类型,利用(1)(2)的结论,直接得出结果. 【详解】解:(1)由题意可得: 25-24=2×24-1×24=24; (2)2n +1-2n =2×2n -1×2n =2n ; (3)1232019202022222++++-=()1232019202022222++++-=1232018201922222++++-... =2-22 =-2 【点睛】此题主要考查了数字变化规律,认真观察、仔细思考,善用联想是解决这类问题的方法,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:2n +1-2n =2n 成立. 25.一列数a 1,a 2,a 3,…,a n ,其中a 1=﹣1,a 2=111a -,a 3=211a -,…,a n =111n a --.(1)求a 2,a 3的值;(2)求a 1+a 2+a 3+…+a 2021的值. 【答案】(1)212a =,32a =;(2)1009 【分析】(1)将11a =-代入2111a a =-计算可得2a ,再将2a 代入3211a a =-,可求出3a ;(2)根据规律可得出结果. 【详解】解:(1)把11a =-代入2111a a =-得, 2111(1)2a =--=,把212a =代入3211a a =-得,312112a ==-,∵212a =,32a =; (2)将32a =代入4311a a =-得, 41112a ==-- 同理5111(1)2a ==--, 62a =,71a =-,812a =, ⋯⋯12345678920172018201932a a a a a a a a a a a a ++==++=++=⋯=++, 所以1232021111112121212222a a a a +++⋯+=-++-++-++⋯⋯-+31673122=⨯-+ 1009=.【点睛】本题考查有理数的混合运算,探索数字的变化规律,正确的计算2a ,3a ,4a ,5a ⋯⋯进而得出变化规律是解决问题的关键. 26.观察下列等式:111122=-⨯,1112323=-⨯,1113434=-⨯,将以上三个等式两边分别相加得:111122334++⨯⨯⨯11111122334=-+-+-13144=-=. (1)猜想并写出:1(1)n n =+________. (2)直接写出结果:111112233420182019++++=⨯⨯⨯⨯___________.(3)计算111124466820182020++++⨯⨯⨯⨯.【答案】(1)111n n -+;(2)20182019;(3)10094040【分析】(1)根据题目中的式子,可以写出相应的猜想; (2)先裂项,然后再计算即可;(3)根据题目中式子的特点,每项提取12,再裂项计算即可. 【详解】解:(1)由题意可得:111(1)1n n n n =-++;(2)111112233420182019++++⨯⨯⨯⨯=111111112233420182019-+-+-++- =112019- =20182019; (3)111124466820182020++++⨯⨯⨯⨯=111111111224466820182020⎛⎫-+-+-++- ⎪⎝⎭=111222020⎛⎫- ⎪⎝⎭ =1100922020=10094040【点睛】本题考查了规律型:数字的变化类:探寻数列规律:认真观察、仔细思考,善用联想是解决这类问题的方法. 27.阅读下列材料:11112(123012)23(234123)34(345234)333⨯=⨯⨯-⨯⨯⨯=⨯⨯-⨯⨯⨯=⨯⨯-⨯⨯;由以上三个等式相加,可得1122334345203⨯+⨯+⨯=⨯⨯⨯=.读完以上材料,请你计算下列各题: (1)计算:12233499100⨯+⨯+⨯++⨯(写出过程)(2)直接写出直接:122334(1)n n ⨯+⨯+⨯+⋯+⨯+=_________. (3)计算:123234345181920⨯⨯+⨯⨯+⨯⨯++⨯⨯(写出过程)【答案】(1)333300;(2)()()1123n n n ++;(3)35910 【分析】根据给定等式的变化找出变化规律()()()()()1112113n n n n n n n n +=++--+⎡⎤⎣⎦;(1)根据变化规律将算式展开后即可得出原式=1991001013⨯⨯⨯,此题得解; (2)根据变化规律将算式展开后即可得出原式=()()1123n n n ++,此题得解;(3)通过类比找出变化规律“n (n +1)(n +2)=14[n (n +1)(n +2)(n +3)-(n -1)n (n +1)(n +2)]”,依此规律将算式展开后即可得出结论. 【详解】解:观察,发现规律:112(123012)3⨯=⨯⨯-⨯⨯,123(234123)3⨯=⨯⨯-⨯⨯,134(345234)3⨯=⨯⨯-⨯⨯,…,∵()()()()()1112113n n n n n n n n +=++--+⎡⎤⎣⎦; (1)12233499100⨯+⨯+⨯++⨯=()()()111123012234123 (9910010198991003)33⨯⨯-⨯⨯+⨯⨯-⨯⨯++⨯⨯-⨯⨯ =1991001013⨯⨯⨯ =333300;(2)122334(1)n n ⨯+⨯+⨯+⋯+⨯+=()()()()()()111230122341231121.13..33n n n n n n ++--+⎡⎤⎣⎦⨯⨯-⨯⨯+⨯⨯-⨯⨯++ =()()1123n n n ++;(3)123234345181920⨯⨯+⨯⨯+⨯⨯++⨯⨯=()()()1111234012323451234 (181920211718192044)4⨯⨯⨯-⨯⨯⨯+⨯⨯⨯-⨯⨯⨯++⨯⨯⨯-⨯⨯⨯ =1181920214⨯⨯⨯⨯ =35910 【点睛】本题考查数字的变化类、有理数的混合运算,解答本题的关键是明确题意,发现题目中数字的变化特点,利用类比的数学思想解答.28.用黑白两种颜色的正方形纸片,按黑色纸片数逐渐加1的规律拼成一系列图案,请仔细观察,并回答下列问题:(1)第4个图案中有白色纸片多少张?(2)第n个图案中有白色纸片多少张?(3)第几个图案有白色纸片有2011张?(写出必要的步骤)【答案】(1)13;(2)(3n+1)张(3)第670个图案有白色纸片有2011张,见解析【分析】(1)观察图形的变化可得第4个图案中有白色纸片有3×4+1=13张;(2)结合(1)即可得规律,第n个图案中有白色纸片(3n+1)张;(3)结合(2)发现的规律即可求得白色纸片有2011张是第几个图案.【详解】(1)观察图形的变化可知:第1个图案中有白色纸片张数为:3×1+1=4;第2个图案中有白色纸片张数为:3×2+1=7;第3个图案中有白色纸片张数为:3×3+1=10;第4个图案中有白色纸片张数为:3×4+1=13;(2)根据(1)发现规律:第n个图案中有白色纸片张数为:(3n+1)张.(3)根据(2)可知:3n+1=2011,解得n=670.答:第670个图案有白色纸片有2011张.【点睛】此题考查规律型-图形的变化类,解题的关键是根据图形的变化寻找规律.29.图1是用绳索织成的一片网的一部分,小明为了研究这片网的结点数(V),网眼数(F),边数(E)之间的关系,他采用由特殊到一般的方法进行探索,列表如下:V F E之间(1)表中“∵”处应填的数字为__________;根据上述探索过程,可能猜想,,满足的数量关系是__________.(2)如图2,若网眼形状为六边形,请仿照小明的探索方法,完成下面表格并猜想,,V F E 之间满足的数量关系.根据上述探索过程,可以猜想,,V F E 之间满足的数量关系是________. 【答案】(1)17,1V F E +-=;(2)表见解析,1V F E +-= 【分析】(1)根据表格中的数据可以得到表中“∵”处应填的数字并猜想出V ,F ,E 之间满足的等量关系;(2)根据(1)中的例子,可以猜想出若网眼形状为六边形,V ,F ,E 之间满足的等量关系. 【详解】解:(1)由表格可得, 表中“∵”处应填的数字为17,根据上述探索过程,可以猜想V ,F ,E 之间满足的等量关系为:V+F -E=1, 故答案为:17,V+F -E=1; (2)若网眼形状为六边形 当V=6时,F=1,E=6, 当V=10时,F=2,E=11, 当V=16时,F=4,E=19, 当V=22时,F=6,E=27,则V ,F ,E 之间满足的等量关系为V+F -E=1, 故答案为:V+F -E=1【点睛】30.先阅读下面文字,然后按要求解题.例:123100?+++⋅⋅⋅+=如果一个一个顺次相加显然太繁,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为11002993985051101+=+=+=⋅⋅⋅=+=,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果. (1)补全例题解题过程;123100(1100)(299)(398)(5051)101++++=++++++++=⨯_____=_____.(2)计算:2468100++++⋅⋅⋅+(3)计算:()(2)(3)(99)a a b a b a b a b +++++++⋅⋅⋅++. 【答案】(1)50,5050;(2)2550;(3)1004950a b + 【分析】(1)根据题干中的示例计算即可得解;(2)根据两数之和为102,再乘以数字的个数即可得;(3)将所有的a 相加、所有含b 的式子相加,含b 的代数式利用以上求和方法求解可得. 【详解】解:(1)123100+++⋯+(1100)(299)(398)(5051)++++++⋯++10150=⨯5050=,故答案为:50、5050; (2)2468100++++⋅⋅⋅+1(2100)22100=+⨯⨯10225=⨯ 2550=;(3)原式100(23499)a b b b b b =+++++⋯+99(199)1002a b ⨯+=+1004950a b =+.【点睛】本题主要考查数字的变化规律,解题的关键是熟练掌握(1)1232n n n ++++⋯+=.。
七年级数学(上)探索规律类-问题及答案

七年级数学(上)探索规律类 问题班级 学号 姓名 成绩一、数字规律类:1、一组按规律排列的数:41,93,167,2513,3621,…… 请你推断第9个数是 .2、(2005年山东日照)已知下列等式: ① 13=12; ② 13+23=32; ③ 13+23+33=62;④ 13+23+33+43=102 ;…………由此规律知,第⑤个等式是 .3、(2005年内蒙古乌兰察布)观察下列各式;①、12+1=1×2 ;②、22+2=2×3; ③、32+3=3×4 ;………请把你猜想到的规律用自然数n 表示出来 。
4、(2005年辽宁锦州)观察下面的几个算式:①、1+2+1=4; ②、1+2+3+2+1=9; ③、1+2+3+4+3+2+1=16;④、1+2+3+4+5+4+3+2+1=25,……根据你所发现的规律,请你直接写出第n 个式子 5、(2005年江苏宿迁)观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( ) A .1 B . 2 C .3 D .4 6、(2005年山东济南市)把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行、……,中间用虚线围的一列,从上至下依次为1、5、13、25、……,则第10个数为________。
第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10(第6题图) 第5行 11 -12 13 -14 15 ……………… (第7题图) 7、(05年江苏省金湖实验区)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成如上所示的形式:按照上述规律排下去,那么第10行从左边数第5个数等于 . 二、图形规律类: 8、(2005年云南玉溪)一质点P 从距原点1个单位的A 点处向原点方向跳动,第一次跳动到OA 的中点1A 处,第二次从1A 点跳动到O 1A 的中点2A 处,第三次从2A 点跳动到1条 2条 3条 图1 图2 图 3 O 2A 的中点3A 处,如此不断跳动下去,则第n 次跳动后,该质点到原点O 的距离为 。
北师大版七年级数学上册《探索与表达规律》专项练习(含答案)
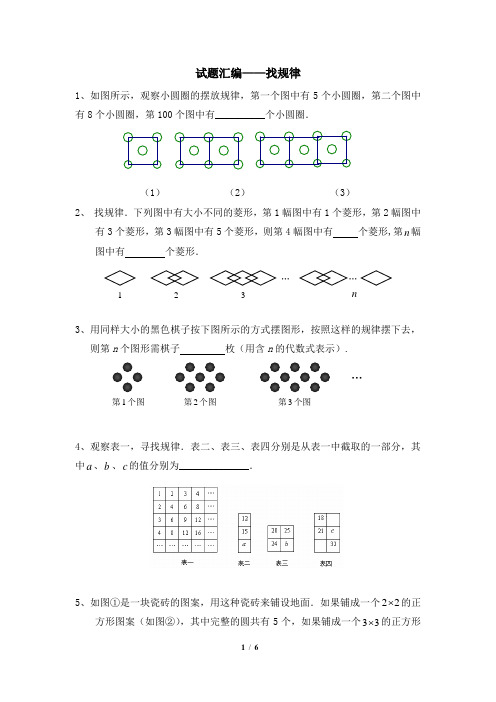
试题汇编——找规律1、如图所示,观察小圆圈的摆放规律,第一个图中有5个小圆圈,第二个图中有8个小圆圈,第100个图中有__________个小圆圈.(1) (2) (3)2、 找规律.下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有 个菱形,第n 幅图中有 个菱形.3、用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n 个图形需棋子 枚(用含n 的代数式表示).4、观察表一,寻找规律.表二、表三、表四分别是从表一中截取的一部分,其中a 、b 、c 的值分别为______________.5、如图①是一块瓷砖的图案,用这种瓷砖来铺设地面.如果铺成一个22⨯的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个33⨯的正方形1 2 3 n … … 第1个图 第2个图 第3个图…图案(如图③),其中完整的圆共有13个,如果铺成一个44⨯的正方形图案(如图④),其中完整的圆共有25个.若这样铺成一个1010⨯的正方形图案, 则其中完整的圆共有 个.6、 如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n 个图案需要用白色棋子 枚(用含有n 的代数式表示,并写成最简形式).○ ○ ○ ○ ○ ○ ○ ○ ○○ ○ ○ ○ ● ● ○ ○ ● ● ● ○○ ● ○ ○ ● ● ○ ○ ● ● ● ○○ ○ ○ ○ ○ ○ ○ ○ ● ● ● ○○ ○ ○ ○ ○7、用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形 需 根火柴棒。
8、将正整数按如图5所示的规律排列下去,若有序实数对(n ,m )表示第n 排,从左到右第m 个数,如(4,2)表示实数9,则表示实数17的有序实数对是 .9、如图 2 ,用n 表示等边三角形边上的小圆圈,f(n)表示这个三角形中小圆圈的总数,那么f(n)和n 的关系是第一排 第二排 第三排 第四排 6 ┅┅ 10 9 87 32 15 410、观察图4的三角形数阵,则第50行的最后一个数是 ( )1-2 3-4 5 -67 -8 9 -10。
初一数学整式规律探索含答案

初一数学整式规律探索含答案规律探索中考要求内容基本要求略高要求较高要求。
学生需要根据特定的问题所提供的资料,合理选用知识和方法,通过代数式的适当变形求代数式的值。
同时,他们需要能够用整式的加减运算对多项式进行变形,进一步解决有关问题。
代式学生需要了解代数式的值概念并能求代数式的值。
他们还需要能根据代数式的值或特征,推断这些代数式反映的规律。
整式有关概念学生需要了解整式及其有关概念。
他们需要理解整式加减运算法则并能进行简单的整式加减运算。
重难点学生需要能根据图、表、数、式中的排列特征,探究其中蕴藏的数式规律。
课前预德国著名大科学家XXX(1777~1855)出生在一个贫穷的家庭。
XXX在还不会讲话就自己学计算,在三岁时有一天晚上他看着父亲在算工钱时,还纠正父亲计算的错误。
长大后,他成为当代最杰出的天文学家和数学家。
他在物理的电磁学方面有一些贡献,现在电磁学的一个单位就是用他的名字命名。
数学家们则称呼他为“数学王子”。
他八岁时进入乡村小学读书。
教数学的老师是一个从城里来的人,觉得在一个穷乡僻壤教几个小猢狲读书,真是大材小用。
而他又有些偏见:穷人的孩子天生都是笨蛋,教这些蠢笨的孩子念书不必认真,如果有机会还应该处罚他们,使自己在这枯燥的生活里添一些乐趣。
这一天正是数学教师情绪低落的一天。
同学们看到老师那抑郁的脸孔,心里畏缩起来,知道老师又会在今天捉这些学生处罚了。
“你们今天替我算从1加2加3一直到100的和。
谁算不出来就罚他不能回家吃午饭。
”老师讲了这句话后就一言不发的拿起一本小说坐在椅子上看去了。
教室里的小朋友们拿起石板开始计算:“1加2等于3,3加3等于6,6加4等于10……”一些小朋友加到一个数后就擦掉石板上的结果,再加下去,数越来越大,很不好。
有些孩子的小脸孔涨红了,有些手心、额上渗出了汗来。
还不到半个小时,XXX拿起了他的石板走上前去。
“老师,答案是不是这样?”数学老师本来想怒吼起来,可是一看石板上整整齐齐写了这样的数:5050,他惊奇起来,因为他自己曾经算过,得到的数也是5050,这个8岁的小鬼怎么这样快就得到了这个数值呢?XXX发现了一种计算级数1+2+3+。
(完整版)七年级数学整式的加减探索规律(习题及答案)

探索规律(习题)➢例题示范例1:观察图1至图4中小圆圈的摆放规律,并按这样的规律继续摆放,记第n个图中小圆圈的个数为M,则M=__________(用含n的代数式表示).…图1 图2 图3 图4思路分析做图形规律的题,我们一般从两个方面来研究:(1)观察图形的构成.(2)转化.观察本题的图形,发现后面的图形总比前面的图形多3个小圆圈,可以采用分类的手段进行解决.分成原来的和增加的两类.①2+3×1②2+3×2③2+3×3④2+3×4则第n个:2+3n=3n+2.验证:当n=1时,3n+2=5,成立.故第n个图形中有(3n+2)个小圆圈.(想一想,还有其他观察角度吗?)例2:观察下列球的排列规律(其中●是实心球,○是空心球):…从第1个球起到第2 014个球止,共有实心球________个.思路分析①判断该题是循环规律,查找重复出现的结构,即循环节;②观察图形的变化规律,发现每10个球为一个循环,每个循环节里有3个实心球.故2 014÷10=201…4,201×3=603;③再从某个循环节开始查前4个球,发现有2个实心球,故总数为603+2=605(个).➢巩固练习1.如下数表是由从1开始的连续自然数组成,观察规律并完成下列各题.123456781011121314151617181920212223242526272829303132333435369…(1)表中第8行的最后一个数是_____,它是自然数______ 的平方,第8行共有________个数;(2)用含n 的代数式表示:第n 行的第一个数是_________, 最后一个数是_________,第n 行共有_________个数. 2. 将1,-2,3,-4,5,-6,…按一定规律排成下表:(1)第8行的数是_________________________________; (2)第50行的第一个数是_______.3. 下列图形由边长为1的正方形按某种规律排列而成,依此规律,则第8个图形中正方形有( )…图3图2图1A.38个 B.41个 C.43个D.48个4.如下图所示,摆第1个“小屋子”要5枚棋子,摆第2个要11枚棋子,摆第3个要17枚棋子,则摆第30个要_________枚棋子.…第3个第2个第1个5. 下列图案由边长相等的黑白两色正方形按一定规律拼接而成,依此规律,第n 个图案中白色正方形的个数为_________.…图3图2图16. 观察下列图形,根据图形及相应点的个数的变化规律,第n 个图形中点的个数为__________.图5图4图1图2图3…7. 如图1,一等边三角形的周长为1,将这个等边三角形的每边三等分,在每边上分别以中间的一段为边作等边三角形,然后去掉这一段,得到图2;再将图2中的每一段作类似变形,得到图3;按上述方法继续下去得到图4,则第4个图形的周长为________,第n 个图形的周长为________________.…图1 图2 图38. 一个纸环链,纸环按“红黄绿蓝紫”的顺序重复排列,截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )红 黄 绿 蓝 紫 红 黄 绿 … … 黄 绿 蓝 紫 A .2 012B .2 013C .2 014D .2 0159. 小时候我们就用手指练习过数数,一个小朋友按图中的规则练习数数,数到2 013时对应的手指头是( ) A .大拇指B .食指C .小拇指D .无名指大拇指1234567891011121314151617181910. 如图,平面内有公共端点的八条射线OA ,OB ,OC ,OD ,OE ,OF ,OG ,OH ,从射线OA 开始按逆时针方向依次在射线上写出数字1,2,3,4,5,6,7,8,9,….(1)“20”在射线______________上; (2)请任意写出三条射线上的数字排列规律; (3)“2 015”在哪条射线上?➢ 思考小结1. 我们学习了数的规律、式的规律、图形规律、循环规律等,它们都有对应的操作方法.(1)数与式的规律:①_________;②_________;③处理符号;④验证. (2)图形规律:①观察图形的构成:____________________;②转化:________________________________________. (3)循环规律:①________________;②____________________.HD【参考答案】➢巩固练习1.(1)64,8,15;(2)(n-1)2+1(或n2-2n+2),n2,(2n-1).2.(1)29,-30,31,-32,33,-34,35,-36;(2)-1 226.3. C4.1795.5n+36.n2-n+17.6427,143n-⎛⎫⎪⎝⎭8. B9. C10.(1)OD(2)射线OA:8n-7;射线OB:8n-6;射线OC:8n-5;射线OD:8n-4;射线OE:8n-3;射线OF:8n-2;射线OG:8n-1;射线OH:8n.任选三个即可.(3)在射线OG上.➢思考小结1.(1)①标序号;②找结构.(2)①分类,去重,补形;②转化为数的规律或其他图形的规律.(3)①确定起始位置;②找循环节.。
七年级数学探索规律——循环规律(人教版)(专题)(含答案)

一、单选题(共10道,每道10分)
1.观察下列一组数的排列:1,2,3,4,3,2,1,2,3,4,3,2,1,…,那么第2019个数是( )
A.1 B.2
C.3 D.4
答案:C
解题思路:
分析可得:这列数6个一组“1,2,3,4,3,2”形成循环;
因此可以判断具有循环规律,循环周期为6,循环节为“1,2,3,4,3,2”;
盒子左边露出来的部分“白黄蓝白黄蓝白”,是2个周期还多余一颗白色的珠子;
盒子右边露出来的部分“蓝白黄蓝”,是一颗蓝色的珠子和1个周期.
左右两边多余的两颗珠子“白”和“蓝”要构成一个周期,中间还差一颗黄色的珠子,根据周期为3,这串珠子被放在盒子里的颗数应该是 ( 为自然数),因为2020=3×673+1,易得四个选项中只有选项B符合题意.
故选D.
试题难度:三颗星知识点:略
6.现有一串彩色的珠子,按“白黄蓝”的顺序重复排列,其中有一部分放在盒子里,如图所示,则这串珠子被放在盒子里的颗数可能是( )
A.2018 B.2020
C.2019 D.2021
答案:B
解题思路:
分析:
由题意,一串彩色的珠子按“白黄蓝”的顺序重复排列,说明是循环规律,且循环周期为3.
青蛙是沿着一个圆圈跳的,这是循环规律,循环节为5,2,1,3,循环周期为4,因为114÷4=38……2,所以经过114次后,它停在1对应的点上,故选A.
试题难度:三颗星知识点:略
试题难度:三颗星知识点:略
3.探索规律: 的个位数字为3, 的个位数字为9, 的个位数字为7, 的个位数字为1, 的个位数字为3,…,则 的个位数字为( )
A.1 B.3
七上数学每日一练:探索图形规律练习题及答案_2020年填空题版
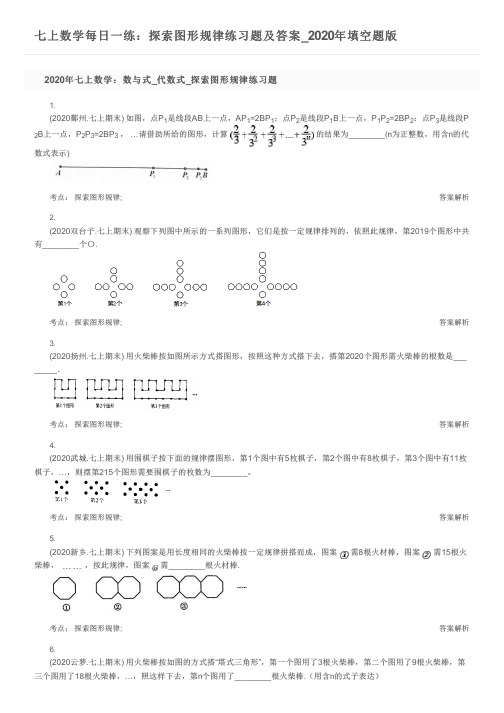
七上数学每日一练:探索图形规律练习题及答案_2020年填空题版答案解析答案解析答案解析答案解析答案解析2020年七上数学:数与式_代数式_探索图形规律练习题1.(2020鄞州.七上期末) 如图,点P 是线段AB 上一点,AP =2BP ;点P 是线段P B 上一点,P P=2BP :点P 是线段P B 上一点,P P =2BP , …请借助所给的图形,计算的结果为________(n 为正整数,用含n 的代数式表示)考点: 探索图形规律;2.(2020双台子.七上期末) 观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有________个〇.考点: 探索图形规律;3.(2020扬州.七上期末) 用火柴棒按如图所示方式搭图形,按照这种方式搭下去,搭第2020个图形需火柴棒的根数是________.考点: 探索图形规律;4.(2020武城.七上期末) 用围棋子按下面的规律摆图形,第1个图中有5枚棋子,第2个图中有8枚棋子,第3个图中有11枚棋子,…,则摆第215个图形需要围棋子的枚数为________。
考点: 探索图形规律;5.(2020新乡.七上期末) 下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案需8根火材棒,图案 需15根火柴棒, ,按此规律,图案 需________根火材棒.考点: 探索图形规律;6.(2020云梦.七上期末) 用火柴棒按如图的方式搭“塔式三角形”,第一个图用了3根火柴棒,第二个图用了9根火柴棒,第三个图用了18根火柴棒,…,照这样下去,第n 个图用了________根火柴棒.(用含n 的式子表达)1112112232233答案解析答案解析答案解析答案解析答案解析考点: 探索图形规律;7.(2019诸暨.七上期末) 如图,甲、乙两动点分别从正方形ABCD 的顶点,A ,C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2019次相遇在________边上(填AB ,B C ,CD 或AD ).考点: 探索图形规律;正方形的性质;8.(2019鄞州.七上期末) 下列每个三角形中的4个数之间都有相同的规律,根据这种规律,第4个三角形中的中间数字x 为________,第n 个三角形的中间数字用含n 的代数式表示为________.考点: 探索图形规律;9.(2019沈河.七上期末) 如图,把一个面积为1的正方形等分成两个面积为 的长方形,接着把面积为的长方形等分成两个面积为的长方形,再把面积为的长方形等分成两个面积为 的长方形,如此下去,利用图中示的规律计算=________; =________.考点: 探索图形规律;10.(2019皇姑.七上期末) 如图,找出其变化的规律,则第1345个图形中黑色正方形的数量是________.考点: 探索图形规律;2020年七上数学:数与式_代数式_探索图形规律练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:。
【七年级数学】七年级上数学探索与表达规律训练题(北师大版含答案)

七年级上数学探索与表达规律训练题(北师大版含答案)
七年级上数学探索与表达规律训练题(北师大版含答案)(30分钟 50分)
一、选择题(每小题4分,共12分)
1( ,
+ + =1- ,…请根据上面的规律计算
+ + +…+ =
6(4,5,-6,7,-8,…
(1)它的每一项你认为可用怎样的式子表示?
(2)它的第100个数是多少?
(3)
6【解析】根据图形可知第一个图形中阴影部分小正方形个数为4=2+2=1×2+2,第二个图形中阴影部分小正方形个数为8=6+2=2×3+2,第三个图形中阴影部分小正方形个数为14=12+2=3×4+2,…
所以第n个图形中阴影部分小正方形个数为n(n+1)+2
答案n(n+1)+2
7【解析】(1)9+5=14(枚)
故摆成第四个图案需要14枚棋子
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需5+3×(n-1)
=5+3n-3=( 3n+2)枚棋子
(3)3×1)100+1×100=-100
(3)当n=2018时,(-1)2018+1×2018=2018,
所以2018是其中的第2018个数
9【解析】(1)①因为5+2=7,
所以左边的三位数是275,右边的三位数是572,。
初一数学规律探索之数字的变化规律专题训练(附答案)
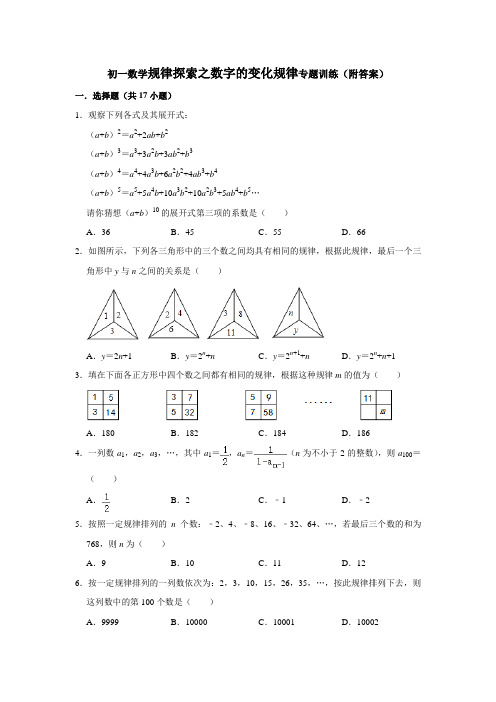
初一数学规律探索之数字的变化规律专题训练(附答案)一.选择题(共17小题)1.观察下列各式及其展开式:(a+b)2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3(a+b)4=a4+4a3b+6a2b2+4ab3+b4(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5…请你猜想(a+b)10的展开式第三项的系数是()A.36B.45C.55D.662.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是()A.y=2n+1B.y=2n+n C.y=2n+1+n D.y=2n+n+1 3.填在下面各正方形中四个数之间都有相同的规律,根据这种规律m的值为()A.180B.182C.184D.1864.一列数a1,a2,a3,…,其中a1=,a n=(n为不小于2的整数),则a100=()A.B.2C.﹣1D.﹣25.按照一定规律排列的n个数:﹣2、4、﹣8、16、﹣32、64、…,若最后三个数的和为768,则n为()A.9B.10C.11D.126.按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第100个数是()A.9999B.10000C.10001D.100027.已知整数a1,a2,a3,a4…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|…依此类推,则a2017的值为()A.﹣1009B.﹣1008C.﹣2017D.﹣20168.一列数按某规律排列如下:,,,,,,,,,,…,若第n个数为,则n=()A.50B.60C.62D.719.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为()A.﹣1007B.﹣1008C.﹣1009D.﹣2018 10.1261年,我国南宋数学家杨辉用图中的三角形解释二项和的乘方规律,比欧洲的相同发现要早三百多年,我们把这个三角形称为“杨辉三角”,请观察图中的数字排列规律,则a,b,c的值分别为()A.a=1,b=6,c=15B.a=6,b=15,c=20C.a=15,b=20,c=15D.a=20,b=15,c=611.已知整数a0,a1,a2,a3,a4,…,满足下列条件:a0=0,a1=﹣|a0+1|,a2=﹣|a1+2|,a3=﹣|a2+3|,…,以此类推,a2019的值是()A.﹣1009B.﹣1010C.﹣2018D.﹣202012.仔细观察,探索规律:则22019+22018+22017+…+2+1的个位数字是()A.1B.3C.5D.713.如图,是按一定规律排成的三角形数阵,按图中数阵的排列规律,第9行从左至右第5个数是()A.2B.C.5D.14.现定义一种变换:对于一个由有限个数组成的序列S0,将其中的每个数换成该数在S0中出现的次数,可得到一个新序列S1,例如序列S0:(4,2,3,4,2),通过变换可生成新序列S1:(2,2,1,2,2),若S0可以为任意序列,则下面的序列可作为S1的是()A.(1,2,1,2,2)B.(2,2,2,3,3)C.(1,1,2,2,3)D.(1,2,1,1,2)15.对于每个正整数n,设f(n)表示n(n+1)的末位数字.例如:f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),…则f(1)+f(2)+f(3)+…+f(2012)的值为()A.6B.4022C.4028D.670816.大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是103,则m的值是()A.9B.10C.11D.1217.a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是,已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2019=()A.3B.﹣2C.D.二.填空题(共18小题)18.如图,在x轴的正半轴上依次间隔相等的距离取点A1,A2,A3,A4,…,A n,分别过这些点做x轴的垂线与反比例函数y=的图象相交于点P1,P2,P3,P4,…P n,再分别过P2,P3,P4,…P n作P2B1⊥A1P1,P3B2⊥A2P2,P4B3⊥A3P3,…,P n B n﹣1⊥A n﹣1P n,垂足分别为B1,B2,B3,B4,…,B n﹣1,连接P1P2,P2P3,P3P4,…,P n﹣1P n,得﹣1到一组Rt△P1B1P2,Rt△P2B2P3,Rt△P3B3P4,…,Rt△P n﹣1B n﹣1P n,则Rt△P n﹣1B n﹣1P n的面积为.19.古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为a1,第二个三角数记为a2…,第n个三角数记为a n,计算a1+a2,a2+a3,a3+a4,…由此推算a399+a400=.20.按一定规律排列的一列数:21,22,23,25,28,213,…,若x、y、z表示这列数中的连续三个数,猜想x、y、z满足的关系式是.21.找出下列各图形中数的规律,依此,a的值为.22.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a+b+c=.23.按一定规律排列的一列数依次为:,1,,,,,…,按此规律,这列数中的第100个数是.24.将从1开始的自然数按以下规律排列,例如位于第3行、第4列的数是12,则位于第45行、第8列的数是.25.已知:(n=1,2,3,…),记b1=2(1﹣a1),b2=2(1﹣a1)(1﹣a2),…,b n=2(1﹣a1)(1﹣a2)…(1﹣a n),则通过计算推测出b n的表达式b n=.(用含n的代数式表示)26.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为.27.将被3整除余数为1的正整数,按照下列规律排成一个三角形数阵,则第20行第19个数是.28.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系式是.29.观察“田”字中各数之间的关系:则c的值为.30.下面是按一定规律排列的一列数:,,,,…那么第n个数是.31.观察下面的单项式:a,﹣2a2,4a3,﹣8a4,…根据你发现的规律,第8个式子是.32.设a1,a2,a3……是一列正整数,其中a1表示第一个数,a2表示第二个数,依此类推,a n表示第n个数(n是正整数).已知a1=1,4a n=(a n+1﹣1)2﹣(a n﹣1)2,则a2018=.33.下面每个表格中的四个数都是按相同规律填写的:根据此规律确定x的值为.34.我们可以用符号f(a)表示代数式.当a是正整数时,我们规定如果a为偶数,f(a)=0.5a;如果a为奇数,f(a)=5a+1.例如:f(20)=10,f(5)=26.设a1=6,a2=f(a1),a3=f(a2)…;依此规律进行下去,得到一列数:a1,a2,a3,a4…(n为正整数),则2a1﹣a2+a3﹣a4+a5﹣a6+…+a2013﹣a2014+a2015=.35.设一列数中相邻的三个数依次为m、n、p,且满足p=m2﹣n,若这列数为﹣1,3,﹣2,a,﹣7,b…,则b=.三.解答题(共10小题)36.先观察下列等式,然后用你发现的规律解答下列问题.……(1)计算=;(2)探究=;(用含有n的式子表示)(3)若的值为,求n的值.37.观察下列各式:1×5+4=32…………①3×7+4=52…………②5×9+4=72…………③……探索以上式子的规律:(1)试写出第6个等式;(2)试写出第n个等式(用含n的式子表示),并用你所学的知识说明第n个等式成立.38.观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第n个数记为a n.(1)请写出29后面的第一个数;(2)通过计算a2﹣a1,a3﹣a2,a4﹣a3,…由此推算a100﹣a99的值;(3)根据你发现的规律求a100的值.39.有依次排列的3个数:3,9,8,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:3,6,9,﹣1,8,这称为第一次操作;做第二次同样的操作后也可产生一个新数串:3,3,6,3,9,﹣10,﹣1,9,8,继续依次操作下去.问:从数串3,9,8开始操作第一百次以后所产生的那个新数串的所有数之和是多少?40.阅读材料:求1+2+22+23+24+…22017的值.解:设S=1+2+22+23+24+…+22016+22017,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22017+22018,将下式减去上式得:2S﹣S=22018﹣1,即S=22018﹣1,即1+2+22+23+24+…22017=22018﹣1请你仿照此法计算(1)1+2+22+23+24 (29)(2)1+5+52+53+54…+5n(其中n为正整数).41.阅读材料:求1+2+22+23+24+…+22019的值.解:设S=1+2+22+23+24+…+22019,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22019+22020将下式减去上式得2S﹣S=22020﹣1即S=22020﹣1即1+2+22+23+24+…=22020﹣1请你仿照此法计算:(1)1+2+22+23+24+…+220(2)1+5+52+53+54+…+5n(其中n为正整数).42.观察下面三行数:﹣2,4,﹣8,16,﹣32,64 …①0,6,﹣6,18,﹣30,66…②﹣1,2,﹣4,8,﹣16,32…③(1)第①、②、③行第n个数分别为;;.(2)取每行数的第九个数,计算这三个数的和.43.对于数轴上的A,B,C三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“联盟点”.例如数轴上点A,B,C所表示的数分别为1,3,4,此时点B是点A,C的“联盟点”.(1)若点A表示数﹣2,点B表示数2,下列各数﹣,0,4,6所对应的点分别为,C1,C2,C3,C4,其中是点A,B的“联盟点”的是;(2)点A表示数﹣10,点B表示数30,P为数轴上一个动点:①若点P在点B的左侧,且点P是点A,B的“联盟点”,求此时点P表示的数;②若点P在点B的右侧,点P,A,B中,有一个点恰好是其它两个点的“联盟点”,写出此时点P表示的数.44.观察下列式子,并探索它们的规律:,=,………(1)尝试写出第四个式子:(2)通过以上式子,你发现了什么规律,试用正整数n表示出该规律:(3)借助以上规律,化简式子:45.观察下列等式(1)13=×12×22;(2)13+23=×22×32;(3)13+23+33=×32×42;(4)13+23+33+43=×42×52;…根据上述等式的规律,解答下列问题:(1)写出第5个等式:;(2)写出第n个等式(用含有n的代数式表示);(3)设s是正整数且s≥2,应用你发现的规律,化简:×s2×(s+1)2﹣×(s﹣1)2×s2.参考答案:一.选择题(共17小题)1.解:(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6;(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7;第7个式子系数分别为:1,8,28,56,70,56,28,8,1;第8个式子系数分别为:1,9,36,84,126,126,84,36,9,1;第9个式子系数分别为:1,10,45,120,210,252,210,120,45,10,1,则(a+b)10的展开式第三项的系数为45.故选:B.2.解:∵观察可知:左边三角形的数字规律为:1,2,…,n,右边三角形的数字规律为:2,22,…,2n,下边三角形的数字规律为:1+2,2+22,…,n+2n,∴y=2n+n.故选:B.3.解:由前面数字关系:1,3,5;3,5,7;5,7,9,可得最后一个三个数分别为:11,13,15,∵3×5﹣1=14,;5×7﹣3=32;7×9﹣5=58;∴m=13×15﹣11=184.故选:C.4.解:根据题意得,a2==2,a3==﹣1,a4==,a5==2,…,依此类推,每三个数为一个循环组依次循环,∵100÷3=33…1,∴a100是第34个循环组的第一个数,与a1相同,即a100=.故选:A.5.解:由题意,得第n个数为(﹣2)n,那么(﹣2)n﹣2+(﹣2)n﹣1+(﹣2)n=768,当n为偶数:整理得出:3×2n﹣2=768,解得:n=10;当n为奇数:整理得出:﹣3×2n﹣2=768,则求不出整数.故选:B.6.解:∵第奇数个数2=12+1,10=32+1,26=52+1,…,第偶数个数3=22﹣1,15=42﹣1,35=62﹣1,…,∴第100个数是1002﹣1=9999,故选:A.7.解:a1=0,a2=﹣|a1+1|=﹣|0+1|=﹣1,a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,…,所以n是奇数时,结果等于﹣;n是偶数时,结果等于﹣;a2017=﹣=﹣1008.故选:B.8.解:,,,,,,,,,,…,可写为:,(,),(,,),(,,,),…,∴分母为11开头到分母为1的数有11个,分别为,∴第n个数为,则n=1+2+3+4+…+10+5=60,故选:B.9.解:a1=0,a2=﹣|a1+1|=﹣|0+1|=﹣1,a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,a6=﹣|a5+5|=﹣|﹣2+5|=﹣3,a7=﹣|a6+6|=﹣|﹣3+6|=﹣3,…以此类推,经过前几个数字比较后发现:从第二个数字开始,如果顺序数为偶数,最后的数值是其顺序数的一半的相反数,即a2n=﹣n,则a2018=﹣=﹣1009,故选:C.10.解:根据图形得:每个数字等于上一行的左右两个数字之和,∴a=1+5=6,b=5=10=15,c=10+10=20,故选:B.11.解:a0=0,a1=﹣|a0+1|=﹣|0+1|=﹣1,a2=﹣|a1+2|=﹣|﹣1+2|=﹣1,a3=﹣|a2+3|═﹣|﹣1+3|=﹣2,a4=﹣|a3+4|═﹣|﹣2+4|=﹣2,a5=﹣|a4+5|=﹣|﹣2+5|=﹣3;a6=﹣|a5+6|=﹣|﹣3+6|=﹣3;a7=﹣|a6+7|=﹣|﹣3+7|=﹣4;……由此可以看出,这列数是0,﹣1,﹣1,﹣2,﹣2,﹣3,﹣3,﹣4,﹣4,……,(2019+1)÷2=1010,故a2019=﹣1010,故选:B.12.解:22019+22018+22017+…+2+1=(2﹣1)×(22019+22018+22017+…+2+1)=22020﹣1,∵21=2,22=4,23=8,24=16,25=32,26=64,…,2020÷4=505,∴22020的末个位数字是6,∴22020﹣1的个位数字是5,故选:C.13.解:由图形可知,第n行最后一个数为=,∴第8行最后一个数为==6,则第9行从左至右第5个数是=,故选:B.14.解:A、∵2有3个,∴不可以作为S1,故A选项错误;B、∵2有3个,∴不可以作为S1,故B选项错误;C、3只有1个,∴不可以作为S1,故C选项错误;D、符合定义的一种变换,故D选项正确.故选:D.15.解:∵f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),f(4)=0,f(5)=0,f(6)=2,f(7)=6,f(8)=2,f(9)=0,…,∴每5个数一循环,分别为2,6,2,0,0…∴2012÷5=402..2∴f(1)+f(2)+f(3)+…+f(2012)=2+6+2+0+0+2+6+2+…+2+6=402×(2+6+2)+8=4028.故选:C.16.解:∵底数是2的分裂成2个奇数,底数为3的分裂成3个奇数,底数为4的分裂成4个奇数,∴m3有m个奇数,∵2n+1=103,n=51,∴奇数103是从3开始的第52个奇数,∵=44,=54,∴第52个奇数是底数为10的数的立方分裂的奇数的其中一个,即m=10.故选:B.17.解:∵a1=3,∴a2==﹣2,a3=,a4==,a5==3,∴该数列每4个数为一周期循环,∵2019÷4=504…3,∴a2019=a3=,故选:C.二.填空题(共18小题)18.解:设OA1=A1A2=A2A3=…=A n﹣2A n﹣1=a,∵x=a时,y=,∴P1的坐标为(a,),∵x=2a时,y=,∴P2的坐标为(2a,),∴Rt△P1B1P2的面积=×a×(﹣),Rt△P2B2P3的面积=×a×(﹣),Rt△P3B3P4的面积=×a×(﹣),…,∴△P n﹣1B n﹣1P n的面积=×a×[﹣]=×1×(﹣)=.故答案为:.19.解:∵;;;…∴;∴.故答案为:1.6×105或160000.20.解:∵21×22=23,22×23=25,23×25=28,25×28=213,…,∴x、y、z满足的关系式是:xy=z.故答案为:xy=z.21.解:根据题意得出规律:14+a=15×16,解得:a=226.故答案为:226.22.解:根据左上角+4=左下角,左上角+3=右上角,右下角的数为左下和右上的积加上1的和,可得6+4=a,6+3=c,ac+1=b,可得:a=10,c=9,b=91,所以a+b+c=10+9+91=110,故答案为:11023.解:按一定规律排列的一列数依次为:,,,,,,…,按此规律,第n个数为,∴当n=100时,=,即这列数中的第100个数是,故答案为:.24.解:观察图表可知:第n行第一个数是n2,∴第45行第一个数是2025,∴第45行、第8列的数是2025﹣7=2018,故答案为2018.25.解:根据以上分析b n=2(1﹣a1)(1﹣a2)…(1﹣a n)=.26.解:a1=0,a2=﹣|a1+1|=﹣|0+1|=﹣1,a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,a6=﹣|a5+5|=﹣|﹣2+5|=﹣3,a7=﹣|a6+6|=﹣|﹣3+6|=﹣3,…,所以,n是奇数时,a n=﹣(n﹣1),n是偶数时,a n=﹣,∴a2019=﹣(2019﹣1)=﹣1009.故答案为:﹣1009.27.解:由图可得,第一行1个数,第二行2个数,第三行3个数,…,则前20行的数字有:1+2+3+…+19+20=210个数,∴第20行第20个数是:1+3(210﹣1)=628,∴第20行第19个数是:628﹣3=625,故答案为:625.28.解:∵观察可知:各三角形中左边第一个数的数字规律为:1,2,…,n,右边第二个数的数字规律为:2,22,…,2n,下边第三个数的数字规律为:1+2,2+22,…,n+2n,∴最后一个三角形中y与n之间的关系式是y=2n+n.故答案为y=2n+n.29.解:经过观察每个“田”左上角数字依此是1,3,5,7等奇数,此位置数为15时,恰好是第8个奇数,即此“田”字为第8个.观察每个“田”字左下角数据,可以发现,规律是2,22,23,24等,则第8数为28.观察左下和右上角,每个“田”字的右上角数字依次比左下角大0,2,4,6等,到第8个图多14.则c=28+14=270.故答案为:270或28+14.30.解:∵分子分别为1、3、5、7,…,∴第n个数的分子是2n﹣1,∵4﹣3=1=12,7﹣3=4=22,12﹣3=9=32,19﹣3=16=42,…,∴第n个数的分母为n2+3,∴第n个数是.故答案为:.31.解:第八项为﹣27a8=﹣128a8.32.解:∵4a n=(a n+1﹣1)2﹣(a n﹣1)2,∴(a n+1﹣1)2=(a n﹣1)2+4a n=(a n+1)2,∵a1,a2,a3……是一列正整数,∴a n+1﹣1=a n+1,∴a n+1=a n+2,∵a1=1,∴a2=3,a3=5,a4=7,a5=9,…,∴a n=2n﹣1,∴a2018=4035.故答案为4035.33.解:观察可知:3a=21,解得:a=7,∴b=14,∴x=21×14+7=301.故答案为:301.34.解:观察,发现规律:a1=6,a2=f(a1)=3,a3=f(a2)=16,a4=f(a3)=8,a5=f(a4)=4,a6=f(a5)=2,a7=f(a6)=1,a8=f(a7)=6,…,∴数列a1,a2,a3,a4…(n为正整数)每7个数一循环,∴a1﹣a2+a3﹣a4+…+a13﹣a14=0,∵2015=2016﹣1=144×14﹣1,∴2a1﹣a2+a3﹣a4+a5﹣a6+…+a2013﹣a2014+a2015=a1+a2016+(a1﹣a2+a3﹣a4+a5﹣a6+…+a2015﹣a2016)=a1+a7=6+1=7.故答案为:7.35.解:根据题意得:a=32﹣(﹣2)=11,则b=112﹣(﹣7)=128.故答案为:128.三.解答题(共10小题)36.解:(1)原式=1﹣﹣+﹣+﹣+﹣=1﹣=;(2)原式=1﹣﹣+﹣+﹣+…+﹣=1﹣=;(3)=+…+==由=,解得n=17,经检验n=17是方程的根,∴n=17.37.解:(1)第6个等式为11×15+4=132;(2)由题意知(2n﹣1)(2n+3)+4=(2n+1)2,理由:左边=4n2+6n﹣2n﹣3+4=4n2+4n+1=(2n+1)2=右边,∴(2n﹣1)(2n+3)+4=(2n+1)2.38.解:(1)29后面的第一位数是37;(2)由题意:a2﹣a1,=2,a3﹣a2=3,a4﹣a3=4…由此推算a100﹣a99=100;(3)a100=2+2+3+4+…+100=1+×100=505139.解:一个依次排列的n个数组成一个数串:a1,a2,a3,…,a n依题设操作方法可得新增的数为:a2﹣a1,a3﹣a2,a4﹣a3,a n﹣a n﹣1所以,新增数之和为:(a2﹣a1)+(a3﹣a2)+(a4﹣a3)+…+(a n﹣a n﹣1)=a n﹣a1原数串为3个数:3,9,8第1次操作后所得数串为:3,6,9,﹣1,8根据(*)可知,新增2项之和为:6+(﹣1)=5=8﹣3第2次操作后所得数串为:3,3,6,3,9,﹣10,﹣1,9,8根据(*)可知,新增4项之和为:3+3+(﹣10)+9=5=8﹣3按这个规律下去,第100次操作后所得新数串所有数的和为:(3+9+8)+100×(8﹣3)=520 (本题(10分),直接写出正确答案得3分)40.解:(1)设S=1+2+22+23+24 (29)则2S=2+22+23+24 (210)∴2S﹣S=210﹣1,即S=210﹣1,则1+2+22+23+24…+29=210﹣1;(2)设S=1+5+52+53+54…+5n,则5S=5+52+53+54…+5n+1,∴5S﹣S=5n+1﹣1,即4S=5n+1﹣1,则S=1+5+52+53+54…+5n=.41.解:(1)设S=1+2+22+23+24+ (220)将等式两边同时乘以2得:2S=2+22+23+24+25+…+221将下式减去上式得2S﹣S=221﹣1即S=221﹣1即1+2+22+23+24+…+220=221﹣1;(2)设S=1+5+52+53+54+…+5n,将等式两边同时乘以5得5S=5+52+53+54+…+5n+1将下式减去上式得5S﹣S=5n+1﹣1即4S=5n+1﹣1,S=即1+5+52+53+54+…+5n=.42.解:(1)∵第1行中,第1个数=(﹣2)1=﹣2,第2个数=(﹣2)2=4,第3个数=(﹣2)3=﹣8,…,故第n个数=(﹣2)n.第2行数等于第1行相应的数加2;第3行数等于第1行相应的数的一半;故答案为:(﹣2)n;(﹣2)n+2;(﹣2)n;(2)当n=9时,(﹣2)n=﹣512;(﹣2)n+2=﹣510;(﹣2)n=﹣256;∴这三个数的和=﹣1278.43.解:(1)C1A=,C1B=,C1B=2C1A,故C1符合题意;C2A=C2B=2,故C2不符合题意;C3A=6,C3B=1,故C3不符合题意;C4A=8,C4B=4,C4A=2C4B,故C4符合题意,故答案为:C1或C4.(2)①设点P表示的数为x,i.当点在点A左侧时,则30﹣x=2(﹣10﹣x),解得x =﹣50.所以点表示的数为﹣50;ii.如图,当点在线段AB上且时,则30﹣x=2(x+10),解得x=.所以点表示的数为;iii.如图,当点在线段AB上且时,则x+10=2(30﹣x),解得x=.所以点表示的数为.综上所述,当点P在点B的左侧时,点P表示的数为﹣50或或.②当P为A、B联盟点时:设点P表示的数为x,∵P A=2PB,∴x+10=2(x﹣30),解得x=70,即此时点P表示的数70;当A为P、B联盟点时:设点P表示的数为x,∵P A=2AB,∴x+10=80,解得x=70,即此时点P表示的数70;当B为A、P联盟点时:设点P表示的数为x,∵AB=2PB,∴40=2(x﹣30),解得x=50,即此时点P表示的数50;当B为P、A联盟点时:设点P表示的数为x,∵PB=2AB,∴x﹣30=80,解得x=110,即此时点P表示的数110,故答案为:70、50、110.44.解:(1)由题意知,第四个式子为=﹣,故答案为:=﹣;(2)第n个式子为=﹣,故答案为:=﹣;(3)原式=2(1﹣+﹣+﹣+…+﹣)=2×(1﹣)=2×=.45.解:(1)第5个等式为13+23+33+43+53=×52×62,故答案为:13+23+33+43+53=×52×62.(2)第n个等式为13+23+33+43+…+n3=×n2×(n+1)2;(3)原式=13+23+33+43+…+s3﹣[13+23+33+43+…+(s﹣1)3]=13+23+33+43+…+s3﹣13﹣23﹣33﹣43﹣…﹣(s﹣1)3=s3。
【七年级数学代数培优竞赛专题】专题4 找规律【含答案】

专题4 找规律知识解读1.探索数列中的规律现阶段的数列多为等差数列(后一个数与前一个数的差都相等)、等比数列(后一个数与前一个数的商都相等),也有的数列是某几个数的循环。
2.探索等式中的规律题目条件所提供的等式都是一般规律的具体应用,因此将所提供的等式一般化是找寻规律的常用方法.3.探索图案中的规律图案中蕴含的规律,一般可从数和形两个角度来探寻.培优学案典例示范1.探索数列中的规律例1(1)有一列数:1,-2,4,-8,16,-32,…则这列数的第8个数是,第n个数是 .(用含n的代数式表示)(2)有一列数:20,10,n,n,19,…则这列数的第9个数是,第n个数是 .(用含n的代数式表示)【提示】(1)思路一:先看符号:正、负、正、负循环,可用12319190++++=来表示;再看绝对值,后一个数的绝对值都是前一个数的绝对值的2倍,因此第n个数的绝对值是第一个数的绝对值乘(n-1)个2.思路二:看整列数,可以发现后一个数都是前一个数的-2倍,因此第n个数是第一个数乘以(n-1)个-2.(2)先看符号,负、正、负、正循环,可用20来表示;再看绝对值,分子都是1,后一个分母比前一个分母大2,因此第n个数的分母是第一个数的分母加上(n-1)个2.【技巧点评】一个数列:10,200,5,…,1,2如果满足3-4=5-1=…=1-3=5-7=p那么这个数列是等差数列,2=15+(n-1)p.一个数列:13,11,9,…,3,17如果满足19那么这个数列是等比数列,21=23等差数列和等比数列及其派生出的数列(将原等差数列或等比数列的每个数或加、或减、或乘以、或除以一个相同的非零数而生成的新数列)是找规律题中常见的数列.跟踪训练1(1)下面一组按规律排列的数:1,2,4,8,16,…第2015个数是 ; (2)已知一列数2,8,26,80,…,按此规律,则第n 个数是 (用含n 的代数式表示)例2 有一列数:1111112612203042,,,,,,,则这列数的第n 个数是 (用含n 的代数式表示)【提示】分子都是1,分母既不是等差数列,也不是等比数列. 思路一:第一个分母是12⨯,第二个是23⨯,第三个是34⨯思路二:从乘方的角度考虑,第一个分母是211+,第二个是222+,第三个是233+【技巧点评】遇到非等差或非等比数列时,从乘方的角度考虑,常常会有突破. 跟踪训练2有一组数1,2,5,10,17,26请观察规律,则第10个数为 .例3 有若干个数,第一个数记为1a ,第二个数记为2a ,第三个数记为3a 第n 个数记为n a ,若112a =-,从第二个数起,每个数都等于“1与它前面的那个数的差的倒数”.(1)试计算2a = ,3a = ,4a = ; (2)根据以上结果,请你写出2015a = ,2016a = .【提示】先根据条件计算2a ,3a ,4a ,可以发现,这n 个数是12-,23,3这三个数在循环.【技巧点评】 有的数列是一组数12,,,n a a a 在循环,找出这个数列是哪些数在循环是解决这类问题的关键.跟踪训练3观察下列各式:133=,239=,3327=,4381=,53243=,63729=,依照这个规律,20153的末位数字是 .例4 将1,12-,13,14-,15,16-按一定规律排列如下:第一行 1第二行 12- 13第三行 14- 15 16-第四行17 18- 19 110- 请你写出第20行从左到右第10个数是 .【提示】从数的排列方式可以看出,第n 行就有n 个数,因此,前面19行共有12319190++++=个数,第20行从左到右第10个数应该是所给数列中的第200个数.【技巧点评】这类问题是将一个有规律的数列与数的位置排列结合起来,因此需要在原来的基础上再去探寻数的位置的排列规律.跟踪训练4将正奇数按下表排成5列:第1列 第2列 第3列 第4列 第5列第1行 1 3 5 7 第2行 15 13 11 9第3行 17 19 21 23 第4行 31 29 27 25根据上面规律,2007应在第 行第 列.2.探索等式中的规律例5 观察下列各式:332211129492344+==⨯⨯=⨯⨯;3332211123369163444++==⨯⨯=⨯⨯;33332211123410016254544+++==⨯⨯=⨯⨯(1)若n 为正整数,试猜想3333123n ++++等于多少? (2)请利用你的猜想比较3333123100++++与()25000-的大小.【提示】当2n =时,()23322211122322144+=⨯⨯=⨯⨯+;当3n =时,()2333222111233433144++=⨯⨯=⨯⨯+,【技巧点评】将所提供的每一个式子一般化,即当n 为这些特殊值时,把原来的式子转化为含n 的式子. 跟踪训练5 观察下列各式:1121=-21221+=- 2312221++=-猜想:(1)236312222+++++= ;(2)若n 是正整数,那么2312222n +++++= .3.探索图案中的规律例6 图4-1是由一些点组成的图形,按此规律,在第n 个图形中,点的个数为 .【提示】思路一:分别写出每个图形中点的个数,得到一个数列,再去探寻数列的规律. 思路二:从形的角度入手,从第三、第四个图很容易看出是图形上面两个点再加上一个n 层的三角形,因此点的个数有这样的规律:1n =时,21+;2n =时,213++;3n =时,2135+++;4n =时,21357++++【技巧点评】这类图形的找规律问题,通常都可以从数和形两个角度来切入.跟踪训练6如图4-2,图①中有1个平行四边形,图②中有3个平行四边形,图③中有5个平行四边形,则图⑩中有 个平行四边形.培优训练直击中考1.★(2017·湖北荆州)如图4-3,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n 个图案中有2017个白色纸片,则n 的值为( )A.671B.672C.673D.6742.★(2017·辽宁丹东)观察下列数据:510172622345---,,,,,,它们是按一定规律排列的,依照此规律,第11个数据是 . 3.★(2017·湖北黄石)观察下列各式:11111222=-=⨯ 111112112232233+=-+-=⨯⨯ 1111111131122334223344++=-+-+-=⨯⨯⨯按以上规律,写出第n 个式子的计算结果(n 为正整数).(写出最简计算结果即可)4.★(2017·黑龙江绥化)古希腊数学家把数1,3,6,10,15,21叫做三角数,它有一定的规律.若把第一个三角数记为1a ,第二个三角数记为2a ,,第n 个三角数记为n a ,计算12a a +,23a a +,34a a +,由此推算399400a a += .5.★(2017·四川遂宁)求1232222n ++++的和,解法如下:解:设1232222n S =++++①2312222n S +=+++②②-①得:122n S +=- 所以1231222222n n +++++=-.参照上面的解法:计算:23201713333+++++= .6. ★(2017·山东束庄)一列数123,,,a a a 满足条件:112a =,111n n a a -=-(2n ≥,n 为整数),则2017a = .挑战竞赛1.★★(希望杯试题)在以下两个数串中:1,3,5,7,1991,1993,1995,1997,1999,和1,4,7,101990,1993,1996,1999,,同时出现在这两个数串中的数共有()A.333个B.334个C.335个D.336个2.★★(希望杯试题)将111111,23456---,,,,,按一定规律排成下表:从表中可以看到第4行中,自左向右第3个数是9,第5行中从左向右第2个数是112-,那么第199行中自左向右第8个数是,第1998行中自左向右第11个数是 .3.★★(迎春杯试题)一串数排成一行,它们的规律是这样的:头两个数都是1,从第三个数开始,每一个数都是前两个数的和,也就是1,1,2,3,5,8,13,21,34,55,问:这串数的前100个数中(包括第100个数),有多少个偶数?4.★★(华杯赛试题)自然数按下表的规律排列:(1)求上起第10行,左起第13列的数;(2)数127应在上起第几行、左起第几列?5.★★★(湖北省竞赛试题)按下列规律排成一列数:11,12,21,13,22,31,14,23,32,4 1,15,24,33,42,51,16,…(*),在(*)中左起第m个数记为()F m,当()1=2001F m时,求m的值和这m个数的积.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级规律探索题答案 Document number:NOCG-YUNOO-BUYTT-UU986-1986UT前言:七年级上册数学期中考试,主要考察书本前2章,想要考试取得好的成绩,首先应一般能力:①基本知识、基本技能;②计算能力;其次要想获得高分必须具备高分能力:①观察、猜想、推理、验证的能力;②数形结合思想的建立;③分类讨论思想的建立;④方程思想的建立;对于重点中学学生,尤为重要。
高分能力是今后学习领先的有力保障,需要大量练习、总结、体会,七年级涉及的仅仅是一部分。
一、规律探索类题型规律探索型问题是指在一定条件下,探索发现有关数学对象所具有的规律性或不变性的问题,它往往给出了一组变化了的数、式子、图形等条件,要求学生通过:①读题 ②观察 ③分析 ④猜想 ⑤验证,来探索对象的规律。
它体现了“特殊到一般”、“数形结合”等数学思想方法,考察学生的分析、解决问题能力。
题型可涉及填空、选择或解答。
【题型分类】 【1、数字问题】最好具备数列的有关知识(小学奥数有涉及),实际考察的是:经历探索事物间的数量关系,用字母表示数和代数式表示的过程,建立初步的符号感,发展抽象思维,进一步使学生体会到代数式是刻画现实世界的有效数学模型。
如: 1、正整数规律1、2、3、4、5、、、、可以表示为n (其中n 为正整数) 2、奇数规律1、3、5、7、9、、、、可以表示为21n -(其中n 为正整数) 3、偶数规律2、4、6、8、10、、、、可以表示为2n (其中n 为正整数) 4、正、负交替规律变化一组数,不看他们的绝对值,只看其性质,为正负交替 (1)、-、+、-、+、-、+、-、+可以表示为(1)n - (2)、+、-、+、-、+、-、+、-可以表示为1(1)n +- 5、平方数规律1、4、9、16、、、、可以表示为2n (其中n 为正整数),能看得出:上面的规律数+1、+2、-1、-26、等差数列常识按一定次序排列的一列数就叫数列。
例如:(1) 1,2,3,4,5,6,… (2) 1,2,4,8,16,32;A 、一个数列中从左至右的第n 个数,称为这个数列的第n 项。
如,数列(1)的第3项是3,数列(2)的第3项是4。
一般地,我们将数列的第n 项记作a n 。
B 、数列中的数可以是有限多个,如数列(2)(4),也可以是无限多个,如数列(1)(3)(带省略号)。
概念:干个数排成一列称为数列,数列中的每一个数称为一项,其中第一项称为首项(记作:1a ),最后一项称为末项(记作:n a )。
后项与前项之差都相等的数列称为等差数列,后项与前项之差称为公差(记作:d )。
其中:1(1)n a a n d =+-, 11n a a n d-=+,数列的和1()2n n a a nS +⨯= (记得住就记,记不住就推理)方法说明:掌握3个原则:①数据表面上看来排列无序,且形式不一致,那么要进行数据变形,使之形式一致;②一组数中的每个数进行数据分解,有时可快速得出规律;③对数据做一些简单的运算看出规律,如:加一加、减一减,乘一乘、除一除 例1 观察一列数:1,-,3611,259,167,95,43--……根据规律,请你写出第10个数是 。
例2 古希腊数学家把1,3,6,10,15,21,… 叫做三角形数,根据它的规律,则第100个与第98个的差为 ________练习:(1)观察一列数:21,52-,103,174-,265,376-……根据规律,请你写出第10个数是 (2)按一定规律排列的一列数依次为11113102635---11,,,,,,,215按此规律排列下去,这列数中第七个数是(3)某种细胞开始有2个,1小时后分裂成4并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1个,按此规律,5小时后细胞存活数是____,n 小时后细胞存活数是____ 【2、图形规律】根据一组相关图形的变化规律,从中总结图形变化所反映的规律。
解决图形规律问题的方法有两种:一种是数形结合,将图形转化成数字规律,用数字规律的解决问题;一种是通过图形的直观性,观察图形的变化,主要从各图形的形状、方向、数量、大小及各组成部分的相对位置入手,从中找出变化规律。
例3 观察图给出的四个点阵,s 表示每个点阵中的点的个数,按照图形中的点的个数变化规律,猜想第n 个点阵中的点的个数s 为( ) A 、32n -B 、31n -C 、41n +D 、43n -例4 若按下图方式摆放餐桌和椅子,请探索规律并填表: 餐桌张数 1234…..10n可坐人数练习:(1)观察下列图形,则第n 个图形中三角形的个数是( )A 、22n +B 、44n +C 、44n -D 、4n(2) 如图是一组有规律的图案, 第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……第8个图案由_____个基础图形组成,第n (n 是正整数)个图案中由 ___ 个基础图形组成。
(3) 下列图案是晋商大院窗格的一部分,其中○”代表窗纸上所贴的剪纸,则第n 个图中所贴剪纸“○”的个数为 .【3、循环排列规律】循环排列规律是运动着的规律,我们只要根据题目的已知部分分析出图案或数据每隔几个就会循环出现,看看最后所求的与循环的第几个一致即可,关键是找出“循环节数”。
其次,就是利用“余数”。
例5 如图所示,数轴被折成90︒,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。
先让圆周上数字2所对应的点与数轴上的数3所对应的点重合,数轴固定,圆紧贴数轴沿着数轴的正方向滚动,那么数轴上的数2009将与圆周上的数字 重合。
(1(2(3………………第1个第2个第3个(1) (2)(3)……9876543例6 手的示意图,在各个手指间标记字母A 、B 、C 、D .请你按图中箭头 所指方向(即A →B →C →D →C →B →A →B →C…的方式)从A 开始数连续的 正整数1,2,3,4…,当数到12时,对应的字母是____;当字母C 第 201次出现时,恰好数到的数是____;当字母C 第2n+1次出现时 (n 为正整数),恰好数到的数是_______(用含n 的代数式表示). 练习:(1)如图所示,圆的周长为4个单位长度,在圆的4等分点处标上数字0,1,2,3。
先让圆周上数字0所对应的点与数轴上的数1-所对应的点重合,再让数轴按逆时针方向绕在该圆上,那么数轴上的数2006-将与圆周上的数字 重合。
(2)观察下图中正方形四个顶点所标的数字规律,可知数2011应标在( )A 、第502个正方形的左下角B 、第502个正方形的右下角C 、第503个正方形的左上角D 、第503个正方形的右下角 (3)观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称) 【4、算式规律】应对的一般原则:①找出等式中的各个部分;②找出等式中的各个部分中不变的部分;③找出等式中的各个部分中变化的部分、并寻找他们的变化规律。
例7 1+2+3+…+100=经过研究,这个问题的一般性结论是(1)123 (2)n n n +++++=,其中n是正整数。
现在我们来研究一个类似的问题:1223......(n 1)n ⨯+⨯+++=观察下面三个特殊的等式:将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯ 读完这段材料,请你思考后回答: 例8 观察下列三行数:(1)第①行数按什么规律排列(2)第②③行数与第①行数分别有什么关系(3)取每行数的第n 个数,这三个数的和能否等于-1278,如果能,指出是每行的第几个数,并求出这三个数;如果不能,请说明理由。
练习:3210-5-4-3-2-10-1, 2, -4, 8, -16, 32,…; ① -2, 4, -8, 16, -32, 64,…; ②(1)观察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,请你在观察规律之后并用你得到的规律填空:2____________________50⨯+=, 第n 个式子呢 ________________________ (2)观察下列各式,你会发现什么规律3×5=15,而15=241-5×7=35,而35=261-……11×13=143,而143=2121-将你猜想到的规律用只含一个字母的式子表示出来:___________________________。
(3)下列图是由同型号黑白两种颜色的三角形瓷砖按一定规律铺设的图形。
仔细观察图形可知:图①有1块黑色的瓷砖,可表示为21)11(1⋅+=; 图②有3块黑色的瓷砖,可表示为22)21(21⋅+=+;图③有3块黑色的瓷砖,可表示为23)31(321⋅+=++实践探索:(1)请在图④的虚线框内画出第4个图形(只须画出草图)(2)第10个图形有 ________ 块黑色的瓷砖(直接填写结果) (3)第n 个图形有多少块黑色的瓷砖(用含n 的代数式表示) 【5、数表规律】兼具数字规律和图形规律的特点,难度加大。
例9 将111111,,,,,,23456---按一定规律排列如下:第1行 1 第2行 12-13第3行 14-15 16-第4行1718-19 110-第5行 111 112- 113 114- 115…请你写出第20行从左至右第10个数是 。
例10 (1) 在2008年10月的月历中(见图1),任意圈出一竖列上相邻的三个数,设中间的一个为a ,则用含a 的整式表示这三个数(从小到大排列)分别是 ____ 。
图1(2)现将连续自然数1至2008按图中的方式排成一个长方形的数阵,用一个正方形框出9个数(见图2)①图中框出的这9个数的和是 ; ②在图中,能否使一个正方形框出的9个数之和等于2007 若不可能,请说明理由;若有可能,请求出该正方形框出的9个数中的最小数和最大数。
(写出详细的解题过程) 练习:(1)已知一列数:1,―2,3,―4,5,―6,7,… 将这列数排成如下所示的形式:按照上述规律排下去,那么第10行从左边数第5个数等于 . 第1行 1 第2行 -2 3第3行 -4 5 -6 第4行 7 -8 9 -10 第5行 11 -12 13 -14 15 ………………(2)将正偶数排成5列,如下表:日一二三 四 五 六1 2 3 4 567891011 12 13 14 15 16 1718 19 20 21 22 23 24 2526 27 28 29 30 311 2 3 4 5 6 7 8 9 10 14 15 16 17 21 22 23 24 28 29 30 31 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 …………………1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008行 第3行18 20 22 24………2826A 、第25行,第1列B 、第125行,第2列C 、第250行,第1列D 、第250行,第2列 (3)观察一列数表:1 2 3 4 … 第一行 2 3 4 5 … 第二行 3 4 5 6 … 第三行 4 5 6 7 … 第四行 ┆ ┆ ┆ ┆ 根据数表所反映的规律,猜想第6行与第6列的交叉点上的数应为多少第n 行与第n 列交叉点上的数应为多少(用n 表示) 【5、其它规律】等比数列 如果一个数列从第二项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。
