维随机游走
随机游走离散型随机变量的随机漫步模型

随机游走离散型随机变量的随机漫步模型随机游走是一种描述随机变量在一条离散路径上从一个状态跳转到另一个状态的模型。
在该模型中,随机变量在每次转移时根据一定的概率进行状态的跳转,使得其在状态空间中进行“随机漫步”。
本文将介绍随机游走的概念、离散型随机变量以及随机漫步模型的基本原理。
一、随机游走的概念随机游走(Random Walk)是一种数学模型,用于描述在离散路径上随机变量的运动轨迹。
在随机游走过程中,随机变量从当前状态跳转到下一个状态的概率是随机的,并且其转移规律通常遵循一定的概率分布。
随机游走常用于模拟各种现实中的问题,如股票价格的变化、传染病的传播等。
二、离散型随机变量离散型随机变量(Discrete Random Variable)指的是在一定的取值范围内,可能取到有限个或可列个数值的随机变量。
与连续型随机变量不同,离散型随机变量的取值仅限于某些特定的数值。
常见的离散型随机变量包括二项分布、泊松分布等。
三、随机漫步模型随机漫步模型(Random Walk Model)是一种描述随机变量以随机方式在状态空间中移动的数学模型。
在随机漫步模型中,随机变量在每次转移时根据一定的概率进行状态的跳转,使得其在状态空间中进行随机的移动。
具体的转移规律通常由转移概率矩阵来描述。
在离散型随机变量的随机漫步模型中,随机变量的状态空间是有限个或可列个状态。
随机漫步模型可以用一个状态转移矩阵来表示,矩阵的元素表示从一个状态转移到另一个状态的概率。
通过迭代计算,可以得到随机变量在每个状态下的概率分布,从而对其进行建模和分析。
随机漫步模型在实际应用中具有广泛的意义。
例如,在金融领域中,可以利用随机漫步模型来预测股票价格的变化趋势;在物理学领域中,可以使用随机漫步模型来模拟原子或分子的扩散过程等。
总结:随机游走离散型随机变量的随机漫步模型是一种描述随机变量在离散路径上随机跳转的数学模型。
通过随机漫步模型,我们可以对离散型随机变量的状态进行建模和分析,为实际问题的解决提供参考。
随机过程中的随机游走

随机游走是随机过程中一种重要的模型,其在多个领域都有广泛的应用,包括物理学、金融学、生物学等。
随机游走的基本思想是描述一个在一系列随机步骤中随机移动的过程。
在随机游走中,我们关注的是一个在一个状态空间中移动的随机变量。
这个状态空间可以是一维、二维甚至更高维度的。
随机游走中的每一步移动都是随机的,通常是根据某种概率分布来决定的。
最常见的随机游走模型是一维随机游走,其中随机变量在每个时间步长内以概率 p 向右移动一步,以概率 q 向左移动一步,p + q = 1。
这样的随机游走可以模拟许多现实世界中的情况,比如一个颗粒在液体中的扩散、股票价格的变化等。
随机游走可以用一种简单的数学模型来描述,即马尔可夫链。
马尔可夫链是一种具有“无记忆”的特性,即在给定当前状态下,未来状态的转移只依赖于当前状态,与过去的状态无关。
这种特性使得马尔可夫链成为描述随机游走的理想模型。
利用马尔可夫链的转移矩阵,我们可以计算随机游走在不同时间步长内到达各个状态的概率。
随机游走不仅有理论上的意义,还有很多实际应用。
在物理学中,随机游走可以用来研究粒子在溶液中的扩散行为。
根据随机游走模型,可以计算出粒子在不同时间段内从起始位置到达各个位置的概率分布。
这些概率分布可以与实验结果进行比较,从而验证实验数据与理论模型的一致性。
在金融学中,随机游走被广泛应用于股票价格预测和风险管理。
根据随机游走模型,股票价格的变动可以看作是一系列随机变量的累积。
根据已有的历史数据,可以估计出股票价格的随机变动的概率分布,并利用这些概率分布来预测未来的股票价格趋势。
在生物学中,随机游走可以用来研究细胞运动行为和蛋白质折叠过程。
细胞在背景噪声的影响下随机移动,这种运动可以用随机游走来描述。
蛋白质折叠是一个复杂且具有多种可能路径的过程,随机游走可以用来模拟蛋白质在其折叠过程中的构象变化。
随机游走作为一种重要的随机过程模型,不仅在理论研究中具有重要地位,也在实际应用中发挥着重要作用。
随机游走的自相关系数

随机游走的自相关系数随机游走是一种常见的数学模型,常用于描述随机过程中的移动。
它可以用来研究许多领域,如金融市场、物理学、生物学等。
在随机游走中,自相关系数是一个重要的指标,用于衡量随机过程中的相关性。
让我们了解一下什么是随机游走。
随机游走是一种模型,描述了一个物体在每个时间步中随机移动的情况。
在一维情况下,物体可以向左或向右移动,每次移动的距离可以是固定的或服从某个特定的概率分布。
在二维或更高维的情况下,物体可以在各个方向上移动。
在随机游走中,自相关系数是一个重要的统计量。
它用来衡量随机过程中两个变量之间的相关性。
自相关系数的取值范围在-1到1之间,其中-1表示完全负相关,1表示完全正相关,0表示没有相关性。
自相关系数越接近于1或-1,表示两个变量之间的关联越强。
随机游走的自相关系数可以通过计算相邻步长之间的相关性得到。
例如,假设我们有一个随机游走模型,物体在每个时间步中向左或向右移动一个单位距离。
我们可以计算相邻步长之间的自相关系数,来衡量物体移动的趋势是否存在相关性。
随机游走的自相关系数在金融市场中有广泛的应用。
在股票市场中,投资者经常使用随机游走模型来预测股票价格的走势。
他们通过计算股票价格的自相关系数,来判断价格是否存在长期的趋势。
如果自相关系数接近于1,意味着价格存在明显的上涨或下跌趋势;如果自相关系数接近于0,意味着价格呈现随机波动。
除了金融市场,随机游走的自相关系数还可以应用于物理学和生物学领域。
在物理学中,随机游走模型可以用来描述分子在溶液中的扩散过程。
研究人员可以通过计算分子的自相关系数,来了解分子在溶液中的运动规律。
在生物学中,随机游走模型可以用来描述细胞的移动过程。
科学家可以通过计算细胞的自相关系数,来研究细胞的迁移行为和群体行为。
随机游走的自相关系数是一个重要的统计量,用于衡量随机过程中的相关性。
它在金融市场、物理学和生物学等领域都有广泛的应用。
通过计算自相关系数,我们可以了解随机游走模型中变量之间的关联程度,从而预测未来的趋势和行为。
概率论中的马尔可夫链与随机游走

概率论中的马尔可夫链与随机游走概率论是数学的一个重要分支,研究随机事件的规律性。
其中,马尔可夫链与随机游走是概率论中常见的概念和模型。
本文将介绍马尔可夫链和随机游走的基本概念、性质和应用,并分析它们在实际问题中的作用。
一、马尔可夫链的基本概念马尔可夫链是指具有马尔可夫性质的随机过程。
马尔可夫性质是指,在给定当前状态下,未来的状态只依赖于当前状态,与过去的状态无关。
马尔可夫性质可以用条件概率表示,即对于任意两个状态 i 和 j,以及任意正整数 n,有:P(X_n=j | X_0=i, X_1=xi_1, X_2=xi_2,...,X_{n-1}=xi_{n-1}) =P(X_n=j | X_{n-1}=xi_{n-1})其中,X_0, X_1, ..., X_n 表示随机过程在不同时刻的状态。
二、马尔可夫链的性质1. 马尔可夫链的状态空间马尔可夫链的状态空间是指所有可能状态的集合。
状态空间可以是有限的,也可以是无限的。
2. 马尔可夫链的转移概率矩阵转移概率矩阵是马尔可夫链的核心概念,它用来描述从一个状态转移到另一个状态的概率。
如果状态空间是有限的,转移概率矩阵是一个方阵,其元素表示从一个状态到另一个状态的转移概率。
3. 马尔可夫链的平稳分布马尔可夫链的平稳分布是指在长时间内,马尔可夫链的状态分布趋于稳定且不随时间变化的分布。
平稳分布与转移概率矩阵有关,可以通过求解状态转移方程得到。
三、马尔可夫链的应用1. 随机游走模型随机游走是马尔可夫链在数理金融学、统计物理学等领域的重要应用之一。
随机游走模型可以用来描述在离散状态空间中,随机过程在各个状态间的随机跳跃。
2. PageRank算法PageRank算法是谷歌搜索引擎中应用的一种基于马尔可夫链的排序算法。
该算法通过将互联网看做一个巨大的马尔可夫链,根据页面之间的链接关系概率进行页面排序。
3. 马尔可夫链蒙特卡洛方法马尔可夫链蒙特卡洛方法是一种基于马尔可夫链的随机模拟方法,用于求解复杂的数学问题。
二维随机游走 概率计算

二维随机游走概率计算
二维随机游走是一种概率过程,它描述了一个粒子在二维平面上的随机运动。
在每一个时间步长内,粒子有相等的概率向四个方向(上、下、左、右)移动一个单位距离。
随机游走的概率计算涉及到组合数学和概率论的知识。
假设我们从原点(0,0)出发,经过n个时间步长后,粒子到达点(x,y)的概率为:
P(x,y,n) = C(n,(n+x+y)/2) * C((n+x+y)/2,(n+y-x)/2) * (1/4)^n
其中,C(n,k)表示从n个元素中取出k个元素的组合数,即C(n,k) = n!/(k!(n-k)!)。
解释如下:
1) 要到达(x,y),粒子需要向右移动(n+x-y)/2次,向上移动(n+y-x)/2次。
2) 在n个时间步长中,有(n+x+y)/2次是向右或向上移动。
3) 从n个时间步长中选择(n+x+y)/2个时间步长向右或向上移动,有C(n,(n+x+y)/2)种方式。
4) 在选定的(n+x+y)/2个时间步长中,有(n+y-x)/2次是向上移动,剩余的是向右移动,有C((n+x+y)/2,(n+y-x)/2)种方式安排这些向上移动。
5) 每次移动的概率是1/4。
通过上述公式,我们可以计算出粒子在二维随机游走中到达任意点
(x,y)的概率。
需要注意的是,当n是奇数时,如果x+y是奇数,则概率为0,因为粒子无法到达该点。
E02.多维随机游走及应用

多维随机游走及应用
摘要
本文从一维和二维随机游走开始探究,基于组合数学和概率论的有关理论, 利用 Bernoulli 概型及其叠加推导得到了从一确定点出发到达任意随机点的概 率; 然而在三维随机游走问题上,不能直接利用 Bernoulli 概型,因而首先引入了 一个有放回的摸球问题,再通过该问题得到三维随机变量的分布概型,从而解决 了三维随机游走中到达任意随机点的概率问题,并且通过这个思想推导了多维随 机游走的相关结论.最后,本文将得到的结论应用在环形随机游走中, 得到相关结 论.
\ a + b(mod 2) ⎧0, N ≡ ⎪ ⎪ ⎪ i + a i + a i −a N −i +b N −i +b N −i −b ⎤. P(B ) = ⎨ N −b ⎡ i i N −i 2 2 2 2 2 ( ) ( ) + + ⋅ ⋅ C p q m n C p q C m n 2 ⎥ i i ⎪∑ ⎢ N ⎦ ⎪ i =a ⎣ ⎪ ⎩ N ≡ a + b(mod 2), i ≡ a(mod 2)
i =1
G
数, β 为 δ i = 1 的个数.则有 α − β = a , α + β = G , G − a = 2β .故 G ≡ a (mod 2) . I. G ≡ \ a (mod 2) 时, P(B ) = 0 .
即此时是不可能到达 (a, b ) 的;同时,若 G ≡ \ a (mod 2) ,有 G ≡ \ − a (mod 2) ,即
新高考视角下的随机游走与马尔科夫过程

随机游走与马尔科夫过程一.基本原理1.转移概率:对于有限状态集合S ,定义:)|(1,i n j n j i X X P P ==+=为从状态i 到状态j 的转移概率.2.马尔可夫链:若ij i n j n i i n i n j n P X X P X X X X P n ==⋅⋅⋅==+==-==+-)|(),,,|(101101,即未来状态1+n X 只受当前状态n X 的影响,与之前的021,,,X X X n n ⋅⋅⋅--无关.3.一维随机游走模型设数轴上一个点,它的位置只能位于整点处,在时刻0=t 时,位于点)(+∈=N i i x ,下一个时刻,它将以概率α或者β(1),1,0(=+∈βαα)向左或者向右平移一个单位.若记状态i t X =表示:在时刻t 该点位于位置)(+∈=N i i x ,那么由全概率公式可得:)|()()|()()(1111111+==++=-==+-==+⋅+⋅=i t i t i t i t i t i t i t X X P X P X X P X P X P 另一方面,由于αβ==+==+-==+)|(,)|(1111i t i t i t i t X X P X X P ,代入上式可得:11-+⋅+⋅=i i i P P P βα.进一步,我们假设在0=x 与),0(+∈>=N m m m x 处各有一个吸收壁,当点到达吸收壁时被吸收,不再游走.于是,1,00==m P P .随机游走模型是一个典型的马尔科夫过程.进一步,若点在某个位置后有三种情况:向左平移一个单位,其概率为a ,原地不动,其概率为b ,向右平移一个单位,其概率为c ,那么根据全概率公式可得:11-+⋅+⋅+⋅=i i i i P c P b P a P 有了这样的理论分析,下面我们看全概率公式及以为随机游走模型在2019年全国1卷中的应用.二.典例分析.例1.(2019全国1卷).为了治疗某种疾病,研制了甲、乙两种新药,希望知道哪种新药更有效,为此进行动物试验.试验方案如下:每一轮选取两只白鼠对药效进行对比试验.对于两只白鼠,随机选一只施以甲药,另一只施以乙药.一轮的治疗结果得出后,再安排下一轮试验.当其中一种药治愈的白鼠比另一种药治愈的白鼠多4只时,就停止试验,并认为治愈只数多的药更有效.为了方便描述问题,约定:对于每轮试验,若施以甲药的白鼠治愈且施以乙药的白鼠未治愈则甲药得1分,乙药得1-分;若施以乙药的白鼠治愈且施以甲药的白鼠未治愈则乙药得1分,甲药得1-分;若都治愈或都未治愈则两种药均得0分.甲、乙两种药的治愈率分别记为α和β,一轮试验中甲药的得分记为X .(1)求X 的分布列;(2)若甲药、乙药在试验开始时都赋予4分,(0,1,,8)i p i = 表示“甲药的累计得分为i 时,最终认为甲药比乙药更有效”的概率,则00p =,81p =,11i i i i p ap bp cp -+=++(1,2,,7)i = ,其中(1)a P X ==-,(0)b P X ==,(1)c P X ==.假设0.5α=,0.8β=.(i)证明:1{}i i p p +-(0,1,2,,7)i = 为等比数列;(ii)求4p ,并根据4p 的值解释这种试验方案的合理性.解析:(1)由题意可知X 所有可能的取值为:1-,0,1()()11P X αβ∴=-=-;()()()011P X αβαβ==+--;()()11P X αβ==-则X 的分布列如下:X1-01P ()1αβ-()()11αβαβ+--()1αβ-(2)0.5α= ,0.8β=0.50.80.4a ∴=⨯=,0.50.80.50.20.5b =⨯+⨯=,0.50.20.1c =⨯=(i)()111,2,,7ii i i p ap bp cp i -+=++=⋅⋅⋅ 即()110.40.50.11,2,,7i i i i p p p p i -+=++=⋅⋅⋅整理可得:()11541,2,,7ii i p p p i -+=+=⋅⋅⋅()()1141,2,,7i i i i p p p p i +-∴-=-=⋅⋅⋅{}1i i p p +∴-()0,1,2,,7i =⋅⋅⋅是以10p p -为首项,4为公比的等比数列(ii)由(i)知:()110144i ii i p p p p p +-=-⋅=⋅78714p p p ∴-=⋅,67614p p p -=⋅,……,01014p p p -=⋅作和可得:()880178011114414441143p p p p p ---=⋅++⋅⋅⋅+===-18341p ∴=-()4401234401184144131144441434141257p p p p p --∴=-=⋅+++==⨯==--+4p 表示最终认为甲药更有效的.由计算结果可以看出,在甲药治愈率为0.5,乙药治愈率为0.8时,认为甲药更有效的概率为410.0039257p =≈,此时得出错误结论的概率非常小,说明这种实验方案合理.注:1.虽然此时学生未学过全概率公式,但命题人也直接把11-+⋅+⋅+⋅=i i i i P c P b P a P 给出,并没有让考生推导这个递推关系,实际上,由前面的基本原理,我们可以看到,这就是一维随机游走模型.习题1.足球是一项大众喜爱的运动.2022卡塔尔世界杯揭幕战将在2022年11月21日打响,决赛定于12月18日晚进行,全程为期28天.校足球队中的甲、乙、丙、丁四名球员将进行传球训练,第1次由甲将球传出,每次传球时,传球者都等可能的将球传给另外三个人中的任何一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,第n 次触球者是甲的概率记为n P ,即11P =.(1)求3P (直接写出结果即可);(2)证明:数列14n P ⎧⎫-⎨⎬⎩⎭为等比数列,并判断第19次与第20次触球者是甲的概率的大小.解析:(1)由题意得:第二次触球者为乙,丙,丁中的一个,第二次触球者传给包括甲的三人中的一人,故传给甲的概率为13,故313P =.(2)第n 次触球者是甲的概率记为n P ,则当2n ≥时,第1n -次触球者是甲的概率为1n P -,第1n -次触球者不是甲的概率为11n P --,则()()1111101133n n n n P P P P ---=⋅+-⋅=-,从而1111434n n P P -⎛⎫-=-- ⎪⎝⎭,又11344P -=,14n P ⎧⎫∴-⎨⎬⎩⎭是以34为首项,公比为13-的等比数列.则1311434n n P -⎛⎫=⨯-+ ⎪⎝⎭,∴181931114344P ⎛⎫=⨯-+> ⎪⎝⎭,192031114344P ⎛⎫=⨯-+< ⎪⎝⎭,1920P P >,故第19次触球者是甲的概率大。
随机游走方差的计算公式

随机游走方差的计算公式随机游走(Random Walk,缩写为RW),又称随机游动或随机漫步,是一种数学统计模型,它是一连串的轨迹所组成,其中每一次都是随机的。
它能用来表示不规则的变动形式,如同一个人酒后乱步,所形成的随机过程记录。
因此,它是记录随机活动的基本统计模型。
Random Walk是随机过程(Stochastic Process)的一个重要组成部分,通常描述的是最简单的一维Random Walk过程。
下面给出一个例子来说明:考虑在数轴原点处有一只蚂蚁,它从当前位置(记为x(t))出发,在下一个时刻(x(t+1))以的概率向前走一步(即x(t+1)=x(t)+1),或者以的概率向后走一步(即x(t+1)=x(t)-1),这样蚂蚁每个时刻到达的点序列就构成一个一维随机游走过程。
本质上Random Walk是一种随机化的方法,在实际上生活中,例如醉汉行走的轨迹、花粉的布朗运动、证券的涨跌等都与Random Walk有密不可分的关系。
Random Walk已经被成功地应用到数学,物理,化学,经济等各种领域。
当前研究者们已经开始将Random Walk应用到信息检索、图像分割等领域,并且取得了一定的成果,其中一个突出的例子就是Brin和Page利用基于Random Walk的PageRank技术创建了Google公司。
随机游走的形式有:马尔可夫链或马可夫过程:一维随机游走也可以看作马尔可夫链,其状态空间由整数给出。
布朗运动醉汉走路(drunkard’s walk)莱维飞行(Lévy flight)随机游走(random walk)矩阵可以看做是马尔科夫链的一种特例。
喝醉的酒鬼总能找到回家的路,喝醉的小鸟则可能永远也回不了家。
一维、二维随机游走过程中,只要时间足够长,我们最终总能回到出发点; 三维网格中随机游走,最终能回到出发点的概率只有大约34%;四维网格中随机游走,最终能回到出发点的概率是19.3%;八维空间中,最终能回到出发点的概率只有7.3%;。
随机游走

随机游走本来是“物理上布朗运动”相关的分子,还是微观粒子的运动形成的一个模型。
现在过多的谈到随机游走假说是数理金融中最重要的假设,它把有效市场的思想与物理学中的布朗运动联系起来,由此而来的一整套的随机数学方法成为构建数理金融的基石。
(其研究的机理已经在股票研究中应用很广泛)编辑本段何谓随机游走?“随机游走”(random walk)是指基于过去的表现,无法预测将来的发展步骤和方向。
这一术语应用到股市上,则意味着股票价格的短期走势不可预知,意味着投资咨询服务、收益预测和复杂的图表模型全无用处。
在华尔街上,“随机游走”这个名词是个讳语,是学术界杜撰的一个粗词,是对专业预言者的一种侮辱攻击。
若将这一术语的逻辑内涵推向极致,便意味着一只戴上眼罩的猴子,随意向报纸的金融版面掷一些飞镖,选出的投资组合就可与投资专家精心挑选出的一样出色编辑本段随机游走模型随机游走模型的提出是与证券价格的变动模式紧密联系在一起的。
最早使用统计方法分析收益率的著作是在1900年由路易·巴舍利耶(Louis Bachelier)发表的,他把用于分析赌博的方法用于股票、债券、期货和期权。
在巴舍利耶的论文中,其具有开拓性的贡献就在于认识到随机游走过程是布朗运动。
1953年,英国统计学家肯德尔在应用时间序列分析研究股票价格波动并试图得出股票价格波动的模式时,得到了一个令人大感意外的结论:股票价格没有任何规律可寻,它就象“一个醉汉走步一样,几乎宛若机会之魔每周仍出一个随机数字,把它加在目前的价格上,以此决定下一周的价格。
”即股价遵循的是随机游走规律。
随机游走模型有两种,其数学表达式为:Y t =Y t-1 +e t ①Y t =α+Y t-1 +e t ②式中:Y t 是时间序列(用股票价格或股票价格的自然对数表示); e t 是随机项,E(e t )=0;Var(e t )=σ 2 ;α是常数项。
模型①称为“零漂移的随机游走模型”,即当天的股票价格是在前一天价格的基础上进行随机变动。
一种基于随机游走的多维数据推荐算法

L I F a n g a L I Y o n g - j i n 2
( S c h o ol o f Co mp u t e r , Hu b e i I n s t i t u t e o f Te c h n o l o g y, Hu a n g s hi 4 3 5 0 0 0, Ch i n a )
( Sc h ol o f o mp C u t e r ci S e n c e , Na t i o n a l Un i v e r s i t y o f De f e ns e Te c h n o l o g y, Ch a n g s h a 4 1 0 0 7 3 , Ch i n a ) 。
c o mme n d e r a l g o r i t h m. F i r s t , t h i s p a p e r b u i l t a mu l t i d i me n s i o n a l r e c o mme n d e r s y s t e m mo d e l u s i n g u s e r s ’c o n t e x t , 8 e -
基于内容的推荐方法对用户以前访问过的商品进行分析并将与其相似的未知商品推荐给用户这种方法主要是对商品的资料如大小类别生产商等进行分析然后将未知的商品与之比较以发现相似的商品4
第4 O 卷
2 0 1 3年 1 1 月
第1 1 期
计
算
机
科
学
ቤተ መጻሕፍቲ ባይዱ
Co mp u t e r S c i e n c e
Vo 1 . 4 0 NO . 1 1 Nov 2 01 3
一
种 基 于 随机 游 走 的 多维 数 据 推 荐算 法
计算物理随机游走

通过分子动力学模拟,可以研究不同成分、结构对材料性能的影 响,为新材料的设计和开发提供理论指导。
材料制备工艺优化
分子动力学模拟可用于优化材料的制备工艺,提高材料的性能和 稳定性。
量子计算在处理大规模数据中的潜力
量子计算原理
大规模数据处理
量子计算可应用于处理大规模数据,通过量子叠加 和量子纠缠等特性,实现高效的数据分析和挖掘。
随机游走具有马尔可夫性质,即下一步的状态仅 与当前状态有关,与历史状态无关。
03 路径依赖性
尽管每一步是随机的,但长期行为可能呈现出一 定的规律性,如扩散现象。
一维、二维及三维随机游走
一维随机游走
01
粒子在一条直线上进行左右随机移动,位置随时间变化形成一
维随机序列。
二维随机游走
02
粒子在平面上进行上下左右随机移动,位置变化构成二维随机
用
布朗运动与扩散现象
01
02
03
布朗运动
悬浮在液体或气体中的微 粒受到周围分子的无规则 碰撞而产生的无规则运动。
扩散现象
物质分子从高浓度区域向 低浓度区域转移的过程, 其速率与浓度梯度和扩散 系数有关。
随机游走模型
描述布朗运动和扩散现象 的常用模型,通过模拟大 量粒子的随机运动来揭示 宏观规律。
化学反应动力学过程模拟
01
化学反应速率
描述化学反应快慢的物理量,与反应物浓度、温度等因素有关。
02
随机游走模型在化学反应中的应用
通过模拟反应物分子的随机运动,可以研究反应速率、反应机理等动力
学过程。
03
Monte Carlo模拟
一种基于随机数的计算方法,可用于模拟复杂的化学反应过程。
《基于随机游走的基因功能预测研究及应用》范文

《基于随机游走的基因功能预测研究及应用》篇一一、引言随着生物信息学和基因组学的飞速发展,对基因功能的研究已经从传统的实验方法转向了计算预测。
基因功能的预测与解读在生物学、医学和药物研发等领域具有极其重要的价值。
本文将介绍一种基于随机游走的基因功能预测方法,并探讨其在实际应用中的效果和价值。
二、随机游走基因功能预测方法1. 算法原理随机游走算法是一种模拟生物分子运动轨迹的算法,它可以通过模拟分子在空间中的随机运动来研究分子的性质和行为。
在基因功能预测中,我们可以通过构建基因网络,将基因看作网络中的节点,基因之间的相互作用看作边,然后利用随机游走算法在基因网络中模拟基因的“运动”,从而推断出基因的功能。
2. 算法步骤(1)构建基因网络:根据基因之间的相互作用、表达模式等数据,构建基因网络。
(2)初始化随机游走:在基因网络中选择一个起始节点,开始随机游走。
(3)游走过程:在游走过程中,根据节点的连接关系和权重,计算游走到下一个节点的概率,并按照概率进行游走。
(4)功能预测:根据游走过程中访问的节点信息,结合已知的基因功能数据,预测目标基因的功能。
三、实验结果与分析1. 数据集与实验设置我们使用了一个包含数千个基因的公开数据集进行实验。
在实验中,我们将基因网络构建为无向加权网络,并设置了不同的游走步长和游走次数进行实验。
2. 实验结果通过随机游走算法,我们成功地预测了大量基因的功能。
与已知的基因功能数据相比,我们的预测结果具有较高的准确性和可靠性。
此外,我们还发现了一些新的基因功能,这些功能在之前的研究中并未被报道过。
3. 结果分析我们的实验结果表明,基于随机游走的基因功能预测方法是一种有效的预测方法。
该方法能够充分利用基因网络中的信息,通过模拟基因的“运动”来推断基因的功能。
此外,该方法还具有较高的准确性和可靠性,能够为生物学、医学和药物研发等领域提供有力的支持。
四、应用案例1. 疾病相关基因挖掘基于随机游走的基因功能预测方法可以用于疾病相关基因的挖掘。
随机游走分析

随机游走分析随机游走是一种数学模型,用于描述在随机过程中物体或者概念的随机移动。
在金融领域,随机游走分析可以被用来预测股票价格的变化,以及其他一些与市场相关的现象。
本文将探讨随机游走分析的基本原理、应用以及一些相关的扩展内容。
1. 随机游走的定义和基本原理随机游走是指一个物体或者概念在一定时间内的随机移动轨迹。
在随机游走模型中,物体在每个时间步骤中向左或者向右移动的概率是相等的,且每一步都是独立且随机的。
这种模型可以被形象地比作一只蚂蚁在一条直线上的随机行走。
数学上,随机游走可以用一个数列来表示,其中每一项代表物体在每个时间步骤中的位置。
该数列可以被描述为:S_t = S_{t-1} + \epsilon_t其中,S_t 表示在第 t 个时间步骤时物体的位置,S_{t-1} 表示在第t-1 个时间步骤时物体的位置,\epsilon_t 是一个随机变量,表示在第 t 个时间步骤中物体的移动方向(向左或向右)。
2. 随机游走的应用2.1 股票价格预测随机游走分析在金融领域被广泛应用于股票价格的预测。
根据随机游走的原理,股票价格的变化可以被视为一个随机过程。
通过分析历史股票价格的随机游走模型,可以得出未来一段时间内股票价格的预测。
在随机游走模型中,假设股票价格在每个时间步骤中上涨或下跌的概率是相等的,且每个时间步长的涨跌幅度是独立且随机的。
通过计算历史股票价格序列的平均涨幅,可以得到股票价格的长期趋势。
然后,通过模拟股票价格的随机游走轨迹,可以预测未来一段时间内的价格波动。
2.2 经济市场分析除了股票价格预测,随机游走分析还可以应用于其他经济市场的分析。
例如,在外汇市场中,汇率的变化也可以被视为随机游走模型,通过模拟随机游走轨迹可以预测未来汇率的趋势。
此外,随机游走分析还可以应用于商品市场、利率市场等其他金融领域的分析,帮助预测市场的走势和风险。
通过深入理解随机游走的原理,金融从业者可以更好地把握市场机会,进行决策和风险管理。
随机游走

RMR实例
随机游走概述
一维随机游走
一维随机游走
上述问题可以用杨辉三角来看:
当n趋于无穷的时候,就可以与中心极限定理相联系
一维随机游走模拟结果图:
高维随机游走模拟
二维模拟:
一个25000步伐的二维随机游走
三维模拟:
高斯随机游走
带重启的随机游走(RWR)
• Random walk with restart :从一个节点开始,在每一步游 走时面临两个选择:或者移动到一个随机选择的邻点;或 者跳回起点。 • RWR最初是为图像分割而提出的一个算法,它反复的探究 一个网络的总体结构去估计两个节点之间的亲和力程度 (亲和力分数),这个算法只考虑一个参数 r :“重启概率” (1-r的概率移动到某个邻点) 这个过程反复迭代进行下去直到走遍所有节点,此时得到的 概率向量包含所有节点与起点的亲和力分数。 另外,RWR的起点也可以选择一个起点集合(多个起点组成 的集合)。
随机游走(Random Walk)
问题直观:
• 有个醉汉走在回家路上,由于酒醉未醒,分不清家往哪边走。假如 家在东面n的位置,醉汉处在m(m<n)位置。醉汉每一个时间单位 走一步,向东(家的方向)或者向西(酒吧的方向)的概率皆为 1/2。 这个醉汉的行为就可用random walk 来模拟。
ห้องสมุดไป่ตู้
这是一个简单的一维随机游走问题模型,从这个模型中我们可以对随机游走 有一个直观上的感受:每一步都是随机的。
什么是随机游走
随机游走是由一系列随机步伐(steps)所形成的活动模型。 比如: 液体或空气中分子的运动; 动物的觅食; 股票的价格波动; 一个赌徒的财产状况… 这些都可以模型为random walks(尽管现实中他们可能不是真 正的随机) • Karl Pearson在1905年第一次提出了random walk,如今已被应 用在诸多领域:生态学、经济学、心理学、计算机科学、物 理学、化学、生物学等。
TheOne-DimensionalRandomWalk:一维随机游走

previous index nextThe One-Dimensional Random WalkMichael Fowler, UVa Physics 6/8/07Flip a Coin, Take a StepThe one-dimensional random walk is constructed as follows:You walk along a line, each pace being the same length.Before each step, you flip a coin.If it’s heads, you take one step forward. If it’s tails, you take one step back.The coin is unbiased, so the chances of heads or tails are equal.The problem is to find the probability of landing at a given spot after a given number of steps, and, in particular, to find how far away you are on average from where you started.Why do we care about this game?The random walk is central to statistical physics. It is essential in predicting how fast one gas will diffuse into another, how fast heat will spread in a solid, how big fluctuations in pressure will be in a small container, and many other statistical phenomena.Einstein used the random walk to find the size of atoms from the Brownian motion.The Probability of Landing at a Particular Place after n StepsLet’s begin with walks of a few steps, each of unit length, and look for a pattern.We define the probability function f N (n) as the probability that in a walk of N steps of unit length, randomly forward or backward along the line, beginning at 0, we end at point n. Since we have to end up somewhere, the sum of these probabilities over n must equal 1.We will only list nonzero probabilities.For a walk of no steps, f0(0) = 1.For a walk of one step, f1(–1) = ½, f1(1) = ½.For a walk of two steps, f2(–2) = ¼, f2(0) = ½, f2(2) = ¼.It is perhaps helpful in figuring the probabilities to enumerate the coin flip sequences leading to a particular spot.For a three-step walk, HHH will land at 3, HHT, HTH and THH will land at 1, and for thenegative numbers just reverse H and T. There are a total of 23 = 8 different three-step walks, so the probabilities of the different landing spots are: f 3(–3) = 1/8 (just one walk), f 3(–1) = 3/8 (three possible walks), f 3(1) = 3/8, f 3(3) = 1/8.For a four-step walk, each configuration of H’s and T’s has a probability of (½)4 = 1/16.So f 4(4) = 1/16, since only one walk—HHHH—gets us there.f 4(2) = ¼; four different walks, HHHT, HHTH, HTHH and THHH, end at 2.f 4(0) = 3/8, from HHTT, HTHT, THHT, THTH, TTHH and HTTH.Probabilities and Pascal’s TriangleIf we factor out the 1/2N , there is a pattern in these probabilities:n–5 –4 –3 –2 –1 0 1 2 3 4 5 f 0(n ) 1 2f 1(n ) 1 1 22f 2(n ) 1 2 1 23f 3(n ) 1 3 3 1 24f 4(n ) 1 4 6 4 1 25f 5(n ) 1 5 10 10 5 1This is Pascal’s Triangle —every entry is the sum of the two diagonally above. These numbers are in fact the coefficients that appear in the binomial expansion of (a + b )N .For example, the row for 25f 5(n ) mirrors the binomial coefficients:()554322345510105a b a a b a b a b ab b +=+++++.)To see how these binomial coefficients relate to our random walk, we write:()()()()()(5a b a b a b a b a b a b +=+×+×+×+×+and think of it as the sum of all products that can be written by choosing one term from each bracket. There are 25 = 32 such terms (choosing one of two from each of the five brackets), so the coefficient of a 3b 2 must be the number of these 32 terms which have just 3 a ’s and 2 b ’s.But that is the same as the number of different sequences that can be written by rearranging HHHTT, so it is clear that the random walk probabilities and the binomial coefficients are the same sets of numbers (except that the probabilities must of course be divided by 32 so that they add up to one).Finding the Probabilities Using the Factorial FunctionThe efficient way to calculate these coefficients is to use the factorial function. Suppose we have five distinct objects, A, B, C, D, E. How many different sequences can we find: ABCDE, ABDCE, BDCAE, etc.? Well, the first member of the sequence could be any of the five. The next is one of the remaining four, etc. So, the total number of different sequences is 5×4×3×2×1, which is called “five factorial” and written 5!But how many different sequences can we make with HHHTT? In other words, if we wrote down all 5! (that’s 120) of them, how many would really be different?Since the two T’s are identical, we wouldn’t be able to tell apart sequences in which they had been switched, so that cuts us down from 120 sequences to 60. But the three H’s are also identical, and if they’d been different there would have been 3! = 6 different ways of arranging them. Since they are identical, all six ways come out the same, so we have to divide the 60 by 6, giving only 10 different sequences of 3 H’s and 2 T’s.This same argument works for any number of H’s and T’s. The total number of different sequences of m H’s and n T’s is (m + n)!/((m!)(n!)), the two factorials in the denominator coming from the fact that rearranging the H’s among themselves, and the T’s among themselves, gives back the same sequence.It is also worth mentioning that in the five-step walk ending at –1, which has probability 10/25, the fourth step must have been either at 0 or –2. Glancing at Pascal’s Triangle, we see that the probability of a four-step walk ending at 0 is 6/24, and of ending at –2 is 4/24. In either case, the probability of the next step being to –1 is ½, so the total probability of reaching –1 in five steps is ½×6/24 + ½×4/24. So the property of Pascal’s triangle that every entry is the sum of the two diagonally above is consistent with our probabilities.Picturing the Probability DistributionIt’s worth visualizing this probability distribution to get some feel for the random walk. For 5 steps, it looks like:Let’s now consider a longer walk. After 100 steps, what is the probability of landing on the integer n?This will happen if the number of forward steps exceeds the number of backward steps by n (which could be a negative number).That is,forward backward forward backward 100n n nn n −=+=from which()()11forward backward 22100,100.n n n =+=−nNote that in the general case, if the total number of steps N is even, are both even or both odd, so n , the difference between them, is even, and similarly odd N means odd n . forward backward ,n nThe total number of paths ending at the particular point n , from the heads and tails argument above, is()()()()()()11forward backward 22100!100!.!!100!100!n n n n =+−To find the actual probability of ending at n after 100 steps, we need to know what fraction of all possible paths end at n . (Since the coin toss is purely random, we take it all possible paths are equally likely). The total number of possible 100-step walks is 100302 1.2610≅×.We’ve used Excel to plot the ratio: (number of paths ending at n )/(total number of paths) for paths of 100 random steps, and find:The actual probability of landing back at the origin turns out to be about 8%, as is(approximately) the probability of landing two steps to the left or right. The probability oflanding at most ten steps from the beginning is better than 70%, that of landing more than twenty steps away well below 5%.(Note : It’s easy to make this graph yourself using Excel. Just write -100 in A1, then =A1 + 2 in A2, then =(FACT(100))/(FACT(50 - A1/2)*FACT(50+A1/2))*2^-100 in B1, dragging to copy these formulae down to row 101. Then highlight the two columns, click ChartWizard, etc.)It is also worth plotting this logarithmically, to get a clearer idea of how the probabilities are dropping off well away from the center.This looks a lot like a parabola—and it is! Well, to be precise, the logarithm of the probability distribution tends to a parabola as N becomes large, provided n is much less than N , and in fact this is the important limit in statistical physics.The natural log of the probability of ending the path at n tends to ln C –n 2/200, where the constant C is the probability (of ending the path exactly where it began. )100100!/50!50!/2This means that the probability P (n ) itself is given by:2200(),0.08.n P n CeC −=≅This is called a Gaussian probability distribution. The important thing to notice is how rapidly it drops once the distance from the center of the distribution exceeds 10 or so. Dropping one vertical space is a factor of 100!*Deriving the Result from Stirling’s Formula(This more advanced material is not included in Physics 152.)For large N , the exponential dependence on n 2 can be derived mathematically using Stirling’s formula ln . That formula follows from !ln n n n n ≅−[]00ln !ln1ln 2ln 3ln ln ln ln nnn n xdx x x x =++++≅=−=−∫…n n n .For a walk of N steps, the total number of paths ending at n is()()()()1122!!!N N n N n +−.To find the probability P (n ) we took one of these paths, we divide by the number of all possible paths, which is 2N .Applying Stirling’s formula()()()()()1122!1ln ln .2!!ln ln ln ln 2222222ln ln ln ln 22222N N P n N n N n N n N n N n N n N n N n N N N N N n N n N n N n N N N ⎛⎞=⎜⎟⎜⎟+−⎝⎠+++−−−⎛⎞⎛⎞⎛⎞⎛⎞⎛⎞⎛⎞≅−−+−+−⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠⎝⎠⎝⎠⎝⎠++−−⎛⎞⎛⎞⎛⎞⎛⎞=−−−⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠⎝⎠then approximating21ln ln ln 12ln 22222N n N n N n n N N ±⎛⎞⎛⎞⎛=+±≅±−⎜⎟⎜⎟⎜⎝⎠⎝⎠⎝N ⎞⎟⎠(using for small x ) the right-hand side becomes just .()2ln 1/2x x x ±≅±−2/2n N −Actually, we can even get the multiplicative factor for the large N limit (n much less than N ) using a more accurate version of Stirling’s formula, 12ln !ln ln 2.n n n n n π≅−+ This gives()2/2.n NP n −=For N = 100, this gives P (0) = 0.08, within 1%, as we found with Excel. The normalization can be checked in the limit using the standard result for the Gaussian integral, remembering that P (n ) is only nonzero if N – n is even.So, How Far Away Should You Expect to Finish?Since forward and backward steps are equally likely at all times, the expected average finishing position must be back at the origin. The interesting question is how far away from the origin, on average, we can expect to land, regardless of direction. To get rid of the direction, we compute the expected value of the square of the landing distance from the origin, the “mean square” distance, then take its square root. This is called the “root mean square” or rms distance.For example, taking the probabilities for the five step walk from the figure above, and adding together +5 with –5, etc., we find the expectation value of n2 is:2⋅1/32⋅52 + 2⋅5/32⋅32 + 2⋅10/32⋅12 = 160/32 = 5.That is, the rms distance from the origin after 5 steps is √5. In fact,The root mean square distance from the origin after a random walk of n unit steps is √n.A neat way to prove this for any number of steps is to introduce the idea of a random variable. If x1 is such a variable, it takes the value +1 or –1 with equal likelihood each time we check it. In other words, if you ask me “What’s the value of x1?” I flip a coin, and reply “+1” if it’s heads, “–1” if it’s tails. On the other hand, if you ask me “What’s the value of x12?” I can immediately say “1” without bothering to flip a coin. We use brackets ‹› to denote averages (that is, expectation values) so ‹x1› = 0 (for an unbiased coin), ‹x12› = 1.The endpoint of a random walk of n steps can be written as a sum of n such variables:Path endpoint = x1 + x2 + … + x n.The expectation value of the square of the path length is then:‹(x1 + x2 + … + x n)2›On squaring the term inside, we get n2 terms. n of these are like ‹x12› and so must equal 1. All the others are like ‹x1x2›. But this is the product of two different coin tosses, and has value +1 for HH and TT, –1 for HT and TH. Therefore it averages to zero, and so we can throw away all the terms having two different random variables. It follows that‹(x1 + x2 + … + x n)2› = n,It follows that the rms deviation is √n in the general case.Density Fluctuations in a Small Volume of GasSuppose we have a small box containing N molecules of gas. We assume any interaction between the molecules is negligible, they are bouncing around inside the box independently.If at some instant we insert a partition down the exact middle of the box, we expect on average to find 50% of the molecules to be in the right-hand half of the box.The question is: how close to 50%? How much deviation are we likely to see? Is 51% very unlikely?Since the N molecules are moving about the box in a random fashion, we can assign a random variable y n to each molecule, where y n = 1 if the n th molecule is in the right hand half, y n = 0 if the nth molecule is in the left-hand half of the box, and the values 1 and 0 are equally probable. The total number of molecules N R in the right-hand half of the box is then:N R = y 1 + y 2 + … +y N .This sum of N random variables looks a lot like the random walk! In fact, the two are equivalent. Define a random variable x n by:y n = ½(1 + x n ).Since y n takes the values 0 and 1 with equal probability, x n takes the values –1 and +1 with equal probability—so x n is identical to our random walk one-step variable above. Therefore,N R = y 1 + y 2 + … +y N = ½ N + x 1 + x 2 + … x N .Evidently the sum of an N -step random walk gives the deviation of the number of molecules in half the container from N /2. Therefore, from our random walk analysis above, the expectation value of this deviation is √N . For example, if the container holds 100 molecules, we can expect a ten percent or so deviation at each measurement.But what deviation in density can we expect to see in a container big enough to see, filled with air molecules at normal atmospheric pressure? Let’s take a cube with side 1 millimeter. This contains roughly 1016 molecules. Therefore, the number on the right hand side fluctuates in time by an amount of order √1016 = 108. This is a pretty large number, but as a fraction of the total number, it’s only 1 part in 108!The probability of larger fluctuations is incredibly small. The probability of a deviation of m from the average value N /2 is:22()m NP m Ce−=.So the probability of a fluctuation of 1 part in 10,000,000, which would be 10√N , is of order , or about 10-85. Checking the gas every trillionth of a second for the age of the universe200e −wouldn’t get you close to seeing this happen. That is why, on the ordinary human scale, gases seem so smooth and continuous. The kinetic effects do not manifest themselves in observable density or pressure fluctuations—one reason it took so long for the atomic theory to be widely accepted.previous index next。
随机游走模型(RandomWalkMobility)
随机游⾛模型(RandomWalkMobility)随机游⾛模型由⾸先由爱因斯坦在1926年以数学⽅式描述。
由于⾃然界中的许多实体会以不可预知的⽅式移动,因此随机游⾛模型⽤来描述这种不稳定的移动。
在这种移动模型中,移动节点随机选择⼀个⽅向和速度来从当前位置移动到新的位置。
新的速度和⽅向分别从预定义的范围【speedmin,speedmax】和【0,2】。
移动节点的每次移动会以恒定的时间间隔t或恒定的⾏进距离d进⾏,结束后会计算新的⽅向和速度。
如果此模型的移动节点到达模拟边界,则它将从模拟边界“弹回”,其⾓度有⼊射⽅向确定,然后沿着这条路径继续移动。
许多随机游⾛模型已经被研究,包括⼀维,⼆维,三维和d-维游⾛。
在1921年,Polya证明在⼀维或⼆维的随机游⾛能够完全确定地返回远点,这⼀特征确保随机游⾛模型代表了⼀种移动模型----可以测试移动节点在其起点附近的移动,不⽤担⼼移动节点因游⾛⽽永远回不到起点。
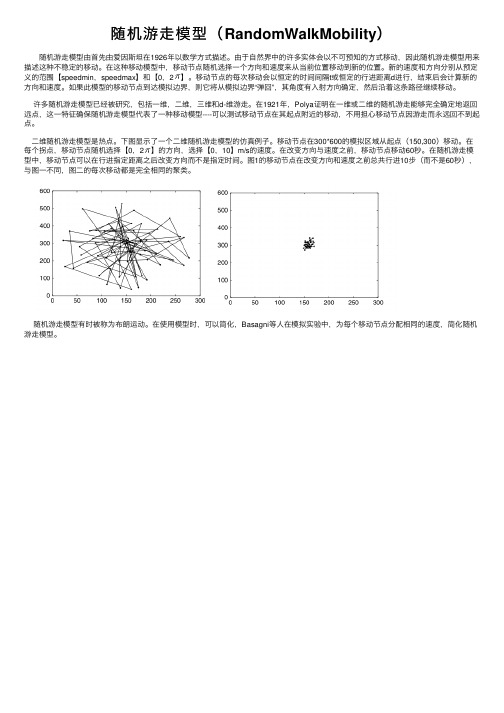
⼆维随机游⾛模型是热点。
下图显⽰了⼀个⼆维随机游⾛模型的仿真例⼦。
移动节点在300*600的模拟区域从起点(150,300)移动。
在每个拐点,移动节点随机选择【0,2】的⽅向,选择【0,10】m/s的速度。
在改变⽅向与速度之前,移动节点移动60秒。
在随机游⾛模型中,移动节点可以在⾏进指定距离之后改变⽅向⽽不是指定时间。
图1的移动节点在改变⽅向和速度之前总共⾏进10步(⽽不是60秒),与图⼀不同,图⼆的每次移动都是完全相同的聚类。
随机游⾛模型有时被称为布朗运动。
在使⽤模型时,可以简化,Basagni等⼈在模拟实验中,为每个移动节点分配相同的速度,简化随机游⾛模型。
随机游走与布朗运动

随机游走与布朗运动随机游走和布朗运动是数学中两个常见而重要的概念。
它们的应用涵盖了许多领域,包括经济学、物理学和生物学等。
在这篇文章中,我们将探讨这两个概念的意义、性质和应用。
一、随机游走随机游走是指在一个空间中由一些随机事件所决定的移动过程。
在数学中,随机游走可以用一个概率模型来描述。
这个模型通过指定每一步移动的可能性来定义了随机游走的性质。
最简单的随机游走是一维随机游走。
在这种情况下,我们想象在一个数轴上有一个“醉汉”从原点出发,每次他会朝着左边或右边走一步。
如果左右移动的概率相等,那么这个“醉汉”的行走轨迹就是一个随机游走。
虽然这个模型看上去很简单,实际上囊括了许多真实世界中的情况。
例如,在股票市场中,股价的波动也可以被看作一种随机游走。
在这种情况下,每次股票价格的变化也可以用一个随机过程来建模。
二、布朗运动布朗运动是一种描述随机运动的过程,其中粒子沿任意方向移动,它受到来自周围环境的不断碰撞的影响。
这个过程是不规则的,但总体上呈现出均匀随机的趋势。
布朗运动最初在物理学中被描述为小颗粒在液体中的运动。
这个过程可以看作是受到大量分子碰撞的效果。
因此,布朗运动也被称作“分子碰撞运动”。
尽管这个模型最初是由物理学家来研究的,但它也被广泛应用于其他领域。
在金融学中,股票价格的波动也可以用布朗运动来进行建模。
三、随机游走和布朗运动的区别尽管随机游走和布朗运动都是描述随机过程的概念,但它们之间还是有一些重要的区别。
首先,由于布朗运动是在连续空间中进行的,而随机游走是在离散空间中进行的,因此布朗运动在数学上更加复杂。
其次,随机游走是由离散的事件所驱动的,而布朗运动则是连续的。
因此,随机游走的行动是分离的,每一步的方向和大小都是随机的,而布朗运动则是持续不断的行动,并且从一开始就存在一个随机的初态和一个终态。
最后,随机游走可以看作是在一个固定的空间中进行的,而布朗运动是在一个可变的空间中进行的。
这个空间的状态是通过小颗粒可以发生碰撞来变化的。
随机游走定义的概念错误及纠正

数学学习与研究㊀2021 28随机游走定义的概念错误及纠正随机游走定义的概念错误及纠正Һ高㊀宏㊀(清华大学,北京㊀100084)㊀㊀ʌ摘要ɔ本文分析了随机游走定义将单个质点的位移与时间之间的数量关系假设为随机变量的基本概念错误,以及用刻画大量重复试验中随机事件发生可能性的概率来度量随机游走每一步向右或向左可能性的研究方法错误.随机游走定义中的概念错误会导致随机游走研究对象发生错位,使研究对象从一个质点改变为大量质点,从而会得出与事实不符的结论.本文基于白噪声序列的基本概念,重新定义了随机游走,并分别推导出随机游走样本轨道性质和随机变量性质.ʌ关键词ɔ随机游走;样本轨道;随机变量一㊁引言随机游走(RandomWalk)是随机过程学科中用于描述动态随机现象的一种基本随机过程,其他重要的随机过程都可由它构造出来.随机游走不仅在随机过程理论中占有相当重要的地位,而且是自然科学㊁工程技术和社会科学研究动态随机现象的重要数学工具.液体中悬浮微粒的布朗运动㊁光纤陀螺中的随机游走误差和股票市场中的价格波动等随机现象均可用随机游走过程进行描述.本文分析了随机过程教科书在定义随机游走时,将一个质点的位移与时间之间的数量关系假设为随机变量的基本概念错误,以及用刻画大量重复试验中随机事件发生可能性的概率来度量随机游走每一步向右或向左可能性的研究方法错误.随机游走定义的概念错误无形中会导致研究对象从一个质点改变为质点集合,只能用描述大量质点空间位置分布的统计特性来刻画一个质点的运动规律,从而会得出一系列与事实不符的结论.本文基于白噪声序列的基本概念重新定义了随机游走,并分别推导出随机游走过程的样本轨道性质和随机变量性质,可为自然科学㊁工程技术和社会科学提供正确的理论㊁方法及工具.二㊁随机游走定义错误分析随机游走有两种形式的定义:一是对质点每一步的位移概率进行定义,二是将每一步的位移定义为独立同分布随机变量.1.基于概率的定义定义1㊀假设质点只能在数轴x的整数点上移动(如图1所示),t=0时质点处于原点,每隔Δt时间,质点随机地以概率p或概率q=1-p向右或向左移动一个单位,且每次移动相互独立,若记第i次的移动为Δx(i),则Δx(i)分别以p和概率q=1-p取值+1和-1,那么质点经n步移动或t=nΔt时刻的位置可表示为:x(n)=ðni=1Δx(i)(1)则称x(n)为从原点出发的一维简单随机游动[1-4].图1㊀质点随机游走当p=q=0.5时,x(n)被称为 简单对称随机游走 ,此时可用抛硬币来模拟简单随机游走x(n).每隔Δt时间,抛掷一枚质量均匀的硬币,如果第i次抛硬币结果为正面向上,则Δx(i)=1,质点往右移动1个单位;如果第i次抛硬币结果为反面向上,则Δx(i)=-1,质点向左移动1个单位,则第n次抛硬币后质点的位置为x(n).随机现象在个别试验中的观察结果是随机的,呈现出不确定性,但是在大量重复试验中其结果又具有某种固有的统计规律.例如,如果只抛掷一次硬币,其结果完全随机,无法预测;但是随着抛硬币次数的增多,硬币正反面出现的频率会逐渐稳定于数值0.5附近,则称数值0.5为硬币正反面出现的概率.因此,概率是在随机试验次数n充分大时,用来刻画随机事件发生可能性大小的一个数量指标.概率p和q是指随机游走的步数n充分大时,质点向右移动的步数和向左移动的步数与总步数n之比.概率不能用来描述当n=1时的随机事件发生的可能性.对于n=1时的抛硬币试验,硬币正面出现的频率不是为1,就是为0,根本不存在频率的稳定值.定义1的错误在于将概率用于度量当n=1时的随机事件发生可能性大小,意味着如果只抛掷一次硬币,会同时出现正㊁反面向上的错误结果.二㊁基于随机变量的定义定义2㊀假设质点在x轴上随机移动,质点在t=0时处于原点,每隔Δt时间,质点随机移动一次,若记ΔX(i)为第i次的质点位移,并设ΔX(1),ΔX(2), ,ΔX(n)独立同分布,则称随机变量,表示为:X(n)=ðni=1ΔX(i)(2)则称x(n)为从原点出发的一维随机游走[5-6].若P[ΔX(i)=1]=P[ΔX(i)=-1]=0.5,则称X(n)为一维对称简单随机游走.由于ΔX(i)的数学期望和方差分别为E[ΔX(i)]=0,D[ΔX(i)]=1,因此有:E[X(n)]=0(3)D[X(n)]=n(4)随机过程是定义在ΩˑT上的二元函数X(ω,t).对于固定的状态ω,X(ω,t)是时间t的函数,称为样本函数或样本轨道,简记为x(t);对于固定的时间t,X(ω,t)是ω的函数,. All Rights Reserved.数学学习与研究㊀2021 28称为随机变量,简记为X(t).随机试验中的一次 测量结果 与随机过程中的一个样本函数x(t)相对应,样本函数x(t)描述了人们实际观察到的随机现象随时间演变过程,因此x(t)也被称为随机过程的一个 实现 .图2为随机过程X(ω,t)㊁随机变量X(t)和样本函数x(t)三者之间的关系示意图.图2㊀随机过程定义图中的三条样本函数曲线x1(t),x2(t)和x3(t)可分别看成三个随机运动质点的位移曲线,所有质点在t1时刻的位置x1(t1),x2(t1)和x3(t1)就是随机变量X(t1)在t1时刻的取值.因此,随机过程X(ω,t)即可看成所有样本轨道x(t)的集合,也可看成所有随机变量X(t)的集合.从图2可以看出,随机变量X(t)和样本函数x(t)描述的是完全不同的物理现象.随机变量X(t)用来描述质点集合在某一时刻的位置分布,样本函数x(t)则用来描述一个质点的位移随时间变化过程.定义2用随机变量X(t)来描述一个质点在t时刻的位移,无形中将研究对象从一个质点改变为大量质点,势必会用随机变量X(t)的统计特性来刻画一个质点的随机游走运动规律,得出与事实不符的错误结论.3.质点位移与时间之间的数量关系观察图1中质点位移x(t)随时间t的变化过程,无论质点做确定性运动还是随机性运动,在每一个确定的时刻,都有唯一一个确定的质点位置与时间 一一对应 ,因此质点位移x(t)与时间t之间的数量关系为函数关系.从物理学角度看,质点位移x(t)无疑是时间t的函数.从随机过程的角度看,质点位移是固定ω时的随机过程X(ω,t),即随机过程X(ω,t)中的一条样本轨道x(t),而非随机变量X(t).但是,定义1和定义2均将质点位移与时间之间的数量关系假设为随机变量,使研究对象从一个质点改变为质点集合,无形中导致样本轨道研究对象错误,由此必然会推导出一系列与事实不符的错误结论.三㊁随机游走样本轨道性质为区别随机游走过程中的随机变量和样本轨道,随机变量用大写的X(t)表示,样本轨道用小写的x(t)表示.1.一阶差分性质为方便起见,我们直接用序号n表示时间nΔt,因此随机游走的质点位移x(n)是以时间顺序记录的一系列数据,其一阶差分为:Δx(n)=x(n)-x(n-1)(5)质点随机游走的位移变化(一阶差分)Δx(n)是完全随机的,Δx(n)的时间序列图像,如图3所示.图3㊀Δx(n)时间序列图像假设:一维随机游走的质点向右和向左移动的概率分别为p和q,则时间序列Δx(n)的算数平均值可表示为:m=limnңɕ1nðni=1Δx(i)=p-q(6)式中,算数平均值m的物理意义为时间序列Δx(n)中的直流分量.因此,对于一维对称简单随机游走,p=q=0.5,Δx(n)的时间均值m和方差σ2分别为:m=limnңɕ1nðni=1Δx(i)=0(7)σ2=limnңɕ1nðni=1Δx(i)2=1(8)另外,随机游走的质点位移在各个Δt区间上的位移变化Δx(i)相互独立,表明随机游走样本轨道的一阶差分Δx(i)互不相关,其自相关函数为:r(k)=limnңɕ1nðni=1Δx(i)Δx(i-k)=δ(k)(9)式中,δ(k)为单位冲击序列,其定义为:δ(k)=1,k=00,kʂ0{(10)表明仅在时间间隔k=0时,Δx(i)才具有相关性,只要两个Δx(i)之间的时间间隔不为0,就互不相关.由维纳-欣钦定理可知,平稳随机信号的自相关函数与其功率谱密度之间构成一对傅立叶变换,可得Δx(n)的功率谱密度函数为:S(f)=1(11)Δx(n)的功率谱密度在整个频率轴(-ɕ,+ɕ)上为常数,表明Δx(n)为白噪声序列.由于白噪声序列的自相关函数为 单位冲击序列 ,其功率谱密度为 常数 ,在数学上具有处理简单㊁计算方便等突出优点,因此白噪声序列是一个理想化的数学模型,在随机现象的理论研究中具有相当重要的地位.基于白噪声序列的基本概念,可给出随机游走样本函数的定义:定义3㊀若时间序列x(n)的一阶差分Δx(n)=w(n),w(n)为定义在为[-ɕ,+ɕ]上零均值不相关白噪声序列,则称x(n)为随机游走.定义3可作为推导随机游走其他命题的基本假设(公理),也可被称为随机游走运动定律.2.位移公式随机游走x(n)的一阶差分Δx(n)在区间[0,n]上的算数平均值为:Δx(n)=1nðni=1Δx(i)(12). All Rights Reserved.数学学习与研究㊀2021 28Δx(n)的物理意义,表示随机游走的质点在区间[0,n]上的平均速度,或是随机序列Δx(n)在区间[0,n]上的直流分量.由式(5)的一阶差分Δx(n)和式(12)的算数平均值Δx(n),可得随机游走位移公式为:x(n)=Δx(n)㊃n(13)表明一维简单随机游走质点的位移等于其平均速度与时间的乘积,即随机游走的位移与步数n成正比.根据大数定律,算数平均值Δx(n)反映了Δx(n)序列中的确定性部分,当n充分大时,Δx(n)趋于一个接近于0的常数.因此,随机游走位移x(n)随步数n线性增长,与物理学中机械运动质点位移与时间成正比的结论完全一致.随着步数n的增加,随机游走的质点会逐渐远离原点.即使随机游走的步数n充分大时,Δx(n)也不等于零.这是因为Δx(n)中包含了所有频率的谐波分量,在[0,n]有限区间上的Δx(n)序列不可能对w(n)中的所有谐波分量进行整周期截取,因此 频谱泄漏效应 会导致时间序列Δx(n)中出现直流分量.从式(13)可以看出,随机游走的位移特性完全取决于其在区间[0,n]上的平均速度Δx(n),由于Δx(n)也是一随机序列,其方差为:[7]σ2a=σ2n=1n(14)方差σ2a反映了平均速度Δx(n)的波动程度.当n较小时,平均速度Δx(n)变化剧烈,位移x(n)表现出很强的随机性;当n充分大时,平均速度Δx(n)的波动逐渐变小,Δx(n)趋于一个常数,位移x(n)就变为一条斜率为Δx(n)的直线.3.频域性质随机过程样本函数在时域无法用确定性的数学解析式来描述,但是在频域可用确定性的数学解析式表示.例如,式(11)的功率谱密度函数就是随机游走样本轨道一阶差分在频域的解析表达式.任何复杂的运动均由众多频率不同的简谐运动叠加而成.研究随机游走的频域特性,能够发现隐藏在随机游走现象下的确定性运动,从而能揭示出在时域看不到的确定性特征及规律.对式(5)随机游走x(n)的一阶差分Δx(n)进行迭代,有:x(n)=ðni=1Δx(i)(15)表明随机游走x(n)是Δx(n)序列在[0,n]区间上的累加.随机游走位移x(n)不仅与当前时刻的Δx(n)有关,而且与之前所有时刻的Δx(1),Δx(2), ,Δx(n-1)都有关,表明x(n)具有很强的记忆性.从信号与系统的角度来看,随机游走x(n)是白噪声序列w(n)通过如图4所示的系统后所产生的输出响应.图4㊀随机游走系统模型由于系统输入w(n)的功率谱密度为常数,因此系统输出x(n)的功率谱密度就完全取决于系统的传递函数特性,可把对随机现象统计规律的研究转变为对确定性系统特性的研究.图4所示的系统由开关和累加器两个元件组成.开关的功能是将定义在[-ɕ,+ɕ]上的白噪声序列w(n)在[0,t]区间上截断,将w(n)变换为Δx(n),累加器的作用是对[0,t]区间上的所有Δx(i)进行累加运算并产生输出.开关将定义在[-ɕ,+ɕ]上的w(n)截断为定义在[0,t]上Δx(n),不可能对w(n)中所有谐波分量进行整周期截断,从而会使Δx(n)中出现直流分量.累加器对Δx(n)中的直流分量累加运算,就会在输出序列x(n)中产生线性趋势.累加器的幅频特性为:[8]|H(Ω)|=12sinΩ2()(16)式中,Ω为角频率.从式(16)的累加器幅频特性可以看出,累加器具有低通滤波特性,导致Δx(n)通过累加器后,原时间序列中的低频谐波分量得到增强,高频谐波分量大幅衰减,因此系统输出x(n)是信号能量集中在低频段的红噪声序列.此外,累加器具有记忆性,表明当前时刻的系统输出x(n)不仅与当前时刻的系统输入w(n)有关,而且与之前所有时刻的系统输入w(n)有关.因此,随机游走的质点位移x(n)具有很强的 相关性 或 记忆性 .四㊁随机游走随机变量性质1.增量数字特征假设:有N个质点同时从原点出发,在x轴上做定义3所描述的随机游走,N个质点在第i步的位置x1(i),x2(i),,xN(i)就是随机变量X(i)在t=iΔt时刻的取值或状态,N个质点的样本轨道在第i步的一阶差分Δx1(i),Δx2(i), ,ΔxN(i)就是随机变量X(i)的增量ΔX(i)在t=iΔt时刻的取值或状态,如图5所示.图5㊀随机游走增量. All Rights Reserved.数学学习与研究㊀2021 28由于白噪声过程为各态历经随机过程,因此ΔX(n)的统计平均在概率意义上等于Δx(n)的时间平均,有:E[ΔX(n)]=limnңɕ1nðni=1Δx(i)=m=0(17)D[ΔX(n)]=limnңɕ1nðni=1Δx(i)2=σ2=1(18)即P[ΔX(i)=1]=P[ΔX(i)=-1]=0.5,表明当质点数量N充分大时,所有质点每随机移动一步,向右移动的质点数量与向左移动的质点数量趋于相等.2.随机变量数字特征由式(15)随机游走样本轨道位移x(n),可直接写出随机变量模型:X(n)=ðni=1ΔX(i)(19)表明随机游走X(n)是大量独立同分布随机变量ΔX(n)之和.根据中心极限定理,当n充分大时,X(n)服从或近似服从正态分布.根据式(17)和式(18)的E[ΔX(n)]和D[ΔX(n)],可由式(19)计算出随机变量X(n)的数学期望和方差:E[X(n)]=ðni=1E[ΔX(i)]=0(20)D[X(n)]=ðni=1D[ΔX(i)]=n(21)即X(n)服从参数为(0,n)的正态分布,与大量布朗粒子的空间位置分布规律相同,表明大量质点的随机游走是一种与布朗运动类似的扩散现象;当n充分大时,X(n)将变为一族从原点发出的射线.所有样本轨道x(n)在第n步时的位置就是随机变量X(n)在第n步时的状态,因此所有样本轨道x(n)在第n步时的位置服从均值为0和方差为n的正态分布.图6所示为8个质点的随机游走样本轨道,质点随步数n的增加而远离原点.图6㊀随机游走样本轨道五㊁随机游走问题重新求解1905年,英国数学家卡尔㊃皮尔逊(KarlPearson)在‘自然“杂志上公开求解随机游走(RandomWalk)问题:如果一个酒鬼醉得非常严重,完全丧失方向感,走路时每步的方向完全随机.问经过一段时间以后,在哪里找到他的可能性最大.1921年,匈牙利数学家乔治㊃波利亚(GeorgePolya)在研究了随机游走问题后,假设随机游走每一步的概率p=q=0.5,证明了P[X(n)=0,i.o.]=1,即一维简单随机游走的质点返回原点的概率为1.日本数学家角谷静夫通俗地将其表述为:喝醉的酒鬼最终会找到回家的路(Adrunkmanwilleventuallyfindhiswayhome).假设:P[X(n)=0,i.o.]=1成立,则有:P[D[X(n)]=0,i.o.]=1(22)表明随机游走X(n)的步数n充分大时,其方差D[X(n)]=0的概率也为1,与式(4)和式(21)D[X(n)]=n的结论矛盾.根据式(13)的随机游走位移公式,从原点出发的一维简单随机游走质点相对原点的位移x(n)与步数n成正比,表明随着步数n的增加,喝醉的酒鬼会逐渐远离原点.六㊁结论本文指出了随机游走定义中的两个基本概念错误:①将质点位移与时间之间的数量关系抽象为随机变量的基本概念错误;②用刻画大量重复试验中随机事件发生可能性的概率来度量随机游走每一步向右或向左可能性的研究方法错误.随机游走定义中的两个基本概念错误无形中导致随机游走样本轨道研究对象发生错位,使研究对象从一个质点改变为质点集合,只能用刻画随机变量的空间统计特性来描述一个质点的时间运动规律,从而会得出一系列与事实不符的结论.本文基于白噪声序列的基本概念,重新定义了随机游走,分别推导出单个随机游走质点的运动规律和大量随机游走质点的统计特性,可全面㊁系统地阐明随机游走过程的现象㊁特征及规律;同时证明了在微观上表现出很强随机性的随机游走,在宏观上具有总体的确定性和稳定性.ʌ参考文献ɔ[1]JosephRudnick.ElementsoftheRandomWalk:AnintroductionforAdvancedStudentsandResearchers[M].Cambridge:CambridgeUniversityPress,2010.[2]SheldonM.Ross.应用随机过程:概率模型导论[M].龚光鲁,译.北京:人民邮电出版社,2016.[3]何书元.随机过程[M].北京:北京大学出版社,2008.[4]林元烈.应用随机过程[M].北京:清华大学出版社,2002.[5]RickDurrett.Probability:TheoryandExamples[M].Cambridge:CambridgeUniversityPress,2019.[6]钱敏平,龚光鲁,陈大岳,等.应用随机过程[M].北京:高等教育出版社,2017.[7]常建平,李海林.随机信号分析[M].北京:科学出版社,2006.[8]徐守时,谭勇,郭武.信号与系统:理论㊁方法和应用[M].北京:中国科学技术大学出版社,2018.. All Rights Reserved.。
知识点:数学上奇怪的定理(二年级)

知识点:数学上奇怪的定理(二年级)假设有一条水平直线,从某个位置出发,每次有50%的概率向左走1米,有50%的概率向右走1米。
按照这种方式无限地随机游走下去,最终能回到出发点的概率是多少?答案是100%。
在一维随机游走过程中,只要时间充足长,我们最终总能回到出发点。
现在考虑一个喝醉的酒鬼,他在街道上随机游走。
假设整个城市的街道呈网格状分布,酒鬼每走到一个十字路口,都会概率均等地选择一条路(包括自己来时的那条路)继续走下去。
那么他最终能够回到出发点的概率是多少呢?答案也还是100%。
刚开始,这个醉鬼可能会越走越远,但最后他总能找到回家路。
不过,醉酒的小鸟就没有这么幸运了。
假如一只小鸟飞行时,每次都从上、下、左、右、前、后中概率均等地选择一个方向,那么它很有可能永远也回不到出发点了。
事实上,在三维网格中随机游走,最终能回到出发点的概率只有大约34%。
这个定理是数学家波利亚(GeorgePólya)在1921年证明的。
随着维度的增加,回到出发点的概率将变得越来越低。
在四维网格中随机游走,最终能回到出发点的概率是19.3%,而在八维空间中,这个概率只有7.3%。
定理:你永远不能理顺椰子上的毛。
想象一个表面长满毛的球体,你能把所有的毛全部梳平,不留下任何像鸡冠一样的一撮毛或者像头发一样的旋吗?拓扑学告诉你,这是办不到的。
这叫做毛球定理(hairyballtheorem),它也是由布劳威尔首先证明的。
用数学语言来说就是,在一个球体表面,不可能存有连续的单位向量场。
这个定理能够推广到更高维的空间:对于任意一个偶数维的球面,连续的单位向量场都是不存有的。
毛球定理在气象学上有一个有趣的应用:因为地球表面的风速和风向都是连续的,所以由毛球定理,地球上总会有一个风速为0的地方,也就是说气旋和风眼是不可避免的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设事件 R :共走了N 步, N N ,到达了点a1 , a2 ,...,an ,其中 a i n
*
表示在坐标轴 x i 上的坐标(假设 ai 0 ), a N . n i 记 i 1 a ,则:
i 1
i
P R
N a1 N a2
j1 a1
...
N an jn an
j2 a2
ai ji ai ji ai B1, ,B2 ,...,Bn n B j ji 2 2 2 p j C p q Gn j i j 1
环形随机游走
定理4:在一个环上,有M 个点,各点之间的距离相等,且均为一个 单位长度.假设一点从某点 O 出发,每一次沿环上移动一个单位长 度,假设向顺时针方向移动一个单位的概率为 p ,向逆时针方向移 动一个单位的概率为 q ,且 p, q 0 , p q 1 . 设事件 A :走了N 步后到达点 a (点与点顺时针方向相距 a ,逆时 * a N , N N M a 针方向相距 ), .则:
华东师范大学第二附属中学 作者:高二(7)班 顾韬 景琰杰 指导教师:张成鹏
研究背景
“随机游走”(random walk)是指基于 过去的表现,无法预测将来的发展步骤和方向. 随机游走问题最早来源于“梅茵街的醉汉”问 题:一个醉汉从酒店出发,向左和向右走分别有 一个概率,那么他回到家的概率是多少?这是一 个有趣的概率问题,引起了我的兴趣,同时,在思 考解决这个问题的基础上,我想是否也可以解决 在二维坐标平面内的随机游走问题,甚至是在多 维空间内的?在环上进行的随机游走问题呢? 于是,我试图去解决这些问题.
为方便表示,不妨记 C C C G B D q r q r 即为每一次摸球摸到白 A B D , A B D(事实上 p ,, 球、黑球和红球的概率),有 p q r 1 .
a1 n a2 n an n a1 ,a2 ,..., an p , n
n
n
P M
G n 1,
2
n
Aj
j 1 n
i 1
Ak k 1
n
PM G
B1, , B2 ,..., Bn n
pj j
B j 1
n
多维随机游走
通过这个问题,多维随机游走也可以类比于三维随机游走得出结 果.
多维随机游走
猜想 假设在一个 n 维坐标空间上随机游走,从原点出发.向x i 轴 正方向移动的概率为 pi ,向 x i 轴负方向移动的概率为 q i ,其 中 i 1,...,n , n 且 pi , qi 0 , pi qi 1 .
\ a b c d e f mod2 0, N g a d g a d g a d N bc e f N ac d f g ,h g h N g h PT Cg 2 p 2 q 2 GN p q m n s t h b e g a d hbe hbe hbe N g h c f N g h c f N g h c f 2 2 2 C 2 p 2 q 2 C p q , N g h h N a b c d e f mod2 , g amod2 , h bmod2 .
一维随机游走
推论1. 假设一点从点 i 出发,在数轴 x上一维随机游走, 向右走的概 率为 p,向左走的概率为q ,且 p, q 0, p q 1. * 设事件 A:共走了N 步, N N ,到达了点 j, j i N . 则.
\ j i(mod2) 0, N P( A) N j i N j i N j i . 2 2 2 C p q ,N j i(mod2) N
i a
i
二维随机游走
定理2. 假设一点在二维坐标系 xOy 上进行随机游走,从原点出发, 每一次沿坐标轴移动一个单位,向右走的概率为p ,向左走的概率 为q ,向上走的概率为 m ,向下走的概率为n , 且 p, q, m, n 0, p q m n 1. * 设总步数为 N . 设事件B :共走了N 步, n N ,到达了点 a, b (假设 a, b 0), a b N. 运用两次Bernoulli概型的叠加,可得:
n
n
多维随机游走
引理2 一个袋子中有 A1个 a1 球,A2 个a2 球,…,Ak 个ak 球(各球形状 大小均无差异). 现有放回的从袋子中摸球,问:在n 次摸球中恰 好摸到 B1个 a1 球,B2 个a2 球,…, Bk个ak 球的概率是多少? 设上述事件为事件 M .
n A i . 每次有 Ai 个样本点,又因为共摸球n 次,所以样本点共有 i 1 i 1 Aj p 可得 n 设 j ,则 n Ai B , B ,..., B
A A B D,
三维随机游走
则上式可表示为:
a,b a b na b PS Gn pqr
a,b Gn pa qb 1 p q
nab
三维随机游走
定理3. 假设一点在一个三维坐标空间 x y z 上进行随机游走,从 原点出发,每一次沿坐标轴移动一个单位,向 x轴正方向移动的概率 为 p , 向 x轴负方向移动的概率为q ,向 y 轴正方向移动的概率为m, s ,向 z 轴 向 y 轴负方向移动的概率为n ,向 z 轴正方向移动的概率为 负方向移动的概率为 t ,且 p, q, m, n, s, t 0 , p q m n s t 1 . * abc N 设事件 T :共走了 N 步, n N ,到达了点 a, b, c , (暂时假设 a, b, c 0 ). g a g a g a h b h b h b bc a c g ,h p q g m nh s t N g h Cg 2 p 2 q 2 Ch 2 p 2 q 2 PT GN g a h b
\ a b c d mod2, 0, i N bd i a c i a c i a c N i bd N i bd N i bd i i N i PB C N p q m n Ci 2 p 2 q 2 Ci 2 m 2 n 2 , i a c i a b c d mod2.
一维随机游走
推论2:从零点出发在数轴上一维随机游走, 向右走的概率为 p , 向左走的概率为 q ,且 p, q 0, p q 1 . * 设事件 A :在 N 步之内(包括第N 步)到达了点 a, a N , N N . 则 i a i a i a N P( A) C 2 p 2 q 2 ,其中 i amod2 .
2 维随机游走
在得到了二维随机游走的结果后,由于 2 维可以看作是 n个二 维情况的简单叠加,因此我们可以以类似的方法将2 n 几个Bernoulli 概型进行叠加,从而得到维随机游走的结论.然而,由于每一次使用 k k N k Bernoulli概型时,它的分布 CN p q 中的 N 总是一个变量,所以 得到的表达式是十分复杂的,也不易于计算.因此,本文中并没有给 出计算.
P A C
i 1
u
N a iM 2 N
N a iM N a iM N a2iM N a2iM 2 2 p q p q
其中 u max u : u M N , u N
N a M
.
项目的未来期望
1、寻找并建立更好的模型。 2、尝试解决解决树上的随机游走问题。 3、给出三维、多维随机游走的渐进公式, 方便实际运用。
C
N g h c 2 N g h
p
N g h c 2
q
N g h c 2
三维随机游走
推论4:一质点在一个三维坐标空间Oxyz上随机游走,从点 d , e, f 出发.向x 轴正方向移动的概率为 p ,向x 轴负方向移动的概率为q , 向 y 轴正方向移动的概率为m,向 y 轴负方向移动的概率为 n ,向 z 轴 正方向移动的概率为 s,向 z 轴负方向移动的概率为 t , 且 p, q, m, n, s, t 0 , p q m n s t 1 . * 设事件 T:共走了N 步, N N ,到达了点 a, b, c (假设 a, b, c 0 , a d , b e ,c f ), a b c N .则:
一维随机游走
定理1. 假设在一维坐标轴 x轴上一维随机游走,从原点出发,向右走 的概率为 p,向右走的概率为q ,且 p, q 0, p q 1 .
设事件 A 为:共走了N 步, n N * ,到达了点 a, a N . 运用Bernoulli概型,可得:
\ a(mod2) 0, N P( A) N a N a k 2 2 C N p q ,N a(mod2)
三维随机游走
引理1 一个袋子中有 A个白球, B 个黑球,D个红球(各球形状大小均 无差异). 现有放回的从袋子中摸球,问:在n 次摸球中恰好摸到 a
个白球, b 个黑球,( n a b 个红球)的概率是多少? 设上述事件为事件 S ,可得:
a b Cn Cn Aa Bb D na b PS A B Dn
\ amod2 0, i N b i a i a i a N i b N i b N i b i i N i 2 2 2 2 2 2 PB C N p q m n Ci p q Ci m n , i a i amod2
