(完整版)2018上海初三数学一模压轴题汇总各区2325题

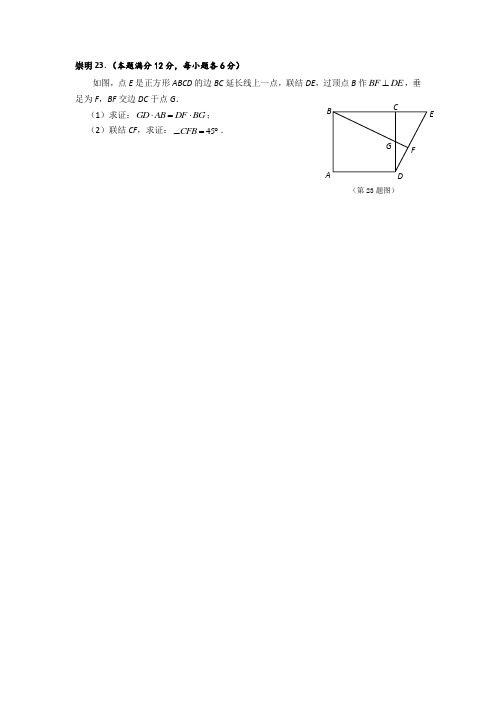
崇明23．（本题满分12分，每小题各6分）如图，点E 是正方形ABCD 的边BC 延长线上一点，联结DE ，过顶点B 作BF DE ⊥，垂足为F ，BF 交边DC 于点G ． （1）求证：GD AB DF BG ⋅=⋅； （2）联结CF ，求证：45CFB ∠=︒．（第23题图）ABDECGF崇明24．（本题满分12分，每小题各4分）如图，抛物线24yx bx c =-++过点(3,0)A ，(0,2)B ．(,0)M m 为线段OA 上一个动点（点AB 和抛物线分别交于点P 、N ． （（N 的坐标；（APM △相似，求点M 的坐标．（第24题图） （备用图）崇明25．（本题满分14分，第(1)小题4分，第(2)小题5分，第(3)小题5分）如图，已知ABC △中，90ACB ∠=︒，8AC =，4cos 5A =，D 是AB 边的中点，E 是AC 边上一点，联结DE ，过点D 作DF DE ⊥交BC 边于点F ，联结EF ．（1）如图1，当DE AC ⊥时，求EF 的长；（2）如图2，当点E 在AC 边上移动时，DFE ∠的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出DFE ∠的正切值；（3）如图3，联结CD 交EF 于点Q ，当CQF △是等腰三角形时，请直接写出．．．．BF 的长．（第25题图1） ABCD FE BD FE CA（第25题图2）BDFECA（第25题图3）如图，已知在Rt△ABC中，∠ACB=90°，AC＞BC，CD是Rt△ABC的高，E是AC 的中点，ED的延长线与CB的延长线相交于点F．（1）求证：DF是BF和CF的比例中项；（2）在AB上取一点G，如果AE：AC=AG：AD，求证：EG：CF=ED：DF．平面直角坐标系xOy 中（如图），已知抛物线23y ax bx =++与y 轴相交于点C ，与x 轴正半轴相交于点A ，OA OC =，与x 轴的另一个交点为B ，对称轴是直线1x =，顶点为P ．（1）求这条抛物线的表达式和顶点P 的坐标；（2）抛物线的对称轴与x 轴相交于点M ，求∠PMC 的正切值； （3）点Q 在y 轴上，且△BCQ 与△CMP 相似，求点Q 的坐标．金山25. （本题满分14分，第（1）小题3分，第（2）小题5分，第（3）小题6分）如图，已知在△ABC中，45,cos5AB AC B===，P是边AB一点，以P为圆心，PB为半径的Pe与边BC的另一个交点为D，联结PD、AD．（1）求△ABC的面积；（2）设PB =x，△APD的面积为y，求y关于x的函数关系式，并写出定义域；（3）如果△APD是直角三角形，求PB的长．青浦23．（本题满分12分，第（1）小题4分，第（2）小题8分）如图8，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CD CA CE CB⋅=⋅．（1）求证：∠CAE＝∠CBD；（2）若BE ABEC AC=，求证：AB AD AF AE⋅=⋅．ABDEF图8如图9，在平面直角坐标系xOy 中，抛物线()20y axbx c a =++>与x 轴相交于点A （-1，0）和点B ，与y 轴交于点C ，对称轴为直线1x =．（1）求点C 的坐标（用含a 的代数式表示）；（2）联结AC 、BC ，若△ABC 的面积为6，求此抛物线的表达式；（3）在第（2）小题的条件下，点Q 为x 轴正半轴上一点，点G 与点C ，点F 与点A 关于点Q 成中心对称，当△CGF 为直角三角形时，求点Q 的坐标．图9如图10，在边长为2的正方形ABCD 中，点P 是边AD 上的动点（点P 不与点A 、点 D 重合），点Q 是边CD 上一点，联结PB 、PQ ，且∠PBC ＝∠BPQ ． （1）当QD ＝QC 时，求∠ABP 的正切值； （2）设AP =x ，CQ =y ，求y 关于x 的函数解析式；（3）联结BQ ，在△PBQ 中是否存在度数不变的角，若存在，指出这个角，并求出它的度数；若不存在，请说明理由．图10QP D C BA备用图A BCD黄浦23、（本题满分12分）如图，BD 是ABC △的角平分线，点E 位于边BC 上，已知BD 是BA 与BE 的比例中项.（1）求证：12CDE ABC ∠=∠（2）求证：AD CD AB CE ⋅=⋅ED CB A在平面直角坐标系xOy 中，对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-. （1）求抛物线的表达式，并写出其顶点坐标；（2）现将此抛物线沿y 方向平移若干个单位，所得抛物线的顶点为D ，与y 轴的交点为B ,与x 轴负半轴交于点A ，过点B 作x 轴的平行线交所得抛物线于点C ，若AC BD ∥，试求平移后所得抛物线的表达式.如图，线段5AB =，4AD =，90A ∠=︒，DP AB ∥，点C 为射线DP 上一点，BE 平分ABC ∠交线段AD 于点E （不与端点A 、D 重合）.（1）当ABC ∠为锐角，且tan 2ABC ∠=时，求四边形ABCD 的面积； （2）当ABE △与BCE △相似时，求线段CD 的长；（3）设DC x =，DE y =，求y 关于x 的函数关系式，并写出定义域.PDBA P EDC BA已知四边形ABCD中，∠BAD=∠BDC=90°，2=⋅．BD AD BC（1）求证：AD∥BC；（2）过点A作AE∥CD交BC于点E．请完善图形并求证：2=⋅．CD BE BC如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++的对称轴为直线x =1，抛物线与x 轴交于A 、B 两点（点A 在点B 的左侧），且AB =4，又P 是抛物线上位于第一象限的点，直线AP 与y 轴交于点D ，与对称轴交于点E ，设点P 的横坐标为t ． （1）求点A 的坐标和抛物线的表达式； （2）当AE :EP =1:2时，求点E 的坐标；（3）记抛物线的顶点为M ，与y 轴的交点为C ，当四边形CDEM 是等腰梯形时，求t 的值．松江25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知△ABC中，∠ACB=90°，AC=1，BC=2，CD平分∠ACB交边AB与点D,P是射线CD上一点，联结AP．（1）求线段CD的长；（2）当点P在CD的延长线上，且∠P AB=45°时，求CP的长；（3）记点M为边AB的中点，联结CM、PM，若△CMP是等腰三角形，求CP的长．如图，已知在△ABC 中，∠BAC =2∠B ，AD 平分∠BAC ， DF //BE ，点E 在线段BA 的延长线上，联结DE ，交AC 于点G ，且∠E =∠C ．（1）求证：2AD AF AB =⋅； （2）求证：AD BE DE AB ⋅=⋅．（第23题图）ABDCEFG抛物线23(0)y ax bx a =++≠经过点A （1-，0），B （32且与y 轴相交于点C ．（1）求这条抛物线的表达式； （2）求∠ACB 的度数；（3）设点D 是所求抛物线第一象限上一点，且在对称轴的右侧，点E 在线段AC 上，且DE ⊥AC ， 当△DCE 与△AOC 相似时，求点D 的坐标．（第24题图）闵行25．（共3小题，第（1）小题4分，第（2）小题6分，第（3）小题4分，满分14分）如图，在Rt △ABC 中，∠ACB =90°，AC =4，BC =3，CD 是斜边上中线，点E 在边AC 上，点F 在边BC 上，且∠EDA =∠FDB ，联结EF 、DC 交于点G ． （1）当∠EDF =90°时，求AE 的长；（2）CE = x ，CF = y ，求y 关于x 的函数关系式，并指出x 的取值范围； （3）如果△CFG 是等腰三角形，求CF 与CE 的比值．（备用图）ABDC（第25题图）AB DCEFG浦东23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图，已知，在锐角△ABC 中，CE ⊥AB 于点E ，点D 在边AC 上， 联结BD 交CE 于点F ，且DF FB FC EF ⋅=⋅. （1）求证：BD ⊥AC ；（2）联结AF ，求证：AF BE BC EF ⋅=⋅.A （第23题图）DEFBC浦东24．（本题满分12分，每小题4分）已知抛物线y＝ax2＋bx＋5与x轴交于点A(1，0)和点B(5，0)，顶点为M．点C在x轴的负半轴上，且AC＝AB，点D的坐标为(0，3)，直线l经过点C、D．（1）求抛物线的表达式；（2）点P是直线l在第三象限上的点，联结AP，且线段CP是线段CA、CB的比例中项，求tan∠CPA的值；（3）在（2）的条件下，联结AM、BM，在直线PM上是否存在点E，使得∠AEM=∠AMB.若存在，求出点E（第24题图）浦东25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知在△ABC 中，∠ACB=90°，BC =2，AC =4，点D 在射线BC 上，以点D 为圆心，BD 为半径画弧交边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ． （1）求证：△EFG ∽△AEG ；（2）设FG =x ，△EFG 的面积为y ，求y 关于x 的函数解析式并写出定义域； （3）联结DF ，当△EFD 是等腰三角形时，请直接．．写出FG 的长度．（第25题备用图）ABC（第25题备用图）ABC虹口23．（本题满分12分，第（1）题满分6分，第（2）题满分6分）如图，在△ABC中，点D、E分别在边AB、AC上，DE、BC的延长线相交于点F，且EF DF BF CF⋅=⋅．（1）求证AD AB AE AC⋅=⋅；（2）当AB=12，AC=9，AE=8时，求BD的长与△△ADEECFSS的值．分4分）如图，在平面直角坐标系xOy中，抛物线与x轴相交于点A（-2,0）、B（4,0），与y轴交于点C（0，-4），BC与抛物线的对称轴相交于点D．（1）求该抛物线的表达式，并直接写出点D的坐标；（2）过点A作AE⊥AC交抛物线于点E，求点E的坐标；（3）在（2）的条件下，点F在射线AE上，若△ADF∽△ABC，求点F的坐标．分4分）已知AB=5，AD=4，AD∥BM，3cos5B=（如图），点C、E分别为射线BM上的动点（点C、E都不与点B重合），联结AC、AE，使得∠DAE=∠BAC，射线EA交射线CD于点F．设BC=x，AFy AC=．（1）如图1，当x=4时，求AF的长；（2）当点E在点C的右侧时，求y关于x的函数关系式，并写出函数的定义域；（3）联结BD交AE于点P，若△ADP是等腰三角形，直接写出x的值．普陀23. （本题满分12分）已知：如图9，四边形ABCD 的对角线AC 和BD 相交于点E ，2,AD DC DC DE DB ==⋅．求证：（1）BCE ADE V V ∽；（2）··AB BC BD BE =．图9Bx普陀24．（本题满分12分，每小题满分各4分）如图10，在平面直角坐标系中，已知抛物线22y ax ax c +=+（其中a c 、为常数，且0a <）与x 轴交于点A ，它的坐标是()3, 0-，与y 轴交于点B ，此抛物线顶点C 到x 轴的距离为4．（1）求该抛物线的表达式； （2）求CAB ∠的正切值；（3）如果点P 是抛物线上的一点，且ABP CAO ∠=∠，试直接写出点P 的坐标．普陀25．（本题满分14分，第（1）小题满分3分，第（1）小题满分5分，第（1）小题满分6分）如图11，BAC ∠的余切值为2，AB =D 是线段AB 上的一动点（点D 不与点A B 、重合），以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上，且点F 在点E 的右侧．联结BG ，并延长BG ，交射线EC 于点P ．（1）点D 在运动时，下列的线段和角中，______是始终保持不变的量（填序号）；①AF ； ②FP ； ③BP ； ④BDG ∠； ⑤GAC ∠； ⑥BPA ∠； （2）设正方形的边长为x ，线段AP 的长为y ，求y 与x 之间的函数关系式，并写出定义域；（3）如果PFG V 与AFG V 相似，但面积不相等，求此时正方形的边长．备用图图11P ACC E F嘉定23．（本题满分12分，每小题6分）如图6，已知梯形ABCD 中，AD ∥BC ，CD AB =，点E 在对角线AC 上，且满足BAC ADE ∠=∠.（1）求证：BC DE AE CD ⋅=⋅；（2）以点A 为圆心，AB 长为半径画弧交边BC 于点F ，联结AF .求证：CA CE AF ⋅=2.图6嘉定24．（本题满分12分，每小题4分）已知在平面直角坐标系xOy （如图7）中，已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .（1）求该抛物线的表达式；（2）设该抛物线的对称轴与x 轴的交点为C ， 第四象限内的点D 在该抛物线的对称轴上，如果 以点A 、C 、D 所组成的三角形与△AOB 相似， 求点D 的坐标；（3）设点E 在该抛物线的对称轴上，它的纵坐标是1， 联结AE 、BE ，求ABE ∠sin .嘉定25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）在正方形ABCD 中，8=AB ，点P 在边CD 上，43tan =∠PBC ，点Q 是在射线BP 上的一个动点，过点Q 作AB 的平行线交射线AD 于点M ，点R 在射线AD 上，使RQ 始终与直线BP 垂直．（1）如图8，当点R 与点D 重合时，求PQ 的长； （2）如图9，试探索：MQRM的比值是否随点Q 的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；（3）如图10，若点Q 在线段BP 上，设x PQ =，y RM =，求y 关于x 的函数关系式，并写出它的定义域．图8图9图10静安23. （本题满分12分，其中第1小题6分，第2小题6分）已知：如图，梯形ABCD 中，//,,DC AB AD BD AD DB =⊥，点E 是腰AD 上一点，作45EBC ∠=o ，联结CE ，交DB 于点F ． （1）求证：ABE V ∽DBC V ； （2）如果56BC BD =，求BCE BDA S S V V 的值．静安24. （本题满分12分，第1小题4分，第2小题8分）在平面直角坐标系xOy中（如图），已知抛物线25 3y ax bx=+-经过点(1,0)A-、(5,0)B．（1）求此抛物线顶点C的坐标；（2）联结AC交y轴于点D，联结BD、BC，过点C作CH BD⊥，垂足为点H，抛物线对称轴交x轴于点G，联结HG，求HG的长．静安25. （本题满分14分，第1小题4分，第2小题6分，第3小题4分）已知：如图，四边形ABCD 中，090,,,BAD AD DC AB BC AC <∠≤==o o平分BAD ∠．（1）求证：四边形ABCD 是菱形；（2）如果点E 在对角线AC 上，联结BE 并延长，交边DC 于点G ，交线段AD 的延长线于点F （点F 可与点D 重合），AFB ACB ∠=∠，设AB 长度是a （a 实常数，且0a >），,AC x AF y ==，求y 关于x 的函数解析式，并写出定义域；（3）在第（2）小题的条件下，当CGE V 是等腰三角形时，求AC 的长．（计算结果用含a 的代数式表示）长宁23．（本题满分12分，第（1）小题6分，第（2）小题6分）如图，在∆ABC 中，点D 在边BC 上，联结AD ，∠ADB=∠CDE ， DE 交边AC 于点E ，DE 交BA 延长线于点F ，且DF DE AD ⋅=2． （1）求证：BFD ∆∽CAD ∆； （2）求证：AD AB DE BF ⋅=⋅．F EDA第23题图长宁24．（本题满分12分，每小题4分）在直角坐标平面内，直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ，且与x 轴的另一个交点为点B . 点D 在该抛物线上，且位于直线AC 的上方．（1）求上述抛物线的表达式；（2）联结BC 、BD ，且BD 交AC 于点E ，如果∆ABE 的面积与∆ABC 的面积之比为4:5，求∠DBA 的余切值；（3）过点D 作DF ⊥AC ，垂足为点F ，联结CD . 若∆CFD 与∆AOC 相似，求点D 的坐标．备用图第24题图长宁25．（本题满分14分，第（1）小题3分，第（2）小题6分，第（3）小题5分） 已知在矩形ABCD 中，AB =2，AD =4. P 是对角线BD 上的一个动点（点P 不与点B 、D 重合），过点P 作PF ⊥BD ，交射线BC 于点F . 联结AP ，画∠FPE =∠BAP ，PE 交BF 于点E .设PD=x ，EF =y ．（1）当点A 、P 、F 在一条直线上时，求 ABF 的面积；（2）如图1，当点F 在边BC 上时，求y 关于x 的函数解析式，并写出函数定义域； （3）联结PC ，若∠FPC =∠BPE ，请直接写出PD 的长．备用图 备用图图1DCBA DCBA F EP D CB A 第25题图徐汇23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图在△ABC中，AB=AC，点D、E、F分别在边BC、AB、AC上，且∠ADE=∠B，∠ADF=∠C，线段EF交线段AD于点G．（1）求证：AE=AF；（2）若DF CFDE AE,求证：四边形EBDF是平行四边形．徐汇24．（本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）如图，在平面直角坐标系xOy 中，直线y =kx （k ≠0）沿着y 轴向上平移3个单位长度后，与x 轴交于点B （3,0），与y 轴交于点C ，抛物线2y x bx c =++过点B 、C 且与x 轴的另一个交点为A ．（1）求直线BC 及该抛物线的表达式；（2）设该抛物线的顶点为D ，求△DBC 的面积；（3）如果点F 在y 轴上，且∠CDF =45°，求点F 的坐标．徐汇25．（本题满分14分，第（1）小题3分，第（2）小题7分，第（3）小题4分）已知，在梯形ABCD中，AD∥BC，∠A=90°，AD=2，AB=4，BC=5，在射线BC任取一点M，联结DM，作∠MDN=∠BDC，∠MDN的另一边DN交直线BC于点N（点N在点M 的左侧）．（1）当BM的长为10时，求证：BD⊥DM；（2）如图（1），当点N在线段BC上时，设BN=x，BM=y，求y关于x的函数关系式，并写出它的定义域；（3）如果△DMN是等腰三角形，求BN的长．杨浦23．（本题满分12分，第（1）小题5分，第（2）小题7分）已知：梯形ABCD中，AD//BC，AD=AB，对角线AC、BD交于点E，点F在边BC上，且∠BEF=∠BAC.（2）当EF//DC时，求证：AE=DE.（第23题图）杨浦24．（本题满分12分，第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，抛物线2221y x mx m m =-+--+交 y 轴于点为A ，顶点为D ，对称轴与x 轴交于点H .（1）求顶点D 的坐标（用含m 的代数式表示）；（2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线22y x x =-+的位置，求平移的方向和距离；（3）当抛物线顶点D 在第二象限时，如果∠ADH =∠AHO ，求m 的值.（第24题图）杨浦25．（本题满分14分，第（1）、（2）小题各6分，第（3）小题2分）已知：矩形ABCD 中，AB =4，BC =3，点M 、N 分别在边AB 、CD 上，直线MN 交矩形对角线AC 于点E ，将△AME 沿直线MN 翻折，点A 落在点P 处，且点P 在射线CB 上. （1）如图1，当EP ⊥BC 时，求CN 的长； （2）如图2，当EP ⊥AC 时，求AM 的长；（3）请写出线段CP 的长的取值范围，及当CP 的长最大时MN 的长.（备用图）（图1） A B C D NP ME（图2） A B C D N P M E （第25题图）A B C D奉贤23．（本题满分 12 分，每小题满分各 6 分）已知：如图 8，四边形90ABCD DCB ∠=︒，，对角线 BD ⊥AD ，点 E 是边 AB 的中点，CE 与 BD 相交于点 F ，2·BD AB BC =． （1） 求证：BD 平分∠ABC ；（2） 求证：··BE CF BC EF ＝．奉贤24. （本题满分 12 分，每小题满分各 4 分）如图9，在平面直角坐标系xOy 中，抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ，与y 轴相交于点(0,3)C -，经过点A 的射线AM 与y 轴相交于点E ，与抛物线的另一个交点为点F ，且13AE EF =． （1）求这条抛物线的表达式，并写出它的对称轴； （2）求FAB ∠的余切值；（3）点D 是点C 关于抛物线对称轴的对称点，点 P 是 y 轴上一点，且AFP DAB ∠=∠，求点 P 的坐标．奉贤25．（本题满分 14 分，第（1）小题满分 3 分，第（1）小题满分 5 分，第（1）小题满分 6 分）已知：如图10，在梯形ABCD 中，//,90,2AB CD D AD CD ∠===o，点E 在边AD上（不与点A 、D 重合），45,CEB EB ∠=o与对角线AC 相交于点F ，设DE x =．（1）用含x 的代数式表示线段CF 的长；（2）如果把CAE V 的周长记作CAE C V ，BAF V 的周长记作BAF C V ，设CAEBAFC y C =V V ，求y 关于x 的函数关系式，并写出它的定义域； （3）当ABE ∠的正切值是35时，求AB 的长．如图，ABC V 中，AB AC =，过点C 作//CF AB 交ABC V 的中位线DE 的延长线于F ，联结BF ，交AC 于点G . （1）求证：AE EGAC CG=； （2）若AH 平分BAC ∠，交BF 于H ，求证：BH 是HG 和HF 的比例中项.设,a b 是任意两个不等实数，我们规定：满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间，表示为[],a b ，对于一个函数，如果它的自变量x 与函数值y 满足：当m x n ≤≤时，有m y n ≤≤，我们就此称此函数是闭区间[],m n 上的“闭函数”。