八年级几何习题(角平分线性质和线段垂直平分线性质习题)
专题02 垂直平分线与角平分线(解析版)八年级数学下册期末综合复习专题提优训练(北师大版)

2020-2021学年八年级数学下册期末综合复习专题提优训练(北师大版)专题02 垂直平分线与角平分线【典型例题】1.如图,△ABC 中,△ABC =25°,△ACB =55°,DE ,FG 分别为AB ,AC 的垂直平分线,E ,G 分别为垂足; (1)直接写出△BAC 的度数;(2)求△DAF 的度数;(3)若BC 的长为30,求△DAF 的周长.【答案】(1)100BAC ∠=︒;(2)20DAF ∠=︒;(3)30DAF C =【分析】 (1)由题意直接根据三角形内角和定理计算,得到答案;(2)由题意根据线段垂直平分线的性质、等腰三角形的性质计算;(3)根据线段垂直平分线的性质、三角形的周长公式计算,得到答案.【详解】解:(1)△△ABC +△ACB +△BAC =180°,△△BAC =180°﹣25°﹣55°=100°;(2)△DE 是线段AB 的垂直平分线,△DA =DB ,△△DAB =△ABC =25°,△FG 是线段AC 的垂直平分线,△AF =CF ,△△F AC =△ACB =55°,△△DAF =△BAC ﹣△DAB ﹣△F AC =100°﹣25°﹣55°=20°;(3)△BC =30,由(2)可知, AD =BD ,F A =FC ,△C △DAF =AD +DF +F A =BD +DF +FC =BC =30.【点睛】本题考查的是线段的垂直平分线的性质以及三角形内角和定理,等腰三角形性质,熟练掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.【专题训练】一、选择题1.如图,在Rt ABC 中,90,B AD ∠=︒平分BAC ∠,交BC 于点D ,DE AC ⊥,垂足为点E ,若1BD =,则DE 的长为( )A .12B .1C .2D .6【答案】B【分析】根据△B =90°,AD 平分△BAC ,DE △AC ,再根据角平分线的性质得到DE =BD =1.【详解】△90B ∠=︒,△DB AB ⊥,又△AD 平分BAC ∠,DA AC ⊥,△由角平分线的性质得1DE BD ==. 故选:B【点睛】本题主要考查了角平分线的性质,灵活运用角平分线的性质处理问题.2.如图,在ABC 中,直线ED 是线段BC 的垂直平分线,直线ED 分别交BC 、AB 于点D 、点E ,已知BD =3,ABC 的周长为20,则AEC 的周长为( )A .14B .20C .16D .12【答案】A【分析】 根据线段的垂直平分线的性质得到EC =EB ,BC =2BD =6,根据三角形的周长公式计算即可.【详解】△ED 是线段BC 的垂直平分线,△EC =EB ,BC =2BD =6,△△ABC 的周长为20,△AB +AC +BC =20,△AB +AC =14,△△AEC 的周长=AC +AE +EC =AC +AE +EB =AC +AB =14,故选:A .【点睛】本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.3.如图,在ABC 中,AD BC ⊥,垂足为D ,EF 垂直平分AC ,交AC 于点F ,交BC 于点E ,BD DE =,若ABC 的周长为26cm ,5AF =cm ,则DC =( )A .8cmB .7cmC .10cmD .9cm【答案】A【分析】根据线段垂直平分线和等腰三角形性质得出AB=AE=CE,能推出2DE+2EC=16,即可求解.【详解】解:△AD△BC,BD=DE,EF垂直平分AC△AB=AE=EC△△ABC周长是26cm,AF=5cm△AC=10cm△AB+BC=16cm△AB+BE+EC=16cm即2DE+2EC=16cm△DE+EC=8cm△DC=DE+EC=8cm故选A.【点睛】本题主要考查了等腰三角形的性质,线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端的距离相等时解题的关键.4.如图,在Rt△ABC中,△ACB=90°,AC=3,BC=4,BE平分△ABC,CD△AB于D,BE与CD相交于F,则CF的长是()A.1B.43C.53D.2【答案】B【分析】过点E作EG△AB于点G,由EG△AB,CD△AB,可得EG△CD,由平行线的性质可得△GEB=△EFC;在Rt△ABC 中,由勾股定理求得AB的值;由HL判定Rt△EBC△Rt△EBG,由全等三角形的性质可得△CEB=△EFC及AG 的值,进而可判定CF=CE.设CF=EG=EC=x,则AE=3-x,在Rt△AEG中,由勾股定理得关于x的方程,解得x 的值即为CF 的长.【详解】解:过点E 作EG △AB 于点G ,如图:△CD △AB 于D ,△EG △CD ,△△GEB =△EFC ,△在Rt △ABC 中,△ACB =90°,△EC △CB ,又△BE 平分△ABC ,EG △AB ,△EG =EC .在Rt △ABC 中,△ACB =90°,AC =3,BC =4,△AB =5.在Rt △EBC 和Rt △EBG 中,EB EB EC EG=⎧⎨=⎩, △Rt △EBC △Rt △EBG (HL ),△CEB =△GEB ,BG =BC =4,△△CEB =△EFC ,AG =AB ﹣BG =5﹣4=1,△CF =CE .设CF =EG =EC =x ,则AE =3﹣x ,在Rt △AEG 中,由勾股定理得:(3﹣x )2=x 2+12,解得x =43△CF 的长是43.故选:B.【点睛】本题考查了勾股定理、角平分线的性质定理及等腰三角形的判定等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.5.如图,在△ABC中,△B=15°,△C=30°,MN是AB的垂直平分线,PQ是AC的垂直平分线,已知S△ANQ则BC的长为()A B.3C.3D.2+【答案】B【分析】根据线段垂直平分线的性质得出AQ=CQ,BN=AN,根据等腰三角形的性质和已知条件得出△BAN=△B=15°,△CAQ=△C=30°,根据三角形外角性质得出△ANQ=△B+△BAN=30°,△AQN=△C+△CAQ=60°,求出△NAQ=90°,再根据三角形的面积求出AQ,最后求出BC即可.【详解】解:△MN是AB的垂直平分线,PQ是AC的垂直平分线,△AQ=CQ,BN=AN,△△B=15°,△C=30°,△△BAN=△B=15°,△CAQ=△C=30°,△△ANQ=△B+△BAN=15°+15°=30°,△AQN=△C+△CAQ=30°+30°=60°,△△NAQ=180°﹣△ANQ﹣△AQN=90°,△NQ=2AQ,AN==,△S△ANQ=,2△12⨯AQ 解得:AQ =1(负数舍去),即CQ =AQ =1,AN =BN NQ =2AQ =2,△BC =BN +NQ +CQ 2+1=3故选:B .【点睛】本题考查了含30°角的直角三角形的性质,线段垂直平分线的性质,勾股定理,三角形的面积,三角形的外角性质,等腰三角形的性质等知识点,能综合运用知识点进行推理和计算是解此题的关键.二、填空题6.如图,在△ABC 中,△C =90°,AP 平分△CAB ,且PC =3,PB =5,则点P 到边AB 的距离是 ______________【答案】3【分析】作PH △AB 于H .直接根据角平分线的性质求解即可.【详解】解:作PH △AB 于H ,如图,△AP 平分△CAB ,且△C =90°,△3PH PC ==,即点P 到边AB 的距离是3.故答案为3.【点睛】此题主要考查了角平分线的性质,熟练掌握角平分线性质定理是解答此题的关键.7.如图,在△ABC 中,△C =90°,DE 垂直平分斜边AB ,分别交AB 、BC 于D 、E ,若△CAB =△B +28°,则△CAE=__.【答案】28︒【分析】先根据直角三角形的两锐角互余可得31,59B CAB ∠=︒∠=︒,再根据垂直平分线的性质可得AE BE =,然后根据等腰三角形的性质可得31B BAE ∠=∠=︒,最后根据角的和差即可得.【详解】解:△在ABC 中,90C ∠=︒,△90CAB B ∠+∠=︒,又△28CAB B ∠=∠+︒,△31,59B CAB ∠=︒∠=︒,△DE 垂直平分斜边AB ,△AE BE =,△31BAE B ∠=∠=︒,△593128CAE CAB BAE ∠=∠-∠=︒-︒=︒,故答案为:28︒.【点睛】本题考查了直角三角形的两锐角互余、等腰三角形的性质、线段垂直平分线的性质等知识点,熟练掌握等腰三角形的性质和线段垂直平分线的性质是解题关键.8.如图,在△ABC 中,AB =6,AC =8,BC =11,AB 的垂直平分线分别交AB ,BC 于点D 、E ,AC 的垂直平分线分别交AC ,BC 于点F 、G ,则△AEG 的周长为__.【答案】11.【分析】根据线段垂直平分线的性质可得EA=EB,GA=GC,所以可求出△AEG的周长.【详解】解△DE是线段AB的垂直平分线,△EA=EB,同理,GA=GC,△△AEG的周长=AE+EG+GA=EB+EG+GC=BC=11,故答案为:11.【点睛】本题考查了线段垂直平分线的性质.线段垂直平分线上的点到线段两端点的距离相等.9.如图,在四边形ABCD中,△A=90°,AD= 6,连接BD,BD△CD,△ADB=△C.若P是BC边上一动点,则DP长的最小值为__________.【答案】6【分析】根据垂线段最短得出当DP△BC时,DP的长度最小,求出△ABD=△CBD,根据角平分线的性质得出AD=DP=6,即可得出选项.【详解】解:△BD△CD,△△BDC=90°,△△C+△CBD=90°,△△A=90°△△ABD+△ADB=90°,△△ADB=△C,△△ABD=△CBD,当DP△BC时,DP的长度最小,△AD△AB,△DP=AD,△AD=6,△DP的最小值是6,故答案为:6.【点睛】本题考查了角平分线的性质,三角形内角和定理和垂线段最短等知识点,能知道当DP△BC时,DP的长度最小是解此题的关键.10.如图,等腰三角形ABC的面积为24,底边BC为12,点P在边BC上,且BP:PC=3:1,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDP周长的最小值为___________.【答案】8.【分析】如图作AH△BC于H,连接AD.由EG垂直平分线段AC,推出DA=DC,推出DP+DC=AD+DP,可得当A、D、P共线时,DP+DC的值最小,最小值就是线段AP的长,此时,△CDP周长的最小,求出AP的长即可.【详解】解:如图作AH△BC于H,连接AD.△EG垂直平分线段AC,△DA=DC,△DP+DC=AD+DP,△当A、D、P共线时,DP+DC的值最小,最小值就是线段AP的长,△12×12•AH=24,△AH=4,△AB=AC,AH△BC,△BH=CH=6,△BP:PC=3:1,△CP=PH=3,△AP5,△DP+DC的最小值为5.△△CDP周长的最小值为5+3=8;故答案为:8.【点睛】本题考查轴对称﹣最短问题、线段的垂直平分线的性质、等腰三角形的性质、勾股定理等知识,解题的关键是学会利用轴对称,解决最短问题,属于中考常考题型.三、解答题11.如图,在△ABC中,AB=AC,BE平分△ABC,DE△BC,交AB于点D,交AC于点E.(1)求证:BD=DE;(2)若△DEB=30°且DE=3,求AD的长度.【答案】(1)见解析;(2)3.【分析】(1)由BE平分△ABC,DE△BC可得△DBE=△DEB,可得结论;(2)通过证明△ADE为等边三角形,可得AD=DE=3.【详解】证明:(1)△BE平分△ABC,△△ABE=△EBC,△DE△BC,△△DEB=△EBC,△△DBE=△DEB,△BD=DE;(2)△△DEB=△DBE=30°=△EBC,△△ABC=60°,△AB=AC,△△ABC是等边三角形,△△ABC=△ACB=△A=60°,△DE△BC,△△ADE=△ABC=60°,△AED=△C=60°,△△ADE是等边三角形,△AD=DE=3.【点睛】本题考查了等腰三角形的性质,角平分线的性质,平行线的性质,等边三角形的判定和性质,灵活运用这些性质进行推理是本题的关键.,的垂直平分线交于点P.12.如图,ABC中,边AB BC==.(1)求证:PA PB PC(2)点P是否也在边AC的垂直平分线上?请说明理由.【答案】(1)见解析;(2)在,理由见解析【分析】(1)根据线段的垂直平分线的性质可求得,P A=PB,PB=PC,则P A=PB=PC.(2)根据线段的垂直平分线的性质的逆定理,可得点P在边AC的垂直平分线上.【详解】解:(1)证明:△边AB、BC的垂直平分线交于点P,△P A=PB,PB=PC.△P A=PB=PC.(2)△P A=PC,△点P 在边AC 的垂直平分线上.【点睛】此题主要考查线段垂直平分线的性质定理及逆定理:(1)线段垂直平分线上的点和这条线段的两个端点的距离相等;(2)和一条线段的两个端点的距离相等的点,在这条线段的垂直平分线上.13.如图,AD 为△ABC 的角平分线,DE △AB 于点E ,DF △AC 于点F ,连接EF 交AD 于点O .(1)求证:△DEF =△DFE ;(2)求证:AD 垂直平分EF .【答案】(1)见解析;(2)见解析【分析】(1)根据角平分线的性质证明即可得解;(2)根据已知条件证明Rt △AED △Rt △AFD (HL )和△△DEO DFO ≅即可得解;【详解】(1)△AD 为△ABC 的角平分线,DE △AB ,DF △AC ,△DE =DF ,△△DEF =△DFE ;(2)根据已知条件可得△AED =△AFD =90°,在Rt △AED 和Rt △AFD 中,DE DF AD AD=⎧⎨=⎩, △Rt △AED △Rt △AFD (HL ),△△ADE =△ADF ;在△DEO 和△DFO 中, DEO DFO DE DFEDO FDO ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△△DEO DFO ≅,△EO FO =,EOD FOD ∠=∠,△∠EOD +∠FOD =180°,△∠EOD =∠FOD =90°,△AD 垂直平分EF .【点睛】本题主要考查了角平分线的垂直平分线的判定与性质,结合等三角形证明是解题的关键.14.如图,在ABC 中,AB AC =,AB 的垂直平分线交AB 于M ,交AC 于N .(1)若70ABC ∠=︒,求A ∠的度数;(2)连接NB ,若8cm AB =,NBC 的周长是14cm ,求BC 的长.【答案】(1)40°;(2)6cm【分析】(1)由AB =AC 可得△C =△ABC =70°,由三角形内角和可得△A =40°;(2)由(1)可知BN =AN ,由此可得BN +NC =AN +NC =AC =AB =8cm ,再由C △BNC =BN +CN +BC =14cm ,可得BC =14-8=6(cm ).【详解】解:(1)△AB =AC ,△△ABC =△ACB =70°,△△A =180°-70°-70°=40°;(2)MN 是AB 的垂直平分线,△AN =BN ,△BN +CN =AN +CN =AC ,△AB =AC =8cm ,△BN +CN =8cm ,△C △BNC =BN +CN +BC =14(cm ),△BC =14﹣8=6(cm ).【点睛】本题考查等腰三角形性质,三角形内角和,线段垂直平分线性质,三角形周长,掌握等腰三角形性质,三角形内角和,线段垂直平分线性质,三角形周长是解题关键.15.如图,△ABC 中,AD 平分△BAC ,DG △BC 且平分BC ,DE △AB 于E ,DF △AC 于F .(1)求证:BE =CF ;(2)如果AB =8,AC =6,求AE ,BE 的长.【答案】(1)证明见解析,(2)AE =7,BE =1.【分析】(1)连接DB 、DC ,先由角平分线的性质就可以得出DE =DF ,再证明△DBE △△DCF 就可以得出结论; (2)由条件可以得出△ADE △△ADF 就可以得出AE =AF ,进而就可以求出结论.【详解】解:(1)证明:连接DB 、DC ,△DG △BC 且平分BC ,△DB =DC .△AD 为△BAC 的平分线,DE △AB ,DF △AC ,△DE =DF .在Rt △DBE 和Rt △DCF 中DB DC DE DF =⎧⎨=⎩, Rt △DBE △Rt △DCF (HL ),△BE =CF .(2)在Rt △ADE 和Rt △ADF 中AD AD DE DF =⎧⎨=⎩,△Rt△ADE△Rt△ADF(HL).△AE=AF.△AC+CF=AF,△AE=AC+CF.△AE=AB﹣BE,△AC+CF=AB﹣BE,△AB=8,AC=6,△6+BE=8﹣BE,△BE=1,△AE=8﹣1=7.即AE=7,BE=1.【点睛】本题考查了角平分线的性质的运用,中垂线的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.16.如图,已知Rt△ABC中,△ACB=90°,CD△AB于点D,△BAC的平分线分别交BC,CD于点E、F.(1)试说明△CEF是等腰三角形;(2)若点E恰好在线段AB的垂直平分线上,猜想:线段AC与线段AB的数量关系,并说明理由;(3)在(2)的条件下,若AC=2.5,求△ABE的面积.【答案】(1)见解析;(2)AB=2AC,理由见解析;(3)12【分析】(1)求出△B=△ACD,根据三角形的外角性质求出△CFE=△CEF,根据等腰三角形的判定得出即可;(2)求出△B=△CAE=△BAE,根据三角形内角和定理求出△B=30°,再求出答案即可;(3)求出高EM的长,求出AB的长,再根据三角形的面积公式求出即可.【详解】解:(1)△CD△AB,△△CDB=90°,△△B+△BCD=90°,△△ACB=90°,△△ACD+△BCD=90°,△△ACD=△B,△AE平分△BAC,△△CAE=△BAE,△△ACD+△CAE=△B+△BAE,即△CFE=△CEF,△CF=CE,即△CEF是等腰三角形;(2)AB=2AC,理由是:△E在线段AB的垂直平分线上,△AE=BE,△△B=△BAE,△△CAE=△BAE,△ACB=90°,△3△B=90°,△△B=30°,△AB=2AC;(3)△AC=2.5,△AB=2AC=5,由(2)得,△CAB=60°,△AE平分△CAB,△△CEA =30°,设CE 为x ,则AE 为2x ,AC ,x ,过E 作EM △AB 于M ,△EM =CE =6,△△ABE 的面积S =12AB EM ⋅=12⨯5. 【点睛】本题考查勾股定理、等腰三角形的判定、含30°角的直角三角形的性质,解题关键是熟练运用所学知识,整合已知条件,解决综合问题.17.如图1,在△ABC 中,AD △BC ,垂足为D ,E 为AC 上一点,BE 交AD 于点F ,△ABC =45°,FD =CD . (1)请写出BE 与AC 的位置关系,并说明理由;(2)如图2,连接DE ,求证:△BED =△DEC ;(3)若AD =4,CD =2,在直线BC 上方的平面内是否存在点P ,使得△BFP 为等腰直角三角形.若存在,请直接写出点P 到直线BC 的距离.【答案】(1)BE △AC ,见解析;(2)见解析;(3)存在,4或6或3【分析】(1)证明△BDF △△ADC ,得到△DBF =△DAC ,由△BFD =△AFE 证得△BDF =△AEF =90°,即可得到结论;(2)过点D 作DM △AC ,DN △BE ,根据△BDF △△ADC ,得到BF =AC ,BDF ADC SS =,推出DM =DN ,证得ED 平分△BEC ,由此得到结论;(3)根据勾股定理求出AC 由△BDF △△ADC ,得到BF =AC =DF =DC =2,BD =AD =4,分三种情况:当△PBF =90°,BP =BF 时, 当△P ′FB =90°,P ′F =BF 时, 当△BP ″F =90°,BP ″=FP ″时, 根据等腰直角三角形的性质解答即可.【详解】(1)证明:如图①中,△AD △BC ,△△ADB =90°,△△ABC =45°,△△ABD =△BAD =45°,△BD =DA ,△DF =DC ,△BDF =△ADC =90°,△△BDF △△ADC (SAS ).△△DAC =△CBE ,△△BFD =△AFE ,△△BDF =△AEF =90°,△BE △AC .(2)解:如图,过点D 作DM △AC ,DN △BE ,△△BDF △△ADC ,△BF =AC ,BDF ADC SS =,△DM =DN ,△ED 平分△BEC ,△△BED =△DEC ;(3)解:如图2-1中,满足条件的点P 有3个.在Rt △ADC 中,△AD =4,CD =2,△AC ,△△BDF △△ADC ,△BF =AC =DF =DC =2,BD =AD =4,当△PBF =90°,BP =BF 时,作PM △CB 交CB 的延长线于M . 易证△PMB △△BDF ,△PM =BD =4,△点P 到直线BC 的距离为4;当△P ′FB =90°,P ′F =BF 时,作P ′H △BC 于H ,FG △P ′H 于G . 易证:P ′G =BD =4,GH =DF =2,△P ′H =4+2=6,△P ′到直线BC 的距离为6;当△BP ″F =90°,BP ″=FP ″时,作P ″N △BC 于N .易证P ″N =2PM DF +=3,△P″到直线BC的距离为3,综上所述,满足条件的点P到直线BC的距离为4或6或3.【点睛】此题考查全等三角形的判定及性质,等腰直角三角形的性质,勾股定理,角平分线的判定及性质,熟记各定理并熟练应用解决问题是解题的关键.18.在△ABC中,若AD是△BAC的角平分线,点E和点F分别在AB和AC上,且DE△AB,垂足为E,DF△AC,垂足为F(如图(1)),则可以得到以下两个结论:①△AED+△AFD=180°;②DE=DF.那么在△ABC中,仍然有条件“AD是△BAC的角平分线,点E和点F,分别在AB和AC上”,请探究以下两个问题:(1)若△AED+△AFD=180°(如图(2)),则DE与DF是否仍相等?若仍相等,请证明;否则请举出反例.(2)若DE=DF,则△AED+△AFD=180°是否成立?(只写出结论,不证明)【答案】(1)DE=DF,理由见解析;(2)不一定成立【分析】(1)过点D作DM△AB于M,DN△AC于N,DM=DN,△DME△△DNF,DE=DF;(2)如图,若DE、DF在点D到角的两边的垂线段与顶点A的同侧则一定不成立;【详解】(1)DE=DF.理由如下:过点D作DM△AB于M,DN△AC于N,△AD平分△BAC,DM△AB,DN△AC,△DM=DN,△△AED+△AFD=180°,△AFD+△DFN=180°,△△DFN=△AED,△△DME△△DNF(AAS),△DE=DF;(2)不一定成立.如图,若DE、DF在点D到角的两边的垂线段与顶点A的同侧则一定不成立,经过(1)的证明,若在垂线段上或两侧则成立,所以不一定成立..【点睛】本题主要考查角平分线的性质,难点在于熟练和灵活的应用角平分线要点;19.根据图片回答下列问题.(1)如图①,AD平分△BAC,△B+△C=180°,△B=90°,易知:DB____DC.(2) 如图②,AD平分△BAC,△ABD+△ACD=180°,△ABD<90°,求证:DB=DC.(3)如图③,四边形ABCD中,△B=45°△C=135°,DB=DC AB−AC=________.【答案】(1)=;(2)见解析;(3)【分析】(1)利用HL判断出△ADC△△ADC,即可得出结论;(2)先构造出△ACD△△AED,得出DC=DE,△AED=△C,在判断出DE=DB,即可得出结论;(3)利用(2)结论得出DE=DB,再判断出△BDE=90°,利用勾股定理求出BE即可得出结论.【详解】解:证明:(1)△△B+△C=180°,△B=90°,△△C=90°,△AD平分△BAC,△△DAC=△BAD,△AD=AD,△△ACD△△ABD(AAS),△BD=CD;(2)如图②,在AB边上取点E,使AC=AE,△AD平分△BAC,△△CAD=△EAD,△AD=AD,AC=AE,△△ACD△△AED(SAS),△DC=DE,△AED=△C,△△C+△B=180°,△AED+△DEB=180°,△△DEB=△B,△DE=DB,△DB=DC;(3)如图③,连接AD,在AB上取一点E使AE=AC,同(2)的方法得,AE =AC ,CD =DE =BD =2,△△DEB =△B =45°,△△BDE =90°,根据勾股定理得,BE =,△AB -AC =BE =故答案为:【点睛】本题是四边形综合题,考查全等三角形的判定和性质,角平分线的性质,等腰直角三角形的性质,勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形,属于中考常考题型.20.如图①,△ABC 中,△ABC ,△ACB 的平分线交于O 点,过O 点作BC 平行线交AB ,AC 于E ,F . (1)试说明:EO =BE ;(2)探究图①中线段EF 与BE ,CF 间的关系,并说明理由;(3)探究图②,△ABC 中若△ABC 的平分线与△ABC 的外角平分线交于O ,过点O 作BC 的平行线交AB 于E ,交AC 于F ,这时EF 与BE ,CF 的关系又如何?请直接写出关系,不需要说明理由.【答案】(1)证明见解析;(2)EF BE CF =+,理由见解析;(3)EF BE CF =-【分析】(1)由题意易得△EOB =△EBO ,△ABO =△OBC ,则有△EOB =△ABO ,进而问题得证;(2)由题意易得△FOC =△OCB ,△FCO =△OCB ,则有△FCO =△FOC ,然后可得CF =OF ,由(1)得BE =OE ,进而问题可求解;(3)同理(1)(2)可得:BE=OE,CF=OF,然后问题可求解.【详解】证明:(1)△EF△BC,△△EOB=△EBO,△BO平分△ABC,△△ABO=△OBC,△△EOB=△ABO,△BE=OE;=+,理由如下:(2)解:EF BE CF△EF△BC,△△FOC=△OCB,△CO平分△ACB,△△FCO=△OCB,△△FCO=△FOC,△CF=OF,由(1)得:BE=OE,△EF=BE+CF;(3)解:EF=BE-CF,理由如下:同理(1)(2)可得:BE=OE,CF=OF,△EF=OE-OF=BE-CF.【点睛】本题主要考查角平分线的定义及平行线的性质,熟练掌握角平分线的定义及平行线的性质是解题的关键,也要熟练掌握“双平等腰”模型.。
线段的垂直平分线和角平分线重难点专练

专题02线段的垂直平分线和角平分线重难点专练(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2020·上海市曹杨第二中学附属学校八年级期中)如图,D 为BAC Ð的外角平分线上一点,过D 作DE AC ^于E ,DF AB ^交BA 的延长线于F ,且满足FDE BDC Ð=Ð,则下列结论:①CDE V ≌BDF V ;②CE AB AE =+;③BDC BAC Ð=Ð;④DAF CBD Ð=Ð.其中正确的结论有( ).A .1个B .2个C .3个D .4个【答案】D【分析】根据角平分线上的点到角的两边距离相等可得DE=DF ,再证明FDB EDC Ð=Ð,即可证明Rt △CDE 和Rt △BDF 全等;根据全等三角形对应边相等可得CE=BF ,利用“HL”证明Rt △ADE 和Rt △ADF 全等,可得AE=AF ,然后求出CE=AB+AE ;∠FDE 与∠BAC 都与∠FAE 互补,可得∠FDE=∠BAC ,于是可证BDC BAC Ð=Ð;利用外角定理得2∠DAF=∠ABC+∠ACB=∠ABD+∠DBC +∠ACB ,由Rt △CDE ≌Rt △BDF 可得∠ABD=∠DCE ,BD=DC ,故∠DBC=∠DCB ,于是可证明∠DAF=∠CBD .【详解】解:∵AD 平分∠CAF ,DE ⊥AC ,DF ⊥AB ,∴DE=DF ,DFB DEC Ð=Ð=90o∵FDE BDC Ð=Ð,∴FDB EDC Ð=Ð,在Rt △CDE 和Rt △BDF 中FDB CDE DFB DEC Ð=ÐìïÐ=Ðí,∴Rt △CDE ≌Rt △BDF ,故①正确;∴CE=BF ,在Rt △ADE 和Rt △ADF 中,,AD AD DE DF =ìí=î∴Rt △ADE ≌Rt △ADF ,∴AE=AF ,∴CE=AB+AF=AB+AE ,故②正确;∵DFA DEA Ð=Ð=90o ,∴∠EDF+∠FAE=180o ,∵∠BAC+∠FAE=180o ,∴∠FDE=∠BAC ,∵∠FDE=∠BDC ,∴∠BDC =∠BAC ,故③正确;∵∠FAE 是△ABC 的外角,∴2∠DAF=∠ABC+∠ACB=∠ABD+∠DBC +∠ACB ,∵Rt △CDE ≌Rt △BDF ,∴∠ABD=∠DCE ,BD=DC ,∴∠DBC=∠DCB ,∴2∠DAF=∠DCE +∠DBC +∠ACB=∠DBC +∠DCB=2∠DBC ,∴∠DAF=∠CBD ,故④正确;综上所述,正确的结论有①②③④共4个.故选:D .【点睛】要二次证明三角形全等.2.(2021·上海金山区·八年级期末)下列命题中,是假命题的是()A .两条直角边对应相等的两个直角三角形全等 ;B .每个命题都有逆命题;C .每个定理都有逆定理;D .在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上.【答案】C【分析】根据全等三角形的判定,命题与定理及角平分线的判定等知识一一判断即可.【详解】解:A .两条直角边对应相等的两个直角三角形,符合两三角形的判定定理“SAS”;故本选项是正确;B 、每个命题都有逆命题,所以B 选项正确;C 、每个定理不一定有逆定理,所以C 选项错误;D 、在一个角的内部(包括顶点)且到角的两边距离相等的点,在这个角的平分线上,正确.故选C .【点睛】本题考查了全等三角形的判定,命题与定理以及角平分线的判定方法,熟练利用这些判定定理是解题关键.3.(2021·上海市康城学校八年级期末)下列命题的逆命题是真命题的是( ).A .若a b =,则a b=B .同位角相等,两直线平行C .对顶角相等D .若0a >,0ba >,则0a b +>【答案】B【分析】分别写出各选项中命题的逆命题,然后判断其真假即可.【详解】解:A 、逆命题为:若∣a ∣=∣b ∣,则a=b ,是假命题;B 、逆命题为:两直线平行,同位角相等,是真命题;故选:B.【点睛】本题考查了互逆命题的知识,会判断命题的真假,正确写出原命题的逆命题是解答的关键.4.(2021·上海八年级期末)下列命题中,是真命题的是()A.三角形的外角大于三角形的任何一个内角B.线段的垂直平分线上的任一点与该线段两个端点能构成等腰三角形C.三角形一边的两个端点到这边上的中线所在的直线的距离相等D.面积都相等的两个三角形一定全等【答案】C【分析】A、B、D均可举反例说明错误,C选项可构造图形证明.【详解】解:A.钝角三角形与钝角相邻的外角小于该角,原命题是假命题,故该选项不符合题意;B.如果该点在线段上,那么不能构成等腰三角形,原命题是假命题,故该选项不符合题意;C.当该中线为等腰三角形底边上的中线时,根据三线合一即可得出这两个端点到这边上的中线所在的直线的距离相等,当三角形不是等腰三角形或中线不是等腰三角形底边上的中线时,如图所示,AD为△ABC的中线,BF⊥AD,CE⊥AD,∵AD为△ABC的中线,∴BD=CD,∵BF⊥AD,CE⊥AD,∴∠BFD=∠CED=90°,∵∠ADB=∠EDC,∴△BDF≌△CDE(AAS),∴BF=CE,综上,三角形一边的两个端点到这边上的中线所在的直线的距离相等,原命题是真命题,故该选项符合题意;D.如果是一个钝角三角形和锐角三角形,某边相等且该边上的高相等,但它们不全等,原命题是假命题,故该选项不符合题意;故选:C.【点睛】本题考查判断命题的真假,主要考查三角形外角的性质,等腰三角形的性质和判定,垂直平分线的性质,全等三角形的判定与性质.说明一个命题是假命题只需要举一个反例,判断一个命题是真命题需要证明它.5.(2020·上海市曹杨第二中学附属学校八年级期中)下列定理中,没有逆定理的是().A.两直线平行,同旁内角互补B.线段垂直平分线上的任意一点到这条线段两个端点的距离相等C.等腰三角形两个底角相等D.同角的余角相等【答案】D【分析】把一个命题的条件和结论互换就得到它的逆命题.再分析逆命题是否为真命题.【详解】解:A、逆命题是:同旁内角互补,两直线平行,是真命题,故本选项不符合题意;B、逆命题是:到线段两个端点的距离相等的点在这条线段的垂直平分线上,是真命题,故本选项不符合题意;C、逆命题是:如果三角形有两个角相等,那么这个三角形是等腰三角形,是真命题,故本选项不符合题意;项符合题意.故选:D.【点睛】本题主要考查了互逆定理的知识,如果一个定理的逆命题是假命题,那这个定理就没有逆定理.6.(2019·上海全国·八年级课时练习)如图,在△ABC中,AD平分∠BAC,DE⊥AB 于E,ABCS V=15,DE=3,AB=6,则AC长是( )A.4B.5C.6D.7【答案】A【分析】根据角平分线上的点到角的两边的距离相等可得AC边上的高,再利用S△ABD+S△ACD=S△ABC,即可得解.【详解】解:作DF⊥AC于F,如图:∵AD平分∠BAC,DE⊥AB,DF⊥AC,∴DE=DF=3,∵S△ABD+S△ACD=S△ABC,∴1163AC315 22´´+´´=,∴AC=4.故选:A.【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.7.(2020·上海闵行区·八年级期中)如图,在△ABC中,∠ACB=90°,CH⊥AB,垂足E ,那么下列结论中一定正确的是( )A .DA=DEB .AC=EC C .AH =EHD .CD =ED【答案】D【分析】根据题意可以分析出A 、B 、C 三个选项要成立同时成立,所以D 选项一定正确,可以通过证明()ACD AED AAS @V V ,验证D 选项正确.【详解】解:可以分析出A 、B 、C 选项任何一个成立,那么都可以得到CH 是AE 的垂直平分线,那么就可以推出其他两个选项也都成立,但这是不可能的,所以A 、B 、C 都不一定正确,D 选项一定正确,证明如下:∵//DE BC ,∴AED ABC Ð=Ð,∵CH AB ^,∴90ABC BCH Ð+Ð=°,∵90ACB Ð=°,∴90ACD BCH Ð+Ð=°,∴ABC ACD AED Ð=Ð=Ð,∵AD 平分BAC Ð,∴CAD EAD Ð=Ð,在ACD △和AED V 中,CAD EAD ACD AED AD AD Ð=ÐìïÐ=Ðíï=î,∴()ACD AED AAS @V V ,∴CD ED =.本题考查全等三角形的性质和判定,垂直平分线的性质,解题的关键是掌握这些性质定理进行证明.8.(2019·上海市市西初级中学八年级期末)下列命题中,逆命题是真命题的是( )A .全等三角形的对应角相等;B .同旁内角互补,两直线平行;C .对顶角相等;D .如果0,0a b >>,那么0a b +>【答案】B【分析】先分别写出各命题的逆命题,再分析是否为真命题,需要分别分析各题设是否能推出结论,从而利用排除法得出答案.【详解】解:A.全等三角形的对应角相等的逆命题为对应角相等的三角形全等是假命题,所以A 选项不符合题意;B.同旁内角互补,两直线平行的逆命题为两直线平行,同旁内角互补是真命题,所以B 选项符合题意;C.“对顶角相等”的逆命题是“相等的角是对顶角”是假命题,所以C 选项不符合题意;D. 如果0,0a b >>,那么0a b +>的逆命题为如果0a b +>,那么0,0a b >>是假命题,所以D 选项不符合题意.故选:B .【点睛】本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.9.(2019·上海七年级期末)如图,下面是利用尺规作∠AOB 的角平分线OC 的作法,在用尺规作角平分线过程中,用到的三角形全等的判定方法是( )A .ASAB .SASC .SSSD .AAS如图,根据题意可得:OE=OD,EG=DG,OG=OG,进一步即可根据SSS判定△OEG≌△ODG,可得∠BOC=∠AOC,从而可得答案.【详解】解:如图,由作图可知:OE=OD,EG=DG,OG=OG,所以△OEG≌△ODG(SSS),所以∠BOC=∠AOC,即OC是∠AOB的平分线.所以用到的三角形全等的判定方法是SSS.故选:C.【点睛】本题考查了尺规作角平分线以及全等三角形的判定与性质,属于基本题型,正确理解题意、熟练掌握基础知识是解题的关键.10.(2020·上海市静安区实验中学八年级课时练习)如果三角形二条边的中垂线的交点在第三条边上,那么,这个三角形是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形【答案】A【分析】根据题意,画出图形,用线段垂直平分线的性质结合等腰三角形的性质,三角形内角和定理解答.【详解】如图,CA、CB的中点分别为D、E,CA、CB的垂直平分线OD、OE相交于点O,且点O落在AB边上,连接CO,∵OD 是AC 的垂直平分线,∴OC=OA ,∠A=∠ACO ,同理OC=OB ,∠B=∠BCO ,∵∠A+∠ACO+∠B+∠BCO=180°,∴∠ACO +∠BCO=12´180°=90°,∴∠C 是直角.故选:A .【点睛】本题主要考查了线段的垂直平分线的性质,等腰三角形的性质,三角形内角和定理.熟记线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.11.(2020·上海市云岭实验中学八年级月考)如图,已知ABC V ,求作一点P ,使P 点到CAB Ð的两边的距离相等,且PA PB =.下列确定P 点的方法正确的是( )A .P 为CAB Ð,ABC Ð两角平分线的交点B .P 为CAB Ð的平分线与AB 的垂直平分线的交点C .P 为AC ,AB 两边上的高的交点D .P 为AC ,AB 两边的垂直平分线的交点【答案】B【分析】根据角平分线及线段垂直平分线的判定定理作答.【详解】∵P 点到CAB Ð的两边的距离相等,∴P 在CAB Ð的平分线上.∵PA PB =,∴P 在AB 的垂直平分线上.即P 为CAB Ð的平分线与AB 的垂直平分线的交点.故选:B .【点睛】线及线段垂直平分线的性质是解答此题的关键.12.(2019·上海全国·八年级课时练习)如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )A.△ABC的三条中线的交点B.△ABC三边的中垂线的交点C.△ABC三条角平分线的交点D.△ABC三条高所在直线的交点.【答案】C【分析】由于凉亭到草坪三条边的距离相等,所以根据角平分线上的点到边的距离相等,可知是△ABC三条角平分线的交点.由此即可确定凉亭位置.【详解】解:∵凉亭到草坪三条边的距离相等,∴凉亭选择△ABC三条角平分线的交点.故选:C.【点睛】本题主要考查的是角平分线的性质在实际生活中的应用.主要利用了利用了角平分线上的点到角两边的距离相等.13.(2020·上海虹口区·九年级二模)已知在ABC中,小明按照下列作图步骤进行尺规作图(示意图与作图步骤如表),那么交点O是△ABC的()示意图作图步骤(1)分别以点B、C为圆心,大于12BC长为半径作圆弧,两弧分别交于点M、N,联结MN 交BC于点D;(2)分别以点A、C为圆心,大于12AC长为半径作圆弧,两弧分别交于点P、Q,联结PQ 交AC于点E;(3)联结AD、BE,相交于点OA .外心B .内切圆的圆心C .重心D .中心【答案】C【分析】根据尺规作图得到AD 、BE 是△ABC 的中线,根据重心的概念判断即可.【详解】解:由尺规作图可知,MN 、PQ 分别是线段BC 、AC 的垂直平分线,∴点D 、E 分别是BC 、AC 的中点,∴AD 、BE 是△ABC 的中线,∴点O 是△ABC 的重心,故选:C .【点睛】本题考查的是中线的尺规作图及三角形重心的概念:三角形的重心是三角形三条中线的交点,掌握三角形重心的概念是解题的关键.14.(【新东方】初中数学1234初二上)如图在ABC V 中,ABC Ð和ACB Ð的平分线交于点G ,过点G 作//EF BC 交AB 于E ,交AC 于F ,过点G 作GD AC ^于D ,下列四个结论:其中正确的结论有( )个.①EF BE CF =+;②90BGC A Ð=°+Ð;③点G 到ABC V 各边的距离相等;④设GD m =,AE AF n +=,则AEF S mn =△;⑤AEF V 的周长等于+AB AC 的和.A .1B .2C .3D .4【答案】C【分析】①根据∠ABC 和∠ACB 的平分线相交于点G 可得出∠EBG =∠CBG ,∠BCG =∠FCG ,再由EF ∥BC 可知∠CBG =∠EGB ,∠BCG =∠CGF ,故可得出BE =EG ,GF =CF ,由此可得出结论;②先根据角平分线的性质得出∠GBC +∠GCB =12(∠ABC +∠ACB ),再由三角形内角和定理即可得出结论;③根据三角形角平分线的性质即可得出结论;④连接AG ,由三角形的面积公式即可得出结论;⑤根据BE=EG,GF=CF,进行等量代换可得结论.【详解】解:①∵∠ABC和∠ACB的平分线相交于点G,∴∠EBG=∠CBG,∠BCG=∠FCG.∵EF∥BC,∴∠CBG=∠EGB,∠BCG=∠CGF,∴∠EBG=∠EGB,∠FCG=∠CGF,∴BE=EG,GF=CF,∴EF=EG+GF=BE+CF,故①正确;②∵∠ABC和∠ACB的平分线相交于点G,∴∠GBC+∠GCB=12(∠ABC+∠ACB)=12(180°-∠A),∴∠BGC=180°-(∠GBC+∠GCB)=180°-12(180°-∠A)=90°+12∠A,故②错误;③∵∠ABC和∠ACB的平分线相交于点G,∴点G也在∠BAC的平分线上,∴点G到△ABC各边的距离相等,故③正确;④连接AG,作GM⊥AB于M,如图所示:∵点G是△ABC的角平分线的交点,GD=m,AE+AF=n,∴GD=GM=m,∴S△AEF=12AE•GM+12AF•GD=12(AE+AF)•GD=12nm,故④错误.⑤∵BE=EG,GF=CF,∴AE+AF+EF=AE+AF+EG+FG=AE+AF+BE+CF=AB+AC,即△AEF的周长等于AB+AC的和,故⑤正确,故选:C.【点睛】本题考查了等腰三角形的判定与性质、角平分线的性质、平行线的性质、三角形内角和定理等知识;熟练掌握角平分线的性质、三角形内角和定理及三角形内心的性质是解题的关键.15.(【新东方】初中数学1222初二上)如图,在ABC V 中,45,ABC AD BEÐ=°,分别为,BC AC 边上的高,,AD BE 相交于点F ,连接CF ,则下列结论:①BF AC =;②FCD DAC Ð=Ð;③CF AB ^;④若2BF EC =,则FDC △周长等于AB 的长.其中正确的有( )A .①②B .①③④C .①③D .②③④【答案】B【分析】证明△BDF ≌△ADC ,可判断①;求出∠FCD =45°,∠DAC <45°,延长CF 交AB 于H ,证明∠AHC =∠ABC +∠FCD =90°,可判断③;根据①可以得到E 是AC 的中点,然后可以推出EF 是AC 的垂直平分线,最后由线段垂直平分线的性质可判断④.【详解】解:∵△ABC 中,AD ,BE 分别为B C 、AC 边上的高,∠ABC =45°,∴AD =BD ,∠DAC 和∠FBD 都是∠ACD 的余角,而∠ADB =∠ADC =90°,∴△BDF ≌△ADC (ASA ),∴BF =AC ,FD =CD ,故①正确,∵∠FDC =90°,∴∠DFC =∠FCD =45°,∵∠DAC =∠DBF <∠ABC=45°,∴∠FCD ≠∠DAC ,故②错误;延长CF 交AB 于H ,∵∠ABC =45°,∠FCD =45°,∴∠AHC =∠ABC +∠FCD =90°,∴CH⊥AB,即CF⊥AB,故③正确;∵BF=2EC,BF=AC,∴AC=2EC,∴AE=EC=12 AC,∵BE⊥AC,∴BE垂直平分AC,∴AF=CF,BA=BC,∴△FDC的周长=FD+FC+DC=FD+AF+DC=AD+DC=BD+DC=BC=AB,即△FDC的周长等于AB,故④正确,综上:①③④正确,故选B.【点睛】本题考查了全等三角形的性质与判定,也考查了线段的垂直平分线的性质与判定,也利用了三角形的周长公式解题,综合性比较强,对学生的能力要求比较高.<二、解答题16.(2020·上海市曹杨第二中学附属学校八年级期中)如图,在ABCV中,2ACB BÐ=Ð,BACÐ平分线AO交BC于点D,点H为AO上一动点,过H作直线l AO^于H,分别交直线AB、AC、BC于点N、E、M.=;(1)当直线l经过点C时(如图2),求证:BN CD(2)当M是线段BC的中点时,写出线段CE和线段CD之间的数量关系,并证明;(3)请直接写出BN、CE和CD之间的数量关系.【答案】(1)见解析;(2)CD=2CE,证明见解析;(3)当点M在线段BC上时,CD=BN+CE;当点M在BC的延长线上时,CD=BN-CE;当点M在CB的延长线上时,CD=CE-BN.【分析】(1)连接ND,先由已知条件证明DN=DC,再证明BN=DN即可;(2)当M是BC中点时,CE和CD之间的等量关系为CD=2CE,过点C作CN'⊥AO交AB于N'.过点C作CG∥AB交直线l于G,再证明△BNM≌△CGM问题得证;(3)BN、CE、CD之间的等量关系要分三种情况讨论:①当点M在线段BC上时;②当点M在BC的延长线上时;③当点M在CB的延长线上时;由(2)即可得出结论.【详解】(1)证明:连接ND,如图2所示:∵AO平分∠BAC,∴∠BAD=∠CAD,∵直线l⊥AO于H,∴∠AHN=∠AHE=90°,∴∠ANH=∠AEH ,∴AN=AC ,∴NH=CH ,∴AH 是线段NC 的中垂线,∴DN=DC ,∴∠DNH=∠DCH ,∴∠AND=∠ACB ,∵∠AND=∠B+∠BDN ,∠ACB=2∠B ,∴∠B=∠BDN ,∴BN=DN ,∴BN=DC ;(2)解:当M 是BC 中点时,CE 和CD 之间的数量关系为CD=2CE ,理由如下:过点C 作CN'⊥AO 交AB 于N',过点C 作CG ∥AB 交直线l 于点G ,如图3所示:由(1)得:BN'=CD ,AN'=AC ,AN=AE ,∴∠ANE=∠AEN ,NN'=CE ,∵CG ∥AB ,∴∠ANE=∠CGE ,∠B=∠BCG ,∴∠CGE=∠AEN ,∴CG=CE ,∵M 是BC 中点,∴BM=CM ,在△BNM 和△CGM 中,B BCG BM CM NMB GMC Ð=Ðìï=íïÐ=Ðî∴△BNM ≌△CGM (ASA ),∴BN=CG,∴CD=BN'=NN'+BN=2CE;(3)解:BN、CE、CD之间的等量关系:当点M在线段BC上时,CD=BN+CE;理由如下:过点C作CN'⊥AO交AB于N',如图3所示:由(2)得:NN'=CE,CD=BN'=BN+CE;当点M在BC的延长线上时,CD=BN-CE;理由如下:过点C作CN'⊥AO交AB于N',如图4所示:同(2)得:NN'=CE,CD=BN'=BN-CE;当点M在CB的延长线上时,CD=CE-BN;理由如下:过点C作CN'⊥AO交AB于N',如图5所示:同(2)得:NN'=CE,CD=BN'=CE-BN.【点睛】本题是三角形综合题目,考查了全等三角形的判定与性质,线段垂直平分线的性质,等腰三角形的判定与性质、平行线的性质等知识;熟练掌握等腰三角形的判定与性质是解17.(2020·上海同济大学附属实验中学)如图,△ABC 中,AB =AC ,∠BAC +∠BDC=180°.(1)求证:AD 为∠BDC 的平分线;(2)若∠DAE=12∠BAC ,且点E 在BD 上,直接写出BE 、DE 、DC 三条线段之间的等量关系_______.【答案】(1)见解析;(2)DE= B E+DC.【分析】(1)过A 作AG ⊥BD 于G ,AF ⊥DC 于F ,先证明∠BAG=∠CAF ,然后证明△BAG ≌△CAF得到AG=AF ,最后由角平分线的判定定理即可得到结论;(2)过A 作∠CAH=∠BAE ,证明△EAD ≌△HAD ,得到AE=AH ,再证明△EAB ≌△HAC 中,即可得出BE 、DE 、DC 三条线段之间的等量关系.【详解】证明:(1)如图1,过A 作AG ⊥BD 于G ,AF ⊥DC 于F ,∵AG ⊥BD ,AF ⊥DC ,∴∠AGD=∠F=90°,∴∠GAF+∠BDC=180°,∵∠BAC+∠BDC=180°,∴∠GAF=∠BAC ,∴∠GAF-∠GAC=∠BAC-∠GAC ,∴∠BAG=∠CAF ,在△BAG 和△CAF 中90AGB F BAG CAFAB AC ìÐ=Ð=ïÐ=Ðíï=îo∴△BAG ≌△CAF (AAS ),∴AG=AF ,∴∠BDA=∠CDA ,(2)BE 、DE 、DC 三条线段之间的等量关系是DE= B E+DC ,理由如下:如图2,过A 作∠CAH=∠BAE 交DC 的延长线于H ,∵∠DAE=12∠BAC ,∴∠DAE=∠BAE+∠CAD ,∵∠CAH=∠BAE ,∴∠DAE=∠CAH+∠CAD=∠DAH ,在△EAD 和△HAD 中EAD HAD AD ADADE ADH Ð=Ðìï=íïÐ=Ðî,∴△EAD ≌△HAD (ASA ),∴DE=DH ,AE=AH ,在△EAB 和△HAC 中AB AC BAE CAH AE AH =ìïÐ=Ðíï=î,∴△EAB ≌△HAC (SAS ),∴BE=CH ,∴DE=DH=DC+CH=DC+BE ,∴DE=DC+BE.故答案是:DE=DC+BE.【点睛】本题考查了全等三角形的性质和判定,角平分线的判定定理,线段和差的证明,掌握截长法和补短法是解答此题的突破口.18.(2019·上海外国语大学秀洲外国语学校八年级期中)如图,A、B两村在一条小河的同一侧,要在河边建一水厂向两村供水(1)若要使自来水厂到两村的距离相等,厂址应选在哪个位置?(2)若要使自来水厂到两村的输水管用料最省,厂址应选在哪个位置?请用尺规作图,将上述两种情况下的自来水厂厂址分别在图(1)(2)中标出,并保留作图痕迹.【答案】(1)见解析;(2)见解析.【分析】(1)作出AB的垂直平分线与河岸交于点P,则点P满足到AB的距离相等.(2)作出点A关于河岸的对称点C,连接CB,交于河岸于点P,连接AP,则点P能满足AP+PB最小.【详解】(1)根据垂直平分线的性质:垂直平分线上的点到线段两个端点的距离相等知,作出AB的垂直平分线与河岸交于点P,则点P满足到AB的距离相等.(2)作出点A关于河岸的对称点C,连接CB,交于河岸于点P,连接AP,则点P能满足AP+PB最小,理由:AP=PC,三角形的任意两边之和大于第三边,当点P在CB的连线上时,CP+BP是最小的.【点睛】本题考查了垂直平分线的性质,轴对称的性质和距离之和最短问题,熟悉性质及距离之和最短问题的作法是关键.19.(2019·上海外国语大学附属大境初级中学八年级月考)如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.(2)当∠BPC=125°时,∠A= .(3)当n=60°时,EB=7,BC=12,DC的长为.【答案】(1)∠BPC=90°+12n,推理过程见解析;(2)70°;(3)5.【分析】(1)根据角平分线的性质得∠ABC=2∠PBC,∠ACB=2∠PCB,再根据三角形内角和定理求得∠A=-180°+2∠BPC,即可求证∠BPC=90°+12 n;(2)根据(1)可知∠BPC=90°+12n,把∠BPC=125°代入原式求出n即为∠A的度数;(3)当n=60°时,即可求出∠BPC=120°,作辅助线在CB上截取CG=CD,可证出△CPG≌△PCD(SAS),即可得出∠DPO=∠GPC,PD=PG,再可证出△BEP≌△BGP,即可得出BE=BG,即可求出DC.【详解】解:(1)∵DB 、CE 分别为∠ABC ,∠ACB 的平分线,∴∠ABC=2∠PBC ,∠ACB=2∠PCB.∵∠A=180°-(∠ABC+∠ACB),∴∠A=180°-2(∠PBC+∠PCB),∴∠A=180°-2(180°-∠BPC),∴∠A=-180°+2∠BPC ,∴2∠BPC=180°+∠A ,∴∠BPC=90°+ 12∠A,∴∠BPC=90°+12n (2)由(1)知∠BPC=90°+12∠A ∴当∠BPC=125°时,∠A =2×(125°-90°)= 70°;(3)在CB 上截取CG=CD ,连接GP ,Q CE 平分BCA Ð∴∠GCP=∠PCD ,在△PCD 和△PCG 中,CD CG GCP PCD PC PC ìïÐÐíïî===∴△PCD ≌△CGP (SAS ),∴∠GPC=∠CPD ,PG=PD ,由∠BPG+∠GPC=120°,又∵∠BPG+2∠GPC=180°,解得:∠BPG=∠GPC=∠FPC=60°在△BEP 和△BGP 中,EBP GBP BP BPBPE BPG ÐÐìï=íïÐÐî== ∴△BEP ≌△BGP (ASA ),∴BE=BG ,∴CG=BC-BG=BC-BE=12-7=5∴CD=CG=5.【点睛】本题考查了三角形的内角和定理,角平分线的定义以及三角形全等的判定与性质,难度较大.20.(2021·上海浦东新区·七年级期末)如图,AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,垂足分别为点E ,F ,DB =DC .(1)求证:BE =CF ;(2)如果BD//AC ,∠DAF =15°,求证:AB =2DF .【答案】(1)见解析;(2)见解析.【分析】(1)证明DE DF =,90E DFC Ð=Ð=°;进而证明 Rt BDE Rt DFC D @D ,即可解决问题;(2)根据平行线的性质和含30°的直角三角形的性质解答即可.【详解】证明:(1)AD Q 平分BAC Ð,DE AB ^, DF AC ^,DE DF \=,90BED DFC Ð=Ð=°;在Rt BDE D 和Rt DFC D 中,BD CD DE DF =ìí=î,Rt BDE Rt DFC(HL)\D @D,BE CF \=;(2)AD Q 平分BAC Ð,15DAF Ð=°,30BAC \Ð=°,BAD DAF Ð=Ð,//BD AC Q ,30DBE BAC \Ð=Ð=°,DAF BDA Ð=Ð,BAD BDA \Ð=Ð,AB BD \=,在Rt BDE D 中,30DBE Ð=°,2BD DE \=,2AB DE \=,AD Q 平分BAC Ð,DE AB ^, DF AC ^,DE DF \=,2AB DF \=.【点睛】本题主要考查了全等三角形的判定、角平分线的性质及其应用等几何知识点,熟悉相关性质是解题的关键.21.(2021·上海金山区·八年级期末)已知:如图,ABC D 中,,,AB AC BD CE =分别是,AC AB 上的中线,,BD CE 相交于点O ,联结OA DE ,.求证:(1)OB OC =;(2)OA 垂直平分DE .【答案】(1)见解析;(2)见解析.【分析】(1)利用三角形的全等,得到一对对应角,后利用等角对等边证明即可;(2)逆用线段垂直平分线的判定证明即可.【详解】(1)∵,,AB AC BD CE =分别是,AC AB 上的中线,∴BE=CD ,∠EBC=∠DCB ,∵BC=CB ,∴△EBC ≌△DCB ,∴∠ECB=∠DBC ,∴OB=OC ;(2)设AO 与DE 的交点为F ,∵△EBC ≌△DCB ,∴EC=DB ,∵OB=OC ;∴OD=OE ,∴点O 在线段DE 的垂直平分线上,∵AE=AD ,∴点A 在线段DE 的垂直平分线上,∴直线AO 是线段DE 的垂直平分线,∴OA 垂直平分DE .【点睛】本题考查了等腰三角形的性质,三角形的全等,中线的定义,垂直平分线的判定和性质,同一个三角形中,等角对等边,熟练掌握线段垂直平分线的逆定理是解题的关键.22.(2019·上海七年级单元测试)如图,直线AB 、CD 交于点O ,∠AOM =90°(1)如图1,若OC 平分∠AOM ,求∠AOD 的度数;(2)如图2,若∠BOC =4∠NOB ,且OM 平分∠NOC ,求∠MON 的度数【答案】(1)135°;(2)54°【分析】(1)根据角平分线的定义求出∠AOC =45°,然后根据邻补角的定义求解即可;(2)设∠NOB =x °,∠BOC =4x °,根据角平分线的定义表示出∠COM =∠MON =12∠CON ,再根据∠BOM 列出方程求解x ,然后求解即可.【详解】解(1)∵∠AOM =90°,OC 平分∠AOM ,∴∠AOC =12∠AOM =12×90°=45°,∵∠AOC +∠AOD =180°,∴∠AOD =180°-∠AOC =180°-45°=135°,即∠AOD 的度数为135°;(2)∵∠BOC =4∠NOB∴设∠NOB =x °,∠BOC =4x °,∴∠CON =∠COB -∠BON =4x °-x °=3x °,∵OM 平分∠CON ,∴∠COM =∠MON =12∠CON =32x °,∵∠BOM =32x +x =90°,∴x =36°,∴∠MON =32x °=32×36°=54°,即∠MON 的度数为54°.【点睛】本题考查了对顶角、邻补角,角平分线的定义,此类题目熟记概念并准确识图是解题的关键,(2)难点在于根据∠BOM 列出方程.23.(2021·上海八年级期末)作图:已知ABC V 和线段r ,请在ABC V 内部作点P ,使得点P 到AC 和BC 的距离相等,并且点A 到点P 的距离等于定长r .(不写作法,保留痕迹)【答案】图见解析.【分析】根据题意点P 到AC 和BC 的距离相等,可知点P 在ACB Ð的角平分线上,点A 到点P 的距离等于定长r ,可知点P 在以点A 为圆心,以定长r 为半径的圆上,由此作图即可.【详解】如图,先作ACB Ð的角平分线,再以点A 为圆心,以定长r 为半径作圆弧,圆弧与ACB Ð角平分线的交点即为点P .【点睛】本题主要考查角平分线的画法,属于基础题,需要有一定的画图能力,熟练掌握角平分线的画法是解题的关键.24.(2020·上海市松江区民办茸一中学八年级月考)已知:如图,在△EBC 中,作∠EBA =∠C ,AB 交EC 于点A ,作BD 平分∠ABC 交AC 于点B ,F 是BD 上一点,联结EF ,点G 是EF 上一点,且有GB =GD .求证:EF ⊥BD .【答案】证明见解析.【分析】先利用三角形外角的性质和角平分线的定义得出EBD EDB Ð=Ð,从而得出BE DE =,再根据GB =GD 可得E 、G 在BD 的垂直平分线上,从而可得结论.证明:∵BD 平分∠ABC ,∴ABD DBC Ð=Ð,∵EBA C Ð=Ð,∵,EBD ABD EDB D EB C BC A Ð+=ÐÐ=Ð+ÐÐ,∴EBD EDB Ð=Ð,∴BE DE =,∵GB =GD ,∴E 、G 在BD 的垂直平分线上,即EF ⊥BD .【点睛】本题考查线段垂直平分线的判定,三角形外角的性质,等角对等边.理解到线段两端距离相等的点到线段的垂直平分线上是解题关键.25.(2019·上海同济大学实验学校八年级月考)已知点P 是ABC V 的BAC Ð平分线上一点,连接PB ,PC .(1)如图1,若AB AC =,证明:PB PC=(2)如图2,若PB PA =,45ABC Ð=°,2Ð=ÐPBC PAC ,证明:BP BC =(3)如图,若AB BC AC ==,点E 是AC 的中点,当PC PE +的最小时PE CP 值为______.【答案】(1)见解析;(2)见解析;(3)12【分析】(1)要求证PB PC =,根据全等三角形的判定证明≌BAP CAP △△即可;(2)根据等腰三角形的性质以及角平分线的性质可得出3ABC ABP Ð=Ð,可得:30CBP Ð=°,要证BP BC =,继续做辅助线求证三角形全等,即可求解;(3)根据AB BC AC ==可知ABC V 是等边三角形,由题意PC PE +的最小时,即BE 为直线时,根据正三角形重心的性质求解.(1)证明:∵AP 平分BAC Ð∴BAP CAP Ð=Ð∴在BAP △和CAP V 中AB AC BAP CAP AP AP =ìïÐ=Ðíï=î∴≌BAP CAP △△(SAS )∴PB PC=(2)令2Ð=PBC α,PAC a Ð=∵45ABC Ð=°∴452Ð=-ABP α°∵AP BP=∴452Ð=Ð=-ABP BAP α°∵AP 平分BAC Ð∴BAP PAC Ð=Ð即452-=αα°15a =°∴15Ð=Ð==ÐBAP PAC ABP °,30CBP Ð=°在75=Rt KPB △°作PK AC ^于G连BG∵有等腰ABP△∴PK ^平分AB∴AG BG =,Ð=ÐBAC APG∵30Ð==Ð+ÐBAC ABP GBP °∴15Ð=GBP °∴在Rt AKG △中,60Ð=AGK °Rt KGB △中,60Ð=KGB °∴60BGC Ð=°∴BG 平分ÐKGC作BQ AC ^延长线于Q ,∴=BK BQ∴在Rt CBQ V 中,30Ð==Ð+ÐGBC GBC CBQ°∵15Ð=GBC °∴15Ð=CBQ °在Rt QBC V 中75Ð=BCQ °∴在BKP △和QBC V 中KPB BCQ KBP CBQBK BQ Ð=ÐìïÐ=Ðíï=î∴≌BKP QBC△△∴BP BC=成立得证.(3)∵AB BC AC ==,∴ABC V 是等边三角形,∵AP 是BAC Ð的平分线,∴延长AP 交BC 于点D ,则AD 是BC 垂直平分线,∴PB CP =,∴PC PE +最小即为PB PE +最小,∴BE 为一条线段时PB PE +最小,∵BE 、AD 是BAC V 的中线交于点P ,∴P 为BAC V 的重心,。
八年级竞赛培优训练 线段的垂直平分线与角平分线的性质 含解析

线段的垂直平分线与角平分线的性质【思维入门】1.如图1-3-1,在△ABC 中,∠ABC =50°, ∠ACB =60°,点E 在BC 的延长线上,∠ABC 的平分线BD 与∠ACE 的平分线CD 相交于点D ,连结AD .下列结论不正确的是( )A .∠BAC =70°B .∠DOC =90° C .∠BDC =35°D .∠DAC =55°2.如图1-3-2,BD 是∠ABC 的平分线,P 是BD 上的一点,PE ⊥BA 于点E ,PE =4 cm ,则点P 到边BC 的距离为____cm.图1-3-23.如图1-3-3,在Rt △ABC 中,∠A =90°,∠ABC 的平分线BD 交AC 于点D ,AD =5,BC =12,则△BDC 的面积是____.图1-3-34.如图1-3-4,在△ABC 中,DE ,FG 分别是△ABC 的边AB ,AC 的垂直平分线,若BC =10,则△ADF 的周长是多少?图1-3-45.已知,如图1-3-5所示,AB =AC ,BD =CD ,DE ⊥AB 于点E ,DF ⊥AC 于点F,求证:DE=DF.【思维拓展】6.如图1-3-6,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC的长是()5A.3 B.4C.6D.7.已知△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=32,且BD∶CD=9∶7,则D到AB的距离为()A.18 B.16 C.14 D.128.如图1-3-7,直线l1,l2,l3表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则供选择的地址有()A.1处B.2处C.3处D.4处Array 9.如图1-3-8,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为____.。
八年级数学垂直平分线的性质(人教版)(含答案)

垂直平分线的性质(人教版)一、单选题(共12道,每道8分)1.下列命题中正确的命题有( )①线段垂直平分线上任一点到线段两端距离相等;②线段上任一点到垂直平分线两端距离相等;③经过线段中点的直线只有一条;④点P在线段AB外且PA=PB,过P作直线MN,则MN是线段AB的垂直平分线;⑤过线段上任一点可以作这条线段的中垂线.A.1个B.2个C.3个D.4个答案:A解题思路:试题难度:三颗星知识点:垂直平分线的性质2.下列说法:①P是线段AB上的一点,直线经过点P且⊥AB,则是线段AB的垂直平分线;②直线经过线段AB的中点,则是线段AB的垂直平分线;③若AP=PB,且直线垂直于线段AB,则是线段AB的垂直平分线;④经过线段AB的中点P且垂直于AB的直线是线段AB的垂直平分线.其中正确的个数有( )A.1个B.2个C.3个D.4个答案:A解题思路:试题难度:三颗星知识点:垂直平分线的性质3.如图,在△ABC中,DE是线段AB的垂直平分线,交BC于点D,交AB于点E,连接AD,下列结论一定成立的是( )A.ED=CDB.∠DAC=∠BC. D.∠B+∠ADE=90°答案:D解题思路:试题难度:三颗星知识点:垂直平分线的性质4.如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )A.AB=ADB.AC平分∠BCDC.AB=BDD.△BEC≌△DEC答案:C解题思路:试题难度:三颗星知识点:垂直平分线的性质5.如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线DE交AB于点D,交BC于点E,且AE平分∠BAC,下列关系式不成立的是( )A.AC=2ECB.∠B=∠CAEC.∠DEA=2∠BD.BC=3EC答案:A解题思路:试题难度:三颗星知识点:垂直平分线的性质6.如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )A.在AC,BC两边高线的交点处B.在AC,BC两边中线的交点处C.在AC,BC两边垂直平分线的交点处D.在∠A,∠B两内角平分线的交点处答案:C解题思路:试题难度:三颗星知识点:垂直平分线的性质7.如图,在△ABC中,AB=AC=20cm,将△ABC对折,使A与B重合,折痕为DE,连接BD,若△BCD的周长为27cm,则BC的长为( )cm.A.10B.9C.7D.13答案:C解题思路:试题难度:三颗星知识点:轴对称图形的性质8.如图,在Rt△ABC中,∠B=90°,DE是AC的垂直平分线,交AC于点D,交BC于点E,连接AE.已知∠BAE=10°,则∠C的度数为( )A.30°B.40°C.50°D.60°答案:B解题思路:试题难度:三颗星知识点:垂直平分线的性质9.如图,在△ABC中,AB=AC,DE垂直平分AC,交AB于点D,交AC于点E,连接CD,∠A=50°,则∠DCB的度数是( )A.15°B.30°C.50°D.65°答案:A解题思路:试题难度:三颗星知识点:垂直平分线的性质10.如图,在△ABC中,分别以点A和点B为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC 的周长为( )A.7B.14C.17D.20答案:C解题思路:试题难度:三颗星知识点:垂直平分线的性质11.如图,锐角三角形ABC中,直线为BC的中垂线,直线为∠ABC的角平分线,与相交于P点,连接CP.若∠A=60°,∠ACP=24°,则∠ABP的度数是( )度A.24B.30C.32D.36答案:C解题思路:试题难度:三颗星知识点:垂直平分线的性质12.如图,△ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E,F,连接EF,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③;④EF一定平行BC.其中正确的是( )A.①②③B.②③④C.①③④D.①②③④答案:A解题思路:试题难度:三颗星知识点:垂直平分线的性质。
部编数学八年级上册专题22角平分线和垂直平分线结合(解析版)含答案

专题22 角平分线和垂直平分线结合1.如图,△ABC 是等腰三角形,AB =AC ,∠BAC =45°,过点A 作AD ⊥BC 于点D ,过点B 作BE ⊥AC 于点E ,AD ,BE 交于点F ,H 为AB 的中点,连接EH ,CH ,FH ,则下列说法正确的个数为( )①∠BAD =∠CBE ;②EH ⊥AB ;③CE =12AF ;④AE =CE +CF ;⑤S △EFH =S △EHC .A .2个B .3个C .4个D .5个【答案】C【解析】【分析】先根据等腰三角形的性质可得22.5,67.5BAD CAD ABC ACB Ð=Ð=°Ð=Ð=°,再根据直角三角形的性质可得22.5CBE Ð=°,由此可判断①;先判断出Rt ABE △是等腰直角三角形,再根据等腰三角形的三线合一即可判断②;先根据三角形全等的判定定理证出BCE AFE @V V ,根据全等三角形的性质可得BC AF =,在AE 上截取GE CE =,连接BG ,从而可得BG BC =,再根据等腰三角形的性质可得67.5,45BGC CBG Ð=°Ð=°,从而可得12<CE BC ,据此可判断③;先根据等腰三角形的三线合一可得AD 垂直平分BC ,从而可得BF CF =,再证出Rt CEF V 是等腰直角三角形,从而可得CE EF =,然后根据线段和差可得AE BE CE CF ==+,即可判断④;过点H 作HM AC ^于点M ,作HN BE ^于点N ,先根据等腰三角形的三线合一可得EH 平分AEB Ð,再根据角平分线的性质可得HM HN =,然后根据三角形的面积公式即可判断⑤.【详解】解:,45,AB AC BAC AD BC =Ð=°^Q ,122.5,67.52BAD CAD BAC ABC ACB \Ð=Ð=Ð=°Ð=Ð=°,BE AC ^Q ,9022.5CBE ACB \Ð=°-Ð=°,BAD CBE \Ð=Ð,说法①正确;,45BE AC BAC ^Ð=°Q ,Rt ABE \V 是等腰直角三角形,AE BE =,H Q 为AB 的中点,EH AB \^(等腰三角形的三线合一),说法②正确;在BCE V 和AFE △中,22.590CBE FAE BE AE CEB FEA Ð=Ð=°ìï=íïÐ=Ð=°î,()BCE AFE ASA \@V V ,BC AF \=,如图,在AE 上截取GE CE =,连接BG ,则BE 垂直平分CG ,BG BC \=,67.5,18045BGC BCG CBG BGC BCG \Ð=Ð=°Ð=°-Ð-Ð=°,BGC CBG \Ð>Ð,2BC CG CE \>=,即12<CE BC ,12CE AF \<,说法③错误;,AB AC AD BC =^Q ,AD \垂直平分BC ,BF CF \=,22.5BCF CBF \Ð=Ð=°,45EFC BCF CBF \Ð=Ð+Ð=°,Rt CEF \V 是等腰直角三角形,CE EF =,BE EF BF CE CF \=+=+,又AE BE =Q ,AE CE CF \=+,说法④正确;如图,过点H 作HM AC ^于点M ,作HN BE ^于点N ,Rt ABE Q V 是等腰直角三角形,EH 是AB 边上的中线,EH ∴平分AEB Ð(等腰三角形的三线合一),HM HN \=,1122EFH EHC S S EF HN CE HM \=×=×=V V ,说法⑤正确;综上,说法正确的个数为4个,故选:C .【点睛】本题考查了等腰三角形的判定与性质、三角形全等的判定定理与性质、线段垂直平分线的判定与性质、角平分线的性质等知识点,熟练掌握各判定定理与性质是解题关键,较难的是⑤,通过作辅助线,利用到角平分线的性质定理.2.如图,BAC Ð的角平分线与BC 的垂直平分线DG 交于点,,D DE AB DF AC ^^,垂足分别为E F 、,若9,10AF BC ==,则ABC V 的周长为( )A .19B .28C .29D .38【答案】B【解析】【分析】连接BD 、DC ,证△BDE ≌△CDF ,可得CF=BE ,根据角平分线性质可知AE=AF ,即可求周长.【详解】解:连接BD 、DC ,∵AD 平分∠ BAC ,,DE AB DF AC ^^,∴DE=DF ,∵AD=AD ,∴Rt △ADE ≌Rt △ADF ,∴AE=AF=9,∵DG 垂直平分BC ,∴BD=DC ,∴Rt △BDE ≌Rt △CDF ,∴BE=CF ,ABC V 的周长=AB+AC+BC=AF-CF+AE+BE+BC=2AF+BC=28,故选:B .【点睛】本题考查了角平分线的性质、垂直平分线的性质、全等三角形的判定与性质,解题关键是依据已知条件,恰当作辅助线,构造全等三角形.3.如图,∠BAC与∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于点F,交AB于点G.有下列结论:①GA=GP;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④FP=FC,其中正确的结论有( )A.1个B.2个C.3个D.4个【答案】D【解析】【分析】①根据角平分线的性质和平行线的性质即可得到结论;②根据角平分线的性质和三角形的面积公式即可求出结论;③根据线段垂直平分线的性质即可得结果;④根据角平分线的性质和平行线的性质即可得到结果.【详解】解:①∵AP平分∠BAC,∴∠CAP=∠BAP,∵PG∥AD,∴∠APG =∠CAP ,∴∠APG =∠BAP ,∴GA =GP ;②∵AP 平分∠BAC ,∴P 到AC ,AB 的距离相等,∴S △PAC :S △PAB =AC :AB ,③∵BE =BC ,BP 平分∠CBE ,∴BP 垂直平分CE (三线合一),④∵∠BAC 与∠CBE 的平分线相交于点P ,可得点P 也位于∠BCD 的平分线上,∴∠DCP =∠BCP ,又∵PG ∥AD ,∴∠FPC =∠DCP ,∴∠FPC =∠BCP ,∴FP =FC ,故①②③④都正确.故选:D .【点睛】本题主要考查了角平分线的性质和定义,平行线的性质,垂直平分线的判定,等腰三角形的性质,根据角平分线的性质和平行线的性质解答是解题的关键.4.如图,ABC V 中,60BAC Ð=°,ABC Ð、ACB Ð的平分线交于E ,D 是AE 延长线上一点,且120BDC Ð=°.下列结论:①120Ð=°BEC ;②DB DE =;③2BDE BCE Ð=Ð.其中所有正确结论的序号有( ).A .①②B .①③C .②③D .①②③【答案】D【解析】【详解】分析:根据三角形内角和等于180°求出∠ABC+∠ACB ,再根据角平分线的定义求出∠EBC+∠ECB ,然后求出∠BEC=120°,判断①正确;过点D 作DF ⊥AB 于F ,DG ⊥AC 的延长线于G ,根据角平分线上的点到角的两边的距离相等可得DF=DG ,再求出∠BDF=∠CDG ,然后利用“角边角”证明△BDF 和△CDG 全等,根据全等三角形对应边相等可得BD=CD ,再根据等边对等角求出∠DBC=30°,然后根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义求出∠DBE=∠DEB ,根据等角对等边可得BD=DE ,判断②正确,再求出B ,C ,E 三点在以D 为圆心,以BD 为半径的圆上,根据同弧所对的圆周角等于圆心角的一半可得∠BDE=2∠BCE ,判断③正确.详解:∵60BAC Ð=°,∴18060120ABC ACB Ð+Ð=°-°=°,∵BE 、CE 分别为ABC Ð、ACB Ð的平分线,∴12EBC ABC Ð=Ð,12ECB ACB Ð=Ð,∴11()1206022EBC ECB ABC ACB Ð+Ð=Ð+Ð=´°=°,∴180()18060120BEC EBC ECB Ð=°-Ð+Ð=°-°=°,故①正确.如图,过点D 作DF AB ^于F ,DG AC ^的延长线于G ,∵BE 、CE 分别为ABC Ð、ACB Ð的平分线,∴AD 为BAC Ð的平分线,∴DF DG =,∴36090260120FDG Ð=°-°´-°=°,又∵120BDC Ð=°,∴120BDF CDF Ð+Ð=°,120CDG CDF Ð+Ð=°.∴BDF CDG Ð=Ð,∵在BDF V 和CDG V 中,90BFD CGD DF DGBDF CDG Ð=Ð=°ìï=íïÐ=Ðî,∴BDF V ≌()CDG ASA V ,∴DB CD =,∴1(180120)302DBC Ð=°-°=°,∴30DBC DBC CBE CBE Ð=Ð+Ð=°+Ð,∵BE 平分ABC Ð,AE 平分BAC Ð,∴ABE CBE Ð=Ð,1302BAE BAC Ð=Ð=°,根据三角形的外角性质,30DEB ABE BAE ABE Ð=Ð+Ð=Ð+°,∴DEB DBE Ð=Ð,∴DB DE =,故②正确.∵DB DE DC ==,∴B 、C 、E 三点在以D 为圆心,以BD 为半径的圆上,∴2BDE BCE Ð=Ð,故③正确,综上所述,正确结论有①②③,故选D .点睛:本题考查了角平分线的性质,全等三角形的判定与性质,等角对等边的性质,圆内接四边形的判定,同弧所对的圆周角等于圆心角的一半性质,综合性较强,难度较大,特别是③的证明.第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题5.已知:△ABC 是三边都不相等的三角形,点P 是三个内角平分线的交点,点O 是三边垂直平分线的交点,当P 、O 同时在不等边△ABC 的内部时,那么∠BOC 和∠BPC 的数量关系是___.【答案】4360BOC BPC Ð=Ð-°【解析】【分析】根据三角形角平分线的性质以及三角形内角和定理,即可得到2180BAC BPC Ð=Ð-°;再根据三角形垂直平分线的性质以及三角形内角和定理,即可得到2BOC BAC Ð=Ð,进而得出BOC Ð和BPC Ð的数量关系.【详解】解:BP Q 平分ABC Ð,CP 平分ACB Ð,12PBC ABC \Ð=Ð,12PCB ACB Ð=Ð,180()BPC PBC PCB \Ð=°-Ð+Ð180(=°-11)22ABC ACB Ð+Ð1180()2ABC ACB =°-Ð+Ð1180(180)2BAC =°-°-Ð1902BAC =°+Ð,即2180BAC BPC Ð=Ð-°;如图,连接AO .Q 点O 是这个三角形三边垂直平分线的交点,OA OB OC \==,OAB OBA \Ð=Ð,OAC OCA Ð=Ð,OBC OCB Ð=Ð,1802AOB OAB \Ð=°-Ð,1802AOC OAC Ð=°-Ð,360()BOC AOB AOC \Ð=°-Ð+Ð360(18021802)OAB OAC =°-°-Ð+°-Ð,22OAB OAC=Ð+Ð2BAC=Ð2(2180)BPC =Ð-°4360BPC =Ð-°,故答案为:4360BOC BPC Ð=Ð-°.【点睛】本题考查了三角形的垂直平分线与角平分线,熟练掌握三角形的垂直平分线与角平分线的性质是解题的关键.三、解答题6.同学们,等边三角形、等腰直角三角形都是最常见的几何图形.(1)如图1,以等边ABC V 的边BC 为腰作等腰直角BCD △,其中90DBC Ð=°,BD BC =,点D 、点A 都是在BC 的同侧,延长BD 、CA 交于点M ,连接AD ,求MAD ∠的度数;(2)如图2,在(1)的条件下,作BN 平分DBC Ð交AC 于点N ,求证:MD CN =;(3)如图3,将图(1)的CBD V 沿着BC 翻折得到1CBD △,连接1AD ,P 为1AD 中点,连接BP 并延长交1CD 于点Q ,请猜测CQ 、BP 、PQ 三条线段之间的数量关系,并证明你的结论.【答案】(1)45MAD Ð=°;(2)见解析;(3)PQ BP CQ=+【解析】【分析】(1)ABC V 为等边三角形,BDC V 为等腰直角三角形可求;(2)作60EMA Ð=°交AD 延长线于E ,再证明AME BCN V V ≌即可求出CN DM =;(3)在PQ 上截取PG BP =连AG CG 、,得到1AB BD =,知道P 1AD 中点,可得1111,2BP AD ABP PBD ABD ^Ð=Ð=Ð,知道BP AP ^,得到AP 为BG 垂直平分线,再用角之间的关系可以推出PQ BP CQ 、、三者关系.【详解】解:(1)如图,∵ABC V 为等边三角形∴60;ABC BAC ACB AB AC BC Ð=Ð=Ð=°==∵BDC V 为等腰直角三角形∴90DBC Ð=°,BD BC BA==∴30;75DBA DAB BDA Ð=°Ð=Ð=°∴18045MAD DAB BAC Ð=°-Ð-Ð=°(2)如图,作60EMA Ð=°交AD 延长线于E∵90,60MBC ACB Ð=°Ð=°∴30;BMA ABM ACB EMAÐ=Ð=°Ð=Ð∴AB AM BC==∵BN 平分MBCÐ∴45NBC EAM Ð=Ð=°∴()AME BCN ASA V V ≌∴ME CN=603030;304575EMD EDM Ð=°-°=°Ð=°+°=°∵∴75MED MDE Ð=Ð=°∴ME DM=∴CN DM=(3)如图,在PQ 上截取PG BP =连AG CG、∵1,AB BC BD BC==∴1AB BD =∵P 为1AD 中点∴1111,2BP AD ABP PBD ABD ^Ð=Ð=Ð∵160,90,ABP CBD Ð=°Ð=°∴1150ABD Ð=°∴11175,15ABP PBD BAD AD B Ð=Ð=°Ð=Ð=°∵BP AP^∴AP 为BG 垂直平分线∴,75AG AB AC AGB ABG ==Ð=Ð=°∴180105,AGQ AGB AGC ACGÐ=°-Ð=°Ð=Ð∵1105,ACQ ACB BCD Ð=Ð+Ð=°∴AGQ ACQÐ=Ð∴AGQ AGC ACQ ACG Ð-Ð=Ð-Ð,即GCQ CHQ Ð=Ð∴GQ CQ =∴PQ PG QG PB CQ=+=+【点睛】此题考查的是等腰直角三角形的性质、三角形全等的性质和判定、垂直平分线的性质,掌握等腰直角三角形的性质和三角形全等的性质和判定,灵活作辅助线是解题的关键.7.如图,在ABC V 中,42B Ð=°,50C Ð=°,通过尺规作图,得到直线DE 和射线AF ,仔细观察作图痕迹,完成下列问题:(1)直线DE 是线段AB 的________线,射线AF 是EAC Ð的________线;(2)求EAF Ð的度数.【答案】(1)线段垂直平分;角平分(2)23°【解析】【分析】(1)根据作图痕迹判断即可;(2)根据角平分线的性质、线段垂直平分线的性质进行求解即可;(1)解:根据作图痕迹可知,直线DE 是线段AB 的线段垂直平分线;射线AF 是EAC Ð的角平分线;(2)∵DE 垂直平分AB∴AE BE=∴42BAE B Ð=Ð=°∵50C Ð=°∴180180504828BAC B C Ð=°-Ð-Ð=°-°=-°°∴884246EAC BAC BAE Ð=Ð-Ð=°-°=°∵AF 平分EACÐ∴11462322EAF EAC Ð=Ð=´°=°【点睛】本题主要考查线段垂直平分线的性质、角平分线的性质,掌握相关性质并灵活应用是解题的关键.8.某地有两所大学和两条相交叉的公路,如图所示(点M ,N 表示大学,AO ,BO 表示公路).现计划修建一座物资仓库,希望仓库到两所大学的距离相等,到两条公路的距离也相等.(1)你能确定仓库应该建在什么位置吗?在所给的图形中画出你的设计方案;(2)阐述你设计的理由.【答案】(1)仓库在线段MN 的垂直平分线和∠AOB 的平分线的交点上.(2)角的平分线的性质和线段垂直平分线的性质.【解析】【详解】试题分析:(1) 连接MN ,分别以之为圆心进而画圆求解,做出其垂直平分线DE(2)再以O为圆心,任意长为半径,做角平分线考点:基本作图点评:解答本题的关键是熟练掌握几种基本变换的作图方法,准确找到关键点的对应点.9.如图,两条公路OA与OB相交于点O,在∠AOB的内部有两个小区C与D,现要修建一个市场P,使市场P到两条公路OA、OB的距离相等,且到两个小区C、D的距离相等.(1)市场P应修建在什么位置?(请用文字加以说明)(2)在图中标出点P的位置(要求:用尺规作图,不写作法,保留作图痕迹,写出结论).【答案】(1)详见解析;(2)详见解析.【解析】【分析】(1)直接利用角平分线的性质以及线段垂直平分线的性质分析得出答案;(2)直接利用角平分线的作法以及线段垂直平分线的作法得出答案.【详解】(1)点P应修建在∠AOB的角平分线和线段CD的垂直平分线的交点处;(2)如图所示:点P即为所求.【点睛】此题主要考查了应用设计与作图,正确掌握角平分线的性质以及线段垂直平分线的性质是解题关键.10.有公路l1同侧、l2异侧的两个城镇A,B,如下图.电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条公路l1,l2的距离也必须相等,发射塔C 应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置.(保留作图痕迹,不要求写出画法)【答案】答案作图见解析【解析】【分析】根据题意知道,点C应满足两个条件,一是在线段AB的垂直平分线上;二是在两条公路夹角的平分线上,所以点C应是它们的交点.【详解】解:连接A,B两点,作AB的垂直平分线,作两直线交角的角平分线,交点有两个.(1)作两条公路夹角的平分线OD或OE;(2)作线段AB的垂直平分线FG;则射线OD,OE与直线FG的交点C1,C2就是所求的位置.考点:作图-应用与设计作图11.如图,七年级(1)班与七年级(2)班的学生分别在M、N两处参加植树劳动,现要设一个茶水供应点,使茶水供应点到两个班的距离相等(不写作法、要求保留作图痕迹).(1)若茶水供应点P设在道路AB上,请你作出点P;(2)若茶水供应点Q设在道路AB、AC的交叉区域内,并且使点Q到两条道路的距离相等,请你作出点Q.【答案】(1)MN的垂直平分线与AB的交点;(2)∠BAC的平分线与MN的垂直平分线的交点.【解析】【详解】解:(1)线段MN的垂直平分线与AB的交点即为点P,如下图:(2)点Q是∠BAC的平分线与线段MN的垂直平分线的交点,如下图:12.请你先在BC上找一点P,使点P到AB、AC的距离相等,再在射线AP上找一点Q,使QB=QC.【答案】见解析【解析】【分析】利用网格特点作∠BAC 的平分线交BC 于P ,则根据角平分线的性质得点P 到AB 、AC 的距离相等,再利用网格特点过BC 的中点作BC 的垂线交AP 于Q ,则根据线段垂直平分线的性质得QB =QC .【详解】解:如图,点P 和点Q 为所作.13.如图所示,已知AOB Ð和两点M 、N ,求作一点P ,使得点P 到AOB Ð的两边距离相等且PM PN =.【答案】详见解析【解析】【分析】要使点P 到AOB Ð的两边距离相等,则P 应在AOB Ð的角平分线上,要使PM PN =,则点P 在MN 的垂直平分线上,那么满足题设的点P 就是MN 的垂直平分线与AOB Ð的角平分线的交点.【详解】要使点P 到AOB Ð的两边距离相等,则P 应在AOB Ð的角平分线上,要使PM PN =,则点P 在MN 的垂直平分线上,那么满足题设的点P 就是MN 的垂直平分线与AOB Ð的角平分线的交点,作AOB Ð的角平分线C O ,再作线段MN 的垂直平分线交OC 于点P ,如图所示:【点睛】本题是对角平分线的性质和垂直平分线性质的考查,熟练掌握角平分线的性质和垂直平分线性质是解决本题的关键.14.如图,点M,N分别是∠AOB的边OA,OB上的点,OM=3,ON=7,在∠AOB内有一点G,到边OA,OB的距离相等,且满足GM=GN.(1)尺规作图:画出点G(要求:保留作图痕迹);(2)试证明:∠OMG+∠ONG=180°;(3)若P,Q分别是射线OA,OB上的动点,且满足GP=GQ,则当OP=4时,OQ的长度为 .【答案】(1)见解析;(2)见解析;(3)4或6【解析】【分析】(1)作OP平分∠AOB,作线段MN的垂直平分线EF,EF交OP于点G,点G即为所求;(2)证明△OGK≌△OGH(AAS),推出OK=OH,GK=GH,由GM=GN,∠GKM=∠GHN=90°,推出Rt△GKM≌Rt△GHN(HL),再利用全等三角形的性质,四边形内角和定理解决问题;(3)首先求出OK=OH=5,PK=1,然后分两种情形分别求解即可解决问题.【详解】解:(1)如图,点G即为所求.(2)证明:作GK⊥OA于K,GH⊥OB于H.∵∠GOK=∠GOH,∠GKO=∠GHO=90°,OG=OG,∴△OGK≌△OGH(AAS),∴OK=OH,GK=GH,∵GM=GN,∠GKM=∠GHN=90°,∴Rt△GKM≌Rt△GHN(HL),∴∠KGM=∠HGN,∴∠MGN=∠KGH,∵∠KGH+∠AOB=180°,∴∠MGN+∠AOB=180°,∴∠OMG+∠ONG=180°;(3)如图,∵OK=OH,MK=NH,∴OM+ON=OK﹣KM+OH+HN=2OK=10,∴OK=OH=5,∵OP=4,∴PK=5﹣4=1,∵GP=GQ,∴当点Q在线段OH上时,OQ=OP=4,当点Q′在OH的延长线上时,OQ′=5+1=6,故答案为4或6.【点睛】本题考查作图−复杂作图,角平分线的性质,线段的垂直平分线的性质,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.15.(1)如图1,利用网格线,作出三角形关于直线l的对称图形.(2)如图2,利用网格线:①在BC上找一点P,使点P到AB和AC的距离相等;②在射线AP上找一点Q,使QB=QC.【答案】(1)见解析;(2)①见解析;②见解析.【解析】【分析】(1)直接利用轴对称图形的性质得出对应点位置,再顺次连接即可;(2)①借助网格作出∠CAB的角平分线,则∠CAB的角平分线与BC的交点即为所求;②借助网格作出线段BC的垂直平分线,则线段BC的垂直平分线与射线AP的交点即为所求.【详解】解:(1)如图所示:;(2)①如图所示,点P即为所求;②如图所示,点Q即为所求.【点睛】此题主要考查了作轴对称图形、角平分线的性质以及线段垂直平分线的性质,正确借助网格作图是解题关键.16.已知直线l及位于其两侧的两点A,B,如图:∠.(1)在图①中的直线l上求一点Q,是直线l平分AQB(2)能否在直线l上找一点,使该点到点A,B的距离之差的绝对值最大?若能,直接在图②作出该点的位置,若不能,请说明理由.【答案】答案详见解析【解析】【详解】分析:(1)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,由三角形全等的判定定理求出△BDQ≌△B′DQ,再由三角形全等的性质可得出;(2)根据两点之间线段最短,连接AB,线段AB交直线l于点O,则点O为所求.详解:(1)如图,作点A关于直线l的对称点A¢,连接BA¢并延长交直线l于点Q,点Q即为所求.(2)如图:作点B关于直线l的对称点B¢,连结AB¢并延长交直线l于点P,点P即为所求.点睛:此题主要考查了两点之间线段最短、线段的垂直平分线的性质及角平分线的性质,熟知各题的知识点是解题关键.17.如图,方格纸上画有AB 、CD 两条线段,按下列要求作图.(保留作图痕迹)(1)请你在图(1)中画出线段AB 关于CD 所在直线成轴对称的图形.(2)请你在图(2)中添上一条线段,使图中3条线段组成一个轴对称图形,画出所有情形.(3)如图(3),已知AOB Ð和C 、D 两点,求作一点P ,使PC PD =,且P 到AOB Ð两边的距离相等.【答案】见解析【解析】【详解】分析:(1)做BO ⊥CD 于点O ,并延长到B′,使B′O=BO ,连接AB 即可;(2)轴对称图形沿某条直线折叠后,直线两旁的部分能完全重合.(3)作出∠AOB 的平分线;作出CD 的中垂线;找到交点P 即为所求.详解:(1)(2)如图所示:(3)如图所示:作CD 的中垂线和ADB Ð的平分线,两线交点即为点P .点睛:1)(2)两个小题考查对称轴作图,掌握画图的方法和图形的特点是解题的关键;(3)本题考查了角平分线的作法以及垂直平分线的作法,解答此题要明确两点:(1)角平分线上的点到角的两边的距离相等;(2)中垂线上的点到两个端点的距离相等.18.(1)作图题:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵黄桷树.如图,要求黄桷树的位置点P到边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种黄桷树的位置点P(不写作法,保留作图痕迹).(2)用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)【答案】(1)图形见解析(2)图形见解析【解析】【详解】试题分析:(1)到边AB、BC的距离相等的点在∠ABC的平分线上,到点A、D的距离相等的点在线段AD 的垂直平分线上,点P即角平分线和垂直平分线的交点.(2)根据轴对称图形的法则去画即可,有多种图形.试题解析:(1)作出∠ABC的角平分线,作出线段AD的中垂线,交点即为点P.(2)所作图形如下所示:。
北师大版 八年级数学 线段的垂直平分线,角平分线

线段的垂直平分线,角平分线课前测试【题目】课前测试如图,在△ABC中,∠B=70°,DE是AC的垂直平分线,且∠BAD:∠BAC=1:3,则∠C的度数是度.【答案】44【解析】由DE垂直平分AC可得∠DAC=∠DCA;∠ADB是△ACD的外角,故∠DAC+∠DCA=∠ADB又因为∠B=70°⇒∠BAD=180°﹣∠B﹣∠BAD,由此可求得角度数.解:设∠BAD为x,则∠BAC=3x,∵DE是AC的垂直平分线,∴∠C=∠DAC=3x﹣x=2x,根据题意得:180°﹣(x+70°)=2x+2x,解得x=22°,∴∠C=∠DAC=22°×2=44°.故填44°.本题考查的是线段垂直平分线的性质(垂直平分线上任意一点,和线段两端点的距离相等),难度一般.考生需要注意的是角的比例关系的设法,应用列方程求解是正确解答本题的关键.【难度】3【题目】课前测试如图,在△ABC中,∠C=90°,AM是∠CAB的平分线,CM=20cm,那么M到AB的距离为.【答案】20cm.【解析】过点D作DM⊥AB于D,根据角平分线上的点到角的两边距离相等可得DM=CM.解:如图,过点D作DM⊥AB于D,∵∠C=90°,AM是∠CAB的平分线,∴DM=CM=20cm,即M到AB的距离为20cm.故答案为:20cm.本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质是解题的关键.【难度】2知识定位适用范围:北师大版,八年级知识点概述:本章重点部分是线段的垂直平分线和角平分线。
了解,掌握线段的垂直平分线的做法和性质以及角平分线的定义,性质。
能熟练的利用线段的垂直平分线和角平分线来做题适用对象:成绩中等偏下的学生注意事项:熟练掌握线段的垂直平分线以及角平分线的性质重点选讲:①线段的垂直平分线性质的几何应用②角平分线性质的几何应用③线段的垂直平分线和角平分线性质的解答题应用知识梳理知识梳理1:线段的垂直平分线线段的垂直平分线:定理:线段垂直平分线上的点到这条线段上的两个端点的距离相等。
(北师版)八年级数学下册 第一章 三角形的证明 辅导讲义
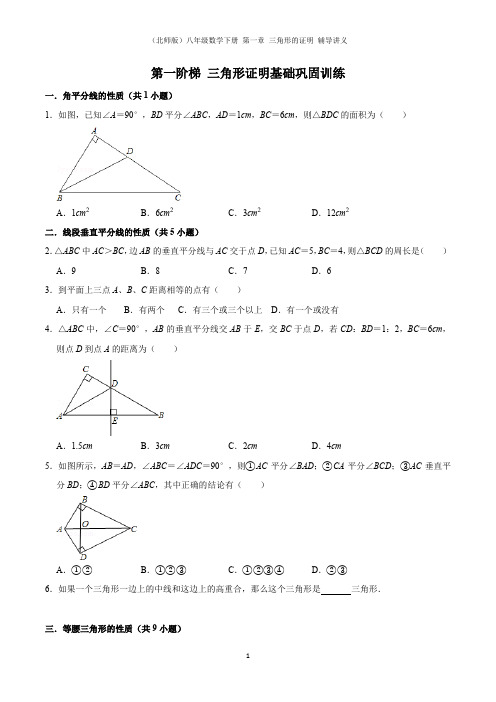
第一阶梯三角形证明基础巩固训练一.角平分线的性质(共1小题)1.如图,已知∠A=90°,BD平分∠ABC,AD=1cm,BC=6cm,则△BDC的面积为()A.1cm2B.6cm2C.3cm2D.12cm2二.线段垂直平分线的性质(共5小题)2.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是()A.9B.8C.7D.63.到平面上三点A、B、C距离相等的点有()A.只有一个B.有两个C.有三个或三个以上D.有一个或没有4.△ABC中,∠C=90°,AB的垂直平分线交AB于E,交BC于点D,若CD:BD=1:2,BC=6cm,则点D到点A的距离为()A.1.5cm B.3cm C.2cm D.4cm5.如图所示,AB=AD,∠ABC=∠ADC=90°,则①AC平分∠BAD;②CA平分∠BCD;③AC垂直平分BD;④BD平分∠ABC,其中正确的结论有()A.①②B.①②③C.①②③④D.②③6.如果一个三角形一边上的中线和这边上的高重合,那么这个三角形是三角形.三.等腰三角形的性质(共9小题)7.等腰三角形周长是32cm,一边长为10cm,则其他两边的长分别为()A.10cm,12cm B.11cm,11cm C.11cm,11cm或10cm,12cm D.不能确定8.等腰三角形周长为36cm,两边长之比为4:1,则底边长为()A.16cm B.4cm C.20cm D.16cm或4cm9.一个等腰而非等边的三角形,它的所有的内角平分线、中线和高的条数为()A.9B.6C.7D.310.等腰三角形的周长为22cm,其中一边的长是8cm,则其余两边长分别为.11.顶角为60°的等腰三角形,两个底角的平分线相交所成的角是°.12.AB边上的中线CD将△ABC分成两个等腰三角形,则∠ACB=度.13.如果等腰三角形一腰上的高与腰的夹角为30°,则该三角形的顶角的度数为.14.如图,△ABC中,AB=AC,O是△ABC内一点,且∠OBC=∠OCB,求证:AO⊥BC.15.如图,在△ABC中,AB=AC,CD为AB边上的高,求证:∠BCD=∠A.四.等腰三角形的判定与性质(共1小题)16.△ABC中,AB=AC,∠ABC=36°,D,E是BC上的点,∠BAD=∠DAE=∠EAC,则图中等腰三角形有个.五.等边三角形的性质(共2小题)17.如图,等边△ABC中,E,D在AB,AC上,且EB=AD,BD与EC交于点F,则∠DFC=度,18.如图所示,△ABC、△ADE与△EFG都是等边三角形,D和G分别为AC和AE的中点,若AB=4时,则图形ABCDEFG外围的周长是.六.等边三角形的判定(共2小题)19.三角形中有两条中线分别平分它的两个内角,则这个三角形是()A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形20.已知a,b,c是△ABC的三边,且a2+b2+c2=ab+ac+bc,则△ABC是()A.等腰三角形B.直角三角形C.等边三角形D.等腰直角三角形第二阶梯三角形证明能力提升训练一.直角三角形全等的判定(共1小题)1.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC =()A.28°B.59°C.60°D.62°二.角平分线的性质(共1小题)2.如图,已知∠A=90°,BD平分∠ABC,AD=1cm,BC=6cm,则△BDC的面积为()A.1cm2B.6cm2C.3cm2D.12cm2三.线段垂直平分线的性质(共3小题)3.已知△ABC中,AD⊥BC于点D,且BD=CD,若AB=3,则AC=.4.M、N、A、B是同一平面上的四个点,如果MA=MB,NA=NB,则点、在线段的垂直平分线上.5.△ABC中,AB比AC大2cm,BC的垂直平分线交AB于D,若△ACD的周长是14cm,则AB=,AC=.四.等腰三角形的性质(共6小题)6.等腰三角形周长为36cm,两边长之比为4:1,则底边长为()A.16cm B.4cm C.20cm D.16cm或4cm7.一个等腰而非等边的三角形,它的所有的内角平分线、中线和高的条数为()A.9B.6C.7D.38.已知:等腰三角形的周长为50厘米,若底边长为x厘米,则x的取值范围是.9.如图:△ABC中,∠B=∠C,E是AC上一点,ED⊥BC,DF⊥AB,垂足分别为D、F,若∠AED=140°,则∠C=度,∠A=度,∠BDF=度.10.分别以等腰三角形的腰与底边向三角形外作正三角形,其周长为24和36,求等腰三角形的周长.11.在△ABC中,AB=AC,它的两条边分别为3cm,4cm,那么它的周长为多少.五.等腰三角形的判定与性质(共5小题)12.如图,在△ABC中,已知∠ABC和∠ACB的平分线相交于点F.过点F作DF∥BC,交AB于点D,交AC于点E.若BD=4,DE=9,则线段CE的长为()A.3B.4C.5D.613.如图,在△ABC中,AB=AC=10,点D为BC上一点,过点D分别作DF∥AC交AB于点F,DE∥AB交AC于点E.求四边形AFDE的周长.14.在△ABC中,AB≠AC,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.(1)如图1,写出图中所有的等腰三角形.猜想:EF与BE、CF之间有怎样的关系,并说明理由.(2)如图2,△ABC中∠ABC的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB 于E,交AC于F.图中还有等腰三角形吗?如果有,分别指出它们.写出EF与BE、CF关系,并说明理由.15.如图,AD是△ABC的角平分线,过点D作直线DF∥BA,交△ABC的外角平分线AF于点F,DF与AC交于点E.求证:DE=EF.16.如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC,请判断△ADE是不是等边三角形,并说明理由.六.等边三角形的性质(共3小题)17.如图,等边三角形ABC的边长为2,则它的高为.18.△ABC是等腰三角形,AB=AC,分别以两腰为边向外作等边△ADB和等边△ACE,若∠DAE=∠DBC,则∠BAC的度数为.19.如图,已知等边△ABC边长为1,D是△ABC外一点且∠BDC=120°,BD=CD,∠MDN=60°.求证:△AMN的周长等于2.七.等边三角形的判定(共1小题)20.三角形中有两条中线分别平分它的两个内角,则这个三角形是()A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形第三阶梯三角形的证明综合训练(一)一、填空题1.如图,修建抽水站时,沿着倾斜角为30°的斜坡铺设管道,若量得水管AB的长度为80米,那么点B 离水平面的高度BC的长为米.2.如果一个三角形的一条角平分线恰好是对边上的高,那么这个三角形是三角形.3.如图,已知AC=DB,要使△ABC≌△DCB,只需增加的一个条件是或.4.命题“全等三角形的对应角相等”的逆命题是,这个逆命题是(填“真”或“假”).5.如图,一个顶角为40°的等腰三角形纸片,剪去顶角后,得到一个四边形,则∠1+∠2=度.6.在△ABC中,已知AB=AC,AD是中线,∠B=70°,BC=15cm,则∠BAC=,∠DAC=,BD=cm.7.已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC 于E,若BC=10 cm,则△ODE的周长cm.第7题图第8题图8.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是度.9.如图,△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若DC=7,则点D到AB的距离DE=.10.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为.二、选择题11.等腰三角形底边上的高与底边的比是1:2,则它的顶角等于()A.60°B.90°C.120°D.150°12.下列两个三角形中,一定全等的是()A.有一个角是40°,腰相等的两个等腰三角形B.两个等边三角形C.有一个角是100°,底相等的两个等腰三角形D.有一条边相等,有一个内角相等的两个等腰三角形13.到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点14.△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于点D,若BC=a,则AD等于()A.B.C.D.15.如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为()A.30°B.36°C.45°D.70°三、解答题16.如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°.求:(1)∠ABC的度数;(2)AD、CD的长.17.已知:如图,△ABC中,AB=AC,∠A=120度.(1)用直尺和圆规作AB的垂直平分线,分别交BC、AB于点M、N(保留作图痕迹,不写作法).(2)猜想CM与BM之间有何数量关系,并证明你的猜想.四、证明题18.已知:如图,CE⊥AB,BF⊥AC,CE与BF相交于D,且BD=CD.求证:D在∠BAC的平分线上.19.已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD.求证:BD=DE.五、阅读下面的题目及分析过程,并按要求进行证明.20.阅读下面的题目及分析过程,并按要求进行证明.已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.求证:AB=CD.分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB =CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.第四阶梯三角形的证明综合训练(二)一、填空题:1.三角形三个角的度数之比为1:2:3,它的最大边长等于16cm,则最小边长是cm.2.已知等腰三角形的一个角是36°,则另两个角分别是.3.Rt△ABC中,锐角∠ABC和∠CAB的平分线交于点O,则∠BOA=.4.如图,在△ABC中,∠B=115°,AC边的垂直平分线DE与AB边交于点D,且∠ACD:∠BCD=5:3,则∠ACB的度数为度.第4题图第5题图5.如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,则BC=.6.如图,将矩形纸片ABCD沿BD对折,使点C落在E处,BE与AD相交于点O,写出一组相等线段、相等角(不包括矩形的对边、对角).7.如图,将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′,若AC=1,则图中阴影部分的面积为.8.命题“全等三角形的对应角相等”的逆命题是,这个逆命题是(填“真”或“假”).9.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是度.10.如图,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,则PD的长为.二、选择题:11.在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B =∠C中,能确定△ABC是直角三角形的条件有()A.1个B.2个C.3个D.4个12.到△ABC的三条边距离相等的点是△ABC的()A.三条中线交点B.三条角平分线交点C.三条高的交点D.三条边的垂直平分线交点13.如图,在等边三角形ABC中,BD⊥BC,过A作AD⊥BD于D,已知△ABC周长为M,则AD=()A.B.C.D.14.在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于D,AB=a,则DB等于()A.B.C.D.15.已知Rt△ABC中,∠C=90°,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A.24cm2B.36cm2C.48cm2D.60cm216.如图,在△ABC中,AB=AC,AB的垂直平分线交BC的延长线于E,交AC于F,∠A=50°,AB+BC =16cm,则△BCF的周长和∠EFC分别为()A.16cm,40°B.8cm,50°C.16cm,50°D.8cm,40°17.如图所示,已知△ABC中,AB=AC,∠BAC=90°,直角△EPF的顶点P是BC中点,两边PE、PF 分别交AB、AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形;③S四边形AEPF=S△ABC;④EF=AP.当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),上述结论中始终正确的有()A.①④B.①②C.①②③D.①②③④18.如图,△ABC中,AB=AC,点D在AC边上,且BD=BC=AD,则∠A的度数为()A.30°B.36°C.45°D.70°三、解证题:19.如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N.(1)求△AEN的周长.(2)求∠EAN的度数.(3)判断△AEN的形状.20.已知:如图,D是等腰△ABC底边BC上一点,它到两腰AB、AC的距离分别为DE、DF,当D点在什么位置时,DE=DF?并加以证明.21.如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.以其中三个条件为题设,填入已知栏中,一个论断为结论,填入下面求证栏中,使之组成一个真命题,并写出证明过程.已知:.求证:.证明:22.如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.(1)求证:∠PCD=∠PDC;(2)求证:OP是线段CD的垂直平分线.23.已知:如图,△ABC中,AB=AC,∠A=120度.(1)用直尺和圆规作AB的垂直平分线,分别交BC、AB于点M、N(保留作图痕迹,不写作法).(2)猜想CM与BM之间有何数量关系,并证明你的猜想.24.如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD.(1)求证:BE=AD;(2)求证:AC是线段ED的垂直平分线;(3)△DBC是等腰三角形吗?并说明理由.参考答案第一阶梯三角形证明基础巩固训练一.角平分线的性质(共1小题)1.C;二.线段垂直平分线的性质(共5小题)2.A;3.D;4.D;5.B;6.等腰;三.等腰三角形的性质(共9小题)7.C;8.B;9.C;10.7cm、7cm或8cm、6cm;11.60或120;12.90;13.120°或60°;四.等腰三角形的判定与性质(共1小题)16.6;五.等边三角形的性质(共2小题)17.60;18.15;六.等边三角形的判定(共2小题)19.C;20.C;第二阶梯三角形证明能力提升训练一.直角三角形全等的判定(共1小题)1.B;二.角平分线的性质(共1小题)2.C;三.线段垂直平分线的性质(共3小题)3.3;4.M;N;AB;5.8cm;6cm;四.等腰三角形的性质(共6小题)6.B;7.C;8.0<x<25;9.50;80;40;五.等腰三角形的判定与性质(共5小题)12.C;六.等边三角形的性质(共3小题)17.;18.20°;七.等边三角形的判定(共1小题)20.C;第三阶梯三角形的证明综合训练(一)一、填空题1.40;2.等腰;3.∠ABC=∠DCB;AC=DB;4.对应角相等的三角形是全等三角形;假;5.220;6.40°;20°;7.5;7.10;8.10;9.7;10.2;二、选择题11.B;12.C;13.B;14.C;15.B;第四阶梯三角形的证明综合训练(二)一、填空题:1.8;2.72°,72°或36°,108°;3.135°;4.40;5.6;6.DE=DC,∠OBD=∠ODB等.;7.;8.对应角相等的三角形是全等三角形;假;9.10;10.2;二、选择题:11.D;12.B;13.B;14.A;15.A;16.A;17.C;18.B;三、解证题:21.在△ABD和△ACE中,AB=AC,AD=AE,BD=CE;∠1=∠2;。
八年级上学期数学期末专题:点段垂直平分线与角平分线综合(原题和解析)

【期末压轴题】专题04:线段的垂直平分线与角平分线综合(原卷版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在△ABC 中,CD 是AB 边上的高,BE 平分△ABC ,交CD 于点E ,BC =6,DE =3,则△BCE 的面积是( )A .9B .7C .10D .18 2.如图,△ABC 中,△A =△ACB ,CP 平分△ACB ,BD ,CD 分别是△ABC 的两外角的平分线,下列结论中:△CP △CD △△P =12A ∠△BC =CD △01902D A ∠=-∠△PD //AC ,其中正确的结论有( )A .1个B .2个C .3个D .4个 3.如图,ABC 中,CAB ∠和CBA ∠的角平分线交于点P ,连接P A 、PB 、PC ,若PAB △、PBC 、PAC △的面积分别为1S 、2S 、3S ,则( )A .123S S S <+B .123S S S =+C .123S S S >+D .无法确定1S 与()23S S +的大小4.如图,AD 是ABC 中BAC ∠的角平分线,DE AB ⊥于点E ,26ABC S =△,4DE =,7AB =,则AC 长是( )A .5B .6C .7D .85.如图,ΔABC 的三边AB 、BC 、CA 的长分别为20,30,40,其三条角平分线将ΔABC 分为三个三角形,则S ΔABO △S ΔBCO △S ΔAOC 等于( )A .1△1△1B .2△3△4C .1△2△3D .3△4△5 6.在下列各原命题中,逆命题是假命题的是( )A .两直线平行,同旁内角互补;B .如果两个三角形全等,那么这两个三角形的对应边相等;C .如果两个三角形全等,那么这两个三角形的对应角相等;D .两个相等的角是对顶角.7.如图,已知AF AB =,60FAB ∠=︒,AE AC =,60EAC ∠=︒,CF 和BE 交于O 点,则下列结论::△CF BE =;△120COB ∠=︒;△OA 平分FOE ∠;△OF OA OB =+.其中正确的有( )A .△△B .△△△C .△△△△D .△△△ 8.如图,点A ,B ,C 在一条直线上,ABD △,BCE 均为等边三角形,连接AE 和CD ,AE 分别交CD 、BD 于点M 、P ,CD 交BE 于点Q ,连接PQ ,BM .下列结论:△ABE DBC ≌;△60DMA ∠=︒;△BPQ 为等边三角形;△MB 平分AMC ∠.其中结论正确的有( )A .1个B .2个C .3个D .4个 9.如图,在△ABC 中,AB =AC ,△BAC =46°,△BAC 的平分线与AB 的垂直平分线OD 交于点O ,点E 在BC 上,点F 在AC 上,连接EF .将△C 沿EF 折叠,点C 与点O 恰好重合时,则△OEC 的度数( )A .90°B .92°C .95°D .98°10.如图,在△ABC 中,△BAC 和△ABC 的平分线AE ,BF 相交于点O ,AE 交BC 于E ,BF 交AC 于F ,过点O 作OD △BC 于D ,下列三个结论:△△AOB =90°+△C ;△当△C =60°时,AF +BE=AB ;△若OD=a ,AB +BC +CA =2b ,则S △ABC =ab .其中正确的个数是( )A .1个B .2个C .3个D .0个 11.如图,正ABC 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有( )个△60AFB ∠=︒ △连接FC ,则CF 平分BFD ∠ △3BF DF = △BF AF FC =+A .4B .3C .2D .112.如图,在ABC 中,BC AC =,90ACB ∠=︒,AD 平分BAC ∠,BE AD ⊥交AC 的延长线于F ,垂足为E .则下列结论不正确的是( )A .AD BF =B .CF CD =C .AC CD AB +=D .BE CF =二、填空题 13.如图,△ABC 的外角△DBC 、△ECB 的角平分线交于点M ,△ACB 的角平分线与BM 的反向延长线交于点N ,若在△CMN 中存在一个内角等于另一个内角的2倍,则△A 的度数为 _______14.已知:△ABC 是三边都不相等的三角形,点P 是三个内角平分线的交点,点O 是三边垂直平分线的交点,当P 、O 同时在不等边△ABC 的内部时,那么△BOC 和△BPC 的数量关系是___.15.如图,在四边形ABCD 中,//AD BC ,AB AC =,6BC =,DBC △面积为18,AB的垂直平分线MN 分别交AB ,AC 于点M ,N ,若点P 和点Q 分别是线段MN 和BC 边上的动点,则PB PQ +的最小值为______.16.如图,AB 为等腰直角ABC 的斜边,E 为AB 的中点,F 为AC 延长线上的一个动点(F 与点C 不重合),线段FB 的垂直平分线交线段CE 于点O ,D 垂足.当F 点运动时,给出下列四个结论.其中一定正确的结论有______(请填写正确序号).△点O 到ABF 三个顶点的距离相等;△⊥OF OB ;FC AB +=;△AEC BOF S S <△△ 17.如图,反比例函数k y x=的图象经过点(-1,-,点A 是该图象第一象限分支上的动点,连结AO 并延长交另一支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC 与x 轴交于点P ,连结BP .在点A 运动过程中,当BP 平分△ABC时,点A 的坐标是____________.18.如图,在ABC 中,△ACB =45°,AD △BC ,BE △AC ,AD 与BE 相交于点F ,连接并延长CF 交AB 于点G ,△AEB 的平分线交CG 的延长线于点H ,连接AH ,则下列结论:△△EBD =45°;△AH =HF ;△ABD △CFD ;△CH =AB +AH ;△BD =CD ﹣AF .其中正确的是 ___.(只填写序号)19.如图,在ABC 中,AB 、AC 的垂直平分线分别交BC 于D 、E 两点,并且相交于点F ,且70DFE ∠=︒,则DAE ∠的度数是______.20.如图,AP ,BP 分别平分△ABC 内角△CAB 和外角△CBD ,连接CP ,若△ACP =130°,则△APB =___.三、解答题21.已知,如图1,射线PE 分别与直线AB 、CD 相交于E 、F 两点,△PFD 的平分线与直线AB 相交于点M ,射线PM 交CD 于点N ,设△PFM =α,△EMF =β,且2(35)αβα-+-0=.(1)α=____ °,β=______ °;直线AB 与CD 的位置关系是_______ ;(2)如图2,若点G 是射线MA 上任意一点,且△MGH=△PNF ,试找出△FMN 与△GHF 之间存在的数量关系,并证明你的结论:(3)若将图中的射线PM 绕着端点P 逆时针方向旋转(如图3),分别与AB 、CD 相交于点M 和点N ,时,作△PMB 的角平分线MQ 与射线FM 相交于点Q ,问在旋转的过程中1FPN Q∠∠的值变不变?若不变,请求出其值;若变化,请说明理由. 22.如图1,将线段AB 平移至CD ,使A 与D 对应,B 与C 对应,连AD 、BC .(1)填空:AB 与CD 的关系为__________,B 与D ∠的大小关系为__________. (2)如图2,若60B ∠=︒,F 、E 为BC 的延长线上的点,∠=∠EFD EDF ,DG 平分CDE ∠交BE 于G ,求FDG ∠.(3)在(2)中,若B α∠=,其它条件不变,则FDG ∠=__________.23.如图1所示,已知点E 在直线AB 上,点F ,G 在直线CD 上,且EFG FEG ∠=∠,EF 平分AEG ∠.(1)判断直线AB 与直线CD 是否平行,并说明理由.(2)如图2所示,H 是AB 上点E 右侧一动点,EGH ∠的平分线GQ 交FE 的延长线于点Q ,设Q α∠=,EHG β∠=.△若40HEG ∠=︒,20QGH ∠=︒,求Q ∠的度数.△判断:点H 在运动过程中,α和β的数量关系是否发生变化?若不变,求出α和β的数量关系;若变化,请说明理由.24.如图,已知△ABC 和△CDE 均是等边三角形,点B 、C 、E 在同一条直线上,AE 与BD 交于点O ,AE 与CD 交于点G ,AC 与BD 交于点F ,连结OC 、FG ,(1)求证:BD =AE , 并求出△DOE 的度数;(2)判断△CFG的形状并说明理由;(3)求证:OA+OC=OB;(4)判断下列两个结论是否正确,若正确请说明理由:△OC平分△FOG;△CO平分△FCG.25.在平面直角坐标系中,已知点A(0,a),B(b,0),其中a,b满足:(x+b)(x +2)=x2+ax+6(a,b为常数).(1)求点A,B的坐标;(2)如图1,D为x轴负半轴上一点,C为第三象限内一点,且△ABC=△ADC=90°,AO=DO,DB平分△ADC.过点C作CE△DB于点E,求证:DE=OB;(3)如图2,P为y轴正半轴上一动点,连接BP,过点B在x轴下方作BQ△BP,且BQ=BP,连接PC,PQ,QC.在(2)的条件下,设P(0,p),求△PCQ的面积(用含p的式子表示).26.在△ABC中,AB=CD△AB于点D,CD.(1)如图1,当点D是线段AB中点时,△AC的长为;△延长AC至点E,使得CE=AC,此时CE与CB的数量关系为,△BCE与△A 的数量关系为.(2)如图2,当点D不是线段AB的中点时,画△BCE(点E与点D在直线BC的异侧),使△BCE=2△A,CE=CB,连接AE.△按要求补全图形;△求AE的长.27.如图1,已知线段AC△y轴,点B在第一象限,且AO平分△BAC,AB交y轴于点D,连接OB,OC.(1)可以判断AOD的形状为三角形(直接写答案);(2)若OE平分△AOB且△B=2△BAO,证明:AO=BE+OB;(3)如图2,若点B,C关于y轴对称,AO△BO,点M为OA上一点,且△ACM=45°,点B的坐标为(3,1),求点M的坐标.28.如图,已知点B(-2,0),C(2,0),A为y轴正半轴上一点,点D为第二象限内的一个动点,M在BD的延长线上,CD交AB于点F,且△ABD=△ACD.(1)求证:△BDC=△BAC;(2)求证:DA平分△CDM;(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,△BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出△BAC的度数?【期末压轴题】专题04:线段的垂直平分线与角平分线综合(解析版)学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,在△ABC中,CD是AB边上的高,BE平分△ABC,交CD于点E,BC=6,DE=3,则△BCE的面积是()A.9B.7C.10D.18【标准答案】A【思路点拨】作EH△BC于点H,根据角平分线的性质得出EH=DE,最后根据三角形的面积公式进行求解.【精准解析】如图,作EH△BC于点H,△BE平分△ABC,CD是AB边上的高,EH△BC,△EH=DE=3,△1163922BCES BC EH=⋅=⨯⨯=△.故选A.【名师指导】本题考查角平分线的性质,熟练掌握角的平分线上的点到角的两边的距离相等是解题的关键.2.如图,△ABC中,△A=△ACB,CP平分△ACB,BD,CD分别是△ABC的两外角的平分线,下列结论中:△CP△CD△△P=12A∠△BC=CD△01902D A∠=-∠△PD//AC,其中正确的结论有()A.1个B.2个C.3个D.4个【标准答案】D【思路点拨】根据邻补角平分线性质可判断△;根据三角形外角与角平分线定义列出等式2△PBG=△A+2△PCB,△PBG=△P+△PCB,可判断△,根据外角性质与角平分线定义,结合三角形内角和△BCD+△CBD=12BCF∠+12CBE∠=1902A︒+∠可判断△,利用等腰三角形性质与外角性质,可得△DBC=△A,可得△D=90°12DBC-∠,得出2△D+△DBC=180°,当△A=60°时,△D=△DBC=60°成立,可判断△,根据△DBC=△A=△ACB,利用平行线判定定理可判断△.【精准解析】解:△△BCA+△BCF=180°,CP平分△ACB,CD平分△FCB,△△PCB=12BCA∠,△DCB=12BCF∠,△△PCD=△PCB+△DCB =12BCA∠+()11118090 222BCF BCA BCF∠=∠+∠=⨯︒=︒,△CP△CD;故△正确;延长CB到G,△BD平分△CBE,△△EBD=△DBC,△△EBD=△PBA,△CBD=△PBG,△△PBA =△PBG,△△ABG=2△GBP,△△ABG=△A+△ACB,即2△PBG=△A+2△PCB,△PBG=△P+△PCB,△△PBG=12△A+△PCB,△△P=12△A,△CD 平分△BCF ,△△BCD =12BCF ∠, △DBC =12CBE ∠, △△BCD +△CBD =12BCF ∠+12CBE ∠, =()()1122A ABC A ACB ∠+∠+∠+∠, =()1122A ABC ACB A ∠+∠+∠+∠, =1902A ︒+∠, △△D=180°-(△BCD +△CBD )=180°-11909022A A ︒-∠=︒-∠, 故△正确;△AB =BC ,△△BAC =△ACB ,△2△DBC =△EBC =△A +△ACB =2△A ,△△DBC =△A ,△△D =90°12DBC -∠, △2△D +△DBC =180°,当△A =60°时,△D =△DBC =60°,△BC =CD ,故△不正确,△△DBC =△A =△ACB ,△PD△AC ,故正确的结论有4个.故选D .【名师指导】本题考查三角形内角与外角平分线,等腰三角形性质,三角形外角性质,三角形内角和,平行线判定,掌握三角形内角与外角平分线定义,等腰三角形性质,三角形外角性质,三角形内角和,平行线判定是解题关键.3.如图,ABC 中,CAB ∠和CBA ∠的角平分线交于点P ,连接PA 、PB 、PC ,若PAB △、PBC 、PAC △的面积分别为1S 、2S 、3S ,则( )A .123S S S <+B .123S S S =+C .123S S S >+D .无法确定1S 与()23S S +的大小【标准答案】A【思路点拨】过点P 分别作PD △AB ,PE △BC ,PF △AC ,垂足分别为D ,E ,F ,运用三角形面积公式,三角形三边关系定理判断即可.【精准解析】过点P 分别作PD △AB ,PE △BC ,PF △AC ,垂足分别为D ,E ,F ,△CAB ∠和CBA ∠的角平分线交于点P ,△PD =PE =PF =h ,△1S =1h 2AB ,2S =1h 2BC ,3S =1h 2AC ,△23()S S +=1h 2BC +1h 2AC =1()h 2AC BC +, △AC +BC >AB ,△23()S S +>1S ,△123S S S <+,△A 符合题意,B ,C ,D 都不符合题意,故选A .【名师指导】本题考查了角的平分线的性质定理,三角形的面积公式,三角形的三边关系定理,灵活运用角的平分线的性质和三角形三边关系定理是解题的关键.4.如图,AD 是ABC 中BAC ∠的角平分线,DE AB ⊥于点E ,26ABC S =△,4DE =,7AB =,则AC 长是( )A .5B .6C .7D .8【标准答案】B【思路点拨】 作DF △AC 于F ,如图,根据角平分线定理得到DE =DF =4,再利用三角形面积公式和S △ADB +S △ADC =S △ABC 得到12×4×7+12×4×AC =26,然后解一次方程即可.【精准解析】解:作DF △AC 于F ,如图,△AD 是△ABC 中△BAC 的角平分线,DE △AB ,DF △AC ,△DE =DF =4,△S △ADB +S △ADC =S △ABC , △12×4×7+12×4×AC =26,△AC =6,故选:B .【名师指导】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等,三角形的面积公式等知识,解题的关键是学会添加常用辅助线,学会利用面积法构建方程解决问题. 5.如图,ΔABC 的三边AB 、BC 、CA 的长分别为20,30,40,其三条角平分线将ΔABC 分为三个三角形,则S ΔABO △S ΔBCO △S ΔAOC 等于( )A.1△1△1B.2△3△4C.1△2△3D.3△4△5【标准答案】B【思路点拨】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是20,30,40,所以面积之比就是2:3:4.【精准解析】解:过点O作OD△AC于D,OE△AB于E,OF△BC于F,△点O是内心,△OE=OF=OD,△S△ABO:S△BCO:S△CAO=12•AB•OE:12•BC•OF:12•AC•OD=AB:BC:AC=2:3:4,故选:B.【名师指导】本题主要考查了角平分线上的一点到两边的距离相等的性质及三角形的面积公式.做题时应用了三个三角形的高是相等的,这点是非常重要的.6.在下列各原命题中,逆命题是假命题的是()A.两直线平行,同旁内角互补;B.如果两个三角形全等,那么这两个三角形的对应边相等;C.如果两个三角形全等,那么这两个三角形的对应角相等;D.两个相等的角是对顶角.【标准答案】C【思路点拨】先写出逆命题,再根据相关性质,定义判断即可.【精准解析】解:A逆命题是同旁内角互补,两直线平行,是真命题,△A不符合题意;B 逆命题是如果两个三角形的对应边相等,那么这两个三角形全等,是真命题,△B 不符合题意;C 逆命题是如果两个三角形的对应角相等,那么这两个三角形全等,是假命题,△C 符合题意;D 逆命题是如果两个角是对顶角,那么这两个角相等,是真命题,△D 不符合题意;故选C .【名师指导】本题考查了命题,互逆命题,命题的真假,熟练确定逆命题,灵活运用相关知识判断是解题的关键.7.如图,已知AF AB =,60FAB ∠=︒,AE AC =,60EAC ∠=︒,CF 和BE 交于O 点,则下列结论::△CF BE =;△120COB ∠=︒;△OA 平分FOE ∠;△OF OA OB =+.其中正确的有( )A .△△B .△△△C .△△△△D .△△△【标准答案】C【思路点拨】 证明ABE AFC ∆≅∆,由全等三角形的性质得到BE CF =,可得AEB ACF ∠=∠,则60CON CAE MOB ∠=∠=︒=∠,得出180120BOC CON ∠=︒-∠=︒;ABE AFC S S ∆∆=,得到AP AQ =,利用角平分线的判定定理得AO 平分EOF ∠,在OF 上截取OD OB =,根据SAS 可证明FBD ABO ∆≅∆,得出DF OA =,由此可以解决问题.【精准解析】解:△AB AF =,AC AE =,60FAB EAC ∠=∠=︒,FAB BAC EAC BAC ∴∠+∠=∠+∠,即FAC BAE ∠=∠,在ABE ∆与AFC ∆中,AB AF BAE FAC AE AC =⎧⎪∠=∠⎨⎪=⎩,()ABE AFC SAS ∴∆≅∆,BE FC ∴=,AEB ACF ∠=∠,故△正确,180EAN ANE AEB ∠+∠+∠=︒,180CON CNO ACF ∠+∠+∠=︒,ANE CNO ∠=∠,60CON CAE MOB ∴∠=∠=︒=∠,180120BOC CON ∴∠=︒-∠=︒,故△正确,连接AO ,过A 分别作AP CF ⊥与P ,AM BE ⊥于Q ,如图1,ABE AFC ∆≅∆,ABE AFC S S ∆∆∴=, ∴1122CF AP BE AQ =,而CF BE =, ∴=AP AQ ,OA ∴平分FOE ∠,所以△正确,在OF 上截取OD OB =,60BOF ∠=︒,OBD ∴∆是等边三角形,BD BO ∴=,60DBO ∠=︒,FBD ABO ∴∠=∠,BF AB =,()FBD ABO SAS ∴∆≅∆,DF OA ∴=,OF DF OD OA OB ∴=+=+;故△正确;故选:C . 【名师指导】本题考查了等边三角形的性质、全等三角形的判定和性质、角平分线的判定定理等知识,利用全等三角形面积相等证明高相等是解决问题的关键.8.如图,点A ,B ,C 在一条直线上,ABD △,BCE 均为等边三角形,连接AE 和CD ,AE 分别交CD 、BD 于点M 、P ,CD 交BE 于点Q ,连接PQ ,BM .下列结论:△ABE DBC ≌;△60DMA ∠=︒;△BPQ 为等边三角形;△MB 平分AMC ∠.其中结论正确的有( )A .1个B .2个C .3个D .4个【标准答案】D【思路点拨】 由等边三角形的性质得出AB =DB ,△ABD =△CBE =60°,BE =BC ,得出△ABE =△DBC ,由SAS 即可证出△ABE △△DBC ;由△ABE △△DBC ,得出△BAE =△BDC ,根据三角形外角的性质得出△DMA =60°;由ASA 证明△ABP △△DBQ ,得出对应边相等BP =BQ ,即可得出△BPQ 为等边三角形;由△ABE △△DBC 得到△ABE 和△DBC 面积等,且AE =CD ,从而证得点B 到AE 、CD 的距离相等,利用角平分线判定定理得到点B 在角平分线上.【精准解析】解:△△ABD 、△BCE 为等边三角形,△AB =DB ,△ABD =△CBE =60°,BE =BC ,△△ABE =△DBC ,△PBQ =60°,在△ABE 和△DBC 中,AB DB ABE DBC BE BC =⎧⎪∠=∠⎨⎪=⎩△△ABE △△DBC (SAS ),△△正确;△△ABE △△DBC ,△△BAE =△BDC ,△△BDC +△BCD =180°-60°-60°=60°,△△DMA =△BAE +△BCD =△BDC +△BCD =60°,△△正确;在△ABP 和△DBQ 中,60BAP BDQ AB DB ABP DBQ ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩△△ABP △△DBQ (ASA ),△BP =BQ ,△△BPQ 为等边三角形,△△正确;△△ABE △△DBC△AE =CD ,S △ABE =S △DBC ,△点B 到AE 、CD 的距离相等,△B 点在△AMC 的平分线上,即MB 平分△AMC ;△△正确;故选:D .【名师指导】本题考查了等边三角形的性质与判定、全等三角形的判定与性质、角平分线的判定定理;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.9.如图,在△ABC 中,AB =AC ,△BAC =46°,△BAC 的平分线与AB 的垂直平分线OD 交于点O ,点E 在BC 上,点F 在AC 上,连接EF .将△C 沿EF 折叠,点C 与点O 恰好重合时,则△OEC 的度数( )A .90°B .92°C .95°D .98°【标准答案】B【思路点拨】 仔细分析题意,可连接BO ,CO ,根据角平分线性质和中垂线性质不难得到△OAB =△OBA ;然后结合三角形内角和定理以及等边对等角可得△ABC 的度数;接下来根据全等三角形的判定易得△ABO △△ACO ,进而结合全等三角形的性质可得△OCB 的度数;最后根据折叠变换的性质得出EO =EC ,由等边对等角以及三角形内角和定理的知识即可求出△OEC 的度数.【精准解析】解:连接BO ,CO ,△△BAC=46°,△BAC的平分线与AB的中垂线交于点O,△△OAB=△OAC=23°,△OD是AB的垂直平分线,△OA=OB,△OA=OB,△OAB=23°,△△OAB=△ABO=23°,△AB=AC,△△ABC=△ACB=67°,△△OBC=△ABC-△ABO=67°-23°=44°,△AB=AC,△OAB=△OAC,AO=AO,△△ABO△△ACO(SAS),△BO=CO,△△OBC=△OCB=44°,△点C沿EF折叠后与点O重合,△EO=EC,△△EOC=△OCE=44°,△△OEC=180°-△EOC-△OCE=180°-2×44°=92°,故选:B.【名师指导】本题考查了线段垂直平分线上的点到线段两端点的距离相等的性质,等腰三角形三线合一的性质,等边对等角的性质,以及翻折变换的性质,综合性较强,难度较大,作辅助线,构造出等腰三角形是解题的关键.10.如图,在△ABC中,△BAC和△ABC的平分线AE,BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD△BC于D,下列三个结论:△△AOB=90°+△C;△当△C=60°时,AF+BE=AB;△若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的个数是()A .1个B .2个C .3个D .0个【标准答案】B【思路点拨】 由角平分线的定义结合三角形的内角和的可求解△AOB 与△C 的关系,进而判定△;在AB 上取一点H ,使BH =BE ,证得△HBO △△EBO ,得到△BOH =△BOE =60°,再证得△HAO △△F AO ,得到AF =AH ,进而判定△正确;作OH △AC 于H ,OM △AB 于M ,根据三角形的面积可证得△正确.【精准解析】解:△△BAC 和△ABC 的平分线相交于点O ,△△OBA =12△CBA ,△OAB =12△CAB ,△△AOB =180°−△OBA −△OAB =180°−12△CBA −12△CAB=180°−12(180°−△C )=90°+12△C ,△错误;△△C =60°,△△BAC +△ABC =120°,△AE ,BF 分别是△BAC 与ABC 的平分线,△△OAB +△OBA =12(△BAC +△ABC )=60°,△△AOB =120°,△△AOF =60°,△△BOE =60°,如图,在AB 上取一点H ,使BH =BE ,△BF 是△ABC 的角平分线,△△HBO =△EBO ,在△HBO 和△EBO 中,BH BE HBO EBO BO BO =⎧⎪∠=∠⎨⎪=⎩,△△HBO △△EBO (SAS ),△△BOH =△BOE =60°,△△AOH =180°−60°−60°=60°,△△AOH =△AOF ,在△HAO 和△F AO 中,HAO FAO AO AO AOH AOF ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△HAO △△F AO (ASA ),△AF =AH ,△AB =BH +AH =BE +AF ,故△正确;作OH △AC 于H ,OM △AB 于M ,△△BAC 和△ABC 的平分线相交于点O ,△点O 在△C 的平分线上,△OH =OM =OD =a ,△AB +AC +BC =2b△S △ABC =12×AB ×OM +12×AC ×OH +12×BC ×OD =12(AB +AC +BC )•a =ab ,△正确. 故选:B .【名师指导】本题主要考查了三角形内角和定理,三角形外角的性质,三角形全等的性质和判定,正确作出辅助线证得△HBO △△EBO ,得到△BOH =△BOE =60°,是解决问题的关键.11.如图,正ABC 和正CDE △中,B 、C 、D 共线,且3BC CD =,连接AD 和BE 相交于点F ,以下结论中正确的有( )个△60AFB ∠=︒ △连接FC ,则CF 平分BFD ∠ △3BF DF = △BF AF FC =+A .4B .3C .2D .1【标准答案】A【思路点拨】根据“手拉手”模型证明BCE ACD ≌,从而得到CBE CAD ∠=∠,再结合三角形的外角性质即可求解60AFB ACB ∠=∠=︒,即可证明△;作CM BE ⊥于M 点,CN AD ⊥于N 点,证明CEM CDN ≌,结合角平分线的判定定理即可证明△;利用面积法表示BCF △和DCF 的面积,然后利用比值即可证明△;利用“截长补短”的思想,在AD 上取点Q ,使得FC FQ =,首先判断出FCQ 为等边三角形,再结合“手拉手”模型推出BCF ACQ ≌即可证明△.【精准解析】解:△△ABC 和CDE △均为等边三角形,△60ACB ECD ∠=∠=︒,AC BC =,EC DC =,△ACB ACE ECD ACE ∠+∠=∠+∠,△BCE ACD ∠=∠,在BCE 和ACD △中, BC AC BCE ACD EC DC =⎧⎪∠=∠⎨⎪=⎩△()BCE ACD SAS ≌,△CBE CAD ∠=∠,△AFB CBE CDA ∠=∠+∠,ACB CDA CAD ∠=∠+∠,△60AFB ACB ∠=∠=︒,故△正确;△如图所示,作CM BE ⊥于M 点,CN AD ⊥于N 点,则90CME CND ∠=∠=︒,△BCE ACD ≌,△CEM CDN ∠=∠,在CEM 和CDN △中,CME CND CEM CDN CE CD ∠=∠⎧⎪∠=∠⎨⎪=⎩△()CEM CDN AAS ≌,△CM CN =,△CF 平分BFD ∠,故△正确;△如图所示,作FP BD ⊥于P 点, △1122BCF S BF CM BC FP ==,1122DCF S DF CN CD FP ==, △11221122BCFDCF BF CM BC FP S S DF CN CD FP ==, △CM CN =,△整理得:BF BC DF CD=, △3BC CD =,△33BF CD DF CD==, △3BF DF =,故△正确;△如图所示,在AD 上取点Q ,使得FC FQ =,△60AFB ACB ∠=∠=︒,CF 平分BFD ∠,△120BFD ∠=︒,1602CFD BFD ∠=∠=︒, △FCQ 为等边三角形,△60FCQ ∠=︒,CF CQ =,△60ACB ∠=︒,△ACB ACF FCQ ACF ∠+∠=∠+∠,△BCF ACQ ∠=∠,在BCF △和ACQ 中,BC AC BCF ACQ CF CQ =⎧⎪∠=∠⎨⎪=⎩△()BCF ACQ SAS ≌,△BF AQ =,△AQ AF FQ =+,FQ FC =,△BF AF FC =+,故△正确;综上,△△△△均正确;故选:A .【名师指导】本题考查等边三角形的判定与性质,全等三角形的判定与性质等,理解等边三角形的基本性质,掌握全等三角形中的辅助线的基本模型,包括“手拉手”模型,截长补短的思想等是解题关键.12.如图,在ABC 中,BC AC =,90ACB ∠=︒,AD 平分BAC ∠,BE AD ⊥交AC 的延长线于F ,垂足为E .则下列结论不正确的是( )A .AD BF =B .CF CD =C .AC CD AB +=D .BE CF =【标准答案】D【思路点拨】 A.根据BC AC =,90ACB ∠=︒可知45CAB ABC ∠=∠=︒,再由AD 平分BAC ∠可知22.5BAE EAF ∠=∠=︒,在Rt ACD ∆与Rt BFC ∆中,90EAF F ∠+∠=︒,90FBC F ∠+∠=︒,可求出EAF FBC ∠=∠,由BC AC =可求出Rt ADC Rt BFC ∆≅∆,故可求出AD BF =;B.由选项A中Rt ADC Rt BFC ∆≅∆可直接得出结论;C.由选项A中Rt ADC Rt BFC ∆≅∆可知,CF CD =,故AC CD AC CF AF +=+=,22.5CBF EAF ∠=∠=︒,在Rt AEF ∆中,9067.5F EAF ∠=︒-∠=︒,根据45CAB ∠=︒可知,18067.5ABF EAF CAB ∠=︒-∠-∠=︒,即可求出AF AB =,即AC CD AB +=;D.由选项C可知,ABF ∆是等腰三角形,由于BE AD ⊥,故12BE BF =,在Rt BCF ∆中,若BE CF =,则30CBF ∠=︒,与选项B中22.5CBF ∠=︒相矛盾,故BE CF ≠;【精准解析】解:A.BC AC =,90ACB ∠=︒,45CAB ABC ∴∠=∠=︒, AD 平分BAC ∠,22.5BAE EAF ∴∠=∠=︒,在Rt ACD ∆与Rt BFC ∆中,90EAF F ∠+∠=︒,90FBC F ∠+∠=︒,EAF FBC ∴∠=∠,BC AC =,EAF FBC ∠=∠,BCF AEF ∠=∠,Rt ADC Rt BFC ∴∆≅∆,AD BF ∴=;故选项A 正确; B.选项A 中Rt ADC Rt BFC ∆≅∆,CF CD ∴=,故选项B 正确; C.选项A 中Rt ADC Rt BFC ∆≅∆,CF CD ∴=,AC CD AC CF AF +=+=,22.5CBF EAF ∠=∠=︒,∴在Rt AEF ∆中,9067.5F EAF ∠=︒-∠=︒,45CAB ∠=︒,18018067.54567.5ABF F CAB ∴∠=︒-∠-∠=︒-︒-︒=︒,AF AB ∴=,即AC CD AB +=,故C 正确;D.由选项C 可知,ABF ∆是等腰三角形,BE AD ⊥,12BE BF ∴=, 在Rt BCF ∆中,若BE CF =,则30CBF ∠=︒,与选项B 中22.5CBF ∠=︒相矛盾,故BE CF ≠,故选项D 错误;故选:D .【名师指导】本题考查的是线段垂直平分线的性质及等腰三角形的判定与性质,熟知线段垂直平分线的性质及等腰三角形的判定与性质是解答此题的关键.二、填空题13.如图,△ABC 的外角△DBC 、△ECB 的角平分线交于点M ,△ACB 的角平分线与BM 的反向延长线交于点N ,若在△CMN 中存在一个内角等于另一个内角的2倍,则△A 的度数为 _______【标准答案】60︒或90︒或120︒【思路点拨】根据ECB ∠,DBC ∠的角平分线交于点M ,可求得1902M A ∠=︒-∠,延长 CB 至F ,根据BM 为ABC ∆的外角DBC ∠的角平分线,可得 BN 是ABC ∆的外角ABF ∠的平分线, 根据CN 平分 ACB ∠,得到2ACB NCB ∠=∠,则有NBF NCB N ∠=∠+∠,可得 2ABF ACB N ∠=∠+∠,可求得12N A ∠=∠;再根据NCM NCF BCM ∠=∠+∠1122ACB BCE =∠+∠90=︒,分四种情况:△290MCN N ∠=∠=︒;△ 290MCN M ∠=∠=︒;△2M N ∠=∠;△2N M ∠=∠,分别讨论求解即可. 【精准解析】 解:外角ECB ∠,DBC ∠的角平分线交于点 M ,()12MCB MBC ECB DBC ∴∠+∠=∠+∠ ()11801802ACB ABC =︒-∠+︒-∠ ()13602ACB ABC =︒-∠-∠ ()13601802A =︒-︒+∠⎡⎤⎣⎦ ()11802A =︒+∠ 1902A =+∠︒△()11180180909022M MCB MBC A A ⎛⎫∠=︒-∠+∠=︒-︒+∠=︒-∠ ⎪⎝⎭; 如图示,延长CB 至F ,BM 为ABC ∆的外角DBC ∠的角平分线,BN ∴是ABC ∆的外角ABF ∠的平分线,2ABF NBF ∴∠=∠, CN 平分ACB ∠,2ACB NCB ∴∠=∠,NBF NCB N ∠=∠+∠,222NBF NCB N ∴∠=∠+∠,即2ABF ACB N ∠=∠+∠,又ABF ACB A ∠=∠+∠,△2ACB N ACB A ∠+∠=∠+∠2A N ∴∠=∠,即12N A ∠=∠; NCM NCF BCM ∠=∠+∠1122ACB BCE =∠+∠ 11802=⨯︒ 90=︒;如果CMN ∆中,存在一个内角等于另一个内角的2倍,那么分四种情况:△290MCN N ∠=∠=︒,则45N ∠=︒, 290A N ∠=∠=︒;△290MCN M ∠=∠=︒,则45M ∠=︒, 45N ∠=︒,290A N ∠=∠=︒;△2M N ∠=∠,则1190222A A ︒-∠=⨯∠,解得 60A ∠=︒;△2N M ∠=∠,则1129022A A ⎛⎫∠=︒-∠ ⎪⎝⎭,解得 120A ∠=︒. 综上所述,A ∠的度数是60︒或90︒或120︒.【名师指导】本题是三角形综合题,考查了三角形内角和定理、外角的性质,角平分线定义等知识;灵活运用三角形的内角和定理、外角的性质进行分类讨论是解题的关键.14.已知:△ABC 是三边都不相等的三角形,点P 是三个内角平分线的交点,点O 是三边垂直平分线的交点,当P 、O 同时在不等边△ABC 的内部时,那么△BOC 和△BPC 的数量关系是___.【标准答案】4360BPC ∠-︒【思路点拨】根据三角形角平分线的性质以及三角形内角和定理,即可得到2180BAC BPC ∠=∠-︒;再根据三角形垂直平分线的性质以及三角形内角和定理,即可得到2BOC BAC ∠=∠,进而得出BOC ∠和BPC ∠的数量关系.【精准解析】解:BP 平分ABC ∠,CP 平分ACB ∠,12PBC ABC ∴∠=∠,12PCB ACB ∠=∠, 180()BPC PBC PCB ∴∠=︒-∠+∠180(=︒-11)22ABC ACB ∠+∠ 1180()2ABC ACB =︒-∠+∠ 1180(180)2BAC =︒-︒-∠ 1902BAC =︒+∠, 即2180BAC BPC ∠=∠-︒;如图,连接AO .点O 是这个三角形三边垂直平分线的交点,OA OB OC ∴==,OAB OBA ∴∠=∠,OAC OCA ∠=∠,OBC OCB ∠=∠,1802AOB OAB ∴∠=︒-∠,1802AOC OAC ∠=︒-∠,360()BOC AOB AOC ∴∠=︒-∠+∠360(18021802)OAB OAC =︒-︒-∠+︒-∠,22OAB OAC =∠+∠2BAC =∠2(2180)BPC =∠-︒4360BPC =∠-︒,故答案为:4360BPC ∠-︒.【名师指导】本题考查了三角形的垂直平分线与角平分线,熟练掌握三角形的垂直平分线与角平分线的性质是解题的关键.15.如图,在四边形ABCD 中,//AD BC ,AB AC =,6BC =,DBC △面积为18,AB 的垂直平分线MN 分别交AB ,AC 于点M ,N ,若点P 和点Q 分别是线段MN 和BC 边上的动点,则PB PQ +的最小值为______.【标准答案】6【思路点拨】连接AQ ,过点D 作DH BC ⊥于H .利用三角形的面积公式求出DH ,由题意得: PB PQ AP PQ AQ +=+≥,求出AQ 的最小值,AQ 最小值是与DH 相等,也就是AQ BC ⊥时,根据面积公式求出DH 的长度即可得到结论.【精准解析】解:连接AQ ,过点D 作DH BC ⊥于H .△DBC △面积为18,BC =6, △1182BC DH =, △6DH =,△MN 垂直平分线段AB ,△PA PB =,△PB PQ AP PQ AQ +=+≥,△当AQ 的值最小时,PB PQ +的值最小,根据垂线段最短可知,当AQ BC ⊥时,AQ 的值最小,△//AD BC ,△AQ =DH =6,△PB PQ +的最小值为6.故答案为:6.【名师指导】本题考查轴对称最短问题,平行线的性质,三角形的面积,线段的垂直平分线的性质等知识,把最短问题转化为垂线段最短是解题关键.16.如图,AB 为等腰直角ABC 的斜边,E 为AB 的中点,F 为AC 延长线上的一个动点(F 与点C 不重合),线段FB 的垂直平分线交线段CE 于点O ,D 垂足.当F 点运动时,给出下列四个结论.其中一定正确的结论有______(请填写正确序号).△点O 到ABF 三个顶点的距离相等;△⊥OF OB ;FC AB +=;△AEC BOF S S <△△【标准答案】△△△【思路点拨】如图,连接AO ,根据等腰三角形的性质得到CE △AB ,求得OA =OB ,根据线段垂直平分线的性质得到OF =OB ,得到点O 到△ABF 三个顶点的距离相等,故△正确;设BC 交OF 于J ,根据全等三角形的性质得到△CAO =△CBO ,求得△CAO =△CFJ ,得到△JOB =△JCF =90°,根据垂直的定义得到OF △OB ,故△CE =AC ,AC +CF =AF ,显然AF不一定等于AB 、故△错误;根据等腰直角三角形的性质得到AE =CE =BE =12AB ,CE △AB ,求得△ACE 面积为12AE •CE =12BE 2,得到△BOF 面积为12OF •OB =12OB 2,于是得到S △AEC <S △BOF ,故△正确.【精准解析】解:如图,连接AO ,△CA =CB ,AE =EB ,△CE △AB ,△OA =OB ,△OD 垂直平分线段BF ,△OF =OB ,△OA =OF =OB ,△点O 到△ABF 三个顶点的距离相等,故△正确;设BC 交OF 于J ,在△ACO 与△BCO 中,AC BC CO CO AO BO =⎧⎪=⎨⎪=⎩, △△ACO △△BCO (SSS ),△△CAO =△CBO ,△OA =OF ,△△CAO =△CFJ ,△△CFJ =△OBJ ,△△CJF =△OJB ,△△JOB =△JCF =90°,△OF △OB ,故△正确;CE =AC ,AC +CF =AF ,显然AF 不一定等于AB 、故△错误;△△ABC 为等腰直角三角形,E 为AB 中点,△AE =CE =BE =12AB ,CE △AB ,△△ACE 面积为12AE •CE =12BE 2,△OF △OB ,OF =OB ,△△BOF 面积为12OF •OB =12OB 2,在Rt △OBE 中,OB 为斜边,BE 为直角边,△OB >BE , △12BE 2<12OB 2,△S △AEC <S △BOF ,故△正确.故答案为:△△△.【名师指导】本题考查了全等三角形的判定和性质,线段垂直平分线的性质,三角形的面积公式,正确的识别图形是解题的关键.17.如图,反比例函数k y x =的图象经过点(-1,-),点A 是该图象第一象限分支上的动点,连结AO 并延长交另一支于点B ,以AB 为斜边作等腰直角三角形ABC ,顶点C 在第四象限,AC 与x 轴交于点P ,连结BP .在点A 运动过程中,当BP 平分△ABC 时,点A 的坐标是____________.【标准答案】)2 【思路点拨】把点(-1,-)代入反比例函数k y x=,求出k . 连接OC ,过点A 作AE △x 轴于E ,过点C 作CF △x 轴于F ,则有△AOE △△OCF ,进而可得出AE =OF 、OE =CF ,根据角平分线的性质及三角形面积可得出AP CP =,易证APE CPF ,利用三角形性质可得出CF AE =即OE AE =A 的坐标为(a (a >0),由OE AE =可求出a 值,进而得到点A 的坐标.【精准解析】解:把点(-1,-k y x=得: k=−1×(-△y = 连接OC ,过点A 作AE △x 轴于E ,过点C 作CF △x 轴于F ,如图所示.△△ABC 为等腰直角三角形,△OA =OC ,OC △AB ,△△AOE +△COF =90°.△△COF +△OCF =90°,△△AOE =△OCF .在△AOE 和△OCF 中,90AEO OFC AOE OCF OA OC ∠∠︒⎧⎪∠∠⎨⎪⎩==== , △△AOE △△OCF (AAS ),△AE =OF ,OE =CF .设点P 到AB 的距离为h ,△BP 平分△ABC ,△h PC =,△1·21·2ABP CBP h AB S AP AB CP S BC PC BC ==== △,APE CPF AEP CFP ∠=∠∠=∠,△APECPF , △CF CP AE AP ==, △OE AE =. 设点A的坐标为(a , 解得:a或a =(舍去),2=, △点A的坐标为)2, 故答案为:)2.【名师指导】本题考查了反比例函数图象上点的坐标特征、全等三角形的判定与性质、角平分线的性质、三角形的面积、相似三角形的判定与性质以及等腰直角三角形,构造全等三角形,利用全等三角形的对应边相等是解题的关键.18.如图,在ABC 中,△ACB =45°,AD △BC ,BE △AC ,AD 与BE 相交于点F ,连接并延长CF 交AB 于点G ,△AEB 的平分线交CG 的延长线于点H ,连接AH ,则下列结论:△△EBD =45°;△AH =HF ;△ABD △CFD ;△CH =AB +AH ;△BD =CD ﹣AF .其中正确的是 ___.(只填写序号)【标准答案】△△△△△【思路点拨】△根据45ACB ∠=︒,BE AC ⊥,即可得解;△先证明EH 是AF 的垂直平分线,根据垂直平分线的性质即可得结论;△根据“边角边”即可证明ABD CFD ≌;△根据ABD CFD ≌可得AB CF =,再结合CH CF FH =+进而可以判断CH AB AH =+; △由DF AD AF =-结合△即可得结论.【精准解析】解:△△BE AC ⊥,90BEA BEC ∴∠=∠=︒,45ACB =︒∠,9045EBD ACB ∴∠=︒-∠=︒,故△正确;△EH 是AEB ∠的角平分线,1452HEB HEA AEB ∴∠=∠=∠=︒, 45HEB EBC ∴∠=∠=︒,//EH BC ∴,AD BC ⊥,AD EH ∴⊥,90AOE FOE ∴∠=∠=︒,9045OAE HEA ∴∠=︒-∠=︒,9045OFE HEB ∠=︒-∠=︒,45OAE OFE ∴∠=∠=︒,AE FE ∴=,又EH 平分AEB ∠,EH ∴是AF 的垂直平分线,AH HF ∴=,故△正确;。
垂直平分线与角平分线(习题及答案).

垂直平分线与角平分线(习题)➢复习巩固1.到三角形三条边的距离都相等的点是这个三角形的()A.三条中线的交点B.三条高的交点C.三条边的垂直平分线的交点D.三条角平分线的交点2.如图,在△ABC 中,AF 平分∠BAC,AC 的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C 的度数为.第2 题图第3 题图3.如图,AD 是∠BAC 的平分线,DE⊥AB 于点E,若S△ABC=6,AB=4,AC=3,则线段DE 的长为.4.如图,P 是∠AOB 平分线上的一点,PC⊥OA,PD⊥OB,垂足分别为C,D,连接CD.求证:OP 是CD 的垂直平分线.5.如图,点P 为锐角∠ABC 内一点,点M 在边BA 上,点N 在边BC 上,且PM=PN,∠BMP+∠BNP=180°.求证:BP 平分∠ABC.16.如图,点D 在边AC 上,∠ABD+∠ABC =180°,CE 平分∠ACB 交AB 于点E,连接DE.求证:DE 平分∠ADB.7.如图,在△ABC 中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:①作∠BAC 的平分线AM 交BC 于点D;②作边AB 的垂直平分线EF,EF 与AM 相交于点P;③连接PB,PC.若∠ABC=70°,则∠BPC 的度数为.8.如图,已知△ABC(AC<BC),求作:(不写作法,保留作图痕迹)(1)BC 边上的高;(2)在BC 上确定一点P,使PA+PC=BC.9.如图,已知线段a,利用尺规求作以a 为底、以2a 为高的等腰三角形.(不写作法,保留作图痕迹)10.如图,有三幢公寓楼分别建在点A,点B,点C 处,AB,AC,BC 是连接三幢公寓楼的三条道路,要修建一超市P,按照设计要求,超市要在△ABC 的内部,且到A,C 的距离必须相等,到两条道路AC,AB 的距离也必须相等,请利用尺规作图确定超市P 的位置.(不写作法,保留作图痕迹)【参考答案】➢复习巩固1. D2. 24°3. 12 74.证明略;提示:先证Rt△POC≌Rt△POD(HL),得到OC=OD,由“到一条线段两个端点距离相等的点,在这条线段的垂直平分线上”求证5.证明略;提示:过点P 分别作PD⊥AB 于D,PE⊥BC 于E,先证△PMD≌△PNE(AAS),得到PD=PE,再由“在一个角的内部,到角的两边距离相等的点在这个角的平分线上”求证6.证明略;提示:过点E 分别作EF⊥AC 于F,EH⊥BD 于H,EG⊥BC 于G,证EF=EG=EH,求证7. 80°8.作图略提示:(1)过直线外一点作已知直线的垂线;(2)作线段AB 的垂直平分线9.作图略10.作图略提示:作线段AC 的垂直平分线和∠CAB 的角平分线;。
人教版八年级数学上角平分线和线段垂直平分线(一)教案导学案教学设计同步练习课时作业试卷含答案解析

角平分线和线段垂直平分线【要点梳理】知识点1. 角的平分线的性质及判定定理:1.如图∵OP 平分∠AOB ,点P 在射线OP 上,PC ⊥OA 于C ,PD ⊥OB 于D∴ ( )2.∵PC ⊥OA 于C ,PD ⊥OB 于D ,PC = PD ,∴ ( ) 答案:PC=PD (角平分线上的点到角两边的距离相等) OP 平分∠AOB (到角两边距离相等的点在角的平分线上)知识点2. 线段的垂直平分线的性质及判定定理:1.线段垂直平分线性质:线段垂直平分线上的点与这条线段两个端点的 .2.线段垂直平分线的判定:与一条线段两个端点 的点,在这条线段的垂直平分线上.3.线段的垂直平分线是到这条线段两端点距离相等的点的集合.答案:1、距离相等 2、距离相等知识点3. 角的平分线和线段的垂直平分线的应用:1.三角形的三条 交于一点,并且这一点到三条边的距离相等。
2.三角形的 交于一点,这点到三角形三个顶点的距离相等。
3.如图,321l l l 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )A 、一处B 、二处C 、三处D 、四处4.如图,在△ABC 中,AB =AC ,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别为E ,F .下列推理中正确的个数是 .①AD 上任意一点到点C ,B 的距离相等;②AD 上任意一点到AC ,AB 的距离相等;③BD =CD ,AD ⊥BC ;④∠BDE =∠CDF答案:1、角平分线2、三条边的垂直平分线3、A 4、4【例题选析】例1 如图4,AB=AD ,BC=CD ,AC 、BD 相交于点E .由这些条件可以得出若干结论,请你写出其中三个正确结论(不要添加字母和辅助线,不要求证明).答案:∠DAE=∠BAE;DE=BE; ∠DCE=∠BCEl 3l 2l 1P D C BOA F D E CB AG NC FB D E A例2.如图,∠A =∠B =90°,M 是AB 的中点,DM 平分∠ADC ,求证:CM 平分∠BCDMDB C A答案:如图:过点M 作MN 与CD 垂直,先用AAS 证明△AMD 与△NMD 全等,得MN=AM,由M 为AB 中点可知,AM=BM,所以BM=NM ,又因为CM 是公共边,根据HL 可证明△MBC 与△MNC 全等,所以CM 平分∠BCD 。
角平分线、中垂线性质定理专题复习 (原卷)

【期末复习】浙教版八年级上册提分专题:角平分线、中垂线性质定理【角平分线】1.如图,△ABC的∠ABC和∠ACB的角平分线BE,CF相交于点O,∠A=60°,则∠BOC 的大小为()A.110°B.120°C.130°D.150°2.如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,则∠A1=.∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2009BC的平分线与∠A2009CD 的平分线交于点A2010,得∠A2010,则∠A2010=.3.如图,在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=70°,则∠BOA= ,∠DAE= .第3题第4题第5题第6题4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E.若BD=4,DE=7,则线段EC的长为()A.3B.4C.3.5D.25.如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°.则∠FEC的度数为()A.10°B.20°C.30°D.60°6.如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是()A.30°B.40°C.50°D.60°7.如图,点O是△ABC角平分线的交点,过点O作MN∥BC分别与AB,AC相交于点M,N,若AB=5,BC=8,CA=7,则△AMN的周长为.8.如图,Rt△ABC的两直角边AB、BC的长分别是9、12.其三条角平分线交于点O,将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于()A.1:1:1B.1:2:3C.3:4:5D.2:3:49.如图,在△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,若BC=10,点D到AB的距离为4,则DB 的长为()A.6B.8C.5D.4第8题第9题第10题第12题10.如图,AB∥CD,∠CAB和∠ACD的平分线相交于H点,E为AC的中点,若EH=4.则AC=()A.8B.7C.6D.911.到三角形的三条边距离相等的点()A.是三条角平分线的交点B.是三条中线的交点C.是三条高的交点D.以上答案都不对12.如图,点P是∠AOB内的一点,PC⊥OA于点C,PD⊥OB于点D,连接OP,CD.若PC=PD,则下列结论不一定成立的是()A.∠AOP=∠BOP B.∠OPC=∠OPDC.PO垂直平分CD D.PD=CD13.如图,在△ABC中,∠A=90°,AB=3,AC=4,BC=5,∠ABC与∠ACB的平分线交于点O,过点O作OD ⊥AB于点D,则AD的长为第13题第14题第15题第16题14.如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P,且与AB垂直,若AD=8,则点P到BC的距离是15.如图,Rt△ABC中,∠C=90°,AC=BC=6,AD为∠BAC的平分线,DE⊥AB垂足为E,则△DBE的周长等于16.如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为()A.3cm2B.4cm2C.4.5cm2D.5cm217.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于点E,交AC于点F,过点G作GD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BGC=90°+∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则S△AEF=mn.其中正确的结论有第17题第18题第19题第20题18.如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,已知CD=4.则AC的长为.19.如图,已知△ABC,∠BAC=80°,∠ABC=40°,若BE平分∠ABC,CE平分外角∠ACD,连接AE,则∠AEB的度数为.20.如图,已知∠ABC、∠EAC的角平分线BP、AP相交于点P,PM⊥BE,PN⊥BF,垂足分别为M、N.现有四个结论:①CP平分∠ACF;②∠BPC=∠BAC;③∠APC=90°﹣∠ABC;④S△APM+S△CPN>S△APC.其中结论正确的为.(填写结论的编号)21.如图,已知∠ABC、∠ACB的平分线相交于点O,EF过点O且EF∥BC.(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;(2)若∠BOC=130°,∠1:∠2=3:2,求∠ABC、∠ACB的度数.22.如图1,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC,交AB于点E,交AC于点F.(1)若AB=4,AC=5,求△AEF的周长.(2)过点O作OH⊥BC于点H,连接OA,如图2.当∠BAC=60°时,试探究OH与OA的数量关系,并说明理由.23.如图,AD是△ABC中∠BAC的平分线,DE⊥AB于点E,BD=4,∠B=30°,S△ACD=7,求AC的长.24.在△ABC中,AD是角平分线,∠B<∠C,(1)如图(1),AE是高,∠B=50°,∠C=70°,求∠DAE的度数;(2)如图(2),点E在AD上.EF⊥BC于F,试探究∠DEF与∠B、∠C的大小关系,并证明你的结论;(3)如图(3),点E在AD的延长线上.EF⊥BC于F,试探究∠DEF与∠B、∠C的关系是(直接写出结论,不需证明).【线段垂直平分线】1.如图,在△ABC中,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F,连接AE、AF,若△AEF的周长为2,则BC的长是()A.2B.3C.4D.无法确定第1题第2题第3题2.如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是()A.2B.4C.6D.83.如图,在△ABC中,BC边上两点D、E分别在AB、AC的垂直平分线上,若BC=24,则△ADE的周长为()A.22B.23C.24D.254.如图,已知∠B=20°,∠C=25°,若MP和QN分别垂直平分AB和AC,则∠P AQ等于()A.80°B.90°C.100°D.105°第4题第5题第7题5.如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为()cmA.3B.4C.7D.116.元旦联欢会上,同学们玩抢凳子游戏,在与A、B、C三名同学距离相等的位置放一个凳子,谁先抢到凳子谁获胜.如果将A、B、C三名同学所在位置看作△ABC的三个顶点,那么凳子应该放在△ABC的()A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边垂直平分线的交点7.如图,在Rt△ABC中,∠BAC=90°,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若DE=3,AE =5,则△ACE的周长为.8.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠F AC=68°,则∠B的度数为.第8题第9题第10题9.如图,△ABC中,已知∠C=90°,DE是AB的垂直平分线,若∠DAC:∠DAB=1:2,那么∠BAC=度.10.如图,已知△ABC的面积为8cm2,BP为∠ABC的角平分线,AP垂直BP于点P,则△PBC的面积为cm2.11.如图,AD是△ABC的角平分线,AD的垂直平分线交BC的延长线于点F.求证:∠F AC=∠B.12.在△ABC中,∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,(1)如图(1),连接AM、AN,求∠MAN的度数;(2)如图(2),如果AB=AC,求证:BM=MN=NC.。
中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题(含答案解析)

中考数学复习----《角的平分线与线段的垂直平分线》知识点总结与专项练习题(含答案解析)知识点总结1.角平分线的定义:角的内部把角平均分成两个相等的角的射线叫做角的平分线。
2.角平分线的性质:①平分角。
②角平分线上任意一点到角两边的距离相等。
3.角平分线的判定:角的内部到角两边相等的点一定在角平分线上。
4.角平分线的尺规作图:具体步骤:①以角的顶点O为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M、N。
如图①。
②分别以点M与点N为圆心,大于MN长度的一半为半径画圆弧,两圆弧交于点P。
如图②。
③连接OP,OP即为角的平分线。
5.线段的垂直平分线的定义:过线段的中点且与线段垂直的直线是这条线段的垂直平分线。
6.垂直平分线的性质:①垂直且平分线段。
②垂直平分线上任意一点到这条线段两个端点的距离相等。
7.垂直平分线的判定:到线段两端点距离相等的点一定在线段的垂直平分线上。
8.垂直平分线的吃规作图:具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M、N。
如图①②连接MN,过MN的直线即为线段的垂直平分线。
如图②练习题1、(2022•鄂尔多斯)如图,∠AOE=15°,OE平分∠AOB,DE∥OB交OA于点D,EC⊥OB,垂足为C.若EC=2,则OD的长为()A.2 B.2C.4 D.4+2【分析】过点E作EH⊥OA于点H,根据角平分线的性质可得EH=EC,再根据平行线的性质可得∠ADE的度数,再根据含30°角的直角三角形的性质可得DE的长度,再证明OD=DE,即可求出OD的长.【解答】解:过点E作EH⊥OA于点H,如图所示:∵OE平分∠AOB,EC⊥OB,∴EH=EC,∵∠AOE=15°,OE平分∠AOB,∴∠AOC=2∠AOE=30°,∵DE∥OB,∴∠ADE=30°,∴DE=2HE=2EC,∵EC=2,∴DE=4,∵∠ADE=30°,∠AOE=15°,∴∠DEO=15°,∴∠AOE=∠DEO,∴OD=DE=4,故选:C.2、(2022•北京)如图,在△ABC中,AD平分∠BAC,DE⊥AB.若AC=2,DE=1,则S △ACD=.【分析】过D点作DH⊥AC于H,如图,根据角平分线的性质得到DE=DH=1,然后根据三角形面积公式计算.【解答】解:过D点作DH⊥AC于H,如图,∵AD平分∠BAC,DE⊥AB,DH⊥AC,∴DE=DH=1,∴S△ACD=×2×1=1.故答案为:1.3、(2022•黑龙江)在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,CD=.【分析】过点D作DE⊥AB于E,利用勾股定理列式求出AB,再根据角平分线上的点到角的两边距离相等可得CD=DE,然后根据△ABC的面积列式计算即可得解.【解答】解:如图,过点D作DE⊥AB于E,∵∠C=90°,AC=6,BC=8,∴AB===10,∵AD平分∠CAB,∴CD=DE,∴S△ABC=AC•CD+AB•DE=AC•BC,即×6•CD+×10•CD=×6×8,解得CD=3.故答案为:3.4、(2022•宜昌)如图,在△ABC中,分别以点B和点C为圆心,大于BC长为半径画弧,两弧相交于点M,N.作直线MN,交AC于点D,交BC于点E,连接BD.若AB=7,AC=12,BC=6,则△ABD的周长为()A.25 B.22 C.19 D.18【分析】根据题意可知MN垂直平分BC,即可得到DB=DC,然后即可得到AB+BD+AD =AB+DC+AD=AB+AC,从而可以求得△ABD的周长.【解答】解:由题意可得,MN垂直平分BC,∴DB=DC,∵△ABD的周长是AB+BD+AD,∴AB+BD+AD=AB+DC+AD=AB+AC,∵AB=7,AC=12,∴AB+AC=19,∴△ABD的周长是19,故选:C.5、(2022•湖北)如图,在矩形ABCD中,AB<BC,连接AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧交于点M,N,直线MN分别交AD,BC于点E,F.下列结论:①四边形AECF是菱形;②∠AFB=2∠ACB;③AC•EF=CF•CD;④若AF平分∠BAC,则CF=2BF.其中正确结论的个数是()A.4 B.3 C.2 D.1【分析】根据题意分别证明各个结论来判断即可.【解答】解:根据题意知,EF垂直平分AC,在△AOE和△COF中,,∴△AOE≌△COF(ASA),∴OE=OF,∴AE=AF=CF=CE,即四边形AECF是菱形,故①结论正确;∵∠AFB=∠FAO+∠ACB,AF=FC,∴∠FAO=∠ACB,∴∠AFB=2∠ACB,故②结论正确;∵S四边形AECF=CF•CD=AC•OE×2=AC•EF,故③结论不正确;若AF平分∠BAC,则∠BAF=∠FAC=∠CAD=90°=30°,∴AF=2BF,∵CF=AF,∴CF=2BF,故④结论正确;故选:B.33.(2022•鄂尔多斯)如图,在△ABC中,边BC的垂直平分线DE交AB于点D,连接DC,若AB=3.7,AC=2.3,则△ADC的周长是.【分析】根据线段垂直平分线的性质可得BD=CD,进一步即可求出△ADC的周长.【解答】解:∵边BC的垂直平分线DE交AB于点D,∴BD=CD,∵AB=3.7,AC=2.3,∴△ADC的周长为AD+CD+AC=AB+AC=6,故答案为:6.34.(2022•青海)如图,在Rt△ABC中,∠ABC=90°,ED是AC的垂直平分线,交AC 于点D,交BC于点E,∠BAE=10°,则∠C的度数是.【分析】根据线段垂直平分线的性质可得AE=EC,从而可得∠EAC=∠C,然后利用三角形内角和定理可得∠EAC+∠C=80°,进行计算即可解答.【解答】解:∵ED是AC的垂直平分线,∴AE=EC,∴∠EAC=∠C,∵∠ABC=90°,∠BAE=10°,∴∠EAC+∠C=180°﹣∠BAE﹣∠ABC=80°,∴∠EAC=∠C=40°,故答案为:40°.。
线段垂直平分线和角平分线的性质(习题课)

变式:如图,在△ABC中,BD平分∠ABC, ∠A=90°, DA=6cm,BC=10cm,求△BDC的面积.
E
∟
性质重现
(一)线段垂直平分线的性质 线段垂直平分线上的点到这条线段两端 点的距离相等。
(二)角平分线的性质:
角平分线上的点到角两边的距离相等
生活中的应用
例3、如图,初一(3)班与初一(4)班两个班的学 生分别在M、N两处参加植树劳动,现要在道路AB、AC 的交叉区域内设一个茶水供应点P,使P到两条道路的 距离相等,且使PM=PN,请你找出P点。
10.1线段垂直平分线
线和段角和平角(分习平线题分性课质线)的性应质用的 应用
性质再现
一、线段垂直平分线的性质
线段垂直平分线上的点到这条线段 两端点的距离相等。
几何语言:∵OB,AO=OB)
∴AC=BC
A
O
B
几何中的应用
例1:在△ABC中,边BC的垂直平分线分别交AB、BC 于点E、D;BE=6, BC=10,求△BCE的周长。
B
P .N
.M
A
C
作法:∠BAC的平分线与线段NM中垂线的交点 P就是所求的点。
作业:
课后习题
图9
变式练习
1、在△ABC中, 边BC的垂直平分线分别交AB、BC 于点E、D, AB=10,AC=6,△ACE的周长为 16 。
2、在△ABC中,边BC的垂直平分线分别交AB、图 B9 C于点
E 、D,△ACE的周长为16cm, ⊿ABC的周长为24cm则
BD长为
4 cm。
图9
3、如图,在△ABC中,AB的垂直平分线分别交AB、 BC于点D、E,AC的垂直平分线分别交AC、BC于点F、 G,若BC=20,则△AEG的周长为多少?
垂直平分线与角平分线综合 练习题(带答案))

垂直平分线与角平分线综合 题集一、垂直平分线(1)(2)1.如图,中,,垂直平分,交于点,交于点,且.若,求的度数.若周长,,求长.【答案】(1)(2)..【解析】(1)(2)∵垂直平分,垂直平分,∴,∴,∵,∴,∴.∵周长,,∴,即,∴.【标注】【知识点】作三角形的高,中线和角平分线(1)(2)2.的两边和的垂直平分线分别交于点、.若,求的周长.若,求.【答案】(1)(2)..【解析】(1)(2)∵边、的垂直平分线分别交于、,∴,,∴的周长.∵的两边,的垂直平分线分别交于,,∴,,∴,.∵,①∴.∵,∴,即.②由①②组成的方程组.解得,故答案为:.【标注】【知识点】三角形的周长与面积问题3.在中,,,的垂直平分线交于,的垂直平分线交于.求证:.【答案】证明见解析.【解析】连接、,∵,,∴,∵的垂直平分线交于,的垂直平分线交于,∴,,∴,,,∵,∴,∴是等边三角形,∴,∴.【标注】【知识点】等边三角形的构造4.已知中,是的平分线,的垂直平分线交的延长线于.求证:.【答案】证明见解析.【解析】∵是的平分线,∴,∵是的垂直平分线,∴,,∵,,∴.【标注】【能力】推理论证能力【知识点】线段的垂直平分线的性质定理【知识点】角分线性质定理5.中,是线段的垂直平分线,垂足为点,是上一点,.求证:点在线段的垂直平分线上.【答案】(1)证明见解析.【解析】(1)连接,是线段的垂直平分线,,,,在的垂直平分线上.【标注】【知识点】线段的和差的证明【知识点】线段的垂直平分线的性质定理【知识点】线段的垂直平分线的判定定理【知识点】等边三角形的性质【思想】数形结合思想【能力】运算能力【能力】推理论证能力6.如图,四边形中,的垂直平分线与的垂直平分线交于点,且.求证:点一定在的垂直平分线上.【答案】证明见解析.【解析】连接、,∵点是、的垂直平分线的交点,∴,,又∵,∴,∴点一定在的垂直平分线上.【标注】【知识点】作线段的垂直平分线(1)(2)7.如图,已知等腰三角形中,,点、分别在边、上,且,连接、,交于点.判断与的数量关系,并说明理由.求证:过点、的直线垂直平分线段.【答案】(1)(2)相等,证明见解析.证明见解析.【解析】(1)(2).在和中,,∴≌,∴.∵,∴,由()可知,∴,∴,∵,∴点、均在线段的垂直平分线上,即直线垂直平分线段.【标注】【知识点】线段的垂直平分线的性质定理【知识点】SAS【知识点】全等三角形的对应边与角【能力】推理论证能力二、角平分线8.如图,平分,于,于,,.若,则.【答案】【解析】∵平分,,,∴,∵,,∴,即,解得.故答案为:.【标注】【知识点】角分线性质定理9.如图,在中,,平分,,,则点到的距离为.【答案】【解析】∵,,∴.∵平分,,∴点到的距离等于,即点到的距离等于.【标注】【知识点】角分线性质定理A. B. C. D.10.如图,的三边、、的长分别,,,是三条角平分线的交点,则( ).【答案】C 【解析】∵是三条角平分线的交点,∴点到各边的距离相等,即、、的高相等,∵、、的长分别,,,∴,故答案为.【标注】【知识点】与中线或等分线有关的等积变换A.B.C.D.11.如图,三条公路把、、三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,则这个集贸市场应建在( ).在、两边高线的交点处在、两边中线的交点处在、两内角平分线的交点处在、两边垂直平分线的交点处【答案】C 【解析】内角平分线上的点到,距离相等,内角平分线上的点到,距离相等,∴要到三条公路距离相等,应在,内角平分线交点处满足到,,距离相等.故选.【标注】【知识点】角分线性质定理A. B. C. D.12.如图,点是的两外角平分线的交点,下列结论:①;②点到、的距离相等;③点到的三边的距离相等;④点在的平分线上.以上结论正确的个数是().【答案】C【解析】如图,过点作于,作于,作于,∵点是的两外角平分线的交点,,,∴点在的平分线上,故②③④正确,只有点是的中点时,,故①错误,综上所述,正确的是②③④.【标注】【知识点】角分线性质定理【知识点】角平分线判定定理三、角分线的角度模型(1)(2)(3)(4)13.完成下列各题:如图 ,、分别是中和的平分线,则与的关系是 (直接写出结论).如图 ,、分别是两个外角和的平分线,则与的关系是 ,请证明你的结论.如图 ,、分别是一个内角和一个外角的平分线,则与的关系是 ,请证明你的结论.利用以上结论完成以下问题:如图,已知:,点 、 分别是射线、上的动点,的外角的平分线与角的平分线相交于点,猜想的大小是否变化?请证明你的猜想.图图图图【答案】(1)(2)(3)(4). ..的大小没有变化,证明见解析.【解析】(1)理由如下:如图 ,∵ ,,分别是,的角平分线,∴ ,∴.(2)(3)(4)图如图 ,∵ 平分 ,∴ ,同理可证: ,∴ ,∵ ,∴,∴ .图∵ 平分 , 平分 ,∴ ,∵ 是 的外角,∴ ,∵ 是 的外角,∴ ,∴.根据⑶可得: ,∵ ,∴ ,∴ 的大小不会变化始终为 .【标注】【知识点】三角形-内角角分线;三角形-外角角分线;三角形-内外角角分线(1)(2)(3)14.回答下列问题.探索发现:如图,在中,点是内角和外角的角平分线的交点,试猜想与之间的数量关系,并证明你的猜想.图迁移拓展:如图,在中,点是内角和外角的等分线的交点,即,,试猜想与之间的数量关系,并证明你的猜想.图应用创新:已知,如图,、相交于点,、、的角平分线交于点,,,则 .图【答案】(1),证明见解析.(2)(3),证明见解析.【解析】(1)(2)(3)∵点是内角和外角的角平分线的交点,∴,,∵是的外角,∴,∴∴∵是的外角,∴,∴.∵是的外角,∴,∴,∵,,∴,∵是的外角,∴,∴.∵、、的角平分线交于点,∴由()的结论知,,,∴,故答案为:.【标注】【知识点】三角形-内外角角分线(1)15.阅读下面的材料,并解决问题:已知在中,.如图(1),、的角平分线交于点,则可求得.如图(2),、的三等分线交于点、,则 .如图(3),、的等分线交于点、、……,则.;(用含的代数式)(2)(3)图图图如图,,、的三等分线交于点、,若,,求的度数;(要求写出解答过程)如图,,的三等分线分别与的平分线交于点,,若,,求的度数为 (不要求写出解答过程).【答案】(1)(2)(3); ;.【解析】(1)(2)(3)是的外角,,、是的三等分线,,在中,,又是的平分线,,.只需抓住加.则等分,下面两个小角之和为,.【标注】【知识点】三角形-内角角分线。
八年级数学线段的垂直平分线的性质和判定(人教版)(基础)(含答案)

线段的垂直平分线的性质和判定(人教版)(基础)一、单选题(共11道,每道9分)1.下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的一条直线垂直平分线段AB.其中不正确的个数有( )A.1个B.2个C.3个D.4个答案:A解题思路:根据线段垂直平分线的性质定理和判定定理,①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB,符合性质定理,是正确的;②若PA=PB,EA=EB,则直线PE垂直平分线段AB,符合判定定理,是正确的;③若PA=PB,则点P必是线段AB的垂直平分线上的点,符合判定定理,是正确的;④若EA=EB,则点E在AB垂直平分线上,但是平面内过一点的直线有无数条,不能确定是垂直平分线,所以错误;综上④错误,故选A试题难度:三颗星知识点:略2.如图,AC=AD,BC=BD,则有( )A.CD垂直平分ABB.AB垂直平分CDC.AB与CD互相垂直平分D.CD平分∠ACB答案:B解题思路:AC=AD,根据到线段两个端点距离相等的点在这条线段的垂直平分线上,所以A在CD的垂直平分线上;BC=BD,所以B在CD的垂直平分线上.两点确定一条直线,则AB垂直平分CD.故选B.试题难度:三颗星知识点:略3.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C,D,下列结论不一定成立的是( )A.DE=CEB.OE平分∠DECC.OE垂直平分CDD.CD垂直平分OE答案:D解题思路:A:因为OE平分∠AOB,EC⊥OA,ED⊥OB,所以DE=CE成立;B:由题可知∠DOE=∠COE,∠ODE=∠OCE=90°,可证△DOE≌△COE(AAS)所以∠OED=∠OEC,故OE平分∠DEC成立;C:由选项A,B可知DE=CE,OD=OC,所以点E和点O分别在线段CD的垂直平分线上,所以OE垂直平分CD成立;D:点C和点D均不在线段OE的垂直平分线上,所以CD垂直平分OE不成立;故选D试题难度:三颗星知识点:略4.平面内,过直线外一点作已知直线的垂线最终都转化为下列哪一种基本作图( )A.作一个角等于已知角B.作一条线段等于已知线段C.作已知角的角平分线D.作已知线段的垂直平分线答案:D解题思路:过直线外一点作已知直线的垂线可以先在直线上作一条线段,使直线外的一点在这条线段的垂直平分线上,再作这条线段的垂直平分线.故选D.试题难度:三颗星知识点:略5.如图1,已知A为直线MN外一点,求作直线AB,使AB⊥MN.如图2用尺规作图作出直线AB,下列叙述:①任取一点P;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.其中错误的是( )A.①B.②C.③D.④答案:A解题思路:过点A作直线AB,使AB⊥MN的作法为:①任取一点P,使点P和点A位于直线MN的异侧;②以点A为圆心,AP长为半径作弧,交MN于C,D两点;③分别以点C,点D为圆心,以大于长为半径作弧,两弧交MN下方于一点B;④作直线AB.直线AB即为所求.要保证以AP为半径的弧与直线MN有交点,点P与点A应位于直线MN异侧,①错误.故选A.试题难度:三颗星知识点:略6.如图1,已知线段MN,在MN上求作一点O,使OM=ON.如图2用尺规作图作出了点O,下列作图语言叙述正确的是( )A.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.B.分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.C.以点M为圆心,任意长为半径作弧,再以点N为圆心,大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求.D.分别以点M,点N为圆心,任意长为半径作弧,两弧相交于点A和点B;作直线AB,直线AB即为所求.答案:B解题思路:在MN上求作一点O,使OM=ON可以转化为作线段MN的垂直平分线,与MN的交点即为点O.正确作法为:分别以点M,点N为圆心,以大于长为半径作弧,两弧相交于点A和点B;作直线AB交MN于点O,点O即为所求;要找到MN垂直平分线上的两点,需要保证以相同长为半径作弧,且两弧有交点,所以此半径应大于,故选项A,C,D错误.故选B.试题难度:三颗星知识点:略7.如图,以C为圆心,以大于点C到AB的距离为半径作弧交AB于点D,E,再以D,E为圆心,以大于DE为半径作弧,两弧交于点F,作射线CF,则( )A.CF平分∠ACBB.CF垂直平分DEC.CF平分ABD.CF垂直平分AB答案:B解题思路:由题意可知,点C到D,E两点的距离相等,点F到D,E两点的距离相等,所以点C和点F 均在线段DE的垂直平分线上,所以CF垂直平分DE;故选B试题难度:三颗星知识点:略8.如图,某地由于居民增多,要在公路边增加一个公共汽车站,A,B是路边两个新建小区,要使两个小区到车站的路程一样长,这个公共汽车站C应建在( )A.点A到l的垂线与l的交点处B.线段AB的垂直平分线上任意某点处C.线段AB的垂直平分线和l的交点处D.点B到l的垂线与l的交点处答案:C解题思路:由题意可得,点C到A,B两点的距离相等,所以C在AB的垂直平分线上,因为C在l上,所以这个公共汽车站C应建在线段AB的垂直平分线和l的交点处.故选C试题难度:三颗星知识点:略9.如图,某公园的三个出口A,B,C构成△ABC,想要在公园内修建一个公共厕所,要求到三个出口距离都相等,则公共厕所应该在( )A.三条边的垂直平分线的交点B.三个角的角平分线的交点C.三角形三条高的交点D.三角形三条中线的交点答案:A解题思路:∵公共厕所到出口A,B的距离相等∴公共厕所在线段AB的垂直平分线上,同理,公共厕所在线段BC的垂直平分线上所以,公共厕所应该在三条边的垂直平分线的交点故选A试题难度:三颗星知识点:略10.电信部门要在S区修建一座手机信号发射塔,按照设计要求,发射塔到两个城镇A,B的距离必须相等,到两条高速公路OC,OD的距离也必须相等,则发射塔应建在( )A.∠COD的平分线上任意某点处B.线段AB的垂直平分线上任意某点处C.∠COD的平分线和线段AB的交点处D.∠COD的平分线和线段AB垂直平分线的交点处答案:D解题思路:由题意可得,发射塔到两个城镇A,B的距离相等,所以发射塔要建在AB的垂直平分线上,又因为发射塔到两条高速公路OC,OD的距离也相等,所以发射塔要建在∠COD的平分线上,所以发射塔应建在线段AB垂直平分线和∠COD的平分线的交点处;故选D试题难度:三颗星知识点:略11.如图,△ABC,AB>AC>BC,边AB上存在一点P,使得PA+PC=AB,下列描述正确的是( )A.P是AC的垂直平分线与AB的交点B.P是BC的垂直平分线与AB的交点C.P是∠ACB的平分线与AB的交点D.P是以点B为圆心,AC长为半径的弧与边AB的交点答案:B解题思路:因为PA+PB=AB,要使PA+PC=AB即PB=PC,即点P在BC的垂直平分线上所以点P为线段BC的垂直平分线与AB的交点故选B试题难度:三颗星知识点:略。
平面几何的垂直平分线与平行线与角平分线与相交角练习题

平面几何的垂直平分线与平行线与角平分线与相交角练习题平面几何的垂直平分线、平行线、角平分线与相交角练习题一、垂直平分线1. 已知线段AB的中点为M,延长线段AB的垂直平分线相交于点O。
若AM = 4cm,MB = 6cm,求线段AO和线段OB的长度。
解析:由于垂直平分线将线段AB等分,所以线段AO和线段OB 的长度相等,设其长度为x,则有AO = OB = x。
又因为线段AM和线段MB的长度已知,根据线段分割定理可得,AM : MB = AO : OB。
代入已知数据可得4 : 6 = x : x,化简得2 : 3 = 1 : x,解得x = 3。
故线段AO和线段OB的长度均为3cm。
2. 已知四边形ABCD中,线段AB的中点为O,垂直平分线AC和BD相交于点E。
若AE = 6cm,DE = 10cm,求线段AB的长度。
解析:由于垂直平分线将线段AC和线段BD等分,所以线段AE和线段DE的长度相等,设其长度为x,则有AE = DE = x。
又因为线段AB的中点为O,根据线段分割定理可得,AE : EC = BO : OD。
代入已知数据可得6 : x = BO : 10,化简得6x = 10BO,再代入AE = DE = x得6x = 10x,解得x = 0,这显然不符合实际。
因此,题目中所给的条件是矛盾的,无解。
二、平行线1. 已知平行线l和m分别与线段AB相交于点C和点D,若AC =3cm,BC = 5cm,CD = 6cm,求BD的长度。
解析:由于平行线l和m与线段AB相交,根据平行线分割定理可得,AC : CB = CD : BD。
代入已知数据可得3 : 5 = 6 : BD,化简得3BD = 30,解得BD = 10。
故BD的长度为10cm。
2. 已知平行线l和m分别与线段AB相交于点C和点D,且AC =2BC,CD = 4cm,求BD的长度。
解析:由于平行线l和m与线段AB相交,根据平行线分割定理可得,AC : CB = CD : BD。
第03讲 线段的垂直平分线、角平分线性质、尺规作图(3大考点6种解题方法)(原卷版)

第03讲线段的垂直平分线、角平分线性质、尺规作图(3大考点6种解题方法)考点考向一.角平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.注意:①这里的距离是指点到角的两边垂线段的长;②该性质可以独立作为证明两条线段相等的依据,有时不必证明全等;③使用该结论的前提条件是图中有角平分线,有垂直角平分线的性质语言:如图,∵C 在∠AOB的平分线上,CD⊥OA,CE⊥OB∴CD=CE二.线段垂直平分线的性质(1)定义:经过某一条线段的中点,并且垂直于这条线段的直线,叫做这条线段的垂直平分线(中垂线)垂直平分线,简称“中垂线”.(2)性质:①垂直平分线垂直且平分其所在线段.②垂直平分线上任意一点,到线段两端点的距离相等.③三角形三条边的垂直平分线相交于一点,该点叫外心,并且这一点到三个顶点的距离相等.三.作图—基本作图基本作图有:(1)作一条线段等于已知线段.(2)作一个角等于已知角.(3)作已知线段的垂直平分线.(4)作已知角的角平分线.(5)过一点作已知直线的垂线.四.作图—复杂作图复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.五.作图—应用与设计作图应用与设计作图主要把简单作图放入实际问题中.首先要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.六.作图—代数计算作图代数计算作图是实际问题中要求所作图形具备一定的条件,如角的度数或边的长度.(1)根据题意计算出图形所具备的条件,边长,角度等,在网格纸上作图或利用圆规和直尺作图.(2)直接利用尺规作图做出符合题意的图形.如在数轴上找到表示无理数的点.要熟悉几何图形的性质和5种基本作图的步骤,才能灵活运用熟练作图.考点精讲一.角平分线的性质(共5小题)1.(2021秋•温岭市期末)如图,OP平分∠AOB,E为OA上一点,OE=4,P到OB的距离是2,则△OPE 的面积为()A.2B.3C.4D.82.(2021秋•北仑区期中)如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC的长是()A.2B.3C.4D.53.(2021秋•东阳市期末)如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N 为圆心,大于MN长为半径画弧,两弧交于点O,作射线AO,交BC 于点E.已知CE=3,BE=5,则AC的长为()A.8B.7C.6D.54.(2021秋•新昌县期末)如图,AB∥CD,BP和CP分别平分∠ABC和∠BCD,AD过点P且与AB垂直.若AD=8,BC=10,则△BCP的面积为()A.16B.20C.40D.805.(2021秋•诸暨市校级月考)如图,在△ABC中,AC=6cm,AB=9cm,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连接DE,已知DE=2cm,BD=3cm.求:(1)线段BC的长;(2)若∠ACB的平分线CF交AD于点O,且O到AC的距离是acm,请用含a的代数式表示△ABC的面积.二.线段垂直平分线的性质(共8小题)6.(2021秋•海曙区期末)如图,△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,若∠EAG=40°,则∠BAC的度数是()A.140°B.130°C.120°D.110°7.(2021秋•温州期末)如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若△ABC与△ABE的周长之差为4,则AE的长为()A.1B.2C.3D.48.(2021秋•余杭区月考)如图,在△ABC中,DE是AC的中垂线,分别交AC、AB于点D、E,若△BCE 的周长为8,BC=3,求AB的长.9.(2021秋•义乌市期中)如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF =90°,AF=3,AE=4.(1)求边BC的长;(2)求出∠BAC的度数.10.(2021秋•柯桥区月考)已知:如图,△ABC中,∠A=90°,BC的垂直平分线DE交BC于点E,交AC于点D.(1)若∠C=35°,求∠DBA的度数;(2)若△ABD的周长为30,AC=18,求AB的长.11.(2021秋•余杭区期中)如图,△ABC中,∠BAC=130°,AB,AC的垂直平分线分别交BC于点E,F,与AB,AC分别交于点D,G,则∠EAF的度数为()A.65°B.60°C.70°D.80°12.(2021秋•上城区期中)如图,在△ABC中,AD是BC边上的高线,AD的垂直平分线分别交AB,AC 于点E,F.(1)若∠DAC=20°,求∠FDC的度数;(2)试判断∠B与∠AED的数量关系,并说明理由.13.(2021秋•西湖区期末)如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=()A.50°B.80°C.90°D.100°三.作图—基本作图(共4小题)14.(2021秋•鄞州区期中)如图,在△ABC中,∠B=65°,∠C=30°,分别以点A和点C为圆心,大于AC的长为半径画弧,两弧相交于点M、N,作直线MN,交BC于点D,连接AD,则∠BAD的度数为()A.45°B.55°C.60°D.65°15.(2021秋•诸暨市期末)下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是()A.①B.②C.①②D.无16.(2021秋•新昌县期末)如图,已知△ABC.(1)请用直尺和圆规作∠ABC的角平分线BD,交AC于点D.(保留作图痕迹,不写作法)(2)在(1)的条件下,若∠A=100°,∠C=28°,求∠BDA的度数.17.(2021秋•余姚市期末)如图,在△ABC中,CE⊥AB于点E.(1)用尺规作BD⊥AC,垂足为点D.(不写作法,保留痕迹)(2)在(1)所画的图中,若BE=CD.求证:AB=AC.四.作图—复杂作图(共5小题)18.(2021秋•临海市期末)如图,已知△ABC,点D在边AB上.(1)求作点D,使点D到点B,C的距离相等;(尺规作图,保留作图痕迹,不写作法)(2)连接DC,已知∠B=32°,求∠ADC的度数.19.(2021秋•缙云县期末)(拓展创新)如图所示,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点以顶点分别按下列要求画三角形.(1)使三角形的三边长分别为3,2,;(在图①中画一个即可)(2)使三角形为钝角三角形且面积为4.(在图②中画一个即可)20.(2021秋•新昌县期中)如图,在△ABC中,AB>AC,按以下步骤作图:分别以点B和点C为圆心,大于BC长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D;连结CD.(1)则MN是BC的线.(2)若AB=8,AC=4,求△ACD的周长.21.(2021秋•西湖区校级期中)如图,已知△ABC.(1)尺规作图:①作出△ABC的角平分线CD;②作出BC的中垂线交AB于点E.(2)连结CE,若∠ABC=60°,∠A=40°,则∠DCE=.22.(2021秋•拱墅区期中)如图,△ABC中,AC>AB.(1)作AB边的垂直平分线交BC于点P,作AC边的垂直平分线交BC于点Q,连接AP,AQ.(尺规作图,保留作图痕迹,不需要写作法)(2)在(1)的条件下,若BC=14,求△APQ的周长.五.作图—应用与设计作图(共6小题)23.(2021秋•临海市期末)如图,在5×5的网格纸中,△ABC的三个顶点都在格点上.请仅用直尺,按要求画图.(1)在图1中画出过点B的直线l,使其平分△ABC的面积;(2)在图2中画出线段BD,使其平分∠ABC,且点D在格点上.24.(2021秋•椒江区期末)如图,两条公路OA,OB相交于点O,在∠AOB内部有两个村庄C,D.为方便群众接种新冠疫苗,该地决定在∠AOB内部再启动一个方舱式接种点P,要求同时满足:(1)到两条公路OA,OB的距离相等.(2)到两村庄C,D的距离相等.请你用直尺和圆规作出接种点P的位置(保留作图痕迹).25.(2021秋•宁波期末)定义:如果三角形的两个内角α和β满足α+2β=90°,那么我们称这样的三角形为“类直角三角形”.如图,在△ABC中,∠C=90°,AC=8,BC=6.请把这个三角形分割成两个三角形,使得其中一个为“类直角三角形”,并求出这个“类直角三角形”的面积.(备注:要求尺规作图)26.(2021秋•婺城区校级月考)如图,在7×6的方格中,△ABC的顶点均在格点上.试按要求画出线段EF(E,F均为格点),各画出一条即可.27.(2021春•南岗区校级月考)如图,网格中的每个小正方形的边长都是2,线段交点称做格点.(1)画出△ABC的高CD;(2)连接格点,用一条线段将图中△ABC分成面积相等的两部分;(3)直接写出△ABC 的面积是.28.(2021春•鼓楼区校级月考)我们知道,三角形具有性质:三条角平分线相交于一点,三条中线相交于一点.事实上,三角形还具有性质:三条高所在直线相交于一点.如图,在由小正方形组成的4×3的网格中,三角形的顶点都在小正方形的格点上.请运用上述三角形的性质,在该网格中,仅用无刻度的直尺,作出AC边上的高BH,再作出BC边上的高AK.(不写作法,保留作图痕迹)六.作图—代数计算作图(共1小题)29.(2021秋•诸暨市期中)如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中解答下面问题.(1)图中线段AB的两端点都落在格点(即小正方形的顶点)上,求出AB的长度;(2)再以AB为一边画一个等腰三角形ABC,使点C在格点上,且另两边的长都是无理数;(3)请直接写出符合(2)中条件的等腰三角形ABC 的顶点C的个数.巩固提升一、单选题1.(2021·衢州市实验学校教育集团(衢州学院附属学校教育集团)八年级期末)如图,在,OA OB 上分别截取,OD OE ,使OD OE =,再分别以点,D E 为圆心,以大于12DE 的长为半径作弧,两弧在AOB ∠内交于点C ,作射线,OC OC 就是AOB ∠的角平分线.这是因为连结,CD CE ,可得到COD COE ≌,根据全等三角形对应角相等,可得COD COE ∠=∠.在这个过程中,得到COD COE ≌的条件是( )A .SASB .AASC .ASAD .SSS2.(2021·浙江八年级期末)如图是用直尺和圆规作一个角等于已知角的示意图,说明O O ∠'=∠的依据是( )A .SASB .SSSC .AASD .ASA3.(2020·浙江八年级期末)ABC 内找一点P ,使P 到B 、C 两点的距离相等,并且P 到C 的距离等于A 到C 的距离.下列尺规作图正确的是( )A .B .C .D .4.(2020·浙江八年级期末)如图,在AOB ∠的两边上,分别取OM ON =,再分别过点M 、N 作OA 、OB 的垂线,交点为P ,画射线OP ,则OP 平分AOB ∠的依据是( )A .SSSB .SASC .AASD .HL5.(2020·浙江八年级期末)如图,已知ABC ,求作一点P ,使P 到A ∠的两边的距离相等,且PA PB =、下列确定P 点的方法正确的是( )A .P 为AB ∠∠、两角平分线的交点B .P 为AC AB 、两边上的高的交点 C .P 为AC AB 、两边的垂直平分线的交点D .P 为A ∠的角平分线与AB 的垂直平分线的交点二、填空题 6.(2019·浙江八年级期末)如图,依据尺规作图的痕迹,计算∠α=________°.7.(2019·浙江杭州·八年级月考)用直尺和圆规作一个角等于已知角的示意图如下,则要说明D O C DOC '''∠=∠,需要证明D O C DOC '''∆∆≌,则两个三角形全等的依据是________(写出全等简写).8.(2018·浙江全国·)用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC =∠BOC 的依据是_______.9.(2020·浙江高照实验学校八年级月考)如图,在ABC 中,∠C =90°,∠B =30°,以点A 为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于12MN的长为半径画弧,两弧交于P,连接AP并延长交BC于点D,则∠ADB=_____度.10.(2019·浙江杭州市·)尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于12CD长为半径画弧,两弧交于点P,作射线OP.由作法得△OCP≌△ODP的根据是_________.三、解答题11.(2019·浙江八年级期中)如图,在△ABC中,AB=AC,∠ABC=76°.(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.12.(2021·浙江八年级期末)电信部门要修建一座电视信号发射塔,如图,按照设计要求,发射塔到两个城镇A,B的电网必须相等,到两条高速公路m和n的距离也必须相等,发射塔应修建在什么位置,从图中标出.(保留作图痕迹,说明理由)13.(2020·浙江)已知ABC ,用尺规作图:(1)作AC 边上的中线;(2)画AB 边上的高.14.(2019·浙江宁波·八年级期中)某小区为方便M 、N 两幢住宅楼的住户投放分类后的垃圾,拟在小区主路AB AC 、的交叉区域内设置一个垃圾投放点P ,现要求P 点到两条道路的距离相等,且使PM PN =,请你通过尺规作图找出这一P 点(不写作法,保留作图痕迹)15.(2020·浙江八年级期末)已知:线段c 和αβ∠∠,求作:ABC ,使得AB c A B αβ=∠=∠∠=∠,,(不写作法,但保留作图痕迹)16.(2020·浙江)已知线段a 及锐角α,用直尺和圆规作ABC ,使B α∠=∠,AB BC a ==.17.(2020·浙江)如图,线段a ,利用直尺和圆规按照下列要求作出图形.(保留作图痕迹,不要求写作法)(1)作一个等边三角形,边长为a ;(2)在第(1)题的图中,作一个α∠,使30︒=α.18.(2020·浙江八年级期末)如图,BAC ∠和点D .在BAC ∠内部,试求作一点P ,使得点P 到BAC ∠两边的距离相等,同时到点A ,D 的距离也相等.(不写作法,保留作图痕迹)19.(2021·浙江八年级期末)如图,已知ABC ,请按下列要求作图:(1)作BC边上的中线.(2)用直尺和圆规作ABC的角平分线CG.≌(使点D与A对应,点E与B对应,点F与C对应).(3)用直尺和圆规作DEF,使DEF ABC20.(2020·浙江八年级期中)如图,已知ABC(1)用直尺和圆规按下列要求作图:(保留作图痕迹)在BC上作点D,使点D到AB和AC的距离相等;过BE AD交CA的延长线于E;点B作//(2)若AF BE⊥,垂足为F,证明BF EF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在△ABC 中, D 为 BC 中点, BAC 的平分线 AE 于 E, EF ⊥AC 交 AC 的延长线于 G,
E
10.已知,如图,在 Rt△ABC 中,∠ACB=90°,AC=BC,D 为 BC 中点,CE⊥AD 于 E,BF∥AC 交 CE 的延长线于点 F,求证: C AB 垂直平分 DF.
A Q R B P S C
3 .已知,如图, ∠C=90°, 若∠1=∠2, BC=10,BD=6,则 D 到 AB 边的距离是
B
C D
2 1
A
教
4.如图,∠C=90°,DE 垂直平分 AB,∠1:∠2 = 2:3,则 ∠BAC= 度
C
2 1
D
学
A
E
B
挑选学生到 黑板写出自 己的解题步 骤
5.如图,△ABC 中,AD 平分∠BAC,BD=CD,DE、DF 分 A 别垂直于 AB、AC,垂足分别为 E、F,求证:EB=FC 过
E A D B F
教
学
过
四、课堂小结 角平分线的性质和线段垂直平分线的性质是本章的重点,同 学们一定要活学活用,遇到题目时能将角平分线的性质和线段垂直 平分线的性质运用到解题当中。 五、课后作业 报纸“第一期”的 2、3 版面。
程
板 书 设 计 教 学 反 思
E B AB、BC 的垂直平分线交于△ABC 内一点 P,求证:PA=PB=PC. (三)知识拓展与提高练习 7 .如图, CE ⊥ AB 于点 E,BD⊥AC A 于点 D, BD、 CE 交于 点 O,且 AO 平分∠ BAC, 求证: OB=OC.
E O B C D
8.如图,△ABC BAC=120°,D、 点,DE⊥AB,GF BC=15cm,求 EG
A D B E G F C
中 , AB=AC , ∠ F 分别为 AB、AC 的中 ⊥AC,E、G 在 BC 上, 的长度.
9. 如图, DE ⊥ BC 交 ∠ ⊥AB 于 F,EG 求证:BF=CG
A
F B D C G
课题
角平分线性质和线段垂直平分线性质习题课
课型
习题课
教学 目标 具体 要求 教学 重点 难点 教学 方法 学习 方法 教学 工具
1.知识与技能目标:通过题组训练,深化对角平分线性质和线段垂直平分线性质的 理解。 2.过程与方法目标:经历典例的思考与反思的过程,体会利用角平线性质和垂直平 分线性质来解题的思想方法,提升解题的应变能力。 3.情感态度与价值观目标:通过作图、欣赏、设计,来培养学生的审美观念及创新 能力。 重点:掌握线段的垂直平分线、角的平分线的性质,并能应用到具体的题目当中。 难点:线段的垂直平分线和角的平分线的性质的应用。 习题讲解法 习题练习法 三角板、PPT 课件 教师活动 (一)例题精选 例 1 张庄、李庄、马庄的位置如图所示,每两个村庄之间都有 笔直的公路相连,他们计划共同投资达一眼机井,希望机井的位置 到三条道路的距离相等,试确定机井的位置.
马庄 李庄 张庄
学生活动
教 学 过 程 例 2 如图,用直尺和圆规在途中的直线 MN 上找一点 P,使点 P 到射线 OA 和 OB 的距离相等。 B M A N O
学生回答教 师讲解例题 中提出的问 题
(二)练习精选 1. △ABC 中,AB=AC,BC=5cm,作 AB 的垂直平分线交另 一腰 AC 于 D, 连结 BD, 如果△BCD 的周长 17cm, 则腰长为 ( ) A.12cm; B.6cm; C.7cm; D.5cm. 学生做练习 2.如图,已知,△ABC 中 AQ=PQ,PR=PS,PR⊥AB 于 R, 题 PS⊥AC 于 S,则三个结论①AS=AR;②QP∥AR;③△BRP≌△ QSP 中( ) A.全部正确 B.仅①和②正确 C.仅①正确 D.仅①和③正确
