数字电路习题解答习题解答组合
数字电路第三章习题答案
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B
数字电路第三章习题答案
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当 电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在B、 C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
3531736半加器的设计1半加器真值表2输出函数3逻辑图输入输出被加数a加数b4逻辑符号31837ab改为用与非门实现函数表达式变换形式
3-1 分析图示电路，分别写出M=1,M=0时的逻辑函数表达式
即M＝1时，对输入取反，M＝0时不取反。
数字电路第三章习题答案
3-2 分析图示补码电路，要求写出逻辑函数表达式，列出真值表。
3-10 试用与非门设计一个逻辑选择电路。
S1、S0为选择端，A、B为数据输入端。 选择电路的功能见下表。选择电路可 以有反变量输入。
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B FS 1 S 0A B S 1 S 0(A B )S 1 S 0(A BA)B
数字电路第三章习题答案
3-5
Ai 0 0 0 0 1 1 1 1
Si Ai BiCi Ai BiCi Ai BiCi Ai BiCi
数电组合逻辑电路习题含答案)
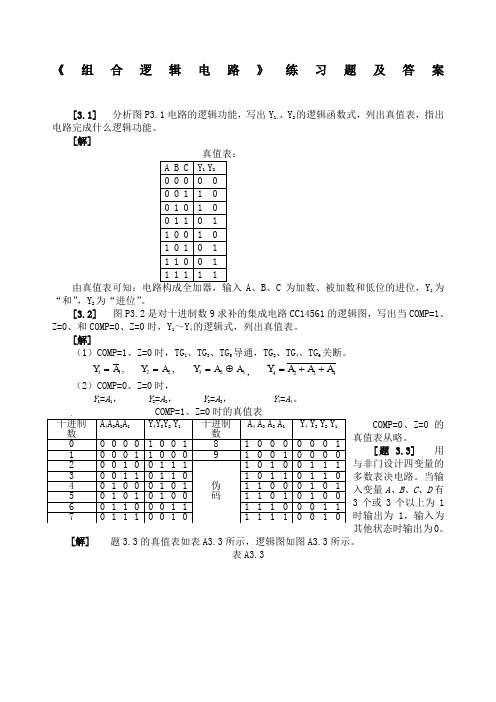
《组合逻辑电路》练习题及答案[3.1] 分析图P3.1电路的逻辑功能，写出Y 1、、Y 2的逻辑函数式，列出真值表，指出电路完成什么逻辑功能。
[解]A 、B 、C 为加数、被加数和低位的进位，Y 1为“和”，Y 2为“进位”。
[3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图，写出当COMP=1、Z=0、和COMP=0、Z=0时，Y 1～Y 4的逻辑式，列出真值表。
[解]（1）COMP=1、Z=0时，TG 1、TG 3、TG 5导通，TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===， 4324A A A Y ++= （2）COMP=0、Z=0时，Y 1=A 1， Y 2=A 2， Y 3=A 3， Y 4=A 4。
COMP=1、Z=0时的真值表 COMP=0、Z=0的真值表从略。
[题 3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1，输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示，逻辑图如图A3.3所示。
表A3.3[3.4] 有一水箱由大、小两台泵M L 和M S 供水，如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作；水位低于C 点而高于B 点时M S 单独工作；水位低于B 点而高于A 点时M L 单独工作；水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。
真值表中的C B A 、C B A 、C B A 、C AB 为约束项，利用卡诺图图A3.4(a)化简后得到： C B A M S +=， B M L =（M S、M L的1状态表示工作，0状态表示停止）。
【数电】组合逻辑电路习题(含答案)
《组合逻辑电路》练习题及答案[3.1]分析图P3.1电路的逻辑功能，写出Y1、、Y2的逻辑函数式，列出真值表，指出电路完成什么逻辑功能。
[解]、Z=0A、1时A3.3所示。
P3.4所示。
M S单独工点时M L和要求电路真值表中的C A 、C B A 、C B A 、C AB 为约束项，利用卡诺图图A3.4(a)化简后得到：C B A M S +=， B M L =（M S 、M L的1状态表示工作，0状态表示停止）。
逻辑图如图A3.4(b)。
[3.5] 设计一个代码转换电路，输入为4位二进制代码，输出为4位循环码。
可以采用各种逻辑功能的门电路来实现。
[解] 题3.5的真值表如表A3.5所示。
D 4、D 3与足上述控制要求的逻辑电路，给出控制四个指示灯状态的高、低电平信号。
74LS148的逻辑图如图P3.7所示，其功能表如表P3.7所示。
表 P3.7 74LS148的功能表A 、B 、C 、L 1、0为0000～2）工作，P3.10输 入21O 123用外加与非门实现之，如图A3.10所示。
[3.11] 画出用4线-16线译码器74LS154（参见题3.9）和门电路产生如下多输出逻辑函数的逻辑图。
[解]电路图如图A3.11所示。
[3.12] 用3线-8线译码器74LS138和门电路设计1位二进制全减器电路。
输入为被减数、减数和来自低位的借位；输出为两数之差及向高位的借位信号。
[解] 设a i 为被减数，b i 为减数，c i-1为来自低位的借位，首先列出全减器真值表，然后将Di ，Ci 表达式写成非-与非形式。
最后外加与非门[3.13] 74LS153[解] [3.14]如表P3.14 [解][3.15][解] [3.16] [解] 与4选1[3.17][解] 则 D =41507632 如图A3.17所示。
[3.18] 用8选1数据选择器CC4512（参见题3.14）产生逻辑函数[解] 将Y 变换成最小项之和形式。
数字电路习题解答习题解答-组合
01
11 1
10 1
1 1 1
4、 用卡诺图法化简下列各式。 AB C 00 0 1 1 01 1 1 11 1 1 10 1 1
(3) F=AB+AB+BC+AC = A+B+C
1、用布尔代数化简逻辑函数表达式。
(1) F=(A+B)(A B) = A B (2) F=A+ABC+ABC+CB+C B = A+BC+BC (3) F=AB+A B+AB+AB = 0 (4) F=(A+B+C)(A+B+C) = (A+B)+CC = A+B (5) F=ABCD+ABD+BCD+ABCD+BC = AB+BC+BD (6) F=AC+ABC+BC+ABC = BC (7) F=AB+ABC+A(B+AB) = 0 (8) F=(A+B)+(A+B)+ (AB)(AB) = 0
F= A0A1A2A3+A4A5A6A7+A8A9A10A11+A12A13A14A15 = A0A1A2A3A4A5A6A7A8A9A10A11A12A13A14A15
只有当变量A0~A15全为0时，F = 1；否则，F = 0。 因此，电路的功能是判断变量是否全部为逻辑“0”。
分析下图所示逻辑电路，列出真值表，说明其逻辑关系。
由真值表可知：M=1 时，完成8421 BCD码到格雷码的转换；
数字电子基础部分答案（康华光）第04章_组合逻辑习题解答
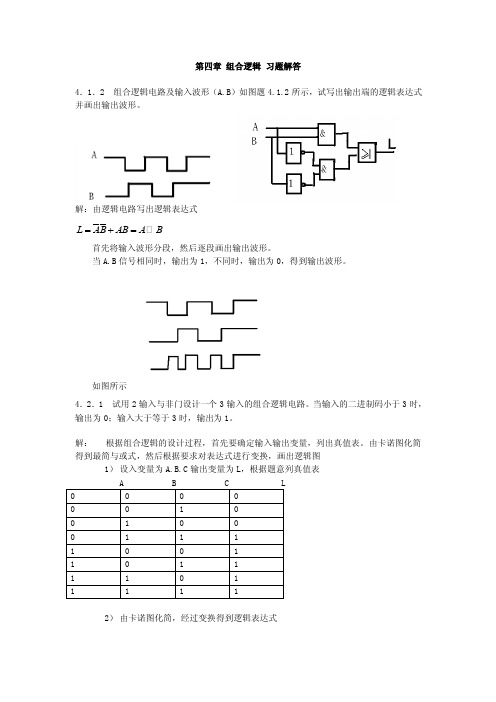
第四章组合逻辑习题解答4．1．2 组合逻辑电路及输入波形（A.B）如图题4.1.2所示，试写出输出端的逻辑表达式并画出输出波形。
解：由逻辑电路写出逻辑表达式=+=L AB AB A B首先将输入波形分段，然后逐段画出输出波形。
当A.B信号相同时，输出为1，不同时，输出为0，得到输出波形。
如图所示4．2．1 试用2输入与非门设计一个3输入的组合逻辑电路。
当输入的二进制码小于3时，输出为0；输入大于等于3时，输出为1。
解：根据组合逻辑的设计过程，首先要确定输入输出变量，列出真值表。
由卡诺图化简得到最简与或式，然后根据要求对表达式进行变换，画出逻辑图1）设入变量为A.B.C输出变量为L，根据题意列真值表2）由卡诺图化简，经过变换得到逻辑表达式L A BC A BC=+=*3）用2输入与非门实现上述逻辑表达式4．2．7 某足球评委会由一位教练和三位球迷组成，对裁判员的判罚进行表决。
当满足以下条件时表示同意；有三人或三人以上同意，或者有两人同意，但其中一人是叫教练。
试用2输入与非门设计该表决电路。
解： 1）设一位教练和三位球迷分别用A和B.C.D表示，并且这些输入变量为1时表示同意，为0时表示不同意，输出L表示表决结果。
L为1时表示同意判罚，为0时表示不同意。
由此列出真值表输入输出A B C D L2）由真值表画卡诺图由卡诺图化简得L=AB+AC+AD+BCD由于规定只能用2输入与非门，将上式变换为两变量的与非——与非运算式 *******L AB AC AD BCD AB AC AD B CD ==3）根据L 的逻辑表达式画出由2输入与非门组成的逻辑电路4．3．3 判断图所示电路在什么条件下产生竞争冒险，怎样修改电路能消除竞争冒险?解： 根据电路图写出逻辑表达式并化简得*L A B BC =+当A=0，C=1时，L B B =+ 有可能产生竞争冒险，为消除可能产生的竞争冒险，增加乘积项使AC ，使 *L A B BC A C =++ ，修改后的电路如图4.4.4 试用74HC147设计键盘编码电路，十个按键分别对应十进制数0～9，编码器的输出为8421BCD码。
【数电】组合逻辑电路习题(含答案)
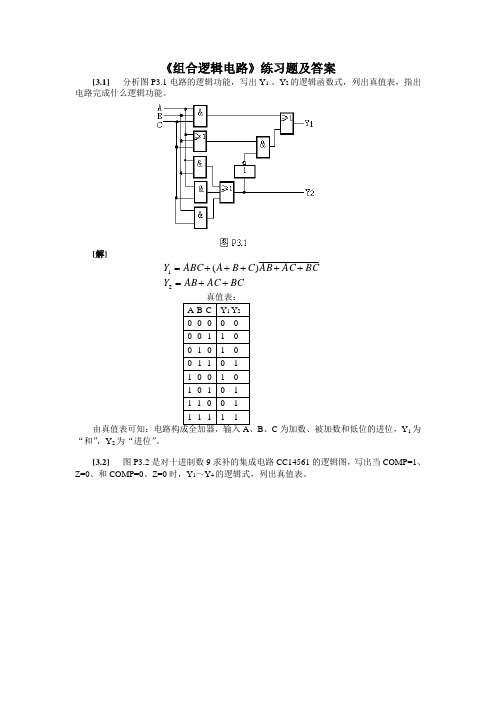
《组合逻辑电路》练习题及答案[3.1] 分析图P3.1电路的逻辑功能，写出Y 1、、Y 2的逻辑函数式，列出真值表，指出电路完成什么逻辑功能。
[解]BCAC AB Y BC AC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位，Y 1为“和”，Y 2为“进位”。
[3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图，写出当COMP=1、Z=0、和COMP=0、Z=0时，Y 1～Y 4的逻辑式，列出真值表。
[解]（1）COMP=1、Z=0时，TG 1、TG 3、TG 5导通，TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===， 4324A A A Y ++=（2）COMP=0、Z=0时，Y 1=A 1， Y 2=A 2， Y 3=A 3， Y 4=A 4。
COMP =0、Z=0的真值表从略。
[题3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1，输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示，逻辑图如图A3.3所示。
ABCD D ABC D C AB CD B A BCD A Y ++++=BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[3.4] 有一水箱由大、小两台泵M L 和M S 供水，如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时，检测元件给出高电平；水面高于检测元件时，检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作；水位低于C 点而高于B 点时M S 单独工作；水位低于B 点而高于A 点时M L 单独工作；水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路，要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。
基础电子技术 习题解答 第8章 组合数字电路习题解答
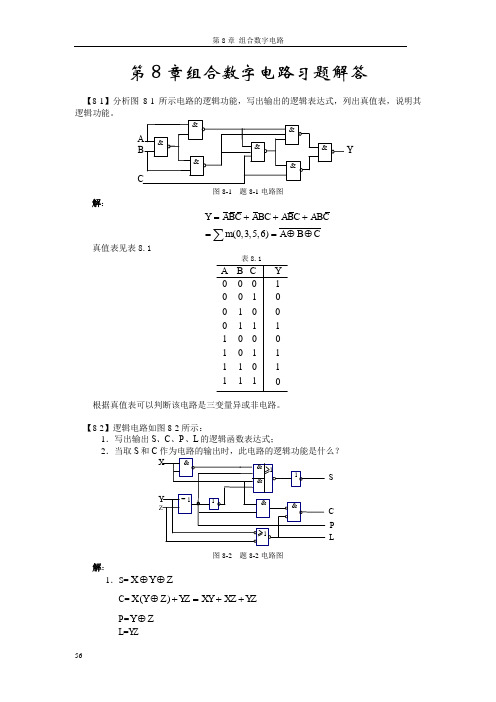
第8章组合数字电路习题解答【8-1】分析图8-1所示电路的逻辑功能，写出输出的逻辑表达式，列出真值表，说明其逻辑功能。
A B &&&&&&&CY图8-1 题8-1电路图解：(0,3,5,6)Y ABC ABC ABC ABC m A B C=+++==⊕⊕∑真值表见表8.1表8.1Y C B A 10001000010011100101110111111000根据真值表可以判断该电路是三变量异或非电路。
【8-2】逻辑电路如图8-2所示：1．写出输出S 、C 、P 、L 的逻辑函数表达式；2．当取S 和C 作为电路的输出时，此电路的逻辑功能是什么？=1&&1&&11&1XYZSC P L图8-2 题8-2电路图解：1．S=X Y Z ⊕⊕C =()X Y Z YZ XY XZ YZ ⊕+=++ P =Y Z ⊕ L =YZ2．当取S 和C 作为电路的输出时，此电路为全加器。
【8-3】 图8-3为由三个全加器构成的电路，试写出其输出F 1，F 2，F 3，F 4的表达式。
A iB iC i-1S i C iA iB iC S i C iA iB iC i-1S i C iX YZ12F 3F 4i-1图8-3 题8-3电路图解：F 1=X Y Z ⊕⊕ 2()F X Y Z =⊕⋅3F XY Z =⊕ 4F XYZ =【8-4】图8-4为集成4位全加器74LS283和或非门构成的电路，已知输入DCBA 为BCD8421码，写出B 2 B 1的表达式，并列表说明输出''''A B C D 为何种编码？A 3A 2A 1A 0S 3 S 2S 1 S 0C 0C 4D' C' B' A'74LS283D C B AB 3 B 2B 1B 041>1>1>图8-4 题8-4电路图解：21B B D B A D C D CB CA ==++++=++若输入DCBA 为BCD8421码，列表可知D 'C 'B 'A '为BCD2421码。
数字电路 第2章习题解答
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。 a、b两图常用于扩展输入 端。 能否用于扩展TTL电路？ 为什么？
F2 A B C D E
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
不能用于扩展TTL电路。 在a图中，当C、D、E中 有低电平输入时，分立元 件与门输入到TTL电路的 电平已大于其VILmax，在逻 辑上可能相当于1，这样 分立元件与门已实现不了 “与”功能了。
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
不能用于扩展TTL电路。 在b图中，当C、D、E均 为低电平时，三个二极管 均截止，100kΩ电阻会使 TTL或非门输入相当于逻 辑1，因而，分立元件或 非门实现不了“或”运算 。
2-21 图2-53中所示门电路均为CMOS电路， 写出各电路输出的表达式。
错误。 ⒉A=0，无论B、C取何值，AB=AC=0 ，故运算
错误。 ⒊1+B=1，A=B=1时，AB=1，故运算正确。
填空
采用5V电压供电的 CMOS门的抗干扰噪 声容限比5V电压供电的TTL门的抗干扰 噪声容限要（ 宽 ）。
TTL门带同类门的负载能力比CMOS门带 同类门的负载能力要（ 弱 ）。
F(A,B,C,D) =∑m（3，5，6，7，10） 约束条件：∑d（0，1，2，4，8）= 0。
用公式法化简函数 F ABCD ABD ACD
回答下列各题
•门电路组成的电路如图所示，请写出F1、 F2的逻辑表达式，当输入如图所示信号波 形时，画出F1、F2端的波形。
A
&
1
C
EN
TTL
&
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
AB CD 00 01 11 10
00
1
01 1 1
1
11
10 1 1
1
设输入只有原变量没有反变量，试用或非门实现下列 函数组合电路：
(1) F(A,B,C,D) = (A+B+C)(A+B) (A+B+C)(B+C)
[解] 先由 F→ F’，在由 F’→ F，得： F = A + B+C
(2) F(A,B,C,D) = Σ(0,1,5,7,10,11,12,13,14,15)
只有当变量A0~A15全为0时，F = 1；否则，F = 0。 因此，电路的功能是判断变量是否全部为逻辑“0”。
分析下图所示逻辑电路，列出真值表，说明其逻辑关系。
X0 X1 X2 X3
A1 A0
这是一个四选一的数据选择器。 真值表如下：
F
A1 A0
F
00
X0
01
X1
10
X2
11
X3
[解] F = A1A0X0 + A1A0X1 + A1A0X2 + A1A0X3
如图所示为数据总线上的一种判零电路，写出F的逻辑表达式， 说明该电路的逻辑功能。
A0
A3 A4
A7
F
A8
A11 A12
A15
[解]
F= A0A1A2A3+A4A5A6A7+A8A9A10A11+A12A13A14A15 = A0A1A2A3A4A5A6A7A8A9A10A11A12A13A14A15
0
0111 0
1000 1
1001 1
1010 1
1011
1
1100 1
1101 0
1110 0
1111 0
F = AB + BD + BC D + ABC (或ACD)
T2.15 用红、黄、绿三个指示灯表示三台设备的工作情况：绿灯亮 表示全部正常；红灯 亮表示有一台不正常；黄灯亮表示有两台不正 常；红、黄灯全亮表示三台都不正常。列出控制电路真值表，并选 出合适的集成电路来实现。
F = AC ABD BCD = (A+C)(A+B+C)(B+C+D) 两次求反后得： F = (A+C) + (A+B+C) + (B+C+D)
(2) F(A,B,C,D) = A+B + B+C AB
[解] 两次求反后得：
F = A+B + B+C + A+B
设输入只有原变量而无反变量，试用最少的三级与非门 实现下列函数：
分析下图所示逻辑电路，其中S3、S2、S1、S0为控制输入端， 列出真值表，说明 F 与 A、B 的关系。
S3 S2
A
F2
B
F1
S1 S0
F1 = A + BS0 + BS1 F2 = ABS2 + ABS3 F = F1F2 = A + BS0 + BS1
S1 S0
F1
S3 S2
F2
00
A
00
1
01
AB
0 1 A+B
10
AB
1 0 A+B
F
11
0
11
A
S3 S2 S1 S0 00×× 01×× 10×× 11××
F=F1F2
F1 F1 F1 F1
S3 S2 S1 S0 ××00 ××01 ××10 ××11
F=F1F2 A AB AB 0
分析下图所示逻辑电路，列出真值表，说明其逻辑功能。
1-15 写出下面逻辑图的函数表达式，要求表出每一级门的输出。
A
AB
B
C
CD
AB(CD+CD)
D
C
CD+CD
D
CD
第一级门
第二级门
第三级门
1-20 输入信号A、B、C的波形如下所示。试画出F1、F2的波形图。
A
B
F1
F2
A
A
B
B
C
C
F1
解：
F2
F1 = A⊕B
F2 = F1⊕C
分析下图所示的逻辑电路，写出表达式并进行简化。
由真值表可知：M=1 时，完成8421 BCD码到格雷码的转换； M=0 时，完成格雷码到8421 BCD码的转换。
在有原变量又有反变量的输入条件下，用与非门设计实现 下列函数的组合电路：
(1) F(A,B,C,D) = Σ(0,2,6,7,10,13,14,15) = ABD ABD BC CD (2) F(A,B,C,D) = Σ(2,4,5,6,7,10) + φ(0,3,8,15) = AB BD
然后，两次求反即可。 ②先求对偶式的最简与非表达式：F’=(A+B)(A+C) =A B AC
再对F’求对偶式：F=(A+B)+(A+C) ③先求F的反函数：F= AB+AC
再对 F 三次求反得：F= (A+B)+(A+C)
(2) F(A,B,C,D) = Σm(0,1,2,4,6,10,14,15) = A+B+C + A+B+C + A+D + C+D
AB CD 00 01 11 10
00
1
01
11
11
11
10 1 1 1 1
AB CD 00 01 11 10
00
11
01
111
11
11
10 1
11
设输入既有原变量又有反变量，用或非门设计实现下列 函数的组合电路：
(1) F(A,B,C,D) = Σ(0,1,2,4,6,10,14,15)
[解] F = AC + ABD +BCD
01
0
11 0
10 0 0
已知输入信号A,B,C,D的波形如下图所示，选择适当的集成逻辑门 电路，设计产生输出 F 波形的组合电路（输入无反变量）。
AB CD 00 01 11 10
00
111
01 1 1
1
11 1
1
10
1
ABCD F
0000
0
0001
1
0010
0
0011
1
0100
1
0101
1
0110
当 M= 1 时：
Y3 = X3
X1
Y1
Y2 = X2 + X3
M
Y1 = X1 + X2
Y0 = X0 + X1
当 M= 0 时：
X2
Y2
Y3 = X3
X3
Y3
Y2 = X2 + X3
Y1 = X1 + X2 + X3
Y0 = X0 + X1 + X2 + X3
列真值表如下：
M= 1 的真值表
X3 X2 X1 X0
M= 0 的真值表
X3 X2 X1 X0
0000
0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
Y3 Y2 Y1 Y0
0000
0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
(2) F=ABCD+ABC D+AB+AD+ABC =AB+AD
AB C 00 01 11 10
AB CD 00 01 11 10
00
11
01 1 1 1
01
1
10 0 0 0
11
1
10
11
4、 用卡诺图法化简下列各式。
(3) F=AB+AB+BC+AC = A+B+C
AB C 00 01
0
1
11 1
AB C 00 01
0
11 1
11 10 11
AB CD 00 01 11 10
00
11
01
111
11 1
1
10
111
用卡诺图法化简下列各式。
(7) F(A,B,C,D) = Σm(0,1,2,5,6,7,8,9,13,14) (8) F(A,B,C,D) = Σm(0,13,14,15) + Σφ(1,2,3,9,10,11)
A B
F
F = AB + B = AB
A
B
F
C
F = AB BABC CABC = AB + AC + BC + BC = AB + BC + BC
分析下图所示的逻辑电路，写出表达式并进行简化。
A
AD
BD
B
BD
F
BC
C CD
D
[解]
F = AD AD BD BD BC CD C
经化简后为：
F = AD + BD + C
AB CD 00 01 11 10
00 1
1
01 1 1 1 1
11
1
10 1 1 1
AB CD 00 01 11 10