机械动力学大作业
机械动力学大作业

曲柄连杆机构的建模与仿真
曲柄连杆机构如图1所示,曲柄AC长90mm,OC距离300mm。
计算β=300时曲柄的v、θ、θ’。
1-1仿真测试
通过ADAMS/View建立的如图1-1-1所示的模型:
图1-1-1曲柄连杆模型
(1)在工具栏中单击仿真控制按钮。
(2)系统打开参数设置对话框,设置为Forever,Steps为0.01,如图1-1-2所示。
图1-2运动仿真
(3)点击开始仿真图标
(4)模型开始运动。
如果曲柄逆时针转动,对旋转运动(Motion_1)单击鼠标右键,选择Modify,在Function(time)一栏的数据前面加上“-”。
开始仿真。
1-2测试仿真结果
(1)在ADAMS工具菜单的Measure中选择,在To Point栏中输入PART3,即曲柄;
(2)在Characteristic栏中选择Translation velocity 以测其速度。
(3)选择Cylindrical坐标系,并选择R选项。
(4)设置完毕单击Apply按钮,弹出测量窗口如图1-2-1曲柄连杆运行一周的速度分量图。
图1-2-1 qubingliangan 测量曲线
(5)重复((1)~(3)步再测量节点2、3沿Y轴方向的速度分量,测量结果如图1-2-2:
图1-2-2 qubingliangan2、3测量曲线。
机械动力学大作业

机械动力学大作业
一、问题及要求
建立单自由度杆机构(有无滑块均可)动力学模型,由静止启动,选择一个固定驱动力矩,绘制原动件在一周内的运动关系线图,具体
机构及参数自拟。
、建立模型
建立如图一所示机构:已知驱动力矩M=20Nm阻力矩M=10 Nm 杆1长120mm转动惯量为J i=0.16kgm2 ;杆3质量为1kg,转动惯量为
j3=0.16kgm2;杆2质量、转动惯量忽略,其他参数如图所示。
求:建立系统运动方程。
二、求解过程
M3图一
方法:利用等效力学模型法进行动力学分析
解:取杆1为等效件,有
f w3
M v= Mi - M3—(1)
jv=ji+02+j3)(—y ⑵
< XWj/
w3120 3
—二—=一=0.75 Wi 160 4
又有(2)可知J V为常数则可知:
Ki
M v=J v i
则错误!未找到引用源。
四、采用ADAMS软件或Matlab/Simulink 环境,建立机械系统的动力学模型,借助软件进行求解计算和结果分析。
(1)利用Adams软件,建模后如图:
图2
图3
(2)当杆1由图1所示位置开始运动一周,机构运动时间为0.03秒, 利用Adam漱件分析杆件1角加速度错误!未找到引用源。
随时间的变化关系图,如图4所示:
图 线系关动运的内周一在件动原
4
图
uoqB 」曰|总3。
\/」e[n6uv
0/SS3
y
s s C6唾
二 N 2
I 」善E。
机械动力学大作业

单自由度杆机构的Adams动力学仿真摘要:文章分析了单自由度的铰链机构的动力学问题,已知原动件曲柄的转矩,绘制输出件摆杆的运动曲线。
首先在Adams软件中构造连杆,添加三个连杆,使其成一定角度,相互连接。
再在两杆之间添加转动副,并且头尾连杆与地相连。
并在曲柄处加转矩,最后进行仿真,并绘出相应图表。
关键词:铰链机构;Adams仿真1、机构模型的建立根据题目要求,选择一个铰链四杆机构——曲柄摇杆机构为模型,其结构简图如图1所示。
其中,曲柄1为原动件。
图1曲柄摇杆机构简图在Adams软件中,建立该曲柄摇杆机构的模型如图2所示。
图2 Adams中的曲柄摇杆机构模型曲柄摇杆机构各连杆的惯性参数参考表1。
杆件的材料均选择钢材(密度ρ=7.801×10-6 kg•mm-3,杨氏模量E=2.07×105 N•mm-2,泊松比μ=0.29)。
表1 传动导杆机构各部件惯性参数2、利用Adams软件添加约束和力矩杆1和地之间有转动副,杆1和杆2、杆2和杆3之间有转动副,杆3和地之间有转动副。
杆1为原动件,在杆1上添加转矩。
转矩大小为30。
图3约束与转矩3、进行仿真点击仿真按钮,开始仿真,选择仿真时间为2s,可以观察到该机构各个时间的运动状态如图4和图5所示。
(a)T=0时刻(b)T=1时刻图4仿真过程中机构模型的运动状态(a)T=1.2时刻(b)T=2时刻图5仿真过程中机构模型的运动状态结论当原动件曲柄的转矩取为30时,点击“后处理”,可以绘制出输出件摆杆的位移曲线、角速度曲线、加速度曲线分别如图10、图11和图12所示。
图10输出件摆杆的位移曲线图11输出件摆杆的角速度曲线图12输出件摆杆的角加速度曲线参考文献[1]陈立平,张云清,任卫群.机械系统动力学分析及ADAMS应用教程[M].北京:清华大学出版社.2005.。
机械动力学作业

仿真运动结束后的如图1-5所示。
图1-5仿真运动结束后的图
建立测量(滑块的位移、速度、加速度)
1)鼠标右键单击需要测量的部件,系统打开右键快捷菜单,选择Measure;
2)系统打开参数对话框,将Characteristic设为CM Position,Component设为X,测量X向位移;
图1-1曲柄滑块机构
本次所使用的运动仿真软件是ADAMS2012版,启动ADAMS/View程序,打开ADAMS软件,进行新建模型,然后在检查和设置建模基本环境,准备工作都完成后,就开始进行几何建模,建模完成图如下图1-2所示。
进行施加运动副和驱动,施加铰接副,在曲柄同地面框架连接,和曲柄连杆之间的连接,以及在连杆和滑块上处通过铰接副将连杆和滑块连接。滑块和地面也要进行棱柱副连接。运动副施加完成后的图,如图1-3所示。
3)点击Apply,出现空白的测量窗口;
4)重复上述步骤,将Characteristic设为CM Velocity,新建测量速度;
5)重复上述步骤,将Characteristic设为CM Acceleration,新建测量加速度;
测量后测得结果如图1-6,1-7,1-8所示。
图1-6滑块位移图
图1-7滑块速度图
图1-3运动副施加完成后的图
定义曲柄的运动
①在主工具箱的运动工具集,选择旋转运动工具图标 ,显示定义旋转运动对话框;
②在Set up栏,输入360;选择JOINT_1,完成转速设置。
定义曲柄运动后,如图1-4所示。
图1-4定义曲柄运动
对曲柄滑块机构进行仿真分析
1)仿真分析
机械原理课程大作业

机械原理课程大作业基于MATLAB平面连杆机构运动学和动力学分析指导老师:王玉丹目录作业一:平面连杆机构运动学分析第2页作业二:平面连杆机构动力学分析第15页作业一L(AE)=70mm,L(AB)=40mm,L(EF)=60mm,L(DE)=35mm,L(CD)=75m m,L(BC)=50mm,原动件以等角速度W1=10rad/s回转。
试以图解法求在θ1=50°时C点的速度和加速度.对机构进行运动分析,写出C点的位置、速度及加速度方程。
解题过程:令AB=r1, BC=r2, CD=r3, DE=r4,AE=r6,EF=r8, AF=r7,角EAF=θ1。
分析:对机构进行位置分析由封闭形ABCDEA可得:r1+r2=r6+r3+r4 (1)由封闭图形AEFA可得:r7=r6+r8 (2)将(1)(2)两式整理可得:r2-r3-r4=-r1+r6-r8+r7=r6【一】(1)位置方程:【二】速度方程:【三】加速度方程:【四】根据位置方程式编制如下函数:【五】进行数据输入,运行程序进行运算。
根据上面分析的θ1 的极限位置取θ1 的范围为40°-55°并均分成15个元素:输出的P、矩阵的第二列到第四列分别是θ2 、θ3 、4θ4 的值,第一列是AF杆的长度r1’。
【六】第二步根据速度方程式编写如下函数:根据第一步得到的数据进行数据输入,运行程序计算各速度值。
程序如下:程序运行得到q矩阵,第一行到第三行分别是a2、a3、a4 的值,第四行是杆AF上滑块运动的速度,即F点的速度。
【七】第三步编写加速度计算函数:【八】根据第一步和第二步输入数据,运行程序得到各加速度的值:【1】计算C点在θ1 =55°,w1 =10rad/s时的速度,加速度:总结数据绘出各构件的位置、速度和加速度的表格如下:【2】输出图像1)角位置程序及输出的图像:2)F点速度程序及输出的图像:3)角加速度程序及输出的图像:4)F点的加速度程序及输出图像:作业二在图示的正弦机构中,已知:L(AB)=100mm,h1=120mm,h2=80mm, W1=10rad/s(常数),滑块2和构件3的重量分别为,G2 =40 N 和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
机械系统动力学大作业

《机械系统动力学》课程作业小组成员:王凌飞 20150702081t王毅 20150702041 指导教师:***学院:机械工程学院专业:机械工程重庆大学机械工程学院二〇一五年十一月机械系统动力学大作业一、 问题描述图1为汽车结构简化模型:图1 汽车结构简化模型图2为汽车结构受力分析:图2 受力分析图已知22120.64m 4000kg 2000N s/m r m c c ====⋅121220000N/m0.9m1.4m k k l l ====r :车辆的回转半径。
初始条件为:0x x θθ====。
外部冲击力矩:)(10t δ。
试用MATLAB 中的ode45函数求解并画出0-5s 内的位移x 和转角θ的响应。
单位冲击函数()t δ的定义:1,()0,t t t δ=⎧=⎨≠⎩,其图像如图3所示。
00.511.5tδ图3 单位冲击函数图像二、求解过程1.系统运动方程不考虑冲击力矩,由图2机构受力分析得到系统运动方程如下:0)()()()(112221112221=-+++-+++θθk l k l x k k c l c l x c c x m (1) 0)()()()(222121112212122211222=++-+++-+θθk l k l x l k l k c l c l x l c l c x mr (2) 考虑t=0时刻,系统受到一个冲击力矩)(10t δ,此时运动学方程表示为:0)()()()(112221112221=-+++-+++θθk l k l x k k c l c l x c c x m (3) 222222211221122112211()()()()10()mr c l c l x l c l c k l k l x l k l k t θθθδ+-+++-++= (4)2.运动方程一阶常微分方程组形式令,,,,4321x x x x x x ====θθ 则t=0时:12212222114121221133422222422112221142211111223()/()/()/()/[10()/()()()]/x x x c c x m l c l c x m k k x m l k l k x m x x x l c l c x l c l c x l k l k x l k l k x mr =⎧⎪=-+---+--⎪⎨=⎪⎪=---+---+⎩ t>0时:12212222114121221133422222422112221142211111223()/()/()/()/[()/()()()]/x x x c c x m l c l c x m k k x m l k l k x m x x x l c l c x l c l c x l k l k x l k l k x mr =⎧⎪=-+---+--⎪⎨=⎪⎪=---+---+⎩ 3. MATLAB 程序求解运动方程ode45函数主程序文件solution.m ,如下所示: clc;clear;r=0.8; m=4000; c1=2000; c2=2000; k1=20000; k2=20000; l1=0.9; l2=1.4; t0=0; tf=5;x0=[0,0,0,0];[t,x]=ode45('f1',[t0 tf],x0); subplot(3,1,1) plot(t,x);subplot(3,1,2) plot(t,x(:,1)); subplot(3,1,3) plot(t,x(:,3));ode45函数微分关系函数文件f1.m ,如下所示:function xdot=f1(t,x) r=0.8; m=4000; c1=2000; c2=2000; k1=20000; k2=20000; l1=0.9; l2=1.4; t0=0; tf=5;xdot=zeros(4,1); xdot(1)=x(2);xdot(2)=-(c1+c2)/m*x(2)-(l2*c2-l1*c1)/m*x(4)-(k1+k2)/m*x(1)-(l2*k2-l1*k1)/m*x(3);xdot(3)=x(4); if t<=0xdot(4)=10/(m*r*r)-(c2*l2-c1*l1)/(m*r*r)*x(2)-(c2*l2*l2+c1*l1*l1)/(m*r*r)*x(4)-(k2*l2-k1*l1)/(m*r*r)*x(1)-(l1*l1*k1+l2*l2*k2)/(m*r*r)*x(3); elsexdot(4)=-(c2*l2-c1*l1)/(m*r*r)*x(2)-(c2*l2*l2+c1*l1*l1)/(m*r*r)*x(4)-(k2*l2-k 1*l1)/(m*r*r)*x(1)-(l1*l1*k1+l2*l2*k2)/(m*r*r)*x(3); end在MATLAB 中运行以上两个程序,即可得0~5s 内汽车系统的位移x 与转角θ的响应。
机械动力学-典型习题

1 k eq 1 k1 k 2 k eq m 1 k3
n
fn
2 6 1 .8 6 ra d / s
n
2
4 1 .6 8 H z
Machinery Dynamics
机械动力学
Raymond Ding ©
6.3 如图所示的系统,重物挂在弹簧上,静变形为δ s 。现
( t ) A n 2 sin n t y
n 2 f n
( t ) m ax A n g y
2
A
g
n
2
0 .0 1 m
Machinery Dynamics
机械动力学
Raymond Ding ©
6.2 如图所示的系统,m=2.5kg,k1=k2=2×105N/m,
Байду номын сангаас
将其重新挂在未变形弹簧的下端,并给予向上的初速度u0 ,求重物的位移响应和从开始运动到首次通过平衡位置 的时间。 y ( t ) A sin( n t )
n
k /m
g /s
y (t ) 0 s y (t ) 0 u 0
Machinery Dynamics
机械动力学
Raymond Ding ©
机械动力学习题课 Chapter A Exercises Analysis of Machinery Dynamics
Machinery Dynamics
机械动力学
Raymond Ding ©
6.1 一物体搁置在水平台面上。当台面沿竖直方向作频率
为5Hz的简谐振动,要使物体不跳离台面,试问对台面的 振幅有何限制? y ( t ) A sin n t
机械系统动力学作业

6
3)、工作辊有大质量差时
图 3-5 在上下工作辊有很大的质量和质量差下固有频率的变化趋势
图 3-6 在上下工作辊有很大的质量和质量差下上下工作辊的主振型差的变化趋势 以上两图是在 m3=30,m2 逐渐减小的情况下得到的,当上下工作辊有很大的质量并且有相对大的差 距时,这里只是对这种变化情况分析 f 和 dh 的变化趋势。由上图 3-5 和图 3-6 可知,在 f4 下,上下工作辊 振型有变化,但是还是维持在很大的高度情况;而在 f3 的情况下有较大的 dh 变化。
各阶振型的图形表示为:
第一阶
第二阶
第三阶
图 2-1 各阶主振型图示
4
第四阶
三、当各参数变化时的分析和优化 3.1 参数[k]和[m]变化对系统的影响
由(2.4)式可知影响固有频率 f 和各阶主振型的因素有[k]和[m]的变化引起,所以这只对这两种情况 进行 MATLAB 计算并画出图形来对比和分析各参数变化时对系统的影响。且影响轧件质量的只要是由上下 工作辊的上下振型差距(dh)决定的。
f2
f3
151.83
481.92
表 2-4 第二阶 -0.4947 -0.2159 0.4555 0.7079
各阶主振型 第三阶 -0.0763 0.7039 0.7019 -0.0778
机械动力学作业

机械动力学作业1、机械动力学的研究内容机械动力学是一门基于Newton力学,研究机械系统宏观动态行为的学科。
该学科的研究对象包括几乎所有具有机械功能的系统,其研究范围涵盖了这类系统的建模与仿真、动力学分析与设计、动力学控制、运行状态监测和故障诊断等。
该学科的主要任务是采用尽可能低的代价使产品在设计、研制、运行各阶段具有最佳的动力学品质。
机械动力学是机械原理的主要组成部分。
它研究机械在运转过程中的受力、机械中各构件的质量与机械运动之间的相互关系,是现代机械设计的理论基础。
研究机械运转过程中能量的平衡和分配关系。
主要研究的是:在已知外力作用下,求具有确定惯性参量的机械系统的真实运动规律;分析机械运动过程中各构件之间的相互作用力;研究回转构件和机构平衡的理论和方法;机械振动的分析;以及机构的分析和综合等等。
研究内容概况6个方面:1、在已知外力作用下,求具有确定惯性参量的机械系统的真实运动规律;分析机械运动过程中各构件之间的相互作用力;研究回转构件和机构平衡的理论和方法;机械振动的分析;以及机构的分析和综合等等。
为了简化问题,常把机械系统看作具有理想、稳定约束的刚体系统处理。
对于单自由度的机械系统,用等效力和等效质量的概念,可以把刚体系统的动力学问题转化为单个刚体的动力学问题;对多自由度机械系统动力学问题一般用拉格朗日方程求解。
机械系统动力学方程常常是多参量非线性微分方程,只在特殊条件下可直接求解,一般情况下需要用数值方法迭代求解许多机械动力学问题可借助电子计算机分析计算机根据输入的外力参量、构件的惯性参量和机械系统的结构信息,自动列出相应的微分方程并解出所要求的运动参量。
2、分析机械运动过程中各构件之间的相互作用力。
这些力的大小和变化规律是设计运动副的结构、分析支承和构件的承载能力以及选择合理润滑方法的依据。
在求出机械真实运动规律后可算出各构件的惯性力,再依据达朗伯原理用静力学方法求出构件间的相互作用力。
机械动力学第二章作业(答案)

第二章习题2- 1如图2-1所示,长度为L 、质量为m 的均质刚性杆由两根刚度为k 的弹簧系住,求杆绕O 点微幅振动的微分方程。
222...2..011T J 2231V 2(sin )(1cos )222()0m 0322ml L Lk mg dT V dtmg k L θθθθθθθ==⋅=⋅+-+=⎛⎫++= ⎪⎝⎭解:设系统处于静平衡位置时势能为,当杆顺时针偏转角时动能:势能:由能量守恒原理,得化简得:2- 2如图2-2所示,质量为m 、半径为r 的圆柱体,可沿水平面作纯滚动,它的圆心O 用刚度为k 弹簧相连,求系统的振动微分方程。
22 (2)2..0111T J ,2221V ()2()03m 02m r J mr k r dT V dtk θθθθθθ⎛⎫=+= ⎪⎝⎭=+=+=解:设系统处于静平衡位置时势能为,当杆顺时针偏转角时动能:势能:由能量守恒原理,得化简得:2- 3如图2-3所示,质量为m 、半径为R 的圆柱体,可沿水平面作纯滚动,与圆心O 距离为a 处用两根刚度为k 的弹簧相连,求系统作微振动的微分方程。
图2- 1 图2- 22.222..220111T J ,2221V (2)[()]2()032()02m R J mR k R a dT V dt mR k R a θθθθθ⎛⎫=+= ⎪⎝⎭=⋅++=++=解:设系统处于静平衡位置时势能为动能:势能:由能量守恒原理,得化简得: 2- 4求图2-4所示弹簧-质量-滑轮系统的振动微分方程(假设滑轮与绳索间无滑动)。
2.222....0111T J ,2221V ()2()0()02m r J Mr k r dT V dt x r x r M m x kx θθθθθ⎛⎫=+= ⎪⎝⎭=⋅+===++=解:设系统处于静平衡位置时势能为动能:势能:由能量守恒原理,得其中,,化简得: 2- 5质量可忽略的刚性杆-质量-弹簧-阻尼器系统参数如图2-5所示,2L 杆处于铅垂位置时系统静平衡,求系统作微振动的微分方程。
动力学大作业-史忠辉

二、运动简图
三、物理几何参数分析
杆件1长度 L1 杆件2长度 L2 杆件3长度 L3 机架间距离 L4
杆2伸出长度
l 杆件2质量
杆1转动惯量
J1 杆件1角速度
杆2转动惯量
J2 杆1与竖竖直线 夹角
m2
ω1
四、受力分析
1.初始状态:颚式破碎机未放入破碎物,整个 机构只受由电机提供的驱动力矩M1,处于空转 状态。 2.工作状态:物料进入颚式破碎机,机构受到 物料对其产生的阻力F。 3.整个机构中,由于等效杆件1与杆件3的质量 影响较小,忽略不计;杆件2可视为均匀杆质 ,质量为m2;系统摩擦力忽略不计。
机械动力学大作业
——颚式破碎机
组员:史忠辉、弓震、张帆、 王振汉、吴博
作业内容
一、内容简介
颚式破碎机俗称颚破,又名老虎口。由动颚和静 颚两块颚板组成破碎腔,模拟动物的两颚运动而 完成物料破碎作业的破碎机。
一、内容简介
颚式破碎机的工作部分是两块 颚板,一是固定颚板,垂直 (或上端略外倾)固定在机体 前壁上,另一是活动颚板,位 置倾斜,与固定颚板形成上大 下小的破碎腔。活动颚板对着 固定颚板做周期性的往复运动。 分开时,物料进入破碎腔,成 品从下部卸出;靠近时,使装 在两块颚板之间的物料受到挤 压,弯折和劈裂作用而破碎。
史忠辉:动力学求解、讲述ppt 弓震 :ppt制作、动力学求解、运动简图 张帆:受力分析、ppt制作、动力学求解 王振汉:方案提供、确定物理参数、动力学 求解 吴博:关键问题的提出与解决、动力学求解
恳请老师、同学指正
五、动力学模型
五、动力学模型
五、动力学模型
六、关键问题提出及解决
关键问题1:颚式破碎机破碎时动力不足无法碎石 解决方法:由M=F×R(不考虑方向,只考虑大小) 可知,增大F或者增大R来增大力矩M,考虑到实际情 况,增大力F合适 关键问题2:如何增大颚式破碎机的破碎比 解决方法:通过控制破碎机的动鄂和定鄂的距离来调 整破碎比 关键问题3:发动机和破碎机之间的槽轮之间是通过带 传动传动的,如果发生打滑怎么办? 解决方法:当破碎机负荷工作时,皮带出现打滑,需 要控制进料的粒度和大小来调整。
机械原理大作业凸轮机构有关公式

机械原理大作业凸轮机构有关公式凸轮机构是机械传动中常见的一种机构,具有转动曲线的特点,可以将驱动轴的转动运动通过凸轮的滚动轮廓来实现对从动件的相应动作控制。
在凸轮机构的设计和分析中,有一些与凸轮曲线有关的公式是十分重要的。
一、凸轮曲线方程凸轮曲线是指凸轮的滚动轮廓,可以通过数学方法来表示。
常见的凸轮曲线方程有圆弧、椭圆、正弦曲线等。
其中,最常用的是圆弧和直线的组合,这种凸轮曲线被称为简谐凸轮曲线。
简谐凸轮曲线方程可以表示为:y = r (1 - cos(θ - θ0))其中,r为凸轮半径,θ为凸轮角度,θ0为凸轮曲线的初相位差。
凸轮在其中一角度θ的位置的坐标可以通过此公式计算得出。
二、凸轮曲线的导数和导数变化率在凸轮机构的设计和分析中,对凸轮曲线的导数和导数变化率也有相当重要的影响。
凸轮的导数表示了凸轮曲线的斜率,而导数的变化率表示了凸轮曲线的曲率。
凸轮曲线的导数可以表示为:dy/dθ = r sin(θ - θ0)凸轮曲线的导数变化率可以表示为:d²y/dθ² = r cos(θ - θ0)通过对凸轮的导数和导数变化率的计算和分析,可以确定从动件的运动状态和速度变化情况,进而进行凸轮机构的设计和优化。
三、凸轮压力和压力角在凸轮机构中,凸轮和从动件之间存在着压力作用。
对于凸轮的任何一个位置,凸轮所施加的压力可以通过力的分解计算得出,并且可以利用凸轮的转角来表示。
凸轮的压力可以表示为:F = P * r * cos(θ - θ0)其中,P为压力系数,r为凸轮半径,θ为凸轮角度,θ0为凸轮曲线的初相位差。
凸轮的压力角可以表示为:φ = atan(dy/dθ)其中,dy/dθ为凸轮曲线的导数。
凸轮的压力角可以用来描述凸轮的主动件施加力的方向和作用范围,对凸轮机构的设计和分析具有指导意义。
以上是凸轮机构常见的几个重要的公式,通过这些公式可以计算和分析凸轮机构的运动学和动力学性能,为凸轮机构的设计和优化提供指导。
机械动力学大作业ppt课件

2
dJV () d
M1
F阻
V3
1
J1A
JS 2
L1 L1
x
2
m2
EF L1 L1 x
2
m3
(xsin e)L1
(L1 x)
2
..
1
.
2
2
dJV () d
11
12
小组分工
方利升:动力学建模、动力学模型求解、ppt制作 游小峰:提出方案、动力学模型求解、ppt制作 何顺清:受力分析、确定物理参数、动力学模型求解、ppt制作 刘 锐:关键问题的提出与解决、动力学模型求解、讲述ppt
13
谢谢观看
THANK YOU
14
பைடு நூலகம்
2(xsin e)(L1 x)
2
可求出来 x x()
2 L1 1 L1 x
v3 2 CE (xsin e)L1
1
1
(L1 x)
则MV MV ()
9
10
05
章节 PART 动力学模型
利用微分方程:
M(V )
JV
()
1
.
2
7
05
章节 PART 动力学模型
取杆1为等效件,求解杆1的角加速度
MV
M1 F阻
V3
1
JV
J1A
J
S
2
2 1
2
m2
vs2
1
2
机械动力学第二次大作业孟富强

动力学方程
J12 q1 J 22 q2 Q2
J11q1 J12q2 Q1
进行Adams建模,对模型进行仿真
04
小组成员
学号 S318070019
姓名 龚锐
任务 讨论选择何种结构,参与物理参数、动力学方程等的计算。
S318070034
刘易
讨论选择何种结构,参与物理参数、动力学方程等的计算。制作PPT并根据小组其他成员意见 修改PPT,并在制作过程中核对计算。 讨论选择何种结构,参与物理参数、动力学方程等的计算。进行Adams建模及运动学仿真。
02
建立模型
该机构自由度为2,其主要参数如下:
齿轮号 1 齿数 56 模数 2 分度圆锥角 45
2
2'
44
30
2
2
45
45
3
62
2
45
03
模型求解
q1
M1 ↓ J1 Z1
q2
0
1
J2+J2' M3 ↑
MH↓
2-2' Z3
H
J3
JH
0
1
由表格法得到如下数据
惯性系数
14 2 5 2 J11 J1 J 2 J 2 (8070039
孟富强 讨论选择何种结构,参与物理参数、动力学方程等的计算。画机构简图,进行计算并求出最 王路遥 后的动力学方程。 讨论选择何种结构,参与物理参数、动力学方程等的计算。解决计算过程遇到的问题,参与 徐文龙 仿真过程。
S318070060
S318070073
感谢聆听 批评指导
机械动力学第二次大作业
DIRECTORY 目录
01
研究生机械动力学与动态特性分析课程大作业
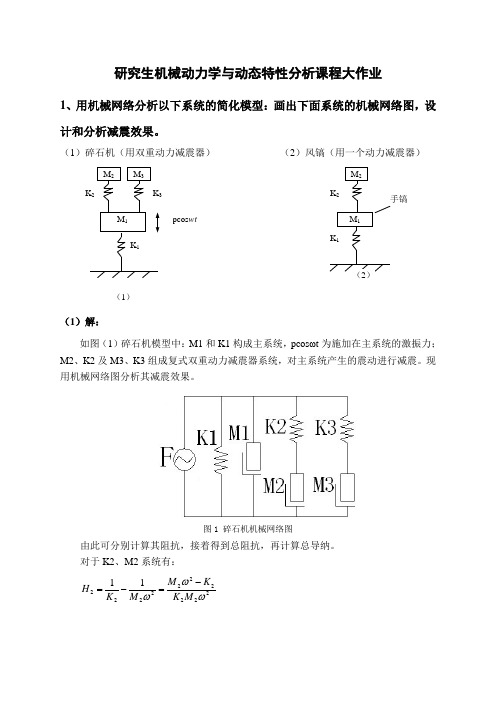
研究生机械动力学与动态特性分析课程大作业1、用机械网络分析以下系统的简化模型:画出下面系统的机械网络图,设计和分析减震效果。
(1)碎石机(用双重动力减震器) (2)风镐(用一个动力减震器)(1)解:如图(1)碎石机模型中:M1和K1构成主系统,pcos ωt 为施加在主系统的激振力;M2、K2及M3、K3组成复式双重动力减震器系统,对主系统产生的震动进行减震。
现用机械网络图分析其减震效果。
图1 碎石机机械网络图由此可分别计算其阻抗,接着得到总阻抗,再计算总导纳。
对于K2、M2系统有:222222222211ωωωM K K M M K H -=-= M 1 M 2K 2K 1 手镐M 1 M 2M 3K 2K 3K 1pcos wt(1)(2)222222221K M M K H Z -==ωω 同理有,对于K3、M3系统:233323233311ωωωM K K M M K H -=-= 323233331K M M K H Z -==ωω 由此可以计算总阻抗为:))(()()())()((32322223322222232332322221132323322222221132211K M K M M K K M M K K M K M K M M K K M M K K M M K M K Z Z M K Z ---+-+---=-+-+-=++-=ωωωωωωωωωωωωωωω 所以总导纳为:233222222323323222211323222)()())()(())((1ωωωωωωωωωM K K M M K K M K M K M M K K M K M Z H -+-+-----== 由此,在M1上作用)cos()(t p t F ω=的激励后,激励振幅为0≥p ,可以求出M1的振动幅值相应为:233222222323323222211323222)()())()(())((ωωωωωωωωωM K K M M K K M K M K M M K pK M K M p H X -+-+---•--=•= 当M1的振动幅值X=0时,即减振效果达到了最好,为此应有:0))((323222=--K M K M ωω解此方程有:222ω=M K 或 233ω=M K 因此,对于碎石机双重动力减震器的设计应该使得222ω=M K 和233ω=M K ,这样才能得到最佳的减振效果。
中石油(北京)机械动力学第一次在线作业

作业第1题动力学反问题是已知机构的(),求解输入转矩和各运动副反力及其变化规律。
您的答案:B题目分数:0.5此题得分:0.5批注:动力学反问题概念第2题动力学正问题是给定机器的输入转矩和工作阻力,求解机器的()。
您的答案:A题目分数:0.5此题得分:0.5批注:动力学正问题概念第3题动态静力分析适用于分析()。
您的答案:A题目分数:0.5此题得分:0.5批注:动力学分类第4题动态静力分析应用于()。
您的答案:C题目分数:0.5此题得分:0.5批注:动力学分类第5题动力分析是()。
您的答案:D题目分数:0.5此题得分:0.5批注:动力分析概念第6题弹性动力分析考虑构件的()。
您的答案:D题目分数:0.5此题得分:0.5批注:弹性动力学分析第7题设机构中的活动构件数位6,含低副数目为2,含高副数目为3,则构件的自由度数为()。
您的答案:B题目分数:0.5此题得分:0.5批注:自由度概念第8题对于不存在多余约束和()的机构,动态静力分析是一个静定问题。
您的答案:A题目分数:0.5此题得分:0.5批注:自由度知识点第9题在高速运动下,惯性载荷是周期性波动的,是引起()的主要激励。
您的答案:A题目分数:0.5此题得分:0.5批注:机构的摆动力和摆动力矩第10题平衡的实质就是采用构件质量再分配等手段完全地或部分地消除()。
您的答案:C题目分数:0.5此题得分:0.5批注:平衡概念第11题质量代换是将构件的质量用若干集中质量来代换,使这些代换质量与原有质量在()上等效。
您的答案:B题目分数:0.5此题得分:0.5批注:质量代换概念第12题两点静代换适用于构件的()恰在两铰链连线上的情况。
您的答案:C题目分数:0.5此题得分:0.5批注:两点静代换第13题两点动代换后的系统与原有系统在()上是完全等效的。
您的答案:D题目分数:0.5此题得分:0.5批注:两点动代换第14题您的答案:B题目分数:0.5此题得分:0.5批注:机构的摆动力和摆动力矩第15题机械动力学是研究机械在力作用下的运动和机械在运动中产生的力的科学。
机械动力学期末试题(卷)与答案解析

机械动力学期末试题(卷)与答案解析一、判断题(每小题2分;共30题;共60分)1、机构平衡问题在本质上是一种以动态静力分析为基础的动力学综合;或动力学设计。
()2、平衡是在运动设计完成之前的一种动力学设计。
(X )3、平衡分析着眼于全部消除或部分消除引起震动的激振力。
()4、优化平衡就是采用优化的方法获得一个绝对最佳解。
(X)5、在动力分析中主要涉及的力是驱动力和生产阻力。
()6、通路定理是用来判断能否实现摆动力完全平衡的理论。
(X )7、惯性力的计算是建立在主动构件作理想运动的假定的基础上的。
()8、当取直线运动的构件作为等效构件时;作用于系统上的全部外力折算到该构件上得到等效力。
()9、无论如何;等效力与机械驱动构件的真实速度无关。
()10、等效质量和等效转动惯量与机械驱动构件的真实速度无关。
()11、摆动力的平衡一定会导致机械结构的复杂化。
(X)12、综合平衡不仅考虑机构在机座上的平衡;同时也考虑运动副动压力的平衡和输入转矩的平衡。
()13、作用于等效构件上的等效力(或等效力矩)所作的功等于作用于系统上的外力所作的功。
(X )14、机器人操作机是一个多自由度的闭环的空间机构。
(X)15、速度越快;系统的固有频率越大。
(X)16、两点动代换后的系统与原有系统在静力学上是完全等效的。
(X)17、质量代换是将构件的质量用若干集中质量来代换;使这些代换质量与原有质量在运动学上等效。
()18、平衡的实质就是采用构件质量再分配等手段完全地或部分地消除惯性载荷。
()19、对于不存在多余约束和多个自由度的机构;动态静力分析是一个静定问题。
(X)20、弹性动力分析考虑构件的弹性变形。
()21、优化综合平衡是一个多目标的优化问题;是一种部分平衡。
()22、摆动力的完全平衡常常会导致机械结构的简单化。
(X)23、机构摆动力矩完全平衡的条件为机构的质量矩为常数。
(X)24、机构摆动力完全平衡的条件为机构的质量矩为常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机电工程学院有限元分析及应用Ansys软件大作业
学号:S314070061
专业:机械工程
学生姓名:郭海山
任课教师:钟宇光
2014年12月18日
一.题目要求:
采用ADAMS软件或Matlab/Simulink环境,建立简单机械系统的动力学模型,借助软件进行求解计算和结果分析。
建立单自由度杆机构(有无滑块均可)动力学模型,由静止启动,选择一固定驱动力矩,,具体机构及参数自拟。
二.模型及结构分析:
利用ADAMS建立如下图1所示单自由度机构模型:
图1单自由度机构模型
结构简图如下图2:
图2 机构简图
曲柄1长度为24cm,质量为1.69kg
滑块2质量为15.6kg
导杆3长度为80cm,质量为5.19kg
部件的材料都是钢,
Material Density: 7.801E-006 kg/mm**3
三.建模:
1.启动adams/view,新建模型model_1。
单位设置成MMKS-mm,kg,N,s,deg。
存储位置设在桌面。
设置工作环境后,利用主工具箱里的基本建模工具,先后建立曲柄1、滑块2和导杆3。
2.曲柄和地面之间,曲柄和连杆之间,连杆和滑块之间,都是转动副。
滑块和地面之间是移动副。
在A,B,C分别放,再在B点添加进行约束。
3.现在给曲柄一个匀速转动。
其值如下图3所示:
图3
最后得到模型如下图4所示:
图4
四.仿真:
标签页 simulation.选择下面图标。
修改仿真时间参数如下图5:
图5
完成仿真观察机构运动状况。
图6为第0.97S时的仿真图像
图6
图7为第2.91S时的仿真图像
图7
图8为第8.24S时的仿真图像
图8
五.数据分析:
运用后处理命令查看个原动件曲柄1的位移,速度加速度随时间变化的图像。
1.原动件位移关系图9:
2.原动件速度关系图10:
图10原动件在x,y,z的速度关系3.原动件加速度关系图11:
图11 曲柄2的加速度变化沿X轴方向曲线
图12曲柄2的加速度变化沿y轴方向曲线
图13曲柄2的加速度变化沿z轴方向曲线。
