计算机组成原理中的三种校验方式上课讲义
(完整版)计算机组成原理作业讲解1_4章答案解析

1.1 概述数字计算机的发展经过了哪几个代?各代的基本特征是什么?略。
1.2 你学习计算机知识后,准备做哪方面的应用?略。
1.3 试举一个你所熟悉的计算机应用例子。
略。
1.4 计算机通常有哪些分类方法?你比较了解的有哪些类型的计算机?略。
1.5 计算机硬件系统的主要指标有哪些?答:机器字长、存储容量、运算速度、可配置外设等。
答:计算机硬件系统的主要指标有:机器字长、存储容量、运算速度等。
1.6 什么是机器字长?它对计算机性能有哪些影响?答:指CPU一次能处理的数据位数。
它影响着计算机的运算速度,硬件成本、指令系统功能,数据处理精度等。
1.7 什么是存储容量?什么是主存?什么是辅存?答:存储容量指的是存储器可以存放数据的数量(如字节数)。
它包括主存容量和辅存容量。
主存指的是CPU能够通过地址线直接访问的存储器。
如内存等。
辅存指的是CPU不能直接访问,必须通过I/O接口和地址变换等方法才能访问的存储器,如硬盘,u盘等。
1.8 根据下列题目的描述,找出最匹配的词或短语,每个词或短语只能使用一次。
(1)为个人使用而设计的计算机,通常有图形显示器、键盘和鼠标。
(2)计算机中的核心部件,它执行程序中的指令。
它具有加法、测试和控制其他部件的功能。
(3)计算机的一个组成部分,运行态的程序和相关数据置于其中。
(4)处理器中根据程序的指令指示运算器、存储器和I/O设备做什么的部件。
(5)嵌入在其他设备中的计算机,运行设计好的应用程序实现相应功能。
(6)在一个芯片中集成几十万到上百万个晶体管的工艺。
(7)管理计算机中的资源以便程序在其中运行的程序。
(8)将高级语言翻译成机器语言的程序。
(9)将指令从助记符号的形式翻译成二进制码的程序。
(10)计算机硬件与其底层软件的特定连接纽带。
供选择的词或短语:1、汇编器2、嵌入式系统3、中央处理器(CPU)4、编译器5、操作系统6、控制器7、机器指令8、台式机或个人计算机9、主存储器 10、VLSI答:(1)8,(2)3,(3)9,(4)6,(5)2,(6)10,(7)5,(8)4,(9)1,(10)7计算机系统有哪些部分组成?硬件由哪些构成?答:计算机系统硬件系统和软件系统组成。
校验和纠错

计算机组成原理 校验和纠错
3、循环冗余校验码 3.1、循环冗余码的概念 循环冗余码(简称CRC码)广泛应用在计 算机网络和通信中。
计算机组成原理 校验和纠错
传送的信息是一串是k位二进制序列,在发 送时,被一个预先选择的“生成多项式” 相除,“生成多项式”长r+1位,相除后得 到r位余数就是校验位,它拼接到原k位有 效 信 息 后 面 即 形 成 k+r 位 的 循 环 冗 余 校 验 码——CRC码。
计算机组成原理 校验和纠错
如果只一位出错,例如,第2字节的第a5位 在传输过程中由0变成了1,校验器就会从 第2字节的横向校验位和第a5位的纵向校 验位上发现错误,并能确定出错位置。
计算机组成原理 校验和纠错
在通常情况下,并不知道一个数据块里有几 个二进制位发生了错误,所以,几乎不把交 叉校验看作是改正错误的办法,而是把它看 作辨认错误的手段。然而与简单的奇、偶校 验相比,交叉校验要保险得多。
计算机组成原理
计算机组成原理 校验和纠错
1、奇偶校验
二进制信息在存取、传送过程中难免会发生 诸如1误变为0,0误变成1的错误。为了保证 信息的正确性,通过软件的方法,对原始数 据进行扩充,加入适当的“校检码”或“纠 错码”,再与原始数据信息一起进行编码, 使之具有发现错误的能力,有的甚至能指出 错误所在的准确位置并自动纠正。
计算机组成原理 校验和纠错
3.2、CRC码计算 传送信息时生成CRC码以及接收时对CRC码校 验都要与“生成多项式”相除,这里除法是 “模2运算”,即二进位运算时不考虑进位 和借位。
计算机组成原理 校验和纠错
做模2除法时,上商的原则是当部分余数 首位为1时商取1,反之商取0,然后按模2 减,求部分余数,这个余数不计高位。当 被除数逐位除完时,最后余数的位数比除 数少一位,该余数就是校验位,它拼接在 有效信息后面组成CRC码。
西电计算机组成原理7

2
校验及纠错码
海明码(Hamming Code) 以8位M+4位K为例,希望校验方案产生效果如 下: 如果故障字全为0,则表示没有检测到差错。 如果故障字仅有1位为1,则表示4个校验位中一 个位出错,不需要纠正。 如果故障字有多位为1,则故障位的数值表示出 错数据位的位置,将这个数据位取反即可纠正。
27
定点数加减运算
只要运算结果超出所能表示的数据范围,就会 发生溢出。发生溢出时,运算结果肯定是错误 的。只要发现运算结果产生溢出,就必须采取 措施防止溢出发生。最简单有效的方法就是增 加补码的二进制编码长度。 只有当两个同符号的数相加(或者是相异符号 数相减)时,运算结果才有可能溢出。而在异 符号的数相加(或者是同符号数相减)时,永 远不会产生溢出。
22
定点数加减运算
例3.2 若两个定点整数-63和-35,利用补 码加法求-63+(-35)=? 解:根据题意,用8位二进制补码表示-63和 -35: [-63]补=11000001 [-35]补=11011101 则[-63+(-35)]补=10011110
23
定点数加减运算
例3.3 若两个定点整数63和35,利用补码减法求63-35=? 解:根据题意,用8位二进制补码表示63和35: [63]补=00111111 [35]补=00100011 而[63-35]补=[63]补+[-35]补 ; 同时,[-35]补 =[[35]补]求补 =11011101,从而求出: 00111111 +11011101 100011100 得到[63-35]补=00011100。
30
定点数加减运算
溢出的判定 (1) 双符号位判决法 若采用两位表示符号,即00表示正号、11表 示负号,一旦发生溢出,则两个符号位就一定 不一致,利用判别两个符号位是否一致便可以 判定是否发生了溢出。 若运算结果两符号分别用S2S1表示,则判别溢 出的逻辑表示式为: VF=S2⊕S1
计算机组成原理课件第三章计算机中的数据表示

基于BCD码进行加减乘除等运算,需考虑进位和借位 问题。
数值型数据运算方法
01
加法运算
通过加法器实现,考虑进位问题。
乘法运算
通过移位和加法操作实现,考虑乘 积的符号和绝对值问题。
03
02
减法运算
通过减法器或加法器配合取反操作 实现,考虑借位问题。
除法运算
通过比较和减法操作实现,考虑商 的符号和余数问题。
计算机组成原理课件第三章 计算机中的数据表示
• 数据表示概述 • 数值型数据的表示 • 非数值型数据的表示 • 数据的逻辑结构与物理结构 • 数据校验与纠错技术 • 计算机中数据表示的应用与发展趋
势
01
数据表示概述
数据表示的定义与重要性
定义
数据表示是指将数据以某种形式编码成 计算机能够识别和处理的形式。它是计 算机科学中的基础概念,涉及到计算机 内部数据的存储、传输和处理方式。
CRC是一种广泛使用的数据校验方法,它通过发送方和接收方共同约定一个多项式,然后发送方在数 据后添加冗余位,使得整个数据能够被该多项式整除。
接收方在接收到数据后,也会使用同样的多项式进行除法运算。如果余数为0,则说明数据正确;如果余 数不为0,则说明数据在传输过程中出现了错误。
纠错编码技术简介
纠错编码技术是一种能够自动纠正数据传输过程中所发生错误的方法。它通过在数据中添加冗余信息,使得接收方能够根据 这些冗余信息来检测和纠正错误。
跨语言文本处理。
汉字编码
GB2312
GBK
简体中文编码标准,收录6763个 常用汉字和682个非汉字图形字符, 采用双字节编码。
扩展GB2312,收录21003个汉字 和图形符号,支持繁体中文和简 体中文。
计算机组成原理课程介绍

计算机组成原理课程
四、教学方法
填鸭似的 灌入式 学生参与思索的 启发式 激发学生主动探求答案积极性的 激发式
老师授课时 在每个章节处安排疑点 在每一堂课的前后连接处提出悬念 激发学生学习的兴趣和探索的欲望,引导学生主动思考
(10)控制单元的设计(4 学时) 组合逻辑设计:组合逻辑控制单元框图、微操作节拍安 排、组合逻辑设计举例。 微程序设计:微程序控制单元框图及工作原理、微指令 的编码方式、微指令地址的形成方式、微指令格式、微程序 设计举例。
计算机组成原理课程
二、教材选择
选用普通高等教育 “十一五” 国家级规划教材《计算机组 成原理第 2 版》(唐朔飞编著,高等教育出版社, 2008 年 1月) 该教材是面向 21 世纪课程教材《计算机组成原理》的第 2 版。
计算机组成原理教学设计
哈尔滨工业大学 唐朔飞
2009年10月30日
计算机组成原理教学设计
课程的内容体系 教材选择 课程讲授 作业安排 实验环节 考题设计 成绩评定
计算机组成原理教学设计
一、课程的内容体系
1.基本描述 课程名称:计算机组成原理 课程英文名称:Principles of Computer Organization 课程性质:计算机科学与技术专业必修的核心专业基础课 总学时:68 讲课学时:52 实验学时:16 先修课程:计算机导论、数字逻辑设计、汇编语言程序设计 后续课程:计算机接口技术、计算机系统结构、操作系统等
哈工大是国家 “985” 重点建设的大学,哈工大计算机 科学与技术学科被认定为国家一级重点学科,我们的人才 培养理念是 “研究型、个性化、精英式” 人才。
计算机组成原理6

可靠性编码
例如,把二进制码0111和1100转换成Gray码:
如果已知Gray码,求对应的二进制码
Bn=Gn Bi=Bi+1 Gi (i<n)
可靠性编码
“五笔”、“搜狗拼音”等。
由外到内
计算机内部
由内到外
输入码有若干:拼音码、字型码、区位码… …
拼音码: da
字型码: dddd
“大”
汉字信息的编码
❖汉字国标码(输入码)
➢ 国家标准GB2312-80编码字符集,称为国标码,每个汉字采用 双字节编码,每个字节使用低7位,最高位为0。
第一个字节
0XXXXXXX 76543210
检查接送的码字 发现 / 改正错误
奇偶校验
❖奇偶校验码
➢ 在数据信息上附加一个校验位,值取决于信息中‘1’的个数 和校验方式
➢ 奇校验:加上校验码位后数据中’1’的个数为奇数 ➢ 偶校验:加上校验码位后数据中’1’的个数为偶数 ➢ 校验位的值=数据位依次异或的结果
❖ 简单奇偶校验
例:假定信息位8位,奇、偶校验位在末尾
(91.76)10 = (1001 0001 . 0111 0110)BCD (0110 0000 0001 .0010)BCD =(601.2)10
计算机中数值的表示
❖ 余3码
➢ BCD码+0011 ➢ 特点:对9的自补码:自身按位取反,可得到对9的补码。
✓ 十进制数字5的余3码为1000,5对9之补是9-5=4,而4的余3码是0111, 它正好是5的余3码1000按位取反而得。
计算机组成原理机器数的定点与浮点、非数值数据的编码表示和数据校验码 (1)

13:41
11
§2.3 机器数的定点与浮点表示
2)精度 所谓精度是指一个数所含有效数值位的位数。 一般来说机器字长越长,它所表示的数的有效位数就越多, 精度就越高:对于字长相同的定点数与浮点数来说,浮点 数虽然扩大了数的表示范围,但这正是以损失精度为代价 的,也就是数轴上各点的排列更稀疏了。
13:41
13:41
10
§2.3 机器数的定点与浮点表示
三、 定点数和浮点数比较
定点数据表示简单,省硬件;浮点数据表示较麻烦, 价格较贵。从以下几个方面来比较它们性能上的主要差距。 1)数值的表示范围 假设定点数和浮点数的字长相同,浮点表示法所能表示的 数值范围将远远大于定点表示法,但是此范围指的只是数 的上下限,它们之间是一些不连续的点,而不是—段连续 的区间。 对于定点数而言,各个点在数轴上的分布是均匀的; 而对于浮点数而言,各个点在数轴上的分布是不均匀的。 越靠近数轴的原点,两个相邻的浮点数之间的距离就越近。
13:41 8
§2.3 机器数的定点与浮点表示
4.浮点数的表示范围
尾数部分给出有效数字的位数,决定了浮点数的表示 精度,尾数占的位数越大,浮点数的表示精度就越高; 阶码部分指明小数点在数据中的位置,决定了浮点 数的表示范围,阶码占的位数越大,浮点数的表示范围 就越大; 通常希望数据表示的范围越大越好、精度越高越好, 但是由于计算机的存储字长是一定的,不能两者兼顾。
• --------在取回这样的浮点数到运算器执行运算时,必须先恢 复该隐藏位。
13:41
7
§2.3 机器数的定点与浮点表示
4. 浮点数的表示范围(阶码用移码表示,尾数用补码表示)
Es,E1 … Em ; Ms . M1 … Mn
“计算机组成原理”中信息校验码的探讨

“计算机组成原理”中信息校验码的探讨【摘要】本文针对“计算机组成原理”中信息校验码的特点,结合多年从事“计算机组成原理”课程的教学经验,探讨了一种“计算机组成原理”结合实例,使用实例法讲解了信息校验码的难点问题。
【关键词】“计算机组成原理”;实例法;信息校验码0 引言“计算机组成原理”是计算机相关专业的一门核心专业基础课,主要讨论计算机基本的部件构成和组成方式,也包括基本的运算操作原理和单元设计思想、操作方式及其实现,“模拟电子技术”、“数字逻辑”是它的先导课程,它的后继课程如“操作系统”、”编译原理”、“汇编语言程序设计”等,它学好与否直接影响着后继课程的学习,“计算机组成原理”在这些课程之间起着承上启下的作用[1-4]。
学习过程中学生普遍感到“计算机组成原理”课程涉及的内容多、抽象、难度大、难学、难懂,“教师难教,学生怕学”的现象在各高校普遍存在,如何把握课程的主线和重点培养学生的学习兴趣、提高教学效果,是从事本课程教学的教师在不断探讨的问题[1];结合多年“计算机组成原理”的教学经验,对学生难理解的信息校验问题提出实例教学法。
1 信息校验问题信息校验问题95%的学生对奇偶校验是能正确理解,但是对海明码校验只有50%的学生能正确理解,如何让更多学生顺利理解海明校验码以及其他校验方法,是一直上课教师思考的问题。
结合遇到的一个问题,通过这个问题的解决,可以让同学们更好的理解海明校验码。
1.1 问题的提出问题如下,有1000瓶一模一样的药,其中至多有一瓶是毒药或者没有毒药,任何喝下毒药的生物都会在一星期之后死亡。
现在,有10只小白鼠和一星期的时间,如何检验出哪瓶瓶子里有毒药或者证明没有毒药?1.2 解决问题算法小白鼠喝了药后,有中毒和不中毒2种情况,一个星期后,有死亡和未死亡2种情况,符合二进制的特征。
在二进制中,10位二进制数可以表示的范围为0000000000至1111111111,转换为十进制为0~1023。
计算机组成原理(校验码)

生成多项式应满足以下条件:
生成多项式的最高位和最低位必须为1。 当被传送信息(CRC码)任何一位发生错误 时,被生成多项式做除后应该使余数不为0。 不同位发生错误时,应该使余数不同。 对余数继续做除,应使余数循环。
CRC举例
信息码为101,生成多项式为:11101,求 其CRC。 解题步骤如下: 1、左移4位得1010000 2、模2除生成多项式得余数为:0011 3、生成传输码为:1010011
出错的位置。
海明码举例
例:0100 解题步骤如下:
n=4,k取3即可 I4=0,I3=1,I2=0,I1=0 各个位的排列规则如下:
7 I4 6 I3 5 I2 4 P3 3 I1 2 P2 1 P1
海明码举例
按如下公式计算校验位的值:
P3= I4 ⊕ I3 ⊕ I2 P2= I4 ⊕ I3 ⊕ I1 P1= I4 ⊕ I2 ⊕ I1
2k>=n+k+1
校验码的生成
[第一步]信息码的权展开式乘以xk,也就是信息
码左移k位。
[第二步] 给出生成多项式。注意,生成多项式的
最高次幂就是校验位的位数,最低次幂必须为0。
[第三步] 第一步所得的多项式除以生成多项式。
所得余数就是校验位的权展开式。注意,该除法 运算是模2运算,即加减时按“异或”进行。
C1 C2 C3 C4 C5 C6 C7 偶校验
海明码
海明码的组成: 由数据位及校验位组合而成的 ,数据位和校验位 交叉排列。
实现原理: 在数据中加入校验位,并把数据的每一个二进制位 分配在几个奇偶校验组中。
海明码计算步骤
根据信息位的位数n确定校验码的位数k 确定校验码的位置 求出校验位的值
计算机组成原理-第4章 存储器-5(校验) [兼容模式]
![计算机组成原理-第4章 存储器-5(校验) [兼容模式]](https://img.taocdn.com/s3/m/d69cb00b6bd97f192279e9a3.png)
• Time redundancy
– is especially helpful for transient or intermittent faults. – Eg, using transactions(回滚,rollback)
• Physical redundancy
– Eg, 747s have four engines but can fly on three – RAID
CRC校验码
CRC(Cyclic Redundancy Check)
• CRC:各类介质存储器、数据通信 • 基于模2运算:不考虑进位和借位
• 模2加减运算:异或(相同为“0”,不同为“1”) • 模2乘:按模2加求部分积之和 • 模2除:按模2减求部分余数 – 部分余数首位为1,商1 – 部分余数首位为0,商0 – 每上商一次,部分余数减少一位。 – 部分余数位数少于除数位数时,结束
分解 i 2 j1 2 j 2 ... 2 j x ( j1 j 2 ... j x )
得:H3由P1和P2校验,H5由P1和P4校验, H6由P2和P4校验,H7由 P1、P2和P4校验, 。。。 即:Pi参与第j1、j2、…、jx个校验位的计算(P1参与H3、H5、H7、…)
• 由电磁干扰或者硬件故障所导致 • 软错误:很少损坏字位,但是并不会避免物理损坏 ,这是可修正的; • 硬错误:会损坏DRAM中的字位而成为物理缺陷, 从而造成数据错误的反复发生。
• 硬盘:数据失效率高达6%(厂商:2%)
– 错误类型:位跳变(可由ECC纠错),物理损坏
容错计算FAULT-TOLERANT COMPUTING
1位纠错海明码的应用
• 上述海明码称为单纠错码(SEC)
计算机组成原理中的三种校验方式

为了使一个系统能检查和纠正一个差错, 为了使一个系统能检查和纠正一个差错,码间最小距离必须至 少是“ 。最小距离为3时 或能纠正一个错,或能检二个错, 少是“3”。最小距离为 时,或能纠正一个错,或能检二个错, 但不能同时纠一个错和检二个错。 但不能同时纠一个错和检二个错。编码信息纠错和检错能力的 进一步提高需要进一步增加码字间的最小距离。 进一步提高需要进一步增加码字间的最小距离。
参与的校验位 P1 P2 P2 P3 P3,P1 P3,P2 P3,P2,P1 P4 P4,P1 P4,P2 P4,P2,P1 P4,P3 P4,P3,P1 P4,P3,P2 P4,P3,P2,P1 P1
4,2,1 (7=4+2+1)
• 各校验位形成公式: 各校验位形成公式: P1=D0⊕D1⊕D3⊕D4⊕D6⊕D8⊕D10 (1) P2 =D0⊕D2⊕D3⊕D5⊕D6⊕D9⊕D10 (2) P3=D1⊕D2⊕D3⊕D7⊕D8⊕D9⊕D10 (3) P4=D4⊕D5⊕D6⊕D7⊕D8⊕D9⊕D10 (4) 按上述方式Pi的取值是采用偶校验时的取值 当采用奇校验 的取值是采用偶校验时的取值, 按上述方式 的取值是采用偶校验时的取值,当采用奇校验 则取反。 连同数据位一起形成了海明码的各位。 时,Pi则取反。这样 连同数据位一起形成了海明码的各位。 则取反 这样Pi连同数据位一起形成了海明码的各位 用海名位号改写P4~P1: 用海名位号改写P P1= H3⊕H5⊕H7⊕H9⊕H11 ⊕H13 ⊕H15 P2= H3⊕H6⊕H7⊕H10⊕H11 ⊕H14 ⊕H15 P3= H5⊕H6⊕H7⊕H12 ⊕H13 ⊕H14 ⊕H15 P4= H9⊕H10⊕H11⊕H12⊕H13 ⊕H14 ⊕H15
• 在接收端校验检测: • 偶校验:P=C ⊕ X0 ⊕X1 ⊕…⊕Xn-1 ⊕
计算机组成原理--海明码的编码和校验方法(易懂)

计算机组成原理--海明码的编码和校验⽅法(易懂)海明码(也叫汉明码)具有⼀位纠错能⼒。
本⽂以1010110这个⼆进制数为例解释海明码的编码和校验⽅法。
编码 确定校验码的位数x 设数据有n位,校验码有x位。
则校验码⼀共有2x种取值⽅式。
其中需要⼀种取值⽅式表⽰数据正确,剩下2x-1种取值⽅式表⽰有⼀位数据出错。
因为编码后的⼆进制串有n+x位,因此x应该满⾜2x-1 ≥ n+x 使不等式成⽴的x的最⼩值就是校验码的位数。
在本例中,n=7,解得x=4。
确定校验码的位置 校验码在⼆进制串中的位置为2的整数幂。
剩下的位置为数据。
如图所⽰。
位置1234567891011内容x1x21x3010x4110 求出校验位的值 以求x2的值为例。
为了直观,将表格中的位置⽤⼆进制表⽰。
位置00010010001101000101011001111000100110101011内容x1x21x3010x4110 为了求出x2,要使所有位置的第⼆位是1的数据(即形如**1*的位置的数据)的异或值为0。
即x2^1^1^0^1^0 = 0。
因此x2 = 1。
同理可得x1 = 0, x3 = 1, x4 = 0。
位置00010010001101000101011001111000100110101011内容01110100110 因此1010110的海明码为01110100110。
校验 假设位置为1011的数据由0变成了1,校验过程为: 将所有位置形如***1, **1*, *1**, 1***的数据分别异或。
***1: 0^1^0^0^1^1 = 1 **1*: 1^1^1^0^1^1 = 1 *1**: 1^0^1^0 = 0 1***: 0^1^1^1 = 1 以上四组中,如果⼀组异或值为1,说明该组中有数据出错了。
***1 **1* 1***的异或都为1,说明出错数据的位置为1011。
海明码简单分析确定校验位个数海明码的码组长度需要符合:2^r – 1 (r代表校验位个数)为什么是这个公式呢?因为:只有这样才能保证校验位⾜够覆盖整个需要校验的码组。
“计算机组成原理”中信息校验码的探讨

“计算机组成原理”中信息校验码的探讨【摘要】本文针对“计算机组成原理”中信息校验码的特点,结合多年从事“计算机组成原理”课程的教学经验,探讨了一种“计算机组成原理”结合实例,使用实例法讲解了信息校验码的难点问题。
【关键词】“计算机组成原理”;实例法;信息校验码0 引言“计算机组成原理”是计算机相关专业的一门核心专业基础课,主要讨论计算机基本的部件构成和组成方式,也包括基本的运算操作原理和单元设计思想、操作方式及其实现,“模拟电子技术”、“数字逻辑”是它的先导课程,它的后继课程如“操作系统”、”编译原理”、“汇编语言程序设计”等,它学好与否直接影响着后继课程的学习,“计算机组成原理”在这些课程之间起着承上启下的作用[1-4]。
学习过程中学生普遍感到“计算机组成原理”课程涉及的内容多、抽象、难度大、难学、难懂,“教师难教,学生怕学”的现象在各高校普遍存在,如何把握课程的主线和重点培养学生的学习兴趣、提高教学效果,是从事本课程教学的教师在不断探讨的问题[1];结合多年“计算机组成原理”的教学经验,对学生难理解的信息校验问题提出实例教学法。
1 信息校验问题信息校验问题95%的学生对奇偶校验是能正确理解,但是对海明码校验只有50%的学生能正确理解,如何让更多学生顺利理解海明校验码以及其他校验方法,是一直上课教师思考的问题。
结合遇到的一个问题,通过这个问题的解决,可以让同学们更好的理解海明校验码。
1.1 问题的提出问题如下,有1000瓶一模一样的药,其中至多有一瓶是毒药或者没有毒药,任何喝下毒药的生物都会在一星期之后死亡。
现在,有10只小白鼠和一星期的时间,如何检验出哪瓶瓶子里有毒药或者证明没有毒药?1.2 解决问题算法小白鼠喝了药后,有中毒和不中毒2种情况,一个星期后,有死亡和未死亡2种情况,符合二进制的特征。
在二进制中,10位二进制数可以表示的范围为0000000000至1111111111,转换为十进制为0~1023。
校验码辅导讲座
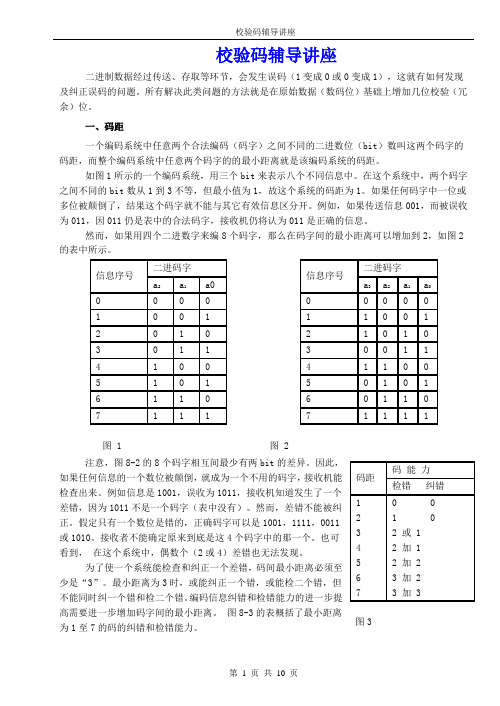
校验码辅导讲座二进制数据经过传送、存取等环节,会发生误码(1变成0或0变成1),这就有如何发现及纠正误码的问题。
所有解决此类问题的方法就是在原始数据(数码位)基础上增加几位校验(冗余)位。
一、码距一个编码系统中任意两个合法编码(码字)之间不同的二进数位(bit )数叫这两个码字的码距,而整个编码系统中任意两个码字的的最小距离就是该编码系统的码距。
如图1所示的一个编码系统,用三个bit 来表示八个不同信息中。
在这个系统中,两个码字之间不同的bit 数从1到3不等,但最小值为1,故这个系统的码距为1。
如果任何码字中一位或多位被颠倒了,结果这个码字就不能与其它有效信息区分开。
例如,如果传送信息001,而被误收为011,因011仍是表中的合法码字,接收机仍将认为011是正确的信息。
然而,如果用四个二进数字来编8个码字,那么在码字间的最小距离可以增加到2,如图2的表中所示。
图 1图 2注意,图8-2的8个码字相互间最少有两bit 的差异。
因此,如果任何信息的一个数位被颠倒,就成为一个不用的码字,接收机能检查出来。
例如信息是1001,误收为1011,接收机知道发生了一个差错,因为1011不是一个码字(表中没有)。
然而,差错不能被纠正。
假定只有一个数位是错的,正确码字可以是1001,1111,0011或1010。
接收者不能确定原来到底是这4个码字中的那一个。
也可看到, 在这个系统中,偶数个(2或4)差错也无法发现。
为了使一个系统能检查和纠正一个差错,码间最小距离必须至少是“3”。
最小距离为3时,或能纠正一个错,或能检二个错,但不能同时纠一个错和检二个错。
编码信息纠错和检错能力的进一步提高需要进一步增加码字间的最小距离。
图8-3的表概括了最小距离为1至7的码的纠错和检错能力。
图3码距越大,纠错能力越强,但数据冗余也越大,即编码效率低了。
所以,选择码距要取决于特定系统的参数。
数字系统的设计者必须考虑信息发生差错的概率和该系统能容许的最小差错率等因素。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k 1 2~4 5~11 12~26 27~57
r(最小) 2 3 4 5 6
2r-1≥k+r (3.19) (一位出错并纠错并发现两位错) 码距为4
由3.19式计 算可得
2、编码规则
若海明码的最高位号为m,最低位号为1,即: HmHm-1…H2H1,则此海明码的编码规律:
(1)校验位与数据位之和为m,每个校验位Pi在海 明码中被分在位号2i-1的位置,其余各位为数据位, 并按从低向高逐位依次排列的关系分配各数据位。
海明码位号 参与校验的校验位位号 H1 P1 1 H2 P2 2 H3 D0 2,1 (3=2+1) H4 P3 4 H5 D1 4,1 (5=4+1) H6 D2 4,2 (6=4+2) H7 D3 4,2,1 (7=4+2+1) H8 P4 8 H9 D4 8,1 (8=8+1) H10 D5 8,2 (10=8+2) H11 D6 8,2,1 (11=8+2+1) H12 D7 8,4 (12=8+4) H13 D8 8,4,1 (13=8+4+1) H14 D9 8,4,2 (14=8+4+2) H15 D10 8,4,2,1 (15=8+4+2+1)
◇强调指出:海明码校验方法以奇偶校验法为基础, 其校验位不是一个而是一组。海明码校验方法能 够检测出具体错误并纠正。
◇ 海明码的最低目标是能纠正一位错,因此要求 海明码的码距大于或等于3。
海明校验码是Richard Hamming于1950年提出的,目 前仍广泛使用的一种编码方法。
1、原理 (1)特点:能检测出两位同时出错、亦能检测出一位出错
例如:八位信息‘10101011’中共有5个‘1’, 附加校验位后变为九位。
若采用奇校验,则附加的校验位应取‘0’值, 保证1的个数为奇数个即 0 10101011 ;
若采用偶校验则附加的校验位应取‘1’值即 1 10101011 。
奇偶校验的特点:
1、奇偶校验法可检出数据传送过程中奇数个 数位出错的情况;
即:
H15 H14 H13 H12 H11 H10 H9 H8 H7 H6 H5 H4 H3 H2 H1 D10 D9 D8 D7 D6 D5 D4 P4 D3 D2 D1 P3 D0 P2 P1 海明码的每一位用多个校验位一起进行校验, 被校验的位号等于校验它的各校验位位号和; 各校验位的值为它参与校验的数据位的异或。
2、实际中两位同时出错的概率极低,奇偶校
验法简便可靠易行,但它只能发现错误,却不知
错在何处,因而不能自动纠正。
为了使一个系统能检查和纠正一个差错,码间最小距离必须至 少是“3”。最小距离为3时,或能纠正一个错,或能检二个错, 但不能同时纠一个错和检二个错。编码信息纠错和检错能力的 进一步提高需要进一步增加码字间的最小距离。
C =X0 ⊕X1 ⊕…⊕Xn-1
如果采用偶校验,则这组数据加上校验码位后数据 中‘1’的个数应为偶数个。偶校验位形成公式:
C =X0 ⊕X1 ⊕…⊕Xn-1
• 在接收端校验检测:
• 偶校验:P=C ⊕ X0 ⊕X1 ⊕…⊕Xn-1 • 奇校验:P=C ⊕ X0 ⊕X1 ⊕…⊕Xn-1
• 若P=0则无错或有偶数位错,若P=1则有奇数位 错
计算机组成原理中的三种校验方 式
1 奇偶校验法
奇偶校验法是计算机中广泛采用的检查传输数据准 确性的方法。奇偶校验法的原理是:
在每组数据信息上附加一个校验位,校验位的取值 (0或1)取决于这组信息中‘1’的个数和校验方式(奇 或偶校验)。
如果采用奇校验,则这组数据加上校验码位后数据 中‘1’的个数应为奇数个。奇校验位形成公式:
并能自动纠错。 (2)实现原理:
在k个数据位之外加上r个校验位,从而形成一个k十r位 的新码字,当某一位出错后,就会引起相关的几个校验位 的值发生变化,从而达到检错、纠错的目的。
k 位 ( 信 息 位 ) R 位 ( 校 验 位 )
数据位k与校验位r的对应关系:
2r≥k+r+1 (3.18)(一位出错并纠错)
参与的校验位 P1 P2 P2 P1 P3 P3,P1 P3,P2
P3,P2,P1 P4 P4,P1 P4,P2 P4,P2,P1 P4,P3 P4,P3,P1 P4,P3,P2 P4,P3,P2,P1
• 各校验位形成公式: P1=D0⊕D1⊕D3⊕D4⊕D6⊕D8⊕D10 (1) P2 =D0⊕D2⊕D3⊕D5⊕D6⊕D9⊕D10 (2) P3=D1⊕D2⊕D3⊕D7⊕D8⊕D9⊕D10 (3) P4=D4⊕D5⊕D6⊕D7⊕D8⊕D9⊕D10 (4)
按上述方式Pi的取值是采用偶校验时的取值,当采用奇校验 时,Pi则取反。这样Pi连同数据位一起形成了海明码的各位。
用海名位号改写P4~P1:
P1= H3⊕H5⊕H7⊕H9⊕H11 ⊕H13 ⊕H15 P2= H3⊕H6⊕H7⊕H10⊕H11 ⊕H14 ⊕H15 P3= H5⊕H6⊕H7⊕H12 ⊕H13 ⊕H14 ⊕H15 P4= H9⊕H10⊕H11⊕H12⊕H13 ⊕H14 ⊕H15
(2)海明码的每一位码Hi(包括数据位和校验位本 身)由多个校验位校验,其关系是被校验的每一位位
号要等于校验它的各校验位的位号之和。这样安排
的目的,是希望校验的结果能正确反映出出错位的位
号。
1以校验11位数据。设: D10D9D8D7D6D5D4D3D2D1D0为11个数据位, P4P3P2P1分别为四个校验码,则编码规则是: ‐ 海明码的总位数H等于数据位与校验位之和; ‐ 每个校验位Pi排放在2i-1的位置,如P4排放 在第24-1=8位,其余数据位依序排列。
• 码能力 • 码距 检错 纠错
1 00 2 10 3 2或1 4 2加1 5 2加2 6 3加2 7 3加3
码距越大,纠错能力越强,但数据 冗余也越大,即编码效率低了。所 以,选择码距要取决于特定系统的 参数。
2 海明码校验方法
◇ 海明码是一种比较常用的纠错码,它实际上是 一种多重奇偶校验码。其基本思想是将被检验 码分成多个组,每组配备一个奇偶校验位完成 该组的奇偶校验位的功能。当被校验码中某一 位出错时,将会有相关的多个小组出现奇偶校 验错,根据这些组的出错情况便可将错误定位 到某一位上从而即可纠正过来。
