五年级中环杯详解

合集下载

第十一届中环杯数学思维能力训练五年级选拔赛解析

34m/s 340m/s 27s
【解析】让火车和声音行驶相同的时间，那么声音比火车多行驶了 27 秒，也就是多行驶了所以火车行驶的时间是 9180 340 34 30 秒，所以火车拉响汽笛 27 340 9180 米，时距离小明 34 30 1020 米。 7、某校五年级的同学，每人都订阅了《青少年科技报》、《小朋友》、《故事大王》、《少年科学》、《少年文艺》中的至少 2 种刊物，那么，这个年级至少要有（235）名学生，才能保证他们中至少有 10 个人订的报刊杂3 607 ，所以第 2010 位上的数字是第 607 个三位数的个位，即为 706
的个位 6。 4、一个长 42 厘米、宽 24 厘米、高 36 厘米的长方体木块，表面涂上红漆，再把它锯成若干个相同大小的小正方形体且没有废料。则表面没有涂上红漆的小正方体至少有（40）块。【考点】最大公约数，最值思想，立体图形表面染色。
13 10 1 2 6 8 9
4 5
3 11 12
4、有 6 个边长是 2 厘米的等边三角形，2 个边长是 2 厘米的正方形，如图，请你选取其中的一些或全部，分别拼出一个六边形和一个八边形，请画出多边形的拼法。
2厘米
【考点】图形的拼合。【解析】六边形：
2厘米
八边形：
4
3s 2 y A① ，只需凑出 x y 则可替换成 s ，故可由 ① 3 ② 2 得： 3 s 3 x B ②
21s 3 A 2 B s
1 (3 A 2 B) 21
3、将自然数按从小到大的顺序无间隔地排成一列：123456789101112 ，则左起第 2010 位上的数字是（6）。【考点】页码问题。【解析】一位数共有 9 个数码，两位数共有 180 个数码，三位数共有 2700 个数码。

第十三届中环杯五年级初赛试题附答案分析 2

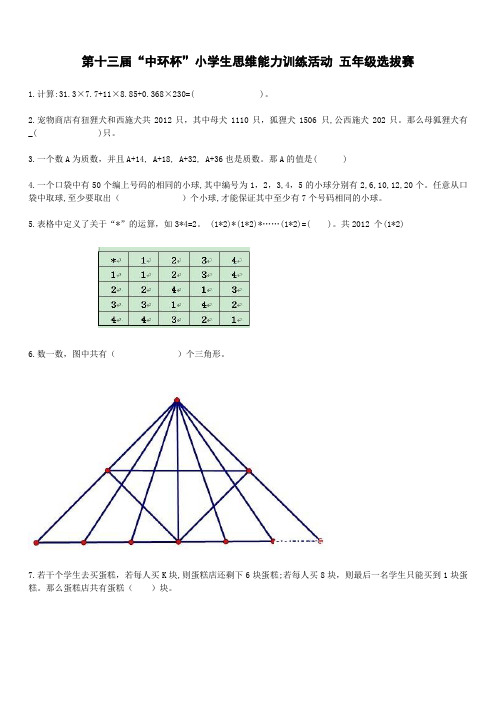
第十三届“中环杯”小学生思维能力训练活动五年级选拔赛1.计算:31.3×7.7+11×8.85+0.368×230=()。

2.宠物商店有狃狸犬和西施犬共2012只，其中母犬1110只，狐狸犬1506 只,公西施犬202只。

那么母狐狸犬有_( )只。

3.一个数A为质数，并且A+14, A+18, A+32, A+36也是质数。

那A的值是( )4.一个口袋中有50个编上号码的相同的小球,其中编号为1，2，3,4，5的小球分别有2,6,10,12,20个。

任意从口袋中取球,至少要取出（）个小球,才能保证其中至少有7个号码相同的小球。

5.表格中定义了关于“*”的运算，如3*4=2。

(1*2)*(1*2)*……(1*2)=()。

共2012 个(1*2)6.数一数，图中共有（）个三角形。

7.若干个学生去买蛋糕，若每人买K块,则蛋糕店还剩下6块蛋糕;若每人买8块，则最后一名学生只能买到1块蛋糕。

那么蛋糕店共有蛋糕（）块。

8.—张正方形纸，如图所示折叠后,构成的图形中，角x的度数是（）。

9.A、B两地相距66千米，甲、丙两人从A地向B地行走，乙从B地向AI地行走。

甲每小时行12千米，乙每小时行10千米,丙每小时行8千米。

三人同时出发（）小时后, 乙刚好走到甲、丙两人距离的中点。

10.有（）个形如abcdabcd的数能被18769 整除。

11.小明带24个自制的纪念品去伦敦奥运会卖。

早上每个纪念品卖7英镑，卖出的纪念品不到总数的一半。

下午他对每个纪念品的价格进行打折，折后的价格仍是—个整数。

下午他卖完了剩下的纪念品。

全天共收入120英镑。

那么早上他卖出了（）个纪念品。

12.如图，在一个四边形ABCD中，AC,BD相交于点O。

作三角形DBC的高DE，联结AE。

若三角形ABO的面积与三角形DCO的面积相等，且DC=17厘米，DE=15厘米，则阴影部分的面积为( )平方厘米。

13.五名选手在一次数学竞赛中共得414分;毎人得分互不相等且都是整数，并且其中得分最高的选手得了92分，那么得分最低的选手至少得（）分，最多得（）分。

第十六届中环杯五年级初赛解析

第十六届“中环杯”五年级(初赛)解析1、计算：. 171720.1522015_______3203⨯+⨯+=【分析】原式 371777317=20++2015=20++2015=49+2015=206420320332020⎛⎫⨯⨯ ⎪⎝⎭2、要使得算式成立，方框内应填的数是________.111{[(1451)]4}7234⨯⨯⨯--+= 【分析】原式变为：11[144]41434⨯⨯-+= 11(144)103411443046⨯⨯-=⨯-==3、把61本书分给某个班级的学生，如果其中至少有1人能分到至少3本书，你们这个班最多有________人.【分析】抽屉原理.（60-1）÷2=30（人）4、有一个数，除以3余数是1，除以5余数是2，那么这个数除以15的余数是________. 【分析】设这个数为3k+1，（3k+1）除以5余2则k 最小为2，所以这个数最小为75、如图，一个三角形的三个内角分别为、和，其中x 、y 都(53)x y +︒(320)x +︒(1030)y +︒是正整数，则x+y =________.【分析】根据内角和180度得：53320103018081313081013x y x y x y y x+++++=+==-由于都是正整数所以x=13，y=2，和为156、三个数两两之间的最大公约数分别是3、4、5，那么这三个数的和最小是________.（5x+3y ）°（10y+30）°（3x+20）°【分析】 A B C 设这三个数为、、不妨设：()A B =A=12a A C =B=15b a b c =1B C =C=20c 12152047⎧⎧⎪⎪⇒⎨⎨⎪⎪⎩⎩（，）3（，）4，，（，）5所以这三个数最小为：、、，和为7、对字母a~z 进行编码（a=1，b=2.，…，z=26），这样每个英文单词（所有单词的字母都认为是小写字母）都可以算出其所有字母编码的乘积p.比如单词good ，其对应的p 值为7×15×15×4=6300（因为g=7,0=15，d=4）.如果某个合数无法表示成任何单词（无论这个单词是不是有意义）的p 值，这样的合数就称为“中环数”.最小的三位数“中环数”为________.【分析】(方法一)要为“中环数”，则分解出的质因子至少有大于26的质因子：大于26的质数为29,31,37…,29×4=116，肯定是中环数，所以只要再验算小于107是否还有中环数，这时会发现106是最小的一个；(方法二)绝大多数小朋友的方法，直接从最小的三位合数开始试.100，102，104，105，106，然后发现106是第一个满足的，.所以答案是106. 106253=⨯8、甲、乙两人同时骑自行车从A 地到C 地，路上会经过B 地.骑了一会，甲问乙：“我们骑了多少公里了？”乙回答：“我们骑的路程相当于这里到B 地距离的.”又骑了10公13里后，甲又问：“我们还要骑多少公里才能到达C 地？”乙回答：“我们还要骑的路程相当于这里到B 地距离的.”A 、C 两地相距________公里（答案写为分数形式）13【分析】3yA第一次对话点在D ，第二次对话点在E.不妨设AD 为x ，则BD 为3x ；设EC 为y ，则BE 为3y.根据题意有，，则AC 的长为：. 03x 3y 1+=()4440443310333x y=x y ==++⨯9、如果一个数不是11的倍数，但是移除一个任意位上的数码后，它就变成了11的倍数了（比如111就是这样的数，无论移除其个位、十位或百位数码，都变成了11的倍数），这样的数定义为“中环数”.四位“中环数”有________个（如果不存在，就写0）.【分析】设这样的四位数为，则根据题意：，由于a 和b 都abcd 11a |b+d-c b |a+d-cc |a+d-bd a c b⎧⎪⎪⎨⎪⎪⎩ 有有有11 有有有11 有有有有有有11|+-是一位数，只能是.那么，则.所以不存在这样的四位数. b=c 11,11||d a 0,0a d ==10、有一天，小明带了100元去购物，在第一家店买了若干件A 商品，在第二家店买了若干件B 商品，在第三家店买了若干件C 商品，在第四家店买了若干件D 商品，在第五家店买了若干件E 商品，在第六家店买了若干件F 商品.六种商品的价格各不相同且都是整数元，小明在六家店里花的钱相同.则小明还剩________元. 【分析】设在每家店都花了x 元，根据题意x 最少含有6个因数. 因为，所以x 最小为，()()()6512111=+=+⨯+22312⨯=而其他的情况花的钱都会超出100这个范围，所以不用考虑，所以剩下（元）. 10012628-⨯=11、将长为31厘米的一条绳子分成三段，每段的长度都是整数，任取其中的两段作为一个长方形的长与宽，可以构成三个长方形.这三个长方形面积之和的最大值为________平方厘米.【分析】设将绳子分成长为a 、b 、c 的三段，则这三个长方形的面积之和，而，当a 、b 、c 的22222()[()()()]6a b c a b a c b c ab ac bc ++--+-+-++=31a b c ++=差最小时面积和最大，即a 、b 、c 取10、10、11，面积和为（平101010111011320⨯+⨯+⨯=方厘米）.12、如图12-1所示，小明从A->B ，毎次都是往一个方向走三格，然后转90度后再走一格，例如图12-2中，从点C 出发可以走到八个位置.那么小明至少走________次才能从点A 到达点B.第12题【分析】答案如图，最少5次.A13、如图，一个大正方形被分割成六个小正方形，如果两个小正方形之间有多于一个的公共点，那么称它们为相邻的.将1、2、3、4、5、6填人右图，每个小正方形内填一个数字，使得相邻的小正方形内数之差永远不是3.不同的填法有________种.【分析】先从相邻最多的F 填起，发现1至6都可以填，有6种，不妨假设填了1，此时发现ABDE 都不能与1的差等于3，所以只能ABDE 为2、3、5、6中的一个；此时发现C 确定为4，一种填法，A 可以有4种（2、3、5、6随便一个），不妨设A 填2，B 有2种填法，D ，E 有2种填法：6×4×2×2=96（种）.14、如图，在梯形ABCD 中，CD=2AB ，点E,F 分别为AD,AB 的中点.若三角形CDG 的面积减去四边形AEGF 的面积等于平方厘米（其中k 为正整教），为了使得梯形24kABCD 的面积为一个正整数，则k 的最小值为________.【分析】22b h.AB a CD ==设，，高为min S =h 224h 23k24k 24k24111k 4h h=222241k h=224k h=12k k=33()124k 4CDG AEGF CDG DEG AEGF DEG CDE a a ah S S S S S S S S a a a a S ah ⨯÷=+⨯÷=-=∴-+∴-=∴⨯⨯-⨯⨯∴∴=⨯=∴= 梯△△△△△△A D F 梯（A B +C D ）（）（+）（）=为整数A B CDFE15、一间房间里住着3个人（小王、小张、小李）和1只狗.毎天早上，3 人起床后都会去做一些曲奇饼干，这样他们饿的话可以随时吃这些饼干.一天早上，小王第—个出门去上班，出门前他将1块曲奇饼干丢给了狗，然后带走并吃掉了剩下的1/3；小张第二个出门去上班，出门前他将1块曲奇饼干丢给了狗，然后带走并吃掉了剩下的1/3；小李第三个出门去上班，出门前他将1块曲奇饼干丢给了狗，然后带走并吃掉了剩下的1/3；晚上，3个人都回到家以后，他们将1块曲奇饼干丟给了狗，然后平分并吃掉了剩下的饼干.在整个过程中，所有的曲奇饼干都不需要被掰碎.那么，小王吃掉的饼干数最少为________块. 【分析】设晚上每人分得n 块，则总数为是整数， 2228165{[(31)1]1}13338n n ++÷+÷+÷+=n 至少为7，总数为79，所以吃掉的饼干数最少为（块）. 7917333-+=16、两辆车在高速公路上行驶，相距100米，两车的速度都是60公里/时.高速公路上设置了不同的速度点（速度点之间相距很远）.每辆车在经过第一个速度点之后，速度都立刻提高到 80公里/时；经过第二个速度点之后，速度都立刻提高到100公里/时；经过第三个速度点之后，速度都立刻提高到120公里/时.当两辆车都经过第三个速度点之后，两车相距________米.【分析】两车在同样的两个速度点之间速度相同相邻速度点之间用的时间也相同 ∴后车需要晚小时到达每个速度点，当后车到达第三速度点时，前车已经离开小时.所0.1600.160以前车在后车前（km ）=200（m ） 0.11200.260⨯=17、这是一个由72个相同小四边形组成的图形，有一些四边形被病毒感染变成黑色.当某个健康的小四边形（白色），其周围至少有两个相邻的小四边形被感染时，则该四边形也将被感染变黑，依次扩散开来.那么至少再增加________个病毒源（即黑色小四边形），可以使整个大图形都被感染.（相邻是指两个小四边形有公共边).①【分析】如右上图所示：标红色阴影的四个区域，他们有共同的特征：比如①红色阴影他所在的红色菱形的外面即使全被感染，菱形内也不会感染，当把①变为病源就可以了其他三个红色阴影一样的道理，所以至少增加4个病源，当然；经验算有了这四个以后，整个图都可以被感染了.18、如图，四边形PQRS 满足PQ=PS=25厘米，QR=RS=15厘米，作ST//QR 与PQ 交于点T.若PT=15厘米，则TS=________厘米（注意：由于我们知道△PQR 与△PSR{PQ =PSQR =RS }的形状和大小完全相同，所以两个三角形的面积相等）.【分析】如图, 3h.=h h 5PB PA =设高为，2=h 5133h=h2510122(15)h=(3)h2510321=(3)h=152101021315224PTS TSRQ PTS TSRQ AB a S a a S a a S S a a h a a ===+++++⨯⨯⨯+== △四边形△四边形，设TSS19、我们用表示一个数的反序数（如果从右往左读一个数，就会得到一个新数，这个新A 数就是原数的反序数，比如=94321），用S （n ）表示数n 的数码和（比如S 12349（123）=1+2+3=6）.有如下的两个条件：（1） n=S （n ）；⨯S(n)（2）找到的所有质因数，计算这些质因数的平方和，再除以2，将结果中的所有0n 移除，最后还是得到n （比如所有质因数平方和除以2后的结果为3025，那么移除0之后变为325）.满足这两个条件的正整数n=________. 【分析】19911729⨯=22927173127(73127)2107291729=⨯+÷=→T S Q R 第18题20、沿着虚线将右图划分为若干“中环块”（表格内每个小正方形的面积均为1），任意两个相邻“中环块”的面积均不同（如果两个“中环块”有至少一条公共边，就称为相邻“中环块”）.图中标了一些数字，每个数字都表示其所在“中环块”的面积.每个“中环块”中可能不含数字，可能含有一个数字，也可能含有多个相同的数字.每列中都画有两个圆圈，其中一个圆圈在表格中，另一个在表格下方.在表格内的圆圈中填上圆圈所在“中环块”的面积，并把这个数字填在与之同列的表格下方圆圈内.最后，表格下方的七个圆圈从左至右构成一个七位数，这个七位数为________.【分析】答案如图55555555522222223333331117777777444444444145432135374541○ ○ 1 4 5 4 7 3 ○ 4 5 ○ 1 ○ 3 4 1 2 3 4 5 ○ ○ ○ ○ ○ ○ ○ ○ ○。

十三届五年级中环杯选拔赛答案

7. 【答案】 97 块
3 能被 8 K 整除。先用盈亏问题思考，人数 6 7 8 K ，即1 所以 K 7 ，
即学生人数是 13 人。所以蛋糕共有 13 8 7 97 块 8. 【答案】 75 9. 【答案】 3.3
66 12 8 2 10 3.3 （小时）
所以 a3 28 。所以 a2 a3 8 。 17. 【答案】 623
2012 y 6 x y 2012 y x y 6 。 6 x 7 y 2012 7 x y 2012 x x y 2012 x 7
1 1 DE EC 15 8 60cm 2 。 2 2
13. 【答案】52，79 如果要考虑最低的得分，那么其余几人的得分要尽量高，则为 91、90、89，则得解为 52。如要考虑最多得分，那要用平均思想解答。 414－92＝322， 322 ÷4＝80.5，则其余四人的分数分别为 82、81、80、79。 14. 【答案】 C 由 D 与 E 所讲的话可判断出 D 与 E 两人间至少有一人是说谎者；若 C 说实话，则 AB 两人均说谎，说谎人数超过两人，矛盾，故 C 是说谎者，因此 AB 两人都说实话，可推知写字的人是 C 。 15. 【答案】18.75 或 6.25 此题两解。第二次相遇，可能在中点的左面，也可能在中点的右面。首先求出 AB 两地的距离：300×2÷（60－40）＝30 分钟，（60＋40）×30 ＝3000 米。再求第二次相遇两人分别走的时间之差，得到两个结果：18.75 分钟或 6.25 分钟。 16. 【答案】 8 首先当 m 2 时，要使得
（1）根据 x y

第九届中环杯数学思维能力训练五年级决赛解析

3
）。
【考点】约数与倍数、质因数分解【解析】设 a, b m ， a Am ， b Bm ，那么 a b 185 可化简成
3
A3m3 Bm 185 ，即 m A3m2 B 185 5 37 ，所以 m 5 ， 25 A3 B 37 ，
第九届“中环杯”小学生思维能力训练活动五年级决赛
一、填空题： 1、 99
999 的尾数为（
99
）。
99
【考点】周期问题【解析】9 的幂的尾数周期是：9，1。 99 是奇数，所以 99
999 的尾数是 9。 b c b c b c b c 注：幂运算需要注意的地方： a a a ， a a a ，
那么从费用上来考虑应选择丙队。
4、如图，三角形 ABC 、三角形 ACD 与三角形 AEF 均为等边三角形， AE BC ，
AF CD ， GH AE 。如果三角形 ABC 的面积是 10cm2 ，那么三角形 EGH 的面积是
多少？
A
A
B E D G C F
H
D
C
B
【考点】直线型面积的计算，平行线比例关系【解析】在直角三角形 AEG 中， EAG 30 ，所以有 EG
所以 285 头牛可以吃 840 285 180 8 天。
2
【答案】8 天 10、 A 、 B 、 C 三人进行小口径步枪射击比赛，每个人射击 6 次，并且都得了 71 分，三人共 18 次的得分情况从小到大排列为：1、1、1、2、2、3、3、5、5、10、10、10、20、20、20、25、 25、 50。已知 A 首先射击两次，共得 22 分；请根据条件判断，是（） C 第一次射击只得 3 分，（填 A 、 B 或 C ）击中了靶心（击中靶心得 50 分）。【考点】逻辑推理【解析】 A 得 71 分，且前两次得到 22 分，那么 A 不可能有一次得到 50 分，且 22 2 20 ，后四次得到 71 22 49 分，如果其中没有 25 分，那么最多还有 2 个 20 分，不管取多少个 20 分，都不可能取到 49 分，所以 49 25 20 3 1 。再考虑 C ，后面 5 次要拿到 68 分，如果其中有一次 50 分，那么剩下 4 次要拿到 18 分，只能是18 10 5 2 1 。所以 C 可能击中靶心。最后考虑 B ，如果 B 击中了靶心，那么他其余 5 次要拿到 21 分，那么还剩下的 20 分和 25 分只能是 C 拿， 3 个 10 分页必须至少由 C 拿 2 个，71 3 20 25 10 10 3 ，C 还得拿 1 个 3 分，但是 3 分已经没有了，矛盾。【答案】 C 二、动手动脑题： 1、50 个数排成一行，除了第 1 个数以外，每个数的 3 倍加 1 恰好等于它后面那个数。这一行最左边的几个数是这样的：0、1、4、13 ，那么，最右边的数除以 7 余几？【考点】周期问题，余数定理【解析】利用余数加法定理和乘法定理，可得到这些数除以 7 的余数，依次为：0、1、4、 6、5、2、0、1、4、6、5、2，不难看出其中的周期性，以“0、1、4、6、5、2”为一个周期。 50 6 8 2 ，所以最右边的数除以 7 余 1。【答案】1 2、甲、乙两人的信纸一样多，信封也一样多，甲写一封信用一张信纸，乙写一封信用三张信纸。结果甲的信封用完时还剩 40 张信纸，乙的信纸用完时还剩 60 个信封。原来他们各有多少个信封和多少张信纸？【考点】盈亏问题【解析】每封信： 1 张信纸多 40 张信纸 3 张信纸多 60 个信封第二个条件可以转化为每封信： 3 张信纸，少 60 3 180 张信纸所以信封有 40 180 3 1 110 个，信纸有110 1 40 150 张。【答案】信封有 110 个，信纸有 150 张。

第十五届中环杯中小学生思维能力训练活动五年级决赛试卷及解析

第15届中环杯决赛试题解析（五年级）一、填空题A （本大题共8小题，每题6分，共48分）：1. 计算：1331649113157112015157++⨯+⨯=++________. 【答案】2 【解答】133164911315711201515731313199315711201515711311130571151331157231231++⨯+⨯+++++=⨯++⎛⎫⨯++ ⎪⎝⎭=⨯⨯⨯++=⨯= 2. 老师布置了一些数学回家作业。

由于小明基础不好，所以小明收到的题目数量比小王收到的题目数量多20道。

若两人收到的题目数量之比为4:3，则小明回家需要完成________道题目。

【答案】80【解答】设小明收到了4x 道题目，则小王收到了3x 道题目，根据题意432020x x x -=⇒=，所以小明需要完成442080x =⨯=道题目。

3. 如图，正八边形的边长为1，将其进行下图的切割，切割后灰色部分面积与斜线部分面积之差为________（大减小）。

【答案】14【解答】如下图，,A B 与,C D 抵消，剩下的中间的正方形可以切割为四个等腰直角三角形，其中三个与灰色部分抵消，留下的一个面积就是14【说明】考察等腰直角三角形用斜边表示的面积公式4. 在一组英文字母串中，第一个字母串1a A =、第二个字母串2a B =，之后每个字母串()3n a n ≥都是由1n a -后面跟着2n a -的反转构成的。

比如321a a a BA ==（我们用i a 表示i a 的反转，就是从右往左读这个字母串得到的结果，比如ABB BBA =、AABA ABAA =），432a a a BAB ==，543a a a BABAB ==，654a a a BABABBAB ==。

那么，这组字母串的前1000个中，有________个是回文字母串（所谓的回文字母串，就是指从左往右读与从右往左读相同，比如ABA 、AABAA ）【答案】667【解答】通过尝试，我们发现只有3a 、6a 、9a 、、999a 不是回文字母串，别的都是，那么可以直接得到答案：一共只有333个非回文字母串，剩下的1000333667-=个都是回文字母串。

第十五届中环杯初赛五年级试题解析

第十五届中环杯初赛五年级试题解析Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++，其中 m,，n 是两个互质的正整数，则10______m n +=。

【考点】分数计算【答案】110 分析：2016910920110162020=-=⨯+=原式。

2、D 老师家里有五个烟囱，这五个烟囱正好从矮到高排成一排，相邻两个烟囱之间的高度差为 2 厘米，其中最高的烟囱又正好等于最矮的两个烟囱的高度之和，则五个烟囱的高度之和是________厘米。

【考点】等差数列，方程【答案】50分析：设这五个烟囱分别为 x-4，x-2，x ，x+2，x+4，则 x+4=x-2+x-4，x=10，和为 5x=50。

3、已知()()22332014a b c d =+⨯-，其中 a 、b 、c 、d 是四个正整数，请你写出满足条件的一个乘法算式：___________。

【考点】数的拆分，分解质因数【答案】答案不唯一分析：2014=1×2014=2×1007=19×106=38×53()()22335932+⨯-4、一个长方体的长、宽分别为 20 厘米、15 厘米，其体积的数值与表面积的数值相等，则它的高为______厘米（答案写为假分数）。

【考点】立体几何，方程【答案】6023分析：设高为 h ，则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=，则。

5、一次中环杯比赛，满分为 100 分，参赛学生中，最高分为 83 分，最低分为 30 分（所有的分数都是整数），一共有 8000 个学生参加，那么至少有_____个学生的分数相同。

【考点】抽屉原理【答案】149分析：833015480005414881481149-+=÷=+=，…,。

第十五届“中环杯”初赛五年级试题解析

第十五届“中环杯”小学生思维能力训练活动五年级选拔赛1、已知2468135713572468m n++++++-=++++++，其中 m,，n 是两个互质的正整数，则10______m n +=。

【考点】分数计算【答案】110 分析：2016910920110162020=-=⨯+=原式。

【考点】等差数列，方程【答案】50分析：设这五个烟囱分别为 x-4，x-2，x ，x+2，x+4，则 x+4=x-2+x-4，x=10，和为 5x=50。

3、已知()()22332014a b c d =+⨯-，其中 a 、b 、c 、d 是四个正整数，请你写出满足条件的一个乘法算式：___________。

【考点】立体几何，方程【答案】6023分析：设高为 h ，则 ()60201520152015223h h h h ⨯⨯=⨯++⨯=，则。

【考点】抽屉原理【答案】149分析：833015480005414881481149-+=÷=+=，…,。

6、对 35个蛋黄月饼进行打包，一共有两种打包规格：大包袋里每包有9 个月饼，小包装里每包有 4个月饼。

第十四届五年级中环杯初赛真题(含详解)

18. 如图， ABCD 是边长为 6 的正方形， ADGH 是一个梯形，点 E、F 分别是 AD、GH 的中点， HF 6，EF 4，EF GH 。联结 HE 并延长交 CD 于点 I ，作 IJ HA ，则 IJ = ________。
19. 如图所示，甲、乙两只蚂蚁在下列圆周上运动。 AC 为大圆的直径，点 B 在 AC 上， AB、BC 分别为两个小圆的直径。甲蚂蚁在大圆上顺时针爬行，乙蚂蚁在两个小圆上沿着箭头所指方向绕“8”字爬行（ A B C B A ）。甲蚂蚁与乙蚂蚁在某一时刻同时从 A 点出发，然后不断地爬行，速度比为 v甲：v乙 =3 : 2 。经过 T1 分钟，两只蚂蚁相遇。接下来，
7. 某次射箭比赛，满分是 10 份，初赛阶段淘汰所有参赛者的 50%。已知进入复赛的选手平均分比全体选手的平均分高 2 分，且进入复赛选手的平均分是 8 分。则被淘汰选手的平均分是_________。
8. 有若干本书和若干本练习本。如果按每 1 本书配 2 本练习本分给一些学生，那么练习本分完时还剩 2 本书；如果按每 3 本书配 5 本练习本分给另一些学生，那么书分完时还剩 1
31 30
7. 某次射箭比赛，满分是 10 份，初赛阶段淘汰所有参赛者的 50%。已知进入复赛的选手平均分比全体选手的平均分高 2 分，且进入复赛选手的平均分是 8 分。则被淘汰选手的平均分是_________。【分析】设共有 2n 人，则进入复赛的选手为 n 人、被淘汰的选手也为 n 人。全体选手平均分为 6 分，总分为 6 2n 12n 分，进入复赛选手总分为 8 n 8n 分，所以被淘汰的选手总分为 12n 8n 4n 分，平均分为 4n n 4分 8. 有若干本书和若干本练习本。如果按每 1 本书配 2 本练习本分给一些学生，那么练习本分完时还剩 2 本书；如果按每 3 本书配 5 本练习本分给另一些学生，那么书分完时还剩 1

第十三届中环杯五年级初赛试题+解析

A O D
B
E
C
分析：因为 SABO SDCO ，所以 SABC SDCB ，由于两个三角形共用底边 BC，所以两个三角形 BC 边上的高相等，于是 AD 与 BC 平行，所以三角形 ACE 中，CE 边上的高为 15 厘米。又在直角三角形 CDE 中，由勾股定理，可知
CE 2 CD2 DE 2 172 152 (17 15)(17 15) 64 ，于是 CE=8 厘米
与1号同色或与5号不同色此时7号线段同时与56号相邻只有一种染色方法与2号线段同时与57相邻只有一种染色方法与1段同时与67号相邻只有一种染色方法与3号同色10号线段同时与89号相邻只有一种染色方法与2号同色综上此时有3号线段与5号同色此时7号线段有2种选择或与1号同色或与2号同色此时8号线段同时与57号相邻只有一种选择9号线段同时与67号相邻只有一种选择号同色此时10号线段也有种染色方法综上共有24
个，1。 6、数一数，图中共有多少个三角形？
分析：
这张图里有 (6 5 4 3 2 1) 2 42 个。
增加一条线，多了 12 个，增加了 2 条线，多了 24 个
两条线一起还增加了一个所以一共有 42 24 1 67 个。 7、若干个小学生去买蛋糕，若每人买 K 块，则蛋糕店还剩下了 6 块蛋糕，若每人买 8 块，则最后一名学生只能买到 1 块蛋糕，那么蛋糕店共有蛋糕多少块？分析：盈亏问题，第一次，每人买 K 快，盈 6 块第二次，每人买 8 块，亏 8 1 7 块人数为 (6 7) (8 K ) 13 (8 K ) ，显然 13 是质数，而 8 K 小于 13，所以 8 K 1 ，共有 13 个学生，蛋糕店有 13 8 7 97 或 13 7 6 97 块蛋糕。 8、一个正方形纸，如图所示折叠后，构成的图形中角 x 的度数是多少？

第十一届中环杯数学思维能力训练五年级决赛解析

2、将一堆练习本平均分给班上的同学，每人可得到 12 本；如果只分给男生，则每个男生可以比原来多分到 9 本。那么该班男生人数与女生人数的比是（ 4 : 3 ）。【考点】比和比例。【解析】平分给全班，每人有 12 本；平分给男生，每人有 12 9 21 本。所以全班人数和男生人数的比是 21:12 7 : 4 ，那么男生人数与女生人数的比是 4 : 3 。 3、 10 个小朋友的平均身高是 1.5 米，其中有一些低于 1.4 米的，他们的平均身高是 1.2 米；另一些高于 1.4 米的，他们的平均身高是 1.6 米。那么最多有（3）人的身高恰好是 1.4 米。【考点】平均数问题，列方程解应用题中设而不求的方法。【解析】假设身高低于 1.4 米的有 x 人，高于 1.4 米的有 y 人：
第十一届“中环杯”小学生思维能力训练活动五年级决赛
一、填空题： 1、计算： 201120111949 19501950 2009 （18891889）。【考点】速算与巧算，乘法意义，重码数。【解析】
201120111949 19501950 2009 1001 20111949 1950 2009 1001 20111949 1949 2009 2009 1001 1949 1949 2009 10011889 18891889
335
9 ，它的个位数字是 9。
6、有 61 只乒乓球，将它们放在 20 个盒子里，不允许有空盒子，每个盒子里最多放 5 只乒乓球，那么最少有（5）个盒子里的乒乓球数量相同。【考点】抽屉原理。【解析】每个盒子尽量放不同数量的乒乓球，1 2 3 4 5 15 ， 61 15 4 1 如果只有 4 个盒子里的乒乓球数量相同，那么最多只能放 60 个乒乓球，所以最少有 5 个盒子里的乒乓球数量相同。 7、如图，两个等腰直角三角形重叠在一起，阴影部分为重合部分，阴影部分的面积是（21.5）平方厘米。

第十四届中环杯五级决赛详解

第十四届中环杯五年级决赛一、填空题（每题 5 分，共 50 分）1 1. 计算：×× 297+22 2×(3 -1 )=_________【剖析】原式 =11××73+1.09 ×11× 27+4=11 ×× 100+4=1199+4=12032. 420× 814× 1616 除以 13 的余数为 __________【剖析】 420× 814×1616≡ 4× 8× 4≡ 128≡ 11(mod13)3.五年级有甲乙两班，甲班学生人数是乙班学生人数的5/7，假如从乙班调 3 人去甲班，甲班学生人数就是乙班学生人数的4/5，甲班原有学生_________人【剖析】本来人数比为甲：乙=5: 7=15: 21 ，人数调整后代数比为甲：乙=4 : 5=16 : 20 ，前后两次总人数不变，所以将总人数变成[(5+7),(4+5)]=36份，比率调整如上，发现人数调整为1份，所以 1 份为 3 人，所以甲班原有学生15× 3=45 人。

4. 已知 990× 991× 992× 993= 966428 A91B40，则AB =【剖析】因为99 丨 990，所以 99 丨966428 A91B40所以 99 丨 96+64+28+ A9 + 1B +40 → 99 丨AB +247→AB=505.如图，△ ABC 面积为 60，E、F 分别为 AB 和 AC 上的点，知足 AB=3AE ，AC=3AF ，点D 是线段 BC 上的动点，设△ FBD 的面积为 S1, △ EDC 的面积为 S2，则 S1× S2的最大值为__________.【剖析】因为AEAF1，所以 EF ∥ BC AB AC32所以 S EBD = S FBD =S1→ S1+S2=S EBC=S ABC =403和一准时，差越小，积越大，所以当S1 =S2时，即 D 为中点时， S1× S2最大为 20×20=4006．如，在每个方框中填入一个数字，使得乘法式建立，个算式乘的最大和最小的之差 __________.【剖析】易得，乘数中下方数的十位1，因十位数字乘上边的数获得的三位数，百位上的 2 乘上边的数获得的四位数。

第十二届中环杯数学思维能力训练五年级决赛解析

SABC AB CQ 2 12 6 2 36 平方厘米；
1 3 3 ；所以 CP AC ；所以 SPBC SABC ； 4 4 4 1 1 因为 MN BC ；所以 SPMN SPBC ； 3 3
因为 AP AC 所以 SPMN SABC
【考点】数字谜，质数，【解析】积的个位数等于两个因数的个位数乘积的个位数；一位质数有 2、3、5、7； 2 3 6, 2 5 10, 2 7 14, 3 5 15, 3 7 21, 5 7 35 ；其中符合积的个位数也是质数的只有 3 5 15 或 5 7 35 ；故积的个位数是 5。

所以 ACQ 180 AQC A 180 90 45 45 ,

BCQ 180 BQC A 180 90 45 45 ;
所以 A ACQ, B BCQ ；所以 AQ CQ, BQ CQ ；所以 AQ BQ CQ AB 2 12 2 6 厘米；
4
2、如图，三角形 ABC 是等腰直角三角形，斜边 AB 12 厘米， MN 是 BC 的， AP 是 AC 的求三角形 PMN 的面积。
1 3
1 ， 4
【考点】等腰直角三角形求面积，等高模型【解析】连接 BP ；过点 C 作 CQ AB ，垂足为 Q ；因为三角形 ABC 是等腰直角三角形；所以 C 90 , A B 45 ；

3 1 1 SABC 36 4 9 平方厘米。 4 3 4
3、有一个棱长为 20 厘米的大正方体，在它的每个顶点处按图所示的方法各作一个小正方体（图中表示的是在一个顶点处作小正方体的方法），于是得到八个小正方体。在这些小正方体空位中，上面四个的棱长为 12 厘米，下面四个的棱长为 13 厘米，所有这八个小正方体公共部分的体积是多少立方厘米？

十二届五年级中环杯决赛答案

4/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
年新好好新
年
年
新年好新好
（2）18 (2 5) 2 4 18
5/5
1/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
有 8889,8888889, 其中不能被 9 整除的最小数是 8889 ，其次为 8888889 。所以能够被 27 整除但不能被 81 整除的第二小数是 80000001 。 8. 答：9 分成三种情况，得 n 1 10 11 n 9 11 n 10 10 2671 ，所以
2/5
第十二届“中环杯”中小学生思维能力训练活动五年级决赛答案
2011÷4＝502„„3，所以木块从左向右翻转 2011 次，“13”在右面(如下图)。此时左面是“3”，后面是“11”，下面是“9”。
木块从前向后翻转 1 次，“9”在正面；翻转 2 次，“11”在正面；翻转 3 次，“7”在正面；翻转 4 次，“5”在正面。所以木块从前向后翻转 4 次，又回到初始状态。 2012÷4＝503„„0，所以最后木块正面的数字是 5。 2. 答：9 平方厘米我们知道，4 个同样的等腰直角三角形可以拼成一个正方形。如图，以斜边 AB 为正方形的边长。
因为正方形的面积是＝AB2＝122＝144(平方厘米)，所以，三角形 ABC 的面积＝144÷4＝ 36(平方厘米)。 1 3 1 又因为在等腰直角三角形 ABC 中，MN＝ BC，PC＝(1－ )AC＝ AC，所以三角形 PMN 的 4 3 4 1 1 1 3 1 1 1 面积是： ×MN×PC＝ × × ×BC×AC＝ ×BC×AC＝ S△ABC＝ ×36＝9(平方厘 2 2 3 4 8 4 4 米)。 3. 答：80 立方厘米如图，上面四个棱长为 12 厘米的小正方体在大正方体的上底面内交出一个边长为 12＋12 －20＝4(厘米)的正方形，由此可知它们的公共部分是一个长方体，底面为 4×4＝16(平方厘米)的正方形，高 12 厘米。

5年级中环杯答案

bb
14
20
；
第十六届“中环杯”中小学生思维能力训练活动五年级决赛
城隍喵
【第 4 题】一位父亲要将他的财产分给他的孩子：首先将 1000 元以及剩余财产的财产的
1 给老大，其次将 2000 元以及剩余 10
1 1 给老二，再次将 3000 元以及剩余财产的给老三，以此类推。结果发现每个孩子都分到了相同 10 10 数量的财产。这位父亲一共有 ________ 个孩子。
第十六届“中环杯”中小学生思维能力训练活动五年级决赛
城隍喵
【第 6 题】一个瓶子里有 1001 个蓝球、 1000 个红球、 1000 个绿球，同时小明手中还有足够的这三种颜色的球。接下来，小明每次从瓶子中取出两个球，然后再按照下面的规则将一个球或两个球放入瓶中。 ⑴如果取出一个蓝球、一个绿球，则放回去一个红球； ⑵如果取出一个红球、一个绿球，则放回去一个红球； ⑶如果取出两个红球，则放回去两个蓝球； ⑷如果取出的两个球不是上面 3 种情况，则放回去一个绿球。不断重复上述操作，直到瓶中只剩下一个球为止。剩下的一个球是 ________ 球（填“红” 、 “蓝” 、 “绿” 或“不确定” ）。【分析与解】操作类问题；奇偶性。取球的情况拿出的两个球 ⑴ ⑵ ⑶ ⑷ 放回的一个球或两个球红、蓝、绿三种颜色的球的个数变化蓝球个数红球个数绿球个数
老大分得 1000 81000 1000
1 9000 元； 10
即每个孩子都分到了 9000 元；这位父亲一共有 81000 9000 9 个孩子。（方法二）因为每个孩子都分到了相同数量的财产；所以老大与老二分得财产相同；老大分得 1000 元以及剩余财产（这里的剩余我们记为 A ）的老二分得 2000 元以及剩余财产（这里的剩余我们记为 B ）的那么 A 的

第十二届中环杯五年级初赛详解

5 ，所以 abc 98 的末位数字为 2 或 7 ，所以 abc 98 462 或 77 或 847 ，所，以 abc 560
或 175 或 945 ，由于这个数能被 3 整除，所以其各位数字和能被 3 整除，经验证，只有 98175 符合要求，所以这个五位数为 98175 ，其各位数字和 30 。 3. 从 1, 2, 3, 4 , 2000 共 2000 个正整数中，最多能取出（
Hale Waihona Puke 共有（）种不同的入座方式种不同的入座方式。【考点】 2012 年第十二届中环杯初赛（五年级）年第十二届中环杯初赛；排列组合，插空法；【解析】如下图，座位选择共有座位选择共有 ACEG , ACEH , ACFH , ADFH , BDFH ，共 5 种（或者可以这
上海学而思教材研发中心
5、、 7 11 的整除判断；【考点】 2012 年第十二届中环杯初赛（五年级）年第十二届中环杯初赛；数论， 3、的整除判断【解析】方法一：能被 3 、 5、 7 、 11 整除，既能被 [3,5,7,11] 1155 整除，五位数中最
大的为 99330 ，但有相同的数字，字比 99330 小一些的是 98175 ，各各位数字不同，其数字和为 30 。方法二：考虑最大，则设这个五位数为 98abc ，由于这个数能被 7 、 11 整除，故这个数能被 77 整除，即能 abc 98 被 77 整除，由于这个数能被 5 整除，所以 c 0或

十三届五年级中环杯决赛答案

第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
一、填空题： 1. 答： 25502400
1 3 1 3 1 2 3 2 3 2 99 3 99 3 99 1 3 1 3 1 1 2 3 2 3 2 1 99 3 99 3 99 1 99
13225, 24336 ，满足我们的要求。
3/6
第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
2. 答： 486 设对一个 2 k 的表格进行染色，有 N k 种染色方法。假设 2 k 表格的最后一列
的颜色从上到下依次 R、G，则对于 2 k 1 的表格，所增加的一列可以有 3 种染色方法，如下图。从而得到递推式： Nk 1 3Nk 。利用乘法原理我们得 N1 3 2 ，所以 N5 2 35 486
用相似模型我们知道
4/6
第十三届“中环杯”中小学生思维能力训练活动五年级决赛答案
知道 AE 、 BF 与 GC 交于同一点，这个点就是点 H ，所以点 H 在线段 GC 上。 20 16 cm 。过点 I 作 KJ AB ，则利用相似如图 5，我们推出 GH GC CH 4 9 9 16 KI GI GH 16 9 5 c m从而推出模型我们有，而 K I I J K J A D ， IJ IB AB 5 45 80 1 1 16 80 640 2 KI cm ，所以 SGHI GH KI cm 61 2 2 9 61 549
R 2T 1 20 X 2T R X 19 。由于这里一共出现了 10 个字母，代表了 10 个 F 1 S

第八届中环杯数学思维能力训练五年级选拔赛解析

3
S1 S4 9 S2 S3 ，将 S1 S4 S2 S3 9 代入，可得： S1 S3 S4 S2 9
S2 S3 9 S3 S2 9 ，即 S3 9 。
注：本题的重要思想是，通过寻找图形的各个部分的面积的等量关系去求不规则图形的面积。这种方法在面对很多看似无法下手的题目的时候有很好的效果。 3、有三个盒子，其中一个装两只黑球，另一个装两只白球，还有一个装了黑球、白球各一个，但是三个盒子上的标签全贴错了。现要求从一个盒子里摸出一个球就能确定三个盒子中的球色，应该如何去做？【考点】逻辑推理。【解析】三个盒子上的标签全贴错了，那么可能的错误的贴法是：正确错误可能一错误可能二 2黑 1黑1白 2白 2白 2黑 1黑1白 1黑1白 2白 2黑
那么我们从贴有“1 黑 1 白”标签的盒子入手：如果摸出来的是黑色球，那么是错误可能一：“1 黑 1 白”的应该贴“2 黑”，“2 黑”的应该贴“2 白”，“2 白”应该贴“2 黑”；
4
如果摸出来的是白色球，那么是错误可能二：“1 黑 1 白”的应该贴“2 白”，“2 白”的应该贴“2 黑”，“2 白”应该贴“1 黑 1 白”。 4、张家和李家共同拥有一块如图所示的平行四边形的田地，田地的中间有一用于灌溉的圆形池塘，点 O 为圆心，现在他们两家想用一条直线把这块田平均分配，并且中间的池塘也要平均分配，你能为他们设计一个分配方案吗？把你的设计图画在原图上，如有必要，请作简要文字说明。【考点】图形的分割。【解析】用一条直线可以把长方形、正方形、圆、 O 平行四边形分成形状、大小完全相同的两部分，而且这样的直线有无数条，每条都经过图形的中心点。回到本题，只需要作出平行四边形的中心点，即作出两条对角线，它们的交点就是平行四边形的中心点，那么该点和圆心 O 确定的直线即所求直线。 5、如图是由边长为 3cm 和 4cm 的两个正方形组成，请按尺寸在发给你的彩纸上画上这一图形，再将它剪成 3 块，拼成一个大的正方形，并求这个大正方形的边长是多少？