高考数学解题模板及做题技巧

合集下载

高考数学答题万能模板

高考数学答题万能模板一、问题分析在高考数学答题过程中，我们常常遇到各种类型的题目，而每个题目又有不同的解题思路和方法。

为了提高答题效率和准确性，我们可以使用以下的万能模板来辅助解答。

二、万能模板1. 解决方案模板当遇到复杂的数学问题时，我们可以使用以下的解决方案模板来有条理地解答问题：- 问题陈述：清晰地陈述题目所给的条件和要求。

问题陈述：清晰地陈述题目所给的条件和要求。

- 思路分析：分析问题的关键点和难点，明确解题思路。

思路分析：分析问题的关键点和难点，明确解题思路。

- 公式运用：根据问题所涉及的数学知识，选择适当的公式或定理进行运用。

公式运用：根据问题所涉及的数学知识，选择适当的公式或定理进行运用。

- 计算过程：按照步骤进行计算，注意每一步的细节和注意事项。

计算过程：按照步骤进行计算，注意每一步的细节和注意事项。

- 最终结果：得出最终的答案，并且注意核对答案的有效性和合理性。

最终结果：得出最终的答案，并且注意核对答案的有效性和合理性。

2. 图形解析模板当遇到涉及图形的题目时，我们可以使用以下的图形解析模板来进行问题分析和解答：- 给定图形的特点描述。

- 根据特点分析，确定所需解题的步骤和方法。

- 运用几何相关定理和公式，进行计算和推理。

- 最后给出答案及解答的过程。

3. 数据分析模板当遇到涉及数据分析的题目时，我们可以使用以下的数据分析模板来进行问题分析和解答：- 给定数据的描述和要求。

- 理清问题的思路和逻辑，确定解题的步骤。

- 运用统计学知识和相关公式，进行数据分析和计算。

- 最后给出答案及解答的过程。

三、总结高考数学答题万能模板可以提供一个结构化的解题方法和思路，帮助我们更有效地解答各种类型的数学题目。

在使用模板时，我们要根据实际题目的要求和题型，灵活运用模板的内容，以达到解题的目的。

希望这份高考数学答题万能模板能对您有所帮助！。

高考数学解答题答题模板

典例1 (12分)已知m ＝(cos ωx ，3cos(ωx ＋π))，n ＝(sin ωx ，cos ωx )，其中ω>0，f (x )＝m·n ，且f (x )相邻两条对称轴之间的距离为π2.(1)若f (α2)＝－34，α∈(0，π2)，求cos α的值；(2)将函数y ＝f (x )的图象上各点的横坐标伸长到原来的2倍，纵坐标不变，然后向左平移π6个单位长度，得到函数y ＝g (x )的图象，求函数y ＝g (x )的单调递增区间．审题路线图 (1)f (x )＝m·n ――――→数量积运算辅助角公式得f (x )――→对称性周期性求出ω()2f α−−−−和差公式cos α (2)y ＝f (x )―――→图象变换y ＝g (x )―――→整体思想g (x )的递增区间评分细则 1.化简f (x )的过程中，诱导公式和二倍角公式的使用各给1分；如果只有最后结果没有过程，则给1分；最后结果正确，但缺少上面的某一步过程，不扣分；2．计算cos α时，算对cos(α－π3)给1分；由cos(α－π3)计算sin(α－π3)时没有考虑范围扣1分；3．第(2)问直接写出x 的不等式没有过程扣1分；最后结果不用区间表示不给分；区间表示式中不标出k ∈Z 不扣分；没有2k π的不给分．跟踪演练1 已知函数f (x )＝3sin ωx cos ωx ＋cos 2ωx －12(ω>0)，其最小正周期为π2.(1)求f (x )的表达式；(2)将函数f (x )的图象向右平移π8个单位长度，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y ＝g (x )的图象，若关于x 的方程g (x )＋k ＝0在区间[0，π2]上有且只有一个实数解，求实数k 的取值范围．解 (1)f (x )＝3sin ωx cos ωx ＋cos 2ωx －12＝32sin 2ωx ＋cos 2ωx ＋12－12＝sin(2ωx ＋π6)，由题意知f (x )的最小正周期T ＝π2，T ＝2π2ω＝πω＝π2，所以ω＝2，所以f (x )＝sin(4x ＋π6)．(2)将f (x )的图象向右平移π8个单位长度后，得到y ＝sin(4x －π3)的图象；再将所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，得到y ＝sin(2x －π3)的图象，所以g (x )＝sin(2x －π3)，因为0≤x ≤π2，所以－π3≤2x －π3≤2π3，所以g (x )∈[－32，1]．又g (x )＋k ＝0在区间[0，π2]上有且只有一个实数解，即函数y ＝g (x )与y ＝－k 在区间[0，π2]上有且只有一个交点，由正弦函数的图象可知－32≤－k <32或－k ＝1，解得－32<k ≤32或k ＝－1，所以实数k 的取值范围是(－32，32]∪{－1}.典例2 (12分)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c .已知a ＝3，cos A ＝63，B ＝A ＋π2.(1)求b 的值； (2)求△ABC 的面积．审题路线图 (1)利用同角公式、诱导公式→求得sin A 、sin B →利用正弦定理求b (2)方法一余弦定理求边c →S ＝12ac sin B方法二用和角正弦公式求sin C →S ＝12ab sin C评分细则 1.第(1)问：没求sin A 而直接求出sin B 的值，不扣分；写出正弦定理，但b 计算错误，得1分．2．第(2)问：写出余弦定理，但c 计算错误，得1分；求出c 的两个值，但没舍去，扣2分；面积公式正确，但计算错误，只给1分；若求出sin C ，利用S ＝12ab sin C 计算，同样得分．跟踪演练2 已知a ，b ，c 分别为△ABC 三个内角的对边，且3cos C ＋sin C ＝3a b， (1)求B 的大小；(2)若a ＋c ＝57，b ＝7，求AB →·BC →的值．解 (1)∵3cos C ＋sin C ＝3ab，由正弦定理可得：3cos C ＋sin C ＝3sin Asin B， ∴3cos C sin B ＋sin B sin C ＝3sin A ， 3cos C sin B ＋sin B sin C ＝3sin(B ＋C )3cos C sin B ＋sin B sin C ＝3sin B cos C ＋3cos B sin C ， sin B sin C ＝3sin C cos B ， ∵sin C ≠0，∴sin B ＝3cos B ， ∴tan B ＝3，又0<B <π，∴B ＝π3.(2)由余弦定理可得：2ac cos B ＝a 2＋c 2－b 2＝(a ＋c )2－2ac －b 2，整理得：3ac ＝(a ＋c )2－b 2，即：3ac ＝175－49. ∴ac ＝42，∴AB →·BC →＝－BA →·BC →＝－|BA →||BC →|·cos B ＝－ac ·cos B ＝－21.典例3 (12分)下表是一个由n 2个正数组成的数表，用a ij 表示第i 行第j 个数(i ，j ∈N *)，已知数表中第一列各数从上到下依次构成等差数列，每一行各数从左到右依次构成等比数列，且公比都相等．已知a 11＝1，a 31＋a 61＝9，a 35＝48.a 11 a 12 a 13 … a 1n a 21 a 22 a 23 … a 2n a 31 a 32 a 33 … a 3n … … … … … a n 1 a n 2 a n 3 … a nn(1)求a n 1和a 4n ；(2)设b n ＝a 4n(a 4n －2)(a 4n －1)＋(－1)n ·a n 1(n ∈N *)，求数列{b n }的前n 项和S n .审题路线图数表中项的规律―→确定a n 1和a 4n ――→化简b n 分析b n 的特征―――――→选定求和方法分组法及裂项法、公式法求和评分细则 (1)求出d 给1分，求a n 1时写出公式结果错误给1分；求q 时没写q >0扣1分； (2)b n 写出正确结果给1分，正确进行裂项再给1分； (3)缺少对b n 的变形直接计算S n ，只要结论正确不扣分； (4)当n 为奇数时，求S n 中间过程缺一步不扣分．跟踪演练3 已知数列{a n }是各项均不为0的等差数列，公差为d ，S n 为其前n 项和，且满足a 2n ＝S 2n －1，n ∈N *.数列{b n }满足b n ＝1a n ·a n ＋1，n ∈N *，T n 为数列{b n }的前n 项和． (1)求数列{a n }的通项公式；(2)若对任意的n ∈N *，不等式λT n <n ＋8·(－1)n 恒成立，求实数λ的取值范围．解 (1)a 21＝S 1＝a 1，∵a 1≠0，∴a 1＝1. ∵a 22＝S 3＝a 1＋a 2＋a 3，∴(1＋d )2＝3＋3d ，解得d ＝－1或2.当d ＝－1时，a 2＝0不满足条件，舍去，∴d ＝2. ∴数列{a n }的通项公式为a n ＝2n －1. (2)∵b n ＝1a n a n ＋1＝1(2n －1)(2n ＋1)＝12(12n －1－12n ＋1)， ∴T n ＝12(1－13＋13－15＋…＋12n －1－12n ＋1)＝n 2n ＋1. ①当n 为偶数时，要使不等式λT n <n ＋8·(－1)n 恒成立，只需不等式λ<(n ＋8)(2n ＋1)n ＝2n ＋8n ＋17恒成立即可．∵2n ＋8n≥8，等号在n ＝2时取得，∴λ<25.②当n 为奇数时，要使不等式λT n <n ＋8·(－1)n 恒成立，只需不等式λ<(n －8)(2n ＋1)n ＝2n －8n －15恒成立即可．∵2n －8n 是随n 的增大而增大，∴n ＝1时，2n －8n 取得最小值－6，∴λ<－21.综上①②可得λ的取值范围是(－∞，－21).典例4 (12分)如图，四棱锥P —ABCD 的底面为正方形，侧面P AD ⊥底面ABCD ，P A ⊥AD ，E ，F ，H 分别为AB ，PC ，BC 的中点．(1)求证：EF ∥平面P AD ； (2)求证：平面P AH ⊥平面DEF .审题路线图 (1)条件中各线段的中点――――→设法利用中位线定理取PD 中点M ―――――→考虑平行关系长度关系平行四边形AEFM ―→AM ∥EF ――――→线面平行的判定定理EF ∥平面P AD (2)平面P AD ⊥平面ABCD P A ⊥AD ―――→面面垂直的性质P A ⊥平面ABCD ―→P A ⊥DE ――――――――→正方形ABCD 中E 、H 为AB 、BC 中点DE ⊥AH ――――→线面垂直的判定定理DE ⊥平面P AH ――――→面面垂直的判定定理平面P AH ⊥平面DEF评分细则 1.第(1)问证出AE綊FM给2分；通过AM∥EF证线面平行时，缺1个条件扣1分；利用面面平行证明EF∥平面P AD同样给分；2．第(2)问证明P A⊥底面ABCD时缺少条件扣1分；证明DE⊥AH时只要指明E，H分别为正方形边AB，BC中点得DE⊥AH不扣分；证明DE⊥平面P AH只要写出DE⊥AH，DE⊥P A，缺少条件不扣分．跟踪演练4(2015·北京)如图，在三棱锥V－ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝2，O，M分别为AB，VA的中点．(1)求证：VB ∥平面MOC ； (2)求证：平面MOC ⊥平面VAB ； (3)求三棱锥V －ABC 的体积．(1)证明因为O ，M 分别为AB ，VA 的中点，所以OM ∥VB ，又因为VB ⊄平面MOC ，OM ⊂平面MOC ，所以VB ∥平面MOC .(2)证明因为AC ＝BC ，O 为AB 的中点，所以OC ⊥AB .又因为平面VAB ⊥平面ABC ，且OC ⊂平面ABC ，所以OC ⊥平面VAB . 又OC ⊂平面MOC ，所以平面MOC ⊥平面VAB .(3)解在等腰直角三角形ACB 中，AC ＝BC ＝2，所以AB ＝2，OC ＝1，所以等边三角形VAB 的面积S △VAB ＝ 3. 又因为OC ⊥平面VAB .所以三棱锥C －VAB 的体积等于13·OC ·S △VAB ＝33，又因为三棱锥V －ABC 的体积与三棱锥C －VAB 的体积相等，所以三棱锥V －ABC 的体积为33.典例5 (12分)如图，AB 是圆O 的直径，C 是圆O 上异于A ，B 的一个动点，DC 垂直于圆O 所在的平面，DC ∥EB ，DC ＝EB ＝1，AB ＝4.(1)求证：DE⊥平面ACD；(2)若AC＝BC，求平面AED与平面ABE所成的锐二面角的余弦值．审题路线图(1)(2)CA、CB、CD两两垂直―→建立空间直角坐标系―→写各点坐标―→求平面AED与平面ABE的法向量―→将所求二面角转化为两个向量的夹角评分细则 1.第(1)问中证明DC ⊥BC 和AC ⊥BC 各给1分；证明DE ∥BC 给1分；证明BC ⊥平面ACD 时缺少AC ∩DC ＝C ，AC ，DC ⊂平面ACD ，不扣分．2．第(2)问中建系给1分；两个法向量求出1个给2分；没有最后结论扣1分；法向量取其他形式同样给分．跟踪演练5 如图，在几何体ABCDQP 中，AD ⊥平面ABPQ ，AB ⊥AQ ，AB ∥CD ∥PQ ，CD ＝AD ＝AQ ＝PQ ＝12AB ，(1)证明：平面APD ⊥平面BDP ； (2)求二面角A —BP —C 的正弦值．方法一 (1)证明设AQ ＝QP ＝1，则AB ＝2，易求AP ＝BP ＝2，由勾股定理可得BP ⊥AP ，而AD ⊥平面ABPQ ，所以BP ⊥DA ，又AP ∩AD ＝A ，故BP ⊥平面APD .而BP ⊂平面BDP ，所以平面APD ⊥平面BDP .(2)解设M 、N 分别为AB 、PB 的中点，连接CM ，MN ，CN .易得CM ⊥平面APB ，MN ⊥PB ，故∠CNM 为二面角A —BP —C 的平面角．结合(1)计算可得，CM ⊥MN ，CM ＝1， MN ＝22，CN ＝62，于是在Rt △CMN 中，sin ∠CNM ＝63. 所以二面角A —BP —C 的正弦值为63. 方法二 (1)证明如图所示，建立空间直角坐标系，点A 为坐标原点，设AB ＝2，依题意得A (0,0,0)，B (0,2,0)，C (0,1,1)，D (0,0,1)， Q (1,0,0), P (1,1,0)，BP →＝(1，－1,0)，AP →＝(1,1,0)，AD →＝(0,0,1)，那么BP →·AP →＝0，BP →·AD →＝0，因此，BP ⊥AP ，BP ⊥AD .又AP ∩AD ＝A ，故BP ⊥平面APD ，而BP ⊂平面BDP ，所以平面APD ⊥平面BDP .(2)解设平面CPB 的一个法向量为n ＝(x ，y ，z )，而BC →＝(0，－1,1)，则BP →·n ＝0，BC →·n ＝0，那么x －y ＝0，－y ＋z ＝0，令x ＝1可得n ＝(1,1,1)．又由题设，平面ABP 的一个法向量为m ＝(0,0,1)．所以，cos 〈m ，n 〉＝m·n|m||n |＝33，可得sin 〈m ，n 〉＝63. 所以二面角A —BP —C 的正弦值为63.典例6 (12分)2015年12月10日，我国科学家屠呦呦教授由于在发现青蒿素和治疗疟疾的疗法上的贡献获得诺贝尔医学奖．以青蒿素类药物为主的联合疗法已经成为世界卫生组织推荐的抗疟疾标准疗法．目前，国内青蒿人工种植发展迅速．调查表明，人工种植的青蒿的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性，现将这三项的指标分别记为x ，y ，z ，并对它们进行量化：0表示不合格，1表示临界合格，2表示合格，再用综合指标ω＝x ＋y ＋z 的值评定人工种植的青蒿的长势等级：若ω≥4，则长势为一级；若2≤ω≤3，则长势为二级；若0≤ω≤1，则长势为三级．为了了解目前人工种植的青蒿的长势情况，研究人员随机抽取了10块青蒿人工种植地，得到如下结果：(1)在这10块青蒿人工种植地中任取两地，求这两地的空气湿度的指标z 相同的概率； (2)从长势等级是一级的人工种植地中任取一块，其综合指标为m ，从长势等级不是一级的人工种植地中任取一块，其综合指标为n ，记随机变量X ＝m －n ，求X 的分布列及其均值．审题路线图 (1)对事件进行分解―→求出从10块地中任取两块的方法总数―→求出空气湿度指标相同的方法总数―→利用古典概型求概率(2)确定随机变量X的所有取值―→计算X取各个值的概率―→写分布列―→求均值评分细则 1.第(1)问中，列出空气湿度相同的情况给2分；计算概率只要式子正确给2分；2．第(2)问中，列出长势等级的给2分，只要结果正确无过程不扣分；计算概率时每个式子给1分；分布列正确写出给1分．跟踪训练6(2016·课标全国乙)某公司计划购买2台机器，该种机器使用三年后即被淘汰，机器有一易损零件，在购进机器时，可以额外购买这种零件作为备件，每个200元．在机器使用期间，如果备件不足再购买，则每个500元．现需决策在购买机器时应同时购买几个易损零件，为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数，得下面柱状图：以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率，记X 表示2台机器三年内共需更换的易损零件数，n表示购买2台机器的同时购买的易损零件数．(1)求X的分布列；(2)若要求P(X≤n)≥0.5，确定n的最小值；(3)以购买易损零件所需费用的均值为决策依据，在n＝19与n＝20之中选其一，应选用哪个？解(1)由柱状图并以频率代替概率可得，一台机器在三年内需更换的易损零件数为8,9,10,11的概率分别为0.2，0.4,0.2,0.2，从而P(X＝16)＝0.2×0.2＝0.04；P(X＝17)＝2×0.2×0.4＝0.16；P(X＝18)＝2×0.2×0.2＋0.4×0.4＝0.24；P(X＝19)＝2×0.2×0.2＋2×0.4×0.2＝0.24；P(X＝20)＝2×0.2×0.4＋0.2×0.2＝0.2；P(X＝21)＝2×0.2×0.2＝0.08；P(X＝22)＝0.2×0.2＝0.04.所以X的分布列为(2)由(1)知P((3)记Y表示2台机器在购买易损零件上所需的费用(单位：元)．当n＝19时，E(Y)＝19×200×0.68＋(19×200＋500)×0.2＋(19×200＋2×500)×0.08＋(19×200＋3×500)×0.04＝4 040(元)．当n ＝20时，E (Y )＝20×200×0.88＋(20×200＋500)×0.08＋(20×200＋2×500)×0.04＝4 080(元)．可知当n ＝19时所需费用的均值小于n ＝20时所需费用的均值，故应选n ＝19.典例7 (12分)(2015·山东)平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为32，且点⎝⎛⎭⎫3，12在椭圆C 上． (1)求椭圆C 的方程；(2)设椭圆E ：x 24a 2＋y 24b 2＝1，P 为椭圆C 上任意一点，过点P 的直线y ＝kx ＋m 交椭圆E 于A ，B 两点，射线PO 交椭圆E 于点Q . (ⅰ)求|OQ ||OP |的值；(ⅱ)求△ABQ 面积的最大值．审题路线图 (1)椭圆C上点满足条件―→求出a 222e a b c =+已知离心率基本量法求得椭圆C 方程(2)①P 在C 上，Q 在E 上――→P 、Q 共线设坐标代入方程―→求出|OQ ||QP |. ②直线y ＝kx ＋m 和椭圆E 方程联立――→通法研究判别式Δ并判断根与系数的关系―→ 用m ，k 表示S △OAB ―→求S △OAB 最值―――――――→利用①得S △ABQ和S △OAB关系得S △ABQ 最大值评分细则 1.第(1)问中，求a 2－c 2＝b 2关系式直接得b ＝1，扣1分；2．第(2)问中，求|OQ ||OP |时，给出P ，Q 坐标关系给1分；无“Δ>0”和“Δ≥0”者，每处扣1分；联立方程消元得出关于x 的一元二次方程给1分；根与系数的关系写出后再给1分；求最值时，不指明最值取得的条件扣1分．跟踪演练7 已知中心在原点O ，焦点在x 轴上，离心率为32的椭圆过点(2，22)．(1)求椭圆的方程；(2)设不过原点O 的直线l 与该椭圆交于P ，Q 两点，满足直线OP ，PQ ，OQ 的斜率依次成等比数列，求△OPQ 面积的取值范围．解 (1)由题意可设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)，则c a ＝32(其中c 2＝a 2－b 2，c >0)，且2a 2＋12b 2＝1，故a ＝2，b ＝1. 所以椭圆的方程为x 24＋y 2＝1.(2)由题意可知，直线l 的斜率存在且不为0.故可设直线l ：y ＝kx ＋m (m ≠0)，设P (x 1，y 1)，Q (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2＋4y 2＝4，消去y ，得(1＋4k 2)x 2＋8kmx ＋4(m 2－1)＝0，则Δ＝64k 2m 2－16(1＋4k 2)(m 2－1)＝16(4k 2－m 2＋1)>0，且x 1＋x 2＝－8km1＋4k 2，x 1x 2＝4(m 2－1)1＋4k 2，故y 1y 2＝(kx 1＋m )(kx 2＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2，因为直线OP ，PQ ，OQ 的斜率依次成等比数列，所以y 1x 1·y 2x 2＝k 2x 1x 2＋km (x 1＋x 2)＋m 2x 1x 2＝k 2，即m 2－4k 24(m 2－1)＝k 2. 又m ≠0，所以k 2＝14，即k ＝±12.由于直线OP ，OQ 的斜率存在，且Δ>0，得0<m 2<2，且m 2≠1，设d 为点O 到直线l 的距离，则d ＝|2m |5，|PQ |＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2]＝5(2－m 2)，所以S ＝12|PQ |d ＝m 2(2－m 2)<m 2＋2－m 22＝1(m 2≠1)，故△OPQ 面积的取值范围为(0,1)．典例8 (12分)已知定点C (－1,0)及椭圆x 2＋3y 2＝5，过点C 的动直线与椭圆相交于A ，B 两点．(1)若线段AB 中点的横坐标是－12，求直线AB 的方程；(2)在x 轴上是否存在点M ，使MA →·MB →为常数？若存在，求出点M 的坐标；若不存在，请说明理由．审题路线图 (1)设AB 的方程y ＝k (x ＋1)→待定系数法求k →写出方程(2)设M 存在即为(m ，0)→求MA →·MB →→在MA →·MB →为常数的条件下求m →下结论评分细则 (1)不考虑直线AB 斜率不存在的情况扣1分； (2)不验证Δ>0，扣1分；(3)直线AB 方程写成斜截式形式同样给分； (4)没有假设存在点M 不扣分；(5)MA →·MB →没有化简至最后结果扣1分，没有最后结论扣1分．跟踪演练8 已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为12，以原点为圆心，椭圆的短半轴长为半径的圆与直线7x －5y ＋12＝0相切． (1)求椭圆C 的方程；(2)设A (－4,0)，过点R (3,0)作与x 轴不重合的直线l 交椭圆C 于P ，Q 两点，连接AP ，AQ 分别交直线x ＝163于M ，N 两点，若直线MR ，NR 的斜率分别为k 1，k 2，试问：k 1k 2是否为定值？若是，求出该定值，若不是，请说明理由．解 (1)由题意得⎩⎨⎧c a ＝12，127＋5＝b ，a 2＝b 2＋c 2，∴⎩⎪⎨⎪⎧a ＝4，b ＝23，c ＝2，故椭圆C 的方程为x 216＋y 212＝1.(2)设直线PQ 的方程为x ＝my ＋3， P (x 1，y 1)，Q (x 2，y 2)，由⎩⎪⎨⎪⎧x 216＋y 212＝1，x ＝my ＋3，∴(3m 2＋4)y 2＋18my －21＝0. ∴y 1＋y 2＝－18m 3m 2＋4，y 1y 2＝－213m 2＋4，由A ，P ，M 三点共线可知y M 163＋4＝y 1x 1＋4，∴y M ＝28y 13(x 1＋4).同理可得y N ＝28y 23(x 2＋4)，∴k 1k 2＝y M 163－3×y N 163－3＝9y M y N 49＝16y 1y 2(x 1＋4)(x 2＋4)∵(x 1＋4)(x 2＋4)＝(my 1＋7)(my 2＋7) ＝m 2y 1y 2＋7m (y 1＋y 2)＋49∴k 1k 2＝16y 1y 2m 2y 1y 2＋7m (y 1＋y 2)＋49＝－127，为定值．典例9 (12分)(2015·课标全国Ⅱ)已知函数f (x )＝ln x ＋a (1－x )． (1)讨论f (x )的单调性；(2)当f (x )有最大值，且最大值大于2a －2时，求a 的取值范围．审题路线图求f ′(x )――→讨论f ′(x )的符号f (x )单调性―→f (x )最大值―→解f (x )max >2a －2.(2)分类讨论，每种情况给2分，结论1分；(3)求出最大值给2分；(4)构造函数g(a)＝ln a＋a－1给2分；(5)通过分类讨论得出a的范围，给2分．跟踪演练9已知函数f(x)＝(ax2＋bx＋c)e x在[0,1]上单调递减且满足f(0)＝1，f(1)＝0.(1)求a的取值范围；(2)设g(x)＝f(x)－f′(x)，求g(x)在[0,1]上的最大值和最小值．解(1)由f(0)＝1，f(1)＝0，得c＝1，a＋b＝－1，则f(x)＝[ax2－(a＋1)x＋1]e x，f′(x)＝[ax2＋(a－1)x－a]e x.依题意对任意x∈(0,1)，有f′(x)<0.当a>0时，因为二次函数f(x)＝ax2＋(a－1)x－a的图象开口向上，而f′(0)＝－a<0，所以有f′(1)＝(a－1)e<0，即0<a<1；当a＝1时，对任意x∈(0,1)有f′(x)＝(x2－1)e x<0，f(x)符合条件；当a＝0时，对于任意x∈(0,1)，f′(x)＝－x e x<0，f(x)符合条件；当a <0时，因f ′(0)＝－a >0，f (x )不符合条件．故a 的取值范围为0≤a ≤1. (2)因g (x )＝(－2ax ＋1＋a )e x ， g ′(x )＝(－2ax ＋1－a )e x .(ⅰ)当a ＝0时，g ′(x )＝e x >0，g (x )在x ＝0处取得最小值g (0)＝1，在x ＝1处取得最大值g (1)＝e.(ⅱ)当a ＝1时，对于任意x ∈(0,1)有g ′(x )＝－2x e x <0，g (x )在x ＝0处取得最大值g (0)＝2，在x ＝1取得最小值g (1)＝0.(ⅲ)当0<a <1时，由g ′(x )＝0得x ＝1－a2a>0.①若1－a 2a ≥1，即0<a ≤13时，g (x )在[0,1]上单调递增，g (x )在x ＝0处取得最小值g (0)＝1＋a ，在x ＝1处取得最大值g (1)＝(1－a )e.②若1－a 2a <1，即13<a <1时，g (x )在x ＝1－a 2a 处取得最大值121()2e ,2aaa g a a--=在x ＝0或x ＝1处取得最小值，而g (0)＝1＋a ，g (1)＝(1－a )e ，则当13<a ≤e －1e ＋1时，g (x )在x ＝0处取得最小值g (0)＝1＋a ；当e －1e ＋1<a <1时，g (x )在x ＝1处取得最小值g (1)＝(1－a )e.典例10 (12分)(2015·课标全国Ⅱ)设函数f (x )＝e mx ＋x 2－mx . (1)证明：f (x )在(－∞，0)单调递减，在(0，＋∞)单调递增；(2)若对于任意x 1，x 2∈[－1,1]，都有|f (x 1)－f (x 2)|≤e －1，求m 的取值范围．审题路线图 (1)求导f ′(x )＝m (e mx －1)＋2x →讨论m 确定f ′(x )符号→证明结论(2)条件转化为(|f (x 1)－f (x 2)|)max ≤e －1――→结合(1)知f (x )min ＝f (0)⎩⎪⎨⎪⎧f (1)－f (0)≤e －1f (－1)－f (0)≤e －1→⎩⎪⎨⎪⎧e m －m ≤e －1e －m＋m ≤e －1→构造函数g (t )＝e t－t －e ＋1→研究g (t )单调性→寻求⎩⎪⎨⎪⎧g (m )≤0g (－m )≤0的条件→对m 讨论得适合条件的范围评分细则(1)求出导数给1分；(2)讨论时漏掉m＝0扣1分；两种情况只讨论正确一种给2分；(3)确定f′(x)符号时只有结论无中间过程扣1分；(4)写出f(x)在x＝0处取得最小值给1分；(5)无最后结论扣1分；(6)其他方法构造函数同样给分．跟踪演练10已知函数f(x)＝ln x＋1x.(1)求函数f(x)的单调区间和极值；(2)若对任意的x>1，恒有ln(x－1)＋k＋1≤kx成立，求k的取值范围；(3)证明：ln 222＋ln 332＋…＋ln n n 2<2n 2－n －14(n ＋1) (n ∈N *，n ≥2)．(1)解 f ′(x )＝－ln xx2，由f ′(x )＝0⇒x ＝1，列表如下：因此函数f (x )的增区间为(0,1)，减区间为(1，＋∞)，极大值f (1)＝1，无极小值． (2)解因为x >1，ln(x －1)＋k ＋1≤kx ⇔ln (x －1)＋1x －1≤k ⇔f (x －1)≤k ，所以f (x －1)max ≤k ，∴k ≥1，(3)证明由(1)可得f (x )＝ln x ＋1x ≤f (x )max ＝f (1)＝1⇒ln x x ≤1－1x ，当且仅当x ＝1时取等号．令x ＝n 2 (n ∈N *，n ≥2)．则ln n 2n 2<1－1n 2⇒ln n n 2<12(1－1n2)<12(1－1n (n ＋1))＝12(1－1n ＋1n ＋1)(n ≥2)， ln 222＋ln 332＋…＋ln n n2 <12(1－12＋13)＋12(1－13＋14)＋…＋12(1－1n ＋1n ＋1) ＝12(n －1＋1n ＋1－12)＝2n 2－n －14(n ＋1).。

高考数学统计与概率大题解题模板

统计与概率大题解题模板一、随机抽样和用样本估计总体模板一、频率分布直方图1、频率分布直方图的性质：（1）小矩形的面积=组距×频率/组距=频率，所以各小矩形的面积表示相应各组的频率.这样，频率分布直方图就以面积的形式反映了数据落在各个小组内的频率大小；（2）在频率分布直方图中，各小矩形的面积之和等于1；（3）频数/相应的频率=样本容量.2、频率分布直方图反映了样本在各个范围内取值的可能性，由抽样的代表性利用样本在某一范围内的频率，可近似地估计总体在这一范围内的可能性.3、频率分布直方图中的纵坐标为频率组距，而不是频率值.例1-1.某城市100户居民月平均用电量(单位：度)，以[160180)，、[180200)，、[200220)，、[220240)，、[240260)，、[260280)，、]280[300，分组的频率分布直方图如图.（1）求直方图中x 的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量为[220240)，、[240260)，、[260280)，、]280[300，的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220240)，的用户中应抽取多少户？【解析】（1）由(0.0020.00950.0110.01250.0050.0025)201x ++++++⨯=得：0.0075x =，∴直方图中x 的值是0.0075；（2）月平均用电量的众数是2202402302+=，∵(0.0020.00950.011)200.450.5++⨯=<，∴月平均用电量的中位数在[220240)，内，设中位数为a ，由(0.0020.00950.011)200.0125(220)0.5a ++⨯+⨯-=得：224a =， ∴月平均用电量的中位数是224；（3）月平均用电量为[220240)，的用户有0.01252010025⨯⨯=户，月平均用电量为[240260)，的用户有0.00752010015⨯⨯=户，月平均用电量为[260280)，的用户有0.0052010010⨯⨯=户，月平均用电量为]280[300，的用户有0.0025201005⨯⨯=户，抽取比例11125151055==+++，∴月平均用电量在[220,240)的用户中应抽取12555⨯=户.模板二、茎叶图1、绘制茎叶图的关键是分清茎和叶，如数据是两位数，十位数字为“茎”，个位数字为“叶”；如果是小数时，通常把整数部分作为“茎”，小数部分作为“叶”，解题时要根据数据的特点合理选择茎和叶.2、利用茎叶图进行数据分析时，一般从数据分布的对称性、中位数、稳定性等几个方面来考虑. 例1-2.某中学高二（2）班甲、乙两名学生自进入高中以来，每次数学考试成绩情况如下：甲：95、81、75、91、86、89、71、65、76、88、94、110、107；乙：83、86、93、99、88、103、98、114、98、79、78、106、101. 画出两人数学成绩的茎叶图，并根据茎叶图对两人的成绩进行比较. 【解析】甲、乙两人数学成绩的茎叶图如图所示：从这个茎叶图上可以看出，乙同学的得分情况是大致对称的，中位数是98；甲同学的得分情况，也大致对称，中位数是88，乙同学的成绩比较稳定，总体情况比甲同学好.模板三、散点图1、两个变量的关系2、散点图：将样本中n 个数据点()i i x y ，(1i =，2，…，n )描在平面直角坐标系中得到的图形.3、正相关与负相关：（1）正相关：如果一个变量的值由小变大时，另一个变量的值也由小变大，这种相关称为正相关.（2）负相关：如果一个变量的值由小变大时，另一个变量的值由大变小，这种相关称为负相关. 4、最小二乘法：设x 、y 的一组观察值为()i i x y ，(1i =，2，…，n )，且回归直线方程为ˆˆˆybx a =+.当x 取值i x (1i =，2，…，n )时，y 的观察值为i y ，差ˆi i y y -(1i =，2，…，n )刻画了实际观察值i y 与回归直线上相应点纵坐标之间的偏离程度，通常是用离差的平方和，即21()ni i i Q y a bx ==--∑作为总离差，并使之达到最小.这样，回归直线就是所有直线中Q 取最小值的那一条.由于平方又叫二乘方，所以这种使“离差平方和最小”的方法，叫做最小二乘法. 5、回归直线方程的系数计算公式例1-3.一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，收集数据如下：（1）y 与x 是否具有线性相关关系？（2）如果y 与x 具有线性相关关系，求y 关于x 的回归直线方程. 审题路线图：→→→【解析】（1）画散点图如下：由图可知y 与x 具有线性相关关系；（2）列表、计算：1102211055950105591.70.66838500105520ˆ1iii ii x y x ybxx ==⋅-⋅⋅-⨯⨯==≈-⨯-⋅∑∑，91.70.668ˆ55.6ˆ549ay bx =-=-⨯=，即所求的回归直线方程为：0.66859ˆ 4.6y x =+.构建答题模板：第一步：列表i x 、i y 、i i x y ；第二步：计算x ，y ，21ni i x =∑，1ni i i x y =∑；第三步：代入公式计算ˆb 、ˆa 的值；第四步：写出回归直线方程；第五步：反复回顾，查看是否有重复或遗漏情况，明确规范书写答题.模板四、古典概型例1-4.袋中有五张卡片，其中红色卡片三张，标号为1、2、3；蓝色卡片两张，标号为1、2. （1）从以上五张卡片中任取两张，求这两张卡片颜色不同且标号之和小于4的概率；（2）向袋中再放入一张标号为0的绿色卡片，从这六张卡片中任取两张，求这两张卡片颜色不同且标点之和小于4的概率.审题路线图：确定概率模型→列出所有取卡片的结果(基本事件)→构成事件的基本事件→求概率. 规范解答：【解析】（1）标号为1、2、3的三张红色卡片分别记为A 、B 、C ，标号为1、2的两张蓝色卡片分别记为D 、E ，从五张卡片中任取两张的所有可能的结果为：AB 、AC 、AD 、AE 、BC 、BD 、BE 、CD 、CE 、DE 共10种，由于每一张卡片被取到的机会均等，因此这些基本事件的出现是等可能的，从五张卡片中任取两张，这两张卡片颜色不同且它们的标号之和小于4的结果为：AD 、AE 、BD ，共3种，∴这两张卡片颜色不同且它们的标号之和小于4的概率为310；（2）记F 是标号为0的绿色卡片，从六张卡中任取两张的所有可能的结果为：AB 、AC 、AD 、AE 、AF 、BC 、BD 、BE 、BF 、CD 、CE 、CF 、DE 、DF 、EF 共15种，用于每一张卡片被取到的机会均等，因此这些基本事件的出现是等可能的，从六张卡片中任取两张，这两张卡片颜色不同且它们的标号之和小于4的结果为：AD 、AE 、BD 、AF 、BF 、CF 、DF 、EF ，共8种， ∴这两张卡片颜色不同且它们的标号之和小于4的概率为815. 构建答题模板：第一步：列出所有基本事件，计算基本事件总数；第二步：将所求事件分解为若干个互斥的事件或转化为其对立事件(也许不用分解，但分解必要注意互斥)；第三步：分别计算每个互斥事件的概率；第四步：利用概率的加法公式求出问题事件的概率；第五步：反复回顾，查看是否有重复或遗漏情况，明确规范书写答题.二、概率与统计之超几何分布与二项分布离散型随机变量的分布列、数学期望与方差1、关于离散型随机变量分布列的计算方法如下：（1）写出ξ的所有可能取值；（2）用随机事件概率的计算方法，求出ξ取各个值的概率；（3）利用（1）、（2）的结果写出ξ的分布列. 2、常见的特殊离散型随机变量的分布列：（1）两点分布，分布列为(0p -、1q -)，其中01p <<，且1p q +=；（2）二项分布，分布列为(00p 、11p 、22p 、…、k kp 、…、n np )，其中k k n kk n p C p q -=，0k =、1、2、…、n ，且01p <<，1p q +=，k k n k k n p C p q -=可记为(,,)b k n p .3、对离散型随机变量的期望应注意：（1）期望是算术平均值概念的推广，是概念意义下的平均；（2）()E ξ是一个实数，由ξ的分布列唯一确定，即作为随机变量ξ是可变的，可取不同值，而()E ξ是不变的，它描述ξ取值的平均状态；（3）()1122n n E x p x p x p ξ=++⋅⋅⋅++⋅⋅⋅直接给出了E ξ的求法，即随机变量取值与相应概率值分别相乘后相加.4、对离散型随机变量的方差应注意：（1）()D ξ表示随机变量ξ对()E ξ的平均偏离程度，()D ξ越大表明平均偏离程度越大，说明ξ的取值越分散；反之()D ξ越小，ξ的取值越集中，在()E ξ来描述ξ的分散程度.（2）()D ξ与()E ξ一样也是一个实数，由ξ的分布列唯一确定.模板一、超几何分布——离散型随机变量的分布列、期望与方差（1）超几何分布的特征：①在小范围内不放回的随机抽取；②每次抽取相互影响；③每次抽取的可能性一直变化；（2）超几何分布的题型：在含有M 件次品的N 件产品中任取n 件(n M N ≤≤)，其中恰有X 件次品；（3）超几何分布的分布列、期望与方差：①分布列：()k n k M N MnNC C P X k C --⋅==，012k n =⋅⋅⋅，，，，，k ∈N ；②期望：0()[()]nk nME X k P X k N ===⋅=∑； ③{}22()()()[()]()(1)nk nM N M N n D X k E x P X k N N =--==-⋅=-∑. 例2-1.已知一个袋中装有3个白球和3个红球，这些球除颜色外完全相同.（1）每次从袋中取一个球，取出后不放回，直到取到一个红球为止，求取球次数ξ的分布列和数学期望()E ξ；（2）每次从袋中取一个球，取出后放回接着再取一个球，这样取3次，求取出红球次数η的分布列、数学期望和方差()D η.审题路线图：取到红球为止→取球次数的所有可能1、2、3、4→求对应次数的概率→列分布列→求()E ξ.取出后放回，这是条件→每次取到红球的概率相同→三次独立重复试验→利用公式. 规范解答：【解析】（1）ξ的可能取值为1、2、3、4，31(1)62P ξ===，333(2)6510P ξ==⨯=， 3233(3)65420P ξ==⨯⨯=，32131(4)654320P ξ==⨯⨯⨯=，故ξ的分布列为：17()123421020204E ξ=⨯+⨯+⨯+⨯=；（2）取出后放回，取球3次，可看作3次独立重复试验，∴1~(2)2B η，，η的可能取值为0、1、2、3，0033111(0)()()228P C η==⋅⋅=，1123113(1)()()228P C η==⋅⋅=，2213113(2)()()228P C η==⋅⋅=，3303111(4)()()228P C η==⋅⋅=，故ξ的分布列为：∴()322E η=⨯=，113()3224D η=⨯⨯=. 构建答题模板：第一步：确定离散型随机变量的所有可能性；第二步：求出每个可能性的概率；第三步：画出随机变量的分布列；第四步：求期望和方差；第五步：反复回顾，查看是否有重复或遗漏情况，明确规范书写答题.如本题可重点查看随机变量的所有可能值是否正确；根据分布列性质检查概率是否正确.模板二、二项分布及其应用（1）二项分布的特征：①在小范围内有放回的随机抽取或在大范围内任意随机抽取；②每次抽取相互独立；③每次抽取的可能性保持不变；（2）二项分布的题型：在n 次独立重复试验中，设事件A 发生的次数为X ，在每次试验中事件A 发生的概率为p ；（3）二项分布的分布列、期望与方差：①分布列：~(,)X B n p ，n 为试验次数，p 为试验成功率，()(1)k kn k n P X k C p p -==-，0,1,2,,k n =⋅⋅⋅，k ∈N ；②期望：()E X np =； ③()(1)D X np p =-.例2-2.某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为23，中奖可以获得2分；方案乙的中奖率为25，中奖可以获得3分；未中奖则不得分.每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品.（1）若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X ，求3≤X 的概率；（2）若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？【解析】（1）由已知得，小明中奖的概率为23，小红中奖的概率为25，且两人中奖与否互不影响，记“这2人的累计得分3≤X ”的事件为A ，则事件A 的对立事件为“5X =”， ∵224(5)3515P X ==⨯=，∴11()1(5)15P A P X =-==，即这两人的累计得分3≤X 的概率为1115；（2）设小明小红都选择方案甲抽奖中奖次数为1X ，都选择方案乙抽奖中奖次数为2X ，则这两人选择方案甲抽奖累计得分的数学期望为1()2E X ⨯，选择方案乙抽奖累计得分的数学期望为2()3E X ⨯，由已知可得12~(2)3X B ，，22~(2)5X B ，，∴124()233E X =⨯=，224()255E X =⨯=，从而18()23E X ⨯=，212()35E X ⨯=，∴12()2()3E X E X ⨯>⨯，∴他们都选择方案甲进行抽奖时，累计得分的数学期望较大.模板三、统计概率的综合应用例2-3.某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量(单位：克)重量的分组区间为，(495500]，，…，(510515]，，由此得到样本的频率分布直方图，如图所示.（1）根据频率分布直方图，求重量超过505克的产品数量.（2）在上述抽取的40件产品中任取2件，设X 为重量超过505克的产品数量，求X 的分布列及期望.（3）在上述抽取的40件产品中任取5件产品，求恰有2件产品的重量超过505克的概率. 【解析】（1）重量超过505克的产品数量是40(0.0550.015)12⨯⨯+⨯=件；（2）X 的所有可能取值为0、1、2，021********(0)130C C P X C ⋅===，11122824056(1)130C C P X C ⋅===，20122824011(2)130C C P X C ⋅===， X 的分布列为：X 的期望561139()01213013013065E X =⨯+⨯+⨯=；（3）设在上述抽取的40件产品中任取5件产品，恰有2件产品的重量超过505克为事件A ，则322812540231()703C C P A C ⋅==. 变式1：第三问改为：从流水线上任取5件产品，设Y 为重量超过505克的产品数量，求Y 的分布列、期望、方差.【解析】从流水线上任取5件产品服从二项分布：Y 可取：0、1、2、3、4、5；超过505克的产品发生的概率为0.3p =，则~(50.3)Y B ，， 005055(0)(1)0.70.16807P Y C p p -==-==， 115111455(1)(1)0.30.70.36015P Y C p p C -==-=⨯=，225222355(2)(1)0.30.70.3087P Y C p p C -==-=⨯=，335333255(3)(1)0.30.70.1323P Y C p p C -==-=⨯=，44544455(4)(1)0.30.70.02835P Y C p p C -==-=⨯=，555555(5)(1)0.30.00243P Y C p p -==-==，则Y 的分布列为：Y 的期望()50.3 1.5E Y =⨯=，方差()50.30.7 1.05D Y =⨯⨯=.变式2：某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条抽流水线上各抽取40件产品作为样本算出他们的重量(单位：克).重量落在(495510]，的产品为合格品，否则为不合格.表一为甲流水线样本频率分布表，图一为乙流水线样本的频率分布直方图.（1）根据上表数据在答题卡上作出甲流水线样本的频率分布直方图；（2）若以频率作为概率，试估计从乙流水线上任取5件产品，恰有3件产品为合格品的概率；（3）由以上统计数据完成下面22⨯列联表，并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.附：下面的临界值表供参考：(参考公式：22()()()()()n ad bcKa b a c c d b d-=++++，其中n a b c d=+++).在平面直角坐标系中做出频率分布直方图，甲流水线样本的频率分布直方图如下：（2）由图1知，乙样本中合格品为：(0.060.090.03)54036++⨯⨯=，故合格品的频率为360.940=， ∴可估计从乙流水线上任取一件产品该产品为合格品的概率0.9P =，设ξ为从乙流水线上任取5件产品中的合格品数，则~(50.9)B ξ，， ∴3325(3)0.90.10.0729P C ξ===，即从乙流水线上任取5件产品，恰有3件产品为合格品的概率为0.0729；（3）22⨯列联表如下：∵22()80(120360) 3.117 2.706()()()()66144040n ad bc K a b a c c d b d -⨯-==≈>++++⨯⨯⨯， ∴有90%的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.课后作业1. 某学生对其亲属30人的饮食习惯进行了一次调查，并用茎叶图表示30人的饮食指数.(说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主.)（1）根据茎叶图，帮助这位学生说明其亲属30人的饮食习惯；（2）根据以上数据完成下列22⨯列联表：（3）能否有99%的把握认为其亲属的饮食习惯与年龄有关，并写出简要分析.【答案】（1）30位亲属中50岁以上的人多以食蔬菜为主，50岁以下的人多以食肉为主；（2）表格见解析；（3）有，分析见解析.【解析】【分析】（1）根据茎叶图，分析题中数据即可得出结果.（2）根据茎叶图，补充完善列联表，计算观测值即可求解.【详解】（1）30位亲属中50岁以上的人多以食蔬菜为主，50岁以下的人多以食肉为主；（2）补全22⨯列联表：（3）230(42168)10 6.63512182010K ⨯⨯-⨯==>⨯⨯⨯，有99%的把握认为其亲属的饮食习惯与年龄有关.2. 某网站就“民众是否支持加大修建城市地下排水设施的资金投入”进行投票.按照北京暴雨前后两个时间收集有效投票，暴雨后的投票收集了50份，暴雨前的投票也收集了50份，所得统计结果如下表：已知工作人员从所有投票中任取一个，取到“不支持投入”的投票的概率为25. （1）求列联表中的数据x ､y ､A ､B 的值；（2）绘制条形统计图，通过图形判断本次暴雨是否影响到民众对加大修建城市地下排水设施的投入的态度？（3）能够有多大把握认为北京暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关？【答案】（1）40x =，10y =，60A =，40B =；（2）条形统计图答案见解析，暴雨影响到民众对加大修建城市地下排水设施的投入的态度；（3）有99.9%把握.【解析】【分析】（1）先求出y的值，再求,,B x A的值；（2）先求出暴雨前后的支持率和不支持率，画出条形统计图，再通过图形判断本次暴雨是否影响到民众对加大修建城市地下排水设施的投入的态度.（3）利用独立性检验求解即可.【详解】（1）设“从所有投票中抽取一个，取到不支持投入的投票”为事件A，由已知得302()1005yP A+==，∴10y=，40B=，40x=，60A=；（2）由（1）知北京暴雨后支持为404505=，不支持率为41155-=，北京暴雨前支持率为202505=，不支持率为23155-=，条形统计图如图：由图可以看出暴雨影响到民众对加大修建城市地下排水设施的投入的态度；（3）22100(30402010)5016.7810.828505040603K⨯⨯-⨯==≈>⨯⨯⨯，故至少有99.9%把握认为北京暴雨对民众是否赞成加大对修建城市地下排水设施的投入有关.【点睛】方法点睛：独立性检验的解题步骤：（1）2*2列联表；（2）提出假设：设p与q没有关系；（3）根据列联表中的数据2K计算的值；（4）根据计算得到的随机变量2K的观测值作出判断.3. 电视传媒公司为了解某地区观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.（1）根据已知条件完成下面的22⨯列联表，并据此资料判断是否有95%的把握认为“体育迷”与性别有关？（2）将日均收看该体育节目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.附：22()()()()()n ad bcKa b a c c d b d-=++++【答案】（1）列联表答案见解析，没有95%的把握认为“体育迷”与性别有关；（2）7 10 .【解析】【分析】（1）根据频率分布直方图，计算体育迷的人数，再结合条件依次填入22⨯列联表，并计算2K ，并和临界值3.841比较后进行判断；（2）首先由频率分布直方图计算“超级体育迷”的人数，在通过编号列举的方法，利用古典概型的计算公式计算概率.【详解】（1）由频率分布直方图可知，在抽取的100人中，“体育迷”有25人，从而完成22⨯列联表如下：将22⨯列联表中的数据代入公式计算，得22100(30104515)100 3.030 3.8417525455533K ⨯⨯-⨯==≈<⨯⨯⨯，∴没有95%的把握认为“体育迷”与性别有关；（2）由频率分布直方图可知“超级体育迷”为5人，设123,,a a a 是3名男超级体育迷，12,b b 是2名女超级体育迷，从而一切可能结果所组成基本事件为：12()a a ，､13()a a ，､23()a a ，､11()a b ，､12()a b ，､ 21()a b ，､22()a b ，､31()a b ，､32()a b ，､12()b b ，，则由10个基本事件组成，而且这些基本事件的出现是等可能的，用A 表示“任选2人中，至少有1人是女性”这一事件，则A 由11()a b ，､12()a b ，､21()a b ，､22()a b ，､31()a b ，､32()a b ，､12()b b ，这7个基本事件组成，因而7()10P A =.4. 2015年7月9日21时15分，台风“莲花”在我国广东省陆丰市甲东镇沿海登陆，给当地人民造成了巨大的财产损失，适逢暑假，大学生小张调查了当地某小区的100户居民由于台风造成的经济损失，将收集的数据分成[02000),、[2000,4000)、[4000,6000)、[6000,8000)、[800010000],五组作出频率分布直方图，如图：（1）台风后居委会号召小区居民为台风重灾区捐款，小张调查的100户居民捐款情况如表格，在表格空白处填写正确数字，并说明是否有95%以上的把握认为捐款数额多于或少于500元和自身经济损失是否到4000元有关？（2）将上述调查所得到的频率视为概率.现在从该地区大量受灾居民中，采用随机抽样方法每次抽取1户居民，抽取3次，记被抽取的3户居民中自身经济损失超过4000元的人数为ξ.若每次抽取的结果是相互独立的，求ξ的分布列，期望()E ξ和方差()D ξ.【答案】（1）答案见解析，有；（2）分布列见解析，()0.9E ξ=，()0.63D ξ=. 【解析】【分析】（1）由频率分布直方图可求出抽取的100户中，经济损失不超过4000元的户数，经济损失超过4000元的户数，从而可补全列联表，进而可求出2K ，得出结论；（2）由题意知ξ的取值可能有0、1、2、3，符合二项分布，则3~(3)10B ξ，，从而利用二项分布的概率公式求出各自对应的概率，进而可得ξ的分布列，期望()E ξ和方差()D ξ. 【详解】（1）由频率分布直方图可知，在抽取的100户中，经济损失不超过4000元的有1002000(0.000150.00020)70⨯⨯+=户，则经济损失超过4000元的有30户，则表格数据如下：22100(60102010) 4.76280207030K ⨯⨯-⨯=≈⨯⨯⨯，∵4.762 3.841>，2( 3.841)0.05P K ≥=，∴有95%以上把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关；（2）由频率分布直方图可知抽到自身经济损失超过4000元居民的频率为0.3，将频率视为概率，由题意知ξ的取值可能有0、1、2、3，符合二项分布，则3~(3)10B ξ，，003337343(0)()()10101000P C ξ==⋅⋅=，112337441(1)()()10101000P C ξ==⋅⋅=，221337189(2)()()10101000P C ξ==⋅⋅=，33033727(3)()()10101000P C ξ==⋅⋅=，从而ξ的分布列为：3()30.910E np ξ==⨯=，37()(1)30.631010D np p ξ=-=⨯⨯=. 5. 私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成下表：（1）完成被调查人员的频率分布直方图．（2）若从年龄在[15,25)（[25,35)的被调查者中各随机选取2人进行追踪调查，求恰有2人不赞成的概率．（3）在(2)在条件下，再记选中的4人中不赞成．．．“车辆限行”的人数为ξ，求随机变量ξ的分布列和数学期望．【答案】（1）见解析（2（2275（3）见解析【解析】【详解】试题分析：（1）根据频率等于频数除以总数，再求频率与组距之比得纵坐标，画出对应频率分布直方图．（2）先根据2人分布分类，再对应利用组合求概率，最后根据概率加法求概率，（3）先确定随机变量，再根据组合求对应概率，列表可得分布列，最后根据数学期望公式求期望. 试题解析：（1（（2（由表知年龄在[)15,25内的有5人，不赞成的有1人，年龄在[)25,35 内的有10人，不赞成的有4人，恰有2人不赞成的概率为：()11122464442222510510C C C C C 4246666222C C C C 1025104522575P ξ==⋅+⋅=⋅+⋅==（（3（ ξ的所有可能取值为：0（1（2（3（()226422510C C 45150C C 22575P ξ==⋅==（()21112646442222510510C C C C C 415624102341C C C C 1045104522575P ξ⋅==⋅+⋅=⋅+⋅==（ ()124422510C C 461243C C 104522575P ξ==⋅=⋅==（所以ξ的分布列是：所以ξ的数学期望5E ξ=（ 6. 某商场举行的“三色球”购物摸奖活动规定：在一次摸奖中，摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球，再从装有1个蓝球与2个白球的袋中任意摸出1个球，根据摸出4个球中红球与蓝球的个数，设一、二、三等奖如下：其余情况无奖且每次摸奖最多只能获得一个奖级．（1）求一次摸奖恰好摸到1个红球的概率；（2）求摸奖者在一次摸奖中获奖金额x的分布列与期望E（x）．【答案】（1）（2）X的分布列为EX==4元【解析】【详解】（1）设A i表示摸到i个红球，B i表示摸到i个蓝球，则与相互独立（i=0，1，2，3）∴P（A1）==（2）X的所有可能取值为0，10，50，200P（X=200）=P（A3B1）=P（A3）P（B1）=P（X=50）=P（A3）P（B0）==P（X=10）=P（A2）P（B1）==P（X=0）=1﹣=∴X的分布列为EX==4元7. 以下茎叶图记录了甲､乙两组个四名同学的植树棵树､乙组记录中有一个数据模糊，无法确认，在图中以X表示.（1）如果8X=，求乙组同学植树棵树的平均数和方差；（2）如果9X=，分别从甲､乙两组中随机选取一名同学，求这两名同学的植树总棵树Y的分布列和数学期望.【答案】（1）平均数为354，方差为1116；（2）分布列答案见解析，数学期望：19.【解析】【分析】（1）利用平均数和方差公式求出即可；（2）根据题意可得Y 的可能取值为17，18，19，20，21，分别求出Y 取不同值的概率，即可得出分布列，求出期望.【详解】（1）当8X =时，由茎叶图可知，乙组同学的植树棵数是：8，8，9，10， ∴平均数为889103544x +++==，方差为2222213535353511[(8)(8)(9)(10)]4444416s =-+-+-+-=；（2）当9X =时，由茎叶图可知，甲组同学的植树棵树是：9，9，11，11，乙组同学的植树棵数是：9，8，9，10，分别从甲､乙两组中随机选取一名同学，共有4416⨯=种可能的结果，这两名同学植树总棵数Y 的可能取值为17，18，19，20，21，事件“17Y =”等价于“甲组选出的同学植树9棵，乙组选出的同学植树8棵”， ∴该事件有2种可能的结果，21(17)168P Y ===，事件“18Y =”等价于“甲组选出的同学植树9棵，乙组选出的同学植树9棵”， ∴该事件有4种可能的结果，41(18)164P Y ===，事件“19Y =”等价于“甲组选出的同学植树9棵，乙组选出的同学植树10棵，或甲组选出的同学植树11棵，乙组选出的同学植树8棵”， ∴该事件有224+=种可能的结果，41(19)164P Y ===，事件“20Y =”等价于“甲组选出的同学植树11棵，乙组选出的同学植树9棵”， ∴该事件有4种可能的结果，41(20)164P Y ===，事件“21Y =”等价于“甲组选出的同学植树11棵，乙组选出的同学植树10棵”， ∴该事件有2种可能的结果，21(21)168P Y ===，∴随机变量Y 的分布列为：∴11()17181920211984448E Y =⨯+⨯+⨯+⨯+⨯=.8. 语文成绩服从正态分布2(100,17.5)N ，数学成绩的频率分布直方图如图，如果成绩大于135的则认为特别优秀.（1）这500名学生中本次考试语文、数学特别优秀的大约各多少人？（2）如果语文和数学两科都特别优秀的共有6人，从（1）中的这些同学中随机抽取3人，设三人中两科都特别优秀的有X 人，求X 的分布列和数学期望.(附公式：若2~(,)X N μσ，则()0.68P X μσμσ-<≤+=，(22)0.96P X μσμσ-<≤+=).【答案】（1）语文有10人，数学有12人；（2）分布列见解析，98.【解析】【分析】（1）利用正态分布的对称性求出语文成绩特别优秀的概率，从而可估计出语文成绩特别优秀人数，由频率分布直方图可求出数学成绩特别优秀的频率，用频率来衡量概率，从而可求出数学成绩特别优秀的人数；（2）结合（1）可知数学语文单科优秀的有10人，则X 的所有可能取值为0、1、2、3，然后求出各自对应的概率即可列出分布列，求得数学期望【详解】（1）∵语文成绩服从正态分布2(10017.5)N ，，∴语文成绩特别优秀概率为11(135)(10.96)0.022P P X =≥=-⨯=， ∴数学成绩特别优秀的概率为230.0016200.0244P =⨯⨯=， ∴语文特别优秀的同学有5000.0210⨯=人，数学特别优秀的同学有5000.02412⨯=人；（2）语文数学两科都优秀的有6人，单科优秀的有10人，X 的所有可能取值为0、1、2、3，3103163(0)14C P X C ===，2110631627(1)56C C P X C ⋅===， 1210631615(2)56C C P X C ⋅===，363161(3)28C P X C ===， ∴X 的分布列为：19()0123145656288E X =⨯+⨯+⨯+⨯=. 9. 张明要参加某单位组织的招聘面试.面试要求应聘者有7次选题答题的机会(选一题答一题)，若答对4题即终止答题，直接进入下一轮，否则被淘汰.已知张明答对每一道题的概率都为12. （1）求张明进入下一轮的概率；（2）设张明在本次面试中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望. 【答案】（1）12；（2）分布列答案见解析，数学期望：9316. 【解析】【分析】（1）分情况讨论张明进入下一轮的概率；（2）由条件可知4,5,6,7ξ=，理解随机变量对应的事件，写出概率分布列，计算数学期望.。

高考数学高分答题模板

高考数学高分答题模板高考数学答题黄金模板1选择填空题易错点归纳：九大模块易混淆难经历考点分析，如概率和频率概念混淆、数列求和公式经历错误等，强化基础知识点经历，躲开因为知识点失误造成的客观性解题错误。

针对审题、解题思路不严谨如集合题型未考虑空集情形、函数问题未考虑定义域等主观性因素造成的失误进行专项训练。

答题方法：选择题十大速解方法：排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感受法、分析选项法;填空题四大速解方法：直截了当法、专门化法、数形结合法、等价转化法。

2突破解答题三角函数：考点题型归纳：通常考察正弦、余弦公式、三角形差不多性质、三种差不多三角函数之间的转化与角度的化简。

通常题型：Q1：带入求值，化简等;Q2：利用正弦、余弦公式转化，依照角度取值范畴确定正负号，求某角某边等。

答题方法：七大解题思想：如巧用数形结合、化归转化等方法解题。

概率统计：考点题型归纳：通常考察排列、组合运用分布列排列、期望运算等知识点。

通常题型：Q1：求某条件的概率;Q2：利用Q1所求的概率，求分布列以及期望。

答题方法：如互斥时刻和对立事件的巧妙运用等数列：考点题型归纳：通常考察通项公式和求和公式的运用。

通常题型：Q1：求某一项，求通项公式，求数列和通式;Q2：证明，求新数列第N项和，绝对值比较等。

答题方法：如通项公式三大解法：和作差，积作商，找规律叠加化简等;求和公式三大解法：直截了当公式，错位相减，分组求和等。

立体几何：通常题型：Q1：证明线面，线线，面面垂直等;Q2：求距离，求二面角等。

答题方法：如直截了当逻辑法：面面，线面，线面垂直平行等性质的运用;空间向量法：线面垂直，平行时用向量如何表达，公式;等面积、体积法：找到最方便运算的图形。

解析几何：考点题型归纳：椭圆，双曲线，抛物线方程的长短轴性质，离心率等，直线与圆锥曲线联立，求解某点，证明某直线与圆锥曲线的关系等。

通常题型：Q1：求圆锥曲线方程式;Q2：证明某点在某线某面上，求位置关系，求直线方程等。

高考数学万能解题模板总结(高考必备)

高考数学万能解题模板总结（高考必备）1、选择填空题1）易错点归纳九大模块易混淆难记忆考点分析，如概率和频率概念混淆、数列求和公式记忆错误等，强化基础知识点记忆，避开因为知识点失误造成的客观性解题错误。

针对审题、解题思路不严谨如集合题型未考虑空集情况、函数问题未考虑定义域等主观性因素造成的失误进行专项训练。

2）答题方法选择题十大速解方法：排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法。

填空题四大速解方法：直接法、特殊化法、数形结合法、等价转化法。

2、解答题答题技巧与模板1）三角变换与三角函数的性质问题一、解题路线图①不同角化同角①降幂扩角①化f（x）=Asin（ωx+φ）+h①结合性质求解。

二、构建答题模板①化简：三角函数式的化简，一般化成y=Asin（ωx+φ）+h的形式，即化为“一角、一次、一函数”的形式。

①整体代换：将ωx+φ看作一个整体，利用y=sinx，y=cosx的性质确定条件。

①求解：利用ωx+φ的范围求条件解得函数y=Asin（ωx+φ）+h的性质，写出结果。

①反思：反思回顾，查看关键点，易错点，对结果进行估算，检查规范性。

2）解三角形问题一、解题路线图①化简变形；①用余弦定理转化为边的关系；①变形证明。

①用余弦定理表示角；①用基本不等式求范围；①确定角的取值范围。

二、构建答题模板①定条件：即确定三角形中的已知和所求，在图形中标注出来，然后确定转化的方向。

①定工具：即根据条件和所求，合理选择转化的工具，实施边角之间的互化。

①求结果。

①再反思：在实施边角互化的时候应注意转化的方向，一般有两种思路：一是全部转化为边之间的关系；二是全部转化为角之间的关系，然后进行恒等变形。

3）数列的通项、求和问题一、解题路线图①先求某一项，或者找到数列的关系式。

①求通项公式。

①求数列和通式。

二、构建答题模板①找递推：根据已知条件确定数列相邻两项之间的关系，即找数列的递推公式。

高中数学解答题答题模板(11个)

Asin(ωx＋φ)＋h 的形式或 y＝Acos(ωx＋φ)＋h 的形式． π 如：f(x)＝2sin2x＋3 ＋1.
第二步：根据 f(x)的表达式求其周期、最值．
第三步：由 sin x、cos x 的单调性，将“ωx＋φ”看作一个整体，转化为解不等式问题．
第四步：明确规范表述结论．
π (2)∵－1≤sin2x＋3≤1， π ∴－1≤2sin2x＋3＋1≤3.
π π π ∴当 2x＋3＝2＋2kπ，k↔Z，即 x＝12＋kπ，k↔Z 时，f(x)取得最大值 3； π π 5π 当 2x＋＝－＋2kπ，k↔Z，即 x＝－＋kπ，k↔Z 时，f(x)取得最小值－1. 3 2 12
高中数学解答题答题模板（11个）
【模板特征概述】数学解答题是高考数学试卷中的一类重要题型，通常是高考的把关题和压轴题，具有较好的区分层次和选拔功能．目前的高考解答题已经由单纯的知识综合型转化为知识、方法和能力的综合型解答题．在高考考场上，能否做好解答题，是高考成败的关键，因此，在高考备考中学会怎样解题，是一项重要的内容．本节以著名数学家波利亚的《怎样解题》为理论依据，结合具体的题目类型，来谈一谈解答数学解答题的一般思维过程、解题程序和答题格式，即所谓的“答题模板”． “答题模板”就是首先把高考试题纳入某一类型，把数学解题的思维过程划分为一个个小题，按照一定的解题程序和答题格式分步解答，即化整为零．强调解题程序化，答题格式化，在最短的时间内拟定解决问题的最佳方案，实现答题效率的最优化.
模板 1 【例 1】
三角函数的周期性、单调性及最值问题
已知函数 f(x)＝2cos x· π sinx＋3 － 3sin2x＋sin xcos x＋1. (1)求函数 f(x)的最小正周期； (2)求函数 f(x)的最大值及最小值； (3)写出函数 f(x)的单调递增区间．审题路线图规范解答不同角化同角→降幂扩角→化 f(x)＝Asin(ωx＋φ) ＋h→结合性质求解．

高考数学专题04 函数的奇偶性黄金解题模板

专题04 函数的奇偶性【高考地位】函数的奇偶性是函数的一个重要性质，几乎是每年必考的内容，例如判断和证明函数的奇偶性，利用函数的奇偶性解决实际问题．【方法点评】一、函数奇偶性的判断使用情景：一般函数类型解题模板：第一步确定函数的定义域；第二步判断其定义域是否关于原点对称；第三步若是，则确定()f x 与()f x -的关系；若不是，则既不是奇函数也不是偶函数；第四步得出结论. 例1 判断下列函数的奇偶性：(1)22()99f x x x =-+-；(2) 1()(1)1x f x x x -=++；(3)24()33x f x x -=+-.【点评】确定函数的奇偶性时，必须先判定函数定义域是否关于原点对称．若对称，再验证()()f x f x -=±或其等价形式()()0f x f x -±=是否成立．【变式演练1】下列函数中，既是偶函数又在区间()0,+∞上单调递增的是（）A. 1y x=B. lg y x =C. cos y x =D. 22x y x =+ 【答案】B考点：函数的奇偶性.【变式演练2】函数的图象（）A. 关于轴对称B. 关于轴对称C. 关于原点对称D. 关于直线对称【答案】B【解析】由为偶函数可得. 函数的图象关于y 轴对称,选B.【变式演练3】设函数()y f x =的定义域为R ，并且满足()()()f x y f x f y -=-，且(2)1f =，当0x >时，()0f x >. （1）求(0)f 的值；（2）判断函数()f x 的奇偶性,并给出证明；（3）如果()(2)2f x f x ++<，求x 的取值范围．【答案】（1）(0)0f =；（2）函数()y f x =为奇函数；（3）{|1}x x <；【解析】试题分析：（1）利用赋值法，求)0(f 的值，即令y x =，能求出)0(f ；（2）利用函数奇偶性的定义，判断函数)(x f 的奇偶性，即令0=x ,可得到)(y f 与)(y f -的关系；（3）由奇偶性及()()()f x y f x f y -=-，对()(2)2f x f x ++<进行转化，可得到(2)(4)()(4)f x f f x f x +<-=-，然后再利用定理证明)(x f 在R 上的单调性，即可求出x 的取值范围（3）任取12,x x R∈，不妨设12x x >，则120x x ->，1212()()()f x x f x f x -=-因为当0x >时，()0f x > 所以12()0f x x ->，即12()()0f x f x ->，所以12()()f x f x >所以函数()y f x =在定义域R 上单调递增. 因为()()()f x y f x f y -=- 所以()()()f x f x y f y =-+所以211(2)(2)(2)(42)(4)f f f f f =+=+=--= 因为()(2)2f x f x ++< 所以()(2)(4)f x f x f ++<所以(2)(4)()(4)f x f f x f x +<-=- 因为函数()y f x =在定义域R 上单调递增所以24x x +<-，从而1x <，所以x 的取值范围为{|1}x x < 考点：1.抽象函数及其应用；2.函数的奇偶性与单调性综合应用；二、利用函数的奇偶性求函数的解析式解题模板：第一步首先设出所求区间的自变量x ；第二步运用已知条件将其转化为已知区间满足的x 的取值范围；第三步利用已知解析式确定所求区间相应的函数的表达式.例2 ．已知函数()f x 是定义在R 上的奇函数，当0x ≥时， ()()=1f x x x +，求出函数()f x 的解析式. 【答案】()()1,0{1,0x x x x x x +≥-<.考点：求函数的解析式．【点评】（1）已知函数的奇偶性求解析式的题目，一般是求哪个区间，则设未知数在哪个区间，然后化为已知区间求解；（2）本题是求函数()f x 在R 上的解析式，一定不要忘记0=x 时，函数()f x 的值. 例3 若函数()f x 是奇函数，()g x 是偶函数，且其定义域均为{,1}x x R x ∈≠±.若()1()1f xg x x +=-，求()f x ，()g x 的解析式. 【答案】2()1xf x x =-，()211g x x =-.【点评】这里运用了构造法，把符合要求的奇函数与偶函数构造出来，问题也就解决了，构造的关键是运用奇、偶函数的概念，并联系方程组的知识.【变式演练4】已知定义在R 上的函数)(x f y =是偶函数，且0≥x 时，)22ln()(2+-=x x x f . 当0<x 时，求)(x f 解析式；【答案】)22ln()(2++=x x x f .试题解析：0<x 时，0>-x ，∴)22ln()(2++=-x x x f ，∵)(x f y =是偶函数，∴)()(x f x f =-，0<x 时，)22ln()(2++=x x x f .【变式演练5】已知函数是奇函数．（1）求实数的值；（2）用定义证明函数在上的单调性；（3）若对任意的，不等式恒成立，求实数的取值范围．【答案】（1）（2）见解析（3）考点：函数的简单性质的综合运用．【高考再现】1.【2017全国二文】已知函数()f x 是定义在R 上的奇函数，当(,0)x ∈-∞时，32()2f x x x =+,则(2)f =【答案】12【解析】(2)(2)[2(8)4]12f f =--=-⨯-+= 【考点】函数奇偶性【名师点睛】(1)已知函数的奇偶性求函数值或解析式，首先抓住奇偶性讨论函数在各个区间上的解析式，或充分利用奇偶性得出关于()f x 的方程，从而可得()f x 的值或解析式.(2)已知函数的奇偶性求参数，一般采用待定系数法求解，根据()()0f x f x ±-=得到关于待求参数的恒等式，由系数的对等性得参数的值或方程(组)，进而得出参数的值.2. 【2016高考浙江文数】已知函数()f x 满足：()f x x ≥且()2,xf x x ≥∈R .（） A.若()f a b ≤，则a b ≤ B.若()2bf a ≤，则a b ≤ C.若()f a b ≥，则a b ≥ D.若()2b f a ≥，则a b ≥ 【答案】B3. 【2016高考山东理数】已知函数f (x )的定义域为R .当x <0时，3()1f x x =- ；当11x -≤≤ 时，()()f x f x -=-；当12x >时，11()()22f x f x +=- .则f (6)= （）（A ）−2 （B ）−1（C ）0（D ）2【答案】D考点：1.函数的奇偶性与周期性；2.分段函数.【名师点睛】本题主要考查分段函数的概念、函数的奇偶性与周期性，是高考常考知识内容.本题具备一定难度.解答此类问题，关键在于利用分段函数的概念，发现周期函数特征，进行函数值的转化.本题能较好的考查考生分析问题解决问题的能力、基本计算能力等.4.【2016高考天津理数】已知f (x )是定义在R 上的偶函数，且在区间（-∞，0）上单调递增.若实数a 足1(2)(2)a f f ->-，则a 的取值范围是______.【答案】13(,)225.【2015高考广东，理3】下列函数中，既不是奇函数，也不是偶函数的是（） A ．xe x y += B ．x x y 1+= C ．x xy 212+= D ．21x y += 【答案】A ．【考点定位】函数的奇偶性判断．【名师点睛】本题主要考查函数的奇偶性判断和常见函数性质问题，但既不是奇函数，也不是偶函数的判断可能较不熟悉，容易无从下手，因此可从熟悉的奇偶性函数进行判断排除，依题易知B 、C 、D 是奇偶函数，排除得出答案，属于容易题．6.【2015高考福建，文3】下列函数为奇函数的是( ) A ．y x =．x y e = C ．cos y x = D ．x x y e e -=-【答案】D【解析】函数y x =和x y e =是非奇非偶函数； cos y x =是偶函数；x x y e e -=-是奇函数，故选D ．【考点定位】函数的奇偶性．【名师点睛】本题考查函数的奇偶性，除了要掌握奇偶性定义外，还要深刻理解其定义域特征即定义域关于原点对称，否则即使满足定义，但是不具有奇偶性，属于基础题． 7.【2015高考安徽，文4】下列函数中，既是偶函数又存在零点的是（）（A ）y =lnx （B ）21y x =+ （C ）y =sinx （D ）y =cosx 【答案】D8.【2015高考天津，文7】已知定义在R 上的函数||()21()x m f x m -=-为实数为偶函数,记0.5(log 3),a f =2b (log 5),c (2)f f m ==,则,,a b c ,的大小关系为（）(A) b c a << (B) b c a << (C) b a c << (D) b c a << 【答案】B【解析】由()f x 为偶函数得0m =,所以0,52log 3log 32121312,a =-=-=-=2log 521514b =-=-=,0210c =-= ,所以b c a <<,故选B.【考点定位】本题主要考查函数奇偶性及对数运算.【名师点睛】函数是高考中的重点与热点,客观题中也会出现较难的题,解决此类问题要充分利用相关结论.函数()0,1x my ab a a -=+>≠的图像关于直线x m = 对称,本题中求m 的值,用到了这一结论,本题中用到的另一个结论是对数恒等式:()log 0,1,0a NaN a a N =>≠>.9.【2015新课标2文12】设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是（）A ．1,13⎛⎫ ⎪⎝⎭B ．()1,1,3⎛⎫-∞+∞ ⎪⎝⎭UC ．11,33⎛⎫- ⎪⎝⎭D ．11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U 【答案】A10. 【2015高考广东，文3】下列函数中，既不是奇函数，也不是偶函数的是（）A ．2sin y x x =+ B ．2cos y x x =- C ．122xx y =+D ．sin 2y x x =+ 【答案】A【解析】函数()2sin f x x x =+的定义域为R ，关于原点对称，因为()11sin1f =+，()11sin1f -=-，所以函数()2sin f x x x =+既不是奇函数，也不是偶函数；函数()2cos f x x x =-的定义域为R ，关于原点对称，因为()()()()22cos cos f x x x x x f x -=---=-=，所以函数()2cos f x x x =-是偶函数；函数()122xx f x =+的定义域为R ，关于原点对称，因为()()112222x xx x f x f x ---=+=+=，所以函数()122x x f x =+是偶函数；函数()sin 2f x x x =+的定义域为R ，关于原点对称，因为()()()sin 2sin 2f x x x x x f x -=-+-=--=-，所以函数()sin 2f x x x =+是奇函数．故选A ．【考点定位】函数的奇偶性．【名师点晴】本题主要考查的是函数的奇偶性，属于容易题．解题时一定要判断函数的定义域是否关于原点对称，否则很容易出现错误．解本题需要掌握的知识点是函数的奇偶性，即奇函数：定义域关于原点对称，且()()f x f x -=-；偶函数：定义域关于原点对称，且()()f x f x -=．11.【2015高考山东，文8】若函数21()2x x f x a+=-是奇函数，则使3f x >（）成立的x 的取值范围为( )（A ）( ) (B)() （C ）0,1（）（D ）1,+∞（）【答案】C12.【2015高考北京，文3】下列函数中为偶函数的是（）A ．2sin y x x = B ．2cos y x x = C ．ln y x = D ．2xy -=【答案】B【考点定位】函数的奇偶性.【名师点晴】本题主要考查的是函数的奇偶性，属于容易题．解题时一定要判断函数的定义域是否关于原点对称，否则很容易出现错误．解本题需要掌握的知识点是函数的奇偶性，即奇函数：定义域关于原点对称，且()()f x f x -=-；偶函数：定义域关于原点对称，且()()f x f x -=．13.【2014全国2，文15】偶函数)(x f y =的图像关于直线2=x 对称，3)3(=f ，则)1(-f =________．【答案】3【解析】因为)(x f y =的图像关于直线2=x 对称，故(3)(1)3f f ==，又因为)(x f y =是偶函数，故(1)(1)3f f -==．【考点定位】函数的奇偶性及对称性.【名师点睛】本题考查了函数的奇偶性，函数图象的对称性，属于中档题目，根据函数图象的对称性及奇偶性，找到未知与已知之间的关系，从而由已知即可求得未知.14. 【2015高考新课标1，理13】若函数f (x )=2ln()x x a x ++为偶函数，则a = 【答案】115.【2014上海,理20】（本题满分14分）本题有2个小题，第一小题满分6分，第二小题满分1分.设常数0≥a ，函数aa x f x x -+=22)(（1）若a =4，求函数)(x f y =的反函数)(1x fy -=；（2）根据a 的不同取值，讨论函数)(x f y =的奇偶性，并说明理由.【答案】（1）121()2log 1x fx x -+⎛⎫=+ ⎪-⎝⎭，(,1)(1,)x ∈-∞-+∞U ；（2）1a =时()y f x =为奇函数，当0a =时()y f x =为偶函数，当0a ≠且1a ≠时()y f x =为非奇非偶函数．【解析】试题分析：（1）求反函数，就是把函数式2424x x y +=-作为关于x 的方程，解出x ，得1()x f y -=，再把此式中的,x y 互换，即得反函数的解析式，还要注意的是一般要求出原函数的值域，即为反函数的定义域；（2）讨论函数的奇偶性，我们可以根据奇偶性的定义求解，在0a =，1a =这两种情况下，由奇偶性的定义可知函数()f x 具有奇偶性，在01a a ≠≠且时，函数的定义域是2log x a ≠，不关于原点对称，因此函数既不是奇函数也不是偶函数．【反馈练习】1. 【2018届河北省衡水市高三上学期第三次调研考试数学（理）试题】下列函数中，在[]1,1-上与函数2cos 2xy =的单调性和奇偶性都相同的是（） A. 22xxy -=- B. 1y x =+ C. ()22y x x =+ D. 22y x =-+【答案】D【解析】函数2cos 2x y =在[]1,0-上递增，在[]0,1上递减，且函数2cos 2x y =为偶函数，而22y x =-+也在[]1,0-上递增，在[]0,1上递减，且函数22y x =-+为偶函数，即22y x =-+与函数2cos 2x y =的单调性和奇偶性都相同，故选D. 考点：函数的奇偶性．2. 【2017届广西省高三上学期教育质量诊断性联合考试数学（文）试卷】已知定义在R 上的奇函数()f x在[)0,+∞上递减，若()()321f x x a f x -+<+对[]1,2x ∈-恒成立，则a 的取值范围为（） A. ()3,-+∞ B. (),3-∞- C. ()3,+∞ D. (),3-∞ 【答案】C3. 【2018届高河北省衡水中学三9月大联考数学（理）试题】已知函数()f x 为R 内的奇函数，且当0x ≥时， ()1cos xf x e m x =-+-，记()22a f =--， ()1b f =--， ()33c f =，则a ， b ， c 间的大小关系是（）A. b a c <<B. a c b <<C. c b a <<D. c a b << 【答案】D【解析】函数()f x 是奇函数，则()001cos00,0f e m m =-+-=∴=，即当0x ≥时， ()1xf x e =-+，构造函数()()g x xf x =，满足()()g x g x -=，则函数()g x 是偶函数，则()()'11xg x ex =-+，当0x ≥时， 1,11xe x ≥+≥，据此可得： ()'0g x ≤，即偶函数()g x 在区间[)0,+∞上单调递减，且： ()()()()()22,11,3a g g b g g c g =-==-==，结合函数的单调性可得： ()()()123g g g >>，即： c a b <<. 本题选择D 选项.点睛：对于比较大小、求值或范围的问题，一般先利用函数的奇偶性得出区间上的单调性，再利用其单调性脱去函数的符号“f ”，转化为考查函数的单调性的问题或解不等式(组)的问题，若f (x )为偶函数，则f (－x )＝f (x )＝f (|x |)．4.【2018届山西省山大附中等晋豫名校高三年级第四次调研诊断考试数学理试题】若对,R x y ∀∈，有()()()3f x y f x f y +=+-，则函数()()221xg x f x x =++在[]2017,2017-上的最大值与最小值的和为（）A. 4B. 6C. 9D. 12 【答案】B【解析】对,R x y ∀∈，有()()()3f x y f x f y +=+-，令0x y ==，有()()()()0003,03f f f f =+-=，令y x =-，有()()()03f f x f x =+--，则()()6f x f x +-=，令()()3h x f x =-，则()()0h x h x +-=，则()h x 为奇函数，又设函数()221xx x ϕ=+， ()x ϕ为奇函数，则()()()3g x x h x ϕ=++，而()()x h x ϕ+为奇函数，由于奇函数在关于原点对称的单调区间内的最大值与最小值互为相反数，则()g x 的最大值与最小值之和为6.选B.5.【山西省45校2018届高三第一次联考理数试卷】若函数是偶函数，则__________．【答案】12-6．【2018届江西省新余市第一中学毕业年级第二模拟考试理科数学试题】函数()y f x =与()y g x =有相同的定义域，且都不是常值函数，对于定义域内的任何x ，有()()0f x f x +-=， ()()1g x g x -=，且当0x ≠时， ()1g x ≠，则()()()()21f x F x f xg x =+-的奇偶性为__________．【答案】偶函数【解析】由条件，得()()()()()()()22111f x f xF x f x f xg xg x---=+-=----()()()()()()()()()()2211f xg x f x g x f x f x g xf xg x g x-⋅-⋅-+⋅=-=--()()()()()()()()()()()()2=111f xg x f x f x g x f x f xf x F xg x g x g x-⋅-⋅+==+=---，故()()()()21f xF x f xg x=+-为偶函数，故答案为偶函数.7. 已知)(xf为奇函数，当0>x时，56)(2+-=xxxf，则当0<x时，=)(xf____.【答案】562---xx考点：1、函数的奇偶性；2、分段函数的解析式.8. 下列说法中：①若2()(2)2f x ax a b x=+++（其中[21,4]x a a∈-+）是偶函数，则实数2b=；②22()20082008f x x x--③已知()f x是定义在R上的奇函数，若当[0,)x∈+∞时，()(1)f x x x=+,则当x R∈时，()(1)f x x x=+；④已知()f x是定义在R上的不恒为零的函数，且对任意的,x y R∈都满足()()()f x y x f y y f x⋅=⋅+⋅，则()f x是奇函数；其中正确说法的序号是（注：把你认为是正确的序号都填上）．【答案】①②③④【解析】试题分析：①若()()222f x ax a b x=+++是定义在[21,4]a a-+上的偶函数，则214020a aa b-++=⎧⎨+=⎩，所以12ab=-⎧⎨=⎩，①正确；②()2220082008f x x x =-+-的定义域为{}2008,2008-，则函数转化(){}0,2008,2008f x x =∈-，所以()f x 既是奇函数与又是偶函数；②正确；③当(),0x ∈-∞时，()0,x -∈+∞，则()()1f x x x -=--，根据奇函数()()f x f x -=-，所以()()()1,,0f x x x x =-∈-∞，所以当x R ∈时，()()1f x x x =+，③正确；④令1x y ==，得到：()10f =，令1x y ==-，得到：()()121f f =--，所以()10f -=，令1y =-，则有()()f x f x -=-，所以函数()f x 为奇函数，④正确。

高考数学解答题常考公式及答题模板

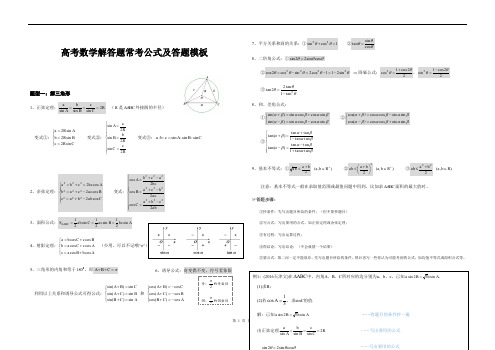
第 1 页高考数学解答题常考公式及答题模板题型一：解三角形1、正弦定理：R CcB b A a 2sin sin sin === （R 是ABC ∆外接圆的半径）变式①：⎪⎩⎪⎨⎧===C R c B R b A R a sin 2sin 2sin 2 变式②：⎪⎪⎪⎩⎪⎪⎪⎨⎧===Rc C R bB R aA 2sin 2sin 2sin 变式③：CB A c b a sin :sin :sin ::=2、余弦定理：⎪⎪⎩⎪⎪⎨⎧-+=-+==+=C ab b a c B ac c a b A bc c b a cos 2cos 2cos 2222222222 变式：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+=-+=-+=ab c b a C ac b c a B bc a c b A 2cos 2cos 2cos 2222222223、面积公式：A bc B ac C ab S ABC sin 21sin 21sin 21===∆ 4、射影定理：⎪⎩⎪⎨⎧+=+=+=A b B a c A c C a b Bc C b a cos cos cos cos cos cos （少用，可以不记哦^o^）5、三角形的内角和等于 180，即π=++C B A6、诱导公式：奇变偶不变，符号看象限利用以上关系和诱导公式可得公式：⎪⎩⎪⎨⎧=+=+=+A C B B C A C B A sin )sin(sin )sin(sin )sin( 和 ⎪⎩⎪⎨⎧-=+-=+-=+A C B B C A CB A cos )cos(cos )cos(cos )cos(7、平方关系和商的关系：①1cos sin 22=+θθ ②θθθcos sin tan =8、二倍角公式：①θθθcos sin 22sin =②θθθθθ2222sin 211cos 2sin cos 2cos -=-=-= ⇒降幂公式：22cos 1cos 2θθ+=，22cos 1sin 2θθ-= ③θθθ2tan 1tan 22tan -=8、和、差角公式：①⎩⎨⎧-=-+=+βαβαβαβαβαβαsin cos cos sin )sin(sin cos cos sin )sin(②⎩⎨⎧+=--=+βαβαβαβαβαβαsin sin cos cos cos(sin sin cos cos cos(））③⎪⎪⎩⎪⎪⎨⎧+-=--+=+βαβαβαβαβαβαtan tan 1tan tan )tan(tan tan 1tan tan )tan( 9、基本不等式：①2ba ab +≤),(+∈R b a ②22⎪⎭⎫ ⎝⎛+≤b a ab ),(+∈R b a ③222b a ab +≤ ),(R b a ∈注意：基本不等式一般在求取值范围或最值问题中用到，比如求ABC ∆面积的最大值时。

2023高考数学答题技巧及方法模板

2023高考数学答题技巧及方法模板对学习内容越熟悉，对解题的基本思路和方法就越熟悉，能背的数字和公式就越多，能把局部和整体有机地结合成一个整体，形成跳跃式思维，能大大加快解题速度。

下面是小编为大家带来的高考数学答题技巧及方法模板，希望大家能够喜欢！高考数学答题模板1选择填空题1、答题方法高考数学选择题速解方法：排除法、假设条件法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法;数学填空题速解方法：直接法、特殊化法、数形结合法、等价转化法。

2、易错点归纳数学易混淆难记忆考点分析：概率和频率概念混淆、数列求和公式记忆错误等，强化基础知识点记忆，避开因为知识点失误造成的客观性解题错误。

2解答题数学解答题是高考数学试卷中的一类重要题型，通常是高考的把关题和压轴题。

1、三角函数考察正弦、余弦公式、三角形基本性质、三种基本三角函数之间的转化与角度的化简。

三角函数是以角度为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

常见的三角函数包括正弦函数、余弦函数和正切函数。

不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

答题方法：巧用数形结合、化归转化等方法解题。

例1：设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，a=2sinabA(1)求B的大小。

(2)求cosA+sinC的取值范围。

2、概率统计考察排列、组合运用分布列罗列、期望计算等知识点。

概率所研究的内容一般包括随机事件的概率、统计独立性和更深层次上的规律性。

对于任何事件的概率值一定介于0和1之间。

有一类随机事件，它具有两个特点：第一，只有有限个可能的结果;第二，各个结果发生的可能性相同。

具有这两个特点的随机现象叫做“古典概型”。

3、数列考察通项公式和求和公式的运用。

数列是以正整数集(或它的有限子集)为定义域的函数，是一列有序的数。

数列中的每一个数都叫做这个数列的项。

排在第一位的数称为这个数列的第1项(通常也叫做首项)，排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项，通常用an表示。

备战高考技巧大全之高中数学黄金解题模板：专题21三角形中的最值问题答案解析

；（2）由余弦定理和基本不等式，有 a2 b2 16 ab 2ab ，ab 16，
2
3
S ABC
3 ab 4 3 ，当且仅当 a b 时等号成立，故为等边三角形．
4
试题解析：
（ 2）由题知，
c 4， C
，∴ S ABC
3
3 ab ．∵由余弦定理可知：
a2 b2
c2
2ab cosC ，
4
Байду номын сангаас
a2 b2 16 ab 2ab ，∴ ab 16．当且仅当“ a b ”时等号成立，
4
4
【变式演练 1 】已知 ABC 外接圆的半径为 6 ，若面积 S ABC a 2 (b c) 2 且
sin B sin C 4 ，则 sin A 3
【答案】 sin A
8 256
，
.
17 17
， S ABC 的最大值为
考点： 1．正弦定理； 2．解斜三角形．
【变式演练 2 】在 ABC 中，角 A ， B ， C 的对边分别为 a ， b ， c ，已知 c cos B (2 a b) cosC ．
tan B b
sin B cos A
sin B
sin Acos B 2sin C sin B , 也即 sin A cosB 2sin C cos A sin B cos A , 故
cos A
1
sin( A B) 2 sin C cos A ,也即 2 cos A 1, 则 A 60 0 ,由正弦定理可得 a 2sin A 3 ,
.本题以三角形的外接
圆的半径及 tan A

高考数学专题24 数列求和方法黄金解题模板

专题24 数列求和方法【高考地位】数列是高中数学的重要内容,又是高中数学与高等数学的重要衔接点,其涉及的基础知识、数学思想与方法,在高等数学的学习中起着重要作用,因而成为历年高考久考不衰的热点题型,在历年的高考中都占有重要地位。

数列求和的常用方法是我们在高中数学学习中必须掌握的基本方法，是高考的必考热点之一。

此类问题中除了利用等差数列和等比数列求和公式外，大部分数列的求和都需要一定的技巧。

下面，就近几年高考数学中的几个例子来谈谈数列求和的基本方法和技巧。

【方法点评】方法一公式法解题模板：第一步结合所求结论，寻找已知与未知的关系；第二步根据已知条件列方程求出未知量；第三步利用前n 项和公式求和结果例1.设}{n a 为等差数列，n S 为数列}{n a 的前n 项和，已知77=S ，7515=S ，n T 为数列}{nS n的前n 项和，求n T ．【评析】直接应用公式求和时，要注意公式的应用范围，如当等比数列公比为参数(字母)时，应对其公比是否为1进行讨论．常用的数列求和公式有：等差数列前n 项和公式： 11()(1)22n n n a a n n S na d +-==+．等比数列前n 项和公式：111(1)(1)(1)11n n n na q S a q a a q q q q =⎧⎪=--⎨=≠⎪--⎩．自然数方幂和公式：1123(1)2n n n +++⋅⋅⋅+=+ 22221123(1)(21)6n n n n +++⋅⋅⋅+=++333321123[(1)]2n n n +++⋅⋅⋅+=+【变式演练1】已知{a n }是等差数列，a 1+a 2=4，a 7+a 8=28，则该数列前10项和S 10等于（） A.64 B.100 C.110 D.120 【答案】B考点：等差数列通项公式及求和方法二分组法解题模板：第一步定通项公式：即根据已知条件求出数列的通项公式；第二步巧拆分：即根据通项公式特征，将其分解为几个可以直接求和的数列；第三步分别求和：即分别求出各个数列的和；第四步组合：即把拆分后每个数列的求和进行组合，可求得原数列的和.例2. 已知数列{a n }是3＋2－1,6＋22－1,9＋23－1,12＋24－1，…，写出数列{a n }的通项公式并求其前n 项S n .【变式演练2】在已知数列11a =， 22a =，且()2221nn n a a +-=--， *n N ∈，则2017S 的值为（） A. 201610101⨯- B. 10092017⨯ C. 201710101⨯- D. 10092016⨯ 【来源】【全国百强校】河北省2017届衡水中学押题卷理数 II 卷【答案】C【解析】由递推公式可得：当n 为奇数时， 24n n a a +-= ，数列{}21n a - 是首项为1，公差为4的等差数列，当n 为偶数时， 20n n a a +-= ，数列{}21n a - 是首项为2，公差为0的等差数列，()()20171320172420161100910091008410082220171010 1.S a a a a a a =+++++++=+⨯⨯⨯+⨯=⨯-本题选择C 选项.【方法点睛】分组转化法求和的常见类型(1)若a n ＝b n ±c n ，且{b n }，{c n }为等差或等比数列，可采用分组求和法求{a n }的前n 项和；(2)通项公式为a n ＝⎩⎪⎨⎪⎧b n ，n 为奇数，c n ，n 为偶数的数列，其中数列{b n }，{c n }是等比数列或等差数列，可采用分组求和法求和.【变式演练3】已知{}n a 是等差数列，{}n b 是等比数列，且23b =，39b =，11a b =，144a b =．（1）求{}n a 的通项公式；（2）设n n n c a b =+，求数列{}n c 的前n 项和．【答案】（1）21(1,2,3,)n a n n =-=；（2）2312n n -+．考点：1、等差数列；2、等比数列．方法三裂项相消法解题模板：第一步定通项公式：即根据已知条件求出数列的通项公式；第二步巧裂项：即根据通项公式特征准确裂项，将其表示为两项之差的形式；第三步消项求和：即把握消项的规律，准确求和. 例 3. 已知数列{}n a :12,1233+,123444++,…, 123910101010+++,…,若11n n n b a a +=⋅，那么数列{}n b 的前n 项和n S 为（）A ．1n n + B ．41n n + C. 31n n + D ．51nn +【答案】B【变式演练4】已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列{11.n n a a +}的前100项和为（）A ．100101 B ．99101C ．99100D ．101100 【答案】A 【解析】试题分析：由a 5=5，S 5=15，可知11,1a d == ()1111111n n n a n a a n n n n +∴=∴==-++ 10011111110011223100101101101S ⎛⎫⎛⎫⎛⎫∴=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭考点：数列求和方法四错位相减法解题模板：第一步巧拆分：即根据通项公式分解为等差数列和等比数列乘积的形式；第二步确定等差、等比数列的通项公式；第三步构差式：即写出n S 的表达式，然后两边同时乘以等比数列的公比得到另外一个式子，两式作差；第四步求和：根据差式的特征准确求和.例 4. 已知数列{}n a 满足11a =， 122n n n a a a +=+.记2nn nC a =，则数列{}n C 的前n 项和12...n C C C +++=__________．【答案】2n n ⋅【变式演练5】已知数列{}n a 的前n 项和为n S ，且122n n S +=-（*n ∈N ）. (Ⅰ) 求数列{}n a 的通项公式；(Ⅱ) 令n n b na =，求数列{}n b 的前n 项和n T . 【答案】（Ⅰ）2nn a =；（Ⅱ）1(1)22n n T n +=-+.(Ⅱ) 由(Ⅰ)，2n n n b na n ==⨯. 则1212222n n T n =⨯+⨯++⨯，所以231212222n n T n +=⨯+⨯++⨯，则212222nn n T n +-=+++-⨯12(12)212n n n +-=-⨯-1(1)22n n +=--.所以1(1)22n n T n +=-+考点：1、数列的通项公式；2、数列求和.【方法点睛】对于递推公式确定的数列的求解，通常可以通过递推公式的变换，转化为等差或等比数列问题，有时也用到一些特殊的转化方法与特殊数列，此法称为辅助数列法.常用转化方法：变换法、待定系数法、加减法、累加法、迭代法等.【变式演练6】已知等差数列{}n a 的前n 项和为n S ，且93=S ，731,,a a a 成等比数列. （1）求数列{}n a 的通项公式；（2）若数列{}n a 的公差不为0，数列{}n b 满足nn n a b 2)1(-=，求数列{}n b 的前n 项和n T .【答案】（1）1n a n =+；（2）22)1(1+⋅-=+n n n T .【解析】试题分析：（1）由题意可知，利用93=S ，731,,a a a 成等比数列，从而可求出数列{}n a 的通项公式，数列{}n b考点：1.等差数列的综合；2.等比数列的综合；3.错位相减法的运用.方法五倒序相加法例5.函数()()()*112321,11,,1x n x e n f x g x f x a g g g g n N e n n n n --⎛⎫⎛⎫⎛⎫⎛⎫==-+=++++∈ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭，则数列{}n a 的通项公式为__________．【答案】21n a n =-【解析】由()()1111x x x xe ef x f x e e -----===-++，函数()11x x e f x e -=+为奇函数， ()()()()()()211211112g x g x f x f x f x f x +-=-++--+=-+-+，由()11x x e f x e -=+为奇函数， ()()110f x f x ∴-+-=， ()()22g x g x ∴+-=，∵*12321,n n a g g g g n N n n n n -⎛⎫⎛⎫⎛⎫⎛⎫=++++∈⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，①考点：倒序相加法求和.【变式演练7】已知函数321(),().212x F x x x -=≠- （1）求122009()()()201020102010F F F +++的值；（2）已知数列11{}2,()n n n a a a F a +==满足,求证数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列；（3）已知nn n b 212-=，求数列{}n n a b 的前n 项和n S . 【答案】(1) S=60272. (2)见解析；（3）n S =1242n n-+-。

高考文科数学解答题解题模板

(2)由余弦定理及 C＝π3得 7＝a2＋b2－2ab·12，即(a＋b)2－3ab＝7， 8 分得分点⑤ 又 S＝12ab·sin C＝ 43ab＝323，所以 ab＝6，10 分得分点⑥ 所以(a＋b)2－18＝7，a＋b＝5，11 分得分点⑦ 所以△ABC 的周长为 a＋b＋c＝5＋ 7. 12 分得分点⑧
3an，同时 a2＝3a1， ∴数列{an}的通项公式为 an＝3n－1，n∈N*.
(2)设 bn＝|3n－1－n－2|，n∈N*，则 b1＝2，b2＝1. 当 n≥3 时，由于 3n－1>n＋2，
故 bn＝3n－1－n－2，n≥3.
设数列{bn}的前 n 项和为 Tn，
则 T1＝2，T2＝3，
当
(1)证明：直线 BC∥平面 PAD； (2)若△PCD 的面积为 2 7，求四棱锥 P－ABCD 的体积.
规范解答 (1)证明在平面 ABCD 中，因为∠BAD＝∠ABC＝90°. 所以 BC∥AD，1 分得分点① 又 BC⊄平面 PAD，AD⊂平面 PAD. 所以直线 BC∥平面 PAD.3 分得分点② (2)解如图，
PN＝
14 2x
等.
2.注意利用第(1)问的结果：在题设条件下，在第(2)问的求解过程
中，证明 CM⊥AD 时，利用第(1)问证明的结果 BC∥AD.
3.写明得分关键：对于解题过程中的关键点，有则给分，无则没分.所以在解立体几何类解答题时，一定要写清得分关键点，如第 (1)问中一定要写出 BC⊄平面 PAD，AD⊂平面 PAD 两个条件，否则不能得全分.在第(2)问中，证明 PM⊥平面 ABCD 时，一定写全三个条件，如平面 PAD∩平面 ABCD＝AD，PM⊥AD 一定要有，否则要扣分.再如第(2)问中，一定要分别求出 BC，AD 及 PM，再计算几何体的体积.

高中数学万能解题模板及解题方法

高中数学万能解题模板及解题方法高中数学万能解题模板及解题方法高中数学万能解题模板及解题方法 1、高中数学万能解题模板：特值检验法对于具有一般性的数学问题，我们在解题过程中，可以将问题特殊化，利用问题在某一特殊情况下不真，则它在一般情况下不真这一原理，达到去伪存真的目的。

2、高中数学万能解题模板：极端性原则将所要研究的问题向极端状态进行分析^p ，使因果关系变得更加明显，从而达到迅速解决问题的目的。

极端性多数应用在求极值、取值范围、解析几何上面，很多计算步骤繁琐、计算量大的题，一但采用极端性去分析^p ，那么就能瞬间解决问题。

3、高中数学万能解题模板：剔除法利用已知条件和选择支所提供的信息，从四个选项中剔除掉三个错误的答案，从而达到正确选择的目的。

这是一种常用的方法，尤其是答案为定值，或者有数值范围时，取特殊点代入验证即可排除。

4、高中数学万能解题模板：数形结合法由题目条件，作出符合题意的图形或图象，借助图形或图象的直观性，经过简单的推理或计算，从而得出答案的方法。

数形结合的好处就是直观，甚至可以用量角尺直接量出结果来。

5、高中数学万能解题模板：递推归纳法通过题目条件进行推理，寻找规律，从而归纳出正确答案的方法。

6、高中数学万能解题模板：顺推破解法利用数学定理、公式、法则、定义和题意，通过直接演算推理得出结果的方法。

7、高中数学万能解题模板：逆推验证法将选择支代入题干进行验证，从而否定错误选择支而得出正确选择支的方法。

8、高中数学万能解题模板：正难则反法从题的正面解决比较难时，可从选择支出发逐步逆推找出符合条件的结论，或从反面出发得出结论。

9、高中数学万能解题模板：特征分析^p 法对题设和选择支的特点进行分析^p ，发现规律，归纳得出正确判断的方法。

：10、高中数学万能解题模板：估值选择法有些问题，由于题目条件限制，无法(或没有必要)进行精准的运算和判断，此时只能借助估算，通过观察、分析^p 、比较、推算，从面得出正确判断的方法。

高考数学高分技巧,不同题型的答题套路,轻松搞定数学8大学习法

高考数学高分技巧,不同题型的答题套路，轻松搞定数学 8 大学习法数学习题无非就是数学概念和数学思想的组合应用，弄清数学基本概念、基本定理、基本方法是判断题目类型、知识范围的前提，是正确把握解题方法的依据。

只有概念清楚，方法全面，遇到题目时，就能很快的得到解题方法，或者面对一个新的习题，就能联想到我们平时做过的习题的方法，达到迅速解答。

弄清基本定理是正确、快速解答习题的前提条件，特别是在立体几何等章节的复习中，对基本定理熟悉和灵活掌握能使习题解答条理清楚、逻辑推理严密。

反之，会使解题速度慢，逻辑混乱、叙述不清。

01、抓好基础那么如何抓基础呢?1、看课本;2、在做练习时遇到概念题是要对概念的内涵和外延再认识，注意从不同的侧面去认识、理解概念。

3、理解定理的条件对结论的约束作用，反问：如果没有该条件会使定理的结论发生什么变化?4、归纳全面的解题方法。

要积累一定的典型习题以保证解题方法的完整性。

5、认真做好我们网校同步课堂里面的每期的练习题，采用循环交替、螺旋式推进的方法，克服对基本知识基本方法的遗忘现象。

02、制定好计划和奋斗目标复习数学时，要制定好计划，不但要有本学期大的规划，还要有每月、每周、每天的小计划，计划要与老师的复习计划吻合，不能相互冲突，如按照老师的复习进度，今天复习到什么知识点，就应该在今天之内掌握该知识点，加深对该知识点的理解，研究该知识点考查的不同侧面、不同角度。

在每天的复习计划里，要留有一定的时间看课本，看笔记，回顾过去知识点，思考老师当天讲了什么知识，归纳当天所学的知识。

可以说，每天的习题可以少做，但这些归纳、反思、回顾是必不可少的。

望你在制定计划时注意。

03、克服盲目做题而不注重归纳的现象做习题是为了巩固知识、提高应变能力、思维能力、计算能力。

学数学要做一定量的习题，但学数学并不等于做题，在各种考试题中，有相当的习题是靠简单的知识点的堆积，利用公理化知识体系的演绎而就能解决的，这些习题是要通过做一定量的习题达到对解题方法的展移而实现的，但，随着高考的改革，高考已把考查的重点放在创造型、能力型的考查上。

高考数学答题模板12个

高考数学答题模板12个1500字高考数学答题模板12个1. 解方程模板：首先列出方程：a(x - m)^2 + n = b然后展开方程：ax^2 - 2amx + am^2 + n = b移项并化简：ax^2 - 2amx + am^2 + n - b = 0将方程视为一元二次方程，使用求根公式：x = （2am ±√(4a(b-n) + 4a^2m^2)）/ (2a)化简并整理得最终答案。

2. 圆的相关模板：圆的标准方程：(x - a)^2 + (y - b)^2 = r^2其中，圆心为 (a, b)，半径为 r。

根据题目给出的条件，代入方程中求解。

3. 三角形的模板：勾股定理：a^2 + b^2 = c^2 （三角形中，a、b 为直角边，c 为斜边）根据给出的条件，利用勾股定理求解。

4. 几何图形的模板：首先画出几何图形，标出已知的条件和需要求解的量。

根据已知条件，利用几何定理、相似性原理等，搭建等式或者比例关系，并解方程求解。

5. 求导模板：根据给出的函数关系，利用求导公式对函数进行求导。

注意计算过程的细节，利用链式法则、乘积法则等进行计算。

最后化简求解得结果。

6. 极限求解模板：对于一般的函数极限求解，可以利用函数极限的性质进行求解。

根据题目的要求，利用夹逼准则、洛必达法则等方法求解极限。

7. 统计问题模板：根据题目的要求计算平均数、方差、标准差等统计量。

注意计算过程的细节，并进行适当的整理和化简。

8. 概率问题模板：根据已知的概率模型和条件，利用概率公式计算概率。

注意计算过程的细节，并进行适当的整理和化简。

9. 计算题模板：根据题目给出的计算式和条件，一步一步进行计算。

注意计算的细节，进行适当的化简和整理。

10. 综合题模板：综合题一般包含多个题目要求，根据每个小题的要求进行分析和求解。

先分析每个小题的要求，并给出解题思路。

然后分别解答每个小题，并按照题目要求进行整理和化简。

高考数学答题模板：解题法则

高考数学答题模板：解题法例编者按：高考前的第一轮复习正在火热进行中，同学们要利用这些复习的时间增强学习，查词典数学网为大家整理了高考数学答题模板，在高三数学第一轮复习时，给您最实时的帮助 !下边给出十种简捷奇妙的解法。

供你参照。

一、“抓住特点，逆施倒行”;二、“火眼金睛，一眼洞穿”;三、“察看思虑，估量判断”;四、“多思少算，特值判断”;五、运动变化，巧用极端”;六、“数形联合，巧用直观”;七、“敢于清除，擅长清除”;八、“注意均衡，巧用对称”;九、“等价转变，活用定义”;十、“巧用包含，坚决清除”。

要练说，得练听。

听是说的前提，听得正确，才有条件正确模拟，才能不停地掌握高一级水平的语言。

我在教课中，注意听闻联合，训练少儿听的能力，讲堂上，我特别重视教师的语言，我对少儿说话，注意声音清楚，高低起伏，抑扬有致，富裕吸引力，这样能惹起少儿的注意。

当我发现有的少儿不专心听他人讲话时，就随时夸奖那些静听的少儿，或是让他重复他人说过的内容，抓住教育机遇，要求他们专心听，专心记。

平常我还经过各样兴趣活动，培育少儿边听边记，边听边想，边听边说的能力，如听词对词，听词句说意思，听句子辩正误，听故事叙述故事，听谜语猜谜底，听智力故事，动脑筋，出想法，听儿歌上句，接儿歌下句等，这样幼儿学得生动开朗，轻松快乐，既训练了听的能力，增强了记忆，又发展了思想，为说打下了基础。

以上十种方法，配合应用就能够使得选择填空题解答又快又准。

比方，有些方程的解，我们能够翻过来用选择支代入考证，这就是逆向代入法，它比直接求解对号入坐有时要来得快。

再比方估值法，某年一道高考题是说，一个正方体的表面积是 a 的平方，那么，它的外接球的表面积是：题目中给出了四个选择支，我们预计圆的表面积比它的内接正方体的表面积要大一些，但也大不到哪里去，有两个答案说，外接球的表面积，分别是正方体表面积的六倍多和九倍多，明显应当清除另一个选择支，所求的表面积是正方体表面积的1.01 倍，明显，也不对。

备战高考技巧大全之高中数学黄金解题模板：专题32不等式的证明技巧答案解析

【高考地位】
证明数列不等式，因其思维跨度大、构造性强，需要有较高的证明技巧。

这类问题的求解策略往往是：通过多角度观察所给数列通项的结构，
深入剖析其特征，抓住其规律进行恰当地选择不等式的证明技巧
. 在高考中常常以解答题出现，其试题难度属中高档题. 【方法点评】
方法一
比较法使用情景：一般不等式证明
解题模板：第一步
通过两个实数a 与b 的差或商的符号（范围）确定a 与b 大小关系；
第二步得出结论. 例1设实数,a b 满足
a b ，求证：4422()a b ab a b ．
【答案】详见解析
. 【解析】试题分析：作差，分解因式，配方，判断符号
. 试题解析：作差得442233()
()()a b ab a b a a b b b a 3
3222()()()()a b a b a b a ab b 2223()[()]24b a
b a b ．因为a b ，所以,a b 不同时为0，故223()024b a
b ，2()0a b ，所以2223()[()]02
4b a b a b ，即有4422()a b ab a b ．考点：不等式的证明
. 【点评】两个多项式的大小比较常用的两种方法是作差法和作商法
. 【变式演练1】设
0b a ，求证：a
b b a b a b a . 【答案】详见解析. 考点：不等式的证明.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高考数学解题模板及做题技巧
高考数学解题重点是思维过程、规范解答和反思回顾，结合着具体题型给出了具有可
操作性的答题程序。

下面是数学解题模板及做题技巧，希望大家能够举一反三，对答题有
所帮助。

数学不好的人五大特征高中数学最无耻的得分技巧高考考场上数学拿高分的技巧如何
判断函数的对称性与周期性
三角变换与三角函数的性质问题
1、解题路线图
①不同角化同角
②降幂扩角
③化fx=asinx++h
④结合性质求解。

2、构建答题模板
①化简：三角函数式的化简，一般化成y=asinx++h的形式，即化为一角、一次、一
函数的形式。

②整体代换：将x+看作一个整体，利用y=sinx，y=cosx的性质确定条件。

③求解：利用x+的范围求条件解得函数y=asinx++h的性质，写出结果。

④反思：反思回顾，查看关键点，易错点，对结果进行估算，检查规范性。

点击查看：高考数学万能解题法
解三角形问题
1、解题路线图
1①化简变形;②用余弦定理转化为边的关系;③变形证明。

2①用余弦定理表示角;②用基本不等式求范围;③确定角的取值范围。

2、构建答题模板
①定条件：即确定三角形中的已知和所求，在图形中标注出来，然后确定转化的方向。

②定工具：即根据条件和所求，合理选择转化的工具，实施边角之间的互化。

③求结果。

④再反思：在实施边角互化的时候应注意转化的方向，一般有两种思路：一是全部转化为边之间的关系;二是全部转化为角之间的关系，然后进行恒等变形。

学习学不下去了可以看下这本书，淘宝搜索《高考蝶变》购买
数列的通项、求和问题
1、解题路线图
①先求某一项，或者找到数列的关系式。

②求通项公式。

③求数列和通式。

2、构建答题模板
①找递推：根据已知条件确定数列相邻两项之间的关系，即找数列的递推公式。

②求通项：根据数列递推公式转化为等差或等比数列求通项公式，或利用累加法或累乘法求通项公式。

③定方法：根据数列表达式的结构特征确定求和方法如公式法、裂项相消法、错位相减法、分组法等。

④写步骤：规范写出求和步骤。

⑤再反思：反思回顾，查看关键点、易错点及解题规范。

利用空间向量求角问题
1、解题路线图
①建立坐标系，并用坐标来表示向量。

②空间向量的坐标运算。

③用向量工具求空间的角和距离。

2、构建答题模板
①找垂直：找出或作出具有公共交点的三条两两垂直的直线。

②写坐标：建立空间直角坐标系，写出特征点坐标。

③求向量：求直线的方向向量或平面的法向量。

④求夹角：计算向量的夹角。

⑤得结论：得到所求两个平面所成的角或直线和平面所成的角。

解析几何中的探索性问题
1、解题路线图
①一般先假设这种情况成立点存在、直线存在、位置关系存在等
②将上面的假设代入已知条件求解。

③得出结论。

2、构建答题模板
①先假定：假设结论成立。

②再推理：以假设结论成立为条件，进行推理求解。

③下结论：若推出合理结果，经验证成立则肯。

定假设;若推出矛盾则否定假设。

④再回顾：查看关键点，易错点特殊情况、隐含条件等，审视解题规范性。

高考数学选择填空题答题模板
1易错点归纳：
九大模块易混淆难记忆考点分析，如概率和频率概念混淆、数列求和公式记忆错误等，强化基础知识点记忆，避开因为知识点失误造成的客观性解题错误。

针对审题、解题思路不严谨如集合题型未考虑空集情况、函数问题未考虑定义域等主
观性因素造成的失误进行专项训练。

答题方法设计：
选择题十大速解方法：排除法、增加条件法、以小见大法、极限法、关键点法、对称法、小结论法、归纳法、感觉法、分析选项法;
填空题四大速解方法：直接法、特殊化法、数形结合法、等价转化法。

高考数学解答题答题模板
⑵三角函数
考点题型归纳：
通常考察正弦、余弦公式、三角形基本性质、三种基本三角函数之间的转化与角度的化简。

通常题型：
Q1：带入求值，化简等;
Q2：利用正弦、余弦公式转化，根据角度取值范围确定正负号，求某角某边等。

答题方法设计：
七大解题思想：如巧用数形结合、化归转化等方法解题。

⑶概率统计
考点题型归纳：
通常考察排列、组合运用分布列罗列、期望计算等知识点。

通常题型
Q1：求某条件的概率;
Q2：利用Q1所求的概率，求分布列以及期望。

答题方法设计：
如互斥时间和对立事件的巧妙运用等
⑷数列
考点提醒归纳：
通常考察通项公式和求和公式的运用。

通常题型
Q1：求某一项，求通项公式，求数列和通式;
Q2：证明，求新数列第N项和，绝对值比较等。

答题方法设计：
如通项公式三大解法：和作差，积作商，找规律叠加化简等;
求和公式三大解法：直接公式，错位相减，分组求和等。

⑸立体几何
考点题型归纳：
通常题型
Q1：证明线面，线线，面面垂直等;
Q2：求距离，求二面角等。

答题方法设计：
如直接逻辑法：面面，线面，线面垂直平行等性质的运用;
空间向量法：线面垂直，平行时用向量如何表达，公式;
等面积、体积法：找到最方便计算的图形。

⑹解析几何
考点题型归纳：
椭圆，双曲线，抛物线方程的长短轴性质，离心率等，直线与圆锥曲线联立，求解某点，证明某直线与圆锥曲线的关系等。

通常题型
Q1：求圆锥曲线方程式;
Q2：证明某点在某线某面上，求位置关系，求直线方程等。

答题模板设计：
四步理清解题思路。

⑺导数函数
考点提醒归纳：
题型通常为求函数表达式，求某函数值，求某常数值，求单调区间，最大最小值，证明等。

答题模板设计：
七步理清解题思路。

高考数学压轴题答题模板
考点提醒归纳：
压轴题通常为解析几何和函数导数的题型，难度较大。

答题方法设计：
课程主要讲解解答压轴题的解题思路，如复杂问题简单化、运动问题静止化、一般问题特殊化等思维方法，以求突破。

感谢您的阅读，祝您生活愉快。