流体力学第五章3-4节
合集下载
工程流体力学第五章 相似原理和量纲分析
弹性力比： k F 'e dp' A' K ' A' dV ' V ' k k 2 K l F
Fe
dp A
KAdV V
K－体积模量 kK－体积模量比例尺
k k kK
K'
2
1
kF 1 2 2 k kl k
力的比例尺
也可写成:
' '2
2
2
K
柯西数 是惯性力与弹 性力的比值
2 2
推导过程
角速度比例尺:
' ' l ' k k l kl
注：确定了长度比例尺和速度比例尺，一切运动相似比例尺都可以推导出来。
注：*运动粘度比例尺的推导
d F A dy
F ma V a dy 1 则： A d dy m V A d dy A d 1
相似原理
如何去做模型？
第五章 相似原理和量纲分析
数学 分析 理论分析 数值计算 模型实验
解决流体 力学问题 的方法
实验研究
基础：相似原理 相似原理与模型试验研究方法不仅广泛应用于流体力 学，而且广泛应用于传热、燃烧过程机理等的研究中。
第一节 流动的力学相似
表 征 流 动 过 程 的 物 理 量
第五章 相似原理和量纲分析
xcli@
L/O/G/O
相似原理
相似原理 实物 模型
相似理论：
模型流场再现实物流场的准则——指导模型实验 实验结果推广到原型以及应用到相似的流动中
本章内容
1 2 3 4 1 5 流动的力学相似 动力相似准则 流动相似条件 近似模型实验 Click to add title in here 量纲分析法 连续方程
Fe
dp A
KAdV V
K－体积模量 kK－体积模量比例尺
k k kK
K'
2
1
kF 1 2 2 k kl k
力的比例尺
也可写成:
' '2
2
2
K
柯西数 是惯性力与弹 性力的比值
2 2
推导过程
角速度比例尺:
' ' l ' k k l kl
注：确定了长度比例尺和速度比例尺，一切运动相似比例尺都可以推导出来。
注：*运动粘度比例尺的推导
d F A dy
F ma V a dy 1 则： A d dy m V A d dy A d 1
相似原理
如何去做模型？
第五章 相似原理和量纲分析
数学 分析 理论分析 数值计算 模型实验
解决流体 力学问题 的方法
实验研究
基础：相似原理 相似原理与模型试验研究方法不仅广泛应用于流体力 学，而且广泛应用于传热、燃烧过程机理等的研究中。
第一节 流动的力学相似
表 征 流 动 过 程 的 物 理 量
第五章 相似原理和量纲分析
xcli@
L/O/G/O
相似原理
相似原理 实物 模型
相似理论：
模型流场再现实物流场的准则——指导模型实验 实验结果推广到原型以及应用到相似的流动中
本章内容
1 2 3 4 1 5 流动的力学相似 动力相似准则 流动相似条件 近似模型实验 Click to add title in here 量纲分析法 连续方程
大学物理：第五章 流体力学 (Fluid Mechanics)
上海交通大学 物理系
Aneurysm(动脉瘤)
若处动脉的半径增大N倍 血液流速就缩小N2倍 病灶处的压强大幅度上降 由于该处血管壁薄，使血 管容易破裂。
上海交通大学 物理系
Atherosclerosis（动脉粥样硬化）
动脉病变从内膜开始。一 般先有脂质和复合糖类积 聚、出血及血栓形成，纤 维组织增生及钙质沉着， 并有动脉中层的逐渐蜕变 和钙化，病变常累及弹性 及大中等肌性动脉，
?
? hB=0.5m
P0
?
0
1 2
v
2 c
ghc
Pc
1 2
v
2 A
ghA
PA
vc 2ghA 6 m / s
B,C点
1 2
v
2 c
ghc
Pc
1 2
v
2 B
ghB
PB
SBvB SCvC
PB P0 0.85g
PB P0 ghD
hD 0.85m
上海交通大学 物理系
一柱形容器，高1m、截面积为5x10-2 m2，储满水 ，在容器底部有一面积为2x10-4 m2 的水龙头，问 使容器中的水流尽需多少时间？
度变小，压强变大
压力
上海交通大学 物理系
马格纳斯效应
上海交通大学 物理系
机翼受到的举力
Q：用机翼上、下的流速变化，讨论其受到的升力，是否合理
上海交通大学 物理系
上海交通大学 物理系
压强的范围
太阳中心 地球中心 实验室能维持的最大压强 最深的海沟 尖鞋跟对地板 汽车轮胎 海平面的大气压 正常的血压 最好的实验室真空
四、液流连续原理(Principle of continuity of flow)
Aneurysm(动脉瘤)
若处动脉的半径增大N倍 血液流速就缩小N2倍 病灶处的压强大幅度上降 由于该处血管壁薄，使血 管容易破裂。
上海交通大学 物理系
Atherosclerosis（动脉粥样硬化）
动脉病变从内膜开始。一 般先有脂质和复合糖类积 聚、出血及血栓形成，纤 维组织增生及钙质沉着， 并有动脉中层的逐渐蜕变 和钙化，病变常累及弹性 及大中等肌性动脉，
?
? hB=0.5m
P0
?
0
1 2
v
2 c
ghc
Pc
1 2
v
2 A
ghA
PA
vc 2ghA 6 m / s
B,C点
1 2
v
2 c
ghc
Pc
1 2
v
2 B
ghB
PB
SBvB SCvC
PB P0 0.85g
PB P0 ghD
hD 0.85m
上海交通大学 物理系
一柱形容器，高1m、截面积为5x10-2 m2，储满水 ，在容器底部有一面积为2x10-4 m2 的水龙头，问 使容器中的水流尽需多少时间？
度变小，压强变大
压力
上海交通大学 物理系
马格纳斯效应
上海交通大学 物理系
机翼受到的举力
Q：用机翼上、下的流速变化，讨论其受到的升力，是否合理
上海交通大学 物理系
上海交通大学 物理系
压强的范围
太阳中心 地球中心 实验室能维持的最大压强 最深的海沟 尖鞋跟对地板 汽车轮胎 海平面的大气压 正常的血压 最好的实验室真空
四、液流连续原理(Principle of continuity of flow)
流体力学第5章管内不可压缩流体运动PPT课件
10
5.1.1 层流与湍流流动
2、流态的判别： （1）临界流速
11
5.1.1 层流与湍流流动
2、流态的判别： （1）临界流速
缺点：临界流速的值随着管径以及工作 液粘度的变化而变化，并不是一个常数， 作为判别标准并不实用。
12
5.1.1 层流与湍流流动
2、流态的判别：
（2）临界雷诺数 对于圆管而言，雷诺数：Re
43
5.2.3 湍流流动中的粘性底层
【粘性底层 】
粘性底层的厚度为：
14.14 d Re
粘性底层的厚度与雷诺数成反比，即：流速 越高，Re数越大——粘性底层的厚度越薄； 流速越低，Re数越小——粘性底层的厚度越 厚。
虽然，粘性底层的厚度仅有几个mm的量级， 但却可能严重影响水流的流动阻力。
d2
0 .1 2
（3）管路中的最大速度： u m a2 x v 2 6 1m 2 /s
（4）壁面处的最大切应力：
m a x 2 p lr 0 22 7 5 3 0 .0 0 6 5 10 .8 3 N 0 /m 6 2
32
33
5.2 湍流流动及沿程摩擦阻力计算
【内容提要】 本节简要介绍紊流理论及湍流沿程阻力 系数的计算
umaxp14lp2
r02
pd2
16l
v q A V(p 1 p d 2 2 )d /4 4/1
2 l (8 p 1 p 2 )d 2 p2 d u ma 3l2 3l22
x
26
5.1.4 圆管道内层流流动及粘性摩擦损失
hf
p
v pd 2
32 l
水平等径管
p 32lv d 2
结论：层流状态，水 头损失与速度呈线性 关系。
5.1.1 层流与湍流流动
2、流态的判别： （1）临界流速
11
5.1.1 层流与湍流流动
2、流态的判别： （1）临界流速
缺点：临界流速的值随着管径以及工作 液粘度的变化而变化，并不是一个常数， 作为判别标准并不实用。
12
5.1.1 层流与湍流流动
2、流态的判别：
（2）临界雷诺数 对于圆管而言，雷诺数：Re
43
5.2.3 湍流流动中的粘性底层
【粘性底层 】
粘性底层的厚度为：
14.14 d Re
粘性底层的厚度与雷诺数成反比，即：流速 越高，Re数越大——粘性底层的厚度越薄； 流速越低，Re数越小——粘性底层的厚度越 厚。
虽然，粘性底层的厚度仅有几个mm的量级， 但却可能严重影响水流的流动阻力。
d2
0 .1 2
（3）管路中的最大速度： u m a2 x v 2 6 1m 2 /s
（4）壁面处的最大切应力：
m a x 2 p lr 0 22 7 5 3 0 .0 0 6 5 10 .8 3 N 0 /m 6 2
32
33
5.2 湍流流动及沿程摩擦阻力计算
【内容提要】 本节简要介绍紊流理论及湍流沿程阻力 系数的计算
umaxp14lp2
r02
pd2
16l
v q A V(p 1 p d 2 2 )d /4 4/1
2 l (8 p 1 p 2 )d 2 p2 d u ma 3l2 3l22
x
26
5.1.4 圆管道内层流流动及粘性摩擦损失
hf
p
v pd 2
32 l
水平等径管
p 32lv d 2
结论：层流状态，水 头损失与速度呈线性 关系。
流体力学第5章 相似性原理和量纲分析
几何相似只有一个长度比例尺，几何相似是力学 相似的前提
二、运动相似
❖ 流场中所有对应点上对应时刻的流速方向相同大小成比例。
v3' 3
v1'
v2'
1
2
3
v3''
v1 v1
v2 v2
v3 v3
v v
kv
v1''
1
2
kv——速度比例尺
v2''
A
A
o
系统1：v
l t
o
系统2：v l t
时间比例尺 加速度比例尺
1/ p
7.5k,kpkv2'
0.001207, kv 4416(Pa)
22.5, 有
F F ' F ' 1.261104(N)
kF
k
k
2
l
k
2
v
M M ' 2030(N m)
k
k
3k
l
2
v
第五节 量纲分析法
❖一、量纲分析的概念和原理 ❖ 量纲是指物理量的性质和类别。例如长度和质量， 它们分别用 [ L ] ， [ M ]表达。 ❖而单位除表示物理量的性质外，还包含着物理量的 大小，如同为长度量纲的米，厘米等单位。
如何进行模型实验： (1) 几何相似（模型和实物、攻角、位置等）； (2) 确定相似准则数； (3) 确定模型尺度和速度； (4) 实验数据整理(无因次形式)； (5) 试验值与实际值之间的换算。
完全相似：两个流动的全部相似准则数对应相等。不可能实现。 部分相似：满足部分相似准则数相等。
近似的模型试验：在设计模型和组织模型试验时，在 与流动过程有关的定性准则中考虑那些对流动过程起 主导作用的定性准则，而忽略那些对过程影响较小的
流体力学第五章
5.2 边界层流动
5.2 边界层流动
*
0
u 1 u e e
dy
5.2 边界层流动
**
0
u eue
u 1 u dy e
5.2 边界层流动
平面边界层流动方程
边界层近似假定 1. 纵向偏导数远小于横向偏导数
5.2 边界层流动
边界层分离
理想流体能量转换过程 边界层内粘性对机械能的耗散使得流体微团在逆 压区 MF 段间的某个点处 V 降为零，后来的质点 将改道进入主流区，使来流边界层与物面分离； 在分离点下游区域，受逆压作用而发生倒流。
5.2 边界层流动
边界层分离
分离点：紧邻壁面顺流区与倒流区分界点。 边界层分离的必要条件：粘性、逆压梯度。
湍流边界层摩阻系数大
0.664 C fL Re x
C fT
0.0576 /5 Re 1 x
5.2 边界层流动
边界层分离
边界层流动：流体质点受惯性力、粘性力和压力 作用；粘性力阻滞流体质点运动，使流体质点减 速和失去动能；压力的作用取决于绕流物体形状； 顺压梯度有助于流体加速前进，而逆压梯度阻碍 流体运动。
研究方法：实验、数值(RANS、LES、DNS)
5.1 粘流的基本特性
层流、紊流速度型 紊流粘性应力比层流大
5.2 边界层流动
边界层概念的提出
高 Re流动，惯性力远大于粘性力，研究忽略粘 性的流动有实际意义。 阻力、分离、涡扩散等问题，无粘解与实际相 差甚远。 研究表明：虽然 Re很大，但在靠近物面的薄层 流体内，沿物面法向存在很大的速度梯度，粘 性力与惯性力相当而不可忽略。 Prandtl把物面附近粘性力起重要作用的薄层称 为边界层。
流体力学课件 第五章 流动阻力
斜直线分布
r hf 1 g grJ 2 l 2
du grh f dr 2l
抛物线分布
2.流速分布 3.流量
Q
r0 0
gh f 2 2 u (r0 r ) 4l
gh f 2 2 gh f 4 (r0 r ) 2 rdr d 4l 128l
（3）粗糙区
莫迪
§5-7 局部损失计算
一、边界层理论
1.边界层：贴近平板存在 较大切应力、粘性影响不能 忽略的这一层液体 。
2.边界层的厚度：当流速达到 边界层的厚度顺流增大，即δ是x的函数。
处时，它
3.转捩点，临界雷诺数 转捩点：在x=xcr处边界层由层流转变为紊流的过渡点。
临界雷诺数： Recr
三、总水头损失
hw h f h j
i 1 i 1 n n
§5-2 流体流动的两种型态
一、雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行 实验，提出了流体运动存在两种型态：层流和紊流。
1 4
(a)
hf 5
(b)
2
3
(c)
1.层流 ：管中水流呈层状流动，各层的流体质点互不掺混的 流动状态。
四、湍流切应力分布和流速分布
1.切应力分布
du 2 du 2 1 2 L ( ) dy dy
摩擦切应力 普朗特混合长度 ： 附加切应力
y L ky 1 r0
k 称为卡门常数
k 0.36 ~ 0.435
2.流速分布 （1）近壁层流层： 管壁切应力
du u 0 dy y
§5-6 湍流的沿程损失
一、湍流沿程损失计算
流体力学课后习题答案第五章
第五章 量纲分析和相似原理5-1 假设自由落体的下落距离S 与落体的质量m,重力加速度g 及下落时间t 有关，试用瑞利法导出自由落体下落距离的关系式。
解： c b a t g m S ][][][][=c b a T LT M L )()()(2-=2202:1:0:===+-==b c c b T b L aM2Kgt S = 5-3 已知文丘里流量计喉管流速v 与流量计压强差Δp 、主管直径d 1、喉管直径d 2、以及流体的密度ρ和运动粘滞系数ν有关，试用π定理确定流速关系式。
解： 0),,,,,(21=∆νρd d p v f取ρ,,2d v 为基本量11121c b a d v p ρπ∆=，222212c b a d v d ρπ=，33323c b a d v ρνπ= 111][][][][:21c b a d v p ρπ=∆111)()()(3121c b a ML L LT T ML ----=1,0,22:31:1:11111111===-=--+=-=c b a a T c b a L c Mρπ21v p ∆= 212d d =π 333][][][][:23c b a d v ρνπ= 得 011333===c b a23vd νπ=0),,(2212=∆vd d d v p f νρ),(21212νρvd d d f v p =∆)(Re,122d d p v Φ=∆ρ )(Re,12d d pv Φ∆=ρ 5-4 球形固体颗粒在流体中的自由沉降速度f u 与颗粒的直径d 、密度s ρ以及流体的密度ρ、动力黏滞系数μ，重力加速度g 有关。
试用π定理证明自由沉降速度关系式,f s f u d u f ρρρμ⎡=⎢⎣。
解： 0),,,,,(=g d u f s f μρρ取ρ,,d u f 为基本量333232111321,,c b a f c b a f s c b a f d u d u d u gρμπρρπρπ===计算有121-=d u gf π ρρπs =2 ρμπd u f =3 ),(2ρμρρd u f u dg f s f =,f s f u d u f ρρρμ⎡=⎢⎣ 5-6 用水管模拟输油管道。
《流体力学》第五章孔口管嘴管路流动
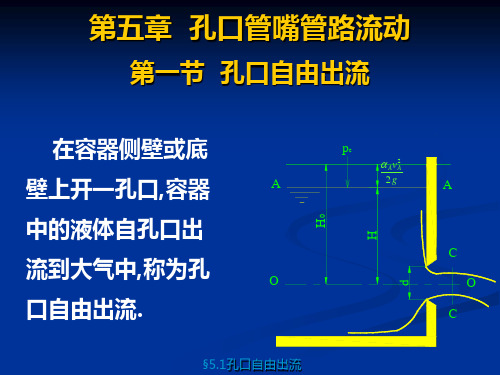
2g
A
C O
C
(C
1)
vc2 2g
(ZA
ZC )
pA
pC
Av
2 A
2g
令
H0
(Z A
ZC )
pA
pC
AvA2
2g
§5.1孔口自由出流
1
则有
vc
c 1
2gH0
H0
(Z A
ZC )
pA
pC
AvA2
2g
H0称为作用水头,是促使
力系数是不变的。
§5.4 简单管路
SH、Sp对已给定的管路是一个定数，它综合 反映了管路上的沿程和局部阻力情况，称为 管路阻抗。
H SHQ2
p SpQ2
简单管路中，总阻力损失与体积流量平方成 正比。
§5.4 简单管路
例5-5：某矿渣混凝土板风道，断面积为1m*1.2m, 长为50m，局部阻力系数Σζ=2.5，流量为14m3/s, 空气温度为20℃，求压强损失。
2v22
2g
1
vc2 2g
2
vc2 2g
令 H0 (H1 ζH12:局)液部体p阻1 经力p孔2系口数处1v的122g1 2v22
1
H1 H
H2
2
2
H0 (1 2 ) 2vcg2突ζ然2:液扩体大在的收局缩部断阻面力之系后数 C
C
§5.2 孔口淹没出流
1
c 1
2gH0
Q A 2gH0 A 2gH0
出流
H0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1
第三节 相似理论基础
相似概念 具体来说，两相似流动应几何相似 、运动相似、 动力相似。
表征
流动
按性 质分
过程
的物
理量
描述几何形状的
如长度、面积、体积等
描述运动状态的
如速度、加速度、体积流量等
描述动力特征的
如质量力、表面力、动量等
几何
相似 流 应
运动
动
满 足
相似
相
的 条
动力 似 件
相似
03:13:30
Fp v p Fmvm
Fv
l 2v3
动力粘度比例尺:
p m
p p m m
lv
03:13:30
有了模型与原型的密度比例尺，长 度比例尺和速度比例尺，就可由它 同济大学航空航天与们力确学学定院所有动力学量的比例尺1。4
第三节 相似理论基础
边界条件和初始条件相似：流场相应边界性质相同，如固体壁 面，自由液面等。对于非恒定流动，要满足初始条件相似。
03:13:30
同济大学航空航天与力学学院
8
第三节 相似理论基础
体积流量比例尺:
l
3 p
Q
Qp Qm
lm3 t p
l 3 t
l 2t
tm
l
2 p
运动粘度比例尺:
p m
tp lm2
l 2 t
lv
tm
03:13:30
同济大学航空航天与力学学院
9
第三节 相似理论基础
动力相似：在对应位置和对应瞬时，流场中各种成分的力（惯 性力、质量力、压差力和粘性力）矢量图都相似，即相应点力 的大小成比例，方向相同。并且各种成分力的相似比例数也相 同，即力多边形相似。
常选惯性力为特征力，将其它作用力与惯性力相 比，组成一些准则，由这些准则得到的准则数 （准数）在相似流动中应该是相等的。
03:13:30
同济大学航空航天与力学学院
16
第三节 相似理论基础
（1）雷诺准则——粘性力是主要的力
Ip Im Tp Tm
粘滞力
T A du lv
dy
03:13:30
惯性力
长度比尺 l lp / lm 时间比尺 t t p / tm 作用力比尺 F Fp / Fm
03:13:30
同济大学航空航天与力学学院
10
第三节 相似理论基础
质点达朗贝尔原理
作用于质点上的主动力Ｆ，约束力ＦＮ，虚加惯性
力ＦＩ在形式上组成平衡力系．
Ｆ
ｍ
ＦＩ
F FN FI 0
Ｆ＝ｍａ ＦＮ
vp tp
mlm3
vm tm
l22v
其中：
p m
为流体的密度比尺。
03:13:30
同济大学航空航天与力学学院
13
第三节 相似理论基础
力矩（功，能）比例尺:
M
Mp Mm
Fpl p Fmlm
F l
l3v2
压强（应力）比例尺:
Fp
p
pp pm
Ap Fm
F A
v2
Am
功率比例尺:
P
Pp Pm
Fｘ FNｘ FIｘ 0
Fｙ FNｙ FIｙ 0 Fｚ FNｚ FIｚ 0
03:13:30
惯性力是人为地、假想地加上去的， 并不真实的作用在物体上。达朗贝尔 原理从形式上将动力学问题转化为静 力学问题，它并不改变动力学问题的 实质，质点实际上也并不平衡。
“动”代表研究对象是动力学问题。
综上所述，要使模型流动和原型流动相似，需 要两者在时空相似的条件下受力相似。
动力相似（受力相似）用相似准则（相似准数） 的形式来表示，即：要使模型流动和原型流动 动力相似，需要这两个流动在时空相似的条件 下各相似准则都相等。
03:13:30
同济大学航空航天与力学学院
15
第三节 相似理论基础
动力相似的流动，相应点上的力多边形相似， 相应边（即同名力）成比例。
第三节 相似理论基础
模型通常是指与原型有同样的运动规律，各运动参数存 在固定比例关系的缩小物。
为使模型流动能表现出实型流动的主要现象和特性，并 从模型流动上预测出实型流动的结果，就必须使两者在 流动上相似，即两个互为相似流动的对应部位上对应物 理量都有一定的比例关系。
03:13:30
同济大学航空航天与力学学院
同济大学航空航天与力学学院
5
第三节 相似理论基础
面积比尺
A
Ap Am
lp2 lm2
l2
体积比尺
V
Vp Vm
lp3 lm3
3l
03:13:30
同济大学航空航天与力学学院
6
第三节 相似理论基础
运动相似：以几何相似为前提。 流体质点流过相应的位移所用时 间成比例。即两个流动相应点速 度方向相同,大小成比例。
“静”代表研究问题所用的方法是静力学方
同济大学航空航天与力学学院 法。
11
第三节 相似理论基础
T G P I 0
Tp Gp Pp I p
Tm Gm Pm
Im
力的比尺 T G p I
03:13:30
同济大学航空航天与力学学院
12
第三节 相似理论基础
又由牛顿定律可知：
F
pl
3 p
I ma l3 l l 2v2
t2
vplp vmlm
p m
(Re) p (Re) m
同济大学航空航天与力学学院
17
第三节 相似理论基础
无量纲数 Re vl
雷诺数——表征惯性力与粘性力之比 两流动相应的雷诺数相等，粘性力相似
纪念英国的物理学家奥斯本•雷诺（1842-1942），他于1882年 在他的一篇实验报告中提出了这个符号。但是动力相似理 论却是10年后由另外一位英国物理学家提出的，即瑞利爵 士（1842-1919），一位诺贝尔奖获得者。
同济大学航空航天与力学学院
2
第三节 相似理论基础
几何相似：流场几何形状相似，相应长度成比例，相应角度相 等。几何相似还可认为包括流场相应边界性质相同，如固体壁 面，自由液面等。
03:13:30
同济大学航空航天与力学学院
3
第三节 相似理论基础
几何相似的难点： 1、无法使粗糙度成比例缩小 2、用细粉末来代替河床上的物质，会出现内聚力，
不能模拟沙粒的特性； 3、模型尺寸减小，毛细作用影响显著；
……
03:13:30
同济大学航空航天与力学学院
4
第三节 相似理论基础
对应边成比例， 对应角相等。
p1 m1 p2 m2来自l p1 lm1lp2 lm2
lp3 lm3
.......
lp lm
l
长度比尺 l lp / lm
03:13:30
速度场相似
03:13:30
同济大学航空航天与力学学院
7
第三节 相似理论基础
速度比尺 u u p / um
u
up um
vp vm
v
v
lp lm
/ /
tp tm
lp lm
tm tp
l t
时间比尺 t t p / tm
加速度比尺
a
ap am
up um
/tp / tm
up um
tm tp
l t2
注：长度比例尺和速度比例尺确定所 有运动学量的比例尺。