27对数与对数函数
专题27 对数函数的图像和性质(一)(解析版)

专题27 对数函数的图像和性质(一)题组1 对数函数的图像1.已知函数f (x )=133,1log ,1x x x x ⎧≤⎪⎨>⎪⎩则函数y =f (1-x )的大致图象是( )A. B. C. D.【答案】D【解析】先画出函数f (x )=133,1log ,1x x x x ⎧≤⎪⎨>⎪⎩的草图,令函数f (x )的图象关于y 轴对称,得函数f (-x )的图象,再把所得的函数f (-x )的图象,向右平移1个单位,得到函数y =f (1-x )的图象,故选:D.2.函数f (x )=10x 与函数g (x )=lgx 的图象 A.关于x 轴对称 B.关于y 轴对称 C.关于原点对称 D.关于y=x 对称【答案】D【解析】因为f (x )=10x 与函数g (x )=lgx 是一对反函数,所以其图象关于y=x 对称. 故选D. 3.函数f (x )=ln|11xx+-|的大致图象是( ) A. B. C. D.【答案】D【解析】因为()()11lnln 11x xf x f x x x-+-==-=-+-,所以函数()f x 是奇函数,图象关于原点对称,可排除,A C ;由()2ln30f =>,可排除B ,故选D.4.函数f (x )=log 2(x+1)与g (x )=2﹣x +1在同一直角坐标系下的图象大致是( )A. B. C. D.【答案】B 【解析】定义域为,函数为增函数;定义域为,函数为减函数,所以结合指数函数对数函数的性质可知B 图像正确5.已知函数f(x)=-x 2+2,g(x)=log 2|x |,则函数F(x)=f(x)·g(x)的图象大致为( )A. B. C. D.【答案】B【解析】由题意得,函数()(),f x g x 为偶函数,∴函数()()()F x f x g x =为偶函数,其图象关于y 轴对称, 故只需考虑0x >时的情形即可.由函数()(),f x g x 的取值情况可得,当0x >时,函数()F x 的取值情况为先负、再正、再负, 所以结合各选项得B 满足题意.故选B. 6.设函数()()21ln 11f x x x=+-+,则使()()21f x f x >-成立的x 的取值范围是( ) A.1,13⎛⎫ ⎪⎝⎭B.()1,1,3⎛⎫-∞+∞ ⎪⎝⎭C.11,33⎛⎫- ⎪⎝⎭D.11,,33⎛⎫⎛⎫-∞+∞ ⎪⎪⎝⎭⎝⎭【答案】A【解析】因为函数()()21ln 11f x x x =+-+定义域为R ,关于原点对称, 且()()()()()2211ln 1ln 111f x x x f x xx -=+--=+-=++-, 所以函数()f x 是偶函数, 又()f x 在()0,∞+是增函数, 所以()()21f x f x >-等价于()()21fx f x >-,所以2213410x x x x >--+<,, 解得113x <<,故选:A7.函数2()ln(1)x xe ef x x --=+在[3,3]-的图象大致为( )A. B. C . D.【答案】C【解析】函数2()ln(1)x xe ef x x --=+,则2()()ln(1)x xe ef x f x x ---==-+,所以()f x 为奇函数,排除B 选项; 当x →+∞时,2()ln(1)x xe ef x x --=→+∞+,所以排除A 选项; 当1x =时,11 2.720.37(1) 3.4ln(11)ln 20.69e e e ef -----==≈≈+, 排除D 选项;综上可知,C 为正确选项, 故选:C. 8.函数()1ln 1y x x=-+的图象大致为( ) A. B. C. D.【答案】A【解析】0x >时,函数为减函数,排除B ,10x -<<时,函数也是减函数,排除D ,又1x =时,1ln 20y =->,排除C ,只有A 可满足.故选:A. 9.函数()()22ln 11x f x x +=+的大致图像为( )A. B. C. D.【答案】B【解析】因为()()22ln 11x f x x +=+是由()22ln xg x x=向左平移一个单位得到的, 因为()22ln ()(0)()xg x g x x x --==≠-,所以函数()22ln xg x x=为偶函数,图像关于y 轴对称, 所以()f x 的图像关于1x =-对称,故可排除A ,D 选项; 又当2x <-或0x >时,2ln 10x +>,()210x +>, 所以()0f x >,故可排除C 选项 故选:B .10.在同一直角坐标系中,函数11,log (02a x y y x a a ⎛⎫==+> ⎪⎝⎭且1)a ≠的图象可能是( ) A. B. C. D.【答案】D【解析】当01a <<时,函数xy a =过定点(0,1)且单调递减,则函数1x y a=过定点(0,1)且单调递增,函数1log 2a y x ⎛⎫=+⎪⎝⎭过定点1(,0)2且单调递减,D 选项符合;当1a >时,函数x y a =过定点(0,1)且单调递增,则函数1x y a =过定点(0,1)且单调递减,函数1log 2a y x ⎛⎫=+ ⎪⎝⎭过定点1(,02)且单调递增,各选项均不符合.故选:D11.函数()24ln x f x x=的部分图象大致为( )A. B. C. D.【答案】A【解析】因为()24ln x f x x =是偶函数,排除B ,当01x <<时,ln 0x <,()204ln x f x x=<,排除C , 当x e =时()214ef e =>,排除D.故选:A.12.已知函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=x 2﹣2x ﹣3,求当x≤0时,不等式f (x )≥0整数解的个数为( ) A.4 B.3 C.2 D.1 【答案】A【解析】由函数为奇函数可知当x≤0时,不等式f (x )≥0整数解的个数与0x ≥时()0f x ≤的个数相同,由奇函数可知()00f =,由2230x x --≤得()()320x x -+≤,所以整数解为1,2,3,所以满足题意要求的整数点有4个 13.若x 1,x 2是方程2x =12⎛⎫ ⎪⎝⎭+1-1x 的两个实数解,则x 1+x 2=________.【答案】-1 【解析】 ∵2x =1112x-+⎛⎫⎪⎝⎭,∴2x =112x -,∴x =1x-1,∴x 2+x -1=0. ∴x 1+x 2=-1. 故答案:-114.已知函数()lg f x x =.(1)画出函数()y f x =的草图,并根据草图求出满足()1f x >的x 的集合; (2)若0a b <<,且()()f a f b >,求证:1ab <. 【答案】(1)图见解析,(0,110)∪(10,+∞).(2)证明见解析 【解析】(1)画出函数()y f x =的草图,如图所示:令()1f x =,则lg 1,lg 1x x ==±,可得10x =或110x =. 故满足()1f x >的x 的集合为1(0,)(10,)10⋃+∞. (2)证明:若0a b <<,且()()f a f b >,则lg lg a b >. 当01a b <<≤时, lg lg a b >显然成立且1ab <.当01a b <≤≤,因为lg lg a b >则lg lg lg +lg 0lg 01a b a b ab ab -><⇒<⇒<,成立 当1a b ≤<时, lg lg a b >不成立. 综上所述1ab <成立.15.已知函数2()4||3f x x x =-+,(1)试证明函数()f x 是偶函数;(2)画出()f x 的图象;(要求先用铅笔画出草图,再用黑色签字笔描摹,否则不给分) (3)请根据图象指出函数()f x 的单调递增区间与单调递减区间;(不必证明)(4)当实数k 取不同的值时,讨论关于x 的方程24||3x x k -+=的实根的个数;(不必求出方程的解) 【答案】(1)详见解析(2)详见解析(3)增区间()()+∞-,2,0,2减区间)2,0(),2,(--∞(4)①当1k <-时,方程无实数根;②当1k =-或3k >时,方程有两个实数根;③当3k =时,方程有三个实数根;④当13k -<<时,方程有四个实数根【解析】(1)()f x 的定义域为R ,且2()()4||3f x x x -=---+ 24||3()x x f x =-+=故()f x 为偶函数; (2)如图(3)递增区间有:()()+∞-,2,0,2 递减区间有:)2,0(),2,(--∞ (4)根据图象可知,①当1k <-时,方程无实数根;②当1k =-或3k >时,方程有两个实数根; ③当3k =时,方程有三个实数根; ④当13k -<<时,方程有四个实数根; 16.已知函数f (x )=x ln x -x .(1)设g (x )=f (x )+|x -a |,a ∈R.e 为自然对数的底数.①当32a e=-时,判断函数g (x )零点的个数; ②1,x e e ⎡⎤∈⎢⎥⎣⎦时,求函数g (x )的最小值.(2)设0<m <n <1,求证:()2201mf n m +<+ 【答案】(1)① g (x )有且仅有两个零点.②a -e.(2)证明见解析 【解析】(1)①当32a e =-时, g (x )=x ln x -x +|x +32e |=x ln x +32e, g′(x )=1+ln x ,当0<x <1e 时,g′(x )<0;当x >1e时,g′(x )>0; 因此g (x )在(0,1e )上单调递减,在(1e,+∞)上单调递增,又434412424g =0e e e e e -⎛⎫-=> ⎪⎝⎭,g (1e )=-1e +23322e e e-=<0,g (1)=32e >0, 所以g (x )有且仅有两个零点. ②(i )当a ≤1e时,g (x )=x ln x -x +x -a =x ln x -a , 因为x ∈[1e ,e ],g′(x )=1+lnx ≥0恒成立, 所以g (x )在[1e ,e ]上单调递增,所以此时g (x )的最小值为g (1e )=-1e-a .(ii )当a ≥e 时,g (x )=x ln x -x +a -x =x ln x -2x +a ,因为x ∈[1e ,e],g′(x )=ln x -1≤0恒成立, 所以g (x )在[1e ,e ]上单调递减,所以此时g (x )的最小值为g (e )=a -e .(iii )当1e <a <e 时,若1e≤x ≤a ,则g (x )=x ln x -x +a -x =x ln x -2x +a , 若a ≤x ≤e ,则g (x )=x ln x -x +x -a =x ln x -a , 由(i ),(ii )知g (x )在[1e,a ]上单调递减,在[a ,e ]上单调递增, 所以此时g (x )的最小值为g (a )=a ln a -a , 综上有:当a ≤1e 时,g (x )的最小值为-1e-a ;当1e<a <e 时,g (x )的最小值为a ln a -a ; 当a ≥e 时,g (x )的最小值为a -e . (2)设h (x )=221xx +, 则当x ∈(0,1)时,h′(x )=()()222211x x -+>0,于是h (x )在(0,1)单调递增,又0<m <n <1,所以h (m )<h (n ), 从而有()()()2222ln 111m f n f n h n n n m n ⎛⎫+<+=-+ ⎪++⎝⎭设φ(x )=22ln 11n n -++,x >0 则φ′(x )=()()()222222114011x xx x x x --=≥++因此φ(x )在(0,+∞)上单调递增,因为0<n <1,所以φ(n )<φ(1)=0,即ln n -1+221n +<0, 因此()2222ln 1011m f n n n m n ⎛⎫+<-+< ⎪++⎝⎭ 即原不等式得证.17.已知函数f (x )=xln x ,g (x )=-x 2+ax -2(e 为自然对数的底数,a ∈R ). (1)判断曲线y =f (x )在点(1,f (1))处的切线与曲线y =g (x )的公共点个数; (2)当1[,]x e e∈时,若函数y =f (x )-g (x )有两个零点,求a 的取值范围. 【答案】(1)答案不唯一,见解析;(2)3<a ≤e +2e+1. 【解析】(1)()1f x lnx '=+, 所以切线的斜率()11k f ='=, 又()10f =,所以曲线在点(1,0)处的切线方程为1y x =-,由221y x ax y x ⎧=-+-⎨=-⎩,得2(1)10x a x +-+=,由△22(1)423(1)(3)a a a a a =--=--=+-可得,当△0>时,即1a <-或3a >时,有两个公共点,当△0=时,即1a =-或3a =时,有一个公共点,当△0<时,即13a -<>时,没有公共点,(2)2()()2y f x g x x ax xlnx =-=-++,由0y =,得2a x lnx x =++, 令2()h x x lnx x =++,则2(1)(2)()x x h x x -+'=,当1[x e ∈,]e 时,由()0h x '=,得1x =,所以()h x 在1[e ,]e 上单调递减,在[1,]e 上单调递增,因此()()13min h x h ==,由11()21h e e e =+-,()21h e e e =++,比较可知()1h h e e ⎛⎫> ⎪⎝⎭,所以,结合函数图象可得,当231a e e <++时,函数()()y f x g x =-有两个零点.18.根据函数f(x)=log 2x 的图像和性质解决以下问题:(1)若f(a)>f(2),求a 的取值范围;(2)求y =log 2(2x -1)在[2,14]上的最值.【答案】(1) (2,+∞) (2) 最小值为log 23,最大值为log 227【解析】(1)由函数2()log f x x =的单调性及()(2)f a f >,即可求出a 的取值范围;(2)根据定义域为[2,14],表示出21x -的取值范围,结合对数函数的性质,即可求得最值.试题解析:函数f (x )=log 2x 的图象如图:(1)因为f (x )=log 2x 是增函数,故f (a )>f (2),即log 2a >log 22,则a >2.所以a 的取值范围为(2,+∞).(2)∵2≤x ≤14,∴3≤2x -1≤27,∴log 23≤log 2(2x -1)≤log 227.∴函数y =log 2(2x -1)在[2,14]上的最小值为log 23,最大值为log 227. 题组2 对数函数的性质 19.已知定义在R 上的函数()y f x =满足()()()111f x f x f x -=+=-,当[]12x ∈,时,2()log f x x =,若方程()0f x ax -=在()0+∞,上恰好有两个实数根,则正实数a 的值为( )A.2log ee B.1ln 2e C.12 D.2【答案】C【解析】由()()()111f x f x f x -=+=-,可知()f x 为偶函数,且一条对称轴为1x =,再由()()11f x f x +=-,可得()2()f x f x +=,即函数()f x 的周期为2.根据[]12x ∈,时,2()log f x x =作出函数()f x 的草图,如图所示:方程()0f x ax -=在()0+∞,上恰好有两个实数根,∴函数y ax =与()y f x =的图象在y 轴右侧有两个交点,设y ax =与2log y x =相切时,切点坐标为()020log x x ,,由1ln2y x '=,得2000log 1ln2x x x =,解得02x e =>.∴由图象可知,当直线y ax =过点()21,时,方程()0f x ax -=在()0+∞,上恰好有两个实数根,12a ∴=.故选:C .20.已知函数2|1|,0()log ,0x x f x x x +≤⎧=⎨>⎩,若方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<,则()3122341x x x x x ++的取值范围是( ). A.(1,)-+∞B.[1,1)-C.(,1)-∞D.(]1,1- 【答案】D 【解析】函数()21,0|log ,0x x f x x x ⎧+⎪=⎨>⎪⎩,的图象如下:根据图象可得:若方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<,则11x a +=-,21x a +=,23log x a =-,24log x a =.(01)a <≤122x x +=-,32a x -=,42a x =∴则31222344()22221222a a a a a x x x x x ---++=-⋅+=-⋅. 令2a t ,(1t ∈,2],而函数2y t t=-在(1,2]单调递增. 所以211t t -<-≤,则21212a a ∴-<-. 故选:D.21.函数()log 1xa f x a x =-有两个不同的零点,则实数a 的取值范围是( ) A.()1,10B.()1,+∞C.0,1D.()10,+∞【答案】B【解析】函数()f x 有两个零点等价于1x y a ⎛⎫= ⎪⎝⎭与log a y x =的图象有两个交点,当01a <<时同一坐标系中做出两函数图象如图(2),由图知有一个交点,符合题意;当1a >时同一坐标系中做出两函数图象如图(1),由图知有两个交点,不符合题意,故选B.22.已知函数()2,11,12x a x f x x a x ⎧+≤⎪=⎨+>⎪⎩,其中a R ∈.如果函数()f x 恰有两个零点,则a 的取值范围为()A.1,2⎛⎤-∞- ⎥⎝⎦ B.[)2,-+∞ C.12,2⎡⎤--⎢⎥⎣⎦ D.12,2⎡⎫--⎪⎢⎣⎭【答案】D【解析】当1x ≤时,(]2,2x y a a a =+∈+,当1x >时,11,22y x a a ⎛⎫=+∈++∞ ⎪⎝⎭,两段均为增函数,函数()f x 恰有两个零点,可得102200a a a ⎧+<⎪⎪⎨+≥⎪⎪<⎩,解得12,2a ⎡⎫∈--⎪⎢⎣⎭.故选:D23.给出下列四个结论:(1)若集合A ={x,y },B ={0,2x },且A=B ,则x =1,y =0;(2)若函数f (x )的定义域为(-1,1),则函数f (2x +1)的定义域为(-1,0);(3)函数1()f x x =的单调减区间是{}0x x ≠;(4)若()()()f x y f x f y +=⋅,且(1)2f =,则(2)(4)(2014)(2016)(2018)2018(1)(3)(2013)(2015)(2017)f f ff f f f f f f +++++=其中不正确的有______.【答案】(3)【解析】(1)因为A=B ,所以20,0,1x y x x x ≠==∴=,故(1)正确;(2)因为函数f (x )的定义域为(-1,1),所以121110x x -<+<∴-<<,故(2)正确; (3)函数1()f x x =的单调减区间是(,0)-∞和(0,)+∞,故(3)错误;(4)因为()()()f x y f x f y +=⋅,所以(1)()(1)2()f x f x f f x +=⋅=,因此(2)(4)(2014)(2016)(2018)210092018(1)(3)(2013)(2015)(2017)f f f f f f f f f f +++++=⨯=,故(4)正确; 故答案为:(3)题组3 对数值大小比较24.已知1275a -⎛⎫= ⎪⎝⎭,1357b ⎛⎫= ⎪⎝⎭,25log 7c =,则a 、b 、c 的大小关系是( ).A.b a c <<B.c b a <<C.c a b <<D.b c a <<【答案】C 【解析】12125757a -⎛⎫=⎛⎫= ⎝⎭⎪⎭⎪⎝<135()7b =,225log log 107c =<=因此c a b <<故选:C.25.函数()log (2)a f x ax =-(0a >且1a ≠)在[]0,3上为增函数,则实数a 的取值范围是()A.2,13⎛⎫ ⎪⎝⎭ B.(0,1) C.20,3⎛⎫⎪⎝⎭ D.[)3,+∞【答案】C【解析】因为0a >且1a ≠,令2t ax =-,所以函数2t ax =-在[]0,3上为减函数, 所以函数log a y t =应是减函数,()f x 才可能是增函数,∴01a <<,因为函数()f x 在[]0,3上为增函数,由对数函数性质知230a ->,即23<a , 综上023a <<. 故选:C .26.设3log 7a =, 1.12b =, 3.10.8c =,则( )A.b a c <<B.a c b <<C.c b a <<D.c a b << 【答案】D【解析】因为333log 7(log 3,log 9)a =∈,所以(1,2)a ∈; 1.122b =>; 3.100.80.81c =<=; 所以c a b <<,故选D.27.三个数0.76,60.7,0.7log 6的大小顺序是( )A.60.70.7log 60.76<<B.60.70.70.76log 6<<C.0.760.7log 660.7<<D.60.70.70.7log 66<< 【答案】A 【解析】因为0.70661>=,6000.70.71<<=,0.70.7log 6log 10<=;所以60.70.7log 60.76<<.故选:A.28.已知0.42x =,2lg 5y =,0.425z ⎛⎫= ⎪⎝⎭,则下列结论正确的是( ) A.x y z <<B.y z x <<C.z y x <<D.z x y <<【答案】B【解析】0.40221x =>=,2lg lg105y =<=,0.4021525z ⎛⎫<= ⎪⎝⎫⎭⎭⎛=⎪⎝,又0z >,即01z <<.因此,y z x <<.故选:B.。
对数与对数函数

对数与对数函数 知识梳理1、对数式log a N 可看作一记号,表示底为a (a >0,且a ≠1),幂为N 的指数工表示方程xa N =(a >0,且a ≠1)的解. 也可以看作一种运算,即已知底为a (a >0,且a ≠1)幂为N ,求幂指数的运算. 因此,对数式log a N 又可看幂运算的逆运算.为a >0,a ≠1时,log x N a a N x =⇔= 【扩展】两类对数① 以10为底的对数称为常用对数,10log N 常记为lg N .② 以无理数e=2.71828…为底的对数称为自然对数,log e N 常记为ln N .以后解题时,在没有指出对数的底的情况下,都是指常用对数,如100的对数等于2,即lg1002=.说明:在例1中,10log 0.010.01,log 10ln10e 应改为lg 应改为. 2、对数的运算法则如果a >0且a ≠1,M >0,N >0,那么:(1)log log log a a a MN M N =+ (2)log log log aa a MM N N=- (3)log log ()n a a M n Mn R =∈3、画出函数2log xy =的图象, 再利用电脑软件画出0.5log .x y =的图象42-2-4-55探究:选取底数(a a >0,且a ≠1)的若干不同的值,在同一平面直角坐标系内作出相应的对数函数的图象.观察图象,你能发现它们有哪些特征吗?画出4log y x =,3log y x =,13log y x =和14log y x =提问:通过函数的图象,你能说出底数与函数图象的关系吗?函数的图象有何特征,性质又如何?先由学生讨论、交流,教师引导总结出函数的性质. (投影) 图象的特征函数的性质(1)图象都在y 轴的右边 (1)定义域是(0,+∞) (2)函数图象都经过(1,0)点 (2)1的对数是0(3)从左往右看,当a >1时,图象逐渐上升,当0<a <1时,图象逐渐下降 .(3)当a >1时,log xa y =是增函数,当0<a <1时,log a y x =是减函数. (4)当a >1时,函数图象在(1,0)点右边的纵坐标都大于0,在(1,0)点左边的纵坐标都小于0. 当0<a <1时,图象正好相反,在(1,0)点右边的纵坐标都小于0,在(1,0)点左边的纵坐标都大于0 .(4)当a >1时x >1,则log a x >00<x <1,log a x <0 当0<a <1时x >1,则log a x <00<x <1,log a x <0由上述表格可知,对数函数的性质如下(先由学生仿造指数函数性质完成,教师适当启发、引导):a >10<a <1图象性 质(1)定义域(0,+∞); (2)值域R ; (3)过点(1,0),即当x =1,y =0; (4)在(0,+∞)上是增函数在(0,+∞)是上减函数精讲精练(1)对数运算的例题【例1】将下列指数式化为对数式,对数式化为指数式:(1)712128-=; (2)327a =; (3)1100.1-=;(4)12log 325=-; (5)lg0.0013=-; (6)ln100=4.606.【例2】求证:(1)log n a a n =; (2)log log log a a a MM N N-=.【例3】试推导出换底公式:log log log c a c bb a= (0a >,且1a ≠;0c >,且1c ≠;0b >).【例4】化简与求值:(1)221(lg 2)lg2lg5(lg 2)lg212++-+ ;(2)2log (4747)++-.【例5】若2510a b ==,则11a b+= . (教材P 83 B 组2题) 【例6】 (1)方程lg lg(3)1x x ++=的解x =________;(2)设12,x x 是方程2lg lg 0x a x b ++=的两个根,则12x x 的值是 .【例7】(1)化简:532111log 7log 7log 7++;(2)设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅= ,求实数m 的值.(2)对数函数图象和性质的例题【例1】比较大小:(1)0.9log 0.8,0.9log 0.7,0.8log 0.9; (2)3log 2,2log 3,41log 3.【例2】求下列函数的定义域:(1)2log (35)y x =-;(2)0.5log (4)3y x =-.【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <,求实数a 的取值范围.【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.【例5】讨论函数0.3log (32)y x =-的单调性.【例6】(05年山东卷.文2)下列大小关系正确的是( ). A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<【例7】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系?课堂作业(1)对数幂的运算1. 将下列指数式与对数式互化,有x 的求出x 的值 .(1)12155-=(2)42log x = (3)1327x =(4)1()644x= (5)lg0.0001x = (6)5ln e x =2.求log log log ,a b c b c Na⋅⋅∈+的值(a,b,c R 且不等于1,N >0).3.计算331log log 5533+的值.4、判断下列式子是否正确,a >0且a ≠1,x >0且a ≠1,x >0,x >y ,则有(1)log log log ()a a a x y x y ⋅=+ (2)log log log ()a a a x y x y -=-(3)log log log aa a xx y y=÷ (4)log log log a a a xy x y =- (5)(log )log n a a x n x = (6)1log log a a x x=- (7)1log log n a a x x n=5. 用log a x ,log a y ,log a z 表示出(1)(2)小题,并求出(3)、(4)小题的值.(1)log a xyz =____________; (2)23log 8a x y =______________________;(3)75log (42)z ⨯=______________; (4)5lg 100=_____________________; 6. 已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a - 7、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 8、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a a a x m n x+==-则等于( )A 、m n +B 、m n -C 、()12m n +D 、()12m n -9、如果方程2lg (lg5lg7)lg lg5lg70x x +++= 的两根是,αβ,则αβ 的值是( )A 、lg5lg 7B 、lg 35C 、35D 、351 10、已知732log [log (log )]0x =,那么12x -等于( )A 、13 B 、123 C 、122 D 、13311. 若2log 2,log 3,m n a a m n a +=== 。
对数

(1) y = log
0.3
( x − 2) − 3
(2,+∞)上递减
(2) y = log 3 ( x − 2 ) + 5
(3) y = log (4) y = log 0 .3 0 .3 2) (3 + 2 x − x
(2,+∞)上递增
(−1,1)上递减 (1,3)上递增
(3,+∞)上递减 1 (−∞,− )上递增 2
问题2:对数函数的图象有几种情况? 问题2 对数函数的图象有几种情况?
5
(a> (a>1)
y y=ax y=x 1 y=logax
(0<a<1)
y = ax y
y=x
·
O 1
·
1 x
·
O1
·
x y=logax
(二)对数函数的图象和性质:
6
a >1
y
0 <a <1
y=logax (a>1 ) > y
右侧总是底大图低. 当a>1 和0<a<1时,在x=1右侧总是底大图低. , x=1右侧总是底大图低
动态演示 图象分析
18
谢谢指导!
1. log23
log23.5
同底对数式比较 大小的步骤 步骤: 大小的步骤: 1、判断底数a的范围 判断底数a
解:∵y= log2x 中底数 2>1
∴ y= log2x在(0,+∞)上 是增函数 ∵ 3<3.5 ∴ log23 < log23.5
log0.20.7
练习4.已知下列不等式,比较正数m,n的大小 练习4.已知下列不等式,比较正数m,n的大小 (1)若log3m < log3n 则 m
对数函数

对数与对数运算一、对数的定义一般地,如果 ()1,0≠>a a a 的b 次幂等于N , 就是 N a b =,那么数 b 叫做 以a 为底 N 的对数,记作 b N a =log ,a 叫做对数的底数,N 叫做真数。
特别提醒:1、对数记号log a N 只有在01a a ≠且>,0N >时才有意义,就是说负数和零是没有对数的。
2、记忆两个关系式:①log 10a =;②log 1a a =。
3、常用对数:我们通常将以10为底的对数叫做常用对数。
为了简便, N 的常用对数N 10log , 简记作:lg N 。
例如:10log 5简记作lg 5 ; 5.3log 10简记作lg 3.5。
4、自然对数:在科学技术中常常使用以无理数e 为底的对数,以e 为底的对数叫自然对数。
为了简便,N 的自然对数N e log ,简记作:ln N 。
如:3log e 简记作ln 3;10log e 简记作ln10。
二、对数运算性质:如果 0,1,0,0,a a M N n R ≠∈>>> 有:log ()log log a a a MN M N =+log log log aa a MM N N=- log log () n a a M n M n R =∈ 特别提醒:1、对于上面的每一条运算性质,都要注意只有当式子中所有的对数记号都有意义时,等式才成立。
如[]2log (3)(5)--是存在的,但[]222log (3)(5)log (3)log (5)--=-+-是不成立的。
2、注意上述公式的逆向运用:如lg5lg 2lg101+==;三、对数的换底公式及推论: 对数换底公式:()log log 0,1,0,1,0log m a m NN a a m m N a=≠≠>>> 两个常用的推论:(1)1log log =⋅a b b a (2)1log log log =⋅⋅a c b c b a四、两个常用的恒等式:N a N a =log , log log m n a a nb b m=()0,1,0,0a a b N ≠>>>类型一 指数式与对数式的相互转化例1:将下列指数式与对数式进行互化.(1)3x =127; (2)⎝ ⎛⎭⎪⎫14x =64;(3)5-12 =15; (4)log 24=4;(5)lg0.001=-3;(6)log2-1(2+1)=-1.解析:(1)log 3127=x .(2) log 14 64=x .(3)log 515=-12.(4)(2)4=4.(5)10-3=0.001.(6)(2-1)-1=2+1.练习1:将下列指数式与对数式进行互化.(1)e 0=1;(2)(2+3)-1=2-3;(3)log 327=3;(4)log 0.10.001=3. 答案:(1)ln1=0.(2)log (2+3)(2-3)=-1.(3)33=27.(4)0.13=0.001.练习2:将下列对数式与指数式进行互化.(1)2-4=116;(2)53=125;(3)lg a =2;(4)log 232=5.答案:(1)log 2116=-4. (2)log 5125=3. (3)102=a . (4)25=32. 类型二 对数基本性质的应用 例2:求下列各式中x 的值.(1)log 2(log 5x )=0; (2)log 3(lg x )=1;解析:(1)∵log 2(log 5x )=0,∴log 5x =1,∴x =5. (2)∵log 3(lg x )=1,∴lg x =3,∴x =103=1 000.练习1:已知log 2(log 3(log 4x ))=log 3(log 4(log 2y ))=0,求x +y 的值.80 练习2:已知4a =2,lg x =a ,则x =__10____. 类型三 对数的运算法则例3:计算(1)log a 2+log a 12(a >0且a ≠1);(2)log 318-log 32;(3)2log 510+log 50.25;解析:(1)log a 2+log a 12=log a (2×12)=log a 1=0.(2)log 318-log 32=log 3(18÷2)=log 39=2.(3)2log 510+log 50.25=log 5100+log 50.25=log 5(100×0.25)=log 525=2. 练习1:计算log 535+2log 22-log 5150-log 514的值.4练习2:计算:2log 510+log 50.25的值为____2____. 类型四 带有附加条件的对数式的运算例4:lg2=a ,lg3=b ,试用a 、b 表示lg108,lg1825. 解析:lg108=lg(27×4)=lg(33×22)=lg33+lg22=3lg3+2lg2=2a +3b .lg 1825=lg18-lg25=lg(2×32)-lg 10222=lg2+lg32-lg102+lg22=lg2+2lg3-2+2lg2=3a +2b -2.练习1:已知lg2=0.301 0,lg3=0.477 1,求lg 45.0.8266 练习2:若lg x -lg y =a ,则lg(x 2)3-lg(y2)3等于( D )A .a 2B .aC .3a2 D .3a 类型五 应用换底公式求值例5: 计算:lg 12-lg 58+lg12.5-log 89·log 278.解析:lg 12-lg 58+lg12.5-log 89·log 278=lg 12-lg 58+lg 252-lg9lg8·lg8lg27=lg ⎝ ⎛⎭⎪⎫12×85×252-2lg33lg3=1-23=13.练习1: 计算(log 2125+log 425+log 85)·(log 52+log 254+log 1258).13 练习2: log 89·log 32的值为( A )A .23B .1C .32 D .2 类型六 应用换底公式化简例6: 已知log 89=a ,log 25=b ,用a 、b 表示lg3.解析:∵log 89=lg9lg8=2lg33lg2=a ,①又∵log 25=lg5lg2=1-lg2lg2=b ,②由①②消去lg2可得:lg3=3a2 1+b.练习1:已知log 23=a ,log 37=b ,则log 1456=( A )A .ab +3ab +1 B .a b +3 ab +1 C .b +3ab +1 D .ab -3ab +1练习2: 已知log 72=p ,log 75=q ,则lg5用p 、q 表示为( B )A .pqB .q p +qC .1+pq p +q D .pq1+pq1、使对数log a (-2a +1)有意义的a 的取值范围为( B )A .0<a <12且a ≠1B .0<a <12C .a >0且a ≠1D .a <122、已知x 、y 为正实数,则下列各式正确的是( A )A .2lg x +lg y 2=2lg x +2lg yB .2lg(x +y )=2lg x ·2lg yC .2(lg x ·lg y )=2lg x +2lg yD .2lg(xy )=2lg x ·2lg y3、若lg2=a ,lg3=b ,则lg12lg15等于( A )A .2a +b 1-a +bB .2a +b1+a +bC .a +2b 1-a +bD .a +2b1+a +b4、.log 52·log 425等于( C )A .-1B .12 C .1D .2 5、化简log 1a b -log a 1b 的值为( A )A .0B .1C .2log a bD .-2log a b1.已知log 7[log 3(log 2x )]=0,那么x -12等于( C )A .13B .123 C .122D .1332.若f (10x )=x ,则f (3)的值为( B )A .log 310B .lg3C .103D .310 3.如果lg x =lg a +3lg b -5lg c ,那么( C )A .x =a +3b -cB .x =3ab5cC .x =ab 3c 5D .x =a +b 3-c 34.方程2log 3x =14的解是( C )A .33 B .3 C .19D .95.e ln3-e -ln2等于( C )A .1B .2C .52D .36.若log (1-x )(1+x )2=1,则x =_____-3___. 7.若log x (2+3)=-1,则x =___2-3_____. 8.已知log 32=a ,则2log 36+log 30.5=____2+a ____. 9. (1)设log a 2=m ,log a 3=n ,求a 2m +n 的值;12. (2)设x =log 23,求22x +2-2x +22x+2-x 的值.103. 10. 已知log a x +3log x a -log x y =3(a >1).(1)若设x =a t ,试用a 、t 表示y ;y =at 2-3t +3(t ≠0).(2)若当0<t ≤2时,y 有最小值8,求a 和x 的值.a =16,x =64.对数函数一、对数函数的定义:函数x y a log =)10(≠>a a 且叫做对数函数。
人教A版数学必修第一册期末复习:对数与对数函数课件

技巧点拨
➢ 无论题型如何变化,都是围绕对数函数的单调性
方法
总结
➢ 弄清对数函数的单调性是解题的关键
➢ 注意有时需对底数字母参数进行讨论
过关检测
1.设a,b,c均为正数,且2a=
的大小关系是 ( A )
A.a<b<c
C.c<a<b
a>0
b>0
c>0
2a>1
0<
1
2
1
>0
2
,
在 , 单调递减
×
×
常考题型
1
例 4 当 0<x≤2时,4x<logax,则 a 的取值范围是( B )
题
型
二
对
数
函
数
的
图
象
及
应
用
A. 0,
2
2
B.
C.(1, 2)
2,1源自2D.( 2,2)
易知0<a<1
依图知需满足 >
>
<a<1
当0<x<1时,y<0
当0<x<1时,y>0
核心考点
1.换底公式的两个重要结论
常
用
结
论
(1)logab=
1
log
(2)log =
log
其中a>0且a≠1,b>0且b≠1,m≠0,n∈R.
核心考点
2.对数函数的图象与底数大小的比较
常
用
结
论
如图,作直线y=1,则该直线与四个函数图象交点的横坐标为相应
高三:对数与对数函数

这时f(x)=log4(-x2+2x+3).
由-x2+2x+3>0得-1<x<3,即函数定义域为(-1,3). 令g(x)=-x2+2x+3. 则g(x)在(-1,1)上单调递增,在(1,3)上单调递减. 又y=log4x在(0,+∞)上单调递增,
所以f(x)的单调递增区间是(-1,1),单调递减区间是
则f(a2)+f(b2)=________. 解析:由f(ab)=1得ab=10,于是f(a2)+f(b2)=lg a2 +lg b2=2(lg a+lg b)=2lg(ab)=2lg 10=2. 答案:2
1.在运用性质logaMn=nlogaM时,要特别注意条件,在
无M>0的条件下应为logaMn=nloga|M|(n∈N*,且n为偶数).
1 4 3 1 = ×(5lg 2-2lg 7)- × lg 2+ (lg 5+2lg 7) 2 3 2 2 5 1 = lg 2-lg 7-2lg 2+ lg 5+lg 7 2 2 1 1 1 1 = lg 2+ lg 5= lg(2×5)= . 2 2 2 2
(2)由 2a=5b=m 得 a=log2m,b=log5m, 1 1 ∴a+b=logm2+logm5=logm10. 1 1 ∵a+b=2, ∴logm10=2,即 m2=10. 解得 m= 10(∵m>0).
A.0,
(
B. 2 ,1 2
)
2 2
C.(1, 2)
D.( 2,2)
[自主解答]
(1)由1-x>0,知x<1,排除选项A、
B;设t=1-x(x<1),因为t=1-x为减函数,而y=ln t 为增函数,所以y=ln(1-x)为减函数,可排除D选C.
对数与对数函数

2.已知 1<a<b<a2, 比较 logab, logba, loga a , logb a , 1 的大小. b b 2 a a 2 解: 由 1<a<b<a 可知: loga b <0, logb b <0, logab>1. ∴0<logba<1. ∵ 0>log a a>log a b, ∴logaa <logb a . b b b b 2> 1 log b= 1 , 又 logba= 1 log a 2 b 2 2 b 1 a ∴ logab>logba> 2 >logb b >loga a . b 3.已知 logm4>logn4, 比较 m, n 的大小. 解: 由已知 logm4>logn4, 可分情况讨论如下: ①当 m>1, 0<n<1 时, logm4>0, logn4<0, 原不等式成立. ∴m>1>n>0; ②当 m>1, n>1 时, 由 logm4>logn4>0 得: log4m<log4n. ∴n>m>1; ③当 0<m<1, 0<n<1 时, 由 0>logm4>logn4 得: log4m<log4n. ∴0<m<n<1. 综上所述: m, n 的大小是 m>1>n>0 或 n>m>1 或 0<m<n<1.
对数与对数函数
一、对数
如果 a(a>0, a1)的 b 次幂等于 N, 即 ab=N, 那么数 b 叫做 以 a 为底 N 的对数, 记作 logaN=b, 其中 a 叫做对数的底数, N 叫做真数, 式子 logaN 叫做对数式. 常用对数: (lgN), 自然对数: (lnN).
对数运算和对数函数

对数与对数函数一、相关知识点1.对数的定义:如果()1,0≠>=a a N a x 且,那么数x 叫做以a 为底,N 的对数,记作N x a log =,其中a 叫做对数的底数,N 叫做真数。
2.几种常见对数(1)()1,0≠>a a 且①01log =a ; ②1log =a a ; ③N a Na =log ; ④N a N a =log .(两个对数恒等式) (2)对数的重要公式:①换底公式:()0,1,log log log >=N b a b aN aNb均为大于零且不等于;②abba log 1log =,推广:da d c cb b a log log log log =⋅⋅. (3)对数的运算法则:如果0,0,1,0>>≠>N M a a 且,那么 ①()Na M a MN aloglog log += ; ②NaM a N Malog log log -=; ③()R n n MaM a n∈=log log ;④b a b a mnnm log log = . 3.反函数,只需了解:指数函数xa y =与对数函数xa y log =互为反函数,它们的图象关于直线x y =对称。
题型一:对数的化简和求值1.计算:(1)2110025lg 41lg ÷⎪⎭⎫ ⎝⎛-;(2)32log 2450lg 2lg 5lg +⋅+;(3)()232031027.0252lg 3.0lg 21000lg 8lg 27lg --⎪⎭⎫⎝⎛-⨯+-++-+;(4)()222lg 20lg 5lg 8lg 325lg +++. 2.已知()[]0lg log log 25=x ,求x 的值.3.已知0>a ,且1≠a ,m a =2log ,n a =3log ,求nm a +2的值能力提高:(1).设m ba==52,且211=+ba ,则=m ; (2).若632==b a ,求证:c b a 111=+题型二:(1)对数函数的基本性质题型一:基本性质1.函数()()223lg +-=x x f 恒过定点_______________________2.如果0log log 2121<<y x ,那么()(A)1<<x y ; (B)1<<y x ;(C)y x <<1; (D)x y <<1.3.已知()x x f a log =,()x x g b log =,()x x r c log =,()x x h d log =的图象如图所示则a ,b ,c ,d 的大小为A.b a d c <<<;B.a b d c <<<;C.b a c d <<<;D.d c b a <<<4.若函数()⎪⎩⎪⎨⎧<⎪⎭⎫⎝⎛+≥=)()(4214log 2x x f x x x f ,则⎪⎭⎫⎝⎛23f 的值是( ) A.21; B.1; C.23; D.2 5.若点()b a ,在x y lg =图像上,1≠a ,则下列点也在此图像上的是()A.⎪⎭⎫⎝⎛b a ,1;B. ()b a -1,10;C.⎪⎭⎫⎝⎛+1,10b a ; D.()b a 2,2. 6.函数()()13log 2+=xx f 的值域为7.为了得到函数103lg+=x y 的图像,只需把函数x y lg =的图像上所有的点( ) A.向左平移3个单位长度,再向上平移1个单位长度; B.向右平移3个单位长度,再向上平移1个单位长度; C.向左平移3个单位长度,再向下平移1个单位长度; D.向右平移3个单位长度,再向下平移1个单位长度.8.若函数()()()101≠>--=a a a a k x f xx且在R 上既是奇函数,又是减函数()()k x x g a +=log 的图象是( )9.对于函数()x f 定义域中任意的()2121,x x x x ≠,有如下结论: ①()()()2121x f x f x x f ⋅=+; ②()()()2121x f x f x x f +=⋅; ③()()02121>--x x x f x f ; ④()()222121x f x f x x f +<⎪⎭⎫ ⎝⎛+. 当()x x f lg =时,上述结论中正确结论的序号是. 能力提高:1.已知函数()22log 21+-=a y x 的值域是R ,求a 的取值范围.2.已知函数()()1log 22++=ax ax x f 的定义域为全体实数,求a 的取值范围.3.已知函数()()1log 22++=ax axx f 的值域域为全体实数,求a 的取值范围。
对数公式及对数函数的总结

对数公式及对数函数的总结对数是数学中的一个重要概念。
如果一个数N可以表示为a的x次方(a>0且a≠1),那么x就是以a为底N的对数,记作x=logaN。
其中a称为底数,N称为真数。
负数和零没有对数。
对数式与指数式可以互相转化:x=logaN等价于ax=N (a>0,a≠1,N>0)。
常用的对数有lgN(即以10为底N的对数)和lnN(即以自然常数e为底N的对数)。
自然常数e≈2..对数函数是指函数y=logax(a>1或0<a<1)的图像。
它的定义域为正实数集,值域为实数集。
对数函数的图像经过点(1,0),在(0,+∞)上是增函数,在(0,1)上是减函数。
当x=1时,y=0.对数函数既非奇函数也非偶函数。
对数公式在数学中有广泛的应用。
例如,可以用对数公式计算各种对数值,如log26-log23=2,log212+log25=log=3,等等。
还可以用对数公式来解对数的值,如lg14-2lg7+lg7/lg18-2lg2-(-1)=log0.5,以及2(lg2+lg5)+log3(4/27)的值等。
在第一象限内,a越大图像越靠下,在第四象限内,a越大图像越靠上。
总之,对数及其函数在数学中有着广泛的应用,是不可或缺的数学工具。
4、已知a>b>c,那么a>b>c。
3、设a=log3π,b=log23,c=log32,则a>b>c。
2、如果a>b>logc1,那么B选项___c。
5、如果a>1,且a-x-logaxy。
1、已知函数f(x)=logx,如果f(ab)=1,则f(a)+f(b)=2.6、设函数f(x)={x-1,x<2;2logx-1,x≥2},那么f(f(2))=2log2-1.7、设函数f(x)满足:当x≥4时,f(x)=1/x;当x<4时,f(x)=f(x+1),那么f(2+log23)=1/7.参数问题部分无需改写。
对数与对数函数-高考数学复习课件

故有ቊ
解得1< a ≤3.
6 − 2≥0,
(2)(2024·河南郑州模拟)设函数 f ( x )=ln| x +3|+ln| x -3|,则
f ( x )( A
)
A. 是偶函数,且在(-∞,-3)上单调递减
B. 是奇函数,且在(-3,3)上单调递减
C. 是奇函数,且在(3,+∞)上单调递增
因为0< a < b ,所以ln a <0,ln b >0,
所以0< a <1, b >1,
所以-ln a =ln b , 所以ln a +ln b =ln( ab )=0,
1
所以 ab =1,则 b = ,
2
所以 a +2 b = a + .
2
令 g ( x )= x + (0< x <1),
a >1
0< a <1
图象
定义域
(0,+∞)
值域
性质
R
过定点 (1,0)
,即 x = 1
时, y = 0
a >1
0< a <1
当 x >1时, y >0 ;
当0< x <1时, y <0
性质
在(0,+∞)上是 增
数
函
当 x >1时, y <0 ;
当0< x <1时, y >0
在(0,+∞)上是 减
内容索引
必备知识
自主梳理
关键能力
重点探究
课时作业
巩固提升
必备知识 自主梳理
[知识梳理]
知识点一 对数与对数运算
1. 对数的概念
如果 ax = N ( a >0,且 a ≠1),那么数 x 叫做以 a 为底 N 的对数,记作
对数函数及其性质,对数的公式互化,详尽的讲解

§2.2对数函数2.2.1对数与对数运算1.对数的概念一般地,如果a x=N (a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=log a N,其中a叫做对数的底数,N叫做真数.说明:(1)实质上,上述对数表达式,不过是指数函数y=a x的另一种表达形式,例如:34=81与4=log381这两个式子表达是同一关系,因此,有关系式a x=N⇔x=log a N,从而得对数恒等式:a log a N=N.(2)“log”同“+”“×”“”等符号一样,表示一种运算,即已知一个数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面.(3)根据对数的定义,对数log a N(a>0,且a≠1)具有下列性质:①零和负数没有对数,即N>0;②1的对数为零,即log a1=0;③底的对数等于1,即log a a=1.2.对数的运算法则利用对数的运算法则,可以把乘、除、乘方、开方的运算转化为对数的加、减、乘、除运算,反之亦然.这种运算的互化可简化计算方法,加快计算速度.(1)基本公式①log a(MN)=log a M+log a N (a>0,a≠1,M>0,N>0),即正数的积的对数,等于同一底数的各个因数的对数的和.②log a MN=log a M-log a N(a>0,a≠1,M>0,N>0),即两个正数的商的对数,等于被除数的对数减去除数的对数.③log a M n=n·log a M (a>0,a≠1,M>0,n∈R),即正数的幂的对数等于幂的底数的对数乘以幂指数.(2)对数的运算性质注意点①必须注意M>0,N>0,例如log a[(-3)×(-4)]是存在的,但是log a(-3)与log a(-4)均不存在,故不能写成log a[(-3)×(-4)]=log a(-3)+log a(-4).②防止出现以下错误:log a(M±N)=log a M±log a N,log a(M·N)=log a M·log a N,log a M N=log a Mlog a N,log a M n =(log a M )n . 3.对数换底公式在实际应用中,常碰到底数不为10的对数,如何求这类对数,我们有下面的对数换底公式:log b N =log c Nlog c b(b >0,且b ≠1;c >0,且c ≠1;N >0).证明 设log b N =x ,则b x =N .两边取以c 为底的对数,得x log c b =log c N .所以x =log c N log c b ,即log b N =log c Nlog c b.换底公式体现了对数运算中一种常用的转化,即将复杂的或未知的底数转化为已知的或需要的底数,这是数学转化思想的具体应用.由换底公式可推出下面两个常用公式:(1)log b N =1log N b 或log b N ·log N b =1 (N >0,且N ≠1;b >0,且b ≠1);(2)log bn N m =mnlog b N (N >0;b >0,且b ≠1;n ≠0,m ∈R ).题型一 正确理解对数运算性质对于a >0且a ≠1,下列说法中,正确的是( ) ①若M =N ,则log a M =log a N ; ②若log a M =log a N ,则M =N ; ③若log a M 2=log a N 2,则M =N ; ④若M =N ,则log a M 2=log a N 2.A .①与③B .②与④C .②D .①、②、③、④解析 在①中,当M =N ≤0时,log a M 与log a N 均无意义,因此log a M =log a N 不成立. 在②中,当log a M =log a N 时,必有M >0,N >0,且M =N ,因此M =N 成立. 在③中,当log a M 2=log a N 2时,有M ≠0,N ≠0,且M 2=N 2,即|M |=|N |,但未必有M =N .例如,M =2,N =-2时,也有log a M 2=log a N 2,但M ≠N .在④中,若M =N =0,则log a M 2与log a N 2均无意义,因此log a M 2=log a N 2不成立. 所以,只有②成立. 答案 C点评 正确理解对数运算性质公式,是利用对数运算性质公式解题的前提条件,使用运算性质时,应牢记公式的形式及公式成立的条件.题型二 对数运算性质的应用求下列各式的值:(1)2log 32-log 3329+log 38-5log 53;(2)lg25+23lg8+lg5·lg20+(lg2)2;(3)log 52·log 79log 513·log 734.分析 利用对数的性质求值,首先要明确解题目标是化异为同,先使各项底数相同,才能使用性质,再找真数间的联系,对于复杂的真数,可以先化简再计算.解 (1)原式=2log 32-(log 332-log 39)+3log 32-3 =2log 32-5log 32+2+3log 32-3=-1.(2)原式=2lg5+2lg2+lg 102·lg(2×10)+(lg2)2=2lg(5×2)+(1-lg2)·(lg2+1)+(lg2)2 =2+1-(lg2)2+(lg2)2=3.(3)∵log 52·log 79log 513·log 734=12log 52·2log 73-log 53·13log 74=-lg2lg5·lg3lg7lg3lg5·13·lg4lg7=-32.点评 对数的求值方法一般有两种:一种是将式中真数的积、商、幂、方根利用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;另一种方法是将式中的和、差、积、商运用对数的运算法则将它们化为真数的积、商、幂、方根,然后化简求值.题型三 对数换底公式的应用计算:(log 2125+log 425+log 85)(log 52+log 254+log 1258).分析 由题目可获取以下主要信息:本题是一道对数化简求值题,在题目中各个对数的底数都各不相同.解答本题可先通过对数换底公式统一底数再进行化简求值. 解 方法一 原式=⎝⎛⎭⎫log 253+log 225log 24+log 25log 28⎝⎛⎭⎫log 52+log 54log 525+log 58log 5125=⎝⎛⎭⎫3log 25+2log 252log 22+log 253log 22⎝⎛⎭⎫log 52+2log 522log 55+3log 523log 55=⎝⎛⎭⎫3+1+13log 25·(3log 52) =13log 25·log 22log 25=13.方法二 原式=⎝⎛⎭⎫lg125lg2+lg25lg4+lg5lg8⎝⎛⎭⎫lg2lg5+lg4lg25+lg8lg125 =⎝⎛⎭⎫3lg5lg2+2lg52lg2+lg53lg2⎝⎛⎭⎫lg2lg5+2lg22lg5+3lg23lg5 =⎝⎛⎭⎫13lg53lg2⎝⎛⎭⎫3lg2lg5=13.点评 方法一是先将括号换底,然后再将底统一;方法二是在解题方向还不清楚的情况下,一次性地统一为常用对数(当然也可以换成其他非1的正数为底),然后再化简.上述方法是不同底数对数的计算、化简和恒等证明的常用方法.已知log (x +3)(x 2+3x )=1,数x 的值.错解 由对数的性质可得x 2+3x =x +3. 解得x =1或x =-3.错因分析 对数的底数和真数必须大于0且底数不等于1,这点在解题中忽略了.正解 由对数的性质知⎩⎪⎨⎪⎧x 2+3x =x +3,x 2+3x >0,x +3>0且x +3≠1.解得x =1,故实数x 的值为1.对数的定义及其性质是高考中的重要考点之一,主要性质有:log a 1=0,log a a =1,a log a N =N (a >0,且a ≠1,N >0).1.(高考)方程9x -6·3x -7=0的解是________. 解析 ∵9x -6·3x -7=0,即32x -6·3x -7=0 ∴(3x -7)(3x +1)=0 ∴3x =7或3x =-1(舍去) ∴x =log 37. 答案 log 372.(高考)设g (x )=⎩⎪⎨⎪⎧e x ,x ≤0,ln x ,x >0,则g ⎝⎛⎭⎫g ⎝⎛⎭⎫12=____. 解析 g ⎝⎛⎭⎫12=ln 12<0,g ⎝⎛⎭⎫ln 12=eln 12=12, ∴g ⎝⎛⎭⎫g ⎝⎛⎭⎫12=12. 答案 121.对数式log (a -3)(7-a )=b ,实数a 的取值围是( )A .(-∞,7)B .(3,7)C .(3,4)∪(4,7)D .(3,+∞) 答案 C解析 由题意得⎩⎪⎨⎪⎧a -3>0,a -3≠1,7-a >0,解得3<a <7且a ≠4.2.设a =log 32,则log 38-2log 36用a 表示的形式是( )A .a -2B .3a -(1+a )2C .5a -2D .-a 2+3a -1 答案 A解析 ∵a =log 32,∴log 38-2log 36=3log 32-2(log 32+1) =3a -2(a +1)=a -2. 3.log 56·log 67·log 78·log 89·log 910的值为( )A .1B .lg5 C.1lg5D .1+lg2答案 C解析 原式=lg6lg5·lg7lg6·lg8lg7·lg9lg8·lg10lg9=lg10lg5=1lg5.4.已知log a (a 2+1)<log a 2a <0,则a 的取值围是( )A .(0,1) B.⎝⎛⎭⎫0,12 C.⎝⎛⎭⎫12,1 D .(1,+∞) 答案 C解析 由题意,得⎩⎪⎨⎪⎧0<a <1,2a >1,∵a >0,a ≠1,log a (a 2+1)<log a 2a ,∴0<a <1.∴12<a <1.5.已知函数f (x )=a x -1+log a x (a >0,a ≠1)在[1,3]上最大值与最小值之和为a 2,则a 的值为( )A .4 B.14 C .3 D.13答案 D6.若方程(lg x )2+(lg7+lg5)lg x +lg7·lg5=0的两根为α,β,则αβ等于( )A .lg7·lg5B .lg35C .35 D.135答案 D解析 ∵lg α+lg β=-(lg7+lg5)=-lg35=lg 135∴α·β=135.7.已知f (log 2x )=x ,则f ⎝⎛⎭⎫12=________. 答案 2解析 令log 2x =12,则212=x ,∴f ⎝⎛⎭⎫12=212= 2.8.log (2-1)(2+1)=________. 答案 -1解析 log 2-1(2+1)=log 2-1(2+1)(2-1)2-1=log (2-1)12-1=-1.9.已知lg2=0.301 0,lg3=0.477 1,lg x =-2+0.778 1,则x =________. 答案 0.06解析 ∵lg2=0.301 0,lg3=0.477 1,而0.301 0+0.477 1=0.778 1,∴lg x =-2+lg2+lg3, 即lg x =lg10-2+lg6.∴lg x =lg(6×10-2),即x =6×10-2=0.06.10.(1)已知lg x +lg y =2lg(x -2y ),求log 2xy的值;(2)已知log 189=a,18b =5,试用a ,b 表示log 365. 解 (1)lg x +lg y =2lg(x -2y ), ∴xy =(x -2y )2,即x 2-5xy +4y 2=0. 即(x -y )(x -4y )=0,解得x =y 或x =4y , 又∵⎩⎪⎨⎪⎧x >0,y >0,x -2y >0,∴x >2y >0,∴x =y ,应舍去,取x =4y .则log 2x y =log 24y y =log 24=lg4lg 2=4.(2)∵18b =5,∴log 185=b, 又∵log 189=a , ∴log 365=log 185lg 1836=blog 18(18×2)=b 1+log 182=b 1+log 18189=b 1+(1-log 189)=b2-a. 11.设a ,b ,c 均为不等于1的正数,且a x =b y =c z ,1x +1y +1z =0,求abc 的值.解 令a x =b y =c z =t (t >0且t ≠1),则有1x =log t a ,1y =log t b ,1z =log t c ,又1x +1y +1z=0,∴log t abc =0,∴abc =1. 12.已知a ,b ,c 是△ABC 的三边,且关于x 的方程x 2-2x +lg(c 2-b 2)-2lg a +1=0有等根,试判定△ABC 的形状.解 ∵关于x 的方程x 2-2x +lg(c 2-b 2)-2lg a +1=0有等根, ∴Δ=0,即4-4[lg(c 2-b 2)-2lg a +1]=0.即lg(c2-b2)-2lg a=0,故c2-b2=a2,∴a2+b2=c2,∴△ABC为直角三角形.2.2.1对数与对数运算(一)学习目标1.理解对数的概念,能进行指数式与对数式的互化.2.了解常用对数与自然对数的意义.3.理解对数恒等式并能用于有关对数的计算.自学导引1.如果a(a>0且a≠1)的b次幂等于N,就是a b=N,那么数b叫做以a为底N的对数,记作b=log a N,其中a叫做对数的底数,N叫做真数.2.对数的性质有:(1)1的对数为零;(2)底的对数为1;(3)零和负数没有对数.3.通常将以10为底的对数叫做常用对数,以e 为底的对数叫做自然对数,log 10N 可简记为lg N ,log e N 简记为ln N .4.若a >0,且a ≠1,则a b =N 等价于log a N =b . 5.对数恒等式:a log a N =N (a >0且a ≠1).一、对数式有意义的条件例1 求下列各式中x 的取值围:(1)log 2(x -10);(2)log (x -1)(x +2);(3)log (x +1)(x -1)2.分析 由真数大于零,底数大于零且不等于1可得到关于x 的不等式(组),解之即可. 解 (1)由题意有x -10>0,∴x >10,即为所求.(2)由题意有⎩⎪⎨⎪⎧ x +2>0,x -1>0且x -1≠1,即⎩⎪⎨⎪⎧x >-2,x >1且x ≠2,∴x >1且x ≠2. (3)由题意有⎩⎪⎨⎪⎧(x -1)2>0,x +1>0且x +1≠1,解得x >-1且x ≠0,x ≠1.点评 在解决与对数有关的问题时,一定要注意:对数真数大于零,对数的底数大于零且不等于1.变式迁移1 在b =log (a -2)(5-a )中,实数a 的取值围是( ) A .a >5或a <2 B .2<a <5 C .2<a <3或3<a <5 D .3<a <4 答案 C解析 由题意得⎩⎪⎨⎪⎧5-a >0a -2>0a -2≠1,∴2<a <5且a ≠3.二、对数式与指数式的互化例2 将下列对数形式化成指数形式或将指数形式转化为对数形式:(1)54=625; (2)log 128=-3;(3)⎝⎛⎭⎫14-2=16; (4)log 101 000=3. 分析 利用a x =N ⇔x =log a N 进行互化. 解 (1)∵54=625,∴log 5625=4.(2)∵log 128=-3,∴⎝⎛⎭⎫12-3=8. (3)∵⎝⎛⎭⎫14-2=16,∴log 1416=-2. (4)∵log 101 000=3,∴103=1 000.点评 指数和对数运算是一对互逆运算,在解题过程中,互相转化是解决相关问题的重要途径.在利用a x =N ⇔x =log a N 进行互化时,要分清各字母分别在指数式和对数式中的位置.变式迁移2 将下列对数式化为指数式求x 值:(1)log x 27=32; (2)log 2x =-23;(3)log 5(log 2x )=0; (4)x =log 2719;(5)x =log 1216.解 (1)由log x 27=32,得x 32=27,∴x =2723=32=9.(2)由log 2x =-23,得2-23=x ,∴x =1322=322.(3)由log 5(log 2x )=0,得log 2x =1,∴x =21=2.(4)由x =log 2719,得27x =19,即33x =3-2,∴x =-23.(5)由x =log 1216,得⎝⎛⎭⎫12x =16,即2-x =24, ∴x =-4.三、对数恒等式的应用例3 (1)a log a b ·log b c ·log c N 的值(a ,b ,c ∈R +,且不等于1,N >0);(2)412(log 29-log 25).解 (1)原式=(a log a b )log b c ·log c N =b log b c ·log c N =(b log b c )log c N=c log c N =N .(2)原式=2(log 29-log 25)=2log 292log 25=95.点评 对数恒等式a log a N =N 中要注意格式:(1)它们是同底的;(2)指数中含有对数形式;(3)其值为真数.变式迁移3 计算:3log 35+(3)log 315.解 原式=5+312log 315=5+(3log 315)12=5+15=655.1.一般地,如果a (a >0,a ≠1)的b 次幂等于N ,就是a b =N ,那么b 叫做以a 为底N 的对数,记作log a N =b ,其中a 叫做对数的底数,N 叫做真数.2.利用a b =N ⇔b =log a N (其中a >0,a ≠1,N >0)可以进行指数与对数式的互化. 3.对数恒等式:a log a N =N (a >0且a ≠1).一、选择题1.下列指数式与对数式互化不正确的一组是( ) A .100=1与lg1=0B .27-13=13与log 2713=-13C .log 312=9与912=3D .log 55=1与51=5 答案 C2.指数式b 6=a (b >0,b ≠1)所对应的对数式是( )A .log 6a =aB .log 6b =aC .log a b =6D .log b a =6 答案 D3.若log x (5-2)=-1,则x 的值为( ) A.5-2 B.5+2C.5-2或5+2 D .2- 5 答案 B4.如果f (10x )=x ,则f (3)等于( ) A .log 310 B .lg3 C .103 D .310 答案 B解析 方法一 令10x =t ,则x =lg t , ∴f (t )=lg t ,f (3)=lg3.方法二 令10x =3,则x =lg3,∴f (3)=lg3.5.21+12·log 25的值等于( )A .2+ 5B .2 5C .2+52D .1+52答案 B解析 21+12log 25=2×212log 25=2×2log 2512=2×512=2 5.二、填空题6.若5lg x =25,则x 的值为________. 答案 100解析 ∵5lg x =52,∴lg x =2,∴x =102=100.7.设log a 2=m ,log a 3=n ,则a 2m +n 的值为________. 答案 12解析 ∵log a 2=m ,log a 3=n ,∴a m =2,a n =3, ∴a 2m +n =a 2m ·a n =(a m )2·a n =22×3=12.8.已知lg6≈0.778 2,则102.778 2≈________. 答案 600解析 102.778 2≈102×10lg6=600. 三、解答题9.求下列各式中x 的值(1)若log 3⎝⎛⎭⎫1-2x 9=1,则求x 值;(2)若log 2 003(x 2-1)=0,则求x 值. 解 (1)∵log 3⎝⎛⎭⎪⎫1-2x 9=1,∴1-2x 9=3 ∴1-2x =27,即x =-13 (2)∵log 2 003(x 2-1)=0 ∴x 2-1=1,即x 2=2 ∴x =±210.求x 的值:(1)x =log224;(2)x =log 93;(3)x =71-log 75; (4)log x 8=-3;(5)log 12x =4.解 (1)由已知得:⎝⎛⎭⎫22x =4,∴2-12x =22,-x2=2,x =-4.(2)由已知得:9x =3,即32x =312.∴2x =12,x =14.(3)x =7÷7log 75=7÷5=75.(4)由已知得:x -3=8, 即⎝⎛⎭⎫1x 3=23,1x =2,x =12. (5)由已知得:x =⎝ ⎛⎭⎪⎫124=116.2.2.1 对数与对数运算(二)学习目标1.掌握对数的运算性质及其推导.2.能运用对数运算性质进行化简、求值和证明.自学导引1.对数的运算性质:如果a >0,a ≠1,M >0,N >0,那么, (1)log a (MN )=log a M +log a N ;(2)log a MN=log a M -log a N ;(3)log a M n =n log a M (n ∈R ).2.对数换底公式:log a b =log c blog c a.一、正确理解对数运算性质例1 若a >0,a ≠1,x >0,y >0,x >y ,下列式子中正确的个数有( ) ①log a x · log a y =log a (x +y ); ②log a x -log a y =log a (x -y );③log a xy=log a x ÷log a y ;④log a (xy )=log a x ·log a y .A .0个B .1个C .2个D .3个 答案 A解析 对数的运算实质是把积、商、幂的对数运算分别转化为对数的加、减、乘的运算.在运算中要注意不能把对数的符号当作表示数的字母参与运算,如log a x ≠log a ·x ,log a x 是不可分开的一个整体.四个选项都把对数符号当作字母参与运算,因而都是错误的. 点评 正确理解对数运算性质公式,是利用对数运算性质公式解题的前提条件. 变式迁移1 若a >0且a ≠1,x >0,n ∈N *,则下列各式正确的是( )A .log a x =-log a 1xB .(log a x )n =n log a xC .(log a x )n =log a x nD .log a x =log a 1x答案 A二、对数运算性质的应用例2 计算:(1)log 535-2log 573+log 57-log 51.8;(2)2(lg 2)2+lg 2·lg5+(lg 2)2-lg2+1; (3)lg 27+lg8-lg 1 000lg1.2;(4)(lg5)2+lg2·lg50. 分析 利用对数运算性质计算.解 (1)原式=log 5(5×7)-2(log 57-log 53)+log 57-log 595=log 55+log 57-2log 57+2log 53+log 57-2log 53+log 55 =2log 55=2.(2)原式=lg 2(2lg 2+lg5)+(lg 2-1)2=lg 2(lg2+lg5)+1-lg 2=lg 2+1-lg 2=1.(3)原式=32lg3+3lg2-32lg3+2lg2-1=3lg3+6lg2-32(lg3+2lg2-1)=32.(4)原式=(lg5)2+lg2·(lg2+2lg5)=(lg5)2+2lg5·lg2+(lg2)2=(lg5+lg2)2=1.点评 要灵活运用有关公式.注意公式的正用、逆用及变形使用. 变式迁移2 求下列各式的值:(1)log 535+2log 122-log 5150-log 514;(2)[(1-log 63)2+log 62·log 618]÷log 64. 解 (1)原式=log 5(5×7)-2log 2212+log 5(52×2)-log 5(2×7)=1+log 57-1+2+log 52-log 52-log 57=2.(2)原式=[log 262+log 62·log 6(3×6)]÷log 622 =log 62(log 62+log 63+1)÷(2log 62)=1.三、换底公式的应用例3 (1)设3x =4y =36,求2x +1y的值;(2)已知log 189=a,18b =5,求log 3645. 解 (1)由已知分别求出x 和y . ∵3x =36,4y =36, ∴x =log 336,y =log 436,由换底公式得: x =log 3636log 363=1log 363,y =log 3636log 364=1log 364,∴1x =log 363,1y =log 364, ∴2x +1y =2log 363+log 364 =log 36(32×4)=log 3636=1.(2)∵log 189=a,18b =5,∴log 185=b .∴log 3645=log 1845log 1836=log 18(9×5)log 18(18×2)=log 189+log 1851+log 182=a +b 1+log 18189=a +b2-a .点评 指数式化为对数式后,两对数式的底不同,但式子两端取倒数后,利用对数的换底公式可将差异消除.变式迁移3 (1)设log 34·log 48·log 8m =log 416,求m ; (2)已知log 1227=a ,求log 616的值.解 (1)利用换底公式,得lg4lg3·lg8lg4·lg mlg8=2,∴lg m =2lg3,于是m =9.(2)由log 1227=a ,得3lg32lg2+lg3=a ,∴lg3=2a lg23-a ,∴lg3lg2=2a3-a .∴log 616=4lg2lg3+lg2=42a 3-a +1=4(3-a )3+a.1.对于同底的对数的化简常用方法是:(1)“收”,将同底的两对数的和(差)化成积(商)的对数; (2)“拆”,将积(商)的对数拆成对数的和(差).2.对于常用对数的化简要充分利用“lg5+lg2=1”来解题. 3.对于多重对数符号对数的化简,应从向外逐层化简求值.一、选择题1.lg8+3lg5的值为( )A .-3B .-1C .1D .3 答案 D解析 lg8+3lg5=lg8+lg53=lg1 000=3. 2.已知lg2=a ,lg3=b ,则log 36等于( ) A.a +b a B.a +b bC.a a +bD.b a +b 答案 B解析 log 36=lg6lg3=lg2+lg3lg3=a +bb.3.若lg a ,lg b 是方程2x 2-4x +1=0的两个根,则⎝⎛⎭⎫lg ab 2的值等于( ) A .2 B.12 C .4 D.14答案 A解析 由根与系数的关系,得lg a +lg b =2,lg a ·lg b =12,∴⎝⎛⎭⎫lg ab 2=(lg a -lg b )2 =(lg a +lg b )2-4lg a ·lg b=22-4×12=2.4.若2.5x =1 000,0.25y =1 000,则1x -1y等于( )A.13 B .3 C .-13 D .-3 答案 A解析 由指数式转化为对数式:x =log 2.51 000,y =log 0.251 000, 则1x -1y =log 1 0002.5-log 1 0000.25=log 1 00010=13.5.设函数f (x )=log a x (a >0,且a ≠1),若f (x 1x 2…x 2 005)=8,则f (x 21)+f (x 22)+…+f (x 22 005)的值等于( )A .4B .8C .16D .2log a 8 答案 C解析 因为f (x )=log a x ,f (x 1x 2…x 2 005)=8,所以f (x 21)+f (x 22)+…+f (x 22 005) =log a x 21+log a x 22+…+log a x 22 005=2log a |x 1|+2log a |x 2|+…+2log a |x 2 005| =2log a |x 1x 2…x 2 005|=2f (x 1x 2…x 2 005)=2×8=16. 二、填空题6.设lg2=a ,lg3=b ,那么lg 1.8=__________.答案 a +2b -12解析 lg 1.8=12lg1.8=12lg 1810=12lg 2×910=12(lg2+lg9-1)=12(a +2b -1). 7.若log a x =2,log b x =3,log c x =6,则log abc x 的值为____. 答案 1解析 log abc x =1log x abc =1log x a +log x b +log x c∵log a x =2,log b x =3,log c x =6∴log x a =12,log x b =13,log x c =16,∴log abc x =112+13+16=11=1.8.已知log 63=0.613 1,log 6x =0.386 9,则x =________. 答案 2解析 由log 63+log 6x =0.613 1+0.386 9=1. 得log 6(3x )=1.故3x =6,x =2. 三、解答题9.求下列各式的值: (1)12lg 3249-43lg 8+lg 245; (2)(lg5)2+2lg2-(lg2)2.解 (1)方法一 原式=12(5lg2-2lg7)-43·32lg2+12(2lg7+lg5) =52lg2-lg7-2lg2+lg7+12lg5 =12lg2+12lg5=12(lg2+lg5) =12lg10=12. 方法二 原式=lg 427-lg4+lg7 5=lg42×757×4=lg(2·5)=lg 10=12.(2)方法一 原式=(lg5+lg2)(lg5-lg2)+2lg2=lg10·lg 52+lg4=lg ⎝⎛⎭⎫52×4=lg10=1. 方法二 原式=(lg10-lg2)2+2lg2-lg 22 =1-2lg2+lg 22+2lg2-lg 22=1.10.若26a =33b =62c ,求证:1a +2b =3c .证明 设26a =33b =62c =k (k >0),那么 ⎩⎪⎨⎪⎧6a =log 2k ,3b =log 3k ,2c =log 6k ,∴⎩⎪⎨⎪⎧1a =6log 2k=6log k 2,1b =3log 3k =3log k3,1c =2log 6k =2log k6.∴1a +2b=6·log k 2+2×3log k 3 =log k (26×36)=6log k 6=3×2log k 6=3c,即1a +2b =3c. 2.2.2 对数函数及其性质1.对数函数的概念形如y =log a x (a >0且a ≠1)的函数叫做对数函数. 对于对数函数定义的理解,要注意:(1)对数函数是由指数函数变化而来的,由指数式与对数式关系知,对数函数的自变量x 恰好是指数函数的函数值y ,所以对数函数的定义域是(0,+∞);(2)对数函数的解析式y=log a x中,log a x前面的系数为1,自变量在真数的位置,底数a 必须满足a>0,且a≠1;(3)以10为底的对数函数为y=lg x,以e为底的对数函数为y=ln x.实际上,观察对数函数的图象不难发现,对数函数中的值y =log m n 有以下规律:(1)当(m -1)(n -1)>0,即m 、n 围相同(相对于“1”而言),则log m n >0;(2)当(m -1)(n -1)<0,即m 、n 围相反(相对于“1”而言),则log m n <0.有了这个规律,我们再判断对数值的正负就很简单了,如log 213<0,log 52>0等,一眼就看出来了!题型一 求函数定义域求下列函数的定义域:(1)y =log 3x -12x +3x -1;(2)y =11-log a (x +a ) (a >0,a ≠1).分析 定义域即使函数解析式有意义的x 的围. 解 (1)要使函数有意义,必须{2x +3>0,x -1>0,3x -1>0,3x -1≠1同时成立,解得⎩⎨⎧x >-32,x >1,x >13,x ≠23. ∴x >1. ∴定义域为(1,+∞).(2)要使原函数有意义,需1-log a (x +a )>0, 即log a (x +a )<1=log a a .当a >1时,0<x +a <a ,∴-a <x <0. 当0<a <1时,x +a >a ,∴x >0.∴当a >1时,原函数定义域为{x |-a <x <0}; 当0<a <1时,原函数定义域为{x |x >0}.点评 求与对数函数有关的定义域问题,首先要考虑:真数大于零,底数大于零且不等于1,若分母中含有x ,还要考虑不能使分母为零.题型二 对数单调性的应用(1)log 43,log 34,log 4334的大小顺序为( )A .log 34<log 43<log 4334B .log 34>log 43>log 4334C .log 34>log 4334>log 43D .log 4334>log 34>log 43(2)若a 2>b >a >1,试比较log a a b ,log b ba ,logb a ,log a b 的大小.(1)解析 ∵log 34>1,0<log 43<1,log 4334=log 43⎝⎛⎭⎫43-1=-1, ∴log 34>log 43>log 4334.答案 B(2)解 ∵b >a >1,∴0<ab<1.∴log a a b <0,log b ba ∈(0,1),logb a ∈(0,1).又a >b a >1,且b >1,∴log b ba<log b a ,故有log a a b <log b ba<log b a <log a b .点评 比较对数的大小,一般遵循以下几条原则:①如果两对数的底数相同,则由对数函数的单调性(底数a >1为增;0<a <1为减)比较. ②如果两对数的底数和真数均不相同,通常引入中间变量进行比较.③如果两对数的底数不同而真数相同,如y =log a 1x 与y =log a 2x 的比较(a 1>0,a 1≠1,a 2>0,a 2≠1).当a 1>a 2>1时,曲线y 1比y 2的图象(在第一象限)上升得慢.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2.而在第一象限,图象越靠近x 轴对数函数的底数越大.当0<a 2<a 1<1时,曲线y 1比y 2的图象(在第四象限)下降得快.即当x >1时,y 1<y 2;当0<x <1时,y 1>y 2即在第四象限,图象越靠近x 轴的对数函数的底数越小. 已知log a 12<1,那么a 的取值围是________.分析 利用函数单调性或利用数形结合求解.解析 由log a 12<1=log a a ,得当a >1时,显然符合上述不等式,∴a >1;当0<a <1时,a <12,∴0<a <12. 故a >1或0<a <12.答案 a >1或0<a <12点评 解含有对数符号的不等式时,必须注意对数的底数是大于1还是小于1,然后再利用相应的对数函数的单调性进行解答.理解会用以下几个结论很有必要:(1)当a >1时,log a x >0⇔x >1,log a x <0⇔0<x <1;(2)当0<a <1时,log a x >0⇔0<x <1,log a x <0⇔x >1.题型三 函数图象的应用若不等式2x -log a x <0,当x ∈⎝⎛⎭⎫0,12时恒成立,数a 的取值围. 解要使不等式2x<logax 在x ∈⎪⎭⎫ ⎝⎛21,0时恒成立,即函数y=logax 的图象在⎪⎭⎫ ⎝⎛21,0恒在函数y=2x 图象的上方,而y=2x 图象过点⎪⎭⎫⎝⎛2,21.由图可知,loga 21>2,显然这里0<a<1,∴函数y=logax 递减. 又loga21>2=log 2a a ,∴a2>21,即a>2221⎪⎭⎫ ⎝⎛.∴所求的a 的取值围为2221⎪⎭⎫⎝⎛<a<1.点评 原问题等价于当x ∈⎪⎭⎫ ⎝⎛21,0时,y1=2x 的图象在y2=logax 的图象的下方,由于a 的大小不确定,当a>1时,显然y2<y1,因此a 必为小于1的正数,当y2的图象通过点⎪⎭⎫⎝⎛2,21时,y2满足条件,此时a 0=2221⎪⎭⎫⎝⎛.那么a 是大于a 0还是小于a 0才满足呢?可以画图象观察,请试着画一画.这样可以对数形结合的方法有更好地掌握.设函数f(x)=lg(ax2+2x+1),若f(x)的值域是R,数a的取值围.错解∵f(x)的值域是R,∴ax2+2x+1>0对x∈R恒成立,即{a>0Δ<0⇔{a>04-4a<0⇔a>1.错因分析出错的原因是分不清定义域为R与值域为R的区别.正解函数f(x)=lg(ax2+2x+1)的值域是R⇔真数t=ax2+2x+1能取到所有的正数.当a=0时,只要x>-12,即可使真数t取到所有的正数,符合要求;当a≠0时,必须有{a>0Δ≥0⇔{a>04-4a≥0⇔0<a≤1.∴f(x)的值域为R时,实数a的取值围为[0,1].本节容在高考中考查的形式、地位与指数函数相似,着重考查对数的概念与对数函数的单调性,考查指数、对数函数的图象、性质及其应用.1.(高考)已知函数f(x)=11-x的定义域为M,g(x)=ln(1+x)的定义域为N,则M∩N等于()A .{x |x >-1}B .{x |x <1}C .{x |-1<x <1}D .∅解析 由题意知M ={x |x <1},N ={x |x >-1}. 故M ∩N ={x |-1<x <1}. 答案 C2.(高考)下列不等式成立的是( ) A .log 32<log 23<log 25 B .log 32<log 25<log 23 C .log 23<log 32<log 25 D .log 23<log 25<log 32解析 ∵y =log 2x 在(0,+∞)上是增函数, ∴log 25>log 23>log 22=1.又y =log 3x 在(0,+∞)上为增函数,∴log 32<log 33=1.∴log 32<log 23<log 25. 答案 A3.(全国高考)若x ∈(e -1,1),a =ln x ,b =2ln x ,c =ln 3x ,则( ) A .a <b <c B .c <a <b C .b <a <c D .b <c <a解析 ∵1e <x <1,∴-1<ln x <0.令t =ln x ,则-1<t <0. ∴a -b =t -2t =-t >0.∴a >b . c -a =t 3-t =t (t 2-1)=t (t +1)(t -1), 又∵-1<t <0,∴0<t +1<1,-2<t -1<-1,∴c -a >0,∴c >a . ∴c >a >b . 答案 C1.已知函数f (x )=1+2x 的定义域为集合M ,g (x )=ln(1-x )的定义域为集合N ,则M ∩N 等于( )A .{x |x >-1}B .{x |x <1}C.⎩⎨⎧⎭⎬⎫x |-12<x <1 D .∅答案 C2.已知函数f (x )=lg 1-x 1+x,若f (a )=12,则f (-a )等于( )A.12 B .-12 C .-2 D .2 答案 B解析 f (-a )=lg 1+a1-a =-lg ⎝ ⎛⎭⎪⎫1+a 1-a -1=-lg 1-a 1+a=-f (a )=-12.3.已知a =log 23,b =log 32,c =log 42,则a ,b ,c 的大小关系是( )A .c <b <aB .a <b <cC .b <c <aD .c <a <b 答案 A解析 因为a =log 23>1,b =log 3 2<1,所以a >b ;又因为2>3,则log 32>log 33=12,而log 42=log 22=12,所以b >12,c =12,即b >c .从而a >b >c .4.函数f (x )=lg|x |为( )A .奇函数,在区间(0,+∞)上是减函数B .奇函数,在区间(0,+∞)上是增函数C .偶函数,在区间(-∞,0)上是增函数D .偶函数,在区间(-∞,0)上是减函数 答案 D解析 已知函数定义域为(-∞,0)∪(0,+∞),关于坐标原点对称,且f (-x )=lg|-x |=lg|x |=f (x ),所以它是偶函数.又当x >0时,|x |=x ,即函数y =lg|x |在区间(0,+∞)上是增函数.又f (x )为偶函数,所以f (x )=lg|x |在区间(-∞,0)上是减函数.5.函数y =a x 与y =-log a x (a >0,且a ≠1)在同一坐标系中的图象只可能为( )答案 A解析 方法一 若0<a <1,则曲线y =a x 下降且过(0,1),而曲线y =-log a x 上升且过(1,0);若a >1,则曲线y =a x 上升且过(0,1),而曲线y =-log a x 下降且过(1,0).只有选项A 满足条件.方法二 注意到y =-log a x 的图象关于x 轴对称的图象的表达式为y =log a x ,又y =log a x 与y =a x 互为反函数(图象关于直线y =x 对称),则可直接选定选项A.6.设函数f (x )=log 2a (x +1),若对于区间(-1,0)的每一个x 值都有f (x )>0,则实数a 的取值围为( )A .(0,+∞) B.⎝⎛⎭⎫12,+∞ C.⎝⎛⎭⎫12,1 D.⎝⎛⎭⎫0,12 答案 D 解析 已知-1<x <0,则0<x +1<1,又当-1<x <0时,都有f (x )>0,即0<x +1<1时都有f (x )>0,所以0<2a <1,即0<a <12.7.若指数函数f (x )=a x (x ∈R )的部分对应值如下表:则不等式log a (x -1)<0答案 {x |1<x <2}解析 由题可知a =1.2,∴log 1.2(x -1)<0, ∴log 1.2(x -1)<log 1.21,解得x <2, 又∵x -1>0,即x >1,∴1<x <2. 故原不等式的解集为{x |1<x <2}.8.函数y =log a x (1≤x ≤2)的值域为[-1,0],那么a 的值为________.答案 12解析 若a >1,则函数y =log a x 在区间[1,2]上为增函数,其值域不可能为[-1,0]; 故0<a <1,此时当x =2时,y 取最小值-1,即log a 2=-1,得a -1=2,所以a =12.9.已知函数f (x )=⎩⎪⎨⎪⎧(3a -1)x +4a ,x <1log a x ,x ≥1是实数集R 上的减函数,那么实数a 的取值围为__________.答案 ⎣⎡⎭⎫17,13解析 函数f (x )为实数集R 上的减函数,一方面,0<a <1且3a -1<0,所以0<a <13,另一方面,由于f (x )在R 上为减函数, 因此应有(3a -1)×1+4a ≥log a 1,即a ≥17.因此满足题意的实数a 的取值围为17≤a <13.10.已知f (x )=1+log 2x (1≤x ≤4),求函数g (x )=f 2(x )+f (x 2)的最大值和最小值. 解 ∵f (x )的定义域为[1,4], ∴g (x )的定义域为[1,2].∵g (x )=f 2(x )+f (x 2)=(1+log 2x )2+(1+log 2x 2) =(log 2x +2)2-2, 又1≤x ≤2,∴0≤log 2x ≤1. ∴当x =1时,g (x )min =2;当x =2时,g (x )max =7.学习目标1.掌握对数函数的概念、图象和性质.2.能够根据指数函数的图象和性质得出对数函数的图象和性质,把握指数函数与对数函数关系的实质.自学导引1.对数函数的定义:一般地,我们把函数y=log a x(a>0,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).对数函数y =log a x (a >0且a ≠1)和指数函数y =a x _(a >0且a ≠1)互为反函数.一、对数函数的图象例1 下图是对数函数y =log a x 的图象,已知a 值取3,43,35,110,则图象C 1,C 2,C 3,C 4相应的a 值依次是( )A.101,53,34,3B .53,101,34,3C .101,53,3,34 D .53,101,3,34 答案 A解析 方法一 因为对数的底数越大,函数的图象越远离y 轴的正方向,所以C1,C2,C3,C4的a 值依次由大到小,即C1,C2,C3,C4的a 值依次为101,53,34,3. 方法二 过(0,1)作平行于x 轴的直线,与C1,C2,C3,C4的交点的横坐标为(a1,1),(a2,1),(a3,1),(a4,1),其中a1,a2,a3,a4分别为各对数的底,显然a1>a2>a3>a4,所以C1,C2,C3,C4的底值依次由大到小.点评 函数y=logax (a>0,且a ≠1)的底数a 的变化对图象位置的影响如下:①上下比较:在直线x=1的右侧,底数大于1时,底数越大,图象越靠近x 轴;底数大于0且小于1时,底数越小,图象越靠近x 轴.②左右比较:(比较图象与y=1的交点)交点的横坐标越大,对应的对数函数的底数越大. 变式迁移1 借助图象比较m ,n 的大小关系:(1)若logm5>logn5,则m n ;(2)若logm0.5>logn0.5,则m n.答案 (1)< (2)>二、求函数的定义域例2 求下列函数的定义域:(1)y =3log 2x ;(2)y =log 0.5(4x -3);(3)y =log (x +1)(2-x ).分析 定义域即使函数解析式有意义的x 的围.解 (1)∵该函数是奇次根式,要使函数有意义,只要对数的真数是正数即可, ∴定义域是{x |x >0}.(2)要使函数y =log 0.5(4x -3)有意义,必须log 0.5(4x -3)≥0=log 0.51,∴0<4x -3≤1.解得34<x ≤1. ∴定义域是⎩⎨⎧⎭⎬⎫x |34<x ≤1. (3)由⎩⎪⎨⎪⎧ x +1>0x +1≠12-x >0,得⎩⎨⎧ x >-1x ≠0,x <2即0<x <2或-1<x <0,所求定义域为(-1,0)∪(0,2).点评 求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数;三是按底数的取值应用单调性,有针对性的解不等式.变式迁移2 求y =log a (4x -3)(a >0,a ≠1)的定义域.解 log a (4x -3)≥0.(*)当a >1时,(*)可化为log a (4x -3)≥log a 1,∴4x -3≥1,x ≥1.当0<a <1时,(*)可化为log a (4x -3)≥log a 1,∴0<4x -3≤1,34<x ≤1. 综上所述,当a >1时,函数定义域为[1,+∞),当0<a <1时,函数定义域为⎝⎛⎦⎤34,1.三、对数函数单调性的应用例3 比较大小:(1)log 0.81.5与log 0.82;(2)log 35与log 64.分析 从比较底数、真数是否相同入手.解 (1)考查对数函数y =log 0.8x 在(0,+∞)是减函数,∵1.5<2,∴log 0.81.5>log 0.82.(2)log 35和log 64的底数和真数都不相同,找出中间量“搭桥”,再利用对数函数的单调性,即可求解.∵log 35>log 33=1=log 66>log 64,∴log 35>log 64.点评 比较两个对数值的大小,常用方法有:①底数相同真数不同时,用函数的单调性来比较;②底数不同而真数相同时,常借助图象比较,也可用换底公式转化为同底数的对数后比较;③底数与真数都不同,需寻求中间值比较.变式迁移3 比较下列各组中两个值的大小:(1)log 0.52.7,log 0.52.8; (2)log 34,log 65;(3)log a π,log a e (a >0且a ≠1).解 (1)∵0<0.5<1,∴对数函数y =log 0.5x 在(0,+∞)上是减函数.又∵2.7<2.8,∴log 0.52.7>log 0.52.8.(2)∵y =log 3x 在(0,+∞)上是增函数,∴log 34>log 33=1.∵y =log 6x 在(0,+∞)上是增函数,∴log 65<log 66=1.∴log 34>log 65.(3)当a >1时,y =log a x 在(0,+∞)上是增函数.∵π>e ,∴log a π>log a e.当0<a <1时,y =log a x 在(0,+∞)上是减函数.∵π>e ,∴log a π<log a e.综上可知,当a >1时,log a π>log a e ;当0<a <1时,log a π<log a e.例4 若-1<log a 34<1,求a 的取值围. 分析 此不等式为对数不等式且底数为参数.解答本题可根据对数函数的单调性转化为一般不等式求解,同时应注意分类讨论.解 -1<log a 34<1⇔log a 1a <log a 34<log a a . 当a >1时,1a <34<a ,∴a >43. 当0<a <1时,1a >34>a ,∴0<a <34. ∴a 的取值围是⎝⎛⎭⎫0,34∪⎝⎛⎭⎫43,+∞. 点评 (1)解对数不等式问题通常转化为不等式组求解,其依据是对数函数的单调性.(2)解决与对数函数相关的问题时要遵循“定义域优先”原则.(3)若含有字母,应考虑分类讨论.变式迁移4 已知log a (2a +1)<log a 3a <0,求a 的取值围.解 log a (2a +1)<log a 3a <0(*)当a >1时,(*)可化为⎩⎨⎧ 0<2a +1<10<3a <12a +1<3a, 解得⎩⎪⎨⎪⎧ -12<a <00<a <13a >1,∴此时a 无解.当0<a <1时,(*)可化为⎩⎨⎧ 2a +1>13a >12a +1>3a ,解得⎩⎨⎧ a >0a >13a <1,∴13<a <1. 综上所述,a 的取值围为⎝⎛⎭⎫13,1.1.求对数函数定义域要注意底数中是否含有自变量,此时底数大于0且不等于1.2.应用对数函数的图象和性质时要注意a >1还是0<a <1。
27【数学】2.2.2《对数函数及其性质》(2)教案(人教A版必修1)
课题:§2.2.2对数函数(二)教学任务:(1)进一步理解对数函数的图象和性质;(2)熟练应用对数函数的图象和性质,解决一些综合问题;(3)通过例题和练习的讲解与演练,培养学生分析问题和解决问题的能力.教学重点:对数函数的图象和性质.教学难点:对对数函数的性质的综合运用. 教学过程: 一、回顾与总结1. 函数x y x y x y lg ,log ,log 52===的图象如图所示,回答下列问题. (1)说明哪个函数对应于哪个图象,并解释为什么?(2)函数x y a log =与x y a1log =,0(>a 且)0≠a 有什么关系?图象之间又有什么特殊的关系?(3)以x y x y x y lg ,log ,log 52===的图象为基础,在同一坐标系中画出x y x y x y 1015121log ,log ,log ===的图象.(4)已知函数x y x y x y x y a a a a 4321log ,log ,log ,log ====的图象,则底数之间的关系:.教○1 ○2 ○3 log =y xa 1 log =y x a2 log =y x a3 log =y xa 42. 完成下表(对数函数x y a log =,0(>a 且)0≠a 的图象和性质)10<<a 1>a图 象定义域 值域 性 质3. 根据对数函数的图象和性质填空.○1 已知函数x y 2log =,则当0>x 时,∈y ;当1>x 时,∈y ;当10<<x 时,∈y ;当4>x 时,∈y .○1 已知函数x y 31lo g =,则当10<<x 时,∈y ;当1>x 时,∈y ;当5>x 时,∈y ;当20<<x 时,∈y ;当2>y 时,∈x .二、应用举例例1. 比较大小:○1 πa log ,e alog ,0(>a 且)0≠a ; ○2 21log 2,)1(log 22++a a )(R a ∈. 解:(略)例2.已知)13(log -a a 恒为正数,求a 的取值范围.解:(略)[总结点评]:(由学生独立思考,师生共同归纳概括). . 例3.求函数)78lg()(2-+-=x x x f 的定义域及值域. 解:(略)注意:函数值域的求法.例4.(1)函数x y a log =在[2,4]上的最大值比最小值大1,求a 的值;(2)求函数)106(log 23++=x x y 的最小值. 解:(略)注意:利用函数单调性求函数最值的方法,复合函数最值的求法.例5.(2003年上海高考题)已知函数xxx x f -+-=11log 1)(2,求函数)(x f 的定义域,并讨论它的奇偶性和单调性. 解:(略)注意:判断函数奇偶性和单调性的方法,规范判断函数奇偶性和单调性的步骤.例6.求函数)54(log )(22.0++-=x x y x f 的单调区间. 解:(略)注意:复合函数单调性的求法及规律:“同增异减”. 练习:求函数)23(log 221x x y --=的单调区间.三、作业布置考试卷一套。
最经典总结-对数与对数函数

(3)底数不同,真数相同的对数值,可利用函数图象或比较其倒数大小来进行.
解简单的对数不等式
先利用对数的运算性质化为同底的对数值,再利用对数函数的单调性转化为一般不等式求解
求解对数型函数的定义域、单调性(区间)、奇偶性、最值(值域)等性质
[答案]C
考向三 简单的对数不等式的解法
3.若f(x)=lgx,g(x)=f(|x|),则g(lgx)>g(1)时,x的取值范围是______.
[解析]当g(lgx)>g(1)时,f(|lgx|)>f(1),由f(x)为增函数得|lgx|>1,从而lgx>1或lgx<-1,解得0<x< 或x>10.
[答案]D
8.若f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上递减,则a的取值范围为()
A.[1,2)B.[1,2]
C.[1,+∞)D.[2,+∞)
[解析]令函数g(x)=x2-2ax+1+a=(x-a)2+1+a-a2,对称轴为x=a,要使函数在(-∞,1]上递减,则有 即 解得1≤a<2,即a∈[1,2).
[解析]∵2a=5b=m>0,∴a=log2m,b=log5m,
∴ + = + =logm2+logm5=logm10=2.
∴m2=10,∴m= .
[答案]
题型二 对数函数的图象及应用(重点保分题,共同探讨)
(1)已知函数y=loga(x+c)(a,c为常数,其中a>0,a≠1)的图象如图,则下列结论成立的是()
第5讲 对数与对数函数
◆高考导航·顺风启程◆
最新考纲
常见题型
1.理解对数的概念及其运算性质,知道用换底公式将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.
基本初等函数之对数与对数函数,附练习题

对数与对数函数(讲义)知识点睛一、对数与对数的运算1.对数(1)如果x a N =(a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做对数的底数,N 叫做真数.常用对数:10log lg N N =;自然对数:e log ln N N =.(2)当a >0,且a ≠1时,x a N =⇔log a x N =.(3)负数和零没有对数;log 10a =,log 1a a =.2.对数的运算性质(1)如果a >0,且a ≠1,M >0,N >0,那么①log ()log log a a a M N M N ⋅=+;②log log log aa a MM N N=-;③log log ()n a a M n M n =∈R .(2)换底公式:log log log c a c bb a=(a >0,且a ≠1;c >0,且c ≠1;b >0).(3)log (010)a b a b a a b =>≠>,;.二、对数函数及其性质1.定义:一般地,函数log (0,1)a y x a a =>≠且叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞).2.对数函数log (0,1)a y x a a =>≠且的图象和性质:0<a <1a >1图象定义域(0,+∞)值域R性质①过定点(1,0),即x =1时,y =0②在(0,+∞)上是减函数②在(0,+∞)上是增函数3.对数函数底数变化与图象分布规律1log a y x =;②log b y x =;③log c y x =;④log d y x =,则有0<b <a <1<d <c ,即:x ∈(1,+∞)时,log log log log a b c d x x x x <<<;x ∈(0,1)时,log log log log a b c d x x x x >>>.4.反函数对数函数与指数函数互为反函数,互为反函数的两个函数的图象关于直线y x =对称.精讲精练1.把下列指数式化为对数式,对数式化为指数式.(1)32=8_______________;(2)415625-=_______________;(3)13127=3-_______________;(4)lg 0.0013=-_____________;(5)0.3log 2=a _____________;(6)ln x =_____________.2.求下列各式的值.(1)43log (927)⨯(2)1lg lg 4lg 52++(3)661log 12log 2-(4)22333399(log 2)(log )log log 422++⋅(5)2345log 3log 4log 5log 2⋅⋅⋅(6)48525(log 5log 5)(log 2log 2)++3.已知234log [log (log )]0x =,则x 的值为_________.4.已知3485log 4log 8log log 25m ⋅⋅=,那么m 的值为()A .9B .18C .12D .275.已知4823log 3x y ==,,则x +2y 的值为()A .3B .8C .4D .log 486.已知log 3a m =,log 2a n =,那么a 2m +3n =()A .17B .72C .108D .317.已知lg lg 2lg(2)x y x y +=-,则xy的值为_________.8.设lg a ,lg b 是方程2x 2-4x +1=0的两个实根,则2(lg )ab的值等于()A .2B .12C .4D .149.已知函数()lg f x x =.若()1f ab =,则22()()f a f b +=_____.10.下列函数表达式中是对数函数的是()A .0.01log (0)y x x =>B .22log y x =C .2log (2)(2)y x x =+>-D .2ln(1)y x =+11.若点(a ,b )在lg y x =图象上,且a ≠1,则下列点也在此图象上的是()A .1()b a ,B .(10a ,1-b )C .10(1)b a+,D .(a 2,2b )12.若函数log ()a y x b =+(a >0,a ≠1)的图象过两点(-1,0)和(0,1),则()A .a =2,b =2B .2a b ==C .a =2,b =1D .a b ==13.直接写出下列函数的定义域:311log (2)_______________2345log (3)_______________16_______________ln(1)x y x y y y y x y x -=-====-=+=+();();();();();().14.已知()f x 的定义域为[0,1],则函数12[log (3)]y f x =-的定义域是_____________.15.函数212log (613)y x x =++的值域为()A .RB .[8,+∞)C .(-∞,-2]D .[-3,+∞)16.函数log a y x =在区间[2,π]上最大值比最小值大1,则a =__________.17.下列判断不正确的是()A .22log 3.4log 4.3<B .0.20.3log 0.4log 0.4<C .67log 7log 6>D .30.3log log 4π<18.为了得到函数3lg10x y +=的图象,只需把函数lg y x =的图象上所有的点()A .向左平移3个单位长度,再向上平移1个单位长度B .向右平移3个单位长度,再向上平移1个单位长度C .向左平移3个单位长度,再向下平移1个单位长度D .向右平移3个单位长度,再向下平移1个单位长度19.函数21log (01)1a x y a a x +=>≠-,的图象过定点P ,则点P 的坐标为()A .(1,0)B .(-2,0)C .(2,0)D .(-1,0)20.已知函数()log (1)a f x x =+,()log (1)a g x x =-(a >0,且a ≠1).(1)求函数()()f x g x +的定义域;(2)判断函数()()f x g x +的奇偶性,并说明理由.21.设a ,b ∈R 且a ≠2,定义在区间(-b ,b )上的函数1()lg12axf x x+=+满足:()()0f x f x +-=.(1)求实数a 的值;(2)求b 的取值范围.22.已知关于x 的方程212log 210x a x ⋅--=有实数根,求a 的取值范围.23.已知函数2log [(21)]a y x a x a =--+的定义域为R ,求实数a 的取值范围.回顾与思考________________________________________________________________________________________________________________________________________________________________________【参考答案】1.(1)2log 83=;(2)51log 4625=-;(3)2711log 33=-;(4)3100.001-=;(5)0.32a =;(6)e x =2.(1)11;(2)1;(3)12;(4)4;(5)1;(6)543.644.A 5.A 6.B 7.48.A 9.210.A 11.D 12.A13.(1)(2)+∞,;(2)(0)+∞,;(3)2(1]3,;(4)(0;(5)(12)(23)⋃,,;(6)(10)(02]-⋃,,14.5[22,15.C16.2π或2π17.D18.C 19.B20.(1)(-1,1);(2)偶函数,证明()()()()f x g x f x g x -+-=+21.(1)2a =-;(2)102b ≤<22.02a ≤<23.33(11)(1122,-⋃+对数与对数函数(随堂测试)1.函数22()log (2)f x x x a =-+的值域为[0,+∞),则正实数a 等于()A .1B .2C .3D .42.求函数2log (4)(01)a y x x a a =->≠,且的单调递减区间.【参考答案】1.B2.当01a <<时,f (x )的单调递减区间为(0,2];当1a >时,f (x )的单调递减区间为[2,4)对数与对数函数(作业)1.求下列各式的值.(1)lg +(2)553log 10log 0.125+(3)22(lg 2)(lg 5)lg 4lg 5++⋅(4)22lg 5lg83+(5)20321log log ()52-+-(6)231lg 25lg 2lg log 9log 22+-⨯2.下列对数运算中,一定正确的是()A .lg()lg lg M N M N +=⋅B .ln ln n M n M =C .lg()lg lg M N M N⋅=+D .lg log lg a b b a=3.已知3log 2a =,那么33log 22log 6-用a 表示是()A .5a -2B .-a -2C .3a -(1+a )2D .3-a 2-14.设a ,b ,c 均为不等于1的正实数,则下列等式中恒成立的是()A .log log log a c c b b a ⋅=B .log log log a c c b a b ⋅=C .log ()log log a a a bc b c =⋅D .log ()log log a a a b c b c+=+5.已知x ,y 为正实数,则下列式子中正确的是()A .lg lg lg lg 222x y x y +=+B .lg()lg lg 222x y x y +=⋅C .lg lg lg lg 222x y x y⋅=+D .lg()lg lg 222x y x y⋅=⋅6.设方程22(lg )lg 30x x --=的两实根是a ,b ,则log log a b b a +等于()A .1B .-2C .-4D .103-7.在(2)log (5)a y a -=-中,实数a 的取值范围是()A .5a >或2a <B .23a <<或35a <<C .25a <<D .34a <<8.函数()ln1xf x x =+-的定义域为()A .(0,+∞)B .(1,+∞)C .(0,1)D .(0,1)∪(1,+∞)9.已知函数12()2log f x x =的值域为[-1,1],则函数()f x 的定义域为()A .22B .[11]-,C .1[2]2,D .2(])2-∞⋃∞,+10.已知3log 6a =,5log 10b =,7log 14c =,则()A .c b a >>B .b c a >>C .a c b >>D .a b c>>11.已知2log 3.45a =,4log 3.65b =,3log 0.31()5c =,则()A .a b c >>B .b a c >>C .a c b >>D .c a b>>12.函数12log 2y x =+的单调增区间为()A .()-∞∞,+B .(2)-∞-,C .(2)-∞+,D .(2)(2)-∞-⋃∞,,+13.若函数log (01)a y x a =<<在区间[a ,2a ]上的最大值是最小值的3倍,则a的值为()A .22B .24C .12D .1414.函数log (2)5a y x =-+过定点()A .(1,0)B .(3,1)C .(3,5)D .(1,5)15.当a >1时,在同一坐标系中,函数x y a -=与log a y x =的图象大致是()A .B .C .D .16.设函数()(01)x x f x ka a a a -=->≠,在()-∞+∞,上既是奇函数又是增函数,则()log ()a g x x k =+的图象是()A .B .C .D .17.已知函数e 1(1)()ln (1)x x f x x x ⎧-=⎨>⎩≤,则(ln 2)f 的值为_________.18.函数12log (1)()2(1)x x x f x x ⎧⎪=⎨⎪<⎩≥的值域是_________________.19.已知13log 2a =,0.62b =,4log 3c =,则a ,b ,c 的大小关系为_____________.20.给出下列命题:12log 2log a a x x =;2函数2log (1)y x =+是对数函数;3函数1ln1xy x+=-与ln(1)ln(1)y x x =+--的定义域相同;4若log log a a m n <,则m n <.其中正确的命题是_________.21.已知函数()f x 在[0)+∞,上是增函数,()(||)g x f x =-,若(lg )(1)g x g >,求x 的取值范围.22.设函数212log (0)()log ()(0)xx f x x x >⎧⎪=⎨-<⎪⎩,若()()f a f a >-,求实数a 的取值范围.23.已知函数3()2log f x x =+(1≤x ≤9),求函数22[()]()y f x f x =+的最大值.【参考答案】24.(1)1;(2)3;(3)1;(4)2;(5)4;(6)12-25.D26.B27.B28.D29.D30.B31.B32.A33.D34.C35.B36.B37.C38.A39.C40.141.(2)-∞,42.a <c <b43.③44.11010x <<45.1a >或10a -<<46.22阅读材料反函数趣谈在指数函数2x y =中,x 为自变量,y 为因变量.如果把y 当成自变量,x 当成因变量,同学们思考一下,x 是不是y 的函数?在指数函数2x y =中,过y 轴正半轴上任意一点作x 轴的平行线,与2x y =的图象有且只有一个交点.另一方面,根据指数与对数的关系,由指数式2x y =可得到对数式2log x y =.这样,对于任意一个(0)y ∈+∞,,通过式子2log x y =,在R 中都有唯一确定的x 和它对应.此时,可以把y 作为自变量,x 作为y 的函数,这时我们就说2log x y =((0))y ∈+∞,是函数2x y =()x ∈R 的反函数.注意到,在函数2log x y =中,y 是自变量,x 是函数,但是习惯上,我们通常用x 表示自变量,y 表示函数,因此我们对调函数2log x y =中的字母,把它写成2log y x =,这样,对数函数2log y x =((0))x ∈+∞,是指数函数2x y =()x ∈R 的反函数.由前面的讨论可知,指数函数2x y =()x ∈R 与对数函数2log y x =((0))x ∈+∞,是互为反函数的.类似地,我们可以得到对数函数log (01)a y x a a =>≠,且和指数函数x y a =(01)a a >≠,且互为反函数.在上面的讨论过程中我们发现,过y 轴正半轴上任意一点作x 轴的平行线,与2x y =的图象有且只有一个交点,这就保证了对于任意一个(0)y ∈+∞,,都有唯一确定的2log x y =和它对应,进而才能得到反函数.这就启发我们,不是任意的函数都存在反函数的,只有一一对应的函数才存在反函数.一一对应的函数是指值域中的每一个元素y 只有定义域中的唯一的一个元素x 和它相对应,即定义域中的元素x 和值域中的元素y ,通过对应法则y=f (x )存在着一一对应关系.清楚了反函数存在的条件后,我们接下来讨论反函数的性质.通过画出指数函数2x y =与对数函数2log y x =的图象后,我们发现它们是关于直线y=x 对称的,也就是互为反函数的两个函数的图象是关于直线y=x 对称的.这与我们前面的分析也是一致的,原函数与反函数是定义域、值域互换,对应法则互逆.研究反函数的性质离不开函数的单调性和奇偶性,下面的结论同学们可以自己尝试证明.一个函数与它的反函数在相应区间上单调性是一致的,也就是说如果原函数在某个区间上是单调递增(减)的,那么它的反函数在相应区间上也是单调递增(减)的.关于奇偶性,如果一个奇函数存在反函数,那么它的反函数也是奇函数;一般情况下偶函数是不存在反函数的,例外情况是f (x )=C (C 为常数).学习了反函数这种重要的工具,它可以帮助我们解决很多问题.当原函数的性质不容易研究时,我们可以考虑研究它的反函数.比如当直接求原函数的值域比较困难时,可以通过求其反函数的定义域来确定原函数的值域,来看一道具体的例题.【例】已知函数10110x xy =+,求它的值域.解析:先计算它的反函数,由10110x x y =+得到(110)10x x y +=,解得101x y y =-,反函数即为lg 1y x y =-,反函数的定义域为原函数的值域,也就是01y y >-,原函数的值域即为(01),.练习题1.下列函数中,有反函数的是()A .22y x x=+B .||y x =C .2lg y x =D .11y x =-2.函数21x y =-的反函数为_____________.3.已知函数1212x x y -=+,求它的值域.【参考答案】1.D2.2log (1)y x =+3.(-1,1)。
对数公式及对数函数的总结
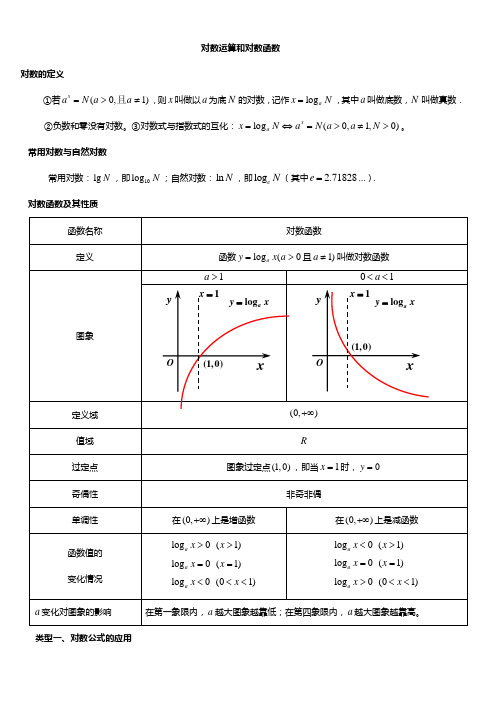
对数运算和对数函数对数的定义①若(0,1)x a N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数。
③对数式与指数式的互化:log (0,1,0)xa x N a N a a N =⇔=>≠>。
常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). 对数函数及其性质类型一、对数公式的应用1计算下列对数=-3log 6log 22 =⋅31l o g12log 2222=+2lg 5lg =61000lg=+64log 128log 22 =⨯)24(log 432 =++)2log 2)(log 3log 3(log 9384=++3log 23log 2242 =⋅16log 27log 32 =+-2log 90log 5log 333=++c b a 842log log log =+++200199lg 43lg 32lg=++32log 8log 8log 842 =+25.0log 10log 255 =-64log 325log 225 =)))65536(log (log (log log 22222 解对数的值:18lg 7lg 37lg214lg -+- 0 =-+-1)21(2lg 225lg-1 13341log 2log 8⎛⎫-⨯ ⎪⎝⎭的值0 提示:对数公式的运算如果0,1,0,0a a M N >≠>>,那么(1)加法:log log log ()a a a M N MN += (2)减法:log log log a a aMM N N-= (3)数乘:log log ()na a n M M n R =∈ (4)log aN a N = (5)log log (0,)b n a a nM M b n R b=≠∈(6)换底公式:log log (0,1)log b a b NN b b a=>≠且 (7)1log log =⋅a b b a (8)a b b a log 1log =类型二、求下列函数的定义域问题 1函数)13lg(13)(2++-=x xx x f 的定义域是)1,31(-2设()x x x f -+=22lg,则⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为 ()()4,11,4 --3函数()lg(1)f x x =+的定义域为( ]1,0()0,1( - )提示:(1)分式函数,分母不为0,如0,1≠=x xy 。
高中数学对数和对数函数知识点与例题讲解

对数与对数函数1.对数(1)对数的定义:如果a b=N(a>0,a≠1),那么b叫做以a为底N的对数,记作logaN=b.(2)指数式与对数式的关系:a b=NlogaN=b(a>0,a≠1,N>0).两个式子表示的a、b、N三个数之间的关系是一样的,并且可以互化.(3)对数运算性质:①log a(MN)=log a M+log a N.②log aMN=log a M-log a N.③logaM n=nlogaM.(M>0,N>0,a>0,a≠1)④对数换底公式:logbN= l oglogaaNb(a>0,a≠1,b>0,b≠1,N>0).2.对数函数(1)对数函数的定义函数y=log a x(a>0,a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).注意:真数式子没根号那就只要求真数式大于零,如果有根号,要求真数大于零还要保证根号里的式子大于零,底数则要大于0且不为1对数函数的底数为什么要大于0且不为1呢?在一个普通对数式里a<0,或=1的时候是会有相应b的值的。
但是,根据对数定义:log a a=1;如果a=1或=0那么log a a就可以等于一切实数(比如log11也可以等于2,3,4,5,等等)第二,根据定义运算公式:log a M^n=nlogaM如果a<0,那么这个等式两边就不会成立(比如,log(-2)4^(-2)就不等于(-2)*log(-2)4;一个等于1/16,另一个等于-1/16)(2)对数函数的图象yyy =l ogxa>(1)a1O1xOxy =l o g a x (<a <1) 0底数互为倒数的两个对数函数的图象关于x 轴对称. (3)对数函数的性质: ①定义域:(0,+∞). ②值域:R.③过点(1,0),即当x=1时,y=0.④当a >1时,在(0,+∞)上是增函数;当0<a <1时,在(0,+∞)上是减函数.基础例题题型1(对数的计算) 1.求下列各式的值. (1)35 log +25log2-1 21 50log - 514 log ;(2)log5 2 1 25 ×lo g 3 1 8 ×lo g 5 1 9. 练习题1.计算:lg 1 2 -lg5 8 +lg12.5-log 89·log 278;3.log535+21log2-log51502 -log514;3.log2125×log318×log519.1loglog4log3 4.399222.5.lg5lg2lg41(6).log24lglog27lg2log33222 7.2lg2lg3111lg0.36lg823例2.已知实数x、y、z满足3x=4y=6z>1.(1)求证:2x+1y=2z;(2)试比较3x、4y、6z的大小.练习题.已知log189=a,18b=5,用a、b表示log3645.题型二:(对数函数定义域值域问题)例1.已知函数fxlog22xx1aax的定义域为集合A,关于x的不等式22 的解集为B,若AB,求实数a的取值范围.2.设函数2ylog(ax2x2)定义域为A.2(1)若AR,求实数a的取值范围;(2)若2log(ax2x2)2在x[1,2]上恒成立,求实数a的取值范围.2练习题1.已知函数2 fxlgax2x1(1)若fx的定义域是R,求实数a的取值范围及fx的值域;(2)若fx的值域是R,求实数a的取值范围及fx的定义域2求函数y=2lg (x -2)-lg (x -3)的最小值.题型三(奇偶性及性) 例题1.已知定义域为R 的函数f (x )为奇函数足f(x +2)=-f(x),当x ∈[0,1]时,f(x)=2x -1.(1)求f(x)在[-1,0)上的解析式; (2)求f(1 log24)的值. 2 4.已知f (x )=l o g 1[3-(x -1)2],求f (x )的值域.3 5.已知y =l o g a (3-a x )在[0,2]上是x 的减函数,求a 的围.4.已知函数f(x)lg(2x)lg(2x).(Ⅰ)求函数yf(x)的定义域;(Ⅱ)判断函数yf(x)的奇偶性;(Ⅲ)若f(m2)f(m),求m的取值范围.练习题1.已知函数f(x)=loga(x+1)-loga(1-x)(a>0,a≠1)(1)求f(x)的定义域;(2)判断f(x)的奇偶性,并给出证明;(3)当a>1时,求使f(x)>0的x的取值范围2.函数f(x)是定义在R上的偶函数,f(0)0,当x0时,1f(x)logx.2 (1)求函数f(x)的解析式;(2)解不等式2f(x1)2;3.已知f(x)是定义在R上的偶函数,且x0时,1f(x)log(x1).2 (Ⅰ)求f(0),f(1);(Ⅱ)求函数f(x)的表达式;(Ⅲ)若f(a1)1,求a的取值范围.题型4(函数图像问题)例题1.函数f(x)=|log2x|的图象是yy111x-11xOOAByy111x1xOOCD6.求函数y=log2|x|的定义域,并画出它的图象,指出它的单调区间.f(x)=|lgx|,a,b为实数,且0<a<b.(1)求方程f(x)=1的解;(2)若a,b满足f(a)=f(b)=2fa b2,求证:a·b=1,a b2 >1.练习题:1.已知a0且a1,函数f(x)log(x1)a,1g(x)log a,记F(x)2f(x)g(x)1x(1)求函数F(x)的定义域及其零点;(2)若关于x的方程2 F2.已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.(1)求k的值;(2)设g(x)=log44xa?237.函数y=log2|ax-1|(a≠0)的对称轴方程是x=-2,那么a等于题型五:函数方程1方程lgx+lg(x+3)=1的解x=___________________.5.已知函数f(x)= 1()2x,x4,则f(2+log23)的值为f(x1),x4,4.已知函数f(x)log a(axx)(a0,a1为常数). (Ⅰ)求函数f(x)的定义域;(Ⅱ)若a2,x1,9,求函数f(x)的值域;(Ⅲ)若函数f(x)ya的图像恒在直线y2x1的上方,求实数a的取值范围.1xxyloglog(2x8).5.已知函数22242(Ⅰ)令tlog2x,求y关于t的函数关系式及t的取值范围;(Ⅱ)求函数的值域,并求函数取得最小值时的x的值.8.设函数f(x)=lg(1-x),g(x)=lg(1+x),在f(x)和g(x)的公共定义域内比较|f(x)|与|g(x)|的大小.您好,欢迎您阅读我的文章,本WORD文档可编辑修改,也可以直接打印。
高三数学对数与对数函数试题答案及解析

高三数学对数与对数函数试题答案及解析1.设命题函数的定义域为;命题对一切的实数恒成立,如果命题“”为假命题,求实数的取值范围.【答案】a≤2.【解析】分别求出命题p,q成立的等价条件,利用p且q为假p,q至少有一个为假命题,故其反面为:p,q都为真命题;先求出p,q都为真命题时实数k的取值范围,再求其在实集上的补集就是所求实数k的取值范围.试题解析:要使函数的定义域为R,则不等式对于一切x∈R恒成立,若a=0,则不等式等价为-x>0,解得x<0,不满足恒成立.若a≠0,则满足条件,即,解得,即a>2,所以p:a>2.记,∴要使3x-9x<a对一切的实数x恒成立,则a>,即q:a>.要使p且q为假,则p,q至少有一个为假命题.当p,q都为真命题时,满足∴p,q至少有一个为假命题时有a≤2,即实数a的取值范围是a≤2.【考点】复合命题的真假.2.函数y=(x2-4x+3)的单调递增区间为()A.(3,+∞)B.(-∞,1)C.(-∞,1)∪(3,+∞)D.(0,+∞)【答案】B【解析】令u=x2-4x+3,原函数可以看作y=u与u=x2-4x+3的复合函数.令u=x2-4x+3>0,则x<1或x>3.∴函数y=(x2-4x+3)的定义域为(-∞,1)∪(3,+∞).又u=x2-4x+3的图象的对称轴为x=2,且开口向上,∴u=x2-4x+3在(-∞,1)上是减函数,在(3,+∞)上是增函数.而函数y=u在(0,+∞)上是减函数,∴y=(x2-4x+3)的单调递减区间为(3,+∞),单调递增区间为(-∞,1).3.函数y=的定义域为________.【答案】(-2,8]【解析】由题意可知,1-lg(x+2)≥0,整理得lg(x+2)≤lg 10,则,解得-2<x≤8,故函数y=的定义域为(-2,8].4.函数y=(x2-6x+17)的值域是________.【答案】(-∞,-3]【解析】令t=x2-6x+17=(x-3)2+8≥8,y=为减函数,所以有≤=-3.5.(5分)(2011•湖北)里氏震级M的计算公式为:M=lgA﹣lgA,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A为0.001,则此次地震的震级为级;9级地震的最大的振幅是5级地震最大振幅的倍.【答案】6,10000【解析】根据题意中的假设,可得M=lgA﹣lgA=lg1000﹣lg0.001=6;设9级地震的最大的振幅是x,5级地震最大振幅是y,9=lgx+3,5=lgy+3,由此知9级地震的最大的振幅是5级地震最大振幅的10000倍.解:根据题意,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则M=lgA﹣lgA=lg1000﹣lg0.001=3﹣(﹣3)=6.设9级地震的最大的振幅是x,5级地震最大振幅是y,9=lgx+3,5=lgy+3,解得x=106,y=102,∴.故答案耿:6,10000.点评:本题考查对数的运算法则,解题时要注意公式的灵活运用.6.设a=log54,b=(log53)2,c=log45,则 ()A.a<c<b B.b<c<a C.a<b<c D.b<a<c 【答案】D【解析】因为log45>1,0<log54<1,0<log53<1,所以(log53)2<log53<log54,所以b<a<c,选D.7.函数f(x)=㏑x的图象与函数g(x)=x2﹣4x+4的图象的交点个数为()A.0B.1C.2D.3【答案】C【解析】在同一个坐标系中,画出函数f(x)=㏑x 与函数g(x)=x2﹣4x+4=(x﹣2)2的图象,如图所示:故函数f(x)=㏑x的图象与函数g(x)=x2﹣4x+4的图象的交点个数为2,故选C.8.函数的值域为 .【答案】【解析】由得 ,所以函数的定义域是:设点=所以,,所以答案填:【考点】1、对数函数的性质;2、数形结合的思想.9.定义“正对数”:现有四个命题:①若,则;②若,则;③若,则;④若,则.其中的真命题有.(写出所有真命题的编号)【答案】①③④【解析】对于①:当时,有,此时;当时,有,此时;当时,有,此时,而综合知①正确对于②:令,则,而,故不成立,②错误对于③:当时,有,或,或验证知: 成立;当时,有,或,或,验证知:成立;当时,成立,故③正确对于④:分四种情况讨论:当时,不妨令,有此时成立;同理,当或或时,成立,故④正确综合知①③④正确10.如果函数的图像过点,则________.【答案】1【解析】依题意得.所以.【考点】1.函数的知识.2.数列的求和公式.3.极限的运算.11..【答案】2【解析】由对数运算法则得:.【考点】对数运算.12.已知函数f(x)=lg(1-x)+lg(1+x)+x4-2x2.(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性;(3)求函数f(x)的值域.【答案】(1)(-1,1)(2)f(x)是偶函数(3)(-∞,0]【解析】(1)由得-1<x<1,所以函数f(x)的定义域为(-1,1).(2)由f(-x)=lg(1+x)+lg(1-x)+(-x)4-2(-x)2=lg(1-x)+lg(1+x)+x4-2x2=f(x),所以函数f(x)是偶函数.(3)f(x)=lg(1-x)+lg(1+x)+x4-2x2=lg(1-x2)+x4-2x2,设t=1-x2,由x∈(-1,1),得t∈(0,1].所以y=lg(1-x2)+x4-2x2=lgt+(t2-1),t∈(0,1],设0<t1<t2≤1,则lgt1<lgt2,<,所以lgt1+(-1)<lgt2+(-1),所以函数y=lgt+(t2-1)在t∈(0,1]上为增函数,所以函数f(x)的值域为(-∞,0].13.设a是实数,讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实数解的个数.【答案】两个【解析】原方程等价于方程组即在同一坐标系下作直线y=a 与抛物线y=-x2+5x-3(1<x<3)的图象,由图可知,当1<a≤3或a=时,原方程只有一个实数解;当3<a< 时,原方程有两个不同的实数解.14.求下列各式的值.(1)log535+2-log5-log514;(2)log2×log3×log5.【答案】(1)2(2)-12 【解析】(1)原式=log 5+2=log 553-1=2.(2)原式==-12.15. 已知m 、n 为正整数,a >0且a≠1,且log a m +log a+log a+…+log a=log a m +log a n ,求m 、n 的值.【答案】【解析】左边=log a m +log a+log a+…+log a=log a=log a (m +n),∴已知等式可化为log a (m +n)=log a m +log a n =log a mn. 比较真数得m +n =mn ,即(m -1)(n -1)=1. ∵m 、n 为正整数,∴解得16. 若点(a,b)在y=lgx 的图象上,a≠1,则下列点也在此图象上的是( )A .(,b)B .(10a,1-b)C .(,b+1)D .(a 2,2b)【答案】D【解析】∵点(a,b)在函数y=lgx 的图象上, ∴b=lga,则2b=2lga=lga 2,故点(a 2,2b)也在函数y=lgx 的图象上.17. 已知实数a,b 满足等式2a =3b ,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中可能成立的关系式有( ) A .①②③ B .①②⑤ C .①③⑤ D .③④⑤【答案】B【解析】设2a =3b =k, 则a=log 2k,b=log 3k.在同一直角坐标系中分别画出函数y=log 2x,y=log 3x 的图象如图所示,由图象知:a<b<0或0<b<a 或a=b.18. 已知函数f(x)=|log 2x|,正实数m,n 满足m<n,且f(m)=f(n),若f(x)在区间[m 2,n]上的最大值为2,则m,n 的值分别为( )A .,2B .,4C .,D .,4【答案】A【解析】f(x)=|log2x|=则函数f(x)在(0,1)上是减函数,在(1,+∞)上是增函数, 又m<n且f(m)=f(n),则0<m<1,n>1,∴0<m2<m<1,∴f(m2)>f(m)=f(n),即函数f(x)在区间[m2,n]上的最大值为f(m2).由题意知f(m2)=2,即-log2m2=2,∴m=,由f(m)=f(n)得-log2=log2n,∴n=2.19.已知函数,则的值是()A.B.C.D.【答案】A【解析】因为函数,所以,,所以=,选A.【考点】分段函数,对数运算,指数运算.20.已知,不等式成立,则实数a的取值范围是_____________.【答案】【解析】由绝对值的几何意义,,所以恒成立,须恒成立.所以,故答案为.【考点】绝对值的几何意义,对数函数的性质.21.已知函数.(1)若,当时,求的取值范围;(2)若定义在上奇函数满足,且当时,,求在上的反函数;(3)若关于的不等式在区间上有解,求实数的取值范围.【答案】(1);(2);(3).【解析】(1)这实质上是解不等式,即,但是要注意对数的真数要为正,,;(2)上奇函数满足,可很快求出,要求在上的反函数,必须求出在上的解析式,当时,,故,当然求反函数还要求出反函数的定义域即原函数的值域;(3)可转化为,这样利用对数函数的性质得,变成了整式不等式,问题转化为不等式在区间上有解,而这个问题通常采用分离参数法,转化为求相应函数的值域或最值.试题解析:(1)原不等式可化为 1分所以,, 1分得 2分(2)因为是奇函数,所以,得 1分当时,2分此时,,所以 2分(3)由题意, 1分即 1分所以不等式在区间上有解,即 3分所以实数的取值范围为 1分【考点】(1)对数不等式;(2)分段函数的反函数;(3)不等式有解问题.22.______________.【答案】【解析】.故填.本题关键是对数的基本运算.同底的对数的加减运算,运算法则是底数不变真数相乘或相除.结合对数的性质及可得结论.【考点】1.对数的性质.2.对数的加减运算.23.已知函数(1)若x=2为的极值点,求实数a的值;(2)若在上为增函数,求实数a的取值范围.【答案】(1);(2)【解析】(1)通过求导可得.又因为x=2是极值点.即可求得.(2)通过对对数的定义域可得符合题意的不等式.在上恒成立.所以转化为研究二次函数的最值问题.通过对称轴研究函数的单调性即可得到结论.本题的的关键是对含参的函数的最值的讨论.以二次的形式为背景紧扣对称轴这个知识点.试题解析:(1)因为.因为x=2为f(x)的极值点.所以即.解得.又当时.从而x=2为f(x)的极值点成立. (2)因为f(x)在区间上为增函数.所以.在区间上恒成立. ①当时. 在上恒成立.所以f(x)在上为增函数.故符合题意.②当时.由函数f(x)的定义域可知,必须有时恒成立.故只能.所以在区间上恒成立.令g(x)= .其对称轴为.因为.所以<1.从而g(x) 在上恒成立.只需要g(3) 即可.由g(3)= .解得:.因为.所以.综上所述. 的取值范围为.【考点】1.对数函数的知识点.2.最值问题.3.含参的讨论.24.关于的不等式(为实常数)的解集为,则关于的不等式的解集为 .【答案】【解析】,则.由题意得:不等式的解为.所以,不等式即为,.【考点】1、一元二次不等式、指数不等式及对数不等式的解法;2、韦达定理.25.函数的定义域为_____________.【答案】【解析】解得:.【考点】求函数的定义域26.的值为( )A.B.C.D.【答案】B【解析】.【考点】1、对数的性质及求值;2、三角函数的恒等变换及化简求值.27.给出下列命题:①在区间上,函数,,,中有三个是增函数;②若,则;③若函数是奇函数,则的图象关于点对称;④已知函数则方程有个实数根,其中正确命题的个数为()A.B.C.D.【答案】C【解析】①在区间上,,是减函数,,是增函数,错误;②如图在第一象限,底数越大,函数的图像越高,∴,正确;③函数的图像向右平移一个单位,得到的图像,对称中心为(1,0),正确;④或或或,正确.【考点】幂函数,对数函数,指数函数的图像与性质.28.已知,则()A.B.C.D.【答案】D【解析】,且,.【考点】指数与对数运算29.已知数列满足,且,则的值是( ) A.B.C.D.【答案】D【解析】由可以推出,数列是以3为公比的等比数列,故,故.【考点】等比数列性质和对数运算.30.已知函数.(1)求函数的定义域,并判断的奇偶性;(2)用定义证明函数在上是增函数;(3)如果当时,函数的值域是,求与的值.【答案】.解:(1),函数是奇函数.(2)设、算、证、结(3),【解析】思路分析:(1)由,求得计算知函数是奇函数.另证:对任意0,(2)利用“定义”“设、算、证、结”。
高三数学对数与对数函数试题答案及解析

高三数学对数与对数函数试题答案及解析1.函数的单调递增区间为()A.(0,+∞)B.(-∞,0)C.(2,+∞)D.(-∞,-2)【答案】D【解析】首先由得函数的定义域为(-∞,-2) (2,+∞);再令,则在(0,+∞)是减函数,又因为在(-∞,-2)上是减函数;由复合函数的单调性可知:函数的单调递增区间为(-∞,-2);故选D.【考点】复合函数的单调性.2.已知函数为奇函数则实数的值为【答案】1【解析】由奇函数得:,,,因为,所以【考点】奇函数3.计算.【答案】2【解析】【考点】对数式的运算.4.已知函数为常数,其中的图象如右图,则下列结论成立的是()A.B.C.D.【答案】D【解析】由图可知,的图象是由的图象向左平移个单位而得到的,其中,再根据单调性易知,故选D.【考点】对数函数的图象和性质.5.设且.若对恒成立,则的取值范围是()A.B.C.D.【答案】D【解析】时显然不成立.当时,结合图象可知:.【考点】对数函数与三角函数.6.函数的定义域是A.[1,2]B.C.D.【答案】C【解析】根据函数定义域的要求得:.【考点】(1)函数的定义域;(1)对数函数的性质.7. (1)解方程:(2)已知命题命题且命题是的必要条件,求实数m的取值范围【答案】(1);(2).【解析】(1)解对数方程,一般把利用对数的运算法则把对数方程变形为,转化为代数方程,但解题过程中要注意对数函数的定义域,即,;(2)这类问题的解决,首先要把两个命题化简,本题中命题化为:,命题是命题的必要条件,说明由命题成立可推导出命题也成立,若把命题成立时的变量的集合分别记为,从集合角度,即有,由此我们可得出关于的不等关系,从而求出的取值范围. 试题解析:(1)解:由原方程化简得,即:所以,,解得.(2)解:由于命题是的必要条件,所以,所以.【考点】(1)对数方程;(2)充分与必要条件.8.函数f(x)=ln是________(填“奇”或“偶”)函数.【答案】奇【解析】因为f(-x)=ln=ln=-ln=-f(x),所以f(x)是奇函数.9.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b的取值范围是________.【答案】(3,+∞)【解析】因为f(a)=f(b),即|lga|=|lgb|,所以a=b(舍去)或b=,得a+2b=a+.又0<a<b,所以0<a<1<b.令f(a)=a+,则f′(a)=1-<0,所以f(a)在a∈(0,1)上为减函数,得f(a)>f(1)=1+2=3,即a+2b的取值范围是(3,+∞).10.设a=lge,b=(lge)2,c=lg,则a、b、c的大小关系是________.【答案】a>c>b【解析】本题考查对数函数的增减性,由1>lge>0,知a>b.又c=lge,作商比较知c>b,故a>c>b.x|,正实数m、n满足m<n,且f(m)=f(n),若f(x)在区间[m2,n]上的最大值为2, 11.已知函数f(x)=|log2则m+n等于()A.-1B.C.1D.2【答案】B【解析】由函数f(x)=|log2x|的图象知,当m<n且f(m)=f(n),得mn=1,且0<m<1<n.∴0<m2<m<1<n.∵f(x)在区间[m2,n]上的最大值为2,∴|log2m2|=2,∴m=,n=2,∴m+n=.12.设则a,b,c的大小关系为A.a<c<b B.b<a<c C.a<b<c D.b<c<a【答案】B【解析】因为所以显然,所以的值最大.故排除A,D选项.又因为,所以.即.综上.故选B.本小题关键是进行对数的运算.【考点】1.对数的运算.2.数的大小比较的方法.13.已知f(x)是定义域为实数集R的偶函数,∀x1≥0,∀x2≥0,若x1≠x2,则<0.如果f=,4f()>3,那么x的取值范围为()A.B.C.∪(2,+∞)D.∪【答案】B【解析】依题意得,函数f(x)在[0,+∞)上是减函数,不等式4f()>3等价于f()>,f(||)>f,||<,即-<<,由此解得<x<2,故选B.14.计算:lg-lg+lg7=.【答案】【解析】原式=lg4+lg2-lg7-lg8+lg7+lg5=2lg2+(lg2+lg5)-2lg2=.15.已知函数.(1)若,当时,求的取值范围;(2)若定义在上奇函数满足,且当时,,求在上的反函数;(3)若关于的不等式在区间上有解,求实数的取值范围.【答案】(1);(2);(3).【解析】(1)这实质上是解不等式,即,但是要注意对数的真数要为正,,;(2)上奇函数满足,可很快求出,要求在上的反函数,必须求出在上的解析式,当时,,故,当然求反函数还要求出反函数的定义域即原函数的值域;(3)可转化为,这样利用对数函数的性质得,变成了整式不等式,问题转化为不等式在区间上有解,而这个问题通常采用分离参数法,转化为求相应函数的值域或最值.试题解析:(1)原不等式可化为 1分所以,, 1分得 2分(2)因为是奇函数,所以,得 1分当时,2分此时,,所以 2分(3)由题意, 1分即 1分所以不等式在区间上有解,即 3分所以实数的取值范围为 1分【考点】(1)对数不等式;(2)分段函数的反函数;(3)不等式有解问题.16.设,则之间的关系是()A.B.C.D.【答案】A【解析】由函数的图象可知,又由函数的图象可得该函数在上单调增,因为,则,综上所述选A.【考点】1.对数函数;2.幂函数的单调性17.使不等式(其中)成立的的取值范围是.【答案】【解析】即,而,所以,,答案为.【考点】对数函数及其性质18.已知,,,,则()A.B.C.D.【答案】C【解析】,,,因为且,所以.【考点】对数的运算.19.设函数的定义域为,值域为,若的最小值为,则实数的值为.【答案】.【解析】由题意函数的值域为,,则,当即时,,;当即时,,,.【考点】对数函数的值域.20.设,则( )A.B.C.D.【答案】D【解析】因为,所以.【考点】对数比较大小21.函数,其中满足且∥,则_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.7 对数与对数函数
一、知识点
1.对数的定义:如果a x =N (a >0且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数. 2.对数的性质与运算及换底公式
(1)对数的性质(a >0且a ≠1):①log a 1=0;②log a a =1;③a log a N =N . (2)对数的换底公式:log a b =log c b
log c a (a ,c 均大于0且不等于1,b >0).
(3)对数的运算法则:如果a >0且a ≠1,M >0,N >0,那么
①log a (M ·N )=log a M +log a N ,②log a M
N =log a M -log a N ,③log a M n =n log a M (n ∈R ).
3.对数函数的图像与性质
a >1
0<a <1
图像
定义域 (0,+∞)
值域 R 定点 过点(1,0)
单调性 在(0,+∞)上是增函数 在(0,+∞)上是减函数
函数值正负
当x >1时,y >0; 当0<x <1,y <0 当x >1时,y <0;
当0<x <1时,y >0
4.反函数:a 线y =x 对称.
5.求复合函数y =f (g (x ))的单调区间的步骤:(1)确定定义域;(2)将复合函数分解成基本初等函数y =f (u ),u =g (x );(3)分别确定这两个函数的单调区间;(4)若这两个函数同增或同减,则y =f (g (x ))为增函数,若一增一减,则y =f (g (x ))为减函数,即“同增异减”. 二、考点分析
考点一 对数式的化简与求值
1.(2013·陕西高考)设a ,b ,c 均为不等于1的正实数, 则下列等式中恒成立的是( )
A .log a b ·log c b =log c a
B .log a b ·log c a =log c b
C .log a (bc )=log a b ·log a c
D .log a (b +c )=log a b +log a c 2.计算下列各题:
(1)lg 37+lg 70-lg 3-(lg 3)2-lg 9+1; (2)12lg 3249-4
3lg 8+lg 245
考点二 对数函数的图像及应用
3.(1)已知lg a +lg b =0,则函数f (x )=a x 与函数g (x )=-log b x 的图像可能是( )
(2)当0<x ≤1
2
时,4x <log a x ,则a 的取值范围是( )
A.⎝
⎛⎭⎫0,
22 B.⎝⎛⎭
⎫2
2,1 C .(1,2) D .(2,2) 4.(2014·安徽皖南八校三联)若函数f (x )=log a (x +b )的大致图像如图,
其中a ,b 为常数,则函数g (x )=a x +b 的大致图像是( )
考点三 对数函数的性质及应用
5.已知函数f (x )=log 4(ax 2+2x +3).(1)若f (1)=1,求f (x )的单调区间;
(2)是否存在实数a ,使f (x )的最小值为0?若存在,求出a 的值;若不存在,说明理由.
6.已知f (x )=log a (a x -1)(a >0且a ≠1).(1)求f (x )的定义域;(2)判断函数f (x )的单调性.
三、巩固练习
1.(2013·重庆高考)函数y =
1
log 2(x -2)
的定义域是( )
A .(-∞,2)
B .(2,+∞)
C .(2,3)∪(3,+∞)
D .(2,4)∪(4,+∞)
2.函数y =log a (3x -2)(a >0,a ≠1)的图像经过定点A ,则A 点坐标是( )
A.⎝⎛⎭⎫0,23
B.⎝⎛⎭⎫2
3,0 C .(1,0) D .(0,1)
3.(2013·全国卷Ⅱ)设a =log 32,b =log 52,c =log 23,则( )
A .a >c >b
B .b >c >a
C .c >b >a
D .c >a >b
4.(2014·深圳调研)设f (x )为定义在R 上的奇函数,当x >0时,f (x )=log 3(1+x ),则f (-2)=( )
A .-1
B .-3
C .1
D .3
5.(2013·广东高考)函数y =
lg (x +1)
x -1
的定义域是( ) A .(-1,+∞) B .[-1,+∞) C .(-1,1)∪(1,+∞) D .[-1,1)∪(1,+∞) 6.函数y =lg
1
|x +1|
的大致图像为( )
7.设函数f (x )=⎩
⎪⎨⎪⎧
21-
x ,x ≤1,
1-log 2x ,x >1,则满足f (x )≤2的x 的取值范围是( )
A .[-1,2]
B .[0,2]
C .[1,+∞)
D .[0,+∞) 8.函数y =1-lg (x +2)的定义域为( )
A .(0,8]
B .(2,8]
C .(-2,8]
D .[8,+∞) 9.若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数,且f (2)=1,则f (x )=( )
A .log 2x B.1
2
x C .log 12
x
D .2x -
2
10.(2013·全国卷Ⅱ)设a =log 36,b =log 510,c =log 714,则( )
A .c >b >a
B .b >c >a
C .a >c >b
D .a >b >c
11.设函数f (x )=⎩⎪⎨⎪⎧
log 12x ,x >0,log 2(-x ),x <0,若f (m )<f (-m ),则实数m 的取值范围是( )
A .(-1,0)∪(0,1)
B .(-∞,-1)∪(1,+∞)
C .(-1,0)∪(1,+∞)
D .(-∞,-1)∪(0,1) 12.已知函数f (x )=log a |x |在(0,+∞)上单调递增,则( )
A .f (3)<f (-2)<f (1)
B .f (1)<f (-2)<f (3)
C .f (-2)<f (1)<f (3)
D .f (3)<f (1)<f (-2) 13.下列区间中,函数f (x )=|ln(2-x )|在其上为增函数的是( )
A .(-∞,1] B.⎣⎡⎦⎤-1,43 C.⎣⎡⎭⎫0,3
2 D .[1,2) 14.(2013·四川高考)lg 5+lg 20的值是________.
15.(2013·南京模拟)若log 2a 1+a 2
1+a <0,则a 的取值范围是________.
16.(2013·北京高考)函数f (x )=⎩⎪⎨⎪⎧
log 12x ,x ≥1,
2x ,x <1的值域为________.
17.函数y =log 12
(x 2-6x +17)的值域是________.
18.设2a =5b =m ,且1a +1
b
=2,则m =________.
19.(2013·无锡模拟)若f (x )=lg x ,g (x )=f (|x |),则g (lg x )>g (1),x 的取值范围是________. 20.(2014·长春模拟)设f (x )=log a (1+x )+log a (3-x )(a >0,a ≠1),且f (1)=2.
(1)求a 的值及f (x )的定义域.(2)求f (x )在区间⎣⎡⎦⎤0,3
2上的最大值.
21.已知f (x )=log a x (a >0且a ≠1),如果对于任意的x ∈⎣⎡⎦⎤
13,2都有|f (x )|≤1成立,试求a 的取值范围.。
